0 引言
接地网是变电站、发电厂的重要组成部分,接地网性能的好坏直接影响工作人员及电气设备的安全[1-3]。由于接地网常年埋于地下,接地网导体常常因受土壤侵蚀而无法正常工作,目前已经发生了多起因接地网造成事故的事例,因此需要对接地网进行故障诊断,为电力系统稳定运行提供保障[4-5]。目前提出的很多方法难以得到准确的结果,实际上凭借经验进行停电开挖判断,具有盲目性并且无法直观成像[6]。
电阻抗成像(Electrical Impedance Tomography, EIT)技术具有非入侵、无损伤、结构简单、易于操作且成本低廉等优点,有广阔的应用前景[7]。然而提高图像质量和分辨率是当前电阻抗成像领域的一大挑战[8],特别是EIT技术应用于接地网故障诊断领域,由于接地网的测量电压数据有限,不足以反映重构目标的基本特征,且接地网中导体和土壤的电阻率数量级相差巨大使其系统矩阵病态性严重,因此EIT逆问题具有不适定性[9]。
为了克服EIT逆问题的不适定性,国内外学者提出了具有各种技术的逆问题方法。其中,B. S. Kim[10]提出了自适应阈值的网格细化方法,能在一定程度上提高图像质量。但对于接地网而言,网格剖分单元太多会加剧逆问题病态性且计算时间增加。2012年,刘杰等[11]设计了一套基于电阻抗成像的接地网故障诊断自动测量系统,在接地网电压循环测量原理的基础上获得更多的测量电压数据,然而该系统逆问题成像具有病态性,只能判断接地网腐蚀的区域,不能准确定位。EIT不适定问题通常需要加入正则化求解,Tikhonov正则化是常用的方法之一[12-14]。因此为了改善逆问题病态性,2015年代锋[15]将Tikhonov正则化方法应用到接地网电阻抗成像中,使迭代求解过程的稳定性得到很大提高,在一定程度上克服了逆问题的病态性,但Tikhonov正则化是局部收敛的,对于具有多种不同介质的接地网模型,尤其在接地网导体和土壤数量级相差巨大的情况下,迭代过程很难收敛。此外,牛顿类算法对迭代初值要求比较苛刻[16],对于图样已经丢失的老旧变电站,场域剖分单元初值很难预先给定,因此需要一种能够对初值要求宽松的全局收敛方法。2003年,T. M. Wu[17]在传统牛顿法中引入辅助同伦函数,避免因初值选取不当而发散的问题。2008年,徐桂芝等[18]提出将同伦延拓法与牛顿类算法相结合,应用于四介质的三维电阻抗成像问题,证明了该算法具有大范围收敛性。2017年,N. Mostashiri等[19]将同伦延拓法应用在空间并联机器人数值求解运动学问题中,指出该方法减轻了传统数值方法的初始取值不当及收敛困难等问题。2020年,Wang Mengran等[20]从数学角度证明了同伦延拓法在求解非线性方程组中的可行性。此外,在文献[21-24]表明同伦延拓法不依赖于矩阵方程的初始值,计算使得误差较大的初始值接近真实电阻率,克服迭代过程中的局部收敛性问题。
因此,为了改善接地网电阻抗成像逆问题的病态性,本文将传统的同伦延拓法与Tikhonov正则化相结合,提出了具有全局收敛性的Homotopy-Tikhonov算法(HT-GN)。在最佳迭代初值和最佳正则化参数基础上对比了该算法与Tikhonov算法的接地网重建图像,然后分析了不同迭代初值、不同正则化参数对接地网成像的影响,最后进行了接地网不同腐蚀程度的仿真成像,并针对轻腐蚀情况进行了接地网实验成像,验证了该方法收敛性能最优,腐蚀位置更清晰,可更好地改善接地网电阻抗成像的病态性问题。
1 接地网电阻抗成像原理
接地网电阻抗成像原理是通过在接地网的引下线注入电流,测量其他引下线之间的电压来确定未知介质电阻率分布的问题,其正、逆问题关系如图1所示。

图1 接地网正、逆问题关系图
Fig.1 Diagram of forward and inverse problems of grounding grid
在接地网电阻抗建模中,需假设以下几个条件:①施加直流电,忽略位移电流;②不考虑接地网引下线的面积;③成像场域是各向同性的;④电导率与电流密度无关。接地网电阻抗成像的数学问题是从狄利克雷-诺依曼图中反演电阻率。根据Maxwell方程组,场域内满足拉普拉斯方程,边界满足狄利克雷边界条件和诺依曼边界条件,接地网电阻抗成像的数学模型表示为[25]
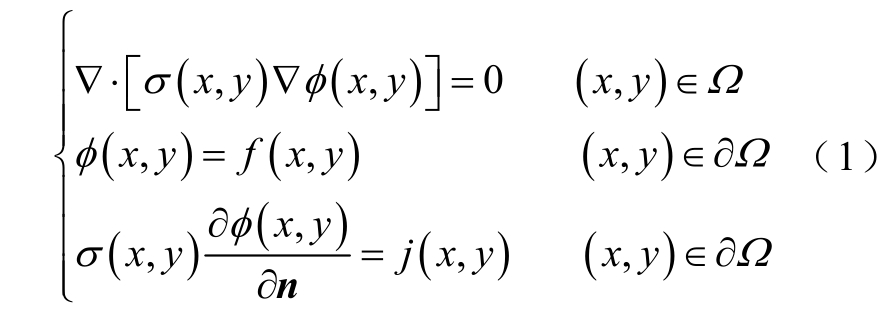
式中,σ为场域内的电导率分布;φ为场域内的电位分布;Ω为待求解的场域,Ω∂为场域Ω的边界;f为已知边界电位;j为流入场域Ω的电流密度;n为场域Ω的外法向单位向量。
EIT逆问题可以表示为如式(2)的非线性方程组。
式中,U(ρ)为注入直流电后,对应电阻率分布ρ的计算电压;V为测量电压; ρ为采用有限元法得到的N个剖分单元的电阻率,ρ=[ρ1 ρ2 ρ3 ⋅⋅⋅ ρN ]T 。
实际上,由于各种误差存在,很难得到U(ρ)和V的等式关系,通常用最小二乘法构造误差函数,即求解满足计算电压和测量电压的差值在一定范围内的电阻率分布,其EIT逆问题数学模型为
式(3)是一个典型的非线性方程组的优化问题,为了使误差最小,对其进行求导,并且采用迭代法逼近真值。
2 Homotopy-Tikhonov算法(HT-GN)的求解
2.1 Tikhonov正则化原理
由于EIT逆问题具有不适定性,为了得到接地网的电阻率分布情况,通常加入经典的Tikhonov正则化算法,该算法由Tikhonov在20世纪60年代初提出,工程上广泛使用,其构造的泛函为
式中,α为Tikhonov正则化参数,通过L曲线法求得;L为正则化矩阵,这里取单位阵;ρ0为初始电阻率。
式(5)是在式(4)基础上得到的忽略高阶项的电阻率迭代式,是电阻抗成像中典型的基于Tikhonov正则化的高斯牛顿迭代法(Gauss-Newton)。

式中, k为迭代次数,k=1,2,3,…;J为雅克比矩阵,Δρ为电阻率变化量,ΔU(ρ)为对应Δρ的电压变化量,ΔU(ρ)=JΔρ。
2.2 Homotopy原理
基于Tikhonov正则化的高斯牛顿迭代法具有局部收敛性质,Homotopy具有全局收敛性,文献[26]指出常用的数学同伦方法有牛顿同伦、定点同伦、定尺度仿射同伦等,由定点同伦构造的HT-GN算法方程表述为
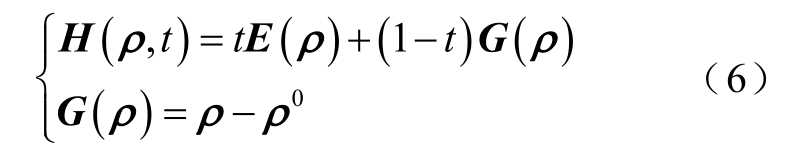
式中,t为Homotopy参数,取值[0,1];ρ0为已知量。对于接地网而言,令G(ρ)=ρ−ρ0,E(ρ)=F′(ρ),t=k/K,其中k=1,2,3,…,K,K为电阻率初始值求取的迭代次数。
2.3 HT-GN算法
基于Tikhonov正则化的高斯牛顿算法具有自校正的性质,只要给予恰当的初值,均能够收敛到最终解,但是该方法对初值要求苛刻,接地网导体和土壤的电阻率数量级相差巨大,且当接地网拓扑未知的情况下,很难预先给定较好的初值,因此,本文引入对初值要求宽松的Homotopy法,得到基于Homotopy-Tikhonov算法(HT-GN)的接地网电阻抗成像故障诊断方法。
定义Eρ)是式(4)中F(ρ)的一阶导数,即
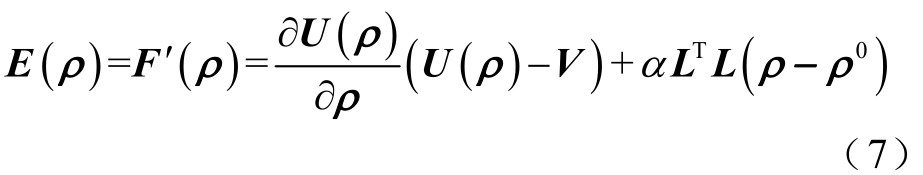
将式(7)代入式(6)得到基于HT-GN算法的定点同伦表达式为

因此,式(9)为基于HT-GN算法的第一阶段迭代表达式,目的是获得新的贴近接地网真实电阻率的初值。

式中,![]() 表示式(8)对电阻率ρ求一阶偏导,并忽略高阶项。
表示式(8)对电阻率ρ求一阶偏导,并忽略高阶项。
最终,得到基于HT-GN算法的第一阶段为式(10),并将其得到的新的初值代入式(11),不断迭代直至收敛,得到反映接地网腐蚀情况的电阻率分布。
当k=1,2,3,…,K时

当k<K时


图2 HT-GN算法流程
Fig.2 HT-GN algorithm flow chart
根据文献[26]对Homotopy法进行讨论,K选取经验值15。当迭代次数小于等于设定值K时,按照式(10)更新电阻率,当迭代次数大于K时,按照式(11)更新电阻率,这样式(10)就为式(11)提供一个比较好的初始值,Homotopy-Tikhonov(HTGN)的部分算法流程如图2所示。 HT-GN算法的接地网成像流程为:首先输入接地网引下线的测量电压、初始电阻率、雅克比矩阵,初始化电压误差、电压误差精度、Homotopy迭代次数;然后通过正问题有限元法计算引下线上的电压,代入式(10)进行Homotopy第一阶段迭代运算,满足k=K时,获得新的初始电阻率ρK;最后将ρK代入式(11),求解电阻率分布ρ,并将计算电压和测量电压相比较,满足w<e则停止迭代,输出电阻率分布ρ,否则继续通过有限元计算引下线电压,更新电阻率,直至满足迭代条件为止。
3 仿真成像
为了验证HT-GN算法在改善接地网电阻抗成像病态性的效果,本文通过COMSOL仿真软件建立接地网正、逆问题模型, 图3a为2×2接地网正问题的二维模型,“田”字轮廓为接地导体部分,选择截面积为40mm×4mm的镀锌扁钢构建边长为40cm的拓扑结构,电阻率为1.67×10−7Ω⋅m 。接地网导体中上部分小矩形是腐蚀部分,腐蚀电阻率为1×10−6Ω⋅m 。其余为土壤部分,电阻率为200Ω⋅m。注入1A的直流电,采用循环测量模式得到测量电压数据。图3b是接地网未知拓扑结构的逆问题模型,该模型边长为40cm,与接地扁钢拓扑大小一致,根据有限元法对其进行三角形剖分,其中网格剖分单元数为200个,网格剖分节点数为117个。

图3 接地网正、逆问题模型
Fig.3 Model of forward and inverse problems of grounding grid
在Matlab仿真平台下,首先计算最佳迭代初值,并且通过L曲线法求取最佳正则化参数,在二者基础上进行HT-GN算法和Tikhonov算法的接地网电阻抗成像,并引入电压相对误差进行图像质量评价;其次研究不同迭代初值和不同正则化参数对HT-GN算法的接地网电阻抗成像的影响,结合收敛精度和电压相对误差,定性和定量地分析HT-GN算法在改善接地网病态性问题上的效果;最后运用HT-GN算法分别对轻腐蚀、重腐蚀和断裂三种情况进行接地网仿真成像,验证HT-GN算法在改善接地网电阻抗成像逆问题病态性上的优越性。
3.1 HT-GN算法与Tikhonov算法的成像对比
首先根据文献[27]的公式计算接地网电阻抗成像迭代初值ρ0,即
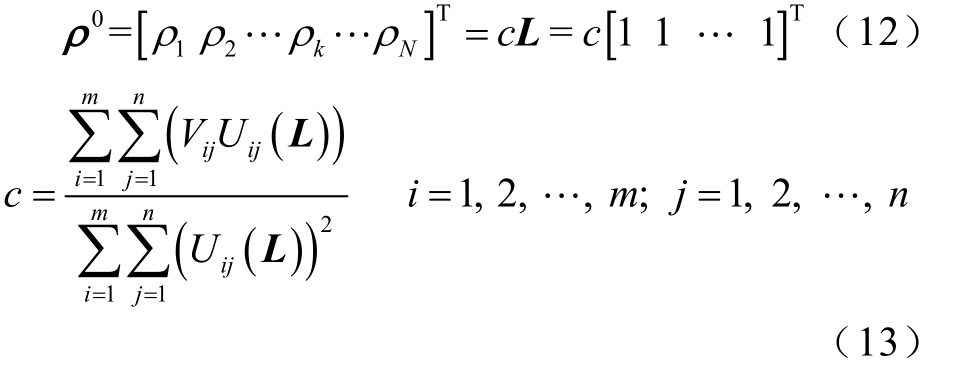
式中,m为循环注入电流次数;n为测量电压数量。经计算,本文接地网每个剖分单元最佳电阻率初值为6.51×10−7Ω⋅m。
由于电阻抗成像算法需要较优正则化参数来克服逆问题的病态性,因此两种迭代算法的正则化参数α均通过L曲线法求解。HT-GN算法的最佳正则化参数分两部分,第一部分为0.482,第二部分为0.446,Tikhonov算法的最佳正则化参数取为0.482。二者的L曲线如图4所示。
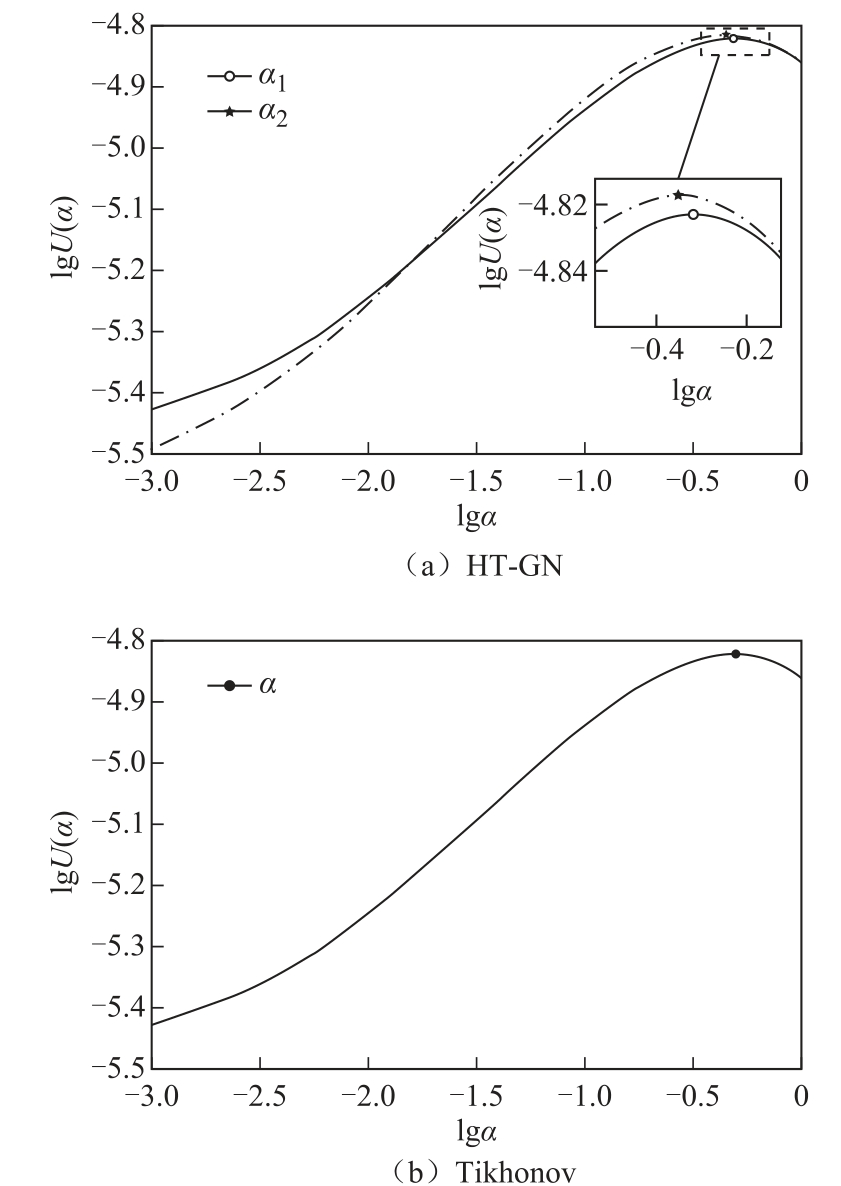
图4 HT-GN算法和Tikhonov算法L曲线
Fig.4 L curves of HT-GN algorithm and Tikhonov algorithm
最后在最佳迭代初值和正则化参数基础上,对两种算法分别进行接地网电阻抗成像,设置迭代精度为1×10−12,迭代上限为50次。图5a、图5b、图 5c分别为无腐蚀情况下、有腐蚀情况下的HT-GN算法和Tikhonov算法的接地网剖分单元图、色彩云图及三维地形图。
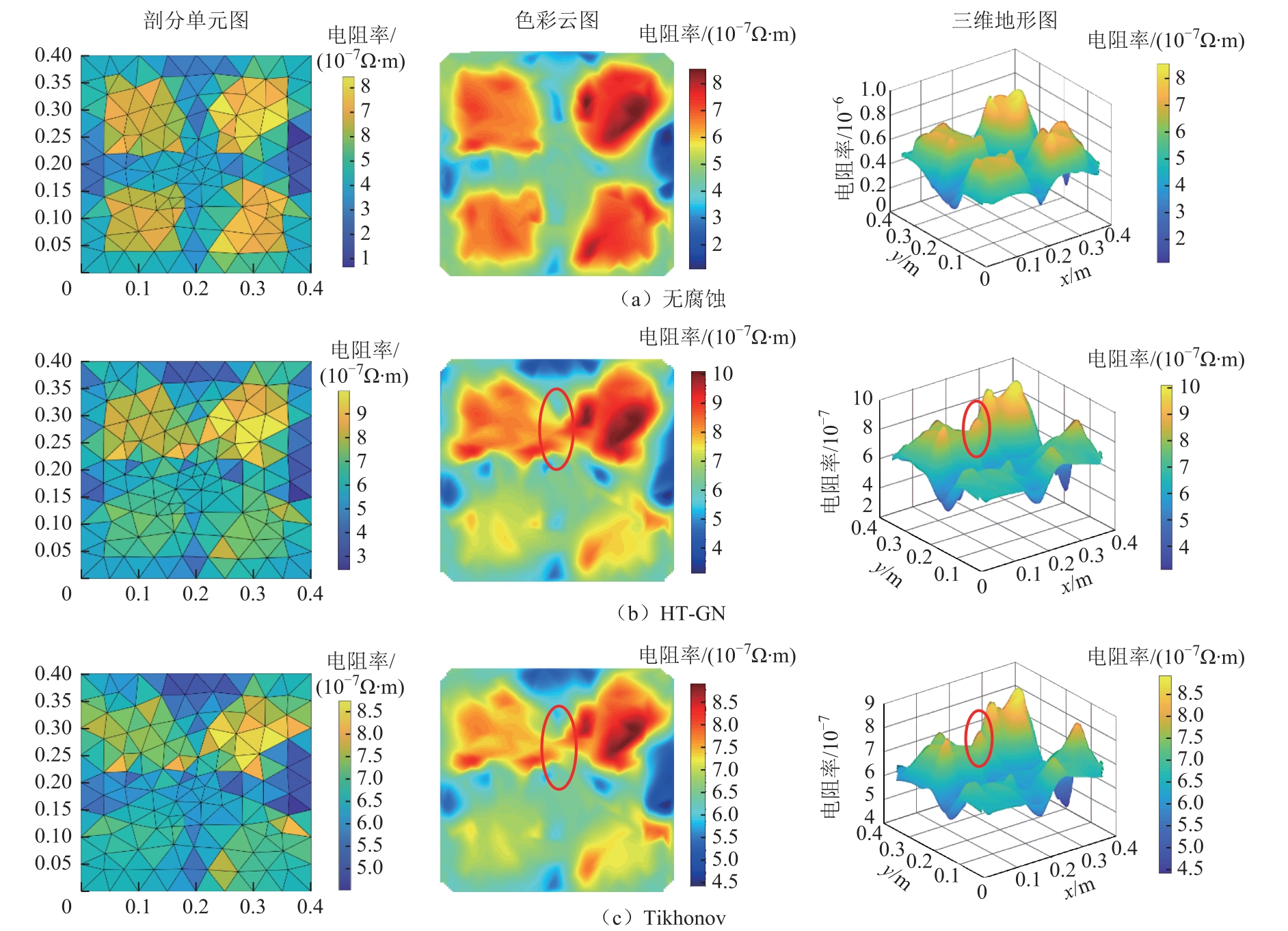
图5 HT-GN算法和Tikhonov算法接地网重构图像对比图
Fig.5 Comparison of reconstruction images of ground grid by HT-GN algorithm and Tikhonov algorithm
从图5可以看出,针对剖分单元图和色彩云图,四块类似方形部分代表土壤,“田”字轮廓代表接地网导体,在有腐蚀的位置两个方形土壤相连。针对三维地形图,凸起的四部分代表土壤,其余凹陷部分代表接地网导体,在腐蚀位置两块土壤相连,有较小的凸起。对比无腐蚀情况的接地网图像,可以明显看出两种重建算法均能反映2×2接地网中的扁钢、腐蚀区域及土壤分布,但两种算法的图像也不尽相同。本文提出的HT-GN算法在剖分单元成像、色彩云图成像及三维地形图成像下能更清晰完整地呈现腐蚀区域。因此,在最佳迭代初值和正则化参数前提下,HT-GN算法重建的接地网腐蚀图像清晰度优于Tikhonov算法。
为了进一步定量分析基于HT-GN算法的接地网图像质量情况,本文引入电压相对误差评价重构图像,其定义为
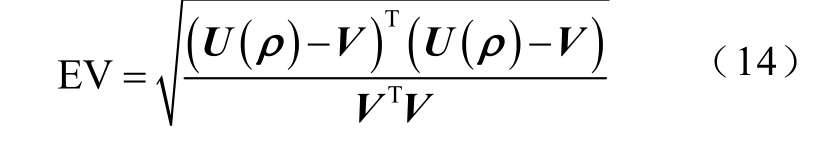
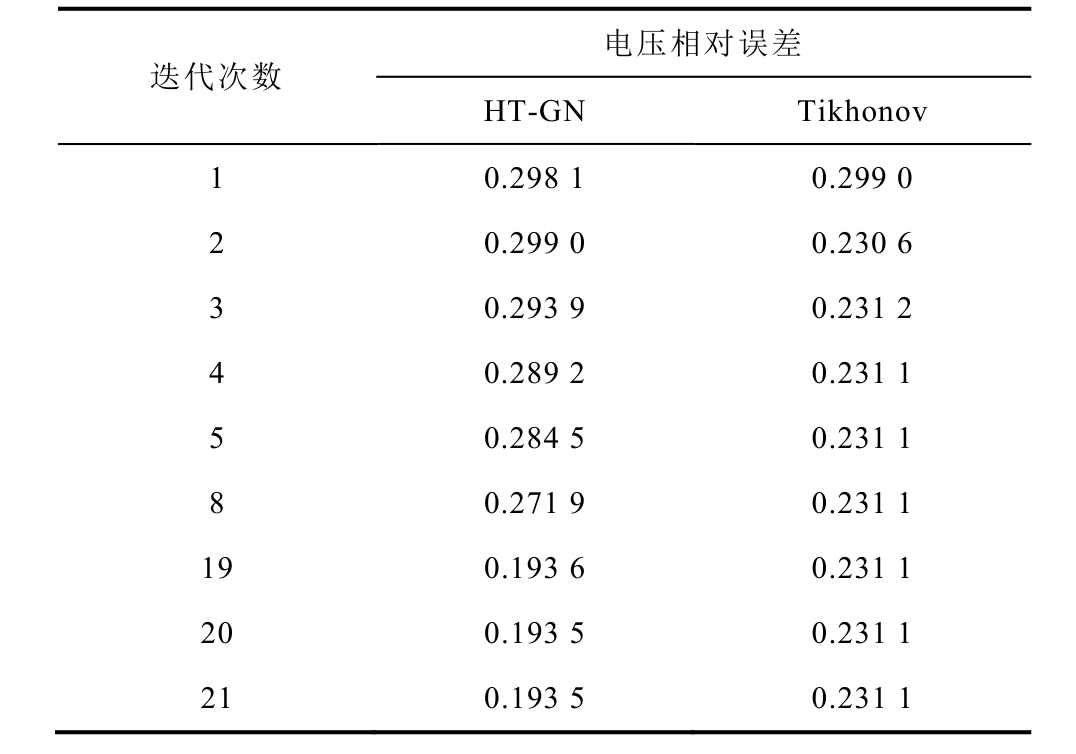
根据最佳迭代初值和正则化参数,两种算法的电压相对误差对比情况如图6所示,同时为了直观地展现两种算法的电压相对误差数值,表1为选取了部分迭代次数下的电压相对误差结果。由表1可见,基于Tikhonov算法的接地网电阻抗成像在迭代4次开始EV数值逐渐趋于稳定,而HT-GN算法在迭代了19次才开始变得平缓,但是在二者EV均稳定后,HT-GN算法的电压相对误差要更小。显然HTGN算法在最佳迭代初值和最佳正则化参数前提下,无论是直观还是定量对比,在图像精度上均优于Tikhonov算法。
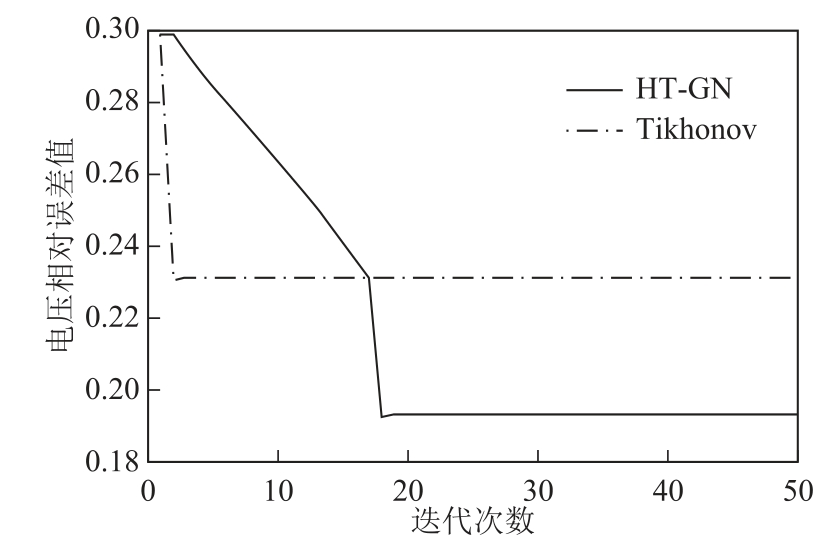
图6 电压相对误差对比图
Fig.6 Voltage relative error comparison diagram
表1 HT-GN算法和Tikhonov算法的电压相对误差
Tab.1 Voltage relative error of HT-GN algorithm and Tikhonov algorithm
电压相对误差 迭代次数 HT-GN Tikhonov 1 0.298 1 0.299 0 2 0.299 0 0.230 6 3 0.293 9 0.231 2 4 0.289 2 0.231 1 5 0.284 5 0.231 1 8 0.271 9 0.231 1 19 0.193 6 0.231 1 20 0.193 5 0.231 1 21 0.193 5 0.231 1
3.2 迭代初值的影响
对于多介质且介质之间电导率数量级差别大的模型,例如本文的接地网模型,HT-GN算法是适用的,它提高了图像的精度,且对初值的要求比较宽松。文献[26]提到Homotopy基本上对任意初始值均具有全局收敛性,但是针对接地网模型,HT-GN算法能否完全消除对初值的依懒性,需要进行大量的探究。3.1节已经求出较好的电阻率迭代初值,因此本文为了探究HT-GN算法的接地网电阻抗成像对初值的依赖性,分别取最佳迭代初值的0.2倍、0.5倍、1倍、1.2倍和1.5倍,图7为不同初值下HTGN算法的接地网重建图像。
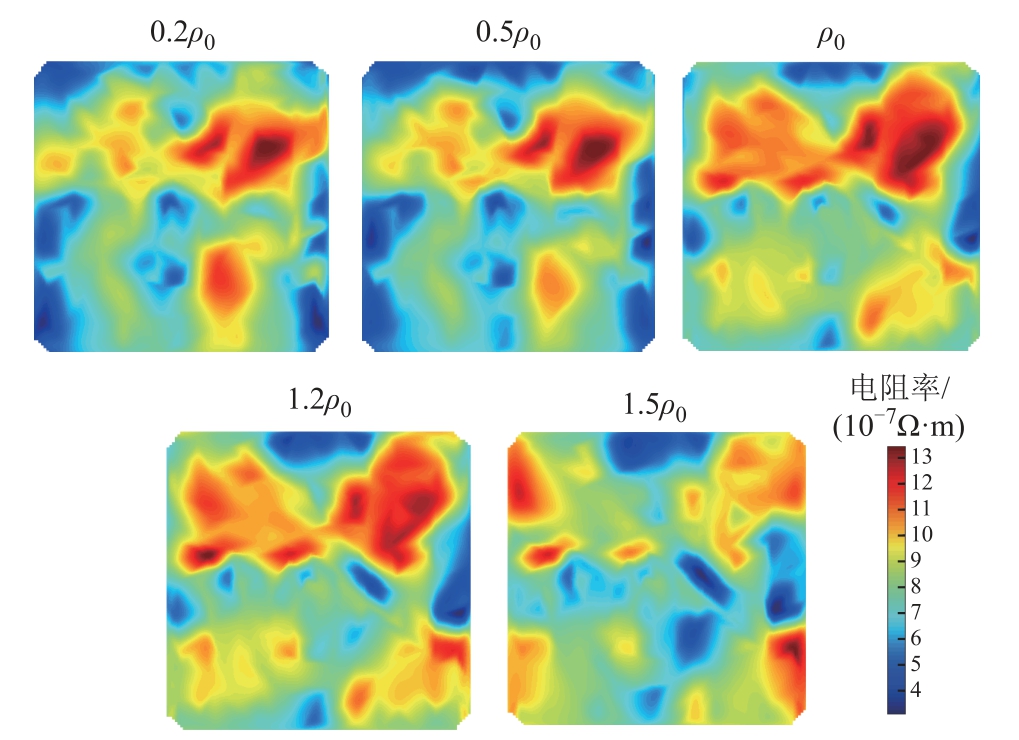
图7 不同迭代初值的接地网重建图像
Fig.7 Reconstruction images of ground grid with different initial iteration values
由图7所示,在已有的图像基础上,由式(12)求得的最佳迭代初值反映接地网腐蚀情况最好,病态性问题较轻。为了直观验证结论,引入计算电压和测量电压的2范数作为收敛精度进行定量分析。图8为五种初值下HT-GN算法的接地网图像收敛曲线。

图8 不同迭代初值的HT-GN算法收敛曲线
Fig.8 Convergence curves of HT-GN algorithm with different initial iteration values
从图8的结果可以看出,收敛精度在迭代初期变化大,随着迭代次数不断增加,收敛精度变化幅度越来越小,在迭代15~20次之间趋于平稳,稳定之后的收敛精度见表2。从表中可以看出,按照文献[27]取的初值,其收敛精度一直是最佳的。就目前取的初值,HT-GN算法的接地网图像均能收敛,进一步证实其对初值的要求比较宽松。
表2 不同迭代初值的收敛精度
Tab.2 The convergence precision of different initial values of iterations

初值倍数 0.2倍 0.5倍 1倍 1.2倍 1.5倍收敛精度/10-12 3.661 2.501 1.774 1.800 1.988
3.3 正则化参数的影响
对于HT-GN算法,正则化参数包含两部分:第一部分正则化参数的目的是计算出更贴近真实电阻率的迭代初值;第二部分正则化参数的目的是在该迭代初值基础上更加精确地迭代到真值。因此为了进一步探索正则化参数对基于HT-GN算法的接地网电阻抗成像的影响,本文提出HT-GN算法的第一部分正则化参数仍然根据3.1节L曲线法求解,而第二部分参数设置为以下五种数值,分别为0.04、0.08、0.4、0.8、2。图9为不同正则化参数下HT-GN算法和Tikhonov算法的接地网重建图像。

图9 不同正则化参数的接地网腐蚀成像图
Fig.9 Corrosion images of grounding grid with different regularization parameters
从图9可以看出,当正则化参数α=0.04时,Tikhonov算法的接地网图像不收敛,无法反映腐蚀情况,而HT-GN算法能够显示出腐蚀位置;随着α的增加,两种算法的接地网腐蚀情况反映逐渐明显,但是当正则化参数太大,如α=2,与HTGN算法相比,Tikhonov算法的接地网腐蚀成像不明显。因此,HT-GN算法的接地网腐蚀位置成像受正则化参数影响较小,同时在正则化参数相同情况下该算法重建图像清晰度、完整性均优于Tikhonov算法。
3.4 腐蚀程度的影响
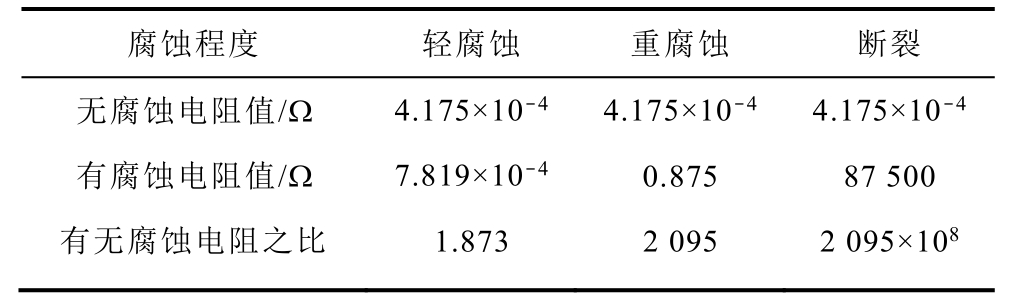
上文接地网腐蚀位置的电阻率设为1×10−6Ω⋅m ,镀锌扁钢电阻率为1.67×10−7Ω⋅m ,土壤电阻率为200Ω⋅m,其结果表明HT-GN算法更好地改善了接地网电阻抗成像逆问题的病态性,为了进一步研究不同腐蚀程度下,HT-GN算法的接地网成像逆问题改善情况,本文设置了轻腐蚀、重腐蚀和断裂三种情况,接地扁钢长度为0.4m,腐蚀长度为0.07m,具体参数见表3。当腐蚀位置的电阻率大小是1×10−6Ω⋅m 时,经计算,有、无腐蚀的电阻之比为1.873:1,定义为轻腐蚀;同理,当腐蚀位置电阻率大小是2×10−3Ω⋅m 时,有、无腐蚀之比为2 095:1,定义为重腐蚀;当腐蚀的电阻大小是200Ω⋅m,与土壤电阻率一致时,定义为断裂情况,具体成像结果如图10所示。

图10 不同腐蚀程度的接地网腐蚀成像图
Fig.10 Corrosion imaging of grounding grid with different corrosion degrees
表3 三种腐蚀程度的电阻值
Tab.3 Resistance values for three corrosion degrees
腐蚀程度 轻腐蚀 重腐蚀 断裂 无腐蚀电阻值/Ω 4.175×10-4 4.175×10-4 4.175×10-4有腐蚀电阻值/Ω 7.819×10-4 0.875 87 500 有无腐蚀电阻之比 1.873 2 095 2 095×108
由图10可见,在相同腐蚀程度下,与Tikhonov算法相比, HT-GN算法的接地网图像腐蚀位置更清晰,且腐蚀程度越大,这种情况越明显。为了定量分析此结论,借助电压相对误差进行图像质量评价,图11为两种算法在不同腐蚀程度下的电压相对 误差情况。
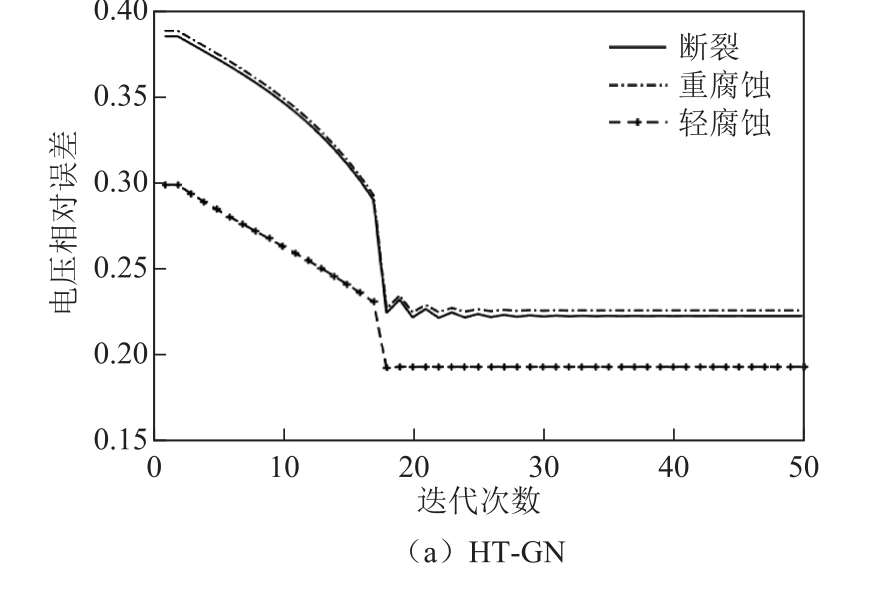

图11 不同腐蚀程度的电压相对误差对比
Fig.11 Comparison of voltage relative errors with different corrosion degrees
表4数据取自图11中电压相对误差稳定后的数值,可以明显看出,每种腐蚀情况下,HT-GN算法接地网成像的电压相对误差小于Tikhonov算法,改善接地网逆问题病态性问题效果更好,图像精度更高。
表4 三种腐蚀程度的电压相对误差
Tab.4 Voltage relative error for three corrosion degrees

算法 电压相对误差 轻腐蚀 重腐蚀 断裂 HT-GN 0.193 5 0.226 2 0.222 9 Tikhonov 0.231 1 0.293 2 0.290 6
4 实验验证
本文为了验证HT-GN算法能够改善接地网的病态性,选用40mm×4mm的镀锌扁钢,搭建3×3的接地网模型,每个网格长度为0.5m,恒流源注入1A的直流电,测量系统采集电压数据上传至计算机,最后导入Matlab进行电阻抗成像。图12为3×3接地网模型,电压循环测量系统获取电压数据,该系 统由电流注入和电压采集通道的自动切换模块、高精度模数转换模块、数据传输模块和人机交互模块四部分组成。

图12 3×3接地网模型
Fig.12 3×3 grounding grid model
电压测量采用四电极法,以减少两电极系统的接触阻抗对接地网成像的影响,测量节点个数为16,测量方式为循环测量,即以第16节点为参考,将一组电极,如1-2、1-3、…1-15、2-3、…2-15、…14-15中的前一个电极作为电流注入点,后一个电极作为电流流出点,依次循环,最终得到105×13个测量电压数据。
此次实验是在已知接地网图样或者已经通过其他方法重建了接地网拓扑的情况下[28],在实验室里模拟了接地网一处和二处腐蚀情况。由于接地网土壤和扁钢电阻率数量级相差大,镀锌扁钢电阻率为1.67×10−7Ω⋅m,而土壤电阻率通常为200Ω⋅m,因此在电阻抗逆问题成像中可以忽略土壤只留下扁钢。仿真对比了接地网重腐蚀、轻腐蚀、断裂三种情况,其中接地网轻腐蚀图像精度最高,按照轻腐蚀中有、无腐蚀电阻率之比为1.873:1的标准,本实验选用长度为50cm的镀锌扁钢,测得电阻大小为2.519mΩ,用绝缘细绳将断开的镀锌扁钢与另外长度为10cm的镀锌扁钢绑紧,此时电阻值为4.169mΩ,有无腐蚀之比为1.655:1,能够满足轻腐蚀的成像需要,因此本文在轻腐蚀状态下接地网模拟了1处和2处腐蚀情况。

图13 一处接地网腐蚀的示意图和成像图
Fig.13 Diagram and imaging of a grounding grid corrosion
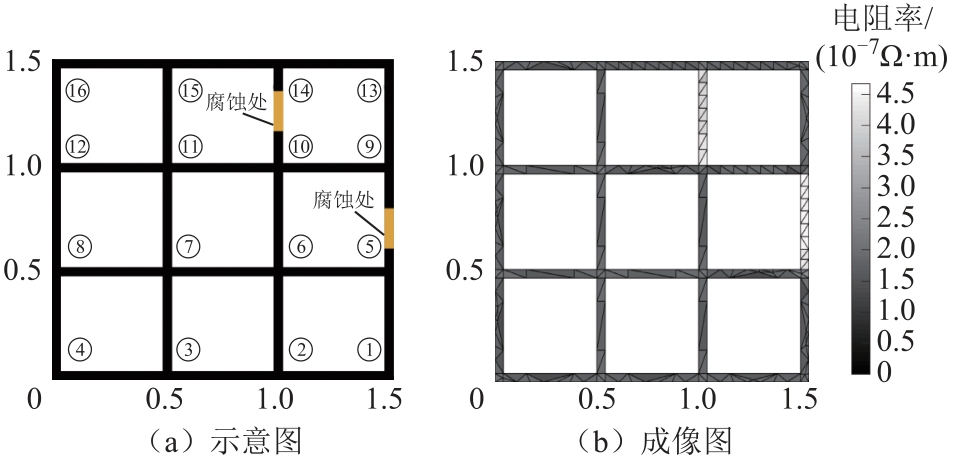
图14 两处接地网腐蚀的示意图和成像图
Fig.14 Schematic diagram and imaging of two grounding grid corrosion
图13a和图13b分别为一处腐蚀的接地网成像的示意图和对应的逆问题成像图。同理,图14a和图14b分别为两处腐蚀的接地网成像的示意图和对应的逆问题成像图。两个逆问题成像图均能清晰地显示出腐蚀的数量和位置,验证了该方法在改善接地网病态性问题上的可行性。
5 结论
为了克服接地网扁钢和土壤电阻率数量级相差巨大,改善接地网电阻抗成像病态性问题,本文提出了基于Homotopy-Tikhonov算法(HT-GN)的接地网电阻抗成像故障诊断方法。借助COMSOL 和Matlab两个仿真软件,对接地网进行了电阻抗成像。仿真和实验结果表明,基于HT-GN算法的接地网图像改善病态性效果更好。主要结论如下:
1)在求取的最佳迭代初值和最佳正则化参数基础上,对比了HT-GN算法和Tikhonov算法的接地网重建图像,仿真结果表明基于HT-GN算法重构的接地网图像腐蚀位置更加清晰,且收敛后的电压相对误差更小,优于Tikhonov算法重建的接地网图像,但迭代次数相对较多。
2)针对HT-GN算法的接地网电阻抗成像,分别对比了最佳迭代初值与该初值的0.2~1.5倍、最佳正则化参数与其他正则化参数的接地网重构图像,仿真结果表明采用HT-GN算法的接地网图像在几种迭代初值条件下均能收敛,并且在最佳迭代初值和最佳正则化参数条件下腐蚀区域成像效果最好,图像清晰度最高。进一步验证了在接地网电阻抗成像中,该方法对电阻率迭代初值要求更加宽松且成像效果与正则化参数的选取密切相关。
3)仿真设置了接地网轻腐蚀、重腐蚀、断裂三种情况,结果表明采用HT-GN算法均能反映接地网腐蚀位置,且轻腐蚀状态下电压相对误差最小,随着腐蚀程度加大,接地网腐蚀区域成像越明显。同时接地网实验验证了轻腐蚀条件下该方法重建图像的可行性。
因此,本文提出的基于HT-GN算法的接地网电阻抗成像腐蚀位置更清晰,收敛效果最好,更好地改善了电阻抗成像逆问题的病态性,为解决接地网腐蚀定位成像提供了一种新方法,推动了电阻抗成像技术在接地网中的实际应用,有利于解决实际工程问题。
[1] 张波, 何金良, 曾嵘. 电力系统接地技术现状及展望[J]. 高电压技术, 2015, 41(8): 2569-2582.
Zhang Bo, He Jinliang, Zeng Rong. State of art and prospect of grounding technology in power system[J]. High Voltage Engineering, 2015, 41(8): 2569-2582.
[2] 王思华, 杨桐, 段启凡, 等. 基于DT法和粗糙集理论的接地网安全性状态评定[J]. 电力系统保护与控制, 2017, 45(2): 48-54.
Wang Sihua, Yang Tong, Duan Qifan, et al. Evaluation of security state in grounding grid based on DT method and rough set[J]. Power System Protection and Control, 2017, 45(2): 48-54.
[3] 陈伟伟, 吕盼, 纪凤坤, 等. 基于多维度检测与Petri网的变电站接地故障风险评估[J]. 电力系统保护与控制, 2019, 47(23): 152-159.
Chen Weiwei, Lü Pan, Ji Fengkun, et al. Risk assessment of substation grounding fault based on multidimensional detection and Petri net[J]. Power System Protection and Control, 2019, 47(23): 152-159.
[4] 王晓宇, 何为, 杨帆, 等. 基于微分法的接地网拓扑结构检测[J]. 电工技术学报, 2015, 30(3): 73-78, 89.
Wang Xiaoyu, He Wei, Yang Fan, et al. Topology detection of grounding grids based on derivative method[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 73-78, 89.
[5] 史庆岩, 何为, 杨帆. 基于模拟退火遗传算法的接地网故障磁场诊断方法研究[J]. 电力系统保护与控制, 2012, 40(20): 52-55, 67.
Shi Qingyan, He Wei, Yang Fan. Magnetic fault diagnosis of grounding gird based on simulated annealing genetic algorithm[J]. Power System Protection and Control, 2012, 40(20): 52-55, 67.
[6] 李星, 杨帆, 余晓, 等. 基于内源式电阻抗成像的接地网缺陷诊断逆问题研究[J]. 电工技术学报, 2019, 34(5): 902-909.
Li Xing, Yang Fan, Yu Xiao, et al. Research on the inverse problem of grounding grid fault diagnosis based on inner-source EIT[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 902-909.
[7] 夏慧, 刘国强, 黄欣, 等. 注入电流式磁声成像平面模型的逆问题研究[J]. 电工技术学报, 2017, 32(4): 147-153.
Xia Hui, Liu Guoqiang, Huang Xin, et al. The inverse problem study of plane model based on magnetoacoustic tomography with current injection[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 147-153.
[8] 章伟睿, 张涛, 史学涛, 等. 基于差分迭代的电阻抗成像算法研究[J]. 电工技术学报, 2021, 36(4): 747-755.
Zhang Weirui, Zhang Tao, Shi Xuetao, et al. An algorithm of electrical impedance tomography based on differential iteration[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 747-755.
[9] Bera T K, Biswas S K, Rajan K, et al. Projection error propagation-based regularization (PEPR) method for resistivity reconstruction in electrical impedance tomography (EIT)[J]. Measurement, 2014, 49(1): 329-350.
[10] Kim B S, Kim K Y, Kim S. Image reconstruction using adaptive mesh refinement based on adaptive thresholding in electrical impedance tomography[J]. Nuclear Engineering and Design, 2014, 270: 421-426.
[11] 刘杰. 基于电阻抗成像测量原理的接地网腐蚀诊断系统设计[D]. 重庆: 重庆大学, 2012.
[12] 赵宏晨, 刘晓明, 杨滢璇, 等. 基于分数阶Tikhonov正则化方法的电弧反演研究[J]. 电工技术学报, 2019, 34(1): 84-91.
Zhao Hongchen, Liu Xiaoming, Yang Yingxuan, et al. Research on arc inversion based on fractional Tikhonov regularization method[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 84-91.
[13] Noschese S, Reichel L. Some matrix nearness problems suggested by Tikhonov regularization[J]. Linear Algebra and Its Applications, 2015, 502: 366-386.
[14] Morigi S, Reichel L, Sgallari F. Fractional Tikhonov regularization with a nonlinear penalty term[J]. Journal of Computational and Applied Mathematics, 2017, 324: 142-154.
[15] 代锋. 接地网的电阻抗成像系统与方法研究[D]. 重庆: 重庆大学, 2015.
[16] Vazquez-Leal H, Marin-Hernandez A, Khan Y, et al. Exploring collision-free path planning by using homotopy continuation methods[J]. Applied Mathematics and Computation, 2013, 219(14): 7514-7532.
[17] Wu T M. A study of convergence on the Newtonhomotopy continuation method[J]. Applied Mathematics and Computation, 2003, 168(2): 1169-1174.
[18] Wu Huanli, Xu Guizhi, Yu Hongli, et al. Three dimensional electrical impedance tomography in thorax complete model[C]//2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, 2008: 466-469.
[19] Mostashiri N, Akbarzadeh A, Rezaei A. Implementing the homotopy continuation method in a hybrid approach to solve the kinematics problem of spatial parallel robots[J]. Intelligent Service Robotics, 2017, 10(3): 257-270.
[20] Wang Mengran, Li Jing. The feasibility of homotopy continuation method for a nonlinear matrix equation[J]. Mathematical Problems in Engineering, 2020: 1-13. DOI:10.1155/2020/1787058.
[21] 秦伟刚, 王超. 乳腺肿瘤同伦LM算法EIT图像重建[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(5): 506-512.
Qin Weigang, Wang Chao. Image reconstruction of breast tumors using homotopy LM algorithm in electrical impedance tomography[J]. Journal of Tianjin University(Science and Technology), 2016, 49(5): 506-512.
[22] Liu Shutian, Lei Jingzhe, Li Z H, et al. Generalized flow pattern image reconstruction algorithm for electrical capacitance tomography[J]. Nuclear Engineering and Design, 2011, 241(6): 1970-1980.
[23] Nor H M, Md Ismail A I, Majid A A. A new homotopy function for solving nonlinear equations[C]//AIP Conference Proceedings, American Institute of Physics, 2013, 1557(1): 21-25.
[24] Huang Qingqun, Zhu Zhibin, Wang Xiangling. A predictor–corrector algorithm combined conjugate gradient with homotopy interior point for general nonlinear programming[J]. Applied Mathematics and Computation, 2013, 219(9): 4379-4386.
[25] 张晓菊. 基于牛顿—拉弗逊正则化算法的开放式电阻抗成像研究[D]. 重庆: 重庆大学, 2009.
[26] 徐桂芝, 李颖, 杨硕, 等. 生物医学电阻抗成像技术[M]. 北京: 机械工业出版社, 2010.
[27] Cheney M, Isaacson D, Newell J C, et al. NOSER: an algorithm for solving the inverse conductivity problem[J]. International Journal of Imaging Systems and Technology, 1990, 2(2): 66-75.
[28] 王文东, 胡绪权, 徐正玉, 等. 基于形态滤波的接地网拓扑检测[J]. 电工技术学报, 2021, 36(7): 3685-3692.
Wang Wendong, Hu Xuquan, Xu Zhengyu, et al. Topology detecting method of grounding grids based on morphological filtration[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 3685-3692.
作者简介
闫孝姮 女,1984年生,博士,副教授,研究方向为电磁探测与成像。
E-mail:xiaohengyan@163. com
林晓雪 女,1996年生,硕士研究生,研究方向为电磁探测与成像。
E-mail:1604006222@qq. com(通信作者)