0 引言
阻抗匹配是一种提高能量传输效率的常见手段,当负载阻抗与源阻抗互为共轭复数时即可使系统的功率传输效率达到最大。在一些特殊情况下,如无线电能传输[1-2]、微波系统[3-4]、声电换能[5-6]、弱电网并网[7-8]等场合,系统的源阻抗和负载阻抗可能会发生动态变化,使系统失去匹配。而自动阻抗匹配技术,可以使系统时刻保持匹配状态,极大地提高了系统的稳定性。
目前对于阻抗匹配算法的研究主要集中于智能算法,如遗传算法、粒子群算法和神经网络算法等[9–12]。这些智能算法在理论上可以获得较好的匹配,但建模较为复杂,所需的迭代时间长,计算量大,往往需要专门的数字处理器,增加了系统的开发成本。
Q值法是由Y. Sun和J. K. Fidler在1996年提出的一种匹配网络计算方法[13],使用该方法对已知的源阻抗和负载阻抗进行匹配,只需确定合适的负载品质因数Q0,即可完成相应Π型(或T型)匹配网络的参数设计。B. K. Chung和Liao Ruijin等也针对Q值法开展了后续研究和完善工作[14-15]。
本文针对传统自动阻抗匹配方法匹配时间较长的问题,提出了一种自动阻抗匹配方法。该方法利用T型网络器件的解空间截面确定Q0,再通过Q值法计算网络参数。与智能算法相比,所需计算量大大减小。在Matlab平台上对使用该方法的自动阻抗匹配系统进行仿真,并通过样机进行实验验证,结果表明该方法与经典的遗传算法自动阻抗匹配相比,能够在保证较好匹配效果的前提下大幅减少匹配时间。
1 Q值法基础理论
阻抗匹配网络大致可分为L型、Π型、T型以及复合型网络。其中L型网络的匹配范围有限,只能处理源阻抗大于负载阻抗或源阻抗小于负载阻抗中的一种情况。而复合型网络则较为复杂,较多的网络器件会让自动阻抗匹配网络的设计和控制更加困难。Π型网络和T型网络是互相对偶的网络,它们可以匹配完整的阻抗圆且只需要三个器件[16]。本文主要以T型网络为例进行研究,可以通过对偶关系得到Π型网络的设计方法。
由诺顿定理可知,任何T型网络都可表示为图1所示电路,其中G1、G2分别为源阻抗R1和负载阻抗R2的倒数,L1、L2、C为T型网络的组成元件。若负载不为纯电阻,其虚部亦可折算进L2。为方便讨论,本文仅考虑源阻抗和负载阻抗为纯电阻的情况。
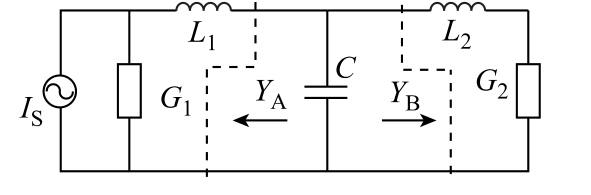
图1 T型网络
Fig.1 T type network
记T型网络无源器件的阻抗分别为XL1、XL2和BC,即

如图1所示,G1、L1和G2、L2分别组成了一个L型网络,定义这两个L型网络的品质因数Q1和Q2分别为
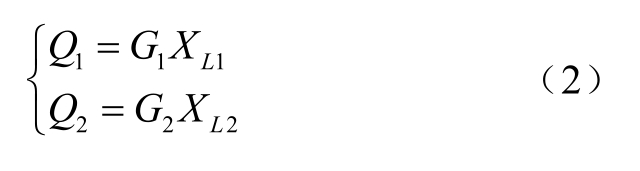
如图1所示,引入YA表示G1和L1的串联导纳,YB表示G2和L2的串联导纳,由导纳性质可知
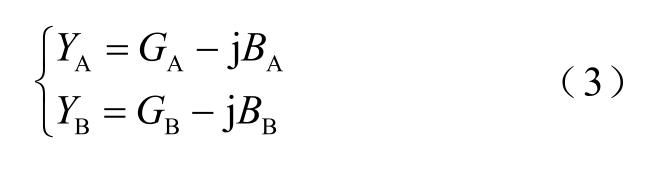
计算可得
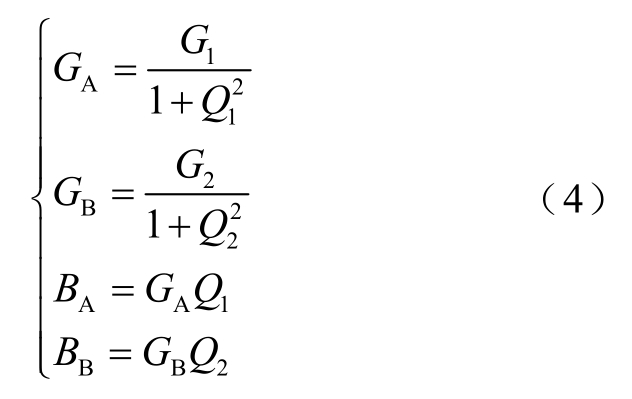
为使网络能够匹配,需要满足
式中,YA为YA的共轭。将式(3)代入式(5)可得

定义T型网络的负载品质因数Q0为
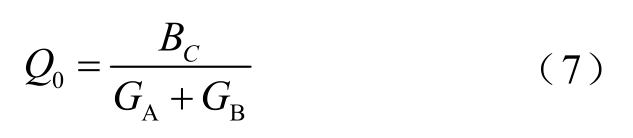
由式(4)、式(6)可得
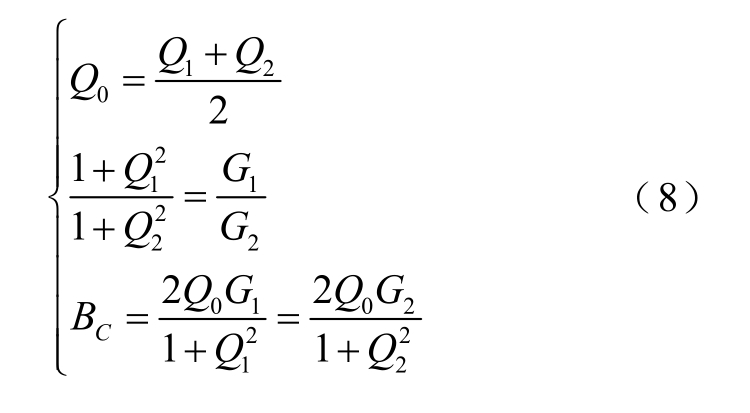
进一步可推得T型网络的设计条件为

式中,k为导纳比,k=G1/G2。在满足式(9)条件下求解式(8)可得

将式(10)回代到式(2)、式(4)、式(7)中,可得T型网络参数的计算公式为
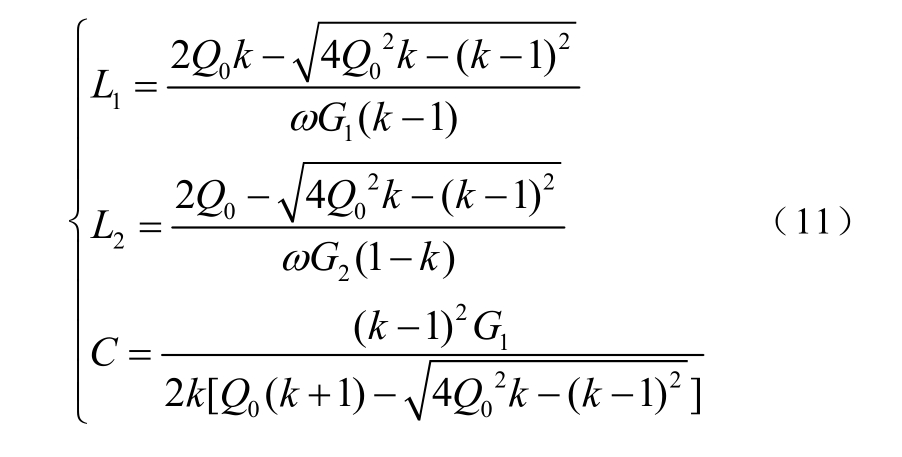
2 基于Q值法的自动阻抗匹配网络设计
2.1 自动阻抗匹配方法的理论分析
使用Q值法可以在已知源阻抗和负载阻抗的情况下得到很好的匹配效果,但当阻抗发生变化时,系统便会失去匹配。
为了研究匹配网络参数L1、L2和C关于G1、G2和Q0的关系,取G1为X轴,G2的倒数R2为Y轴,如图2所示,分别做L1、L2和D的函数图像,其中D为C的倒数,具体参数见表1。其中G1、G2的取值范围都是常见的源阻抗和负载阻抗范围,据此可算出k的范围。将k的范围代入式(9),可以得到Q0在k<1和k≥1两种情况时的下限。当k=0.01时(此时G1=0.01、G2=1),有Q0≥![]() /2;当k=10时(此时G1=0.05、G2=0.005),有Q0≥1.5,所以当Q0∈[1.5,
/2;当k=10时(此时G1=0.05、G2=0.005),有Q0≥1.5,所以当Q0∈[1.5, ![]() /2]时可恰好满足设计条件。由式(11)可以看出Q0的范围越大,可调器件的范围也越大,但是可调器件的范围是有限的,所以Q0的范围不宜过大。为了留有裕度,表1中将Q0的范围进行了放大处理。为了便于描述,后文下标中带有min的参数即为该参数取值范围的最小值,带max为取值范围的最大值。
/2]时可恰好满足设计条件。由式(11)可以看出Q0的范围越大,可调器件的范围也越大,但是可调器件的范围是有限的,所以Q0的范围不宜过大。为了留有裕度,表1中将Q0的范围进行了放大处理。为了便于描述,后文下标中带有min的参数即为该参数取值范围的最小值,带max为取值范围的最大值。

图2 T型网络参数与G1、R2及Q0间的关系
Fig.2 Relationship between T-network parameters and G1, R2 and Q0
表1 仿真参数
Tab.1 Simulation parameters

参 数数 值 输出频率f/kHz 100 源导纳G1/S [0.01, 0.05] 负载导纳G2/S [0.005, 1] 导纳比k [0.01, 10] Q0 [3, √99]
观察图2可知L1、L2和D的变化趋势大致相同,两个曲面之间所夹的空间即为器件在Q0∈[Q0min , Q0max]时解的范围。取Q0=Q0min 时的器件最大值作为可调器件的取值上限,记作L1max、L2max和Dmax;取Q0=Q0max时的器件最小值为可调器件的取值下限,记作L1min、L2min和Dmin。这样即可在可调器件设计范围最小的同时保证匹配网络能对设计范围内的G1、G2进行匹配。以L1为例,过L1max和L1min作一平行G1轴的截面,截面方程为
L1的解空间截面如图3所示,由图3可知该截面穿过整个解空间,且仅为G1、G2的函数,如此便可通过G1、G2确定L1的大小。由式(11)可以推出
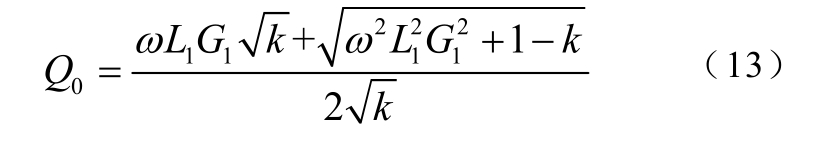
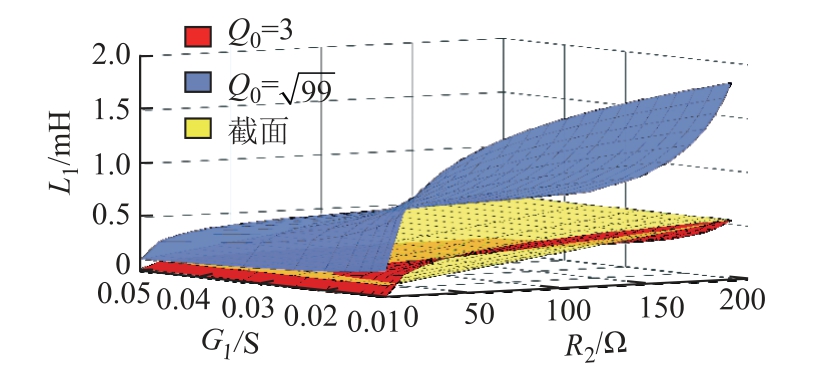
图3 L1的解空间截面
Fig.3 The cross section of L1’s solution space
由式(13)可以求出Q0,再通过式(11)计算其他参数,便可得到一组完整的匹配参数。式(13)若要有意义,需满足条件
若不满足式(14)条件,可对L2以类似方法也构建一个平面,其平面方程与Q0的公式为
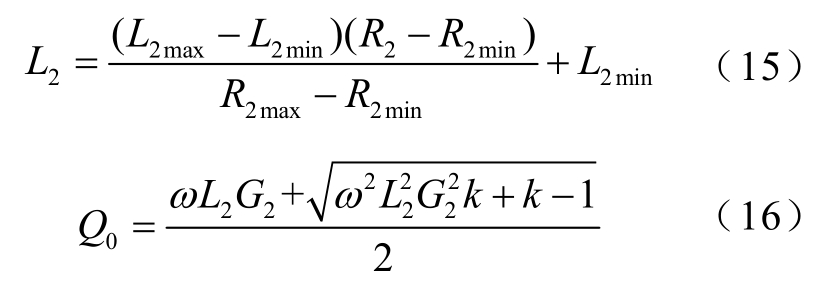
式(15)成立所需满足条件
分析式(14)、式(17)可知,两式中一式不成立时另一式必然成立,故使用这种方法必然可以得到一个Q0,并以此反求出其他参数。当式(14)、式(17)同时成立时,由于L1和L2的函数不同,两者求出的Q0也未必相同,因此可以得到两组匹配参数。将由L1求得的参数记为参数1,由L2求得的参数记作参数2。若L1、L2和C的参数可连续变化,则两组参数皆可完成匹配,从损耗角度考虑应选择Q0较小的方案进行匹配[13]。
这种匹配方法因为利用了解空间的截面,本文称其为截面法。
2.2 自动阻抗匹配网络的设计
匹配网络的整体电路如图4所示,主要由源阻抗与负载阻抗测量电路、可调器件和控制器组成。其中阻抗测量电路主要用于测量外部阻抗,得到G1、G2交由系统运算。控制器主要负责进行运算和判断,以及对可调器件的控制。可调器件通过改变自身参数使系统得到匹配。

图4 T型自动阻抗匹配网络
Fig.4 T-network automatic impedance matching network
可调器件是系统得以实现的基础。目前常见的可调电容有真空电容器、变容二极管和电容阵列等。其中真空电容器的器件分辨率取决于选用的电机齿数;变容二极管可无级调节,但可承受的功率较小;电容阵列是较为经济便捷的方案,但当阵列级数增加时,其误差的累积会使系统的匹配精度降低。
为了便于在Matlab中建模仿真,本文最终选用电容阵列作为实现方案,其结构如图5所示。由于使用了电容的倒数D,因此将电容串联。可调电容的第1级电容大小为Dmin的倒数,后N级的电容大小为Dunit与2的N-1次幂的积的倒数,其中Dunit=(Dmax-Dmin)/2N。通过控制相应的开关开合即可控制L1、L2和D在设计范围内以2-N精度变化。
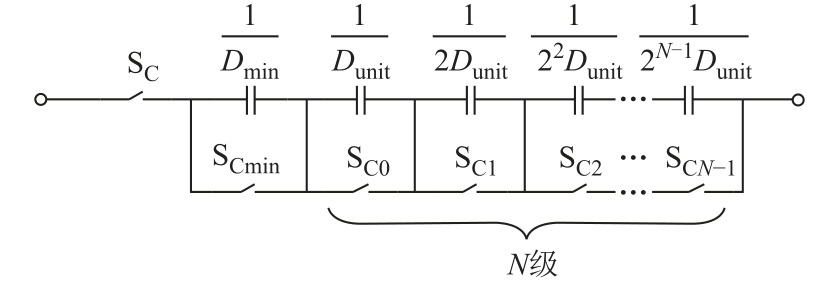
图5 可调电容模块结构
Fig.5 Adjustable capacitor module structure
相较于可调电容,高精度的可调电感目前实现还较为困难。常见的方案有滚筒线圈、磁控电感和电感阵列[17-18]。其中滚筒线圈的器件分辨率取决于选用的电机齿数,且不能承受太大的功率;磁控电感可以无极调节感量,但控制难度较高,非线性较大;电感阵列是较为经济便捷的方案,但当阵列级数增加时,其误差的累积会使系统的匹配精度降低。
本文选用电感阵列作为实现方案,其具体电路结构如图6所示,由N+1级电感和开关的并联结构串联而成。第1级电感大小为Lxmin,后N级的电感大小为Lxunit与2的N-1次幂的积。其中Lxunit=(Lxmax-Lxmin)/2N,下标中的x可为1或2。

图6 可调电感模块结构
Fig.6 Adjustable inductance module structure
2.3 自动阻抗匹配网络的匹配流程
在通信系统中经常使用反射系数Г来衡量系统的匹配程度,反射系数Г为

式中,Z1为系统源阻抗,Z1=R1+jX1;Z2为系统的负载阻抗,Z2=R2+jX2。一般来说,反射系数的模越小,系统的匹配度越高,当|Г|=0时系统便达到了完全匹配。所以让系统不断扫描计算Г,当|Г|大于预先设定的阈值时,认为系统失配,匹配器开始工作。具体匹配流程如图7所示。首先,系统通过源阻抗和负载阻抗测量模块测得Z1和Z2,进而得到G1、G2。 随后将G1、G2代入式(12)求得L1,并检验其是否满足式(14),若是不满足则直接将L1舍去;若是满足则将L1代入式(13)求得Q0,再将Q0代回式(11)求得L2和C值。由于T型网络器件的值不连续,只能将可调器件调节到最为接近的值,记这组参数为参数1。引入误差d为
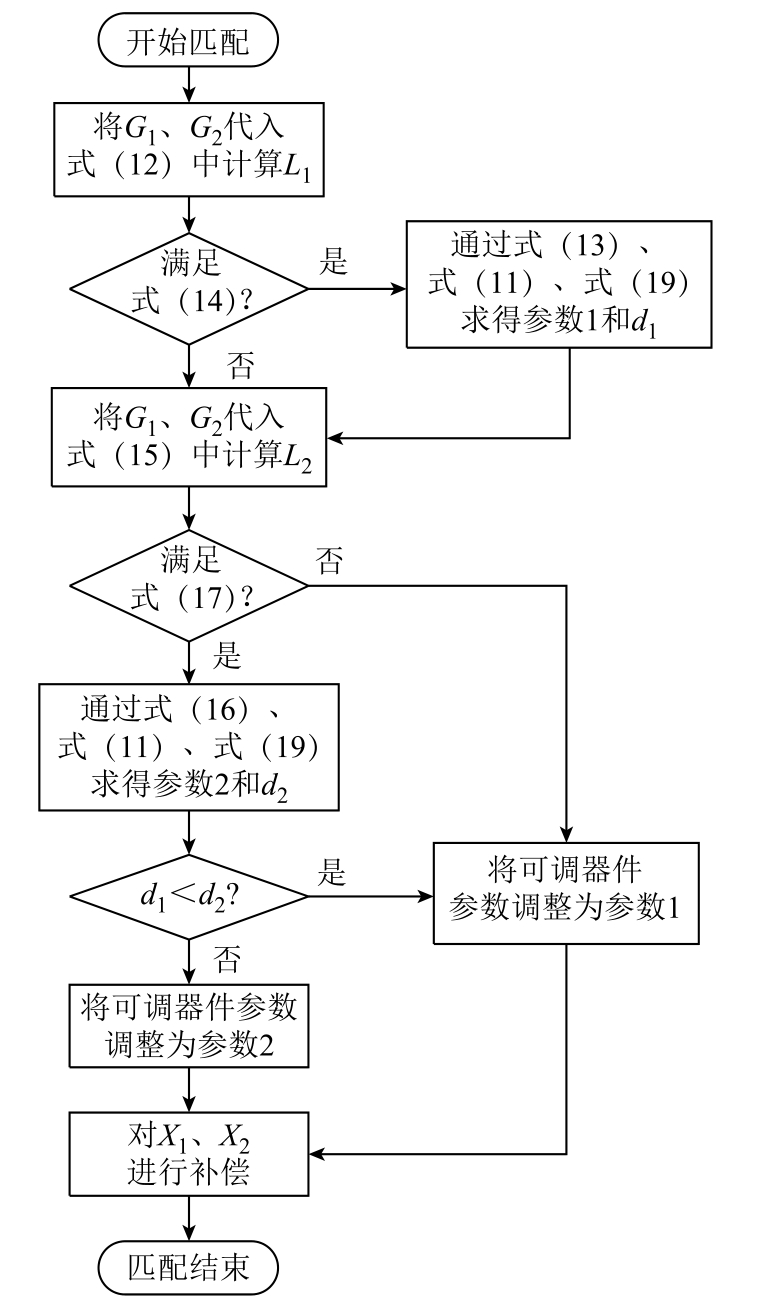
图7 匹配流程
Fig.7 Matching flow chart
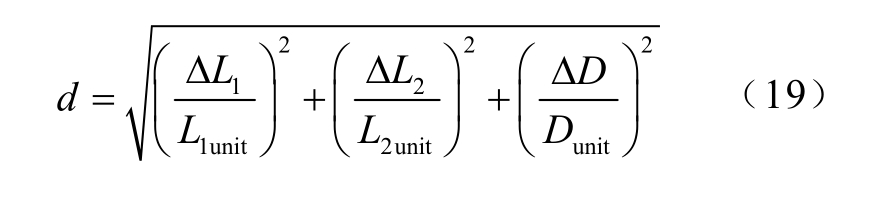
d代表了离散的器件值与运算得到的理想值之间的偏差,其中ΔL1表示L1离散化后产生的误差,其他参数以此类推,将参数1与理想值的误差记作d1。再按类似的流程将G1、G2代入式(15)求出L2,检验其是否满足式(17),若是满足条件则继续求出参数2,以及参数2的误差d2;若是不满足则直接舍去L2。根据前文讨论可知至少会有一组参数,若只得到一组参数则选用这组参数;若有两组参数则选用误差较小的参数作为匹配参数。接下来要用L1、L2补偿X1、X2,若X2<0,负载为容性,则L2要再加上X2/ω的电感量;若X2>0,负载为感性,则L2要减去X2/ω的感量。若补偿后超出了L2的范围,则需要在L2和负载之间串联电感或电容来补偿,或在设计L2时提前留出足够的余量用于补偿,L1同理。
3 对于自动阻抗匹配网络的仿真
为了研究设计网络时Q0范围和可调器件级数N对于最终匹配效果的影响,现设计四个匹配网络,其Q0和N分别见表2,其他参数与表1一致。
表2 网络参数
Tab.2 Network parameters
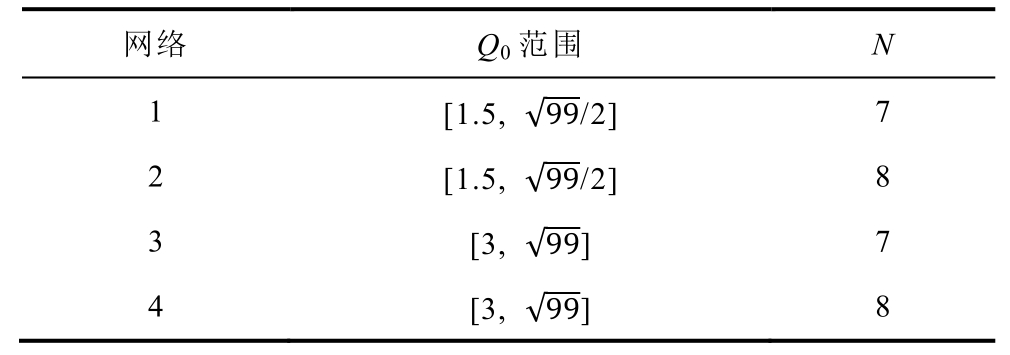
网络 Q0范围 N1 [1.5, √99/2] 7 2 [1.5, √99/2] 8 3 [3, √99] 7 4 [3, √99] 8
在Matlab中分别对四个网络进行建模,使其在不同的源阻抗与负载阻抗下完成匹配,记录其完成匹配后反射系数模的大小,分析结果如图8所示。 由图8的整体趋势可以看出,截面法在负载阻抗较小时误差较大,其主要原因是反射系数受负载阻抗的影响很大。对于Q值法设计的电路,当负载阻抗为纯电阻时,有
式中,dr为负载电阻相对于设计值发生的偏移量[15]。负载越小,相同的偏移量造成的影响就越明显。另外,在负载电阻较小时,截面与解空间边缘的不吻合也是一个影响因素。建议在设计匹配网络时对负载阻抗的下界留出一定的设计冗余,以抵消相应的误差,提高系统匹配的准确度。
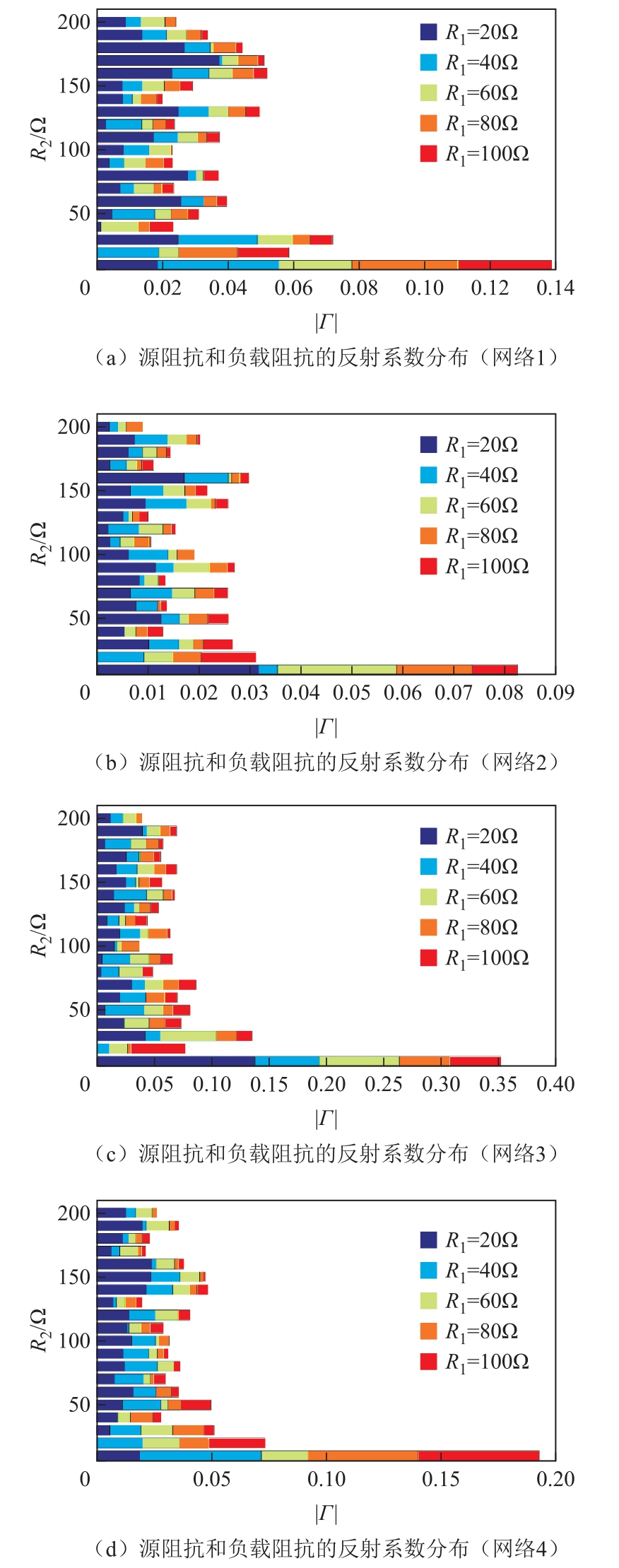
图8 四组匹配网络关于源阻抗和负载阻抗的 反射系数分布图
Fig.8 Reflection coefficient distribution of four matching networks on source impedance and load impedance
对比观察图8可知,当Q0的范围减小或可调器件的调节精度提高时,系统的匹配精度也会相应提高。因此当系统的匹配精度达不到预期时,可行的对策有:①缩小之前设计时Q0留下的冗余;②增大N以提高器件精度。但当N=8时电容电感阵列中最大器件已是最小器件的128倍,若使用1%精度的器件,则最大器件的误差已大于最小器件的值。此时应考虑选用更高精度的器件,或改用可无极调节的可控器件,重新设计网络。
为了比较截面法和常见启发式算法的匹配精度和匹配时间,在Matlab中使用表2的网络2作为匹配网络,对源阻抗R1=50Ω的交流源分别使用截面法和遗传算法进行匹配。两种算法完成匹配后的反射系数模和完成匹配的时间分别如图9a、图9b所示,其中匹配时间使用了对数坐标。可以看到截面法在负载阻抗较小时匹配误差较大,而在其他情况下截面法与遗传算法的误差在一个量级。与此同时,遗传算法所需的匹配时间是截面法的100倍,截面法直接求解的运算速度比需要迭代的遗传算法要快很多。

图9 截面法与遗传算法的反射系数和匹配时间比较图
Fig.9 Comparison of reflection coefficient and matching time between cross section method and genetic algorithm
4 实验验证
为了验证截面法的匹配性能,搭建自动阻抗匹配系统如图10所示。系统结构与图4一致,但去掉了源阻抗检测模块,自动阻抗匹配系统的源阻抗由程序设定为50Ω。在负载前有采样模块可采样电压、电流和相位,用于计算负载阻抗。使用表2的网络1作为匹配网络,计算匹配网络各级参数见表3。

图10 阻抗匹配网络实验验证图
Fig.10 Experimental verification of impedance matching network
表3 阻抗匹配网络器件各级参数
Tab.3 Parameters of impedance matching network device
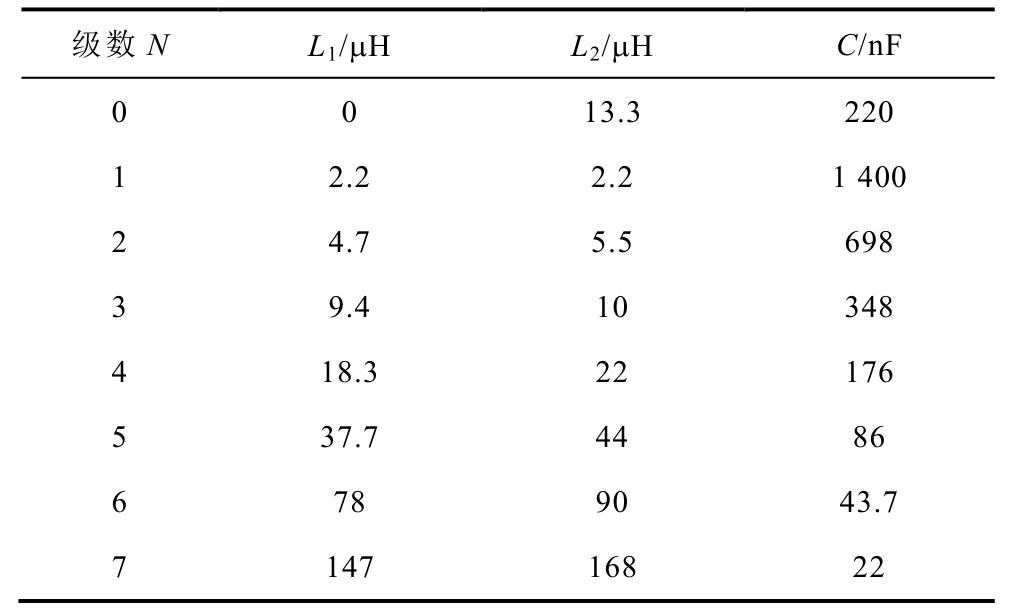
级数N L1/μH L2/μHC/nF 0 0 13.3 220 1 2.2 2.2 1 400 2 4.7 5.5 698 3 9.4 10 348 4 18.3 22 176 5 37.7 44 86 6 78 90 43.7 7 147 168 22
表3中的电容电感都为1%精度的标准器件,非标称值的器件是由多个器件串并联得到的。
系统的控制器选用TMSLF2812 DSP,控制器可以接收采样模块采集的电压电流和相位信号,并依此计算出负载阻抗和反射系数。当反射系数模大于0.1时系统开始使用截面法匹配,并输出控制信号驱动阻抗匹配网络改变自身参数以完成匹配。
使用一个24V电源为系统供电,使用TH2817LCR数字电桥测量匹配网络匹配完成的等效阻抗。
作为对照,使用遗传算法对同样的负载进行匹配。由于遗传算法在DSP2812上较难实现,故控制器只负责将负载阻抗的值传输给上位机,在PC端使用遗传算法求出相应参数,再将参数下发给控制器。控制器驱动阻抗匹配网络完成匹配。
实验得到的匹配情况如图11所示。可以看到,由于器件参数都只是理想参数的近似,加上器件自身存在的误差,截面法和遗传算法都存在较大波动,匹配效果不如理想的仿真情况。而截面法在保证相近匹配精度的情况下,相较遗传算法计算量更小,占用资源更少,更易实现,体现了一定实用性。
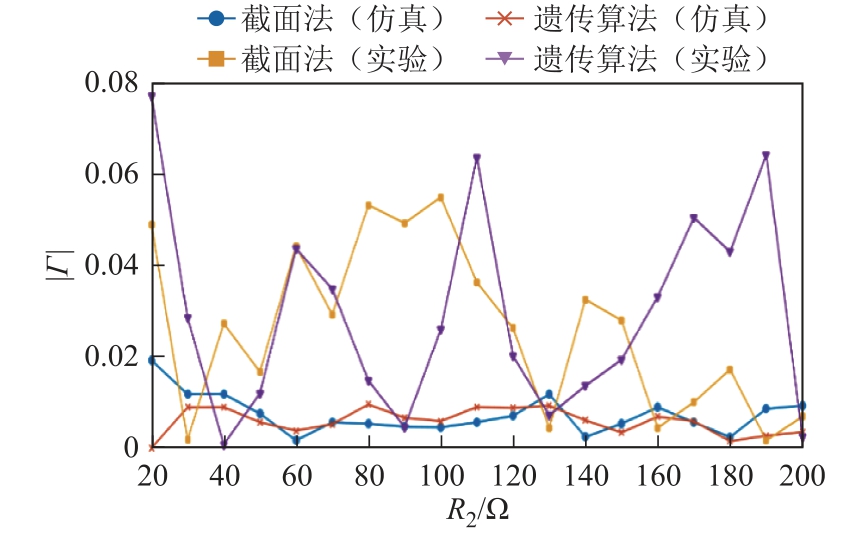
图11 截面法和遗传算法在仿真和实验中得到的反射系数模与负载电阻之间的关系图
Fig.11 Diagram of the relationship between the reflection coefficient and the load resistance which obtained through the cross section method and genetic algorithm in the simulation and experiment
5 结论
本文在Q值法的基础上,针对传统自动阻抗匹配算法匹配时间较长,耗费资源较多的问题,提出一种新的自动阻抗匹配算法,并以该算法为核心设计了一个自动阻抗匹配系统。在Matlab平台上建立该方法的仿真分析模型,仿真结果表明该方法的匹配性能与负载电阻的大小有关。分析比较了负载品质因数Q0和可调器件级数N对匹配网络匹配效果的影响。通过样机测试对该算法进行实验验证,并与使用遗传算法的自动阻抗匹配方法进行比较,结果显示本文提出的基于Q值法的自动阻抗匹配算法在大多数场合通过简单的计算即可达到较好的匹配效果,并且匹配速度快,占用资源少,较容易实现。
本文提出的自动阻抗匹配系统设计简单,只需确定源阻抗和负载阻抗的范围即可快速设计出整个匹配网络,适用于对匹配速度有较高要求的应用场合。例如在无线电能传输系统中,若接收端负载或线圈位置发生变化,传输效率就会受到影响。若在交流电源和发射线圈之间增加一自动阻抗匹配环节,可针对负载端的阻抗变化进行快速匹配,则能极大地提高系统传输效率和稳定性。
[1] 李树凡, 王丽芳, 郭彦杰, 等. 基于整流性负载补偿的无线充电系统T型阻抗匹配网络设计方法的优化[J]. 电工技术学报, 2017, 32(24): 9-16.
Li Shufan, Wang Lifang, Guo Yanjie, et al. Optimization of design method of T-type impedance matching network for wireless charging system based on rectified load compensation[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 9-16.
[2] 赵鱼名, 王智慧, 苏玉刚, 等. 基于T型CLC谐振网络的恒压型电场耦合电能传输系统负载自适应技术[J]. 电工技术学报, 2020, 35(1): 106-114.
Zhao Yuming, Wang Zhihui, Su Yugang, et al. Load adaptive technology of constant voltage electric-field coupled power transfer system based on T-CLC resonant network[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 106-114.
[3] Li Zhuo, Hao Kaizi, Wang Xin, et al. Design of dualband wide-angle RF/IR beam combiner based on impedance matching[J]. IET Microwaves Antennas & Propagation, 2020, 14(1): 7-14.
[4] Wong Y C, Mahmod N M, Radzi S A, et al. Adaptive boundary impedance matching network algorithm for multi frequency standards RF front-end[J]. AEUInternational Journal of Electronics and Communications, 2016, 70(10): 1449-1456.
[5] 谭坚文, 廖瑞金, 邓思建, 等. 高强度聚焦超声换能器的宽带阻抗匹配[J]. 电工技术学报, 2014, 29(11): 141-146.
Tan Jianwen, Liao Ruijin, Deng Sijian, et al. Broadband impedance matching for high intensity focused ultrasound transducer[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 141-146.
[6] 赵能桐, 杨鑫, 陈钰凯, 等. 考虑超磁致伸缩材料非均匀性的大功率电声换能器阻抗特性[J]. 电工技术学报, 2021, 36(10): 1999-2006.
Zhao Nengtong, Yang Xin, Chen Yukai, et al. The impedance characteristics of high power electroacoustic transducer considering the inhomogeneity of giant magnetostrictive material[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 1999-2006.
[7] 涂春鸣, 高家元, 李庆, 等. 具有复数滤波器结构锁相环的并网逆变器对弱电网的适应性研究[J]. 电工技术学报, 2020, 35(12): 2632-2642.
Tu Chunming, Gao Jiayuan, Li Qing, et al. Research on adaptability of grid-connected inverter with complex coefficient-filter structure phase locked loop to weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2632-2642.
[8] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335.
Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[9] 熊智挺, 谭阳红, 易如方, 等. 射频自动阻抗匹配的分层遗传算法实现[J]. 计算机工程与应用, 2013, 49(23): 261-265.
Xiong Zhiting, Tan Yanghong, Yi Rufang, et al. RF impedance automatic-matching with multilevel genetic arithmetic[J]. Computer Engineering and Applications, 2013, 49(23): 261-265.
[10] 杨晓博, 李阳, 肖朝霞, 等. 改进粒子群算法的自动阻抗匹配技术[J]. 重庆大学学报, 2016, 39(6): 41-48.
Yang Xiaobo, Li Yang, Xiao Zhaoxia, et al. Automatic impedance matching based on improved particle swarm optimization algorithm[J]. Journal of Chongqing University, 2016, 39(6): 41-48.
[11] Briones E, Ruiz-Cruz R, Briones J, et al. Particle swarm optimization of nanoantenna-based infrared detectors[J]. Optics Express, 2018, 26(22): 28484-28496.
[12] Li Yang, Dong Weihao, Yang Qingxin, et al. An automatic impedance matching method based on the feedforward-backpropagation neural network for a WPT system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3963-3972.
[13] Sun Y, Fidler J K. Design method for impedance matching networks[J]. IEE Proceedings-Circuits, Devices and Systems, 1996, 143(4): 186-194.
[14] Chung B K. Q-based design method for T network impedance matching[J]. Microelectronics Journal, 2006, 37(9): 1007-1011.
[15] Liao Ruijin, Tan Jianwen, Wang Hua. Q-based design method for impedance matching network considering load variation and frequency drift[J]. Microelectronics Journal, 2011, 42(2): 403-408.
[16] Sun Y, Fidler J K. Determination of the impedance matching domain of passive LC ladder networks: theory and implementation[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 1996, 333B(2): 141-155.
[17] 刘校销, 郑涛, 黄婷. 基于等效漏电感参数辨识的磁控式并联电抗器匝间故障保护方案[J]. 电工技术学报, 2020, 35(1): 134-145.
Liu Xiaoxiao, Zheng Tao, Huang Ting. Protection scheme based on the identification of equivalent leakage inductance against turn-to-turn fault of magnetically controlled shunt reactor[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 134-145.
[18] 郑涛, 刘校销. 磁控式并联电抗器容量调节暂态过程及其对匝间保护的影响[J]. 电工技术学报, 2021, 36(5):1052-1063.
Zheng Tao, Liu Xiaoxiao. Power regulation transient process of magnetically controlled shunt reactor and its impact on protection against turn-to-turn faults[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1052-1063.