0 引言
特高压并联电抗器在电网中主要起无功补偿、 抑制工频电压升高的作用,作为特高压变电站的主设备之一,对特高压交流输电网络的安全稳定运行至关重要。但是由于其工作原理及结构特点,并联电抗器的振动噪声较变电站内其他设备更为明显[1], 对变电站周边的环境影响很大,同时长期振动也会给设备的安全可靠运行带来风险。工程上目前常用隔声罩对电抗器的噪声进行治理,会实现20dB以上的降噪效果,有效地改善了厂界噪声,但是其对电抗器本体振动的改善无效果,且由此带来的占地面积大、成本增加、检修维护困难、消防隐患等问题不可忽视。因此对特高压并联电抗器的振动进行分析并从振源进行控制十分必要,近年来越来越多的研究也集中于特高压电抗器的振动方面。.
文献[2-6]从理论上分析了电抗器的振动机理及部分影响因素,侧重于电抗器振动产生的机理研究及分析;文献[7]开展了特高压并联电抗器振动测试,分析了振动频谱特性,提出优化现场运行电抗器噪声的方法;祝丽花、刘松等通过数值仿真及对运行中电抗器油箱的振动测试,讨论了变压器及电抗器振动机理的区别,分析了电抗器的振动特性,研究了基于电抗器振动的监测方法[8-13];文献[14-16]采用有限元数值仿真方法,分析电抗器产生振动噪声的主要原因,提出在基础和电抗器箱底之间增加橡胶隔振器的改进方法,该措施有助于降低电抗器的辐射噪声及设备对基础振动的传递,但是不会改善电抗器本体的振动;文献[17]对电抗器的振动噪声进行测试,并评估其对电站环境的影响,但是未对电抗器本体的振动机理及控制进行深入研究和讨论;张鹏宁等基于硅钢片磁致伸缩特性,同时考虑磁致伸缩及麦克斯韦力的影响,证明了麦克斯韦力是并联电抗器模型铁心振动的主要原因,但是其采用的电抗器模型为变压器模型铁心中部开尺寸一定的气隙,与采用垫块构成多组气隙的实际电抗器产品铁心结构有较大差异,因此铁心电磁力的分布及结构的振动响应也与实际产品差别较大[18]。
综上所述,目前对特高压并联电抗器振动的研究主要集中于电抗器设备外部的试验测试分析及有限元数值仿真。由于内部复杂的电磁场环境并浸没于绝缘油中,难以直接对铁心振动进行测试,因此对于电抗器铁心振动的分析和测试研究较少。
本文以一台型号为BKDF—240000/1000的特高压并联电抗器为研究对象,从振动产生的机理入手进行分析,通过磁-机械多场耦合,利用有限元法对电抗器的铁心电磁力进行计算,并通过光纤测振传感器对铁心各部位的振动加速度进行了测试。结合仿真分析与试验测试,对影响电抗器振动的主要因素进行了研究。
1 铁心振动机理
电抗器铁心通过绕组励磁,产生频率与工频一致的交变磁场,为了降低铁心心柱磁导率,使阻抗与电流基本成正比,防止电抗器在工作中磁饱和,电抗器心柱存在由非导磁材料组成的气隙,因此铁心饼间会随着磁感应强度的变化产生交变的电磁力——麦克斯韦力。另外硅钢片叠积而成的铁轭在磁通密度变化时存在磁致伸缩效应,麦克斯韦力与磁致伸缩变化的频率均为2倍工频,即为电抗器的主要振动频率。电抗器工作磁通密度较低(通常小于1.4T),磁致伸缩远低于麦克斯韦力导致的振动,因此一般认为铁心饼的麦克斯韦力是电抗器振动的主要因素。
对于瞬态磁场定义磁矢势A,存在
式中,B为磁通密度;μ为磁导率;H为磁场强度。
对于绕组激励电流密度为J的瞬态磁场,则可由式(2)解得磁矢势A,进而求得磁通密度B。
式中,σ为电导率。
铁心饼间电磁力是由于磁场作用,在铁心气隙与铁心饼分界面的表面应力,由麦克斯韦应力张量对面域进行积分,可将电磁力表示为

式中,Ω为气隙与铁心饼分界面的积分域;I为单位矩阵。
忽略铁心阻尼,由连续多自由度系统振动微分方程可对铁心的振动进行计算。
式中,x为位移矢量;M为铁心的质量矩阵;K为刚度矩阵,与铁心的结构及材料参数相关。
2 铁心振动仿真与试验
2.1 计算模型
图1为铁心模型,包括绕组、铁轭、心柱、磁分路及气隙,铁心采用双柱串联结构,即包含两个安装有线圈的心柱。电抗器铁心外部为绝缘油,铁心气隙材料的磁导率与绝缘油一致,故计算时以绝缘油代替气隙。考虑到几何结构与磁路的对称性,磁场计算采用1/2模型以提高计算效率,而振动仿真采用全模型,以避免对称模态丢失。为计算油箱对铁心磁场分布及结构刚度的影响,铁心模型外部装配有电抗器油箱,材料为Q355。表1为计算模型的基本参数。

图1 铁心模型
Fig.1 Model of core
表1 模型参数
Tab.1 Model parameters

参 数 数值(型号) 频率f/Hz 额定容量Sn/Mvar 额定电压Un/kV 硅钢片 外形尺寸(长×宽×高)/(mm×mm×mm) 50 240 1 100/3 B30P100 5 780×2 400×4 550铁心总重W/kg 132 000
2.2 磁场仿真
铁心磁场仿真以正弦交变电压对绕组励磁,电压幅值为![]() 倍的额定电压,即898kV,对电抗器的瞬态磁场进行求解。
倍的额定电压,即898kV,对电抗器的瞬态磁场进行求解。
图2为磁场计算结果,其中图2a是电压为0、电流为峰值时刻铁心的磁密分布云图,图2b为一个周期内(20ms)心柱中部及端部的磁通密度时程计算结果。由图2可得,心柱中部和端部磁通密度峰值分别约为1.37T和1.2T,因此硅钢片磁通未饱和,其磁致伸缩导致的振动可以忽略。

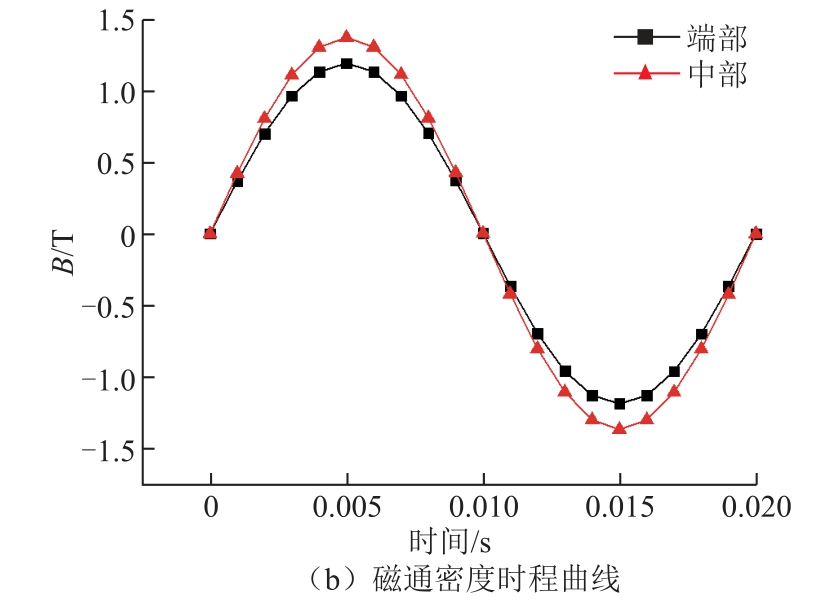
图2 磁场计算结果
Fig.2 Calculation results of magnetic field
图3为5ms时刻铁心饼间电磁力的计算结果,可得铁心饼的两个表面电磁力方向相反,在电磁力作用下,相邻的两个铁心饼互相吸引。

图3 铁心电磁力
Fig.3 Electromagnetic force of core
由于在心柱不同位置漏磁分布不同,因此不同铁心饼的电磁力有差异。定义心柱最下端铁心饼的饼号为1,则由下至上不同位置铁心饼的电磁力及磁通密度分布如图4所示,可得两端部电磁力较小,而中部电磁力最大,最大相差约30%,且沿高度方向对称,与铁心饼磁通密度变化规律一致。

图4 电磁力及磁通密度分布
Fig.4 Distribution of electromagnetic force & magnetic flux density
2.3 振动仿真
振动仿真时,首先对结构底部约束进行模态分析,其次以铁心饼间电磁力作为激励源,进行基于模态叠加法的振动响应分析。
铁心模型各部位的振动加速度仿真结果如图5所示,可得铁心振动具有对称性,即沿中面两侧振动基本相同。振动最大位置位于上磁分路边缘,加速度约为2.52g。底部由于采用固定约束,因此振动加速度很小。上铁轭中部由于两个心柱的作用,其振动加速度约为1.5g,两个旁轭中部的振动加速度约为0.5g。

图5 铁心振动仿真
Fig.5 Core vibration simulation
2.4 铁心振动试验
为了进一步对特高压并联电抗器的铁心振动进行研究,本文通过光纤振动传感器对电抗器铁心进行了振动测试,传感器采用ABS材质封装以避免金属可能导致绝缘击穿、局部过热等影响电抗器性能的问题。共计布置6个测点M1~M6,分别位于铁心上铁轭中部、上磁分路边缘、旁轭中部以及下铁轭中部,测试方向均为传感器固定面的法向。图6a为测点位置示意,图6b为安装于测点M1位置的传感器。


图6 铁心振动测点
Fig.6 Measuring points of core vibration test
测试结果表明,振动加速度最大处位于磁分路边缘处,即测点M2位置。图7为额定电压激励时测点M2的振动加速度时程曲线,图8为M2的振动加速度频谱,可得M2位置振动加速度为2.38g。振动的主要频率分量为100Hz,有一定的2倍频分量,但占比很小。

图7 M2振动加速度时程曲线
Fig.7 Time-history curve of acceleration

图8 M2振动加速度频谱
Fig.8 Vibration acceleration spectrum
振动测试与仿真分析各测点的加速度结果对比见表2,可得测试数据与仿真结果基本相同,其中振动较大的M1、M2及M3误差介于5%~6%,验证了电抗器铁心振动仿真分析方法及结果的准确性。测点M4、M5、M6的误差相对较大,约为10%~15%,主要原因在于上述测点的振动加速度值较小,较小的差值也会导致较大的误差率。
表2 结果对比
Tab.2 Data comparison

测点 振动加速度/g ()%st s−误差 仿真s 试验t M1 1.47 1.4 4.76 M2 2.52 2.38 5.56 M3 2.13 2.26 -6.10 M4 0.48 0.43 10.42 M5 0.48 0.41 14.58 M6 0.13 0.12 7.69
从振动加速度的绝对数值来看,除了测点M3以外,其余测点的计算值均略大于实测值。仿真与实测存在误差可能的原因包括:①测试传感器与仿真结果振动加速度最大位置不完全相同;②实际产品安装时存在一定的预应力,与计算模型不完全一致;③实际铁心置于绝缘油中,存在一定的阻尼,仿真计算仅考虑了恒定的模态阻尼,与实际有一定的差异;④测试电压有一定的波动。
3 铁心振动影响因素分析
由第1节式(3)及式(4)可得,在铁心结构一定的前提下,影响电抗器铁心振动的主要因素为铁心饼间的电磁力以及铁心的刚度。电磁力与铁心磁通密度相关,而磁通密度与激励电压成正比,因此本文通过改变激励电压研究不同电磁力对振动的影响。铁心刚度则主要和气隙垫块的材料相关,本文分别采用不同的气隙垫块材料进行分析。
3.1 电磁力
3.1.1 不同激励电压的振动仿真
分别设置激励电压为70%、80%、90%的额定电压,进行铁心振动仿真和试验测试。结合额定电压激励的仿真结果,铁心饼电磁力及最大振动加速度仿真数据如图9所示。

图9 电压对电磁力和加速度的影响
Fig.9 Influence of voltage on electromagnetic force and acceleration
由图9仿真结果,与激励电压为额定值相比较,90%电压下铁心振动加速度与电磁力均降低19%,80%电压下铁心振动加速度与电磁力均降低36%,激励电压为70%时,振动加速度和电磁力均降低51%。
结合第1节中关于电磁力的理论分析可得,对 于结构确定的电抗器,铁心的振动加速度及电磁力与电压的变化满足关系
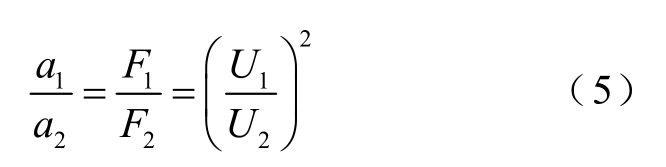
式中,U1、U2分别为不同的激励电压;F1、F2分别为U1、U2激励时铁心的电磁力;a1、a2分别为U1、U2激励时铁心的振动加速度。
3.1.2 不同激励电压的振动试验
在不同激励电压下开展电抗器铁心振动测试,各测点的振动加速度如图10所示。与仿真结果一致,振动加速度最大位置位于磁分路,由于结构的对称性,测点M4与M5的振动加速度基本相同。由测试数据可得,电压与加速度变化关系同样满足式(5),进一步验证了理论分析。

图10 不同测点的振动加速度
Fig.10 Vibration acceleration of different points
3.2 气隙垫块材料
3.2.1 不同气隙垫块的振动仿真
在额定电压激励下,分别采用A、B两种不同的非导磁材料作为气隙垫块对铁心模型进行振动仿真,两种材料的属性见表3,存在较大差异的参数是弹性模量,垫块B材料的弹性模量是垫块A的5.1倍,因此刚度更高。图11所示为两种不同的气隙垫块。
铁心刚度会影响模态计算结果,使自振频率发 生变化。标记铁心长度方向为x向,宽度方向为y向,高度方向为z向,不同气隙垫块的铁心模态计算结果见表4。
表3 气隙垫块参数
Tab.3 Parameters of air-gap spacer
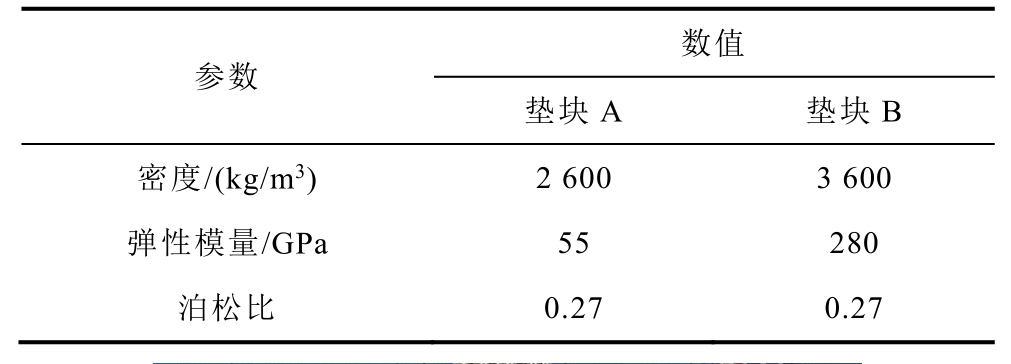
参数 数值 垫块A 垫块B 密度/(kg/m3) 2 600 3 600 弹性模量/GPa 55 280 泊松比 0.27 0.27

图11 气隙垫块
Fig.11 Air-gap spacers
表4 模态结果
Tab.4 Modal results

阶次 垫块A 垫块B 频率/Hz 振型 频率/Hz 振型 1 25.3 沿z向平动 28.2 沿z向平动 2 26.7 沿x向平动 32.8 沿x向平动 3 41.8 沿y向平动 43.9 沿y向平动 4 104.2 绕z向转动 106.5 绕z向转动 5 110.3 绕x向转动 115.0 绕x向转动 6 131.1 绕y向转动 142.6 绕y向转动
由表4可得,采用垫块B铁心刚度增加,自振频率较采用垫块A有所增大,但是由于铁轭的结构相同,铁心整体刚度变化不大,因此各阶模态振型基本相同。
图12为采用垫块B的铁心模型振动仿真结果, 结合图5可得,采用垫块A及垫块B时,最大加速度分别为2.52g及1.62g,采用垫块B铁心最大加速度可降低约36%,其他位置的加速度也有较大幅度的降低。因此提高气隙垫块的刚度对降低铁心的振动加速度有明显的效果。

图12 振动仿真结果(垫块B)
Fig.12 Core vibration simulation results with spacer B
3.2.2 不同气隙垫块的振动试验
采用额定电压激励,对气隙材料为垫块B的电抗器铁心进行振动测试,与采用垫块A的电抗器对比,各测点振动加速度如图13所示。
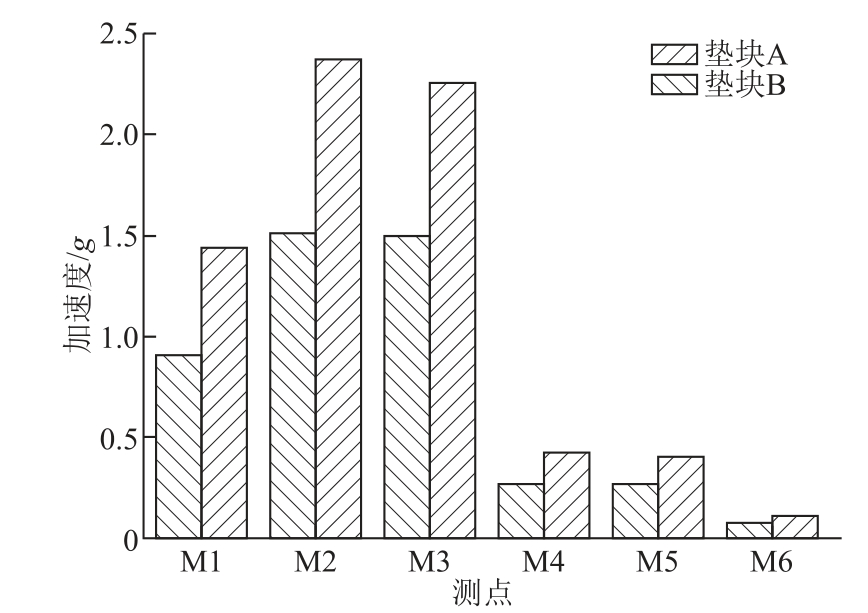
图13 垫块材料的影响
Fig.13 Acceleration of air-gap spacer material at different point
测试结果与仿真分析结果一致,采用垫块B可以使电抗器的磁分路及上铁轭中部振动加速度明显降低,其中磁分路位置测点M2降低约35%,而下铁轭中部测点M6振动加速度变化不大,主要是由于其与箱底固定约束,其振动加速度大小在很大程度上取决于箱底的刚度,气隙垫块的材料影响不大。
因此,采用刚度更高的垫块材料可以实现铁心振动加速度的降低,有助于从振源进行电抗器的振动控制。
4 铁心振动控制
综上所述,对电抗器铁心振动影响的主要因素包括铁心饼的电磁力以及铁心的刚度,因此对电抗器铁心的振源可考虑从上述两方面采取措施,另外在振动传递路径上采取措施,对于降低铁心的振动也有一定的帮助。
4.1 减小电磁力
结合式(1)及式(3)可得,铁心电磁力与磁密满足关系
式中,S为铁心饼的面积。穿过铁心饼的磁通Φ满足
则式(6)可转换为
故减小电磁力需取较小的设计磁通密度B,由式(7)可得需增加铁心饼面积S,基于绝缘距离考虑的油箱内壁尺寸等同样需要增大,由此会导致电抗器的重量明显增加。
以BKDF—240000/1000的特高压并联电抗器为例,若将设计磁通密度降低0.1T,振动会降低约7%~9%,噪声会降低约1~2dB,但是综合考虑磁通密度变化对原材料、运输费用等的影响,电抗器总成本会增加约18%~23%,经济性不佳。
4.2 提高铁心刚度
如前文对不同气隙垫块材料仿真结果可知,采用刚度更高的气隙垫块材料有助于提高铁心心柱刚度,可以有效地实现电抗器铁心的振动控制。由于气隙垫块材料成本在并联电抗器的总成本中占比很小,因此该方法对成本的影响几乎可以忽略。
另外,合理设计铁轭截面的宽高比,可以提高铁轭的刚度,从而降低铁心振幅。图14所示为电抗器铁轭截面的优化示意。

图14 铁轭截面优化
Fig.14 Optimization of yoke section
由于通过铁轭的总磁通恒定,设计磁通密度为定值,因此铁轭的截面积Ssec保持不变,即
截面惯性矩I为评估铁轭截面沿铁心心柱轴向抗弯性能的主要参数,优化前后截面惯性矩分别为

显然地,对于图中两种截面,I1<I2,截面2的抗弯能力更强,刚度更高,在相同电磁力的作用下,其振幅更小。由于优化前后铁轭的截面积相同,因此铁心的质量和成本都不会增加,即通过优化铁轭截面的方法不会对电抗器总成本有明显的影响。
4.3 铁心有效隔振
铁心与油箱之间设置如图15所示的橡胶-纸板复合隔振装置,可以有效地降低振动传递,同时对于避免铁心共振也有明显的效果。

图15 铁心隔振装置
Fig.15 Core vibration isolation system
但是由于特高压电抗器隔振装置的绝缘纸板为薄板大尺寸结构,直接测试其刚度及振动传递特性比较困难,因此本文采用小尺寸样件与金属质量块组成隔振系统,以小样件的试验台测试结果计算电抗器隔振装置的隔振效率。
样件面积Asample与测试质量块Msample满足关系式(12),即样件的受压状态与实际隔振装置相同。

式中,M和A分别为电抗器的铁心质量及隔振装置的面积。
通过样件的振动台扫频测试得到系统的自振频率fsample,其与橡胶刚度kr及纸板刚度kp的关系为

橡胶刚度kr可由其弹性模量E、厚度H及形状系数Ssample计算得到,橡胶刚度rk为
联立式(13)、式(14),即可求出纸板的刚度kp。
复合隔振结构的等效刚度ksys可由式(15)进行计算。

式中,Ssys为电抗器隔振装置中橡胶板的形状系数;Sp为纸板的刚度修正系数,与A/Asample及其压强相关,取1.0~1.5。
从而可计算得电抗器电磁力振动频率f与电抗器隔振系统自振频率之比λ为

则电抗器器身隔振结构的振动传递率η计算式为

式中,ζ为阻尼比,对于电抗器器身隔振结构,ζ取0.13~0.15。
从而计算得隔振效率ε为
由上述分析可得,电抗器隔振装置的隔振效率主要取决于橡胶材料的弹性模量以及隔振装置的尺寸。对于特高压电抗器的隔振装置,隔振效率不小于75%时可取得较好的振动控制效果。由于复合隔振装置的成本很低,且无需对电抗器的设计方案进行调整,因此其对总成本的影响很小。
5 结论
1)通过磁-机械多场耦合,采用有限元法对特高压并联电抗器的铁心电磁力及振动进行了仿真,通过光纤振动传感器对电抗器铁心振动进行测试,验证了仿真分析的准确性,同时分析了仿真与测试误差的原因。
2)通过仿真和试验研究不同电压及不同气隙垫块对电抗器铁心振动的影响,得到了测试电压与铁心振动加速度的关系,结果表明刚度更高的气隙垫块材料有助于降低铁心振动。
3)从振动源及传递路径分别讨论分析了电抗器铁心的振动控制方法,结果表明减小电磁力、采用刚度更高的气隙垫块材料、优化铁轭截面及铁心隔振均会实现振动的控制,但是通过设计降低磁通密度,减小铁心电磁力会大幅增加电抗器的总成本,而其他措施则不会对成本有明显的影响。
[1] GB/T 1094.6—2011 电力变压器第6部分: 电抗器[S]. 2011.
[2] 杨敏, 仲兆平, 严青, 等. 220kV城市户内变电站声场模拟与分析[J]. 东南大学学报(自然科学版), 2010, 40(6): 1226-1231.
Yang Min, Zhong Zhaoping, Yan Qing, et al. Simulation and analysis of sound field in 220 kV urban indoor substations[J]. Journal of Southeast University(Natural Science Edition), 2010, 40(6): 1226-1231.
[3] 王起司. 油浸式电抗器振动噪音研究[D]. 大连: 大连理工大学, 2013.
[4] 陈德志, 张玉庸, 白保东, 等. 不同温度及谐波下硅钢片电磁-力特性与变频电机振动[J]. 电工技术学报, 2020, 35(22): 4647-4656.
Chen Dezhi, Zhang Yuyong, Bai Baodong, et al. Electromagnetic-force and vibration of silicon steel sheet and variable frequency motor under different temperature and harmonic[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4647-4656.
[5] 闫荣格, 赵文月, 陈俊杰, 等. 基于谐波注入的串联电抗器的减振研究[J]. 电工技术学报, 2020, 35(16): 3445-3452.
Yan Rongge, Zhao Wenyue, Chen Junjie, et al. Research on vibration reduction of series reactor based on harmonic injection[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3445-3452.
[6] 刘骥, 张明泽, 李凯, 等. 电抗器铁芯振动噪声的多场耦合分析方法[J]. 电机与控制学报, 2016, 20(9): 17-25.
Liu Ji, Zhang Mingze, Li Kai, et al. Multi-field coupling research on iron-core vibration noise of power reactor[J]. Electric Machines and Control, 2016, 20(9): 17-25.
[7] 谭黎军, 陈洪波, 欧强, 等. 特高压并联电抗器运行振动与噪声特性研究[J]. 变压器, 2016(7): 43-46.
Tan Lijun, Chen Hongbo, Ou Qiang, et al. Research on vibration and noise characteristics of UHV shunt reactor [J]. Transformer, 2016(7): 43-46.
[8] Zhu Lihua, Yang Yimei, Yang Qingxin, et al. Electromagnetic vibration of saturable reactor considering magnetostriction and damping effect[C]// Biennial IEEE Conference on Electromagnetic Field Computation, Miami, US, 2017,DOI:10.1109/CEFC.2016.7816019.
[9] 刘松, 祝丽花, 王斌, 等. 基于三维磁特性电抗器电磁振动分析[J]. 电气应用, 2019, 38(3): 35-40.
[10] 潘超, 苏昊, 蔡国伟, 等. 变压器直流偏磁下异常电流表征振动特性研究[J]. 电工技术学报, 2020, 35(9):1868-1879.
Pan Chao, Su Hao, Cai Guowei, et al. Research on characterization of core vibration by abnormal current of DC bias transformer[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1868-1879.
[11] 孙喜桂. 大型油浸式电抗器噪声机理研究[D]. 大连: 大连理工大学, 2016.
[12] 李冰, 王泽忠, 刘海波, 等. 直流偏磁下500kV单相变压器振动噪声的试验研究[J]. 电工技术学报, 2021, 36(13): 2801-2811.
Li Bing, Wang Zezhong, Liu Haibo, et al. Experiment on vibro-acoustic characteristic of 500kV singlephase transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2801-2811.
[13] 肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615.
Xiao Yang, Song Jinyuan, Qu Renhao, et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2607-2615.
[14] 葛德馨. 特高压并联电抗器铁心振动研究及仿真分析[D]. 济南: 山东大学, 2017.
[15] Yan Rongge, Gao Xu, Zhu Lihua, et al. Research on three-dimensional stress distribution of reactor core[J]. IEEE Transactions on Applied Superconductivity, 2016, 26: 06020044.
[16] 吴书煜, 马宏忠, 姜宁, 等. 基于多物理场耦合的特高压并联电抗器振动噪声仿真分析与实验研究[J]. 电力自动化设备, 2020, 40(3): 122-127.
Wu Shuyu, Ma Hongzhong, Jiang Ning, et al. Simulation analysis and experimental research on vibration and noise of UHV shunt reactor based on multi physical field coupling[J]. Electric Power Automation Equipment, 2020, 40(3): 122-127.
[17] 周兵, 王延召, 胡静竹, 等. 基于振动测量的并联电抗器声场计算[J]. 高压电器, 2019, 55(11): 105-112.
Zhou Bing, Wang Yanzhao, Hu Jingzhu, et al. Sound field calculation of shunt reactor based on vibration measurement[J]. High Voltage Apparatus, 2019, 55(11): 105-112.
[18] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5273-5281.