0 引言
高压断路器作为动作型控制和保护设备,其可靠性是保证电力系统安全稳定运行的基础[1-2]。在分闸、合闸和储能等操动状态下,断路器部件动作产生强烈的冲击,易引发各种机械故障。国际大电网会议调查表明,断路器机械故障占比61%[3]。振动信号蕴含大量机械部件状态信息,利用非侵入式振动信号辨识断路器操动过程机械状态取得了较好的实践效果[4-5]。经典振动特征提取方法包括短时能量法[6]、包络分析[7]、功率谱[8]和希尔伯特-黄变换[9]等。断路器动作产生的振动波通过透射、反射和衍射等传输过程呈现出非平稳、非线性特点,在时域和频域均有繁杂的结构特征[10]。由于缺少定量描述信号细节变化的特征,上述方法在精准描述信号局部变化和辨识复杂故障方面受到限制。
近年来出现将断路器复杂振动信号化繁为简的分解和分段处理方法。文献[11]利用自适应噪声集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)将振动信号自适应拆分,求取各分量的样本熵构成特征向量。文献[12]通过S变换的模值矩阵进行时域、频域分段,以振动信号在不同时段和频段的最大局部奇异值作为特征量。文献[13]对小波包变换后各频段振动信号进行等时间分段,以各子块能量作为特征量。通过提取拆解信号的总体特征,可以较好地描述信号局部细节,但在刻画非平稳信号的波形突变、功率分布和频谱形态等关键特征指标方面缺乏针对性。
断路器在实际运行中不会频繁操作,造成积累现场数据样本困难,限制了人工神经网络、聚类分析等需要较多训练样本智能辨识方法的应用。支持向量机(Support Vector Machine, SVM)适用于小样本分类问题,但是其准确率在很大程度上依赖参数的选取[14]。分群粒子群优化-支持向量机(Grouped Particle Swarm Optimization-SVM, GPSO-SVM)算法通过分群粒子群(Grouped Particle Swarm Optimization, GPSO)优化SVM函数参量,提高搜索效率和辨识准确率。
根据断路器振动信号经CEEMDAN分解后频域谱线聚集性特点,以感知功率谱波形变化、主峰分布、描述非平稳信号细节特征,提出在极坐标下定义的谱形状熵特征提取方法,由GPSO-SVM模型进行分类辨识。实验结果表明,本文方法能够挖掘波形细节变化特征且未占用过多时间开销,具有工程应用价值。
1 断路器操动状态辨识流程
振动信号是断路器操动机构各部件动作产生冲击性能量及在固体介质传播的体现[15]。非平稳振动信号频域谱特征与断路器操动状态直接相关,基于谱形状熵的断路器操动状态辨识新方法流程如图1所示。

图1 断路器操动状态辨识流程
Fig.1 Circuit breaker operation state identification process
通过CEEMDAN将断路器非平稳振动信号逐步拆解并求取频率分量的功率谱,利用故障敏感因子筛选体现故障状态本质特征的模态分量,再由发散因子增强对频域主峰敏感度,在极坐标下定义感知波形变化、功率分布和频谱形态的谱形状熵特征,最后以GPSO-SVM模型对所提取的特征量进行状态辨识。
2 振动信号处理及谱形状熵特征
2.1 CEEMDAN分解算法
CEEMDAN是一种有效解决模态混叠问题的自适应分解算法[16]。在原始信号s(t)中添加具有标准正态分布的白噪声Vi(t),将多次经验模态分解得到的分量E(∙)求取平均值作为最终实际分量[17],第k个残余信号rk(t)和第k+1阶模态分量IMFk+1(t)为
式中,rk-1(t)为第k-1个残余信号;IMFk(t)为CEEMDAN分解得到的第k阶模态分量;kε为第k个模态分量的信噪比系数;kE为信号经验模态分解后的第k个分量,k∈Z。直至残余信号的极点个数不超过2个时停止分解。
以高压断路器合闸过程为例,利用CEEMDAN算法将正常合闸振动信号分解9次,得到不同特征尺度的9个IMF分量和1个残余分量,如图2所示。

图2 CEEMDAN各分量时域波形
Fig.2 Time waveforms of CEEMDAN components
计算各IMF分量功率谱得到图3中的PIMF波形。随着分解阶数增加,逐步剥离出原信号的高频信息,实现各阶PIMF包含主峰区域的有效划分。幅值较大的PIMF1~PIMF5主峰频率均大于1kHz,是构成原信号频率结构的主要成分,自PIMF6后信号频率和幅值急剧下降,是经机构部件传输后振动水平大幅衰减子波的集合。

图3 CEEMDAN各分量功率谱
Fig.3 Power spectrum of CEEMDAN components
2.2 有效模态分量的筛选
高压断路器机械故障多是由正常状态逐步演化形成,故障与正常状态的振动信号存在不同程度的相似性。将文献[18]提出的故障敏感因子修正为二次表达式λp,使计算结果为正数,消除符号影响。利用λp筛选包含主要特征的IMF分量,λp的计算公式为
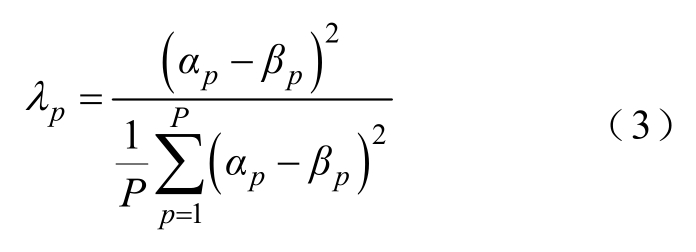
式中,αp为故障信号与其各IMF分量的相关系数;βp为该故障IMF分量与同工况下正常信号的相关系数。
计算CEEMDAN各分量故障敏感因子如图4所示,各工况下第6阶IMF分量的敏感因子均大幅降低,选取前5阶IMF分量即可反映出故障主要特征。

图4 各阶分量故障敏感因子
Fig.4 Fault sensitivity factor of each order component
2.3 谱形状熵的提出
断路器振动信号经CEEMDAN分解后功率谱线具有较强聚集性,为准确描述各分量功率谱波形蕴含的设备状态信息,提出在极坐标下定义的谱形状熵特征提取方法。由发散因子δ对波形进行发散处理,提高对主峰区域的敏感度,根据信息熵理论中发生概率较小事件所含信息量反而较大的理念,以谱形状熵量化信号功率分布和频谱形态特征。计算步骤如下:
(1)在极坐标下,根据极径尺度ω和极角尺度b,将极坐标以极点为中心、呈辐射状划分为若干等面积子区域,划分公式为
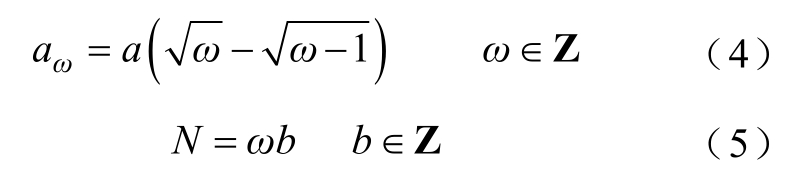
式中,a为在极径方向划分子区域的基值;ω为在极径方向划分的段数;aω为极径方向每段划分的长度;b为等分极角的段数;N为极坐标下划分子区域的个数。
(2)将笛卡尔坐标下功率谱波形的频率和幅值(xj,yj )经发散因子δ在极坐标(tj,θj)中发散。
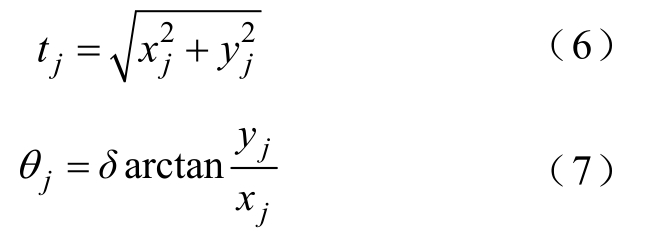
δ=4时原本只存在于0~90°极角范围的功率谱波形扩展到0~360°,极径维持不变。
(3)以波形散布在子区域频数构建信息熵的概率函数,重新定义为极坐标下感知波形变异和功率主峰分布的谱形状熵特征,计算公式为

式中,qf为波形散布在第q个子区域的频数。
2.4 断路器振动信号谱形状熵特征
谱形状熵对操动状态进行细节特征刻画,建立起特征量与机械故障及部件状态间的联系。断路器谱形状熵提取过程为:
(1)将CEEMDAN分解前5阶IMF分量功率谱波形的横、纵坐标分别采用极差法和最大值法进行归一化,其中最大值法能够保留各分量幅值比例关系,维持原始波形信息完备性。
(2)经归一化处理,极径最大值为2,此时极径基值a与极径段数ω满足

暂定a=0.353,ω=16,b=32,将极坐标划分为512个等面积子区域。
(3)将各IMF功率谱波形,经发散因子δ转换到极坐标下。由于篇幅有限,图5展示各状态类型前2阶IMF功率谱波形。功率谱中幅值较小的点被 限定在零极轴附近,幅值较大的点沿零轴逆时针旋转发散,使主峰区域数据散布在同一子区域的概率降低,从而增强敏感程度。


图5 各状态前2阶分量功率谱极坐标图
Fig.5 Polar coordinates of power spectrum of the first two components of each state
(4)统计各PIMF散布在极坐标子区域的频数,由式(8)计算谱形状熵特征。
依据4.1节数据样本,得到谱形状熵见表1。各PIMF至少存在两个及以上的值与其他状态类型存在较大差异,使断路器谱形状熵特征在各状态之间具有特异性分布。
表1 谱形状熵特征值
Tab.1 Eigenvalues of spectral shape entropy

状态类型 谱形状熵 PIMF1 PIMF2 PIMF3 PIMF4 PIMF5正常合闸 19.369 16.978 14.365 12.619 9.890 弹簧疲劳 28.939 13.510 9.407 8.727 8.598 铁心卡涩 33.362 18.466 11.717 7.969 9.076 轴销脱落 20.901 15.124 14.888 12.978 11.270
3 GPSO-SVM辨识模型
针对传统粒子群算法存在易陷入局部最优问题,GPSO算法可以在不增加粒子个数和维度的情况下将粒子群一分为二,分别用于全局搜索和局部搜索[19],粒子位置Xid的更新公式[20-21]为
式中,k为迭代次数;d为粒子群处理数据的维度;i为粒子的序列号。
全局搜索粒子群速度![]() 的更新公式为
的更新公式为
式中,Vm为全局搜索粒子最大速度。
局部搜索粒子群速度![]() 的更新公式为
的更新公式为

式中,χ为惯性权重;c1、c2、c3为学习因子;ξ、η为介于(0,1)之间的随机数;Pid为粒子搜索到的历史最优解;Pgd为整个群体搜索到的最优解;Psd为全局搜索粒子群的全局历史最优解(k,i,d,g,s∈Z)。
SVM目标是寻找一个超平面将样本分成两类,当样本集线性不可分时,需引入惩罚因子和核函数来进行分析[22]。径向基核函数不仅局部性能良好,且具有较少的参数[23-25]。径向基核函数K(xτ, x)表达式为
式中,g为径向基核函数参数,用于控制函数的作用范围;xτ为特征向量;x为核函数中心。
设样本数据为y,m,n=1,2,…,e,e为样本数量,则SVM优化方程为

式中,γm和nγ为拉格朗日乘子;C为惩罚因子,用于控制对错分样本的惩罚程度。
GPSO-SVM辨识模型利用GPSO对SVM惩罚函数参量C和径向基核函数参量g进行优化,提高了搜索效率和辨识准确率。
4 实验及结果分析
4.1 断路器振动信号样本库的建立
建立ZN63—12型高压断路器操动及故障模拟实验平台,由加速度振动传感器、霍尔型电流传感器、开关状态操控设备、信号采集装置以及上位机组成,实验平台示意图如图6所示。
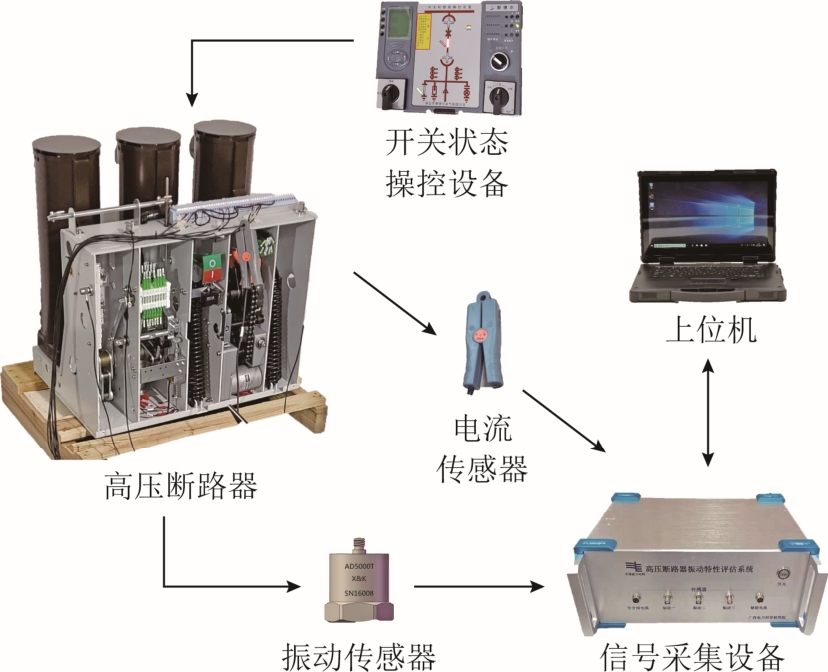
图6 实验平台示意图
Fig.6 Schematic diagram of experimental platform
利用开关状态操控设备控制高压断路器合闸、分闸和储能状态的切换,通过强磁座将振动传感器吸附在操动机构顶壁中部,钳形电流传感器夹在电流控制线圈,以电流启动时刻作为振动采集触发信号,上位机采用I5CPU、16G内存的便携加固工控机,设置采样率为25.6kHz,每次操作记录时间为0.5s。
分、合闸振动信号由冲击子波叠加形成,具有相似的结构特征,均可用本文算法进行分析。以合闸振动信号为例进行算法验证。
谱形状熵表征信号细节变化具有独特优势,除差异明显的轴销脱落故障(摘除连接轴销模拟)外,还设置与正常状态差异较小的潜伏性故障,如合闸弹簧疲劳(减少合闸弹簧预压缩模拟)、合闸铁心卡涩(铁心中混入异物模拟)。对四种状态各重复进行50次实验,构建200组振动信号组成的高压断路器数据样本库。
4.2 谱形状熵算法参数优化
谱形状熵算法中极径尺度ω和极角尺度b分别从不同角度反映对波形敏感度。为研究尺度参数对谱形状熵算法性能的影响,设置ω和b各6组,选取60%样本库数据作为训练集,其余40%经GPSOSVM进行状态辨识,结果如图7所示。

图7 谱形状熵尺度参数优化
Fig.7 Optimization of spectral shape entropy parameters
辨识准确率高于95%时,谱形状熵算法的极径尺度和极角尺度分别介于14~18、28~40之间。当尺度参数增大到一定限值,辨识准确率反而有所降低。通过单步长调节极径尺度ω和极角尺度b,对当前辨识准确率最高为97.5%时的尺度参数邻域做进一步辨识实验,得到辨识准确率优先、子区域数量较少的最佳参数为ω=16、b=30,此时GPSO寻优结果C=0.064、g=0.887。
4.3 不同模式识别算法比较
为验证基于谱形状熵的GPSO-SVM辨识模型效率,对最佳参数下的谱形状熵特征选用SVM、粒子群优化支持向量机(PSO-SVM)、分群粒子群优化支持向量机(GPSO-SVM)、反向神经网络(Back Propagation Neural Network, BPNN)、K近邻(K-Nearest Neighbor, KNN)五种分类方法对比识别效果。
取ZN63—12型高压断路器振动样本库中60%数据用于训练模型,其余40%数据用于测试。各分类方法输入谱形状熵特征后经过训练和测试,识别准确率和时间开销如图8所示。

图8 不同模式识别算法辨识结果
Fig.8 Identification results of different algorithms
BPNN算法耗时较多,时间开销少的KNN辨识准确率较低。GPSO-SVM寻优过程未占用过多时间开销,辨识准确率与SVM和PSO-SVM相比得到有效提升。
最优参数下的GPSO-SVM辨识详细情况如图9所示。轴销脱落、弹簧疲劳两类故障分类正确,两例铁心卡涩故障被分类到正常合闸状态中,总体识别准确率为97.5%。

图9 GPSO-SVM模型辨识情况
Fig.9 The identification results of GPSO-SVM model
铁心卡涩作为一种延时故障,其振动信号能量分布和频谱形态与正常状态相似,只是某些部件能量传递发生延后,其动触头激烈撞击事件及能量仍较为接近,因此误判为正常状态。总体分类准确率满足现场需求,时间开销也较为理想。
广西某变电站现场检修中,由机械特性测试仪测试发现某台ZN63—12型断路器合闸时间偏大、最大速度偏低,进行3次合闸操作获取异常样本振动信号。将该断路器正常状态历史数据与现场异常状态的振动信号进行对比,结果如图10所示。二者波形轮廓接近,异常信号冲击变化不明显且存在一定延时。

图10 正常与异常状态的振动信号
Fig.10 Vibration signals under normal and abnormal states
提取正常及异常信号谱形状熵特征,见表2。除第5阶分量,各阶分量的谱形状熵特征在正常和异常状态间均存在较显著的差异性分布。利用GPSO-SVM模型进行状态辨识,判定为弹簧疲劳故障。经对断路器拆解检查发现合闸弹簧发生锈蚀,验证了本文方法准确有效。
表2 正常信号与异常信号的谱形状熵特征
Tab.2 Spectral shape entropy characteristics of normal and abnormal signals
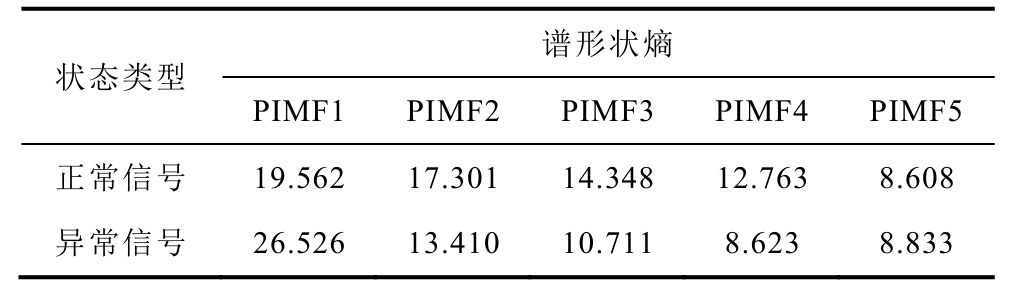
状态类型 谱形状熵 PIMF1 PIMF2 PIMF3 PIMF4 PIMF5正常信号 19.562 17.301 14.348 12.763 8.608 异常信号 26.526 13.410 10.711 8.623 8.833
5 结论
由振动信号判别断路器操动状态是一种非侵入式测试方法,现场实用化的关键在于选取信号精准特征及优化辨识模型。
1)谱形状熵可有效刻画非平稳信号的波形变化和功率主峰分布特征,且性能稳定。当极径尺度和极角尺度分别介于14~18、28~40之间,采用本文辨识算法准确率均≥95%。
2)GPSO-SVM辨识模型相较于BPNN、SVM和PSO-SVM时间开销略有增加,但有效提高了操动状态辨识准确率,尤其对断路器机构卡涩和弹簧疲劳等潜伏性故障具有较好的辨识能力。
3)断路器因储能方式、操动部件结构不同而有所差异,通过更新GPSO-SVM模型训练集中的谱形状熵特征,可使算法对断路器操动状态辨识具有通用性,在现场带电测试和故障监测中有广阔的应用前景。
[1] 杨秋玉, 王栋, 阮江军, 等. 基于振动信号的断路器机械零部件故障程度识别[J]. 电工技术学报, 2021, 36(13): 2880-2892.
Yang Qiuyu, Wang Dong, Ruan Jiangjun, et al. Fault severity estimation method for mechanical parts in circuit breakers based on vibration analysis[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2880-2892.
[2] 王昱皓, 武建文, 马速良, 等. 基于核主成分分析-SoftMax的高压断路器机械故障诊断技术研究[J]. 电工技术学报, 2020, 35(增刊1): 267-276.
Wang Yuhao, Wu Jianwen, Ma Suliang, et al. Mechanical fault diagnosis research of high voltage circuit breaker based on kernel principal component analysis and SoftMax[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 267-276.
[3] Heising C R, Janssen A L J, Lanz W, et al. Summary of CIGRE 13.06 Working Group world wide reliability data and maintenance cost data on high voltage circuit breakers above 63kV[C]//IEEE Industry Applications Society Meeting, Rome, Italy, 1994: 2226-2234.
[4] 杨秋玉, 阮江军, 张灿, 等. 基于定量递归分析的高压断路器机械缺陷辨识及应用[J]. 电工技术学报, 2020, 35(18): 3848-3859.
Yang Qiuyu, Ruan Jiangjun, Zhang Can, et al. Study and application of mechanical defect identification for high-voltage circuit breakers using recurrence quantification analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3848-3859.
[5] 游颖敏, 王景芹, 舒亮, 等.断路器保护特性测试电流的自适应控制策略[J]. 电工技术学报, 2020, 35(15): 3203-3213.
You Yingmin, Wang Jingqin, Shu Liang, et al. Research on adaptive current control method in circuit breaker protection characteristic test[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3203-3213.
[6] 马强, 荣命哲, 贾申利. 基于振动信号小波包提取和短时能量分析的高压断路器合闸同期性的研究[J]. 中国电机工程学报, 2005, 25(13): 149-154.
Ma Qiang, Rong Mingzhe, Jia Shenli. Study of switching synchronization of high voltage breakers based on the wavelet packets extraction algorithm and short time analysis method[J]. Proceedings of the CSEE, 2005, 25(13): 149-154.
[7] 张佩, 周秀萍. 基于振声时三维图的高压断路器机械故障诊断方法[J]. 高压电器, 2014, 50(12): 121-125.
Zhang Pei, Zhou Xiuping. Mechanical fault diagnosis of high voltage circuit breaker based on threedimensional vibration-acoustics-time diagram[J]. High Voltage Apparatus, 2014, 50(12): 121-125.
[8] 赵洋, 曾庆军. 采用功率谱估计法的真空断路器振动分析[J]. 电气应用, 2009, 28(9): 62-65.
Zhao Yang, Zeng Qingjun. Vibration analysis of vacuum circuit breaker by power spectrum estimation method[J]. Electrical Application, 2009, 28(9): 62-65.
[9] 李建鹏, 赵书涛, 夏燕青. 基于双谱和希尔伯特-黄变换的断路器故障诊断方法[J]. 电力自动化设备, 2013, 33(2): 115-119,125.
Li Jianpeng, Zhao Shutao, Xia Yanqing. Fault diagnosis based on bispectrum and Hilbert-Huang transform for circuit breaker[J]. Electric Power Automation Equipment, 2013, 33(2): 115-119, 125.
[10] 曹宇鹏, 罗林, 王乔, 等. 基于卷积深度网络的高压真空断路器机械故障诊断方法[J]. 电力系统保护与控制, 2021, 49(3): 39-47.
Cao Yupeng, Luo Lin, Wang Qiao, et al. Fault diagnosis of high-voltage vacuum circuit breaker with a convolutional deep network[J]. Power System Protection and Control, 2021, 49(3): 39-47.
[11] 赵书涛, 马莉, 朱继鹏, 等. 基于CEEMDAN样本熵与FWA-SVM的高压断路器机械故障诊断[J]. 电力自动化设备, 2020, 40(3): 181-186.
Zhao Shutao, Ma Li, Zhu Jipeng, et al. Mechanical fault diagnosis of high voltage circuit breaker based on CEEMDAN sample entropy and FWA-SVM[J]. Electric Power Automation Equipment, 2020, 40(3): 181-186.
[12] 黄南天, 陈怀金, 林琳, 等. 基于S变换和极限学习机的高压断路器机械故障诊断[J]. 高压电器, 2018, 54(6): 74-80.
Huang Nantian, Chen Huaijin, Lin Lin, et al. Mechanical fault diagnosis of high voltage circuit breakers based on S⁃transform and extreme learning machine[J]. High Voltage Apparatus, 2018, 54(6): 74-80.
[13] 陈欣昌, 冯玎, 林圣. 基于深度自编码网络的高压断路器操作机构机械故障诊断方法[J]. 高电压技术, 2020, 46(9): 3080-3088.
Chen Xinchang, Feng Ding, Lin Sheng. Mechanical fault diagnosis method of high voltage circuit breaker operating mechanism based on deep auto-encoder network[J]. High Voltage Engineering, 2020, 46(9): 3080-3088.
[14] 范贤浩, 刘捷丰, 张镱议, 等. 融合频域介电谱及支持向量机的变压器油浸纸绝缘老化状态评估[J]. 电工技术学报, 2021, 36(10): 2161-2168.
Fan Xianhao, Liu Jiefeng, Zhang Yiyi, et al. Aging evaluation of transformer oil-immersed insulation combining frequency domain spectroscopy and support vector machine[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2161-2168.
[15] 罗翔. 一起基于声电联合检测的特高压GIS断路器局部放电缺陷诊断分析与处理[J]. 电气技术, 2018, 19(6): 107-111, 116.
Luo Xiang. Diagnosis analysis and disposal of partial discharge in GIS using ultrasonic associated with electromagnetic wave method[J]. Electrical Engineering, 2018, 19(6): 107-111, 116.
[16] Torres M E, Colominas M A, Schlotthauer G, et al. A complete ensemble empirical mode decomposition with adaptive noise[J]. Brain Research Bulletin, 2011, 125(3): 4144-4147.
[17] 刘友波, 吴浩, 刘挺坚, 等. 集成经验模态分解与深度学习的用户侧净负荷预测算法[J]. 电力系统自动化, 2021, 45(24): 57-64.
Liu Youbo, Wu Hao, Liu Tingjian, et al. User-side net load forecasting method integrating empirical mode decomposition and deep learning[J]. Automation of Electric Power Systems, 2021, 45(24): 57-64.
[18] 张梅军, 唐建, 何晓晖. EEMD方法及其在机械故障诊断中的应用[D]. 北京: 国防工业出版社, 2015.
[19] 毕立恒, 朱彦齐. 基于分群粒子群算法的平面度误差评定研究[J]. 计量学报, 2019, 40(6): 980-985.
Bi Liheng, Zhu Yanqi. Flatness error evaluation based on grouped particle swarm optimization algorithm[J]. Acta Metrologica Sinica, 2019, 40(6): 980-985.
[20] 卢辉斌, 周绯菲, 孙金伟. 一种改进粒子群优化算法在入侵检测中的应用[J]. 燕山大学学报, 2013, 37(2): 124-128,147.
Lu Huibin, Zhou Feifei, Sun Jinwei. Application of improved particle swarm optimization algorithm in intrusion detection[J]. Journal of Yanshan University, 2013, 37(2): 124-128,147.
[21] 谢国民, 倪乐水. 基于IABC优化SVM的变压器故障诊断[J]. 电力系统保护与控制, 2020, 48(15): 156-163.
Xie Guomin, Ni Leshui. Transformer fault diagnosis based on an artificial bee colony-support vector machine optimization algorithm[J]. Power System Protection and Control, 2020, 48(15): 156-163.
[22] Iqbal A, Singh G K. PSO based controlled six-phase grid connected induction generator for wind energy generation[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 41-49.
[23] Ali M Z, Shabbir M N S K, Liang Xiaodong, et al. Machine learning-based fault diagnosis for single-and multi-faults in induction motors using measured stator currents and vibration signals[J]. IEEE Transactions on Industry Applications, 2019, 55(3): 2378-2391.
[24] Miao Di. Research on fault diagnosis of high-voltage circuit breaker based on support vector machine[J]. International Journal of Pattern Recognition & Artificial Intelligence, 2019, 33(6): 603-608.
[25] 谢桦, 亚夏尔·吐尔洪, 陈昊, 等. 基于支持向量机算法的配电线路时变状态预测方法[J]. 电力系统自动化, 2020, 44(18): 74-80.
Xie Hua, Yaxar Turgun, Chen Hao, et al. Prediction method for time-variant states of distribution line based on support vector machine algorithm[J]. Automation of Electric Power Systems, 2020, 44(18): 74-80.