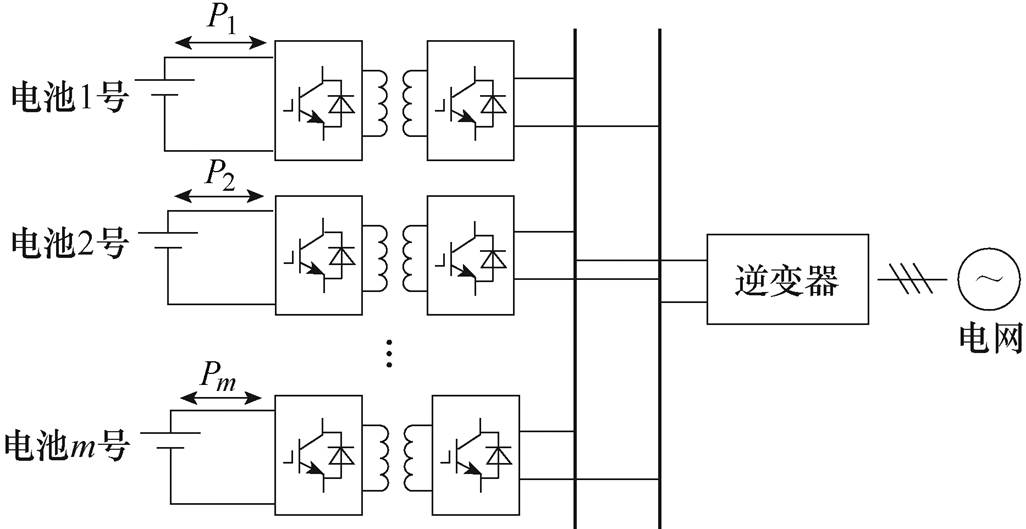
图1 电池模块分散接入的储能系统
Fig.1 Energy storage system with distributed access of battery modules
摘要 针对三端口双向DC-DC变换器（TP BDC）在端口电压不匹配时无功回流大、软开关范围小以及效率低的问题，该文提出一种以最小无功为目标的效率优化控制策略。分析TP BDC各端口的电压电流特性，基于占空比控制和相量分析法建立各端口功率模型。通过构建最小无功优化问题并求解最优控制量，在宽电压范围内减小TP BDC的无功回流。进一步分析TP BDC在优化控制下的软开关特性，提出最优控制量的选取策略。实验结果表明，该文所提优化控制策略使TP BDC在宽电压工况下具有更小的无功回流和更宽的软开关范围，从而显著提升变换器在端口电压不匹配及轻载条件下的传输效率。
关键词：三端口双向DC-DC变换器 最小无功 优化控制策略 相量分析法
随着社会经济的快速发展，能源危机和环境问题也日益严重。风能、太阳能等可再生能源的使用可以有效解决这些问题。作为可再生能源整合过程的重要组成部分，储能技术也得到了广泛的应用，它能够对系统输出功率进行平抑，提高电能质量和系统供电的可靠性与稳定性[1-3]。储能电池既需要放电也需要充电，这就要求储能变流器的功率可实现双向流动，因此双向直流变换器广泛应用于储能系统中[4]。图1所示为基于双向直流变换器的电池模块分散接入储能系统，P为对应商品的功率。
图1 电池模块分散接入的储能系统
Fig.1 Energy storage system with distributed access of battery modules
电池模块分散接入能有效避免木桶短板效应并大幅减小电池筛选成本。但上述储能系统的端口间协调控制困难、结构复杂且当二端口结构并联数过多时会出现环流、稳定性的问题[5-6]。采用多端口双向DC-DC变换器（Multi-Port Bidirectional DC-DC Converter, MP BDC）代替上述二端口并联的结构，从而达到简化结构、提高系统稳定性及母线电压质量、降低成本的目的[7]。图2所示为基于MP BDC的电池分散接入储能系统。目前，针对三端口双向DC-DC变换器（Three-Port Bidirectional DC-DC Converter, TP BDC）的研究最为广泛。
对于TP BDC，单移相（Single Phase-Shift, SPS）控制是最基本的控制策略[8]。然而，当电压不匹配及轻载运行时，SPS控制下TP BDC的无功回流增大，并且部分开关管会失去软开关特性，导致变换器的效率降低。文献[9]提出了一种脉宽调制加二次侧移相的控制策略，采用该控制策略可以实现功率解耦，极大地消除循环电流，减小传导损耗且在一定条件下能够扩大软开关范围，但未给出具体的最优控制量表达式。文献[10]应用叠加定理将变换器分解为多个子电路，推导出电感电流的统一表达式，分析了移相控制下的软开关范围。文献[11]分析移相控制的死区时间与负载电流，并详细讨论了死区时间对软开关范围和效率的影响，提出通过调整死区时间来减小开关管损耗提高效率。文献[12]提出了一种输出电压模型预测控制和梯度下降算法的混合优化控制策略，能够实现减小回流功率提升效率的目的。上述两个文献详细分析了能使变换器提升效率的控制方法，但其具体的控制及建模过程比较复杂。文献[13-14]以多谐振DC-DC变换器为对象，对多谐振的结构进行设计，通过控制频率在宽电压范围内实现软开关并提高效率。此种频率控制方法只面向特定的谐振结构，并不适用于所有的DC-DC变换器。文献[15]提出了一种移相加频率控制方法，该方法可以控制端口功率，以变换器电流最小推导出最优移相角的表达式，在较宽的电压范围内可以提高变换器的效率，但其并未对开关管的软开关范围进行分析。
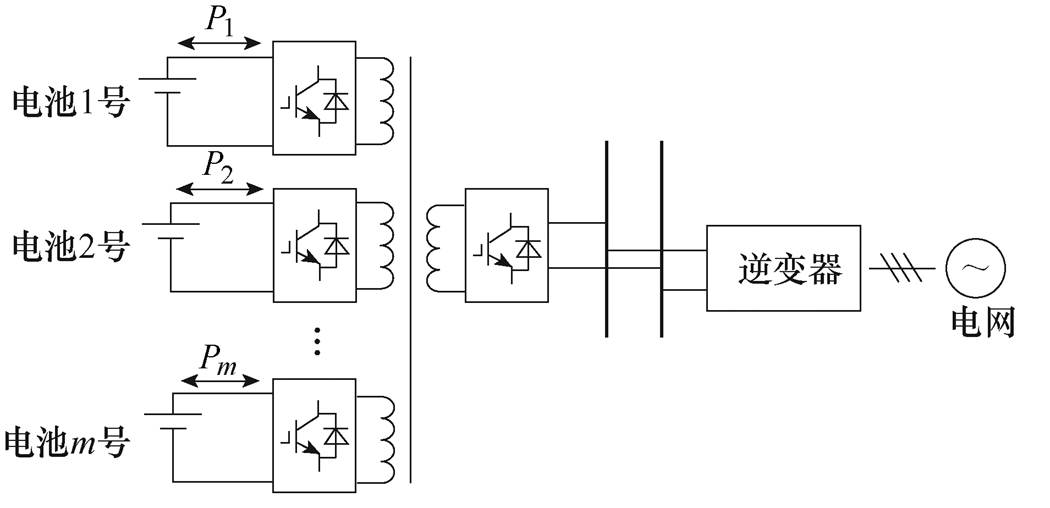
图2 基于MP BDC的电池模块分散接入的储能系统
Fig.2 Energy storage system with distributed access of battery modules based on MP BDC
为解决TP BDC在电压不匹配时无功回流大、效率低的问题，本文提出一种以无功最小为目标的优化控制策略。该优化控制策略采用相量分析法建立TP BDC的功率模型，构建无功优化问题并求得最优解，使TP BC在宽电压范围内具有更小的无功回流、更宽的软开关范围，从而提升变换器的传输效率。最后，通过搭建的实验样机，验证了所提出优化控制策略的有效性。
TP BDC拓扑结构如图3所示。该拓扑结构主要由三个H桥结构和一个三绕组高频变压器组成。图中，N1
N2N3为变压器电压比，V1、V2、V3为三个端口直流侧的电压，C1、C2、C3为三个端口直流侧的电容，L2、L3分别为变压器端口2和端口3的漏感与外接电感之和，utr1、utr2、utr3为三个H桥的桥臂中点电压，iL2、iL3分别为电感L2和L3的电流，i1为端口1侧的绕组电流。定义图3中箭头的方向为电流正方向。定义端口1、2的电压比K12=N1/N2，端口1、3的电压比K13=N1/N3。
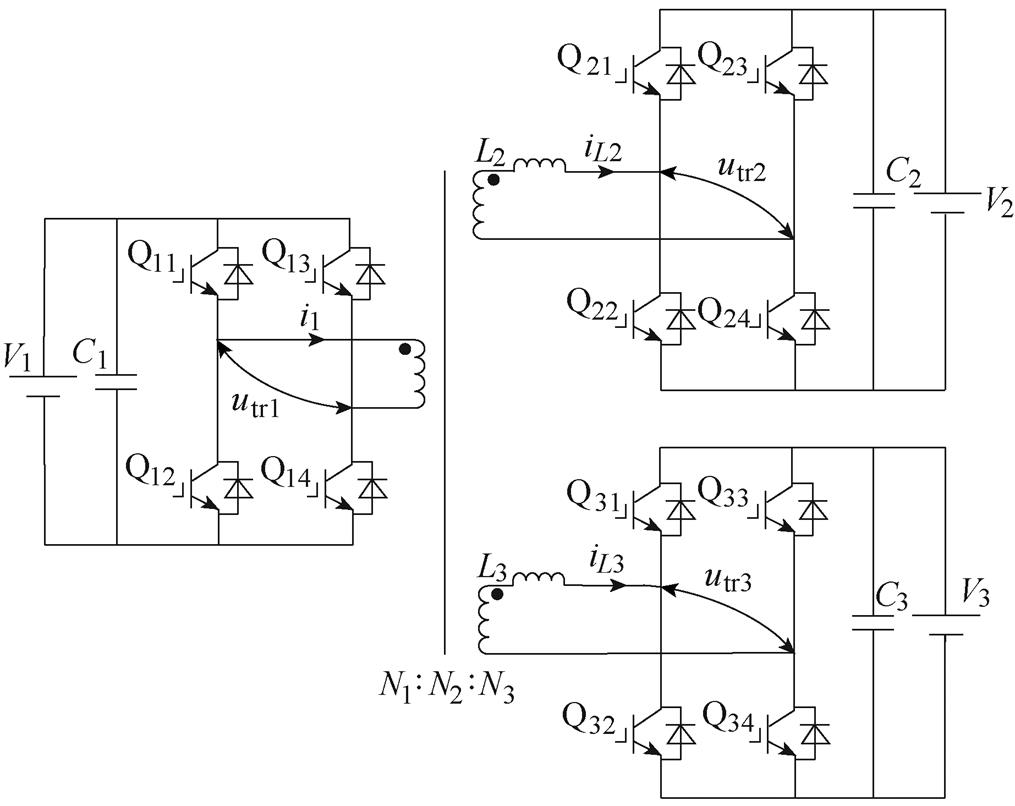
图3 TP BDC拓扑结构
Fig.3 Topology of TP BDC
TP BDC在SPS控制下，其变压器一次侧、二次侧H桥两桥臂的中点电压均为两电平，TP BDC在SPS下的波形如图4所示。从图中看出，三个H桥的中点电压utr1、utr2、utr3均为占空比为50%的方波。j12为utr1与utr2间的移相角，j13为utr1与utr3间的移相角。定义utr1超前utr2时j12＞0，反之j12＜0；utr1超前utr3时j13＞0，反之j13＜0。
为了解决SPS控制下变换器效率低、软开关范围小的问题，本文提出了一种优化控制策略。以端口电压V1＞V2＞V3为例进行具体讨论，根据伏秒平衡原理引入端口1和端口2中H桥的桥内移相角，则变换器在优化控制下的波形如图5所示。
从图5中可以看出，引入内移相角后端口1和端口2的H桥中点电压为三电平电压，端口3的H桥中点电压仍为两电平。j12为端口1和端口2的桥间移相角，j13为端口1和端口3的桥间移相角，j11为端口1的桥内移相角，j22为端口2的桥内移相角。dj12、dj13、dj11、dj22为四个移相角的移相占空比，且dj12=j12/p、dj13=j13/p、dj11=j11/p、dj22=j22/p。
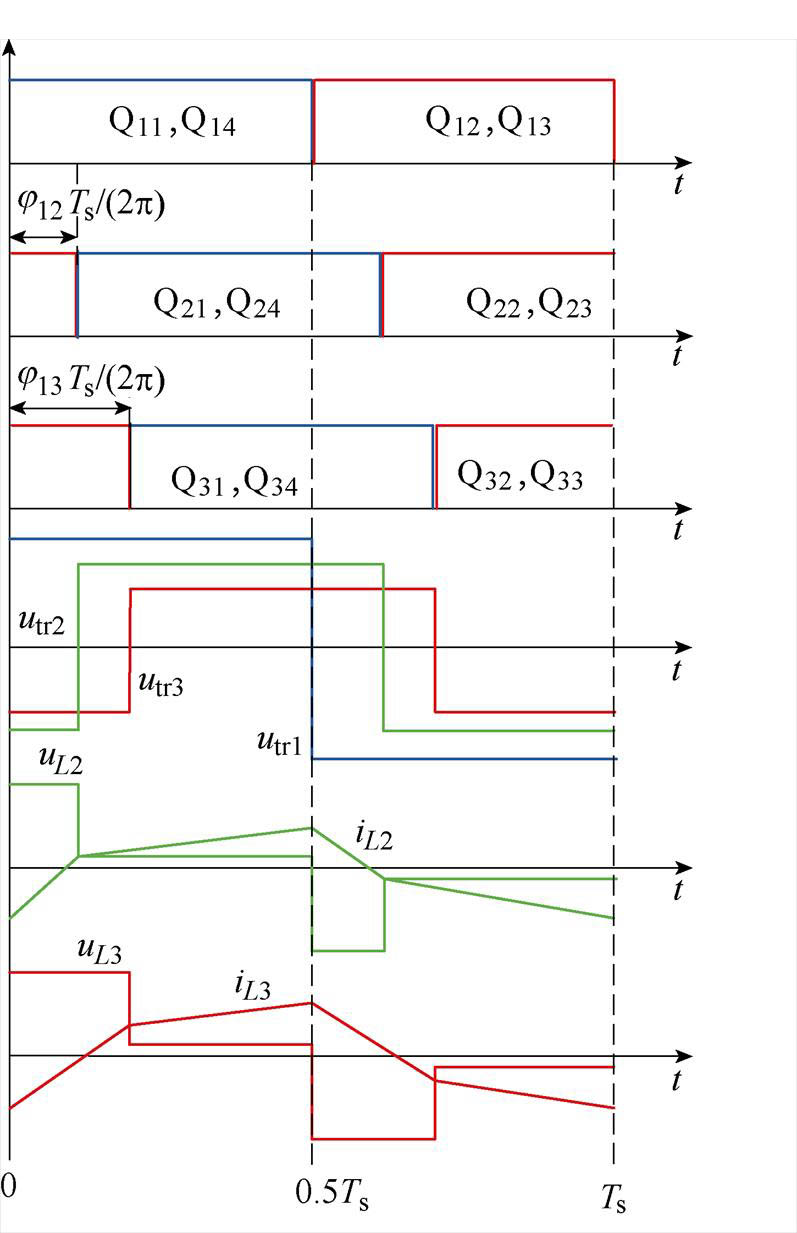
图4 TP BDC在SPS下的波形
Fig.4 Waveforms of TP BDC under SPS
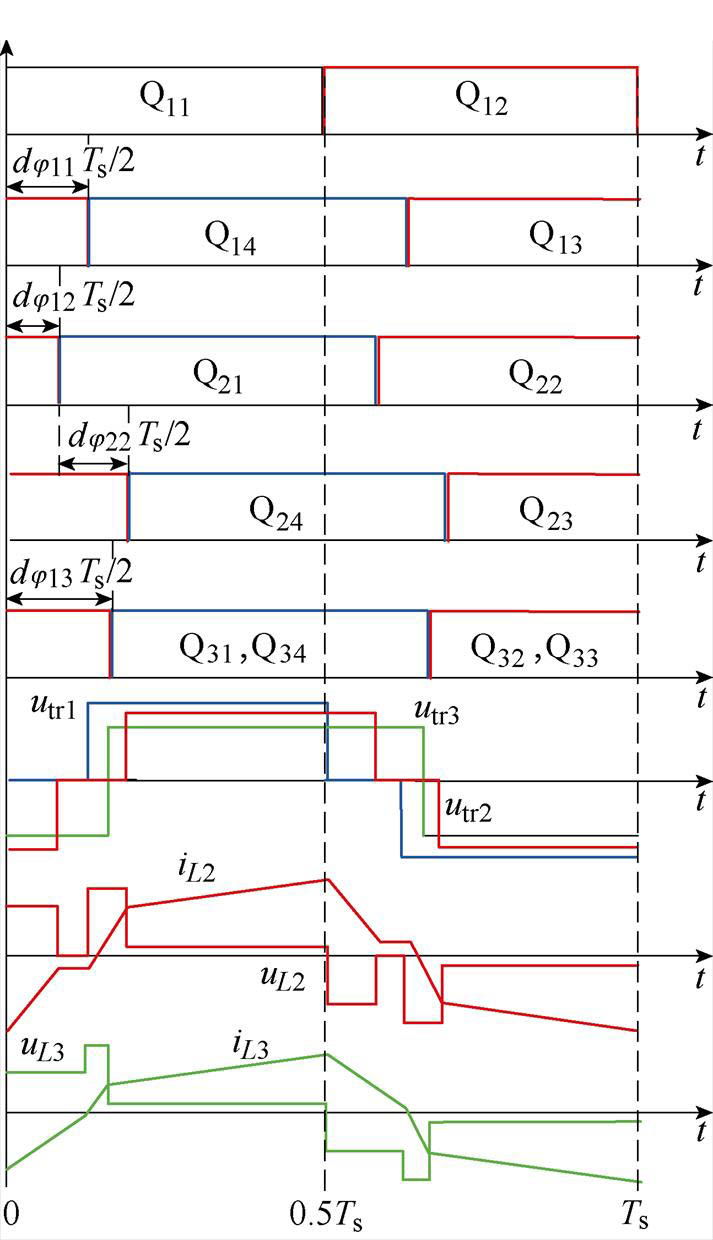
图5 TP BDC在优化控制下的波形
Fig.5 Waveforms of TP BDC under optimal control
为了解决三端口变换器在多重控制下功率模型复杂的问题，本文采用统一相量分析法来对变换器进行分析。相量分析法通过傅里叶级数分解，将变换器的状态方程转化为稳态相量表达式，建立复功率模型，对该功率模型进行详细分析[16]。该方法不用对特定的开关状态进行分析，能够大大简化分析过程。
TP BDC在优化控制下的工作波形如图5所示，TP BDC中三个端口的H桥中点电压均为交流方波电压，所以该变换器中的H桥结构可用交流方波电压等效。在相量分析中，方波电压用基波正弦电压等效，又根据移相控制与变换器拓扑结构特性，变换器可等效为如图6所示的正弦等效电路[17-19]。
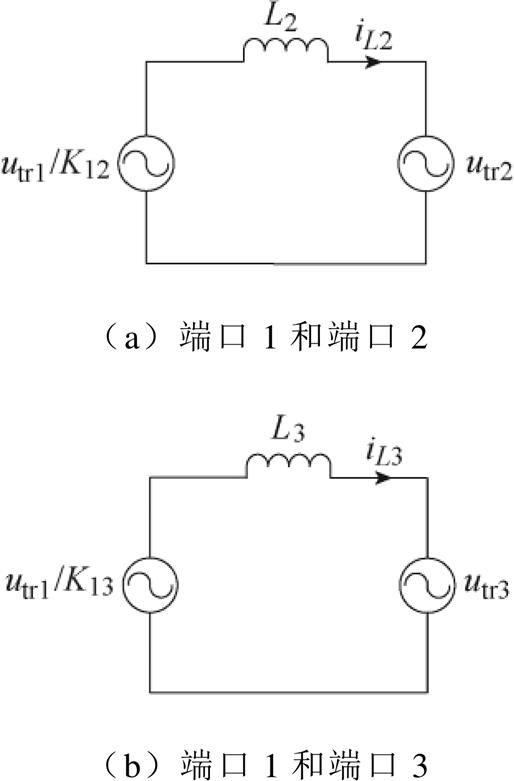
图6 TP BDC的正弦等效电路
Fig.6 Sinusoidal equivalent circuit of TP BDC
将开关管Q11、Q14、Q21、Q24、Q31、Q34所对应的驱动信号定义为G1～G6。同桥臂中另一开关管的驱动信号定义为F1～F6，则Gk（k=1, 2,…, 6）与Fk互补。移相控制下开关管驱动信号的傅里叶级数形式为
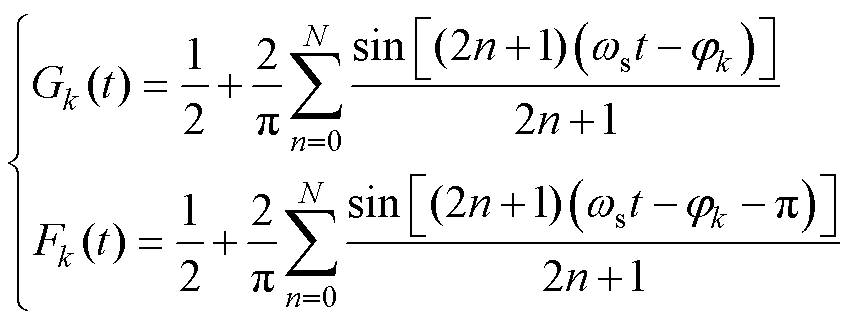（1）
式中，ws为开关角频率；jk为以Q11开通时刻为零点时Gk的相位。根据图5所示的电压电流波形及图6所示的正弦等效电路，应用相量分析法，可以得到三个端口H桥中点电压的基波分量分别为
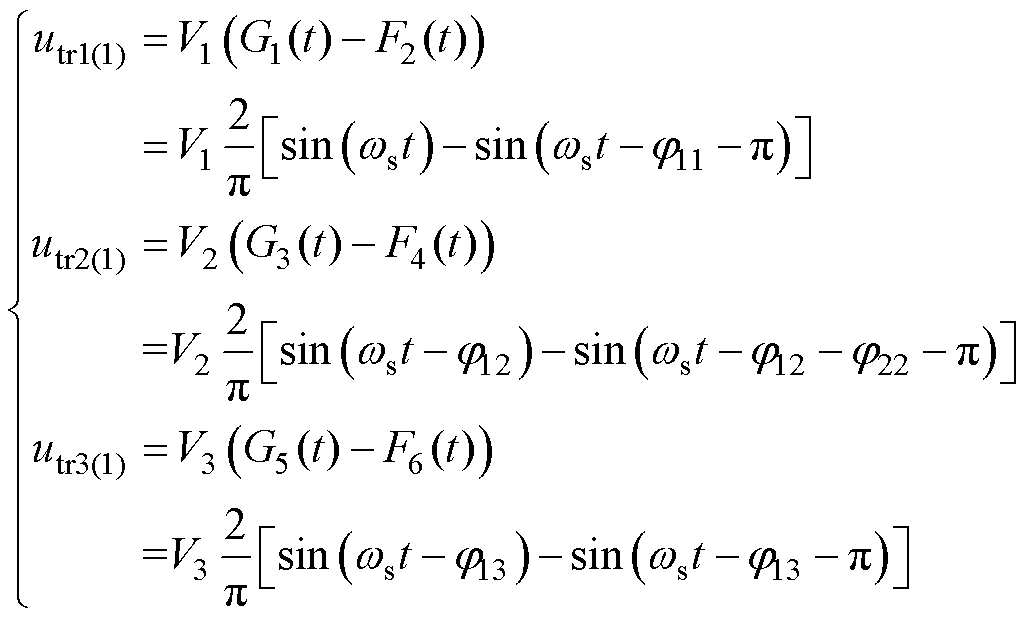（2）
则可以得到中点电压基波分量的相量形式为
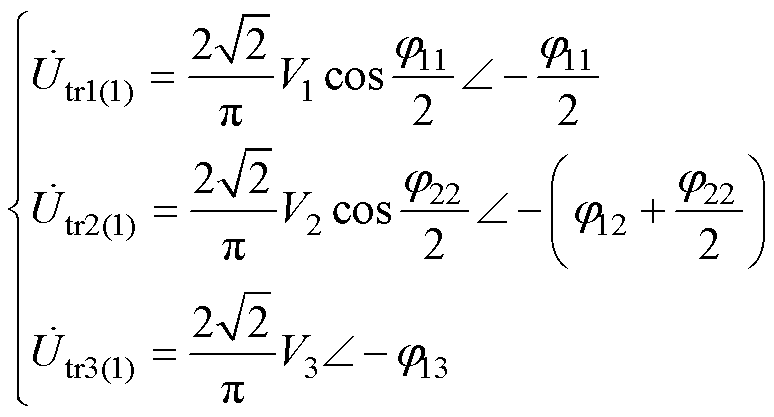（3）
根据图6及式（3）所示中点电压表达式，可以得到端口1和端口2等效回路中H桥中点电压和电感电流的相量分析如图7a所示，端口1和端口3等效回路中H桥中点电压和电感电流的相量分析如图7b所示。
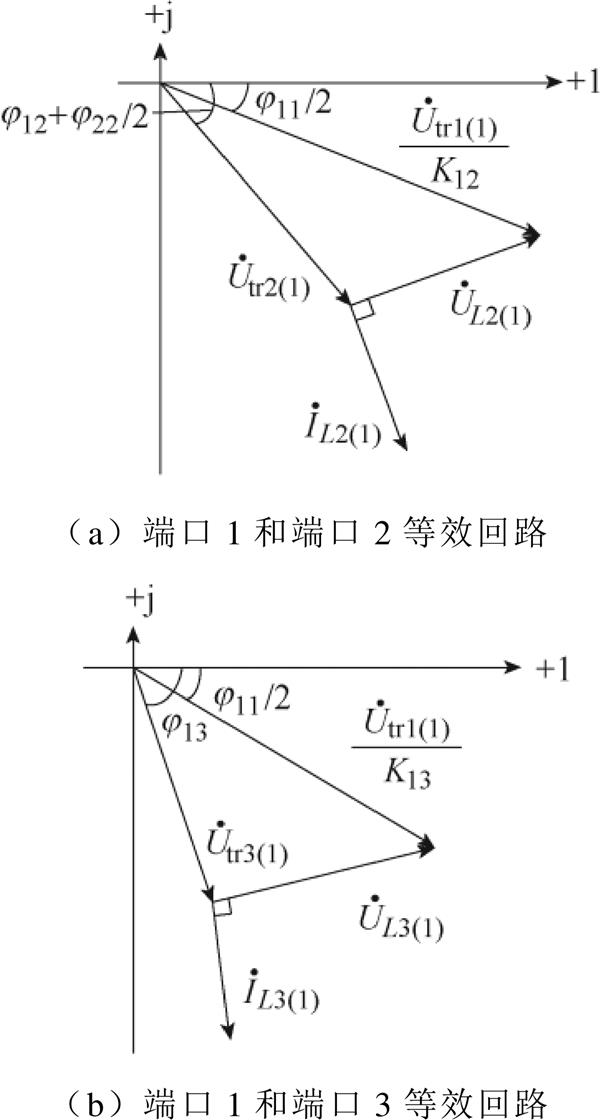
图7 等效回路中电压电流的相量分析
Fig.7 Phasor analysis diagrams of voltage and current in equivalent circuit
根据图7a中端口1和端口2等效回路的相量，可得变换器稳态运行情况下，回路电压电流基波分量的稳态相量表达式为
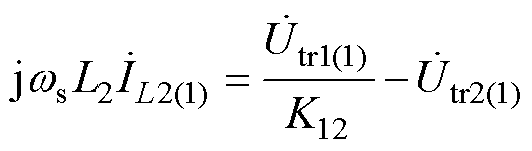（4）
结合式（3）和式（4）可以得到端口2电感电流的相量表达式为
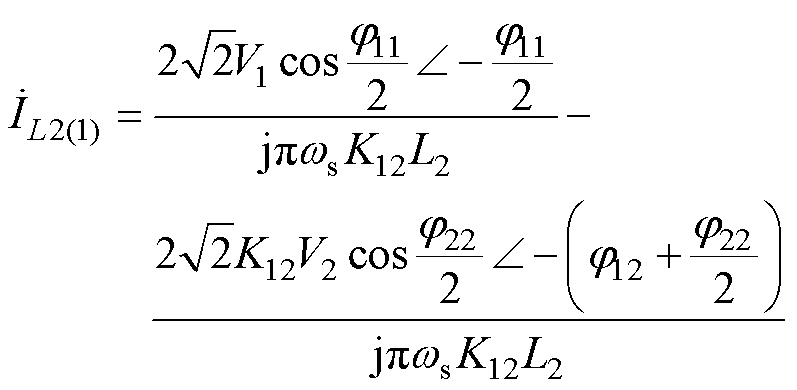（5）
根据式（3）和式（5）及复功率计算式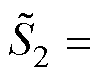
（
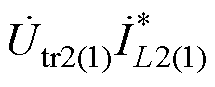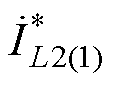为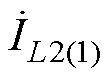
的共轭），可以得到，端口2的有功功率P2和无功回流Q2分别为
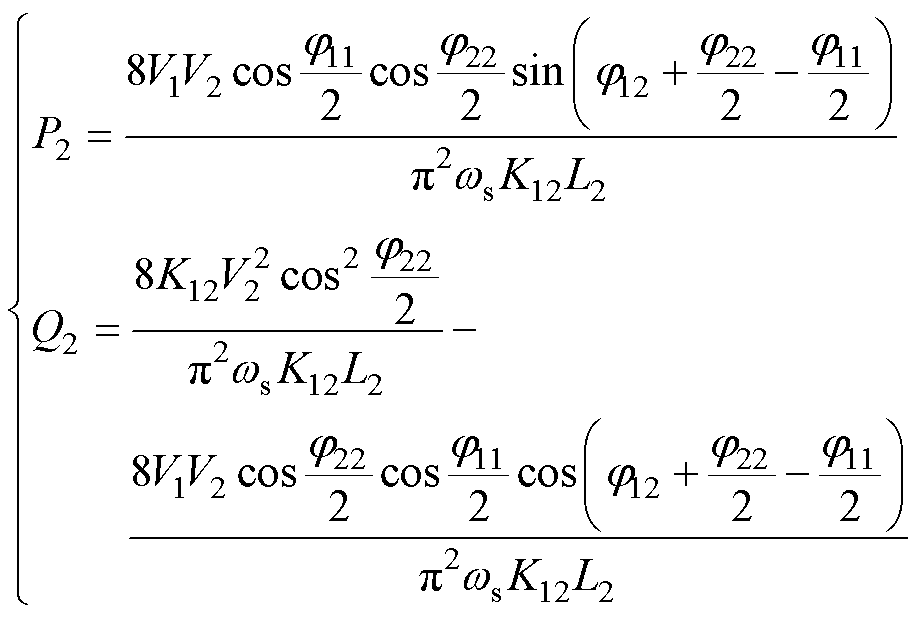（6）
为了方便分析，将有功功率和无功回流标幺化，以端口2有功功率最大值P2N=8V1V2/(p2wsK12L2)为基准值，则根据式（6），可以得到端口2有功功率和无功回流的标幺值分别为
（7）
式中，k21为端口2、1的电压传输比，k21=K12V2/V1。
同理，根据图7b中端口1和端口3等效回路的相量，结合式（3）可以得到端口3的电感电流表达式为
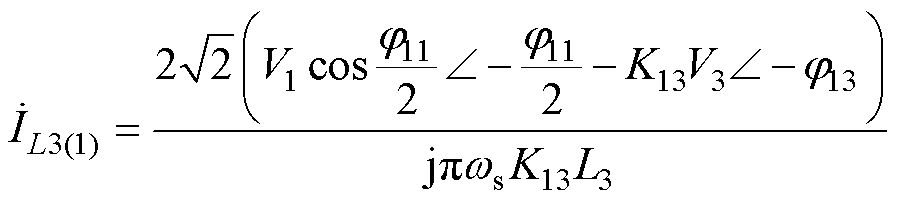（8）
根据式（3）和式（8）及复功率计算式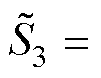
（
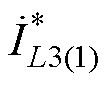为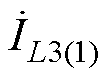
的共轭），可以得到，端口3的有功功率P3和无功回流Q3分别为
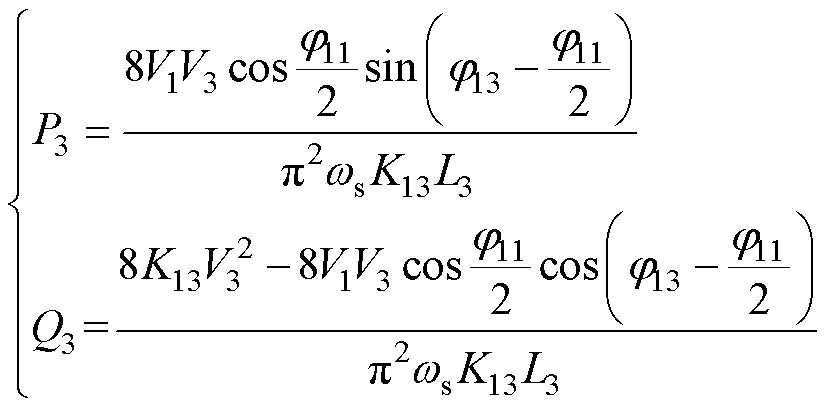（9）
以端口3有功功率最大值P3N=8V1V3/(p2wsK13L3)为基准值，则根据式（9），可以得到端口3有功功率和无功回流的标幺值分别为
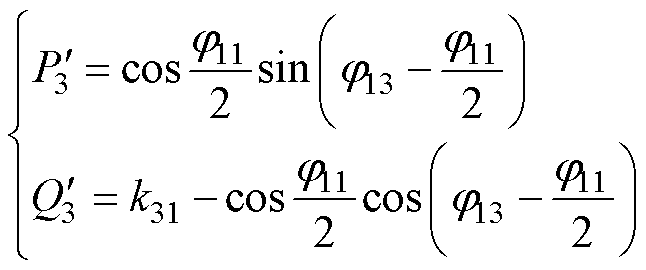（10）
式中，k31为端口3、1的电压传输比，k31=K13V3/V1。
基于无功优化的控制策略采用移相加占空比的控制方式。首先应用相量分析法得到端口2和端口3的有功功率及无功回流的表达式；然后根据得到的功率模型构建无功最优化问题；最后在给定有功功率和电压传输比的情况下以无功回流最小为目标进行最优移相角的求解。
根据图7a所示端口1和端口2等效回路的相量及式（7）所示端口功率可以确定，滞后端口无功回流存在为零的情况。当端口2的H桥中点电压utr2和电感电流iL2同向时，对应端口2无功回流达到最小且为零，此时端口1和端口2等效回路中电压电流相量如图8所示。
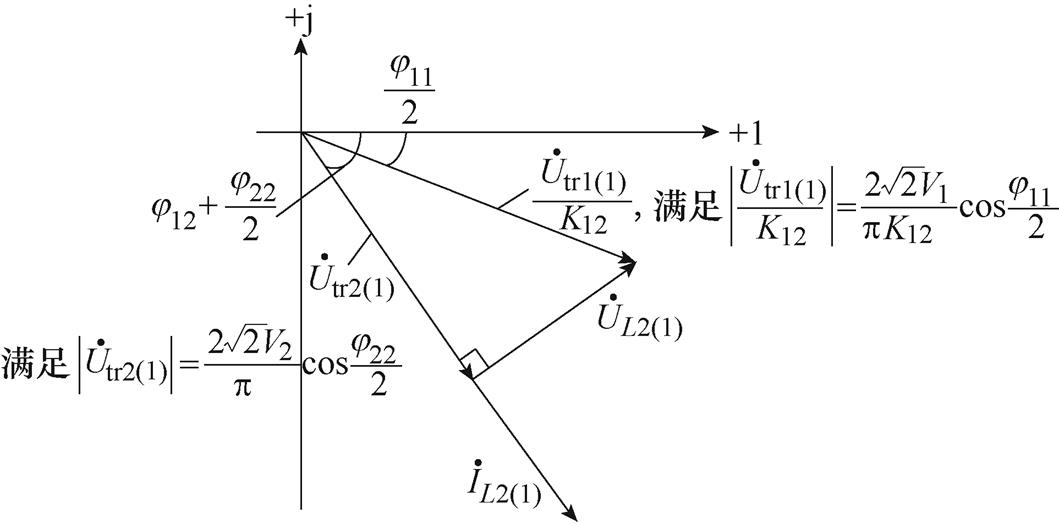
图8 端口2无功最小对应的相量
Fig.8 Phasor diagram corresponding to the minimum reactive power of port 2
根据图8所示无功回流最小的相量可以确定，端口2无功回流取最小值零时，其移相角满足
（11）
根据图7b所示端口1和端口3等效回路的相量及式（10）所示端口功率可以确定，滞后端口无功回流存在为零的情况。当端口3的H桥中点电压utr3与电感电流iL3同向时，对应端口3无功回流达到最小且为零，此时端口1和端口3等效回路中电压电流相量如图9所示。
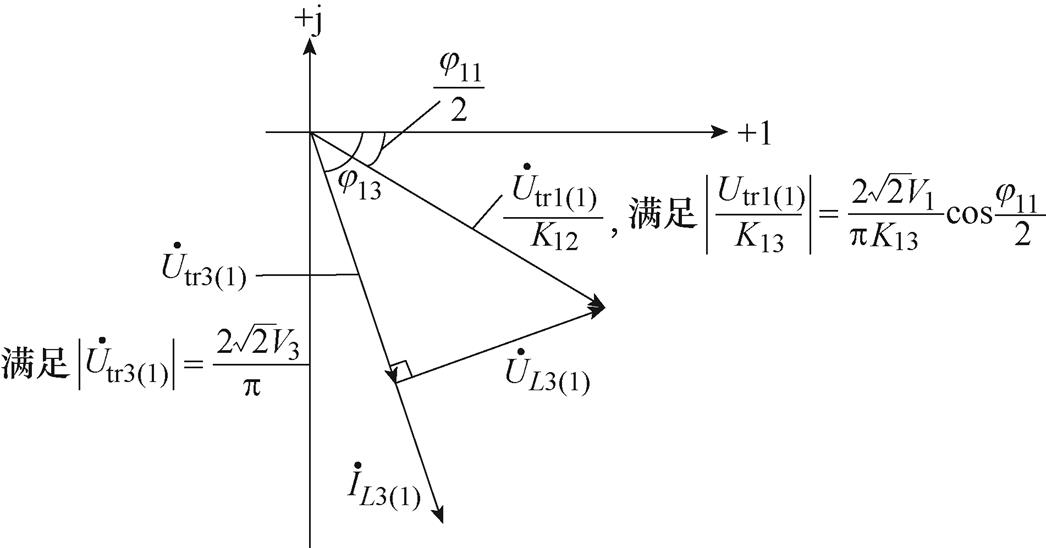
图9 端口3无功最小对应的相量
Fig.9 Phasor diagram corresponding to the minimum reactive power of port 3
则根据图9所示无功回流最小的相量可以确定，端口3无功回流取最小值零时，其移相角满足
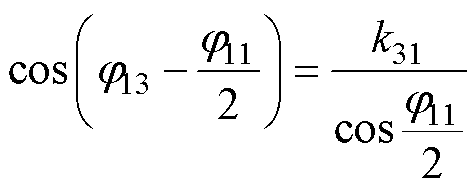（12）
结合式（7）、式（10）～式（12）中的有功功率标幺值可以确定端口2和端口3的无功回流最小时，各最优移相角的表达式为
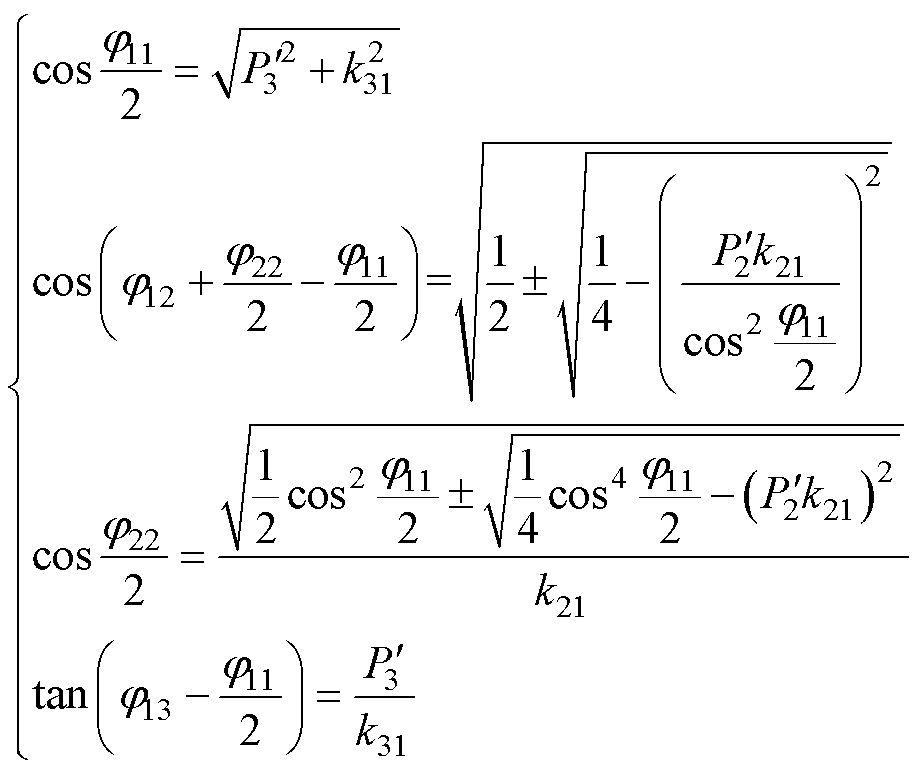（13）
若保证式（13）所示最优移相角均有解，则其有功功率和电压传输比应满足如式（14）所示的约束条件；若不满足其约束条件，则SPS控制下无功回流最小，此时端口1和端口2内移相角为零，即为SPS控制。
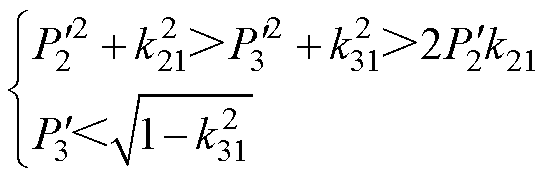（14）
综上所述，提出的无功最小为目标的优化控制策略见表1。
表1 TP BDC优化控制策略
Tab.1 Optimal control strategy of TP BDC
条件状态优化控制量 满足式（13） 不满足j11=0 满足式（13） 不满足j22=0
TP BDC的开关管要实现零电压软开关（Zero Voltage Switching, ZVS），需要满足：在开关管导通之前，其反并联二极管先导通，即电流先从反并联二极管流过。由此可知，讨论开关管的ZVS问题实际为讨论端口电流问题。根据TP BDC拓扑结构及变压器的工作特性，变压器一次电流等于折算后的二次电流和，因此对一次电流的分析可以转化为对二次侧两个端口电流的分析。通过对图4所示SPS控制下变换器的电感电流进行稳态分析，可以得到开关管实现ZVS要满足
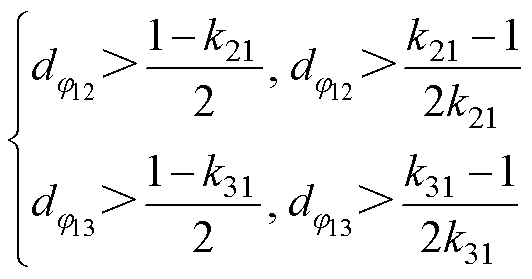（15）
对图5所示优化控制下变换器的电感电流进行稳态分析，可以得到，优化控制下开关管ZVS的范围要分情况进行分析。当有功功率标幺值及电压传输比满足式（14）时，变换器开关管实现ZVS的条件如式（16）所示；当有功功率标幺值及电压传输比不满足式（14）中第一个不等式时，开关管实现ZVS的条件如式（17）所示；当有功功率标幺值及电压传输比不满足式（14）时，开关管实现ZVS的条件如式（15）所示。
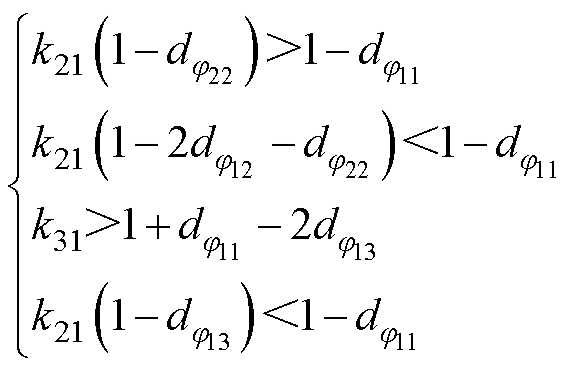（16）
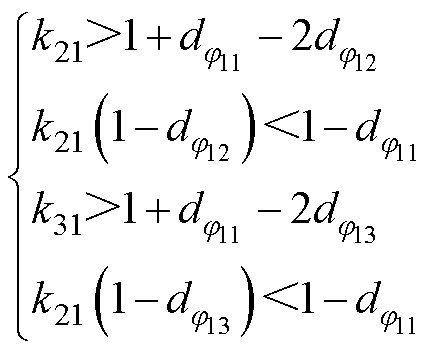（17）
以k21=0.6，k31=0.4为例，对TP BDC在SPS控制下和优化控制下的软开关范围进行分析，如图10所示为TP BDC在两种控制下的ZVS范围，图10a为SPS控制，图10b为优化控制。图10中，斜线阴影部分为端口1、端口3开关管实现ZVS的范围，点阴影部分为端口1、端口2开关管实现ZVS的范围，方格阴影部分为端口1、端口2和端口3开关管均实现ZVS的范围，其余空白部分为只有端口1开关管实现ZVS的范围。对比分析图10a和图10b可以清楚地看到，TP BDC在优化控制下的各端口的ZVS范围要大于在SPS控制下的ZVS范围，所以提出的基于无功最小的优化控制策略能够扩大开关管的软开关范围。
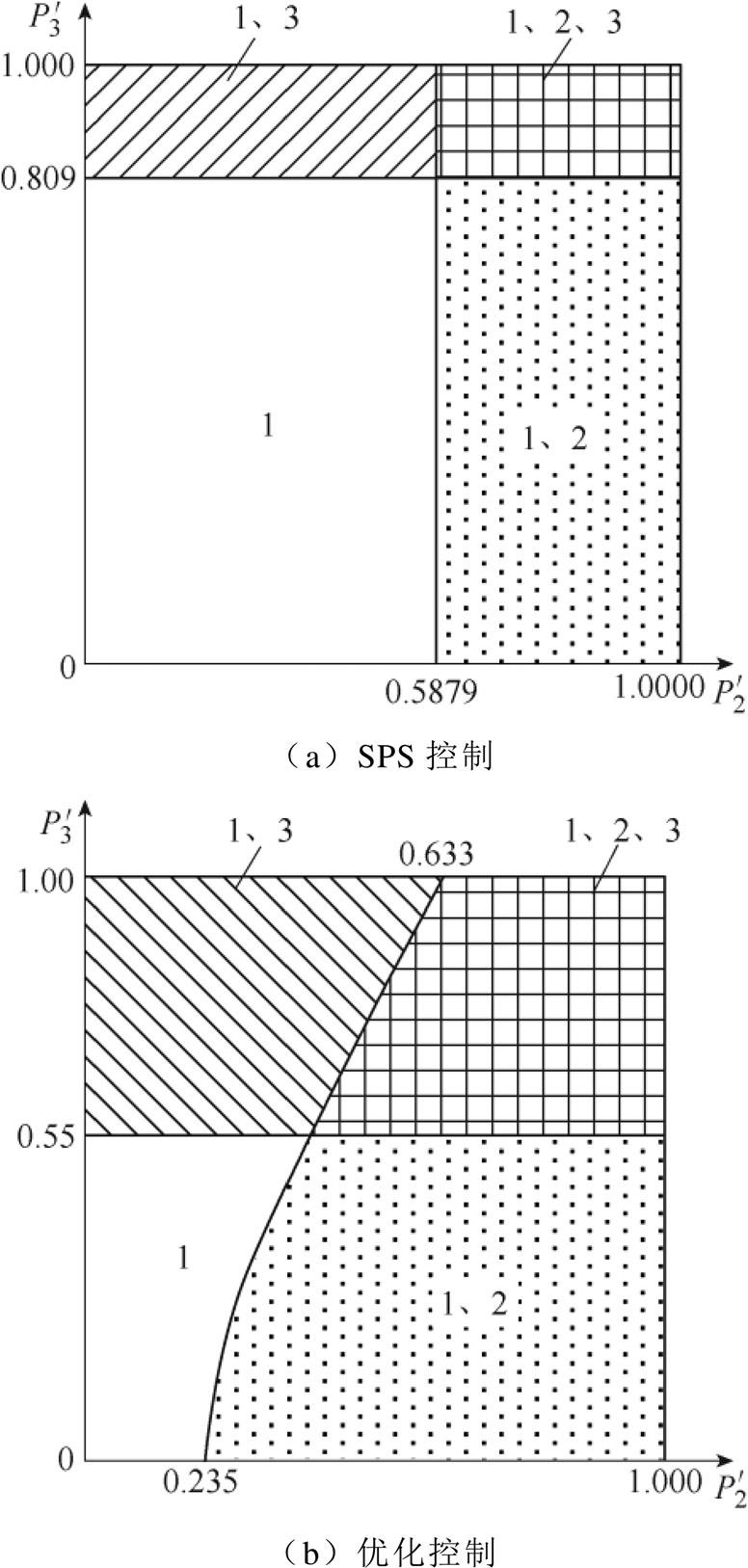
图10 TP BDC的ZVS范围
Fig.10 The ZVS range of TP BDC
由以上推导分析可以得到TP BDC在优化控制下的最优移相角的具体控制流程，图11为TP BDC的最优控制量选取策略。
结合图11，TP BDC最优控制量选取策略阐述如下：
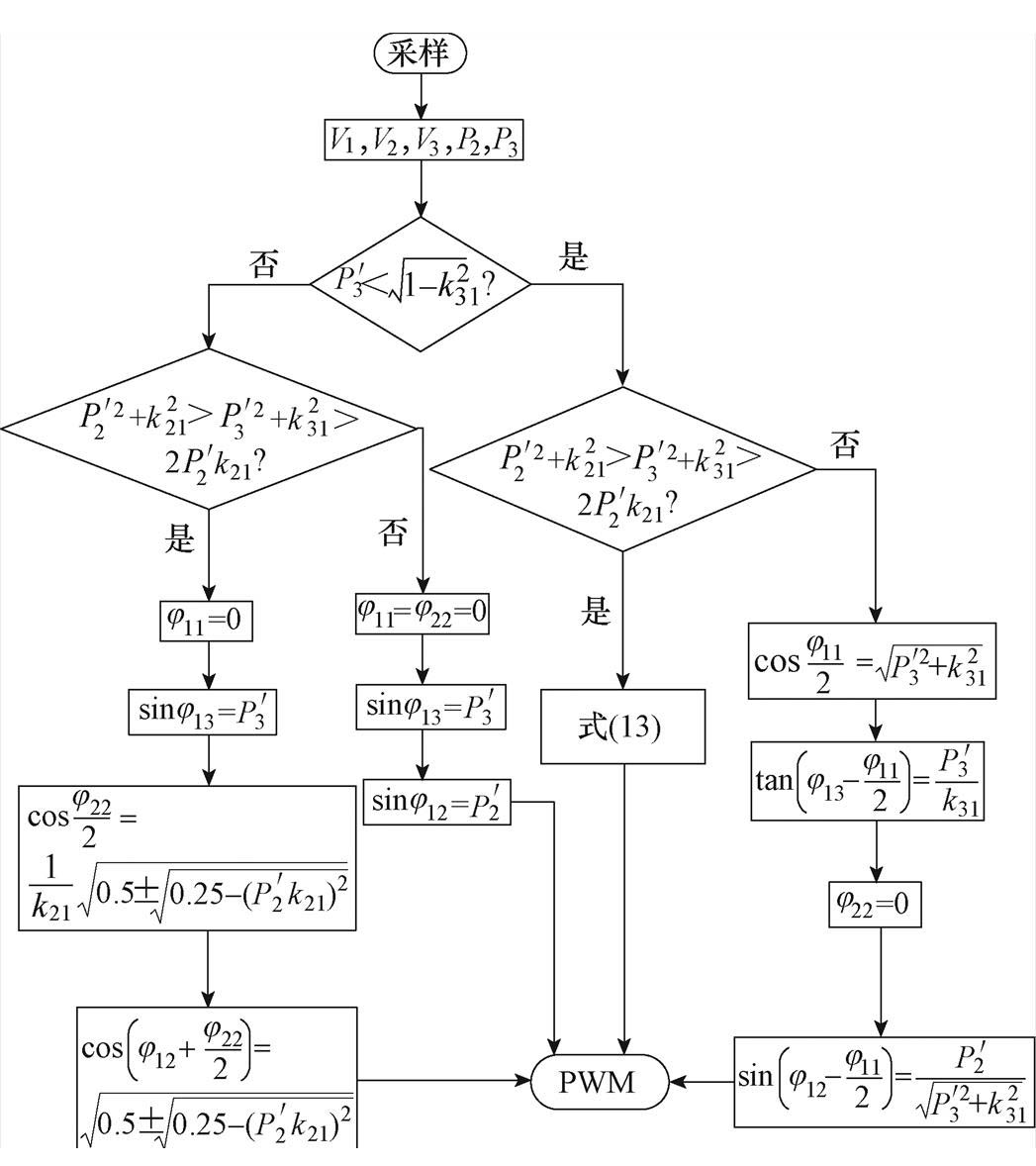
图11 TP BDC最优控制量选取策略
Fig.11 The selection strategy of optimal control quantity of TP BDC
（1）对端口电压电流进行采样并计算电压传输比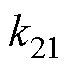
、
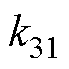及功率标幺值
、
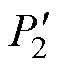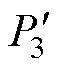，后对电压传输比及有功功率标幺值进行判断。若电压传输比及有功功率标幺值满足式（14），则端口2和端口3的无功回流均可达到最小值零，最优移相角表达式如式（13）所示。
（2）若电压传输比及有功功率标幺值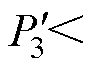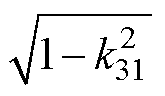满足
不满足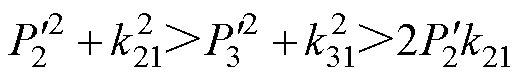
，则端口3的无功回流可达到最小值零，而端口2的无功回流不可为零，最优移相角的表达式如图11最右侧流程中公式所示。
（3）若电压传输比及有功功率标幺值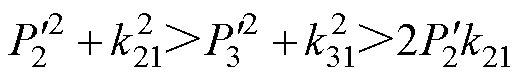满足不满足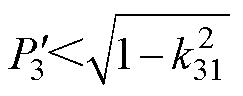
，则端口2的无功回流可达到最小值零，而端口3的无功回流不可为零，最优移相角的表达式如图11最左侧流程中公式所示。
（4）若电压传输比及有功功率标幺值不满足式（14），则端口2和端口3的无功回流均不可达到最小值零，两个端口内移相角均为零，控制方式为SPS控制。
为了验证上述无功优化控制策略的有效性，本文搭建了以TMS320F28335为控制器的TP BDC样机。图12所示为TP BDC的实验装置，其电路参数见表2。本文利用所建的实验平台分别对SPS控制和优化控制下的三端口变换器进行实验。
图12 TP BDC实验装置
Fig.12 Experimental prototype of TP BDC
表2 TP BDC实验电路参数
Tab.2 The experiment circuit parameters of TP BDC
参 数数 值 开关频率fs/kHz20 端口1直流电压V1/V100 端口2直流电压V2/V60 端口3直流电压V3/V40 端口2外接电感L2/mH69 端口3外接电感L3/mH63 变压器电压比N1N2N3111
图13为端口2传输功率P2=100W，端口3传输功率P3=120W时，SPS控制下变换器的电压电流波形。三个H桥桥臂中点电压utr1、utr2、utr3的波形如图13a所示，端口1绕组电流i1及端口2、端口3外接电感电流iL2、iL3的波形如图13b所示。
图14为端口2传输功率P2=100W，端口3传输功率P3=120W时，优化控制下变换器的电压电流波形。三个H桥桥臂中点电压utr1、utr2、utr3的波形如图14a所示，端口1绕组电流i1及端口2、端口3外接电感电流iL2、iL3的波形如图14b所示。SPS控制下，变换器H桥中点电压均为两电平电压。优化控制下引入了端口1和端口2的桥内移相角，端口1和端口2的H桥中点电压为三电平电压，端口3的H桥中点电压仍为两电平。
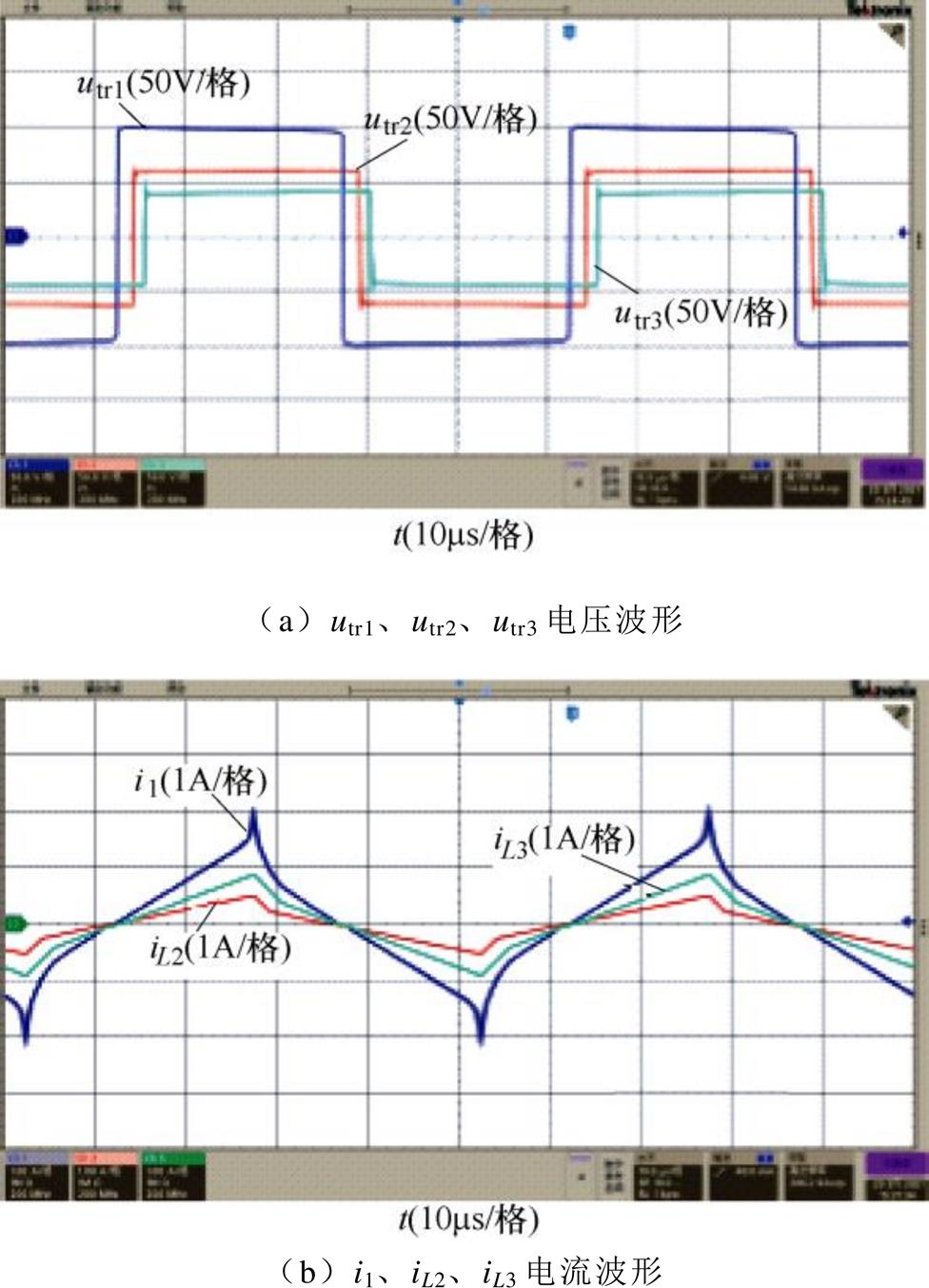
图13 P2=100W，P3=120W时SPS控制下的波形
Fig.13 Waveforms of SPSat P2=100W, P3=120W
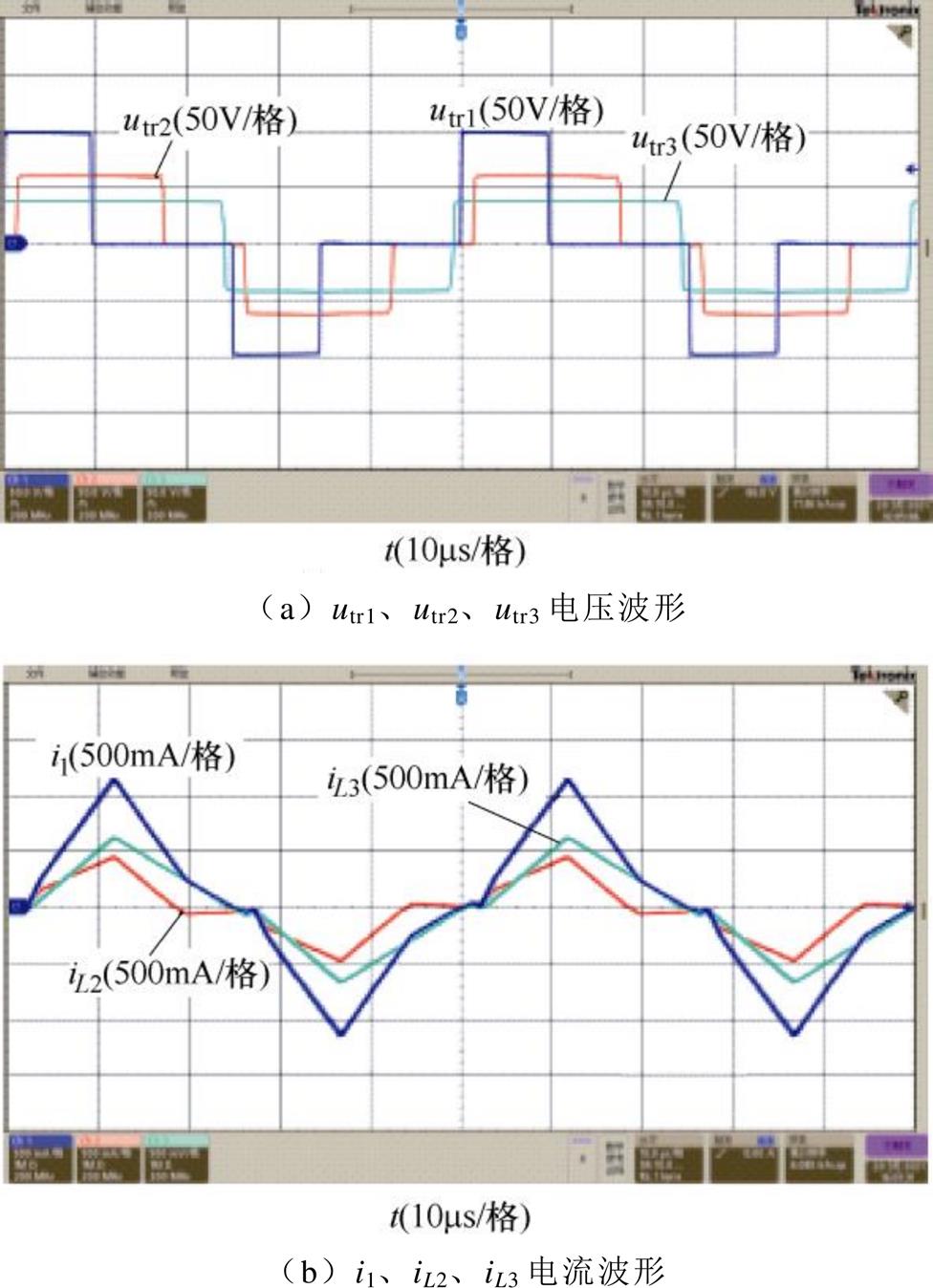
图14 P2=100W，P3=120W时优化控制下的波形
Fig.14 Waveforms of optimal controlat P2=100W, P3=120W
图15为P2=100W，P3=120W时，两种控制方式下开关管Q24的uDS、uGS及电感电流iL2的波形。根据2.2节的分析并结合图3所示电流正方向，开关管Q24实现ZVS，则在其导通之前电流iL2＞0。由图15a中A点可以确定，在Q24导通之前iL2＜0，所以此时为硬开关；图15b中B点可以确定，在Q24导通之前iL2＞0，所以此时为软开关。由此可确定优化控制下开关管的ZVS范围大于SPS控制下的ZVS范围。
图16、图17分别为不同功率时两种调制方式下变换器的无功回流曲线以及效率曲线。
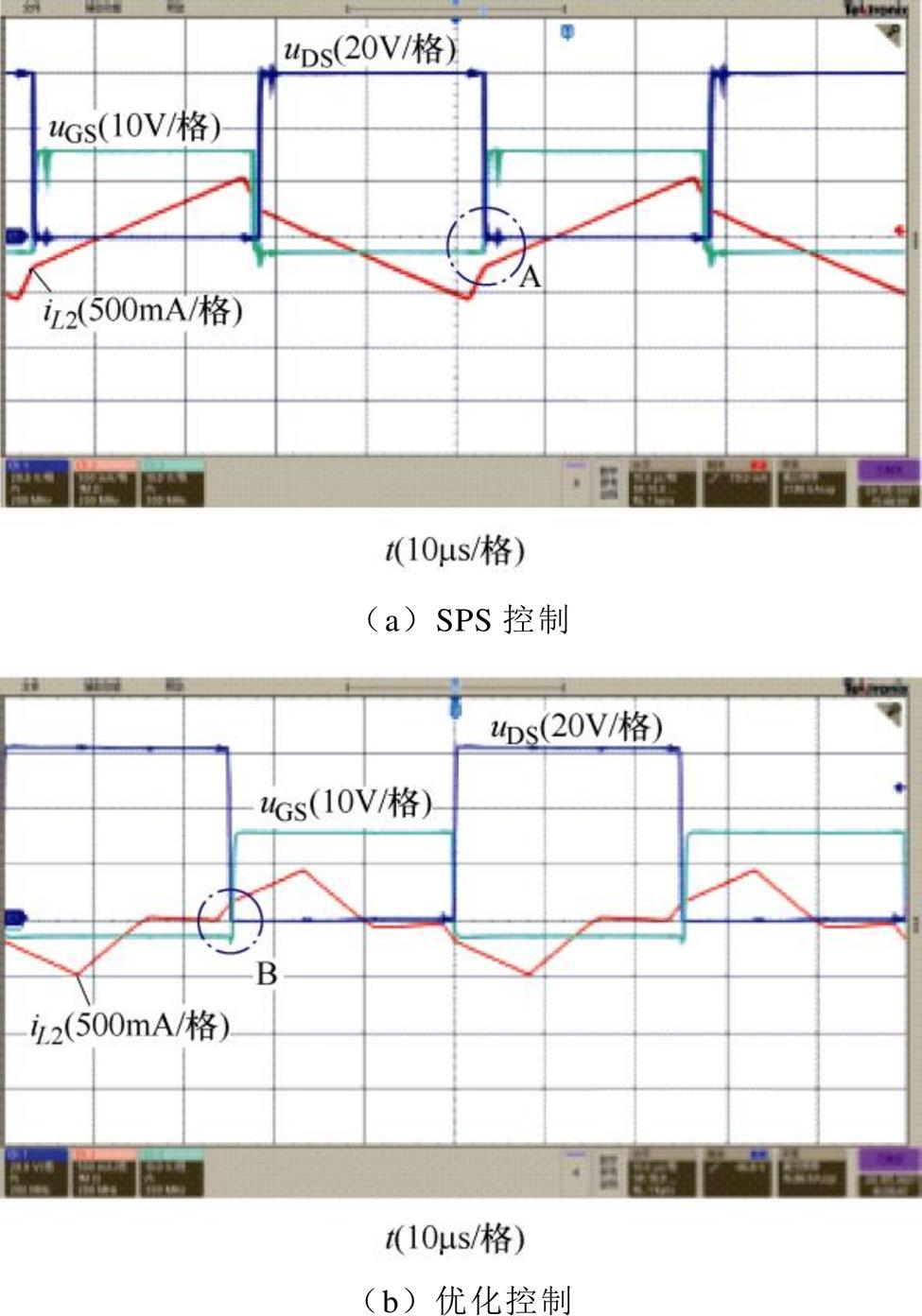
图15 P2=100W，P3=120W时，两种控制方式下开关管Q24的uDS、uGS及iL2的波形
Fig.15 Waveforms of uDS、uGS and iL2 of two control modes at P2=100W, P3=120W
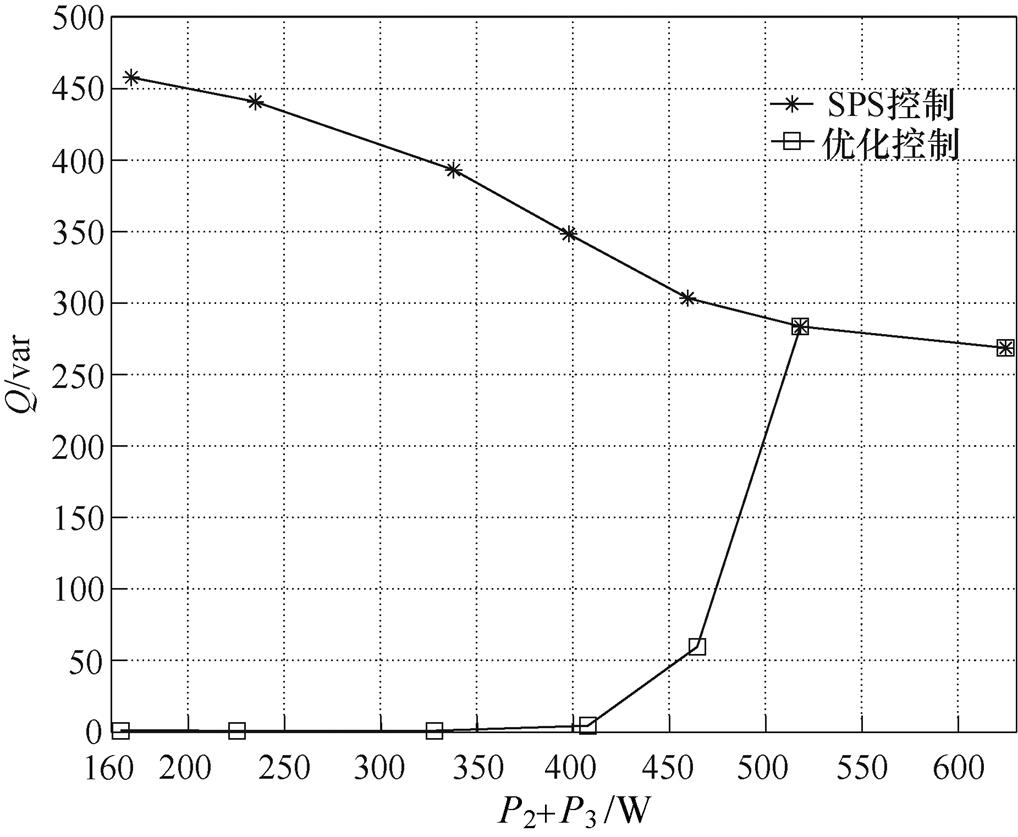
图16 两种调制方式下的无功回流曲线
Fig.16 The reactive power return curves under two modulation modes
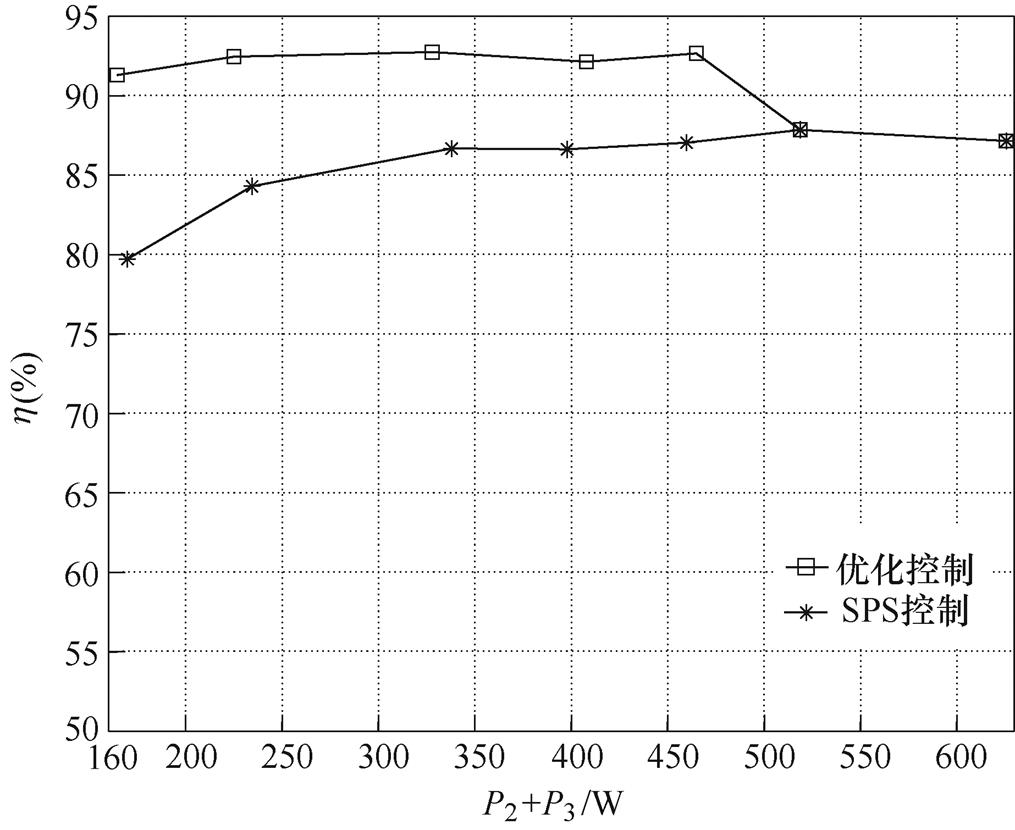
图17 两种调制方式下的效率曲线
Fig.17 The Efficiency curves under two modulation modes
从图16可以看出，当功率及电压传输比满足两个优化条件（见式（14））时，优化控制下变换器的各端口无功回流均为零，远小于SPS下的无功回流。当功率及电压传输比不满足其中一个优化条件时，会出现一个端口无功回流不为零的情况，使得变换器无功有所增长，但仍远小于SPS控制下的无功回流。当功率及电压传输比两个优化条件都不满足时，优化控制实际为SPS控制，二者无功回流一致。从图17可以看出，在端口电压不匹配的情况下，优化控制下变换器的效率大于SPS下的效率，且优化控制的优势在轻载的条件下尤其明显。
本文采用相量分析法对TP BDC进行分析，建立了各个端口的功率模型，简化了分析过程。根据功率模型构建无功回流最优问题，结合相量中电压电流相量的位置关系，得到了确定的功率和电压传输比下，无功回流最小时的最优移相角的表达式。通过实验验证了所提出的以无功最小为目标的优化控制策略的有效性。实验结果表明，与传统的单移相控制相比，该优化控制策略在输入输出电压不匹配时，能够降低端口无功回流，扩大开关管ZVS范围，从而提高变换器功率传输的效率，尤其提高了轻载时的效率。
参考文献
[1] Sheikh Jakir Hossain, Biswajit Dipan Biswas, Rojan Bhattarai, et al. Operational value-based energy storage management for photovoltaic (PV) integrated active power distribution system[J]. IEEE Transa- ctions on Industry Applications, 2019, 55(5): 5320- 5330.
[2] Poh Chiang Loh, Ding Li, Yi Kang Chai, et al. Autonomous operation of hybrid microgrid with AC and DC subgrids[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2214-2223.
[3] 朱晓荣, 孟凡奇, 谢志云. 基于虚拟同步发电机的直流微DC-DC变换器控制策略[J]. 电力系统自动化, 2019, 43(21): 132-140.
Zhu Xiaorong, Meng Fanqi, Xie Zhiyun. Control strategy of DC-DC converter in DC microgrid based on virtual synchronous generator[J]. Automatic of Electric Power Systems, 2019, 43(21): 132-140.
[4] 刘计龙, 朱志超, 肖飞, 等. 一种面向舰船综合电力系统的模块化三端口直流变换器[J]. 电工技术学报, 2020, 35(19): 4085-4096.
Liu Jilong, Zhu Zhichao, Xiao Fei, et al. A modular three-port DC-DC converter for vessel integrated power system[J]. Transactions of China Electro- technical Society, 2020, 35(19): 4085-4096.
[5] 陈强, 李睿, 蔡旭. 链式储能系统电池侧二次脉动功率的抑制方法[J]. 电工技术学报, 2015, 30(8): 231-237.
Chen Qiang, Li Rui, Cai Xu. Method of second-order ripple power suppression for battery in cascaded H-bridge storage system[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 231-237.
[6] 李建林, 徐少华, 惠东. 百MW级储能电站用PCS多机并联稳定性分析及其控制策略综述[J]. 中国电机工程学报, 2016, 36(15): 4034-4047.
Li Jianlin, Xu Shaohua, Hui Dong. A review of stability analysis and control strategy of multi-parallel PCS for hundred MW level energy storage power station[J]. Proceedings of the CSEE, 2016, 36(15): 4034-4047.
[7] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292-304.
[8] Zhao Biao, Song Qiang, Liu Wenhua, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.
[9] Zhang Junjun, Wu Hongfei, Qin Xiaoqing, et al. PWM plus secondary-side phase-shift controlled soft- switching full-bridge three-port converter for rene- wable power systems[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11): 7061-7072.
[10] 余雪萍, 涂春鸣, 肖凡, 等. 三端口隔离DC-DC变换器软开关特性研究[J]. 电工技术学报, 2021, 36(23): 5014-5026.
Yu Xueping, Tu Chunming, Xiao Fan, et al. Soft switching characteristics of the three-port isolated DC-DC converter[J]. Transactions of China Electro- technical Society, 2021, 36(23): 5014-5026.
[11] Zhao Lei, Li Haoyu, Hou Yue, et al. Operation analysis of a phase-shifted full-bridge converter during the dead-time inverval[J]. IET Power Electro- nics, 2016, 9(9): 1777-1783.
[12] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3030-3040.
[13] 李微, 王议锋, 韩富强, 等.一种隔离型三端口双向LCLC多谐振直流变换器[J]. 电工技术学报, 2018, 33(14): 3231-3244.
Li Wei, Wang Yifeng, Han Fuqiang, et al. An isolated three-port bidirectional LCLC multi-resonant DC-DC converter[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3231-3244.
[14] 王萍, 陈博, 王议锋, 等.一种多谐振隔离双向DC-DC变换器[J]. 电工技术学报, 2019, 34(8): 1667-1676.
Wang Ping, Chen Bo, Wang Yifeng, et al. A multi resonant bidirectional DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(8): 1667-1676.
[15] Ngoc Dat Dao, Dong-Choon Lee, Quoc Dung Phan. High-efficiency SiC-based isolated three-port DC/DC converter for hybrid charging stations[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10455-10465.
[16] 沙广林, 王聪, 程红, 等. 移相控制的双有源桥DC-DC变换器统一相量分析法[J]. 电工技术学报, 2017, 32(18): 175-185.
Sha Guanglin, Wang Cong, Cheng Hong, et al. Unified phasor analytical method for bidirectional dual-active-bridge DC-DC converter under phase- shift control[J]. Transactions of China Electro- technical Society, 2017, 32(18): 175-185.
[17] Zhao Biao, Song Qiang, Liu Wenhua, et al. Universal high-frequency-link characterization and practical fundamental-optimal strategy for dual-active-bridge DC-DC converter under PWM plus phase-shift control[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6488-6494.
[18] 李广地, 阮杰, 王昆, 等. 一种混合调制型三路输出DC-DC变换器[J]. 电工技术学报, 2019, 34(22): 4719-4727.
Li Guangdi, Ruan Jie, Wang Kun, et al. A hybrid modulated triple-output DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(22): 4719-4727.
[19] 杨玉岗, 赵金升. 高增益对称双向LCLC谐振变换器的研究[J]. 电工技术学报, 2020, 35(14): 3007- 3017.
Yang Yugang, Zhao Jinsheng. Research on high-gain symmetric bidirectional LCLC resonant converter[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3007-3017.
Control Strategy of Three-Port Bidirectional DC-DC Converter Based on Reactive Power Optimization
Abstract The three-port bidirectional DC-DC converter (TP BDC) suffers high reactive power, narrow soft switching range, and low efficiency when the port voltages do not match. Thus, this paper proposes a control strategy for the efficiency optimization of TP BDC, which aims to minimize the reactive power. The voltage and current characteristics of each port are analyzed. On this basis, the power model of each port is established with the duty cycle control and phasor analysis. By constructing and solving the minimum reactive power optimization problem, the reactive power of TP BDC is reduced in a wide voltage range. Furthermore, this paper analyzes the soft switching characteristics of TP BDC under the optimal control. The selection strategy of optimal control parameters is subsequently proposed. The experimental results show that TP BDC has lower reactive power and wider soft switching range under wide voltage conditions by applying the proposed optimal control strategy. Consequently, the transmission efficiency of the converter is significantly improved under port voltage mismatch and light load conditions.
keywords：Three-port bidirectional DC-DC converter (TP BDC), minimum reactive power, optimal control strategy, phasor analysis method
DOI: 10.19595/j.cnki.1000-6753.tces.210451
中图分类号：TM46
黄 珺 男，1986年生，博士，工程师，研究方向为高频功率变换技术。E-mail: hj2018@hebut.edu.cn（通信作者）
付亚楠 女，1998年生，硕士研究生，研究方向为三端口双向DC-DC变换器。E-mail: nanhebei@126.com
收稿日期 2021-04-02
改稿日期 2021-07-21
智能电网保护和运行控制国家重点实验室开放课题项目（SGNR0000KJJS1907542）和河北省高等学校科学技术研究项目（QN2019041）资助。
（编辑 陈 诚）