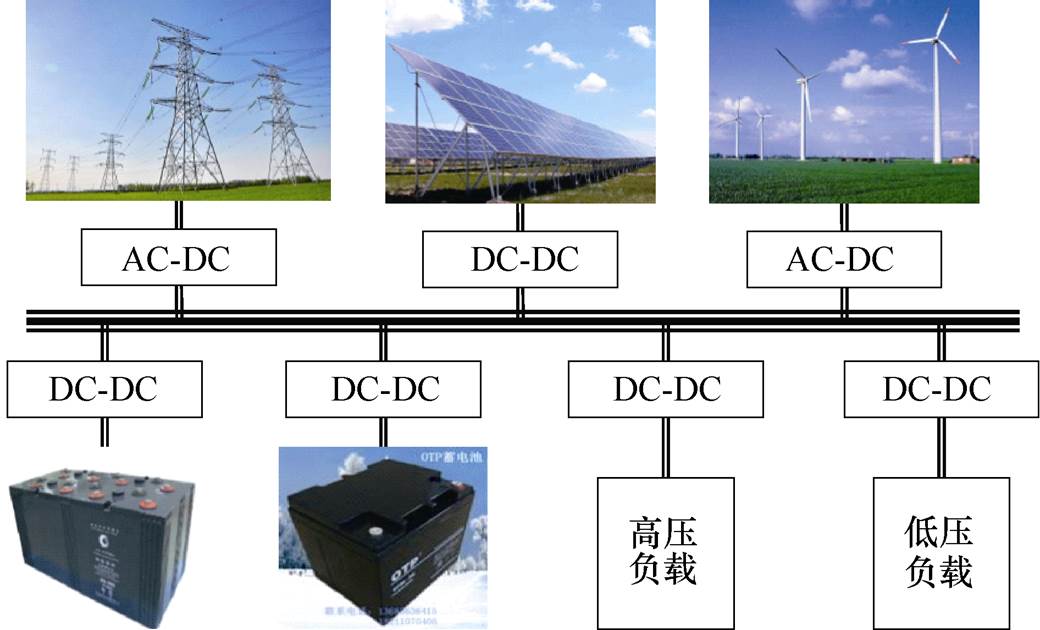
图1 混合储能微电网
Fig.1 Hybrid energy storage microgrid
摘要 混合储能微电网具有非线性、强耦合、负载扰动强、并/离网模式切换灵活等特性,针对传统控制难以取得理想效果的问题,该文将二阶线性自抗扰控制(2nd-LADRC)技术引入微电网负载端接口变换器的控制中。首先,根据状态空间平均法对被控对象进行分析并提取模型信息,根据状态方程与传递函数从系统层面设计2nd-LADRC控制器;然后,通过频域分析,验证2nd-LADRC控制器的收敛性和抗扰性,探讨观测器带宽与抗扰性能之间的关联,并运用Lyapunov理论分析应用2nd-LADRC控制器时的系统稳定性,得出系统在工程意义上是稳定的;最后,设计一台40kW实验样机,模拟在微电网和负载功率波动时不同控制策略的实验场景。实验结果验证了2nd-LADRC控制方法的可行性和有效性。
关键词:混合储能微电网 状态空间平均法 二阶线性自抗扰控制 频域分析 Lyapunov理论
当今时代,能源短缺和环境问题逐渐成为人们关注的焦点。这促使新能源(如风能、太阳能等)在社会的发展中扮演愈发重要的角色[1-3]。而以往传统的电能变换技术已经不能满足人们对新能源变换器高性能、高效率的要求,高频电能变换技术在新能源系统中发挥着举足轻重的作用[4-5]。近年来,随着碳化硅(SiC)、氮化镓(GaN)等宽禁带电力电子器件在工程领域的不断发展,小型化、高频化逐步成为分布式能源变换器的发展方向[1]。在直流微电网应用中,这些具有高频、高可靠性和高效率等优势的新型器件,不仅降低了功率器件损耗,同时能够大幅提高DC-DC变换器的工作频率和效率[6]。但直流微电网是一个融合多种分布式能源和负载的系统,加之与交流电网频繁的能量交互,常表现出间歇性、时变性的特性。这就会给直流母线和输出侧接口的电压造成较大冲击,使其难以维持在一个合理的波动范围内,进而影响微电网中多种接口变换器的稳定运行,严重时会导致保护动作使其停止工作。因此,对于微电网的各个控制模块来说,拥有较强的鲁棒性和抗扰能力就显得尤为重要。
目前,主要通过接口变换器的控制环节改造来实现对电能质量的优化。根据目前研究中的建模分析可知,蓄电池和超级电容储能系统均具有典型的非线性特性,与此同时,DC-DC变换器也是一个非线性结构[7-8]。然而,对于一个非线性的、不连续的系统,经典PI控制的结果通常不理想[9]。在过去的几年里,很多学者将其他一些先进的算法,如粒子群、神经网络算法应用到变换器的控制中[10-11]。然而,这些算法的过程太过复杂,且对系统的精确数学模型有严格的要求,这两者在现实中很难得到。
自抗扰控制技术[12]是由韩京清提出的,是一种在传统比例-积分-微分(Proportion-Integration- Differentiation, PID)控制基础上发展起来的新型非线性控制策略。该控制方法具备鲁棒性强、抗干扰能力强的特点[13-14]。目前自抗扰控制(Active Dis- turbance Rejection Control, ADRC)技术已初步应用于有源电力滤波器控制[15]、电机控制[16]和静止无功发生器控制[17]。但是传统的自抗扰控制器参数众多、分析困难、难以在工程中推广应用。因此Gao Zhiqiang教授和他的团队开发出线性自抗扰控制(Linear Active Disturbance Rejection Control, LADRC)策略,此方法继承了传统非线性自抗扰的核心功能,
并将大多数参数进行整合,使其与带宽呈线性相关,大大简化了调参过程,方便了自抗扰控制的工程化应用[18]。基于线性自抗扰理论,有些学者通过分离传统的耦合观测器与模型误差,提出了一种基于扩张状态观测器(Extended State Observer, ESO)的逆变器电流控制策略,改进了观测器的鲁棒性[19]。在文献[20]中,提出了一种基于ESO的超局域模型,并从无差拍方法的电压基准中减去观测到的扰动。当电网电压出现不平衡时,类似的技术还被用于有源前端整流器,以实现稳定控制[21]。在文献[22]中,ESO被用于预测模型,并将干扰抑制作为速度控制回路的并行观测器。可见,LADRC理论已经初步扩展到了多个领域。然而,关于基于LADRC的微电网接口变换器控制的完整理论、证明和实验分析的研究还很少。
本文利用线性自抗扰控制策略的优点,并结合扩张状态观测器的思想,处理微电网运行中难以取得理想控制效果的问题。该方法无需依赖摄动产生模型或直接测量,即可观测扰动并获得估计进而补偿不确定性带来的问题。首先分析了微电网接口处的数学模型。根据对直流微电网数学模型的分析,将已知的部分模型信息集成到ESO的系数矩阵中构成模型辅助的ESO,在观测器带宽不变的情况下提高观测和估计的精度。并通过频域分析法和Lyapunov理论分析了应用二阶线性自抗扰控制(Second- Order Linear Active Disturbance Rejection Control, 2nd-LADRC)技术系统的收敛性、抗扰性和稳定性,也揭示了观测器带宽与抗扰性能之间的对应关系。最后,通过数字仿真和40kW样机的物理实验,验证了所提控制策略的正确性和可行性。
混合储能微电网如图1所示。本文主要针对母线与负载之间的降压接口变换器的电压控制技术进行探究和讨论。变换器拓扑结构如图2所示。图1中,Cin为输入电容,Cout为输出电容,vin(t)为输入电压,vo(t)为输出电压,Rload为负载,S1~S12为SiC MOSFET,L1~L6为电感。图2a中,降压接口处采用的是6路交错并联型变换器结构,由于动态过程相似,仅对单路进行分析。

图1 混合储能微电网
Fig.1 Hybrid energy storage microgrid
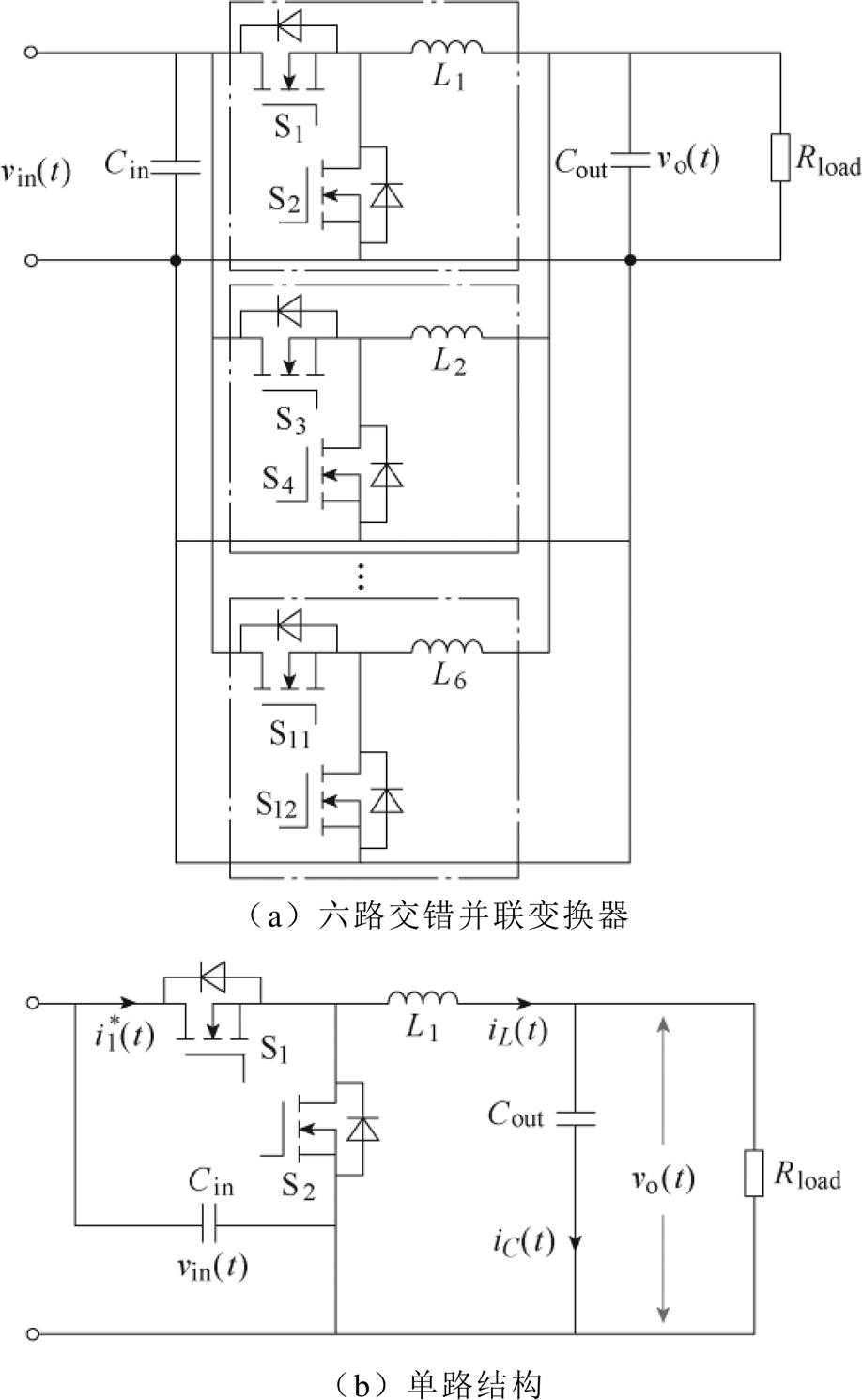
图2 变换器拓扑结构
Fig.2 Converter topology
为了简化分析与数学建模,假设电路均为理想器件,且同步整流过程处于理想状态。针对一个周期内,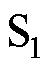 的开通与关断,将电路的工作状态在每个周期
的开通与关断,将电路的工作状态在每个周期 内分成
内分成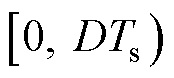 与
与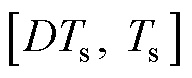 两部分,在这两个时间段内互补导通,即工作状态1和工作状态2,其中,
两部分,在这两个时间段内互补导通,即工作状态1和工作状态2,其中,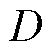 为占空比。
为占空比。
工作状态1即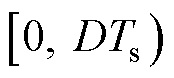 时段,
时段,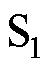 导通、
导通、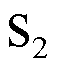 关断。电感电压
关断。电感电压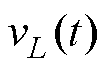 与电容电流
与电容电流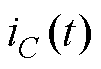 分别为
分别为
 (1)
(1)
输入电流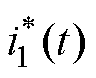 即为电感电流
即为电感电流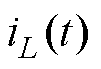 ,输出电压
,输出电压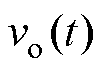 即为电容电压。将式(1)写成状态方程与输出方程式为
即为电容电压。将式(1)写成状态方程与输出方程式为
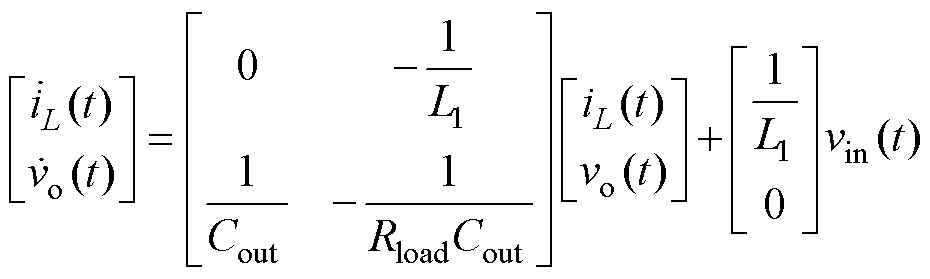 (2)
(2)
 (3)
(3)
工作状态2即 时段,
时段,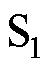 截止、
截止、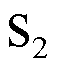 导通。在此工作状态下,状态方程与输出方程式为
导通。在此工作状态下,状态方程与输出方程式为
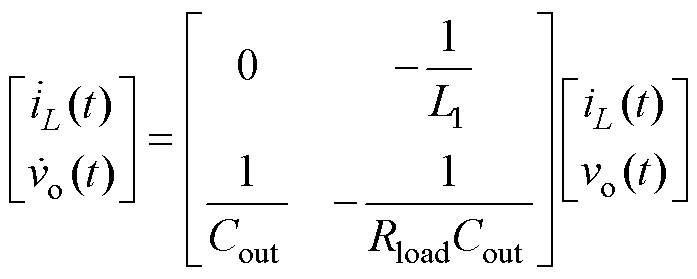 (4)
(4)
根据状态空间平均法[23],整理出Buck变换器输出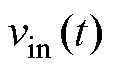 对控制变量的传递函数
对控制变量的传递函数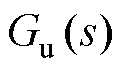 为
为
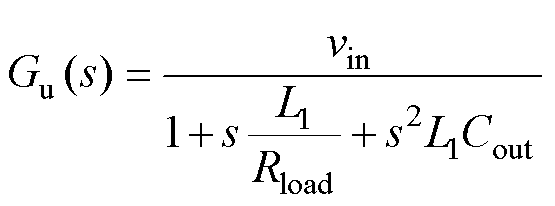 (5)
(5)
根据第1节的建模与分析,可知被控对象为二阶系统,因此2nd-LADRC与其最为匹配,控制器结构如图3所示。
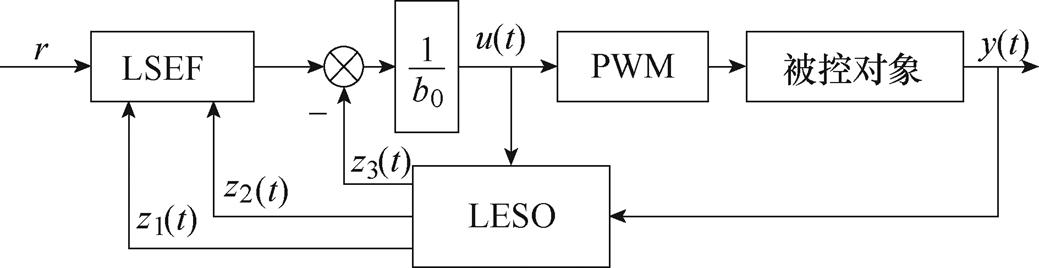
图3 2nd-LADRC控制器
Fig.3 2nd-LADRC controller
图3中,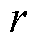 为负载侧电压参考值;
为负载侧电压参考值;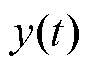 为输出;
为输出;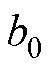 为控制增益;
为控制增益;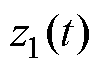 为
为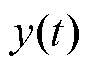 的观测值;
的观测值;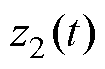 为
为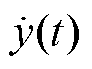 的观测值;
的观测值;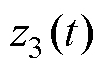 为总扰动的观测值;
为总扰动的观测值;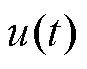 为含有控制信息信号流,其物理含义为MOSFET的触发信号。
为含有控制信息信号流,其物理含义为MOSFET的触发信号。
由于模型的所有信息均可通过LESO进行观测与补偿,因此LADRC是一种不依赖模型信息也能达到较好动态性能的控制策略。在无模型辅助时,未知总扰动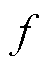 包含了所有的外扰与模型信息、控制增益以及它们受参数偏移等不确定性因素影响的变化量,它们全都依靠ESO观测并补偿。为达到更好的控制品质,本文对LESO的系数矩阵做了进一步改造,即把经过分析获得的部分模型信息从
包含了所有的外扰与模型信息、控制增益以及它们受参数偏移等不确定性因素影响的变化量,它们全都依靠ESO观测并补偿。为达到更好的控制品质,本文对LESO的系数矩阵做了进一步改造,即把经过分析获得的部分模型信息从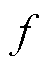 中分离,写入LESO的系数矩阵中。对式(5)进行Laplace反变换得到
中分离,写入LESO的系数矩阵中。对式(5)进行Laplace反变换得到
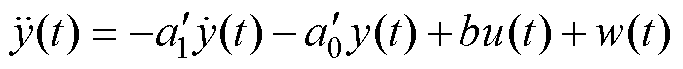 (6)
(6)
其中
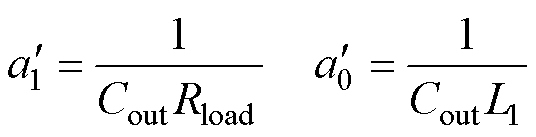
假设 未知,
未知,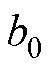 为
为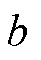 的已知部分,则式(6)又可写成
的已知部分,则式(6)又可写成
 (7)
(7)
其中
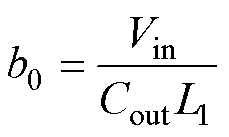
式中,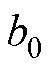 为设定的控制器增益值;
为设定的控制器增益值;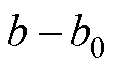 仅包括控制增益因参数偏移等不确定性因素影响的变化量。经过分析微电网的部分模型信息,并将其分离,实际的未知总扰动
仅包括控制增益因参数偏移等不确定性因素影响的变化量。经过分析微电网的部分模型信息,并将其分离,实际的未知总扰动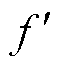 表示为
表示为
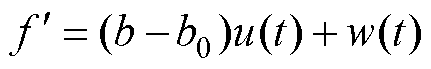 (8)
(8)
选取状态变量: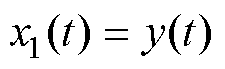 ,
,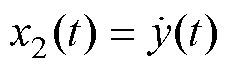 ,
,
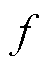 ,则
,则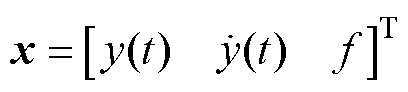 为包括了扰动的扩张状态,将式(7)转化为连续的状态空间描述,即
为包括了扰动的扩张状态,将式(7)转化为连续的状态空间描述,即
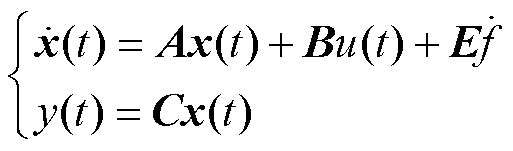 (9)
(9)
其中
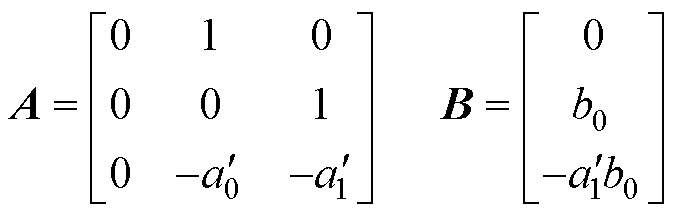
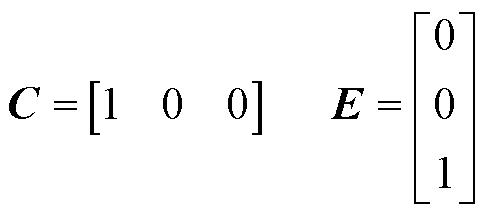
对应的连续LESO为
 (10)
(10)
式中,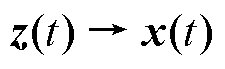 ,
,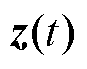 为扩张状态观测器的状态变量矩阵;
为扩张状态观测器的状态变量矩阵; 为状态变量导数矩阵;
为状态变量导数矩阵; 为需要结合被控对象设计的状态观测器增益矩阵。
为需要结合被控对象设计的状态观测器增益矩阵。
由于 未知且通过校正可以估计出来,因而略去
未知且通过校正可以估计出来,因而略去 ,故观测器方程又可写成
,故观测器方程又可写成
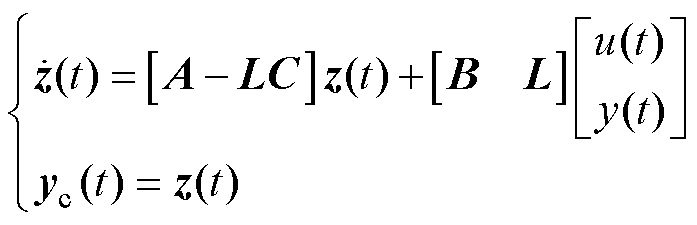 (11)
(11)
针对此三阶LESO,线性状态误差反馈律为PD控制率。为了避免给定值快速变化所导致的系统振荡,采用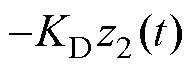 代替
代替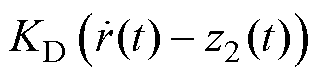 ,则线性状态误差反馈应为
,则线性状态误差反馈应为
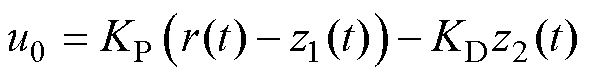 (12)
(12)
式中,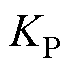 和
和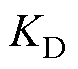 为控制器放大系数。经过带宽参数化[24],取
为控制器放大系数。经过带宽参数化[24],取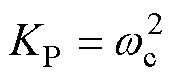 ,
,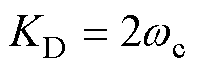 ,
,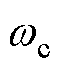 为控制器带宽。
为控制器带宽。
与其对应的扰动补偿环节为
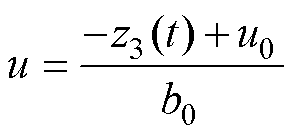 (13)
(13)
根据极点配置方法[20],对上述LESO做如下配置
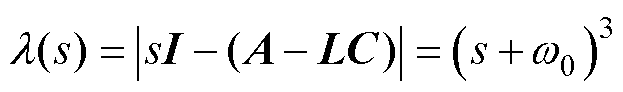 (14)
(14)
式中, 为观测器带宽;
为观测器带宽;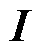 为单位矩阵。计算得观测器增益矩阵
为单位矩阵。计算得观测器增益矩阵
 (15)
(15)
根据式(10)、式(13)、式(15),可以得到具有模型信息的二阶LADRC结构,结合模型信息的2nd-LADRC结构如图4所示。
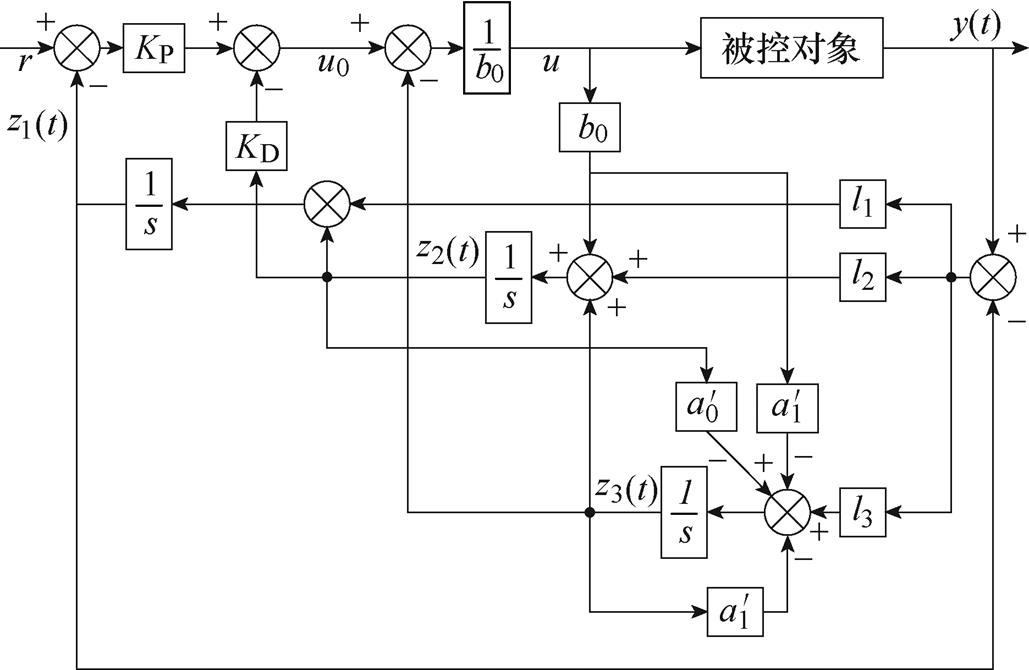
图4 结合模型信息的2nd-LADRC结构
Fig.4 2nd-LADRC structure combining model information
根据式(11)可知,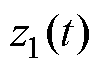 、
、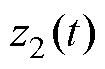 、
、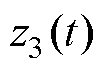 的传递函数分别为
的传递函数分别为
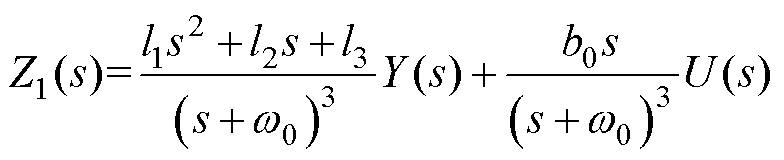 (16)
(16)
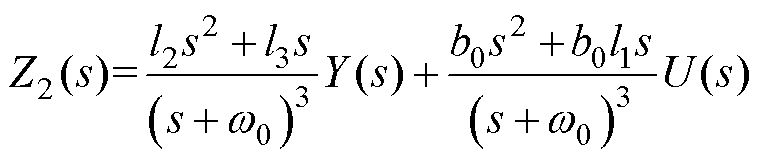 (17)
(17)
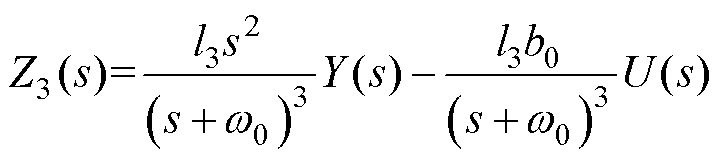 (18)
(18)
式中,为了使分析具有典型性,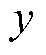 和
和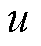 均取振幅为
均取振幅为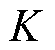 的阶跃信号,即
的阶跃信号,即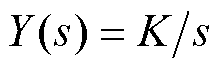 和
和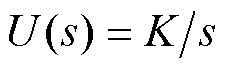 。
。
跟踪误差可表示为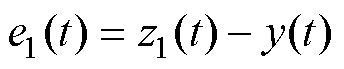 ,
,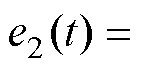
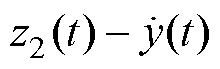 ,
,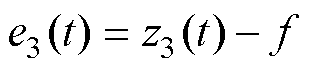 。根据式(9)可得
。根据式(9)可得
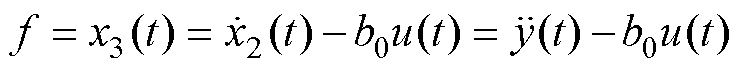 (19)
(19)
通过Laplace变换并结合式(16)~式(18)可得
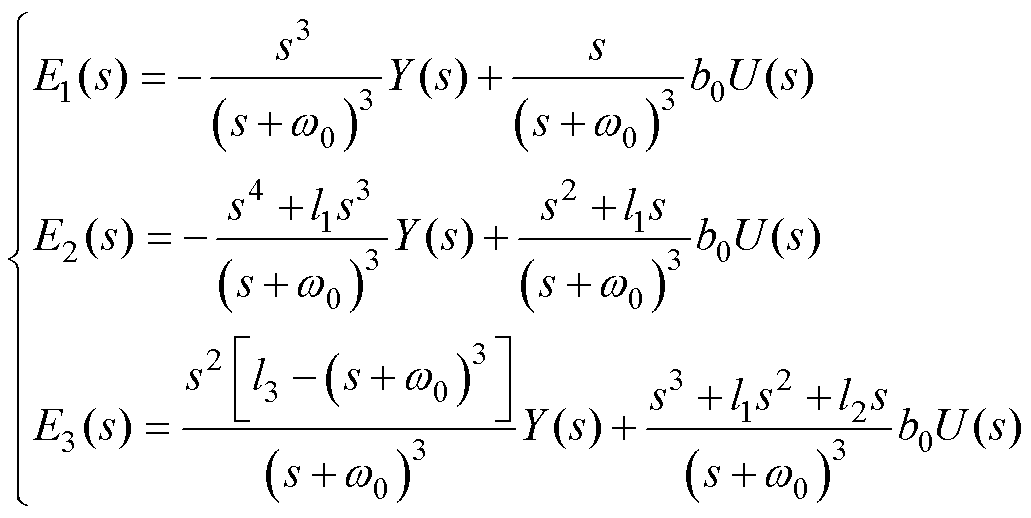 (20)
(20)
稳态误差可表示为
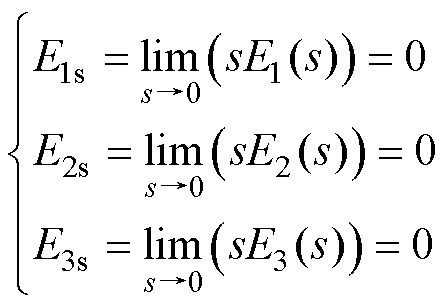 (21)
(21)
由式(21)可知,LESO具有较好的收敛性,可以实现对系统状态变量和广义扰动的无偏估计。
由式(11)~式(13)可得
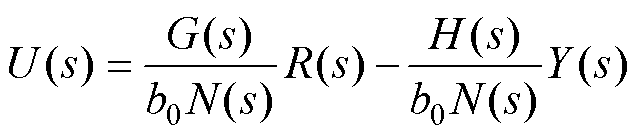 (22)
(22)
其中
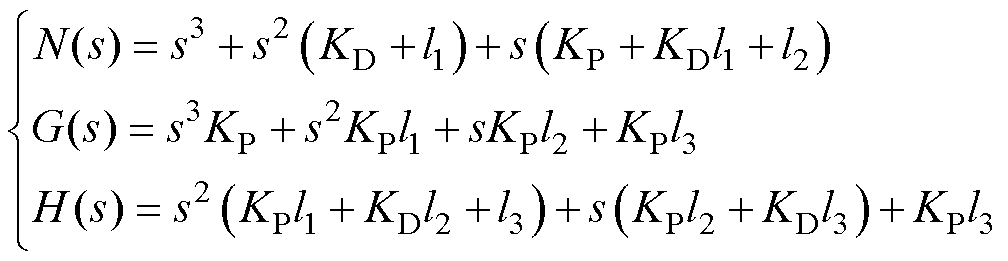
根据式(19),将可视被控对象表示为
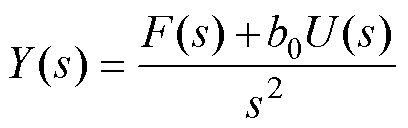 (23)
(23)
结合式(22)、式(23),可将图4所示的结合模型信息2nd-LADRC结构简化如图5所示。根据图5,可得其闭环传递函数为
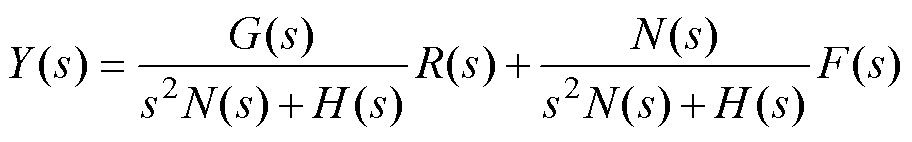 (24)
(24)
式中,跟踪项只与线性误差反馈控制率系数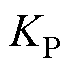 和
和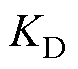 有关。图6为LADRC的扰动传递函数频率特性曲线,可以看出,随着w0增加,LADRC的扰动抑制能力有所增强。
有关。图6为LADRC的扰动传递函数频率特性曲线,可以看出,随着w0增加,LADRC的扰动抑制能力有所增强。
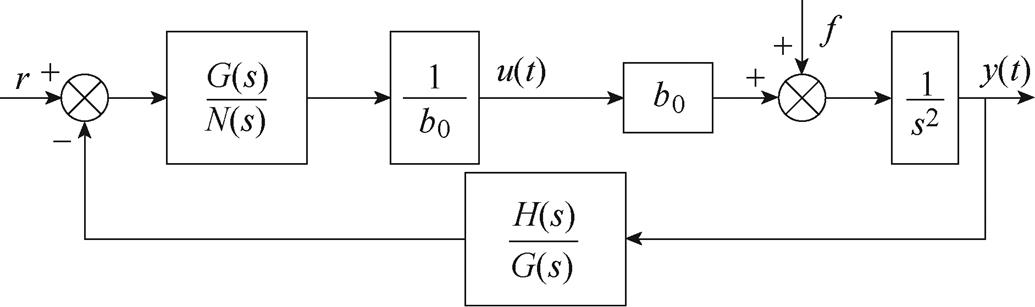
图5 2nd-LADRC简化结构
Fig.5 Simplify the structure of 2nd-LADRC
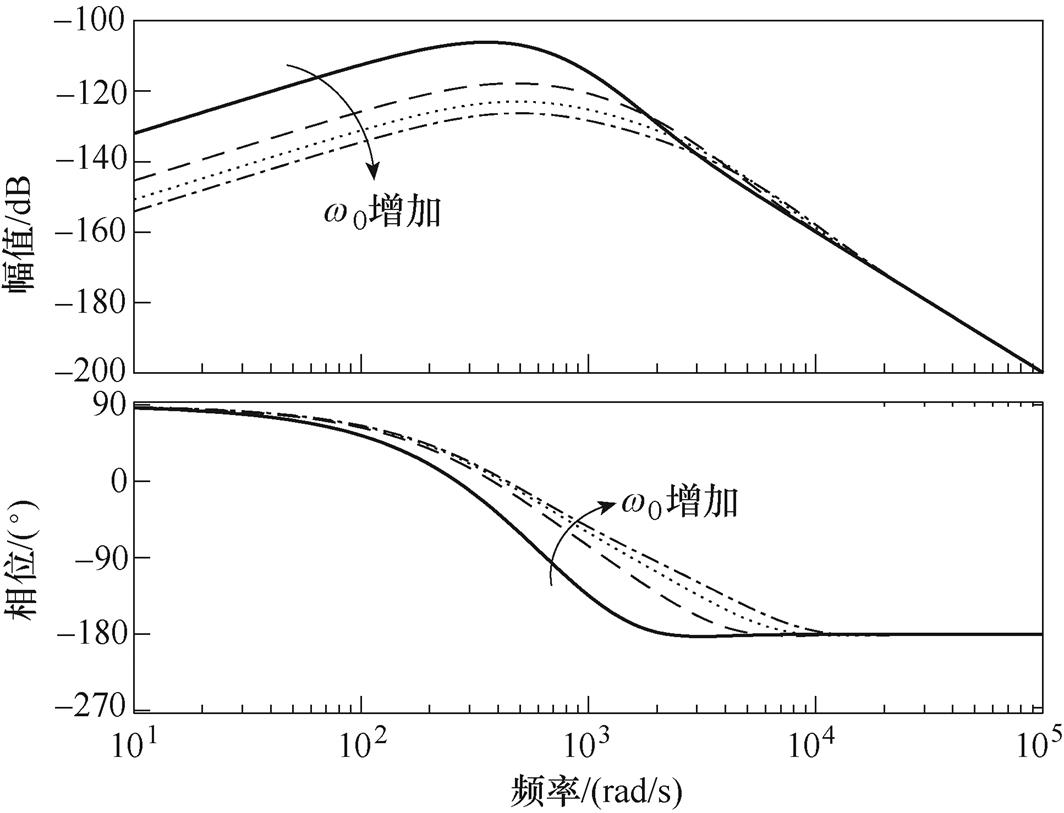
图6 2nd-LADRC抗扰性能分析
Fig.6 Immunity analysis of 2nd-LADRC
针对本文所提的模型,证明其稳定性。根据式(11)的分析,可知
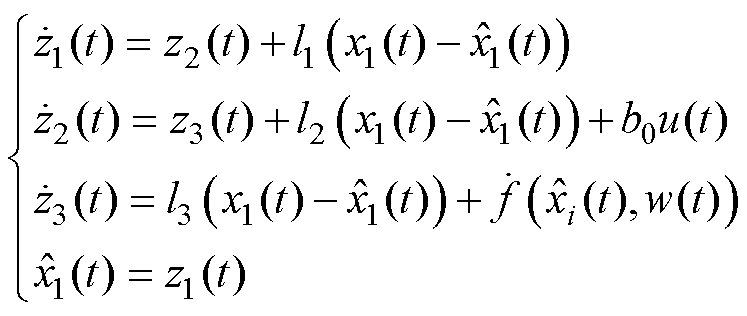 (25)
(25)
其中
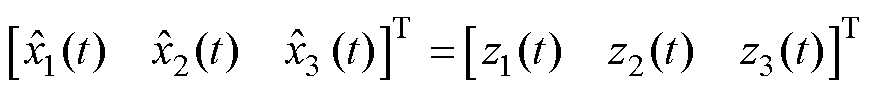
选取增益为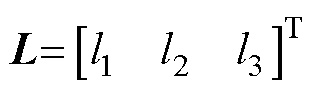 ,设
,设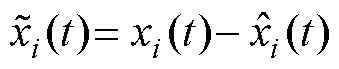 ,
,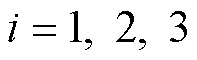 ,由式(25)得LESO的估计误差计算式为
,由式(25)得LESO的估计误差计算式为
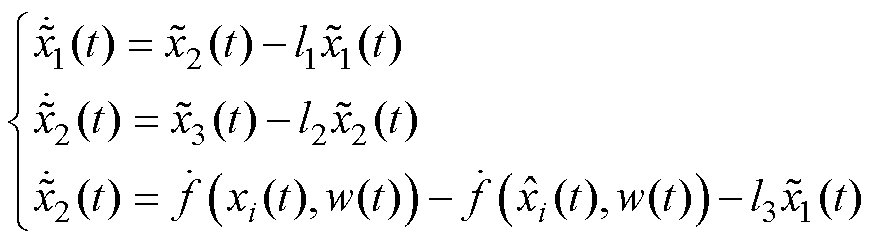 (26)
(26)
设 ,
,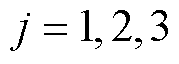 ,式(26)可变成
,式(26)可变成
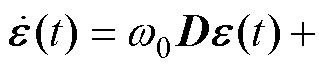
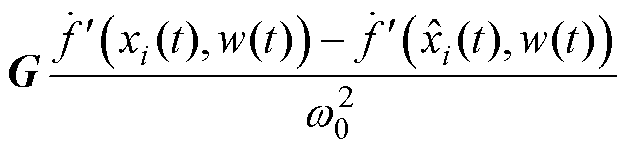 (27)
(27)
其中
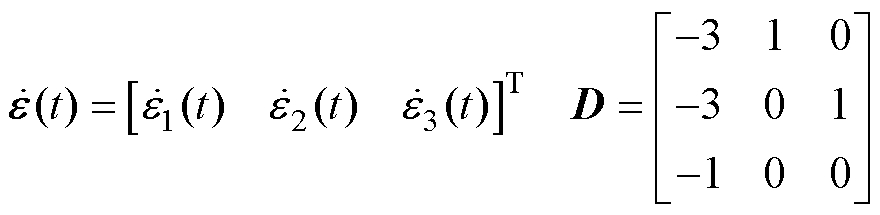

由式(14)可知,LESO的双重极点配置在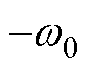 处,则
处,则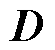 是Hurwitz稳定的。存在一个正定的Hermitian矩阵P,使满足
是Hurwitz稳定的。存在一个正定的Hermitian矩阵P,使满足
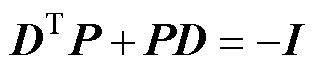 (28)
(28)
其中
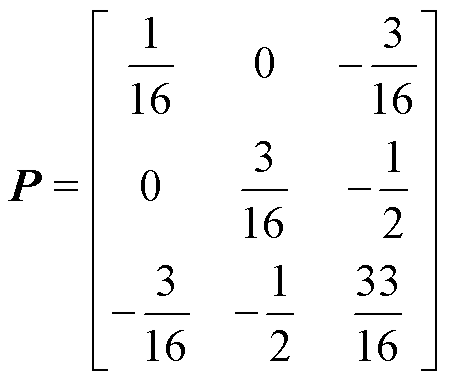
定义Lyapunov函数 ,则结合式(27)、式(28)有
,则结合式(27)、式(28)有
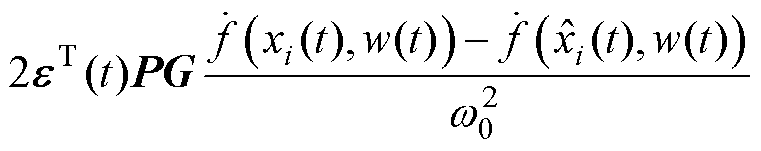 (29)
(29)
由于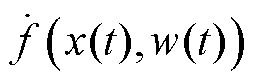 在定义域内满足Lipschitz连续条件,那么存在一个常数c,使得对于所有的
在定义域内满足Lipschitz连续条件,那么存在一个常数c,使得对于所有的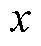 、
、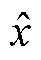 和
和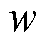 都有
都有
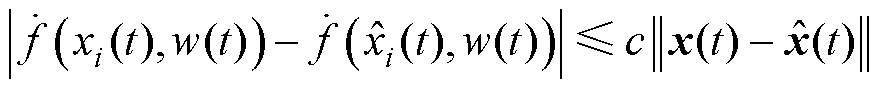 (30)
(30)
成立。则
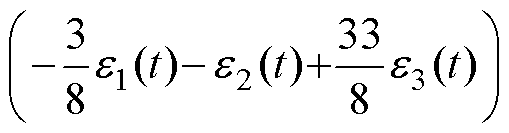
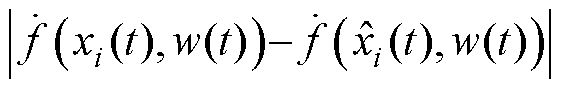
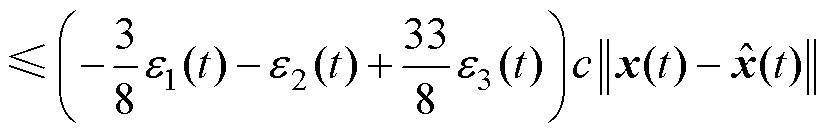 (31)
(31)
根据(27)、式(28),可得
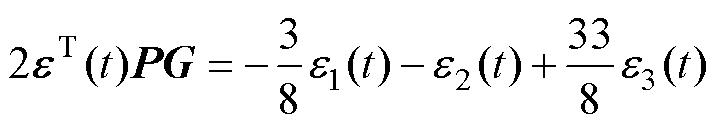 (32)
(32)
从而 可满足
可满足
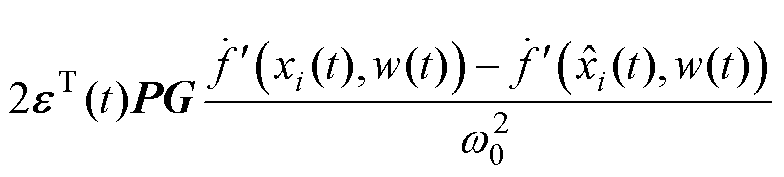
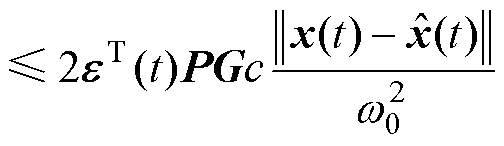 (33)
(33)
当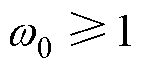 ,有
,有
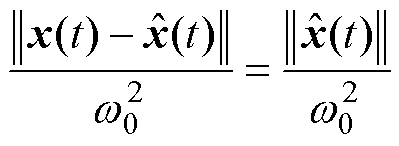
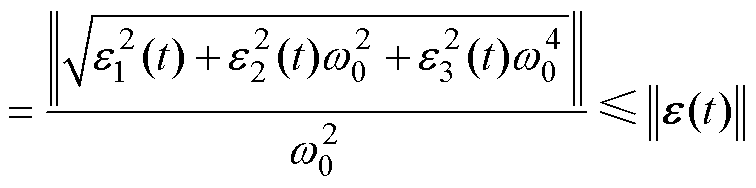 (34)
(34)
同时又由于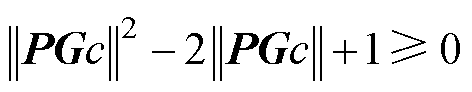 ,故
,故
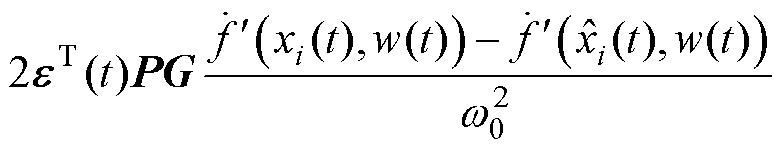
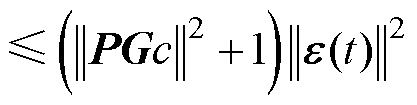 (35)
(35)
由式(29)、式(35)可得
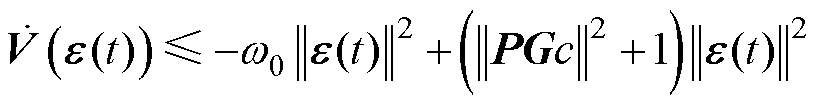 (36)
(36)
当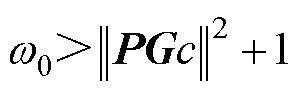 时,
时,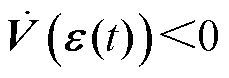 根据Lyapunov渐近稳定的意义,有
根据Lyapunov渐近稳定的意义,有
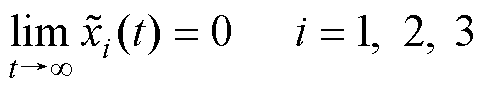 (37)
(37)
成立。根据上述推导并结合式(37)可知,Lyapunov渐近稳定性定理成立。故当时间趋于无穷时,线性扩张状态观测器的估计误差为零,即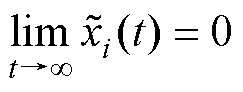 ,
,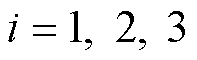 。因此LESO是收敛的。在控制目标中,
。因此LESO是收敛的。在控制目标中,
假定控制的目标是被控对象的输出跟踪有界输入信号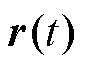 ,为了方便表述,令
,为了方便表述,令
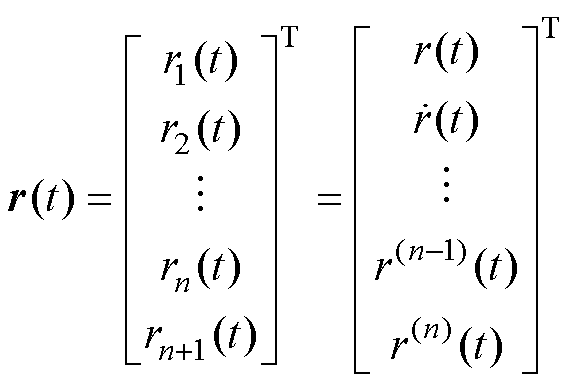 (38)
(38)
在自抗扰控制过程中,由式(13)可知,经典自抗扰控制反馈控制率为
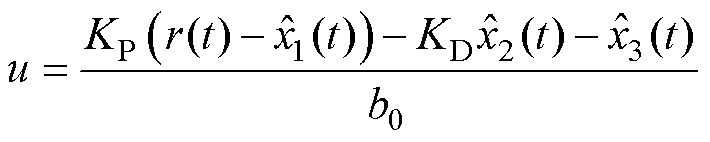 (39)
(39)
设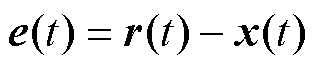 ,由式(39)得
,由式(39)得

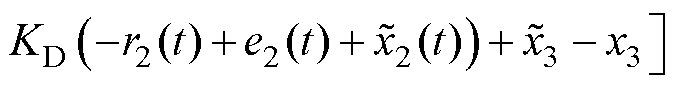 (40)
(40)
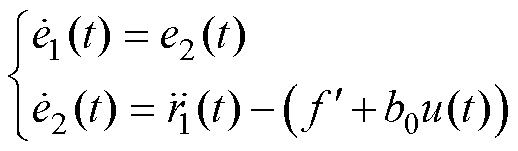 (41)
(41)
为避免线性跟踪微分器的噪声放大效应,一般在LADRC中不应用微分信号。此外在LESO设计精确的情况下,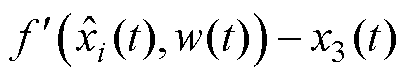 可忽略不计。故式(41)又可以写为
可忽略不计。故式(41)又可以写为
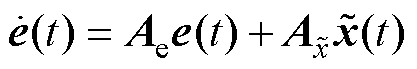 (42)
(42)
其中
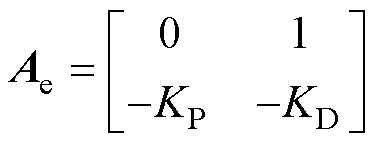
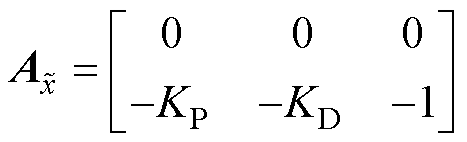

由于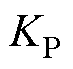 、
、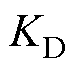 使特征多项式
使特征多项式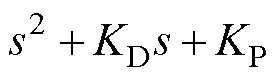 满足Routh判据,故
满足Routh判据,故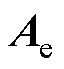 是Hurwitz稳定的。为了参数整定方便,取
是Hurwitz稳定的。为了参数整定方便,取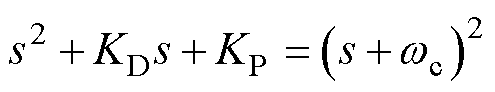 ,算得
,算得 ,
,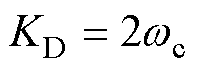 。由式(37)可知,
。由式(37)可知,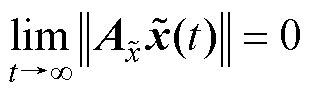 ,所以
,所以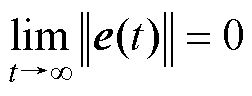 。根据Lyapunov理论可知,LADRC是渐近稳定的,等价于工程意义上的稳定。
。根据Lyapunov理论可知,LADRC是渐近稳定的,等价于工程意义上的稳定。
为了验证本文所提控制策略的可行性以及理论分析的准确性,搭建了一台40kW样机进行了实验验证。实验样机中开关管采用Infineon公司的SiC,IMZ120R045M1。直流母线电压控制器样机,如图7a所示。本文所述的微电网系统由上位机、电网、风电、光伏、电池、超级电容器、电子负载及其接口变换器组成,其中风力发电、光伏发电、蓄电池、超级电容器等被可编程电源取代。本文研究重点的是直流母线与负载之间的6路交错并联Buck变换器系统参数,见表1。为了简化实验程序,在测试过程中采用可编程电源模拟母线电压的各种特性,如图7所示。
分别对母线处电压突增、突降以及负载侧加、减载4个工况进行测试。为了验证所提2nd-LADRC策略的性能,将PI策略和2nd-LADRC策略分别用作电压外环控制器在不同的工况下进行对比分析,如图8~图11所示。通过最大超调量s%和恢复时间tv来展示实际运行中的抗扰性。从图8可以观察到,当6路交错并联Buck变换器运行在10kW的功率下,同时在输入侧出现一个电压正向突变时,超调降至94%,恢复时间缩短1/3。显然,与经典PI策略相比,2nd-LADRC限制了输出电压的波动范围并缩减了输出电压波动的恢复时间。图9中,显示了在输入侧电压骤降和10kW负载运行条件下的输出电压比较波形。当2nd-LADRC应用其中时,可以看出,在电压骤降期间输出电压的波动幅度与PI相同,而速度响应得到了显著的优化,即输出电压恢复时间的有效缩短。这得益于扩张状态观测器对扰动信号的观测、估计和补偿。可以看出,无论输入侧电压骤升还是骤降,本文提出的2nd-LADRC策略都可以成功增强抗扰性,这与理论分析的结论一致。图10a、图10b分别为输入电压550V、电压环给定450V且负载增加10kW时,采用PI控制器、2nd-LADRC策略的动态响应。可以看出,采用PI策略时,输出电压的波动幅度约为33.5V,恢复时间为260ms,在相同的运行条件下,6路交错并联Buck变换器的电压响应波动和恢复时间明显大于采用2nd-LADRC时的响应。此外,图11a、图11b分别给出了PI和2nd-LADRC在减载工况下的测试结果。从输出电压波形中可以看出,与PI相比,2nd-LADRC策略的恢复时间和电压波动都得到了有效的缩短。
表1 系统参数
Tab.1 System parameters

参 数数 值 输入电容Cin/mF40 输出电容Cout/mF90 变换器电感L1~L6/mH100 功率Pr/kW40 开关频率fc/kHz100 母线电压/V550 电压环参考电压值/V450

图7 测试平台
Fig.7 Experimental prototype
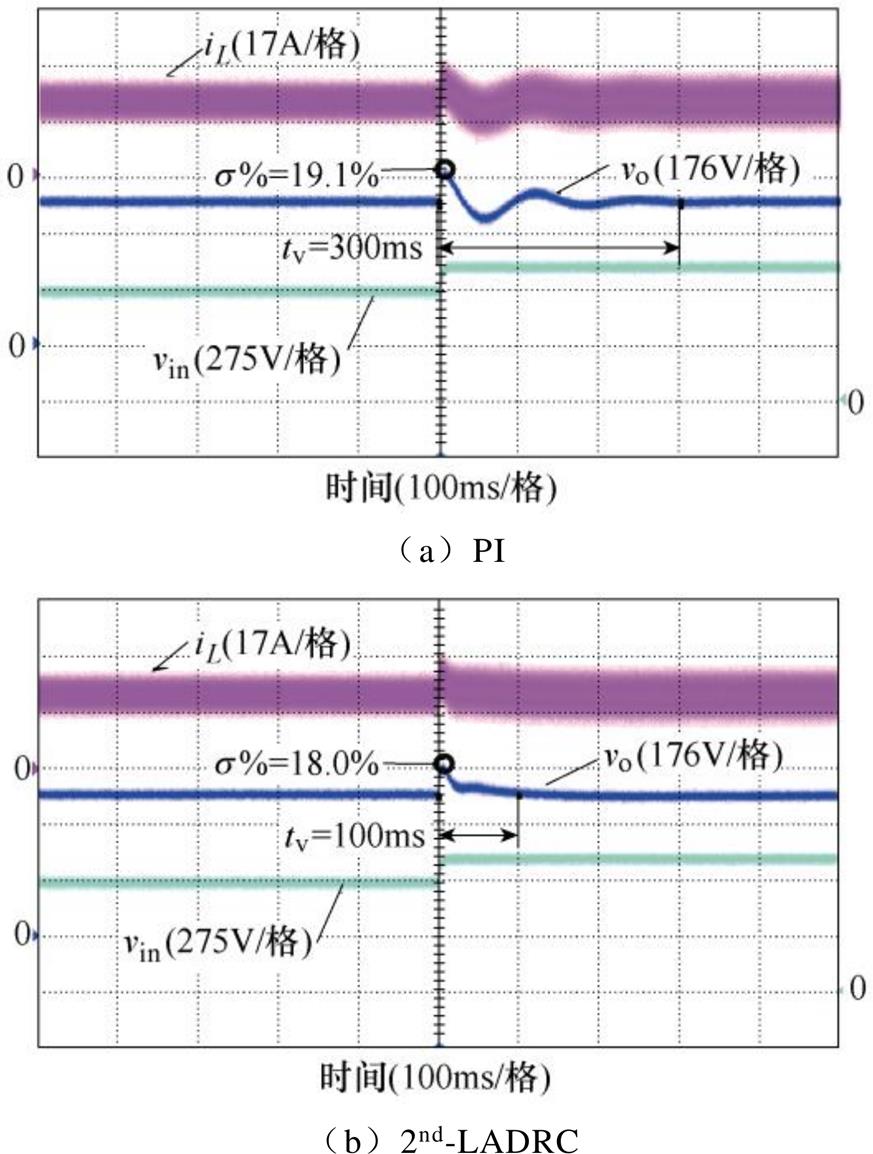
图8 母线电压突增下的动态响应
Fig.8 Dynamic response of bus voltage surge
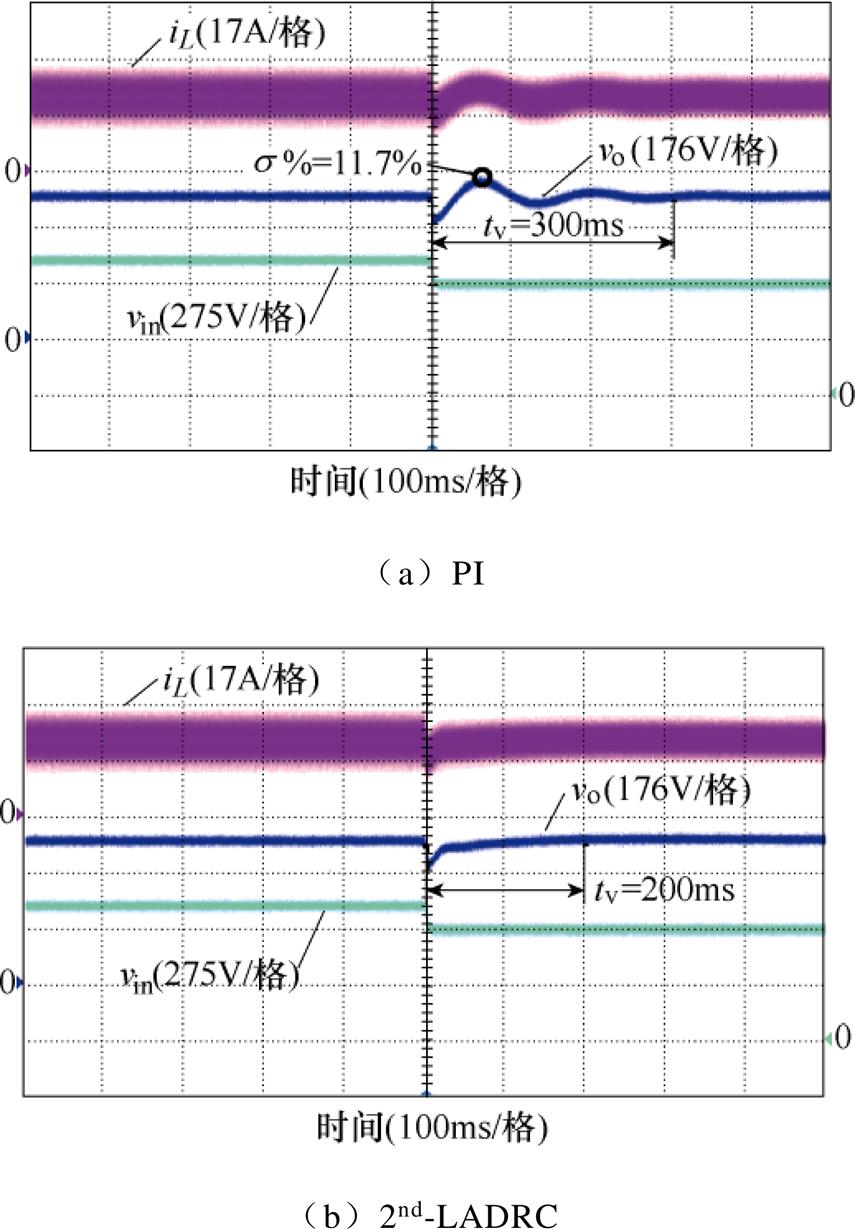
图9 母线电压突降下的动态响应
Fig.9 Dynamic response of bus voltage drop
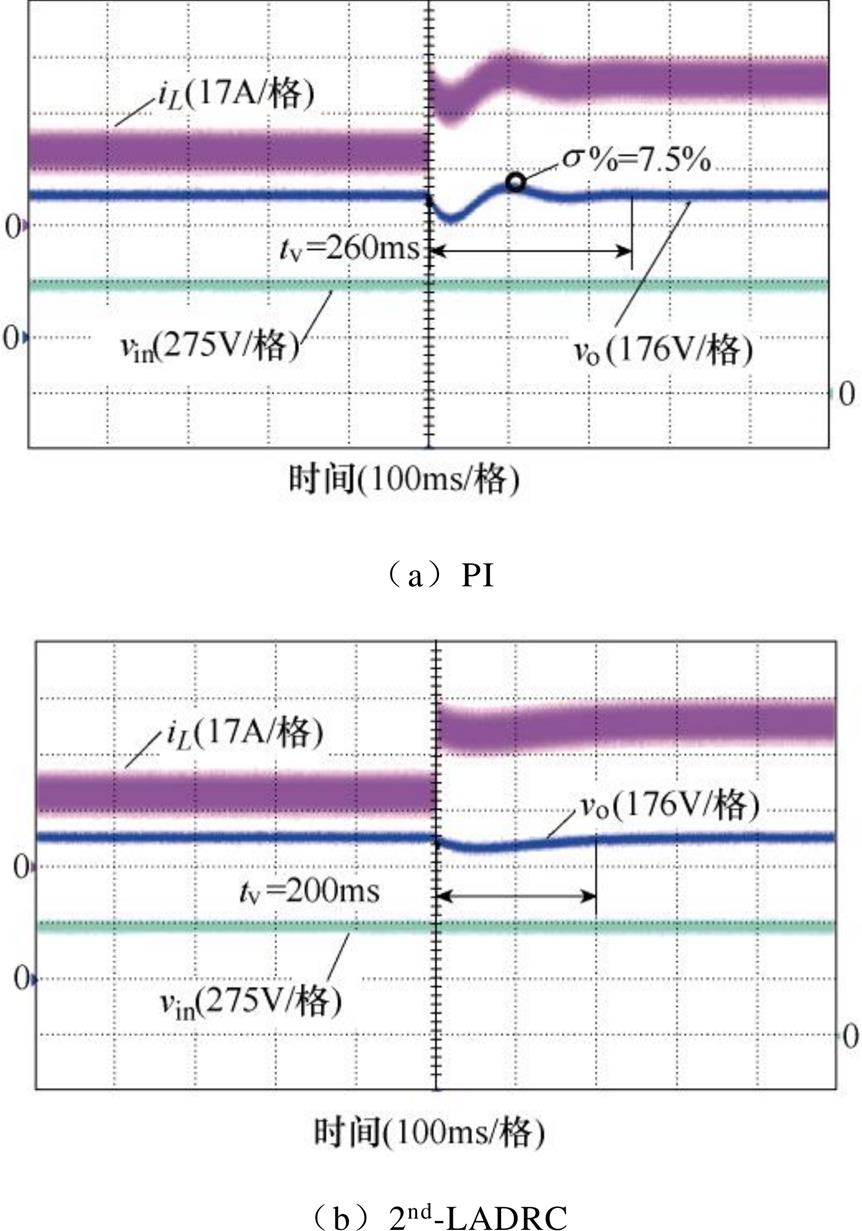
图10 负载增加时的动态响应
Fig.10 Dynamic response as load increases
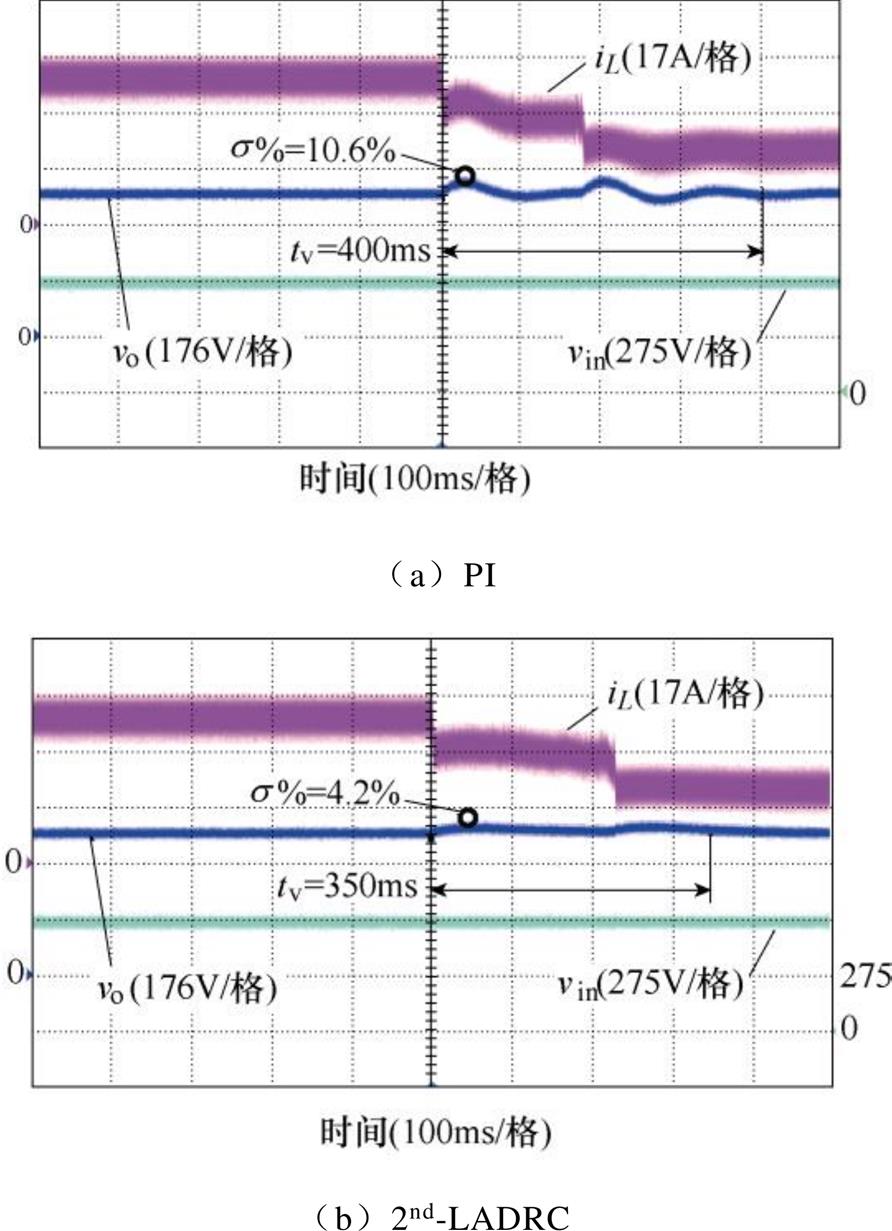
图11 负载减少时的动态响应
Fig.11 Dynamic response to load reduction
根据实验结果的对比可知,在负载变化的工况下采用2nd-LADRC策略和PI策略与输入侧电压变化时采用2nd-LADRC策略和PI策略有着相似的对应关系。输出电压的超调较PI有所降低,电感电流的波动也有所减弱;此外,2nd-LADRC的调节速度明显快于PI。这都使输出侧的电能质量有所提高,进而有效地减弱了扰动对负载的冲击。
本文以混合储能微电网的输出侧接口变换器为研究对象,利用二阶线性自抗扰控制策略优化了输出电压的电能质量。首先,依据状态空间平均法对被控对象的数学模型进行分析与总结。然后,依据状态空间表达式从系统层面对2nd-LADRC控制器进行LESO设计。并在复频域,分析了2nd-LADRC控制器的收敛性与抗扰性,探讨了观测器带宽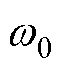 与抗扰性的关联。此外,运用Lyapunov稳定性原理,分析了本文所设计的2nd-LADRC控制器的稳定性。最后,基于40kW接口变换器样机,分别对不同工况下经典PI和2nd-LADRC两种策略进行实验测试。结果表明,2nd-LADRC的性能明显优于PI,验证了所提控制策略的正确性、有效性和可行性。需要指出的是,由于引入了2nd-LADRC控制策略,系统参数设计复杂度会有所提高。对于参数整定及其边界确定,后续会深入研究。希望本文能对混合储能微电网接口变换器的控制优化和鲁棒性提高提供新的思路。
与抗扰性的关联。此外,运用Lyapunov稳定性原理,分析了本文所设计的2nd-LADRC控制器的稳定性。最后,基于40kW接口变换器样机,分别对不同工况下经典PI和2nd-LADRC两种策略进行实验测试。结果表明,2nd-LADRC的性能明显优于PI,验证了所提控制策略的正确性、有效性和可行性。需要指出的是,由于引入了2nd-LADRC控制策略,系统参数设计复杂度会有所提高。对于参数整定及其边界确定,后续会深入研究。希望本文能对混合储能微电网接口变换器的控制优化和鲁棒性提高提供新的思路。
参考文献
[1] 孟准, 王议锋, 杨良. 一种适用于小功率可再生能源的单相高频双Buck全桥并网逆变器[J]. 电工技术学报, 2017, 32(8): 220-228.
Meng Zhun, Wang Yifeng, Yang Liang. A single- phase high frequency dual-Buck full-bridge inverter for small-scale renewable source application[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(8): 220-228.
[2] Huenteler J, Niebuhr C, Schmidt T S. The effect of local and global learning on the cost of renewable energy in developing countries[J]. Journal of Cleaner Production, 2016, 128: 6-21.
[3] 李春杰, 黄文新, 李朋, 等. 一种基于磁组合式变压器的AC-DC高频变换器[J]. 电工技术学报, 2016, 31(8): 19-26.
Li Chunjie, Huang Wenxin, Li Peng, et al. An AC-DC high frequency converter based on magnetic- combination transformer[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 19-26.
[4] Ahmed H F, Cha H, Khan A A, et al. A family of high-frequency isolated single-phase Z-source AC- AC converters with safe-commutation strategy[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7522-7533.
[5] Singaravel M M R, Daniel S A. MPPT with single DC-DC converter and inverter for grid connected hybrid wind-driven PMSG-PV system[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(8): 4849- 4857.
[6] Fei Chao, Yang Yuchen, Li Qiang, et al. Shielding technique for planar matrix transformers to suppress common-mode EMI noise and improve efficiency[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1263-1272.
[7] 李微, 周雪松, 马幼捷, 等. 三端口直流微网母线电压控制器及多目标控制[J]. 电工技术学报, 2019, 34(1): 92-102.
Li Wei, Zhou Xuesong, Ma Youjie, et al. Three-port DC microgrid bus voltage controller and multi- objective control[J]. Transactions of China Elec- trotechnical Society, 2019, 34(1): 92-102.
[8] 佟子昂, 武建文, 马速良, 等. 一种基于主动电压扰动的直流微网负载均流控制策略[J]. 电工技术学报, 2019, 34(24): 5199-5208.
Tong Ziang, Wu Jianwen, Ma Suliang, et al. A load current-sharing control strategy for DC microgrid converters based on active voltage disturbance[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5199-5208.
[9] Chang Xiaoyong, Li Yongli, Zhang Weiya, et al. Active disturbance rejection control for a flywheel energy storage system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 991-1001.
[10] 阳同光, 桂卫华. 基于粒子群优化自适应反推光伏并网逆变器控制研究[J]. 中国电机工程学报, 2016, 36(11): 3036-3044.
Yang Tongguang, Gui Weihua. Research on a particle swarm optimization adaptive backstepping control method of grid-connected inverters[J]. Proceedings of the CSEE, 2016, 36(11): 3036-3044.
[11] 周振雄, 石硕. 基于DRNN自整定准PR控制的光伏并网系统研究[J]. 太阳能学报, 2017, 38(11): 2932-2940.
Zhou Zhenxiong, Shi Shuo. Research on quasi-PR control based on DRNN of selftuning for photovoltaic grid-connected system[J]. Acta Energiae Solaris Sinica, 2017, 38(11): 2932-2940.
[12] 韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
[13] Wu Dan, Chen Ken. Frequency-domain analysis of nonlinear active disturbance rejection control via the describing function method[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3906-3914.
[14] Chen Wenhua, Yang Jun, Guo Lei. Disturbance- observer-based control and related methods-an over- view[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1083-1095.
[15] 马幼捷, 赵健, 周雪松, 等. 并联混合型有源电力滤波器的线性自抗扰控制及稳定性分析[J]. 电网技术, 2012, 36(11): 211-216.
Ma Youjie, Zhao Jian, Zhou Xuesong, et al. A linear auto disturbance rejection controller for shunt hybrid active power filters and its stability analysis[J]. Power System Technology, 2012, 36(11): 211-216.
[16] 徐海珍, 张兴, 刘芳, 等. 基于微分补偿环节虚拟惯性的虚拟同步发电机控制策略[J]. 电力系统自动化, 2017, 41(3): 96-102.
Xu Haizhen, Zhang Xing, Liu Fang, et al. Control strategy of virtual synchronous generator based on differential compensation virtual inertia[J]. Auto- mation of Electric Power Systems, 2017, 41(3): 96- 102.
[17] Xu Rong, Yu Yong, Yang Rongfeng, et al. A novel control method for transformerless H-bridge cascaded STATCOM with star configuration[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(3): 1189-1202.
[18] Gao Zhiqiang. Scaling and bandwidth-parameterization based controller tuning[C]//American Control Con- ference, Denver, USA, 2003: 4989-4996.
[19] Wang Baochao, Xu Yongxiang, Shen Zhaoyuan, et al. Current control of grid-connected inverter with LCL filter based on extended-state observer estimations using single sensor and achieving improved robust observation dynamics[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(7): 5428-5439.
[20] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[21] Yang Haitao, Zhang Yongchang, Liang Jiejunyi, et al. Robust deadbeat predictive power control with a discrete-time disturbance observer for PWM rectifiers under unbalanced grid conditions[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(1): 287-300.
[22] Song Zhanfeng, Zhou Fengjiao, Zhang Zhen. Parallel- observer-based predictive current control of per- manent magnet synchronous machines with reduced switching frequency[J]. IEEE Transactions on Indu- strial Informatics, 2019, 15(1): 6457-6467.
[23] 王瑶. 基于状态空间平均模型的电压控制SIDO Buck变换器稳定性分析[J]. 中国电机工程学报, 2018, 38(6): 1810-1817, 1918.
Wang Yao. Stability analysis for voltage controlled single-inductor dual-output Buck converter based on state space average model[J]. Proceedings of the CSEE, 2018, 38(6): 1810-1817, 1918.
Voltage Stabilization Strategy for Load-Side Interface Converter of Microgrid Combined with Active Disturbance Rejection Control
Abstract Hybrid energy storage microgrid has the characteristics of non-linearity, strong coupling, strong load disturbance, and flexible switching of parallel/off-grid modes. Aiming at the problem that traditional control is difficult to achieve ideal results, this paper introduces the second-order linear active disturbance rejection control technology (2nd-LADRC) into the control of the interface converter at the load end of the microgrid. First, this paper analyzes the controlled object and extracts model information according to the state-space average method, and designs the 2nd-LADRC controller from the system level according to the state equation and transfer function. Then through frequency domain analysis, the convergence and anti-interference of 2nd-LADRC are verified, the relationship between the bandwidth of the observer and the anti-interference performance is discussed, and the system stability when the 2nd-LADRC controller is applied is analyzed using Lyapunov theory. It is concluded that the system is stable from the perspective of engineering application. Finally, a 40kW experimental prototype is designed to simulate the experimental scenarios of different control strategies when the microgrid and load power fluctuate. The experimental results verify the feasibility and effectiveness of the 2nd-LADRC control method.
keywords:Hybrid energy storage micro grid, state space average method, second order linear active disturbance rejection controller, frequency domain analysis, Lyapunov theory
DOI: 10.19595/j.cnki.1000-6753.tces.210371
中图分类号:TM46
陶 珑 男,1994年生,博士研究生,研究方向为混合储能微电网的能量转换与先进控制策略。E-mail: taolongtl@126.com
王议锋 男,1981年生,副教授,博士生导师,研究方向为新能源发电与电能变换。E-mail: wayif@tju.edu.com(通信作者)
收稿日期 2021-03-19
改稿日期 2021-07-04
国家自然科学基金资助项目(51977146)。
(编辑 陈 诚)