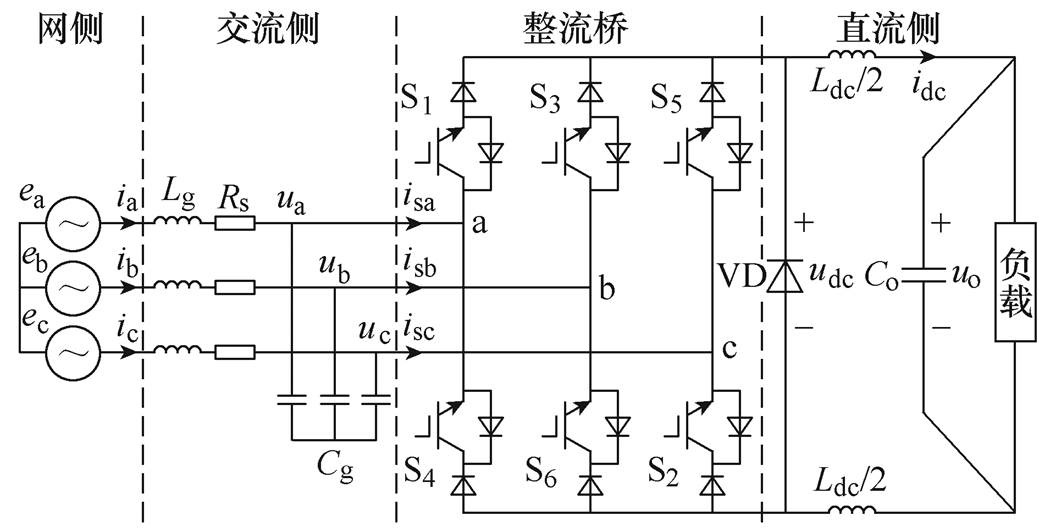
图1 PWM电流源型整流器主电路拓扑
Fig.1 The main circuit of PWM current-source rectifier
摘要 三相电流源型PWM整流器作为低压直流配电系统有源前端时，因网侧LC滤波环节和直流侧电容的存在使系统控制难度增加。首先，在同步旋转坐标系下建立电压定向数学模型，通过控制网侧电流d轴与q轴分量，完成系统有功、无功功率的独立控制；其次，基于相量法提出一种电容电流补偿方法，仅构建电容电压前馈通道，实现间接电流控制策略下功率因数校正；然后，采用电容电压反馈有源阻尼法对网侧LC谐振进行抑制，详细分析反馈增益对系统稳定性的影响；此外，该文通过在内环引入直流侧电感电流反馈以及阻尼因子，进一步改善系统性能；之后，利用频域法与根轨迹法对整个控制环路进行分析，辅助Matlab/SISO设计工具，在离散域中直接优化设计控制器零点位置与环路增益；最后，通过仿真和实验结果验证了所提出方法的可行性和有效性。
关键词：电流源型整流器 多环路 有源阻尼 功率因数补偿 控制器设计
近年来，社会对直流负荷的需求显著增加，包括LED照明设备、具有变频功能的家用电器、电动汽车以及数据中心等。与此同时，可再生能源中诸如光伏电池、燃料电池、储能单元等均属于直流电源。若利用低压直流配电系统将两者合理接入，可有效减少功率变换环节，从而改善系统效率、可靠性并降低成本[1-3]。
目前在通信、楼宇供电等应用领域中，低压直流配电系统母线电压标准尚未完善，为兼容所用交流设备，考虑用电设备中元器件选型和生产设计的合理性，直流母线电压控制在380～400V附近[4-5]。由于对功率处理能力以及输入电流正弦化的要求，多采用PWM电压源型整流器（Voltage Source Rectifier, VSR）获得直流电压。然而针对未来以数据中心为代表，对配电系统有更高可靠性、更高效率要求的背景下，该拓扑存在两个不利因素：①直流母线电容器影响系统寿命与可靠性[6]；②两级拓扑结构导致系统效率降低[7]。
与VSR不同，PWM电流源型整流器（Current Source Rectifier, CSR）具有降压输出、抑制输出短路电流、输入滤波器尺寸小、直接启动等优点[8-9]，使其在低压直流配电系统具有较大的应用前景。
目前针对CSR控制策略方面，国内外学者进行了一些研究工作[10-17]。文献[10-13]在同步旋转坐标系下将网侧电流分解为d轴和q轴分量，分别采用比例积分（Proportional Integral, PI）控制器进行控制，具有良好的性能。文献[14]提出基于幅相控制的间接电流控制策略，相比于直接电流控制，其网侧电流动态响应较慢，但控制环路简单且易于整定。文献[15]基于非线性微分几何理论的输入/输出精确线性化方法，实现三相CSR动态模型大范围的线性化以及状态变量的解耦控制。该方法可获得较理想的效果，但在轻载条件下准确度降低，系统容易不稳定。文献[16-17]将有限控制集模型预测控制运用于CSR整流器中，具有无需PI参数整定、网侧谐波小、动态响应快等优点，但运算量较大。以上文献中仅涉及对直流侧电流的跟踪控制，而当三相CSR应用于低压直流配电系统时，其需要实现对输出电压的控制。针对上述问题，文献[18-20]采用了直流输出电压外环、直流侧电流内环的双闭环控制策略，但目前尚未有文献对网侧电流谐波抑制、电容电流补偿以及控制器参数设计给出系统的解决方案。
本文针对低压直流配电系统下三相CSR网侧与直流侧的控制要求，首先，在dq坐标系下建立电压定向大信号数学模型，通过调节网侧电流矢量d轴分量和q轴分量，实现有功功率与无功功率的独立控制。其次，基于十二扇区空间矢量调制策略，采用解析法估算网侧电流谐波，并通过迭代优化滤波器参数；同时，基于相量法提出一种电容电流补偿方法，仅通过构建电容电压前馈通道，实现间接电流控制策略下功率因数校正。然后，采用电容电压反馈有源阻尼法对网侧LC谐振进行抑制，详细分析反馈增益对系统稳定性的影响。此外，该文通过在内环引入直流侧电感电流反馈以及阻尼因子，进一步改善系统动态性能。利用频域法与根轨迹法对整个控制环路进行分析，辅助Matlab/SISO设计工具，兼顾快速性与稳定性，在离散域中直接优化控制器零点位置与环路增益。最后，采用基于模型的设计方法将离散模型直接转化为控制代码，实现算法的快速验证。仿真和实验结果验证了本文所提出控制策略以及参数设计的正确性。
三相CSR作为低压直流配电系统有源前端整流器时，Co为直流侧接电容，PWM电流源型整流器主电路拓扑如图1所示。ex、ux、ix、isx分别为x相网侧电压、交流侧电压、网侧电流、交流侧电流，x=a, b, c；Lg、Cg分别为交流滤波电感和滤波电容，用于滤除高频开关分量；Rs为交流滤波电感及线路等效电阻；为保证开关Sk（k=1,…, 6）具有反向电压阻断能力，文中采用绝缘栅双极型晶体管（Insu- lated Gate Bipolar Transistor, IGBT）与二极管串联结构；整流器输出侧并联二极管VD，不仅可以简化控制逻辑，还能有效降低续流过程的导通损耗；电感Ldc均分为感值相同的两个电感，分别置于正、负直流母线端，将有效降低共模噪声电流。
图1 PWM电流源型整流器主电路拓扑
Fig.1 The main circuit of PWM current-source rectifier
当采用空间矢量调制策略时，由于二极管VD的续流作用，零矢量作用时间内电流无需流经对应桥臂，从而实现降低导通损耗以及简化控制逻辑的目的[7]。同时，为了降低整流器开关损耗，本文采用十二扇区电流空间矢量调制策略，如图2所示。在一个PWM开关周期Ts内，参考电流空间矢量Iref通过相邻两个有效电流矢量和零矢量合成得到，当Iref处于扇区1时，有效矢量与零矢量分别为I1、I6和I0，根据安秒平衡法则以及矢量合成原理得到
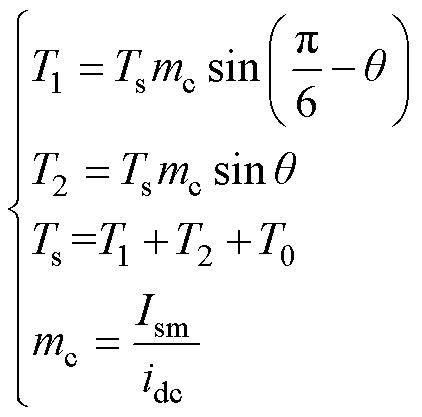（1）
式中，T1、T2和T0分别为矢量I6、I1和I0的作用时间；q 为电流矢量扇区角；Ism为交流侧基波电流幅值；idc为直流侧电感电流；mc为调制因数，mc∈[0, 1]。
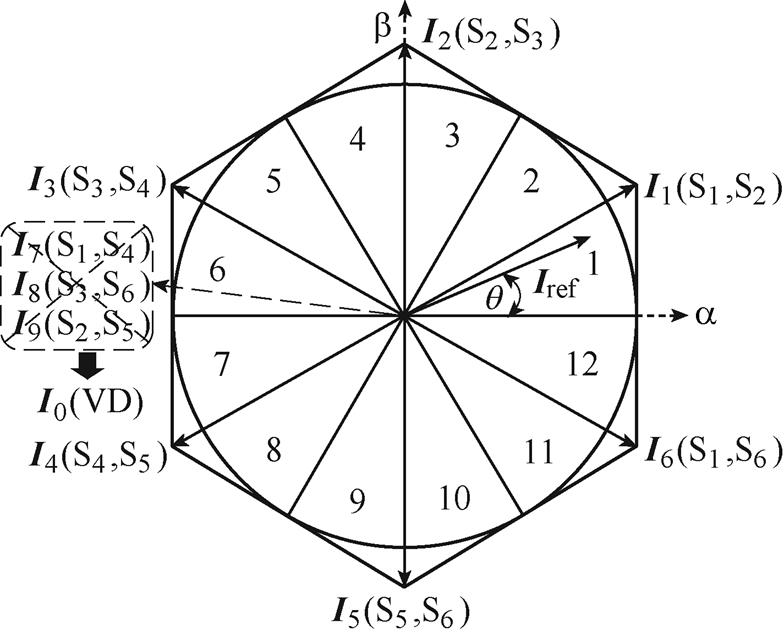
图2 十二扇区电流空间矢量
Fig.2 Current space vector diagram with twelve sectors
当矢量I1作用时，a相经S1与直流侧相连，有isa=idc；当矢量I6作用时，有isa=idc；当矢量I0作用时，有isa=0。假设三相网侧电压为理想电压源，且忽略直流侧电流纹波，有idc=Idc，得到一个开关周期内a相交流侧电流有效值为
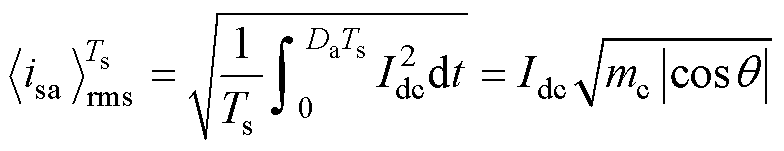（2）
将式（2）扩展到基波周期中，a相交流侧电流有效值为
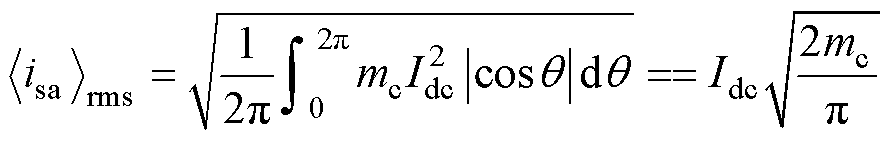（3）
通过减去式（3）中交流侧基波电流分量有效值，得到a相交流侧纹波电流有效值为
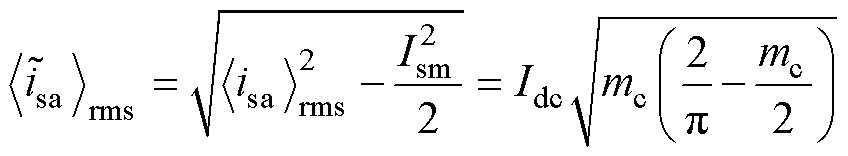（4）
由于高频谐波分量主要分布在载波频率以及其整数倍附近，且谐波幅值依次衰减，CSR交流侧等效电路如图3所示。故简化为CSR交流侧仅含有基波分量与高频开关分量，利用叠加定理将整流器交流侧分别等效如下。
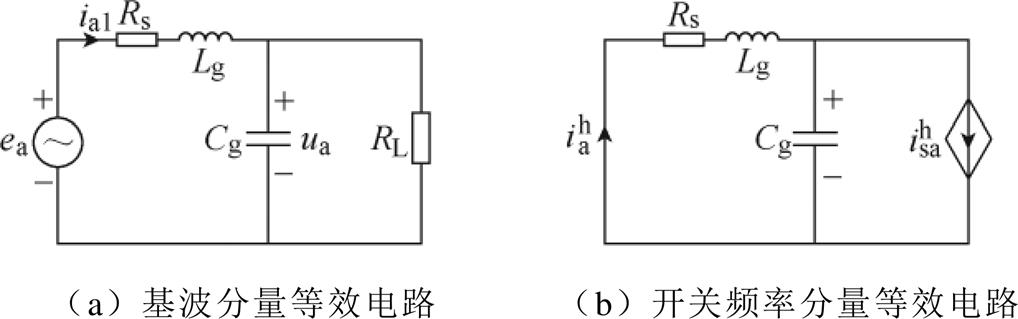
图3 CSR交流侧等效电路
Fig.3 AC-side equivalent circuit of the CSR
（1）针对基频分量，当采用合理的控制策略时网侧电流、电压实现同相位，其直流侧等效为电阻负载，如图3a所示，其中
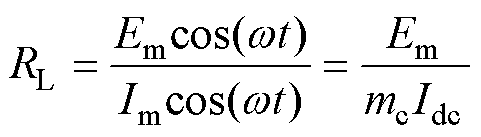（5）
式中，w 为基波角频率；Em为网侧基波电压幅值；Im为网侧基波电流幅值。
（2）针对高频开关分量，将直流输出侧等效为受控电流源，其频率为开关频率，如图3b所示。
为了满足入网电气设备电流谐波的要求，需要对LC滤波器进行合理设计。根据上述分析，得到网侧电流谐波分量有效值为
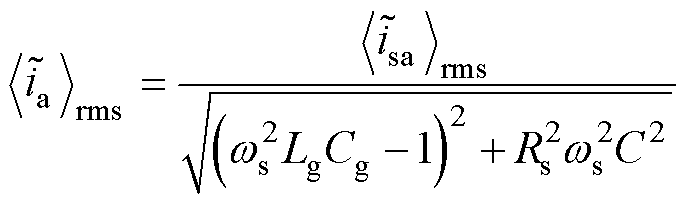（6）
式中，ws为开关角频率，ws=2p/Ts。
根据总谐波畸变率（Total Harmonic Distortion, THD）的定义，得到
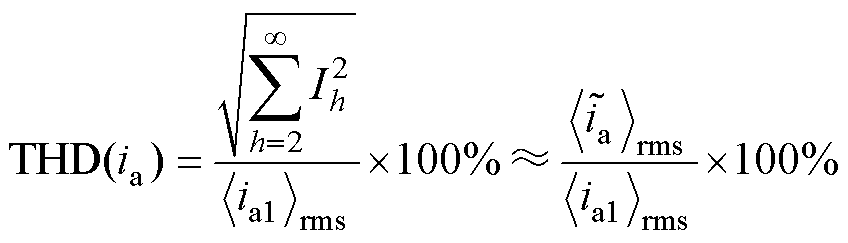（7）
式中，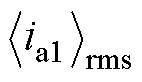
为a相网侧基波电流有效值。
由式（6）、式（7）可知，增大L、C可有效降低网侧电流谐波。然而电感值过大将引起系统体积、质量及成本的增加；而滤波电容过大将引起功率因数降低以及启动冲击电流增大。迭代优化LC滤波器参数，以保证网侧电流谐波畸变率小于5%，因此根据IEEE 1459-2010标准，整流器输入功率因数（Power Factor, PF）可表示为
（8）
式中，j 为网侧电压与网侧电流的相位。
假设三相电网电压平衡且仅含有基波分量，得到三相CSR在dq坐标系下系统大信号模型为
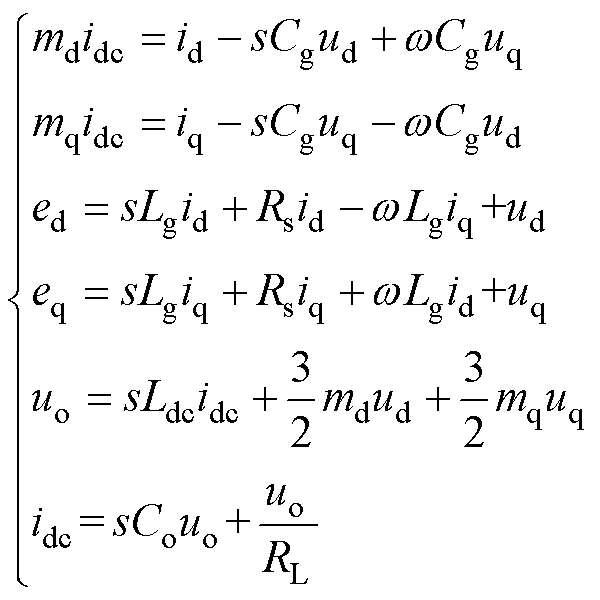（9）
式中，ud、uq、ed、eq、id、iq、md、mq分别为交流滤波电容电压、网侧电压、网侧电流和占空比的d轴、q轴分量；uo为直流侧输出电压。
根据瞬时功率理论，三相CSR系统有功功率与无功功率可分别表示[21]为
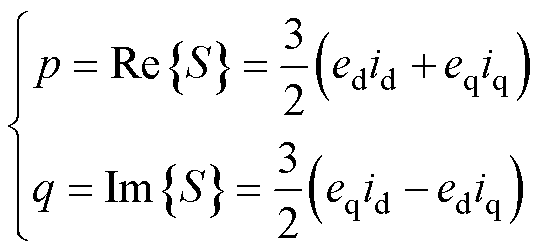（10）
式中，S为复功率；p为有功功率；q为无功功率。
通过将d轴定向于网侧电压矢量，有eq=0，则式（10）可简化为
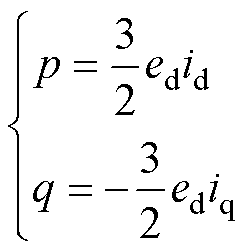（11）
由式（11）可知，当网侧电压稳定时，系统有功功率、无功功率独立控制即转化为对id、iq的 控制。
针对三相CSR系统的控制目标，实现直流侧输出电压恒定、输入功率因数校正及网侧电流正弦化，本文采用含无功功率前馈的双闭环控制策略，三相CSR系统控制框图如图4所示。首先，直流侧输
出电压uo与给定值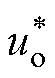
进行比较，其误差信号经外环控制器Gv(s)，得到直流侧电感电流给定值
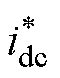；然后，与idc进行比较，经内环控制器Gi(s)得到网侧电流d轴分量控制量
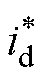，由此可实现对有功功率的控制。由于系统工作在单位功率因数，则令网侧电流q轴分量控制量
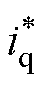=0。由于uo和idc均为直流量，因此Gv(s)和Gi(s)采用PI控制器可实现系统的无静差控制。
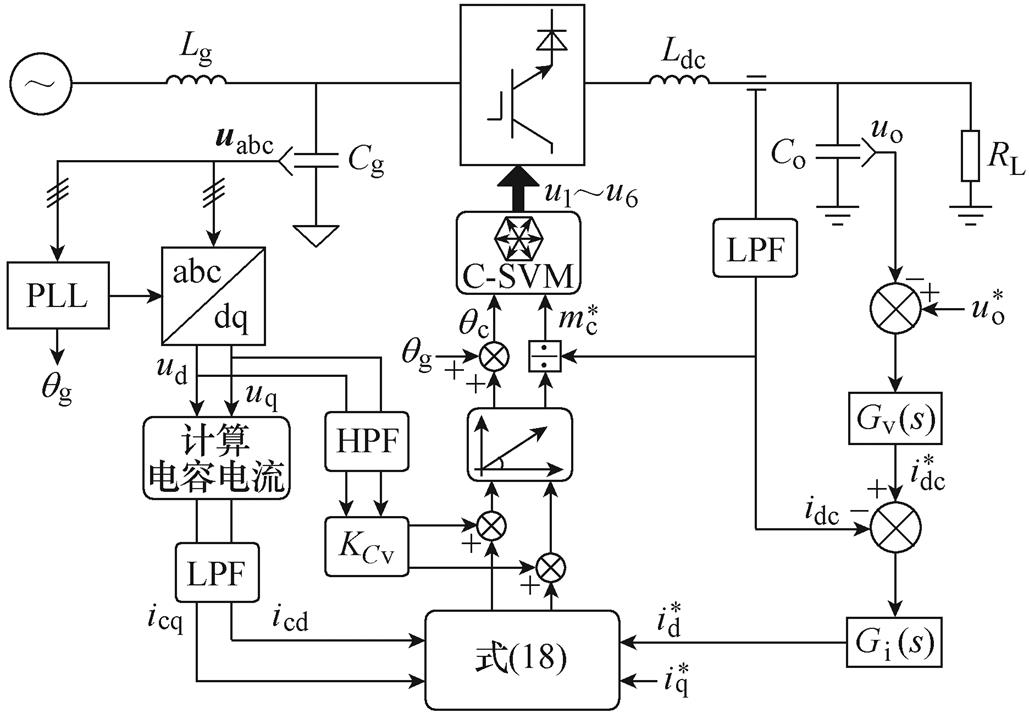
图4 三相CSR系统控制框图
Fig.4 Control block diagram of three-phase CSR
当三相CSR采用间接电流控制策略时，交流侧参考电流表示为
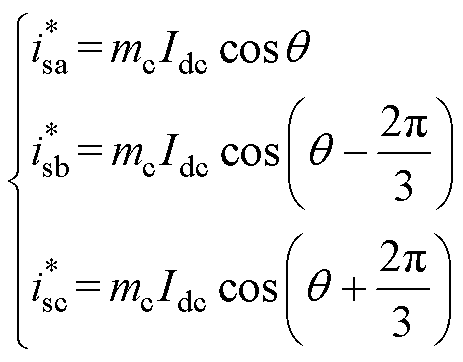（12）
为了方便分析，忽略滤波电感压降，作出CSR单相基波相量，如图5所示。由于滤波电容电流
（x=a, b, c）的影响，当系统采用间接电流控制策略时，会造成网侧基波电流分量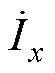
相位超前于网侧电压
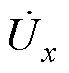，形成功率因数角j，如图5a所示，导致整流器无法实现单位功率因数运行。
忽略整流器及滤波电路中功率损耗，根据功率守恒理论有
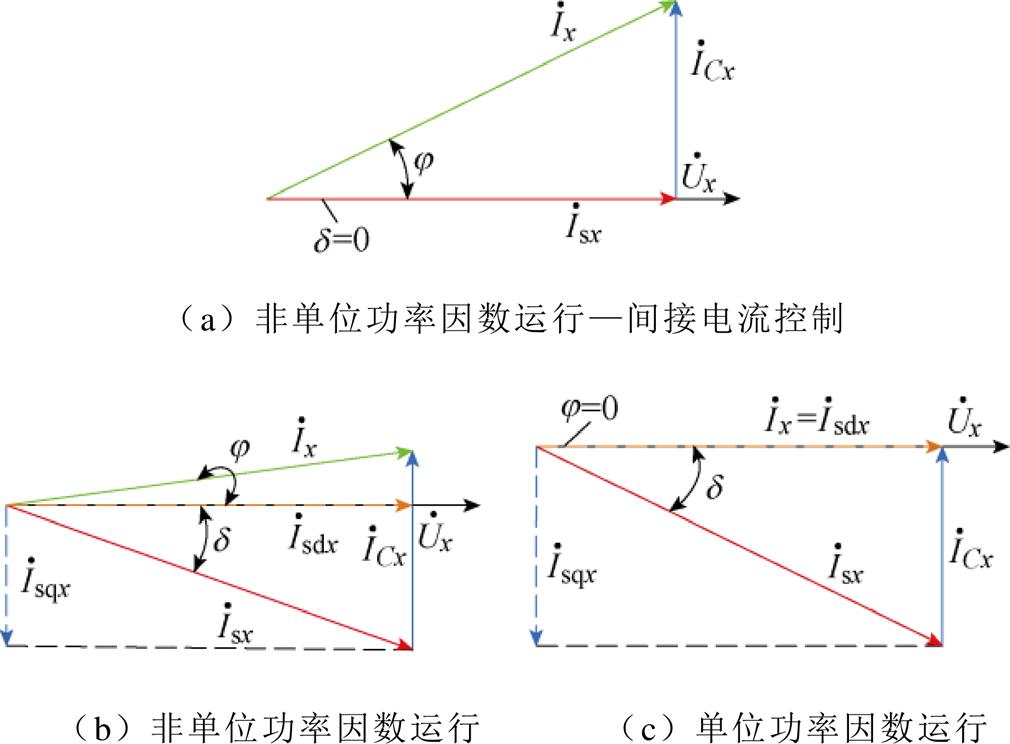
图5 CSR交流侧相量
Fig.5 Phasor diagram of AC-side of CSR
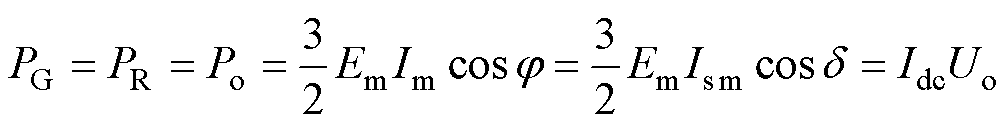（13）
式中，PG、PR和Po分别为网侧输入有功功率、交流侧输入有功功率以及直流侧输出功率；d 为网侧基波电压与交流侧基波电流相位。
联立式（1）和式（13），得到
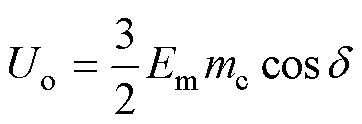（14）
由式（13）和式（14）可知，当输出功率和输出电压保持恒定时，通过增加调制因数mc，可增大d 值，从而减小j 值，提高三相CSR输入功率因数，如图5所示，以下进行详细的定量分析。
根据图5及式（13）得到以下复数关系表达式为
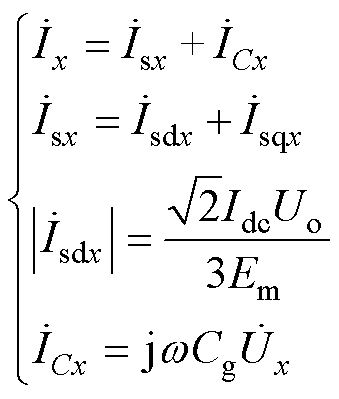（15）
（16）
式中，
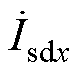为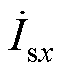
中有功电流分量，与网侧电压同相位；
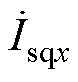为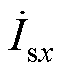中无功电流分量，滞后网侧电压90°。
由式（15）和式（16）可知，通过控制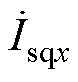，可逐步抵消滤波电容电流，当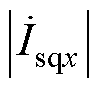
=
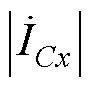时，即满足j =0，整流器输入侧对外将呈现纯电阻特性，实现单位功率因数运行。
根据上述分析，经补偿dq坐标系下相量关系如图6所示，在电网电压定向dq坐标系中利用相量法，分别对交流滤波电容电流iCd、iCq进行补偿，得到交流侧控制参考电流为
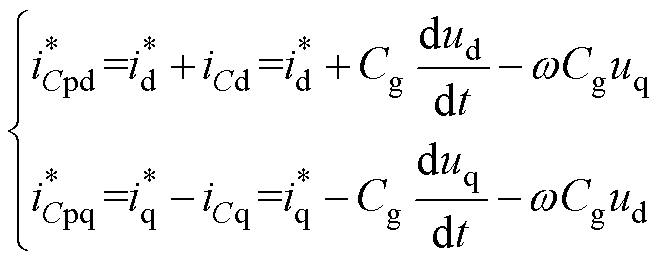（17）
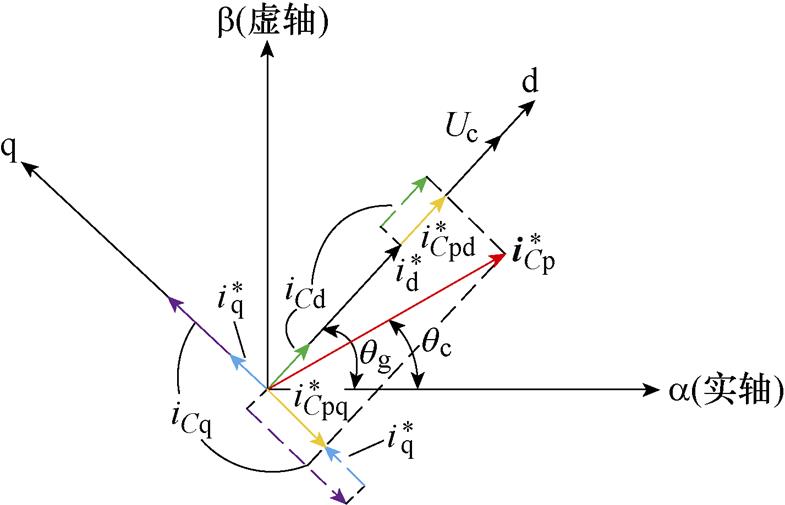
图6 经补偿dq坐标系下相量关系
Fig.6 Vector diagram in the d-q-axis with compensation
为了降低系统灵敏度与噪声的影响，忽略电容电流中的微分项，仅考虑稳态项，有
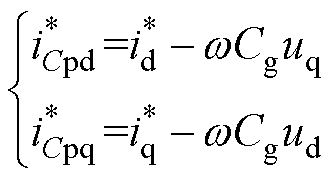（18）
dq坐标系下电容电流仅通过电容电压计算得到，相应可求得
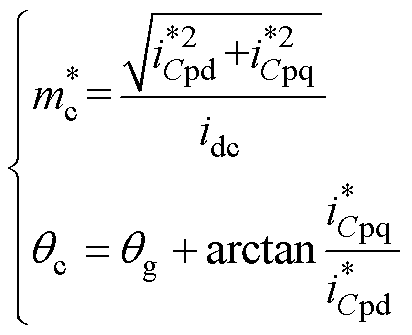（19）
由于网侧LC滤波器存在，三相CSR易受到PWM谐波或系统阶跃响应的影响，引起系统谐振。此外，线路电感因电源阻抗、传输线路以及隔离变压器而增加，使谐振频率点向低频偏移，将会造成更为严重的低频谐振。为了有效抑制谐振，常采用将阻尼电阻串联、并联接在LC滤波电路中，共包括四种位置样式。由于电流将流过这些阻尼电阻，必然造成损耗增加，从而限制其在大功率应用场合中的性能。有源阻尼法则通过改变系统控制环路来增加LC滤波器阻尼，从而有效克服了无源阻尼电阻发热问题。根据引入反馈变量的不同，包括电感电流反馈、电感电压反馈、电容电压反馈和电容电流反馈四种有源阻尼方法[22]，如图7所示，其中KLi、KLv、KCv、KCi和分别为对应的反馈增益。
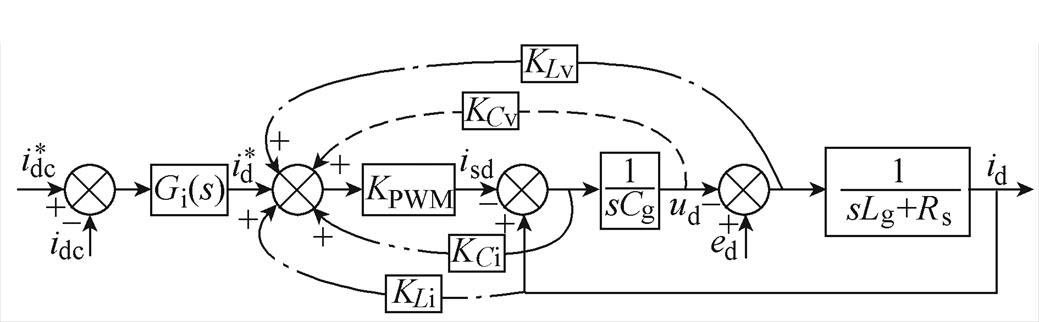
图7 不同变量反馈下的有源阻尼方法
Fig.7 Active damping methods with possible variable feedbacks
然而电感电压、电容电流的获取需要增加微分环节，将可能引入噪声干扰；而电感电流的获取需要在网侧增加电流传感器，因此本文采用电容电压反馈有源阻尼法，得到交流侧电流到网侧电流的传递函数为
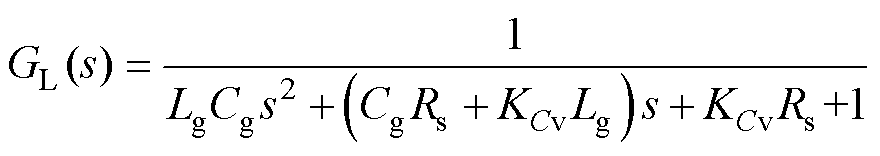（20）
由式（20）计算出阻尼系数x 和谐振频率wr为
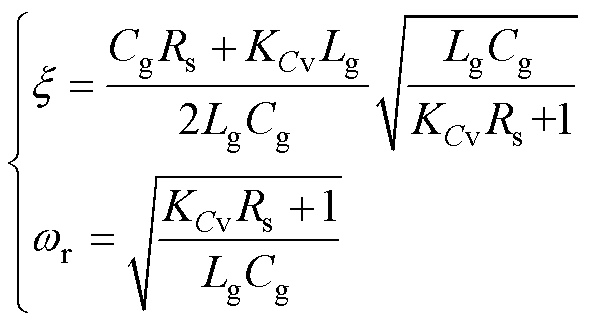（21）
通过式（21）可知，增大反馈增益KCv能有效提高阻尼系数，然而KCv过大会造成调制系数mc输出饱和。为了解决该问题，在反馈环路中引入高通滤波器，电容电压反馈环路框图如图8所示，此时交流侧电流到网侧电流的传递函数为
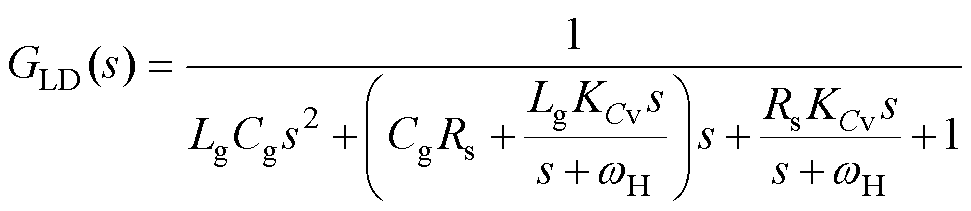（22）
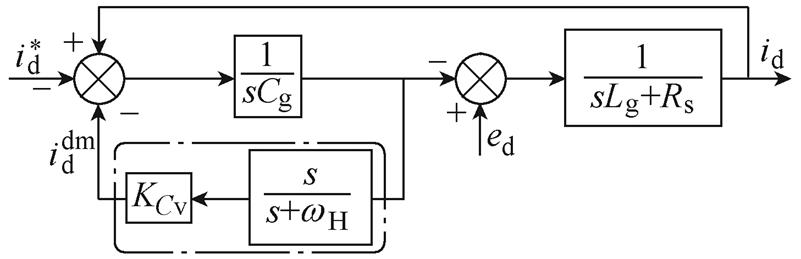
图8 电容电压反馈环路框图
Fig.8 Block diagram of the capacitor-voltage feedback loop
当反馈增益KCv在（0, 1）范围内不断增大时，不同KCv取值下GL(s)的幅频特性曲线如图9所示，LC谐振尖峰被逐渐衰减，并最终呈现过阻尼特性。从GLD(s)零极点位置分布来看，不同KCv对滤波器传递函数零极点位置影响如图10所示，当KCv为零或较小时，系统存在一对共轭极点和一个实数极点，在共同作用下呈现谐振特性；随着KCv不断增大，共轭极点阻尼系数逐渐减小，此后转化为两个实数极点，使系统呈现过阻尼特性。综合考虑，选取反馈增益KCv=0.2，在有效抑制谐振的同时不造成电流控制器输出饱和。
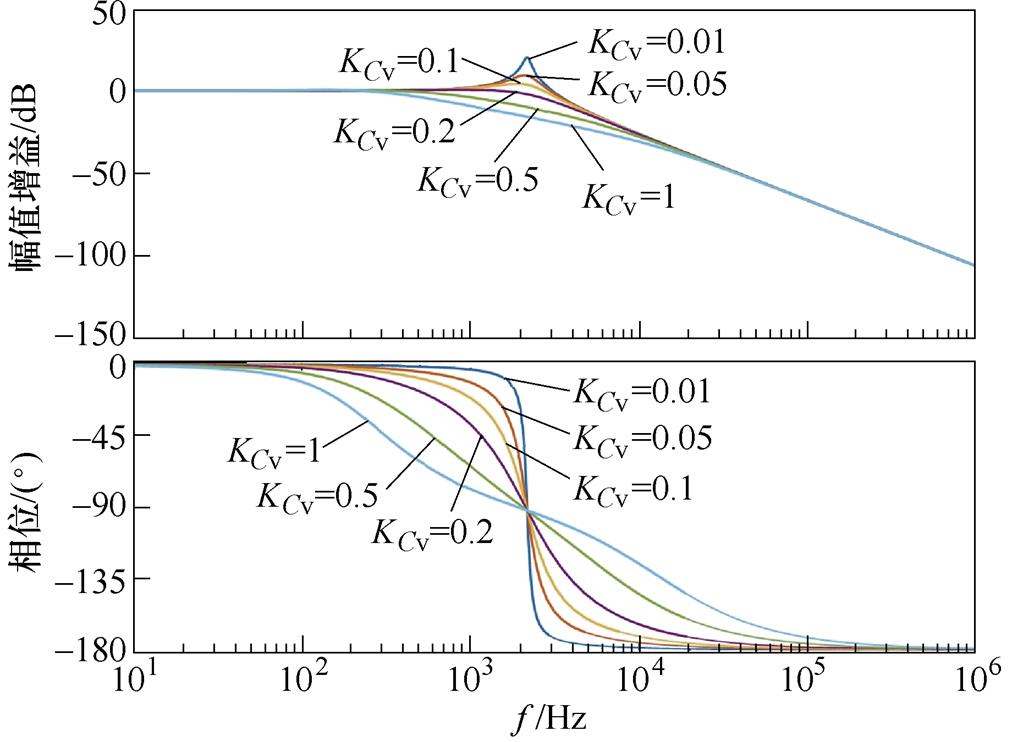
图9 不同KCv取值下GL(s)的幅频特性曲线
Fig.9 Bode diagrams of GL(s) with different KCv
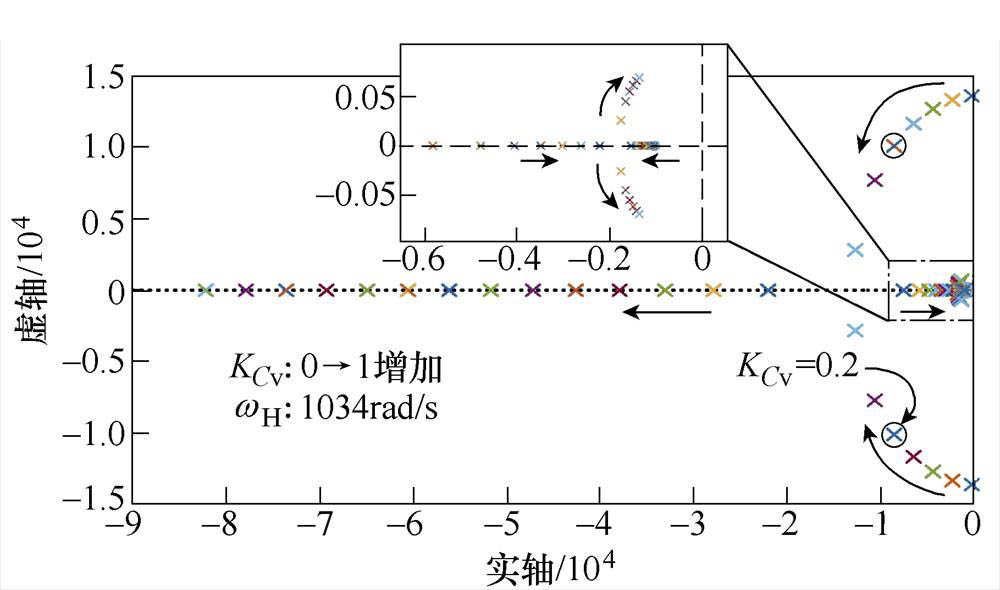
图10 不同KCv对滤波器传递函数零极点位置影响
Fig.10 Impact of different KCv gain on the filter pole-zero locations
根据本文所提出控制策略得到三相CSR双闭环控制框图，如图11所示。
图11a中给出了系统在连续s域中双闭环控制框图，Gi(s)和Gv(s)的表达式分别为
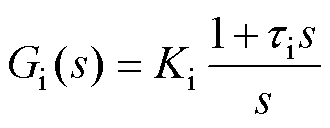（23）
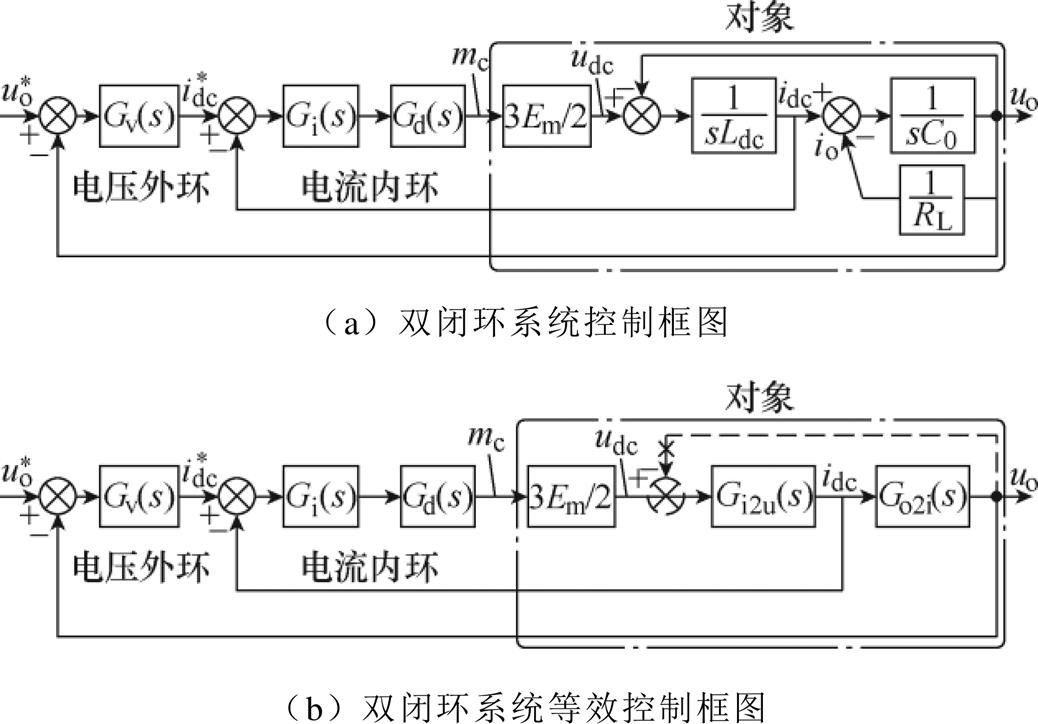
图11 连续s域中双闭环系统控制框图
Fig.11 Control block diagram of the closed-loop system in the continuous s-domain
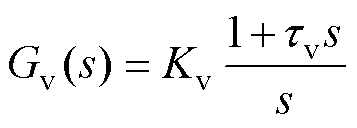（24）
式中，Ki、ti分别为电流内环控制器的增益系数和时间系数；Kv、tv分别为电压外环控制器的增益系数和时间系数。
当整流器系统采用数字控制时，程序计算会引起1个采样时间的延迟，而对称PWM因零阶保持作用，产生0.5个采样时间延迟[23]。因此，在控制环路中总时间延迟的传递函数可表示为
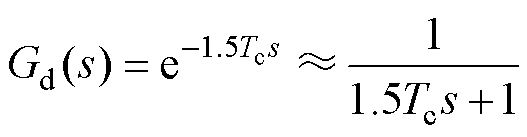（25）
式中，Tc为数字控制系统采样时间。
由于被控模型与电流内环存在交联，利用Mason定理得到等效控制框图，如图11b所示，包括两部分组成：整流器输出电压udc到直流侧电感电流idc的传递函数Gi2u(s)；直流侧电感电流idc到负载输出电压uo的传递函数Go2i(s)，即
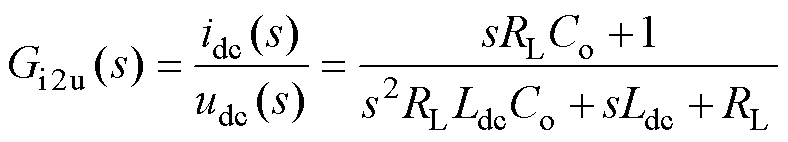（26）
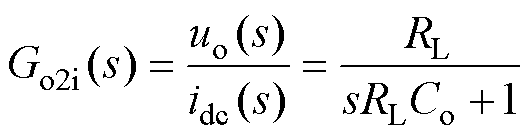（27）
联立式（23）、式（25）和式（26），得到电流内环开环传递函数为
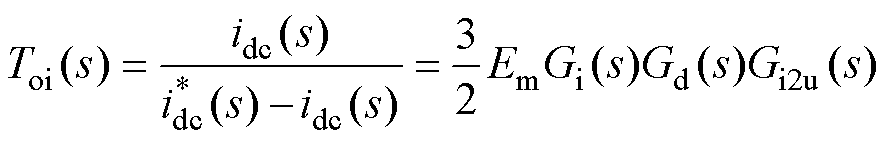（28）
令电流内环控制器Gi(s)=1，得到Toi(s)未经校正的Bode图如图12所示，由于直流侧电感、电容的存在，将引起电流内环的低频LC振荡，并影响系统的动态性能。为了解决该问题，本文通过在电流内环中增加直流侧电感电流来反馈阻尼环路，并引入阻尼因子KD，含直流侧阻尼反馈环路的系统闭环控制框图如图13所示。在KD由0逐渐增加到0.5的过程中，系统谐振峰值由57.8dB（162Hz处）逐渐降低，有效抑制直流侧谐振尖峰；但随着KD继续增大，传递函数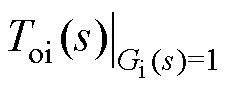
幅值增益在1.5～2.5kHz范围内出现小谐振尖峰，从而对电流内环设计产生不利影响，故选取KD=0.05。
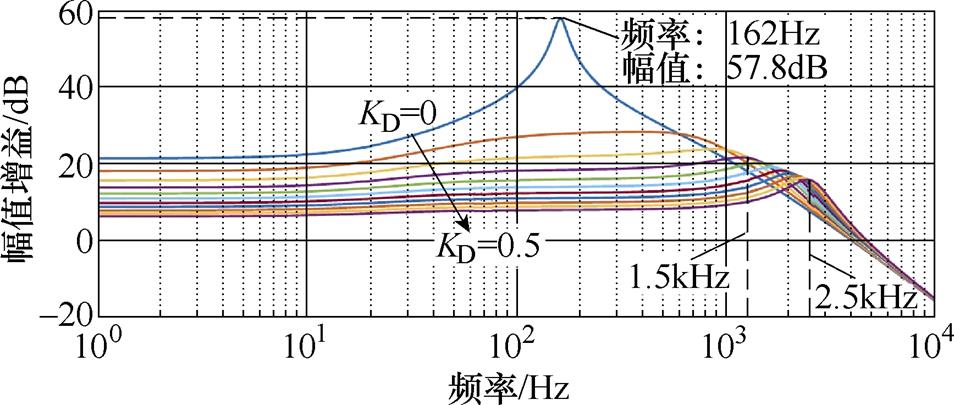
图12 不同KD取值时电流内环开环幅频特性曲线
Fig.12 Bode diagram of inner current open-loop with different values of KD
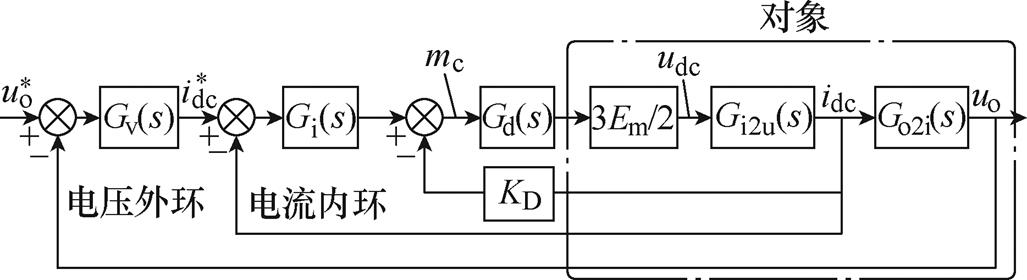
图13 含直流侧阻尼反馈环路的系统闭环控制框图
Fig.13 Control block diagram of the closed-loop system with DC-side damping feedback loop
为了实现数字控制，需要将所设计的控制模型进行离散化处理。
首先，应用Tustin变换将电流内环控制器Gi(s)和电压外环控制器Gv(s)进行离散化，得到
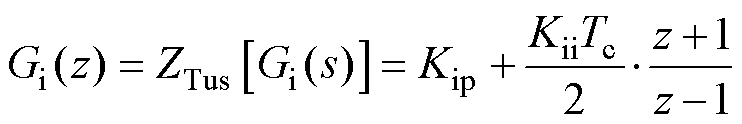（29）
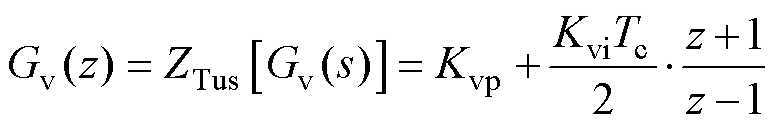（30）
式中，Kip=Kiti；Kii=Ki；Kvp=Kvtv；Kvi=Kv。
对式（26）应用零阶保持变换，得到离散域传递函数为
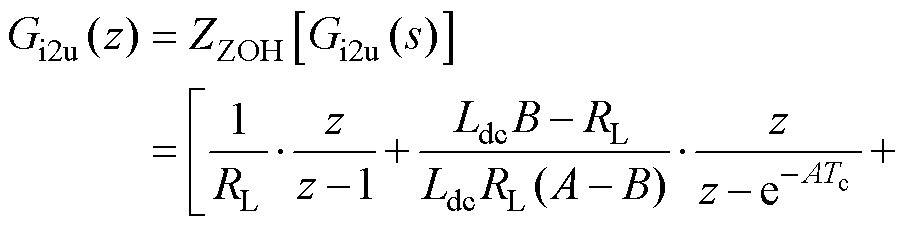
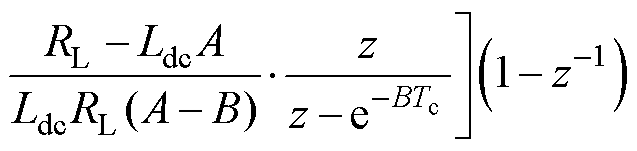（31）
其中
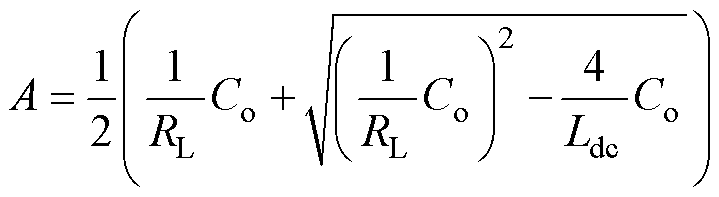
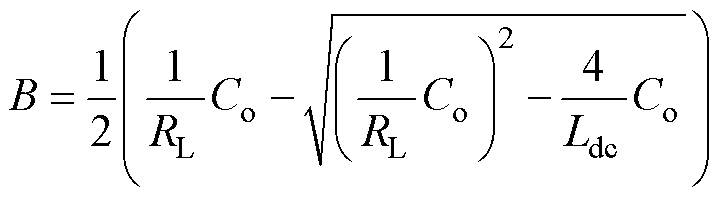
由于直流侧电感电流与负载输出电压保持同步采样，被控模型将不会产生附加延迟。因此，对式（27）应用脉冲响应不变法，得到其离散域传递函数为
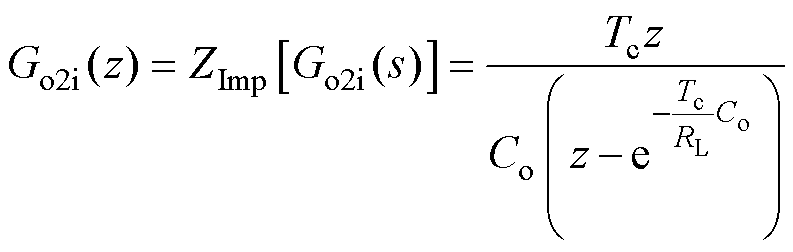（32）
因此，建立双闭环控制系统离散域模型，如图14所示，并分别得到系统离散域电流内环开环、闭环传递函数分别为
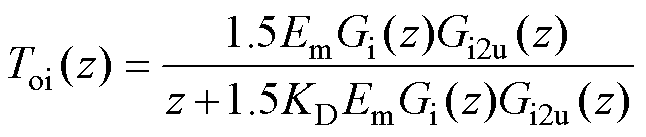（33）
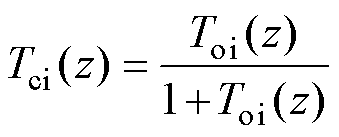（34）
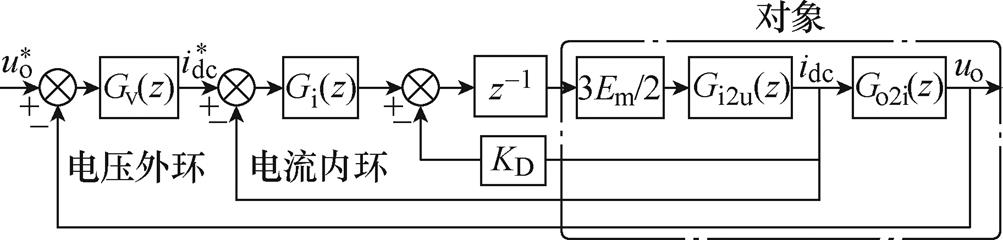
图14 闭环系统离散域控制框图
Fig.14 Control block diagram of the closed-loop system in discrete-time domain
电流内环传递函数为四阶系统，若要兼顾动态响应速度与系统稳定性，需要合理设置电流内环控制器参数。对于电流内环的设计，本文利用Matlab/ SISO设计工具，通过配置Gi(z)零点位置与增益大小，使系统具有所期望的性能。首先，保持Ki不变，逐渐改变Gi(z)中零点位置，即改变ti的大小，得到电流内环开环Bode图和根轨迹，如图15所示。
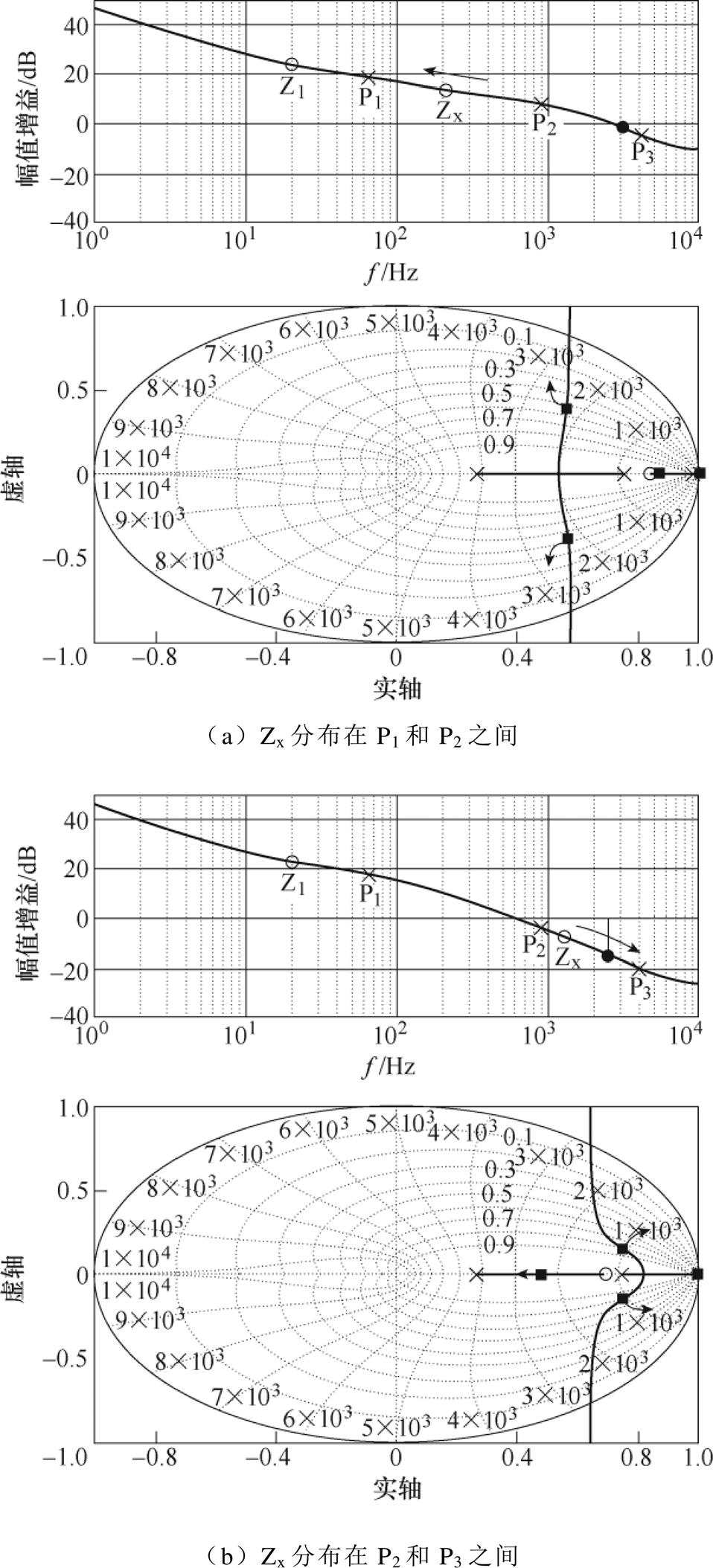
图15 Gi(z)零点位置对系统的影响
Fig.15 Influence of Gi(z) zero position on system performance
令电流内环开环传递函数极点、零点在Bode图中对应的位置分别记作P1、P2、P3、Z1和Zx，如图15a所示，Zx为Gi(z)的零点位置。
（1）当Zx放置于P1和P2之间时，电流内环闭环传递函数中存在1对共轭极点，随着Zx逐渐向极点P1靠近，系统阻尼比不断减小，增益裕度降低，最终导致系统不稳定；相反，随着Zx向极点P2靠近，同时闭环共轭极点逐渐向原点逼近，其对系统影响逐渐显现，但始终保持过阻尼特性。
（2）当Zx放置于P2和P3之间时，Zx穿越P2后，系统根轨迹如图15b所示，共轭极点已成为主导极点，随着向P3接近以及穿越的过程中，系统维持欠阻尼特性，随着阻尼比不断减小，响应速度及跟随能力明显增强，但同时引起电流内环超调量的增加。
为了保证电流内环快速跟随性能，首先将Zx设置在P2和P3间频段内；然后通过局部优化零点位置和增益值，使共轭复数极点阻尼比接近0.707，从而使系统获得良好的动、静态性能。最终确定电流内环控制器参数：Ki=126，ti=1.7×10-4。补偿后电流内环开环、闭环传递函数伯德图如图16所示，开环传递函数的增益裕度为15.1dB（＞6dB），相位裕度为58.1°（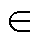
30°～60°），中频段以-20dB斜率经过0dB，且具有较宽的频率范围，系统带宽为935Hz，满足电流内环性能设计要求。
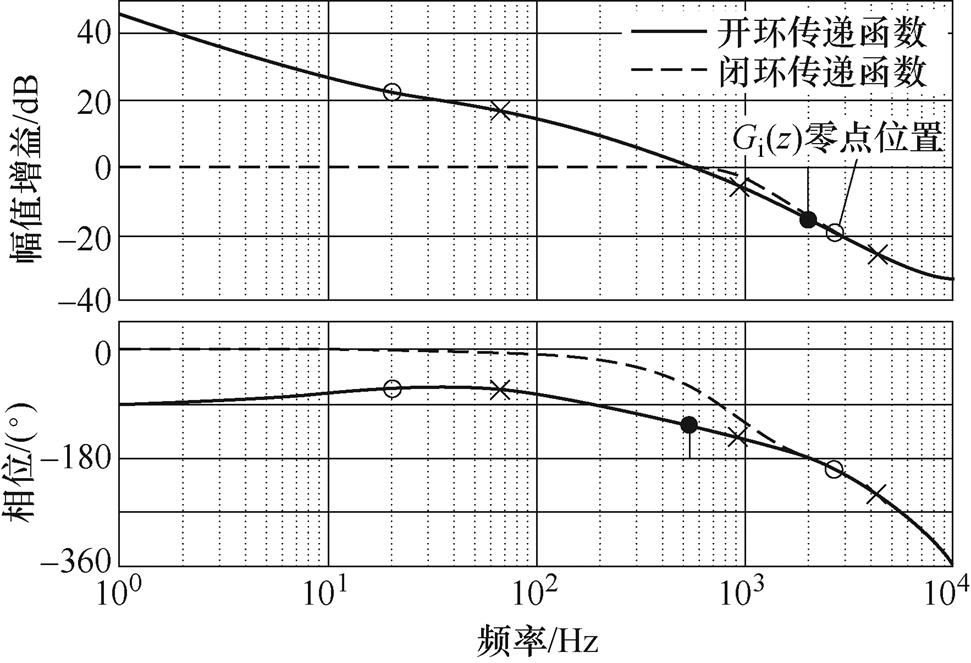
图16 电流内环开环、闭环传递函数伯德图
Fig.16 Bode diagrams of inner current open and closed-loop transfer functions
根据图14所示，列写出系统离散域电压外环开环、闭环传递函数为
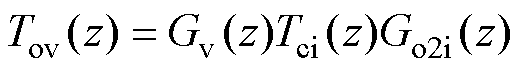（35）
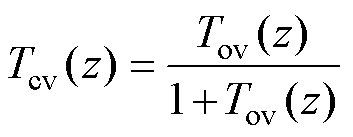（36）
针对高阶系统，同样利用Matlab/SISO设计工具对Gv(z)进行优化设计，最终确定Kv=14，tv=8.7× 10-3。补偿后电压外环开环、闭环传递函数伯德图如图17所示，此时系统稳定，相位裕度为78.5°，系统带宽为115Hz，约为电流内环带宽的1/10，故满足系统性能设计要求。
图17 电压外环开环、闭环传递函数伯德图
Fig.17 Bode diagrams of outer voltage open and closed-loop transfer functions
本文基于Matlab/Simulink搭建三相CSR仿真模型，分析系统稳态、动态运行性能，从而验证所提出方法的正确性。表1给出了仿真所需参数。
表1 三相CSR系统参数
Tab.1 System parameters of three-phase CSR
参 数数 值 网侧基波电压幅值Em/V311 交流滤波电感Lg/mH0.45 交流滤波电容Cg/mF12 直流侧电感Ldc/mH2×2.4 直流侧电容Co/mF100 开关频率fs/kHz20 电网基波频率/Hz50 直流侧输出电压uo/V380
图18为三相CSR稳态运行时的仿真结果，可以看出，分别工作在阻性负载4.5kW（半载）和9kW（满载）时，网侧电流均呈现正弦化，其满载时THD仅为1.58%，满足IEEE 519标准；网侧电压、电流始终保持同相位，有功、无功功率独立稳定输出，无功功率在零值附近作较小幅值波动，功率因数大于0.99。
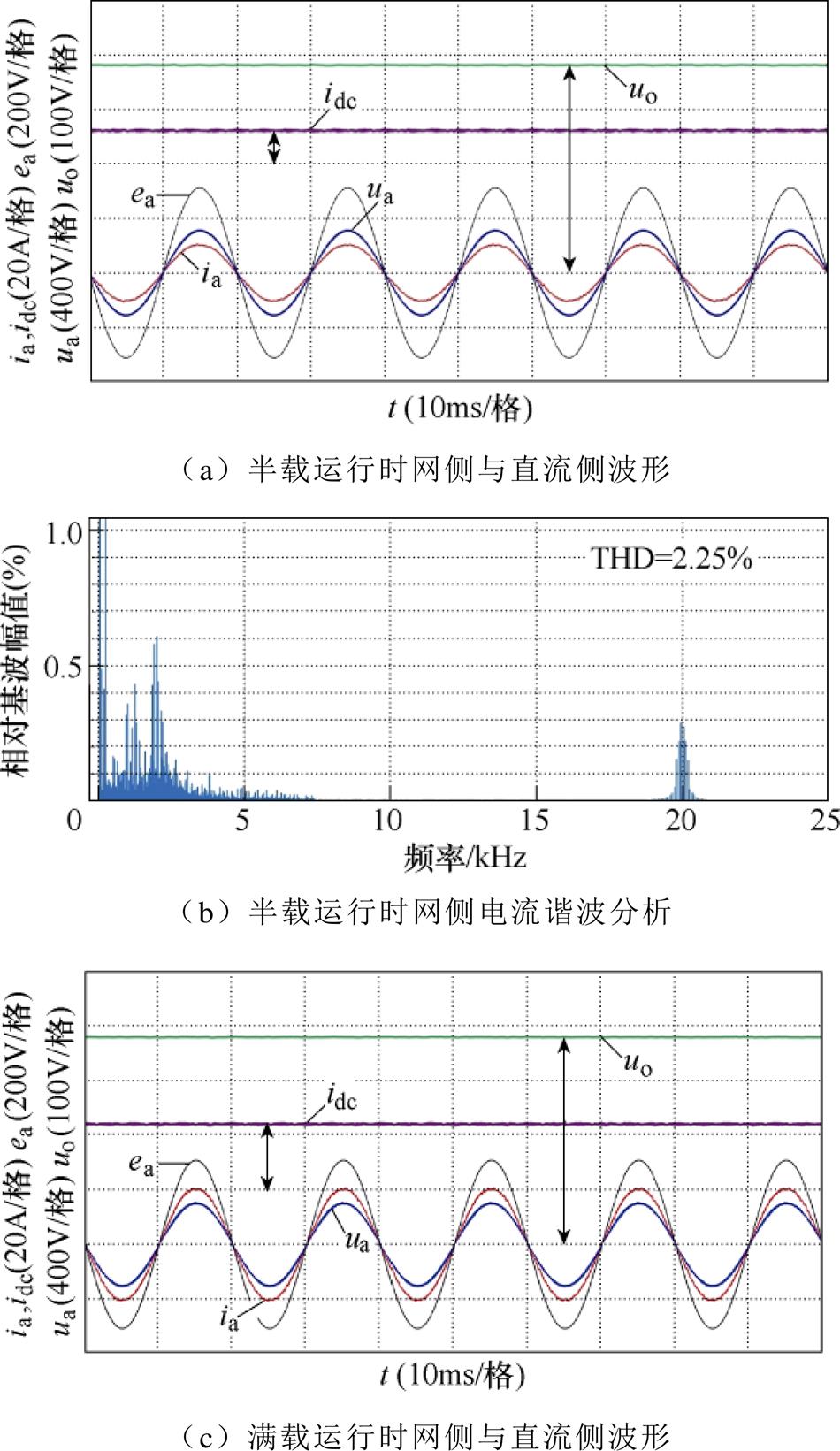
图18 稳态运行仿真结果
Fig.18 Simulation results of steady-state operation
图19给出了负载阶跃变化20%的仿真结果。结果表明，在突加、突减运行两种工况下，直流侧输出电压均能在10ms内完成对给定值的跟踪，电压波动均小于25V，同时网侧电流在突变过程中无明显畸变，始终实现对电网电压的相位跟踪。
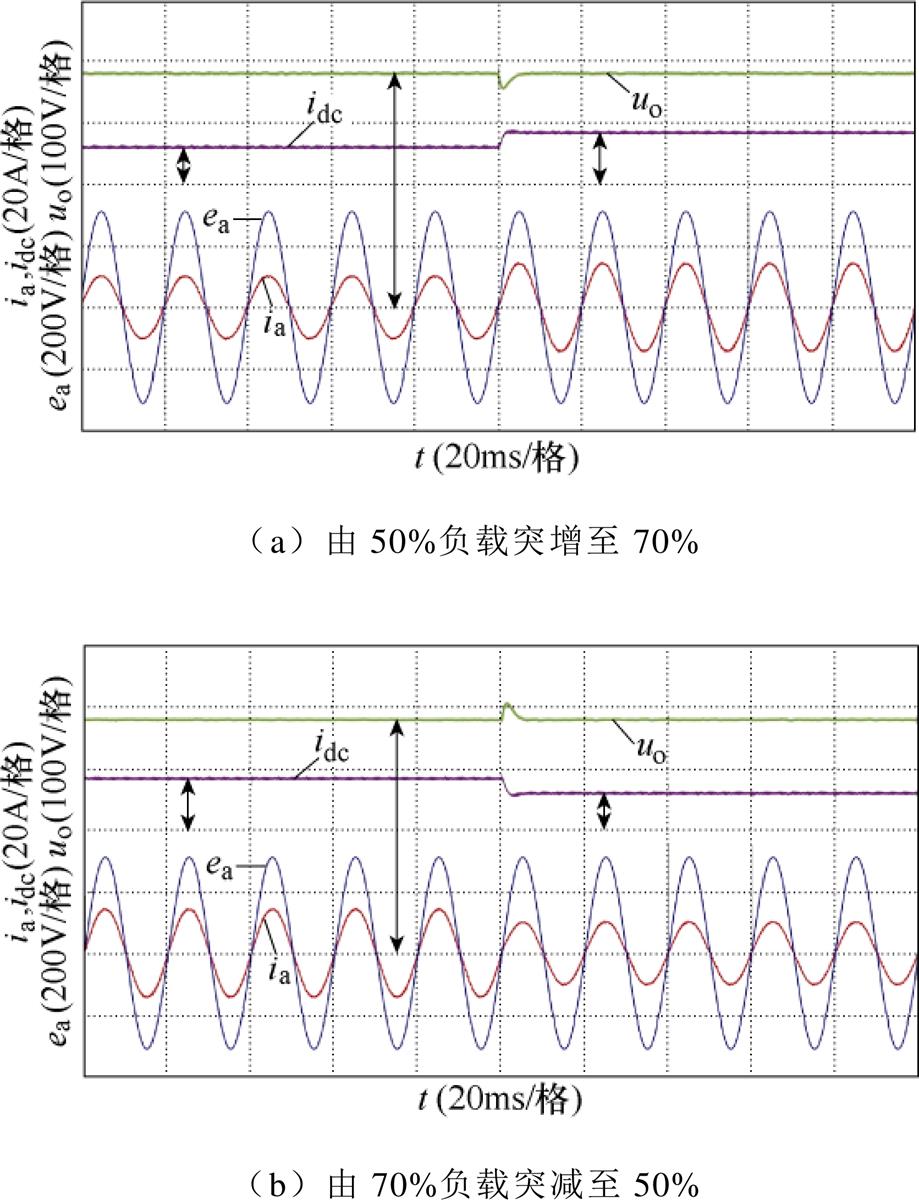
图19 瞬态响应仿真结果
Fig.19 Simulation results of transient response
通过搭建一台三相CSR实验样机，对提出控制策略进行验证，实验样机如图20所示。整流器交流侧连接三相可编程电网模拟器（Chroma-61830），而直流侧连接电子负载（IETCH-IT8626）。其中主控制芯片采用TMS320F28335+CPLD，开关管采用FF100R12RT4，串联二极管分别采用MEA75-12DA和MEK75-12DA，交、直流侧滤波电感分别采用非晶合金磁心AMCC-32和AMCC-100，实验电气参数与仿真参数设置一致。
图20 三相CSR实验平台
Fig.20 Experimental setup of three-phase CSR
本文软件部分采用基于模型的设计方法，通过Embedded Target Library外设功能模块和常用算法模块构建Simulink模型，如图21所示，并根据硬件环境合理配置模块，最终生成所需程序代码。
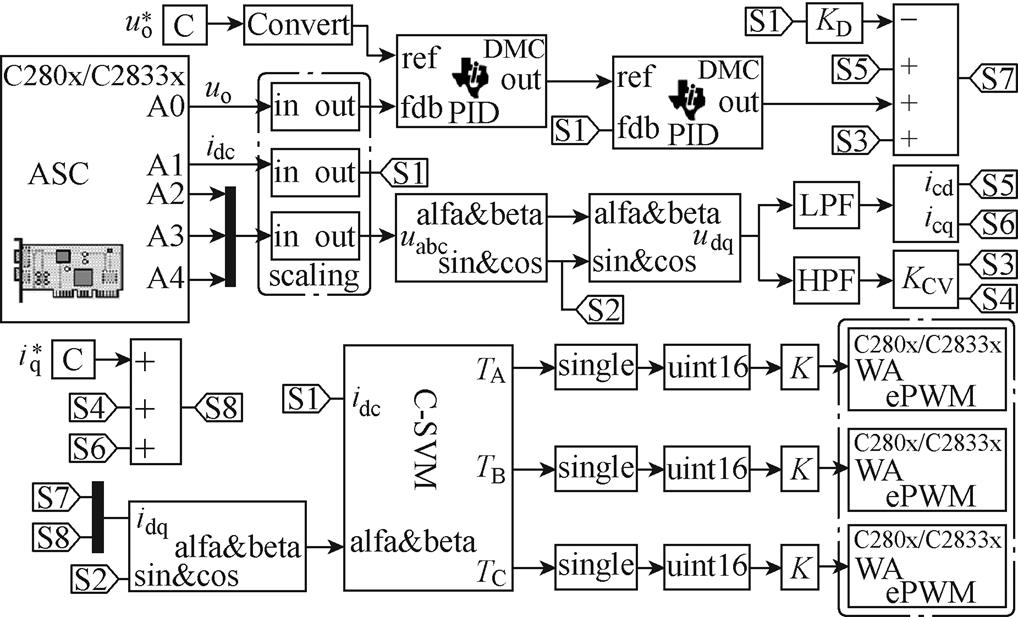
图21 基于模型设计的Simulink模型
Fig.21 Simulink model of model-based design
图22给出了采用与未采用有源阻尼控制策略时网侧电流波形，图中，t1为算法使能开始时刻，可以看出，使能前网侧电流ia谐波含量明显，而使能后网侧电流ia谐波分量得到有效抑制，具有更好的正弦特性。
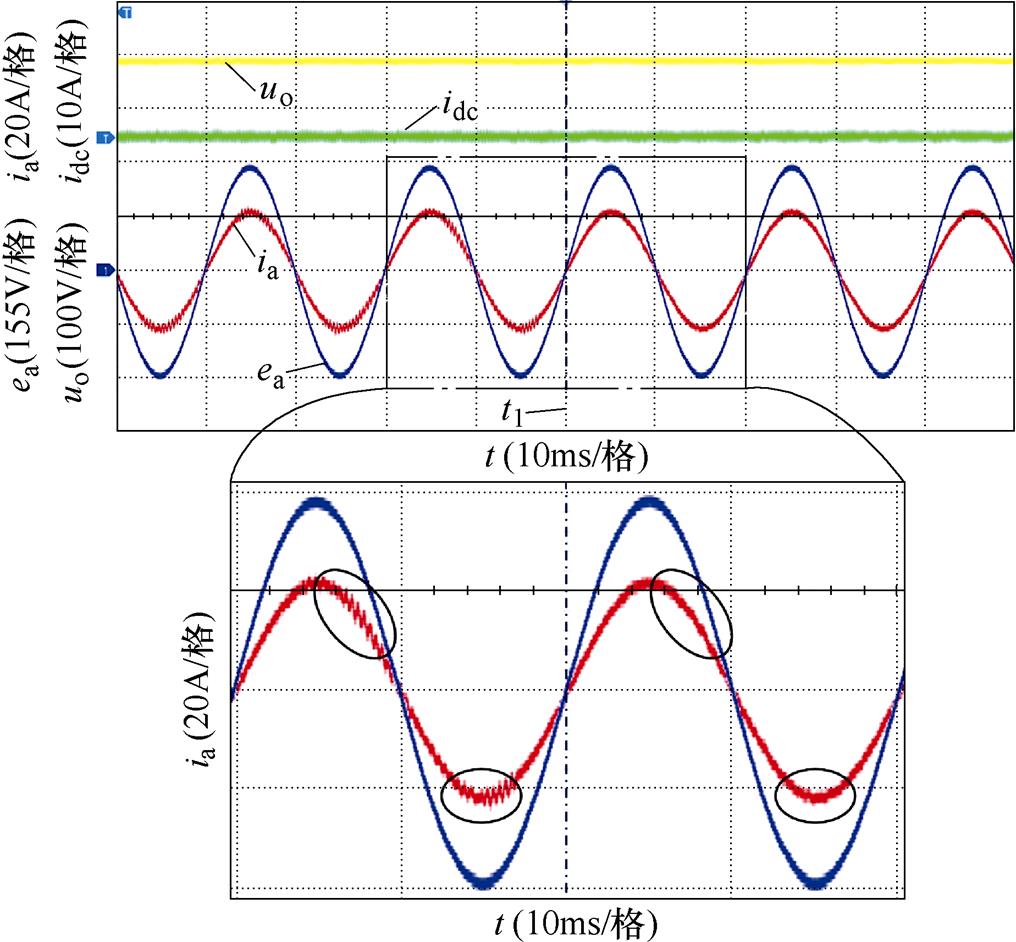
图22 采用与未采用有源阻尼法时网侧电流波形
Fig.22 Grid-side current waveforms with and without active damping method
图23给出了阻性负载分别为4.5kW（半载）和9kW（满载）情况下，系统稳态运行时网侧电压、网侧电流、直流侧电感电流以及输出电压的实验波形。实验结果表明，本文所设计的三相CSR系统，在不同运行工作点下，网侧电流均能准确跟踪网侧电压相位，实现单位功率因数运行；同时网侧电流正弦化，其半载、满载THD值分别为3.64%和2.43%，均小于5%，能够有效抑制网侧电流的谐波畸变；直流侧输出电压uo保持380V稳定输出，实现对给定电压的无静差控制，且与仿真结果保持 一致。
图23 稳态运行实验结果
Fig.23 Experimental results of steady-state operation
图24a为系统以40%负荷带载起动时动态响应实验结果，网侧电流ia仅在5ms内便实现对电网电压相位的快速跟踪，同样直流侧输出电压uo在10ms内稳定至给定值，整个响应过程无超调。图24b为满载情况下突减20%负载时的实验结果，直流侧电感电流idc能快速下降至稳定值，且过程无超调；uo虽然存在过冲，但其波动幅值小于30V，调节时间小于10ms。
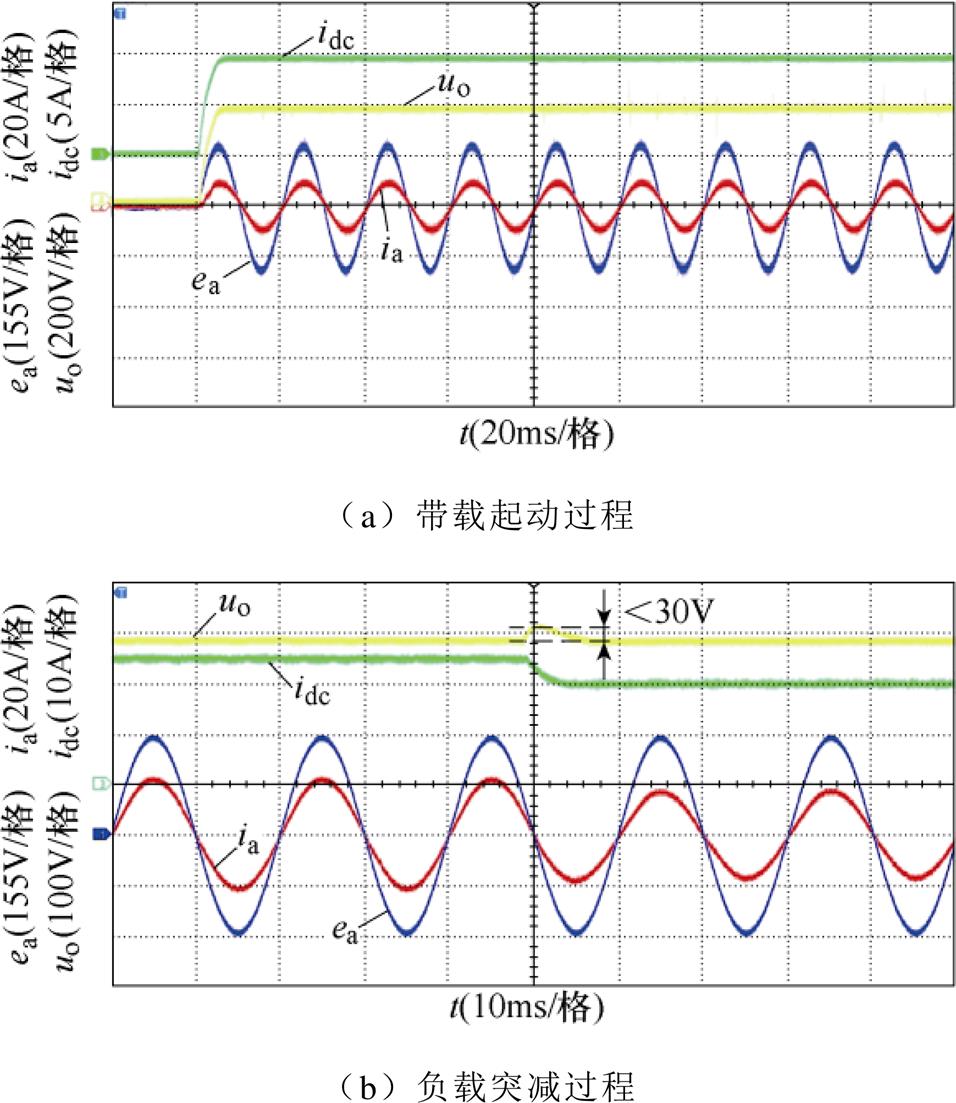
图24 瞬态响应实验结果
Fig.24 Experimental results of transient response
因此，通过上述实验证明了本文提出的控制策略与参数设计方法能够使三相CSR系统具有良好的稳态、动态性能。
考虑三相CSR应用于低压直流配电系统时的控制要求，基于dq坐标系建立电压定向数学模型，实现系统有功、无功功率独立控制。基于相量法提出一种电容电流补偿方法，构建电容电压前馈通道，并采用电容电压反馈有源阻尼法对网侧LC谐振进行抑制。同时，引入直流侧电感电流反馈以及阻尼因子，改善其环路性能。利用频域法与根轨迹法优化控制器零点位置与环路增益。通过仿真与实验验证，得到如下结论：
1）基于直流侧电压、电流双闭环控制方法简化了有功功率和无功功率的控制架构，省去了网侧电流传感器，具有良好的工程应用价值。
2）本文所提出的控制策略使系统具有良好的稳态、动态性能，其中网侧电压电流保持同相位，有效改善网侧电流谐波且输出电压稳定。
3）采用基于模型的设计方法，提高了控制算法的开发效率。
参考文献
[1] Ganesan S I, Pattabiraman D, Govindarajan R K, et al. Control scheme for a bidirectional converter in a self- sustaining low-voltage DC nanogrid[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(10): 6317- 6326.
[2] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution net- work[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[3] 郭伟, 赵洪山. 基于事件触发机制的直流微电网多混合储能系统分层协调控制方法[J]. 电工技术学报, 2020, 35(5): 1140-1151.
Guo Wei, Zhao Hongshan. Coordinated control method of multiple hybrid energy storage system in DC microgrid based on event-triggered mechanism[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1140-1151.
[4] Dong Dong, Cvetkovic I, Boroyevich D, et al. Grid interface bidirectional converter for residential DC distribution systems-part one: high-density two-stage topology[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1655-1666.
[5] Schrittwieser L, Leibl M, Haider M, et al. 99.3% efficient three-phase Buck-type all-SiC swiss rectifier for DC distribution systems[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 126-140.
[6] Wang Huai, Blaabjerg F. Reliability of capacitors for DC-link applications in power electronic converters: an overview[J]. IEEE Transactions on Industry Appli- cations, 2014, 50(5): 3569-3578.
[7] Stupar A, Friedli T, Minibock J, et al. Towards a 99% efficient three-phase Buck-type PFC rectifier for 400V DC distribution systems[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1732-1744.
[8] Bai Zhihong, Ruan Xinbo, Zhang Zhongchao. A generic six-step direct PWM (SS-DPWM) scheme for current source converter[J]. IEEE Transactions on Power Electronics, 2010, 25(3): 659-666.
[9] 张强, 吴延飞, 张保顺, 等. 基于三相电流型五电平整流器的空间矢量脉宽调制算法[J]. 电工技术学报, 2020, 35(24): 5134-5141.
Zhang Qiang, Wu Yanfei, Zhang Baoshun, et al. Space vector pulse width modulation strategy based on three-phase five-level current source rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5134-5141.
[10] Bai Zhihong, Ma Hao, Xu Dewei, et al. Control strategy with a generalized DC current balancing method for multimodule current-source converter[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 366-373.
[11] 张丽霞, 颜湘武, 康伟, 等. 基于空间电流矢量的动力蓄电池组测试系统变流技术[J]. 电工技术学报, 2010, 25(9): 122-128.
Zhang Lixia, Yan Xiangwu, Kang Wei, et al. Con- verting technology based on the current mode SVPWM on the power accumulator battery testing system[J]. Transactions of China Electrotechnical Society, 2010, 25(9): 122-128.
[12] Zhang Lixia, Kang Wei, Wang Yansong. Study on output characteristic of bi-direction current source converters[J]. IET Power Electronics, 2012, 5(7): 929-934.
[13] 郭强, 刘和平, 彭东林, 等. 电流型PWM整流器多环控制策略及其参数设计[J]. 中国电机工程学报, 2015, 35(5): 1193-1202.
Guo Qiang, Liu Heping, Peng Donglin, et al. A multi- loop control strategy and parameter design for current-source PWM rectifiers[J]. Proceedings of the CSEE, 2015, 35(5): 1193-1202.
[14] 李玉玲, 鲍建宇, 张仲超. 间接电流控制可调功率因数电流型PWM变流器[J]. 中国电机工程学报, 2007, 27(1): 51-55.
Li Yuling, Bao Jianyu, Zhang Zhongchao. Indirect current control adjustable power factor current source PWM converter[J]. Proceedings of the CSEE, 2007, 27(1): 51-55.
[15] 朱晓荣, 彭咏龙, 李和明, 等. 电流型PWM整流器的非线性控制[J]. 中国电机工程学报, 2007, 27(28): 96-101.
Zhu Xiaorong, Peng Yonglong, Li Heming, et al. Nonlinear control of current-source PWM rectifier[J]. Proceedings of the CSEE, 2007, 27(28): 96-101.
[16] Gao Hang, Wu Bin, Xu Dewei, et al. A model predictive power factor control scheme with active damping function for current source rectifiers[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2655-2667.
[17] Gao Hang, Wu Bin, Xu Dewei, et al. Model predictive control scheme with active damping function for current source rectifiers[J]. IET Power Electronics, 2017, 10(7): 717-725.
[18] Xu Fan, Guo Ben, Xu Zhuxian, et al. Paralleled three-phase current-source rectifiers for high-efficiency power supply applications[J]. IEEE Transactions on Industry Applications, 2015, 51(3): 2388-2397.
[19] Nussbaumer T, Heldwein M L, Gong G, et al. Comparison of prediction techniques to compensate time delays caused by digital control of a three-phase Buck-type PWM rectifier system[J]. IEEE Transa- ctions on Industrial Electronics, 2008, 55(2): 791- 799.
[20] Xu Fan, Guo Ben, Tolbert L M, et al. An all-SiC three-phase Buck rectifier for high-efficiency data center power supplies[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2662-2673.
[21] Salo M, Tuusa H. A vector controlled current-source PWM rectifier with a novel current damping method[J]. IEEE Transactions on Power Electronics, 2000, 15(3): 464-470.
[22] Bai Zhihong, Ma Hao, Xu Dewei, et al. Resonance damping and harmonic suppression for grid-connected current source converter[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3146-3154.
[23] Wang Xiongfei, Loh P C, Blaabjerg F. Stability analysis and controller synthesis for single-loop voltage-controlled VSIs[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7394-7404.
A Multiple Loops Control Strategy Based on DC Link Voltage of Current Source PWM Rectifiers
Abstract When the three-phase current source PWM rectifier is employed as the active front-end in low-voltage DC distribution systems, the difficulty and complexity of the control system increase due to the existence of input LC filter and DC bus capacitor. Firstly, a voltage-oriented mathematical model is established in the synchronous rotating reference frame. A compensation scheme of capacitance current based on phasor method is proposed, which guarantees that only by capacitor-voltage feedforward path the input power factor can be kept at unity. Secondly, as an alternative damping method, the capacitor-voltage feedback is used to suppress the LC resonance, and the influence of the feedback gains on the stability of the system is discussed. Furthermore, the system’s dynamic performance is further improved by adopting DC-side inductor-current feedback and damping factor. The active power and reactive power of the system are controlled independently by d-axis and q-axis components of the grid side current. The control loops are analyzed using the frequency-response method and the root locus analysis, and supported with Matlab/SISOTOOL, the zero position and loop gains of the controllers are straightforward designed in the z-domain. Finally, the simulation and experimental results verify the feasibility and effectiveness of the proposed method.
keywords：Current source rectifier, multiple loops, active damping, power factor compensation, controller design
DOI: 10.19595/j.cnki.1000-6753.tces.210274
中图分类号：TM46
郭 强 男，1984年生，博士，研究方向为功率变换器控制技术。E-mail: guoqiang@cqut.edu.cn
周琛力 男，1996年生，硕士研究生，研究方向为电流源型整流器建模与控制等。E-mail: Zhouchenli@2018.cqut.edu.cn（通信作者）
收稿日期 2021-03-03
改稿日期 2021-04-19
重庆市教委科学技术研究计划资助项目（KJQN202001128）。
（编辑 陈 诚）