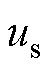 、
、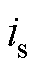 为网侧电压和网侧电流;
为网侧电压和网侧电流; 为网侧电感;
为网侧电感;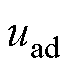 为a点、d点之间的输入电压;
为a点、d点之间的输入电压;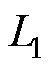 和
和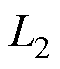 为耦合电感,
为耦合电感,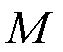 为互感;
为互感;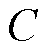 、
、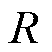 、
、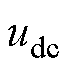 分别为直流侧支撑电容、负载电阻、直流侧输出电压;
分别为直流侧支撑电容、负载电阻、直流侧输出电压;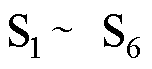 为功率开关管;该拓扑共有3个桥臂,每个桥臂的上下开关管互补导通。
为功率开关管;该拓扑共有3个桥臂,每个桥臂的上下开关管互补导通。摘要 五电平整流器由于具有大功率输出能力、网侧电流谐波小的特性而被广泛应用于高压电力传输变换场合。该文以耦合电感五电平整流器为研究对象,针对传统模型预测外环采用PI控制存在的动态性能差、抗扰动能力差的问题,提出滑模模型预测控制(SMMPC)算法。首先,分析整流器的五电平产生原理,在此基础上建立外环与内环控制所需的动态方程。然后,针对该整流器详细设计滑模模型预测控制算法。最后,仿真和实验结果均表明,该滑模模型预测算法不仅保留了模型预测固定开关频率、延时误差小的优点,同时与PI模型预测控制相比,其动态响应速度与抗扰动能力更加优异。
关键词:五电平整流器 耦合电感 滑模控制 模型预测控制
随着电力电子技术的发展,单相脉冲宽度调制(Pulse Width Modulation, PWM)整流器因具有能单位功率因数运行、直流电压控制简单、能量双向流动等优点,被广泛应用于铁路、可再生能源、直流输电系统中[1-3]。多电平整流器因谐波含量低、功率器件承受电压低,所以更适用于高压大功率场合。目前常见的多电平拓扑结构有级联H桥型、二极管中点钳位型和飞跨电容型[4-6]三种。当增加电平时,级联H桥多电平结构会大幅增加所需元器件个数,且需要考虑直流侧电容电压平衡问题;二极管钳位型拓扑结构需要增加较多的钳位二极管;飞跨电容型则需要增加许多电容器,从而增大换流器体积。根据具体应用场合,学者们还提出了多种改良多电平拓扑,文献[7]设计了一种具有升降压功能的五电平拓扑结构。文献[8]设计了一种级联七电平拓扑结构,相对传统七电平拓扑结构,有较少的开关器件。文献[9-11]提出了基于耦合电感的单相五电平变流器拓扑结构,该拓扑结构具有开关器件少、无需电容电压平衡等优点。
模型预测控制(Model Predictive Control, MPC)具有概念简单、动态性能好、适用范围广等优点。传统的有限集模型预测控制利用了开关器件的离散特性,在一个周期内计算所有开关矢量,选择使目标函数误差最小的开关矢量,作用于下个周期。由于一个周期内仅采用一个开关矢量,为了实现精确控制,需要很高的采样频率和数据计算速度,且存在开关频率不固定的情况。为此,学者们对传统有限集模型预测控制进行了各种研究和改进。文献[12-13]将模型预测应用于整流器和有源滤波器上,并将矢量作用时间应用于固定开关频率中。文献[14-15]提出在模型预测控制算法中引入空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)技术的调制函数,通过设计调制函数对其寻优,能明显固定开关频率。文献[16-17]提出了无差拍模型预测的控制方法,可以有效地消除因采样和计算带来的延时误差。
在模型预测中,外环常采用PI控制来生成参考电流,然后应用于模型预测的目标函数中,因此PI控制的效果会直接影响内环模型预测的效果。这种PI模型预测控制(PI Model-Predictive Control, PIMPC)中的PI参数是根据系统参数来设定的,在整个运行过程中,PI参数无法自动改变,这使得其在系统参数发生变化时无法快速控制。而滑模控制具有良好的动态响应能力,对系统参数变化有较强的鲁棒性[18-20],因此可考虑外环用滑模控制来生成参考电流。
综合上述考虑,本文针对传统PIMPC算法存在的开关频率不固定、动态响应速度慢、抗扰动性能差的问题,结合滑模控制与模型预测控制的优点,提出了滑模模型预测控制(Sliding-Mode Model- Predictive Control, SMMPC)算法。首先,通过分析耦合电感单相五电平PWM整流器的拓扑原理,得到了外环与内环控制所需数学模型。然后,针对传统PI控制在参数变化时动态响应速度慢的问题,在两相同步旋转坐标系下设计了滑模控制外环。之后,针对传统模型预测存在采样计算延时,开关频率不固定的问题,将模型预测与无差拍控制,空间矢量调制相结合,在两相静止坐标系下设计了模型预测内环,并构建了整体控制框架。最后,对提出的SMMPC与传统的PIMPC进行仿真和实验比较。
图1为含耦合电感的五电平整流器拓扑结构,图中,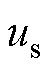 、
、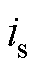 为网侧电压和网侧电流;
为网侧电压和网侧电流; 为网侧电感;
为网侧电感;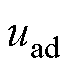 为a点、d点之间的输入电压;
为a点、d点之间的输入电压;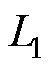 和
和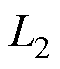 为耦合电感,
为耦合电感,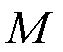 为互感;
为互感;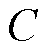 、
、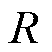 、
、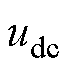 分别为直流侧支撑电容、负载电阻、直流侧输出电压;
分别为直流侧支撑电容、负载电阻、直流侧输出电压;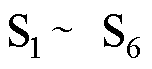 为功率开关管;该拓扑共有3个桥臂,每个桥臂的上下开关管互补导通。
为功率开关管;该拓扑共有3个桥臂,每个桥臂的上下开关管互补导通。
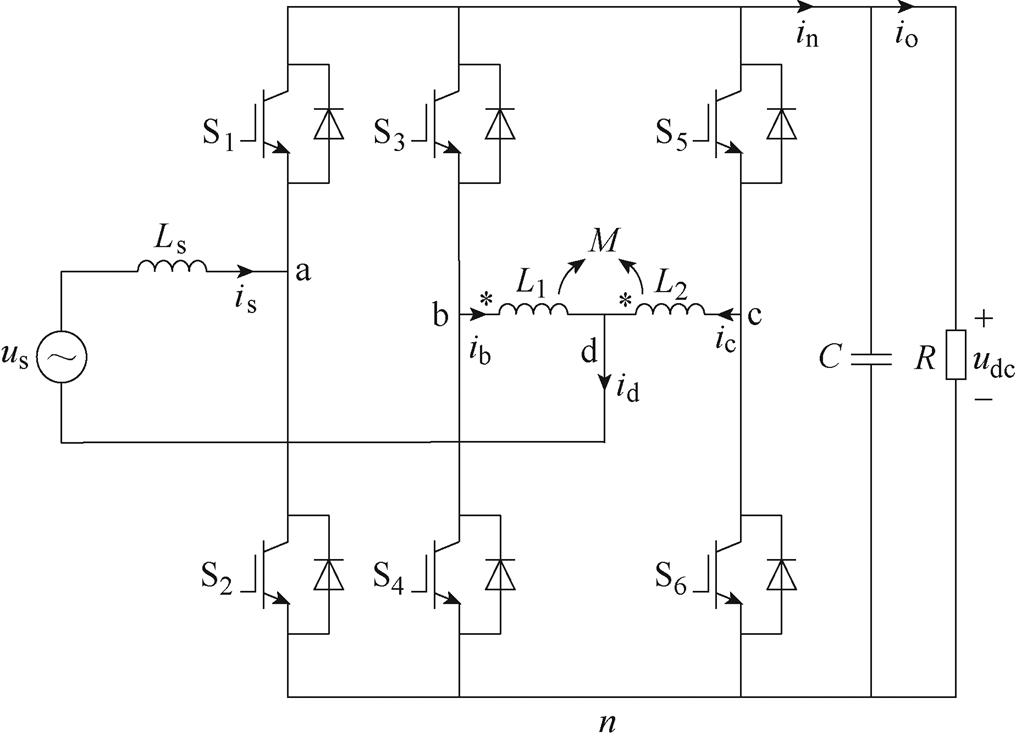
图1 含耦合电感的五电平整流器拓扑结构
Fig.1 Five-level rectifier topology with coupled inductors
耦合电感的电压表示为
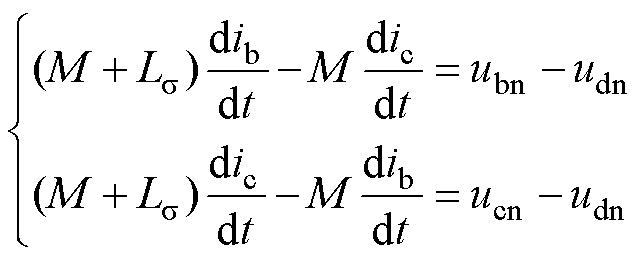 (1)
(1)
式中,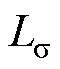 为耦合电感的漏感;ubn、udn、ucn为节点电压;ib、ic为节点电流。
为耦合电感的漏感;ubn、udn、ucn为节点电压;ib、ic为节点电流。
根据基尔霍夫定律有
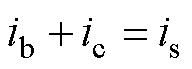 (2)
(2)
将式(1)代入式(2),可以得到
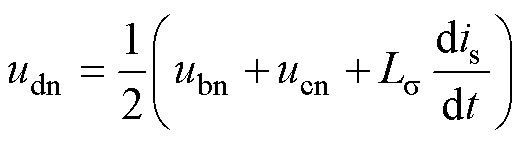 (3)
(3)
通常情况下,电感的漏感被设计的非常小,在大多数情况下,其影响可以忽略不计,因此式(3)可以写成
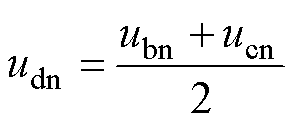 (4)
(4)
根据式(4)可以推出输入电压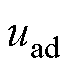 为
为
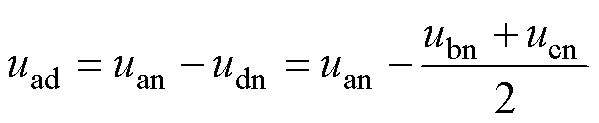 (5)
(5)
设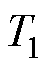 、
、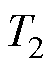 、
、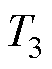 为各桥臂的开关状态,则理想二值逻辑开关函数为
为各桥臂的开关状态,则理想二值逻辑开关函数为
 (6)
(6)
开关函数K可以表示为
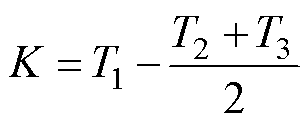 (7)
(7)
则输入电压和直流侧电流可表示为
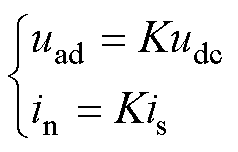 (8)
(8)
根据式(3)~式(8)可以给出该拓扑结构的具体开关状态,见表1。
表1 含耦合电感的五电平整流器开关状态
Tab.1 Switching state of five-level rectifier with coupled inductors
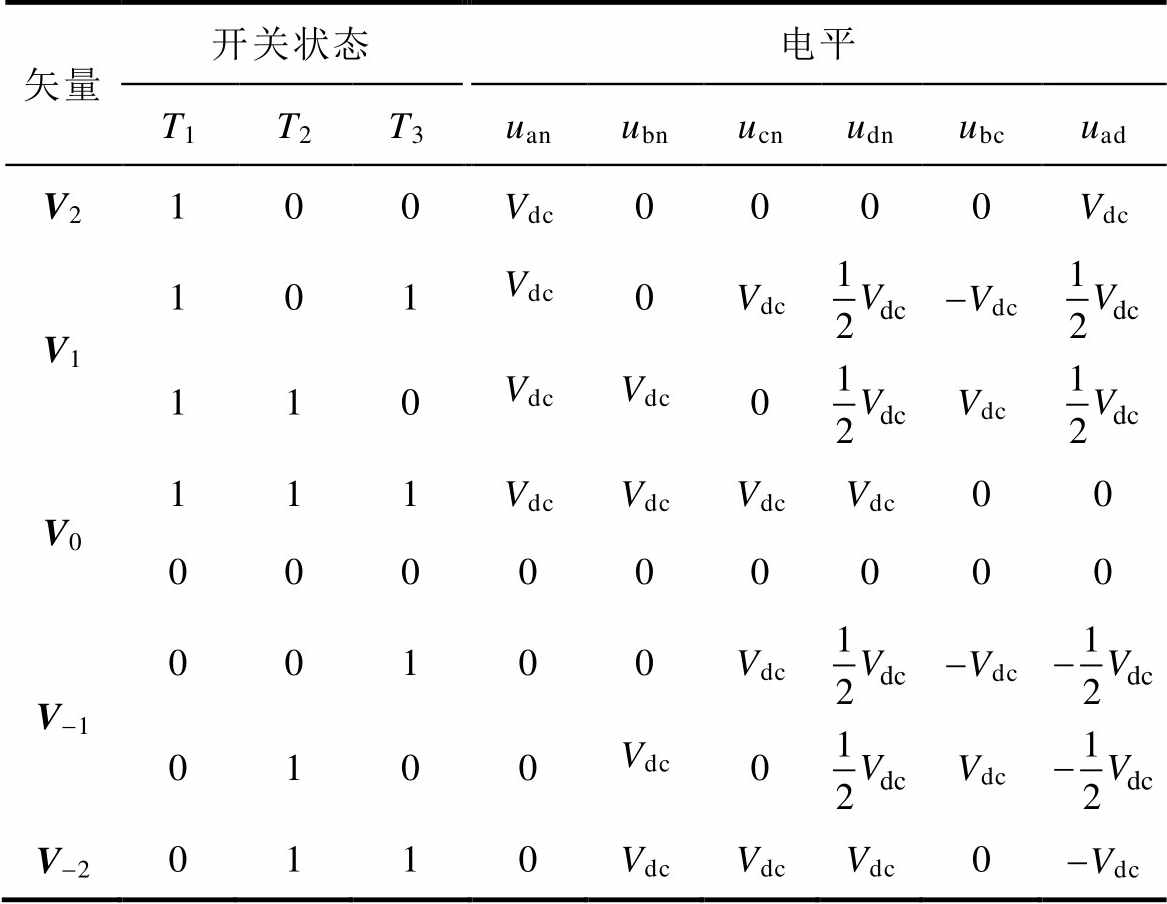
矢量开关状态电平 T1T2T3uanubnucnudnubcuad V2100Vdc0000Vdc V1101Vdc0Vdc-Vdc 110VdcVdc0Vdc V0111VdcVdcVdcVdc00 000000000 V-100100Vdc-Vdc 0100Vdc0Vdc V-20110VdcVdcVdc0-Vdc
图2为整流器五电平工作状态,表1中的五种矢量对应图中五个电平,其中, 的具体开关状态选择根据空间矢量调制策略的扇区划分以及开关作用顺序来进行设定。
的具体开关状态选择根据空间矢量调制策略的扇区划分以及开关作用顺序来进行设定。
根据图1中的拓扑结构,在不考虑线路和滤波电感 内阻的情况下,根据基尔霍夫定律,可得
内阻的情况下,根据基尔霍夫定律,可得
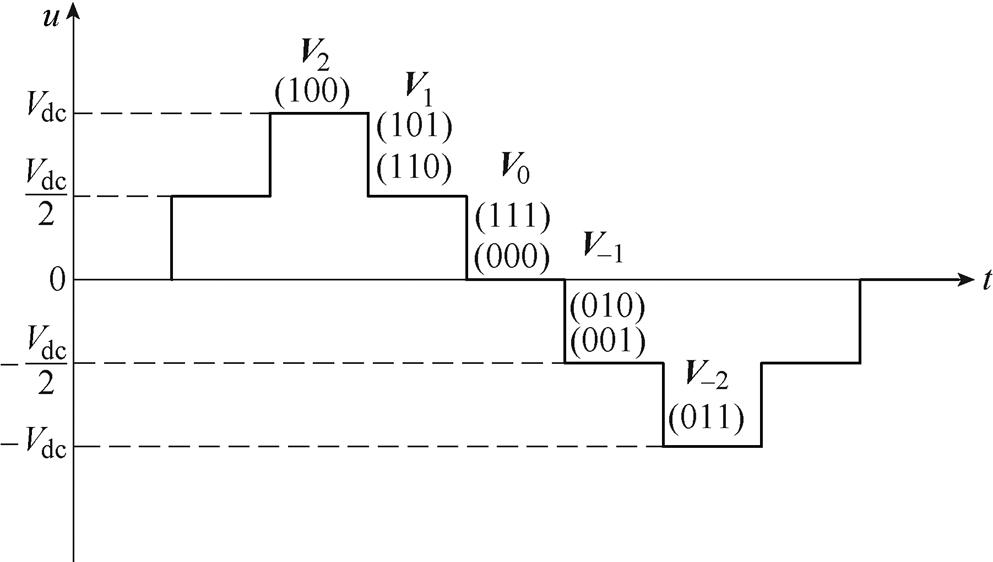
图2 整流器五电平工作状态
Fig.2 Rectifier five-level working state
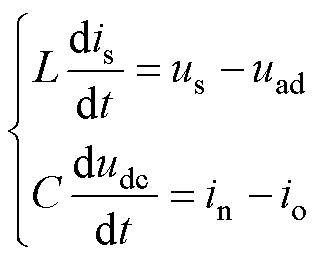 (9)
(9)
由于单相系统所得到的网侧电压与网侧电流均为标量,无法直接进行坐标变换。为了生成对系统精确控制的电压、电流矢量,需要构建一个滞后实际值 的电压电流虚拟量。将虚拟量与实际值叠加即可得到网侧电压与网侧电流矢量。
的电压电流虚拟量。将虚拟量与实际值叠加即可得到网侧电压与网侧电流矢量。
根据上述方法,网侧电压和网侧电流在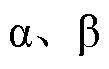 坐标系下可以表示为
坐标系下可以表示为
 (10)
(10)
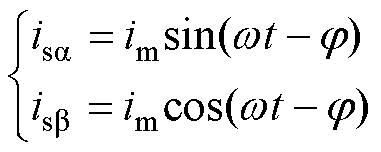 (11)
(11)
式中,usa、usb、isa、isb 分别为网侧电压和网侧电流在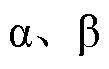 轴的分量;um、im为网侧电压、网侧电流的幅值;j 为网侧电压电流的相位差。
轴的分量;um、im为网侧电压、网侧电流的幅值;j 为网侧电压电流的相位差。
将电流由ab 坐标系进行Park变换得到dq坐标系下的电流为
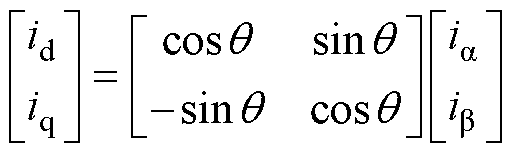 (12)
(12)
由式(9)~式(12),可以分别得出整流器在两种坐标系下的动态方程为
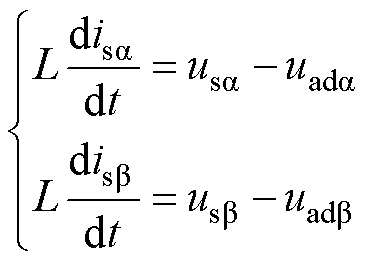 (13)
(13)
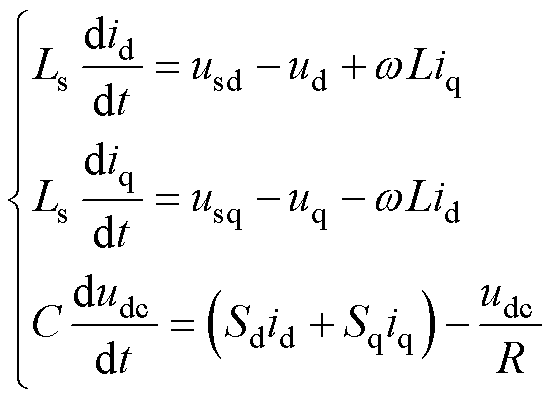 (14)
(14)
式中,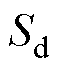 、
、 为d、q坐标轴下数学模型的输入控制变量;
为d、q坐标轴下数学模型的输入控制变量;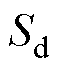 用于控制变流器直流侧电压
用于控制变流器直流侧电压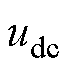 ,
, 控制无功电流
控制无功电流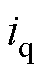 。
。
2.1.1 滑模控制设计
滑模控制的思想是根据系统当前状态的偏差及其各阶导数有规律地改变控制律,使系统快速从初始状态到达滑模面,并在滑模面上按照预期的运动轨迹做滑动模态运动,而电压外环的作用是使直流侧的实际电压值能跟踪给定电压值。因此可将滑模面s设计为
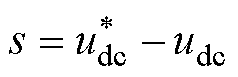 (15)
(15)
对式(15)求导得
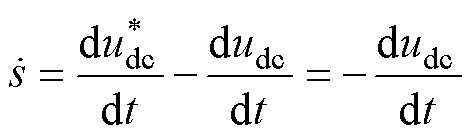 (16)
(16)
根据式(14)和式(16)可得
为了保证直流电压能从任意初始状态运动到滑模面,且拥有良好的运动性能和误差范围,需要选用合适的趋近律。本文在设计时选取幂次趋近律作为滑动模态趋近律,即
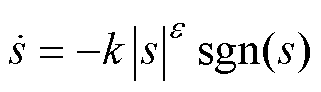 (18)
(18)
式中,k、e 为幂次趋近律系数,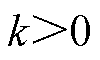 ,
,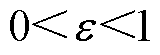 。
。
通过选取一组合适的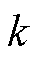 、
、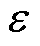 使系统能更快地进入滑模面。结合式(17)、式(18)可得
使系统能更快地进入滑模面。结合式(17)、式(18)可得
在dq坐标系下,式(8)中输入电压可以表示为
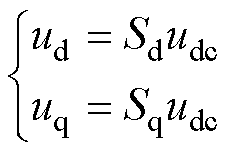 (20)
(20)
当系统达到稳态时有![]() ,无功分量
,无功分量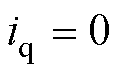 ,
,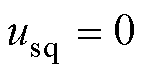 ,将其代入式(14)可得
,将其代入式(14)可得
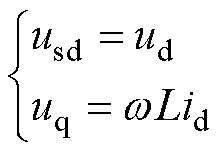 (21)
(21)
将式(20)代入式(21)有
 (22)
(22)
将式(22)代入式(19),可得内环参考电流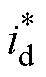 为
为
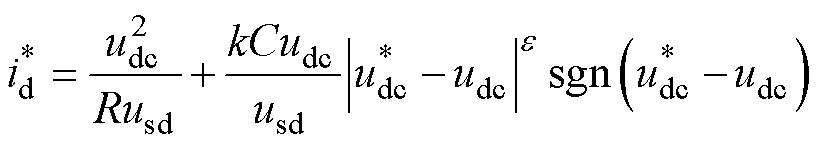 (23)
(23)
2.1.2 存在性证明
在滑模面附近的点根据运行状态的不同分为三类,如图3所示。
(1)运动到滑模面附近,从滑模面某一点穿越过去,称之为常点,如图3中A点所示。
(2)运动到滑模面附近,从某一侧背离滑模面,称之为起点,如图3中B点所示。
(3)运动到滑模面附近,从某一侧趋向于滑模,称之为止点,如图3中C点所示。

图3 滑模面上点的三种状况
Fig.3 Three conditions of points on the sliding surface
当滑模面的一定区域内所有的点都是止点时,说明该区域的点能构成滑动模态运动。只有当该滑动模态区域存在时,滑模控制才满足控制的要求。为此则需满足
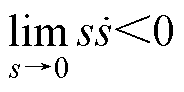 (24)
(24)
根据式(15)和式(18),当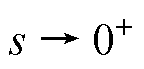 时有
时有 、
、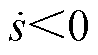 ,此时满足
,此时满足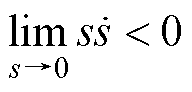 ;当
;当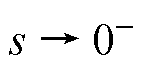 时有
时有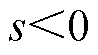 、
、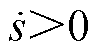 ,此时也满足
,此时也满足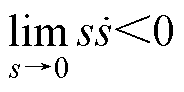 。
。
2.2.1 目标函数设计
传统模型预测在一个周期内仅采用一个开关矢量,控制精度不足,导致稳态性能差,电流谐波畸变率高。同时开关频率不固定,影响开关管使用寿命。本文将空间矢量调制技术与模型预测算法结合来解决上述问题。
首先,对式(13)进行离散化得
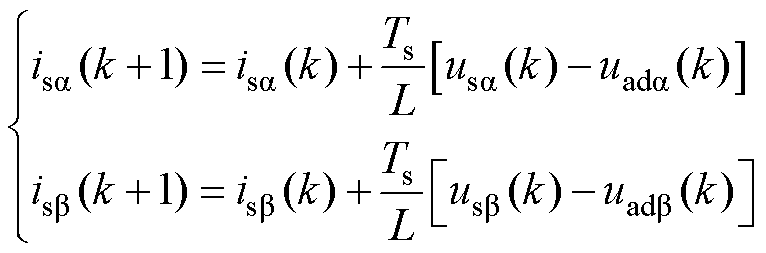 (25)
(25)
为了减小实际系统中硬件采样和计算过程中产生的延迟误差,这里采用无差拍控制,使用k+2时刻的电流值进行计算完成系统控制。
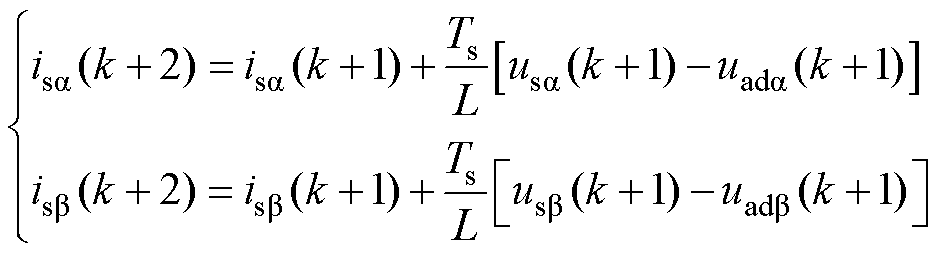 (26)
(26)
设目标函数为
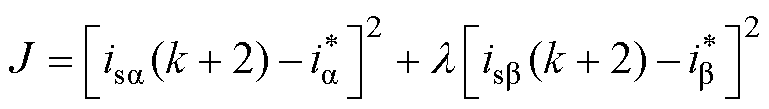 (27)
(27)
式中,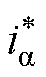 、
、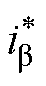 为参考电流在k+2时刻的a、b 轴分量;
为参考电流在k+2时刻的a、b 轴分量;
l 为权重系数。
根据面积等效原理引入空间矢量调制,可以在一个开关周期内应用多种矢量状态,从而达到精确跟踪的目的。图4为单矢量作用与多矢量作用的电流对比。可以看出,当一个周期仅作用一种开关状态时,电流难以精确跟踪给定值,开关频率不固定;当一个周期内作用多矢量时,电流能更好地跟踪给定电流。
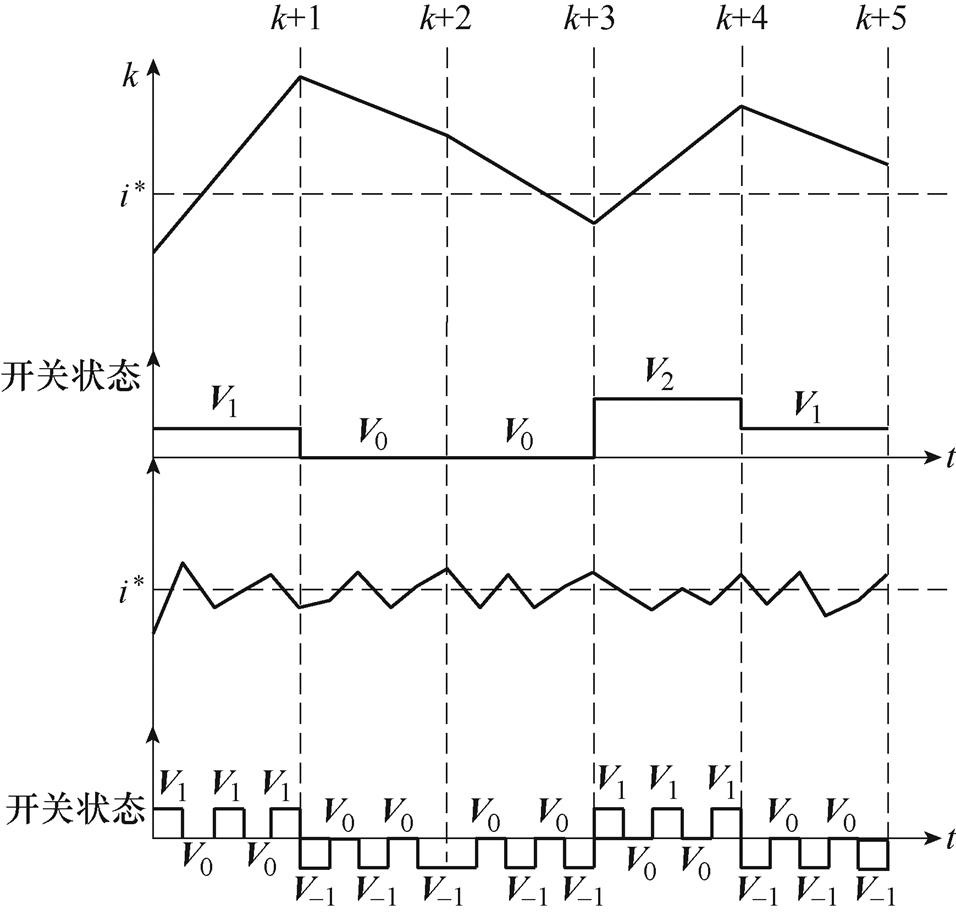
图4 单矢量作用与多矢量作用电流对比
Fig.4 Single vector action and multi-vector action current comparison chart
2.2.2 引入空间矢量调制
图5给出了基于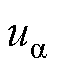 的SVPWM区域矢量划分情况。根据参考电压所在扇区的不同,可以选择不同的开关矢量进行电压合成。
的SVPWM区域矢量划分情况。根据参考电压所在扇区的不同,可以选择不同的开关矢量进行电压合成。
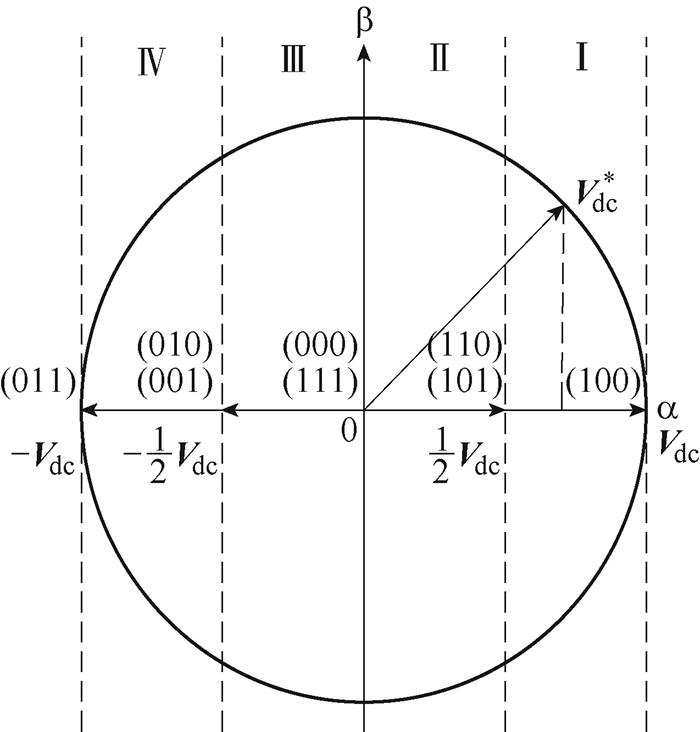
图5 电压矢量区间
Fig.5 Voltage vector interval
根据表1可以看出,小矢量和零矢量存在冗余矢量。为了保证耦合电感电流平衡、优化开关频率,在进行矢量合成时,考虑以下几点:
(1)每次开关状态变化仅有一对桥臂发生变化。
(2)在一个开关周期内,开关状态的作用顺序是轴对称的。
(3)小矢量的两冗余矢量作用时间相同。
在满足以上三个条件的情况下进行矢量作用时间和作用顺序的设计。以第Ⅰ扇区为例,矢量作用顺序为V1+→V2→V1-→V2→V1+。上述作用顺序中V1+和V1-代表对ubc作用效果相反的冗余矢量。具体作用矢量为(101)→(100)→(110)→(100)→(101)。作用时间为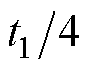 →
→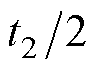 →
→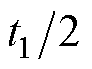 →
→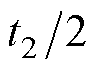 →
→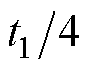 。
。
根据伏秒平衡原则有
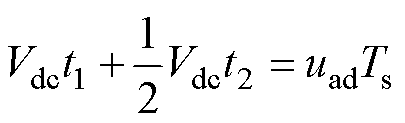 (28)
(28)
其中
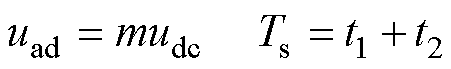
式中,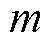 为调制函数;t1、t2为矢量V1、V2的作用时间;Ts为PWM开关周期。
为调制函数;t1、t2为矢量V1、V2的作用时间;Ts为PWM开关周期。
将式(26)、式(28)代入式(27),由于b 轴分量为0,因此取l=0。可得
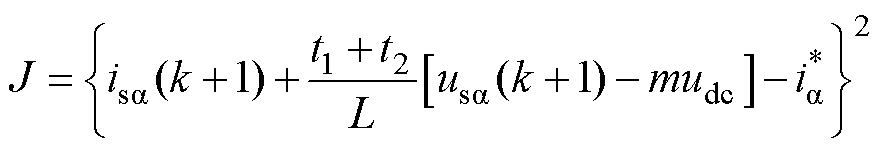 (29)
(29)
由式(29)可以看出,合适的调制函数可以使目标函数达到最小。
联立式(26)~式(29),求目标函数J对时间t1的偏导,可以求出k+1时刻的最佳调制函数为
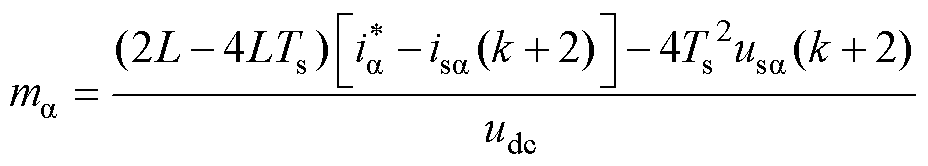 (30)
(30)
该单相五电平PWM整流器外环采用滑模控制,内环采用改进型模型预测。滑模外环对系统参数不敏感,能有效降低因系统参数的改变带来的扰动。改进型模型预测内环能够有效地固定开关频率,提高稳态电流波形,降低电流谐波含量。为了保证滑模外环与模型预测内环在同一坐标系下运算,对滑模输出参考电流进行坐标变换,系统整体控制系统如图6所示。
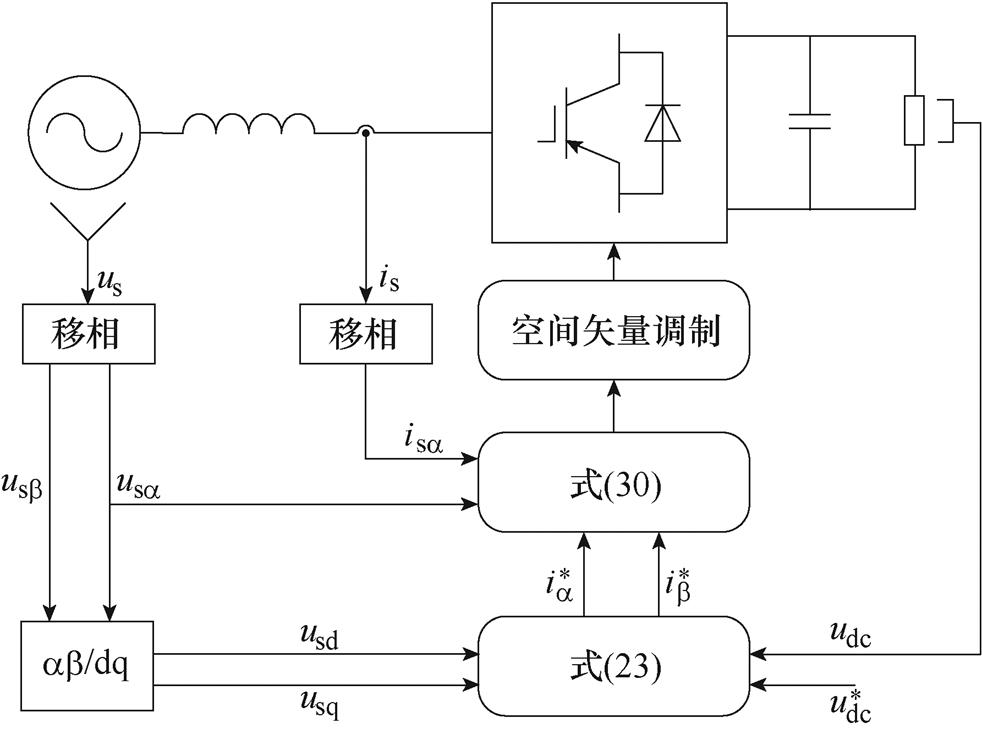
图6 滑模模型预测控制系统
Fig.6 Sliding mode model predictive control system diagram
为了证明SMMPC算法的正确性和有效性,首先在Matlab/Simulink中搭建了基于单相五电平PWM整流器的传统PIMPC算法和SMMPC算法仿真,仿真系统参数见表2。
表2 仿真系统参数
Tab.2 Simulation system parameters

参 数数 值 网侧电压幅值us/V47 直流侧给定电压68 网侧输入电感Ls/mH2.7 耦合电感自感L1, L2/mH3 耦合电感互感M/mH3 直流侧支撑电容C/mF4.6 直流侧负载R/W11.7 开关频率f/kHz1
图7为采用SMMMPC时的整流器输入电压波形。图8为两种不同控制算法在不同工况下的直流侧电压波形。图8a为启动过程中的输出电压波形,可以看出两种算法最终都能到达给定电压。滑模模型预测能够更快地到达稳定状态;图8b为给定电压由68V突增到78V时两种控制策略的直流侧电压波形,可以看出,当采用PIMPC时,电压经过一段时间才达到稳定状态,而采用SMMPC时,输出电压很快就到达稳态值;图8c为负载突增时的输出电压波形,电阻由17.5W 变成11.7W。可以看出,采用PIMPC时输出电压有较大的电压跌落,经过较长时间的调整重新到达稳定值,而采用SMMPC时输出电压几乎无电压跌落。从仿真结果来看,SMMPC的动态性能和抗扰动性能均优于PIMPC,可以大大减少系统调节所需的时间。
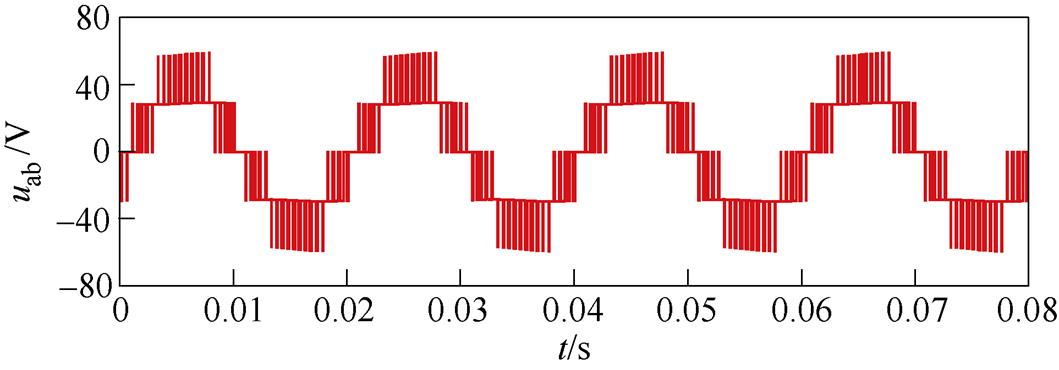
图7 输入电压波形
Fig.7 Input voltage waveform
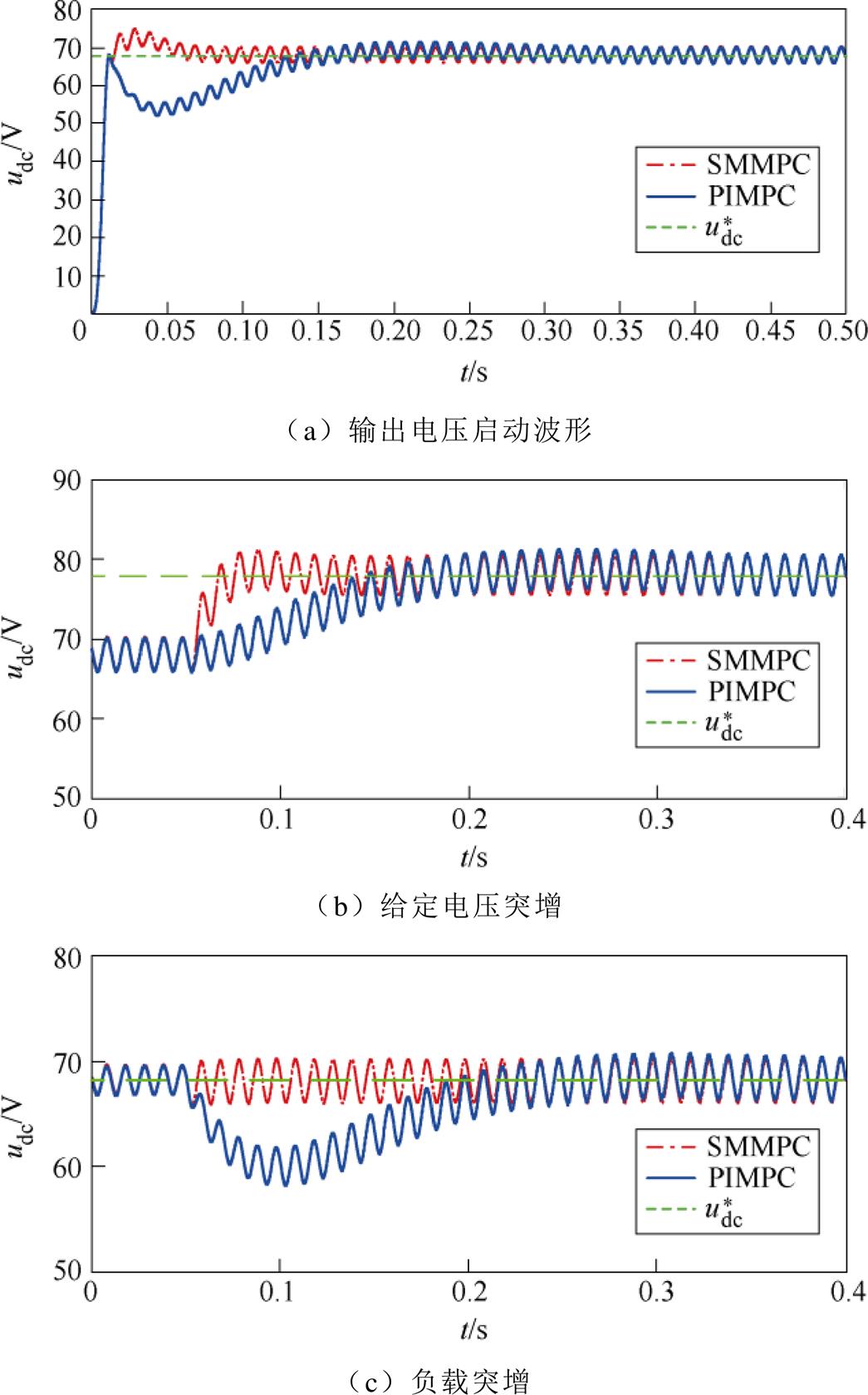
图8 不同工况下两种控制策略的直流侧电压波形
Fig.8 DC side voltage waveforms of two control strategies under different working conditions
图9为两种算法在系统达到稳态时的网侧电压电流波形。在两种算法下网侧电压和电流均能保持一致,实际系统运行时能使j =0°。
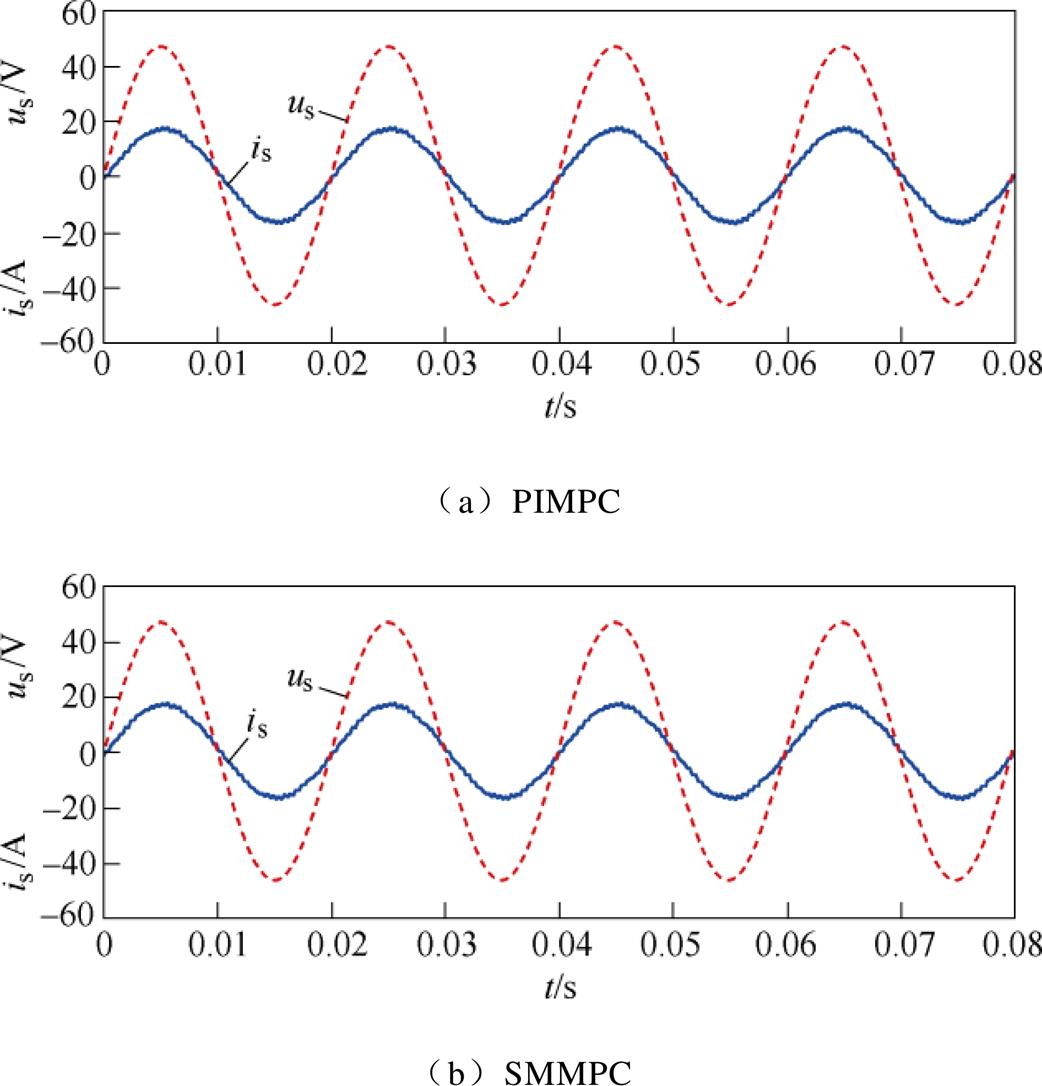
图9 稳态下网侧电压电流波形
Fig.9 Waveforms of grid-side voltage and current in steady state
图10为两种控制算法的快速傅里叶变换(Fast Fourier Transform, FFT)分析结果。PIMPC的总谐波畸变率(Total Harmonic Distortion, THD)为3.27%,SMMPC的THD为3.19%。可以看出,SMMPC谐波含量更低,且能够有效地提高动态性能。
为了进一步验证算法的优越性,搭建了小功率实验平台。实验具体参数与仿真参数一致。图中序号①~ 分别为上位机、直流负载、网侧电源、示波器、dSPACE、转接板、主电路与驱动板、耦合电感、网侧滤波电感、采样电路、直流电源。
分别为上位机、直流负载、网侧电源、示波器、dSPACE、转接板、主电路与驱动板、耦合电感、网侧滤波电感、采样电路、直流电源。
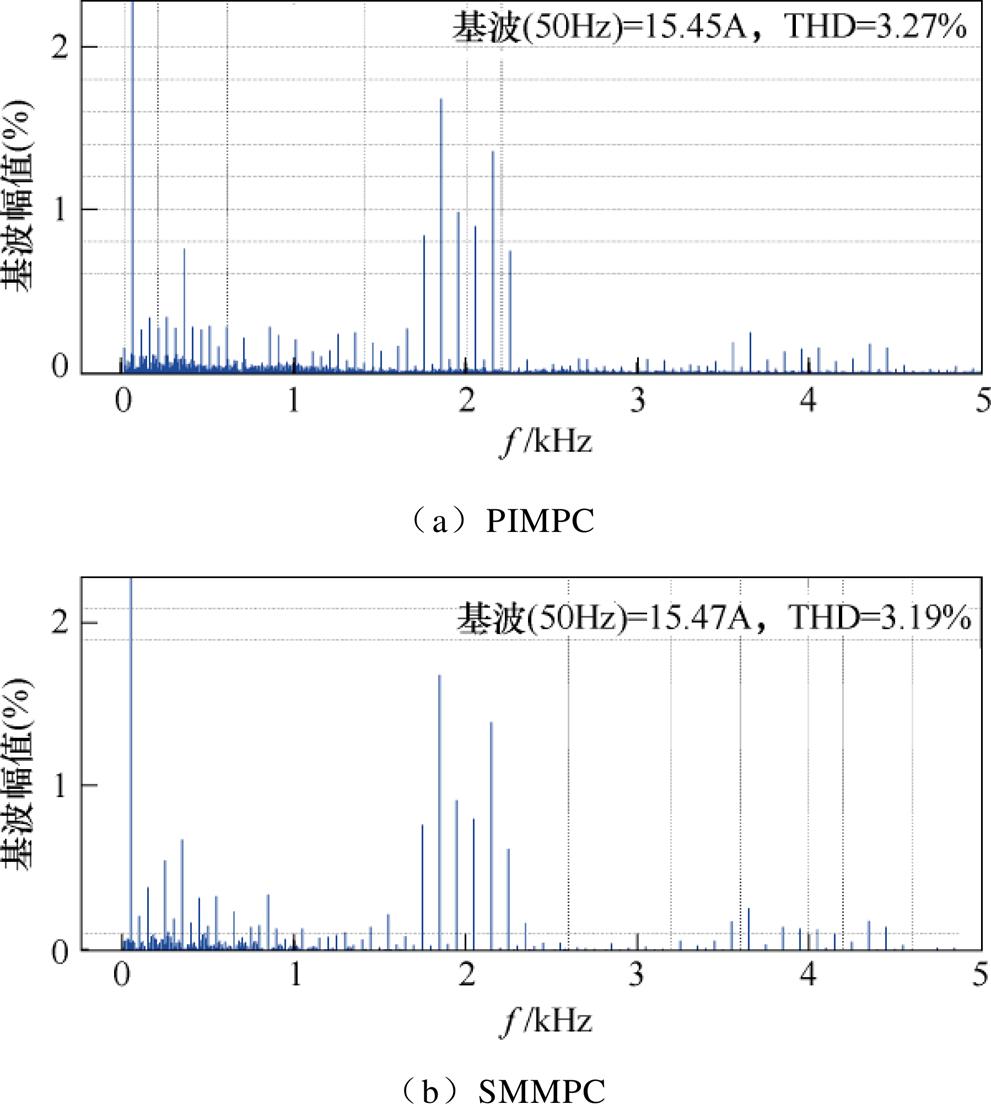
图10 仿真网侧电流THD
Fig.10 THD of simulation grid-side current

图11 实验平台
Fig.11 Experiment platform
图12给出了整流器在PIMPC和SMMPC下稳态时网侧电压电流的波形。由图可以看出,两种情况下的电压与电流相位相同,说明两种算法都能实现单位功率因数运行。
图13给出分别在PIMPC和SMMPC下启动过程的直流侧电压和网侧电流波形。由图可以出,两种控制策略到达稳态所需的时间分别为180ms和40ms,两者拥有近似的冲激电压与冲击电流,SMMPC策略下的启动速度更快,电压波形更加平滑。
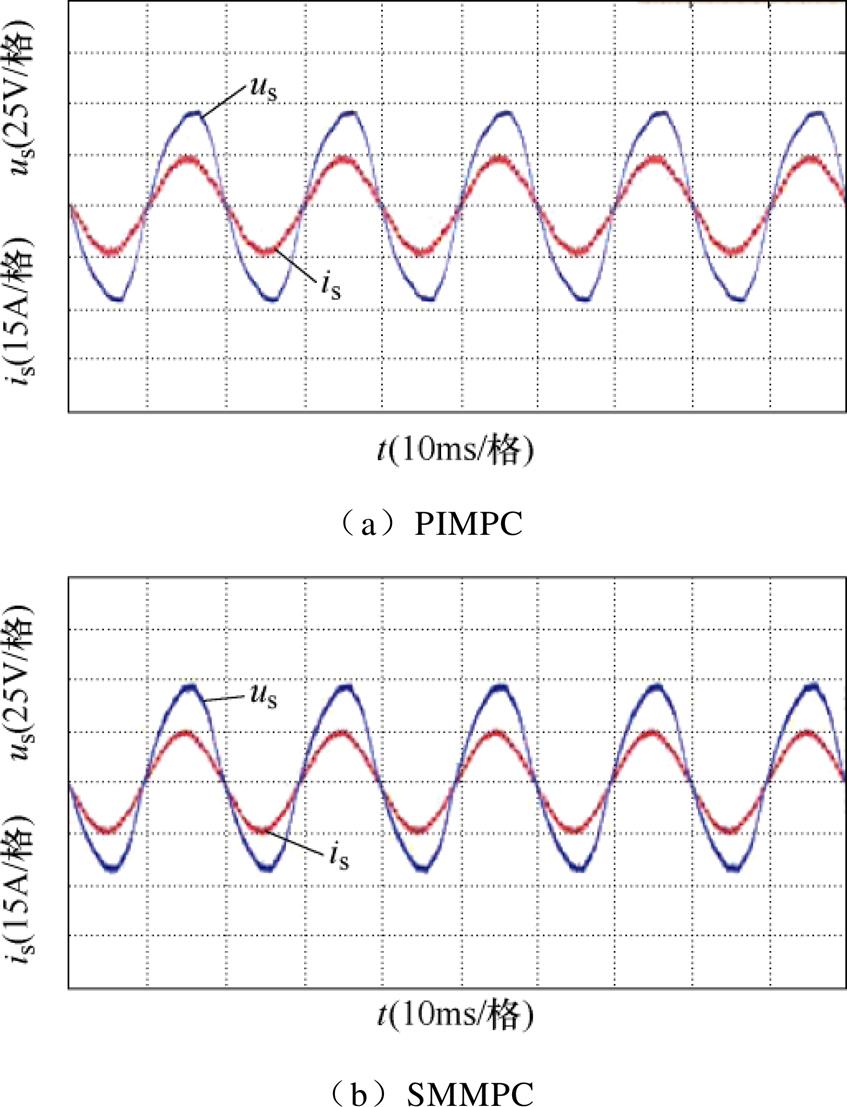
图12 稳态时网侧电压电流波形
Fig.12 Grid-side voltage and grid-side current waveforms in steady state
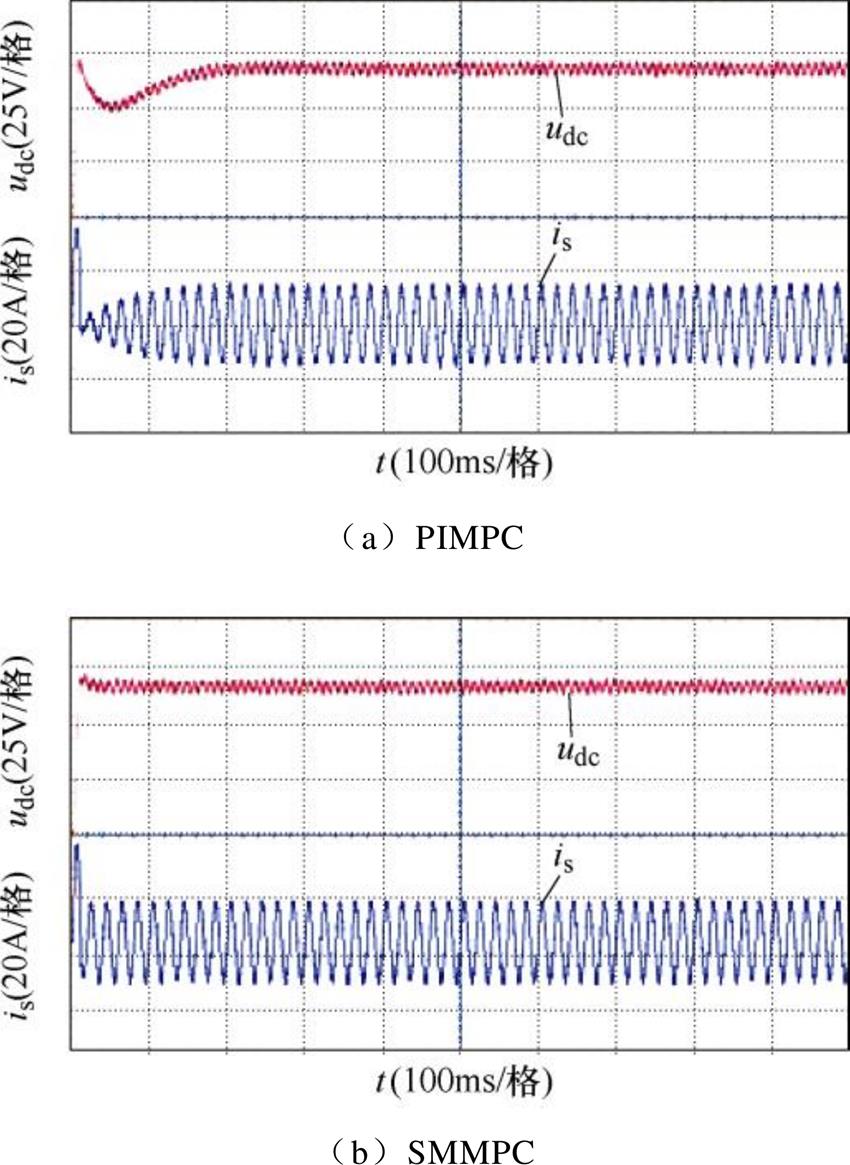
图13 启动过程直流输出电压和网侧电流波形
Fig.13 DC side output voltage and grid side current waveforms during startup
图14给出了两种控制策略在给定电压突变下的实验结果。实验中给定电压由68V突变为78V。可以看出,采用PIMPC策略时,直流电压与网侧电流经过110ms重新到达给定值;采用SMMPC策略时,直流电压经过40ms重新到达给值,网侧电流经过20ms即可到达新稳定状态。从实验结果可以看出,SMMPC在给定电压突变时,网侧电流和直流侧电压能迅速到达新稳定状态。说明SMMPC策略在电压给定突变时比PIMPC拥有更好的动态性能。
图15给出了两种算法在负载突变时的实验波形。在实验中,负载电阻由17.5W 变成11.7W,可以看出,当采用PIMPC时电压经过140ms的跌落后,重新回到给定值,网侧电流也经过同样时间到达新稳定状态;当采用SMMPC时直流电压和网侧电流能几乎无调节过程,迅速到达稳定状态。说明SMMPC策略在负载突变时具有更好的抗扰动能力。
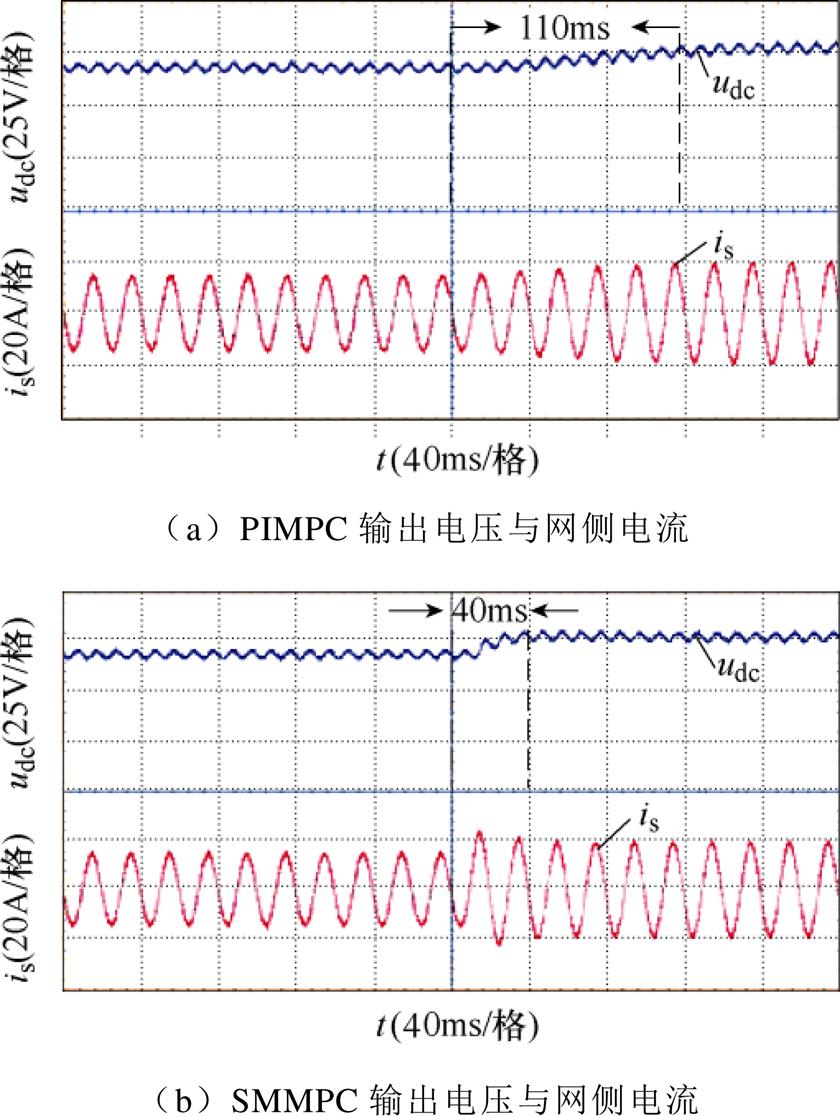
图14 给定电压突增实验波形
Fig.14 Experimental waveforms of a given voltage surge
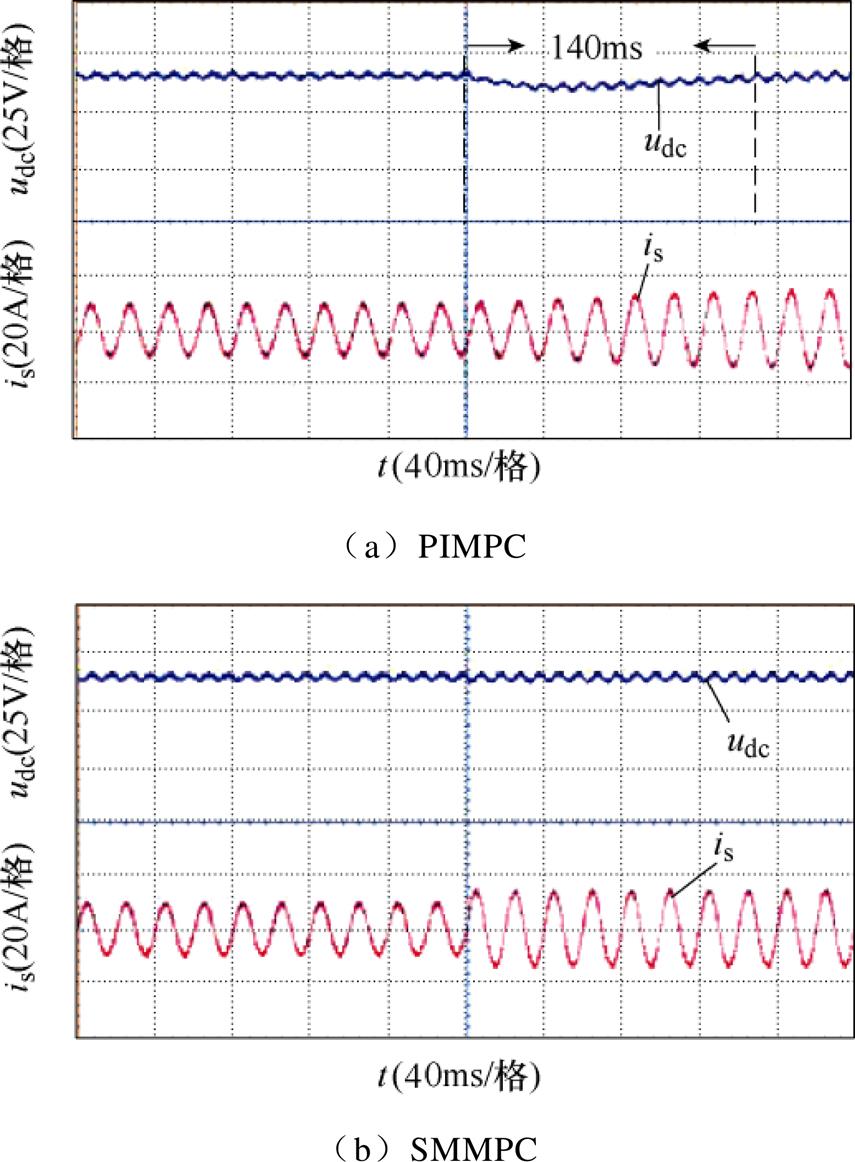
图15 负载突变实验波形
Fig.15 Experimental waveforms of sudden load change
本文针对传统的PIMPC算法出现的问题,设计了SMMPC策略。传统的PIMPC算法采用PI控制,在控制回路中生成参考电流,但在系统遇到扰动时,根据系统参数设计的PI参数无法自动调整,导致动态性能变差。滑模控制优秀的动态响应能力及对系统参数的不灵敏性恰好弥补了上述缺陷。与外环PI内环模型预测控制策略相比,本文所提出的控制策略具有更快的动态响应速度、更小的动态电压降落和更强的抗干扰能力。本文所提的滑模模型预测控制策略也可以为其他整流器的控制提供借鉴。
参考文献
[1] 徐殿国, 李彬彬, 周少泽. 模块化多电平高压变频技术研究综述[J]. 电工技术学报, 2017, 32(20): 104-116.
Xu Dianguo, Li Binbin, Zhou Shaoze. Over view of the modular multilevel converter based high voltage motor drive[J]. Transactions of China Electro- technical Society, 2017, 32(20): 104-116.
[2] 李永东, 徐杰彦, 杨涵棣, 等. 多电平变换器拓扑结构综述及展望[J]. 电机与控制学报, 2020, 24(9): 1-12.
Li Yongdong, Xu Jieyan, Yang Handi, et al. Overview and prospect of multilevel converter topology[J]. Electric Machines and Control, 2020, 24(9): 1-12.
[3] Xu Qianming, Ma Fujun, He Zhixing, et al. Analysis and comparison of modular railway power conditioner for high-speed railway traction system[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 6031-6048.
[4] Luo Rui, He Yingjie, Liu Jinjun. Research on the unbalanced compensation of delta-connected cascaded H-bridge multilevel SVG[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8667-8676.
[5] 王付胜, 郑德佑, 杜成孝, 等. 一种具有漏电流抑制能力的ANPC 型五电平调制策略及其载波实现方法[J]. 中国电机工程学报, 2018, 38(24): 7326-7337.
Wang Fusheng, Zheng Deyou. Du Chengxiao, et al. An ANPC five-level modulation strategy with leakage current suppression and its carrier implementation method[J]. Proceedings of the CSEE, 2018, 38(24): 7326-7337.
[6] Hu Yihua, Gan Chun, Cao Wenping, et al. Split converter-fed SRM drive for flexible charging in EV/ HEV applications[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6085-6095.
[7] 杨国良, 张玉娜, 陈泰余, 等. 单相升降压型五电平逆变器拓扑及控制[J]. 电工技术学报, 2019, 34(14): 2922-2935.
Yang Guoliang, Zhang Yuna, Chen Taiyu, et al. Topology and control strategy of a single-phase buck- boost five-level inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2922-2935.
[8] 张琦, 李江江, 孙向东, 等. 单相级联七电平逆变器拓扑结构及其控制方法[J]. 电工技术学报, 2019, 34(18): 3843-3853.
Zhang Qi, Li Jiangjiang, Sun Xiangdong, et al. Topology and control method of single-phase cascaded seven-level inverter[J]. Transactions of China Electro- technical Society, 2019, 34(18): 3843-3853.
[9] Li Zixin, Wang Ping, Li Yaohua, et al. A novel single-phase five-level inverter with coupled indu- ctors[J]. IEEE Transactions on Power Electronics, 2012, 27(6): 2716-2725.
[10] Zhao Lu, Ge Qiongxuan, Li Zixin, et al. A novel single-phase five-level rectifier with coupled indu- ctors[C]//International Conference on Electrical Machines and Systems, Busan, Korea, 2013: 26-29.
[11] 朱艺锋, 岳豪, 赵海龙, 等. 含耦合电感的四管五电平整流器模型预测控制[J]. 电网技术, 2021, 45(2): 768-754.
Zhu Yifeng, Yue Hao, Zhao Hailong, et al. Model predictive control of four-tube five-level rectifier with coupled inductors[J]. Power System Technology, 2021, 45(2): 768-754.
[12] Luca T, Zanchetta P, Watson A, et al. Modulated model predictive control for a three-phase active rectifier[J]. IEEE Transactions on Industry Appli- cations, 2015, 51(2): 1610-1620.
[13] Zhang Yongchang, Peng Yubin. Model predictive current control with optimal duty cycle for three- phase grid-connected AC/DC converters[C]//IEEE Electronics and Application Conference and Exposition (PEAC), Shanghai, China, 2014: 837-842.
[14] 邓知先, 宋文胜, 曹梦华. 单相PWM整流器模型预测电流控制算法[J]. 中国电机工程学报, 2016, 36(11): 2996-3004.
Deng Zhixian, Song Wensheng, Cao Menghua. A model predictive current control scheme for single- phase PWM rectifiers[J]. Proceedings of the CSEE, 2016, 36(11): 2996-3004.
[15] Gregor R, Barrero F, Toral S L, et al. Predictive-space vector PWM current control method for asymmetrical dual three-phase induction motor drives[J]. IET Electric Power Applications, 2010, 4(1): 26-34.
[16] 宋智威, 熊成林, 黄路, 等. 基于牛顿插值的单相整流器功率前馈无差拍控制[J]. 电网技术, 2018, 42(11): 3623-3629.
Song Zhiwei, Xiong Chenglin, Huang Lu, et al. Power feedback-forward and deadbeat control of single- phase rectifier based on Newton interpolation[J]. Power System Technology, 2018, 42(11): 3623-3629.
[17] 杨立永, 杨烁, 张卫平, 等. 单相PWM整流器改进无差拍电流预测控制方法[J]. 中国电机工程学报, 2015, 35(22): 5842-5850.
Yang Liyong, Yang Shuo, Zhang Weiping, et al. The improved deadbeat predictive current control method for single-phase PWM rectifiers[J]. Proceedings of the CSEE, 2015, 35(22): 5842-5850.
[18] Li Shihua, Zhou Mingming, Yu Xinghuo. Design and implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 1879-1891.
[19] 李景灏, 吴爱国. 基于离散趋近律与无差拍双闭环结构的单相LCL型PWM整流器控制策略[J]. 电工技术学报, 2021, 36(6): 1290-1303.
Li Jinghao, Wu Aiguo. A double closed-loop control method for single-phase PWM rectifiers with LCL filter based on discrete reaching law and deadbeat algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1290-1303.
[20] 吴璟玥. 单相PWM整流器新型控制策略在车载充电器中的研究[D]. 广州: 华南理工大学, 2018.
Sliding Mode Model Predictive Control of Single-Phase Five-Level Rectifier
Abstract Five level rectifier is widely used in high voltage power transmission and transformation because of its high power output capacity and low harmonic current at the grid side. The traditional model with PI control has poor dynamic performance and poor disturbance resistance when predicting the outer ring. Therefore, this paper proposes a sliding-mode model-predictive control (SMMPC) algorithm. Firstly, the working principle of the rectifier is analyzed, and the mathematical models for outer ring and inner ring control are established. Then, a sliding mode model predictive control algorithm is designed in detail for the rectifier. Both simulation and experimental results show that the sliding mode model prediction algorithm not only retains the advantages of fixed switch frequency and small delay error, but also has faster dynamic response and stronger anti-disturbance ability than PI model prediction control.
keywords:Five-level rectifier, coupled inductance, sliding mode control, model predictive control
DOI: 10.19595/j.cnki.1000-6753.tces.210197
中图分类号:TM461
朱艺锋 男,1979年生,博士,副教授,研究方向为功率变流器的建模与控制。E-mail: zyfny@hpu.edu.cn
赵海龙 男,1998年生,硕士研究生,研究方向为功率变流器的建模与控制。E-mail: zhaohailong0829@163.com(通信作者)
收稿日期 2021-02-05
改稿日期 2021-07-16
国家自然科学基金项目(U1504518, U1804143)、河南省矿山电力电子装置与控制创新型科技团队项目(CXTD2017085)和河南省科技攻关计划项目(192102210228)资助。
(编辑 陈 诚)