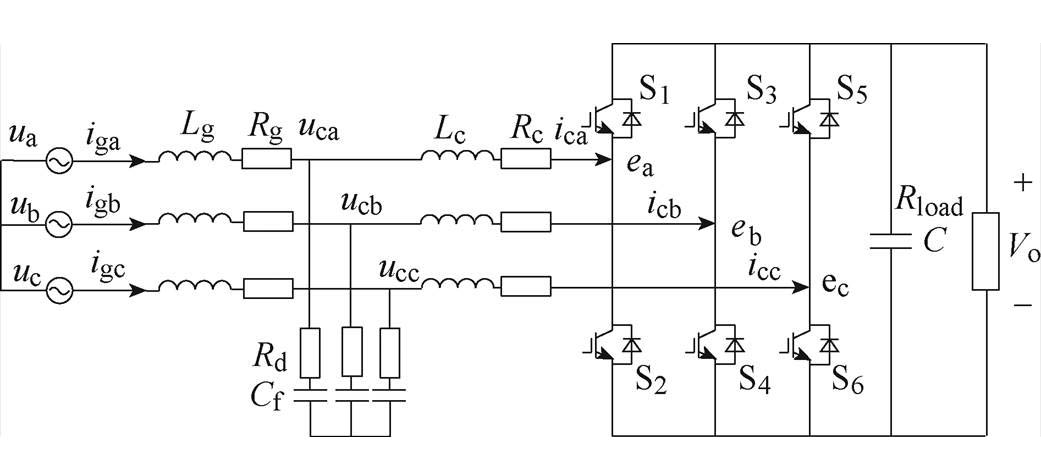
图1 虚拟同步整流器电路拓扑
Fig.1 Topology of virtual synchronous rectifier
摘要 虚拟同步机技术可使电力电子变换器表现出类似同步电机的阻尼和惯量特性,从而促进电源或负荷与电网的友好交互。然而,因实际电网运行工况较为复杂,电网电压畸变将导致虚拟同步变换器的并网电流发生严重畸变。为此,该文提出一种适用于畸变电网下的虚拟同步整流器电流谐波抑制方法。首先,运用阻抗分析法,研究电网谐波电压对虚拟同步整流器并网电流的影响机制;其次,基于阻抗分析,提出一种电网谐波电压前馈的方法,通过增大谐波频率处的网侧阻抗,削弱电网谐波电压对并网电流的影响,实现对电流谐波的抑制;最后,采用小信号分析法,研究前馈因子的取值方法,并评估系统的稳态与动态性能。仿真和实验结果证明了该研究方法的正确性和有效性。
关键词:电网电压畸变 虚拟同步整流器 谐波抑制 阻抗分析 前馈因子
随着经济和科技的迅速发展,新能源发电装机比例不断上升[1]。然而,在带来电能的同时,新能源发电技术因引入大量高频、低惯性的电力电子装置而给传统电网造成了较大冲击[2]。由于虚拟同步机能够模拟同步电机的阻尼特性,为电网提供适度的惯量支撑,因此该技术受到了广泛关注。
虚拟同步机技术是将电力电子装置按照同步电机的数学模型进行建模和控制的一种新兴变换器控制方法。文献[3-4]提出了电流型虚拟同步机,通过构造可模拟同步电机定子电气特性的电流环指令来模拟同步电机的转子惯性、一次调频特性及励磁调节机理。然而电流型虚拟同步机在电路外特性上等效于受控电流源,无法在弱电网下提供电压支撑。为了克服这个问题,文献[5]提出了电压型虚拟同步机方案。文献[6]将虚拟同步机技术应用于三相整流器中,从负荷侧实现了对电网的支撑。文献[7-9]研究了多虚拟同步机并联系统,通过建立小信号模型,分析了重要控制参数对并联系统稳定性的影响,为扩充基于虚拟同步机的变换器系统的容量提供了理论依据。
然而,以上对虚拟同步机的研究多集中于理想电网情形。针对弱电网情形,文献[10]提出了一种自适应无功功率补偿策略,减小了虚拟同步机因输出功率耦合而引起的功率控制误差。文献[11]从序阻抗分析的角度,指出相较于直流侧电容虚拟惯性控制的负荷变换器,负荷虚拟同步机因中低频段与电网的阻抗特性基本一致,在弱电网中,具有更好的运行稳定性。针对电网不平衡和故障情形,文献[12]采用复数滤波器分离虚拟同步整流器控制中的正负序分量,结合虚拟阻抗法,改变负序电流的大小与相位,减小了不平衡电网工况下直流侧电压的脉动。文献[13]提出了一种不平衡电压灵活补偿策略,运用虚拟同步机与电网友好交互的特性,充分利用并网变换器的剩余容量,改善了不平衡电网下公共连接点处的电能质量。更多情形下的实际应用中,受非线性负载的影响,电网中总含有一些低次谐波,虚拟同步机将运行于畸变电网。此时,若不对控制策略做出改进,则虚拟同步机并网电流的畸变率很有可能超出并网标准,产生较大的谐波污染。对于传统变换器在畸变电网下的谐波抑制,目前已有较为成熟的控制方法。文献[14-16]采用多谐振控制技术,实现了对变换器不同次谐波电流的抑制,然而其控制过程中的计算量较大,将给CPU带来很大的负担。文献[17-20]采用重复控制技术,通过改变基波及谐波频率处的控制环路增益,实现对电流谐波分量的无静差控制。文献[21-22]采用电网电压前馈策略,通过在变换器调制波中引入电网电压分量,减弱电网电压对并网电流的影响,从而抑制电流谐波。但由于虚拟同步机控制与常规的电流电压双闭环控制在控制机理、参数设计方面存在较大差异,适用于传统变换器的电流谐波抑制方法难以直接应用于虚拟同步变换器中。
本文首先阐述了虚拟同步整流器的控制原理,进而运用阻抗分析法,研究了电网谐波电压对虚拟同步整流器并网电流的影响。从增加电流谐波频率处网侧阻抗的角度出发,提出了一种基于电网谐波电压前馈的虚拟同步整流器电流谐波抑制方法,并运用小信号分析法,研究了前馈因子的取值,最后评估了系统的稳态与动态性能。仿真和实验结果证明了所提控制方法可有效抑制畸变电网情形下虚拟同步整流器的电流谐波,提升控制品质。
本文研究的虚拟同步整流器采用如图1所示的LCL型滤波的三相全桥拓扑结构。图中,ua、ub、uc为三相输入电压,iga、igb、igc为整流器的网侧电流,ica、icb、icc为变换器侧电流,uca、ucb、ucc为滤波电容支路电压,ea、eb、ec为整流器三相桥臂的中点电压。虚拟同步整流器交流侧采用LCL型滤波方式,Lg和Rg为网侧滤波电感和其附加电阻,Lc和Rc为变换器侧滤波电感和其附加电阻,Cf和Rd为电容支路的滤波电容和阻尼电阻,C为直流侧稳压电容,Rload为直流侧负载电阻,采用的开关器件为6个含反并联二极管的IGBT(S1~S6)。Vo为虚拟同步整流器的输出电压。

图1 虚拟同步整流器电路拓扑
Fig.1 Topology of virtual synchronous rectifier
虚拟同步整流器在整流器的控制中嵌入同步电机的数学模型,从而模拟同步电机的转子惯性和励磁调节机理。同步电机的转矩惯量方程和励磁调节方程分别为
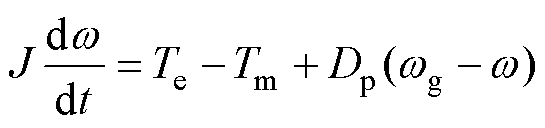 (1)
(1)
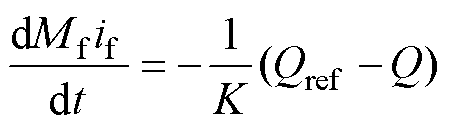 (2)
(2)
式中,J为虚拟惯量;Te为虚拟电磁转矩;Tm为虚拟机械转矩;Dp为虚拟阻尼;w 为虚拟转速;wg为电网角频率;Mfif为虚拟励磁磁链;K为无功调节系数;Qref为无功功率参考值;Q为实际整流器发出的无功功率。进一步地,为充分模拟同步电机的电磁暂态关系,补充为矢量方程的表达形式,即
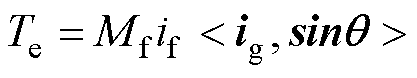 (3)
(3)
式中, 表示矢量的内积运算;
表示矢量的内积运算;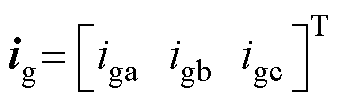 ;
;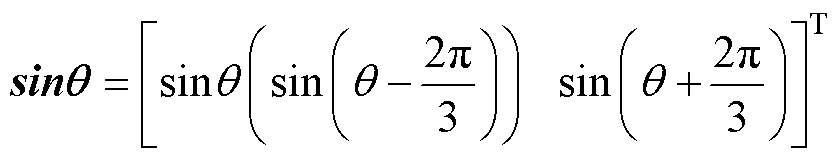 ,θ为虚拟相位。虚拟同步整流器的虚拟内电动势为
,θ为虚拟相位。虚拟同步整流器的虚拟内电动势为
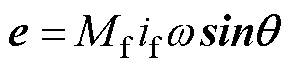 (4)
(4)
式中,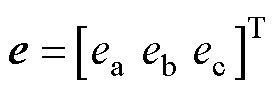 ,
,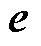 为实际控制中所需的调制波。
为实际控制中所需的调制波。
结合式(5)和式(6)描述的三相整流器的瞬时有功功率P和瞬时无功功率Q,可以实现对三相整流器的虚拟同步控制。
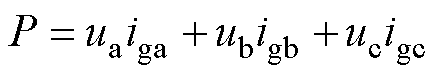 (5)
(5)
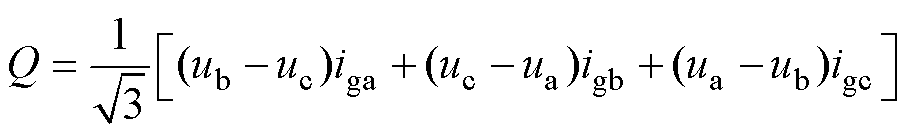 (6)
(6)
为了研究电网谐波电压对虚拟同步整流器的影响,本节对虚拟同步整流器进行阻抗分析。虚拟同步整流器单相支路的s域电路模型如图2所示。
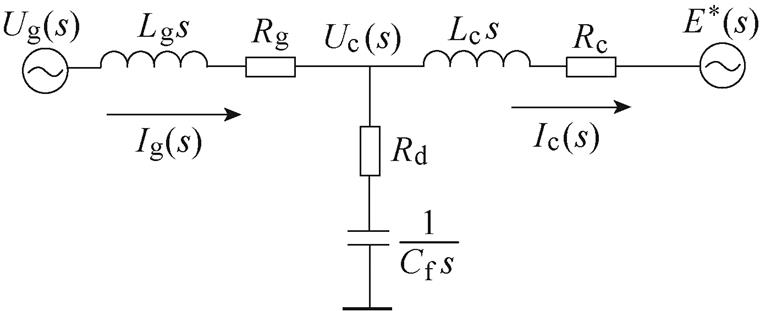
图2 虚拟同步整流器单相s域电路模型
Fig.2 Single phase circuit model of virtual synchronous rectifier in s domain
图2中,Ug(s)、Ig(s)、Ic(s)分别为图1中网侧电压、网侧电流、变换器侧电流的s域表达。考虑PWM增益为1,由虚拟同步机算法得到的指令电压E*(s)即为整流器桥臂中点的等效电压。由图2所示的s域模型,可得
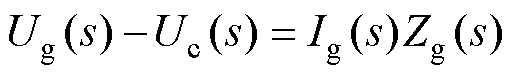 (7)
(7)
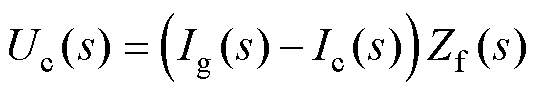 (8)
(8)
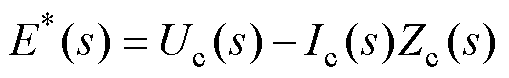 (9)
(9)
式中,Zg(s)=Lgs+Rg;Zf(s)=1/(Cfs)+Rd;Zc(s)=Lcs+Rc。联立式(7)~式(9),可解出网侧电流为
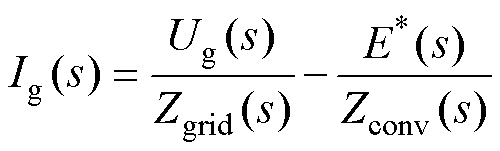 (10)
(10)
式中,Zgrid(s)为网侧阻抗;Zconv(s)为变换器侧阻抗,可分别表示为
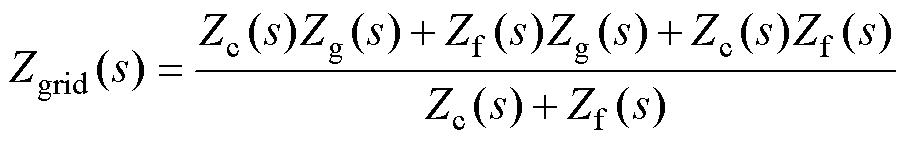 (11)
(11)
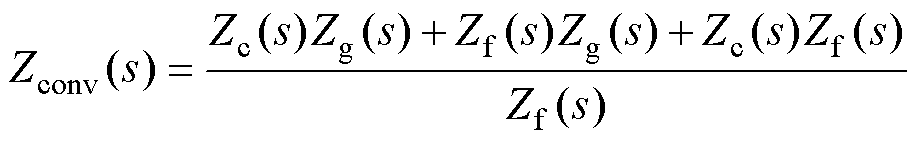 (12)
(12)
由式(10)可知,虚拟同步整流器的网侧电流由两部分组成:一部分由网侧电压和网侧阻抗决定;另一部分由桥臂中点电压和变换器侧阻抗决定。传统的虚拟同步整流器桥臂中点电压由式(4)给出,此时,若虚拟同步整流器运行于畸变电网工况,电网的谐波电压将在网侧阻抗的作用下产生谐波电流。若相应谐波电压频率处的网侧阻抗不够大,则网侧电流的畸变率很可能超出并网标准,产生较大的谐波污染。为了减小电网谐波电压对并网电流的影响,应增加谐波电压频率处的网侧阻抗,同时为了不影响虚拟同步整流器正常输送功率,基波频率处的阻抗应尽可能保持不变。从此角度出发,本文提出了一种电网谐波电压前馈的方法,通过在调制波中注入电网谐波电压,使得桥臂中点电压和变换器侧阻抗产生的电流分量同样包含谐波,以此减小电网谐波电压对网侧电流的影响。
为了实现电网谐波电压的前馈,首先需要提取电网谐波电压。因为电网谐波电压的组成复杂,直接提取谐波分量较为困难,若能有效提取基波分量,再用网侧总电压减去网侧电压的基波分量,便可有效提取网侧谐波电压。本文使用广义二积分器进行电网谐波电压的提取,其由两个积分器级联组成谐振器,如图3所示。

图3 广义二积分器结构框图
Fig.3 The structure of second order generalized integrator
图3中,ui为输入信号,wh为谐振角频率,h为阻尼调节系数,uo1和uo2为两路相互正交的输出信号。由结构框图,可得传递函数为
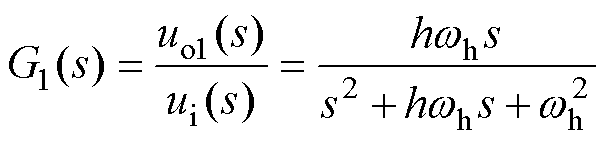 (13)
(13)
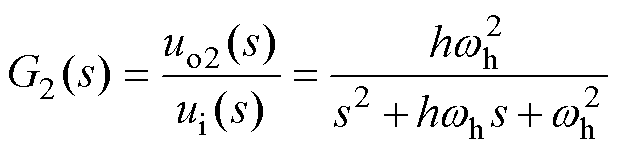 (14)
(14)
由传递函数可知,G1(s)表现出带通滤波特性,其中wh决定中心角频率,h决定带宽。根据上述的电网谐波电压提取思路,可使用广义二积分器先提取电网电压的基波分量。取wh=100p(rad/s),为确定较好的带宽,分别取h为0.1、0.5、1、1.5和2,做出G1(s)伯德图如图4所示。
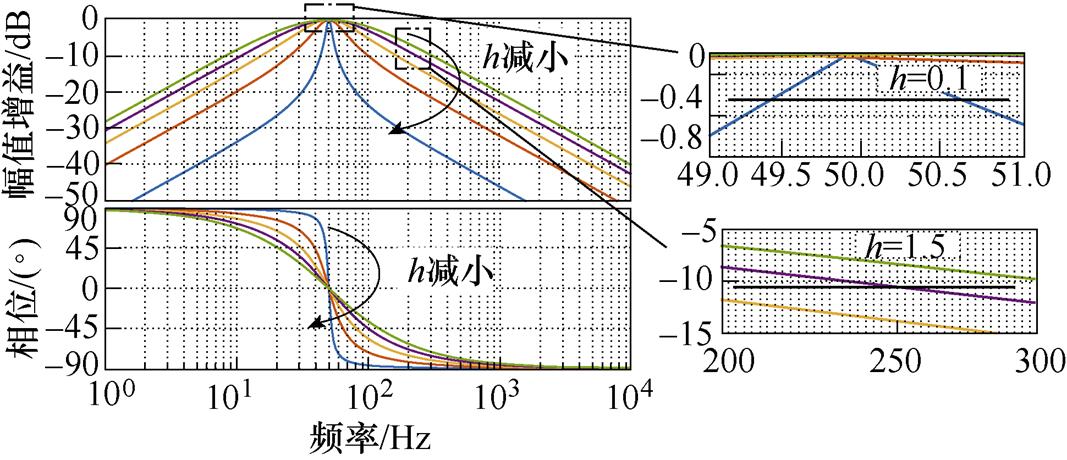
图4 不同h值的G1(s)伯德图
Fig.4 Bode diagram of G1(s) with different h
注意到实际电网电压的频率会发生一定的偏移,虚拟同步整流器在电网发生频率跌落时,具有工作在下垂控制模式给电网提供有功支撑的功能,但此时的电网频率已显著偏离基频,为使得在此种情形下也具有较好的补偿效果,阻尼调节系数不宜取小。结合国家电力系统的标准:规定容量在3 000MW以下的系统,频率允许偏差为 (50±0.5)Hz,当电网电压的基频在49.5~50.5Hz之间发生变化时,希望提取到的电网电压基频信号衰减不超过5%, 以保证后续的控制效果。对应到伯德图中,即49.5~50.5Hz之间,SOGI的 端的幅值增益不小于-0.446dB,当h变化时,以这条直线去截图4所示的伯德图,可得到阻尼调节系数h应大于0.1以保证较好的带宽。同时注意到,SOGI在提取基波信号时,会保留附近频率处一定幅值的谐波次信号,从而使最终提取到的谐波信号产生稍许的衰减,虽然后续运用的比例微分的前馈方式会对这种幅值上的衰减起到补偿效果,但理应在信号的提取过程中尽可能保持较少的信号衰减。在三相电网中,6k±1次的谐波成分较多,因此希望5次谐波的信号可以保持在70%以上,即对应于SOGI的
端的幅值增益不小于-0.446dB,当h变化时,以这条直线去截图4所示的伯德图,可得到阻尼调节系数h应大于0.1以保证较好的带宽。同时注意到,SOGI在提取基波信号时,会保留附近频率处一定幅值的谐波次信号,从而使最终提取到的谐波信号产生稍许的衰减,虽然后续运用的比例微分的前馈方式会对这种幅值上的衰减起到补偿效果,但理应在信号的提取过程中尽可能保持较少的信号衰减。在三相电网中,6k±1次的谐波成分较多,因此希望5次谐波的信号可以保持在70%以上,即对应于SOGI的 端在250Hz处可以提供超过-10.5dB的幅值增益,当h变化时,以这条直线去截所对应的伯德图,可得到阻尼调节系数h应小于1.5。
端在250Hz处可以提供超过-10.5dB的幅值增益,当h变化时,以这条直线去截所对应的伯德图,可得到阻尼调节系数h应小于1.5。
另一方面,阻尼调节系数h将影响SOGI提取信号时的快速性,借助Matlab/Simulink工具,评估这种影响。图5给出了当阻尼调节系数取0.1和1.414时,SOGI的uo1端对电网基波信号的提取结果(换言之,对220cos(wt)的响应情况)。从图中可以发现,当h=0.1时,系统至少需要0.2s以获取完全的电网基波信息;当h=1.414时,系统仅需不足0.02s的时间,即一个电周期之内就可以完全跟随住电网基波信号,在下一个电周期就可以发挥出较好的谐波抑制效果。其余h取值情形下,SOGI的响应时间见 表1。综合考虑,本文选取h=1.414。
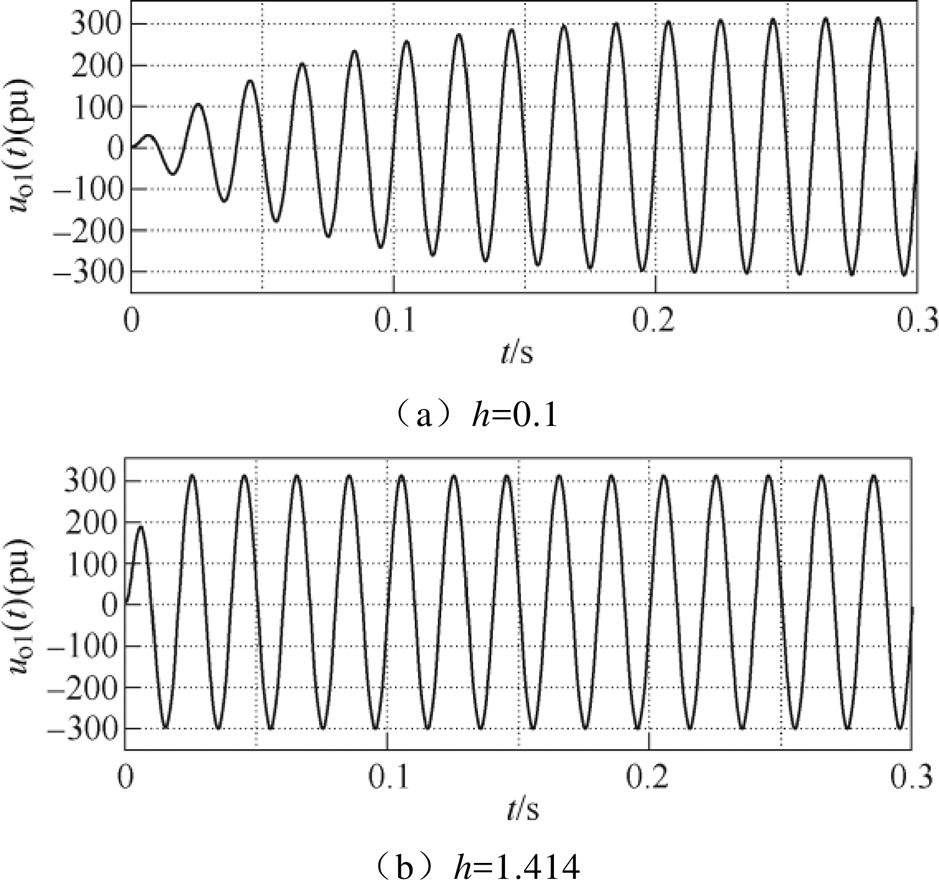
图5 不同h值的SOGI响应曲线
Fig.5 SOGI response curves with different h values
表1 不同h取值时SOGI的响应时间
Tab.1 SOGI responses time with different h values

阻尼系数hSOGI响应时间/s 0.50.06 0.70.04 10.02 1.5<0.02
通过广义二积分器,可以得到电网电压的谐波分量Uh(s)为
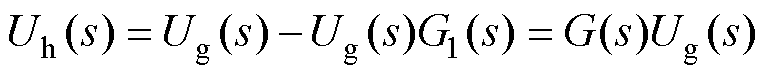 (15)
(15)
其中
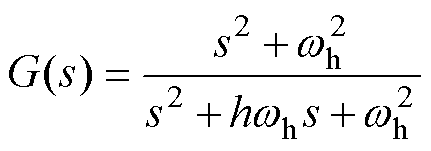
基于电网谐波电压的前馈方法,推导虚拟同步整流器的网侧阻抗和变换器侧阻抗。为简化分析,前馈因子先假设为1,即电网谐波电压全前馈。此时,虚拟同步整流器单相支路的s域电路模型如图6所示。
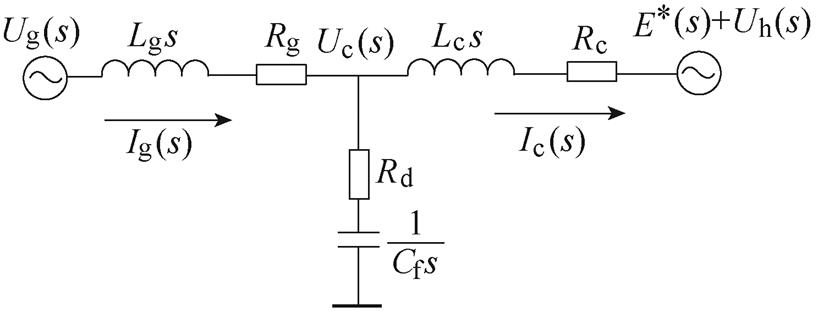
图6 含电网谐波电压前馈的虚拟同步整流器单相s域电路模型
Fig.6 Single-phase circuit model of virtual synchronous rectifier in s domain with grid harmonic voltage feedforward
由图6可知,此时虚拟同步整流器桥臂处的指令电压发生了变化,可得此时的网侧阻抗和变换器侧阻抗分别为
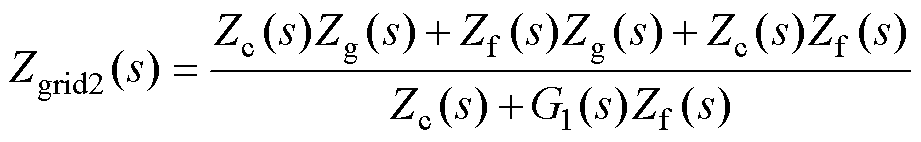 (16)
(16)
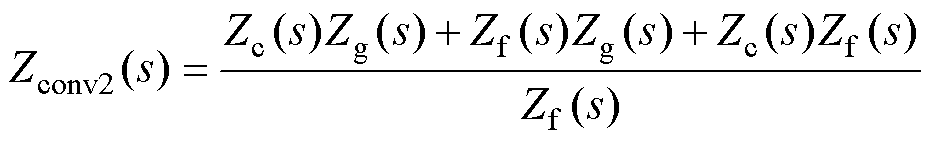 (17)
(17)
对比式(11)与式(12),在电网谐波电压前馈的作用下,虚拟同步整流器的变换器侧阻抗没有受到影响,而网侧阻抗发生了变化。图7给出了加入电网谐波电压前馈前后的网侧阻抗伯德图。从图中可以发现,加入电网谐波电压前馈以后,虚拟同步整流器基波频率处的网侧阻抗没有发生变化,其仍可以正常地输送功率。而低次谐波频率处的网侧阻抗显著增加,可以有效地减弱畸变电网下的谐波电压对虚拟同步整流器并网电流的影响,提升电流 品质。
在阻抗分析中,为简化分析以评估电网谐波电压前馈对网侧阻抗的影响,选取了前馈因子为1。事实上,电网谐波电压全前馈并非是最好的选择,在进行前馈时,需同时考虑整个系统的稳态与动态性能。本节采用小信号分析法,结合虚拟同步整流器的控制原理,研究前馈因子的取值方法。
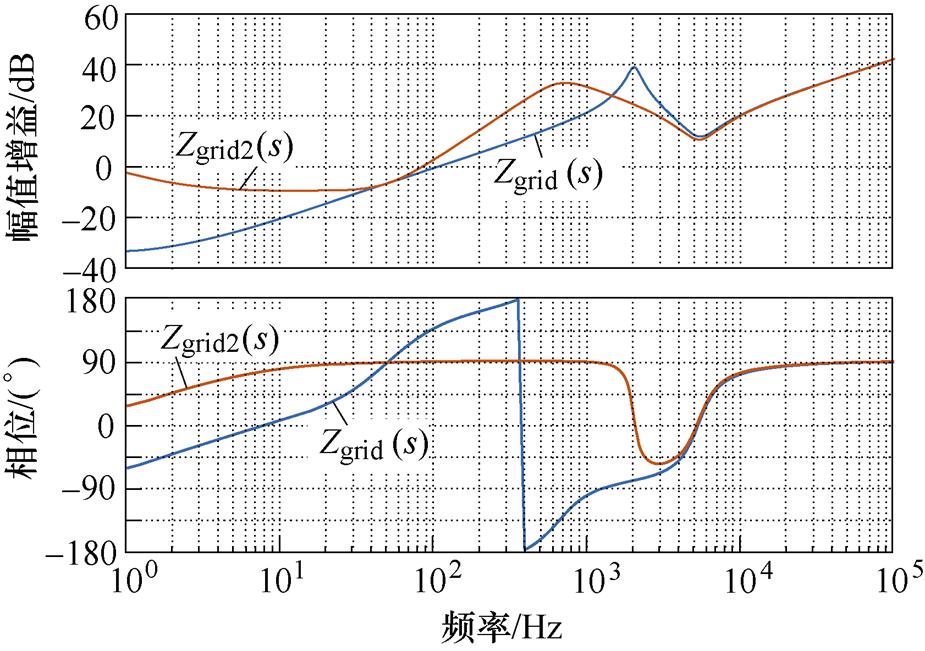
图7 网侧阻抗对比伯德图
Fig.7 Comparsion Bode diagram of grid impedance
在电网谐波电压的实际提取过程中,会产生一定的时间滞后,考虑在前馈因子中引入微分环节进行补偿,设前馈因子表达式F(s)为
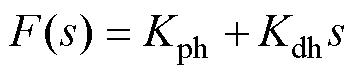 (18)
(18)
式中,Kph为前馈因子中的比例系数;Kdh为前馈因子中的微分系数。
经谐波电压前馈补偿后的新调制波为
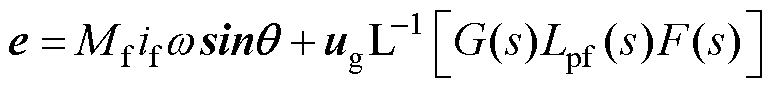 (19)
(19)
式中,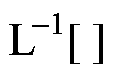 为拉普拉斯逆变换;
为拉普拉斯逆变换;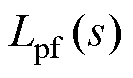 为低通滤波器表达式;
为低通滤波器表达式;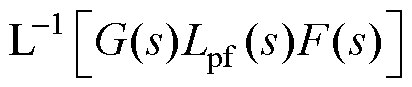 对应的是电网电压的谐波提取及前馈这一信号处理过程的时域表达式。
对应的是电网电压的谐波提取及前馈这一信号处理过程的时域表达式。
将式(19)等式两边分别与 做内积,可得
做内积,可得
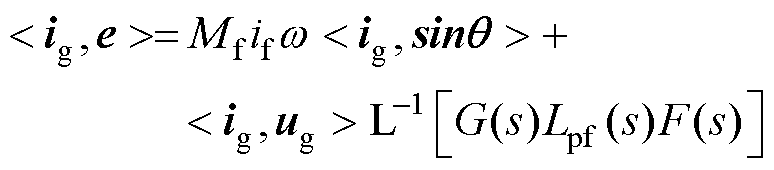 (20)
(20)
由电路关系易知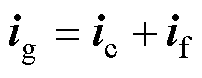 ,则可得
,则可得
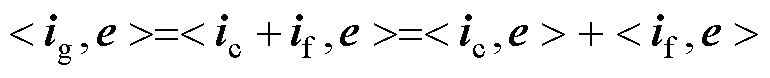 (21)
(21)
式中,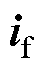 为交流侧滤波电容支路电流矢量。因电容支路上的电流低频分量极少,所以
为交流侧滤波电容支路电流矢量。因电容支路上的电流低频分量极少,所以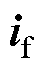 与
与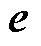 基本不产生有功功率,可认为
基本不产生有功功率,可认为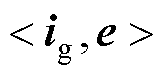 近似表述了虚拟同步整流器的变换器侧有功功率。忽略由于滤波电感的附加电阻引起的有功损耗,结合式(3),可将式(20)简化为
近似表述了虚拟同步整流器的变换器侧有功功率。忽略由于滤波电感的附加电阻引起的有功损耗,结合式(3),可将式(20)简化为
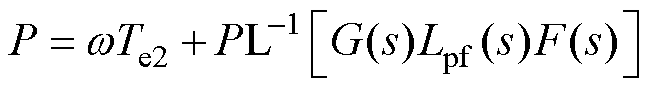 (22)
(22)
从而可得新的虚拟电磁转矩为
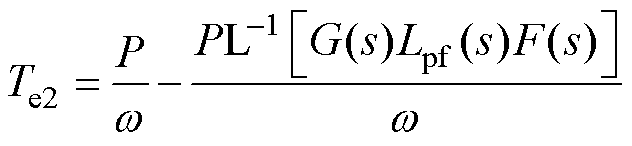 (23)
(23)
对比传统的虚拟同步整流器算法,在电网谐波电压前馈的作用下,新的虚拟电磁转矩含有一项与前馈因子相关的修正转矩,显然,前馈因子的取值将影响到虚拟同步整流器的性能。
虚拟同步机算法将三相整流器模拟成同步电机进行控制,因而可将其电路等效为反电动势与电枢电抗的串联,可得简化的系统单相简化模型如图8所示。
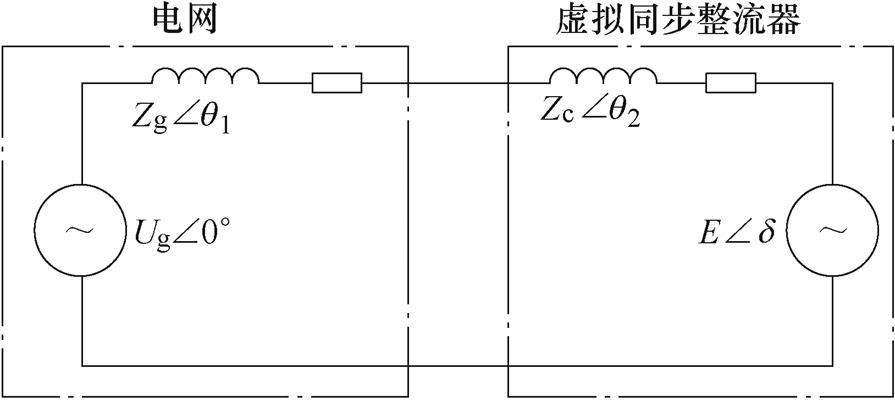
图8 虚拟同步整流器与电网的系统简化模型
Fig.8 Simplifed model of grid and virtual synchronous rectifier
由图8可得,系统的网侧有功功率为
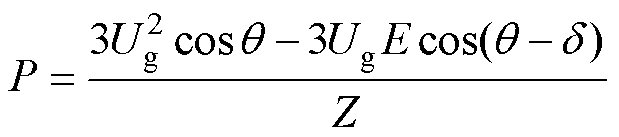 (24)
(24)
式中,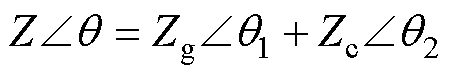 ;d 为功角,由于虚拟同步整流器的内电动势滞后于电网电压,因此d 为负
;d 为功角,由于虚拟同步整流器的内电动势滞后于电网电压,因此d 为负
值。对式(24)在稳态工作点处进行小信号化得
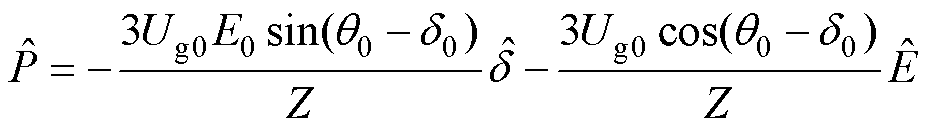 (25)
(25)
式中,上标“ ”表示的是小信号量;下标“0”表示的是稳态量。
”表示的是小信号量;下标“0”表示的是稳态量。
在大电网情形下,虚拟同步整流器的有功环和无功环耦合很弱,可忽略式(25)中的第二项,得
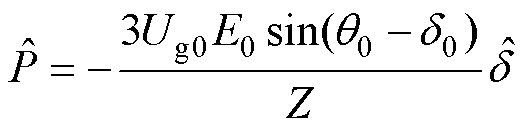 (26)
(26)
为书写方便,令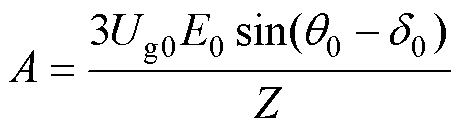 ,这是一个与主电路参数及系统稳态工作点相关的常数。
,这是一个与主电路参数及系统稳态工作点相关的常数。
同样地,将式(1)、式(23)进行小信号化,可得到电网谐波电压前馈下的虚拟同步整流器的小信号模型框图,如图9所示。图中,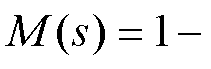
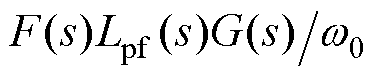 。
。
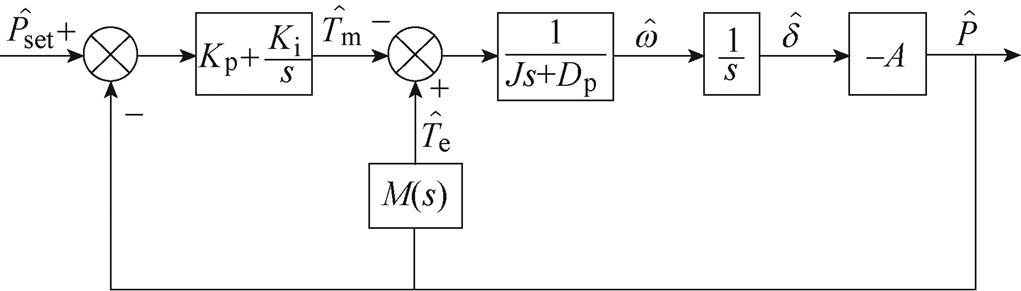
图9 基于电网谐波电压前馈的虚拟同步整流器的小信号模型框图
Fig.9 Small signal control block diagram of virtual synchronous rectifier with grid harmonic voltage feedforward
经推导,图9中输入输出间的开环传递函数为
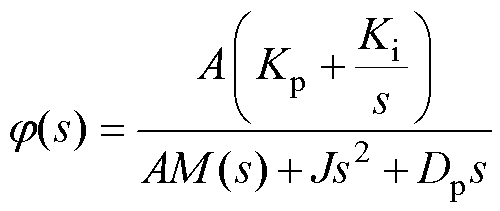 (27)
(27)
为使系统拥有足够的相位裕度,以避免受到扰动后的振荡风险,设计系统的相位裕度g>30°。在功率控制目标为20kW、0kvar时,使用Matlab软件为辅助工具,做出相位裕度g 与前馈因子Kph与Kdh参数的三维关系,如图10所示。从图中可以发现,随着Kph参数的增加,系统的相位裕度在增加,反映系统稳定性在上升,快速性在下降;随着Kdh参数的增加,系统的相位裕度在减小,事实上为避免微分环节引入噪声信号,Kdh参数也不宜选取过大。综合考虑,选取Kph=0.9,Kdh=0.001。
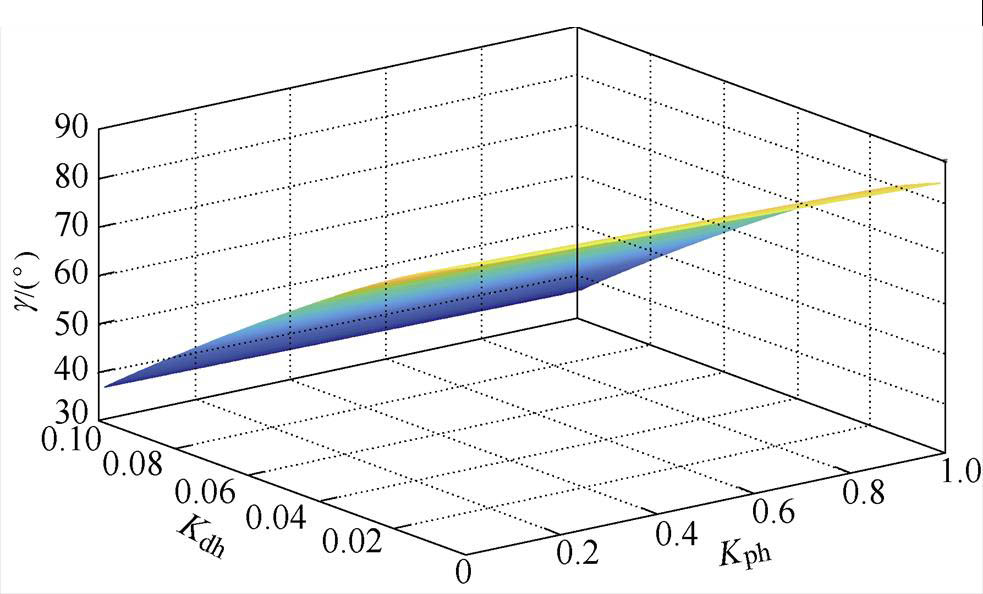
图10 相位裕度与前馈因子的三维关系
Fig.10 Relationship among the phase angle and feedforward factors
当选取Kph=0.9,Kdh=0.001时,系统的阶跃响应 的曲线如图11所示。从图中可以发现,相较于无电压前馈算法,加入谐波电压前馈算法后,系统的峰值时间、调节时间几乎无变化,超调量增加了约3.7%,这是可接受的。因此,整个系统的动态响应情况仍然良好。
的曲线如图11所示。从图中可以发现,相较于无电压前馈算法,加入谐波电压前馈算法后,系统的峰值时间、调节时间几乎无变化,超调量增加了约3.7%,这是可接受的。因此,整个系统的动态响应情况仍然良好。
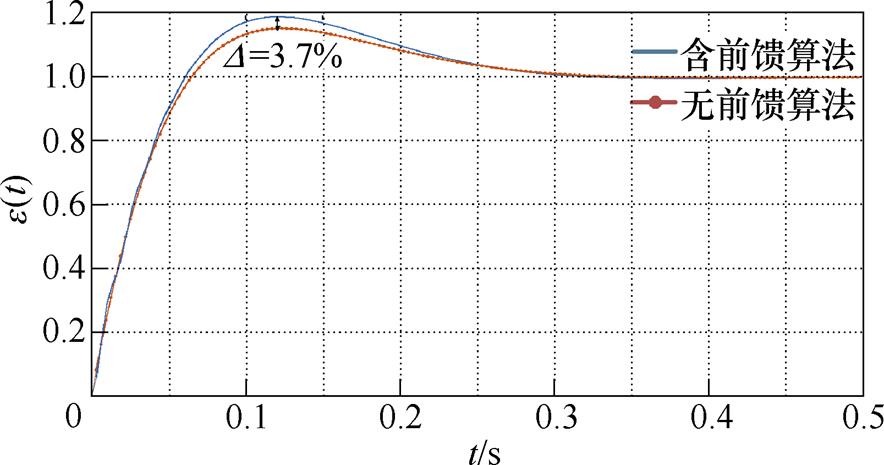
图11 加入前馈算法前后虚拟同步整流器的阶跃响应对比曲线
Fig.11 Virtual synchronous rectifier step response curves with and without feedforward method of harmonic grid voltage
采用电网谐波电压前馈方法后的虚拟同步整流器控制框图如图12所示。图中,vharm和ecom分别为电网电压的谐波提取量及前馈量矢量。

图12 含电网谐波电压前馈法的虚拟同步整流器的控制框图
Fig.12 Control block of virtual synchronous rectifier with feedforward method of harmonic grid voltage
本文基于Matlab/Simulink仿真平台搭建了采用谐波电压前馈方法的虚拟同步整流器仿真模型,以证明畸变电网情形下所提控制算法对谐波电流抑制的有效性,仿真中采用的具体参数见表2。值得说明的是,实验中,变换器与配电柜的连接导线较长,为充分考虑连接导线内阻的影响,将其内阻等效为网侧滤波电感的内阻,因此网侧滤波电感的内阻值较大。
在虚拟同步整流器并网后,设定工作状态为输出有功功率20kW,无功功率0kvar,此时电网电压质量良好。为模拟电网电压畸变,1~3s向电网电压中注入4%的5次谐波和3%的7次谐波。参考GB/T 14549—93《电能质量公用电网谐波》标准中提及的380V配电网的电压总谐波畸变率应小于5%,奇次谐波畸变率应小于4%,此时的电网情况已相当恶劣。1~2s虚拟同步整流器采用传统控制算法,2s后采用含电网谐波电压前馈的虚拟同步算法。图13为仿真过程中虚拟同步整流器输出的有功功率和无功功率,图14为采用电网谐波电压前馈算法前后的三相电流对比,图15给出了其快速傅里叶变换(Fast Fourier Transform, FFT)分析结果,图16为虚拟同步整流器的虚拟同步频率。
表2 仿真参数
Tab.2 Simulation parameters
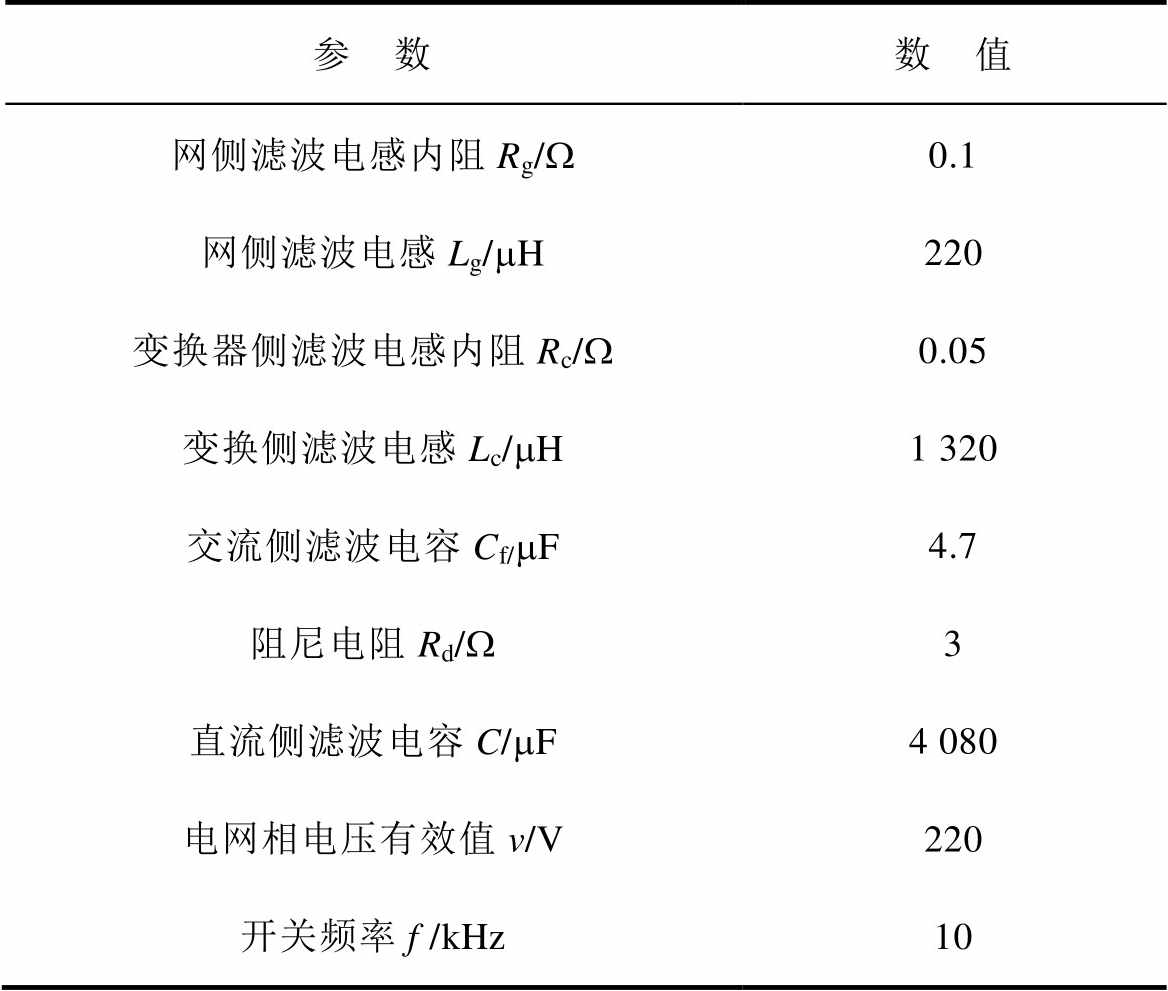
参 数数 值 网侧滤波电感内阻Rg/W0.1 网侧滤波电感Lg/mH220 变换器侧滤波电感内阻Rc/W0.05 变换侧滤波电感Lc/mH1 320 交流侧滤波电容Cf/mF4.7 阻尼电阻Rd/W3 直流侧滤波电容C/mF4 080 电网相电压有效值v/V220 开关频率f /kHz10
由图13~图16可知,虚拟同步整流器工作于电网质量良好情形时,输出功率可准确跟随给定值,电流质量良好,可充分模拟同步电机的同步机制,良好跟踪电网频率。当电网电压发生畸变时,虚拟同步整流器的网侧电流将发生严重畸变,由图15的FFT分析对比结果可知,此时的电流总谐波畸变率(Total Harmonic Distortion, THD)达到了13.83%,远超并网标准,将带来严重的谐波污染。同时,因有功功率、无功功率由电流与电压计算而得(见式(5)、式(6)),畸变的交流电压和并网电流将使得有功功率、无功功率产生严重的周期性波动。这将降低虚拟同步整流器的控制品质,使得虚拟同步频率也产生大幅波动,无法准确跟踪电网频率。在启用电网谐波电压前馈算法后,虚拟同步整流器的网侧谐波电流得到了很好的抑制,电流THD降至5%以下,符合并网标准,虚拟同步整流器输出的有功功率和无功功率波动减小。同时,在电网谐波电压前馈的作用下,由于引入了修正的虚拟电磁转矩,虚拟同步机在畸变电网下的同步机制得到了改善,仍可较好地追踪电网频率。仿真结果充分说明了算法的有效性。
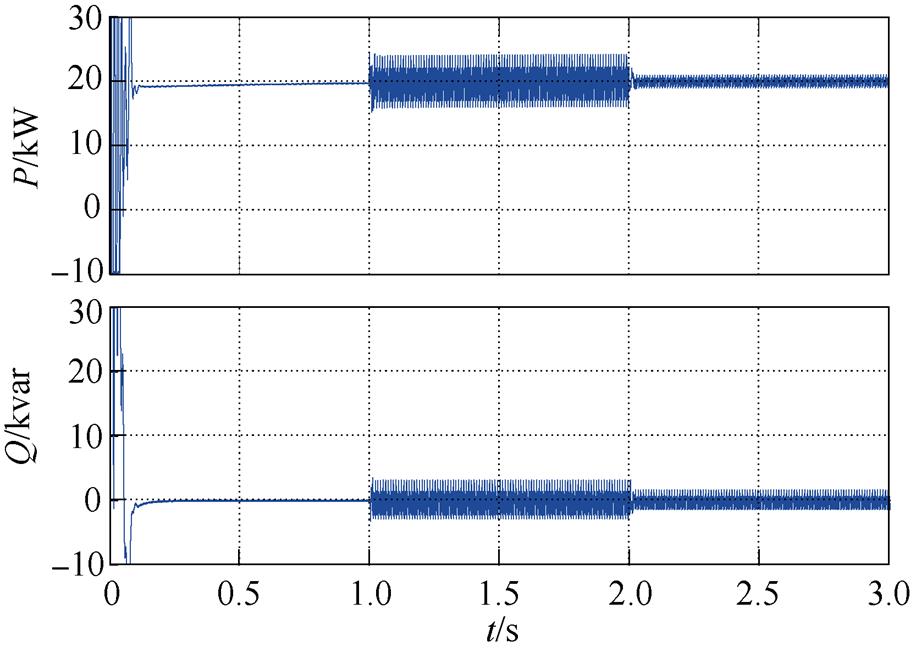
图13 虚拟同步整流输出的有功功率、无功功率仿真结果
Fig.13 Simulation results of output active power, reactive power of virtual synchronous rectifier
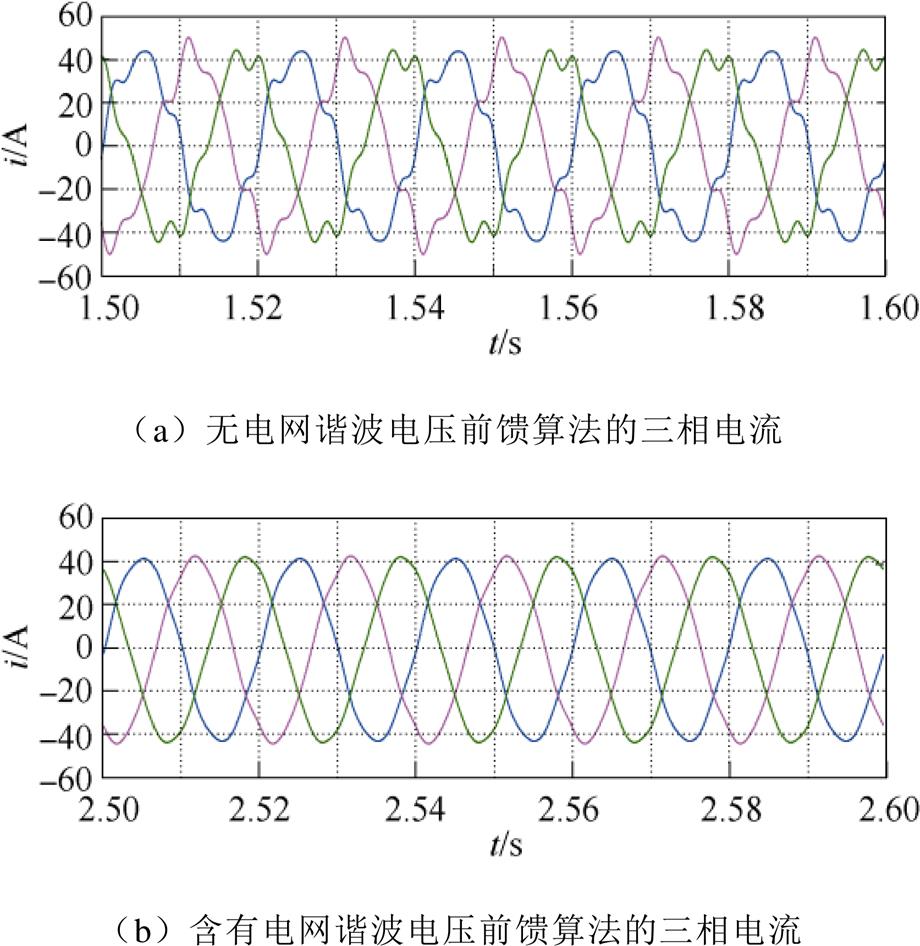
图14 虚拟同步整流器三相电流的对比仿真结果
Fig.14 Comparsion simulation results of three phase current of virtual synchronous rectifier
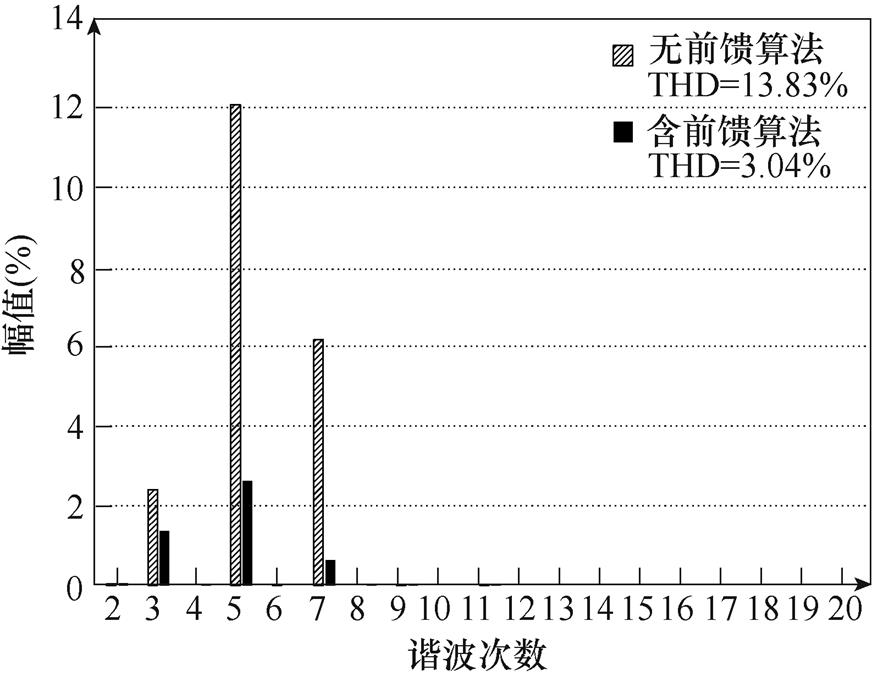
图15 三相电流FFT分析的对比结果
Fig.15 Comparsion results of FFT analysis of three phase current
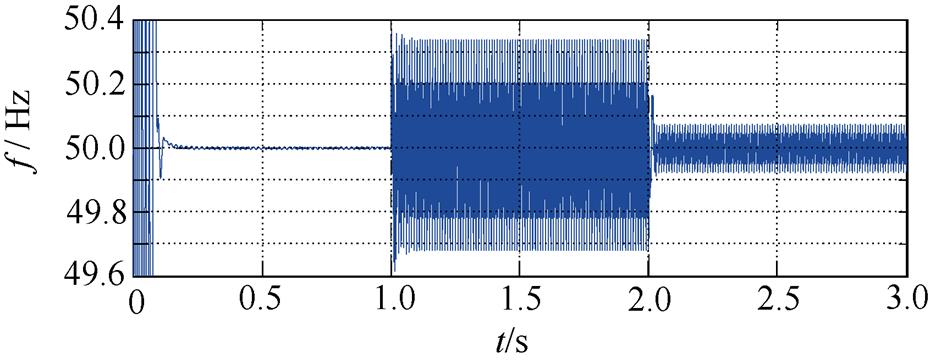
图16 虚拟同步整流器的虚拟频率仿真结果
Fig.16 Simulation results of virtual frequency of virtual synchronous rectifier
为充分验证电网谐波电压前馈算法对工作于畸变电网下的虚拟同步整流器的电流谐波抑制的有效性,搭建了基于DSP+FPGA的数字控制平台,实验平台的原理框图如图17所示,实物如图18所示。整个平台主要由DSP+FPGA的数字控制、LCL滤波电路、功率变换和直流负载构成,在20kW功率等级下对本文所提的控制算法进行实验验证。实验所用的电路参数与仿真参数相一致。
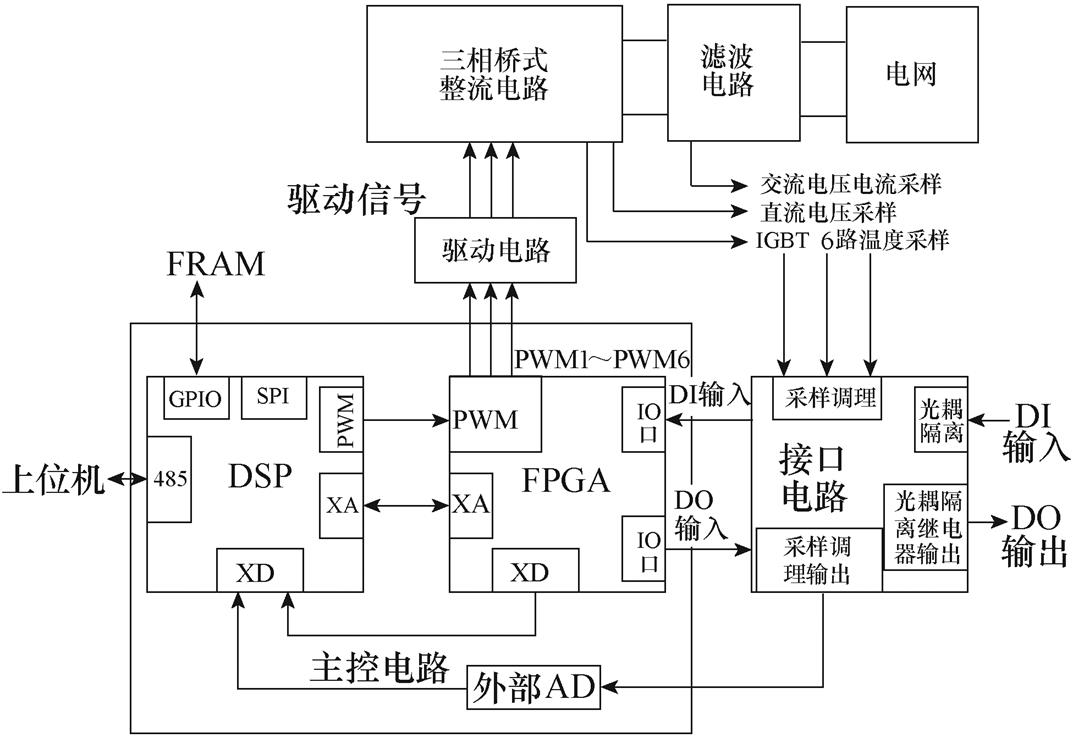
图17 实验平台原理框图
Fig.17 Experimental platform functional diagram

图18 虚拟同步整流器实验平台实物
Fig.18 Experimental platform of virtual synchronous rectifier
虚拟同步整流器输入端接实验室交流电网,因实验室电力负载复杂,交流电压波形不理想,存在低频谐波分量,虚拟同步整流器实际工作于畸变电网情形。首先不引入谐波电压前馈算法,虚拟同步整流器工作于20kW稳态工况时的三相电流和A相电压波形如图19所示,A相电压、电流与输出的有功功率、无功功率波形如图20所示。图20中,有功功率与无功功率采用DA导出,实验所用DA的参考电压为10V,采用单极性供电,因此示波器上显示的0~10V即对应于实际需显示的物理量的最小值至最大值。设置有功功率的显示范围为0~20kW。因无功功率有感性与容性之分,因此其零点处为中间位置。因实际电网工况的波动,实际的输入电压有效值略高于标准值,约为240V。从图中的A相电压波形可以发现,虚拟同步整流器的交流输入电压存在畸变,波形的峰顶与峰谷处存在削顶,其THD分析结果显示,电网电压总畸变率约为2.8%,其中5次谐波含量较大,约2%。在虚拟同步控制算法的作用下,虚拟同步整流器的输出功率仍可跟随功率指令。然而不引入谐波电压前馈算法时,虚拟同步整流器于谐波频率处的阻抗较低,由于电网谐波电压的作用,网侧电流产生了严重畸变。根据如图21所示的THD分析结果,此时的电流总畸变率高达16.46%,5次谐波含量约为16%,3次谐波含量约为3.2%,将给电网带来严重的谐波污染。
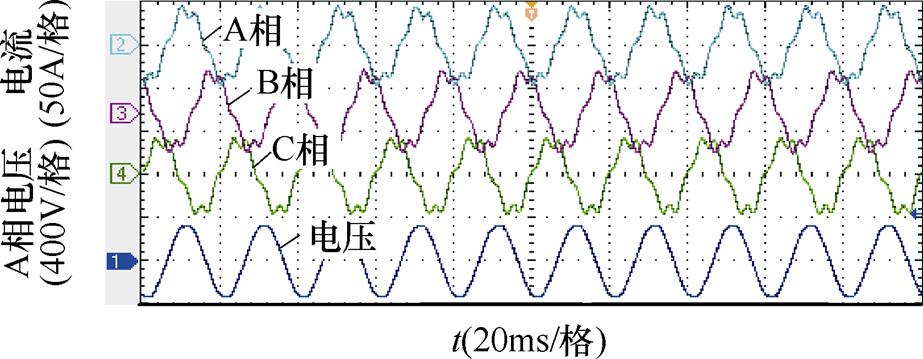
图19 无谐波电压前馈算法时虚拟同步整流器的三相电流与A相电压波形
Fig.19 Waveforms of three phase current and voltage (phase A) of virtual synchronous rectifier without feedforward method of harmonic grid voltage
采用本文所提算法的三相电流与A相电压波形如图22所示。由图可知,此时的三相电流波形正弦度高,且与电压的相位准确对应。由图21中的分析可知,此时的网侧电流THD为3.6%,低于5%的变换器并网标准,最高的单次谐波为7次谐波,其含量约为1.6%,小于单次谐波3%的标准。对比两种情况下的THD分析结果可知,采用本文所提算法后,虚拟同步整流器的并网电流质量得到了很大程度的提高,其在电网电压畸变工况下的适应性也得到了提升。
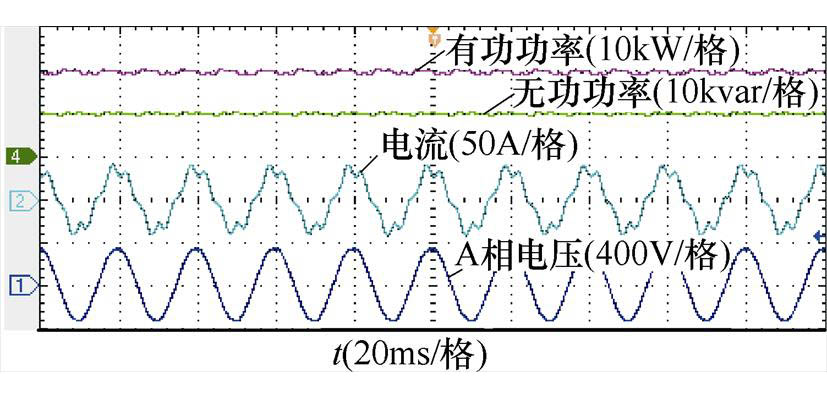
图20 无谐波电压前馈算法时A相电压、电流与输出的有功功率、无功功率波形
Fig.20 Waveforms of current and voltage(phase A), active power, reactive power of virtual synchronous rectifier without feedforward method of harmonic grid voltage
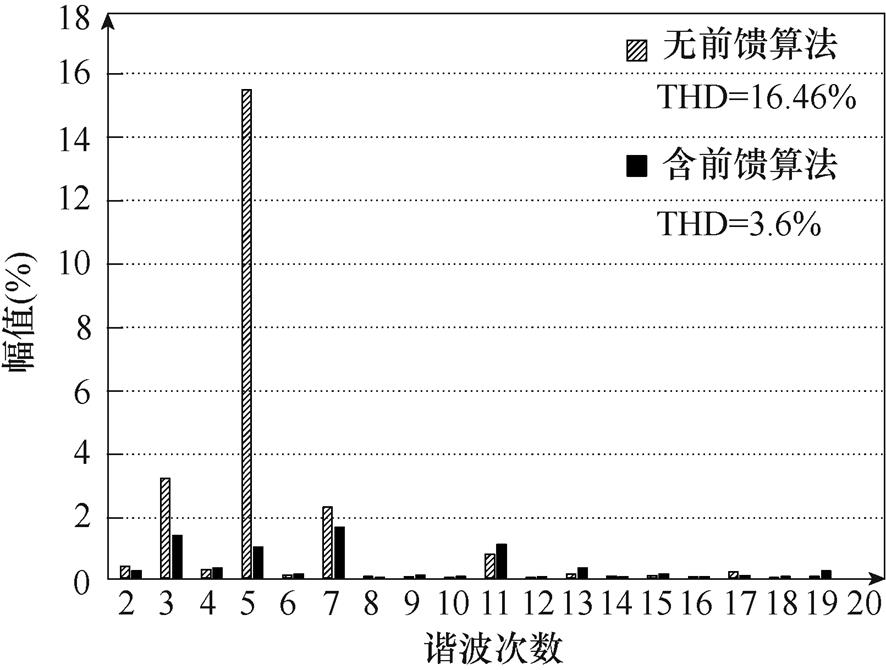
图21 谐波电压前馈算法使用前后的电流THD分析结果
Fig.21 The current THD analysis result of virtual synchronous rectifier before and after using feedforward method of harmonic grid voltage
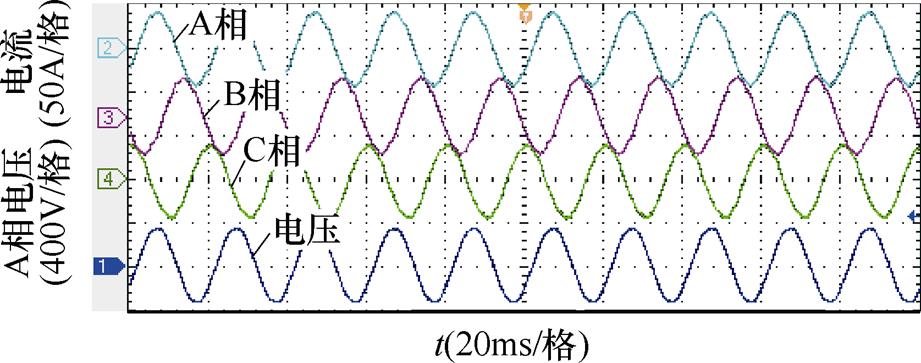
图22 采用谐波电压前馈算法后三相电流与A相电压波形
Fig.22 Waveforms of three phase current and voltage(phase A) of virtual synchronous rectifier with feedforward method of harmonic grid voltage
采用本文方法后,虚拟同步整流器输出的直流侧电压和交流侧三相电流波形如图23所示,可以发现,此时的直流侧电压平稳无波动,直流输出为740V。虚拟同步整流器的A相电压、电流和输出有功功率、无功功率波形如图24所示,图中显示的有功功率约为19.4kW,无功功率约为-0.2kvar,负号仅表示无功功率为感性,而与大小无关。由于网侧电流质量的提升,虚拟同步整流器输出的功率脉动减小,控制性能得到了提升,与仿真结果相吻合。
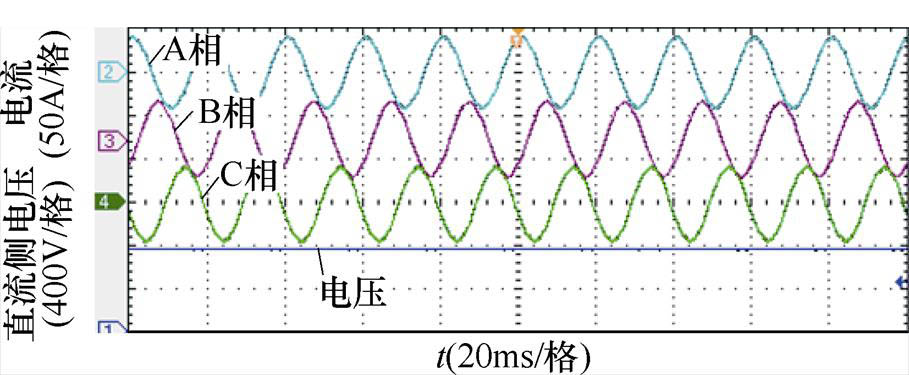
图23 采用谐波电压前馈算法后的三相电流与直流侧电压波形
Fig.23 Waveforms of three phase current and DC voltage of virtual synchronous rectifier with feedforward method of harmonic grid voltage
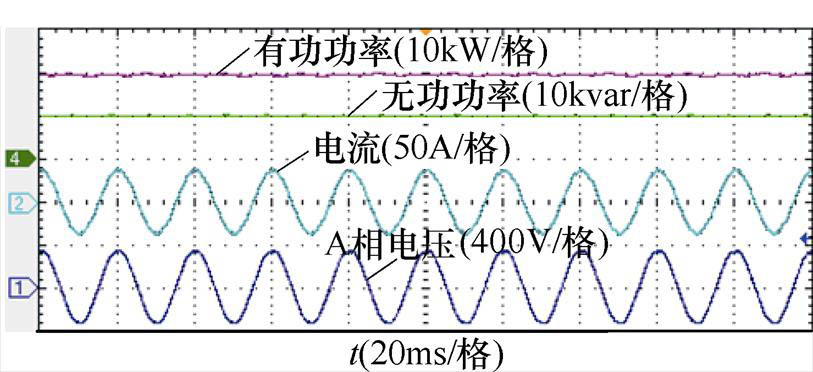
图24 采用谐波电压前馈算法后虚拟同步整流器的A相电压电流与输出有功功率、无功功率波形
Fig.24 Waveforms of current and voltage(phase A), active power, reactive power of virtual synchronous rectifier with feedforward method of harmonic grid voltage
本文针对畸变电网下虚拟同步整流器的网侧电流畸变严重和虚拟同步控制品质降低的问题,从阻抗分析入手,提出了一种电网谐波电压前馈的方法,并结合小信号分析法,选取了合适的前馈因子,改善了网侧电流品质,提升了工作于畸变电网下的虚拟同步整流器的性能,得到如下结论:
1)采用本文方法后,虚拟同步整流器抑制谐波电流的能力增强。在实验室谐波种类丰富,THD为2.8%的交流电网输入下,可将并网电流的THD从16.46%降至3.6%。
2)采用小信号分析法研究电网谐波电压的前馈因子取值范围,在提升虚拟同步整流器并网电流质量的同时可保证其控制的稳定性,使系统具有充足的相位裕度。
3)采用电网谐波电压前馈法提升了虚拟同步整流器在不同电网工况下的适应性,完成了20kW功率等级的实验验证,为大功率虚拟同步整流器的实际运用提供了实验依据。
参考文献
[1] 尹伟华. 2018年以来我国电力供需形势及问题对策研究[J]. 中国物价, 2018(11): 65-67.
Yi Weihua. Research on power supply and demand situation and countermeasures in China since 2018[J]. China Price, 2018(11): 65-67.
[2] 李明节, 于钊, 许涛, 等. 新能源并网系统引发的复杂振荡问题及其对策研究[J]. 电网技术, 2017, 41(4): 1035-1042.
Li Mingjie, Yu Zhao, Xu Tao, et al. Study of complex oscillation caused by renewable energy integration and its solution[J]. Power System Technology, 2017, 41(4): 1035-1042.
[3] Chen Yong, Hesse R, Turschner D, et al. Improving the grid power quality using virtual synchronous machines[C]//International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 2011: 1-6.
[4] Sakimoto K, Miura Y, Ise T. Stabilization of a power system with a distributed generator by a virtual synchronous generator function[C]//8th International Conference on Power Electronics, Jeju, Korea (South), 2011: 1498-1505.
[5] Zhong Qingchang, Weiss G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transa- ctions on Industrial Electronics, 2011, 58(4): 1259- 1267.
[6] Ma Zhenyu, Zhong Qingchang, Joseph D Yan. Synchronverter-based control strategies for three- phase PWM rectifiers[C]//2012 7th IEEE Conference on Industrial Electronics and Applications, Singapore, 2012: 225-230.
[7] 张波, 颜湘武, 黄毅斌, 等. 虚拟同步机多机并联稳定控制及其惯量匹配方法[J]. 电工技术学报, 2017, 32(10): 42-52.
Zhang Bo, Yan Xiangwu, Huang Yibin, et al. Stability control and inertia matching method of multi-parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 42-52.
[8] 颜湘武, 贾焦心, 王德胜, 等. 基于P/w“导纳”的并联虚拟同步机功频响应建模与分析[J]. 电工技术学报, 2020, 35(15): 3191-3202.
Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al. Modeling and analysis of active power-frequency response of parallel VSGs using a P/w “admit- tance”[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3191-3202.
[9] 涂春鸣, 谢伟杰, 肖凡, 等. 多虚拟同步发电机并联系统控制参数对稳定性的影响分析[J]. 电力系统自动化, 2020, 44(15): 77-86.
Tu Chunming, Xie Weijie, Xiao Fan, et al. Influence analysis of control parameters of parallel system with multiple virtual synchronous generators on stability[J]. Automation of Electric Power Systems, 2020, 44(15): 77-86.
[10] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
Jiang Jingya, Wang Wei, Wu Xuezhi, et al. Power decoupling strategy in virtual synchronous generator based on adaptive reactive power compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2747-2756.
[11] 刘一锋, 周小平, 洪乐荣, 等. 虚拟惯性控制的负荷变换器接入弱电网的序阻抗建模与稳定性分析[J]. 电工技术学报, 2021, 36(4): 843-856.
Liu Yifeng, Zhou Xiaoping, Hong Lerong, et al. Sequence impedance modeling and stability analysis of load converter with virtual inertia control con- nected to weak grid[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 843-856.
[12] 缪惠宇, 梅飞, 张宸宇, 等. 基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J]. 电工技术学报, 2019, 34(17): 3622-3630.
Miao Huiyu, Mei Fei, Zhang Chenyu, et al. Three phase unbalanced control strategy for virtual syn- chronous rectifier based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3622-3630.
[13] 年珩, 教煐宗, 孙丹. 基于虚拟同步机的并网逆变器不平衡电压灵活补偿策略[J]. 电力系统自动化, 2019, 43(3): 123-129.
Nian Heng, Jiao Yingzong, Sun Dan. Flexible com- pensation strategy of unbalanced voltage for grid- connected inverter based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2019, 43(3): 123-129.
[14] 姚骏, 夏先锋, 陈西寅, 等. 风电并网用全功率变流器谐波电流抑制研究[J]. 中国电机工程学报, 2012, 32(16): 17-25.
Yao Jun, Xia Xianfeng, Chen Xiyin, et al. Harmonic currents suppression for full size power grid- connection converter used for wind power gen- eration[J]. Proceedings of the CSEE, 2012, 32(16): 17-25.
[15] Jong-Kyu Kim, Jong-Hyun Lee, Hea-Gwang Jeong, et al. Improvement of grid-connected inverter systems with PR controllers under the unbalanced and distorted grid voltage[C]//Proceedings of The 7th International Power Electronics and Motion Control Conference, Harbin, China, 2012: 1183-1187.
[16] 徐君, 陈文杰, 徐德鸿, 等. 电网低次谐波电压下双馈风电系统定子谐波电流抑制[J]. 电力系统自动化, 2011, 35(8): 87-92.
Xu Jun, Chen Wenjie, Xu Dehong, et al. Stator harmonic current suppression strategy for doubly-fed wind power generator system influenced by low-order harmonic voltage of grid[J]. Automation of Electric Power Systems, 2011, 35(8): 87-92.
[17] Chen Dong, Zhang Junming, Qian Zhaoming. An improved repetitive control scheme for grid- connected inverter with frequency-adaptive capa- bility[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 814-823.
[18] 江法洋, 郑丽君, 宋建成, 等. LCL型并网逆变器重复双闭环控制方法[J]. 中国电机工程学报, 2017, 37(10): 2944-2954.
Jiang Fayang, Zheng Lijun, Song Jiancheng, et al. Repetitive-based dual closed-loop control approach for grid-connected inverters with LCL filters[J]. Proceedings of the CSEE, 2017, 37(10): 2944-2954.
[19] 高吉磊, 张雅静, 林飞, 等. 单相PWM整流器谐波电流抑制算法研究[J]. 中国电机工程学报, 2010, 30(21): 32-39.
Gao Jilei, Zhang Yajing, Lin Fei, et al. Research on harmonic current elimination method of single-phase PWM rectifiers[J]. Proceedings of the CSEE, 2010, 30(21): 32-39.
[20] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198.
Zhao Qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5189-5198.
[21] Wang Xuehua, Ruan Xinbo, Liu Shangwei, et al. Full feedforward of grid voltage for grid-connected inverter with LCL filter to suppress current distortion due to grid voltage harmonics[J]. IEEE Transactions on Power Electronics, 2010, 25(12): 3119-3127.
[22] Li Weiwei, Ruan Xinbo, Pan Donghua, et al. Full-feedforward schemes of grid voltages for a three-phase LCL-type grid-connected inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2237-2250.
A Harmonic-Current Suppression Method for Virtual Synchronous Rectifier Based on Feedforward of Grid Harmonic Voltage
Abstract The virtual synchronous machine technology can make power electronic converters exhibit damping and inertia characteristics similar to conventional synchronous machines, which is beneficial to the friendly interaction of power sources or loads with the grid. However, due to the complicated conditions of the actual grid, the distortion of grid voltage always leads to serious grid-connected current distortion of virtual synchronous converters. Thus, this paper proposes a harmonic-current suppression method for the virtual synchronous rectifier to solve this problem. Firstly, the influence mechanism of grid harmonic voltage on grid-connected current of virtual synchronous rectifier was investigated through impedance analysis. Secondly, a feedforward method of grid harmonic voltage was proposed accordingly. By increasing the grid-side impedance at the harmonic frequency, the influence of grid harmonic voltage on grid-connected current was weakened, then the current harmonics were suppressed accordingly. Finally, the selection method of feedforward factor was developed by small signal analysis, and the system steady-state and dynamic performance was evaluated. Simulation and experimental results verified the proposed method.
keywords:Distortion of grid voltage, virtual synchronous rectifier, harmonic suppression, impedance analysis, feedforward factor
DOI: 10.19595/j.cnki.1000-6753.tces.210318
中图分类号:TM461
徐 健 男,1996年生,硕士研究生,研究方向为整流器、逆变器的先进控制技术。E-mail: xujian@nuaa.edu.cn
曹 鑫 男,1981年生,教授,博士生导师,研究方向为开关磁阻电机、新能源并网技术。E-mail: caoxin@nuaa.edu.cn(通信作者)
收稿日期 2021-03-18
改稿日期 2021-05-09
国家自然科学基金资助项目(51877107)。
(编辑 陈 诚)