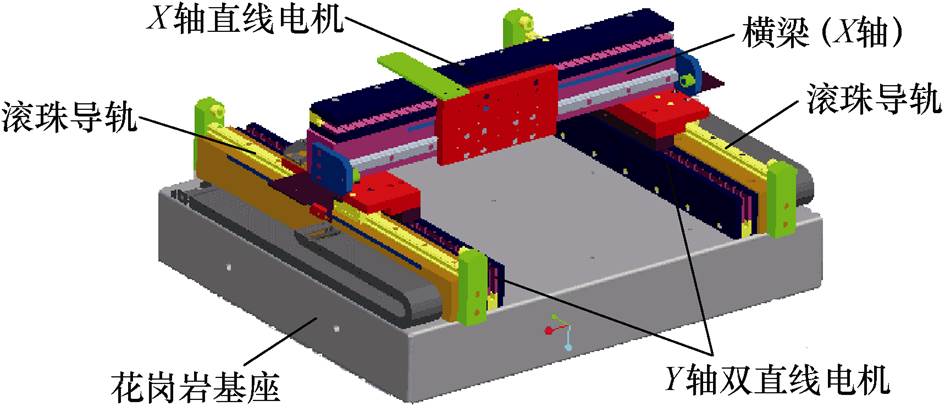
图1 直驱H型平台结构
Fig.1 Direct drive H-type platform structure
摘要 为了解决系统同步误差对永磁直线同步电机（PMLSM）驱动H型平台轮廓跟踪精度的影响，该文将并联轴位置不同步引起的横梁偏转角定义为等效同步误差，以此构建适用于直驱H型平台的融合误差模型。同时，建立基于融合误差的非线性耦合模型，将系统控制目标由轮廓跟踪转变为融合误差收敛。采用反馈线性化对以融合误差为状态变量的非线性耦合动态方程进行解耦线性化。针对线性模型，设计自适应积分滑模控制器（AISMC），削弱反馈线性化控制对系统数学模型的强依赖性，提高系统对负载扰动和参数摄动的鲁棒性。实验结果表明，所提出的控制方法不仅能有效提高系统的轮廓精度和同步精度，而且增强了系统的鲁棒性。
关键词：直驱H型平台 同步误差 轮廓控制 反馈线性化 自适应积分滑模控制
数控机床加工技术正在向高速度、高精度的方向发展[1]。永磁直线同步电机（Permanent Magnet Linear Synchronous Motor, PMLSM）驱动H型平台，采取三轴协同运动，具有响应速度快、定位精度高和可靠性强的优点，被广泛应用于自动化精密加工等领域[2-3]。但由于受机械耦合、平行轴参数不匹配以及负载扰动等因素的影响，平行轴间会产生运动的不同步，进而导致轮廓加工精度下降。因此，研究考虑同步误差影响的轮廓控制结构对直驱H型平台的应用具有重要意义。
轮廓加工精度作为衡量多轴运动平台系统性能的重要指标，早期控制系统设计的目标都是尽可能减小单轴的跟踪误差[4]。然而，对于多轴系统的运动控制，通常给出的任务是要同时控制单轴运动，使其跟踪所期望的轮廓[5]。一旦系统进给量增加，受轴间协调度、系统带宽及外部扰动影响，只靠单轴跟踪精度不能保证相应的系统轮廓跟踪性能[6]。目前，对直驱H型平台的研究主要集中在同步控制和直接轮廓控制[7]。同步误差作为直驱H型平台所具有的特异性误差，其存在会导致系统机械结构耦合，引起系统振荡，影响伺服系统控制性能[8]。为此，文献[9]一方面设计了互补滑模位置控制器提高系统鲁棒性；另一方面采用交叉耦合控制结构提高系统同步性能。文献[10]提出一种基于直驱H型平台集总参数动力学模型的前馈解耦控制策略，提高同步控制性能。但是，同步跟踪性能的提高只能间接改善轮廓加工精度[11]。对于直驱H型平台轮廓控制结构主要有任务坐标法[12]、切线-轮廓控制[13]和交叉耦合控制[14]等。然而以上结构都是基于线性近似的处理方式，不适用于非线性被控对象的轮廓跟踪任务[15]。为此，文献[16]将轮廓跟踪误差分为切线误差与等效轮廓误差，将跟踪误差在期望轮廓坐标点法向上的投影定义为等效轮廓误差，以等效误差作为被控量进行控制器设计，在跟踪非线性轮廓时取得较好的轮廓控制效果。但在直驱H型平台轮廓控制系统中，由于受同步误差影响，等效轮廓误差收敛于零时，真实轮廓误差并不收敛于零。
反馈线性化作为一种基于微分几何的非线性控制方法，可将耦合非线性系统转化为独立的线性子系统，已在混合励磁同步电机[17]、无刷双馈电机[18]和异步电机[19]等交流伺服系统中得到应用，但反馈线性化方法对系统数学模型具有依赖性，因此鲁棒性不强，在实际系统应用中存在局限性。在伺服系统鲁棒控制方法中，滑模控制对系统外部扰动及参数摄动具有较强的鲁棒性，且实现简单，成为提高伺服系统控制性能的有效手段之一[20]。
为此，本文提出一种考虑同步误差影响的融合误差模型，将直驱H型平台轮廓控制问题转化为融合误差的收敛性问题。为方便轮廓控制器设计，采用反馈线性化对以融合误差为状态变量的耦合非线性动态方程进行解耦线性化。针对线性子系统分别设计自适应积分滑模控制器（Adaptive Integrated Sliding Mode Controller, AISMC），降低反馈线性化控制对系统数学模型的依赖性，提高直驱H型平台伺服系统轮廓控制精度，增强系统鲁棒性。最后，通过实验验证所提控制方法的可行性和有效性。
直驱H型平台是数控机床中特殊的一种平面运动机构，该直驱平台由一个X轴方向的PMLSM和两个Y轴方向的PMLSM共同驱动，具有高刚度、大推力和高加速度的优点，直驱H型平台结构如图1所示。
图1 直驱H型平台结构
Fig.1 Direct drive H-type platform structure
根据PMLSM的运动学模型与直驱H型平台工作原理，系统数学模型可表示为
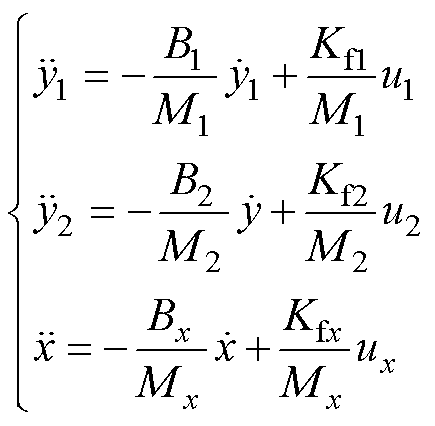（1）
式中，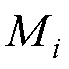
、
、
、
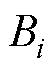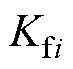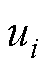分别为单轴动子质量、粘滞摩擦因数、推力系数和控制输入（
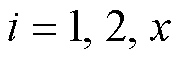）；y1、y2和x为单轴动子位置。
将式（1）写为矩阵的形式为
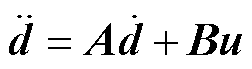（2）
其中
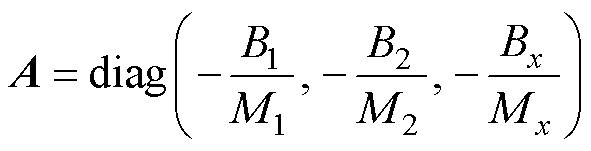
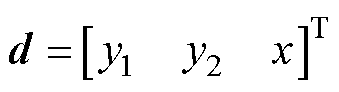
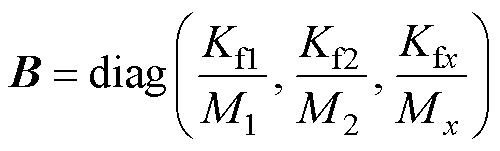
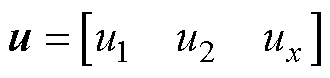
多轴运动平台伺服系统的轮廓误差定义为实际轮廓到期望轮廓的最短距离。在跟踪过程中要实时获取非线性轮廓的轮廓误差精确值较为困难，因此一般采取建立轮廓误差模型进行估计。
在忽略直驱H型平台伺服系统同步误差的情况下，即认为并联轴位置跟踪同步，则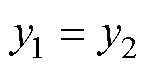
。以Y1轴测量的位置
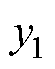为例，将实际轮廓表示为代数方程的形式
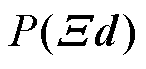。根据文献[16]，直驱H型平台的等效误差模型如图2所示。图中，d为实际轮廓的点，dm为期望轮廓的点，若等效轮廓误差定义为
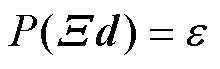，当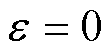
时，则表示实际轮廓准确跟踪期望轮廓，真正的轮廓误差
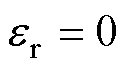。同时，定义切线误差为轮廓跟踪误差在切线方向的投影量，即
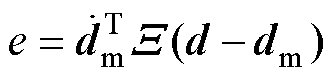，保证控制目标到达期望位置。等效误差模型可以表示为
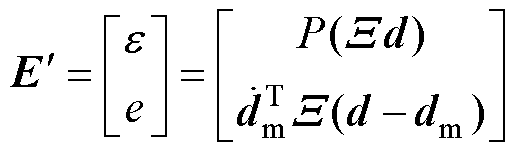（3）
其中
式中，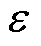
为等效轮廓误差；
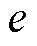为切线误差。
图2 等效误差模型原理
Fig.2 Schematic of equivalent error model
H型平台等效误差模型是建立在忽略直驱H型平台伺服系统同步误差的情况下，但由于并联电机之间存在的机械耦合、动态不匹配以及永磁直线同步电机的抗干扰能力差等因素，两台并联直线电机之间不可避免地产生运动不同步，导致横梁（X轴）偏转[21]。图3为融合误差模型原理，可以看出，偏转角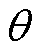
的存在，导致实际运动轮廓变为
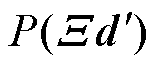，在忽略系统同步误差的情况下，等效轮廓误差
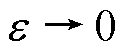时，并不能保证实际轮廓误差
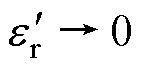。因此，将偏转角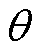定义为等效同步误差，表示为
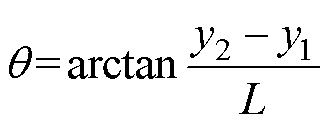（4）
式中，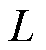
为两平行滚珠导轨间的距离。
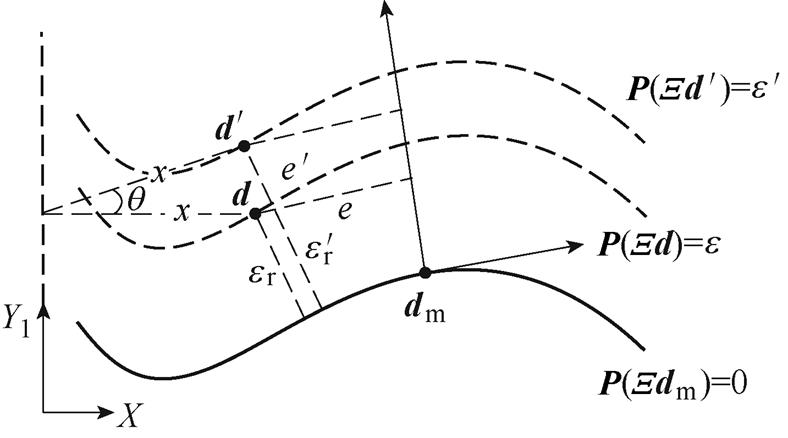
图3 融合误差模型原理
Fig.3 Schematic of integrated error model
当横梁偏转角
时，轨迹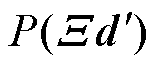
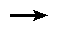
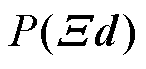，进而保证等效轮廓误差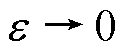时，实际轮廓误差。
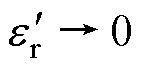为此，将等效同步误差引入等效误差模型，构建适用于直驱H型平台的融合误差模型。融合误差模型可以表示为
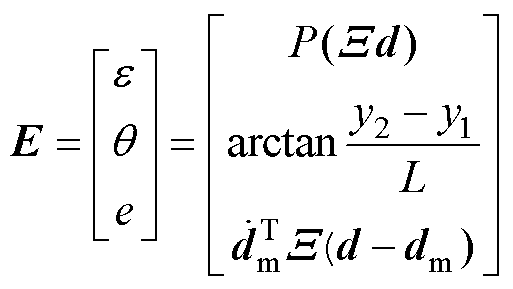（5）
建立融合误差模型后，将融合误差模型式（5）做二次微分后结合原状态方程式（2），得到以融合误差为状态变量的非线性耦合动态方程为
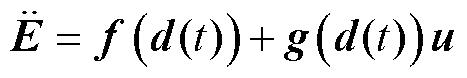（6）
其中
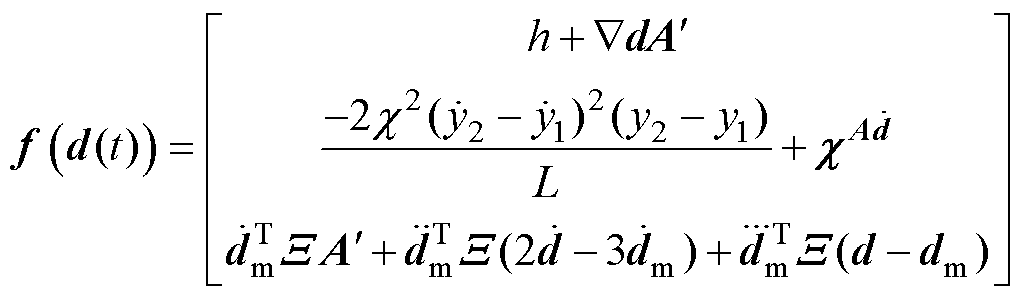
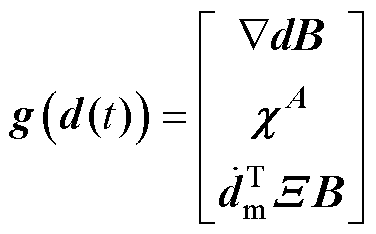
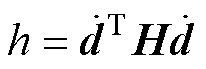
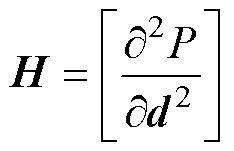
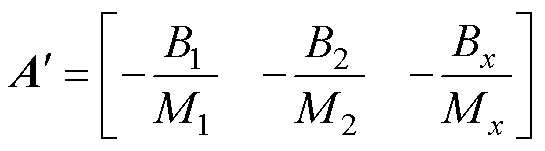
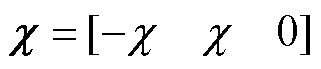
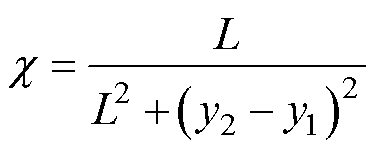
综上所述，当直驱H型平台系统转换成融合误差动态方程后，原始系统轮廓跟踪控制目标也转换为对广义坐标与期望轮廓间的误差量进行控制的新目标。同时，系统不再单独进行同步控制和轮廓控制，而是以融合误差为控制量进行轮廓控制器设计。
虽然以融合误差作为被控量直接控制误差信号会使轮廓控制的目标更明确，但式（6）为耦合非线性系统，增加了控制器的设计难度。为此，本文采用反馈线性化对式（6）进行解耦线性化，针对独立的线性系统分别设计AISMC保证系统稳定，即融合误差收敛于零。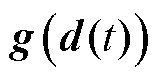
由电机动子质量与电机的物理参数组成，为非奇异矩阵，伺服系统可完全线性化。
为了消去式（6）中非线性部分
，选取输入控制律为
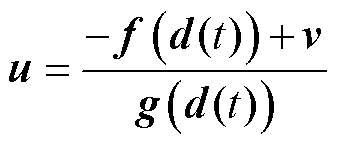（7）
式中，v为新的等价控制输入，代入式（6）可以得到3个独立的线性系统，有
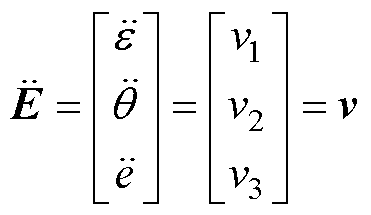（8）
式中，v1、v2和v3分别为Y1轴、Y2轴和X轴对应的等价控制输入。
反馈线性化控制是基于直驱H型平台标称模型，未考虑实际系统的扰动因素，因此对负载扰动和参数摄动的鲁棒性不强，在实际应用中有很大的局限性。为了提高轮廓控制系统的鲁棒性和稳定性，对解耦线性化后的融合误差动态系统设计自适应积分滑模控制器。
系统式（8）的积分滑模面定义为
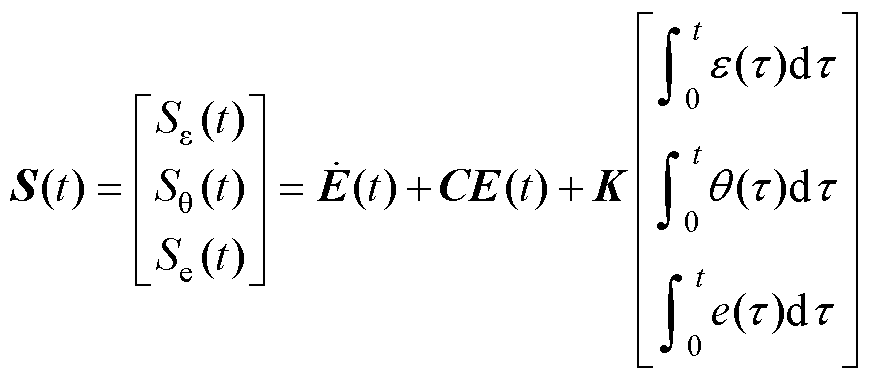（9）
式中，
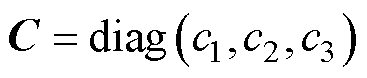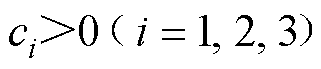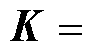
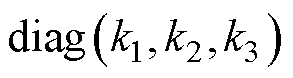且
；
且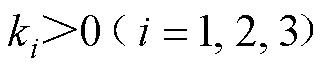
为控制增益。对于式（9）设计的具有常数控制增益矩阵C和K的滑模面，可能引起控制系统的振荡，激发系统的未知动力学[9]。为了解决这个问题，设计自适应律在线调整增益值以进一步提高系统控制性能。
控制增益的自适应律可以设计为
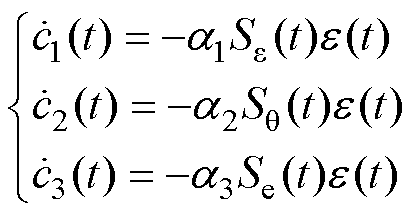（10）
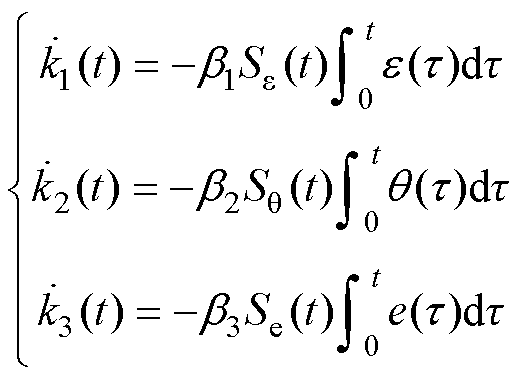（11）
式中，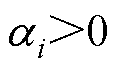
，
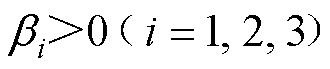均为常数。
定理1对于式（8）所描述的系统，随着积分滑模面式（9）的变化，如果使用具有自适应律式（10）和式（11）的控制器式（12），则融合误差E渐近收敛于零。
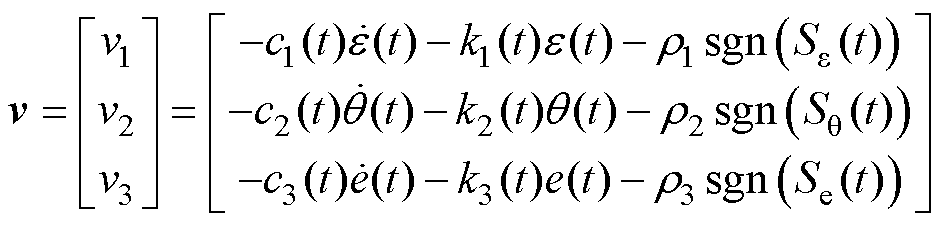（12）
式中，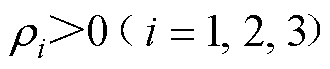
为切换增益。
证明：对3个独立的系统定义李雅普诺夫函数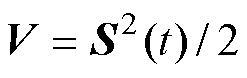
。存在
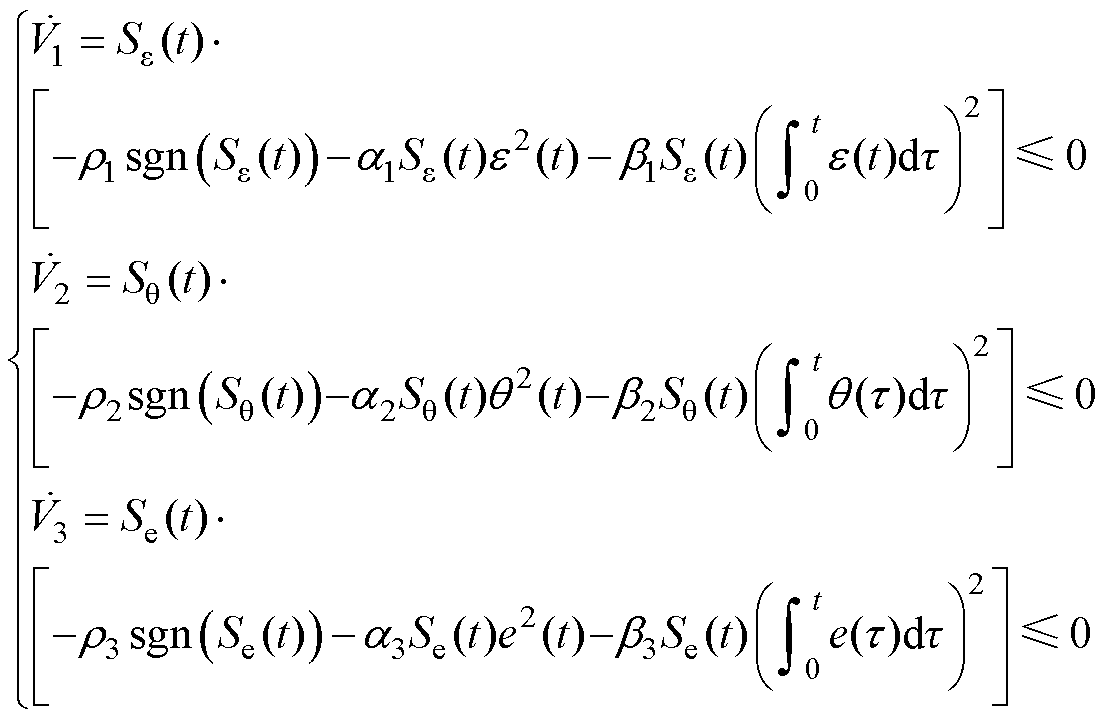（13）
根据李雅普诺夫稳定性理论，式（13）满足滑模可达性条件。
为削弱符号函数引起的系统抖振现象，用饱和函数代替符号函数。因此，自适应积分滑模控制律可以重新表示为
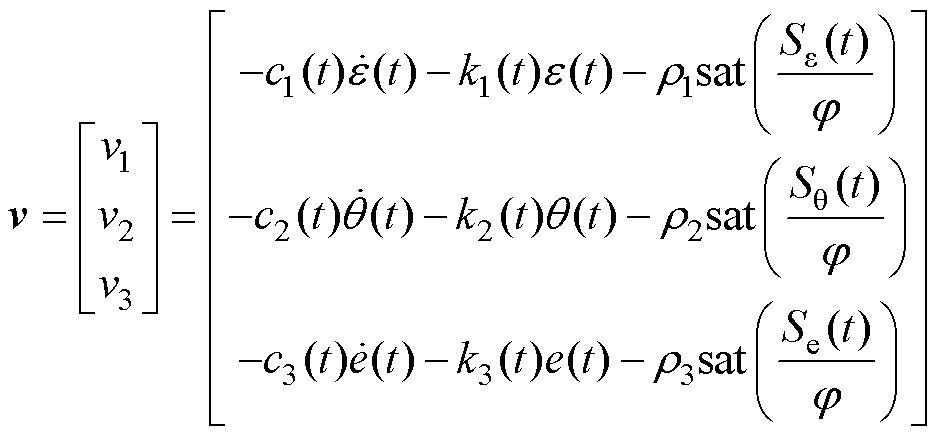（14）
式中，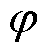
为边界层厚度；
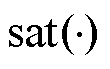为饱和函数。
综上所述，可得直驱H型平台控制系统框图如图4所示。点画线内部分可表示为反馈线性化后的线性系统。
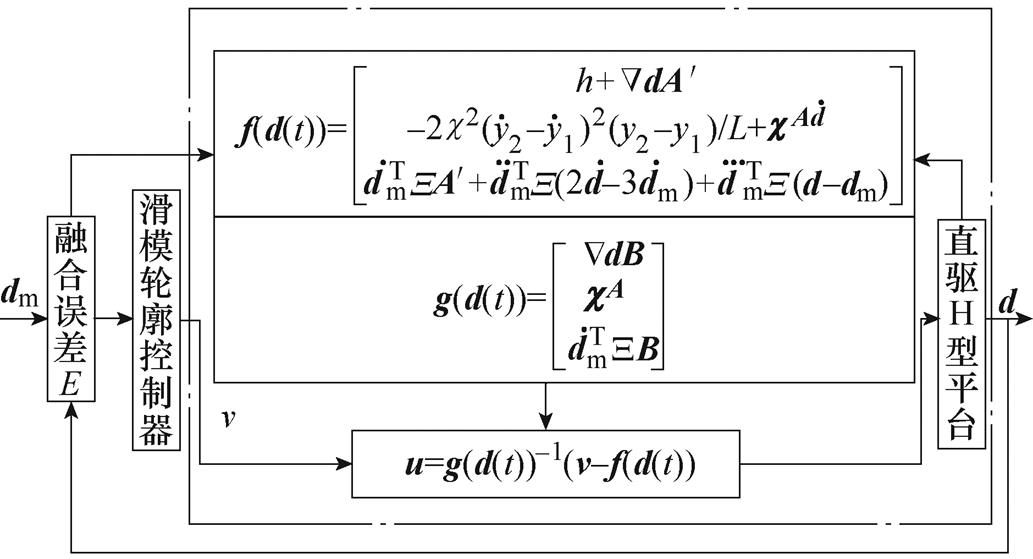
图4 直驱H型平台控制系统结构
Fig.4 Direct drive H-type platform control system structure drawing
为验证所提轮廓控制方法的可行性和有效性，进行实验分析。直驱H型实验平台如图5所示，系统主要由永磁直线同步电机（行程范围为360mm）、ZMP运动控制卡、AKD伺服驱动器、Mercury II直线光栅尺（分辨率为0.05mm）等组成。上位机通过SynqNet总线与控制卡连接实现了直驱生控制电压伺服系统的搭建；伺服驱动器根据控制卡的输出产驱动PMLSM的运行，直驱H型平台实验系统框图如图6所示。
图5 直驱H型实验平台
Fig.5 Direct drive H-type experimental platform
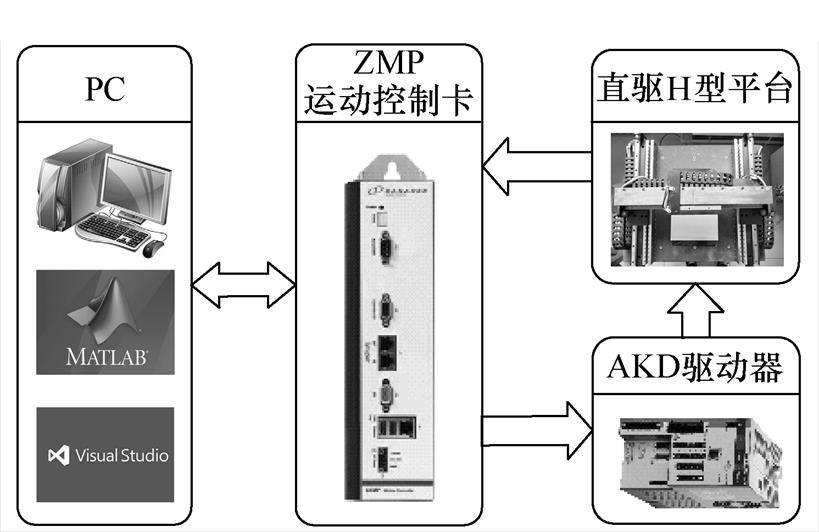
图6 实验系统框图
Fig.6 Block diagram of experimental system
给定椭圆期望轮廓，各单轴的给定输入分别为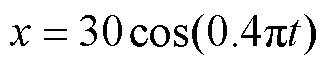
mm，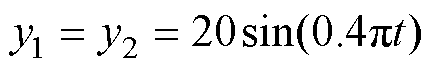
mm。通过与等效误差模型进行对比，验证所提出的融合误差模型在直驱H型平台轮廓控制上的优越性。同时，分别进行空载和负载为2kg的轨迹跟踪实验，验证系统的鲁棒性。为了便于比较，将基于等效误差模型控制方法下的同步误差响应曲线经式（4）转换成等效同步误差响应曲线。
直驱H型平台单轴PMLSM参数：Y1、Y2轴永磁直线电机，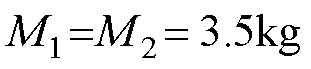
，
，
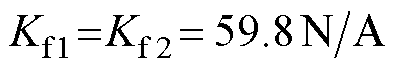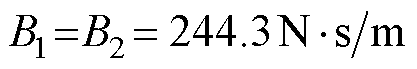。X轴永磁直线电机，
，
，
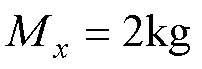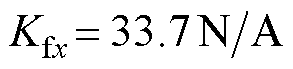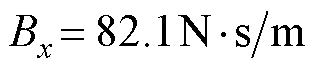。通过不断调节参数使系统运行状态良好，自适应积分滑模控制器参数见表1。针对积分滑模控制的积分饱和问题，在实验中对积分项施加饱和限制。
表1 AISMC参数设置
Tab.1 Parameters setting of AISMC
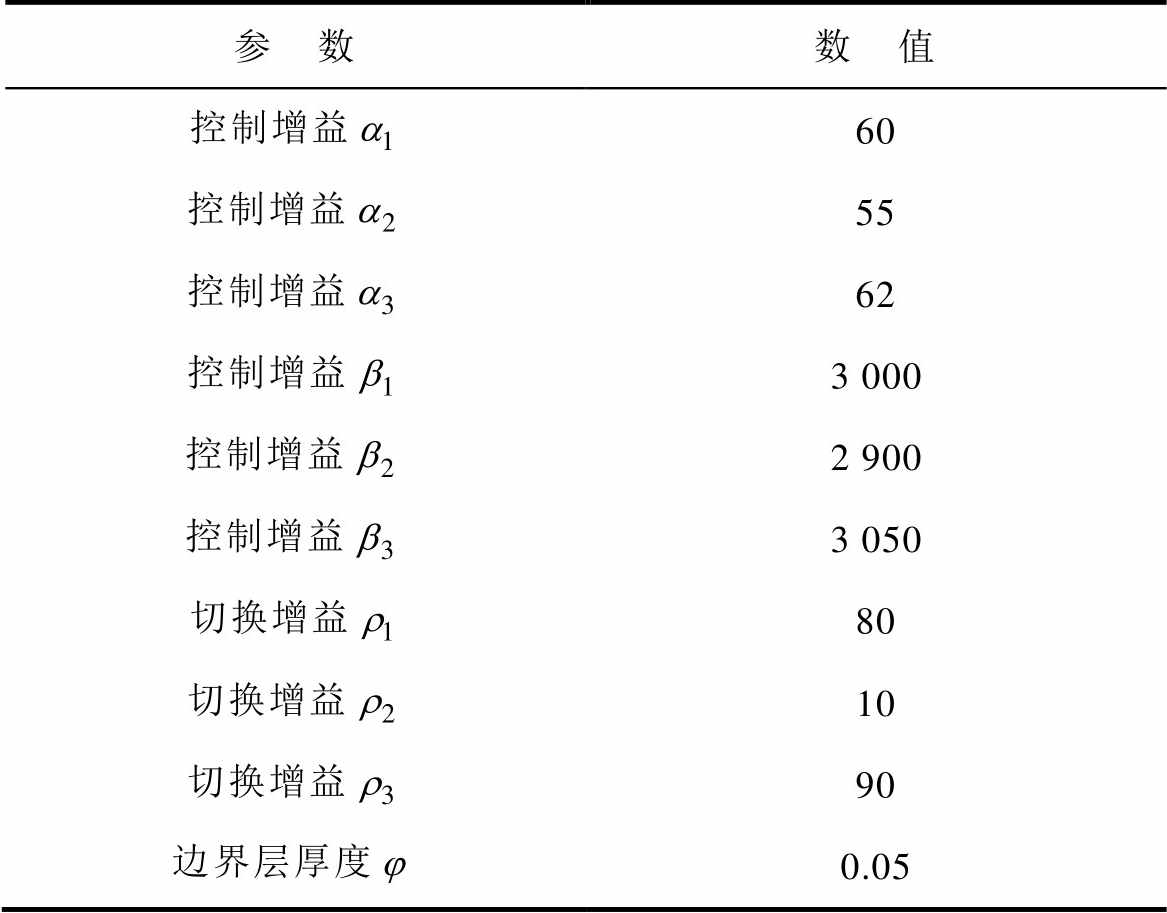
参 数数 值 控制增益60 控制增益55 控制增益62 控制增益3 000 控制增益2 900 控制增益3 050 切换增益80 切换增益10 切换增益90 边界层厚度0.05
为评价基于不同控制方法的轮廓控制系统性能，定义平均值R和方均根（Root Mean Square, RMS）为
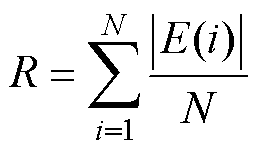（15）
（16）
式中，N为误差信号序列长度。
（1）空载实验：在直驱H型平台空载运行时，伺服系统仍然会受到固有推力波动、摩擦力等因素的影响，实验结果如图7和图8所示。表2列出了具体实验结果数据。从图7c与图8c的等效轮廓误差响应曲线可以明显看出，基于融合误差模型的伺服控制策略具有更高的轮廓控制精度；从图7b和图8b等效同步误差响应曲线可以看出，基于融合误差模型设计的轮廓控制器综合同步误差的控制量补偿于单轴伺服系统，以此提高系统同步控制精度，削弱同步误差影响，保证轮廓跟踪精度；从图7a与图8a切线误差响应曲线可以看出，所提方法也能有效提高单轴的跟踪性能。
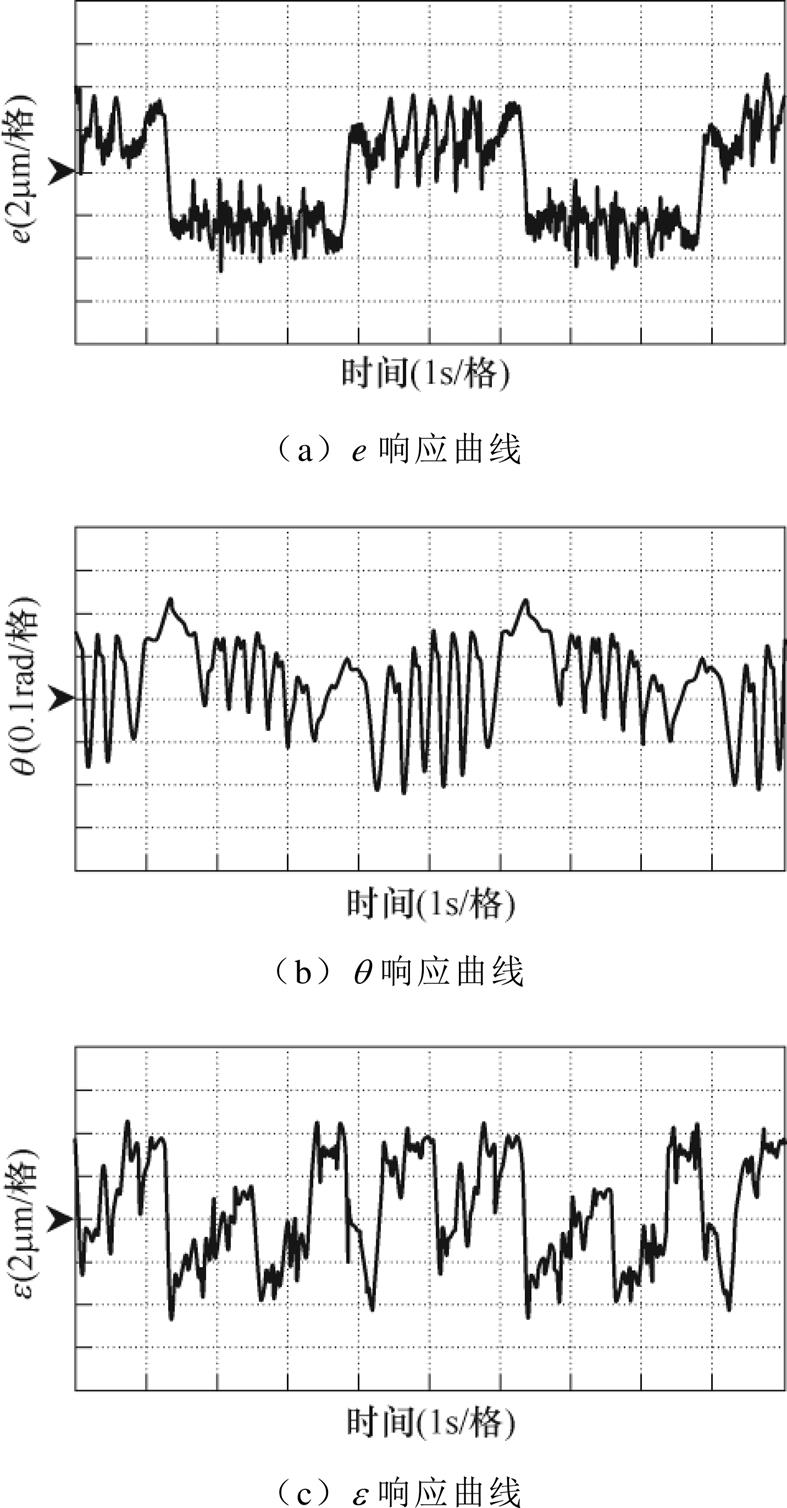
图7 空载状态下响应曲线（等效误差模型）
Fig.7 Response curves under no load condition (equivalent error model)
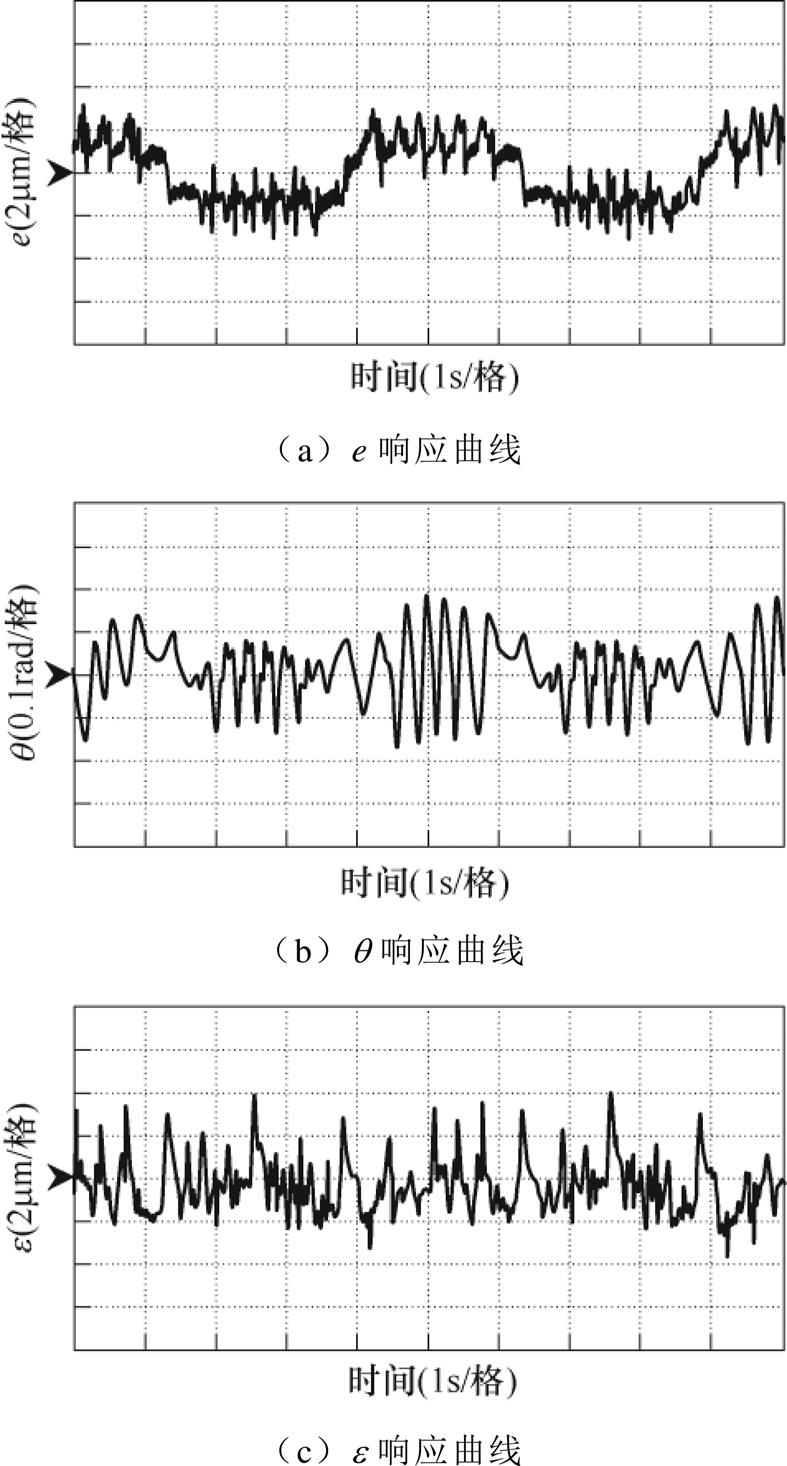
图8 空载状态下响应实验（融合误差模型）
Fig.8 Response curves under no load condition (integrated error model)
表2 空载时两种控制策略误差数据统计
Tab.2 Error data statistics of two control strategies in no-load condition
性能指标等效误差融合误差 em/mm1.7741.289 erms/mm1.9241.429 0.0890.055 0.1050.069 2.0911.183 2.4071.319
（2）负载实验：在直驱H型平台负载（负载为2kg）运行时，实验结果如图9和图10所示。通过图9与图10可以明显看出，基于融合误差模型的伺服控制策略在负载条件下与等效误差模型相比仍然具有更高的控制精度。表3列出了具体实验结果数据。
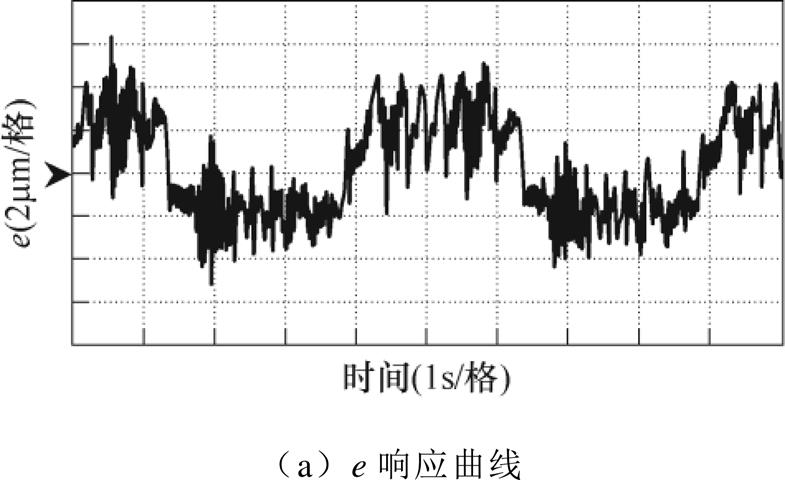
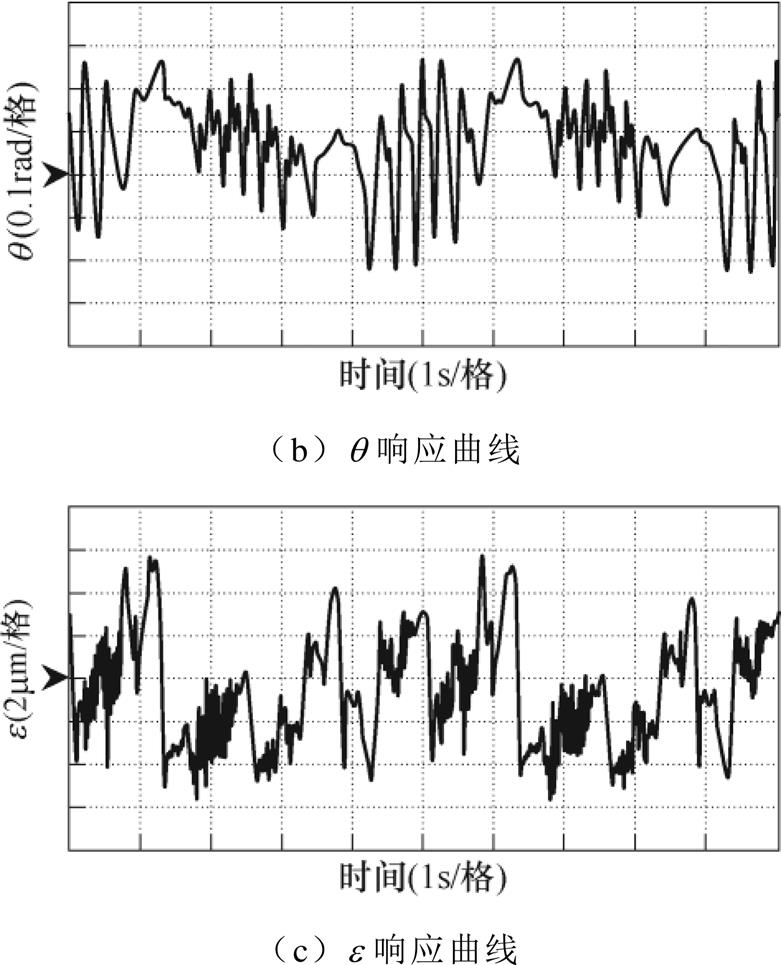
图9 负载状态下响应实验（等效误差模型）
Fig.9 Response curves under load condition (equivalent error model)
图10 负载状态下响应实验（融合效误差模型）
Fig.10 Response curves under load condition (integrated error model)
表3 负载时两种控制策略误差数据统计
Tab.3 Error data statistics of two control strategies in load condition
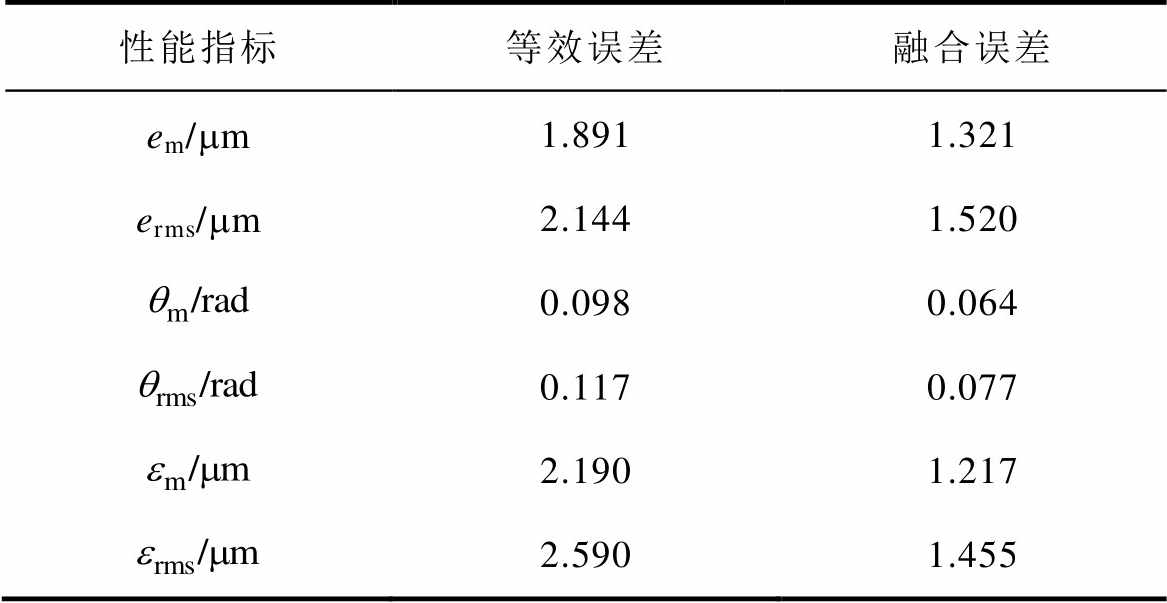
性能指标等效误差融合误差 em/mm1.8911.321 erms/mm2.1441.520 0.0980.064 0.1170.077 2.1901.217 2.5901.455
由图8和图10的实验结果可以看出，在空载情况下，切线误差在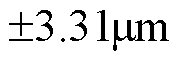
之间波动，等效同步误差在
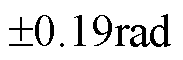之间波动，等效轮廓误差在
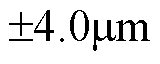之间波动；在进行负载实验时，切线误差稳定在
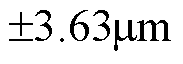之间波动，等效同步误差稳定在
之间波动，等效轮廓误差稳定在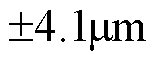
之间波动。同时结合表2与表3的实验数据可以看出，加入负载前后系统控制精度变化不大。由实验结果可得，融合误差模型能有效地削弱同步误差对轮廓控制性能的影响，同时轮廓精度和同步精度得到显著提高。基于反馈线性化设计的AISMC轮廓控制器能有效抑制负载扰动对轮廓跟踪精度的影响，提高系统的鲁棒性。
为了提高直驱H型平台轮廓控制性能，提出了一种考虑同步误差影响的反馈线性化滑模轮廓跟踪控制方法。通过实验得到以下结论：
1）融合误差模型能够有效地削弱同步误差对轮廓控制性能的影响，同时轮廓精度和同步精度得到显著提高。
2）采用反馈线性化对以融合误差为状态量的耦合非线性系统进行解耦线性化，对解耦后的线性子系统进行轮廓控制器设计，控制律易于实现。
3）AISMC轮廓控制器增强了系统鲁棒性，克服了负载扰动对轮廓控制精度的影响。
参考文献
[1] 叶宇豪, 彭飞. 多电机同步运动控制技术综述[J]. 电工技术学报, 2021, 36(14): 2922-2935.
Ye Yuhao, Peng Fei. Overview of multi-motor synchronous motion control technology[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(14): 2922-2935.
[2] Zhang Zongxue. The IT2FNN synchronous control for H-type gantry stage driven by dual linear motors[C]// Chinese Control And Decision Conference, Chongqing, China, 2017: 4790-4795.
[3] 王璨, 李国冲, 杨桂林, 等. 基于生物智能环状耦合的嵌入式永磁同步直线电机高精度位置协同控制研究[J]. 电工技术学报, 2021, 36(5): 935-943.
Wang Can, Li Guochong, Yang Guilin, et al. Research on position cooperative control of high-precision embedded permanent magnet synchronous linear motor based on biological intelligence loop coup- ling[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 935-943.
[4] 李争, 肖宇, 孙鹤旭, 等. 基于速度前瞻的双轴直线电机交叉耦合控制策略[J]. 电工技术学报, 2021, 36(5): 973-983.
Li Zheng, Xiao Yu, Sun Hexu, et al. Speed pro- spective based cross-coupling control strategy for dual-axis linear motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 973-983.
[5] Ma Jun, Chen Silu, Liang Wenyu, et al. Robust decentralized controller synthesis in flexure-linked H-gantry by iterative linear programming[J]. IEEE Transactions on Industrial Informatics, 2019, 15(3): 1698-1708.
[6] Teo C S, Tan K K, Lim S Y, et al. Dynamic modeling and adaptive control of a H-type gantry stage[J]. Mechatronics, 2007, 17(7): 361-367.
[7] 罗品奎, 金建新, 李小平, 等. 双直线电机的H型运动平台同步控制研究[J]. 电气与自动化, 2013, 62(7): 158-161.
Luo Pinkui, Jin Jianxin, Li Xiaoping, et al. Research on dual linear motor synchronous control in H-type stage[J]. Electrical and Automation, 2013, 62(7): 158-161.
[8] Iván García-Herreros, Kestelyn X, Gomand J, et al. Model-based decoupling control method for dual- drive gantry stages: a case study with experimental validations[J]. Control Engineering Practice, 2013, 21(3): 298-307.
[9] 原浩, 赵希梅. 基于全局任务坐标系的直驱XY平台学习互补滑模轮廓控制[J]. 电工技术学报, 2020, 35(10): 2141-2148.
Yuan Hao, Zhao Ximei. Learning complementary sliding mode contouring control based on global task coordinate frame for direct drive XY table[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2141-2148.
[10] Tajima S, Sencer B, Shamoto E. Accurate inter- polation of machining tool-paths based on FIR filtering[J]. Precision Engineering, 2018, 32(52): 332-344.
[11] 王丽梅, 张宗雪. H型精密运动平台交叉耦合模糊PID同步控制[J]. 沈阳工业大学学报, 2018, 40(1): 1-5.
Wang Limei, Zhang Zongxue. Cross-coupled fuzzy PID synchronous control for H-type precision motion platform[J]. Journal of Shenyang University of Technology, 2018, 40(1): 1-5.
[12] 陈晓, 赵文祥, 吉敬华. 考虑边端效应的双边直线永磁游标电机模型预测电流控制[J]. 电工技术学报, 2019, 34(1): 49-57.
Chen Xiao, Zhao Wenxiang, Ji Jinghua. Model predictive current control of double-side linear vernier permanent magnet machines considering end effect[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 49-57.
[13] Hu Chuxiong, Hu Zhipeng, Zhu Yu, et al. Advanced GTCF-LARC contouring motion controller design for an industrial X-Y linear motor stage with experi- mental investigation[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 3308-3318.
[14] Peng Xiaoyan, Jia Mingfei. Fuzzy sliding mode control based on longitudinal force estimation for electro mechanical braking systems using BLDC motor[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1): 142-151.
[15] Chen Shyh-Leh, Wu Kai-Chiang. Contouring control of smooth paths for multi-axis motion systems based on equivalent errors[J]. IEEE Transactions on Control Systems Technology, 2007, 15(6): 1151-1158.
[16] 王丽梅, 金抚颖, 孙宜标. 基于等效误差的直线电机XY平台二阶滑模控制[J]. 中国电机工程学报, 2010, 30(6): 88-92.
Wang Limei, Jin Fuying, Sun Yibiao. Second order sliding mode control for linear motor XY table based on equivalent errors method[J]. Proceedings of the CSEE, 2010, 30(6): 88-92.
[17] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear syn- chronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[18] 夏超英, 张耀华, 郭海宇. 无刷双馈电机反馈线性化控制方法[J]. 电工技术学报, 2020, 35(7): 1387- 1397.
Xia Chaoying, Zhang Yaohua, Guo Haiyu. Feedback linearization control approach of brushless doubly fedmachine[J]. Transactions of China Electrotechni- cal Society, 2020, 35(7): 1387-1397.
[19] 李鹏瀚, 王杰, 吴飞. 双馈风电机组次同步控制相互作用的反馈线性化滑模变结构抑制[J]. 电工技术学报, 2019, 34(17): 3661-3671.
Li Penghan, Wang Jie, Wu Fei. Sub-synchronous control interaction mitigation for DFIGs by sliding mode control strategy based on feedback lineari- zation[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3661-3671.
[20] 王勃, 王天擎, 于泳, 等. 感应电机电流环非线性积分滑模控制策略[J]. 电工技术学报, 2021, 36(10): 2039-2048.
Wang Bo, Wang Tianqing, Yu Yong, et al. Nonlinear integral sliding mode control strategy for current loop of induction motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2039-2048.
[21] Li Chao, Chen Zheng, Yao Bin. Adaptive robust synchronization control of a dual-linear-motor-driven gantry with rotational dynamics and accurate online parameter estimation[J]. IEEE Transactions on Indu- strial Informatics, 2017, 14(7): 3013-3022.
A Contour Tracking Control Method of Direct Drive H-Type Platform Considering the Influence of Synchronization Error
Abstract In order to reduce the influence of system synchronization error on the contour tracking accuracy of the H-type platform driven by permanent magnet linear synchronous motor (PMLSM), the beam deflection angle caused by the position mismatch of parallel axis is defined as the equivalent synchronization error, and the integrated error model is hence built suitable for the direct drive H-type platform. At the same time, a nonlinear coupling model based on integrated error is established to transform the control target from contour tracking to fusion error convergence. Feedback linearization is used to decouple the nonlinear coupled dynamic equation with integrated error as state variable. For linear models, an adaptive integrated sliding mode controller (AISMC) is designed to reduce the strong dependence of feedback linearization control on the mathematical model of the system and improve the robustness of the system to load disturbances and parameter perturbations. The experimental results show that the proposed control method can not only improve the contour precision and synchronization precision, but also enhance the robustness of the system.
keywords：Direct drive H-type platform, synchronization error, contour control, feedback linearization, adaptive integral sliding mode control
DOI: 10.19595/j.cnki.1000-6753.tces.201037
中图分类号：TM351
张 康 男，1995年生，博士研究生，研究方向为直线电机伺服系统及其控制。E-mail: zdzxzk@163.com
王丽梅 女，1969年生，教授，博士生导师，研究方向为交流伺服系统及其控制。E-mail: wanglm@sut.edu.cn（通信作者）
收稿日期 2020-08-14
改稿日期 2020-12-18
国家自然科学基金资助项目（51875366）。
（编辑 崔文静）