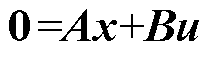（1）
摘要 针对中低频轻载工况下感应电机变频调速系统存在的转速与电流振荡问题，该文提出一种引入虚拟电抗的感应电机变频调速系统V/f控制方法。首先，建立感应电机变频调速系统的数学模型，在此基础上分析V/f控制下感应电机变频调速系统的稳态性能。然后，分析引入虚拟电抗的感应电机变频调速系统的根轨迹，证明了引入虚拟电抗可提升感应电机变频调速的稳定性，达到抑制感应电机变频调速在轻载中低频工况下振荡的目的。最后，通过Matlab/Simulink仿真和大功率感应电机变频调速系统的实验平台，验证了采用该文所提的引入虚拟电抗的V/f控制方法，可实现感应电机变频调速系统在中低频轻载工况下低转速脉动和低电流振荡运行。
关键词：感应电机变频调速系统 V/f控制 虚拟电抗 轻载低频工况下
随着感应电机控制技术的不断进步，感应电机控制系统的性能也在不断提升，对于大功率矿井提升机、风机、水泵等应用领域，由于其转动惯量过大、要求成本低，因此在中低频轻载工况下感应电机系统普遍采用V/f控制技术[1-3]。由于V/f控制不依赖感应电机模型参数，所以具有良好的稳定性和可靠性。然而，感应电机V/f控制在中低频轻载工况下容易出现不稳定的情况，从工程实践中可知，造成系统不稳定的原因有以下几种：①输出接有正弦LRC滤波器的电源系统，滤波器中的电容对交流感应电机的附加励磁会导致感应电机内部磁场产生改变从而引起系统振荡；②感应电机处于轻载甚至于空载的情况下转差率约等于零，齿槽所形成的磁阻转矩会引起感应电机磁场的不稳定；③超高效电机在轻载中低频运行时，电机内部处于过励磁的状态，会引起超高效电机磁链的不稳定，从而引发系统振荡。
针对感应电机变频调速系统的不稳定性问题，文献[4-8]对其不稳定性的原因作了较为系统的分析，为了进一步研究在V/f控制中感应电机的稳定性，构造了感应电机的状态方程并对其进行了小信号分析，得到了随感应电机参数变化的系统稳定性的变化趋势。文献[9-13]对如何提高感应电机V/f控制系统的稳定性进行研究，通过分析感应电机不同参数对系统振荡的影响，提出一种转差补偿策略来消除系统的振荡。文献[14]提出了一种新型感应电机电压矢量控制算法，通过对定子电压进行坐标变换，得到电机的无功电流，调节PI调节器使无功电流保持恒定来改善异步电机在极低速运行的稳定性。文献[15]分析了感应电机的中低频振荡原因，通过检测逆变器的输入电流中负序电流的间隔时间，并与逆变器的载波频率进行比较，来达到判定感应电机系统是否会出现中低频振荡的目的。文献[16]提出了一种增强感应电机V/f控制性能的策略，通过降低逆变器输出电压的频率和幅值，从而降低感应电机定子电流中的振荡分量，达到改善感应电机系统稳定性的目的。文献[17]针对感应电机变频调速系统在中低频工况下容易出现振荡的问题，提出了一种将电流闭环和死区补偿相结合的控制策略。文献[18-19]提出了一种开环系统稳定控制的通用方法，该方法可用于感应电机、永磁同步电机或其他电机驱动，将频率的设定值通过频率补偿来进行调整，以减轻电机控制系统的振荡。文献[20]提出了一种新的感应电机中低频振荡抑制方法，对磁通与电流分量进行带通滤波和比例控制，通过电流反馈补偿来增强感应电机系统的稳定性。文献[21-22]在感应电机风电系统的虚拟同步控制策略中引入虚拟阻抗，建立了定子电压控制模型以及发电机输出阻抗模型，实现了感应电机系统的解耦稳定运行。
针对感应电机在中低频轻载工况下V/f控制的不稳定问题，本文提出了一种全新的用虚拟电抗代替实体电抗的感应电机变频调速系统的稳定控制策略。此外，本文还对引入不同大小的电抗、引入实体电抗、引入虚拟电抗等情况下的感应电机变频调速系统的稳态性能进行了详细分析。与传统构建观测器、增加滤波环节等方法相比，本文所提的引入虚拟电抗的感应电机变频调速系统的控制策略，具有算法简单、控制效果更好、成本更低、实施更便捷等优势。最后，通过Matlab/Simulink仿真和大功率感应电机实验平台对本文所提控制策略的有效性和可行性进行了验证。
在dq旋转坐标系下，以定子电流和定子磁链为状态变量，当感应电机系统稳定运行时，感应电机系统的五阶状态方程[8, 23-24]为
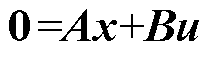（1）
其中
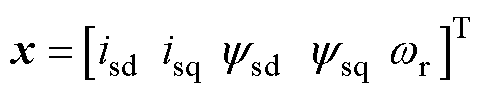
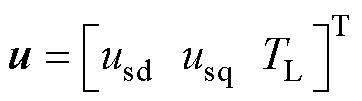
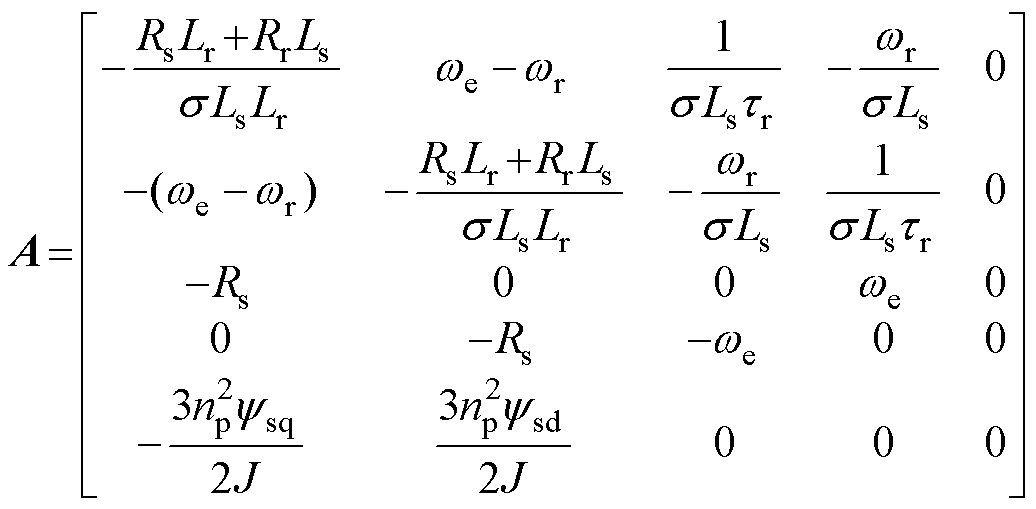
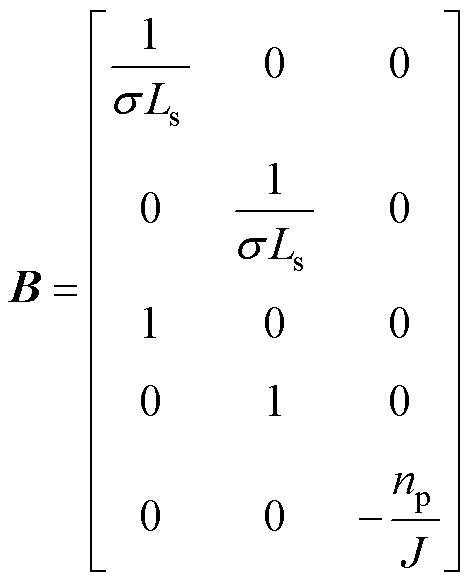
式中，usd、usq为感应电机的定子d、q轴电压；
、
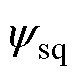为感应电机的d、q轴磁链；isd、isq为感应电机的d、q轴电流；Rs为定子电阻；Rr为转子电阻；Ls为定子电感；Lr为转子电感；
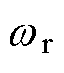为转子角频率；
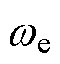为定子电角频率；Te为电磁转矩；np为电机的极对数；J为机械转动惯量；TL为负载转矩；
为电机的漏磁系数；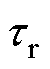
为转子电磁时间常数，
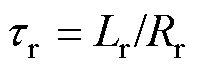。该系统处于稳态时，状态方程左侧的状态变量的导数可视为零。在中低频轻载工况下，感应电机稳定运行时转子转速很接近同步转速，所以
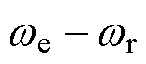≈0。
感应电机变频调速系统稳定运行时，V/f控制方法下感应电机输出的定子电压[8]为
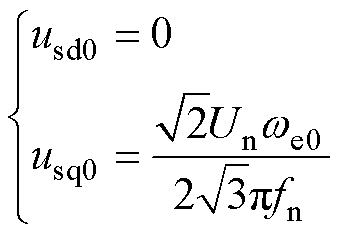（2）
式中，Un为额定电压；fn为额定频率；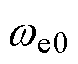
为稳态工作点上的定子电角速度；usd0、usq0为稳态工作点上的d、q轴电压。
感应电机的转矩方程为
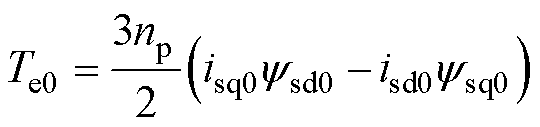（3）
式中，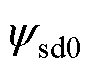
、
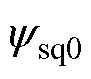分别为稳态工作点上的d、q轴磁链；isd0、isq0分别为稳态工作点上的d、q轴电流。
根据式（1）和式（3），可得感应电机系统的定子磁链方程为
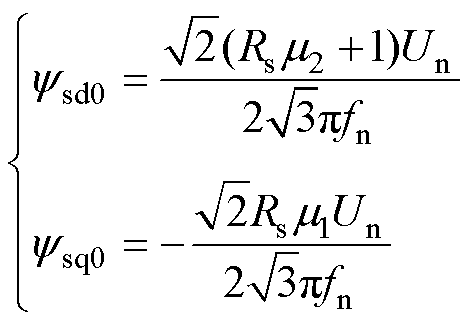（4）
由于感应电机的同步角速度与给定转速相同，结合式（1）和式（4）可得感应电机系统的定子电流方程为
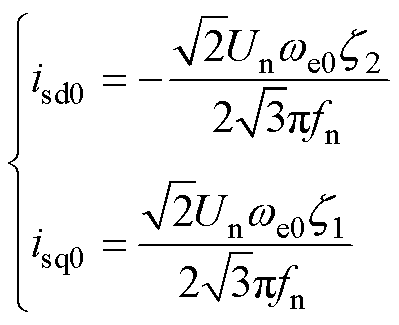（5）
其中
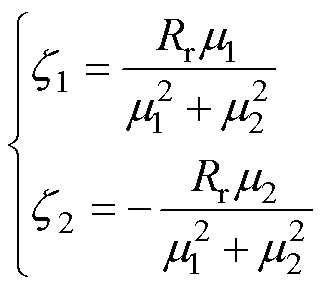
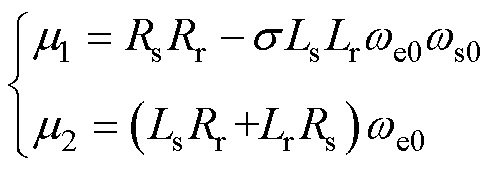
式中，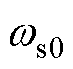
为稳态工作点上的转差角频率；
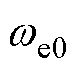为稳态工作点上的定子电角频率。
将式（4）和式（5）代入式（3），可得稳态工作点下的感应电机的转矩状态方程为
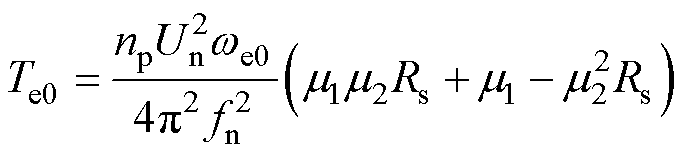（6）
感应电机变频调速系统原理如图1所示。电网通过变频器、正弦滤波器、变压器向感应电机供电，其中，正弦变频电源与感应电机构成变频调速系统。在中低频轻载工况下，感应电机变频调速系统存在不稳定问题，本节通过建立小信号模型详细分析了感应电机变频调速系统的稳定性。
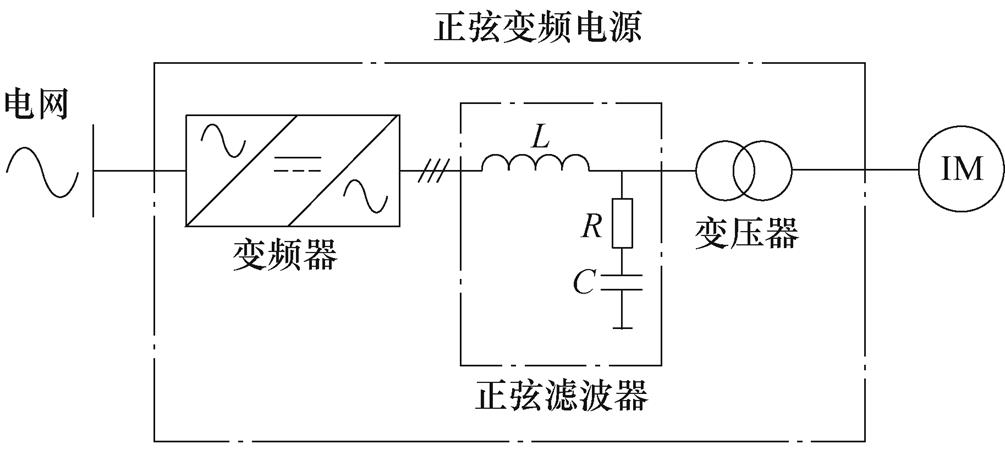
图1 感应电机变频调速系统原理
Fig.1 The principle diagram of variable frequency speed control system of induction motor
当感应电机稳定运行时，在稳态工作点的基础上通过引入微小的扰动，可得感应电机变频调速系统的线性化小信号模型为
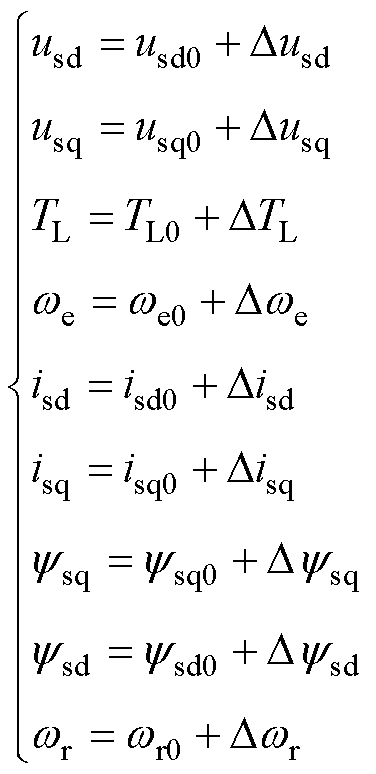（7）
式中，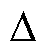
为小信号扰动量。
将式（7）代入感应电机系统状态方程式（1）中，经线性化处理，可得感应电机变频调速系统的小信号状态方程的特征矩阵At为
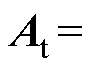
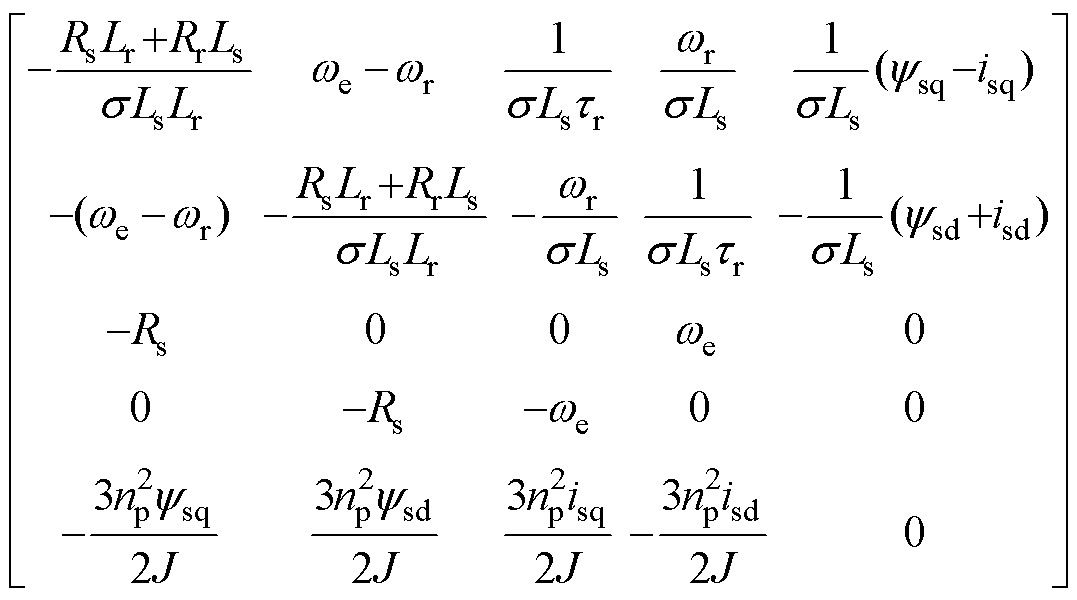（8）
为了得到感应电机变频调速系统的根轨迹，则有
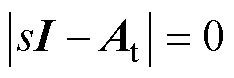（9）
将表1中感应电机的参数代入式（9）中进行求解，可得感应电机变频调速系统的5个极点，包括一个实部极点和两对共轭极点。如果极点全部分布在s域的左半平面，说明感应电机变频调速系统是稳定的；反之，则系统不稳定。感应电机变频调速系统的根轨迹图，如图2所示。可知，感应电机变频调速系统的根轨迹有极点位于s域的右半平面，所以此系统存在不稳定的运行情况。
通过分析发现，增大感应电机的定子电抗可以解决感应电机变频调速系统的不稳定问题。图3给出了定子电抗变化情况下的感应电机变频调速系统的根轨迹图。由图3可知，随着感应电机的定子电抗增加，根轨迹有进入s域左半平面的趋势。当其定子电抗增加到一定值时，感应电机变频调速系统的根轨迹完全进入左半平面，系统从不稳定变为稳定。由图3可知，当定子电抗增加为8.745mH时，感应电机变频调速系统的极点全部位于s域的左半平面，感应电机变频调速系统趋向于稳定。
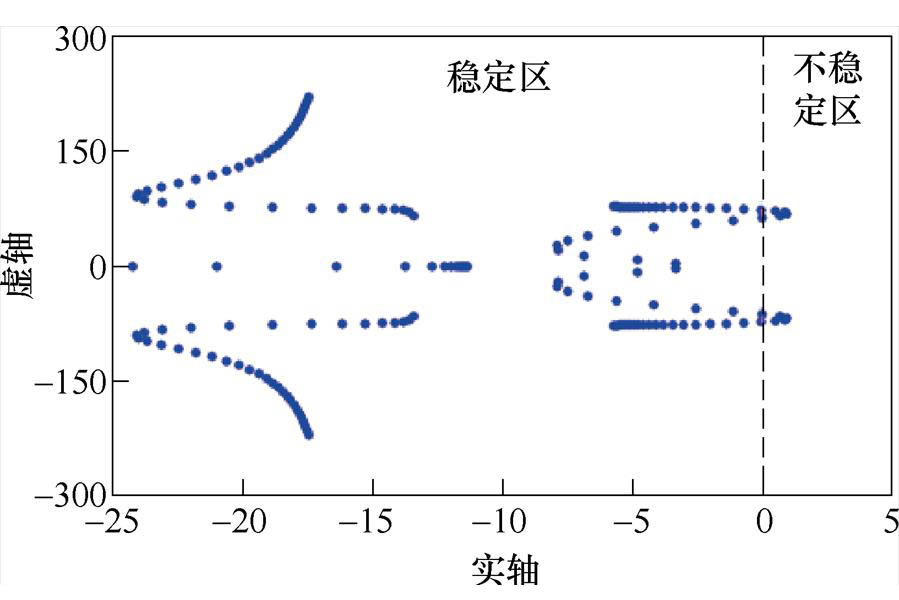
图2 正常情况下感应电机变频调速系统根轨迹图
Fig.2 Root locus of induction motor variable frequency speed control system under normal conditions
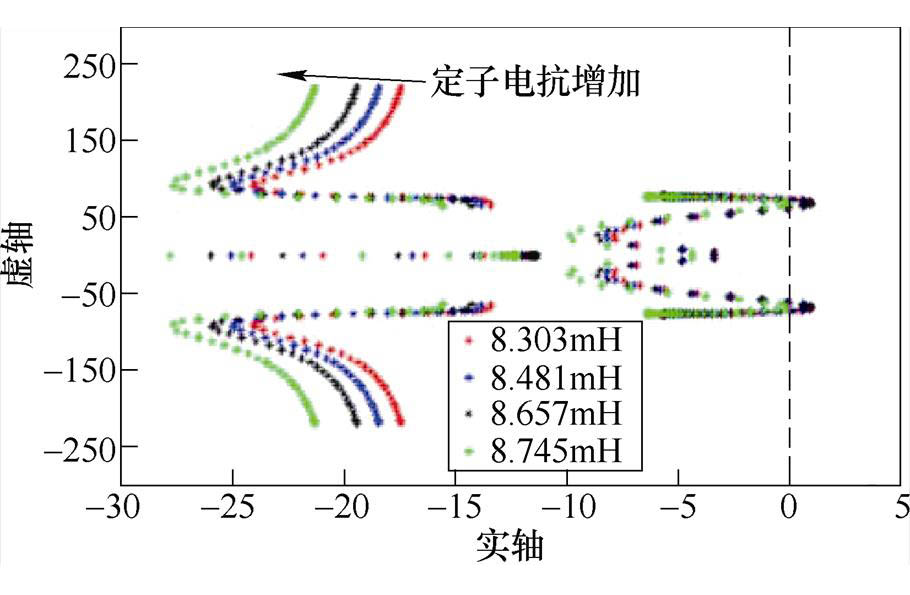
图3 定子电抗变化情况下感应电机变频调速系统根轨迹图
Fig.3 Root locus of induction motor variable frequency speed control system under stator reactance variation
通过上述感应电机变频调速系统稳定性分析可知，增大感应电机定子电抗可使系统稳定。然而，在实际工程应用中改变感应电机内部参数非常困难，且不具备工程实用价值。为此，提出了在感应电机变频调速系统中引入外部电抗的方法来提升系统的稳定性。引入外部电抗后感应电机变频调速系统的等效电路如图4所示。
由图4可知，将引入的外部电抗与感应电机的定子电抗串联，可等效为感应电机的定子电抗增大，提高了变频调速系统中感应电机定子端电压，从而来提升感应电机变频调速系统的稳定性。然而，实际工程应用中在感应电机变频调速系统中引入外部电抗，存在体积过大、工程成本增加、系统效率降低等一系列问题。此外，当实验的感应电机功率不一致时，还存在外部电抗匹配不方便的调节问题。为此，本文研究了在电源控制器中引入虚拟电抗，达到引入同等参数值外部电抗相同效果的目的。
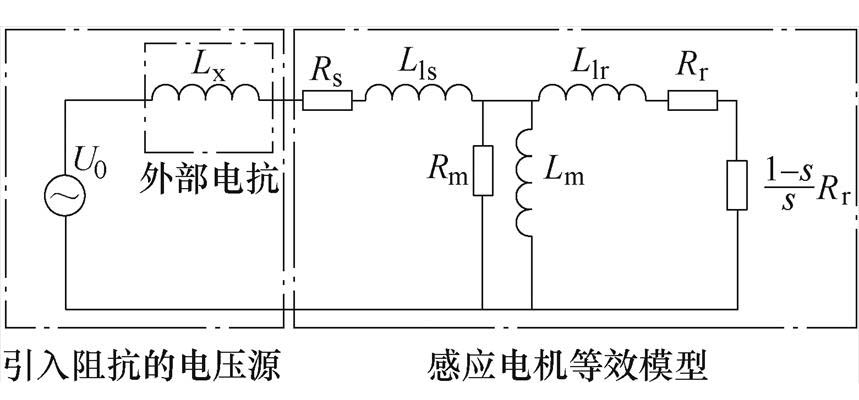
图4 引入外部电抗后感应电机变频调速等效电路
Fig.4 Equivalent circuit diagram of induction motor variable frequency speed control system after introducing external reactance
在电源控制器中，引入虚拟电抗的传递函数Gv表达式为
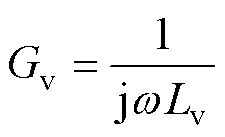（10）
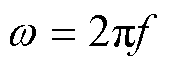（11）
式中，Lv为引入的虚拟电感；f为电源控制器的给定频率；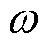
为电源控制器的给定角频率。
令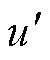
为引入虚拟电抗后感应电机定子端的电压，将定子端的电压分解到d轴和q轴上得
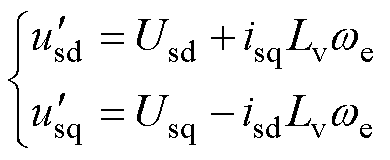（12）
将式（12）中的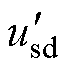
和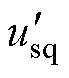
代入式（1）中，可列写出引入虚拟电抗的感应电机变频调速系统的状态方程为
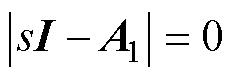（13）
其中
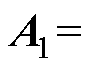
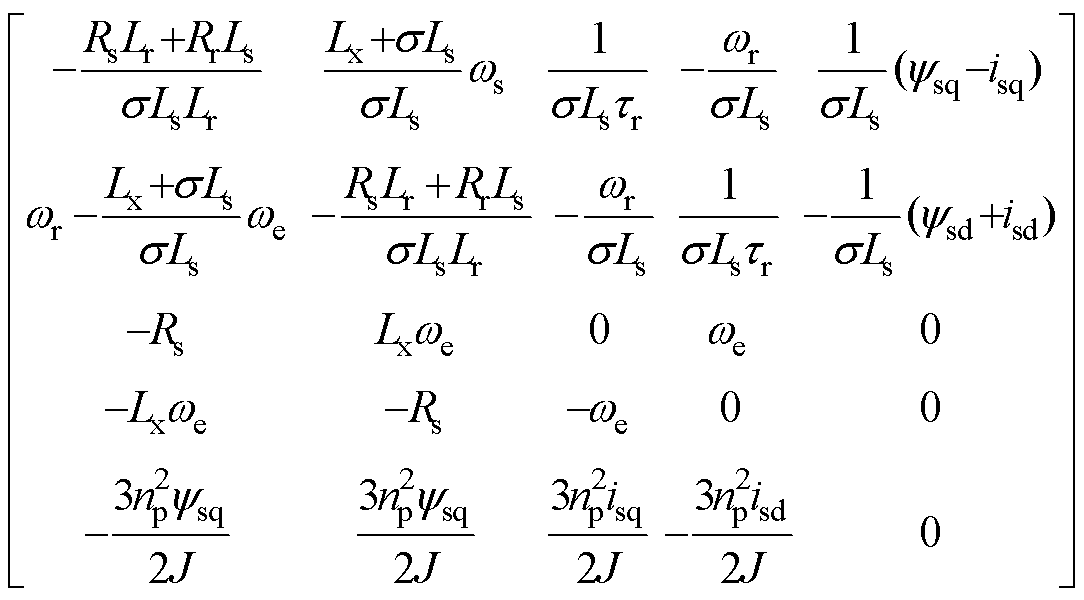
对式（13）中感应电机变频调速系统矩阵进行求解，可绘制引入虚拟电抗的变频调速系统根轨迹图，如图5所示。图中，Zs为感应电机定子电抗，Zs=8.30mH，Zx为引入的虚拟电抗，Zx=0.041 021mH（2.5%的基值电抗）。当定子电抗为Zs+4Zx时，感应电机变频调速系统的极点全部位于s域的左半平面，感应电机变频调速系统趋向于稳定。对比图3和图5可知，在感应电机变频调速系统中引入适量的虚拟电抗也可使系统稳定，达到抑制变频调速系统振荡、改善其不稳定性的目的。
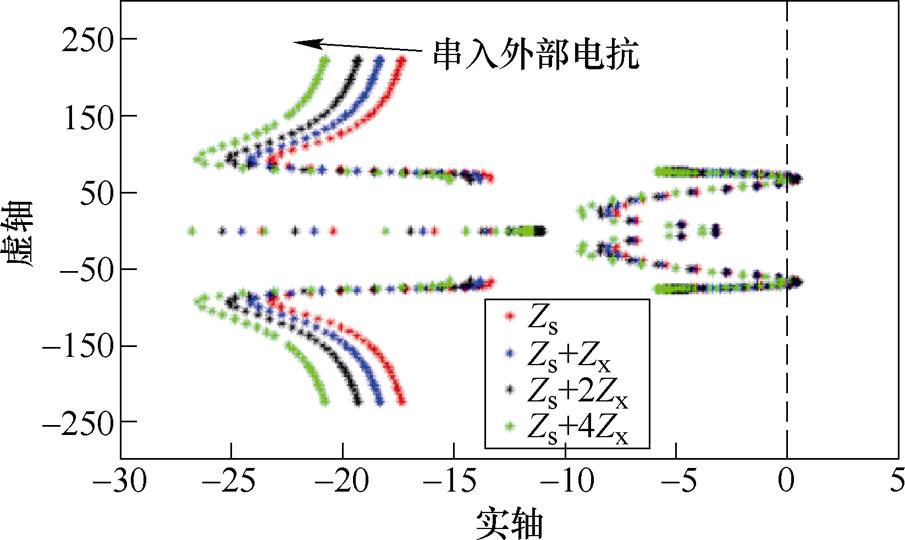
图5 引入虚拟电抗时感应电机变频调速系统根轨迹图
Fig.5 Root locus of induction motor variable frequency speed control system with virtual reactance
在引入虚拟电抗的同时也改变了变频调速系统的时间常数，所以在引入虚拟电抗时还应考虑虚拟电抗和定子电阻的匹配性，使得引入虚拟电抗后变频调速系统的时间常数尽量和引入之前保持一致。此外，设计虚拟电抗也应考虑到系统中存在的干扰信号的影响。变频调速系统在引入虚拟电抗后，为了减小系统的噪声及其放大效应对变频调速系统的影响，通常在感应电机变频调速系统中还加入一个二阶低通滤波器LPF，有
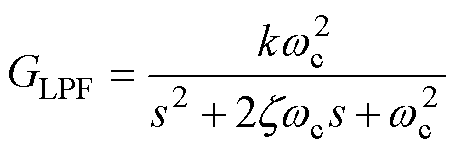（14）
式中，
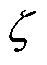为阻尼比；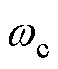
为无阻尼自振角频率。
为了验证本文所提引入虚拟电抗的感应电机变频调速系统V/f控制方法的有效性和可行性，在Matlab/Simulink平台中搭建了感应电机变频调速系统，仿真使用的感应电机参数见表1。感应电机变频调速系统引入不同大小的外部电抗的仿真结果，如图6～图11所示。感应电机变频调速系统引入虚拟电抗与外部电抗的对比仿真结果，如图12～图17所示。
本节给出了13Hz和15Hz工况下，感应电机变频调速系统的转速、d轴电流及A相定子电流的仿真结果。
表1 900kW感应电机参数
Tab.1 Parameters of 900kW induction motor
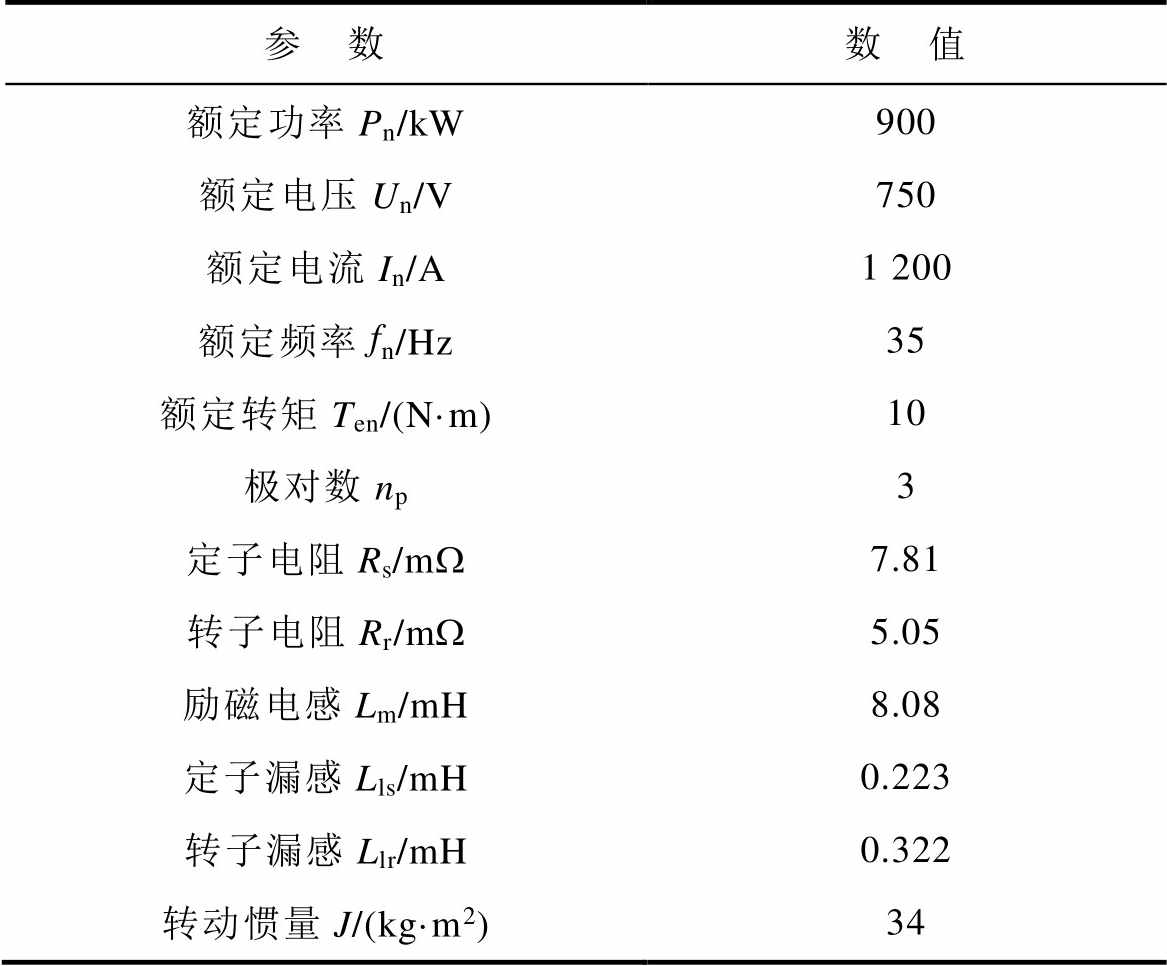
参 数数 值 额定功率Pn/kW900 额定电压Un/V750 额定电流In/A1 200 额定频率fn/Hz35 额定转矩Ten/(N·m)10 极对数np3 定子电阻Rs/mW7.81 转子电阻Rr/mW5.05 励磁电感Lm/mH8.08 定子漏感Lls/mH0.223 转子漏感Llr/mH0.322 转动惯量J/(kg·m2)34
图6给出了13Hz工况下，没有引入电抗、引入5%基值电抗大小的外部电抗、引入10%基值电抗大小的外部电抗的感应电机转速对比仿真结果。由图6可知，在没有引入电抗的情况下，感应电机转速出现大幅振荡，振荡峰峰值高达±35r/min。在引入5%基值电抗大小的外部电抗后，感应电机转速振荡幅度明显下降；引入10%基值电抗大小的外部电抗后，感应电机转速振荡得到进一步抑制，转速振荡峰峰值低至±1.5r/min。图7给出了13Hz工况下，没有引入电抗、引入5%基值电抗大小的外部电抗、引入10%基值电抗大小的外部电抗的感应电机d轴电流对比仿真结果。仿真结果表明，引入10%基值电抗大小的外部电抗后，感应电机d轴电流趋于稳定，没有出现振荡的现象。
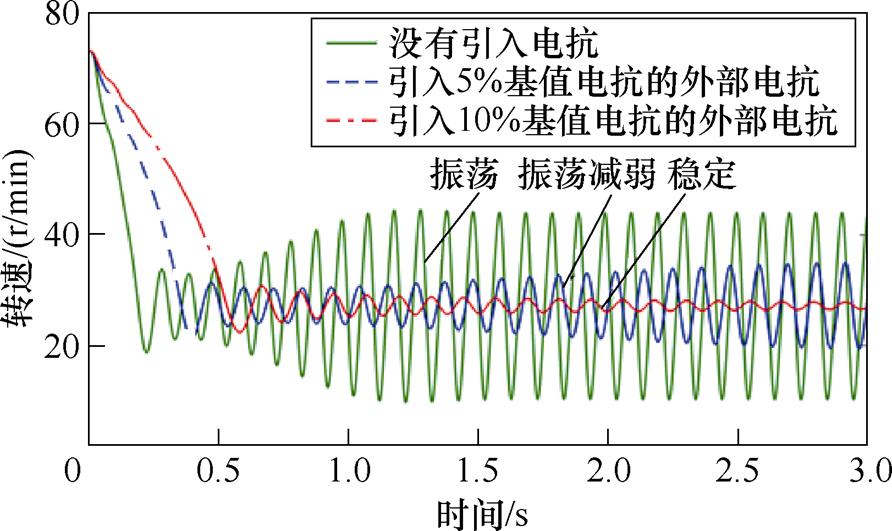
图6 13Hz工况下引入不同比例外部电抗后感应电机转速仿真结果
Fig.6 Simulation results of speed under 13Hz operating condition with different proportion of external reactance
图8给出了13Hz工况下，没有引入电抗、引入5%基值电抗大小的外部电抗、引入10%基值电抗大小的外部电抗的感应电机A相定子电流对比仿真结果。在没有引入电抗的情况下，感应电机A相定子电流出现明显畸变。在引入10%基值电抗大小的外部电抗后，感应电机A相定子电流畸变现象得到抑制，出现较好的正弦波形。上述仿真结果分析可知，通过增加引入电抗的大小，可以达到抑制感应电机转速、电流振荡的目的，表明引入适量大小的外部电抗可使感应电机变频调速系统趋于稳定。
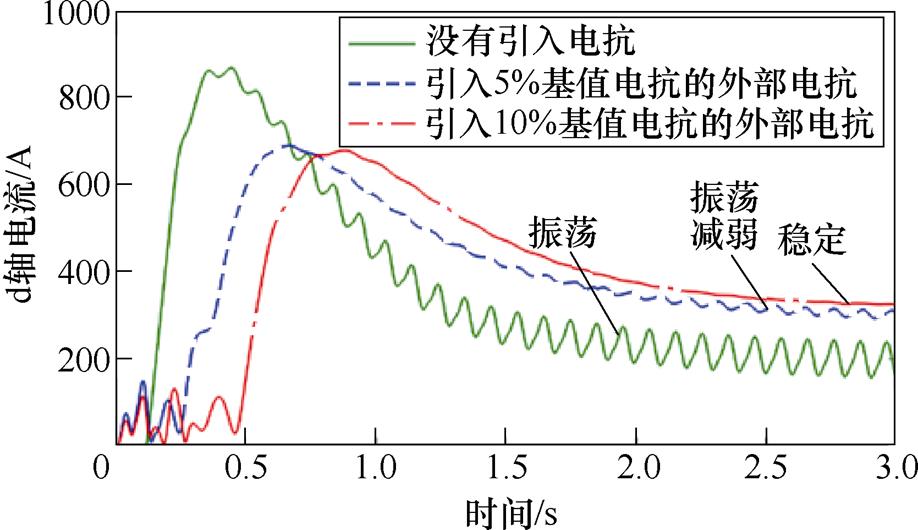
图7 13Hz工况下引入不同比例外部电抗后感应电机d轴电流仿真结果
Fig.7 Simulation results of d-axis current under 13Hz operating condition with different proportion of external reactance
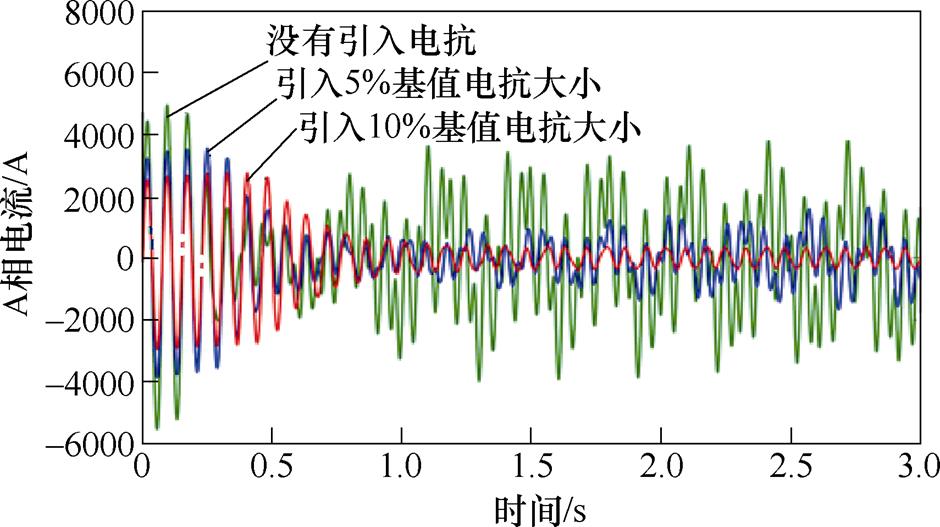
图8 13Hz工况下引入不同比例外部电抗后感应电机A相定子电流仿真结果
Fig.8 Simulation results of phase A stator current under 13Hz operating condition with different proportion of external reactance
15Hz工况下引入不同比例基值电抗后感应电机转速仿真结果如图9所示。对比图9和图6可知，在15Hz的工况下感应电机转速仿真结果和13Hz的结果基本保持一致。15Hz工况下引入不同比例基值电抗后感应电机d轴电流仿真结果如图10所示。对比图10和图7的仿真结果可以看出，在没有引入外部电抗的情况下，15Hz工况下的d轴电流的波动明显小于13Hz的工况下。15Hz工况下引入不同比例基值电抗后感应电机A相电流仿真结果如图11所示。而对比图11和图8的仿真结果可以看出，在引入10%基值电抗大小的外部电抗情况下，15Hz工况下的A相定子电流的波动明显小于13Hz的工况下。上述仿真结果分析可知，通过适量的增加外部电抗的大小，可以达到抑制感应电机转速、电流振荡的目的，同时提高系统运行频率也能起到一定的抑制振荡效果。
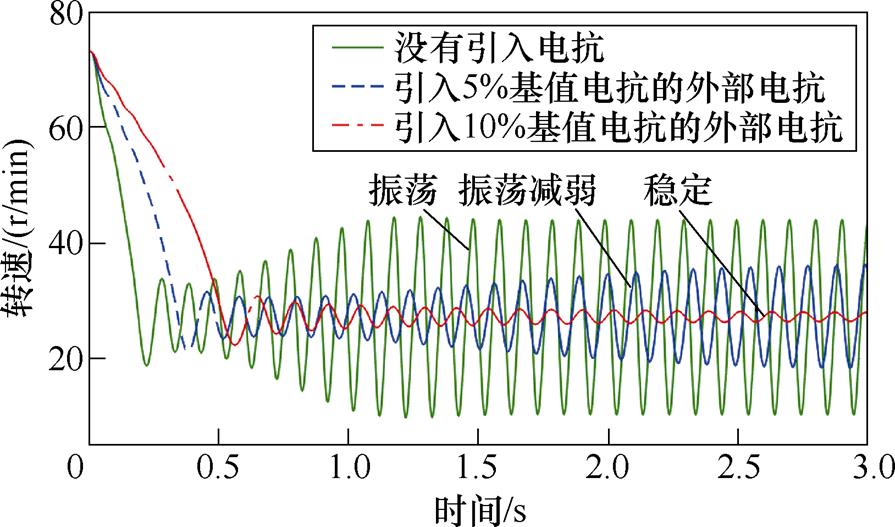
图9 15Hz工况下引入不同比例基值电抗后感应电机转速仿真结果
Fig.9 Simulation results of speed under 15Hz operating condition with different proportion of external reactance
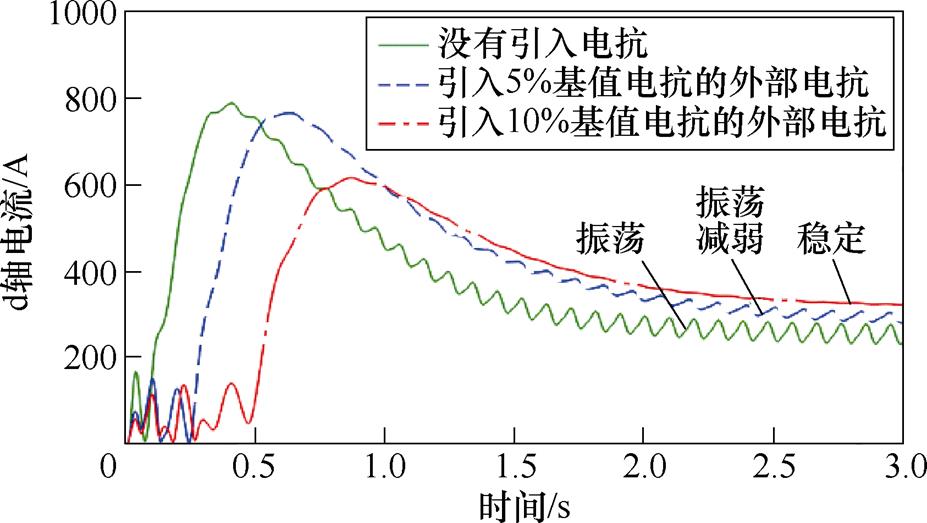
图10 15Hz工况下引入不同比例基值电抗后感应电机d轴电流仿真结果
Fig.10 Simulation results of d-axis current under 15Hz operating condition with different proportion of external reactance
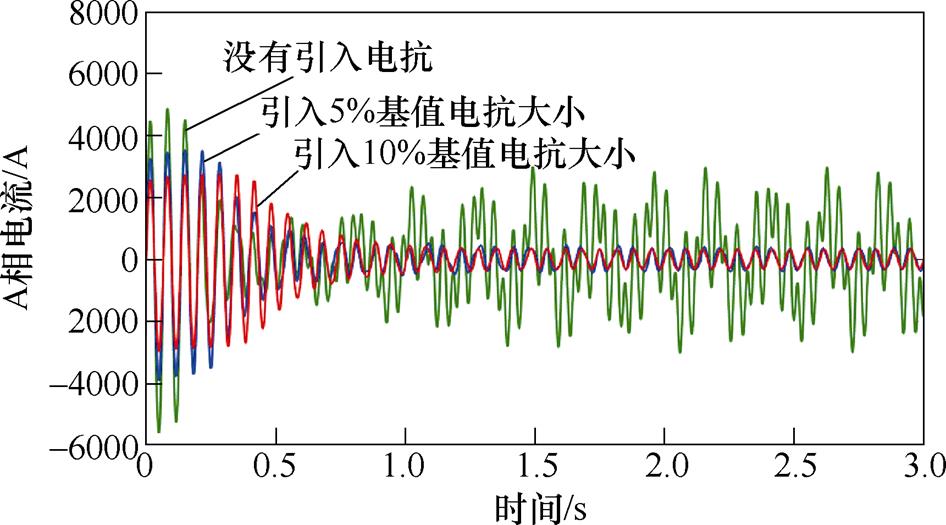
图11 15Hz工况下引入不同比例基值电抗后感应电机A相电流仿真结果
Fig.11 Simulation results of phase A stator current under 15Hz operating condition with different proportion of external reactance
本节给出了13Hz工况下，引入虚拟电抗和外部电抗的感应电机变频调速系统的转速、d轴电流及A相定子电流的对比仿真结果。
13Hz工况下引入虚拟电抗和外部电抗后的感应电机转速对比仿真结果（5%基值电抗大小）如图12所示。可知，在没有引入电抗的情况下，感应电机转速出现大幅振荡。在引入外部电抗后，感应电机转速振荡明显减小；引入同等大小虚拟电抗后，感应电机转速从振荡变为稳定。13Hz工况下引入虚拟电抗和外部电抗后的感应电机d轴电流对比仿真结果（5%基值电抗大小）如图13所示。可知，引入虚拟电抗后，感应电机d轴电流趋于稳定，没有出现波动。13Hz工况下引入虚拟电抗和外部电抗后的感应电机A相定子电流对比仿真结果（5%基值电抗大小）如图14所示。可知，在没有引入电抗的情况下，感应电机A相定子电流畸变明显。在引入虚拟电抗后，感应电机A相定子电流畸变现象得到抑制，出现较好的正弦波形。上述仿真结果分析可知，通过引入虚拟电抗，可以达到抑制感应电机转速、电流振荡的目的，而且比引入实体电抗效果更好。
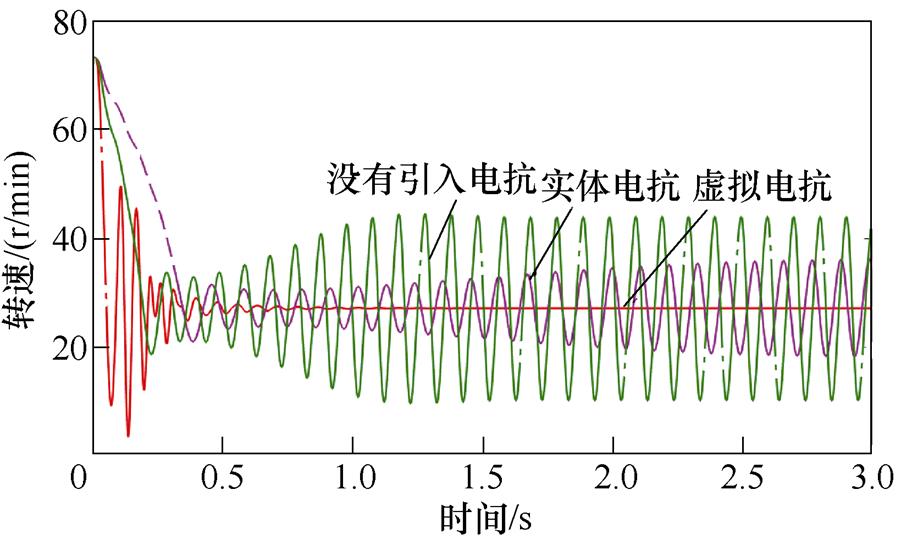
图12 13Hz工况下引入虚拟电抗和外部电抗后的感应电机转速对比仿真结果（5%基值电抗大小）
Fig.12 Simulation results of speed comparison with virtual reactance and solid reactance at 13Hz (5% base value reactance)
图13 13Hz工况下引入虚拟电抗和外部电抗后的感应电机d轴电流对比仿真结果（5%基值电抗大小）
Fig.13 Simulation results of d-axis comparison with virtual reactance and solid reactance at 13Hz (5% base value reactance)
图15～图17给出了在13Hz的工况下引入10%大小基值电抗的虚拟电抗和外部电抗的对比仿真结果。通过仿真结果可知，引入虚拟电抗的情况下，感应电机转速、d轴电流、A相电流的波动明显小于引入外部电抗的情况，同时调整时间也更短。进一步证明了增大引入虚拟电抗的大小，感应电机变频调速系统的稳定性会更好。
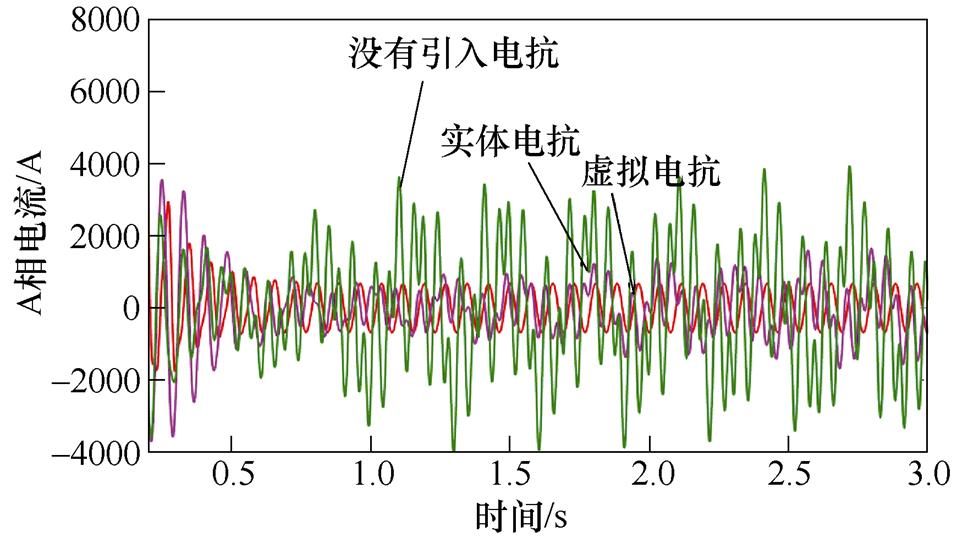
图14 13Hz工况下引入虚拟电抗和外部电抗后的感应电机A相定子电流对比仿真结果（5%基值电抗大小）
Fig.14 Simulation results of phase A current comparison with virtual reactance and solid reactance at 13Hz (5% base value reactance)
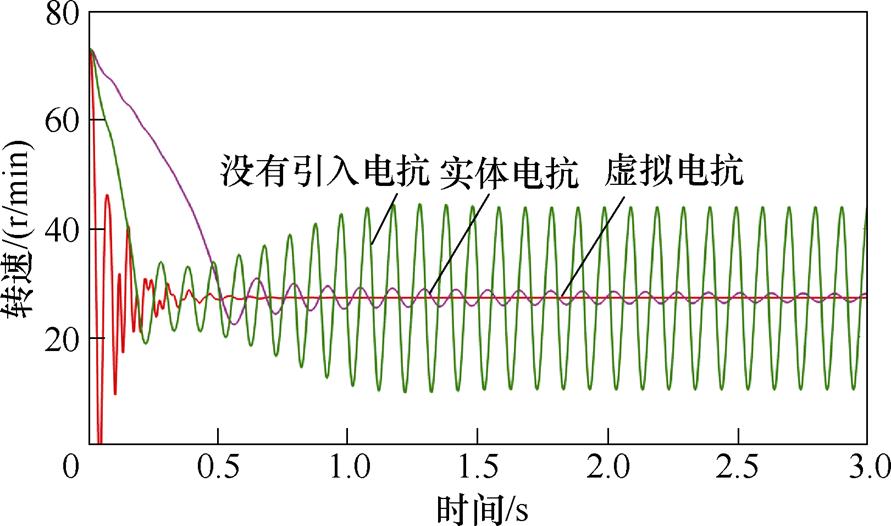
图15 13Hz工况下引入虚拟电抗和外部电抗后的感应电机转速对比仿真结果（10%基值电抗大小）
Fig.15 Simulation results of speed comparison with virtual reactance and solid reactance at 13Hz (10% base value reactance)
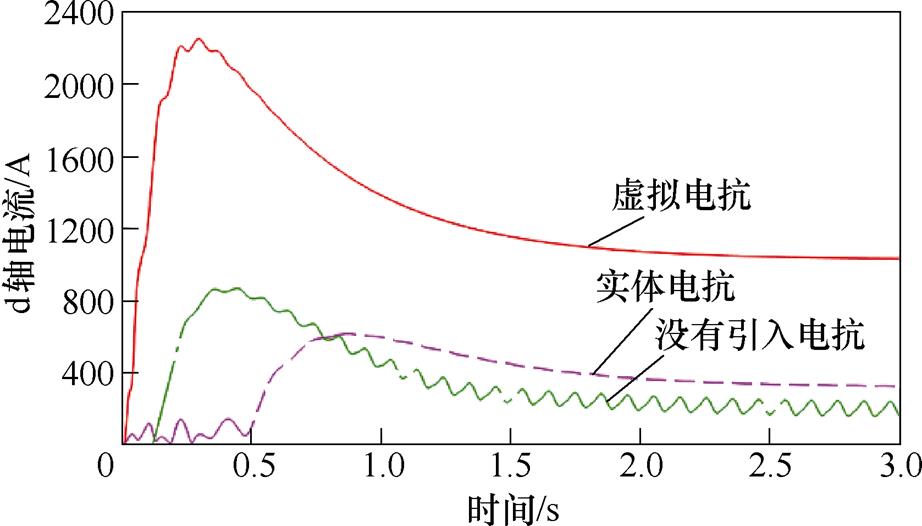
图16 13Hz工况下引入虚拟电抗和外部电抗后的感应电机d轴电流对比仿真结果（10%基值电抗大小）
Fig.16 Simulation results of d-axis comparison with virtual reactance and solid reactance at 13Hz (10% base value reactance)
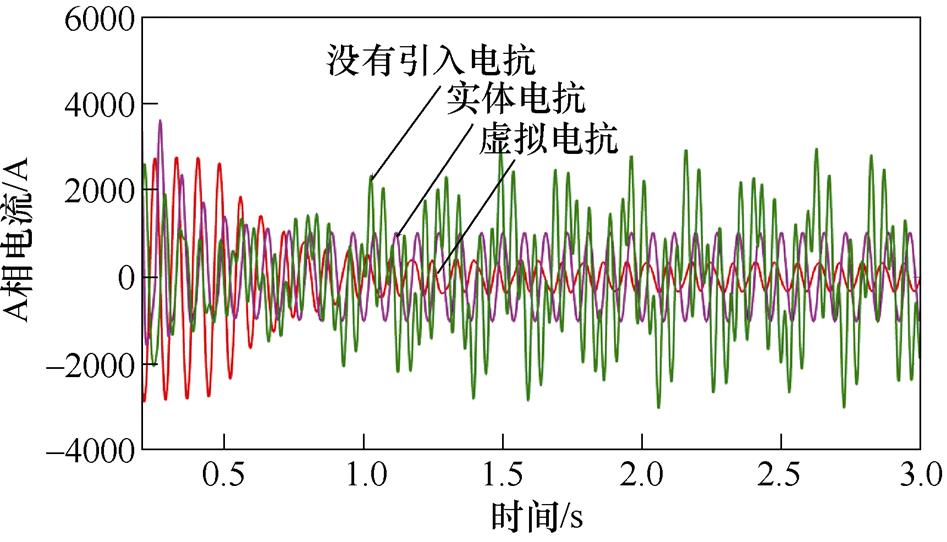
图17 13Hz工况下引入虚拟电抗和外部电抗后的感应电机A相定子电流对比仿真结果（10%基值电抗大小）
Fig.17 Simulation results of phase A current comparison with virtual reactance and solid reactance at 13Hz (10% base value reactance)
为了进一步验证本文所提控制方法的有效性和可行性，在大功率感应电机变频调速系统实验平台上进行了实验，感应电机变频调速系统实验平台如图18所示，感应电机系统参数见表1。图19给出了感应电机变频调速系统实验平台的逻辑框图。感应电机变频调速系统实验平台的主电路由中点钳位型三电平变频器、LRC正弦滤波器和2 500kV·A变压器组成。变频器采用英飞凌公司的IGBT模块，作用是将直流母线的直流电逆变成可控的三相交流电，变频器的开关频率为2kHz。感应电机变频调速系统中的电源控制器选用倍福公司CX2020控制器，功率控制器选用TI公司DSP TMS320F28335，电源控制器与功率控制器之间通过Ether CAT总线连接，本文所提的控制方法在电源控制器中实现。
图18 大功率感应电机变频调速系统实验平台
Fig.18 The platform experimental platform of high power induction motor variable frequency speed control system
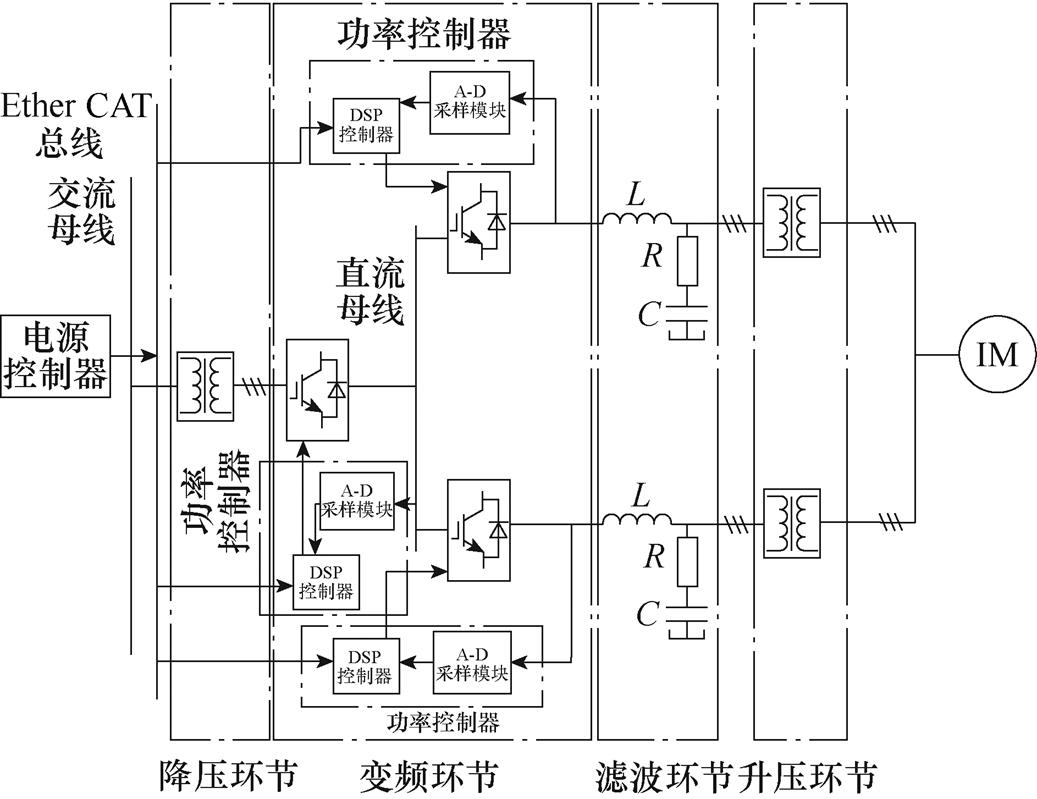
图19 感应电机变频调速系统实验平台逻辑框图
Fig.19 Logic block diagram of induction motor variable frequency speed control system experiment platform
本节给出了13Hz和15Hz工况下，感应电机变频调速系统引入不同量值的虚拟电抗后的转速、三相及A相定子电流的实验结果。实验对比了没有引入虚拟电抗和引入了5%和10%基值电抗大小的虚拟电抗的实验波形，如图20～图31所示。
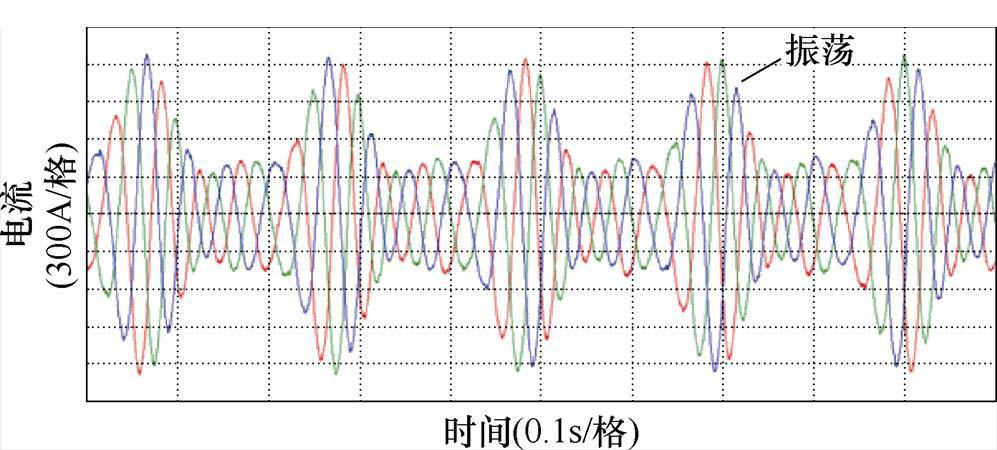
图20 在13Hz工况下运行没有引入虚拟电抗的三相电流实验波形
Fig.20 Experimental waveforms of three-phase current without virtual reactance at 13Hz
由图20和图21可知，在13Hz工况下没有引入电抗的情况时感应电机电流和转速出现大幅振荡，三相电流的振荡峰峰值高达到±900A，转速的波动的峰峰值高达到40r。由图22和图23可知，在1.5s后，感应电机变频调速系统中引入5%基值电抗大小的虚拟电抗，感应电机的电流和转速的振荡相对于没有引入虚拟电抗的情况大幅减弱，感应电机变频调速系统可以稳定运行。由图24和图25可知，在1.5s后，感应电机变频调速系统中引入10%基值电抗大小的虚拟电抗，感应电机的三相电流和转速的波动更加减小。由图20～图25可得，适量增加引入虚拟电抗的大小可以有效地解决该变频调速系统中感应电机不稳定运行的问题，实验结果与第3节中的仿真结果一致。
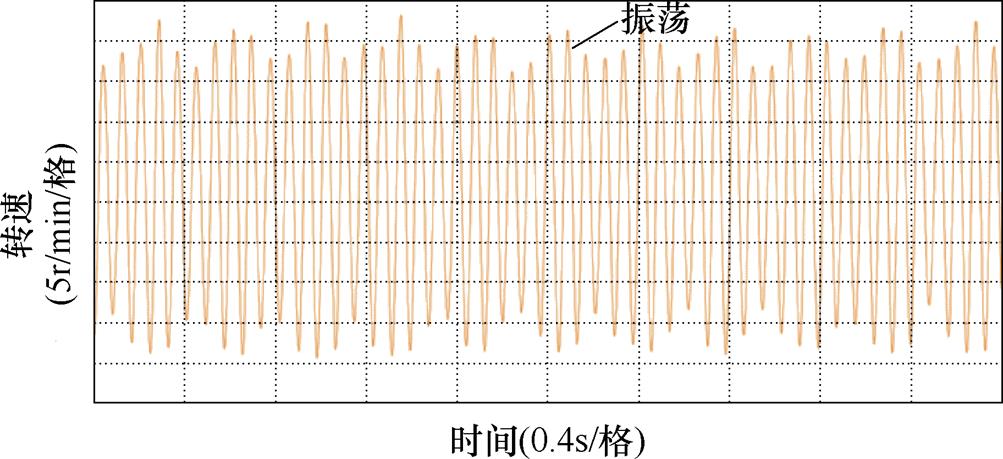
图21 在13Hz工况下运行没有引入虚拟电抗的转速实验波形
Fig.21 Experimental waveform of speed without virtual reactance at 13Hz
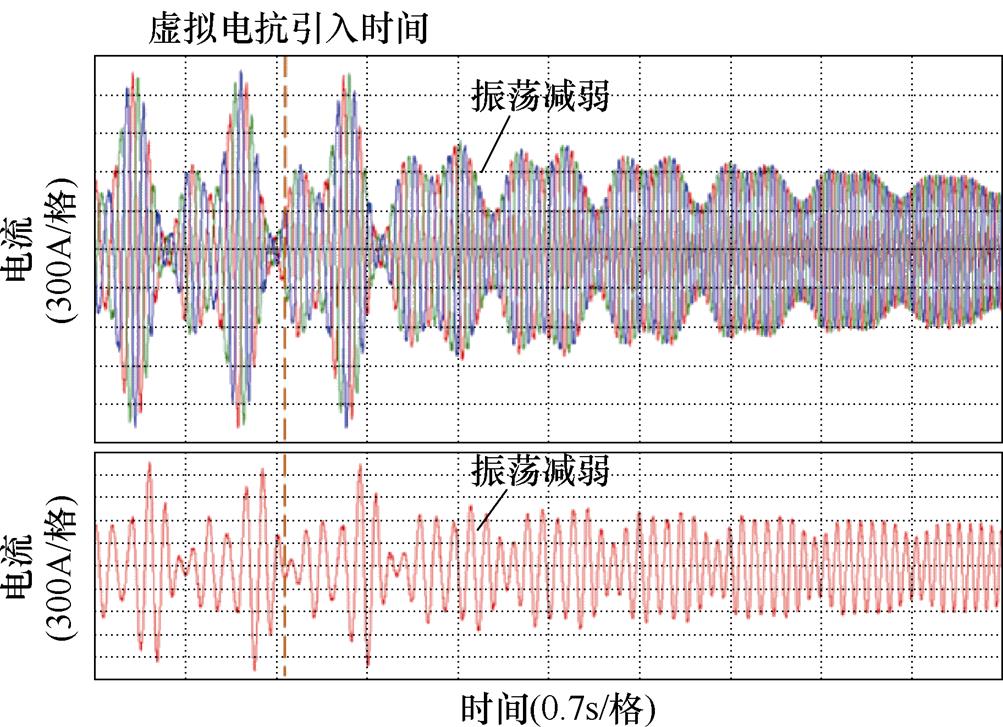
图22 在13Hz工况下引入虚拟电抗的感应电机系统三相电流实验波形（5%基值电抗大小）
Fig.22 Experimental waveforms of three-phase current with virtual reactance at 13Hz (5% base value reactance)
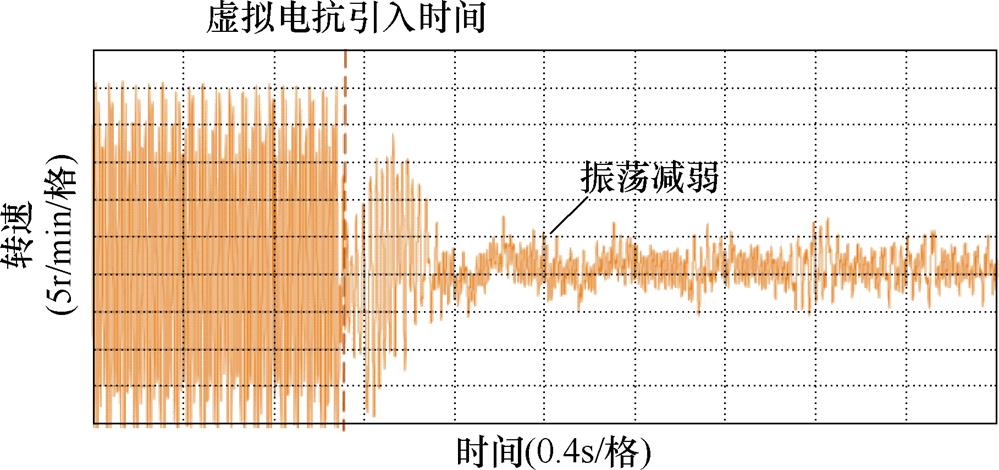
图23 在13Hz工况下引入虚拟电抗的感应电机系统转速实验波形（5%基值电抗大小）
Fig.23 Experimental waveform of speed with virtual reactance at 13Hz (5% base value reactance)
由图26和图27可知，在15Hz工况下没有引入虚拟电抗的情况下，感应电机的三相电流和转速同样会出现大幅振荡，但随着频率的上升，振荡周期比13Hz工况下减少。由图28和图29可以看出，在15Hz工况下，在1.5s后，感应电机变频调速系统中引入5%基值电抗大小的虚拟电抗，通过观察感应电机的三相电流和转速，其也是处于稳定运行的状态。对比图22和图23可知，提高感应电机系统给定频率，三相电流和转速的波动会减小，系统的稳定性更好。由图30和图31可知，在1.5s后，感应电机变频调速系统中引入10%基值电抗大小的虚拟电抗，感应电机的三相电流和转速的波动比图24和图25中更进一步减弱，电机稳定运行。上述实验结果验证了，通过适量地增加虚拟电抗的大小，或者提高系统的运行频率，均可达到使感应电机变频调速系统稳定运行的目的。
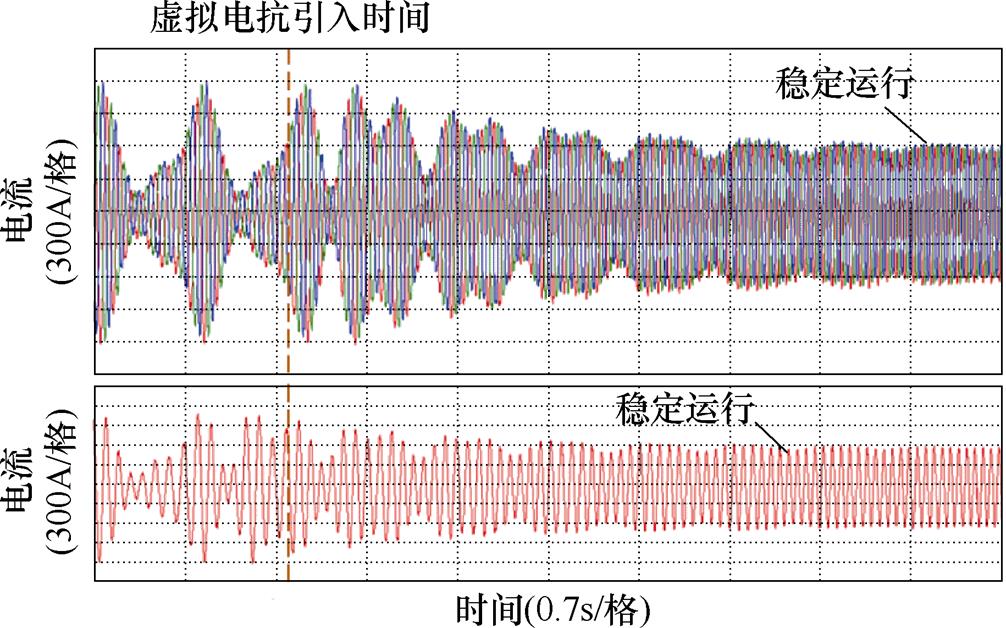
图24 在13Hz工况下引入虚拟电抗（10%基值电抗大小）的感应电机系统三相电流实验波形
Fig.24 Experimental waveforms of three-phase current with virtual reactance (10% base value reactance) at 13Hz
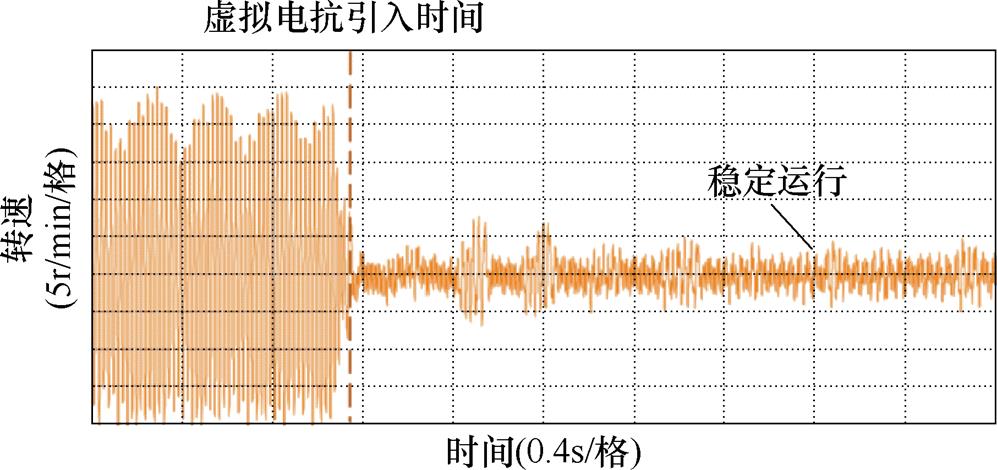
图25 在13Hz工况下引入虚拟电抗（10%基值电抗大小）的感应电机系统转速实验波形
Fig.25 Experimental waveform of speed with virtual reactance (10% base value reactance) at 13Hz
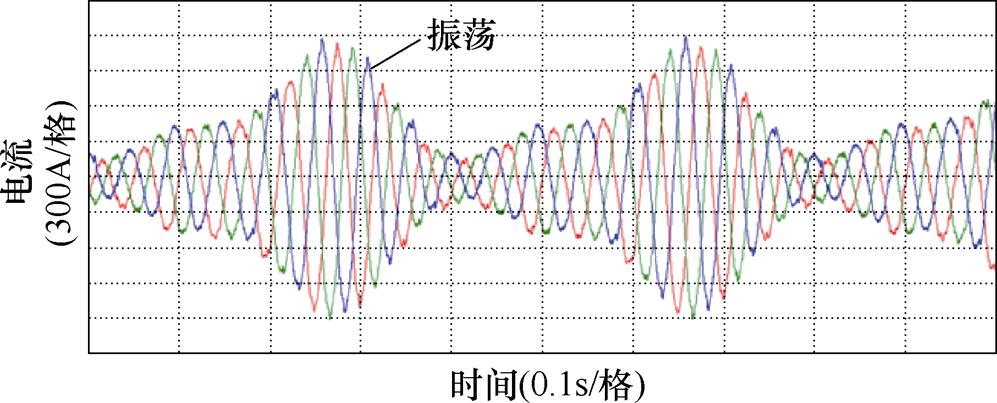
图26 在15Hz工况下运行没有引入虚拟电抗的三相电流实验波形
Fig.26 Experimental waveforms of three-phase current without virtual reactance at 15Hz
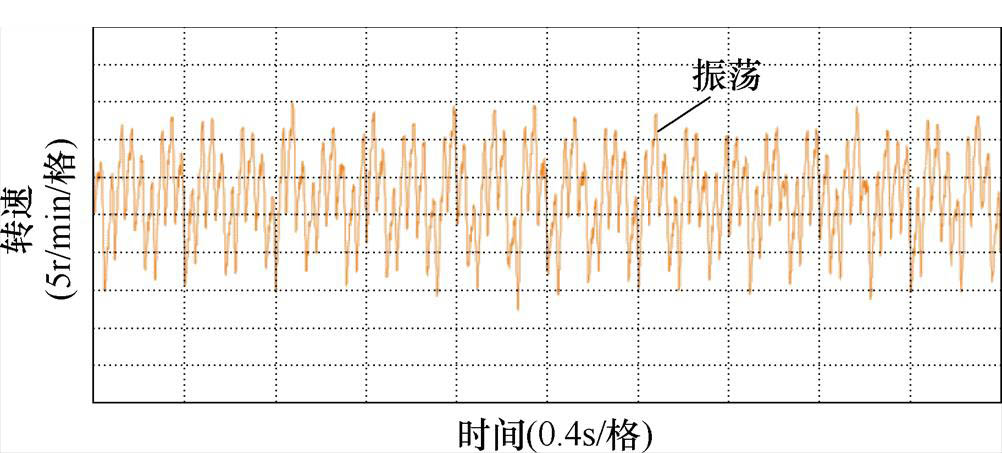
图27 在15Hz工况下运行没有引入虚拟电抗的转速实验波形
Fig.27 Experimental waveform of speed without virtual reactance at 15Hz
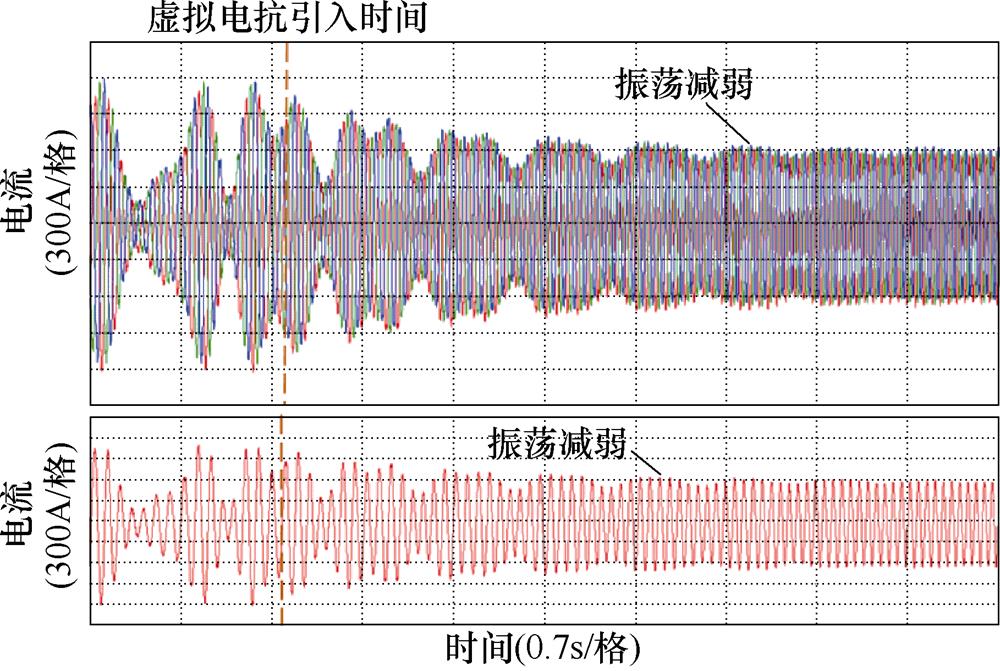
图28 在15Hz工况下引入虚拟电抗（5%基值电抗大小）的感应电机系统三相电流实验波形
Fig.28 Experimental waveforms of three-phase current with virtual reactance (5% base value reactance) at 15Hz
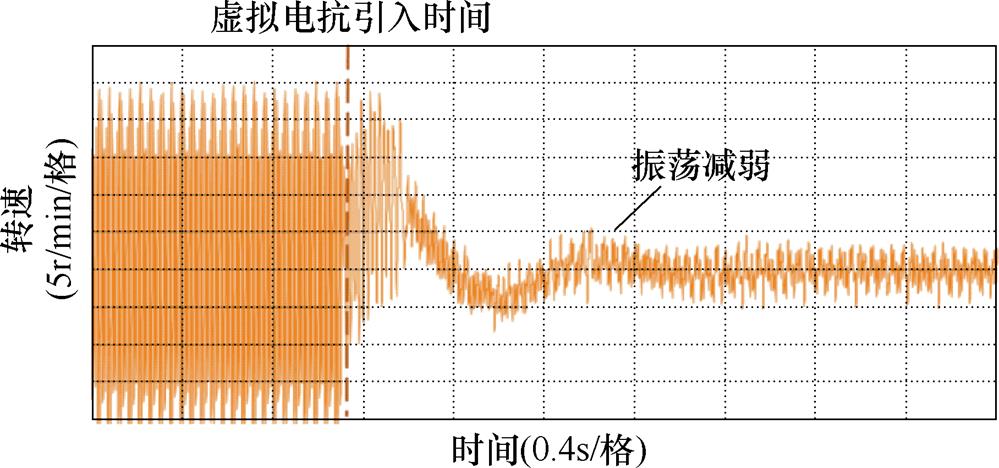
图29 在15Hz工况下引入虚拟电抗（5%基值电抗大小）的感应电机系统转速实验波形
Fig.29 Experimental waveform of speed with virtual reactance (5% base value reactance) at 15Hz
为了解决感应电机变频调速系统在中低频轻载工况下存在转速波动与电流振荡的问题，本文提出了一种引入虚拟电抗的感应电机变频调速系统V/f控制方法。本文结论如下：
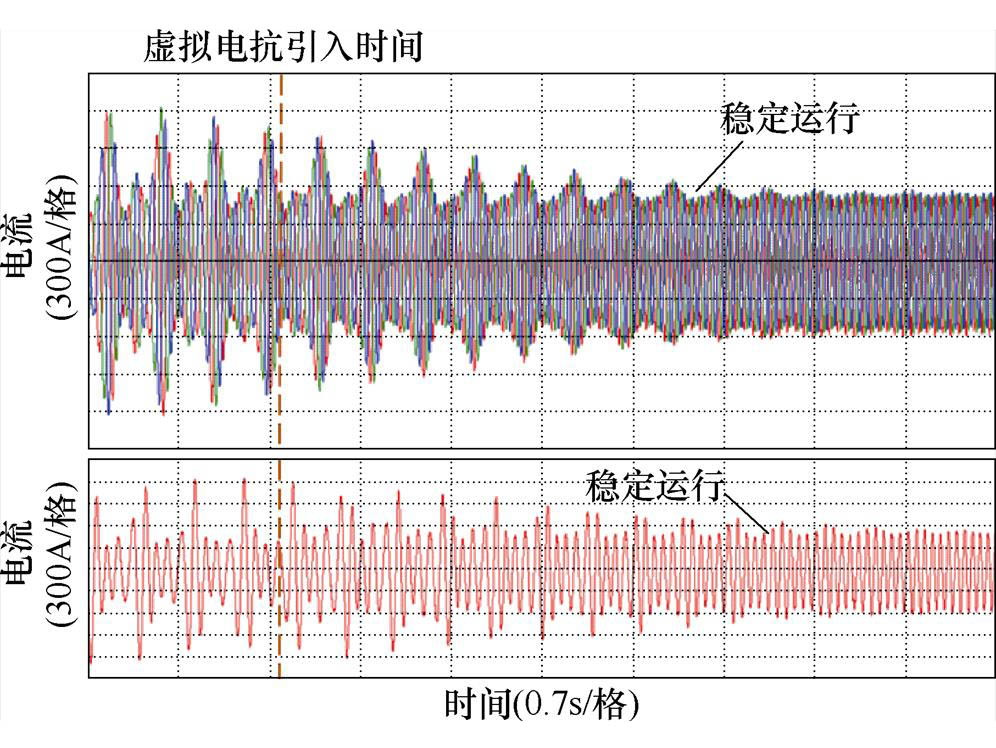
图30 在15Hz工况下引入虚拟电抗（10%基值电抗大小）的感应电机系统三相电流实验波形
Fig.30 Experimental waveforms of three-phase current with virtual reactance (10% base value reactance) at 15Hz
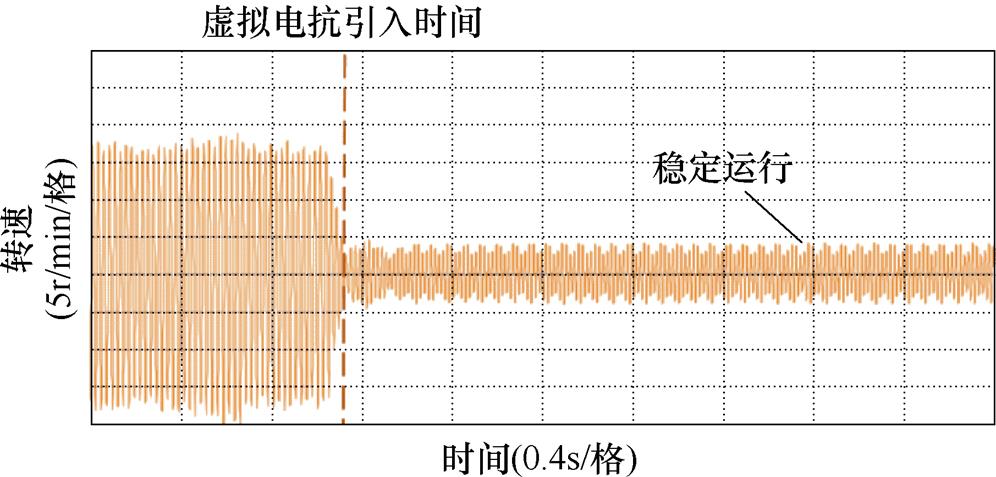
图31 在15Hz工况下引入虚拟电抗（5%基值电抗大小）的感应电机系统转速实验波形
Fig.31 Experimental waveform of speed with virtual reactance (5% base value reactance) at 15Hz
1）通过分析没有引入电抗与引入虚拟电抗的根轨迹图，可知增加感应电机的定子电抗大小，可提升感应电机变频调速系统的稳定性。当引入适量大小的虚拟电抗时，能达到抑制感应电机变频调速系统振荡，改善其不稳定性的目的。
2）通过对比5%和10%基值电抗大小的虚拟电抗仿真实验结果，可知增加适量虚拟电抗的值，感应电机变频调速系统将越来越稳定。
3）通过对比引入同等大小的虚拟电抗和实体电抗的仿真实验结果，可知引入虚拟电抗可实现感应电机变频调速系统在中低频轻载工况下的低转速脉动和低电流振荡运行，且比引入外部电抗的控制效果更好。
参考文献
[1] 钟志宏, 方晓春, 王晓帆, 等. 考虑零速/极低速稳定性的异步电机转差频率与定子电阻耦合补偿策略[J]. 电工技术学报, 2020, 35(增刊1): 192-202.
Zhong Zhihong, Fang Xiaochun, Wang Xiaofan, et al. A coupling compensation strategy for slip frequency and stator resistance of induction motor considering the stability near zero speed[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 192-202.
[2] 陈君, 孟彦京, 段明亮, 等. 一种高起动转矩的感应电机起动方法[J]. 电工技术学报, 2017, 32(9): 32-39.
Chen Jun, Meng Yanjing, Duan Mingliang, et al. A starting method of induction motor with high starting torque[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 32-39.
[3] 王琛琛, 齐龙, 苟立峰, 等. 基于无速度传感器的异步电机并联加权矢量控制[J]. 电工技术学报, 2015, 30(10): 131-137, 156.
Wang Chenchen, Qi Long, Gou Lifeng, et al. Speed sensorless weighted vector control of parallel connected induction motors drive[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 131- 137, 156.
[4] 陈伟. 异步电机无速度传感器系统轻载稳定性与低速性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
[5] 陈伟, 于泳, 杨荣峰, 等. 异步电机自适应全阶观测器算法低速稳定性研究[J]. 中国电机工程学报, 2010, 30(36): 33-40.
Chen Wei, Yu Yong, Yang Rongfeng, et al. Low speed stability research of adaptive full-order observer for induction motor[J]. Proceedings of the CSEE, 2010, 30(36): 33-40.
[6] 孙涓涓, 李永东. 异步电机定子电压定向矢量控制系统的改进[J]. 电工技术学报, 2002, 17(2): 29-33.
Sun Juanjuan, Li Yongdong. Improvement of voltage oriented vector control system for induction motor[J]. Transactions of China Electrotechnical Society, 2002, 17(2): 29-33.
[7] 陈伟, 金辛海, 蔡亮, 等. 异步电机V/f控制系统轻载稳定性仿真研究[J]. 中国电机工程学报, 2013, 33(增刊1): 211-218.
Chen Wei, Jin Xinhai, Cai Liang, et al. Light load stability simulation of IM V/f drive system[J]. Proceedings of the CSEE, 2013, 33(S1): 211-218.
[8] 陈斌. 感应电机无速度传感器控制的若干关键技术研究[D]. 杭州: 浙江大学, 2015.
[9] Chen Bin, Yao Wenxi, Kevin L, et al. A novel stator flux oriented V/f control method in sensorless indu- ction motor drives for accuracy improvement and oscillation suppression[C]//2014 IEEE Energy Con- version Congress and Exposition (ECCE), Pittsburgh, PA, 2014: 5092-5099.
[10] 陈伟, 杨荣峰, 于泳, 等. 新型感应电机V/F控制系统稳定性方法[J]. 电机与控制学报, 2009, 13(增刊1): 11-14.
Chen Wei, Yang Rongfeng, Yu Yong, et al. Novel stability improvement method for V/F controlled induction motor drive system[J]. Electric Machines and Control, 2009, 13(S1): 11-14.
[11] Zhao Xiaodan, Tsuji M, Inaki Y, et al. Steady-state and transient characteristics of a high-performance V/ƒ control system of induction motor[C]//2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, 2012: 1-6.
[12] 李洪亮, 姜建国, 周中正. 异步电机V/F控制系统起动和某频段振荡问题[J]. 电机与控制学报, 2017, 21(1): 90-97.
Li Hongliang, Jiang Jianguo, Zhou Zhongzheng. V/F control method of induction motor's starting and oscillation in a certain frequency band[J]. Electric Machines and Control, 2017, 21(1): 90-97.
[13] 陈伟, 杨荣峰, 于泳, 等. 具有低速高性能的电压定向V/F控制方法[J]. 电机与控制学报, 2010, 14(1): 7-11.
Chen Wei, Yang Rongfeng, Yu Yong, et al. Novel stator voltage oriented V/F control method capable of high performance at low speed[J]. Electric Machines and Control, 2010, 14(1): 7-11.
[14] 陈伟, 杨荣峰, 王高林, 等. 新型电压矢量控制算法极低速性能研究[J]. 中国电机工程学报, 2010, 30(15): 99-105.
Chen Wei, Yang Rongfeng, Wang Gaolin, et al. Very low speed performance research of novel voltage vector control method for IM[J]. Proceedings of the CSEE, 2010, 30(15): 99-105.
[15] 李红梅, 李忠杰, 刘良成. 逆变器供电下异步电动机低频振荡现象的研究[J]. 电工技术学报, 2000, 15(3): 16-19.
Li Hongmei, Li Zhongjie, Liu Liangcheng. Analysis low frequency oscillation of inverter fed asyn- chronous motor[J]. Transactions of China Electro- technical Society, 2000, 15(3): 16-19.
[16] Yang Shuying, Cao Pengpeng, Chang Liuchen, et al. Droop control based stabilizing method for V/f PWM inverter fed induction motor drive system[C]//2015 IEEE 28th Canadian Conference on Electrical and Computer Engineering (CCECE), Halifax, NS, 2015: 1078-1082.
[17] 乔鸣忠, 夏益辉, 朱鹏, 等. 基于电流闭环和死区补偿的变频驱动调速系统低频振荡抑制[J]. 电工技术学报, 2014, 29(11): 126-133.
Qiao Mingzhong, Xia Yihui, Zhu Peng, et al. Low- frequency oscillation restrain method of induction motor fed by inverter based on current close-loop and dead-time compensation[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 126-133.
[18] Al-Taee M A, AlZu'bi H S, Al-Din M S, et al. Stable and highly efficient operation of open-loop controlled PM synchronous motor drive[C]//2008 5th Inter- national Multi-Conference on Systems, Signals and Devices, 2008: 1-6.
[19] Liu Jingbo, Nondahl T A, Schmidt P B, et al. Generalized stability control for open-loop operation of motor drives[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2517-2525.
[20] Lee K, Chen Bin, Yao Wenxi, et al. Stability analysis and mitigation of oscillation in an induction machine[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 3767-3776.
[21] 谢震, 孟浩, 张兴. 基于定子虚拟阻抗的双馈风电机组虚拟同步控制策略[J]. 电力系统自动化, 2018, 42(9): 157-163.
Xie Zhen, Meng Hao, Zhang Xing. Virtual syn- chronous control strategy of DFIG-based wind turbines based on stator virtual impedance[J]. Auto- mation of Electric Power Systems, 2018, 42(9): 157-163.
[22] 谢震, 张兴. 基于虚拟阻抗的双馈风力发电机高电压穿越控制策略[J]. 中国电机工程学报, 2012, 32(27): 16-23.
Xie Zhen, Zhang Xing. High voltage ride-through control strategy of doubly fed induction wind generators based on virtual impedance[J]. Pro- ceedings of the CSEE, 2012, 32(27): 16-23.
[23] 陈闯, 王勃, 于泳, 等. 基于改进指数趋近律的感应电机滑模转速观测器研究[J]. 电工技术学报, 2020, 35(增刊1): 155-163.
Chen Chuang, Wang Bo, Yu Yong, et al. An improved exponential reaching law based-sliding mode observer for speed-sensorless induction motor drives[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 155-163.
[24] 梅杨, 王梁, 黄伟超. 间接矩阵变换器-异步电机调速系统的优化模型预测控制[J]. 电工技术学报, 2019, 34(14): 2884-2893.
Mei Yang, Wang Liang, Huang Weichao. An optimized model predictive control method for the induction motor drives fed by an indirect matrix converter[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2884-2893.
The Stability Control of Induction Motor Variable Frequency Speed Regulation System Injected with Virtual Reactance under Low Frequency and Light Load Condition
Abstract In order to solve the oscillation of speed and current in the induction motor variable frequency speed control system under low frequency and light load conditions, this paper proposes a V/f control method with virtual reactance of induction motor variable frequency speed control system. First, the mathematical model of induction motor variable frequency speed control system is established, and the steady-state performance of the system under V/f control has been analyzed. The root locus of the system with virtual reactance is then analyzed. It is shown that the virtual reactance injection can further improve the stability and suppress the oscillation of the system under low frequency and light load conditions. Finally, the simulation and high-power induction motor variable frequency speed control system experiment verify that the proposed V/f control method with virtual reactance injection can realize low speed ripple and low current oscillation operation under low-frequency and light load conditions.
keywords：Induction motor variable frequency speed control system, V/f control, virtual reactance, low frequency and light load conditions
DOI: 10.19595/j.cnki.1000-6753.tces.201291
中图分类号：TM346+.2
易 山 男，1996年生，硕士研究生，研究方向为电力电子与电力传动。E-mail: cesareyi@163.com
卢子广 男，1963年生，教授，博士生导师，研究方向为微电网、电力电子变流系统、电机系统控制等。E-mail: luzg@gxu.edu.cn（通信作者）
收稿日期 2020-09-25
改稿日期 2021-02-10
广西自然科学基金资助项目（2018GXNSFDA138008）。
（编辑 崔文静）