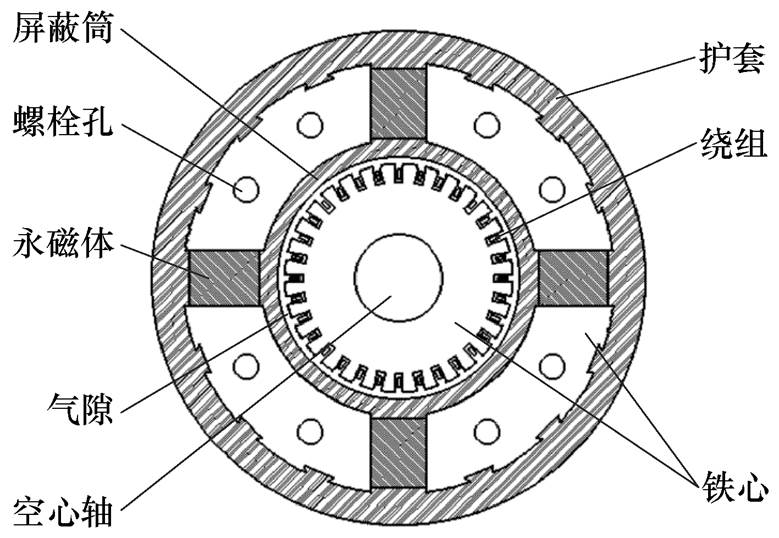
图1 ORPMPCPA整体结构
Fig.1 Overall structure diagram of ORPMPCPA
摘要 为探究被动补偿式外转子永磁脉冲发电机(ORPMPCPA)的放电特性,在综合考虑放电过程中被动补偿作用对电枢绕组电感的影响以及机电能量转换造成转速变化等因素的基础上,建立ORPMPCPA对负载放电的数学模型,对ORPMPCPA放电时的脉冲电流形成过程、能量转化过程以及相关因素对脉冲电流波形的影响进行仿真分析。结果表明,ORPMPCPA能在瞬间将转子内部储存的动能转化为强脉冲电能,且通过改变外电路中触发延迟角、两相绕组组合方式和外接电感数值,实现对脉冲电流波形的灵活调节。通过对比分析样机测试结果和仿真结果,证明所提出的ORPMPCPA放电特性分析方法的准确性。
关键词:被动补偿脉冲发电机 永磁励磁 外转子 脉冲电流波形 放电特性
电能的存储是脉冲功率电源面向工程应用的关键所在,目前广泛使用的电容储能脉冲电源通常体积庞大,储能密度难以提高,且放电频次和循环寿命低;电感储能技术能够实现更高的储能密度,但其可靠性低[1-2]。
补偿脉冲发电机(Compensated Pulsed Alter- nator, CPA)是一种集惯性储能、机电能量转换和脉冲电流压缩成形于一体的特殊同步发电机,具有储能密度高、放电频次高和波形易于调节的优点[3-5]。但CPA的驱动电机一般需要配合滑动离合器和增速齿轮箱来带动脉冲发电机运转,其结构复杂,在脉冲放电的冲击下可靠性低[6]。
补偿脉冲发电机的类型很多,按补偿方式可分为主动补偿、被动补偿和选择被动补偿,不同补偿方式可以获得不同的脉冲电流波形,可根据负载需求选择合适的补偿方式[7-9]。当不同补偿形式的CPA应用于各类负载的脉冲电源系统时,其放电特性是普遍关注的研究内容之一。文献[10]从负载特性的角度出发来对主动补偿脉冲发电机主要参数进行计算,进而可以框定出样机的总体尺寸,然后再通过电磁程序反复的迭代运算,得到优化的样机参数。文献[11]中设计了一台两相四极并由短路的励磁绕组实现补偿作用的脉冲发电机,以电磁轨道炮为负载建立了放电过程的数学模型,以弹丸加速比为目标函数,使用差分进化算法对输出电流波形进行了优化,并与有限元法取得结果进行对比分析,说明通过建立数学模型能够显著提高仿真效率和仿真灵活性。文献[12]提出了一种通过调节励磁绕组和补偿绕组匝数比例的方法来改变对电枢绕组沿交轴和直轴侧的补偿效果,并利用有限元软件对相应的输出性能进行分析,分析结果表明,采用此方法可以使单相脉冲发电机的输出电流波形更接近平顶波。文献[13]证实了通过改变电枢绕组和补偿绕组间的相位,可实现对选择被动补偿脉冲发电机输出功率波形的有效调节。
CPA目前广泛采用内转子结构以配合电励磁方式进行励磁,由于其需要足够大的励磁电流来保证磁场强度,因而励磁绕组的发热现象十分严重,且脉冲发电机转速较高,电励磁所需的电刷与换向片在大电流高转速下运行时易发生故障[14]。CPA还可采用外转子结构结合永磁励磁,以提高储能密度和功率密度,省去外部励磁装置,减小故障率。文献[15]设计了一台外转子表贴式永磁脉冲发电机,补偿方式为被动补偿,对其空载和负载性能进行了仿真分析,根据设计方案制造了等比例缩小的样机,对样机的脉冲电流波形进行了测量,证明了设计方案的可行性。文献[16]利用解析法对采用永磁励磁和外转子结构的补偿脉冲发电机进行了分析,建立了样机的空载、负载简化解析模型,并通过有限元方法进行了验证。文献[17]针对一台空心外转子补偿脉冲发电机进行了研究,其采用被动补偿方式以及Halbach阵列磁极结构,并通过有限元法分析了放电过程中电枢绕组阻抗、永磁体退磁风险和屏蔽筒涡流分布,验证了该结构可以达到预期的设计要求。
本文在综合考虑放电过程中被动补偿作用对电枢绕组电感的影响和机电能量转换造成转速变化等因素的前提下,建立了被动补偿式外转子永磁脉冲发电机(Outer Rotor Permanent Magnet Passively Compensated Pulsed Alternator, ORPMPCPA)对负载放电的数学模型,基于该模型进行了ORPMPCPA放电特性的仿真分析,并通过搭建样机测试平台,将相应实验结果和仿真结果进行对比以证实所提出的分析方法的准确性,以期为有效提高ORPMPCPA系统的功率等级以及进一步拓展其工程应用提供可靠的理论依据。
本文中补偿脉冲发电机的转子通过一个共用的转子护套与其驱动电机的转子相连,省去了连接部件和变速箱,在提高储能密度的同时亦能确保系统运行的可靠性。由于采用永磁体励磁,故可避免在高转速下经由换向器对励磁绕组通入大电流进行励磁,从而降低发生故障的可能性;此外,钕铁硼永磁材料具有很高的磁能积,可提高脉冲发电机的功率密度,减小脉冲发电机体积[18-22]。通过采用外转子切向式磁极结构,永磁体放置于转子铁心内部,且永磁体较厚,可以削弱转子旋转时产生的离心力对转子磁极的影响,工作过程中永磁体不易发生损坏[23]。采用被动补偿的方式,可减小电枢绕组电感以增大输出电流,同时将屏蔽筒固定于外转子内侧,在转子旋转时产生的离心力作用下使屏蔽筒压向转子铁心,有利于避免运行过程中定转子发生刮碰。采用电角度相差90°的两相正交绕组,减小两相绕组间的电磁耦合,有利于对输出电流波形进行调整。外转子被动补偿永磁脉冲发电机的整体结构如图1所示,主要参数见表1。
将ORPMPCPA系统作为铜铝异质金属板电阻焊的供电电源以研究该系统的放电特性。基于铜铝异质金属板电阻焊的工艺特点,相应的负载可等效为一个电阻Rl和一个电感Ll串联。ORPMPCPA放电等效电路如图2所示,其中两相绕组输出电压用两个电压源Uwa和Uwb表示,每相电枢绕组的电阻用Rwa和Rwb表示,每相电枢绕组电感用Lwa和Lwb表示,S1~S8为晶闸管,两相输出电压分别经过一个全波半可控整流桥整流后并联为负载供电。

图1 ORPMPCPA整体结构
Fig.1 Overall structure diagram of ORPMPCPA
表1 ORPMPCPA的主要参数
Tab.1 Main parameters of ORPMPCPA
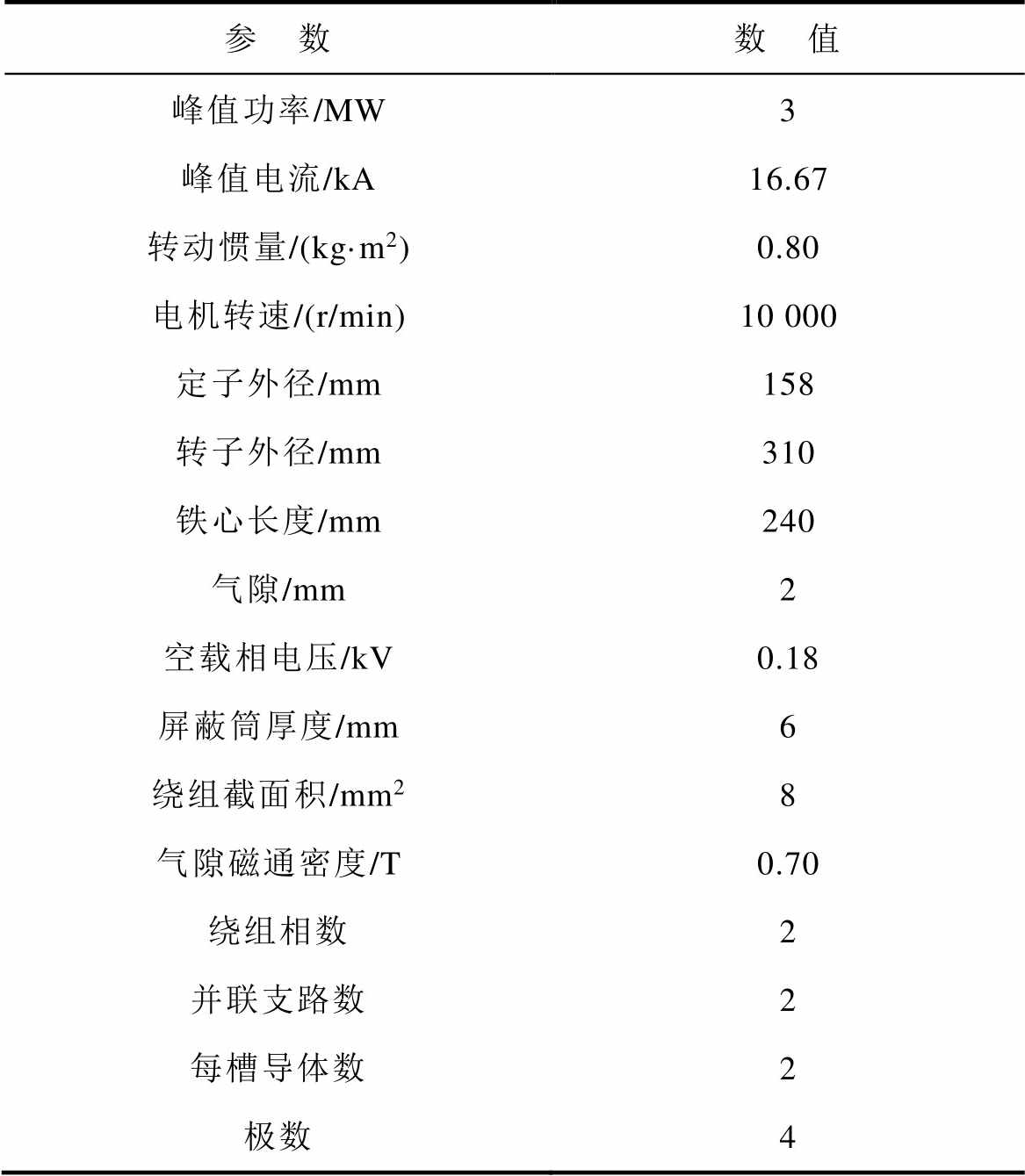
参 数数 值 峰值功率/MW3 峰值电流/kA16.67 转动惯量/(kg·m2)0.80 电机转速/(r/min)10 000 定子外径/mm158 转子外径/mm310 铁心长度/mm240 气隙/mm2 空载相电压/kV0.18 屏蔽筒厚度/mm6 绕组截面积/mm28 气隙磁通密度/T0.70 绕组相数2 并联支路数2 每槽导体数2 极数4
实际上,对铜铝异质金属板进行电阻焊接时,铜板和铝板分别作为电阻以串联方式连接,故电阻Rl为
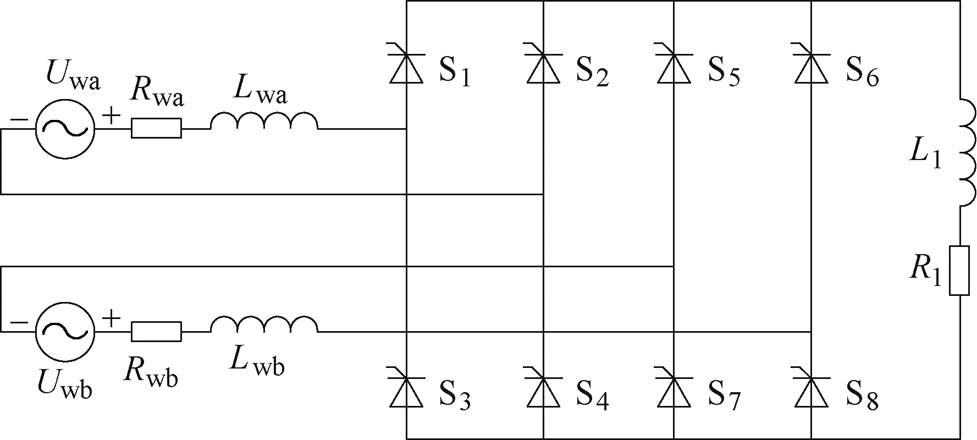
图2 ORPMPCPA放电等效电路
Fig.2 Equivalent circuit for ORPMPCPA discharge
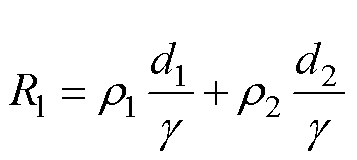 (1)
(1)
式中,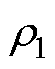 为铜的电阻率;d1为铜板的厚度;
为铜的电阻率;d1为铜板的厚度;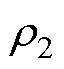 为铝的电阻率;d2为铝板的厚度;
为铝的电阻率;d2为铝板的厚度;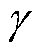 为金属板间的接触面积。
为金属板间的接触面积。
流经两金属板的脉冲电流大小发生变化时,在两块金属板上会产生电感Ll,其值可大致估算为
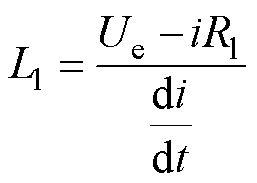 (2)
(2)
式中,Ue为负载端电压;i为负载电流;t为时间。
基于铜铝异质金属板电阻焊的实际工况要求,根据式(1)和式(2)可确定出电阻Rl的电阻值为2.5mW,电感Ll的电感值为0.5mH。
对于一般发电机来说,电枢绕组的电感与绕组的排布方式、组成材料的导磁性能及饱和情况等因素有关,而ORPMPCPA中屏蔽筒产生的被动补偿作用会进一步对电枢绕组电感产生影响。由于放电过程中ORPMPCPA电枢绕组电感的影响因素十分复杂,本文将电枢绕组电感分为电枢绕组内自感、气隙漏电感、槽漏电感和端部漏电感四个部分来进行计算。
ORPMPCPA电枢绕组的内自感Li可以按照一般电机的设计经验计算,一般发电机的绕组内自感经验公式[24]为
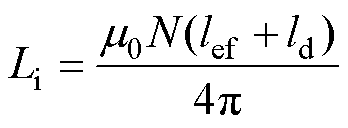 (3)
(3)
式中,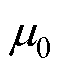 为空气中的磁导率;N为电枢绕组每相串联匝数;lef为电枢绕组有效长度;ld为电枢绕组端部长度。
为空气中的磁导率;N为电枢绕组每相串联匝数;lef为电枢绕组有效长度;ld为电枢绕组端部长度。
在ORPMPCPA放电时,电枢绕组的气隙漏电感的形成过程较为复杂,为了简化计算流程,同时由于每极每相电枢绕组沿径向的厚度远远小于其周向长度和定子的直径,因而可以忽略电枢绕组的径向厚度,将电枢绕组等效为贴在定子铁心表面的电流层。为了进一步简化计算,将放电瞬间的ORPMPCPA内部磁场视为二维稳定场,形成的气隙磁场近似为平行平面场,同时将定转子铁心材料的磁导率和屏蔽筒的电导率视为无穷大。将等效电流层的电流密度J按照傅里叶级数法,沿空间分布展开后的谐波函数为
 (4)
(4)
式中,Jm为电枢绕组电流密度幅值;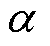 为每极每相电枢绕组在定子铁心外表面的张角;Im为电枢绕组流过的电流幅值;rs为定子铁心外半径。
为每极每相电枢绕组在定子铁心外表面的张角;Im为电枢绕组流过的电流幅值;rs为定子铁心外半径。
由于气隙磁场中没有电流流过,因而气隙内磁场矢量磁位AZ的拉普拉斯方程的极坐标形式可以表示[25-26]为
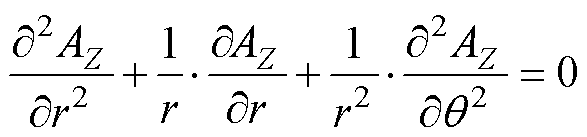 (5)
(5)
通过分离变量法对式(5)进行求解,可以得到方程的通解为
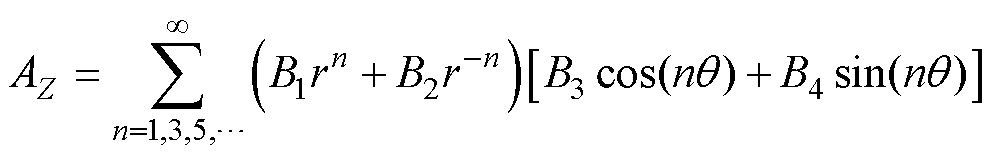 (6)
(6)
式中,B1~B4为通解中的待定系数。
由于矢量磁位AZ满足周期性边界条件,且关于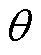 对称,则
对称,则
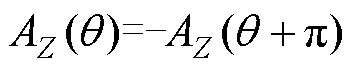 (7)
(7)
将式(7)代入式(6)可以计算得到B3=1,B4=0,则式(6)变为
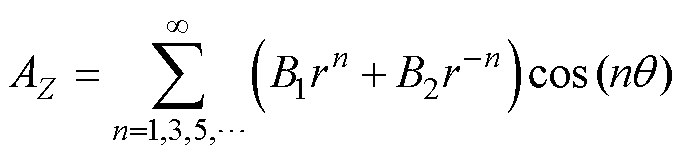 (8)
(8)
由于定子铁心材料的磁导率为无穷大,气隙中的磁导率为0,则定子铁心外壁的磁场强度切向分量为0,磁场强度方向总是与铁心内表面垂直,因而当r=rs时,根据电磁场理论可知,气隙磁场强度切向分量 =J,又因为
=J,又因为
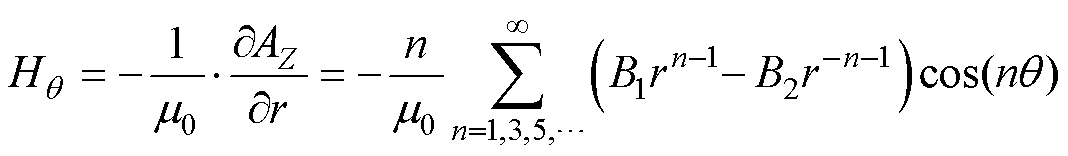 (9)
(9)
则可得到
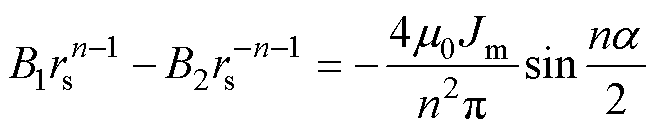 (10)
(10)
又因为
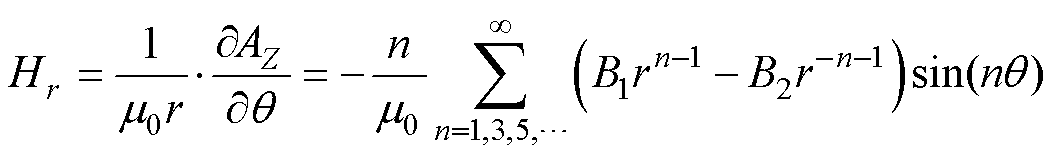 (11)
(11)
由于屏蔽筒的电导率为无穷大,rc为屏蔽筒内半径,当r=rc时,气隙磁场强度径向分量Hr=0,则可得
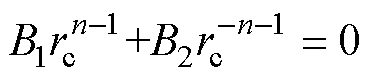 (12)
(12)
结合式(10)和式(12)可以得到
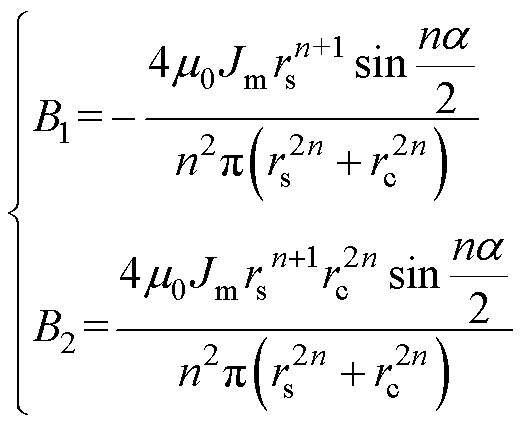 (13)
(13)
将式(13)中的B1和B2代入到式(9)和式(11)中可得,当ORPMPCPA放电时,气隙磁场强度为
 (14)
(14)
由于ORPMPCPA采用屏蔽筒进行被动补偿的方式,气隙磁场分布均匀,因此放电过程中,每极电枢绕组电流产生的磁场能量为
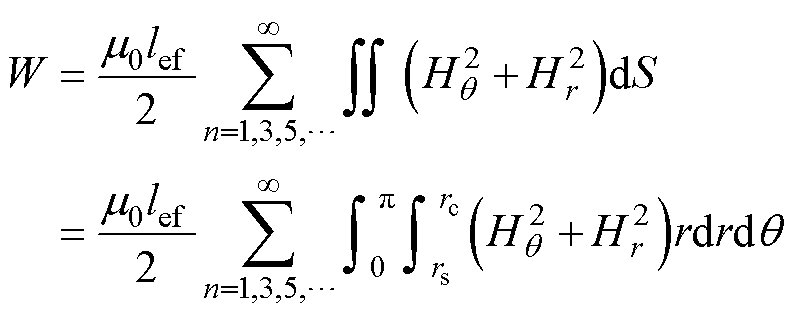 (15)
(15)
将式(14)中 和
和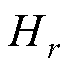 代入式(15)后可得
代入式(15)后可得
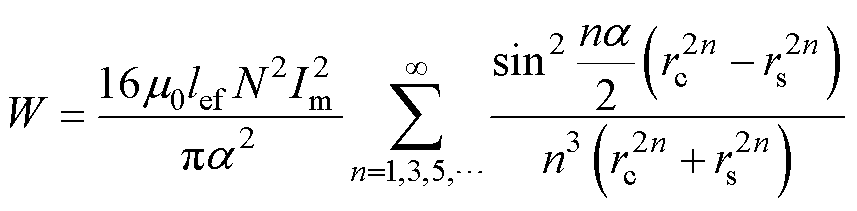 (16)
(16)
根据电感的磁场储能公式W=LI2/2,结合式(16)得到每极电枢绕组对应的气隙漏电感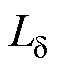 为
为
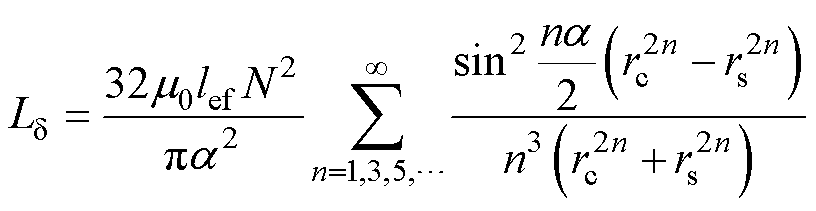 (17)
(17)
ORPMPCPA定子开槽用于放置电枢绕组,对于单层绕组来说,槽漏感的大小主要取决于槽型结构,单层整距开口槽绕组的槽漏电感可以计算[27]为
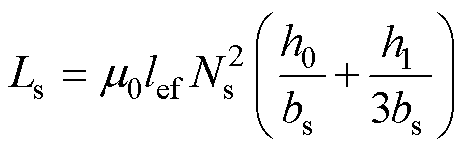 (18)
(18)
式中,Ns为定子每槽导体数;h0为定子槽口高;h1为定子槽内绕组高度;bs为定子槽宽度。
由于绕组端部得到了同样的补偿,按照电枢绕组有效部分长度与其端部长度的比例,进而得到电枢绕组端部漏电感的计算公式[28]为
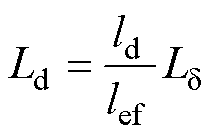 (19)
(19)
结合式(3)、式(17)~式(19),可以得到ORPMPCPA在放电过程中电枢绕组暂态电感的计算公式为
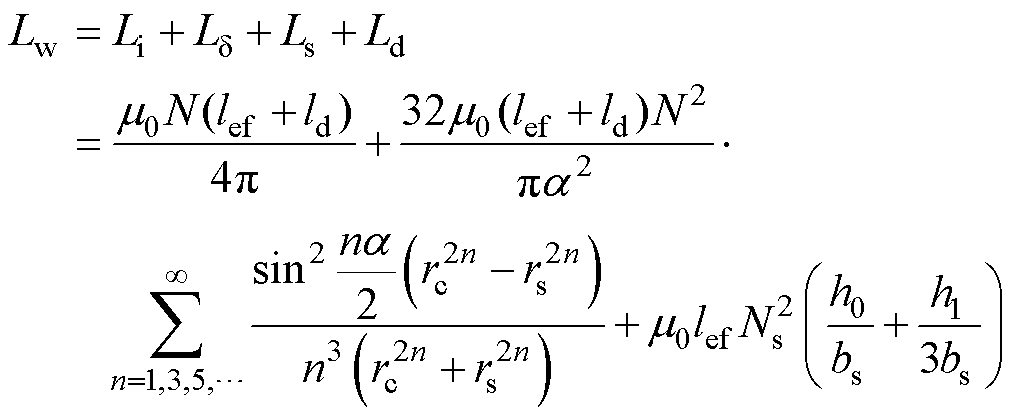 (20)
(20)
由于ORPMPCPA两相绕组的电角度相差90°,因此两相绕组相互独立,没有磁链耦合,根据图2中等效电路,并忽略晶闸管及导电线路压降,同时考虑补偿脉冲发电机放电过程中转速变化,则电压方程式可写成
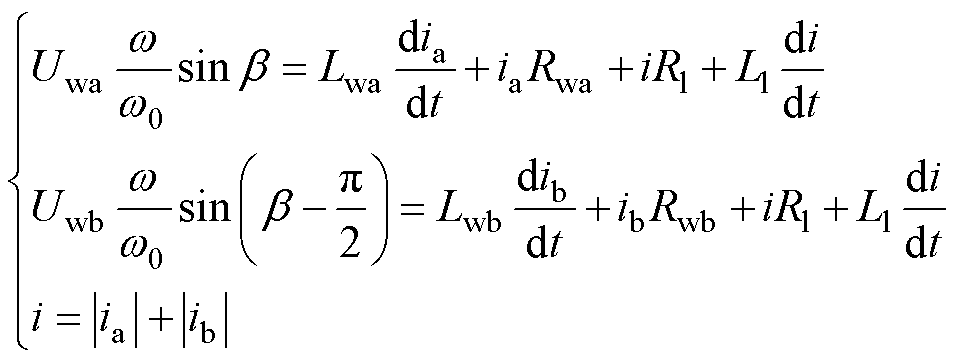 (21)
(21)
式中, 为转子电角度;
为转子电角度;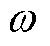 为转子电角速度;
为转子电角速度;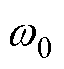 为转子额定电角速度;ia和ib分别为两相绕组电流。
为转子额定电角速度;ia和ib分别为两相绕组电流。
放电过程中两相绕组产生的电磁转矩为
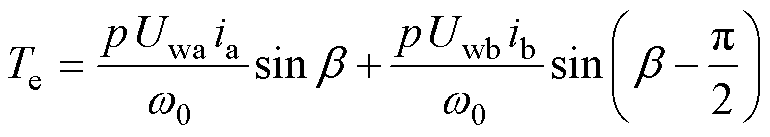 (22)
(22)
式中,p为极对数。
ORPMPCPA在运行过程中达到的转矩平衡方程为
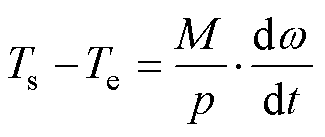 (23)
(23)
式中,Ts为驱动电机电磁转矩,当ORPMPCPA放电时,原动机停止供电,因而Ts=0;M为转子转动惯量。
将式(22)代入式(23)可以得到放电过程中机电能量转化关系为
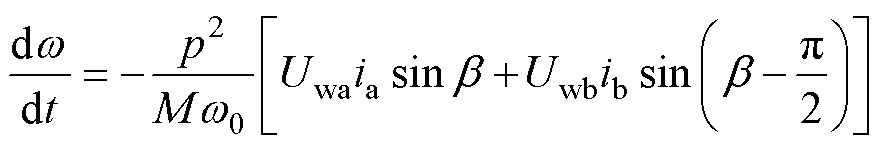 (24)
(24)
基于上述的ORPMPCPA放电数学模型,利用Matlab对ORPMPCPA放电时的输出性能进行仿真模拟。设置的初始条件为:转子转速为10 000r/min,A相绕组触发延迟角取为0°,B相绕组触发延迟角取为自然换流点135°。ORPMPCPA系统放电时负载端电压和脉冲电流波形如图3所示。
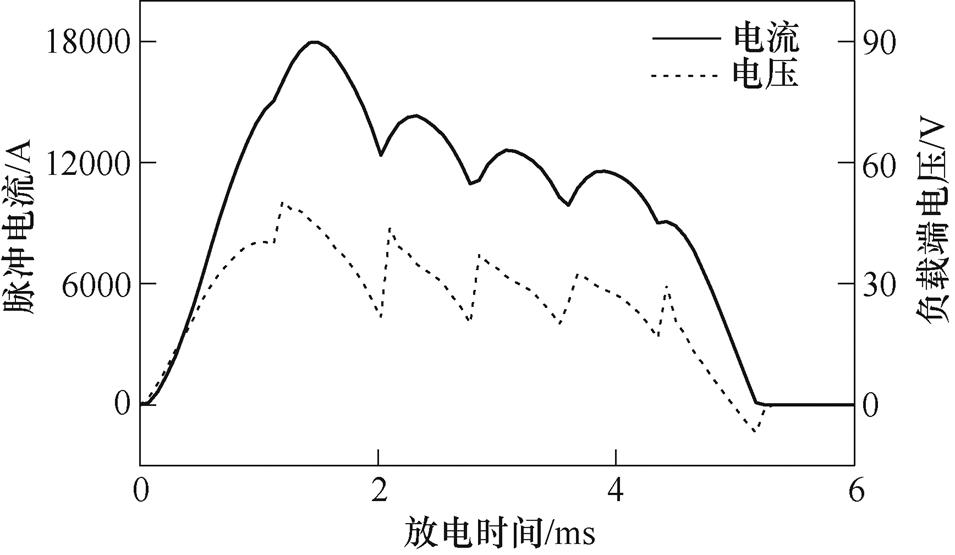
图3 ORPMPCPA系统放电时负载端电压和脉冲电流波形
Fig.3 Waveforms of voltage and current at load side during discharge of ORPMPCPA system
从图3中可以看出,在整个放电过程中,脉冲电流的脉宽约为5ms,幅值达到18 000A,且根据式(21)可知,负载上的脉冲电流为两相绕组电流经过整流后的叠加,因而脉冲电流波形出现多个波峰。随着放电的进行,ORPMPCPA的动能逐渐转化为电能,因而其转速不断下降,造成ORPMPCPA的输出电压逐渐下降。ORPMPCPA采用两相电压波形叠加的方式对负载供电,在放电过程中,当某一相绕组过零时,负载端电压变化较为剧烈。此外,由于负载中有电感存在,当负载端电压过零时,负载中电流正处于减小阶段,电感释放储能,维持电流流动,此时晶闸管没有立即关断,因而使得负载端电压出现一部分负值。负载端电压幅值约为50.3V,端电压幅值相对空载时较小,主要原因为ORPMPCPA内阻抗的分压效果。
ORPMPCPA在进行放电过程中,其产生的电磁转矩体现为制动性质,进而实现机械能到电能的转换,ORPMPCPA系统放电时制动转矩和转子转速波形如图4所示。可以看出,ORPMPCPA在额定状态进行放电时,作用在转子上制动转矩的峰值达到3.26kN·m。此外,根据式(22)可以看出,放电过程中电磁转矩受两相绕组电流共同作用,体现为叠加性质,因而电磁转矩的变化趋势与负载中脉冲电流变化趋势相近,但由于处于制动状态,电磁转矩为负值。ORPMPCPA转速从10 000r/min下降到9 926r/min,转速下降幅度很小,对ORPMPCPA空载反电动势的影响可以忽略不计,因而在一次放电后可以继续进行满足负载要求的放电。
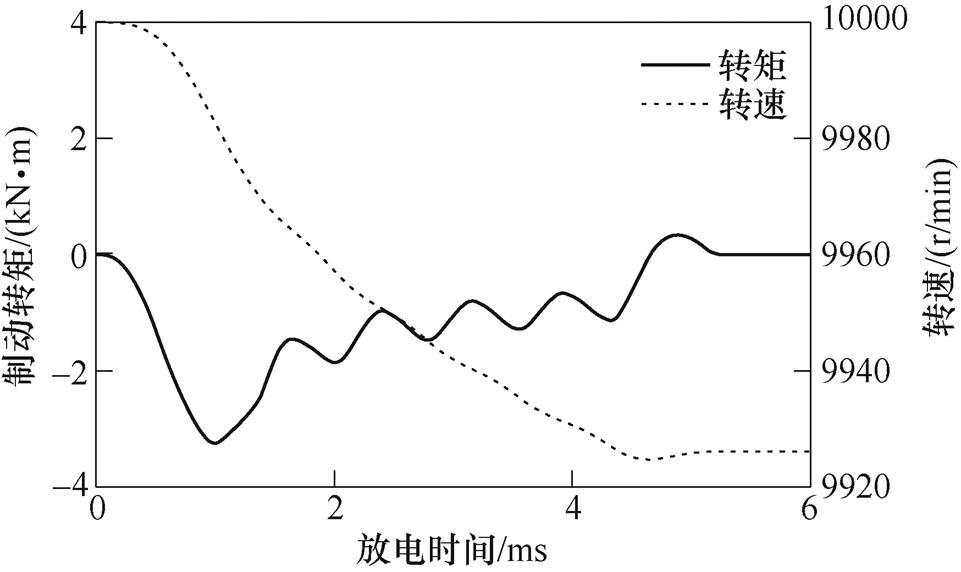
图4 ORPMPCPA放电过程中制动转矩与转子转速波形
Fig.4 Waveforms of braking torque and rotating speed during discharge of ORPMPCPA system
基于上述分析获得的ORPMPCPA输出脉冲电流幅值、脉宽以及可实现连续放电的特点可以预期,该ORPMPCPA可作为电阻焊机的脉冲功率电源,当进一步提高ORPMPCPA功率等级和增大输出脉冲电流幅值时,其亦可用于驱动电磁导轨炮。永磁体励磁结构在应用于大功率脉冲发电机中时,最容易出现饱和的部位为定子齿部,在大功率永磁脉冲发电机设计时,可通过选择合适的极槽配合,使得定子齿宽加大以及调整气隙磁通密度等方式,避免饱和现象的发生。
对于CPA来说,电机参数确定之后,脉冲电流波形的调节范围比较有限[29]。但是选取不同的触发延迟角,对脉冲电流波形的影响依然很大。
通过控制A相绕组触发延迟角在0°~90°之间等间隔变化,控制B相绕组触发延迟角始终为135°,以此来分析不同触发延迟角对脉冲电流波形的影响。不同A相绕组触发延迟角下脉冲电流波形如图5所示。
从图5中可以看出,随着触发延迟角增大,脉冲电流的脉宽随之减小,同时脉冲电流波形出现的第一个峰值相应减小且出现时刻相对前移,可以说改变脉宽是以牺牲第一脉冲峰值为代价的,但这种调节方式具有动态灵活的特点,可以作为波形细调方法。不同的触发延迟角对应的脉冲电流波形相差较大,当需要峰值电流更大时,触发延迟角可以取的相对较小,当需要减小脉宽时,触发延迟角可以取值相对较大。
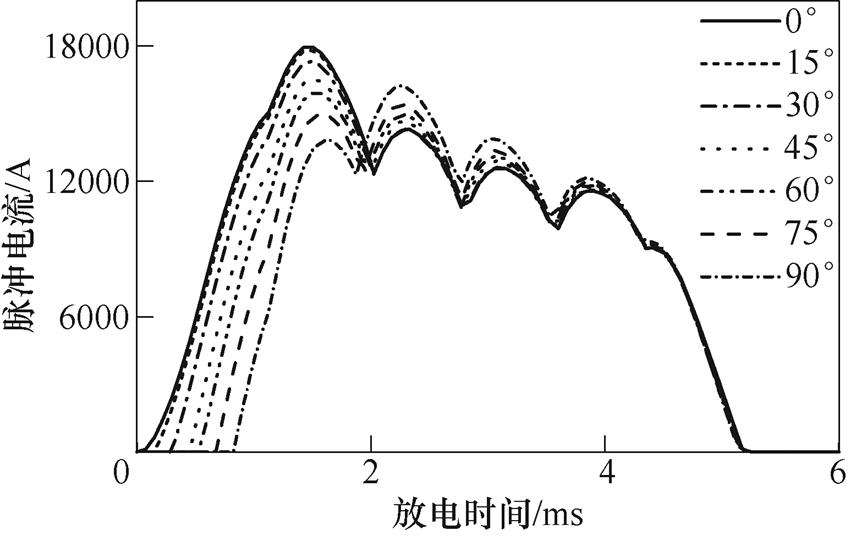
图5 不同触发延迟角下ORPMPCPA脉冲电流波形
Fig.5 Discharge current waveforms of ORPMPCPA under different triggering angles
ORPMPCPA两相电枢绕组正交分布,两绕组之间不存在电磁耦合,因而能独立输出电压,可以根据需要在CPA外部进行串、并联组合,调节电压电流等级,获得不同的脉冲电流波形。图6为A、B两相分别经过整流桥后并联放电、串联放电和单相放电时的脉冲电流波形。
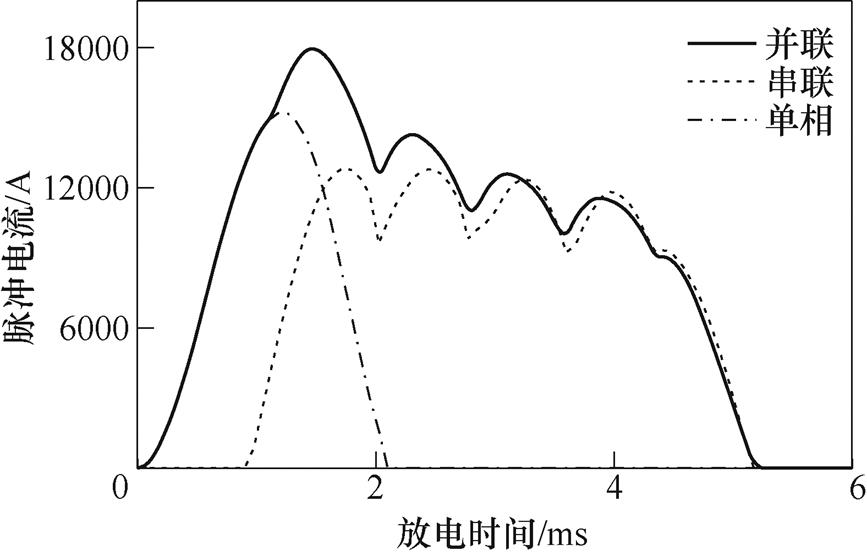
图6 两相绕组不同连接方式下ORPMPCPA脉冲电流波形
Fig.6 Discharge current waveforms of ORPMPCPA under different connection modes of two phase winding
由图6可知,两相绕组分别整流后并联在一起对负载放电时,脉冲电流峰值最大,为单相放电时峰值的1.2倍,且脉宽约是单相放电脉宽的2.5倍,这是由于单相放电时,无法通过多个电流波形叠加的方法增加脉宽,只能产生一个尖顶脉冲。当两相绕组分别整流后串联放电时,可以产生一个近似的平顶波,但其脉冲电流峰值反而比单相放电时小,这是因为串联时,两个电枢绕组之间产生了耦合,使得CPA内部电感增大,导致脉冲电流峰值减小,且由于仿真时A相先导通,B相导通时间滞后,而仅当A、B两相晶闸管全部导通时才能在串联电路中产生电流,所以串联时的脉宽相比并联时的要小。
负载侧串联不同电感时,ORPMPCPA脉冲电流波形如图7所示。可以看出,随着负载侧的电感值增大,脉冲电流脉宽略微变宽,幅值逐渐减小,脉冲电流波形曲线更接近于平顶矩形波,这是因为负载电感值变大时,电流上升率变小,脉冲的上升时间更长,同时电流下降率变小。
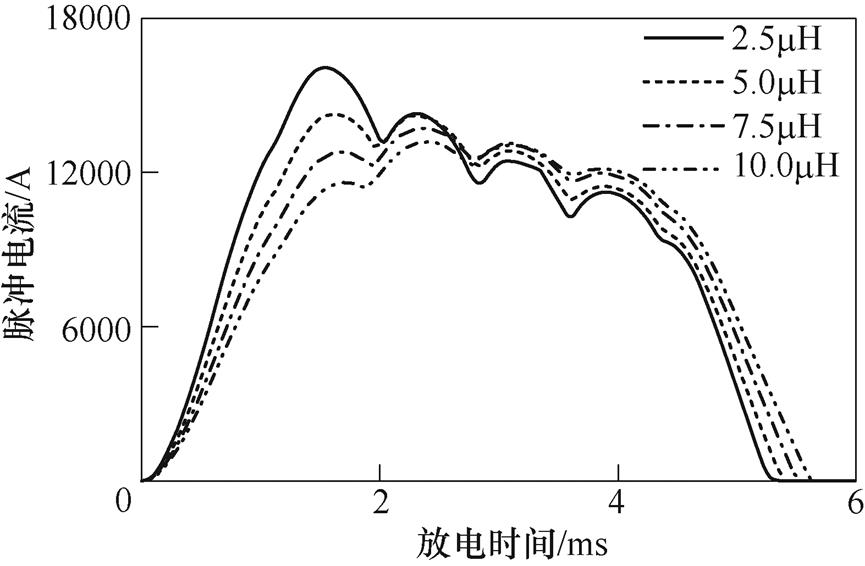
图7 负载侧串联不同电感时ORPMPCPA脉冲电流波形
Fig.7 Discharge current waveforms of ORPMPCPA with different inductors in series at load side
为了验证分析方法的准确性,对研制的ORPMPCPA样机的放电特性进行测试,搭建的ORPMPCPA样机放电测试平台如图8a所示,对应的测试原理如图8b所示。
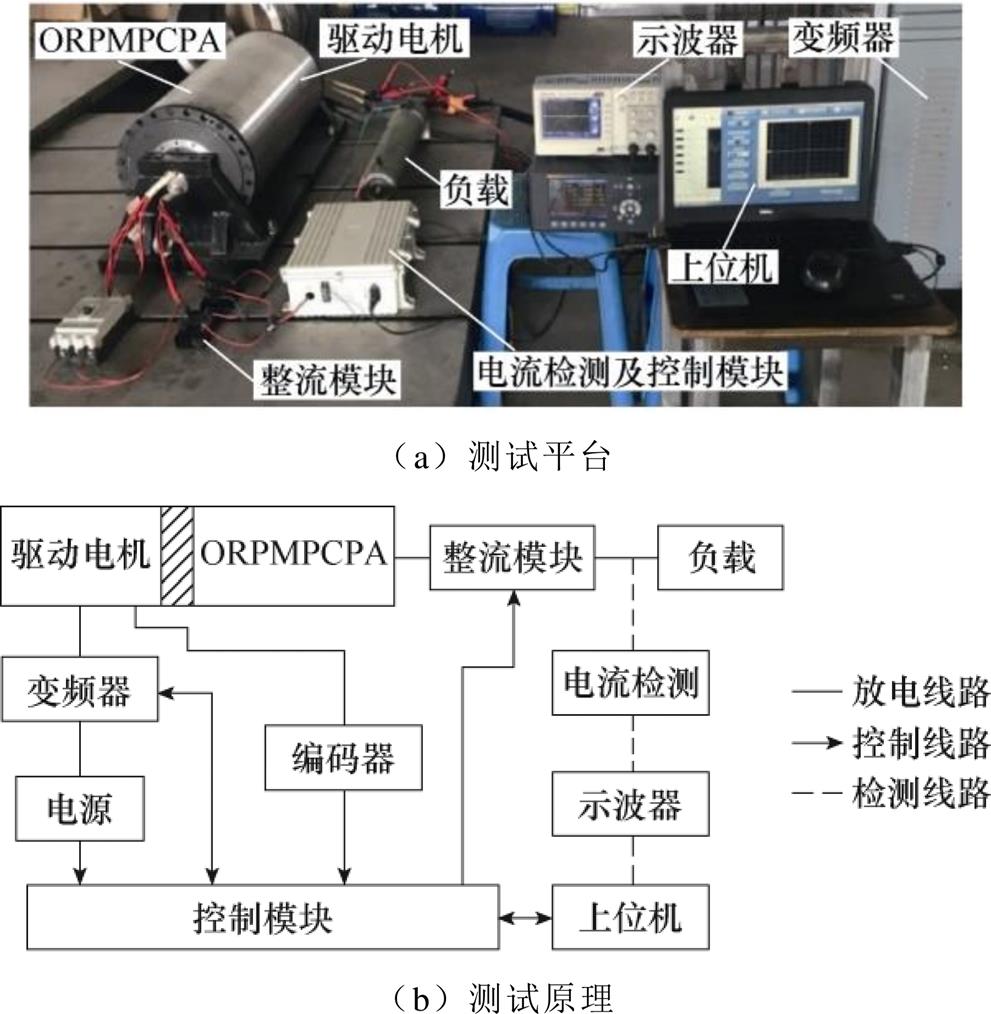
图8 ORPMPCPA样机放电测试平台
Fig.8 Discharge test platform for ORPMPCPA prototype
当ORPMPCPA转速达到额定,且两相绕组并联放电时脉冲电流波形的测试结果和仿真结果如图9所示。图中,实验脉冲电流波形是采用TDS2012C型数字存储示波器和Rogowski线圈测得,相应的波形数据同步上传至上位机中。
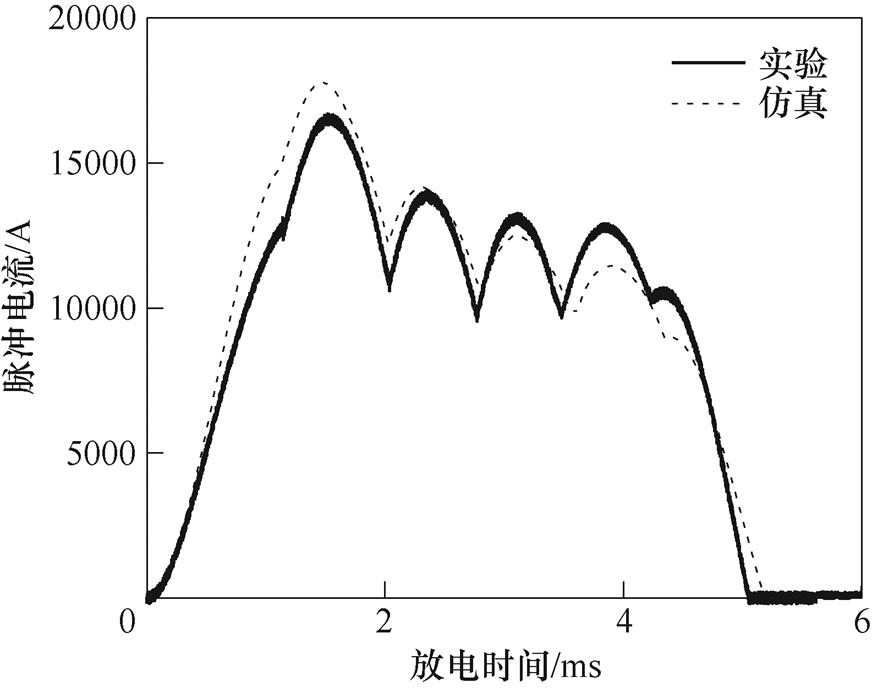
图9 两相绕组并联放电时脉冲电流波形
Fig.9 Pulse current waveforms under two phase winding discharge in parallel
从图9可知,实验测得的脉冲电流峰值为17 360A,脉冲宽度约为5.05ms,两相分别整流后并联在一起进行波形叠加,进而形成多个波峰,与仿真得到的波形基本一致,但实验测得的脉冲电流波形在幅值上要小于仿真结果,主要是由于线路中的接线电阻、整流器件压降等在仿真时未做考虑。
此外,从图9可以看出,实验测得的脉冲电流波形和仿真得到的脉冲电流波形在开始阶段无交叉,在超过2ms后则存在交叉。产生此现象的原因是由于两相绕组导通状态和导线电感(此部分电感在仿真时被忽略不计)综合作用所致。在放电开始阶段,由于A相在0°触发延迟角先导通,脉冲电流从零开始逐渐增加,随后B相在135°触发延迟角处导通,两相绕组同时放电维持电流上升至峰值,随后逐渐下降,故在2ms前的放电过程中,脉冲电流波形出现一个波峰,而实测电路比仿真电路多了一部分导线电感,因而实测波形的电流上升速率、下降速率和脉冲电流峰值均比仿真时要低,所以实测电流波形和仿真电流波形在此阶段不出现交叉现象;超过2ms后,并联的两相绕组均保持导通状态直至最后关断,两相绕组输出的电流波形经过整流后产生叠加,相应的电流波形出现多个波峰,由于导线电感对电流变化的阻碍作用,使得实测电流波形的波峰下降幅度比仿真电流波形的波峰下降幅度更小,因而实测电流波形和仿真电流波形之间发生交叉。
两相绕组串联放电时脉冲电流波形的测试结果与仿真结果如图10所示。可以看出,测试得到的两相绕组串联放电时脉冲电流波形与仿真得到的脉冲电流波形同样为近似平顶波,且受到放电回路中未做考虑的部分阻抗影响,测试波形峰值相比仿真波形峰值略有减小。
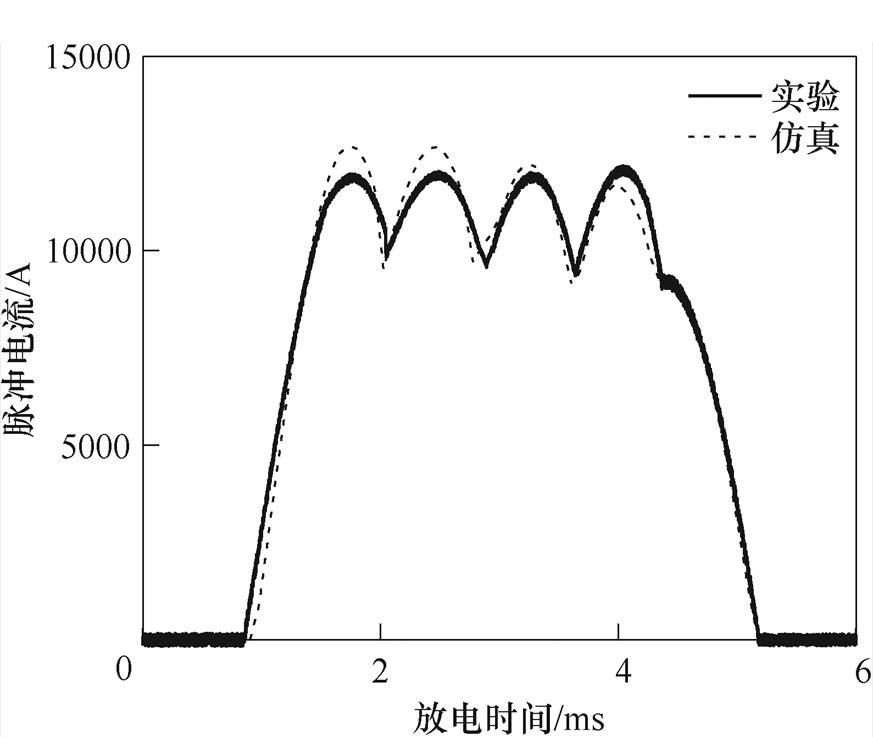
图10 两相绕组串联放电电流波形
Fig.10 Pulse current waveforms under two phase winding discharge in series
单相绕组放电时脉冲电流波形的测试结果与仿真结果如图11所示。可以看出,单相绕组放电时,会产生一个尖顶脉冲,且电流峰值介于两相绕组并联放电时峰值和两相绕组串联放电时峰值之间,这是因为两相并联时ORPMPCPA内部阻抗比单相放电时小,放电电流峰值更大,而串联时虽然输出电压有所增加但是内部阻抗增加带来的影响更大,所以放电电流峰值相对单相放电时要小。
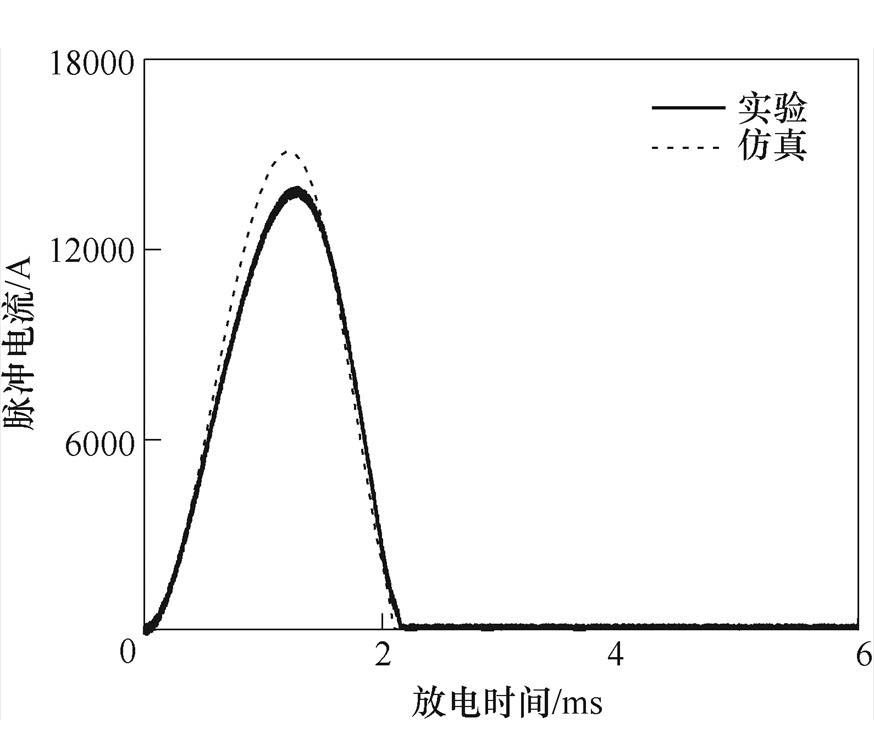
图11 单相绕组放电电流波形对比
Fig.11 Comparison of discharge current waveforms for single phase winding
实际上,由于ORPMPCPA运行时大部分时间处于空载状态,对负载放电时间仅有几毫秒,故机体的发热量不大;实验过程中,利用测温枪对转子外壳的温度进行了测量,结果表明,当ORPMPCPA在自然冷却状态下长时间以额定转速空载运行时,转子外壳温度在50℃以内,且在进行单次放电后并无明显温升,因而无需采用强制冷却。在ORPMPCPA放电过程中,由于屏蔽筒的存在,定子电枢绕组产生的磁场被压缩在气隙中,不会对转子磁场产生影响,对永磁体起到了保护作用,防止其退磁现象的发生,且放电前后测得ORPMPCPA的空载反电动势波形基本一致。上述事实说明,ORPMPCPA能够安全稳定运行。
本文研究了一种被动补偿式、外转子、永磁体励磁的脉冲发电机,建立了在考虑补偿作用对电感影响和机电能量转化作用下,其对负载放电的数学模型,并对其放电特性进行仿真分析,最后通过实验结果进行对比验证,得出以下结论:
1)ORPMPCPA结构简单,采用永磁体励磁,在高转速下转子无需励磁电流和换向器,运行时更加安全稳定,且屏蔽筒可对电枢绕组起到很好的补偿作用,进而可实现瞬时大电流放电。
2)ORPMPCPA采用外转子结构可提高转子储能密度,放电过程中,转子内部储存的动能可在瞬间转化为强脉冲电能,且一次放电后,转子转速下降很小,可以实现连续放电。
3)ORPMPCPA中两相绕组正交,实现绕组间电气解耦,通过改变外电路中触发延迟角、两相绕组组合方式和串联电感值,可以改变放电电流的脉宽和峰值,从而实现对脉冲放电波形的灵活调节。
4)不同绕组组合方式下脉冲放电电流波形的样机测试结果和仿真结果基本吻合,验证了本文所提出的放电电流分析方法的准确性。
参考文献
[1] 马山刚, 于歆杰, 李臻. 用于电磁发射的电感储能型脉冲电源的研究现状综述[J]. 电工技术学报, 2015, 30(24): 222-228, 236.
Ma Shangang, Yu Xinjie, Li Zhen. A review of the current research situation of inductive pulsed-power supplies for electromagnetic launch[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 222-228, 236.
[2] Hameer S, van Niekerk J L. A review of large-scale electrical energy storage[J]. International Journal of Energy Research, 2015, 39(9): 1179-1195.
[3] Zhu Bofeng, Lu Junyong, Wang Jie, et al. A com- pulsator driven reluctance coilgun-type electromagnetic launcher[J]. IEEE Transactions on Plasma Science, 2017, 45(9): 2511-2518.
[4] 袁培, 于克训, 黄福勇, 等. 用于高能脉冲激光器直驱式电源系统的主动补偿脉冲发电机的电磁设计与实验分析[J]. 中国电机工程学报, 2016, 36(9): 2528-2537.
Yuan Pei, Yu Kexun, Huang Fuyong, et al. Elec- tromagnetic design and experimental analysis of the active compensation pulse alternator for the high- energy pulsed laser direct-drive power system[J]. Proceedings of the CSEE, 2016, 36(9): 2528-2537.
[5] Zhao Weiduo, Wu Shaopeng, Cui Shumei, et al. A fractional slot multiphase air-core compulsator with concentrated winding[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1387-1393.
[6] Wan Yuan, Cui Shumei, Wu Shaopeng, et al. Shock- resistance rotor design of a high-speed PMSM for integrated pulsed power system[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1399-1405.
[7] Ye Caiyong, Liang Xin, Yang Jiangtao, et al. Feasibility analysis of a multidisk axial flux com- pensated pulsed alternator[J]. IEEE Transactions on Plasma Science, 2019, 47(5): 2412-2418.
[8] Nguyen B S, Yen W W, Chao C P, et al. A new high-efficiency power management circuit for a novel two-phase compensated pulse alternator[J]. IEEE Transactions on Plasma Science, 2020, 48(9): 3176- 3187.
[9] Kulkarni A S, Thomas M J. Performance analysis of a self-excited passive compulsator driving a railgun with field winding excited by a secondary armature[J]. IEEE Transactions on Plasma Science, 2019, 47(10): 4738-4744.
[10] 袁培, 于克训, 叶才勇. 10kJ高能脉冲激光器直驱式电源系统的分析和设计[J]. 电工技术学报, 2013, 28(11): 223-230.
Yuan Pei, Yu Kexun, Ye Caiyong. Analysis and design of a 10kJ directly driven power supply system for high energy pulsed lasers[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 223- 230.
[11] 陶雪峰, 刘昆. 空心补偿脉冲发电机设计与仿真[J].电工技术学报, 2018, 33(9): 1931-1937.
Tao Xuefeng, Liu Kun. Design and simulation of an air-core compulsator[J]. Transactions of China Elec- trotechnical Society, 2018, 33(9): 1931-1937.
[12] Zhao Weiduo, Wang Xuejiao, Wu Shaopeng, et al. Research on the compensation matching design and output performance for two-axis-compensated com- pulsators[J]. IEEE Transactions on Plasma Science, 2019, 47(5): 2445-2451.
[13] Li Jiangtao, Yan Xiaohui, Lü Li, et al. Pulsed power regulation in selective passively compensated pulsed alternator[J]. IEEE Transactions on Magnetics, 2012, 48(11): 3875-3878.
[14] McNab I R. Pulsed power options for large EM launchers[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1352-1357.
[15] Wang Haoze, Liu Kun, Yu Xiang, et al. Design, analysis, and testing of a novel permanent magnet compulsator[J]. IEEE Transactions on Plasma Science, 2015, 43(4): 1040-1048.
[16] 王昊泽, 刘昆, 张立, 等. 两相永磁被动补偿脉冲发电机研制[J]. 高电压技术, 2018, 44(3): 914-919.
Wang Haoze, Liu Kun, Zhang Li, et al. Development of two-phase passive permanent magnet com- pulsator[J]. High Voltage Engineering, 2018, 44(3): 914-919.
[17] Vats P, Singh B. Design and analysis of air core outer rotor Halbach array compulsator[J]. IEEE Transa- ctions on Plasma Science, 2020, 48(10): 3663-3669.
[18] 甘志伟, 缪冬敏, 王云冲, 等. 宽转速范围永磁同步发电机系统稳压控制及参数优化[J]. 电工技术学报, 2020, 35(8): 1624-1633.
Gan Zhiwei, Miao Dongmin, Wang Yunchong, et al. Voltage stabilization control and parameters optimi- zation for wide-speed-range permanent magnet synchronous generator systems[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1624- 1633.
[19] 刘毓希, 李立毅, 曹继伟, 等. 短时高过载永磁同步电机电磁热研究[J]. 电工技术学报, 2019, 34(11): 2296-2305.
Liu Yuxi, Li Liyi, Cao Jiwei, et al. Electromagnetic thermal analysis for short-term high-overload permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2296-2305.
[20] Zhang Zhuoran, Geng Weiwei, Liu Ye, et al. Feasi- bility of a new ironless-stator axial flux permanent magnet machine for aircraft electric propulsion application[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 30-38.
[21] 夏加宽, 康乐, 詹宇声, 等. 表贴式三相永磁同步电机极槽径向力波补偿模型及参数辨识[J]. 电工技术学报, 2021, 36(8): 1596-1606.
Xia Jiakuan, Kang Le, Zhan Yusheng, et al. The model of pole slot radial force wave compensation for surface-mounted three-phase permanent magnet synchronous motor and parameter identification[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1596-1606.
[22] 高起兴, 王晓琳, 顾聪, 等. 基于多耦合特性的整体支撑式超高速微型永磁电机设计[J]. 电工技术学报, 2021, 36(14): 2989-2999.
Gao Qixing, Wang Xiaolin, Gu Cong, et al. Design of ultra high speed micro permanent magnet motor with integrated support type based on multi coupling characteristics[J]. Transactions of China Electro- technical Society, 2021, 36(14): 2989-2999.
[23] 孙少男, 冯桂宏, 李岩, 等. 切向结构永磁同步电机磁钢径向并联组合研究[J]. 电工技术学报, 2021, 36(1): 131-140.
Sun Shaonan, Feng Guihong, Li Yan, et al. The performance impact of radial parallel permanent magnet in spoke-type permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 131-140.
[24] Jumayev S, Borisavljevic A, Boynov K, et al. Indu- ctance calculation of high-speed slotless permanent magnet machines[J]. COMPEL-the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2015, 34(2): 413-427.
[25] 张守首, 郭思源. 基于子域分析模型的实心转子感应电机磁场解析[J]. 电工技术学报, 2021, 36(20): 4285-4296.
Zhang Shoushou, Guo Siyuan. Analytical solution of magnetic field in solid rotor induction machine based on subdomain model[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4285-4296.
[26] 饶凡, 吴旭升, 高嵬, 等. 两极永磁电机静态内外磁场研究[J]. 电工技术学报, 2021, 36(14): 2936- 2944.
Rao Fan, Wu Xusheng, Gao Wei, et al. Study on internal and external magnetic field of static two-pole permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2936-2944.
[27] Laksar J. Improved calculation of the slot leakage inductance of different slot shapes[J]. Electrical Engineering, 2020, 102(3): 1129-1139.
[28] Li Ge. The inductance computation for the passive compulsator[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(4): 1033-1036.
[29] Tao Xuefeng, Liu Kun, Wang Haoze. Modeling of an air-core compulsator and the pulse shaping using optimization algorithm[J]. IEEE Transactions on Plasma Science, 2019, 47(1): 611-618.
Discharge Characteristics of Outer Rotor Permanent Magnet Passively Compensated Pulsed Alternator
Abstract In order to clarify the discharge characteristics of outer rotor permanent magnet passively compensated pulsed alternator (ORPMPCPA), the influence of passive compensation on the inductance of armature winding was taken into account, the change in the rotating speed due to the electromechanical energy conversion was considered, and thus the discharge mathematical model of ORPMPCPA for the load was established. The forming process of pulse current and conversion process of energy as well as the influence of relative factors on the pulse current waveform of ORPMPCPA were simulated and analyzed. The simulated results reveal that under the working condition, the kinetic energy stored in the rotor can be instantaneously transformed into the strong pulse electric energy, and the pulse discharge current waveform can be flexibly adjusted through changing the trigger angle, two-phase winding combination mode and external inductance value. Through comparing the experimental results of the prototype and the simulation results, the accuracy of the proposed analysis method for the discharge characteristics is proved.
keywords:Passively compensated pulsed alternator, permanent magnet excitation, outer rotor, pulse current waveform, discharge characteristic
DOI: 10.19595/j.cnki.1000-6753.tces.201270
中图分类号:TM35
陈亚千 男,1990年生,博士研究生,研究方向为特种电机及其控制。E-mail: chenyaqian@sut.edu.cn
张炳义 男,1954年生,教授,博士生导师,研究方向为特种电机及其控制、电子电气机械一体化。E-mail: zhangby@sut.edu.cn(通信作者)
收稿日期 2020-09-22
改稿日期 2020-11-24
国家重大科学仪器设备开发专项资助项目(2012YQ05024207)。
(编辑 崔文静)