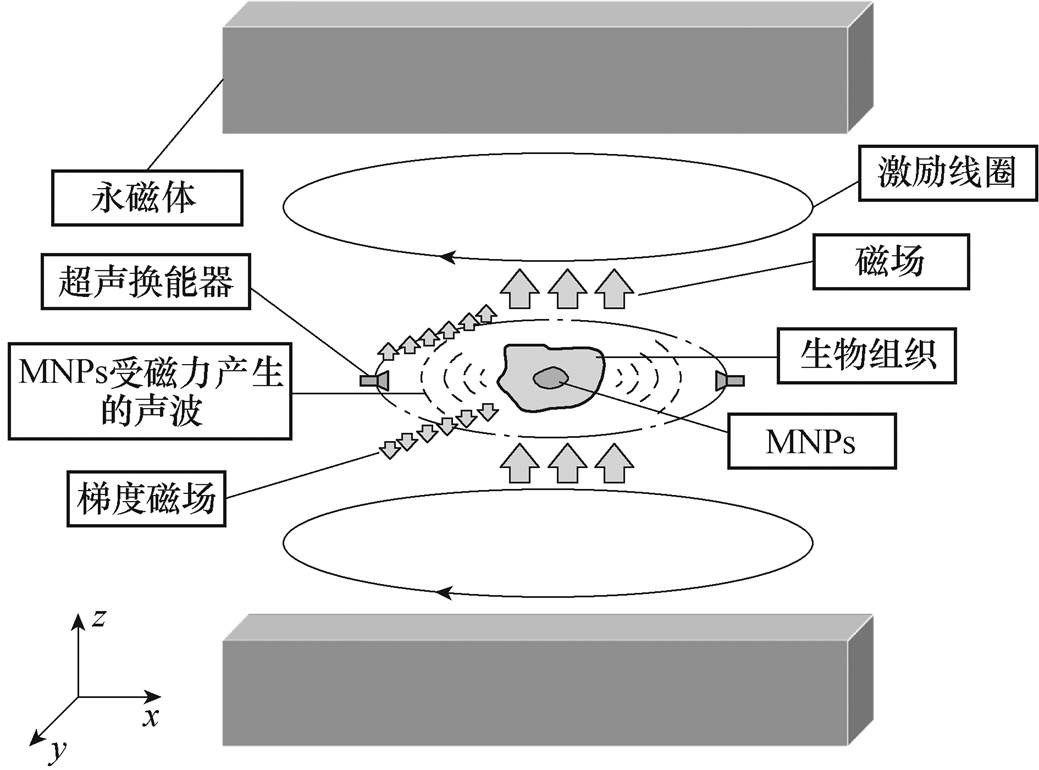
图1 MACT-MI原理
Fig.1 Schematic diagram for MACT-MI
摘要 感应式磁声磁粒子浓度成像（MACT-MI）是一种基于磁声耦合效应的磁性纳米粒子（MNPs）浓度成像新方法，为降低激励源幅值、增大磁声信号的信噪比，该文提出一种加入相同极性永磁体的MACT-MI新思路。根据Langevin顺磁理论，研究加入相同极性的永磁体后MACT-MI的电磁学与声学特性，进而对磁体系统进行设计，同时构建浓度渐变模型，采用多物理场仿真软件COMSOL对MACT-MI的物理过程进行求解，得到磁通密度、磁力和声压的二维分布及其对应的一维曲线。研究结果表明，加入相同极性永磁体后，MNPs受到的磁力更强，从而激发信噪比更大的磁声信号，有利于声信号的获取，在所设计的磁体系统激励下，MNPs产生的声压呈上下对称分布且方向相反，浓度均匀模型中声压的峰值出现在浓度边界处，浓度渐变模型声压的峰值出现在渐变中心处。研究结果可为成像装备的设计以及MACT-MI的后续实验乃至临床应用提供研究基础。
关键词：磁性纳米粒子 相同极性永磁体 感应式磁声磁粒子浓度成像 磁力 声压
磁性纳米粒子（Magnetic Nanoparticles, MNPs）是纳米技术与传统磁性材料相结合的一类新型材料，由于其独特的物理、化学、热力学以及力学性质，MNPs在医学应用上呈现出极大的潜力，现已经广泛应用于磁共振造影剂[1-2]、细胞标记和分 离[3-4]、药物递送[5-6]和热疗[7]等研究领域。然而，随着纳米医学的飞速发展，这些应用对磁粒子监控成像技术提出了更高的要求，探索一种用于检测MNPs的高分辨率成像方法刻不容缓。闫孝姮团队最近提出了一种基于MNPs浓度的感应式磁声成像方法 ——感应式磁声磁粒子浓度成像（Magneto-Acoustic Concentration Tomography of Magnetic nanoparticles with magnetic Induction, MACT-MI），利用电-磁-声场结合的耦合效应进行探测与成像，融合了电磁技术、超声技术的优势，兼具无创、对比度好、灵敏度高以及高空间分辨率等优点，有望进一步提高成像分辨率，为肿瘤治疗提供依据[8]。
将MNPs应用于磁声成像是近年来研究的热点。2006年，J. Oh等通过借鉴Oldenburg于2005年提出的磁致振动光学相干断层扫描，首次将MNPs作为标记物来检测小鼠肝脏中的巨噬细胞，并用实验证明相比于光学，超声波更容易实现内部振动信号的检测[9]。2009年，M. Mehrmohammadi等为了降低线圈和组织的热约束，提出脉冲磁声成像的方法，并且探究了脉冲磁动信号对磁纳米粒子浓度的依赖性，研究结果表明，MNPs可以作为脉冲磁声成像的造影剂[10]。2012年，He Bin等基于磁声效应对嵌入仿体中的MNPs进行实验研究，通过采集样品周围的超声信号，并利用反投影重建声源图像，为医学中病变组织检测提供了一种无损检测新技术[11]。2016年，G. Podaru等通过实验证明了当暴露于脉冲磁场和交变磁场时，超声波是MNPs产生的[12]。2018年，Yan Xiaoheng等研究了MNPs对磁声成像的影响，理论上证明MNPs能让磁声信号更明显、分布更均匀[13]。2019年，张帅等提出基于时间反演的磁动力超声成像方法，能快速准确地获得磁纳米粒子的尺寸和位置信息[14]。同年，M. Fink等提出了一种定量的磁动力超声反算法，可以定量测定组织中MNPs浓度的空间分布，该方法可以确定空间粒子浓度的数量级[15]。2020年，Shi Xiaoyu等提出感应式磁声磁粒子浓度成像方法，该方法对MNPs的浓度进行成像[8]。同年，Yan Xiaoheng等提出一种基于矩量法的MACT-MI逆问题的数值计算方法，进行了不同形状模型下声源与超顺磁纳米粒子浓度的图像重建[16]。
本课题组在前期的研究中发现，MACT-MI在当前装置条件下磁声信号信噪比较低，不利于实验工作的开展。为增大磁声信号的信噪比，本文从增大MNPs所受磁场的方向开展研究，在成像过程中引入相同极性的永磁体，并基于经典朗之万顺磁性理论，建立了MNPs浓度与磁力声源关系的数学物理模型。研究了磁体系统的设计，分析了有无永磁体对MNPs磁力和声压的影响，同时建立了成像目标体的浓度渐变模型，研究了在该磁体系统的激励下渐变浓度对MACT-MI成像过程的影响，为MACT- MI的后续实验乃至临床应用奠定基础。
MACT-MI原理如图1所示，对被MNPs标记的生物组织，施加由Maxwell线圈产生的时变磁场和由相同极性永磁体产生的恒定均匀静磁场，MNPs被磁化后会受到磁力的作用，在组织中发生振动产生超声波，MNPs在生物组织中分布的浓度不同导致所受磁力不同，进而致使所产生的声压信号不同。利用超声换能器检测含有浓度信息的声压信号，应用时间反演法以及有限差分法重构出MNPs的浓度分布图像，其中，Maxwell线圈和永磁体产生的磁场方向均为z轴正方向。
图1 MACT-MI原理
Fig.1 Schematic diagram for MACT-MI
与其他成像方法类似，MACT-MI主要分为正问题和逆问题两个部分。所谓正问题是指对于某些物理过程，若已知该物理过程的内部参数，根据系统的约束规律以及某些特定条件来确定系统的某些可观测变量，而与之相反的过程则称为逆问题[14, 17-21]。对正问题的研究有助于分析成像方法理论的可行 性[22]，本文主要对MACT-MI的正问题进行研究，以物理场类别进行划分[23]，MACT-MI的正问题又可分为电磁场正问题和声场正问题两部分。
1.2.1 电磁场正问题
在无磁场作用时，MNPs在基液中磁矩取向杂乱无章，平均磁矩为零，对外不显磁性。当MNPs受到磁场B的作用时，所受磁力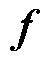
为
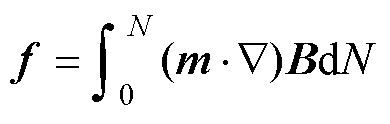（1）
式中，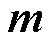
为MNPs的磁矩；
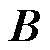为MNPs周围的磁通密度；N为单位体积内MNPs的数量，即MNPs的浓度。
对其在笛卡尔坐标系下展开为
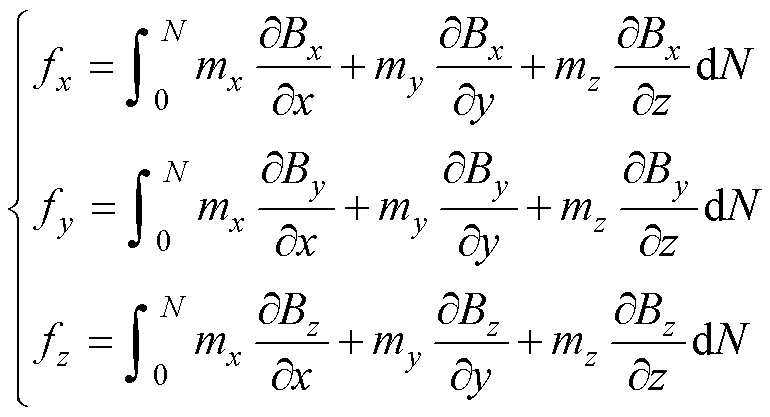（2）
式中，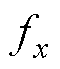
、
、
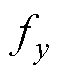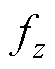分别为磁力f在x、y和z方向上的分量；
、
、
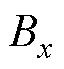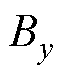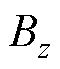分别为磁通密度B在x、y和z方向上的分量；
、
、
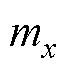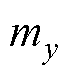分别为磁矩m在x、y和z方向上的分量。
根据Langevin经典顺磁理论，当对单位体积内数量为N的MNPs施加单方向磁场时，MNPs被磁化，单个MNPs固有磁矩的空间取向与外加磁场方向一致，大小为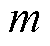
，且磁化强度服从Langevin规律，即
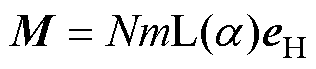（3）
式中，M为磁化强度；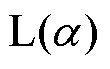
为Langevin函数，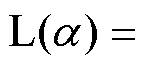
，
；
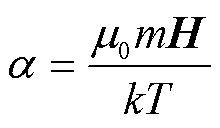为外磁场强度；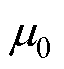
为真空磁导率；
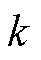为玻耳兹曼常数；
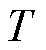为温度（K）；
为与外加磁场方向相同的单位矢量。
MNPs的磁化强度
为小体元DV内的全部MNPs磁矩矢量和与DV之比，即
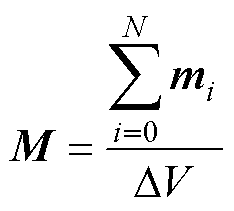（4）
式中，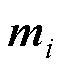
为单个MNPs的磁矩。
当磁体系统提供的磁场可以视为仅有z方向时，将式（3）和式（4）代入式（1），可得磁力表达式为
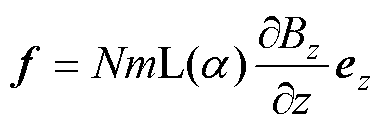（5）
激励线圈中施加的交变电流及其产生的所有物理量及导出量都是时变矢量，而任何时变矢量都可以表示为空间矢量和时间的乘积。假设Maxwell线圈对MNPs仅施加笛卡尔坐标系下z方向的交变磁场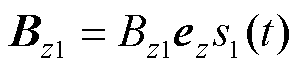
，其中，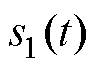
为磁场的时间函数，
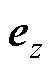为z方向的单位矢量；假设永磁体在MNPs处产生的磁场为均匀磁场
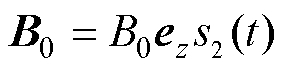，B0恒定，时间函数
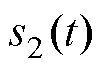=1。
在无永磁体时，MNPs周围的磁场仅由Maxwell线圈提供，Langevin函数中的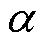
可以描述为
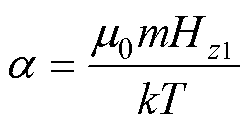（6）
式中，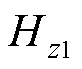
为Maxwell线圈在研究区域（Region of Interest, ROI）产生的磁场强度。
由Maxwell线圈和永磁体组成的磁体系统在ROI产生的磁场强度为
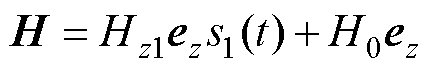（7）
式中，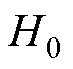
为永磁体在ROI产生的磁场强度。
此时Langevin函数中的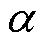转变为
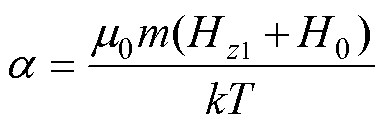（8）
当磁体系统所提供的外磁场强度大小超过饱和磁场强度Hs时，MNPs的磁化强度趋于饱和，基本不再随外磁场的增大而增大，此时数量浓度为N的磁饱和MNPs的饱和磁化强度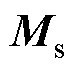
可以简化[24]为
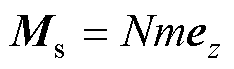（9）
由此可得，饱和MNPs所受磁力为
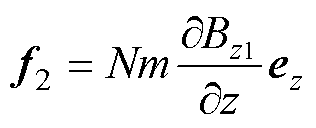（10）
因此，MNPs所受磁力与MNPs浓度、ROI的磁场梯度和ROI的磁场强度有关，当ROI的磁场强度低于饱和磁场强度Hs时，采用式（5）对MNPs所受磁力进行计算，当ROI的磁场强度高于饱和磁场强度Hs时，采用式（10）对MNPs所受磁力进行计算。
1.2.2 磁体系统设计
在文献[8]研究的MACT-MI中，以Maxwell线圈作为磁体系统，以此来提供z方向的磁场和梯度磁场，没有采用其他方式来增大MNPs所受磁场。对相同极性的永磁体进行合理设计，可以在中心区域提供较为均匀的磁场。同时，为使ROI的磁场尽可能的均匀，本文采用双磁环结构的永磁体。MACT-MI磁体系统示意图如图2所示，Maxwell线圈和相同极性的永磁体组合在一起构成MACT- MI的磁体系统，MNPs所受的梯度磁场分量仅由Maxwell线圈提供，而MNPs所受磁场分量由Maxwell线圈和永磁体共同提供。
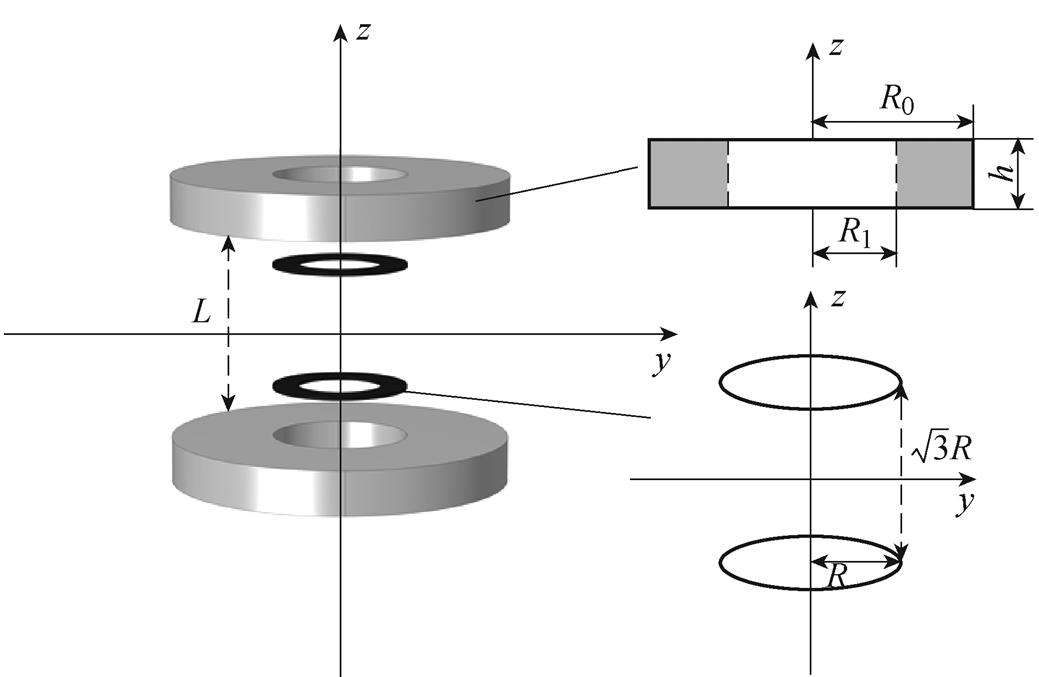
图2 MACT-MI磁体系统示意图
Fig.2 Schematic diagram of MACT-MI magnet system
与z轴同轴的Maxwell线圈会在z方向上产生均匀梯度磁场，在ROI产生的磁场可近似为
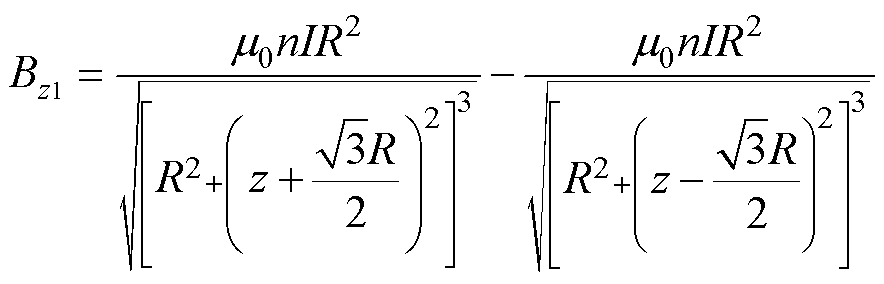（11）
式中，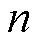
为Maxwell线圈的匝数；
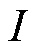为通过Maxwell线圈的电流；
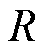为Maxwell线圈的平均半径。
双磁环结构永磁体在ROI产生的磁场可近似为
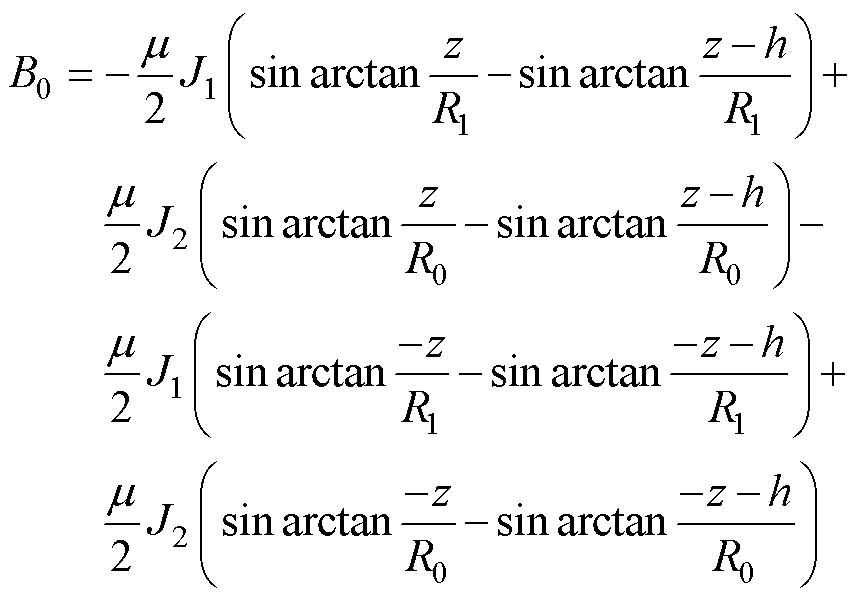（12）
其中
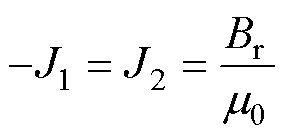
式中，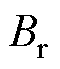
为永磁体的表面磁通密度；R0为磁环的外径；R1为磁环的内径；h为磁环的厚度；J1为磁环内表面的磁化电流密度；J2为磁环外表面的磁化电流密度。
因此，磁体系统在ROI产生的磁场可以表示为
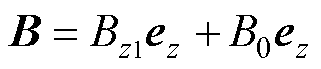（13）
1.2.3 声场正问题
声场传播的过程是声压的时空变化过程，即每个时刻每个位置的声压都在变化，基于牛顿第二定律、质量守恒定律以及描述压强、温度与体积等状态参数关系的物态方程，在理想流体媒质的假设条件下，可以推导出有源线性声压波动方程为
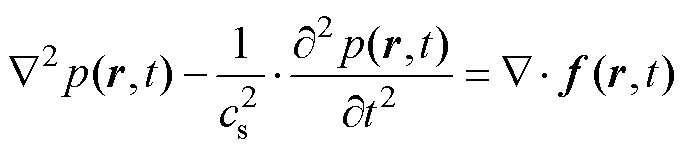（14）
式中，
为无界空间中的任意一点的位置矢量；
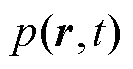为声压场的时空分布；
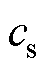为生物组织内的声速；
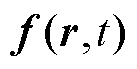为超顺磁纳米粒子受到的磁力；磁力散度
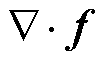即为声源项。以Maxwell线圈通电之前为初始时刻，此时成像体中无梯度磁场，即
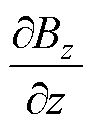=0，MNPs不受磁力，即不存在声源，可以认为初始条件为
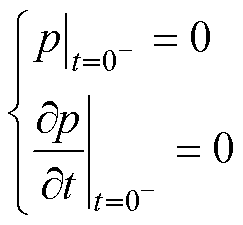（15）
根据无界空间格林函数法，结合卷积特性求解式（13），可得到无界声场的解析解为
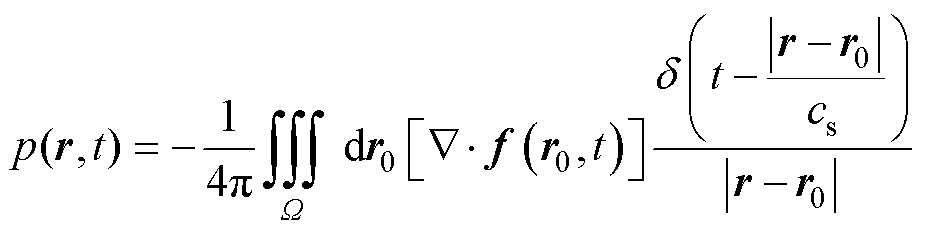（16）
式中，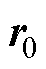
为源点位置矢量；
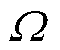为空间积分区域。
MACT-MI对恒定磁场的要求与成像方法密切相关，要求在ROI磁场只有z方向分量且分布均匀，为了营造MACT-MI成像所需的恒定磁场，本文采用双磁环结构的永磁体对MACT-MI所需的恒定磁场进行单独设计。恒定磁场的磁体系统由牌号为N50的圆柱形永磁体钕铁硼、夹件以及磁屏蔽板组成，具体结构如图3所示。
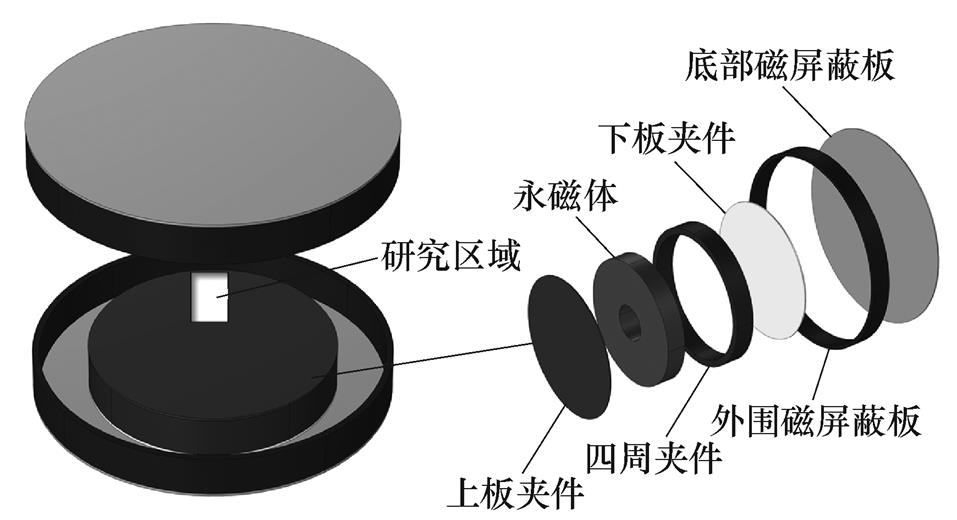
图3 恒定磁场磁体系统结构示意图
Fig.3 Schematic diagram of the structure of a constant magnetic field magnet system
同时考虑到MACT-MI所需的磁场由Maxwell线圈和永磁体共同提供，目前MACT-MI的ROI为底面半径为25mm，高为50mm的圆柱体[25]，若要在该区域内产生相对均匀的梯度磁场至少需要平均半径为80mm的Maxwell线圈，则双磁环结构的永磁体上下两磁环的距离要大于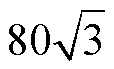
mm，因此设定该系统部件的材料参数[26-28]以及几何尺寸见表1。
设永磁体的磁化方向为z轴正方向，与z轴同轴放置且两磁环距离为L。随着距离L的增大，轴线上的磁通密度分布曲线会由中心凸起向中心凹陷过渡[29]。因此，在某一间距时，双磁环中心附近存在磁通密度相对较强且均匀性较好的空间。
本文采用COMSOL中的三维磁场分析模块对双磁环结构的永磁体进行设计，为使ROI内的磁场
表1 恒定磁场磁体系统的材料属性以及几何尺寸
Tab.1 Material properties and geometric dimensions of the constant magnetic field magnet system
部件名称材料名称尺寸/ mm×mm×mm相对磁导率电导率/ (S/m) 上板夹件无磁不锈钢105×21.0081×106 四周夹件铝板105×95×3015×107 永磁体钕铁硼N5095×27×301.051×10-16 下板夹件无磁不锈钢105×21.0081×106 外围磁屏蔽板钢板152×26002×107 底部磁屏蔽板钢板152×142×306002×107
尽可能均匀，将L设为可变参数，在距离为150～170mm范围内以步长0.02mm进行参数化扫描，以磁通密度的均匀度
作为衡量磁场均匀性的参量，即
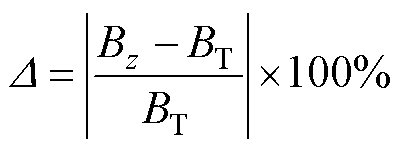（17）
式中，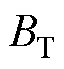
为基点处的磁通密度z方向分量。
结果表明，当L=160.82mm时能提供最为均匀的磁场，xOz截面上的磁通密度z分量如图4所示。在截面中取截线AB并绘制出磁通密度z分量曲线如图5所示，其中截线的起止点A、B坐标分别为（0, 0, 50）、（0, 0, -50）。
图4 ROI中xOz截面上的磁通密度z分量
Fig.4 The magnetic flux density z component on the xOz section of ROI
以作为衡量磁场均匀性的参量时需要选定基点，由于双磁环结构永磁体与z轴同轴，且上下对称，故选取C（0, 0, 0）点作为基点，该点处的磁通密度z轴分量为0.12T左右，满足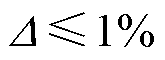
的区域如图6所示，即当L=160.82mm时，ROI附近的磁通密度相对较强且均匀性较好，满足MACT-MI的成像需求。
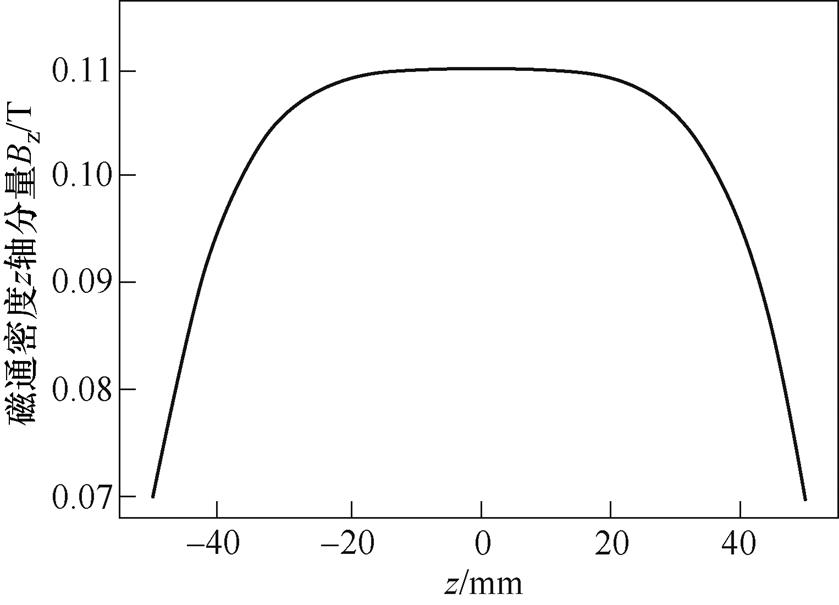
图5 ROI中截线AB的磁通密度z分量
Fig.5 The magnetic flux density z component of the section AB of ROI
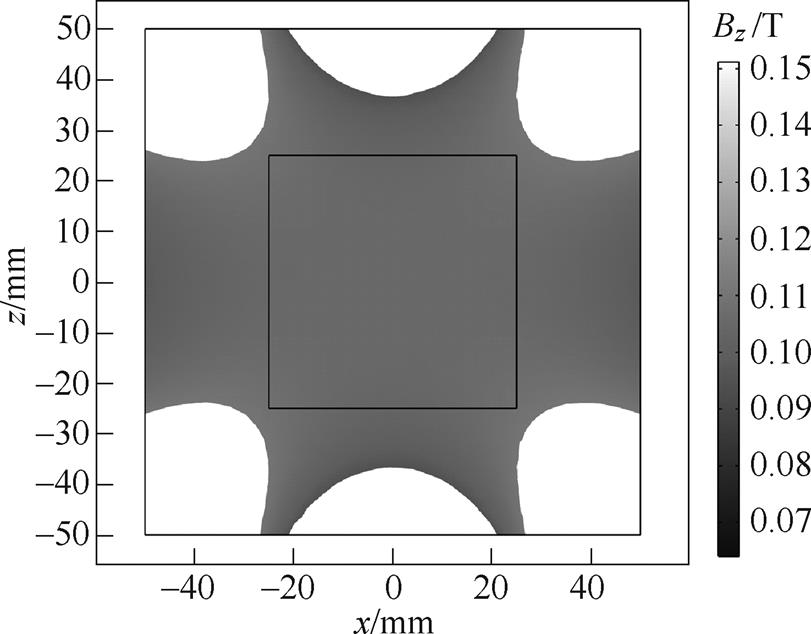
图6 满足D≤1%的区域
Fig.6 The area that the uniformity of less than 1%
因此，该系统在ROI产生的磁场只有单一分量且均匀分布，故在下文进行电-磁-声多物理场耦合仿真计算时，可将恒定磁场以常数代入。
为了验证加入永磁体后，MNPs受力公式的正确性，仿真中采用Maxwell线圈和永磁体组合的方式为MNPs提供外部磁场，MNPs周围的磁通密度z分量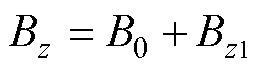
，其中，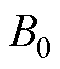
为相同极性永磁体所提供的恒定磁场分量，
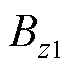为Maxwell线圈提供的时变磁场分量。以z轴摆放，磁体系统示意图如图7所示。图7a中，ROI的磁场由Maxwell线圈和相同极性永磁体共同产生，图7b中，ROI的磁场仅由Maxwell线圈产生，对两种激励方式在电磁场中进行对比仿真。
Maxwell线圈的结构参数见表2，在Maxwell线圈中通入反向的窄脉冲电流，其应满足在电流波形下降到零时刻时无反极性振荡[30]，故设定激励电流为正弦衰减截断波信号，即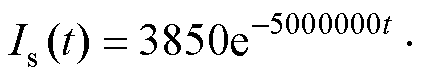
，通入电流的时间特性如图8所示，电流在0.2ms附近达到峰值，且持续时间为2ms。
图7 磁体系统示意图
Fig.7 Schematic diagram of the magnet system
表2 Maxwell线圈的结构参数
Tab.2 Structural parameters of Maxwell coils
参 数数 值 外径/mm175 内径/mm145 宽度/mm15 高度/mm4 匝数10 厚度/mm1.5
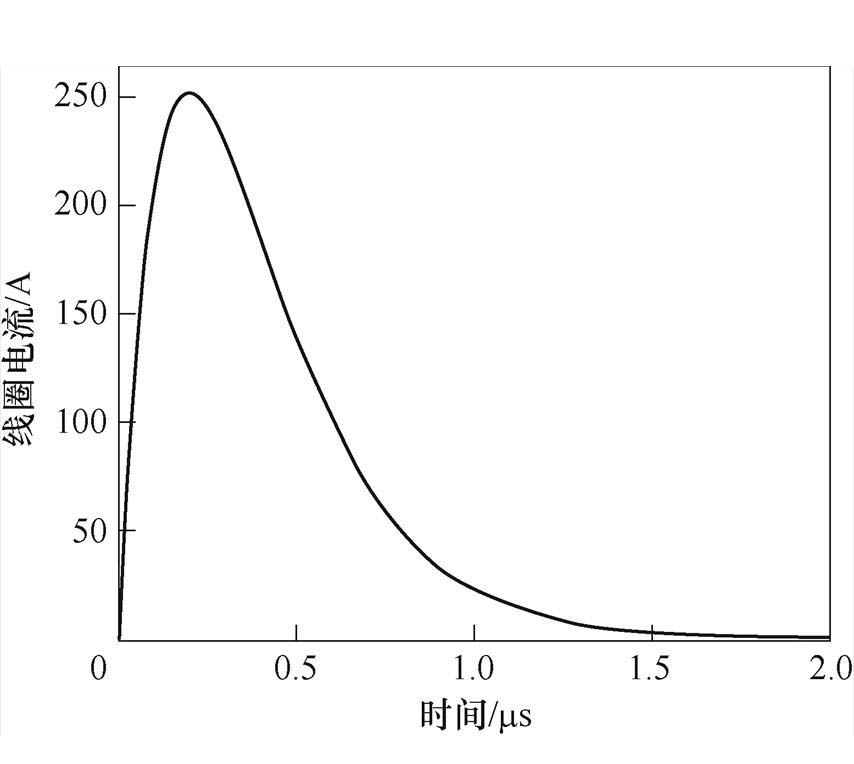
图8 线圈电流
Fig.8 Coil current
利用COMSOL建立二维轴对称生物组织模型，如图9所示，以底面半径25mm，高50mm的圆柱体来模拟生物组织，且忽略生物组织的磁属性，设置相对磁导率为1；将半径为5mm的球体嵌入生物组织以模拟MNPs集群，并且MNPs参数取自美国Ferrotec公司的水溶性超顺磁性纳米颗粒EMG 304，其规格见表3[11, 25]。
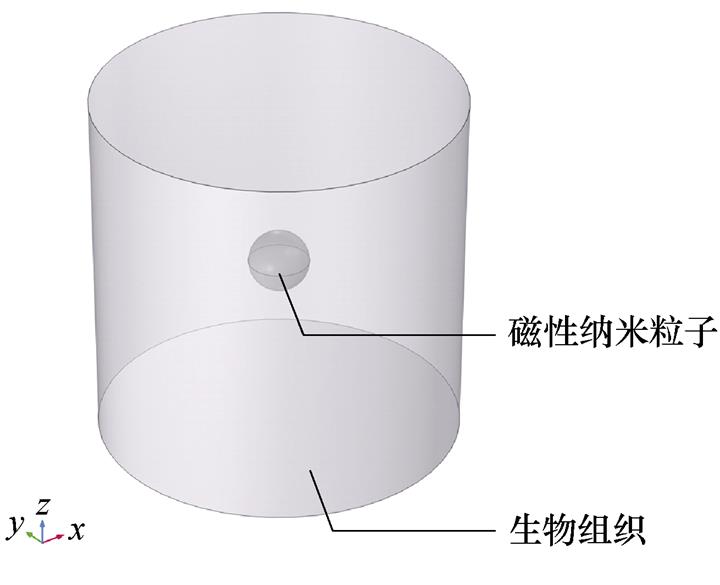
图9 生物组织模型
Fig.9 Biological tissue model
表3 EMG 304规格
Tab.3 EMG 304 specifications
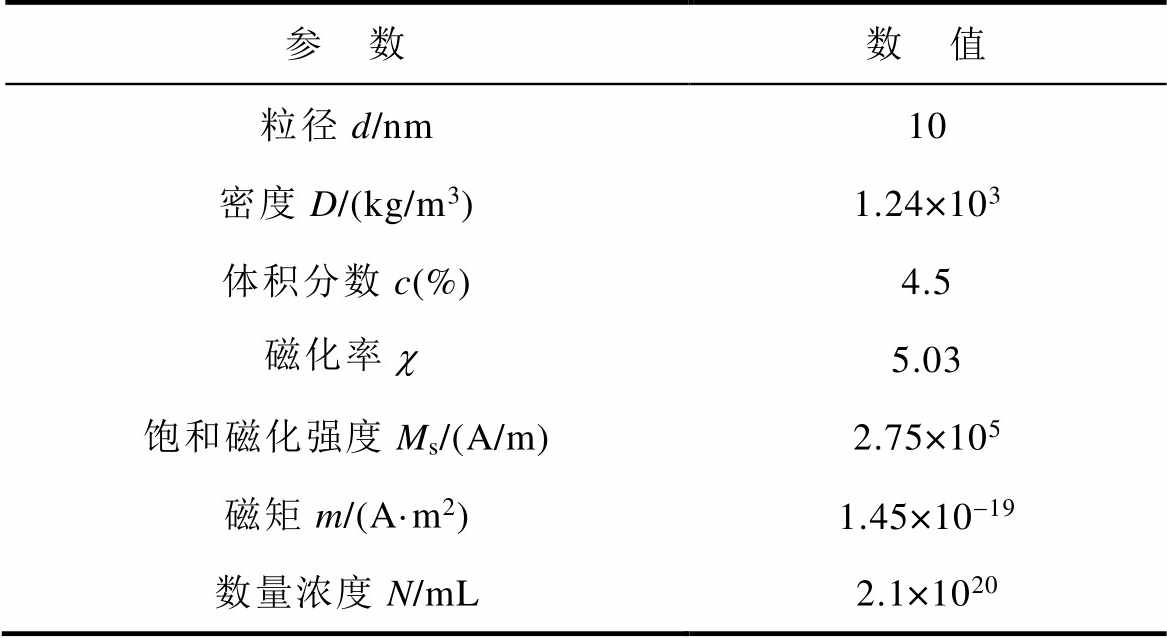
参 数数 值 粒径d/nm10 密度D/(kg/m3)1.24×103 体积分数c(%)4.5 磁化率5.03 饱和磁化强度Ms/(A/m)2.75×105 磁矩m/(A·m2)1.45×10-19 数量浓度N/mL2.1×1020
注：m=pd3Ms/6；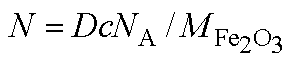
。
由式（5）和式（10）可知，MNPs的浓度是影响磁力的一个重要因素，如果不对MNPs的浓度进行限制，理论上浓度越大成像效果越好，但是考虑到实际MACT-MI最终的应用场合为活体实验，如果粒子溶液浓度过大会严重影响肾脏功能，因此在实际使用时粒子的浓度不能过高[6]。通过文献[12]可知，EMG 304溶液的铁含量已经超过了食品药品监督管理局（Food and Drug Administration, FDA）所批准的铁含量，在实验时需要将其稀释，故在仿真中设定MNPs浓度为1×1016/mL。
由式（3）可知，MNPs的磁化强度与外磁场之间的关系为非线性的Langevin函数，当外磁场从零开始增加时，MNPs的磁化强度随之迅速增大，当外磁场强度大小超过饱和磁场强度Hs时，MNPs的磁化强度趋于饱和，一般将饱和磁场强度定义为MNPs溶液磁化强度达到饱和磁化强度80%时的磁场强度，此时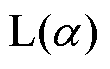
中的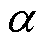
=5，饱和磁场强度的表达式[23]为
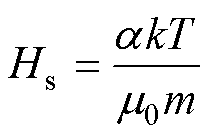（18）
按照表3中EMG 304的参数进行计算，可得该样品的饱和磁场强度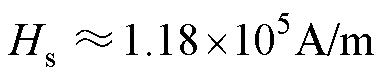
，当磁体系统在ROI产生的磁场强度高于
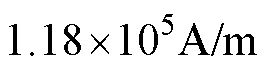时，采用式（10）计算MNPs所受磁力，当磁体系统在ROI产生的磁场强度低于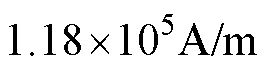时，采用式（5）计算MNPs所受磁力。
利用COMSOL多物理场问题数值分析软件求解Maxwell线圈与相同极性的永磁体组成的MACT- MI磁体系统在脉冲电流激励下产生的磁力，并与仅以Maxwell线圈作为磁体系统时进行对比。由于Maxwell线圈会在其中心区域产生零磁场点[31]，故将MNPs集群中心置于（0, 15），而相同极性的永磁体和Maxwell线圈构成的磁体系统不存在零磁场点，故将MNPs集群中心置于（0, 0）。两种磁体系统在ROI产生的磁场分布如图10所示，图10a中，Maxwell线圈与永磁体组成的MACT-MI磁体系统在MNPs集群区域产生的磁通密度约为0.12T，而图10b中，MNPs集群所在区域的磁场仅由Maxwell线圈产生，磁通密度约为0.009T。
Maxwell线圈和永磁体组成的磁体系统在ROI产生的磁场强度约为9.55×104A/m，单Maxwell线圈在ROI产生的磁场强度约为7.2×103A/m，均低于EMG 304样品的饱和磁场强度Hs，故均采用式（5）计算MNPs所受磁力。在0.5ms时，ROI的磁力分布如图11所示，磁力只作用于被MNPs标记的生物组织，这是因为MNPs相较于周围组织粒子数量较多，且具有较大磁化率，在磁场激励下受到较大的磁力，由此为声场提供声源；图11a中的MNPs所受磁力分布较为均匀，大小基本一致，而图11b中磁力分布略微不均匀，这是由于Maxwell线圈产生的磁场为线性梯度场。
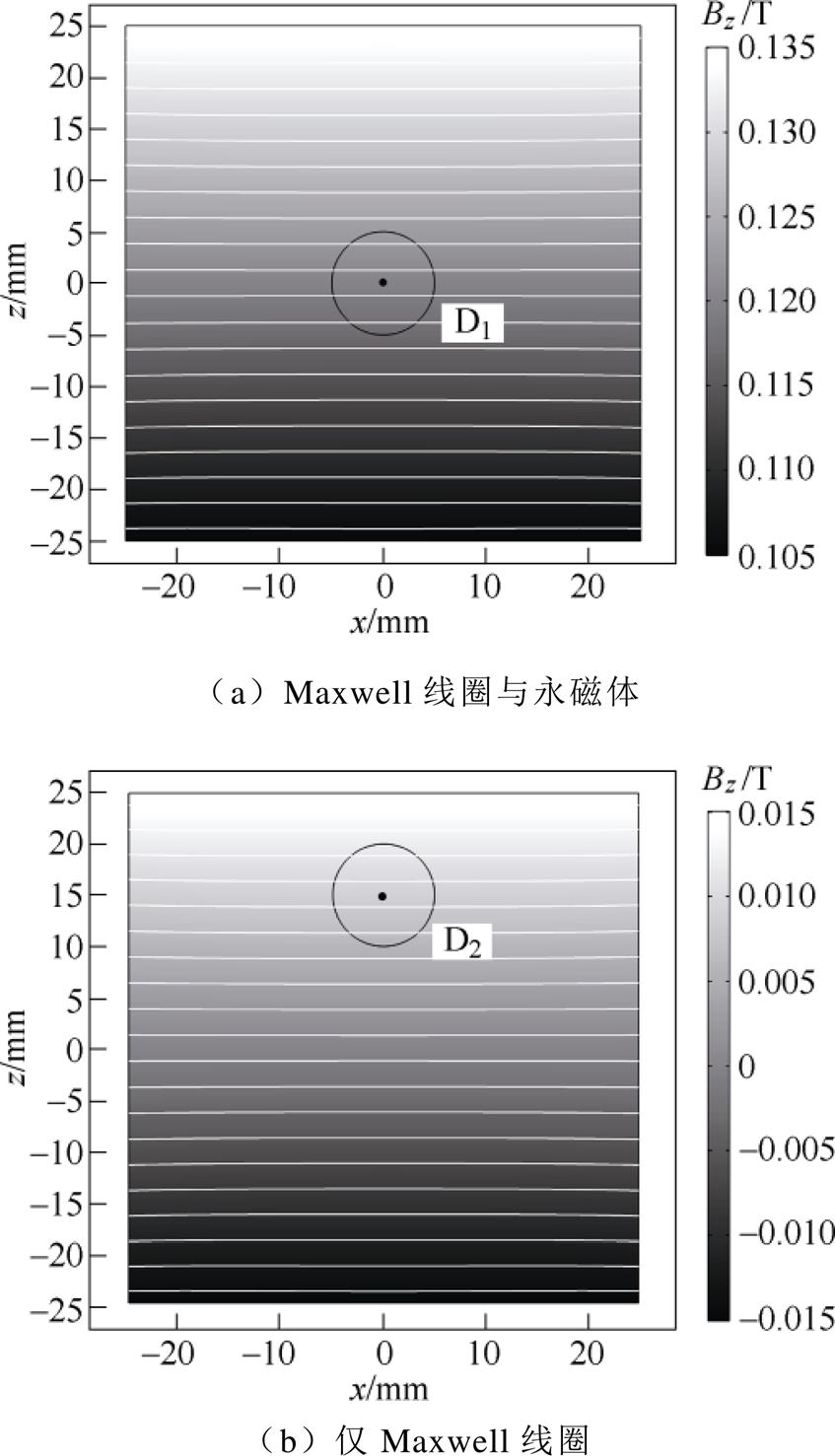
图10 磁体系统在ROI的xOz截面上产生的磁通密度
Fig.10 Magnetic flux density generated by the magnet system on the xOz section of ROI
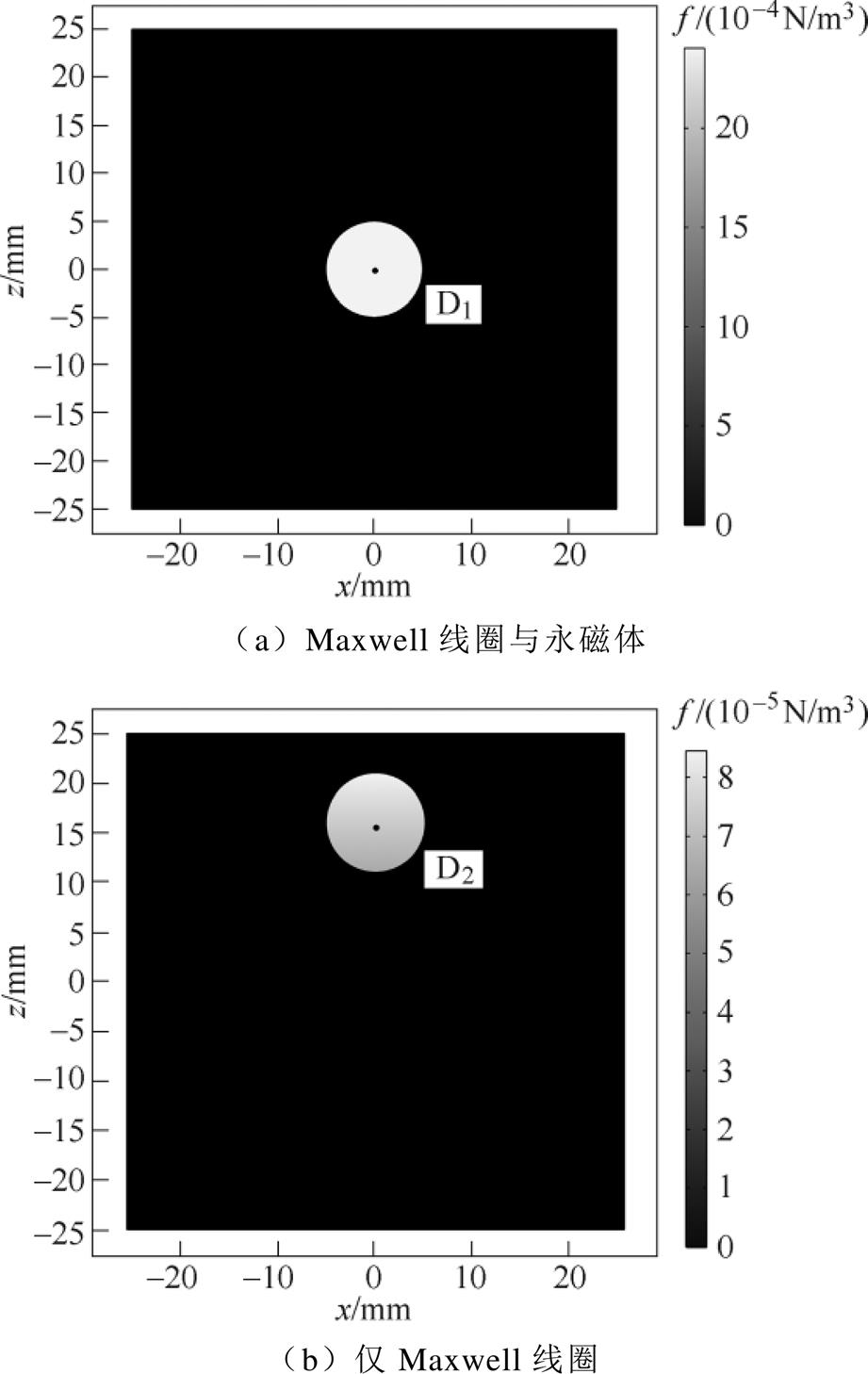
图11 t =0.5ms磁力分布
Fig.11 Magnetic force distribution of t =0.5ms
为了研究在两种磁体系统激励下磁力随时间的变化规律，取MNPs集群中心处的D1和D2点，并绘制出磁力随时间的变化曲线，磁力对比如图12所示。Maxwell线圈激励下的磁力明显小于Maxwell线圈与永磁体共同作用下的磁力，进而验证了MACT- MI成像新方法的正确性及优越性。
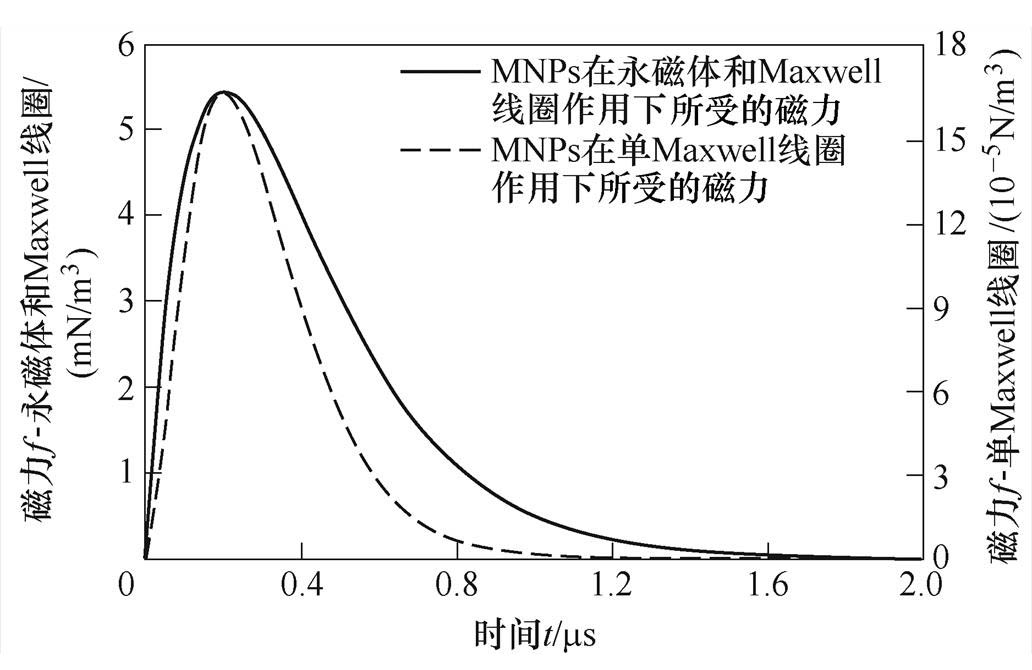
图12 磁力对比
Fig.12 Magnetic force comparison
钕铁硼表面的磁通密度为1.4～1.45T，双磁环永磁体可在ROI内产生0.115～0.125T的磁通密度，在该范围内以步长0.000 5T进行参数化扫描21个点，分别计算出对应磁力大小，为观察磁力随外磁场的瞬态变化规律，选取0.5ms时的D1点作为观测点，并绘制出磁力随永磁体表面磁通密度的变化如图13所示，MNPs所受磁力与外磁场的磁通密度呈正相关，但MNPs所受磁力的增长趋势逐渐减缓且数值变化不大，这是由于永磁体和Maxwell线圈组成的磁体系统使得MNPs接近饱和状态，以至于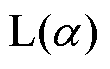的增长趋势逐渐减缓。
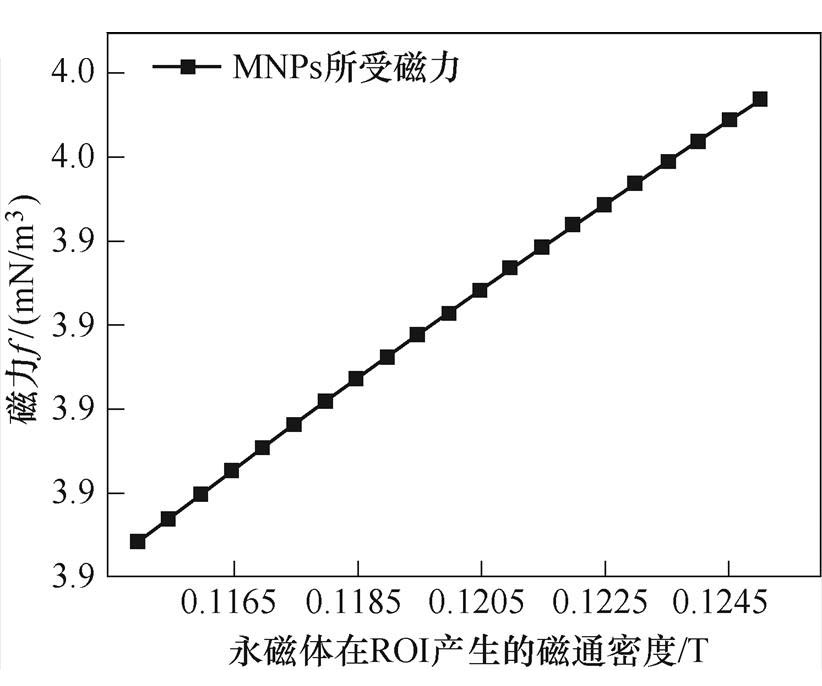
图13 磁力随永磁体表面磁通密度的变化
Fig.13 Variation of magnetic force with the magnet flux density of the permanent magnet
假定模型内为声学均匀条件，根据两种磁体系统下磁力的仿真结果，进行电-磁-声多物理场耦合求解并进行对比，两种磁体系统激励下的声压分布如图14所示。图14a中，MNPs集群上下边缘声压明显，z方向上声压分布较为均匀，且由于偶极声源特性，声压对称分布，方向相反；而图14b的声压分布与图14a大致相同，只是声压信号较为微弱。
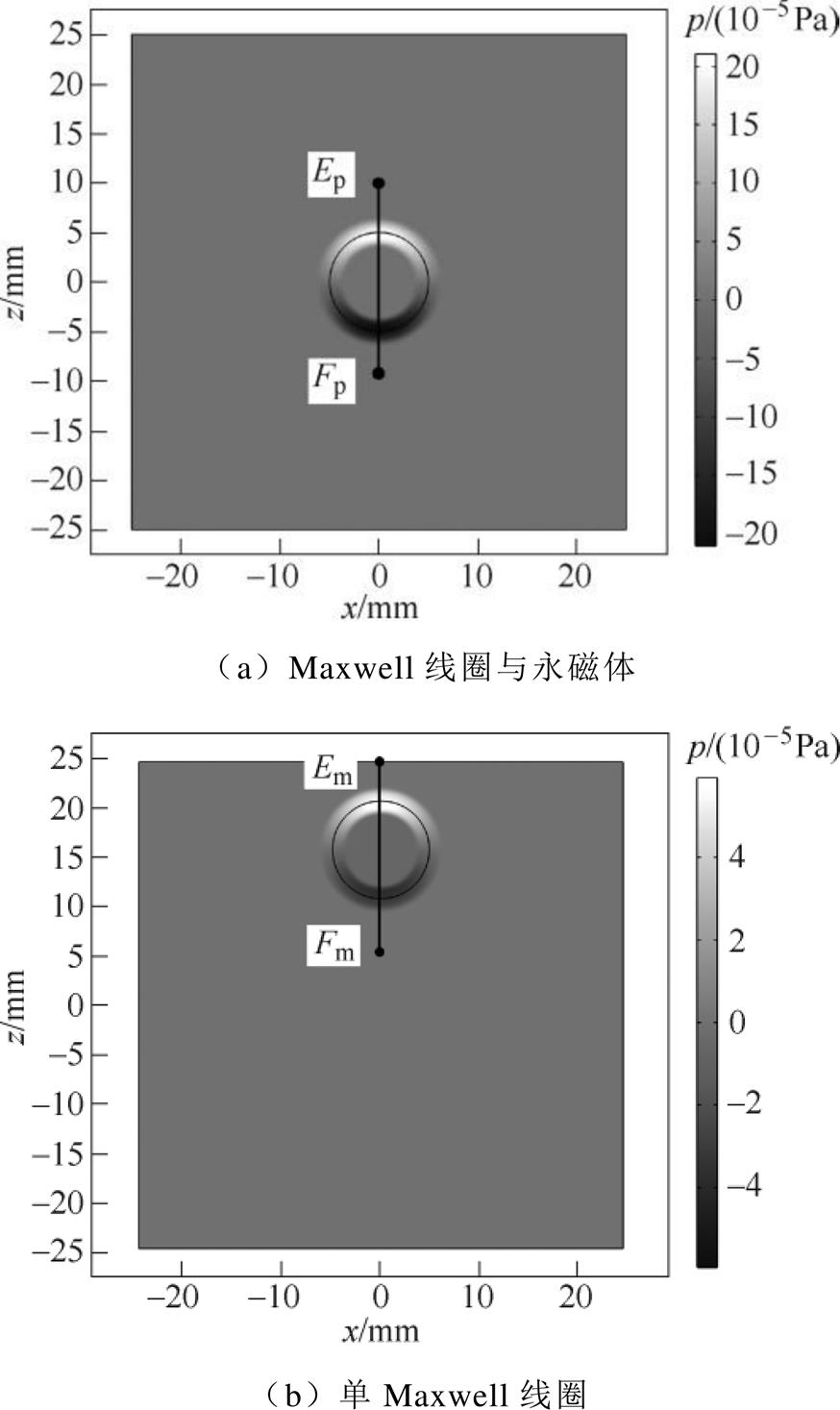
图14 t =1ms时两种磁体系统的声压分布
Fig.14 Sound pressure distribution of the two magnet systems at t =1ms
为了研究在两种磁体系统激励下声压与位置的变化规律，取xOz平面上的截线，并绘制出1ms时刻声压曲线，t =1ms声压分布曲线如图15所示，其中截线的起止点Ep、Fp和Em、Fm的坐标分别为（0, 10）、（0, -10）和（0, 25）、（0, 5）。在两种磁体系统的激励下，声压峰值均出现在MNPs集群边界处，峰值间距与集群直径相等；图15a中，上下边界声压方向相反、大小相等；但在图15b中，MNPs集群上边缘处的声压略大于下边缘处的声压，这是由于在Maxwell线圈的作用下，ROI附近产生的磁场为均匀梯度场。
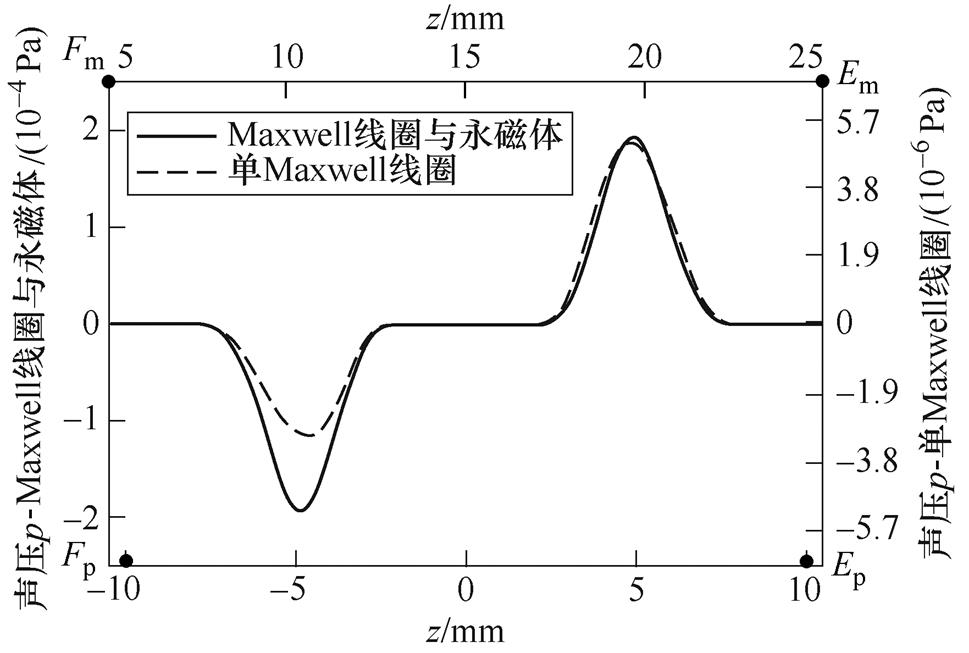
图15 t =1ms时两种磁体系统的声压分布曲线
Fig.15 Sound pressure distribution curves of the two magnet systems at t =1ms
考虑到实际生物组织环境，MNPs的浓度分布是弥散渐变的，因此建立浓度连续变化模型，对其进行电-磁-声多物理场耦合求解，并与均匀浓度模型进行对比。渐变模型中MNPs浓度沿着径向变化，可表示为
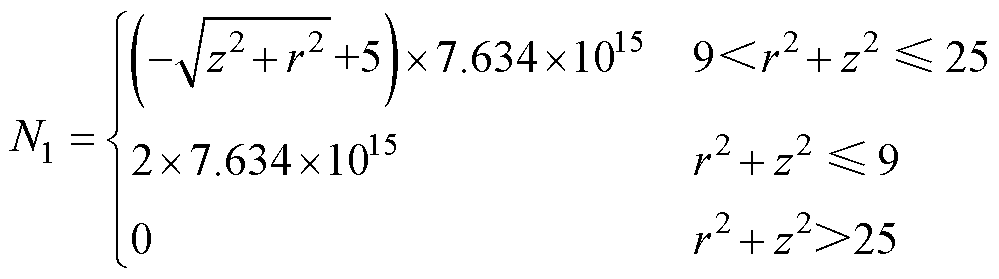（19）
式中，r和z为圆柱坐标系下的r坐标分量和z坐标分量，r=z=7.634×1015mm，这是因为两种模型中MNPs的平均浓度相同。
均匀浓度模型与渐变浓度模型的声压分布如图16所示。在单z方向磁体系统激励下，浓度均匀模型的声压分布与浓度渐变模型的声压分布有着较为明显的区别，在图16a中，声压主要集中在MNPs集群的上下边界处，z方向上声压分布较为均匀；而在图16b中，声压不止分布在集群边缘，整个集群的声压分布更为均匀，且集群中内声压要大于边界处声压，这是由于边界处的MNPs浓度要低于内层浓度。同时，由于偶极声源特性，两种模型产生的声压大小相等，方向相反。
进一步地，为了研究两种浓度分布模型下声压与位置的变化规律，分别取截线GuHu和GgHg并绘制出t =1ms时的声压曲线，如图17所示，其中截线的起止点坐标分别为Gu（0, 10）、Hu（0, -10）、Gg（0, 10）和Hg（0, -10）。对于均匀浓度模型，其上下边界处声压方向相反，声压峰值出现在边界处，峰值间距与集群直径相等；对于渐变浓度模型，其声压峰值出现在集群中内部渐变区域中心附近，究其原因，边界区域的MNPs浓度是渐变的，会导致声压波形变宽，波形中心即为渐变区域中心。
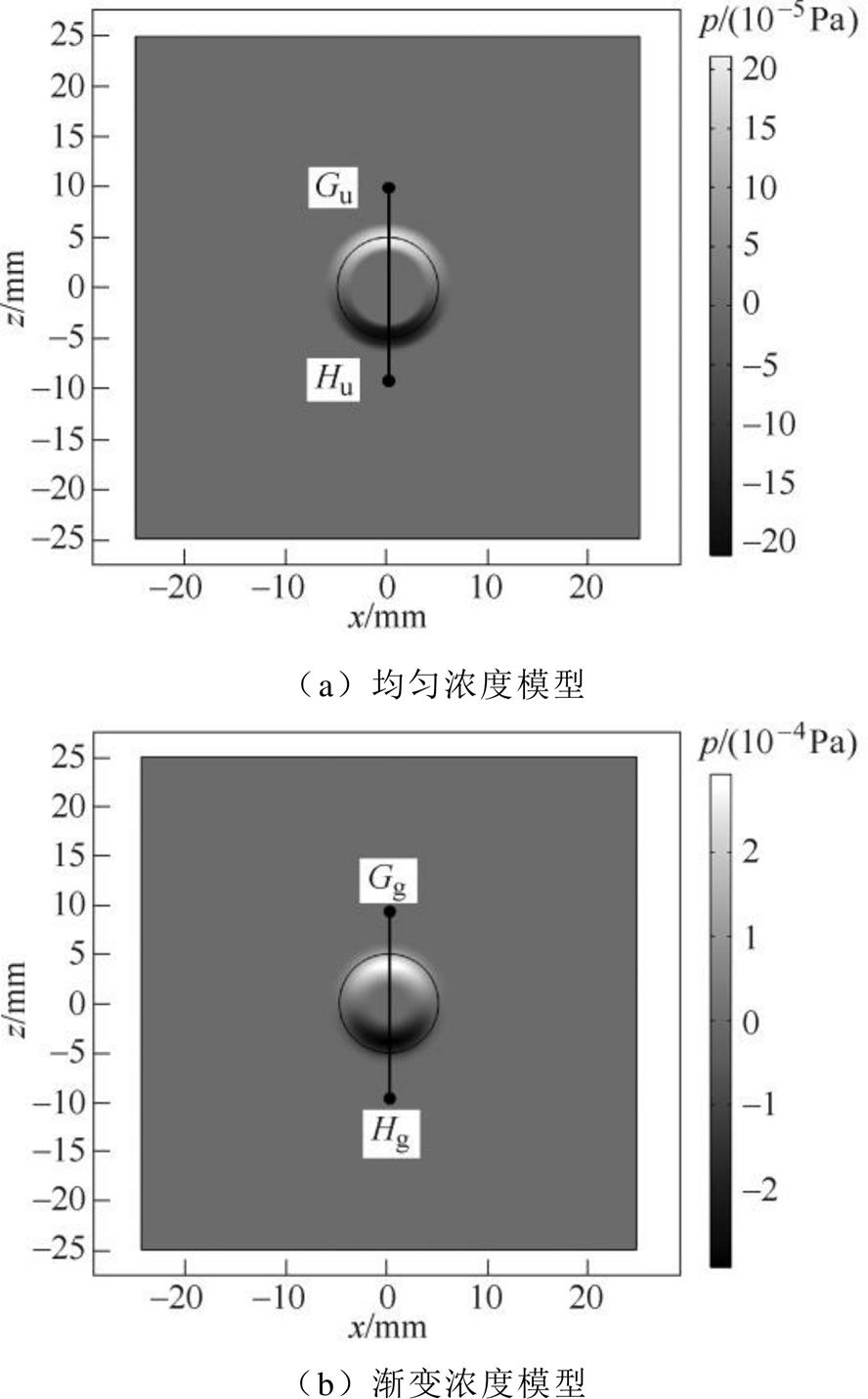
图16 t =1ms时不同浓度模型的声压分布
Fig.16 Sound pressure distribution for different concentration models at t =1ms
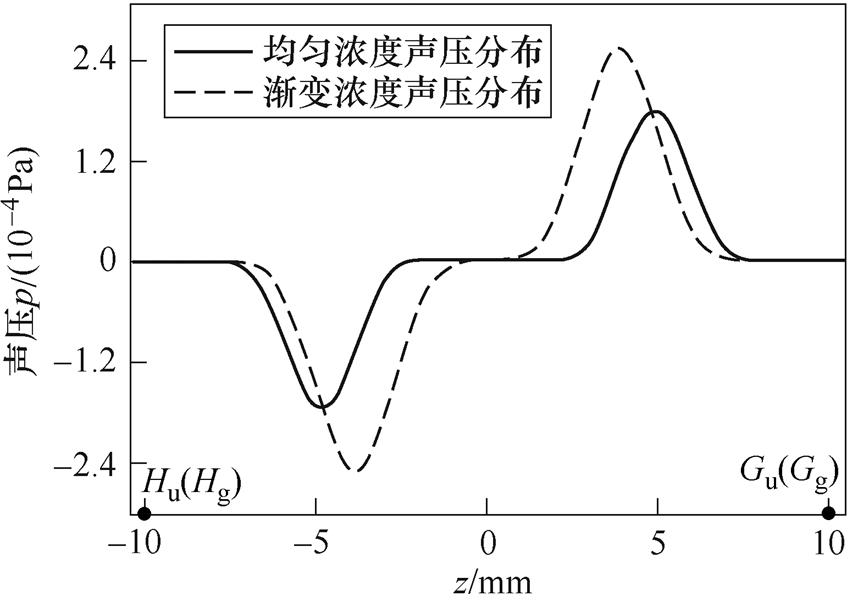
图17 t =1ms时不同浓度模型的声压曲线
Fig.17 Sound pressure curves for different concentration models at t =1ms
为提高MACT-MI声压信号信噪比，本文开展了基于增大MNPs所受磁场的研究，对磁体系统进行了设计，重点研究了在该系统的激励下，MACT- MI成像的物理过程。包括MACT-MI加入永磁体后的磁力公式、磁体系统的磁场计算公式、永磁体存在与否对磁力以及声压的影响、浓度渐变对声压分布的影响。主要结论如下：
1）未饱和的MNPs所受磁力与MNPs浓度、磁场梯度以及磁场强度有关，且均呈正相关；磁饱和的MNPs所受磁力仅与MNPs浓度和磁场梯度 有关。
2）采用双磁环结构的圆柱形永磁体，可在ROI附近产生磁通密度相对较强且均匀度小于1%空间，为MACT-MI的后续实验乃至临床应用奠定基础。
3）Maxwell线圈与永磁体组成的磁体系统比以Maxwell线圈作为磁体系统多一个恒定的均匀磁场分量，在相同的激励条件下，能增大MNPs的磁化强度，进而使得MNPs所受磁力及其产生的声压更大，对解决MACT-MI实验过程中磁声信号微弱的问题具有指导意义。
4）磁力和永磁体的表面磁通密度呈正相关。在所设计的磁体系统激励下，声压沿磁场方向上下对称分布且方向相反，浓度均匀模型的声压峰值出现在边界处，渐变浓度模型的声压峰值出现在渐变区域中心附近。
MACT-MI是一种能对MNPs进行定量检测的非侵入式成像方法，该方法采用接收超声的方式来获取MNPs的浓度信息，但在前期的研究中发现，磁声信号微弱，不利于实验工作的开展，为了从根本上提高磁声信号的信噪比，本文提出了一种MACT-MI新思路，从增大MNPs所受磁场的角度出发，对磁体系统进行设计，通过双磁环结构的永磁体增大MNPs周围的磁场，进而使MNPs的磁化强度增大，与单Maxwell线圈对比仿真发现，磁力和声压均有明显提升，使得MACT-MI的研究更加深入，但缺乏实验对磁体系统产生的磁场和MNPs所受磁力进一步研究。除此之外，在进行声源及声压的数值计算时，本文是基于人体内部声速均匀进行计算的，而在实际情况中，不同组织声速一般是不均匀的，在研究中也需要具体考虑。总之，本文对MACT-MI做了一些深入研究，完善了MACT-MI基础理论体系，为该方法的进一步实验乃至临床研究奠定了基础。
参考文献
[1] Moffat B. A novel polyacrylamide magnetic nano- particle contrast agent for molecular imaging using MRI[J]. Molecular Imaging, 2003, 2(4): 324-332.
[2] Nitin N, Laconte L, Zurkiya O, et al. Fun- ctionalization and peptide-based delivery of magnetic nanoparticles as an intracellular MRI contrast agent[J]. JBIC Journal of Biological Inorganic Chemistry, 2004, 9(6): 706-712.
[3] Lewin M, Carlesso N, Tung C H, et al. Tat peptide- derivatized magnetic nanoparticles allow in vivo tracking and recovery of progenitor cells[J]. Nature Biotechnology: The Science and Business of Bio- technology, 2000, 18(4): 410-414.
[4] Mccloskey K E, Chalmers J J, Zborowski M. Magnetic cell separation: characterization of mag- netophoretic mobility[J]. Analytical Chemistry, 2003, 75(24): 6868-6874.
[5] Arruebo M, Fernández-Pacheco R, Ibarra M R, et al. Magnetic nanoparticles for drug delivery[J]. Drug Development Research, 2010, 67(3): 55-60.
[6] Sun C, Lee J, Zhang Miqin. Magnetic nanoparticles in MR imaging and drug delivery[J]. Advanced Drug Delivery Reviews, 2008, 60(11): 1252-1265.
[7] Ito A, Shinkai M, Honda H, et al. Heat-inducible TNF-alpha gene therapy combined with hyperthermia using magnetic nanoparticles as a novel tumor- targeted therapy[J]. Cancer Gene Therapy, 2001, 8(9): 649-654.
[8] Shi Xiaoyu, Liu Guoqing, Yan Xiaoheng, et al. Simulation research on magneto-acoustic con- centration tomography of magnetic nanoparticles with magnetic induction[J]. Computers in Biology and Medicine, 2020, 119(10): 1-7.
[9] Oh J, Feldman M, Kim J, et al. Detection of magnetic nanoparticles in tissue using magneto-motive ultra- sound[J]. Nanotechnology, 2006, 17(16): 4183-4190.
[10] Mehrmohammadi M, Oh J, Aglyamov S, et al. Pulsed magneto-acoustic imaging[J]. IEEE Engineering in Medicine and Biology Society, 2009, 20(9): 4771- 4774.
[11] Hu Gang, He Bin. Magnetoacoustic imaging of magnetic iron oxide nanoparticles embedded in biological tissues with microsecond magnetic stimu- lation[J]. Applied physics letters, 2012, 100(1): 3741- 3743.
[12] Podaru G, Chikan V, Prakash P. Magnetic field induced ultrasound from colloidal superparamagnetic nanoparticles[J]. Journal of Physical Chemistry C, 2016, 120(4): 2386-2391.
[13] Yan Xiaoheng, Zhang Ying, Liu Guoqiang. Simula- tion research on effect of magnetic nanoparticles on physical process of magneto-acoustic tomography with magnetic induction[J]. Chinese Physics B, 2018, 27(10): 382-389.
[14] 张帅, 李子秀, 张雪莹, 等. 基于时间反演的磁动力超声成像仿真与实验[J]. 电工技术学报, 2019, 34(16): 3303-3310.
Zhang Shuai, Li Zixiu, Zhang Xueying, et al. The simulation and experiment of magneto-motive ultrasound imaging based on time reversal method[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3303-3310.
[15] Fink M, Lyer S, Alexiou C, et al. Quantitative imaging of the iron-oxide nanoparticle- concentration for magnetic drug targeting employing inverse magnetomotive ultrasound[J]. Current Directions in Biomedical Engineering, 2019, 5(1): 417-419.
[16] Yan Xiaoheng, Xu Zhengyang, Chen Weihua, et al. Implementation method for magneto-acoustic con- centration tomography with magnetic induction (MACT-MI) based on the method of moments[J]. Computers in Biology and Medicine, 2021, 128(10): 1-11.
[17] 周德全, 石天明. 基于ANSYS的电阻层析成像传感器敏感场三维分析[J]. 电气技术, 2008, 9(3): 30-33.
Zhou Dequan, Shi Tianming. Three-dimensional analysis of electrical resistance tomography sensor fields based on ANSYS[J]. Electrical Engineering, 2008, 9(3): 30-33.
[18] 张帅, 侯琬姣, 张雪莹, 等. 基于真实乳腺模型的感应式磁声成像正问题[J]. 电工技术学报, 2016, 31(24): 126-133, 149.
Zhang Shuai, Hou Wanjiao, Zhang Xueying, et al. Forward problem in magnetoacoustic tomography with magnetic induction based on real model of breast[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 126-133, 149.
[19] 李星, 杨帆, 余晓, 等. 基于内源式电阻抗成像的接地网缺陷诊断逆问题研究[J]. 电工技术学报, 2019, 34(5): 902-909.
Li Xing, Yang Fan, Yu Xiao, et al. Research on the inverse problem of grounding grid fault diagnosis based on inner-source EIT[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 902-909.
[20] 刘亮, 苏盛, 曹一家, 等. 基于Kalman滤波的持续卫星时间同步攻击防护方法[J]. 电力系统自动化, 2020, 44(10): 119-126.
Liu Liang, Su Sheng, Cao Yijia, et al. Kalman filtering based protection method of sustained satellite time synchronization attack[J]. Automation of Electric Power Systems, 2020, 44(10): 119-126.
[21] 贺中华, 何为, 贺玉成, 等. 皮肤烧伤深度检测的单边核磁共振浅层成像磁体系统[J]. 电工技术学报, 2019, 34(3): 449-458.
He Zhonghua, He Wei, He Yucheng, et al. Unilateral nuclear magnetic resonance superficial imaging magnet system for skin burn depth assessme[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 449-458.
[22] 刘婧, 刘国强. 电粒子成像方法及其正问题数值研究[J]. 电工技术学报, 2020, 35(22): 4621-4626.
Liu Jing, Liu Guoqiang. Electrical particles imaging method and numerical study on the forward problem[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4621-4626.
[23] 刘运华, 张波, 谢帆, 等. 多尺度和多物理场的电力电子变换器建模方法初探[J]. 电力系统自动化, 2020, 44(16): 61-69.
Liu Yunhua, Zhang Bo, Xie Fan, et al. Preliminary study on modeling methods with multiscale and multiphysics for power electronic converters[J]. Auto- mation of Electric Power Systems, 2020, 44(16): 61-69.
[24] Tobias K, Thorsten M B. Magnetic particle imaging[M]. Berlin: Springer-Verlag, 2012.
[25] Yan Xiaoheng, Pan Ye, Chen Weihua, et al. Simulation research on the forward problem of magnetoacoustic concentration tomography for mag- netic nanoparticles with magnetic induction in a saturation magnetization state[J]. Journal of Physics D: Applied Physics, 2020, 54(7): 1-10.
[26] 胡剑雄. 面向人体手指血糖无创核磁共振监测的多层Halbach型永磁体的研制[D]. 南京: 东南大学, 2017.
[27] Okada T, Matsumori H, Kosaka, et al. Hybrid excitation flux switching motor with permanent magnet placed at middle of field coil slots and high filling factor windings[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2019, 3(3): 248-258.
[28] 李长生, 马彪, 宋艳磊, 等. 无磁钢的研究概况和我国无磁钢的发展思路[J]. 河南冶金, 2014, 22(1): 1-7, 12.
Li Changsheng, Ma Biao, Song Yanlei, et al. The research progress and development ideas of non- magnetic steels in China[J]. Henan Metallurgy, 2014, 22(1): 1-7, 12.
[29] 底楠, 赵建林, 王志兵. 永磁体双磁环结构的磁场均匀性分[J]. 中国激光, 2009, 36(9): 2290-2294.
Di Nan, Zhao Jianlin, Wang Zhibing. Analysis on magnetic field homogeneity of dual-ring permanent magnets[J]. Chinese Journal of Lasers, 2009, 36(9): 2290-2294.
[30] 刘国强. 磁声成像技术[M]. 北京: 科学出版社, 2014.
[31] 刘洋洋, 杜强, 柯丽, 等. 磁性粒子成像线型零磁场设计及性能分析[J]. 电工技术学报, 2020, 35(10): 2088-2097.
Liu Yangyang, Du Qiang, Ke Li, et al. Design and analysis of magnetic field-free line in magnetic particle imaging[J]. Transactions of China Electro- technical Society, 2020, 35(10): 2088-2097.
Simulation of the Influence of Permanent Magnets of the Same Polarity on the Magneto-Acoustic Concentration Tomography of Magnetic Nanoparticles with Magnetic Induction Process
Abstract Magneto-acoustic concentration tomography of magnetic nanoparticles (MNPs) with magnetic induction (MACT-MI) is a new method for concentration imaging of MNPs based on the magneto-acoustic coupling effect. To reduce the excitation source amplitude and increase the signal-to-noise ratio of the magneto-acoustic signal, a new idea was proposed in this paper: the same polarity as the permanent magnet was added in the MACT-MI. According to the Langevin paramagnetic theory, the electromagnetic and acoustic characteristics of MAT-MI after adding permanent magnets with the same polarity were studied, the magnet system was designed, and the concentration gradient model was established. By multi-physics simulation software COMSOL, the 2D distribution of magnetic flux density, magnetic force and sound pressure and the corresponding 1D curve were obtained, which clearly show the physical process of MAT-MI. This conclusion indicates that adding permanent magnets of the same polarity, MNPs receive stronger magnetic force and can obtain magneto-acoustic signals with a larger signal-to-noise ratio, which is conducive to the acquisition of acoustic signals. At the excitation of the magnet system, the sound pressure generated by MNPs is symmetrically distributed up and down and in opposite directions. At the uniform concentration model, the sound pressure peak appears at the concentration boundary, and the peak of the sound pressure of the concentration gradient model appears at the center of the gradient. The results can provide a research foundation for the design of imaging equipment, follow-up experiments and clinical applications of MACT-MI.
keywords：Magnetic nanoparticles, the same polarity permanent magnet, magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction (MACT-MI), magnetic force, sound pressure
DOI: 10.19595/j.cnki.1000-6753.tces.210218
中图分类号：TM12
闫孝姮 女，1984年生，博士，副教授，研究方向为电磁探测与成像。E-mail: xiaohengyan@163.com
李政兴 男，1997年生，硕士研究生，研究方向为电磁探测与成像。E-mail: lizhengxing163@163.com（通信作者）
收稿日期 2021-02-19
改稿日期 2021-04-28
2019年辽宁省自然科学基金指导项目（2019-ZD-0039）和2020年辽宁省教育厅科学研究基础研究项目（LJ2020JCL003）资助。
（编辑 陈 诚）