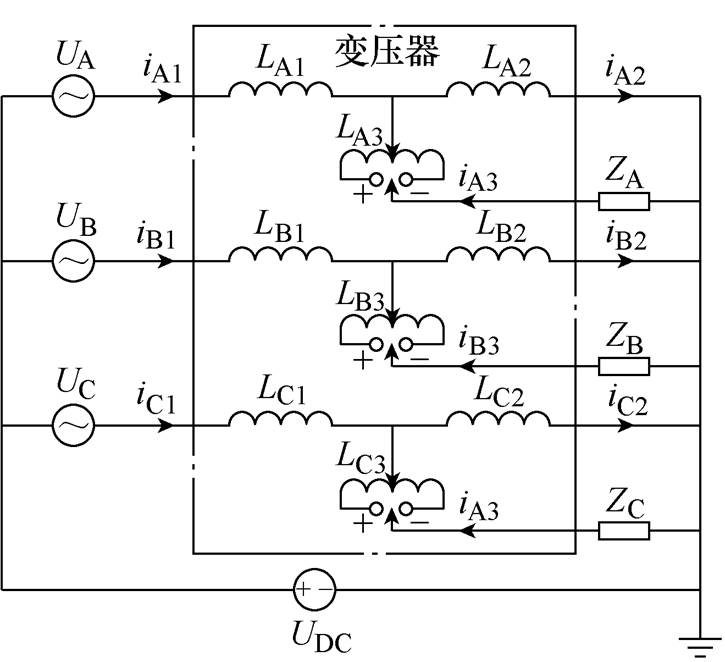
图1 500kV变压器直流偏磁时电路模型
Fig.1 Equivalent circuit diagram of 500kV transformer during DC bias
摘要 为准确分析电力变压器在地磁感应电流(GIC)作用下的温升特性,该文通过建立某500kV三相共体油浸式电力变压器的电磁-流热场耦合三维仿真模型,计算变压器满负载运行及不同GIC作用下其内部构件的损耗密度和温度场分布,并依据IEEE C57.163标准,计算GIC作用下变压器内部构件的动态温升曲线。仿真计算结果与设计值的良好吻合说明了该文计算结果的正确性。同时发现,受GIC影响后,电力变压器的夹件、拉板、油箱等的涡流损耗分布极不均匀,且随GIC电流的增加而增大。GIC脉冲作用下的变压器金属构件局部温度会急剧上升,在100A直流脉冲下,变压器主柱拉板的局部温升达到允许限值。研究结果可为GIC作用下大型变压器的耐受性能分析提供重要参考依据。
关键词:大型变压器 地磁感应电流 损耗密度 温度场 温升曲线
地磁感应电流(Geomagnetically Induced Current, GIC)是地磁场发生强烈扰动(磁暴)时的强感应电场在导电体内产生的感应电流,持续时间为几秒到几小时。由于GIC的频率小于0.01Hz,对变压器而言,可将其视为缓慢变化的直流[1],故与高压直流输电引起的变压器直流偏磁现象类似,GIC在变压器中的流动会导致铁心半周饱和及漏磁增大,引起变压器金属构件的涡流损耗增加,在一定条件下有可能会使变压器内部的局部温升超过允许的限制[2]。而温度是影响变压器寿命的关键因素之一,即变压器的温度越大,其预期寿命就会越短,有必要准确掌握GIC作用下变压器的温升特性,提高其运行可靠性。
GIC通常多发于高纬度地区,国内外研究者分别从GIC电流水平监测及其对电力系统的影响、GIC对电力变压器的励磁电流、无功损耗、振动、噪声、温升等的影响及抑制策略等方面进行了若干研究[3-6]。其中,对GIC作用下电力变压器的温升特性研究主要包括试验研究和数值计算等。文献[7]选取了最易受直流偏磁影响的单相三柱式变压器进行温升试验,发现其在200AGIC电流作用下的夹件局部温升约110℃。文献[8]给出了某110kV单相单柱旁轭变压器空载和负载试验中振动、噪声、绕组热点温升和结构件温升、油色谱等的测试结果,发现直流偏磁下变压器绕组热点温升和结构件温升显著增大,当直流达到36A时,低压绕组热点温升和拉板上部最高温升均超过90K,且油中出现碳氢气体。试验研究虽能够较贴切实际,但受制于试验条件如电源容量限制、试验周期和成本等诸多因素影响,研究者更多的是借助于数值计算或与试验研究结合的方法探究变压器的温升特性。根据变压器的有限元分析模型,文献[9]依据GIC作用下不同铁心结构的变压器励磁电流和磁通分布计算结果,计算了自耦变压器铁心螺栓和油箱夹件的损耗和温升,发现铁心螺栓存在产生局部过热的风险,且变压器温升与直流持续时间线性相关。文献[10]计算分析了GIC作用下变压器的油箱损耗特性及其影响因素(变压器类型、功率因数、并联磁路等),认为降压变压器的油箱损耗大于升压变压器,且在功率因数为0.9时变压器油箱的损耗和温升将会最严重。文献[11-12]计算了GIC作用下单相自耦变压器的损耗和温升变化规律,指出变压器铁心以及邻近夹件在
GIC作用下温升较小,但拉板处是最容易快速温升的变压器组件。文献[13]依据GIC作用下变压器油箱三维模型的损耗和温升计算结果,指出油箱前壁中心处为其损耗最大值和热点位置,同时依据变压器内部油的热对流速度确定了其温升速率。文献[14-15]基于某500kV单相变压器的电路-磁路模型的计算结果,发现变压器内部结构件的损耗随着直流偏磁程度的增加而增大,当铁心饱和时,结构件的涡流损耗增幅将加剧。文献[16]根据某壳式变压器的三维有限元模型分析了变压器的绕组电流、损耗密度分布及温升变化,同时指出,如果变压器采用非磁性材料金属构件,可长时间承受200A直流和短时间承受400A直流电流影响,并通过试验进行了验证。综上,现有研究大都对变压器空载运行下的损耗进行计算分析,对受GIC影响的变压器温升特性的研究尚不多见,且实际GIC为低至中等水平直流下伴随一些短时间内较高的峰值,其对变压器温升特性的影响程度尚不清楚,需要进一步研究。
我国虽处于中低纬度地区,但随着太阳活动的增强及我国超/特高压输电工程的快速发展,GIC对电力系统安全稳定运行的威胁也越来越大。为进一步理解和掌握GIC作用下的变压器温升特性,本文以某500kV三相共体变压器为对象,基于电磁场和流热场耦合模型,计算其在不同GIC条件下满负载运行时的损耗和温升特性,据此分析评估变压器的GIC耐受能力,并给出降低变压器GIC温升的防范措施建议,为大型主变压器的安全可靠运行提供参考。
针对GIC作用下的变压器电磁特性,本文在此采用场路耦合模型进行计算,分别描述如下。
1.1.1 电路方程
对高电压等级和大容量的有载调压自耦变压器来说,因需要较多电压档位进行调压,通常采用正反调压的调压方式。相应地,可得GIC或直流电流作用下此类三相自耦变压器的电路模型如图1所示。图中,UA、UB和UC为三相交流电压源;LA1、LB1和LC1为三相串联绕组(高压)漏感;LA2、LB2和LC2为三相公共绕组(中压)漏感;LA3、LB3和LC3为三相调压绕组漏感;ZA、ZB和ZC为三相负载;UDC为直流偏置激励。此处,通过在变压器中性点施加直流来进行不同GIC作用下的变压器电磁特性计算。

图1 500kV变压器直流偏磁时电路模型
Fig.1 Equivalent circuit diagram of 500kV transformer during DC bias
依据图1所示的变压器电路,可列写电路方程为
 (1)
(1)
式中,RA1、RB1和RC1为三相串联绕组电阻;RA2、RB2和RC2为三相公共绕组电阻;RA3、RB3和RC3为三相调压绕组电阻;NA1、NB1和NC1为三相串联绕组匝数;NA2、NB2和NC2为三相公共绕组匝数;NA3、NB3和NC3为三相调压绕组匝数;jA、jB和jC为三相磁通;iA1、iB1和iC1为三相串联绕组电流;iA2、iB2和iC2为三相公共绕组电流;iA3、iB3和iC3为三相负载电流。
1.1.2 磁场方程
在变压器三维交变电磁场中,由麦克斯韦方程可得到其矢量磁位方程为
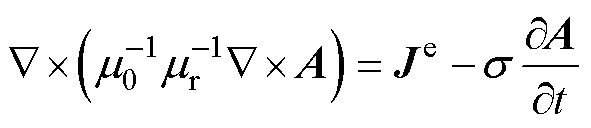 (2)
(2)
式中,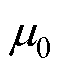 为自由空间磁导率;
为自由空间磁导率;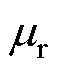 为相对磁导率;
为相对磁导率; 为外部电流密度;
为外部电流密度; 为电导率;A为矢量磁位;
为电导率;A为矢量磁位;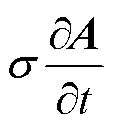 为涡流密度。
为涡流密度。
依据式(2)可得到变压器的磁场分布。此外,变压器的电路方程计算得出的激励电流ik以外部电流密度的形式耦合到磁场方程中,然后通过硅钢片的磁化曲线(B-H曲线)得到的铁心交变磁通jk反馈到电路方程实现场路耦合,其存在对应关系为
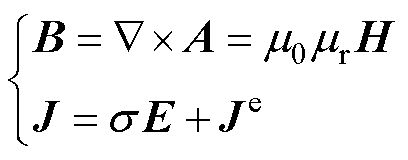 (3)
(3)
式中,B为磁感应强度;H为磁场强度;J为电流密度;E为电场强度。
联合求解式(1)~式(3),可得出直流偏磁时500kV变压器的励磁电流、负载电流和磁通分布等,从而为变压器的损耗及温升计算提供数据支持。
变压器损耗包括铁损、铜损和杂散损耗等,其中,铁损主要由磁滞损耗和涡流损耗组成,有
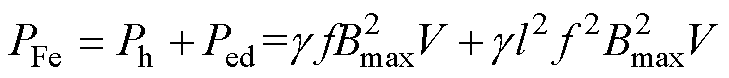 (4)
(4)
式中,Ph为铁心磁滞损耗;Ped为铁心涡流损耗;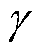 为铁心磁滞系数;f为电流频率;Bmax为铁心磁感应强度最大值;V为铁心体积;l为硅钢片厚度。
为铁心磁滞系数;f为电流频率;Bmax为铁心磁感应强度最大值;V为铁心体积;l为硅钢片厚度。
铜损由直流电阻损耗和涡流损耗组成,有
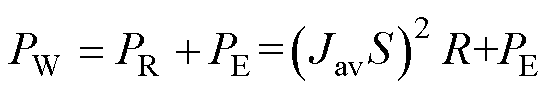 (5)
(5)
式中,PW为绕组总损耗;PR为直流电阻损耗;PE为绕组涡流损耗;Jav为绕组电流密度有效值;S为导线截面积;R为绕组电阻。
大型变压器绕组的涡流损耗能达到绕组总损耗的10%以上[17],特别在受GIC影响后涡流损耗会明显增大,因此不能忽略。对于漏磁引起的绕组涡流损耗分为径向和轴向两部分,其中,绕组不同部位的涡流损耗[18]为
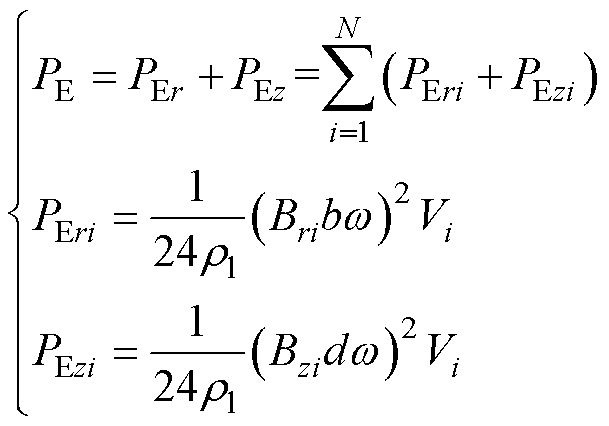 (6)
(6)
式中,PE为绕组总涡流损耗;PEr和PEz分别为绕组径向和轴向涡流损耗;PEri和PEzi分别为绕组第i个单元的径向和轴向涡流损耗;w 为角速度;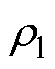 为导线电阻率;Bri为绕组第i个单元的径向磁感应强度;Bzi为绕组第i个单元的轴向磁感应强度;b为导体厚度;d为导体高度;Vi为绕组第i个单元的体积。
为导线电阻率;Bri为绕组第i个单元的径向磁感应强度;Bzi为绕组第i个单元的轴向磁感应强度;b为导体厚度;d为导体高度;Vi为绕组第i个单元的体积。
变压器的杂散损耗主要指油箱、夹件、拉板等金属部件在漏磁通下产生的涡流损耗。由于变压器金属结构不规则且磁通密度分布不均匀,利用已有解析公式和半经验公式计算的损耗误差较大,因此,本文在此通过式(2)计算得到的涡流密度可求得各单元的涡流损耗为
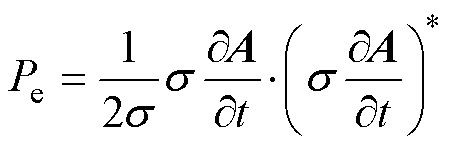 (7)
(7)
式中,Pe为涡流损耗。
油浸式变压器运行中的损耗所转化的热量通过绝缘油的循环对流进行散热冷却,通常将变压器油视为不可压缩性流体,认为其流动遵循质量守恒定律、动量守恒定律和能量守恒定律,其在直角坐标下可分别表示为
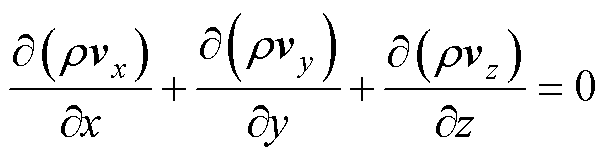 (8)
(8)
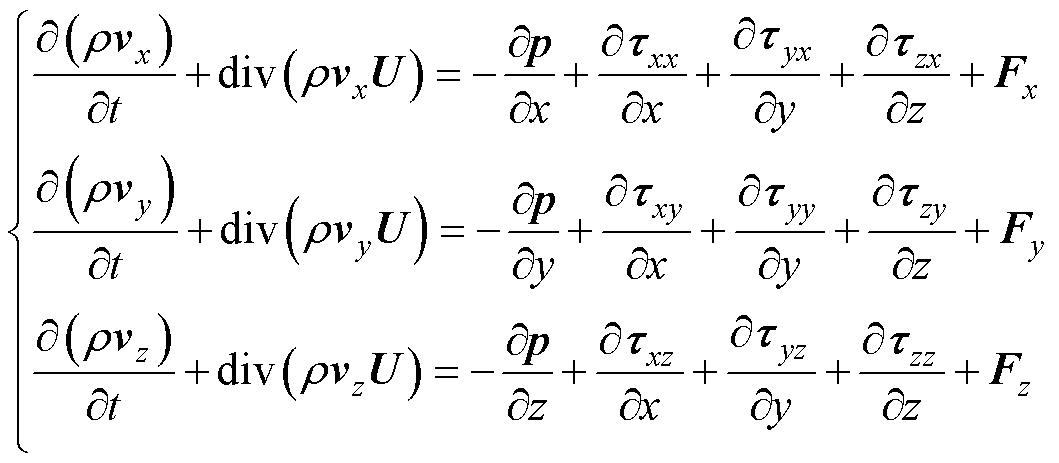 (9)
(9)
 (10)
(10)
式中,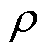 为流体密度;vx、vy、vz分别为x、y、z三个方向上的速度分量;U为速度矢量;p为微元体上的压力;Fx、Fy、Fz均为微元体上的体积力;
为流体密度;vx、vy、vz分别为x、y、z三个方向上的速度分量;U为速度矢量;p为微元体上的压力;Fx、Fy、Fz均为微元体上的体积力;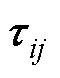 为分子黏性作用在微元体表面上黏性应力的分量;l 为导热系数;T为温度;cp为比定压热容;ST为流体内热源。
为分子黏性作用在微元体表面上黏性应力的分量;l 为导热系数;T为温度;cp为比定压热容;ST为流体内热源。
变压器的铁心、绕组、油箱和夹件等通过热传导使热量从温度高的地方传至温度较低的地方,故热传导方程为
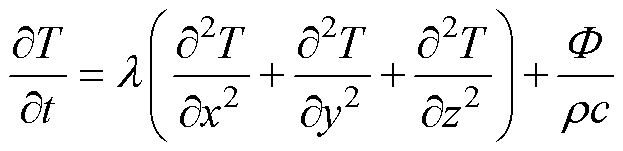 (11)
(11)
式中,r 为物体密度;c为物体比热容;F 为单位时间单位体积热源的发热量。
在固液交界面上,固体和液体的热耦合是靠表面传热进行的,表面传热的计算公式为
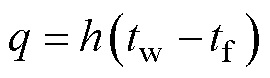 (12)
(12)
式中,q为发热量;h为表面传热系数;tw为固体表面温度;tf为流体温度。
变压器内外部只要有温度差,就会有热辐射,物体表面的辐射程度是受表面辐射率影响的,辐射的热转移斯特凡玻耳兹曼定律为
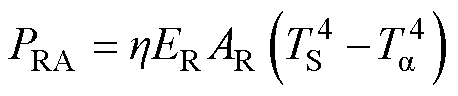 (13)
(13)
式中,PRA为辐射热量;h 为斯特凡玻耳兹曼常数;ER为表面发射率;AR为表面积;TS为表面平均温度;Ta 为周围环境温度。
以一台型号为OSFSZ-525000/525的三相五柱式自耦变压器为研究对象,额定容量为525MV·A/ 525MV·A/105MV·A,额定电压为525kV/345kV/ 34.5kV,空载电流百分数为0.03%,阻抗电压百分数为:高/中6.9%;高/低72.6%;中/低63.5%,绕组匝数为398/762/132,冷却方式为自然油循环。因实际变压器绕组线饼数较多且机械结构较为复杂,且散热器为内部油循环必不可少的一部分,在建模计算时进行简化和假设:
(1)将圆筒绕组进行分层以更为接近绕组线饼和油道的结构,用箱体代替片式散热器,忽略垫块、绝缘纸筒等绝缘件。
(2)忽略铁磁材料的磁滞损耗。
(3)绕组电流密度在导体内认为均匀分布。
(4)考虑到非平均损耗密度作为流热模型热源的导入,磁路模型和流热模型的结构应保持一致。
图2为所建立的变压器三维有限元模型。当电路模型计算得到的激励电流施加到变压器绕组上时,会产生线圈直流电阻损耗,同时部分漏磁会在变压器结构件中感应出涡流电流,引起结构件发热。在电磁暂态计算模型中边界条件设定如下:
(1)磁场求解域边界为平行边界条件,即磁动势的切向分量在边界处设置为零。
(2)电磁场计算所用材料属性为各向同性,见表1,铁心B-H曲线如图3所示。

图2 变压器三维有限元模型
Fig.2 Three-dimensional finite element model of transformer
表1 电磁场材料属性
Tab.1 Electromagnetic field material properties

材料相对介电常数相对磁导率电导率/(S/m) 硅钢 (铁心)1B-H曲线— 铜 (绕组)114.6×107 钢 (夹具和油箱)14004.800 8×10-7 绝缘油110.01
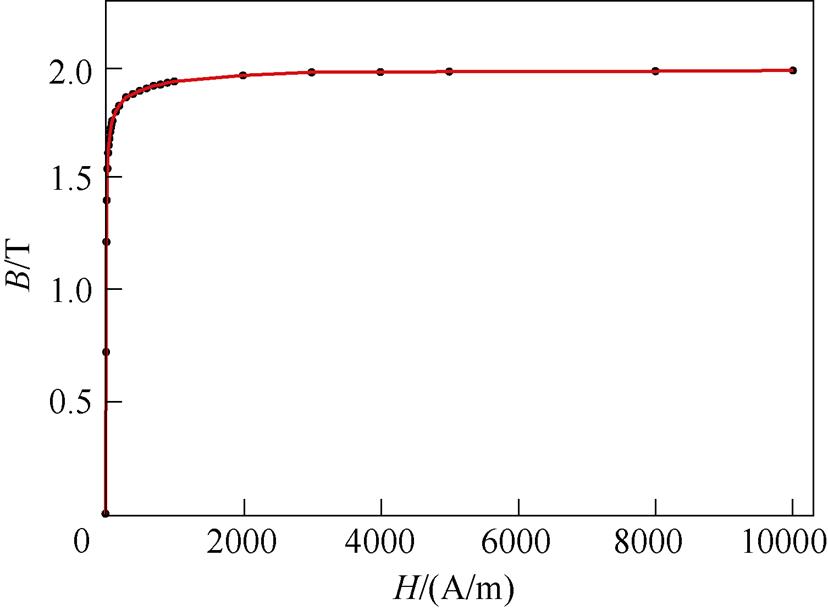
图3 铁心B-H曲线
Fig.3 Iron core B-H curve
因自然油循环变压器是一内部油流为自然对流的封闭容器,受热膨胀上升后的油从油箱出口流出经过外部冷却装置散热后从油箱入口流入。在流热物理模型中边界条件设定如下:
(1)油箱外壁表面传热系数设为15W/(m2·K),环境温度恒定为20℃,散热器表面传热系数为143W/(m2·K)。
(2)铁心热源以总损耗形式施加,其余热源以非平均损耗密度形式施加,流场采用层流模型,流热场模型采用瞬态求解。
(3)变压器固体材料属性为常数,绝缘油材料属性为随温度变化的拟合函数,分别见表2和表3。
表2 流热场固体材料属性
Tab.2 Solid material properties
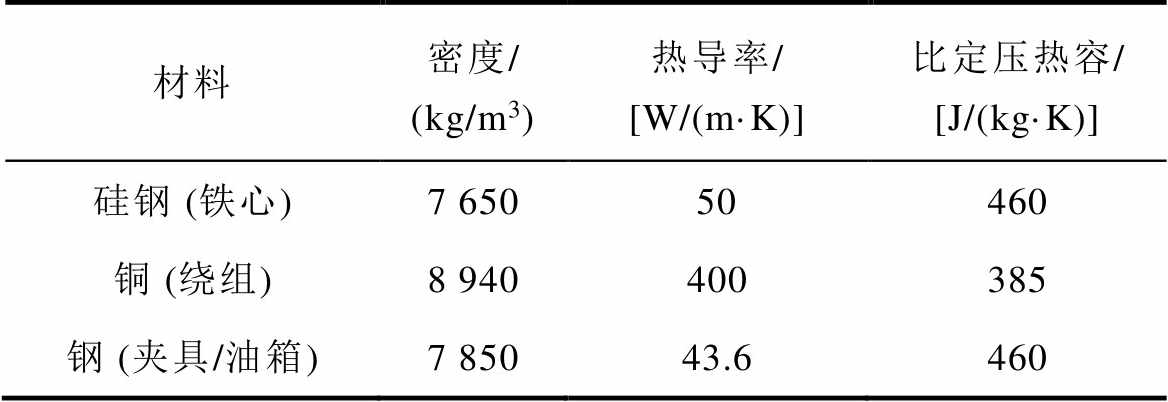
材料密度/ (kg/m3)热导率/ [W/(m·K)]比定压热容/ [J/(kg·K)] 硅钢 (铁心)7 65050460 铜 (绕组)8 940400385 钢 (夹具/油箱)7 85043.6460
表3 流热场绝缘油材料属性
Tab.3 Insulating oil material properties

性 质拟合函数 密度/(kg/m3)1 055.046 07-0.581 753 034T 比定压热容/[J/(kg·K)]13 408.149 1+123.044 152T-0.335T2 热导率/[W/(m·K)]0.134 299 084-8.049 738 22×10-5T 粘度/(Pa·s)91.452 5-1.332 270T+0.007 776 8T2
变压器多物理场有限元模型包括磁、温度场单元实体类型和流场单元类型,各单元离散化程度选择线性单元类型,计算网格要同时适用于电磁和热流场物理属性特征,因此网格要尽量规则且单元大小和增长率不宜过大。变压器网格剖分如图4所示,对绕组、铁心柱、散热器、夹件等采用扫掠网格剖分,其中绕组网格为六面体单元类型,绝缘油网格主要为四面体单元类型。在计算GIC作用下变压器的温升特性时,首先通过场路耦合计算出变压器满负载运行不同GIC影响时的损耗,然后将变压器各
图4 变压器网格剖分
Fig.4 Transformer meshing
部件的损耗导入热流场模型作为传热接口的热源计算其温升,流热场对电磁场无影响,该过程为顺序耦合。据此可得本文的多物理场耦合计算过程如图5所示。此处,场路模型采用的是直接耦合法,热场中的热源对流体加热使流体受热膨胀产生流动,流场流速的大小影响热场表面传热的大小,因此流热场模型亦采用直接耦合法。
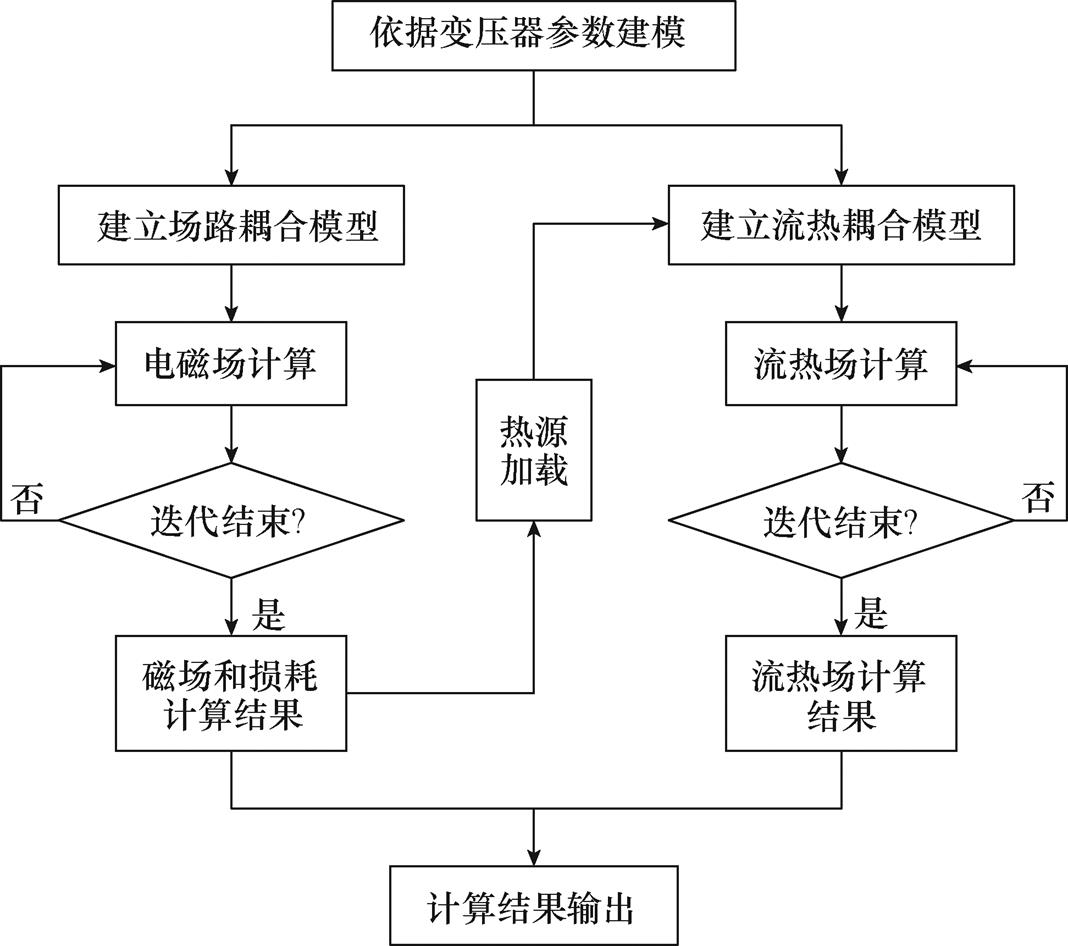
图5 电磁-流热场耦合计算过程
Fig.5 Electromagnetic-fluid thermal field coupling calculation process
分别对变压器额定负载下和GIC作用下的变压器损耗计算结果进行分析。
3.1.1 额定负载下变压器电磁及损耗结果
由于在高中运行调压最小分接的工况下变压器损耗最大,所引起的温升最为严重[19],因此选择此运行方式进行损耗和温升的仿真计算。
图6为变压器高中最小分接额定负载运行时的A相电流和磁感应强度计算结果。其中,图中所给磁感应强度云图对应于B相绕组所在的铁心柱的磁感应强度达最大值时刻。此处,根据变压器铭牌参数,其对应的高压绕组、中压绕组和负载的电流有效值分别为577.4A、456.2A和1 033.6A,且变压器铁心的磁感应强度约在1.7T左右。显然,计算结果与变压器设计参数吻合良好,说明了计算结果的准确性。
表4为变压器高中最小分接额定负载运行时各部件的总损耗计算结果与厂家的相关设计值。由表4可见,本文计算结果与设计值吻合良好,说明了本文计算模型及计算结果的合理性和准确性。其中,漏磁分布的计算误差是绕组损耗结果产生偏差的主要原因。同时,由于在有限元建模时未考虑油箱加强筋以及箱盖和侧壁等连接处为非直角连接等因素,致使油箱损耗计算结果偏高。此外,因为未考虑连接螺栓等产生的附加损耗、拉板和夹件的磁滞损耗等原因将会导致铁心、夹件和拉板损耗导致的计算结果偏低。
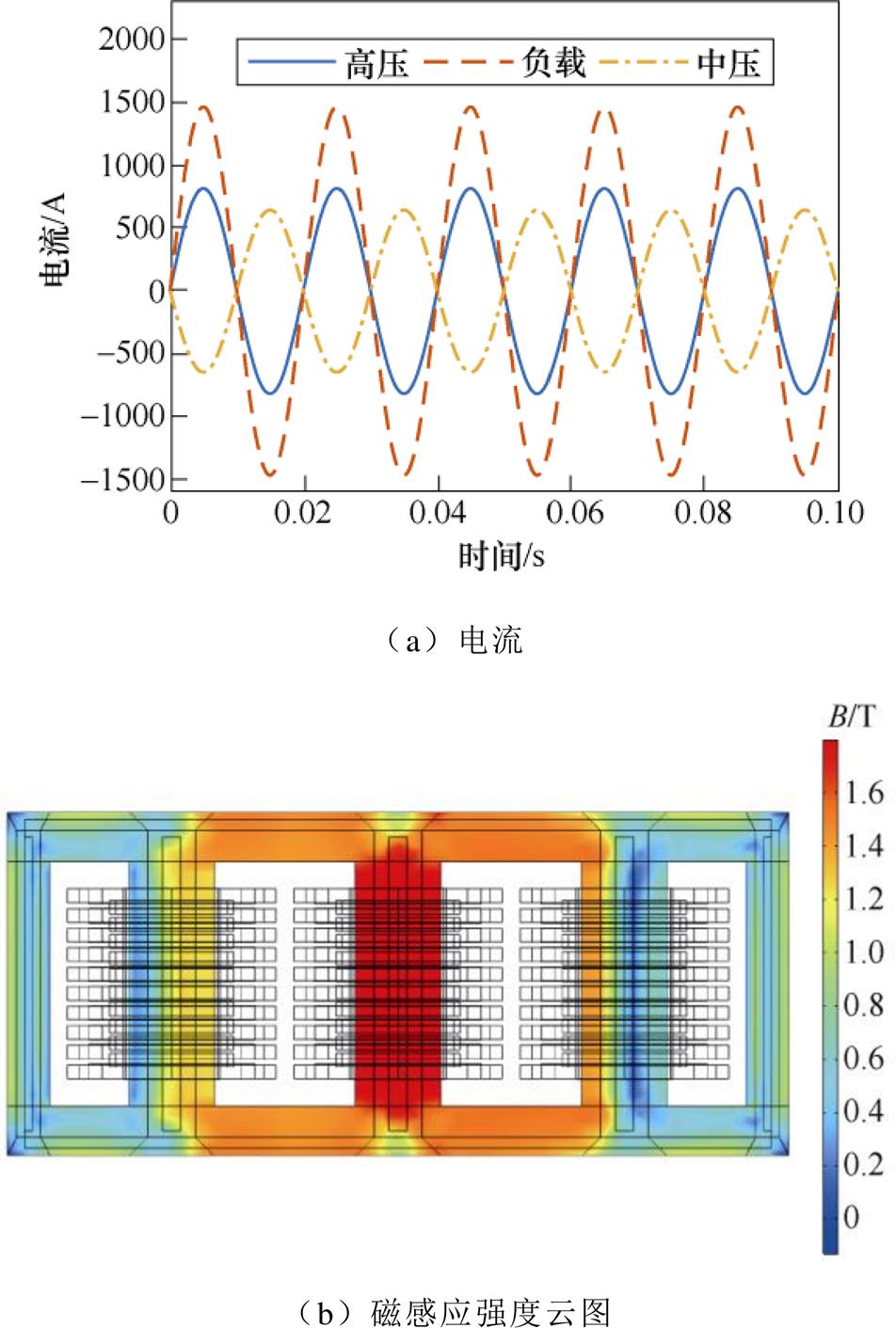
图6 变压器的电流和磁感应强度
Fig.6 Current and magnetic induction of transformer
表4 变压器各部件的损耗计算结果
Tab.4 Total loss of several components of transformer
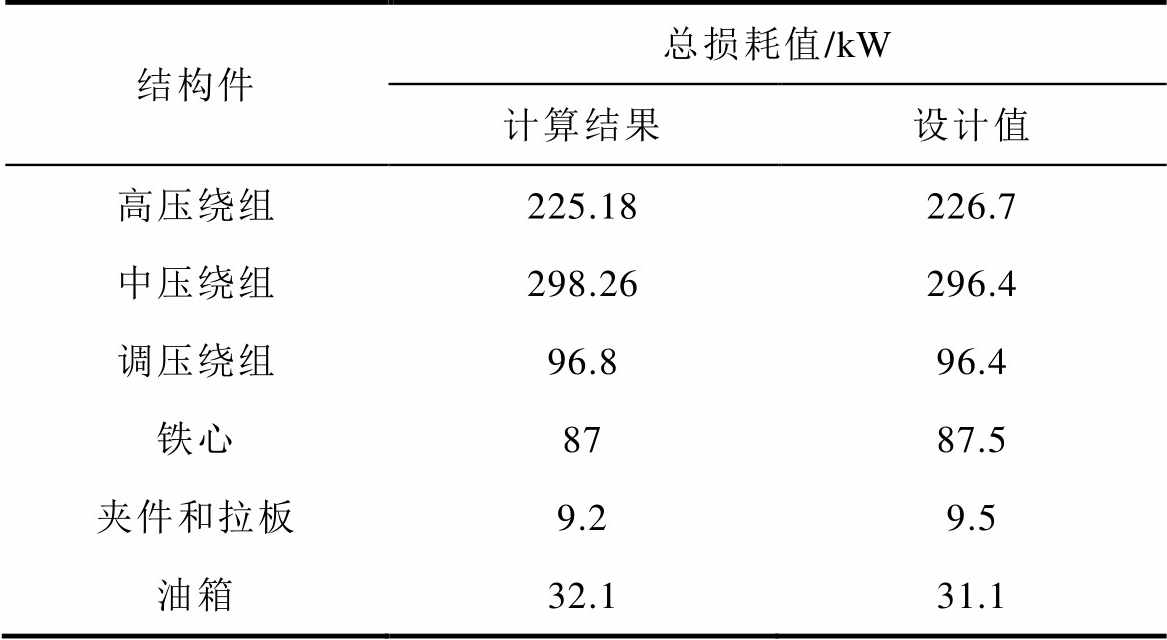
结构件总损耗值/kW 计算结果设计值 高压绕组225.18226.7 中压绕组298.26296.4 调压绕组96.896.4 铁心8787.5 夹件和拉板9.29.5 油箱32.131.1
图7为电力变压器的杂散损耗密度分布。可见,变压器油箱涡流损耗主要集中分布在绕组上下方和两侧,顶部损耗密度最高达66kW/m3,最大损耗密度出现在靠近绕组的夹件局部位置,达700kW/m3。
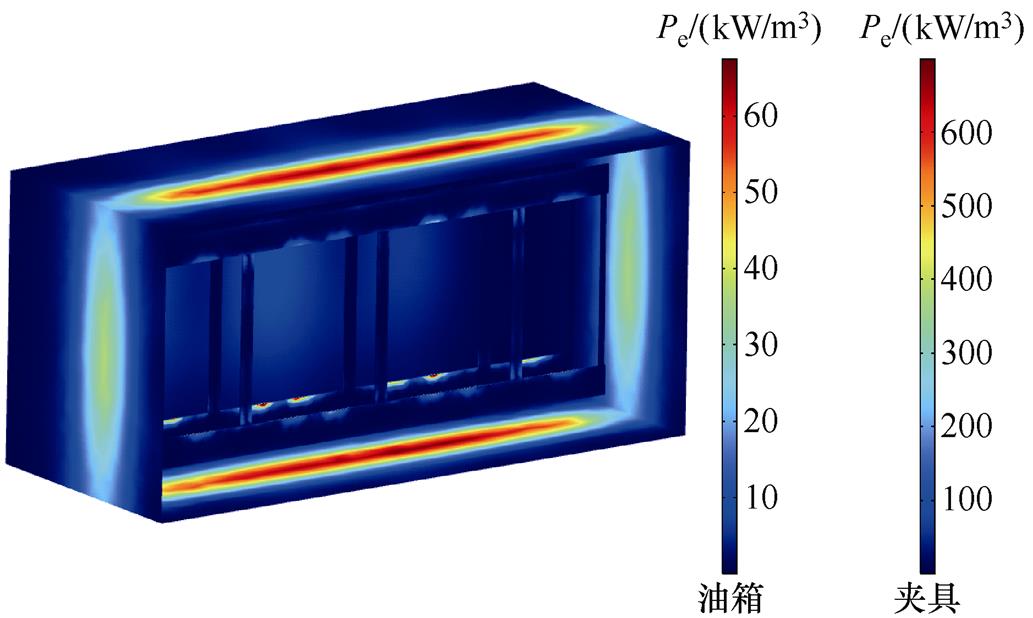
图7 额定下变压器杂散损耗密度分布
Fig.7 Transformer stray loss density distribution under rated conditions
3.1.2 GIC作用下时的变压器损耗
以50A直流的情形为例进行分析,对应的变压器杂散损耗密度分布如图8所示。由图可见,损耗密度最大值出现在绕组端部对应的夹件区域,约为3.5MW/m3。由于主柱拉板位于绕组和铁心主柱之间,直流偏磁时,其损耗密度大幅度增加。变压器油箱的损耗密度最大值出现在绕组正上方的油箱顶部区域,最大值约为610kW/m3。
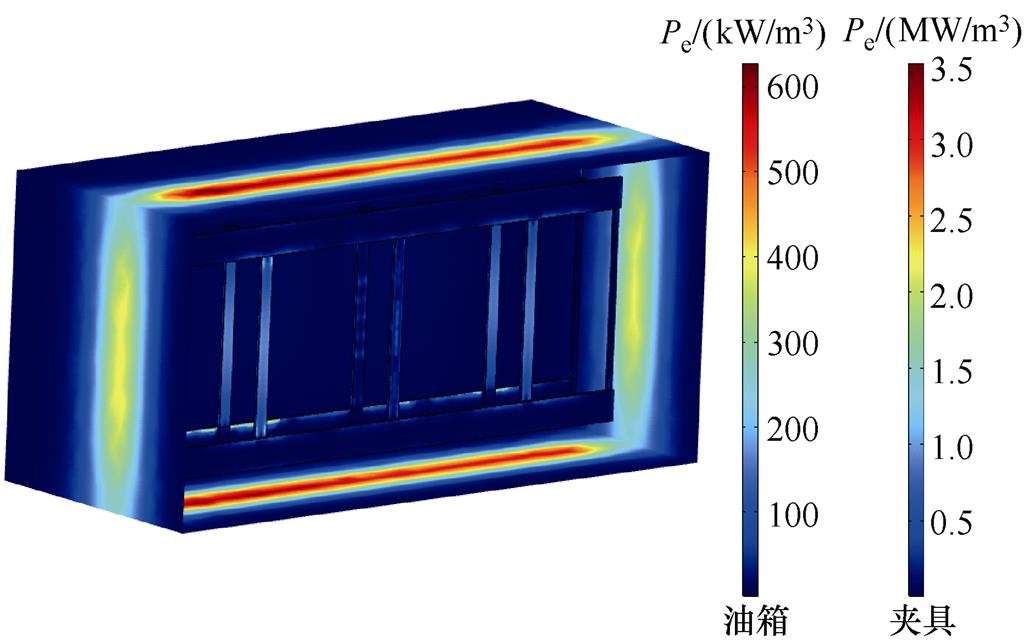
图8 50A直流下变压器杂散损耗密度分布
Fig.8 Transformer stray loss density distribution under 50A DC current
表5列出了在变压器满负载时不同GIC条件下各部件总损耗的变化,可知变压器各部件的总损耗随GIC的增加而增大。由于自耦变压器一、二次绕组都有直流的通入,因此其损耗都会有所增加,且在大直流下损耗的增幅变大,但调压绕组相比于高、中压绕组在直流影响下的损耗增加较小。夹件、油箱等杂散损耗在直流影响下的增长倍数远大于绕组损耗,考虑其损耗分布的不均匀性,需要关注所引起的局部温升过高的问题。
表5 GIC作用下变压器各部件总损耗结果
Tab.5 Total loss of transformer components under GIC
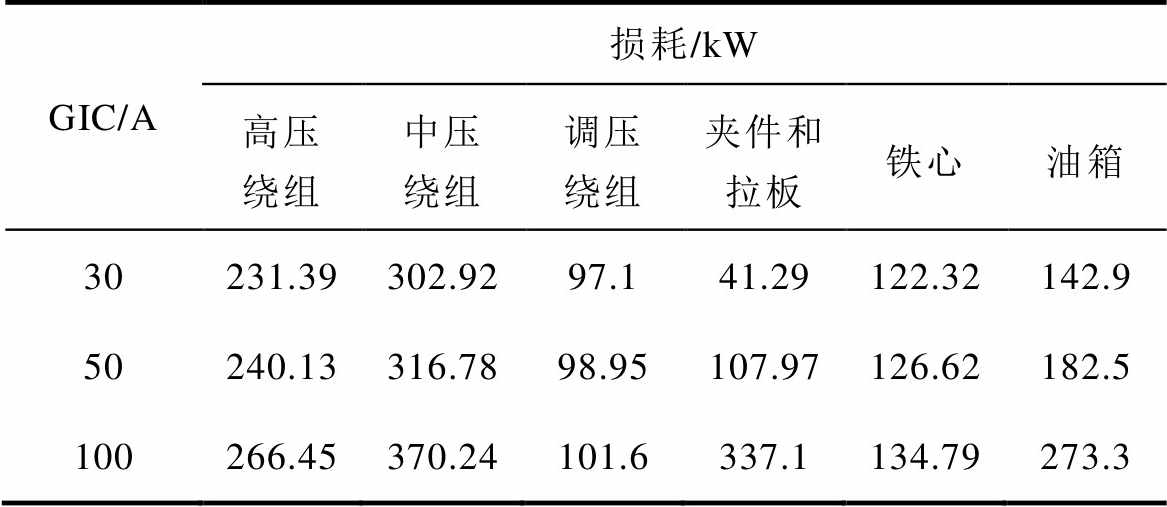
GIC/A损耗/kW 高压绕组中压绕组调压绕组夹件和拉板铁心油箱 30231.39302.9297.141.29122.32142.9 50240.13316.7898.95107.97126.62182.5 100266.45370.24101.6337.1134.79273.3
分别对变压器额定负载下和GIC作用下的变压器热流场计算结果进行分析。
3.2.1 额定负载下变压器温升结果
图9为将损耗结果导入流热模型计算得到的变压器温度基本稳定后的温度场、流场分布和绕组热点温升曲线结果。由图可见,由于绝缘油的流动将热量带到油箱顶部通过出口流入散热器,热油经过散热器冷却后流入油箱底部,各绕组温度从底部到顶部逐渐增高,各绕组的热点位置位于绕组顶部第一层处,由流场分布可知,在散热器出入口附近流速较高,约为0.06m/s。由温升曲线可知,各绕组热点温度随时间呈指数形式上升,在10h后基本达到稳定。变压器绕组热点温度计算结果与设计值对比见表6,两者吻合良好,验证了流热场模型的合理性。

图9 变压器热流场计算结果
Fig.9 Heat flow field calculation results of transformer
表6 额定下绕组热点温升计算结果
Tab.6 Hot spot temperature rise of windings under rated conditions (单位: ℃)
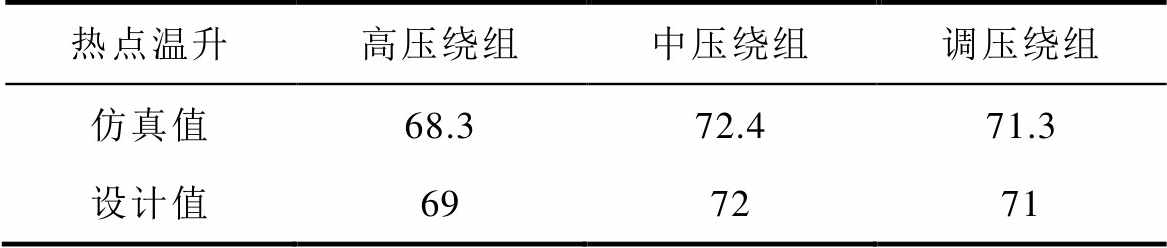
热点温升高压绕组中压绕组调压绕组 仿真值68.372.471.3 设计值697271
3.2.2 GIC作用下变压器温升结果
实际GIC通常表现为数小时内连续大量低至中等水平的窄脉冲,期间并夹杂着小于数分钟的高峰值。根据IEEE C57.163中的建议,在计算变压器受GIC影响下的各部件的温升曲线时,GIC应为半连续直流电流,对于每种直流情况,可采用如图10所示的周期性动态直流[20],以此通过施加动态损耗计算变压器各部件温度分布和温升曲线。图中,Ipeak为每种GIC的大小,Ibase=30%Ipeak,其中时间tb1= 60min,tb2=20min,tp=2min,通过此周期性动态电流可近似地模拟数小时的GIC事件。
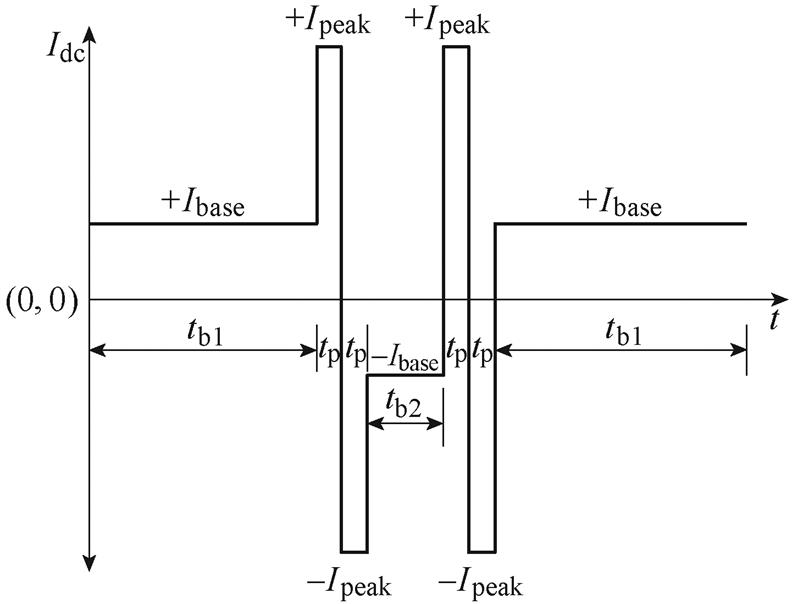
图10 模拟的GIC电流
Fig.10 Simulated GIC current
在变压器高中最小分接满负载运行时温度达到稳态时,通入每种模拟的GIC电流,重复两个周期后来表示整个GIC事件。以表5中最为严重的Ipeak= 100A时情况为例,计算得出温度最大时的温度分布如图11所示。由图可知,较大的直流电流通入绕组,绕组整体温度也升高明显,由于三相磁路不对称等因素所引起三相绕组损耗的差异,A、C相绕组热点温度最高比B相大5℃左右,绕组热点位于绕组上端部,其中中压绕组温升最高,其热点温度为123.6℃,因绕组涡流损耗增加较大,绕组最低温度位置并不位于最下端。由于主柱拉板损耗密度比较集中,且拉板所处位置散热能力弱,在100A直流脉冲下,变压器最高温度出现在主柱拉板处,高达133℃。非平均热源的加载使油箱热点位置也对应于其涡流损耗集中的位置,因油箱有较好的散热条件,其热点温升远低于夹件和绕组。
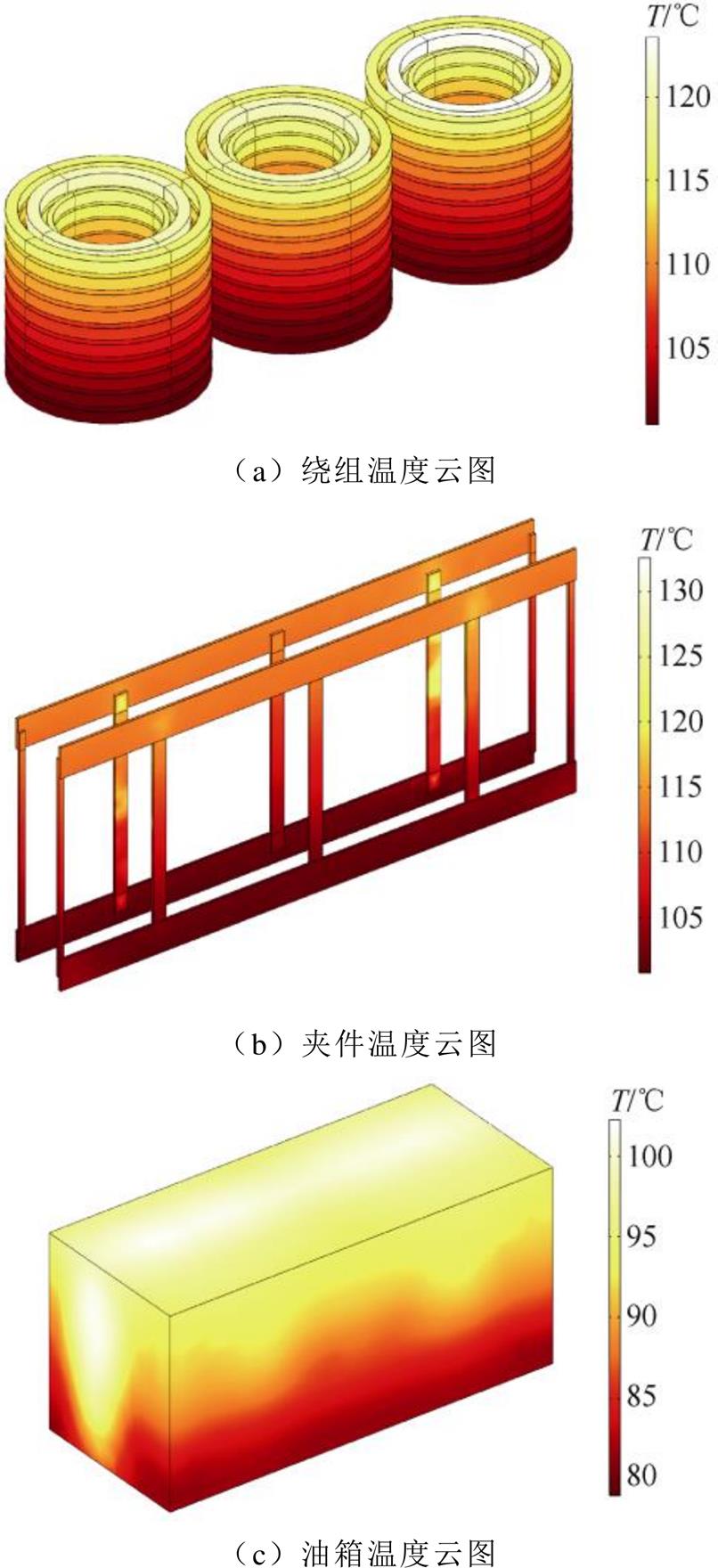
图11 Ipeak=100A时变压器部件温度分布
Fig.11 Temperature distribution of transformer components when Ipeak is 100A
绕组热点和夹具、油箱热点在Ipeak分别为50A、100A时温升曲线如图12所示,由图可知,在Ibase直流阶段,绕组温度随时间逐渐上升,而夹具和油箱热点温度短时间急剧上升,这是因为在额定情况下,夹具和油箱损耗值较低,温度不会出现明显升高,但由于其对直流的存在很敏感,在直流通入后涡流损耗值会成倍地增加。
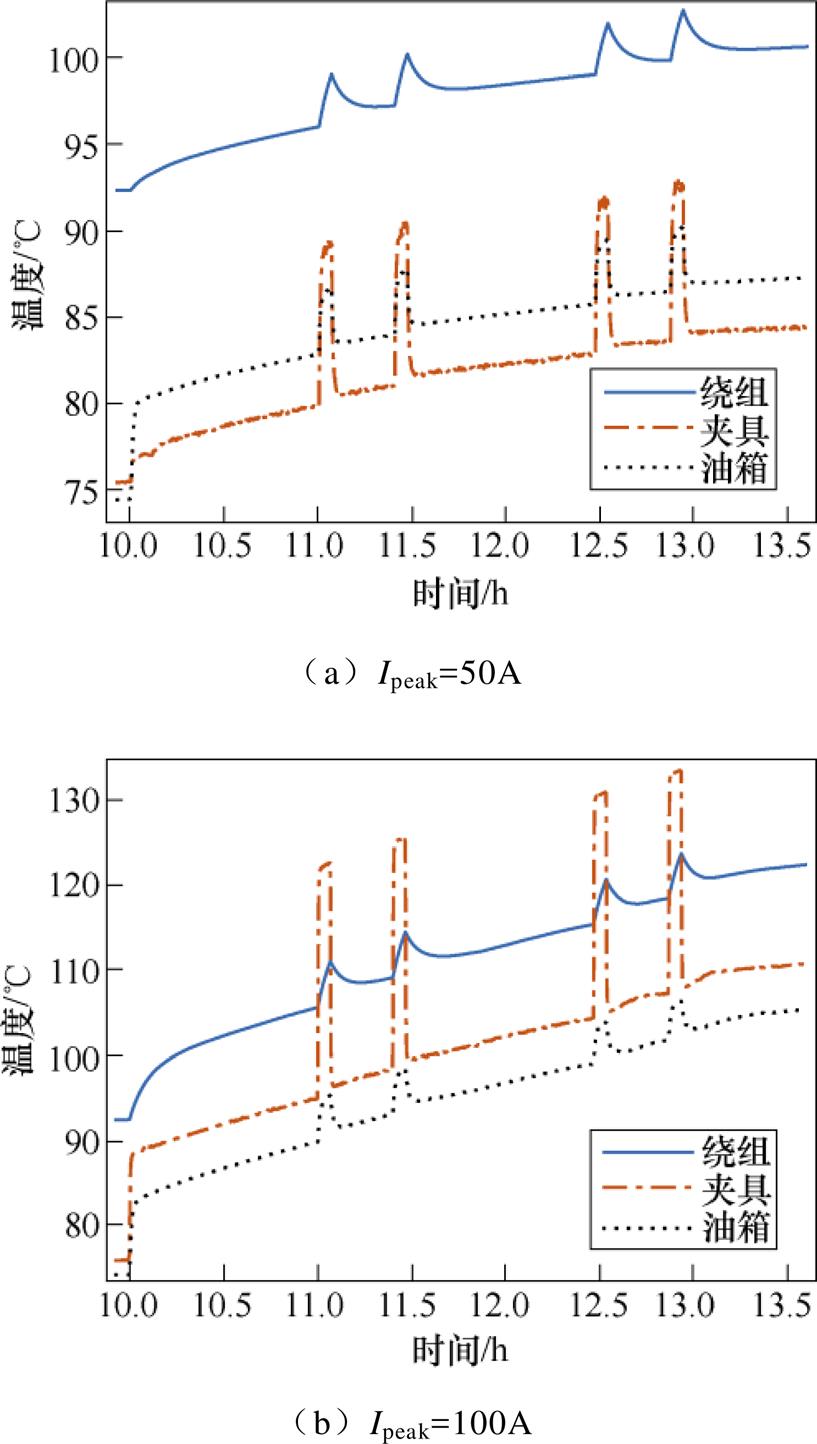
图12 绕组、夹具和油箱热点的动态温升曲线
Fig.12 Dynamic temperature rise curves of winding, clamping and the hot spot of tank
在每一个Ipeak直流脉冲阶段,由于阶跃损耗的作用,热点温度急剧升高,当阶跃损耗开始下降时,热点温度就会急剧降低,在热点温度降到一定数值后其下降速度会有所减缓。相对于环境温度20℃,在第四个50A直流脉冲阶段,绕组热点温升为82.8℃,夹具热点温升为73.3℃,油箱热点温升为69.9℃,其中100A直流脉冲阶段绕组热点温升达103.6℃,夹具热点温升高达113℃。
由图12b可知,对于变压器初始温度较高时,如在环境温度40℃下,此时变压器绕组热点温度将超过IEEE/IEC中的长时GIC事件绝缘材料耐热水平限值140℃,若直流脉冲高达100A时的GIC持续时间过久时,将会导致绝缘材料恶化,而夹具热点短时温度将达到153℃,接近短时GIC绝缘耐受限值160℃。因此,在GIC脉冲为100A时该变压器仍有足够承受能力,但在某些条件下会出现变压器内部局部过热而接近绝缘耐受限值。相应地,在更高GIC水平下该变压器的安全运行将会受到严重威胁。
由温升结果可见,GIC对变压器的影响具有短时和温升剧烈的特点,即使变压器具有足够的抗GIC干扰的能力,但变压器的累积效应会加速其老化,甚至发生故障和损坏,为降低GIC引起变压器局部过热,优化变压器设计,可采用以下防范措施:
(1)因GIC引起变压器涡流损耗的严重增加是变压器温升的主要原因,故可以通过改善变压器构件的结构或材料进行防范,绕组线圈导线采用逐层换位式连接;拉板、夹件等结构件适当开槽或采用非导磁性材料;对于高漏磁区域(如夹件和拉板的连接处)的局部过热问题,可通过在局部加设磁屏蔽来降低局部涡流损耗值。
(2)GIC引起变压器漏磁增加的原因是变压器铁心磁通半波饱和,因此对于直流偏磁或GIC高发地区,在变压器制造过程中建议采用高导磁材料铁心,通过增加铁心饱和裕度来提高变压器GIC电流的耐受阈值。若条件允许,也可在变压器内部安装补偿绕组,当检测到GIC流入到变压器绕组时,使补偿绕组产生反向直流磁动势来抵消GIC产生的磁动势,从而降低铁心的饱和程度。
(3)对运行中的变压器来说,针对GIC主要通过中性点侵入变压器进而对其造成威胁,可在变压器中性点采用相关直流偏磁抑制措施,如在中性点串接小电阻、电容器等,或者在中性点安装反向补偿装置,根据检测到的GIC脉冲电流,自动向变压器中性点注入与GIC大小相同的反向直流电流。
本文基于电磁-热流场计算模型,以一台三相五柱自耦变压器为研究对象,计算了在不同GIC影响下变压器的损耗和温升,主要结论如下:
1)在满负载运行工况下计算变压器各部件的损耗和绕组热点温升,与设计值吻合较好,误差在±3.5%以内,验证了本分析方法的有效性。
2)变压器在GIC作用下,夹件、拉板等杂散损耗增加明显且随直流偏磁程度增加而增大,局部损耗密度远大于整体损耗密度,大直流的注入不仅会引起绕组涡流损耗的增加还会导致直流电阻损耗明显增大,进而引起绕组整体特别是端部热点温度升高。
3)在不同GIC事件作用下的变压器温升仿真结果发现,该变压器在GIC水平为100A时依旧有足够的耐受能力但已接近允许限值,其中在主柱拉板的局部温升最为严重。
参考文献
[1] 王泽忠, 黄天超. 变压器GIC-Q动态关系分析[J]. 电工技术学报, 2021, 36(9): 1948-1955.
Wang Zezhong, Huang Tianchao. Analysis of GIC-Q dynamic relationship of transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1948- 1955.
[2] 王丰华, 周翔, 高沛, 等. 基于绕组热分布的改进油浸式变压器绕组热点温度计算模型[J]. 高电压技术, 2015, 41(3): 895-901.
Wang Fenghua, Zhou Xiang, Gao Pei, et al. Improved thermal circuit model of hot spot temperature in oil-immersed transformers based on heat distribution of winding[J]. High Voltage Engineering, 2015, 41(3): 895-901.
[3] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013.
Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(5): 1006-1013.
[4] 李冰, 王泽忠, 刘海波, 等. 直流偏磁下500kV单相变压器振动噪声的试验研究[J]. 电工技术学报, 2021, 36(13): 2801-2811.
Li Bing, Wang Zezhong, Liu Haibo, et al. Experiment on vibro-acoustic characteristic of 500kV single- phase transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2801- 2811.
[5] 王泽忠, 黄天超. 变压器地磁感应电流-无功功率动态关系分析[J]. 电工技术学报, 2021, 36(9): 1948- 1955.
Wang Zezhong, Huang Tianchao. Analysis of geo- magnetically induction current-reactive power dynamic relationship of transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1948-1955.
[6] 王泽忠, 司远, 刘连光. 地磁暴对电力系统稳定性的影响[J]. 电工技术学报, 2021, 37(7): 1780-1788.
Wang Zezhong, Si Yuan, Liu Lianguang. Influence of geomagnetic storms on the stability of power system[J]. Transactions of China Electrotechnical Society, 2021, 37(7): 1780-1788.
[7] Takasu N, Oshi T. An experimental analysis of DC excitation of transformers by geomagnetically indu- ced currents[J]. IEEE Transactions on Power Delivery, 1994, 9(2): 1173-1182.
[8] 张书琦, 汪可, 李金忠, 等. 单相单柱旁轭变压器空负载工况下的直流偏磁关键性能测试[J]. 中国电机工程学报, 2019, 39(14): 4334-4344, 4281.
Zhang Shuqi, Wang Ke, Li Jinzhong, et al. Tests of DC bias key performances of power transformer with single-phase three-limb core under no-load and rated- load conditions[J]. Proceedings of the CSEE, 2019, 39(14): 4334-4344, 4281.
[9] Price P R. Geomagnetically induced current effects on transformers[J]. IEEE Power Engineering Review, 2002, 22(6): 62-62.
[10] Zhang Bing, Liu Lianguang, Liu Yilu, et al. Effect of geomagnetically induced current on the loss of transformer tank[J]. IET Electric Power Applications, 2010, 4(5): 373-379.
[11] Picher P, Bolduc L. Study of the acceptable DC current limit in core-form power transformers[J]. IEEE Transactions on Power Delivery, 1997, 12(1): 257-265.
[12] Torriano F, Campelo H, Picher P, et al. Experimental and numerical thermofluid study of a disc-type transformer winding scale model[C]//XXIIth Inter- national Conference on Electrical Machines, Lausanne, 2016: 2833-2839.
[13] Vakhnina V V, Shapovalov V A, Kuznetsov V N, et al. The influence of geomagnetic storms on thermal processes in the tank of a power transformer[J]. IEEE Transactions on Power Delivery, 2015, 30(4): 1702- 1707.
[14] 韩金华, 杨晓辉, 王丰华, 等. 500kV电力变压器直流偏磁损耗特性的仿真研究[J]. 高压电器, 2015, 51(5): 40-46.
Han Jinhua, Yang Xiaohui, Wang Fenghua, et al. Simulation study of DC bias loss characteristics of 500kV power transformer[J]. High Voltage Apparatus, 2015, 51(5): 40-46.
[15] 杨晓辉, 王丰华, 段若晨, 等. 500kV电力变压器直流偏磁耐受性能的仿真研究[J]. 电力系统保护与控制, 2014, 42(14): 60-66.
Yang Xiaohui, Wang Fenghua, Duan Ruochen, et al. Simulation study of DC bias enduring ability of 500kV power transformer[J]. Power System Pro- tection and Control, 2014, 42(14): 60-66.
[16] Nishiura R, Yamashita S, Kano S. Simulation analysis of geomagnetically-induced currents (GIC) effects on shell-form transformers[C]//IEEE Power & Energy Society General Meeting, Vancouver, BC, 2013: 1-5.
[17] Xia Yunyan, Han Yongsen, Liu Jinhui. Calculation of winding loss and temperature rise of large power transformer under DC magnetic biasing[C]//Inter- national Conference on the Properties and Appli- cations of Dielectric Materials, Xi’an, 2018: 590-593.
[18] 尹忠东, 魏文思. 基于有限元算法的变压器绕组涡流效应分析及损耗计算[J]. 智慧电力, 2018, 46(5): 71-77.
Yin Zhongdong, Wei Wensi. Analysis of eddy current effect and loss calculation of transformer winding based on finite element algorithm[J]. Smart Power, 2018, 46(5): 71-77.
[19] 刘弘景, 张丹丹, 李伟, 等. 大型油浸式变压器绕组温度场的有限元分析[J]. 高压电器, 2019, 55(12): 83-89.
Liu Hongjing, Zhang Dandan, Li Wei, et al. Finite element analysis for temperature field of winding in large oil-immersed transformer[J]. High Voltage Apparatus, 2019, 55(12): 83-89.
[20] IEEE Std. C57.163-2015 IEEE guide for establishing power transformer capability while under geomag- netic disturbances[S]. 2015.
Calculation of Temperature Rise of Large Transformer under Geomagnetically Induced Current
Abstract To accurately analyze the feature of temperature rise of power transformer under the action of geomagnetically induced current (GIC), an electromagnetic-flow and heat field coupling 3D simulation model for a 500kV three-phase integrated oil-immersed power transformer is proposed in this paper. The loss density and temperature field distribution of internal components of power transformer under different GICs are calculated when the transformer is operated at rated load. Meanwhile, the dynamic temperature rise curve of internal components of power transformer under different GICs is obtained according to the IEEE C57.163 standard. The simulation results are in good agreement with the designed results. In addition, the eddy current loss distribution of the clamp, pulling plate and oil tank of the power transformer is uneven after being affected by GIC, and increases with the increase of the GIC. With the action of GIS pulse, the local temperature of metal components of the transformer rises rapidly and approaches the permissible limit for the pulling plate of main column at the 100A DC pulse. The results can provide a reference for the tolerance performance analysis of large transformer under the action of GIC.
keywords:Power transformer, geomagnetically induced current (GIC), loss density, temperature field, temperature rise
DOI: 10.19595/j.cnki.1000-6753.tces.201312
中图分类号:TM411
朱 涛 男,1995年生,硕士研究生,研究方向为电力变压器直流偏磁、变压器温度场。E-mail: 1344098230@qq.com
王丰华 女,1973年生,博士,副教授,研究方向为电力变压器振声监测及装备智能化、电力变压器直流偏磁、电力系统接地技术等。E-mail: fhwang7723@sjtu.edu.cn(通信作者)
收稿日期 2020-09-29
改稿日期 2021-01-30
(编辑 崔文静)