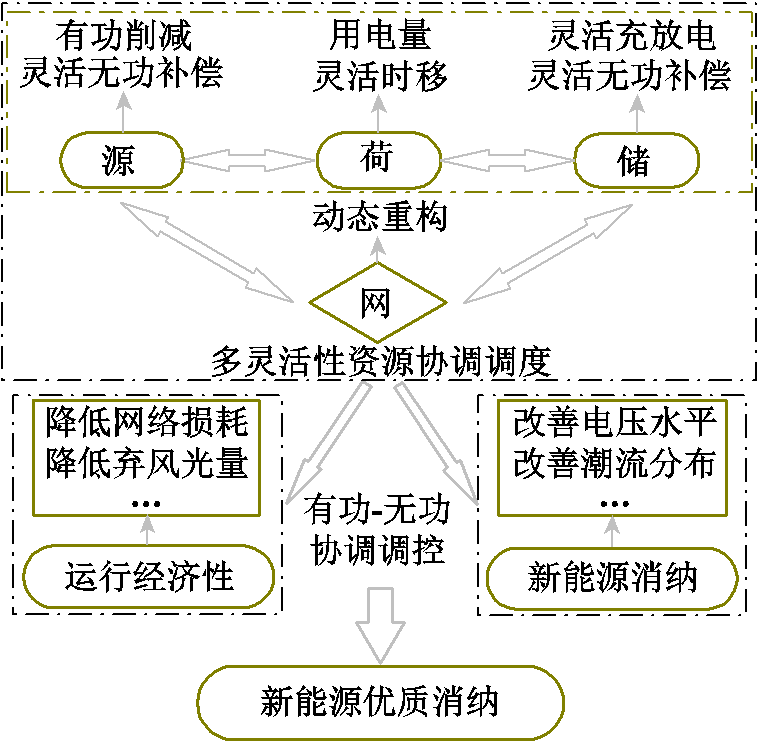
图1 面向高比例新能源消纳的多灵活性资源协调调度机理示意图
Fig.1 Schematic diagram of coordinated dispatching of multi-flexible resources for high-proportion renewable energy accommodation
摘要 针对双碳目标下高比例新能源并网造成的灵活性调节资源匮乏及高效消纳难题,该文提出一种考虑多灵活性资源协调调度的配电网新能源消纳策略。首先,建立多灵活性资源灵活互动特性的刻画方法,兼顾配电网新能源消纳水平与经济运行,构建考虑多灵活性资源协调调度的新能源优化消纳模型;然后,为寻找优化消纳模型非支配解的可行域,基于双层嵌套结构建立多目标优化求解方法,并提出一种复合型线性化策略,将复杂的多目标非线性非凸优化消纳模型转换为多目标混合整数线性优化问题,实现优化消纳模型的高效求解;最后,采用IEEE 33节点测试系统和中国某地级市110kV配电网,验证所提消纳策略的有效性和适应性。
关键词:配电网 新能源 多灵活性资源 灵活互动 多目标混合整数优化
2021年3月15日,习近平主席提出构建以新能源为主体的新型电力系统。预计到2030年,我国风光装机总量将超过12亿kW[1-2]。国家“十四五”规划提出坚持集中式和分布式并举,大力提升风电和光伏发电规模[3]。
新能源出力具有较强的间歇性和波动性,高比例新能源并入配网,导致灵活调节资源需求大幅增加[4-6],新能源的高效优质消纳成为难题。国家发改委发布指导意见,明确提出要强化源网荷储各环节间协调互动,充分挖掘系统灵活性调节能力和需求侧资源[7]。
目前已有大量研究考虑大电网灵活性资源建立新能源消纳模型,以解决大规模新能源场站的弃风弃光现象[8-12]。然而,配电网和大电网在运行边界、网络结构、运行特征等方面存在较大差异,两者的新能源消纳限制因素、灵活性资源类型和协同运行方式等并不相同[13]。因此,现有研究提出的考虑多种灵活性资源的大电网新能源消纳模型,难以适用于配电网。
现有文献通常考虑电源侧、网络侧、负荷侧和储能侧等单环节的灵活性资源研究配电网的新能源优化消纳策略。针对节点电压是限制新能源并网消纳的瓶颈这一问题,文献[14-15]利用光伏逆变器的灵活性进行连续动态无功补偿,通过改善节点电压质量以提高新能源消纳量。配电网重构基于网架灵活性,能够有效缓解电压越限、线路过载等新能源消纳的限制因素。文献[16]利用静态重构优化配电网拓扑结构,提升新能源消纳电量。然而,风光出力和负荷均具有时变特性,静态重构显然难以适应该特点。为此,文献[17-19]基于动态重构建立新能源消纳策略。文献[20-21]提出基于分布式电源出力优化调控和配网重构的主动配电网新能源消纳策略,但其仅针对单一时段建模,难以考虑多时段灵活性调节措施的协调性。此外,文献[16-21]基于生成树或虚拟潮流模型模拟网架灵活性,须添加较多辅助变量,大大增加了建模难度和求解难度。合理利用荷储灵活性有助于平滑新能源出力波动。文献[22-23]提出了基于储能和可控负荷优化调度的新能源消纳策略,灵活利用可控负荷的时移特性及储能装置的充放电特性来提升配电网新能源消纳水平,但其忽略了储能的无功调节能力,因而无法有效利用储能的灵活性解决新能源并网引起的电压越限问题。
配电网新能源优化消纳模型属于非凸非线性的大规模优化求解问题。文献[22-23]采用粒子群算法对加权转换的单目标优化消纳模型进行求解,但智能算法存在易陷入局部最优、寻优时间长等问题,且难以合理确定权重系数。二阶锥松弛和线性化方法具有易获得全局最优解、求解效率高等优点,得到了广泛应用。文献[20-21, 24]利用凸化松弛潮流约束,将非凸新能源优化消纳模型转换为混合整数二阶锥优化问题,但该方法要求模型能够严格满足二阶锥松弛准确性条件,适应性相对较差;文献[18-19]采用线性化方法将非线性单目标的新能源优化消纳模型转换为混合整数线性规划问题,提高了计算效率,但其难以适用于多目标优化消纳模型的求解。
综上所述,现有研究对灵活性措施的考虑较为单一,难以满足高比例新能源并网消纳的灵活性需求,且传统网架灵活性建模复杂,消纳模型难以高效求解。为此,本文通过对多种灵活性资源的有效建模,充分挖掘和协调配电网不同环节有功/无功灵活资源调节潜力,以消除限制配电网新能源消纳的制约因素,并提出消纳模型高效求解方法。
风光等间歇式发电资源大量并网,导致配电网灵活调节资源捉襟见肘,高效、经济消纳成为难题。配电网多灵活性资源的灵活互动特性能够有效应对新能源出力的不确定性,提高配电网的安全经济运行水平。本节基于源网荷储不同环节,深入分析多灵活性资源的协调调度对新能源消纳水平提升的作用机理,然后,基于多目标优化理论,建立计及多灵活性资源协调调度的配电网新能源优化消纳模型。该模型综合考虑灵活互动约束、潮流以及安全运行等约束,以新能源消纳电量最大和配电网总运行成本最小为目标,充分挖掘配电网消纳潜力,实现新能源的经济、优质消纳。
高比例新能源并网后,有功-无功协调调控能够有效缓解电压越限、线路过载等消纳限制性因素的制约作用,有助于提升配电网的消纳能力与经济运行水平[24]。源荷储侧灵活性资源通过合理调整出力和用电需求,可大幅降低净负荷的波动性和峰谷差;充分聚合各环节的动态无功补偿能力,能够有效缓解高比例新能源并网的无功需求;灵活改变网络拓扑可消除网络阻塞,为多环节灵活性资源的灵活互动和优化调度提供通道。面向高比例新能源消纳的多灵活性资源协调调度机理示意图如图1所示。

图1 面向高比例新能源消纳的多灵活性资源协调调度机理示意图
Fig.1 Schematic diagram of coordinated dispatching of multi-flexible resources for high-proportion renewable energy accommodation
在运行经济性方面,通过协调调度多灵活性资源有功/无功输出,能够减少弃电成本、网络损耗等配网运行成本;在新能源消纳方面,多灵活性资源协调调度大幅改善配网节点电压水平和潮流分布,避免高比例新能源并网引起的电压越限、线路过载等问题,尽可能减少或消除消纳限制因素制约作用,提高新能源消纳量。可见,通过全方位多环节的多灵活性资源协调调度有助于实现新能源的经济、优质消纳。
1.2.1 目标函数1:新能源消纳电量最大
以配网新能源消纳电量最大为目标函数1,即
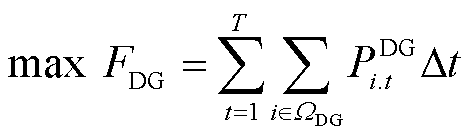 (1)
(1)
式中,FDG为配网全天内的新能源消纳电量;t为时段标识,t=1, 2,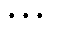 , T;Dt为时段间隔;T为时段总数,本文取Dt=1h,T=24;PDG i.t为节点i处新能源实际消纳的有功功率;WDG为风光对应节点集合。
, T;Dt为时段间隔;T为时段总数,本文取Dt=1h,T=24;PDG i.t为节点i处新能源实际消纳的有功功率;WDG为风光对应节点集合。
1.2.2 目标函数2:配电网运行成本最小
多灵活性资源协调调度策略的多样化将导致迥异的新能源消纳电量与配电网运行成本。为合理利用多灵活性资源的灵活互动特性,本文在考虑弃电成本、购电成本和网损成本的基础上,进一步计及多灵活性资源协调调度成本,以配电网运行总成本最低为目标函数2,即
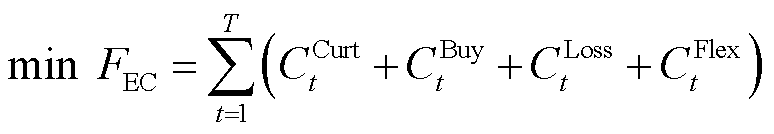 (2)
(2)
式中,FEC为配电网日运行成本;CCurt t、CBuy t和CLoss t分别为配电网的弃电成本、购电成本和网损成本;CFlex t为配电网的多灵活性资源协调调度成本。具体计算公式为
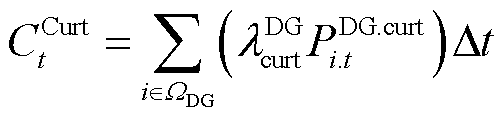 (3)
(3)
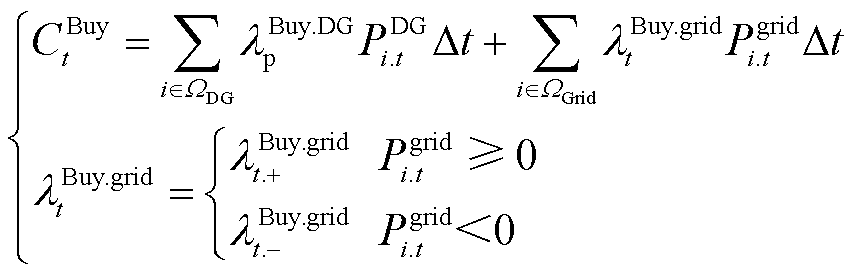 (4)
(4)
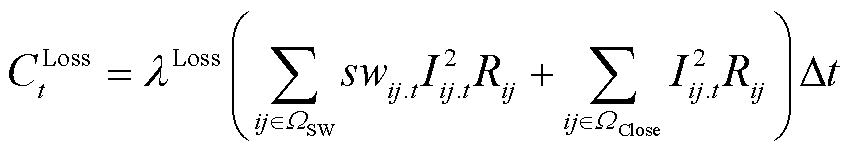 (5)
(5)
式中,PDG.curt i.t为节点i处新能源有功削减量;lDGcurt和lBuy.DGp分别为新能源弃电惩罚成本系数和上网电价;Pgrid i.t、lBuy.grid t.+和lBuy.grid t.-分别为根节点i和上级电网交互的有功功率以及购、售电价;lLoss为网损成本系数;swij.t为支路ij的遥控开关状态,“1”表示闭合,“0”表示断开;Iij.t和Rij分别为支路ij的电流值和电阻值;WGrid、W SW和WClose分别为根节点集合、网络中存在遥控开关的支路集合和常闭支路集合。
配电网多灵活性资源协调调度成本CFlex t由新能源灵活无功补偿成本CDG t、配网动态重构开关动作成本CSW t、可控负荷灵活调控成本CDR t以及储能灵活充放电和无功补偿成本CESS t组成,具体为
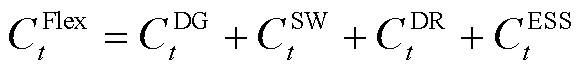 (6)
(6)
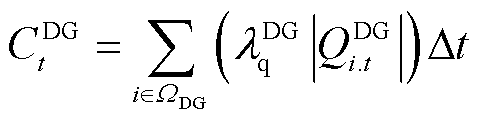 (7)
(7)
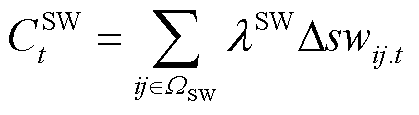 (8)
(8)
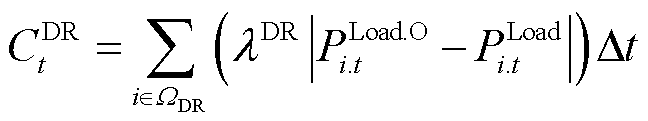 (9)
(9)
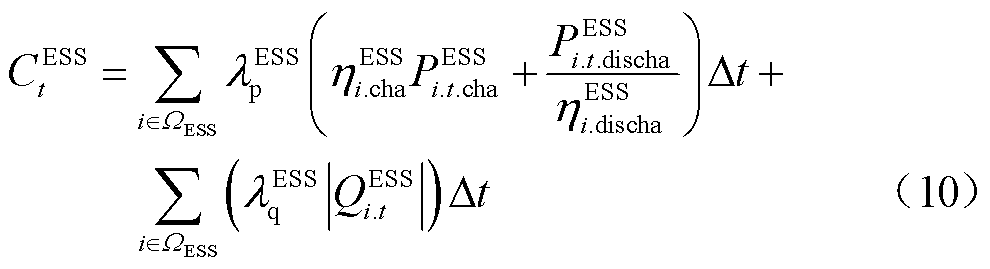
式中,lDGq为新能源无功辅助服务单位补偿系数;lSW为开关动作成本系数;lDR为可控负荷的单位调度成本;lESSp和lESSq分别为储能单位充放电和无功功率的折旧系数;QDG i.t和QESS i.t分别为节点i处新能源和储能在t时段的动态无功补偿功率;Dswij.t为支路ij遥控开关的动作次数;PLoad.O i.t和PLoad i.t分别为节点i处可控负荷原始功率和灵活性时移后的负荷功率;PESS i.t.cha和hESS i.cha分别为节点i处储能的充电功率和效率;PESS i.t.discha和hESS i.discha分别为节点i处储能的放电功率和效率;W DR和WESS分别为可控负荷和储能接入的节点集合。
1.3.1多灵活性资源的灵活互动约束
为合理刻画配电网多灵活性资源的灵活互动特性,需要分别对电源侧、网络侧、负荷侧和储能侧的灵活性建模。
1)电源端灵活性
风电和光伏电站既能输出有功功率,又能快速、连续地进行动态无功补偿[25],其参与多灵活性资源的协调调度需要考虑功率因数限制和逆变器容量约束,即
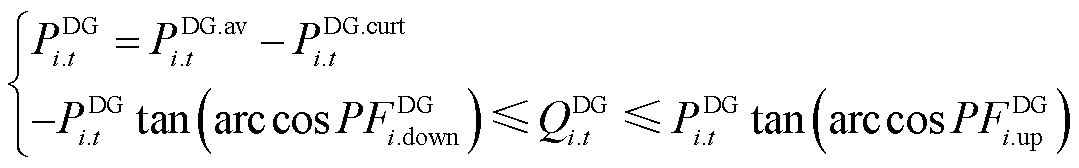 (11)
(11)
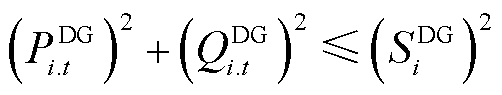 (12)
(12)
式中,PDG.av i.t为节点i处新能源输出有功功率;PFDG i.down和PFDG i.up分别为节点i处新能源功率因数限值;SDG i为节点i处新能源逆变器容量。
2)网架端灵活性
考虑到过于频繁的开关动作会影响开关稳定性,降低开关寿命,为此,在配网动态重构中需要限制开关动作次数,即
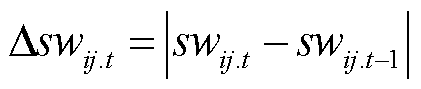 (13)
(13)
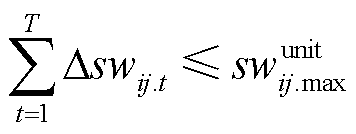 (14)
(14)
式中,swunit ij.max为支路ij的遥控开关在全天内允许的最大动作次数。
此外,重构前后必须保证配电网的辐射状连通性要求。现有研究主要基于生成树和虚拟潮流模型来满足该要求,但须增加较多辅助变量,将会大大增加建模与求解的复杂度。为此,本文考虑配网中所有开关状态,基于供电环路非连通理论,模拟配网重构的辐射状连通性约束,即保证配网中闭合支路数等同于节点总数和电源总数差值,且不存在连通供电环路,具体如式(15)所示[26],其构建的详细步骤见附录。
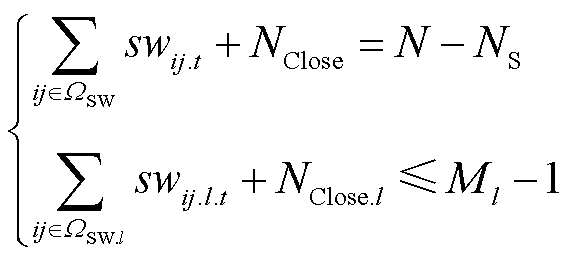 (15)
(15)
式中,N、NS和NClose分别为网络中的节点总数、根节点数量和常闭支路总数;Ml为第l个供电环路中的支路数量,l=1,2, , L,L为网络中供电环路总数;swij.l.t为第l个供电环路中的支路ij的遥控开关状态;W SW.l和NClose.l分别为第l个供电环路中含遥控开关的支路集合和常闭支路数量。
, L,L为网络中供电环路总数;swij.l.t为第l个供电环路中的支路ij的遥控开关状态;W SW.l和NClose.l分别为第l个供电环路中含遥控开关的支路集合和常闭支路数量。
3)负荷端灵活性
部分配网负荷如中央空调、电动汽车等具有较强的可控性,能够实现用电量的跨时空转移,具有良好的削峰填谷效应[27]。式(16)表示可控负荷参与多灵活性资源的协调调度时自身的功率调节能力约束,式(17)表示可控负荷一定时段内的用电总量保持不变。
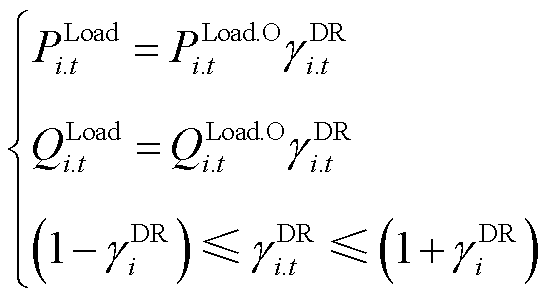 (16)
(16)
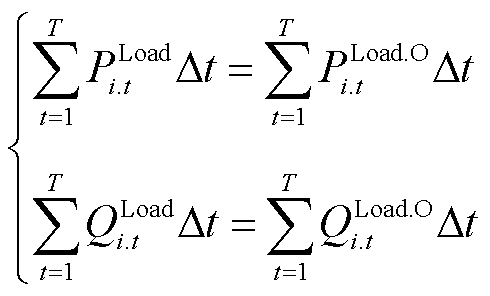 (17)
(17)
式中,QLoad.O i.t和QLoad i.t分别为节点i处可控负荷原始无功功率和灵活性时移后的负荷无功功率;gDR i.t为节点i处可控负荷的负荷时移率,在激励型需求响应中,负荷时移率可由配电网调度人员在响应日的前日确定,并于响应日调度可控负荷;gDR i为节点i处可控负荷功率调节能力限值,其根据可控负荷自身调节能力限制给定。
4)储能端灵活性
为保护储能使用寿命,防止过度充放电,储能在进行充放电灵活性调控时需考虑自身荷电状态约束和平衡约束(如式(18))以及充放电功率约束(如式(19)),具体为[28]
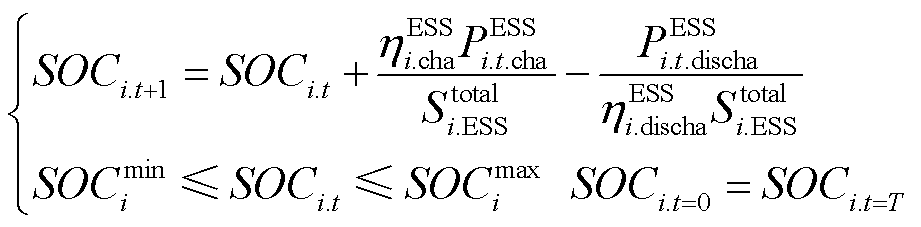 (18)
(18)
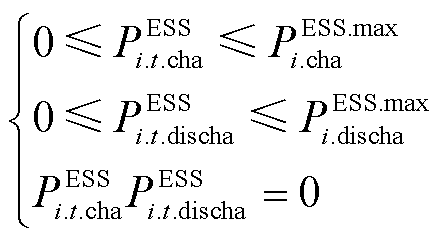 (19)
(19)
此外,储能逆变器利用自身富余容量,结合功率因数运行范围,可在四象限运行范围内进行连续动态无功补偿,储能无功补偿的逆变器约束和功率因数约束分别为
 (20)
(20)
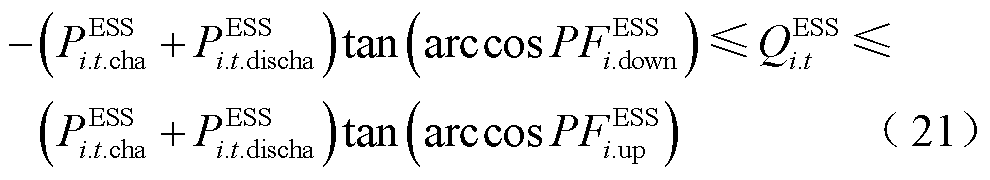
式中,SOCi.t、SOCmin i和SOCmax i分别为节点i处储能的荷电状态和荷电状态限值,SOCi.t=0和SOCi.t=T分别为节点i处储能当日初始和最后的荷电状态; PESS.max i.cha和PESS.max i.discha分别为节点i处储能允许的最大充、放电功率;Stotal i.ESS和SESS i.rate分别为节点i处储能额定容量和储能逆变器容量;PFESS i.up和PFESS i.down分别为节点i处储能功率因数上、下限值。
1.3.2 配电网运行约束
配电网运行需满足潮流约束、静态安全等约束,具体如下所示。
1)支路潮流约束
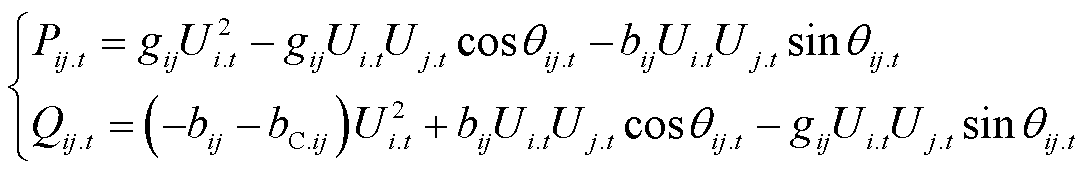 (22)
(22)
式中,Pij.t和Qij.t分别为支路ij的有功功率和无功功率;gij和bij分别为支路ij的电导和电纳;bC.ij为支路ij的对地电纳;qij.t为节点i、j的电压相位差;Ui.t和Uj.t分别为节点i、j的电压幅值。
2)节点功率平衡约束
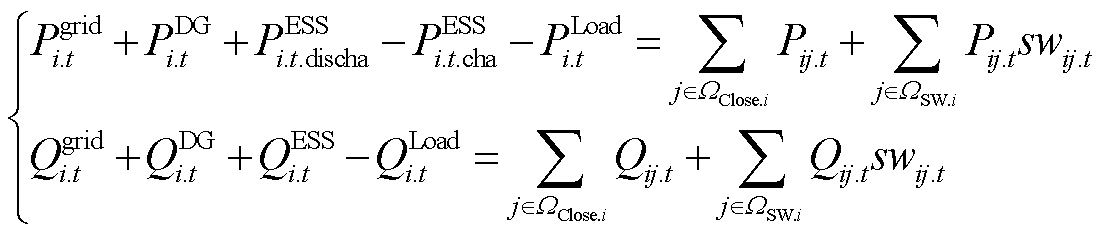 (23)
(23)
式中,WClose.i和WSW.i分别为与节点i相连的常闭支路集合和含遥控开关支路集合;Qgrid i.t为上级电网和根节点i交互的无功功率。
3)节点电压约束
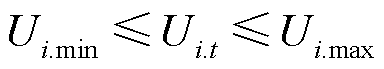 (24)
(24)
式中,Ui.max和Ui.min分别为节点i电压幅值上、下限。
4)支路电流约束
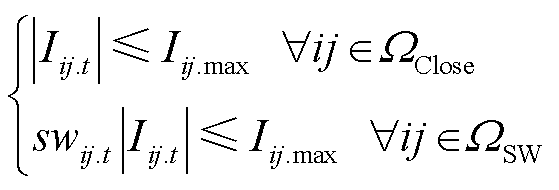 (25)
(25)
式中,Iij.max为支路ij的最大允许载流量。
5)上级电网交互功率约束
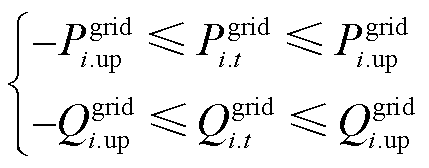 (26)
(26)
式中,Pgrid i.up和Qgrid i.up分别为上级电网和配网根节点i交互的有功和无功功率限值。
本文提出的新能源优化消纳模型具有多目标、多时段耦合、高维混合变量、非线性、非凸等特点,属于大规模多目标混合整数非线性优化问题,采用传统优化算法求解,难以保证所得解的最优性和计算的高效性。为此,本文设计双层嵌套结构高效寻找Pareto最优解集,并选取折中解。为更好地服务于双层嵌套结构的多目标求解,提出了一种复合型线性化策略,将原模型转换为多目标混合整数线性规划(Multi-Objective Mixed Integer Linear Programming, MOMILP)问题,以实现模型的高效求解。
结合变量替换、分段线性化和Big-M法等线性化技术,建立优化消纳模型的复合型线性化策略,依次对不同灵活性资源中的非线性项进行线性化处理,其具体线性化过程如下所示。
2.1.1 电源侧线性化策略
式(4)所示电源侧购电成本和式(7)所示灵活无功补偿成本由于存在分段函数项和绝对值函数项而呈现非线性特征,为此引入辅助变量和二进制变量,并结合Big-M法,将式(4)和式(7)等价线性化为
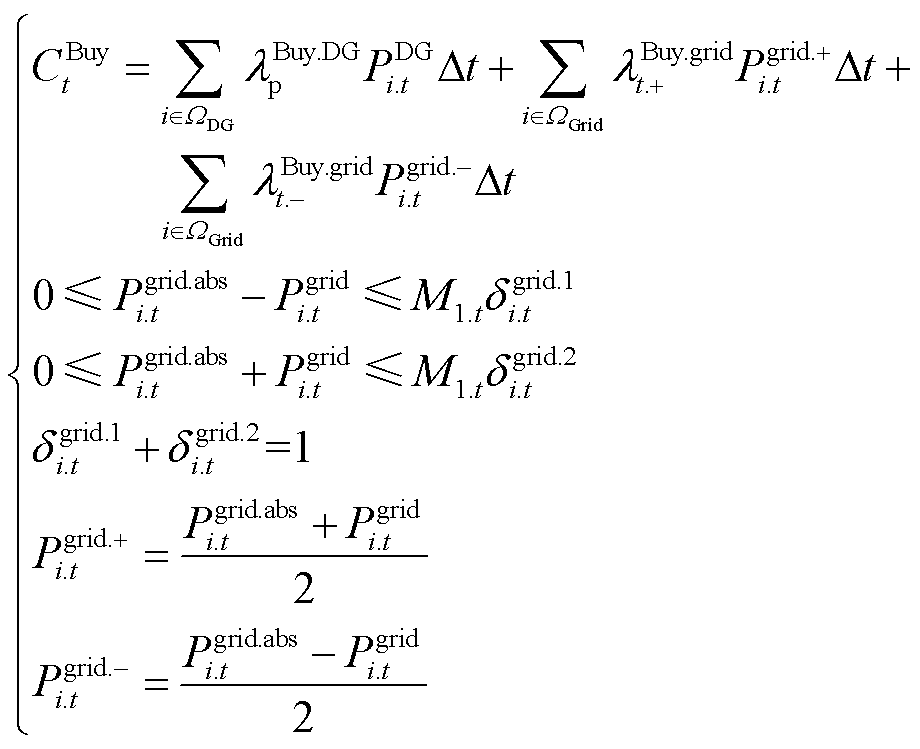 (27)
(27)
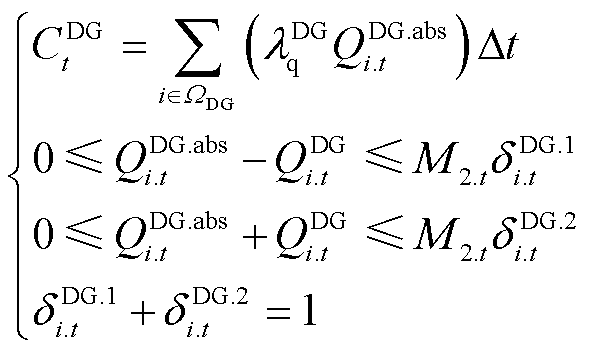 (28)
(28)
式中,Pgrid.+ i.t、Pgrid.- i.t、Pgrid.abs i.t和QDG.abs i.t均为辅助变量,dgrid.1 i.t和dgrid.2 i.t、dDG.1 i.t和dDG.2 i.t均为二进制变量,M1.t和M2.t均为Big-M法中足够大的正数。
此外,式(12)所示电源侧逆变器容量约束由于二次项的存在而呈现非线性特征,可采用分段线性逼近思想,将二阶函数近似为如下一阶线性化形式,其具体推导过程见附录。
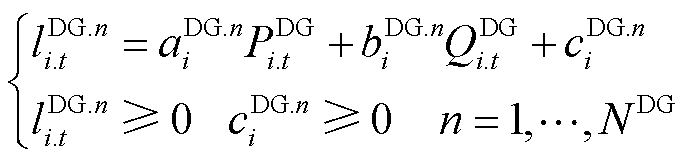 (29)
(29)
式中,n为当前分段编号;aDG.n i、bDG.n i和cDG.n i均为新能源逆变器容量约束的第n条分段线段表达式系数;NDG为新能源逆变器容量约束的线性化分段段数。
2.1.2 电网侧线性化策略
电网侧潮流模型的高度非线性增加了模型求解难度,而基于热启动环境的低非线性度潮流模型准确度高,计算高效[29],为此本文采用该方法将支路潮流约束式(22)线性化为
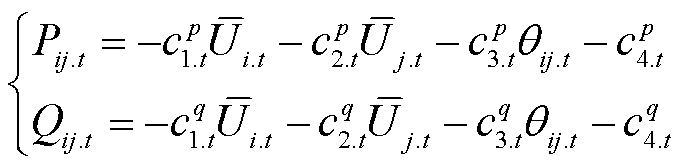 (30)
(30)
式中,cp 1.t,  , cq 4.t为常系数,详见附录式(A2)~式(A4);
, cq 4.t为常系数,详见附录式(A2)~式(A4);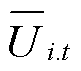 和
和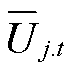 为节点电压幅值二次方变量。此时,节点电压约束式(24)也相应变为
为节点电压幅值二次方变量。此时,节点电压约束式(24)也相应变为
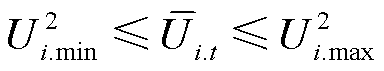 (31)
(31)
此外,电网侧的节点功率平衡约束式(23)由于存在连续变量和离散变量乘积项而呈现非线性特征,可引入辅助变量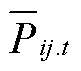 和
和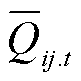 ,并利用Big-M法,将式(23)等价转换为
,并利用Big-M法,将式(23)等价转换为
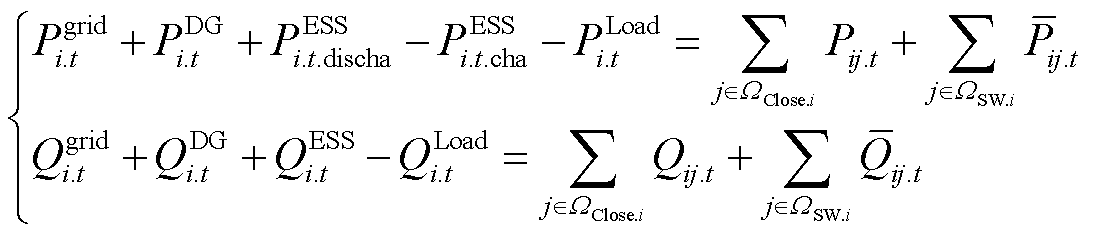 (32)
(32)
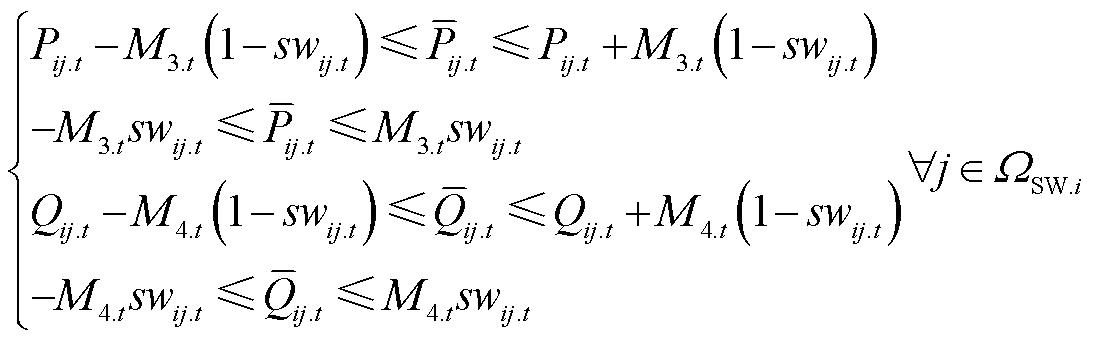 (33)
(33)
式中,M3.t和M4.t为Big-M法中足够大的正数。
针对电网侧的网损成本式(5)和支路电流约束式(25)含有支路电流非线性项,定义支路电流幅值二次方变量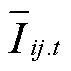 ,令
,令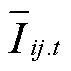 =I2 ij.t,可将
=I2 ij.t,可将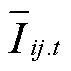 表示为式(34),其详细推导过程见附录。
表示为式(34),其详细推导过程见附录。
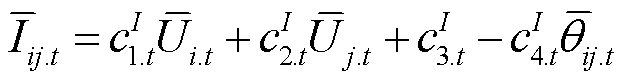 (34)
(34)
式中,cI 1.t,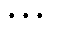 , cI 4.t为常系数,具体表达式见附录式(A10)。此时,可引入辅助变量
, cI 4.t为常系数,具体表达式见附录式(A10)。此时,可引入辅助变量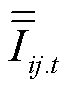 和足够大正数M5.t,利用变量替换和Big-M法将式(5)和式(25)线性化为
和足够大正数M5.t,利用变量替换和Big-M法将式(5)和式(25)线性化为
 (35)
(35)
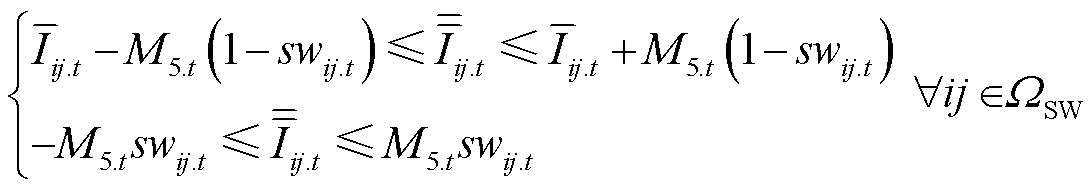 (36)
(36)
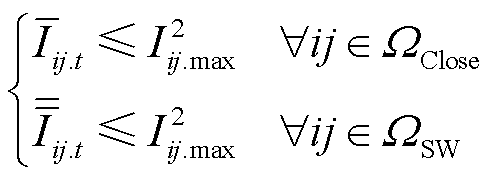 (37)
(37)
针对电网侧的动态重构非线性约束公式(13),引入二进制变量dij.t.1和dij.t.2,以及足够大正数M6.t,利用Big-M法等价线性化处理式(13)中绝对值函数,得到
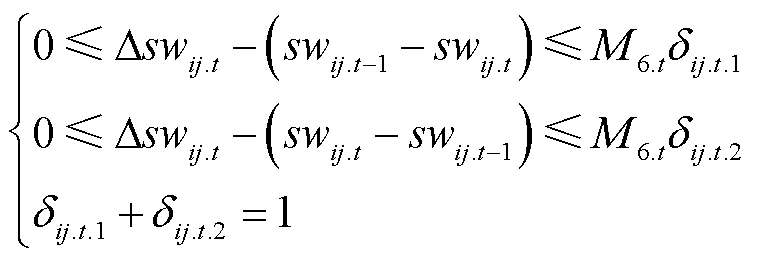 (38)
(38)
2.1.3 负荷侧线性化策略
针对负荷侧的灵活调控成本公式(9)存在绝对值函数项,引入辅助变量和二进制变量,利用Big-M法等价处理为
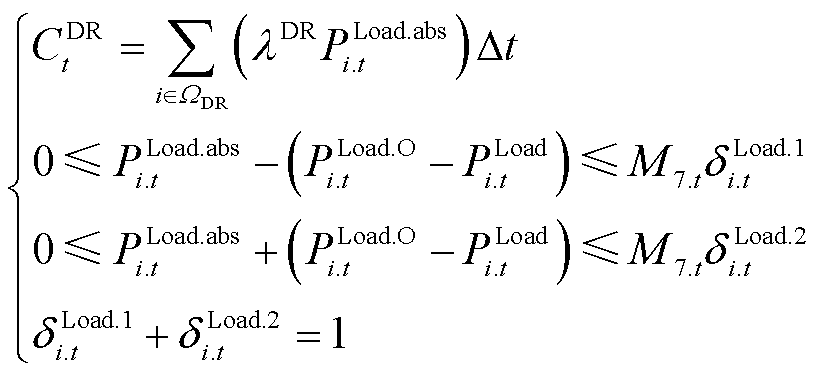 (39)
(39)
式中,PLoad.abs i.t为辅助变量;dLoad.1 i.t和dLoad.2 i.t为二进制变量;M7.t为Big-M法中足够大正数。
2.1.4 储能侧线性化策略
储能侧的运行成本式(10)和充放电功率约束式(19)由于存在绝对值函数和连续变量乘积项而呈现非线性特征,可引入变量,并利用Big-M法对其依次等价线性化为
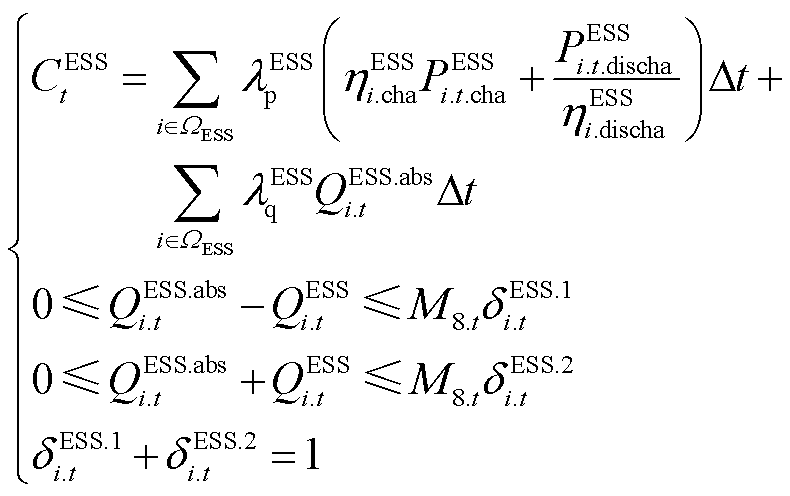 (40)
(40)
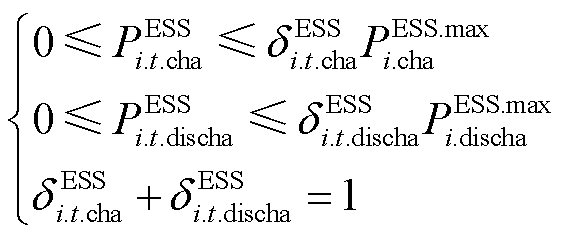 (41)
(41)
式中,QESS.abs i.t为辅助变量;dESS.1 i.t和dESS.2 i.t、dESS i.t.cha和dESS i.t.discha为二进制变量;M8.t为Big-M法中足够大正数。
储能逆变器容量约束式(20)的分段线性化方法同式(12)类似,此处不再赘述,式(20)可转换为
 (42)
(42)
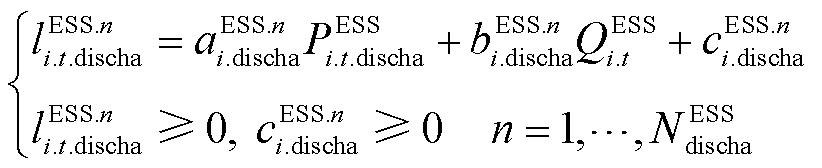 (43)
(43)
式中,aESS.n i.cha, , cESS.n i.discha为储能逆变器容量约束的第n条分段线段表达式系数;NESS cha和NESS discha分别为储能逆变器容量约束的线性化分段段数。
, cESS.n i.discha为储能逆变器容量约束的第n条分段线段表达式系数;NESS cha和NESS discha分别为储能逆变器容量约束的线性化分段段数。
可见,在原始模型的线性化过程中,本文基于等价线性化策略和高准确度的近似线性化策略,处理了经济目标函数中的非线性项以及约束条件中的非线性项,将原模型转换为基于热启动环境下的MOMILP问题,实现了模型的高效求解。
考虑多灵活性资源协调调度将产生迥异的消纳策略,为避免传统多目标求解方法在求解中产生无效支配解,本文设计了基于双层嵌套优化结构的求解方法。首先,基于线性化后的新能源优化消纳模型,确定最优非支配解的可行域,即求解Pareto最优解集中目标函数FDG的区间范围,并将FDG作为外层遍历指标,然后,内层求解在不同外层目标函数FDG指标约束下的内层目标函数FEC最优值,以获得Pareto最优解集。求解流程如图2所示。
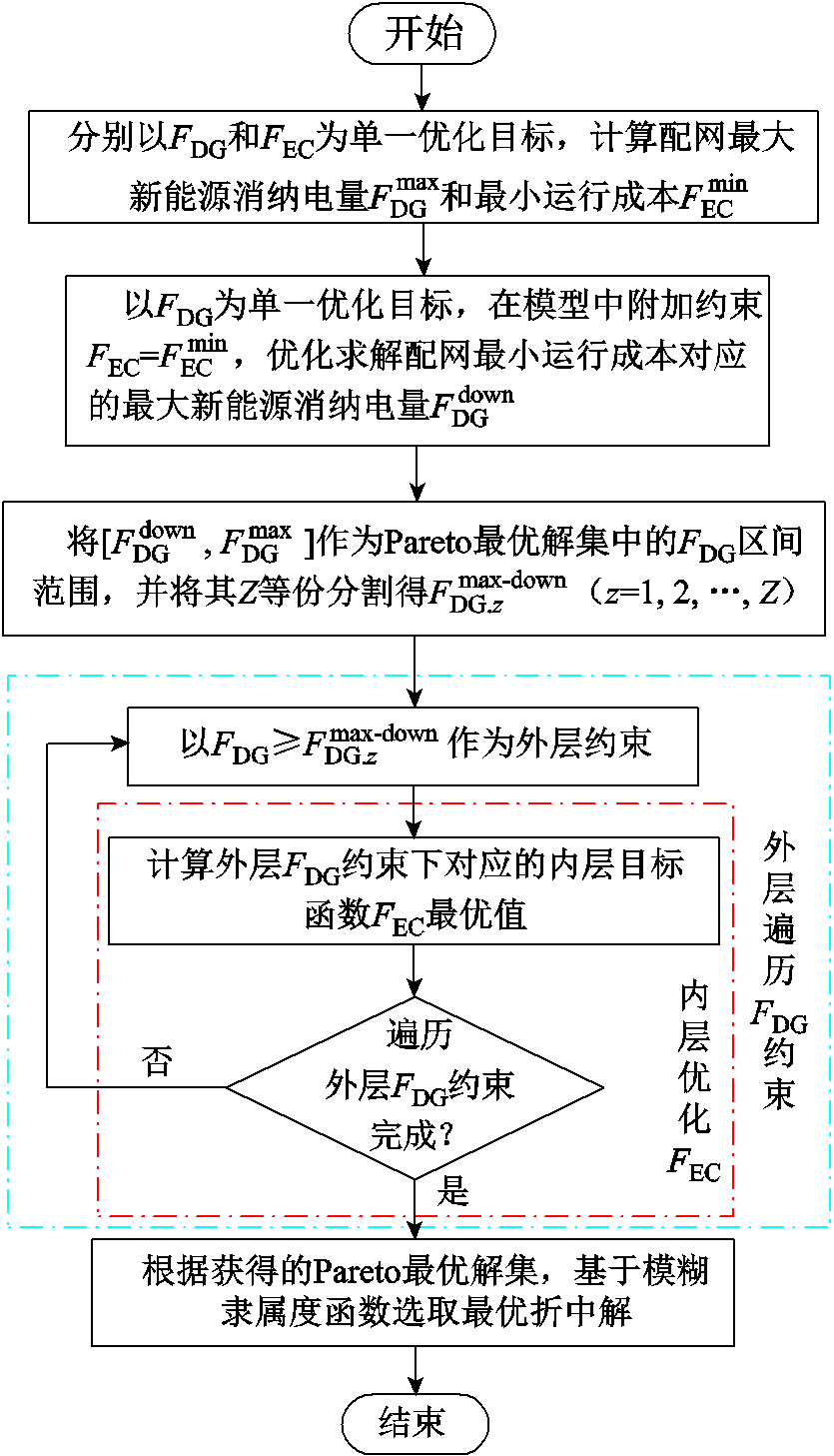
图2 优化消纳模型的求解流程
Fig. 2 Flow chart of the solution for the proposed model
具体步骤简述如下:
(1)在模型中分别仅考虑目标函数FDG和FEC,优化求解配网最大的新能源消纳电量Fmax DG和最小的运行成本Fmin EC。
(2)将FEC=Fmin EC加入优化模型中,求解目标函数FDG,获得配网在最小运行成本时所对应的最大新能源消纳电量Fdown DG。
(3)选取区间[Fdown DG,Fmax DG]作为Pareto最优解集中FDG范围,因为若FDG<Fdown DG,必然存在FEC≥ Fmin EC,即获得无效支配解。
(4)将FDG范围进行Z等份分割得Fmax-downDG.z(z=1, 2,  , Z),并将FDG≥Fmax-downDG.z作为模型外层约束。
, Z),并将FDG≥Fmax-downDG.z作为模型外层约束。
(5)内层优化求解在外层目标函数FDG约束下对应的内层目标函数FEC最优值,经过遍历外层目标函数FDG约束,可以得到Z组Pareto最优解集,并利用模糊隶属度函数[30]选取最优折中解。
步骤(1)、步骤(2)和步骤(5)均涉及求解单目标混合整数线性优化问题,其详细求解流程如图3所示。
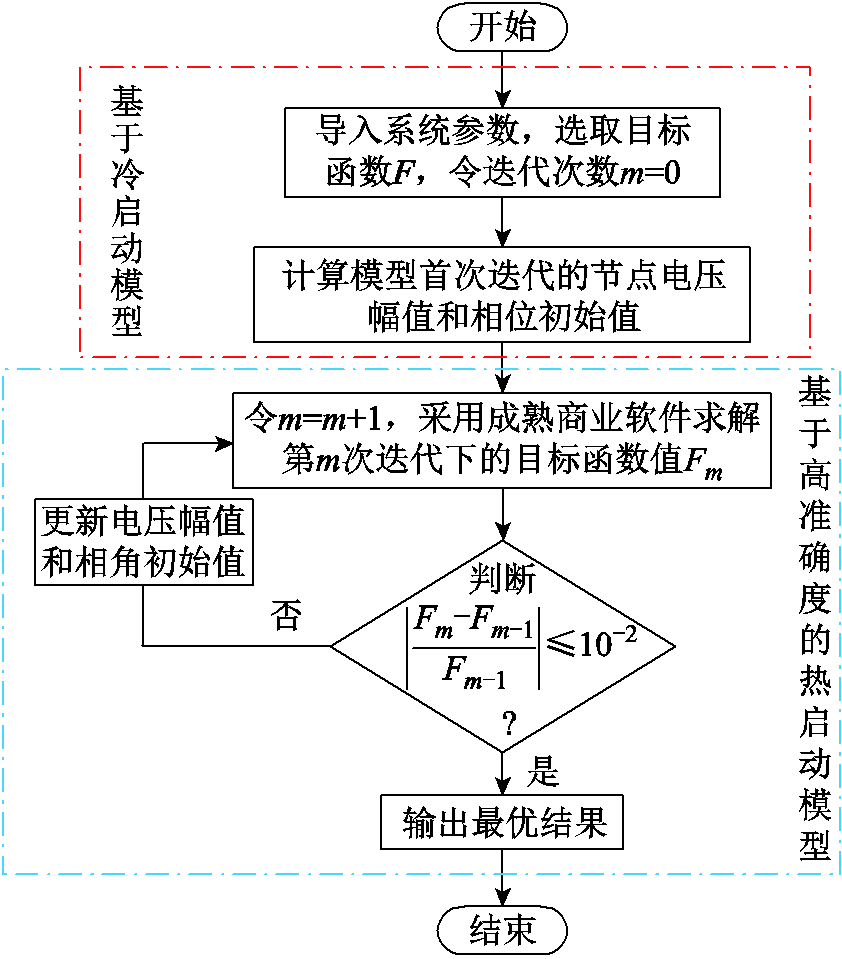
图3 单目标混合整数线性优化问题求解流程
Fig. 3 Flow chart of solving single-objective mixed integer linear optimization problem
值得注意的是,图3中计算模型首次迭代的节点电压和相位初始值,传统方法普遍是基于电网历史运行数据或直流最优潮流获取[29],但电网历史信息难以完整获取,而直流最优潮流则忽略了无功功率和电压幅值,无法保证热启动初值的高质量性,增大了模型收敛难度。为此,本文结合电网实际运行状况,基于支路两端参数的近似假设[31],忽略网络损耗,将原始潮流模型部分简化为式(44)~式(47),用于替换MOMILP模型中的约束式(30)、式(31)、式(34)和式(37),可以将模型转换为无需初值的冷启动模型,通过商业软件直接求解,以提供首次迭代所需的高质量初始值,从而降低模型优化求解的收敛次数,提高求解效率。
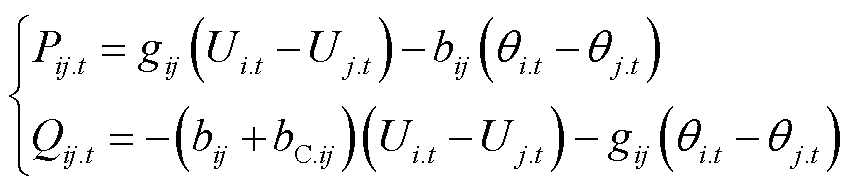 (44)
(44)
 (45)
(45)
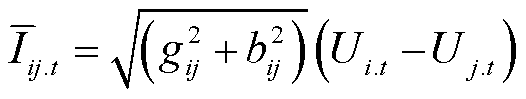 (46)
(46)
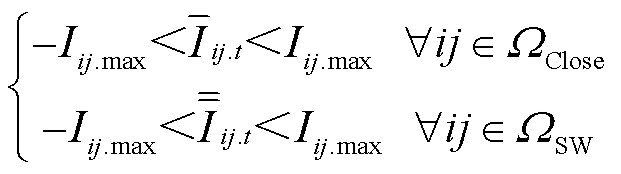 (47)
(47)
本文采用IEEE 33节点系统和某地级市110kV实际配网,基于如下三种方法进行仿真,验证所提方法的有效性,并深入分析多灵活性资源的灵活互动特性对新能源消纳水平的影响。
方法1:本文提出的新能源消纳策略制定方法,即考虑多灵活性资源协调调度制定新能源消纳策略。
方法2:基于文献[18]所提的新能源消纳策略制定方法,即仅考虑配网动态重构制定新能源消纳策略。
方法3:基于文献[22]所提的新能源消纳策略制定方法,即考虑可控负荷和储能装置的灵活有功调节能力制定新能源消纳策略。
采用如图4所示的IEEE33节点配电系统[21,32]进行仿真分析。新能源和储能的接入容量见表1、表2。新能源、遥控开关、可控负荷和储能的技术参数见附表1[33-39],相关经济参数见附表2[39-43]。
图4 IEEE 33节点配电系统
Fig.4 IEEE 33 bus distribution system
表1 新能源配置参数
Tab.1 Configuration parameters of renewable energy

接入节点469132027 容量/kW1 8001 6001 8001 6001 6001 800
表2 储能配置参数
Tab. 2 Configuration parameters of energy storage

接入节点容量/(kW·h)最大充放电功率/kW 14800160 17800160
3.1.1 仿真结果及分析
针对IEEE 33节点系统,采用上述三种方法分别制定配网新能源消纳策略。其中,配网新能源消纳情况和运行成本分别见表3、表4;24个时段的弃风光电量如图5所示;灵活性调控前后系统节点电压和支路载流量时序分布分别如图6和图7所示;多灵活性资源的调控情况如图8和图9所示。
表3 三种方法的仿真结果
Tab. 3 Simulation results under three methods
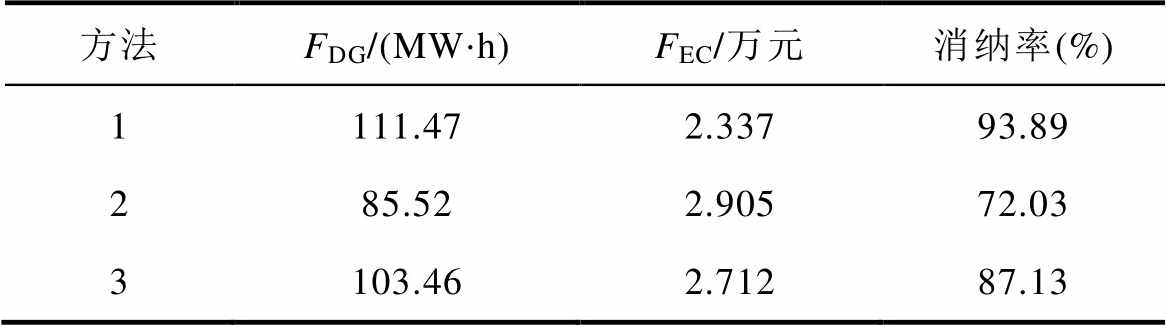
方法FDG/(MW⋅h)FEC/万元消纳率(%) 1111.472.33793.89 285.522.90572.03 3103.462.71287.13
表4 三种方法的经济性成本
Tab. 4 Costs results under three methods (单位:万元)
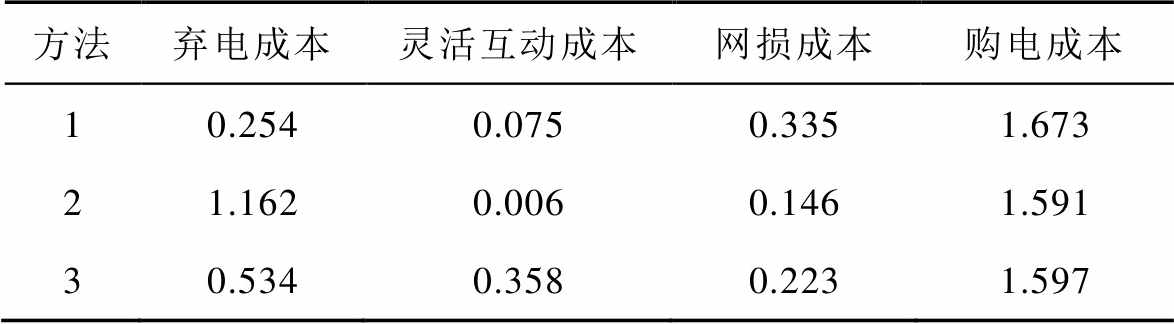
方法弃电成本灵活互动成本网损成本购电成本 10.2540.0750.3351.673 21.1620.0060.1461.591 30.5340.3580.2231.597
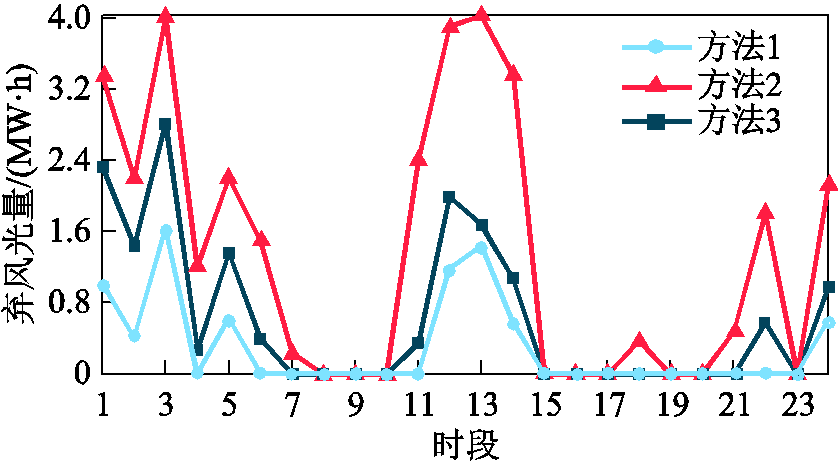
图5 弃风光电量
Fig.5 Renewable energy shedding
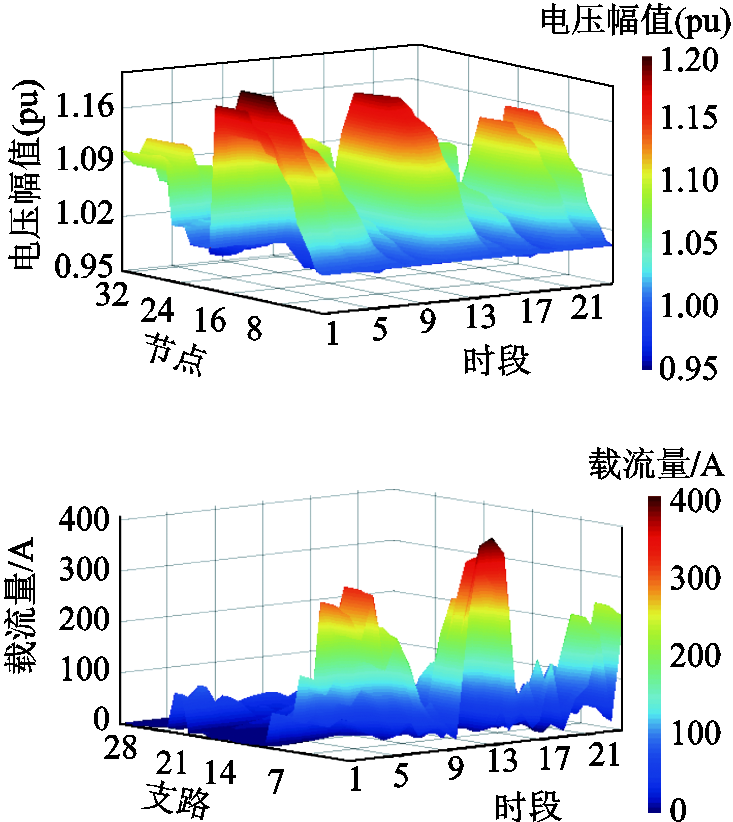
图6 灵活调控前节点电压和支路载流量
Fig.6 Node voltage and branch current before flexible regulation
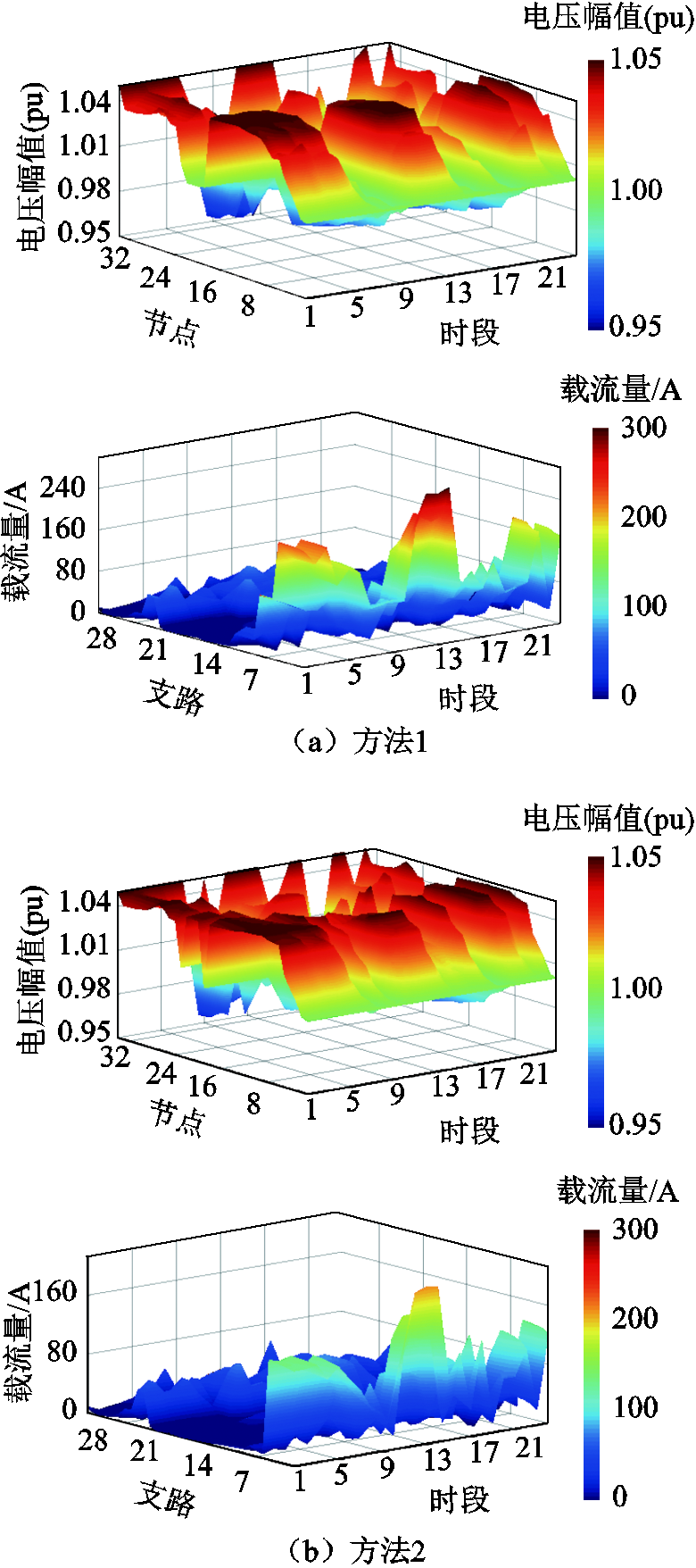

图7 灵活调控后节点电压和支路载流量
Fig. 7 Node voltage and branch current after flexible regulation
由表3和图5可知,本文方法(方法1)所得新能源消纳电量、消纳率及配网运行成本均最优,弃风光时段和弃风光电量最少。与方法2和3相比,新能源消纳电量分别提升了23.28%和7.19%,消纳率分别提高了21.86%和6.76%,运行成本分别降低了24.30%和16.05%,弃风光时段分别降低了7段和4段,弃风光电量分别降低了25.95MW⋅h和8.01MW⋅h。
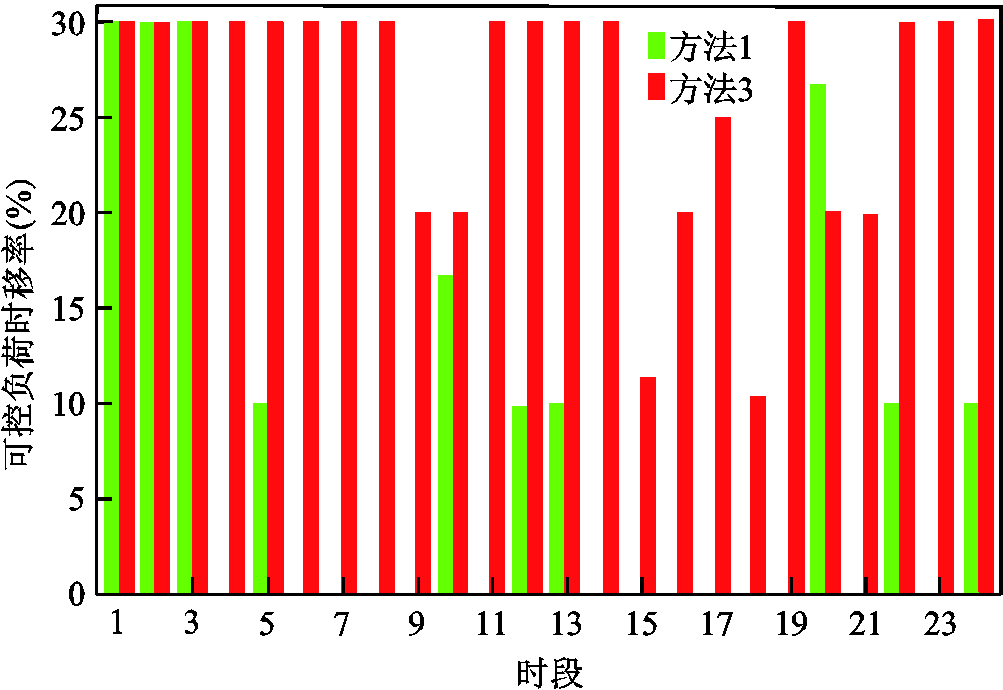
图8 方法1和方法3可控负荷的灵活调控对比
Fig.8 Comparison of flexible regulation of controllable load under method 1 and method 3
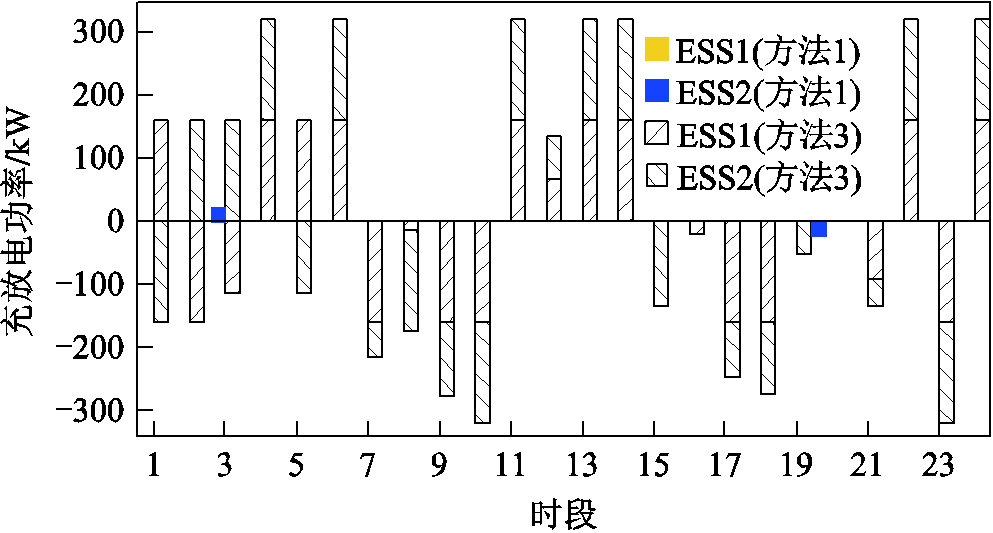
图9 方法1和方法3储能的灵活调控对比
Fig.9 Comparison of flexible regulation of energy storage under method 1 and method 3
由表4可知,相比于方法2和3,本文方法的弃电成本分别下降了0.908万元和0.28万元。尽管本文方法融入了多种灵活性调控措施,但其灵活互动成本相比方法3仍降低了0.283万元。这是由于所提模型兼顾了消纳电量和运行经济性的综合要求,故能合理利用多灵活性资源的灵活互动特性,以最小的运行成本实现新能源最大化消纳,而方法3忽略了系统运行成本。本文方法的网损成本和购电成本均高于方法2和方法3,其原因是本文在利用多灵活性资源的灵活互动特性促进新能源消纳时,会引发逆功率传输,增加了线路损耗,进而增大了网损和新能源购电量和购电费用。
为分析多灵活性资源协调调度对新能源消纳限制因素的缓解作用,图6给出了不考虑灵活性调节措施的系统节点电压和支路载流量情况。可见,高比例新能源接入后,配网出现了大面积节点电压越限和线路过载现象。图7给出了三种方法所得各时段的节点电压和支路载流量情况。方法2与方法3在部分时段的电压水平过高,而本文方法利用多灵活性资源协调调度有效缓解了电压过高的问题,提升了新能源消纳电量。
由图8、图9可知,为提升新能源消纳电量,方法3中可控负荷和储能分别在全天24个时段和23个时段内参与响应,灵活性调控次数分别为24次和23次,本文中可控负荷时移次数和储能充放电次数仅为10次和2次,可控负荷功率时移次数和时移量及储能充放电次数和充放电量均明显降低。
此外,方法1在方法2、方法3灵活性调控措施基础上,同时计及了新能源和储能逆变器灵活动态无功补偿能力,如图10所示,而方法2则根据固定功率因数确定新能源无功功率,方法3未计及二者无功出力,方法2与方法3均没有充分利用新能源和储能的无功补偿作用来缓解消纳的限制因素。
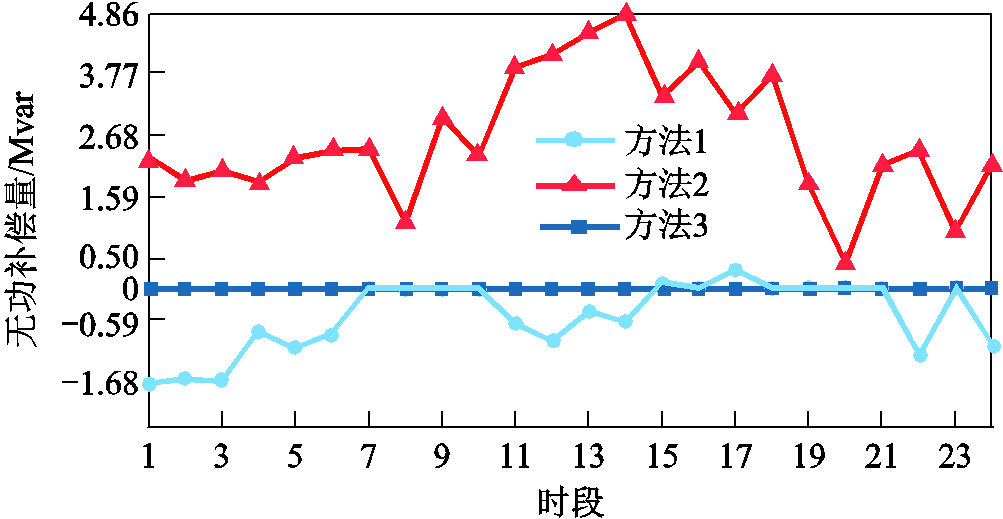
图10 新能源和储能动态无功补偿量
Fig.10 Dynamic reactive power compensation results of renewable energy and energy storage
综上所述,本文方法从整体上协调调度多灵活性资源,最大化利用多环节灵活互动特性消除限制新能源消纳的制约因素。兼顾经济性和消纳电量的综合要求,以增加少量的网损成本和购电成本换取弃电成本的大幅下降,避免了可控负荷和储能等灵活性调节资源的频繁调度。
3.1.2 所提求解方法的计算性能分析
为验证本文提出的优化求解方法,分别选用本文方法、优先目标规划法[44]、模糊决策法[45]、理想点法[46]、多目标粒子群法[47]和ε-约束法[24]求解本文提出的优化消纳模型,计算结果见表5。
由表5可知,与本文方法相比,优先目标规划法和模糊决策法的消纳率分别提升了4.58%和4.56%,但其经济成本分别增加了9.46%和9.24%,这意味着所得消纳策略提升了少量消纳量,但需要付出大量的经济代价。基于理想点法和多目标粒子群算法求解本文模型,需要结合启发式算法,而本文构建的模型涉及大量的非凸和非线性约束、离散和连续型优化变量,使得启发式算法和智能算法出现“维数灾”问题,耗费大量时间后仍无法收敛。基于ε-约束法可实现新能源全额消纳,消纳率提升了6.11%,但其经济成本相对增加了18.53%,更为关键的是,其所得消纳策略导致配网出现了节点电压越限和线路过载的现象。主要原因在于ε-约束法结合二阶锥优化求解本文模型时的松弛间隙最大值为10-2,并不满足二阶锥松弛收敛判据数量级要求[24,48],这表明基于ε-约束法的求解结果是在松弛域内获得,本文模型不满足其求解准确性的充要条件[48]。由此可以看出,与五种现有方法相比,本文提出的双层嵌套结构和复合型线性化策略共济的高效求解方法具有明显优势,可提供更科学的新能源消纳策略。
表5 不同求解算法的计算结果
Tab.5 Calculation results under different solving methods

求解算法FDG/(MW⋅h)消纳率(%)相对量(%)FEC/万元相对量(%) 优先目标规划116.9198.474.582.5589.46 模糊决策法116.8998.454.562.5539.24 理想点法————— 多目标粒子群————— ε-约束法118.731006.112.77018.53 本文算法111.4793.89—2.337—
3.2.1 算例说明
为了进一步验证所提方法的适应性,采用中国某地级市110kV高压配电系统进行仿真分析。为方便分析,将原系统等值简化包含48个节点和48条支路的配电系统,网络拓扑结构如图11所示。新能源装机总容量为358MW(光伏145MW/风电213MW),渗透率为51.79%。新能源和储能电站的相关参数分别见附表3、附表4。
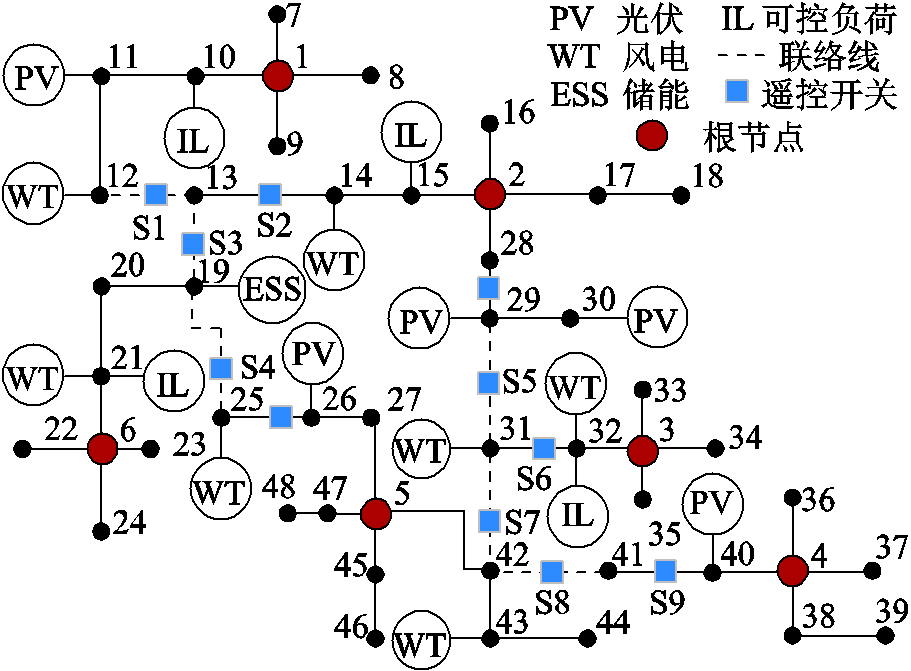
图11 某地级市110 kV配网拓扑
Fig.11 Topology diagram of a practical 110 kV distribution network in China
3.2.2 仿真结果及分析
三种方法的仿真结果见表6。与方法2、方法3相比,本文方法使得新能源消纳电量分别提高了25.23%和7.36%,消纳率分别提高了24.89%和7.26%,总运行成本分别减少了32.14%和10.74%。仿真结果再次验证了多灵活性资源协调调度对促进新能源消纳和降低运行成本的积极作用。
表6 三种方法的仿真结果
Tab.6 Simulation results of three methods

方法FDG/(MW⋅h)FEC/万元消纳率(%) 13412115.1798.65 22551152.1973.76 33161127.5491.39
针对配电网新能源消纳中灵活性资源有功、无功调节与协调运行潜力挖掘不足等问题,本文构建了兼顾新能源消纳量和配电网经济运行水平的配电网多灵活性资源协调调度的新能源优化消纳模型,基于双层嵌套结构和复合型线性化策略,提出了优化消纳模型的高效求解方法。采用IEEE 33节点系统和某实际配网算例验证所提消纳策略的有效性和适应性,并得出如下结论:
1)在深入研究多灵活性资源协调调度对新能源优质消纳作用机理的基础上,通过全面刻画多环节灵活性资源的灵活互动特性,充分发挥多灵活性资源间的协调互动特性,显著提升了新能源消纳电量,大幅降低了配电网运行成本。
2)多灵活性资源的协调调度可充分利用源荷储侧灵活的有功-无功调节能力,以及网络侧灵活传输通道,可大幅改善配网潮流分布和电压水平,有效缓解配电网新能源消纳限制因素的制约作用。
3)多灵活性资源的协调调度策略存在多样化,将导致迥异的消纳策略,而统筹兼顾新能源消纳电量和配电网运行成本,构建多目标优化消纳模型,制定新能源消纳策略,可以经济、有效地协调调度多灵活性资源,达到以配电网运行成本最小化来实现新能源消纳电量最大化的目的。
4)设计双层嵌套结构优化求解方法,并基于复合型线性化策略线性化处理新能源优化消纳模型,能够在保证求解结果最优性的同时,大幅度降低求解难度,有效提升求解效率。
附 录
1. 基于供电环路非连通理论的配网动态重构
基于供电环路非连通理论的配网动态重构步骤如下:
1)获取配电网的拓扑结构、遥控开关、常闭开关等数据信息。
2)设计深度优先搜索算法,搜索构建网络中所有的供电环路。
3)依次计算配电网中的节点总数、根节点数量、常闭支路总数,以及各个供电环路中的支路数量和常闭支路数量。
4)基于上述数据,构建式(15)所示约束。
2. 模型线性化的相关说明
1)式(29)推导
新能源逆变器容量约束式(12)的分段线性化步骤如下:
(1)选取参数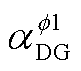 ,
, 和NDG,其中,
和NDG,其中,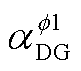 和
和 分别为新能源功率因数角
分别为新能源功率因数角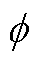 的余角。
的余角。
(2)如附图1所示,将[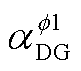 ,
,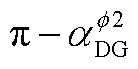 ]的圆弧范围均匀分成NDG份,依次连接各分点(如黄色线段所示),获得NDG条线段,即
]的圆弧范围均匀分成NDG份,依次连接各分点(如黄色线段所示),获得NDG条线段,即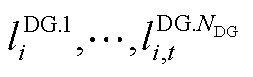 ,任意一条线段可表示为
,任意一条线段可表示为
 (A1)
(A1)

附图1 新能源逆变器容量分段线性化示意图
App.Fig.1 Diagram of piecewise linearization of renewable energy inverter capacity
(3)基于解析几何理论可知,利用NDG条线段对应的线性约束组合可近似约束式(29)。
2)式(30)中的常系数
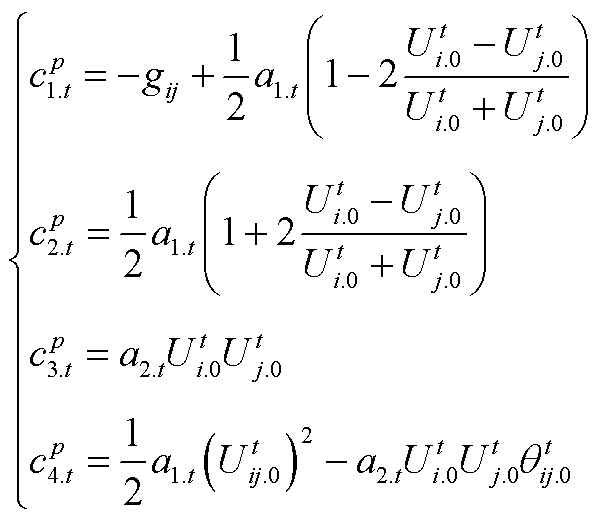 (A2)
(A2)
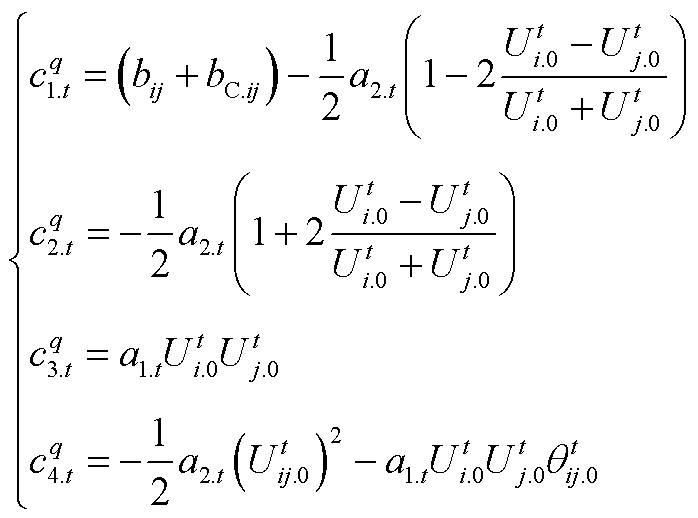 (A3)
(A3)
式中,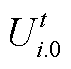 、
、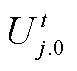 、
、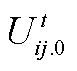 和
和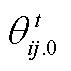 分别为节点i、j的电压幅值初始值、电压幅值初始值差值和电压相位初始值差值,可通过热启动情况下节点电压幅值和相角的初始值获得,并在求解过程中不断迭代更新;a1.t和a2.t为常系数,可表示为
分别为节点i、j的电压幅值初始值、电压幅值初始值差值和电压相位初始值差值,可通过热启动情况下节点电压幅值和相角的初始值获得,并在求解过程中不断迭代更新;a1.t和a2.t为常系数,可表示为
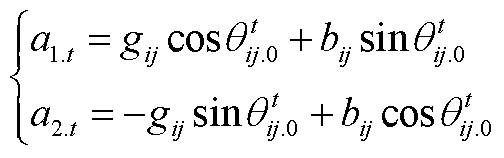 (A4)
(A4)
3)式(34)推导
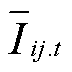 可以表示为
可以表示为
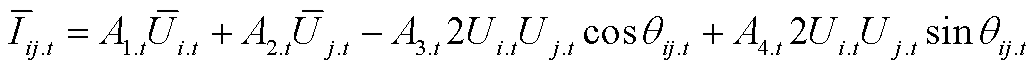 (A5)
(A5)
式中,A1.t,  , A4.t为常系数,其计算表达式为
, A4.t为常系数,其计算表达式为
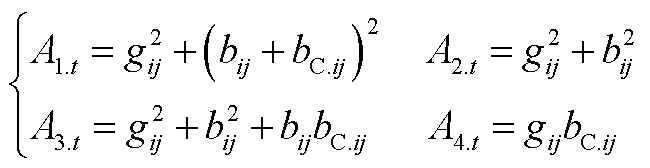 (A6)
(A6)
利用三角函数泰勒级数展开法和交叉项线性化方法,可将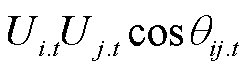 和
和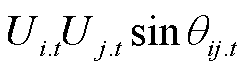 表示为[29]
表示为[29]
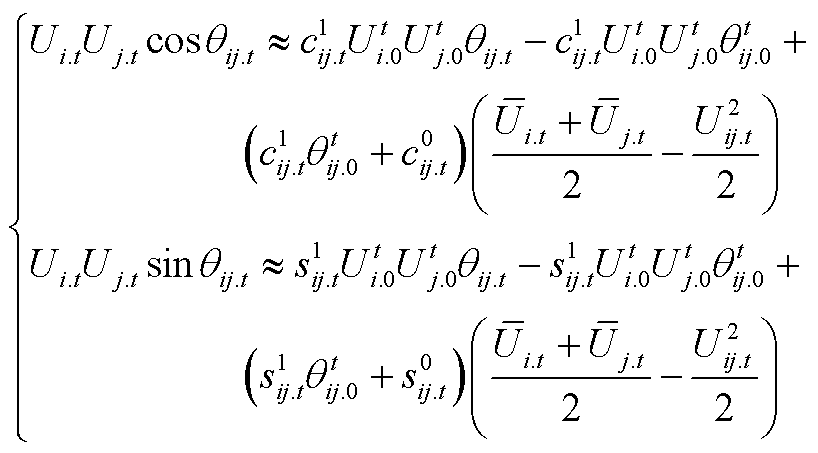 (A7)
(A7)
式中,c1 ij.t、c0 ij.t、s1 ij.t、s0 ij.t分别为
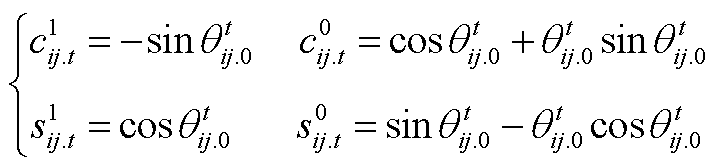 (A8)
(A8)
U2 ij.t为
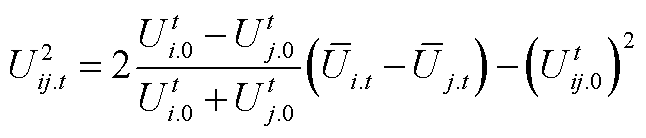 (A9)
(A9)
将式(A7)~式(A9)代入式(A5),可得 的线性表达式(34),其常系数可以表示为
的线性表达式(34),其常系数可以表示为
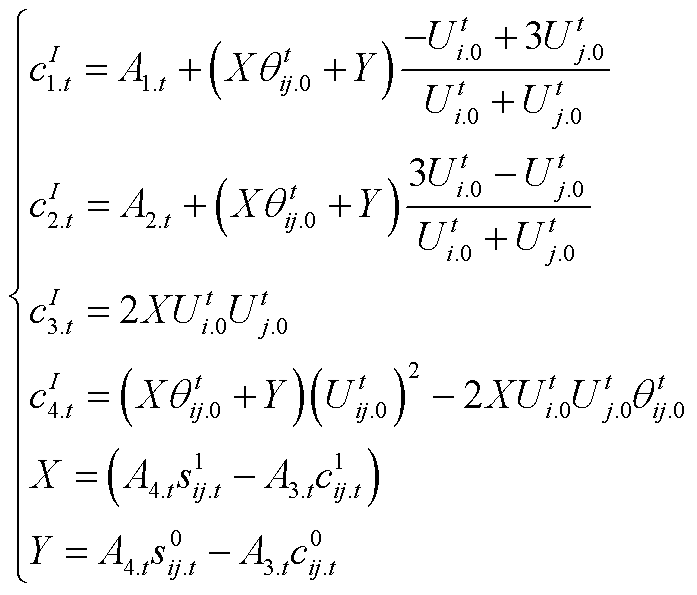 (A10)
(A10)
3. 仿真算例的相关数据
附表1 多灵活性资源灵活互动的技术参数[33-39]
App.Tab.1 Technical parameters of multi-flexible resources flexible interactive[33-39]

参数数值 新能源功率因数限值PFDG i.down和PFDG i.up0.8 遥控开关全天内最大动作次数swunit ij.max3 可控负荷功率调节能力限值gDR i(%)10 储能的初始荷电状态SOCi.t=0(%)50 储能的充放电效率hESS i.cha和hESS i.discha0.95 储能荷电状态上限SOCmax i(%)90 储能荷电状态下限SOCmin i(%)25 储能功率因数限值PFESS i.down和PFESS i.up0.75
附表2 模型经济参数[39-43]
App.Tab.2 Economic parameters for the model[39-43]

参数数值 新能源上网电价lBuy.DGp/[元/(kW·h)]0.3 新能源弃电惩罚系数lDGcurt/[元/(kW·h)]0.35 新能源无功辅助服务补偿系数lDGq/[元/(kvar·h)]0.05 单个开关动作成本系数lSW/(元/次)5 可控负荷单位调度成本系数lDR/[元/(kW·h)]0.4 储能单位充放电折旧系数lESSp/[元/(kW·h)]0.6 储能单位无功功率折旧系数lESSq/[元/(kvar·h)]0.067 售电电价lBuy.grid t.-/[元/(kW·h)]0.3 网损成本系数lLoss /[元/(kW·h)]0.68
附表3 新能源基本参数
App.Tab.3 Parameters of renewable energy
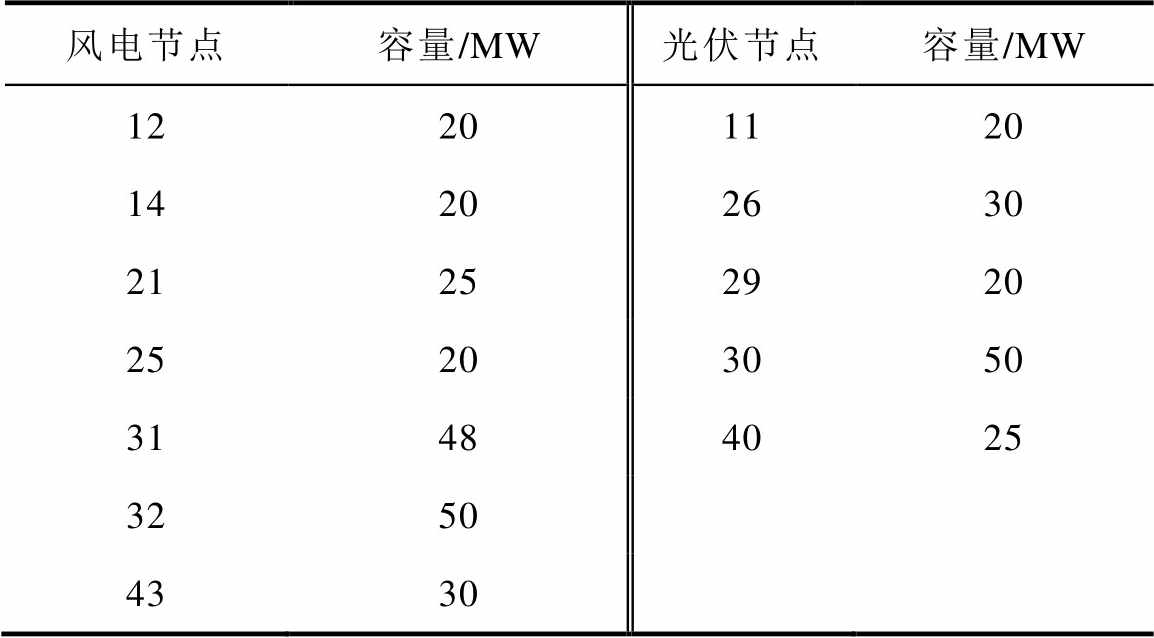
风电节点容量/MW光伏节点容量/MW 12201120 14202630 21252920 25203050 31484025 3250 4330
附表4 储能基本参数
App.Tab.4 Parameters of energy storage

储能节点储能容量/(MW·h)储能最大充放电功率/MW 1952.5
参考文献
[1] 习近平.继往开来,开启全球应对气候变化新征程[EB/OL].人民网,[2020-12-14].http://env.people. com.cn/n1/2020/1214 /c1010-31965084.html.
[2] 央视网.习近平主持召开中央财经委员会第九次会议强调推动平台经济规范健康持续发展把碳达峰碳中和纳入生态文明建设整体布局[EB/OL].[2021-03-15].https://news.cctv.com/2021/ 03/15/ARTIFUhtqyI0GxogiEDWyY28210315.shtml.
[3] 新华社.中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要[EB/OL]. [2021-03-13].http://www.gov.cn/xinwen/2021-03/13/ content_5 59 2681.htm.
[4] Cruz M R M, Fitiwi D Z, Santos S F, et al. Multi-flexibility option integration to cope with large-scale integration of renewables[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 48-60.
[5] 王雪纯, 陈红坤, 陈磊. 提升区域综合能源系统运行灵活性的多主体互动决策模型[J]. 电工技术学报, 2021, 36(11): 2207-2219.
Wang Xuechun, Chen Hongkun, Chen Lei. Multi-player interactive decision-making model for operational flexibility improvement of regional integrated energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2207-2219.
[6] 孙惠, 翟海保, 吴鑫. 源网荷储多元协调控制系统的研究及应用[J]. 电工技术学报, 2021, 36(15): 3264-3271.
Sun Hui, Zhai Haibao, Wu Xin. Research and application of multi-energy coordinated control of generation, network, load and storage[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3264-3271.
[7] 国家发展改革委, 国家能源局. 国家发展改革委国家能源局关于推进电力源网荷储一体化和多能互补发展的指导意见(发改能源规[2021]280号) [EB/OL]. [2021-02-25]. http://www.gov.cn/ zhengce/ zhengceku/2021-03/06/content_5590895.htm.
[8] 徐浩, 李华强. 火电机组灵活性改造规划及运行综合随机优化模型[J]. 电网技术, 2020, 44(12): 4626-4638.
Xu Hao, Li Huaqiang. Planning and operation stochastic optimization model of power systems considering the flexibility reformation[J]. Power System Technology, 2020, 44(12): 4626-4638.
[9] 孙辉, 刘鑫, 贲驰, 等. 含风储一体化电站的电力系统多目标风险调度模型[J]. 电力系统自动化, 2018, 42(5): 94-101.
Sun Hui, Liu Xin, Ben Chi, et al. Multi-objective risk scheduling model of power system containing power station with integrated wind power and energy storage[J]. Automation of Electric Power Systems, 2018, 42(5): 94-101.
[10] 李则衡, 陈磊, 路晓敏, 等. 基于系统灵活性的可再生能源接纳评估[J]. 电网技术, 2017, 41(7): 2187-2194.
Li Zeheng, Chen Lei, Lu Xiaomin, et al. Assessment of renewable energy accommodation based on system flexibility analysis[J]. Power System Technology, 2017, 41(7): 2187-2194.
[11] 周任军, 石亮缘, 汤吉鸿, 等. 多功率曲线协整度约束下的源-荷-储优化协整模型[J]. 中国电机工程学报, 2019, 39(12): 3454-3465.
Zhou Renjun, Shi Liangyuan, Tang Jihong, et al. Source-load-storage optimization cointegration model under multi-power curve cointegration degree constraints[J]. Proceedings of the CSEE, 2019, 39(12): 3454-3465.
[12] 徐箭, 胡佳, 廖思阳, 等. 考虑网络动态特性与综合需求响应的综合能源系统协同优化[J]. 电力系统自动化, 2021, 706(12): 40-48.
Xu Jian, Hu Jia, Liao Siyang, et al. Coordinated optimization of integrated energy system considering dynamic characteristics of network and integrated demand response [J]. Automation of Electric Power Systems, 2021, 706(12): 40-48.
[13] Mahmud N, Zahedi A. Review of control strategies for voltage regulation of the smart distribution network with high penetration of renewable distributed generation[J]. Renewable and Sustainable Energy Reviews, 2016, 64: 582-595.
[14] Verma A, Krishan R, Mishra S. A novel PV inverter control for maximization of wind power penetration[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6364-6373.
[15] Nguyen Q, Padullaparti H V, Lao K, et al. Exact optimal power dispatch in unbalanced distribution systems with high PV penetration[J]. IEEE Transactions on Power Systems, 2019, 34(1): 718-728.
[16] 龚思宇, 魏炜, 徐元孚, 等. 面向分布式电源最大消纳的配电网重构[J]. 电力系统及其自动化学报, 2017, 29(3): 7-11, 41.
Gong Siyu, Wei Wei, Xu Yuanfu, et al. Reconfiguration of distribution network for the maximum consumption of distributed generations[J]. Proceedings of the CSU-EPSA, 2017, 29(3): 7-11, 41.
[17] 刘路宁, 彭春华, 温泽之, 等. 基于配电网动态重构的分布式光伏消纳策略[J]. 电力自动化设备, 2019, 39(12): 56-62.
Liu Luning, Peng Chunhua, Wen Zezhi, et al. Distributed photovoltaic consumption strategy based on dynamic reconfiguration of distribution network[J]. Electric Power Automation Equipment, 2019, 39(12): 56-62.
[18] Lei Shunbo, Hou Yunhe, Qiu Feng, et al. Identification of critical switches for integrating renewable distributed generation by dynamic network reconfiguration[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 420-432.
[19] Wang Chong, Lei Shunbo, Ju Ping, et al. MDP-based distribution network reconfiguration with renewable distributed generation: approximate dynamic programming approach[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 3620-3631.
[20] Capitanescu F, Bilibin I, Romero E R. A comprehensive centralized approach for voltage constraints management in active distribution grid[J]. IEEE Transactions on Power Systems, 2014, 29(2): 933-942.
[21] Capitanescu F, Bilibin I. A tractable two-step MILP-QCP approach to on-line thermal constraint management in large radial active distribution systems[J]. Electric Power Systems Research, 2016, 140: 580-587.
[22] 沙熠, 邱晓燕, 宁雪姣, 等. 协调储能与柔性负荷的主动配电网多目标优化调度[J]. 电网技术, 2016, 40(5): 1394-1399.
Sha Yi, Qiu Xiaoyan, Ning Xuejiao, et al. Multi-objective optimization of active distribution network by coordinating energy storage system and flexible load[J]. Power System Technology, 2016, 40(5): 1394-1399.
[23] 黄伟, 熊伟鹏, 华亮亮, 等. 基于动态调度优先级的主动配电网多目标优化调度[J]. 电工技术学报, 2018, 33(15): 3486-3498.
Huang Wei, Xiong Weipeng, Hua Liangliang, et al. Multi-objective optimization dispatch of active distribution network based on dynamic schedule priority[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3486-3498.
[24] 郑能, 丁晓群, 郑程拓, 等. 含高比例光伏的配电网有功——无功功率多目标协调优化[J]. 电力系统自动化, 2018, 42(6): 33-39, 91.
Zheng Neng, Ding Xiaoqun, Zheng Chengtuo, et al. Multi-objective coordinated optimization of active and reactive power for distribution network integrated with high proportion of photovoltaic generation[J]. Automation of Electric Power Systems, 2018, 42(6): 33-39, 91.
[25] Zhu Xiaonan, Wang Hongliang, Zhang Wenyuan, et al. A novel single-phase five-level Transactionsformer-less photovoltaic (PV) inverter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 329-338.
[26] 徐成司, 董树锋, 朱嘉麒, 等. 基于供电环路非连通条件的配电网辐射状约束描述方法[J]. 电力系统自动化, 2019, 43(20): 82-94.
Xu Chengsi, Dong Shufeng, Zhu Jiaqi, et al. Description method of radial constraints for distribution network based on disconnection condition of power supply loop[J]. Automation of Electric Power Systems, 2019, 43(20): 82-94.
[27] 吴界辰, 艾欣, 胡俊杰. 需求侧资源灵活性刻画及其在日前优化调度中的应用[J]. 电工技术学报, 2020, 35(9): 1973-1984.
Wu Jiechen, Ai Xin, Hu Junjie. Methods for characterizing flexibilities from demand-side resources and their applications in the day-ahead optimal scheduling[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1973-1984.
[28] 白桦, 王正用, 李晨, 等. 面向电网侧、新能源侧及用户侧的储能容量配置方法研究[J]. 电气技术, 2021, 22(1): 8-13.
Bai Hua, Wang Zhengyong, Li Chen, et al. Research on capacity allocation method of energy storage for grid side, new energy side and user side[J]. Electrical Engineering, 2021, 22(1): 8-13.
[29] Yang Zhifang, Bose A, Zhong Haiwang, et al. Optimal reactive power dispatch with accurately modeled discrete control devices: a successive linear approximation approach[J]. IEEE Transactions on Power Systems, 2017, 32, (3): 2435-2444.
[30] Sardou I G, Khodayar M E, Ameli M T. Coordinated operation of natural gas and electricity networks with microgrid aggregators[J]. IEEE Transactions on Smart Grid, 2018, 9(1): 199-210.
[31] Yuan Haoyu, Li Fangxing, Wei Yanli, et al. Novel linearized power flow and linearized OPF models for active distribution networks with application in distribution LMP[J]. IEEE Transactions on Smart Grid, 2017, 9(1): 438-448.
[32] Wang Shouxiang, Chen Sijia, Ge Leijiao, et al. Distributed generation hosting capacity evaluation for distribution systems considering the robust optimal operation of OLTC and SVC[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3): 1111-1123.
[33] Stelt S V D, AlSkaif T, Sark W V. Techno-economic analysis of household and community energy storage for residential prosumers with smart appliances[J]. Applied Energy, 2018(209): 266-276.
[34] Soroudi A, Rabiee A, Keane A. Distribution networks' energy losses versus hosting capacity of wind power in the presence of demand flexibility[J]. Renewable Energy, 2017(102): 316-325.
[35] Cerbantes M C, Fernández-Blanco R, Ortega-Vazquez M A, et al. Incorporating a nodal reactive power pricing scheme into the DisCo’s short-term operation[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 3720-3731.
[36] 赵冬梅, 陶然, 马泰屹, 等. 基于多智能体深度确定策略梯度算法的有功-无功协调调度模型[J]. 电工技术学报, 2021, 36(9):1914-1925.
Zhao Dongmei, Tao Ran, Ma Taiyi, et al. Active and reactive power coordinated dispatching based on multi-agent deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(9):1914-1925.
[37] Lazzeroni P, Repetto M. Optimal planning of battery systems for power losses reduction in distribution grids[J]. Electric Power Systems Research, 2019, 167: 94-112.
[38] 翟世涛, 刘泽槐, 杨家豪, 等. 考虑多时段并网点电压控制的光储容量匹配及优化运行[J]. 电网技术, 2017, 41(6): 1855-1865.
Zhai Shitao, Liu Zehuai, Yang Jiahao, et al. Capacity matching and optimal operation of photovoltaic-storage systems based on multi-period PCC voltage control[J]. Power System Technology, 2017, 41(6): 1855-1865.
[39] 谢琳宇, 唐忠, 黄星宇, 等. 考虑分布式电源和电动汽车不确定性的双层动态配网重构[J]. 电力系统保护与控制, 2020, 48(10): 1-11.
Xie Linyu, Tang Zhong, Huang Xingyu, et al. Bi-layer dynamic reconfiguration of a distribution network considering the uncertainty of distributed generation and electric vehicles[J]. Power System Protection and Control, 2020, 48(10): 1-11.
[40] 杨楠, 董邦天, 黄禹, 等. 考虑不确定性和多主体博弈的增量配电网源网荷协同规划方法[J]. 中国电机工程学报, 2019, 39(9): 2689-2702.
Yang Nan, Dong Bangtian, Huang Yu, et al. Incremental distribution network source-load collaborative planning method considering uncertainty and multi-agent game[J]. Proceedings of the CSEE, 2019, 39(9): 2689-2702.
[41] 麻秀范, 陈静, 余思雨, 等. 计及容量市场的用户侧储能优化配置研究[J]. 电工技术学报, 2020, 35(19): 4028-4037.
Ma Xiufan, Chen Jing, Yu Siyu, et al. Research on user side energy storage optimization configuration considering capacity market[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4028-4037.
[42] 张博, 唐巍, 蔡永翔, 等. 基于一致性算法的户用光伏逆变器和储能分布式控制策略[J]. 电力系统自动化, 2020, 44(2):86-96.
Zhang Bo, Tang Wei, Cai Yongxiang, et al. Distributed control strategy of residential photovoltaic inverter and energy storage based on consensus algorithm[J]. Automation of Electric Power Systems, 2020, 44(2): 86-96.
[43] 周丹, 孙可, 张全明, 等. 含多个综合能源联供型微网的配电网日前鲁棒优化调度[J]. 中国电机工程学报, 2020, 40(14): 4473-4485, 4727.
Zhou Dan, Sun Ke, Zhang Quanming, et al. Day-ahead robust dispatch of distribution network with multiple integrated energy system-based micro-grids[J]. Proceedings of the CSEE, 2020, 40(14): 4473-4485, 4727.
[44] 杨明, 程凤璐, 韩学山. 电力系统实时调度的有效静态安全域法[J]. 中国电机工程学报, 2015, 35(6): 1353-1362.
Yang Ming, Cheng Fenglu, Han Xueshan. Real-time dispatch based on effective steady-state security regions of power system[J]. Proceedings of the CSEE, 2015, 35(6): 1353-1362.
[45] 林凯骏, 吴俊勇, 郝亮亮, 等. 基于非合作博弈的冷热电联供微能源网运行策略优化[J]. 电力系统自动化, 2018, 42(6): 25-32.
Lin Kaijun, Wu Junyong, Hao liangliang, et al. Optimization of operation strategy for micro-energy grid with CCHE systems based on non-cooperative game[J]. Automation of Electric Power Systems, 2018, 42(6): 25-32.
[46] 孙建军, 张世泽, 曾梦迪, 等. 考虑分时电价的主动配电网柔性负荷多目标优化控制[J]. 电工技术学报, 2018, 33(2): 401-412.
Sun Jianjun, Zhang Shize, Zeng Mengdi, et al. Multi-objective optimal control for flexible load in active distribution network considering time-of-use tariff[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 401-412.
[47] 王侨侨, 曾君, 刘俊峰, 等. 面向微电网源–储–荷互动的分布式多目标优化算法研究[J]. 中国电机工程学报, 2020, 40(5): 1421-1432.
Wang Qiaoqiao, Zeng Jun, Liu Junfeng, et al. A distributed multi-objective optimization algorithm for resource-storage-load interaction of microgrid[J]. Proceedings of the CSEE, 2020, 40(5): 1421-1432.
[48] Li Qifeng, Ayyanar R, Vittal V. Convex optimization for DES planning and operation in radial distribution systems with high penetration of photovoltaic resources[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3): 985-995.
An Accommodation Strategy for Renewable Energy in Distribution Network Considering Coordinated Dispatching of Multi-Flexible Resources
Abstract Aiming at the challenges brought by flexible regulation resource scarcity and efficient accommodation with high penetration renewable energy integration under ‘double carbon goal’, an accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources is proposed. The method is established to depict the flexible interaction between multi-flexible resources. Considering both renewable energy accommodation and operating costs of distribution network. The accommodation optimization model for renewable energy is established considering coordinated dispatching of multi-flexible resources. In order to obtain the feasible region of non-dominant solutions of the accommodation optimization model, a multi-objective optimization solution method is established based on bi-layer embedded structure, and the composite linearization strategy is proposed to recast the complex multi-objective, non-linear and non-convex accommodation optimization model to a multi-objective mixed integer linear optimization model so that the accommodation optimization model can be efficiently solved. Finally, the effectiveness and applicability of the proposed accommodation strategy are verified by IEEE 33 bus system and a practical 110 kV distribution network in China.
keywords:Distribution network, renewable energy, multi-flexible resources, flexible interaction, multi-objective mixed integer optimization
DOI:10.19595/j.cnki.1000-6753.tces.211464
中图分类号:TM721
姜云鹏 男,1995年生,博士研究生,研究方向为配电网新能源消纳、区域综合能源系统等。E-mail:yunpeng_jiang@cqu.edu.cn
任洲洋 男,1986年生,副教授,博士生导师,研究方向为电力能源系统低碳运行及规划、人工智能等。E-mail:rzhouyang1108@163.com(通信作者)
国家重点研发计划资助项目(2019YFB1505400)。
收稿日期 2021-09-15
改稿日期 2021-12-15
(编辑 赫蕾)