 (1)
(1)
摘要 准确的风速预测对新能源并网稳定运行具有重要意义。为提高风速预测精度,该文构建基于双重Q学习的动态风速预测模型。首先,构建由五种基础预测算法组成的风速Q学习模型集,充分考虑风速波动情况和属性因素,通过Q学习强化学习算法选取出每时段的最佳预测模型,得到初步的风速预测结果;然后,基于风速预测结果计算预测误差,构建第二阶段的误差Q学习模型库,筛选该模型库中的最佳模型,以修正初步预测值,对误差进行校正,得到最终的预测结果;最后,通过对实际风场不同季节的风速进行预测,验证所提方法的有效性。
关键词:风速预测 Q学习 误差校正 动态模型选择
近年来风力发电技术在全世界得到了广泛的应用和发展。随着越来越多的风电集成到电网中,给电力系统的安全运行带来了巨大的挑战,这主要是由风的间歇性和波动性引起的[1-3]。因此,准确的风速预测对于风电并网及电力系统的稳定运行变得越发重要[4-6]。
现阶段主流的风速的预测方法主要有BP神经网络[7]、极限学习机[8]、核岭回归[9](Kernel Ridge Regression, KRR)等。文献[10]运用小波分解进行数据预处理,利用遗传算法对支持向量机进行参数优选,实现短期风速预测,得到较好的预测效果。文献[11]通过长短时记忆网络(Long-Short Term Memory, LSTM)对风向进行建模,并在预测模型中添加了误差校正环节,验证了误差校正的有效性。现如今,风速预测方法已不仅仅满足于单模型预测,越来越多的国内外学者将集成学习[12-13]、深度学习[14]等方法融入风速预测中,相比于过去的单一预测模型,预测精度得到了一定程度的提高。文献[15]基于多模型融合Stacking集成学习方式对负荷进行预测,相对于单模型预测显著提高了预测精度。
随着人工智能技术的快速发展,无模型的强化学习框架成为近几年的研究热点,通过对当前状态的行为进行奖励或惩罚来提高下一动作的预测精度。其中,Q学习由于所需的参数少、可离线训练等优点已成为最受欢迎的强化学习方法[16]。它可以从最新技术中选择最佳的预测模型,每一步均基于机器学习的预测模型。具体地说,在每个训练步骤中,Q学习代表将从当前的预测模型MI转移到下一个预测模型MJ,从而获得奖励,Q学习代表将从中学习模型选择的最优策略。
本文选取不同的机器学习算法构建基于双重Q学习的动态预测(Dynamic Prediction based on Double Q Learning, DPDQ)模型,对风电场风速序列进行预测。选用支持向量回归(Support Vector Regression, SVR)、核岭回归(Kernel Ridge Regression, KRR)、BP(back propagation)神经网络、深度学习算法LSTM和XGBoost五种机器学习算法组成第一阶段Q学习模型库,通过Q学习筛选出适应本时段的预测算法,得到初步的风速预测结果;第二阶段采用基于不同内核函数的KRR算法、SVR、BP神经网络组成第二阶段Q学习模型库,通过Q学习选取适应度高的模型对第一阶段预测误差进行训练及预测,进而实现对第一阶段预测结果的修正,得到更为准确的风速预测值。最后,将预测结果与实际风场数据进行对比,验证所提模型的有效性。
支持向量回归模型通过将低维数据映射到高维的空间,在高维空间中找到线性可分的超平面,最后再将高维空间的超平面映射回低维空间,以实现支持向量机的预测。但是,将低维的数据映射到高维的空间,在高维空间做计算将会增加模型计算量,也容易过拟合[17]。由此,本文选择径向基核函数代替线性方程中的线性项,可以使原来的线性算法非线性化,即能做非线性回归,此时引进核函数达到了升维的目的,也可以有效地控制过拟合。
BP神经网络是一种多层前馈网络,通过输入信号正向传播和误差信号反向传播对网络参数进行调整,具有很强的非线性映射能力和良好的自组织学习能力[18-19]。BP神经网络模型由输入层、输出层和多个隐藏层组成。输入信号正向传播过程是通过输入向量及各层权重、阈值计算输出向量,再根据输出向量和期望输出向量计算误差;而误差信号反向传播过程则是采用误差梯度下降法更新网络各层权重和阈值,使误差不断减小,直至满足精度要求。
核岭回归[20]基于核技巧将时间序列数据模式非线性地转换为由满足Mercer条件的核函数所确定的某些高维特征空间。回归模型表示为
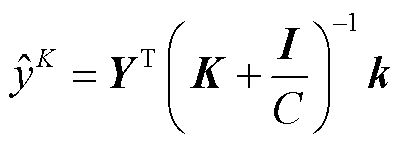 (1)
(1)
式中,Y为输入数据的高维特征空间;K为不同核函数代表的核心矩阵;C为正则化系数;I为N阶单位矩阵;k为输入x通过非线性映射函数内积的向量。
在训练过程中,满足Mercer条件的核函数通过将数据映射到高维特征空间来提高计算能力,增强数据的线性可分性,从而提高了模型回归和分类的准确性、稳定性及泛化能力。内核函数种类及具体表达式如下。
多项式核函数(Polynomial kernel)为
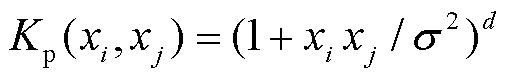 (2)
(2)
高斯核函数(Gaussian kernel)为
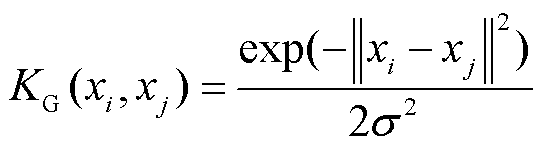 (3)
(3)
正切双曲核函数(tangent hyperbolic kernel)为
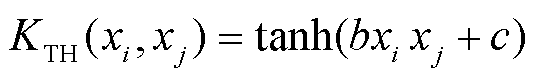 (4)
(4)
Morlet小波核函数(Morlet wavelet kernel)为
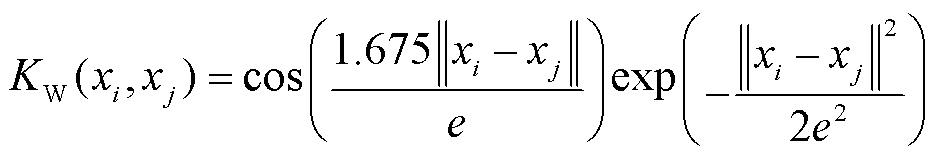 (5)
(5)
墨西哥帽小波核函数(Mexican Hat wavelet kernel)为
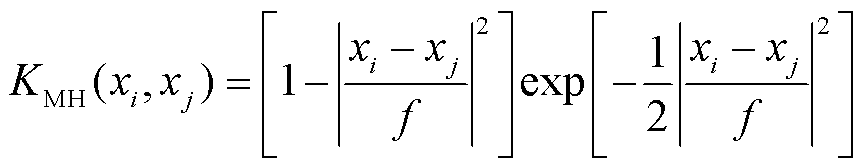 (6)
(6)
式中,s、b、c、e、f为核参数;d为最高次数。
每个记忆细胞在时刻t的状态记为ct。对ct的读取和修改通过对输入门et、遗忘门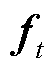 和输出门ot的控制实现。
和输出门ot的控制实现。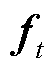 在t时刻接收当前状态xt与上一时刻隐藏层状态yt−1,将所接收状态经由r激活,使遗忘门的输出值均在[0,1]之间。当
在t时刻接收当前状态xt与上一时刻隐藏层状态yt−1,将所接收状态经由r激活,使遗忘门的输出值均在[0,1]之间。当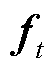 输出为0时,表示上一状态的信息全部丢弃;当
输出为0时,表示上一状态的信息全部丢弃;当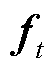 输出为1时,上一状态信息全部保留。et的输入经由非线性函数变换后,与
输出为1时,上一状态信息全部保留。et的输入经由非线性函数变换后,与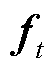 的输出叠加得到更新后的记忆单元状态ct,最后输出门根据非线性函数运算后的ct动态控制得到输出ytL。各变量计算公式为
的输出叠加得到更新后的记忆单元状态ct,最后输出门根据非线性函数运算后的ct动态控制得到输出ytL。各变量计算公式为
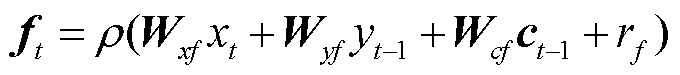 (7)
(7)
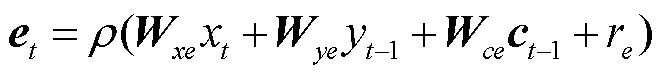 (8)
(8)
 (9)
(9)
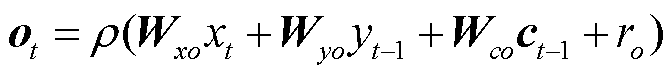 (10)
(10)
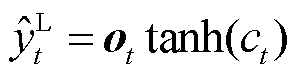 (11)
(11)
式中,Wxf、Wxc、Wxe、Wxo为连接输入信号xt的权重矩阵;Wyf、Wyc、Wyo、Wye为连接隐含层输出信号yt的权重矩阵;Wce、Wcf、Wco为连接神经元激活函数输出矢量ct和门函数的对角矩阵;re、rc、rf、ro为偏置参数;r为激活函数,通常为tanh或Sigmoid函数。采用反向误差传播为本文LSTM的训练算法。
XGBoost算法通过优化结构化损失函数(加入了正则项的损失函数,可以起到降低过拟合的风险)实现弱学习器的生成,并且XGBoost没有采用搜索方法,而是直接利用损失函数的一阶导数和二阶导数值,并通过预排序、加权分位数等技术大大提高了算法的性能。模型形式为
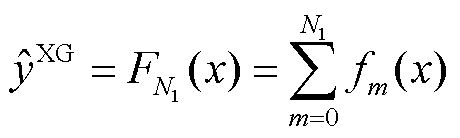 (12)
(12)
式中,N1为树的数量;F为树的集合;fm为第m棵树的相关情况。
强化学习是一种典型的机器学习算法,可与其他预测算法结合,构建出具有高度自适应性的预测模型。本文采用无模型自适应动态规划算法Q学习,在每个时段获取风速预测模型库和误差校正模型库的最优策略。
考虑到风速序列的高变异性,深度学习可对原始数据进行深层特征挖掘,在风速波动剧烈时能更好地预测风速变化趋势,但在细节上可能存在过拟合的现象。而SVR和BP神经网络往往在风速波动较平缓时段,拥有更高的预测精度;在风速波动剧烈时具有较大的预测误差。故选取深度学习算法LSTM、集成学习算法XGBoost、浅层学习算法SVR、BP神经网络和KRR五种算法作为风速预测模型集中的基础模型,以期针对不同波动情况,Q学习能在其中选取到更适合的预测模型,其中KRR选择基于多项式核函数的PKRR。
根据风速预测部分得到的初步预测结果和实际值之差得到的初步预测误差为
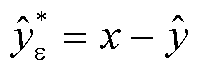 (13)
(13)
式中,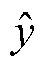 为由风速预测部分得到的初步预测结果;
为由风速预测部分得到的初步预测结果;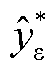 为初步预测误差;x为实测风速值。
为初步预测误差;x为实测风速值。
对于误差校正模型集的选取,由于预测误差的波动性和变异性远没有原始风速序列剧烈,更多的是需要对误差序列进行细节上的预测。因此,本文选取效率较高的SVR、BP神经网络、GKRR、PKRR、MHKRR五种模型构成误差校正模型集。最终的预测结果为
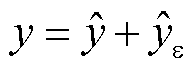 (14)
(14)
式中,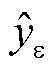 为误差预测结果;y为误差校正后的最终预测结果。
为误差预测结果;y为误差校正后的最终预测结果。
为了训练Q学习代表,首先在马尔可夫决策过程中定义了基于强化学习的动态模型选择的数学框架。通常,Q学习代表根据状态-作用值矩阵Q在一系列状态下采取顺序操作,直到达到最终目标[21]。通过评估当前状态空间的预测效果得到奖励更新Q。状态空间S由当前的预测模型组成,即
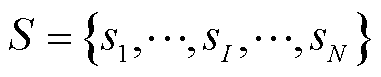 (15)
(15)
式中,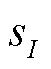 为当前预测模型;N为可选模型的数量。同样,动作空间A由下一步骤的可选预测模型组成,即
为当前预测模型;N为可选模型的数量。同样,动作空间A由下一步骤的可选预测模型组成,即
 (16)
(16)
式中,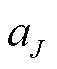 为在下一个预测时间步长从当前预测模型切换到下一预测模型的动作。
为在下一个预测时间步长从当前预测模型切换到下一预测模型的动作。
为了使用Q学习成功地解决马尔可夫决策过程,最核心的部分是通过适当的奖励函数R(s,a)得到奖励矩阵R。本文定义误差和模型排名混合奖励函数为
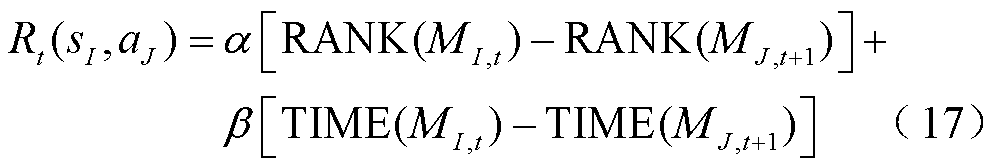
式中,RANK(MI,t)为第t时刻预测模型MI的排名;TIME(MI,t)为第t时刻预测模型MI的计算时间;a、b为权重系数,且满足a+b=1。
由于Q学习为无模型的动态模型选择框架,往往会择优选取模型进行预测,因此当两模型均排名为1时,该项为0,则失去奖惩作用。故选择加权两个Q学习框架,使奖励函数更具普适性。定义状态、行动和奖励后,通过使用Q学习训练数据集Tt训练Q学习动态预测模型。
采用衰变t贪婪方法[22]的Q学习代表从一开始就采取完全随机的动作,同时在学习过程中通过衰减来降低随机性。在Ne次训练之后,Q学习算法最终将收敛到最优策略Q*,该策略用于在Q学习过程中找到最优动作a*。具体步骤如下:
(1)定义模型步长k,预测尺度n,模型库尺寸NM,Q学习数据集Tt,动态预测模型数据集Tc,控制学习的积极性的学习率k,权衡未来回报的折现因子g,训练次数Ne,确保在Tc的每个步骤中,从N个模型中选择最佳模型。图1中Tte和Tce分别为第e步的Q学习数据集及动态预测模型数据集。
(2)初始化Q(s,a),w=1,开始训练。当w<0.3时,以w的概率选择随机动作ae;否则选择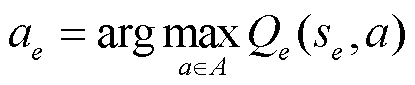 。
。
(3)根据式(17)计算更新奖励矩阵R。
(4)通过式(18)更新Q(s,a)。
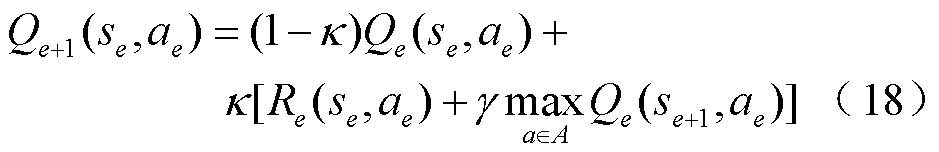
(5)重复步骤(2)~步骤(4)k次,找到每次的最优动作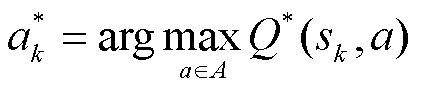 。
。
风速波动的季节性和不可测性给预测模型带来巨大的挑战,因此本文致力于提高风速预测精度的研究提出了基于双重Q学习的两步动态预测模型,具体框架如图1所示。
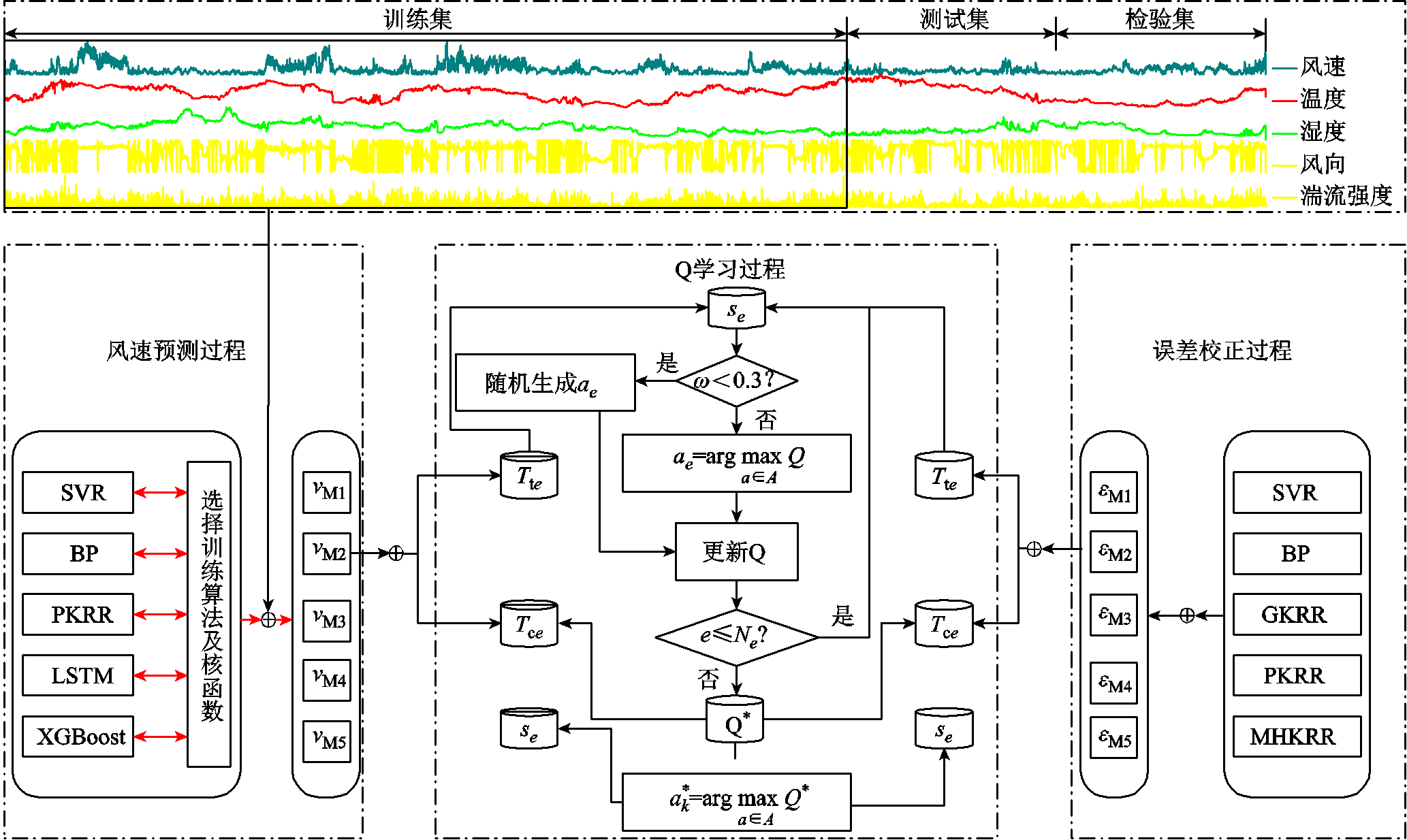
图1 基于双Q学习的动态选择模型框架
Fig.1 Dynamic selection model framework based on double Q learning
为验证所提模型的有效性,选取方均误差e1、相对误差e2和决定系数R2三种评价指标对预测结果进行评价,其中e1、e2预测结果期望为0,R2期待最优为1。
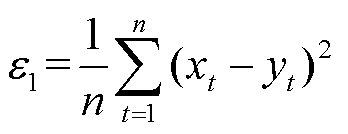 (19)
(19)
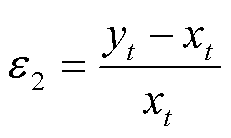 (20)
(20)
 (21)
(21)
选取东北某实际风场2019年1月~2020年12月风速及相关属性数据展开研究,对该风场2020年各季度典型月进行短期风速预测,并对原始数据进行预处理,采用相邻数据互补法替换缺失及异常数据值。原始数据的采样间隔为10min,全年共计52 560个点,取2019年全年数据为训练集,对DPDQ及QWSP模型进行训练。选取2020年3、6、9、12月1~15日数据为测试集,16~30日为检验集(用以检验模型参数设定是否合适)。
本文的训练及测试均在Matlab 2016b环境下运行,采用Intel(R)Core(TM) i5-8500,CPU@3.00GHz,RAM 8.00 GB的微机平台。
为提升模型应用灵活性,本文选取滑动步长为6,即以1h为最小单位尺度。1h的风速预测即可为风电实时并网所需的超短期预测提供参考,也可扩展至24h的日前预测,工程上更具实用性和广泛性。
本文Q学习框架具体参数设置为k=0.1,g=0.8,以确保动态模型选择的学习速度,Ne=100,并充分考虑奖励函数的未来奖惩,选取a=0.9,b=0.1。根据风场实际运行情况,本文选择进行步长为6的日前预测(k=6,n=144),即根据训练集数据的训练结果,采用最佳策略为下一个k步做出模型选择决策。基础模型超参数设置见表1。
表1 不同算法超参数设置
Tab.1 Different algorithm hyperparameter settings

算法超参数设置 LSTM神经元数量40、20,隐藏层层数2树深度5,学习率0.1,树数目300 XGBoost树深度6,学习率0.09,树数目600,最小叶节点样本权重4,随机采样比例0.08,叶子节点分裂最小损失0.1,模型复杂度权重30 BP神经网络单隐含层网络结构,激活函数为Sigmoid函数 SVR惩罚系数0.1,激励因子0.001,自由参数0.1 KRR正则化系数100,核函数选择根据说明选取
关于Q学习奖励函数的设置,目前在人工智能算法中自适应误差函数比较常用,但在训练过程中发现采用自适应误差函数为奖励函数进行的Q学习未能收敛,这是因为预测评估指标的大小不仅取决于预测模型,而且会随着时间而变化。采用从表现较差的模型切换到最佳模型的操作可能仍会收到负回报(由于预测评估指标的下降)。同时,一个预测模型的成熟与否不仅与预测精度有关,还与其所付出的时间成本相关,由此,本文提出了另一种奖励函数对模型效果进行评价,即综合考虑模型排名改进和模型预测时间,见式(17)。两种方法的部分训练结果如图2所示,可以看出,该函数成功收敛,有效地避免了时间序列效应。
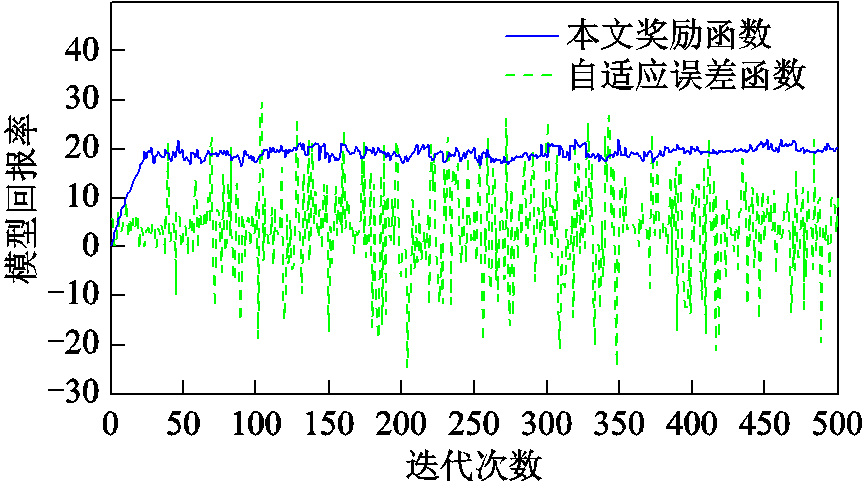
图2 奖励函数收敛情况
Fig.2 Convergence of the reward function
为了使DPDQ模型预测效果达到最优,本文在历史风速数据的基础上添加了多种属性因素作为考量以提高风速预测模型精度。计算了风向(WD)、风速标准差(SD)、湿度(SH)、湍流强度(TI)、风速(WS)、温度(TP)6组序列的Spearman秩序相关系数[23]。当相关系数大于0时两序列为正相关,小于0为负相关,数值越大则相关程度越高。具体结果如图3所示。
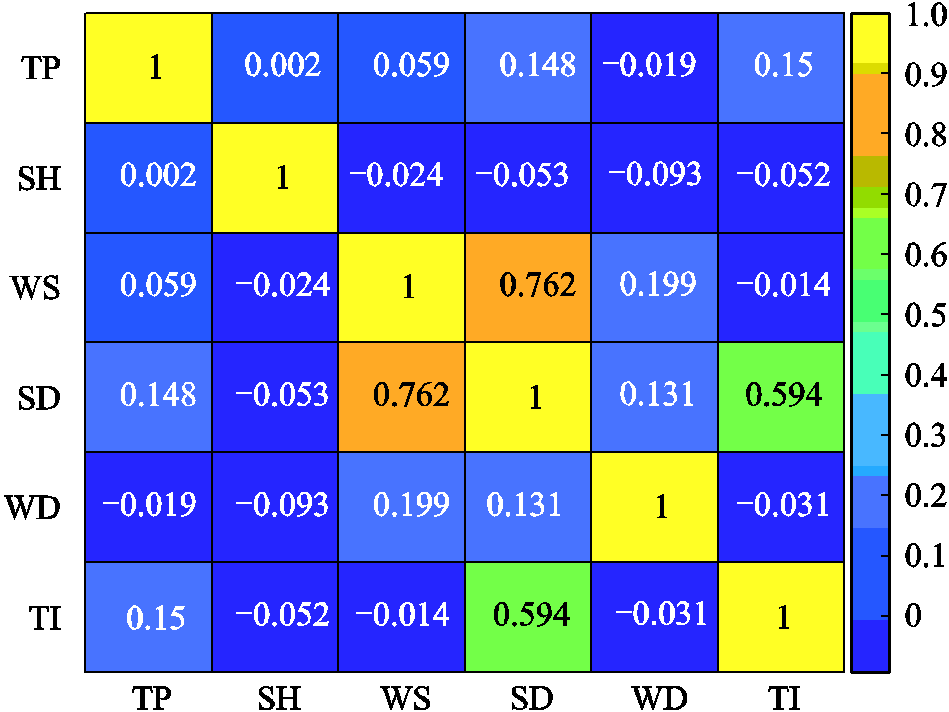
图3 各属性因素相关性
Fig.3 Correlation of each attribute factor
由图3可知,各属性因素与风速之间的相关系数有正有负,其中最高的为风速标准差,可达0.762;与风向的相关程度次之,相关系数为0.199;最低为湍流强度,仅-0.014。选择正相关变量可提升模型预测精度,选择负相关变量会导致模型预测误差增大[24]。由此,根据结果本文选择风速、风速标准差、风向和温度作为输入集,对DPDQ模型进行训练和预测。
东北风场2019年一整年的风速波动情况如图4所示,可以看出该风场风能量密度较大,其中春冬两季风速波动较为剧烈,不同时刻风速差较大,最高风速超过25m/s。而夏秋两季风速多为低于10m/s,波动较为平缓,风能量密度明显低于秋冬季节。
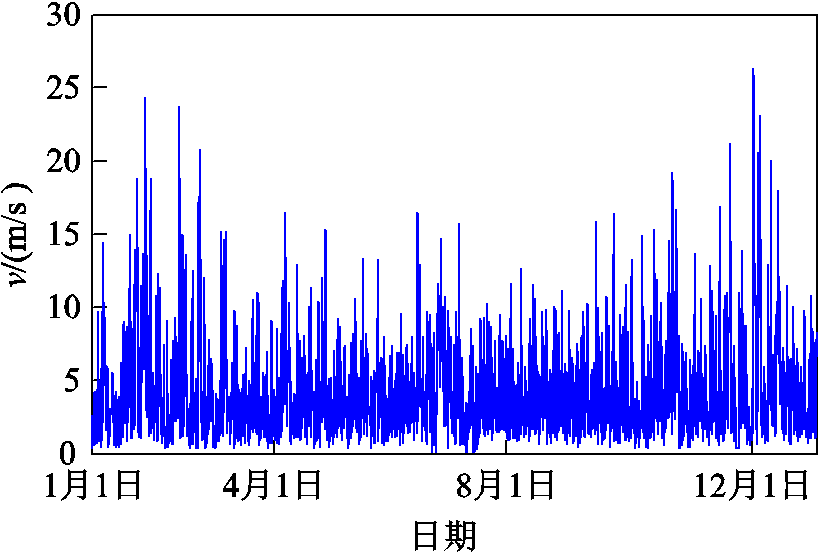
图4 风场2019年风速波动情况
Fig.4 Wind speed fluctuations in the wind farm in 2016
为检验和说明基于Q学习的动态模型选择的有效性,选取单预测模型LSTM和BP神经网络两种不同预测原理的人工智能算法与DPDQ中的风速预测部分(Q learning Wind Speed Prediction, QWSP)进行仿真对比分析,对各季度典型月风速进行滑动步长为6的日前预测。具体预测结果如图5所示。
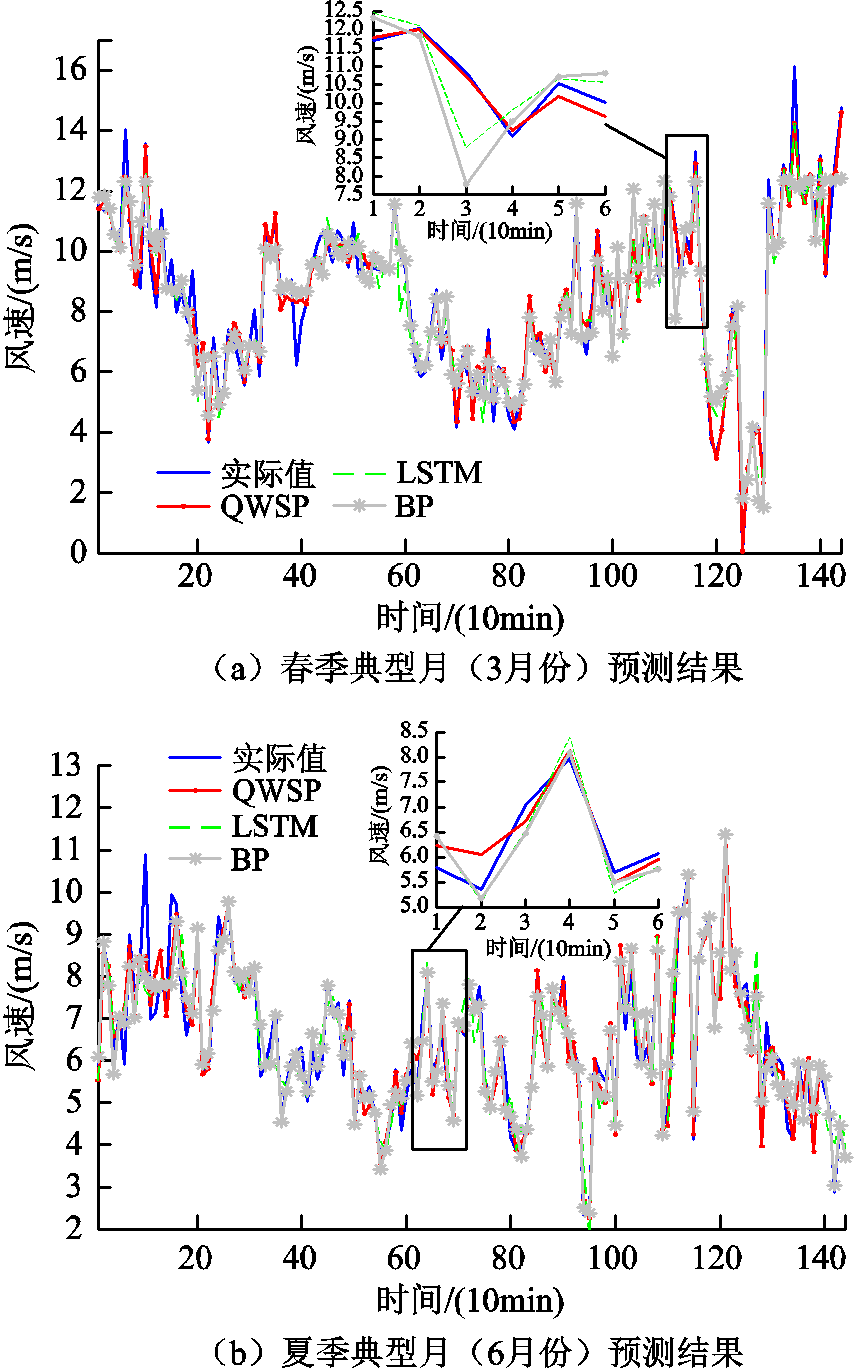
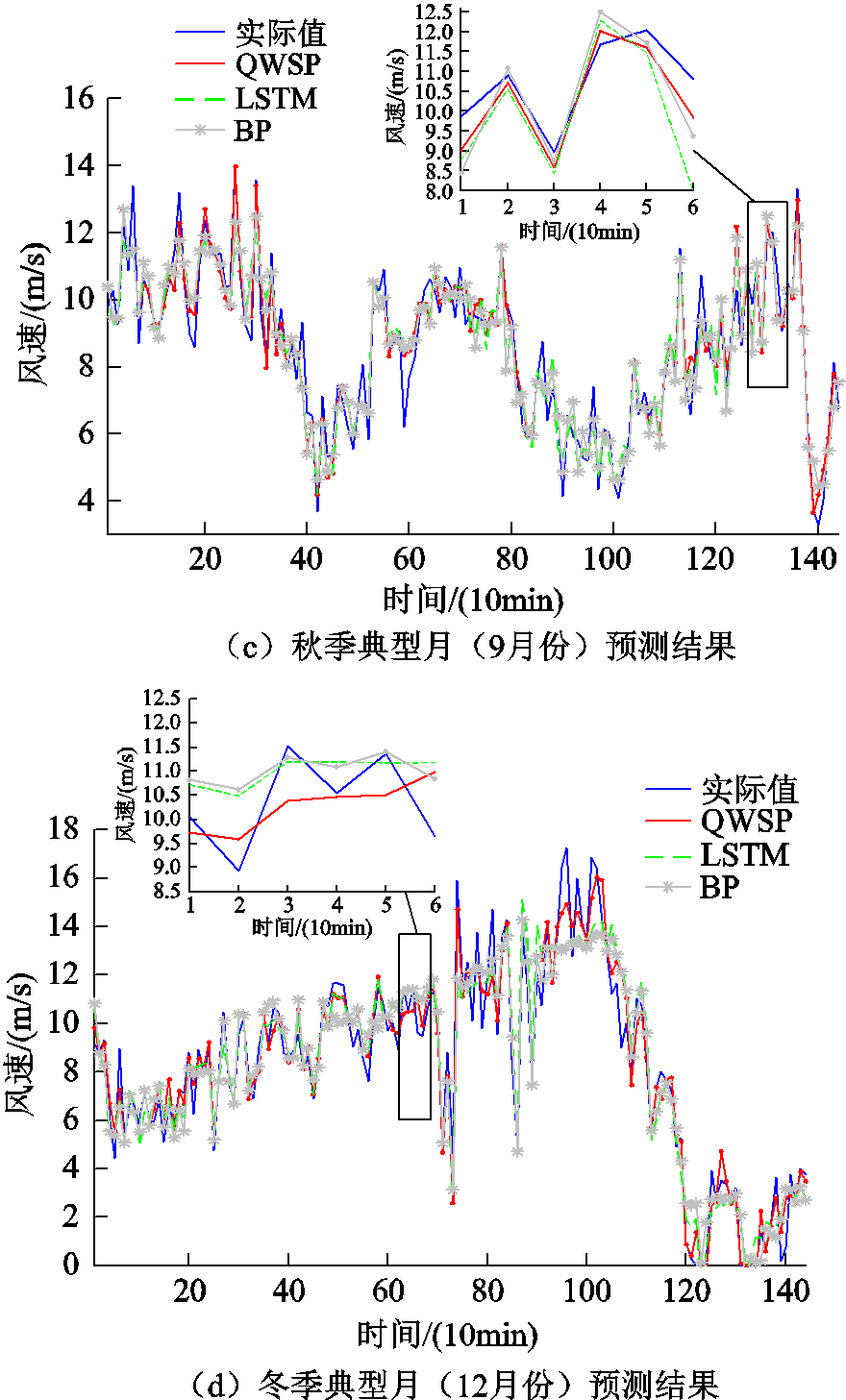
图5 不同方法日前预测结果
Fig.5 Forecast results by different methods
由图5可以看出,QWSP在应对各季节不同的风速波动情况下均能得到良好表现,整体的预测效果优于单一预测模型。而从细节上看,夏季的风速波动较为平缓,风速也较低,春冬季节的风速相对较高。展开图5a中时间序列121~126和图5b中时间序列61~66部分可以看出,各模型均能得到较好的预测效果。图5c中127~132部分,BP神经网络和LSTM由于没有进行动态选择,导致其不能应对所有的风速变化情况,预测结果与实际值偏差较大。而图5d中的细节预测结果则不然,Q学习各时段所选择的预测模型结果见表2。
表2 Q学习在各时段选择模型结果
Tab.2 Q learning to select model results at each time period
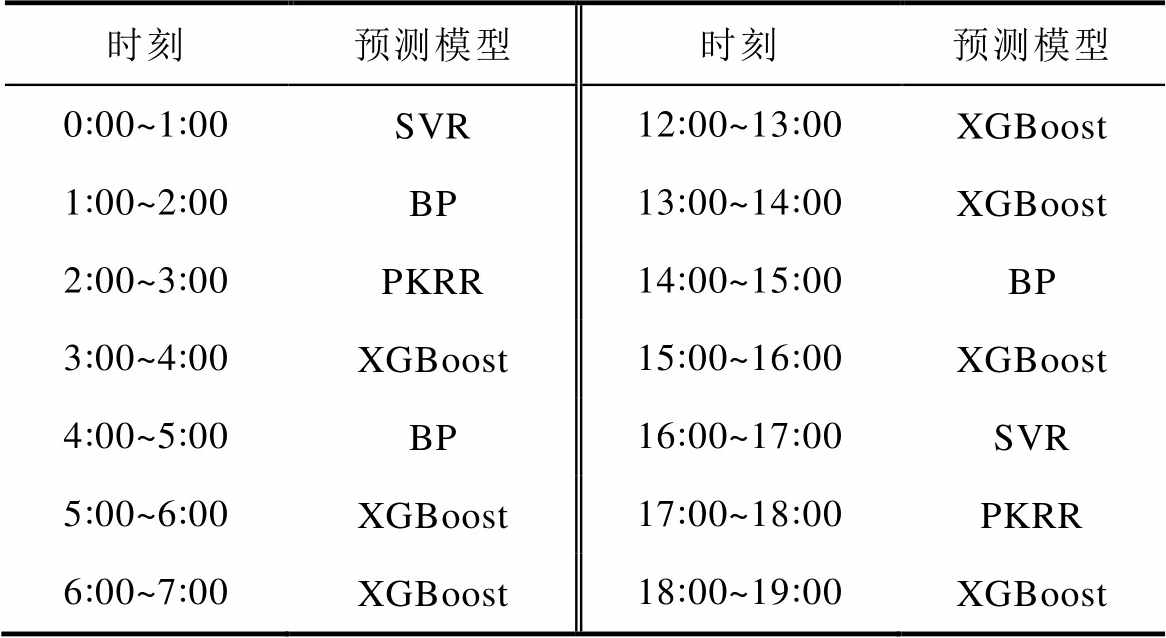
时刻预测模型时刻预测模型 0:00~1:00SVR12:00~13:00XGBoost 1:00~2:00BP13:00~14:00XGBoost 2:00~3:00PKRR14:00~15:00BP 3:00~4:00XGBoost15:00~16:00XGBoost 4:00~5:00BP16:00~17:00SVR 5:00~6:00XGBoost17:00~18:00PKRR 6:00~7:00XGBoost18:00~19:00XGBoost
(续)
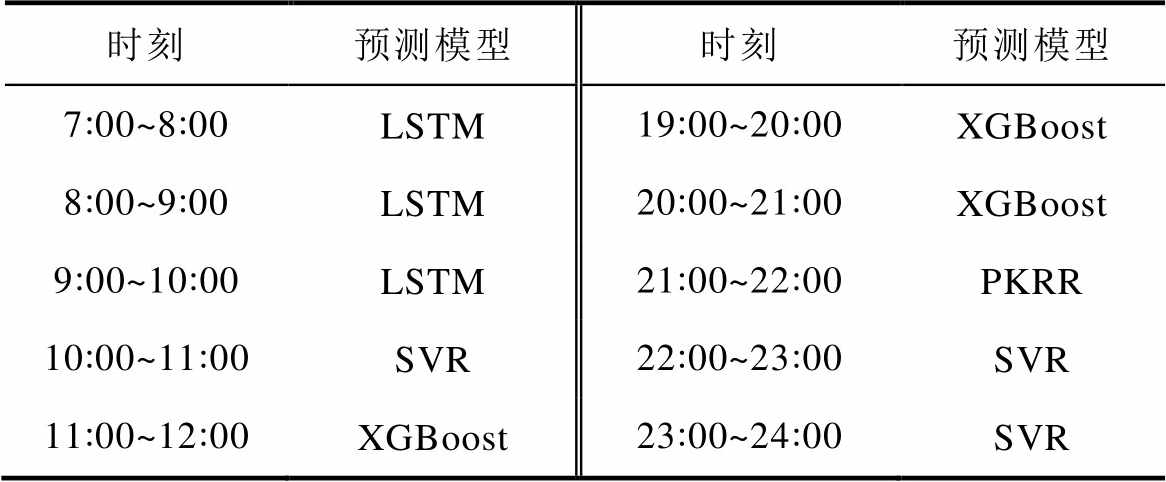
时刻预测模型时刻预测模型 7:00~8:00LSTM19:00~20:00XGBoost 8:00~9:00LSTM20:00~21:00XGBoost 9:00~10:00LSTM21:00~22:00PKRR 10:00~11:00SVR22:00~23:00SVR 11:00~12:00XGBoost23:00~24:00SVR
由表2和图5d中小图可以看出,Q学习在10:00~11:00点之间选择的预测模型为SVR,预测结果偏差大于BP神经网络,这主要是Q学习模型选择失误而导致的预测偏差较大,由于奖励函数机制的设置,本次所选模型的排名应较为靠后,导致本次奖励为负值,在下一次模型选择中实现修正,进而保证预测结果的精度。下一次的预测结果如图6所示,接收到负奖励信号后的Q学习在本次得到了较为准确的预测结果,大部分模型的预测值都更接近实际值。值得说明的是,在0:00~1:00时Q学习选择的SVR模型不是排名第一的,而是随机选择的,这主要是由于首次选择需为后续步骤提供奖励值参考,使后面的模型选择更具逻辑性。
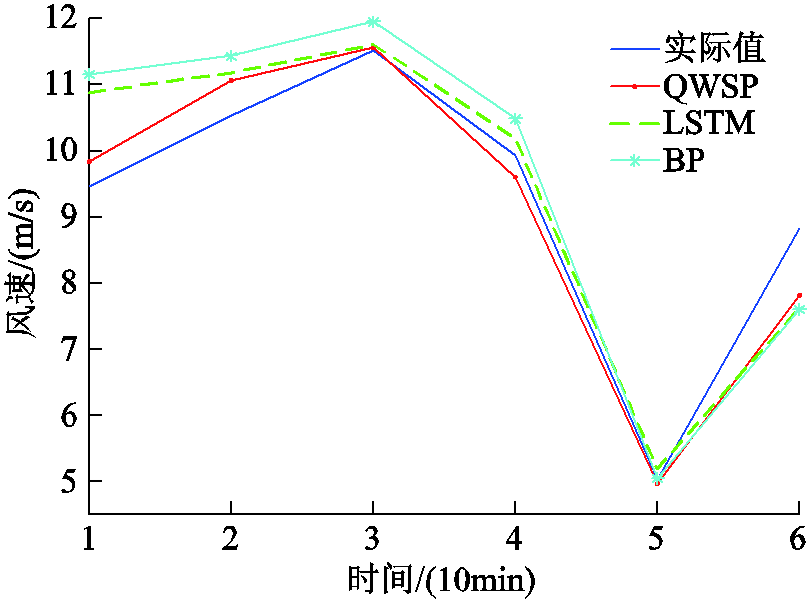
图6 冬季第121~126步预测结果
Fig.6 Forecast results of steps 121-126 in winter
在Q学习的动态选择正确时,预测精度普遍偏高,模型具有较好的稳健性;而当单预测模型过拟合时,将会出现预测误差较大的情况,由于奖励函数的机制,可充分考虑本地奖惩和宏观优势,使模型能够及时得到修正。由此,基于Q学习的模型选择策略,可使风速预测模型性能得到整体提高。
各模型训练及预测时间见表3,深度学习相比于浅层学习所需要的训练时间更长。而Q学习训练Q代理在各基础模型中进行选择,需要153.89s。各季度预测误差见表4。
由表4中数据可知,由于夏季风速波动最小,各模型方均误差均小于0.5(m/s)2,而冬季风速波动大,给模型带来一定的预测难度,导致预测误差ε1也随之增大。本文所提的基于强化学习的动态模型选择使其R2结果在各季度均最接近于1,ε1误差也为三个模型中最小。不同方法夏季的相对误差ε2结果如图7所示。可以看出,QWSP的误差在大多数时刻都小于其他两种方法,验证了本文所提方法的预测精度更高。由图7中误差情况可知,采用本文方法得到初步预测结果对应的误差值同样为非线性波动,因此,本文提出的风速预测模型也适用于预测误差,继而进行误差修正。由于误差的随机波动性远低于原始风速序列,故只需选用效率较高的浅层学习算法进行预测即可。
表3 不同方法运行时间
Tab.3 Different method running time

模型训练时间/s预测时间/s LSTM859.630.467 BP375.810.371 Q学习153.890.012
表4 不同方法短期预测误差
Tab.4 Short-term prediction error results of different methods
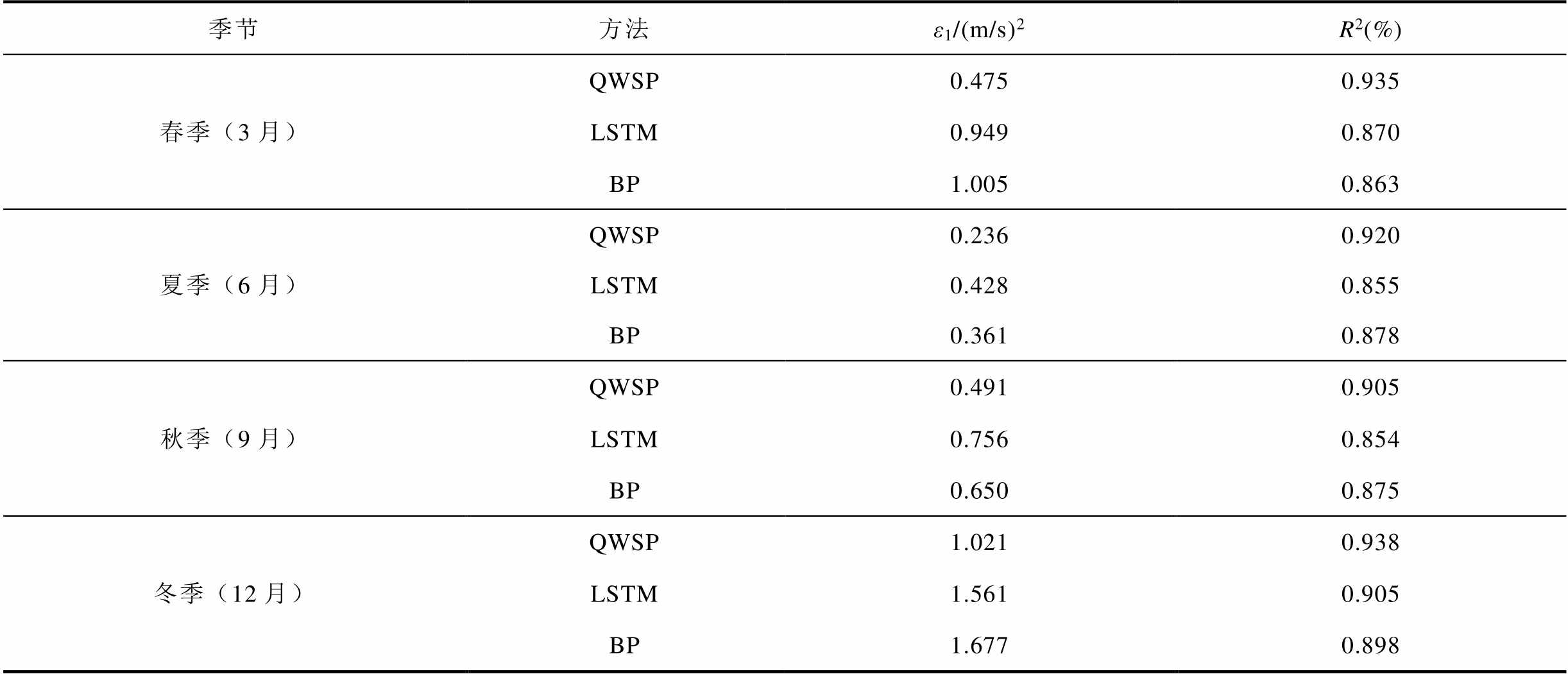
季节方法ε1/(m/s)2R2(%) 春季(3月)QWSP0.4750.935 LSTM0.9490.870 BP1.0050.863 夏季(6月)QWSP0.2360.920 LSTM0.4280.855 BP0.3610.878 秋季(9月)QWSP0.4910.905 LSTM0.7560.854 BP0.6500.875 冬季(12月)QWSP1.0210.938 LSTM1.5610.905 BP1.6770.898

图7 不同方法相对误差ε2
Fig.7 Relative error ε2 of different methods
为验证本文误差校正环节的有效性,利用DPDQ对各季节进行日前风速预测,结果如图8所示。可以看出DPDQ模型在各季节均能达到较好的预测效果,但对于某些风速骤变的极端风况,如图8c中的极值风速点仍存在一定的预测误差,这是不可避免的。对各季节预测值进行误差校验前后的相对误差计算如图9所示。其他误差结果见表5。
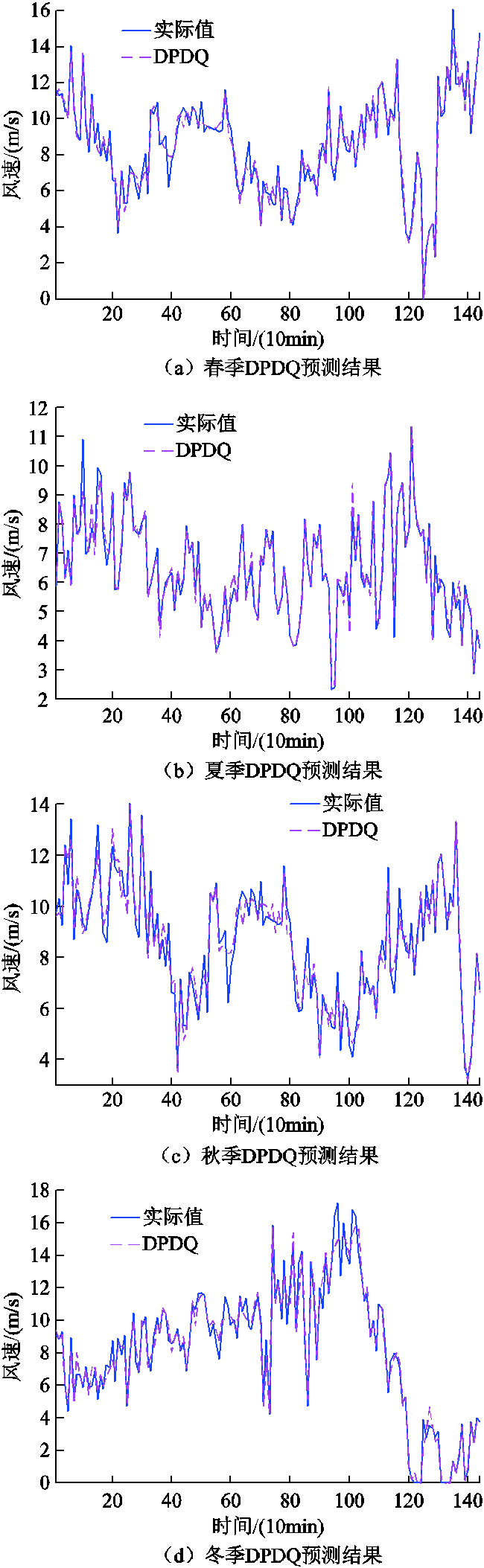
图8 各季节DPDQ预测结果
Fig.8 DPDQ forecast results in each season
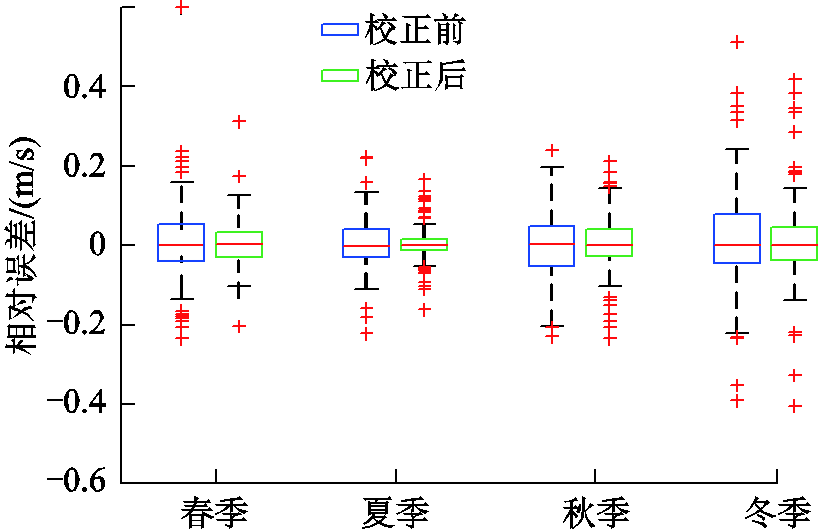
图9 各季节误差校正前后对比
Fig.9 Comparison before and after error correction for each season
表5 DPDQ日前预测误差
Tab.5 DPDQ day-ahead forecast error

季节ε1/(m/s)2R2(%) 春季0.2370.968 夏季0.0950.968 秋季0.2890.944 冬季0.4350.974
图9中右侧框为DPDQ模型的预测误差,左侧框为QWSP的预测误差,可以看出,各季节的预测结果中位数均在0左右,误差上下四分位数有效减小。进一步对比表5中和表4中QWSP的预测误差,不同季节的风速预测结果在进行误差校正后都有所改进,验证了误差校正环节的合理性和必要性。
为了定量分析误差校正部分对预测精度的影响程度,选择校正前后预测结果的|ε2%|误差进行对比,结果如图10所示。从中可以看出,校正前预测误差居于区间大于16中的点在经过校正后,数量明显减少,而多数的点都集中在区间小于4之间。统计多次预测结果可知,校正后预测模型的相对误差与之前相比降低约50%。分析结果表明,误差校正部分可有效减少模型预测误差,提高预测精度。

图10 误差校正前后对比
Fig.10 Comparison before and after error correction
本文构建双重Q学习的动态预测模型,在每个步骤中,Q学习代理从风速预测模型集部分中选择最佳预测模型进行初步风速预测,下一阶段另一个Q学习代表从误差预测模型集中选择最佳预测模型,将误差预测结果输入到误差修正部分,最终提出风速的最优预测策略。结合实测风场数据进行日前风速预测,得出以下结论:
1)Q学习在风速预测部分和误差校正部分都有效选择了每个预测步长的最佳预测模型。
2)误差校正使相对平均误差减少50%左右,说明了误差校正环节对成熟预测模型的有效性。
3)通过构建组合风速预测模型对不同季节典型月进行预测,结果表明DPDQ具有较好的稳健性与适用性。
本文初步探索了将强化学习融入风速预测的可能性,基于此,比较不同强化学习的模型选择功能,如何将其与风速预测结合,构建更全面的误差指标,将成为下一步工作的研究重点。
参考文献
[1] 潘超, 王典, 蔡国伟, 等. 考虑风速时空相关特性的元启发式支配预测模型[J]. 电网技术, 2020, 44(11): 4105-4114.
Pan Chao, Wang Dian, Cai Guowei, et al. Meta-heuristic dominance prediction model considering wind speed spatio-temporal correlation characteristics[J]. Power System Technology, 2020, 44(11): 4105-4114.
[2] 杨茂, 董昊. 基于数值天气预报风速和蒙特卡洛法的短期风电功率区间预测[J]. 电力系统自动化, 2021, 45(5): 79-85.
Yang Mao, Dong Hao. Short-term wind power interval prediction based on wind speed of numerical weather prediction and Monte Carlo method[J]. Automation of Electric Power Systems, 2021, 45(5): 79-85.
[3] 沈小军, 周冲成, 付雪娇. 基于机联网-空间相关性权重的风电机组风速预测研究[J]. 电工技术学报, 2021, 36(9): 1782-1790.
Shen Xiaojun, Zhou Chongcheng, Fu Xuejiao. Wind speed prediction of wind turbine based on the internet of machines and spatial correlation weight[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1782-1790.
[4] 王晨, 寇鹏. 基于卷积神经网络和简单循环单元集成模型的风电场内多风机风速预测[J]. 电工技术学报, 2020, 35(13): 2723-2735.
Wang Chen, Kou Peng. Wind speed forecasts of multiple wind turbines in a wind farm based on integration model built by convolutional neural network and simple recurrent unit[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2723-2735.
[5] Ma J, Fouladirad M, Grall A. Flexible wind speed generation model: Markov chain with an embedded diffusion process[J]. Energy, 2018, 164: 316-328.
[6] 凡航, 张雪敏, 梅生伟, 等. 基于时空神经网络的风电场超短期风速预测模型[J]. 电力系统自动化, 2021, 45(1): 28-35.
Fan Hang, Zhang Xuemin, Mei Shengwei, et al. Ultra-short-term wind speed prediction model for wind farms based on spatiotemporal neural network[J]. Automation of Electric Power Systems, 2021, 45(1): 28-35.
[7] Wang Shouxiang, Zhang Na, Wu Lei, et al. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network[J]. Renewable Energy, 2016, 94: 629-636.
[8] 王琦, 关添升, 秦本双. 基于MRMR的ORELM的短期风速预测[J]. 可再生能源, 2018, 36(1): 85-90.
Wang Qi, Guan Tiansheng, Qin Benshuang. Short-term wind speed prediction of ORELM based on MRMR[J]. Renewable Energy, 2018, 36(1): 85-90.
[9] Naik J, Bisoi R, Dash P K. Prediction interval forecasting of wind speed and wind power using modes decomposition based low rank multi-kernel ridge regression[J]. Renewable Energy, 2018, 129: 357-383.
[10] 罗文, 王莉娜. 风场短期风速预测研究[J]. 电工技术学报, 2011, 26(7): 68-74.
Luo Wen, Wang Lina. Research on short-term wind speed prediction in wind farms[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 68-74.
[11] 唐振浩, 赵赓楠, 曹生现, 等. 基于SWLSTM算法的超短期风向预测[J]. 中国电机工程学报, 2019, 39(15): 4459-4468.
Tang Zhenhao, Zhao Gengnan, Cao Shengxian, et al. Ultra-short-term wind direction prediction based on SWLSTM algorithm[J]. Proceedings of the CSEE, 2019, 39(15): 4459-4468.
[12] 胡梦月, 胡志坚, 仉梦林, 等. 基于改进AdaBoost.RT和KELM的风功率预测方法研究[J]. 电网技术, 2017, 42(2): 536-542.
Hu Mengyue, Hu Zhijian, Wu Menglin, et al. Research on Wind power forecasting method based on improved AdaBoost.RT and KELM algorithm[J]. Power System Technology, 2017, 42(2): 536-542.
[13] 李永刚, 王月, 刘丰瑞, 等. 基于Stacking融合的短期风速预测组合模型[J]. 电网技术, 2020, 44(8): 2875-2882.
Li Yonggang, Wang Yue, Liu Fengrui, et al. Combination model of short-term wind speed prediction based on Stacking fusion[J]. Power System Technology, 2020, 44(8): 2875-2882.
[14] Wang Kejun, Qi Xiaoxia, Liu Hongda, et al. Deep belief network based k -means cluster approach for short-term wind power forecasting[J]. Energy, 2018, 165: 840-852.
[15] 史佳琪, 张建华. 基于多模型融合Stacking集成学习方式的负荷预测方法[J]. 中国电机工程学报, 2019, 39(14): 4032-4042.
Shi Jiaqi, Zhang Jianhua. Load forecasting based on multi-model by stacking ensemble learning[J]. Proceedings of the CSEE, 2019, 39(14): 4032-4042.
[16] Ouyang Tinghui, Zha Xiaoming, Qin Liang, et al. Prediction of wind power ramp events based on residual correction[J]. Renewable Energy, 2019, 136(6): 781-792.
[17] 王贺, 胡志坚, 张翌晖, 等. 基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J]. 电工技术学报, 2014, 29(4): 237-245.
Wang He, Hu Zhijian, Zhang Yihui, et al. Combination forecast of short-term wind speed based on clustering empirical mode decomposition and least square support vector machine[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 237- 245.
[18] 李奎, 李晓倍, 郑淑梅, 等. 基于BP神经网络的交流接触器剩余电寿命预测[J]. 电工技术学报, 2017, 32(15): 120-127.
Li Kui, Li Xiaobei, Zheng Shumei, et al. Prediction of residual current life of AC contactors based on BP neural network[J]. Transactions of the China Electrotechnical Society, 2017, 32(15): 120-127.
[19] 宋建, 束洪春, 董俊, 等. 基于GM(1,1)与BP神经网络的综合负荷预测[J]. 电力建设, 2020, 41(5): 75-80.
Song Jian, Shu Hongchun, Dong Jun, et al. Comprehensive load forecasting based on GM(1,1) and BP neural network[J]. Electric Power Construction, 2020, 41(5): 75-80.
[20] 李勇周, 罗大庸, 刘少强. 邻域保持最大间隔分析的人脸识别[J]. 模式识别与人工智能, 2010, 23(1):23-28.
Li Yongzhou, Luo Dayong Liu Sshaoqiang Face recognition using neighborhood preserving maximal margin analysis of kernel ridge regression[J]. Pattern Recognition and Artificial Intelligence, 2010, 23(1): 23-28.
[21] Yan Jun, He Haibo, Zhong Xiangnan, et al. Q-learning-based vulnerability analysis of smart grid against sequential topology attacks[J]. IEEE Transactions on Information Forensics and Security, 2016, 12(1): 200-210.
[22] Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[J]. Computer Science, 2013.
[23] 康重庆, 夏清, 刘梅. 电力系统负荷预测[M]. 北京:中国电力出版社, 2007.
[24] 朱乔木, 李弘毅, 王子琪, 等. 基于长短期记忆网络的风电场发电功率超短期预测[J]. 电网技术, 2017, 41(12): 3797-3802.
Zhu Qiaomu, Li Hongyi, Wang Ziqi, et al. Short-term wind power forecasting based on LSTM[J]. Power System Technology, 2017, 41(12): 3797-3802.
Dynamic Wind Speed Prediction Model Based on Double Q Learning
Abstract Accurate wind speed prediction is of great significance to the stable operation of new energy grids. In order to improve the accuracy of wind speed prediction, this paper constructs a dynamic wind speed prediction model based on double Q learning. First, build a wind speed Q learning model set consisting of 5 basic prediction algorithms, fully consider wind speed fluctuations and attribute factors, select the best prediction model for each time period through the Q learning, and get the preliminary wind speed prediction results. Calculate the prediction error based on the wind speed prediction result, construct the second-stage error Q learning model library, screen the best model in the model library to correct the preliminary prediction value, obtain the final prediction result. Finally, the effectiveness of the proposed method is verified by predicting the wind speed of the actual wind field in different seasons.
Keywords:Wind speed prediction, Q learning, error correction, dynamic model selection
DOI:10.19595/j.cnki.1000-6753.tces.210272
中图分类号:TM715
李永刚 男,1967年生,教授,博士生导师,研究方向为电气设备诊断、新能源电力系统。E-mail:lygzxm0@163.com
吴滨源 男,1998年生,博士研究生,研究方向为新能源电力系统。E-mail:wby_ncepu@163.com(通信作者)
国家自然科学基金资助项目(51777075)。
收稿日期 2021-03-03
改稿日期 2021-05-30
(编辑 赫蕾)