基于深度强化学习的多能互补发电系统负荷频率控制策略
梁煜东1 陈 峦1 张国洲1 任曼曼2 胡维昊1
(1. 电子科技大学电力系统广域测量与控制四川省重点实验室 成都 611731 2. 国网安徽省电力有限公司电力科学研究院 合肥 230000)
摘要 针对大规模可再生能源接入电网引发的系统调频性能下降的问题,该文提出一种基于数据驱动的风火储多能互补发电系统负荷频率控制方法。首先,通过机理分析建立多区域混合发电系统的数学模型;其次,构建含控制性能标准(CPS)、风电机组弃风(Picast)和动态性能指标的奖励函数,将负荷频率控制问题转换为最大化奖励函数问题,并引入深度确定性策略梯度算法进行求解,通过预学习和在线应用,获得风电机组实际出力情况下的最优自适应协调频率控制策略;最后,从中长期控制性能入手进行分析,通过加入连续阶跃扰动或实际风速扰动仿真,验证所提出方法在改进负荷频率控制性能上的有效性和可行性。仿真结果表明,系统发生扰动时,储能设备的引入及所提的深度确定性策略梯度算法不仅能够更加有效地抑制波动,而且能够在缩短完成负荷频率控制所需调节时间的同时最大限度地减少弃风,提高风电消纳的比例。
关键词:多能互补发电系统 负荷频率控制 深度确定性策略梯度算法 控制性能标准(CPS)指标
0 引言
近年来,为了解决日益突出的能源和环境问题,风火互补发电系统、光水互补发电系统等多能互补发电系统得到快速发展。然而,由于可再生能源具有很强的波动性,随着新能源的大规模接入,其在电网中的渗透率不断提高,随之而来的是传统能源调频能力弱化、电网频率质量急速下降等问题[1-3]。多区域电力系统的负荷频率控制(Load Frequency Control, LFC)是解决负荷变化导致的电网频率问题的重要手段之一,其有助于恢复系统频率并消除联络线间的功率偏差[4]。
常规的LFC方法均基于系统详细模型,其中PID控制器由于其简单高效的控制结构而被广泛使用。文献[5]提出一种基于灰狼优化算法的控制器参数正定设计方案,并采用所提的优化算法获取PI/ PID型负荷频率控制器参数。文献[6]提出一种面向抽水蓄能电站区域负荷频率的分数阶PID控制策略,深入研究了含非线性环节的两区域再热式汽轮机组LFC方法。文献[7]提出一种基于模型预测控制的设计方法,仿真结果表明该方法能够提高负载变化时系统的频率响应能力。上述研究都是通过调节系统控制器参数来实现优化的目的,其本质上属于PI控制。然而,这些方法通常会在控制器参数的估计和调整方面带来极大的实时计算负担,同时忽略了各个区域之间的协调控制,限制了互联区域电力系统的LFC性能。
针对上述方法的不足,近年来,有学者提出将机器学习应用到能源与电力系统的调度优化和控制决策中[8]。文献[9]提出一种基于Q学习算法的控制方法,仿真结果表明该方法相比传统PID控制提高了整个电力系统的鲁棒性与适应性。文献[10]提出一种具备多步预见能力的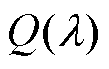 学习算法,该在线回溯算法显式地利用资格迹对将来多步决策的在线强化信息进行高效地回溯操作,能够有效地解决使用单步Q学习算法无法完整评估动作决策优劣性的问题。在文献[10]的基础上,文献[11]将基于相关均衡(Correlated-Equilibrium-Q, CEQ)的学习算法与多步回溯Q学习方法相结合,提出一种全新的多智能体学习算法
学习算法,该在线回溯算法显式地利用资格迹对将来多步决策的在线强化信息进行高效地回溯操作,能够有效地解决使用单步Q学习算法无法完整评估动作决策优劣性的问题。在文献[10]的基础上,文献[11]将基于相关均衡(Correlated-Equilibrium-Q, CEQ)的学习算法与多步回溯Q学习方法相结合,提出一种全新的多智能体学习算法 ,并将该算法应用到控制性能标准(Control Performance Standard, CPS)指令的最优分配问题中。上述研究都提出了基于强化学习的LFC方法,但发电机组生成的命令被离散化,在一定程度上限制了控制性能。同时,复杂电力系统环境高维状态的特性通常让传统强化学习算法面临“维数灾”的困扰,难以找到最优解。谷歌的人工智能团队DeepMind创造性地将深度学习的感知能力与强化学习的决策能力相结合,提出深度强化学习(Deep Reinforcement Learning, DRL)[12],该方法具备了解决大规模强化学习问题的能力。如文献[13]采用深度Q学习算法设计了含电动汽车和大规模光伏的在线调度策略。文献[14]考虑储能系统充放电爬坡和存储电量限值等约束条件,将改进的Q学习算法应用到实时调度周期储能系统中做优化决策。文献[15]将在线Q学习方法与附加控制思想相结合,讨论了其在伺服系统中电机速度最优跟踪控制问题上的应用。
,并将该算法应用到控制性能标准(Control Performance Standard, CPS)指令的最优分配问题中。上述研究都提出了基于强化学习的LFC方法,但发电机组生成的命令被离散化,在一定程度上限制了控制性能。同时,复杂电力系统环境高维状态的特性通常让传统强化学习算法面临“维数灾”的困扰,难以找到最优解。谷歌的人工智能团队DeepMind创造性地将深度学习的感知能力与强化学习的决策能力相结合,提出深度强化学习(Deep Reinforcement Learning, DRL)[12],该方法具备了解决大规模强化学习问题的能力。如文献[13]采用深度Q学习算法设计了含电动汽车和大规模光伏的在线调度策略。文献[14]考虑储能系统充放电爬坡和存储电量限值等约束条件,将改进的Q学习算法应用到实时调度周期储能系统中做优化决策。文献[15]将在线Q学习方法与附加控制思想相结合,讨论了其在伺服系统中电机速度最优跟踪控制问题上的应用。
目前,较少有文献采用先进的连续型深度强化学习算法来解决互联区域电网的负荷频率控制问题,尤其是针对含可再生能源和储能设备的多能互补发电系统。文献[16]提出了一种基于连续动作域的深度强化学习方法来提高单区域电力系统的LFC性能,在一定程度上可以最小化频率偏差,提高控制器响应速度。文献[17]在文献[16]的基础上,针对多区域电力系统提出一种数据驱动协同LFC的方法,以最小化所有区域的区域控制误差信号为目的设置奖励函数,并在英格兰39节点电力系统上仿真测试所提方法的性能。但上述研究都忽略了从中长期角度对电力系统的CPS指标进行分析。此外,考虑到负荷波动的随机性和长期性,这部分内容需要在分析建模中得到妥善处理。
鉴于此,本文提出了一种基于智能体深度强化学习的数据驱动负荷频率协调优化控制方法,以最大程度地减少区域间的频率偏差、计划外的功率交换及提高可再生能源发电消纳为目标。针对仅通过改进控制器和算法提高LFC性能存在的局限性,考虑引入储能设备以进行辅助调频。此外,针对负荷波动长期性和随机性的问题,考虑从中长期角度进行分析,在构造奖励函数时加入CPS指标。最后,通过仿真计算,验证系统发生长期扰动时本文所提出数据驱动LFC方法的可行性和有效性。
1 多能互补发电系统模型
本文在分析三种电源运行特性的基础上,通过 图1展示了具有火电机组、可再生能源风电机组和储能设备的多能互补发电系统模型框架。该电力系统各主要环节的传递函数会在下文进行简要说明。
1.1 负荷频率模型
混合发电系统的发电机-负荷模型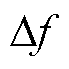 为
为
式中,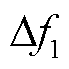 为区域一的频率偏差;
为区域一的频率偏差;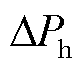 为原动机的输出功率;
为原动机的输出功率; 为储能系统的输出功率;
为储能系统的输出功率; 为区域一、二之间的联络线偏差;
为区域一、二之间的联络线偏差;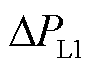 为区域一受到的负荷扰动;
为区域一受到的负荷扰动;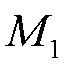 为火电机组的惯性时间系数;
为火电机组的惯性时间系数;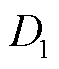 为负荷的频率调节效应系数。
为负荷的频率调节效应系数。
1.2 储能系统模型
储能系统模块包括充放电部分和功率限制部分,动态物理模型为
式中,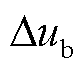 为储能系统模块的控制输入信号;
为储能系统模块的控制输入信号;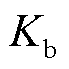 为储能电池单位调节系数;Tb为模块的时间常数。
为储能电池单位调节系数;Tb为模块的时间常数。
1.3 火电机组模型
火电机组模块包括调速器模型和原动机模型[18-19]。调速器功率偏差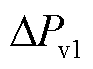 的动态物理模型为
的动态物理模型为
式中,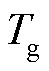 为调速器时间常数;
为调速器时间常数;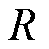 为发电机组的调差系数;
为发电机组的调差系数;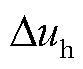 为调速器控制输入信号。
为调速器控制输入信号。
原动机输出功率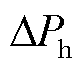 动态物理模型为
动态物理模型为
式中,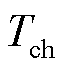 为原动机时间常数。
为原动机时间常数。
1.4 风电机组模型
本文用到了变速恒频双馈风电机组进行两区域负荷频率控制[20-21],该模块包括低频滤波器模型、Washout滤波器模型和发电机组模型。其中低频滤波器频率偏差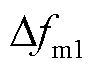 的动态物理模型为
的动态物理模型为
式中,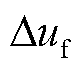 为风电机组控制输入信号;
为风电机组控制输入信号;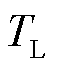 为低频滤波器时间常数。
为低频滤波器时间常数。
Washout滤波器频率偏差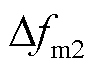 的动态物理模型为
的动态物理模型为
式中,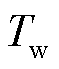 为Washout滤波器时间常数。
为Washout滤波器时间常数。
风力发电机组输出功率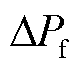 的动态物理模型为
的动态物理模型为
式中,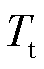 为DFIG发电机组的时间常数;
为DFIG发电机组的时间常数;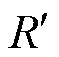 为机组的功频静态特性系数。
为机组的功频静态特性系数。
1.5 联络线功率模型
区域一、二之间的联络线功率偏差动态物理模型为
式中,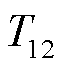 为区域间的同步系数;
为区域间的同步系数; 为区域间的联络线电抗;
为区域间的联络线电抗;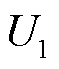 、
、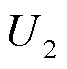 和
和 、
、 分别为区域一、二的端电压和相角;s为变换系数。
分别为区域一、二的端电压和相角;s为变换系数。
1.6 区域控制误差模型
本文采用了联络线功率及频率偏差控制TBC(tie-line bias frequency control)模式,该模式需要同时检测 和
和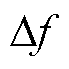 [22],其频率区域控制偏差(Area Control Error, ACE)的计算公式为
[22],其频率区域控制偏差(Area Control Error, ACE)的计算公式为
式中,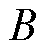 为频率的折算系数。
为频率的折算系数。
2 控制原理
2.1 DDPG自适应控制策略
深度确定性策略梯度算法(Deep Deterministic Policy Gradient, DDPG)是一种基于深度Q学习算法(Deep Q-lenrning, DQN)的改进算法,有效解决了多维连续动作输出的问题。这种优化算法可以在连续的动作空间中运行。此外,类似于其他无模型强化学习算法,DDPG算法可以完成黑盒学习,无需系统的详细数学模型,在运行时只关注状态、动作和奖励值三个部分。
强化学习系统简化框图如图2所示,在学习过程中,智能体和它周围的环境之间存在一个交互过程,可以解释如下:智能体在执行一个动作后,不仅能够从环境中获得瞬时奖赏,也使环境的状态发生了转移。为了获得最优的策略,智能体需要考察一系列状态转移所带来的长期奖赏,这里长期奖赏一般由无限折扣奖赏模型来计算。智能体的强化学习过程就是不断地与环境交互,通过动作的执行从
一个状态转移到另一个状态,并根据环境的瞬时奖赏来计算长期奖赏。
在强化学习算法中,常用的优化目标(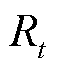 )是在时间
)是在时间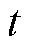 的总的未来回报的期望,即
的总的未来回报的期望,即
式中,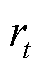 为第一步迭代得到的奖励值;
为第一步迭代得到的奖励值;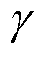 为系数,
为系数,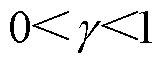 ,可确保
,可确保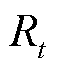 收敛。为了能够方便求解
收敛。为了能够方便求解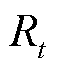 ,可以将式(10)写为迭代公式,即
,可以将式(10)写为迭代公式,即
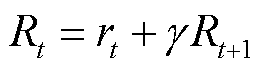 (11)
(11)
在Q学习算法中,如果用状态值和动作值来表示奖励值即函数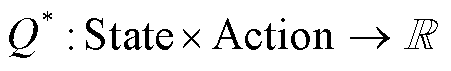 来代替
来代替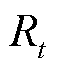 ,那么就可以获得最优动作策略价值函数
,那么就可以获得最优动作策略价值函数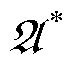 为
为
式中,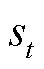 为状态值;at为动作值。
为状态值;at为动作值。
在强化学习算法中,通常情况下环境是未知的,因此函数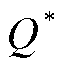 无法直接获得。但已经证明深度神经网络(Deep Neural Network, DNN)是通用的函数逼近器,因此可以被用来近似表达
无法直接获得。但已经证明深度神经网络(Deep Neural Network, DNN)是通用的函数逼近器,因此可以被用来近似表达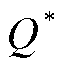 。在本文中,深度神经网络被表示为
。在本文中,深度神经网络被表示为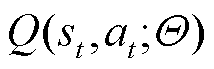 ,其中,
,其中, 代表要求解的参数。因此,当函数
代表要求解的参数。因此,当函数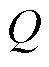 逼近
逼近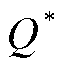 时,
时, 表示最优参数
表示最优参数 ,同时可以得到
,同时可以得到
由于函数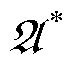 具有最优的动作策略价值。
具有最优的动作策略价值。
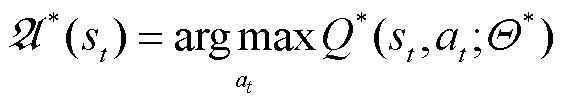 (14)
(14)
所以式(13)可以表示为
因此,可以将深度神经网络的优化目标定义为
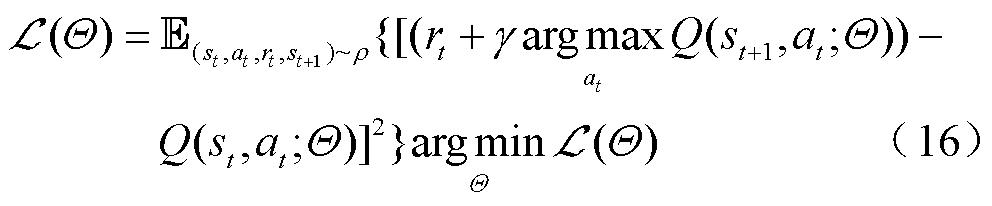
式中,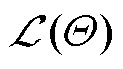 为将包含
为将包含 的优化目标函数作为自变量;
的优化目标函数作为自变量;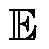 为期望;
为期望;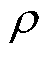 为概率分布。以式(16)为DQN算法的优化目标,但仅当
为概率分布。以式(16)为DQN算法的优化目标,但仅当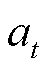 处于离散状态时该优化目标才适用。在本文中,
处于离散状态时该优化目标才适用。在本文中,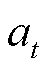 是多维连续的,因此考虑到一种DQN的改进算法——DDPG,该算法使用了深度神经网络
是多维连续的,因此考虑到一种DQN的改进算法——DDPG,该算法使用了深度神经网络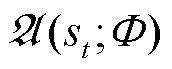 来近似表示最优动作策略函数
来近似表示最优动作策略函数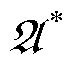 ,其优化目标为
,其优化目标为
式中,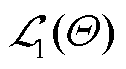 为DQN算法的优化目标;
为DQN算法的优化目标; 为近似动作策略函数
为近似动作策略函数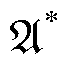 的优化目标。为了使优化过程更加稳定,式(17)中的
的优化目标。为了使优化过程更加稳定,式(17)中的 和
和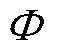 被替换为式(18)中与软更新参数相关的
被替换为式(18)中与软更新参数相关的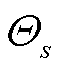 和
和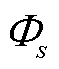 。
。
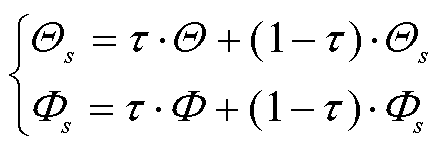 (18)
(18)
式中,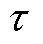 为系数,
为系数,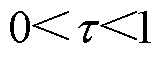 。
。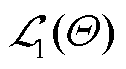 和
和 计算值的期望可以通过蒙特卡洛采样近似估算,因此优化目标可以被重写为
计算值的期望可以通过蒙特卡洛采样近似估算,因此优化目标可以被重写为
式中,N为维数。本文使用随机梯度下降法交替优化两个优化目标,参数更新方法为
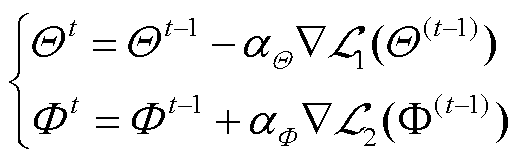 (20)
(20)
DDPG算法包含actor网络和critic网络两部分,该actor-critic框架分别由四个全连接层神经网络构成,见表1。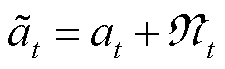 ,
,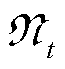 表示随机噪声。在学习阶段,经验记忆库将均匀采样一小批元组信息用于更新actor、critic网络的参数。
表示随机噪声。在学习阶段,经验记忆库将均匀采样一小批元组信息用于更新actor、critic网络的参数。
表1 DDPG算法网络结构
Tab.1 The network structure of DDPG

网络名称输入输出 actor网络 actor目标网络 critic网络 critic目标网络
2.2 基于DDPG算法的控制器设计
2000年以来,国内两大电网公司开始采用北美电力可靠性委员会于1997年提出的CPS指标作为考察频率控制质量的标准。同时,在智能电网发展的大背景下,开发具有自主学习能力的负荷频率控制方法具有重大意义。DDPG算法在运行时只关注状态、动作和奖励值三个部分的特点与CPS控制的获得长期最大收益的特性十分符合,因此,在构造奖励函数时加入CPS指标是合理的[23-24]。其中,CPS标准的考核方法为:① ,
,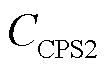 为任意值,则CPS指标合格;②
为任意值,则CPS指标合格;② ,
,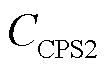 合格,则CPS指标合格;③
合格,则CPS指标合格;③ ,CPS指标不合格。
,CPS指标不合格。
本文通过采用DDPG算法来解决两区域多能电力系统的机组功率分配问题。所提出控制方法的结构模型如图3所示,图中的智能体是一个基于深度神经网络的智能体,该LFC控制器的环境是第1节中的式(1)~式(8)。智能体将接收控制区域中的ACE信号输入,来合理调整发电命令,以减少区域间的频率偏差、计划外的功率以及风电机组的弃风。
该方法包括离线预学习和在线应用两个阶段。离线预学习阶段,预学习过程将迭代更新智能体的所有参数。在每次自学习迭代过程中,智能体将进行动作探索(即生成不同的命令)以与环境(即两区域多能电力系统)进行交互。经过探索,智能体的参数将根据系统区域控制误差和LFC控制器的奖励函数进行更新。在有适当的奖励函数R并考虑环境约束(式(1)~式(8))的情况下,actor的梯度(即控制目标相对于智能体参数的梯度)将被计算和用于更新智能体的所有参数。
在线应用阶段,智能体会针对每一个控制区域,根据自己得到的观测值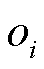 和参数
和参数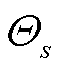 、
、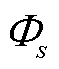 ,计算出动作值(即生成命令)
,计算出动作值(即生成命令)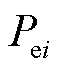 。在本文中,智能体得到的观测值
。在本文中,智能体得到的观测值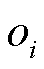 包括区域控制误差的比例、积分和微分值。定义为
包括区域控制误差的比例、积分和微分值。定义为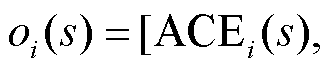
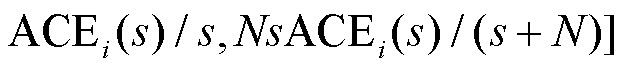 。
。
对两区域多能电力系统LFC模型,本文将频率偏差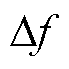 值、联络线功率偏差
值、联络线功率偏差 值、区域控制误差ACE值、风电机组弃风Picast值及CPS1值融入奖励函数中,其定义为
值、区域控制误差ACE值、风电机组弃风Picast值及CPS1值融入奖励函数中,其定义为
奖励函数中引入Picast旨在最大限度地减少弃风,提高风电消纳的比例。当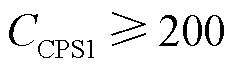 时,CPS指标合格,因此奖励函数中给奖励值-|Picast|2。当
时,CPS指标合格,因此奖励函数中给奖励值-|Picast|2。当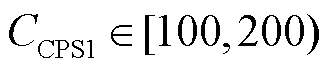 时,CPS2值不合格,因此对CPS2中的ACE值给予较大的惩罚,同时兼顾联络线功率偏差
时,CPS2值不合格,因此对CPS2中的ACE值给予较大的惩罚,同时兼顾联络线功率偏差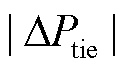 和弃风|Picast|。当
和弃风|Picast|。当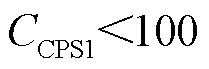 时,CPS1指标不合格,本文引入频率偏差
时,CPS1指标不合格,本文引入频率偏差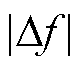 和区域控制误差|ACE|的乘积对较低的CPS1值给予惩罚。
和区域控制误差|ACE|的乘积对较低的CPS1值给予惩罚。
基于提出的DDPG算法框架和控制器参数更新规则,本文采用的算法流程如图4所示。
3 算例分析
3.1 基本参数
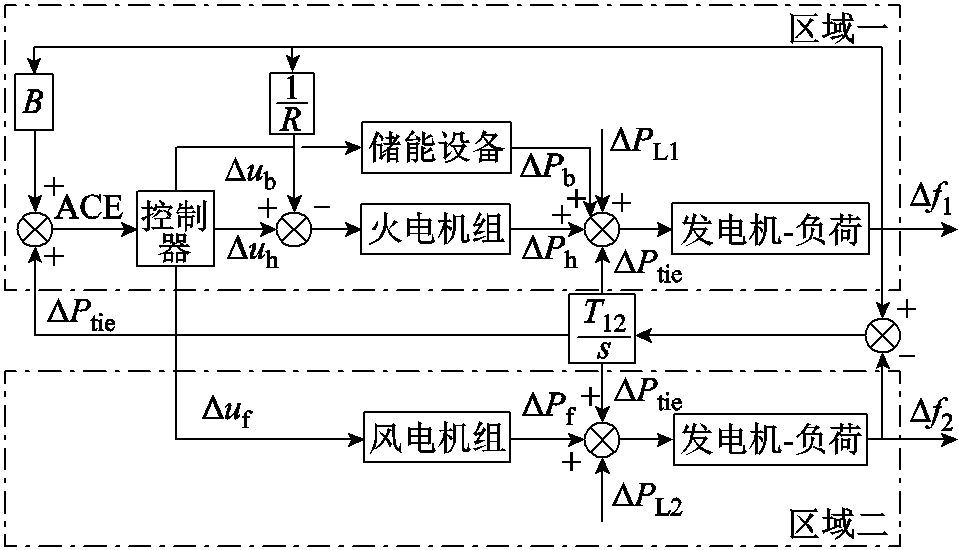
本文采用的算例是一个两区域多能互补电力系统,为验证所设计控制器的控制效果,在Matlab平台进行仿真试验。这两个区域相互连接,结构框图如图5所示,包括火电机组、风电机组惯性时间系数M1、M2以及负荷的频率调节效应系数D1、D2的系统模型控制相关参数选择参考文献[25],见表2。其中,火电机组的出力限制大于或等于30%,风电和储能的容量配比为10:1。
同时本文采用基于深度Q网络的DQN算法应用于控制器作为对照。DQN的critic网络学习率、内存缓存区大小和采样时间分别设置为0.01、3 000和1s,动作被离散为八种不同的生成命令。DDPG的critic网络学习率、actor网络学习率、内存缓冲区大小和采样时间分别设置为0.001、0.000 1、1 000 000和1s。经过多次仿真尝试,奖励函数中的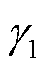 和
和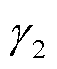 取值为0.1,
取值为0.1,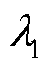 、
、 和
和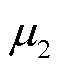 取值为1,
取值为1,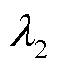 取值为100。
取值为100。
表2 多能互补发电系统的标称参数
Tab.2 Nominal parameters of hybrid power generation system

参数数值参数数值 1/61 1/1200.01 40.3 10.1 0.5451/6 0.4250.2 2.40.1
3.2 储能容量配置对系统的影响
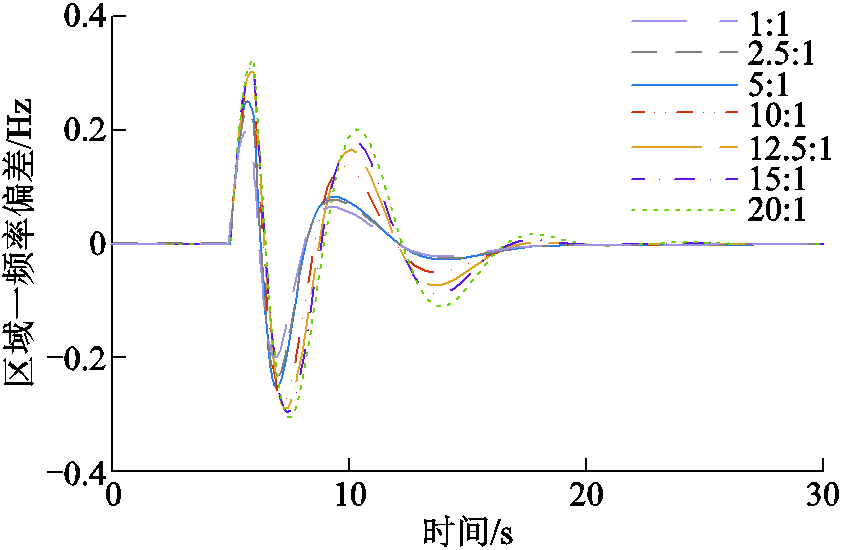
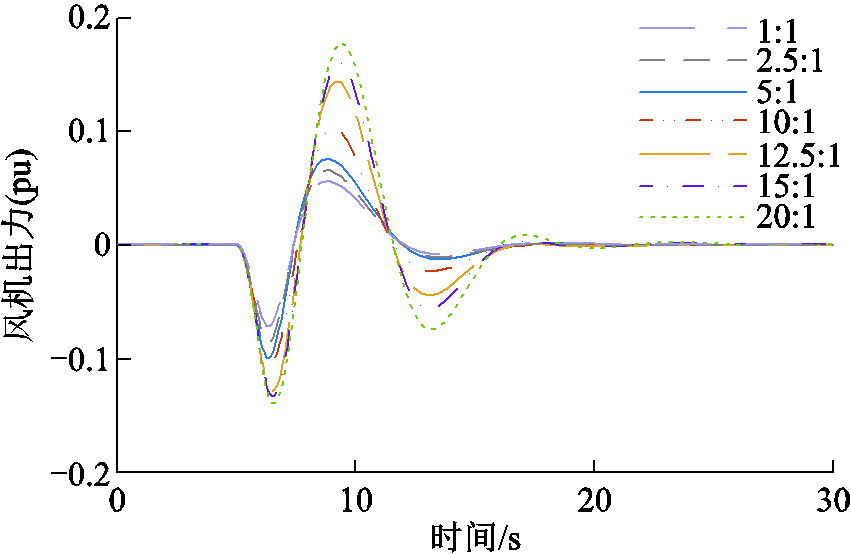
t=5s时,在区域一中设置幅值为0.1(pu),持续时间为1s的扰动以模拟负载突变的工况仿真。图6中比较了PID控制方式下,不同风电储能容量配比的系统动态响应。
从图6中可以看出,随着储能设备容量配比的增加,系统各类型指标的超调量不断减小,而调节时间随着储能配比的升高先减少后增加。
表3中给出了七种容量配比情况下的数值比较,可以得出当风电储能容量配比为10:1时,系统的超调量相对较小,同时能够在波动后迅速恢复稳定,兼顾了超调量和调节时间,总体来说是比较好的选择。
表3 负载突变时七种容量配比情况下的效果对比
Tab.3 Comparison of the effect of seven capacity ratios under load mutation

比较对象风电储能配比调节时间/s最大偏差 1:125.320.476 3 2.5:124.450.489 2 5:123.260.504 6 10:118.970.533 6 12.5:116.550.593 1 15:120.530.610 4 20:121.020.624 3 Pwind1:116.470.159 2 2.5:115.520.166 3 5:113.750.174 8 10:111.380.206 9 12.5:115.860.271 9 15:118.650.291 6 20:119.230.305 6
3.3 中长期控制性能的分析
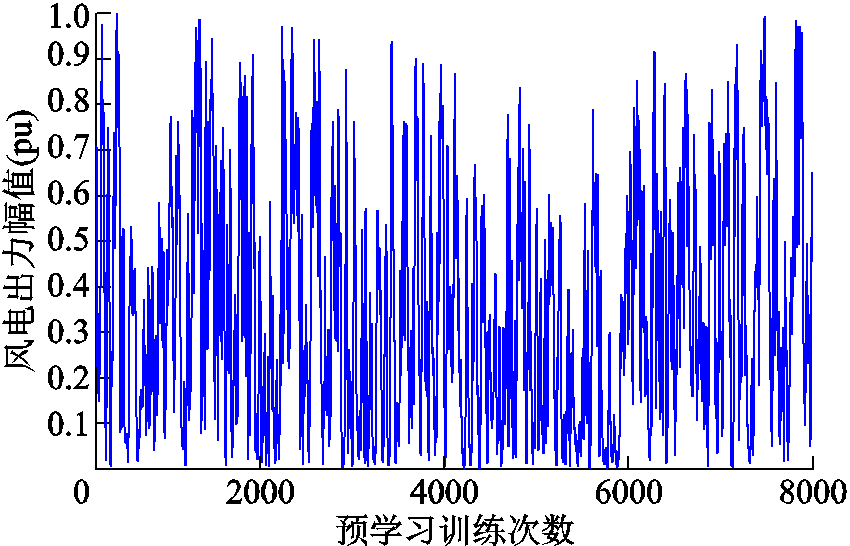
本文控制器首先采用离线模式的预学习方法, 如图7所示,利用四川小金县某风机的一年实际风机出力数据[26]对模型进行一定次数的训练。目的是使actor和critic网络根据训练函数的逻辑更新其内部参数,以适应整个系统,并且得到控制器在风电机组实际出力情况下的控制效果,同时能够应对千变万化的实际风电场出力的随机波动。
其次,考虑到电力系统中负荷波动的长期性与随机性,本文从中长期控制性能入手,通过引入阶跃扰动和实际风速扰动两种扰动方式来检验所提出数据驱动LFC方法的可行性。
3.3.1 阶跃响应扰动
本文在模型区域一采用幅值为0.05(pu),周期为250s的连续阶跃扰动信号,扰动波形如图8所示。测试结果如图9和表4所示。
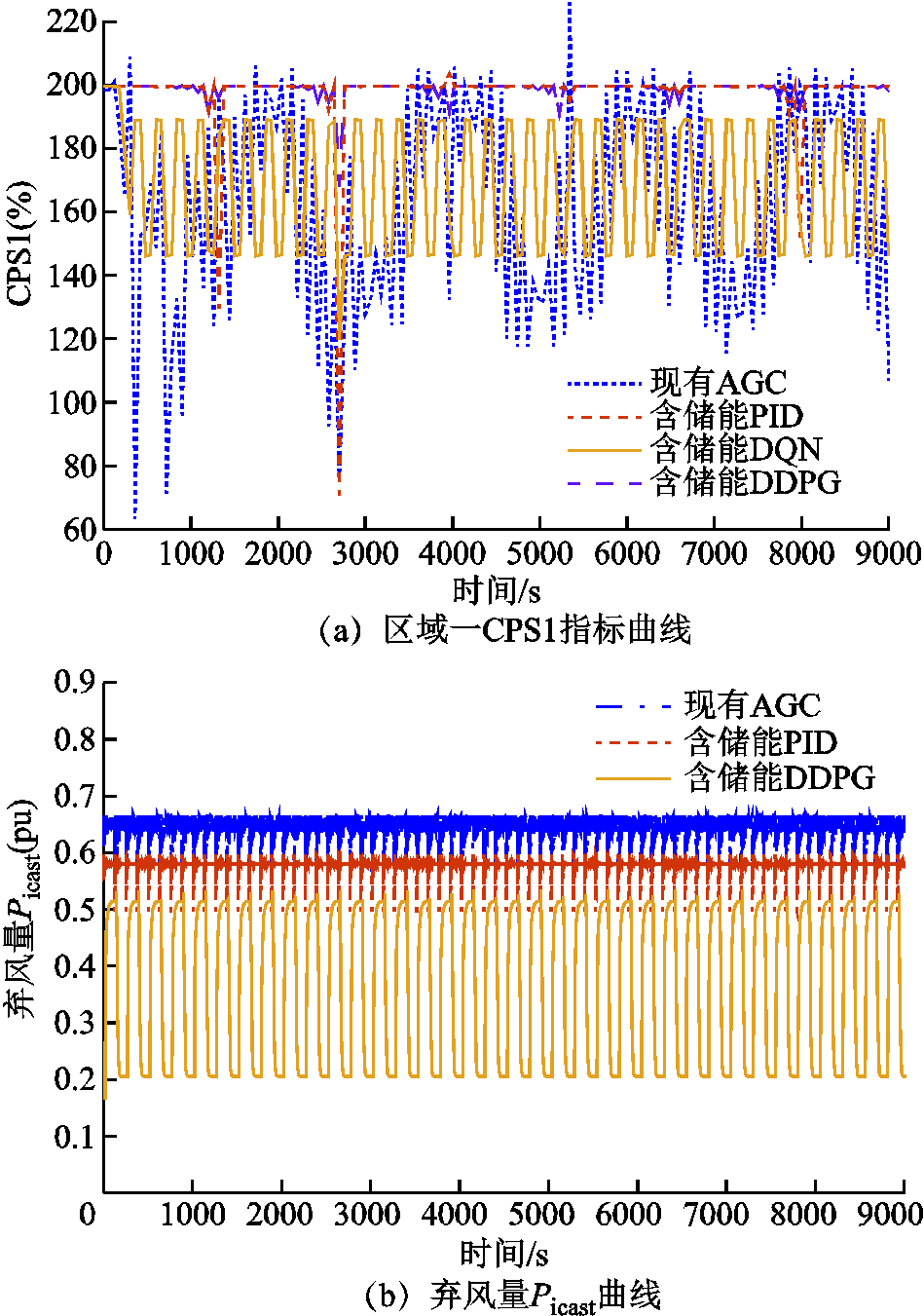
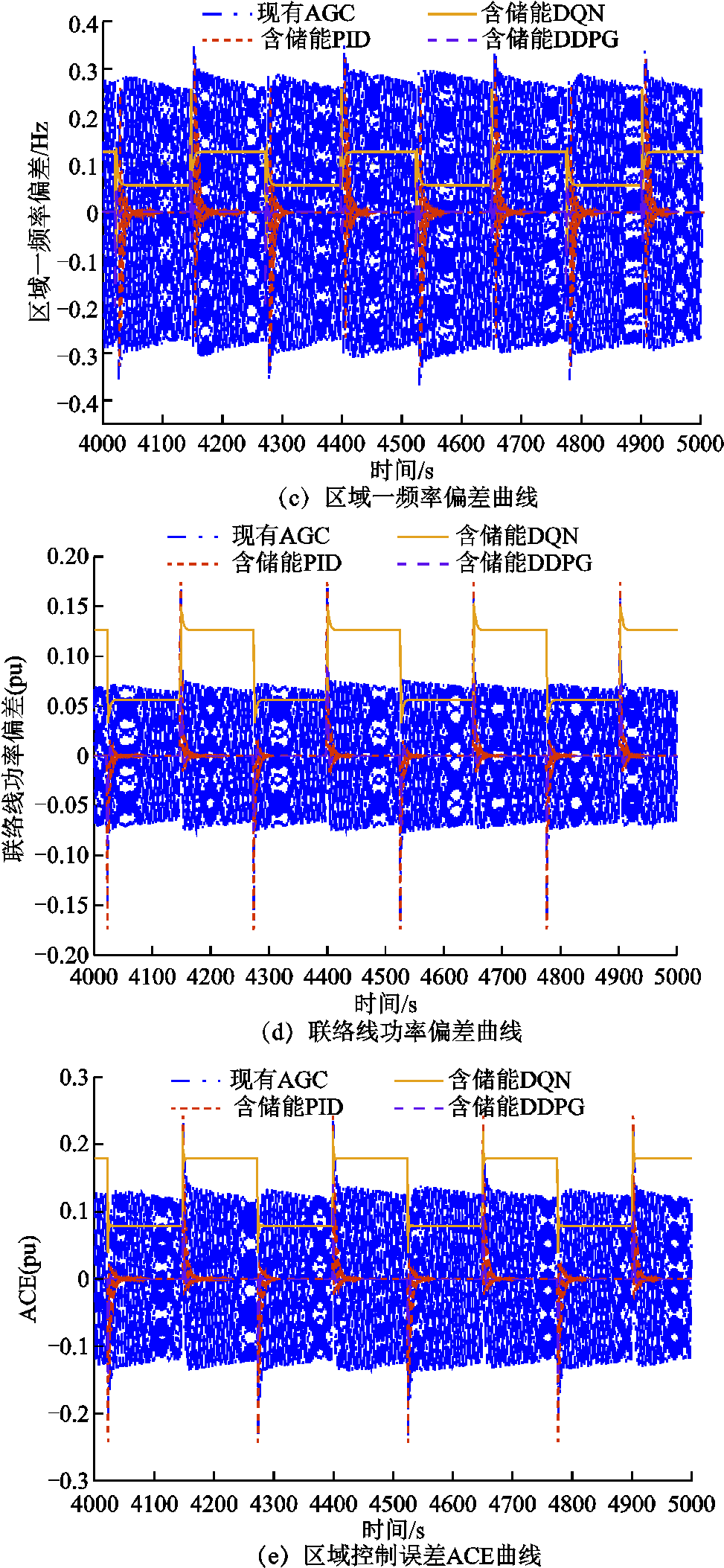
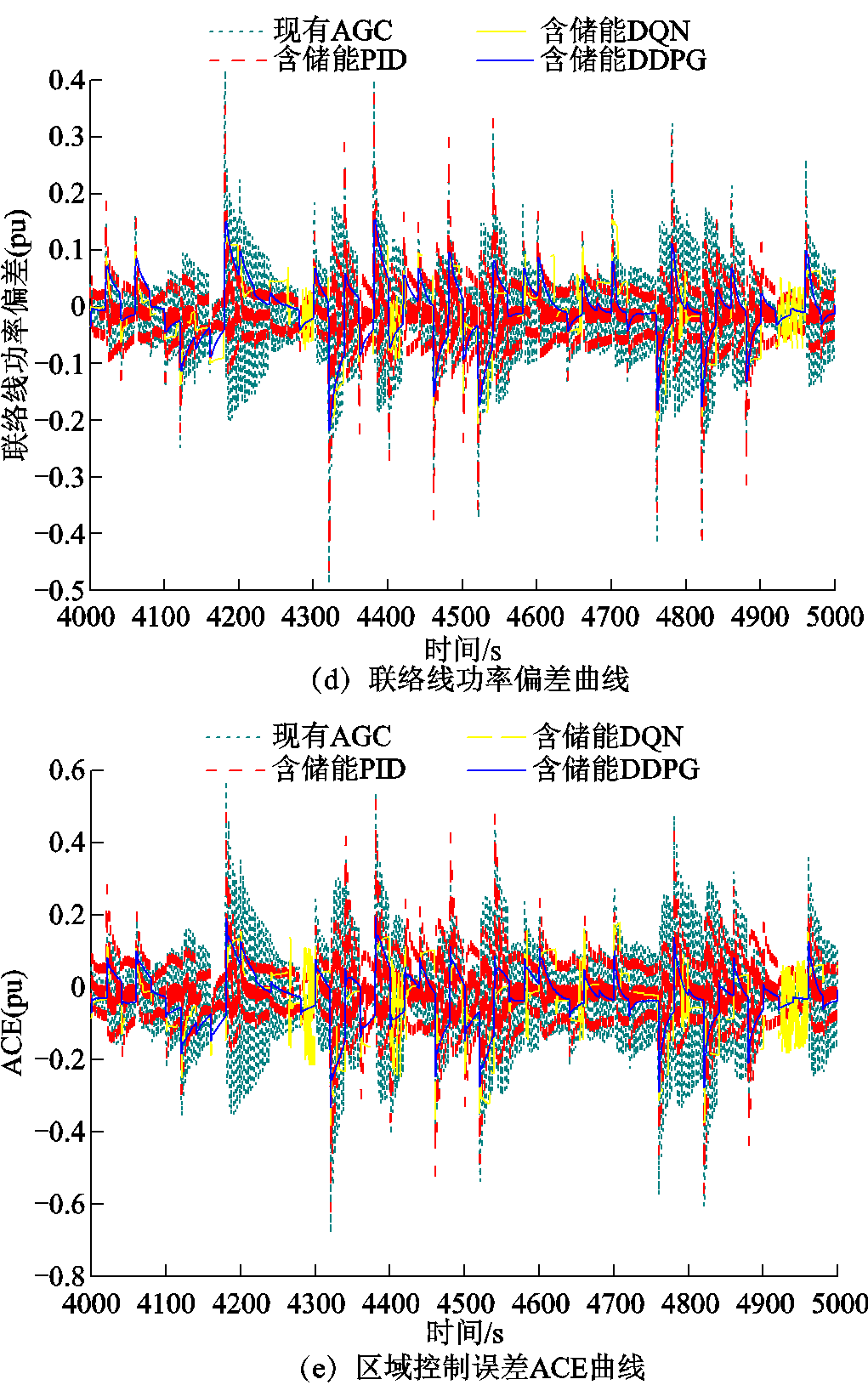
图9提供了四种功率分配协调控制方法(图9c~图9e三张动态性能仿真图截取了仿真时间4 000~ 5 000s):现有自动发电控制(Automation Generation Control, AGC)(无储能PID)、含储能PID、含储能DQN和含储能DDPG。
针对所提出的DDPG算法,根据图9a可得,两种PID控制方法出现了CPS1指标<100%的情况,表明功率分配控制超出了范围。DQN算法的CPS1指标满足CPS评价指标,但是波动较为剧烈。DDPG算法的CPS1控制指标则最为理想。由图9b可得,储能设备的引入以及所提出的DDPG算法在一定程度上减少了风电机组的弃风,其中含储能PID方法相比现有AGC控制的Picast平均值减少了8.40%,DDPG算法相比现有AGC控制和含储能PID方法分别减少了33.12%、26.99%。如图9c~图9e所示,各动态性能指标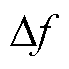 、
、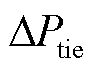 和ACE,DDPG算法相对于PID控制和DQN算法有了显著改进。相比于DQN算法,三种动态指标
和ACE,DDPG算法相对于PID控制和DQN算法有了显著改进。相比于DQN算法,三种动态指标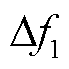 、
、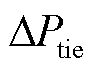 和ACE平均值分别减少了87.91%、94.38%和91.34%,相比于含储能PID方法分别减少了65.63%、54.55%和38.89%,相比现有AGC控制分别减少了93.96%、89.36%和86.59%。说明DDPG算法可以有效减少各动态指标峰值的同时,也可以使系统发生连续阶跃扰动时各指标迅速恢复到0。其中,DQN算法相比含储能PID控制方法效果更差,可能的原因是缺少更加详细的离散化。
和ACE平均值分别减少了87.91%、94.38%和91.34%,相比于含储能PID方法分别减少了65.63%、54.55%和38.89%,相比现有AGC控制分别减少了93.96%、89.36%和86.59%。说明DDPG算法可以有效减少各动态指标峰值的同时,也可以使系统发生连续阶跃扰动时各指标迅速恢复到0。其中,DQN算法相比含储能PID控制方法效果更差,可能的原因是缺少更加详细的离散化。
表4 扰动下的仿真结果
Tab.4 Simulation results under disturbance

扰动方式控制方式CPS1(%)/Hz(pu)|ACE|(pu) 最小值平均值最大值平均值最大值平均值最大值平均值 阶跃响应现有AGC64.73163.90.4840.1820.2040.0470.2920.082 含储能PID71.36198.20.3260.0320.1750.0110.2440.018 DQN120.3168.90.2610.0910.1500.0890.2210.127 DDPG170.9199.30.2010.0110.0930.0050.1420.011 实际风速现有AGC-88.13129.21.6260.1590.7780.0630.7010.089 含储能PID-22.53144.71.4230.1130.6990.0370.6480.051 DQN15.36177.00.8160.0980.2890.0310.4430.046 DDPG179.4191.30.6610.0450.3110.0280.1750.034
综合上述分析及表4,多区域电力系统在发生连续阶跃扰动的情况下,储能设备的引入和所提出的DDPG算法无论是在CPS控制指标、可再生能源发电消纳还是在动态性能方面都较其他三种控制方法更优。
3.3.2 实际风速扰动
考虑到风电场出力的间歇性和波动性,本文采用如图7所示的风电机组实际风速扰动来对系统进行仿真,以验证所提方法的有效性。测试结果如图10和表4所示。
图10提供了四种功率分配控制方法(图10c~图10e三张动态性能仿真图截取了仿真时间 4 000~5 000s):现有AGC控制(无储能PID)、含储能PID、含储能DQN和含储能DDPG。
针对所提出的DDPG算法,根据图10a可得,两种PID控制方法和DQN算法出现了CPS1指标 100%的情况,表明功率分配控制超出了范围。DDPG算法的CPS1控制指标则最为理想,指标值也最接近200%。由图10b可得,储能设备的引入以及所提出的DDPG算法在一定程度上同样减少了风电机组的弃风,其中含储能PID方法相比现有AGC控制的Picast平均值减少了7.44%,DDPG算法相比现有AGC控制和含储能PID方法分别减少了37.75%、32.74%。在动态性能方面,如图10c~图10e所示。两种动态性能指标
100%的情况,表明功率分配控制超出了范围。DDPG算法的CPS1控制指标则最为理想,指标值也最接近200%。由图10b可得,储能设备的引入以及所提出的DDPG算法在一定程度上同样减少了风电机组的弃风,其中含储能PID方法相比现有AGC控制的Picast平均值减少了7.44%,DDPG算法相比现有AGC控制和含储能PID方法分别减少了37.75%、32.74%。在动态性能方面,如图10c~图10e所示。两种动态性能指标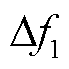 和ACE,DDPG算法相比于DQN算法有了显著改进,平均值分别减少了54.08%和26.09%,相比于含储能PID方法分别减少了60.18%和33.33%,相比于现有AGC控制分别减少了71.70%和61.80%。说明DDPG算法可以有效减少各动态指标峰值的同时,也可以使系统发生实际风速扰动时各指标迅速恢复到0。其中,DDPG算法在
和ACE,DDPG算法相比于DQN算法有了显著改进,平均值分别减少了54.08%和26.09%,相比于含储能PID方法分别减少了60.18%和33.33%,相比于现有AGC控制分别减少了71.70%和61.80%。说明DDPG算法可以有效减少各动态指标峰值的同时,也可以使系统发生实际风速扰动时各指标迅速恢复到0。其中,DDPG算法在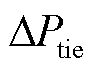 指标控制上较含DQN算法效果较差,可能的原因是缺乏足够次数的预学习训练。
指标控制上较含DQN算法效果较差,可能的原因是缺乏足够次数的预学习训练。
综合上述分析及表4,多区域电力系统在实际风速扰动的情况下,总体来说储能设备的引入和所提出的DDPG算法无论是在CPS控制指标、可再生能源发电消纳还是在动态性能方面都较其他三种控制方法更优。
4 结论
1)提出了一种基于数据驱动的两区域多能电力系统负荷频率控制方法。该方法基于深度强化学习算法,包括离线预学习和在线应用两部分,可直接通过自学习生成控制命令。
2)考虑引入储能设备来克服仅改进控制器控制策略带来的局限性。仿真结果表明储能设备的引入在一定程度上改善了系统的LFC性能和可再生能源的发电消纳能力。
3)考虑所提方法在风电实际出力情况下的控制效果,并且从中长期控制性能入手进行仿真,证明了在电力系统发生连续阶跃扰动或实际风速扰动的情况下,所提DDPG算法比现有AGC控制和DQN算法都能显著降低电力系统的CPS1、风电机组弃风、频率偏差、联络线功率偏差以及区域控制误差等指标,实现了动态性能最优并且能够应对千变万化的实际风电机组出力的随机波动。
本文的仿真模型忽略了各机组的调节死区以及速率限制等问题,这些方面是今后研究更多不同特性新能源接入区域电网需要重点考虑的。
参考文献
[1] 彭思敏, 窦真兰, 凌志斌, 等. 并联型储能系统孤网运行协调控制策略[J]. 电工技术学报, 2013, 28(5): 128-134.
Peng Simin, Dou Zhenlan, Ling Zhibin, et al. Cooperative control for parallel-connected battery energy storage system of islanded power system[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 128-134.
[2] 赵晶晶, 李敏, 何欣芹, 等. 基于限转矩控制的风储联合调频控制策略[J]. 电工技术学报, 2019, 34(23): 4982-4950.
Zhao Jingjing, Li Min, He Xinqin, et al. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4982-4950.
[3] 陈文倩, 辛小南, 程志平. 基于虚拟同步发电机的光储并网发电控制技术[J]. 电工技术学报, 2018, 33(2): 538-545.
Chen Wenqian, Xin Xiaonan, Cheng Zhiping. Control of grid-connected of photovoltaic system with storage based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 538-545.
[4] 常烨骙, 李卫东, 巴宇, 等. 基于运行安全的频率控制性能评价新方法[J]. 电工技术学报, 2019, 34(6): 1218-1229.
Chang Yekui, Li Weidong, Ba Yu, et al. A new method for frequency control performance assessment on operation security[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1218-1229.
[5] 左剑, 谢平平, 李银红, 等. 基于智能优化算法的互联电网负荷频率控制器设计及其控制性能分析[J]. 电工技术学报, 2018, 33(3): 478-489.
Zuo Jian, Xie Pingping, Li Yinhong, et al. Intelligent optimization algorithm based load frequency controller design and its control performance assessment in interconnected power grids[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 478-489.
[6] 单华, 和婧, 范立新, 等. 面向抽水蓄能电站区域负荷频率的分数阶PID控制研究[J]. 电网技术, 2020, 44(4): 1410-1418.
Shan Hua, He Jing, Fan Lixin, et al. Research on fractional order PID control of regional load frequency of pumped storage power station[J]. Power System Technology, 2020, 44(4): 1410-1418.
[7] Wang Haixin, Yang Junyou, Chen Zhe, et al. Model predictive control of PMSG-based wind turbines for frequency regulation in an isolated grid[J]. IEEE Trans actions on Industry Applications, 2018, 54(4): 3077-3089.
[8] 程乐峰, 余涛, 张孝顺, 等. 机器学习在能源与电力系统领域的应用和展望[J]. 电力系统自动化, 2019, 43(1): 15-31.
Cheng Lefeng, Yu Tao, Zhang Xiaoshun, et al. Application and prospects of machine learning in the field of energy and power systems[J]. Automation of Electirc Power Systems, 2019, 43(1): 15-31.
[9] 余涛, 周斌, 陈家荣. 基于Q学习的互联电网动态最优CPS控制[J]. 中国电机工程学报, 2009, 29(19): 13-19.
Yu Tao, Zhou Bin, Chen Jiarong. Q-learning-based dynamic optimal CPS control methodology for interconnected power systems[J]. Proceedings of the CSEE, 2009, 29(19): 13-19.
[10] 余涛, 甄卫国, 叶文加, 等. 基于多步回溯Q学习的自动发电控制指令动态优化分配算法[J]. 控制理论与应用, 2011, 28(1): 58-64.
Yu Tao, Zhen Weiguo, Ye Wenjia, et al. Multi-step backtrack Q-learning based dynamic optimal algorithm for auto generation control order dispatch[J]. Control Theory&Applications, 2011, 28(1): 58-64.
[11] 张孝顺, 余涛, 唐捷. 基于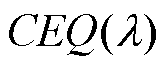 多智能体协同学习的互联电网性能标准控制指令动态分配优化算法[J]. 电工技术学报, 2016, 31(8): 125-133.
多智能体协同学习的互联电网性能标准控制指令动态分配优化算法[J]. 电工技术学报, 2016, 31(8): 125-133.
Zhang Xiaoshun, Yu Tao, Tang Jie. Dynamic optimal allocation algorithm for control performance standard order of interconnected power grids using synergetic learning of multi-agent 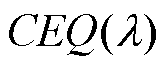 [J]. Transactions of China Electrotechnical Society, 2016, 31(8):125-133.
[J]. Transactions of China Electrotechnical Society, 2016, 31(8):125-133.
[12] 李涛, 胡维昊, 李坚, 等. 基于深度强化学习算法的光伏-抽蓄互补系统智能调度[J]. 电工技术学报, 2020, 35(13): 2757-2768.
Li Tao, Hu Weihao, Li Jian, et al. Intelligent economic dispatch for PV-PHS integrated system: a deep reinforcement learning -based approach[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2757-2768.
[13] Mocanu E, Mocanu D C, Nguyen P H, et al. On-line building energy optimization using deep reinfocement learning[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 3698-3708.
[14] 汪波, 郑文迪. 基于改进Q学习算法的储能系统实时优化决策研究[J]. 电气技术, 2018, 19(2): 54-60, 65.
Wang Bo, Zheng Wendi. Research on real-time optimization decision of energy storage system based on improved Q-learning algorithm[J]. Electrical Engineering, 2018, 19(2): 54-60, 65.
[15] 邹晓敏, 肖曦, 何琪, 等. 基于在线附加Q学习的伺服电机速度最优跟踪控制方法[J]. 电工技术学报, 2019, 34(5): 917-923.
Zou Xiaomin, Xiao Xi, He Qi, et al. Optimal tracking control of servo motor speed based on online supplementary Q-learning[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 917-923.
[16] Yan Ziming, Xu Yan. Data-driven load frequency control for stochastic power systems: a deep reinforcement learning method with continuous action search[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1653-1656.
[17] Yan Ziming, Xu Yan. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4599-4608.
[18] 吴云亮, 孙元章, 徐箭, 等. 基于多变量广义预测理论的互联电力系统负荷-频率协调控制体系[J]. 电工技术学报, 2012, 27(9): 101-107.
Wu Yunliang, Sun Yuanzhang, Xu Jian, et al. Coordinated load-frequency control system in interconnected power system based on multivariable generalized predictive control theory[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 101-107.
[19] Wei Xu, Dong Hu, Gang Lei, et al. System-level efficiency optimization of a linear induction motor drive system[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 285-291.
[20] 张冠锋, 杨俊友, 孙峰, 等. 基于虚拟惯量和频率下垂控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2017, 32(22): 225-232.
Zhang Guanfeng, Yang Junyou, Sun Feng, et al. Primary frequency regulation strategy of DFIG based on virtual inertia and frequency droop control[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 225-232.
[21] 章艳, 高晗, 张萌. 不同虚拟同步机控制下双馈风机系统频率响应差异研究[J]. 电工技术学报, 2020, 35(13): 2889-2900.
Zhang Yan, Gao Han, Zhang Meng. Research on frequency response difference of doubly-fed induction generator system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889-2900.
[22] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039.
Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[23] 余涛, 王宇名, 刘前进, 等. 互联电网CPS调节指令动态最有分配Q-学习算法[J]. 中国电机工程学报, 2010, 30(7): 62-69.
Yu Tao, Wang Yuming, Liu Qianjin, et al. Q-learning-based dynamic optimal allocation algorithm for CPS order of interconnected power grids[J]. Proceedings of the CSEE, 2010, 30(7): 62-69.
[24] 席磊, 余涛, 张孝顺, 等. 基于狼爬山快速多智能体学习策略的电力系统智能发电控制方法[J]. 电工技术学报, 2015, 30(23): 93-101.
Xi Lei, Yu Tao, Zhang Xiaoshun, et al. A fast multi-agent learning strategy based on 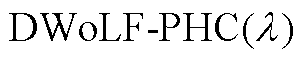 for smart generation control of power systems[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 93-101.
for smart generation control of power systems[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 93-101.
[25] Elgerd O I, Fosha C E. Optimum megawatt-frequency control of multi-area electric energy systems[J]. IEEE Transactions on Power Apparatus and Systems, 1970, PAS-89(4): 556-563.
[26] Zhang Guozhou, Hu Weihao, Cao Di, et al. Data-driven optimal energy management for a wind-solar-diesel-battery-reverse osmosis hybrid energy system using a deep reinforcement learning approach[J]. Energy Conversion and Management, 2021, 227: 113608.
Load Frequency Control Strategy of Hybrid Power Generation System: a Deep Reinforcement Learning—Based Approach
Liang Yudong1 Chen Luan1 Zhang Guozhou1 Ren Manman2 Hu Weihao1
(1. Key Laboratory of Wide-area Mearsurement and Control on Power System of Sichuan Province University of Electronic Science and Technology of China Chengdu 611731 China 2. State grid Anhui Electric Power Co. Ltd Electric Power Research Institute Hefei 230000 China)
Abstract To solve the problem of frequency modulation performance degradation caused by large-scale renewable energy access to the power grid, this paper proposes a data-driven load frequency coordinated optimization control method for hybrid energy system consisted of wind, thermal power and energy storage. Firstly, this paper establishes a mathematical model of the multi-area hybrid energy system through mechanism analysis. Secondly, a reward function with control performance standard (CPS), wind power casting and dynamic performance index is established. The load frequency control problem is transformed into a maximum reward function problem, and the deep deterministic policy gradient (DDPG) algorithm is introduced to solve this problem. Through pre-learning and online application, the optimal adaptive coordinated control strategy can be obtained under acturl output of wind turbine. Finally, the performance of the proposed method in improving the performance of load frequency control (LFC) is verified by stepped disturbance and actual wind speed disturbance. Simulation results show that when the power system is disturbed, the introduction of energy storage equipment and the proposed method can not only suppress fluctuations effectively, but also shorten the adjustment time required by LFC and increase the proportion of wind power consumption.
keywords:Hybrid energy system, load frequency control, deep deterministic policy gradient, control performance standard(CPS) index
DOI:10.19595/j.cnki.1000-6753.tces.210309
中图分类号:TM744
作者简介
梁煜东 男,1997年生,硕士研究生,研究方向为可再生能源发电及其并网技术。E-mail:lydddace@163.com
胡维昊 男,1982年生,教授,博士生导师,研究方向为人工智能在电力系统中的应用、可再生能源发电技术。E-mail:whu@uestc.edu.cn(通信作者)
收稿日期 2021-03-11
改稿日期 2021-07-06
国家重点研发计划(2018YFE0127600)和四川省科技计划(2018HH0146)资助项目。
(编辑 赫蕾)
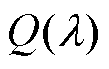 学习算法,该在线回溯算法显式地利用资格迹对将来多步决策的在线强化信息进行高效地回溯操作,能够有效地解决使用单步Q学习算法无法完整评估动作决策优劣性的问题。在文献[10]的基础上,文献[11]将基于相关均衡(Correlated-Equilibrium-Q, CEQ)的学习算法与多步回溯Q学习方法相结合,提出一种全新的多智能体学习算法
学习算法,该在线回溯算法显式地利用资格迹对将来多步决策的在线强化信息进行高效地回溯操作,能够有效地解决使用单步Q学习算法无法完整评估动作决策优劣性的问题。在文献[10]的基础上,文献[11]将基于相关均衡(Correlated-Equilibrium-Q, CEQ)的学习算法与多步回溯Q学习方法相结合,提出一种全新的多智能体学习算法 ,并将该算法应用到控制性能标准(Control Performance Standard, CPS)指令的最优分配问题中。上述研究都提出了基于强化学习的LFC方法,但发电机组生成的命令被离散化,在一定程度上限制了控制性能。同时,复杂电力系统环境高维状态的特性通常让传统强化学习算法面临“维数灾”的困扰,难以找到最优解。谷歌的人工智能团队DeepMind创造性地将深度学习的感知能力与强化学习的决策能力相结合,提出深度强化学习(Deep Reinforcement Learning, DRL)[12],该方法具备了解决大规模强化学习问题的能力。如文献[13]采用深度Q学习算法设计了含电动汽车和大规模光伏的在线调度策略。文献[14]考虑储能系统充放电爬坡和存储电量限值等约束条件,将改进的Q学习算法应用到实时调度周期储能系统中做优化决策。文献[15]将在线Q学习方法与附加控制思想相结合,讨论了其在伺服系统中电机速度最优跟踪控制问题上的应用。
,并将该算法应用到控制性能标准(Control Performance Standard, CPS)指令的最优分配问题中。上述研究都提出了基于强化学习的LFC方法,但发电机组生成的命令被离散化,在一定程度上限制了控制性能。同时,复杂电力系统环境高维状态的特性通常让传统强化学习算法面临“维数灾”的困扰,难以找到最优解。谷歌的人工智能团队DeepMind创造性地将深度学习的感知能力与强化学习的决策能力相结合,提出深度强化学习(Deep Reinforcement Learning, DRL)[12],该方法具备了解决大规模强化学习问题的能力。如文献[13]采用深度Q学习算法设计了含电动汽车和大规模光伏的在线调度策略。文献[14]考虑储能系统充放电爬坡和存储电量限值等约束条件,将改进的Q学习算法应用到实时调度周期储能系统中做优化决策。文献[15]将在线Q学习方法与附加控制思想相结合,讨论了其在伺服系统中电机速度最优跟踪控制问题上的应用。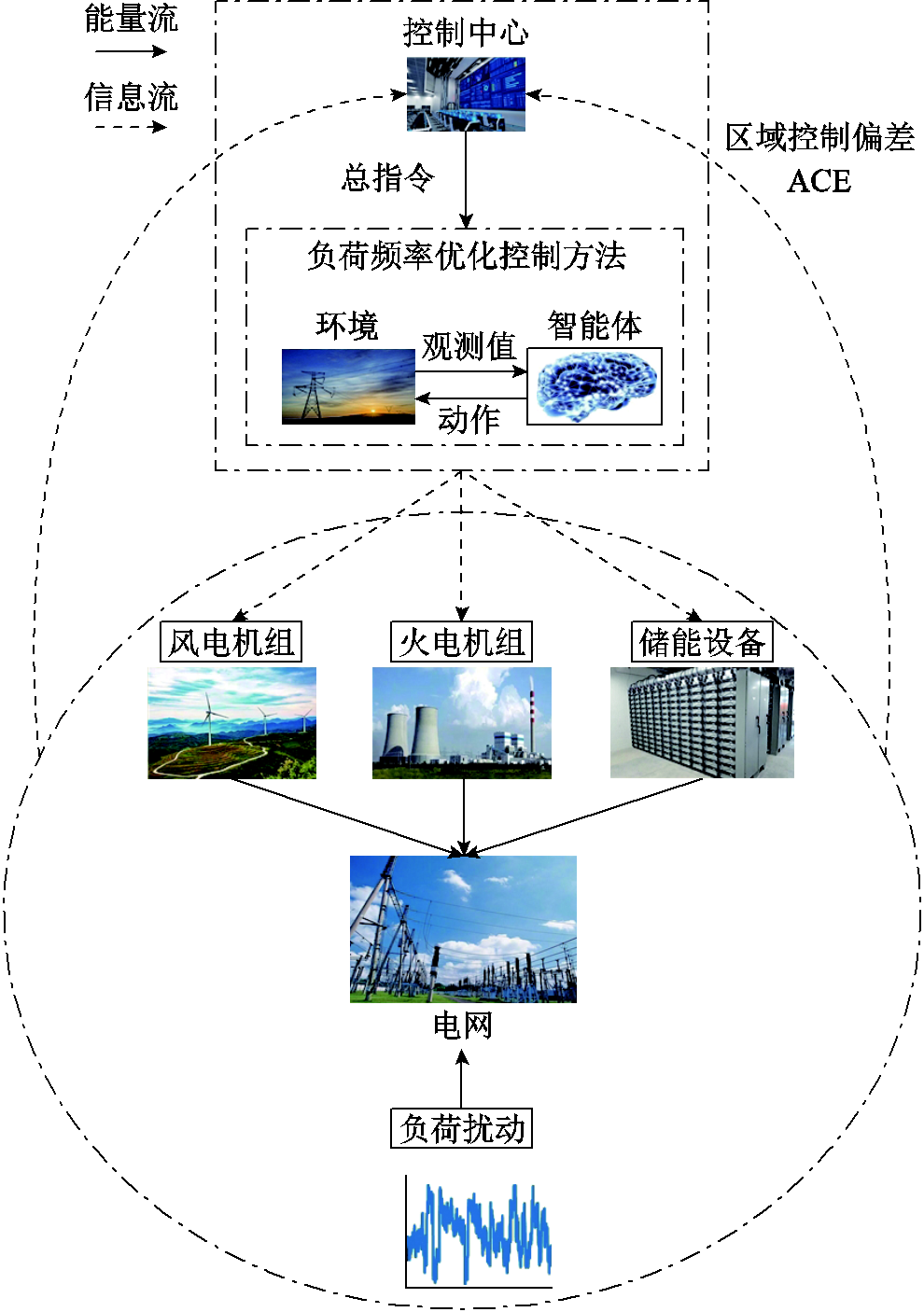
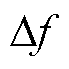 为
为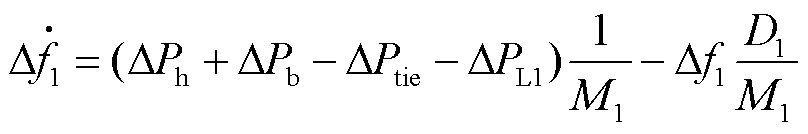 (1)
(1)
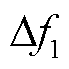 为区域一的频率偏差;
为区域一的频率偏差;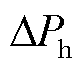 为原动机的输出功率;
为原动机的输出功率; 为储能系统的输出功率;
为储能系统的输出功率; 为区域一、二之间的联络线偏差;
为区域一、二之间的联络线偏差;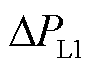 为区域一受到的负荷扰动;
为区域一受到的负荷扰动;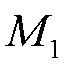 为火电机组的惯性时间系数;
为火电机组的惯性时间系数;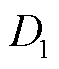 为负荷的频率调节效应系数。
为负荷的频率调节效应系数。 (2)
(2)
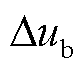 为储能系统模块的控制输入信号;
为储能系统模块的控制输入信号;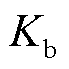 为储能电池单位调节系数;T
为储能电池单位调节系数;T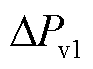 的动态物理模型为
的动态物理模型为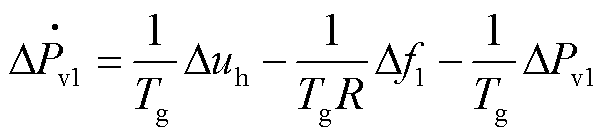 (3)
(3)
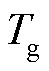 为调速器时间常数;
为调速器时间常数;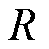 为发电机组的调差系数;
为发电机组的调差系数;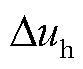 为调速器控制输入信号。
为调速器控制输入信号。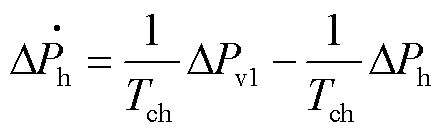 (4)
(4)
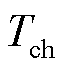 为原动机时间常数。
为原动机时间常数。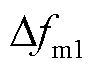 的动态物理模型为
的动态物理模型为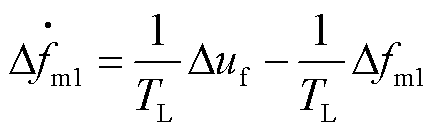 (5)
(5)
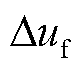 为风电机组控制输入信号;
为风电机组控制输入信号;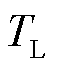 为低频滤波器时间常数。
为低频滤波器时间常数。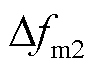 的动态物理模型为
的动态物理模型为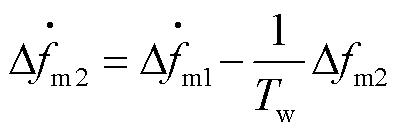 (6)
(6)
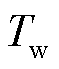 为Washout滤波器时间常数。
为Washout滤波器时间常数。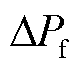 的动态物理模型为
的动态物理模型为 (7)
(7)
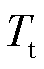 为DFIG发电机组的时间常数;
为DFIG发电机组的时间常数;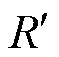 为机组的功频静态特性系数。
为机组的功频静态特性系数。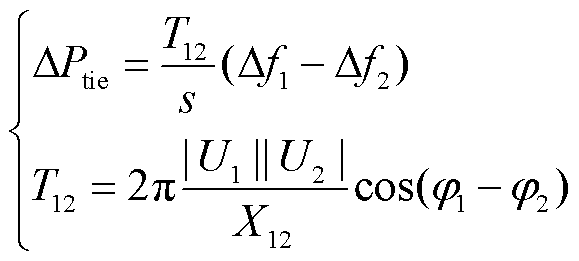 (8)
(8)
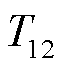 为区域间的同步系数;
为区域间的同步系数; 为区域间的联络线电抗;
为区域间的联络线电抗;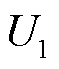 、
、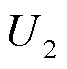 和
和 、
、 分别为区域一、二的端电压和相角;s为变换系数。
分别为区域一、二的端电压和相角;s为变换系数。 (9)
(9)
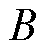 为频率的折算系数。
为频率的折算系数。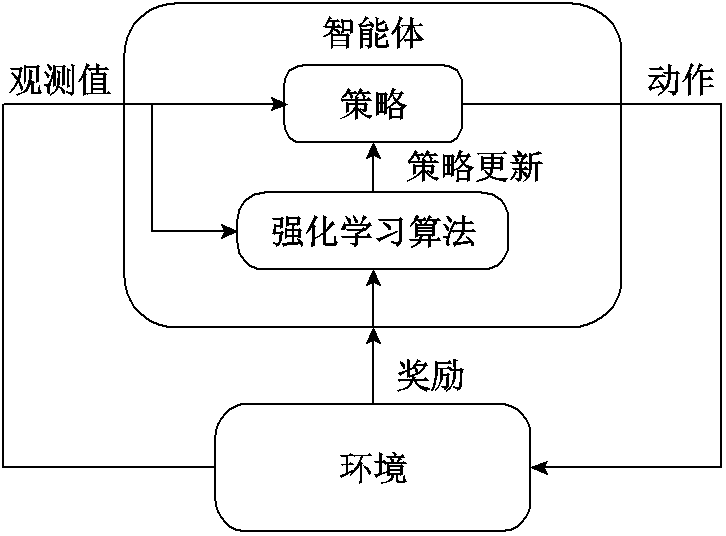
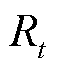 )是在时间
)是在时间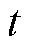 的总的未来回报的期望,即
的总的未来回报的期望,即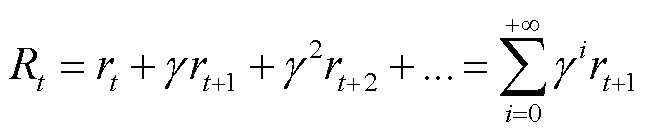 (10)
(10)
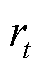 为第一步迭代得到的奖励值;
为第一步迭代得到的奖励值;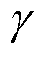 为系数,
为系数,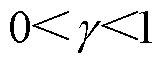 ,可确保
,可确保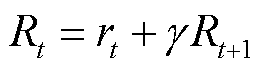 (11)
(11)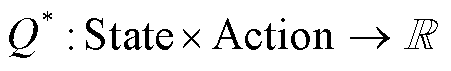 来代替
来代替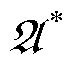 为
为 (12)
(12)
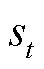 为状态值;a
为状态值;a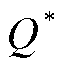 无法直接获得。但已经证明深度神经网络(Deep Neural Network, DNN)是通用的函数逼近器,因此可以被用来近似表达
无法直接获得。但已经证明深度神经网络(Deep Neural Network, DNN)是通用的函数逼近器,因此可以被用来近似表达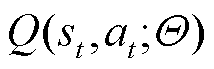 ,其中,
,其中, 代表要求解的参数。因此,当函数
代表要求解的参数。因此,当函数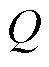 逼近
逼近 ,同时可以得到
,同时可以得到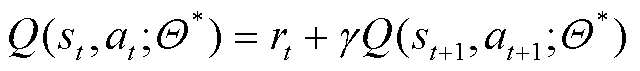 (13)
(13)
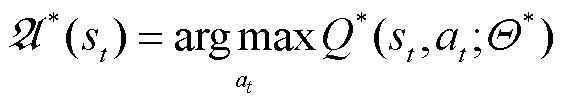 (14)
(14)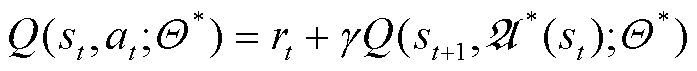 (15)
(15)
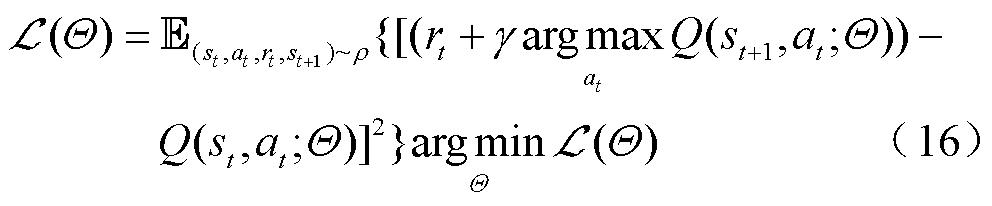
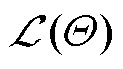 为将包含
为将包含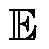 为期望;
为期望;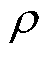 为概率分布。以式(16)为DQN算法的优化目标,但仅当
为概率分布。以式(16)为DQN算法的优化目标,但仅当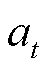 处于离散状态时该优化目标才适用。在本文中,
处于离散状态时该优化目标才适用。在本文中,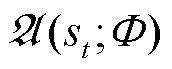 来近似表示最优动作策略函数
来近似表示最优动作策略函数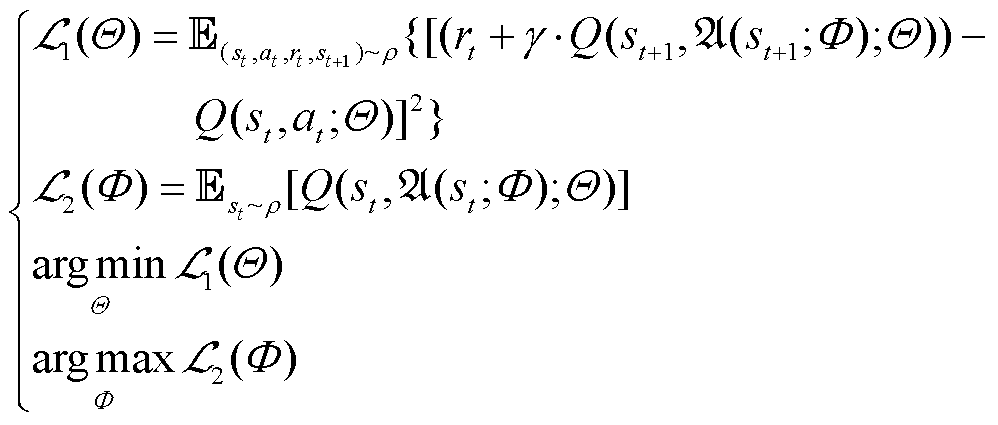 (17)
(17)
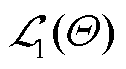 为DQN算法的优化目标;
为DQN算法的优化目标; 为近似动作策略函数
为近似动作策略函数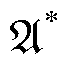 的优化目标。为了使优化过程更加稳定,式(17)中的
的优化目标。为了使优化过程更加稳定,式(17)中的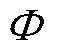 被替换为式(18)中与软更新参数相关的
被替换为式(18)中与软更新参数相关的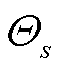 和
和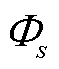 。
。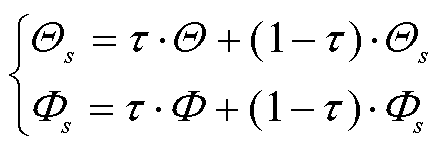 (18)
(18)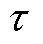 为系数,
为系数,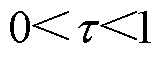 。
。 (19)
(19)
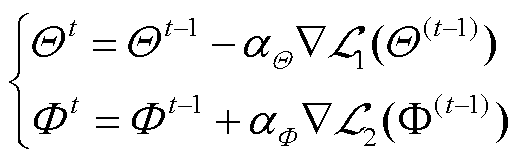 (20)
(20)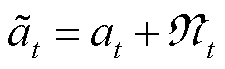 ,
,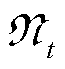 表示随机噪声。在学习阶段,经验记忆库将均匀采样一小批元组信息用于更新actor、critic网络的参数。
表示随机噪声。在学习阶段,经验记忆库将均匀采样一小批元组信息用于更新actor、critic网络的参数。
 ,
,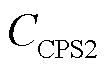 为任意值,则CPS指标合格;②
为任意值,则CPS指标合格;② ,
, ,CPS指标不合格。
,CPS指标不合格。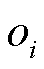 和参数
和参数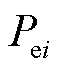 。在本文中,智能体得到的观测值
。在本文中,智能体得到的观测值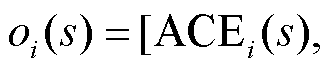
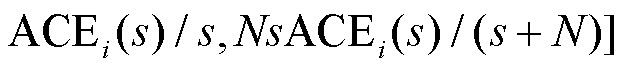 。
。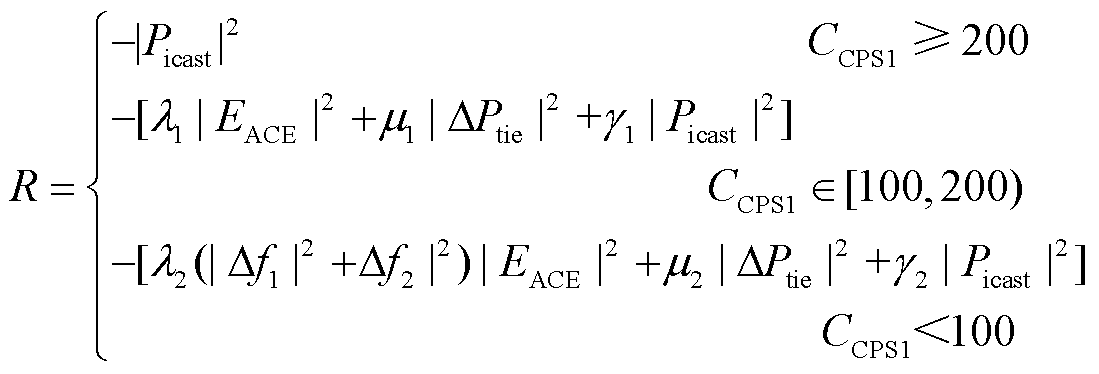 (21)
(21)
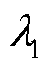 、
、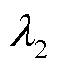 、
、 、
、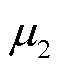 、
、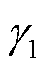 、
、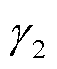 为优化权重值。
为优化权重值。
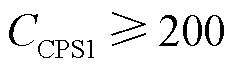 时,CPS指标合格,因此奖励函数中给奖励值-|P
时,CPS指标合格,因此奖励函数中给奖励值-|P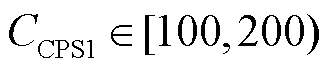 时,CPS2值不合格,因此对CPS2中的ACE值给予较大的惩罚,同时兼顾联络线功率偏差
时,CPS2值不合格,因此对CPS2中的ACE值给予较大的惩罚,同时兼顾联络线功率偏差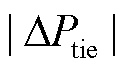 和弃风|P
和弃风|P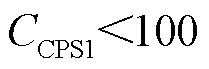 时,CPS1指标不合格,本文引入频率偏差
时,CPS1指标不合格,本文引入频率偏差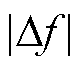 和区域控制误差|ACE|的乘积对较低的CPS1值给予惩罚。
和区域控制误差|ACE|的乘积对较低的CPS1值给予惩罚。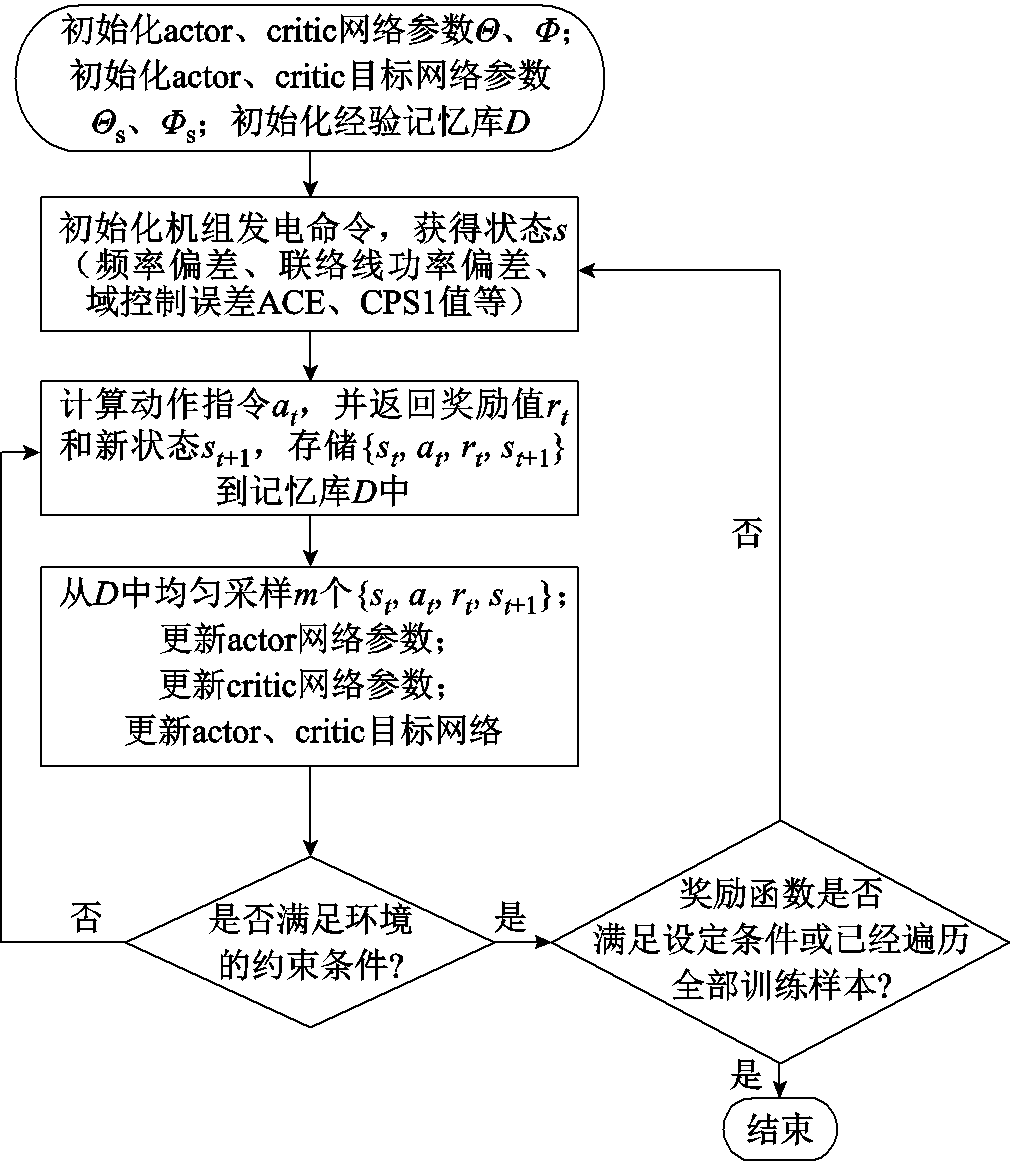



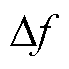 、
、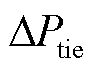 和ACE,DDPG算法相对于PID控制和DQN算法有了显著改进。相比于DQN算法,三种动态指标
和ACE,DDPG算法相对于PID控制和DQN算法有了显著改进。相比于DQN算法,三种动态指标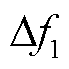 、
、
 100%的情况,表明功率分配控制超出了范围。DDPG算法的CPS1控制指标则最为理想,指标值也最接近200%。由图10b可得,储能设备的引入以及所提出的DDPG算法在一定程度上同样减少了风电机组的弃风,其中含储能PID方法相比现有AGC控制的P
100%的情况,表明功率分配控制超出了范围。DDPG算法的CPS1控制指标则最为理想,指标值也最接近200%。由图10b可得,储能设备的引入以及所提出的DDPG算法在一定程度上同样减少了风电机组的弃风,其中含储能PID方法相比现有AGC控制的P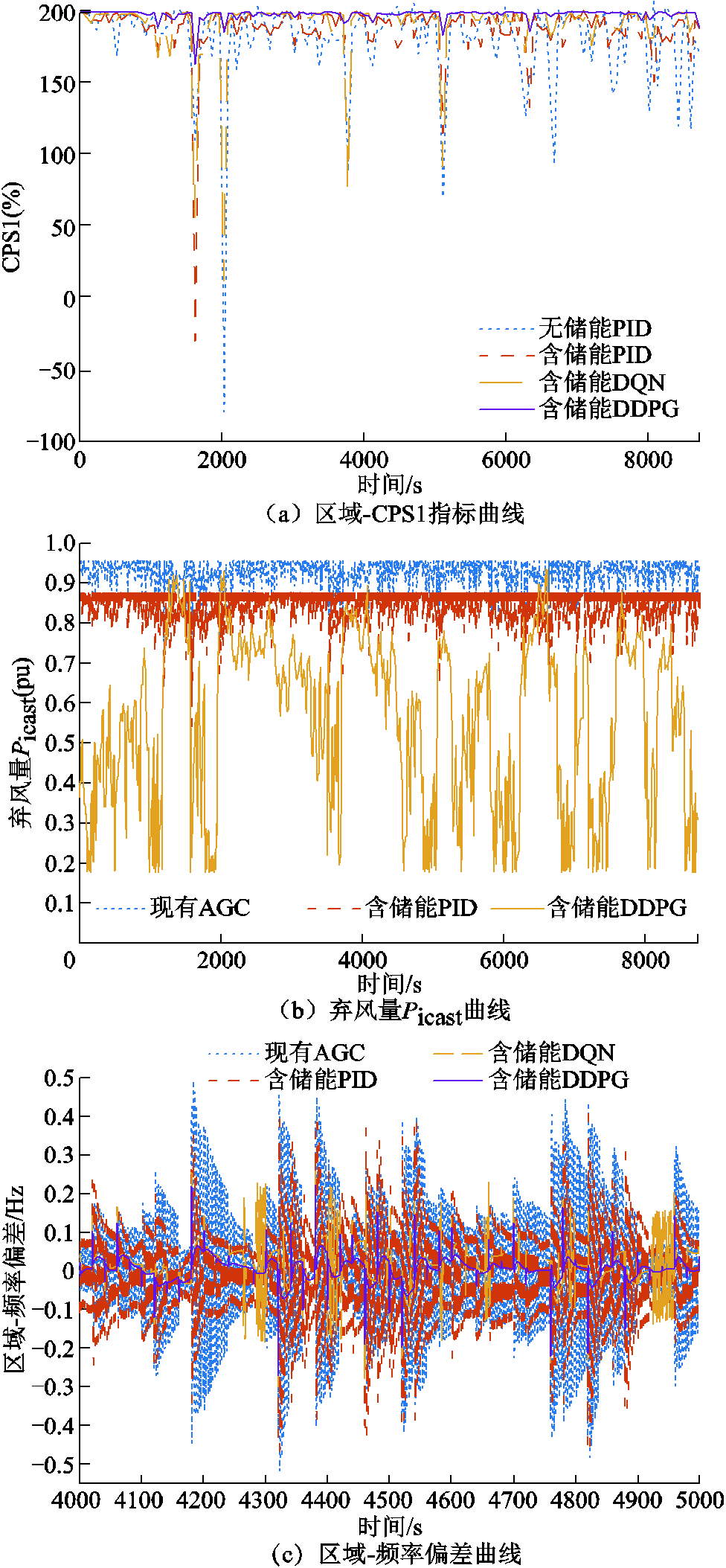
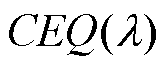 多智能体协同学习的互联电网性能标准控制指令动态分配优化算法[J]. 电工技术学报, 2016, 31(8): 125-133.
多智能体协同学习的互联电网性能标准控制指令动态分配优化算法[J]. 电工技术学报, 2016, 31(8): 125-133.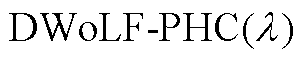 for smart generation control of power systems[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 93-101.
for smart generation control of power systems[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 93-101.