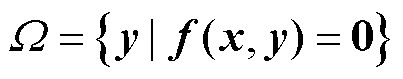（1）
摘要 针对高比例可再生能源并网给交直流电力系统静态电压稳定评估带来的挑战，提出一种含多端柔性直流（VSC-MTDC）的交直流电力系统静态电压稳定域（SVSR）构建方法。该方法根据含VSC-MTDC的交直流电力系统静态电压稳定域边界（SVSRB）的拓扑特性，计及SVSRB搜索过程中换流站控制策略的转换，构建含VSC-MTDC的交直流电力系统SVSRB快速求解的预测-校正模型。首先，该模型借助连续潮流求取出交直流电力系统SVSRB上的初始临界点；然后，根据交直流系统SVSRB上相邻临界点之间的关联，以上一个已求SVSRB临界点为初值，通过所提预测-校正算法求解下一个SVSRB临界点，在此过程中，计及换流站运行参数越限带来的控制策略转换问题，实现SVSRB临界点的准确求解，以提升SVSR的构建精度和效率，增强交直流电力系统的电压稳定态势感知能力；最后，将所提方法应用于含VSC-MTDC的IEEE 5节点测试系统和IEEE 118节点测试系统中进行分析。结果表明，所提方法可实现交直流电力系统SVSR的准确、高效构建。
关键词：交直流系统 多端柔性直流 静态电压稳定域 稳定域边界 控制策略 连续潮流 预测-校正
建立含多端柔性直流（VSC-MTDC）的交直流电网是促进大规模可再生能源消纳、提高电网运行控制能力的有效技术解决方案[1-4]。随着VSC-MTDC技术在电网中广泛应用，其控制策略与电网静态电压稳定关系日趋密切[5-9]。极端情况下，不当的运行控制策略有可能降低交直流电网的电压稳定性，增加电力系统电压稳定评估的复杂度[10-12]。因此，研究含VSC-MTDC的交直流系统电压稳定性评估方法，并提出相关改善措施已成为一个迫切需要解决的问题[13]。
目前，用于交直流电网静态电压稳定性分析的主要方法有灵敏度指标法[14-15]和连续潮流（Continuation Power Flow, CPF）算法[16]。灵敏度指标法通过分析不同控制策略下交直流系统各状态变量的相互变化关系，评估换流站交流公共耦合节点（Point of Common Coupling, PCC）的电压稳定性[17]。该方法可重点监视系统电压稳定薄弱区域的电压稳定性，通过控制换流站功率输出，改善系统的静态电压稳定运行状态[18]，但仅能针对系统特定运行状态下静态电压的稳定性进行分析，难以充分考虑负荷连续变化时，换流站不同控制策略对交流系统静态电压稳定性的影响。CPF通过沿给定的功率增长方向逐步迭代计算，获取交直流系统电压崩溃点处的潮流分布。该方法可有效分析负荷连续变化下直流系统对交流系统静态电压稳定性的影响，进而制定出合理的控制策略，提升系统的电压稳定性。然而，该方法仅能探究特定控制策略和负荷变化下的静态电压稳定性，难以真实反映大规模可再生能源并网所带来的强随机性和不确定性对系统电压稳定性的影响，因此，有必要从全局角度研究高渗透率可再生能源大规模并网下，交直流电力系统的电压稳定性，而静态电压稳定域（Static Voltage Stability Region, SVSR）为研究强随机性和不确定性因素影响下的交直流电网电压稳定性提供了新思路[19-21]。
SVSR表征了在功率注入空间中，满足电力系统电压稳定的所有运行点集合[22]。该方法有效计及了强随机性和不确定性因素对系统电压稳定性的影响，刻画出可保证系统电压稳定的运行区域，有利于电网运行人员深入、全面地分析可再生能源大规模并网对电力系统电压稳定性的影响，但采用SVSR研究系统的电压稳定性时，电压稳定域边界（SVSR Boundary, SVSRB）构建是其首要问题。传统电力系统SVSRB构建主要有近似法和拟合法两种，近似法借助于SVSRB处的潮流方程，通过对SVSR局部边界进行超平面近似，形成表述SVSRB特性的近似解析表达式，进而分析交流系统静态电压稳定性[23]。此类方法可根据实际需要，快速生成SVSR的局部超平面近似边界，但其计算精度低且仅聚焦于交流系统SVSRB近似，难以准确刻画不同控制策略下含VSC-MTDC的交直流系统SVSRB。拟合法通过构建特定换流站控制策略下的CPF模型，遍历各个功率增长方向，获取不同功率增长方向下的交直流系统SVSR临界点，进而拟合所有临界点构成SVSRB[24]。该方法可实现含VSC-MTDC的交直流系统SVSRB的高精度搜索，但存在计算耗时久的不足，难以满足大规模电力系统计算效率要求。为提升SVSRB构建效率，文献[25]以CPF为基础，根据SVSRB拓扑特性，采用边界预测-校正方法实现了SVSR的快速搜索；文献[26]通过建立表征SVSRB临界点的优化模型，通过求解该优化模型以获得各功率增长方向下的SVSR临界点，进而实现SVSR的快速搜索。然而，上述方法仅适用于交流系统SVSR的快速构建，不能有效计及VSC-MTDC控制策略对交直流电力系统SVSR的影响。针对目前VSC-MTDC技术在高压远距离大容量输电、大规模可再生能源并网消纳、区域电网柔性互联等应用前景，有必要进一步对含VSC-MTDC的交直流系统SVSRB构建方法进行深入研究，以提升交直流系统SVSR的构建精度和效率。
为实现不同VSC-MTDC控制策略下交直流电力系统SVSR的准确构建，提升含VSC-MTDC的交直流电力系统SVSRB搜索效率和精度。在文献[25]的基础上，本文进一步提出一种含VSC-MTDC的交直流系统静态电压稳定域边界求解方法。该方法计及VSC-MTDC换流站控制策略对交直流系统电压稳定性的影响，根据SVSRB上相邻鞍结分岔（Saddle Node Bifuvcation, SNB）点之间的关系，构造交直流系统SVSRB快速求解的预测-校正模型，以上一个SNB点为初始点，通过所提模型求解下一个SNB点，实现SVSRB快速、准确构建。最后，将所提方法应用于含VSC-MTDC的IEEE 5节点测试系统和IEEE 118节点测试系统中进行了分析和验证。
电力系统SVSR是定义在功率注入空间内满足系统静态电压稳定的所有运行点集合，其表达式为[25-27]
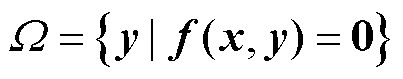（1）
式中，f(x, y)=0为系统潮流方程；x为系统状态变量向量；y为节点注入功率向量。
借助所获取的SVSR，可根据系统运行点与SVSRB的相对位置，直观、定性地评估电力系统的电压稳定性，为电力系统静态电压稳定在线评估与控制提供科学、合理的依据，然而，SVSRB搜索是构建SVSR的首要问题[25-27]。
电力系统SVSRB呈现典型高维非线性拓扑特性，传统构建方法存在计算耗时久、保守性高的不足，严重制约了SVSR在电力系统中的应用。如何准确、高效地构建SVSRB，进而指导电力系统电压稳定在线分析与控制已成为SVSR研究的重点。
为实现SVSRB的快速搜索，文献[25]提出一种用于交流系统SVSRB快速求解的预测-校正模型。
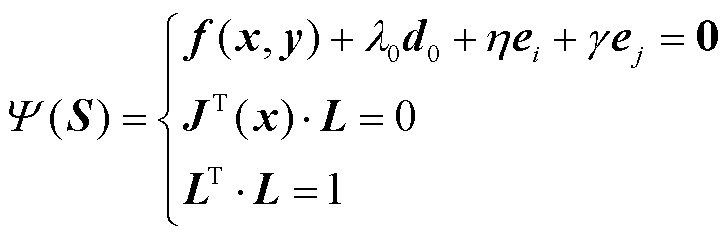（2）
式中，S为SNB点；l0为初始功率增长方向下SNB点对应的负荷裕度；ei与、ej分别为节点i与j有功注入的单位向量；h、g分别为SNB点处节点i、j的有功功率增长量；JT(x)为雅可比矩阵的转置；L为SNB点处雅可比矩阵零特征值的左特征向量；d0为初始功率增长方向，记为
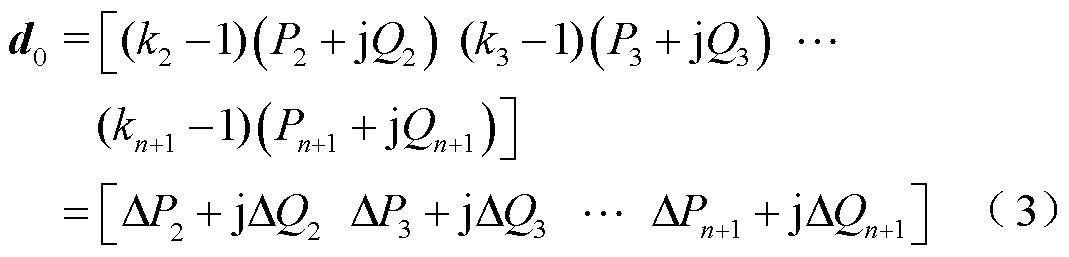
式中，kn+1为随l变化，交流系统节点n+1负荷变化率的乘子；Pn+1+jQn+1为系统初始状态下节点n+1的功率；n+1为交流系统节点个数，其中节点1为平衡节点；DPn+1+jDQn+1为节点n+1的功率变化量。
式（2）将已求SNB点作为已知条件，通过预测-校正算法直接求解下一待求SNB点，可实现SVSRB搜索效率的有效提升。本文借鉴该思路，进一步将其扩展到含VSC-MTDC的交直流电力系统SVSRB搜索中，实现含VSC-MTDC的交直流电力系统SVSRB的快速搜索。
不同于交流系统的SVSR，含VSC-MTDC的交直流系统SVSR受VSC-MTDC换流站控制方式影响较大，在构建含VSC-MTDC的交直流系统SVSR时，需有效计及换流站控制方式对所构建的SVSR的影响。为此，本节提出一种计及VSC-MTDC换流站控制策略影响的交直流系统SVSRB快速求解的预测-校正方法。
VSC-MTDC换流站接口模型如图1所示。图中，PD、ID和Udc分别为换流站直流侧有功功率、直流电流和直流电压；PC和QC分别为换流站电压源换流器（Voltage Source Converter, VSC）交流侧有功功率和无功功率；IC和UC∠qC分别为换流站交流侧电流和电压；ZC、Ztf和Bf分别为相电抗器阻抗、变压器阻抗和滤波器电纳；Uf∠qf为滤波器侧电压；PS和QS分别为换流站向交流系统注入的有功和无功；US∠qS为PCC电压。
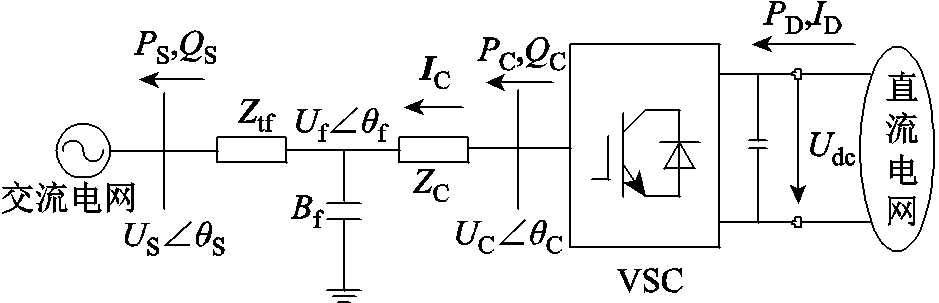
图1 VSC-MTDC接口模型
Fig.1 Interface model of VSC-MTDC
在含VSC-MTDC的交直流系统中，换流站可通过向交流侧注入有功功率PS和无功功率QS，影响交流系统潮流分布。然而，不同控制方式下，换流站向交流侧注入的有功功率和无功功率不同，将导致其对交流系统静态电压稳定性影响也各异。因此，在构建含VSC-MTDC的交直流系统SVSR时，需对换流站不同控制方式下的交直流系统静态电压稳定性进行深入研究。
VSC-MTDC换流站控制方式分为直流侧控制方式和交流侧控制方式两类，其中直流侧控制方式主要有定有功功率控制、定直流电压控制和直流电压下垂控制。
1）定有功功率控制：有功功率为定值，即换流站向交流侧注入的有功功率PS等于其有功功率设定值Pref。
2）定直流电压控制：直流电压Udc为设定值Udc,ref，此时换流站向交流侧注入的有功功率PS为
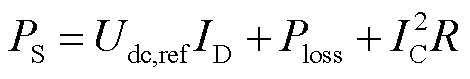（4）
式中，R为变压器与相电抗器等效电阻。
3）直流电压下垂控制：直流系统节点电压Udc与直流系统有功功率注入满足
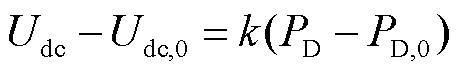（5）
式中，Udc,0和PD,0分别为直流电压下垂控制中直流系统节点电压与有功功率设定值；k为下垂斜率。
此时，换流站向交流侧注入的有功功率PS为
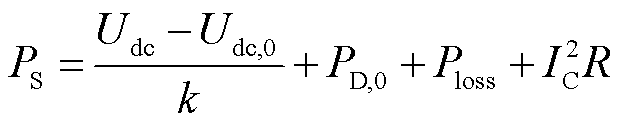（6）
式中，Ploss为换流站损耗。
VSC-MTDC换流站交流侧控制方式主要有定无功功率控制和定交流电压控制。
1）定无功功率控制：无功功率为定值，即换流站向交流侧注入的QS等于其无功功率设定值Qref。
2）定交流电压控制：交流侧电压US为设定值US,ref，此时换流站向交流侧注入的有功功率QS为
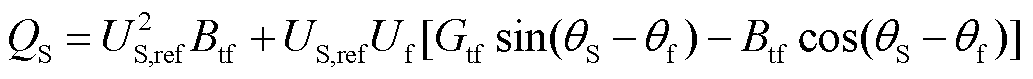（7）
综上所述，在含VSC-MTDC的交直流电力系统中，VSC-MTDC换流站常用控制方式见表1。
表1 典型VSC-MTDC换流站控制方式
Tab.1 Control mode of VSC-MTDC converter station
换流站控制方式直流侧控制方式交流侧控制方式 ①定直流电压控制定无功功率控制 ②定直流电压控制定交流电压控制 ③定有功功率控制定无功功率控制 ④定有功功率控制定交流电压控制 ⑤直流电压下垂控制定无功功率控制 ⑥直流电压下垂控制定交流电压控制
针对表1所示的换流站控制方式，式（8）进一步构建了计及换流站控制方式影响的交直流电力系统CPF模型。
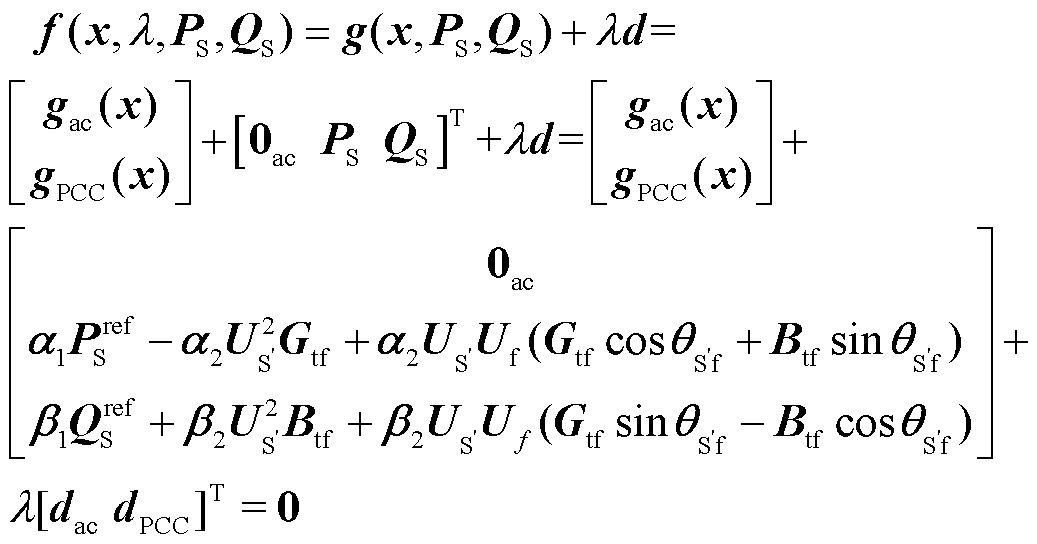（8）
式中，PS和QS分别为换流站向交流系统注入的有功功率和无功功率向量；g(x, PS, QS)为含VSC-MTDC的交直流系统潮流方程；dac为纯交流节点功率增长方向；dPCC为交流系统PCC节点的功率增长方向；gac(x)与gPCC(x)分别为纯交流节点功率平衡方程与交流系统PCC节点常规潮流方程；0ac为与gac(x)矩阵维度相同的零矩阵；US'为PCC节点电压；a1、a2、b1与b2为新增功率参数，当节点i为PCC节点，且其对应的换流站控制方式分别为①、②、③、④、⑤和⑥时，a1i, a2i, b1i与b2i分别为0, 1, 1, 0、0, 1, 0, 1、1, 0, 1, 0、1, 0, 0, 1、0, 1, 1, 0、0, 1, 0, 1；US'为PCC节点电压初值。
由式（8）可知，通过求解不同控制方式下换流站向交流系统注入的PS和QS，可得负荷连续变化下的交直流系统的潮流解，进而获取SNB点处系统潮流分布及其对应的负荷裕度l。但在沿功率增长方向d追踪SVSRB上SNB点过程中，系统运行参数将会发生较大变化，导致换流站交流侧和直流侧控制方式发生转换，相关转换依据如下：
1）交流侧控制方式转换：换流站交流侧通过无功功率控制方式转换以抑制换流母线电压UC越限，使换流母线电压在合理范围内运行。
2）直流侧控制方式转换：以PCC节点电压US设定值作为直流侧控制策略转换依据，以实现在满足直流系统潮流平衡下静态电压稳定性的提升。
2.2节分析表明：采用含VSC-MTDC的CPF可实现计及换流站控制策略转换的交直流系统SNB点的求取，然而若基于该方法遍历各功率增长方向下的SNB点，获取SVSRB，虽可高精度构建SVSRB，但势必加重计算负担。为实现含VSC-MTDC的交直流系统SVSRB快速、准确构建，本节在文献[25]基础上，进一步提出了含VSC-MTDC的交直流系统SVSRB搜索的预测-校正算法，以实现含VSC-MTDC的交直流系统SVSRB上SNB点的快速搜索。本文所提含VSC-MTDC的交直流系统SVSRB搜索模型为
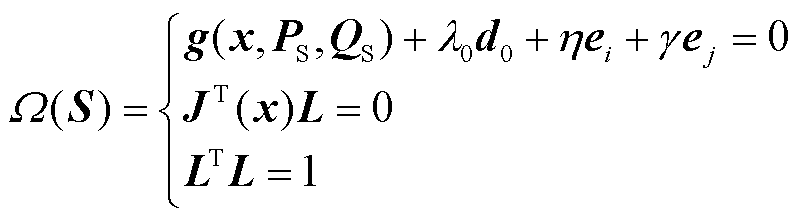（9）
针对上述含VSC-MTDC的交直流系统SVSRB搜索模型，本文所提SVSRB搜索过程如图2所示。
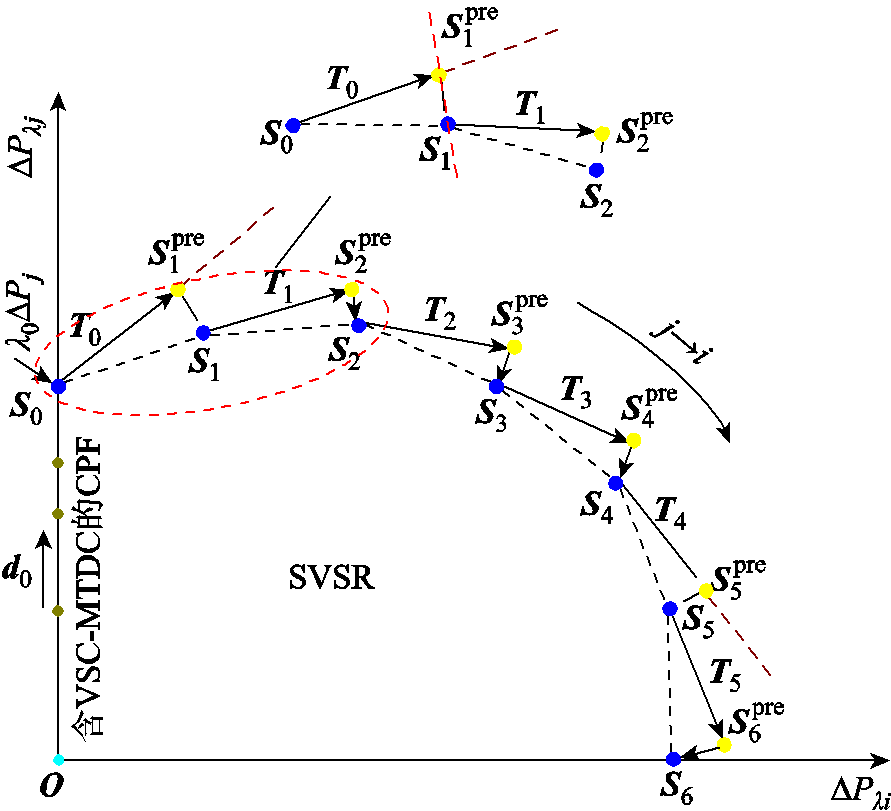
图2 SVSRB上SNB点搜索图示
Fig.2 Exploring the SNB points in SVSRB using the proposed method
SVSRB详细计算原理如下：
1）追踪系统初始SNB点。从图2中基态点O出发，采用式（8）所示的CPF模型沿功率增长方向d0追踪该功率增长方向下的SNB点S0，进而获得该SNB点及其对应的左特征向量L0。
2）根据式（9）所示的搜索模型求取预测点Spre1及其对应的校正点S1的初始值。
定义二维空间中的功率增长方向角u为
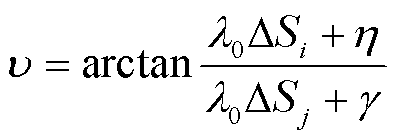（10）
沿u减小方向确定SNB点S0处空间切向量T0为
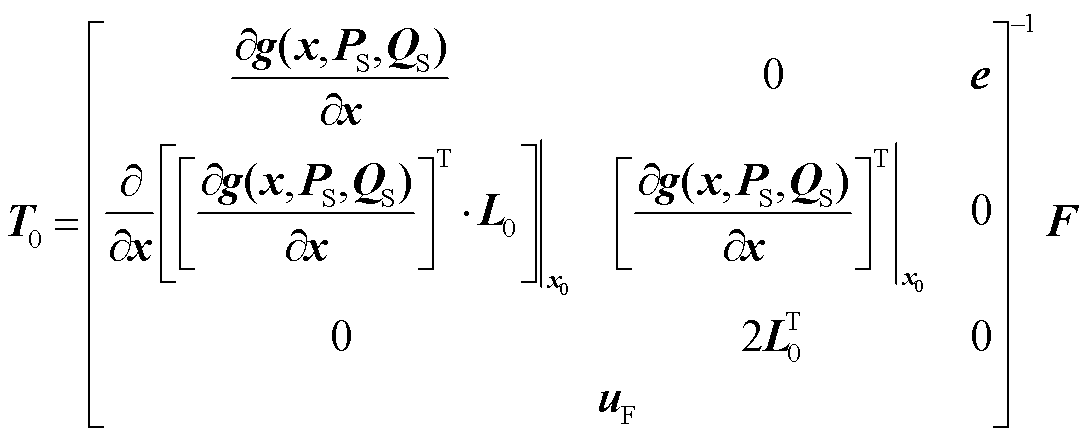（11）
式中，F=[0 …0 1]T为与切向量T0维数相同的列向量；uF=[0 …0 1]为与切向量T0维数相同的行向量。
求得T0后，根据式（12）计算预测点Spre1。
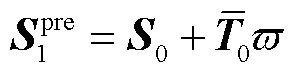（12）
式中，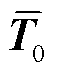
为T0归一化结果；v为交直流系统SVSRB搜索的预测-校正步长。
由式（13）进一步得校正点S1的初始值及其对应PCC的无功功率QPCC和节点电压US。
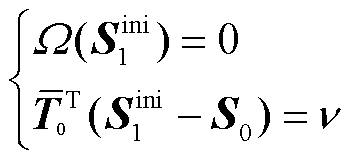（13）
式中，Sini 1为下一SNB点即校正点S1的初始值。
3）若PCC节点对应的换流站采用定无功功率控制，则其无功注入QS为无功设定值；若PCC节点对应的换流站采用定交流电压控制，则其无功注入QS为QPCC。以QS、US和上一SNB点处有功注入PS(0)为初值，参考交直流系统交替迭代算法计算PS(1)，若PS(1)与PS(0)的差值小于设定收敛精度，则执行步骤4）；否则将PS(1)和QS再次代入式（13）进行交流系统迭代计算，然后再执行步骤3），此时，交直流系统交替迭代算法中有功注入初值为PS(1)，直至上一次迭代结果PS(t)与本次迭代结果PS(t+1)的差值满足收敛精度为止，执行步骤4）。
4）换流站控制方式转换。随着SVSRB上所求SNB点逐渐偏离初始SNB点，系统运行参数将发生较大变化。为提高系统静态电压稳定裕度和避免UC越限，需对换流站交流侧和直流侧控制策略进行转换，进而更新步骤3）所得运行数据，详细转换过程如下。
由图1可知，当忽略换流站电阻R和滤波器电抗后，换流站向交流系统注入的有功PS和无功QS为
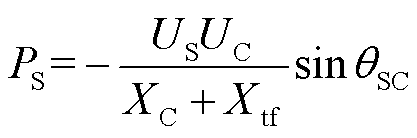（14）
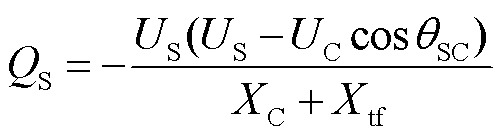（15）
式中，XC为相电抗器电抗；Xtf为变压器电抗。
令X=XC+Xtf，由式（14）和式（15）得
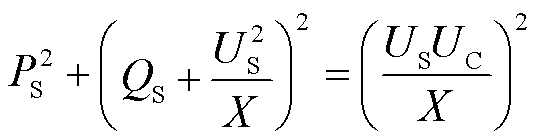（16）
由式（15）可知，理想状态下换流站的工作区域是以(0,-U2S/X)为原点，以USUC/X为半径的圆形区域，如图3中实线圆所示。
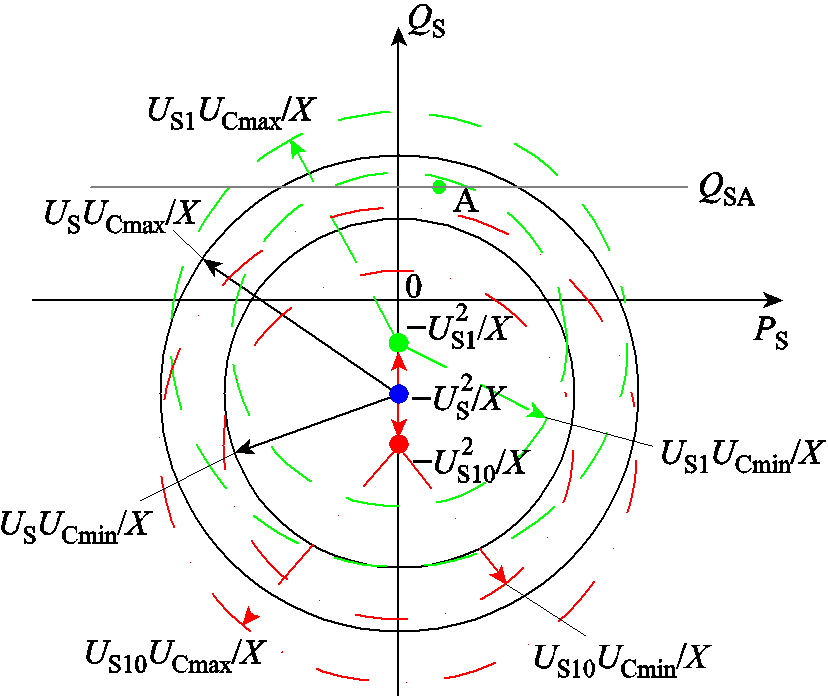
图3 理想状态下换流器的运行范围
Fig.3 Ideal operating range of VSC-MTDC converter station
（1）交流侧控制策略转换
由式（15）可知，VSC电压UC主要与交流系统PCC节点的电压US和注入的无功功率QS有关，因此，设置以下换流站交流侧控制策略转换方案：
①定交流电压控制转换为定无功功率控制。当交流侧控制方式为定交流电压控制时，交流电压设定值为上一SNB点对应PCC节点电压，然而，不同SNB点处PCC节点对应的电压不同，为维持US不变，换流站向交流侧PCC节点注入的无功功率QS可能造成UC越限，如图3中越下限时，换流站的工作区域变为以(0,-U2 S1/X)为原点，以US1UC/X为半径的圆形区域；越上限时，换流站的工作区域变为以(0,-U2S10/X)为原点，以US10UC/X为半径的圆形区域，为维持换流站的稳定运行，其交流侧控制策略由定交流电压控制转换为定无功功率控制，无功功率设定值为上一SNB点处无功功率注入值，继续执行步骤2）、步骤3），当UC仍越限时，令QS为
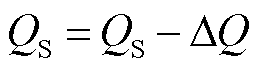（17）
式中，DQ为无功调整步长。当UC越上限时，DQ为正值；当UC越下限时，DQ为负值。
继续执行步骤2）和步骤3），直至UC运行于合理范围内，进而执行直流侧控制策略转换。
②定无功功率控制无功设定值等步长变化。当交流侧控制方式为定无功功率控制时，换流站控制方式保持不变，按式（17）作等步长变化，执行步骤2）、步骤3），直至UC运行于合理范围内，此时，执行直流侧控制策略转换。
（2）直流侧控制策略转换
在SNB点的追踪过程中，交流系统PCC节点的有功功率增长量可等效为
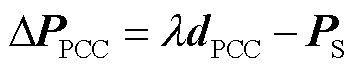（18）
由式（18）可知，通过改变换流站向交流侧注入的有功功率，可改善系统的静态电压稳定裕度，因此，本文以交流系统PCC节点有功注入PS作为换流站直流侧控制策略转换依据，对所求下一个SNB点初始值处电压幅值由低到高的负荷PCC节点所对应的换流站依次进行控制策略转换，其控制策略转换方案为：
①下垂控制转换为定有功功率控制。若下垂控制时换流站向交流系统注入的有功功率小于定有功功率控制时换流站向交流系统注入的有功功率设定值，则如图4中运行点A1®B1所示，换流站由下垂控制转换为定有功功率控制。通过改变换流站向交流系统注入的有功功率PS，有效地减小了交流系统PCC节点的有功功率增加量，增大系统静态电压稳定裕度。
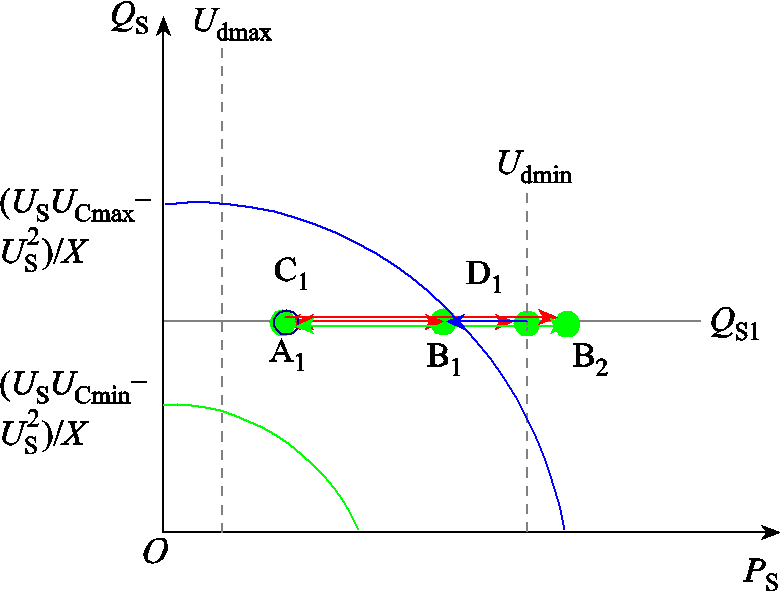
图4 理想状态下直流侧电压约束运行范围
Fig.4 Ideal voltage operating range on the DC side of VSC-MTDC converter station
②定有功功率控制转换为定直流电压控制。当换流站采用定有功功率控制且与其耦合的直流节点电压幅值越限时，换流站由定有功功率控制转换为定直流电压控制，直流电压设定值取该直流节点电压限值，如图4中运行点D1所示。
③定直流电压控制转换为下垂控制。当换流站采用定直流电压控制导致与其未耦合的直流节点电压越限时，换流站由定直流电压控制转换为下垂控制，即换流站直流侧控制策略转换难以提高交流系统静态电压稳定性，如图4中运行点D1®C1所示。
④下垂控制保持不变。当换流站VSC1、VSC2、…、VSC(n-1)采用定有功功率控制，换流站VSC(n)采用下垂控制且PCC(n)节点电压幅值低于限值时，为维持直流系统潮流平衡，换流站n仍采用下垂控制。
⑤定有功功率控制转换为下垂控制。当换流站采用定有功功率控制、直流节点电压幅值越限且存在换流站i采用定直流电压控制时，换流站由定有功功率控制转换为下垂控制，如图4中B2®C1所示。
在所得SNB点初始值处进行交直流交替迭代及换流站控制方式转换，直至求取下一个SNB点S1。继续执行步骤2）～步骤4），搜索SNB点2、3、4、5、6，直至功率增长方向角u小于或等于0°。
需要指出的是：虽然电力系统的SVSRB主要由鞍节分岔（SNB）与极限诱导分岔（Limit Induced Bifurcation, LIB）构成[26-27]，但LIB主要是由发电机无功越限造成的，因此，实际求解过程中，可通过对图5中每一个求得的SNB点进行发电机无功出力校验，以判断系统是否已出现LIB，若无无功出力越限现象，则按上述过程继续搜索下一SNB点；若出现无功越限现象，则基于该SNB相关信息及所提的换流站控制策略转换方法，求解对应的LIB点，然后仍基于所得的SNB点信息，搜索下一SNB点。依次类推，实现含VSC-MTDC的交直流电力系统SVSRB准确求解，即采用所提预测-校正方法搜索交直流系统的SVSRB，其实质仍为求解SVSRB上的SNB点。因此，本文主要关注由SNB点构成的交直流电力系统SVSRB的快速求解。
综上所述，所提含VSC-MTDC的交直流系统二维SVSRB搜索流程如图5所示。
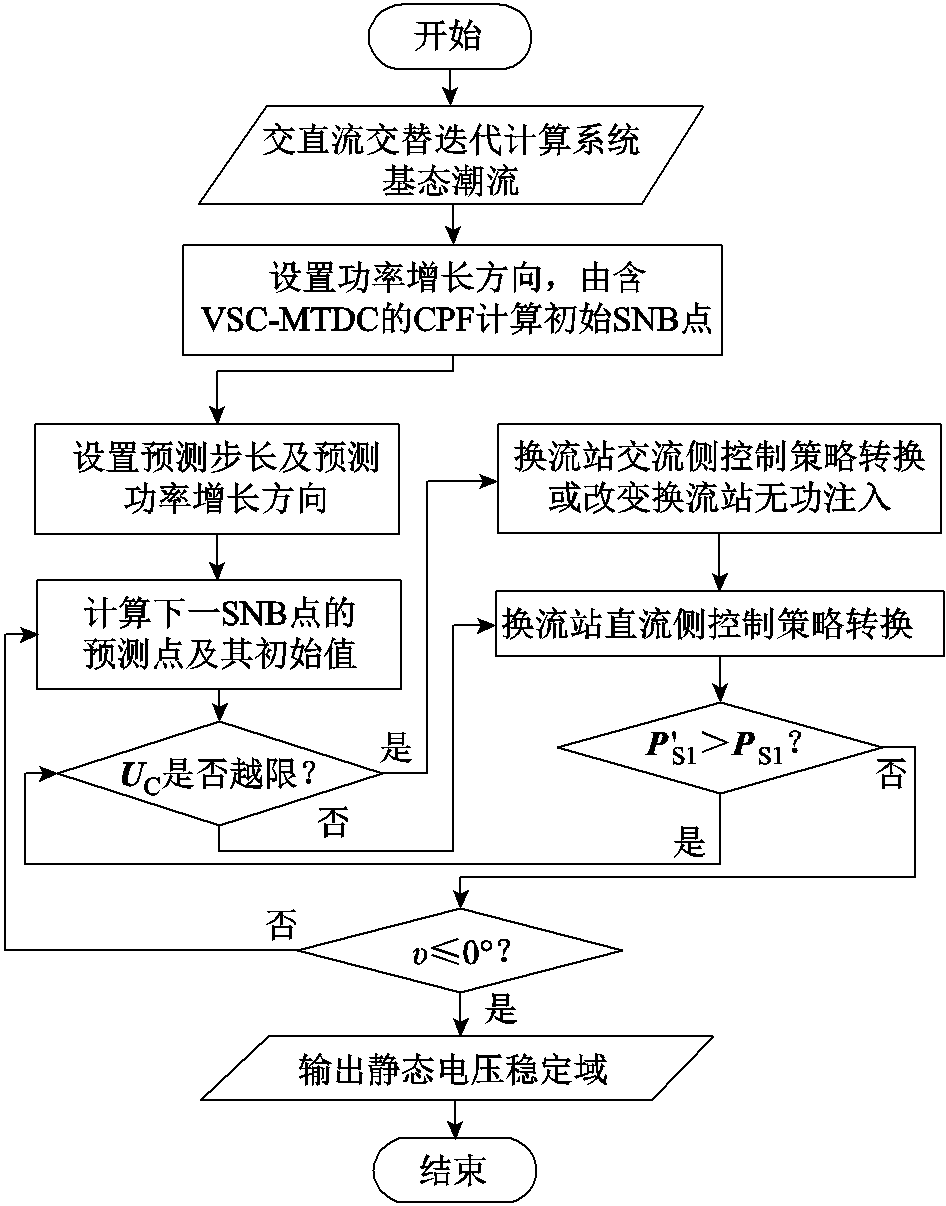
图5 含VSC-MTDC的二维SVSRB计算流程
Fig.5 Flow chart of the proposed 2-dimentional SVSRB tracking
详细步骤如下：
1）确定影响电力系统电压稳定性的关键节点i和j，以节点i和j的有功功率Pi和Pj为坐标轴，构建二维有功功率注入空间。
2）设定功率增长方向d0=[0…DSi…DSj…0]T，其中DSi和DSj分别为0和1，以基态点O为初始点，采用式（9）所提模型，求解d0方向下的SNB点S0，并将S0映射至二维有功注入空间得（0, l0DSj）。
3）以S0为初始点，采用式（12）计算得SNB点S1的预测点Spre 1。
4）以Spre 1为初值，采用式（13）可得校正点S1的初始值Sini 1。
5）判断UC是否越限，若是，类似于2.3节所提方法进行换流站交流侧控制策略转换，采用式（13）计算校正点S1及其对应的PCC有功注入PS1，然后执行步骤6）；若否，直接执行步骤6）。
6）参考2.3节所提方法进行换流站直流侧控制策略转换，计算该控制策略下的校正点S' 1及其对应的PCC有功注入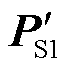
，若存在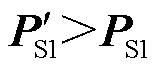
，执行步骤5）；否则，
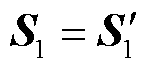，执行步骤7）。
7）判断u是否小于0°，若否，则S0=S1，继续执行步骤3）；若是，则计算结束，可得Pi和Pj为坐标轴的二维有功注入空间内的SVSRB。
本节在2.4节所提二维SVSRB搜索方法的基础上，进一步推导出含VSC-MTDC的交直流系统三维SVSRB计算的预测-校正模型为
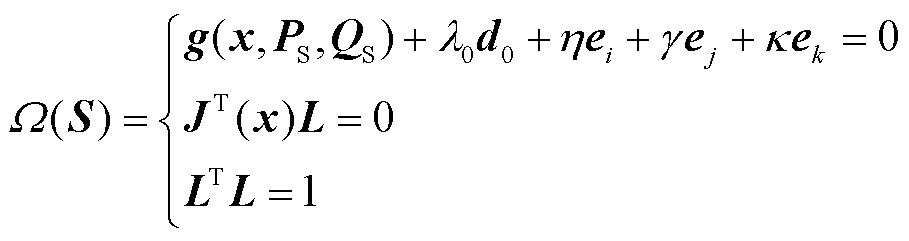（19）
式中，ek为节点k有功注入的单位向量；k为SNB点处节点k的有功功率增长量。
采用式（19）所提预测-校正模型在三维有功注入空间中搜索交直流系统的SVSRB基本原理如图6所示。
具体步骤如下：
1）确定系统电压稳定关键节点i、j和k，以节点i、j、k有功注入为坐标轴，构建三维有功注入空间。
2）令节点i、j的有功功率增长量h和g均为0，采用式（19）所提模型求得图6中三维SVSRB的顶点坐标（0,0,DPkmax）及节点k的最大有功增长量kmax。
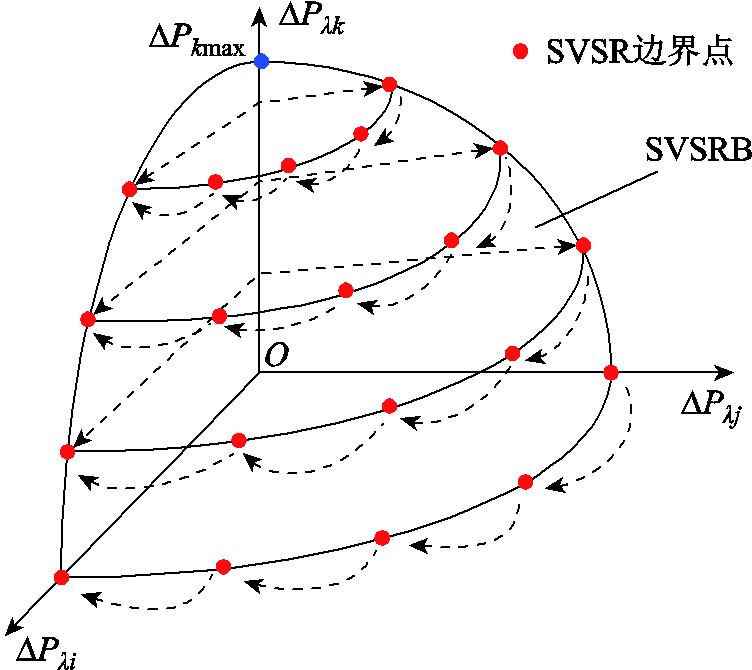
图6 含VSC-MTDC的三维SVSRB搜索原理
Fig.6 Exploring 3-dimensional SVSRB with VSC-MTDC
3）根据二维SVSR构建次数m将kmax等分为
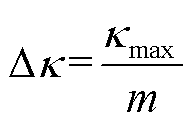（20）
式中，m为预先设定的二维SVSR总构建次数。
4）令t=0。
5）令节点k的有功增长量k=tDk，在k给定条件下，类似第2.3节所提二维SVSRB的预测-校正算法，搜索节点i、j有功注入二维空间内的二维SVSRB，二维SVSRB搜索结束后执行步骤6）。
6）令t=t+1，若t≤m，执行步骤5）；否则，执行步骤7）。
7）三维有功注入空间内SVSRB搜索结束。
针对本文所提含VSC-MTDC的交直流电力系统SVSRB计算方法，本节分别采用含VSC-MTDC的IEEE 5节点测试系统和含VSC-MTDC的IEEE 118节点系统进行分析和验证，验证所提含VSC-MTDC的交直流系统SVSR构建方法的可行性和有效性。
本节以图7所示的含VSC-MTDC的IEEE 5节点测试系统为例[28]，验证所提交直流系统SVSRB搜索模型的准确性和有效性。
3.1.1 二维SVSRB搜索
针对图7所示的IEEE 5节点系统，本节分别在以下两种场景中搜索二维SVSRB：场景1坐标轴为负荷节点有功注入；场景2坐标轴为发电机节点和负荷节点有功注入。
1）场景1
在含VSC-MTDC的交直流系统中，VSC-MTDC换流站直流侧控制方式一般采取直流电压下垂控制以维持直流系统电压稳定[29]，因此，本文假定图7中换流站VSC1、VSC2、VSC3初始控制方式均为直流电压下垂控制。将各VSC换流站交流侧初始控制方式设定为VSC1采用定无功功率控制，换流站VSC2采用定交流电压控制，换流站VSC3采用定无功功率控制。各VSC换流站初始运行参数见表2。
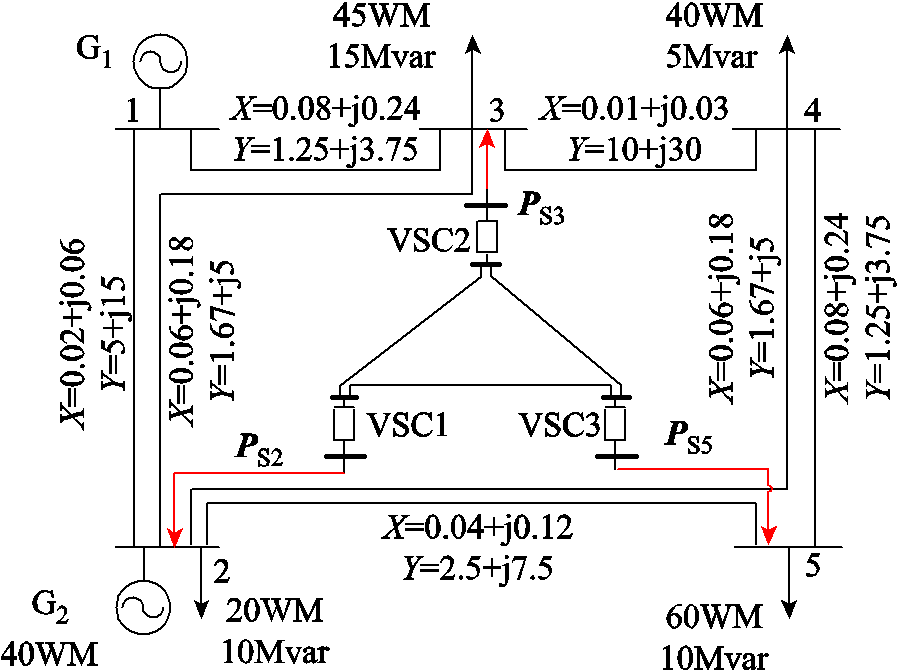
图7 含VSC-MTDC的IEEE 5节点系统
Fig.7 IEEE 5 test system with VSC-MTDC
表2 VSC-MTDC换流站初始运行参数
Tab.2 Initial operating parameters of VSC-MTDC converter stations
换流站编号VSC控制方式直流侧电压Udc(pu)有功功率PS(pu)无功功率QS(pu)下垂斜率交流侧电压US(pu) VSC1⑤1-0.6-0.40.0051 VSC2⑥10.3900.0071 VSC3⑤10.350.050.0051
以节点3和节点4为影响交直流系统电压稳定性的关键节点，在以P3和P4为坐标轴的二维空间内，采用所提方法搜索交直流系统SVSRB，结果如图8所示。
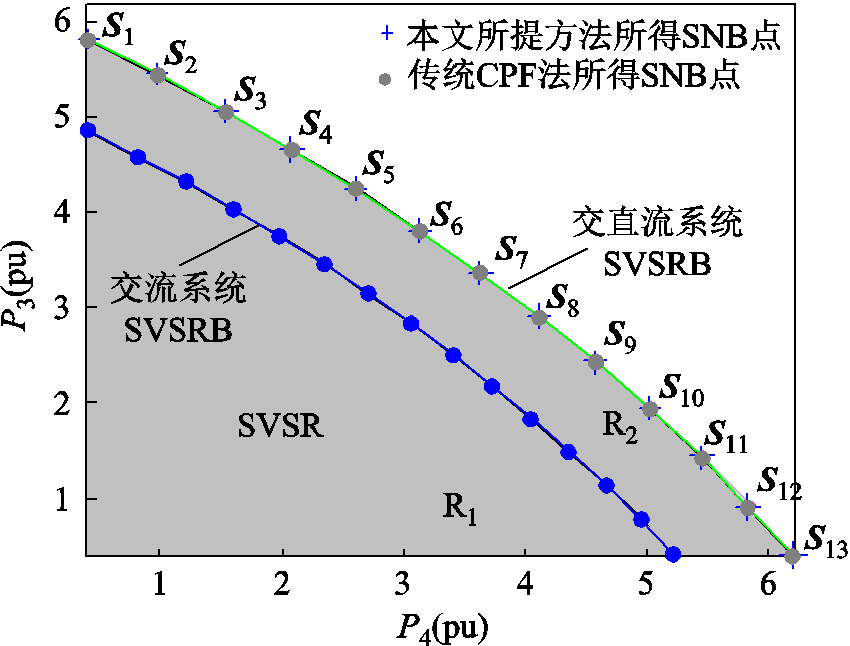
图8 场景1搜索的SVSRB
Fig.8 Tracking SVSRB in scenario 1
设置初始功率增长方向为d=[0 0.60 0 0]T，预测步长为0.70，搜索含VSC-MTDC的IEEE 5节点测试系统二维负荷有功注入空间中的SVSRB。首先，采用式（9）所提模型搜索得图8所示的初始SNB点S1，其对应坐标为（0.400, 5.833）。沿u减小的方向搜索下一SNB点的预测点Spre 1，其对应的坐标为（0.965,5.440），继续沿u减小方向搜索下一SNB点，直至u小于0◦为止，结果如图8所示。
由图8可知：①相对交流系统，含VSC-HVDC的交直流系统在采用合理的换流站控制策略后，可有效提高系统的静态电压稳定裕度（如图中区域R2所示），增强系统的电压稳定运行能力；②本文所提方法与CPF所得SNB点重合，有效地验证了本文所提方法可实现电力系统SVSRB的准确搜索，其各SNB点处换流站控制方式见表3。
表3 场景1中各SNB点处换流站控制策略
Tab.3 Control strategies of converter stations at each SNB point in scenario 1
SNB点控制策略VSC2无功注入/Mvar坐标 S1⑤/③/②98.694(0.400,5.833) S2⑤/③/②98.694(0.975,5.465) S3⑤/③/②98.694(1.524,5.068) S4⑤/③/②98.694(2.070,4.667) S5⑤/③/②98.694(2.603,4.251) S6⑤/③/②98.694(3.120,3.820) S7⑤/③/②98.694(3.622,3.375) S8⑤/③/②98.694(4.107,2.915) S9⑤/③/②98.694(4.572,2.440) S10⑤/③/②98.694(5.018,1.950) S11⑤/③/②98.594(5.443,1.447) S12⑤/③/②98.494(5.845,0.930) S13⑤/③/②98.194(6.226,0.401)
由表3可知，在临界点S1～S10处VSC1/VSC2/VSC3控制方式分别为⑤/③/②，其中VSC2无功注入为98.694Mvar；在临界点S11、S12与S13处仍为⑤/③/②，然而，若VSC2无功注入仍为98.694Mvar，则VSC2在S11、S12与S13处电压幅值将分别为1.102 2(pu)、1.105 8(pu)和1.109 7(pu)，VSC2电压幅值越限，因此，参考2.3节所提方法，将无功功率按步长0.1Mvar进行调节，在S11、S12与S13处无功设定值分别为98.594Mvar、98.494Mvar与98.194Mvar，此时，VSC2电压分别为1.088 3(pu)、1.092 3(pu)和1.095 9(pu)，均在合理运行范围内，验证了所提换流站控制策略转换的有效性和合理性。
图9进一步以CPF为基准，对比了本文所提方法求解的SNB点处系统静态电压稳定裕度及其计算误差。由图9结果可知：本文所提方法搜索的13个SNB点的计算误差均在0.5%以下，最大计算误差为0.493 3%，平均计算误差为0.121 3%。该对比结果表明：采用本文所提方法搜索含VSC-MTDC的交直流系统SNB点具有较高准确性和计算精度。
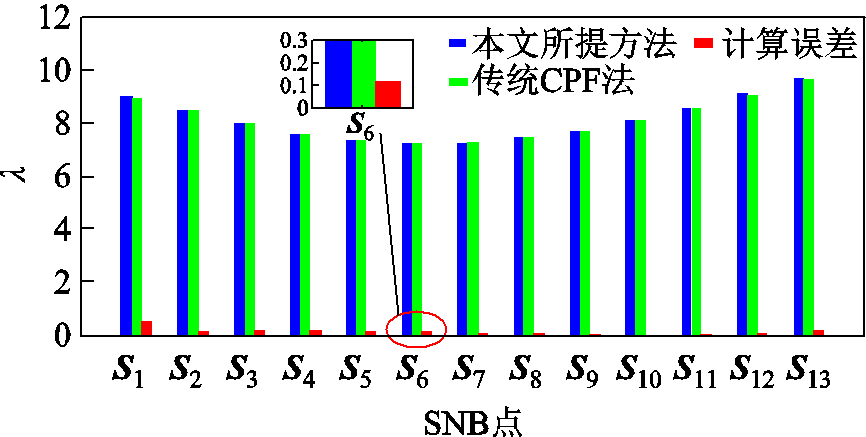
图9 本文所提方法在场景1中的计算误差
Fig.9 Calculation errors of the proposed method in scenario 1
2）场景2
选择发电机节点2和负荷节点4为影响系统电压稳定性的关键节点，以P2和P4为坐标轴，在二维空间内采用本文所提方法构建SVSRB。设初始功率增长方向为d0=[1 0 0 0]T，搜索结果如图10所示，其各SNB点处VSC1/VSC2/VSC3控制方式由基态点的⑤/⑥/⑤转换为⑤/③/⑤。
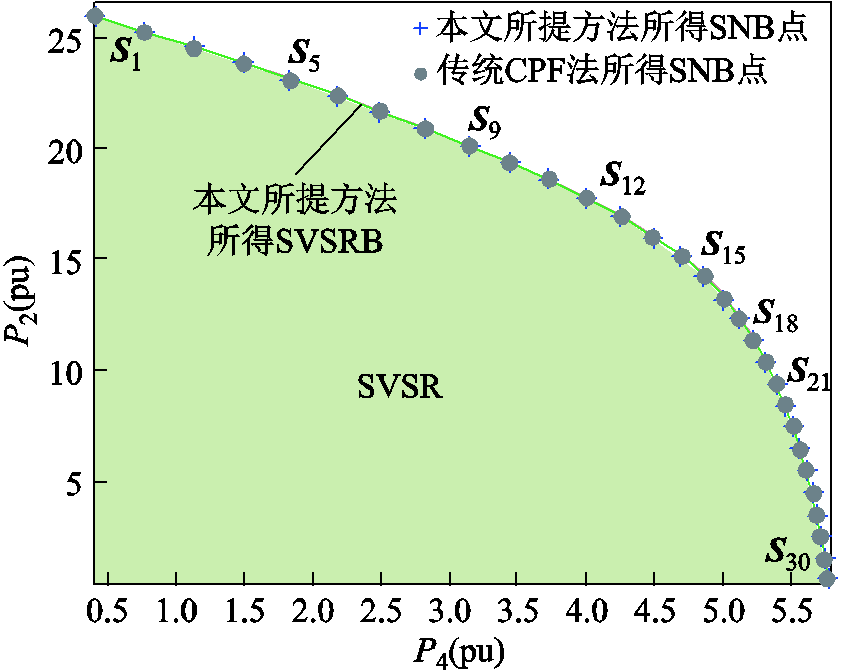
图10 场景2搜索的SVSRB
Fig.10 Tracking SVSRB in scenario 2
图11进一步以CPF搜索结果为基准，对比了本文所提方法与CPF在SNB点处计算所得的系统静态电压稳定裕度。由图中结果可知：在图10所搜索的31个SVSR临界点中，相对CPF，本文所提方法的计算误差均在0.9%以下，最大计算误差为0.801 1%，平均计算误差为0.422 0%。上述计算结果表明采用本文所提方法在构建SVSRB时具有较高的计算精度。
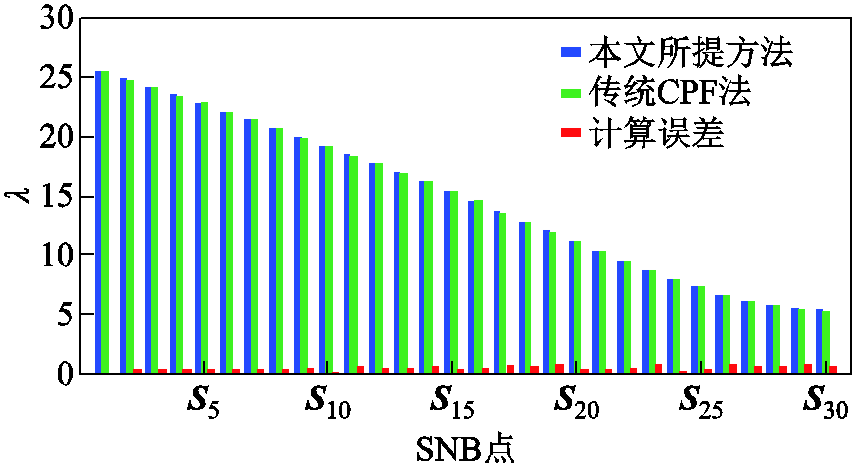
图11 本文所提方法在场景2中的计算误差
Fig.11 Calculation errors of proposed method in scenario 2
3.1.2 计算效率分析
图12进一步对比了本文所提方法与计及换流站控制策略转换的CPF所得SVSRB结果。
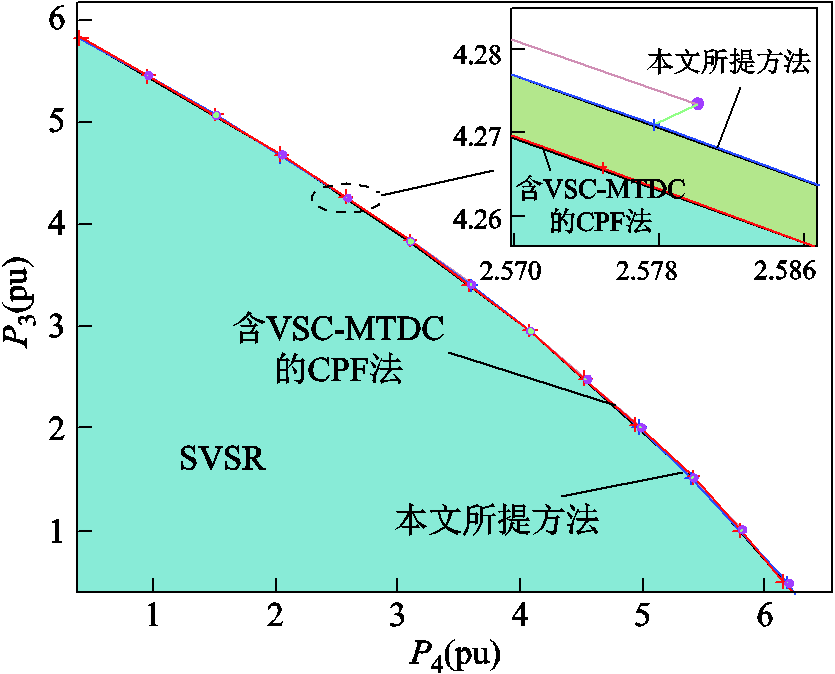
图12 不同算法计算结果对比
Fig.12 Calculation results compared with different methods
由图12结果可知，本文所提方法与计及换流站控制策略转换的CPF所得SNB点完全重合，且求得的SNB点处换流站控制方式与CPF所得SNB点处换流站控制方式均为⑤/③/②，两种方法下各SNB点处换流站控制方式完全相同，验证了所提方法的准确性。
为验证本文所提方法具有较高计算效率，本节在场景1、场景2基础上，进一步对比本文所提方法与CPF搜索SVSRB的计算耗时，结果见表4（计算平台CPU Intel Core i5-4210H，主频2.9MHz，内存8GB）。
表4 不同方法的计算耗时对比
Tab.4 Computational time compared with different methods
场景CPF/s所提算法/s效率提升(%) 1245.1244.2481.95 24434.30168.0896.21
表4结果表明：相对CPF，本文所提方法在实现SVSRB高精度构建的前提下，具有更高的计算效率。其原因为：CPF法需要逐步增加系统负荷水平，进而涉及多次交直流系统换流站控制策略转换，交替迭代计算次数大幅度增加，严重影响SNB点的搜索效率；而本文所提方法通过直接搜索相邻SNB点，减少了不必要的换流站控制策略转换过程，有效地降低了潮流计算迭代次数，提高了系统SNB点的计算效率。
3.1.3 预测步长的选取
在研究SVSRB构建过程中，本节进一步分析了预测步长对所提方法计算精度和效率的影响。
1）以节点3和节点4为电压稳定关键有功注入节点，探究不同预测步长v对SVSRB构建精度影响。
图13为采用本文所提方法，根据不同预测步长v，搜索所得的SVSRB，图中B1为预测步长v＝0.35时，所得的SVSRB；B2为预测步长v＝0.7时，所得的SVSRB；B3为预测步长v＝1.4时，所得的SVSRB。
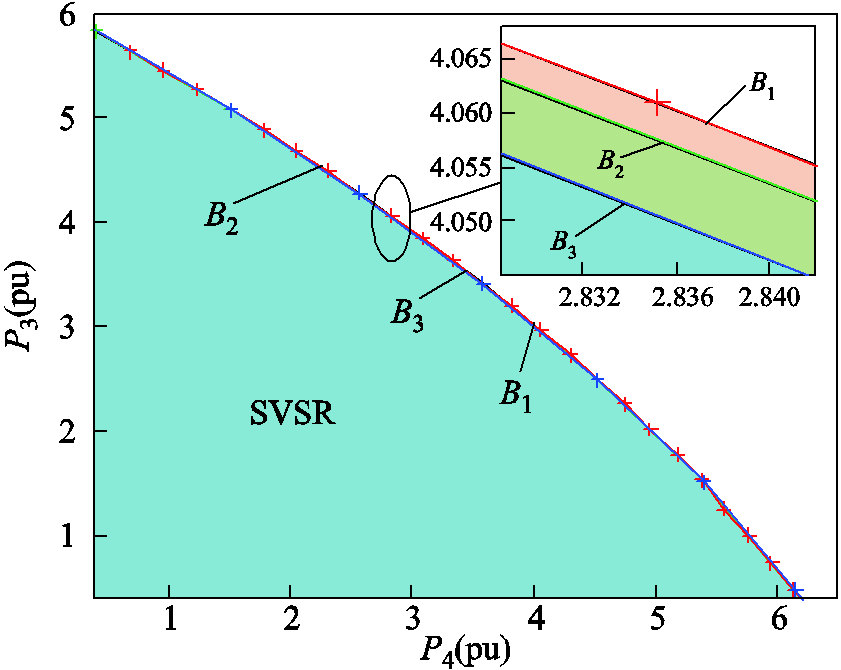
图13 不同预测步长v所得SVSRB结果对比
Fig.13 Tracked SVSRBs with different v
由图13可知：预测步长v＝0.7较v＝1.4所得SVSRB精度更高，保守性更小。当预测步长由v＝0.7变为v＝0.35时SVSRB保守性虽进一步减小，但变化已趋于平缓，呈近似重合状态。
表5进一步对比了不同预测步长v对构建SVSRB效率的影响。
表5 不同预测步长v对SVSRB构建时间的影响
Tab.5 Computational efficiency comparisons of SVSRB with different v
v0.350.701.4 计算时间/s26.9444.2473.03
由表5可知，随着预测步长v的增大，SVSRB的计算耗时逐渐较小。产生上述现象的主要原因为：预测步长v对SVSRB构建效率的影响主要由SNB点搜索数量决定，当预测步长v增大时，SNB点搜索数量相应减少，计算耗时减少。
图13和表5结果表明：当预测步长v减小时，SVSRB保守性降低，精度提高，但这势必会造成SVSRB临界点搜索数量的增多，加重SVSRB求解的计算耗时；而当预测步长v增大时，SVSRB保守性提高，边界构建精度减小，因此，综合考虑交直流系统SVSRB构建精度和计算效率影响，本文中v取值为0.70。
3.1.4 三维SVSR边界搜索
类似上述二维有功注入空间中电力系统SVSR的构建方法，根据2.5节所提的三维SVSR构建方法，本节进一步在三维空间中构建交直流系统的SVSRB。图14给出了以P3、P4、P5为坐标轴构建的SVSRB。图中结果表明：所提方法不仅可用于二维SVSRB的构建，也适用于三维SVSRB的构建。
图14 含VSC-MTDC的IEEE 5节点系统三维SVSRB
Fig.14 3-dimensional SVSRB of IEEE 5 test system with VSC-MTDC
本节进一步将所提方法应用到含VSC-MTDC的IEEE 118节点系统中，以验证该方法的可行性。该系统部分拓扑结构如图15所示，IEEE 118节点测试系统的详细参数详见文献[30]。
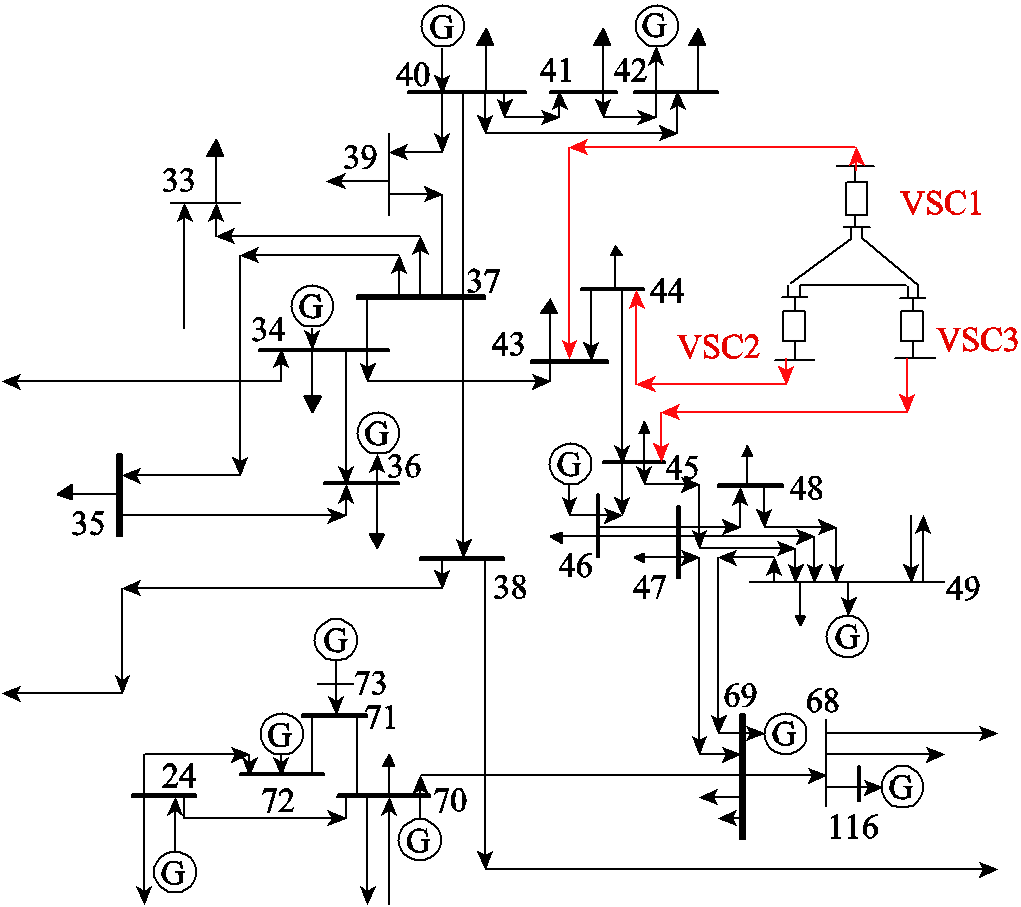
图15 含VSC-MTDC的IEEE 118节点系统部分网络拓扑
Fig.15 Partial network topology of IEEE 118 test system with VSC-MTDC
图15中换流器初始运行参数见表6。选择负荷节点43和44为影响系统电压稳定的关键节点。在以P43、P44为坐标轴的二维空间中，采用本文所提方法搜索SVSRB，结果如图16所述，最终所得其各SNB点处控制方式均为③/⑤/⑤。
表6 含VSC-MTDC的IEEE 188节点系统运行参数
Tab.6 Operating parameters of VSC-MTDC in the modified IEEE 118 test system
换流站编号VSC1VSC2VSC3 换流站控制方式⑤⑤⑤ 直流侧电压Udc(pu)1.0001.0001.000 有功功率PS(pu)-0.6000.2000.300 无功功率QS(pu)-0.1000.0500.050 下垂斜率0.0050.0070.005 交流侧电压US(pu)1.0001.0001.000 下垂有功设定值(pu)-0.5860.2190.362 下垂电压设定值(pu)1.0081.0000.998
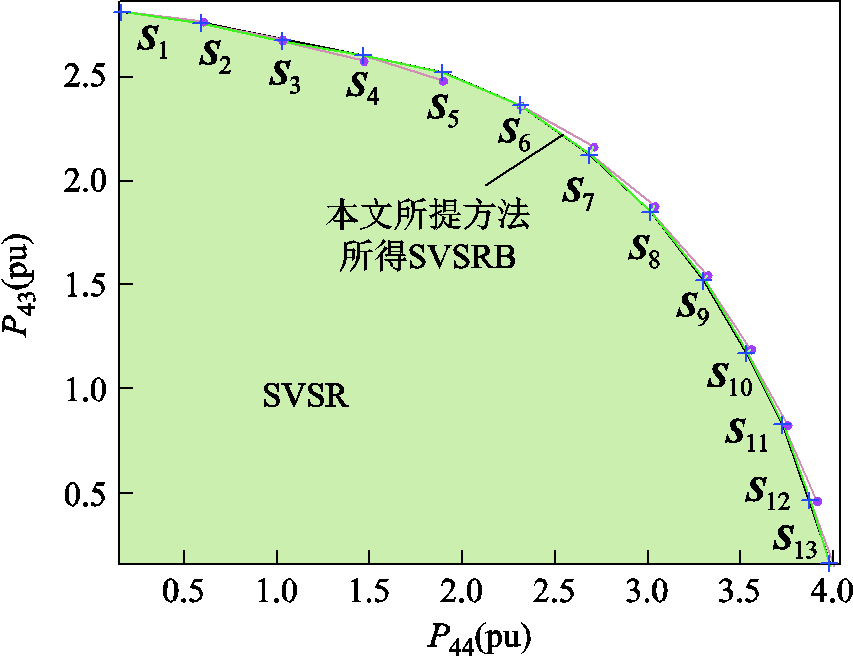
图16 含VSC-MTDC的IEEE 118系统的二维SVSRB
Fig.16 2-dimensional SVSRB of the modified IEEE 118 test system with VSC-MTDC
图17进一步以CPF为基准，对比了所提方法的计算精度。由图17结果可知：本文所提方法搜索的13个SNB点的计算误差均小于0.5%，其中，最大计算误差为0.473 7%，最小计算误差为0.181 6%，平均计算误差为0.354 3%。该结果进一步验证了所
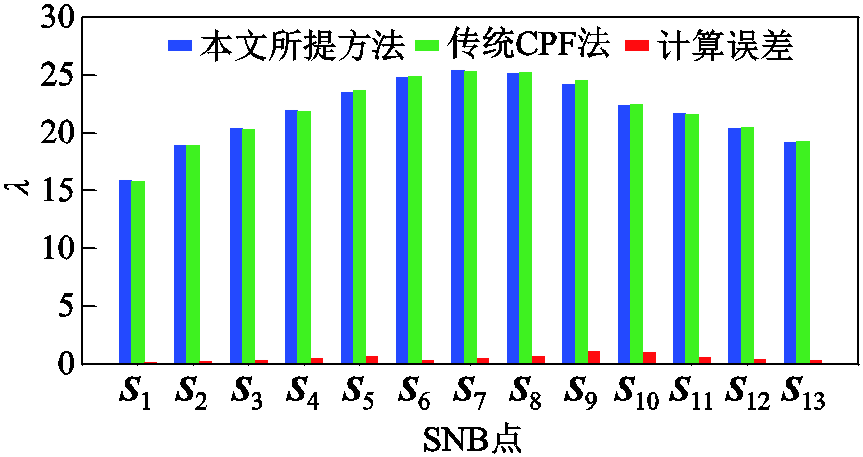
图17 本文所提方法的计算误差
Fig.17 Calculation errors of the proposed method
提方法搜索含VSC-MTDC的交直流系统SNB点具有较高准确性和计算精度。
进一步将负荷节点33、43和44作为影响系统电压稳定的关键节点，在以P43、P44、P33为坐标轴的三维空间中搜索的SVSR，结果如图18所示。
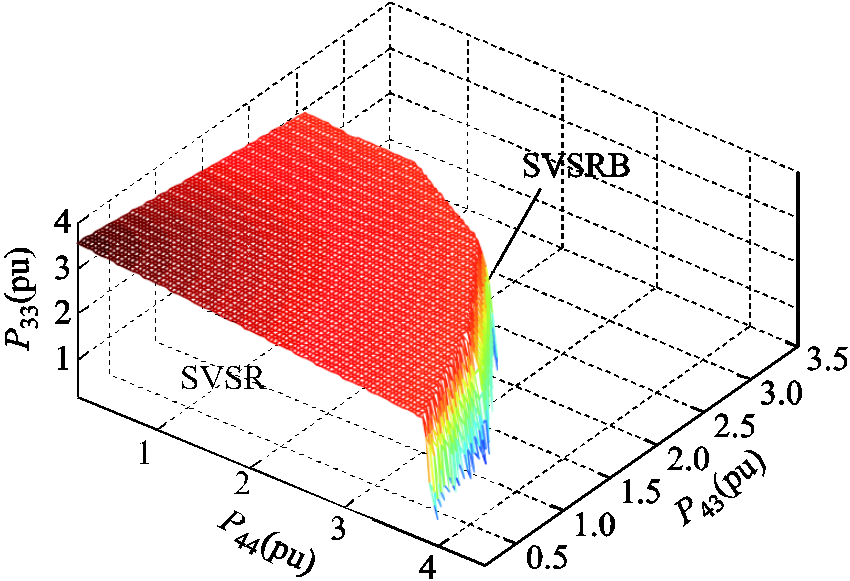
图18 含VSC-MTDC的IEEE 118系统的三维SVSRB
Fig.18 3-dimensional SVSRB of IEEE 118 test system with VSC-MTDC
上述结果表明：所提方法不仅适用于较小规模交直流系统二维和三维SVSR的构建，也适用于较大规模交直流系统二维和三维SVSR构建，验证了所提含VSC-MTDC的交直流电力系统SVSR构建方法在交直流电力系统中应用的可行性和有效性。
本文提出了一种含VSC-MTDC的交直流电力系统SVSR快速构建方法，通过含VSC-MTDC的IEEE 5和IEEE 118节点测试系统对所提方法进行分析、验证，相关结论如下：
1）所提方法有效计及了VSC-MTDC控制策略对交直流系统电压稳定性的影响，实现了含VSC-MTDC的交直流电力系统SNB点准确求解。
2）所提含VSC-MTDC的电力系统SVSRB的求解方法，可在SVSRB搜索过程中，针对VSC-MTDC的参数越限问题，有效调整换流站控制策略和运行参数，实现SVSRB的高精度搜索。
3）所提含VSC-MTDC的交直流电力系统SVSRB快速求解的预测-校正方法，有效计及VSV-MTDC换流站控制策略转换，同步提升交直流电力系统SVSRB的求解精度和计算效率，实现含VSC-MTDC的交直流电力系统SVSR的快速、准确构建。
4）所提交直流电力系统SVSR构建方法，对增强交直流系统静态安全态势感知能力、实现可再生能源大规模并网下的交直流系统电压稳定性评估和预防控制具有一定理论和工程参考价值。
参考文献
[1] 边宏宇, 潘晓杰, 刘芳冰, 等. 多直流馈入背景下的河南电压稳定分析及改善措施研究[J]. 电力系统保护与控制, 2020, 48(21): 125-131.
Bian Hongyu, Pan Xiaojie, Liu Fangbing, et al. Study on voltage stability analysis and improvement measures for Henan province with a background of multiple DC feeding[J]. Power System Protection and Control, 2020, 48(21): 125-131.
[2] 刘英培, 解赛, 梁海平, 等. 计及换流站间电压误差的VSC-MTDC系统自适应下垂控制[J]. 电工技术学报, 2020, 35(15): 3270-3280.
Liu Yingpei, Xie Sai, Liang Haiping, et al. Adaptive droop control of VSC-MTDC system considering voltage error between converter stations[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3270-3280.
[3] 李国庆, 刘先超, 张嵩, 等. 基于MMC的两端TWBS-HVDC直流侧短路故障电流计算方法[J]. 电力系统自动化, 2020, 44(5): 91-100.
Li Guoqing, Liu Xianchao, Zhang Song, et al. Current calculation method of short-circuit fault at DC side for MMC based two-terminal TWBS-HVDC[J]. Automation of Electric Power Systems, 2020, 44(5): 91-100.
[4] 潘超, 米俭, 蔡国伟, 等. 交直流混杂环境下变压器漏电感参数分析方法[J]. 电机与控制学报, 2019, 23(5): 25-33.
Pan Chao, Mi Jian, Cai Guowei, et al. Analysis method of leakage inductance parameters under AC/DC hybrid environment in transformer[J]. Electric Machines and Control, 2019, 23(5): 25-33.
[5] 王长江, 姜涛, 刘福锁, 等.基于轨迹灵敏度的暂态过电压两阶段优化控制[J]. 电工技术学报, 2021, 36(9): 1888-1900.
Wang Changjiang, Jiang Tao, Liu Fusuo, et al. Two-stage optimal control of transient overvoltage based on trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1888-1900.
[6] 张炎, 丁明, 韩平平, 等. 直流闭锁后风电送端系统暂态稳定及控制策略研究[J]. 电工技术学报, 2020, 35(17): 3714-3726.
Zhang Yan, Ding Ming, Han Pingping, et al. Research on transient stability and control strategy of wind power transmission system after DC blocking[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3714-3726.
[7] 朱永强, 刘康, 张泉, 等. 混合微电网交流侧故障传播机理及抑制方法[J]. 电机与控制学报, 2020, 24(4): 5-15.
Zhu Yongqiang, Liu Kang, Zhang Quan, et al. Fault propagation mechanism and suppression method on AC side of hybrid microgrid[J]. Electric Machines and Control, 2020, 24(4): 5-15.
[8] Hussien M G, Liu Yi, Xu Wei. Robust position observer for sensorless direct voltage control of stand-alone ship shaft brushless doubly-fed induction generators[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 363-376.
[9] 刘英培, 解赛, 梁海平, 等.计及换流站间电压误差的VSC-MTDC系统自适应下垂控制[J]. 电工技术学报, 2020, 35(15): 3270-3280.
Liu Yingpei, Xie Sai, Liang Haiping, et al. Adaptive droop control strategy for VSC-MTDC system considering DC voltage errors among converter stations[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3270-3280.
[10] Cao Yijia, Wang Weiyu, Li Yong, et al. A virtual synchronous generator control strategy for VSC-MTDC systems[J]. IEEE Transactions on Energy Conversion, 2018, 33(2): 750-761.
[11] Shah R, Sánchez J C, Preece R, et al. Stability and control of mixed AC-DC systems with VSC-HVDC: a review[J]. IET Generation, Transmission & Distribution, 2018, 12(10): 2207-2219.
[12] 陈厚合, 李国庆, 姜涛. 计及静态电压稳定约束的交直流系统可用输电能力[J]. 电网技术, 2012, 36(2): 75-81.
Chen Houhe, Li Guoqing, Jiang Tao. Available transfer capability of hybrid AC/DC power system considering constraint of static voltage stability[J]. Power System Technology, 2012, 36(2): 75-81.
[13] Zhang Fang, Li Qingquan. Methodology of calculating droop coefficients for stabilising DC voltage in VSC-MTDC system against disturbances[J]. IET Generation, Transmission & Distribution, 2019, 13(4): 521-535.
[14] Moawwad A, EI-Saadany E F, Moursi M, et al. Critical loading characterization for MTDC converters using trajectory sensitivity analysis[J]. IEEE Transactions on Power Delivery, 2018, 33(4): 1962-1972.
[15] 乐健, 廖小兵, 李奔, 等. 基于扩展仿射模型的不确定性静态电压稳定性全局灵敏度分析[J]. 电工技术学报, 2021, 36(13): 2812-2820.
Le Jian, Liao Xiaobing, Li Ben, et al. Global sensitivity analysis of uncertain static voltage stability based on extended affine model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2812-2820.
[16] 陈厚合, 黄亚磊, 姜涛, 等. 含VSC_HVDC的交直流系统电压稳定分析与控制[J]. 电网技术, 2017, 41(8): 2429-2435.
Chen Houhe, Huang Yalei, Jiang Tao, et al. Voltage stability analysis and control for AC/DC system with VSC-HVDC[J]. Power System Technology, 2017, 41(8): 2429-2435.
[17] 潘学萍, 李乐, 黄华, 等. 综合灵敏度和静态电压稳定裕度的直流受端交流系统电压薄弱区域评估方法[J]. 电力自动化设备, 2019, 39(3): 1-8.
Pan Xueping, Li Yue, Huang Hua, et al. Method for evaluating voltage weak area of AC power system at DC receiving end considering sensitivity and static voltage stability margin[J]. Electric Power Automation Equipment, 2019, 39(3): 1-8.
[18] Urquidez O A, Xie Le. Singular value sensitivity based optimal control of embedded VSC-HVDC for steady-state voltage stability enhancement[J]. IEEE Transactions on Power Systems, 2016, 31(1): 216-225.
[19] 李京, 刘道伟, 赵高尚, 等. 基于连续参数追踪的静态电压稳定域边界迁移构建新方法[J]. 电网技术, 2020, 44(2): 465-477.
Li Jing, Liu Daowei, Zhao Gaoshang, et al. A new method for transfer construction of static voltage stability region boundary based on continuous parameter tracking[J]. Power System Technology, 2020, 44(2): 465-477.
[20] 陈中, 严俊, 朱政光, 等. 多馈入交直流混联系统解耦安全域的刻画及应用[J]. 电力系统自动化, 2020, 44(22): 37-44.
Chen Zhong, Yan Jun, Zhu Zhengguang, et al. Characterization and application of decoupling security region in multi-infeed AC/DC hybrid system[J]. Automation of Electric Power Systems, 2020, 44(22): 37-44.
[21] 辛建波, 杨程祥, 舒展, 等. 基于静态安全域的交直流混联大电网关键线路辨识[J]. 电力系统保护与控制, 2020, 48(6): 165-172.
Xin Jianbo, Yang Chengxiang, Shu Zhan, et al. Identification of critical lines in AC/DC hybrid large power grid based on steady-state security region[J]. Power System Protection and Control, 2020, 48(6): 165-172.
[22] 姜涛, 谭洪强, 李雪, 等. 电力系统热稳定安全域边界快速搜索的优化模型[J]. 中国电机工程学报, 2019, 39(22): 6533-6547.
Jiang Tao, Tan Hongqiang, Li Xue, et al. A general optimization model for exploring static thermal security region boundary in bulk power systems[J]. Proceedings of the CSEE, 2019, 39(22): 6533-6547.
[23] 王成山, 许晓菲, 余贻鑫, 等. 电力系统电压稳定域的局部可视化描述及其应用[J]. 中国电机工程学报, 2004, 24(3): 6-10.
Wang Chengshan, Xu Xiaofei, Yu Yixin, et al. Visualization of part of the static voltage stability region in power systems and its application[J]. Proceedings of the CSEE, 2004, 24(3): 6-10.
[24] Iba K, Suzuki H, Egawa M, et al. Calculation of critical loading condition with nose curve using homotopy continuation method[J]. IEEE Transactions on Power Systems, 1991, 6(2): 584-593.
[25] 姜涛, 张明宇, 李雪, 等. 静态电压稳定域局部边界的快速搜索新方法[J]. 中国电机工程学报, 2018, 38(14): 4126-4137, 4318.
Jiang Tao, Zhang Mingyu, Li Xue, et al. A novel algorithm to explore static voltage stability region boundary in power systems[J]. Proceedings of the CSEE, 2018, 38(14): 4126-4137, 4318.
[26] 姜涛, 张明宇, 崔晓丹, 等. 电力系统静态电压稳定域边界快速搜索的优化模型[J]. 电工技术学报, 2018, 33(17): 4167-4179.
Jiang Tao, Zhang Mingyu, Cui Xiaodan, et al. A novel optimization model to explore static voltage stability region boundary in bulk power systems[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4167-4179.
[27] 李雪, 张琳玮, 姜涛, 等. 基于CPU-GPU异构的电力系统静态电压稳定域边界并行计算方法[J/OL]. 电工技术学报, 2021, DOI: 10.19595/j.cnki.1000-6753.tces.201141.
Li Xue, Zhang Linwei, Jiang Tao, et al. Parallel calculation method of power system static voltage stability region boundary based on CPU-GPU heterogeneous[J/OL]. Transactions of China Electrotechnical Society, 2021, DOI: 10.19595/j.cnki. 1000-6753.tces.201141.
[28] Beerten J, Hertem D V, Belmans R. VSC MTDC systems with a distributed DC voltage control-A power flow approach[C]//2011 IEEE Trondheim PowerTech, Trondheim, Norway, 2011: 19-23.
[29] Yogarathinam A, Chaudhuri N R. Stability-constrained adaptive droop for power sharing in AC-MTDC grids[J]. IEEE Transactions on Power Systems, 2019, 34(3): 1955-1965.
[30] Jiang Tao, Bai Lingquan, Jia Hongjie, et al. Spectral clustering-based partitioning of volt/VAR control areas in bulk power systems[J]. IET Generation, Transmission & Distribution, 2016, 11(5): 1126-1133.
A Predictor-Corrector Algorithm for Forming Voltage Stability Region of Hybrid AC/DC Power Grid with Inclusion of VSC-MTDC
Abstract To address the voltage stability assessment of hybrid AC/DC power grid with high permeation of renewable energy, a voltage stability region (SVSR) of the hybrid AC/DC power grid with inclusion of voltage sourced converter based multi-terminal high voltage direct current (VSC-MTDC) is developed in this work. In the light of the topological characteristics of SVSR boundary (SVSRB), a predictor-corrector model is proposed to explore the SVSRB points with regarding the control strategy switching of the VSC-MTDC converter station. The continuation power flow (CPF) is employed to explore the first SVSRB point on the SVSRB, then rest SVSRB points on the SVSRB are explored by the proposed predictor-corrector model with the adjacent explored SVSRB point as the initial point. During this procedure, if the operational parameters of the converter station violate their limits, the control strategy switching of the converter station is switched following the proposed switching condition, which significantly enhance the computational accuracy and efficiency of the SVSRB. The performance of the developed approach is evaluated by the modified IEEE 5 and IEEE 118 test systems with the VSC-MTDC. The results confirm that the proposed predictor-corrector approach exhibits a great performance in the computational accuracy and efficiency for forming the SVSR of the hybrid AC/DC power grid.
Keywords：Hybrid AC/DC power system, voltage sourced converter based multi-terminal high voltage direct current (VSC-MTDC), static voltage stability region, static voltage stability region boundary, control strategy, continuation power flow, predictor-corrector
DOI:10.19595/j.cnki.1000-6753.tces.210281
中图分类号：TM712
姜 涛 男，1983年生，博士，教授，博士生导师，研究方向为电力系统安全性和稳定性、可再生能源集成、综合能源系统。E-mail：t.jiang@aliyun.com
李 雪 女，1986年生，博士，副教授，博士生导师，研究方向为电力系统安全性与稳定性、电力系统高性能计算、电力市场。E-mail：xli@neepu.edu.cn（通信作者）
收稿日期 2021-03-03
改稿日期 2021-04-22
国家自然科学基金（52077029）、国家自然科学基金委员会-国家电网公司智能电网联合基金（U2066208）和国家重点研发计划（2016YFB0900900）资助项目。
（编辑 赫蕾）