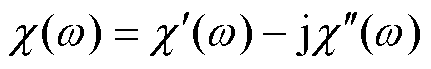 (1)
(1)
摘要 在电力装备的实际运行过程中,可能遭受诸如操作冲击电压、雷电冲击电压等瞬态电压激励的作用。此外,随着电力电子器件在直流输电装备中的大规模应用,装备内部器件的绝缘结构承受的电压不再是传统的交流电压或直流电压,而是正极性重复性方波电压。为了研究这些装备或器件内的绝缘结构在瞬态电压激励下的电场特性,需要在电准静态场下计算其瞬态电场分布。在交变电场中,绝缘材料具有介电弛豫现象,其介电常数在频域上为频变函数。由于瞬态电压激励时间短、变化快,对应的频谱宽。因而,瞬态电压激励下的瞬态电场计算需要考虑材料的介电弛豫特性。为此,该文提出了考虑介质介电弛豫过程的时域有限元法。首先,将材料的介电弛豫现象用时变的介电参数表征,对含时变介电参数的电准静态场控制方程进行时空离散,推导了时域有限元方程和边界电场约束方程;然后,通过对比PEEK材料极化电流的实验测量结果与计算结果,验证了所提方法的有效性;最后,分析了瞬态电压激励下考虑材料介电弛豫特性的复合绝缘结构的瞬态电场分布特性。
关键词:介电弛豫 频变 时域有限元法 边界电场约束方程 电准静态场
绝缘问题是高压电力装备设计和制造中的核心问题之一,导致绝缘问题的原因是高压电力装备的绝缘结构中局部电场超过绝缘材料的许用场强。因此,准确计算电力装备绝缘结构中的电场分布是解决其绝缘问题的关键。在装备的实际运行中,存在如操作冲击电压、雷电冲击电压等瞬态电压激励的作用[1-2]。此外,随着电力电子器件在直流输电装备中的大规模应用,装备内部器件的绝缘结构承受的电压不再是传统的交流电压或直流电压,而是正极性重复性方波电压[3-4]。此时,需要在瞬态电压激励下计算绝缘结构中的瞬态电场分布。
电力装备的瞬态电场计算通常满足电准静态条件,可以忽略变化的磁场感生的电场,此时,电场是近似无旋场[5]。瞬态电场满足的泛定方程是电准静态场下的控制方程。对于具有复杂结构的电力设备而言,其电场分布很难解析得到,只能采用数值计算方法,获得其数值解。对于瞬态电场的数值计算,有众多数值计算方法,如时域有限元法[6]、时间周期有限元法[7]、谐波平衡有限元法[8]和频域有限元法[9]等。其中,时域有限元法操作简单,被广泛应用在电力设备的瞬态电场计算中[10-13]。
在电准静态场下的瞬态电场计算中,材料参数与几何结构决定了瞬态电场的分布。使用时域有限元法计算瞬态电场时,通常将材料用介电和电导模型来考虑,认为材料是各向同性、线性、均匀介质,因而材料的介电常数与电导率是常数[14-15]。为了对材料进行更准确的建模,有许多学者在电场计算中考虑了材料的非线性[12]与各向异性[13],但很少考虑材料自身的介电弛豫现象。
实际上,在交变电场中,电介质呈现介电弛豫现象,介质的介电响应是与频率有关的函数,通常用各种介电弛豫模型表征[16-19]。由于瞬态电压激励时间短、变化快,从而对应的频谱宽。因此,在瞬态电压激励下的瞬态电场计算应该考虑材料的介电弛豫现象,即考虑材料介电常数的频变效应。
从现有文献看,考虑材料频变效应的瞬态电场计算,集中在计算雷电冲击电压下电力设备的瞬态电场,其中包括基于Fourier变换的频域计算[20-21]和时域计算[22-24]。基于Fourier变换的频域计算得到的是雷电冲击电压下瞬态电场的周期稳态响应,而不是瞬态响应。而时域计算能得到瞬态电场的瞬态响应。目前,瞬态电场的时域计算,通常采用有限元法,在Debye模型的基础上,将雷电冲击电压用Dehamel积分来处理[22-23]。这种处理先计算极化强度,再将极化强度代入电位的控制方程求解瞬态电位,增加了一步求解极化强度的过程,实际上增加了额外的计算量。
此外,为了提高高压电力装备的绝缘能力,设备的绝缘结构多采用由多种材料组合而成的复合绝缘结构[5]。对于复合绝缘结构而言,由于界面两侧材料参数的差异导致界面两侧电场强度法向分量的不连续,降低了介质交界面处电场强度的计算精度,进而降低了界面电荷密度的计算精度[25]。而复合绝缘结构中的最大电场强度往往出现在导体表面或介质交界面,这些位置的电场需要准确计算。
为了解决介质分界面处电场强度法向分量的准确计算问题,国内外学者给出了一些解决办法。棱边有限元法选用场矢量作为求解变量,采用棱边单元插值保证场强切向方向连续,而不强制法向方向连续,可以避免通过位函数求解场量而引起的微分误差等问题[26]。与节点有限元相比,棱边有限元法计算代价较高。有限元边界元混合算法先用节点有限元法计算节点电位,再将场域划分成多个由单一介质构成的子域,最后采用边界元法计算子域边界的电场强度法向分量[27]。混合法在介质分界面处计算精度较高,但与传统节点有限元相比多了一步边界元计算。边界电场约束方程法能精确计算Dirichlet边界处的电场强度,并能推广到介质交界面处的电场强度法向分量的计算,此外,还能方便应用在现有的节点有限元程序中[28-29]。
本文直接将表征介电弛豫的介电常数表征为时域函数,并引入电准静态场控制方程,提出考虑介质介电弛豫过程的时域有限元方法。本文首先推导考虑介质介电弛豫时瞬态电场计算的初值–边值问题。然后对控制方程在空间进行有限元离散,时间上进行差分离散,推导瞬态电场计算的时域有限元方程与边界电场约束方程,边界电场约束方程能准确计算边界及介质分界面处的电场强度;最后通过对比计算结果与实验结果验证了本文所提方法的有效性,并给出了复合绝缘结构下瞬态电场的计算结果,分析了绝缘介质介电弛豫响应对电场分布的影响规律。
介电弛豫是指电介质在外电场作用(或移去)后,从瞬时建立的极化状态达到新的极化平衡态的过程。在交变电场中,电介质的介电响应是与频率有关的函数。在频域上,电极化率为复变函数,表示为
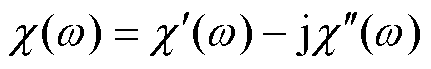 (1)
(1)
式中,χ(ω)为复极化率;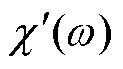 和
和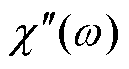 分别为复极化率的实部和虚部。
分别为复极化率的实部和虚部。
复极化率的实部和虚部互为Hilbert变换,满足Kramer-Kronig关系[13]。材料的复极化率可以通过介电响应的频域测量获得。复极化率通常用介电响应模型(介电弛豫模型)表征[13-16]。
根据介电常数和电极化率的关系,复介电常数ε(ω)可以表示为
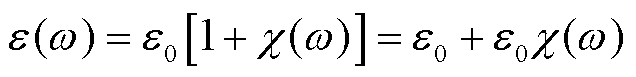 (2)
(2)
式中,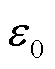 为真空介电常数。
为真空介电常数。
理论上,复极化率的定义域是[0,+∞),因而复介电常数也是定义在[0,+∞)上的复变函数。但是,实际中,对于介电谱的测量不可能测到无穷频率,只能在一定的频率范围内测量,也就是说,实际上复极化率的频率范围为[0, ωc],其中,ωc为宽频测量的截止频率。此时,将复介电常数表示成
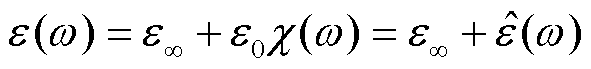 (3)
(3)
式中,ε∞为光频介电常数,包含了自由空间的贡献ε0和ω>ωc时所有极化过程的贡献;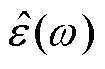 为频变的介电系数,对应于介电弛豫,也称为松弛极化,其定义域为[0, ωc]。
为频变的介电系数,对应于介电弛豫,也称为松弛极化,其定义域为[0, ωc]。
因此,在频域上,如果考虑介电常数的频变效应,电位移矢量D(jω)和电场强度E(jω)满足
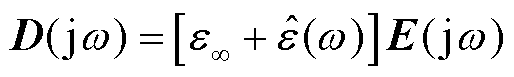 (4)
(4)
而在时域上,如果考虑介质介电常数的频变效应,电位移矢量D和电场强度E满足
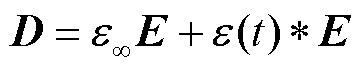 (5)
(5)
式中,ε(t)为时变函数,对应于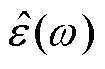 的Fourier反变换;“∗”表示时域卷积。
的Fourier反变换;“∗”表示时域卷积。
式(5)即为电准静态下,考虑介质的介电弛豫现象时电场的本构关系。
联立麦克斯韦方程组中的全电流定律、高斯定理及式(5)所表示的本构关系,此时,电准静态场下,考虑介质的介电弛豫现象,瞬态电场的控制方程可以表示为
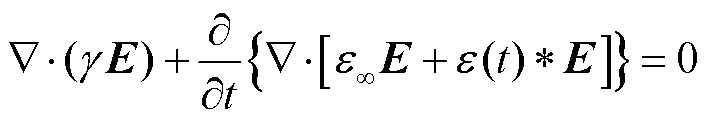 (6)
(6)
式中,γ为介质的电导率。
考虑电准静态场条件,电场为近似无旋场,可以引入标量电位E=−∇φ,因此,式(6)可以用电位表示为
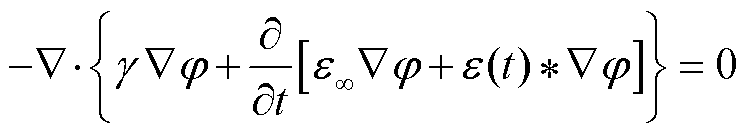 (7)
(7)
对于电准静态场下,考虑介质自身的介电驰豫过程时瞬态电场的初值-边值问题,其场域和边界如图1所示。
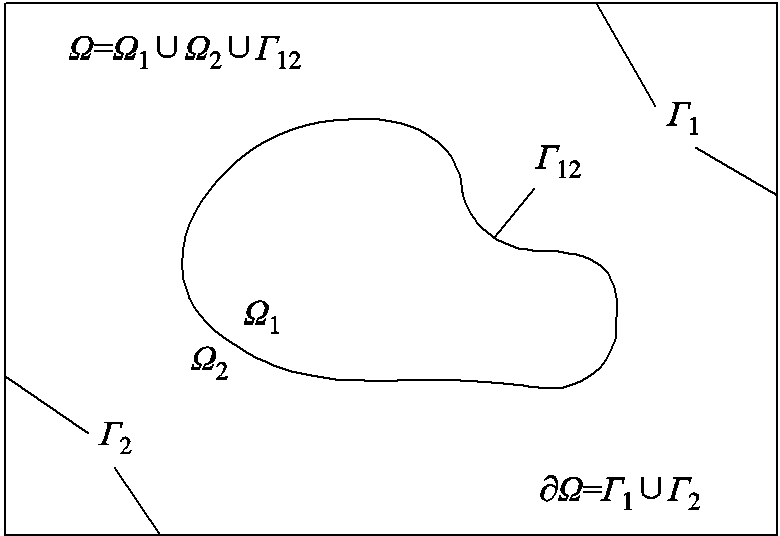
图1 初值-边值问题的场域和边界示意图[29]
Fig. 1 A sketch of the domain and boundary for the initial value and boundary value problem[29]
图1中,场域Ω为凸多边形闭合区域,介质分界面Γ12将场域Ω分割成由不同材料组成的单介质子域Ω1和Ω2,因此Ω=Ω1∪Ω2∪Γ12。其中,∂Ω为场域Ω的边界,Γ1为Dirichlet边界,边界上的电位函数已知,Γ2为Neumann边界,边界上电位的法向倒数已知,且∂Ω = Γ1∪Γ2。
在电准静态场下,对于图1所示的几何模型,考虑介质自身的介电驰豫过程时瞬态电场的初值-边值问题可以表示为
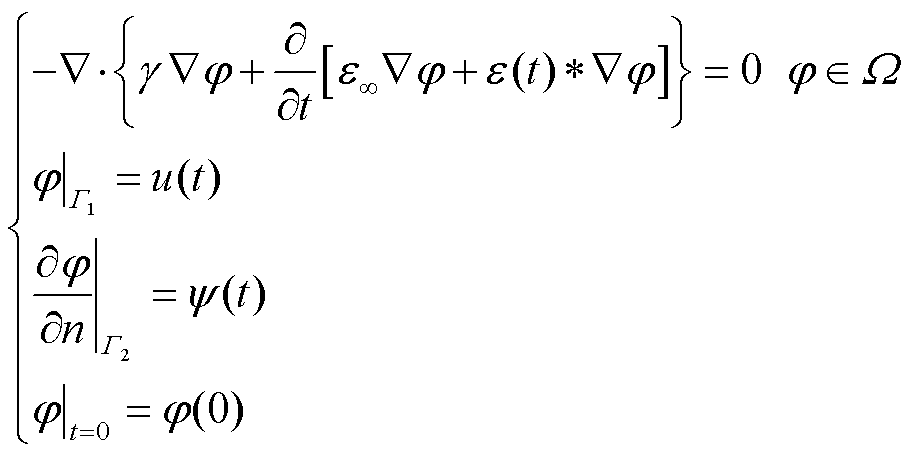 (8)
(8)
式中,u(t)为Dirichlet边界上电位函数;ψ(t)为Neumann边界上电位函数的法向导数;φ(0)为电位初始值。
在介质交界面上,用电位表示的介质交界面上的衔接条件为
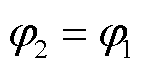 (9)
(9)

式中,n为介质交界面处的单位法向量的方向,其方向由介质1指向介质2。
为了求解上述初值-边值问题,本文采用时域有限元法,在空间上进行有限元离散,将偏微分方程转化为一组代数方程组,在时间上进行差分离散,在每个离散的时间步长上迭代求解代数方程组,获得考虑材料介质弛豫特性的准静态场下的初值-边值问题的时域数值解。
在空间上,将场域Ω离散成m个单元,共有n个节点。其中m个单元中有m1个单元与Dirichlet边界Γ1共线,有m2个单元与Neumann边界Γ2共线。将控制方程在场域中任意一点满足弱化成在控制方程每一个单元上的加权积分满足。因此在每个单元上均能得到一个有限元方程。
选择单元Ωe上的每个节点的形状函数为权函数,在单元Ωe上对方程进行加权积分,利用加权余量法,将方程在任意一点满足放松为在单元Ωe的加权积分满足。对于单元Ωe,其边界为∂Ωe。对于单元Ωe上的节点i,将控制方程乘以节点权函数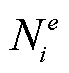 ,并在单元Ωe上做场域积分,得
,并在单元Ωe上做场域积分,得
 (11)
(11)
利用Green公式,式(11)中的积分可分成两部分,分别为对单元的场域积分和对单元边界的边界积分,即
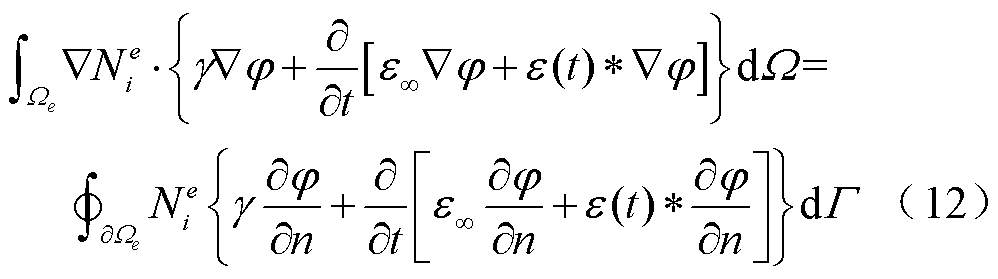
采用Galerkin法,在单元Ωe上,取电位的近似解为
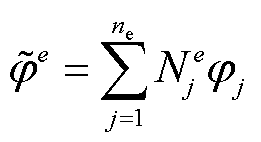 (13)
(13)
式中,φj为单元上第j个节点的节点电位;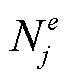 为单元上第j个节点的形状函数。
为单元上第j个节点的形状函数。
将式(13)代入式(12),得
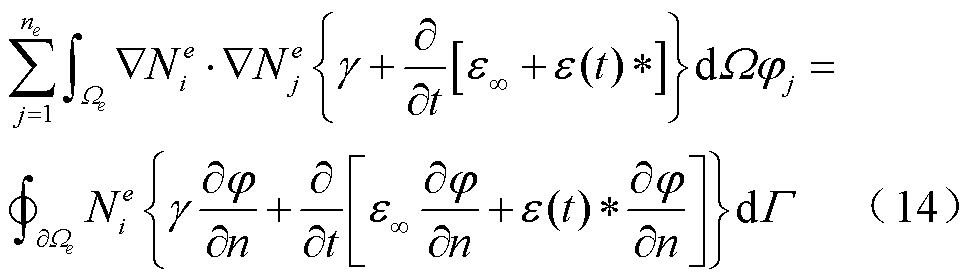
整合所有单元上的有限元方程
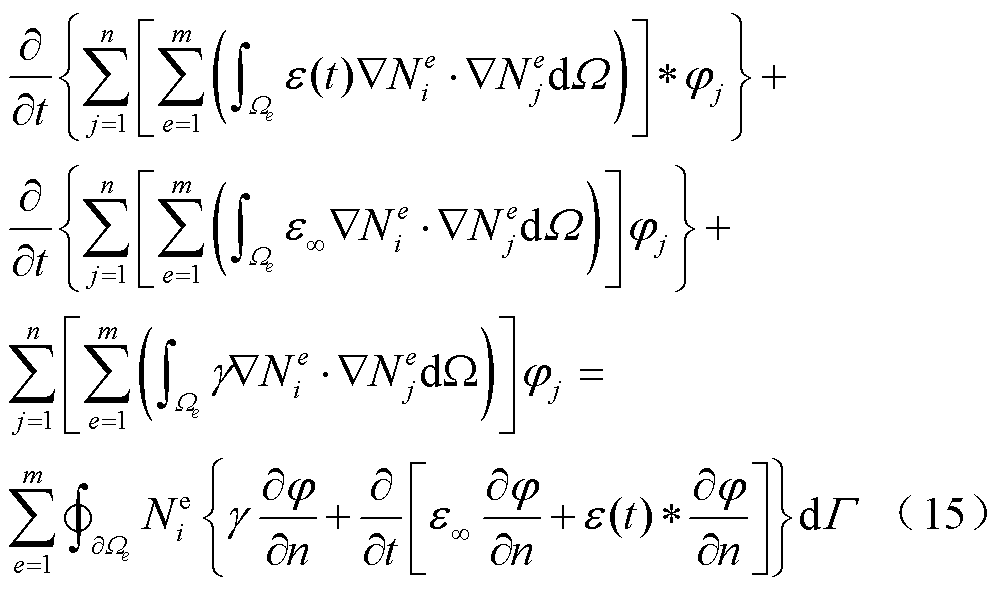
考虑到物理意义,−∂φ/∂n代表电场强度的法向分量En。因此,式(15)中,右端的沿边界的闭合曲线项可以分成三部分:第一部分是沿Dirichlet边界Γ1的曲线积分,其中∂φ/∂n可用−En替代;第二部分是沿Neumann边界Γ2的曲线积分,其中∂φ/∂n可用y替代;第三部分是沿介质分界面Γ12两侧的曲线积分。由于介质分界面两侧的外法线方向相反,n2=−n1。利用介质分界面上的衔接条件式(10),可知式(15)中沿介质分界面Γ12两侧的曲线积分为0。因此,式(15)可写成
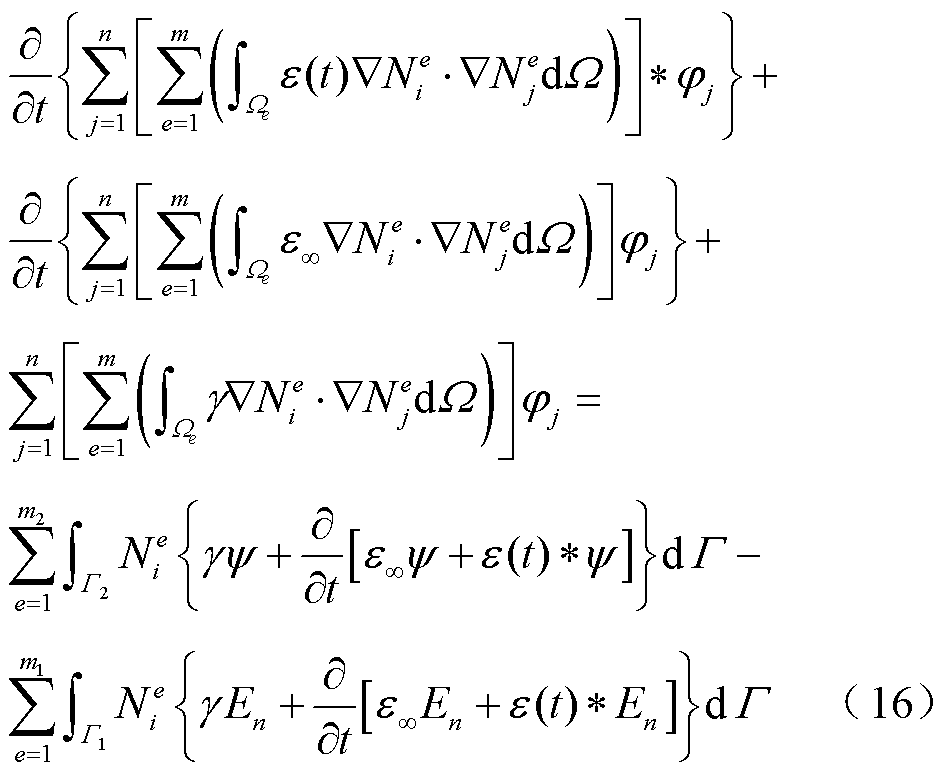
式(16)即为空间离散后的有限元方程,写成矩阵形式为
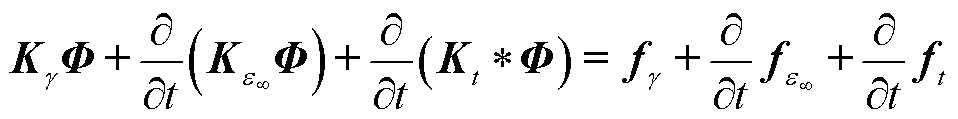 (17)
(17)
式中,Kg、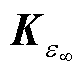 和Kt分别为对应于γ、ε∞和ε(t)的刚度矩阵,且Kt是时变的;fg、
和Kt分别为对应于γ、ε∞和ε(t)的刚度矩阵,且Kt是时变的;fg、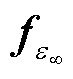 和ft分别为对应于γ、ε∞和ε(t)的边界积分列向量。Kg、
和ft分别为对应于γ、ε∞和ε(t)的边界积分列向量。Kg、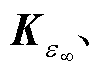 Kt、fg、
Kt、fg、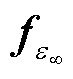 和ff分别表示为
和ff分别表示为
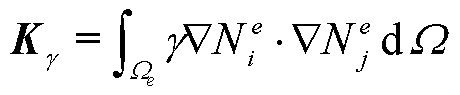 (18)
(18)
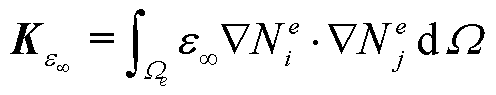 (19)
(19)
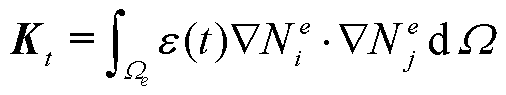 (20)
(20)
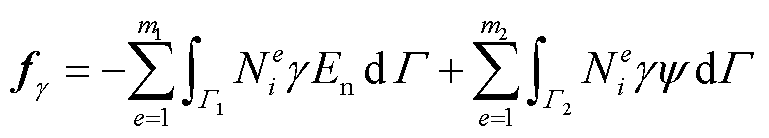 (21)
(21)
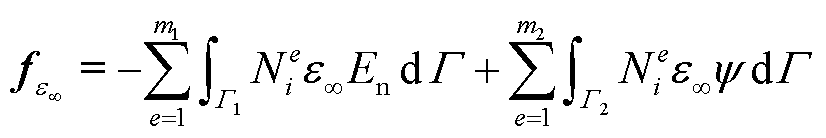 (22)
(22)
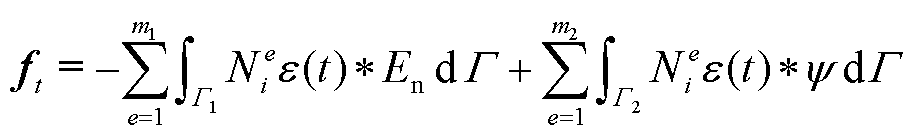 (23)
(23)
由于后向欧拉格式具有无条件稳定性[30],且还能消除由激励突变引起的数值振荡[31]。为了简便,考虑定步长的后向欧拉差分格式,处理式(17)中对时间的偏导数。后向Euler差分格式表示为
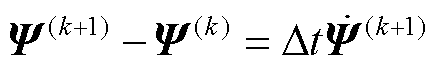 (24)
(24)
式中,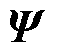 为任意函数;
为任意函数;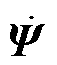 为函数
为函数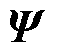 对时间的偏导数;上标k和k+1分别为第k个时间步长和第k+1个时间步长时的量。
对时间的偏导数;上标k和k+1分别为第k个时间步长和第k+1个时间步长时的量。
对于式(17)中的卷积项,利用卷积的微分性质后,再对时间的微分项进行差分处理,有
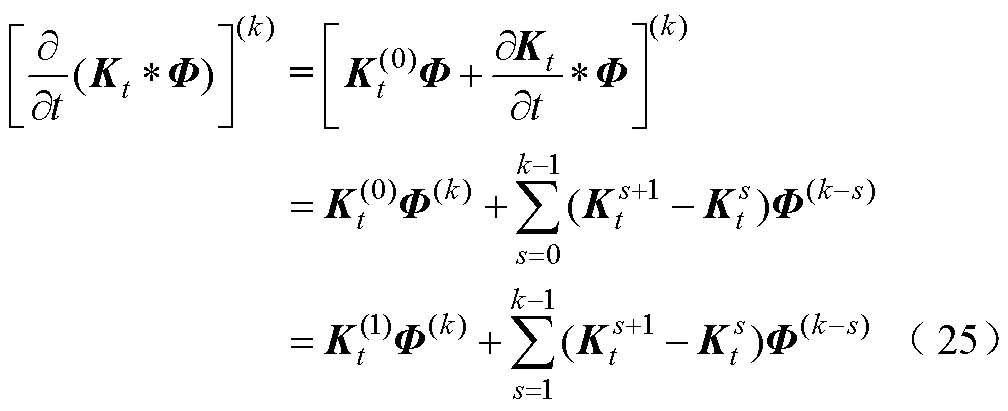
同理
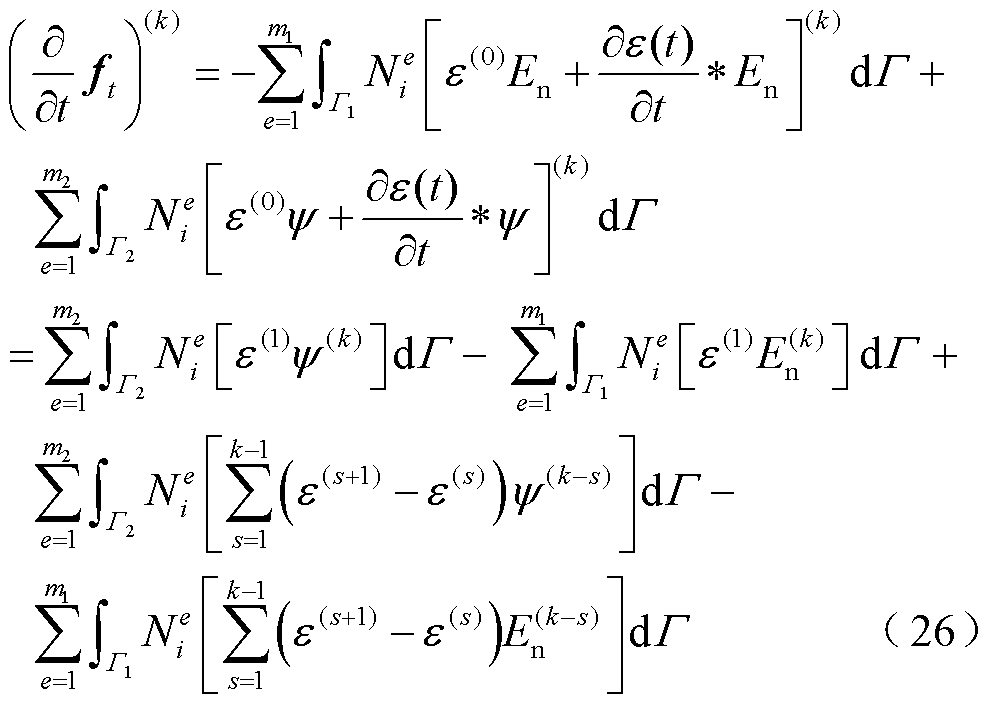
将式(24)~式(26)代入式(17),在第k个时间步长上,有限元方程式(17)可写成
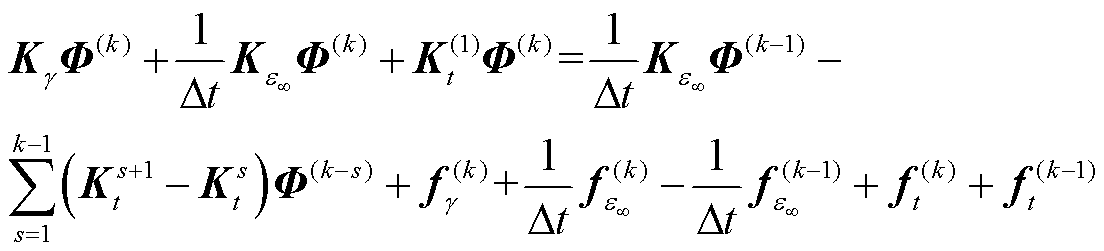 (27)
(27)
式中,ft(k)和ft(k-1)分别为
 (28)
(28)
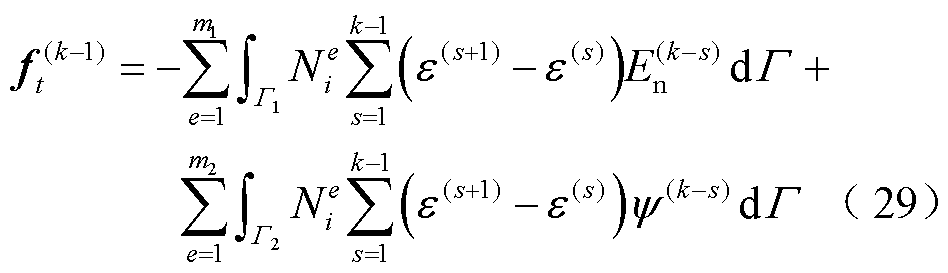
整理式(27),可以将其简写为
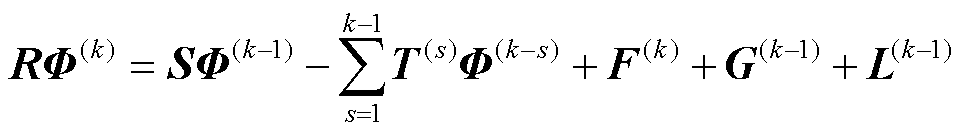 (30)
(30)
式中,各矩阵及向量分别为
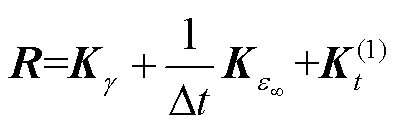 (31)
(31)
 (32)
(32)
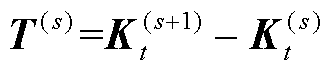 (33)
(33)
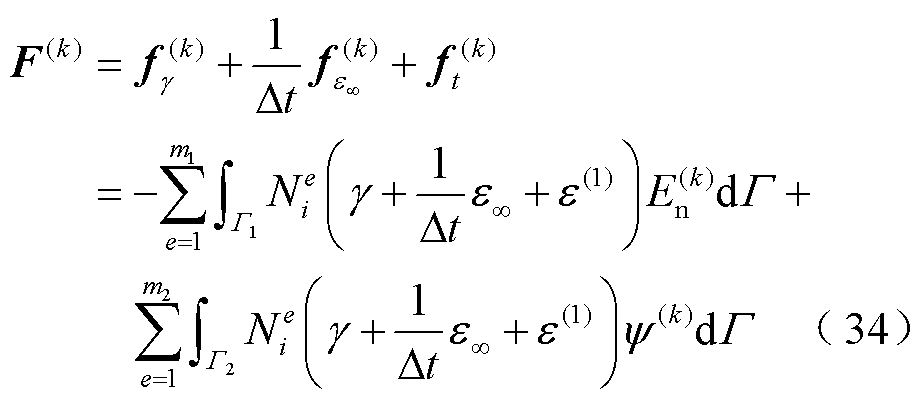
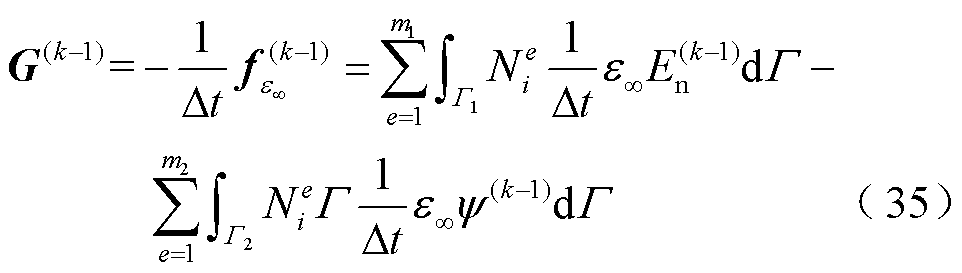
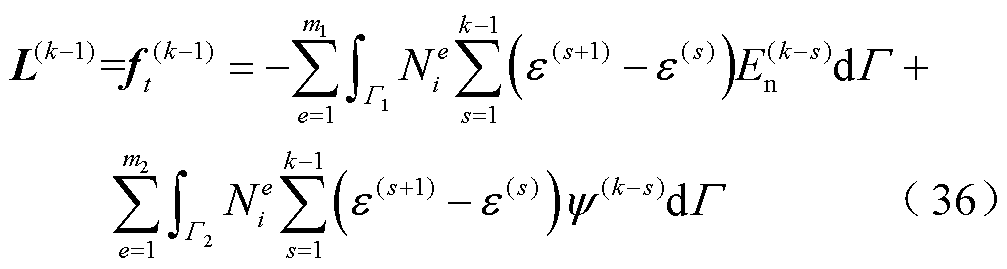
此外,列向量F(k)、G(k−1)、L(k−1)中各元素的表达式fi(k)、gi(k−1)、li(k−1)分别为
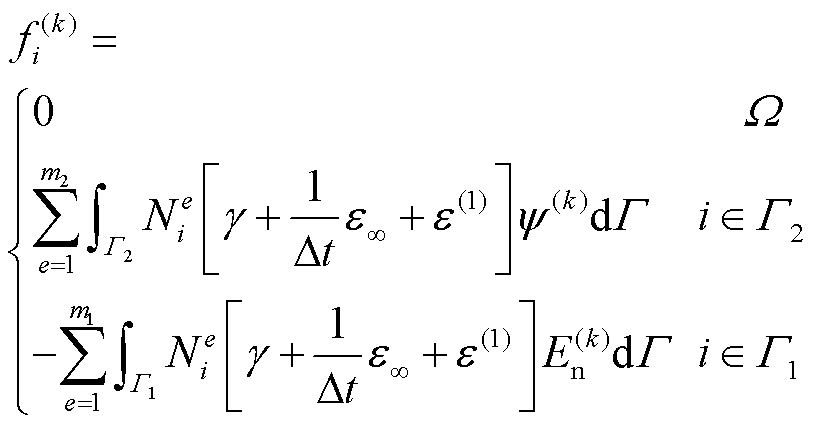 (37)
(37)
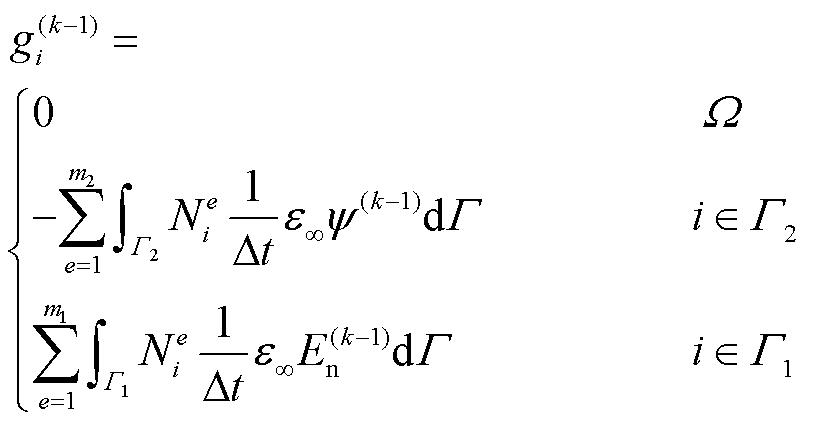 (38)
(38)
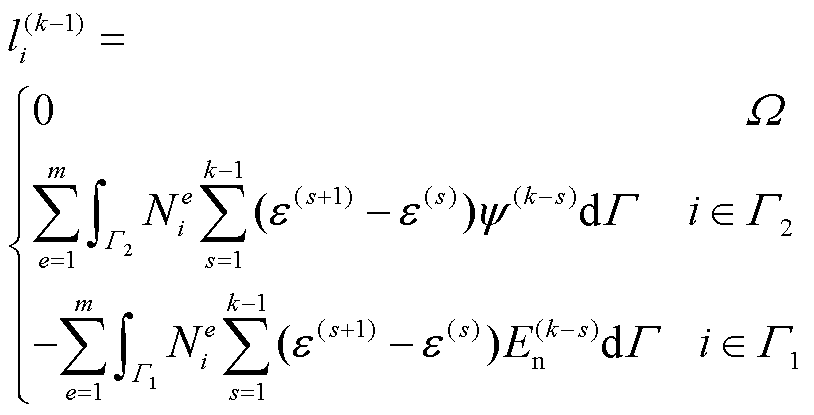 (39)
(39)
式(30)即为初值-边值问题式(8)所对应的时域有限元方程的矩阵形式。在每个时间步长上迭代求解式(30),即可获得电位的时域解。
在复合绝缘结构中,由于介质交界面两侧介质的介电常数不一致,导致介质交界面两侧电场强度的法向分量不连续,从而降低了界面处电场强度的计算精度[25]。为了实现介质交界面处电场强度的准确计算,本文选用边界电场约束方程法[28]求解时域有限元方程式(30)。
设Dirichlet边界Γ1上共有n-n1个节点;场域内非Dirichlet边界节点的节点电位编号在先,依次为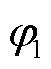 ,
, 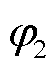 ,×××,
,×××,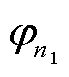 ;Dirichlet边界上已知电位的节点编在后,依次为
;Dirichlet边界上已知电位的节点编在后,依次为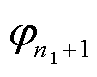 ,
, 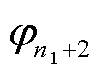 ,×××,
,×××,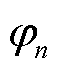 。式(30)可写成分块矩阵形式
。式(30)可写成分块矩阵形式
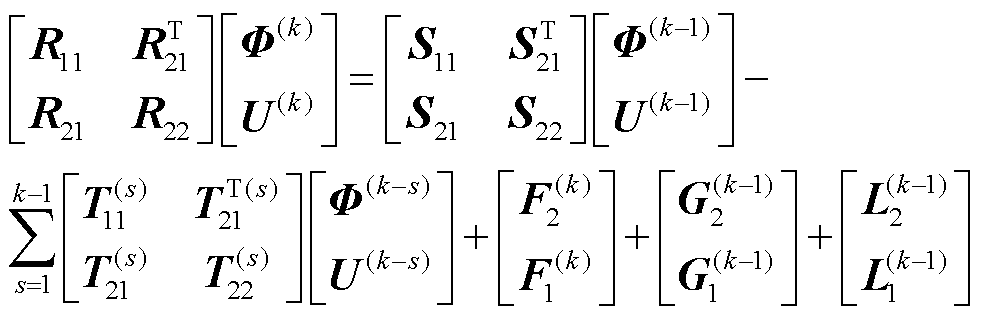 (40)
(40)
式(40)中,待求解的变量分别是Φ(k)和F1(k)中的En(k)。因此,式(40)可分解成两部分
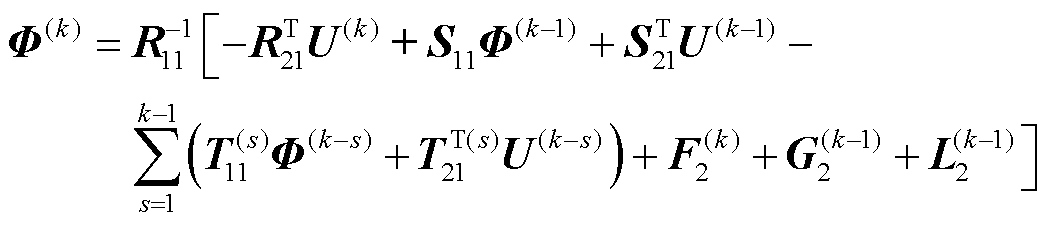 (41)
(41)
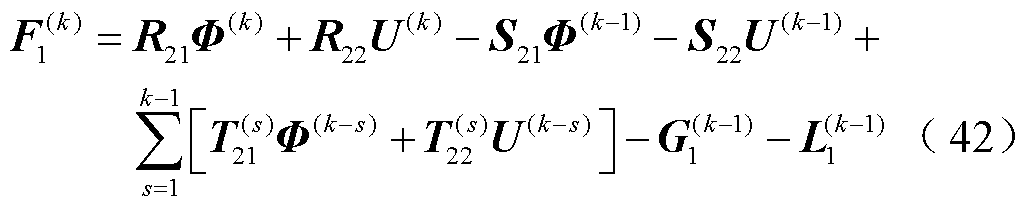
式(41)即为求解电位的时域有限元方程。通常情况下,Dirichlet边界对应于金属电极表面,其电场强度仅有法向分量;即便Dirichlet边界上还有切向分量,式(42)也能完全反映Dirichlet边界上的电场强度法向分量与电位的约束关系。考虑到Neumann边界上的电场强度法向分量已知,称式(42)为电准静态条件下计算边界电场强度法向分量的边界电场约束方程。
利用式(37),式(40)中F1(k)中的元素可表示为
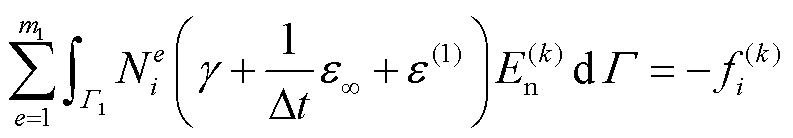 (43)
(43)
采用Galerkin法,在Dirichelt边界上,用边界上节点的电场强度法向分量和节点形状函数插值近似En,有
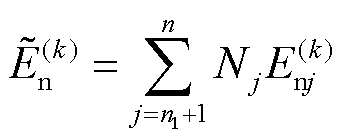 (44)
(44)
将式(44)代入式(43),得
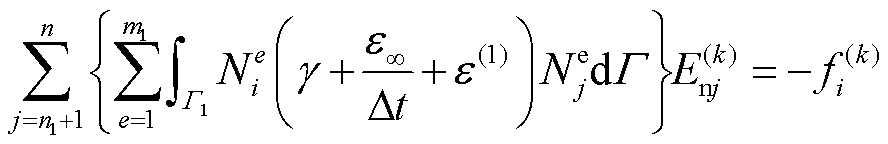 (45)
(45)
将式(45)表示成矩阵形式
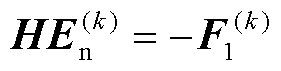 (46)
(46)
式中,刚度矩阵H中各元素hi,j的表达式为
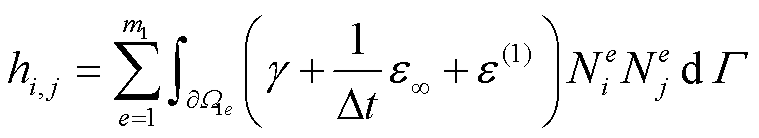 (47)
(47)
同理,G1(k-1)和L1(k-1)分别满足以下矩阵方程
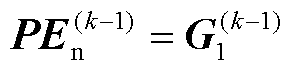 (48)
(48)
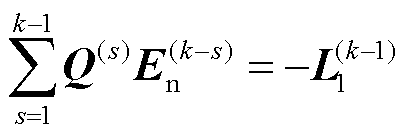 (49)
(49)
式(48)中,刚度矩阵P中各元素pi,j的表达式为
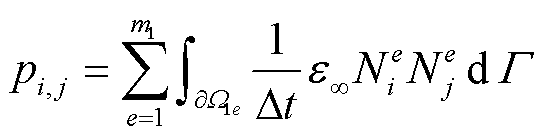 (50)
(50)
式(49)中,刚度矩阵Q中各元素qi,j的表达式为
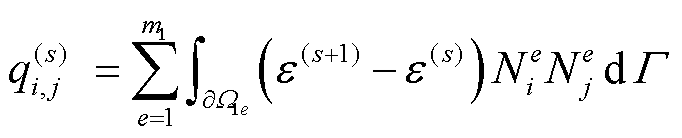 (51)
(51)
将式(46)、式(48)和式(49)代入到式(42)中,时域边界电场约束方程可以表示为
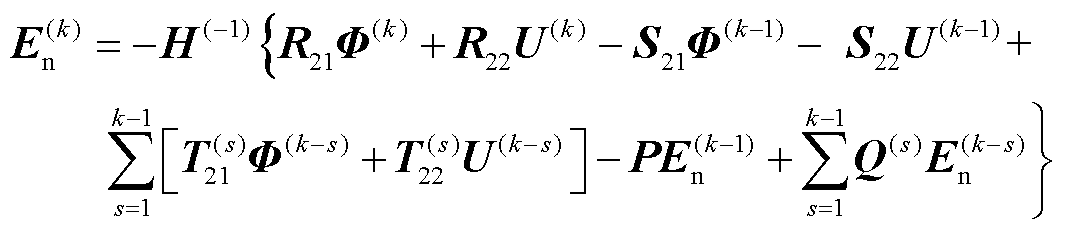 (52)
(52)
在第k个时间步长上,先利用式(41)计算第k个时间步长上的节点电位,再利用式(52)计算第k个时间步长上Dirichlet边界上的电场强度法向分量。交替迭代求解式(41)和式(52),即可求解每个时间点上的瞬态电位和Dirichelt边界上瞬态电场强度的法向分量。
对于由多种材料组合而成的复合绝缘结构,为了求解介质交界面上两侧的电场强度法向分量,需要在计算中做如下处理:将场域Ω分解成若干个只有单一材料组成的子域Ωi,在子域Ωi中每个时刻的节点电位可由式(41)计算得到。再将子域Ωi与其他子域的所有交界面以及子域Ωi上的Dirichlet边界视为等效的Dirichlet边界,此后,利用式(52),便可求解子域Ωi上等效的Dirichlet边界上每个时刻的电场强度法向分量。对所有子域重复上述步骤,即可获得场域中导体表面以及所有介质交界面两侧的电场强度法向分量,从而得到介质交界面处的电荷密度。
考虑介质的介电弛豫过程后,难以找到具有解析解的模型直接验证算法的有效性。为了验证计算方法的有效性,本节选取了刚性压接型IGBT器件中常用的绝缘材料聚醚醚酮(Polyetheretherketone,PEEK)[32],对比了PEEK片在阶跃电压下极化电流的计算结果和实验测量结果。
在PEEK片极化电流的实验中,采用符合IEC 62631:2015标准的三电极法测量PEEK片的极化电流[33]。极化电流测量的实验电路如图2所示,图中Rp为保护电阻,DUT为被测试品,即PEEK片。金属屏蔽箱内为测量极化电流的三电极系统,三电极系统的结构示意图和实物图如图3所示。实验中,通过直流电源对PEEK片施加阶跃电压信号,再通过皮安表采集并记录PEEK片中的体电流。
实验中,考虑到皮安表的最大量程,选择保护电阻Rp=1MΩ,阶跃电压的幅值为1 000V。圆形PEEK片的直径为50mm,厚度为0.1mm[32]。三电极的尺寸参数见表1,三电极的有效面积按照文献[34]进行修正。
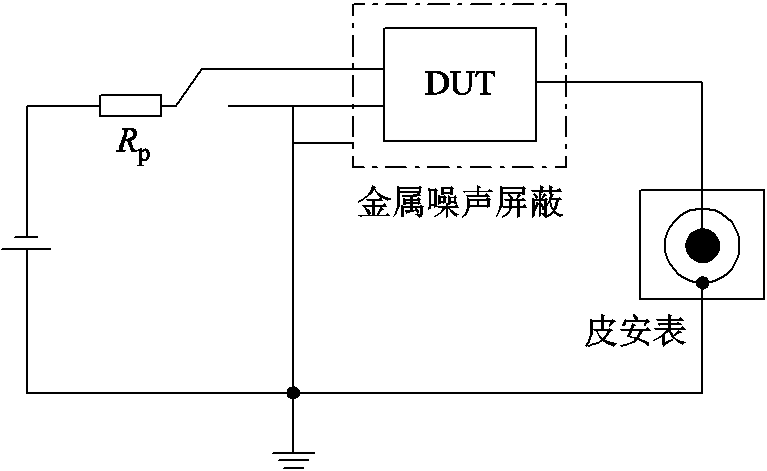
图2 极化电流测量的实验电路
Fig.2 Experimental circuit for polarization current
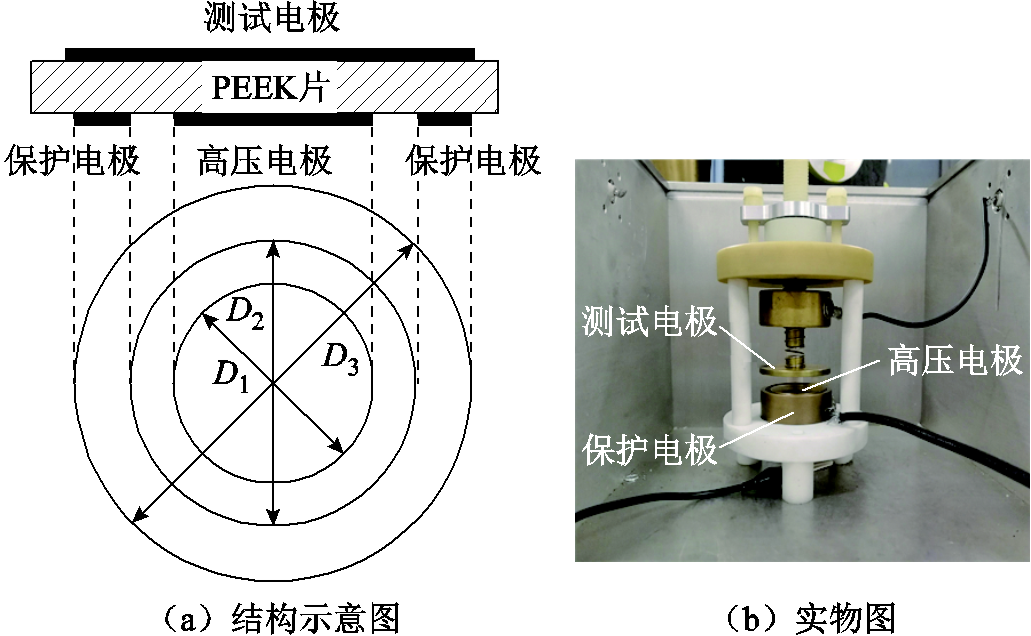
图3 三电极测量系统
Fig.3 Measurement system with three electrodes
表1 三电极的尺寸参数[28]
Tab.1 Parameters of three electrodes[28]

参数数值 D1/mm30 D2/mm36 D3/mm40
由于实际的电介质具有复杂的弛豫过程,其介电弛豫模型较为复杂,在时域上,材料的时变介电系数无法解析表示。为了简化分析,假设PEEK片满足Debye弛豫模型。在Debye弛豫模型下,频域中的复介电常数满足
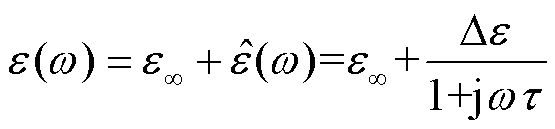 (53)
(53)
式中,Δε=εs−ε∞,εs为静态介电常数,即直流下的介电常数;ε∞为光频相对介电常数,对应于瞬时极化;τ为介电弛豫的弛豫时间。
在时域,时变的介电常数表示为
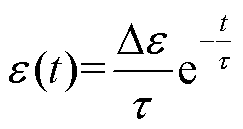 (54)
(54)
在Debye弛豫模型下,假设样品片中的电场均匀分布,则样品片中的电流可以解析表示为[28]
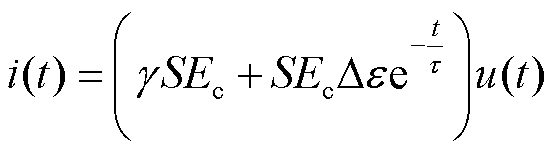 (55)
(55)
式中,γ为电导率;S为样品片的有效面积;u(t)为单位阶跃函数;Ec为样品片中的电场强度。其中,Ec=U/d,U为阶跃电压的幅值,d为样品片的厚度。
根据PEEK片的极化电流测量的实验数据,可以拟合出PEEK片的基本参数,拟合的各参数见表2。
表2 PEEK片的计算参数[32]
Tab.2 Parameters of PEEK for calculation[32]

参数数值 ε∞3.95 ∆ε0.19 τ/s1.95 γ/(S/m)1.02×10−15
为了验证所提计算方法的有效性,本文对比了极化电流的实验结果与用本文方法计算得到的电流的计算结果。在计算中,PEEK片的尺寸和阶跃电压的幅值与实验测量中的参数一致。
计算方法采用本文所提的时域有限元法,PEEK片的基本参数来自表2中的数据。极化电流的数值计算结果与实验测量结果的对比如图4所示。
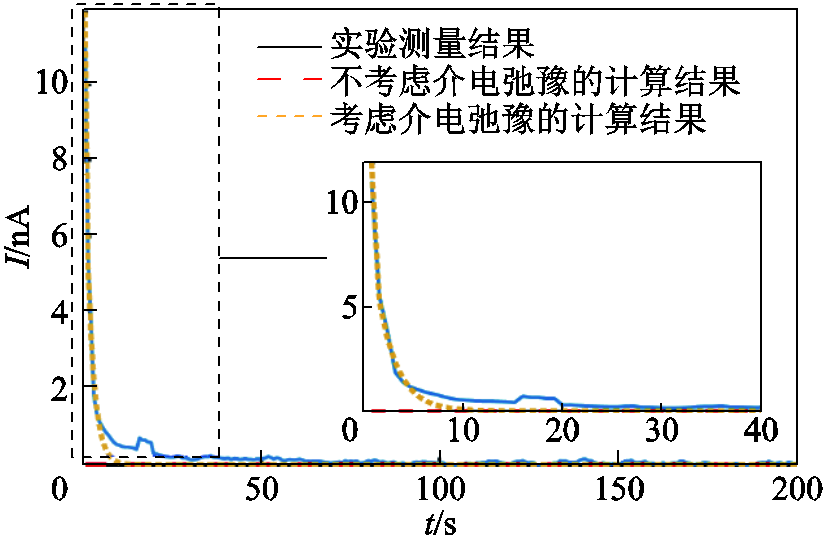
图4 极化电流的实验结果与计算结果对比
Fig.4 Comparison of experimental results and calculation results of polarization current
从图4可以看出,用本文所提的方法计算得到的PEEK片的极化电流与实验测量得到的极化电流基本吻合,从而间接验证了本文所提的时域有限元计算方法的有效性。
选用复合绝缘结构中最简单的双层介质平行板模型作为计算模型,计算模型如图5所示。
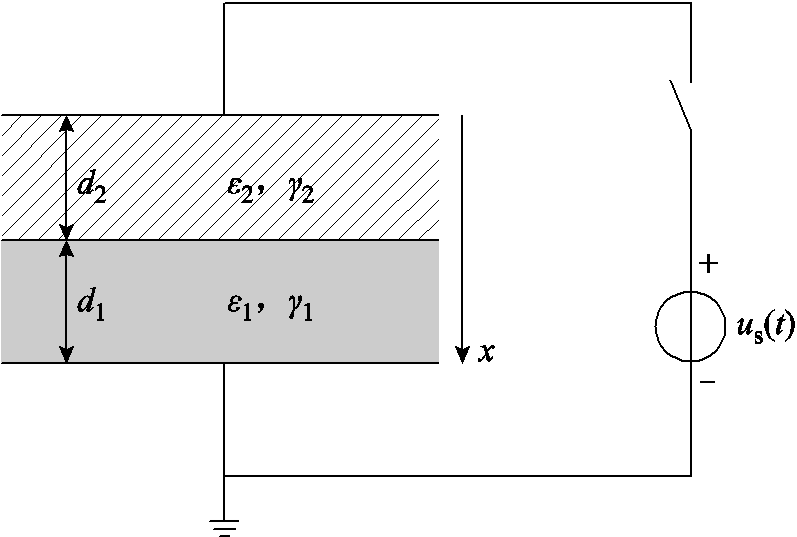
图5 双层介质平行板模型
Fig.5 Model of parallel plate with double-layer dielectrics
为了方便,模型中的两种绝缘材料的介电弛豫均认为满足Debye弛豫模型。模型中,材料1为Polyurethane,对应的时变介电常数的相关参数来自文献[17];材料2为PEEK,对应的时变介电常数的相关参数来自课题组的实验数据。两种材料的厚度均为1mm,Polyurethane和PEEK的参数总结见表3。
表3 两种材料的计算参数
Tab.3 Parameters of two kinds of materials for calculation

材料数值 PolyurethanePEEK εs5.674.11 ε∞4.683.95 ∆ε0.990.19 τ/s9.15×10−71.95 γ/(S/m)1.53×10−121.02×10−15
计算中,电压激励选用如图6所示的正极性周期方波电压,对应于电力电子器件在导通和关断过程中器件承受的工作电压。图6中,Um为正极性周期方波us(t)的幅值,tu和td分别为方波的上升时间和下降时间,α为占空比,Tc为周期。在计算中,取Um=10kV,tu=td=2μs,α=0.5,Tc=100μs。
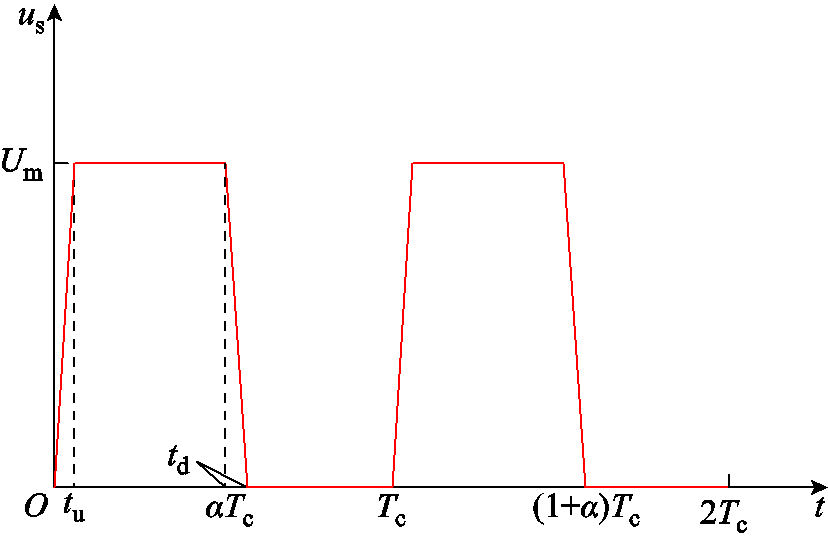
图6 正极性周期方波电压
Fig.6 Positive periodic square waveform voltage
在正极性周期方波电压激励下,是否考虑介电弛豫现象对电场强度与界面电荷密度的影响分别如图7和图8所示。
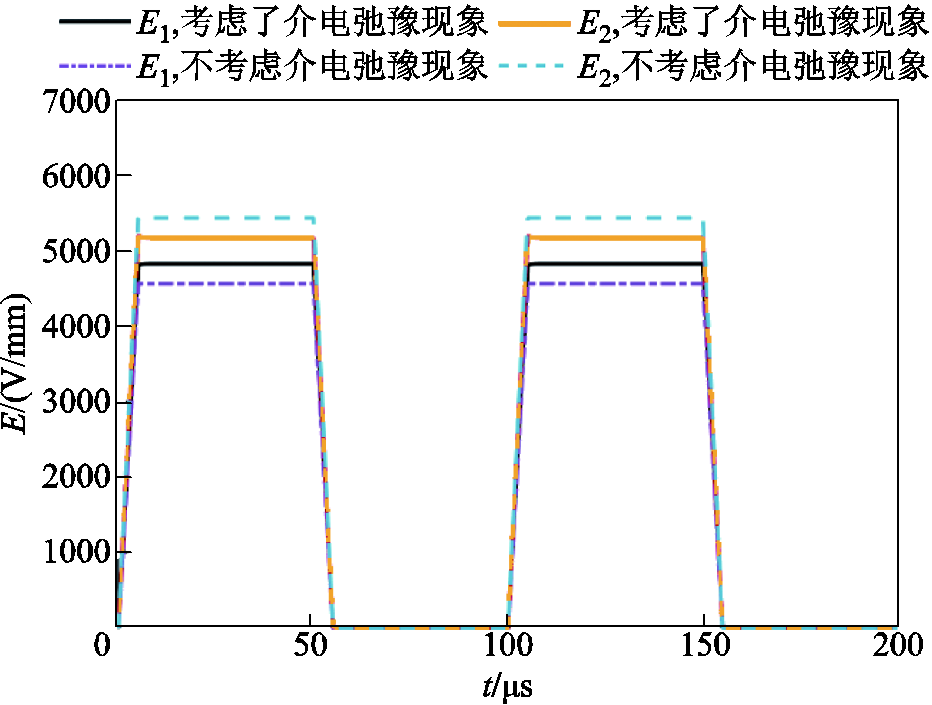
图7 介电弛豫对电场强度的影响
Fig.7 Influence of dielectric relaxation phenomena to the electric field intensity
由图7可知,考虑介电弛豫后,将改变模型中的电场强度分布,增大了介质1中的电场强度,而减小了介质2中的电场强度。对于界面电荷密度而言,介电弛豫对界面电荷密度的影响如图8所示,考虑介电弛豫将显著增加模型中的界面电荷密度。
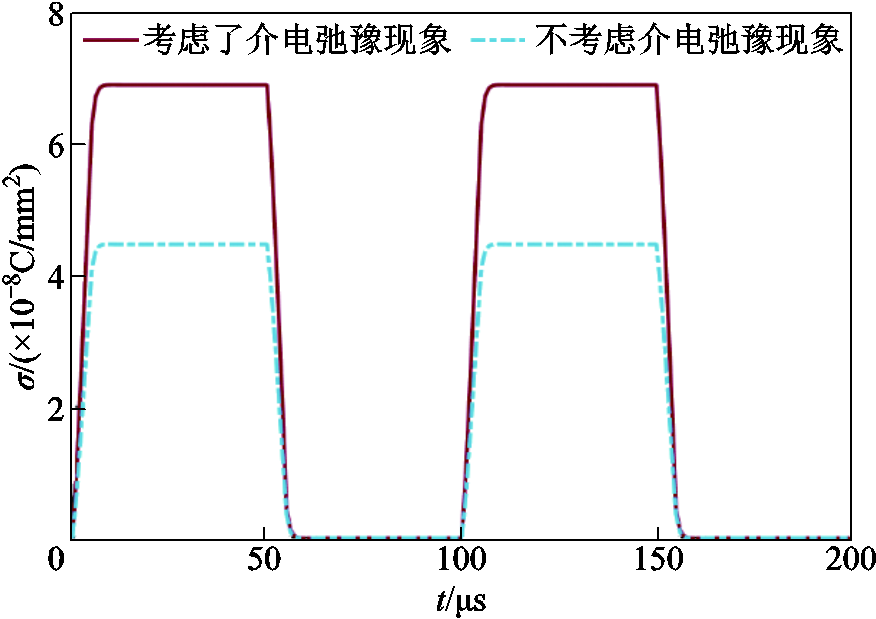
图8 介电弛豫对界面电荷密度的影响
Fig.8 Influence of dielectric relaxation phenomena to the interfacial charge density
考虑介质的介电弛豫过程后,介电常数是时变的,由于Maxwell极化,介质交界面处的界面电荷相比于不考虑介电弛豫时发生变化。而介质交界面处的界面电荷将增强一侧介质中的电场,而减弱另一侧介质中的电场。介质的介电弛豫现象对瞬态电场的影响因不同材料自身介电弛豫而异。因此在瞬态电压激励下的瞬态电场计算,需要考虑介质中介电弛豫现象。
本文提出了考虑材料介电弛豫现象的时域有限元法,主要结论如下:
1)考虑材料的介电弛豫过程,在电准静态场条件下给出了瞬态电场的计算模型,对控制方程进行时空离散后,推导了时域有限元方程和瞬态边界电场约束方程,提出了考虑材料介电弛豫现象的时域有限元法。
2)搭建了用三电极法测量极化电流的实验平台,通过实验获得了PEEK片在阶跃电压下的极化电流。通过对比极化电流的实验结果与用本文所提方法计算得到的计算结果,发现实验结果与计算结果相吻合,从而验证了本文所提的时域有限元法的有效性。
3)将本文所提的时域有限元方法应用到简单的复合绝缘结构,发现考虑介质的介电弛豫过程后,双层介质间的界面电荷密度明显增大,从而显著增强了一侧的电场,削弱了另一侧的电场,表明了瞬态激励下瞬态电场计算时考虑介质介电弛豫过程的必要性。
参考文献
[1] Mitsui K, Wada K. Design of a laminated bus bar optimizing the surge voltage, damped oscillation, and switching loss[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 2737-2745.
[2] Smajic J, Steinmetz T, Ruegg M, et al. Simulation and measurement of lightning-impulse voltage distributions over transformer windings[J]. IEEE Transactions on Magnetics, 2014, 50(2): 553-556.
[3] Deng Erping, Zhao Zhibin, Xin Qingming, et al. Analysis on the difference of the characteristic between high power IGBT modules and press pack IGBTs[J]. Microelectronics Reliability, 2017, 78: 25-37.
[4] 彭程, 李学宝, 张冠柔, 等. 压接型IGBT芯片动态特性实验平台设计与实现[J]. 电工技术学报, 2021, 36(12): 2471-2481.
Peng Cheng, Li Xuebao, Zhang Guanrou, et al. Design and implementation of an experimental platform for dynamic characteristics of press-pack IGBT chip[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2471-2481.
[5] Haus H A, Melcher J R. Electromagnetic fields and energy[M]. Englewood Cliffs, NJ: Prentice-Hall, 1989.
[6] Liu Gang, Li Lin, Ji Feng, et al. Analysis of transient electric field and charge density of converter transformer under polarity reversal voltage[J]. IEEE Transactions on Magnetics, 2012, 48(2): 275-278.
[7] Hara T, Natio, Umoto J. Time-periodic finite element method for nonlinear diffusion equations[J].IEEE Transactions on Magnetics,1985, 21(6): 2261-2264.
[8] Yamada S, Bessho K. Harmonic field calculation by the combination of finite element analysis and harmonic balance method[J]. IEEE Transactions on Magnetics, 1988, 24(6): 2588-2590.
[9] 苑津莎, 张金堂. 计算非线性时变涡流场的有限元方程频域算法[J]. 中国电机工程学报, 1994, 14(3): 7-13.
Yuan Jinsha, Zhang Jintang. Finite element method in frequency domain for nonlinear transient field problems[J]. Proceedings of the CSEE, 1994, 14(3): 7-13.
[10] 刘刚, 李琳, 纪锋, 等. 基于节点电荷电位有限元法的油纸绝缘结构极性反转电场分析[J]. 中国电机工程学报, 2011, 31(25): 132-138.
Liu Gang, Li Lin, Ji Feng, et al. Analysis of polarity reversal electric field of oil-paper insulation based on charge-scalar potential finite element method[J]. Proceedings of the CSEE, 2011, 31(25): 132-138.
[11] Wen Teng, Cui Xiang, Li Xuebao, et al. Characterization of electric field distribution within high voltage press-packed IGBT submodules under condition of repetitive turn-on and turn-off[J]. CSEE Journal of Power and Energy Systems, 2022, 8(2): 609-620.
[12] Badics Z. Charge density-scalar potential formulation for adaptive time-integration of nonlinear electroquasistatic problems[J]. IEEE Transactions on Magnetic, 2011, 47(5): 1138-1141.
[13] 刘刚. 换流变压器交直流复合电场和极性反转电场算法研究[D]. 北京: 华北电力大学, 2012.
[14] 朱洒, 卢智鹏, 王卫东, 等. 基于CE-FEA和小信号分析快速计算逆变器供电下聚磁式场调制电机中永磁体涡流损耗[J]. 电工技术学报, 2020, 35(5): 49-57.
Zhu Sa, Lu Zhipeng, Wang Weidong, et al. Fast calculation of PM eddy current loss in FCFMPM machine under PWM VSI supply based on CE-FEA and small-signal analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 49-57.
[15] 程启问, 万保权, 张建功, 等. 基于误差传递方程的离子流场迎风有限元高精度计算方法[J]. 电工技术学报, 2020, 35(21): 14-20.
Cheng Qiwen, Wan Baoquan, Zhang Jiangong, et al. A highly accurate upwind finite element method for ion-flow field based on the error transport equation[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 14-20.
[16] Jonscher A K. Dielectric relaxation in solids[M]. London: Chelsea Dielectric Press, 1983.
[17] Havriliak S, Negami S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers[J]. Polymer, 1967, 8: 161-210.
[18] Dissado L A, Hill R M. Anomalous low-frequency dispersion, near direct current conductivity in disordered low-dimensional materials[J]. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics, 1984, 80(3): 291-319.
[19] Jonscher A K. Universal relaxation law[M]. London: Chelsea Dielectrics Press,1996.
[20] Yang Xi, Wang Qingyu, Wang Haoran, et al. Transient electric field computation for composite cross-arm in 750 kV AC transmission line under lightning impulse voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(4): 1942-1950.
[21] 杨为, 朱太云, 田宇, 等. 雷电冲击电压下GIS盆式绝缘子暂态电场分析[J]. 高电压技术, 2020, 46(3): 807-814.
Yang Wei, Zhu Taiyun, Tian Yu, et al. Analysis for transient electric field computation of GIS basin insulator under lightning impulse voltage[J]. High Voltage Engineering, 2020, 46(3): 807-814.
[22] Gao Youhua, Wang Erzhi, Li Yanbin, et al. Analysis of transient electric field for epoxy spacer under lightning impulse voltage[J]. IEEE Transactions on Magnetics, 2006, 42(4): 595-598.
[23] 高有华, 王尔智, 曹云东. 500kV GIS盆式绝缘子的暂态电场分析[J]. 电工技术学报, 2001, 16(6): 41-45.
Gao Youhua, Wang Erzhi, Cao Yundong. Transient electric field analysis of 500 kV disc-type spacer[J]. Transactions of China Electrotechnical Society, 2001, 16(6): 41-45.
[24] Preis K, Biro O, Supancic P, et al. Time-domain analysis of quasistatic electric fields in media with frequency-dependent permittivity[J]. IEEE Transactions on Magnetics, 2004, 40(2): 1302-1305.
[25] Egiziano L, Tucci V, Petrarca C, et al. A Galerkin model to study the field distribution in electrical components employing nonlinear stress grading materials[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1999, 6(6): 765-773.
[26] Mur G. Edge elements, their advantages and disadvantages[J]. IEEE Transactions on Magnetics, 1994, 30(5): 3552-3557.
[27] 谢裕清, 李琳. 计算多介质电场节点场强的有限元-边界元法[J]. 华北电力大学学报, 2016, 43(2): 21-26.
Xie Yuqing, Li Lin. Finite element method-boundary element method for calculation of nodal electric field intensity in multi-medium electric field[J]. Journal of North China Electric Power University, 2016, 43(2): 21-26.
[28] 崔翔. 应用边界电场约束方程计算第一类边界上的场强分布[J]. 中国电机工程学报, 1987, 7(1): 53-60.
Cui Xiang. Calculating the field strength distribution on the first type of boundary by using constrained electric field equation on the boundary[J]. Proceedings of the CSEE, 1987, 7(1): 53-60.
[29] Wen Teng, Cui Xiang, Li Xuebao, et al. A time-domain finite element method for the transient electric field and transient charge density on the dielectric interface[J]. CSEE Journal of Power and Energy Systems, 2020, 8(1): 143-154.
[30] Marti J R, Lin J. Suppression of numerical oscillations in the EMTP[J]. IEEE Power Engineering Review, 1989, 9(5): 71-72.
[31] Jin Jianming. The finite element method in electromagnetics[M]. 2nd ed. New York: Wiley, 2002.
[32] 翟宾. PEEK材料介电特性及其影响因素研究[D]. 北京: 华北电力大学, 2020.
[33] IEC 62631:2015 Dielectric and resistive properties of solid insulating materials[S]. Geneva: International Electrotechnical Commission Std, 2015.
[34] Endicott H S. Guard-gap correction for guarded-electrode measurements and exact equations for the two-fluid method of measuring permittivity and loss[J]. Journal of Testing and Evaluation, 1976, 4(3): 188-195.
Abstract In the actual operation of electric power equipment, it may be subjected to transient voltage excitations such as switching surge voltage, lightning impulse voltage and so on. In addition, with the widespread application of power electronic devices in DC power transmission equipment, the voltage that the insulation structure of the internal devices bears is not traditional AC voltage or DC voltage, but positive repetitive square wave voltage. In order to study the electric field characteristics of the insulating structure in these equipment or devices under transient voltage excitation, it is necessary to calculate the transient electric field distribution under the electro-quasistatic field. Insulating materials exhibit dielectric relaxation phenomenon in the alternating electric field, and their permittivity is a frequency-dependent function in the frequency domain. Due to the short duration time and rapid change of the transient voltage, the corresponding frequency spectrum is wide. Therefore, the calculation of the transient electric field under transient voltage excitation needs to consider the dielectric relaxation characteristics. For this reason, this paper proposes a time-domain finite element method which considers the dielectric relaxation process of the materials. In this paper, the dielectric relaxation phenomenon of the material is characterized by the time-varying permittivity. The governing equation is discretized in time and space. The time-domain finite element equation and the constrained electric field equation on the boundary are derived. Then, the effectiveness of the calculation method proposed in this paper is verified by comparing the experimental results and calculation results of the polarization current of PEEK material under the step voltage. Finally, the distribution characteristics of the transient electric field of the combined insulating structure considering the dielectric relaxation characteristics of the material under transient voltage excitation are analyzed.
keywords:Dielectric relaxation, frequency-dependent, time domain finite element method, constrained electric field equation on the boundary, electro-quasistatic field
DOI:10.19595/j.cnki.1000-6753.tces.211540
中图分类号:TM211
文 腾 男,1991年生,博士研究生,研究方向为高压大功率电力电子器件封装绝缘技术,电磁场数值计算。E-mail:wenteng@ncepu.edu.cn
李学宝 男,1988年生,博士,副教授,硕士生导师,研究方向为电磁场理论及应用、高压大功率电力电子器件封装。E-mail:lxb08357@ncepu.edu.cn(通信作者)
收稿日期 2021-09-24
改稿日期 2021-12-21
国家自然科学基金委员会-国家电网公司智能电网联合基金资助项目(U1766219)。
(编辑 郭丽军)