
图1 等效电路模型和电化学模型对比图
Fig.1 Comparison of ECM and EM
摘要 荷电状态(SOC)的准确估计是电池管理系统的重要功能之一。当前,基于模型的方法是实现锂离子电池SOC估计最常用的解决方案。相比于等效电路模型(ECM),由于电化学模型(EM)能够实现耦合电化学机理的SOC估计,逐渐成为下一代高级电池管理系统的研究重点。然而,现有基于模型的锂离子电池SOC估计方法的研究大多集中在ECM上,很少对EM进行系统讨论。为此,该文针对基于EM的SOC估计方法进行了全面综述。首先,概述了EM的建模及参数识别方法;然后,对基于EM的SOC估计方法进行了讨论;最后,针对目前基于EM的SOC估计存在的挑战和未来发展趋势进行了讨论。该文提出的观点有望促进现有基于EM的高级电池管理系统算法的开发和应用。
关键词:锂离子电池 荷电状态 电化学模型 电池管理系统
为了达成“碳达峰、碳中和”目标,电池储能系统在可再生能源发电、智能电网技术和电动汽车方面得到了迅速发展[1-3]。同时,为了提高能源效率和减少对化石燃料的依赖,整个电动汽车行业正在努力寻求实现全球运输电气化的解决方案[4]。锂离子电池作为推动交通电气化的电池储能系统之一,由于其高能量密度、长周期寿命和低自放电率等优点,已成为电动汽车中最广泛使用的储能部件[5]。然而,在复杂的运行工况中,锂离子电池也面临着老化、热失控、机械滥用等一系列问题,这给其在电动汽车上的广泛使用带来极大挑战[6-7]。因此,十分有必要建立高级电池管理系统(Battery Management System, BMS)对电池内部电化学状态进行实时监控,以确保锂离子电池在整个生命周期内能够安全可靠的运行。荷电状态(State of Charge, SOC)作为电池剩余电量的直接表征,能够促使BMS较为准确地确定瞬时峰值功率和健康状态(State of Health, SOH)[8-10],以便及时确保电池在安全范围内运行。因此,准确的SOC估计在电动汽车BMS中起着关键性作用,成为广大学者研究的重点。
迄今为止,国内外学者已对有关车用动力电池SOC的估计方法进行了大量报道[11]。根据现有文献可知,常用SOC估计方法主要分为安时积分法[12-13]、开路电压法[14-15]、基于模型法[16-20]和数据驱动法[21-23]。其中,安时积分法依赖于准确的初始SOC值和高精度电流传感器,开路电压法则需要长时间的搁置以获取准确的SOC估计,这使得二者都不适用于在线应用。同时,随着人工智能技术的发展,数据驱动的方法在电池SOC估计中得到了广泛关注[24-25],比如文献[26-27]针对电池的数据需求提供了一些解决方案,但其因离线数据训练而产生的计算成本仍是一个长期存在的问题。相比之下,基于模型的SOC估计是一种闭环控制,通过结合不同算法能够实现良好的SOC估计。因此,越来越多的研究者将电池SOC估计的研究集中在基于模型的方法上,其估计性能取决于电池模型的选择[28]。现有的电池模型主要包括等效电路模型(Equivalent Circuit Model, ECM)[29-32]和电化学模型(Electrochemical Model, EM)[33-35]。由于具有结构简单、计算效率高以及辨识参数少等特点[36],基于ECM的SOC估计方法[37-40]已经在实车中得到很好的应用。然而,ECM捕获电池内部电化学状态的能力有限,例如电极过电势和电极表面浓度,它们对充电策略及功率预测至关重要,这使得基于ECM的状态估计方法在车用动力电池高级BMS应用中的不足日益凸显。相对而言,EM能够很好地解决这些问题[41],等效电路模型和电化学模型对比如图1所示。同时,由于电池降阶技术的发展[42],EM在模型精度和计算效率之间基本实现了很好的平衡。因此,结合相关智能算法[43],基于EM的SOC估计方法被认为是实现高级BMS应用的最佳选择[44]。

图1 等效电路模型和电化学模型对比图
Fig.1 Comparison of ECM and EM
近年来,大量研究人员从研究进展和发展趋势等方面对电池SOC估计方法进行了全面回顾[45-51],这对基于模型法的SOC估计发展起到了很好的促进作用,意义重大。然而,据作者所知,现有的电池SOC 估计方法的综述文献大多集中在ECM和数据驱动方法的讨论上,鲜有学者对基于EM的SOC估计及其性能进行系统评估和总结。EM由于能够实现耦合电化学机理的电池内部状态估计,逐渐成为下一代高级BMS研究的重点[44,52-54]。为此,本文综合现有国内外文献,对车用电池电化学建模和其相对应的SOC估计方法等关键问题进行了全面探讨。同时,对不同SOC估计方法的局限性进行了系统分析。最后,对现有基于EM的SOC估计存在的挑战和未来发展趋势进行了详细讨论。
电池模型的构建对于高级BMS实现准确估计SOC至关重要[55],EM由于能够较好地观测电池内部状态信息而逐渐成为ECM的替代方案。事实上,EM表征了电池内部锂离子、电化学动力学和材料特性之间的传输过程[56],这些特有优势使其非常适合车用电池的电极浓度估计及充电策略优化[57-58]。为了更好地适应电池实时状态估计,大量文献对各种EM进行了简化和重建,使其重构为具有与SOC估计相关的独特属性[59-60]。目前,锂离子电池EM主要分为四类:伪二维(Pseudo Two-Dimensional, P2D)模型、单粒子(Single Particle, SP)模型、增强型单粒子(Enhanced Single Particle, ESP)模型及多物理耦合(Multiphysical-Coupling, MC)模型,所有这些模型的重构旨在降低计算复杂性的同时保持可接受的模型准确性,以便实现基于EM的电池状态的实时估计。另外,本节也对一些新兴建模方法和影响模型精度的参数识别问题进行了简要阐述。
P2D模型由J. Newman等[61]基于浓溶液和多孔电极理论首先提出。P2D的模型原理图如图2所示。由图2可知,全阶P2D模型主要有五部分组成:多孔正极、多孔负极、隔膜以及两侧电流集流体组成。同时,电池的动态性能由一系列偏微分方程(Partial Differential Equation, PDEs)表征和描述,包括固相的电荷及质量守恒方程,液相电荷及质量守恒方程,以及电极电化学反应动力学方程。这些方程从x和r两个维度描述了电极及电极粒径方向的内部动力学行为。其中,x为电极厚度方向,r为电极粒径方向(如图2所示)。此外,P2D 模型的控制方程和边界条件在表1中进行了总结,表中公式详细推导过程及各参数代表含义详见参考文献[35]。
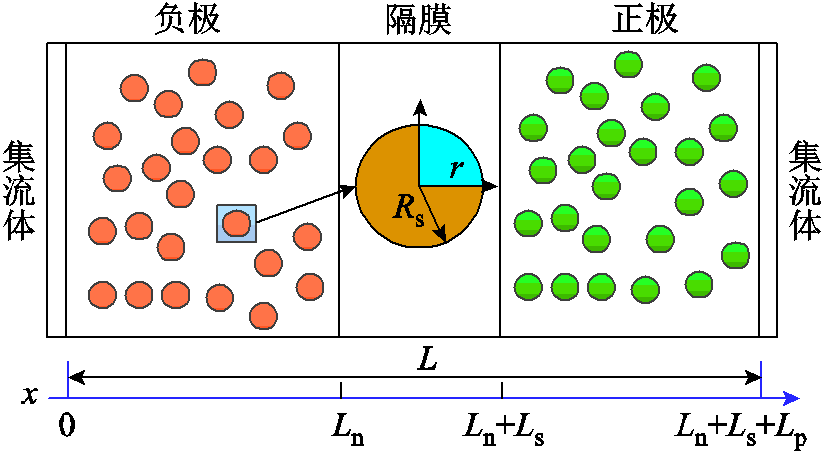
图2 P2D模型的原理图
Fig.2 A schematic of the P2D model
表1 锂离子电池全阶P2D模型控制方程
Tab.1 The governing equation of full order P2D model for lithium-ion battery

描述控制方程边界条件方程式 固相质量守恒方程(1) 液相质量守恒方程(2) 固相电荷守恒方程(3) 液相电荷守恒方程(4) BV动力学方程(5) 交换电流密度(6) 过电势(7) 电池端电压(8)
近年来,P2D模型逐渐成为高级电池管理技术研究的重点,由于是全阶PDEs之间的耦合,P2D模型可以较为全面地提供有关电池内部电化学反应的状态信息,并且融合了大量物理参数。因此,它已经成为用于电池设计和老化机理分析的重要工具[62-64]。事实上,在没有可靠的电池实验数据的情况下,P2D模型预测经常作为虚拟电池来验证其他电池模型的准确性[65]。
随着新兴高级数值方法的应用,简化的P2D模型开始尝试用于锂离子电池参数优化和状态估计。特别是,K. H. Kwon等[66]使用有限元方法(Finite Element Method, FEM)研究电池电极上的电流密度分布。E. Martinez等[67]修改了 P2D 模型中的边界条件,并应用线性方法(Method of Linear, MOL)预测模型端电压,同时不会损失任何精确性。J. N. Reimers等[68]揭示了一种有效的有限差分方法(Finite Difference Method, FDM)和格林函数相结合的方法,可很好地解耦固相和液相偏微分方程,以模拟 P2D 模型的全部物理特性。M. Torchio等[69]详细描述了求解P2D模型的有限体积方法(FiniteVolumeMethod, FVM),以便它能够适合电池设计、模拟和控制应用。此外,G. Plett等[70]比较了应用于P2D模型内部电化学传输函数的四种降阶技术,并认为拉格朗日插值算法产生了最佳的时域仿真结果。值得强调的是,这些新兴数学/数值方法的应用提高了P2D模型的整体计算效率,并使其保持可接受的模型精度,在一定程度上促进其在电池物理特性分析及参数优化中的应用。然而,由于电池全阶P2D模型的PDEs数量相当多,这些数值求解而简化的P2D模型只有极少数能够用于汽车高级BMS中微处理器的实时估计和预测。
SP模型的概念最早由B.S. Haran等[71]提出,每个电极被近似为单个球形粒子,并忽略电解质动力学,其结构如图3所示。
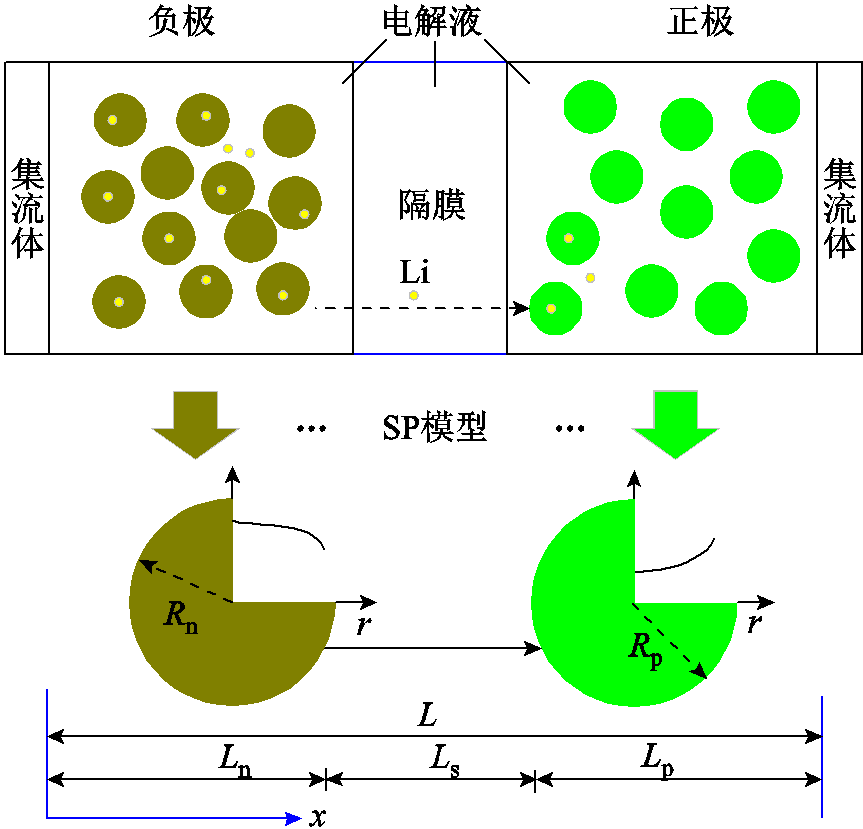
图3 SP模型的结构示意图
Fig.3 A structural diagram of the SP model
根据文献可知,由于能够捕捉基本的内部物理化学反应过程,同时计算成本较低,SP模型近年来在SOC估计领域引起了学者的广泛关注[72-73]。此外,由于SP模型假设多孔电极上锂离子的孔壁通量是均匀的,因此平均孔壁通量可以表示为
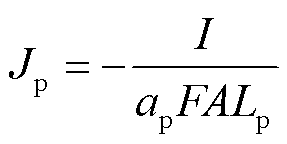 (9)
(9)
 (10)
(10)
式中,Ji为电极平均孔壁通量;Li为电极长度;ai为电极比表面积;下标i表示正负电极(p/n),下同;I为电池输入电流;A为电池电极截面积;F为常数。由于SP模型电解质溶液中不存在锂离子扩散梯度,则电解质电势为零。因此,电池输出电压可以根据等式(1)、式(5)~式(7)计算[65],并表示为
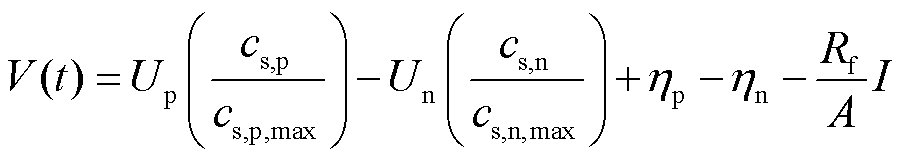 (11)
(11)
式中,V(t)为电池输出电压;Ui为电极电势;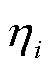 为电极过电势;cs,i电极表面锂离子浓度;cs,i,max为电极可用最大锂离子浓度;Rf为薄膜接触电阻。根据式(11)可知,在求解SP模型时,固体相扩散方程即等式(1)占据了SP模型的主要计算负担,换句话说,固体相扩散方程的简化方法将直接影响SP模型的计算效率和模拟精度。
为电极过电势;cs,i电极表面锂离子浓度;cs,i,max为电极可用最大锂离子浓度;Rf为薄膜接触电阻。根据式(11)可知,在求解SP模型时,固体相扩散方程即等式(1)占据了SP模型的主要计算负担,换句话说,固体相扩散方程的简化方法将直接影响SP模型的计算效率和模拟精度。
鉴于此,在现有SP模型的研究中,固相方程的简化成为学者研究的重点。C. Wang等[74]首先使用扩散长度的概念来简单求解固相扩散方程,得到了较好的仿真精度。然而,由于扩散长度法只有在电极扩散层稳定后才有效,这就导致该方法不适合在瞬态或动态工况下使用[75]。V. R. Subramanian等[76]提出了基于抛物线浓度曲线的假设,从而对固相浓度分布进行计算。这种抛物线近似的方法已经被广泛使用在电池EM固相扩散方程的简化研究[77-78]。此外,徐兴等[79-80]采用FDM法对模型的固相方程进行求解,有助于获得电池电极内每一层的锂离子浓度状态,并基于简化的SP模型对参数进行了辨识。Y. Zhao等[81]比较了针对固体扩散方程的不同简化方法,并展示了这些方法在实际应用中的相对局限性。随后J. Liu等[82]采用Galerkin方法有效地获得固体表面浓度,从而可以用于优化电池充电策略。尽管SP模型相对于P2D模型计算效率有了较大提高,同时在低倍率工况下也适合控制应用,但其结构上的过度简化使其在高倍率动态条件下的仿真精度存在不足[83],这就促使更多研究人员尝试将电解质浓度的变化及电势梯度整合到SP模型中,以提高其仿真精度和适用性。
针对传统SP模型在高倍速率和动态条件下的不足,研究学者已尝试将电解液动力学方程融合到SP模型中,以考虑液相浓度和液相电势对电池输出电压的影响,从而构成一种新的ESP模型[84-86]。图4为ESP 模型结构示意图。从图4可知,通过扩展式(11),电池输出电压即可简单求解得到,即

式中,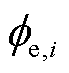 为电极液相电动势。相应地,从式(12)可知,寻求电解质动力学的求解方案已成为ESP模型发展的关键所在。
为电极液相电动势。相应地,从式(12)可知,寻求电解质动力学的求解方案已成为ESP模型发展的关键所在。
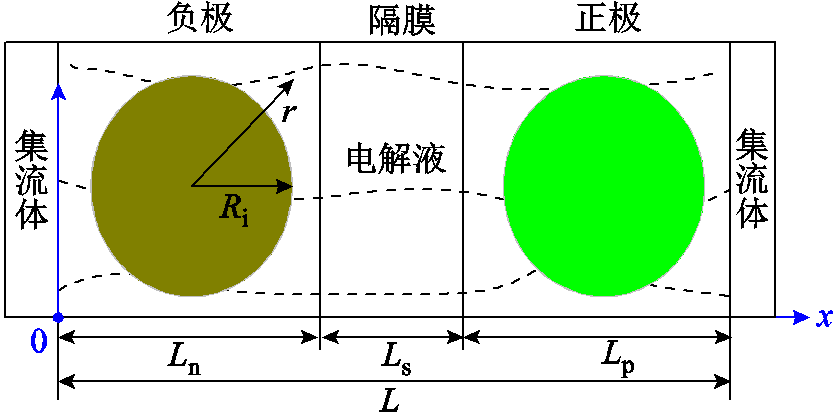
图4 ESP模型的结构原理图
Fig.4 A structural diagram of the ESP model
为此,E. Prada等[87]基于平均电极模型(Average Electrode Model, AEM)[88]提出了初始的ESP模型,并给出了液相电势差及电池输出电压的求解形式。随后,大量学者针对ESP模型中电解质扩散过程的求解进行了广泛的研究,如采用可变分离法[89]、拉普拉斯变换技术[90-91]、Galerkin投影法[92]等对电解液相方程进行降阶。尽管这些数学方法在一定程度上简化了液相方程的复杂度,但是这些方法均以复杂的数学理论为基础,且仅在特定边界条件下求解,使得其在高级BMS中难以在线实现。为了解决此类问题,吕超等[93]提出了多项式近似方法描述电解液浓度的变化趋势,将PDEs转换为易于计算的常微分方程,这种简化方法已经在多种ESP模型的仿真中进行了验证[94-96],结果表明电池模型在高倍率条件下也能达到较好的仿真精度。例如,唐晓鹏等[97]利用多项式近似求解液相浓度分布,建立一种简化的ESP模型,并将其用于SOC/SOH的联合估计。随后,崔纳新等[98]进一步将多项式近似法与域分解法相结合,把电解质动力学方程转换成简单的两态对角线系统。通过与P2D模型和实验结果比较,验证了ESP模型对电池电解质浓度和终端电压的预测精度。庞辉等[34]采用FDM方法对模型电解液方程进行了简化,能够准确预测液相锂离子浓度变化,同时实现了在线仿真应用。此外,V. Kumar等[99-100]提出在电池液相方程中采用体积平均技术进行降阶,从而实现液相常微分方程的求解,使ESP模型的在线应用更具优势。
显然,上述对ESP模型的研究表明,该模型具有高模型精度和低计算负担,这使得它在全阶P2D模型和SP模型之间取得了必要的平衡。因此,ESP 模型的这些优势将有助于基于EM的电池SOC估计中的应用。
尽管上述提到的简化EM模型能够很好地模拟和表征车用动力电池的动态特性,但是随着电动汽车行驶环境的复杂性和行驶里程的增加,锂离子电池的性能将会明显下降,同时异常温度范围下的电池易发生热失控,其容量也将显著减少。因此,锂离子电池老化和热特性耦合EM的开发对于确保整车系统的安全有效运行具有十分重要的意义。近年来,一些学者在简化EM基础上,耦合了电池热和老化特性的影响,重构了多种MC模型,具体开发思路如图5所示。田华等[101]通过建立电化学-热耦合模型,对电池的热特性进行了分析,并详细分析了各部分生热量所占的比例。李俊夫等[102]基于简化的EM对电池老化模型进行了分析,同时对模型参数进行了辨识。杨世春等[103]结合SP模型,开发了电化学-热-老化模型,并将其应用在充电控制策略的优化应用中。这些简化MC模型的出现,为实现锂离子电池全寿命、多环境下的性能仿真提供了重要研究基础。然而,目前针对MC模型的SOC/SOH在线实时估计尚处于前期探索阶段[97, 104-105],且相关研究文献较少,并未形成系统的电化学-热-老化实验验证方案[106-107]。
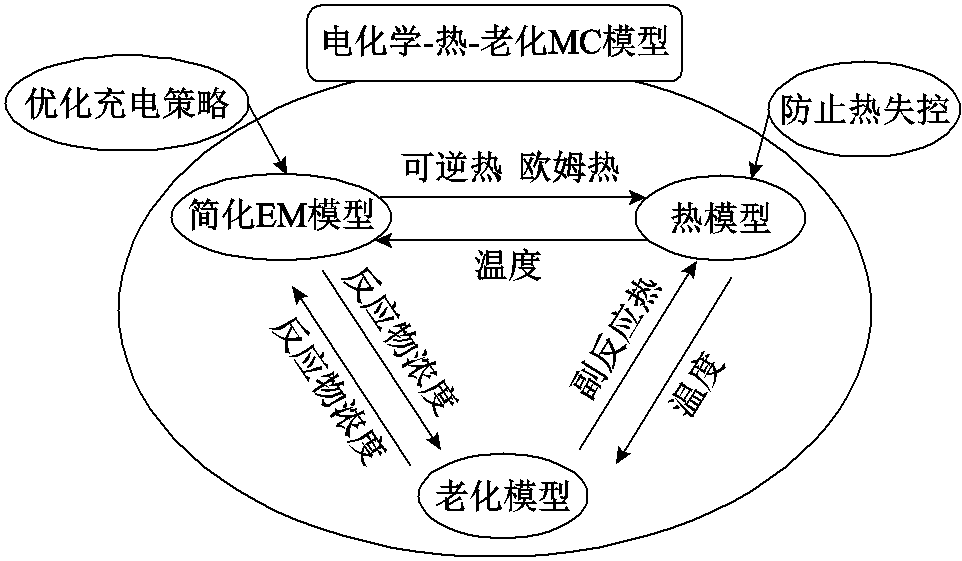
图5 MC模型构建框架
Fig.5 Building framework diagrams of MC model
为了进一步说明上述四种电化学建模方法之间的区别,图6展示了四种简化EM的性能对比图。
除了上述四类电化学建模方法,一些学者开始尝试将电化学机理与ECM相结合,采用多种方式开发了一种基于物理的ECM模型[108-112]。例如,Li Yang等[109]使用FVM开发一种新型基于物理的参数分布ECM,而使ECM的每个组件都和内部电化学特性相结合,提高了模型仿真精度;韩雪冰等[110]提出了一种基于固相浓度扩散的ECM, 解决了传统ECM在低SOC区域表征电池非线性特性差的问题。这些新颖的方法结合了EM和ECM各自优势,确保了模型精度,为锂离子电池EM的广泛应用提供了新的开发思路。
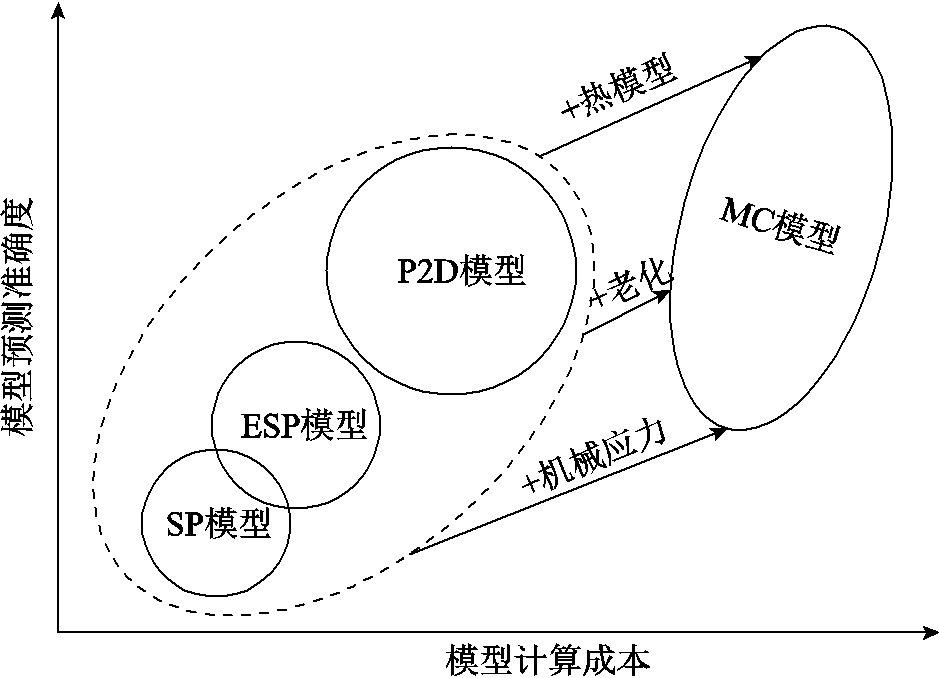
图6 四种简化EMs对比图
Fig.6 Comparison diagram of four simplified Ems
参数的准确识别是EM实现对电池外部特性及内部电化学状态进行表征的关键, 因为参数估计精度进一步决定了EM的准确性[113]。为此,一些学者开始对EM的参数辨识方法进行深入研究[35, 80, 114-119]。例如,徐兴等[80]运用遗传算法对简化EM的固相动力学扩散参数进行辨识,并在多倍率放电及循环工况下验证了算法的准确性。M. A. Rahman等[115]采用粒子群优化法对不同滥用条件下的关键电化学参数进行了提取,验证了估计的参数都在合理的精度范围内。邓忠伟等[116]结合Fisher信息矩阵和非线性最小二乘法对ESP模型的关键参数进行了辨识,并在动态工况下验证了模型精度。考虑到不同老化程度下电池参数会发生变化,V. Ramadesigan等[117]采用基于梯度的局部最小二乘法来估计由于电池老化引起的参数变化,并结合不确定性量化来计算估计参数的置信区间。熊瑞等[118]采用遗传算法对简化EM全寿命周期内的电化学参数进行提取,并根据老化特征参数实现了电池SOH的准确估计。针对电热耦合模型的参数识别问题,G. Correa等[119]提出一种通过二次逼近进行边界优化(Bound Optimization by Quadratic Approximation, BOBYQA)优化算法对电池内部的电化学及热参数进行优化,并根据放电电压和温度曲线对参数精度进行了验证。崔纳新等[35]基于简化的电化学-热耦合模型,将参数进行归类后采用最小二乘法进行逐步识别,并在不同实验工况下获得了较好的辨识效果。尽管上述参数识别方法可能在特定条件下存在不足,例如,遗传算法和粒子优化算法计算成本较高,最小二乘法可能出现局部最优等问题[120],但这些基于EM参数识别的研究成果,有助于提高基于模型的状态估计及控制精度,为EM的广泛使用奠定基础。
众所周知,EM可以很好地描述电池内部电化学状态,特别是,通过了解电极固相表面浓度,有助于在线获取最佳充电策略,从而保护电池在电动汽车运行期间免受过充电和析锂发生[58]。因此,有必要研究基于EM的SOC估计方法。然而,由于电池系统本身具有强非线性、时变特性以及复杂的电化学反应,基于EM的SOC估计仍然是实现高级BMS基本功能的一项具有挑战性任务。
在进行电池SOC估计之前,需要引入SOC的表征方式。一般来说,SOC的定义取决于估计方法中所用的电池模型,且这一直是研究人员讨论的热门话题[121]。对于宏观或经验模型(如ECM),SOC的定义为电池内剩余电荷量(Cremain)与额定容量(Crate)的百分比[122-123]。从理论上讲,SOC可以表示为
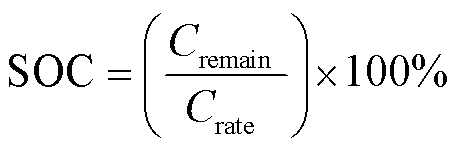 (13)
(13)
然而,对于电化学机理模型(如P2D模型和SP模型),SOC可以分为表面SOC和平均SOC[84]。具体来说,表面SOC和平均SOC根据电化学理论可分别表示为
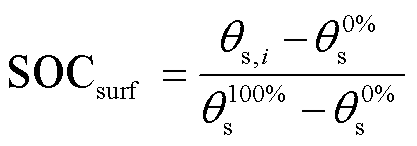 (14)
(14)
 (15)
(15)
这里,首先引入电极利用率的概念,其表示电极固相颗粒的实际锂浓度与最大可用浓度的比值,则有电极利用率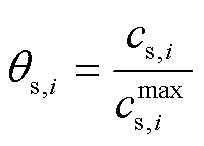 ,
, ,且
,且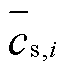 为固相平均锂离子浓度,
为固相平均锂离子浓度,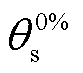 和
和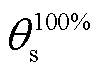 分别代表SOC为0%和100%时的电极利用率。
分别代表SOC为0%和100%时的电极利用率。
应当指出,由于表面SOC和平均SOC分别有助于确定电池瞬时功率的状态信息及其提供电池可用能量的能力[124],因此,基于EM的SOC预测方法已开始受到广泛关注,并在近年来取得了重大进展。到目前为止,基于EM的SOC估计方法主要包括基于滤波的方法、基于观测器的方法和其他方法。图7清楚地展示了这些方法的具体分类。此外,图7中所示方法将在下文中进行详细说明和介绍。
随着简化EMs的发展,基于滤波的方法近年来在SOC估计研究中占有重要地位。目前,现有基于EM的SOC估计算法主要包括扩展卡尔曼滤波(Extended Kalman Filter,EKF)法、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)法、Sigma点卡尔曼滤波(Sigma Point Kalman Filter, SPKF)法、粒子滤波(Particle Filtering, PF)法等。
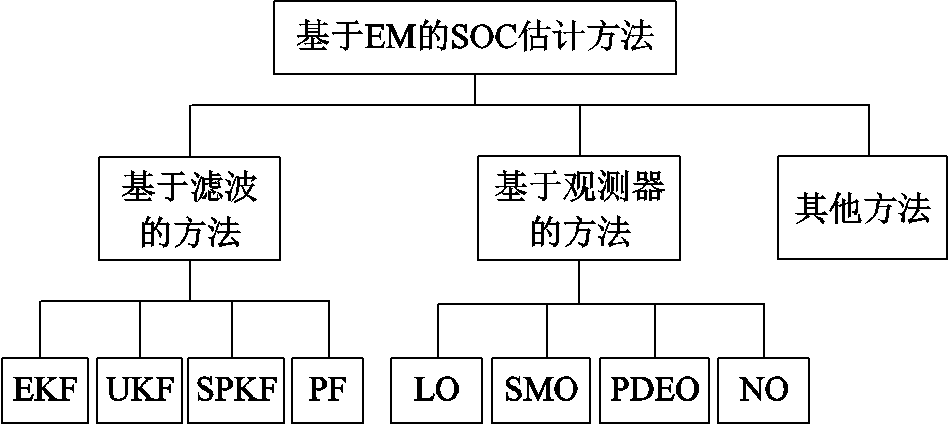
图7 基于EM的SOC估算方法分类
Fig.7 The classification of EM-based SOC estimation method
2.1.1 扩展卡尔曼滤波(EKF)法
基于EKF的SOC估计是由G. Plett等[125]最初在基于ECM的背景下提出的,文献[125]详细描述了如何使用EKF方法结合电池输出电压和电流变量实现对SOC的估计。随后,在基于ECM的SOC估计应用中,EKF 被广泛用于研究解决电池状态估计中的非线性问题[126-127]。
与ECM不同,EM的系统输出方程面临强非线性和可观测性问题[128],这阻碍了EKF在 EM状态估计中的应用。即便如此,近年来使用EKF算法结合EM来估计电池SOC的努力也逐渐凸显成效。R. E. White等[129]首先尝试在SP模型的SOC估计中使用EKF算法,通过简化固相扩散方程实现了EM的线性化处理,同时对电池系统的SOC状态进行估计,但文中缺乏SP模型的可观性证明。为了解决这个问题,D. Domenico等[88]通过假设两电极SOC值相等(即锂离子数量守恒)对模型可观性进行了分析,同时使用FDM方法处理电池SP模型非线化问题,采用EKF算法对电池表面SOC和平均SOC进行了估计。然而,由于SP模型固有的缺陷,这些基于EKF的方法只能在低电流条件下取得良好的效果。因此,为了减少SP模型对SOC估计精度的影响,近年来,部分学者还基于简化P2D/ESP模型开发了一些SOC估计方法[105,130-132],并取得了良好的估计效果,但是对于EM可观性分析描述较少。
此外,考虑到电池参数的不确定性、错误的初始SOC值以及EKF算法中固有的定量噪声,自适应扩展卡尔曼滤波(Adaptive Extended Kalman Filter, AEKF)[133]由于能自动修正这些误差来源而逐渐成为基于EM进行SOC估计的主流选择[134-136]。例如,吕超等[135]在不同运行条件下使用AEKF对简化P2D模型进行了SOC估计,在一定程度上解决了参数不确定性对SOC估计精度的影响,文中AEKF在EM中的详细执行流程如图8所示。李晓宇等[136]结合ESP模型使用AEKF实现了不同温度下的SOC估计,验证了该方法在大温度范围条件下的估计精度和鲁棒性,同时对电池系统的可观性进行了证明,这在一定程度上丰富了AEKF的理论分析,扩展了基于EM的SOC估计在控制领域的适用性。
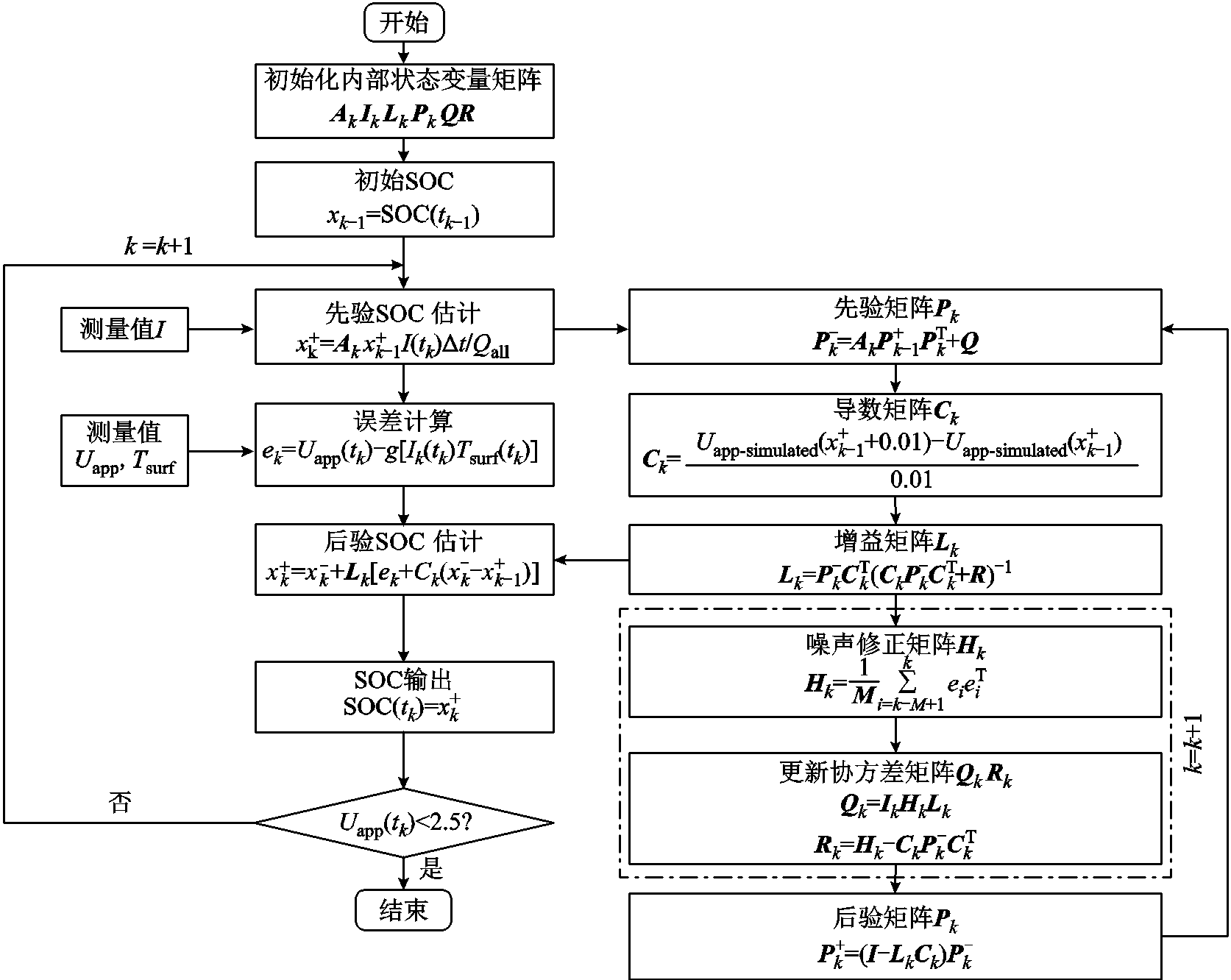
图8 基于EM的AEKF算法流程
Fig.8 The flowchart of EM-based AEKF algorithm
因此,由于 EKF算法可操作强、稳健性较好,逐渐成为基于EM的SOC估算最流行的方法之一。但是,电池EM高度非线性系统中泰勒线性化的处理,使其算法本身也存在固有的缺陷。
2.1.2 无迹卡尔曼滤波(UKF)法
为了克服EKF在线性化处理方面存在的明显缺陷,S. J. Julier等[137]首次提出UKF,可以有效地解决模型系统的非线性化问题。EKF和UKF之间的原理及执行流程的主要差别如图9所示。过去几年,UKF已经被大量使用在ECM中的SOC估计中,算法本身的适用性也已经得到了验证[138-140]。
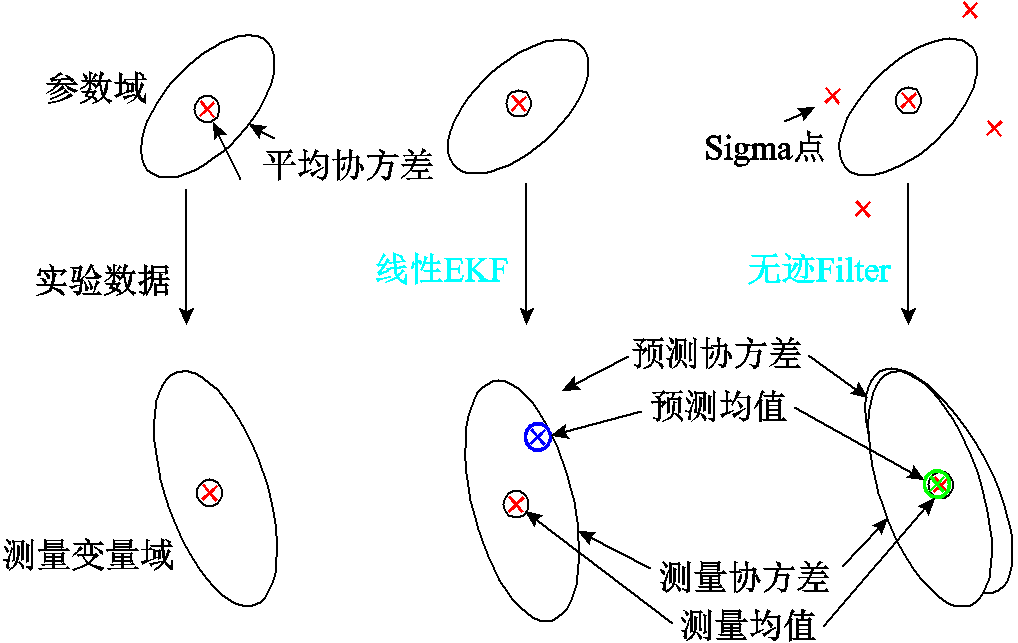
图9 EKF与UKF执行原理比较图
Fig.9 A comparison diagram of the execution of EKF and UKF
近年来,部分学者尝试将UKF应用到基于EM的SOC估算中,R. E. White等[141]采用了简化P2D模型来说明使用UKF进行电池状态估计的过程。相比于EKF, 该方法大大提高了从EM中观察SOC的计算效率和精度。此外,F. Ringbeck等[142]建议使用UKF来解决参数不确定性下的电池状态估计问题,通过结合简化P2D模型实现了电池表面浓度的估计,由此来优化电池充电控制策略,达到了良好效果。最近,为了避免UKF中噪声矩阵的局限性,W. H. Li等[58]探索在ESP模型上使用自适应UKF(AUKF)来观察电池内部状态,包括电极SOC、固相锂浓度和电极过电势,从而准确避免了由于过充电引起的析锂问题。
随着研究的深入,UKF在EM状态估计中的应用得到了一定程度的验证[143-144]。然而,UKF不擅长处理系统高测量噪声以及在复杂工况下鲁棒性差等问题值得学者进一步探讨。
2.1.3 Sigma点卡尔曼滤波(SPKF)法
SPKF算法可以根据选择的系列Sigma点来解决系统输出方程中的非线性问题,而不采用例如EKF中的局部线性化方法[145]。尽管现有SPKF更多应用在基于ECM的SOC估计研究[146-147],但由于SPKF在处理非线性系统过程中优势明显,近年来,相关学者也开始探讨与EM相结合的SOC估计算法。例如,文献[148]中,作者首先采用多模型SPKF框架来实现对电池寿命周期内各个阶段的内部状态估计,认为SPKF能够产生比EKF更好的状态协方差矩阵。然而,关于使用SPKF结合简化EM进行 SOC 估计的实现细节很少描述。此外, Bi Yalan等[149]使用具有等式状态约束的自适应二次方根 SPKF(ASR-SPKF)来提高电池 SOC 估计的准确性,使SPKF算法真正应用在基于EM的SOC 估计中。此外,作者选择ESP模型来评估AEKF、自适应SPKF(ASPKF)和ASR-SPKF 在估计 SOC中的精度和鲁棒性。从表2可知,与AEKF 相比,基于SPKF算法的SOC估计在精度和收敛性上具有突出的优势。
表2 基于AEKF,ASPKF,ASR-SPKF在HPPT测试下的SOC估计性能比较
Tab.2 Comparison of AEKF, ASPKF, and ASR-SPKF on the HPPT test of estimated SOC

算法没有初始SOC误差20% SOC初始误差 RMS误差(%)最大误差(%)RMS误差(%)最大误差(%)收敛时间/s AEKF2.575.602.5020.381116 ASPKF1.683.101.6820.38123 ASR-SPKF1.683.101.7620.38129
2.1.4 粒子滤波(PF)法
与EKF系列算法相比,PF 是另一种使用基于贝叶斯模型选择样本点的非线性滤波器,其优点是可以通过增加粒子数量来任意精确地进行后验密度近似。目前,PF方法已经在车用动力电池ECM状态估计及寿命预测应用中取得了可喜的进展[150-152],这为研究PF与EM的结合进行电池SOC估计提供很好了参考价值。
M. F. Samadi等[153]提出了一种用于监测电池EM表面和平均SOC的PF算法,有效解决了EM的非线性状态估计问题。此外,文献[154]中开发了一种改进的 PF 算法,通过利用 P2D 模型的特殊结构,独立地扫描时间和空间坐标,实现电池EM的SOC及其他状态的估计。仿真结果表明,该方法能够准确地捕捉到存在状态和测量噪声时SOC的变化。然而,以上两种方法都没有经过真实实验验证。为了弥补这一缺点,唐晓鹏等[97]基于简化P2D模型,采用PF算法实现了SOC/SOH的联合估计并进行了实验验证,实验结果证明,该方法有助于实时校对老化电池的SOC估计精度。此外,S. Onori等[155]也将PF方法成功地应用于ESP模型中,并预测和验证了复合材料电极的表面和平均SOC值。值得一提的是,作者还对电池非线性系统的可观性进行了详细的推导和证明,这为滤波算法在EM中的应用提供了理论参考依据。然而,由于计算负担的增加和算法中没有包含新的观测信息[156-157],未来几年,PF方法在EM中的实际应用仍然进一步改进和完善。
此外,国内外学者还开展了一些基于EM的其他滤波方法。特别是,Fan Guodong和Li Xiaoyu等[158-159]分别利用容积卡尔曼滤波(Cubature Kalman Filter, CKF)和自适应容积卡尔曼滤波(Adaptive Cubature Kalman Filter, ACKF)实现了全温度范围下的SOC估计。另外,S. A. Chandra等[160]通过应用粒子群优化(Particle Swarm Optimization, PSO)法开发了一种新颖的电池实时SOC估计,并认为PSO估计的SOC与实验SOC达到了密切的一致性。虽然这些新颖的SOC估计方法在电池EM中没有广泛实际应用,但它们有助于激发研究人员对基于EM的SOC 估计方法产生新的设计思路和方案。
需要强调的是,这些基于滤波方法在各自特定应用条件下实现了自更正系数、误差范围动态估计以及自适应降低传感器噪声影响等诸多优点,使基于EM的SOC 估计获得了较好的精度和鲁棒性,但于此同时,这些滤波方法也存在一定的不足。为方便读者比较,表3总结了现有EM中几种典型的基于滤波法的SOC估计方法,并列出了各自方法的使用局限性。
表3 电池EM中基于滤波方式的SOC估计方法比较
Tab.3 The comparison of existing filtering-based method for EM-based SOC estimation

算法相关文献局限性 EKF[88, 129-132]精度受系统噪声先验知识的影响;线性化的雅可比矩阵计算 AEKF[134-136]部分一阶泰勒展开影响精度;线性化的雅可比矩阵计算
(续)

算法相关文献局限性 UKF[58, 141-144]不擅长高测量噪声;鲁棒性取决于最大采样数据;维度问题 SPKF[148-149]繁重的计算负担和复杂的执行过程 CKF[158-159]高昂的计算和收敛成本 PF[153-155]高的计算成本;没有新观测信息 PSO[160]多维数据导致计算成本增加;有限的进化速度和群体规模
与滤波器类似,基于观测器方法也可通过计算系统误差来实时观测模型状态,但因其不需要考虑系统模型中的测量噪声,同时可用极点配置方法确定模型增益[59, 161],在SOC估计领域中引起了研究学者的极大兴趣。此外,基于观测器的电池SOC 估计的主要原理图如图10所示。由图10可知,设计观测器最关键的一点是准确地获取系统增益。根据这一原理,国内外学者在ECM模型SOC估计的研究方面取得了巨大成功[162-164]。对于电池EM,当前基于观测器的SOC估计方法主要局限于龙塔伯格观测器(Luenberger Observer, LO)法、滑模观测器(Sliding-Mode Observer, SMO)法、PDE观测器(PDEO)法以及非线性观测器(Nonlinear Observer, NO)法。
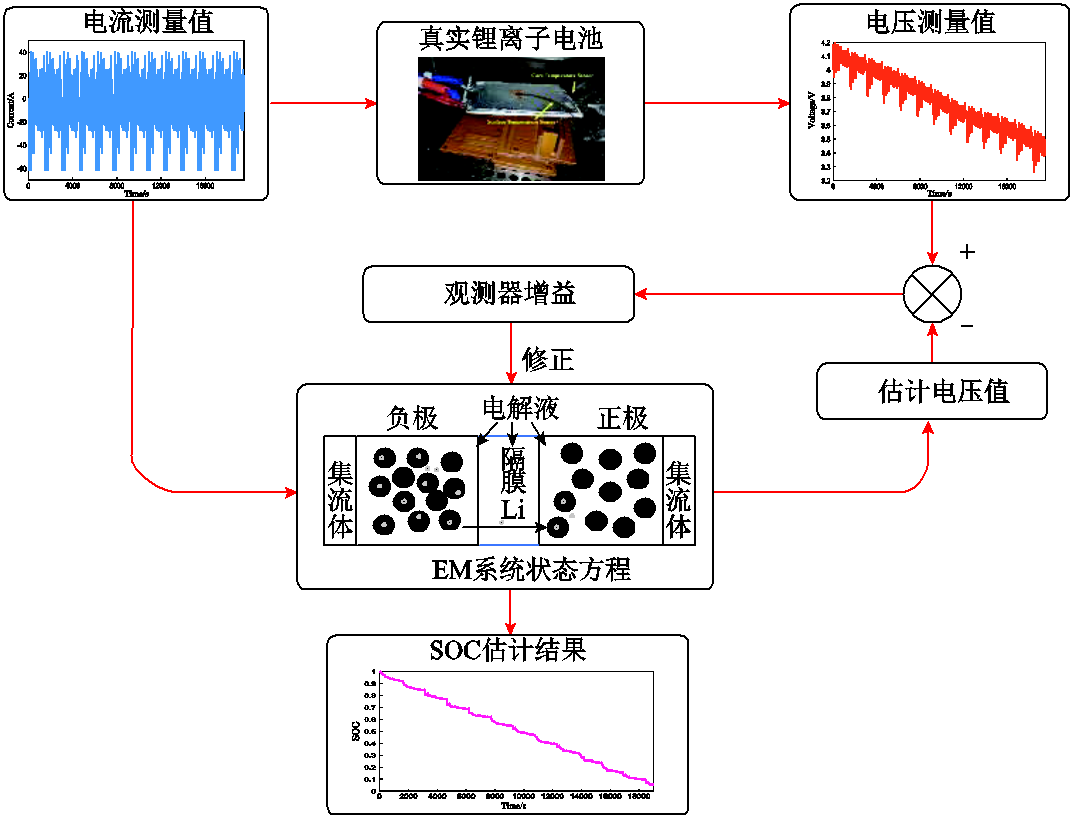
图10 基于观测器的SOC估计原理图
Fig.10 The SOC estimation schematic based on the observer
2.2.1 龙塔伯格观测器(LO)法
LO因为其结构简单,便于调整观测器增益等优点,被研究学者广泛用于预测电池 ECM系统的SOC值[165-166]。然而,由于在EM中强非线性耦合方程导致系统可观性较弱,同时增加了观测器增益系数确定的难度,只有少量文献报道了关于基于LO的SOC估计方法。例如,T. R. Tanim等[90]根据ESP模型提出了基于LO的电池SOC估计方法,其具体的LO估计原理图如图11所示。
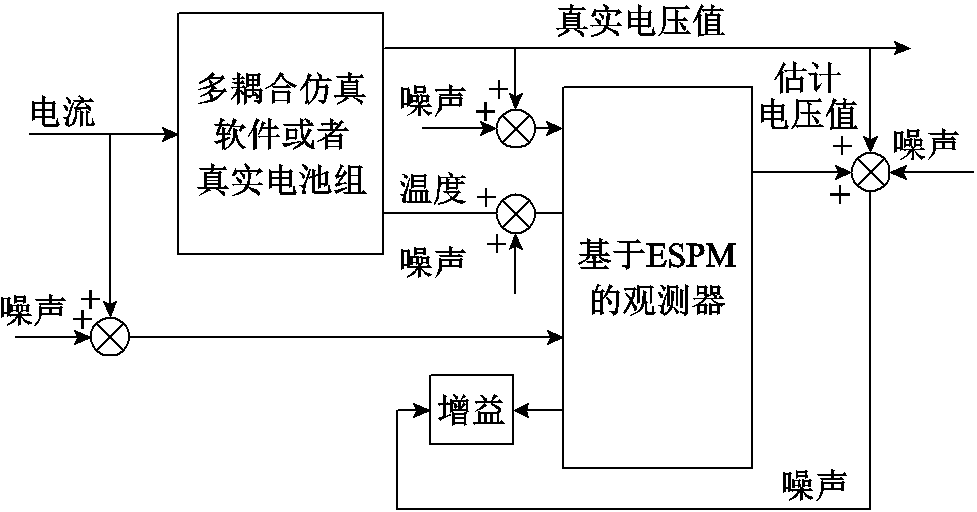
图11 基于LO的SOC估计框图
Fig.11 The block diagram of LO-based SOC estimation
该方法可以在不同的温度条件下准确获取电池实时SOC值,但文中对观测器增益系数的选择描述较少。韩雪冰等[95]将LO与安时积分方法相结合,以改进在线SOC 估算的精度。然而,上述作者都没有针对电池EM系统本身的可观测性和稳定性进行详细说明。鉴于这些缺点,N. Lotfi等[167]基于简化的P2D模型,设计了一个自适应LO,以实现对充电/放电条件下的SOC进行估计,并根据李雅普诺夫理论对系统本身的渐近稳定性进行了详细分析和证明。但是,该方法中观测器的额外输出注入也不可避免地限制了其实际应用范围。因此,为了在BMS中更好地使用 LO来观测SOC状态,Ren Lichao等[168]使用基于ESP模型的闭环观测器结合安时积分法来观测电池SOC,这使得其收敛速度达到30s。
2.2.2 滑模观测器(SMO)法
近年来,SMO也开始被引入到基于EM的SOC估计中。因为该观测器在针对模型误差和不确定性时,可以显示强大的控制鲁棒性[169]。I. S. Kim等[170]首次将 SMO 应用于ECM 进行电池SOC估算,并在实际驾驶条件下降低了计算费用,从而为其在电池 EM 的 SOC 估算中的应用带来了可能。在文献[171]中,通过考虑电池老化现象,作者结合简化EM开发一种基于SMO的状态估计方法,用于预测电极表面SOC,结果表明,提出的方法可用于高级BMS的实时应用。随后,汤爱华等[172]利用EKF算法和SMO分别实现了基于AEM的SOC估计,并在动态条件下比较了两种方法的估计精度。然而,文中并未对电池系统的收敛性和可观测性进行分析。鉴于此,A. Allam等[173]采用了互连SMO的方式,同时实现了对简化EM模型表面和平均SOC的估计,并对互连SMO 的收敛性进行了系统证明。随后几年,针对SMO进行了广泛研究,使其较好地应用于基于EM的SOC估计,但SMO本身的抖振问题仍然令人担忧和迫切需要得到解决。
2.2.3 偏微分方程观测器(PDEO)法
根据电池EM独特的PDE结构,近年来,一些学者设计出一种仅适用于EM的PDEO,用来观测电池内部状态信息。R. Klein等[174]采用以降阶的PDE结构为基础,结合输出注入观测器,用于监控电池单个电极内部的SOC值。值得一提的是,这种PDEO不仅在模拟中得到了广泛的研究,而且在虚拟的电动汽车驱动周期中也得到了验证。紧随其后,S. J. Moura等[175]尝试将自适应反推技术融入到PDEO,用以提高 SOC估算的准确性。基于此,Tang Shuxia和Chen Guangwei等[176-177]利用反推PDEO分别考虑了热和温度对SOC估计的影响,这种方法弥补了传统SOC估计仅在恒温下进行的缺陷。
这些基于PDEO方法的大量研究确实有助于准确估计电池的SOC,但大量复杂的PDE 简化和求解给传统车载控制单元带来了挑战,使 PDEO 难以在嵌入式 BMS 的实际工程应用中得到有效实现。
2.2.4 非线性观测器(NO)法
传统的观测器方法通常会被设定为一个持续固定的系统增益,这使其不能很好地处理系统非线性问题。对于电动汽车用的动力电池系统,恒定增益可能无法准确表示电池模型的动态特性信息。因此,基于文献[178]中的控制理论,NO法首先由夏必忠等[179]引入并应用于基于ECM的SOC估计中。该观测器的一个显著特征是系统增益随着模型空间状态区域的不同权重进行实时变化,真正意义实现了电池模型输出方程的非线性化处理。随后不久,S. Dey等[180]使用NO与SMO方法相结合,从而获取基于EM的SOC估计值。同时还对该方法的稳定性进行了系统分析和证明,从控制角度为NO在电池状态估计中的应用提供了依据。此外,马睿等[181]也在NO领域提出一种基于SP模型的SOC估计方法,并和EKF进行了对比分析,结果显示NO方法在SOC估计上的精度和收敛速度更好。值得注意的是,基于NO的SOC估计方法在EM实际应用中增加了控制器计算成本,并且该方法在SOC估计中的应用并未完全扩展到ESP模型及简化MC模型中。此外,收敛性证明方法需要系统的控制理论支撑,这对实际工程人员来说将是一个巨大的困难。
总之,通过对上述基于观测器SOC估计方法的回顾与总结可知,现有以观测器为基础来实现电池EM的SOC估计方法,各有其优缺点,建议研究人员根据实际操作条件和运行环境做出合理选择。同样地,本文将几种典型的基于观测器的SOC估计方法进行了汇总,并将各自局限性在表4中列出,供读者参考。
表4 用于EM的基于观测器方法SOC估计对比
Tab.4 The comparison of observer-based method for EM-based SOC estimation

观测器文献局限性 LO[90, 95, 167]极点配置复杂;可观性难题 SMO[171-173]抖振影响精度;稳定性证明 PDEO[174-177]理论性强,结构复杂;难以在线应用 NO[180-181]可观性,稳定性难题;使用条件限制,并未扩展在ESP/MC模型
除了使用上述基于滤波方法和基于观测器方法的来估计SOC外,近年来,一些学者还提出了一些新兴方法。吕超等[182]根据设定的电压阈值,同时结合二分法,来迭代更新简化的P2D模型参数,并在不同的运行工况下实现了SOC估计。Bi Yalan等[183]提出了一种EKF和安时积分法混合的方式来获得电池SOC值。具体来说,其主要根据电池的电压误差来定义切换因子,以判断在运行过程中使用哪种方法,从而确保多种条件下SOC误差小于3%。随后,Liu Junfu等[184]根据Nernst方程推导出电压误差与锂离子浓度之间的定量关系,从而进一步实现了更高精度的状态估计。此外,随着人工智能技术的迅速普及,一些数据驱动的SOC估计方法开始在EM中尝试,并初见成效[185],这给准确实现EM的状态估计带来了新的思路和设计方案。
综上所述,相比基于ECM的SOC估计方法,本文介绍的基于EM的SOC估计方法优势主要体现在:①EM模型精度更为准确,能够从电化学机理角度出发反映不同工况下的电池内部电化学反应和充放电特性;②从电池内部固相浓度变化表征SOC,有助于监测全寿命周期内及不同温度下的SOC变化趋势,更具实际意义;③能够扩展SOC估计的应用范围,如实时反应电池的可用功率和有效能量,优化电池充放电策略等[58, 186]。尽管基于EM的SOC估计方法各有其优缺点,甚至部分方法的研究还在初期阶段,但这些努力在一定程度上加速了EM在电池实时状态估计中的应用,为其在高级 BMS中的开发奠定了基础。
随着人们对电动汽车动力系统安全需求的提升以及模型降阶技术的普及,电池EMs的发展越来越受到关注。同时,基于EM的SOC估计方法优势明显,克服了ECM受外界干扰性大,缺乏内部物理机理的缺点,可以有助于处理锂离子电池过充、老化、热失控等问题,在一定程度上推动了电动汽车实现智能化发展的进程。然而,由于电池本身是一个复杂的电化学系统,致使基于EM的SOC估计方法仍然存在诸多不足。如何利用有效的数学手段对EM进行有效降阶并融合多物理特性以实现高效率高精度的在线BMS应用;如何从控制角度出发,灵活处理EM强非线性输出特性以实现对估计算法中系统的可观性及稳定性进行系统分析和证明;如何利用有限的实验数据来验证EM对多种材料电池的适用性问题,都是基于EM的SOC估计方法所面临的严峻挑战。鉴于此,本节主要从三个方面对基于EM的SOC估计的今后研究方向进行展望,希望这些见解可以对未来基于EM的SOC估计算法的改进做出贡献。
1)降阶MC模型的开发
基于模型的SOC估计准确性在一定程度上取决于模型精度,所以,仍然需要先进的电池EM来模拟锂离子电池在各种不确定性和系统干扰下的电化学行为,例如电池老化、热失效、机械疲劳应力等,因此MC模型的开发需要进行深入研究。现有MC模型大多基于全阶复杂P2D模型,不适合高级BMS对模型仿真效率的需求。因此,如何基于现有降阶技术,将电池老化、热效应、机械应力等因素融入现有简化EM,同时保证精度和仿真效率,是以后基于EM开发SOC估计的的前提和方向。
2)自适应参数识别/SOC/SOH的协同估计
目前,现有基于EM的SOC估计方法大多停留在单一因素条件下的研究,忽略了模型参数、SOC与SOH之间的耦合关系。由于EM的参数识别方法仅使用某些操作条件下的数据作为识别目标,没有充分考虑多种工况下电池SOC变化及老化因素的影响。因此,自适应参数识别方法对确定 EM模型精度至关重要。同时,由于SOC估计精度和电池老化程度密切相关,SOH的定时更新在提高电池整个寿命周期内 SOC 估算的准确性方面起到重要作用。因此,如何在基于EM的SOC估计中实现自适应参数识别及SOC/SOH的联合估计,是后续基于EM实现高效准确状态估计的难点和机遇。
3)大数据融合下基于EM的SOC估计
随着车联网与大数据技术的不断发展,数据驱动方法在整车电池实时估计SOC的优势突出,非常适合弥补基于模型方法的不足,即可以利用有效实时的电池工况运行数据,精确地捕获计算密集度相对较低的电池复杂动态。虽然现有大量数据驱动方法已为基于电池ECM的SOC估计取得了令人满意的效果,但很少有基于数据驱动模型来跟踪观测锂离子电池中不可测量电化学状态的动态变化,例如表面SOC及电极过电势。因此,针对于EM在大数据融合下的SOC估计方法需要进一步开发和研究,用于描述可测电压、电流信号与不可测电化学状态之间的复杂关系,这对一些具有重复路线及固定短距离运行的电动汽车高级BMS尤为重要,有助于提升基于EM模型SOC估计的适用性。
随着汽车产业交通电气化需求的提升,EM的开发与有效应用有助于提升高级BMS智能化发展进程,同时,准确的SOC估计是实现BMS其他功能的前提。为此,本文对基于EM的SOC估计算法进行了全面调查和评估,主要包括以下几个部分:
1)在电池电化学建模方面,总结了现有EM的主要分类,较为详细地介绍了常用重构EM分类及相关参数识别方法,强调了各自模型的优缺点及应用背景。
2)在电池SOC估计方面,阐述了基于EM的SOC估计方法的分类,介绍了各自SOC估计方法的原理及最新研究进展,并对其使用的局限性进行了总结。
3)针对现有SOC估计研究现状,分析了基于EM的SOC估计所面临的挑战,同时对未来发展方向进行了展望。
本文旨在对已有车用锂离子电池电化学建模技术及对应SOC估计算法进行总结,以期为广大研究者提供参考,激励产生更多创新性的基于EM的SOC估计思路和方案,并最终促进EM在先进BMS上的开发和应用。
参考文献
[1] Su Tonglun, Lü Nawei, Zhao Zhixing, et al.Safety warning of lithium-ion battery energy storage station via venting acoustic signal detection for grid application[J]. Journal of Energy Storage, 2021, 38: 102498.
[2] Huang Zebo, Mu Anle.Research and analysis of performance improvement of vanadium redox flow battery in microgrid: a technology review[J]. International Journal of Energy Research, 2021, 45(10): 14170-14193.
[3] 王榘, 熊瑞, 穆浩.温度和老化意识融合驱动的电动车辆锂离子动力电池电量和容量协同估计[J].电工技术学报,2020, 35(23): 4980-4987.
Wang Ju, Xiong Rui, Mu Hao. Co-estimation of lithium-ion battery state-of-charge and capacity through the temperature and aging awareness model for electric vehicles[J].Transactions of China Electrotechnical Society. 2020, 35(23): 4980-4987.
[4] Hu Xiaosong, Han Jie, Tang Xiaolin, et al. Powertrain design and control in electrified vehicles: a critical review[J]. IEEE Transactions on Transportation Electrification, 2021, 7(3): 1990-2009.
[5] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426.
Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on comprehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[6] 舒星, 刘永刚, 申江卫, 等. 基于改进最小二乘支持向量机与Box-Cox变换的锂离子电池容量预测[J]. 机械工程学报, 2021, 57: 118-128.
Shu Xing, Liu Yonggang, Shen Jiangwei, et al. Capacity Prediction for lithium-ion batteries based on improved least squares support vector machine and box-cox transformation[J]. Journal of Mechanical Engineering, 2021, 57: 118-128.
[7] 潘海鸿, 张沫, 王惠民, 等. 基于多影响因素建立锂离子电池充电内阻的动态模型[J]. 电工技术学报, 2021, 36(10): 2199-2206.
Pan Haiou, Zhang Mo, Wang Huiming, et al. Establishing a dynamic model of lithium-ion battery charging internal resistance based on multiple factors[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2199-2206.
[8] 刘新天, 何耀, 曾国建, 等. 考虑温度影响的锂电池功率状态估计[J]. 电工技术学报, 2016, 31(13): 155-163.
Liu Xintian, He Yao, Zeng Guojian, et al. State of power estimation for Li-ion battery considering the effect of temperature[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 155-163.
[9] 曹铭, 黄菊花, 杨志平, 等. 车用锂离子动力电池自适应状态联合估计研究[J]. 控制理论与应用, 2020, 37(9): 1951-1962.
Cao Ming, Huang Juhua, Yang Zhiping, et al. Research on adaptive state of charge and state of power joint estimation algorithm of vehicle lithium ion power batteries[J]. Control Theory & Applications, 2020, 37(9): 1951-1962.
[10] 王春雨, 崔纳新, 李长龙, 等. 基于电热耦合模型和多参数约束的动力电池峰值功率预测[J]. 机械工程学报, 2019, 55(20): 28-35.
Wang Chunyu, Cui Naxin, Li Changlong, et al. State of Power prediction based on electro-thermal battery model and multi-parameter constrains for lithium-ion battery[J]. Journal of Mechanical Engineering, 2019, 55(20): 28-35.
[11] Hannan M A, Lipu M S H, Hussain A, et al. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: challenges and recommendations[J]. Renewable and Sustainable Energy Reviews, 2017, 78: 834-854.
[12] Ng K S, Moo C S, Chen Y P, et al. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries[J]. Applied Energy, 2009, 86(9): 1506-1511.
[13] Zhang Shuzhi, Guo Xu, Dou Xiaoxin, et al. A data-driven coulomb counting method for state of charge calibration and estimation of lithium-ion battery[J]. Sustainable Energy Technologies and Assessments, 2020, 40: 100752.
[14] Yu Quanqing, Wan Changjiang, Li Junfu, et al. An open circuit voltage model fusion method for state of charge estimation of lithium-ion batteries[J]. Energies, 2021, 14(7): 1797.
[15] Ren Zhong, Du Changqing, Wu Zhongyi, et al. A comparative study of the influence of different open circuit voltage tests on model‐based state of charge estimation for lithium-ion batteries[J]. International Journal of Energy Research, 2021.
[16] Jiang Bo, Dai Haifeng, Wei Xuezhe, et al. Joint estimation of lithium-ion battery state of charge and capacity within an adaptive variable multi-timescale framework considering current measurement offset[J]. Applied Energy, 2019, 253: 13619.
[17] 刘征宇, 黎盼春, 朱诚诚, 等. 基于组合模型的锂电池参数辨识和电池荷电状态在线联合估计[J]. 中国机械工程,2020, 31(10): 1162-1168.
Liu Zhengyu, Li Pangchun, Zhu Chengcheng, et al. Lithium battery parameter identificaiton and SOC online joint estimation based on combined model[J]. China Mechanical Engineering, 2020, 31(10): 1162-1168.
[18] He Zhigang, Li Yaotai, Sun Yanyan, et al.State-of-charge estimation of lithium ion batteries based on adaptive iterative extended Kalman filter[J]. Journal of Energy Storage, 2021, 39: 102593.
[19] Zou Zhiyue, Xu Jun, Mi Chris, et al. Evaluation of model based state of charge estimation methods for lithium-ion batteries[J]. Energies, 2014, 7(8): 5065-5082.
[20] 蒋聪, 王顺利, 李小霞, 等. 基于改进EKF算法变温度下的动力锂电池SOC估算[J]. 储能科学与技术, 2020, 9(1): 145-151.
Jiang Cong, Wang Shunli, Li Xiaoxia, et al. The estimation method of SOC for power lithium battery based on improved EKF algorithm adaptive to various temperature[J]. Energy Storage and Technology, 2020, 9(1): 145-151.
[21] 王晓兰, 靳皓晴, 刘祥远. 基于融合模型的锂离子电池荷电状态在线估计[J]. 工程科学学报, 2020, 42(9): 1200-1208.
Wang Xiaolan, Jin Haoqing, Liu Xiangyuan. Online estimation of the state of charge of a lithium-ion battery based on the fusion model[J]. China Journal of Engineering, 2020, 42(9): 1200-1208.
[22] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cyle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[23] Xiong Rui, Sun Fengchun, Gong Xianzhi, et al. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles[J]. Applied Energy, 2014, 113: 1421-1433.
[24] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J].电工技术学报, 2020, 35(9): 2051-2062.
Li, Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[25] 贾俊, 胡晓松, 邓忠伟, 等. 数据驱动的锂离子电池健康状态综合评分及异常电池筛选[J]. 机械工程学报, 2021, 57(14): 141-149.
Jia Jun, Hu Xiaosong, Deng Zhongwei, et al. Data-driven comprehensive evaluation of lithium-ion battery state of health and abnormal battery screening[J]. Journal of Mechanical Engineering, 2021, 57(14): 141-149.
[26] Tang Xiaopeng, Liu Kailong, Li Kang, et al. Recovering large-scale battery aging dataset with machine learning[J]. Patterns, 2021, 2(8): 1000302.
[27] Li Weihan, Sengupta N, Dechent P, et al. One-shot battery degradation trajectory prediction with deep learning[J]. Journal of Power Sources, 2021, 506: 230024.
[28] How D N T, Hannan M A, Lipu M S H, et al. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: a review[J]. IEEE Access, 2019, 7: 136116-136136.
[29] Hu Xiaosong, Li Shengbo, Peng Huei. A comparative study of equivalent circuit models for Li-ion batteries[J]. Journal of Power Sources, 2012, 198: 359-367.
[30] Yang Jufeng, Cai Yingfeng, Pan Chaofeng, et al.A novel resistor-inductor network-based equivalent circuit model of lithium-ion batteries under constant-voltage charging condition[J]. Applied Energy, 2019, 254: 113726.
[31] Lai Xin, Wang Shuyu, Ma Shangde, et al. Parameter sensitivity analysis and simplification of equivalent circuit model for the state of charge of lithium-ion batteries[J]. Electrochimica Acta, 2019, 330: 135239.
[32] 庞辉, 郭龙, 武龙星, 等.考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189.
Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society,2021, 36(10): 2178-2189.
[33] Wang Yuhai, Li Junfu, Zhang Jinming, et al. Lithium-iron-phosphate battery electrochemical modelling under a wide range of ambient temperatures[J]. Journal of Electroanalytical Chemistry, 2021, 882: 115041.
[34] 庞辉.基于电化学模型的锂离子电池多尺度建模及其简化方法[J]. 物理学报, 2017, 66(23): 312-322.
Pang Hui. Multi-scale modeling and its simplicaiton method of li-ion battery based on electrochemical model[J]. Acta Physica Sinica, 2017, 66(23): 312-322.
[35] Li Changlong, Cui Naxin, Wang Chunyu, et al.Simplified electrochemical lithium-ion battery model with variable solid-phase diffusion and parameter identification over wide temperature range[J]. Journal of Power Sources, 2021, 497: 229900.
[36] Du Xinhao, Meng Jinhao, Zhang Yingmin, et al. An information appraisal procedure endows reliable online parameter identification to lithium-ion battery model[J]. IEEE Transactions on Industrial Electronics, 2021, DOI:10.1109/TIE.2021-309192.
[37] 来鑫, 李云飞, 郑岳久, 等.基于SOC-OCV优化曲线与EKF的锂离子电池荷电状态全局估计[J]. 汽车工程, 2021, 43(1): 19-26.
Lai Xin, Li Yunfei, Zheng Yuejiu, et al. An Overall estimation of state of charge on SOC-OCV optimization curve and EKF for lithium-ion battery[J]. Automotive Engineering, 2021, 43(1): 19-26.
[38] 马建, 张大禹, 赵轩, 等.基于随机加权自适应容积卡尔曼的电池SOC估计[J]. 中国公路学报,2019, 32(11): 234-244.
Ma Jian, Zhang Dayu, Zhao Xuan, et al. State of charge estimation for battery based on adaptively random weighted cubature Kalman filter[J]. China Journal of Highway and Transport, 2019, 32(11): 234-244.
[39] 李伟, 刘伟嵬, 邓业林.基于扩展卡尔曼滤波的锂离子电池荷电状态估计[J]. 中国机械工程, 2020, 31(3): 321-327.
Li Wei, Liu Weiwei, Deng Yelin. SOC estimation for lithium-ion batteries based on EKF[J]. China Mechanical Engineering, 2020, 31(3): 321-327.
[40] Shen Jiangwei, Xiong Jian, Shu Xing, et al.State of charge estimation framework for lithium-ion batteries based on square root cubature Kalman filter under wide operation temperature range[J]. International Journal of Energy Research, 2021, 45(4): 5586-5601.
[41] Hu Yang, Yin Yilin, Bi Yalan, et al. A control oriented reduced order electrochemical model considering variable diffusivity of lithium ions in solid[J]. Journal of Power Sources, 2020, 468: 228322.
[42] Jokar A, Rajabloo B, Desilets M, et al. Review of simplified Pseudo-two-dimensional models of lithium-ion batteries[J]. Journal of Power Sources, 2016, 327: 44-55.
[43] Xiong Rui, Cao Jiayi, Yu Quanqing, et al. Critical review on the battery state of charge estimation methods for electric vehicles[J]. IEEE Access, 2018, 6: 1832-1843.
[44] Chaturvedi N A, Klein R, Christensen J, et al. Algorithms for advanced battery-management systems[J]. IEEE Control Systems Magazine, 2010, 30(3): 49-68.
[45] 高铭琨, 徐海亮, 吴明铂.基于等效电路模型的动力电池SOC估计方法综述[J]. 电气工程学报, 2021, 16(1): 90-102.
Gao Mingkun, Xu Hailiang, Wu Mingbo. Review of SOC estiamtion methods for power battery based on equivalent circuit model[J]. Journal of Electrical Engineering, 2021, 16(1): 90-102.
[46] 孙冬, 许爽, 李超, 等. 锂离子电池荷电状态估计方法综述[J]. 电池, 2018, 48(4): 284-287.
Sun Dong, Xu Shuang, Li Chao, et al. Review of state of charge estimation method for Li-ion battery[J]. Battery Bimothly, 2018, 48(4): 284-287.
[47] 余运俊,谌新,万晓凤.电动汽车电池荷电状态估计研究综述[J]. 电源学报, 2014(3): 95-102.
Yu Yunjun, Chen Xin, Wan Xiaofeng. Reviewer of estiamting the state of battery charge for electric vehicle[J]. Journal of Power Supply, 2014(3): 95-102.
[48] Dai Haifeng, Jiang Bo, Hu Xiaosong, et al. Advanced battery management strategies for a sustainable energy future: Multilayer design concepts and research trends[J]. Renewable and Sustainable Energy Reviews, 2021, 138: 110480.
[49] Qays M O, Buswig Y, Hossain M L, et al. Recent progress and future trends on state of charge estimation methods to improve battery-storage efficiency: a review[J]. CSEE Journal of Power and Energy Systems, 2020, DOI:10.17775/CSEEJPES. 2019.03060.
[50] Shrivastava P, Soon T K, Idris M Y I B, et al. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries[J]. Renewable and Sustainable Energy Reviews, 2019, 113: 109233.
[51] Lai Xin, Zheng Yuejiu, Sun Tao. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries[J]. Electrochimica Acta, 2018, 259: 566-577.
[52] Hu Xiaosong, Feng Fei, Liu Kailong, et al. State estimation for advanced battery management: Key challenges and future trends[J]. Renewable and Sustainable Energy Reviews, 2019, 114: 109334.
[53] Tian Jiaqiang, Wang Yujie, Chen Zonghai. An improved single particle model for lithium-ion batteries based on main stress factor compensation[J]. Journal of Cleaner Production, 2021, 278: 123456.
[54] 匡柯, 孙跃东, 任东生, 等.车用锂离子电池电化学-热耦合高效建模方法[J]. 机械工程学报, 2021, 57(14): 10-22.
Kuang Ke, Sun Yuedong, Ren Dongsheng, et al. Efficient Approach for electrochemical-thermal coupled modeling of large-format lithium-ion power battery[J]. Journal of Mechanical Engineering, 2021, 57(14): 10-22.
[55] 胡晓松, 唐小林. 电动车辆锂离子动力电池建模方法综述[J]. 机械工程学报, 2017, 53(16): 34-45.
Hu Xiaosong, Tang Xiaolin. Review of modeling techniques for lithium-ion traction battreies in electric vehicles[J]. Journal of Mechanical Engineering, 2017, 53(16): 34-45.
[56] 程昀, 李劼, 贾明, 等. 锂离子电池多尺度数值模型的应用现状及发展前景[J]. 物理学报, 2015, 64(21): 137-152.
Cheng Jun, Li Jie, Jia Ming, et al. Application status and future of multi-scale numerical models for lithium ion battery[J]. Acta Physica Sinica, 2015, 64(21): 137-152.
[57] Kemper P, Li S E, Kum D. Simplification of pseudo two dimensional battery model using dynamic profile of lithium concentration[J]. Journal of Power Sources, 2015, 286: 510-525.
[58] Li Weihan, Fan Yue, Ringbeck F, et al. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter[J]. Journal of Power Sources, 2020, 476: 228534.
[59] Plett G L.锂离子电池荷电状态不同估算方法的综述及讨论(英文)[J]. 汽车安全与节能学报, 2019, 10(3): 249-272.
Plett G L. Review and some perspectives on different methods to estimate state of charge of lithium-ion batteries[J]. Jouneral of Automotive Safety and Energy, 2019, 10(3): 249-272.
[60] 康鑫, 时玮, 陈洪涛.基于锂离子电池简化电化学模型的参数辨识[J]. 储能科学与技术, 2020, 9(3): 969-978.
Kang Xin, Shi Wei, ChenHongtao. Parameter identification based on simplified electrochemical model of lithium ion battery[J]. Energy Storage Science and Technology, 2020, 9(3): 969-978.
[61] Doyle M, Fuller T F, Newman J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell[J]. Journal of the Electrochemical Society, 1993, 140(6): 1526-1533.
[62] Han Sangwoo, Tang Yifan, KhaleghI Rahimian S. A numerically efficient method of solving the full-order pseudo-2-dimensional (P2D) Li-ion cell model[J]. Journal of Power Sources, 2021, 490: 229571.
[63] 方儒卿, 张娜, 李哲. 3类锂离子电池多孔电极模型比较研究及电池正向设计应用[J]. 清华大学学报(自然科学版), 2021, 61(10): 1055-1065.
Fang Ruqing, Zhang Na, Li Zhe. Comparison study of three porous electrode models for the forward design if lithium-ion batteries[J]. Journal of Tsinghua Univerisity ( Science & Technology), 2021, 61(10): 1055-1065.
[64] 蒋跃辉, 艾亮, 贾明, 等.基于动态参数响应模型的动力锂离子电池循环容量衰减研究[J]. 物理学报, 2017, 66(11): 376-386.
Jiang Yuehui, Ai Liang, Jia Ming, et al. Cyclic capacity fading of the power lithium ion battery based on a numerical modeling with dynamic responses[J]. Acta Physica Sinica, 2017, 66(11): 376-386.
[65] Cai L, White R E. Mathematical modeling of a lithium ion battery with thermal effects in COMSOL Inc. Multiphysics (MP) software[J]. Journal of Power Sources, 2011, 196(14): 5985-5989.
[66] Kwon K H, Shin C B, Kang T H, et al. A two-dimensional modeling of a lithium-polymer battery[J]. Journal of Power Sources, 2006, 163(1): 151-157.
[67] Martínez-rosas E, Vasquez-medrano R, Flores-tlacuahuac A. Modeling and simulation of lithium-ion batteries[J]. Computers & Chemical Engineering, 2011, 35(9): 1937-1948.
[68] Reimers J N. Algorithmic Improvements and PDE decoupling, for the simulation of porous electrode cells[J]. Journal of The Electrochemical Society, 2013, 160(6): A811.
[69] Torchio M, Magni L, Gopaluni R B, et al. LIONSIMBA: a Matlab framework based on a finite volume model suitable for Li-ion battery design, simulation, and control[J]. Journal of The Electrochemical Society, 2016, 163(7): A1192.
[70] Rodríguez A, Plett G L, Trimboli m S. Comparing four model-order reduction techniques, applied to lithium-ion battery-cell internal electrochemical transfer functions[J]. eTransportation, 2019, 1: 100009.
[71] Haran B S, Popov B N, White R E. Determination of the hydrogen diffusion coefficient in metal hydrides by impedance spectroscopy[J]. Journal of Power Sources, 1998, 75(1): 56-63.
[72] Guo M, Sikha G, White R E. Single-particle model for a lithium-ion cell: thermal behavior[J]. Journal of the Electrochemical Society, 2011, 158(2): A122.
[73] 程麒豫, 张希, 高一钊, 等.基于降阶电化学模型估算锂离子电池状态[J]. 电池, 2021, 51(2): 121-124.
Cheng Qiyu, Zhang Xi, Gao Yizhao. Estimation staate of Li-ion batttery based on reduced-order electrochemical model[J]. Battery Bimothly, 2021, 51(2): 121-124.
[74] Wang C Y, Srinivasan V. Computational battery dynamics (CBD)—electrochemical/thermal coupled modeling and multi-scale modeling[J]. Journal of Power Sources, 2002, 110(2): 364-376.
[75] Zhang Qi, White R E. Comparison of approximate solution methods for the solid phase diffusion equation in a porous electrode model[J]. Journal of Power Sources, 2007, 165(2): 880-886.
[76] Subramanian V R, Ritter J A, White R E. Approximate solutions for galvanostatic discharge of spherical particles i. constant diffusion coefficient[J]. Journal of The Electrochemical Society, 2001, 148(11): E444.
[77] 李涛, 程夕明, 胡晨华.锂离子电池电化学降阶模型性能对比研究[J]. 物理学报, 2021, 70(13): 423-434.
Li Tao, Cheng Ximing, Hu Chenhua. Comparative study of reduced-order electrochemical models of the lithium-ion battery[J]. Acta Physica Sinica, 2021, 70(13): 423-434.
[78] Li Y, Vilathgamuwa M, Choi S S, et al. Development of a degradation-conscious physics-based lithium-ion battery model for use in power system planning studies[J]. Applied Energy, 2019, 248: 512-525.
[79] 徐兴, 徐琪凌, 王峰, 等. 车用锂离子动力电池电化学模型修正方法研究[J]. 机械工程学报, 2019, 55(12): 128-136.
Xu Xing, Xu Qiling, Wang Feng, et al. Modification method of electrochemical mdoel for vehicular lithium-ion power battery[J]. Journal of Mechanical Engineering, 2019, 55(12): 128-136.
[80] 徐兴, 王位, 陈龙.基于GA的车用锂离子电池电化学模型参数辨识[J]. 汽车工程, 2017, 39(7): 813-821.
Xu Xing, Wang Wei, Chen Long. Parameter identification of electrochemical model for vehicula lithium ion battery based on genetic algorithm[J]. Automobile Engineering, 2017, 39(7): 813-821.
[81] Zhao Yinyin, Choe S Y. Evaluation of order reduction techniques for porous electrode diffusion equation in lithium ion model[J]. SAE Technical Papers, 2014, DOI:10.4271/2014-01-1835.
[82] Liu Ji, Li Guang, Fathy H K. A computationally efficient approach for optimizing lithium-ion battery charging[J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 138(2): 021009.
[83] Mehta R, Gupta A. An improved single-particle model with electrolyte dynamics for high current applications of lithium-ion cells[J]. Electrochimica Acta, 2021, 389: 138623.
[84] Schmidt A P, Bitzer M, Imre Á W, et al. Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell[J]. Journal of Power Sources, 2010, 195(15): 5071-5080.
[85] Li J, Lotfi N, Landers R G, et al. A single particle model for lithium-ion batteries with electrolyte and stress-enhanced diffusion physics[J]. Journal of the Electrochemical Society, 2017, 164(4): A874.
[86] 刘征宇, 杨昆, 魏自红, 等.包含液相扩散方程简化的锂离子电池电化学模型[J]. 物理学报, 2019, 68(9): 251-258.
Liu Zhengyu, Yang Kun, Wei Zihong, et al. Electrochemical model of lithium ion battery with simplified liquid phase diffusion equation[J]. Acta Physica Sinica, 2019, 68(9): 251-258.
[87] Prada E, Di Domenico D, Creff Y, et al. Simplified electrochemical and thermal model of LiFePO4-graphite Li-ion batteries for fast charge applications[J]. Journal of The Electrochemical Society, 2012, 159(9): A1508.
[88] Di Domenico D, Stefanopoulou A, Fiengo G. Lithium-ion battery state of charge and critical surface charge estimation using an electrochemical model-based extended Kalman filter[J]. Journal of Dynamic Systems, Measurement, and Control, 2010, 132(6): 061302.
[89] Guduru A, Northrop P W C, Jain S, et al. Analytical solution for electrolyte concentration distribution in lithium-ion batteries[J]. Journal of Applied Electrochemistry, 2012, 42(4): 189-199.
[90] Tanim T R, Rahn C D, Wang C Y. State of charge estimation of a lithium ion cell based on a temperature dependent and electrolyte enhanced single particle model[J]. Energy, 2015, 80: 731-739.
[91] 杨俊, 张希, 高一钊. 锂电池电化学传递函数模型建模及参数辨识[J]. 电源技术, 2019, 43(7): 1132-1135.
Yang Jun, Zhang Xi, Gao Yizhao. Modeling and parameter idetification of electrochemical transfer function model for lithium battery[J]. Power Technology, 2019, 43(7): 1132-1135.
[92] Fan Guodong, Pan Ke, Canova M, et al. Modeling of Li-ion cells for fast simulation of high C-rate and low temperature operations[J]. Journal of the Electrochemical Society, 2016, 163(5): A666.
[93] Luo Weilin, Lyu Chao, Wang Lixin, et al. An approximate solution for electrolyte concentration distribution in physics-based lithium-ion cell models[J]. Microelectronics Reliability, 2013, 53(6): 797-804.
[94] Luo Weilin, Lü Chao, Wang Lixin, et al. A new extension of physics-based single particle model for higher charge–discharge rates[J]. Journal of Power Sources, 2013, 241: 295-310.
[95] Han Xuebing, Ouyang Minggao, Lu Languang, et al. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part II: Pseudo-two-dimensional model simplification and state of charge estimation[J]. Journal of Power Sources, 2015, 278: 814-825.
[96] Deng Zhongwei, Yang Lin, Deng Hao, et al. Polynomial approximation pseudo-two-dimensional battery model for online application in embedded battery management system[J]. Energy, 2018, 142: 838-850.
[97] Liu Boyang, Tang Xiaopeng, Gao Furong. Joint estimation of battery state-of-charge and state-of-health based on a simplified pseudo-two-dimensional model[J]. Electrochimica Acta, 2020, 344: 136098.
[98] Li Changlong, Cui Naxin, Wang Chunyu, et al. Reduced-order electrochemical model for lithium-ion battery with domain decomposition and polynomial approximation methods[J]. Energy, 2021, 221: 119662.
[99] Senthil Kumar V. Reduced order model for a lithium ion cell with uniform reaction rate approximation[J]. Journal of Power Sources, 2013, 222: 426-441.
[100] Wu Longxing, Liu Kai, Pang Hui. Evaluation and observability analysis of an improved reduced-order electrochemical model for lithium-ion battery[J]. Electrochimica Acta, 2021, 368: 137604.
[101] 田华, 王伟光, 舒歌群, 等. 基于多尺度、电化学-热耦合模型的锂离子电池生热特性分析[J].天津大学学报(自然科学与工程技术版), 2016, 49(7): 734-741.
Tian Hua, Wang Weiguang, Shu Gequn, et al. Analysis of heat generation in a li-ion battery based on a multi-scale and electorchemical-thermal model[J]. Journal of Tianjin University (Science and Technology), 2016, 49(7): 734-741.
[102] Li Junfu, Wang Dafang, Deng Lei, et al. Aging modes analysis and physical parameter identification based on a simplified electrochemical model for lithium-ion batteries[J]. Journal of Energy Storage, 2020, 31: 101538.
[103] Yang Shichun, Gao Xinlei, Li Yalun, et al. Minimum lithium plating overpotential control based charging strategy for parallel battery module prevents side reactions[J]. Journal of Power Sources, 2021, 494: 229772.
[104] Hu Xiaosong, Cao Dongpu, Egardt Bo. Condition monitoring in advanced battery management systems: Moving horizon estimation using a reduced electrochemical model[J]. IEEE/ASME Transactions on Mechatronics, 2017, 23(1): 167-178.
[105] Gao Yizhao, Liu Kailong, Zhu Chong, et al. Co-estimation of state-of-charge and state-of-health for lithium-ion batteries using an enhanced electrochemical model[J]. IEEE Transactions on Industrial Electronics, 2021, DOI: 10.1109/TIE.2021. 3066946.
[106] Wang Yujie, Tian Jiaqiang, Sun Zhendong, et al. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems[J]. Renewable and Sustainable Energy Reviews, 2020, 131: 110015.
[107] Hu Xiaosong, Deng Zhongwei, Lin Xianke, et al. Research directions for next-generation battery management solutions in automotive applications[J]. Renewable and Sustainable Energy Reviews, 2021, 152: 111695.
[108] Zhang Xi, Lu Jinling, Yuan Shifei, et al. A novel method for identification of lithium-ion battery equivalent circuit model parameters considering electrochemical properties[J]. Journal of Power Sources, 2017, 345: 21-29.
[109] Li Yang, Vilathgamuwa M, Farrell T, et al. A physics-based distributed-parameter equivalent circuit model for lithium-ion batteries[J]. Electrochimica Acta, 2019, 299: 451-469.
[110] Zheng Yuejiu, Gao Wenkai, Han Xuebing, et al. An accurate parameters extraction method for a novel on-board battery model considering electrochemical properties[J]. Journal of Energy Storage, 2019, 24: 100745.
[111] Geng Zeyang, Wang Siyang, Lacey M J, et al. Bridging physics-based and equivalent circuit models for lithium-ion batteries[J]. Electrochimica Acta, 2021, 372: 137829.
[112] Pang Hui, Jin Jiamin, Wu Longxing, et al. A comprehensive physics-based equivalent-circuit model and state of charge estimation for lithium-ion batteries[J]. Journal of The Electrochemical Society, 2021, 168(9): 090552.
[113] Lai Q, Ahn H J, Kim Y J, et al. New data optimization framework for parameter estimation under uncertainties with application to lithium-ion battery[J]. Applied Energy, 2021, 295: 117034.
[114] Forman J C, Moura S J, Stein J L, et al. Genetic identification and fisher identifiability analysis of the Doyle–Fuller–Newman model from experimental cycling of a LiFePO4 cell[J]. Journal of Power Sources, 2012, 210: 263-275.
[115] Rahman M A, Anwar S, Izadian A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method[J]. Journal of Power Sources, 2016, 307: 86-97.
[116] Deng Zhongwei, Deng Hao, Yang Lin, et al. Implementation of reduced-order physics-based model and multi-parameters identification strategy for lithium-ion battery[J]. Energy, 2017, 138: 509-519.
[117] Ramadesigan V, Chen K, Burns N A, et al. Parameter estimation and capacity fade analysis of lithium-ion batteries using reformulated models[J]. Journal of the Electrochemical Society, 2011, 158(9): A1048.
[118] Xiong Rui, Li Linlin, Li Zhirun, et al. An electrochemical model based degradation state identification method of Lithium-ion battery for all-climate electric vehicles application[J]. Applied energy, 2018, 219: 264-275.
[119] Munoz P M, Humana R M, Falagüerra T, et al. Parameter optimization of an electrochemical and thermal model for a lithium-ion commercial battery[J]. Journal of Energy Storage, 2020, 32: 101803.
[120] Wang Qiankun, Shen Jiani, Ma Zifeng, et al. Decoupling parameter estimation strategy based electrochemical-thermal coupled modeling method for large format lithium-ion batteries with internal temperature experimental validation[J]. Chemical Engineering Journal, 2021, 424: 130308.
[121] Li Zhe, Huan Jun, Liaw Bor Yann, et al. On state-of-charge determination for lithium-ion batteries[J]. Journal of Power Sources, 2017, 348: 281-301.
[122] How D N T, Hannan M A, Hussain LIPU M S, et al. State-of-charge estimation of li-ion battery in electric vehicles: a deep neural network approach[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5565-5574.
[123] 张振宇, 汪光森, 聂世雄, 等.脉冲大倍率放电条件下磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 1769-1779.
Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al. State of charge estimation of LiFePO4 battery under the condition of high rate pulsed discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1769-1779.
[124] Li Weihan, Cao Decheng, Jöst Dominik, et al. Parameter sensitivity analysis of electrochemical model-based battery management systems for lithium-ion batteries[J]. Applied Energy, 2020, 269: 115104.
[125] Plett G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation[J]. Journal of Power Sources, 2004, 134(2): 277-292.
[126] 戴海峰, 孙泽昌, 魏学哲.利用双卡尔曼滤波算法估计电动汽车用锂离子动力电池的内部状态[J]. 机械工程学报, 2009, 45(6): 95-101.
Dai Haifeng, Sun Zechang, Wei Xuezhe. Estimation of internal states of power lithium-ion batteries used on electric vehicles by dual extended Kalman filter[J]. Journal of Mechanical Engineering, 2009, 45(6): 95-101.
[127] Li Wenqian, Yang Yan, Wang Dongqing, et al. The multi-innovation extended Kalman filter algorithm for battery SOC estimation[J]. Ionics, 2020, 26(12): 6145-6156.
[128] Zhou Xin, Stein J L, Ersal T. Battery state of health monitoring by estimation of the number of cyclable Li-ions[J]. Control Engineering Practice, 2017, 66: 51-63.
[129] Santhanagopalan S, White R E. Online estimation of the state of charge of a lithium-ion cell[J]. Journal of Power Sources, 2006, 161(2): 1346-1355.
[130] Smith k A, Rahn C D, Wang C Y. Model-based electrochemical estimation and constraint management for pulse operation of lithium ion batteries[J]. IEEE Transactions on Control Systems Technology, 2010, 18(3): 654-663.
[131] Stetzel K D, Aldrich L L, Trimboli M S, et al. Electrochemical state and internal variables estimation using a reduced-order physics-based model of a lithium-ion cell and an extended Kalman filter[J]. Journal of Power Sources, 2015, 278: 490-505.
[132] Li Huanhuan, Zhang Wang, Yang Xinrong, et al. State of charge estimation for lithium-ion battery using an electrochemical model based on electrical double layer effect[J]. Electrochimica Acta, 2019, 326: 134966.
[133] 徐保荣, 王兴成, 张齐, 等.自适应扩展卡尔曼滤波电池荷电状态估算方法[J]. 哈尔滨工业大学学报,2021,53(7): 92-98.
Xu Baorong, Wang Xingcheng, Zhang Qi, et al. Adaptive extended Kalman filter for estimating the charging state of battery[J]. Jouranl of Harbing Institute of Technology, 2021,53(7): 92-98.
[134] 邓昊, 杨林, 邓忠伟. 基于电化学机理模型的锂离子电池参数辨识及SOC估计[J]. 上海理工大学学报, 2018, (6): 557-565.
Deng Hao, Yang Lin, Deng Zhongwei. Lithium-ion battery parameter identification and SOC estimaiton based on electrochemical models[J]. Journal of University of Shanghai for Science and Technology, 2018, (6): 557-565.
[135] Lü Chao, Li Junfu, Zhang Lulu, et al. State of charge estimation based on a thermal coupling simplified first-principles model for lithium-ion batteries[J]. Journal of Energy Storage, 2019, 25: 100838.
[136] Fan Guodong, Li Xiaoyu, Zhang Ruigang.Global sensitivity analysis on temperature-dependent parameters of a reduced-order electrochemical model and robust state-of-charge estimation at different temperatures[J]. Energy, 2021, 223: 120024.
[137] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceeding of the IEEE, 2004, 92(3): 401-422.
[138] 谈发明, 赵俊杰, 王琪.动力电池SOC估计的一种新型鲁棒UKF算法[J]. 汽车工程, 2019, 41(8): 944-952.
Tan Faming, Zhao Junjie, Wang Qi. A novel robust UKF algorithm for SOC estiamtion of traction battery[J]. Automotive Engineering, 2019, 41(8):944-952.
[139] Lin Xinyou, Tang Yunliang, Ren Jin, et al. State of charge estimation with the adaptive unscented Kalman filter based on an accurate equivalent circuit model[J]. Journal of Energy Storage, 2021, 41: 102840.
[140] 董祥祥, 武鹏, 葛传久, 等.基于自适应无迹卡尔曼滤波的锂电池荷电状态估计[J]. 电工电能新技术, 2021, 40(2): 58-65.
Dong Xiangxiang, Wu Peng, Ge Chuanjiu, et al. State of charge estimation of Li-ion battery based on adaptive unscented Kalman filter[J]. Adanced Technology of Electrical Engineering and Energy, 2021, 40(2): 58-65.
[141] Santhanagopalan S, White R E. State of charge estimation using an unscented filter for high power lithium ion cells[J]. International Journal of Energy Research, 2010, 34(2): 152-163.
[142] Ringbeck F, Garbade M, Sauer D U. Uncertainty-aware state estimation for electrochemical model-based fast charging control of lithium-ion batteries[J]. Journal of Power Sources, 2020, 470: 228221.
[143] Marelli S, Corno M. Model-based estimation of lithium concentrations and temperature in batteries using soft-constrained dual unscented Kalman Filtering[J]. IEEE Transactions on Control Systems Technology, 2020, 29(2): 926-933.
[144] Feng Fei, Teng Sangli, Liu Kailong, et al. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model[J]. Journal of Power Sources, 2020, 455: 227935.
[145] Sun Changcheng, Lin Huiping, Cai Hui, et al. Improved parameter identification and state-of-charge estimation for lithium-ion battery with fixed memory recursive least squares and sigma-point Kalman filter[J]. Electrochimica Acta, 2021, 387: 138501
[146] Li Di, Ouyang Jian, LI Huiqi, et al. State of charge estimation for LiMn2O4 power battery based on strong tracking sigma point Kalman filter[J]. Journal of Power Sources, 2015, 279: 439-449.
[147] Plett G L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1: Introduction and state estimation[J]. Journal of Power Sources, 2006, 161(2): 1369-1384.
[148] Smiley A, Plett G L. An adaptive physics-based reduced-order model of an aged lithium-ion cell, selected using an interacting multiple-model Kalman filter[J]. Journal of Energy Storage, 2018, 19: 120-134.
[149] Bi Yalan, Choe S Y. An adaptive sigma-point Kalman filter with state equality constraints for online state-of-charge estimation of a Li(NiMnCo)O2/Carbon battery using a reduced-order electrochemical model[J]. Applied Energy, 2020, 258: 113925.
[150] 王学远, 李日康, 魏学哲, 等.基于传荷电阻的锂离子电池剩余寿命预测研究[J]. 机械工程学报, 2021, 57(14): 105-117.
Wang Xueyuan, Li Rikang, Wei Xuezhe, et al. Study on remaining useful life prediction of lithium-ion batteries based on charge transfer resistance[J].Journal of Mechanical Engineering, 2021, 57(14): 105-117.
[151] 焦自权, 范兴明, 张鑫, 等.基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J]. 电工技术学报, 2020, 35(18): 3979-3993.
Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tarcking and remaining useful life predictive method of Li-ion battery based on improved particle filter algorithm.[J]. Transactions of China Electrotechnical Society,2020, 35(18): 3979-3993.
[152] Wang Yujie, Zhang Chenbin, Chen Zhonghai. A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle filter[J]. Journal of power sources, 2015, 279: 306-311.
[153] Samadi m F, Alavi S M M, Saif M. An electrochemical model-based particle filter approach for Lithium-ion battery estimation[C]//Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 2012: 3074-3079.
[154] Tulsyan A, Tsai Y, Gopaluni R B, et al. State-of-charge estimation in lithium-ion batteries: a particle filter approach[J]. Journal of Power Sources, 2016, 331: 208-223.
[155] Bartlett A, Marcicki J, Onori S, et al. Electrochemical model-based state of charge and capacity estimation for a composite electrode lithium-ion battery[J]. IEEE Transactions on Control Systems Technology, 2015, 24(2): 384-399.
[156] 宋宇, 孙富春, 李庆玲. 移动机器人的改进无迹粒子滤波蒙特卡罗定位算法[J]. 自动化学报, 2010, 36(06): 851-857.
Song Yu, Sun Fuchun, Li Qingling. Mobile robot Monte Carlo localization based on improved unscented particle filter[J]. Acta Automatica Sinica, 2010, 36(6): 851-857.
[157] Wang Yujie, Chen Zhonghai. A framework for state-of-charge and remaining discharge time prediction using unscented particle filter[J]. Applied Energy, 2020, 260: 114324.
[158] Fan Guodong. Systematic parameter identification of a control-oriented electrochemical battery model and its application for state of charge estimation at various operating conditions[J]. Journal of Power Sources, 2020, 470: 228153.
[159] Li Xiaoyu, Huang Zhijia, Tian Jindong, et al.State-of-charge estimation tolerant of battery aging based on a physics-based model and an adaptive cubature Kalman filter[J]. Energy, 2021, 220: 119767.
[160] Chandra Shekar A, Anwar S. Real-time state-of-charge estimation via particle swarm optimization on a lithium-ion electrochemical cell model[J]. Batteries, 2019, 5(1): 4.
[161] Zheng Yuejiu, Ouyang Minggao, Han Xuebing, et al. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles[J]. Journal of Power Sources, 2018, 377: 161-188.
[162] Snoussi J, Ben ElghalI S, Zerrougui M, et al. Unknown input observer design for lithium-ion batteries SOC estimation based on a differential-algebraic model[J]. Journal of Energy Storage, 2020, 32: 101973.
[163] Waag W, Fleischer C, Sauer D U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles[J]. Journal of Power Sources, 2014, 258:321-339.
[164] 张云,张承慧,崔纳新.锂离子电池荷电状态估计:非线性观测器方法[J].控制理论与应用,2012, 12: 1639-1644.
Zhang Yun, Zhang Chenghui, Cui Naxin. Estimaiton of state of charge of lithium-ion battery: nonlinear observer method[J]. Control Theory & Application, 2012, 12: 1639-1644.
[165] Hu Xiaosong, Sun Fengchun, Zou Yuan. Estimation of state of charge of a lithium-ion battery pack for electric vehicles using an adaptive luenberger observer[J]. Energies, 2010, 3(9): 1586-1603.
[166] Afri C, Andrieu V, Bako L, et al. State and parameter estimation: a nonlinear luenberger observer approach[J]. IEEE Transactions on Automatic Control, 2017, 62(2): 973-980.
[167] Lotfi N, Landers R G, Li Jie, et al. Reduced-order electrochemical model-based SOC observer with output model uncertainty estimation[J]. IEEE Transactions on Control Systems Technology, 2017, 25(4): 1217-1230.
[168] Ren Lichao, Zhu Guorong, Kang Jianqiang, et al. An algorithm for state of charge estimation based on a single-particle model[J]. Journal of Energy Storage, 2021, 39: 102644.
[169] 何洪文, 熊瑞.基于滑模观测器的锂离子动力电池荷电状态估计[J]. 吉林大学学报(工学版), 2011, 41(3): 623-628.
He Hongwen, Xiong Rui. State of charge estiamiton of lithium-ion power battery suing sliding mode observer[J]. Jouranal of Jilin University (Engineering and Technology Edition), 2011, 41(3): 623-628.
[170] Kim I S. The novel state of charge estimation method for lithium battery using sliding mode observer[J]. Journal of Power Sources, 2006, 163(1): 584-590.
[171] Ahmed R, EL Sayed M, Arasaratnam I, et al. Reduced-order electrochemical model parameters identification and state of charge estimation for healthy and aged li-ion batteries—aged battery model and state of charge estimation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(3): 678-690.
[172] Lin Cheng, Tang Aihua, Xing Jilei. Evaluation of electrochemical models based battery state-of-charge estimation approaches for electric vehicles[J]. Applied Energy, 2017, 207: 394-404.
[173] Allam A, Onori S. An interconnected observer for concurrent estimation of bulk and surface concentration in the cathode and anode of a lithium-ion battery[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7311-7321.
[174] Klein R, Chaturvedi N A, Christensen J, et al. Electrochemical model based observer design for a lithium-ion battery[J]. IEEE Transactions on Control Systems Technology, 2013, 21(2): 289-301.
[175] Moura S J, Chaturvedi N A, Krstic M. Adaptive partial differential equation observer for battery state-of-charge/state-of-health estimation via an electrochemical model[J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(1): 011015.
[176] Tang Shuxia, Camacho-Solorio L, Wang Yebin, et al. State-of-charge estimation from a thermal–electrochemical model of lithium-ion batteries[J]. Automatica, 2017, 83: 206-219.
[177] Chen Guangwei, Liu Zhitao, Su Hongye, et al. Electrochemical-distributed thermal coupled model-based state of charge estimation for cylindrical lithium-ion batteries[J]. Control Engineering Practice, 2021, 109: 104734.
[178] Johansson A, Medvedev A. An observer for systems with nonlinear output map[J]. Automatica, 2003, 39(5): 909-918.
[179] Xia Bizhong, Chen Chaoren, Tian Yong, et al.A novel method for state of charge estimation of lithium-ion batteries using a nonlinear observer[J]. Journal of Power Sources, 2014, 270: 359-366.
[180] Dey S, Ayalew B, Pisu P. Nonlinear robust observers for state-of-charge estimation of lithium-ion cells based on a reduced electrochemical model[J]. IEEE Transactions on Control Systems Technology, 2015, 23(5): 1935-1942.
[181] Liu Yuntian, Ma Rui, Pang Shengzhao, et al.A nonlinear observer soc estimation method based on electrochemical model for lithium-ion battery[J]. IEEE Transactions on Industry Applications, 2020, 57(1): 1094-1104.
[182] Li Junfu, Lai Qingzhi, Wang Lixin, et al.A method for SOC estimation based on simplified mechanistic model for LiFePO4 battery[J]. Energy, 2016, 114: 1266-1276.
[183] Bi Yalan, Zhao Xinchen, Choe Song-Yul A hybrid state of charge estimation method of a LiFePO4/graphite cell using a reduced order model with an extended Kalman filter[C]//American Control Conference (ACC), Philadelphia, USA, 2019: 3155-3160.
[184] Liu Lihua, Zhu Jianguo, Zheng Linfeng. An Effective Method for Estimating State of Charge of Lithium-Ion Batteries Based on an Electrochemical Model and Nernst Equation[J]. IEEE Access, 2020, 8: 211738-211749.
[185] Li Weihan, Zhang Jiawei, Ringbeck Florian, et al. Physics-informed neural networks for electrode-level state estimation in lithium-ion batteries[J]. Journal of Power Sources, 2021, 506: 230034.
[186] Lin Xinfan, Kim Y, Mohan S, et al. Modeling and estimation for advanced battery management[J]. Annual Review of Control, Robotics, and Autonomous Systems, 2019, 2: 393-426.
A Review of SOC Estimation Methods for Lithium-Ion Batteries Based on Electrochemical Model
Abstract Accurate state of charge (SOC) estimation is one of the important functions for battery management system. Currently, the model-based approach is the most widely used solution for lithium-ion battery SOC estimation. Compared with the equivalent circuit model (ECM), the electrochemical model (EM) has gradually become the research focus of the next generation advanced battery management systems due to its ability to estimate the SOC coupled with electrochemical mechanism. However, the existing review studies of the model-based battery SOC estimation methods are mostly focused on ECMs, and the EMs are rarely discussed systematically. For this reason, the EM-based SOC estimation algorithms are reviewed in this paper. First, the modeling and parameter identification methods of EMs are summarized, and the existing approaches to EM-based SOC estimation are discussed. Then, existing challenges and the future prospects of the EM-based SOC estimation are presented. The insights presented in this paper are expected to catalyze the development and application of the EM-based advanced battery management system algorithms.
Keywords: Lithium-ion batteries, state of charge, electrochemical model, battery management system
DOI:10.19595/j.cnki.1000-6753.tces.211030
中图分类号:TM912
武龙星 男,1988年生,博士研究生,研究方向为车用动力电池电化学机理建模及状态估计。E-mail:batterywu@163.com
庞 辉 男,1980年生,博士,副教授,研究方向为车辆动力学与控制理论、新能源车用动力电池/超级电池管理。E-mail:huipang@163.com(通信作者)
收稿日期 2021-07-12
改稿日期 2021-09-07
国家自然科学基金资助项目(51675423)。
(编辑 郭丽军)