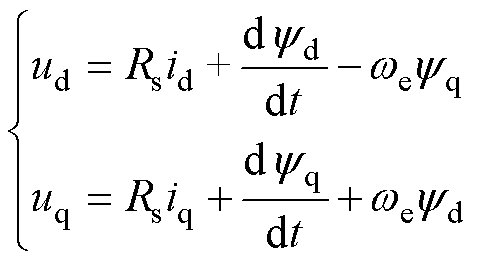 (1)
(1)
摘要 占空比模型预测转矩控制通过优化有效电压矢量的占空比来减小转矩脉动,然而要得到最优有效电压矢量需要进行6次预测,计算量较大,而且第二个电压矢量只能是零矢量,导致转矩脉动仍较大。该文提出一种基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制策略,为了最大限度地降低控制复杂度并减小计算量,设计一种新型开关表,两个有效电压矢量将从开关表中选择,同时提出一种新的占空比计算方法,以期实现转矩与磁链的无差拍控制。实验结果表明,与占空比模型预测转矩控制相比,该文所提方法可以有效减小转矩脉动,实现稳态性能的改善。
关键词:永磁同步电机 模型预测转矩控制 电压矢量 三矢量 新型开关表
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有效率高、功率因数高等优点,被广泛应用于工农业生产、航天航空等诸多领域[1-4]。矢量控制和直接转矩控制作为电机调速领域的两种典型控制方法[5-6],被广泛研究和应用。矢量控制通过将定子电流分解成dq轴分量,并采用比例积分控制器对其进行控制,从而达到线性控制的目的,能够实现良好的稳态性能,但其动态特性受到内部电流环带宽的限制。直接转矩控制根据转矩和定子磁链误差信号以及定子磁链矢量的位置[7],直接从开关表中选择合适电压矢量作用于逆变器,具有控制结构简单、动态响应快等优点,但存在稳态转矩和磁链脉动较大的缺点。目前,学术界提出了多种改进算法来改善传统矢量控制和直接转矩控制方法,以期实现更好的控制效果[8-9]。
近年来,模型预测转矩控制(Model Predictive Torque Control, MPTC)作为一种有效的电机驱动控制方法,受到了越来越多的青睐[10-12]。在MPTC方法中,基于电机逆变器固有的离散性,预测各个电压矢量作用下电机的未来状态,然后设计由预测状态误差(如转矩和定子磁链误差)组成的价值函数,通过最小化价值函数选择下一控制周期的最优电压矢量。MPTC方法的结构简单,能够直接产生作用于逆变器的控制信号,不需要调制器,与直接转矩控制相比,其选择的电压矢量更为准确[13]。然而,在传统MPTC控制方法中,整个控制周期只作用一个电压矢量,即占空比为1,存在转矩与定子磁链脉动较大、开关频率不稳定等问题,无法满足永磁同步电机调速系统不断增长的对转矩和磁链的控制要求。此外,通过对所有电压矢量遍历来选择最优电压矢量,需要进行大量计算,特别是当候选电压矢量较多,如多电平逆变器[14]及多步预测[15]等,会大大增加硬件的计算负担。
为了进一步提高MPTC的控制性能,文献[16-18]将占空比控制引入MPTC,提出了占空比模型预测转矩控制(Duty cycle Model Predictive Torque Control, Duty-MPTC),其在一个控制周期内作用两个电压矢量,即一个有效电压矢量、一个零矢量。选择使价值函数最小的有效电压矢量作为最优电压矢量,然后根据转矩无差拍原理确定一个控制周期内最优电压矢量的作用时间,其余时间作用零矢量。Duty-MPTC控制虽然能够降低电机稳态运行时的转矩脉动,但仍存在不足。首先,这种电压矢量选择和电压矢量作用时间的级联处理不能保证最优矢量和零矢量组合在整个控制周期内是最佳组合。为了解决这个问题,文献[18]使用一个有效电压矢量和一个零矢量的组合代替单个矢量,通过价值函数直接确定矢量组合和矢量持续时间,即使采样频率降低了一半,其在低速时的转矩脉动仍能得到很好抑制。然而,在文献[16, 18]中,第二个电压矢量固定为零矢量,一定程度上限制了稳态性能的改善能力。因此,文献[19]将第二个电压矢量从零矢量扩展到非零电压矢量,通过价值函数对25种电压矢量组合进行循环寻优,能够提高控制系统的稳态性能,但控制算法变得复杂繁琐。此外,文献[20]则通过无差拍方法选择最优电压矢量,为了降低逆变器的开关频率,第二个电压矢量是在最优电压矢量相邻的两个基本矢量与零矢量之间选择,但在计算各个电压矢量的作用时间时只考虑了转矩而忽略了磁链控制。文献[21-23]提出了一种三矢量模型预测的控制方法来改善双矢量模型预测控制的稳态性能,文献[21]在每个扇区用相邻的两个有效电压矢量和零矢量合成一个虚拟电压矢量,由于两电平逆变器有6个扇区,因此可以合成6个虚拟电压矢量,并通过价值函数循环寻优6次选择最优虚拟电压矢量,虽然提高了稳态性能,但6个虚拟电压矢量的选择较为复杂,控制器耗时过多;文献[23]提出了一种双优化三矢量模型预测电流控制方法,该方法在每个采样周期均作用两个有效电压矢量和一个零矢量,但两个有效电压矢量均为遍历寻优所得,第1个有效电压矢量需要寻优6次,第二个有效电压矢量需要寻优5次,有效电压矢量筛选复杂,计算量增加,对硬件要求较高。
为了改善上述Duty-MPTC控制策略的不足,本文提出了一种基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制(Three Vector Model Predictive Torque Control, TV-MPTC)策略。为了快速筛选电压矢量,减小计算量,设计了一种新型开关表,只需要根据转矩误差以及定子磁链矢量所在扇区,就可以从新型开关表中直接选择两个有效电压矢量Vopt1和Vopt2,简化了电压矢量的选取过程,通过合理分配两个有效电压矢量以及零矢量在一个控制周期内的占空比,以实现转矩与磁链的同时无差拍控制。仿真和实验结果均表明,与Duty-MPTC相比,本文所提方法能够在保持动态性能的情况下,有效减小转矩脉动。
本文以表贴式永磁同步电机作为研究对象,为了简化分析,假设永磁同步电机的三相绕组完全对称,不考虑涡流损耗和磁滞损耗,则其在两相旋转dq坐标系下的电压方程可表示为
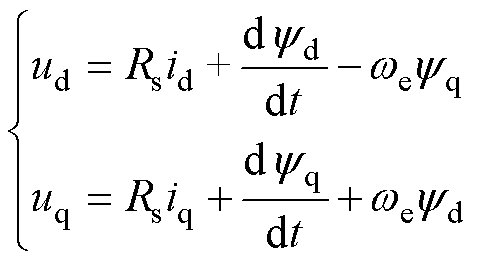 (1)
(1)
式中,ud、uq分别为定子电压在d、q轴的分量;id、iq分别为定子电流在d、q轴的分量;yd、yq分别为定子磁链在d、q轴的分量;Rs为定子电阻;we为电机转子电角速度。此时,磁链方程可表示为
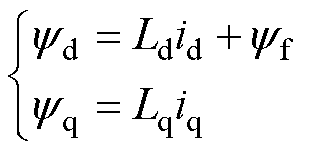 (2)
(2)
式中,Ld、Lq分别为定子电感在d、q轴的分量;yf为永磁磁链。
永磁同步电机的电磁转矩方程可表示为
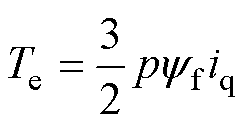 (3)
(3)
式中,Te为电磁转矩;p为电机极对数。
永磁同步电机Duty-MPTC是在传统MPTC基础上引入零电压矢量发展起来的,其将一个控制周期分成两部分,一部分时间施加有效电压矢量,剩余时间施加零矢量,通过调节占空比的大小,可以等效为改变有效电压矢量的幅值。因此,相对于传统MPTC控制,Duty-MPTC可以有效减小转矩脉动,其整体控制原理框图如图1所示。
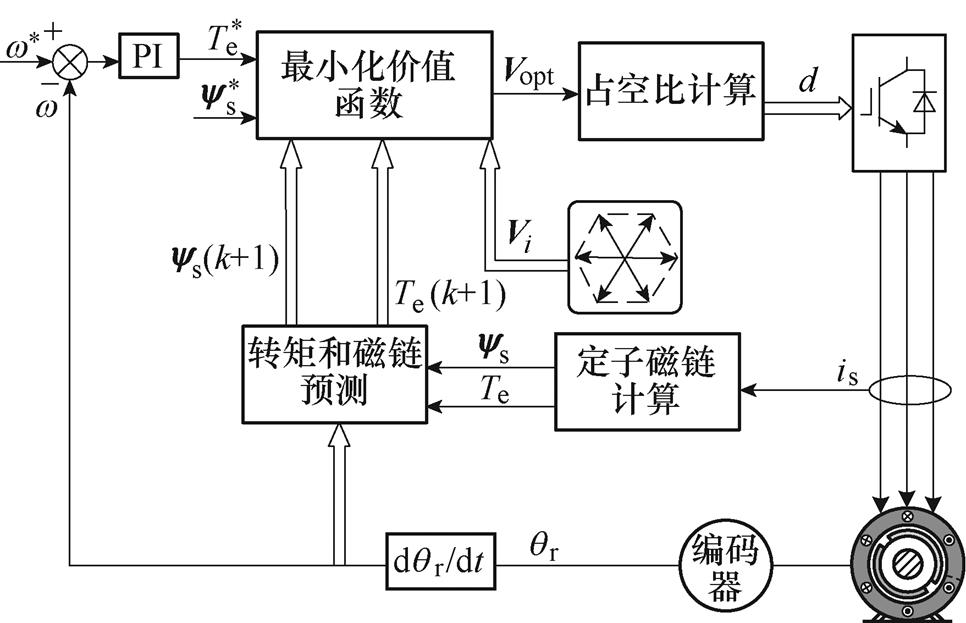
图1 Duty-MPTC原理框图
Fig.1 Control diagram of Duty-MPTC method
应用一阶欧拉公式对表贴式永磁同步电机的数学模型进行离散化,可得k+1时刻定子磁链的预测方程为
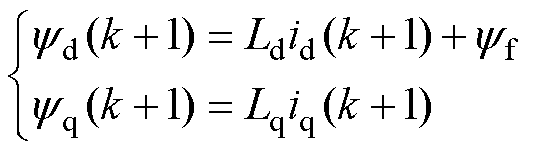 (4)
(4)
式中,yd(k+1)、yq(k+1)分别为k+1时刻定子磁链在d、q轴的分量;id(k+1)、iq(k+1)分别为k+1时刻定子电流在d、q轴的分量。k+1时刻的电磁转矩预测方程为
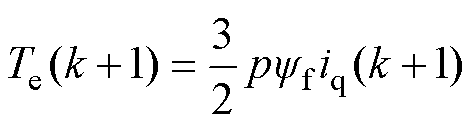 (5)
(5)
其中
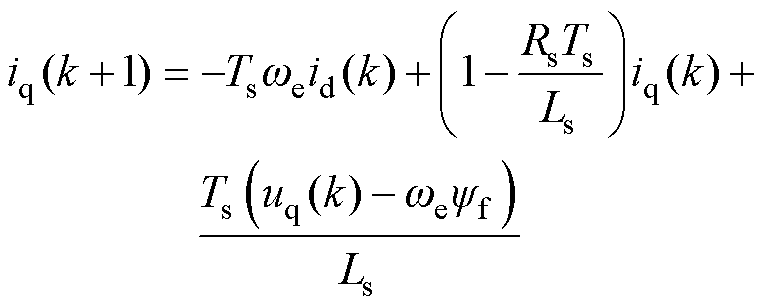 (6)
(6)
式中,id(k)、iq(k)分别为k时刻定子电流在d、q轴的分量;uq(k)为k时刻定子电压在q轴上的分量;Ls为定子电感;Ts为采样周期。
三相两电平电压源型逆变器可以提供8个基本电压矢量,包含6个有效电压矢量以及两个零矢量,电压矢量和扇区划分如图2所示。Duty-MPTC策略通常以转矩和磁链作为控制目标,将转矩和磁链的预测值与给定值代入价值函数中,选取令价值函数最小的电压矢量作为最优电压矢量,常用的价值函数g构造为
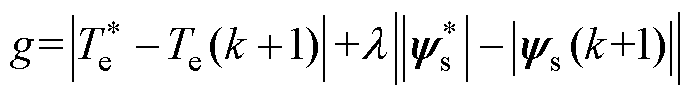 (7)
(7)
式中,l 为定子磁链项的权重系数; 与
与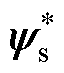 分别为电磁转矩与定子磁链的给定值;
分别为电磁转矩与定子磁链的给定值;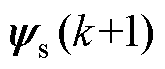 为k+1时刻定子磁链。
为k+1时刻定子磁链。
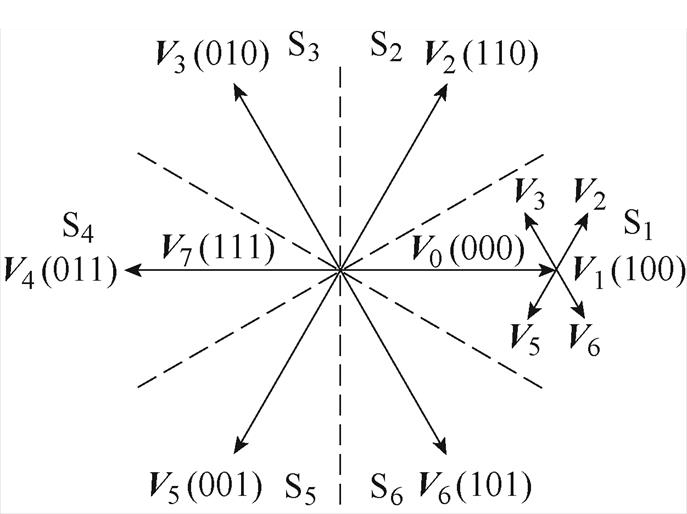
图2 两电平逆变器的电压矢量示意图
Fig.2 Basic voltage vector of two-level inverter
由于定子磁链和转矩的数量级不同,需要设计合适的权重系数来获得满意的控制性能。但到目前为止,权重系数的设计需要反复的调节,缺乏必要的理论指导。因此,本文采用一种取消权重系数的价值函数,通过分析电机转矩与定子磁链矢量的内在关系,可以把对转矩与定子磁链幅值的控制转化为对定子磁链矢量的控制,从而取消了价值函数中权重系数的设计。将定子磁链幅值|ys|和负载角d 作为控制变量,转矩可以表示为
 (8)
(8)
式中,d 为负载角,是磁链ys(k)与d轴之间的角度。
将式(8)对d求导可以得到转矩的微分方程为
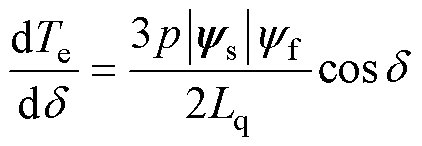 (9)
(9)
将式(9)改写为增量形式并整理后得到
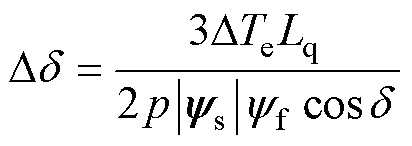 (10)
(10)
式中,Dd 为负载角增量;DTe为电磁转矩增量。
因此,k+1时刻负载角d 的参考值为
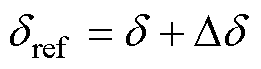 (11)
(11)
根据式(4)、式(10)和式(11)可以得到k+1时刻参考定子磁链在d、q轴上的分量分别为
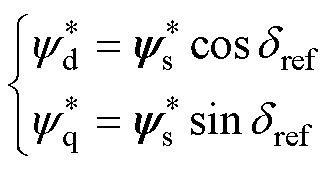 (12)
(12)
基于以上分析,可以构建取消权重系数的价值函数J为
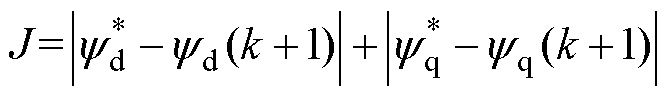 (13)
(13)
三相两电平电压源型逆变器可以提供8个基本电压矢量,包含6个有效电压矢量和两个零矢量,电压矢量和扇区划分如图2所示。有效电压矢量的占空比d可通过转矩无差拍原理得到,即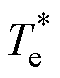 = Te(k+1)。当零矢量和有效电压矢量Vi应用于永磁同步电机时,转矩变化率s0和si分别表示为
= Te(k+1)。当零矢量和有效电压矢量Vi应用于永磁同步电机时,转矩变化率s0和si分别表示为
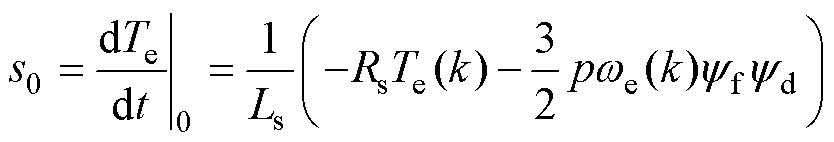 (14)
(14)
 (15)
(15)
利用转矩无差拍原理可得
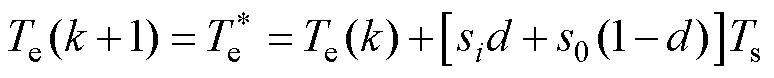 (16)
(16)
则有效电压矢量Vi在一个控制周期内的占空比d可表示为
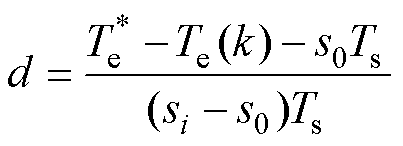 (17)
(17)
分别计算6个有效电压矢量的占空比,并通过预测模型预测k+1时刻的定子磁链,然后通过价值函数式(13)选择使价值函数最小的电压矢量及其占空比,作用于下一控制周期。
本节将从定子磁链矢量和负载角的角度,对PMSM传统模型预测转矩控制的转矩脉动进行定性分析。对于表贴式永磁同步电机,其电磁转矩Te可用定子和转子磁链的幅值来表示,有
 (18)
(18)
对式(18)求导可得
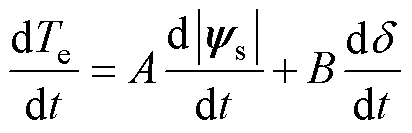 (19)
(19)
其中
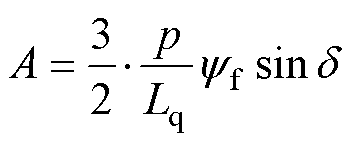 (20)
(20)
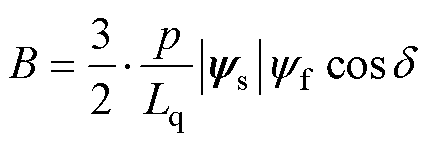 (21)
(21)
离散化后,一个控制周期内转矩变化量可表示为
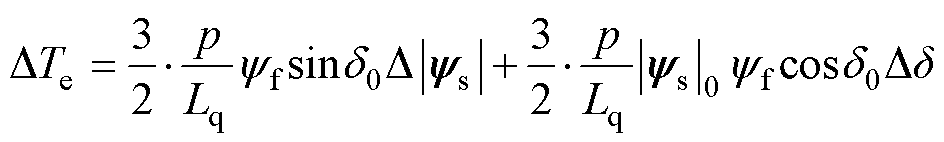 (22)
(22)
式中, 、
、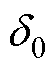 分别为初始时刻的定子磁链幅值与负载角。
分别为初始时刻的定子磁链幅值与负载角。
忽略定子电阻压降,则定子磁链矢量增量与电压矢量的关系可表示为
Dys=usTs (23)
此时,负载角的变化量可表示为
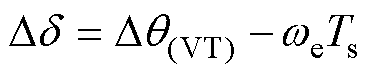 (24)
(24)
式中,Dq(VT)为在一个控制周期内电压矢量Vi(i=0, 1,…, 7)作用下的定子磁链角度变化量。假设定子磁链矢量ys位于第一扇区,电压矢量对转矩和定子磁链的作用如图3所示,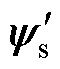 、
、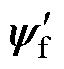 分别为在电压矢量V2作用下的下一采样周期的定子磁链矢量与永磁磁链矢量。从图3可以看出,由电压矢量V2引起的定子磁链角度变化量Dq(VT)与Ts近似成正比,负载角变化量Dd 同样与Ts近似成正比。因此,根据式(22)~式(24)可知,转矩变化量与采样周期近似成正比,即转矩脉动将随采样频率的降低而增大。在传统的MPTC中,最优电压矢量作用于整个控制周期,当采样频率较低时,转矩脉动也会相应变大。因此,为了在较低的采样频率下抑制传统MPTC中的转矩脉动,在一个控制周期内添加零矢量来调节有效电压矢量的作用时间,可以减小转矩脉动,这就是Duty-MPTC的基本控制思想。
分别为在电压矢量V2作用下的下一采样周期的定子磁链矢量与永磁磁链矢量。从图3可以看出,由电压矢量V2引起的定子磁链角度变化量Dq(VT)与Ts近似成正比,负载角变化量Dd 同样与Ts近似成正比。因此,根据式(22)~式(24)可知,转矩变化量与采样周期近似成正比,即转矩脉动将随采样频率的降低而增大。在传统的MPTC中,最优电压矢量作用于整个控制周期,当采样频率较低时,转矩脉动也会相应变大。因此,为了在较低的采样频率下抑制传统MPTC中的转矩脉动,在一个控制周期内添加零矢量来调节有效电压矢量的作用时间,可以减小转矩脉动,这就是Duty-MPTC的基本控制思想。
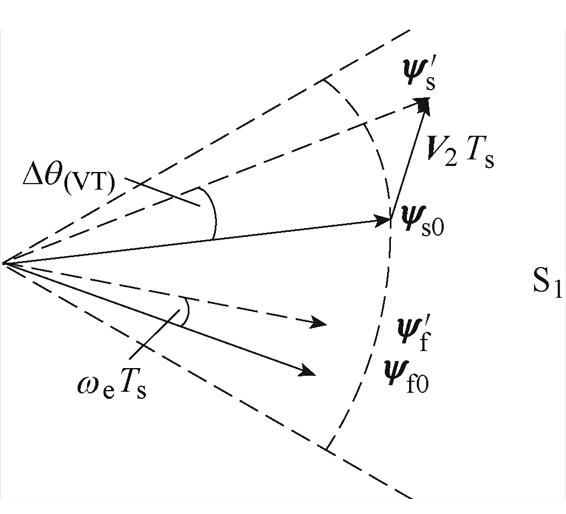
图3 电压矢量对转矩和定子磁链的作用
Fig.3 Effect of voltage vector on torque and stator flux-linkage
但是,由于Duty-MPTC中第二个电压矢量只能是零矢量,因此Duty-MPTC策略中所选有效电压矢量和零矢量的组合不一定是减小转矩脉动的全局最优电压矢量组合。针对这一问题,本文提出一种基于电压矢量快速筛选的TV-MPTC策略,该策略首先根据转矩误差及定子磁链矢量所在扇区,通过新型开关表来选择两个合适的有效电压矢量;然后采用转矩和磁链无差拍原理计算各个电压矢量的占空比;最后在一个控制周期内作用3个电压矢量对电机进行控制,以实现转矩脉动的进一步抑制。
为了快速地选择电压矢量,设计了一种输出多个电压矢量组合而非单个电压矢量的新型开关表,见表1,两个有效电压矢量Vopt1和Vopt2将同时从 新型开关表中选择。开关表的输入是定子磁链矢量所在的扇区以及转矩滞环比较器的输出值ct。表1中V1~V6表示6个有效电压矢量,S1~S6表示1~6号扇区,ct值为1表示增大转矩、为0表示减小转矩。
表1 新型开关
Tab.1 New switching

ct值定子磁链所在扇区 S1S2S3S4S5S6 ct=1V2(110)V3(010)V4(011)V5(001)V6(101)V1(100) V3(010)V4(011)V5(001)V6(101)V1(100)V2(110) ct=0V5(001)V6(101)V1(100)V2(110)V3(010)V4(011) V6(101)V1(100)V2(110)V3(010)V4(011)V5(001)
接下来将解释如何构造新型开关表。假设永磁同步电机转子逆时针旋转,定子磁链位于第一扇区。在这种情况下,应用电压矢量V2(110)将同时增大电磁转矩和定子磁链幅值;应用电压矢量V5(001)时,两者都会减小;应用电压矢量V3(010)将增大电磁转矩,减小定子磁链幅值;而电压矢量V6(101)与V3(010)的作用相反。零矢量V0(000)和V7(111)都会减小电磁转矩,而使定子磁链幅值基本不变。实际上,无论定子磁链偏差符号是什么,本文所提出的有效电压矢量选择方法只涉及转矩偏差。例如,当转矩偏差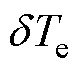 >0时,有效电压矢量的选择如图4所示,有效电压矢量V2和V3对转矩的作用效果相同,都能提高转矩,但对定子磁链的作用效果相反。因此,不管定子磁链幅值是需要增大还是减小,只需合理分配V2、V3以及零矢量在一个控制周期内的占空比,就可以达到转矩与磁链的无差拍控制,从而降低转矩脉动,此时的电压矢量作用效果如图5a所示。当转矩偏差
>0时,有效电压矢量的选择如图4所示,有效电压矢量V2和V3对转矩的作用效果相同,都能提高转矩,但对定子磁链的作用效果相反。因此,不管定子磁链幅值是需要增大还是减小,只需合理分配V2、V3以及零矢量在一个控制周期内的占空比,就可以达到转矩与磁链的无差拍控制,从而降低转矩脉动,此时的电压矢量作用效果如图5a所示。当转矩偏差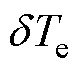 <0时,将从开关表中选择可以减小转矩的电压矢量,有效电压矢量V5、V6都能减小转矩,同时对定子磁链的作用效果相反。因此,通过合理地分配V5和V6以及零矢量在一个控制周期内的占空比,就可以减小转矩与磁链误差,此时的电压矢量作用效果如图5b所示。
<0时,将从开关表中选择可以减小转矩的电压矢量,有效电压矢量V5、V6都能减小转矩,同时对定子磁链的作用效果相反。因此,通过合理地分配V5和V6以及零矢量在一个控制周期内的占空比,就可以减小转矩与磁链误差,此时的电压矢量作用效果如图5b所示。
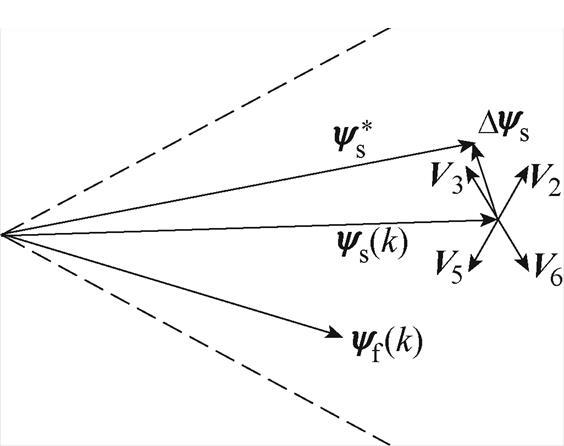
图4 有效电压矢量的选择(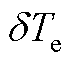 >0)
>0)
Fig.4 Selection of active voltage vectors (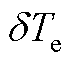 >0)
>0)
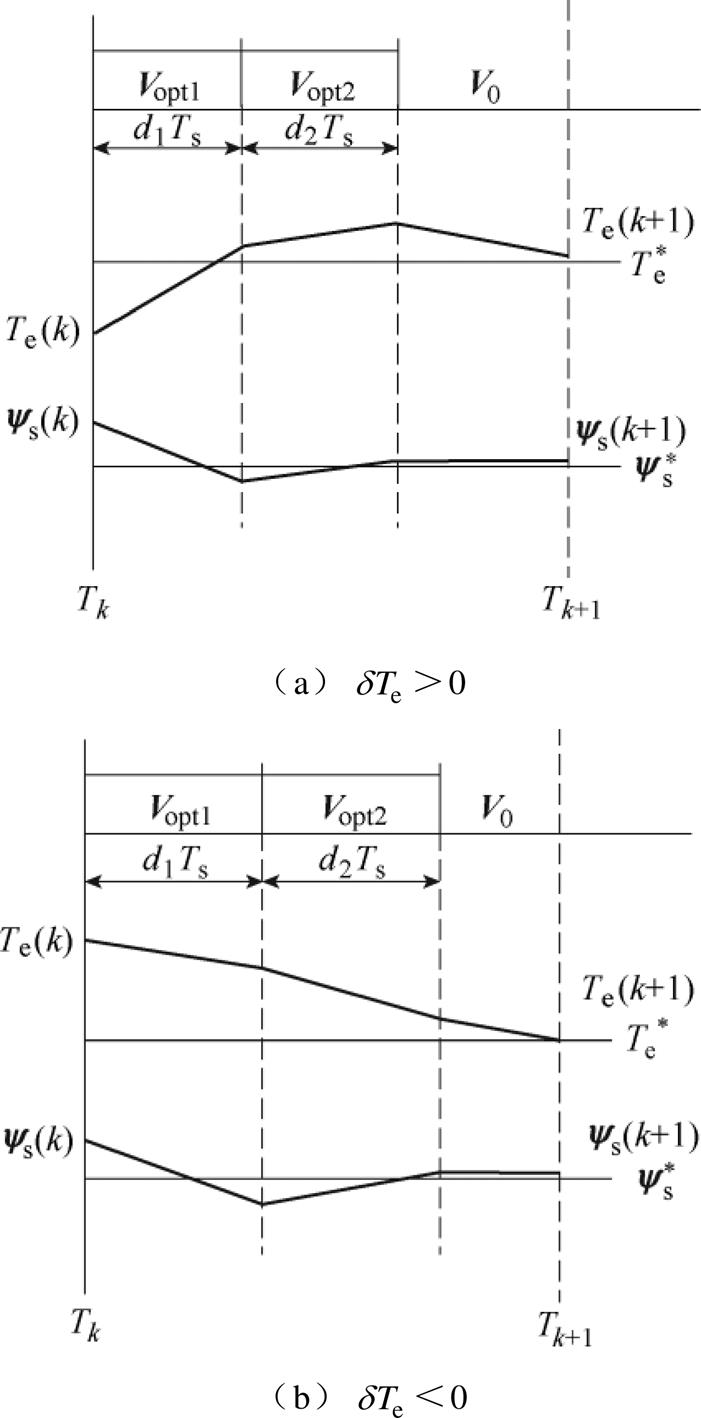
图5 电压矢量作用示意图
Fig.5 Schematic diagram of voltage vector function
通过新型开关表选出合适的电压矢量组合后,一个控制周期内作用两个有效矢量(Vopt1、Vopt2)和一个零矢量来控制PMSM,定义第一个有效电压矢量Vopt1的占空比为d1,第二个有效电压矢量Vopt2的占空比为d2,零矢量的占空比为1-d1-d2。为了有效降低转矩脉动,同时兼顾磁链脉动的抑制,提出了一种基于转矩和磁链差值参数的占空比计算方法。转矩和磁链差值参数定义为
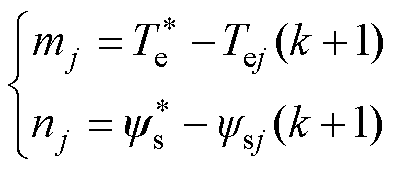 (25)
(25)
式中,mj和nj分别为定义的转矩和磁链差值参数。
两个有效电压矢量占空比的计算基于转矩和磁链无差拍原理,即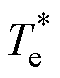 =Te(k+1),
=Te(k+1),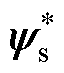 =ys(k+1),由此可得
=ys(k+1),由此可得
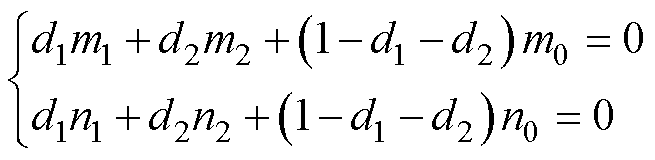 (26)
(26)
式中,m1、m2、m0分别为两个有效电压矢量Vopt1、Vopt2和零矢量V0作用下的转矩差值参数;n1、n2、n0分别为两个有效电压矢量Vopt1、Vopt2和零矢量V0作用下的磁链差值参数。
根据式(26)可以得出d1、d2的计算公式为
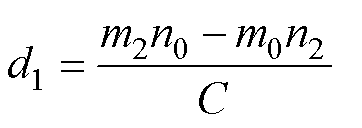 (27)
(27)
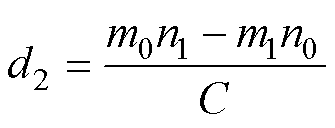 (28)
(28)
其中
C=m1(n2-n0)+m2(n1-n0)+m0(n1-n2)
本文提出的基于电压矢量快速筛选的永磁同步电机TV-MPTC策略以转矩误差及定子磁链矢量所在扇区为依据,通过新型开关表查表的方法快速选择电压矢量,一个控制周期内作用3个电压矢量,并且提出了一种新型的占空比计算方法,同时兼顾了转矩和磁链的无差拍控制。相较于Duty-MPTC策略,所提出的TV-MPTC策略扩大了电压矢量的选择范围,能够进一步抑制转矩脉动,其原理框图如图6所示。
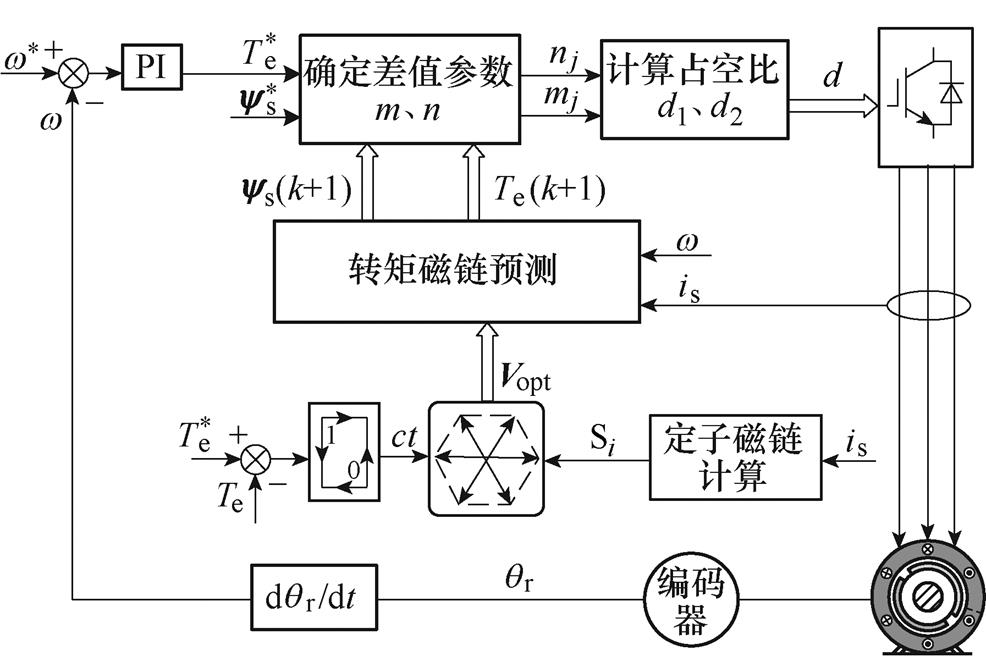
图6 基于电压矢量快速筛选的TV-MPTC原理框图
Fig.6 Control diagram of voltage vector rapid screening-based TV-MPTC
为验证提出的基于电压矢量快速筛选的TV- MPTC策略的有效性,通过Matlab/Simulink对Duty- MPTC策略和TV-MPTC策略进行了对比仿真分析,仿真中的PMSM参数见表2。为了公平比较,Duty- MPTC策略的采样频率设置为20kHz,TV-MPTC策略的采样频率为10kHz。仿真结果如图7~图9所示,波形从上到下依次是转速、电磁转矩和单相定子电流。
首先比较了Duty-MPTC策略和本文所提出的TV-MPTC策略的稳态性能。图7所示为给定转速200r/min、负载转矩为5N·m时,两种控制策略在低速运行下的稳态波形。通过对比图7a、图7b可以看出,相较于Duty-MPTC策略,本文提出的TV-MPTC策略可以有效减小转矩脉动,且在电流质量方面表现更好,其中,Duty-MPTC的电流波形总谐波畸变率(Total Harmonic Distortion, THD)为8.65%,而TV-MPTC的电流波形THD为6.13%。为了进一步分析比较两种控制策略的稳态性能,图8给出两种控制策略在高速800r/min运行情况下的稳态波形。通过图8a、图8b的对比分析可得,TV-MPTC策略有效减小了转矩脉动,且电流谐波含量更少,仅为7.32%,而Duty-MPTC电流THD为10.67%。结合上述仿真分析可得,相比于Duty-MPTC策略,本文提出的TV-MPTC策略具有更好的稳态性能。
表2 永磁同步电机参数
Tab.2 Specifications of the PMSM motor

参 数数 值 极对数p4 永磁磁链yf/Wb0.269 定子电阻Rs/W1.45 定子电感Ls/mH5.05 额定转速nN/(r/min)1 000 额定转矩Te/(N·m)5 转动惯量J/(kg·m2)0.002 77

(a)Duty-MPTC

(b)TV-MPTC
图7 低速稳态仿真波形(200r/min、5N·m)
Fig.7 Steady-state waveforms at low speed (200r/min, 5N·m)
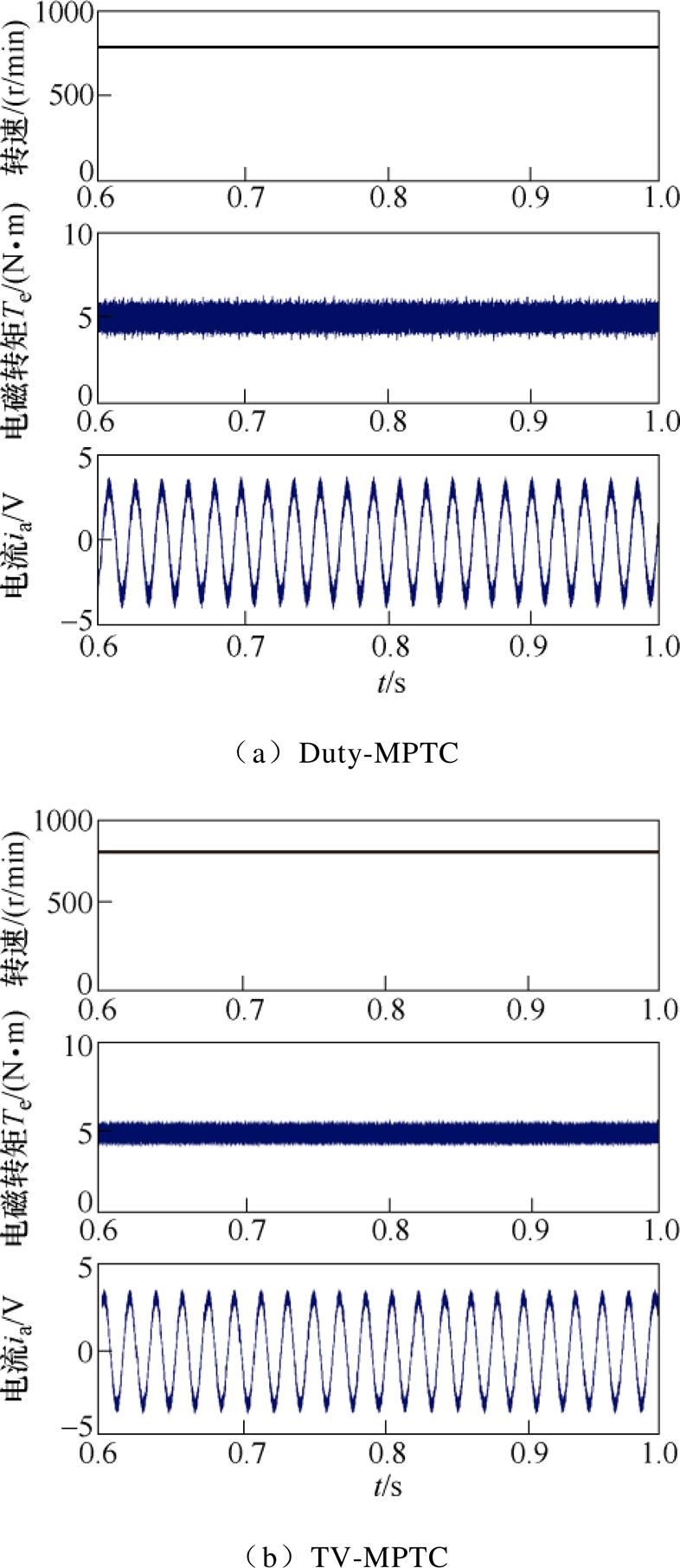
图8 高速稳态仿真波形(800r/min、5N·m)
Fig.8 Steady-state waveforms at high speed (800r/min, 5N·m)
此外,图9所示为两种控制策略的动态性能仿真对比,图示波形的工况条件为:电机在空载情况下由静止加速到500r/min,在0.15s时由空载突加5N·m负载,在0.3s时由5N·m负载突减至空载运行。对比图9a、图9b可知,TV-MPTC和Duty-MPTC具有相似的转速响应性能。在负载突变时,两种控制策略的转速略有波动,但都能够快速跟踪到给定转速,且电流波形在保持良好正弦度的同时能够快速响应转矩的突变,并且所提出的TV-MPTC策略具有更低的转矩波动。

图9 动态仿真波形
Fig.9 Dynamic simulation waveforms
为了验证本文所提出的基于电压矢量快速筛选的永磁同步电机TV-MPTC策略的可行性与有效性,搭建了基于dSPACE1103的永磁同步电机控制实验平台,如图10所示,主要包括dSPACE1103控制器、两电平逆变器、信号调理电路、IGBT驱动电路、永磁同步电机、磁粉制动器以及编码器等。为了更好地验证所提控制策略的有效性,本文将所提TV- MPTC与现有的Duty-MPTC进行了实验对比分析。因为Duty-MPTC一个控制周期作用两个电压矢量,TV-MPTC一个控制周期作用3个电压矢量,为了公平比较,实验中Duty-MPTC的采样频率设置为20kHz,TV-MPTC的采样频率设置为10kHz,用于实验验证的永磁同步电机参数见表2。

图10 实验平台
Fig.10 Experiment platform
图11所示为Duty-MPTC与所提出的TV-MPTC在永磁同步电机带5N·m负载稳定运行于低速200r/min时的稳态实验波形。图11a、图11b中从上到下依次为转速、转矩、单相电流波形。其中,在20kHz采样频率下,Duty-MPTC的平均开关频率为8.23kHz,在10kHz采样频率下,TV-MPTC的平均开关频率为6.35kHz。为了更直观地比较分析,本文采用标准差来衡量这两种控制策略下的转矩脉
动,转矩脉动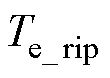 的计算公式为
的计算公式为
 (29)
(29)
其中
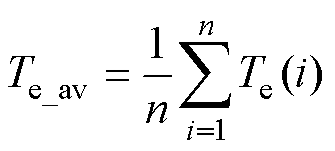
式中,n为存储采样点的个数,是从示波器中保存的实验数值得到的。根据转矩标准差计算公式可以计算出两种控制策略在额定负载5N·m下稳定运行于200r/min时的转矩脉动大小。其中,Duty-MPTC的转矩脉动为0.224N·m,基于电压矢量快速筛选的TV-MPTC的转矩脉动为0.178N·m,与Duty-MPTC相比,本文所提出的TV-MPTC控制使得转矩脉动减小了20.5%。稳态实验波形如图12所示。为了进一步比较分析两种控制策略的稳态性能,对两种控制策略的定子电流谐波进行分析,相电流THD分析(200r/min、5N·m)如图13所示。其中,Duty-MPTC的定子电流THD为10.13%,而TV-MPTC的定子电流THD仅为5.14%。上述分析结果表明,相比于Duty-MPTC,本文所提出的基于电压矢量快速筛选的TV-MPTC在低速时具有更好的稳态性能。

图11 稳态实验波形(200r/min、5N·m)
Fig.11 Measured steady results (200r/min, 5N·m)
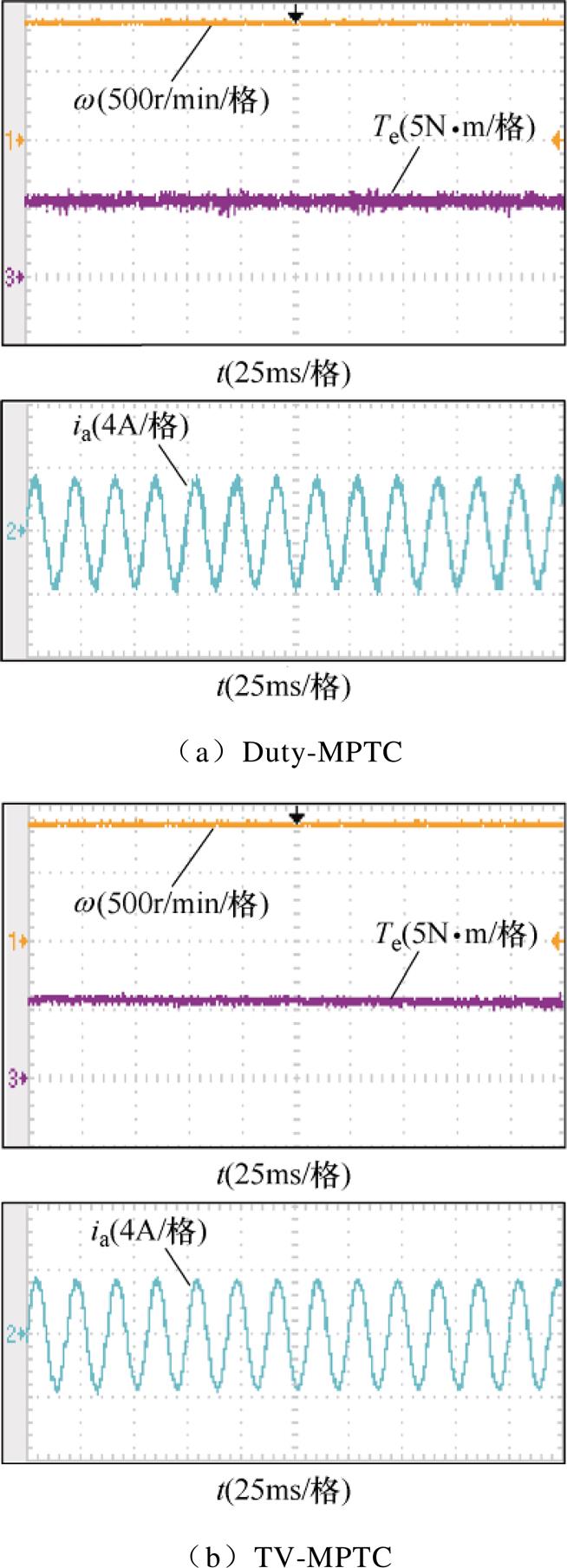
图12 稳态实验波形(800r/min、5N·m)
Fig.12 Measured steady results (800r/min, 5N·m)
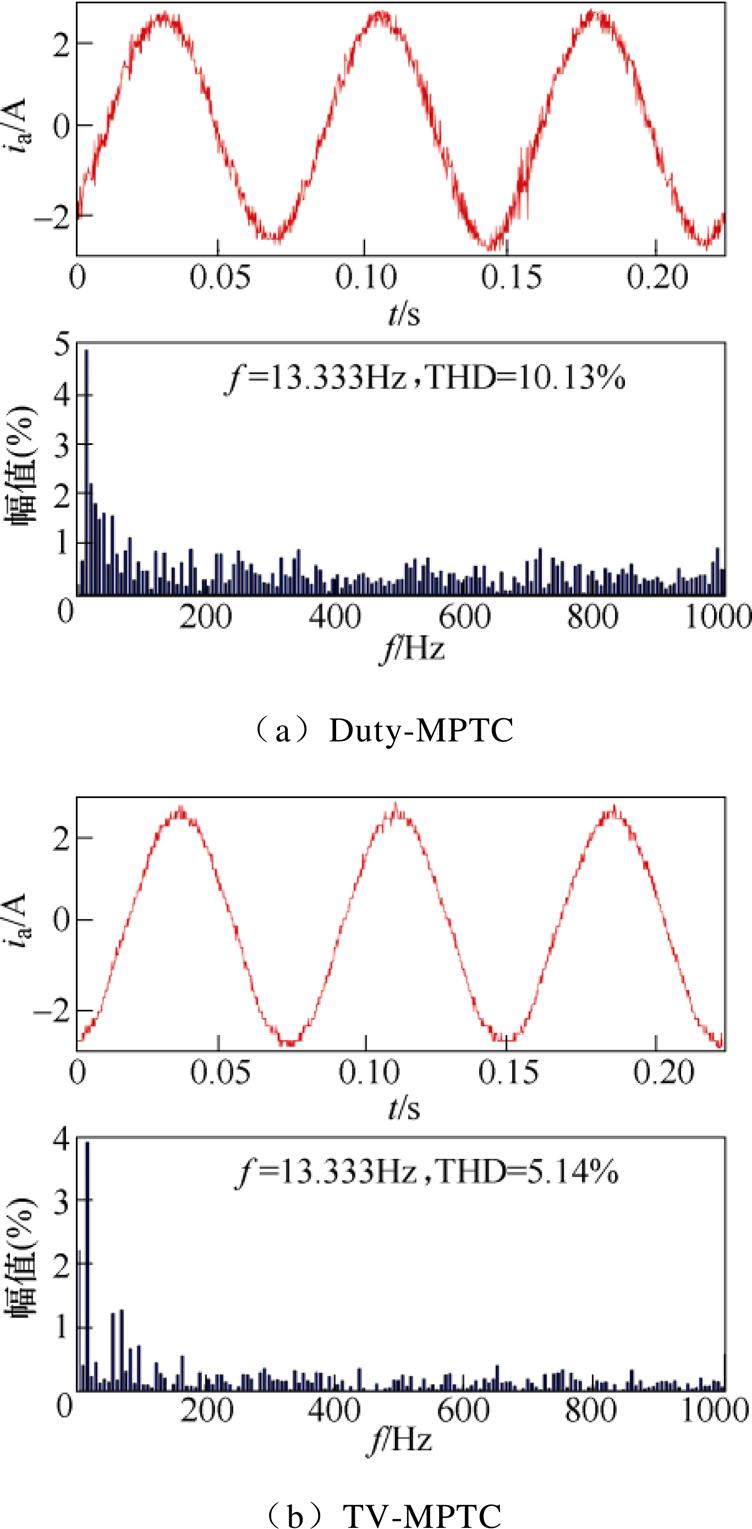
图13 电流THD分析(200r/min、5N·m)
Fig.13 Current THD analysis (200r/min, 5N·m)
此外,图12所示为两种控制策略在5N·m负载下稳定运行于高速800r/min时的稳态实验波形。不难发现,基于电压矢量快速筛选的TV-MPTC具有更小的转矩脉动。图14所示为两种控制策略的电流谐波分析,其中,Duty-MPTC的定子电流THD为12.93%,而TV-MPTC的定子电流THD仅为6.28%,TV-MPTC策略明显降低了谐波含量,改善了波形输出质量。实验结果表明,与Duty-MPTC相比,本文所提出的基于电压矢量快速筛选的TV-MPTC在高速下具有更好的稳态性能。
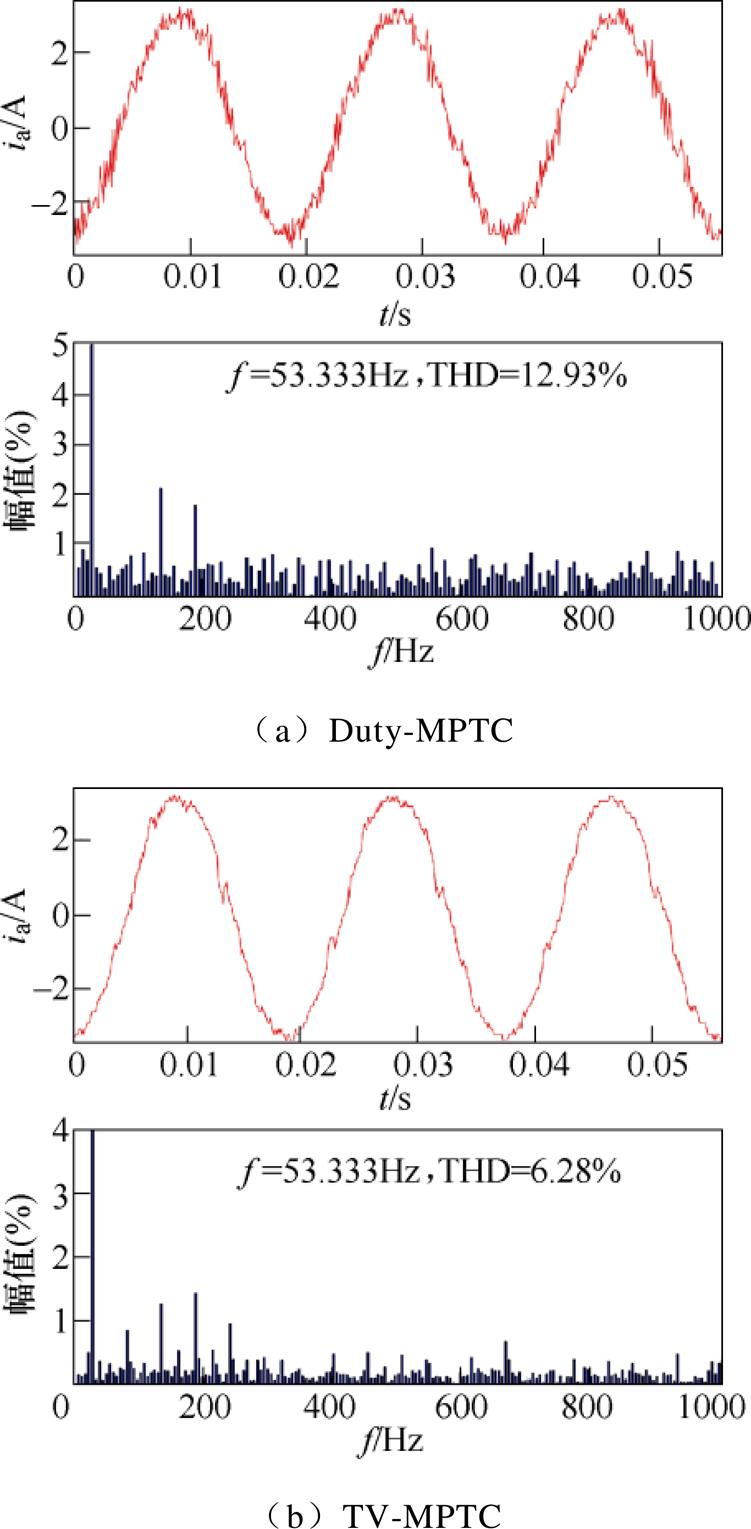
图14 电流THD分析(800r/min、5N·m)
Fig.14 Current THD analysis (800r/min, 5N·m)
为验证本文所提控制策略的动态性能,图15a、图15b分别给出了Duty-MPTC与TV-MPTC策略下永磁同步电机空载起动至给定转速500r/min时的实验波形。实验结果表明,TV-MPTC与Duty-MPTC策略均能实现平稳的起动,起动过程中转速基本无超调,并且基于电压矢量快速筛选的TV-MPTC策略具有更低的转矩脉动。
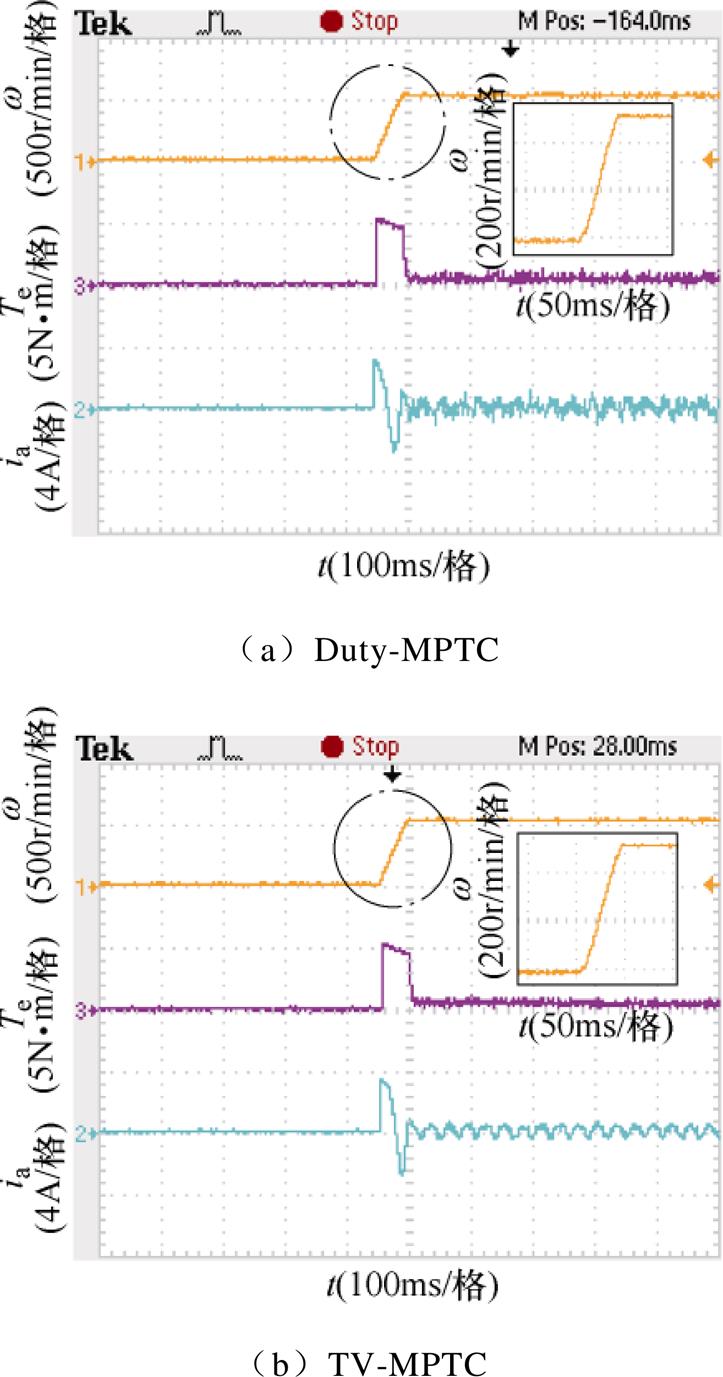
图15 空载起动实验波形
Fig.15 Measured starting results
图16a、图16b所示为Duty-MPTC与TV-MPTC策略下,在电机带5N·m负载稳定运行于500r/min时,负载突减至0N·m时的实验波形。从图16可以看出,在负载突变后,两种控制策略的转速经过轻微波动后可以迅速跟随给定值,两种控制策略下转矩动态响应时间基本相同,表明所提出的基于电压矢量快速筛选的TV-MPTC策略具有良好的动态转矩跟随性能,并且具有更小的转矩脉动与更平滑的电流波形。
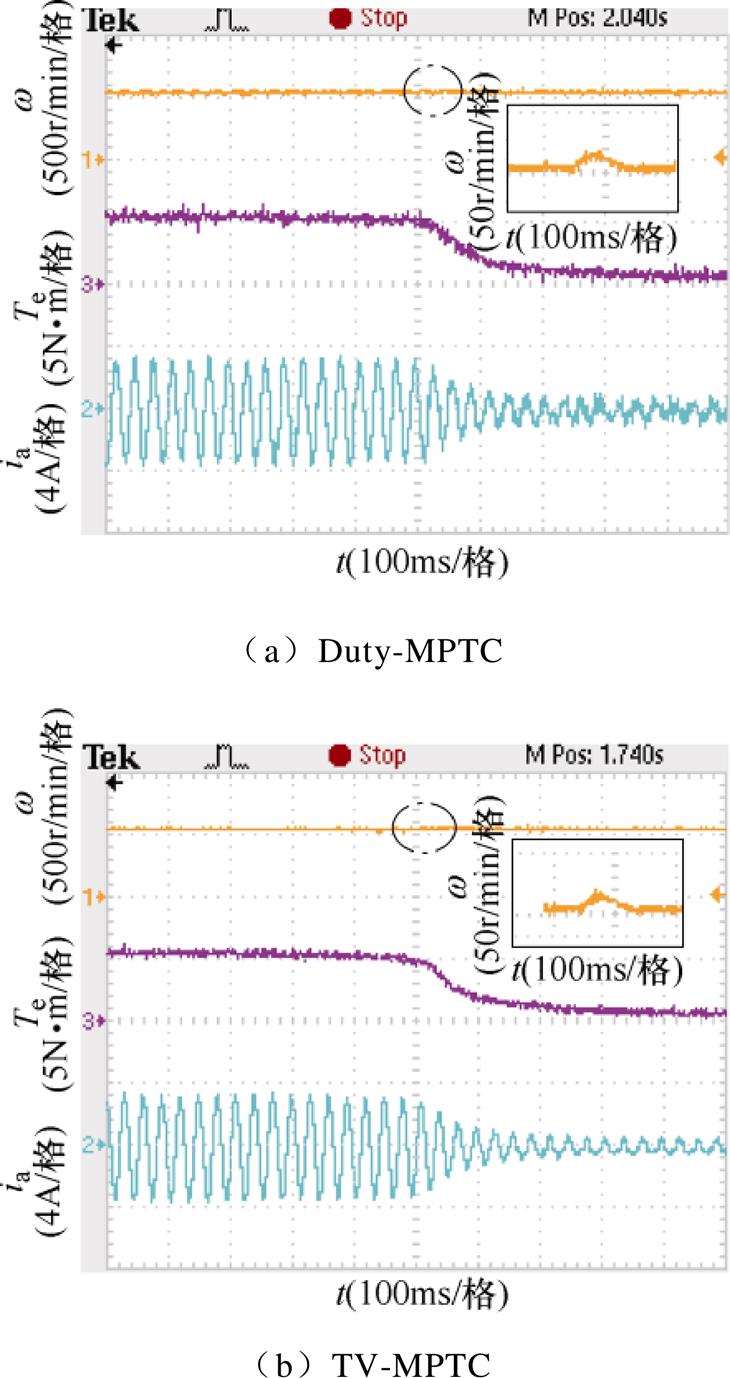
图16 突减负载实验波形
Fig.16 Measured dynamic results of sudden-decreased load
为了验证基于电压矢量快速筛选的TV-MPTC策略的参数鲁棒性,将电阻参数增加20%,电感参数减小20%,并进行了实验。图17为在参数失配情况下,电机带额定负载分别运行于200r/min和800r/min时的实验波形。通过对比无参数失配情况下的实验波形(见图11b和图12b),本文提出的TV-MPTC策略在参数变化前后可以保持类似的控制性能,参数在一定范围内变化,对电机的转矩和电流等影响不大,因此本文提出的TV-MPTC策略具有良好的参数鲁棒性。
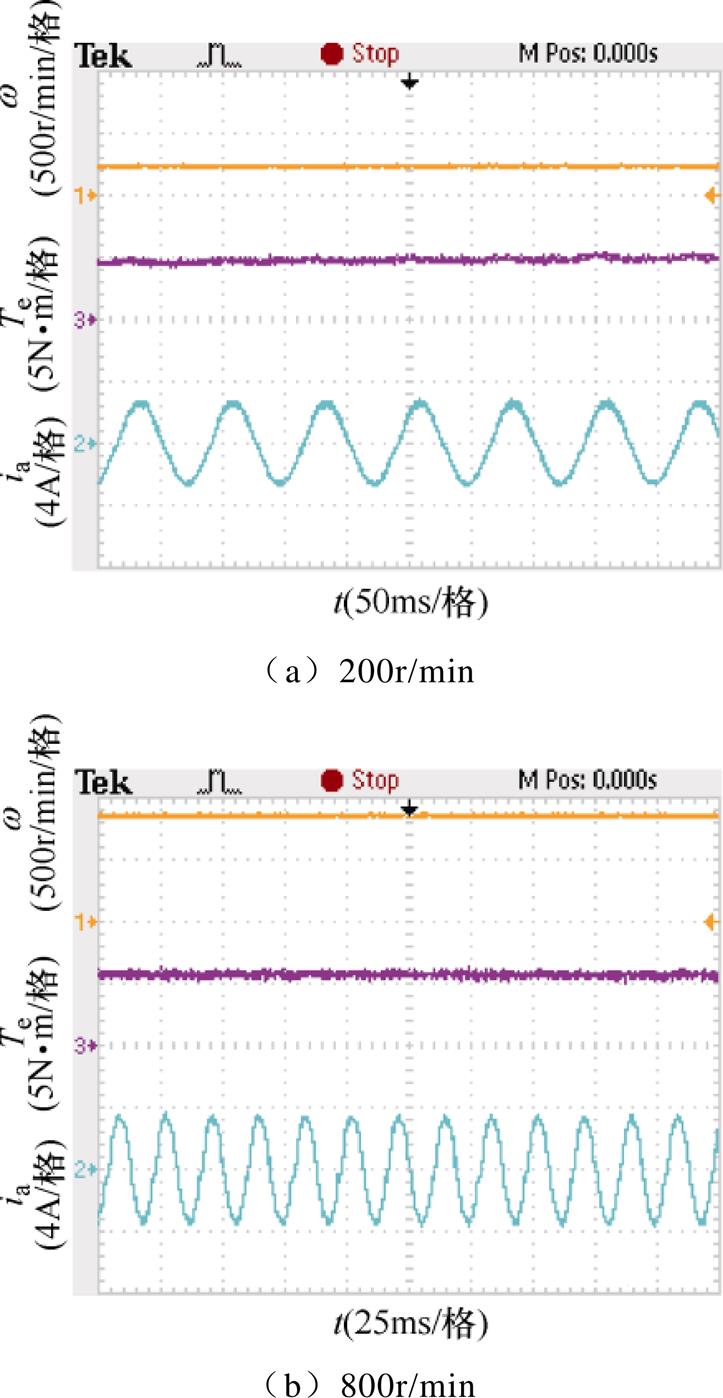
图17 参数失配情况下稳态实验波形(TV-MPTC)
Fig.17 Measured steady results with mismatched parameters (TV-MPTC)
通过实验比较了两种控制策略的计算量,见 表3。在dSPACE控制系统中,Turnaround time作为计算复杂度的度量,其包括dSPACE与控制台之间的通信时间、A-D转换时间、代码实现时间以及数据保存时间,可以直接从dSPACE的控制台中读取。通过表3可知,Duty-MPTC策略的计算时间为28.5ms,而基于电压矢量快速筛选的TV-MPTC策略的计算时间为13.8ms。这表明基于电压矢量快速筛选的TV-MPTC策略能够显著减少算法计算时间,有利于提高控制系统的实用性。
表3 不同控制策略的计算量
Tab.3 Computation burden of different control strategies

控制策略计算时间/ms Duty-MPTC28.5 TV-MPTC13.8
本文针对Duty-MPTC策略下永磁同步电机转矩脉动较大的问题,提出一种基于电压矢量快速筛选的TV-MPTC策略。与Duty-MPTC相比,本文所提出的TV-MPTC可以快速地通过新型开关表直接选择两个有效电压矢量,简化了电压矢量的选取过程,一定程度上降低了控制算法的复杂度,并采用转矩和磁链无差拍原理来计算各个电压矢量在一个控制周期内的作用时间,能够实现对转矩和磁链的综合控制。通过实验分析可得,相比于Duty-MPTC策略,本文所提出的基于电压矢量快速筛选的TV- MPTC策略在稳态下能有效降低电流谐波含量以及转矩脉动,同时具有良好的参数鲁棒性;在转速或转矩突变时,保持快速动态响应的同时,具有更好的稳态性能。
本文所提出的基于电压矢量快速筛选的TV- MPTC策略是以直接转矩控制为基础,同时结合模型预测控制的一种新型控制策略,不仅可以应用于表贴式永磁同步电机,同样可以应用于内置式永磁同步电机;同时,由于该策略具有良好的稳态控制性能以及较低的控制复杂度,因此非常适用于永磁同步电机伺服驱动系统以及直驱应用场合。
参考文献
[1] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[2] 徐奇伟, 孙静, 杨云, 等. 用于混合动力车的复合结构永磁电机电磁优化设计[J]. 电工技术学报, 2020, 35(增刊1): 126-135.
Xu Qiwei, Sun Jing, Yang Yun, et al. Electromagnetic optimization design of compound-structure permanent- magnet motor for hybrid electric vehicle[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S1): 126-135.
[3] 刘细平, 胡卫平, 丁卫中, 等. 永磁同步电机多参数辨识方法研究[J]. 电工技术学报, 2020, 35(6): 1198-1207.
Liu Xiping, Hu Weiping, Ding Weizhong, et al. Research on multi-parameter identification method of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(6): 1198-1207.
[4] 李祥林, 李金阳, 杨光勇, 等. 电励磁双定子场调制电机的多目标优化设计分析[J]. 电工技术学报, 2020, 35(5): 972-982.
Li Xianglin, Li Jinyang, Yang Guangyong, et al. Multi-objective optimization analysis of electric- excitation double-stator field-modulated machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 972-982.
[5] Casadei D, Profumo F, Serra G, et al. FOC and DTC: two viable schemes for induction motors torque control[J]. IEEE Transactions on Power Electronics, 2002, 17(5): 779-787.
[6] Wang Zheng, Chen Jian, Cheng Ming, et al. Field- oriented control and direct torque control for paralleled VSIs fed PMSM drives with variable switching frequencies[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2417-2428.
[7] 吕帅帅, 林辉, 马冬麒. 基于最优占空比调制的永磁同步电机直接转矩控制[J]. 电工技术学报, 2015, 30(增刊1): 35-42.
Lü Shuaishuai, Lin Hui, Ma Donglin. Direct torque control for permanent magnet synchronous motor with optimal duty cycle control[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 35-42.
[8] Zhang Yongchang, Zhu Jianguo. A novel duty cycle control strategy to reduce both torque and flux ripples for DTC of permanent magnet synchronous motor drives with switching frequency reduction[J]. IEEE Transactions on Power Electronics, 2011, 26(10): 3055-3067.
[9] Akrem A M, Pillay P. Novel flux linkage estimation algorithm for a variable flux PMSM[J]. IEEE Transa- ctions on Industry Applications, 2018, 54(3): 2319- 2335.
[10] Zhou Zhanqing, Xia Changliang, Yan Yan, et al. Torque ripple minimization of predictive torque control for PMSM with extended control set[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 6930-6939.
[11] 张晓光, 张亮, 侯本帅. 永磁同步电机优化模型预测转矩控制[J]. 中国电机工程学报, 2017, 37(16): 4800-4809.
Zhang Xiaoguang, Zhang Liang, Hou Benshuai. Improved model predictive torque control of per- manent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(16): 4800-4809.
[12] Wang Fengxiang, Li Shihua, Mei Xuezhu, et al. Model-based predictive direct control strategies for electrical drives: an experimental evaluation of PTC and PCC methods[J]. IEEE Transactions on Industrial Informatics, 2015, 11(3): 671-681.
[13] 张永昌, 杨海涛, 魏香龙. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-73.
Zhang Yongchang, Yang Haitao, Wei Xianglong. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-73.
[14] 夏长亮, 张天一, 周湛清, 等. 结合开关表的三电平逆变器永磁同步电机模型预测转矩控制[J]. 电工技术学报, 2016, 31(20): 83-92.
Xia Changliang, Zhang Tianyi, Zhou Zhanqing, et al. Model predictive torque control with switching table for neutral point clamped three-level inverter-fed permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(20): 83-92.
[15] Tobias G, Quevedo D E. Performance of multi-step finite control set model predictive control for power electronics[J]. IEEE Transactions on Power Electro- nics, 2015, 30(3): 1633-1644.
[16] Davari S A, Khaburi D A, Kennel R. An improved FCS-MPC algorithm for an induction motor with an imposed optimized weighting factor[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(3): 1540-1551.
[17] Zhang Xiaoguang, Hou Benshuai. Double vectors model predictive torque control without weighting factor based on voltage tracking error[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2368-2380.
[18] Zhang Yongchang, Yang Haitao. Model predictive torque control of induction motor drives with optimal duty cycle control[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6593-6603.
[19] Zhang Yongchang, Yang Haitao. Generalized two- vector-based model-predictive torque control of induction motor drives[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3818-3829.
[20] Zhang Yongchang, Yang Haitao. Two-vector-based model predictive torque control without weighting factors for induction motor drives[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(2): 1381-1390.
[21] 徐艳平, 王极兵, 张保程, 等. 永磁同步电机三矢量模型预测电流控制[J]. 电工技术学报, 2018, 33(5): 980-988.
Xu Yanping, Wang Jibing, Zhang Baocheng, et al. Three-vector-based model predictive current control for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(5): 980-988.
[22] Wang Xiaohe, Sun Dan. Three-vector-based low- complexity model predictive direct power control strategy for doubly fed induction generators[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 773-782.
[23] 徐艳平, 王极兵, 周钦, 等. 永磁同步电动机双优化三矢量模型预测电流控制[J]. 中国电机工程学报, 2018, 38(6): 1857-1864, 1923.
Xu Yanping, Wang Jibing, Zhou Qin, et al. Double optimization three-vector-based model predictive current control for permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2018, 38(6): 1857-1864, 1923.
Voltage Vector Rapid Screening-Based Three-Vector Model Predictive Torque Control for Permanent Magnet Synchronous Motor
Abstract The torque ripple can be reduced in the duty cycle model predictive torque control (Duty-MPTC) by optimizing the duty cycle of the active voltage vector. However, obtaining the optimal active voltage vector needs six predictions, which requires a large amount of calculation, and the torque ripple is still large since the second voltage vector in the conventional Duty-MPTC can only be a zero vector. Therefore, in this paper, a new voltage vector rapid screening-based three-vector model predictive torque control (TV-MPTC) for permanent magnet synchronous motor (PMSM) is proposed. In order to minimize the control complexity and reduce the amount of calculation, the two active voltage vectors are selected directly from the new switching table. Also, a new duty cycle calculation method is proposed to achieve the deadbeat control of torque and flux. The experimental results show that compared with the Duty-MPTC method, the proposed TV-MPTC method can effectively reduce the torque ripple, thereby improving the steady-state performance.
keywords:Permanent magnet synchronous motor, model predictive torque control, voltage vector, three-vector, new switching table
DOI: 10.19595/j.cnki.1000-6753.tces.201232
中图分类号:TM351
李祥林 男,1984年生,博士,教授,博士生导师,研究方向为新型永磁电机系统设计分析及其控制等。E-mail: lxllcc@126.com(通信作者)
薛志伟 男,1995年生,硕士研究生,研究方向为永磁同步电机先进控制策略等。E-mail: zhiweixue0503@163.com
收稿日期 2020-09-18
改稿日期 2020-11-11
国家自然科学基金(51877215, 51777216)和山东省自然科学基金(ZR2021YQ33, ZR2019MEE094)资助项目。
(编辑 崔文静)