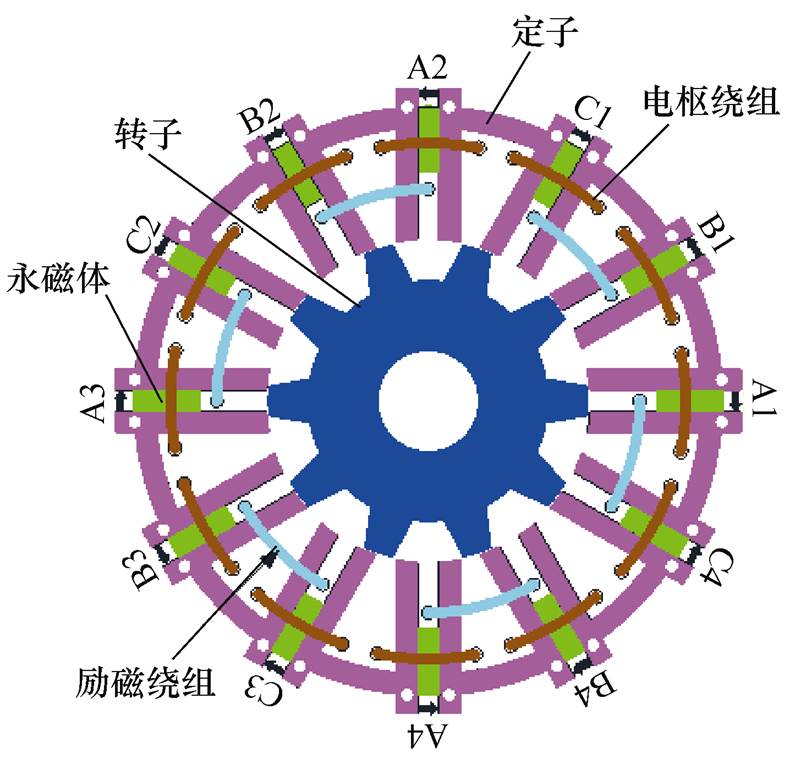
图1 三相12/10极HEFSM拓扑结构示意图
Fig.1 Topology of three-phase 12/10 HEFSM
摘要 混合励磁磁通切换电机(HEFSM)具有永磁磁通切换电机和混合励磁同步电机的优点,通过调节励磁电流实现了调节气隙磁场的目的,这类电机在工业界尤其是电动汽车领域有着广泛的应用前景。该文提出一种针对HEFSM全速范围的优化最大转矩铜耗比(MRTC)控制策略。在低速恒转矩区域,采用优化的励磁电流来提高带负载能力,使铜耗最小,相比励磁电流与电枢电流随机组合策略和零励磁电流控制策略具有更快的响应速度。在恒功率范围,建立电机铜耗的目标函数,以转矩、电流、电压和转速等为约束条件。优化后的负励磁电流和d轴电流不仅可以获得较高的转速和产生磁阻转矩,而且在一定的转矩值下,铜耗最小,实现了转矩与铜耗的最大比值,在扩展电机转速范围的同时提高了效率。最后搭建基于dSPACE1103的电机系统实验平台,验证所提出的控制策略的可行性和有效性。
关键词:混合励磁磁通切换电机 铜耗 励磁电流 最大转矩铜耗比 优化
传统的转子永磁同步电机在高速以及过载运行时,存在电机不稳定、永磁体退磁等问题。永磁磁通切换电机(Permanent Magnet Flux Switching Machine, PMFSM)将永磁体置于定子侧,转子仅由硅钢片叠压而成,既无永磁体也没有绕组,简单的转子结构解决了传统转子永磁电机存在的一些问 题[1-7]。但是PMFSM仅由单一的永磁体励磁,气隙磁场仅由永磁体励磁产生,存在气隙磁场基本恒定、难以调节等缺点。为克服PMFSM的这些缺点,Z. Q. Zhu和花为等提出将一套额外的电励磁绕组添加在PMFSM的定子侧,即混合励磁磁通切换电机(Hybrid Excited Flux-Switching Machine, HEFSM)[8],通过调节励磁电流进而实现调节气隙磁场的目的。在低速区通过正向的励磁电流增强气隙主磁场,实现低速大转矩运行。在高速区通过反向的励磁电流削弱气隙主磁场,拓宽电机的调速范围。这些特性完全符合电动汽车的运行要求,因此混合励磁磁通切换电机未来在工业界有着广泛的应用前景。由于HEFSM中有一套额外的电励磁绕组,虽然增加了系统的灵活性,但是也提高了电机控制系统的难度。国内外对于HEFSM优化控制策略的研究报道并不多,因此研究HEFSM的优化控制策略对于该类混合励磁电机的应用具有重要意义。
文献[9]对于HEFSM提出了最大功率因数控制方法,与传统的“id=0”控制策略相比,在不同的工况下实现了功率因数为1,充分利用了逆变器的容量,并且该算法也适用于其他混合励磁电机系统。文献[10]在HEFSM的高速区弱磁算法中,采用不为零的d轴电流来削弱气隙主磁场进行弱磁升速,在高速区励磁电流则为零,参考电流均通过电压误差调节比较的方法得到,该算法提高了动态响应速度,不依赖于电机电磁参数,算法的通用性较高,提高了电机在弱磁高速区的效率。文献[11]对HEFSM提出了一种线性直接转矩控制策略控制算法,该算法无转矩控制环,仅是调节线性的转矩角,可实现较小的磁链和转矩脉动,并且减少了电枢电流中的谐波分量。文献[12]提出了三相四开关拓扑结构的功率变换器用于HEFSM控制系统,并采用磁链模型预测控制技术,该算法减少了功率器件的个数,抑制了电容电压的下降和偏移,简化了定子磁链的计算过程,但电机的弱磁能力由于直流电压利用率的降低而弱化。文献[13]对于不同的工况要求(低速、大转矩、宽调速范围等),对混合励磁电机控制提出了不同的控制算法,低速区的给定电流不受电压极限的约束,高速区采用分区控制,优化的给定电流在电压极限的条件下得到,这些算法减小了电机的损耗,提高了效率,但对于凸极永磁电机并不适用,无法利用磁阻转矩。
文献[14]针对HEFSM由于加工精度造成绕组的空载反电动势波形不对称、谐波分量较多的问题,对不同相位和谐波次数下的电流进行补偿,使得各高次谐波的电压、电流分量均同相位,得以输出最大的电磁转矩,降低转矩脉动,实现HEFSM的稳定运行。文献[15]提出了一种基于损耗最小的HEFSM控制策略,首先在励磁电流为零时测得电机输出功率以及各种损耗,综合多种工况得到最优的电流分配组合,证明该组合实现了损耗最小,但该方法前期需进行大量的实验测量,比较耗费时间,不能实现给定电流在线自动调节。文献[16]针对一台双三相24/22极PMFSM电机控制系统进行了研究,采用了四矢量的空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)方法对该电机的容错性能进行了分析,针对故障状态下的磁动势,在约束条件下提出了相应的电流补偿策略。文献[17]对单相HEFSM消除死区的措施进行了分析,提出将迭代学习算法应用在HEFSM控制系统中,并进行了相应的仿真分析。文献[18]综述了PMFSM和HEFSM的各种拓扑结构和不同的控制策略,包括优化电机结构参数和采用先进控制策略抑制定位力矩、减小转矩脉动等内容,综合分析,PMFSM和HEFSM在电动汽车领域会有广阔的应用前景。文献[19]针对轴向磁场HEFSM,提出了一种在高速区基于电压差判断弱磁时刻的弱磁控制策略,该弱磁策略可以充分利用逆变器的输出电压,拓宽了电机的调速范围。文献[20]提出了一种针对轴向磁场HEFSM的分区控制策略,在低速区采用单位因数控制策略;在高速区采用一种最大输出功率的弱磁控制策略,提高了电机弱磁运行区域的功率利用率,增强了电机带载能力。
以上一些控制策略研究主要集中在如何提高HEFSM低速区的转矩能力和扩展电机的调速范围,但是对于如何在优化电机铜耗的同时提高电机的转矩、转速范围和效率等问题却关注不多。本文提出一种针对HEFSM全速范围的最大转矩铜耗比控制策略。在低速恒转矩区域,采用优化的励磁电流来提高带负载能力,使铜耗最小,比励磁电流与电枢电流随机组合策略和零励磁电流控制策略具有更快的响应速度。在恒功率范围,建立电机铜耗的目标函数,以转矩、电流、电压和转速等为约束条件。优化后的负励磁电流和d轴电流不仅可以获得较高的转速和产生磁阻转矩,而且在一定的转矩值下,铜耗最小,实现了转矩与铜耗的最大比值,扩展转速范围的同时提高了效率。最后搭建了基于dSPACE 1103控制器的系统实验平台,实验验证了所提出的控制策略对HEFSM驱动系统的可行性和有效性。
本文研究的HEFSM采用经典的三相12/10极拓扑结构,如图1所示,电机定子上有两套绕组,一套电枢绕组,一套直流励磁绕组。12组线圈串联组成直流励磁绕组,励磁绕组放置于永磁体下方靠近电机转子侧,两套绕组和永磁体均在定子侧。

图1 三相12/10极HEFSM拓扑结构示意图
Fig.1 Topology of three-phase 12/10 HEFSM
在HEFSM中向直流励磁绕组中可通入大小和方向均可改变的直流励磁电流,如图2a和图2b所示,此时HEFSM的气隙主磁场由永磁体和额外的励磁电流共同作用产生。在图2a中,通以 向励磁电流所产生的磁通(增磁磁路部分)与永磁体产生磁通方向、路径相同,起到了增强主磁通、增大气隙磁场的目的,定义此时的励磁电流为正向励磁电流;在图2b中,通以
向励磁电流所产生的磁通(增磁磁路部分)与永磁体产生磁通方向、路径相同,起到了增强主磁通、增大气隙磁场的目的,定义此时的励磁电流为正向励磁电流;在图2b中,通以 向励磁电流所产生的磁通(去磁磁路部分)将起到削弱永磁体磁通、减小气隙磁场的目的,定义此时的励磁电流为负向励磁电流。调节气隙磁通密度能力可由励磁电流的大小和方向所决定,这就是“混合励磁”的原理。
向励磁电流所产生的磁通(去磁磁路部分)将起到削弱永磁体磁通、减小气隙磁场的目的,定义此时的励磁电流为负向励磁电流。调节气隙磁通密度能力可由励磁电流的大小和方向所决定,这就是“混合励磁”的原理。
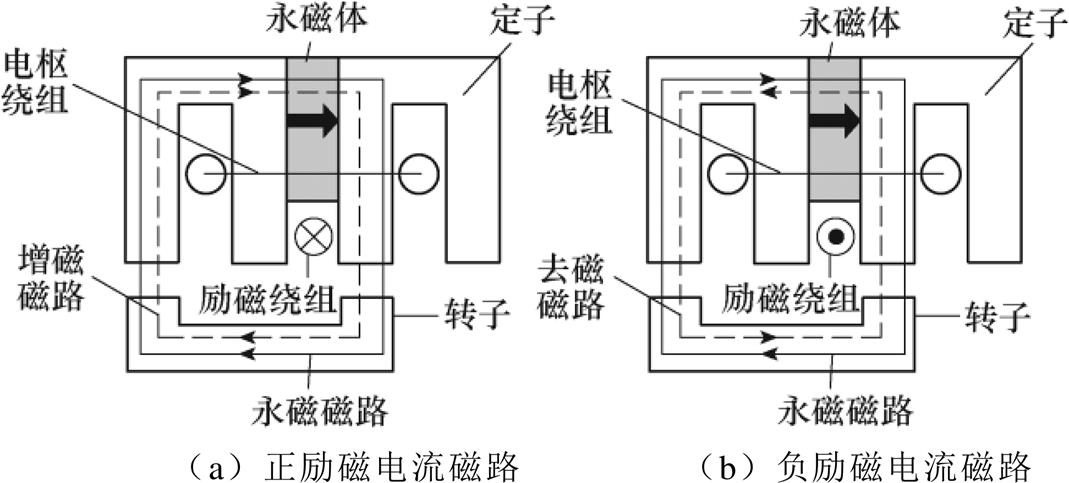
图2 HEFSM工作原理
Fig.2 Operating principle of HEFSM
图3为HEFSM机械特性分区示意图,定义当电机转速小于wN时,电机运行在低速区。当励磁电流if =0时,电机运行在Ⅰ区,工作Ⅰ区最大电磁转矩数值为TN。当电机运行在Ⅱ区时,励磁电流if为正,由于正向电励磁转矩的存在,电机的最大电磁转矩变为Tmax;由电机转速高于wN时,电机反电动势受母线电压和逆变器容量的限制,电机转速不可能无限升高,此时便要通过削弱气隙磁场来提高电机转速。当电机运行在Ⅲ区时,利用反向励磁电流弱磁,当反向励磁电流达到额定值时,HEFSM达到转速wfN,此时若要继续提高电机转速(电机工作在Ⅳ区),就要通过不为零的d轴电流继续削弱气隙磁场,进一步提高电机的转速。励磁电流的存在,提高了HEFSM的最大电磁转矩和最高转速,提高了HEFSM电机控制系统的灵活性。本文将HEFSM这种机械特性分区策略定义为“原始算法”,后文还会提到。
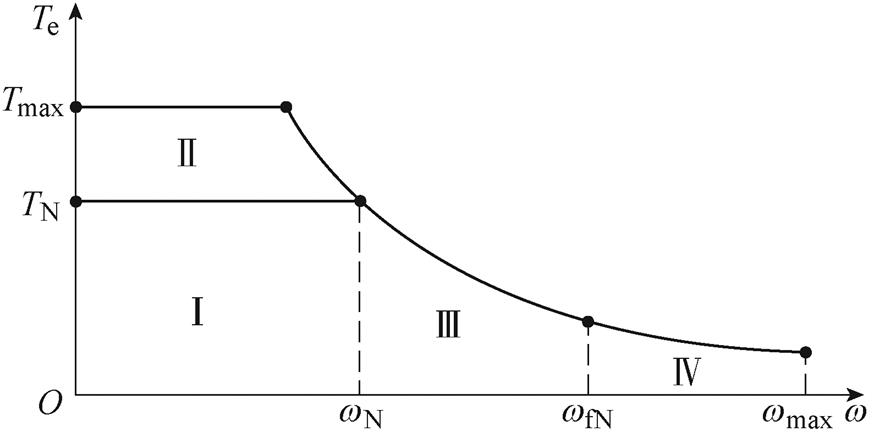
图3 HEFSM机械特性分区示意图
Fig.3 Mechanical characteristic of HEFSM
图4为HEFSM矢量控制系统原理框图,给定转速w*和实时转速w 的误差经过转速PID调节器后得到给定的转矩 ,在
,在 和实时转速w 的输入下通过控制策略的计算得到控制系统的指令电流
和实时转速w 的输入下通过控制策略的计算得到控制系统的指令电流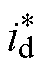 、
、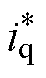 和
和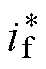 ,
,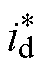 、
、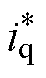 分别和id、iq相比较经过电流PID控制器得到Ud、Uq,经过Park逆变换和SVPWM来控制三相全桥进而得到三相电枢电流;给定励磁电流
分别和id、iq相比较经过电流PID控制器得到Ud、Uq,经过Park逆变换和SVPWM来控制三相全桥进而得到三相电枢电流;给定励磁电流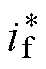 与实时励磁电流if通过滞环比较后控制单相全桥电路,使励磁电流跟随给定值变化。
与实时励磁电流if通过滞环比较后控制单相全桥电路,使励磁电流跟随给定值变化。
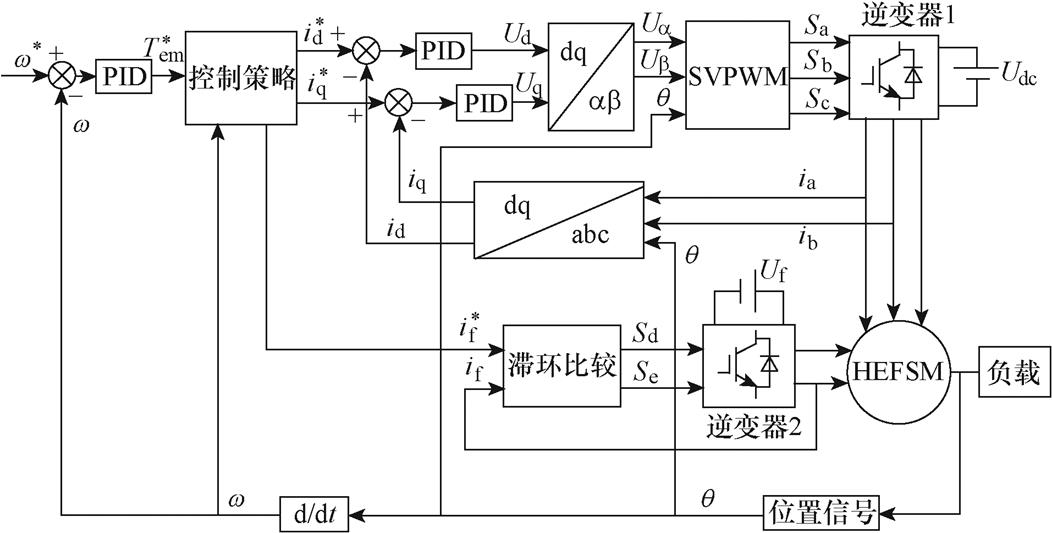
图4 HEFSM矢量控制系统原理框图
Fig.4 Diagram of HEFSM vector control system
HEFSM电压方程在dq轴坐标系下的表达式可写为
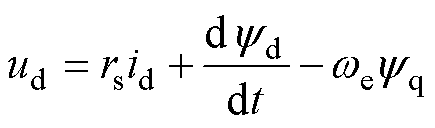 (1)
(1)
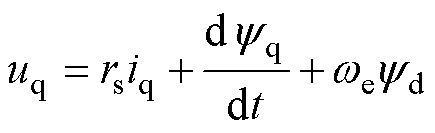 (2)
(2)
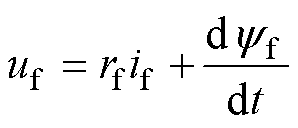 (3)
(3)
式中,ud、uq、id、iq、yd、yq分别为d、q轴电枢电压、电流和磁链;yf为励磁绕组磁链;rs、rf分别为电枢、励磁绕组电阻;if为励磁电流;we为角速度。
忽略温度变化对电阻阻值的影响,HEFSM运行时的铜耗可分为电枢绕组和励磁绕组上的铜耗两部分,总铜耗表达式如式(4)所示。其中,d、q轴电流由三相电枢电流和转子位置信号经Park变换后得到。
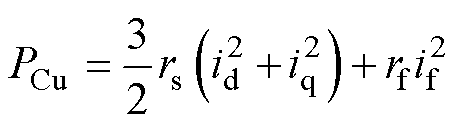 (4)
(4)
式中,PCu为总铜耗。
电机的电磁转矩表达式为
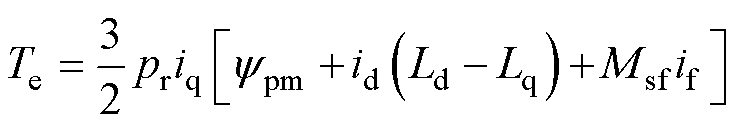 (5)
(5)
式中,Te为HEFSM电磁转矩;pr为转子极对数;Ld、Lq分别为d、q轴电枢电感;ypm为永磁磁链;Msf为电枢与励磁绕组互感。
当HEFSM运行在低速区时,一般采用“id=0”控制算法,该方法灵活简单,便于控制。考虑到HEFSM的d、q轴电感数值上差距很小,式(4)可改写为式(6),HEFSM总电磁转矩表达式改写为式(7),此时电机总铜耗和电磁转矩仅与q轴电流iq和励磁电流if有关,式(6)和式(7)无id项,其余量均为常数。
 (6)
(6)
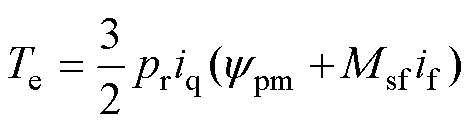 (7)
(7)
由式(7)可知,对于一个给定数值的电磁转矩,会有无数组q轴电流和励磁电流的组合在允许的范围内满足给定,这种控制算法在本文中称为电枢电流和励磁电流组合算法。图5为电机总铜耗随电磁转矩、励磁电流的变化关系,对于任意的电磁转矩Te,令励磁电流if在±ifN约束条件之间变化,即可得到相对应的q轴电流和电机铜耗,对于给定的电磁转矩Te,存在一组(iq, if)组合使得电机总铜耗最小,该组合中的电流为优化电流,实现最大转矩铜耗比(Maximum Ratio of Torque to Copper loss, MRTC)的目标,提高了电机效率。
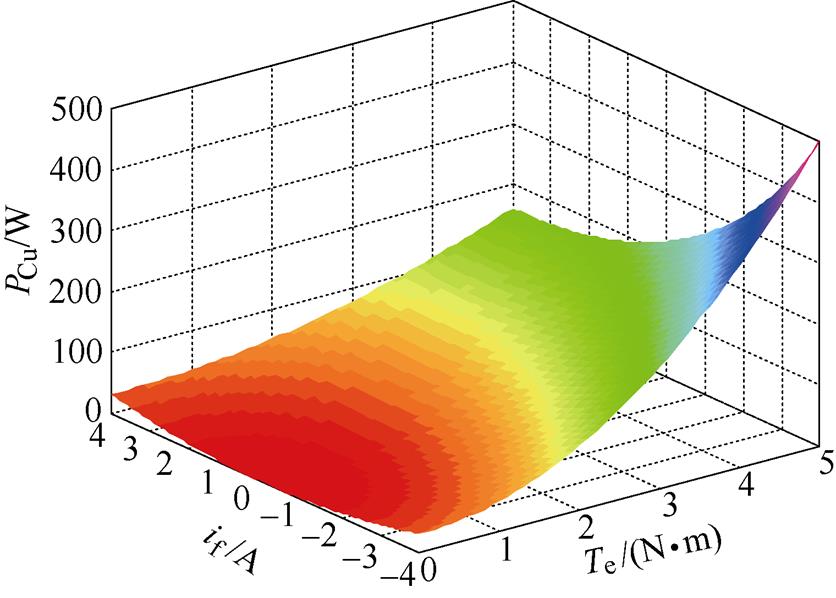
图5 铜耗随Te、if变化关系
Fig.5 Relationship between copper loss and Te, if
通过MRTC算法得到的优化if、iq与电磁转矩Te的关系如图6a和图6b所示,表1给出了不同转矩Te采用MRTC算法得到优化if、iq、PCu之间的数值关系,通过数值拟合的方法将优化励磁电流if和电磁转矩Te的关系拟合为
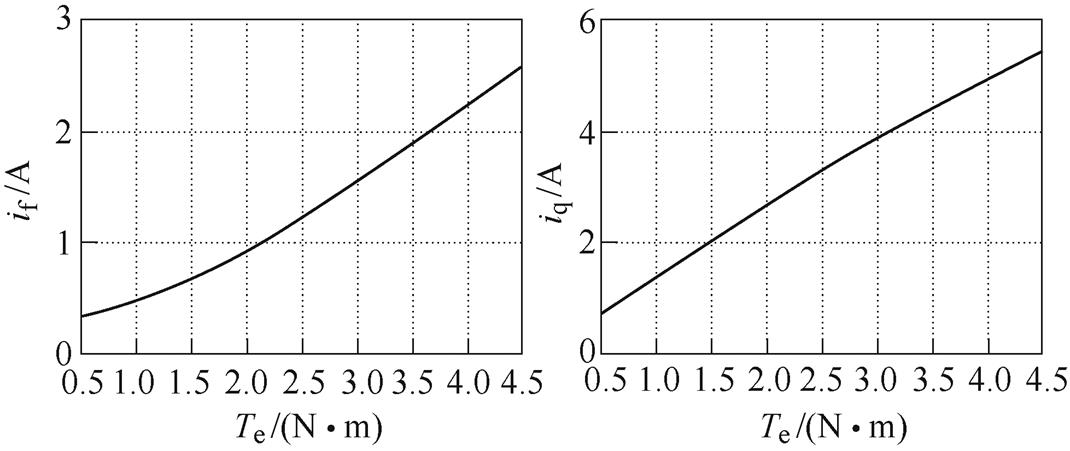
(a)优化if与Te关系 (b)优化iq与Te关系
图6 低速区优化if、iq与Te关系
Fig.6 Optimization of if and iq with Te in low speed region
表1 不同转矩采用MRTC算法得到优化if、iq、PCu数值
Tab.1 Optimization values of if, iq, PCu with Te by MRTC algorithm for different torques
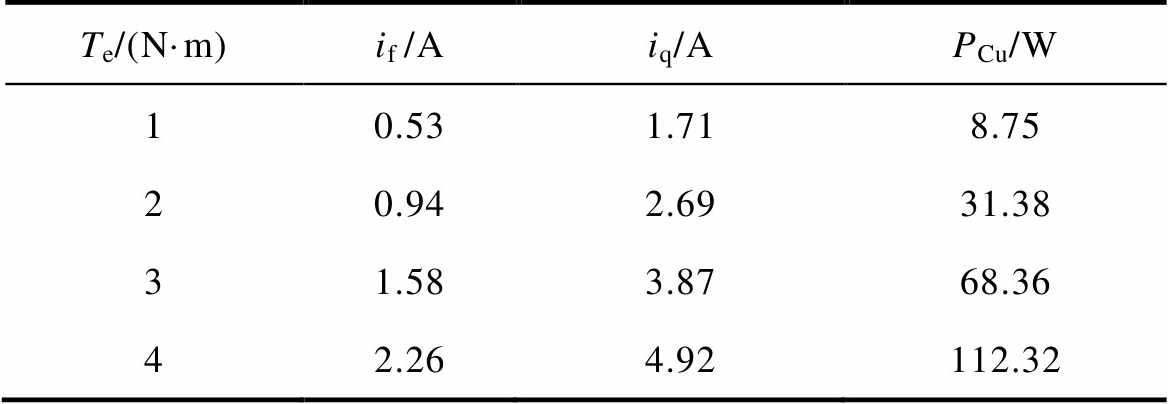
Te/(N·m)if /Aiq/APCu/W 10.531.718.75 20.942.6931.38 31.583.8768.36 42.264.92112.32
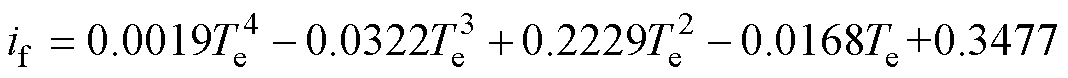 (8)
(8)
在低速区,优化励磁电流if的大小仅和电磁转矩有关,与电机转速无关。
受三相全桥变换器容量以及散热条件限制,电机电流和电压均存在极限值,有
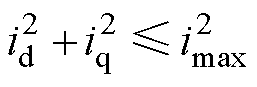 (9)
(9)
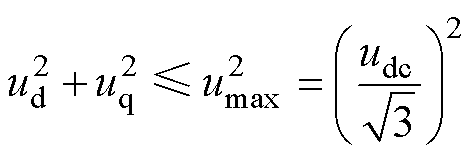 (10)
(10)
式中,imax为电枢电流圆的极限值;umax为电压的极限值;udc为电枢绕组变换器直流侧母线电压。
将式(1)和式(2)代入式(10),考虑电机在稳定运行状态下,并且忽略电机绕组上由电阻产生的压降,式(10)可改写为
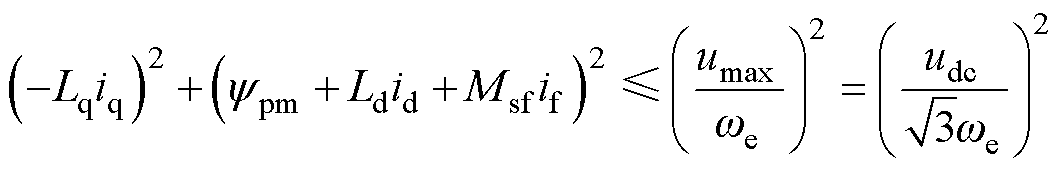 (11)
(11)
从式(9)和式(10)可以看出,两式中均含有dq轴电流分量,可将电压和电流极限用图7来表示,图中,电流极限圆是以(0, 0)点为圆心,imax为半径的圆;电压极限在该图中是以点 为中心,长半轴
为中心,长半轴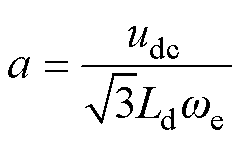 ,短半轴
,短半轴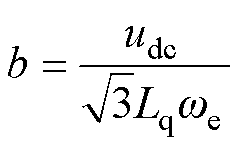 的椭圆。由图7可以看出,当励磁电流保持不变、电机转速升高时,椭圆的半轴变短,中心仍保持在O1不变;当电机转速保持不变、励磁电流变小时,椭圆的半轴长度保持不变,椭圆的中心从O1移动到O2。
的椭圆。由图7可以看出,当励磁电流保持不变、电机转速升高时,椭圆的半轴变短,中心仍保持在O1不变;当电机转速保持不变、励磁电流变小时,椭圆的半轴长度保持不变,椭圆的中心从O1移动到O2。
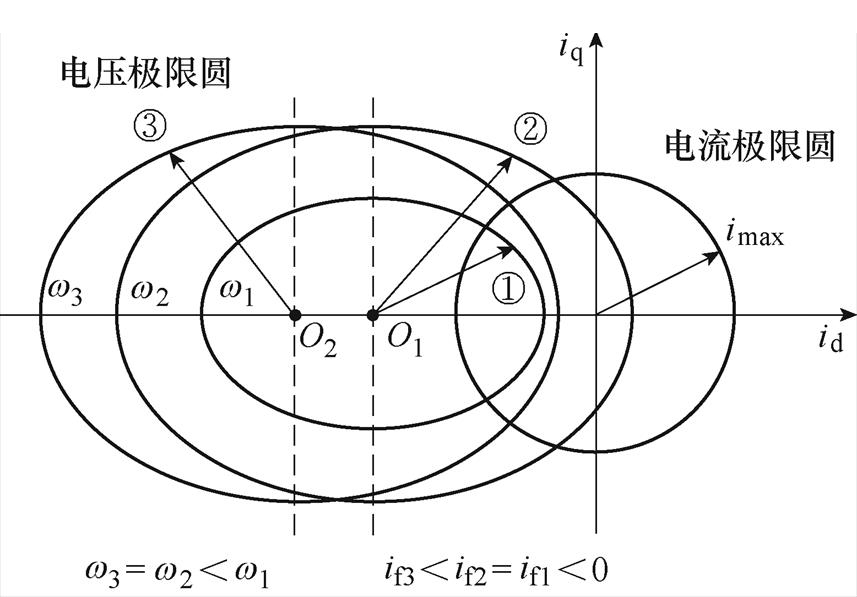
图7 高速区HEFSM电压电流极限圆示意图
Fig.7 Diagram of voltage and current limit circle for HEFSM in high speed region
当电机转速达到wN时,HEFSM的dq轴电压达到额定状态,有
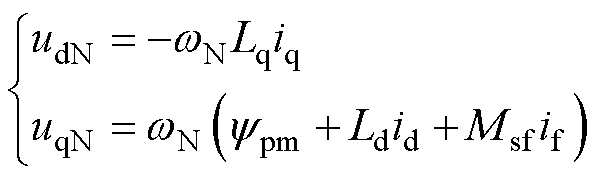 (12)
(12)
在HEFSM运行的高速区,电机转速高于wN,电机反电动势变大,电压开始达到饱和,如果在高速区继续升速,则必须用负的励磁电流减小q轴电压来满足电压极限条件,此时的q轴电压已经达到额定状态,uq=uqN,表达式为
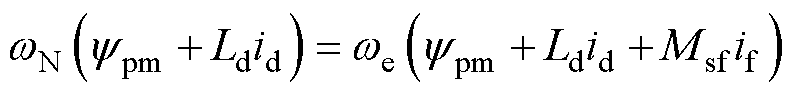 (13)
(13)
该算法下的励磁电流if由式(13)计算得到,有
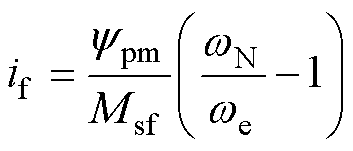 (14)
(14)
此时,d轴电流id仍为零,相对应的q轴电流iq为
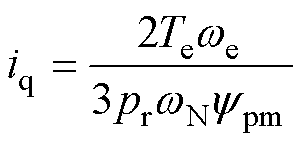 (15)
(15)
当负的励磁电流if达到额定极限值(if =-ifN),此时反向励磁电流不能继续增大,则保持负额定值不变,若要继续提高HEFSM的转速,就需要通过负的d轴电流来削弱永磁磁通,此时的给定d轴电流可由式(13)得到,相对应的q轴电流由转矩方程得到,该状态下的给定电流为
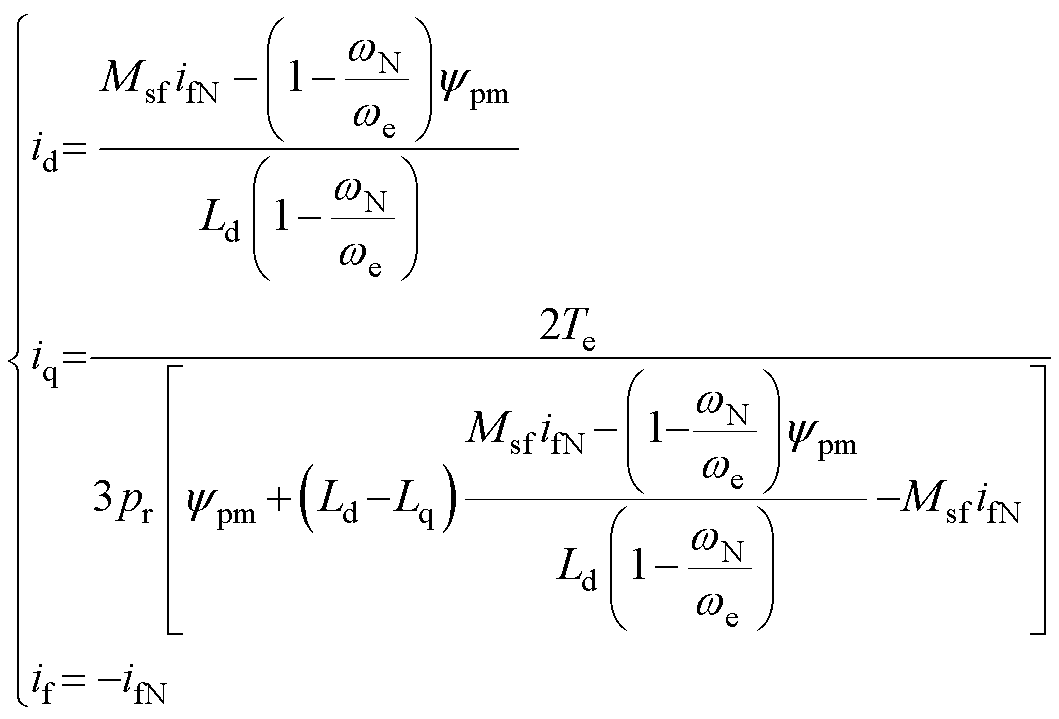 (16)
(16)
以上部分在高速区的弱磁升速算法和低速区的MRTC算法共同组成全速范围内HEFSM矢量控制系统的一种控制算法,命名为“原始算法”,根据不同的转速来确定不同的给定电流,进而实现电流和转速的双闭环控制。
在“原始算法”的高速区中,首先利用负的励磁电流来削弱气隙主磁场调高HEFSM的转速,此时的d轴电流为零;当负励磁电流达到额定值时,再利用不为零的d轴电流来继续减小气隙磁场提高电机转速。原始算法仅相对于同等规格的PMFSM电机获得了更宽广的调速范围。在原始算法中,当励磁电流达到反向额定值时,HEFSM的总铜耗大大增加,这必然会导致电机效率低下,由于存在这些问题,本文对原始算法的高速区算法进行优化,优化目标仍为获得最大转矩铜耗比,对确定的转矩值来说,获得最大的转矩铜耗比即是电机的总铜耗最小,因此该优化问题化归为电机铜耗最小问题。
对于优化电机铜耗,使得总铜耗最小进而实现MRTC的问题,存在着式(5)和式(11)两个约束条件,根据约束条件建立的电机铜耗的目标函数表达式为
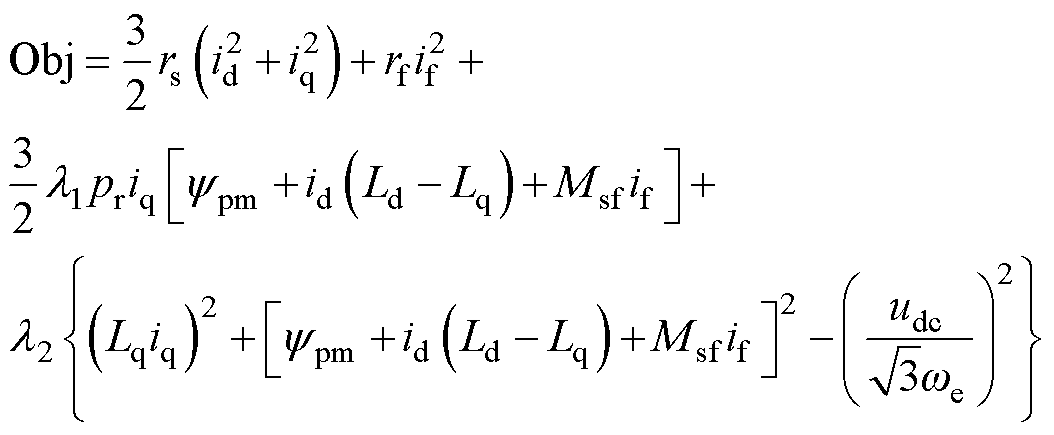 (17)
(17)
式中,Obj为电机总铜耗目标函数;l1为转矩约束条件系数;l2为电压约束条件系数。
在式(17)中,id、iq和if为自变量,Obj为因变量。对于给定的转矩和转速组合,必然存在一组使得HEFSM的总铜耗最小,该最小铜耗值在∂Obj/∂id=0、∂Obj/∂iq=0、∂Obj/∂if =0、∂Obj/∂l1=0、∂Obj/∂l2=0的条件下得到,对以上方程化简可得
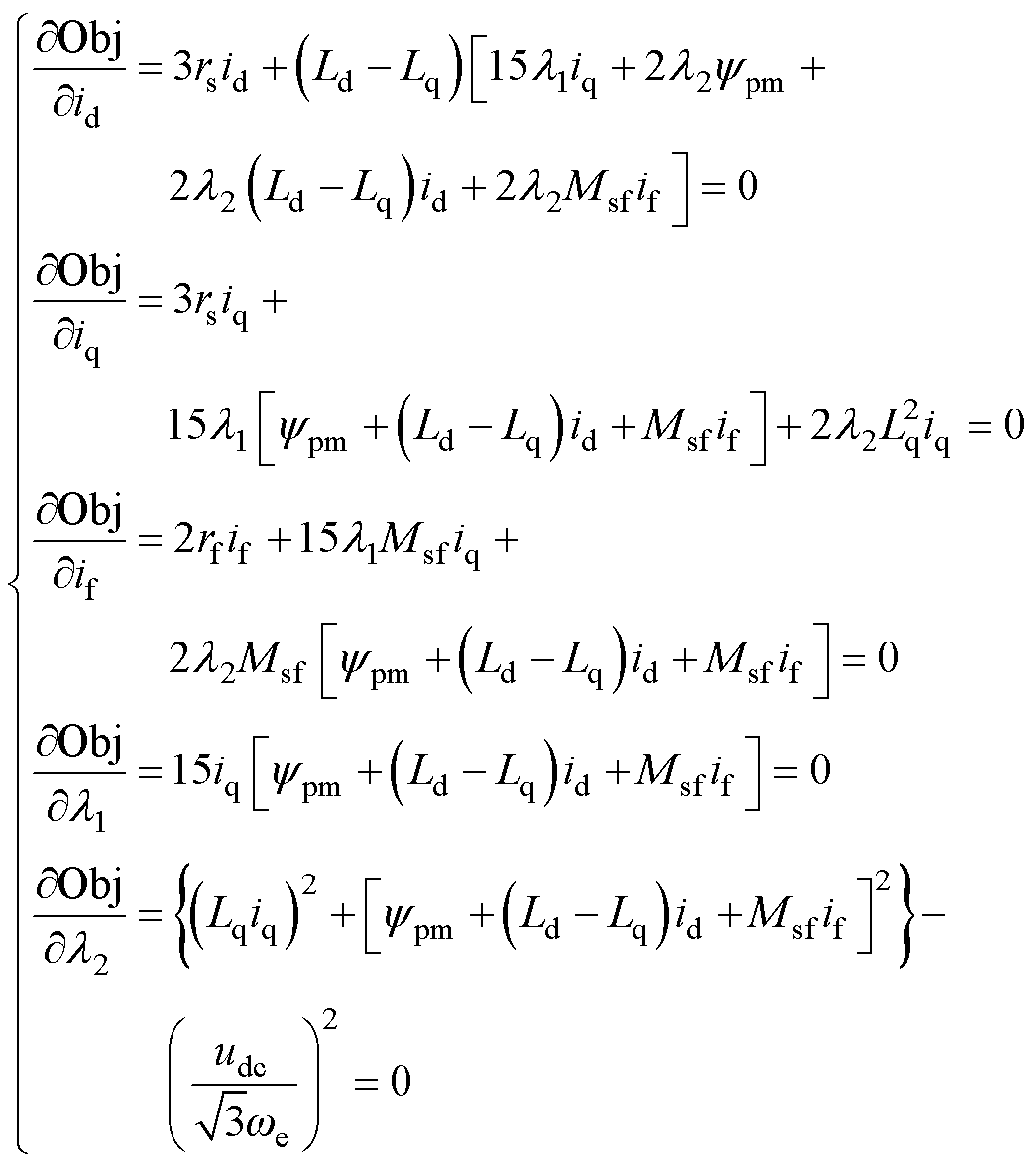 (18)
(18)
对于方程组式(18),为了方便计算,通过合理地省略掉微小数值可将该方程组化简为一个高次非线性方程,接着利用牛顿迭代法求得最优解组合(id, iq, if),使HEFSM在高速区的总铜耗最小,本文将该种在高速区构造拉格朗日乘数来求最优解的算法命名为“优化MRTC算法”。在“优化MRTC算法”中,由于在高速区起始阶段的d轴电流id不为零,HEFSM的磁阻转矩分量得以被利用,在高速区,电机的输出转矩必然会低于低速区的最大转矩,因此在高速区磁阻分量的增加不可忽略,优化算法同时提高了高速区HEFSM的带负载能力。
在方程组式(18)中,转矩Te和转速w 作为已知量,在不同的工况组合(Te, w)下,可求得最优解组合(id, iq, if)。将对应工况的数据存入表格中,当电机运行时,采集到实时的转速w 以及经过转速PI环节的计算转矩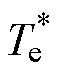 ,查表得到对应的最优目标电流组合(id, iq, if)。
,查表得到对应的最优目标电流组合(id, iq, if)。
图8为全速范围最大转矩铜耗比控制算法的流程,在低速区通过式(8)得到最优的励磁电流,在高速区则通过求解方程组式(18)得到最优目标电流组合(id, iq, if),实现全速范围最大转矩铜耗比控制。
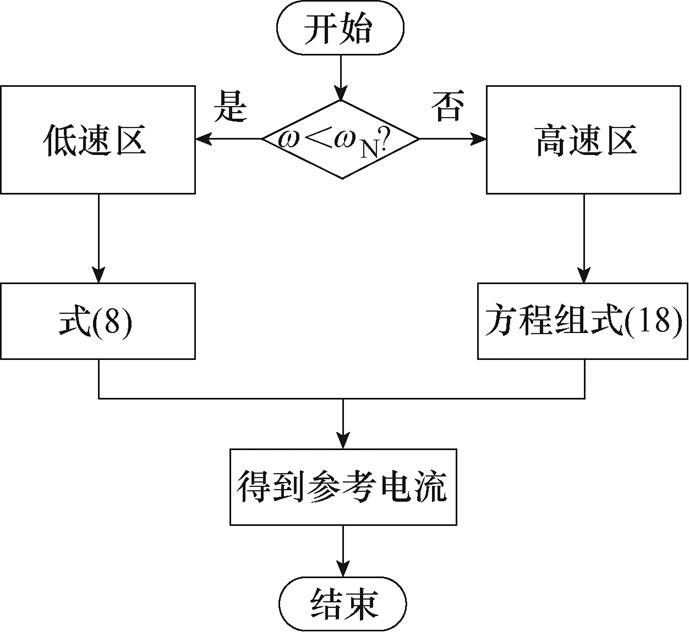
图8 全速范围最大转矩铜耗比控制算法流程
Fig.8 Flow chart of control algorithm of maximum torque copper loss ratio in full speed range
综上所述,本文一共提到了四种不同的控制算法。第一种算法为“if =0”控制算法,HEFSM励磁绕组开路,励磁电流为零,基速以下利用“id=0”的矢量控制,此时的HEFSM相当于一台PMSM或PMFSM。第二种算法为在低速下当“id=0”时,采用电枢电流和励磁电流组合算法,在q轴电流和励磁电流允许的范围内选取优化的(iq, if)组合满足给定的电磁转矩,实现MRTC目标。第三种算法称为原始算法,在低速区采用MRTC算法,在高速区采用分区控制算法,首先利用负的励磁电流削弱气隙磁场来提高电机转速,当反向励磁电流达到额定值时再利用不为零的d轴电流继续削弱气隙主磁场来实现提高电机转速的目的。第四种算法为优化MRTC算法,在全速度范围内采用优化MRTC控制策略,减小电机的铜耗,提升HEFSM电机效率。
为了验证本文控制策略的有效性,搭建如图9所示的HEFSM系统实验平台,主要包括电枢绕组功率变换器(三相全桥)及其驱动、励磁绕组功率变换器(单相全桥)及其驱动、dSPACE 1103、直流稳压电源、磁粉制动器、转矩转速传感器、HEFSM样机等。HEFSM主要参数见表2。
图10为基速以下不同算法起动特性比较结果,图10a采用的是“if =0”算法,图10b采用的是“iq, if组合MRTC算法”。在两种算法下,给定转速为800r/min,起动时负载转矩为1N·m。在“if =0”算法下完成该起动过程需要2s,在iq, if组合MRTC算法下完成该起动过程仅需要1.3s,相比“if =0”算法节约了35%的时间。MRTC算法有较好的起动特性是因为正向励磁电流产生的正电励磁转矩,该正向电励磁转矩相对于算法有更大的加速度,更快地完成起动过程。

图9 HEFSM系统实验平台
Fig.9 Experimental platform of HEFSM system
表2 HEFSM主要参数
Tab.2 Main parameters of HEFSM
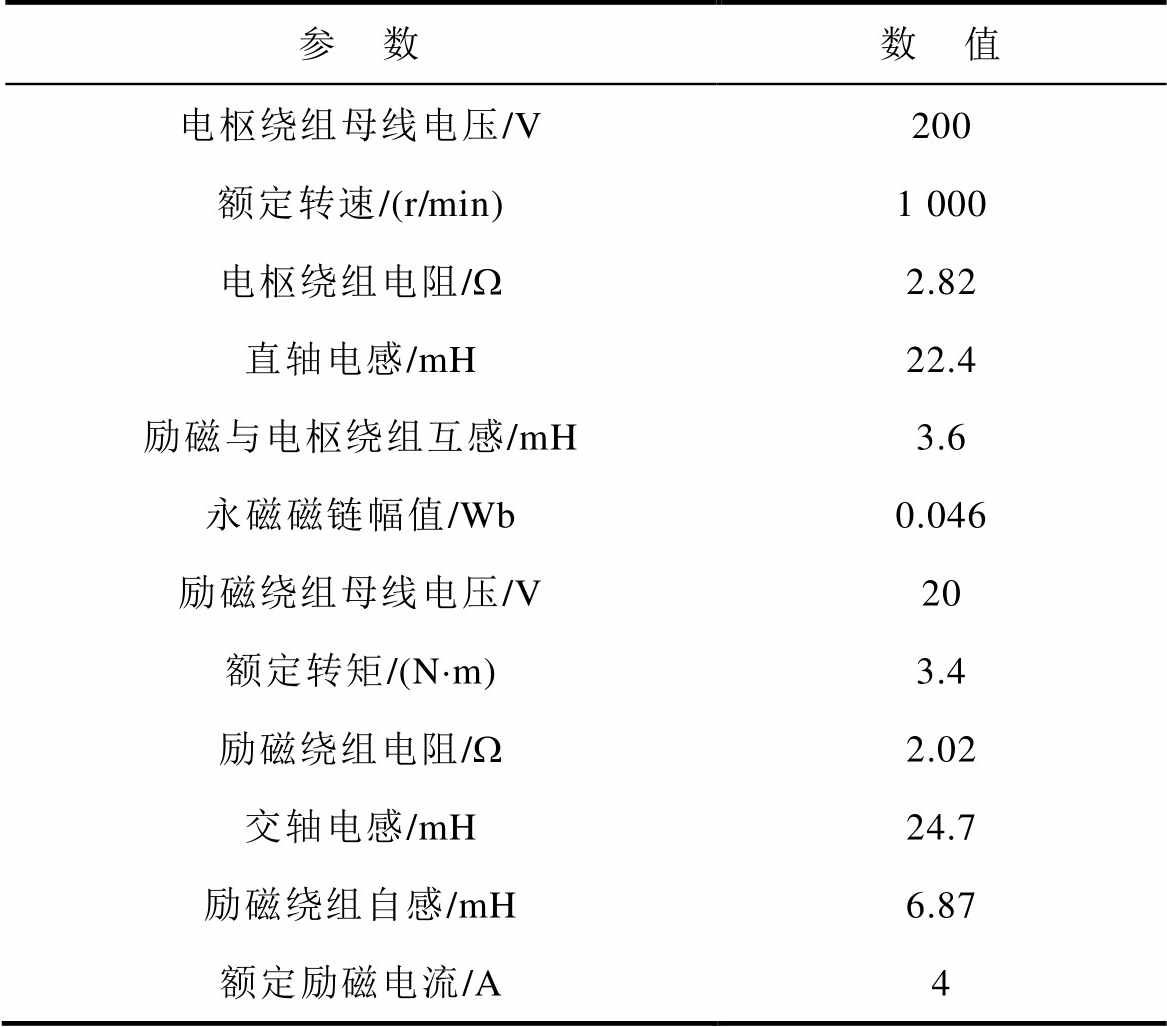
参 数数 值 电枢绕组母线电压/V200 额定转速/(r/min)1 000 电枢绕组电阻/W2.82 直轴电感/mH22.4 励磁与电枢绕组互感/mH3.6 永磁磁链幅值/Wb0.046 励磁绕组母线电压/V20 额定转矩/(N·m)3.4 励磁绕组电阻/W2.02 交轴电感/mH24.7 励磁绕组自感/mH6.87 额定励磁电流/A4
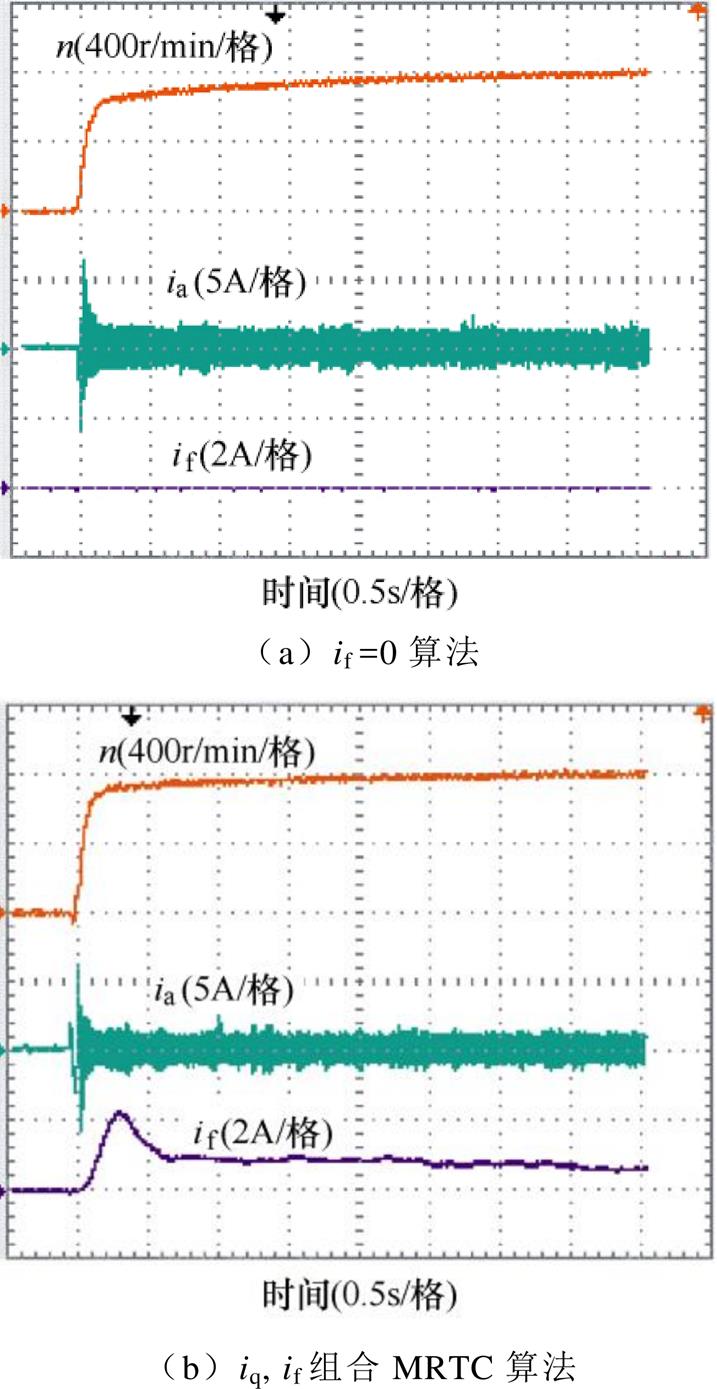
图10 基速以下不同算法下起动特性比较
Fig.10 Comparison of starting characteristics under different algorithms below base speed
图11为基速以下不同算法下负载突变特性比较,图11a采用的是“if =0”算法,图11b采用的是“iq, if组合MRTC算法”。在两种算法下,给定转速均为800r/min,负载转矩由2N·m突变至3N·m。本文实验中负载通过调节磁粉制动器的电流实现负载转矩大小的调节。磁粉制动器回路中串入滑动变阻器,手动调节滑动变阻器改变电流大小,从而实现转矩突变。受磁粉制动器工作特性、磁粉制动器转矩响应速度、手动调节滑动变阻器的快慢、以及滑动变阻器最后到达的位置等各环节影响,两种情况下负载转矩突变实验无法实现前后两次实验完全一致。即图11b所示的工况中,负载突变后,电机输出的电磁转矩大于3N·m,与理想状态存在一定的偏差,采用MRTC算法实际上的负载转矩突变量要大于图11a采用“if =0”算法的转矩突变变化量。在图11a“if =0”算法下,转速变化值为240r/min。在MRTC算法下,转速变化值为140r/min,相比“if =0”算法减小了41.7%。图11b中采用“iq, if组合MRTC算法”,电机能够更加快速地从突加负载的情况下达到新的稳态,转速很快达到之前的给定值800r/min。虽然图11b的工况要比图11a严苛,但采用MRTC算法在负载突变的工况下,转速波动更小,能实现更快的动态响应,间接也说明了采用MRTC算法能够更好地抵抗负载转矩的突变,实现转速快速跟随,提高了HEFSM控制系统的稳定性。
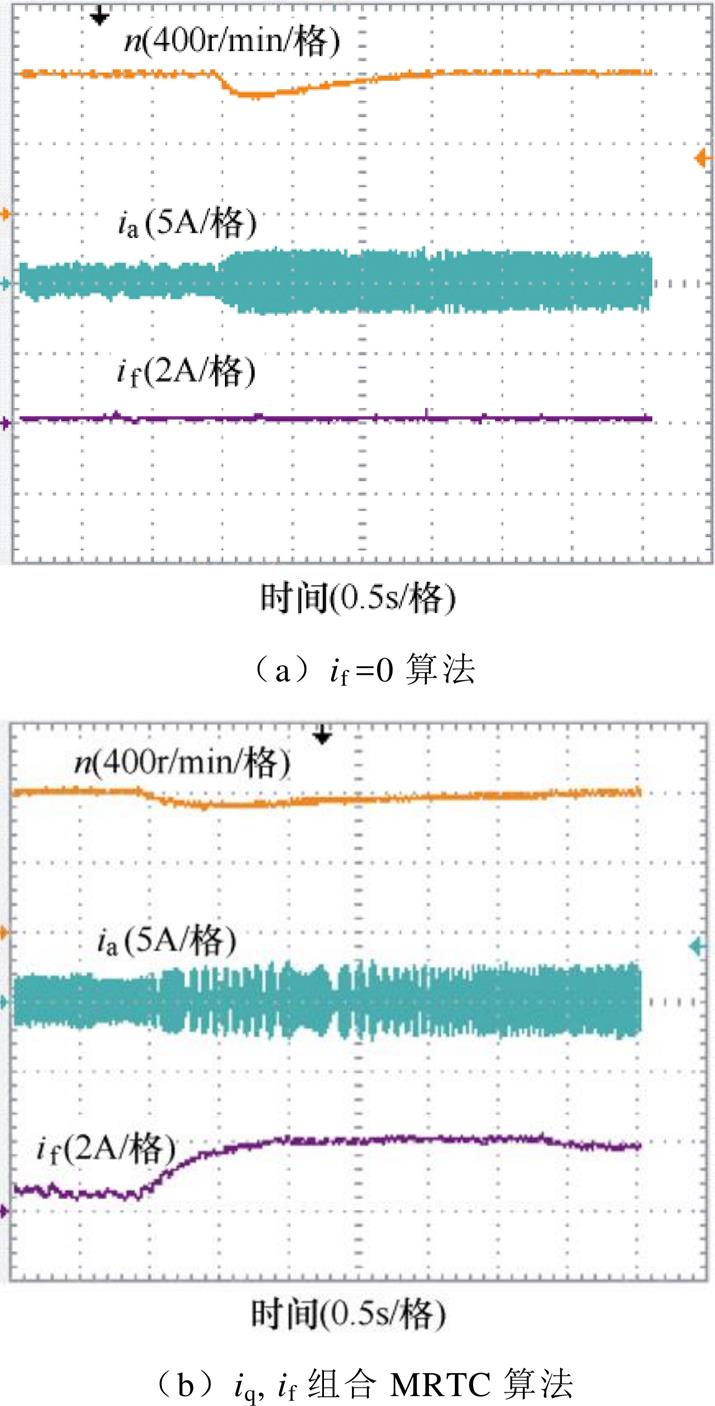
图11 基速以下不同算法下负载突变特性比较
Fig.11 Comparison of load-change characteristics under different algorithms below base speed
图12为中速区采用“优化MRTC算法”下HEFSM控制系统转速突变实验结果,给定转速由800r/min变为1 200r/min,磁粉制动器的负载转矩恒为2.5N·m。该实验结果包含了转速稳定状态到转速突变的动态过程,示波器从上到下依次为实时转速、dq轴电流和励磁电流波形。可以看出,d轴电流id由0A变为-1.2A,不为0的id用来产生正向的磁阻转矩,并且削弱气隙主磁场,提高电机的转速;q轴电流iq由1.7A变为4.0A,通过iq产生的永磁转矩增大;励磁电流if由0.9A变为-1.7A,电励磁转矩由正向变为反向,增大的永磁转矩和非零的磁阻转矩来弥补反向电励磁转矩,维持电机输出的电磁转矩和负载转矩达到平衡。在转速变化的动态过程中,实测转速能够很快地跟随给定。
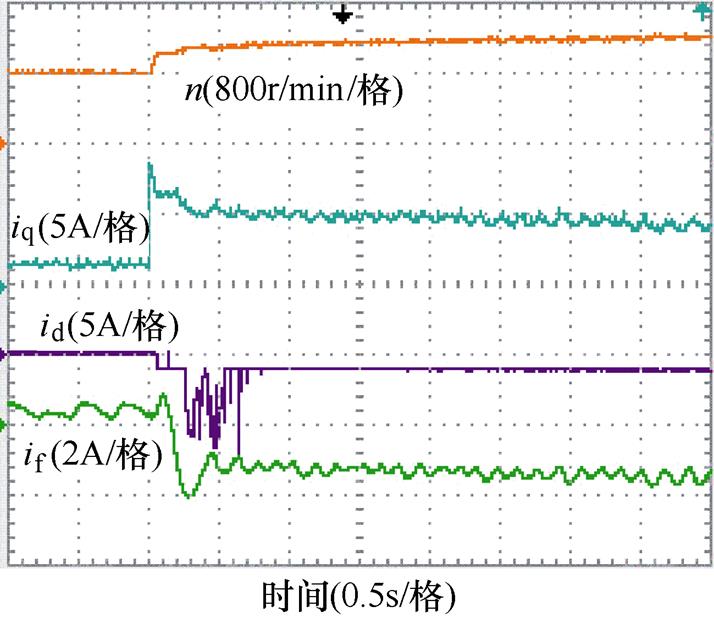
图12 800r/min到1 200r/min转速突变实验结果
Fig.12 Experimental results when speed changes from 800r/min to 1 200r/min
图13为高速区采用“优化MRTC算法”下HEFSM转速突变实验结果。图13a为实测转速、电流波形,图13b为给定转速、电流和实测转速、电流对比结果。给定转速由1 200r/min变为1 700r/min,负载转矩恒为1.5N·m。从实验结果可以看出,d轴电流id由-1.0A变为-2.0A,q轴电流iq由2.5A变为4.5A,励磁电流if由-2.0A变为-2.4A,在转速动态变化的过程中,数值为负的id和if绝对值变大,进一步削弱HEFSM气隙主磁场,提高电机的转速;与此同时,由于电机转速升高,摩擦阻力增大,增大的永磁转矩和非零的磁阻转矩来弥补反向增大的电励磁转矩和摩擦阻力的增加,进而维持电机输出的电磁转矩和负载转矩相等。由图13b可以看出,在转速变化的动态过程中,实测转速和电流能够很好地跟随给定值,验证了采用优化MRTC算法对闭环系统的稳定性。
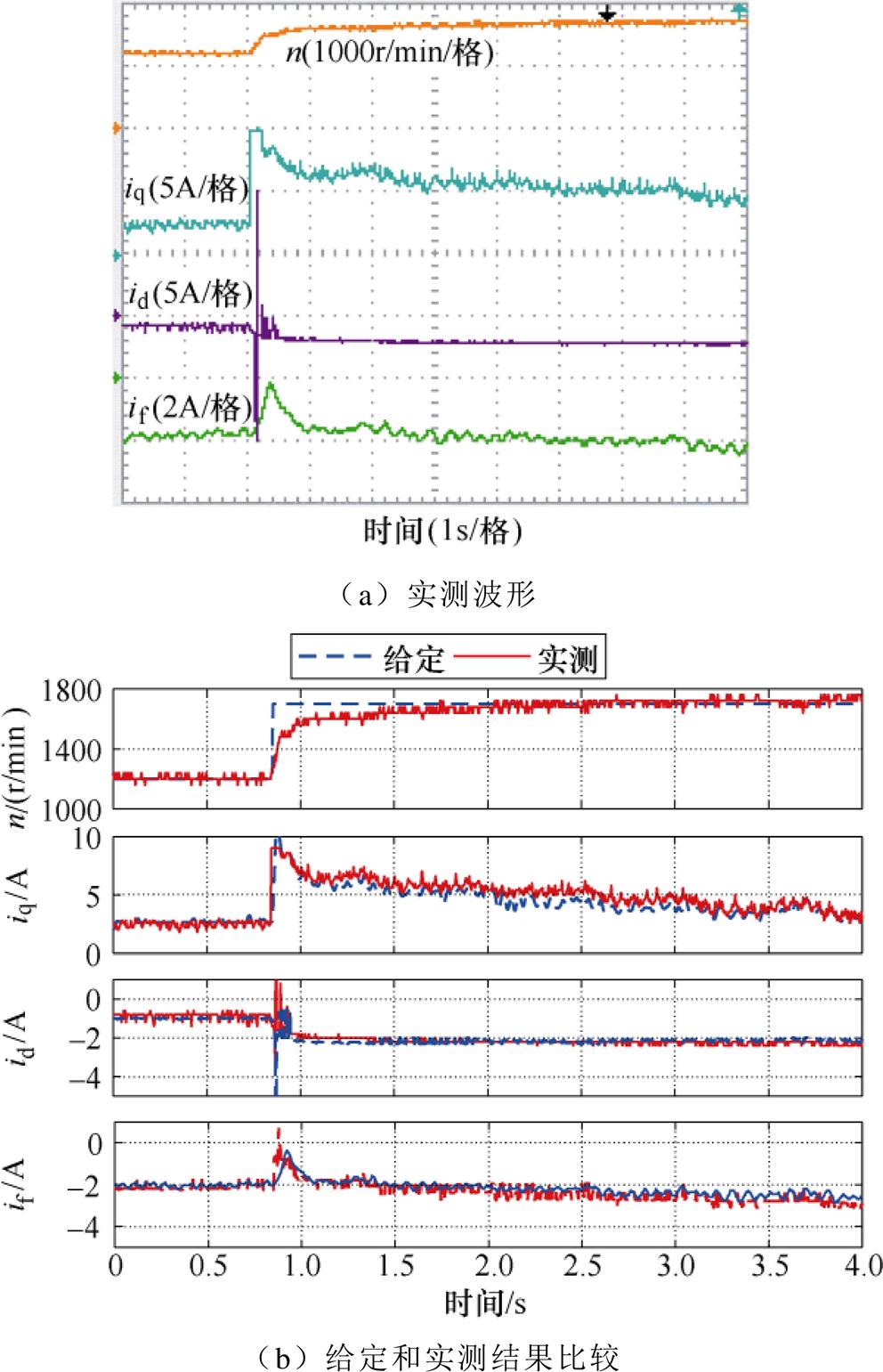
图13 1 200r/min到1 700r/min转速突变实验结果
Fig.13 Experimental results when speed changes from 1 200r/min to 1 700r/min
图14为高速区采用“优化MRTC算法”下HEFSM系统负载突变实验结果,图14a为实测转速、电流波形,图14b为给定转速、电流和实测转速、电流对比结果。负载转矩由原先的2.0N·m变为2.5N·m,突变过程中给定转速保持1 500r/min不变。可以看出,d轴电流id由-1.2A变为-1.6A,电机的磁阻转矩增大;q轴电流iq由1.5A变为4.0A,电机的永磁转矩增大;励磁电流if由-2.4A变为-2.0A,电机的电励磁转矩增大。由图14b可以看出,实测转速和电流能够很好地跟随给定值,HEFSM能够较快地恢复负载突变前的给定转速,dq轴电流和励磁电流达到新的稳定值,验证了采用优化MRTC算法对闭环系统的稳定性。
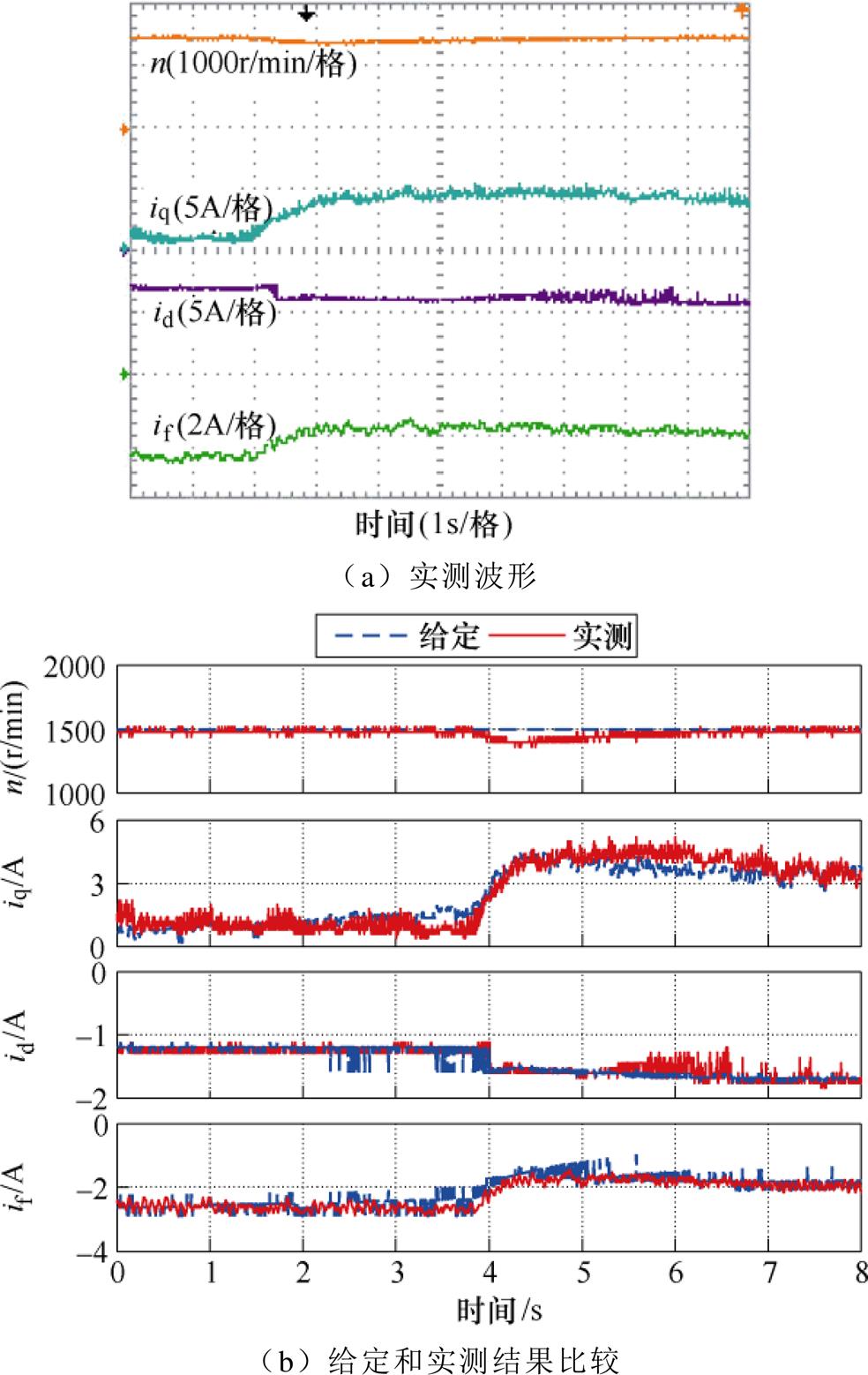
图14 1 500r/min负载突变实验结果
Fig.14 Experimental results when load changes at 1 500r/min
图15为不同算法下HEFSM控制系统的机械特性比较结果,其中,图15a为转矩-转速特性。可以看出,在转速小于1 000r/min的低速区,HEFSM通过优化MRTC算法和原始算法产生的最大转矩值为4.4N·m,大于HEFSM通过“if =0”控制算法产生的最大转矩3.4N·m,这是因为在优化MRTC算法下,HEFSM利用了励磁电流产生的附加电励磁转矩,大于仅通过“if =0”控制算法产生的永磁转矩;在高于1 000r/min的高速运行区,优化MRTC算法可获得最大的电磁转矩,高速区的原始算法采用反向励磁电流来弱磁升速,该反向励磁电流产生的负电励磁转矩分量会造成HEFSM的电磁转矩在1 000~1 100r/min之间较为明显地下降。此外,通过优化MRTC算法HEFSM可获得最大转速2 000r/min,高于通过原始算法和“if =0”控制算法得到的最大转速,从而获得更为宽广的调速范围。图15b为HEFSM采用不同算法下的输出功率-转速特性,在低速区,HEFSM的输出功率和转速成正比,在高速区,通过MRTC算法可获得最大的输出功率,相比其他算法,MRTC算法较为明显地提高了电机的性能。
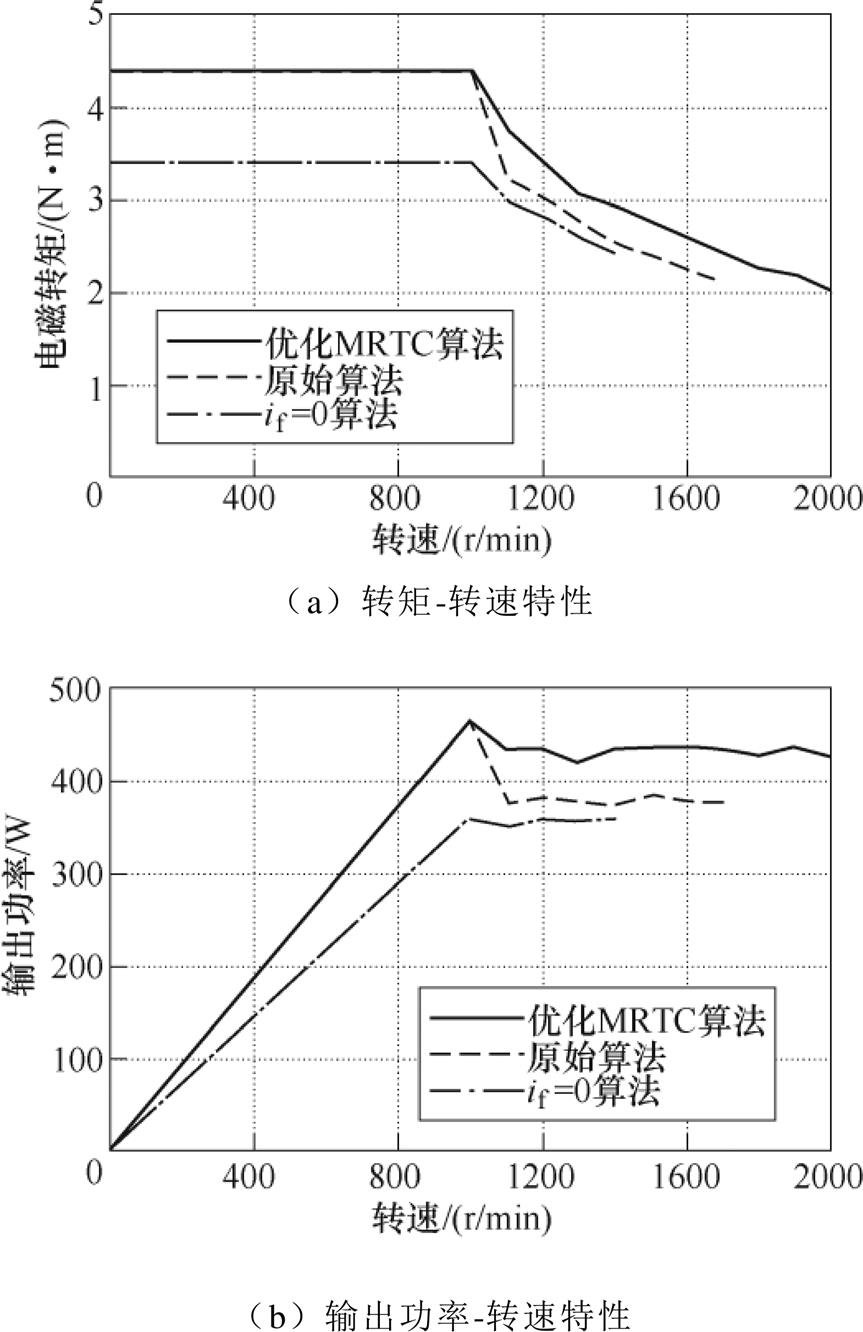
图15 不同算法下实测机械特性比较
Fig.15 Measured mechanic characteristic with different control strategies
图16为高速区HEFSM采用优化MRTC算法和原始算法下铜耗比较结果,转速范围从1 000~1 600r/min。可以看出,通过优化MRTC算法HEFSM的铜耗大大减小。
图17为高速区不同算法下转矩铜耗比结果,可以看出,采用MRTC算法可获得更高的转矩铜耗比,印证了高速区优化MRTC算法的合理性。
图18为不同算法下效率比较结果。可以看出,通过优化MRTC算法减小了HEFSM的铜耗,与原始算法相比,电机的效率得到了明显提高。
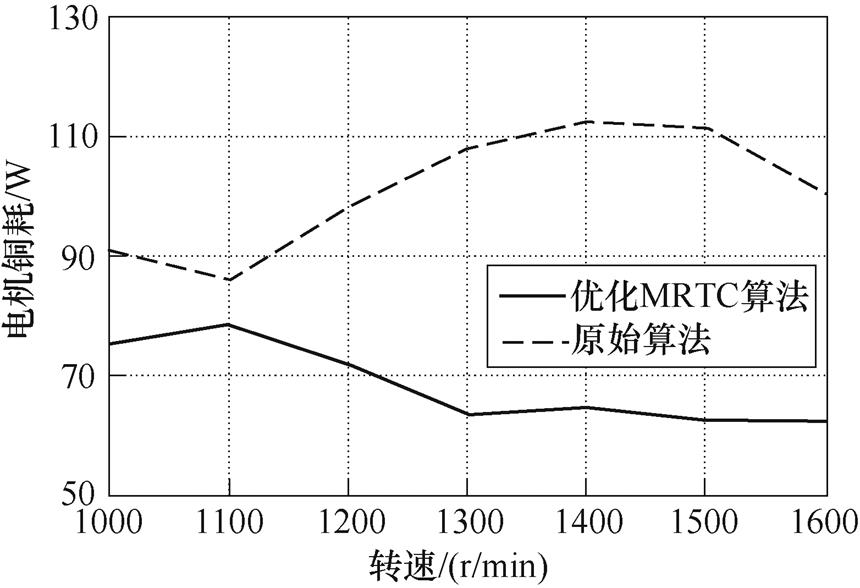
图16 高速区不同算法下HEFSM铜耗比较
Fig.16 Measured copper loss with different control strategies at high speed region
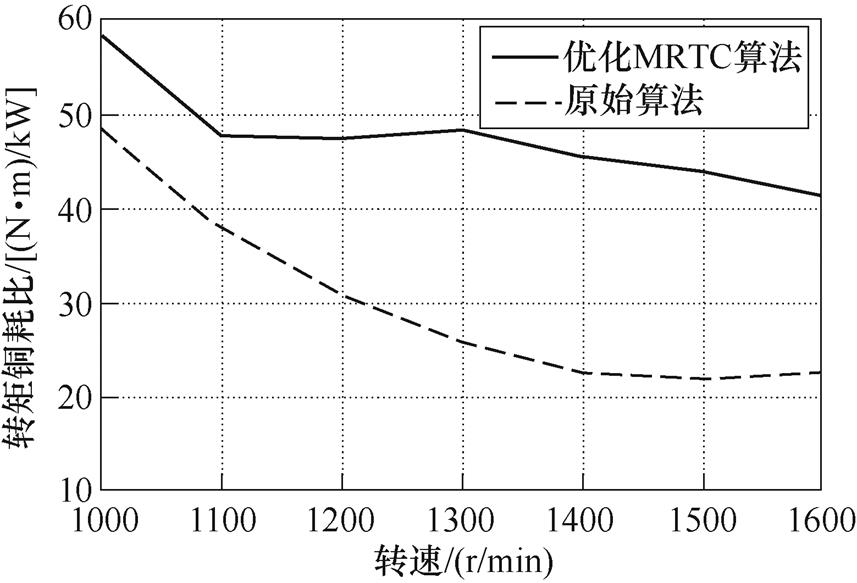
图17 不同算法下转矩铜耗比结果
Fig.17 Comparison of maximum ratio of torque/copper loss with different control strategies
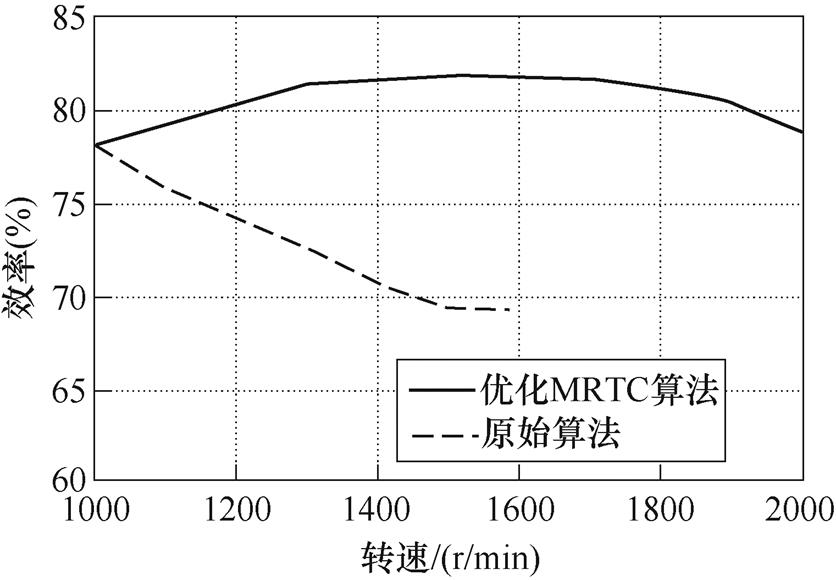
图18 不同算法下效率比较结果
Fig.18 Comparison results of efficiency with different control strategies
本文根据HEFSM的机械特性和矢量控制原理提出了一种基于组合算法的全转速范围MRTC控制策略。在低速区对电枢电流和励磁电流随机组合算法进行了优化,在高速区以电压、转速、转矩、电流等为约束条件建立了电机铜耗的目标函数,对高速区的“原始算法”进行优化,在全速度范围内实现了HEFSM的最大转矩铜耗比控制。搭建了实验系统,对电机系统的稳态、动态响应等进行了实验验证,结果表明,MRTC算法在提高HEFSM的带负载能力和动态响应表现、减小铜耗等方面与优化前算法相比有着明显的改善作用,在扩展电机转速范围的同时提高了效率,实验验证了所提出的控制策略的可行性和有效性。
参考文献
[1] 顾惠, 王宇. 开路及短路组合故障下容错型永磁磁通切换电机转矩冲量平衡控制策略的研究[J]. 电工技术学报, 2020, 35(9): 1931-1944.
Gu Hui, Wang Yu. Research on torque impulse balance control strategy of fault tolerant flux switching permanent magnetic motor under combined open and short circuit faults[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1931-1944.
[2] 程明, 文宏辉, 曾煜, 等. 电机气隙磁场调制行为及其转矩分析[J]. 电工技术学报, 2020, 35(5): 921- 930.
Cheng Ming, Wen Honghui, Zeng Yu, et al. Analysis of airgap field modulation behavior and torque component in electric machines[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 921-930.
[3] 於锋, 程明, 田朱杰, 等. 九相磁通切换永磁电机主动缺相运行控制策略[J]. 电工技术学报, 2019, 34(8): 1626-1635.
Yu Feng, Cheng Ming, Tian Zhujie, et al. Active phase-deficient control of a nine-phase flux-switching permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1626-1635.
[4] 曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012.
Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001- 1012.
[5] 张源, 王宇, 肖文妍, 等. 永磁磁通切换电机转矩冲量平衡控制优化切换控制策略[J]. 电工技术学报, 2019, 34(7): 1404-1412.
Zhang Yuan, Wang Yu, Xiao Wenyan, et al. Optimal switching control strategy for torque impulse balance control of permanent magnet flux switching motor[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1404-1412.
[6] Ullah W, Khan F, Sulaiman E, et al. Torque characteristics of high torque density partitioned PM consequent pole flux switching machines with flux barriers[J]. China Electrotechnical Society Transa- ctions on Electrical Machines and Systems, 2020, 4(2): 130-141.
[7] Ullah W, Khan F, Umair M. Design and optimization of segmented PM consequent pole hybrid excited flux switching machine for EV/HEV application[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2020, 4(3): 206-214.
[8] Hua Wei, Cheng Ming, Zhang Gan. A novel hybrid excitation flux-switching motor for hybrid vehicles[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4728- 4731.
[9] Zhao Jilong, Jing Mengdie, Sun Xiangdong, et al. Unity power factor control of hybrid excited axial field flux-switching mermanent magnet machine[C]// 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-5.
[10] Pothi N, Zhu Ziqiang, Afinowi A A, et al. Control strategy for hybrid-excited switched-flux permanent magnet machines[J]. IET Electric Power Applications, 2015, 9(9): 612-619.
[11] Wang Yu, Deng Zhiquan. Hybrid excitation topo- logies and control strategies of stator permanent magnet machines for DC power system[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4601-4616.
[12] Hua Wei, Huang Wentao, Yu Feng. Improved model predictive flux control strategy for three-phase four switch inverter fed flux reversal permanent magnet machine drives[J]. IET Electric Power Applications, 2017, 11(5): 717-728.
[13] Shinnaka S, Sagawa T. New optimal current control methods for energy-efficient and wide speed-range operation of hybrid-field synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2443-2450.
[14] 董广鹏. 新型混合励磁磁通切换电机的控制策略研究[D]. 南京: 东南大学, 2012.
[15] 廖金国. 混合励磁磁通切换电机优化调磁策略研究[D]. 南京: 东南大学, 2015.
[16] 孟建建. 六相磁通切换永磁电机控制策略与驱动系统研究[D]. 南京: 东南大学, 2017.
[17] 张宗盛. 混合励磁磁通切换型磁阻电机系统的研究[D]. 济南: 山东大学, 2015.
[18] Zhang Gan, Hua Wei, Cheng Ming. Rediscovery of permanent magnet flux-switching machines applied in EV/HEVs: summary of new topologies and control strategies[J]. Chinese Journal of Electrical Engineering, 2016, 2(2): 717-728.
[19] 赵纪龙, 林明耀, 徐妲, 等. 混合励磁轴向磁场磁通切换电机弱磁控制[J]. 中国电机工程学报, 2015, 35(19): 5059-5068.
Zhao Jilong, Lin Mingyao, Xu Da, et al. Flux- weakening control of hybrid excited axial field flux-switching machines[J]. Proceedings of the CSEE, 2015, 35(19): 5059-5068.
[20] 赵纪龙, 景梦蝶, 林明耀, 等. 基于矢量控制的混合励磁轴向磁场磁通切换永磁电机分区控制策略[J]. 中国电机工程学报, 2017, 37(22): 6567-6577.
Zhao Jilong, Jing Mengdie, Lin Mingyao, et al. A zone control scheme of hybrid excited axial field flux-switching permanent magnet machine with vector control[J]. Proceedings of the CSEE, 2017, 37(22): 6567-6577.
Maximum Ratio of Torque to Copper Loss Control of Hybrid Excited Flux Switching Motor Based on Combination Algorithm
Abstract Hybrid excited flux switching machines (HEFSMs) have the advantages of permanent magnet flux switching motor and hybrid excitation synchronous motor. The air gap magnetic field can be adjusted by adjusting the excitation current. This kind of motor has a wide application prospect in industry, especially in the field of electric vehicles. In this paper, an optimized maximum ratio of torque to copper loss control strategy for HEFSM in full speed range is proposed. In the low speed constant torque region, the optimized excitation current is used to improve the load capacity and minimize the copper loss. It has a faster response speed than the random combination strategy of excitation current and armature current and the control strategy of zero excitation current. In the constant power range, the objective function of copper loss is established, and the constraints are torque, current, voltage and speed. The optimized negative excitation current and d-axis current can not only obtain higher speed and reluctance torque, but also achieve the maximum ratio of torque to copper loss under a certain torque value, which can expand the speed range and improve the efficiency. Finally, a motor system experimental platform based on dSPACE1103 is built, and the feasibility and effectiveness of the proposed control strategy are verified by experiments.
keywords:Hybrid excited flux-switching machine, copper loss, excitation current, maximum ratio of torque to copper loss, optimization
DOI: 10.19595/j.cnki.1000-6753.tces.201182
中图分类号:TM351
李 帅 男,1993年生,硕士,工程师,研究方向为电力设备电磁场分析。E-mail: lsgfr4523@163.con
丁 文 男,1981年生,副教授,博士生导师,研究方向为电机系统及其控制、无线电能传输。E-mail: wending@xjtu.edu.cn(通信作者)
收稿日期 2020-09-12
改稿日期 2020-11-20
国家自然科学基金资助项目(51777161, 52077164)。
(编辑 崔文静)