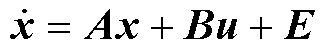 (1)
(1)
摘要 电流传感器受制造工艺与使用环境等因素的影响,在永磁同步电机驱动系统运行时可能失效。为提高系统的容错控制能力,该文提出一种新的基于自适应观测器的单电流传感器矢量控制策略。该策略首先在旋转坐标系下建立电流自适应观测器的数学模型,然后对唯一可测量的相电流进行坐标变换与低通滤波,计算出电流自适应观测器所需要的电流误差信息,并使用粒子群算法对观测器参数进行优化设计。半实物实时仿真结果表明与传统方法相比,所提方法具有更好的动态与稳态性能以及更高的转矩控制精度,并对电机参数具有良好的鲁棒性。
关键词:永磁同步电机 单电流传感器 自适应观测器 粒子群优化算法 低通滤波
永磁同步电机(Permanent Magnet Synchronous Machine,PMSM)具有运行效率高、功率密度高等优点,在工业驱动、船舶推进等领域应用广泛[1-4]。
在永磁同步电机驱动系统中,相电流传感器用来采集电机的相电流信息,是高性能闭环控制中不可或缺的环节。但受制于工艺水平或外部恶劣环境的影响,相电流传感器可能会出现故障[5]。为了提高变频器的可靠性,在相电流传感器出现故障时,一方面要快速准确地诊断出故障类型并定位,为维修人员和用户提供有效的故障信息,大大缩减产品的维修时间;另一方面要具备故障下的容错控制能力,降低变频器因故障停机而可能造成的经济损失和人员伤亡[6]。
相电流传感器故障容错控制策略按照实现的方案可大致分为三类:一是开环控制;二是单相电流传感器控制;三是无电流传感器控制[7-8]。其中,开环控制方案存在较大误差,无法实现高控制精度;无电流传感器控制方案应对外界突变条件时的自抗扰能力弱[9]。文献[10]分别基于电流估算和无电流环对永磁同步电机伺服控制系统实现了矢量控制,但仿真和实验均为空载,未考虑转矩对驱动系统的影响。实际三相永磁同步电机驱动系统具有2~3个相电流传感器,同时出现故障的概率很小,此时可以采用单电流传感器控制方案,利用一个可用电流传感器配合电流重构算法获得完整电流信息,实现三相永磁同步电机驱动系统的矢量控制。文献[11]基于全阶滑模观测器和龙贝格观测器,利用单电流传感器实现了电流重构,但是忽略了空间电流矢量的方向变化,交直轴电流谐波较大,动态性能较差,在低转速工况表现不佳。文献[12]基于卡尔曼滤波器设计了单电流传感器控制算法,但修正电流的计算不够精确,控制性能不佳,电机转矩精度低,有非周期性脉冲尖峰。
永磁同步电机在运行时若发生相电流传感器失效,易导致电机控制发散或过电流,在此情况下可由电流传感器故障诊断算法判别是否是相电流传感器故障。目前,永磁同步电机驱动系统运行时的电流传感器故障诊断方法已有相关研究,主要有基于信号的方法[13]和基于模型的方法[14]。通过这些方法可以诊断出各相电流传感器是处于故障状态还是正常工作状态。在仅剩一相电流传感器非故障时,可应用本文提出的基于自适应观测器的单电流传感器矢量控制策略进行容错控制,在已知电机的转子位置时,通过坐标变换和低通滤波计算出电流自适应观测器所需要的电流误差信息。控制简单,利于工程实践。本文在半实物实时仿真平台上对提出的单相电流传感器矢量控制策略进行了实时仿真。
当PMSM的铁心磁饱和、铁损和涡流损耗忽略不计时,在旋转d-q坐标系下PMSM的电流方程[15]为
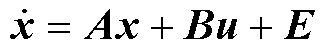 (1)
(1)
其中
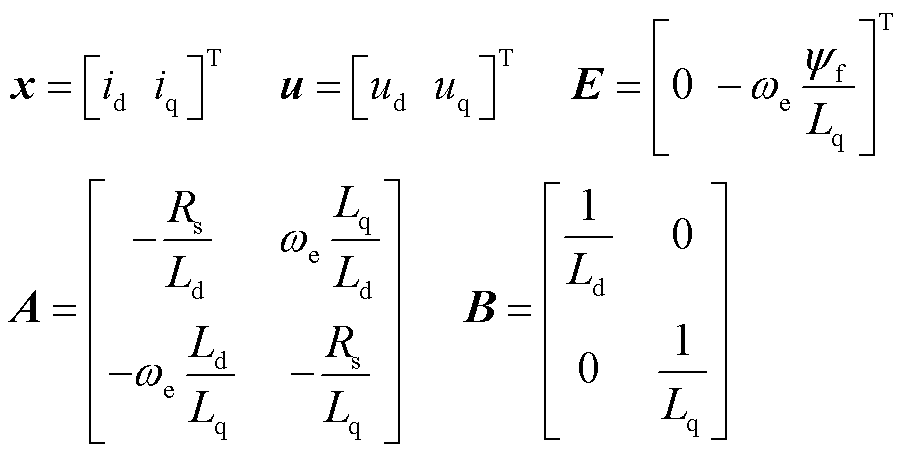
式中,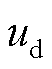 、
、 分别为d、q轴电压;
分别为d、q轴电压; 、
、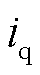 分别为d、q轴电流;
分别为d、q轴电流;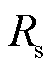 为定子绕组电阻;
为定子绕组电阻;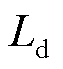 、
、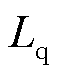 分别为d、q轴电感;
分别为d、q轴电感;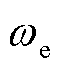 为电机的电角速度;
为电机的电角速度;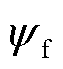 为永磁体磁链。
为永磁体磁链。
电磁转矩方程为
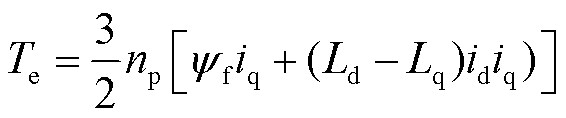 (2)
(2)
式中,np为电机极对数。
直接使用上述方程对交直轴电流进行观测属于开环方式,由于系统的非理想特性,如死区、管压降、电气参数误差等,开环观测可能会导致较大误差甚至发散,因此需要引入闭环环节对观测量进行修正调节。采用式(1)的自适应观测器对交直轴电流进行闭环观测为
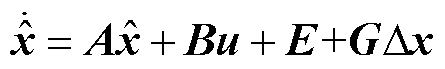 (3)
(3)
式中,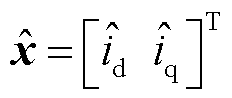 为观测量;电流误差
为观测量;电流误差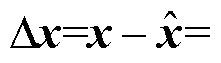
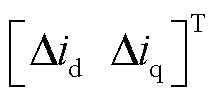 ;系数矩阵
;系数矩阵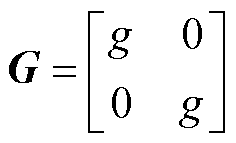 ,g为正实数。
,g为正实数。
下面将介绍在只有一个电流传感器正常工作的情况下,如何计算电流误差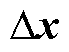 。
。
假定只有一相电流传感器正常工作,该相编号为m,m=0, 1, 2分别对应A、B、C三相,令 为相应的电流采样值,则根据反Park变换[16]有
为相应的电流采样值,则根据反Park变换[16]有
 (4)
(4)
式中,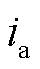 、
、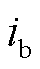 、
、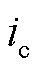 分别为A相、B相、C相电流;
分别为A相、B相、C相电流;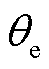 为电角度,可得
为电角度,可得
![]() (5)
(5)
根据观测的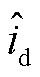 和
和 ,可以计算得
,可以计算得
用式(5)与式(6)相减,可得
![]() (7)
(7)
则
将式(8)两边乘以 并化简可得
并化简可得
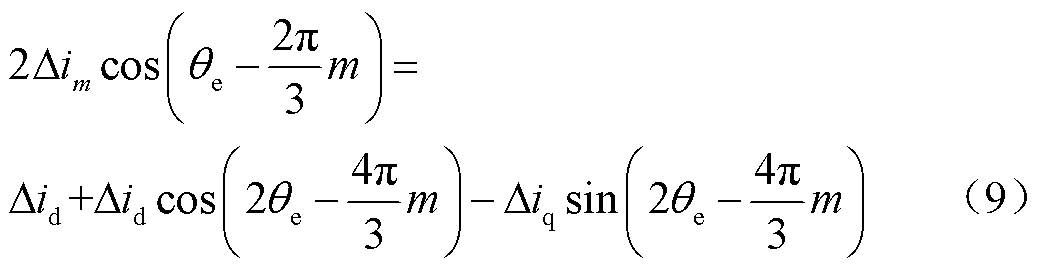
对式(9)进行低通滤波,即可得到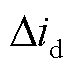 。
。
同理将式(8)两边乘以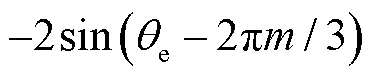 并化简可得
并化简可得
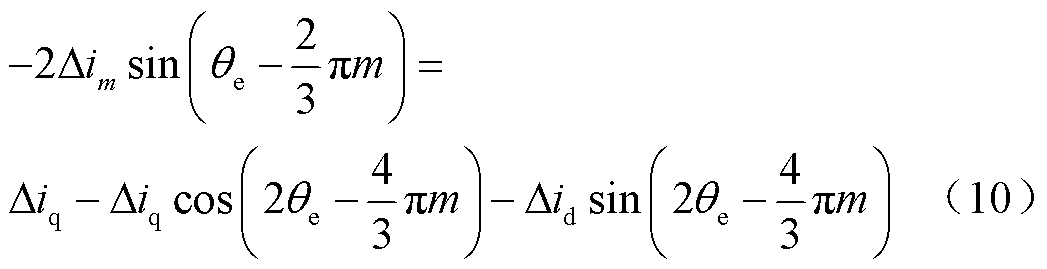
对式(10)进行低通滤波,即可得到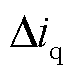 。
。
基于上述结果,可以得到任意一相电流传感器正常工作时的电流误差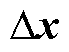 。
。
电流观测器的算法框图如图1所示。

图1 电流观测器的算法框图
Fig.1 Block diagram of the current observer
图1中
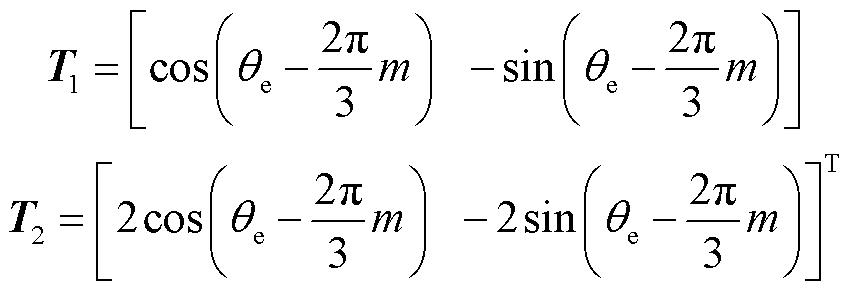
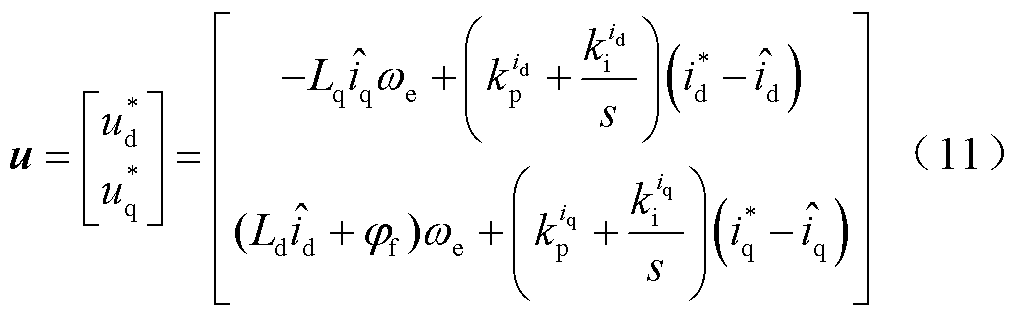
式中,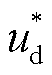 、
、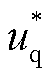 为d、q轴电压参考值;
为d、q轴电压参考值; 、
、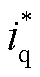 为d、q轴电流参考值;Tf为低通滤器时间常数;
为d、q轴电流参考值;Tf为低通滤器时间常数;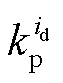 、
、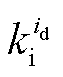 为直轴电流环PI参数;
为直轴电流环PI参数;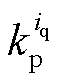 、
、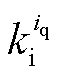 为交轴电流环PI参数,具体设计方法可参考文献[17]。
为交轴电流环PI参数,具体设计方法可参考文献[17]。
三相永磁同步电机闭环控制的反馈电流均可采用观测器观测到的交直轴电流信息。该方案可实现任意单相电流传感器正常工作时的矢量控制。
对如图1所示的电流观测器建立小信号模型,为
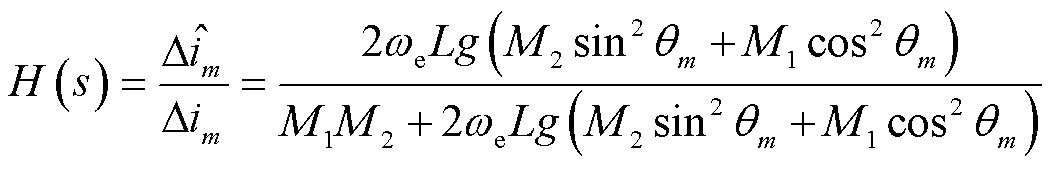 (12)
(12)
其中
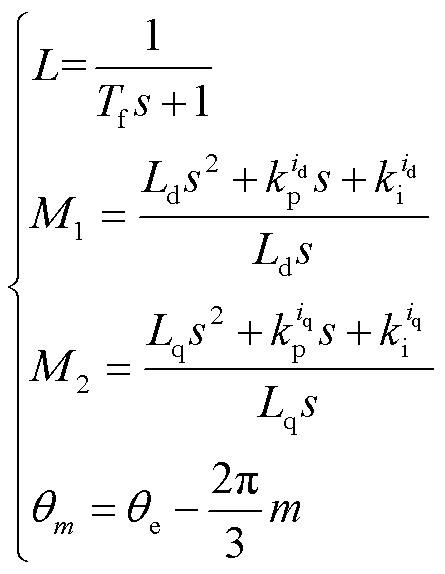 (13)
(13)
需要设计的参数有g和Tf,可变的参数有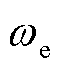 和
和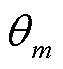 。粒子群算法(Particle Swarm Optimization, PSO)具有概念简明、实现方便、收敛速度快等优点,故采用该方法进行参数设计[18]。下面将具体给出实现步骤。
。粒子群算法(Particle Swarm Optimization, PSO)具有概念简明、实现方便、收敛速度快等优点,故采用该方法进行参数设计[18]。下面将具体给出实现步骤。
1)初始化n组待设计的参数及搜索步长约束
根据经验对参数g和Tf进行初始化,设定n=20,每组参数在式(14)所示的范围内随机选择。
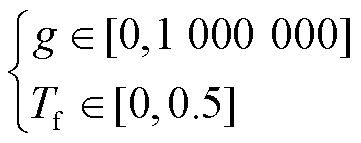 (14)
(14)
搜索步长约束为
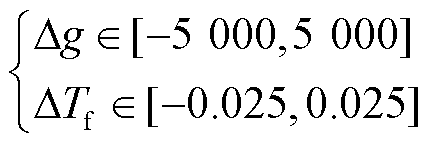 (15)
(15)
2)工况及性能指标设定
假定电机转速工作范围为[-3 000r/min, 3 000r/min],则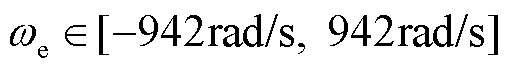 ,均匀划分为20个转速等级;位置角
,均匀划分为20个转速等级;位置角 ,均匀划分为20个位置角度,则总的工况数N=20×20=400。
,均匀划分为20个位置角度,则总的工况数N=20×20=400。
虽然参数g和Tf的解析表达式难以获得,但是在给定具体的工况、转速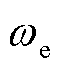 和位置
和位置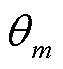 参数时,通过Matlab软件可以计算出闭环系统的各项性能指标。令
参数时,通过Matlab软件可以计算出闭环系统的各项性能指标。令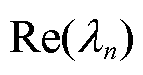 为极点
为极点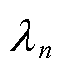 的实部,
的实部,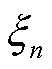 为阻尼,则设计约束条件为
为阻尼,则设计约束条件为
 (16)
(16)
若全部N个工况均满足上述约束条件,则令C=1,否则C=0。C=1意味着系统在N个工况下均稳定,但是稳定裕度尚不明确。
定义P为全部N个工况下所有极点实部的最大值(系统稳定,则P值为负),为了让系统在全工况下均有较大的稳定裕度,P值应尽量小。因此定义适应度函数为
 (17)
(17)
可见适应度函数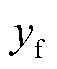 越大,系统的稳定裕度越大,并能满足设定的动态性能(阻尼系数决定)。
越大,系统的稳定裕度越大,并能满足设定的动态性能(阻尼系数决定)。
3)参数与搜索步长更新
根据PSO算法,其位置(即待优化的参数)和速度(即搜索步长)的更新公式[19]为
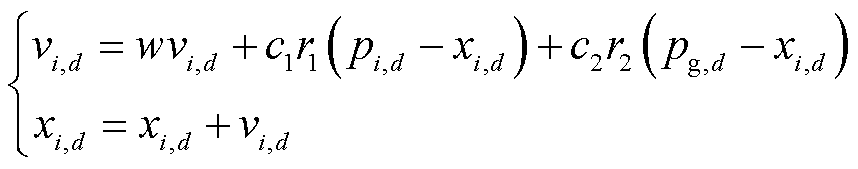 (18)
(18)
式中,i为粒子编号;d为维度编号;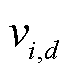 为速度;
为速度;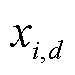 为位置;
为位置; 为自我学习因子;
为自我学习因子;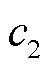 为群体学习因子;
为群体学习因子;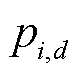 为第i个粒子最优位置;
为第i个粒子最优位置;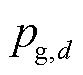 为所有粒子的历史最优位置;
为所有粒子的历史最优位置;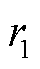 和
和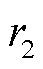 为0~1之间的随机数。
为0~1之间的随机数。
4)收敛判断
当所有粒子的历史最大适应度函数等于最大工况数,或者迭代次数达到设定的次数时,则判定算法收敛。
由上述方法可设计出控制参数g和Tf。
PMSM单电流传感器控制策略的半实物实时仿真验证方案如图2所示,利用Matlab搭建包含电机模型和驱动模型的Simulink仿真模型,利用HDL coder工具箱生成相应的HDL语言,并将其烧写至FPGA芯片;FPGA与DSP通过数据上行和数据下行完成数据传输;DSP实现的主要功能包括电流观测、矢量控制策略、PWM调制;并通过CAN卡连接上位机,实现上位机控制;这样形成一个微型半实物仿真系统。其中,DSP芯片为TI公司的TMS320F28335,FPGA芯片为Cyclone Ⅳ E系列EP4CE115F2317。
在半实物实时仿真中,进行了三种永磁同步电机矢量控制策略的对比:一是两个电流传感器控制方案;二是基于文献[20]的传统电流滑模观测器方案,此方案利用电流空间矢量误差在α、β轴投影,通过电流滑模观测器重构α、β轴电流误差,实现电机驱动系统的单电流传感器控制;三是本文提出的自适应观测器控制方案。

图2 半实物实时仿真平台
Fig.2 Hardware-in-the-loop real-time simulation platform
PMSM参数设计见表1。仿真条件设置为:SVPWM开关频率5 kHz,直流侧电压VDC = 900 V。为了方便比较和直观显示控制性能,本文波形图纵坐标均为相应量的标幺值,基准值为额定值。
表1 PMSM参数设计
Tab.1 PMSM parameter design

参数数值 额定转速/(r/min)3 000 额定转矩/(N∙m)955 额定功率/kW额定电流/A300 500 定子电阻/Ω0.004 1 转子磁链/ Wb0.29 转动惯量/(kg·m2)1.39 d轴电感/mH0.28 q轴电感/mH采样周期/ms死区时间/ms0.61100 5
(续)

参数数值 直轴电流环1.333 直轴电流环19.524 交轴电流环2.905 交轴电流环19.524 观测器参数g170 391 电流滤波时间常数Tf/s0.002 85
表1中的交直轴电流环PI参数由文献[17]给出的PI参数整定算法结合PMSM设计参数计算得到。自适应观测器控制参数g和Tf由2.2节粒子群算法计算得到。
当A相电流传感器可用时,利用单电流传感器控制方法可观测B、C相电流。当电机工作在额定转速、额定转矩工况时,不同控制方案的观测电流和实际电流波形如图3所示。结果表明,本文提出的方法相比于传统电流滑模观测器方案,相电流观测误差更小,观测效果更准确。

图3 不同控制方法的观测电流和实际电流波形
Fig.3 Observed current and actual current curves with different control methods
在额定转速额定负载转矩工况下,不同矢量控制方法的实际交直轴电流波形和频谱如图4所示。其中,为验证矢量控制策略对电机参数d轴电感Ld的鲁棒性,Ld加入了参数摄动,其中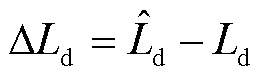 ,
,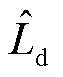 为参数摄动值,
为参数摄动值,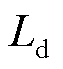 为额定值。结果表明本文自适应观测器方法有一定的2倍基频分量。这是因为由式(9)和式(10)计算d、q轴电流误差时,式中存在2倍基频项,由于低通滤波器时间常数优化设计需折中考虑动态与稳态性能,此误差无法通过低通滤波器完全滤除。
为额定值。结果表明本文自适应观测器方法有一定的2倍基频分量。这是因为由式(9)和式(10)计算d、q轴电流误差时,式中存在2倍基频项,由于低通滤波器时间常数优化设计需折中考虑动态与稳态性能,此误差无法通过低通滤波器完全滤除。
在此工况下,当参数摄动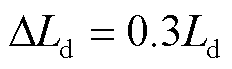 时,采用传统电流滑模观测器控制方案难以使系统稳定,故这里只给出了
时,采用传统电流滑模观测器控制方案难以使系统稳定,故这里只给出了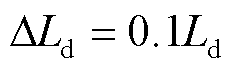 时的波形和频谱。从结果可见,尽管此时参数摄动较小,传统方法的控制性能仍不及本文提出方案。由图4可知,传统电流滑模观测器方案直轴电流id有明显的1倍和2倍基频谐波,交轴电流iq有明显的1倍、2倍和4倍基频谐波,而本文所提方法中交、直轴电流的1倍基频谐波和总电流谐波含量均显著降低。
时的波形和频谱。从结果可见,尽管此时参数摄动较小,传统方法的控制性能仍不及本文提出方案。由图4可知,传统电流滑模观测器方案直轴电流id有明显的1倍和2倍基频谐波,交轴电流iq有明显的1倍、2倍和4倍基频谐波,而本文所提方法中交、直轴电流的1倍基频谐波和总电流谐波含量均显著降低。
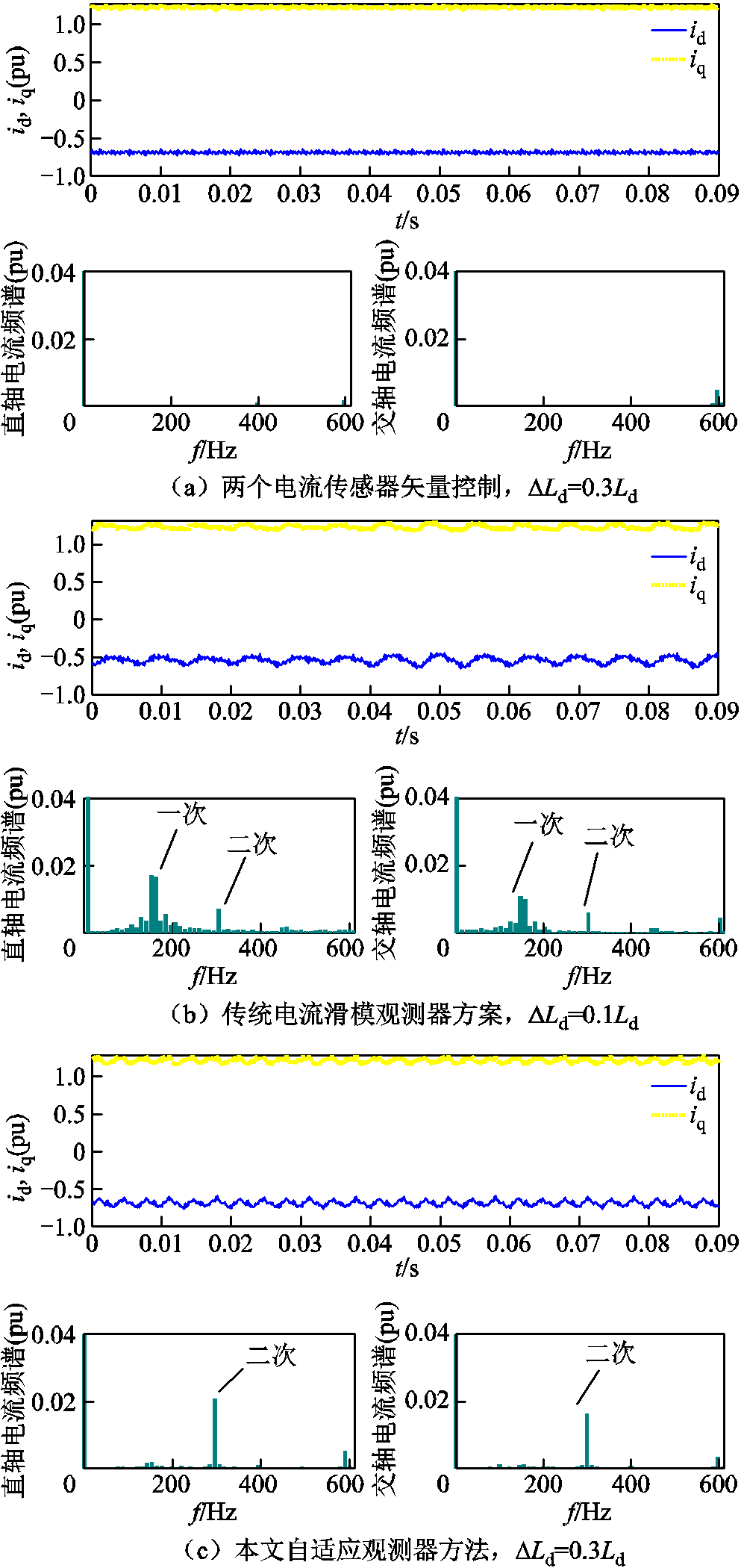
图4 额速额载工况,不同控制方法交直轴电流及频谱
Fig.4 The dq-axis currents and frequency spectrum of different control methods under the rated operating condition
图5为50 r/min转速额定负载工况下,采用两个电流传感器控制策略和本文自适应观测器方法的三相电流波形。其中,为验证矢量控制策略对电机参数定子电阻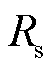 的鲁棒性,
的鲁棒性,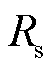 加入了参数摄动,其中
加入了参数摄动,其中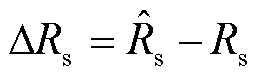 ,
,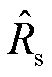 为参数摄动值,
为参数摄动值,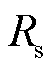 为额定值。传统电流滑模观测器控制方法在此工况下难以稳定运行,故未给出其波形。结果表明,本文方法在50 r/min的极低转速大负载转矩工况能够稳定运行,对电机参数
为额定值。传统电流滑模观测器控制方法在此工况下难以稳定运行,故未给出其波形。结果表明,本文方法在50 r/min的极低转速大负载转矩工况能够稳定运行,对电机参数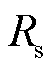 有良好的鲁棒性。
有良好的鲁棒性。
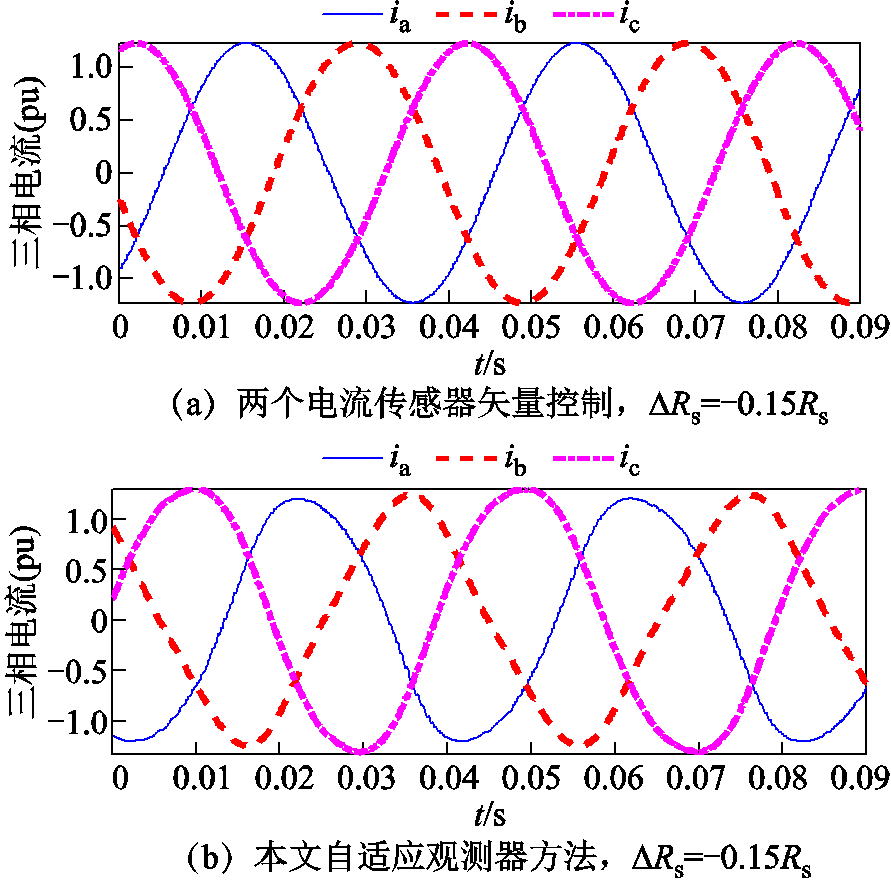
图5 50r/min额载工况不同控制方法三相电流
Fig.5 The three-phase currents of different control methods under 50r/min and rated load condition
表2给出了不同控制策略在不同工况稳态时的交直轴电流谐波大小。为验证矢量控制策略对永磁体磁链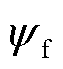 的鲁棒性,工况中加入了参数摄动
的鲁棒性,工况中加入了参数摄动 ,
, 为参数摄动值,
为参数摄动值,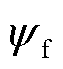 为额定值。表中工况1为额速满载;工况2为70%额定转速满载;工况3为30%额定转速满载。结果表明,采用本文自适应观测器方法的id、iq谐波含量均比传统电流滑模观测器控制方案小。
为额定值。表中工况1为额速满载;工况2为70%额定转速满载;工况3为30%额定转速满载。结果表明,采用本文自适应观测器方法的id、iq谐波含量均比传统电流滑模观测器控制方案小。
表2 不同工况时交直轴电流谐波大小
Tab.2 The dq-axis current harmonics under different working conditions (%)

工况传统电流滑模观测器控制方案两个电流传感器矢量控制本文自适应观测器方法 THD(id)THD(iq) THD(id)THD(iq) THD(id)THD(iq) 16.001.264.461.204.551.28 24.131.181.130.402.320.89 33.471.141.780.442.430.79
GB/T 17626.7—2008《电磁兼容试验和测量技术供电系统及所连设备谐波、谐间波的测量和测量仪器导则》中,THD定义为
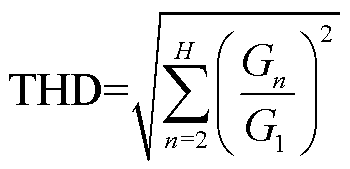
式中,G为谐波分量的有效值,它在表示电流时被I代替,在表示电压时被U代替。
图6给出了不同控制策略在不同工况稳态时的转矩平均相对误差大小。转矩相对误差定义为

式中,观测转矩由观测电流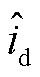 、
、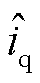 通过式(2)计算得到;实际转矩由实际电流id、iq通过式(2)计算得到;电机参数采用电机实际运行参数。转矩平均相对误差指的是一段时间内转矩相对误差的平均值,反映了矢量控制方法的转矩控制精度。图6结果表明,本文提出的自适应观测器方法转矩控制精度远好于传统电流滑模观测器方案,以3 000 r/min工况为例,本文自适应观测器方法转矩平均相对误差对比传统电流滑模观测器控制方案,由4.45%下降到1.34%,下降幅度达到69.9%。
通过式(2)计算得到;实际转矩由实际电流id、iq通过式(2)计算得到;电机参数采用电机实际运行参数。转矩平均相对误差指的是一段时间内转矩相对误差的平均值,反映了矢量控制方法的转矩控制精度。图6结果表明,本文提出的自适应观测器方法转矩控制精度远好于传统电流滑模观测器方案,以3 000 r/min工况为例,本文自适应观测器方法转矩平均相对误差对比传统电流滑模观测器控制方案,由4.45%下降到1.34%,下降幅度达到69.9%。
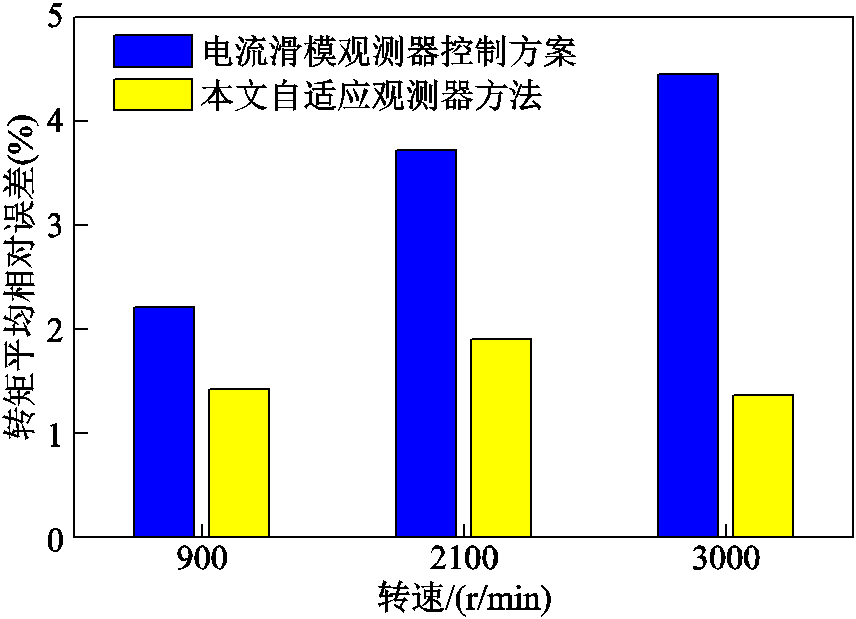
图6 额载工况下不同转速稳态时转矩平均相对误差
Fig.6 The average relative error of torque at different speeds in steady state under rated load torque working condition
图7给出了不同控制策略在额定转速下突加、突卸额定负载转矩的电流波形。为验证矢量控制策略对电机参数交轴电感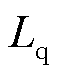 的鲁棒性,工况中加入了参数摄动
的鲁棒性,工况中加入了参数摄动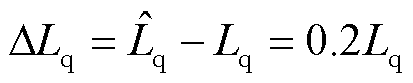 ,
,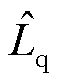 为参数摄动值,
为参数摄动值,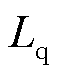 为额定值。结果表明,本文自适应观测器方法的实际交直轴电流有小幅振荡,这是因为电流重构的计算过程利用了低通滤波器,但很快收敛并稳定。传统电流滑模观测器方案中亦存在低通滤波器,不可避免地存在振荡。并且传统电流滑模观测器方案的电流重构过程利用了电流空间矢量,但电流空间矢
为额定值。结果表明,本文自适应观测器方法的实际交直轴电流有小幅振荡,这是因为电流重构的计算过程利用了低通滤波器,但很快收敛并稳定。传统电流滑模观测器方案中亦存在低通滤波器,不可避免地存在振荡。并且传统电流滑模观测器方案的电流重构过程利用了电流空间矢量,但电流空间矢
量与d、q旋转坐标系的夹角难以确定,尤其当转矩突然变化时,此夹角的变化难以跟踪,故动态性能表现不佳。仿真结果表明本文自适应传感器方法交直轴电流振荡幅值和振荡时间明显减小;与两个电流传感器矢量控制性能相近。
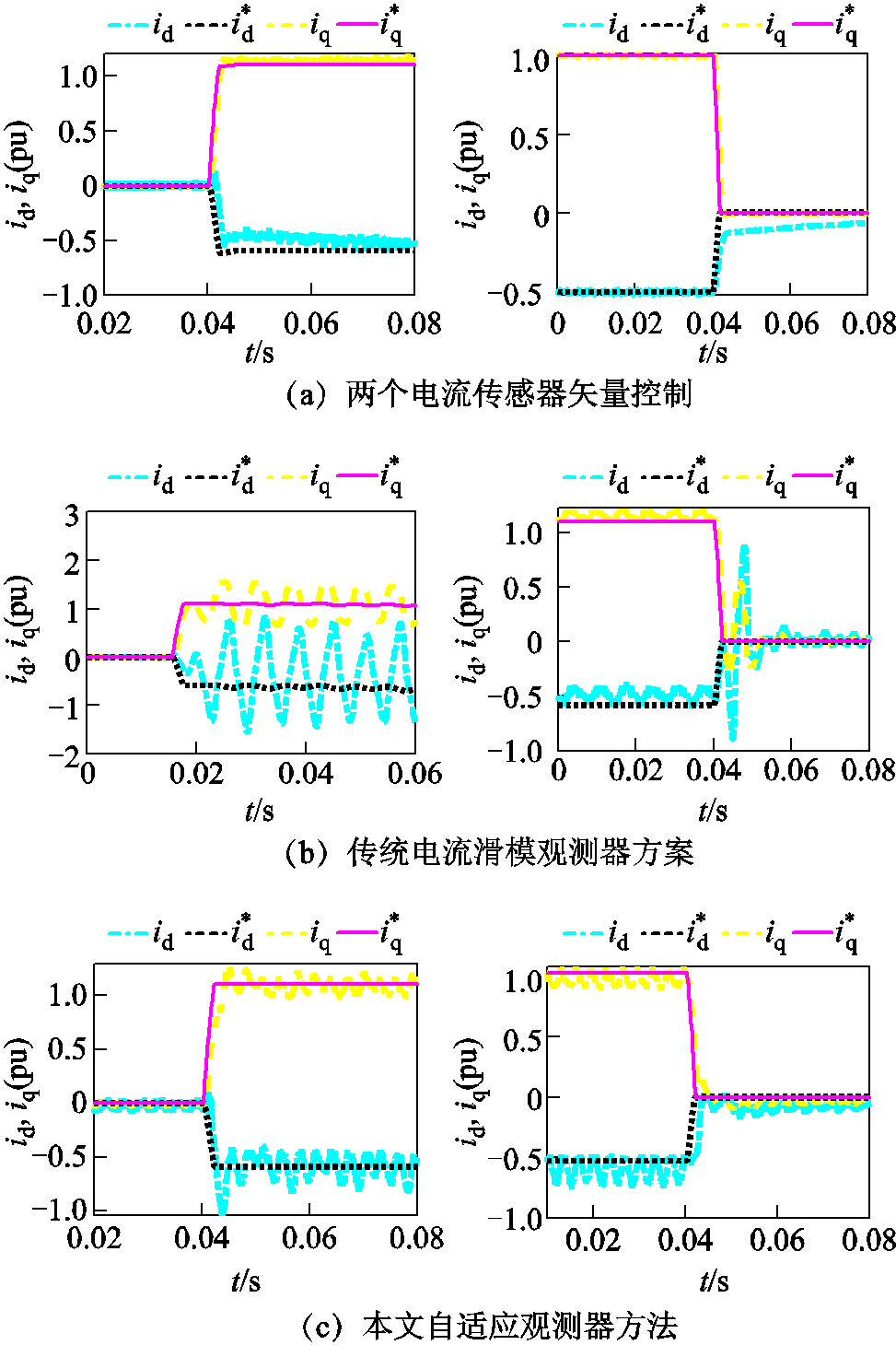
图7 额定转速下突加突卸额定转矩
Fig.7 The dq-axis currents with rated torque added and unloaded suddenly at rated speed working condition
图8给出了不同控制策略在正、负额定转速 (3 000 r/min)范围内运行时的交直轴电流和转速波形,用以评估不同方法的动态性能。在整个运行过程中系统工作在电动与发电两种模式。为验证不同控制策略对电机参数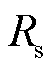 和
和 同时变化的鲁棒性,
同时变化的鲁棒性,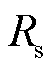 和
和 加入了参数摄动,具体为
加入了参数摄动,具体为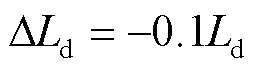 和
和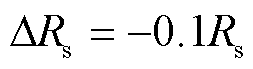 。
。
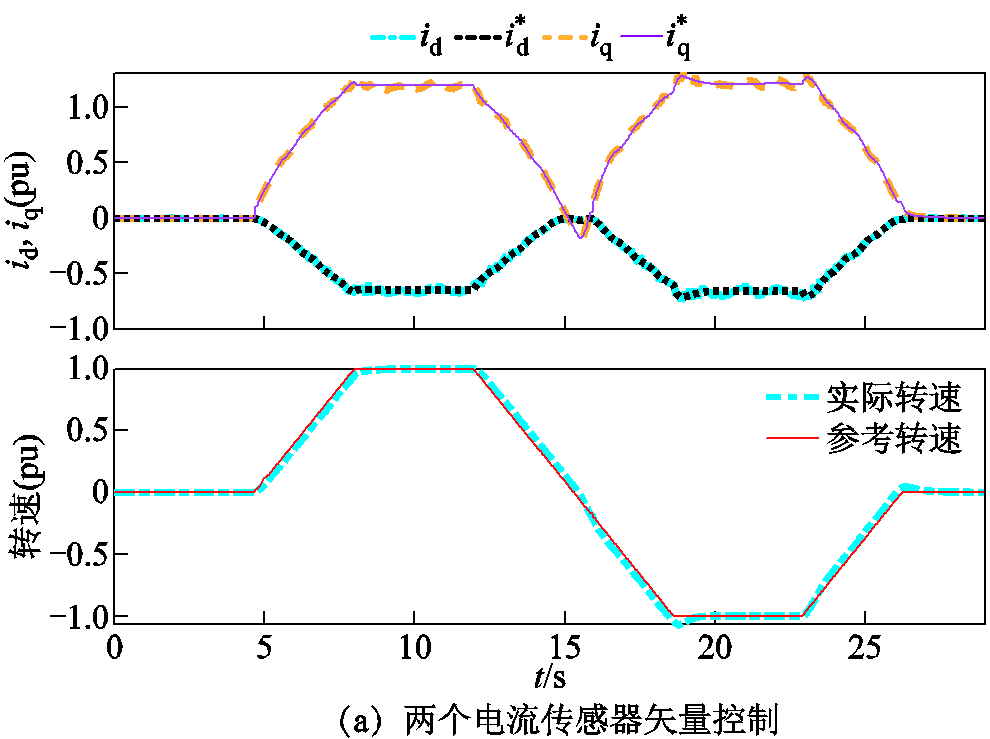
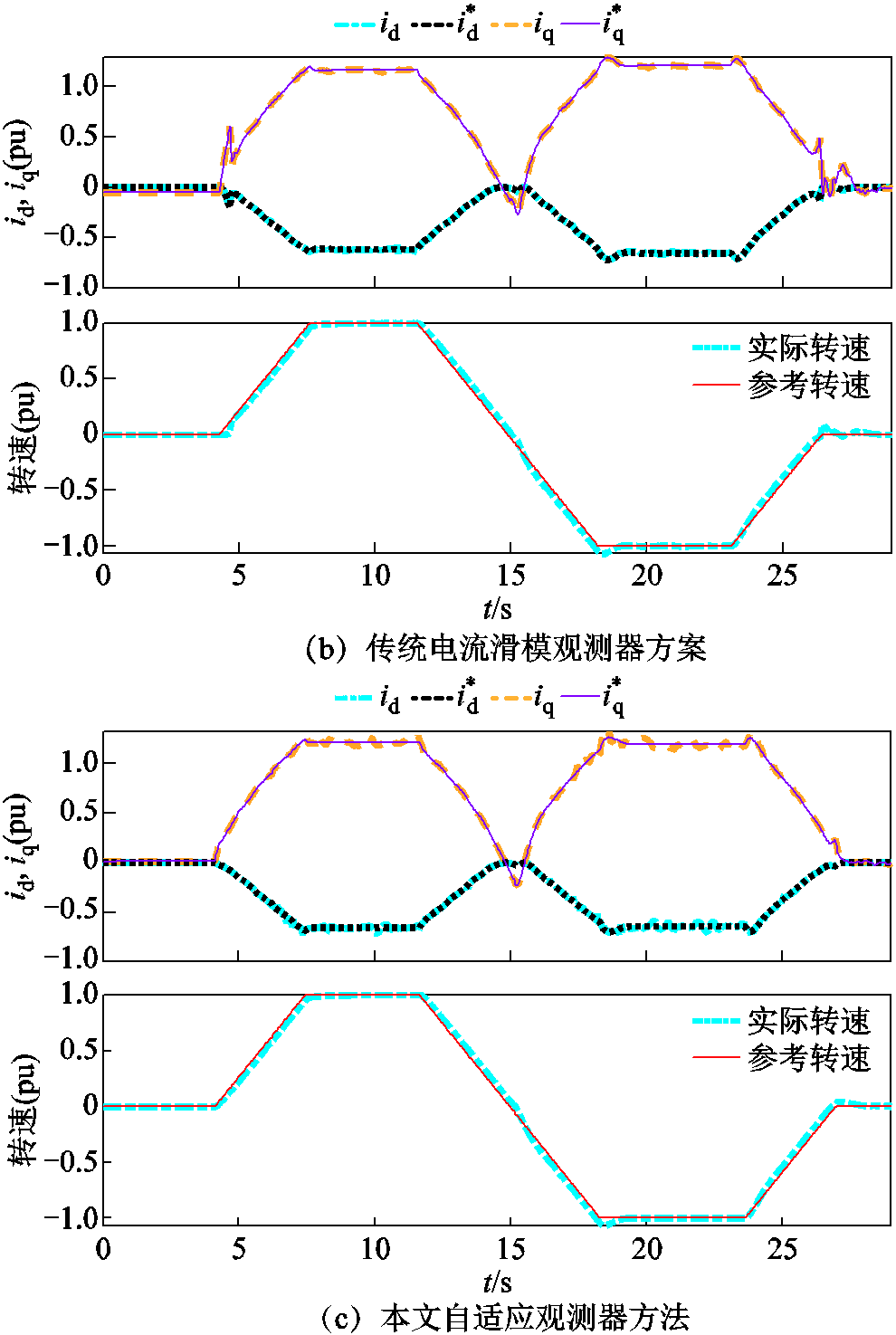
图8 全工况下的电流与速度曲线
Fig.8 Curves of current and speed in the entire operating condition
从全转速工况下电流与速度波形可以看出,传统电流滑模观测器方案在加速阶段交直轴电流变化不够平滑,低速工况存在振荡,动态性能表现不佳。本文自适应观测器方法与两个电流传感器矢量控制方法的转速动态控制性能十分接近,远好于传统电流滑模观测器方案。
本文提出一种基于自适应观测器的三相永磁同步电机单电流传感器矢量控制策略。首先详细介绍了自适应观测器的结构和参数设计方法,然后在半实物实时仿真平台上对提出的单电流传感器矢量控制策略进行仿真验证。与传统方法相比,本文自适应观测器方法基本消除了交直轴电流中的1倍基频谐波,电流总谐波和转矩平均相对误差明显减小,稳态性能显著提升;在突加突卸转矩和转速突变的动态过程中同样具有良好的控制性能,并且对电机参数摄动有较强的鲁棒性。
参考文献
[1] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883-892.
[2] 李垣江, 董鑫, 魏海峰, 等. 表贴式永磁同步电机转速环复合PI无位置传感器控制[J]. 电工技术学报, 2020, 35(10): 2119-2129.
Li Yuanjiang, Dong Xin, Wei Haifeng, et al. Sensorless compound PI control for surface permanent magnet synchronous motor speed regulation system[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2119-2129.
[3] 张伟伟, 肖飞, 刘计龙, 等. 轨道交通车辆永磁同步牵引系统断电区穿越控制策略[J]. 电工技术学报, 2021, 36(16): 3483-3492.
Zhang Weiwei, Xiao Fei, Liu Jilong, et al. Control strategy for power-off area crossing of permanent magnet synchronous traction system of rail transit vehicles[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3483-3492.
[4] He Mingjie, Li Weiye, Peng Jun, et al. Multi-layer quasi three-dimensional equivalent model of axial-flux permanent magnet synchronous machine[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 3-12.
[5] Gao Zhiwei, Cecat C, Ding S X. A survey of fault diagnosis and fault-tolerant techniques—part i: fault diagnosis with model-based and signal-based approaches[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757-3767.
[6] Khil S K E, Jlassi I, Cardoso A J M, et al. Diagnosis of open-switch and current sensor faults in PMSM drives through stator current analysis[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 5925-5937.
[7] 崔宏伟. 永磁同步电机控制系统无电流传感器技术的研究[D]. 兰州: 兰州交通大学, 2018.
[8] An Quntao, Sun Li, Sun Lizhi. Current residual vector-based open-switch fault diagnosis of inverters in PMSM drive systems[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2814-2827.
[9] 应黎明, 杭翠翠, 舒乃秋, 等. 永磁同步电机传感器故障诊断及容错控制[J]. 电机与控制学报, 2020, 24(1): 45-52.
Ying Liming, Hang Cuicui, Shu Naiqiu, et al. Permanent magnet synchronous motor fault diagnosisand fault-tolerant control[J]. Electric Machines and Control, 2020, 24(1): 45-52.
[10] 孙宇航. 永磁同步电机无电流传感器伺服控制技术研究[D]. 杭州: 浙江大学, 2020.
[11] 王国鑫. 永磁电机驱动系统传感器故障诊断与容错控制[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[12] Beng G F H, Zhang Xinan, Vilathgamuwa D M. Sensor fault-resilient control of interior permanent-magnet synchronous motor drives[J]. IEEE/ASME Transactions on Mechatronics, 2015,20(2): 855-864.
[13] Khil S K E, Jlassi I, Estima J O. Current sensor fault detection and isolation method for PMSM drives, using average normalized currents[J]. Control Engineering Practice, 2016, 52(17): 1434-1435.
[14] 袁臣虎, 王岁, 刘晓明, 等. 基于PMSM的EPS系统电流传感器零点误差在线标定策略研究与调控实现[J]. 电工技术学报, 2018, 33(15): 3635-3643.
Yuan Chenhu, Wang Sui, Liu Xiaoming, et al. On line calibration strategy and regulation implementation of EPS system current sensor zero error based on PMSM[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3635-3643.
[15] 连传强, 肖飞, 高山, 等. 基于实验标定及双时间尺度随机逼近理论的内置式永磁同步电机参数辨识[J]. 中国电机工程学报, 2019, 39(16): 4892-4898, 4991.
Lian Chuanqiang, Xiao Fei, Gao Shan, et al. Parameter identification for interior permanent magnet synchronous motor based on experimental calibration and stochastic approximation theory with two time scales[J]. Proceedings of the CSEE, 2019, 39(16): 4892-4898, 4991.
[16] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10): 2130-2140.
Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two-vector-based model predictive flux control of three-level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2130-2140.
[17] Kan Liu, Zhu Z Q. Fast determination of moment of inertia of permanent magnet synchronous machine drives for design of speed loop regulator[J]. IEEE Transactions on Control Systems Technology, 2017, 25(5): 1816-1824.
[18] 赖纪东, 谢天月, 苏建徽, 等. 基于粒子群优化算法的孤岛微电网电压不平衡补偿协调控制[J]. 电力系统自动化, 2020, 44(16): 121-129.
Lai Jidong, Xie Tianyue, Su Jianhui, et al. Coordinated control of voltage unbalance compensation in islanded microgrid based on particle swarm optimization algorithm[J] Automation of Electric Power Systems, 2020, 44(16): 121-129.
[19] 李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59, 76.
Li Jiaxiang, Wang Fengxiang, Ke Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59,76.
[20] 周洪雷. 内置式永磁电机驱动系统电流传感器故障容错控制[D]. 哈尔滨: 哈尔滨工业大学, 2019.
Three-Phase Current Reconstruction Strategy of Permanent Magnet Synchronous Machine Drives Using a Single Current Sensor
Abstract Affected by factors such as manufacturing process and use environment, the current sensor may fail when the permanent magnet synchronous machine drive system is running. To improve the fault-tolerant control ability of the system, a new vector control strategy using a single current sensor is proposed based on the adaptive observer. First, the mathematical model of the current adaptive observer is established in the rotating reference frame; then, the coordinate transformation and low-pass filtering are carried out for the only measurable phase current to calculate the current error information, which is needed by the current adaptive observer. Finally, the particle swarm optimization (PSO) algorithm is employed to design the observer parameters. The hardware-in-the-loop real-time simulation results show that compared with the traditional method, the proposed method has better dynamic and steady-state performance, higher torque control accuracy, and good robustness to motor parameters.
Keywords: Permanent magnet synchronous machine, single current sensor, adaptive observer, particle swarm optimization algorithm, low-pass filtering
DOI:10.19595/j.cnki.1000-6753.tces.210459
中图分类号:TM351
肖 飞 男,1977年生,教授,博士生导师,研究方向为电力电子及电气传动等。E-mail:xfeyninger@qq.com
连传强 男,1986年生,博士,副研究员,研究方向为电机系统及其控制、人工智能。E-mail:wzdslcq@163.com(通信作者)
收稿日期 2021-03-31
改稿日期 2021-06-16
国家自然科学基金青年科学基金资助项目(51807200)。
(编辑 郭丽军)