图1 万能式操作机构示意图
摘要 在万能式断路器合闸时，弹簧所储存的能量以撞击的形式经打击杆传递给连杆机构。由工艺因素引起的打击杆形位偏差对打击杆的断裂过程产生影响，使操作机构的使用寿命远低于设计指标。该文根据多体动力学理论，建立操作机构的虚拟样机模型。通过试验采集储能杠杆和联动轴的运动状态，对虚拟样机的准确性进行验证。然后使用实际产品的测量数据，获得打击杆端点相对滚子的空间形位偏差范围。再使用虚拟样机参数建模表现偏差情况，分析打击杆载荷峰值和裂纹萌生周期的变化。最后假设打击杆上已存在椭圆形裂纹，研究偏差对裂纹尖端应力强度因子的影响。该文给出打击杆空间形位偏差对其断裂过程的影响，可以为设计及工艺改进提供理论指导。
关键词：万能式断路器 断裂过程 偏差影响
万能式断路器作为一种重要的电器开关产品，用于保护低压配电系统免受过电流、逆电流、短路和欠电压等故障的损害[1]。对于断路器的研究，更多关注于触点燃弧特性[2]和短路分断能力[3]等电特性问题。光伏并网中，从原来的接触器、熔断器和万能式断路器并网结构简化为直接断路器并网，这对传统用于配电系统中的万能式断路器机械寿命也提出更高的要求[4]。例如，某分布式光伏并网电站要求1 600A万能式断路器的机械寿命为30 000次。有数据表明，国产与进口断路器的机械寿命差距主要源于操作机构的质量[5-6]。现阶段，在材料性能等本质因素不能发生质变的前提下，通过改善工艺水平降低形位偏差范围能够有效地提高机构的机械寿命，无论在成本还是可行性方面都具有重要的意义。因此，需要研究形位偏差对万能式断路器关键零件断裂过程的影响，为高端产品的制造提供理论指导。
为掌握断路器内零件的工作状态，达到预测机械寿命和故障报警的目的，一些学者通过加速度传感器和角位移传感器监控运行过程中的零件运动状态，再根据这些数据建立判定算法[7-9]。文献[10]对操作机构进行模糊化处理，判定的准确性受样本数量限制。随着计算机仿真技术的进步，通过多体动力学虚拟样机技术，能够对零件的载荷与应力情况进行计算。季良等建立断路器的虚拟样机，对连杆尺寸的最优值问题进行研究，使操作机构的分断速度得到提升[11]。舒亮等基于连续介质理论，根据断路器的多体动力学方程建立仿真模型，计算操作机构内部零件的应力分布情况[12]。此外，一些学者使用虚拟样机技术对断路器内零件位置的平面偏差影响进行研究[13-14]。此类方法可以对断路器零件的工作状态进行研究和优化，但无法给出偏差对关键零件断裂周期的影响。S. H. Park等通过仿真得到断路器内零件的应力分布，将其与材料的拉伸寿命试验相结合，对零件的失效寿命进行预估[15]。胡书通使用有限元软件对零件的裂纹萌生寿命进行计算，提出一种适用于断路器零件的疲劳寿命仿真方法[16]。
断路器接收到脱扣信号时脱扣电磁铁使锁扣解锁，主弹簧释能并推动储能杠杆加速运动。安装于储能杠杆上的打击杆以极高的速度撞击四连杆机构中的上连杆滚子，驱动下连杆带动主轴及触点闭合。该过程中，储能弹簧的绝大多数能量均由打击杆向连杆机构及触点机构传递。因此，打击杆与下连杆棍子之间的接触是合闸动作过程中最关键的能量传递环节。若打击杆断裂，则操作机构及断路器整机将发生机械失效。通过现有的研究成果可以计算平面形位偏差对零件裂纹萌生周期的影响，但未考虑空间形位偏差对裂纹扩展过程的影响。本文首先根据万能式断路器的动作原理，建立多体动力学方程，完成操作机构部分的虚拟样机。然后根据实测得到的打击杆偏差范围，使用虚拟样机计算该零件的载荷变化。再基于断裂力学理论，计算偏差对裂纹萌生周期和裂纹扩展中应力强度因子的影响。最后通过虚拟样机试验及整机小批量机械寿命试验，对研究结果进行验证。本研究将断路器内零件的空间形位偏差与断裂过程相联系，以期为工艺质量控制提供理论指导。
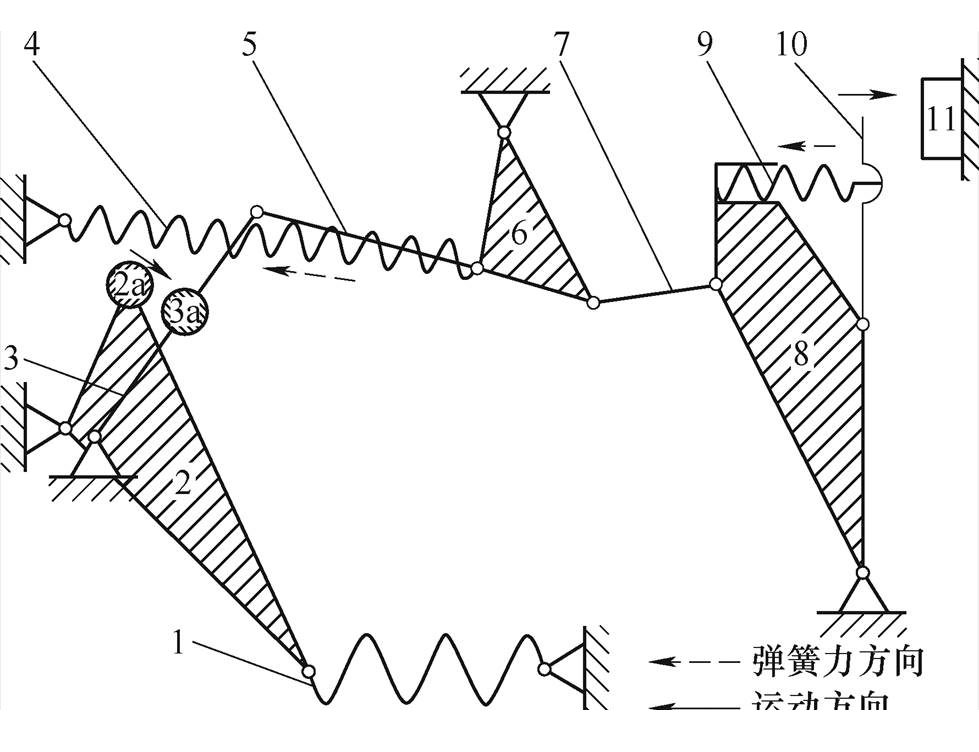
万能式操作机构的结构如图1所示。整套机构由两套四连杆机构组成，其中上连杆组件3、下连杆5和联动轴6构成第一套四连杆机构。联动轴6又与触点连杆7、触头座8组成第二套四连杆机构。图中所示的操作机构已经储能结束，在合闸时储能压簧1迅速释能，推动储能杠杆组件2绕固定于地面的转轴顺时针转动。由于四连杆机构的自由度为1，所以在储能杠杆组件2上的打击杆2a推动上连杆组件3中的滚子3a时，两套连杆机构将共同运动，直至动触点10与静触点11完全闭合。从能量传递的角度出发，储存在储能压簧1中的能量通过打击杆2a撞击滚子3a传递至两套连杆机构中，在合闸动作结束后，剩余的能量被储存在复位拉簧4和触点压簧9中。
图1 万能式操作机构示意图
1—储能压簧 2—储能杠杆组件 2a—打击杆1 3—上连杆组件 3a—滚子 4—复位拉簧 5—下连杆 6—联动轴 7—触点连杆 8—触头座 9—触点压簧 10—动触点 11—静触点
Fig.1 Typical structure of operating mechanics
由于工艺影响，使打击杆的轴心与滚子轴心间存在形位偏差。打击杆偏差示意图如图2所示，以设计值的打击杆轴心端点在xz和yz平面上的投影为坐标原点，建立平面坐标系对打击杆的偏斜进行描述。（yL, zL）与（yR, zR）为打击杆轴心端点在yz平面上的投影坐标，该坐标可通过实际样品测得；qxz为打击杆轴心与x轴在xz平面上的投影夹角；qxy为打击杆轴心与x轴在xy平面上的投影夹角。
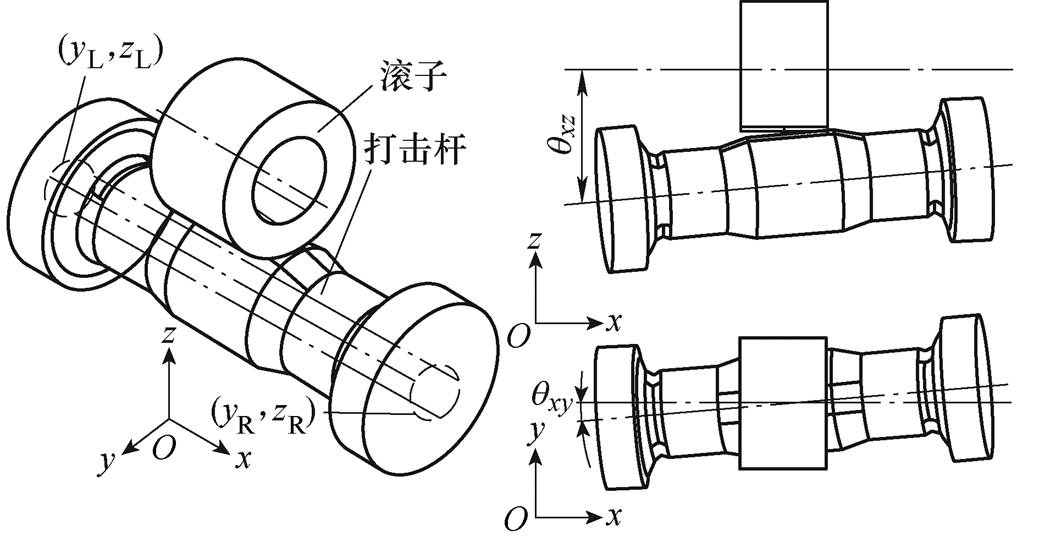
图2 打击杆偏差示意图
Fig.2 Spatial deviation diagram of driving shaft
对5只储能杠杆组件样品进行测量，将形位偏差与各零件的尺寸结合，确定（yL, zL）与（yR, zR）满足
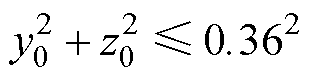（1）
式中，（y0, z0）为打击杆轴心任一端点在yz平面上的投影平面坐标。
通过实测获得的范围，可基于断裂力学理论计算偏差对打击杆断裂过程的影响，研究思路如图3所示。首先，利用三维造型软件建立操作机构的三维实体模型。之后，将三维实体模型导入仿真软件中，建立多体动力学虚拟样机。通过对实际样品进行测量，获得打击杆形位偏差的范围，并将其转为参数化尺寸输入到虚拟样机中，获得偏差对载荷的影响。进一步地，根据偏差及载荷情况，计算打击杆危险表面的裂纹萌生周期。另一方面，假设打击杆上已存在裂纹，计算不同裂纹深度时偏差对裂纹扩展速度的影响。最后，通过方差分析对比形位偏差在裂纹萌生和裂纹扩展中的显著性。
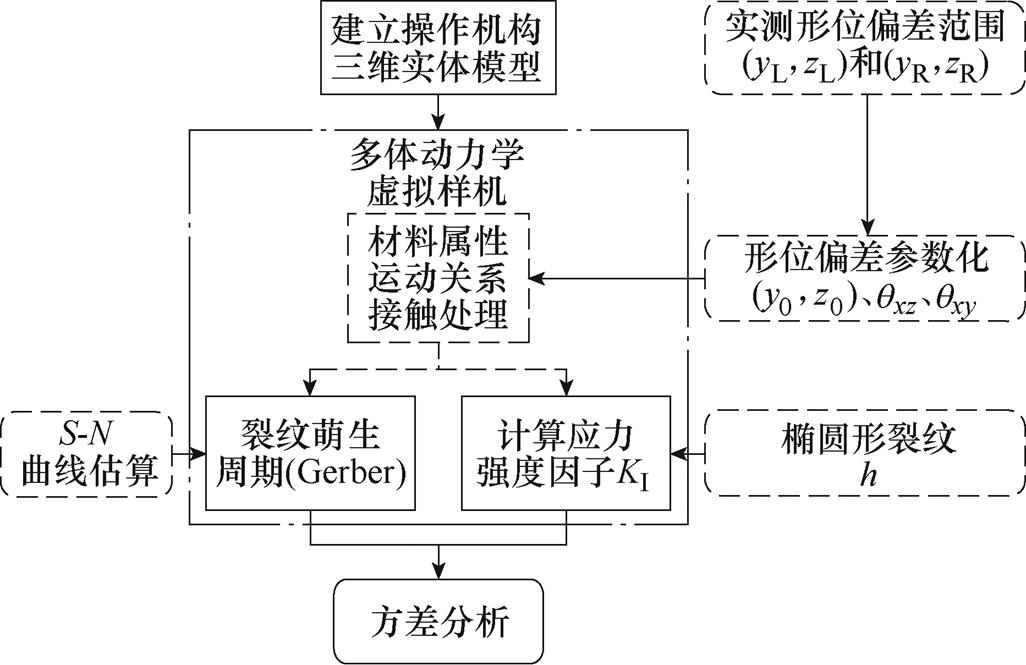
图3 研究思路
Fig.3 Research route
根据1.1节中的动作原理，可以通过建立多体动力学方程对断路器操作机构中各零件运动状态进行描述[14]，有
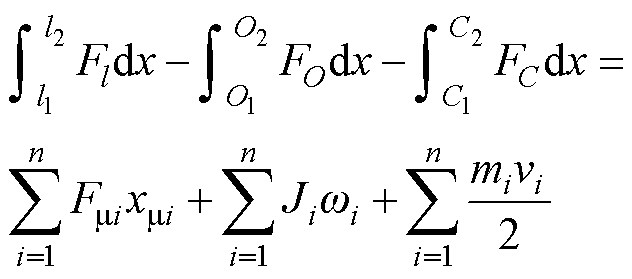（2）
式中，Fl为储能压簧力；FO为触点压簧力；FC为复位拉簧力；n为机构内的零件总数；Fm为运动构件的摩擦力，其中打击杆与滚子间的摩擦因数为0.6[17]，其余摩擦副依照接触零件的材质选取；Ji和wi分别为零件的转动惯量和角速度；mi为各运动部件的归一化质量；vi为各零件的运动速度。
对于多体动力学方程中的各弹簧力，可使用Hooke方程进行计算[14]，有
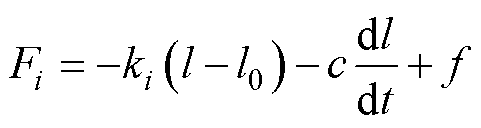（3）
式中，ki为各弹簧的刚度系数；l和l0分别为弹簧的自由长度和初始长度；c为弹簧阻尼系数；f为弹簧预载荷。
在操作机构中，储能压簧的刚度kl=35.5N/mm；触点压簧的总刚度kO=84N/mm；复位拉簧的总刚度kC=11N/mm。
在计算接触力时，需要将Hertz接触公式中的接触深度考虑为沿打击杆轴心分布的变量[18-19]，以计算各偏差下的接触状态。打击杆与滚子间接触力的修正公式为
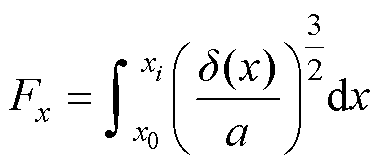（4）
式中，d(x)为接触深度沿打击杆轴心的分布；a为结构常量。
在通过多体动力学方程计算打击杆的受力状态后，可通过连续介质的本构方程对该零件的应力和应变进行计算[12]，有
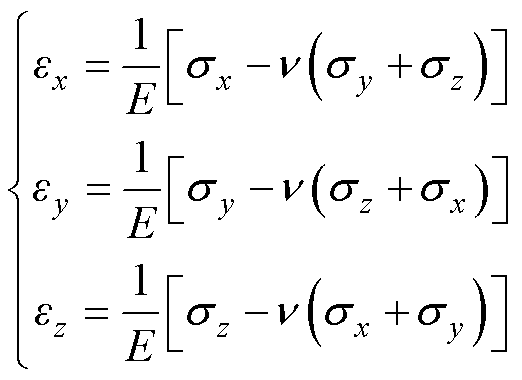
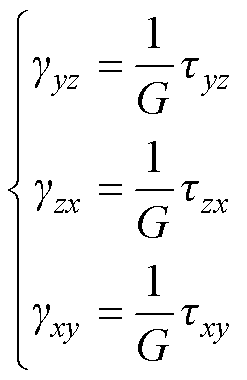（5）
式中，e 为法向应变；s 为法向应力；g 为剪切应变；E为杨氏模量；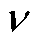
为泊松比；G为剪切模量；t 为剪切应力；x、y、z为直角坐标系的三个轴向。
打击杆与滚子的材质均为轴承钢GCr15，该材料的属性[20]见表1。
表1 GCr15材料属性
Tab.1 Material properties table of GCr15
参 数数 值 密度/(kg/m3)7 810 弹性模量/MPa212 000 泊松比0.29 抗拉强度/MPa981 屈服强度/MPa883
打击杆的断裂过程包含裂纹萌生与裂纹扩展，基于应力计算结果，将S-N曲线与Gerber模型相结合，可以对裂纹的萌生周期进行计算。对GCr15的S-N曲线进行估算，GCr15的S-N曲线经过以下3个点[21]，有
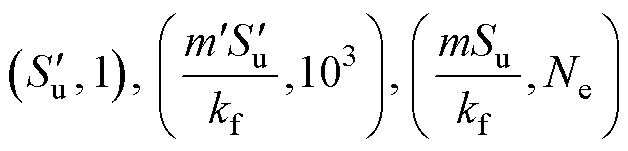（6）
式中，Su为材料的抗拉强度，在工作一定周期后退化为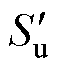
；kf为应力集中系数；Ne为材料的长寿命周期，对于钢取106循环次数；m和
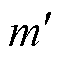为综合修正系数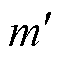，的计算方法为
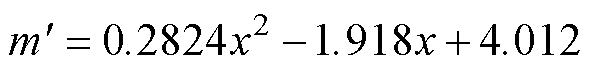（7）
其中
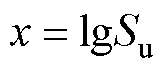
在获得S-N曲线后，通过Gerber模型基于应力计算结果对打击杆的裂纹萌生寿命进行计算[22]，有
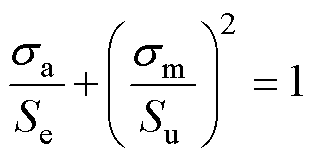（8）
式中，sa为应力幅值；sm为平均应力；Se为疲劳极限；Su为极限抗拉强度。
在断裂过程中，裂纹前端受应力场的作用而不断扩展。该应力场可通过应力强度因子进行描述，有
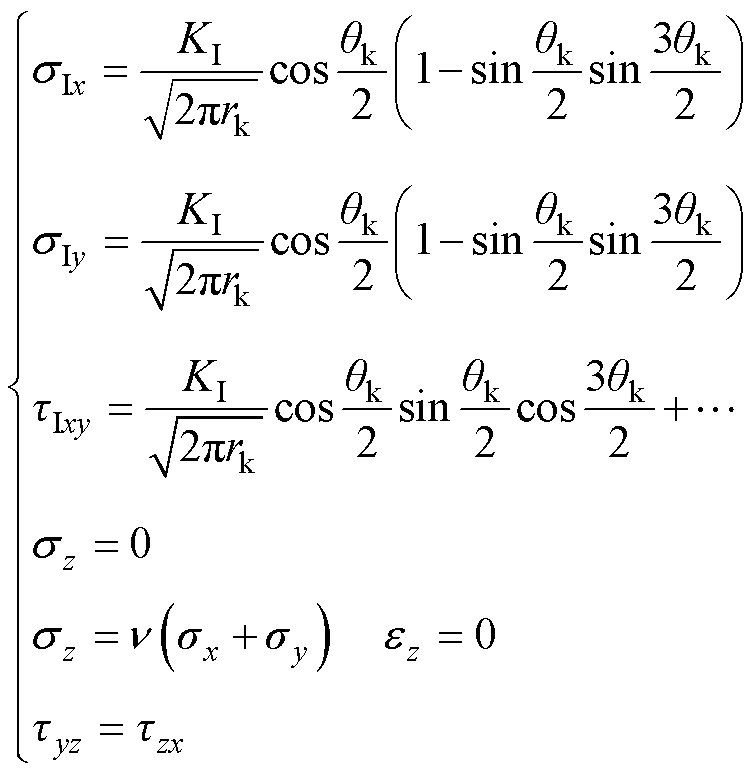（9）
式中，rk和qk为与裂纹面垂直平面上的极坐标；KI为Ⅰ型应力强度因子。对式（9）进行简化[23]，可得
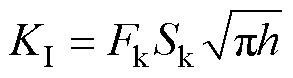（10）
式中，Fk为几何形状系数；Sk为裂纹尖端的作用 应力。
在获得裂纹前端的应力场后，对于裂纹的增量，可通过Pairs公式[23-24]进行计算，有
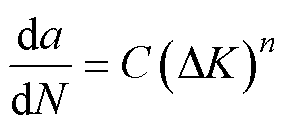（11）
式中，a为裂纹深度；N为裂纹扩展时的断路器动作周期；C和n为材料常数；DK为应力强度因子的幅值。C和n由材料决定，可通过应力强度因子KI对裂纹增速进行评价。
在研究裂纹的扩展过程时，通常将打击杆危险截面上的裂纹考虑为椭圆形裂纹[25]，建立裂纹前端的应力强度因子计算模型。打击杆上的裂纹扩展计算模型如图4所示，其中长轴L0=3mm；短轴自h0～h，代表裂纹的扩展深度；Oi为打击杆轴心；裂纹所在截面的直径j =6mm。
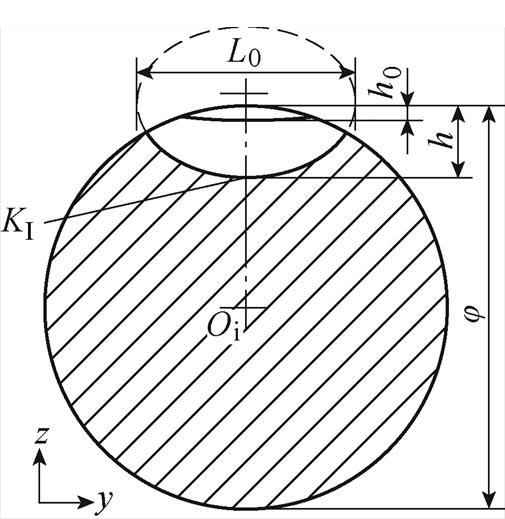
图4 椭圆形裂纹示意图
Fig.4 Schematic diagram of elliptical crack
在完成虚拟样机后，首先需要对形位公差影响下的打击杆载荷进行计算。因打击杆的长度较短，使轴心在各平面上的投影角度qxz、qxy对载荷的影响较小。假设打击杆轴心在波动范围内始终与x轴平行，将平面坐标（y0,z0）转化为极坐标形式（r, qr），在虚拟样机中对r和qr进行参数化，计算偏差引起的打击杆载荷变化，结果如图5所示。
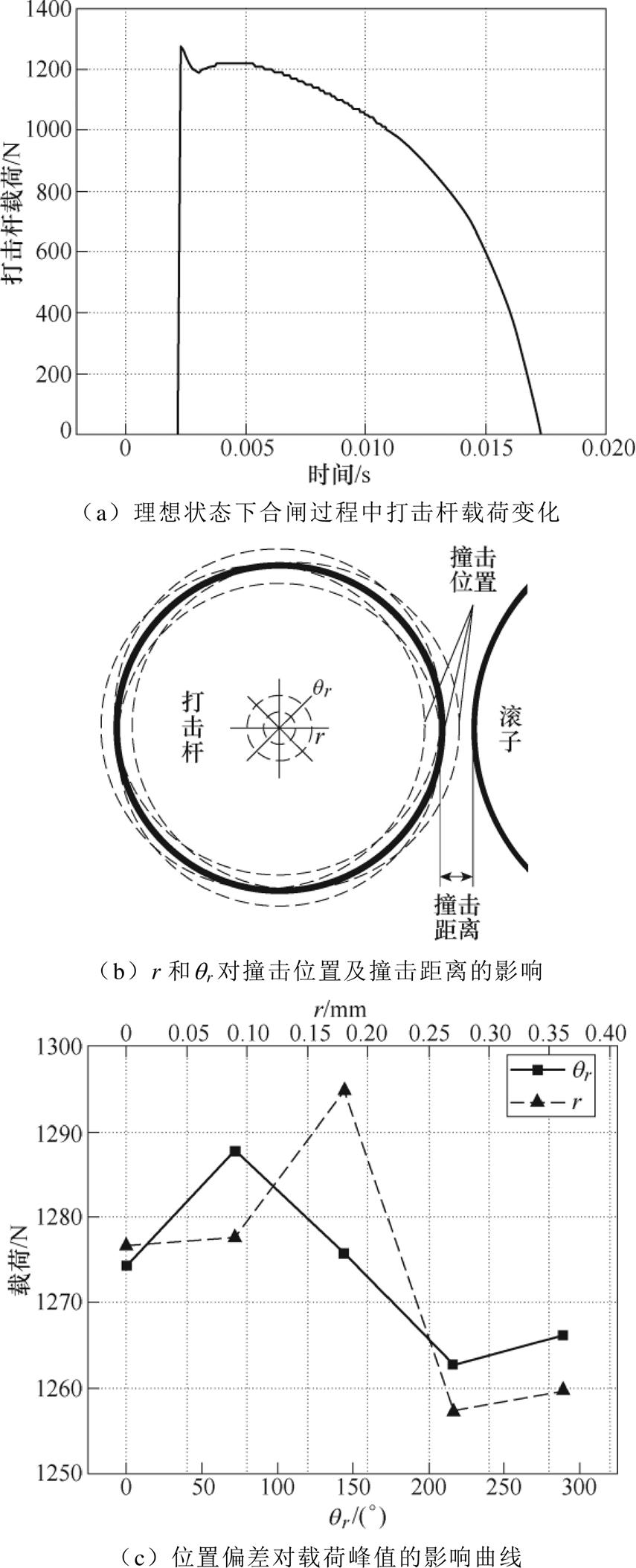
图5 位置偏差对打击杆载荷的影响
Fig.5 Influence of position deviation on the load of driving shaft
在断路器的合闸过程中，打击杆通过撞击滚子完成动能传递，该过程中打击杆的载荷变化如图5a所示。在图5b中，qr影响打击杆与滚子在撞击时的相对位置，该因素将决定撞击位置及撞击时零件的加速度。r影响打击杆与滚子在撞击前的距离，通过改变加速时间使碰撞时的动能发生变化。通过图5c中数据极差分析可知，r较qr的影响更大。因此，偏差主要通过改变打击杆与滚子的相对位置影响载荷。
寿命试验中打击杆的断裂模式如图6所示，打击杆的裂纹位于圆角凹槽处。判断该断裂形式主要受轴向应力作用，应以Ⅰ型裂纹为主。为验证猜测，需要对造成打击杆断裂的主要应力进行分析。
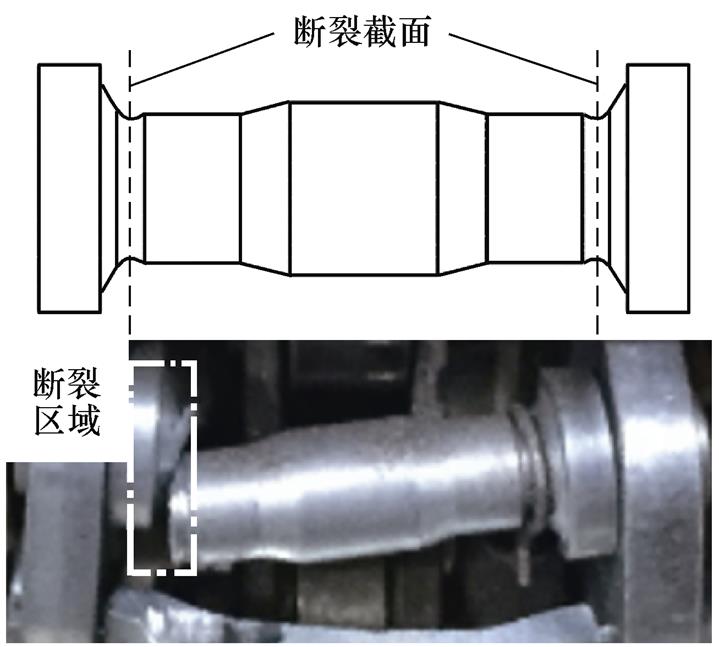
图6 寿命试验中打击杆的断裂模式
Fig.6 Fracture mode of driving shaft in life test
受偏差qxy和qxz作用，打击杆与滚子间的接触区域发生变化，打击杆裂纹萌生区域应力分布云图如图7a所示，裂纹萌生区域的应力峰值也随之改变。为选取造成打击杆断裂的主要应力，需要根据载荷计算结果，分别对qxy与qxz变化时裂纹萌生区域的轴向应力（x轴）、径向应力（y轴）和平均应力（von-Mises）峰值进行单因素分析。
图7 单因素条件下角度偏差对各应力峰值的影响
Fig.7 Influence of angle deviation on peak stress under single factor condition
图7b为单因素影响下各应力的变化情况，qi同时包括qxy和qxz，其中qxy对各应力的影响较小，而qxz增大会引起各应力的明显改变。当qxz增大时，径向应力的变化幅度虽然较大（10.62%），但幅值所限，其并不是引起断裂的主要因素。平均应力的变化幅度（5.23%）虽然大于轴向应力（3.64%），但该应力的数值始终低于轴向应力。
图8为同时考虑qxy和qxz偏差的轴向应力计算结果。对图中数据进行分析，由qxy偏差造成的应力变化为1%，由qxz偏差造成的应力变化为4.47%，在偏差范围内确认qxz是造成应力变化的主要因素。
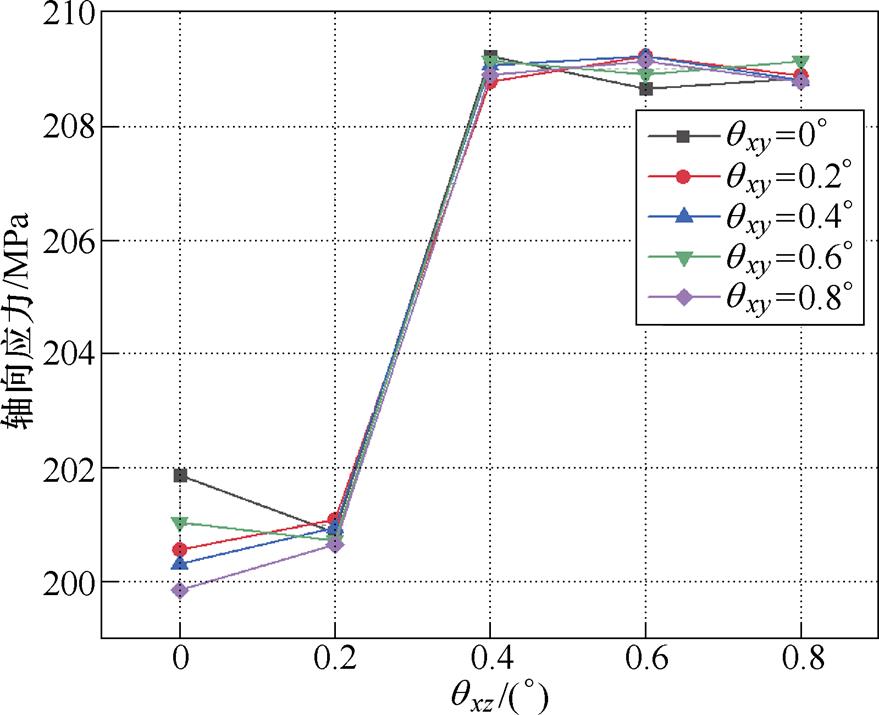
图8 角度偏差对应力峰值的影响
Fig.8 Effect of angle deviation on peak stress
偏差对裂纹萌生周期的影响如图9所示。其中，横坐标为qxz的变化情况，各条折线分别对应qxy的变化。由图中的直观趋势可知，裂纹萌生周期主要受qxz的影响，qxy的影响较小，该趋势与应力计算结果基本相符。
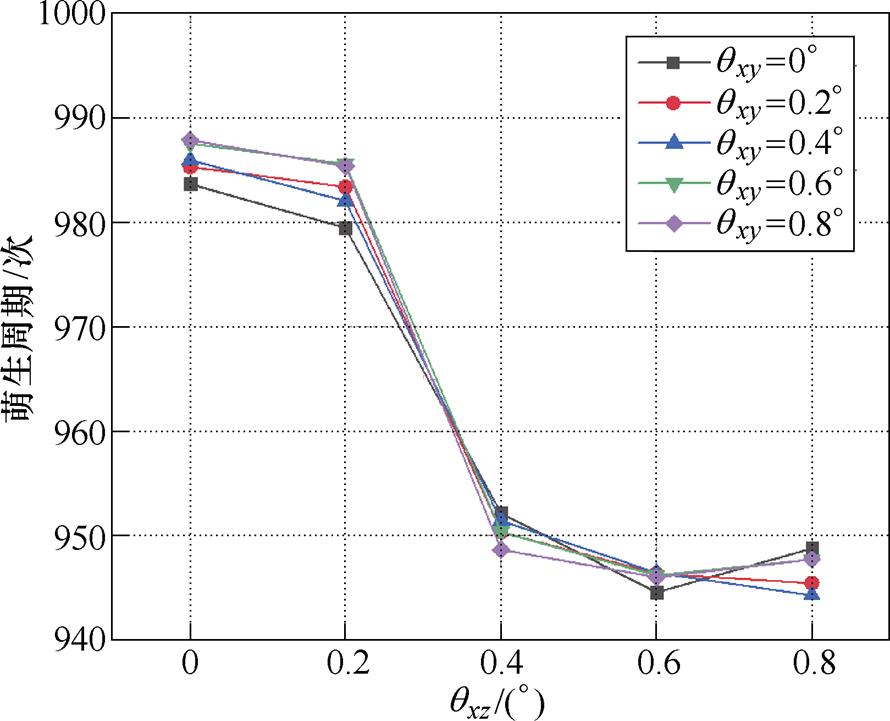
图9 偏差对裂纹萌生周期的影响
Fig.9 Effect of deviation on crack initiation period
为验证图9中的直观趋势是否正确，需要通过方差分析法获得qxy和qxz对裂纹萌生周期的影响程度。在方差分析中，常以P值作为显著性标志。当0.05＞P＞0.01时，该因素高度显著。当P≥0.05时，该因素不显著[26]。因此，由表2中的数据可知，qxz偏差对裂纹萌生周期的影响高度显著，而qxy偏差的影响不显著。表2中，F为效应项和误差项的比值。
表2 裂纹萌生周期结果方差分析
Tab.2 Variance analysis table of crack initiation period
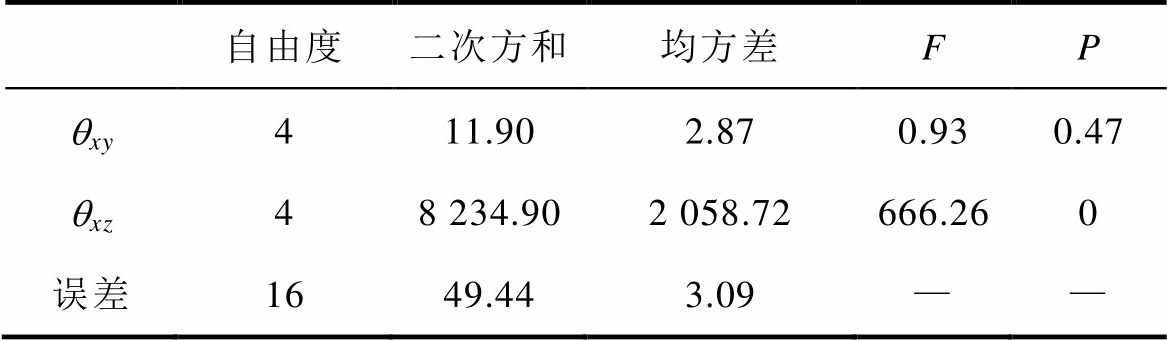
自由度二次方和均方差FP qxy411.902.870.930.47 qxz48 234.902 058.72666.260 误差1649.443.09——
由3.1节中的应力对比结果可知，打击杆的裂纹扩展主要受轴向应力影响，且以Ⅰ型裂纹为主。因此，能够使用椭圆形裂纹模型，计算扩展过程中的裂纹前端的应力强度因子，打击杆裂纹示意及计算云图如图10所示。
根据椭圆形裂纹计算模型，对偏差影响下不同深度时的裂纹前端应力强度因子进行计算。角度偏差对应力强度因子的影响如图11所示。
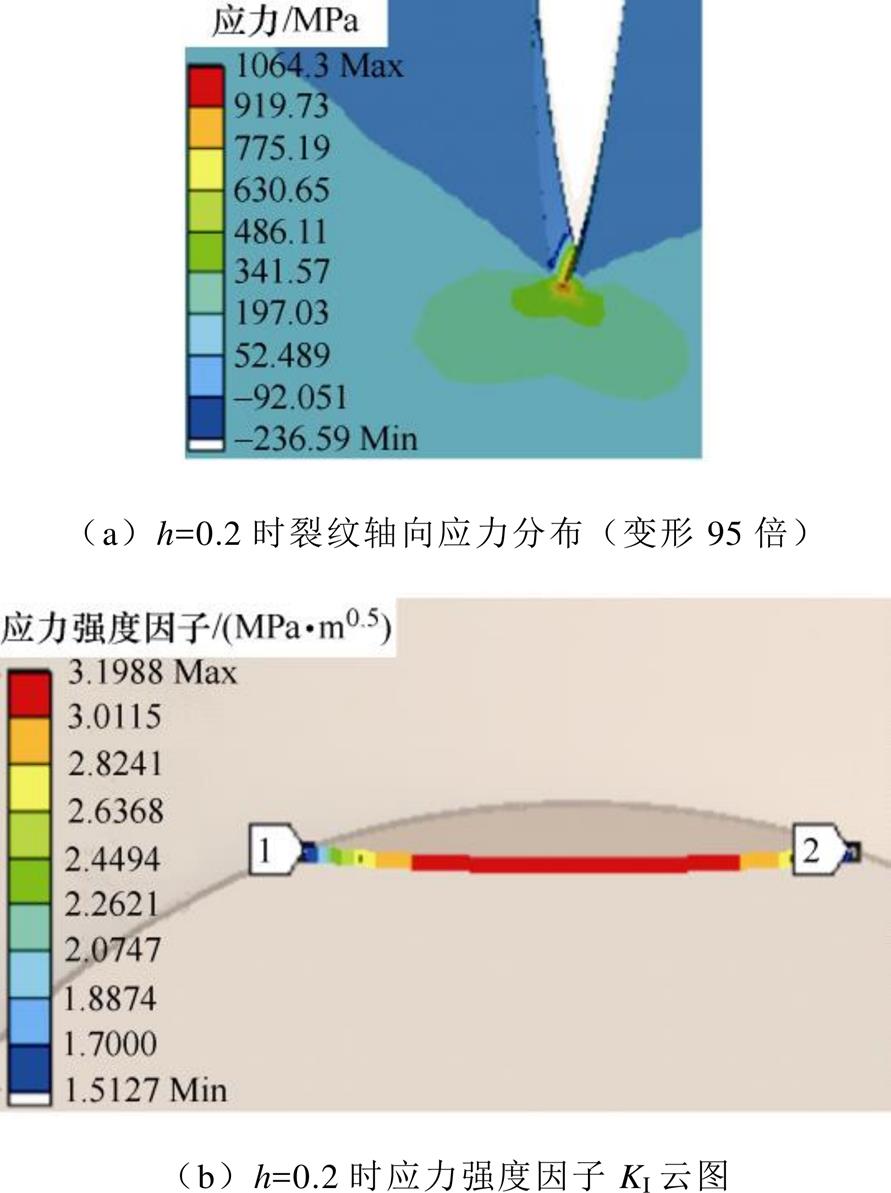
图10 打击杆裂纹示意及计算云图
Fig.10 Crack diagram and calculation nephogram of driving shaft
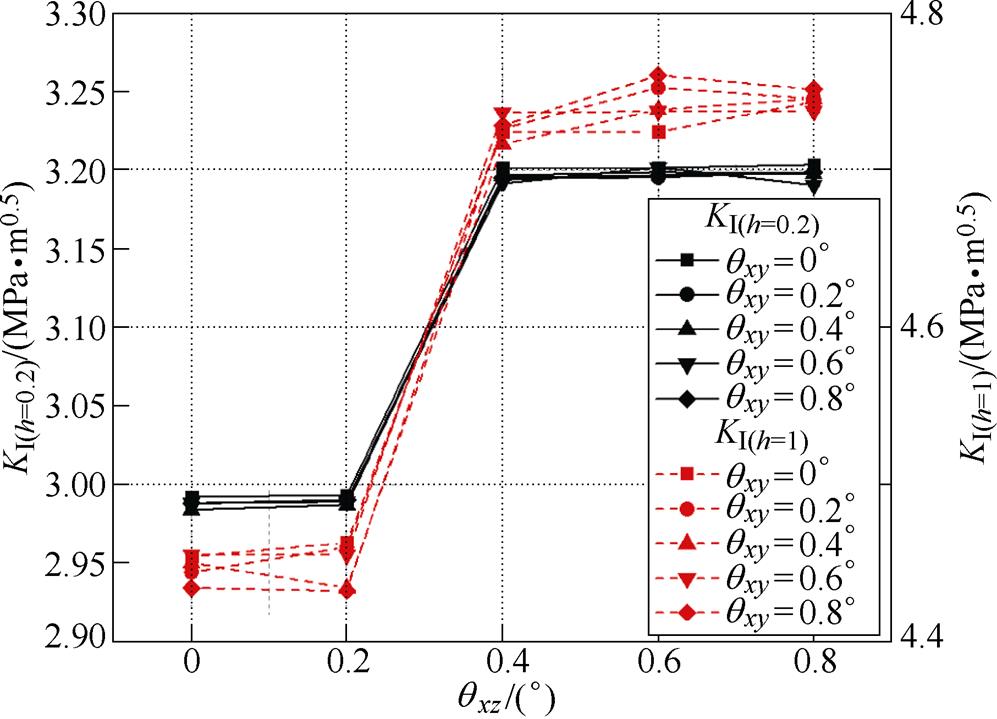
图11 角度偏差对应力强度因子的影响
Fig.11 Effect of angle deviation on crack initiation period
图11中的KI(h=0.2)和KI(h=1)分别为h=0.2mm和h=1mm时的KI。由于图中的KI值均小于GCr15的断裂韧性[27]KIC=105MPa·m0.5，裂纹仍处于扩展过程，此时应力强度因子能够表现裂纹的扩展速度。从图中的直观趋势可以发现，随着裂纹深度的扩展，qxy和qxz影响下的应力强度因子变化幅度增大，但qxz始终为主要因素。
对图9和图11中的数据进行方差分析，计算qxy和qxz因素对断裂过程的影响程度。断裂阶段方差分析见表3。
表3 断裂阶段方差分析
Tab.3 Analysis of variance of fracture stage
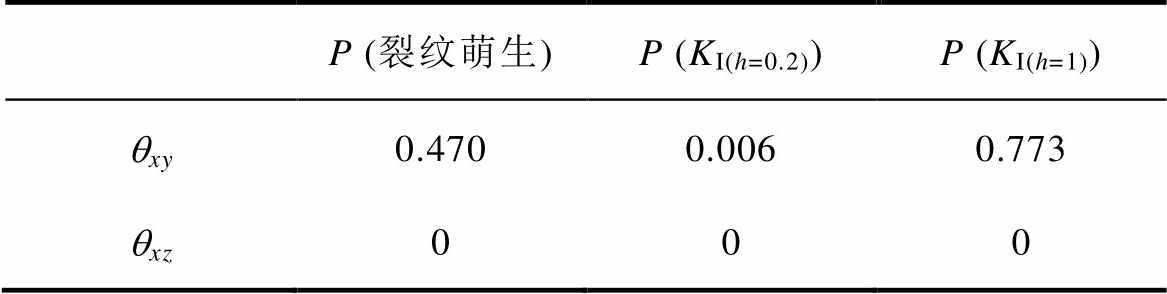
P (裂纹萌生)P (KI(h=0.2))P (KI(h=1)) qxy0.4700.0060.773 qxz000
由表3中的数据可以发现，在裂纹自萌生至扩展的各个阶段，qxz偏差对裂纹的影响均高度显著。qxy仅在裂纹扩展的初期影响高度显著，随裂纹深度的增加显著性降低。由于裂纹扩展初期时的速率较慢，控制qxy偏差可以极大地提高整个断裂过程的持续周期。因此，需要同时对qxz和qxy偏差进行控制，才能保证打击杆的断裂周期满足设计要求。
在完成操作机构的虚拟样机后，需要通过试验对准确性进行验证。若忽略转轴间隙配合等不确定性因素，可认为储能杠杆组件与打击杆的运动情况一致。联动轴作为连杆机构中摇杆，可以表现同在连杆机构内的滚子运动状态。因此，同时对产品中储能杠杆组件和联动轴的运动状态进行测量，可以对虚拟样机进行验证。
文献[12]通过直线激光位移传感器，测量动触头在垂直于触点接触面方向上的直线位移，再通过零件的设计尺寸预测断路器动触头的转动速度。该方法根据直线位移推导机构的整体动作状态，不适用于较复杂的万能式断路器。文献[28-29]通过旋转式电位器测量断路器的转轴位移，根据测量电路的电压波形计算零件的转动速度。旋转式电位器的采样精度较低，在转动时所损耗的能量较多，测量时的误差相对较大。本文的试验系统整体布局如图12a所示，通过精度更高的旋转式编码器作为采样传感器，同时对联动轴和储能杠杆组件的转动状态进行采集，并使用示波器记录编码器输出的脉冲信号。编码器与操作机构的连接方式如图12b所示，编码器的转轴通过弹性联轴器和锥形探头相连，避免因转轴抖动造成编码器损坏。锥形探头通过万能胶与被测转轴的轴端中心孔相连，保证编码器转轴与被测转轴同步旋转。每套测量装置通过螺钉固定在断路器侧板上，保证装置与断路器间不发生相对移动。
图12 验证试验结构布局
Fig.12 Schematic diagram of verification experiment structure
在试验结束后，通过编制程序对示波器采集到的脉冲数据进行处理。获得的运动状态与仿真结果对比如图13所示。
如图13a所示，通过仿真结果和试验的数据对比，试验与仿真中储能杠杆组件的角度变化总体趋势较为相近。由于本研究对储能压簧进行等效处理，未考虑大直径弹簧的阻尼效应及其他损耗，使角度变化值略有相差。在图13b中，因联动轴的总长度较长，且该零件的径向约束位于质心附近，使轴心端点在合闸时会根据模态的振型发生形变，造成0.02s后的运动状态曲线发生抖动。但在合闸过程中，联动轴的仿真与试验趋势基本一致，可以认为现有的虚拟样机能够较准确地表现操作机构的真实动作状态。
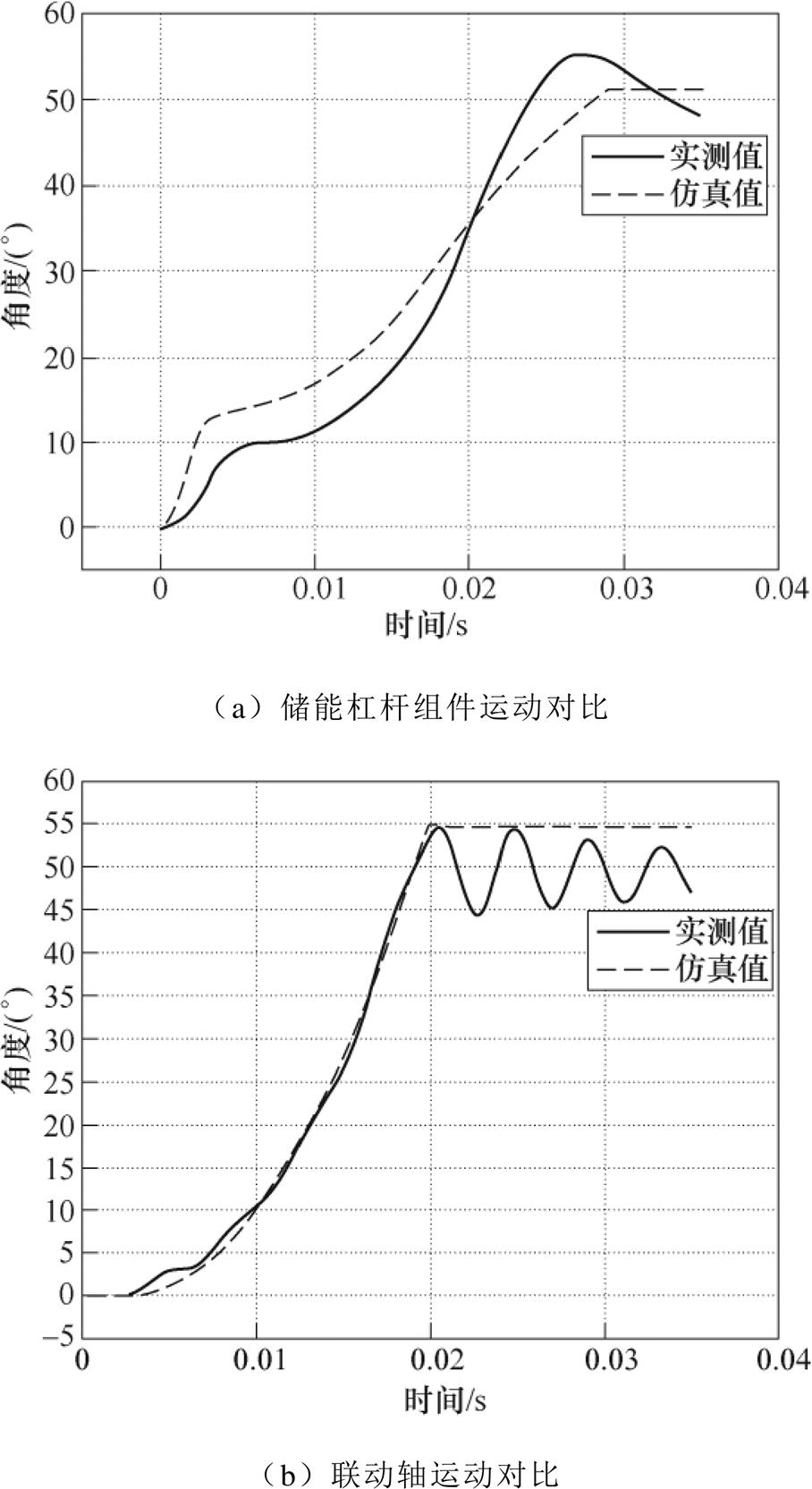
图13 仿真结果与试验对比
Fig.13 Comparison between simulation and experiment
根据偏差对打击杆断裂过程的影响，在断路器的装配过程中对偏差qxy与qxz进行监控，并进行小批量整机寿命试验。为避免不确定性干扰，该试验可对断路器中的次要零件进行维护，以打击杆断裂时的工作周期为机械寿命指标。
表4 断路器机械寿命验证试验
Tab.4 Verification experiment on mechanical life of circuit breaker
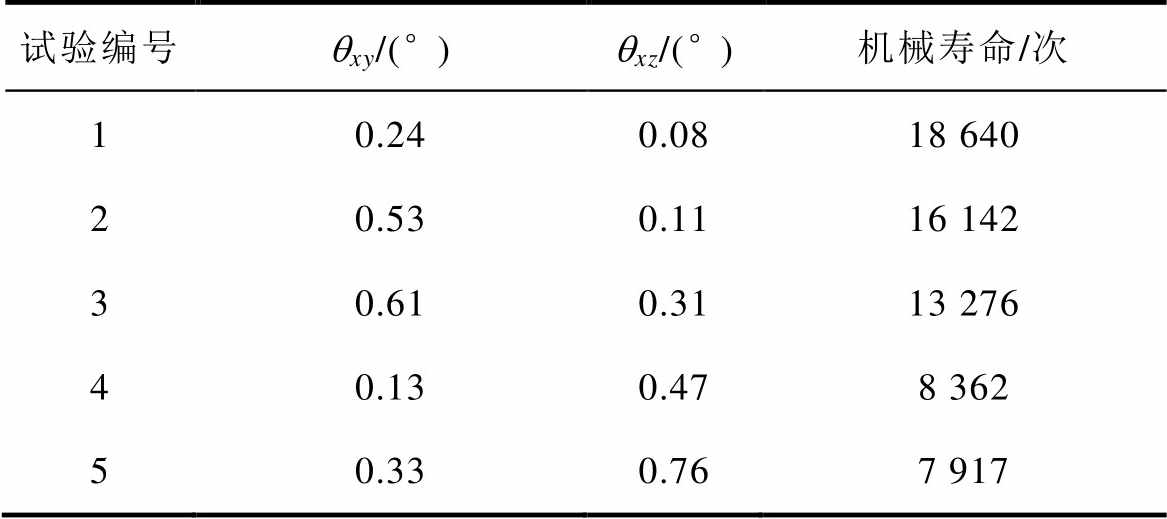
试验编号qxy/(°)qxz/(°)机械寿命/次 10.240.0818 640 20.530.1116 142 30.610.3113 276 40.130.478 362 50.330.767 917
在表4中，当qxz≤0.2°时，即使qxy的值（0.53）较大，打击杆的断裂周期仍能大于15 000次，验证了qxz是影响打击杆断裂失效的主要因素。对于4号和5号试验，虽然qxy、qxz的数值变化较大，但零件的断裂周期相差较小。这一趋势与图9、图11中的趋势相近，当qxz≥0.4°时，偏差对零件的断裂过程影响较小。因此，通过整机寿命试验，能够验证形位偏差对打击杆断裂过程的影响。为解决偏差带来的影响，可在设计阶段对形位公差进行改进，并设计相应的工艺夹具。通过这些手段减少打击杆的空间形位偏差，可以提高断路器的整机寿命。
本文基于断裂力学理论，研究偏差对打击杆断裂过程的影响，提出一种对万能式断路器中空间形位偏差对关键零件断裂过程影响的研究方法。对于万能式断路器操作机构，通过该方法可以从理论上给出偏差的允许极限。所得的结论如下：
1）在对操作机构的虚拟样机进行试验验证时，选用编码器作为传感器，同时对研究对象的上下级运动状态进行检测，能够更好地保证虚拟样机的准确性。
2）对打击杆载荷波动进行研究时，可将操作机构视为平面机构。因空间形位偏差造成的打击杆与滚子相对位置变化，使打击杆承受的载荷发生改变。
3）打击杆受轴向应力的作用而断裂，其形式以Ⅰ型裂纹为主。将空间形位偏差分解为两个平面角度偏差qxy和qxz，当0.2°≤qxz≤0.4°时，该偏差对裂纹萌生及扩展过程均具有高度显著性影响。在裂纹扩展初期，qxy对扩展增量的影响较大。因此，需要通过设计和工艺改进对qxy和qxz同时优化。
参考文献
[1] 游颖敏, 王景芹, 舒亮, 等. 断路器保护特性测试电流的自适应控制策略[J]. 电工技术学报, 2020, 35(15): 3203-3213.
You Yingmin, Wang Jingqin, Shu Liang, et al. Research on adaptive current control method in cir- cuit breaker protection characteristic test[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(15): 3203-3213.
[2] 刘思奇, 沈兵, 庄劲武, 等. 混合型真空限流断路器短燃弧短间隙下的介质强度恢复试验研究[J]. 电工技术学报, 2020, 35(2): 284-291.
Liu Siqi, Shen Bing, Zhuang Jinwu, et al. Experi- mental study on vacuum dielectric recovery of hybrid current limiting circuit breaker with short arcing time and short gap[J]. Transactions of China Electro- technical Society, 2020, 35(2): 284-291.
[3] 张明, 王永兴, 田宇, 等. 气流场驱动下栅片中弧压提升特性的数值分析[J]. 电工技术学报, 2019, 34(13): 2752-2759.
Zhang Ming, Wang Yongxing, Tian Yu, et al. Nume- rical analysis of arc voltage increasing characteristics in plate driven by airflow field[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2752- 2759.
[4] 杨青. 基于美军标对舰用框架式断路器发展趋势的研究[J]. 电器与能效管理技术, 2014(13): 14-19.
Yang Qing. Research on development trend of air circuit breaker in naval ships based on American military standard[J]. Electrical & Energy Management Technology, 2014(13): 14-19.
[5] 杨秋玉, 彭彦卿, 庄志坚. 基于ADAMS的高压断路器弹簧机构动力学仿真与故障分析[J]. 高压电器, 2018, 54(6): 67-73, 80.
Yang Qiuyu, Peng Yanqing, Zhuang Zhijian. Dynamic simulation and failure analysis of spring mechanism of high voltage circuit breaker based on ADAMS[J]. High Voltage Apparatus, 2018, 54(6): 67-73, 80.
[6] 何瑞华, 尹天文. 我国低压电器现状与发展趋势[J].电器与能效管理技术, 2014(1): 1-10, 26.
He Ruihua, Yin Tianwen. Present situation and development trend of low voltage electrical apparatus in China[J]. Electrical & Energy Management Tech- nology, 2014(1): 1-10, 26.
[7] 孟晓承, 韩学山, 许易经, 等. SF6高压断路器机械故障概率的非精确条件估计[J]. 电工技术学报, 2019, 34(4): 693-702.
Meng Xiaocheng, Han Xueshan, Xu Yijing, et al. Imprecise estimation for conditional mechanical outage probabilities of SF6 high voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 693-702.
[8] 杨秋玉, 阮江军, 张灿, 等. 基于定量递归分析的高压断路器机械缺陷辨识及应用[J]. 电工技术学报, 2020, 35(18): 3848-3859.
Yang Qiuyu, Ruan Jiangjun, Zhang Can, et al. Study and application of mechanical defect identification for high-voltage circuit breakers using recurrence quanti- fication analysis[J]. Transactions of China Electro- technical Society, 2020, 35(18): 3848-3859.
[9] 孙曙光, 李勤, 杜太行, 等. 基于一维卷积神经网络的低压万能式断路器附件故障诊断[J]. 电工技术学报, 2020, 35(12): 2562-2573.
Sun Shuguang, Li Qin, Du Taihang, et al. Fault diagnosis of accessories for the low voltage con- ventional circuit breaker based on one-dimensional convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2562-2573.
[10] 赵书涛, 王波, 华回春, 等. 基于马尔科夫模型的直流断路器可靠性评估方法[J]. 电工技术学报, 2019, 34(增刊1): 126-132.
Zhao Shutao, Wang Bo, Hua Huichun, et al. Reliability evaluation method of DC circuit breaker based on Markov model[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 126-132.
[11] 季良, 陈德桂, 刘颖异, 等. 连杆转换位置对MCCB操作机构的影响及其优化[J]. 电工技术学报, 2010, 25(9): 87-91, 121.
Ji Liang, Chen Degui, Liu Yingyi, et al. Analysis and optimization of linkage transfer position for the operating mechanism of MCCB[J]. Transactions of China Electrotechnical Society, 2010, 25(9): 87-91, 121.
[12] 舒亮, 吴浪, 吴桂初, 等. 一种断路器多体动力学仿真方法[J]. 电工技术学报, 2017, 32(5): 41-48.
Shu Liang, Wu Lang, Wu Guichu, et al. A new method of multibody dynamics simulation of circuit breakers[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 41-48.
[13] 闫姿姿, 张敬涛, 王小焕, 等. 框架式真空断路器可靠性影响参数研究[J]. 真空科学与技术学报, 2019, 39(8): 678-682.
Yan Zizi, Zhang Jingtao, Wang Xiaohuan, et al. Design optimization of vacuum circuit-breaker frame- work: a simulation and experimental study[J]. Chinese Journal of Vacuum Science and Technology, 2019, 39(8): 678-682.
[14] 刘超, 赵伟涛, 张强, 等. 真空断路器弹簧操动机构机械特性的仿真与优化[J]. 高压电器, 2019, 55(8): 65-71.
Liu Chao, Zhao Weitao, Zhang Qiang, et al. Simu- lation and optimization for mechanical characteristics of spring operating mechanism in vacuum circuit breaker[J]. High Voltage Apparatus, 2019, 55(8): 65-71.
[15] Park S H, Ahn K Y, Lee B Y. Dynamic analysis and structural design of links in an air circuit breaker to enhance fatigue life[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mecha- nical Engineering Science, 2005, 219(1): 11-18.
[16] 胡书通. 低压断路器操作机构疲劳寿命评估方法及其应用研究[D]. 西安: 西安交通大学, 2014.
[17] 宋宝玉, 古乐, 邢恩辉. 真空条件下GCr15钢摩擦磨损性能研究[J]. 哈尔滨工业大学学报, 2004, 36(2): 238-241.
Song Baoyu, Gu Le, Xing Enhui. Friction and wear properties of GCr15 steel under vacuum condition[J]. Journal of Harbin Institute of Technology, 2004, 36(2): 238-241.
[18] Fei He, Ke Yang, Ning Guo, et al. Study on friction/ wear and contact stress of variable-lead Spiral pair substructure[J]. IOP Conference Series: Materials Science and Engineering, 2019, DOI: 10.1088/1757- 899X/493/1/012047.
[19] 李志农, 刘杰, 卢文秀, 等. 转子系统盘轴松动故障动力学建模和仿真研究[J]. 机械工程学报, 2020, 56(7): 60-71.
Li Zhinong, Liu Jie, Lu Wenxiu, et al. Research on dynamic modeling and simulation of rotors with loose disc[J]. Journal of Mechanical Engineering, 2020, 56(7): 60-71.
[20] 干勇, 田志凌, 董翰, 等. 中国材料工程大典(第3卷): 钢铁材料工程(下)[M]. 北京: 化学工业出版社, 2006.
[21] (美)诺尔曼 E. 道林. 工程材料力学行为—变形、断裂与疲劳的工程方法[M]. 江树勇, 张艳秋, 译. 北京: 机械工业出版社, 2019.
[22] Yeun C P, Changbeom A, Hyoung-Bo S, et al. Failure analysis of fatigue cracking in the tension clamp of a rail fastening system[J]. International Journal of Steel Structures, 2019, 19(5): 1570-1577.
[23] 魏维, 郭文勇, 沈惠杰, 等. 基于ANSYS Workbench的轴套表面裂纹应力强度系数有限元分析研究[J]. 海军工程大学学报, 2019, 31(1): 36-40.
Wei Wei, Guo Wenyong, Shen Huijie, et al. Finite element analysis of stress intensity factor of surface crack in shaft sleeve based on ANSYS Workbench[J]. Journal of Naval University of Engineering, 2019, 31(1): 36-40.
[24] 赵慧, 吕毅, 窦鹏鹏. 三维裂纹扩展轨迹的厚度效应研究[J]. 兵器装备工程学报, 2019, 40(8): 219- 225.
Zhao Hui, Lü Yi, Dou Pengpeng. Research on thickness effect of three-dimensional crack pro- pagation path[J]. Journal of Ordnance Equipment Engineering, 2019, 40(8): 219-225.
[25] Gupta A, Sun W, Bennett C J. Simulation of fatigue small crack growth in additive manufactured Ti- 6Al-4V material[J]. Continuum Mechanics and Thermodynamics, 2020, 32(6): 1745-1761.
[26] 王其亚, 翟国富, 程贤科, 等. 基于正交试验设计的电磁继电器关键调整参数及优化方法[J]. 电工技术学报, 2009, 24(10): 53-58.
Wang Qiya, Zhai Guofu, Cheng Xianke, et al. Key adjusted parameters and optimum method of elec- tromagnetic relay based on orthogonal experimental design[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 53-58.
[27] 闻邦椿. 机械设计手册: 疲劳强度与可靠性设计(单行本)[M]. 5版. 北京: 机械工业出版社, 2016.
[28] 赵洋, 刘汉宇, 曾庆军. 高压真空断路器机械特性在线监测系统研制[J]. 高压电器, 2009, 45(6): 91-95, 101.
Zhao Yang, Liu Hanyu, Zeng Qingjun. Study on on-line monitoring for mechanical characteristics of high voltage vacuum circuit breaker[J]. High Voltage Apparatus, 2009, 45(6): 91-95, 101.
[29] 吴发清. 12kV开关柜断路器机械特性监测与弧光检测的研究[D]. 厦门: 厦门理工学院, 2016.
Fracture Failure Process of Key Part of Air Circuit Breaker Considering Spatial Shape and Position Deviation
Abstract During the closing process of an air circuit breaker (ACB), energy stored in main spring is transferred to four-linkage mechanism through its driving shaft in the form of impact. Position deviations on the striking rod caused by machining and assembly tolerance lead to the fatigue and the final fracture of the driving shaft. This makes operational lifespan of the mechanism inconsistent with the expected design one. Based on multi-body dynamics, a virtual prototype model of the mechanism is established. Accuracy of the virtual prototype is verified by testing rotational positions of two shafts around which the energy storage lever and the linkage shaft rotate. Then, using the measurement data, the spatial deviation range of the end point of the driving shaft relative to the roller is obtained. Then the virtual prototype parameters are used to model the deviation, and the variation of peak load and crack initiation period is calculated. Finally, it is assumed that there is an elliptical-type crack on the driving shaft, and the influence of the deviation on the SIF at the crack tip is studied. In this paper, the influence of the spatial deviation of the driving shaft on its fracture process is given, which can provide theoretical guidance for design and manufacturing.
keywords：Air circuit breaker, fracture process, tolerance effect
DOI: 10.19595/j.cnki.1000-6753.tces.L90305
中图分类号：TM561.1
周 学 男，1982年生，博士，研究方向为航天电器电弧等离子体理论与试验技术。E-mail: zhouxue@hit.edu.cn
李东晖 男，1992年生，助理工程师，研究方向为航天电器可靠性设计及优化。E-mail: ldh920918@qq.com（通信作者）
收稿日期 2020-07-09
改稿日期 2020-10-13
国家自然科学基金资助项目（51707044）。
（编辑 崔文静）