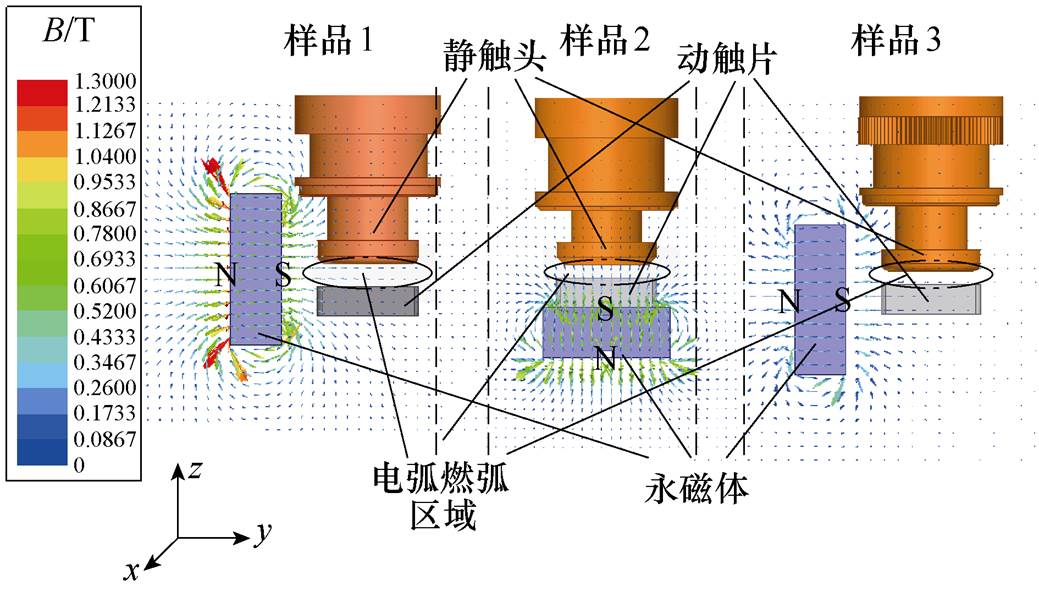
图1 三种磁吹系统仿真
Fig.1 Three magnetic blowing system simulation diagram
摘要 高压直流(HVDC)继电器触头系统结构紧凑,难以利用栅片或产气材料来提高触头的开断性能。通过磁吹系统的外加磁场能够加快电弧的运动速度,提高灭弧能力。永磁体作为磁吹系统的关键部分,其外部磁感应强度分布不均匀,且尺寸对磁场的大小和分布影响较大,这对磁吹系统的设计造成了一定的困扰。针对此问题,该文建立磁吹系统三维有限元模型,重点分析永磁体尺寸对其外部磁场的影响,并建立相关数学模型;分析永磁体外部磁场分布的特点,得出外部磁场分布均匀度与永磁体尺寸的关系。最后,结合高压直流继电器的开断电弧特性,考虑电弧的受力情况及电弧的停滞时间,对永磁体的尺寸、充磁方向及安装位置进行设计,为提升高压直流继电器触头开断性能奠定了理论基础。
关键词:高压直流继电器 磁吹系统 永磁体 直流电弧 三维仿真
高压直流(High Voltage Direct Current, HVDC)继电器是新能源产业中的重要控制元件,对新能源汽车、充电桩等运行过程中的稳定性起着重要作用。在研究高压直流继电器的进程中,目前在理论方面不够深入,虽然某些制造开关电器的厂家以仿制的形式得到了部分产品,但未将理论及技术融于产品开发中,造成国内产品的性能和可靠性指标与国外相比均有一定差距[1]。其中,灭弧系统的合理设计是提升继电器产品性能的关键。
继电器灭弧系统结构紧凑,难以通过添加产气材料和灭弧栅片来提高触头的分断能力[2]。对于直流继电器来说,开断电弧不能像交流系统通过电弧自然过零熄灭,电弧熄灭困难,对触头烧蚀严重,大大降低产品的电寿命和可靠性,采用外加磁场进行吹弧是目前提高触头分断能力的有效方法之一。
外加磁场可使电弧快速运动到触头边缘,拉长电弧,减少电弧的燃弧时间[3]。文献[4-9]在实验和仿真方面验证了外加磁场可以提高电弧的伏安特性,加快电弧熄灭速度,且外加磁场能够降低电弧的停滞时间,减小触头的烧蚀。以上研究成果均假设磁场大小固定、均匀分布,而实际永磁体的外部磁感应强度分布是不均匀的[10],磁场方向随永磁体安装位置的不同而变化,这又恰恰对电弧的运动特性产生极大的影响。吹弧磁场的大小以及方向决定着电弧的运动速度和运动方向。磁场过小会使电弧停滞时间过长、触头烧蚀严重,大大降低开关的电寿命。磁场的方向决定了电弧的运动轨迹,方向不当会使电弧的运动轨迹过长或运动方向错误造成电弧烧蚀触头系统其他零部件。若对永磁体的尺寸和安装位置进行合理设计便能有效改善这些问题。
因此,本文以450V/200A高压直流继电器的磁吹系统为研究对象,建立永磁体三维有限元模型,分析其外部磁场分布特性,并探究永磁体尺寸对其相关特性的影响;建立永磁体尺寸对其外部磁场影响的相关数学模型,为研究磁吹系统提供一定的参考价值。
图1为三种高压直流继电器磁吹系统的三维仿真结果,其中样品1与样品3永磁体的安装位置和大小不同,样品1只含一块永磁体,样品3包含两块永磁体。图2为二者的俯视图。在各自的电弧燃弧区域(见图1中椭圆区域)计算x、y、z 3个方向磁感应强度B的平均值,见表1。通过对比分析可以看到,不同结构的磁吹系统作用在开断电弧燃弧区域的磁感应强度大小及分布明显不同,且在电弧燃弧区域中吹弧磁场分布在三维空间的各个方向。为此有必要对永磁体外部磁场分布的特征及影响其特性的关键因素进行深入分析,探究其合理参数的设计。

图1 三种磁吹系统仿真
Fig.1 Three magnetic blowing system simulation diagram
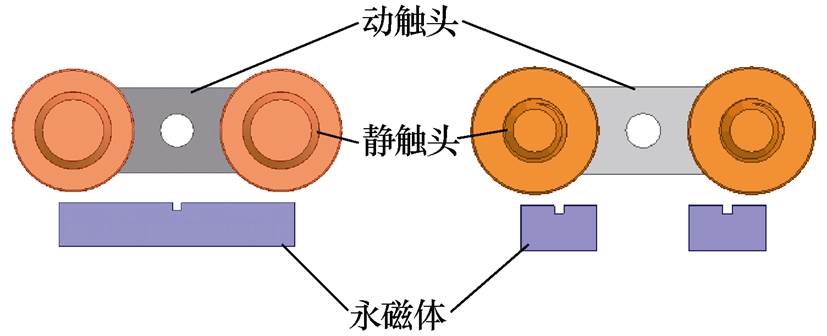
图2 样品1与样品3的俯视图
Fig.2 Top view of sample 1 and sample 3
表1 磁吹系统磁感应强度的分布及大小
Tab.1 Magnetic induction intensity distribution and size of the magnetic blowing system

平均磁感应强度/mT样品 123 x方向9.453.441.5 y方向54.54.344.8 z方向15.52.55.3
文献[11-12]从分子环流模型的角度,搭建永磁体外部磁场分布的数学模型,并分析永磁体的尺寸对横向磁场(平行于充磁方向的磁场)分布的影响。文献[13]基于磁力线划分的方法,建立条形永磁体分布参数模型,与有限元相比大大降低了计算时间。以上研究未分析开路情况下永磁体产生的磁通量达到饱和时的情况及永磁体漏磁问题。
永磁体磁力线分布如图3所示。定义平行于永磁体充磁方向的边为永磁体的高h;垂直于充磁方向的面为底面S;永磁体底面的短边为a,长边为b(图中未示出);永磁体的磁力线设两个底面进出的磁通为主磁通,侧面进出的磁通为漏磁通。本文采用Maxwell三维有限元仿真软件,考虑了漏磁的影响,更全面地对永磁体外部磁场的分布进行分析。
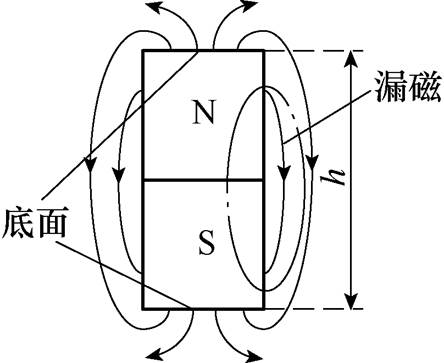
图3 永磁体磁力线分布
Fig.3 Distribution of magnetic field lines of permanent magnets
剩磁Br和内禀矫顽力Hcj是永磁材料的关键参数[14],本文采用钕铁硼稀土永磁材料,其剩磁Br= 1.35T,内禀矫顽力Hcj=1 019kA/m。图4a为永磁体的退磁曲线,Bm、Hm为永磁体工作时对应的剩磁与内禀矫顽力,将其横坐标和纵坐标分别乘以永磁体磁化方向的长度和垂直于磁化方向的截面积,便可得到磁通量Fr与磁动势Fc的关系,Fm、Fm为永磁体工作时对应的磁通量与磁动势,便可得到磁通与磁动势的关系,如图4b所示。
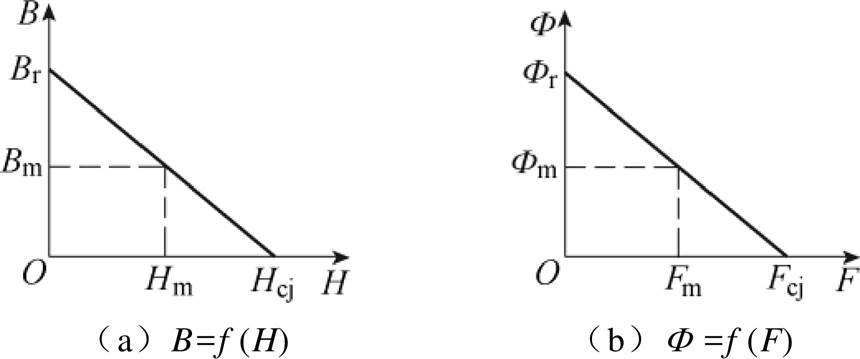
图4 永磁材料特性曲线
Fig.4 Characteristic curves of permanent magnetic material
图5为永磁体三维仿真模型,底面为5.5mm× 14mm的长方形,高为5.5mm。对永磁体底面和中心部位进行磁通量计算,底面磁通量为4.92× 10-6Wb,中心位置的磁通量为7.12×10-6Wb,二者显示永磁体表面的磁通量明显比中心部位的磁通量少,为此不可忽略漏磁产生的影响。为探究永磁体高度对漏磁的影响,对永磁体高度进行单变量特征分析。图6为不同永磁体高度情况下底面磁通量和中心部位磁通量的对比。由图中可以看出,随着永磁体高度的增加,漏磁现象越发明显,而且磁通量呈现饱和趋势。因此,需要对永磁体的高度进行合理设计。
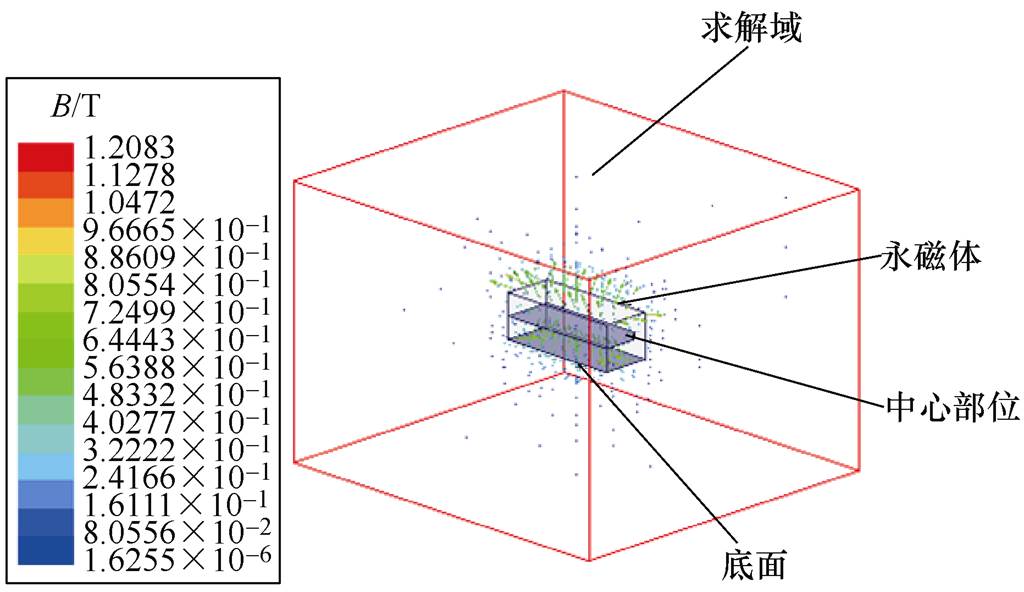
图5 永磁体三维仿真模型
Fig.5 3D simulation model of permanent magnets
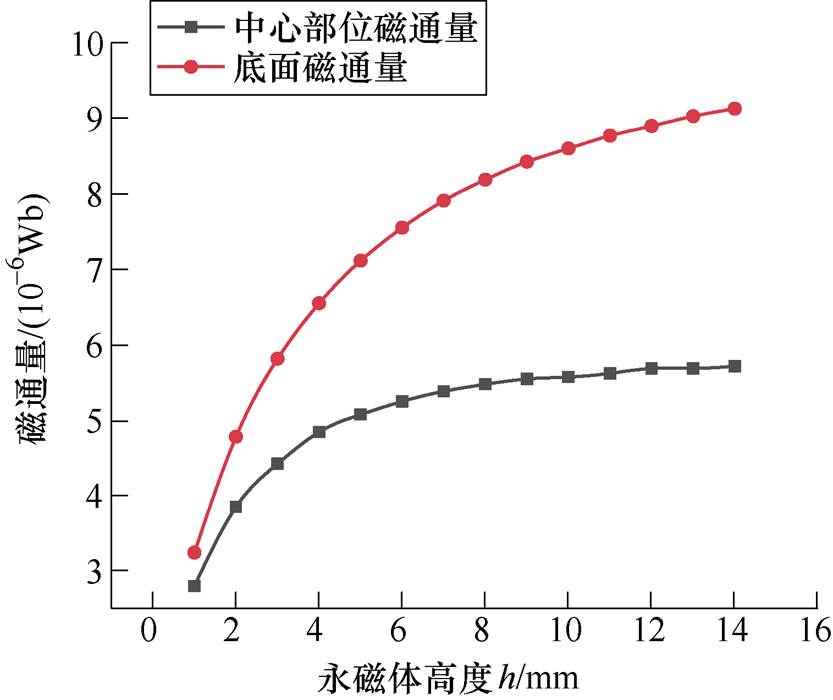
图6 不同永磁体高度仿真对比
Fig.6 Simulation comparison of different permanent magnet heights
为验证仿真模型,本文采用高斯计对永磁体表面的磁感应强度进行测量,如图7所示。探针的测量部位为一个长3mm、宽2mm的长方形,因此仿真模型磁感应强度的计算区域也采用该形状。对两种型号的永磁体的磁感应强度进行测量,其测量点如图8所示。仿真计算结果与测量结果的对比见 表2,其相对误差基本在5%以内,验证了仿真模型的可行性。

图7 高斯计
Fig.7 Gauss meter
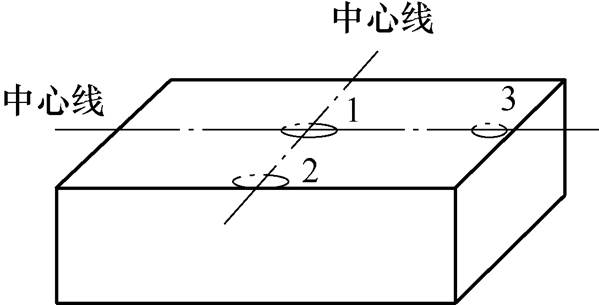
图8 磁通密度测量点
Fig.8 Magnetic induction intensity measuring point
表2 仿真结果与实测值对比
Tab.2 Comparison of simulation results with measured values
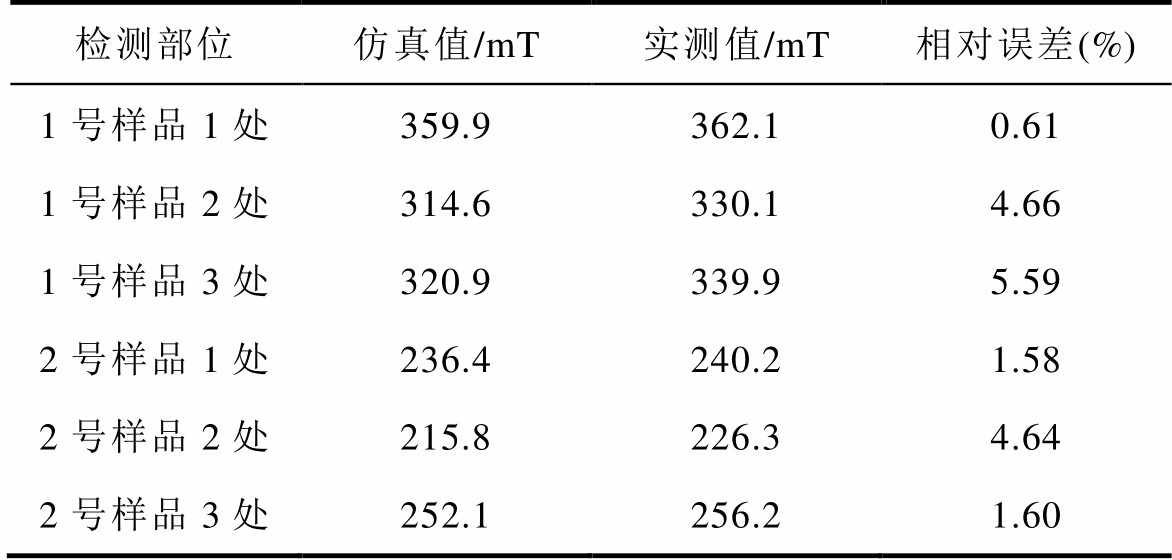
检测部位仿真值/mT实测值/mT相对误差(%) 1号样品1处359.9362.10.61 1号样品2处314.6330.14.66 1号样品3处320.9339.95.59 2号样品1处236.4240.21.58 2号样品2处215.8226.34.64 2号样品3处252.1256.21.60
1.1节的仿真结果表明,永磁体在开路情况下产生的磁通量随着永磁体的高度增加而趋向饱和。永磁体底面的尺寸同样影响着其特性,为此本节主要分析永磁体高度和底面尺寸在开路下对其产生的磁通量的影响,并建立相关数学模型。
图9为永磁体在开路情况下的等效磁路,将永磁体等效成n个磁源串联。永磁体在开路下自身磁阻远小于空气磁阻,可忽略不计。假设永磁体的平均磁场强度为Hc,可建立磁路表达式为
 (1)
(1)
式中,li(i=1, 2,…, n)为每个磁源的长度;Fi为各支路的磁通量;h为永磁体高度;Rairi为空气磁阻;F 为通过永磁体中心的磁通量。
由等效磁路和式(1)可知,随着永磁体高度h的增大,磁通量Fn所经过的磁阻Rairn增大,Hcl2n所提供的磁通量逐渐减小,即表面磁通量逐渐趋向饱和,且漏磁通量也逐渐趋向饱和。因此,随着永磁体高度的增大,永磁体中心磁通量趋于饱和,此时若继续增大永磁体高度将不仅不能加大吹弧磁场,还造成材料浪费。
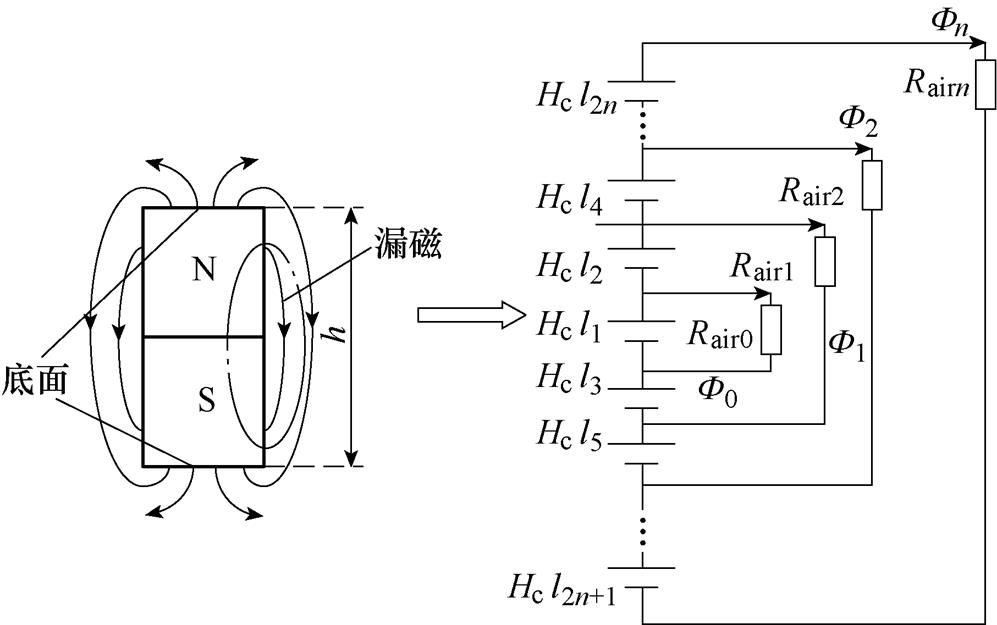
图9 永磁体等效磁路
Fig.9 Permanent magnet equivalent magnetic circuit
由式(1)推导出永磁体中心磁通量的表达式为
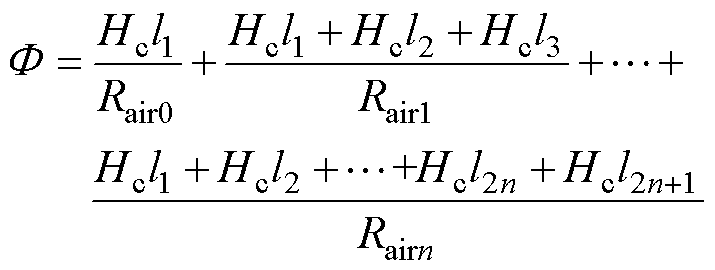 (2)
(2)
由式(2)的最后一项可知,通过永磁体底面的磁通量可以等效为
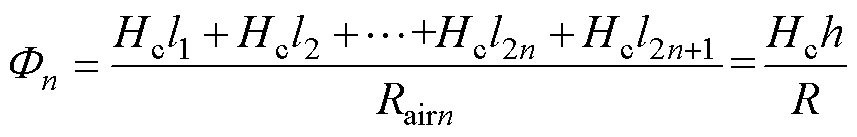 (3)
(3)
式中,R为空气等效磁阻,是关于h的函数,仅需找出R=f (h)即可获取永磁体底面磁通量与永磁体高度的关系。
为探究R=f (h)的关系表达式,对不同型号的永磁体进行高度变化的单变量特征分析,永磁体底面的尺寸见表3,并对底面磁通量进行计算,作为验证模型的对比数据。
定义R=f (h)为m阶函数,其表达式为
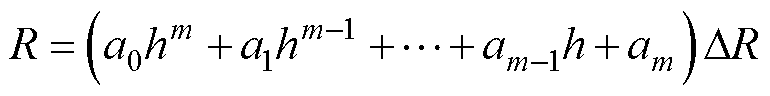 (4)
(4)
式中,DR为外部磁路的单位磁阻;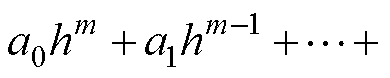
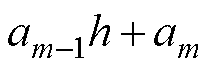 为外部磁路等效路径的长度。
为外部磁路等效路径的长度。
取相同型号高度分别为h1、h2的两个永磁体代入式(3),将二者相除得
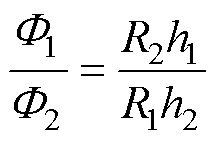 (5)
(5)
表3 不同型号的永磁体底面尺寸
Tab.3 Bottom dimensions of different types of permanent magnets (单位: mm)

样品短边长边 15.55.5 25.514 31010 41414 51020 61430 72020 82630
式中,F1、F2分别为高度h1、h2的永磁体的底面磁通量;R1、R2为对应空气等效磁阻。
将式(4)代入式(5)得
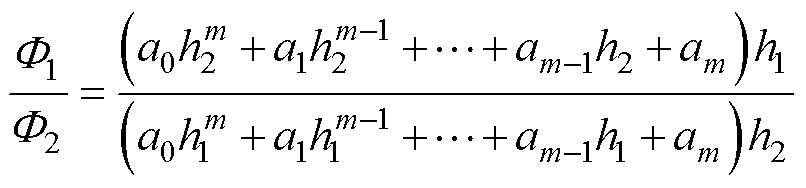 (6)
(6)
式(6)分子除以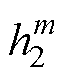 ,分母除以
,分母除以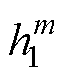 得
得
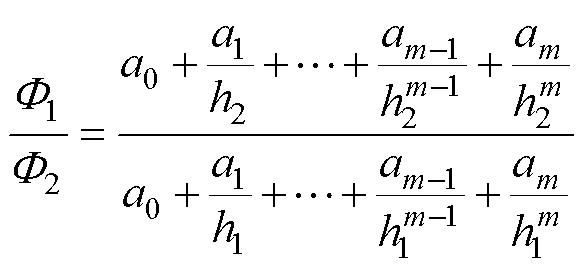 (7)
(7)
由于F1/F2趋于1,因此可令a0=1,其他项随着h的增大可忽略不计,本文只保留a0、a1,即
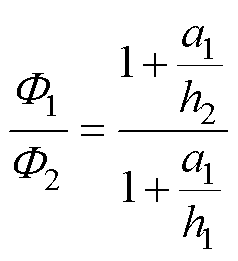 (8)
(8)
对不同型号的永磁体的a1进行计算,结果见表4。
表4 仿真拟合的a1值与公式计算的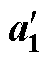 值对比
值对比
Tab.4 Comparison of a1 of simulation fit and 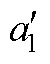 calculated by formula
calculated by formula

样品编号底面宽/mm底面长/mma1/mm/mm误差(%) 15.55.50.940.931.0 25.5141.261.281.6 310101.821.706.5 414142.202.377.7 510202.262.116.6 614302.823.047.8 720203.263.394.0 826304.714.582.8
图10为不同型号永磁体高度的单变量特性分析的仿真结果与通过式(8)计算出的结果对比(F1由仿真数据所得)。由图中可以看出,二者重合度较高,说明式(8)能够较好地描述永磁体高度与其底面磁通量的关系。
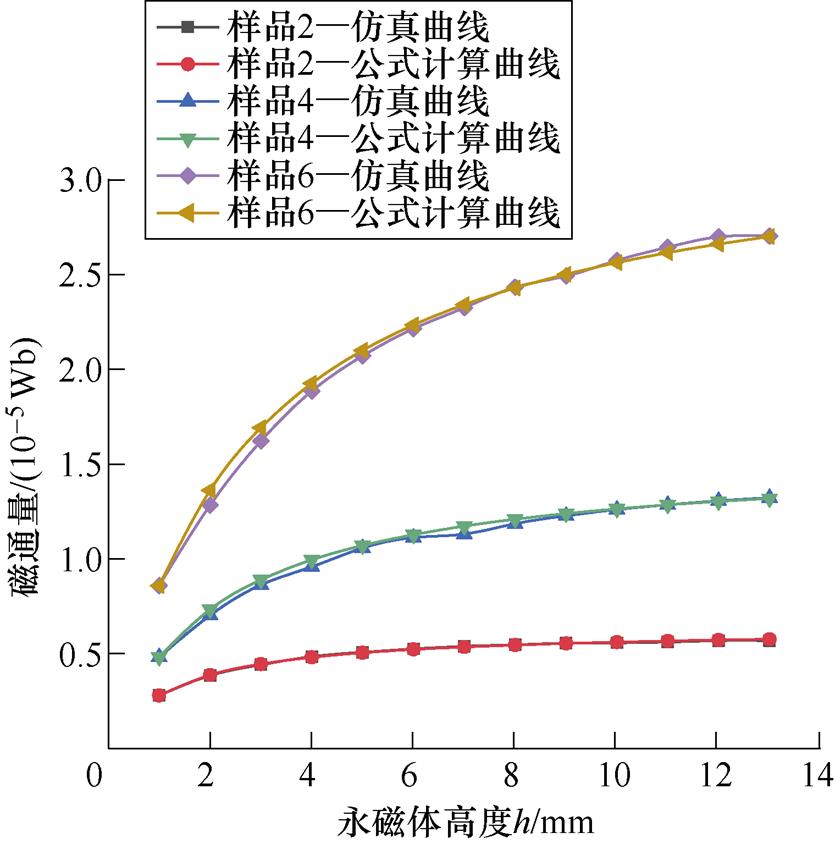
图10 不同型号永磁体高度的单变量特性分析
Fig.10 Univariate characteristics analysis of different specifications of permanent magnet height
不同型号的永磁体对应的a1不同。为进一步探究a1与永磁体底面边长的关系,通过对不同型号永磁体的a1进行分析,发现随着永磁体底面边长a、b的增大,a1也跟着增大,但其所占比重不同。通过对比表4中各型号永磁体随边长增大,a1的变化趋势可发现,短边的增量对a1的增量影响比长边大,为此定义a1与长a和宽b的关系式为
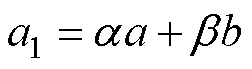 (9)
(9)
式中,a、b 为常数。
通过仿真数据求得a =0.037,b=0.134,并根据式(9)对不同型号的永磁体的a1进行计算。表4为通过式(9)计算的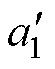 与仿真拟合的a1对比,最大误差为7.8%,可认为该方程能够较为准确地表达a1与底面边长的关系。
与仿真拟合的a1对比,最大误差为7.8%,可认为该方程能够较为准确地表达a1与底面边长的关系。
将式(9)代入式(8)可得任意型号的永磁体在任意两个高度下对应的永磁底面磁通量关系为
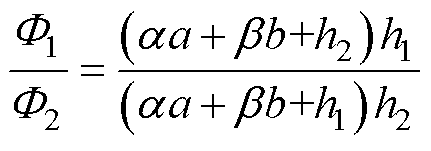 (10)
(10)
通过式(10),可对任意型号永磁体的底面磁通量进行分析计算,设计出合理的永磁体高度,提高永磁体的利用率,避免浪费材料。
第2节分析了永磁体尺寸对其底面磁通量的影响,并建立相关数学模型,但无法确定永磁体在磁吹系统中的安装位置。本节对永磁体外部磁感应强度分布特征进行探究,提出永磁体外部磁感应强度分布的四个阶段,为合理设计永磁体的安装位置提供理论依据。
以永磁体底面的中心为原点,建立磁感应强度三维直角坐标系如图11所示,并对底面积范围内的磁感应强度进行计算。图12为距永磁体底面不同高度d的情况下,永磁体外部磁感应强度Bz的分布。永磁体磁场经过底面后向四周扩散,在d较小时,永磁体边缘除了自身产生的磁场外,还有其相邻区域扩散来的磁场与其进行叠加。随着d的增大,边缘产生的磁场也要向外扩散,中心部位产生的磁场到达边缘的过程中磁场方向逐渐由z方向变成x或y方向,最后转变成z的反方向。为此,永磁体外部磁感应强度的分布特点可以分为四个阶段:第一阶段,当d较小时,永磁体周边的磁感应强度大于中心部位的磁感应强度(见图12a);第二阶段,永磁体外部磁感应强度分布较为均匀(见图12b);第三阶段,中间磁感应强度大于周边磁感应强度(见图12c);第四阶段,中间磁感应强度继续减小,永磁体外部磁感应强度再次趋向均匀分布(见图12d)。该分布趋势与文献[11]一致。
图11 永磁体外部磁感应强度分布三维坐标系
Fig.11 The 3D coordinate system of permanent magnet's external magnetic density distribution
永磁体磁感应强度分布呈对称性,为便于对比分析,取y轴上的磁感应强度分布进行探究。图13为永磁体y轴上的外部磁感应强度Bz分布,由曲线可直观地看到永磁体外部磁感应强度随d变化的四个阶段。永磁体边缘小于2mm的区域磁感应强度Bz迅速减小,为保证开断电弧能够更好地受到吹弧力,应避免该区域作为吹弧磁场的工作区域。图14为外部磁感应强度Bx的分布。由图中可以得出,距离永磁体中心越近,磁感应强度Bx越小。但只在永磁体中心部位附近才能忽略Bx方向的磁场,若欲使用永磁体底面区域内对电弧进行磁吹,需要考虑电弧多方向的受力情况。而如果使用永磁体边缘外的磁场作为吹弧磁场,由于该处Bz相对于Bx较小,可忽略,即可实现单方向吹弧。

图12 永磁体外部磁感应强度三维分布
Fig.12 3D distribution diagram of the external magnetic density of the permanent magnet
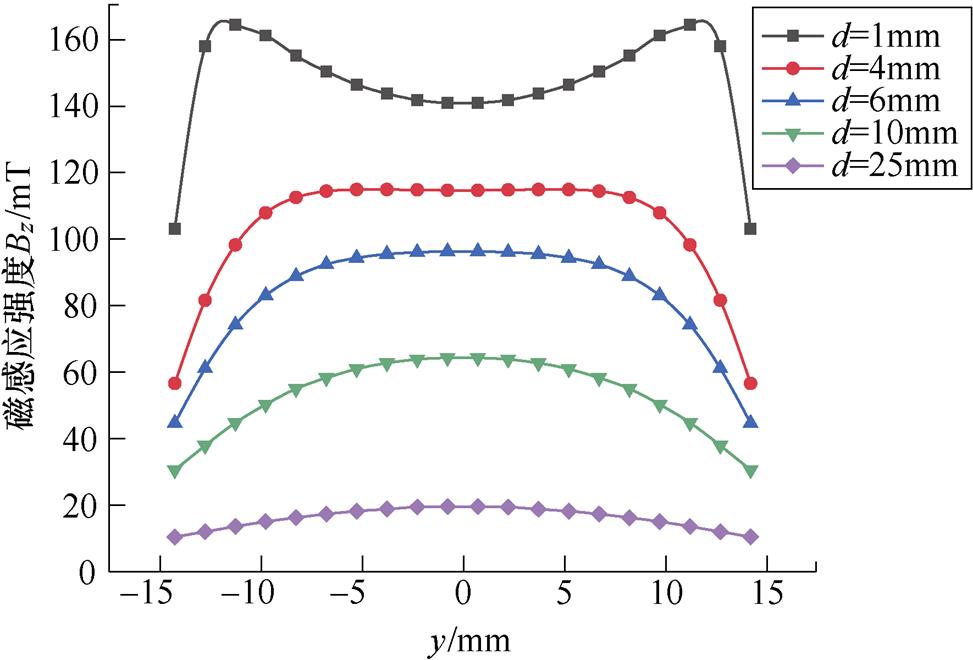
图13 y轴上永磁体的外部磁感应强度分布
Fig.13 Distribution of external magnetic density of permanent magnets on the y-axis
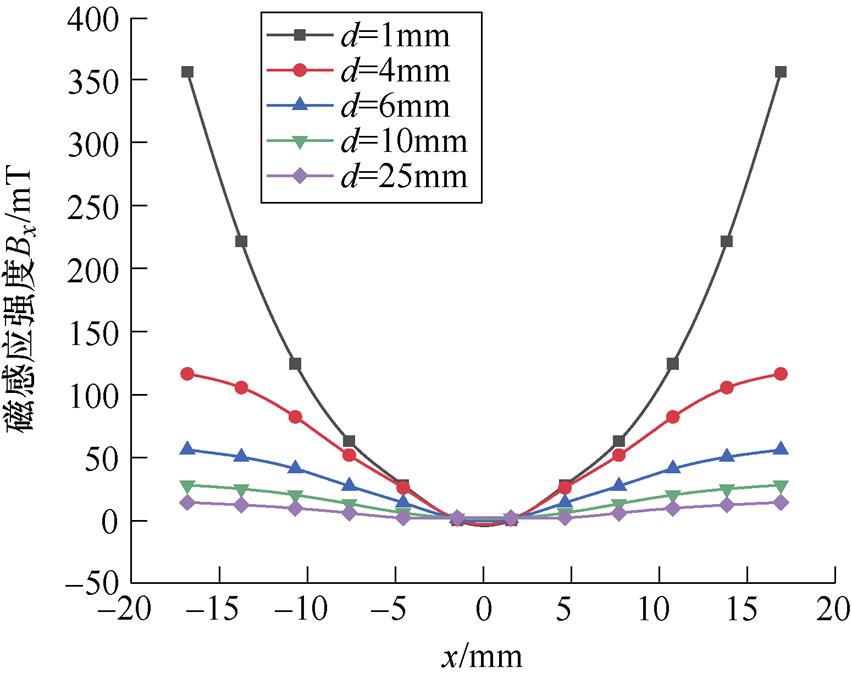
图14 x轴上永磁体Bx磁感应强度分布
Fig.14 Distribution of Bx flux density of permanent magnets on the x-axis
为研究永磁体尺寸对其外部磁感应强度分布的影响,对相同底面(a=30mm, b=16mm)不同高度的永磁体的外部磁感应强度进行对比。定义g =S0/S为永磁体磁感应强度分布均匀度。其中,S0为与原点磁感应强度误差在5%以内的区域面积,S为永磁体底面积。图15为不同永磁体高度下随着d值变化的g 对比。随着d的增大,永磁体的磁感应强度的均匀度g 先增大后下降。随着永磁体高度的增加,均匀度的最大值出现位置越早,如高度大于10mm的永磁体,最大均匀度g 在d<1mm的时候就已出现,且随着永磁体的高度增加,均匀度g 随d的改变其变化速率越快。就高度为6mm的永磁体而言,若永磁体外部磁场的作用区域在d<4mm时,由于工艺误差将造成产品一致性差的问题。通过对永磁体外部磁感应强度分布均匀度的分析,可以确定永磁体的合理安装位置,保证外部磁场分布的一致性。
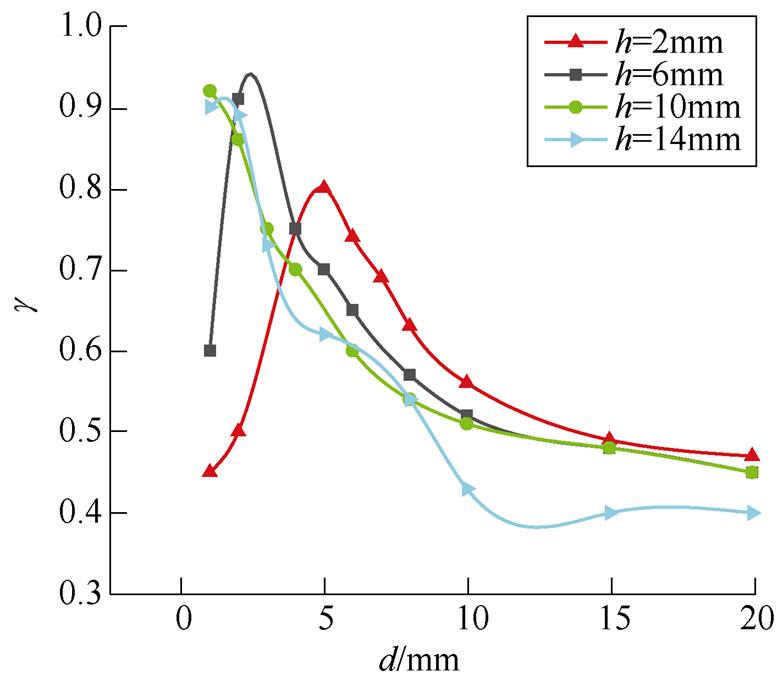
图15 永磁体外部磁场分布均匀度对比
Fig.15 Comparison of the uniformity of the external magnetic field distribution of the permanent magnet
根据3.1节的分析,在永磁体边缘2mm处磁感应强度变化趋势较大,不适合作为磁吹系统的工作区域,因此设计的永磁体边缘应超出电弧燃弧区域的边缘2mm。为留一定的裕量,设计的永磁体边缘大于电弧燃弧区域的边缘3mm,且永磁体中心与燃弧区域的中心在同一水平面上。
所设计的永磁体底面边长a=17mm, b=7mm,通过式(9)确定了a1=1.57mm。并通过式(10)可知,当永磁体高度大于5mm后,其外部磁通随高度的增加增量小于5%,外部磁通量基本达到饱和。因此,所设计的永磁体高度h=5mm。对该型号的永磁体进行三维仿真,分析其外部磁感应强度分布的特点,其外部磁感应强度分布均匀度随d变化的对比如图16所示。当d>5mm以后,磁感应强度分布均匀度的变化趋势较小,为同时保证永磁体能够提供较大的磁场且有较高的分布均匀度,永磁体距离应设计在5mm左右。

图16 永磁体外部磁感应强度分布均匀度
Fig.16 Uniformity of magnetic density distribution of permanent magnets
目前,主要通过实验和仿真两种手段对开断直流电弧进行特性分析[15-19]。由于实验条件和测试手段受到限制,众多电弧内部复杂的物理现象无法通过实验得到,对电弧的深入研究也将受到阻碍,而通过仿真手段建立电弧多物理场耦合模型,能够更直观地对电弧燃烧过程的相关特性进行分析,是深入认识电弧机理的有效方法。本文基于磁流体动力学理论建立开断电弧三维模型,探究外加磁场对电弧运动行为的影响,为合理设计磁吹系统提供理论依据。
以流体动力学控制方程与电磁场方程耦合为基础建立电弧三维模型。流体力学控制方程遵循质量守恒定律、牛顿第二定律和能量守恒定律[20]。电弧仿真基于以下假定条件:
(1)电弧等离子体处于局部热力学平衡状态,且为牛顿层流状态[21]。
(2)鞘层对热场和速度场影响较小,忽略电极鞘层区影响[22]。
(3)不考虑电极及器壁产气、弧柱感应电流、重力等问题。
本文研究的继电器触头系统为双断口,为减小仿真计算量,提升仿真速度,只建立单个断口的简化对称模型。图17为样机一半灭弧室简化模型。为减少网格数,实际建模缩小计算区域,重点分析触头间燃弧区域电弧的运动行为特征。
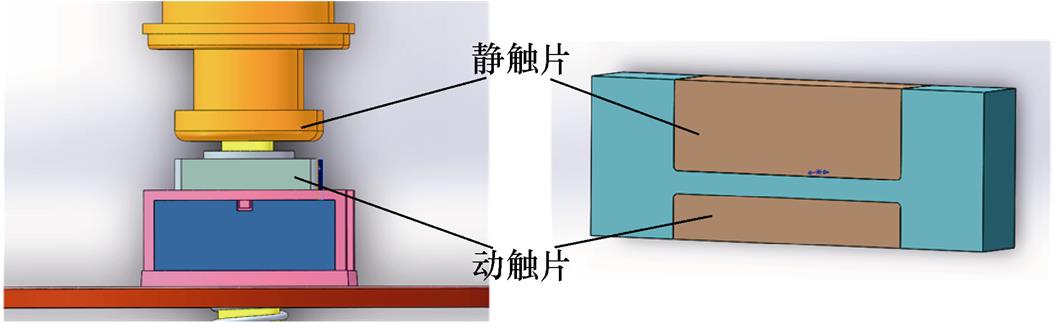
图17 灭弧室简化模型
Fig.17 Simplified model of arc extinguishing chamber
图18为直流200A的稳态电弧仿真结果,靠近电极处电流密度大,焦耳热高,阴阳两极有明显的高温区域。由于电磁感应现象,电弧在燃烧过程中产生自感环形磁场,带电粒子在磁场中受洛伦兹力作用向电弧中心运动。在阴极处电流密度大,产生的磁场大,带电粒子向电弧中心收缩更明显,温度更高,电弧整体呈“钟状”。
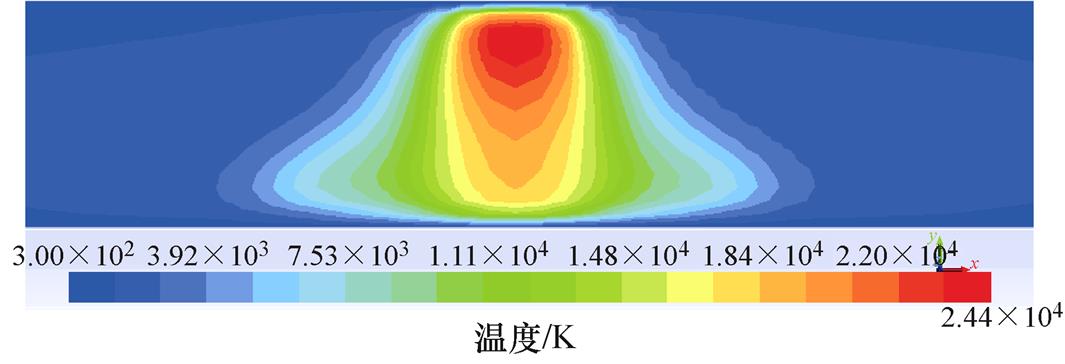
图18 稳态电弧温度分布
Fig.18 Steady-state arc temperature distribution
吹弧磁场为53mT恒定磁场条件下的直流电弧动态仿真结果如图19a所示。电流是在20A/200V、纯阻性负载情况下继电器触头开断过程中的实测时间-电流数据。在外加磁场作用下电弧向触头边缘移动。由于热惯性的原因,电弧经过的区域散热慢,即使电弧运动到触头边缘,触头间依旧存在高温区。图19b为20A开断电弧在磁吹作用下的实验结果。利用高速摄像机拍摄触头通20A电流时的开断电弧现象。高速摄像机帧数为77 000帧,电弧从起弧到熄弧所用时间为0.74ms。仿真中电弧熄灭时间也为0.74ms左右,且仿真电弧模型在整个运动过程中的形态变化与实验基本一致,验证了电弧模型的准确性。
文献[23]研究了永磁体放置位置对电弧电动力的影响。外加磁场的方向决定了电弧的运动方向。本文对永磁体的安装位置和充磁方向进行设计,比较其对电弧运动行为的影响,并分析各自的优势。

图19 仿真结果与实验结果对比
Fig.19 Comparison of simulation results and experimental results
如图20a所示,将永磁体置于动触片下方,永磁体的充磁方向为z方向。由于在电弧燃弧区域y方向的磁场较小,可忽略不计,因此电弧仅在y方向运动,如图20b所示。此时,处于触头中心的电弧运动到触头边缘的距离为5.5mm,并且采用此吹弧方式可以实现触头无极性连接方式,电源正极接在任意一个触头,两端的电弧仅在y方向上运动,避免了电弧向灭弧室中心运动,烧蚀其他零部件。
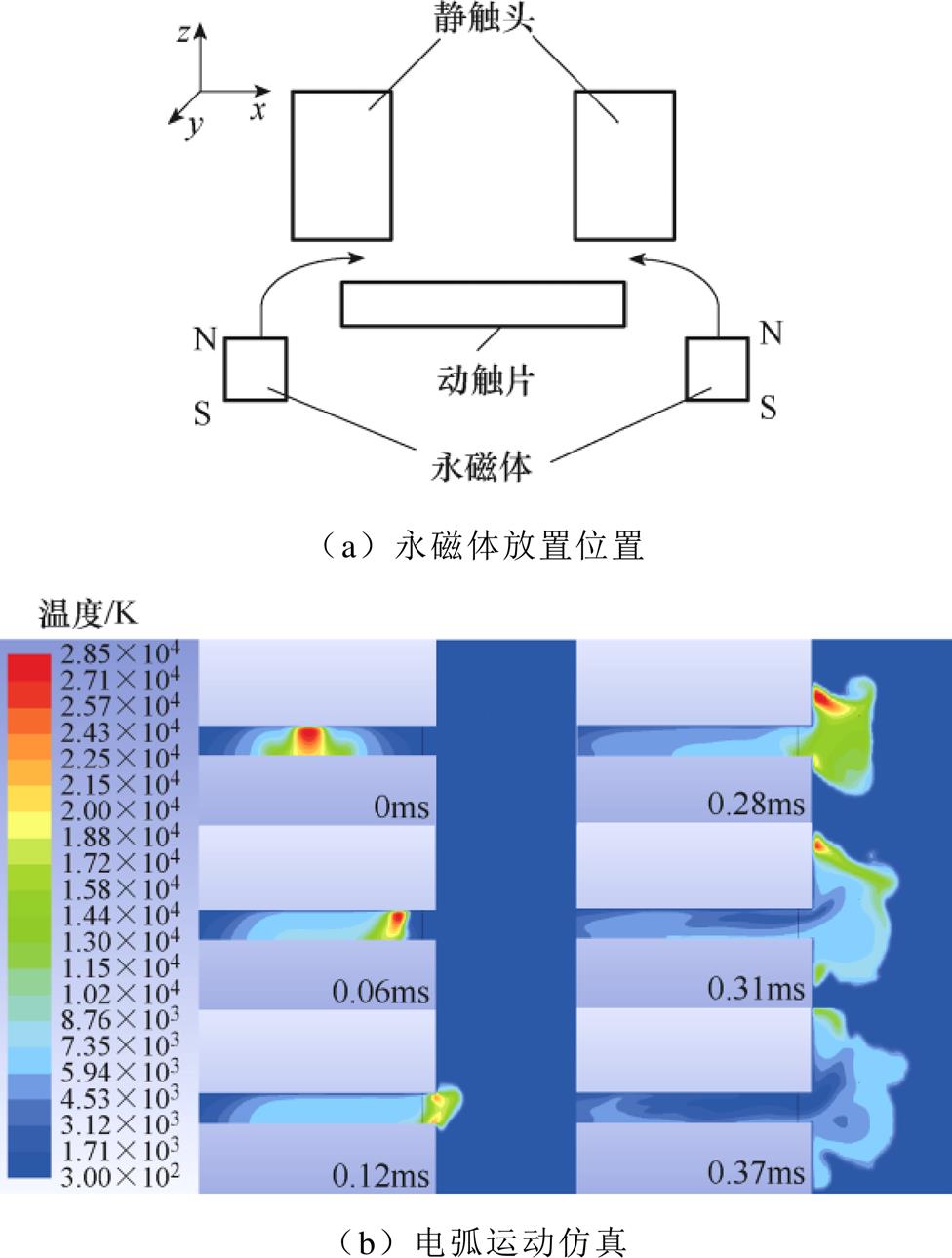
图20 吹弧方式1
Fig.20 The first method of arc blowing
而如果采用图21的吹弧方式2,永磁体依旧放置在动触片下方,充磁方向改为y方向,此时电弧燃弧区域中x方向的磁场可忽略不计,电弧只受到x方向的吹弧力,此时触头中心产生的电弧运动到动触头边缘仅为3mm,电弧可以更快离开触头中心,运动到触头边缘被拉长。但该吹弧方式必须考虑触头的极性问题,防止开断电弧向连杆运动,烧蚀其他零部件。
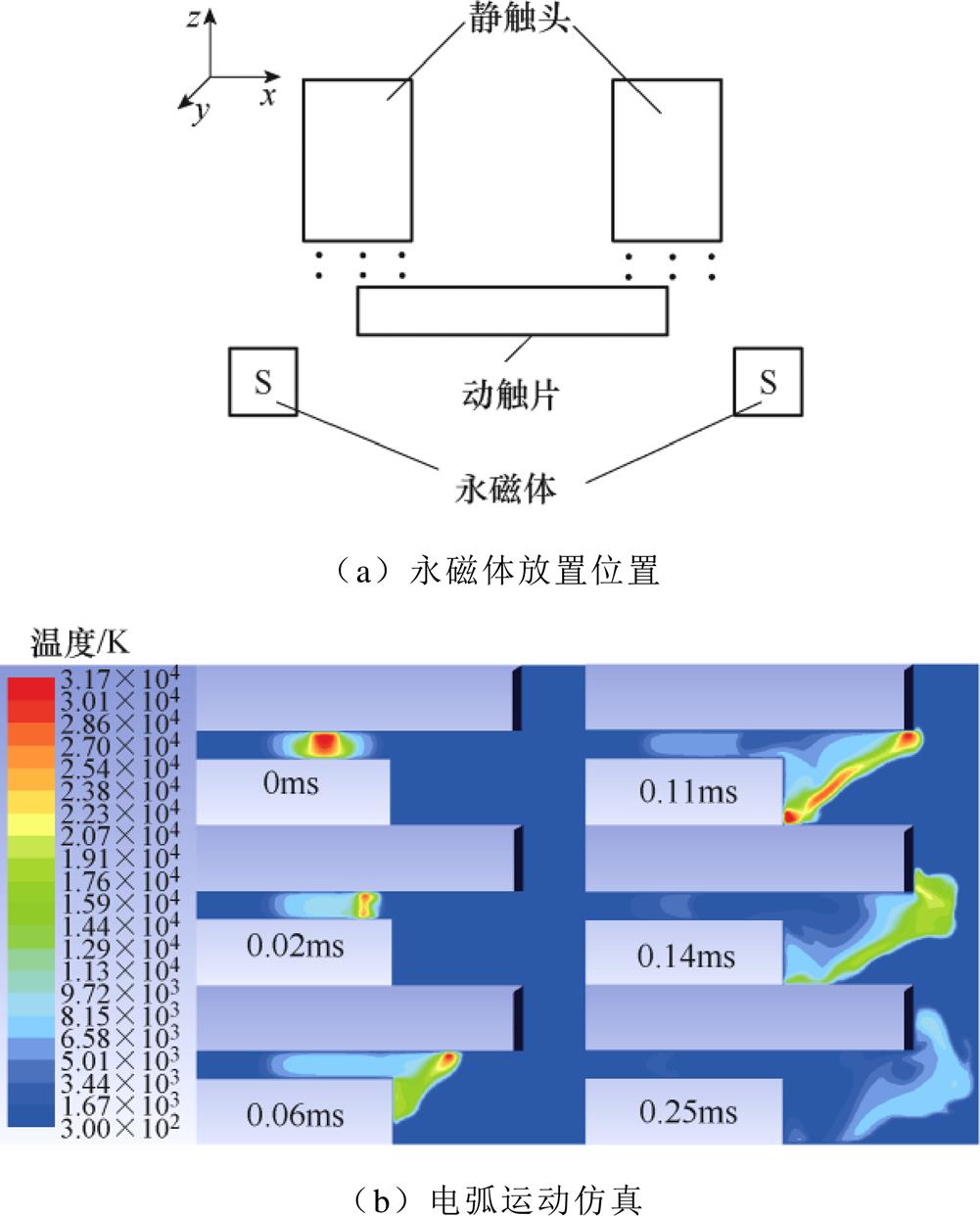
图21 吹弧方式2
Fig.21 The second method of arc blowing
以上两种磁吹方式都可以实现单方向吹弧,而当永磁体安装位置如图22a所示,就需要考虑电弧多方向受力情况。图中点画线框内为永磁体,放置在触头后方,此时在电弧燃弧区域中同时存在x, y方向的磁场。虽然永磁体外部磁感应强度分布呈对称性,在电弧燃弧区域中存在大小相等方向相反的x方向的磁场。但由于电弧起弧位置的随机性,即使永磁体放置在电弧运动区域中心处也无法抵消x方向的吹弧力。图22b左图为电弧受到x, -y方向的磁吹力的仿真结果,该图为静触头的俯视图,即纸面往外为静触头,往里为动触片。由图中可以看到,电弧运动方向为x方向和-y方向的和运动方向,如图22b右图所示。
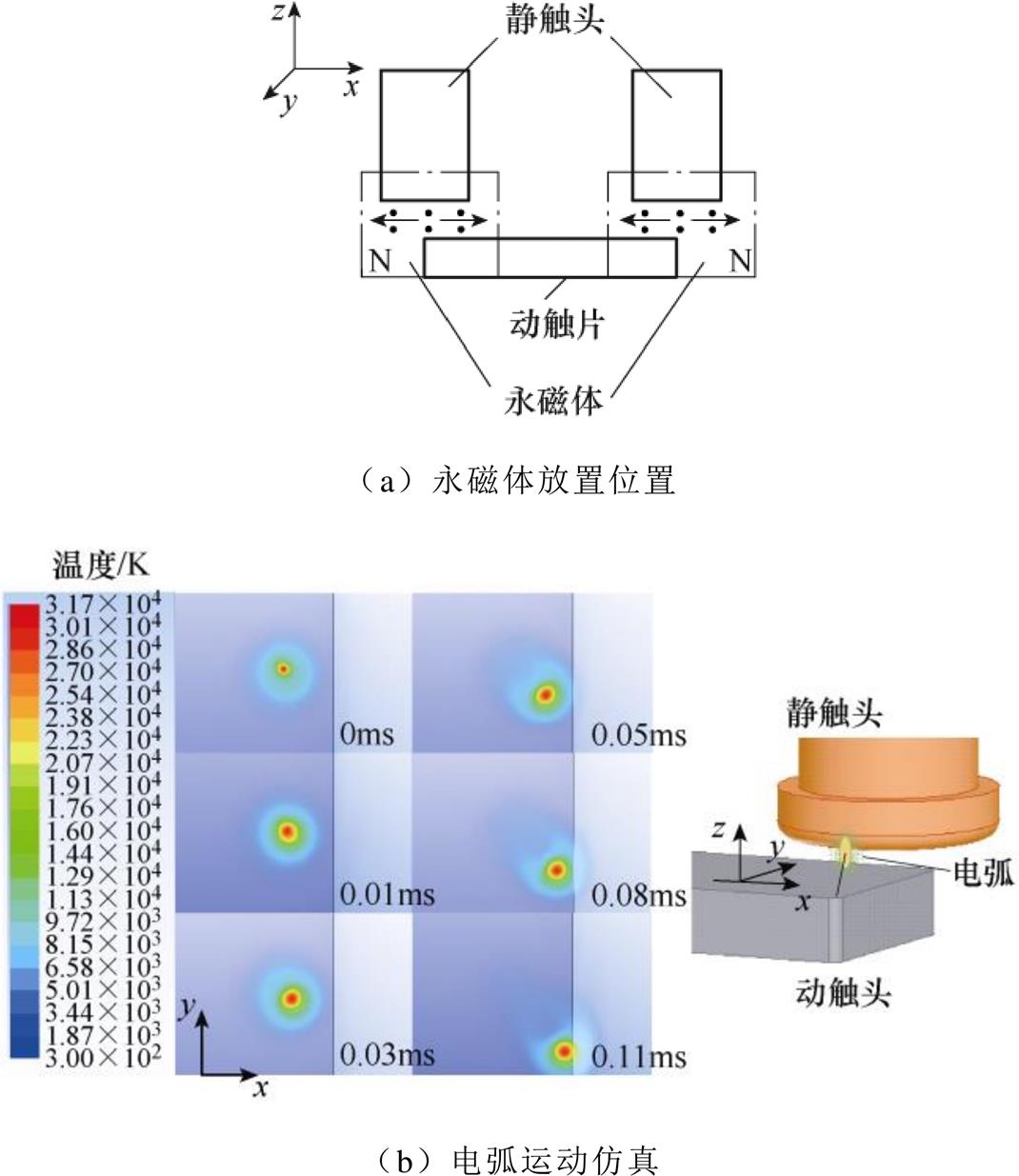
图22 吹弧方式3
Fig.22 The third method of arc blowing
开断电弧生成后受到外加磁场的作用向触头边缘运动所需的时间称为“电弧停滞时间”[9]。电弧停滞时间越长,对触头的烧蚀越严重。本文探究了外加磁感应强度对电弧停滞时间的影响,并进一步对磁吹系统进行改进。
当电弧在动静触头间运动时,由于触头开距较小,电弧弯曲和拉长不明显,电弧电压变化不明显。当电弧运动到触头边缘后,电弧快速弯曲、拉长,电弧电压上升速度变快,因此可通过电弧电压上升率的转折点判断电弧的停滞时间。
如图23所示为相同外加磁感应强度,开断电流等级分别为55A和85A条件下的开断电弧运动行为对比。随着开断电流等级的提高,电弧受到的安培力越大,电弧运动速度越快,停滞时间缩短。当电弧运动到触头边缘后,由于电流等级越大的电弧弧柱半径越大,电弧越不容易变形,电弧电压上升速度慢,电弧越难熄灭,根据实验现象,85A的开断电弧比55A的早0.05ms运动到触头边缘,而将电弧吹出边缘又比55A晚0.08ms,为此有必要增大吹弧磁感应强度。
图24为在不同外加磁感应强度下,电弧电压与电弧电流对比。图中显示,随着外加磁感应强度的增大,电弧停滞时间变短,电弧更快地运动到触头边缘。当电弧运动到触头边缘后,外加磁感应强度越大,电弧拉伸速度更快,弯曲幅度更大,电弧电压上升速度越快,电流下降速度越快,电弧燃弧时间越短,电弧电压趋势与文献[19]一致。因此,增大外加磁感应强度有利于缩短电弧的燃弧时间。
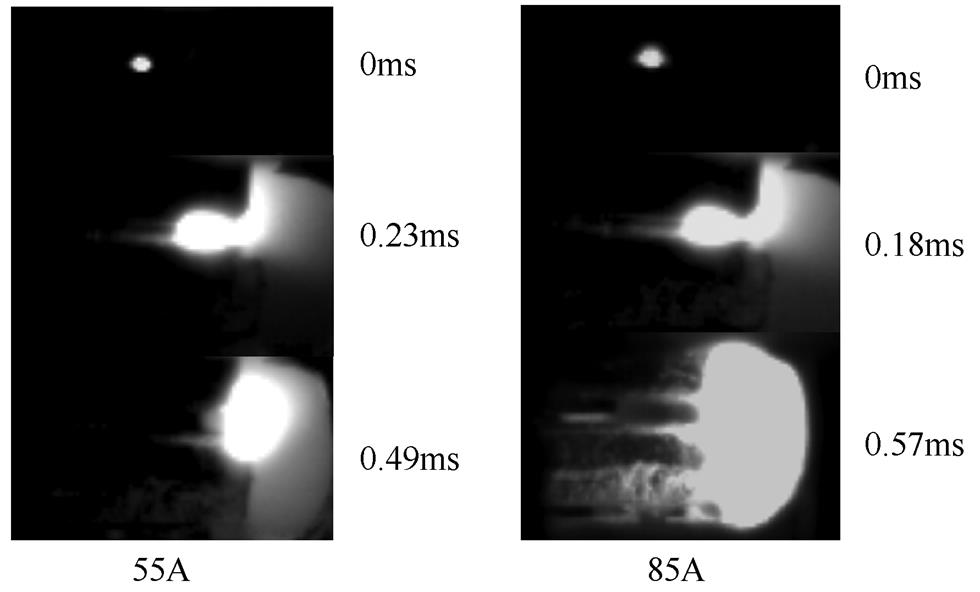
图23 不同电流等级的电弧运动形态
Fig.23 Arc motion patterns of different current levels
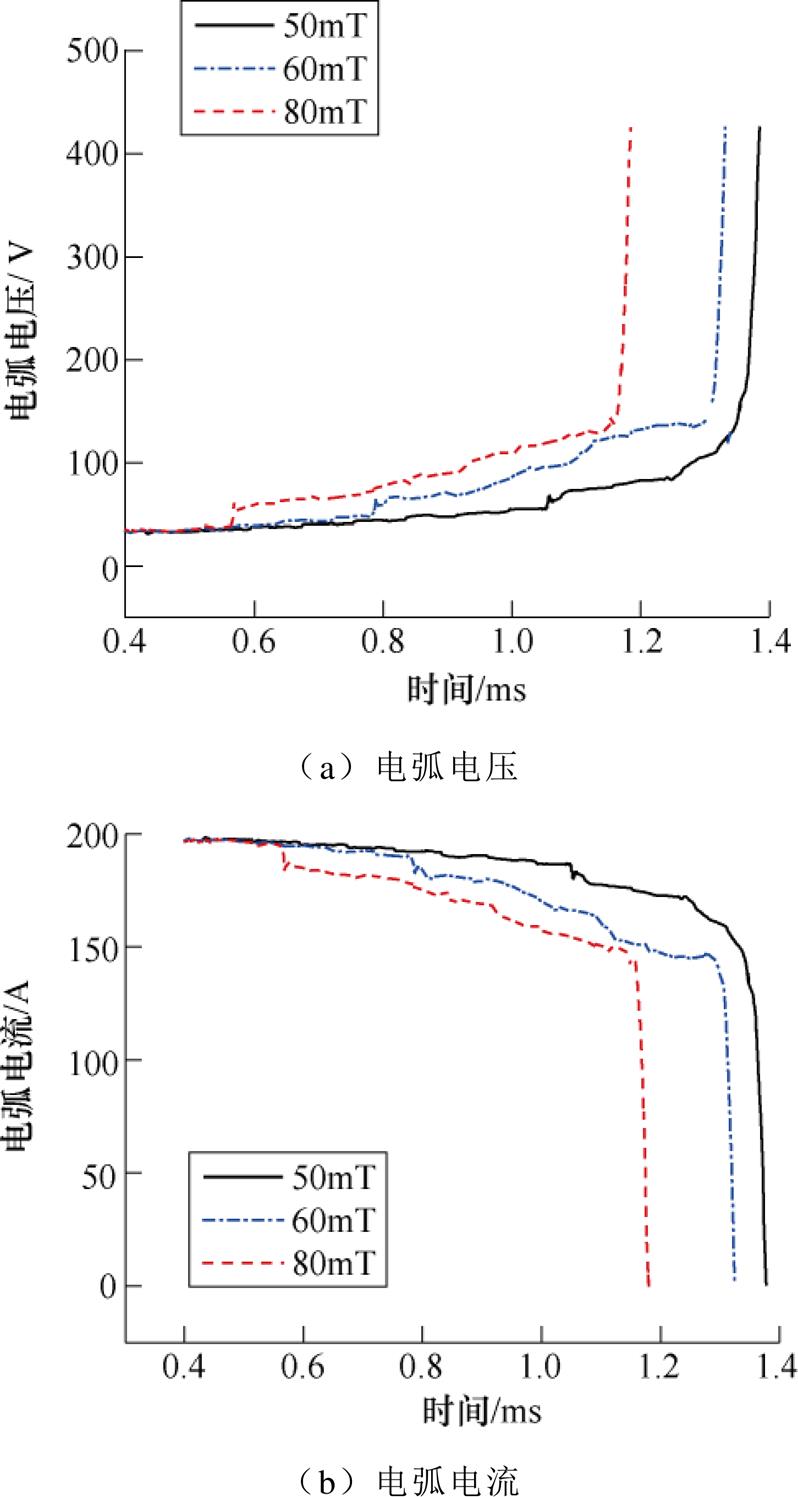
图24 不同外加磁感应强度下电弧电压电流对比
Fig.24 Comparison of arc voltage and current under different applied magnetic fields
虽然通过增大外加磁感应强度能够减小电弧的燃弧时间,但是由于灭弧室空间狭小,加上永磁体磁通量饱和的原因限制了外加磁感应强度的最大值。因此本文对磁吹系统进行了进一步设计。
吹弧方式4如图25所示,在动触片下方和后方同时安装永磁体,将两块永磁体的磁场进行叠加即可大大提高吹弧磁感应强度。表5对比了吹弧方式1和吹弧方式4中Bx、By、Bz 3个方向的磁感应强度大小,发现吹弧方式4依旧能够实现单方向吹弧,并且Bx方向的磁感应强度由原先的54.5mT提高到106.1mT。
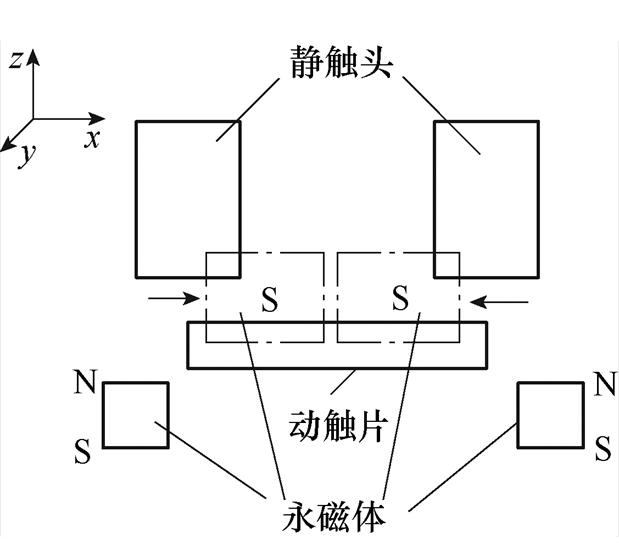
图25 吹弧方式4
Fig.25 The forth method of arc blowing
表5 磁感应强度对比
Tab.5 Comparison of magnetic field strength
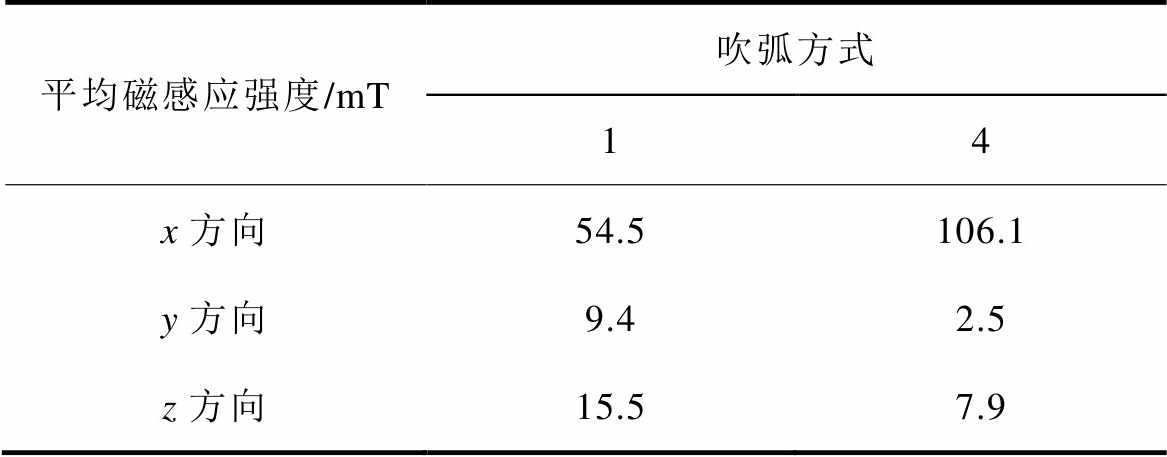
平均磁感应强度/mT吹弧方式 14 x方向54.5106.1 y方向9.42.5 z方向15.57.9
1)建立永磁体尺寸对底面磁通量影响的数学模型,该模型可确定任意底面的永磁体其外部磁通量达到饱和时永磁体的高度,提高永磁体的利用率。
2)探究永磁体外部磁感应强度分布的特征,得出永磁体外部磁感应强度分布随着与永磁体底面距离d的增大可分为四个阶段:第一阶段,永磁体周边的磁感应强度大于中心部位的磁感应强度;第二阶段,永磁体磁感应强度分布较为均匀;第三阶段,中间磁感应强度大于周边磁感应强度;第四阶段,中心磁感应强度继续减小,永磁体外部磁感应强度再次趋向均匀分布。
3)分析永磁体尺寸对外部磁感应强度分布的影响,得出随着永磁体高度的增加,均匀度的最大值出现位置越早,且随着永磁体的高度增加,均匀度g随d改变的变化速率越快。
4)建立开断电弧三维模型,分析了外加磁场的磁吹方向对电弧运动的影响,得出通过改变永磁体的安装位置和充磁方向可以实现单方向吹弧,从而实现触头无极性连接方式。分析了吹弧磁感应强度的增大可以加快电弧熄灭,并提出一种能够提高吹弧磁感应强度的方法。
参考文献
[1] 翟国富, 崔行磊, 杨文英. 电磁继电器产品及研究技术发展综述[J]. 电器与能效管理技术, 2016(2): 1-8.
Zhai Guofu, Cui Xinglei, Yang Wenying. Overview for development of research and technologies of elec- tromagnetic relays[J]. Electrical & Energy Management Technology, 2016(2): 1-8.
[2] 翟国富, 薄凯, 周学, 等. 直流大功率继电器电弧研究综述[J]. 电工技术学报, 2017, 32(22): 251- 263.
Zhai Guofu, Bo Kai, Zhou Xue, et al. Investigation on breaking arc in DC high-power relays: a review[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 251-263.
[3] 翟国富, 周学, 杨文英. 纵向与横向磁场作用下分断直流感性负载时的电弧特性实验[J]. 电工技术学报, 2011, 26(1): 68-74.
Zhai Guofu, Zhou Xue, Yang Wenying. Experiment on DC inductive arcs driven by axial and transverse magnetic fields[J]. Transactions of China Electro- technical Society, 2011, 26(1): 68-74.
[4] 崔彦青. 横向磁场下直流真空断路器中电弧特性及其仿真研究[D]. 天津: 河北工业大学, 2017.
[5] Lindmayer M. Simulation of switching arcs under transverse magnetic fields for DC interruption[J]. IEEE Transactions on Plasma Science, 2016, 44(2): 187-194.
[6] Rau S, Lee W. DC arc model based on 3-D DC arc simulation[J]. IEEE Transactions on Industry Appli- cations, 2016, 52(6): 5255-5261.
[7] Miyagawa H, Sekikawa J. Effect of magnetic blow- out and air flow on break arcs occurring between silver electrical contacts with copper runners[J]. The Institute of Electronics, Information and Communi- cation Engineers, 2017, E100.C(9): 709-715.
[8] Bo Kai, Zhou Xue, Zhai Guofu, et al. Simulation on dwell stage of arcs in bridge type contacts for high- voltage DC relay[C]//2016 IEEE 62nd Holm Con- ference on Electrical Contacts (Holm), Clearwater Beach, FL, 2016: 163-166.
[9] Bo Kai, Zhou Xue, Zhai Guofu. Investigation on arc dwell and restriking characteristics in DC high-power relay[J]. IEEE Transactions on Plasma Science, 2017, 45(6): 1032-1042.
[10] 何永周. 永磁体外部磁场的不均匀性研究[J]. 物理学报, 2013, 62(8): 145-151.
He Yongzhou. Study on the non-uniformity of the external magnetic field of permanent magnets[J]. Acta Physica Sinica, 2013, 62(8): 145-151.
[11] 刘宏娟. 矩形永磁体三维磁场空间分布研究[D]. 北京: 北京工业大学, 2006.
[12] 苟晓凡, 杨勇, 郑晓静. 矩形永磁体磁场分布的解析表达式[J]. 应用数学和力学, 2004, 25(3): 271- 278.
Gou Xiaofan, Yang Yong, Zheng Xiaojing. Analytical expression of magnetic field distribution of rectangular permanent magnet[J]. Applied Mathematics and Mechanics, 2004, 25(3): 271-278.
[13] 梁慧敏, 由佳欣, 罗福彪, 等. 基于磁力线划分的开路条形非线性永磁体分布参数模型[J]. 中国电机工程学报, 2014, 34(9): 1429-1435.
Liang Huimin, You Jiaxin, Luo Fubiao, et al. A distributed parameter model of open circuit nonlinear permanent magnet bars based on magnetic field lines[J]. Proceedings of the CSEE, 2014, 34(9): 1429-1435.
[14] 胡伯平. 稀土永磁材料的现状与发展趋势[J]. 磁性材料及器件, 2014, 45(2): 66-77, 80.
Hu Boping. The status quo and development trend of rare earth permanent magnet materials[J]. Journal of Magnetic Materials and Devices, 2014, 45(2): 66-77, 80.
[15] 伍玉鑫, 王阳明, 杨泽锋, 等. 电弧作用下浸铜碳材料烧蚀过程的数值模拟[J]. 电工技术学报, 2019, 34(6): 1119-1126.
Wu Yuxin, Wang Yangming, Yang Zefeng, et al. Numerical simulation of ablation process of copper- impregnated carbon material under arc action[J]. Transactions of the China Electrotechnical Society, 2019, 34(6): 1119-1126.
[16] 付思, 曹云东, 李静, 等. 触头分离瞬间真空金属蒸气电弧形成过程的仿真[J]. 电工技术学报, 2020, 35(13): 2922-2931.
Fu Si, Cao Yundong, Li Jing, et al. Simulation researches on vacuum metal vapor arc formation at the initial moment of contact parting[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2922-2931.
[17] 蒋原, 李擎, 崔家瑞, 等. 纵向磁场下中频真空电弧的重燃现象分析[J]. 电工技术学报, 2020, 35(18): 3860-3868.
Jiang Yuan, Li Qing, Cui Jiarui, et al. Reignition of intermediate frequency vacuum arc at axial magnetic field[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3860-3868.
[18] 熊德智, 陈向群, 杨杰, 等. 微型断路器弧失效分析及性能优化设计[J]. 电工技术学报, 2019, 34(11): 2333-2341.
Xiong Dezhi, Chen Xiangqun, Yang Jie, et al. Arc extinguishing failure analysis and performance optimization design of miniature circuit breaker[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2333-2341.
[19] 钟昱铭, 熊兰, 杨子康, 等. 计及铜蒸气介质的小电流直流电弧仿真与实验[J]. 电工技术学报, 2020, 35(13): 2913-2921.
Zhong Yuming, Xiong Lan, Yang Zikang, et al. Numerical simulation and experiment of small current DC arc considering copper vapor medium[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2913-2921.
[20] 王福军. 计算流体动力学分析CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
[21] Swierczynski B, Gonzalea J J, Teulet P, et al. Advances in low voltage circuit breaker modeling[J]. Journal of Physics D: Applied Physics, 2004, 37(4): 595-609.
[22] 曹启纯, 刘向军. 高压直流继电器电弧运动仿真分析与实验研究[J]. 电工技术学报, 2019, 34(22): 4699-4707.
Cao Qichun, Liu Xiangjun. Simulation analysis and experimental study on arc motion of high-voltage DC relays[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4699-4707.
[23] 刘佳. 探究永磁体磁性与放置点对电弧电动力的影响[J]. 电器与能效管理技术, 2018(16): 18-20, 31.
Liu Jia. Investigating the influence of magnetism and laying position of permanent magnet on arc’s elec- trodynamic force[J]. Electrical & Energy Manage- ment Technology, 2018(16): 18-20, 31.
福建省2018科技创新领军人才资助项目。
Modeling and Design of Magnetic Blowing System for High Voltage Direct Current Relay
Abstract Due to the compact structure of the HVDC relay contact system, it is difficult to use grids or gas producing materials to improve the breaking performance of the contacts. The arc movement speed can be accelerated by the external magnetic field of the magnetic blowing system, which improves the arc extinguishing ability. As a key part of the magnetic blowing system, the permanent magnet has an uneven distribution of external magnetic induction, and its size has a great influence on the size and distribution of the magnetic field, which causes certain difficulties for the design of the magnetic blowing system. In response to this problem, this paper established a 3D finite element model of the magnetic blowing system, focusing on the analysis of the impact of the permanent magnet size on its external magnetic field, and established a relevant mathematical model. It also analyzed the characteristics of the external magnetic field distribution of the permanent magnet, and obtained the relationship between the uniformity of the external magnetic field distribution and the size of the permanent magnet. Finally, combined with the characteristics of the HVDC relay's breaking arc, this paper designed the size, magnetization direction and installation position of the permanent magnet in the magnetic blowing system by considering the force and stagnation time of the arc. It lays a theoretical foundation for improving the contact breaking performance of HVDC relays.
keywords:High voltage direct current (HVCD) relay, magnetic blowing system, permanent magnet, DC arc, 3D simulation
DOI: 10.19595/j.cnki.1000-6753.tces.201092
中图分类号:TM581
苏伟龙 男,1994年生,硕士,研究方向为电器及其智能化技术。E-mail: 576737933@qq.com
许志红 女,1963年生,教授,博士生导师,研究方向为电器及其智能化技术。E-mail: 641936593@qq.com(通信作者)
收稿日期 2020-08-30
改稿日期 2020-10-30
(编辑 崔文静)