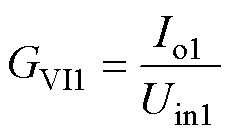 ,补偿网络2电流输出增益
,补偿网络2电流输出增益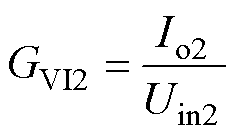 ,同时假设网络无损,则Uin1Iin1=Uo1Io1,Uin2Iin2=Uo2Io2,组合补偿网络电流总的输出增益
,同时假设网络无损,则Uin1Iin1=Uo1Io1,Uin2Iin2=Uo2Io2,组合补偿网络电流总的输出增益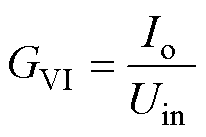 ,则组合补偿网络实现恒流满足的参数关系见表1。
,则组合补偿网络实现恒流满足的参数关系见表1。摘要 针对无线电能传输(WPT)系统线圈相对位置偏移引起传输效率降低、输出电流不稳定和发射线圈过电流问题,提出一种抗偏移恒流输出型WPT系统及其参数配置方法。该系统将LCC-LCC和串联-串联(S-S)补偿网络进行输入串联和输出串联,并采用QDQPs磁耦合结构。在此基础上,通过合理的参数配置,不仅实现了与负载无关的恒流输出,而且可以实现抗x方向、y方向、z方向以及xy方向线圈同时偏移的性能,还可以避免发射线圈过电流。该文分析所提系统的传输特性,从理论上证明了系统具有良好的抗偏移性能。最后,搭建了一个280W实验平台,验证了理论分析的正确性和可行性。
关键词:无线电能传输 抗偏移 恒流输出 组合补偿网络 参数配置
无线电能传输(Wireless Power Transfer, WPT)技术,因其克服传统有线供电方式容易产生电接触电火花、老化磨损和便捷性差等缺点,具有可靠性高、灵活性好、维护费用低及环境亲和力强等优点,近年来得到了迅速的发展。目前,WPT技术在电动汽车、观光车、便携式电子设备、植入式医疗电子设备以及某些特殊应用场合(如化工、矿井、油田钻采、高电压环境、水下探测等)的电能传输等领域展开了广泛的研究,并开始走向商业化[1-7]。
在WPT技术实际应用场合中,发射线圈和接收线圈位置发生偏移是不可避免的。由于接收线圈的位置会影响系统结构参数(线圈自感和互感等),造成系统在恒定输入电压下难以维持输出电压或电流恒定;此外,当接收侧的负载是电池或搅拌机等厨房电器时,在工作过程中等效负载电阻变化较大,这些都会导致系统的各项性能指标(谐振频率、器件应力、输出电压电流、传输功率、传输效率、稳定性等)受到影响[8]。为解决该问题,提高系统抗偏移恒输出性能可从闭环控制技术[9-11]、磁耦合结构[12-15]、补偿网络及参数优化[16-20]这几方面展开研究。对比以上三种抗偏移恒输出方法可看出,闭环控制技术增加了系统的复杂性及所对应的控制成本,有时还需额外增加调节电路,并且涉及频率调节时,易引起频率分裂现象,导致系统稳定性降低。此外,通过调节变换器的占空比来控制系统输出的功率流,当负载和耦合系数变化范围比较大时,系统的调制系数较大,系统控制相对复杂。通常大多数控制器需要射频通信,增加了额外的成本。另外,控制器和通信的速度和准确性可能会导致系统控制的可靠性问题。而采用磁耦合结构和补偿网络的设计和优化可使系统的控制简化,不涉及发射和接收之间的通信问题,但现有磁耦合结构如Q(Quadrature)[11]、DD(Double-D)[12]、BP(Bipolar)[12]、DDQ(Double-D Quadrature)[2]、TP(Tripolar Pad)[15]等线圈的互感随位置变化而剧烈变化的问题或者只存在一个方向的抗偏移特性;现有的补偿网络在接收侧发生偏移(互感M波动较大)或负载大范围变化时造成系统在恒定输入电压下难以输出恒定电压或恒定电流,甚至引起效率降低的问题,同时,其恒压或恒流的输出特性大部分受制于磁耦合结构参数,参数设计自由度相对较低。因此,为实现系统的鲁棒性、控制的简易性、运行的稳定性、应用的普适性,有必要对补偿网络和磁耦合结构进行进一步的研究,以提高系统的抗偏移特性和抗负载扰动的性能以及提高系统参数设计的自由度。
在WPT系统中使用不同的谐振拓扑会对电能输出的恒压恒流、抗偏移、效率等特性产生影响,同时合理地谐振补偿网络设计还可以达到简化电路结构、控制和提高系统性能的效果。在补偿网络的研究方面,近年来,有学者提出将两个具有不同输出性能的补偿网络进行组合[21-24],来达到使系统输出恒定的目的,如文献[21-22]提出LCC-S与S-LCC补偿网络进行组合(输入并联输出串联)实现系统的恒压输出,但系统均采用的是DDQ磁结构,其在线圈平面上只有一个方向的自解耦能力,因此仅存在一个方向(x方向或y方向)的抗偏移性能;文献[23-24]基于DDQ磁耦合结构采用LCC-LCC和串联-串联(Series-Series, S-S)组合补偿网络实现系统恒流输出,但由于系统采用输入并联输出并联的组合,当系统的偏移范围过大时,前级高频逆变电路开关管电流和发射线圈电流存在过电流现象,同时由于采用DDQ磁结构,同样只在一个方向(x方向或y方向)具有良好的抗偏移性能。此外,这些文献虽实现了系统的恒输出性能,但并没有对基于组合补偿网络实现恒输出构造原则进行详细的分析。基于此,本文主要研究基于组合型补偿网络的抗偏移恒流输出型无线电能传输系统及其参数配置原则。首先介绍组合补偿网络拓扑实现恒流输出的构造原则与实现条件;接着详细分析基于LCC-LCC和S-S补偿网络的输入串联输出串联型无线电能传输系统的性能,分析并设计QDQPs(Quadruple-D Quadrature Pads)型磁耦合线圈结构;在此基础上提出在给定偏移和输出电流允许波动范围下的系统参数配置方法,同时分析系统参数的敏感度与软开关实现的方法;最后通过实验验证该理论分析的正确性。
在输入电压恒定的情况下,谐振补偿网络输出电流与发射线圈和接收线圈之间互感的关系与补偿网络的结构有关,有些网络与互感M成正比,有些网络与互感M成反比。如果把这样的一个补偿网络当作一个二端口网络(黑盒子),只考虑输入与输出的关系,若二端口网络1的输出电流与互感M1成正比(如LC-P、LC-LC和LCC-LCC补偿网络[24-25]),二端口网络2的输出电流与互感M2成反比(如S-S补偿网络[26]),通过合理的磁耦合结构设计使得互感M1与互感M2随位置偏移的变化趋势相一致,再将这两个具有互补特性的补偿网络结构串并联组合,就有机会实现整个网络输出电流波动小的目的,从而可实现提升磁耦合系统的抗偏移特性。
根据两个二端口网路的串并联关系,组合网络有四种连接方式:输入串联输出串联(Input Series Output Series, ISOS)、输入串联输出并联(Input Series Output Parallel, ISOP)、输入并联输出串联(Input Parallel Output Series, IPOS)和输入并联输出并联(Input Parallel Output Parallel, IPOP)。假设补偿网络总的输入电压、输入电流、输出电压、输出电流分别为Uin、Iin、Uo和Io,补偿网络1的输入电压、输入电流、输出电压和输出电流分别为Uin1、Iin1、Uo1和Io1,补偿网络2的输入电压、输入电流、输出电压、输出电流分别为Uin2、Iin2、Uo2和Io2,则补偿网络1电流输出增益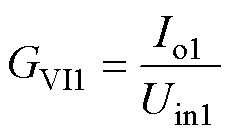 ,补偿网络2电流输出增益
,补偿网络2电流输出增益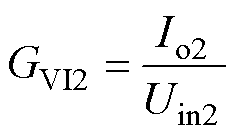 ,同时假设网络无损,则Uin1Iin1=Uo1Io1,Uin2Iin2=Uo2Io2,组合补偿网络电流总的输出增益
,同时假设网络无损,则Uin1Iin1=Uo1Io1,Uin2Iin2=Uo2Io2,组合补偿网络电流总的输出增益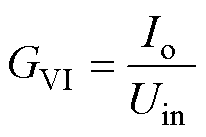 ,则组合补偿网络实现恒流满足的参数关系见表1。
,则组合补偿网络实现恒流满足的参数关系见表1。
表1 两个补偿网络的连接
Tab.1 The connection of two compensating networks

连接方式组合补偿网络结构恒流模式 ISOS ISOP IPOS IPOP
从表1可看出,ISOP和IPOS要实现恒流输出,必须使原两个互补输出的补偿网络在接收负载发生任意位置偏移时具有相同的电流输出增益,这在实际运行时难以保证。因此,四种组合中只有ISOS和IPOP有机会实现系统的恒流输出,但研究表明,IPOP系统当接收线圈偏移范围过大时,系统中流过逆变器开关管的电流会急剧增大[24-25],因此本文研究ISOS型无线电能传输系统。
图1是基于ISOS组合补偿网络WPT系统。图中,UinDC为系统的直流输入电压,Q1~Q4为功率MOSFET,VD1~VD4为高频整流二极管,Lp1、Lp2为发射线圈,Ls1、Ls2为接收线圈,UAB为全桥高频逆变器输出电压即接收侧高频整流电路的输入电压,Req为后级全桥高频整流电容滤波电路的等效负载电阻,Req=8Ro/p2,Ro为负载电阻,R1、R2、Rp1、Rp2、Rs1和Rs2为线圈内阻,Mp1s1和Mp2s2为发射线圈和接收线圈的主耦合互感,Mp1p2和Ms1s2为同侧交叉耦合互感,Mp1s2和Mp2s1是不同侧交叉耦合互感,各同名端如图1标示。L1、C1、Cp1、Lp1和L2、C2、Cs1、Ls1构成LCC-LCC补偿网络,Cp2、Lp2和Cs2、Ls2构成LC-LC串联补偿网络。
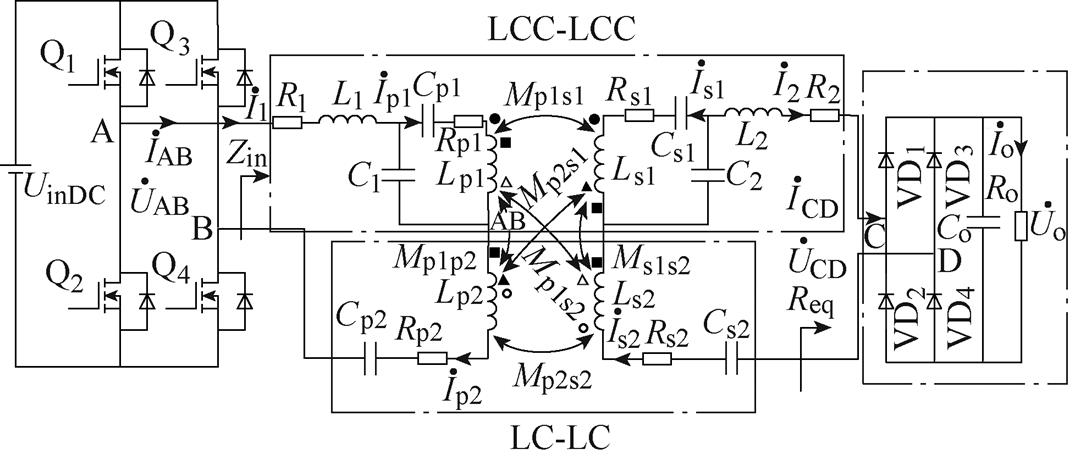
图1 ISOS组合补偿网络WPT系统
Fig.1 ISOS combined compensation network WPT system
在实际应用的电路中,L1和Cp2的串联可以用一个等效的电感Leq1或电容Ceq1来表示,即
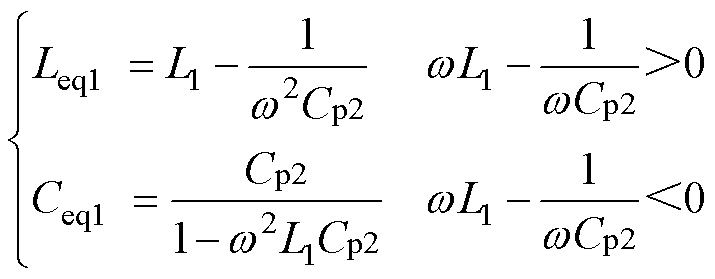 (1)
(1)
同理,L2和Cs2的串联等效电感Leq2和电容Ceq2可表示为
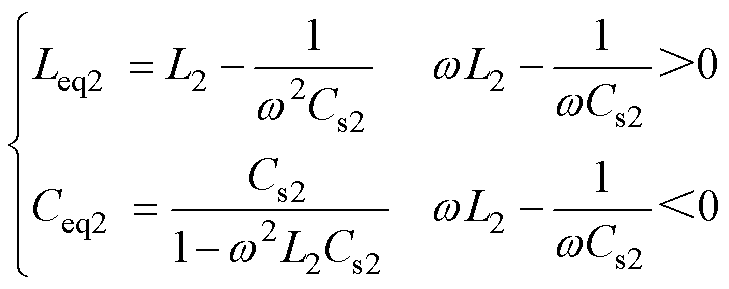 (2)
(2)
假设全桥逆变器开关管的工作角频率为w,则采用基波分析法,图1中全桥逆变器的输出电压为
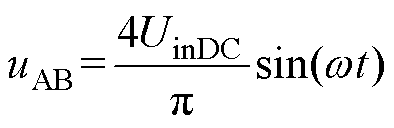 (3)
(3)
系统输出电流为
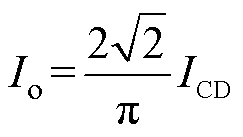 (4)
(4)
列写KVL方程,得到
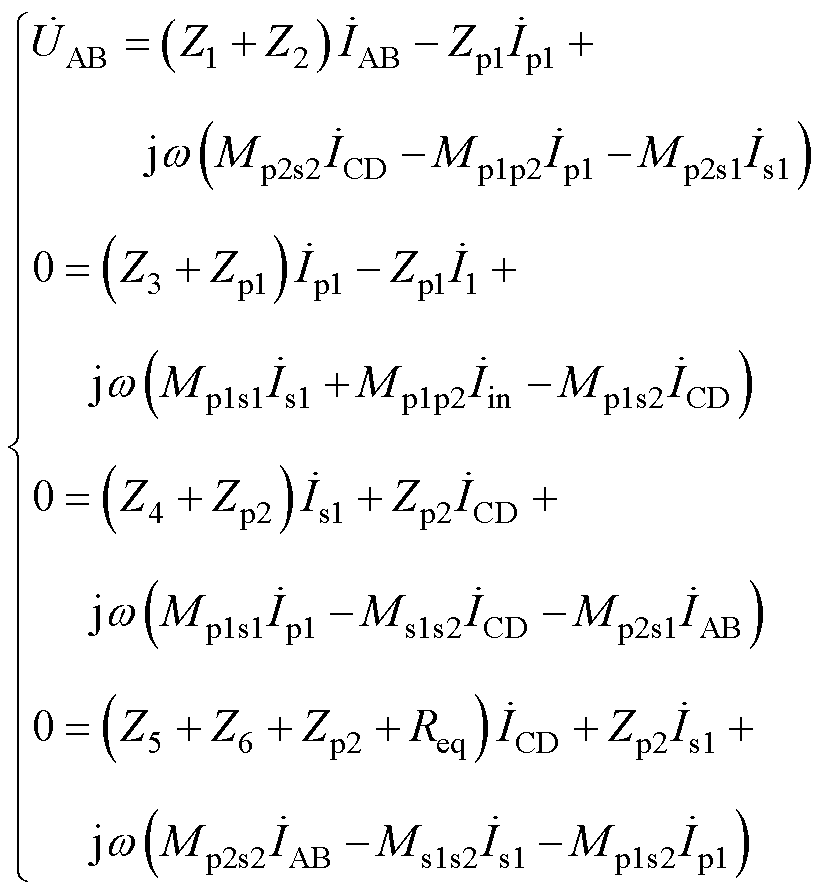 (5)
(5)
其中
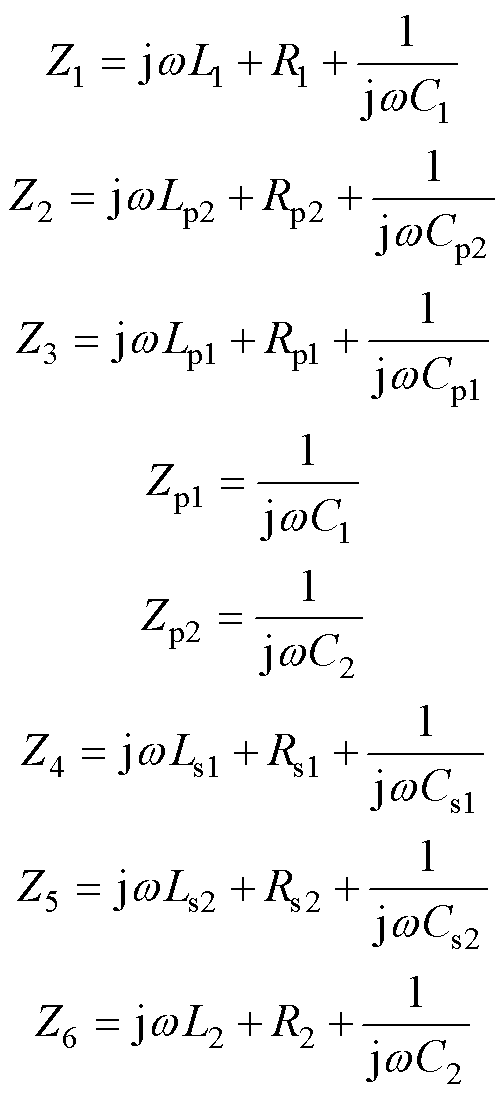
忽略线圈内阻和交叉耦合影响的同时,使电路工作角频率w 满足
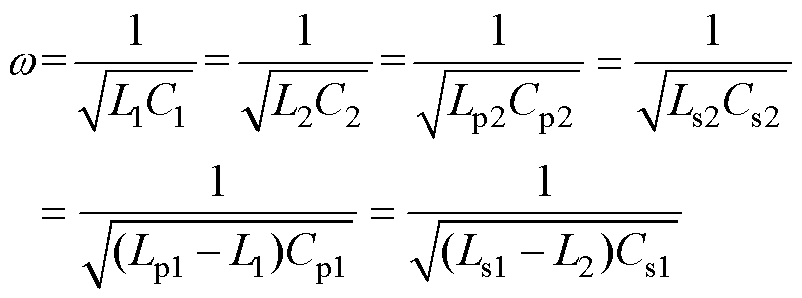 (6)
(6)
则逆变器的输出电流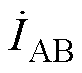 (发射线圈Lp2的电流Ip2)、谐振网络输出电流
(发射线圈Lp2的电流Ip2)、谐振网络输出电流 (接收线圈Ls2的电流
(接收线圈Ls2的电流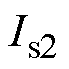 )、发射线圈Lp1的电流
)、发射线圈Lp1的电流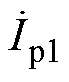 和接收线圈Ls1的电流
和接收线圈Ls1的电流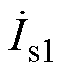 分别为
分别为
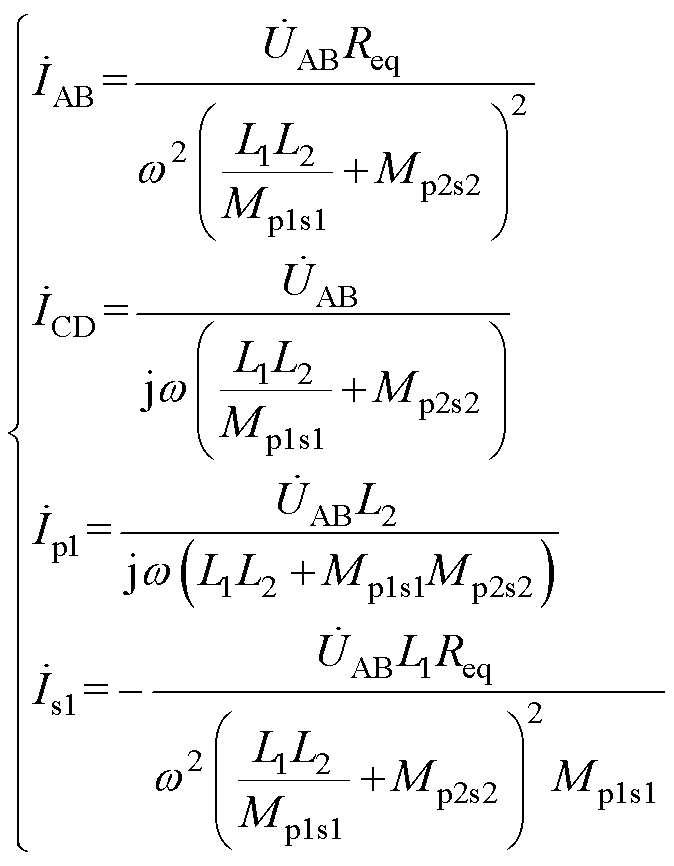 (7)
(7)
从式(4)和式(7)可看出,系统的输出电流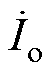 相位滞后谐振网络输入电压
相位滞后谐振网络输入电压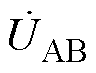 的相位90°,
的相位90°,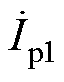 相位超前
相位超前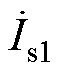 相位90°。同时,当Mp1s1→0,Mp2s2→0时,
相位90°。同时,当Mp1s1→0,Mp2s2→0时,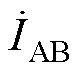 =0;当Mp1s1→0,Mp2s2→0时,
=0;当Mp1s1→0,Mp2s2→0时,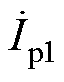 =
=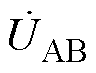 /(jwL1),即接收线圈偏离工作区域时,流过逆变器开关管的电流
/(jwL1),即接收线圈偏离工作区域时,流过逆变器开关管的电流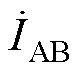 (发射线圈Lp2电流
(发射线圈Lp2电流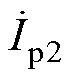 )和发射线圈Lp1电流
)和发射线圈Lp1电流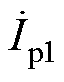 不会急剧增大,克服了IPOP型LCC-LCC和S-S组合补偿网络WPT系统的缺陷[24-25]。
不会急剧增大,克服了IPOP型LCC-LCC和S-S组合补偿网络WPT系统的缺陷[24-25]。
由式(7)中逆变器的输出电流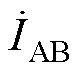 的表达式,得到谐振补偿网络的输入阻抗为
的表达式,得到谐振补偿网络的输入阻抗为
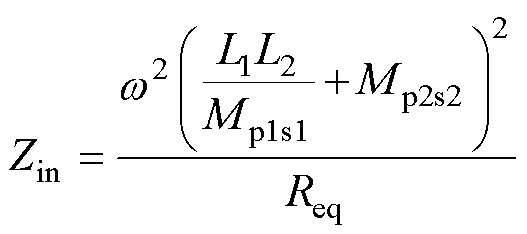 (8)
(8)
从式(8)可看出,输入阻抗呈纯阻性,逆变电路的开关管可实现零相位(Zero Phase Angle, ZPA)。
同时系统的电流输出增益表达式为
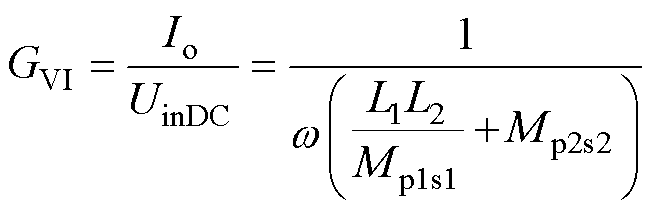 (9)
(9)
从式(9)可以看出,当忽略线圈内阻和交叉耦合时,系统的输出电流解耦于负载电阻,同时通过合理的磁耦合结构设计使Mp2s2和Mp1s1随位置偏移具有相同的变化趋势(同时增大或同时减小),那么GVI可以恒定,即实现系统的恒流输出。
式(5)~式(9)的分析均未考虑交叉耦合的影响。下面考虑交叉耦合的影响,为简化分析,分成以下两种情况考虑。
第一种情况,考虑同侧交叉耦合即Mp1p2和Ms1s2不为零,采用同样的方法可以得到
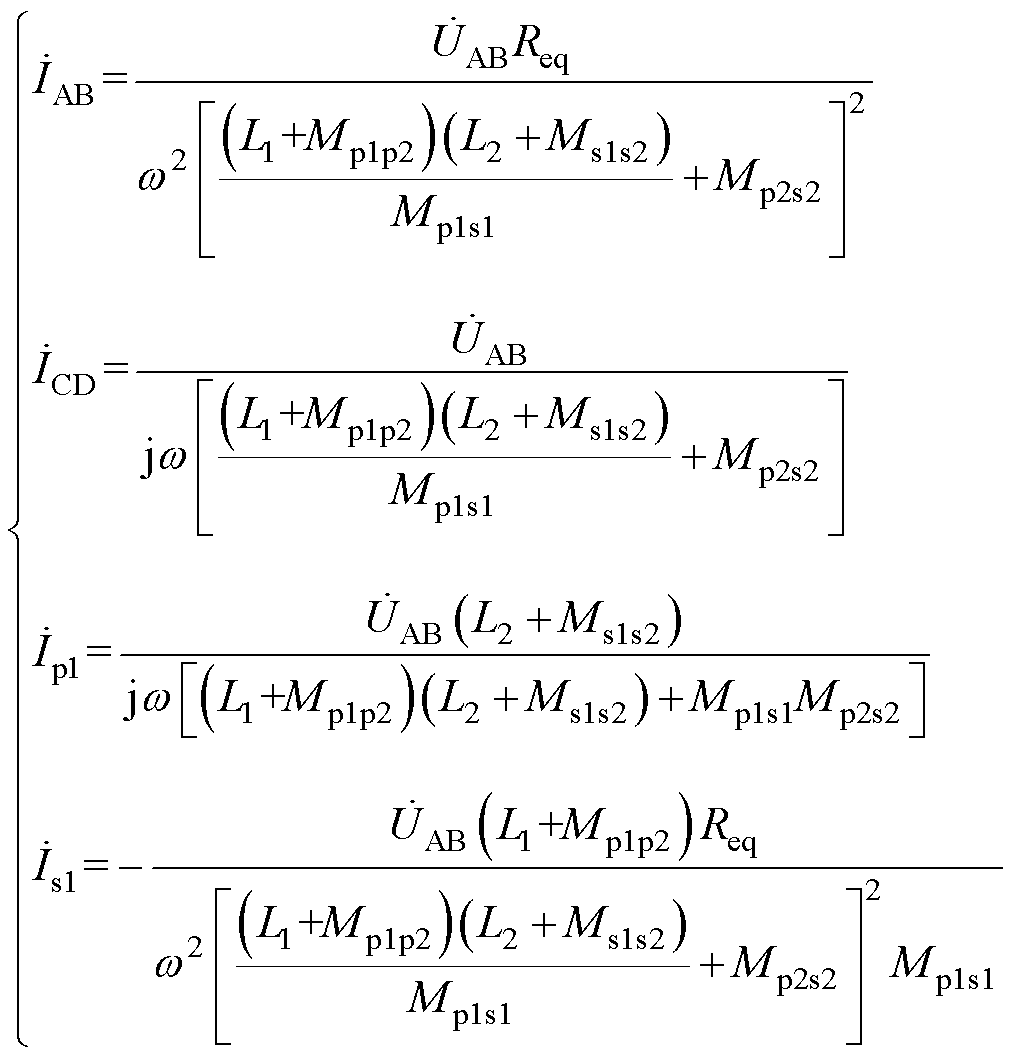 (10)
(10)
从式(10)可以看出,考虑同侧交叉耦合后,谐振补偿网络的输入电流和输出电流、发射线圈和接收线圈上的电流受同侧交叉耦合互感的影响。
第二种情况,考虑不同侧交叉耦合即Mp1s2和Mp2s1不为零,同理可得
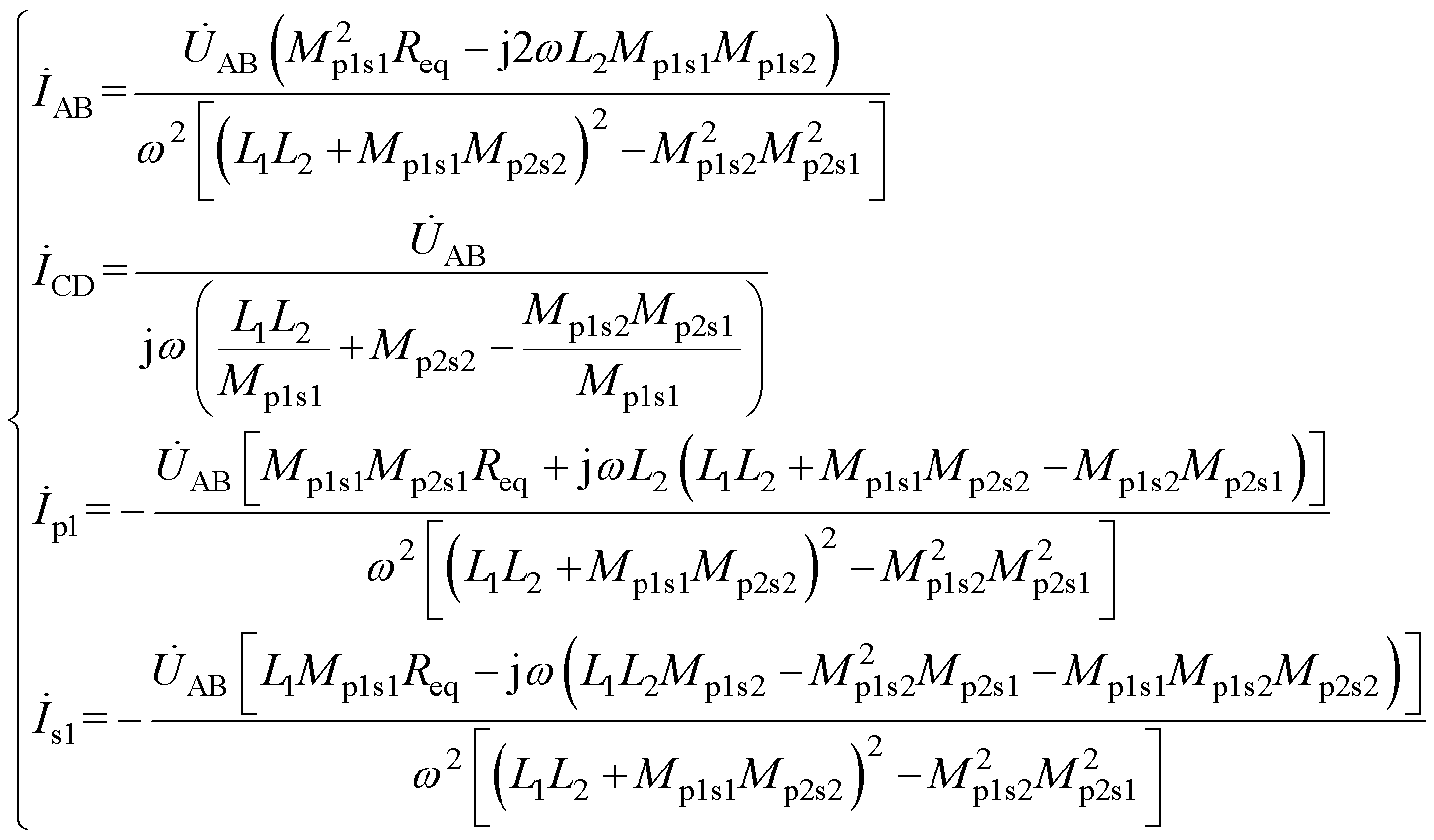 (11)
(11)
从式(11)可以看出,谐振补偿网络的输入电流和输出电流、发射线圈和接收线圈上的电流同样受同侧交叉耦合互感的影响。
考虑线圈内阻后,谐振网络输入电流和输出电流分别为
 (12)
(12)
其中
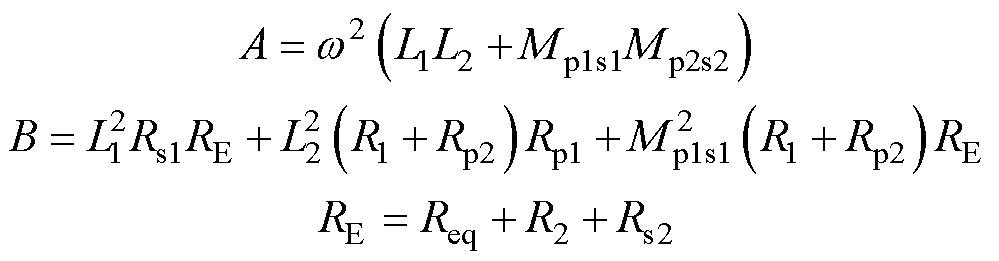
则谐振网络的传输效率的表达式为
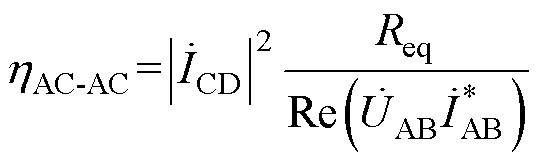 (13)
(13)
式中,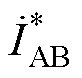 为
为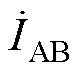 的共轭。
的共轭。
从2.1节分析可知,ISOS补偿网络的输入电流和输出电流受同侧交叉耦合和不同侧交叉耦合的影响,因此实现ISOS型无线电能传输系统的抗偏移恒流输出,磁耦合结构须具有如下性能:①磁结构要有两个发射线圈和两个接收线圈;②当接收线圈位置发生偏移时,线圈的自感维持稳定,主耦合互感Mp1s1和Mp2s2发生变化且Mp2s2和Mp1s1随位置偏移具有相同的变化趋势,同时同侧耦合和不同侧交叉耦合尽可能的小。DDQ具有这样的性质,但是DDQ线圈的横向偏移特性和纵向偏移特性不一 样[24]。为解决这个问题,本文采用QDQPs线圈结构发射侧和接收侧磁结构相同,线圈结构及其参数如图2所示,发射线圈和接收线圈结构的外围尺寸为31.8cm×31.8cm,Lp1和Ls1由4个方形的D线圈串联而成QDP(Quadruple-D Pad),匝数NQDP=7,Lp2和Ls2采用QP(Quadrature Pad),匝数NQP=6,线圈尺寸如图2a所示。同时为增强线圈之间的耦合,加入了铁氧体磁心(由6片尺寸为5.3cm×5.3cm的方形磁心拼接而成,材料为PC95,其初始磁导率为3 300,在25℃下,饱和磁感应强度为530mT,矫顽力9.5A/m),线圈之间的互感如图2b所示。
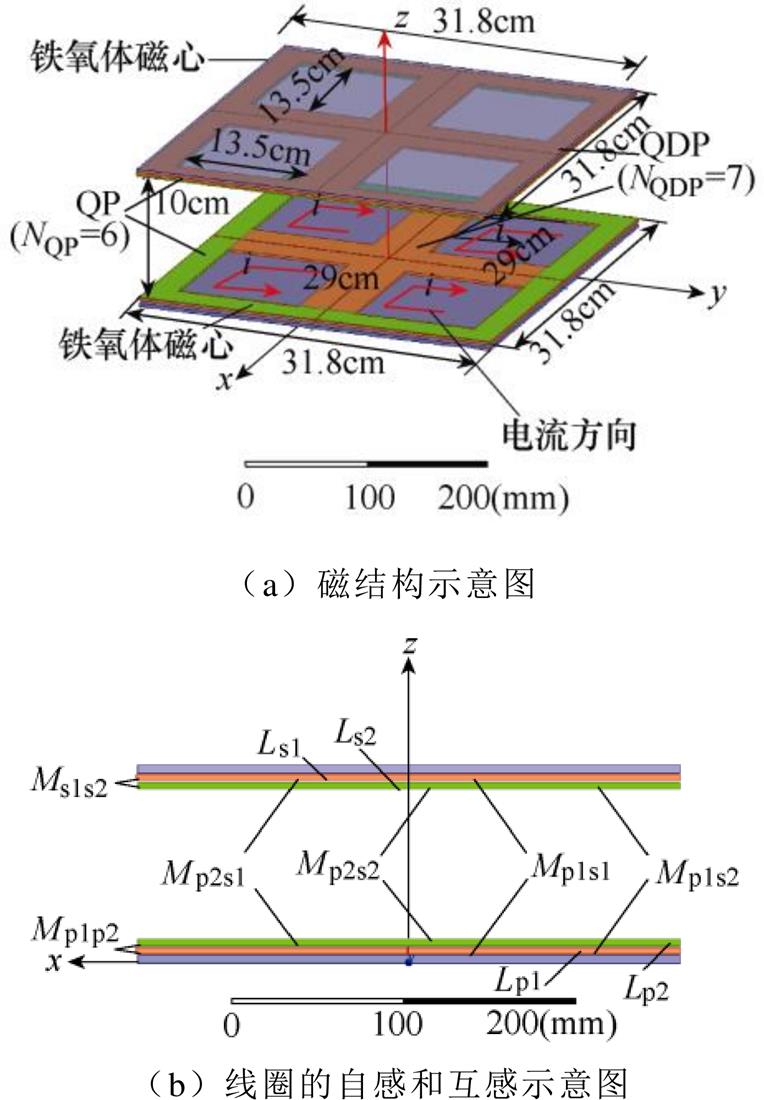
图2 QDQPs磁结构及其参数
Fig.2 Magnetic structure and parameters of QDQPs
为满足磁耦合结构的性能要求②,发射线圈Lp1即QDP的电流方向需如图2a所示,QDP中的任意两个相邻D线圈的电流方向相反,因此产生的磁场大小相等,方向相反,叠加后在QP产生的磁通为零,由于所设计磁结构的发射线圈和接收线圈结构相同,因此不仅能实现同侧QDP与QP的解耦,同时还能实现不同侧QDP与QP的解耦。(QDP线圈Lp1和Ls1由4个方形D线圈串联方式按图2中电流方向标注。)
由于QDQPs采用方形结构,其x方向和y方向的偏移性能相同,故后文将分析x方向和xy方向偏移特性。
QDQPs自感和互感随x方向偏移曲线测量曲线如图3所示。从图中可以看出:①随x方向偏移线圈的自感几乎不变;②主耦合Mp1s1和Mp2s2的数值较大,且随着x方向偏移的增大,Mp1s1和Mp2s2都减小且Mp1s1的数值(两个QDP线圈之间的互感)整体比Mp2s2大(两个QP线圈之间的互感),而交叉耦合(Mp1s2、Mp2s1、Mp1p2和Ms1s2)的数值很小,趋近于零可以忽略不计。
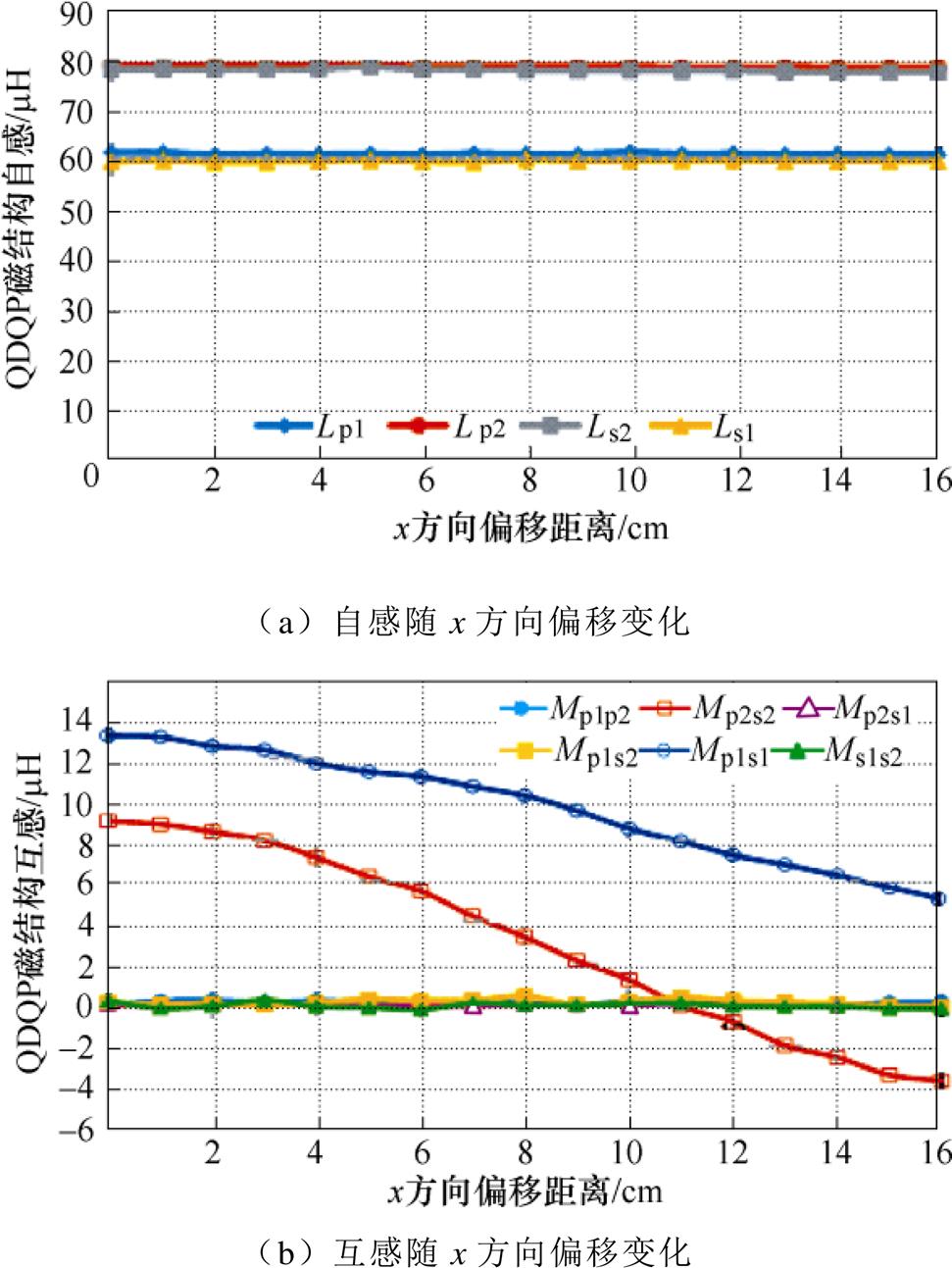
图3 x方向偏移自感和互感测量曲线
Fig.3 x-direction offset self-inductance and mutual inductance measurement curves
据图3b作出Mp2s2和Mp1s1的关系曲线如图4所示,从图中可以看出,Mp2s2和Mp1s1近似呈线性关系,将其关系表示成Mp2s2=aMp1s1+b,其中,a、b为拟合系数,a为无量纲数,b的单位为H,借助Matlab多项式拟合函数拟合可得到a=1.747 5,b=-13.789×10-6H,拟合曲线如图4中虚线所示(此组拟合参数只适合x方向偏移最大距离为12cm,当最大偏移距离改变时,拟合系数要相应改变)。
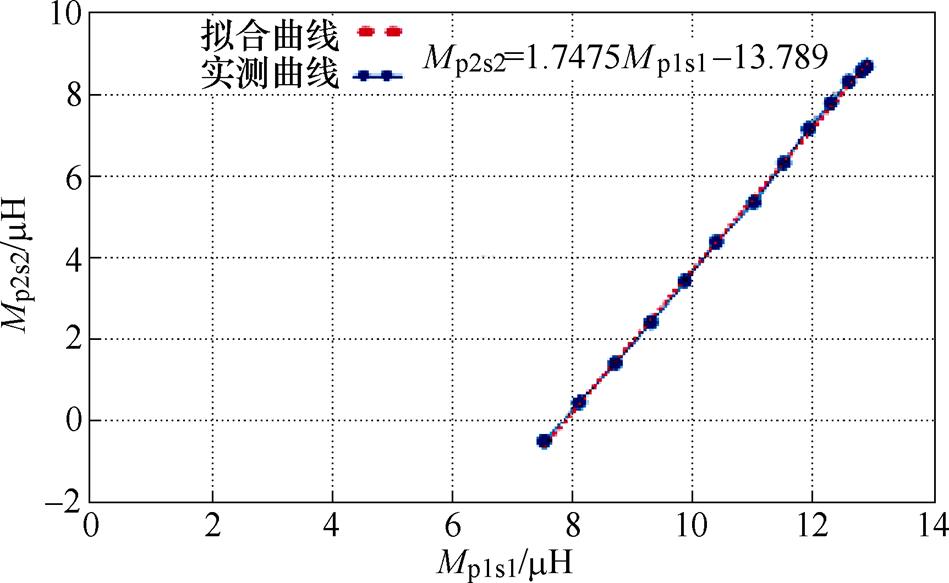
图4 Mp2s2和Mp1s1的关系曲线
Fig.4 The curve of Mp2s2 versus Mp1s1
QDQPs自感和互感随xy方向(对角线方向)偏移曲线测量结果如图5所示。从图中可以看出:①当接收线圈沿xy轴对角线方向偏移时,线圈的自感依然几乎不变;②主耦合Mp1s1和Mp2s2的数值比较大且随着对角线偏移的增大,Mp1s1和Mp2s2都减小。当沿对角线偏移距离小于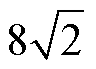 cm时,交叉耦合(Mp1s2、Mp2s1、Mp1p2和Ms1s2)的数值比较小可忽略;当沿对角线偏移距离大于
cm时,交叉耦合(Mp1s2、Mp2s1、Mp1p2和Ms1s2)的数值比较小可忽略;当沿对角线偏移距离大于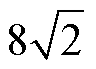 cm时,不同侧交叉耦合Mp1s2和Mp2s1逐渐增大,这个现象会影响补偿谐振补偿网络的输入电流和输出电流、发射线圈和接收线圈上的电流,因此此时Mp1s2和Mp2s1不可再忽略不计。
cm时,不同侧交叉耦合Mp1s2和Mp2s1逐渐增大,这个现象会影响补偿谐振补偿网络的输入电流和输出电流、发射线圈和接收线圈上的电流,因此此时Mp1s2和Mp2s1不可再忽略不计。
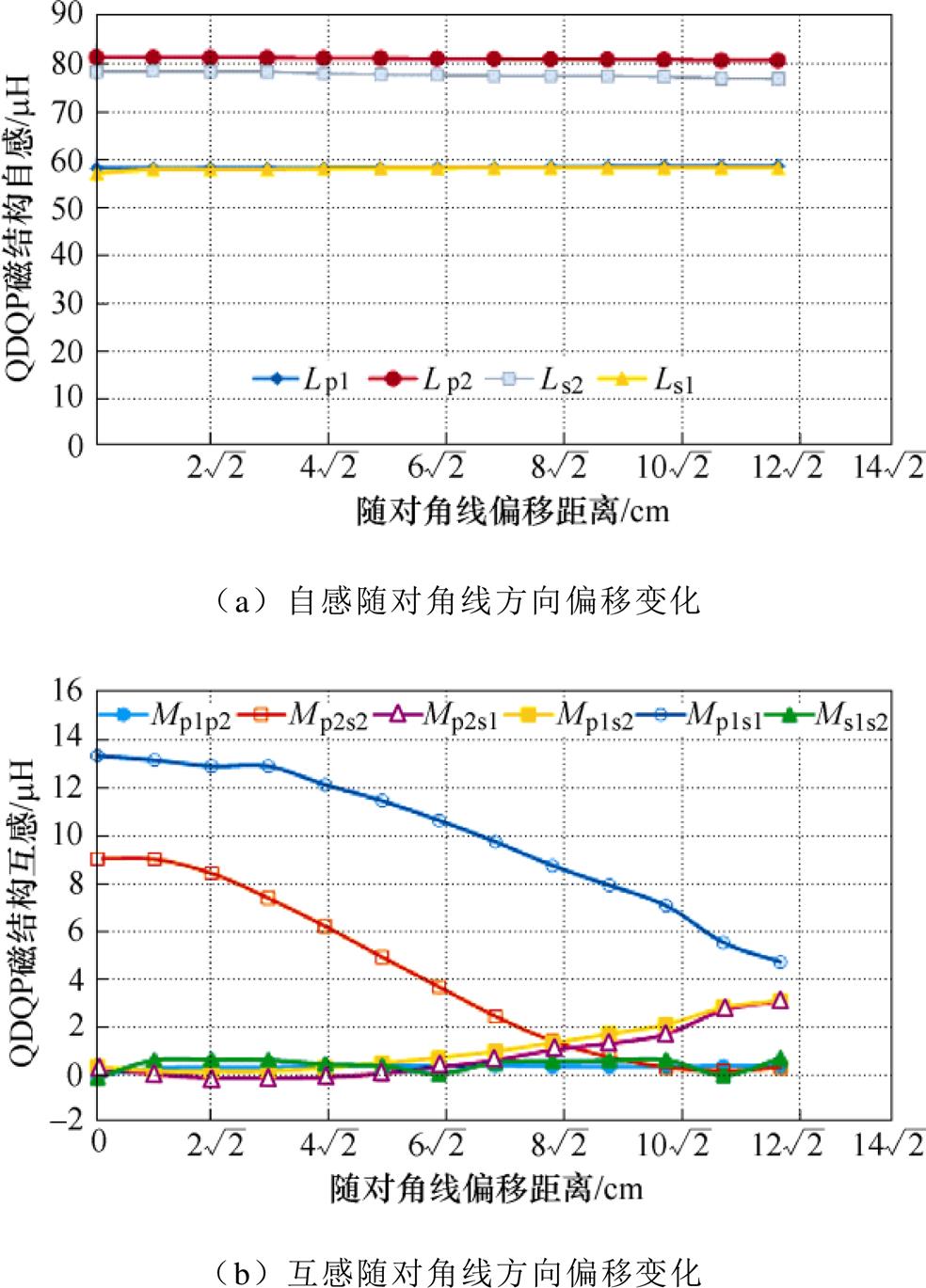
图5 沿对角线方向偏移自感和互感测量曲线
Fig.5 Diagonal direction offset self-inductance and mutual inductance measurement curves
从2.1节谐振网络输出电流ICD的表达式(7)可以看出,输出电流ICD的大小受补偿参数的影响,因此合理的参数配置对系统在一定偏移和负载变化下实现恒流输出至关重要。
先求L1和L2的值。假设发射线圈和接收线圈对准情况下,Lp1与Ls1之间的互感为Mp1s1N,由2.2节分析可以得到Mp2s2N=aMp1s1N+b,则此时电流输出增益表达式为
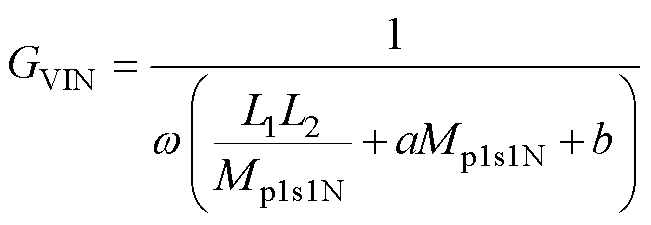 (14)
(14)
设系统允许的输出电流波动比为D(一般取值为5%),则电流输出增益允许的最大值和最小值可以表示为
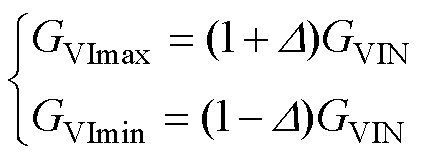 (15)
(15)
若Mp1s1max和Mp1s1min为给定偏移范围下Lp1与Ls1之间的最大互感和最小互感,由于Mp1s1在给定偏移范围内数值大于0,则GVI与Mp1s1之间的大小关系有四种,如图6所示,输出电流增益随Mp1s1先增大后减小,当Mp1s1=Mp1s1opt时,GVI达到最大值GVIopt。
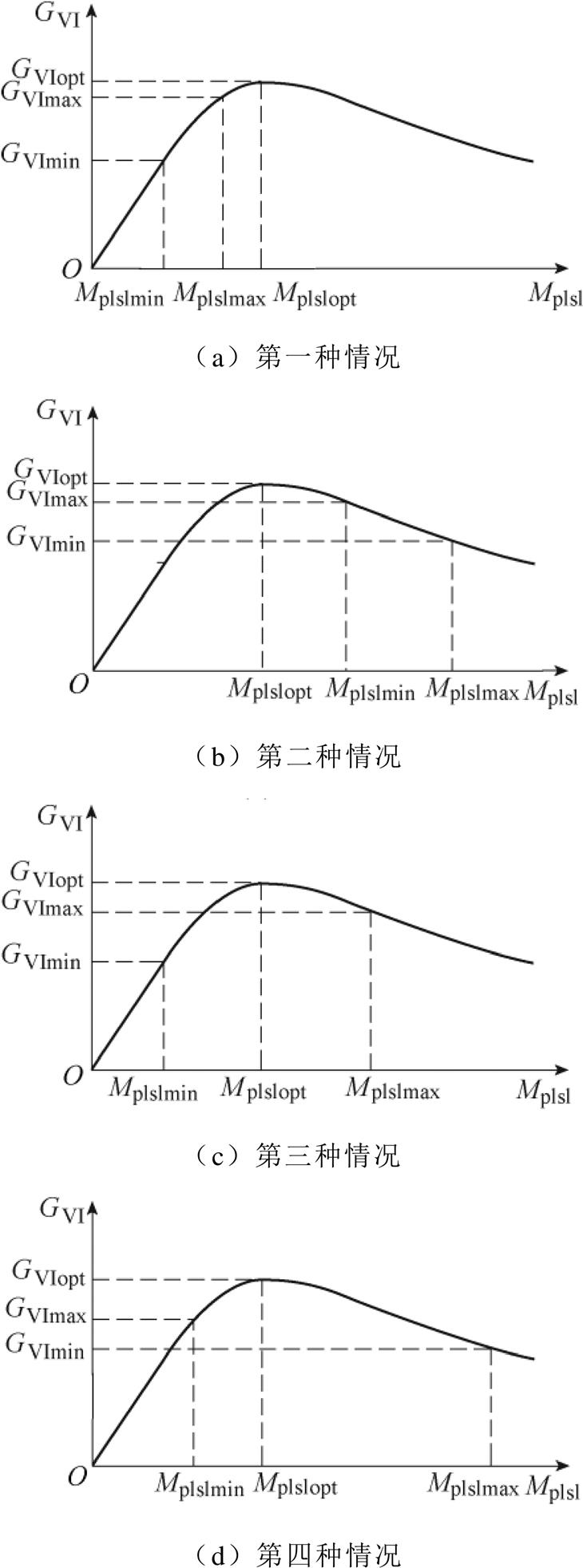
图6 GVI与Mp1s1的关系
Fig.6 Current gain GVI versus varying Mp1s1
由于在参数配置时,L2和L1的关系是任意的,假设L2=lL1,为求得图6中的GVIopt和Mp1s1opt,令
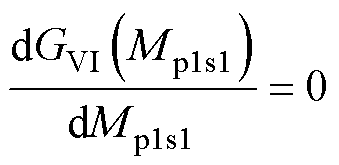 (16)
(16)
从式(16)可得
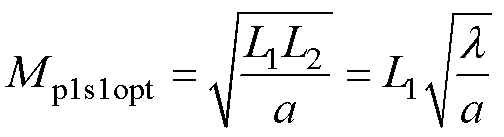 (17)
(17)
则
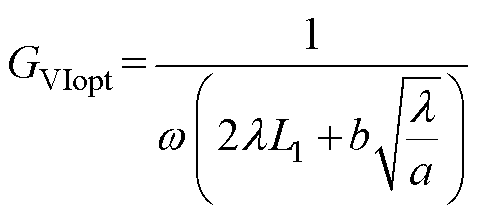 (18)
(18)
第一种情况,如图6a所示,在给定的偏移范围内,GVI(Mp1s1)在[Mp1s1min, Mp1s1max]范围内单调递增,此时系统参数需满足
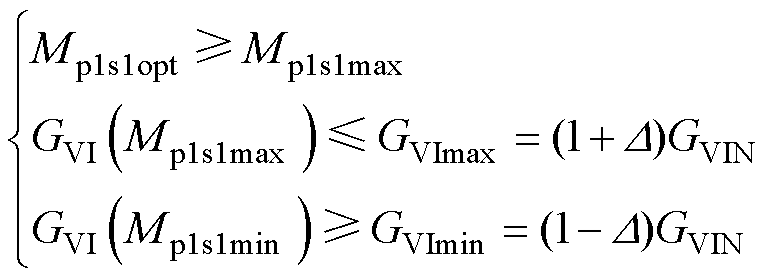 (19)
(19)
求解不等式组式(19)得到
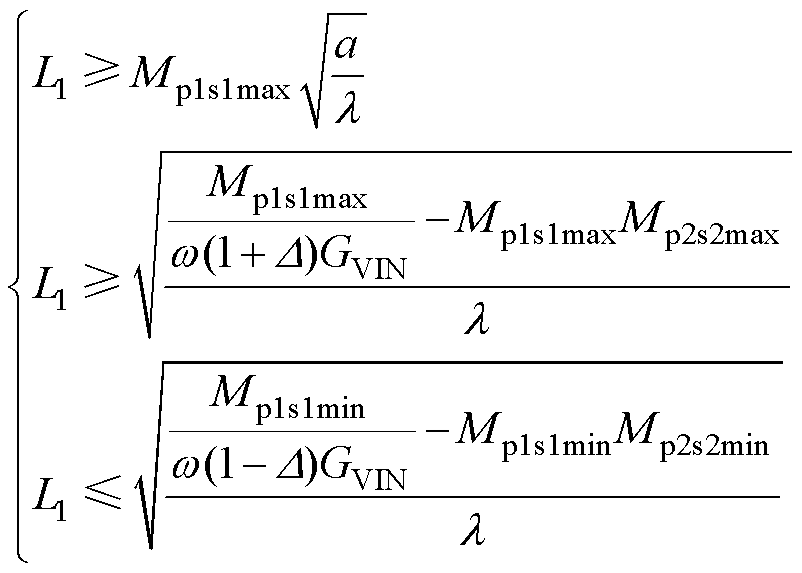 (20)
(20)
如果式(20)无解,则说明系统的偏移工作区不在GVI(Mp1s1)曲线的单调递增区域。
第二种情况,如图6b所示。在给定的偏移范围内,GVI(Mp1s1)在[Mp1s1min, Mp1s1max]范围内单调递减。此时需满足
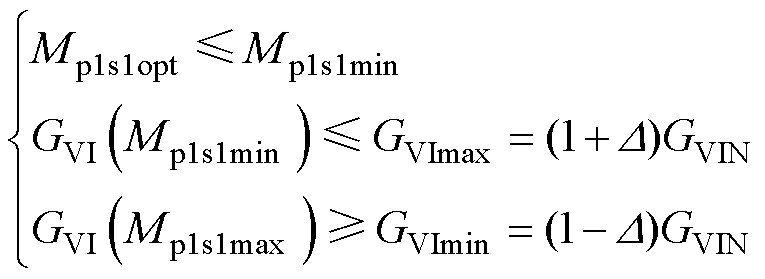 (21)
(21)
求解不等式组式(21)得到
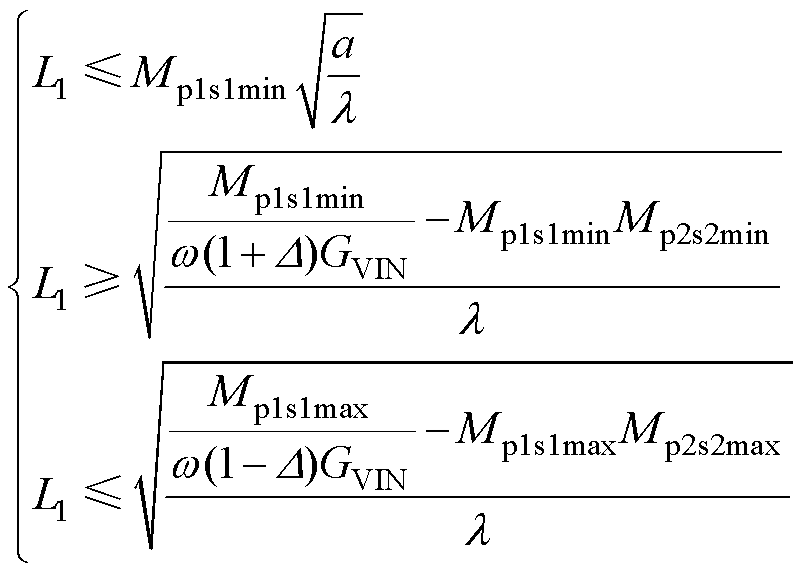 (22)
(22)
如果式(22)无解,则说明工作区不在GVI(Mp1s1)曲线的单调递减区域。
第三种情况,如图6c所示,在给定的偏移范围内,GVI(Mp1s1)在[Mp1s1min, Mp1s1max]区间内先增后减,但GVI(Mp1s1max)≥GVI(Mp1s1min),此时需同时满足
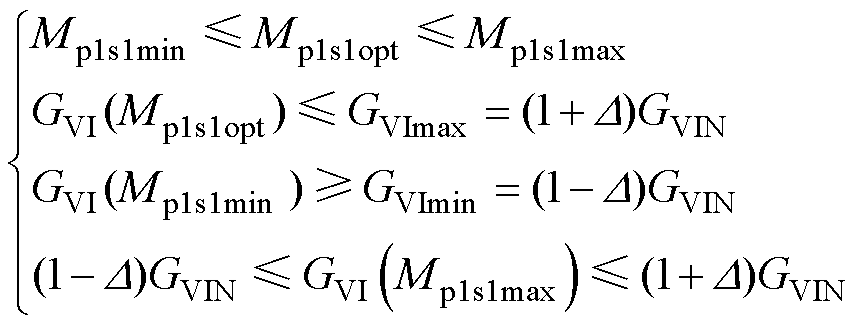 (23)
(23)
求解不等式组式(23)得到
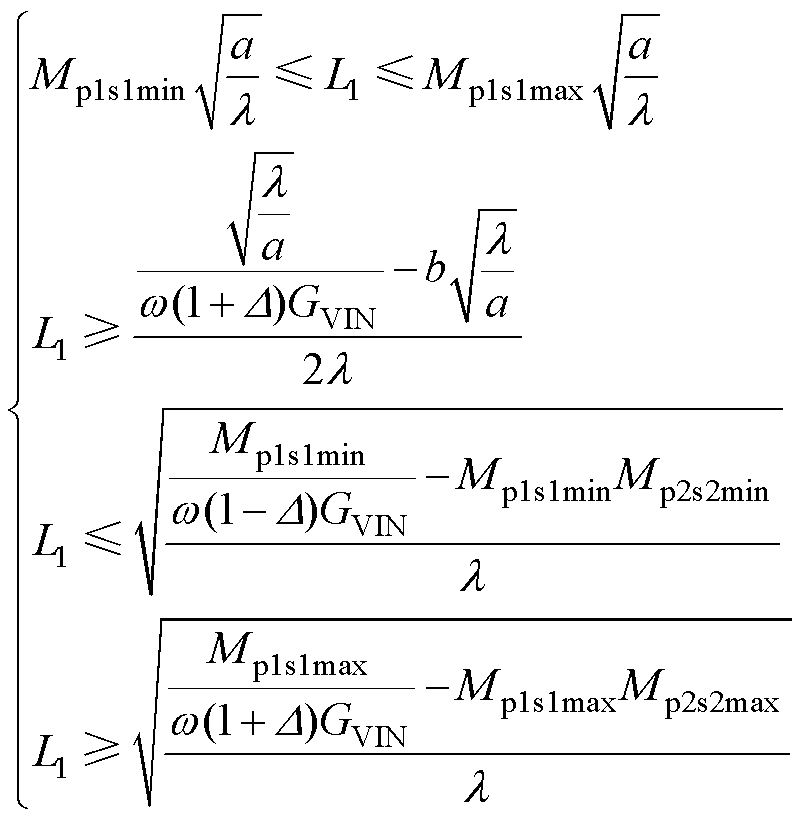 (24)
(24)
如果式(24)无解,则说明工作区不在此区域。
第四种情况,如图6d所示,在给定的偏移范围内,GVI(Mp1s1)在[Mp1s1min, Mp1s1max]范围内先增后减,但GVI(Mp1s1max)≤GVI(Mp1s1min)。此时需同时满足
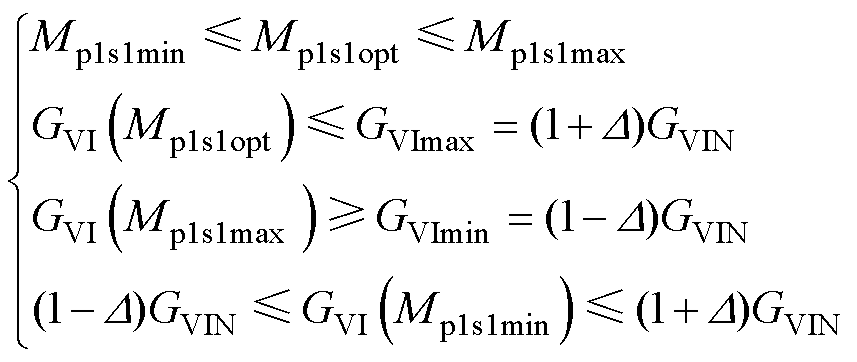 (25)
(25)
求解不等式组式(25)得到
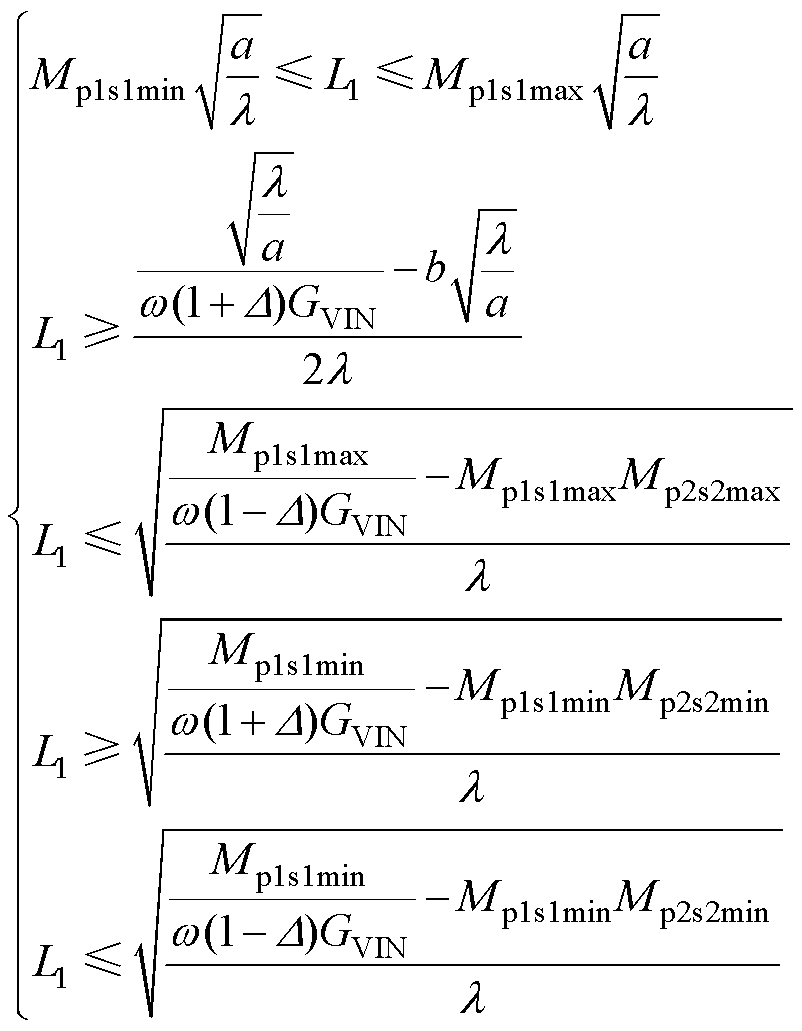 (26)
(26)
如果式(26)无解,则说明工作区不在此区域。只能重新调整偏移范围,重新计算。
综上,系统补偿参数的配置流程如图7所示。为简化分析,后文取l=1。
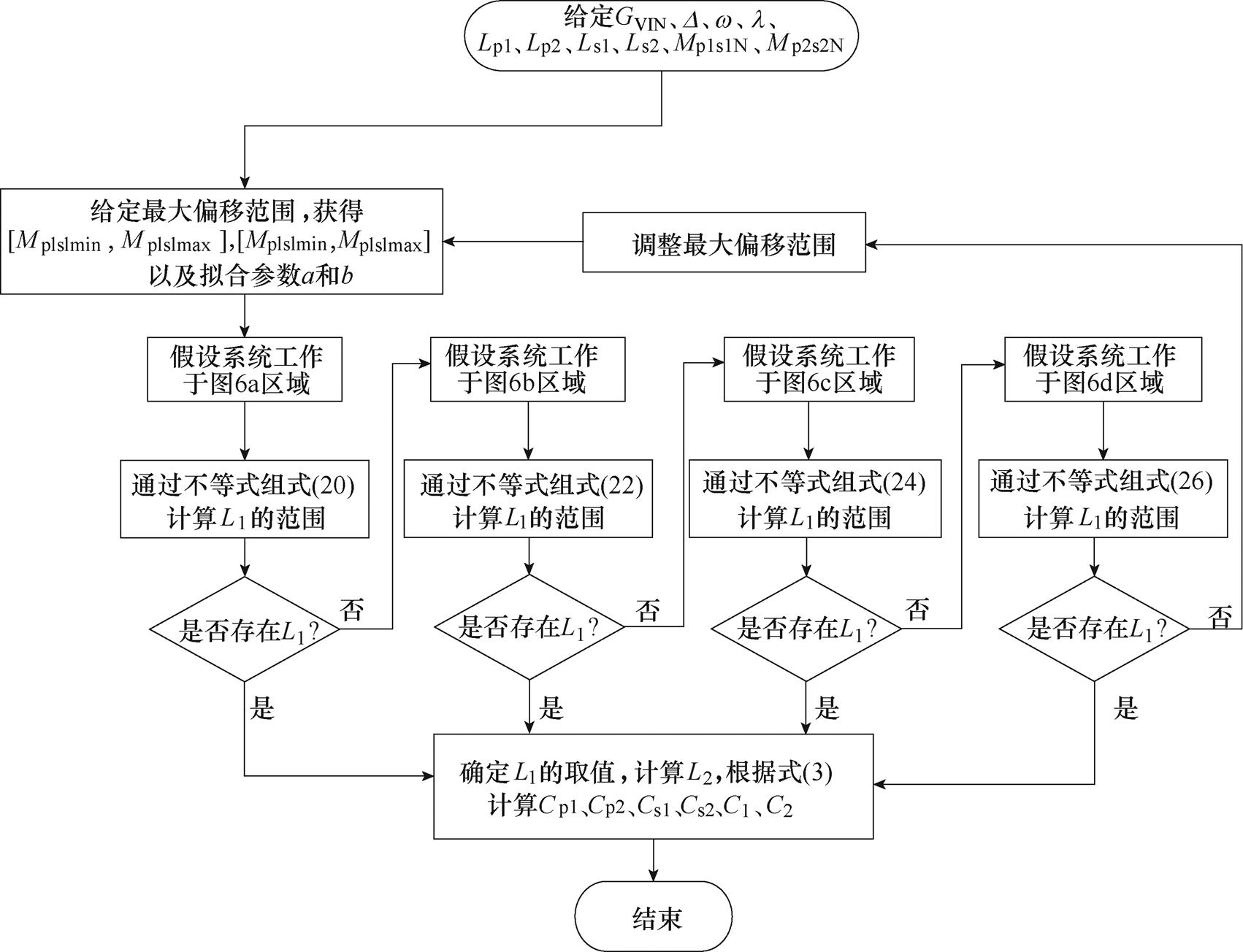
图7 系统补偿参数的配置流程
Fig.7 Flowchart for system compensation parameter configuration
从输入阻抗表达式(8),可看出输入阻抗呈纯阻性,前级高频逆变电路的输入阻抗可实现零相位。为使全桥高频逆变器的开关管实现零电压软开关(Zero Voltage Switching, ZVS)和系统的恒流输出,则输入阻抗需呈弱感性,同时输出电流大小不受影响或者影响很小。
图8显示了归一化输出电流与不同归一化参数和x方向偏移距离的关系,同时为简化系统的控制,系统需实现变负载下的恒流输出性能,因此图8同时给出了归一化输出电流与不同归一化参数和负载电阻Ro大小的关系。
从图8可以看出,当磁结构的接收线圈在x方发生偏移(偏移范围为0~12cm)和系统负载电阻Ro发生变化(变化范围为10~20W,变化量为100%)时,参数Cp1、Cs2、L1和L2变化量(变化量为±10%)输出电流的变化量均小于5%,故可认为Cp1、Cs2、L1和L2的变化对于输出电流的影响很小。因输入阻抗的相位与系统的补偿参数有关,因此可通过调节Cp1、Cs2、L1和L2的大小来调节输入阻抗的相位,以使得系统的输入阻抗呈弱感性。


图8 归一化输出电流与不同归一化参数随x方向偏移和负载电阻Ro变化的关系
Fig.8 Relationship between normalized output current and different normalized parameters x-direction misalignment and load resistance Ro
图9给出了不同归一化Cp1、Cs2、L1和L2条件下输入阻抗的相位随x方向偏移和负载电阻Ro的关系,从图中可看出,L1和L2的变化(变化量为±10%),输入阻抗相位的变化量很小(变化范围在-5°~5°),而Cp1和Cs2的变化(变化量为±10%)对输入阻抗相位的影响相对较大(变化范围在 -20°~40°),此外可看出,Cp1和Cs2减小时,系统的输入阻抗相位增大,故可通过减小Cp1、Cs2参数来使输入阻抗呈弱感性,实现高频逆变桥开关管的ZVS。
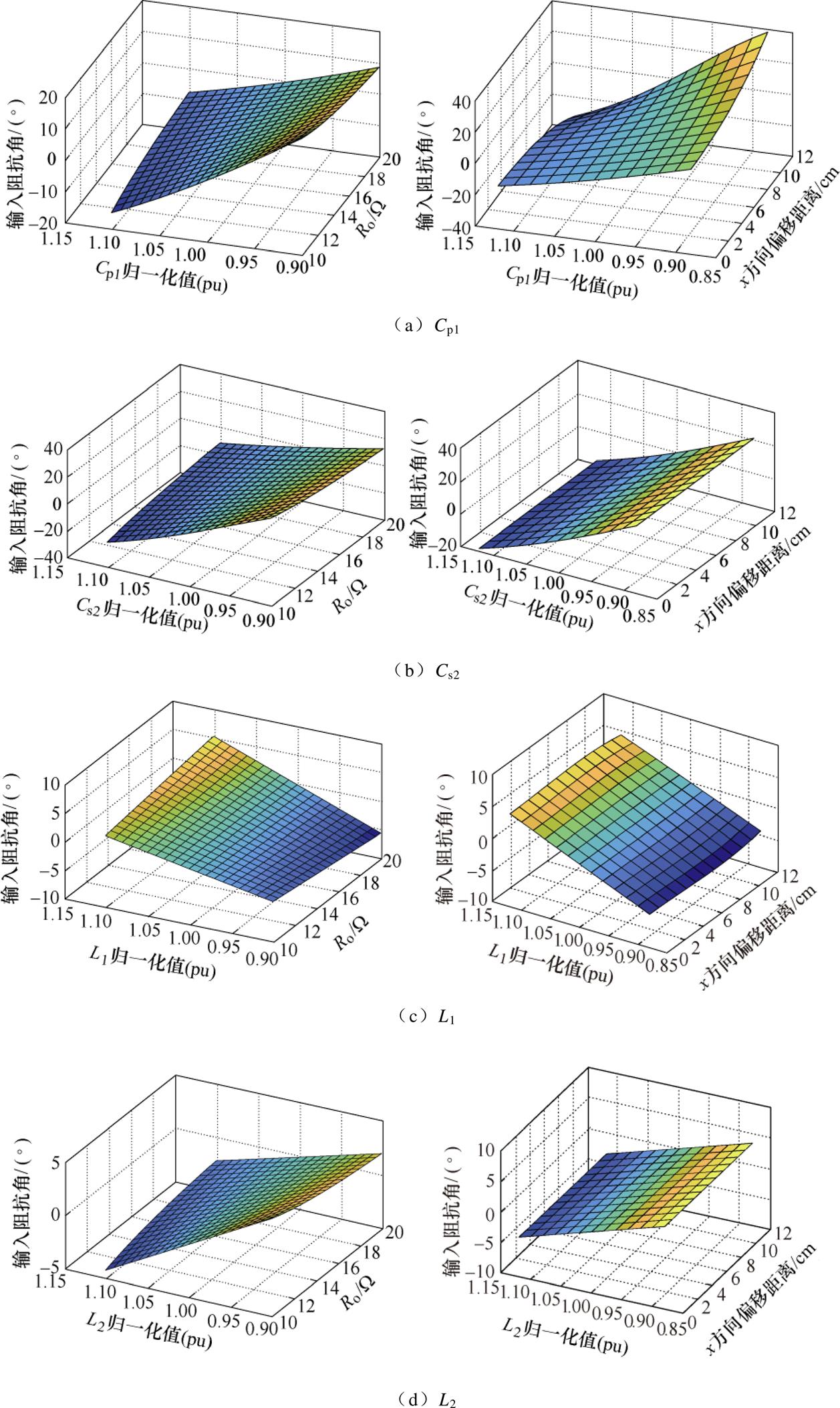
图9 输入阻抗角与不同归一化参数随x方向偏移和负载电阻Ro变化的关系
Fig.9 Phase angle of input impedance versus normalized parameters with x-direction misalignment and load resistance Ro
为验证前述理论分析的正确性,根据2.2节磁结构和2.3节参数配置方法设计并搭建了一个280W的基于QDQPs磁结构的ISOS型WPT系统平台,实验装置如图10所示。

图10 实验装置
Fig.10 Experimental prototype
图10a中①~⑩分别为直流供电电源、全桥逆变器、控制器、发射侧补偿电容、发射线圈、接收线圈、接收侧补偿电容、全桥高频整流滤波电路、电子负载和PX8000功率分析仪。系统指标和详细的参数见表2,控制芯片采用TMS320F28335型DSP,开关管选为IRFP4227,接收侧整流二极管选为MBR20200。图10b为QDQPs磁耦合结构,线圈采用0.1mm×150mm的利兹线,线圈间距离为10cm,其结构和几何参数具体见图2标注,负载电阻采用固纬PEL-2041A可编程直流电子负载。为验证系统的抗偏移性能,系统采用开环控制。
当传输距离为10cm,负载电阻Ro=17.5W,发射线圈和接收线圈对准时,逆变器的输出电压uAB和电流iAB的波形以及接收侧整流桥输入电压uCD与输入电流iCD波形如图11a所示,从图11a中可以看出,逆变电路输出电压和电流相位差为-0.122°,接近零相位差,逆变器的功率MOSFET可实现ZPA。当减小Ceq2后(实际取51.73nF),逆变器的输出电压uAB和电流iAB的波形以及接收侧整流桥输
表2 系统指标与关键参数
Tab.2 System indicators and key parameters

参 数数 值 PoN/W280 f/kHz85 UinDC/V64 a1.747 5 b/mH-13.789 Lp1/mH61.232 Lp2/mH82.616 Ls1/mH59.386 Ls2/mH77.742 Mp1s1N/mH12.873 C1/nF257.8 Cp1/nF73.6 Ceq1/nF50.8 IoN/A4 D(%)5 l1 Rp1/W0.208 Rp2/W0.293 Rs1/W0.204 Rs2/W0.286 Mp2s2N/mH8.640 C2/nF257.8 Cs1/nF76.57 Ceq2/nF54.66
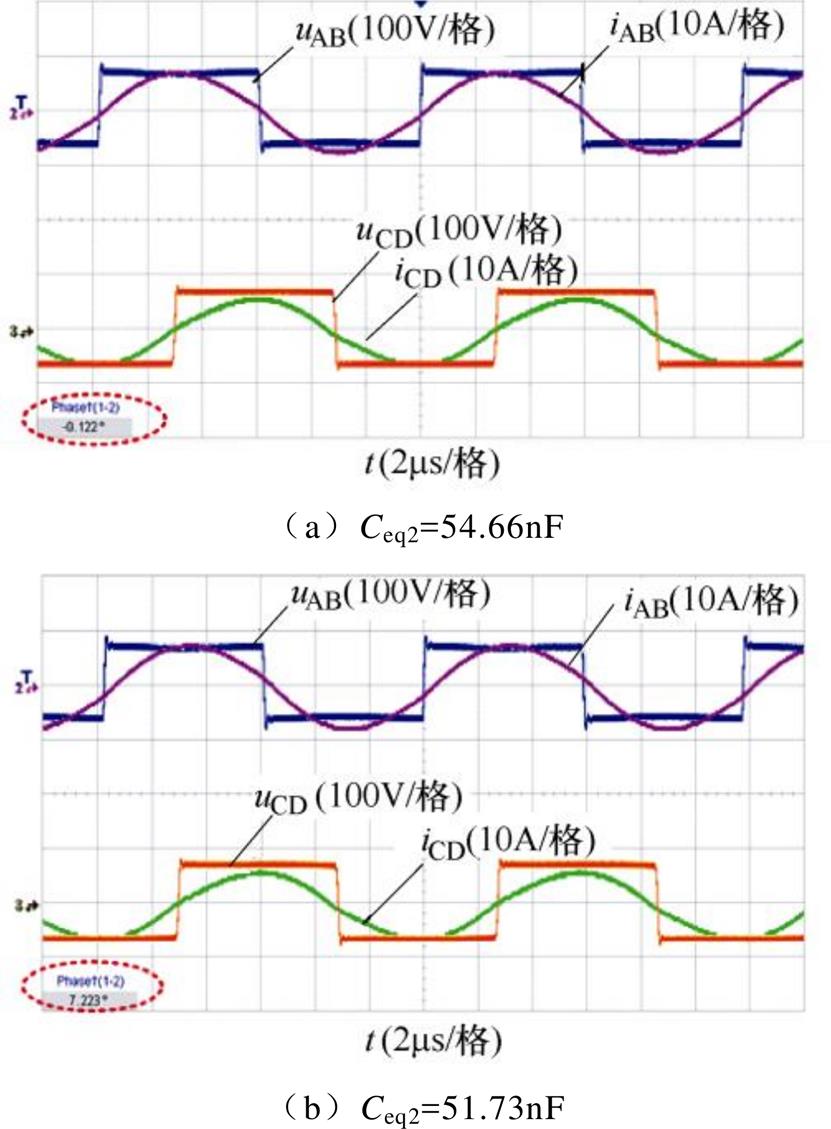
图11 uAB, iA, uCD和iCD的实验波形
Fig.11 Experimental waveforms of uAB, iA, uCD and iCD
入电压uCD与输入电流iCD波形如图11b所示,可看出,逆变电路的输出电压相位超前输出电流相位7.223°,逆变桥的功率MOSFET可以实现ZVS,与2.4节图9的理论分析结论相一致。
当发射线圈和接收线圈对准,负载电阻Ro为10W 和20W 时,逆变器的输出电压uAB和电流iAB的波形以及接收侧整流桥输入电压uCD与输入电流iCD波形如图12所示,从图中可以看出,当负载电阻改变后,功率MOSFET依然可实现ZVS。
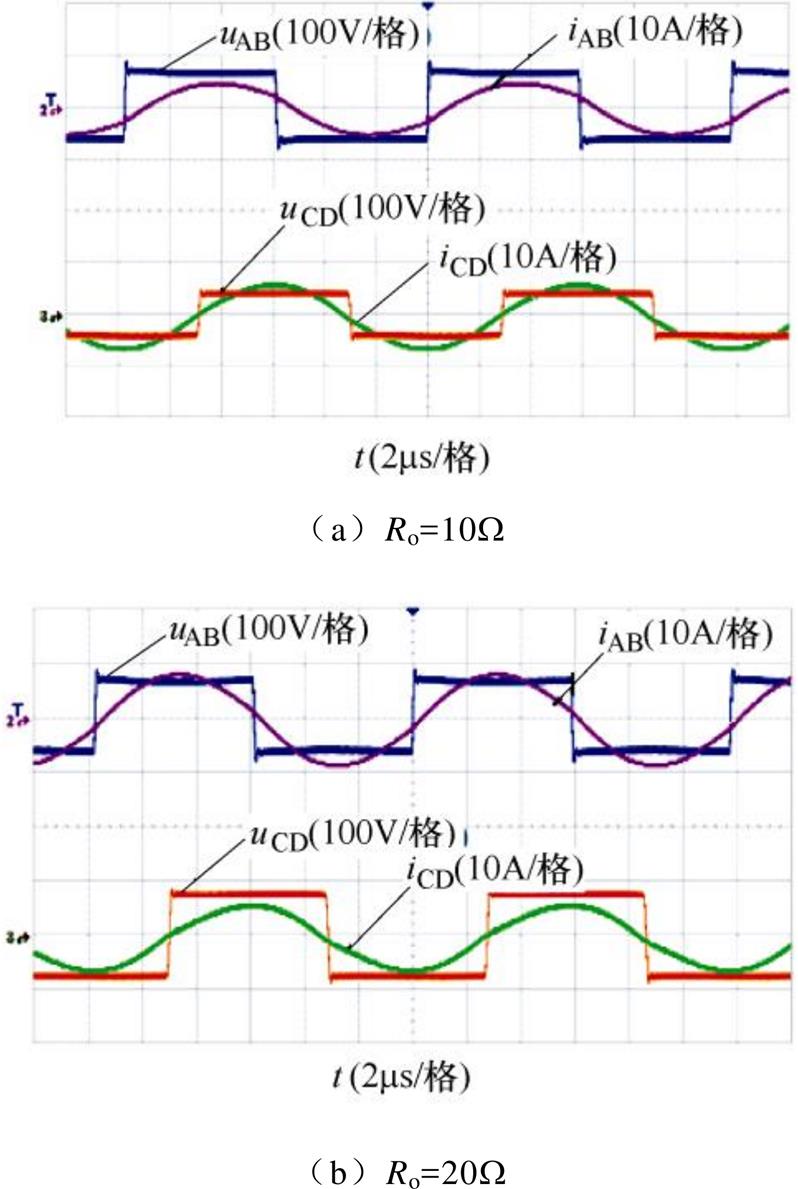
图12 Ro=10W 和20W 时,uAB, iAB, uCD和iCD实验波形
Fig12 Experimetal waveforms of uAB, iAB, uCD and iCD with Ro is 10W and 20W
当x方向偏移距离X为6cm和10cm时,逆变器的输出电压uAB和电流iAB的波形以及接收侧整流桥输入电压uCD与输入电流iAB波形如图13所示,可看出,系统同样可实现ZVS,使系统实现能量的高效传输。
当发射线圈和接收线圈对准时,传输距离为10cm,负载电阻Ro=17.5W,逆变器的输出电压uAB和发射线圈Lp1电流ip1的波形以及接收侧整流桥输入电压uCD与接收线圈Ls1电流is1波形如图14所示,从图中可看出,发射线圈Lp1电流ip1的相位超前接收线圈Ls1电流is1 90°,与2.1节的分析结论一致。
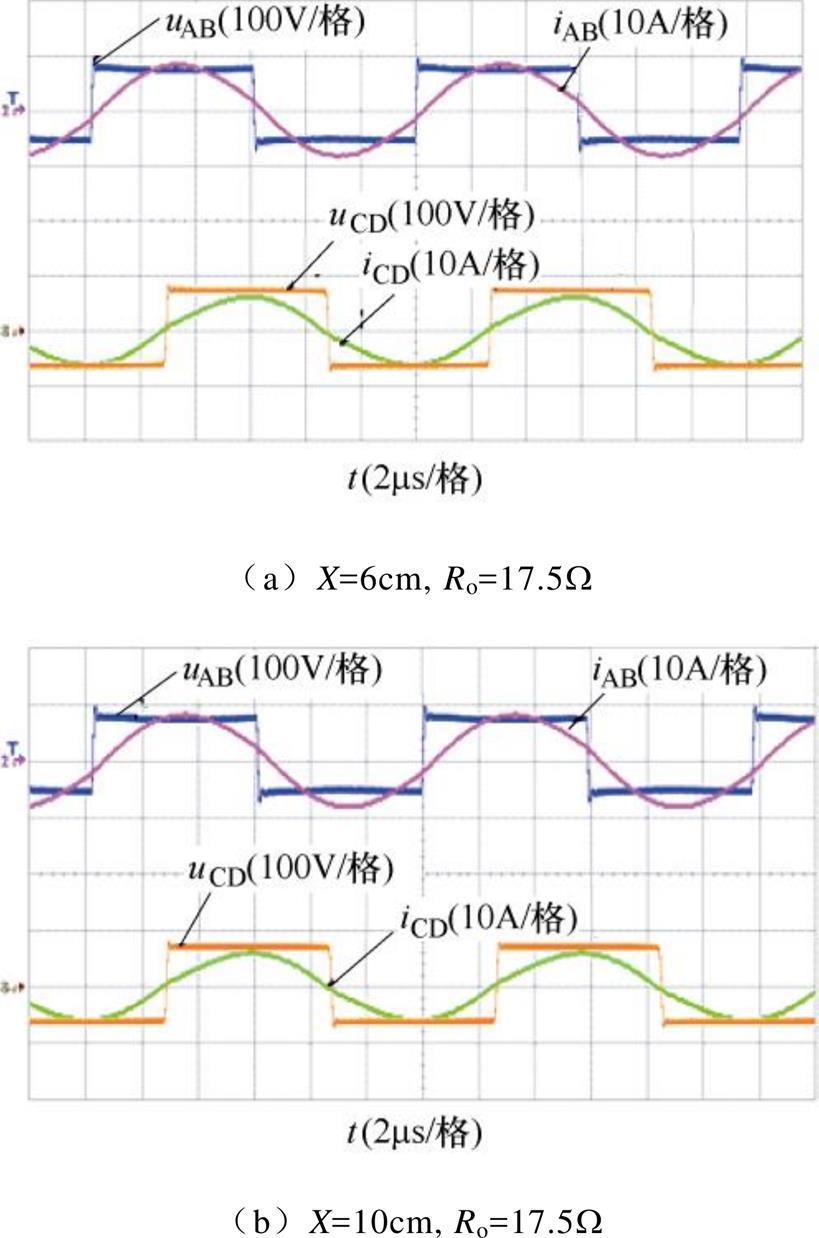
图13 X=6cm和10cm时,uAB, iAB, uCD和iCD实验波形
Fig13 Experimetal waveforms of uAB, iAB, uCD and iCD with X is 6cm and 10cm
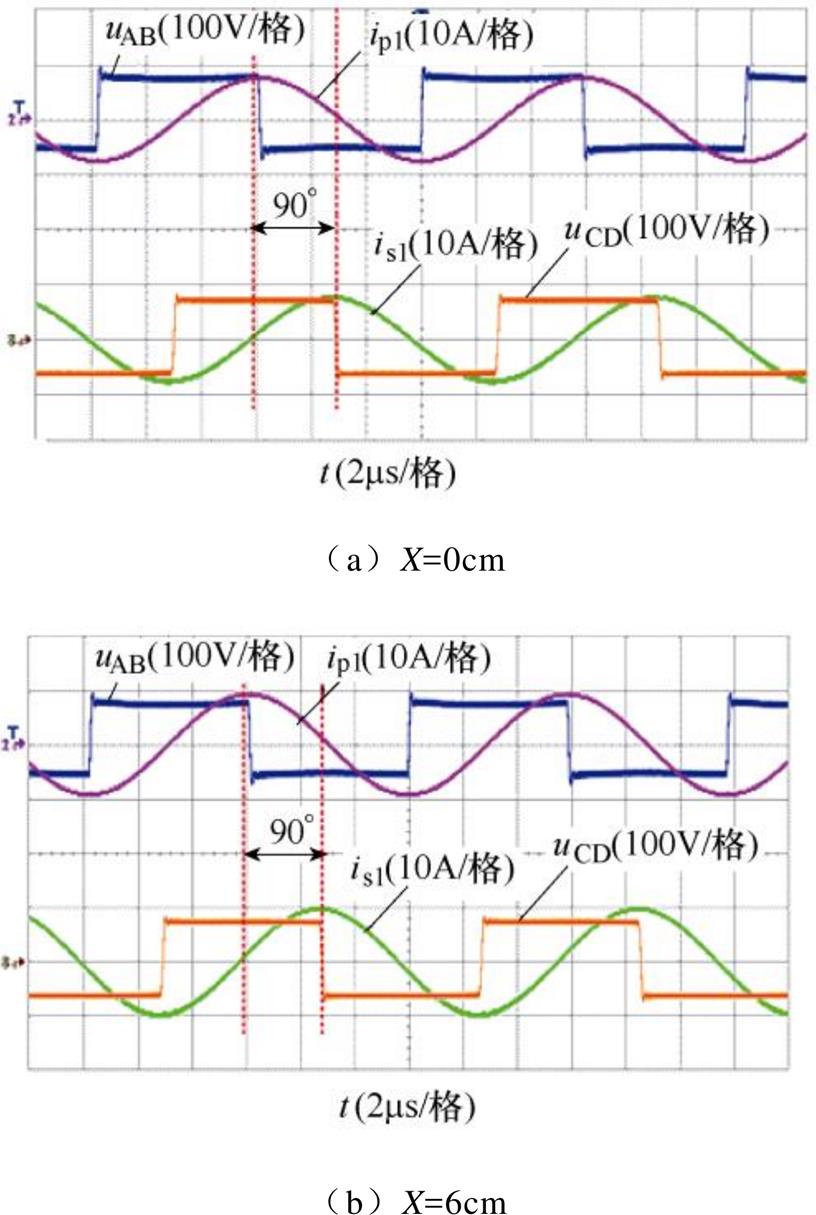
图14 uAB, ip1, uCD和is1的实验波形
Fig14 Experimetal waveforms of uAB, ip1, uCD and is1
图15给出了当接收线圈位置偏离工作区域时(即Mp1s1和Mp2s2接近于0),逆变器的输出电压uAB和电流iAB以及发射线圈Lp1电流ip1的波形。电流iAB的幅值减小是由于接收线圈偏移引起输入阻抗的幅值增大。从图中可看出,当接收线圈位置偏离工作区域过大时,ISOS型无线电能传输系统能够安全可靠的工作,但发射线圈上的电流依然会产生较大的磁场危害外界环境,因此在这种情况下,应该采取相应的控制策略使逆变器停止工作。

图15 接收线圈偏离后,uAB, iAB和ip1的实验波形
Fig15 Experimetal waveforms of uAB, iAB and ip1 when the pickup coils moves far away
当z方向传输距离10cm,负载电阻为17.5W 时,输出电流和传输效率随x方向偏移距离变化曲线如图16所示。从图16的输出电流Io曲线可看出,x方向偏移时,输出电流先增大后减小,当x方向偏移距离在0~10.8cm范围时,输出电流整体均在±5%波动范围内,这个偏移范围比理论设计的12cm小一点,主要是由线圈的内阻造成的;从效率曲线上可看出,当发射线圈和接收线圈对准时(偏移距离为0),效率可达86%且随着x方向的偏移效率逐渐减小。
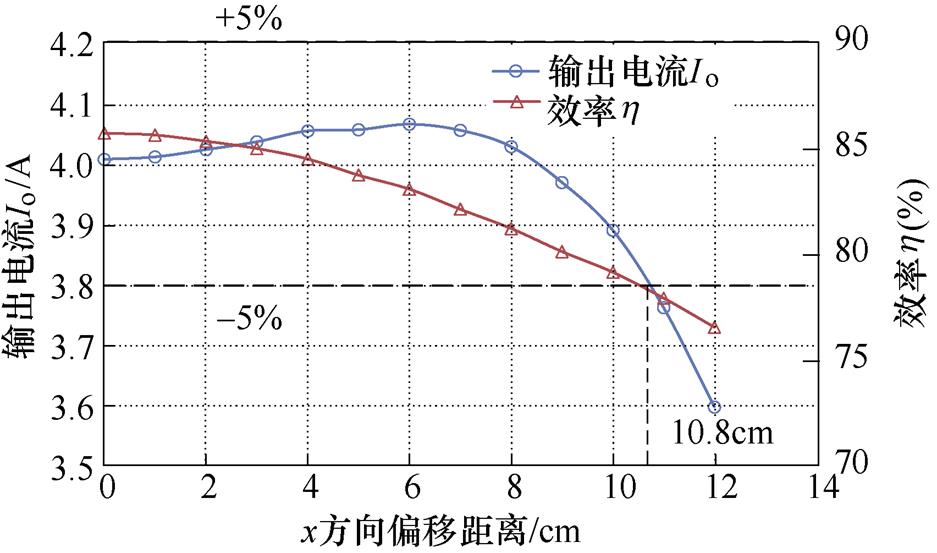
图16 系统输出电流和传输效率随x方向偏移变化
Fig.16 Ouput current and efficiency of the system with x-misalignment
当z方向传输距离10cm,负载电阻17.5W 时,x方向和y方向同时发生偏移,输出电流的情况如图17所示。从图17可以看出,在x和y方向同时偏移距离小于7cm的范围内,输出电流在±5%波动范围内。当超过这个距离后,由2.2节图5的理论分析可知,QDQPs磁耦合线圈结构不同侧交叉耦合互感即Mp1s2和Mp2s1的影响不可忽略,使得系统的输出电流值不断减小(此距离比理论分析的8cm小,是由于线圈内阻的影响)。
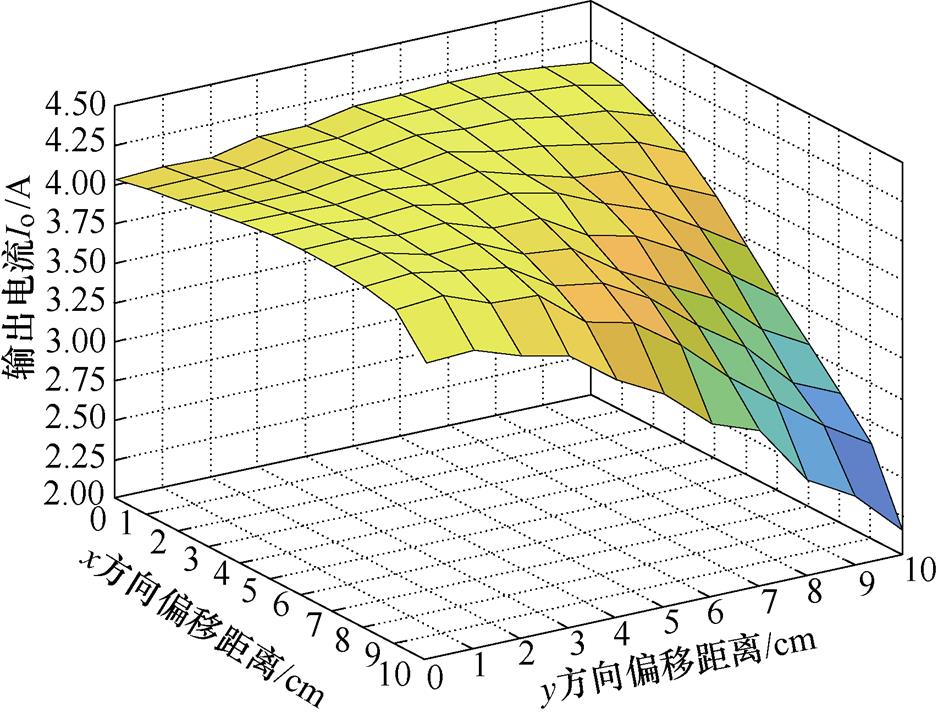
图17 x和y方向同时发生偏移的系统输出电流
Fig.17 Ouput current of the system with x-misalignment and y-misalignment
当负载电阻为17.5W,发射线圈和接收线圈对准时,输出电流和传输效率随z方向传输距离变化
曲线如图18所示。z方向传输距离从7.5cm变化到12.5cm时,系统的输出电流Io先增大后减小,效率均在82.5%以上且在7.7~12.2cm范围内变化时,输出电流在±5%范围内波动。
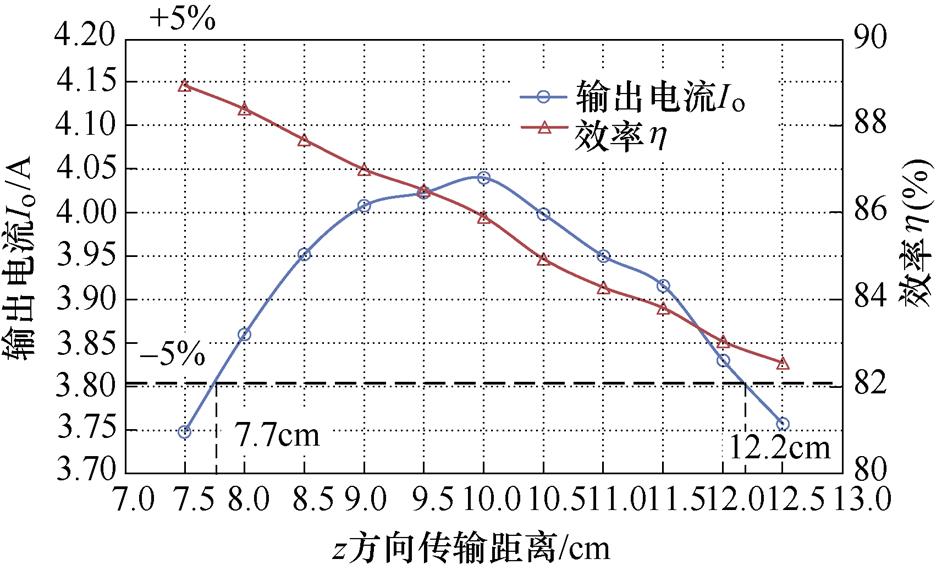
图18 系统输出电流和传输效率随z方向传输距离变化
Fig.18 Ouput current and efficiency of the system with z-axis transmission distance
当负载电阻从10W 变化到20W 时,输出电流和传输效率变化曲线如图19所示。当负载大小变化100%时,输出电流从4.15A变化到3.96A,负载电流波动比均小于±5%,因此系统可实现负载无关性的输出特性。

图19 系统输出电流和传输效率随负载电阻Ro变化
Fig.19 Ouput current and efficiency of the system with load resistance Ro
综合上述的实验结果表明,所设计和研究的基于QDQPs线圈结构的ISOS型恒流输出无线电能传输系统具有良好的抗偏移特性,同时系统可实现输出电流的负载无关性,且避免IPOP型LCC-LCC和S-S组合补偿网络无线电能传输系统前级高频逆变器存在当接收线圈偏离工作区域时,引起的开关电流过电流的现象。
本文研究了基于组合型补偿网络的抗偏移恒流输出型WPT系统,提出了一种通用的系统参数配置方法。
1)两个随位置偏移具有互补输出特性的IPOP组合补偿网络结构和ISOS组合补偿网络结构,通过合理的磁耦合结构设计使得互感M1与互感M2随位置偏移的变化趋势相一致,则有机会实现整个网络输出电流波动小,从而可提升磁耦合系统的抗偏移特性。
2)提出基于LCC-LCC和S-S补偿网络的ISOS型无线电能传输系统补偿网络结构,及在给定偏移范围和允许输出电流波动比下的系统参数配置的一般性通用方法。
3)选择QDQPs型磁耦合结构,其中,LCC-LCC补偿网络采用QDP线圈,S-S采用QP线圈,解决DDQ线圈在线圈平面内只有一个方向(x方向或y方向)具有良好的抗偏移性能。
4)实验结果验证了理论分析的正确性。所设计的基于ISOS型的LCC-LCC和S-S补偿网络WPT系统在负载电阻在10~20W 范围内变化时,x方向(或y方向)偏移范围在0~10.8cm内或x和y方向同时偏移7cm范围内,可实现良好的抗偏移恒流输出效果,波动比在±5%范围之内,同时系统可克服IPOP型当接收线圈偏移范围过大时,系统中流过逆变器开关管电流和发射线圈急剧增大的缺陷。
参考文献
[1] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述(上篇)[J]. 电工技术学报, 2020, 35(6): 1153-1165.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: partⅠ[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1153-1165.
[2] 吴理豪, 张波. 电动汽车静态无线充电技术研究综述(下篇)[J]. 电工技术学报, 2020, 35(8): 1662- 1678.
Wu Lihao, Zhang Bo. Overview of static wireless charging technology for electric vehicles: partⅡ[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1662-1678.
[3] 谢文燕, 陈为. 全方向无线电能传输技术研究进展[J]. 电力系统自动化, 2020, 44(4): 202-221.
Xie Wenyan, Chen Wei. Research progress of omni- directional wireless power transfer technology[J]. Automation of Electric Power Systems, 2020, 44(4): 202-221.
[4] 吴旭升, 孙盼, 杨深钦, 等. 水下无线电能传输技术及应用研究综述[J]. 电工技术学报, 2019, 34(8): 1559-1568.
Wu Xusheng, Sun Pan, Yang Shenqin, et al. Review on underwater wireless power transfer technology and its application[J]. Transactions of China Electro- technical Society, 2019, 34(8): 1559-1568.
[5] 侯佳, 陈乾宏, 任小永, 等. S/SP非接触谐振变换器的时域特性分析[J]. 中国电机工程学报, 2015, 35(8): 1983-1992.
Hou Jia, Chen Qianhong, Ren Xiaoyong, et al. Time-domain analysis of S/SP compensated contact- less resonant converters[J]. Proceedings of the CSEE, 2015, 35(8): 1983-1992.
[6] 范兴明, 高琳琳, 莫小勇, 等.无线电能传输技术的研究现状与应用综述[J]. 电工技术学报, 2019, 34(7): 1353-1380.
Fan Xingming, Gao Linlin, Mo Xiaoyong, et al. Overview of research status and application of wire- less power transmission technology[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1353- 1380.
[7] Germano P, Perriard Y. Battery charger for electric vehicles based on a wireless power transmission[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(1): 66-71.
[8] 薛明, 杨庆新, 王嘉浩, 等. 动态无线供电系统收发端耦合角度对功率影响机理分析[J]. 电工技术学报, 2020, 35(20): 4232-4240.
Xue Ming, Yang Qingxin, Wang Jiahao, et al. Effect mechanism analysis of coupling angle between transmitter and receiver on power in dynamic wireless power supply system[J]. Transactions of China Elec- trotechnical Society, 2020, 35(20): 4232-4240.
[9] 宋凯, 李振杰, 杜志江, 等. 变负载无线充电系统的恒流充电技术[J]. 电工技术学报, 2017, 32(13): 130-136.
Song Kai, Li Zhenjie, Du Zhijiang, et al. Constant current charging technology for variable load wireless charging system[J]. Transactions of China Electro- technical Society, 2017, 32(13): 130-136.
[10] 高立克, 肖静, 姚知洋, 等. 电动汽车无线充电系统的输出功率动态解耦控制[J]. 电力系统自动化, 2019, 43(17): 153-162.
Gao Like, Xiao Jing, Yao Zhiyang, et al. Dynamic decoupling control of output power in wireless charging system for electric vehicle[J]. Automation of Electric Power Systems, 2019, 43(17): 153-162.
[11] Ahmad A, Alam M S, Mohamed A A S. Design and interoperability analysis of quadruple pad structure for electric vehicle wireless charging application[J]. IEEE Transactions on Transportation Electrification, 2019, 5(4): 934-945.
[12] Zhang Jixin, Qu Dawei, Wang Zhu, et al. Analytical magnetic field analysis of misalignment tolerance characteristic of double D pad and bipolar pad[C]// 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC), Beijing, China, 2019: 1573-1578.
[13] 张献, 王杰, 杨庆新, 等. 电动汽车动态无线供电系统电能耦合机构与切换控制研究[J]. 电工技术学报, 2019, 34(15): 3093-3101.
Zhang Xian, Wang Jie, Yang Qingxin, et al. The power coupling mechanism and switching control for dynamic wireless power supply system of electric vehicle[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3093-3101.
[14] 谢文燕, 林苏斌. 无线电能传输磁耦合结构分析与优化[J]. 电气技术, 2014, 15(9): 27-31.
Xie Wenyan, Lin Subin. Analysis and optimization of wireless power transmission magnetic coupling structures[J]. Electrical Engineering, 2014, 15(9): 27-31.
[15] Kim S, Covic G A, Boys J T. Tripolar pad for inductive power transfer systems for EV charging[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5045-5057.
[16] Villa J L, Sallan J, Sanz Osorio J F, et al. Misalignment tolerant compensation topology for ICPT systems[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 945-951.
[17] Feng Hao, Cai Tao, Duan Shanxu, et al. An LCC compensated resonant converter optimized for robust reaction to large coupling variation in dynamic wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6591-6601.
[18] 国玉刚, 崔纳新. LCC-S型无线电能传输系统优化配置及特性研究[J]. 电工技术学报, 2019, 34(18): 3723-3731.
Guo Yugang, Cui Naxin. Research on optimal configuration and characteristics based on LCC-S type wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3723-3731.
[19] Lu Fei, Zhang Hua, Hofmann H, et al. A dual-coupled LCC-compensated IPT system with a compact mag- netic coupler[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(7): 6391-6402.
[20] 任洁, 刘野然, 岳鹏飞, 等. 基于参数优化法的输出抗偏移感应电能传输系统研究[J]. 中国电机工程学报, 2019, 39(5): 1452-1461.
Ren Jie, Liu Yeran, Yue Pengfei, et al. Study on anti-misalignment inductive power transfer system based on parameter optimized method[J]. Proceedings of the CSEE, 2019, 39(5): 1452-1461.
[21] 寇志豪, 杨斌, 陈阳, 等. 二维平面具有抗偏移恒压输出特性的感应式无线充电系统研究[J]. 中国电机工程学报, 2018, 38(15): 4576-4584.
Kou Zhihao, Yang Bin, Chen Yang, et al. Study on IPT charging systems with the characteristics of misalignment tolerant in 2-dimension plane and constant voltage output[J]. Proceedings of the CSEE, 2018, 38(15): 4576-4584.
[22] Chen Yang, Yang Bin, Kou Zhihao, et al. Hybrid and reconfigurable IPT systems with high-misalignment tolerance for constant-current and constant-voltage battery charging[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8259-8269.
[23] Zhao Lei, Thrimawithana D J, Madawala U K. Hybrid bidirectional wireless EV charging system tolerant to pad misalignment[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7079-7086.
[24] 李砚玲, 杜浩, 何正友. 基于双D形正交混合拓扑的感应电能传输系统恒流输出研究[J]. 中国电机工程学报, 2020, 40(5): 942-951.
Li Yanling, Du Hao, He Zhengyou. Research on constant current output of inductive power transfer system with double-D quadrature hybrid topology[J]. Proceedings of the CSEE, 2020, 40(5): 942-951.
[25] Yao Yousu, Wang Yijie, Liu Xiaosheng, et al. A novel parameter tuning method for double-sided LCL compensated WPT system with better comprehensive performance[J] IEEE Transactions on Power Elec- tronics, 2018, 33(10): 8525-8536.
[26] Qu Xiaohui, Han Hongdou, Wong S, et al. Hybrid IPT topologies with constant current or constant voltage output for battery charging applications[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6329-6337.
Research on Anti-Offset Constant-Current Output Wireless Power Transfer System Based on Combined Compensation Network
Abstract For a wireless power transfer (WPT) system, the misalignment of coils can easily cause low transfer efficiency, unstable output current and over-current of transmitting coil. Therefore, this paper proposes a constant current output WPT system and its parameter design method with high anti-offset performance. In the proposed system, the LCC-LCC and S-S compensation network are connected in input series and output series, and the magnetic coupling structure of quadruple-D quadrature pads is adopted. Then, through reasonable parameter configuration, not only the load independent constant current output can be realized, but also anti-x direction, y-direction, z-direction and anti-xy direction can be realized. Moreover, the over-current of the transmitting coil is avoided. By analyzing the transfer property of the proposed system, it is proved theoretically that the system has good anti-offset performance. Finally, an experimental platform with 280W is built to verify the correctness and feasibility of the theoretical analysis.
keywords:Wireless power transfer, anti-offset, constant-current output, combined compensation network, parameter configuration
DOI: 10.19595/j.cnki.1000-6753.tces.210133
中图分类号:TM724
谢文燕 女,1987年生,博士研究生,研究方向为无线电能传输技术和电力电子高频电磁技术。E-mail: xwy@fzu.edu.cn
陈 为 男,1958年生,教授,博士生导师,研究方向为电力电子功率变换、高频磁技术、电磁兼容诊断与滤波器、电磁场分析与应用和电磁检测等。E-mail: chw@fzu.edu.cn(通信作者)
收稿日期 2021-01-24
改稿日期 2021-02-23
国家自然科学基金项目(51407032)和福建省中青年教师教育科研项目(JAT200046, JT180017)资助。
(编辑 陈 诚)