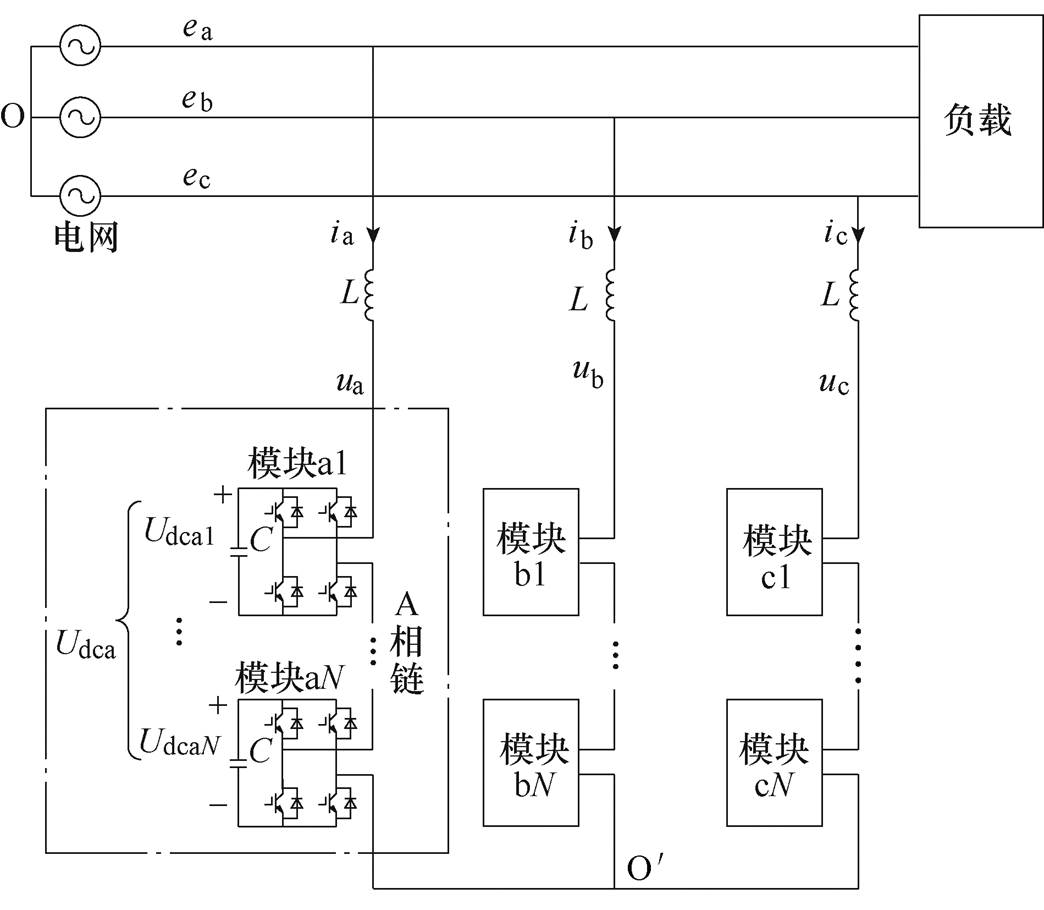
图1 SCHB STATCOM的拓扑结构
Fig.1 SCHB STATCOM topology
摘要 星形级联H桥静止同步补偿器(SCHB STATCOM)补偿负序电流时会产生三相不平衡有功功率,造成相间直流电压不均衡。为了实现相间直流电压均衡,通常需注入零序电压以重新分配三相有功功率。然而,传统的零序电压注入算法普遍基于有功功率的代数模型,方程组求解复杂且无法直观地表明零序电压的产生机理。此外,零序电压的注入将极大地增加STATCOM的输出电压,限制了负序电流的补偿范围。该文借助几何分析方法,构造零序电压相量在三相电流方向上的投影三角形,推导零序电压相量与该三角形外心的几何关系,揭示零序电压的产生机理,从而提出一种新的零序电压计算方法。在此基础上,进一步将零序电压以方波形式注入,提高了STATCOM的直流电压利用率,从而拓宽了负序电流补偿范围。最后,分别在SCHB STATCOM结构10kV/±1Mvar仿真和400V/±7.5kvar实验平台验证该文提出的零序电压注入算法的可行性。
关键词:级联H桥STATCOM 零序电压注入 相间直流电压均衡 负序电流补偿
负序电流是衡量电能质量优劣的一项重要指标,主要由三相不平衡负荷、短路故障、缺相故障等造成。过大的负序电流会给电网造成很多危害[1-3],包括降低发电机和电动机的容量、效率和寿命;增加变压器损耗和降低变压器利用率;增加输电线路损耗;造成三相电网电压不平衡,影响用电设备等。为提高电能质量,静止同步补偿器(Static Synchronous Compensator, STATCOM)在电力系统中常被用于补偿无功功率和负序电流[4-5]。在中高压场合下,星形级联H桥(Star-Connected Cascaded H-Bridge, SCHB)变换器具有模块化和器件少等优点,已被广泛应用于STATCOM场合[6-7]。然而,SCHB STATCOM补偿负序电流时,因级联H桥的各模块直流母线相互独立,负序电流与电网电压作用产生的三相不平衡有功功率会造成三相间直流电压不均衡,直接威胁装置的安全运行。因此,负序电流控制需兼顾三相有功功率平衡,实现相间直流电压均衡。
零序电压注入可重新分配三相有功功率,实现相间直流电压均衡。为了推导零序电压,文献[8]在abc坐标系上建立输入有功功率模型。然而,由于各变量采用三角函数表示,故零序电压的求解算法极其复杂。为简化算法,文献[9]通过Clarke变换,得到零序电压在ab 坐标系上相互垂直的变量。同时,文献[10]利用Park变化与dq坐标系推导零序电压,但仍无法避免反三角函数和开根号运算。文献[11]另辟蹊径,引入延时变量将零序电压转换到dq坐标系上,利用PI调节器直接调节零序电压在dq坐标系上的直流分量,从而实现相间直流电压均衡。然而,上述零序电压的推导方法都是基于有功功率的代数模型,利用不平衡有功功率,通过求解方程组的方式产生零序电压,很难直观地呈现出零序电压的产生机理。
数学语言通常可以借助于三角形、圆形等几何图形形象地展示一个事物的本质机理。因此,国内外学者已经利用几何分析方法探索零序电压的几何意义与产生机理。文献[12]将STATCOM输出电压和电流用相量形式表示,指出STATCOM稳定工作的必要条件是电压相量与电流相量正交,即可保证三相有功功率平衡。为了实现电压电流相量正交,文献[13]提出基于线电压三角形的几何分析方法,通过叠加零序电压相量将三角形的重心转移至三角形的费马点(Fermat Point, FP)。然而费马点求解比较困难,并且该方法只适用于电流平衡的情况。为此,文献[14]考虑不平衡电流,将电压电流相量投影到平面坐标系上,通过设定零序电压相量的坐标,建立电压电流相量内积为0的方程组,从而求解出零序电压的幅值和相位表达式。文献[15]将类似的方法应用在三角形联结的级联桥式STATCOM中推导零序电流的表达式。然而,该方法本质上是在求解方程组,并未从相量图中刻画出零序电压的几何意义。因此,零序电压在STATCOM补偿负序电流时产生机理仍不够明确。
此外,对于一定容量的STATCOM,零序电压注入法限制了负序电流的补偿范围。文献[16-17]详细分析了负序电流与零序电压的关系,发现当负序电流增大时,零序电压急剧增加,尤其当正序电流与负序电流幅值相等时,STATCOM存在一个奇点,即所需注入的零序电压无穷大,严重限制了负序电流的补偿能力。因此,为减小零序电压,确保STATCOM安全可靠运行,负序电流应被限制在一定的范围内。为得到负序电流的补偿范围,文献[18]在abc坐标系上推导了负序电流与STATCOM输出最大电压的关系,但为了简化分析,忽略了负序电流的初始相位,故所得范围不够准确。为增加负序电流的补偿范围,文献[19]将负序电流在dq坐标系上的d轴分量与零序电压结合平衡相间有功功率,利用负序电流q轴分量补偿电网。然而,该方法牺牲了电网负序的补偿效果。为了不影响负序电流补偿性能,通过向基波零序电压中注入谐波来提高直流电压利用率是一种有效的方法,谐波电压不会改变有功功率的重新分配,但可以减小STATCOM输出电压的峰值。在电机应用中通常注入幅值为基波电压1/6的3次谐波分量(以下称为1/6 3次谐波电压)来扩展逆变器的工作范围[20]。文献[21]将3次谐波注入方法应用在级联H桥光伏逆变器中,用于提高逆变器的有功功率均衡能力,从而保证并网有功电流平衡。在此基础上,文献[22]提出利用波峰系数更小的方波替代3次谐波,可进一步增强光伏逆变器的有功功率均衡能力。然而,尚未有学者将方波注入方法应用于SCHB STATCOM场合中探讨负序电流补偿范围的变化情况。
为了阐明零序电压在负序电流补偿时的产生机理,本文借助于几何分析方法,将零序电压相量在三相电流方向上的投影构成三角形,推导了零序电压相量与该三角形外心的几何关系,揭示了零序电压的产生机理,从而提出一种新的零序电压计算方法。为了提高直流电压利用率,扩大系统负序电流补偿范围,本文将零序电压以方波的形式注入,并与传统正弦形式对比,结果表明,以方波形式注入的零序电压可极大地提高负序电流的补偿范围。最后,通过仿真及实验验证了该理论分析的可行性。
图1给出SCHB STATCOM的拓扑结构,每相级联N个H模块。ek为三相电网电压,其中k=a, b, c;uk为STATCOM三相输出电压;ik为三相并网电流;Udckj为每个模块的直流电压,j=1,…,N;Udck为单相直流电压,是由每相中各个模块直流电压相加得到。本文中SCHB STATCOM采用三层控制构架:第一层为双序dq电流控制环,不仅用于调节所有模块的直流电压,而且控制注入电网的正序无功电流和负序电流;第二层为相间直流电压均衡控制环,通过注入零序电压平衡三相相间有功功率,实现三相相间直流电压(Udca, Udcb, Udcc)均衡;第三层为模块直流电压均衡控制,通过调节每个模块输出电压在对应相电流方向上的投影分量实现单相模块间电压相等[23]。本文重点研究相间直流电压均衡控制中零序电压的计算。

图1 SCHB STATCOM的拓扑结构
Fig.1 SCHB STATCOM topology
图2为STATCOM中电网电压和并网电流相量,图中以平衡电网电压A相定向,建立xy坐标系,
则电网电压和电流相量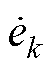 和
和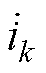 在xy坐标系上分别表示为
在xy坐标系上分别表示为
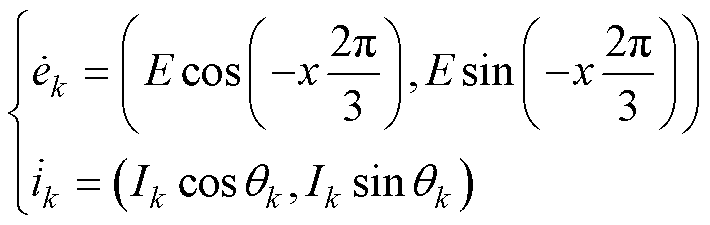 (1)
(1)
式中,x=0, 1, 2分别对应k=a, b, c;E为电网电压幅值;Ik为三相电流幅值;qk为三相电流初始相位。
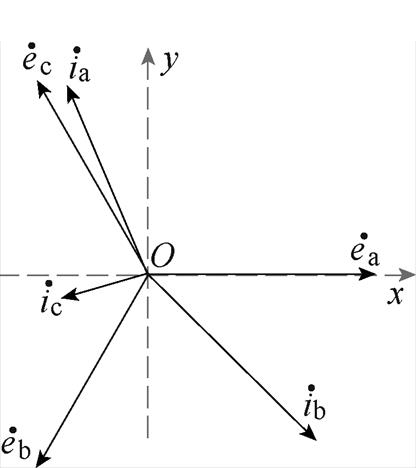
图2 电网电压和并网电流相量
Fig.2 Phasor diagrams of grid voltages and currents
电压相量在电流相量上的投影如图3所示,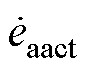 为
为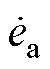 在
在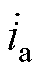 上的投影,该投影与
上的投影,该投影与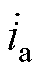 的数量积表征A相电压电流产生的有功功率的大小。另外两相电压相量在对应电流相量上的投影分别记为
的数量积表征A相电压电流产生的有功功率的大小。另外两相电压相量在对应电流相量上的投影分别记为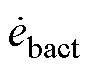 和
和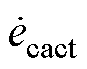 。各相电压的投影相量可以表示为
。各相电压的投影相量可以表示为
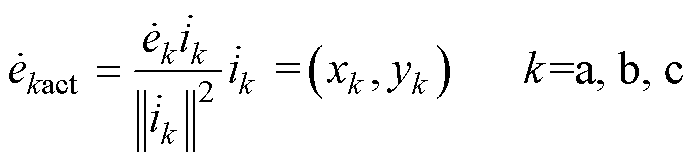 (2)
(2)
其中
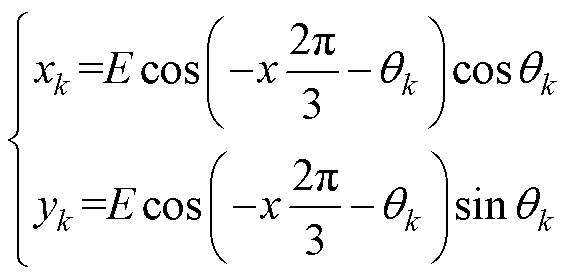
式中,“||*||”为对应相量的模长;xk和yk分别为各投影相量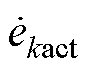 在垂直坐标系上的坐标。为了能够平衡三相间的有功功率,同时不改变输出电流,需要引入零序电压,零序电压相量在电流相量上的投影
在垂直坐标系上的坐标。为了能够平衡三相间的有功功率,同时不改变输出电流,需要引入零序电压,零序电压相量在电流相量上的投影
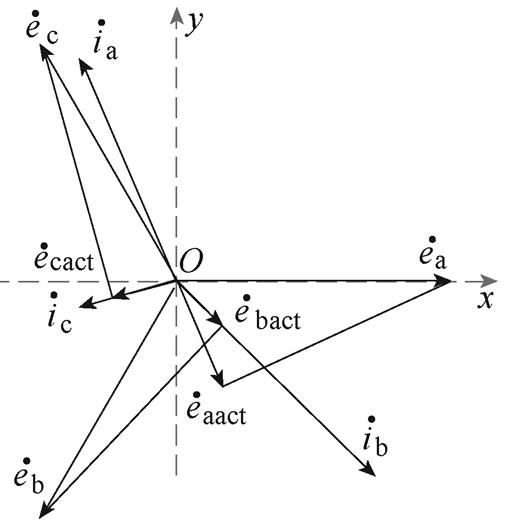
图3 电压相量在电流相量上的投影
Fig.3 The projection of voltage phasors on current phasors
如图4所示。将零序电压相量在各相电流上的投影相量标记为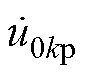 。为实现各相输入有功功率为0,
。为实现各相输入有功功率为0,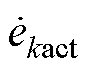 与
与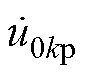 需满足
需满足
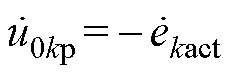 (3)
(3)
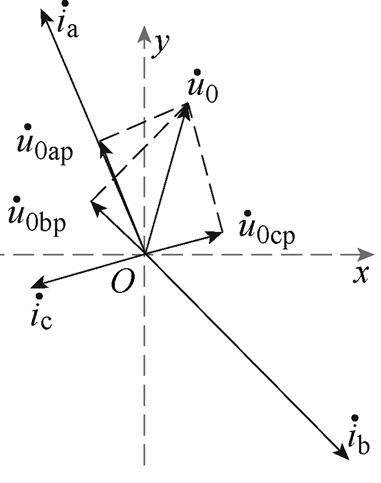
图4 零序电压相量在电流相量上的投影
Fig.4 The projection of zero sequence voltage phasors on current phasors
零序电压相量投影简化示意图如图5所示,各个投影相量的顶点分别记为U、V、W,且零序电压的顶点记为N。根据式(2)和式(3),U、V、W的坐标分别为(-xa, -ya),(-xb, -yb),(-xc, -yc)。由于U、V、W为N在电流方向上的投影,因此连接NU、NV、NW可满足
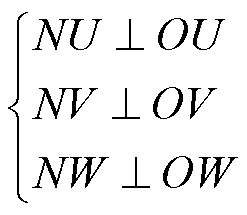 (4)
(4)
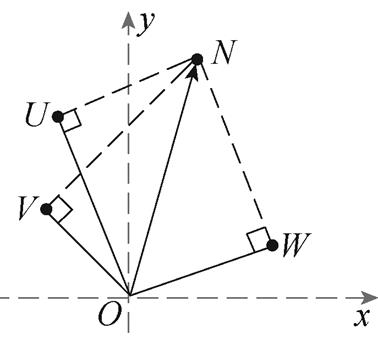
图5 零序电压相量投影简化示意图
Fig.5 Simplified schematic of zero sequence voltage phasors and projections
因此,△UNO、△VNO、△WNO均为直角三角形。令ON的中点为M,根据直角三角形斜边中线定理可知,M到U、V、W距离分别相等,即MU= MV=MW=OM=MN,因此,M为△OVU的外心,零序电压相量与电流相量上的投影之间的关系如图6所示,故零序电压相量与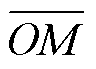 的关系为
的关系为
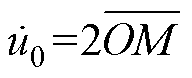 (5)
(5)
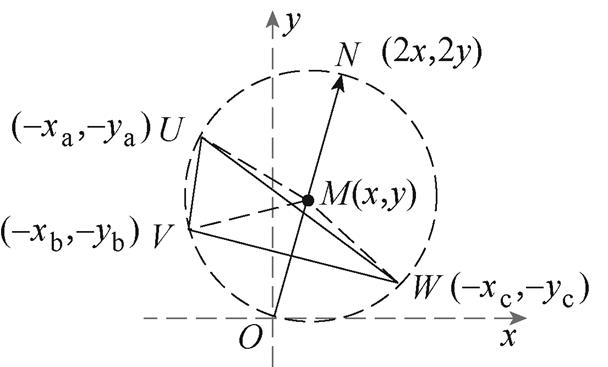
图6 零序电压相量与电流相量上的投影之间的关系
Fig.6 Relationship between zero sequence voltage phasors and projections on current phasors
根据文献[24]的外心求解公式,利用中垂线定理推导出外心M的坐标(x, y)为
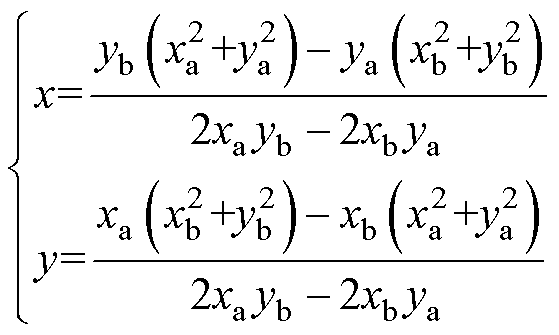 (6)
(6)
将式(2)和式(6)代入式(5),可得零序电压相量的坐标(x0, y0)表达式为
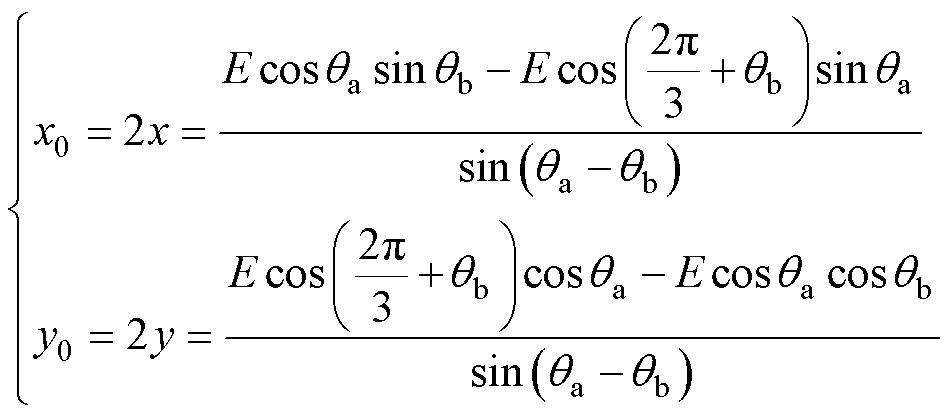 (7)
(7)
根据式(7),可得出零序电压的幅值U0和相位q0分别为
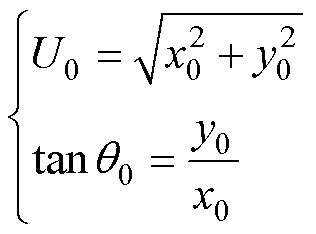 (8)
(8)
由式(7)和式(8)可以看出,当qa-qb=Np(N Z)时,零序电压存在奇点,幅值将趋于无穷大。传统方法中指出当正负序电流幅值相等时,零序电压也将存在奇点[18]。接下来本文将证明它们是等价 关系。
Z)时,零序电压存在奇点,幅值将趋于无穷大。传统方法中指出当正负序电流幅值相等时,零序电压也将存在奇点[18]。接下来本文将证明它们是等价 关系。
通过对式(1)中三相电流进行正负序分离,可以得到A、B相电流的幅值相位与正负序电流之间的关系如式(9)所示,详细推导见附录。
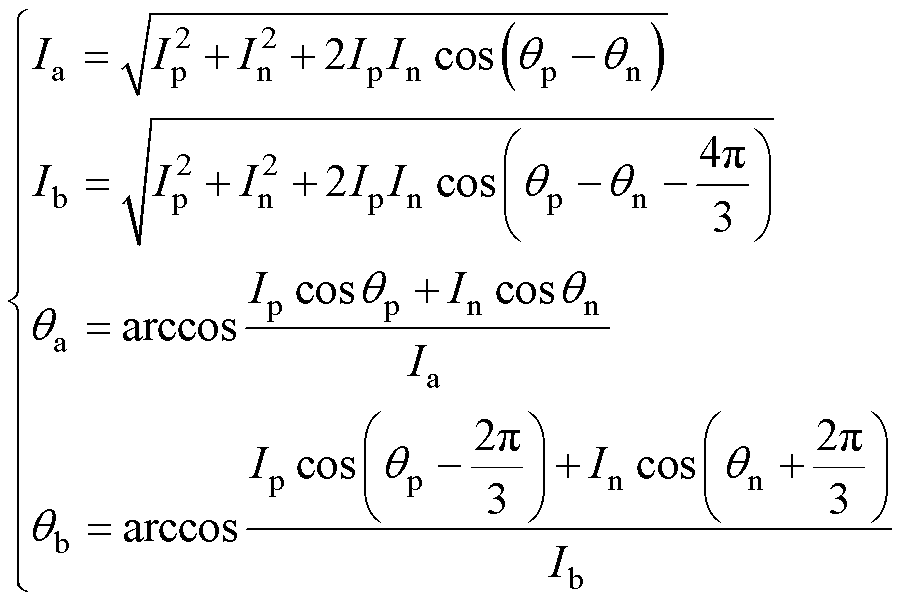 (9)
(9)
式中,Ip、In分别为正、负序电流的幅值;qp、qn分别为正、负电流的初始相位。将式(9)代入式(7)的分母中可以得到
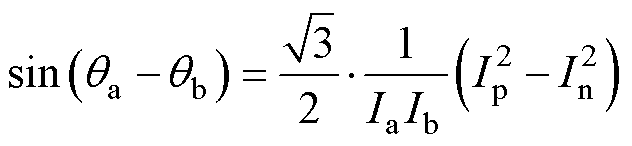 (10)
(10)
根据式(10)可知,qa-qb=Np(N Z)与正负序电流幅值相同是等价的条件,此时零序电压幅值均存在奇点。
Z)与正负序电流幅值相同是等价的条件,此时零序电压幅值均存在奇点。
基波零序电压(Fundamental Frequency Zero- sequence Voltage, FFZV)u0的表达式为
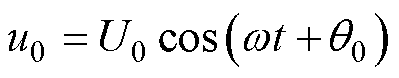 (11)
(11)
式中,零序电压的幅值U0和相位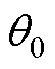 由式(8)计算给定。
由式(8)计算给定。
为了提高直流电压利用率,可以将FFZV用方波输出,且在三相三线制系统中,将FFZV用方波输出不会产生谐波电流。根据方波的傅里叶分解表达式,方波电压的幅值是其分解的基波幅值的4/p 倍。因此,为了不改变输出零序电压的基波分量,该方波电压表示为
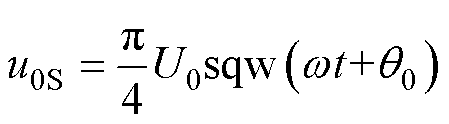 (12)
(12)
其中
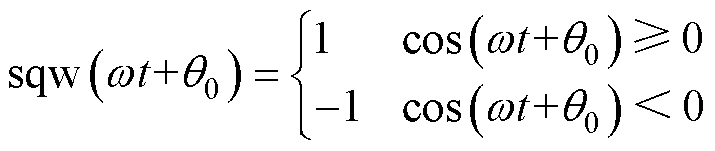
式中,u0S为方波电压,u0S与u0具有相同的基波 电压。
为了进一步提高直流电压利用率,对于正序和负序电压,采用1/6 3次谐波注入的方式。本文为了简化1/6 3次谐波的计算方法,根据文献[22],通过计算三相电压瞬时最大值和最小值的平均值,从而获得1/6 3次谐波电压,其表达式为
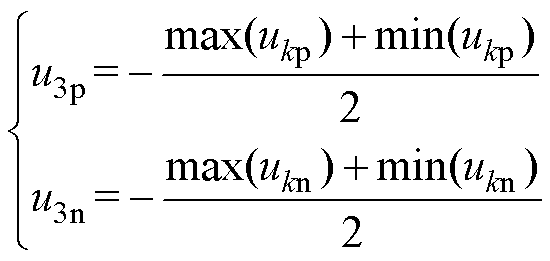 (13)
(13)
式中,u3p、u3n分别为正负序电压的1/6 3次谐波电压;ukp、ukn分别为三相正序和负序电压(k=a, b, c)。结合式(12)和式(13),基于方波的零序电压(Square Wave Zero-sequence Voltage, SWZV)u0SW的表达 式为
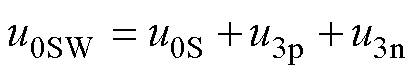 (14)
(14)
在采用SWZV注入时,为了获得负序电流补偿范围,CHB STATCOM输出的三相电压幅值表示为
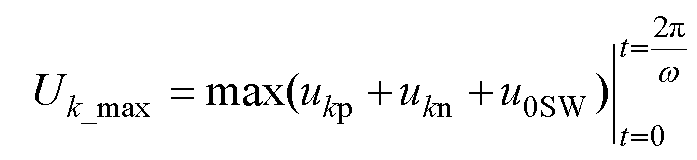 (15)
(15)
根据基尔霍夫电压定律,SCHB STATCOM输出的正序和负序电压可由电网电压和电感电压分 别表示为
 (16)
(16)
式中,L为滤波电感;ikp、ikn分别为三相正序和负序电流,k=a, b, c。
根据式(15),定义SCHB STATCOM输出最大电压为
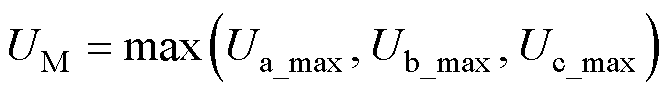 (17)
(17)
为了避免过调制,STATCOM的输出最大电压需满足
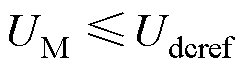 (18)
(18)
式中,Udcref为相间直流电压参考值。当正序电流一定时,UM可视为关于负序电流的函数,故不等式(18)决定了负序电流的范围。
为了获得负序电流范围,以表1中400V/±7.5kvarSCHB STATCOM的主电路参数为算例,将式(14)和式(16)代入式(18),在STATCOM补偿额定正序无功电流的情况下,借助于Maltab软件绘制出负序电流的补偿范围,如图7所示。
表1 400V/±7.5kvar平台参数
Tab.1 Circuit parameters of 400V/±7.5kvar plantform

参 数数 值 级联模块数N5 滤波电感L/mH9 模块直流电压Udc/V84 直流电容C/mF3
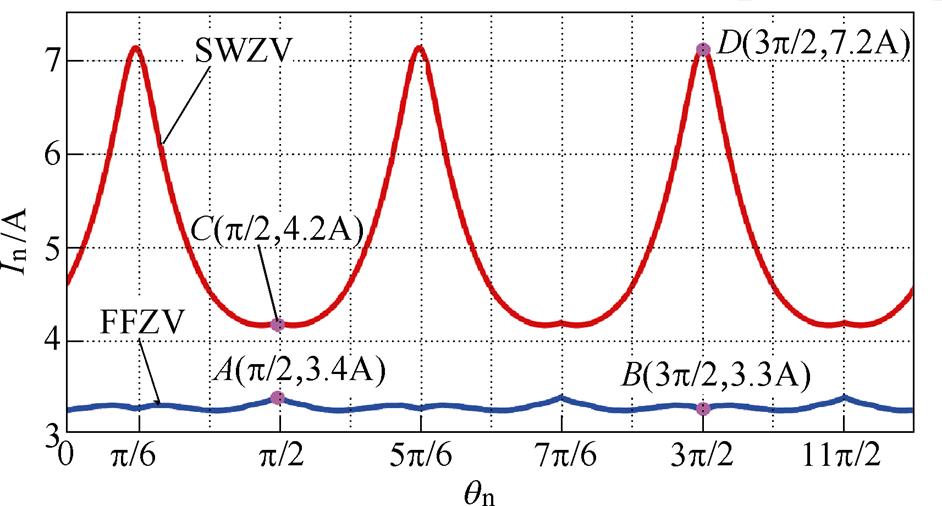
图7 FFZV和SWZV注入下负序电流的补偿范围
Fig.7 The range of negative current compensation under FFZV and SWZV
图7中,In为最大可补偿的负序电流的幅值,qn为负序电流的相位。为与传统正弦零序电压注入方法对比,利用同样的方法,可得到FFZV注入下的负序电流补偿范围。
由图7可以看出,无论采用FFZV注入还是SWZV注入,STATCOM补偿的最大负序电流幅值随着qn呈现周期性变化。当qn=(1+4j)p/6(j=1, 2, 3)时,采用SWZV能够补偿的负序电流幅值最大,达到7.2A,此时采用FFZV仅能够补偿3.3A的负序电流。而在qn=(3+4j)p/6时,采用SWZV的负序电流幅值最小,为4.2A,但仍然大于采用FFZV注入下的最大负序电流幅值3.4A。综合图7及数据分析表明,采用基于方波的零序电压注入法能够有效地拓宽STATCOM补偿负序电流的范围。
为证明本文所提基于几何方法的零序电压计算策略以及基于方波的零序电压注入算法的准确性,在Matlab/Simulink平台搭建10kV/±1Mvar星形CHB STATCOM仿真模型进行仿真证明,仿真平台参数见表2。
表2 10kV/±1Mvar仿真系统参数
Tab.2 Circuit parameters of 10kV/±1Mvar plantform

参 数数 值 级联模块数N12 滤波电感L/mH30 模块直流电压Udc/V800 直流电容C/mF1
为验证所提基于几何方法的零序电压计算策略的有效性和准确性,给出一组仿真对比。
图8给出系统在注入零序电压前后,补偿负序电流的仿真波形。图8a为三相电网电压波形;三相输出电流如图8b所示,正序输出电流30A,在t0时刻后STATCOM输出负序电流In由0A变为2A,相位qn=3p/2,此时不注入零序电压,在t1时刻,负序电流的幅值相位不变,开始注入零序电压均衡直流侧电压,如图8c所示;观察图8d可知,t0时刻后由于未注入零序电压,三相直流侧电压逐渐发散,至t1时刻,系统按照本文所提正弦零序电压计算策略注入后,三相直流侧电压逐渐恢复稳定值9 600V。综上,采用本文所提方法注入正弦零序电压可以稳定三相直流侧电压,由此验证了推导结果正确有效。
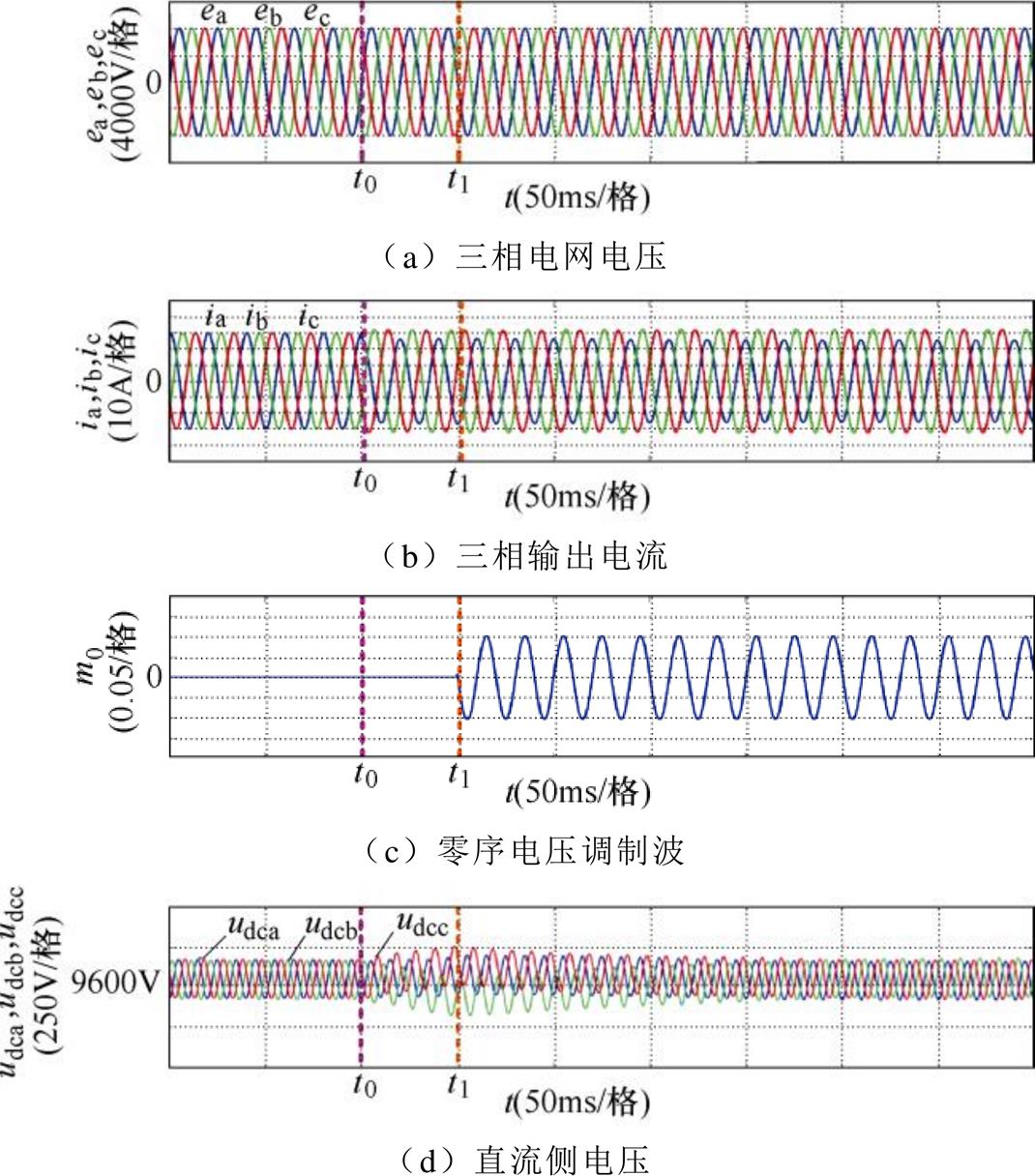
图8 注入零序电压前后系统补偿负序电流仿真波形
Fig.8 Simulation waveforms of system compensated negative sequence current before and after zero sequence voltage injection
图9为对比实验仿真波形。图9a为三相电网电压;图9b为STATCOM三相输出电流,正序输出电流30A,在t0时刻后输出负序电流In由0变为3A,相位qn=3p/2;为补偿负序电流,t0时刻后需要向系统注入零序电压,如图9c~图9g所示,通过本文所提以及文献[8-11]的方法计算得到的零序电压相位和幅值完全相同,结合图9h直流侧电压可知,t0时刻注入零序电压后,三相直流侧电压维持均衡,由此证明本文所提正弦零序电压计算方法与文献[8-11]所述相比,具有相同的准确性和快速性。
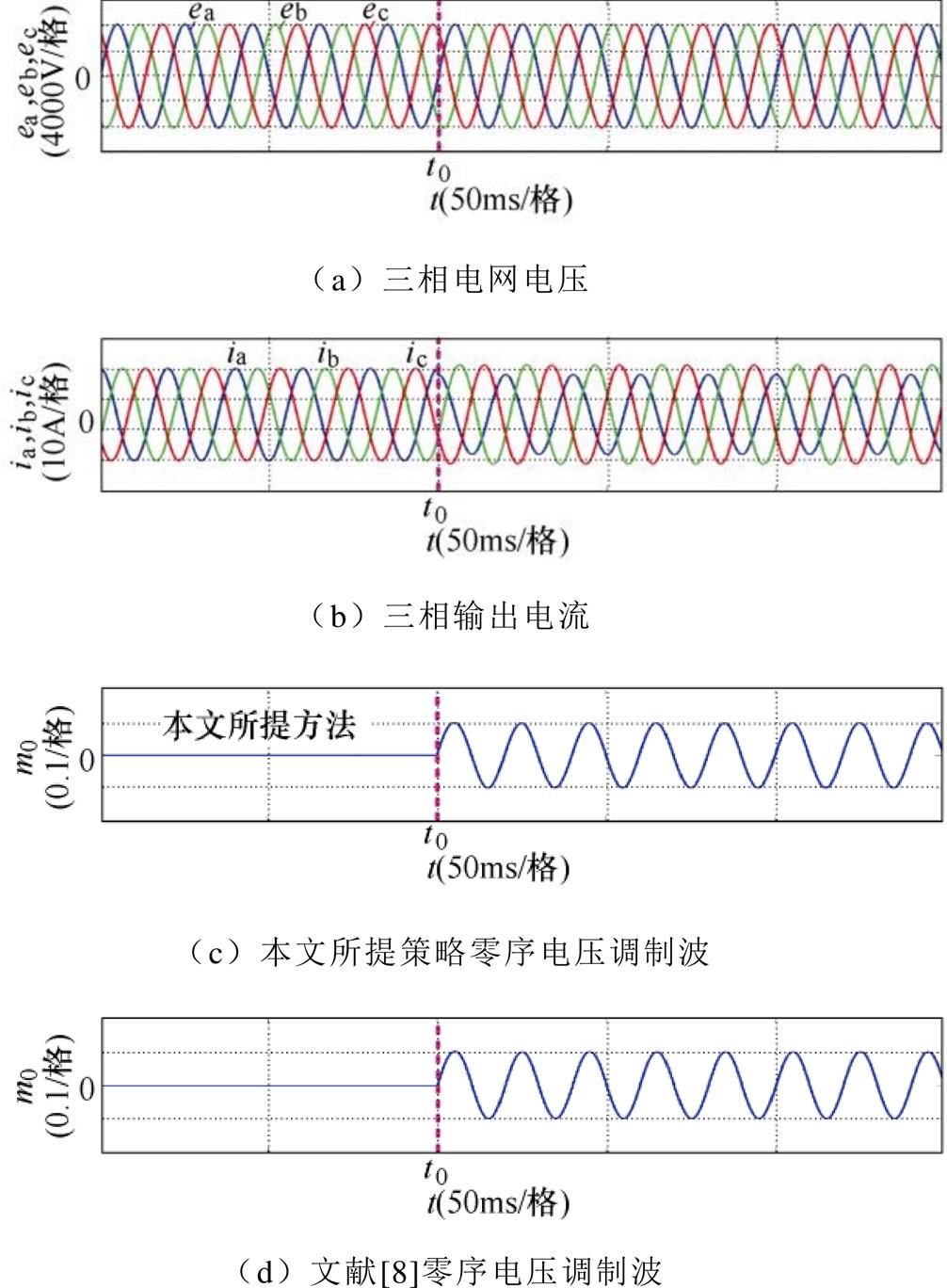
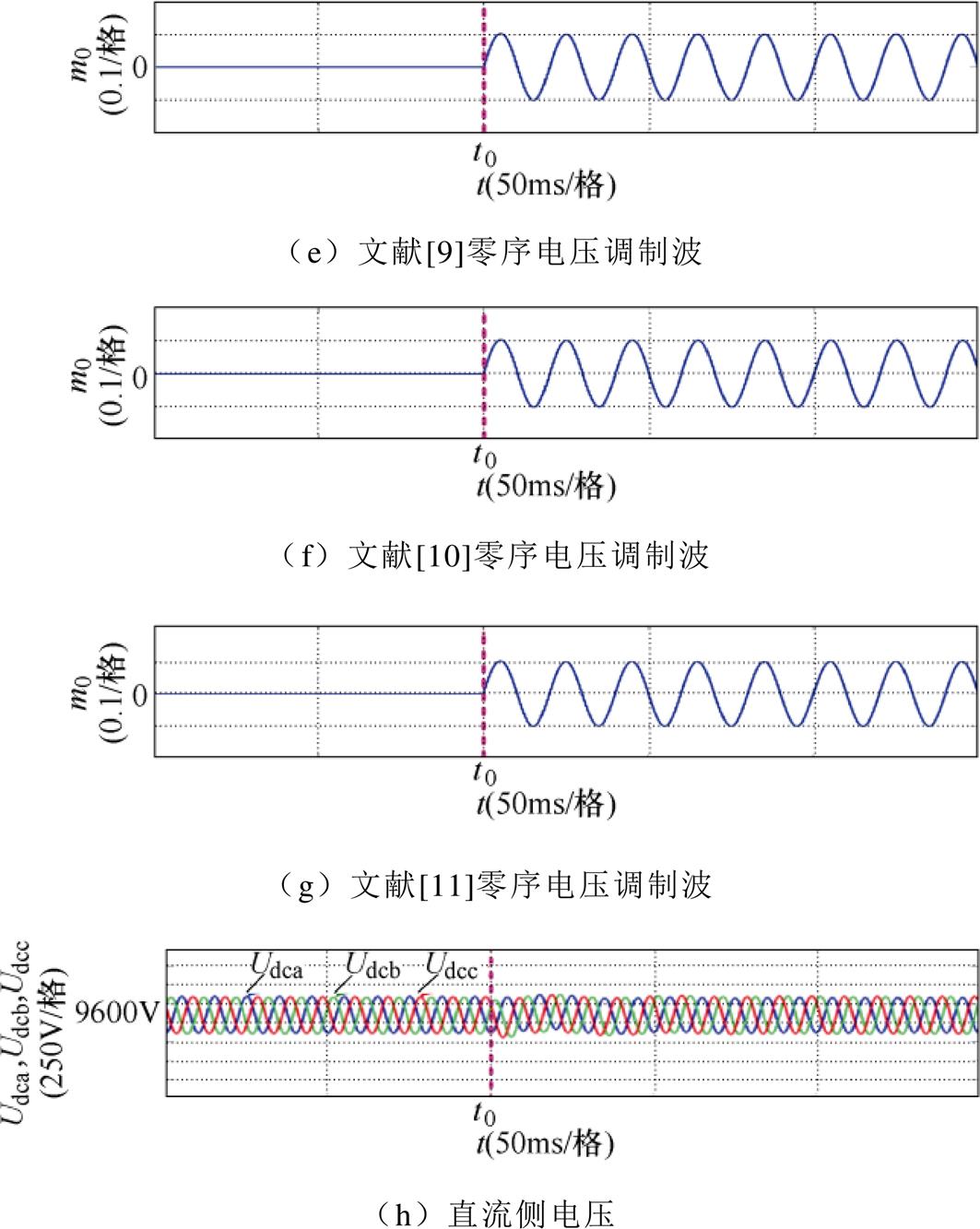
图9 注入零序电压补偿时系统输出仿真波形
Fig.9 Simulation waveforms with zero-sequence voltage compensation
综合比较图8和图9的仿真结果可知,在系统需补偿负序电流场合下,以本文所提计算策略注入相应零序电压可以有效地维持相间直流侧电压均衡,其相间均压效果与文献[8-11]所述相一致。由此验证了本文提出的零序电压计算策略实现相间均压的可行性和准确性。
搭建仿真平台,验证第3节中基于方波的零序电压注入法的可行性及其在负序电流基准切换时的动态性能,仿真参数与4.1节一致。
采用SWZV的负序电流动态切换仿真波形如图10所示。图10a为三相电网电压波形;三相输出电流如图10b所示,正序输出电流为50A,在t0时刻后STATCOM输出负序电流In由6A变为16A,相位qn=3p/2不变;为均衡三相直流电压,根据本文所提计算策略注入SWZV,如图10c所示;图10d显示在动态过程中,三相直流侧电压始终能够维持均衡;图10e为三相调制波电压。

图10 采用SWZV的负序电流动态切换仿真波形
Fig.10 Simulation waveforms with the negative sequence current transition
为验证本文所提基于方波的零序电压注入算法,搭建了400V/±7.5kvar的SCHB STATCOM的样机。样机参数见表1。控制器采用数字信号处理器(Digital Signal Processor, DSP)(TMS320F28335)和现场可编程门阵列(Field-Programmable Gate Array, FPGA)(EPM1270T144C5N)相结合的方式,调制方式采用载波移相正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM),载波频率为1kHz。
考虑到实际示波器通道数有限,设计了基于Labview软件的虚拟示波器。实时的电压电流在采样后进入控制器,控制器通过网络通信将数据发送到计算机,由虚拟示波器显示出波形。
为了验证提出的SWZV注入算法的有效性和补偿范围计算的准确性,向STATCOM注入额定的正序无功电流和In=7.2A、qn=3p/2的负序电流,即图7中的D点。实验结果如图11所示。图11a为三相电网电压波形;图11b为STATCOM输出的三相不平衡电流波形,三相电流的总谐波畸变率(Total Harmonic Distortion, THD)经检测为:A相THD= 1.21%,B相THD=0.67%,C相THD=0.65%;负序电流会造成三相有功功率不平衡,故需注入SWZV电压,如图11c所示;由此三相相间直流电压保持均衡,如图11d所示;图11e和图11f分别为三相输出调制波电压和STATCOM三相输出电压。根据式(18)和图7,由于该实验补偿qn=3p/2下负序电流的最大值,故C相调制波最大值近似为1.0,由此验证了图7中负序电流补偿范围的准确性。需要注意的是,图中mx(x=a, b, c)为输出电压ux关于相间直流电压的归一化后的调制波电压。
为了进一步验证图7中负序电流补偿范围的准确性,选择图7中的C点,此时负序电流的幅值和相位为:In=4.2A, qn=p/2。In=4.2A, qn=p/2采用SWZV的实验波形如图12所示。图12a为三相电网电压波
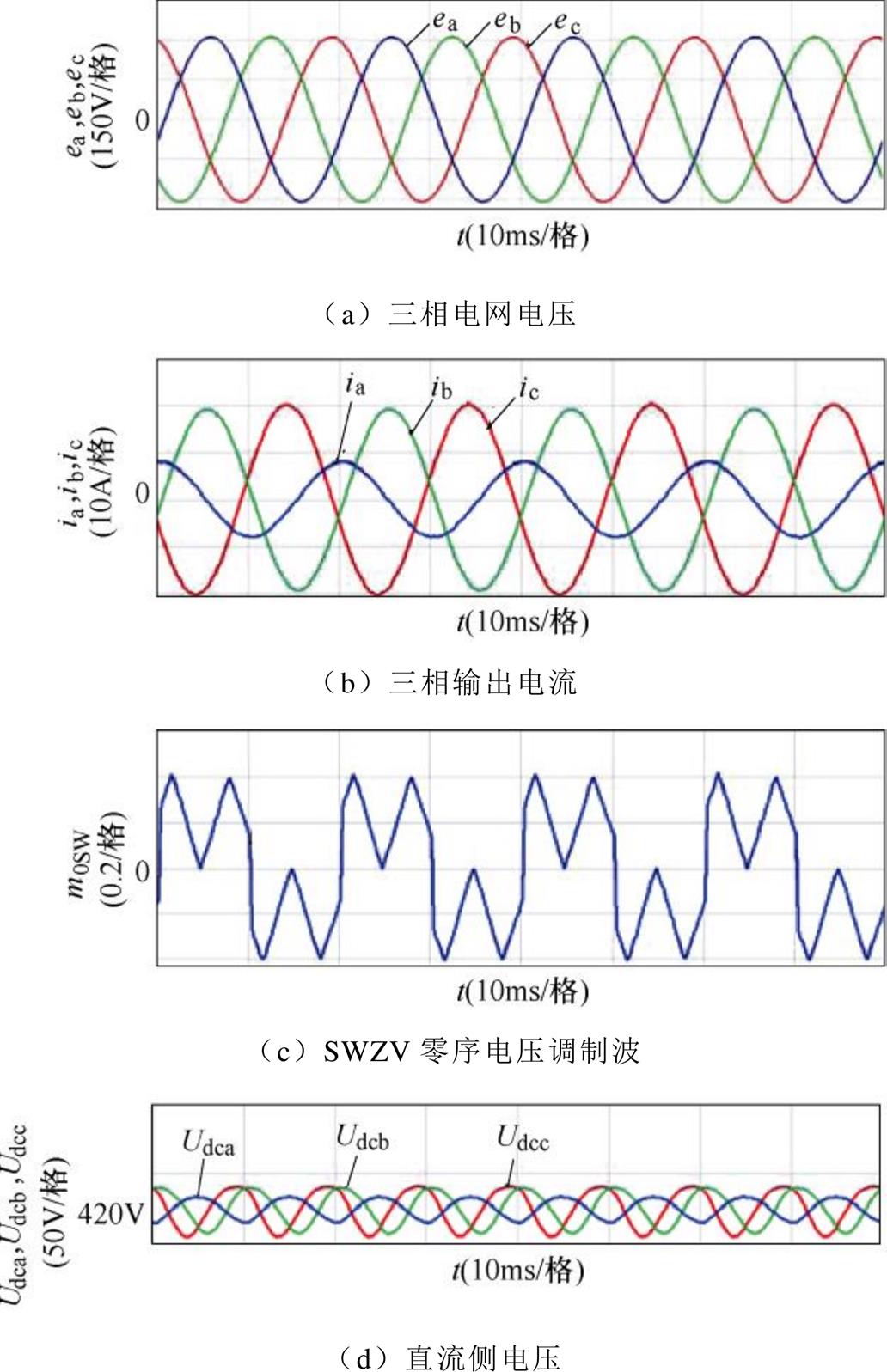
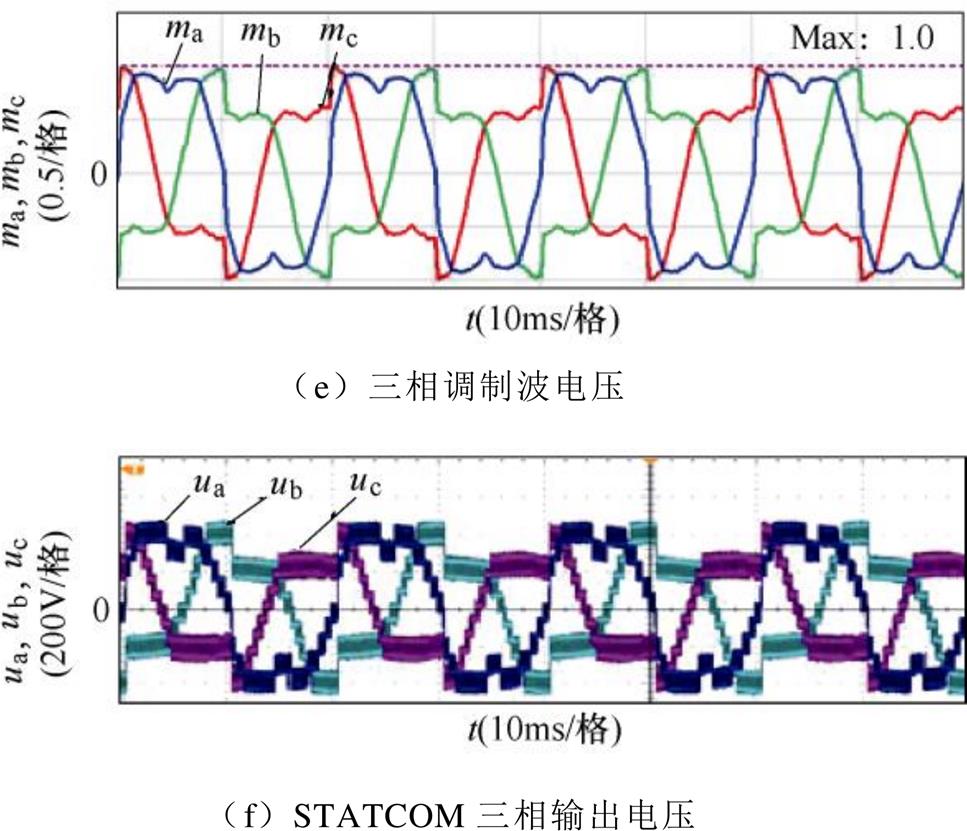
图11 In=7.2A, qn=3p/2采用SWZV的实验波形
Fig.11 Experimental waveforms with SWZV when In=7.2A, qn=3p/2
形;三相输出电流如图12b所示,STATCOM可以很好地控制三相不平衡电流,三相电流THD值经检测为:A相THD=0.62%,B相THD=1.23%,C相THD=1.21%;不仅如此,由于SWZV注入,三相相间直流电压保持均衡,如图12c和图12d所示;图12e为三相调制波电压,从中可以看出,B、C两相调制波最大值近似为1.0,可以证明C点对应的4.2A为STATCOM在qn=p/2下可补偿的最大负序电流,进而验证了图7中负序电流补偿范围的准确性;图12f为STATCOM三相输出电压,由三相调制电压调制而成。
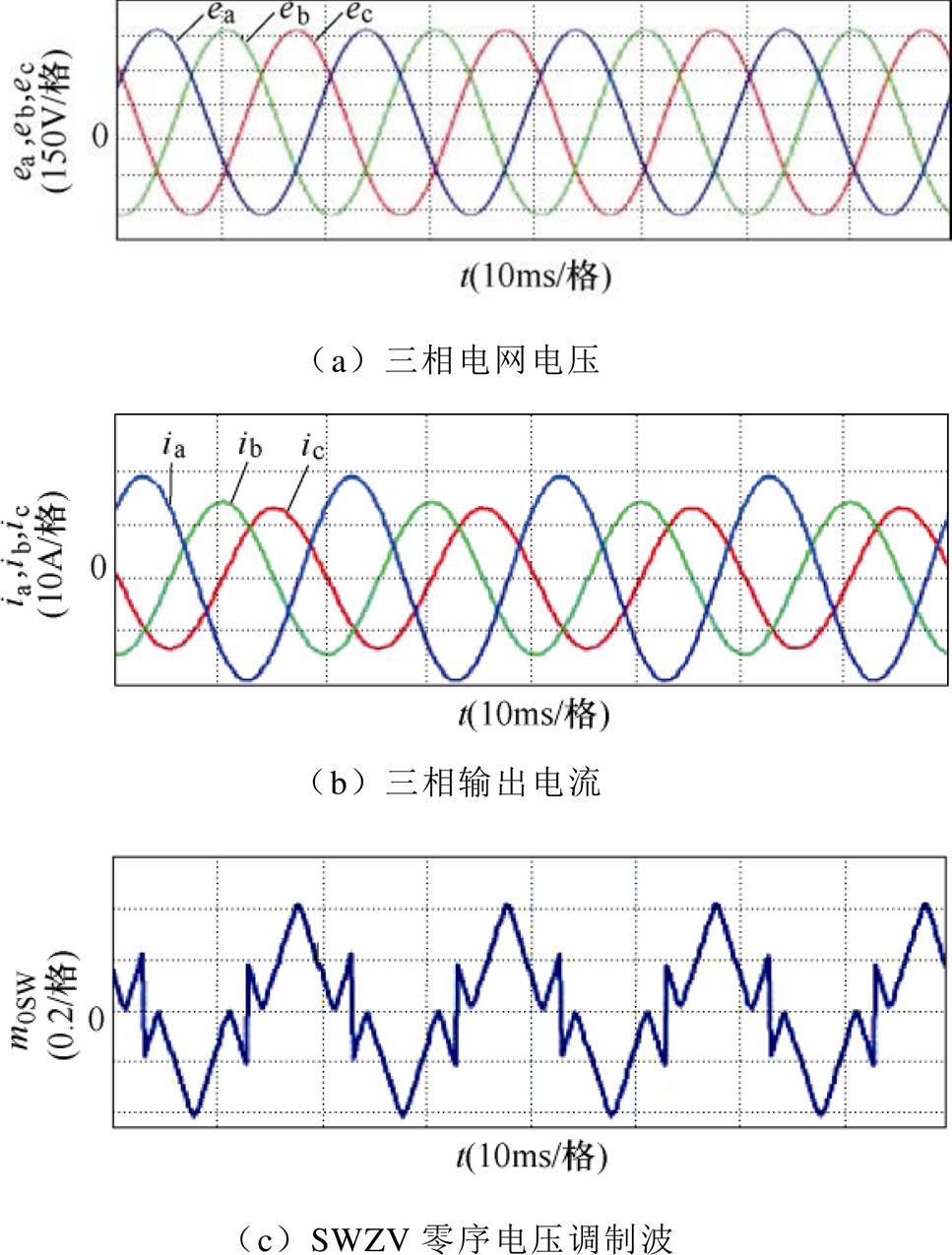
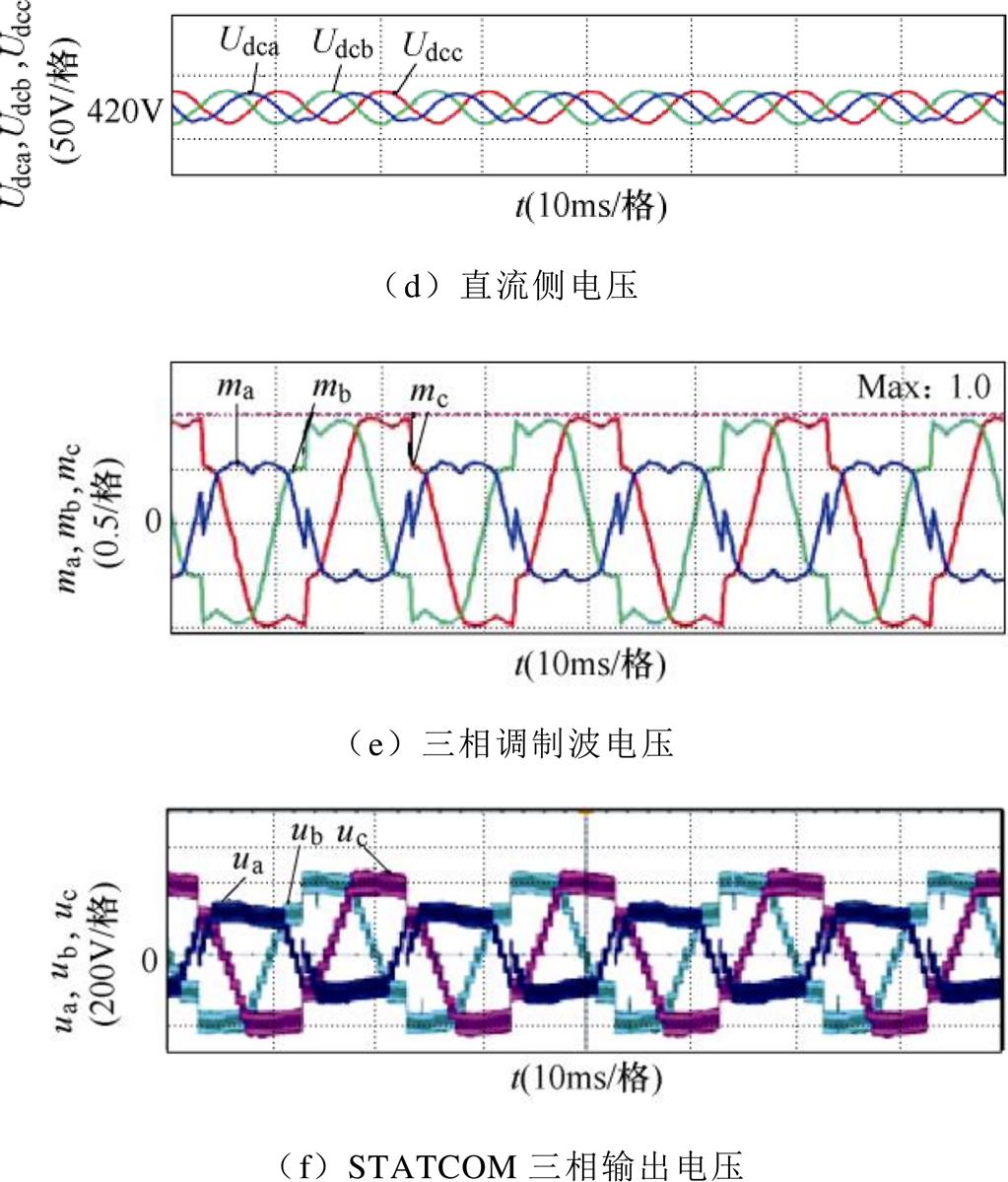
图12 In=4.2A, qn=p/2采用SWZV的实验波形
Fig.12 Experimental waveforms with SWZV when In=4.2A, qn=p/2
为验证本文所提SWZV注入方法的优势,即相同负序电流相位条件下,采用SWZV可以补偿负序电流的幅值更大。具体以负序电流相位在qn=3p/2和qn=p/2两处SWZV和FFZV的最大负序电流补偿能力为判别依据。
采用FFZV注入法并补偿In=3.3A, qn=3p/2的负序电流,即图7的B点,实验波形如图13所示。图13a为三相电网电压;三相输出电流如图13b所示,STATCOM可以很好地控制三相不平衡电流,三相电流THD值经检测为:A相THD=1.20%,B相THD=0.65%,C相THD=0.59%;为了维持三相直流侧电压均衡,STATCOM注入的基波零序电压如图13c所示;三相直流侧电压如图13d所示;图13e为三相调制波电压,其中A相调制波幅值近似为1.0,证明B点为STATCOM采用FFZV后在qn=3p/2下可补偿的最大负序电流。因此,对比图11发现,在qn=3p/2时,FFZV注入可补偿的最大负序电流(3.3A)明显小于采用SWZV注入可补偿的最大负序电流(7.2A);图13f为STATCOM三相输出电压,由三相调制电压调制而成。
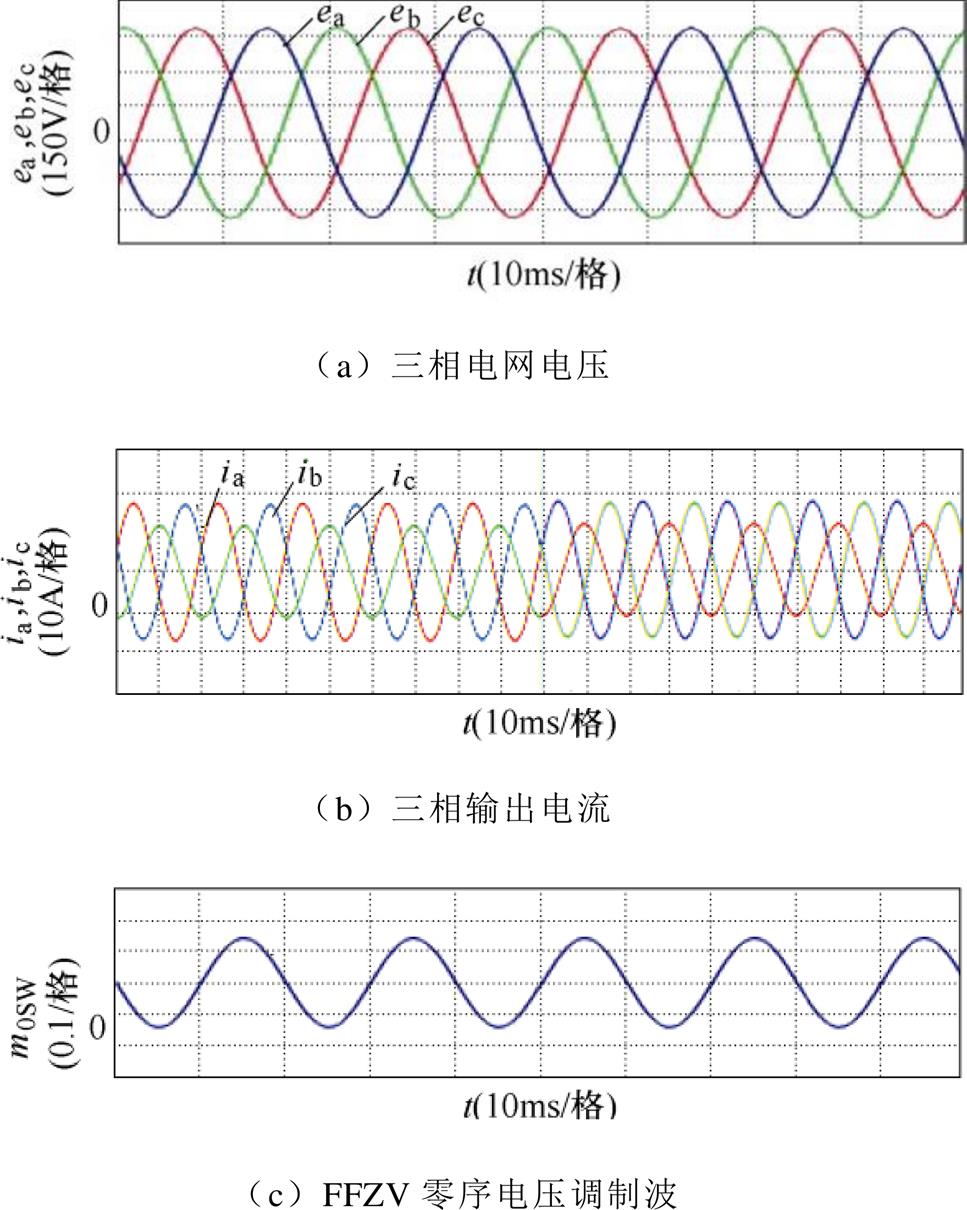
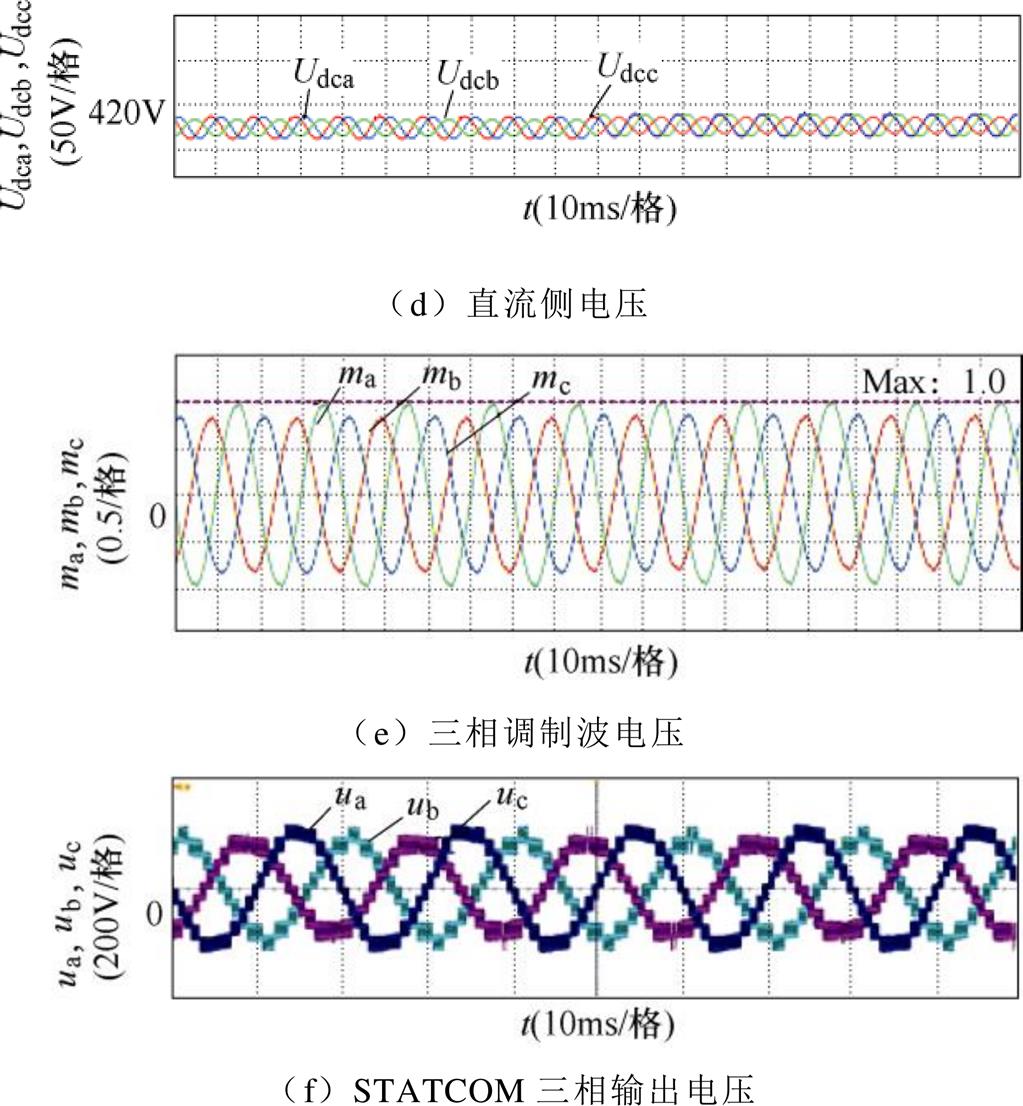
图13 In=3.3A, qn=3p/2采用FFZV的实验波形
Fig.13 Experimental waveforms with FFZV when In=3.3A, qn=3p/2
同样,以图7中的A点为实验条件,此时In= 3.4A,qn=p/2且采用FFZV注入,实验波形如图14所示。图14a为三相电网电压;三相输出电流如图14b所示,STATCOM的三相电流控制稳定,三相电流THD值经检测为:A相THD=0.72%,B相THD= 1.33%,C相THD=1.21%;由于输出电流中的负序分量,需要注入FFZV保持三相相间直流电压均衡,如图14c和图14d所示;图14e为三相调制波电压,其中B、C两相调制波电压幅值最大,近似为1.0,证明STATCOM采用FFZV后在qn=p/2下可补偿的最大负序电流即为3.4A,明显小于相同相位下SWZV注入可补偿的最大负序电流(4.2A);图14f为STATCOM输出电压,由三相调制电压调制而成。综合图11~图14的实验结果,负序电流的补偿范围对比见表3。
结合表3中数据可知,与传统的正弦零序电压注入(FFZV)算法相比,CHB STATCOM采用基于方波的零序电压注入算法(SWZV)能够显著增加负序电流补偿范围。
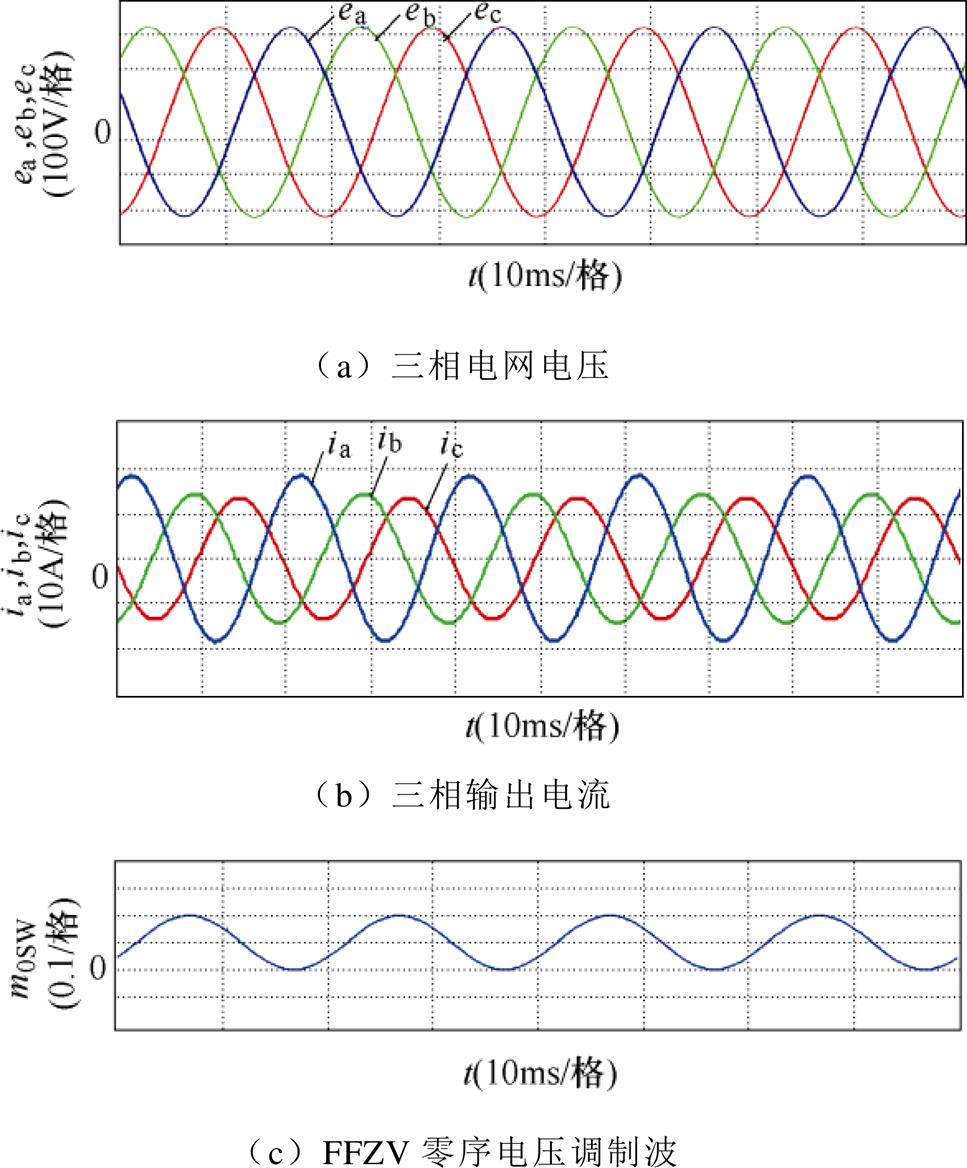
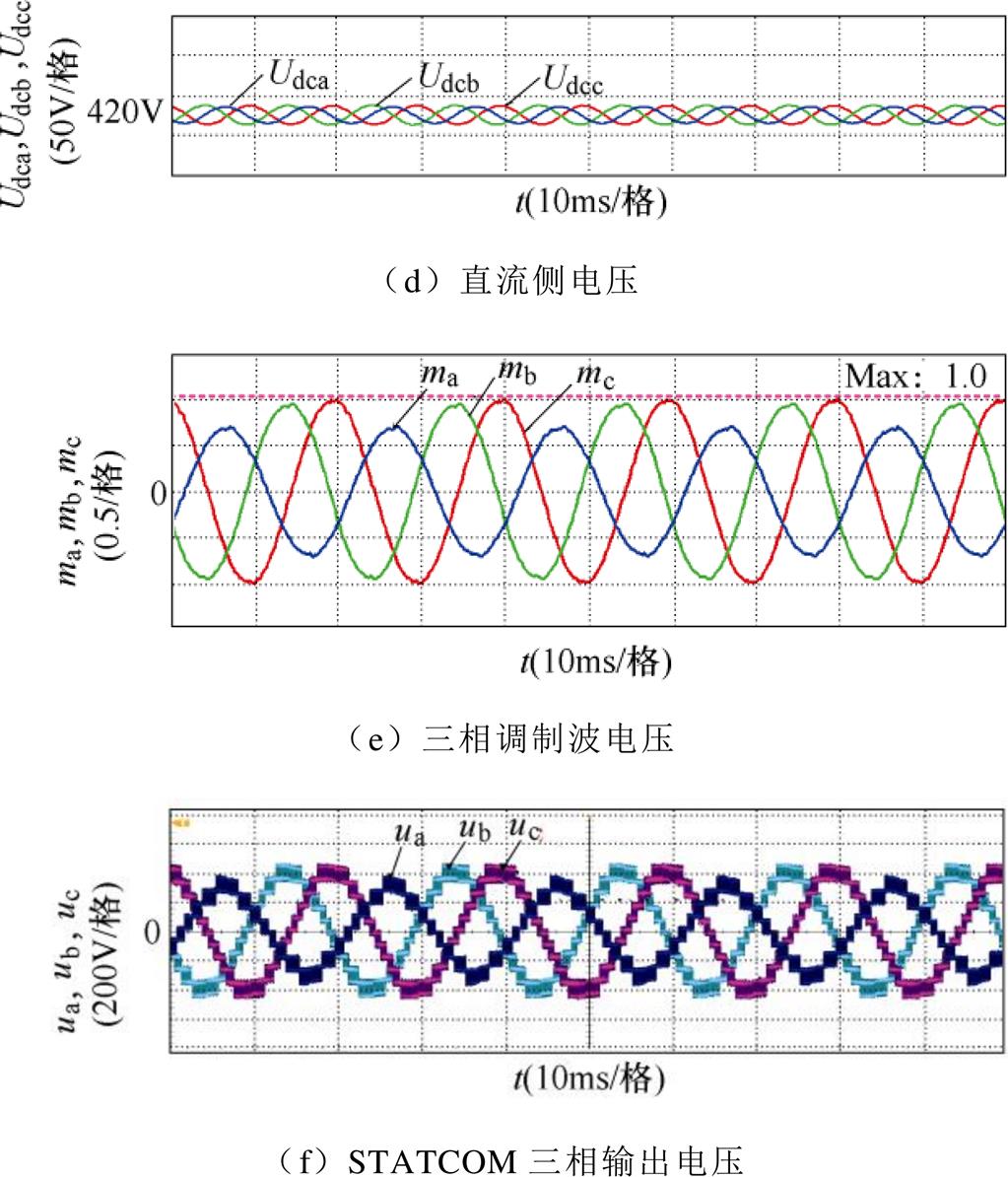
图14 In=3.4A, qn=p/2采用FFZV的实验波形
Fig.14 Experimental waveforms with FFZV when In=3.4A, qn=p/2
表3 不同零序电压注入方法负序电流补偿范围对比
Tab.3 Comparison of negative sequence current compensation range of different zero sequence voltage injection methods
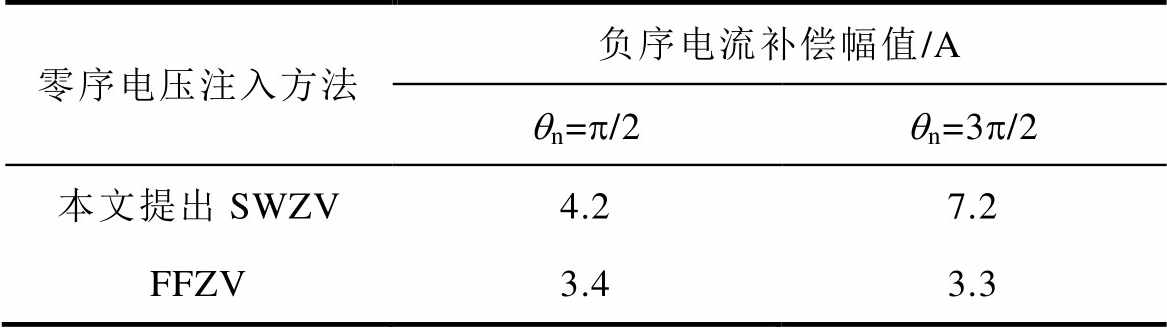
零序电压注入方法负序电流补偿幅值/A qn=p/2qn=3p/2 本文提出SWZV4.27.2 FFZV3.43.3
为了验证SWZV注入下负序电流动态补偿特性,做了一组负序电流切换的实验,其实验波形如图15所示。t0时刻前后,STATCOM在补偿原本的额定无功正序电流15A的基础上分别额外注入In= 4A, qn=p/2和In=10A, qn=3p/2负序电流,如图15a所示。在t0时刻前后,三相输出电流始终得到很好的控制,三相电流THD值经检测为:t0时刻前,A相THD=0.63%;B相THD=1.21%;C相THD=1.32%。t0时刻后,A相THD=1.45%;B相THD=0.77%;C相THD=0.71%。为了均衡三相相间直流电压,需要注入SWZV,由式(14)计算得出,如图15b所示。图15c为三相相间直流电压,在t0时刻前后能够维持均衡。图15d和图15e分别为三相调制波电压和STATCOM输出电压,两者保持一致。
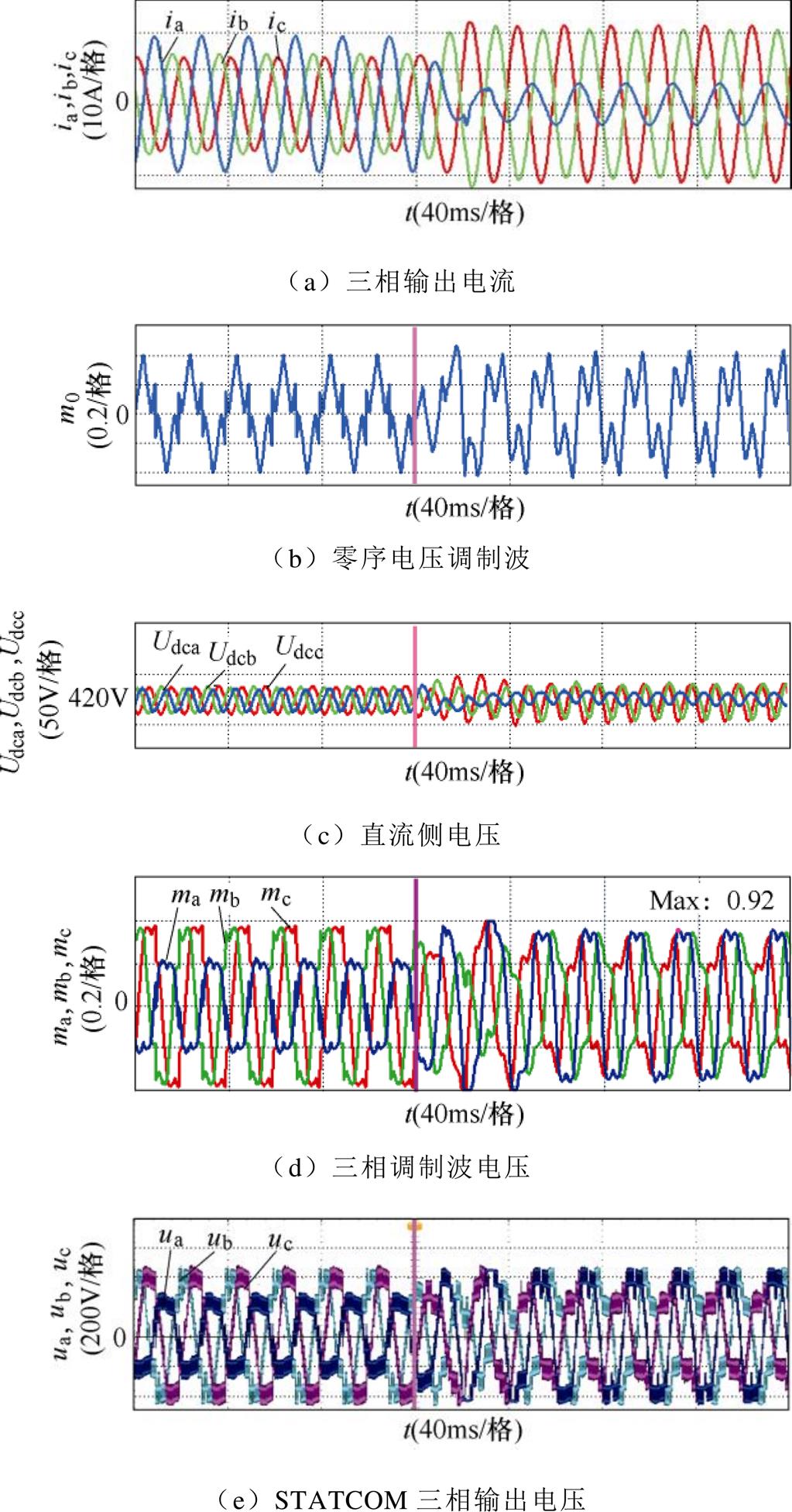
图15 采用SWZV的动态切换实验波形
Fig.15 The experimental waveforms with the negative sequence current transition of SWZV
本文提出基于相量图的零序电压几何分析方法,令零序电压相量在电流相量上的投影抵消输出电压相量在电流相量上投影的有功相量,并将零序电压相量在电流相量上投影的相量构成三角形,推导出零序电压相量与该三角形外心满足相位相同、模长比值为2 1的关系。根据三角形的外心几何性质,本文提出一种新的零序电压计算方法。以此为基础,将零序电压以方波形式注入,提高STATCOM的直流电压利用率。与传统方法比较,本文研究的方法能够有效拓宽其补偿负序电流的范围。最后,分别在10kV/±1Mvar Matlab/Simulink仿真平台和400V/±7.5kvar实验平台上验证了所提控制策略的正确性和可行性。仿真及实验结果表明,本文提出的零序电压注入法不仅能够保证相间直流电压均衡,且较大程度地扩展了SCHB STATCOMN补偿负序电流的范围。
1的关系。根据三角形的外心几何性质,本文提出一种新的零序电压计算方法。以此为基础,将零序电压以方波形式注入,提高STATCOM的直流电压利用率。与传统方法比较,本文研究的方法能够有效拓宽其补偿负序电流的范围。最后,分别在10kV/±1Mvar Matlab/Simulink仿真平台和400V/±7.5kvar实验平台上验证了所提控制策略的正确性和可行性。仿真及实验结果表明,本文提出的零序电压注入法不仅能够保证相间直流电压均衡,且较大程度地扩展了SCHB STATCOMN补偿负序电流的范围。
附 录
根据式(1),三相输出电流的表达式为
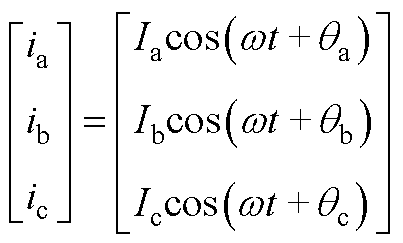 (A1)
(A1)
利用正负序分离,三相输出电流还可表示为正序分量和负序分量叠加,即
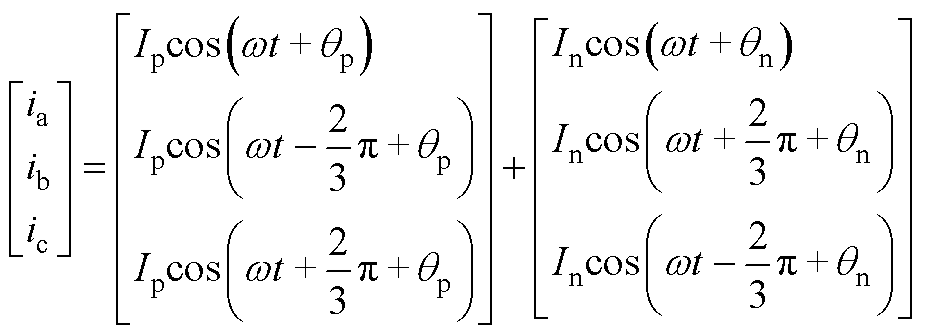 (A2)
(A2)
式中,等号右边第一个式子为正序电流;第二个式子为负序电流。
将式(A2)进行展开并重新合并,结合式(A1),可以得到三相输出电流幅值相位与正负序电流幅值相位的关系为
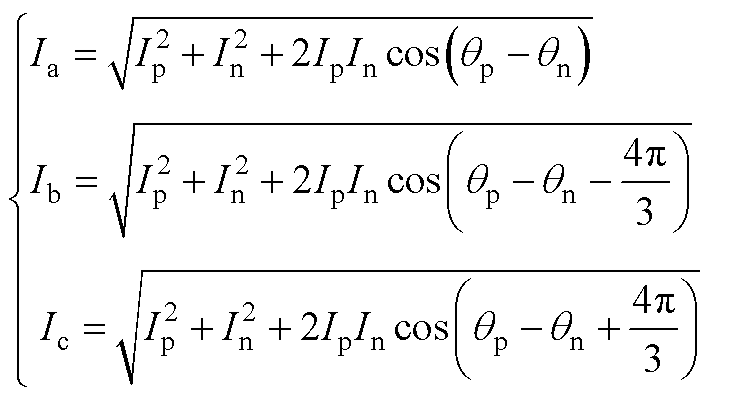 (A3)
(A3)
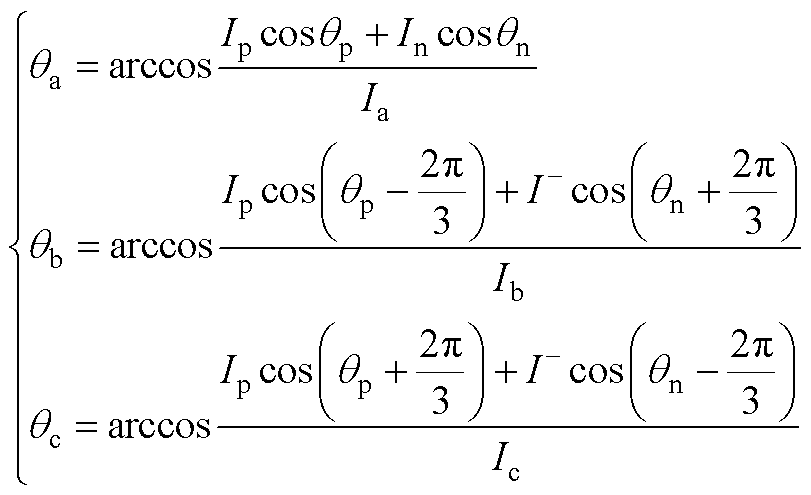 (A4)
(A4)
参考文献
[1] 王涛, 诸自强, 年珩. 非理想电网下双馈风力发电系统运行技术综述[J]. 电工技术学报, 2020, 35(3): 455-471.
Wang Tao, Zhu Ziqiang, Nian Heng. Review of operation technology of doubly-fed induction generator- based wind power system under nonideal grid con- ditions[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 455-471.
[2] 肖非然, 倪周, 闵永智, 等. 一种基于多智能体的多站协同高速铁路不平衡补偿方法[J]. 电工技术学报, 2020, 35(16): 3518-3528.
Xiao Feiran, Ni Zhou, Min Yongzhi, et al. Unbalanced compensation method of multi-station cooperative for high-speed railway based on multi-agent[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(16): 3518-3528.
[3] 游广增, 马斌, 朱毅. 牵引变压器接线方式对谐波和负序的影响研究[J]. 电气技术, 2014, 15(3): 14-18, 40.
You Guangzeng, Ma Bin, Zhu Yi. Study on influence of traction transformer wiring to harmonic and negative sequence[J]. Electrical Engineering, 2014, 15(3): 14-18, 40.
[4] 王轩, 魏宏, 欧朱建, 等. 一种抑制HVDC换相失败的STATCOM补偿方案[J]. 电力系统保护与控制, 2018, 46(5): 135-142.
Wang Xuan, Wei Hong, Ou Zhujian, et al. A STATCOM compensation scheme for suppressing commutation failure in HVDC system[J]. Power System Protection and Control, 2018, 46(5): 135-142.
[5] 刘刚, 张扬, 高志军, 等. 基于不对称分析的高压链式STATCOM的低压穿越控制策略[J]. 电力系统保护与控制, 2015, 43(21): 112-119.
Liu Gang, Zhang Yang, Gao Zhijun, et al. Low voltage ride through control strategy of high voltage cascaded STATCOM based on asymmetric analysis[J]. Power System Protection and Control, 2015, 43(21): 112-119.
[6] 姚钢, 方瑞丰, 李东东, 等. 链式静止同步补偿器的直流电容电压平衡控制策略[J]. 电力系统保护与控制, 2015, 43(18): 23-30.
Yao Gang, Fang Ruifeng, Li Dongdong, et al. DC capacitor voltage balancing control of cascaded static synchronous compensator[J]. Power System Pro- tection and Control, 2015, 43(18): 23-30.
[7] Hatano N, Ise T. Control scheme of cascaded H-bridge STATCOM using zero-sequence voltage and negative-sequence current[J]. IEEE Transaction on Power Delivery, 2010, 25(2): 543-550.
[8] Song Qiang, Liu Wenhua. Control of a cascade STATCOM with star configuration under unbalanced conditions[J]. IEEE Transactions on Power Elec- tronics, 2009, 24(1): 45-58.
[9] Ota J I Y, Shibano Y, Niimura N, et al. A phase- shifted-PWM D-STATCOM using a modular multi- level cascade converter (SSBC)-part I: modeling, analysis, and design of current control[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 279-288.
[10] Chen H, Wu Pingheng, Lee C, et al. Zero-sequence voltage injection for DC capacitor voltage balancing control of the star-connected cascaded H-bridge PWM converter under unbalanced grid[J]. IEEE Transaction on Industry Applications, 2015, 51(6): 4584-4594.
[11] Lu Daorong, Zhu Jianxin, Wang Jiangfeng, et al. A simple zero-sequence-voltage-based cluster voltage balancing control and the negative sequence current compensation region identification for star-connected cascaded H-bridge STATCOM[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8376-8387.
[12] Chen H C, Wu Pingheng, Lee C T, et al. Zero- sequence voltage injection for DC capacitor voltage balancing control of the star-connected cascaded H-bridge PWM converter under unbalanced grid[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 4584- 4594.
[13] 史晏君. 级联多电平STATCOM/BESS的关键控制技术研究[D]. 武汉: 华中科技大学, 2012.
[14] 熊桥坡. 级联多电平静止同步补偿器及其负序补偿若干关键技术研究[D]. 长沙: 湖南大学, 2014.
[15] He Zhixing, Ma Fujun, Xu Qianming, et al. Reactive power strategy of cascaded delta-connected STATCOM under asymmetrical voltage conditions[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2017, 5(2): 784-795.
[16] Du Sixing, Liu Jinjun. A brief comparison of series-connected modular topology in statcom application[C]//2013 IEEE ECCE Asia Downunder, Melbourne, VIC, 2013: 456-460.
[17] Behrouzian E, Bongiorno M. Investigation of negative- sequence injection capability of cascaded H-bridge converters in star and delta configuration[J]. IEEE Transactions on Power Electronics, 2016, 32(2): 1675-1683.
[18] 季振东, 孙毅超, 李东野, 等. 星形和三角形连接的链式H桥STATCOM不平衡补偿分析[J]. 高电压技术, 2015, 41(7): 2435-2444.
Ji Zhendong, Sun Yichao, Li Dongye, et al. Com- parative analysis for unbalance compensation of cascaded H-bridge STATCOMs between star and delta configuration[J]. High Voltage Engineering, 2015, 41(7): 2435-2444.
[19] Neyshabouri Y, Chaudhary S K, Teodorescu R, et al. Improving the reactive current compensation capability of cascaded H-bridge based STATCOM under unbalanced grid voltage[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1466-1476.
[20] 孟繁庆, 易新强, 刘海涛, 等. 三次谐波注入下多相感应电机稳态性能分析[J]. 电工技术学报, 2020, 35(16): 3396-3405.
Meng Fanqing, Yi Xinqiang, Liu Haitao, et al. Steady-state performance analysis of multiphase induction motorwith third-order harmonic injection[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3396-3405.
[21] Yu Yifan, Konstantinou G, Hredzak B, et al. Power balance of cascaded H-bridge multilevel converters for large-scale photovoltaic integration[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(1): 292-303.
[22] Sochor P, Akagi H. Theoretical comparison in energy-balancing capability between star- and delta- configured modular multilevel cascade inverters for utility-scale photovoltaic systems[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(3): 1980-1992.
[23] 朱建鑫, 胡海兵, 陆道荣, 等. 应用于级联STATCOM的高精度低成本全FPGA实时仿真模型研究[J]. 电工技术学报, 2019, 34(4): 777-785.
Zhu Jianxin, Hu Haibing,Lu Daorong, et al. The research on fully FPGA-based real-time simulation with high fidelity and low cost for the cascaded STATCOM[J]. Transactions of China Electro- technical Society, 2019, 34(4): 777-785.
[24] 贺功保. 三角形的六心及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2015.
Zero-Sequence-Voltage Injection Based on Square-Wave to Balance Cluster Voltages for Star-Connected Cascaded STATCOM
Abstract When star-connected cascaded H-bridge STATCOM compensates for the negative sequence current, the active power among clusters will be unbalanced, which will cause unbalanced cluster voltage. To maintain cluster voltage balance, zero sequence voltage is usually injected to redistribute the three-phase active power. However, the traditional calculation algorithms of the zero-sequence voltage are generally derived from the model based on active power, the equations are complicated and the mathematical mechanism is unclear. In addition, the injection of zero sequence voltage will greatly increase the output voltage of STATCOM, thus limiting the compensation range of the negative sequence current. This paper explores the geometric mechanism between zero sequence voltage and other electrical quantities with the help of voltage phasor diagrams, and proposes a special method for solving zero sequence voltage. To extend the range of the negative sequence current, this paper also studies a zero-sequence voltage injection method in the form of a square wave to improve the DC side voltage utilization of STATCOM. Finally, 10kV/±1Mvar star CHB STATCOM simulation platform and 400V/±7.5kvar experimental testbench verify the proposed control method.
keywords:Cascaded H-bridge STATCOM, zero sequence voltage injection, cluster voltage balancing, negative sequence current compensation
DOI: 10.19595/j.cnki.1000-6753.tces.210008
中图分类号:TM461
陆道荣 男,1991年生,博士,研究方向为电能质量治理与多电平变换器控制。E-mail: tcludaorong@nuaa.edu.cn
胡海兵 男,1973年生,博士生导师,教授,研究方向为电能质量治理、多电平变换器控制和谐振变换器等。E-mail: huhaibing@nuaa.edu.cn(通信作者)
收稿日期 2021-01-04
改稿日期 2021-05-11
国家自然科学基金资助项目(52007081)。
(编辑 陈 诚)