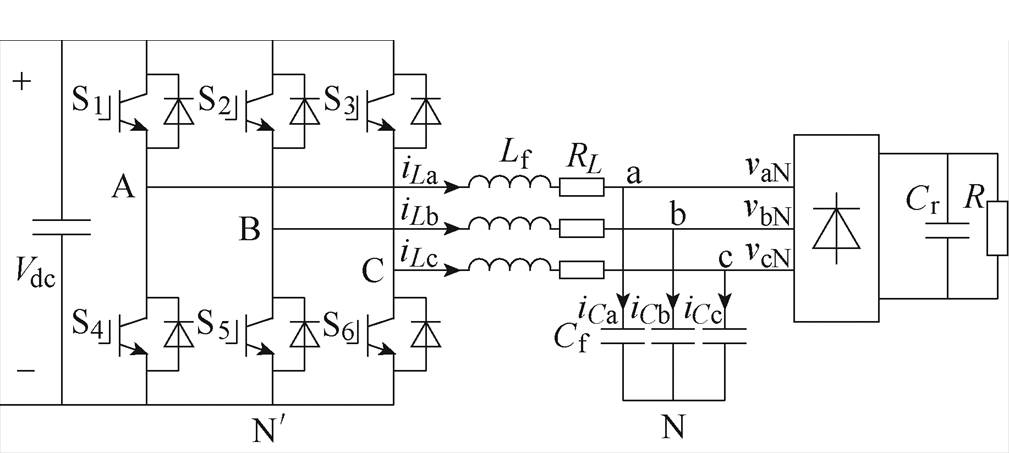
图1 三相离网逆变器拓扑结构
Fig.1 The structure of three phase off-grid inverter
摘要 针对离网逆变器带非线性负载时输出电压存在畸变问题，该文提出一种基于六倍频重复控制器与最优预见控制的复合控制策略，将六倍频重复控制器具有的无差调节和快速调节的优势与最优控制的线性二次型设计方法相结合，仅给定控制加权矩阵和输出加权系数就可求解出状态变量、重复控制器和指令的反馈系数，并保证系统稳定。根据被控对象的状态空间方程和六倍频重复控制器，设计扩大误差方程，将重复控制器参数设计问题转化为线性二次型问题，并通过黎卡提方程对控制参数进行最优整定。最后，搭建一台容量为10kV·A的样机，验证该文所提方法的有效性。
关键词：重复控制 最优预见控制 离网逆变器 非线性负载
随着环境问题和能源危机日益严重，可再生能源，如太阳能和燃料电池，被广泛应用于由分布式发电系统组成的微电网中。微电网可以并网运行或离网运行[1-4]，当微电网运行在离网模式时，逆变器的控制策略对输出电能质量和系统稳定性具有重要的影响[5-12]。
基于内模原理（Internal Model Principle, IMP）的谐振控制器和重复控制器受到了广泛的关注[9-15]。但是，由于重复控制器存在滞后环节，单一的重复控制器动态性能较差，因此很多学者对重复控制器进行不断的改进和完善。文献[16-18]提出了重复控制与PI控制器结合的复合控制策略，该策略对于线性负载有良好的动态性能，但是由于两种控制器之间存在耦合问题[19]，在非线性负载的动态调整过程中会互相影响，调节过程中误差波动较大。文献[12]根据非线性负载所造成的输出电压谐波分布特点提出了奇次重复控制器，将重复控制器的滞后时间缩短了一半。文献[11]提出了六倍频重复控制器，使重复控制器的滞后时间缩短为原来的1/6，在保证控制性能的前提下大大提高了控制器的动态性能。文献[20]提出了双分数阶近似的方法，对六倍频重复控制器进行了改进，解除了采样频率必须是指令频率6的倍数的限制，提高了六倍频重复控制器的适应性，但缺乏相关控制系统的理论分析。
关于重复控制器参数整定的方法，文献[21]给出了相关理论分析和实验验证，但这种参数整定方法在设计补偿器时需要设计较多的参数，同时参数选择不合适会导致系统不能稳定工作。
本文在进行控制器的设计时考虑数字控制带来的一阶滞后环节，在控制中引入状态反馈、重复控制以及预测的指令，通过离散提升技术将输入滞后环节消除并建立扩大误差方程，构建性能指标函数，最后应用线性二次型最优控制优化得到系统的最优预见重复控制器参数。相对于传统的重复控制器整定方式，具有设计思路清晰、设计流程简洁的优点，并且对线性与非线性负载都有出色的稳态性能和动态性能。
三相离网逆变器的拓扑结构如图1所示。图中，Vdc为直流母线电压，S1～S6为开关，Lf为逆变器侧电感，RL为电感Lf的等效内阻，Cf为滤波电容，Cr和R分别为二极管整流的支撑电容和电阻负载；iLa、iLb和iLc为滤波电感电流；iCa、iCb和iCc为滤波电容电流；vaN、vbN和vcN为逆变器输出电压。
图1 三相离网逆变器拓扑结构
Fig.1 The structure of three phase off-grid inverter
本文采用前馈解耦的方法对电感和电容进行解耦[22]。下面以d轴为例，建立三相逆变器状态空间方程。选择d轴输出电压vCd和滤波电容Cf在d轴的电流iCd为状态变量；选择控制器输出的占空比D作为逆变器输入，忽略作为扰动量的负载电流。据此可以推导出状态空间模型为
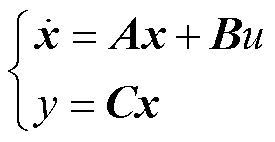（1）
其中
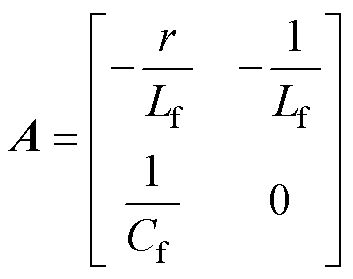
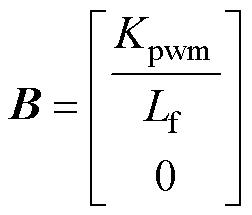
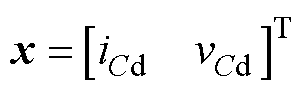
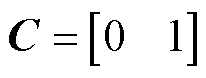
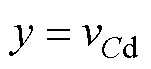
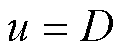
式中，Kpwm为三相逆变桥的传递函数。
由于采用数字控制，生成PWM时存在一拍延时，因此将式（1）离散化，并在输入中加入一阶滞后环节可得
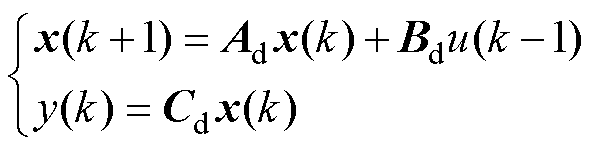（2）
式中，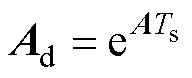
；
；
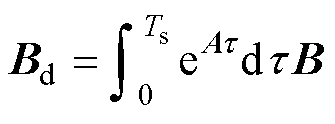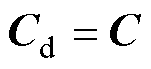；Ts为离散化的采样周期。
重复控制器的基本思想源于控制理论中的内模原理，它是把系统外部信号的动态模型植入控制器内，在稳定的闭环系统中包含外部输入信号的数学模型，即可实现对周期信号的零稳态误差跟踪。典型的重复控制器结构如图2所示。
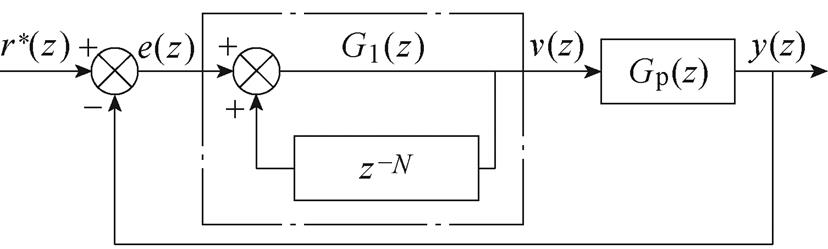
图2 重复控制器结构
Fig.2 Structure of repetitive controller
图2中，r*(z)为指令输入；e(z)为输出与指令的误差；v(z)为控制器输出；y(z)为系统输出；Gp(z)为被控对象的传递函数。
根据图2可得到误差到输出之间的传递函数为
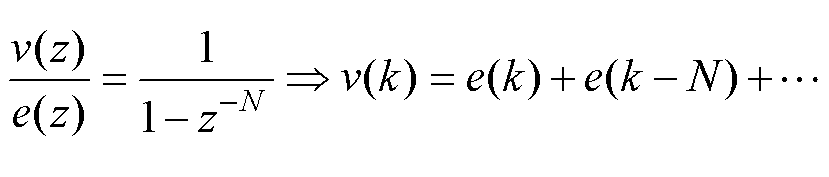（3）
图2中，N=To/Ts，To为输入信号的周期；z-N为延时环节，正反馈回路等效为周期信号的内模。根据式（3）可知，重复控制器实际上每N拍对误差进行一次积累，其作用相当于PI调节器的积分作用。由于每隔一个周期To进行一次“积分”，所以第一个周期内重复控制不起作用，动态响应能力差。根据控制器特点，为了提高重复控制器的动态响应速度，可以适当地减小滞后阶数N，降低重复控制器的“积分”延迟。建立六倍频重复控制器内模[12, 18]，离散结构为
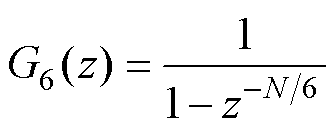（4）
假设指令信号频率fo=50Hz，则典型重复控制器和六倍频重复控制器的“积分”延迟分别为20ms、3.33ms。根据图3中不同控制器的幅频特性可知，降低延迟所带来的影响是改变了控制器的谐振频率。如六倍频重复控制器G6(z)，它只能在6kfo（k=1, 2, 3, …）频率处提供较大增益，实现此频率下的无差控制。
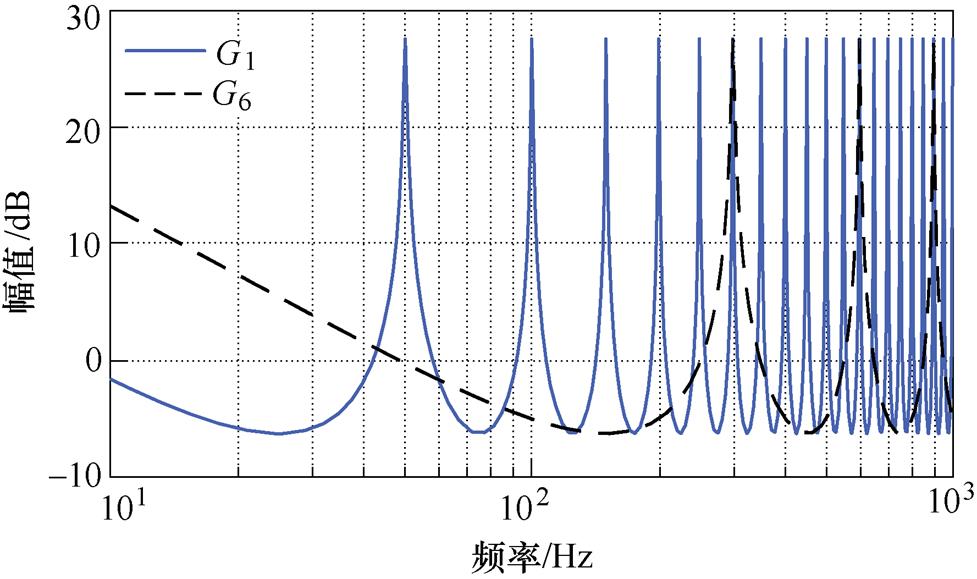
图3 不同重复控制器内模的幅频特性
Fig.3 Amplitude frequency characteristics of inner model of different repetitive controllers
对于三相平衡的离网逆变器在静止坐标系下，输出电压中除去高频分量一般只含有6k±1次谐波分量。控制器G1在相应频率处有较高增益，因此可以实现无差控制，而控制器G6在静止坐标系下不能实现无差控制。
在同步旋转坐标系中，输出电压中的谐波分量会基于坐标系旋转的影响产生相应的变化，不同坐标系的谐波序列对应关系见表1。假设基波角频率为wo且基波旋转方向为正方向，则在旋转坐标系中所有正序性谐波分量的次序需要减1，负序性谐波分量的次序需要加1。因此在dq坐标系中谐波分量变换到6k次频率，符合六倍频重复控制器的幅频特性。即在dq坐标系下，六倍频重复控制器对离网逆变器可以实现无差控制。
表1 不同坐标系的谐波序列对应关系
Tab.1 Corresponding relationship of harmonic sequences in different coordinate systems
静止坐标系中的谐波次序相序旋转坐标系中的谐波次序 1正序0 5负序6 7正序6 11负序12 13正序12 6k+1正序6k 6k-1负序6k
根据式（4）可知，六倍频重复控制的延迟为NTo/6，由于离散延迟只能为整数，因此如果采样频率选取的不合适，使得N/6舍去小数部分只取整数，会导致离散的重复控制器存在频率偏移问题。例如，采样频率为10kHz，指令为50Hz，故N/6=33（整数部分用NI表示）和1/3（小数部分用NF表示）之和，离散下N/6只能取33。图4给出了当前采样频率下重复控制内模在离散域传递函数G6z(z)和连续域传递函数G6s(s)的幅频特性曲线，显然离散域下存在谐振偏移fF=3.03Hz，由6kfo偏移到k(6fo+fF)。
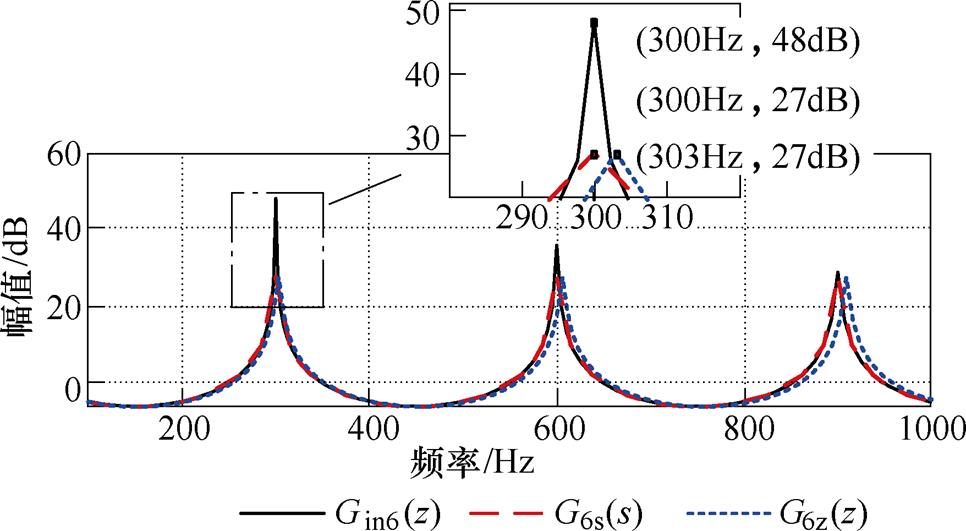
图4 离散和连续域下重复控制内模的幅频特性
Fig.4 Frequency characteristics of internal model with repetitive control in discrete and continuous domains
为了提高六倍频重复控制器的适用范围，根据文献[20]得到分数部分的拟合方程为
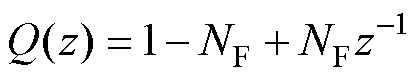（5）
根据式（5）以及整数部分可以得到离散域六倍频重复控制器准内模为
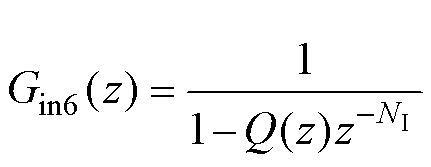（6）
图4中，Gin6(z)为式（6）的幅频特性，从图中可以看到，衰减函数Q(z)不仅起到了低通滤波器的效果提高了控制器的稳定性，还实现了拟合分数部分的作用矫正了谐振峰偏移的问题。
根据前文分析，需要转换到dq坐标系下才能使用六倍频重复控制器。为了简化设计过程，图5给出了d轴的最优预见重复控制系统框图[23]，左边框图为控制器，其中k1i为六倍频重复控制器系数；K2为状态反馈矩阵；K3为一阶滞后环节反馈矩阵；k4i为指令系数；Gin6(z)为离散域六倍频重复控制器准内模，NI为六倍频滞后环节的整数部分；右边为被控对象在离散域的状态方程，如式（2）所示。
根据z变换的性质可知，式（6）中重复控制器Gin6(z)时域形式为
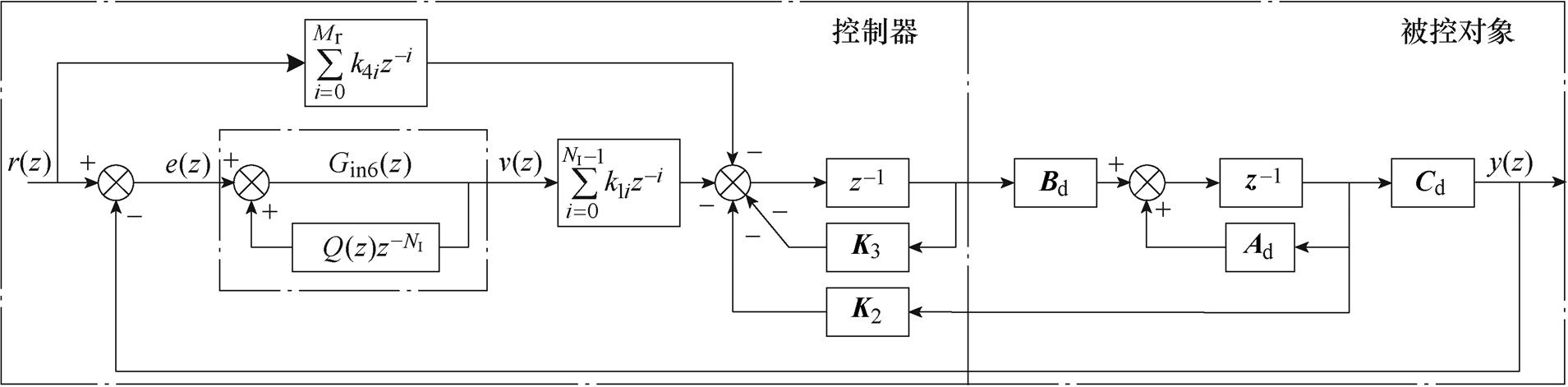
图5 最优预见重复控制系统框图
Fig.5 Structure of optimal preview repetitive control system
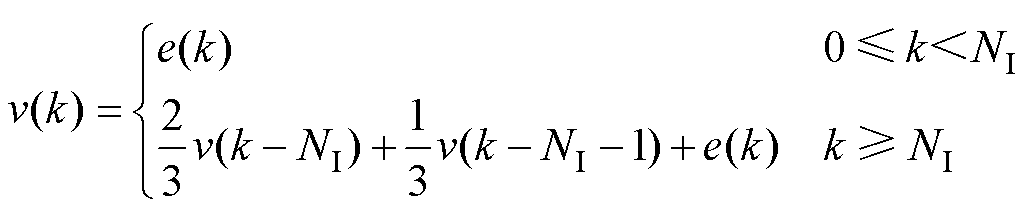（7）
现在对系统输入信号做如下假设：
系统的目标信号为r(k)，且Mr步可预见，Mr步以后取常数，即r(k+1), r(k+2), …, r(k+Mr)已 知，而r(k+j)=r(k+Mr)，j=Mr+1, Mr+2, …，根据假设可得到目标信号系统为
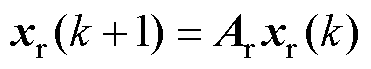（8）
其中
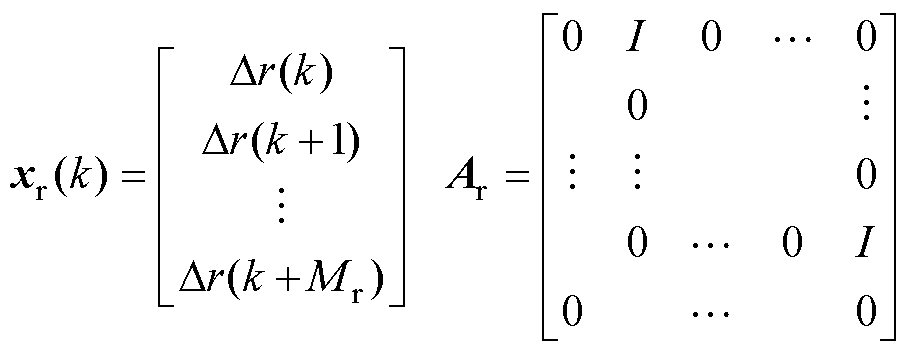
根据重复控制的滞后环节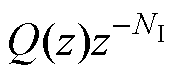
，定义差分算子为
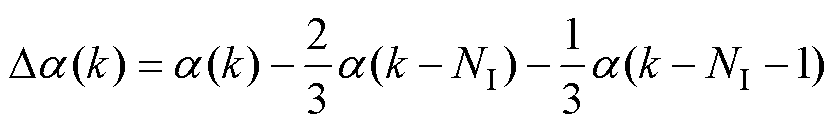（9）
式中，a(k)为任意向量。
根据图5可知系统的误差为
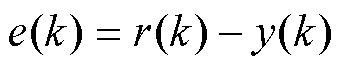（10）
根据式（9）并联立式（2）、式（10）可得系统误差方程为
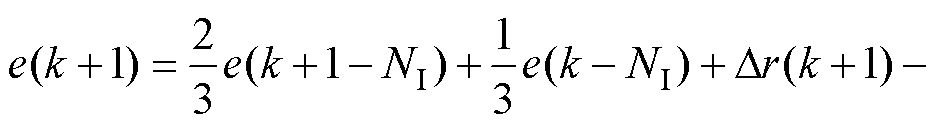
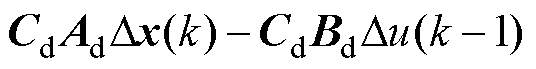（11）
联立式（2）和式（9），可得状态误差方程为
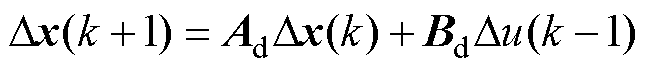（12）
联立式（11）、式（12）可得系统误差方程为
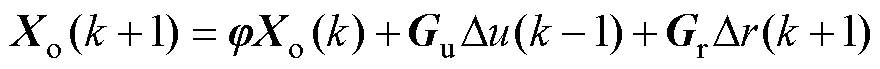（13）
其中
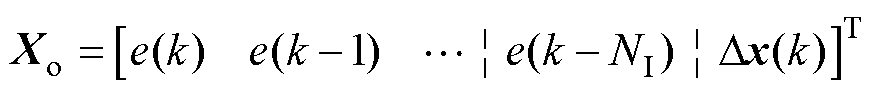
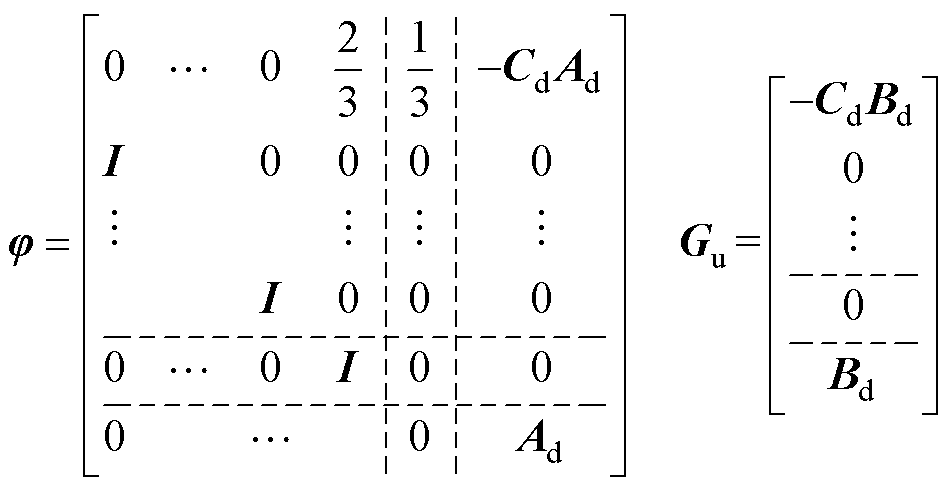
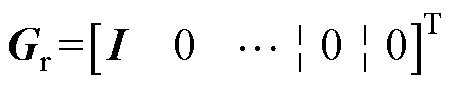
为了消除式（13）中的输入滞后，使用离散提升技术，将Du(k-1)增加到状态向量中，即将式（13）与恒等式Du(k-1)=Du(k)以及式（8）联立，可得系统扩大误差方程为
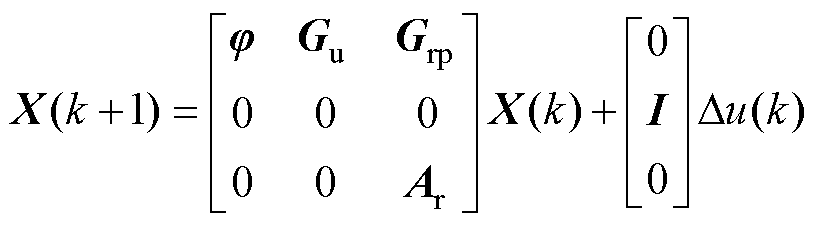（14）
其中
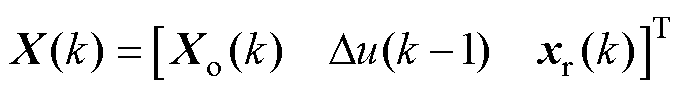
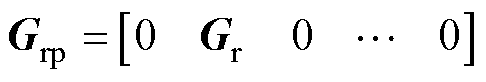
针对系统扩大误差方程式（14），定义二次型性能指标函数为
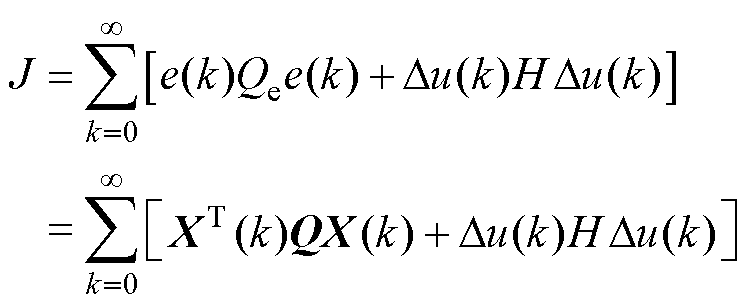（15）
式中，控制加权矩阵Q=diag(Qe, 0, …, 0)，Qe＞0，输出加权系数H＞0。式（15）第一项表示对误差e(k)的要求，Qe值越大，意味着要使J小，需要e(k)更小，也意味着闭环矩阵的特征值处于S平面更远的地方，这样误差e(k)就以更快的速度衰减到零，即动态性能更好；第二项是对控制能量的限制，动态性能越好，需要消耗的控制能量越大。
根据黎卡提方程稳态解，可以得到最优预见控制输入为
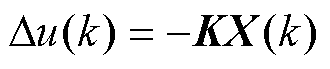（16）
式中，
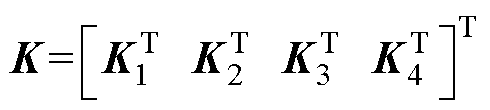，K1∈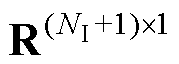
，K2∈R2×1，K3∈R1×1，K4∈
。
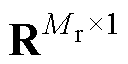根据式（13）和式（14），可以很方便地求解反馈矩阵K。
为了验证本文所提出的复合控制策略，搭建了额定容量为10kV·A的实验平台，实验样机如图6所示，具体实验参数见表2。主电路由3个IGBT半桥组成，逆变器输出采用LC滤波，控制器使用数字信号处理器TMS320F28335。
最优预见重复控制器参数选取：N=fs/fo=200，L取N/6的整数部分为33，衰减函数Q(z)选择式（5），NF取N/6的小数部分为1/3，为了保证系统稳定预见步数取Mr=1，状态加权系数Qe=100，控制加权系数H=1。
根据参考文献[20-21]设计了六倍频重复控制器，参数选取如下：相位超前补偿器为z7，重复控制增益kr=3.5，为了稳定系统采用电容电流反馈，反馈系数为Fi=10，衰减函数Q(z)选择式（5），补偿器选择二阶低通滤波器，截止频率为1kHz。
图6 实验样机
Fig.6 Experimental prototype
表2 三相离网型逆变器参数
Tab.2 Parameters of three phase off grid inverter
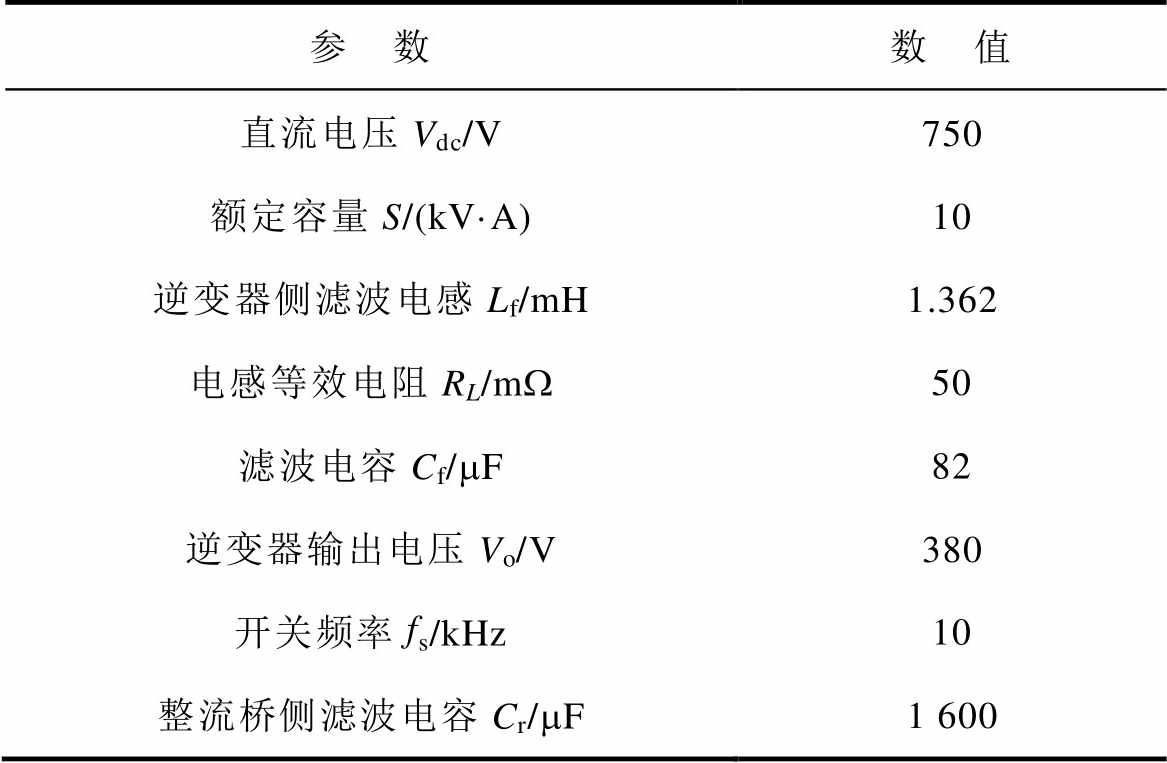
参 数数 值 直流电压Vdc/V750 额定容量S/(kV·A)10 逆变器侧滤波电感Lf/mH1.362 电感等效电阻RL/mW50 滤波电容Cf/mF82 逆变器输出电压Vo/V380 开关频率fs/kHz10 整流桥侧滤波电容Cr/mF1 600
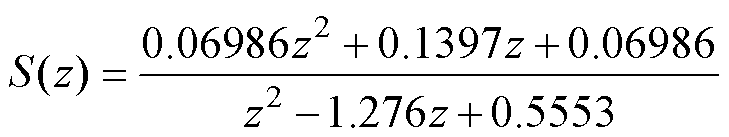（17）
设置了空载到满载的负载切换，验证最极端工况下系统的动态性能及其稳定性。同时为了验证所提出的最优预见重复控制器的性能，在相同工况与负载条件下对比了dq坐标系下的PI控制器以及六倍频重复控制器。
图7～图9依次为采用dq坐标系下的PI控制、六倍频重复控制以及最优预见重复控制在线性与非线性负载条件下的电压与电流波形，以及稳态时电压的快速傅里叶变换（Fast Fourier Transform, FFT）分析。图中，ia、vaN分别为逆变器a相的输出电流与电压。
当逆变器采用PI控制时，由图7a可知，线性负载情况下，调节时间为2ms，输出电压的总谐波畸变率（Total Harmonic Distortion, THD）为1.45%；根据图7b可知，非线性负载情况下输出电压质量则较差，THD达到8.24%。通过图8、图9发现，六倍频重复控制器与本文所提控制策略的动态响应基本一致，线性负载投入后经过5ms后输出电压达到稳态；非线性负载由于存在支撑电容，调节时间长于线性负载，动态响应时间约为一个基波周期。在稳态时逆变器输出电压的THD均不超过2%，优于GB/T 14549—1993[24]规定的5%。所提控制策略通过引入电容电流和输出电压的状态反馈且对输入的一阶滞后环节进行补偿，相较于六倍频重复控制器的电容电流反馈进一步提高了系统的稳定性。对比图8、图9可知，在两种负载情况下所提控制策略的控制效果均好于六倍频重复控制器，说明所提控制策略对线性负载与非线性负载均具有良好的动态与稳态性能。
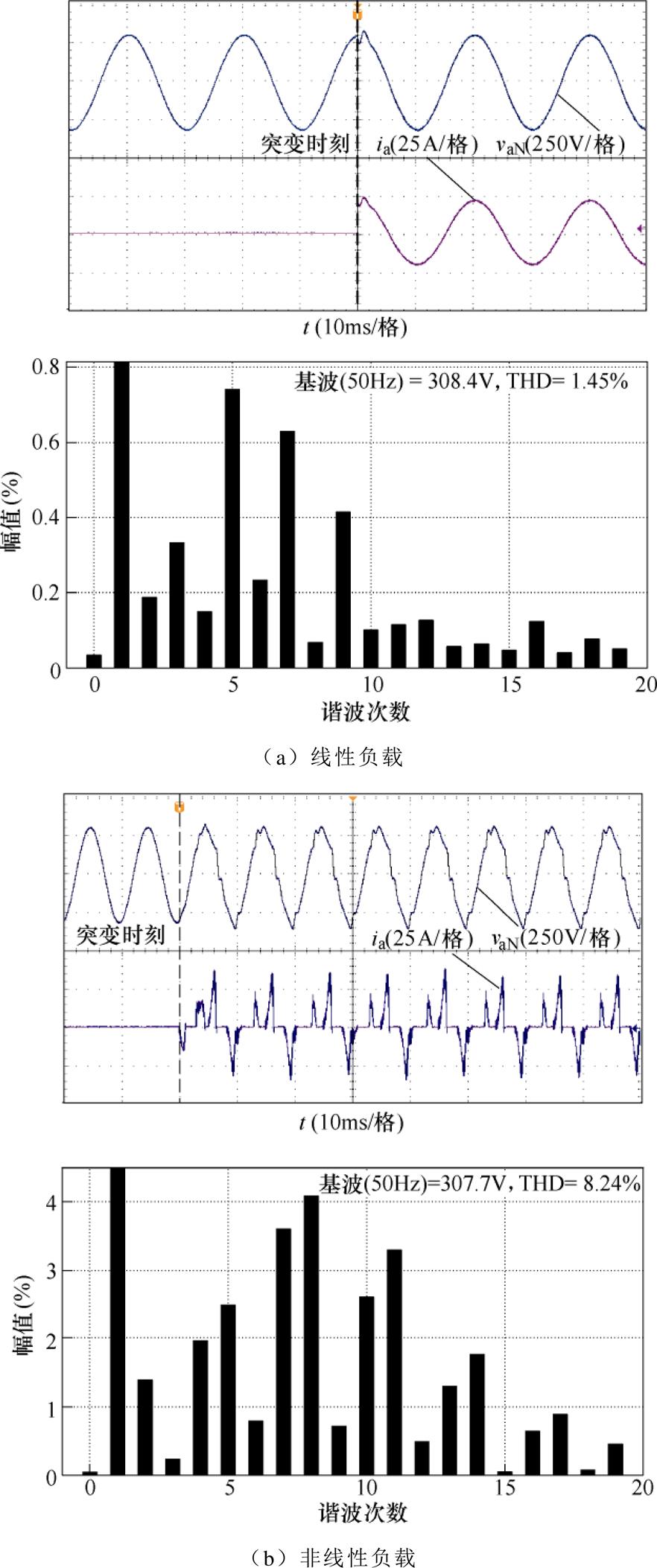
图7 dq坐标系下的PI控制器
Fig.7 PI controller in dq coordinate system
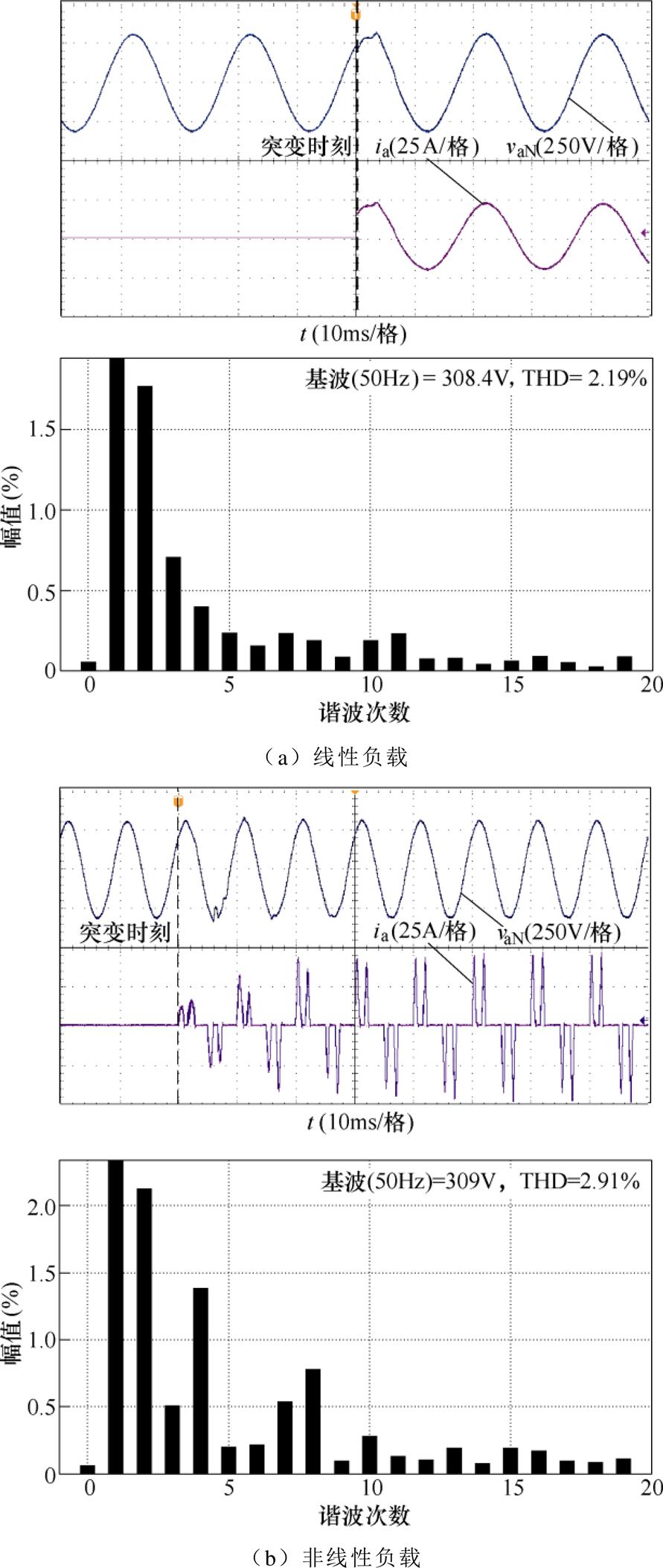
图8 六倍频重复控制器
Fig.8 Six fold repetitive controller
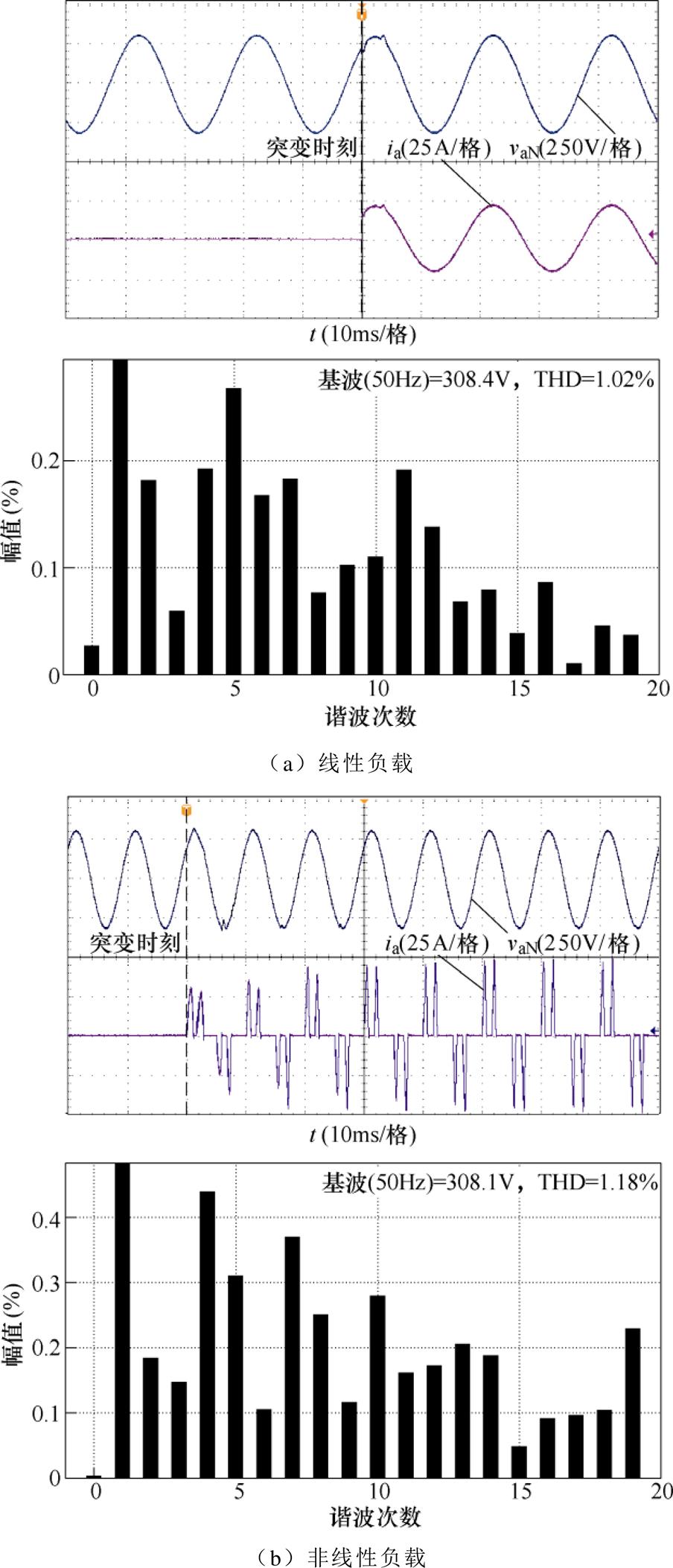
图9 最优预见重复控制器
Fig.9 Optimal preview repetitive controller
本文提出了一种基于六倍频重复控制和最优预见控制的新型控制策略，将重复控制器的整定问题转化为线性二次型性能指标的最优控制问题。相较于传统的重复控制策略，本文控制策略只需要给定性能指标函数即可得到相应的反馈系数，简化了控制参数的整定过程，整定难度大大降低。此外，通过在反馈中加入状态反馈以及一阶滞后环节的反馈，进一步提高了逆变器的稳定性。所提控制策略对于线性负载与非线性负载均具有良好的稳态和动态性能，保证三相逆变器在不同负载条件下均可以快速且准确地跟踪电压指令。
参考文献
[1] 张占俊, 李建文, 董耀, 等. 弱电网下多逆变器并网谐振失稳分析方法[J]. 电气技术, 2020, 21(10): 21-28.
Zhang Zhanjun, Li Jianwen, Dong Yao, et al. Method of resonance instability analysis of multiple grid- connected inverters in weak grid[J]. Electrical Engin- eering, 2020, 21(10): 21-28.
[2] 王晓寰, 张旭东, 郭红强. 基于相位簇扰动的下垂控制并网逆变器孤岛检测[J]. 电工技术学报, 2020, 35(8): 1728-1738.
Wang Xiaohuan, Zhang Xudong, Guo Hongqiang. Islanding detection of droop-controlled grid-connected inverters on phase cluster disturbance[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1728- 1738.
[3] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335.
Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[4] 郭磊磊, 金楠, 李琰琰, 等. 并网逆变器无电网电压传感器模型预测控制[J]. 电工技术学报, 2020, 35(12): 2612-2622.
Guo Leilei, Jin Nan, Li Yanyan, et al. Grid voltage sensorless model predictive control for grid- connected inverters[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2612-2622.
[5] 曹文远, 韩民晓, 谢文强, 等. 基于扰动观测器的电压源型逆变器负载电流前馈控制及参数设计方法[J]. 电工技术学报, 2020, 35(4): 862-873.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. A disturbance-observer-based load current feedforward control and parameter design method for voltage- sourced inverter[J]. Transactions of China Electro- technical Society, 2020, 35(4): 862-873.
[6] Zhou Keliang, Wang Danwei. Digital repetitive controlled three-phase PWM rectifier[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 309- 316.
[7] Hou Qingqing, Hu Cungang, Ye Qiubo, et al. New control strategy based on model predictions and PI for three-phase off-grid inverter[C]//2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 2016: 903-906.
[8] Yang Yunhu, Zhou Keliang, Cheng Ming, et al. Phase compensation multiresonant control of CVCF PWM converters[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3923-3930.
[9] Baek Seunghoon, Cho Younghoon, Yeo Sijun. Improved voltage control scheme for single-phase UPS inverter with repetitive current controller[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, United states, 2019: 1482-1487.
[10] Lorenzini Charles, Flores Jefersonvieira, Pereira Luisfernandoalves, et al. Repetitive controller with low-pass filter compensation applied to Uninter- ruptible Power Supplies (UPS)[C]//IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 2015: 3551-3556.
[11] Jiang Shuai, Cao Dong, Li Yuan, et al. Low-THD, fast-transient, and cost-effective synchronous-frame repetitive controller for three-phase UPS inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(6): 2994-3005.
[12] Zhou Keliang, Low Kay-soon, Wang Danwei, et al. Zero- phase odd-harmonic repetitive controller for a single- phase PWM inverter[J]. IEEE Transactions on Power Electronics, 2006, 21(1): 193-201.
[13] Xin Meiyan, Li Juan, Tan Cuilan, et al. State feedback repetitive control for single-phase inverters[C]//2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 2019: 719-723.
[14] 贾要勤, 朱明琳, 凤勇. 基于状态反馈的单相电压型逆变器重复控制[J]. 电工技术学报, 2014, 29(6): 57-63.
Jia Yaoqin, Zhu Minglin, Feng Yong. State feedback based repetitive control for single-phase inverter[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 57-63.
[15] 张凯, 彭力, 熊健, 等. 基于状态反馈与重复控制的逆变器控制技术[J]. 中国电机工程学报, 2006, 26(10): 56-62.
Zhang Kai, Peng Li, Xiong Jian, et al. State- feedback-with-integral control plus repetitive control for PWM inverters[J]. Proceedings of the CSEE, 2006, 26(10): 56-62.
[16] 张旗, 蔡逢煌, 黄丽梅, 等. 单相程控电流源PI+重复控制[J]. 电工技术学报, 2019, 34(增刊1): 163- 170.
Zhang Qi, Cai Fenghuang, Huang Limei, et al. PI+ repetitive control applied to single-phase pro- grammable standard power source[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 163- 170.
[17] 王斯然, 吕征宇. LCL型并网逆变器中重复控制方法研究[J]. 中国电机工程学报, 2010, 30(27): 69-75.
Wang Siran, Lü Zhengyu. Research on repetitive control method applied to grid-connected inverter with LCL filter[J]. Proceedings of the CSEE, 2010, 30(27): 69-75.
[18] 武健, 何娜, 徐殿国. 重复控制在并联有源滤波器中的应用[J]. 中国电机工程学报, 2008, 28(18): 66-72.
Wu Jian, He Na, Xu Dianguo. Application of repetitive control technique in shunt active power Filter[J]. Proceedings of the CSEE, 2008, 28(18): 66-72.
[19] 张兴, 汪杨俊, 余畅舟, 等. 采用PI+重复控制的并网逆变器控制耦合机理及其抑制策略[J]. 中国电机工程学报, 2014, 34(30): 5287-5295.
Zhang Xing, Wang Yangjun, Yu Changzhou, et al. Mechanism of the control coupling and suppression strategy using PI and repetitive control in grid- connected inverters[J]. Proceedings of the CSEE, 2014, 34(30): 5287-5295.
[20] 徐群伟, 吴俊, 吕文韬, 等. 基于双分数阶快速重复控制的有源电力滤波器电流控制策略[J]. 电工技术学报, 2019, 34(增刊1): 300-311.
Xu Qunwei, Wu Jun, Lü Wentao, et al. Current control strategy of active power filter based on double fractional-order rapid repetitive control[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(S1): 300-311.
[21] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198.
Zhao Qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5189-5198.
[22] Dannehl J, Wessels C, Fuchs F W. Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters[J]. IEEE Transa- ctions on Industrial Electronics, 2009, 56(2): 380- 388.
[23] 廖永龙, 廖福成. 利用提升-预估法设计离散时间时滞线性系统的预见控制器[J]. 控制与决策, 2017, 32(8): 1359-1367.
Liao Yonglong, Liao Fucheng. Design of preview controller for discrete-time linear systems with time delay by using the lifting-predictor method[J]. Control and Decision, 2017, 32(8): 1359-1367.
[24] 全国电压电流等级和频率标准化技术委员会. 电能质量公用电网谐波: GB/T 14549−93[S]. 北京: 中国标准出版社, 1993.
Optimal Preview Control of Three-Phase Inverter Based on Repetitive Control and State-Feedback
Abstract In order to solve the problem of output voltage distortion in off-grid inverter with nonlinear load, a new compound control strategy is proposed in this paper, which is based on six-fold repetitive controller and optimal preview control. The feedback coefficients of state variables, repetitive controllers and instructions can be solved by given a control weighting matrix and output weighting matrix, and the system stability can be guaranteed. According to the state space equation of the controlled object and the six-fold frequency repetitive controller, the extended error equation is designed. The parameter design problem of the repetitive controller is transformed into a linear quadratic problem, and the control parameters are optimally adjusted through the Riccati equation. Finally, a 10kV·A prototype is built to verify the effectiveness of the proposed method.
keywords：Repetitive control, optimal preview control, off-grid inverter, nonlinear load
DOI: 10.19595/j.cnki.1000-6753.tces.201705
中图分类号：TM464
兰梓冉 男，1996年生，硕士研究生，研究方向为逆变器数字控制技术以及重复控制技术。E-mail: 19121443@bjtu.edu.cn
郝瑞祥 男，1975年生，博士，副教授，博士生导师，研究方向为大功率电源、高频开关电源和电力电子变换器的数字控制技术。E-mail: haorx@bjtu.edu.cn（通信作者）
收稿日期 2020-12-29
改稿日期 2021-07-28
（编辑 陈 诚）