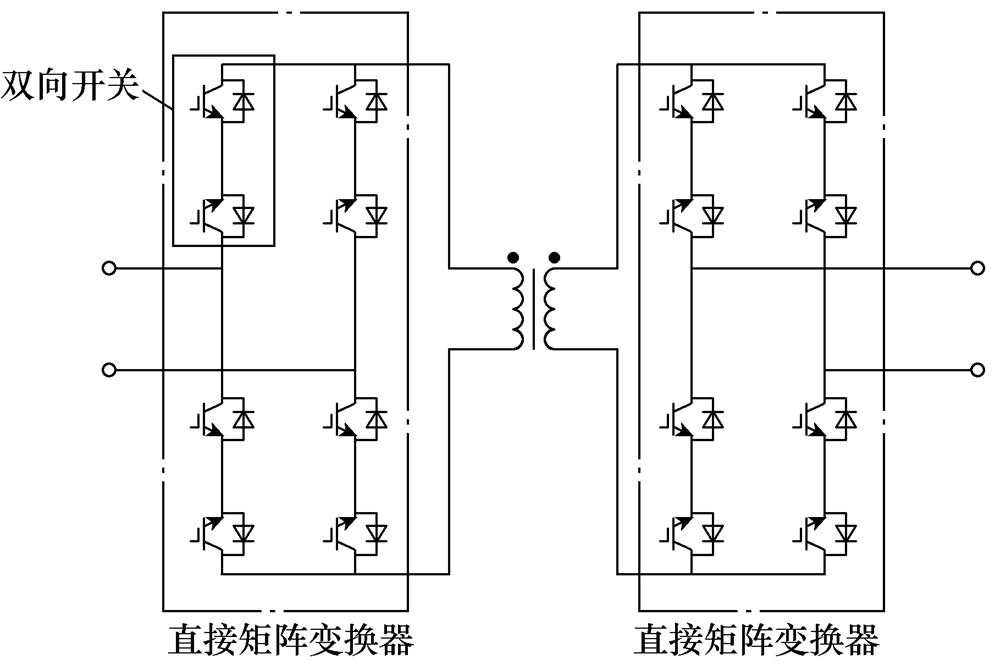
图1 直接矩阵型AC-AC PET
Fig.1 Direct matrix AC-AC PET
摘要 串联谐振间接矩阵型电力电子变压器（PET）通过高频开关并减小直流电容容值可实现高功率密度。然而，小直流电容会改变谐振回路等效电容，并影响高频谐振电流特性，进而影响零电流软开关（ZCS）的实现。该文建立小直流电容下串联谐振间接矩阵型PET等效电路，推导高频电流时域解析表达式，并对ZCS条件下的开关频率进行设计，揭示直流电容和死区时间对开关频率的影响规律。仿真和实验结果验证了该文理论分析的正确性。
关键词：AC-AC电力电子变压器 串联谐振 间接矩阵变换器 高频电流特性 零电流软开关(ZCS) 高功率密度和高效率
电力电子变压器（Power Electronic Transformer, PET），也称固态变压器（Solid-State Transformer, SST），一般是指通过电力电子技术及高频变压器实现的具有但不限于传统工频变压器功能的新型电力电子设备。电力电子变压器一般至少包括传统交流变压器的电压等级变换和电气隔离功能，此外，还包括交流侧无功功率补偿及谐波治理、可再生能源/储能设备直流接入、端口间的故障隔离功能以及与其他智能设备的通信功能等[1-3]；另一方面，PET通过高频开关可以提高变压器的工作频率，同时减小变压器自身的体积和质量，被认为适用于体积和质量受限的场合（如变电站、高铁、轮船、飞机等[4-7]）来替代传统工频变压器。然而，由于需要大量的半导体器件、电感电容等储能或滤波元件，且受到绝缘水平和散热系统体积的限制，PET功率密度的提高一直是一个挑战。另外，由于PET变换环节多，高频环节开关频率高，限制了效率的提高[8-9]。因此，实现AC-AC型PET替代传统工频变压器还需要进一步提高功率密度和效率。
PET一般适用于中高压大功率的场合，本文研究对象为可代替传统工频变压器的AC-AC型PET，该类型的拓扑结构很多，主要可分为级联H桥（Cascaded H-Bridge, CHB）型[10-13]、模块化多电平（Modular Multilevel Converter, MMC）型[14-16]和矩阵型[17-20]。其中，CHB型和MMC型PET都需要大量的直流储能电容，且交流侧需要较大的滤波电感，限制了其功率密度的提高。另外，由于CHB型和MMC型的AC-DC环节大多需要采用PWM或者最近电平调制，部分开关处于硬开关。相比于矩阵型PET型，CHB型和MMC型PET通常具有更多的功能，如无功补偿、直流端口接入等。实际上，在体积和质量受限的场合，PET可牺牲部分功能来换取更高的效率和功率密度。最早使用PET的提出的目的是替代传统变压器，采用直接矩阵变换器[17]，直接矩阵型AC-AC PET如图1所示，但是器件会承受反向电压，因此需要采用双向开关。2008年GE公司提出一种间接矩阵型AC-AC PET[18]，电路拓扑如图2所示，其优点是器件不会承受反向电压，无需双向开关。另外，工频整流和高频逆变环节通过直流电容分离，器件之间的寄生参数不会相互影响，更有利于高频环节的软开关设计。此类PET的缺点是功能简单，但是功率密度和效率相对较高[19-20]。
图1 直接矩阵型AC-AC PET
Fig.1 Direct matrix AC-AC PET
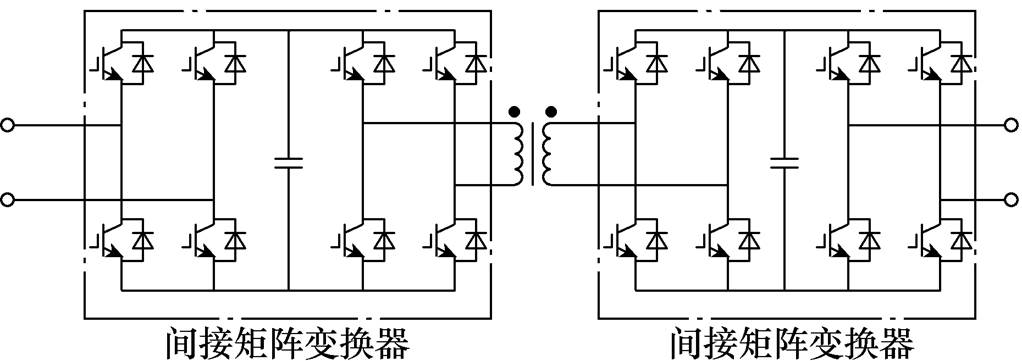
图2 间接矩阵型AC-AC PET
Fig.2 Indirect matrix AC-AC PET
间接矩阵型AC-AC PET也可以看作由工频整流桥和逆变桥以及高频隔离型DC-DC环节组成。其中，为了提高PET的效率，主要是提高高频隔离环节的运行效率，工频整流桥和逆变桥的开关频率仅为50Hz。常用的高频隔离环节拓扑有移相型双有源桥（Dual Active Bridge, DAB）变换器和串联谐振型DAB两种[21-23]。其中移相型DAB的零电压软开关（Zero Voltage Switching, ZVS）范围受负载影响且存在较大的关断损耗[23]。串联谐振型DAB通过合理设计励磁电感和死区时间可实现较大范围的ZVS，通过合理设计开关频率可实现全负载范围的零电流软开关（Zero Current Switching, ZCS）[24-25]。基于此优点，将串联谐振DAB作为高频隔离环节变换器更有利于效率的提高[26]。
串联谐振间接矩阵型PET即将图2高频变压器与谐振电容串联。该类型PET具有矩阵变换器能量直接传输、直流电容小的特点，也具有谐振变换器效率高的优点。但是，输入和输出侧H桥均工作在50Hz开关频率，网侧功率因数不可控，直流电容会在网侧产生无功。减小直流电容不仅可以减小网侧无功，还能进一步提高功率密度。然而，对于串联谐振型DAB来说，直流电容通常远大于谐振电容（10倍以上）[14, 26]，而直流电容的减小使得直流侧不可以再等效为直流电压源来分析，而是会参与谐振，影响谐振频率，如果依然按照原有的串联谐振电容和谐振电感来设计开关频率将无法满足ZCS。另外，死区时间的设置不仅用于避免上下管直通，还用于实现ZVS[25]。因此，减小直流电容和设置死区时间后的高频电流特性需要重新进行分析，以保证ZCS。
现有文献对于串联谐振DAB的分析基本都将直流侧等效为电压源，关于直流电容对于谐振电流影响的分析较少。文献[27]提出了一类直流电容参与谐振的直流变压器拓扑，并分析了小直流电容对于高频谐振电流的影响，但是该文分析的是采用单只开关器件的直流变换器电路，不适用于大功率场合。文献[28]分析了小直流电容下串联谐振型DAB高压侧采用半桥，低压侧采用全桥下的高频电流特性。文献[29-30]分析了串联谐振型DAB高、低压侧都采用半桥结构下的高频电流特性，并给出了ZCS时开关频率与谐振频率的关系。然而，全桥和半桥拓扑中的直流电容在高频开关周期内的充放电特性不同：半桥结构中直流电容存在半个高频开关周期都处于充电的状态，而全桥结构直流电容在半个开关周期即完成充放电，所以，文献[28-30]推导的结果不适用于全桥结构的串联谐振型DAB。另外，只有文献[28]考虑了死区内对直流电容的充放电影响，但是其结论不适用于全桥结构下ZCS开关频率设计。
为了在减小直流电容提高功率密度的同时，实现ZCS，提高效率，本文首先建立了串联谐振间接矩阵型PET等效电路，推导得到了高频开关周期内高频电流的时域解析表达式，并考虑了死区时间的影响，据此计算得到了实现ZCS的开关频率和直流电容、串联谐振电容、谐振电感、死区时间之间的定量关系以及影响规律。最后，通过仿真和实验验证了高频电流特性分析的正确性和ZCS开关频率设计的准确性。
串联谐振间接矩阵型PET电路拓扑如图3所示，串联谐振间接矩阵型PET拓扑由整流桥H1、串联谐振型DAB和逆变桥H2组成。串联谐振型DAB电路拓扑如图4所示，由逆变桥H1、整流桥H2、直流电容C1、直流电容C、高频变压器（High Frequency Transformer, HFT）和串联谐振电容Cr 组成。
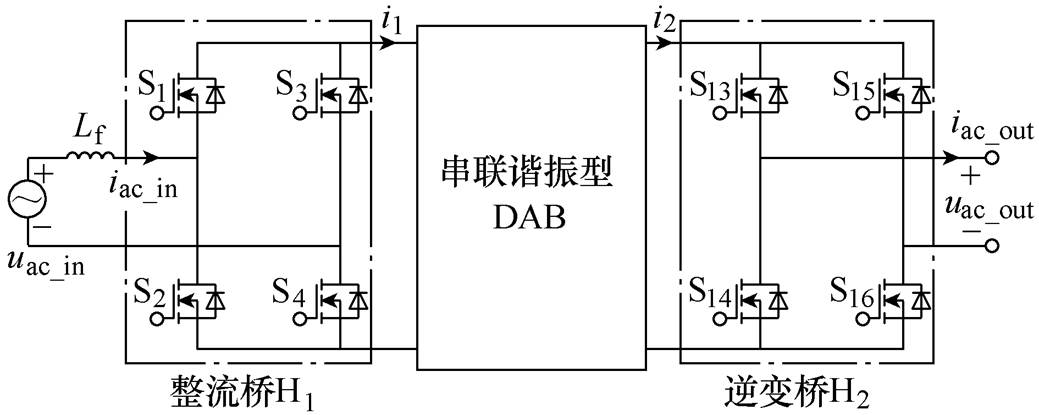
图3 串联谐振间接矩阵型PET电路拓扑
Fig.3 Circuit topology series resonant indirect matrix PET
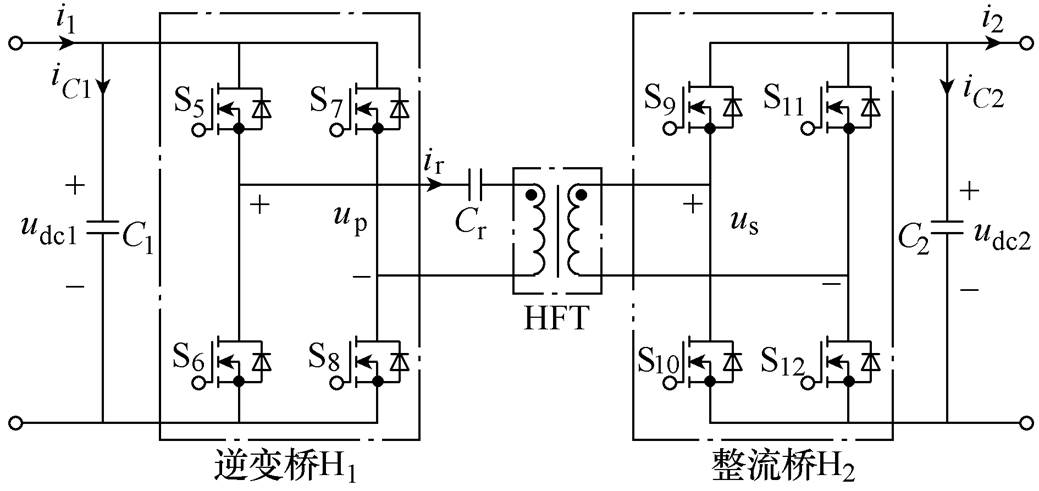
图4 串联谐振型DAB电路拓扑
Fig.4 Circuit topology series resonant DAB
对于整流桥H1，当交流输入电压uac_in为正时，开关S1、S4导通；当uac_in为负时，开关S2、S3导通，直流电压udc1=|uac_in|。直流电压udc1通过串联谐振型DAB变换为udc2，设变压器一次、二次电压比为n
1，则udc2=udc1/n。对于逆变桥H2，采用和整流桥H1同样的控制方法，直流电压udc2被逆变为交流输出电压uac_out，且uac_out=uin/n。低频交流电压、电流、直流电压示意图如图5所示。由于整流桥工作在同步整流状态，无法控制网侧功率因数，则直流电容会在网侧产生无功功率。
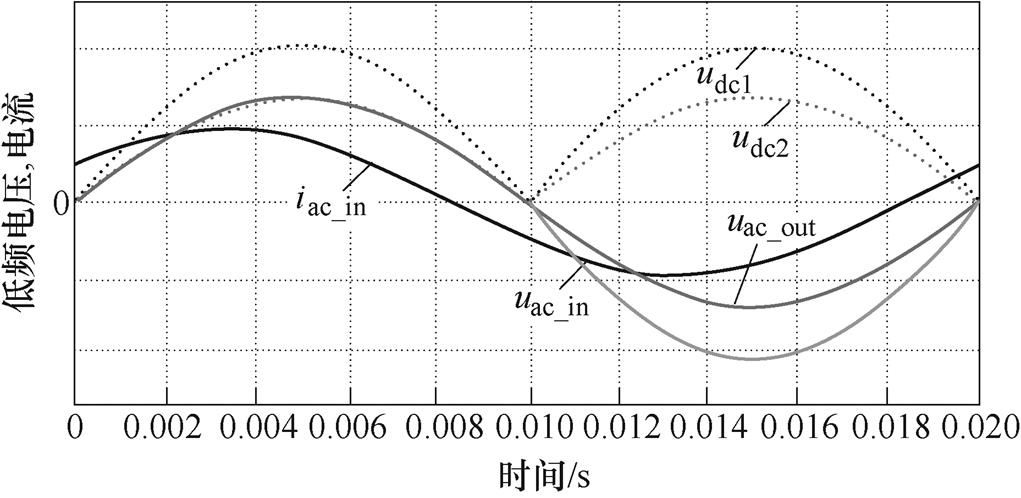
图5 低频交流电压、电流、直流电压示意图
Fig.5 Schematic diagram of low frequency AC voltage, current and DC voltage
对于串联谐振型DAB，采用50%占空比开环控制，开关周期为Ts。通常，串联谐振DAB直流电容远大于谐振电容，因此直流电容对高频谐振环节不会产生影响，直流侧可等效为直流电压源进行分析。由于直流电压是呈现低频波动的，因此高频电压up、us也是含有低频包络的，高频电流ir是含有低频包络的正弦电流。典型的工作波形如图6所示，为了显示方便，图中高频开关频率仅为500Hz，要实现ZCS，只需要满足设计开关周期Ts等于谐振周期Tr与死区时间2Tz之和，即
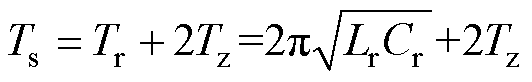（1）
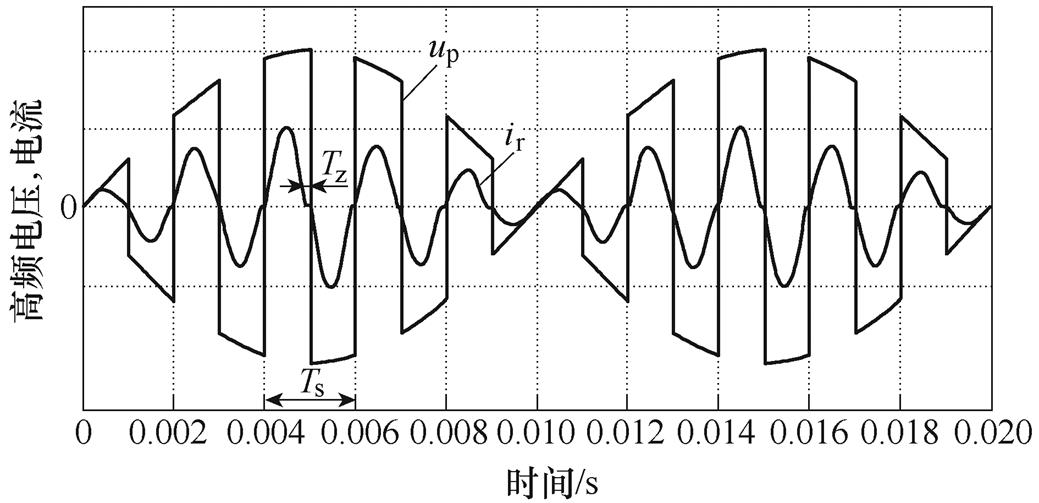
图6 高频电压、电流示意图
Fig.6 Schematic diagram of high frequency voltage and current
本节建立了考虑直流电容在内的高频开关周期等效电路，得到高频电流的时域解析表达式。
在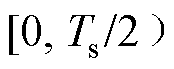 
内，电流路径和等效电路如图7所示，在 
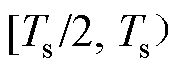内，电流路径和等效电路如图8所示。因为PET输入和输出侧均含有滤波电感，起到了电流滤波的作用，在一个高频开关周期Ts内，低频直流侧输入电流i1和直流侧输出电流i2相对于高频谐振电流ir变化很小，因此i1、i2在高频开关周期Ts时认为是恒定不变的，可等效为电流源模型。根据变压器的电压比n，所有量均折算至变压器一次侧。折算至一次侧的变压器漏感为Lr，谐振电容为Cr，直流电容C2折算至一次侧为C2_eq，直流输出电流i2折算至一次侧为i2_eq，其中，C2_eq=C2/n2，i2_eq=i2/n，iC2_eq=iC2/n。
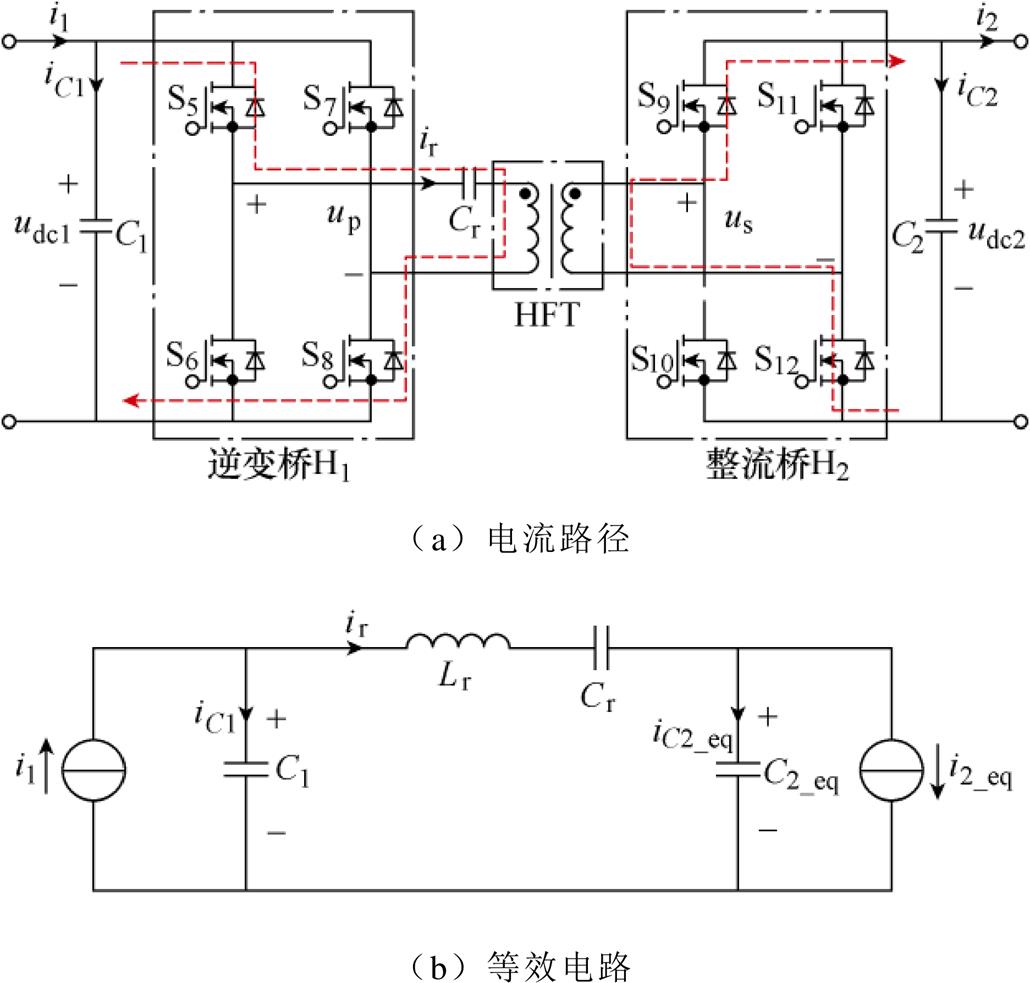
图7 正半周期内电流路径和等效电路
Fig.7 In positive half cycle of current path and equivalent circuit
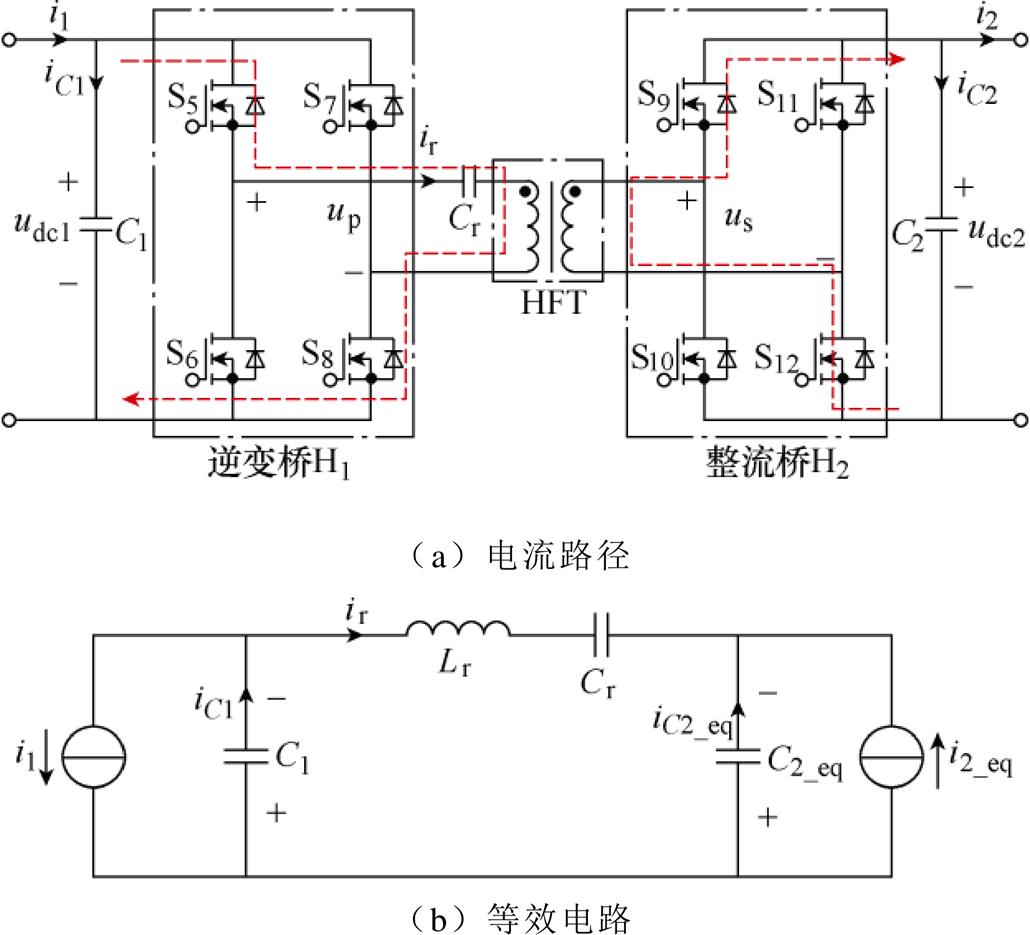
图8 负半周期内电流路径和等效电路
Fig.8 In negative half cycle of current path and equivalent circuit
由于正、负半周具有对称性，因此以正半周期等效电路（见图7b）为例进行分析。根据基尔霍夫电流定律可以得到
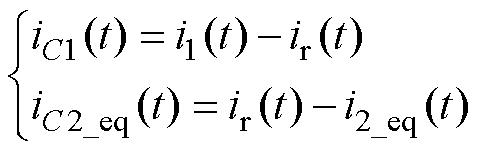（1）
对谐振回路应用基尔霍夫电压定律可以得到
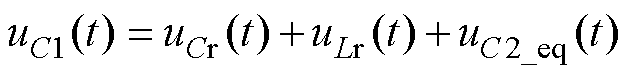（2）
根据电容电压与电容电流的关系可以得到
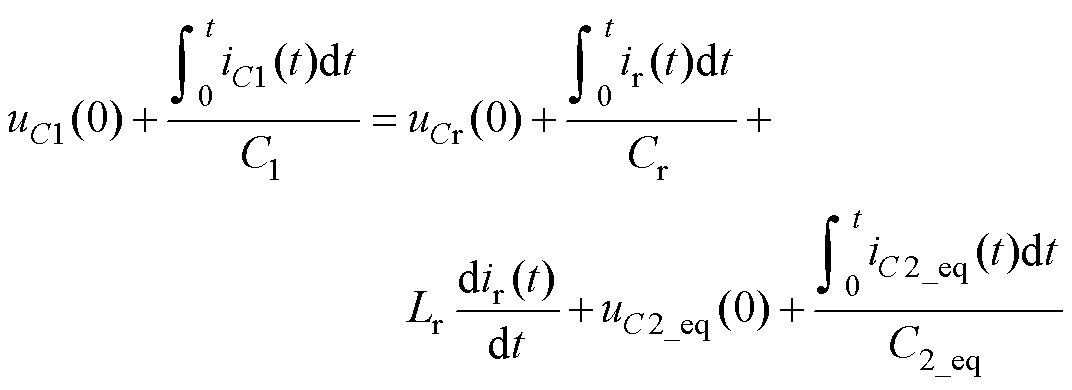（3）
由于等效电路中将输出侧电压折算至输入侧，所以输出电压等于输入电压，由输入功率等于输出功率可得
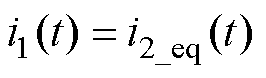（4）
整理式（1）～式（4）可得
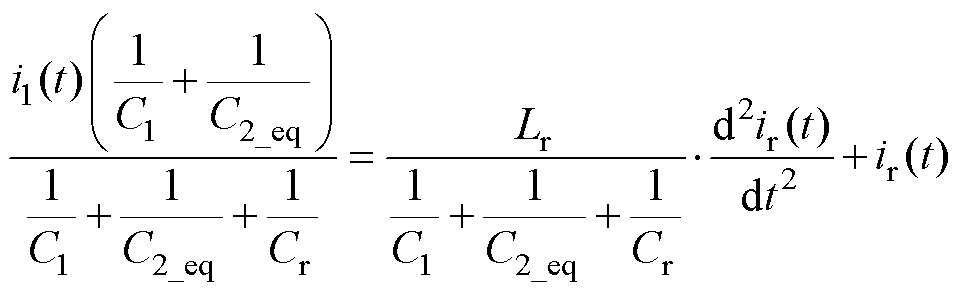（5）
串联谐振回路中包含C1、C2、Cr、Lr，因此谐振角频率wr为
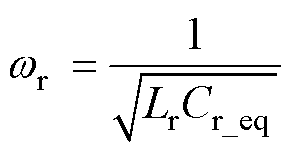（6）
式中，Cr_eq为谐振回路串联等效电容，即
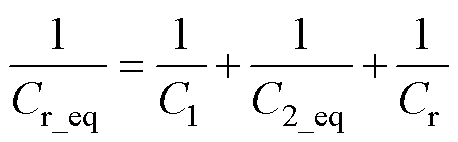（7）
可以看出，考虑直流电容后谐振回路等效谐振电容减小，谐振频率提高。将式（6）和式（7）代入式（5）得到
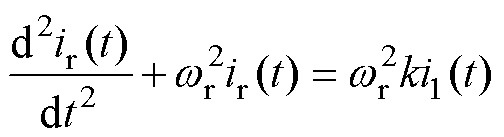（8）
其中
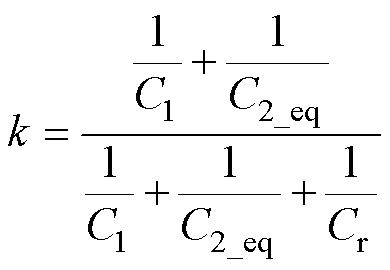（9）
式（9）是二阶常系数非齐次线性微分方程，其解ir(t)由式（9）的特解和对应的齐次线性微分的通解组成，即
（10）
式中，Ir为通解的幅值；q 为通解的初相位。可以看出，高频谐振电流ir(t)在正半周期内含有直流分量ki1，这是与大直流电容下特性不同的。同样地，求解图8b的等效电路，可以得出负半周期电流的解析表达式为
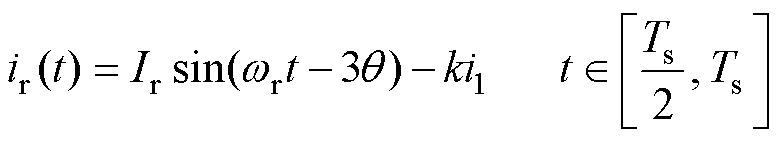（11）
可以看出，高频谐振电流ir(t)在负半周期内含有直流分量-ki1。根据式（10）、式（11），可以得出一个开关周期Ts内的高频电流波形，如图9所示，开关周期正半周高频电流沿着Irsin(wrt-q)+ki1运行，在开关周期负半周，沿着Irsin(wrt-3q)-ki1运行。在一个完整的高频开关周期Ts内，高频电流仍然为正负半周对称的交流电流。
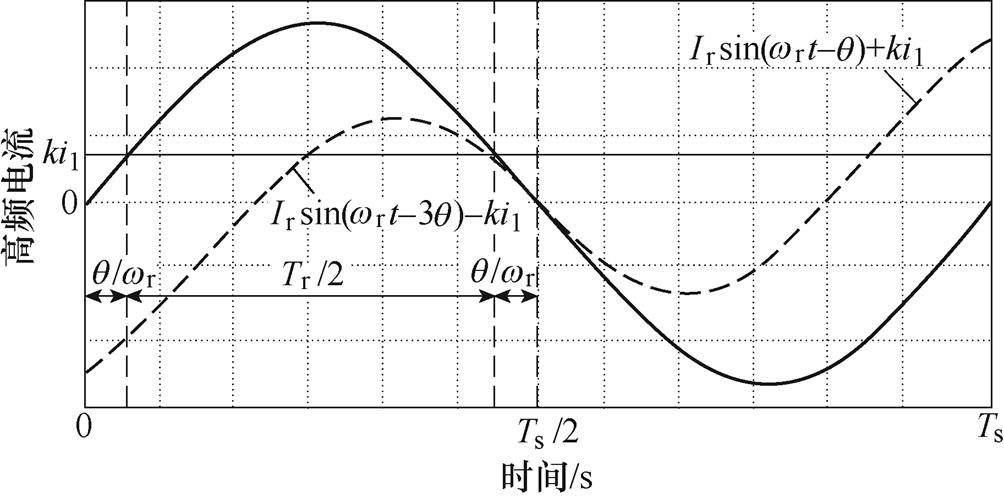
图9 高频电流ir(t)示意图
Fig.9 Diagram of high frequency current ir(t)
本节对ZCS所需开关频率进行了设计，并揭示了直流电容、死区时间对其影响规律。
上述分析在理想情况下，为了防止上下管直通和实现器件ZVS开通，需要设置死区时间，考虑死区后实现ZCS的高频电流示意图如图10所示。
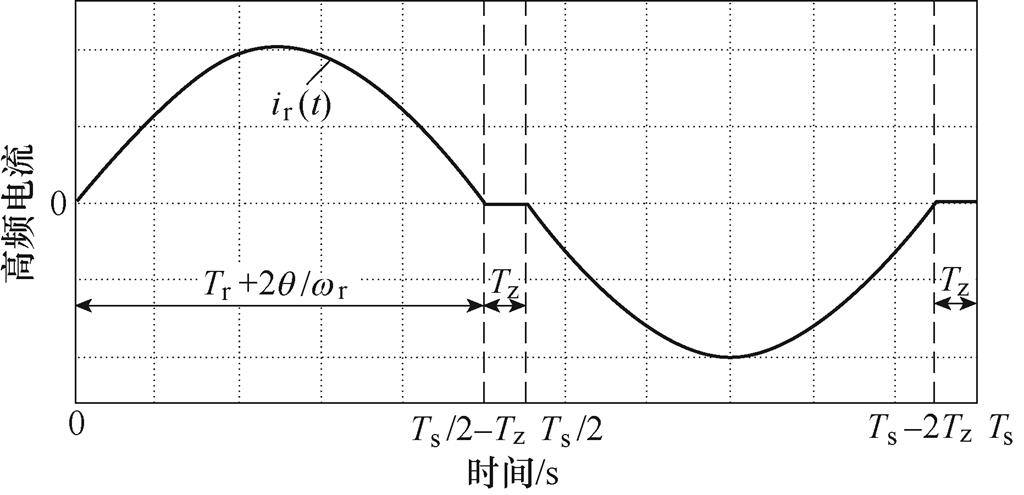
图10 考虑死区后实现ZCS的高频电流示意图
Fig.10 Diagram of high frequency current ir(t) considering dead time achieving ZCS
结合图9、图10可得，实现ZCS的开关周期Ts和谐振周期Tr的关系为
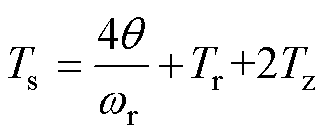（12）
式中，q 为式（10）中ir(t)交流分量的初相位。与式（1）对比看出，直流电容对谐振回路谐振频率的改变和高频电流中直流分量的存在，使得按照式（1）设计无法满足ZCS。为了合理设计开关频率fs，需要准确求解q。
根据串联谐振型DAB关断时刻电流为零的要求，令ir(wr(Ts/2-Tz)-q)=0，代入式（10）可得
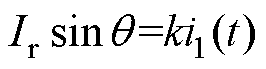（13）
考虑到变换器要保持稳定运行，需要满足直流电容在一个高频开关周期内充放电平衡。根据图7和图8正负半周等效电路可得电容C1电流分别为
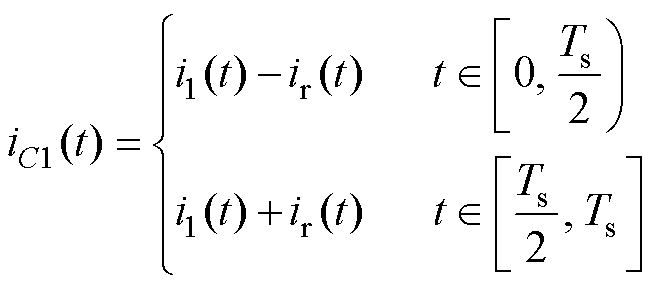（14）
根据图9可知，高频电流ir(t)正负半周大小相等，方向相反，结合式（14）可知，直流电容电流正负半周完全相同。同理可得低压侧直流电容电压电流特性。直流电容电流波形如图11中iC2_eq(t)和iC1(t)所示。根据电容电流和电压的关系可得直流电容电压波形如图12所示。图中，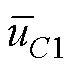
为一个开关周期Ts内的平均值。从图12可以看出，谐振周期内，电容C1、C2充放电，死区时间内，输入直流电流i1(t)对电容C1充电，输出直流电流i2_eq(t)对电容C2放电，在半开关周期内满足充放电平衡。
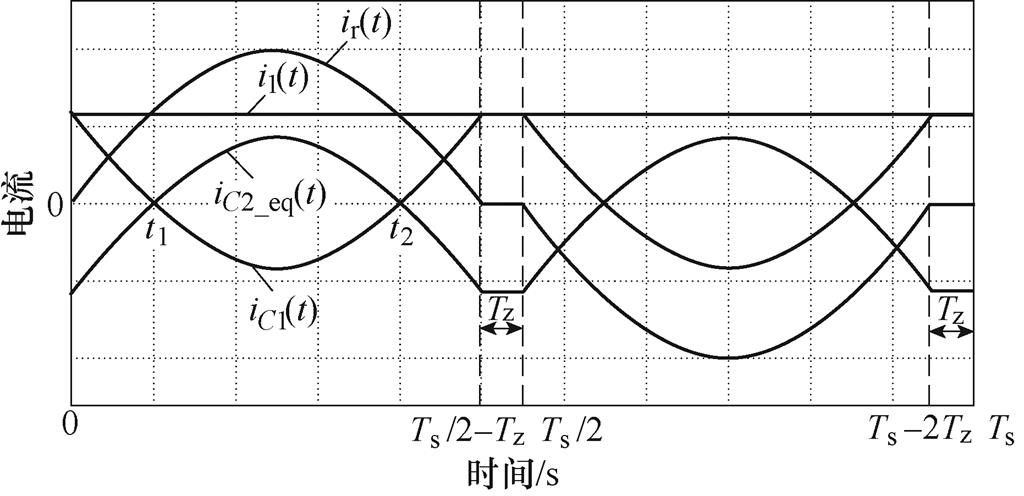
图11 直流电容C1、C2_eq电流波形
Fig.11 Waveforms of currents of DC capacitors C1, C2_ eq
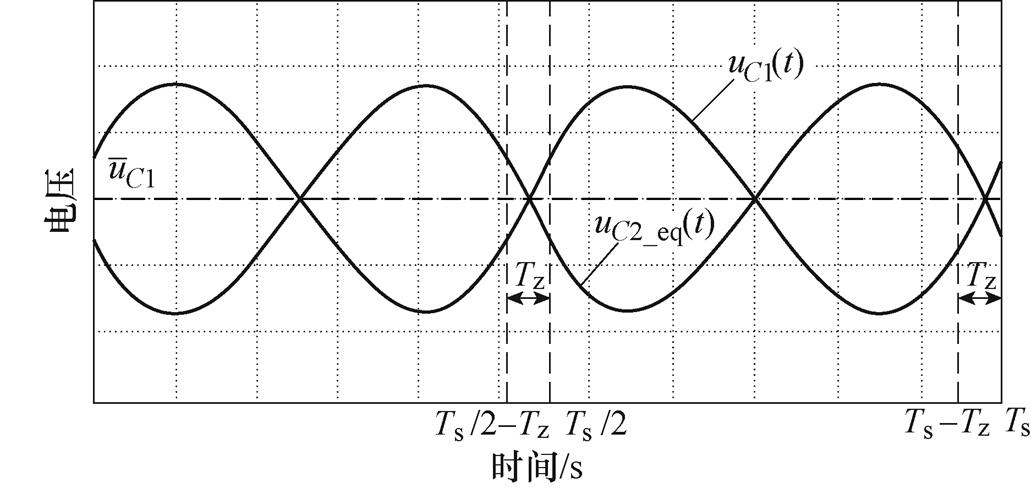
图12 直流电容C1、C2_eq电压波形
Fig.12 Waveforms of voltages of DC capacitors C1, C2_ eq
根据电容C1在半开关周期内充放电平衡可得
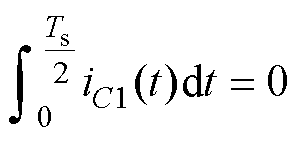（15）
将式（10）、式（14）代入式（15）可得
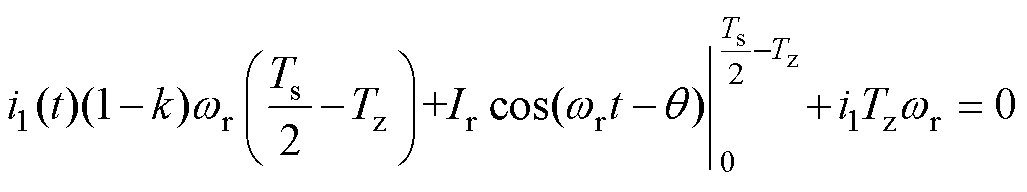（16）
由式（12）可知，wr(Ts/2-Tz)=p+2q，整理后可得
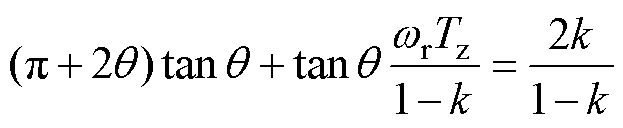（17）
式（17）是初相位q 关于谐振角频率wr、系数k和死区时间Tz的超越方程，说明谐振回路参数和死区时间均会影响初相位q，进而影响ZCS开关频率。从式（17）可以看出，方程中不含i1(t)，说明初相位q 与输入电流大小无关，虽然间接矩阵型PET直流电流在工频周期内是变化的，但是高频电流初相位q 是固定的。求解得到q 后就可计算得到开关频率fs，实现全工频周期内ZCS。
为了揭示直流电容和死区时间对开关频率的影响，定义等效直流电容Cdc_eq=1/(1/C1+1/C2_eq)，为了表征直流电容的大小，定义直流电容与谐振电容的比值为g=Cdc_eq/Cr，则k=1/(1+g)。
当等效直流电容远大于谐振电容时，可得
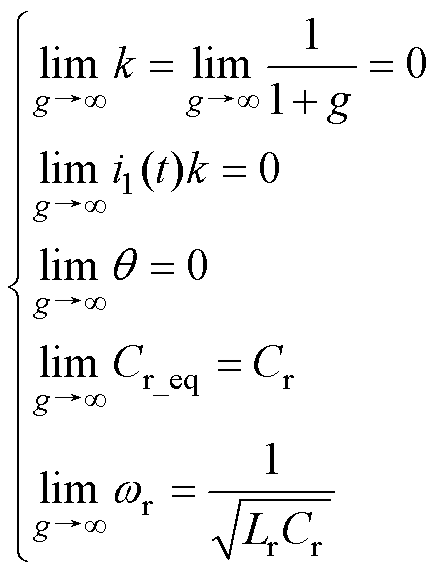（18）
高频电流的表达式可简化为
（19）
高频电流中不含直流分量，且谐振频率与直流电容无关，此时ZCS开关频率设计不需考虑直流电容。
当直流电容较小时，则需要利用计算机求解超越方程式（17）计算开关频率fs。谐振电容Cr=10mF，漏感Lr=8.8mH，根据不同直流电容计算得到不同的fs。以fs与不考虑q 影响计算的开关频率frs=1/(Tr+2Tz)的比值fs/frs作为纵坐标，等效直流电容Cdc_eq与串联谐振电容Cr的比值作为横坐标，绘制关系曲线如图13所示。可以看出，实现ZCS所需的开关频率fs小于只根据谐振参数计算的开关频率frs，原因是高频电流正负半周含有直流分量，延长了过零时刻。随着直流电容减小，fs与frs比值减小。另外可以看出，随着直流电容减小，死区时间变化对开关频率的影响也逐渐增大，且死区时间越小，fs与frs比值越小。
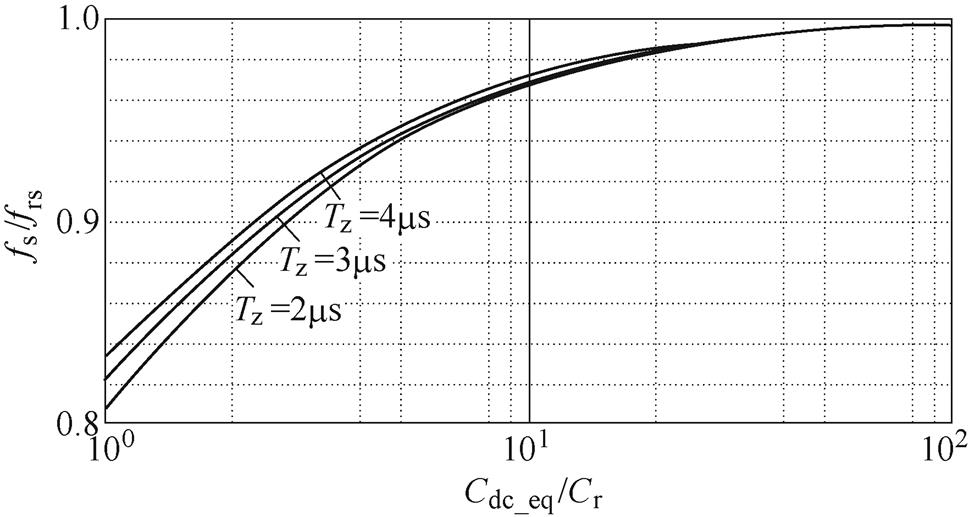
图13 fs/frs-(Cdc_eq/Cr)关系曲线
Fig.13 Relation curves of fs/frs-(Cdc_eq/Cr)
根据上述分析可得，若不考虑直流电容，计算的谐振回路等效电容偏高，开关频率偏低；若考虑直流电容而不考虑高频电流直流分量，开关频率偏高。随着直流电容减小，死区时间变化对开关频率的影响也逐渐增大。
为了证明高频电流特性分析及开关频率设计的正确性，搭建了采用图3所示间接矩阵型AC-AC PET拓扑的仿真模型。初始设计的ZCS开关频率为20kHz，但是由于样机实际参数和设计参数的误差，仿真参数调整为和实验样机一致。具体的仿真参数见表1。
表1 仿真参数
Tab.1 Simulation parameters
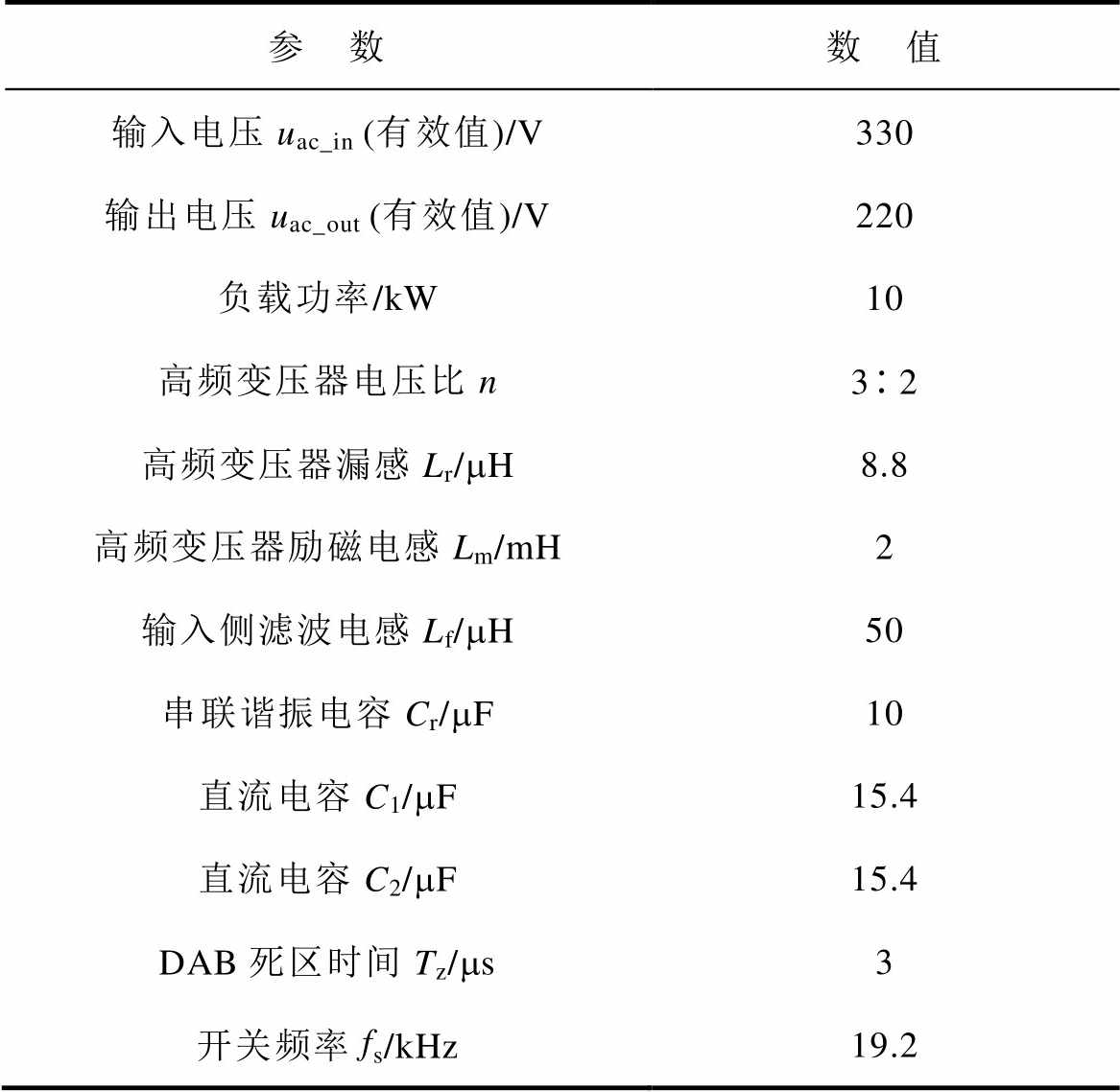
参 数数 值 输入电压uac_in (有效值)/V330 输出电压uac_out (有效值)/V220 负载功率/kW10 高频变压器电压比n32 高频变压器漏感Lr/mH8.8 高频变压器励磁电感Lm/mH2 输入侧滤波电感Lf/mH50 串联谐振电容Cr/mF10 直流电容C1/mF15.4 直流电容C2/mF15.4 DAB死区时间Tz/ms3 开关频率fs/kHz19.2
根据表1仿真参数计算得到开关频率计算结果见表2。
表2 开关频率计算结果
Tab.2 Switching frequency calculation results （单位: kHz）
参 数数 值 不考虑直流电容谐振频率fr1 (Lr, Cr)16.96 考虑直流电容谐振频率fr2 (Lr, Cr, C1, C2)30 不考虑直流电容开关频率fs1 ( fr1, Tz)15.39 不考虑电流直流分量开关频率fs2 ( fr2, Tz)25.4 实现ZCS所需开关频率fs3 ( fr2, Tz, q)19.2
从表2可以看出，不考虑直流电容会导致开关频率计算结果偏小，而不考虑高频电流中直流分量会导致开关频率计算结果偏大。
按照可实现ZCS开关频率fs3=19.2kHz进行仿真，图14为低频开关周期内的波形。从图14a、图14b可以看出，PET实现了330V/220V电压变换的功能，输入电压与输入电流基本同相位，这是因为直流电容C1仅为15.4mF，根据输入电压330V可以计算得到网侧无功电流仅为1.65A，10kW条件下的有功电流为30A，因此功率因数为99.8%，说明小直流电容下可以保证较高的功率因数。由于直流电容减小，因此输出交流电压含有高频波动，可通过增加LC输出进行滤波，由于波动频率为两倍高频开关频率，因此需要的LC体积很小，滤波器相关设计已很成熟，本文不再赘述。在图14c中，逆变桥H1输出高频电压upri和高频电流ipri含有低频包络，与图6吻合。
图15a～图15d为高频开关周期内的波形。从图15a可以看出，高频电压和高频电流同相位，高频环节工作在串联谐振状态，图15b展示了上下管驱动信号与高频电流的波形，可以看出，在工频电压峰值和过零点附近，均实现了ZCS，说明高频电流交流分量初相q 不随低频输入电流的变化而变化，实现了全工频周期内ZCS。图15c、图15d展示了与图15a上图同一时间段高低压侧直流电容电流idc1、idc2和电压udc1、udc2的波形，可以看出，直流电容电流正负开关周期相同，半开关周期内电容充放电平衡，呈现两倍开关频率的波动，与理论分析吻合。
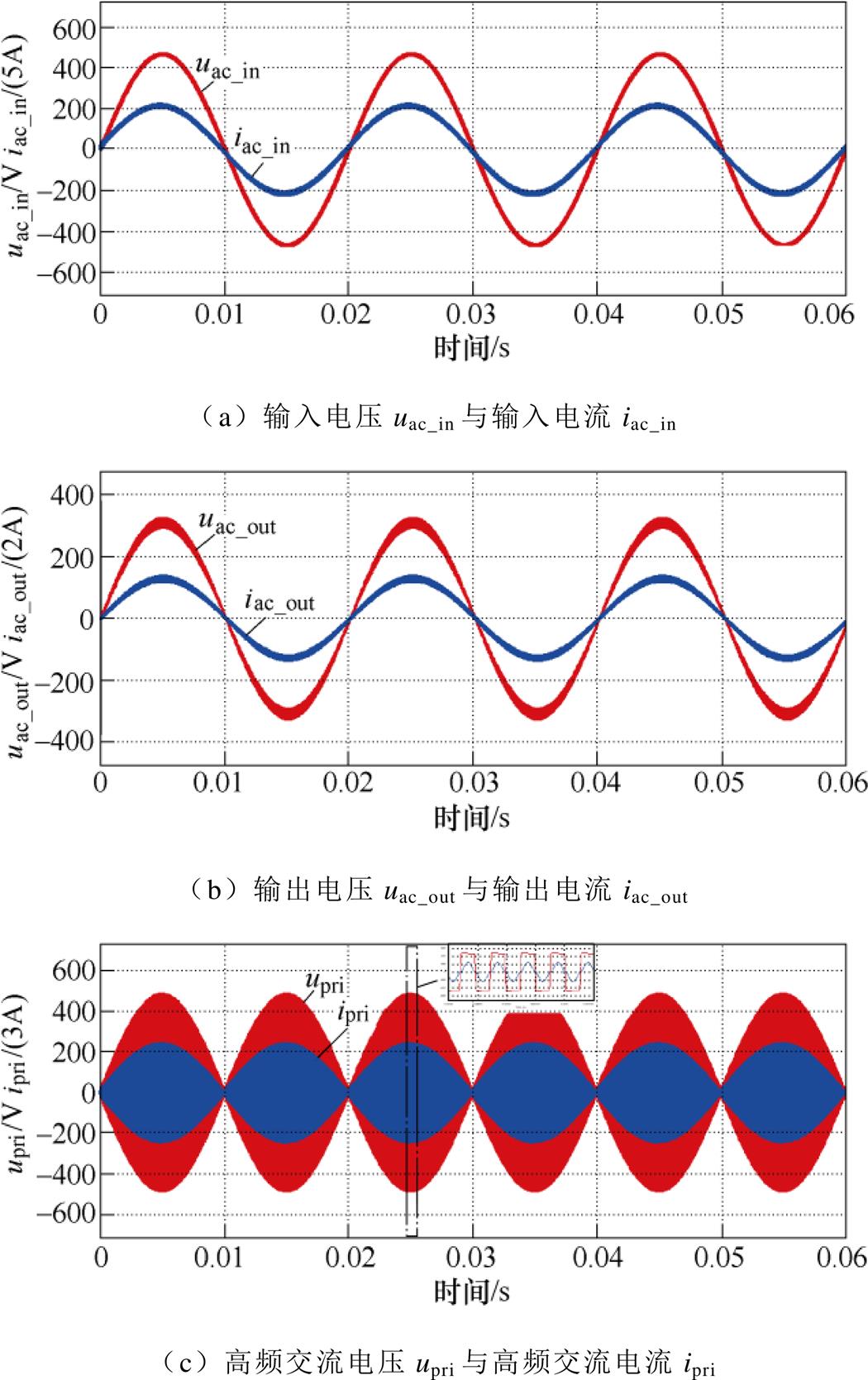
图14 低频开关周期波形
Fig.14 Waveforms in low frequency switching cycle
作为对比，按照fs1=15.39kHz进行仿真，高频电压电流仿真结果如图15e所示。可以看出，开关频率偏低，无法实现ZCS，且会产生无功电流，增加电流应力。按照fs2=25.4kHz进行仿真，仿真结果如图15f所示，可以看出，开关频率偏高，也无法实现ZCS。
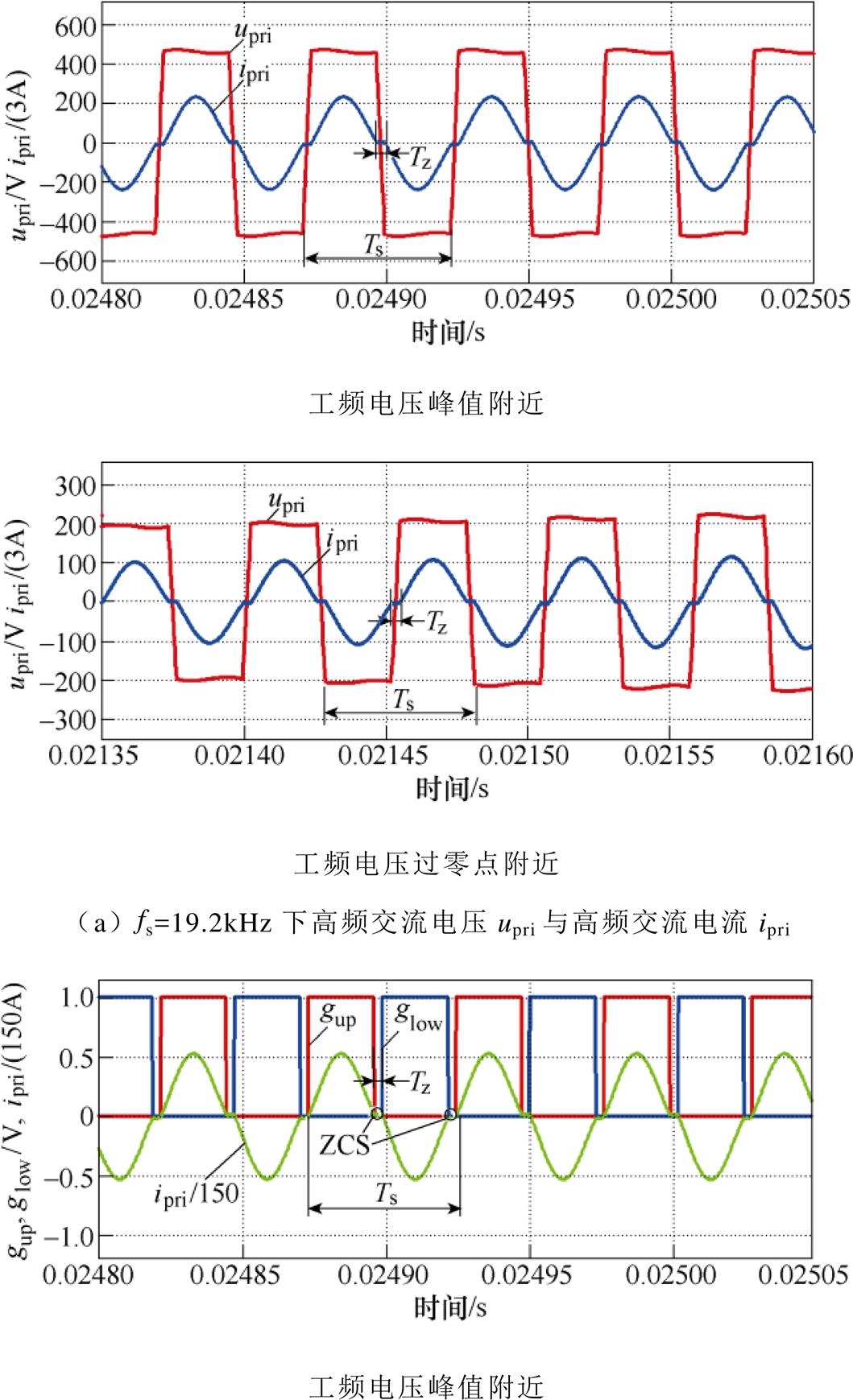
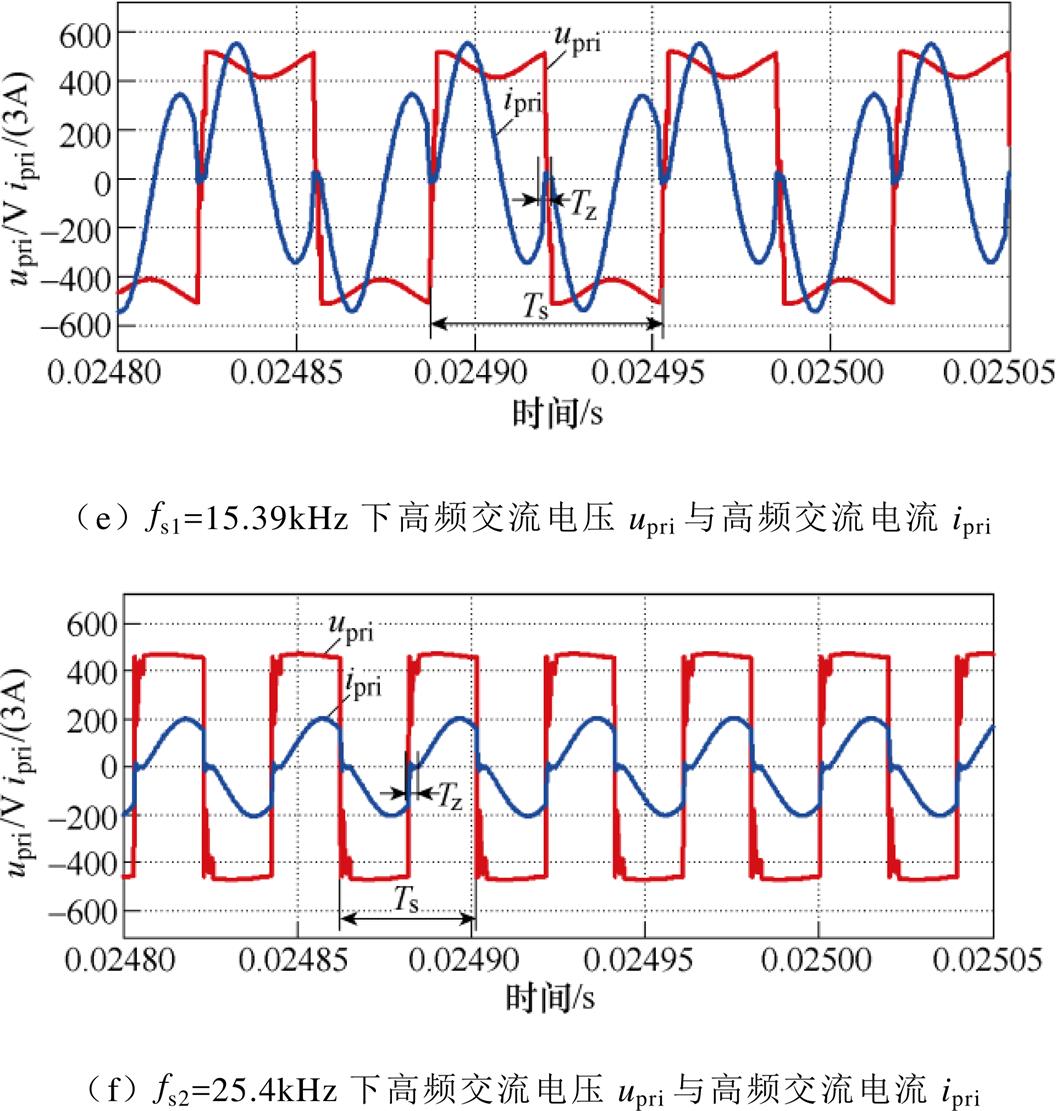
图15 高频开关周期波形
Fig.15 Waveforms in high frequency switching cycle
上述仿真结果说明了高频电流特性分析的正确性，也说明了开关频率设计的准确性。
本文搭建了采用图3所示间接矩阵型AC-AC PET拓扑的实验平台，实验平台原理如图16所示，三相380V电网接至调压器输入端，调压器输出a、b两相间电压调节至330V，接至PET交流输入侧。PET输出接电阻负载。具体的实验平台如图17所示，直流电容的体积与谐振电容体积相当。实验参数和仿真一致。实验采用的器件为Cree 1 700V/300A SiC-MOSFET，器件型号为CAS300M17BM2，控制系统采用ARM+FPGA的架构。
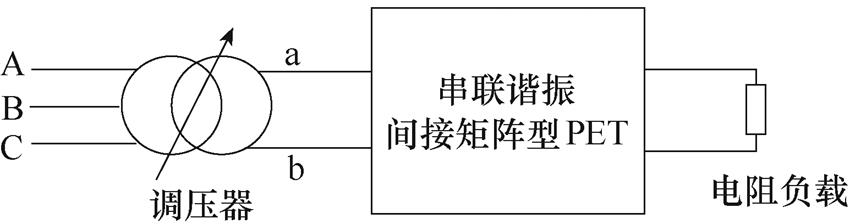
图16 实验平台原理
Fig.16 Schematic diagram of experimental platform
图17 实验平台
Fig.17 Experimental platform
图18为低频开关周期内的波形，图18a中输入电压和输出电压有效值分别为328V和218V，电压比为1.5，实现了电压变换的基本功能，负载功率为10.5kW。图18b中高频电压电流含有低频包络，与理论分析和仿真吻合。图19为高频开关周期内的波形。从图19a可以看出，高频电压和高频电流同相位，高频环节工作在串联谐振状态，从图19b可以看出，在工频电压峰值和过零点附近关断电流均为零，说明实现了全工频周期内ZCS。实验中实现ZCS的开关频率为19kHz，与理论计算和仿真19.2kHz基本吻合。图19c展示了高、低压直流电容电流idc1、idc2和电压udc1、udc2的波形，可以看出，直流电容电流在正负半开关周期内相同，半开关周期内电容充放电平衡，呈现两倍开关频率的波动，与理论分析和仿真吻合。fs1=15.39kHz会导致变压器铁心饱和及器件过电流，因此未在实验中验证。图19d为fs2=25.4kHz下实验结果，未实现ZCS，硬开关会导致开关损耗增加，降低PET效率。通过上述分析可以发现，实验结果和仿真结果基本一致，也进一步证明了理论分析的正确性。
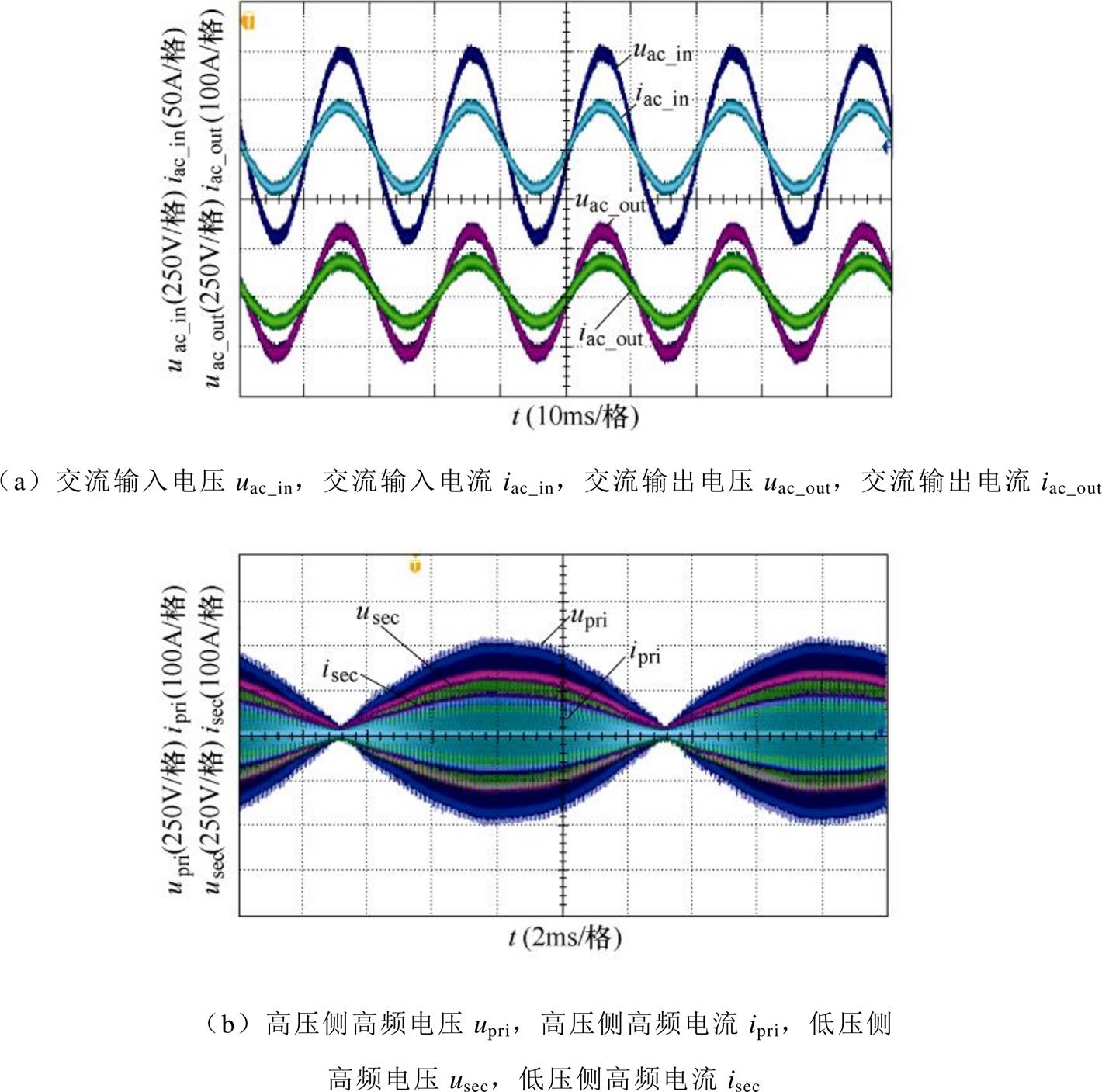
图18 低频开关周期波形
Fig.18 Waveforms in low frequency switching cycle
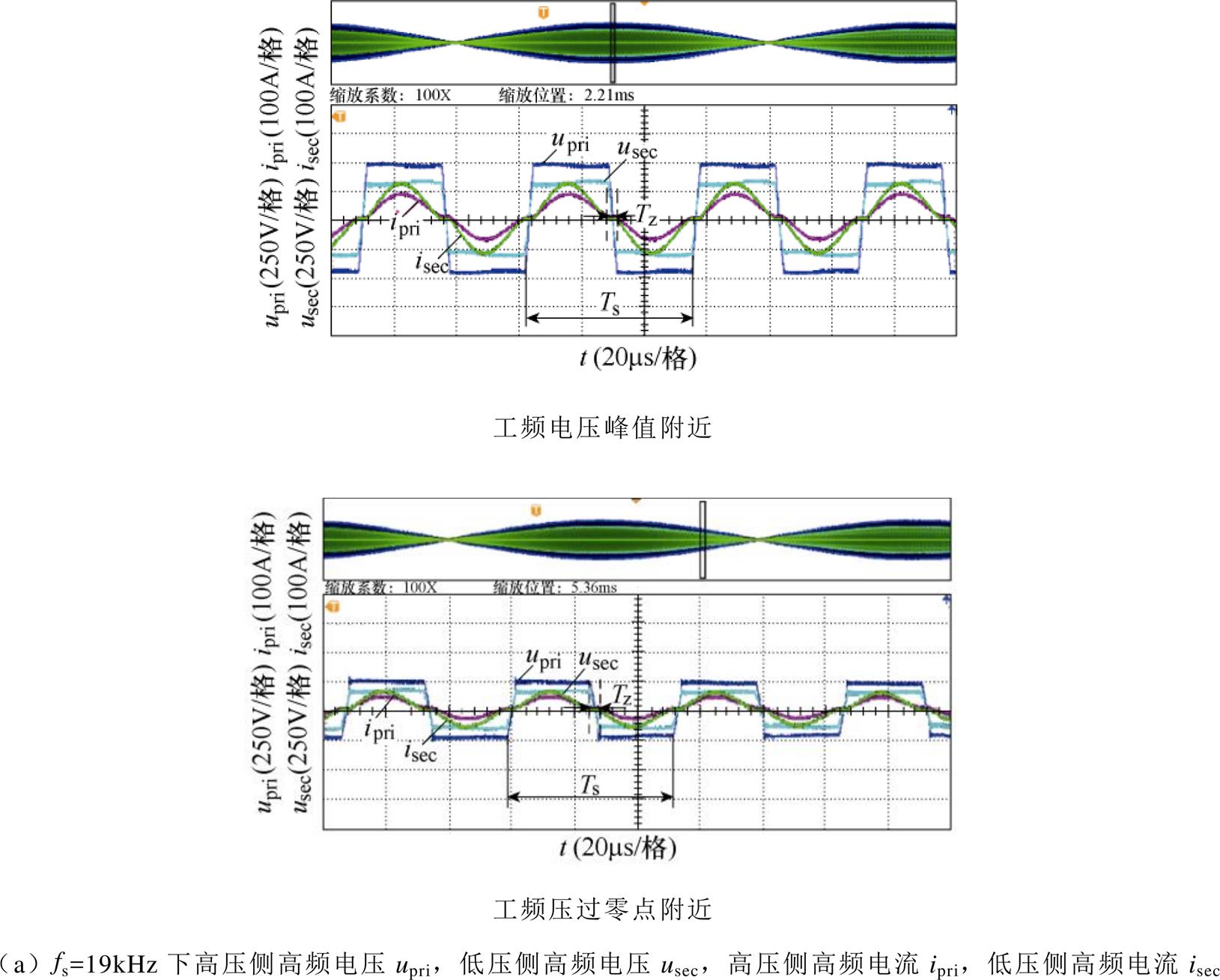
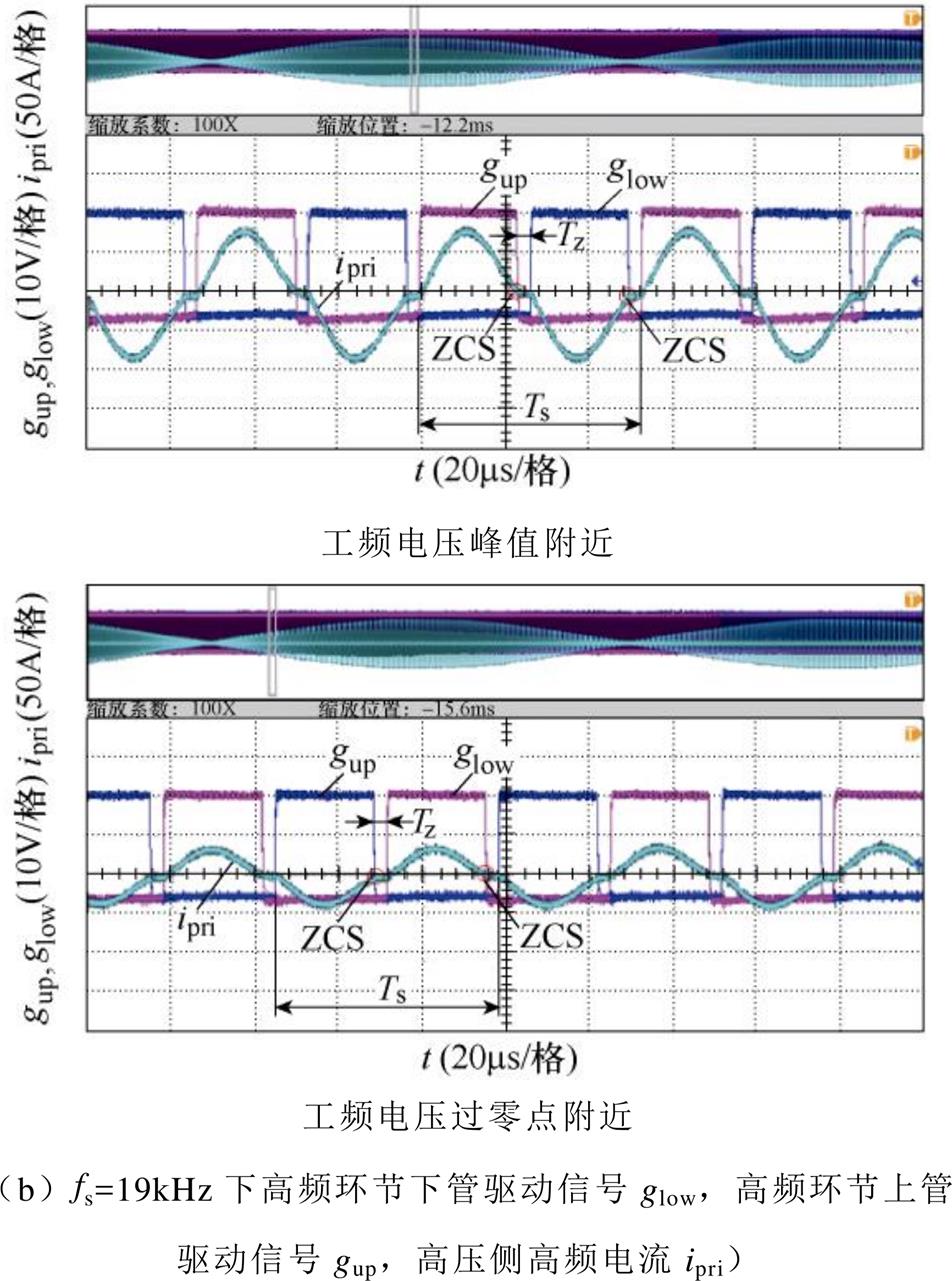
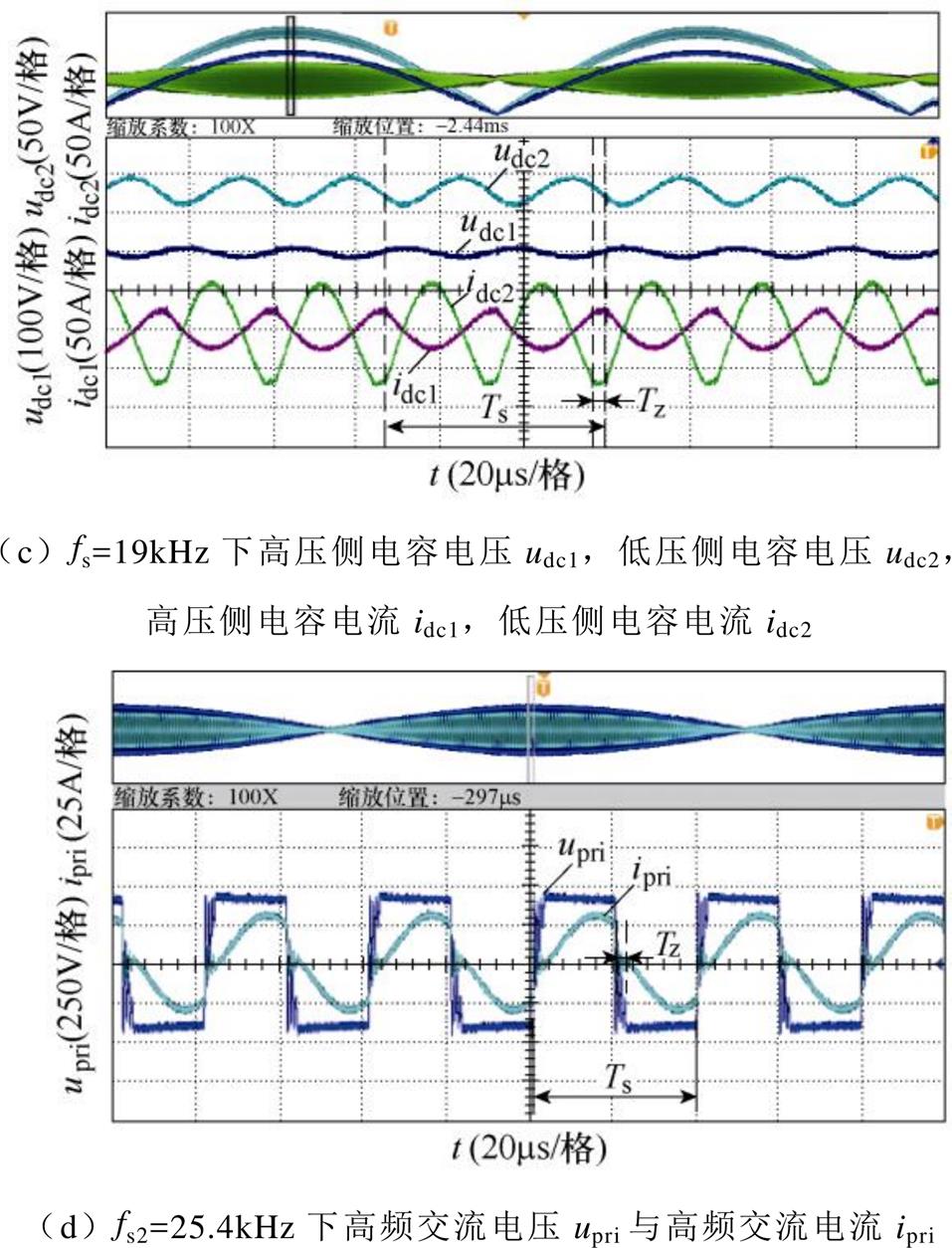
图19 高频开关周期波形
Fig.19 Waveforms in high frequency switching cycle
为了说明开关频率设计对PET效率的重要性，进行了330V/220V不同功率和不同开关频率下的效率测试，测试设备为横河WT1800功率分析仪，效率测试曲线如图20所示。其中，开关频率19kHz下PET峰值效率可达98.86%，原因是串联谐振DAB可实现ZCS和ZVS，整流和逆变桥开关频率仅为50Hz，因此PET开关损耗极低，损耗主要来源于通态损耗。开关频率25.4kHz下效率较19kHz降低最大约1.5%，且功率越大，效率降低越多，原因是25.4kHz相比于19kHz开关频率增加，无法实现ZCS关断，如图19d所示，且功率越大，串联谐振DAB关断电流越大，关断损耗越大。开关频率15.39kHz会导致变压器铁心饱和、器件过电流，因此效率采用计算机热仿真得到，效率较19kHz降低约5%，原因是开关频率过低，串联谐振DAB高频环节会产生大量无功电流，高频电流应力和有效值大幅增加，如图15e所示，导致通态损耗增加，效率降低。
图20 效率曲线
Fig.20 Efficiency curves
本文建立了串联谐振间接矩阵型PET的等效电路，推导了高频电流时域解析表达式。解析表达式表明，高频电流在正负半开关周期内可分解为高频交流分量和直流分量，在一个高频开关周期内仍为正负半周对称的高频交流电流。为实现ZCS，建立了开关频率与直流电容、串联谐振电容、谐振电感、死区时间之间的数学关系，并揭示了直流电容和死区时间对ZCS开关频率的影响规律：若不考虑直流电容，会使开关频率设计偏低；若考虑直流电容而不考虑高频电流直流分量，会导致开关频率设计偏高；死区时间变化对开关频率的影响随着直流电容的减小而增大。最后通过330V/220V 10kW PET仿真和实验验证了高频电流特性分析的正确性和开关频率设计的准确性，实现了减小直流电容的同时高效率运行。
参考文献
[1] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer technolo- gies[J]. Proceedings of the CSEE, 2018, 38(5): 1274- 1289.
[2] 赵争鸣, 冯高辉, 袁立强, 等. 电能路由器的发展及其关键技术[J]. 中国电机工程学报, 2017, 37(13): 3823-3834.
Zhao Zhengming, Feng Gaohui, Yuan Liqiang, et al. The development and key technologies of electric energy router[J]. Proceedings of the CSEE, 2017, 37(13): 3823-3834.
[3] 涂春鸣, 兰征, 肖凡, 等. 模块化电力电子变压器的设计与实现[J]. 电工电能新技术, 2017, 36(5): 42-50.
Tu Chunming, Lan Zheng, Xiao Fan, et al. Design and implementation of modular power electronic trans- former[J]. Advanced Technology of Electrical Engin- eering and Energy, 2017, 36(5): 42-50.
[4] 刘建强, 赵楠, 孙帮成, 等. 基于LLC谐振变换器的电力电子牵引变压器控制策略研究[J]. 电工技术学报, 2019, 34(16): 3333-3344.
Liu Jianqiang, Zhao Nan, Sun Bangcheng, et al. Research on control strategy of power electronic traction transformer based on LLC resonant con- verter[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3333-3344.
[5] 王鹤, 栾钧翔. 变压器的电力电子化演进及其对电压稳定影响综述[J]. 电力系统保护与控制, 2020, 48(16): 171-187.
Wang He, Luan Junxiang. Summary of power electronic evolution of transformer and its influence on voltage stability[J]. Power System Protection and Control, 2020, 48(16): 171-187.
[6] Feng Jianghua, Chu Wenqiang, Zhang Zhixue, et al. Power electronic transformer-based railway traction systems: challenges and opportunities[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1237-1253.
[7] Xu She, Huang A Q, Burgos R. Review of solid-state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 186-198.
[8] Huber J E, Kolar J W. Volume/weight/cost com- parison of a 1MVA 10kV/400V solid-state against a conventional low-frequency distribution transformer[C]// 2014 IEEE Energy Conversion Congress and Expo- sition, Pittsburgh, 2014: 4545-4552.
[9] 李子欣, 高范强, 徐飞, 等. 中压配电网用10kV AC- 750V DC/1MVA电力电子变压器功率密度影响因素研究[J]. 电工电能新技术, 2016, 35(6): 1-6.
Li Zixin, Gao Fanqiang, Xu Fei, et al. Power density analysis of 10kV AC-750V DC/1MVA power elec- tronic transformer for medium voltage distribution grid[J]. Advanced Technology of Electrical Engineering and Energy, 2016, 35(6): 1-6.
[10] Wang Dan, Tian Jie, Mao Chengxiong, et al. A 10kV/400V 500kVA electronic power transformer[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 6653-6663.
[11] 李响, 郝瑞祥, 游小杰, 等. 一种级联电力电子变压器直流电压平衡控制策略[J]. 电工技术学报, 2017, 32(2): 238-245.
Li Xiang, Hao Ruixiang, You Xiaojie, et al. A DC voltage balance control strategy for the cascaded power electronic transformer[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 238- 245.
[12] Liu Tao, Yang Xu, Chen Wenjie, et al. Design and implementation of high efficiency control scheme of dual active bridge based 10kV/1MW solid state transformer for PV application[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4223-4238.
[13] 王杉杉, 王玉斌, 林意斐, 等. 级联型电力电子变压器电压与功率均衡控制方法[J]. 电工技术学报, 2016, 31(22): 92-99.
Wang Shanshan, Wang Yubin, Lin Yifei, et al. Voltage and power balance control for cascaded power electronic transformer[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 92-99.
[14] 李子欣, 王平, 楚遵方, 等. 面向中高压智能配电网的电力电子变压器研究[J]. 电网技术, 2013, 37(9): 2592-2601.
Li Zixin, Wang Ping, Chu Zunfang, et al. Research on medium- and high-voltage smart distribution grid oriented power electronic transformer[J]. Power System Technology, 2013, 37(9): 2592-2601.
[15] Glinka M, Marquardt R. A new AC/AC-multilevel converter family applied to a single-phase con- verter[C]//The Fifth International Conference on Power Electronics and Drive Systems, Singapore, 2003: 16-23.
[16] Glinka M. Prototype of multiphase modular-multilevel- converter with 2MW power rating and 17-level- output-voltage[C]//IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 2004: 2572-2576.
[17] McMurray W. Power converter circuits having a high frequency link. US, 3517300[P]. 1970-6-23.
[18] Raju R N, Zhang R S, Stevanovic L D, et al. AC-AC converter with high frequency link, US, 8644037 B2[P]. 2008-7-15.
[19] Raju R, Dame M, Steigerwald R. Solid-state trans- formers using silicon carbide-based modular building blocks[C]//2017 IEEE 12th International Conference on Power Electronics and Drive Systems, Honolulu, 2017: 1-7.
[20] Wang Hui, Zhang Yichun, Sun Yao, et al. Topology and control method of a single-cell matrix-type solid-state transformer[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2302-2312.
[21] 付超, 武承杰, 孙玉巍, 等. 混合模块化直流固态变压器I: 工作原理及稳态特性分析[J]. 电工技术学报, 2019, 34(增刊1): 141-153.
Fu Chao, Wu Chengjie, Sun Yuwei, et al. Hybrid modular DC solid state transformer I: working prin- ciple and analysis of steady state characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 141-153.
[22] 付超, 高振, 孙玉巍, 等. 混合模块化直流固态变压器Ⅱ: 动态特性及快速响应控制[J]. 电工技术学报, 2019, 34(14): 2980-2989.
Fu Chao, Gao Zhen, Sun Yuwei, et al. Hybrid modular direct current solid state transformer Ⅱ: dynamic characteristic and rapid response control[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2980-2989.
[23] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3030-3040.
[24] Reinold H, Steiner M. Characterization of semi- conductor losses in series resonant DC-DC converters for high power applications using transformers with low leakage inductance[C]//Power Electronics and Applications European Conference, Lausanne, 1999: 1-10.
[25] Lindenmüller L, Alvarez R, Bernet S. Optimization of a series resonant DC/DC converter for traction applications[C]//2012 IEEE Energy Conversion Congress and Exposition, Raleigh, NC, 2012: 2201- 2208.
[26] 杨博, 葛琼璇, 赵鲁, 等. 基于输入串联输出并联的双向全桥串联谐振DC-DC变换器系统控制策略研究[J]. 电工技术学报, 2020, 35(12): 2574-2584.
Yang Bo, Ge Qiongxuan, Zhao Lu, et al. Control strategy of dual bridge series resonant DC-DC converter system based on input series output parallel connection[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2574-2584.
[27] Qin Wei, Wu Xinke, Zhang Junming. A family of DC transformer (DCX) topologies based on new ZVZCS cells with DC resonant capacitance[J]. IEEE Transactions on Power Electronics, 2017, 32(4): 2822-2834.
[28] Rothmund D, Huber J E, Kolar J W. Operating behavior and design of the half-cycle discontinuous conduction-mode series-resonant-converter with small DC link capacitors[C]//2013 IEEE 14th Workshop on Control and Modeling for Power Electronics, Salt Lake City, 2013: 1-9.
[29] Zhu Qianlai, Wang Li, Zhang Liqi. A 10kV DC transformer (DCX) based on current fed SRC and 15kV SiC MOSFETs[C]//2018 IEEE Applied Power Electronics Conference and Exposition, San Antonio, 2018: 149-155.
[30] Zhu Qianlai, Wang Li, Huang A Q, et al. 7.2kV single-stage solid-state transformer based on the current-fed series resonant converter and 15kV SiC MOSFETs[J]. IEEE Transactions on Power Elec- tronics, 2018, 34(2): 1099-1112.
Characteristic Analysis of High-Frequency-Link Current of Series Resonant Indirect Matrix Type Power Electronics Transformer and Switching Frequency Design
Abstract Series resonant indirect matrix type power electronic transformer (PET) can achieve high power density by high frequency switching and reducing dc capacitance. However, small dc capacitors will change the equivalent capacitance of the resonant circuit and affect the high frequency resonant current characteristics. Then, the zero current switching (ZCS) may be lost. In this paper, the equivalent circuit of the series resonant indirect matrix type PET with small dc capacitors is established. Analytical expression of high frequency current in time domain is derived, and switching frequency is designed to achieve ZCS. The influence of dc capacitance and dead time on switching frequency is revealed. Simulation and experimental results verify the correctness of the theoretical analysis.
keywords：AC-AC power electronics transformer, series resonance, indirect matrix converter, high frequency current characteristics, zero current switching (ZCS), high power density and high efficiency
DOI: 10.19595/j.cnki.1000-6753.tces.201715
中图分类号：TM41; TM46
胡钰杰 男，1993年生，博士研究生，研究方向为电力电子变压器。E-mail: huyj@mail.iee.ac.cn
李子欣 男，1981年生，研究员，博士生导师，研究方向为大功率电力电子。E-mail: lzx@mail.iee.ac.cn（通信作者）
收稿日期 2020-12-30
改稿日期 2021-04-28
国家自然科学基金资助项目（52007180）。
（编辑 陈 诚）