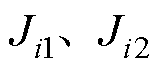 均匀分布。
均匀分布。摘要 针对高功率密度的永磁同步电机电磁转矩波动和永磁体涡流损耗大的问题,提出一种Halbach部分分段结构,永磁体采用Halbach充磁方式,每极分为三段,主磁极采用单侧部分分段,边界磁极与主磁极不等厚且不等宽,并将其永磁体扩展为两种型式,即Hat型和T型。采用精确子域模型法,将求解域划分为槽身、槽口、气隙以及永磁体四个区域,在二维极坐标下计算电机负载气隙磁通密度分布和电磁转矩。建立10极12槽三维电机模型对Hat型、T型以及其他相关五种电机结构进行电磁仿真、分级优化以及对比分析,求出最优Hat型和T型结构。结果表明,Halbach部分分段结构可以降低永磁体涡流损耗、电磁转矩波动以及负载气隙磁通密度总谐波畸变率(THD),T型Halbach部分分段结构的电磁性能高于Hat型,而Hat型Halbach部分分段结构可以进一步减小永磁体体积,节约生产成本。同时,在有限元应力场中建立三维永磁同步电机求解模型,求得等效应力和总变形,确保Hat型和T型Halbach部分分段结构永磁体的机械强度都维持在允许范围内。
关键词:永磁同步电机 精确子域模型法 Halbach部分分段结构 电磁转矩波动 永磁体涡流损耗
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)由于齿槽物理结构、电流谐波以及广泛使用钕铁硼永磁材料等原因[1-3],不可避免地出现了电磁转矩波动和永磁体涡流损耗,导致电机的振动和噪声、电机效率下降以及永磁体温度上升[4-7]。
永磁体部分分段使电机磁场发生畸变,增加了计算Halbach PMSM负载气隙磁场分布和电磁转矩的难度。准确计算负载气隙磁场分布是优化负载气隙磁通密度和减小电机转矩波动的前提,解析法参数调整方便、计算量小、速度快,解析表达式可以直观反映各参数与磁场分布的关系,有利于PMSM的优化。因此,二维解析法常用于表贴式PMSM的磁场计算中,对于改变永磁体参数的结构,常用的解析法为保角变换法和精确子域模型法。保角变换法通常采用无限深单槽模型,利用气隙复数磁导计算PMSM气隙磁通密度分布,但无限深单槽模型无法考虑两槽间的相互影响。文献[8]采用保角变换法推导了计及极间间隔的等宽等厚Halbach PMSM空载气隙磁通密度的表达式。文献[9]采用保角变换法推导了不等宽Halbach PMSM的负载气隙磁通密度、齿槽转矩以及电磁转矩的表达式。精确子域模型法将电机在二维平面内划分为多个子域,求解各个子域的边界条件,得到傅里叶级数形式的解析解。文献[10-13]采用精确子域模型法推导了开口槽结构的PMSM气隙磁通密度的表达式,但定子槽开口宽度仅由槽口宽度决定,与实际电机差别较大。文献[14]采用精确子域模型法推导了永磁体完全分段结构空载气隙磁通密度和齿槽转矩的表达式。文献[15-16]采用精确子域模型法推导了半闭口槽结构的表贴式PMSM在多种充磁方式下的空载和负载气隙磁通密度、齿槽转矩以及电磁转矩的表达式。上述文献对于表贴式PMSM空载和负载气隙磁场分布、齿槽转矩以及电磁转矩的计算具有一定的借鉴意义,但分析和优化的目标十分单一,未考虑改变永磁体结构对电磁转矩波动和永磁体涡流损耗造成的影响,仍需进一步研究和优化。
抑制永磁体涡流损耗最常用的方法是对永磁体进行分段。对于表贴式PMSM,永磁体周向均匀分段更适用于分数槽结构,永磁体非均匀周向分段更适用于整数槽结构[17]。文献[18]研究了PMSM永磁体分段数和输入电流对永磁体涡流损耗和效率的影响。文献[19]提出了一种环形部分分段结构,分析了永磁体完全分段、周向部分分段以及环形部分分段对永磁体涡流损耗的影响,比较了部分分段后永磁体的机械强度。永磁体部分分段的降耗效果虽然不如完全分段,但永磁体完全分段的工艺十分复杂,永磁体需要被切割、绝缘以及重新胶合,会增加工艺难度和成本,减小永磁体机械强度。同时,永磁体部分分段可以保证永磁体的完整性,不需要额外的工艺及成本,符合实际工程的需要。
因此,本文提出一种Halbach部分分段结构来降低永磁体涡流损耗和电磁转矩波动,并将该结构扩展为两种型式,即Hat型和T型。在文献[15-16]的基础上,采用精确子域模型法在二维极坐标下分析两种结构定子开槽后对负载气隙磁场的影响,求解负载气隙磁通密度的表达式。建立10极12槽表贴式PMSM三维模型,在电磁场和应力场中进行仿真分析和分级优化,求解出最优模型,并对Hat型和T型Halbach部分分段结构及其相关结构的电磁性能进行对比分析,验证了Hat型和T型Halbach部分分段结构的优越性。
假设:忽略电机端部效应;铁心磁导率无穷大,忽略电机的饱和效应;定子槽内每个线圈边的电流密度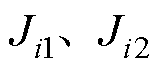 均匀分布。
均匀分布。
Halbach部分分段PMSM的永磁体有两种型式,即Hat型和T型,如图1所示,从图中可以看出,每个磁极由一块主磁极和两块边界磁极组成,充磁角度为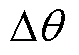 ,主磁极单侧部分分段,边界磁极与主磁极不等宽且不等厚。
,主磁极单侧部分分段,边界磁极与主磁极不等宽且不等厚。
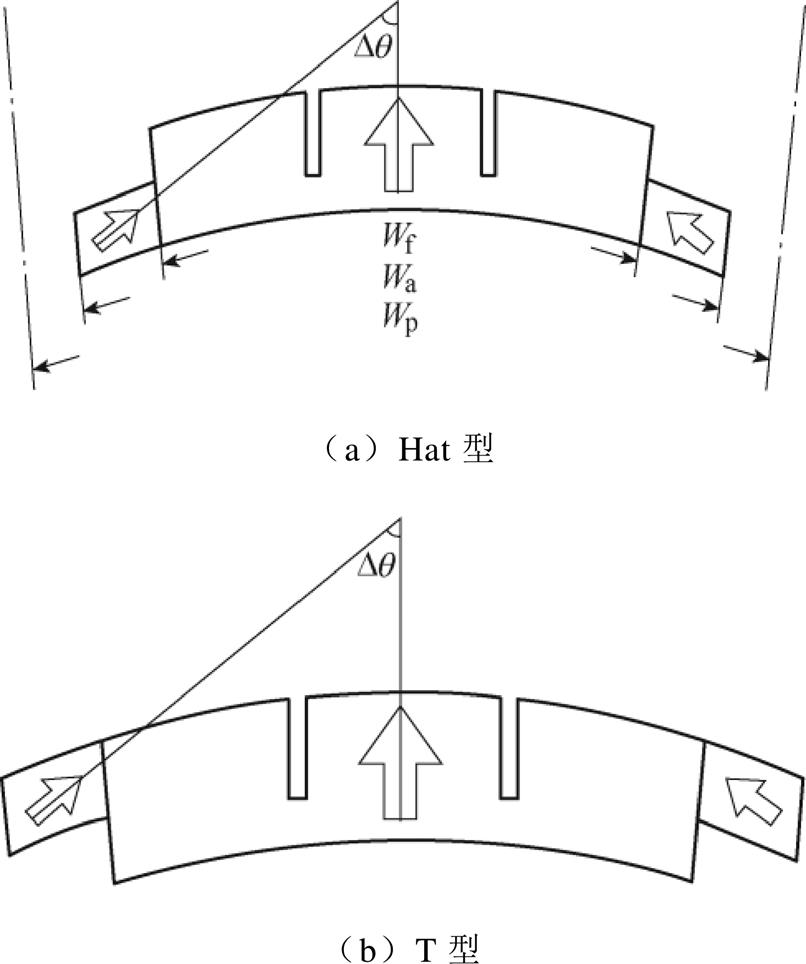
图1 永磁体结构示意图
Fig.1 Schematic diagram of permanent magnet structure
基于精确子域模型法分析定子开槽后的负载气隙磁场,建立Halbach部分分段PMSM解析模型如图2所示,结构1为主磁极,结构2、3为采用一定充磁角度的边界磁极。
图2中, 为转子外半径;
为转子外半径;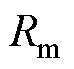 为永磁体外半径;
为永磁体外半径; 为定子铁心内半径;
为定子铁心内半径;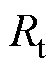 为定子槽顶半径;
为定子槽顶半径;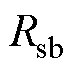 为定子槽底半径;
为定子槽底半径;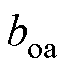 为槽口对应的圆心角;
为槽口对应的圆心角;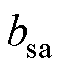 为槽身对应的圆心角;q 为所在位置的机械角度;
为槽身对应的圆心角;q 为所在位置的机械角度;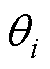 为第i个槽中心的机械角度。空载气隙磁场解析子域:槽子域1i、槽口子域2i、气隙子域3、永磁体子域4。电枢反应磁场解析子域:槽子域1iA、槽口子域2iA、等效气隙子域Ⅰ(包括气隙子域3和不充磁永磁体子域4)。
为第i个槽中心的机械角度。空载气隙磁场解析子域:槽子域1i、槽口子域2i、气隙子域3、永磁体子域4。电枢反应磁场解析子域:槽子域1iA、槽口子域2iA、等效气隙子域Ⅰ(包括气隙子域3和不充磁永磁体子域4)。
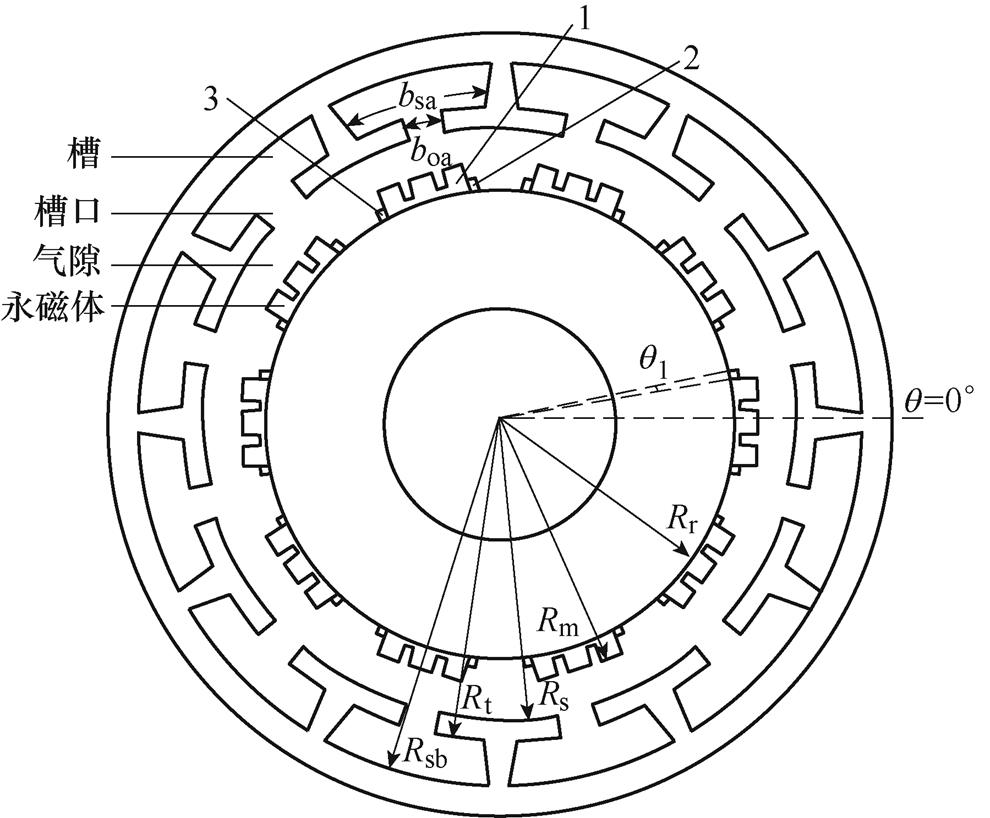
图2 永磁同步电机解析模型
Fig.2 PMSM analysis model
为了便于各子域通解及谐波系数的求解[20],定义了如式(1)所示的函数。
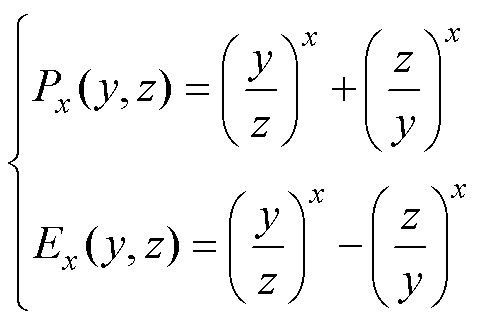 (1)
(1)
1.2.1 矢量磁位表达式及其通解
各子域内空载气隙磁场矢量磁位满足的通解表达式[21-26]为
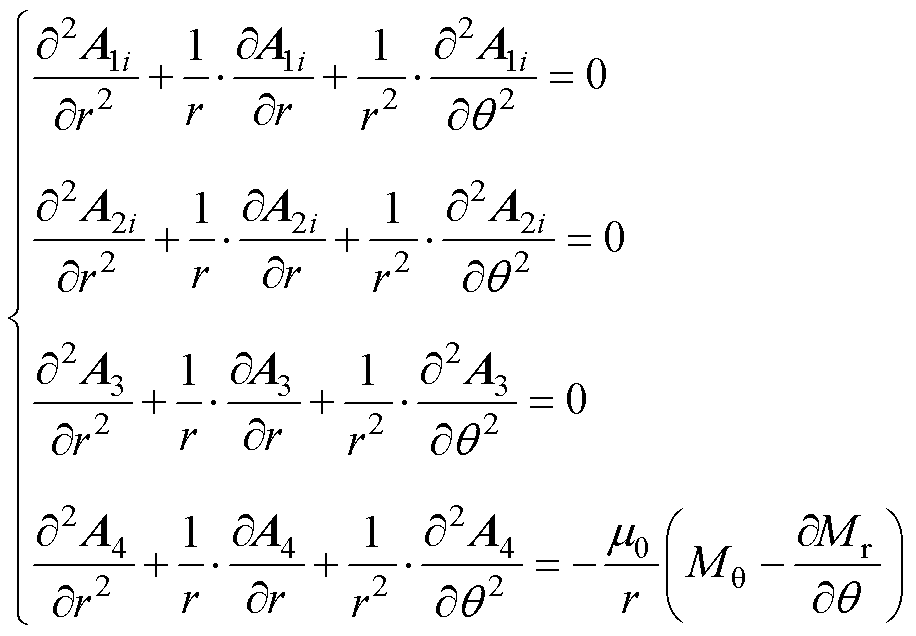 (2)
(2)
式中,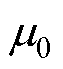 为真空磁导率;
为真空磁导率;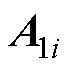 、
、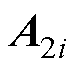 、
、 、
、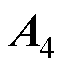 分别为槽、槽口、气隙以及永磁体子域内的矢量磁位;
分别为槽、槽口、气隙以及永磁体子域内的矢量磁位;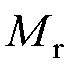 、
、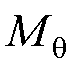 分别为永磁体磁化强度的径向分量和切向分量;r为各子域半径。
分别为永磁体磁化强度的径向分量和切向分量;r为各子域半径。
由式(1)以及分离变量法可求得各子域空载气隙磁场矢量磁位的表达式为
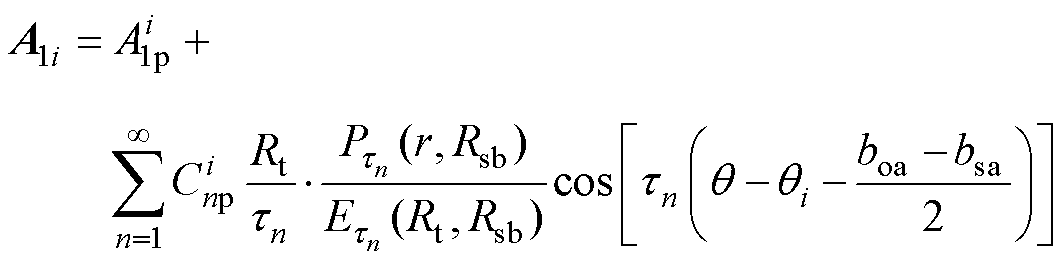 (3)
(3)
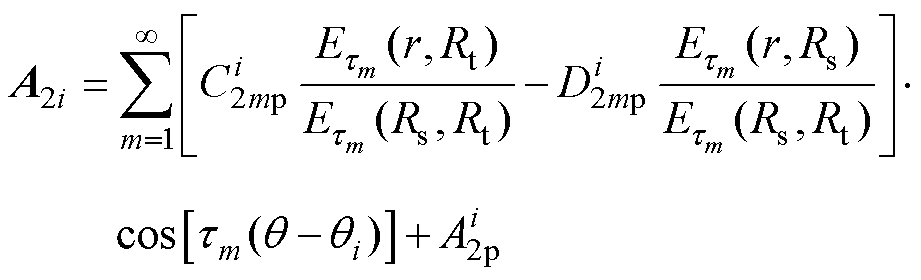 (4)
(4)
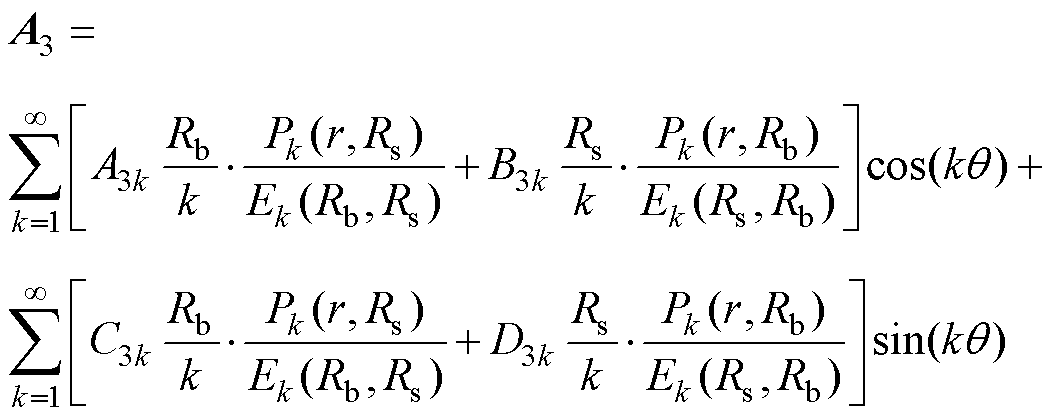 (5)
(5)
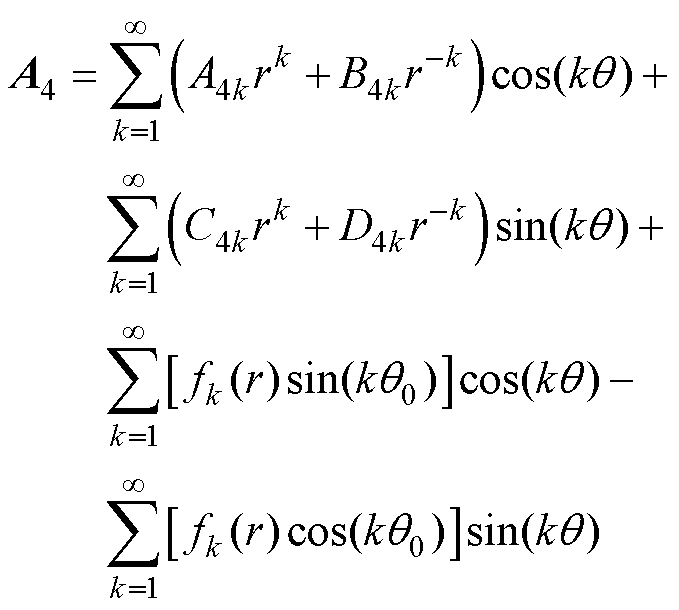 (6)
(6)
其中
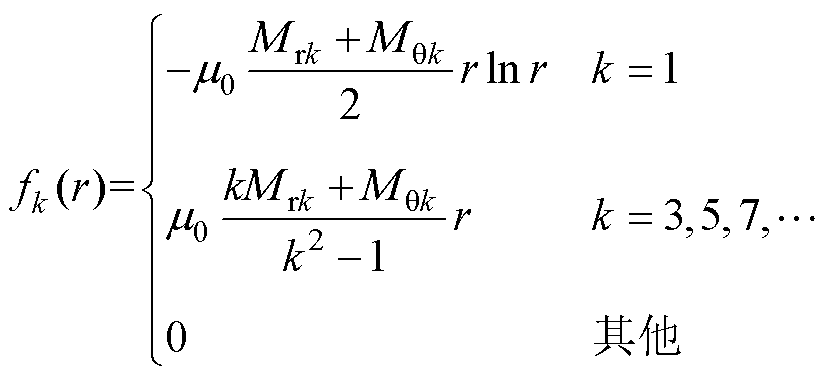 (7)
(7)
式中,n、m、k为对应子域内矢量磁位的傅里叶展开次数; ;
;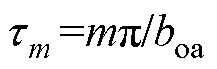 ;
;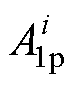 、
、 、
、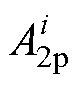 、
、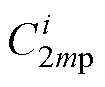 、
、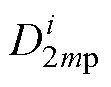 、
、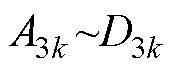 、
、 为空载气隙磁场待定系数;Mrk、Mqk分别为永磁体磁化强度的径向分量和切向分量傅里叶展开系数;Q为定子槽数;
为空载气隙磁场待定系数;Mrk、Mqk分别为永磁体磁化强度的径向分量和切向分量傅里叶展开系数;Q为定子槽数;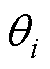 为第i个槽口初始角度,
为第i个槽口初始角度,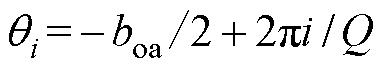 ;
;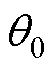 为转子初始位置角。
为转子初始位置角。
1.2.2 各子域边界条件
各子域之间的边界条件为
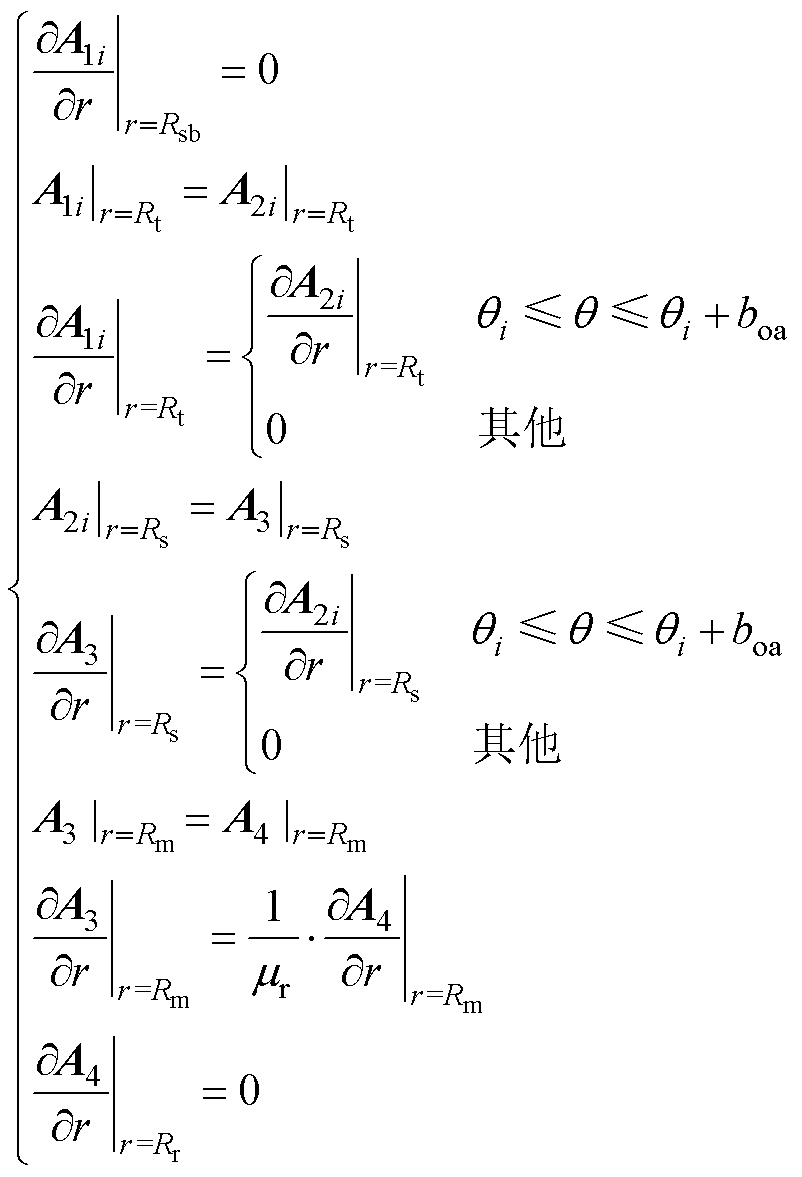 (8)
(8)
根据边界条件,可将永磁体子域的通解表达式进一步求解,有
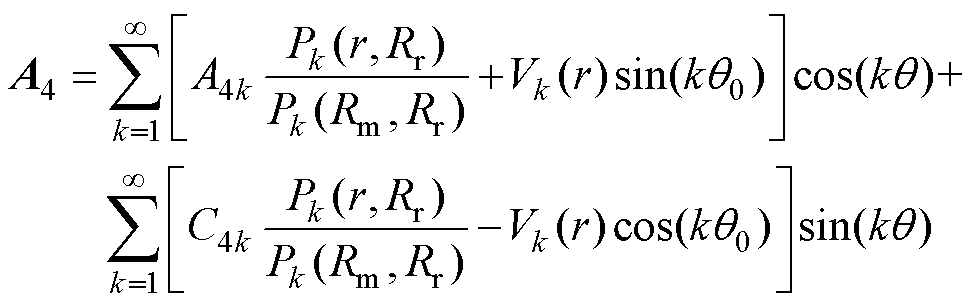 (9)
(9)
其中,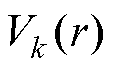 与永磁体磁化方式有关,有
与永磁体磁化方式有关,有
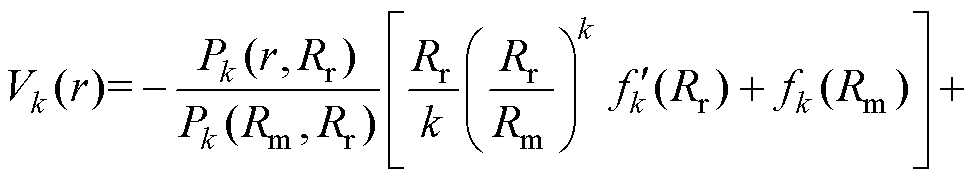
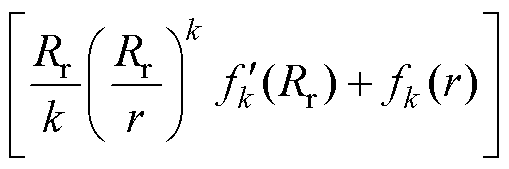 (10)
(10)
由式(10)可以看出,对于不同的永磁体结构,只需将其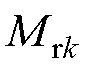 、
、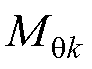 代入式(10),就可以得到特定结构的
代入式(10),就可以得到特定结构的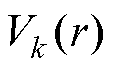 ,进而求出特定结构的空载气隙磁通密度。
,进而求出特定结构的空载气隙磁通密度。
对于平行充磁的永磁体,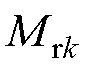 、
、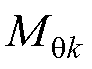 分别为
分别为
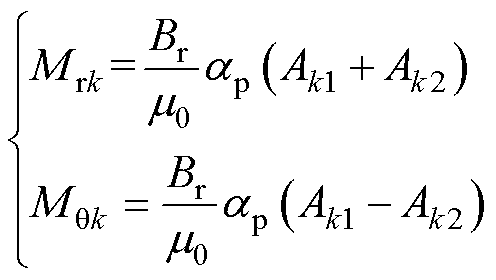 (11)
(11)
其中
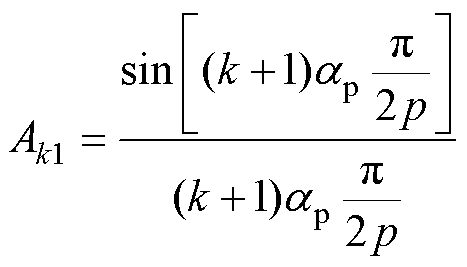 (12)
(12)
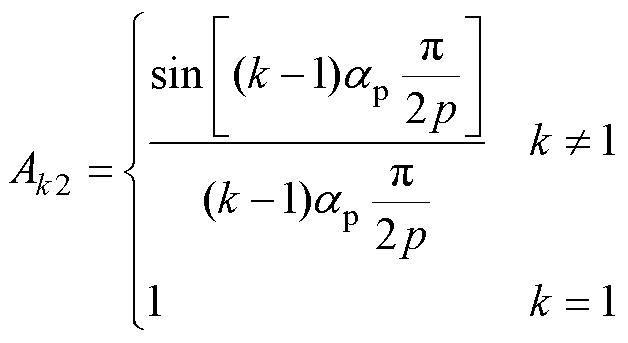 (13)
(13)
式中,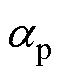 为永磁体极弧系数;
为永磁体极弧系数;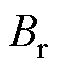 为永磁体剩磁;
为永磁体剩磁; 为极对数。
为极对数。
对于Halbach充磁的永磁体,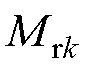 、
、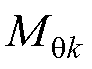 分别为
分别为
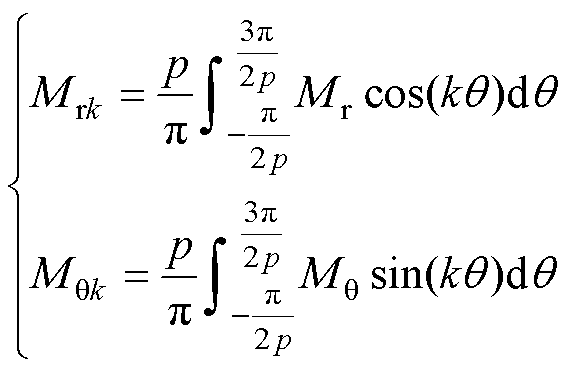 (14)
(14)
对于平行充磁的完全分段永磁体,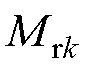 、
、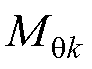 分别为
分别为
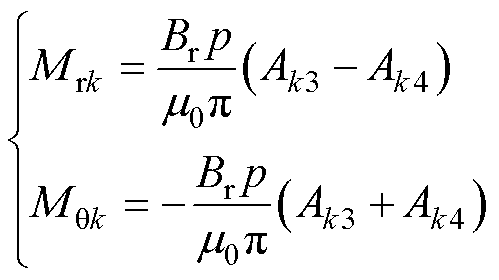 (15)
(15)
其中
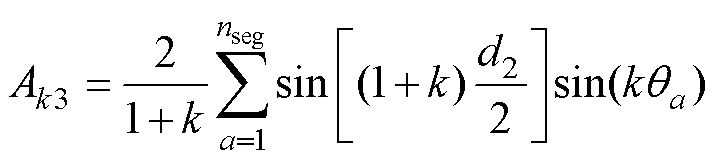 (16)
(16)
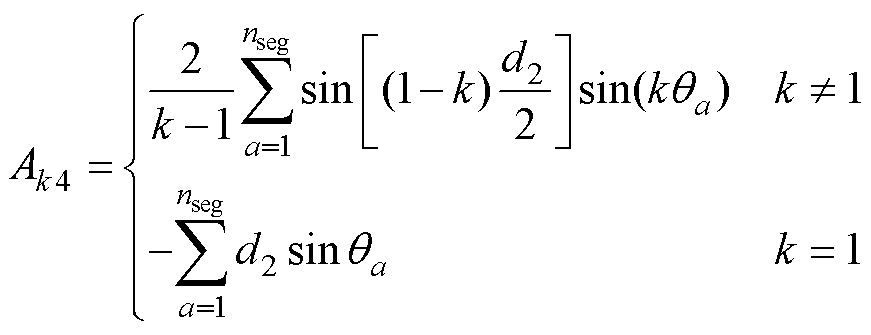 (17)
(17)
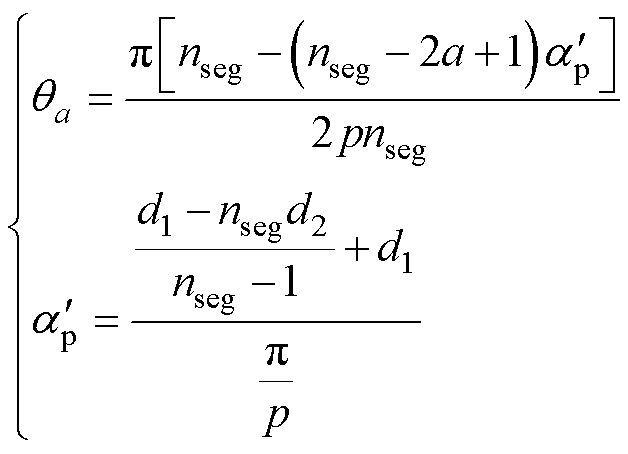 (18)
(18)
式中,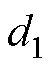 为每极下所有磁块所对应的总极弧宽度;
为每极下所有磁块所对应的总极弧宽度;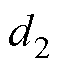 为每块磁块对应的极弧宽度;
为每块磁块对应的极弧宽度;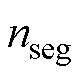 为每极分段数;
为每极分段数;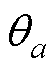 为第a块分段磁块对称轴对应的机械角度。
为第a块分段磁块对称轴对应的机械角度。
1.2.3 空载气隙磁通密度
空载气隙磁通密度径向分量和切向分量分别为
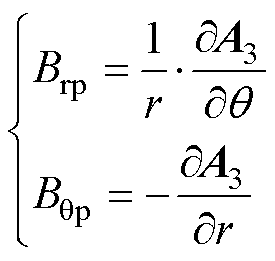 (19)
(19)
联立式(3)~式(6)、式(8),可求得空载气隙磁场待定系数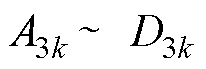 ,具体表达式如式(A6)所示。
,具体表达式如式(A6)所示。
1.3.1 矢量磁位表达式及其通解
在进行电枢反应磁场计算时,可将永磁体与气隙视为同一子域。各子域内电枢反应磁场矢量磁位满足的通解表达式为
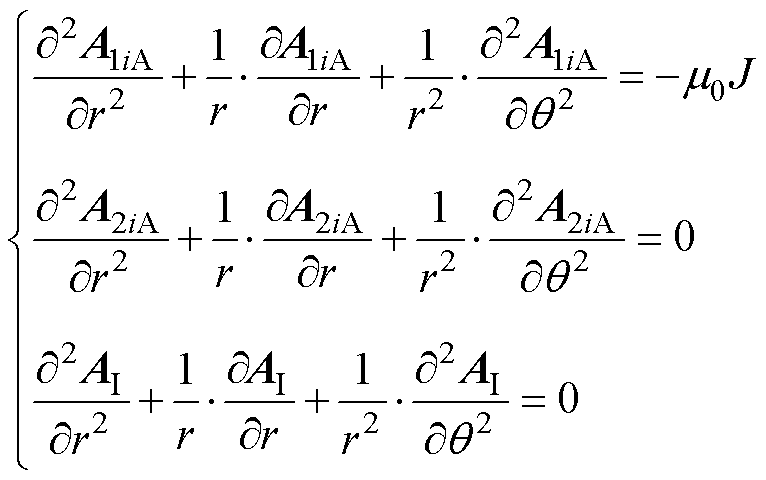 (20)
(20)
其中
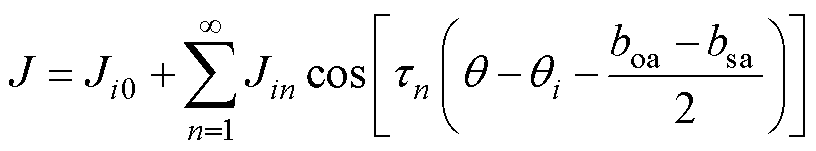 (21)
(21)
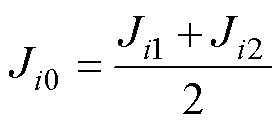 (22)
(22)
式中,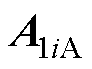 、
、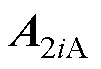 、
、 分别为槽、槽口及等效气隙子域内矢量磁位;Ji0、Jin分别为电流密度的直流、交流分量。
分别为槽、槽口及等效气隙子域内矢量磁位;Ji0、Jin分别为电流密度的直流、交流分量。
由式(1)以及分离变量法可求得各子域电枢反应磁场矢量磁位的表达式为
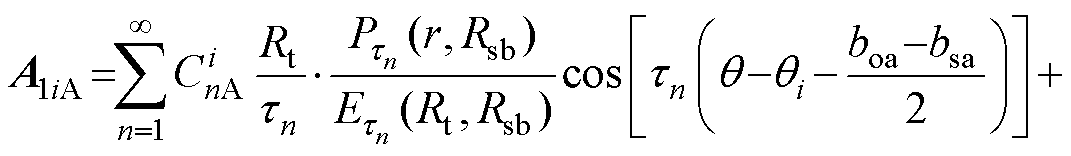
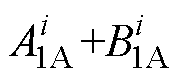 (23)
(23)
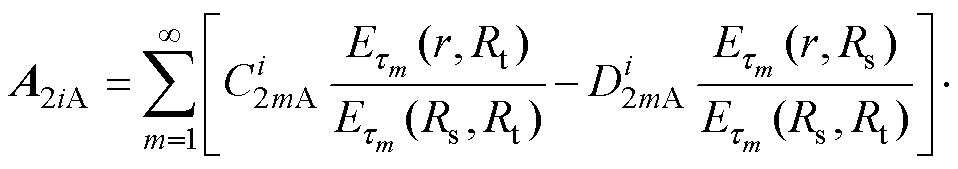
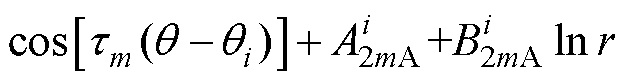 (24)
(24)
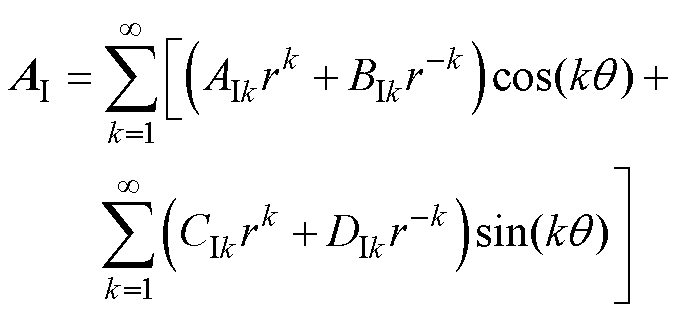 (25)
(25)
式中,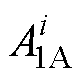 ~
~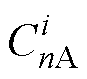 、
、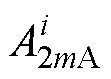 ~
~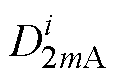 、
、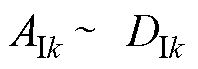 为电枢反应磁场待定系数。
为电枢反应磁场待定系数。
1.3.2 各子域边界条件
各子域之间的边界条件为
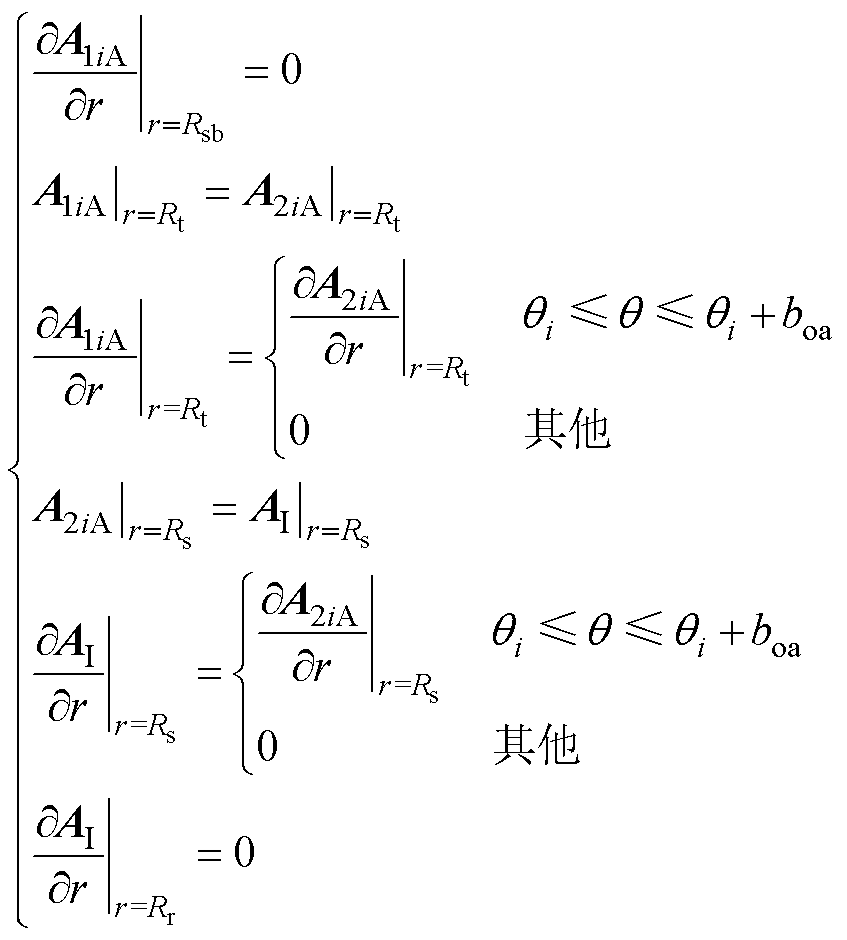 (26)
(26)
1.3.3 电枢反应磁通密度
电枢反应磁通密度径向分量和切向分量分别为
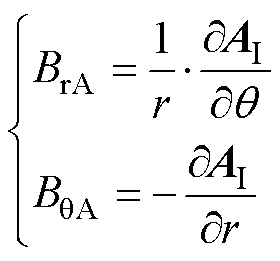 (27)
(27)
联立式(21)~式(26),可求得电枢反应磁场待定系数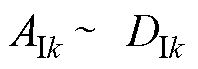 ,具体表达式如式(A14)所示。
,具体表达式如式(A14)所示。
1.4.1 负载气隙磁通密度
根据叠加定理,负载气隙磁通密度径向分量和切向分量分别为
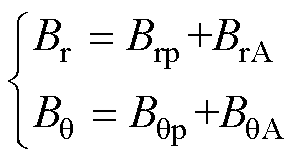 (28)
(28)
1.4.2 Halbach部分分段结构负载气隙磁场计算
在计算电枢反应磁通密度时,永磁体处于不充磁状态,与气隙子域合为等效气隙子域,仅改变永磁体的磁化方式和结构不会对电枢反应磁通密度产生影响。在计算Halbach部分分段结构的负载气隙磁通密度时,首先将Halbach部分分段结构分解为三种简单的永磁体结构;然后将三种简单永磁体结构的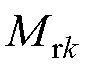 、
、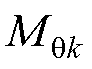 代入式(10)求出
代入式(10)求出 ,进而求出该结构的空载气隙磁通密度,再利用叠加定理合成所提结构的空载气隙磁通密度;最后将Halbach部分分段结构的空载气隙磁通密度和电枢反应磁通密度叠加成负载气隙磁通密度。
,进而求出该结构的空载气隙磁通密度,再利用叠加定理合成所提结构的空载气隙磁通密度;最后将Halbach部分分段结构的空载气隙磁通密度和电枢反应磁通密度叠加成负载气隙磁通密度。
采用叠加原理求取Hat型和T型结构的空载气隙磁通密度时,将图1所示模型的永磁体分解为三部分:第一部分为平行充磁的完全分段永磁体;第二部分为主磁极剩余的两个小永磁体,主磁极结构拆分示意图如图3所示,X1为相邻分段的极弧宽度,X2为分段处极弧宽度,X3为部分分段深度;第三部分为两个边界磁极。
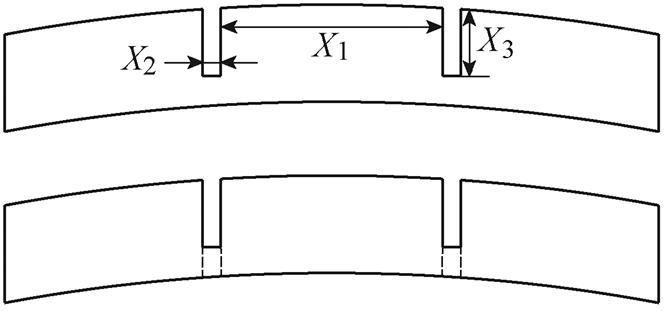
图3 主磁极结构拆分示意图
Fig.3 Main magnetic pole decomposition diagram
以Hat型Halbach部分分段结构为例,求取空载气隙磁通密度,见表1。表中, 为主磁极外半径;
为主磁极外半径;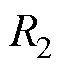 为边界磁极的外半径。
为边界磁极的外半径。
表1 Hat型结构空载气隙磁通密度计算
Tab.1 Calculation of no-load air gap magnetic density of Hat type structure

, , , , ,
Hat型Halbach部分分段结构的负载气隙磁通密度径向分量和切向分量分别为
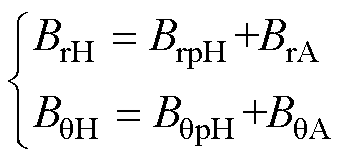 (29)
(29)
在非永磁体参数一定时,Halbach部分分段PMSM的负载气隙磁通密度仅与三个部分的永磁体
外半径 、
、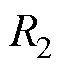 以及
以及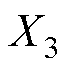 和极弧系数
和极弧系数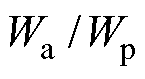 、X1、X2以及
、X1、X2以及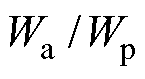 有关。当主磁极外半径
有关。当主磁极外半径 、分段处极弧宽度X2、相邻分段间隔X1以及极间间隔一定时,负载气隙磁通密度与边界磁极外半径
、分段处极弧宽度X2、相邻分段间隔X1以及极间间隔一定时,负载气隙磁通密度与边界磁极外半径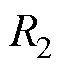 、部分分段深度X3、主磁极极弧系数以及相邻分段间隔有关。因此,对于负载气隙磁通密度的优化主要是对边界磁极厚度h1、部分分段深度X3以及边界磁极角度q1优化。
、部分分段深度X3、主磁极极弧系数以及相邻分段间隔有关。因此,对于负载气隙磁通密度的优化主要是对边界磁极厚度h1、部分分段深度X3以及边界磁极角度q1优化。
1.4.3 电磁转矩计算
由负载气隙磁通密度计算结果,利用麦克斯韦应力张量法,电磁转矩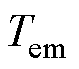 为
为
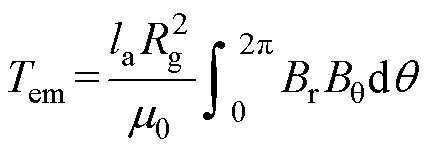 (30)
(30)
式中,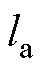 为电机轴向长度;
为电机轴向长度;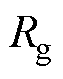 为电磁转矩计算积分半径。
为电磁转矩计算积分半径。
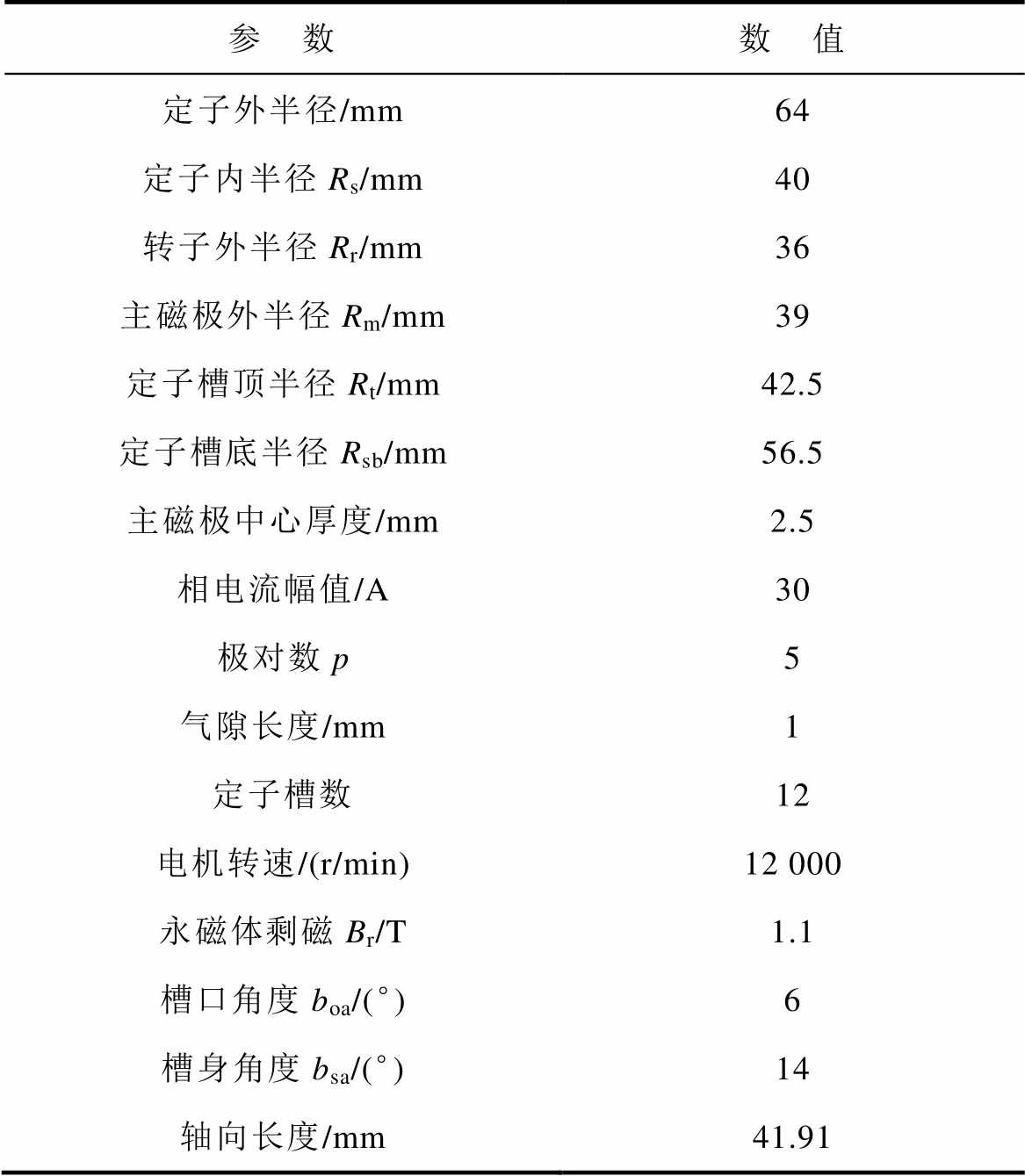
Halbach部分分段结构在Halbach阵列磁场分布正弦度好、磁通密度幅值高等特性的基础上采用主磁极部分分段,使气隙磁通密度波形更加正弦的同时,可以减小永磁体涡流损耗,提高电机的电磁性能。子任务设计方案中,轮毂电机为表贴式PMSM,10极12槽,模型电机的主要参数见表2,在Maxwell中进行参数化建模,建立三维Hat型和T型Halbach部分分段PMSM模型,对Hat型和T型结构的负载气隙磁通密度、电磁转矩、电磁转矩波动以及永磁体涡流损耗等参数进行仿真分析,并比较表贴式结构、部分分段结构、等宽等厚Halbach结构、Hat型和T型Halbach结构、Hat型和T型Halbach部分分段结构的负载气隙磁通密度总谐波畸变率(Total Harmonic Distortion, THD)、电磁转矩、涡流损耗、电磁转矩波动等性能,验证Hat型和T型Halbach部分分段结构的有效性和优越性。
表2 电机模型参数
Tab.2 Parameters of motor model
参 数数 值 定子外半径/mm64 定子内半径Rs/mm40 转子外半径Rr/mm36 主磁极外半径Rm/mm39 定子槽顶半径Rt/mm42.5 定子槽底半径Rsb/mm56.5 主磁极中心厚度/mm2.5 相电流幅值/A30 极对数p5 气隙长度/mm1 定子槽数12 电机转速/(r/min)12 000 永磁体剩磁Br/T1.1 槽口角度boa/(°)6 槽身角度bsa/(°)14 轴向长度/mm41.91
电机负载时Hat型和T型结构气隙中心处的径向磁通密度、切向磁通密度和电磁转矩计算结果对比如图4和图5所示。从图中可以看出,精确子域模型解析法与有限元结果较为接近,验证了解析公式的正确性,为Halbach部分分段PMSM的优化奠定了基础。

图4 负载气隙径向磁通密度和切向磁通密度变化曲线
Fig.4 Variation curves of radial magnetic flux density and tangential magnetic flux density of load air gap
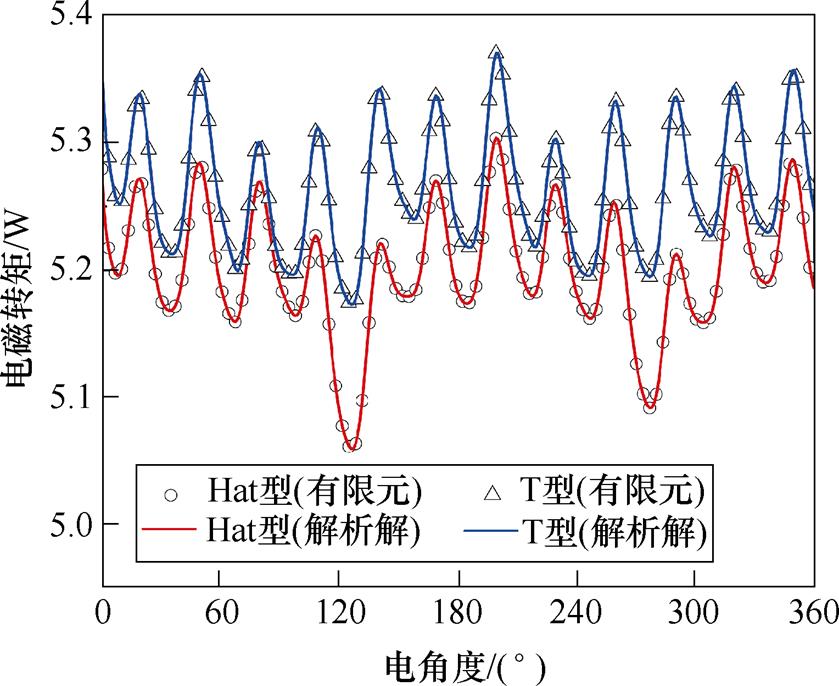
图5 电磁转矩变化曲线
Fig.5 Variation curves of electromagnetic torque
2.2.1 优化思想
对电机结构进行多目标多变量优化时,若对所有参数选取区间内的数据进行扫描分析,会使得寻优的效率非常低下。在变量优化的过程中,负载气隙磁通密度THD是描述负载气隙磁通密度波形正弦程度的重要参数,但仅以负载气隙磁通密度THD为目标筛选最优数据过于片面。这里将分级优化思想引入到电机结构优化中,以负载气隙磁通密度THD为初始目标进行优化分析,缩小数据选取区间,形成的永磁体结构多目标多变量分级优化思 想[27]如下:
(1)以永磁体涡流损耗为目标的寻优过程设为第一级,对于分数槽结构,永磁体适合采用周向均匀分段结构[17],同时,为了维持永磁体的机械强度,部分分段深度应不超过主磁极厚度的65%[19, 28]。
(2)以负载气隙磁通密度THD为目标的寻优过程设为第二级,通过对极间间隔和边界磁极充磁角度进行大范围大步长的仿真,选取负载气隙磁通密度THD数值较小的参数区间,并在此区间范围内进行小步长仿真确定最优极间间隔和边界磁极充磁角度。
(3)在固定的极间间隔和边界磁极充磁角度的基础上,对边界磁极的厚度进行大范围大步长的仿真,选取负载气隙磁通密度THD数值较小的参数区间。
(4)以电磁转矩、转矩波动以及负载气隙磁通密度THD为目标,在筛选出的参数区间范围内进行小步长仿真分析,综合考虑三者的影响,选取最优参数。
2.2.2 优化分析
主磁极的分段深度X3越大,永磁体涡流损耗就越小,但考虑到永磁体主磁极的完整性及其机械强度,X3不能超过主磁极厚度的65%。同时,分数槽结构更适合采用永磁体周向均匀分段。因此,部分分段深度X3=1.625mm,对主磁极进行周向均匀部分分段,即保持分段间隔相同。
改变Hat型和T型Halbach部分分段PMSM模型中的极间间隔qin,在0°~10°内,每隔1°取一个值,得到Hat型和T型结构的负载气隙磁通密度THD随qin变化的曲线,如图6所示,从图中可以看出,随着qin的增大,Hat型和T型结构的负载气隙磁通密度THD逐渐增大,T型结构的负载气隙磁通密度THD的增长速度恒大于Hat型。当qin=0°时,Hat和T型结构的负载气隙THD有最小值,分别为22.33%、21.92%。因此,采用无极间间隔的电机 结构。
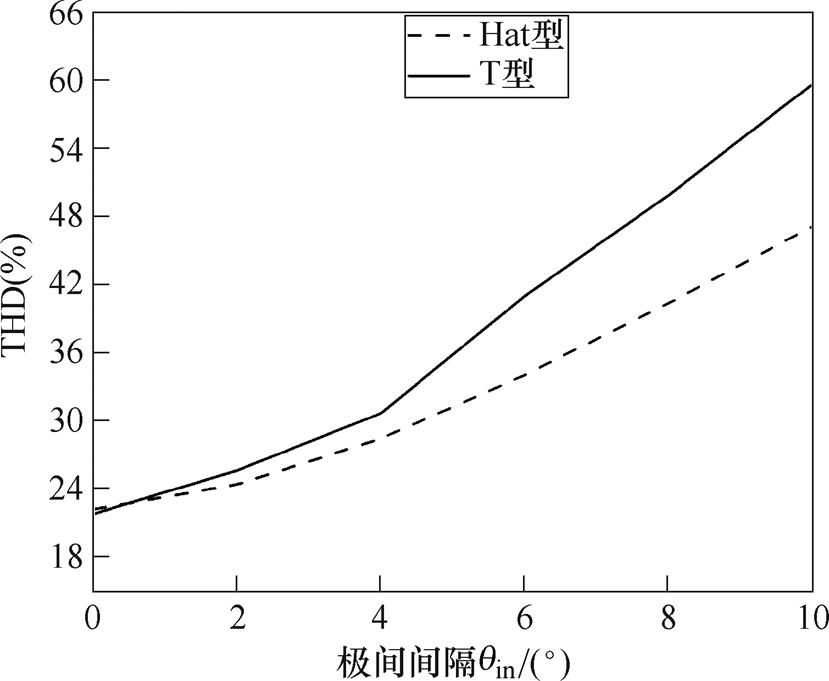
图6 负载气隙磁通密度THD随极间间隔的变化曲线
Fig.6 Variation curves of the load air gap magnetic density THD with the interval between poles
改变Hat型和T型Halbach部分分段PMSM模型中边界磁极的充磁角度 ,在0°~90°内,每隔10°取一个值,仿真后选取一个最优区间即35°~45°,然后在最优区间内每隔1°取一个值,仿真得到Hat型和T型结构的负载气隙磁通密度THD随
,在0°~90°内,每隔10°取一个值,仿真后选取一个最优区间即35°~45°,然后在最优区间内每隔1°取一个值,仿真得到Hat型和T型结构的负载气隙磁通密度THD随 变化的曲线,如图7所示。从图中可以看出,随着
变化的曲线,如图7所示。从图中可以看出,随着 的增大,负载气隙磁通密度THD先减小再增大;在无极间间隔的情况下,Hat型结构的负载气隙磁通密度THD恒大于T型结构。当
的增大,负载气隙磁通密度THD先减小再增大;在无极间间隔的情况下,Hat型结构的负载气隙磁通密度THD恒大于T型结构。当 为39°、40°时,Hat型、T型结构的负载气隙磁通密度THD有最小值21.75%、21.48%。因此,分别选取39°和40°的充磁角度对Hat型和T型结构的边界磁极 充磁。
为39°、40°时,Hat型、T型结构的负载气隙磁通密度THD有最小值21.75%、21.48%。因此,分别选取39°和40°的充磁角度对Hat型和T型结构的边界磁极 充磁。
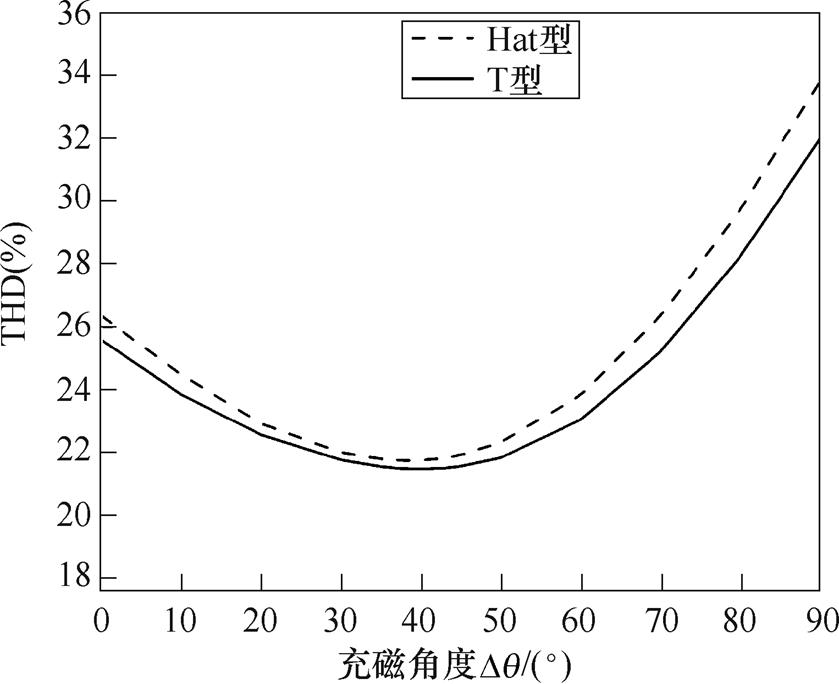
图7 负载气隙磁通密度THD随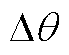 变化的曲线
变化的曲线
Fig.7 Curves of harmonic distortion rate and fundamental wave amplitude with 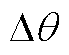
在极间间隔一定时,主磁极与边界磁极角度之和为固定值,通过改变边界磁极角度,使主磁极角度同时变化。改变边界磁极角度q1和边界磁极厚度h1,使q1在2°~12°内,每隔4°取一个值;使h1在0.5~2.5mm内,每隔0.5mm取一个值进行仿真,然后在最优区间内再进行仿真,即在h1间隔不变时,q1在4°~11°内每隔1°选一个值,得到Hat型和T型结构的负载气隙磁通密度THD,见表3、表4。
表3 Hat型结构负载气隙磁通密度THD
Tab.3 The load air gap magnetic density THD of Hat-type structure

q1/(°)THD(%) 0.5mm1mm1.5mm2mm2.5mm 231.0932.1133.8136.4941.17 424.6625.5427.3830.9237.31 523.5423.6024.8428.1934.71 624.0722.2823.0825.3132.22 725.9822.6522.0723.3929.98 829.0424.0621.7521.8828.04 933.1226.4522.2220.8226.26 1038.3830.1723.7321.3024.97 1144.4634.2526.2122.0624.08 1250.8438.5128.9823.5423.95
表4 T型结构负载气隙磁通密度THD
Tab.4 The load air gap magnetic density THD of T-type structure
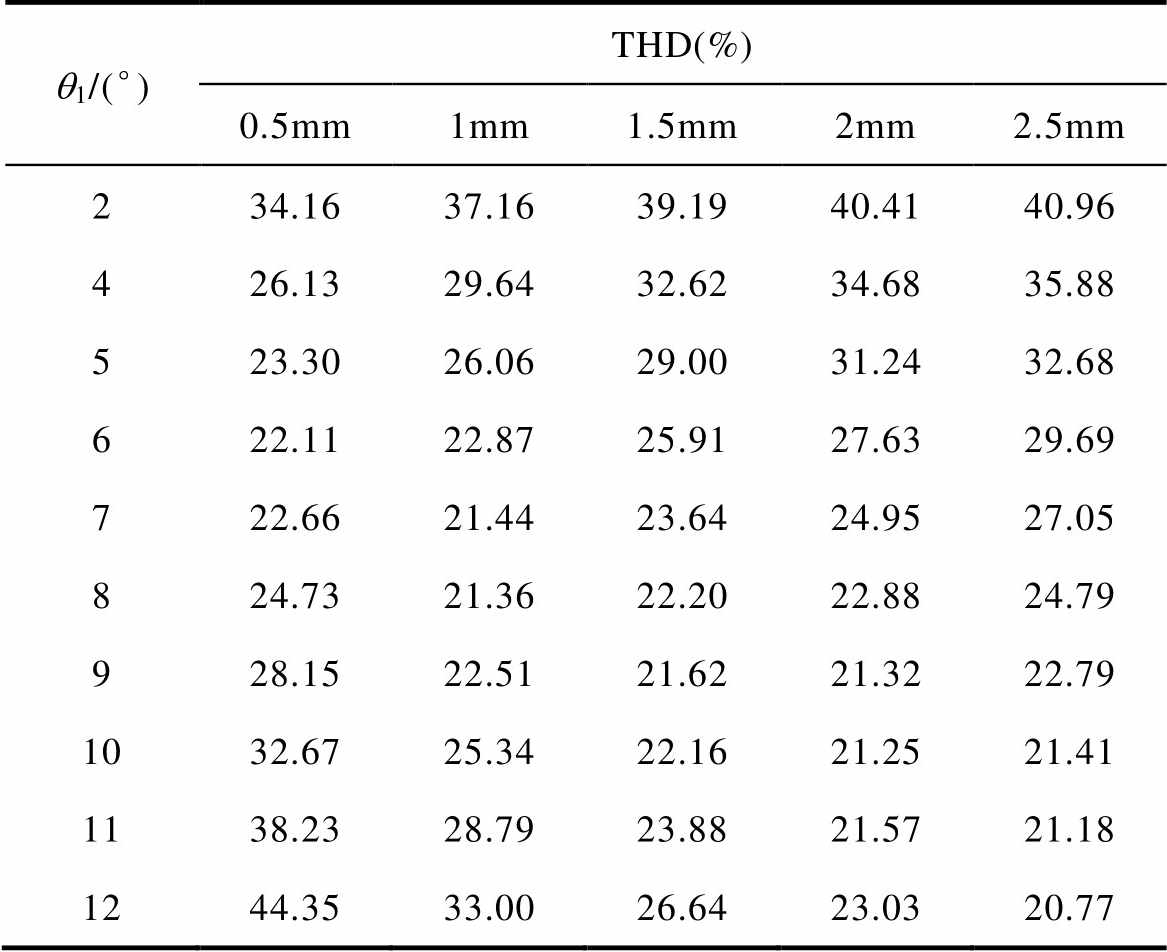
q1/(°)THD(%) 0.5mm1mm1.5mm2mm2.5mm 234.1637.1639.1940.4140.96 426.1329.6432.6234.6835.88 523.3026.0629.0031.2432.68 622.1122.8725.9127.6329.69 722.6621.4423.6424.9527.05 824.7321.3622.2022.8824.79 928.1522.5121.6221.3222.79 1032.6725.3422.1621.2521.41 1138.2328.7923.8821.5721.18 1244.3533.0026.6423.0320.77
从表3、表4可以看出,对于Hat型和T型结构,当h1 时,负载气隙磁通密度THD随着q1的增大先减小再增大;当h1
时,负载气隙磁通密度THD随着q1的增大先减小再增大;当h1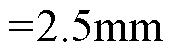 时,负载气隙磁通密度THD随着q1的增大逐渐减小,可以看出,单独改变Halbach边界磁极的厚度或宽度不能对负载气隙磁通密度THD产生很大的改善;当q1较小时,负载气隙磁通密度THD随着h1的增大逐渐增大;当q1逐渐增大时,气隙磁通密度THD随着h1的增大先减小再增大。因此,在此基础上选取负载气隙磁通密度THD偏小的区间再对厚度h1进行仿真选取最优参数,即在q1=6°~9°、h1=1~2mm内,h1每隔0.2mm取一个值对Hat型和T型结构进行仿真。
时,负载气隙磁通密度THD随着q1的增大逐渐减小,可以看出,单独改变Halbach边界磁极的厚度或宽度不能对负载气隙磁通密度THD产生很大的改善;当q1较小时,负载气隙磁通密度THD随着h1的增大逐渐增大;当q1逐渐增大时,气隙磁通密度THD随着h1的增大先减小再增大。因此,在此基础上选取负载气隙磁通密度THD偏小的区间再对厚度h1进行仿真选取最优参数,即在q1=6°~9°、h1=1~2mm内,h1每隔0.2mm取一个值对Hat型和T型结构进行仿真。
Hat型和T型结构的负载气隙磁通密度THD随边界磁极厚度h1和边界磁极角度q1变化的曲线如图8和图9所示,又由表3和表4可知,随着h1的增大,Hat型和T型结构的负载气隙磁通密度THD先减小再增大,当q1=9°、h1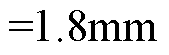 时,Hat型结构的负载气隙磁通密度THD有最小值20.51%,当q1= 9°、h1=
时,Hat型结构的负载气隙磁通密度THD有最小值20.51%,当q1= 9°、h1=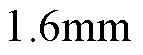 时,T型结构的负载气隙磁通密度THD有最小值21.01%。
时,T型结构的负载气隙磁通密度THD有最小值21.01%。
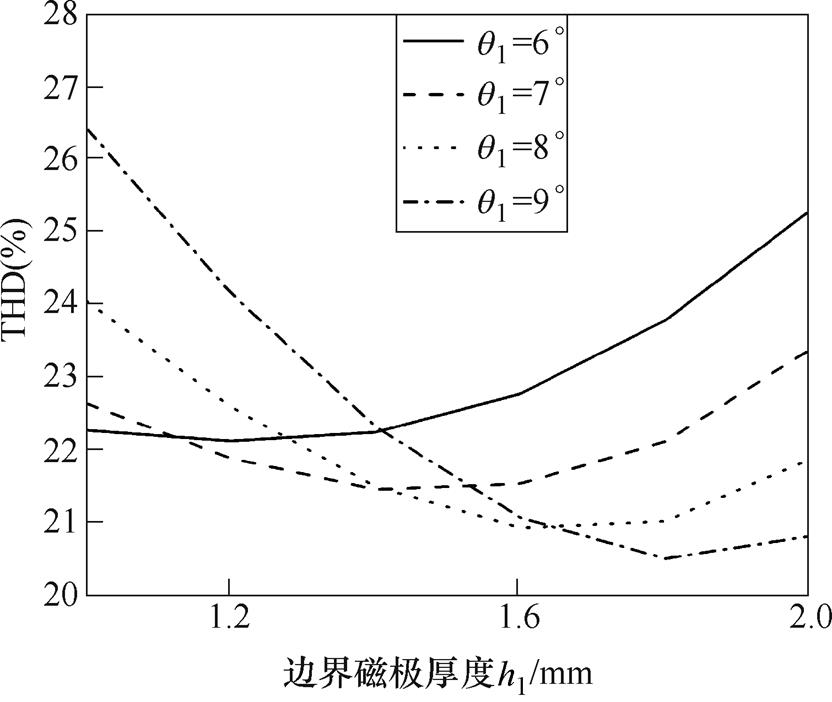
图8 Hat型结构的负载气隙磁通密度THD变化曲线
Fig.8 Variation curves of the load air gap magnetic density THD of Hat-type structure
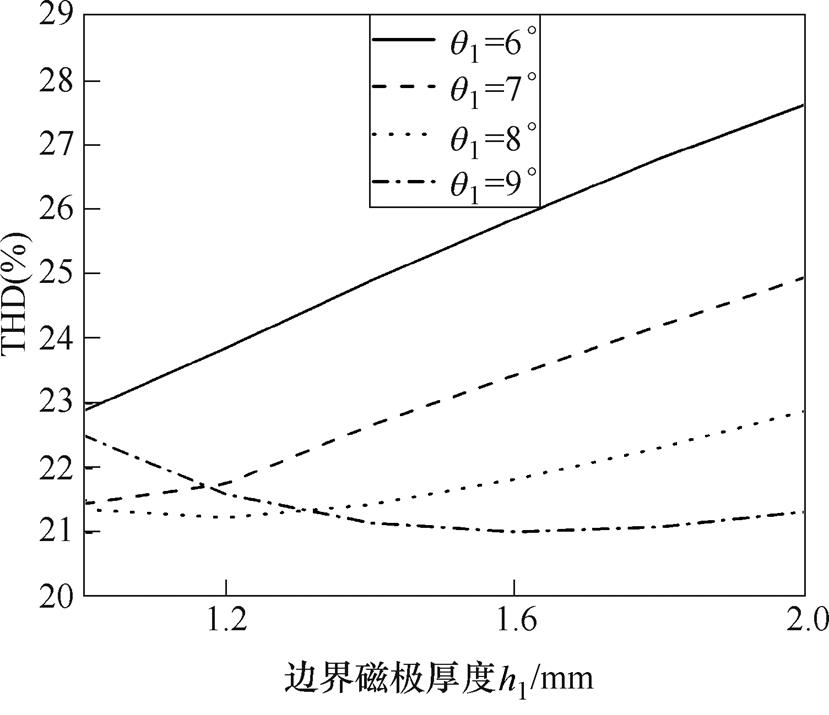
图9 T型结构的负载气隙磁通密度THD变化曲线
Fig.9 Variation curves of the load air gap magnetic density THD of T-type structure
Hat型和T型结构的电磁转矩随边界磁极厚度h1和边界磁极角度q1变化的曲线如图10和图11所示。从图中可以看出,随着h1增大,电磁转矩逐渐增大;随着q1增大,电磁转矩逐渐减小。这是因为对于同种永磁体结构,电磁转矩的大小主要取决于永磁体的用量。
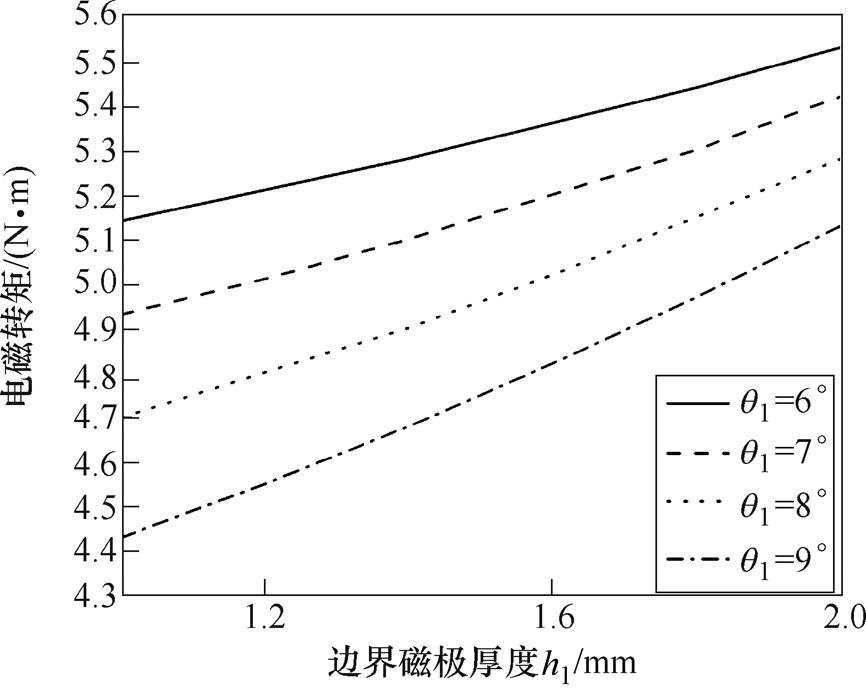
图10 Hat型结构电磁转矩变化曲线
Fig.10 Variation curves of electromagnetic torque of Hat-type structure
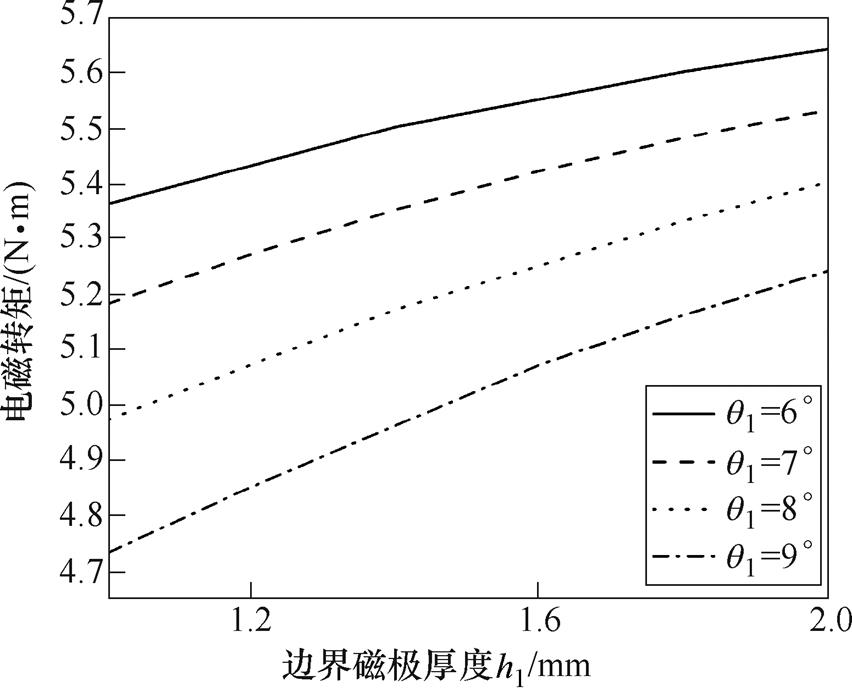
图11 T型结构电磁转矩变化曲线
Fig.11 Variation curves of electromagnetic torque of T-type structure
PMSM稳态运行时,瞬态电磁转矩的最大值为 ,最小值为
,最小值为 ,则电磁转矩波动
,则电磁转矩波动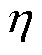 为
为
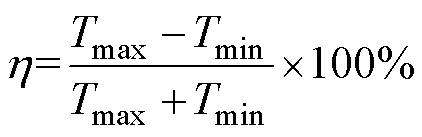 (31)
(31)
Hat型和T型结构的电磁转矩波动见表5和表6。从表中可以看出,Hat型结构的电磁转矩波动在q1为6°或8°时较小,而T型结构在q1为6°~9°时的电磁转矩波动优于Hat型结构,且受q1和h1的影响较小。
为了选取最优的q1和h1,需综合考虑负载气隙磁通密度THD、电磁转矩和电磁转矩波动。对于Hat型结构,为了维持电磁转矩不因为永磁体用量的减少而大幅度降低,q1应选取6°或7°;为了降低电磁转矩波动,使输出转矩更加平稳,q1应选取6°或8°,又考虑到q1=6°时的负载气隙磁通密度THD,因此Hat型结构的最优参数为q1=6°、h1=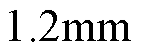 。对于T型结构,为了维持电磁转矩q1应选取6°、7°及8°;为了降低电磁转矩波动,q1应选取7°或9°,又考虑到q1=7°时的负载气隙磁通密度THD,因此,T型结构的最优参数为q1=7°、h1=
。对于T型结构,为了维持电磁转矩q1应选取6°、7°及8°;为了降低电磁转矩波动,q1应选取7°或9°,又考虑到q1=7°时的负载气隙磁通密度THD,因此,T型结构的最优参数为q1=7°、h1=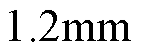 。
。
表5 Hat型结构电磁转矩波动
Tab.5 Electromagnetic torque fluctuation of Hat-type structure
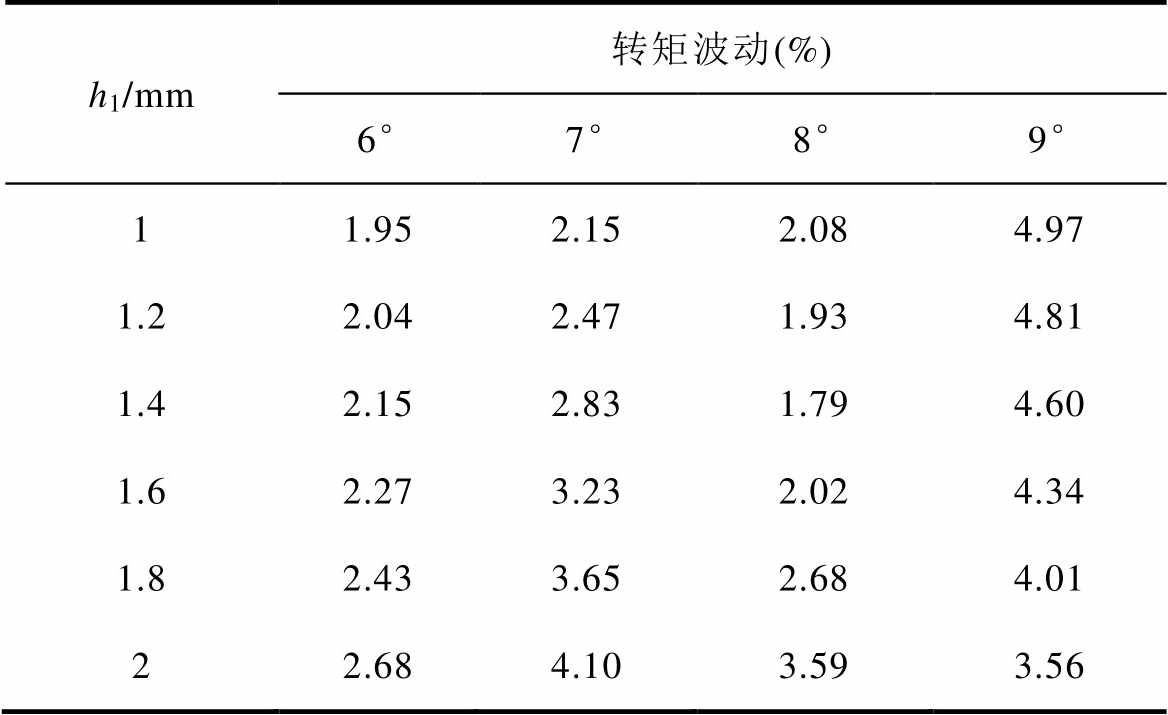
h1/mm转矩波动(%) 6°7°8°9° 11.952.152.084.97 1.22.042.471.934.81 1.42.152.831.794.60 1.62.273.232.024.34 1.82.433.652.684.01 22.684.103.593.56
表6 T型结构电磁转矩波动
Tab.6 Electromagnetic torque fluctuation of T-type structure

h1/mm转矩波动(%) 6°7°8°9° 11.511.651.891.47 1.21.741.672.181.09 1.41.931.732.410.88 1.62.091.792.601.06 1.82.231.852.741.28 22.361.922.921.47
2.2.3 对比分析
为了验证Hat型和T型Halbach部分分段结构的优缺点,在进行PMSM电磁性能的对比分析时,由于相邻永磁体间没有极间间隔,Halbach结构、部分分段结构、表贴式结构的永磁体极弧宽度均为36°。同时,表贴式结构、部分分段结构以及等宽等厚Halbach结构的永磁体厚度等于Hat型和T型Halbach部分分段结构的主磁极厚度。因此,进行对比分析的三种结构之间体积不同,其中 。
。
如图12~图14所示分别为最优Hat型和T型Halbach部分分段结构与表贴式结构的负载气隙磁通密度、电磁转矩以及永磁体涡流损耗的对比。
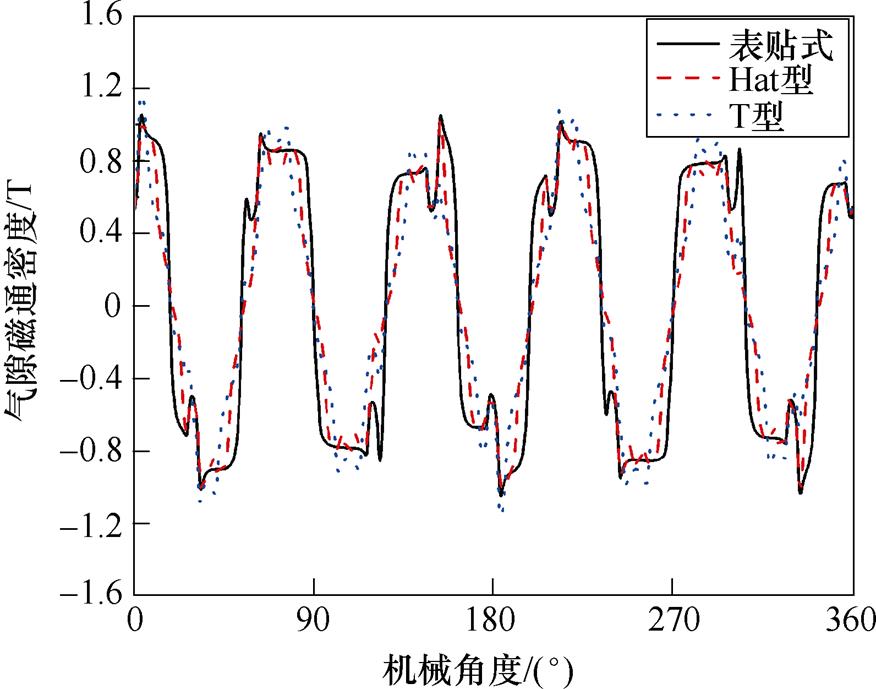
图12 负载气隙磁通密度变化曲线
Fig.12 Load air gap magnetic density curves
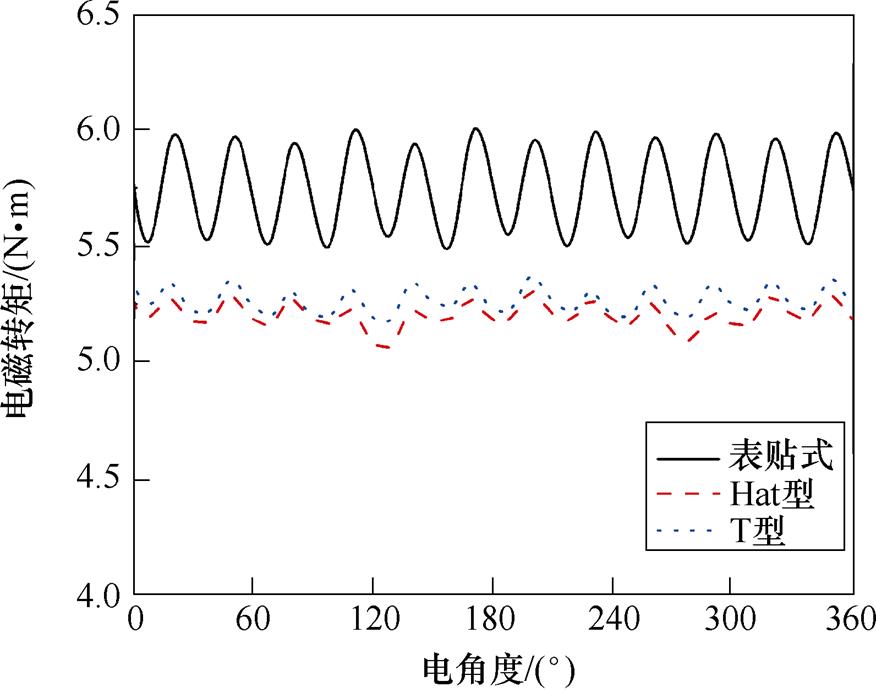
图13 电磁转矩变化曲线
Fig.13 Electromagnetic torque curves
从图12可以看出,Hat型和T型Halbach部分分段结构的负载气隙磁通密度曲线几乎吻合,其中,表贴式结构的负载气隙磁通密度THD为37.34%,而Hat型Halbach部分分段结构的负载气隙磁通密度THD为22.13%,T型Halbach部分分段结构的负载气隙磁通密度THD为21.75%。相比于表贴式结构,采用Hat型和T型Halbach部分分段结构分别降低了15.21%和15.59%的负载气隙磁通密度THD,说明了Hat型和T型Halbach部分分段结构可以大幅度抑制负载气隙磁通密度谐波,改善负载气隙磁通密度波形。
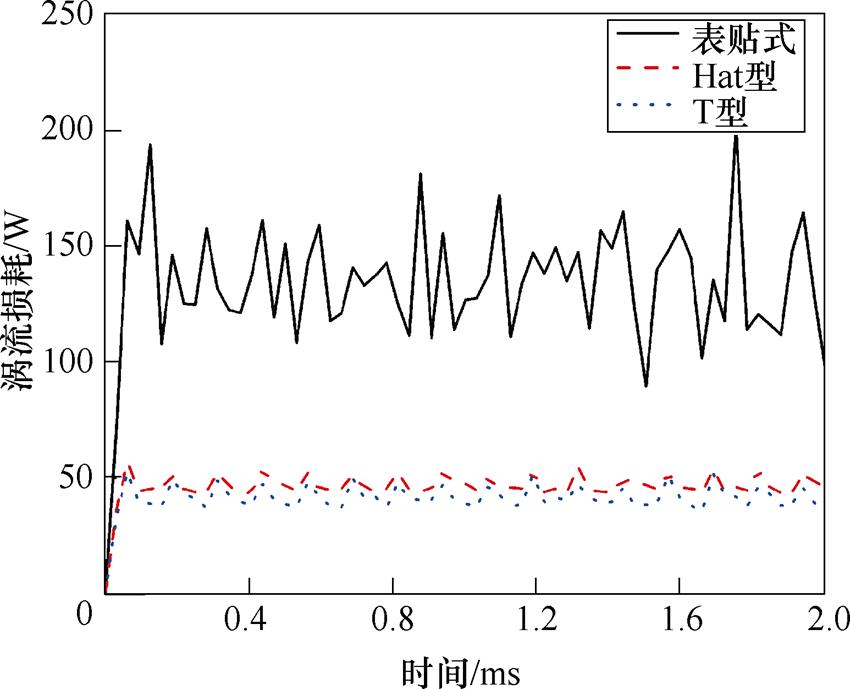
图14 涡流损耗变化曲线
Fig.14 Eddy current loss curves
从图13可以看出,表贴式结构的电磁转矩为5.75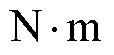 ,电磁转矩波动为4.52%,而Hat型Halbach部分分段结构的电磁转矩为5.2
,电磁转矩波动为4.52%,而Hat型Halbach部分分段结构的电磁转矩为5.2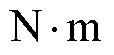 ,电磁转矩波动为2.04%;T型Halbach部分分段结构的电磁转矩为5.26
,电磁转矩波动为2.04%;T型Halbach部分分段结构的电磁转矩为5.26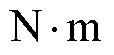 ,电磁转矩波动为1.67%。相比于表贴式结构,采用Hat型和T型Halbach部分分段结构使电磁转矩降低了9.57%和8.52%,电磁转矩波动降低了2.48%和2.85%。永磁体体积的减小不可避免地降低了电磁转矩,但Hat型和T型Halbach部分分段结构可以大幅度减小电磁转矩波动,使电磁转矩更加稳定,T型结构对于电磁转矩波动的优化效果更加显著。虽然T型结构的永磁体体积小于Hat型结构,但T型结构的电磁转矩仍大于Hat型结构,这说明T型结构具有更高的永磁体利用率。
,电磁转矩波动为1.67%。相比于表贴式结构,采用Hat型和T型Halbach部分分段结构使电磁转矩降低了9.57%和8.52%,电磁转矩波动降低了2.48%和2.85%。永磁体体积的减小不可避免地降低了电磁转矩,但Hat型和T型Halbach部分分段结构可以大幅度减小电磁转矩波动,使电磁转矩更加稳定,T型结构对于电磁转矩波动的优化效果更加显著。虽然T型结构的永磁体体积小于Hat型结构,但T型结构的电磁转矩仍大于Hat型结构,这说明T型结构具有更高的永磁体利用率。
从图14可以看出,表贴式结构的永磁体涡流损耗为135.13W,而Hat型Halbach部分分段结构的永磁体涡流损耗为47.03W,T型Halbach部分分段结构的永磁体涡流损耗为41.70W。相比于表贴式结构,采用Hat型和T型Halbach部分分段结构使涡流损耗降低了65.20%和69.14%。说明Hat型和T型Halbach部分分段结构可以大幅度降低涡流损耗,并抑制涡流损耗的波动。
为了进一步验证Hat型和T型Halbach部分分段结构的优缺点,比较了七种不同结构的电磁性能和永磁体体积,不同结构的电磁性能对比见表7,可以看出,七种结构各自具有的优缺点。相比于表贴式结构,部分分段结构在略微改变永磁体体积的情况下,大幅度降低了永磁体涡流损耗,但是这种显著的降耗效果是在牺牲其他电磁性能的基础上达到的,即增加了负载气隙磁通密度THD、提高了电磁转矩波动;相比于表贴式结构,等宽等厚Halbach结构在未改变永磁体体积的情况下,大幅度降低了负载气隙磁通密度THD和电磁转矩波动,但是等宽等厚Halbach结构的电磁转矩过低,不符合实际工程的要求;Hat型和T型Halbach结构在等宽等厚Halbach结构的基础上,降低永磁体体积的同时提高了电磁转矩,提高了永磁体利用率,但仍存在较大的永磁体涡流损耗;Halbach部分分段结构结合了Halbach结构和部分分段结构的优点,相比于表贴式结构,大幅度降低负载气隙磁通密度THD、电磁转矩波动以及永磁体涡流损耗。同时,电磁转矩没有因为永磁体用量的减小而大幅度降低。
表7 不同结构的电磁性能对比
Tab.7 Comparison of electromagnetic properties of different structures

电磁性能负载气隙磁通密度 THD(%)电磁转矩/ (N·m)电磁转矩波动(%)涡流损耗/ W永磁体体积/ cm3 表贴式结构37.345.754.52135.1320.40 部分分段结构38.845.615.6163.1020.04 等宽等厚Halbach结构20.675.022.29104.5620.40 Hat型Halbach结构20.985.302.4386.9717.21 T型Halbach结构21.935.560.8087.2016.75 Hat型Halbach部分分段结构22.135.202.0447.0316.85 T型Halbach部分分段结构21.755.261.6741.7016.39
由表7中的数据计算可得,Hat型Halbach结构单位体积的电磁转矩等于Hat型Halbach部分分段,T型Halbach结构单位体积的电磁转矩大于T型Halbach部分分段结构;T型Halbach结构的单位体积的电磁转矩为最高,T型Halbach部分分段结构次之,这说明T型Halbach结构具有很高的永磁体利用率,在相同的永磁体体积下更容易产生更大的电磁转矩,但Hat型和T型Halbach部分分段结构单位体积的涡流损耗远小于Hat型和T型Halbach结构。相比于Hat型Halbach部分分段结构,T型Halbach部分分段结构具有更大的单位体积的电磁转矩和更小的单位体积的涡流损耗。
综合比较几种结构的负载气隙磁通密度THD、电磁转矩、涡流损耗、永磁体体积等参数,可以看出,相比于表贴式结构,采用Hat型和T型Halbach部分分段结构可以极大地提升电机的电磁性能。同时,Hat型和T型Halbach部分分段结构具有不同的优点,Hat型Halbach部分分段结构的电磁性能略低于T型,但Hat型结构工艺更加简单;T型Halbach部分分段结构的电磁性能更好、永磁体体积更小,具有更加广阔的前景。
在转速为12 000r/min时,在切向离心力和电磁力的作用下,通过Ansys Workbench,仿真得出Hat型和T型Halbach部分分段结构的等效应力和总变形,如图15、图16所示。
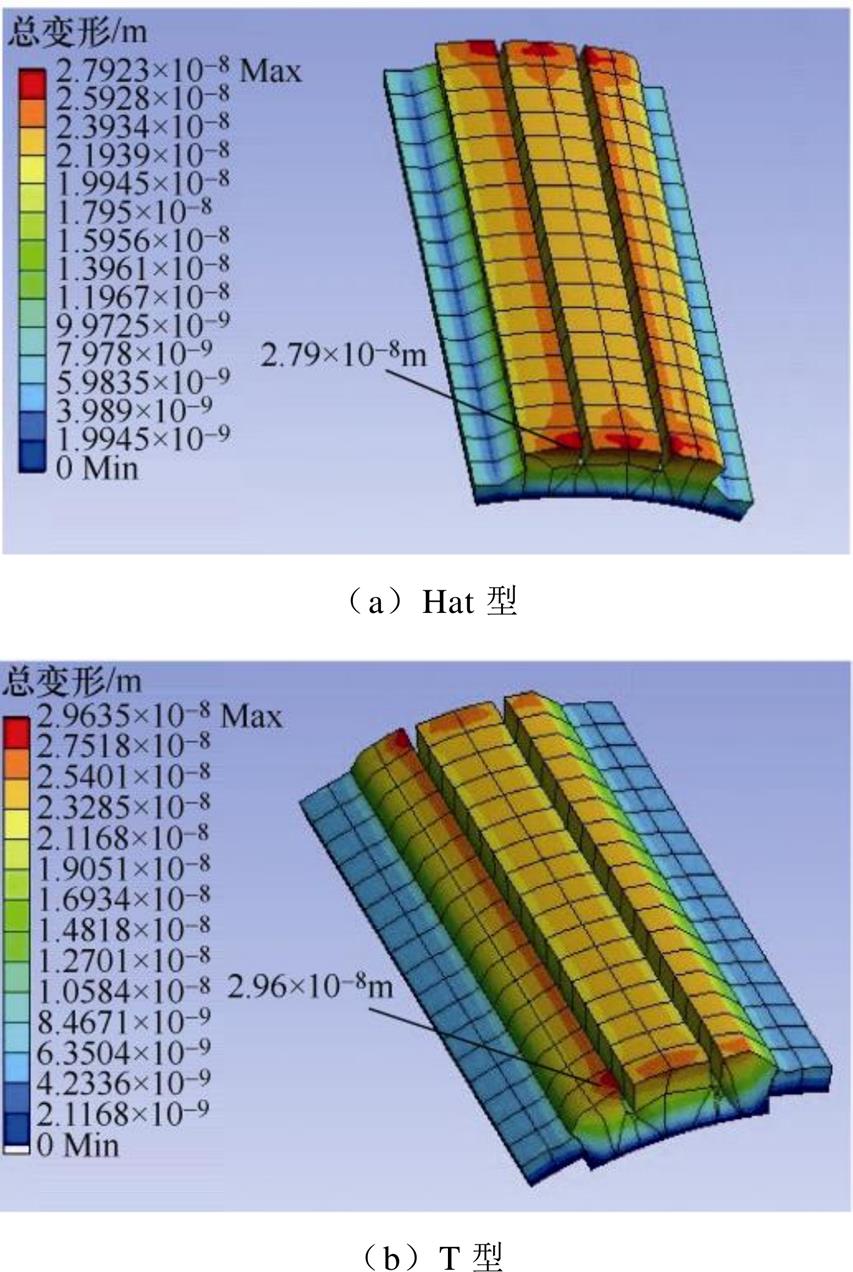
图15 永磁体总变形
Fig.15 Total deformation map of permanent magnets
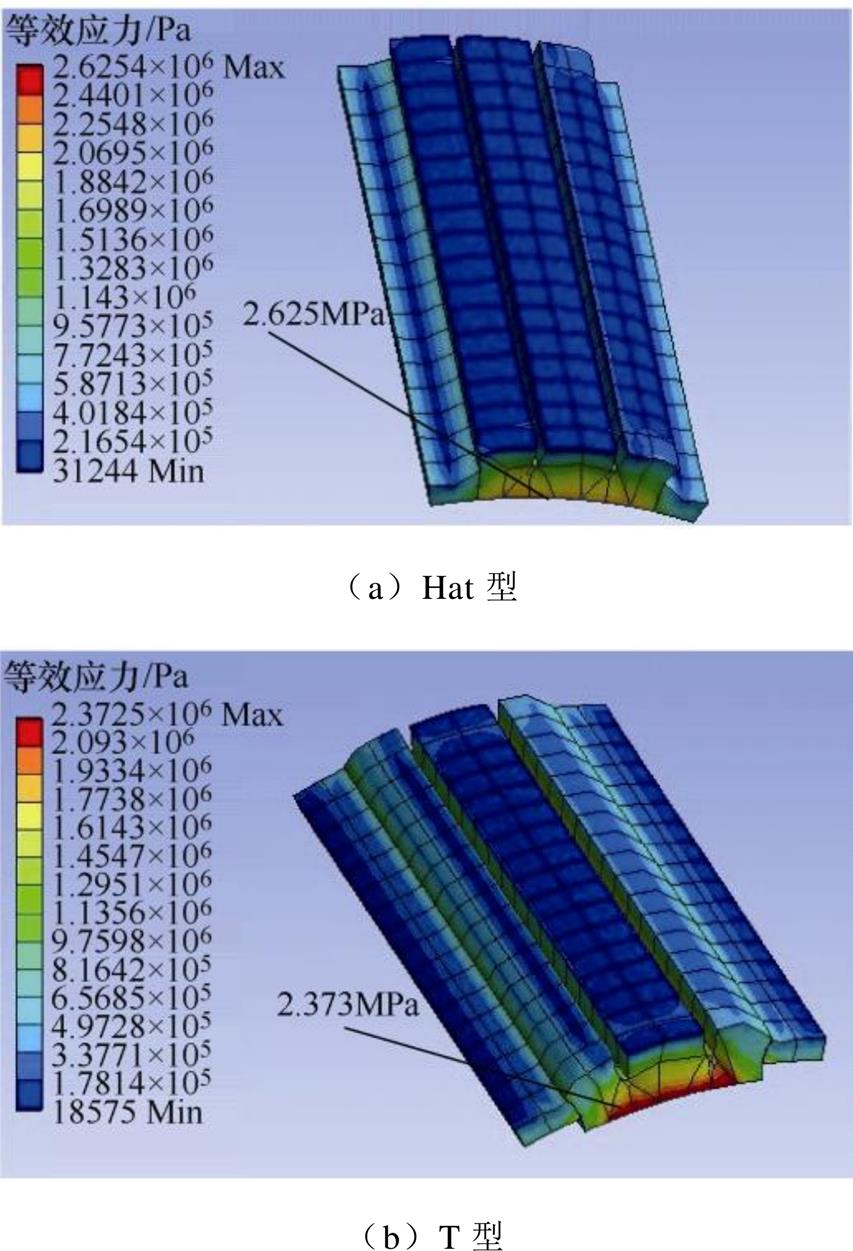
图16 永磁体等效应力
Fig.16 Equivalent stress map of permanent magnets
永磁体总变形如图15所示,显示了Hat型和T型Halbach部分分段结构的永磁体在切向离心力和电磁力的作用下导致的结构变形。可以看出,最大变形发生在永磁体上表面的切口边缘,而发生在永磁体底面结构变形很小,这是因为切口存在于远离轴线的永磁体上表面,并且永磁体底面附着在转子表面上。同时,可以看出,T型Halbach部分分段结构永磁体的最大形变量高于Hat型结构,但Hat型Halbach部分分段结构永磁体表面发生最大形变的面积多于T型结构。
永磁体等效应力如图16所示,显示了由切向离心力和电磁力引起的等效应力。可以看出,最大等效应力发生在永磁体底面,这是因为永磁体附着在转子铁心表面上。同时可以看出,Hat型Halbach部分分段结构的等效应力大于T型结构,而T型Halbach部分分段结构永磁体底面受到最大等效应力的面积多于Hat型结构。Hat型和T型Halbach部分分段结构永磁体最大等效应力分别为2.625MPa和2.373MPa,低于永磁体拉伸应力80MPa。因此,离心力产生的等效应力不会破坏永磁体的机械结构。
本文提出一种Halbach部分分段结构,扩展为Hat型和T型两种型式,在二维极坐标下建立解析模型,推导了电机负载气隙磁通密度的表达式,并验证了解析方法的正确性。同时,利用有限元软件对电机进行电磁场和应力场仿真分析,在固定极间间隔时,对电机进行多变量多目标分级优化,得出最优Hat型和T型Halbach部分分段结构的电机参数,并对相关七种结构的PMSM进行电磁性能对比分析,结果表明:
1)Halbach部分分段结构结合了Halbach结构和部分分段结构的优点,相比于表贴式PMSM,大幅度降低了负载气隙磁通密度THD、永磁体涡流损耗以及电磁转矩波动。相比于表贴式结构、部分分段结构以及等宽等厚Halbach结构,Halbach部分分段结构的各项电磁性能均得到了优化,并维持了永磁体的完整性。
2)相比于Hat型Halbach部分分段结构,T型结构具有更好的电磁性能、更小的永磁体体积以及更高的永磁体利用率,适用于大转矩的实际应用中,但T型结构的工艺更加复杂,会增加生产成本。
3)Halbach部分分段结构永磁体所受拉应力远小于允许值,永磁体机械强度维持在允许范围内。
Halbach部分分段结构在电磁性能优异的情况下,减少了永磁体用量,节约了PMSM的生产成本,适用于实际工程中,具有一定的理论意义和应用价值。但对于Halbach部分分段永磁同步电机边界磁极结构的多样性有待进一步研究。
附 录
重要表达式如下。
当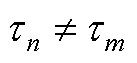 时,有
时,有
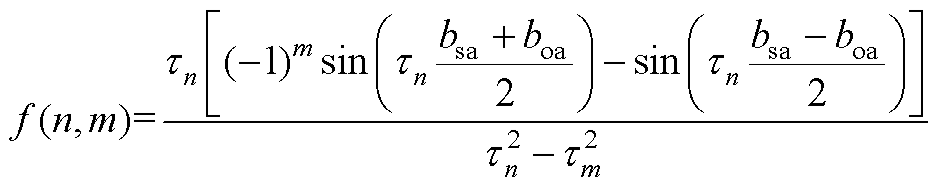 (A1)
(A1)
当 时,有
时,有
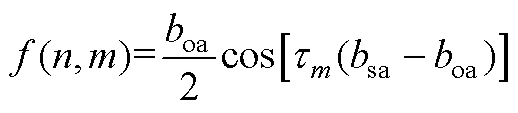 (A2)
(A2)
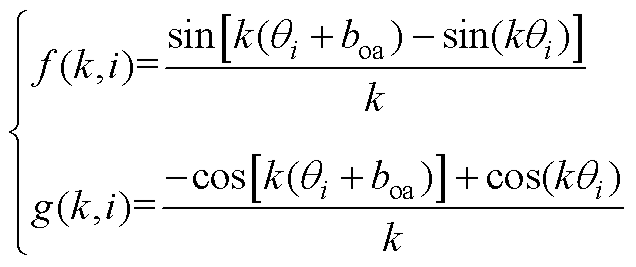 (A3)
(A3)
当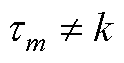 时,有
时,有
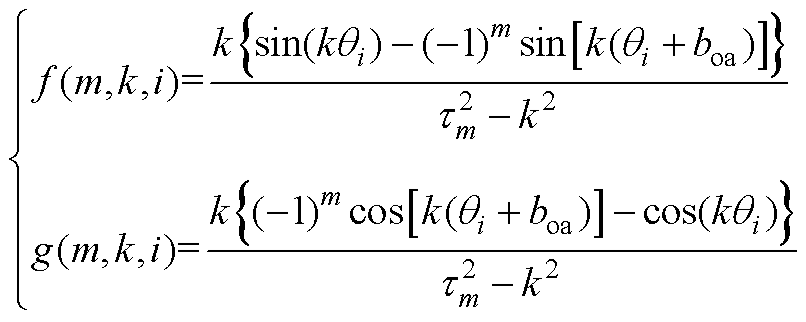 (A4)
(A4)
当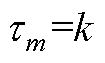 时,有
时,有
 (A5)
(A5)
空载气隙磁场气隙子域待定系数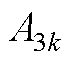 ~
~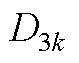 分别为
分别为
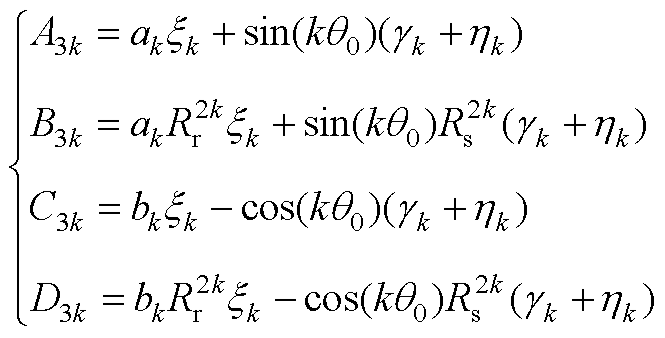 (A6)
(A6)
其中
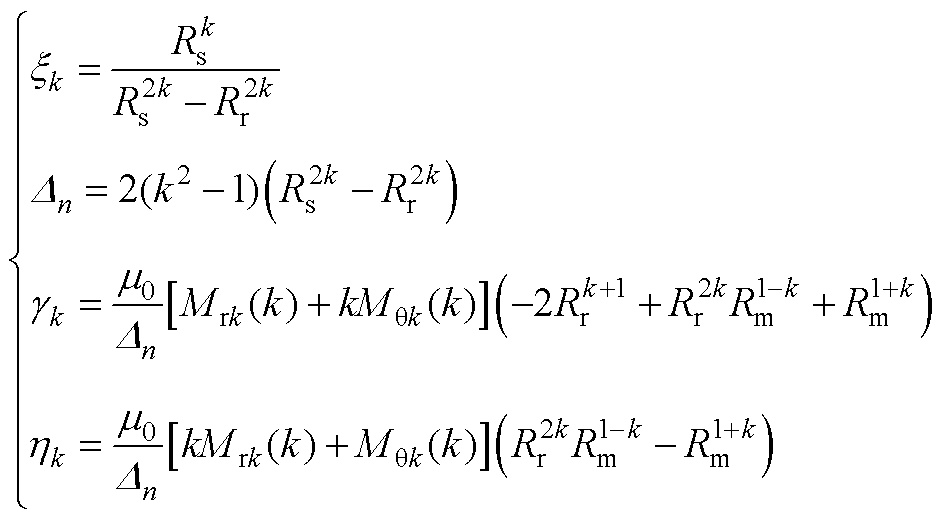 (A7)
(A7)
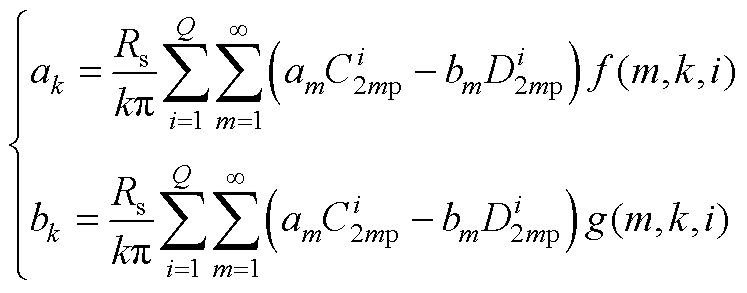 (A8)
(A8)
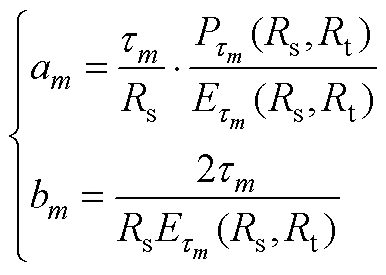 (A9)
(A9)
傅里叶积分求解待定系数为
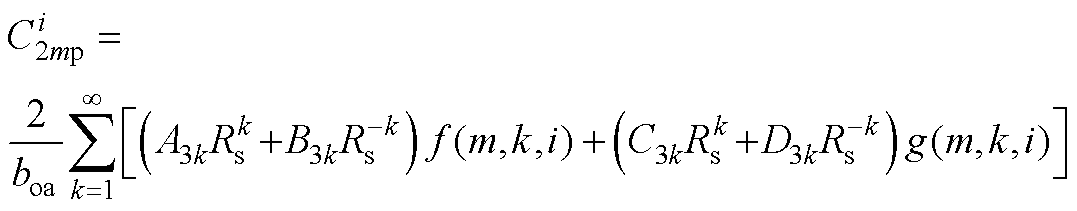 (A10)
(A10)
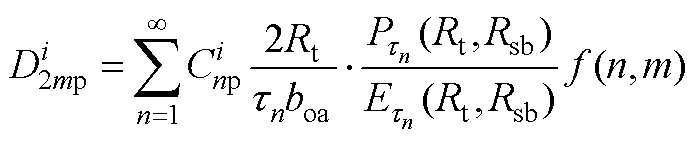 (A11)
(A11)
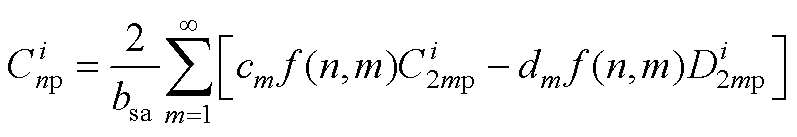 (A12)
(A12)
其中
 (A13)
(A13)
电枢反应磁场等效气隙子域待定系数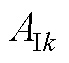 ~
~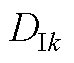 分别为
分别为
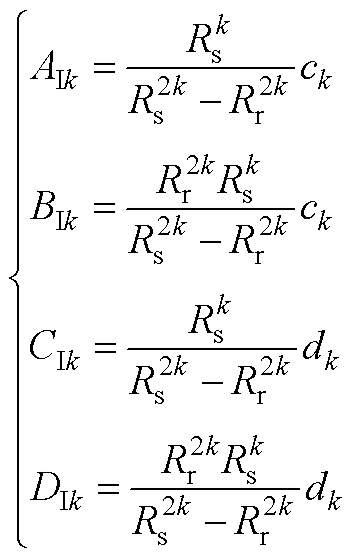 (A14)
(A14)
其中
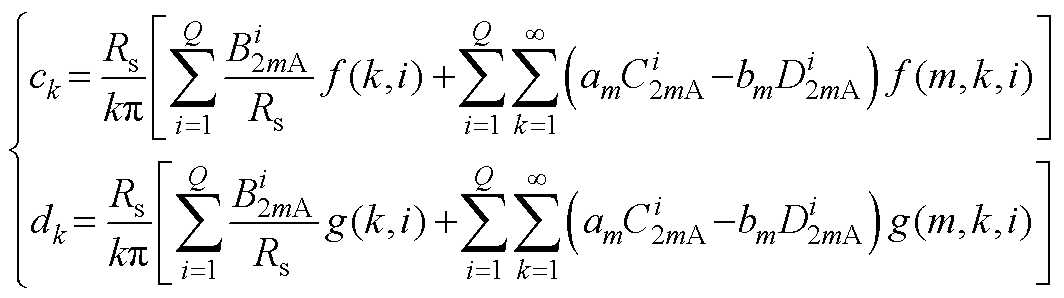 (A15)
(A15)
傅里叶积分求解待定系数,有
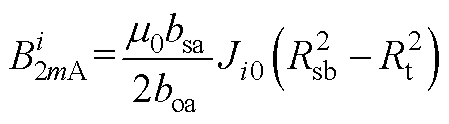 (A16)
(A16)
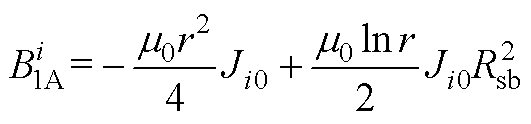 (A17)
(A17)
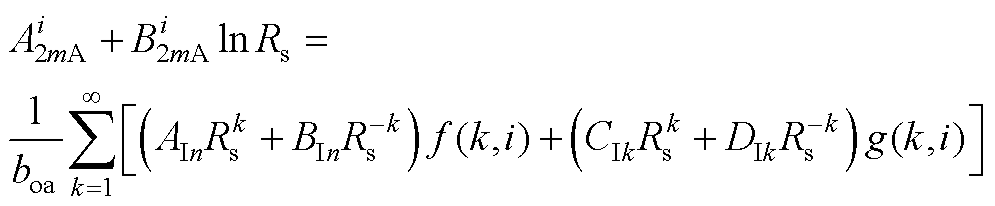 (A18)
(A18)
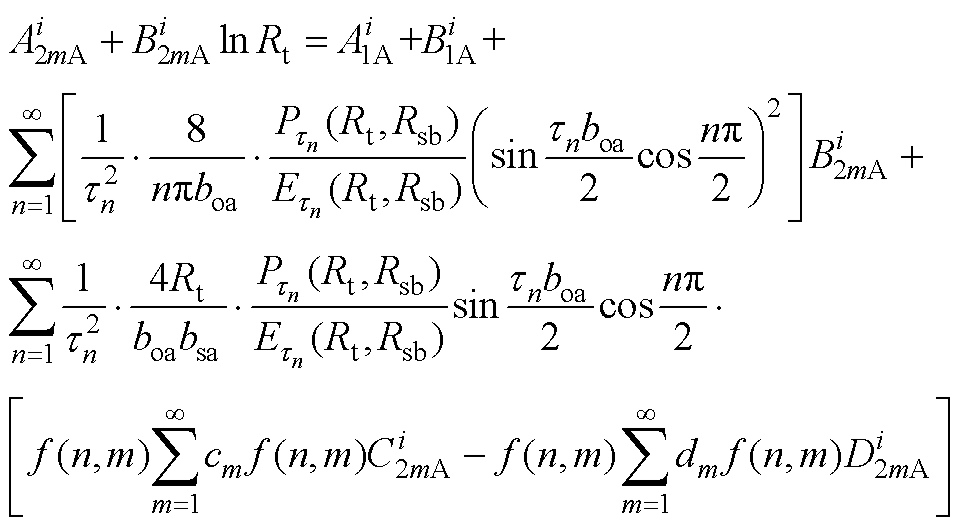 (A19)
(A19)
 (A20)
(A20)
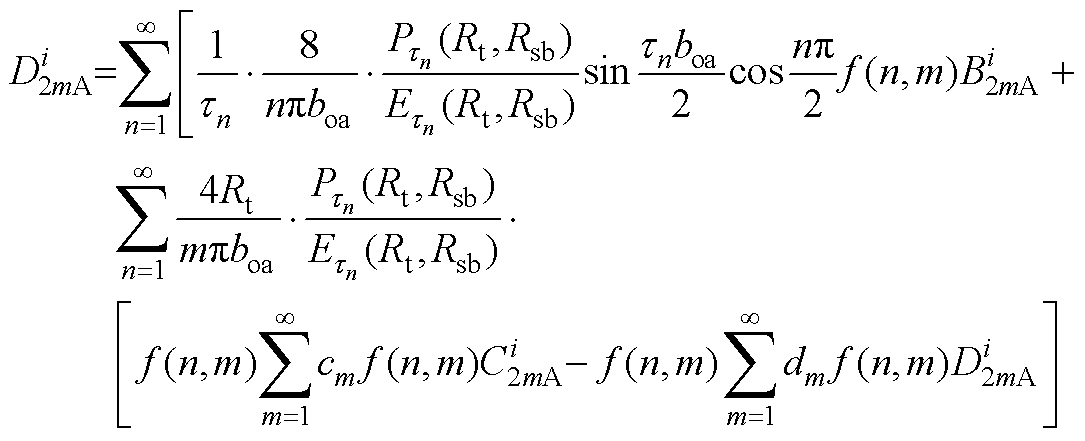 (A21)
(A21)
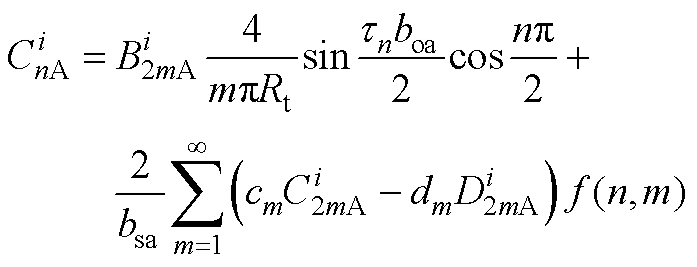 (A22)
(A22)
参考文献
[1] 李勇, 徐兴, 孙晓东, 等. 轮毂电机驱动技术研究概况及发展综述[J]. 电机与控制应用, 2017, 44(6): 1-7, 18.
Li Yong, Xu Xing, Sun Xiaodong, et al. Review and future development of in-wheel motor drive techno- logy[J]. Electric Machines and Control Applications, 2017, 44(6): 1-7, 18.
[2] 石玉君, 程子活, 蹇林旎. 两种典型的场调制型永磁电机的对比分析[J]. 电工技术学报, 2021, 36(1): 120-130.
Shi Yujun, Cheng Zihuo, Jian Linwei. Comparative analysis of two typical field modulated permanent- magnet machines[J]. Transactions of China Electro- technical Society, 2021, 36(1): 120-130.
[3] 孔垂毅, 代颖, 罗建. 电动汽车轮毂电机技术的发展现状与发展趋势[J]. 电机与控制应用, 2019, 46(2): 105-112, 117.
Kong Chuiyi, Dai Ying, Luo Jian. Development status and trend of in-wheel motor technology for electric vehicles[J]. Electric Machines and Control Appli- cations, 2019, 46(2): 105-112, 117.
[4] 程明, 文宏辉, 曾煜, 等. 电机气隙磁场调制行为及其转矩分析[J]. 电工技术学报, 2020, 35(5): 921- 930.
Cheng Ming, Wen Honghui, Zeng Yu, et al. Analysis of airgap field modulation behavior and torque component in electric machines[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 921- 930.
[5] 陈萍, 唐任远, 佟文明, 等. 高功率密度永磁同步电机永磁体涡流损耗分布规律及其影响[J]. 电工技术学报, 2015, 30(6): 1-9.
Chen Ping, Tang Renyuan, Tong Wenming, et al. Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 1-9.
[6] 任庆, 桂祈祯. 基于永磁体温度对车用电机性能影响分析[J]. 机械制造与自动化, 2018, 47(2): 213- 217.
Ren Qing, Gui Qizhen. Influence analysis of temperature of permanent magnet on performance of vehicle motor[J]. Mechanical Engineering & Auto- mation, 2018, 47(2): 213-217.
[7] 张磊, 高春侠. 永磁同步电机磁钢涡流损耗模型及其衡量指标[J]. 电机与控制学报, 2013, 17(7): 46-53.
Zhang Lei, Gao Chunxia. Eddy-current loss model and index for magnets of permanent magnet synchronous motors[J]. Electric Machines and Control, 2013, 17(7): 46-53.
[8] 范坚坚, 吴建华. 计及齿槽极间隔断Halbach型磁钢的PMSM气隙磁场解析分析[J]. 中国电机工程学报, 2010, 30(12): 98-105.
Fan Jianjian, Wu Jianhua. Analytical solution and analysis of airgap magnetic field of PMSM with partition-between-poles Halbach magnet considering effect of slotting[J]. Proceedings of the CSEE, 2010, 30(12): 98-105.
[9] 罗玲, 薛利昆, 吴先宇, 等. Halbach永磁阵列无刷直流电机转矩的解析计算和分析[J]. 电工技术学报, 2017, 32(16): 124-135.
Luo Ling, Xue Likun, Wu Xianyu, et al. Analytical calculation and analysis of torque for brushless DC motors with Halbach magnet array[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 124- 135.
[10] 李深, 章跃进, 周晓燕, 等. 定子开槽表贴式永磁电机转子偏心空载气隙磁场全局解析法[J]. 电机与控制学报, 2014, 18(10): 27-35.
Li Shen, Zhang Yuejin, Zhou Xiaoyan, et al. Exact analytical solution of open circuit air-gap magnetic field for slotted surface-mounted permanent-magnet motors with rotor eccentricity[J]. Electric Machines and Control, 2014, 18(10): 27-35.
[11] Lubin T, Mezani S, Rezzoug A. Exact analytical method for magnetic field computation in the air gap of cylindrical electrical machines considering slotting effects[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1092-1099.
[12] 李节宝, 井立兵, 周晓燕, 等. 表贴式永磁无刷电机直接解析计算方法[J]. 电工技术学报, 2012, 27(11): 83-88.
Li Jiebao, Jing Libing, Zhou Xiaoyan, et al. Exact analytical method for surface-mounted permanent- magnet brushless motors[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 83-88.
[13] 郭思源, 周理兵. 表面埋入式永磁电机磁场解析[J]. 中国电机工程学报, 2015, 35(3): 710-718.
Guo Siyuan, Zhou Libing. Analysis solution of magnetic field surface-inset permanent magnet machines[J]. Proceedings of the CSEE, 2015, 35(3): 710-718.
[14] 杨思雨, 夏长亮, 王慧敏, 等. 磁极分段型表贴式永磁电机建模与分析[J]. 电工技术学报, 2015, 30(增刊2): 49-55.
Yang Siyu, Xia Changliang, Wang Huimin, et al. Modeling and analyzing for surface mounted permanent magnet machine with segmented pole[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 49-55.
[15] 李琛, 章跃进, 井立兵. Halbach阵列半闭口槽永磁电机全局解析法研究[J]. 中国电机工程学报, 2013, 33(33): 85-94.
Li Chen, Zhang Yuejin, Jing Libing. Researches on an exact analytical method of Halbach-array permanent- magnet motors with semi-closed slots[J]. Proceedings of the CSEE, 2013, 33(33): 85-94.
[16] 郭思源, 周理兵, 齐歌. 双三相永磁同步电机电磁性能解析计算[J]. 电工技术学报, 2014, 29(5): 17-28.
Guo Siyuan, Zhou Libing, Qi Ge. Analytical calcu- lateon of electromagnetic performance in dual three- phase permanent magnet brushless AC machines[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 17-28.
[17] Madina P, Poza J, Ugalde G, et al. Analysis of non- uniform circumferential segmentation of magnets to reduce eddy-current losses in SPMSM machines[C]// International Conference on Electrical Machines, Marseille, France, 2012: 79-84.
[18] Lee S H, Oh H S, Kim H S. Experiment research on motor efficiency improvement through the eddy current reduction using segmentation of rotor magnet[C]//International Conference on Electrical Machines and Systems, Sydney, Australia, 2017: 1-4.
[19] Wang Youhua, Ma Jinguang, Liu Chengcheng, et al. Reduction of magnet eddy current loss in PMSM by using partial magnet segment method[J]. IEEE Transa- ctions on Magnetics, 2019, 55(7): 1-5.
[20] Lubin T, Mezani S, Rezzoug A. 2-D exact analytical model for surface-mounted permanent-magnet motors with semi-closed slots[J]. IEEE Transactions on Mag- netics, 2011, 47(2): 479-492.
[21] 倪有源, 王磊, 王群京. 凸形不等厚磁极永磁电机建模与分析[J]. 电工技术学报, 2020, 35(11): 2406-2414.
Ni Youyuan, Wang Lei, Wang Qunjing. Modeling and analysis of permanent magnet machines with salient shape unequal thickness magnets[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2406- 2414.
[22] 杨定伟, 邓兆祥, 张河山, 等. 永磁轮毂电机磁场解析建模[J]. 电工技术学报, 2019, 34(7): 1423- 1433.
Yang Dingwei, Deng Zhaoxiang, Zhang Heshan, et al. Exact analytical solution of magnetic field in permanent magnet in-wheel motor[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1423- 1433.
[23] 梁子漪, 曲荣海, 李大伟, 等. 一种交替极切向励磁游标永磁电机的分析与设计[J]. 电工技术学报, 2020, 35(15): 3173-3181.
Liang Ziyi, Qu Ronghai, Li Dawei, et al. Analysis and design of a vernier permanent magnet motor with alternating pole tangential excitation[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3173-3181.
[24] 杨玉波, 刘国鹏, 陈鹏, 等. 基于子域法的游标混合电机电磁性能解析计算[J]. 电机与控制学报, 2019, 23(9): 9-17, 25.
Yang Yubo, Liu Guopeng, Chen Peng, et al. Elec- tromagnetic performance investigation of vernier hybrid machine[J]. Electric Machines and Control, 2019, 23(9): 9-17, 25.
[25] 倪有源, 刘跃斌, 王群京. 组合磁极结构的永磁电机解析法建模与分析[J]. 电机与控制学报, 2019, 23(1): 52-62.
Ni Youyuan, Liu Yuebin, Wang Qunjing. Analytical modeling and analysis of permanent magnet machine with combined magnetic poles[J]. Electric Machines and Control, 2019, 23(1): 52-62.
[26] 张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 15-26.
Zhang Shoushou, Guo Siyuan. Analytical magnetic field method of permanent magnet synchronous machine considering step-skewed magnets and magnetic slot wedge[J]. Transactions of China Elec- trotechnical Society, 2019, 34(1): 15-26.
[27] 李咸善, 徐浩, 邹芳, 等. 微电网分级优化故障重构[J]. 中国电机工程学报, 2015, 35(24): 6378-6386.
Li Xianshan, Xu Hao, Zou Fang, et al. Micro-grid hierarchical optimization fault reconstruction[J]. Proceedings of the CSEE, 2015, 35(24): 6378-6386.
[28] Wills D A, Kamper M J. Reducing PM eddy current rotor losses by partial magnet and rotor yoke segmentation[C]//International Conference on Elec- trical Machines, Roma, Italy, 2010: 1-6.
Analytical Calculation and Optimization Analysis of Electromagnetic Performance of Halbach Partially-Segmented Permanent Magnet Synchronous Motors with Unequal Width and Thickness
Abstract In order to suppress the electromagnetic torque ripple and reduce the permanent magnet eddy current loss in high power-density permanent magnet synchronous motor, a partially- segmented structure of Halbach is proposed. The permanent magnets is magnetized with Halbach pattern and each pole consists of three sections. The main magnetic pole is segmented on single side. The border magnetic pole and the main magnetic pole are not equal in thickness and width, and the permanent magnet is expanded to Hat type and T type. Using a precise subdomain model method, the solution domain is divided into four regions: slot, slot-opening, air gap and permanent magnet. The magnetic field density of airgap with load and electromagnetic torque is calculated under two- dimensional polar coordinates. A 10-pole/12-slot three-dimensional motor model is established to perform electromagnetic simulation, hierarchical optimization and comparative analysis on Hat-type, T-type and other related five motor structures for finding the optimal Hat-type and T-type structures. The results show that partially-segmented structure of Halbach can reduce the permanent magnet eddy current loss, electromagnetic torque ripple and magnetic field density of airgap with loading. The electromagnetic performance of the partially-segmented structure of the T-type Halbach is higher than that of the Hat type, while the partially-segmented structure of the Hat type Halbach can further reduce the volume of the permanent magnet and save the production cost. Moreover, the equivalent stress and total deformations are calculated based on the three-dimensional finite element stress model of permanent magnetic synchronous motor, which are also in the tolerant range of mechanical strength.
keywords:Permanent magnet synchronous motor, the precise subdomain model method, partially-segmented structure of Halbach, electromagnetic torque ripple, permanent magnet, eddy current loss
DOI: 10.19595/j.cnki.1000-6753.tces.200972
中图分类号:TM351
高锋阳 男,1970年生,教授级高工,研究方向为电机与电器、电机的优化设计。E-mail: 329365048@qq.com
齐晓东 男,1995年生,硕士研究生,研究方向为永磁同步电机的优化设计。E-mail: 782311500@qq.com(通信作者)
收稿日期 2020-08-06
改稿日期 2020-10-26
国家重点研发计划(2018YFB1201602-06)、天津大学和兰州交通大学联合基金(2020056)资助项目。
(编辑 崔文静)