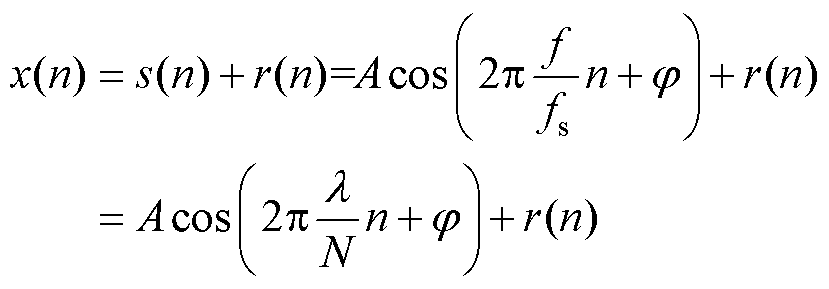 (1)
(1)
摘要 短时波动周期下,来自负频率的频谱泄漏是频域插值算法估计误差的主要来源。为消除频谱泄漏影响以实现任意波动周期下实正弦信号频率的精确估计,该文提出一种基于广义离散时间傅里叶变换(DTFT)插值解析的频率估计算法。该算法利用位于频谱主瓣范围内的任意DTFT谱线构建对应实/虚部的线性方程组,进而通过方程组求解得到基于解析插值DTFT的无偏频率估计公式。此外,考虑实际中加性白噪声的影响,根据频率估计的统计特性分析给出一种简单且有效的迭代方法,从而确保频率估计的方均误差(MSE)在任意波动周期下能够一致逼近无偏频率估计的克拉美罗下届(CRLB)。仿真和实验结果验证了所提算法优于现有的DFT插值算法。
关键词:短时波动周期 频谱泄漏 解析插值DTFT 迭代方法 克拉美罗下届(CRLB)
正弦信号的频率估计是一个经典且重要的信号处理问题,在科学和工程领域具有极为广泛的应用。在电力系统中,频率作为最重要的电能质量参数之一,其变化反映了发电和负载之间的动态平衡[1-3],通过频率及其变化的准确估计可以实现系统的动态过程监测。此外,在计量基准测试和标准溯源等特定应用中,对频率估计精度往往具有更高的要求。
频率估计算法总体上可分为时域和频域两类,频域算法主要基于由快速离散傅里叶变换(Fast Discrete Fourier Transform,FDFT)实现的插值离散傅里叶变换(Interpolated Discrete Fourier Transform, IpDFT),在计算复杂度方面相对于通常需要矩阵求逆的时域方法更具优势(时域为O(N3),频域为O(Nlog2N)[4]),因而在实时频率估计应用中表现出特别的吸引力。但是,过去大多数针对IpDFT频率估计的研究都集中在单频解析信号上[5-9],对于实际中应用更为广泛的实正弦信号,受共轭负频率的频谱长泄漏影响,尤其是在被测信号对应波动周期(Cycles in Record, CiR)较小时,IpDFT存在严重的估计偏差。
短时CiR频谱泄漏问题已引起国内外学者的高度关注并开展了大量研究,提出多种改进IpDFT算法,总体上可分为直接方法和迭代方法。直接方法力求在计及负频率频谱长泄漏基础上直接得到频率估计的解析解。文献[10]提出了一种基于矩形窗的3点IpDFT(a3IpDFT),利用变换构建对应谱线的线性方程组,进而求解得到频率估计的解析解,但仿真结果显示,即便在最优情况下算法方均误差(Mean Square Error, MSE)仍然无法逼近无偏频率估计的克拉美罗下界(Cramer-Rao Lower Bound, CRLB)。文献[11-12]在文献[13]解析泄漏补偿方法基础上,提出了利用信号补零和DFT系数变换的2点IpDFT(z2IpDFT),但补零操作和繁琐的谱线选择判据使得算法计算复杂度相对较高。文献[14-15]基于最大旁瓣衰减窗离散等间隔频谱近似线性比例特性,以求解频谱线性方程组的方式得到了3点IpDFT(m3IpDFT),但鉴于窗函数的数学复杂性增加[16],事实上在高阶情况下很难得到频率估计的解析解,因而无法进一步消除窗函数频谱近似导致的估计偏差。此外,相对矩形窗而言,采用具有更高等效噪声带宽(Equivalent Noise Band Width, ENBW)[17]的最大旁瓣衰减窗,算法MSE在噪声扰动下将无法逼近CRLB。
迭代方法则常以适用于单频解析信号的IpDFT为基础,力求通过迭代不断消除频谱泄漏干扰,从而确保算法最终收敛于频率估计的解析解。文献[18]在最大旁瓣衰减窗频谱近似基础上,提出了一种基于频谱系数加权的单步迭代IpDFT(w3IpDFT),但以经典IpDFT[19]作为其起始解析方式,将导致短时CiR下算法MSE中存在明显的估计偏差。文献[20]对AM算法[21]进行了有效改进,提出了一种利用位于DFT谱线中间的离散时间傅里叶变化(Discrete Time Fourier Transform, DTFT)系数插值的多步迭代算法(eAM)。其基本思想与z2IpDFT类似,即尽量采用幅度最大的频谱系数以降低噪声干扰影响,进而通过不断重构并消除频谱中负频率泄漏分量以逐渐降低频率估计偏差,使得算法MSE最终一致收敛逼近于CRLB,是现有频域估计算法中精度最高的[22]。但由于其核心两点插值方法为有偏频率估计,在估计偏差占主导情况下需要多次计算DTFT系数并进行迭代,这无疑大大增加了算法的计算成本。此外,采用固定0.5Df(Df为频率分辨率)的DTFT系数还使得算法在CiR<1时性能将急剧下降。
基于eAM算法的基本思想,本文提出了一种基于广义DTFT插值的精确频率估计算法。一方面,通过准确解析由任意位置的广义DTFT谱线构成的线性方程组,可以确保算法在任意CiR下得到无偏频率估计;另一方面,通过统计特性分析导出用以优化算法性能的简单迭代方法,可以最大程度地抑制背景噪声干扰以确保算法MSE能够一致逼近CRLB,从而实现任意CiR下频率的精确估计。
假设以采样频率fs进行等间隔均匀离散采样,则N点采样序列x(n)的数学模型可表示为
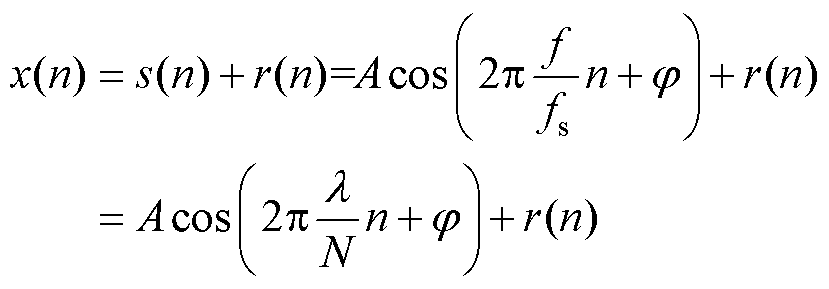 (1)
(1)
式中,n=0, 1,…, N-1ÎN;f、A和j 分别为信号s(n)的频率、幅值和初始相位;r(n)为具有零均值和方差s2的加性高斯白噪声;f/fs=l/N=l+v/N为频域归一化频率,l 在时域中对应于被测信号的波动周期个数,在频域中则表示f在频谱中所处位置。据奈奎斯特采样定律可知,lmax<0.5N,且l 无量纲,其单位通常采用bin标示;l=[l]ÎN,符号[ ]表示四舍五入取整,由Df=fs/N可知,非整余数vÎ[-0.5, 0.5],则N点离散信号x(n)的广义DTFT可表示为
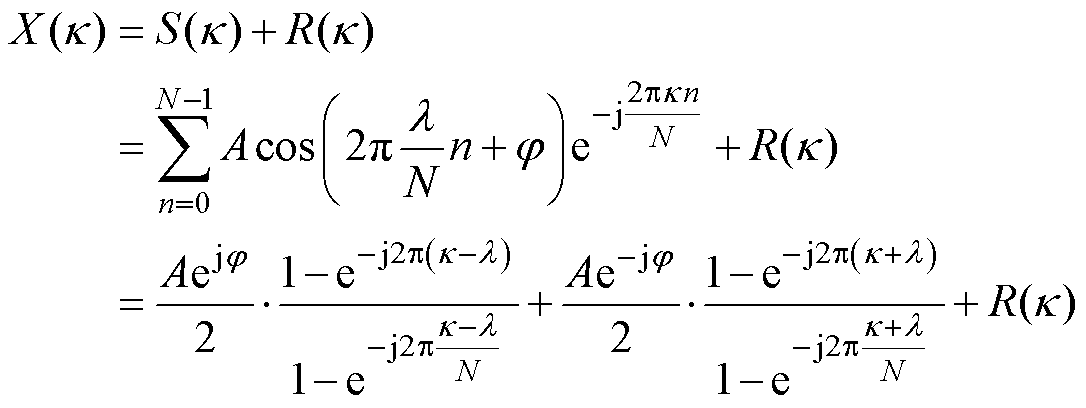
(2)
式中,j为复数单位;R(∙)为宽带噪声的DTFT;第二项为负频率分量引起的频谱长泄漏干扰。值得注意的是,此处参量k 可为任意[0, N-1]范围内的实数,当其为整数时,式(2)即为标准DFT,此时X(k)的等间隔抽样即可表示为X(k|kÎN)。
便于推导,首先忽略噪声项R(∙),通过计算可将式(2)转化为
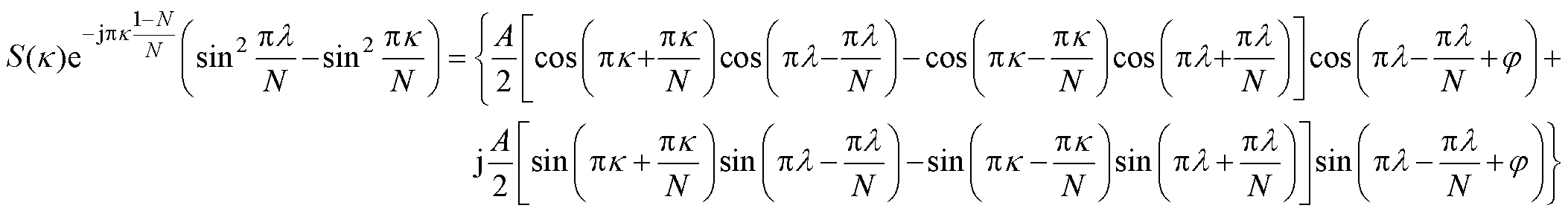 (3)
(3)
将式(2)改写为式(3)所示方程具有两个非常重要的作用:一方面,式(3)中含有3个未知参量l、A和j,可知还需另外两条DTFT谱线{S(k±i)}以形成方程组进行解析;更为重要的一方面在于式(3)左右侧为复数,自然地可分解为对应实部和虚部的方程,这是求解方程组并导出解析插值频率估计的关键。
如式(3)左侧所示,S(k)e-jpk(1-N)/N与未知参量无关,仅由S(k)及其位置索引k 决定,简单起见采用Yk =S(k)e-jpk(1-N)/N表示,则据式(3)可得,对应实部的齐次线性方程组,以矩阵形式表示为
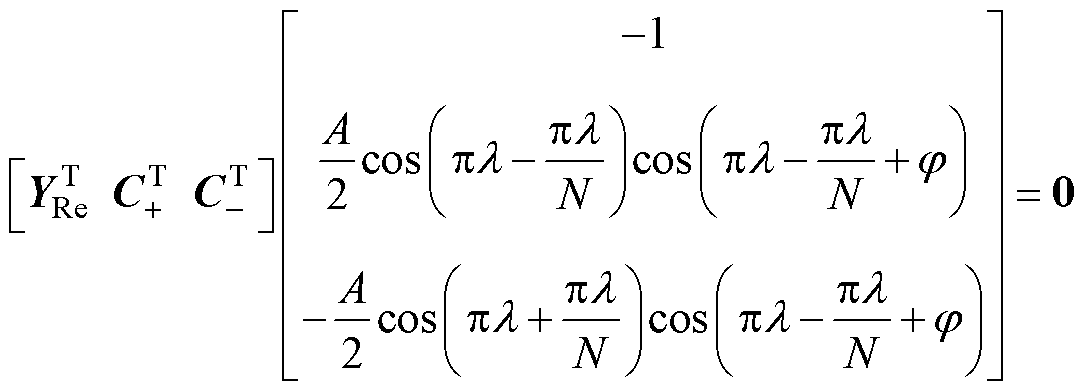 (4)
(4)
方程组式(4)中系数矩阵定义如下
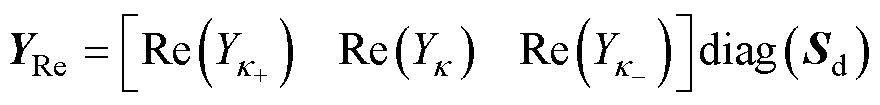 (5)
(5)
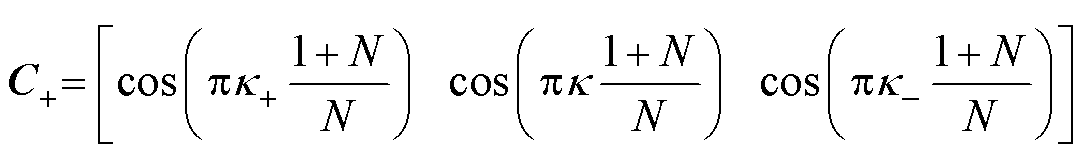 (6)
(6)
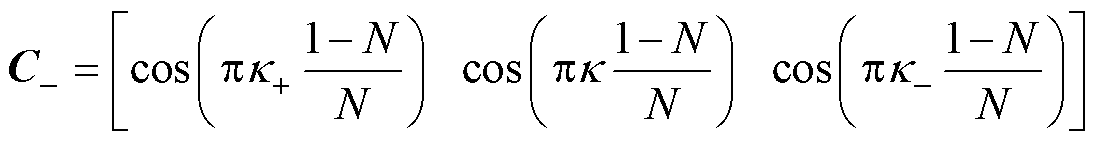 (7)
(7)
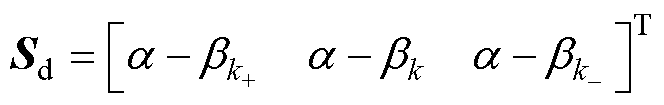 (8)
(8)
其中
k+=k+i k-=k-i a=sin2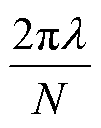 bk=sin2
bk=sin2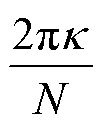
同理,对应虚部的齐次线性方程组为
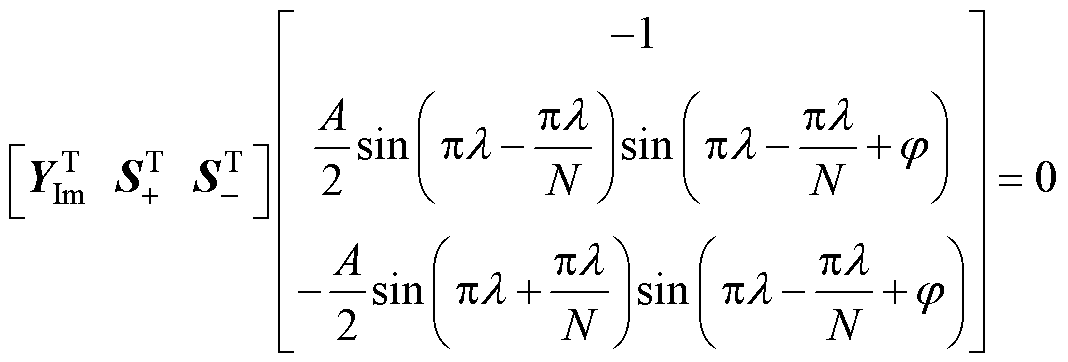 (9)
(9)
方程组式(9)中系数矩阵的相关向量定义如下
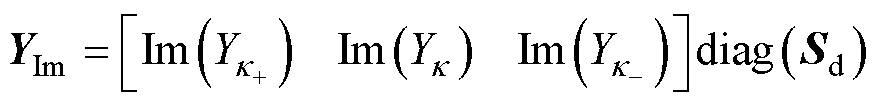 (10)
(10)
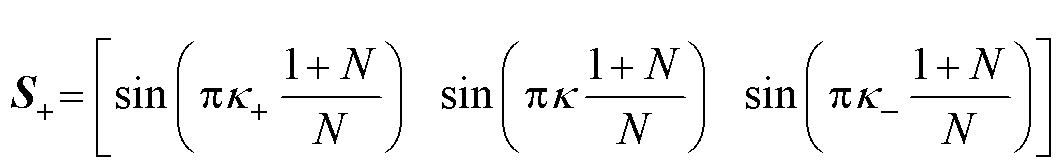 (11)
(11)
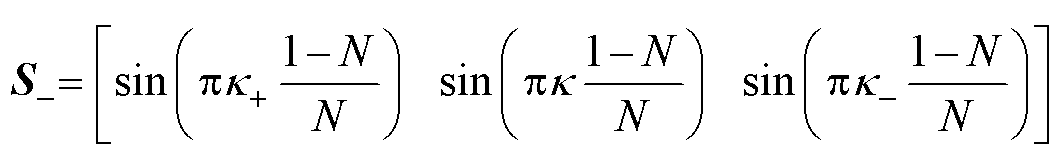 (12)
(12)
在式(4)~式(12)中,需要明确指出的是iÎR+,其范围控制在(0, 0.5],使得所用DTFT谱线全部位于矩形窗谱的主瓣范围内,以确保具有高信噪比。
由于齐次线性方程组式(4)和式(9)必有非零解,则根据线性代数中克莱姆法则(Cramer’s Rule)可知方程组系数矩阵的行列式必然为零[22],即
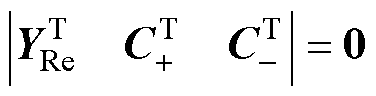 (13)
(13)
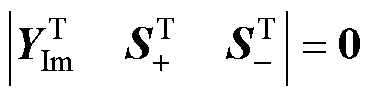 (14)
(14)
虽然据1.2节中各矩阵定义可知,上述方程都仅含有单一的未知变量l,至此可以单独求解式(13)或式(14)而直接得到l 的解析解。但是,当所用DTFT谱线的实部或虚部接近零时,噪声干扰将导致l 估计极为不准确。为防止这种情况的出现,需结合式(13)和式(14)得到用于频率估计的解析插值公式(具体求解过程见附录第1节),结果如下
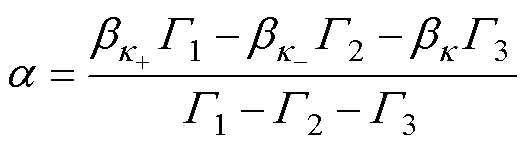 (20)
(20)
其中
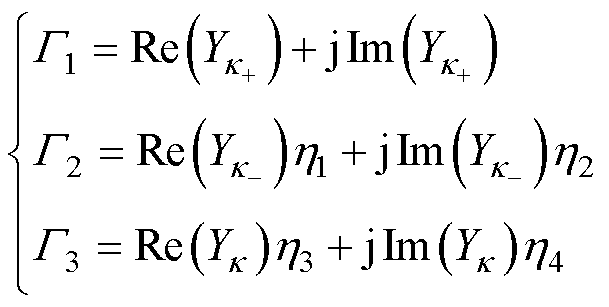 (21)
(21)
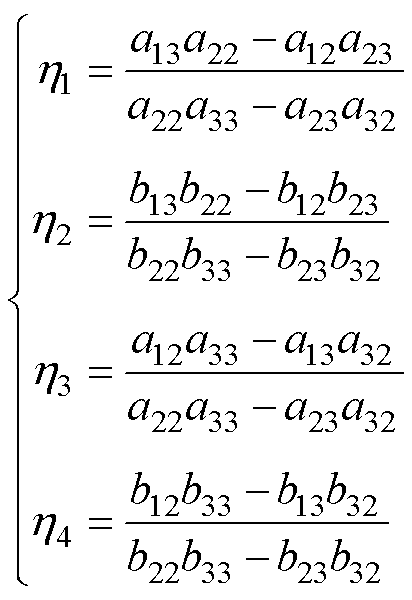 (22)
(22)
在实际应用中,受噪声干扰式(20)所有涉及Gi中采用的DTFT谱线S(∙)都应由观测值X(∙)代替。则令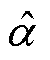 表示由式(20)所得估计值,由此可得基于解析插值DTFT的频率估计为
表示由式(20)所得估计值,由此可得基于解析插值DTFT的频率估计为
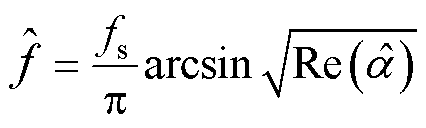 (23)
(23)
第1节通过研究无噪声情况,得到了基于广义插值DTFT的频率估计解析式,本节将分析加性高斯白噪声背景下频率估计算法的性能并得到估计的渐近性质,进而通过简单迭代优化算法性能。
据式(23)可知,频率估计由a 决定,因而首先分析噪声对a 估计的影响。令Qk =R(k )e-jpk(1-N)/N,则背景噪声干扰下a 的估计应准确表示为
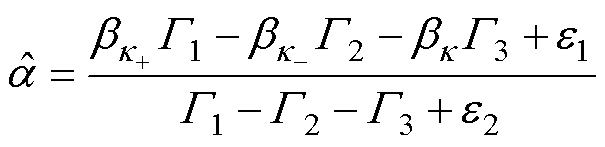 (24)
(24)
其中
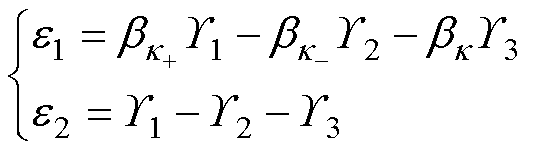 (25)
(25)
参量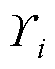 分别表示为
分别表示为
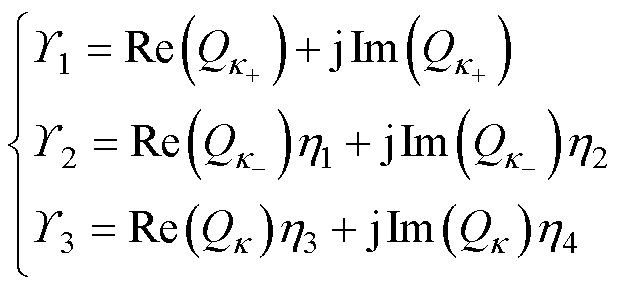 (26)
(26)
由此可得噪声干扰下a 的估计偏差Da 为
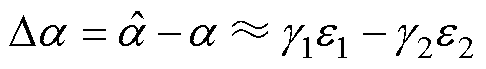 (27)
(27)
其中
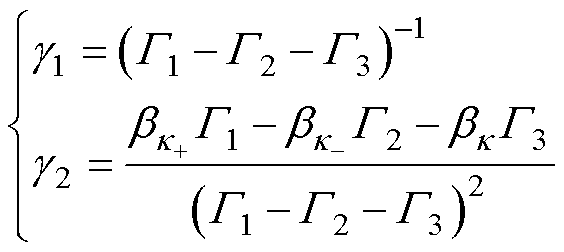 (28)
(28)
由此利用泰勒级数展开,式(23)所示的频率估计解析式可改写为
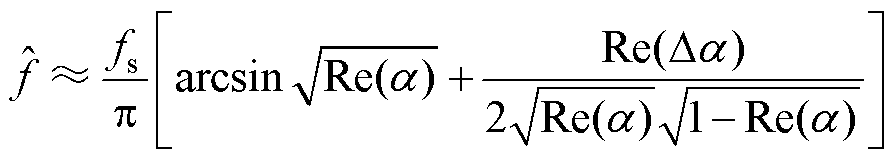
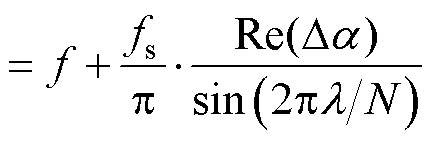 (29)
(29)
则噪声干扰下频率估计的统计偏差为
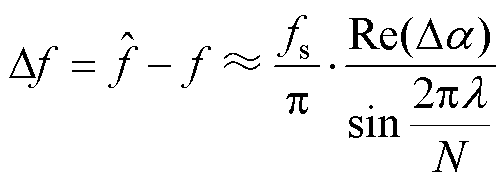 (30)
(30)
由白噪声特性E(e1)=E(e2)=0可知,期望值E(Df)= 0,表明式(23)为频率的无偏估计。
进一步考虑噪声项Qk 之间的相关性,可得频率估计的方差(详细推导过程见附录第2节)为
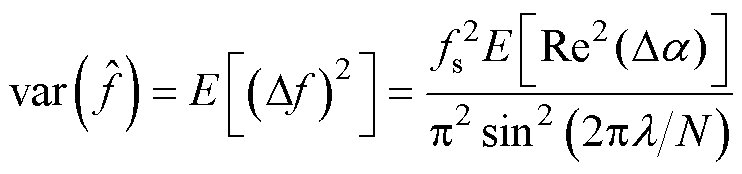 (31)
(31)
式中,E[Re2(Da )]如式(A20)所示。
进一步分析可知,任意频点下式(31)的变化趋势及其量级大小始终由|G1-G2-G3|决定,因而通过分析|G1-G2-G3|即可掌握频率估计的统计方差变化。根据Gi中对应各Yk 定义,将式(2)和式(21)代入G1-G2-G3即可简化为
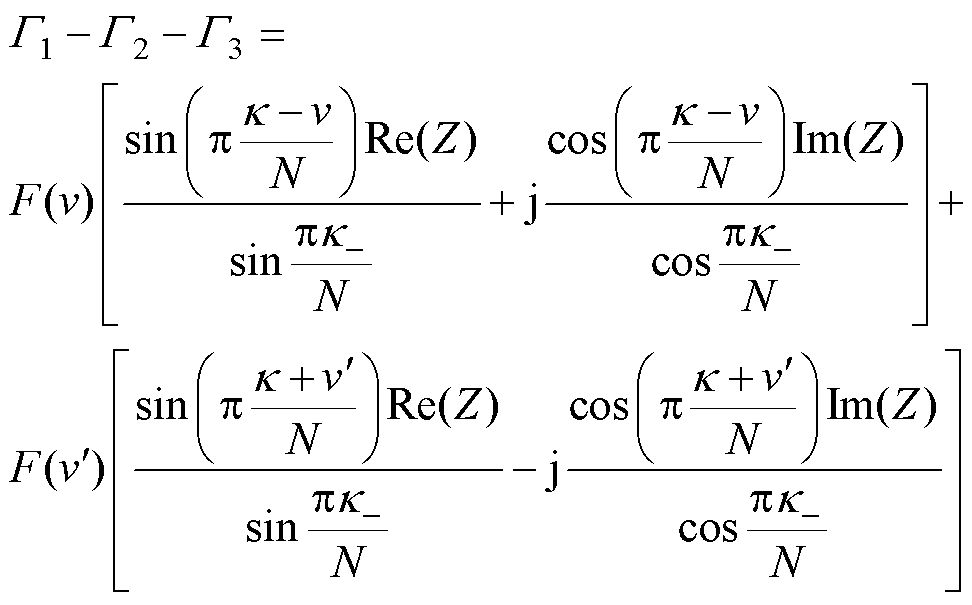 (32)
(32)
式中,Z=(A/2)exp{j[j+pl(N-1)/N]};v′=2k+v;F(v)定义为
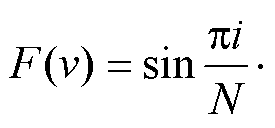
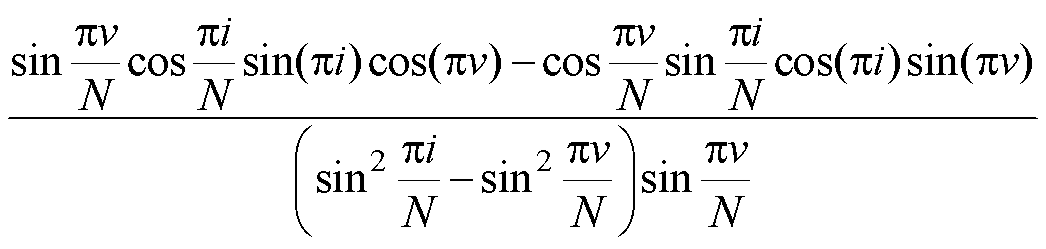 (33)
(33)
通常情况下l>1,此时Gi中的负频率泄漏分量可忽略不计,在中心谱线位置搜索正确的前提下(即k =l),G1-G2-G3可近似为
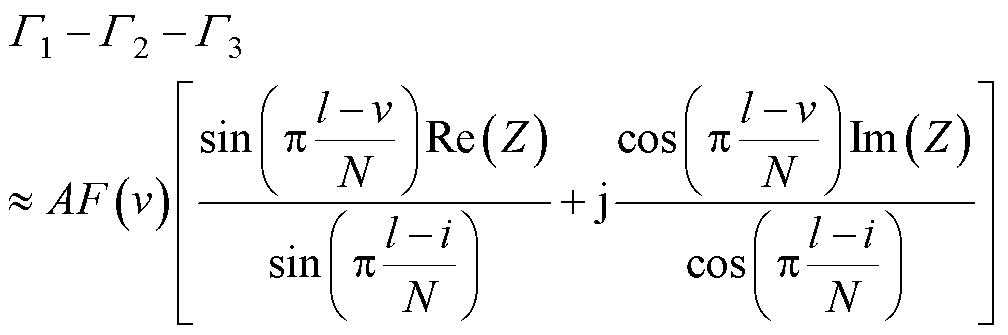 (34)
(34)
根据式(34)可知:
(1)v>0。当Re(Z)=0和Im(Z)=1时,对应|G1-G2-G3|的最大值,此时单一频点下式(31)仅包含Im(g1)时接近其最小值(下界);当Re(Z)=1和Im(Z)=0时,对应|G1-G2-G3|的最小值,此时单一频点下式(31)仅包含Re(g1)时接近其最大值(上界)。
(2)v≤0。当Re(Z)=1和Im(Z)=0时,对应|G1-G2-G3|的最大值,此时单一频点下式(31)仅包含Im(g1)时接近其最小值(下界);当Re(Z)=0和Im(Z)=1时,对应|G1-G2-G3|的最小值,此时单一频点下式(31)仅包含Re(g1)时接近其最大值(上界)。
实际中由于信号相位j 为随机分布,因此取其中值作为平均估计,即Re(Z)=Im(Z)=cos(p/2)。以N= 1 024,A=2,fs=1 024Hz,SNR=40dB,lÎ[2.55, 3.45]和i=0.1为例,对应每一个l 时频率估计方差的理论分布如图1所示。
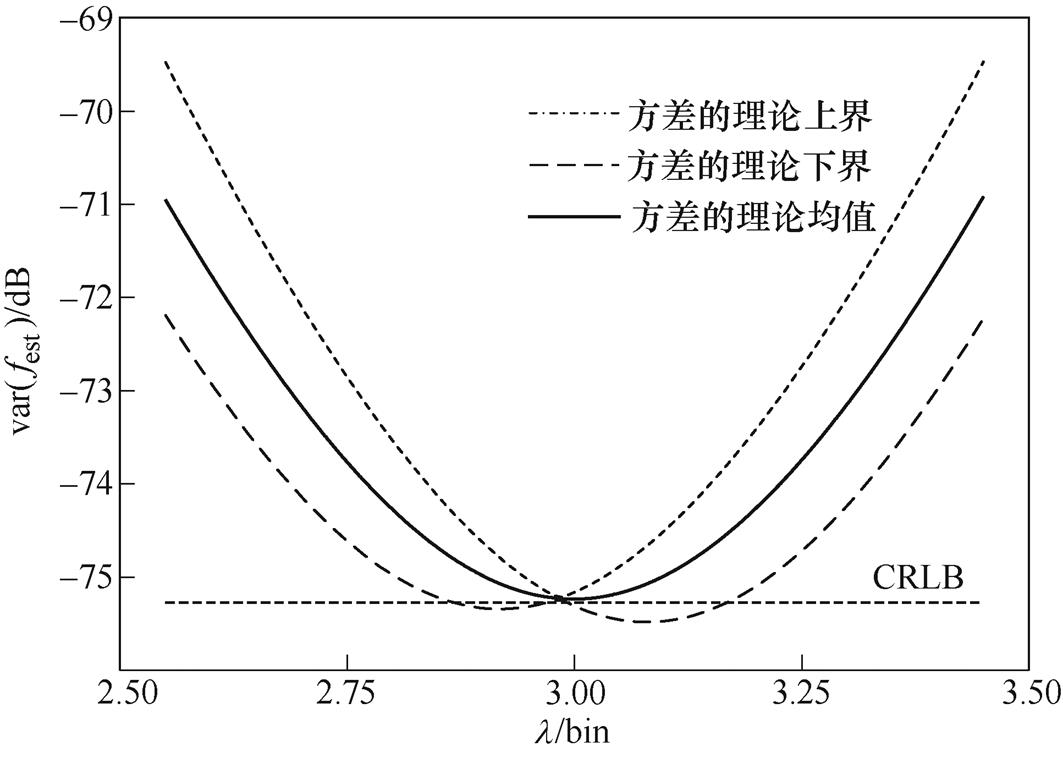
图1 i=0.1时频率估计方差的范围
Fig.1 The range of the variance of frequency estimates with i=0.1
图1结果显示,在i=0.1且相位随机分布前提下,所提频率估计方法的方差在v→0时接近最小值,且最小值十分接近无偏频率估计的CRLB[11]。进一步地,考虑相位在[-p, p]范围内随机变化,i值在0.1~0.5范围内逐渐增大,频率估计方差理论均值的最小值及其与CRLB之比h 见表1。
表1 频率估计的方差最小值
Tab.1 The minimum variance of the frequency estimates

ivar()h 0.12.994 585×10-81.008 822 0.23.002 396×10-81.011 454 0.33.020 767×10-81.017 642 0.43.054 594×10-81.029 038 0.53.112 032×10-81.048 388
据表1结果可知,随着i逐渐增大,频率估计方差最小值逐渐偏离CRLB,但差距十分微小。这表明,算法在i≤0.5范围内性能十分稳定且受i值的影响极小,理论上,随着i→0频率估计方差将完全逼近无偏频率估计的CRLB。
另一更为重要且关键的点在于:该结果表明算法具有可迭代执行的能力,即通过频移(不断迭代),将v≠0时的频率估计转化为v→0时的频率估计,进一步优化提升算法性能,使得v≠0时的频率估计方差能一致逼近于CRLB,从而最大程度地降低噪声对算法的干扰影响。迭代执行程序的具体执行步骤如下所示:
(1)参数初始化,迭代次数m=0,初始频率估计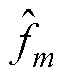 =0。
=0。
(2)通过峰值搜索X(κm)=argmax{|DFT(x)|}得到中心谱线,根据DTFT定义计算辅助谱线X(κm±i)。
(3)据式(23)解析插值得到频率估计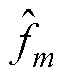 。
。
(4)m=m+1。
(5)中心谱线位置平移:κm+1=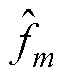 。
。
(6)据DTFT定义计算X(κm+1)及辅助谱线X(κm+1±i)。
(7)据式(23)解析插值再次得到频率估计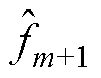 。
。
(8)若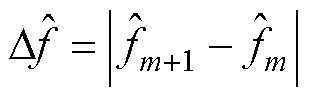 足够小,则跳至步骤(10)。
足够小,则跳至步骤(10)。
(9)否则,重复步骤(4)~步骤(8)。
(10)输出频率估计结果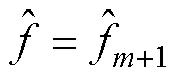 。
。
值得注意的是,虽然理论上i可取任意接近于零的数值,但当i极小时有限字长效应可能导致式(23)的分子和分母接近于零,使得频率估计可能产生无意义的结果[23];且当i低于某一阈值时,受限于采样点数和计算精度限制,频率估计方差几乎保持恒定而无法随着i减小而降低,具体结果见3.1节。
为全面验证算法的有效性和准确性,分别进行三个不同的仿真测试。第一个为分析所用谱线的间隔i对算法在非迭代情况下性能的影响;第二个为验证算法在迭代情况下是否能够一致逼近无偏频率估计的CRLB;第三个为不同性能优异的插值算法与本文算法的性能比对。
噪声干扰情况下,据附录第2节可知,单一谱线及与其他谱线间的统计特性随着谱线间隔i的变化而变化,进而导致不同i值下频率估计方差存在差异。设定信号采样点数N=1 024,幅度A=2,采样频率fs=1 024Hz,信号初始相位在[-p, p]范围内随机变化,对应信号波动周期l 在[2.55, 3.45]以步长0.1逐渐变化;噪声干扰设置为加性高斯白噪声,对应信噪比为SNR=40dB,单一信号条件下重复K= 10 000次独立蒙特卡洛仿真测试,则频率估计的MSE与CRLB之比随i的变化趋势如图2所示。
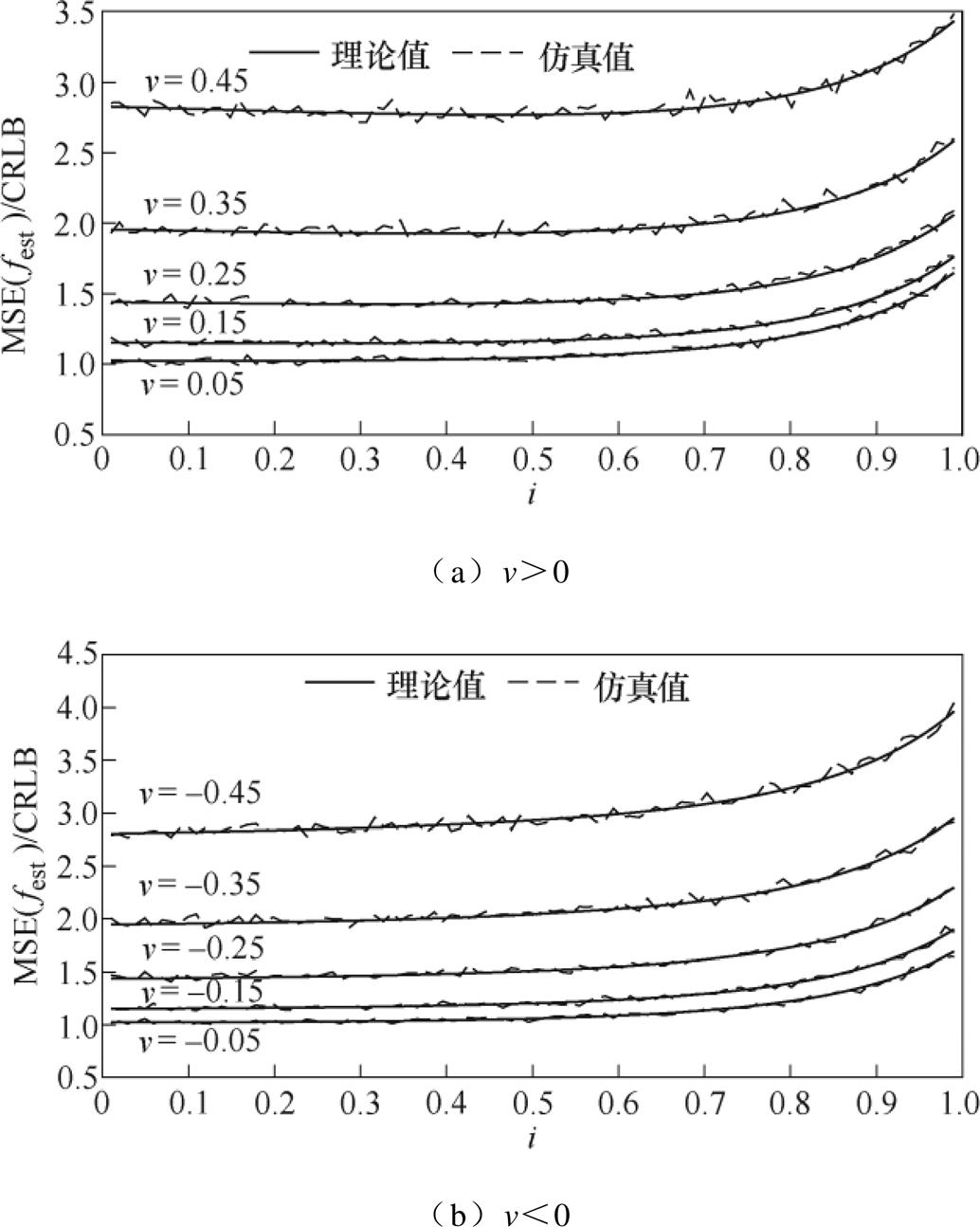
图2 频率估计MSE
Fig.2 The MSE of frequency estimation
图2结果显示:①频率估计的MSE与理论方差结果一致吻合,表明噪声扰动下算法为严格无偏频率估计。②当i≤0.5时,频率估计MSE在单一频率条件下几乎保持恒定,且在v→0时十分接近于CRLB;反之,则随着i的增大而逐渐增大。其原因在于当i≤0.5时,由于所用三条谱线都位于矩形窗主瓣范围内,因而其信噪比相对较高;反之,随着旁瓣衰减,辅助谱线的信噪比则很低,受噪声扰动影响较大。③当i≤0.5时,频率估计MSE不受频率偏移v符号影响,即在v>0或v<0范围内的MSE在量级上几乎相等;当i>0.5时(特别是在i→1时),在v>0范围内的频率估计MSE要小于v<0范围内,其原因在于当v<0时,量级较小的辅助谱线受负频率的频谱泄漏影响将不可忽略。
仍以3.1节中设定的信号为例,对应信号波动周期l 在[2.55, 3.45]则以步长0.02逐渐变化。根据3.1节仿真结果,此处仅考虑i≤0.5范围内取值时的频率估计结果,即对比i>0.5时保持相对最优;同时,考虑实际应用中数值稳定性,此处仅示出i=0.1时的频率估计结果,如图3所示。
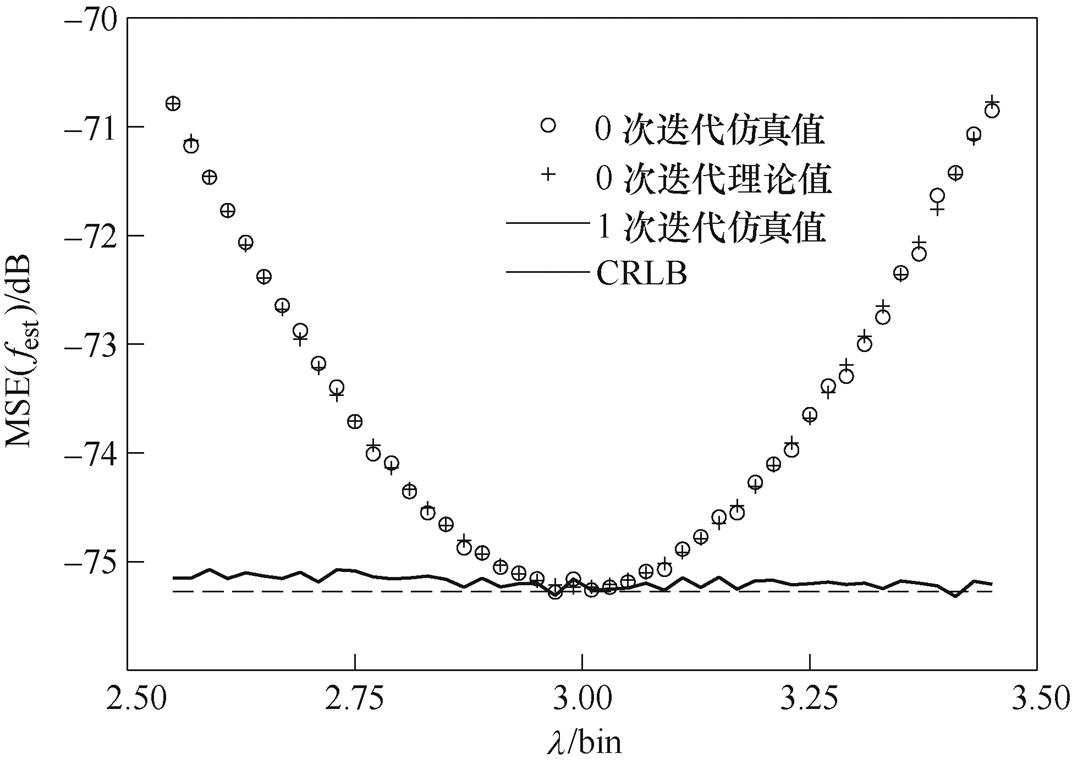
图3 i=0.1时频率估计的MSE
Fig.3 The MSE of frequency estimates when i=0.1
图3结果显示,噪声干扰下虽然所提无偏频率估计算法在频偏v偏离0时无法一致逼近CRLB,但伴随迭代程序的执行,仅需1次迭代频率估计的MSE在频偏vÎ[-0.5, 0.5]全域内都一致趋近于最优估计结果(v→0时),即在任意频偏情况下都十分接近于CRLB。在不显著增加计算复杂度的前提下,迭代执行程序有效降低了算法对频率偏移v的敏感度,极大地提高了算法的鲁棒性。对于i≤0.5范围内其他任意i值,据图2和第2节中算法统计特性分析可知,迭代程序仍有效且在噪声干扰下频偏估计结果将十分接近,不再赘述。
为进一步验证算法在不同波动周期下的有效性和准确性,设定信号波动周期l 在[0.55, 4.45]范围内逐渐变化,其他信号参数保持与3.1节和3.2节一致。由于频域类频率估计算法计算复杂度通常要远远小于时域类参数化算法,分别为O(Nlog2N)和O(N3),因此,仅选取目前为数不多的几种考虑负频率泄漏影响的频域插值算法进行性能比对,包括基于频谱系数加权的w3IpDFT[18]、采用矩阵解析的m3IpDFT[15]、基于补零和DFT系数变换的z2IpDFT[11]、解析插值算法a3IpDFT[10]以及改进的迭代插值DTFT算法eAM[20]。不同插值算法的频率估计MSE结果如图4所示。图4a为SNR=40dB时lÎ[0.55, 4.45]范围内的频率估计结果;图4b为本文算法单步迭代和eAM多步迭代收敛的频率估计结果比对;图4c为SNRÎ[-20, 100]dB范围内l=1.25时的频率估计结果。此外,图4中以aIpDTFT(i, m)表示本文算法,其中i为谱线间隔,m为迭代次数;鉴于在i≤0.5范围内算法性能十分接近,此处仍仅示出i=0.1时的仿真结果。
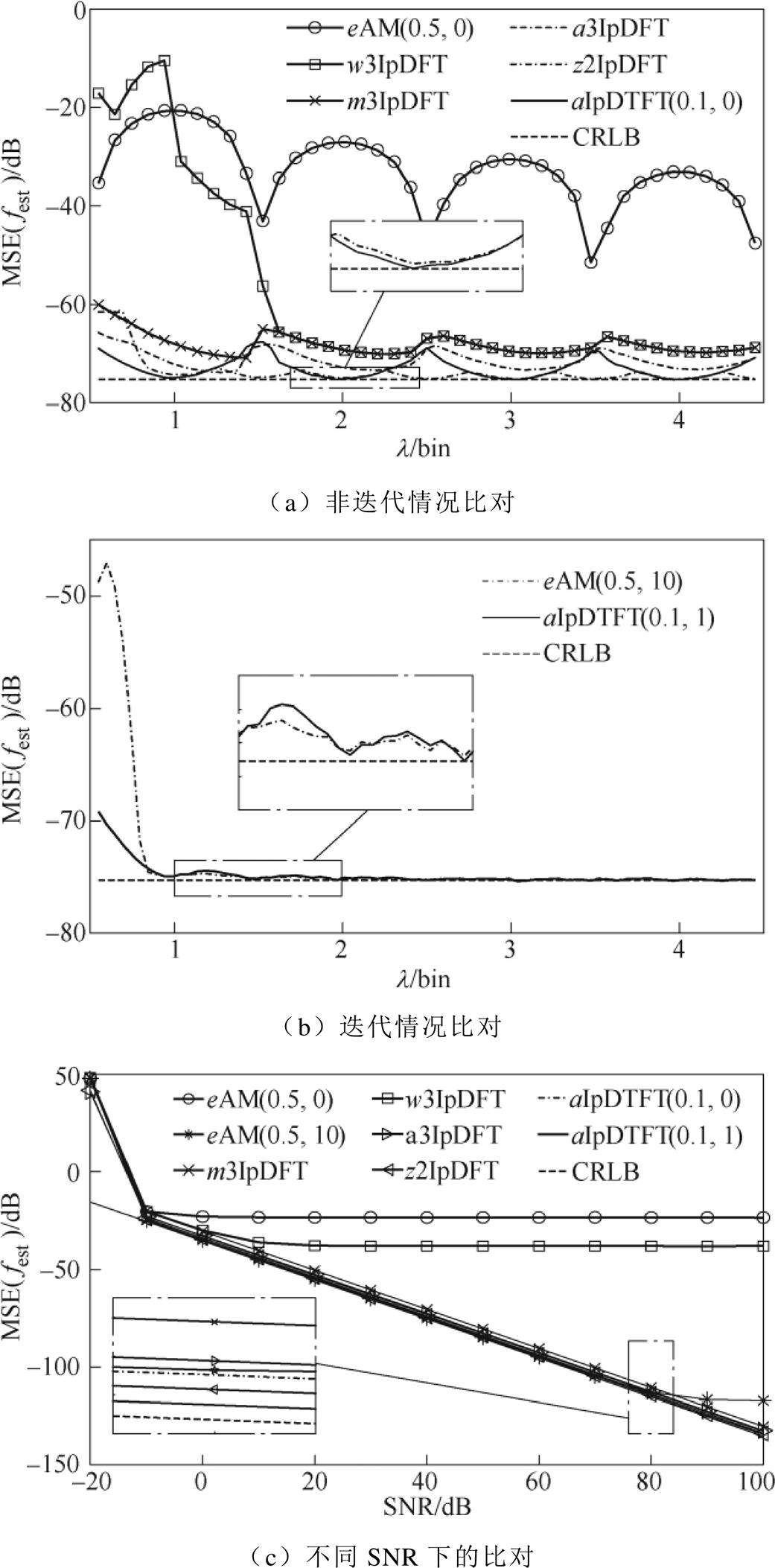
图4 不同算法频率估计性能比对
Fig.4 Comparison of frequency estimation performance of different algorithms
图4a结果显示:①非迭代情况下,本文算法和z2IpDFT整体上要远优于其他参考比对算法。②当信号波动周期l≤1时,本文算法要优于z2IpDFT;当信号波动周期l>1时,在偏移|v|≤0.25范围内两种算法性能十分接近;在0.25<|v|≤0.5范围内z2IpDF要优于本文算法。其原因在于,当|v|≤0.25时两种算法的解析方式极为接近,进一步分析可知,当且仅当i=0.5时两者具有几乎相同的解析插值公式,由3.1节结果可知,两种算法性能相当;而当 0.25<|v|≤0.5时,由于z2IpDFT算法通过补零改变了解析插值中所用谱线,使得其在该范围内的性能与|v|≤0.25时保持一致,因而优于本文算法的非迭代结果。
图4b结果显示:①当信号波动周期l>1时,通过多次不断迭代收敛的eAM算法与本文算法单次迭代结果几乎保持一致,明显受限于多次迭代计算,eAM算法计算量将远远高于本文算法;②当信号波动周期l≤1时,受限于与辅助谱线间隔固定为i=0.5,eAM算法中所用谱线量级极小,受负频率的频谱泄漏影响远大于本文算法(i=0.1),且因未采用信噪比较高的中心峰值谱线,导致算法MSE要远远高于本文算法。
图4c结果显示:①在信号波动周期l=1.25时,此时负频率频谱泄漏干扰相对占主导,非迭代eAM算法和w3IpDFT算法存在明显的估计偏差,因而性能上无法一致逼近CRLB;同理,迭代eAM算法在信噪比SNR>80dB时,因此处迭代次数设定限制无法完全消除估计偏差影响,导致其MSE偏离CRLB。②总体上本文算法(包括迭代)和其他算法对比,因准确计及负频率泄漏使得频率估计结果几乎一致逼近CRLB,在不同SNR情况下本文算法的单次迭代结果依然保持最优。
此外,根据N点FFT计算需要2Nlog2N次实数乘法和3Nlog2N次实数加法运算,单点实数DTFT计算需要2N次实数乘法和2N-2次实数加法运算,对前述不同算法的计算复杂度进行对比,结果见表2,表中右侧数值是根据左侧理论值计算所得。结果显示,总体上w3IpDFT、m3IpDFT和a3IpDFT算法的计算量较为接近且在所有对比算法中相对最小;本文算法(包括1次迭代收敛)和非迭代eAM算法的计算量次之,但在性能上本文算法明显优于非迭代eAM(见图4);eAM算法和z2IpDFT算法的计算量较为接近但要远远大于其他对比算法,通常情况下为保证收敛迭代次数m 3[20],这使得eAM算法随着迭代次数增加其计算量将急剧增加。
3[20],这使得eAM算法随着迭代次数增加其计算量将急剧增加。
综上可知,相较其他插值类算法,虽然本文算法在非迭代情况下未保持全域最优,但在不明显增加计算量的前提下,仅通过单步迭代以优化性能,即能达到最优的频率估计且全域一致逼近CRLB。
表2 不同算法计算复杂度比对
Tab.2 Comparison of the computational complexity of different algorithms
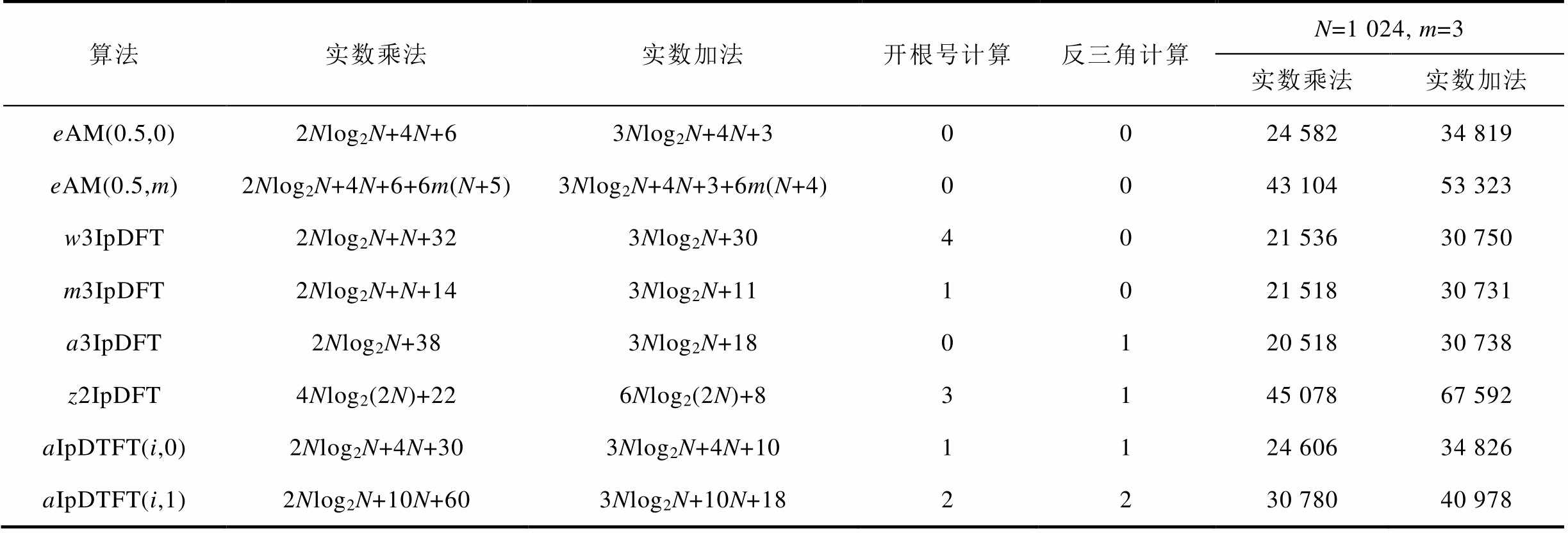
算法实数乘法实数加法开根号计算反三角计算N=1 024, m=3 实数乘法实数加法 eAM(0.5,0)2Nlog2N+4N+63Nlog2N+4N+30024 58234 819 eAM(0.5,m)2Nlog2N+4N+6+6m(N+5)3Nlog2N+4N+3+6m(N+4)0043 10453 323 w3IpDFT2Nlog2N+N+323Nlog2N+304021 53630 750 m3IpDFT2Nlog2N+N+143Nlog2N+111021 51830 731 a3IpDFT2Nlog2N+383Nlog2N+180120 51830 738 z2IpDFT4Nlog2(2N)+226Nlog2(2N)+83145 07867 592 aIpDTFT(i,0)2Nlog2N+4N+303Nlog2N+4N+101124 60634 826 aIpDTFT(i,1)2Nlog2N+10N+603Nlog2N+10N+182230 78040 978
实验验证测试平台如图5所示,以精度为0.05级的DK-56B1三相交直流指示仪表检定装置作为功率信号源,额定输出信号频率为50Hz,信号幅值为5V;以24bit的IOtech数据记录仪作为信号采集装置,采样频率为100kHz。以截取信号采样点数的改变对应于l 变化,对应于每个l 通过单点移动改变信号初始相位,并连续进行10 000次分析。此外,鉴于白噪声扰动下IEEE 1057标准[24]建议的4参量正弦拟合算法(4PSF)提供了频率的最大似然估计,其估计方差非常接近CRLB,因此以该算法估计结果作为基准,其迭代次数设定为6。在lÎ[1, 4]范围内不同算法的频率估计MSE实验结果如图6所示。

图5 实验平台
Fig.5 Experimental platform

图6 实验结果
Fig.6 Experimental results
从图6可看出,实验结果与图4仿真结果基本完全吻合。此处,虽然实验中频率分辨率随着l 增大而增高,频率估计的方差下界将逐渐降低,但本文算法的单步迭代结果在任意频点上仍然与4PSF基准结果基本保持一致,这也再次印证了本文算法的准确性和迭代有效性。
进一步以现场测试信号对算法进行验证,图7所示为一电力机车运行过程中变压器二次电流和电压采样信号,采样频率fs=5kHz。伴随运行状态改变其电流将出现明显波动,对应电压频率也必然会出现变化。以样本点数NÎ{100 25
25 400}改变对应于l变化,以单点移动改变样本信号初始相位。限于篇幅,图8a仅示出N=175和200时基于本文算法的电压基波频率估计结果;而随着l 变化,基于不同算法的电压基波频率估计MSE如图8b所示。
400}改变对应于l变化,以单点移动改变样本信号初始相位。限于篇幅,图8a仅示出N=175和200时基于本文算法的电压基波频率估计结果;而随着l 变化,基于不同算法的电压基波频率估计MSE如图8b所示。

图7 实测电力信号
Fig.7 The measured power signals
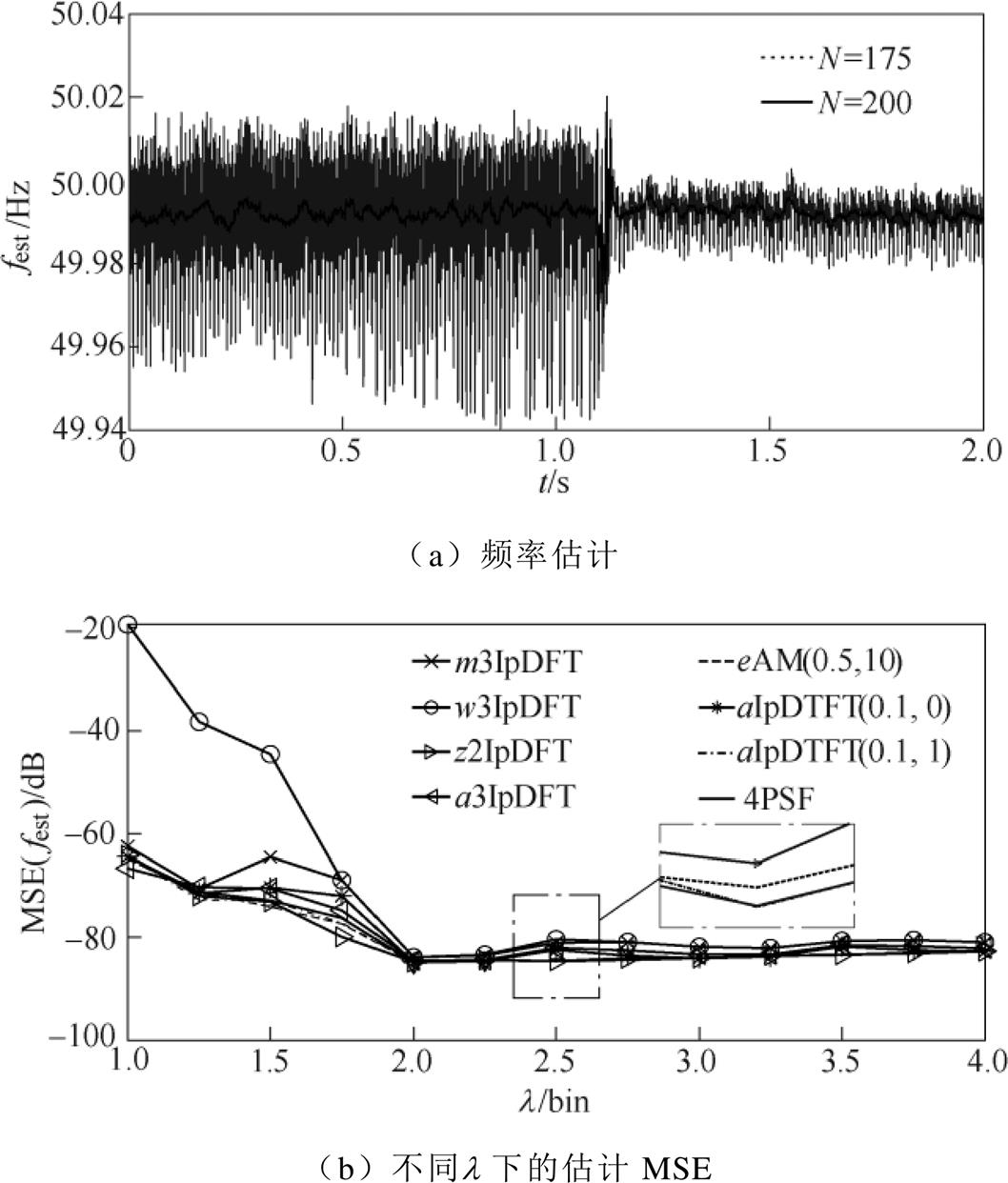
图8 实测电压信号的频率估计
Fig.8 Frequency estimates of measured voltage signals
如图8a所示,当采样点数较小即N≤175时,实测电压信号含有的一定量谐波泄漏干扰导致频率估计波动偏大;随着采样点数增多,谐波泄漏干扰逐渐降低直至忽略不计,频率估计趋于稳定且能够准确反映负载运行状态变化。图8b所示频率估计MSE随l 变化而变化的趋势与图6实验室测试结果基本一致,虽然在l 较小时受限于谐波泄漏干扰,导致与实验室测试结果出现一定偏差,但总体上本文算法的单步迭代频率估计结果依然保持最优,而且极为接近于以4PSF算法为基准近似的CRLB。
针对短时波动周期下实正弦信号频率精确估计问题,首先利用频谱实/虚部线性方程组解析得到了基于广义DTFT插值的无偏频率估计公式,不仅摆脱了对窗函数旁瓣衰减特性的严重依赖,而且打破了以往传统频域插值算法仅限于单频解析信号和离散DFT谱线插值的局限性;进而基于噪声背景下频率估计的统计性能分析导出了算法的迭代执行方式,解决了算法在背景噪声干扰下无法保持全域最优且一致逼近CRLB的问题。
仿真和实验结果显示,一方面,得益于算法解析过程准确计及来自负频率的频谱泄漏干扰,且采用间隔低至0.1Df的DTFT辅助谱线,即便信号波动周期l≤1时算法在未迭代情况下性能仍保持稳定;另一方面,对于噪声干扰影响,算法通过简单有效的迭代执行方式以优化估计性能,在不显著增加计算量和复杂度的前提下,仅需单步迭代即能达到最优的频率估计且全域一致逼近CRLB,在i=0.1时理论上算法最小MSE与CRLB之比接近1.008 822。
对于谐波扰动的多频信号频率估计,在主瓣频谱不存在混叠的前提下,可首先采用本文算法得到单频点的频率粗估计,进一步通过单频点的粗估计实现频谱重构,逐步迭代消除谐波频谱长泄漏的干扰影响,从而再次采用本文算法实现精确频率估计。
这种针对多频信号频率估计的算法具体实现及相应测试结果将在下一步研究工作中详细探讨。
附 录
1. a 的具体求解过程
便于推导,首先将矩阵C+/C-和S+/S-中与位置索引相关的已知三角函数变量分别以aij和bij表示为
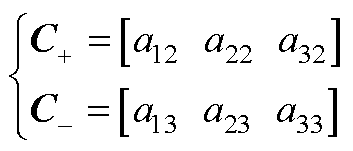 (A1)
(A1)
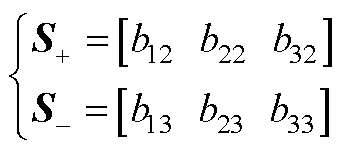 (A2)
(A2)
由此,式(13)和式(14)改写为
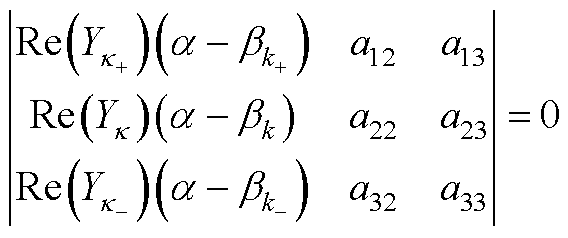 (A3)
(A3)
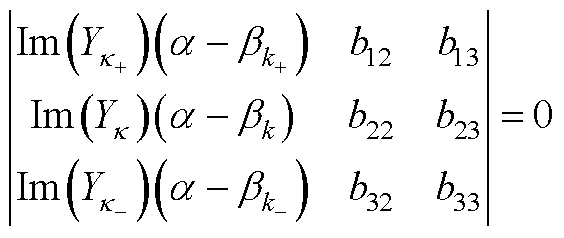 (A4)
(A4)
则根据行列式性质将式(A2)左侧行列式分别进行简化,即
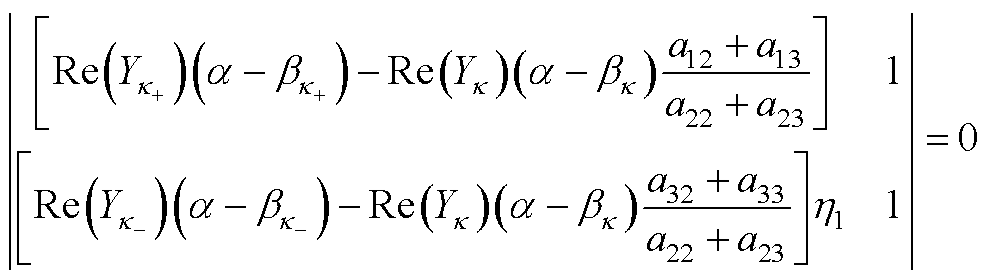 (A5)
(A5)
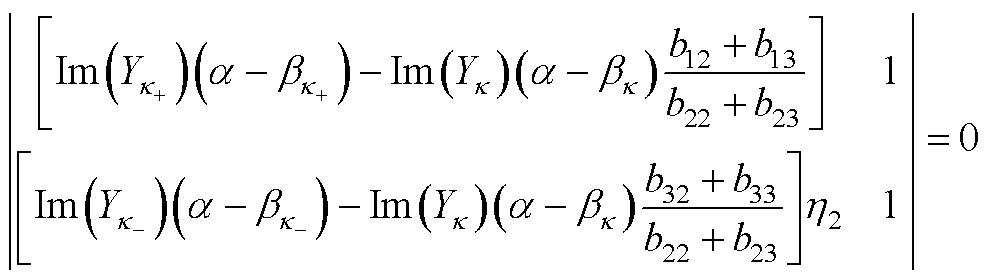 (A6)
(A6)
再次利用行列式性质,将式(A6)虚数部分乘以虚数单位j后与式(A5)实数部分进行合并,进而经过展开计算后可得a 的解析解为
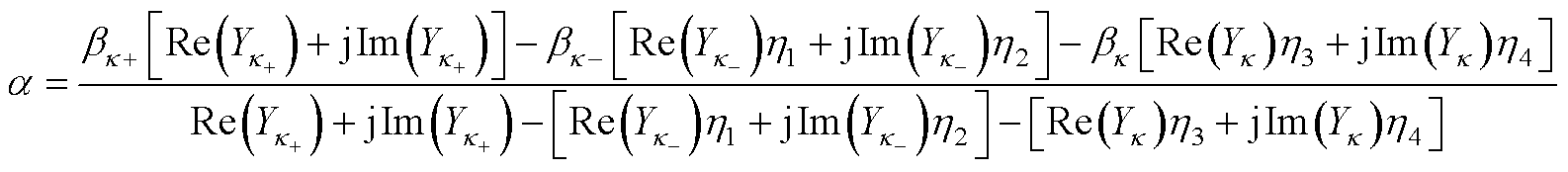 (A7)
(A7)
2. 频率估计的统计方差推导
考虑gi中噪声项Qk 之间的相关性,首先将Da展 开,即
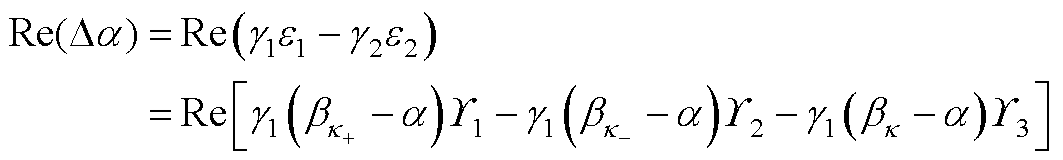 (A8)
(A8)
令a=bk+-a,b=bk--a 和c=bk-a,由于E[Re(Da)]=0,Re(Da)的自相关与方差相等,即
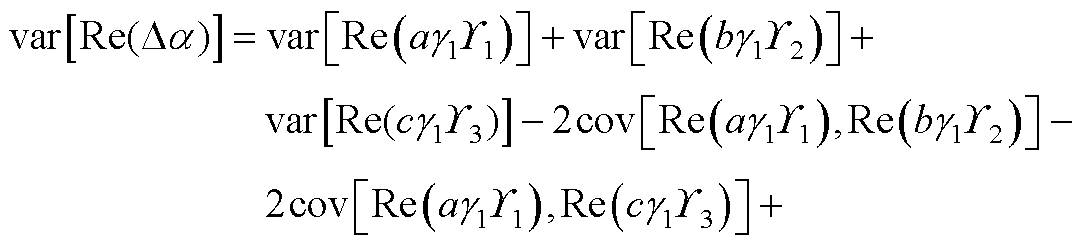
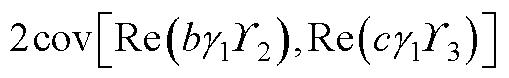 (A9)
(A9)
式中,由于各参量方差及互相关具有相似性,因此,此处仅分别以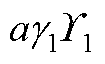 的方差以及
的方差以及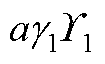 和
和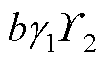 的互相关为例进行推导,即
的互相关为例进行推导,即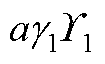 的方差为
的方差为
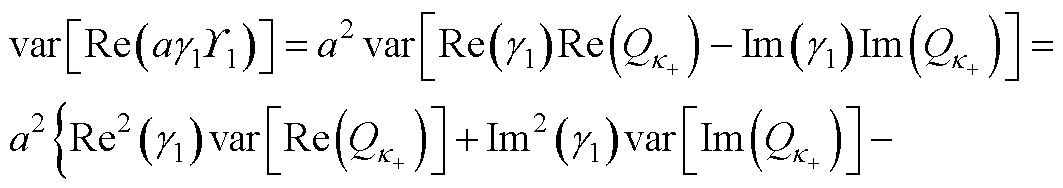
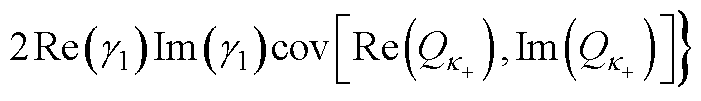 (A10)
(A10)
其中
 (A11)
(A11)
 (A12)
(A12)
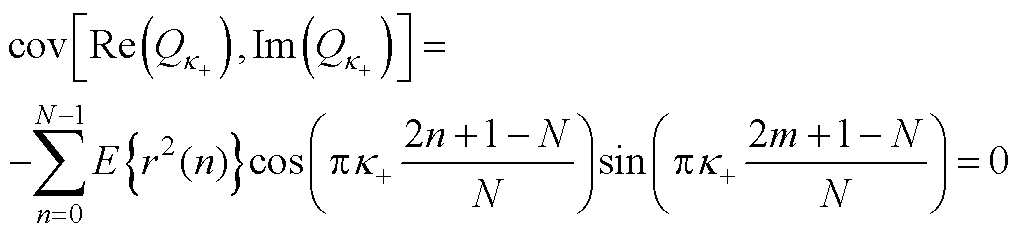 (A13)
(A13)
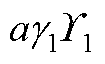 和
和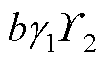 的互相关为
的互相关为
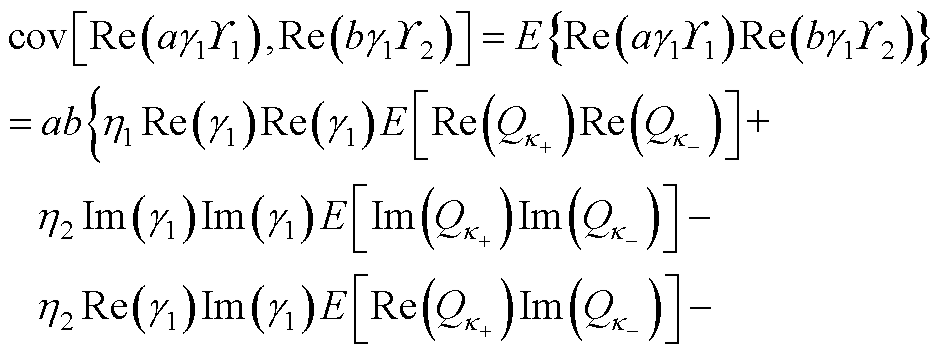
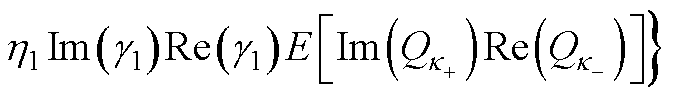 (A14)
(A14)
其中
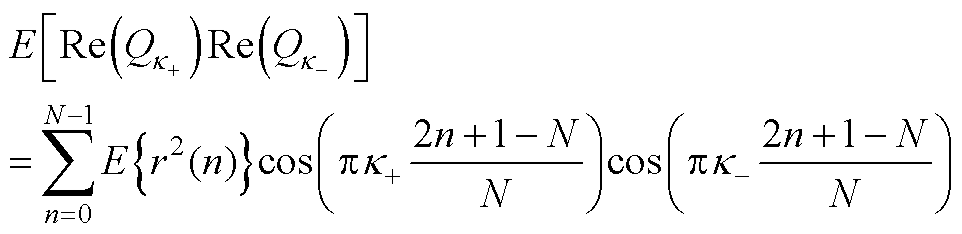
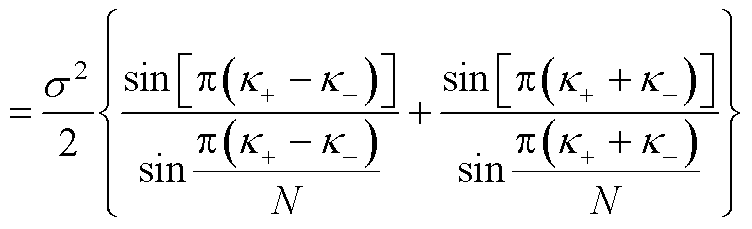 (A15)
(A15)
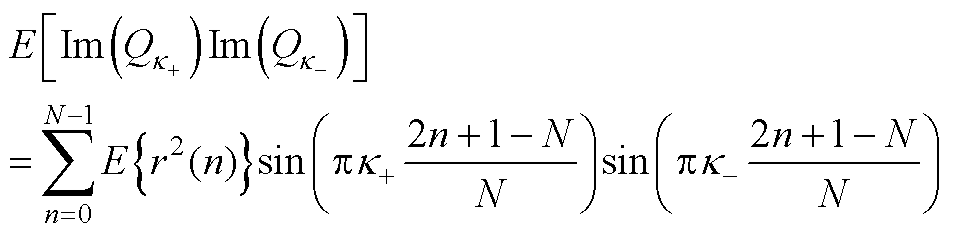
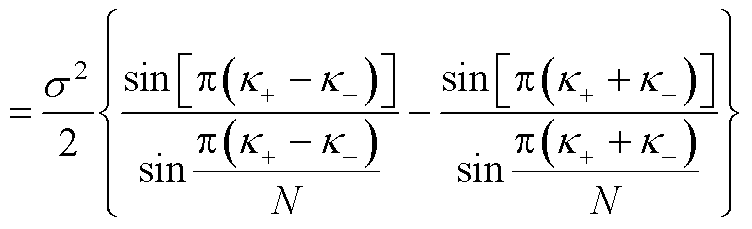 (A16)
(A16)
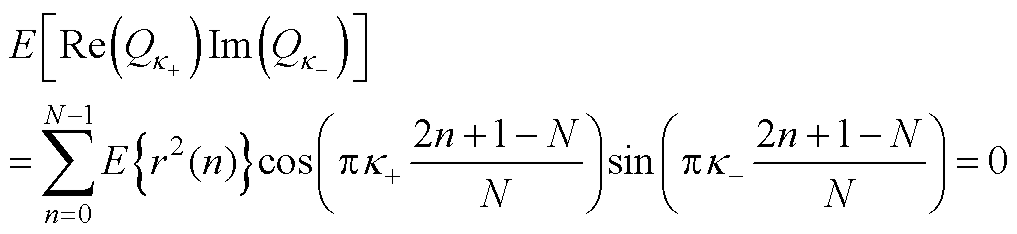 (A17)
(A17)
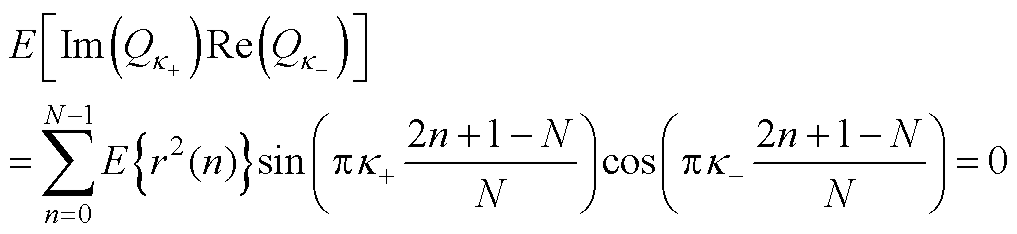 (A18)
(A18)
由此,据式(A10)~式(A18)可得Re(Da)的方差为
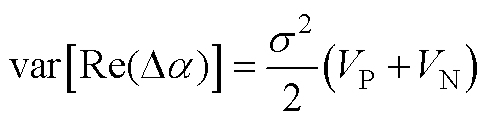 (A19)
(A19)
式中,VP和VN分别为
 (A20)
(A20)
 (A21)
(A21)
参考文献
[1] Sun J, Aboutanios E, Smith D B, et al. Robust frequency, phase, and amplitude estimation in power Systems considering harmonics[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1158-1168.
[2] 张政, 温和, 黎福海, 等. 多水平集单周期电力系统频率测量方法及应用[J]. 电工技术学报, 2017, 32(7): 119-127.
Zhang Zheng, Wen He, Li Fuhai, et al. Multi-level set single-cycle power system frequency measurement method and its application[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 119-127.
[3] 肖勇, 赵伟, 黄松岭. 基于离散傅里叶级数的非同步采样下谐波功率测量算法[J]. 电工技术学报, 2018, 33(7): 1570-1578.
Xiao Yong, Zhao Wei, Huang Songling. Harmonic power measurement algorithm based on discrete fourier series in asynchronous sampling[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(7): 1570-1578.
[4] Jafarpisheh B, Madani S M, Parvaresh F, et al. Power system frequency estimation using adaptive accelerated MUSIC[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(11): 2592-2602.
[5] 杨超, 张淮清, 王耀, 等. 计及全泄漏影响的多点插值离散傅里叶变换校正方法[J]. 电工技术学报, 2020, 35(16): 3385-3395.
Yang Chao, Zhang Huaiqing, Wang Yao, et al. Multipoint interpolated discrete fourier transform correction method considering total leakage effect[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3385-3395.
[6] Shin D, Kwak C, Kim G. An efficient algorithm for frequency estimation from cosine-sum windowed DFT coefficients[J]. Signal Processing, 2020, 166: 107245.1-107245.9.
[7] 孙仲民, 何正友, 臧天磊. 一种混合卷积窗及其在谐波分析中的应用[J]. 电工技术学报, 2016, 31(16): 207-214.
Sun Zhongmin, He Zhengyou, Zang Tianlei. A kind of hybrid convolution window and its application in harmonic analysis[J]. Transactions of China Electro- technical Society, 2016, 31(16): 207-214.
[8] Romano P, Paolone M. Enhanced interpolated-DFT for synchrophasor estimation in FPGAs: theory, implementation, and validation of a PMU prototype[J]. IEEE Transactions on Instrumentation and Measure- ment, 2014, 63(12): 2824-2836.
[9] 翟晓军, 周波. 一种改进的插值FFT谐波分析算法[J]. 中国电机工程学报, 2016, 36(11): 2952-2958.
Zhai Xiaojun, Zhou Bo. An improved interpolated FFT algorithm for harmonic analysis[J]. Proceedings of the CSEE, 2016, 36(11): 2952-2958.
[10] Wang Kai, Wen He, Li Guoqing. Accurate frequency estimation by using three-point interpolated discrete fourier transform based on rectangular window[J]. IEEE Transactions on Industrial Informatics, 2021, 17(1): 73-81.
[11] Sun Yuxin, Zhuang Chungang, Xiong Zhenhua. A scale factor based interpolated DFT for chatter frequency estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(10): 2666-2678.
[12] Sun Yuxin, Zhuang Chungang, Xiong Zhenhua. A switch-based inter-polated DFT for the small number of acquired sine wave cycles[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(4): 846-855.
[13] Hlupic N, Basch D, Fertalj K. A note on optimality of analytical leakage compensation at boundary fre- quencies[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(2): 301-308.
[14] Borkowski J, Kania D, Mroczka J. Interpolated-DFT- based fast and accurate frequency estimation for the control of power[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 7026-7034.
[15] Chen Kuifu, Cao Xu, Li Yangfeng. Sine wave fitting to short records initialized with the frequency retrieved from Hanning windowed FFT spectrum[J]. Measurement, 2009, 42(1): 127-135.
[16] Murakami T, Wang W. An analytical solution to Jacobsen estimator for windowed signals[C]//IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Barcelona, Spain, 2020: 5950-5954.
[17] Belega D, Petri D. Effect of noise and harmonics on sine-wave frequency estimation by interpolated DFT algorithms based on few observed cycles[J]. Signal Processing, 2017, 140: 207-218.
[18] Belega D, Petri D, Dallet D. Frequency estimation of a sinusoidal signal via a three-point interpolated DFT method with high image component interference rejection capability[J]. Digital Signal Processing, 2014, 24: 162-169.
[19] Candan C. A method for fine resolution frequency estimation from three DFT samples[J]. IEEE Signal Process, Lett, 2011, 18(6): 351-354.
[20] Ye S, Sun J, Aboutanios E. On the estimation of the parameters of a real sinusoid in noise[J]. IEEE Signal Processing Letters, 2017, 24(5): 638-642.
[21] Aboutanios E, Mulgrew B. Iterative frequency estimation by interpolation on Fourier coefficients[J]. IEEE Transactions on Signal Processing, 2005, 53(4): 1237-1242.
[22] Horn R A, Johnson C R. Matrix analysis[M]. Cambridge: Cambridge University Pre, 1985.
[23] Lei Fan, Guoqing Qi. Frequency estimator of sinusoid based on interpolation of three DFT spectral lines[J]. Signal Processing, 2018, 144: 52-60.
[24] IEEE standard for digitizing waveform recorders[S]. New Jersey: Piscataway, 2007.
Accurate Frequency Estimation Based on Analytical Interpolated Discrete Time Fourier Transform
Abstract When the cycles in record (CiR) of the signal is small, the spectral leakage from the image component is the main source of estimation errors in the frequency-domain interpolation. To eliminate the influence of spectral leakage and accurately estimate the frequency of a real sinusoidal signal with any CiR, an analytic interpolation algorithm based on generalized DTFT is proposed. The algorithm uses any DTFT spectral lines located in the main lobe of the spectrum to construct a linear equation set corresponding to the real and imaginary parts, and then an unbiased frequency estimator based on analytic interpolated DTFT is obtained. Besides, considering the influence of additive white noise in practice, a simple and effective iterative method is presented based on the analysis of the statistical characteristics of the frequency estimator. The iterative method ensures that the mean square errors (MSE) of the frequency estimation can consistently achieve the Cramer-Rao lower bound (CRLB) of the unbiased frequency estimation under any CiR. Simulation and experimental results confirm that the proposed algorithm is superior to other existing interpolated DFT algorithms.
keywords:Small cycles in record, spectral leakage, analytically interpolated discrete time fourier transform (DTFT), iterative method, Cramer-Rao lower bound (CRLB)
DOI: 10.19595/j.cnki.1000-6753.tces.201667
中图分类号:TM935
杨 超 男,1986年生,博士,研究方向为数字信号处理及其在精密测量、电能计量与电能质量分析中的深度应用。E-mail: 328383369@qq.com(通信作者)
李 波 男,1982年生,硕士,高级工程师,主要从事电气测量以及智能电网测控研究工作。E-mail: libo2010@163.com
收稿日期 2020-12-20
改稿日期 2021-04-27
国家重点研发计划课题(2018YFC0406904)和重庆市重点产业共性关键技术创新专项(重点研发项目)(CSTC2017ZDCY-ZDYFX0045)资助。
(编辑 陈 诚)