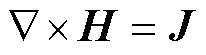 (1)
(1)
摘要 随着城市电力的扩张以及电力需求的增大,为解决地下电缆传输空间用地紧张的问题,新建的直流电缆将敷设在原有的交流隧道中,从而使电缆隧道内电磁场变得更为复杂。该文针对±320kV直流电缆和220kV交流电缆共沟敷设隧道建立电磁场仿真模型;计算隧道内的电磁场分布以及交流电缆在直流电缆上产生的感应电压;分析交直流电缆之间的距离、交流电缆和直流电缆的敷设方式以及单相交流电缆故障对电缆隧道电磁环境的影响,最后根据计算结果提出交直电缆间的最小距离以及交直流电缆的最优敷设方式。
关键词:交直流 电缆 电磁场 敷设方式
由于中国城市扩张以及电力负载增加,我国部分地区高压输电线路逐渐密集,输电走廊资源日益紧缺[1-6]。为保证城市美观和线路的安全运行,越来越多的架空线被电缆所替代,而这一措施却使得电缆隧道空间越来越紧张[7-8]。近年来,高压直流电缆在国内蓬勃发展。为节省土地资源,减少敷设成本,提高单位电缆隧道的输电能力,目前普遍做法是将直流电缆直接敷设在已建成的交流电缆隧道内,因此出现了交直流电缆共沟敷设的情况[9-11]。然而,交流电缆在运行时将在直流电缆上产生电磁感应现象,影响直流电缆正常运行。同时新建的直流电缆将在原交流电缆隧道中产生磁场的叠加,恶化隧道内电磁环境,对运维人员的健康造成严重的危害[12-14]。因此,对交直流共沟敷设隧道内电磁场环境展开研究并提出交直流电缆安全敷设标准十分必要[15]。
近年来,许多学者针对交直流并行敷设的输电走廊进行了研究。文献[16]研究了在考虑离子流条件下交直流混合输电走廊内地面附近的电场分布。文献[17]针对非全线并设的交直流输电走廊电磁耦合进行了分析计算,得到了交直流输电线路接近段的最优位置。文献[18]分析了交流输送功率、交直流输电线路并行长度、两者之间距离、土壤电阻率等因素对电磁环境的影响。
但上述研究都是基于架空线,目前对交直流电缆隧道电磁环境的研究较少,而架空线的运行环境与电缆完全不同。高压直流输电线路由于空气电离,地面附近电场会受到离子流的影响而剧烈增大,而电缆敷设于地下隧道内,其绝缘设计相较于架空输电线路要复杂,绝缘尺寸也远大于架空输电线,因此两者的电磁环境存在明显的差异。但由于我国高压直流电缆运行时间尚短,目前对于电缆隧道的电磁环境评价指标仍参照架空输电线路进行[19]。
本文以±320kV直流电缆线路和220kV交流电缆线路共同敷设的厦门翔安海底隧道段为研究对象,计算了隧道内的电磁场分布以及交流电缆在直流电缆上产生的感应电压;分析了交直流共沟敷设隧道电磁环境的影响因素,研究了交直流电缆之间的距离、交流电缆和直流电缆的敷设方式以及单相交流电缆故障对电缆隧道的电磁环境的影响;最后根据计算结果提出了交直电缆间的最小距离以及交直流电缆的最优敷设方式。
采用有限元方法对隧道磁场进行分析,隧道内的矢量磁位A满足
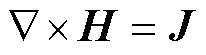 (1)
(1)
 (2)
(2)
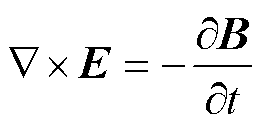 (3)
(3)
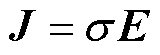 (4)
(4)
式中,H为磁场强度;J为电流密度;B为磁感应强度;E为电场强度;s 为电导率。
图1所示为厦门翔安海底隧道。图1中,给出了两条计算路径,路径1为电缆隧道内距离地面1.5m的位置,该高度一般认为是人体的心脏位置,路径2为电缆隧道中心,同时也是运维人员所处的位置。下文将基于这两条路径上的磁场分布进行分析。

图1 厦门翔安海底隧道
Fig.1 Subsea tunnel of Xiamen Xiang'an
图2为交直流电缆共同敷设模型。厦门±320kV柔性直流输电工程采用导体截面积为1 800mm2的交联聚乙烯电缆,其载流量可达1 617A,而交流侧220kV电缆电流幅值为800A。图中,long表示双回路交流电缆与直流电缆同时向隧道中心位置移动的距离。
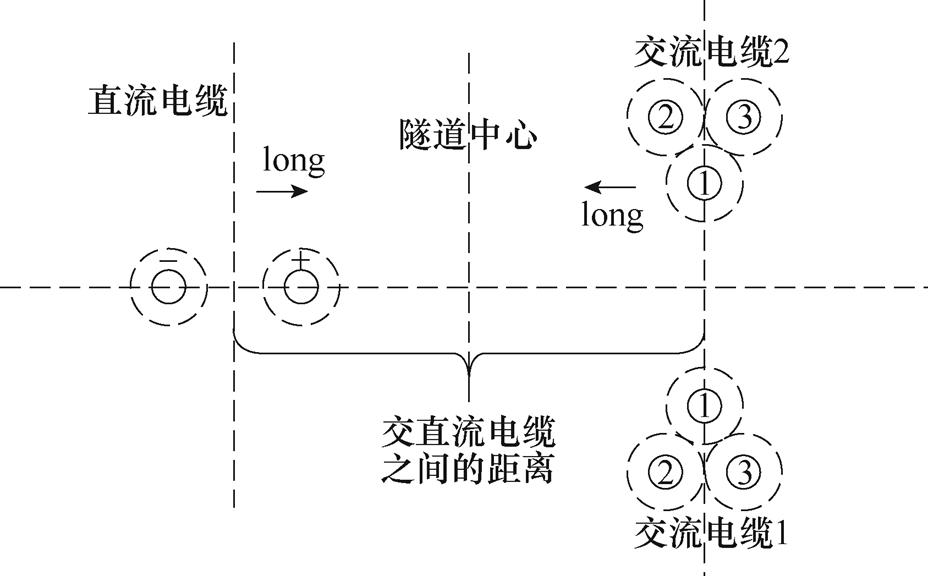
图2 电缆模型
Fig.2 Cable model diagram
参考DL/T 1088—2008《±800kV特高压直流线路电磁环境参数限值》认为,交直流共同敷设隧道中心静态磁场不能超过10mT,交流磁场不能超过500mT。图3给出交直流共同敷设情况下磁场分布云图。图4给出交流与直流电缆距离不同时电缆隧道磁场分布。图4a、图4b分别为路径1和路径2上磁场分布。隧道交直流电缆相距2 300mm,隧道中心与交流电缆和直流电缆的距离相同。交直流电缆共同敷设时隧道磁场满足叠加定理。由图4可知,电缆之间越靠近,隧道中心处的磁感应强度越大。由于满载时直流电缆在隧道走廊中心产生的直流磁感应强度远小于规定的磁场的限值,因此可以将仿
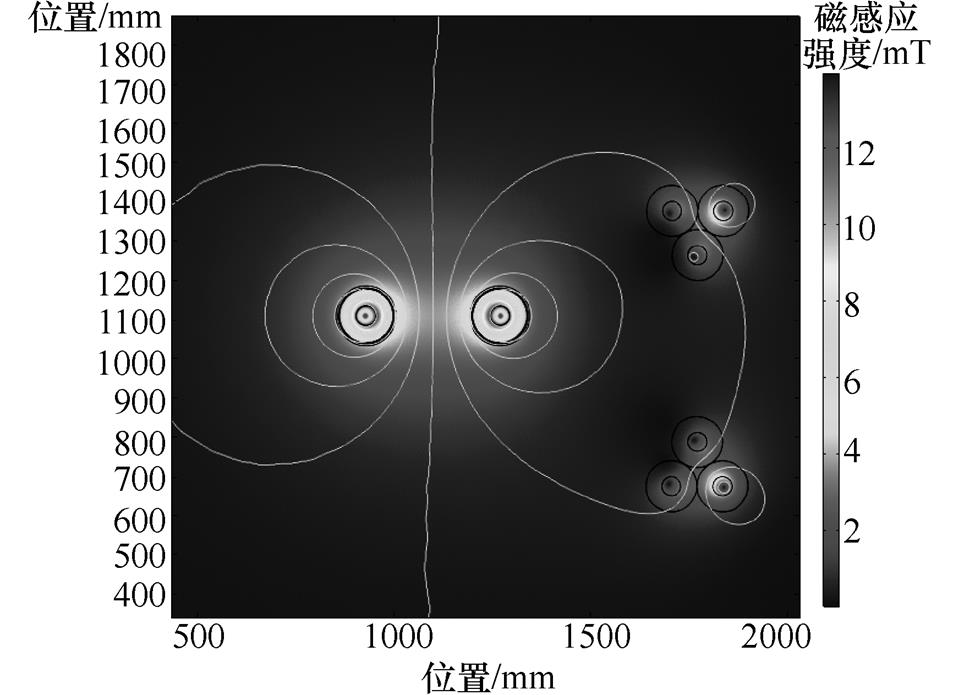
图3 交直流共同敷设时隧道磁场分布
Fig.3 The magnetic field distribution of tunnel when AC and DC cables laying together
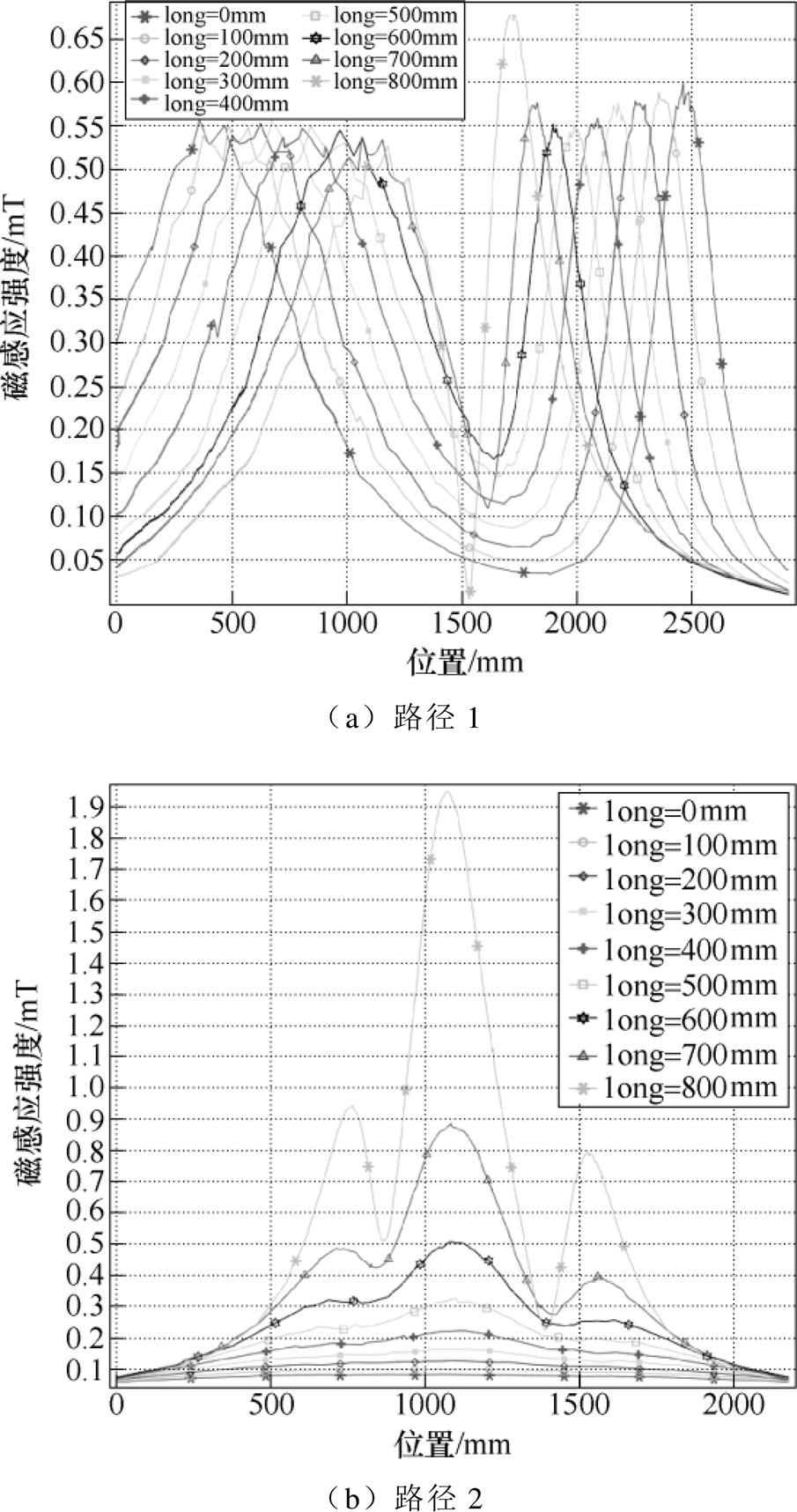
图4 交流与直流电缆距离不同时电缆隧道磁场分布
Fig.4 Magnetic field distribution in cable tunnels with different distances between AC and DC cables
真模型中的直流电缆电流设置为0,单独考虑交流电缆产生的交变磁场。仅考虑交流时电缆不同位置隧道内磁场分布如图5所示,此时的磁场主要集中在交流电缆附近,在long取800mm时隧道中心磁感应强度不符合要求。综上,在交直流电缆共沟敷设情况下,当交流电缆中的电流幅值为800A时,距电缆中心不能小于270mm,而直流电缆的敷设位置对隧道内的磁场环境影响较小。
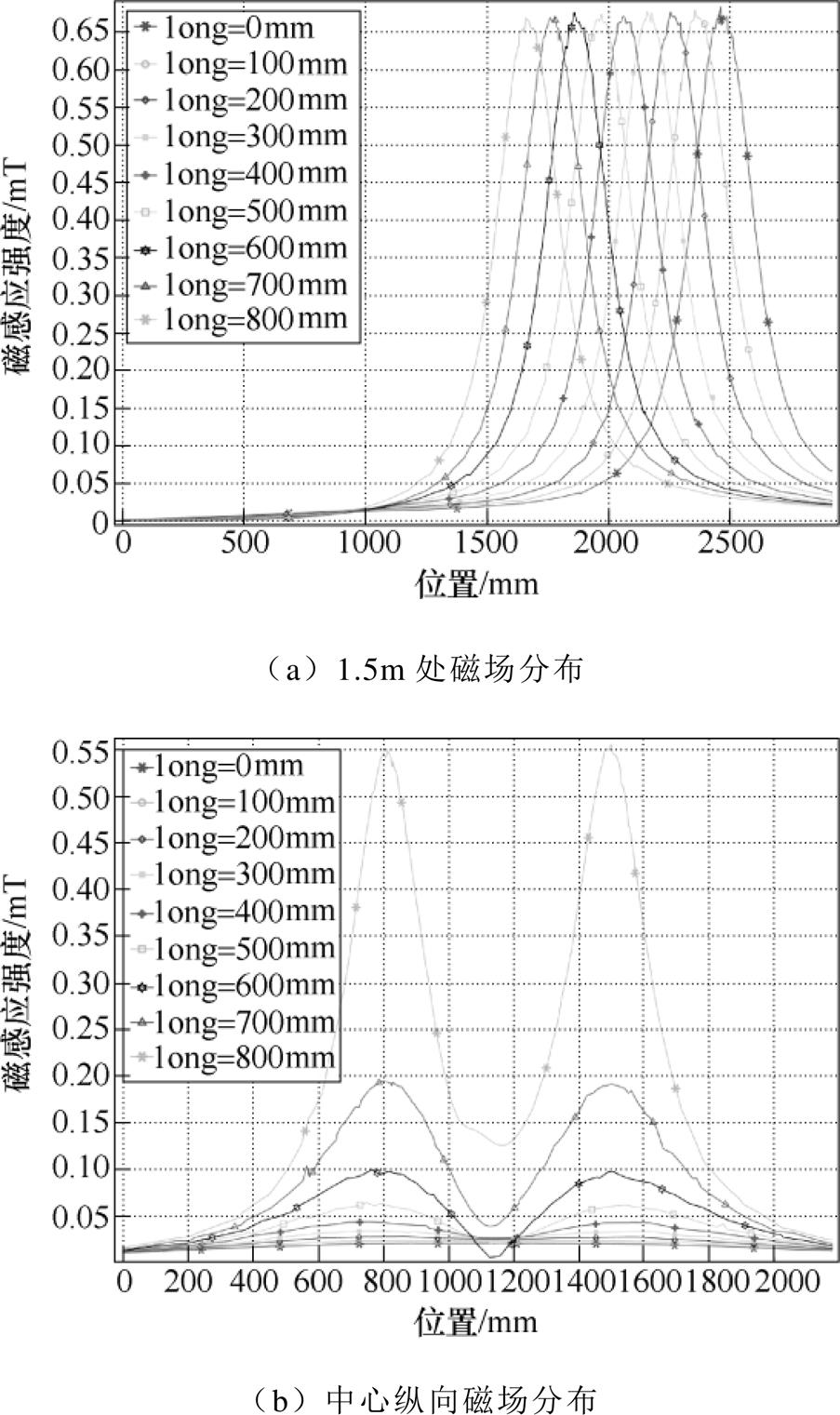
图5 仅考虑交流时电缆不同位置隧道内磁场分布
Fig.5 The distribution of magnetic field with different positions of cable when only considering AC cables
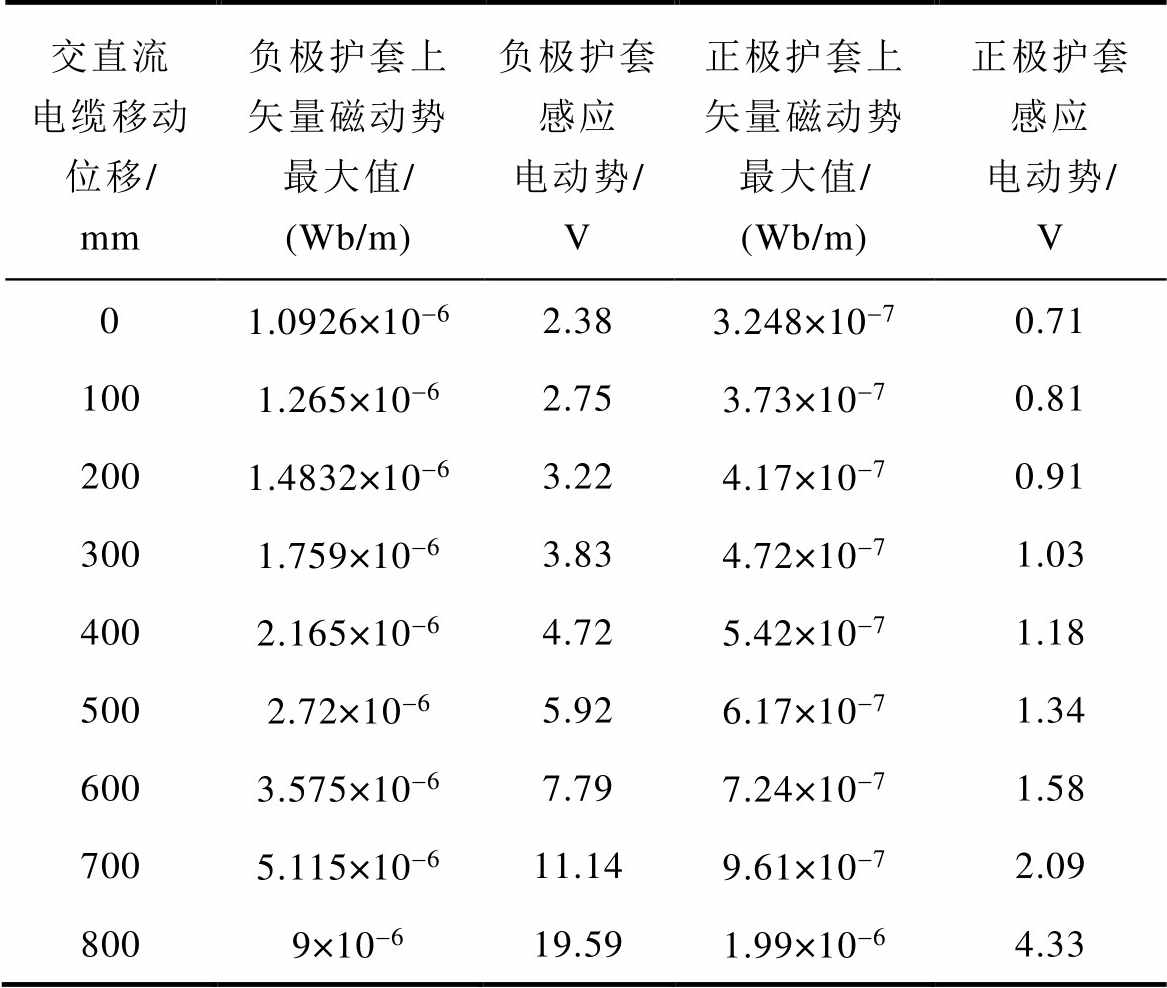
三相电流在交直流共沟敷设的隧道内产生交变电磁场,交流电缆线芯相当于变压器的一次绕组,而直流电缆金属护套相当于二次绕组,在交变磁场作用下直流电缆金属护套上将会产生感应电压。若其值过高不仅会对运维人员的人身安全产生威胁,还会使外护层发生击穿。当外护套两端接地时,护套与大地形成回路,在感应电压的作用下护套上将会产生环流以及环流损耗,该现象不但会极大地影响电缆的载流量,还会提高电缆的运行温度,使电缆的运行寿命降低。因此,准确地计算电缆金属护套感应电压对运行线路的安全稳定运行至关重要。根据建设部和国家质检总局联合颁发的GB 50217—2007《电力工程电缆设计规范》要求,在未采取能有效防止人员任意接触金属防护层的安全措施时,交流单芯电力电缆线路金属层的非直接接地任一点的感应电压不超过50V;若采取不能任意接触金属护层的安全措施,不得大于300V。交直流之间敷设距离对电场的影响主要是考虑交流对直流线芯以及护套产生的感应电压。由于解析法计算电缆金属护套感应电压时,铠装层对护套感应电压的影响是忽略的,因此本文建立了交直流电缆共沟敷设的二维模型,从有限元计算结果中提取护套上的矢量磁位最大值,并根据式(5)、式(6)计算护套上的感应电压。已知直流电缆全长10.7km,交直流共同敷设的长度为9.8km,护套上的感应电压计算结果见表1。由计算结果可知,交流与直流敷设距离越远,护套上产生的感应电压越小,因此正极护套上的感应电压要小于负极。当long取800mm,磁场已超过限值,但电场仍在安全阈值内。因此,在电缆隧道敷设设计时可以优先考虑磁场的影响。

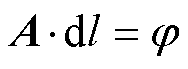 (5)
(5)
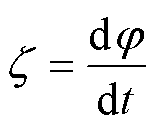 (6)
(6)
式中,j 为磁通;z 为感应电压。
表1 护套上感应电压
Tab.1 The induced voltage on the sheath
交直流电缆移动位移/ mm负极护套上矢量磁动势最大值/ (Wb/m)负极护套感应电动势/ V正极护套上矢量磁动势最大值/ (Wb/m)正极护套感应电动势/ V 01.0926×10-62.383.248×10-70.71 1001.265×10-62.753.73×10-70.81 2001.4832×10-63.224.17×10-70.91 3001.759×10-63.834.72×10-71.03 4002.165×10-64.725.42×10-71.18 5002.72×10-65.926.17×10-71.34 6003.575×10-67.797.24×10-71.58 7005.115×10-611.149.61×10-72.09 8009×10-619.591.99×10-64.33
图6为交流电缆两类典型敷设方式,敷设方式1表示直流电缆与平行排列交流电缆平行敷设。敷设方式2表示直流电缆与三角形排列的交流电缆平行敷设。由于直流电缆护套上的感应电压主要与距离有关,而交流电缆与直流电缆敷设距离较远,交流电缆敷设方式改变产生的感应电压变化较小,因此本节讨论敷设方式对隧道磁场分布的影响。
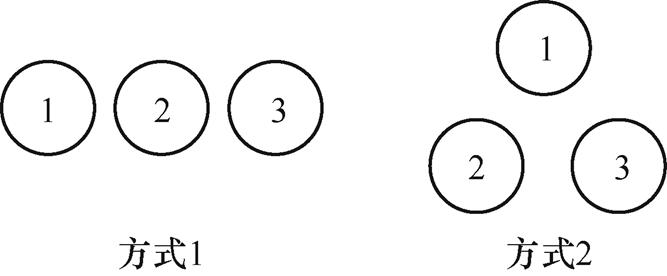
图6 交流电缆敷设方式
Fig.6 The laying method of AC cables
2.3.1 交流敷设方式的影响
首先讨论方式1下,三条交流电缆线路连接不同相电流时对隧道磁场的影响。敷设方式1下磁场分布见表2。可知,当采用方式1敷设交流电缆时,隧道内路径1上磁感应强度最大值可达到0.90mT,最大磁场位于交流电缆侧。路径2上磁感应强度最大值可达0.18mT。
表2 敷设方式1下磁场分布
Tab.2 The magnetic field distribution with laying method 1

1-2-3号电缆上通入的电流形式路径1上的最大磁感应强度/mT路径2上的最大磁感应强度/mT A-B-C0.880.18 A-C-B0.870.18 B-A-C0.870.18 B-C-A0.890.18 C-A-B0.900.18 C-B-A0.890.18
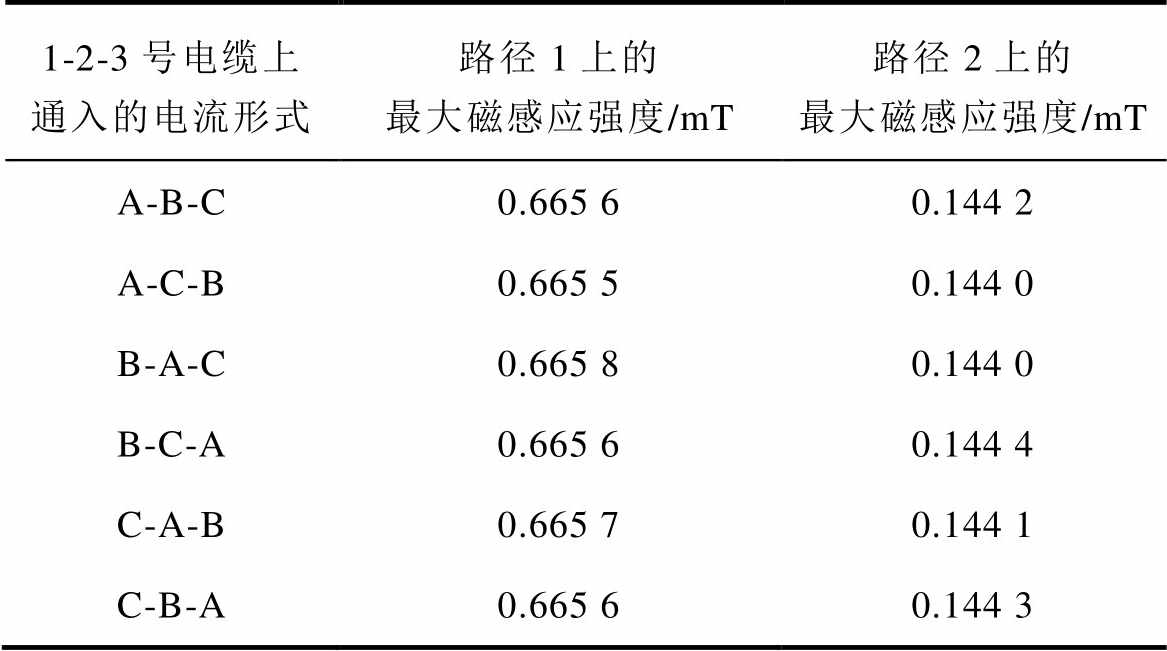
方式2下三条交流电缆线路连接不同相电流时,由于双回路三相电缆所产生的电磁场相互抵消,1-2-3号电缆上连接不同相电流形式时磁场仿真结果接近。采用方式2时抵消程度大于方式1。敷设方式2下磁场分布见表3。因此,可以认为交流采用双回路敷设时,三条电缆上通入不同形式的电流对隧道内磁场影响不大。此时隧道内路径1上磁感应强度最大值为0.665 8mT,隧道路径2上磁感应强度最大值可达0.144 4mT。当采用A-C-B方式敷设时,电缆周围磁感应强度最低。
表3 敷设方式2下磁场分布
Tab.3 The magnetic field distribution with laying method 2
1-2-3号电缆上通入的电流形式路径1上的最大磁感应强度/mT路径2上的最大磁感应强度/mT A-B-C0.665 60.144 2 A-C-B0.665 50.144 0 B-A-C0.665 80.144 0 B-C-A0.665 60.144 4 C-A-B0.665 70.144 1 C-B-A0.665 60.144 3
2.3.2 直流敷设方式的影响
直流电缆的典型敷设方式有两类,如图7所示。方式1为垂直敷设,方式2为水平敷设。直流电缆敷设方式1、2下磁场分布见表4、表5。可知,直流电缆按照方式2敷设时隧道中产生的磁场更小,一个周期内最大磁感应强度为0.67mT,该敷设方式下采用负-正电流时磁场相较另一方式略小,两种敷设方式对磁场的影响并不明显。
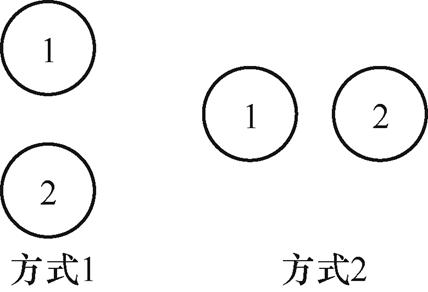
图7 直流电缆敷设方式
Fig.7 DC cable laying method
表4 直流电缆敷设方式1下磁场分布
Tab.4 The magnetic field distribution with DC cable laying method 1

1-2号电缆上通入的电流形式路径1上的最大磁感应强度/mT路径2上的最大磁感应强度/mT 正-负1.220.10 负-正1.210.10
表5 直流电缆敷设方式2下磁场分布
Tab.5 Magnetic field distribution with DC cable laying method 2

1-2号电缆上通入的电流形式路径1上的最大磁感应强度/mT路径2上的最大磁感应强度/mT 正-负0.670.14 负-正0.670.14
当双回路交流电缆对称分布时,由于三相电缆产生的磁感应强度与感应电动势相互叠加使该值大幅度下降。且在电缆故障时刻,当运维检修人员进入隧道进行检修时隧道内电磁环境也应满足职业人员磁场暴露限值。为方便讨论,本节研究了单回路电缆单相停电检修时隧道的磁场分布与直流电缆上感应电动势的值。单相交流与直流电缆共沟示意图如图8所示,图中,long表示单回路交流电缆与直流电缆同时向隧道中心位置移动的距离。图9为交流侧为单回路三相电缆时隧道中心的磁感应强度,此时的交流电缆为B-C-A形式。而隧道中心处的磁感应强度随着long取值越大逐渐变大。当long取800mm时,磁感应强度高达1.1mT。由于静磁场的职业暴露限值较大,可以单独考虑交流电缆所产生的影响。图10所示为仅考虑交流电缆时路径2上的磁感应强度。long取800mm时磁场超过职业人员暴露限值要求。单回路交流电缆护套上感应电动势计算结果见表6。当long取到800mm时,负极上的感应电动势骤然增大到37.71V。
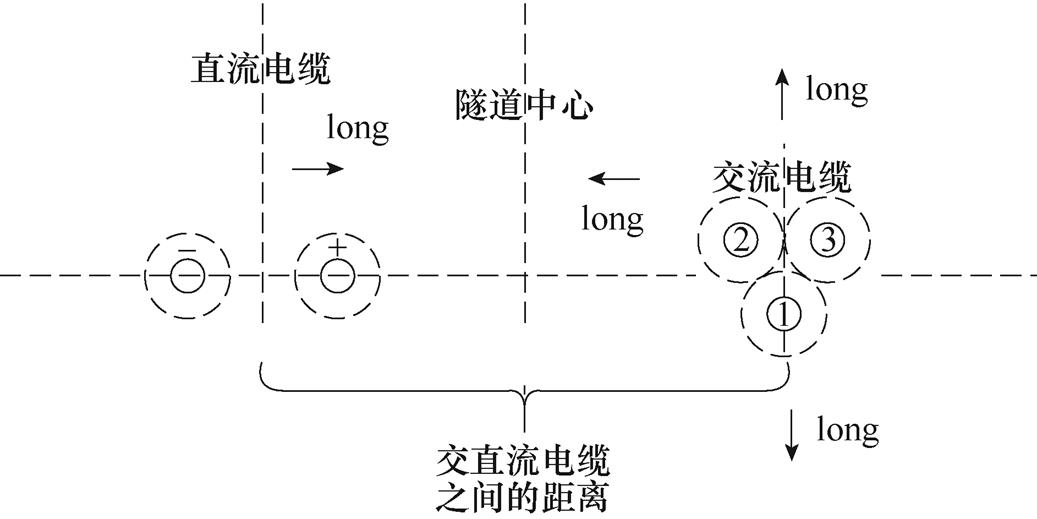
图8 单相交流与直流电缆共沟示意图
Fig.8 Schematic diagram of single-circuit AC and DC cables laying in the same tunnel
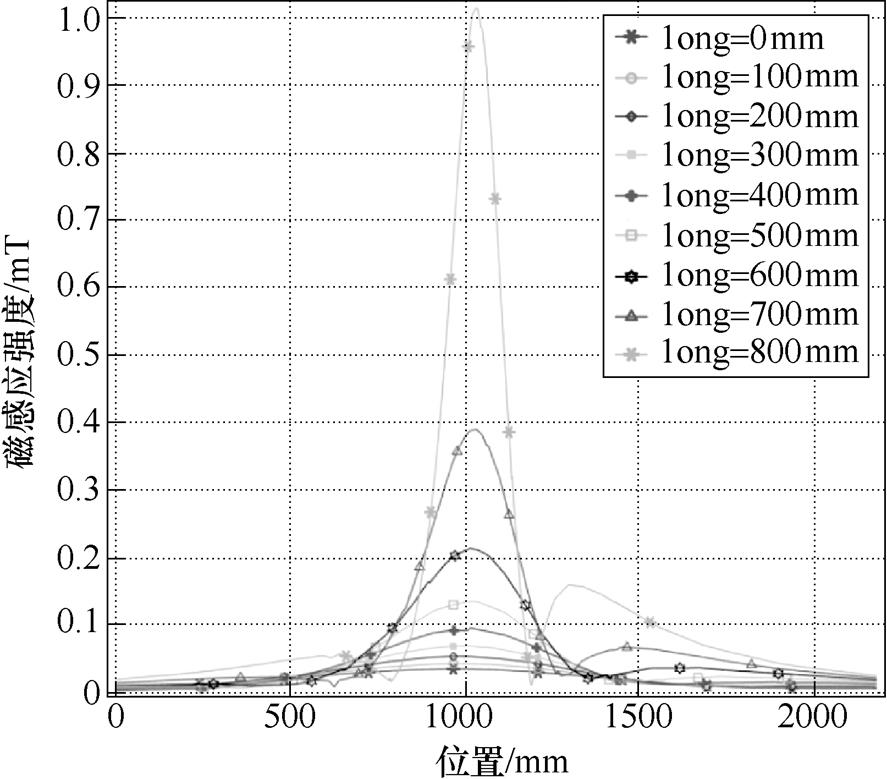
图9 电缆隧道中心磁感应强度
Fig.9 The magnetic induction intensity in the center of the cable tunnel
2.4.1 A相停电
当A相停电时,路径2上磁感应强度分布如图11所示。由于此刻只考虑交流的影响,当long取800mm时已超过了职业人员交流磁场暴露限值,其值为0.87mT。A相停电时电缆护套上感应电动势见表7,同样在long取800mm时不符合要求,其值为77.91V。
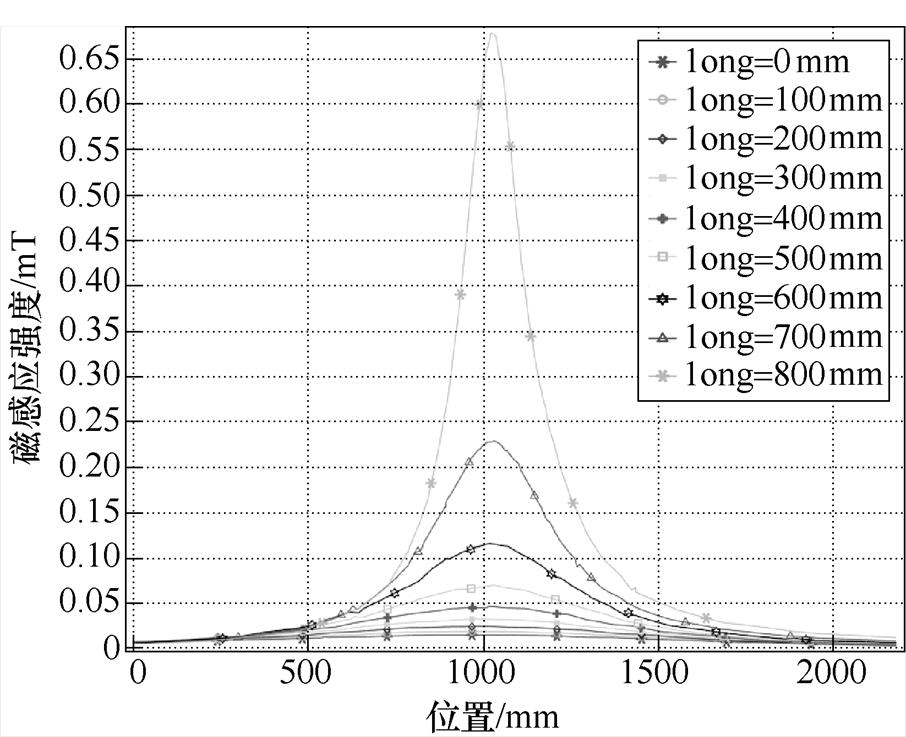
图10 仅考虑交流电缆时电缆隧道中心磁感应强度
Fig.10 The magnetic induction intensity at the center of the cable tunnel when only considering AC cables
表6 单回路交流电缆护套上感应电压
Tab.6 The induced voltage on the sheath of single-circuit AC cable
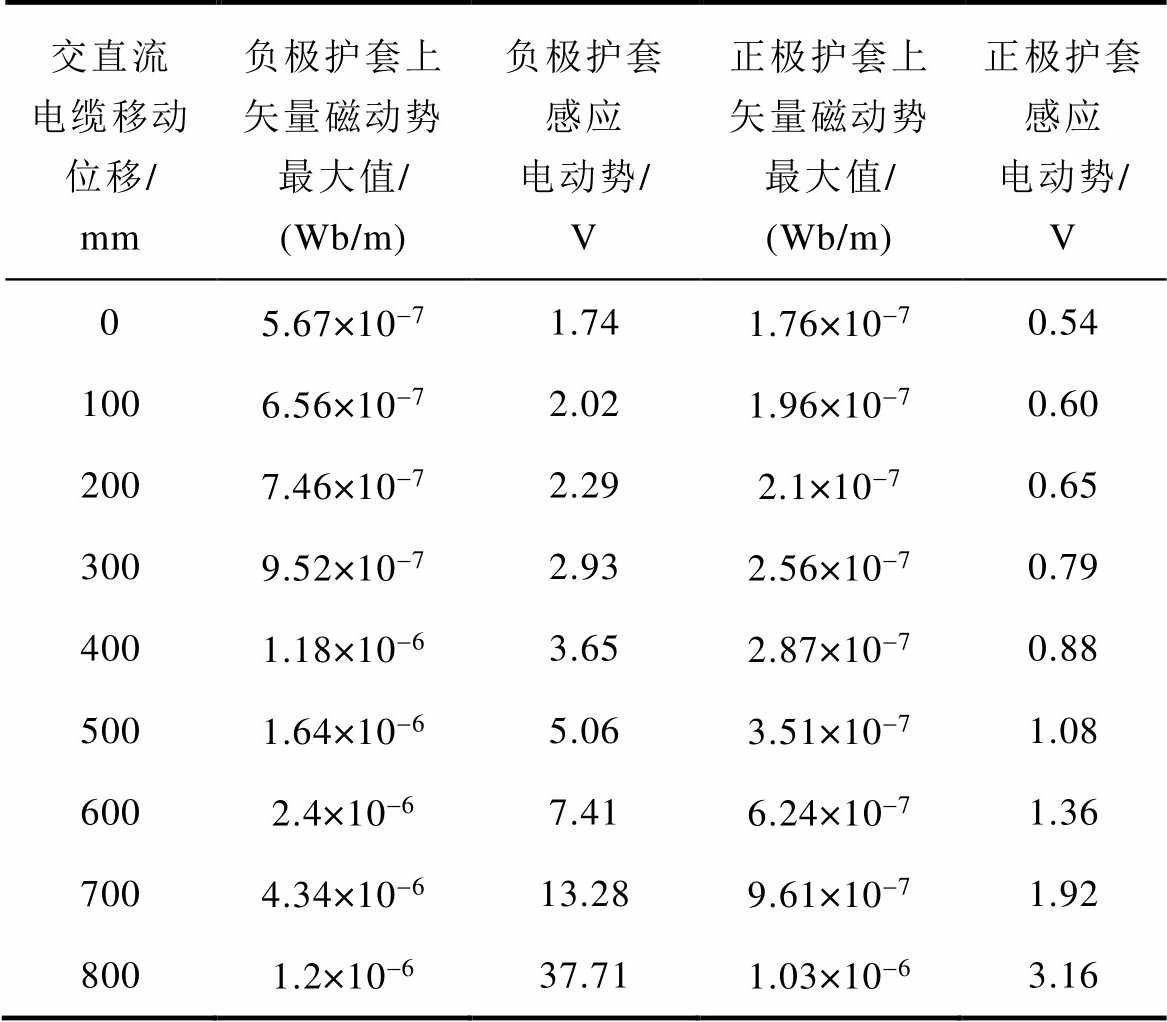
交直流电缆移动位移/ mm负极护套上矢量磁动势最大值/ (Wb/m)负极护套感应电动势/ V正极护套上矢量磁动势最大值/ (Wb/m)正极护套感应电动势/ V 05.67×10-71.741.76×10-70.54 1006.56×10-72.021.96×10-70.60 2007.46×10-72.292.1×10-70.65 3009.52×10-72.932.56×10-70.79 4001.18×10-63.652.87×10-70.88 5001.64×10-65.063.51×10-71.08 6002.4×10-67.416.24×10-71.36 7004.34×10-613.289.61×10-71.92 8001.2×10-637.711.03×10-63.16
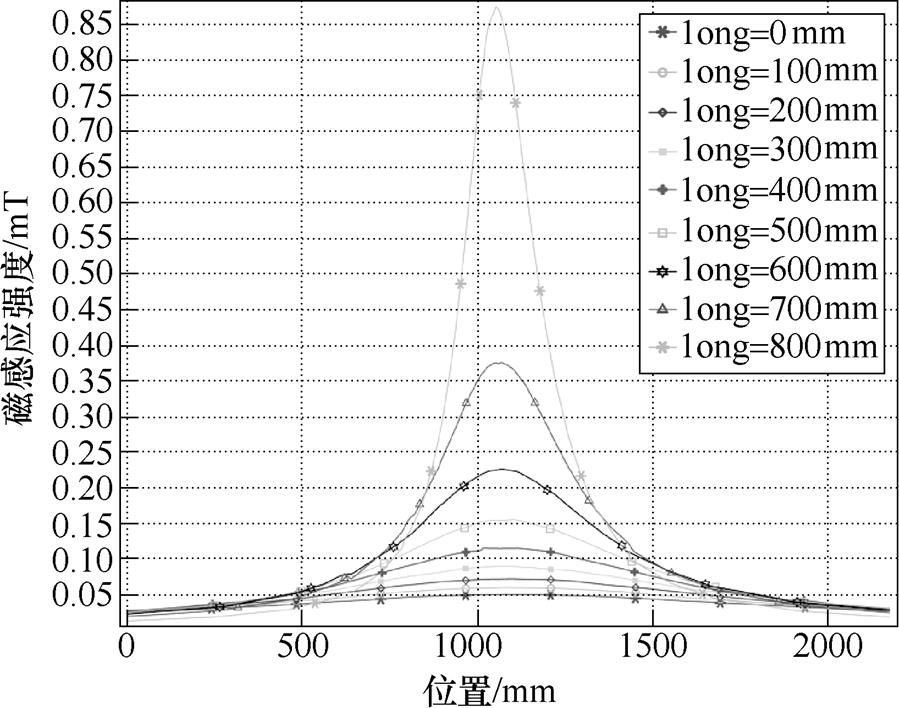
图11 A相停电时路径2上磁感应强度
Fig.11 The magnetic induction intensity on path 2 during phase A power failure
表7 A相停电时电缆护套上感应电动势
Tab.7 The induced voltage on the cable sheath during phase A power failure
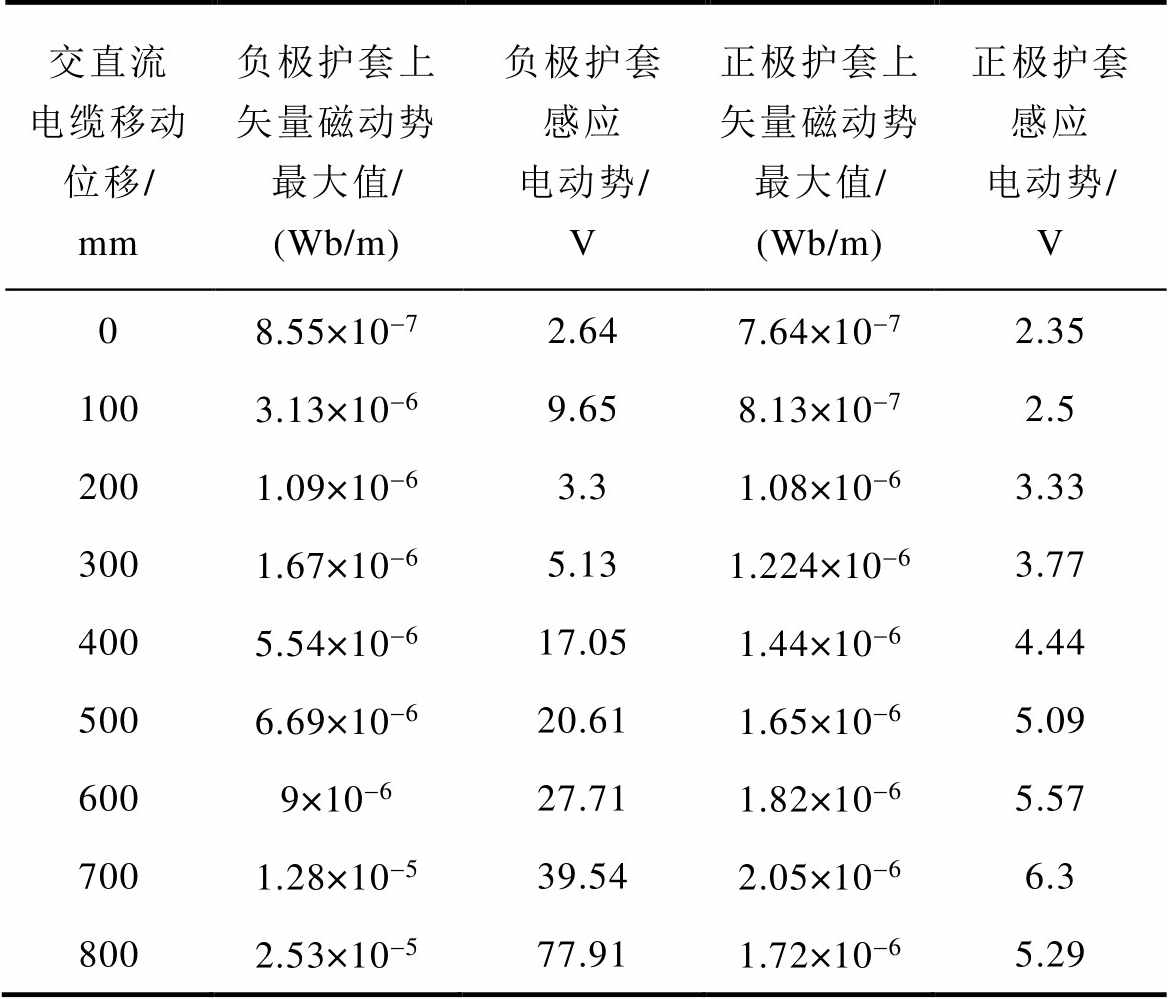
交直流电缆移动位移/ mm负极护套上矢量磁动势最大值/ (Wb/m)负极护套感应电动势/ V正极护套上矢量磁动势最大值/ (Wb/m)正极护套感应电动势/ V 08.55×10-72.647.64×10-72.35 1003.13×10-69.658.13×10-72.5 2001.09×10-63.31.08×10-63.33 3001.67×10-65.131.224×10-63.77 4005.54×10-617.051.44×10-64.44 5006.69×10-620.611.65×10-65.09 6009×10-627.711.82×10-65.57 7001.28×10-539.542.05×10-66.3 8002.53×10-577.911.72×10-65.29
2.4.2 B相停电
当B相停电时,路径2上磁感应强度分布如图12所示。此刻只考虑交流的影响,当long取800mm时远超过了职业人员交流磁场暴露限值,其值为1.1mT。B相停电时电缆护套上感应电动势见表8,同样在long取800mm时不符合要求,负极护套感应电动势值为68.51V。
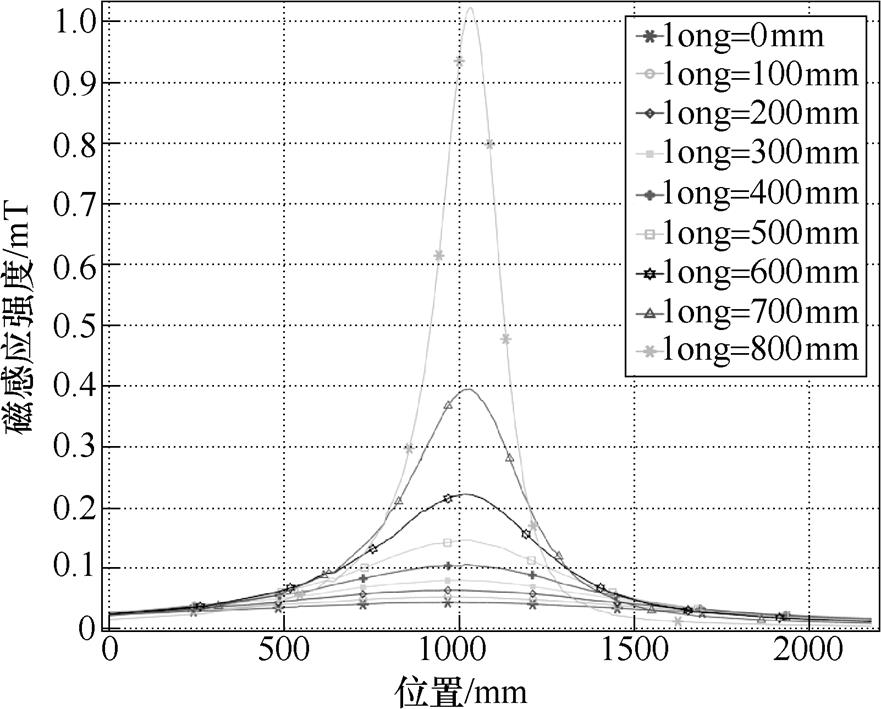
图12 B相停电时路径2上磁感应强度
Fig.12 The magnetic induction intensity on path 2 during phase B power failure
2.4.3 C相停电
当C相停电时,隧道电缆中心磁感应强度分布如图13所示。此刻只考虑交流的影响,当long取800mm时已超过了职业人员交流磁场暴露限值,其值为0.59mT。C相停电时电缆护套上感应电动势见表9,同样在long取800mm时不符合要求,其值为54.1V。
表8 B相停电时电缆护套上感应电动势
Tab.8 The induced voltage on the cable sheath during phase B power failure
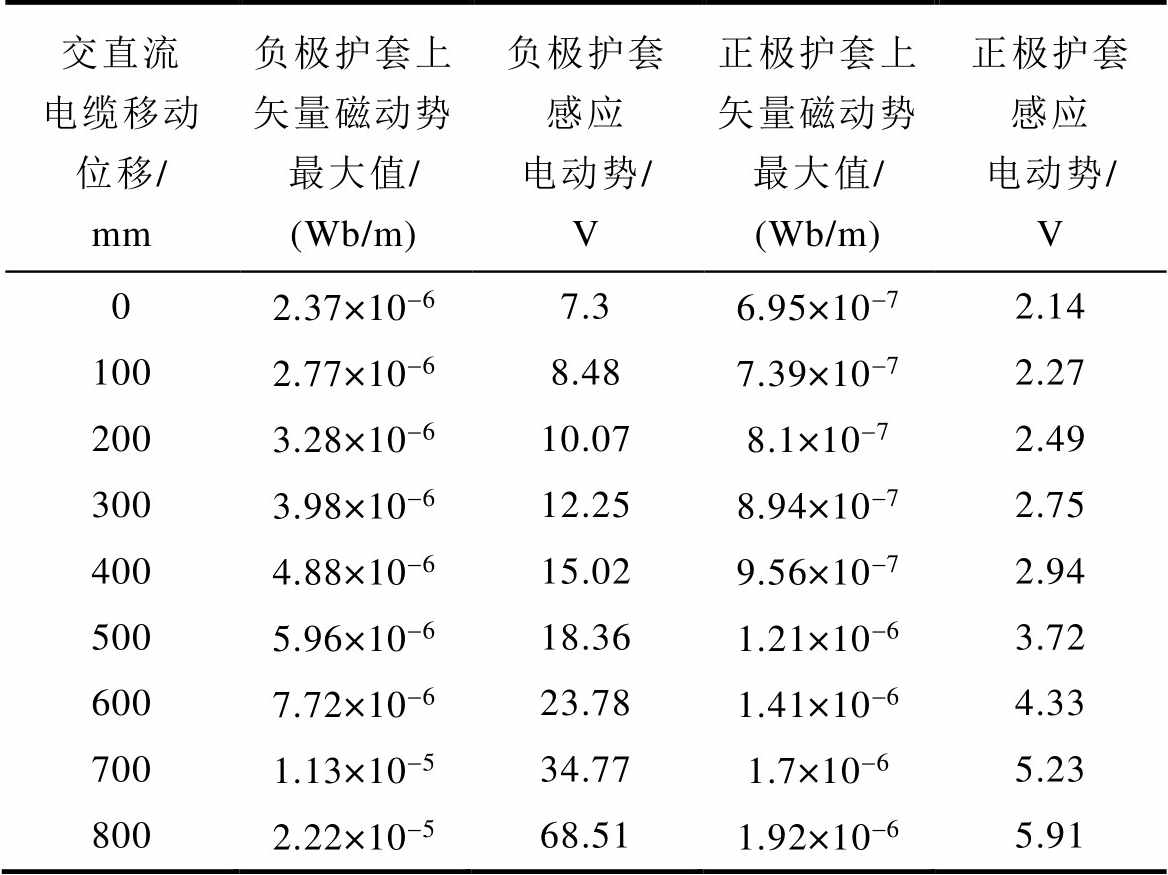
交直流电缆移动位移/ mm负极护套上矢量磁动势最大值/ (Wb/m)负极护套感应电动势/ V正极护套上矢量磁动势最大值/ (Wb/m)正极护套感应电动势/ V 02.37×10-67.36.95×10-72.14 1002.77×10-68.487.39×10-72.27 2003.28×10-610.078.1×10-72.49 3003.98×10-612.258.94×10-72.75 4004.88×10-615.029.56×10-72.94 5005.96×10-618.361.21×10-63.72 6007.72×10-623.781.41×10-64.33 7001.13×10-534.771.7×10-65.23 8002.22×10-568.511.92×10-65.91
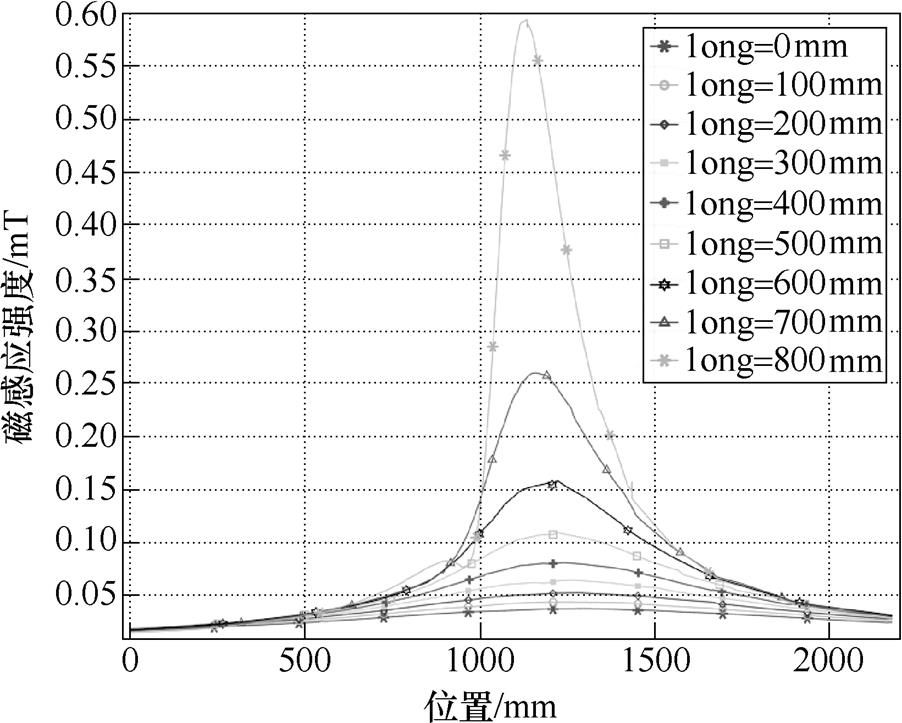
图13 C相停电时路径2上磁感应强度
Fig.13 The magnetic induction intensity on path 2 during phase C power failure
表9 C相停电时电缆护套上感应电动势
Tab.9 The induced voltage on the cable sheath during phase C power failure
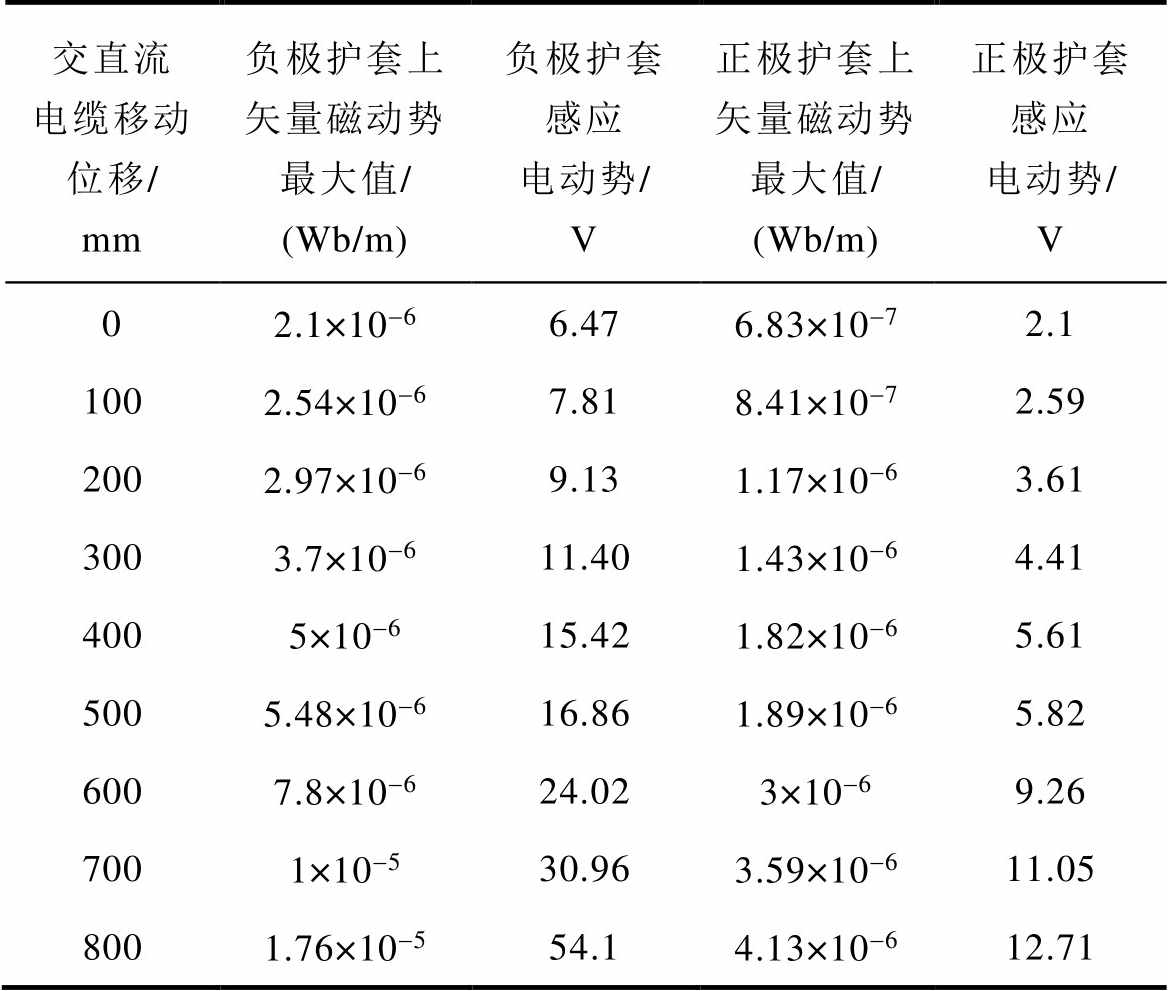
交直流电缆移动位移/ mm负极护套上矢量磁动势最大值/(Wb/m)负极护套感应电动势/ V正极护套上矢量磁动势最大值/ (Wb/m)正极护套感应电动势/ V 02.1×10-66.476.83×10-72.1 1002.54×10-67.818.41×10-72.59 2002.97×10-69.131.17×10-63.61 3003.7×10-611.401.43×10-64.41 4005×10-615.421.82×10-65.61 5005.48×10-616.861.89×10-65.82 6007.8×10-624.023×10-69.26 7001×10-530.963.59×10-611.05 8001.76×10-554.14.13×10-612.71
图14为交流电缆在其垂直线上不同位置时路径2上的磁场分布,long取负数表示交流电缆竖直向上运动,相反,long取正数表示交流电缆垂直向下运动。当long取-400mm时,磁场最小。综上,当交流呈倒三角排列时,交流电缆敷设在直流电缆所处位置水平线下方时有利于减小磁感应强度。

图14 交流电缆在不同位置时路径2上磁场分布
Fig.14 The magnetic field distribution on path 2 with different positions of AC cables
本文分析了交直流共沟敷设隧道电磁环境的影响因素,研究了交直流电缆之间的距离、交流电缆以及直流电缆的敷设方式的影响、单相交流电缆故障对电缆隧道的电磁环境的影响。提出交直流共同敷设时,交流电缆距离隧道中心不能小于270mm,交流电缆与直流电缆之间的距离不能小于540mm,否则隧道内的磁场环境以及电缆护套上的感应电动势将超过规定要求。并发现交流采用三角敷设,通以A-B-C形式电流,直流采用平行敷设,交流电缆敷设在直流电缆所处位置水平线下方时,隧道内的磁感应强度能有效减小。
参考文献
[1] 滕予非, 李小鹏, 林圣, 等. 特高压直流系统接地极线路阻抗监视系统适应性研究[J]. 电工技术学报, 2019, 34(19): 4154-4161.
Teng Yufei, Li Xiaopeng, Lin Sheng, et al. Adapta- bility analysis of fault supervision system for long electrode line of UHVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4154-4161.
[2] 郝黎明, 王东来, 卢铁兵, 等. 计及金属回流线影响的±500kV高压直流输电线路地面合成电场计算分析[J]. 电工技术学报, 2019, 34(12): 2468-2476.
Hao Liming, Wang Donglai, Lu Tiebing. Calculation and analysis of ground-level total electric field under ±500kV HVDC lines considering the influence of metal return lines[J]. Transactions of China Elec- trotechnical Society, 2019, 34(12): 2468-2476.
[3] 谢书鸿, 傅明利, 尹毅, 等. 中国交联聚乙烯绝缘高压直流电缆发展的三级跳: 从160kV到200kV再到320kV[J]. 南方电网技术, 2015, 9(10): 5-12.
Xie Shuhong, Fu Mingli, Yin Yi, et al. Triple jumps of XLPE insulated HVDC cable development in China: from 160kV to 200kV and then to 320kV[J]. Southern Power System Technology, 2015, 9(10): 5-12.
[4] 李永明, 王洋洋, 邹岸新, 等. 超高压输电线工频电场计算的矩量法和表面电荷混合法[J]. 电机与控制学报, 2017, 21(8): 1-8.
Li Yongming, Wang Yangyang, Zou Anxin, et al. Power-frequency electric field calculation of extra high voltage transmission lines by means of the mixed method combining MOM and SCM[J]. Electric Machines and Control, 2017, 21(8): 1-8.
[5] 何青, 李军辉, 邓梦妍, 等. 架空输电导线覆冰冻结系数计算及其影响因素分析[J]. 电工技术学报, 2019, 34(19): 4162-4169.
He Qing, Li Junhui, Deng Mengyan, et al. Calculation and influencing factors of icing freezing coefficient of overhead transmission line[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4162-4169.
[6] 郝建红, 王晖. 不同线型高压直流输电导线表面电场强度分布的计算[J]. 电工技术学报, 2019, 34(增刊1): 14-21.
Hao Jianhong, Wang Hui. Calculation of the surface electric field distribution of high-voltage direct current transmission line[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 14-21.
[7] 王航, 周文俊, 陈杰, 等. 波纹金属护套高压单芯电缆线芯护层互感的解析解[J]. 电工技术学报, 2020, 35(16): 3369-3376.
Wang Hang, Zhou Wenjun, Chen Jie, et al. Analytical solution of the mutual inductance of a HV single conductor cable with corrugated metallic sheath[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3369-3376.
[8] 周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J]. 高电压技术, 2014, 40(9): 2593-2612.
Zhou Yuanxiang, Zhao Jiankang, Liu Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593-2612.
[9] 杜伯学, 李忠磊, 杨卓然, 等. 高压直流交联聚乙烯电缆应用与研究进展[J]. 高电压技术, 2017, 43(2): 344-354.
Du Boxue, Li Zhonglei, Yang Zhuoran, et al. Appli- cation and research progress of HVDC XLPE cables[J]. High Voltage Engineering, 2017, 43(2): 344-354.
[10] 严有祥, 方晓临, 张伟刚, 等. 厦门±320kV柔性直流电缆输电工程电缆选型和敷设[J]. 高电压技术, 2015, 41(4): 1147-1153.
Yan Youxiang, Fang Xiaolin, Zhang Weigang, et al. Cable section and laying of Xiamen ±320kV flexible DC cable transmission project[J]. High Voltage Engineering, 2015, 41(4): 1147-1153.
[11] 严有祥, 朱婷, 陈朝晖, 等. 交直流电缆共同敷设隧道内电磁场环境[J]. 广东电力, 2018, 31(12): 20-26.
Yan Youxiang, Zhu Ting, Chen Chaohui, et al. Electromagnetic environment in utility tunnel with AC and DC cable[J]. Guangdong Electric Power, 2018, 31(12): 20-26.
[12] 刘兵, 阮江军, 韩海宏, 等. 柔性直流输电系统电磁环境分析[J]. 高电压技术, 2009, 35(11): 2747- 2752.
Liu Bing, Ruan Jiangjun, Han Haihong, et al. Analysis of electromagnetic environment of VSC- HVDC[J]. High Voltage Engineering, 2009, 35(11): 2747-2752.
[13] 李新年, 蒋卫平, 李涛. 交直流线路同塔输电对换流变直流偏磁的影响[J]. 电力系统自动化, 2011, 35(11): 87-92.
Li Xinnian, Jiang Weiping, Li Tao. Influence of same-tower AC/DC hybrid transmission lines on DC bias of converter transformer[J]. Automation of Electric Power Systems, 2011, 35(11): 87-92.
[14] 田毅, 黄新波, 田文超, 等. 交直流输电线路离子流场的时域混合有限元法[J]. 电机与控制学报, 2019, 23(10): 85-94.
Tian Yi, Huang Xinbo, Tian Wenchao. Time-domain mixed-hybrid finite element method for analyzing ion-flow field of HVDC and HVAC transmission lines[J]. Electric Machines and Control, 2019, 23(10): 85-94.
[15] 赵鹏, 陈铮铮, 胡凯, 等. 交直流电缆混合敷设的基频电磁感应特性计算与分析[J]. 高电压技术, 2020, 46(2): 576-585.
Zhao Peng, Chen Zhengzheng, Hu Kai, et al. Calculation and analysis of the fundamental frequ- ency electromagnetic induction of hybrid laying AC and DC cable[J]. High Voltage Engineering, 2020, 46(2): 576-585.
[16] Tian Yi, Huang Xinbo, Tian Wenchao, et al. Study on the hybrid ion flow field of HVDC and HVAC transmission lines by the nodal discontinuous Galerkin time-domain method[J]. IET Generation Transmission & Distribution, 2017, 11(1): 209-217.
[17] 朱军, 吴广宁, 曹晓斌, 等. 非全线并行架设的交、直流共用输电走廊线路间电磁耦合计算分析[J]. 高电压技术, 2014, 40(6): 1724-1731.
Zhu Jun, Wu Guangning, Cao Xiaobin, et al. Electromagnetic coupling calculation and analysis of lines non-parallelly erected entirely in one common AC/DC transmission corridor[J]. High Voltage Engineering, 2014, 40(6): 1724-1731.
[18] 任红昕. 并行交直流特高压输电线路耦合干扰研究[D]. 保定: 华北电力大学, 2019.
[19] 何光华, 张培伦. 大截面电缆复杂隧道环境下的敷设和打弯方法[J]. 高电压技术, 2018, 44(增刊2). 174-177.
He Guanghua, Zhang Peilun. Laying and bending methods of large cross-section cable under complex tunnel environment[J]. High Voltage Engineering, 2018, 44(S2): 174-177.
The Influence Factors of Electromagnetic Environment in the Tunnels with DC Cables and AC Cables
Abstract With the expansion of urban power and the increase of the power demand, the alternative current (AC) and direct current (DC) cables will be laid in the same tunnel to solve the shortage of underground cable transmission space, which makes the electromagnetic field of the cable tunnel more complicated. In this paper, the electromagnetic field simulation model was established for ±320kV DC cables and 220kV AC cables co-laying tunnel. Then the electromagnetic field distribution in the tunnel and the induced voltage generated by AC cables on DC cables were calculated. The influence factors of electromagnetic environment in the cable tunnel were analyzed, such as the distance between AC and DC cables, the laying methods of AC cables and DC cables, and single-phase AC cable faults. Finally, the minimum distance between the AC and DC cables and the optimal laying method of the AC and DC cables were proposed.
keywords:AC and DC, cable, electromagnetic field, laying method
DOI: 10.19595/j.cnki.1000-6753.tces.L90547
中图分类号:TM721.1
严有祥 男,1982年生,高级工程师,研究方向为电磁场数值计算。E-mail: yanyouxiang@sina.com
王曙鸿 男,1968年生,教授,博士生导师,研究方向为电磁场数值计算。E-mail: shwang@mail.xjtu.edu.cn(通信作者)
收稿日期 2020-08-06
改稿日期 2020-10-05
(编辑 崔文静)