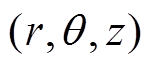 坐标系示意图。
坐标系示意图。摘要 射频电感耦合等离子体(ICP)在实际放电过程中,线圈的构型、电源参数、气压等外部工质条件的变化均会对结果产生较大影响,依靠实验很难得到多外部条件对ICP参数分布的影响机理和规律,因此需要结合仿真和实验的方法进行分析。该文通过建立感性线圈的电磁学有限元模型,分析不同线圈构型下射频电磁场在等离子体内部的空间分布,研究放电参数(线圈构型、功率大小)对等离子体分布影响和E-H模型下放电形态的跳变过程,并观察进入稳定H模式后电源参数的变化规律,为等离子体源的小型化工程应用提供理论基础。实验和仿真计算结果表明:不同线圈匝数在不同功率条件下,电磁场强度变化对等离子功率吸收和功率耦合有较大影响;当工作气压在0~20Pa时,ICP的电子密度呈轴对称分布,随着放电功率、气压的增大,等离子体吸收的功率和电离度也随之增加,其电子密度相应地增大,放电功率的增加会使得环状的等离子体区域随之扩大,在轴向、径向上的分布呈先逐渐增大而后在靠近腔室壁面区域迅速下降。
关键词:电感耦合等离子体 射频功率 放电线圈 参数空间分布
射频感性放电(Inductive Coupled Plasma, ICP)是通过射频电流在感应线圈产生感应磁场分量进而将功率耦合给等离子体。感性耦合等离子体放电能在较宽的气压范围内产生高密度(电子密度可达1017~1018m-3)、大面积的等离子体,且其结构装置简单、放电参数易于调节,在等离子体的电磁波衰减应用上具有很大前景[1]。
电感耦合等离子体的放电过程会经历两种工作模式,即低功率、小电流的容性模式(E模式)和高功率、大电流的感性模式(H模式)。研究初期,国外著名学者J.Hopwood进行了开创性的研究工作,通过Langmuir 探针对平面线圈ICP中的电子能量分布函数(Electron Energy Distribution Function, EEDF)进行了诊断,结果表明ICP是一种高密度等离子体源(可高达1011~1013cm-3),并且通过改变外部条件可以实现参数均匀性优化[2]。V. A. Godyak等对ICP中EEDF和电流密度进行了测量,显示ICP在低气压中存在无碰撞功率吸收现象和电子非局域效应[3]。J. Amorim等在11.4 MHz的Ar-ICP中观察到了E-H模式跳变现象,结果表明模式跳变与电源功率大小、频率、线圈构型、气压参数等因素有关[4]。Rok Zaplotnik采用20 Pa的SO2气体介质,设计了柱状螺旋型感性等离子体放电实验,结果表明受强电场作用下等离子体被约束在射频线圈附近[5]。H.Y.Chang等研究了天线尺寸和腔室长度对等离子参数的影响,发现采用直径较大的线圈可以实现大面积放电,但随着线圈直径的增大,其长度也会增加,因此回路阻抗变大,进而导致天线电压增加,容性耦合随之增强,最终导致等离子体径向不均匀的发生[6-8]。P. L. G. Ventzek等采用二维混合模拟方法研究了单频线圈功率变化对等离子体分布的影响,当4匝线圈输入功率为2kW时,电子密度较高,趋肤深度较小,等离子体主要产生在介质窗附近很薄的区域内,电子被限制在局域在介质窗下方,电子密度的均匀性较差[9]。T. Fukasawa等在实验中发现将输入功率从1kW减小到200W时,电子密度的均匀性先变好后变坏,输入功率为600W时电子密度的均匀性最好[10]。张昀等利用 Langmuir探针测量了不同放电气压对等离子体参数的影响[11]。汪建等对感性放电中放电条件的变化对等离子体的影响进行研究[12],放电过程中容性放电模式(E模式)和感性放电模式(H模式)的转变,功率对等离子体模式跳变的影响和容性放电与感性放电的复杂性进行分析等,至今仍然有许多问题需要继续研究[13-15]。
考虑等离子体技术在电磁波衰减上应用的实际情况,等离子体发生器需要将输入功率高效地耦合给等离子体,能够实现较大面积的均匀性覆盖,在满足衰减需求的同时,尽可能减小发生器的空间尺寸[16-17]。因此如何能够有效地使射频功率传递给等离子体,这涉及射频网络匹配、能量耦合等许多问题[18-19]。为了进一步探索平面型电感耦合系统产生等离子的规律和机理,本文从电感线圈尺寸和电源功率等角度对等离子产生和参数分布特点进行仿真分析和实验现象研究,为下一步实际应用提供理论支撑。
电感耦合等离子体是通过线圈加载射频功率,根据法拉第定律,交变电场伴随着交变磁场,进而感应电磁场在腔室产生等离子体,在电场的作用下,部分粒子中的电子脱离形成自由电子和其他带电粒子,带电粒子在电磁场作用下加速,进而碰撞其他粒子激发更多的电子,最终形成稳定的等离子体[20-21]。图1为平面型ICP的放电腔体结构和根据线圈位置建立的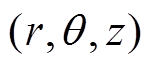 坐标系示意图。
坐标系示意图。
ICP线圈产生的电磁场可以用麦克斯韦方程组描述为
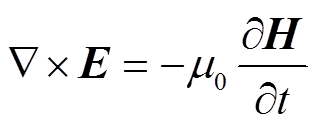 (1)
(1)
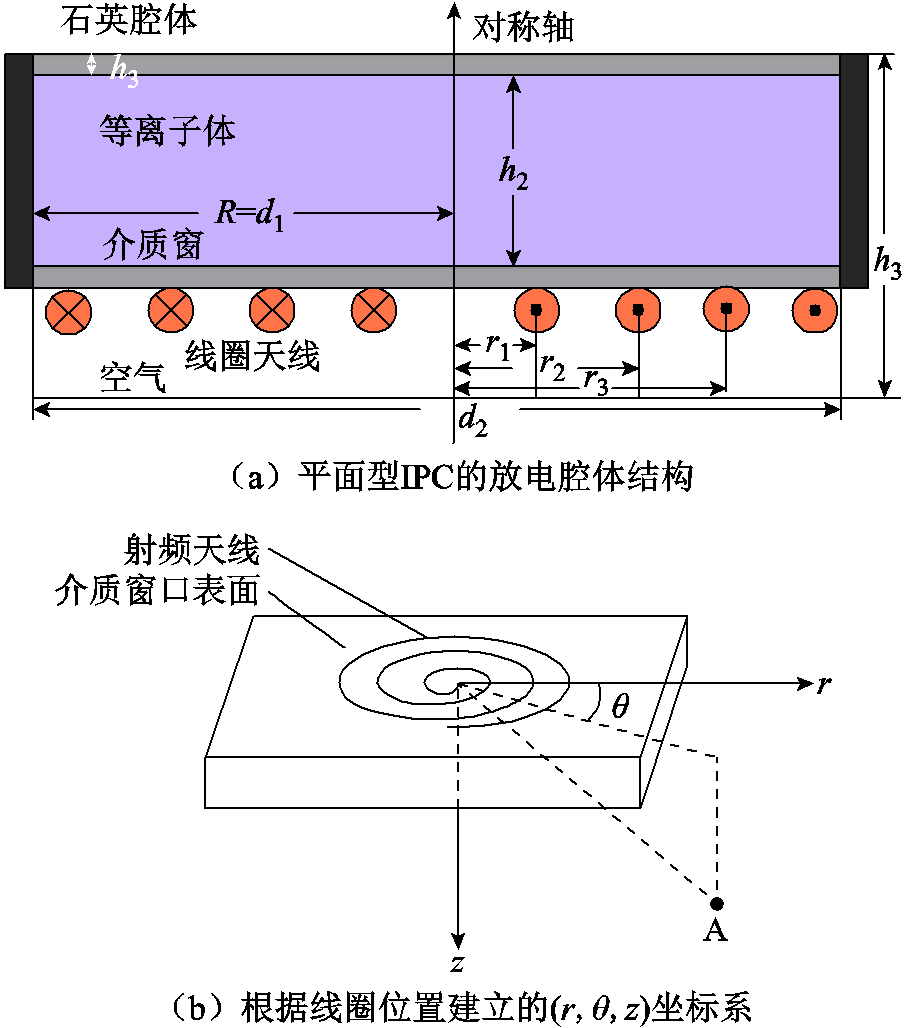
图1 平面型ICP的结构
Fig.1 Schematic diagram of ICP
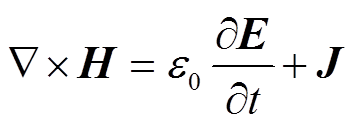 (2)
(2)
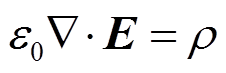 (3)
(3)
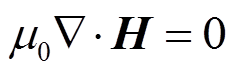 (4)
(4)
电荷密度 和电流密度J满足电荷连续性方程
和电流密度J满足电荷连续性方程
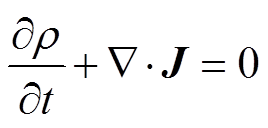 (5)
(5)
电磁场可表示为
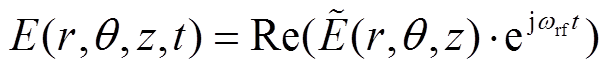 (6)
(6)
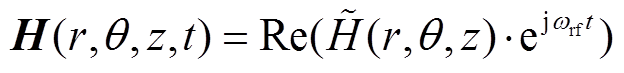 (7)
(7)
式中,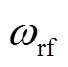 即为射频角频率;
即为射频角频率;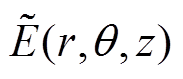 为角向的电场分量;
为角向的电场分量;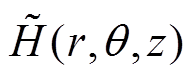 为线圈产生的磁场分量。
为线圈产生的磁场分量。
电感耦合放电等离子体中的粒子之间主要靠欧姆加热和随机加热进行能量的转移。气压较高时,由于电子与中性粒子的碰撞频率较高,欧姆加热起主导作用。这时虽然主等离子体区域的电场不是很强,但是仍然在电子加热中起重要作用。在一段时间内,等离子体吸收的功率平均值为
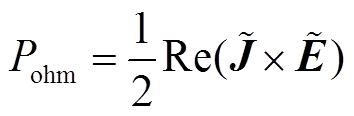 (8)
(8)
式中,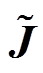 为电流密度;
为电流密度; 为电场分量。根据麦克斯韦方程可以解出电场和电流密度的关系为
为电场分量。根据麦克斯韦方程可以解出电场和电流密度的关系为
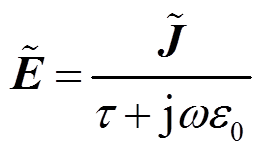 (9)
(9)
式中,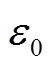 为等离子体的磁导率;
为等离子体的磁导率; 为等离子体角频率;
为等离子体角频率;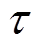 为一个时间周期,
为一个时间周期,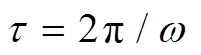 。将式(9)代入式(8)中,可以得到欧姆吸收功率与电流密度的关系为
。将式(9)代入式(8)中,可以得到欧姆吸收功率与电流密度的关系为
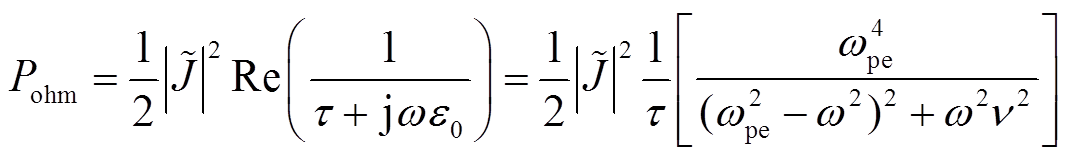 (10)
(10)
式中,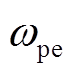 为等离子体的电子频率;v为等离子体碰撞频率。
为等离子体的电子频率;v为等离子体碰撞频率。
气压较高时,满足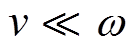 ,可以进一步简化为
,可以进一步简化为
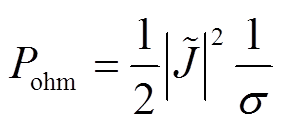 (11)
(11)
而当气压较低时,情况变得不一样,电子与振荡的鞘层之间的碰撞成为主要的加热机制,电磁场的空间分布呈非指数衰减。假设电子初速度为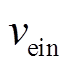 ,鞘层速度为
,鞘层速度为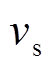 ,电子碰撞后反射回来的速度为
,电子碰撞后反射回来的速度为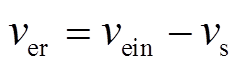 。则可以计算出碰撞过程中发生的转移功率为
。则可以计算出碰撞过程中发生的转移功率为
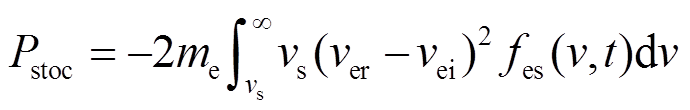 (12)
(12)
式中, 为电子速度在平行于鞘层速度方向上的分布函数,取其近似为麦克斯韦分布,则式(12)积分后得到随机加热过程中的功率为
为电子速度在平行于鞘层速度方向上的分布函数,取其近似为麦克斯韦分布,则式(12)积分后得到随机加热过程中的功率为
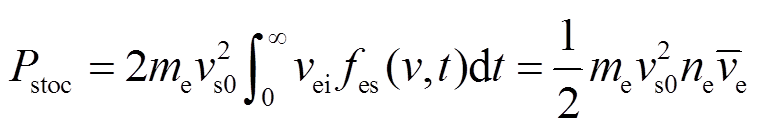 (13)
(13)
式中,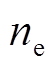 、
、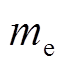 分别为等离子体中的电子密度和质量;
分别为等离子体中的电子密度和质量;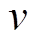 为等离子体碰撞频率;
为等离子体碰撞频率;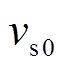 为鞘层速度的幅值;
为鞘层速度的幅值;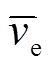 为电子速度的平均值。
为电子速度的平均值。
假设射频线圈为轴对称,则感应产生的磁场有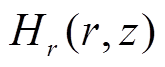 和
和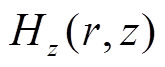 两个分量。放电起始阶段,起激发作用的是线圈产生的感应磁场
两个分量。放电起始阶段,起激发作用的是线圈产生的感应磁场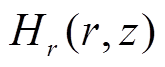 和
和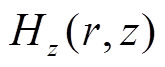 两个分量,以及感应电场的
两个分量,以及感应电场的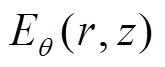 分量。由Faraday定律可知,当等离子体生成后,其中会诱导产生一个角向电场Eθ,这个电场又会在趋肤层中产生一个电流密度Jθ,这个电流与线圈中电流方向相反,并且其大小与半径r呈正比关系。所以圆心处的电场和电流为零,吸收功率也为零,意味着吸收功率呈环形分布[22]。线圈内感应电场可以表示为
分量。由Faraday定律可知,当等离子体生成后,其中会诱导产生一个角向电场Eθ,这个电场又会在趋肤层中产生一个电流密度Jθ,这个电流与线圈中电流方向相反,并且其大小与半径r呈正比关系。所以圆心处的电场和电流为零,吸收功率也为零,意味着吸收功率呈环形分布[22]。线圈内感应电场可以表示为
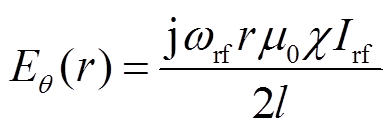 (14)
(14)
式中,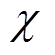 为线圈匝数;
为线圈匝数;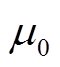 为真空磁导率;
为真空磁导率;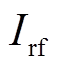 为射频电流;
为射频电流;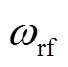 为射频功率源的频率,
为射频功率源的频率, ;r和l分别为线圈径向和轴向上的距离。等离子体吸收的功率为
;r和l分别为线圈径向和轴向上的距离。等离子体吸收的功率为
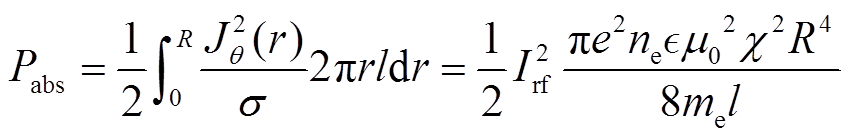 (15)
(15)
式中,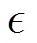 为等效碰撞频率;
为等效碰撞频率;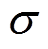 为等离子体有效电导率,即
为等离子体有效电导率,即
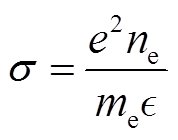 (16)
(16)
式中,e为电子电量。
根据式(15)可知,吸收功率与电子密度呈线性正相关,其关系如图2所示。曲线代表吸收功率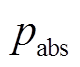 与电子密度
与电子密度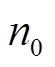 的关系,直线代表损失功率与电子密度的关系,当二者相等时,等离子体达到一个相对平衡的状态。从图2中可以看出,当电流小于某一个最小值Imin时,等离子体一直处于弱容性放电状态。当Irf随射频功率增加时,到达Imin点,等离子体会从容性放电状态跳变到电感放电状态,这就是电感耦合等离子体中的E-H转变现象。
的关系,直线代表损失功率与电子密度的关系,当二者相等时,等离子体达到一个相对平衡的状态。从图2中可以看出,当电流小于某一个最小值Imin时,等离子体一直处于弱容性放电状态。当Irf随射频功率增加时,到达Imin点,等离子体会从容性放电状态跳变到电感放电状态,这就是电感耦合等离子体中的E-H转变现象。
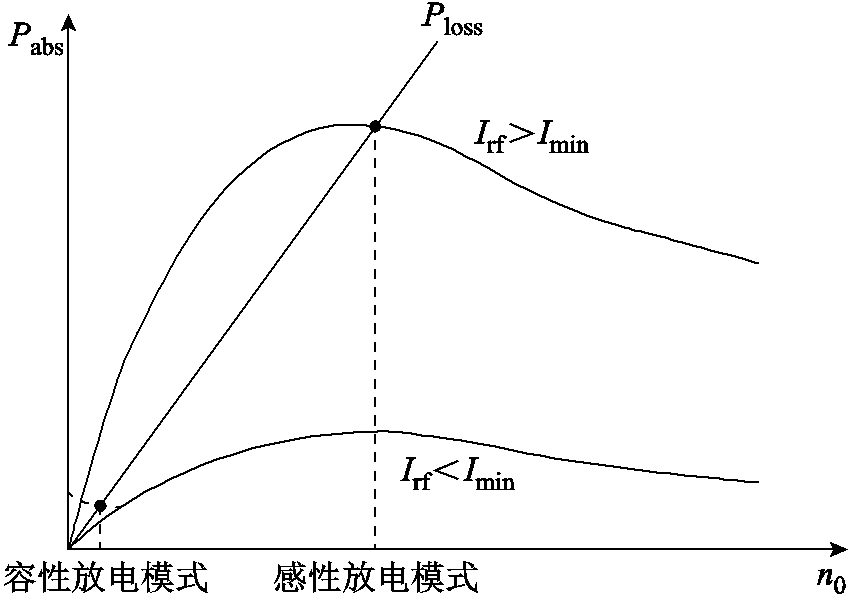
图2 ICP中功率与电子密度关系
Fig.2 Relationship between power and electron density in ICP
当射频源的功率通过匹配电路传输到线圈上,线圈中会产生射频电流和电压,环形的射频电流会在空间中激发产生射频磁场,变化的磁场产生的磁通量又会感应出一个电场,电场驱动电子运动,通过不断地碰撞、电离,将射频功率耦合到等离子体中,因此线圈与等离子体的功率耦合效率至关重要[23]。功率耦合效率定义为
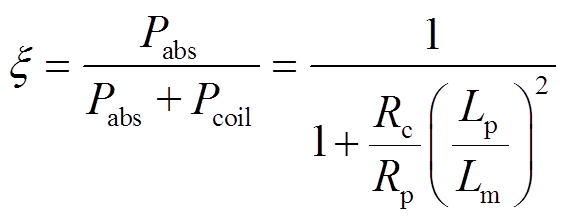 (17)
(17)
式中,Pcoil为线圈上的热损耗功率;Rc为线圈的电阻;Rp和Lp分别为等离子体的电阻和电感;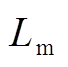 为线圈与等离子体之间的互感。
为线圈与等离子体之间的互感。
从式(17)可以看出,功率耦合效率与线圈和等离子体的参数都相关,对于固定的等离子体参数,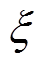 取决于
取决于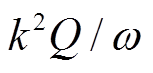 ,k为耦合系数,因此对于确定的射频源频率
,k为耦合系数,因此对于确定的射频源频率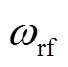 ,耦合效率主要取决于线圈的品质因数Q值,Q越高,等离子体源的功率耦合性能越好。
,耦合效率主要取决于线圈的品质因数Q值,Q越高,等离子体源的功率耦合性能越好。
本文设计的线圈天线是盘香形结构,可视为轴对称形状,射频功率源驱动线圈后,在没有等离子体时,射频磁场的磁力线以线圈平面为对称面环绕分布,如图3a所示。如果在线圈上方的发生器中产生等离子体,则磁场的磁力线如图3b所示,接近等离子体轴心位置主要磁场分量为Hz,远离轴心位置的磁场分量为Hr,总磁场是由射频线圈电流和感应电流所产生的磁场耦合的结果。因为由法拉第定律公式,在等离子体中会诱导出一个角向电场Eθ以及由它产生的电流密度Jθ,并且这个感应电流的方向与射频线圈中的相反,被限制在了等离子体的趋肤层里。由法拉第定律可知,Eθ, Jθ ,可见在靠近等离子体轴心处时,Eθ和Jθ都必须为零。因此,吸收功率密度Pabs在轴心处也为零,由此可见等离子体吸收功率呈现环状的空间分布,与图3中所描述的环状结构一致。
,可见在靠近等离子体轴心处时,Eθ和Jθ都必须为零。因此,吸收功率密度Pabs在轴心处也为零,由此可见等离子体吸收功率呈现环状的空间分布,与图3中所描述的环状结构一致。

图3 射频磁场示意图
Fig.3 Schematic diagram of radio frequency magnetic field
在感性模式中,假设在线圈上方的低气压腔内已经通过容性起辉的方式产生一定电子密度的等离子体,并由此产生一个和线圈电流相反的单匝等离子体电流。等离子体区域的电磁场可以通过式(1)计算获得。
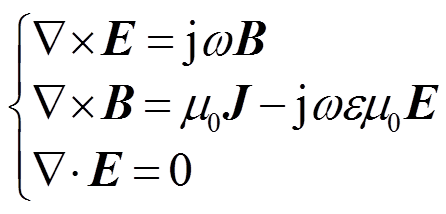 (18)
(18)
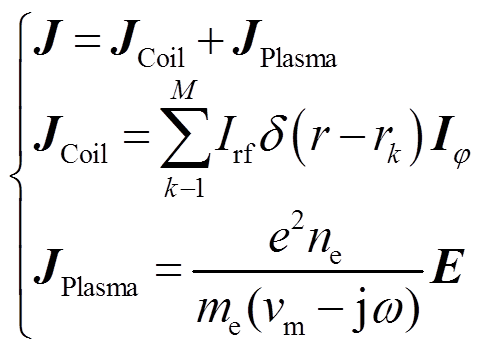 (19)
(19)
式中,E和B分别为空间电场和磁场;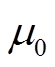 和
和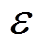 分别为真空磁导率和不同区域内的电介质系数;总的传导电流J为线圈电流JCoil和等离子体极化电流JPlasma之和,其中JCoil通过叠加单圈线圈电流得到;
分别为真空磁导率和不同区域内的电介质系数;总的传导电流J为线圈电流JCoil和等离子体极化电流JPlasma之和,其中JCoil通过叠加单圈线圈电流得到;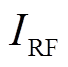 为线圈电流的幅值;M为线圈的匝数;
为线圈电流的幅值;M为线圈的匝数; 为某一单匝线圈距离对称轴的径向位置;
为某一单匝线圈距离对称轴的径向位置;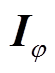 为角向的单位矢量;
为角向的单位矢量;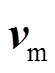 为等离体子碰撞频率;JPlasma由欧姆定律计算获得,空间中的磁场是多匝线圈电流JCoil与“单匝”感应电流JPlasma所产生磁场的总和。
为等离体子碰撞频率;JPlasma由欧姆定律计算获得,空间中的磁场是多匝线圈电流JCoil与“单匝”感应电流JPlasma所产生磁场的总和。
等离子体吸收功率是通过线圈与等离子体之间的耦合来实现的,因此天线线圈的结构会对特性参数的空间分布产生影响。天线线圈具体参数见表1。ICP线圈天线的主要参数包括匝数、均匀度和线圈位置,基本设计原则是满足电磁波衰减效果同时提高能量耦合效率。根据法拉第定律对不同参数下平面线圈的轴向磁感应强度Br(z)进行计算。
表1 天线线圈的具体参数
Tab.1 The parameters of discharge coil

线圈匝数NR1/cmR2/cmR3/cmR4/cm 118——— 21815—— 3181512— 41815128
通过电磁学有限元模型仿真得到盘香型线圈的磁感应强度分布如图4所示。盘香型线圈的磁感应强度在线圈半径1/2处附近达到最大值,由于石英腔体放置于线圈上方,相应的电子密度也在腔体半径1/2处附近达到最大值。这样的结果使等离子体电子密度分布呈圆环状,不均匀性增大。
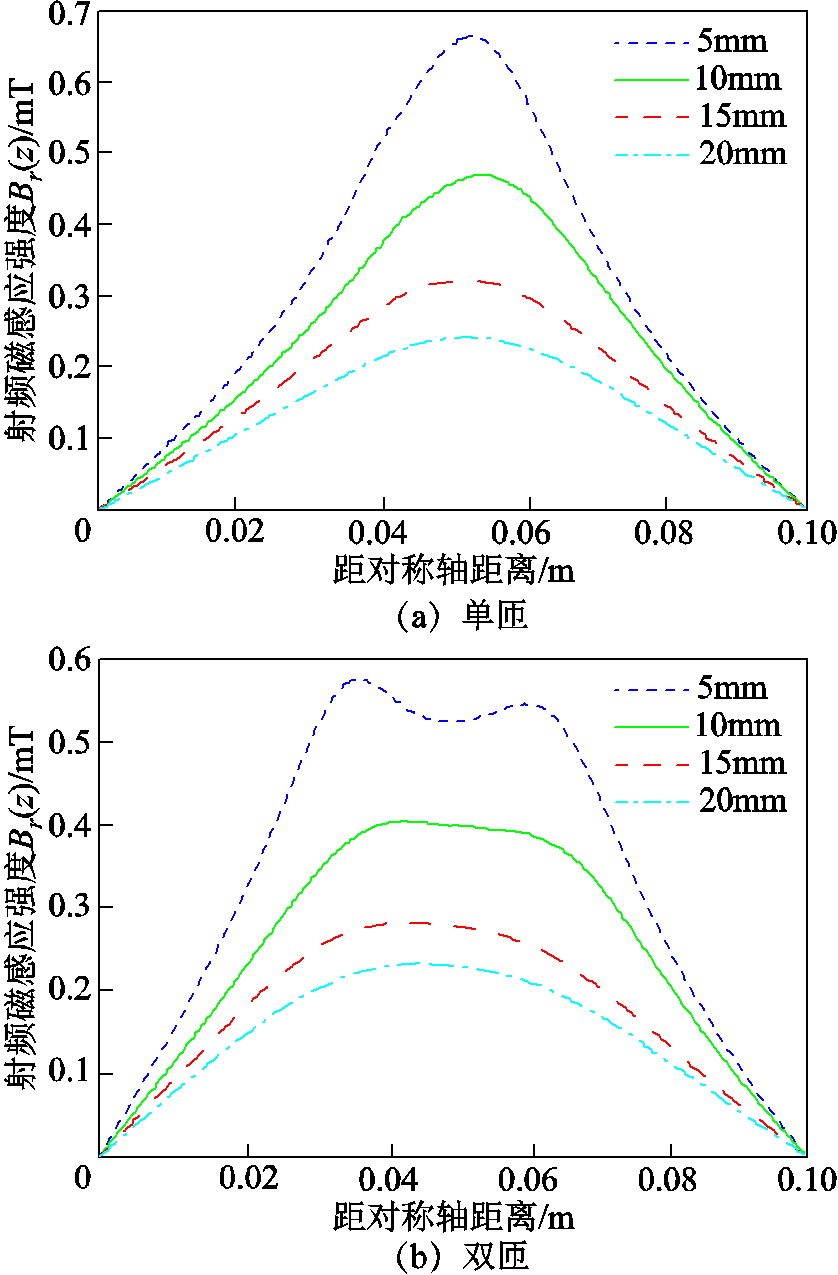
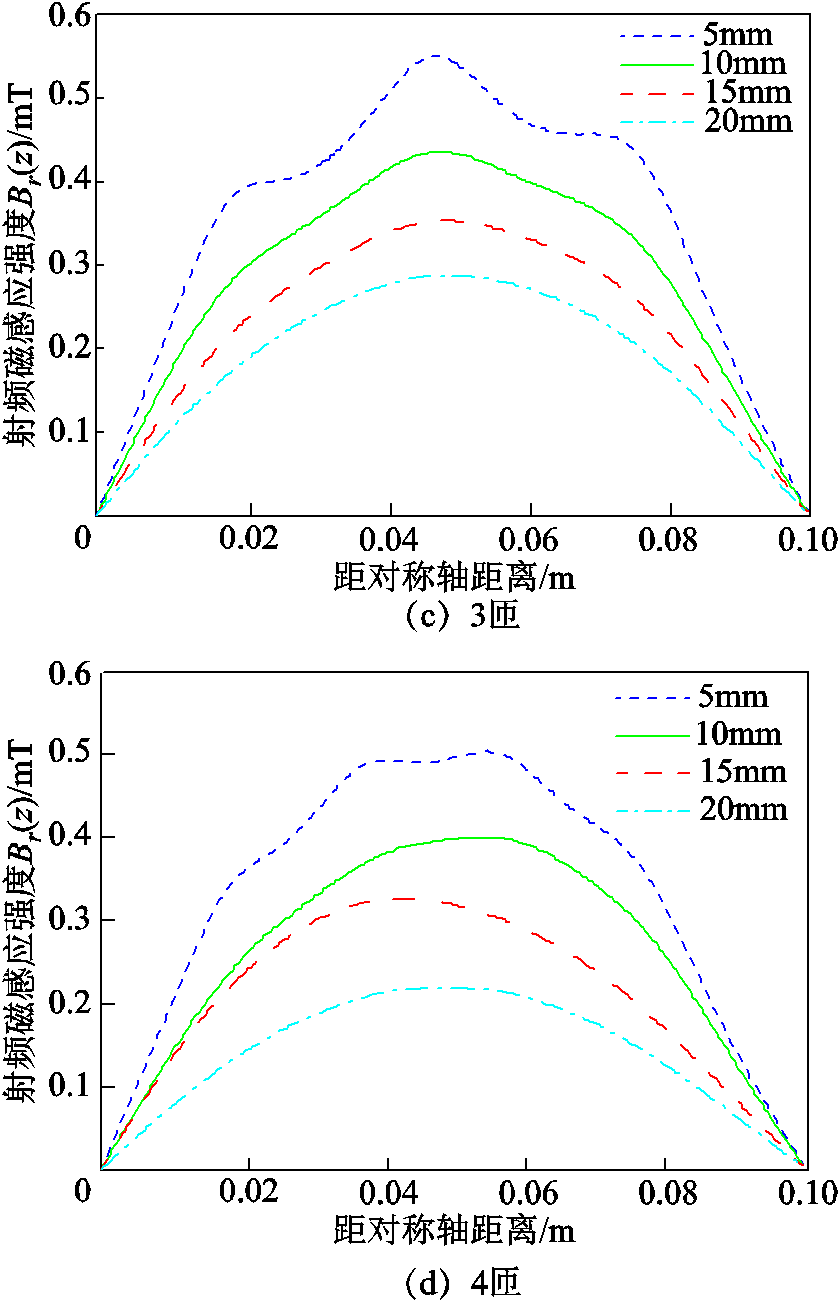
图4 线圈上方不同位置处的射频磁感应强度Br(z)
Fig.4 Magnetic induction intensity at different positions above the coil
图4是放电线圈射频电场的空间分布,射频电场沿径向分布为多峰结构,峰值则是出现在每匝线圈的位置上。由于边界条件设置的约束,射频电场在腔室壁面和对称轴处均为零。由于干涉和补偿作用,位于中部放电线圈上方的电场要强于两边线圈的电场,由此认为射频电场馈入的能量集中在该区域,并被等离子体吸收。
从磁感应强度来看,增加线圈的匝数,线圈电感增大,磁场强度增大,可以明显改善Q值。但是同时线圈的等效电阻和寄生电容也会变大,电阻和电容会增加功率的损耗,从而影响Q值。所以线圈匝数应根据Q值和激发场的分布选取合适的值。
本文根据前期项目设定的固定腔体厚度(2cm)研究电感耦合等离子放电。平面型线圈天线由外径为6mm、内径为4mm的空心铜管绕制而成,铜平面线圈天线的规格分为三种,线圈匝数分别选取1匝、2匝、4匝,分别匹配相同尺寸的放电腔室,天线线圈的参数参照表1。射频电源及匹配系统如图5所示,该系统采用瑞思杰尔公司研制生产的RSG1000型,输出频率13.56MHz,最大输出功率1 000W。

图5 射频电源及匹配系统
Fig.5 RF power supply and matching system
本节首先对典型放电条件下ICP的放电特性进行了研究,放电条件为:薄层石英腔(厚度=2cm),低气压(10mTorr, 1Torr=133.322Pa),工质气体为电正性气体Ar。其放电现象如图6所示。


图6 低气压感性耦合等离子体的放电现象
Fig.6 Discharge phenomenon of ICP at different power rate
低气压感性耦合等离子体的放电过程分为两个典型阶段:第一阶段为E模放电,当功率增加至30W时,腔室内开始起辉,电源功率达到100W时,可以观察到稀薄的等离子体产生,主要分布在电感线圈附近,如图6b、图6f、图6j所示;第二阶段为H模放电,如图6c、图6g、图6k所示,实验过程中当功率上升至150W时,开始进入模式跳变,在150~200W之间均出现跳变式增强的现象,200W之后进入H模式,功率继续增至300W时,不同匝数线圈耦合产生的等离子体亮度和等离子体参数均处于稳定H模式放电,此时放电由线圈的感应电场驱动。ne增加的幅度最大,在容性到感性工作模式的跳变过程中,功率越低容性分量在总耦合功率中占比越大,ne增加导致容性分量降低,提高了总的功率耦合效率。
其次,本节在COMSOL中建立ICP放电的流体模型,对等离子体放电参数的变化规律进行分析,其结果如图7所示。
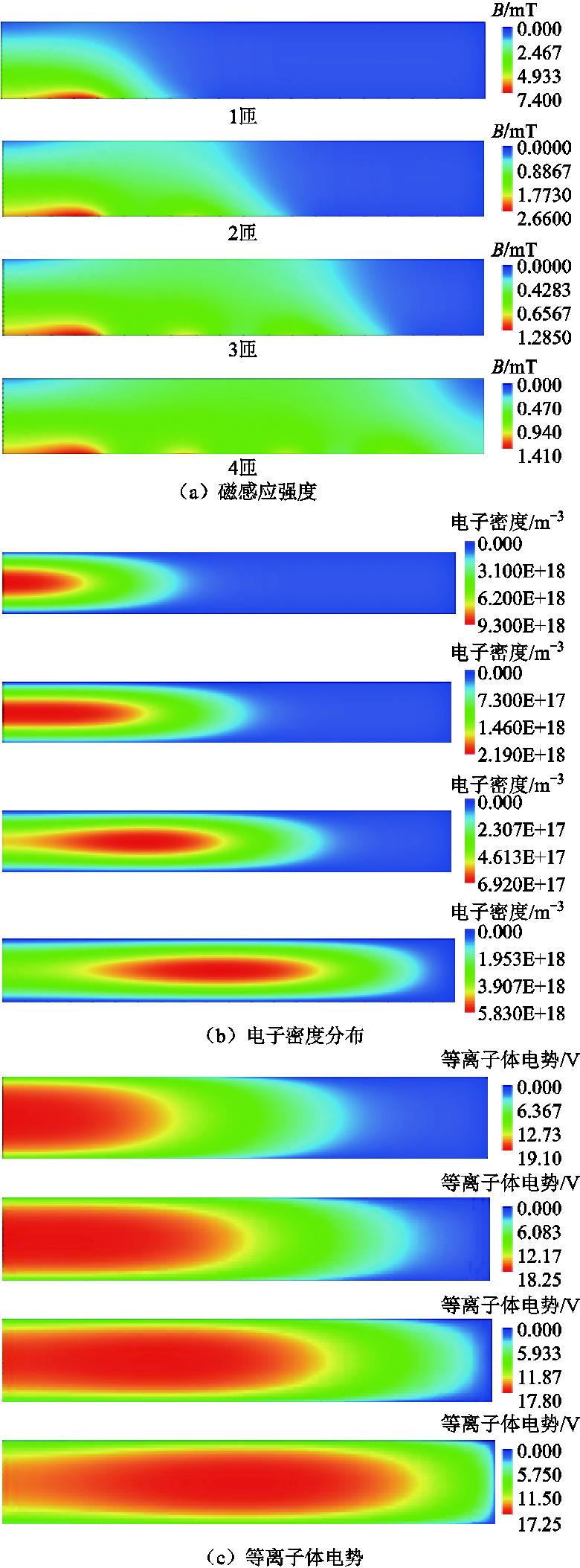
图7 线圈匝数变化对等离子分布影响
Fig.7 The ICP parameter distribution with different coil turns
首先,考虑了不同线圈数下等离子体参数的分布,线圈之间的距离保持在4cm不变,沿腔体对称轴的磁感应强度、沿腔体对称轴的电子密度以及4个线圈(匝数从1~4)的电势分布结果如图7所示。从图7a~图7c结果可以看出随着匝数的增加,在电子扩散和迁移过程中,远离势阱中心区域的电离率受双极势的影响逐渐增大。由图7b可以看出,4匝线圈中,占很大比例的低能电子由于双极电位的限制,无法到达加热场中的强场区,电位分布随着线圈数量的增加,电场强度的峰值远离中心沿径向方向移动,导致的沿径向方向电子发生碰撞反应,由于离子和电子的扩散和重新组合,ne峰随着线圈匝数的增加从0cm移动到11cm。因此,4匝线圈中电子密度分布更均匀,有利于研究电磁波的透射情况。
在四种线圈分布仿真中,选择外部放电条件,压力、温度和功率均相同,电子密度分布沿轴线分布从图8可以直观地看出电子密度ne在核心区达到最高点,随着线圈匝数的增加,电子密度均匀性增大,匝数由椭球形变为鞍形。
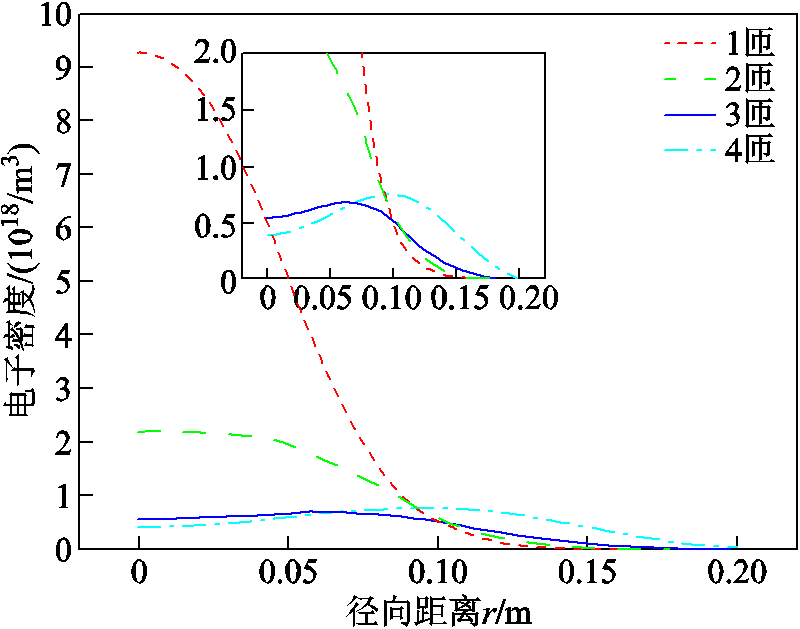
图8 电子密度分布沿轴线分布
Fig.8 Electron density distribution along the axis
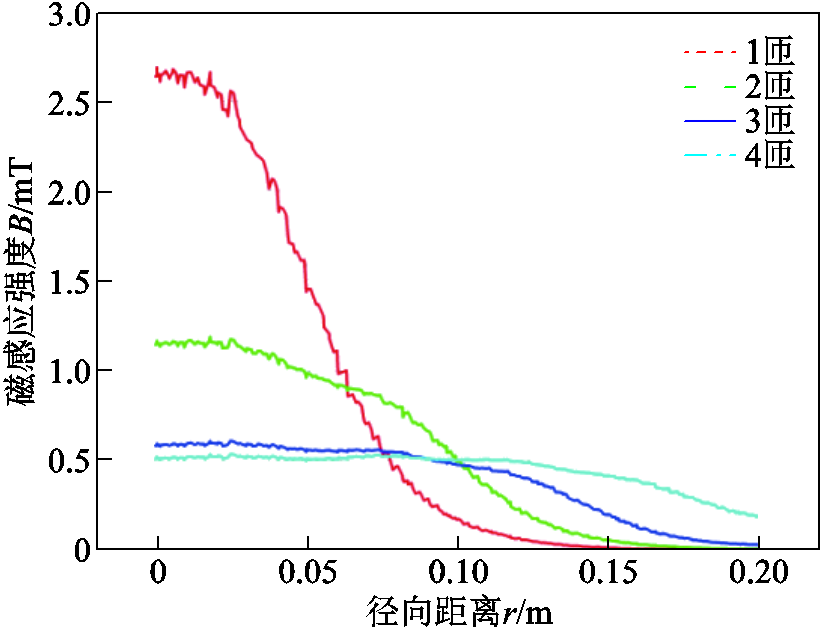
图9 磁感应强度沿轴线分布
Fig.9 Distribution of electromagnetic field induction intensity along the axis
在单匝线圈的作用下,射频功率与石英腔耦合,气体分子在电场力的作用下电离,在腔中心附近的电子加热场中形成电子密度的峰值。在这个范围内,电子受加热场影响,电子的动能增加,电子碰撞增加,因此,等离子体的电离率增加,电子的不均匀性达到峰值。在电场力的作用下,在线圈中心附近的电子密度峰值区形成一个高电位的势阱。随着线圈匝数的增加,等离子体区域增大,峰值减小,峰值电子密度区域远离轴向,主要是由于电子运动产生了抵消部分外电场的反向电场,电子扩散漂移占优势,从图9电磁感应强度也可以看出,随着电场的减小,电子不断向峰两侧扩散。
图10给出了4匝线圈轴向和径向不同位置计算的电子能量分布函数(EEDFs)。可以看出,在高磁场下,电子能量主要集中在低能区域,高能电子(>27eV)明显低于低磁场下的高能电子(>27eV),这主要是低磁场下整体电子密度较低,带电粒子之间碰撞不足造成,高能电子因碰撞而产生的能量转移较小,所占比例高于高磁场区域。在强磁场区域,耦合电能增加,带电粒子间的碰撞增强,因此电子密度普遍较高,同时低能电子基团略有增加,高能电子的尾部随着径向距离的增加而减小,大部分电子集中在低能区域,这是由于足够的粒子碰撞,有利于高能电子的能量转移。
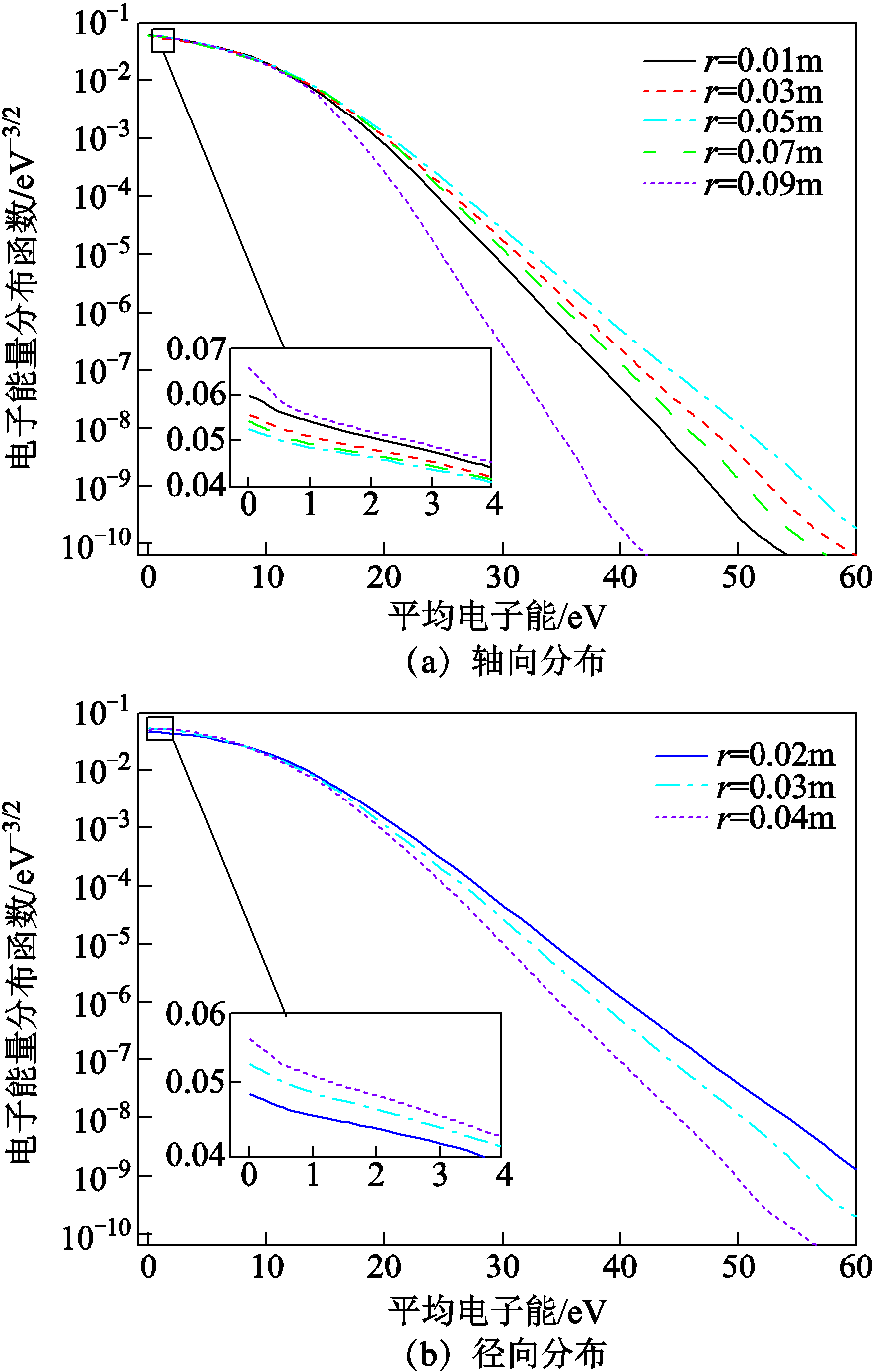
图10 沿轴向和径向分布电子能量分布函数
Fig.10 Electron energy function and distribution along axial and radial directions
在等离子进入H模式后,电子密度峰值超过1012/cm3时,观察电源参数、气压变化情况,放电采用L型电路,自动匹配器的C1电容范围为10~400pF,而C2电容范围为10~1 000pF,因此,根据自动匹配器显示数值可以计算得到对应功率时C1和C2等具体电容值。记录C1和C2的数值如图11所示。
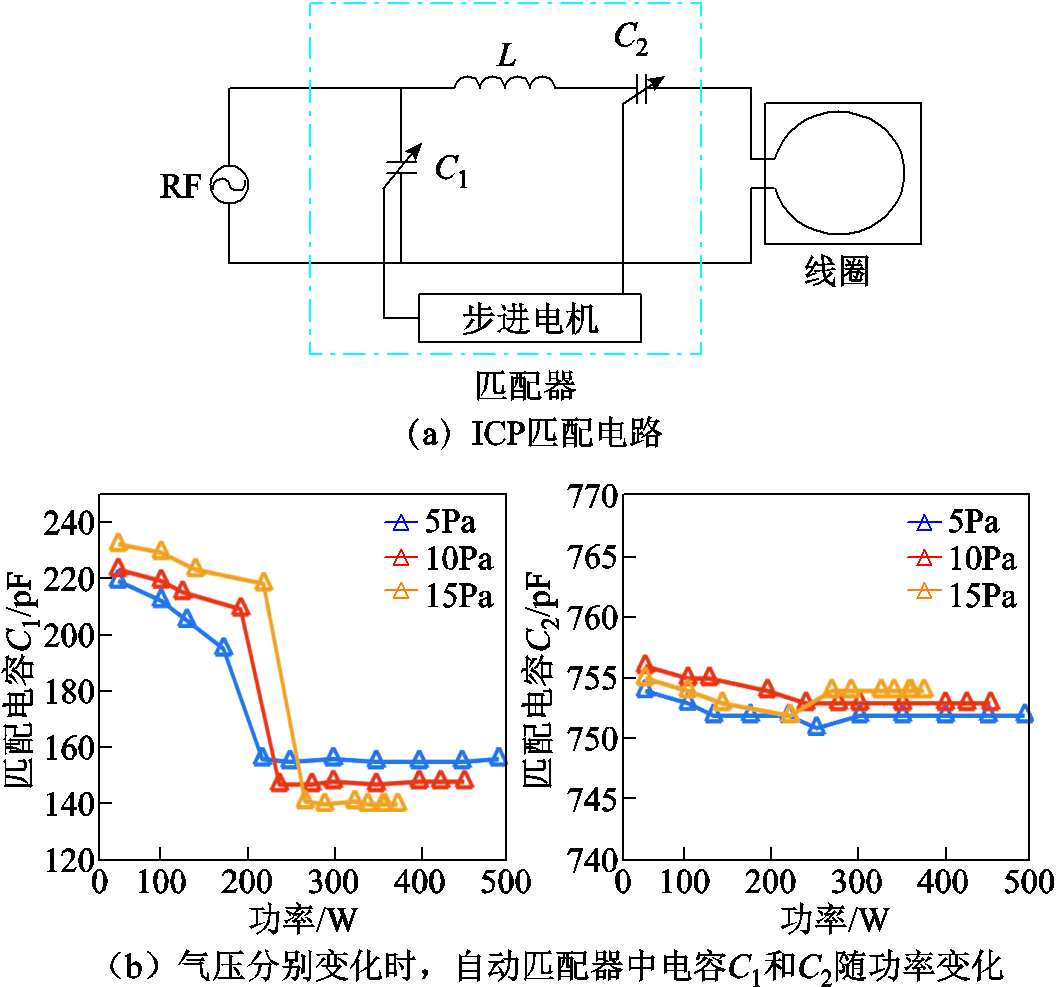
图11 匹配环节电源参数变化
Fig.11 Changes of power parameters in the matching net
从图11b结果中可以看出,当电子密度达到1012/cm3时,射频功率和气压分别为430W(5Pa),390W(10Pa),320W(15Pa),图12随着气压的增大,到达H模式的所需放电功率值在减小。
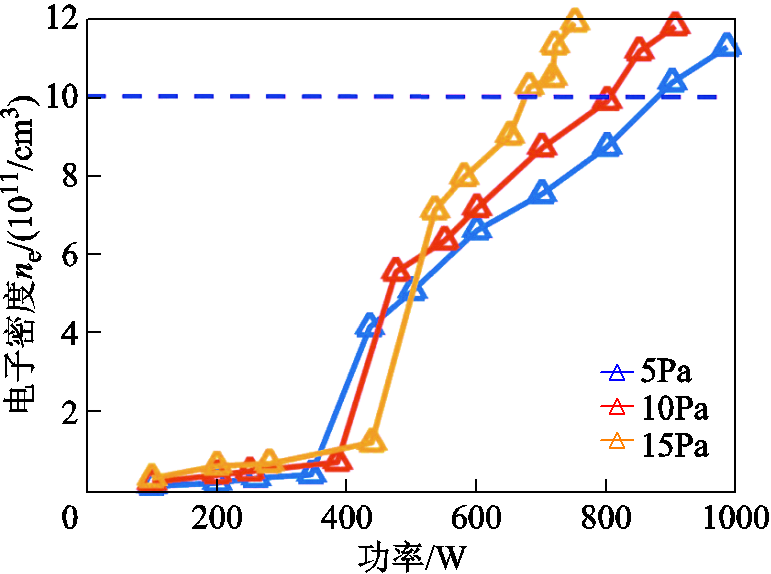
图12 放电气压变化时电子密度随功率变化
Fig.12 Electron density varies with power as discharge pressure changes
最后,实验中选取单匝和4匝这两种情况进行对比分析,通过Langmuir 探针对等离子ne参数在径向分布情况进行诊断,探针的空间位置通过真空直线驱动器控制,间距2 cm,当等离子体源进入稳定的工作状态后,进行数据采集,单匝和4匝线圈的径向ne分布如图13a和图13b所示。
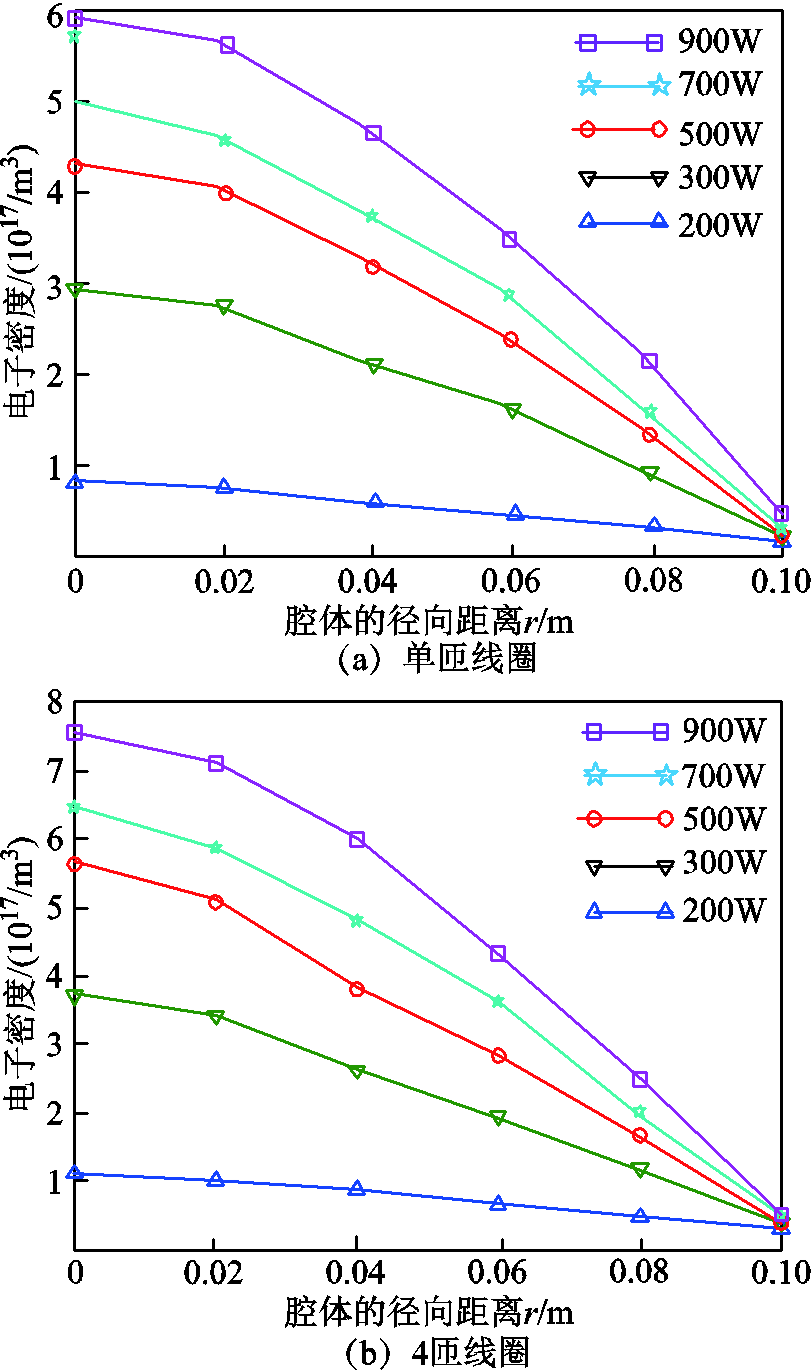
图13 Langmuir 探针诊断的径向ne分布随功率的变化
Fig.13 The radial electron density distribution diagnosed by Langmuir probe varies with power
在10mTorr中,电子的平均自由程λe≈3cm,电子的扩散不受气相碰撞的限制,诊断路径为z=0.01m,单匝和4匝线圈均在900W时ne峰值达到最大值,分别为6.6×1017m-3和7.5×1017m-3,主要原因是在一定范围内随着线圈的增多其电感量也在增多,功率耦合效率会随之提高,这与根据1.2节分析的匝数增多,线圈天线提供更多电感量并且Q值相对更高的结果一致,因此4匝线圈的功率耦合效率相对单匝线圈更好。同时研究发现,图4结果中环向加热电场的强度峰值处在偏离轴心的位置上,但图13结果中电子密度的峰值区位于腔体中心位置(r=0m),远离平面线圈附近,并且随着径向距离的增大,电子密度ne呈减小趋势,这是由于等离子体中的直流双极性电势分布与电场强度不同,电势在腔体中心区域达到最大并形成了一个束缚电子的势阱,可以约束总能量小于器壁电位值的电子,即大量的低能电子被束缚在主等离子体区域内,造成了ne的峰值区远离加热电场强度峰值区。
图14给出了电子温度Te在径向(z=0.01m)距离上的诊断结果,由于H模式中角向的加热电场较小,200W时由于存在一定的容性放电分量,导致Te较高;单匝线圈900W条件下在腔体中心的Te为2.96eV,4匝线圈的Te为2.57eV,除了靠近腔体壁面鞘层部分之外(r>0.09m),Te的空间分布近似均匀分布,Te随功率增大而小幅减小,功率的变化对Te的空间分布影响并不明显,主要原因是随着射频功率的提高而增加,造成单位体积内的碰撞加剧使电子能量得到消耗,导致Te的减小。根据第1节理论分析,电子越靠近线圈的区域Te应该越高,但实验中Langmuir 探针的诊断位置在腔体的中间位置,无法在轴向进行诊断,因此在0.02m<r<0.08m区域内,Te增长趋势不明显。
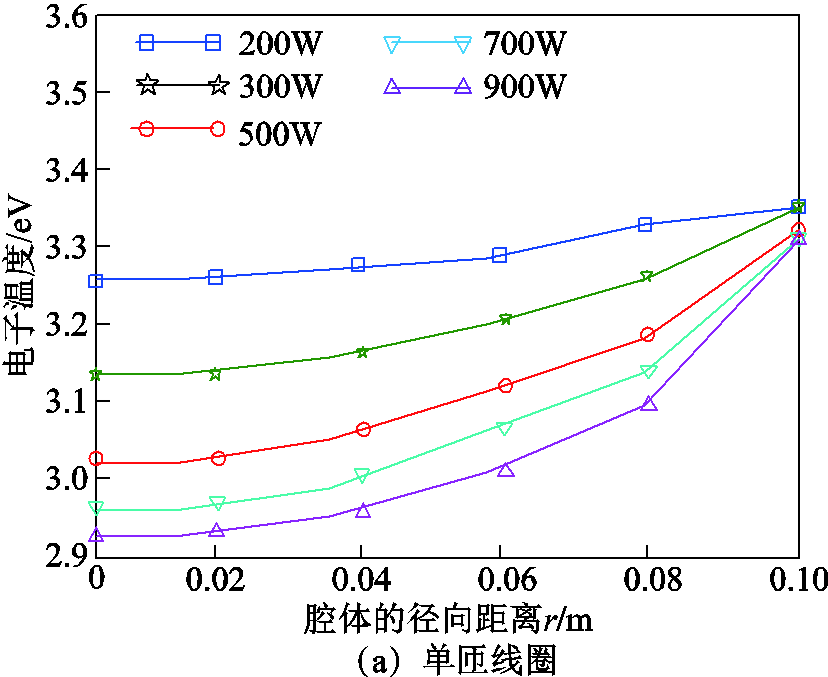
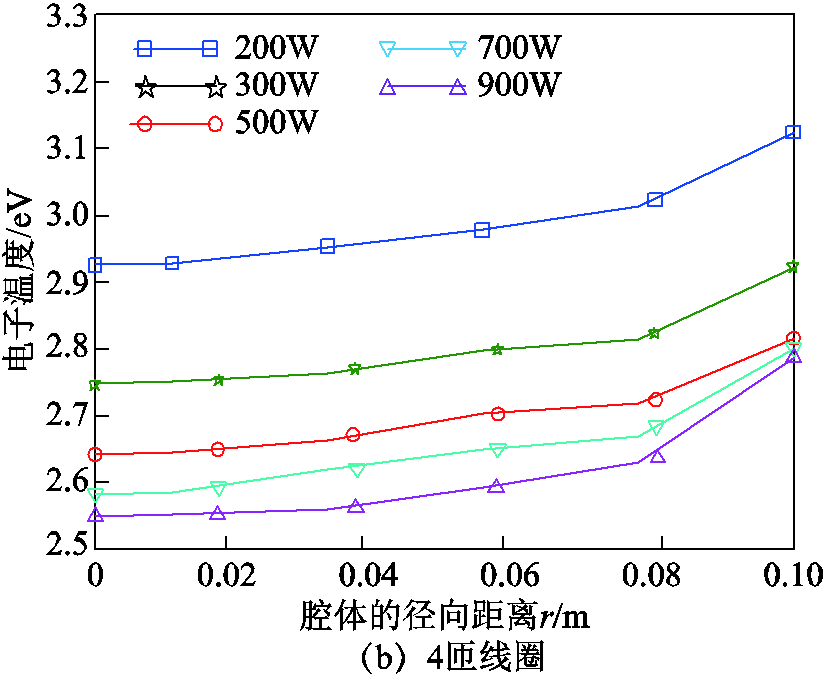
图14 Langmuir探针诊断的径向Te分布随功率的变化(z=0.01m)
Fig.14 The radial electron temperature distribution diagnosed by Langmuir probe varies with power(z=0.01m)
对低气压下平面型ICP功率吸收模式和模式跳变进行了理论分析,并观察了不同线圈匝数随功率变化对E-H模型下ICP放电形态的影响,采用Langmuir探针诊断了典型气压下的Ar-ICP的ne分布,在10mTorr下,结果表明线圈的匝数和构型会对等离子参数分布和耦合效率产生影响,相同功率下4匝线圈的构型参数分布较单匝线圈相对均匀,耦合效率更高,且与不同线圈匝数模式跳变的功率阈值没有太大变化;通过计算不同线圈构型的磁感应强度分布,发现磁感应强度会影响ICP电子密度呈轴对称分布,且射频功率成正比;最后通过实验和COMSOL对平面型ICP参数变化规律进行分析,电子密度达到1012cm3时匹配电路可调电容C1在150pF上下波动,C2在752pF上下波动,一定范围内随着气压增大,进入H模式的放电功率值在不断降低,与仿真得到的结果一致。
参考文献
[1] Xu Shuyan, Ostrikov K N, Li Y, et al. Low-frequency, high-density, inductively coupled plasma sources: operation and applications[J]. Physics of Plasmas, 2001, 8(5): 2549-2557.
[2] Hopwood J, Guarnieri C R, Whitehair S J, et al. Langmuir probe measurements of a radio frequency induction plasma[J]. Journal of Vacuum Science & Technology A, 1993, 11:152-156.
[3] Godyak V A, Alexandrovich B M. Plasma and electrical characteristics of inductive discharge in a magnetic field[J]. Physics of Plasmas, 2004, 11(7): 3553-3560.
[4] Amorim J, Maciel H S, Sudano J P. High-density plasma mode of an inductively coupled radio frequency discharge[J]. Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures Processing, Measurement, and Phenomena, 1991, 9(2): 362-365.
[5] 戴栋, 宁文军, 邵涛. 大气压低温等离子体的研究现状与发展趋势[J]. 电工技术学报, 2017, 32(20): 1-9.
Dai Dong, Ning Wenjun, Shao Tao. A review on the state of art and future trends of atmospheric pressure low temperature plasmas[J]. Transactions of China Electrotechnical Society, 2017, 32(20):1-9.
[6] Lee H C, Chung C W. E-H heating mode transition in inductive discharges with different antenna sizes[J]. Physics of Plasmas, 2015, 22: 053505.
[7] Lee H C, Chung C W. Effect of antenna size on electron kinetics in inductively coupled plasmas[J]. Physics of Plasmas, 2013, 20: 101607.
[8] Jun H S, Chang H Y. Development of 40 MHz inductively coupled plasma source and frequency effects on plasma parameters[J]. Applied Physics Letters, 2008, 92: 041501.
[9] Ventzek P L G, Hoekstra R J, Kushner M J. Two-dimensional modeling of high plasma density inductively coupled sources for materials Proeessing[J]. Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures Processing, Measurement, and Phenomena, 1994, 12(1): 461-477.
[10] Fukasawa T, Nouda T, Nakamura A, et al. RF self-bias characteristics in inductively coupled plasma[J]. Japanese Journal of Applied Physics, 1993, 32: 6076-6079.
[11] 张昀, 王波, 王荷军. 射频感应耦合等离子体郎缪双探针诊断分析[J]. 真空, 2016, 53 (3): 56-61.
Zhang Yun, Wang Bo, Wang Hejun. Langmuir double probe diagnostic analysis of RF inductively coupled plasma[J]. Vacuum, 2016, 53 (3): 56-61.
[12] 汪建. 射频电感耦合等离子体及模式转变的实验研究[D]. 合肥: 中国科学技术大学,2014.
[13] 朱寒, 何湘, 陈秉岩, 等. 容性耦合射频放电等离子体的仿真模拟与实验诊断研究[J]. 电工技术学报, 2019, 34(16): 3504-3511.
Zhu Han, He Xiang, Chen Bingyan, et al. Simulations and experimental diagnostic of capacitively coupled RF discharge plasma[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3504-3511.
[14] 张改玲, 滑跃, 郝泽宇, 等. 13.56MHz/2MHz柱状感性耦合等离子体参数的对比研究[J]. 物理学报, 2019, 68(10): 105202.
Zhang Gailing, Hua Yue, Hao Zeyu, et al. Experimental investigation of plasma parameters in 13.56MHz/2MHz cylindrical inductively coupled plasma[J]. Acta Physica Sinica, 2019, 68(10): 105202.
[15] 李亦非, 付宸聪, 蔡国飙, 等. 微型射频离子推进器放电等离子体全局模型仿真研究[J]. 电工技术学报, 2021, 36(15): 3113-3123.
Li Yifei, Fu Chencong, Cai Guobiao, et al. Global model co-simulation of RF ion thruster based on multi-physical field coupling[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3113-3123.
[16] 桑建华. 飞行器隐身技术[M]. 北京: 航空工业出版社, 2013.
[17] 何湘. 飞机局部等离子体隐身探索研究[D]. 南京: 南京理工大学, 2010.
[18] Wen Deqi, Liu Wei, Gao Fei, et al. A hybrid m Model of radio frequency biase d inductively coupled plasma discharges: description of model and experimental validation in argon[J]. Plasma Sources Science and Technology, 2016, 25(4): 045009.
[19] 苏晨, 徐浩军, 林敏. 封闭式等离子体发生器设计及其放电等离子体参数分布实验研究[J]. 高电压技术, 2013, 39(7): 1668-1673.
Su Chen, Xu Hao Jun, Lin Min. Design on closed plasma generator and experimental study on its plasma parameters distribution[J]. High Voltage Engingeering, 2013, 39 (7): 1668-1673.
[20] 梅丹华, 方志, 邵涛. 大气压低温等离子体特性与应用研究现状[J]. 中国电机工程学报, 2020, 40(4): 1339-1358, 1425.
Mei Danhua, Fang Zhi, Shao Tao. Recent progress on characteristics and applications of atmospheric pressure low temperature plasmas[J]. Proceedings of the CSEE, 2020, 40 (4): 1339-1358, 1425.
[21] 万静, 宁文军, 张雨晖, 等. 气隙宽度对大气压氦气介质阻挡放电多脉冲特性影响的仿真研究[J]. 电工技术学报, 2019, 34(4): 871-879.
Wan Jing, Ning Wenjun, Zhang Yuhui, et al. Influence of gap width on the multipeak characteristics of atmospheric pressure helium dielectric barrier discharges-a numerical approach[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 871-879.
[22] 田微, 盖斐, 张俊敏, 等. 径向放电的等离子体阴极脉冲电子束实验研究[J]. 电工技术学报, 2019, 34(6): 1338-1344.
Tian Wei, Gai Fei, Zhang Junmin, et al. Experiment research on pulse electron beam of plasma cathode with radial discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1338-1344.
[23] 林茂, 徐浩军, 魏小龙, 等. 放电功率变化对电磁波在电感耦合闭式等离子体中的衰减特性[J]. 强激光与粒子束, 2021, 33(6): 065012(1-8).
Lin Mao, Xu Haojun, Wei Xiaolong, et al. Research on attenuation characteristics of electromagnetic wave in ICP plasma based on variation of discharge power[J]. High Power Laser and Particle Beams, 2021, 33(6): 065012(1-8).
Study on Spatial Distribution of Inductive Coupled Plasma Closed Plasma with Discharge Parameter Variation
Abstract In the application of inductive coupled plasma(ICP), such as the coil configuration, power supply parameters, pressure and other external conditions are different, it is difficult to get the mechanism of multiple influences on the ICP parameter distribution, This paper combine the simulation and experiment methods, by the establishment of the inductive coil electromagnetic finite element model, analyzing the radio frequency electromagnetic field under different coil configuration in the spatial distribution within the plasma, then we study the influence of discharge parameters (coil configuration, power rate) on the plasma distribution and E-H model dynamic process. By analyzing its discharge parameters to provides a theoretical basis for the miniaturization engineering application of plasma source.The results of experiment and simulation show that: ①Under different coil turns and different power rates, the variation of electromagnetic field intensity has a great influence on the plasma power absorption and power coupling. ②When pressure the working gas Ar is between 0-20Pa, the electron density of ICP is axismetrically distributed, with the increase of the discharge power and gas pressure, the absorbed power and ionization degree of the plasma also increased. The distribution of electron density in the axial and radial directions increases gradually and then decreases rapidly near the wall of the chamber.
keywords:Inductively coupled plasma, radio frequency power, discharge coil, parameter spatial distribution
DOI:10.19595/j.cnki.1000-6753.tces.210022
中图分类号:TM31
国家自然科学基金资助项目(12075319)。
收稿日期 2021-01-10
改稿日期 2021-04-02
林 茂 男,1988年生,博士,研究方向为低气压等离子体放电。E-mail:496180444@qq.com(通信作者)
徐浩军 男,1965年生,教授,博士生导师,研究方向为等离子体应用技术。E-mail:262432206@qq.com
(编辑 郭丽军)