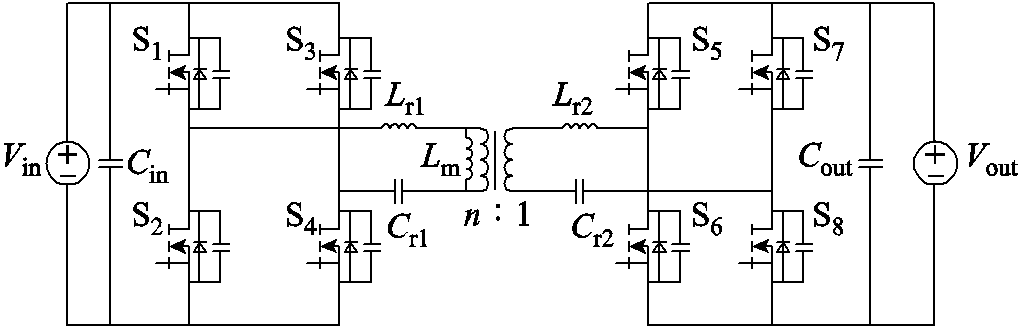
图1 双向CLLC直流变换器拓扑
Fig.1 The topology of bidirectional CLLC DC-DC converter
摘要 CLLC直流变换器的谐振腔参数设计是其稳定运行的保障,但现有的基于基波分析的设计方法并不能实现参数设计的准确与高效。该文从设计的角度出发,首先分析了基波分析在设计上的局限性,接着在CLLC直流变换器时域分析结果的基础上,选取设计中需要考虑的运行模式进行分析,并通过简化处理,建立CLLC直流变换器的简化时域模型,导出了可以用于参数设计的增益公式与边界条件,并讨论不同控制目标下的设计依据。根据该文方法得到的设计公式形式简洁,准确度高,大大简化了设计的步骤。在此基础上,该文给出一套完整的设计思路,并应用该方法设计了一台5kW的CLLC直流变换器样机,仿真与实验的结果均证明了该方法的正确性。
关键词:CLLC直流变换器 谐振腔参数设计 简化时域模型
随着新能源技术、电动汽车充电技术等的不断发展,低损耗、高功率密度、高可靠性的双向DC-DC变换器成为研究的热点[1-9]。在众多双向DC-DC变换器拓扑中,谐振型拓扑因具有易于实现的软开关特性、相对简单的控制方式与较高的功率密度而受到广泛关注。LLC谐振型直流变换器是其中的代表[10-11],但双向LLC拓扑[12]在反向运行时只能降压而不能升压的特点限制了其在某些场合的应用。
为了使LLC型变换器拓扑在正反向运行时都能具有良好的运行特性,有学者提出了对称的CLLC型直流变换器[13-14]拓扑,即在LLC拓扑的基础上,在变压器二次侧额外增添一个谐振电感与谐振电容,使得电路具有完全对称的结构,因此电路的正反向运行时的电路结构完全相同,且均呈现出近似LLC谐振的运行特性。
CLLC直流变换器谐振元件的参数设计是其正常运行的关键保障,参数的设计依赖对CLLC直流变换器的建模分析。一般对其进行建模的方法为基波分析法(First Harmonic Approximation, FHA)[13-16],即将电路中电压电流波形简化为正弦,进而可以利用求解正弦稳态电路的手段对电路进行分析。基波分析法无需对不同开关状态的电路模型进行讨论,很大程度上降低了计算的复杂度,对CLLC谐振腔参数的设计具有一定的指导意义。但基波分析法在简化计算的同时,也加大了分析的误差,利用基波分析法设计出来的谐振腔参数往往有着较大的优化空间,而且基波分析法将整流网络等效为一个恒定电阻,并不适用于电池等非线性负载的情况。
鉴于基波分析法误差较大这一事实,文献[17]试图通过求解CLLC直流变换器在不同模态下的微分方程来对其进行建模,即时域分析法,或称模态分析法。与LLC谐振变换器[18]类似,CLLC直流变换器同样可以分为Pb、Ob、Nb三种运行模态,在不同的频率与负载下,电路的运行模式总是三种模态的组合,结合模态切换的边界条件,利用数值计算的手段可以得到CLLC直流变换器各个状态量在理想情况下的精确值。但由于CLLC电路在各个模态下的电流、电压表达式大多为超越方程组,没有可以明确指导设计的公式,不适合作为参数设计的指导方法。
从上述分析可知,若对CLLC直流变换器进行精确建模,则会失去设计的简易性;而若用基波分析法进行简化,则会失去设计的准确性,因此需要一种折中的建模方案来指导设计。简化时域模型的思想是在时域分析的基础上,通过对关键波形的适当且合理的简化,从而导出可以描述变换器性质的公式,该思想在LLC直流变换器的研究[19-21]中就有所体现。文献[19]通过假定LLC直流变换器欠谐振模式下O模态电流不变,导出了较为准确的增益公式;文献[20]基于相同的假设,利用子区间分析法讨论了LLC直流变换器在PO模式下的边界条件,获得了较为准确的结果。文献[21]总结了LLC直流变换器在各个模式下的简化时域分析结果,给出了各个电气量的表达式。
对波形进行合理简化的思想同样也可以应用于CLLC型直流变换器拓扑。本文在CLLC直流变换器时域分析结果的基础上,主要针对设计中需要考虑的运行情况,建立了CLLC直流变换器的简化时域模型。推导出可用于设计的增益公式以及相应的边界条件。本文所提出的设计流程,相较于传统基于基波分析的设计方法,步骤更加简洁且精度更高,可适用于非线性负载的变换器设计。本文对所提方法进行了仿真验证,并以此为依据设计了一台5kW的样机,仿真和实验的结果均证明了设计的合理性。
CLLC直流变换器的拓扑结构如图1所示,其中开关管S1、S4与S2、S3互补导通,占空比均为50%,变压器二次开关管不施加控制信号。Lr1、Lr2为一次、二次侧谐振电感,Cr1、Cr2为一次、二次侧谐振电容,Lm为励磁电感,n为变压器电压比。为保持电路的对称性,有Lr1=n2Lr2,Cr1= Cr2/n2。

图1 双向CLLC直流变换器拓扑
Fig.1 The topology of bidirectional CLLC DC-DC converter
对CLLC直流变换器应用基波分析法后,可以得到图2所示的等效电路。
图2中,Req为交流等效电阻,且满足[22]
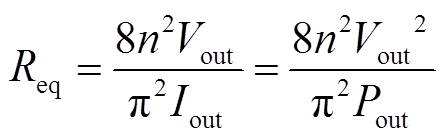 (1)
(1)
式中,Vout为输出电压;Iout为输出电流;Pout为输出功率。
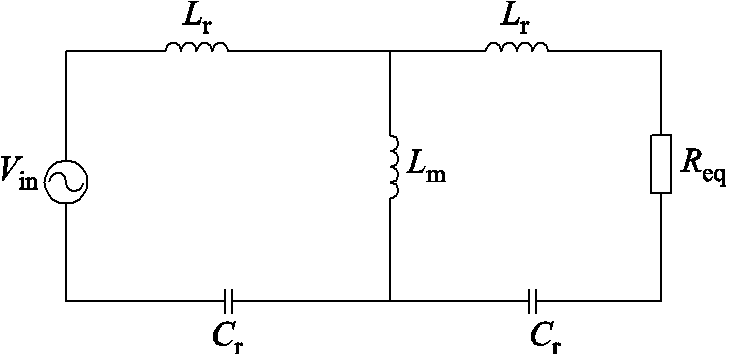
图2 CLLC直流变换器等效电路
Fig.2 Equivalent circuit of CLLC DC-DC converter
通过分压原理,可以得到CLLC直流变换器的基波电压增益为[22]
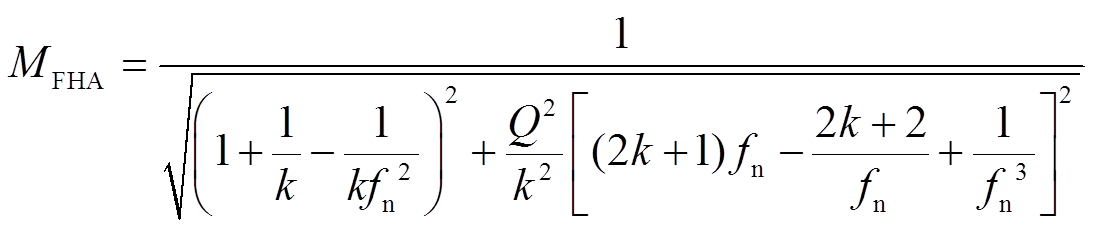 (2)
(2)
式中,MFHA为电压增益;k为电感系数,k=Lm/Lr1; 为谐振频率,
为谐振频率,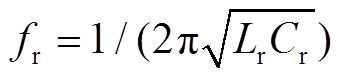 ;
;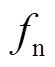 为归一化频率
为归一化频率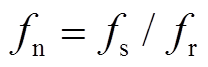 ,
, 为开关频率;Q为品质因数,Q=Zr/Req,Zr为特征阻抗,
为开关频率;Q为品质因数,Q=Zr/Req,Zr为特征阻抗,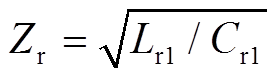 。
。
图3为仿真增益曲线与基波增益曲线的对比,可以看出通过基波分析法得到的理论增益与仿真增益相比存在较大差距,基波分析法在对电压增益的变化率以及增益峰值的描述上均有较大误差。
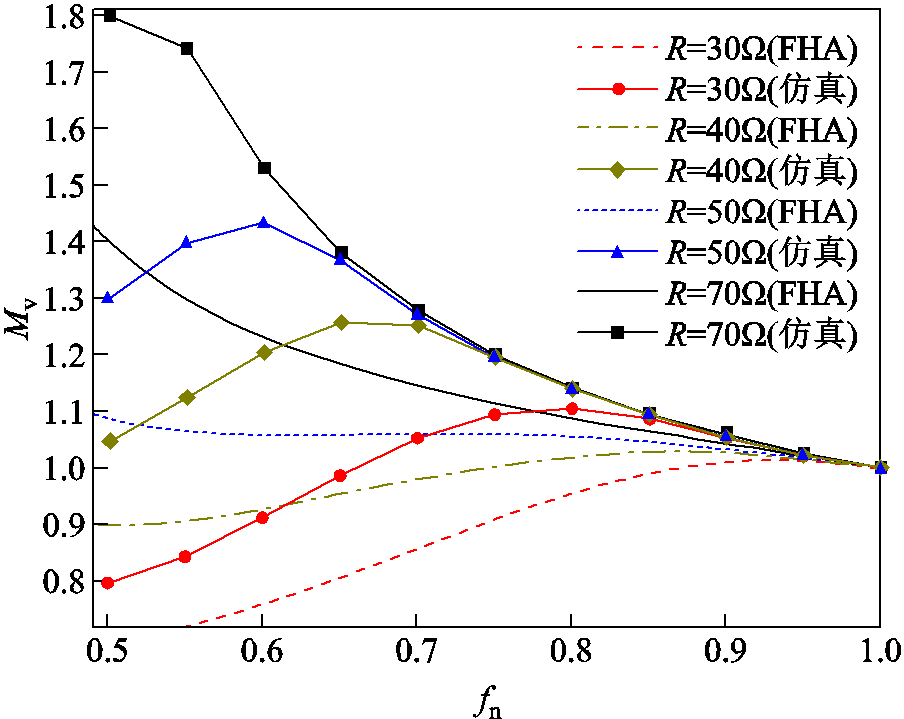
图3 基波分析法与仿真得到的增益对比
Fig.3 Comparison between the gain obtained by fundamental analysis and the gain obtained by simulation
另一方面,当CLLC变换器的输出侧为电池等非线性时变负载时,使用基波分析法进行设计会存在一些困难。以电池充电为例,考虑充电过程,通常会将恒定最大功率充电曲线作为设计依据[23],即假定输出功率保持恒定。在这种情况下,Q不再为常数,而是随着电压增益的变化而变化,若假定输入电压不变,结合式(1)可以推导得出
 (3)
(3)
式(3)表明Q是关于MFHA的函数,在调节输出电压时,Q也处于不断地变化之中,这会给设计带来困难:Q随着频率的减小而降低,而较小的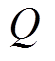 又有利于增益的提高,因此将难以确定何处为最恶劣的运行点[22]。
又有利于增益的提高,因此将难以确定何处为最恶劣的运行点[22]。
文献[22]针对这一点提出了一整套设计方法,在设计时将Q的变化也加以考虑,虽然提高了设计的精度,但也大大增加了设计的复杂度,失去了基波分析法简易的优势。
综上所述,在CLLC变换器的参数设计上,基波分析法的准确性和简易性均有不足,需要一种新的设计思路,本文将通过建立CLLC的简化时域模型来设计参数。
根据时域分析[17]的结果,在欠谐振工况下,CLLC变换器可能存在PbOb、ObPbOb、PbObNb以及PbNb四种工作模式,其中,PbOb模式是一种升压模式,在该模式下CLLC变换器可以实现逆变侧开关管的零电压导通(Zero Voltage Switching, ZVS)与整流侧二极管的零电流关断(Zero Current Switching, ZCS),为理想运行模式,参数的设计应保证CLLC变换器可以在该模式下稳定运行。
当输出功率下降到一定程度时,电路会转入ObPbOb模式运行,由于该模式出现于轻载情况,且此时CLLC变换器的电压增益高于PbOb模式,因此在参数设计时无需考虑该模式。
当开关频率过小或输出功率过大时,CLLC变换器会转入PbObNb模式运行,此时的电压增益变化速度放缓,并呈现出先上升后下降的变化趋势[17],即峰值增益出现在该模式中。同时由于在Nb模态中,一次侧谐振电流是迅速跌落的,使得变压器一次侧开关管的ZVS得不到保证。因此需将PbOb与PbObNb的边界作为设计的考虑因素之一。
在PbObNb模式下,若继续减小频率或是加大输出功率,CLLC变换器会进入PbNb模式,此时电压增益的斜率为正,变换器已无法稳定运行,属于不可工作模式。
经过以上分析可知,用于指导设计的简化时域模型在欠谐振区域应包含:PbOb模式的增益公式、PbOb模式与PbObNb模式的边界条件。
CLLC变换器在PbOb模式下的典型工作波形图如图4所示。
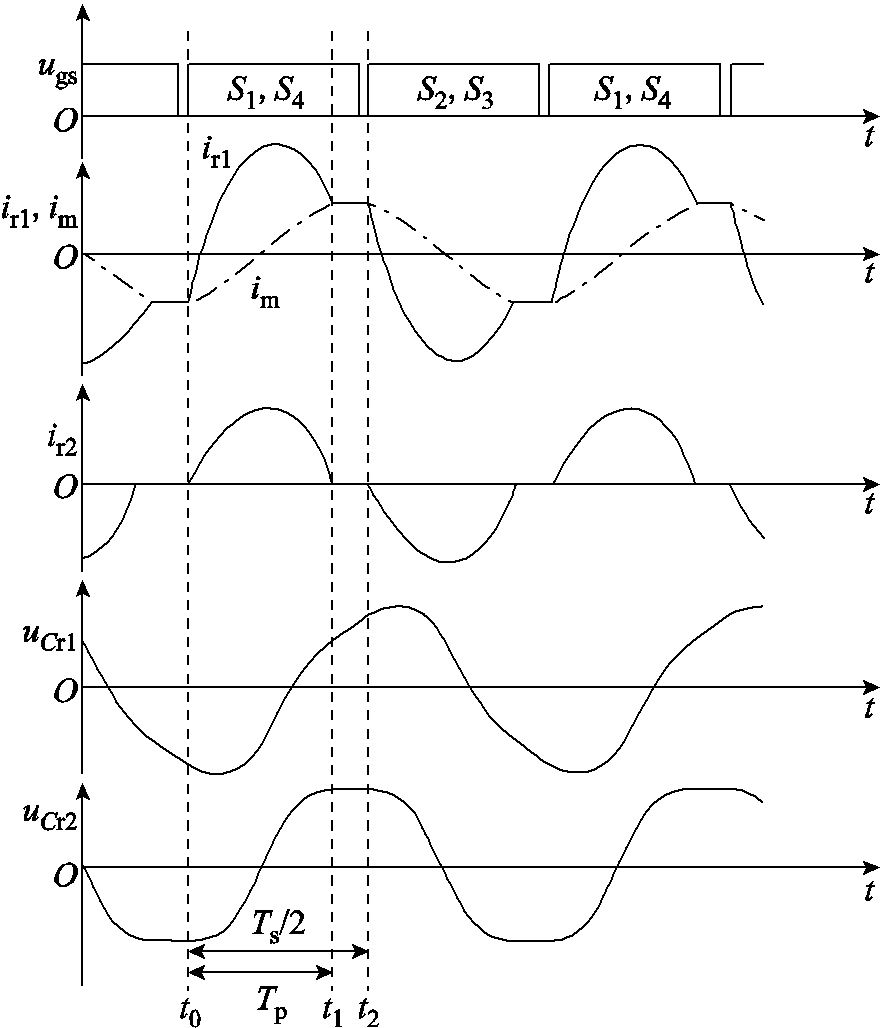
图4 PbOb模式关键波形
Fig.4 The key waveforms of PbOb mode
半个开关周期内,一次侧谐振电流ir1先以近似正弦形式上升(Pb模态),持续时间为Tp,与励磁电流相交后进入Ob模态。在Ob模态内,励磁电感参与谐振,谐振周期加长,励磁电流的变化趋势趋于平缓。实际设计时,励磁电感一般会是一次侧谐振电感的数倍,因此有理由认为在Ob模态下,较大的励磁电感可以将电流保持住。此处做出假设:在Ob模态下,励磁电流保持不变。
Pb模态下,CLLC变换器的等效电路如图5所示,所有参数已归算到一次侧,其中Lr=Lr1=n2Lr2,Cr=Cr1= Cr2 /n2;V2=n2Vout。
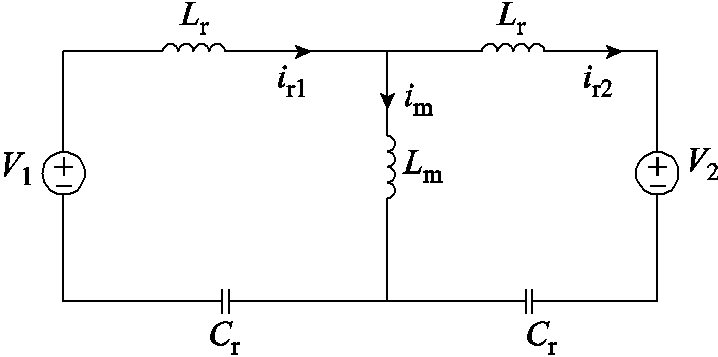
图5 Pb模式等效电路
Fig.5 Equivalent circuit of Pb mode
以 时刻为起点,根据图5可写出谐振电感电流与谐振电容电压的表达式为
时刻为起点,根据图5可写出谐振电感电流与谐振电容电压的表达式为
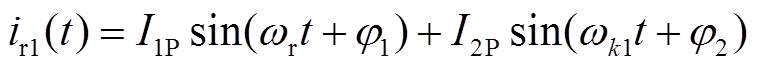 (4)
(4)
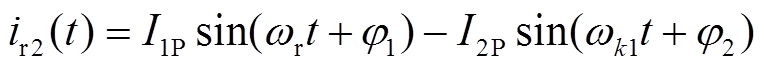 (5)
(5)
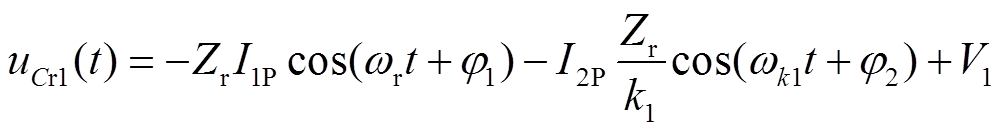 (6)
(6)
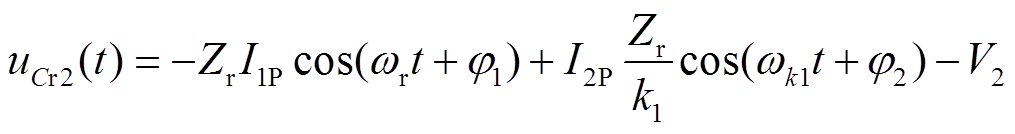 (7)
(7)
式中,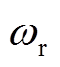 为谐振角频率,且
为谐振角频率,且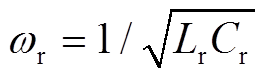 ;系数
;系数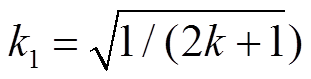 ;ωk1=k1ωr;I1P、I2P、φ1、φ2为未知量。
;ωk1=k1ωr;I1P、I2P、φ1、φ2为未知量。
结合假设条件,经过推导与化简可以得到(详细推导过程在附录中给出)
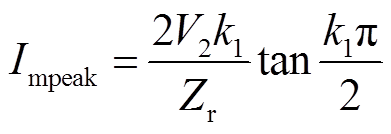 (8)
(8)
 (9)
(9)
式(9)得到的增益与负载无关,这是由于对Ob模态做了简化处理的结果,在这种简化处理下,负载的变化所产生的影响主要体现在PbOb模式与ObPbOb、PbObNb模式的切换边界上。
图6给出了依据式(9)、基波分析法与仿真所得到的增益的对比。可以看出,本文所给出的增益公式能够较好地逼近实际的增益曲线。
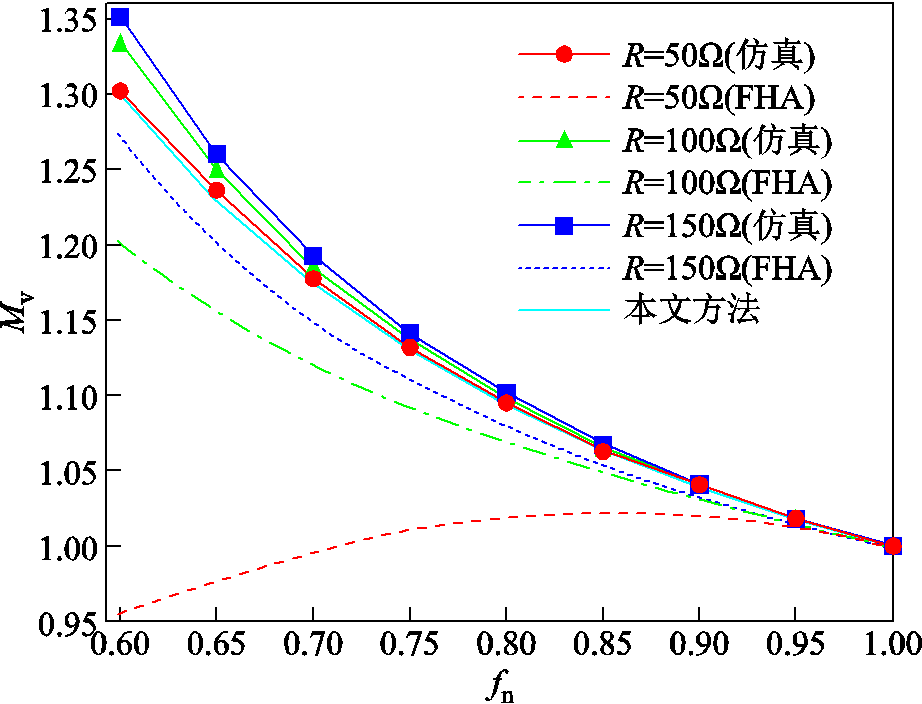
图6 基波分析法本文方法计算得到的增益与仿真得到的增益对比(欠谐振状态)
Fig.6 Comparison between the gain obtained by fundamental analysis, the gain calculated according to the method in this paper and the gain obtained by simulation(under resonance)
如本章第2.2节所述,参数的设计应使得CLLC变换器在升压时能够始终运行在PbOb模式下,即不越过PbOb模式与PbObNb模式的边界,而该边界条件可以描述为:在Ob模态结束前,变压器一次侧谐振电容不会因为过度充电而使变压器二次侧二极管提前导通。由此可以得到关系式
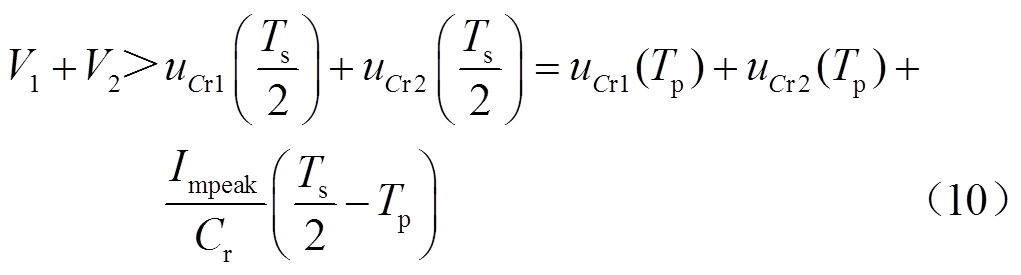
结合2.2小节给出的电压电流表达式,经过推导(见附录)可得
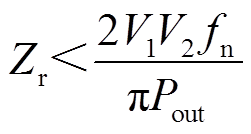 (11)
(11)
式(11)说明在一定功率、频率下,CLLC电路想要维持在PbOb模式运行,Zr的设计不能超过某个最大值。该最大值与V1、V2均有关联,因此对于双向的CLLC直流变换器来说,需要分调压和稳压两种情况讨论。
当目标为恒功率调压时,认为输入电压 保持恒定,而V2=MPOV1,因此式(11)可以改写成
保持恒定,而V2=MPOV1,因此式(11)可以改写成
 (12)
(12)
图7给出了V1=400V、k=7时依据式(12)绘制出的曲线图。由图7可知, 越小,则CLLC变换器越容易保持在PbOb状态,即其载荷能力越强;若保持输出功率不变,所需要的Zr的边界值随频率的下降先减小后增大,在某个频率下有极小值点,该点也是最容易落入PbObNb运行的点。
越小,则CLLC变换器越容易保持在PbOb状态,即其载荷能力越强;若保持输出功率不变,所需要的Zr的边界值随频率的下降先减小后增大,在某个频率下有极小值点,该点也是最容易落入PbObNb运行的点。

图7 输出电压变化时特征阻抗与输出功率的关系
Fig.7 Relationship between characteristic impedance and output power when output voltage changes
当CLLC变换器的目标为恒功率稳压时,此时V2保持不变,V1=V2/MPO,式(11)可以写为
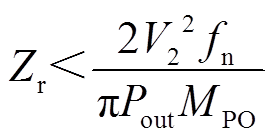 (13)
(13)
图8给出了V2=400V、k=7时依据式(13)绘制出的曲线。由图8可知,在恒输出功率情况下,所需的Zr的边界值随频率的减小呈现出降低的趋势,即频率越小越容易进入PbObNb状态运行。
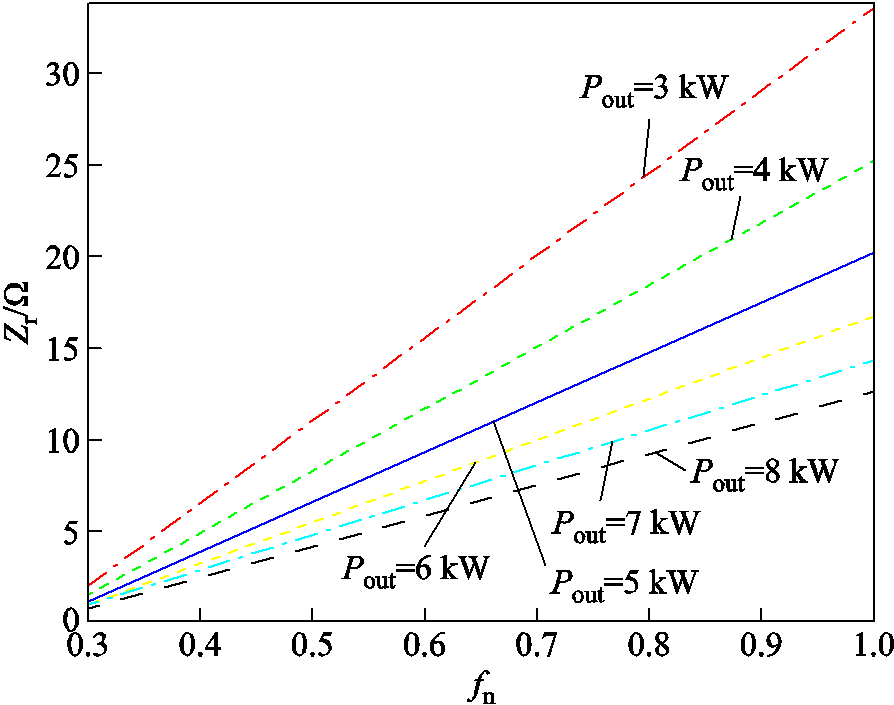
图8 输出电压恒定时特征阻抗与输出功率的关系
Fig.8 The relationship between characteristic impedance and output power at constant output voltage
另外式(9)中隐含了一个边界条件,即增益公式的分母要大于零,解得
 (14)
(14)
基波分析与时域分析的结果均表明,在过谐振区域,增益随着频率的增大而呈现出单调下降的趋势,且负载越轻,下降的趋势越平缓,即降压越困难,最恶劣的情况出现在空载情况下,因此空载增益是设计的指标之一。
另一方面,过谐振工况下,NbPb模式作为过谐振的主要工作模式,对该模式的电压增益的刻画具有重要意义。考虑到在负载较轻时,CLLC变换器通常会辅以多种轻载调节模式来改善增益曲线,如BURST模式、移相模式[24]等,因此在某些设计情况下,NbPb模式的增益曲线仍是参数设计的重要参考依据。
综上所述,过谐振工况下的简化时域模型,应包含NbPb模式电压增益与空载电压增益。
空载对应CLLC变换器的Ob模态,在该模态下变压器二次侧没有电流流过,相当于开路;一次侧谐振电流与励磁电流重合。空载时关键波形如图9所示。
图9 CLLC直流变换器空载时的关键波形
Fig.9 Key waveforms of CLLC DC-DC converter under no load condition
以 时刻为起点,写出谐振电感电流与谐振电容电压的表达式为
时刻为起点,写出谐振电感电流与谐振电容电压的表达式为
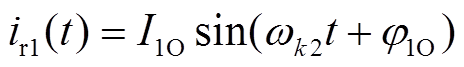 (15)
(15)
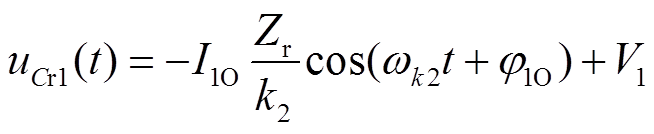 (16)
(16)
式中,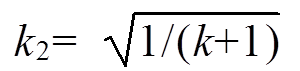 ;ωk2=k2ωr、I1O、φ1O为待求量。
;ωk2=k2ωr、I1O、φ1O为待求量。
推导(见附录)空载电压增益为
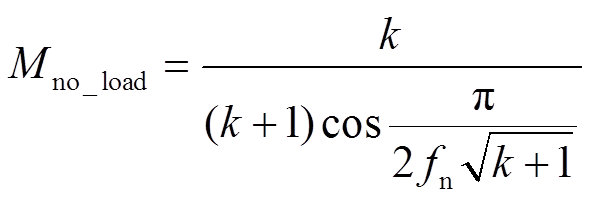 (17)
(17)
在NbPb模式运行下的CLLC变换器共包含Nb与Pb两种模态,典型波形如图10所示,其中Nb模式存在时间很短,变压器一次、二次电流处于迅速跌落状态,谐振电容的电压变化值很小,因此可将Nb模式这一电流降落的阶段忽略,认为电流在开关切换时发生了跳变,则电压增益就可以仅通过Pb模式的电压电流表达式进行求解。
仍以t0时刻为起点,Pb模式的电压电流表达式如式(4)~式(7)所示,结合上述假设,推导(具体过程在附录中给出)得到电压增益的表达式为
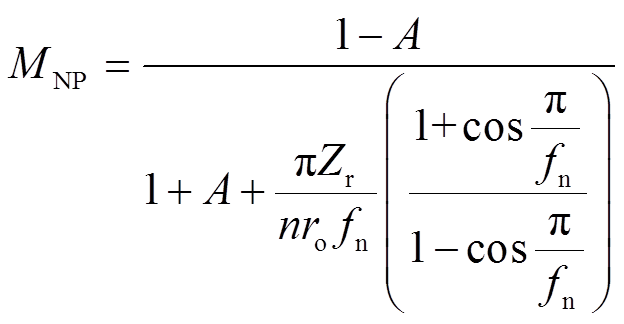 (18)
(18)
其中
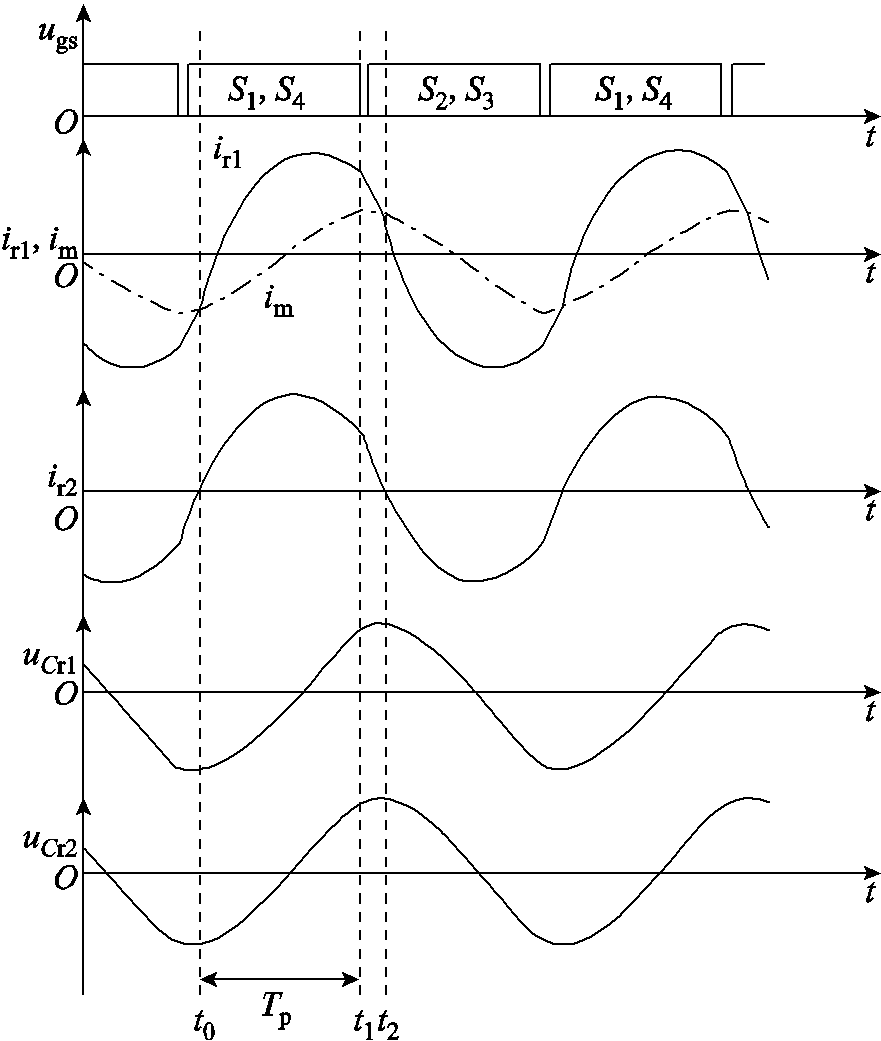
图10 CLLC直流变换器NbPb模式关键波形
Fig.10 Key waveforms of CLLC DC-DC converter of NbPb mode
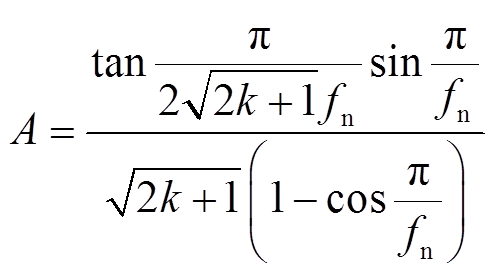 (19)
(19)
式中,ro为输出电阻。与PbOb模式的简化增益表达式不同,NbPb模式增益仍受负载大小的影响。图11给出了分别通过仿真、本文公式以及基波分析法得到的过谐振区域增益曲线的对比。可以看到,无论是满载还是空载,本文导出的公式都可以很好地逼近实际增益曲线,相较于基波分析法,在精度上有了很大的提升。
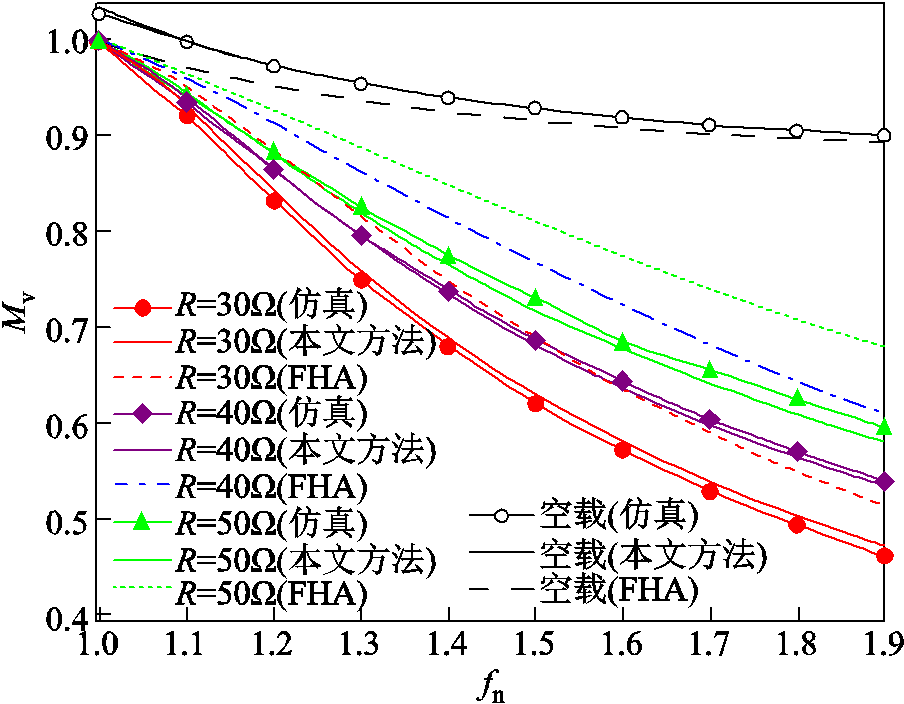
图11 基波分析法本文方法计算得到的增益与仿真得到的增益对比(过谐振状态)
Fig.11 Comparison between the gain obtained by fundamental analysis, the gain calculated according to the method in this paper and the gain obtained by simulation (over resonance)
为验证上述设计思路的可行性,现拟设计一台输入电压为600V,输出电压为360~440V,最大输出功率为5kW的电池充电用CLLC直流变换器样机,拟定谐振频率在125kHz。
在设计前应明确需要考虑的因素,设计CLLC变换器,目标就是要在满足设计需求的基础上,尽可能地提高变换器运行的效率,减小变换器的损耗。为达到此目的,首先应保证CLLC变换器软开关的实现,即在欠谐振区域内,不会因负载过重而从PbOb运行模式落入到PbObNb运行模式。同时在设计时,应尽量减小开关管导通损耗,从式(8)可看出,电感系数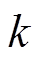 以及特征阻抗Zr越小,励磁电流的峰值就越大,而励磁电流属于环流,减小励磁环流有助于效率的提高,这就要求电感系数
以及特征阻抗Zr越小,励磁电流的峰值就越大,而励磁电流属于环流,减小励磁环流有助于效率的提高,这就要求电感系数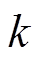 和特征阻抗Zr的值要尽可能大。
和特征阻抗Zr的值要尽可能大。
为使得CLLC变换器在正反向运行时均具有较小的频率改变范围,因此变压器电压比的设计应使正反向运行所需的电压增益范围尽可能地接近。此处选择变压器的电压比为1.5,因此实际的电压增益需求为正向0.9~1.1;反向0.91~1.11。
CLLC变换器正反向运行时结构完全对称,只是负载情况不同,观察式(9)、式(17)可知,在本文模型下,PbOb模式增益与空载增益均只与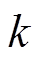 以及开关频率有关,因此结合所需电压增益可直接确定
以及开关频率有关,因此结合所需电压增益可直接确定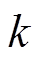 的取值。
的取值。
考虑最小开关频率为谐振频率的0.7倍,将所需的最大增益1.1代入式(9)中可以得到
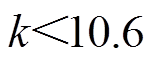 (20)
(20)
考虑轻载时降压的需要,并预计最大频率不应超过谐振频率的两倍,将fn=2以及Mmin=0.9代入到式(17)中可以得到
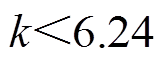 (21)
(21)
综合上述两种情况,最终确定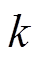 的值为6。则根据式(9)和式(17),理想情况下工作归一化频率为0.8~1.92。
的值为6。则根据式(9)和式(17),理想情况下工作归一化频率为0.8~1.92。
同时验证式(14)所表示的边界条件为
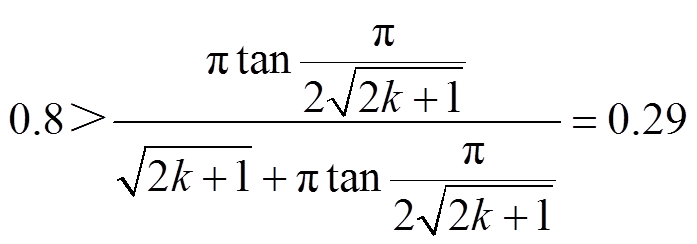 (22)
(22)
如上文所述,特征阻抗的大小直接影响欠谐振工况下CLLC变换器的荷载能力,若Zr过大,则CLLC变换器可能在规定的负载情况下落入PbObNb模式运行,因此Zr应有最大值。
正向运行时,升压状态输入维持600V不变,输出功率为5kW,根据式(12)得到,其最大特征阻抗曲线如图12a所示,可以得到满载运行时,在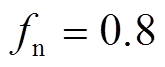 处,Zr的边界值为40.8Ω。
处,Zr的边界值为40.8Ω。
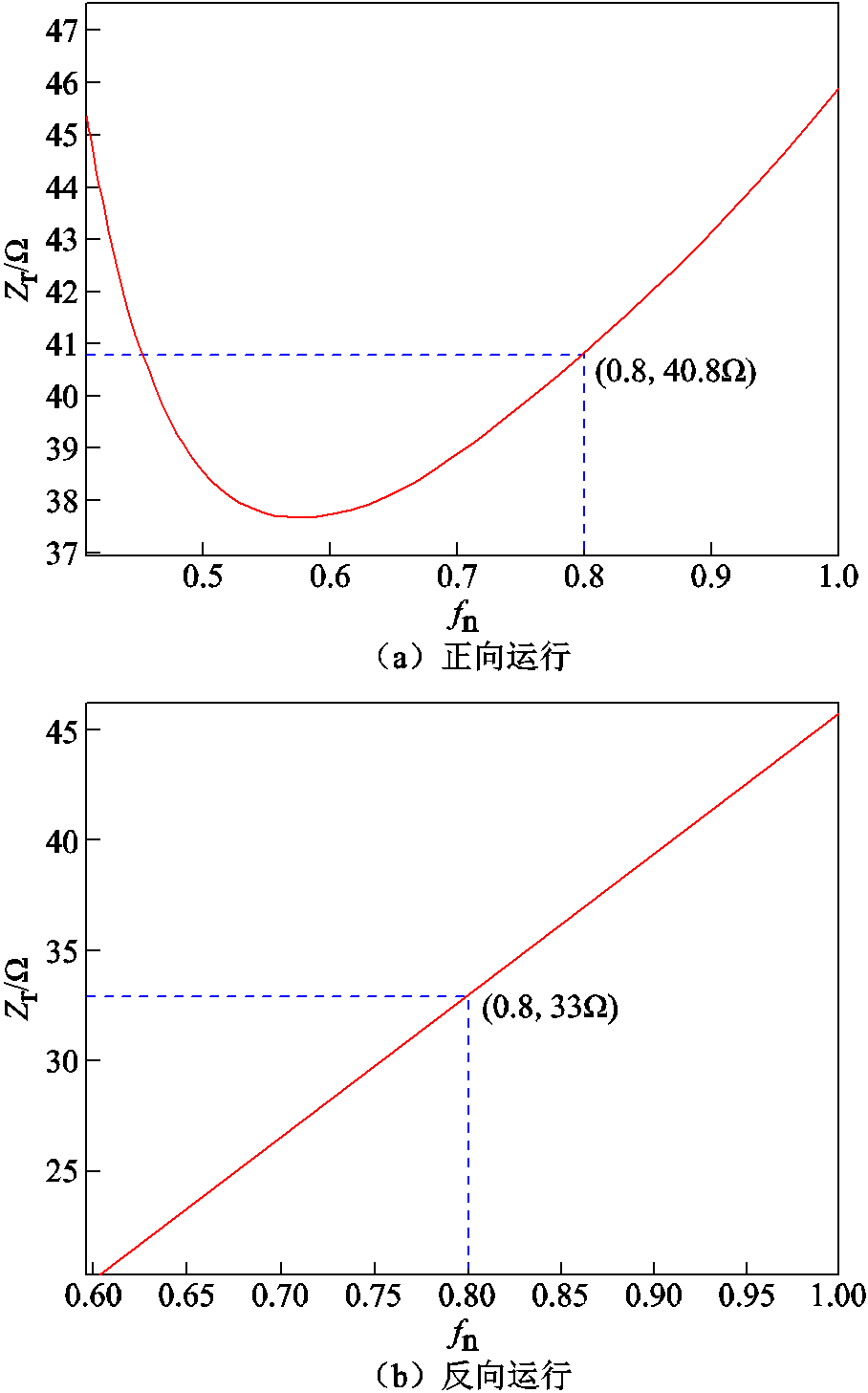
图12 正向稳定运行与反向稳定运行的特征阻抗边界值
Fig.12 Boundary value of characteristic impedance for forward stable operation and reverse stable operation
反向运行时,升压模式下输出电压维持600V不变,根据式(13)做出曲线图12b,可以得到满载运行时,在fn=0.8处,Zr的边界值为33Ω。综合考虑正反向分析情况,最终选择Zr=30Ω。
在设计好参数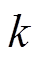 和
和 以后,谐振腔的参数可通过式(23)~式(27)直接给出,最终参数见表1。
以后,谐振腔的参数可通过式(23)~式(27)直接给出,最终参数见表1。
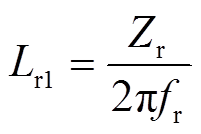 (23)
(23)
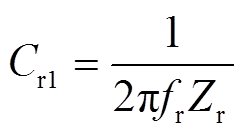 (24)
(24)
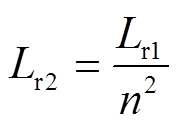 (25)
(25)
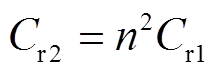 (26)
(26)
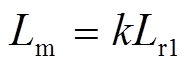 (27)
(27)
表1 CLLC变换器谐振腔参数
Tab.1 The parameters of prototype dual three-phase brushless permanent-magnet AC machine

参数设计值实际值 一次侧谐振电感Lr1/µH38.238.1 一次侧谐振电容Cr1/nF42.542.4 励磁电感Lm/µH229.3230.0 二次侧谐振电感Lr2/µH17.017.1 二次侧谐振电容Cr2/nF95.595.4
在计算出励磁电感后,应验证其设计值是否满足软开关条件。考虑逆变侧开关管的软开关的实现,需要有足够大的励磁电流峰值,使得积累在MOSFET寄生电容中的电荷能够在死区时间内完全释放,因此应满足[25]
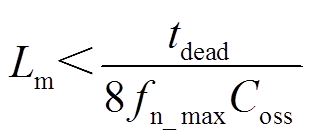 (28)
(28)
式中,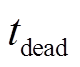 为死区时间;
为死区时间; 为运行时最大归一化频率;
为运行时最大归一化频率;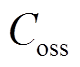 为开关管输出电容值。
为开关管输出电容值。
以C3M0075120K为例,数据手册输出电容为58pF,设定死区时间为200ns,则根据式(28)得到的励磁电感最大值为2.2mH,因此设计值满足软开关需求。
从上述设计过程可以看出,相较于基于基波分析的设计方法,本文提供的设计方法更加简洁高效,且由于文本方法所讨论的边界条件是直接以功率为依据的,因此能够适用于各类负载情况。
为验证参数设计的合理性,依据上述参数在Psim中进行了仿真,图13a是正向运行时固定变压器一次电压恒为600V不变,分别在输出恒5kW、3kW、1kW以及空载输出下的仿真增益曲线,可以看到实际的增益曲线符合预期,证明本文设计方法是有效的。同时,根据式(12),可以计算出理论上在0.8倍谐振频率处,CLLC变换器转入PbObNb运行的功率为6.8kW,实际的仿真功率为7kW左右,证明式(12)具有较高的准确性。
图13b是反向运行时固定变压器一次电压不变,分别在输出功率恒为5kW、3kW、1kW以及空载下的仿真增益曲线。对比CLLC变换器正、反向运行时的增益图可知,除空载外,反向运行时的增益陡度要比正向运行时低,这说明CLLC变换器虽然具有完全的对称性,但正反向运行时负载情况的不同,或者说控制目标的不同仍会使双向运行特性不对称。同时,根据式(13),可以计算出反向运行时,在0.8倍谐振频率处,使CLLC变换器转入PON运行的功率大小为5.5kW,实际的仿真功率为5.8kW左右。在恒5kW的输出功率下,转入PbObNb运行的归一化频率约为0.72。

图13 不同功率条件下样机的电压增益仿真结果
Fig.13 Simulation results of voltage gain of prototype under different power conditions
实验中,测试了CLLC变换器样机在正向运行时,分别在额定负载(Ro=32Ω)、半载(Ro=64Ω)及轻载(Ro=160Ω)时的电压增益。测试时,输入电压始终保持600V不变,实验增益与理论增益的对比结果如图14a所示。同样,反向运行时的增益曲线如图14b所示,负载电阻分别为72Ω、144Ω及360Ω,输入电压为400V不变。测量得到的实验结果与计算结果基本相符。
图15是满载正向运行时,最大增益点处的关键电压、电流波形,此时输出功率为5kW,输入电压为600V,输出电压为440V,实际工作频率约为94kHz,可以看到一次侧开关管实现了零电压开通,二次侧二极管为零电流关断。
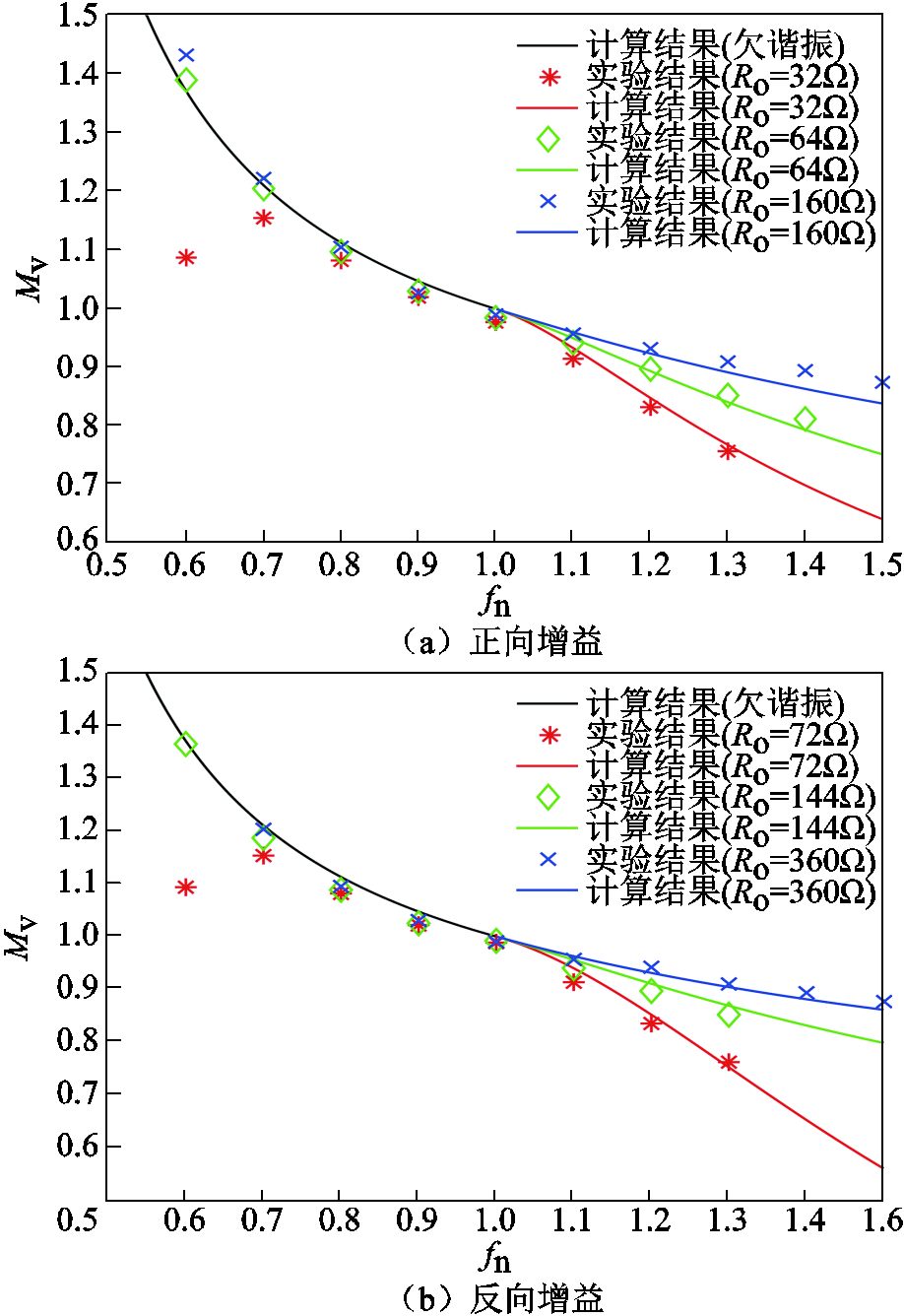
图14 实验得到的增益与本文方法计算得到的增益对比
Fig.14 Comparison between the gain obtained by experiment and the gain calculated according to the method in this paper
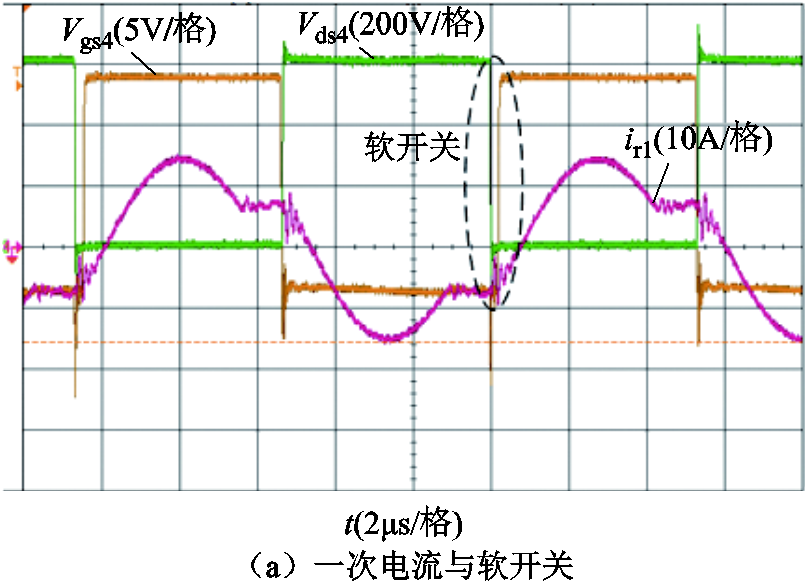
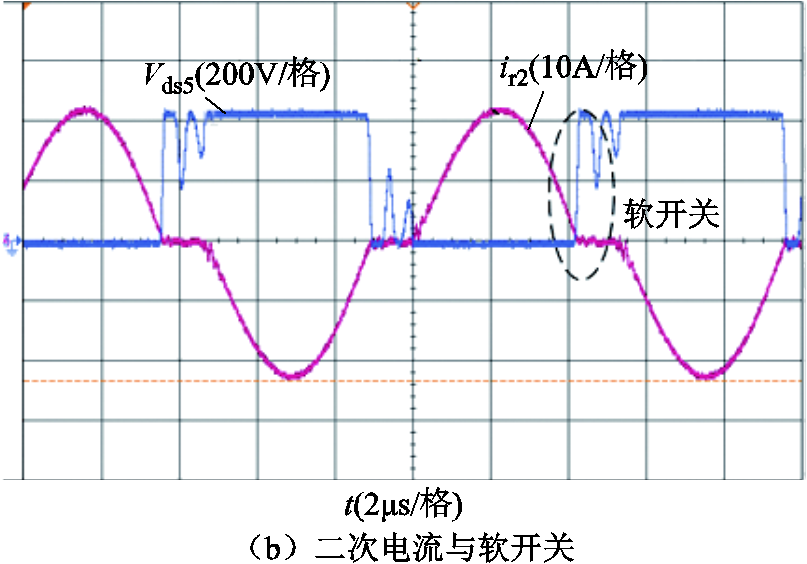
图15 样机在正向最大增益点运行时的关键波形
Fig.15 Key waveforms of the prototype running at the forward maximum gain point
图16是满载正向运行时,最小增益点处的关键电流波形,此时输出功率为5kW,输入电压为600V,输出电压为360V,实际工作频率约为142kHz。

图16 样机在正向最小增益点运行时的关键波形
Fig.16 Key waveforms of the prototype running at the forward minimum gain point
图17是满载反向运行时,最大增益点处的关键电压、电流波形,此时输出功率为5kW,输入电压为360V,输出电压为600V,实际工作频率约为95kHz,可以看到一次侧开关管实现了零电压开通,二次侧二极管为零电流关断。
图18是满载反向运行时,最小增益点处的关键电流波形,此时输出功率为5kW,输入电压为440V,输出电压为600V,实际工作频率约为135kHz。
图19给出了正、反向运行时,本样机在100kHz工作时的效率曲线,测试正向运行效率时,固定输入电压为600V,测试反向运行效率时,固定输入电压为400V。可以看到,由于应用了SiC材料且设计得当,本样机具有较高的效率。
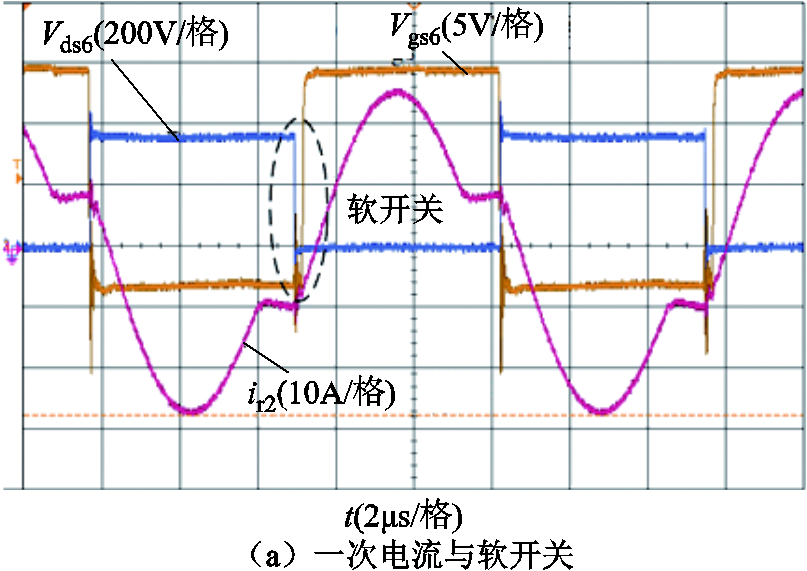
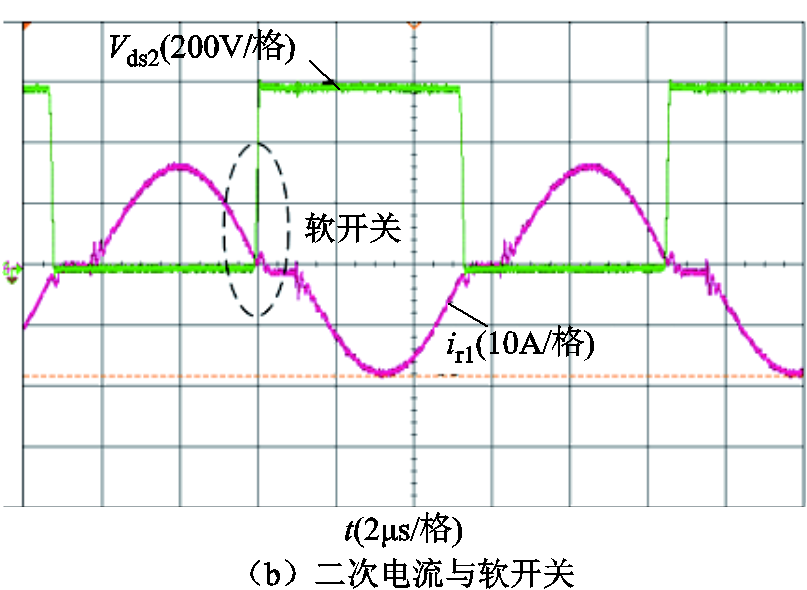
图17 样机在反向最大增益点运行时的关键波形
Fig.17 Key waveforms of the prototype running at the backward maximum gain point
图18 样机在反向最小增益点运行时的关键波形
Fig.18 Key waveforms of the prototype running at the backward minimum gain point
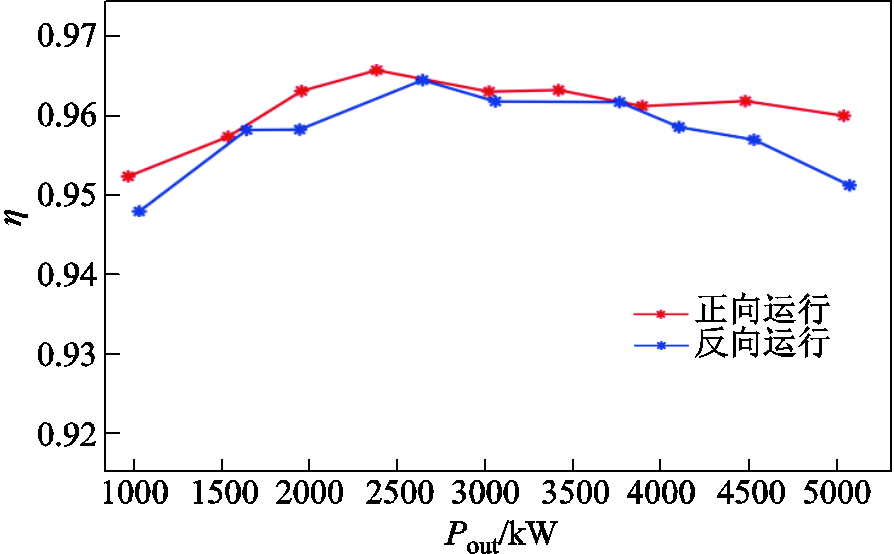
图19 样机工作在100kHz时不同输出功率下的效率曲线
Fig.19 Efficiency curve of the prototype under different output power conditions when working at 100kHz
本文提出了一种双向CLLC谐振型DC-DC变换器的简化时域模型,分析了参数设计所需要的电压增益与边界条件,获得了更为简洁且适用性更广的公式,总结了一套完整的设计方法并依据此设计了一台CLLC变换器样机,仿真和实验的结果均证明了该方法的有效性。
1. 励磁电流峰值Impeak和电压增益MPO的推导过程。
以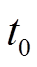 时刻为起点,根据图5可写出谐振电感电流与谐振电容电压的表达式为
时刻为起点,根据图5可写出谐振电感电流与谐振电容电压的表达式为
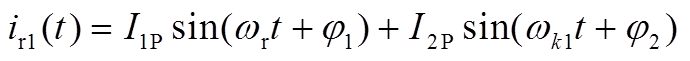 (A1)
(A1)
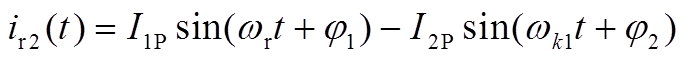 (A2)
(A2)
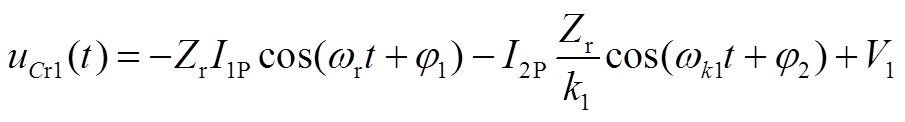 (A3)
(A3)
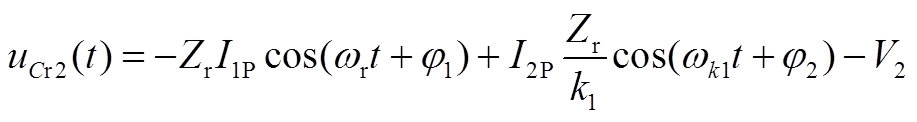 (A4)
(A4)
式中, 为谐振角频率,且
为谐振角频率,且 ;Zr为特征阻抗;系数
;Zr为特征阻抗;系数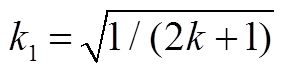 ;ωk1=k1ωr;I1P、I2P、
;ωk1=k1ωr;I1P、I2P、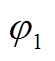 、
、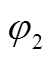 为未知量。
为未知量。
则励磁电流可以表示为
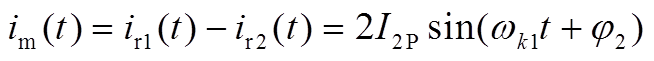 (A5)
(A5)
根据电流的对称性有
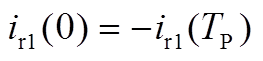 (A6)
(A6)
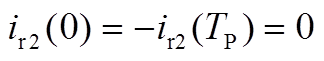 (A7)
(A7)
代入到式(A1)、(A2)中,解得
 (A8)
(A8)
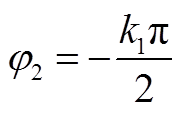 (A9)
(A9)
根据假设,励磁电流在TP时刻到达峰值,并在Ob模态中保持恒定,结合式(A5)、式(A8)、式(A9),励磁电流的峰值可以表示为
 (A10)
(A10)
根据电容电压的对称性有
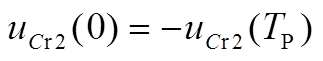 (A11)
(A11)
结合式(A4)、式(A5)、式(A8)、式(A9)、式(A10)、式(A11)可以得到
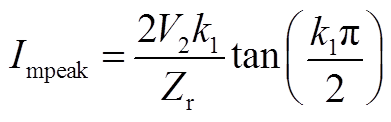 (A12)
(A12)
同时,电容电压的和在半个周期内具有关系式
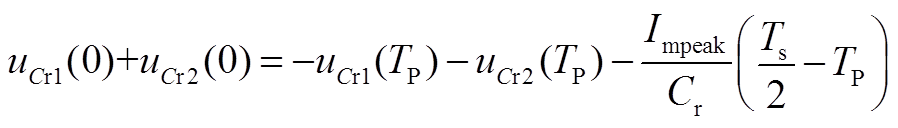 (A13)
(A13)
结合式(A3)、式(A4)、式(A8)、式(A13)得到
 (A14)
(A14)
联立式(A12)、式(A14),得到电压增益的表达式为
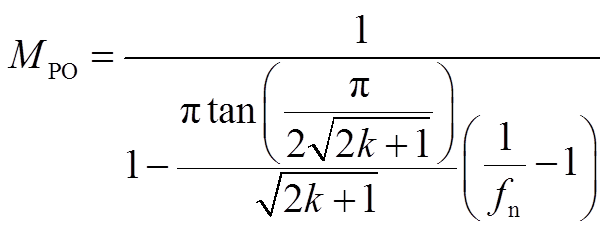 (A15)
(A15)
2. Zr的设计推导过程
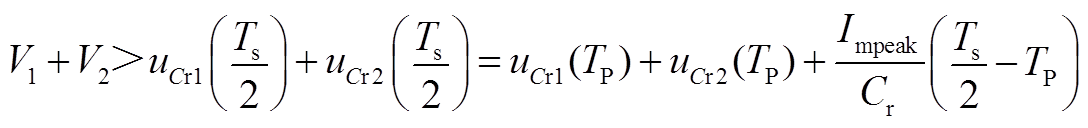 (A16)
(A16)
结合式(A3)、式(A4)、式(A8)、式(A9)、(A14)、(A16)得到
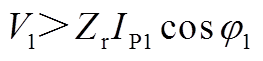 (A17)
(A17)
根据电荷守恒有
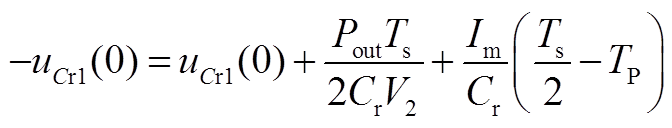 (A18)
(A18)
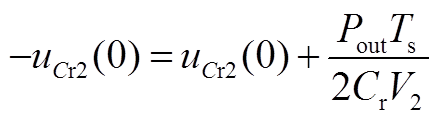 (A19)
(A19)
式中,Pout为输出功率。结合式(A3)、式(A4)、式(A8)、式(A9)、式(A14)、式(A18)、式(A19)可以得到关系式
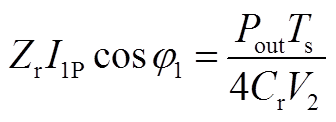 (A20)
(A20)
结合式(A17)、式(A20),化简得到
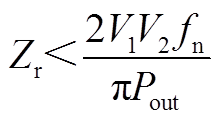 (A21)
(A21)
3. 空载电压增益Mno_1oad的推导过程
 (A22)
(A22)
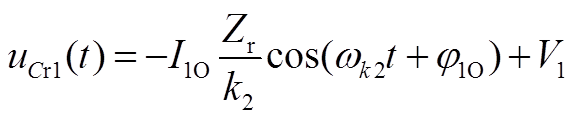 (A23)
(A23)
式中,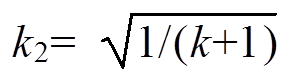 ;ωk2=k2ωr、I1O、φ1O为待求量。
;ωk2=k2ωr、I1O、φ1O为待求量。
根据半个周期内电流的对称性有
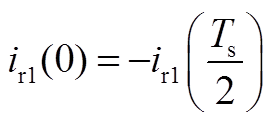 (A24)
(A24)
联立式(A22)、式(A24)解得
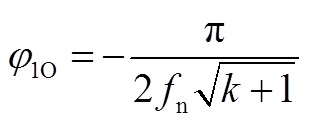 (A25)
(A25)
而根据电容电压得对称性有
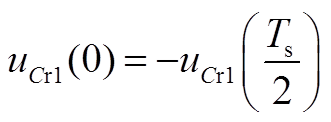 (A26)
(A26)
结合式(A23)、式(A26)可以得到
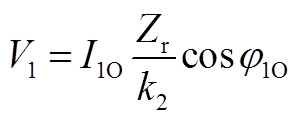 (A27)
(A27)
同时,励磁电感电压又为
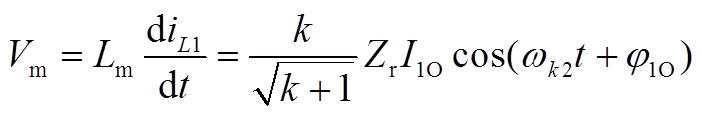 (A28)
(A28)
式(A28)表明,空载情况下励磁电感电压呈现正弦形式,若忽略整流侧二极管压降,假设变换器的空载电压是缓慢建立的,结合变压器二次电压为0可以推知,输出电压应该等于励磁电感电压在半个周期内的最大值,因此有
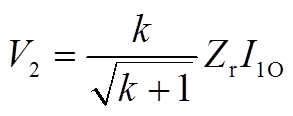 (A29)
(A29)
结合式(A27)、式(A29)可以得到空载电压增益为
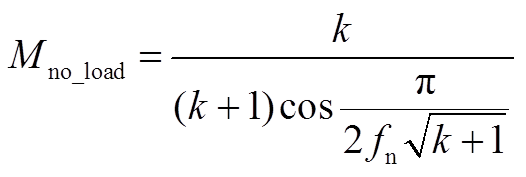 (A30)
(A30)
4. NbPb模式电压增益MNP的推导过程
以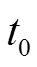 时刻为起点,根据图10可写出谐振电感电流与谐振电容电压的表达式为
时刻为起点,根据图10可写出谐振电感电流与谐振电容电压的表达式为
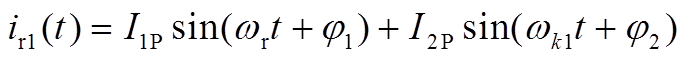 (A31)
(A31)
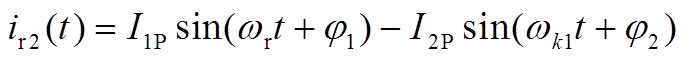 (A32)
(A32)
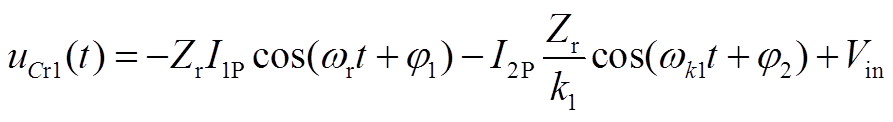 (A33)
(A33)
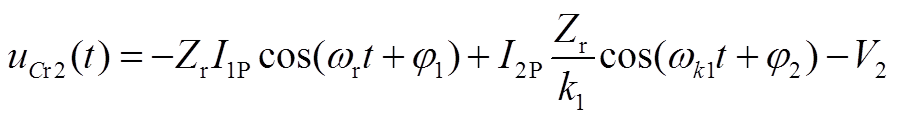 (A34)
(A34)
励磁电流的表达式为
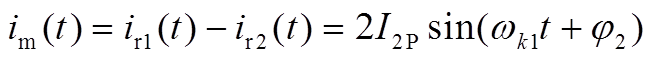 (A35)
(A35)
根据励磁电流的对称性有
 (A36)
(A36)
结合式(A35)、式(A36)得到
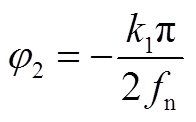 (A37)
(A37)
在初始时刻二次电流为零,因此可以得到
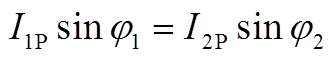 (A38)
(A38)
根据假设,谐振电容的电压在半个开关周期内应是正负对称的,因此有
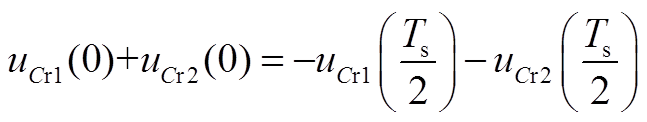 (A39)
(A39)
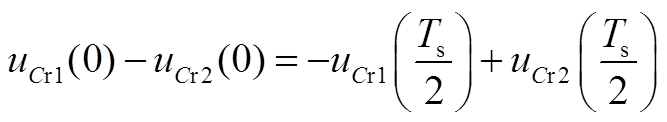 (A40)
(A40)
从式(A39)、式(A40)推知
 (A41)
(A41)
 (A42)
(A42)
输出电流等于半个周期内二次电流的平均值,因此
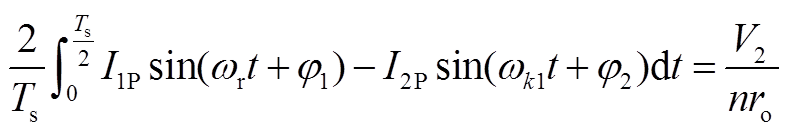 (A43)
(A43)
联立式(A38)、式(A41)、式(A42)、式(A43)整理得到
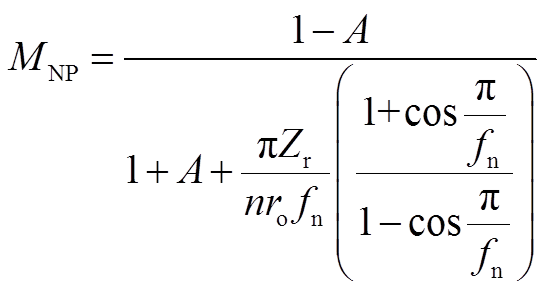 (A44)
(A44)
其中
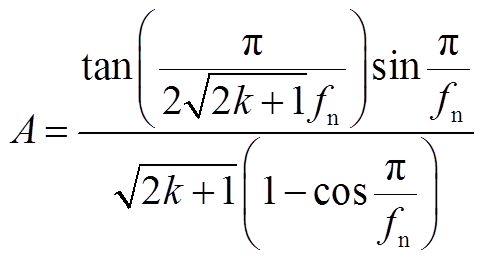 (A45)
(A45)
参考文献
[1] 雷志方, 汪飞, 高艳霞, 等. 面向直流微网的双向 DC-DC变换器研究现状和应用分析[J]. 电工技术学报, 2016, 31(22): 137-147.
Lei Zhifang, Wang Fei, Gao Yanxia, et al. Research status and application analysis of bidirectional DC-DC converters in DC micro-grids[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 137-147.
[2] 师长立, 唐西胜, 李宁宁, 等. 基于全桥隔离双向变换器的直流变换技术[J]. 电工技术学报, 2016, 31(2): 121-127.
Shi Changli, Tang Xisheng, Li Ningning, et al. DC charging technologies based on dual-active-bridge converter[J]. Transaction of China Electrotechnical Society, 2016, 31(2): 121-127.
[3] 杨超, 许海平, 袁志宝, 等. 双PWM控制下三电平半桥隔离型双向DC-DC变换器的全局最小峰值电流研究[J]. 电工技术学报, 2020, 35(8): 1679-1689.
Yang Chao, Xu Haiping, Yuan Zhibao, et al. Global minimum peak current control of the three level isolated half-bridge bi-directional DC-DC converters with PWM-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1679-1689.
[4] Zou S, Lu Jiangheng, Mallik A, et al. 3.3kW CLLC converter with synchronous rectification for plug-in electric vehicles[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 998-1005.
[5] 王朝强, 曹太强, 郭筱瑛, 等. 三相交错并联双向DC-DC变换器动态休眠控制策略[J]. 电工技术学, 2020, 35(15): 3214-3223.
Wang Chaoqiang, Cao Taiqiang, Guo Xiaoying, et al. Dynamic dormancy control strategy of three-phase staggered parallel bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3214-3223.
[6] Deng Junjun, Ji Siqi, Hu Sideng, et al. Design methodology of LLC resonant converters for electric vehicle battery chargers[J]. IEEE Transactions on Vehicular Technology, 2014, 63(4): 1581-1592.
[7] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.
Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.
[8] 杨玉岗, 赵金升. 高增益对称双向LCLC谐振变换器的研究[J]. 电工技术学报, 2020, 35(14): 3007-3017.
Yang Yugang, Zhao Jinsheng. Research on high-gain symmetric bidirectional LCLC resonant converter[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3007-3017.
[9] 杨超, 许海平, 张祖之, 等. PWM 与移相结合控制下的混合三电平隔离型双向DC-DC最小回流功率控制研究[J]. 电工技术学报, 2019, 34(15): 3186-3197.
Yang Chao, Xu Haiping, Zhang Zuzhi, et al. Minimum backflow power control of the hybrid three level isolated bidirectional DC-DC converters based on pwm-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3186-3197.
[10] Musavi F, Craciun M, Gautam D S, et al. An LLC resonant DC-DC converter for wide output voltage range battery charging applications[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5437-5445.
[11] Chang C H, Chang E C, Cheng H L. A high-efficiency solar array simulator implemented by an LLC resonant DC-DC converter[J] . IEEE Transactions on Power Electronics, 2013, 28(6): 3039-3046.
[12] Pledl G, Tauer M, Buecherl D. Theory of operation, design procedure and simulation of a bidirectional LLC resonant converter for vehicular applications[C]// IEEE Vehicle Power and Propulsion Conference, Lille, 2010: 1-5.
[13] Jung J, Kim H, Ryu M, et al. Design methodology of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1741-1755.
[14] 陈启超, 纪延超, 王建赜. 双向 CLLLC 谐振型直流变压器的分析与设计[J]. 中国电机工程学报, 2014, 34(18): 2898-2905.
Chen Qichao, Ji Yanchao, Wang Jianze. Analysis and design of bidirectional CLLLC resonant DC-DC transformers[J]. Proceedings of the CSEE, 2014, 34(18): 2898-2905.
[15] 冯元彬. 基于SiC器件的双向谐振型DC-DC变换器的研究与开发[D]. 广州: 华南理工大学, 2019.
[16] 陈启超, 王建赜, 纪延超. 双向LLC谐振型直流变压器的软启动及功率换向控制[J]. 电工技术学报, 2014, 29(8): 180-186.
Chen Qichao, Wang Jianze, Ji Yanchao. Control scheme of bidirectional LLC resonant DC-DC transformer for soft start and power conversion[J]. Transaction of China Electrotechnical Society, 2014, 29(8): 180-186.
[17] Lü Zheng, Yan Xiangwu, Fang Yukang, et al. Mode analysis and optimum design of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems[C]//2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 1513-1520.
[18] Fang Xiang, Hu Haibing, Shen Z J, et al. Operation mode analysis and peak gain approximation of the LLC resonant converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1985-1995.
[19] 肖文英, 董海兵. 全桥LLC谐振变流器的简化时域模型及其应用[J]. 华东师范大学学报(自然科学版), 2013(5): 119-129.
Xiao Wenying, Dong Haibing. Simplified time domain model of full-bridge LLC resonant converter and its application[J]. Journal of East China Normal Univrsity(Natural Science), 2013(5): 119-129.
[20] 刘硕, 苏建徽, 赖纪东. LLC谐振变换器PO模式增益公式与模式边界条件分析[J]. 电力系统自动化, 2020, 44(6): 164-172.
Liu Shuo, Su Jianhui, Lai Jidong. Analysis on gain formula and mode boundary condition for LLC resonant converter in PO mode[J]. Automation of Electric Power Systems, 2020, 44(6): 164-172.
[21] 孙文进. 隔离型宽增益范围谐振变换器[D]. 南京: 南京航空航天大学, 2018.
[22] 赵烈, 裴云庆, 刘鑫浩, 等. 基于基波分析法的车载充电机CLLC谐振变换器参数设计方法[J]. 中国电机工程学报, 2020, 40(15): 4965-4977.
Zhao Lie, Pei Yunqing, Liu Xinhao, et al. Design methodology of CLLC resonant converters for electric vehicle battery chargers[J]. Proceedings of the CSEE, 2020, 40(15): 4965-4977.
[23] 王菲菲. 双向车载充电机中宽范围CLLC变换器的研究与设计[D]. 杭州: 浙江大学, 2019.
[24] 吕正, 颜湘武, 孙磊, 等. 基于变频-移相混合控制的L-LLC谐振双向DC-DC变换器[J]. 电工技术学报, 2017, 32(4): 12-24.
Lü Zheng, Yan Xiangwu, Sun Lei, et al. A L-LLC resonant bidirectional DC-DC converter based on hybrid control of variable frequency and phase shift[J]. Transactions of China Electrotechnical Society, 2017. 32(4): 12-24.
[25] 冒小晶. 基于 LLC 谐振变换器的高压母线变换器的研究[D]. 南京: 南京航空航天大学, 2012.
Parameter Design Method of CLLC DC-DC Converter Based on Simplified Time Domain Model
Abstract The resonant cavity parameters design of CLLC DC-DC converter is the guarantee of its stable operation, but the existing design method based on first harmonic approximation (FHA) can not achieve accuracy and efficiency. From the point of view of design, this paper firstly analyzed the limitation of FHA. Then, based on the results of time domain analysis of CLLC DC-DC converter, a simplified time domain model of CLLC DC-DC converter was established by reasonably simplifying the waveforms. The gain formula and boundary conditions were derived and the design basis under different load conditions was discussed. The design formulas obtained by this method were simple and accurate, which greatly simplify the design process. On this basis, this paper presented a complete design process and a 5kW CLLC DC-DC converter prototype was made. The simulation and experimental results proved the correctness of the theory.
keywords:CLLC converter, parameter design of resonator, simplified time domain model
DOI: 10.19595/j.cnki.1000-6753.tces.210257
中图分类号:TM46
广东省重点领域研发计划资助项目(2019B090911001)。
收稿日期 2021-03-01
改稿日期 2021-07-12
赵子先 男,1997年生,硕士研究生,研究方向为电力电子变换器及其控制技术。E-mail:epscut_zzx@mail.scut.edu.cn(通信作者)
康龙云 男,1961年生,博士,教授,研究方向为电力电子技术在新能源、电动汽车驱动中的应用。E-mail:lykang@scut.edu.cn
(编辑 郭丽军)