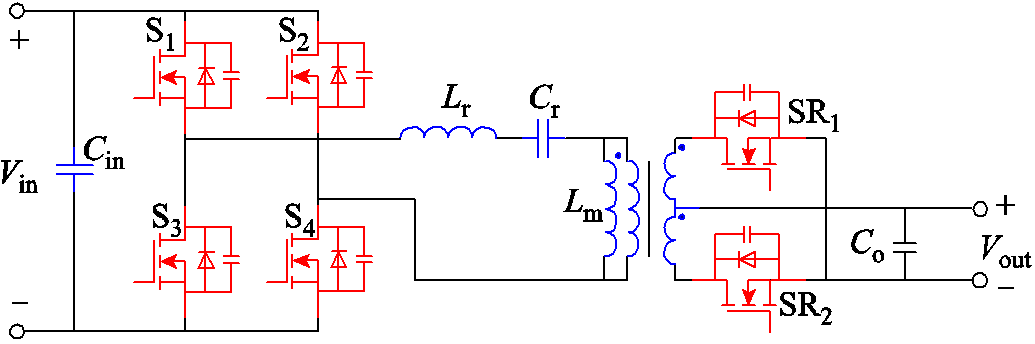
图1 LLC谐振变换器拓扑结构
Fig.1 Topology of LLC converter
摘要 针对LLC谐振变换器工作在高频条件下对平面变压器寄生电容较为敏感的问题，采用磁集成技术对变压器的二次绕组进行优化设计，使得变压器寄生电容和绕组涡流损耗的综合效果最优。该文对平面变压器层间寄生电容的影响因素进行了具体分析，在极坐标系下建立变压器寄生电容的数学模型，并归纳出各影响因素在不同电流情况下的作用效果。该文提出了两种绕组形状的优化设计方案，从减小绕组正对面积的角度改善变压器的寄生电容。利用有限元仿真软件Maxwell，搭建变压器的3D仿真模型，根据仿真结果对比了采用不同优化方案时寄生电容的改善效果，验证了理论分析的可靠性。为了兼顾变换器的寄生电容和涡流损耗，给出了绕组面积设计的优化范围，并确定了最终的优化方案。最后，采用改良后的磁集成平面变压器，搭建了一台500W的样机，效率最高可达97.53%。
关键词：谐振变换器 寄生电容 平面变压器 磁集成 优化设计
依托合理的参数设计，LLC变换器可以同时实现一次侧开关的零电压开通（Zero Voltage Switch, ZVS）和二次侧整流器件的零电流关断（Zero Current Switch, ZCS），具有良好的软开关特性，适用于高频应用场景。然而，该变换器主拓扑的磁性元件数量较多，使用传统分立磁件的LLC谐振变换器难以满足高效高功率密度的技术要求[1-2]。
为此，文献[3]对变压器的结构进行改进，首次提出了矩阵变压器的概念。在此基础上，文献[4]依据磁通抵消原理，将多个分立的平面变压器集成到单个磁心上，显著减小了磁心体积，提高了变换器的功率密度。针对低压大电流的输出场合，文献[4]中的变压器采用一次侧串联和二次侧多匝并联的连接方式，一次侧的串联结构自然实现了各变压器单元二次电流的均分。由于变换器输出电流很大，将4个相同的同步整流管并联使用，进一步降低了整流器件的导通损耗。为了减小漏感和端接损耗，文献[5]把二次绕组置于顶层和底层，将同步整流管和输出电容集成在二次绕组上，最大程度地缩短了二次侧的交流回路，同时将相关的交流损耗降到最低。文献[6]考虑到输入大电流的情况，基于3:1的特殊匝比，提出了一种矩阵变压器一次、二次绕组合并的设计方法，有效地缓解了高频效应引起的电流不均现象。此外，文献[6]提出并验证了变压器终端和过孔交错的概念，进一步改善了多层绕组并联电流不均的现象。文献[7]将矩阵变压器的绕组等效成圆环形，建立了变压器绕组直流电阻模型，并通过求导得出绕组的最佳宽度。但是，上述文献均没有考虑平面变压器因绕组正对面积较大而产生较大的寄生电容，以及寄生电容对变换器电磁干扰（Electromagnetic Interference, EMI）特性造成的影响。
为了缓解绕组间寄生电容带来的不良影响，本文在上述文献的基础上，给出了一种应用于LLC谐振变换器的平面变压器绕组形状优化设计方法。首先基于磁集成的思想，确立了变压器的磁心结构和绕组排布。为了探究多种因素对绕组层间寄生电容的影响，根据变压器的实际结构，采用微元法建立寄生电容的等效模型，推导出不同电流情况下的公式。接着从减小一次、二次绕组正对面积的角度考虑，提出了两种基于绕组形状的优化设计方法。结合磁仿真，对比了不同形状绕组的寄生电容改善效果。为了兼顾变换器的寄生电容和涡流损耗，本文给出了绕组面积设计的优化范围，确定了最终采用的绕组优化方案。最后，搭建了一台500W的样机，给出了实验波形，变换器能够实现软开关，具有较高的变换效率。
本文采用的拓扑结构如图1所示，谐振型LLC变换器主要包括逆变桥、谐振腔、变压器和全波整流四部分[8]。
图1 LLC谐振变换器拓扑结构
Fig.1 Topology of LLC converter
LLC变换器的谐振腔是由串联谐振电感Lr、谐振电容Cr、励磁电感Lm组成的三元件谐振网络。根据Lm是否参与谐振，分别定义了变换器的串联谐振频率fr和并联振频率fm[9]。
LLC谐振变换器采用变频控制。为了充分利用拓扑的软开关特性，保证变换器具有较高的变换效率，LLC变换器的额定工作频率fs通常被设计在fm和fr之间。除此之外，通过调节气隙长度，变压器的励磁电感可代替Lm；变压器一次侧产生的漏感Ll1可作为Lr的一部分参与谐振[10]，进一步提高了变换器的效率。
综上所述，LLC变换器具有高频高效率小型化的应用潜力，但是随着工作频率的不断提升，对变压器等磁性元件的性能提出了更高的要求。
隔离变压器是LLC拓扑的核心部件之一，在高频应用时，其磁心和绕组受趋肤效应、邻近效应、涡流效应等高频效应的不利影响而越发显著，导致变换器的变换效率和工作稳定性降低[11]。
矩阵变压器的磁心集成如图2所示，文献[3]基于磁集成技术与磁通抵消原理，提出了一种典型的四柱矩阵变压器，能够有效地降低磁心损耗，有助于提高变换器的功率密度。
此外，集成后的变压器的高度对称结构降低了变压器的制作难度，使得各矩阵变压器的参数方差更小，避免了因制作工艺欠缺造成的电量不均问题[12-13]。
本文设计的拓扑额定功率为500W，额定输入电压、输出电压分别为220V和55V。采用矩阵变压器的LLC变换器电路如图3所示，为了使变换器工作在额定频率附近时对应输出额定电压，同时保持较高的变换效率，变压器匝比为4:1:1，并采用矩阵变压器的概念[8]进行设计。为避免磁心饱和，实际匝数比为8:2:2。L1g1～L1g4为4个变压器的满感。
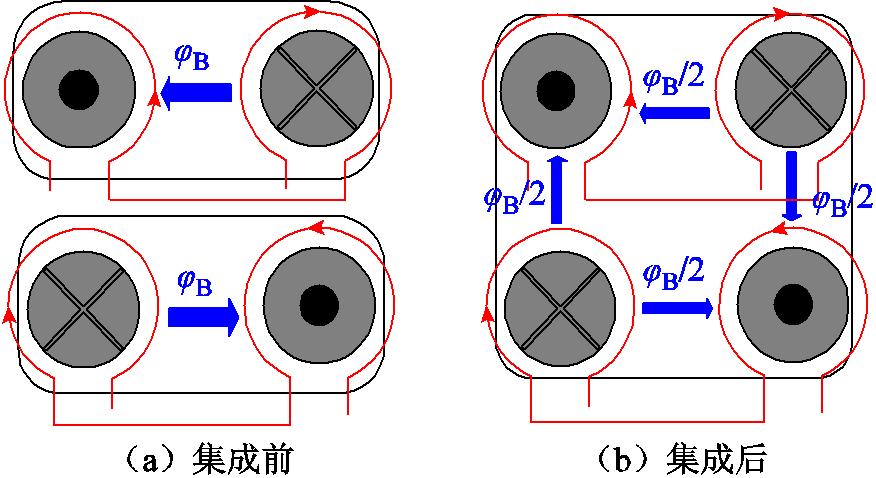
图2 矩阵变压器的磁心集成
Fig.2 Integrated magnetic structure
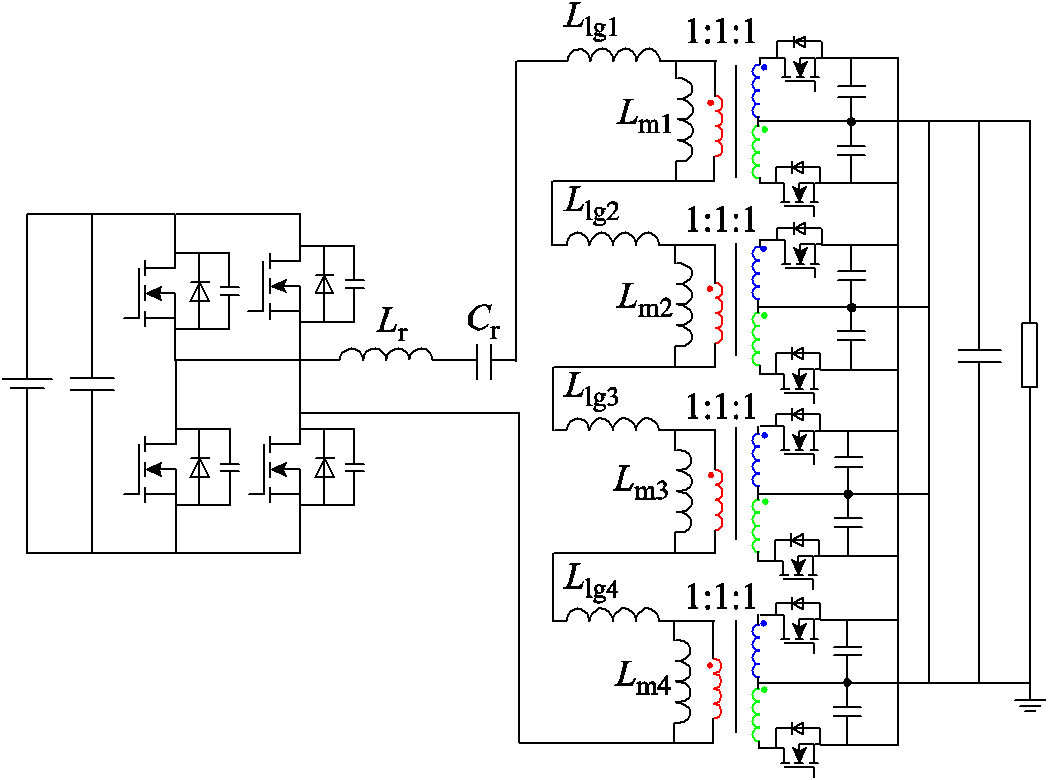
图3 采用矩阵变压器的LLC变换器电路
Fig.3 Circuit diagram of LLC converter with the proposed magnetic design
综上所述，变压器的绕组排布和磁心结构如图4所示。绕组共占用6层印制电路板（Printed circuit Board, PCB），其中一次绕组置于顶层和底层，中间四层为二次绕组，层与层之间通过过孔相连。
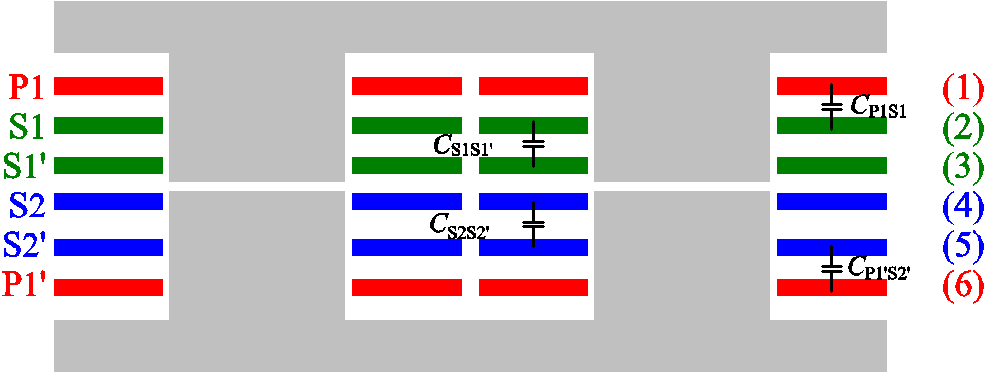
图4 6层PCB绕组变压器的剖面图
Fig.4 Cross-section view of 6 layers PCB transformer
矩阵变压器的绕组排布如图5所示。图5a中箭头代表变换器正半周期的电流流向。图5b以变压器单元TR1为例，说明变压器二次绕组的连接方式。二次电流从“A”点流入，第2、第3层绕组通过“B”点的过孔串联，“C”点外层与中心抽头连接，再与第4层的绕组串联。第4、第5层绕组的连接方式与第2、第3层相同。
图5 矩阵变压器的绕组排布
Fig.5 Winding arrangement of the proposed matrix transformer
寄生电容反映了绕组间因电势差产生的电场强度[14]。对LLC谐振变换器来说，寄生电容的存在不仅损害变换器的EMI特性，还会与电路中的感性元件发生谐振，使得电压、电流波形畸变严重，影响变换器的电能传输和工作效率[15]。为此，本文对变压器绕组层间的寄生电容进行建模，分析了层间寄生电容的影响因素，并从绕组的开口方向和绕组形状两个角度优化了变压器的绕组设计，以达到优化变压器层间寄生电容的目的。
从分析变换器共模噪声的角度，定义集总电容Clump用来表征一次、二次侧寄生电容Cps[16]。高频变压器电容模型如图6所示。
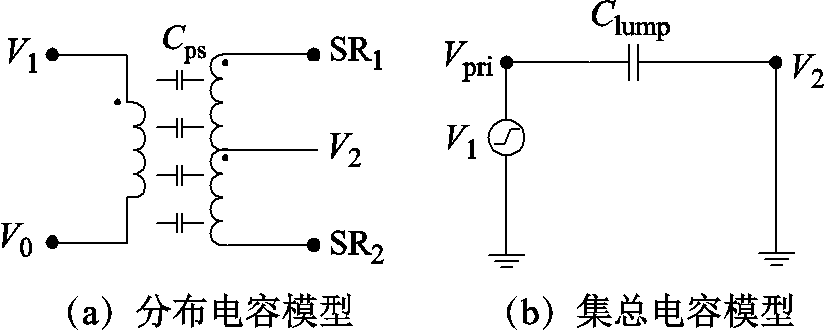
图6 高频变压器电容模型
Fig.6 Capacitance model of high frequency transformer
基于共模噪声推导出的Clump和Cps的关系为
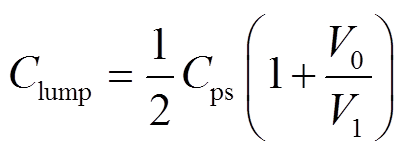（1）
式中，V1、V0分别为变压器一次侧两端口的高、低电位。
通过建立变压器集总电容模型分析一次、二次侧寄生电容Cps能够降低模型的复杂程度，却无法直观地表达出绕组的设计参数对寄生电容的影响，也无法对应到具体的绕组层。
由于平面变压器绕组的面积很大，其上所覆的铜箔阻碍了变压器的电场耦合，因此只需对相邻两层绕组间的寄生电容进行分析。根据图4所示的绕组排布，本文采用的平面变压器的层间寄生电容包括二次绕组层间电容CS1S1′、CS2S2′、一次、二次绕组层间寄生电容CP1S1、CP1′S2′，其他层绕组间的寄生电容则忽略不计。所以上述计算一次、二次侧寄生电容CPS的方法对本文设计的变压器并不适用。
理想电容器的上、下两极板间的电场是均匀的，电场储存的能量为
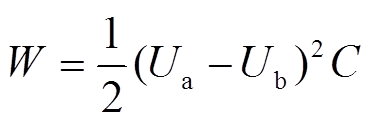（2）
式中，Ua、Ub分别为上、下极板的电势；C为电容值，满足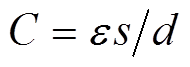
，ε、s、d分别为极板间介质的相对介电常数、极板间正对面积和距离。
而平面变压器的绕组电压沿电流方向降低，显然计算相邻层绕组间的寄生电容时并不能简单地将绕组当成等势体处理，而且不同层绕组的开口角度、绕制方向等差异使得实际情况更加复杂。
由图5可知，产生CS1S1′、CS2S2′的两层绕组流过的电流方向相同；产生CP1S1、CP1′S2′的两层绕组流过电流方向相反。特别地，图中点画线圈出的位置，上层二次绕组S2′对应的下层一次绕组P1′包含了一次侧激励的进出口。因此出现了上层一匝二次绕组正对着下层两段一次绕组的情况。由于CP1S1、CP1′S2′都属于两极板电流相反的情况，区别在于对应的变压器两组相邻绕组出头的角度差并不相等，可以归为一类计算。
根据上述分析，共需要分三种情况建立绕组层间寄生电容模型：单匝同向电流、单匝反向电流和多段单匝反向电流，分别用来分析CP1S1、CP1′S2′，CS1S1′、CS2S2′和CP1′S2′中包含一次电流进出口的特殊情况。
为了简化分析，假设每层绕组的电位沿电流方向均匀分布，即将绕组形状等效为外径为R，内径为r的圆环，每层绕组之间的电位的相互影响忽略不计。将上、下两层绕组放在同一极坐标系下，以角度θ为变量，建立极坐标系。并在该坐标系下分别建立上述三种情况下的变压器绕组层间寄生电容模型。
如图5点画线位置，将变压器一次侧进出口处的绕组标注为P0，P0包含两段绕组，引入参数α表示一次侧激励从流进第6层绕组流经第一组过孔Via1产生的压降比，一次侧的其余7匝绕组以实际电流流向按顺序标注成P1～P7，二次绕组定义为S1、S2。绕组对应的电位示意图如图7所示，定义变压器一次、二次侧的两端电位分别为UA′、UB′和UC′、UD′，一次侧的第n匝绕组两端的高、低电位分别为UAn、UBn(n=1,×××, 7)，二次侧中心抽头一侧的第m匝绕组两端电位分别为UCm、UDm(m=1, 2)。
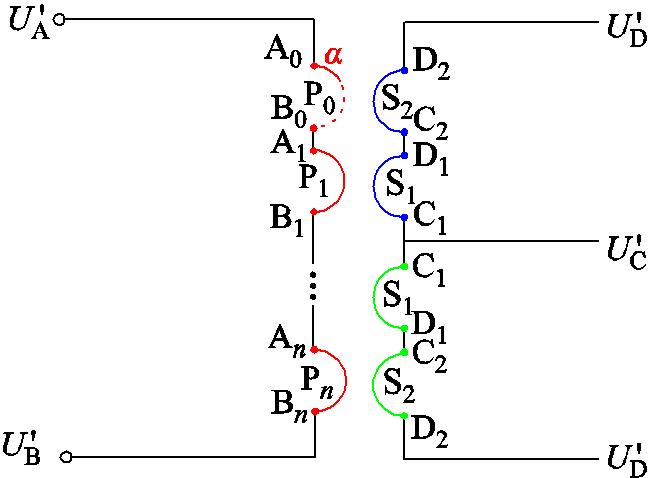
图7 变压器每匝电位示意图
Fig.7 Schematic diagram of the proposed transformer across each winding
上文提到每个变压器单元的匝比都是1:1:1，同时每匝绕组两端的电压差都相同，根据绕组的连接方式可得
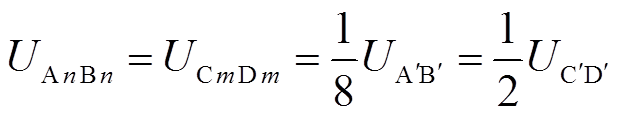（3）
第n匝绕组Pn的高电位UAn为
（4）
同理，第m匝绕组Sm的高电位UCm为
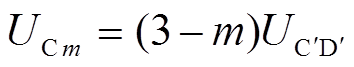m=1,2 （5）
P0包含两段绕组，两端电压差表达式为
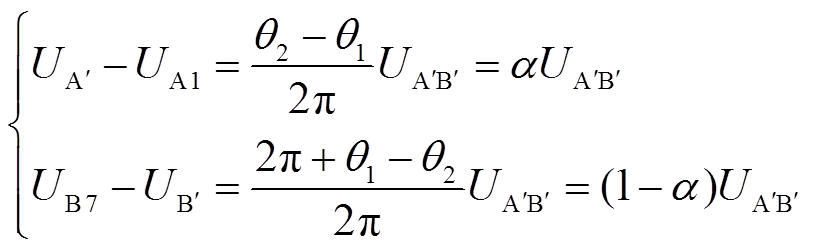（6）
以任意两匝正对的两层相邻一次、二次绕组为例，相邻一次、二次绕组层间寄生电容如图8所示。流过相邻两层一次、二次绕组的电流方向相反，以绕组中心为坐标原点、下层一次绕组的高电位UAn所在位置为初始位置、θ为极角，建立如图8所示的极坐标系，图中实线、虚线箭头的方向分别代表两层绕组的电流方向。
下层一次绕组的瞬时电位的表达式为
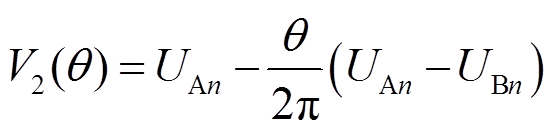（7）
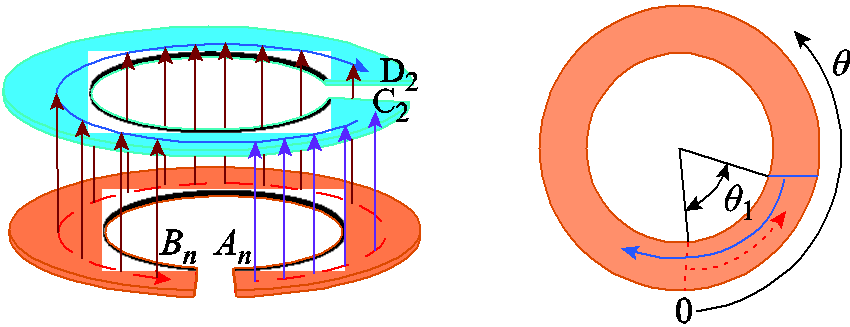
图8 相邻一次、二次绕组层间寄生电容
Fig.8 Parasitic capacitance between adjacent primary and secondary windings
由于实际一次、二次绕组的开口位置并不完全对应，定义该角度差为θ1，可得上层的二次绕组电位V1(θ)为
（8）
结合式（3）～式（5）化简式（6）、式（7），得到
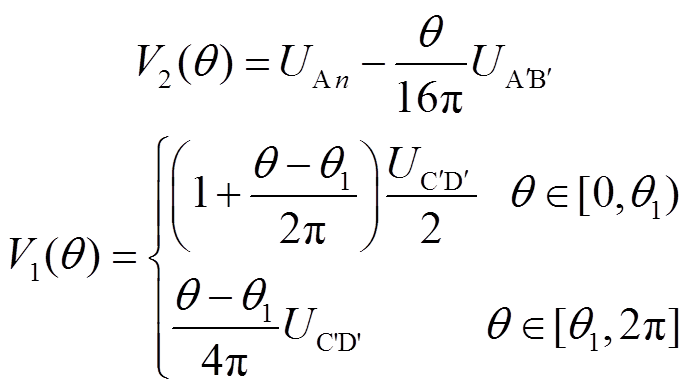（9）
两层绕组的电位差可表达成
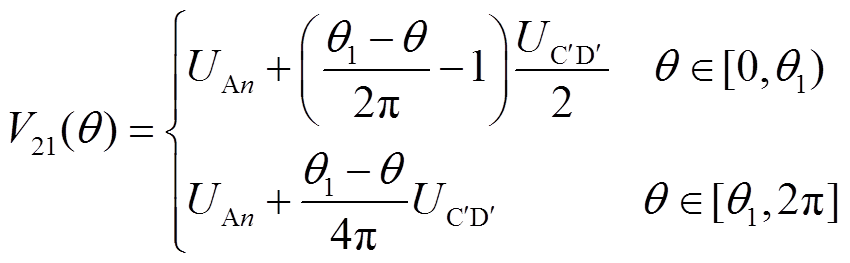（10）
每个变压器单元的二次绕组两端都被输出电容钳位，即UC′=Uo，UD′=0，UC′D′=Uo。根据式（7）和式（10）绘出两层绕组匝间的电位差图，如图9所示。
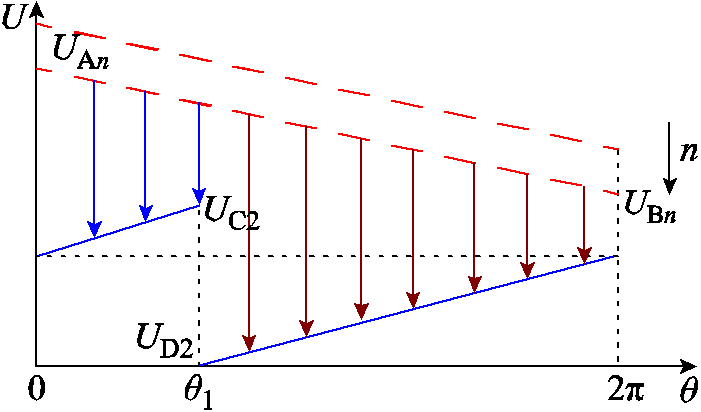
图9 一次绕组与相邻层二次绕组之间的压降
Fig.9 Voltage potential between primary winding and its adjacent secondary winding
从图9中可以直观地看出,两层绕组对应的各匝间绕组寄生电容处于不均衡的状态，越靠近高电位的一次绕组和对应的相邻二次绕组的层间寄生电容越大；绕组出口的角度差也对电位差有较大的影响。理想的绕组设计是保证一次、二次侧出口位置完全正对，即θ1为0。但是一次、二次侧出口正对会使得器件排布较为困难，造成严重的端接损耗。
以同样的方法分析相邻二次绕组间寄生电容，推导过程在此不再赘述。极坐标系下二次绕组层间寄生电容模型如图10所示，相邻二次绕组电流方向一致，对任一角度θ，上、下两层的电位差表达式为
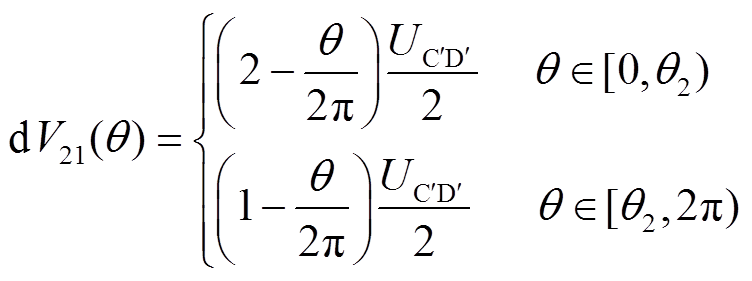（11）
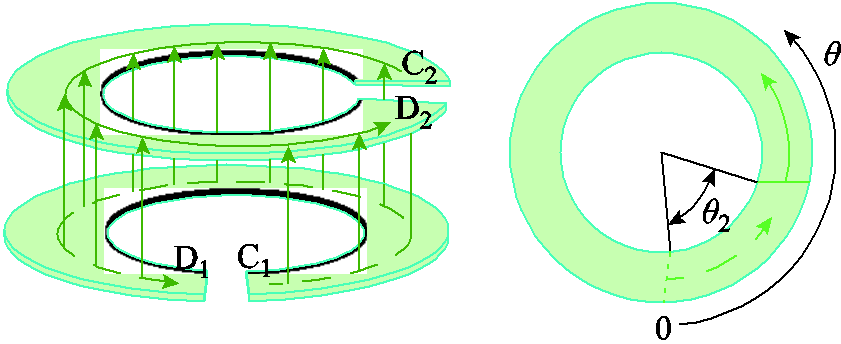
图10 极坐标系下二次绕组层间寄生电容模型
Fig.10 Parasitic capacitance between adjacent secondary windings
根据式（11）做出相邻两层一次、二次绕组的电位差，如图11所示。
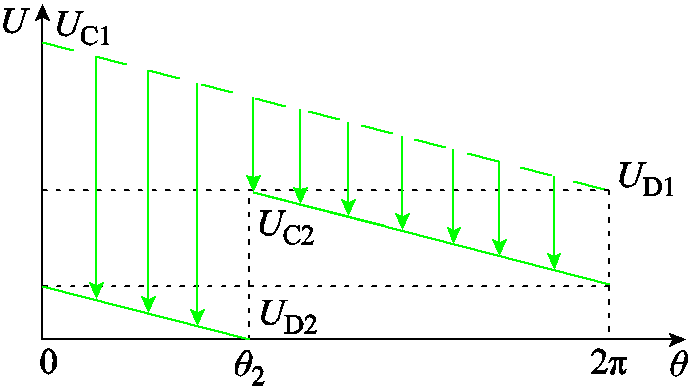
图11 二次绕组与相邻层二次绕组之间的压降
Fig.11 Voltage potential between adjacent secondary windings
从图11可直观地看出，与相邻一次、二次绕组间寄生电容不同，绕组出口处的角度差θ2越大，相邻二次绕组间寄生电容Css反而越小。角度θ2实际与绕组端口宽度有关，为了满足图6中二次绕组的连接形式，各层二次绕组端口的宽度相等，θ2的值是固定不变的。因此，无法通过改变角度改善寄生电容的不利影响。
最后考虑一层二次绕组对应下层两段一次绕组的情况，分析方法与上节类似。
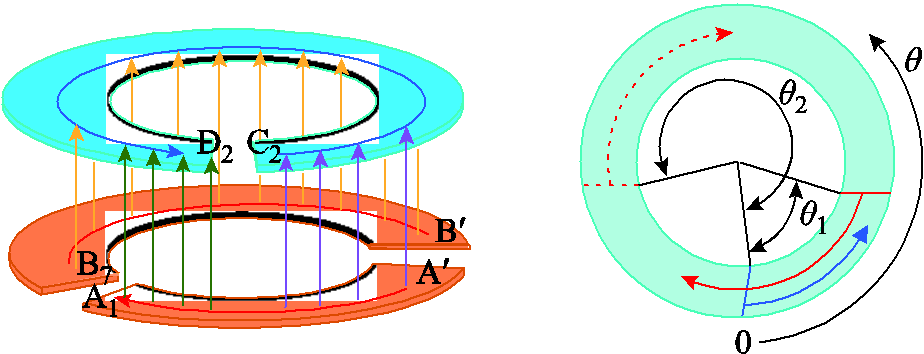
图12 多段一次绕组与二次绕组层间寄生电容模型
Fig.12 Parasitic capacitance between multi-segment primary and secondary windings
上、下两层绕组电位差表达式为
（12）
根据式（12）绘出两层绕组的电位差图，如图13所示。
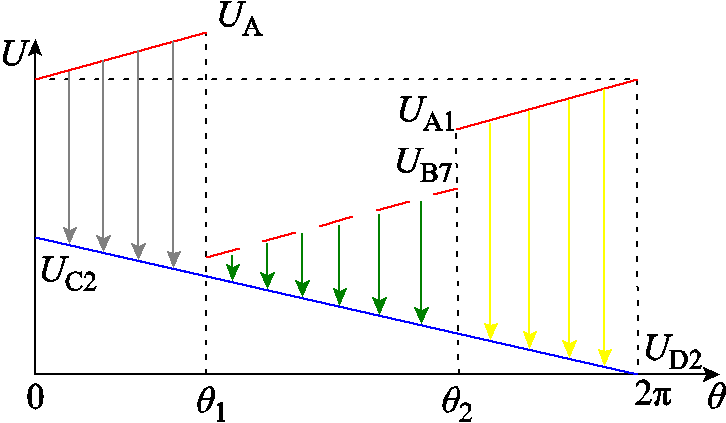
图13 一次绕组P0与相邻二次绕组的电位差
Fig.13 Voltage potential on P0 turn of primary winding and adjacent layer secondary winding
图13表明，为了尽可能减小寄生电容带来的不利影响，α的值应尽可能的小，即θ1、θ2的差值越接近，寄生电容越小，实际设计中，由于绕组外部连接方式和元件布局的限制，α的可调范围有限。
结合微元法的思想，式（2）在极坐标系下可以表述为
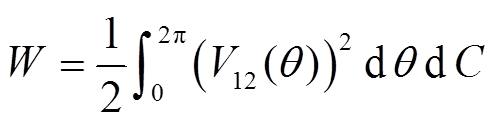（13）
每个微元dθ对应的电容dC为
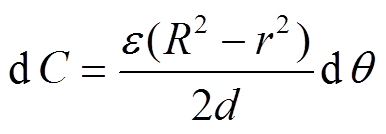（14）
将式（14）与前文推导出的V12(θ)代入式（13），计算出两层绕组之间储存的能量,两层绕组间储存的能量同时满足
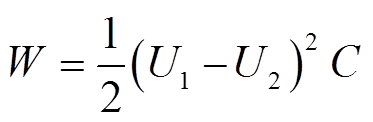（15）
式中，U1、U2分别为上、下两层绕组对应的一组同名端的电位。根据式（12）、式（15）可推导出两匝绕组层间的等效电容C。
根据上述分析结果可知，在变换器参数确定的情况下，变压器绕组层间寄生电容受到相邻两层绕组开口的角度差θ的影响，但是实际设计中，由于外部连接方式的限制，θ的可调范围很小。此外，矩阵变压器一次侧每层PCB通常排布多匝绕组，因此各个元素变压器的层间寄生电容受θ作用的机制将更为复杂，仅靠调节角度差缓解寄生电容不利影响的效果有限。因此本文将进一步分析绕组形状对平面变压器层间电容的影响，通过合理设计绕组的面积，结合角度差θ，达到减小变压器寄生电容的目的。
由于电容容值与极板间距离成反比，与正对面积成正比，考虑到PCB的厚度相对固定，一般通过适当减小绕组面积达到减小层间电容的效果。虽然绕组面积的减小能够减小层间寄生电容的不良影响，但是绕组面积的减小必然导致电流密度的增大，继而导致涡流损耗的增大。因此寄生电容与交流损耗之间存在相互制约的关系，使得绕组面积的大小最终被限制在一定范围内。
为了得到最优的效果，本文在初始绕组设计的基础上提出了两种绕组形状，如图14所示。
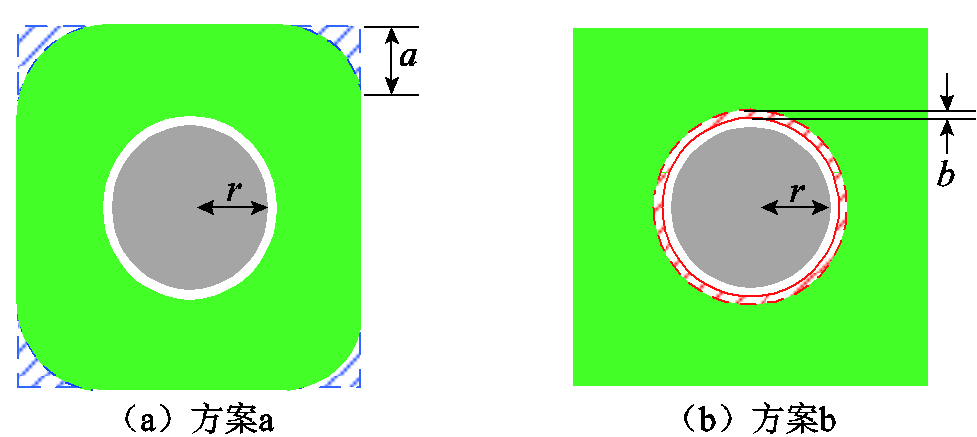
图14 两种绕组形状优化的设计方法
Fig.14 Two design methods of winding optimization
根据图14推导绕组面积公式，阴影部分的面积代表了绕组层间电容正对面积的减小量。两种形状下面积的减小量分别为
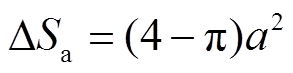（16）
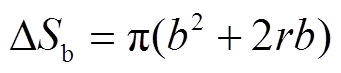（17）
式中，r为绕组的内径；由于面积的减小量相等，即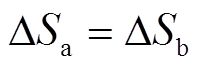
，a、b之间关系为
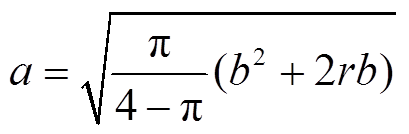（18）
寄生电容与绕组正对面积成正比，而与每层绕组的实际面积无关，所以变压器每层一次、二次绕组面积不需要同时减小来保持每层绕组的面积完全相同。相反地，减小绕组面积反而会使交流损耗增大，涡流效应更严重。因此针对上述两种绕组形状的优化方案首先要确保需要优化的绕组的层数尽可能少。
上文提到，平面变压器的寄生电容主要为相邻层间的寄生电容。从图4看出， CP1S1、CP1′S2′和CS1S1′、CS2S2′都与变压器的第2、5层绕组直接相关。也就是说，变压器的第2、5层绕组的面积同时影响了一次、二次侧层间寄生电容和二次侧寄生电容的大小。从减少寄生电容的角度考虑，对于本文采用的变压器绕组结构，只减小2、5层绕组的面积就能达到相同的效果，同时又能保证带来的损耗增量最小。
初始的变压器绕组如图15a所示。这种二次侧的排布虽然有利于减小过孔长度，但是变压器的第2、5层绕组形状的不对称性在采用图15a的方案时并没有好处。所以将原来的第2、5层的绕组与第3、4层位置的绕组对调，如图15b所示，新的2、5层绕组在四个角的位置都可以采用a方案，而b方案的实施则不受影响。
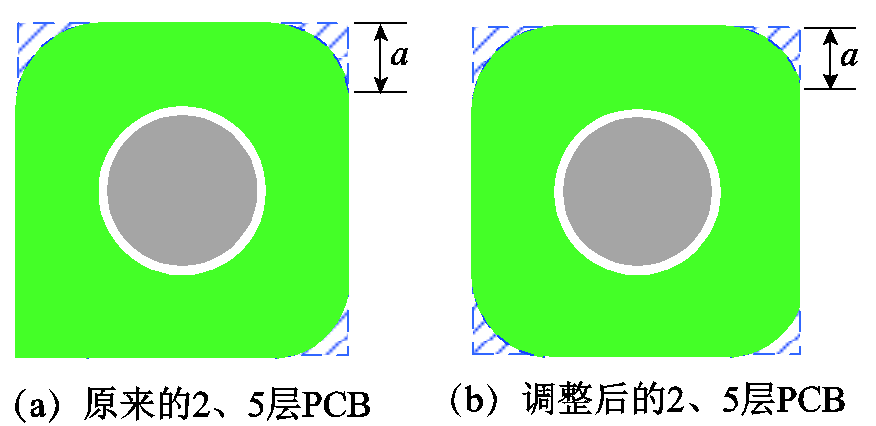
图15 调整前后采用a方案的2、5层PCB
Fig.15 Original and improved PCB layer 2 、5 with method a
鉴于b方案减小的部分两端压降等于进出口处的压降，即单匝绕组的压降，而a方案绕组面积从四个角减小，占的压降显然不是整体的压降，因此只考虑寄生电容的作用，b方案更优。但是变压器气隙附近的漏磁通会在靠近绕组磁柱的部分感应出电流，造成电流不均，b方案面积减小处的电流密度非常大，从损耗的角度考虑，a方案面积减小的位置由于电流的曲率效应（curvature effect），基本无电流流过，a方案带来的交流损耗会更低。
为了对上述两种优化方案进行对比分析，采用电磁仿真软件Maxwell 3D分别搭建仿真模型，如图16所示。
图16 变压器仿真模型（省略上方磁件）
Fig.16 Simulated model for the proposed transformer
为了验证上述两种绕组设计对寄生电容的改善效果，根据式（18）取一系列b的值，对应出一组a的值。通过在静电场中求解变压器的电容矩阵，计算出变压器各部分的寄生电容容值。根据仿真结果绘制的变压器的寄生电容分解图如图17所示。
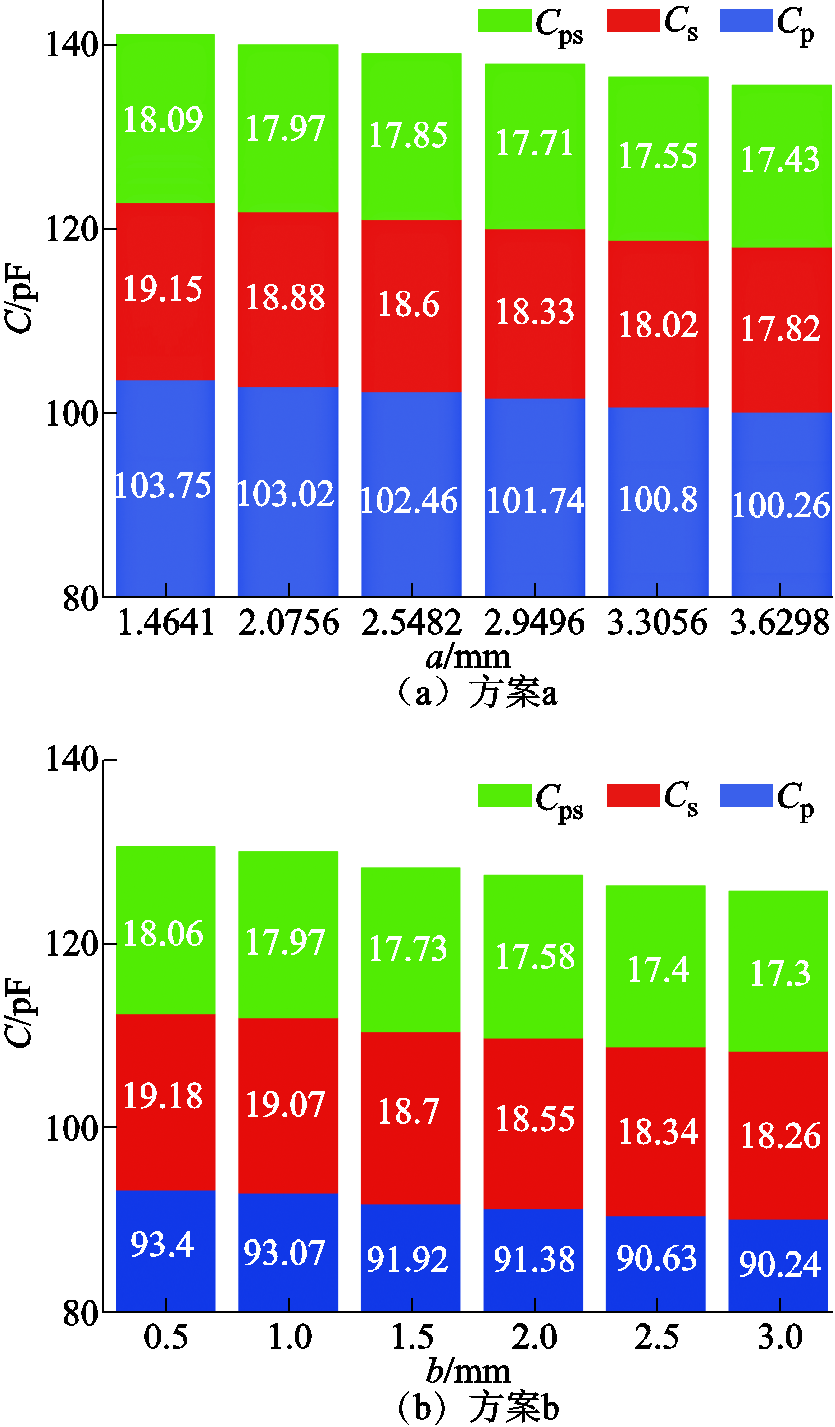
图17 两种绕组形状优化的设计方法寄生电容仿真分解图
Fig.17 Parasitic capacitance breakdown of the two proposed optimized design methods
图17中Cp指的是一次的匝间电容及同层绕组不同匝之间的寄生电容，Cs包括二次绕组的层间电容、二次侧的匝间电容及同层绕组匝间的寄生电容，Cps则代表变压器一次、二次绕组的层间寄生电容。图17表明，采用方案b，在减小相同的绕组面积的情况下，对总的寄生电容的改善效果明显优于a方案，同时Cp、Cs和Cps每个部分都符合相同的规律，变压器一次侧寄生电容Cp占总的寄生电容的比重很大，这与上节的分析一致。
由于绕组形状的改变，在改善寄生电容的同时，影响了电流密度，绕组面积的减小受到损耗的限制。为了探究最优的设计范围，基于Maxwell的瞬态场，仿真得到交流损耗。图18以初始的绕组形状的面积、损耗、电容为基准，绘制了两种方案下的面积-损耗-电容的百分比图。可以观察到，在绕组面积从100%减小到93%的过程中，寄生电容随着面积的减小保持减小的趋势，且b方案的改善效果始终优于a方案；而损耗则相反，a方案的损耗增长总是比b方案要少。图18中阴影的部分兼顾交流损耗和寄生电容，在此面积范围附近优化绕组形状可以得到比较理想的效果。
图18 寄生电容与交流损耗的协调
Fig.18 Coordination of parasitic capacitance and AC loss
本文给出了采用寄生电容优化方法的平面变压器参数设计流程如图19所示，包括变压器的基本参数设计和绕组优化两部分。
首先基于图4、图5给出的磁心结构和绕组排布，结合LLC的参数设计[16-17]，对平面变压器的基本尺寸进行设计，包括确定绕组的内径r、外径R；磁盘的长l、宽w和厚hp；磁柱的截面积Ae、高度hc。鉴于此过程与普通矩阵变压器的参数设计步骤类似，受篇幅限制，本文不展开叙述。
第二部分对应于本文提出的绕组优化方法。完成平面变压器的基本参数设计后，在减小相同的绕组面积的前提下，根据式（16）～式（18），得到一组a、b的值，并将此组参数分别对应两种优化方案进行仿真验证。最后可根据具体的应用场景，综合考虑绕组损耗和寄生电容的影响，从而确定采用具体优化方案和优化值。
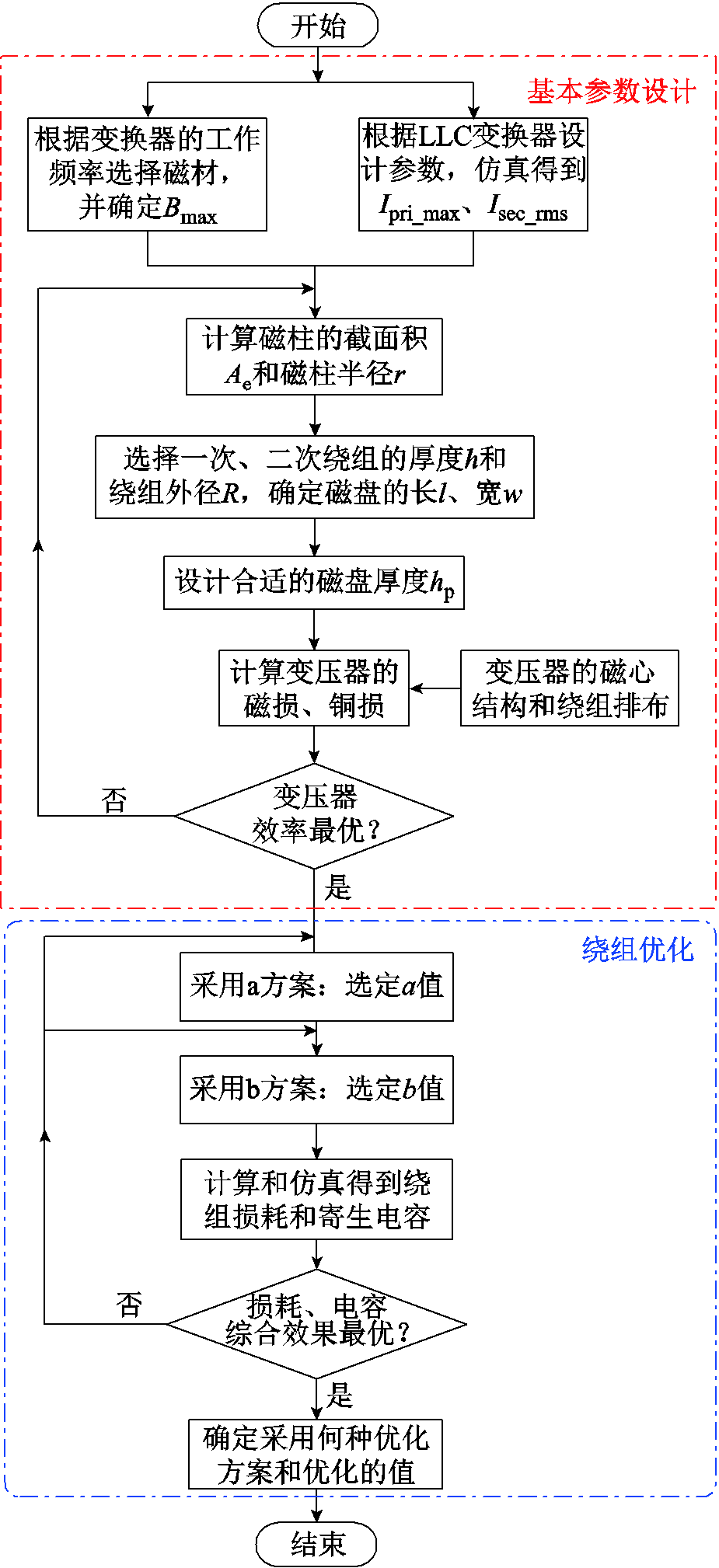
图19 采用绕组优化设计的变压器参数设计流程
Fig.19 Flow chart of the planar transformer design using the proposed winding optimized method
这里，本文所设计的变换器为满足小型高频轻量化的需求，采用500kHz的工作频率。此时，平面变压器一次、二次绕组之间存在较大的寄生电容Cps是出现共模噪声的主要原因之一，导致变换器在开关时刻产生明显的电流尖峰，给开关管的电流应力带来负担，同时给整个变换器带来了严重的EMI问题。另一方面，由于样机的功率等级为500W，两种方案带来的交流绕组损耗的增量对整个变换器的总损耗来说微乎其微。因此，本文着重于寄生电容的改善效果，采用b方案作为最终方案，以达到抑制共模噪声不良影响的目的。
为了验证所提方案的可行性以及理论分析的准确性，本文搭建了一台额定功率500W的样机进行实验验证。变换器的主要参数见表1，实验样机如图20所示。样机采用b方案对绕组进行了优化设计，经计算，取b的值为0.1mm。
表1 LLC谐振变换器样机参数
Tab.1 The parameters of prototype dual three-phase brushless permanent-magnet AC machine
参数数值 串联谐振电感Lr/μH4.7 谐振电容Cr/nF20 励磁电容感Lm/μH70 变压器匝比n14:1:1 额定工作频率fs/kHz500
图20 LLC变换器实验样机
Fig.20 Experimental prototype of the LLC converter
实验波形如图21所示，变换器工作在额定功率500W，额定输入电压220V，频率500kHz的条件下。vG_S为一次侧开关管S1的门极信号，vS、ir分别为一次侧开关管两端电压和流经谐振腔的电流，vD为二次侧同步整流管两端电压。
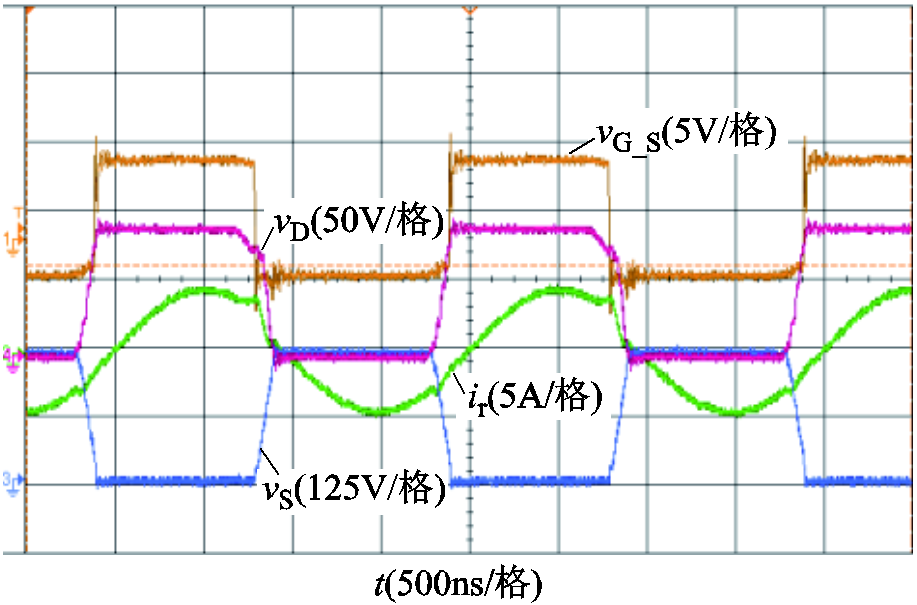
图21 额定工作点实验波形
Fig.21 Experimental waveforms at rating point
图22为变换器在额定点波形细节图，点画线框为一次侧开关管开通过程，由于开通时刻一次侧谐振电流ir的相位滞后于开关管两端电压，即变换器一次侧开关管实现了ZVS开通，开关损耗显著降低。
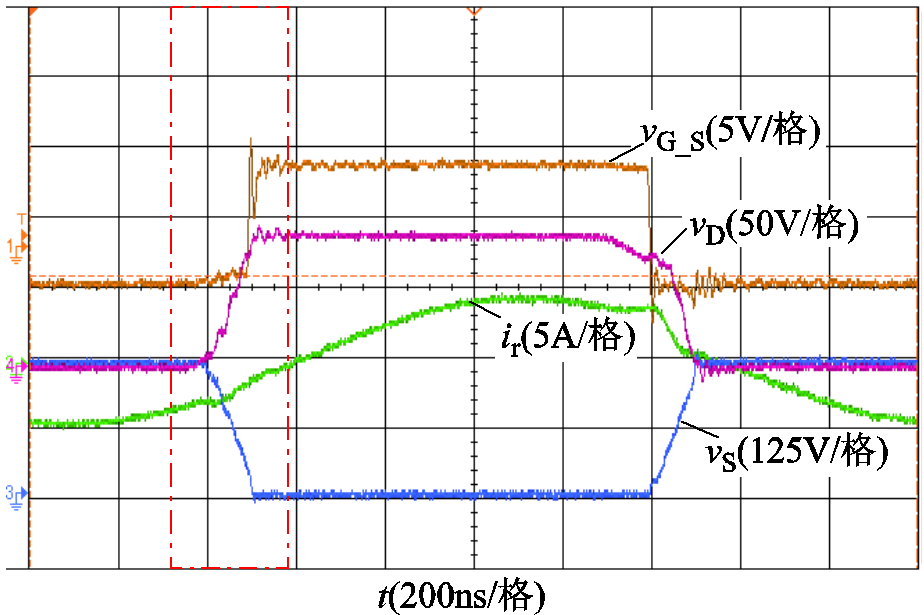
图22 实验波形细节图
Fig.22 Detail of experimental waveforms
本文给出了变换器在不同负载下的测试曲线。变换器效率曲线如图23所示，样机的最高效率到达97.53%。
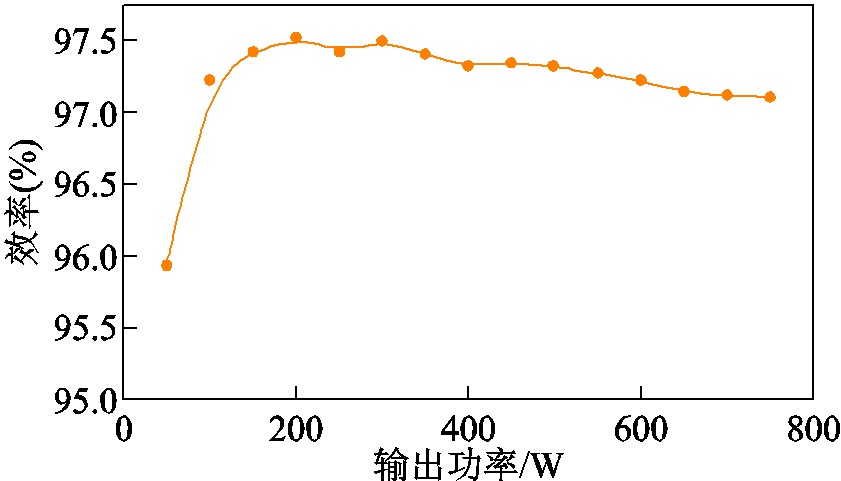
图23 变换器效率曲线
Fig.23 Efficiency curves of the converter with different load
为了缓解绕组层间寄生电容带来的不良影响，本文建立了平面变压器层间寄生电容的数学模型，详细分析了平面变压器寄生电容的产生机制，并对相邻绕组的开口角度和正对面积形状两个方面进行了优化设计，最后结合这两个方面制定了基于LLC谐振变换器的变压器绕组的优化设计方法，使用电磁仿真软件Maxwell搭建了变压器的3D模型，并通过仿真结果对比验证了所提方法的有效性。最后设计了一台500W的实验样机，验证了理论分析的合理性和仿真结果的可行性，最高效率达到97.53%。
参考文献
[1] 王议锋, 杨良, 陈博, 等. 一种拓扑变换型多谐振软开关直流变换器[J]. 电工技术学报, 2018, 33(24): 204-213.
Wang Yifeng, Yang Liang, Chen Bo, et al. A Topology morphing multi-element resonant soft-switching DC-DC converter[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 204-213.
[2] Huang Daocheng, Ji Shua, Lee F C. LLC resonant converter with matrix transformer[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4339-4347.
[3] Ahmed M, Fei Chao, Lee F C, et al. High efficiency two-stage 48V VRM with PCB winding matrix transformer[C]//2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 2017, DOI: 10.1109/ECCE 2016.7855150.
[4] Ahmed M H, Fei Chao, Lee F C, et al. 48-V voltage regulator module with PCB winding matrix transformer for future data centers[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9302-9310.
[5] Cai Yinsong, Mohamed, Li Qiang, et al. Optimal design of megahertz LLC converter for 48-V bus converter application[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 8(1): 495-505.
[6] Fei Chao, Lee F C, Li Qiang. High-efficiency high-power-density LLC converter with an integrated planar matrix transformer for high-output current applications[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 9072-9082.
[7] Huang Daocheng, Ji Shu, Lee F C. LLC Resonant converter with matrix transformer[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4339-4347.
[8] Kim B C, Park K B, Kim C E, et al. LLC resonant converter with adaptive link-voltage variation for a high-power-density adapter[J]. IEEE Transactions on Power Electronics, 2010, 25(9): 2248-2252.
[9] 杨玉岗, 吴晗, 关婷婷. 交错并联LLC谐振变换器的磁集成均流特性[J]. 电工技术学报, 2019, 34(12): 2529-2538.
Yang Yugang, Wu Han, Guan Tingting, The Design and implementation of a dual-CLT resonant soft-switching DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2529-2538.
[10] Fu Minfan, Fei Chao, Yang Yuchen, et al. A two-stage rail grade DC/DC converter based on GaN device[C]// 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019, DOI: 10.1109/APEC.2019.8722095.
[11] Hou Dongbin, Mu Mingkai, Lee F C, et al. New core loss measurement method with partial cancellation concept[C]//2014 IEEE Applied Power Electronics Conference and Exposition - APEC 2014, Fort Worth, TX, USA, 2014, DOI: 10.1109/APEC.2014.6803391.
[12] Cai Yinsong, Ahmed M H, Li Qiang, et al. Optimized design of integrated pcb-winding transformer for MHz LLC converter[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019, DOI: 10.1109/APEC. 2019. 8722181.
[13] Fei Chao, Yang Yuchen, Li Qiang, et al. Shielding technique for planar matrix transformers to suppress common-mode EMI noise and improve efficiency[J]. IEEE Transactions on Industrial Electronics, 2017, 65(2): 1263-1272.
[14] Lu Bing, Liu Wenduo, Liang Yan, et al. Optimal design methodology for LLC resonant converter[C]// Twenty-First Annual IEEE, Applied Power Electronics Conference and Exposition, APEC '06, Dallas, TX, USA, 2006, DOI: 10.1109/APEC.2006.1620590.
[15] Saket M A, Ordonez M, Craciun M, et al. Improving planar transformers for llc resonant converters: paired layers interleaving[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11813-11832.
[16] 王议锋, 陈博, 吕雯, 等. 拓扑变换型LLC-C谐振软开关直流变换器[J]. 电工技术学报, 2019, 34(18): 3810-3820.
Wang Yifeng, Chen Bo, Lü Wen, et al. A topology morphing LLC-C resonant soft-switching DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3810-3820.
[17] 刘瑞欣, 王议锋, 韩富强, 等. 应用于宽输入电压范围的两模式切换型软开关谐振直流变换器[J]. 电工技术学报, 2020, 35(22): 4739-4749.
Liu Ruixin, Wang Yifeng, Han Fuqiang, et al. A two-mode soft-switching resonant DC-DC converter for wide input voltage range applications[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4739-4749.
Optimal Design of Transformer Winding of LLC Converter
Abstract Due to LLC resonant converter is sensitive to the parasitic capacitance of planar transformer at high frequency, the magnetic integration technology is used to optimize the winding of the transformer, so that the comprehensive effect of parasitic capacitance and solid loss of the transformer is optimal. In this paper, the influential factors of parasitic capacitance between layers of planar transformer are analyzed in detail. The mathematical model of parasitic capacitance of transformer is established in polar coordinate system, and the effect of each influential factor under different current conditions is summarized. Two optimal design implementations of winding shape are proposed to improve the parasitic capacitance of transformer by reducing the opposite area of winding. The 3D simulation model of the transformer is built with the FEA simulation software Maxwell. According to the simulation results, the improvement of parasitic capacitance with the two proposed optimal implementations is compared, and the reliability of theoretical analysis is verified. To compromise the parasitic capacitance and solid loss of the transformer, the optimal design range of winding area is given. At the same time, the final implementation is determined. Finally, a 500kHz 500W LLC prototype is demonstrated with the improved magnetically integrated planar transformer, and the peak efficiency of 97.53% is achieved.
keywords：Resonant converter, parasitic capacitance, planer transformer, magnetic integration, optimal design
DOI:10.19595/j.cnki.1000-6753 tces.210250
中图分类号：TM46
国家重点研发计划（2018YFB0904700）和国家自然科学基金重大项目——分布式储能用高频高增益多谐振双向直流变换器及其运行控制（51977146）资助。
收稿日期 2020-02-28
改稿日期 2021-07-12
王议锋 男，1981年生，博士，副教授，研究方向为先进电力电子技术在电网中的应用。E-mail：wayif@tju.edu.cn
陈 博 男，1989年生，博士研究生，研究方向为谐振软开关变换器。E-mail：cb92614@126.com（通信作者）
（编辑 郭丽军）