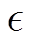，并利用非线性映射将低维空间中的线性不可分的样本点映射到高维线性可分的特征空间中，再对其进行线性回归。摘要 准确的短期电力负荷预测对保证电网安全稳定运行、能量优化管理、提高发电设备利用率和降低运行成本等具有重要作用。传统时间序列分析方法难以学习短期电力负荷数据的非线性特征，因此论文首先将支持向量回归、高斯过程回归和前向神经网络等经典机器学习法应用于短期电力负荷预测的适用性和预测效果进行对比分析；预测评价指标表明机器学习方法能够得到较高的预测精度，适用于处理含强非线性特征的短期电力负荷数据；在此基础上，进一步提出一种基于时间卷积深度学习网络的短期电力负荷预测方法，该模型具有从大样本时间序列中提取特征和实现预测的能力，其模型架构能有效解决深层网络学习的退化问题；最后，以实际电力负荷数据作为算例对所提模型进行测试。实验结果表明，时间卷积网络可以获得更高的预测精度，深度学习方法相较于经典机器学习方法在非线性特征学习方面更具优势。
关键词：短期电力负荷预测 机器学习 支持向量回归 高斯过程回归 时间卷积网络
目前，在各种二次能源应用形式中，电能是最便于生产、输送、分配和利用的一种形式。电能的广泛使用及其相关技术水平的进步为推动人类社会的不断发展做出了重要贡献[1-2]。但是，电能本身具有不易存储的特点，因此在传统电力系统中需要保持发电侧与负荷侧的实时功率平衡。由于负荷侧的实际电能需求是一个受多种因素影响的动态变化过程，因此采用电力负荷预测技术来预测未来电量需求可以为制定发电计划提供数据支持，且有利于实现发电侧和负荷侧的优化调度和电网的经济运行。随着智能电网技术的发展，各种可再生能源越来越多地接入电力系统中，构成各种不同渗透率、不同结构形式的智能微电网。为应对可再生能源所具有的随机性、波动性和周期性等特征对微电网的稳定运行所带来的负面影响，配置电能存储系统已成为一种重要的解决方案[3-5]。但是，受目前储能系统构建、维护成本、能量密度和使用寿命等因素的制约，在微电网实际应用领域中，需要采用先进的能量管理方法和控制策略来保证储能系统在充分发挥储能作用的同时确保整个微电网系统运行的安全性、经济型和可靠性。而对于配置储能系统的微电网能量管理和控制策略的设计和实现，电力负荷的准确预测也是一项必不可少的关键技术。
由此可见，不论是对传统电力系统还是对智能微电网系统而言，系统内部的能量管理均是一项复杂的任务，具体管理方法和策略的有效性及实施效果在很大程度上取决于未来电力负荷需求的预测结果。如果发电量不能满足需求则会导致电网故障，而供过于求又会导致能源和资源的浪费。因此，基于准确的电力系统负荷预测结果不仅可以减少不必要的发电量，从而降低资源浪费，实现节能使用；还可以为输配电规划、用电需求管理、能源市场中的智能化交易等提供重要数据支撑[6-7]。电力负荷预测根据预测时间尺度可以分为：长期预测（以年为单位）、中期预测（以月为单位）、短期预测（以日为单位）和超短期预测（以时、分为单位）。其中，短期电力负荷预测范围可从一天内每小时扩展到一周内每天的负荷，其预测结果对于发电单元的起停安排，提升可再生能源的渗透率及用电需求侧的有效管理等方面均具有重要作用[8-10]。影响短期电力负荷的因素主要有天气条件、假日安排和用户使用习惯等。这些因素的共同作用使得短期电力负荷数据呈现出强非线性、随机性和时变性等特征，这无疑增加了实现准确预测的难度[11-12]。因此，高精度和高鲁棒性的短期电力负荷建模和预测方法一直是电力负荷预测领域的研究重点。国内外研究者的主要研究目标也大多聚焦于采用不同的建模和预测方法来提高短期电力负荷的预测精度。电力负荷预测精度越高，越有利于提高发电设备的利用率和经济调度的有效性[7-8,13]。目前，从建模和预测方法来看，短期电力负荷预测的实现手段主要有基于统计分析的时间序列分析方法和基于数据驱动的机器学习方法[9,14-16]。时间序列分析法在处理平稳序列和学习数据的线性特征方面具有较好的性能，但对于数据的非线性特性处理较差[17-18]；机器学习方法则具有较强的非线性学习能力，因此在处理具有强非线性和随机性等特征的短期电力负荷数据方面具有天然优势。
综上所述，短期电力负荷的预测精度与预测方法的选取和数据自身特点的关系较大。基于此背景，本文首先对实际短期电力负荷数据分别选用几种最具代表性的经典机器学习方法进行建模和预测，从而验证此类方法的有效性。具体选择的方法包括支持向量回归、高斯过程回归和前向神经网络等。然而，经典机器学习方法通常比较适合处理小样本数据，当样本数据量显著增大时通常会出现模型性能下降的问题。因此，本文进一步提出基于时间卷积网络（Temporal Convolution Network, TCN）实现短期电力负荷预测。实验结果表明，TCN深度学习网络具有更好的数据特征提取能力，在对具有强非线性特征的短期电力负荷预测方面可以获得比经典机器学习方法更高的精度。
支持向量回归[19]（Support Vector Regression, SVR）是一种解决函数回归问题的算法，可以用于非线性建模和回归预测等。SVR通过引入不敏感损失函数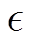，并利用非线性映射将低维空间中的线性不可分的样本点映射到高维线性可分的特征空间中，再对其进行线性回归。
假定训练样本D={(x1, y1), (x2, y2), 
, (xm, ym)}, xi∈Rn,yi∈R。对输入变量与输出变量用式（1）所示的非线性关系进行训练。
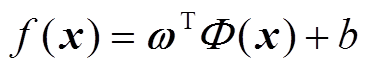（1）
式中，w和b分别为回归系数和截距；F(x)为非线性映射函数。
如果在xi的预测值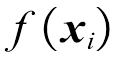
和真实值yi之差不超过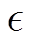，即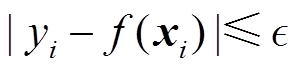
，
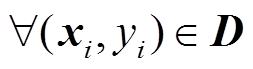，则认为预测值
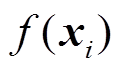是无损的。通过引入松弛变量
、
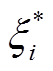和惩罚因子C后，该非线性回归问题可以转换为如式（2）所示的凸优化问题。
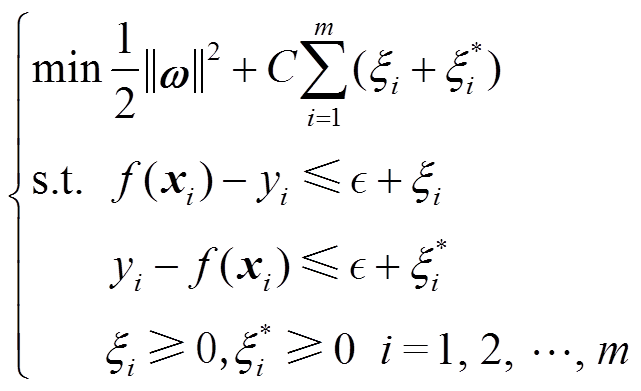（2）
C越大表示对训练误差超过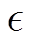的样本惩罚越大，e反映了回归函数的误差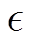，越小说明回归精度越高，误差越小。进一步，通过引入Lagrange乘子a和a*，可得式（2）对应的对偶形式，即
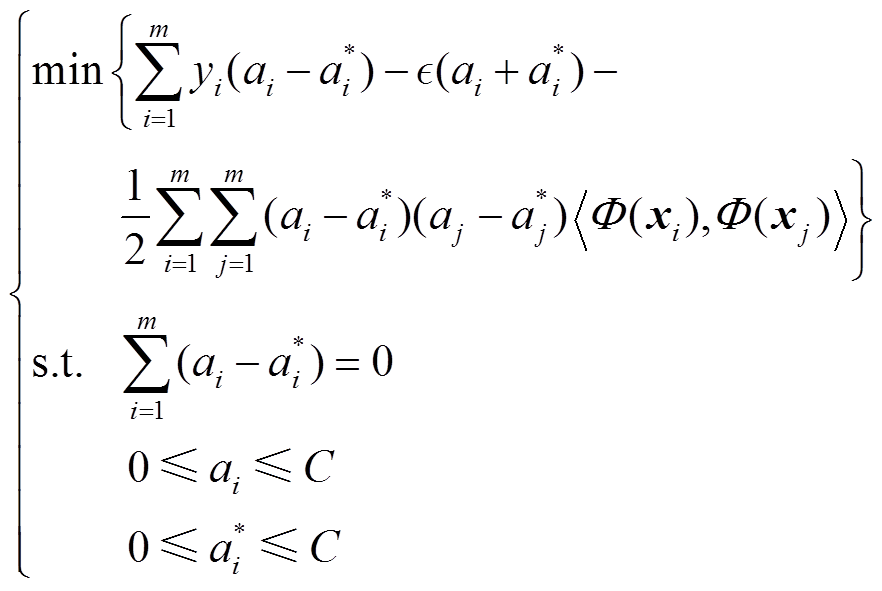（3）
采用核函数k(xi, xj)来代替内积
，并求解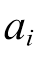
、
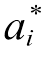和b可得最终的SVR回归函数为
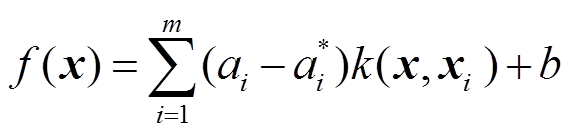（4）
高斯过程回归[20]（Gaussian Process Regression，GPR）是一种将高斯过程作为先验的非参数化模型，其本质也是先将自变量从低维空间映射到高维空间，然后在高维空间对数据进行回归的方法。
假定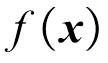
为给定高斯过程先验的一个函数，其均值函数为
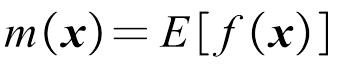，其协方差函数为
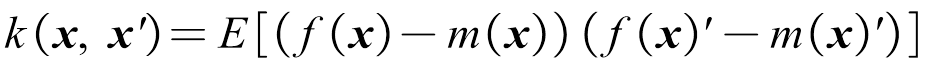
记为
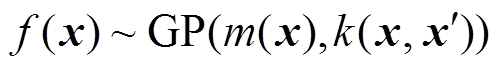
通过对原始数据进行预处理，可以假设均值函数为零，则可简记为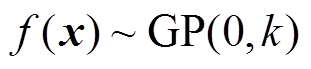
。在此基础上，假设高斯回归过程模型为
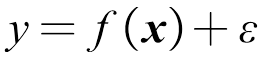（5）
式中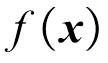，为回归分量；e为零均值和方差为
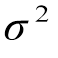的高斯噪声项，即
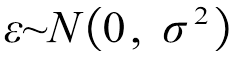。由于f(x)～GP(0, k)，则y的先验分布为y～N(0, K+σ2I)。假设训练集为
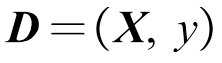。在训练过程中，如有样本x*作为新的输入，那么高斯过程回归模型的任务就是计算与x*相应的输出值y*的条件分布(p(y*|x*, X, y)。K=k(X, X)为n×n阶对称正定的协方差矩阵，矩阵中的项
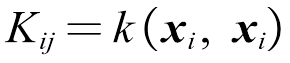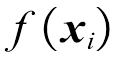度量了和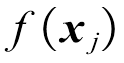
的相关性。当新增一对样本(x*, y*)后，随机向量(f(x1), f(x2),, f(xn), f(x*))=(yT, y*)满足n+1维混合高斯随机分布。进而由贝叶斯定理，采用极大似然估计可以得到y*的条件分布为
式中，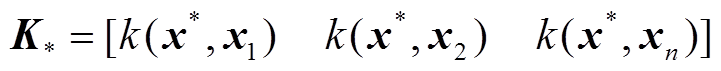
；
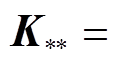
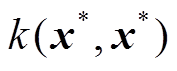。则式（6）的均值就是x*相对应输出值y*的预测值，即
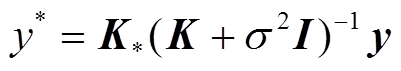（7）
神经网络[21]（Neural Network, NN）是一种由神经元相互连接而成的非线性动态系统。一个基本的前向神经网络由L层和每层Ml（l=1, , L）个节点组成。假设给定输入为x(1), , x(t)，利用神经网络输出下一时刻的预测值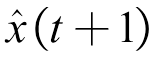
。在第一层网络中，可构造M1个输入变量的线性组合为
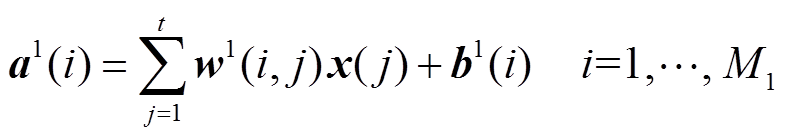（8）
式中，
表示权重；
表示偏差。然后，对每个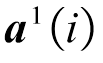
使用非线性激活函数
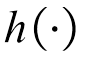进行变换，可得
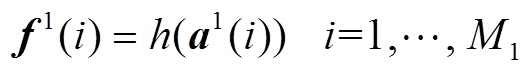（9）
依次在每个后续的网络层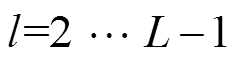
中，对来自前一层的
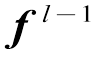的输出再次进行线性组合和非线性变换，可得
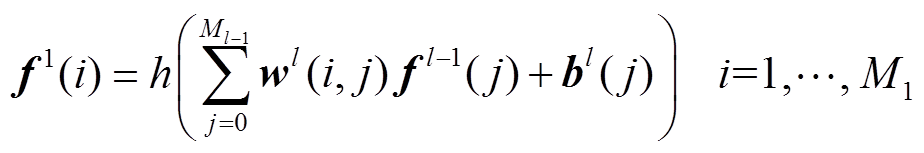（10）
其中，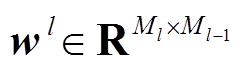
，
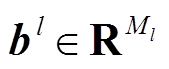。在前向神经网络的输出层（即l=L），可以得到最终的预测值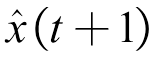为
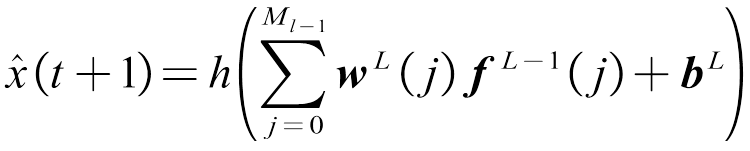（11）
式中，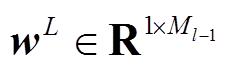
；
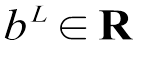。典型前向神经网络结构如图1所示。
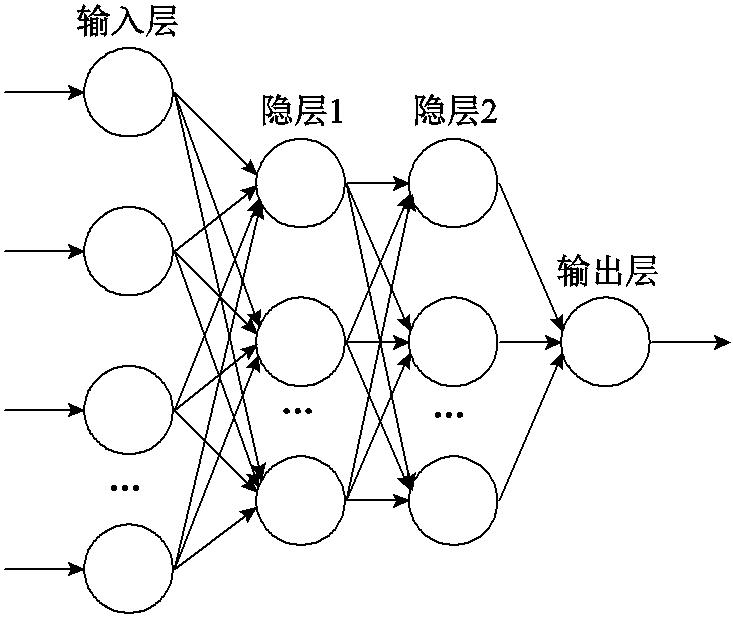
图1 前向神经网络结构
Fig.1 Structure diagram of feedforward neural network
由前述定义可知：短期电力负荷预测的时间范围一般为：未来1天内至未来一周的负荷（具体预测的数据点数还取决于采样频率）。以采样频率1次/h为例，则短期电力负荷预测的时间范围为未来24～168h（也即24～168个数据点）的负荷数据。因此，本文的实验将预测时间范围也设置为该定义范围内。
本小节的实验用于验证采用本文第1小节介绍的三种经典机器学习方法预测短期电力负荷的有效性。采用加拿大某电力公司2016年的电力负荷数据作为原始数据集。该数据集的构成为一个二维数组，即一维时间向量和与时间向量相对应的一维负荷数据向量。选用数据集时间范围为2016年1月1日9时～2016年7月28日8时，总共209天，采样频率为1次/h，因此数据样本总量为5 016h（也即5 016个数据点）的负荷数据。其中，选择前204天（即2016年1月1日9时～2016年7月23日8时）的数据作为预测模型的训练样本，共计4 896h（4 896个数据点）的负荷数据，其时间序列图如图2所示；选择后5天（即2016年7月23日9时～7月28日8时）的数据作为预测模型的测试样本，共计120h（120个数据点）的负荷数据。三种模型的验证实验均在同一硬件平台上完成。具体硬件配置为：操作系统Windows10，处理器Intel Core i7-8700k（12MB高速缓存，最高3.7GHz），内存RAM-32GB- DDR4@1 600MHz，显卡GTX1080 Ti。
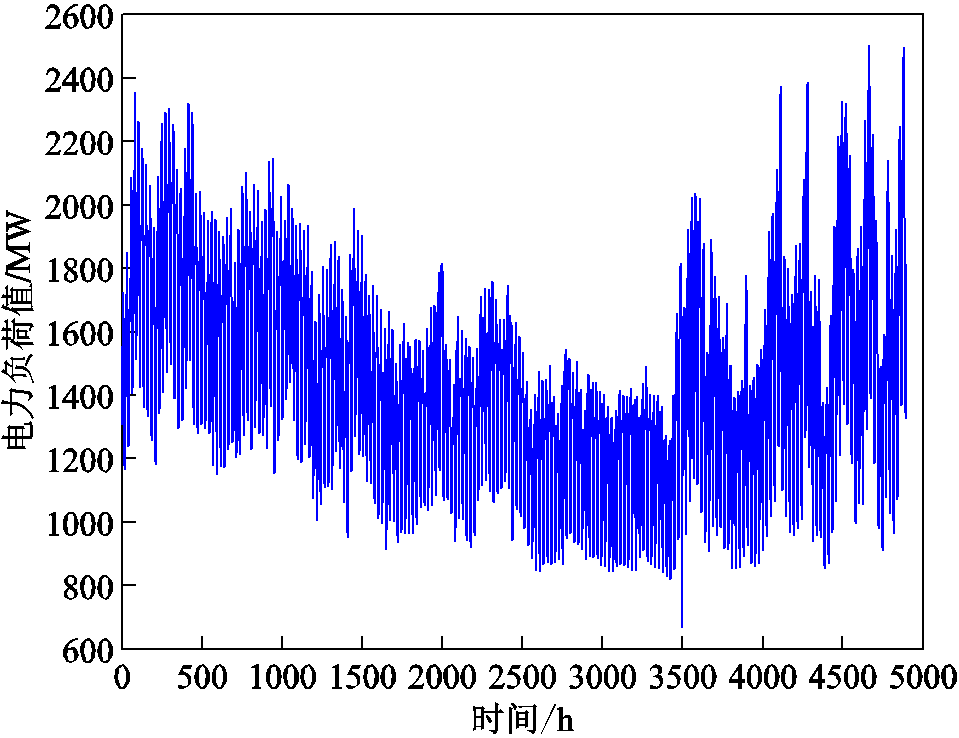
图2 电力负荷数据训练样本
Fig.2 Test samples of electrical load data
为加快机器学习算法的训练速度，提高模型的预测精度并避免训练过程出现饱和，需要对原始电力负荷数据进行数据预处理。本文采用归一化处理方法，其公式为
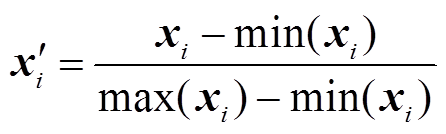（12）
式中，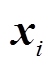
为某一输入样本；
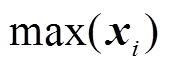为输入样本的最大值；
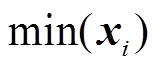为输入样本的最小值；
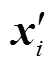为预处理后的数据值。
在得到归一化的样本数据集后，将此样本数据集划分为训练集和测试集，分别对预测模型进行训练和验证。由于基于归一化的输入数据得到的模型预测输出也为归一化的数据，因此，为了使模型的预测输出与真实负荷数据有相同量纲并能进行比较，还需对模型的预测输出进行反归一化操作。反归一化公式为
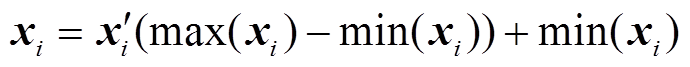（13）
为比较不同建模方法的预测效果，本文分别采用平均绝对误差（Mean Absolute Error, MAE）和方均根误差（Root Mean Squared Error, RMSE）作为负荷预测精度的评价指标[22]，其计算公式分别为
（14）
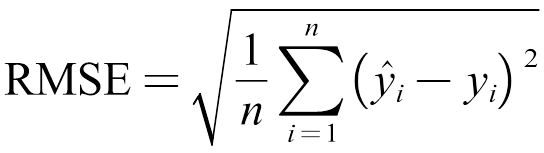（15）
式中，n为训练或者测试样本的数目；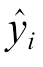
为某个时刻的电力负荷预测值；
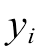为同一时刻的电力负荷实际测量值。
MAE表示预测值和真实值之间绝对误差的平均值，可以准确描述实际预测误差的大小；RMSE表示预测值和真实值之间残差的标准偏差，反映了样本的离散程度。MAE和RMSE的值越小，表明模型的预测性能越好。
利用经过预处理的实验数据，以及SVR、GPR、BP(back propagation)神经网络三种经典机器学习建模方法，实现短期电力负荷预测。其中，对于每种建模方法，分别尝试选用几种不同的核函数（LK、RBK、PK）或隐藏层神经元个数h的参数配置模式进行预测建模，以此获得算法的最佳参数配置。所有模型的训练次数（epoch）和学习率（lr）等参数设置相同，epoch=500，lr=0.01。具体参数配置信息和预测性能评价指标结果见表1。
表1 不同模型预测性能对比
Tab.1 Comparison of precision among different models
建模方法参数配置MAERMSE SVRLinear Kernel (LK)0.3640.468 Radial Basis Kernel (RBK)0.3660.469 Polynomial Kernel (PK)0.3720.468 GPRSquare Kernel (SK)0.4250.521 Cubic Kernel (CK)0.4110.511 Linear Kernel (LK)0.4220.520 BPh=300.3450.425 h=500.3010.389 h=1000.4210.512
为更清晰地对比每种建模方法在不同参数配置下的预测效果，将预测指标值做如图3所示的柱状图显示。可以看出，不同模型配合不同核函数或隐藏层神经元个数的配置所得到的MAE值和RMSE值存在一定差异，其中BP神经网络模型在h=50时所对应的两个指标值最低，分别为MAE=0.301和RMSE=0.389；SVR模型次之，GPR模型两个误差值最高。但对比同一模型的不同参数配置发现，SVR模型和GPR模型的MAE值和RMSE值变化范围较小，表明这两种模型选用不同的核函数都能取得不错的预测效果，即不同核函数对模型预测性能影响差异不大。
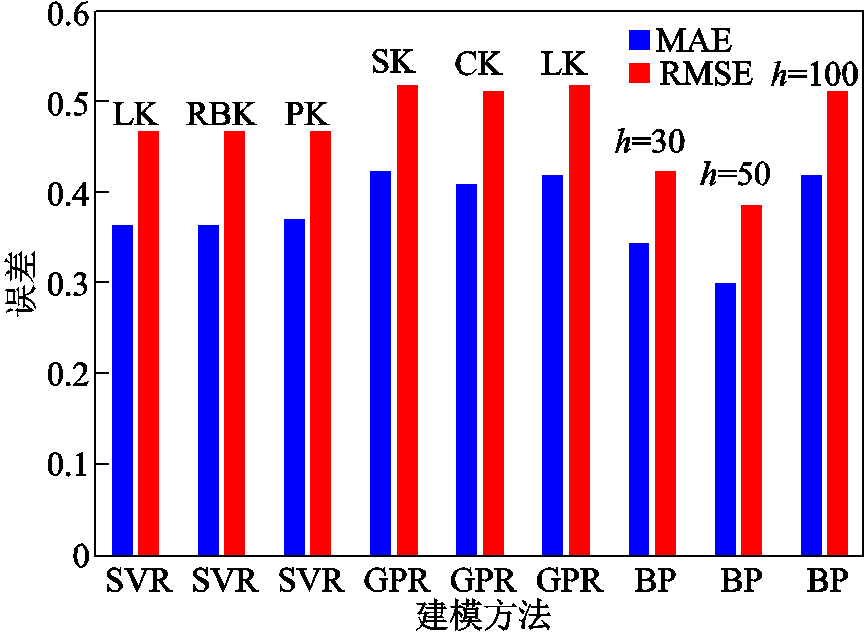
图3 对比模型误差柱状图
Fig.3 Histogram of different models’ prediction metrics
由前述实验结果可知，机器学习方法在处理具有非线性特性的数据建模和预测问题方面具有一定的优势。但是经典机器学习方法通常适用于处理小样本数据[23-24]。由于智能电表等各种测量装置的普及和广泛使用，电力负荷数据量显著增大。为提高机器学习方法处理大样本数据预测的能力，越来越多的学者开始尝试应用深度学习网络这一新型机器学习方法来解决短期电力负荷预测问题。目前，应用于时间序列数据建模和预测的深度学习模型主要有循环神经网络[25]（Recurrent Neural Network, RNN）及其改进算法包括长短期记忆网络[26]（Long Short-Term Memory, LSTM）和门控循环单元[27]（Gate Recurrent Unit, GRU）等。其中，标准RNN在处理长序列时易发生梯度爆炸和梯度消失，模型训练较为困难；LSTM的设置参数过多，存在过学习风险；GRU的参数相对LSTM的参数较少，但其相对于LSTM少一个门单元，在数据量很大的情况下，其数据表达能力弱于LSTM。基于此，本文提出采用更适合处理长时间序列的TCN模型来实现短期电力负荷预测。
TCN是一种基于卷积神经网络（Convolution Neural Network, CNN）的新型架构。与一般CNN不同，TCN采用扩大因果卷积和残差块等结构[28-30]，使其具有从大样本时间序列中提取特征和实现预测的能力，并且可以在网络训练过程中有效解决深层次网络的性能退化问题。文献[28]对比了TCN与RNN、LSTM和GRU等循环神经网络在多种典型序列模型预测问题的性能表现，结果表明TCN通常可以获得更好的预测精度，可以作为时间序列预测建模的一种有效手段。
3.1.1 TCN建模
假设给定输入序列为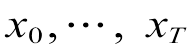
，期望预测得到的输出为
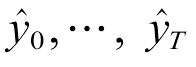。预测输出与输入序列的关系式为
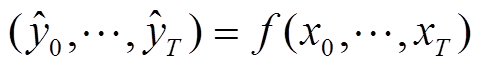（16）
式中，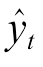
仅与t时刻及t时刻之前的输入序列
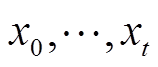有关，而与任何未来的输入
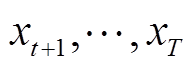无关。TCN建模即建立输入序列和输出序列的映射关系f，其目标函数是最小化实际输出（
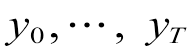）和预测值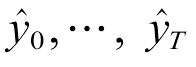（）之间的误差损失。
3.1.2 扩大因果卷积
因果卷积（causal convolutions）最初是在WaveNets[31]网络中提出，用于学习t时刻之前的输入音频数据
，来预测t+1时刻的输出。与RNN相比，使用因果卷积的模型中没有使用循环连接，因此时间序列数据能够并行输入，从而可以获得更快的网络训练速度，特别是对于大样本时间序列的训练更具优势[32]。但是，标准因果卷积在处理大样本时间序列时，需要通过堆叠很多网络层或者使用很大的卷积核来增大神经网络中神经元的感受野。为此，TCN采用扩大因果卷积（Dilated Causal Convolution, DCC）技术来达到提升感受野的同时而不会显著增加计算成本。DCC是一种对输入序列进行跳步操作的卷积运算，其表达式为
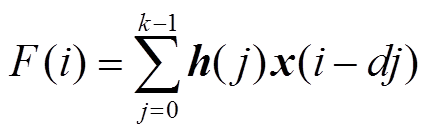（17）
式中，F(i)为对序列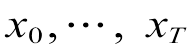（）中第i个元素的卷积结果；
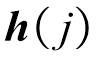为滤波器（也称卷积核，对于一维序列其卷积核大小K=1´k）；d为扩大因子（当d=1时，即为标准因果卷积）。
DCC的结构如图4所示（图中参数K=1´2，d=2l-1，l为隐层层数）。与标准因果卷积相比，DCC可以在相同网络层数的情况下，使输出y能尽可能多地关联到输入x。结合扩大因果卷积的多层堆叠还可以使深度学习网络以较少的网络层就能达到非常大的感受野[20]。此外，通过卷积核在输入数据上的滑动操作，使得TCN可以处理可变长度的输入。因此配合模型输入数据的更新（即将前一时刻的预测值作为新息加入到输入中），可以不断地计算并输出新的预测值。
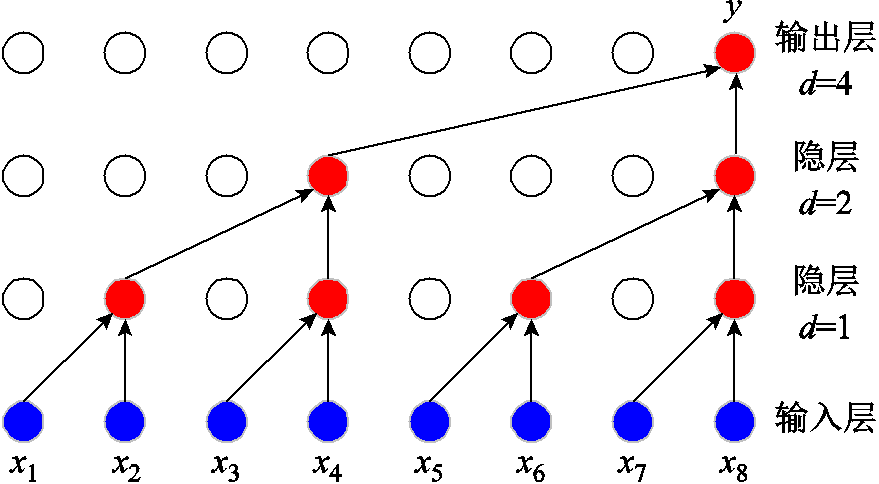
图4 扩大因果卷积结构
Fig.4 Structure of dilated causal convolution
3.1.3 残差块
残差块（Residual Block，RB）主要为解决深度学习网络的退化问题而提出，其核心思想是引入一个跳过一层或多层的“跳连接”操作[33]。假设x是残差块的输入，残差块的输出o如式（18）所示，它是经过线性变化并通过激活函数映射的输出结果。由于在实际中残差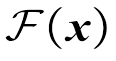
不会为0，故深度学习网络中的堆叠层总能学习到新的特征，因此深层网络的学习性能不会发生退化[21]。
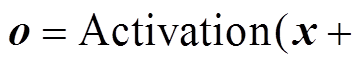
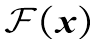) （18）
式中，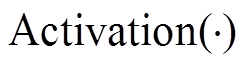
为激活函数。
残差块结构如图5所示。在TCN建模时，使用RB和DCC相结合的网络结构，可以有效提高TCN模型的特征学习能力和鲁棒性。
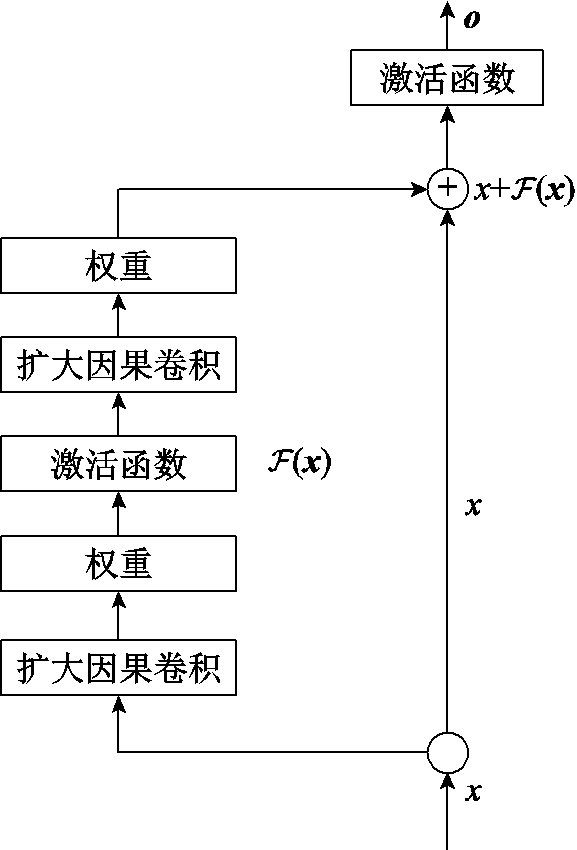
图5 残差块结构
Fig.5 Structure of residual block
为验证TCN模型实现短期电力负荷预测的有效性，并与本文第2节所采用的经典机器学习方法的预测结果进行对比分析，在本小节中继续采用相同的电力负荷数据作为原始数据集。
3.2.1 TCN参数设置
由式（17）可知，TCN模型中的扩大因子d和卷积核大小K是决定TCN模型预测性能的主要参数。此参数的选择目前尚无理论指导，一般均需通过实验对比取得。因此为确定此参数，本文借鉴文献[34]的方法，即通过选取不同d值和不同K值进行组合，然后对每一组合参数的TCN模型进行训练，最后通过对比不同参数配置的TCN模型的MAE值和RMSE值来确定最佳参数。其中，扩大因子d分别取值为2、4、8和16；卷积核K分别取为1×3、1×5和1×7，两组参数共构成12种组合形式，见表2。所有参数组合的TCN训练次数（epoch）和学习率（lr）设置相同，即epoch=500，lr=0.01。12种TCN模型训练后的精度对比结果如图6所示。
表2 TCN模型参数组合
Tab.2 TCN models of different parameter settings
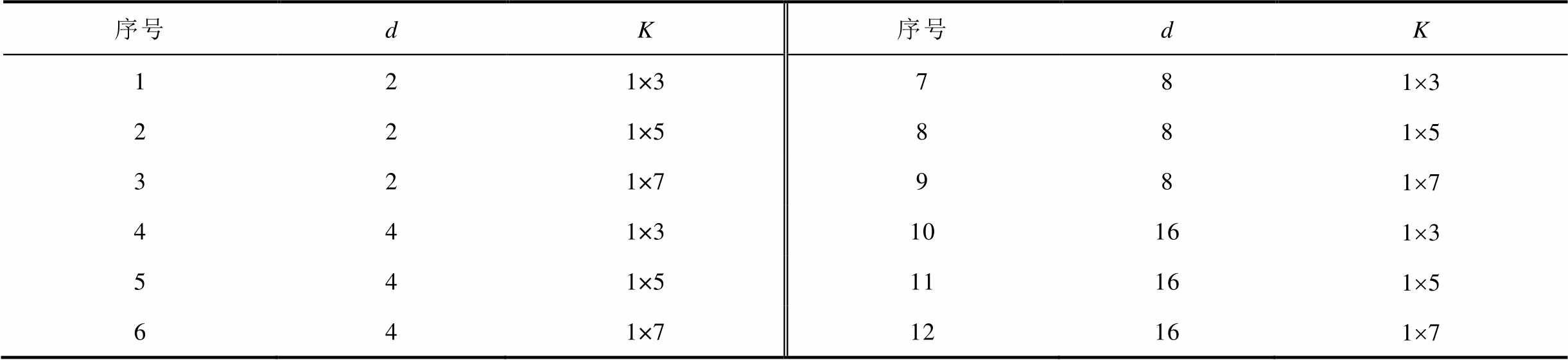
序号dK序号dK 121×3781´3 221×5881´5 321×7981´7 441×310161´3 541×511161´5 641×712161´7
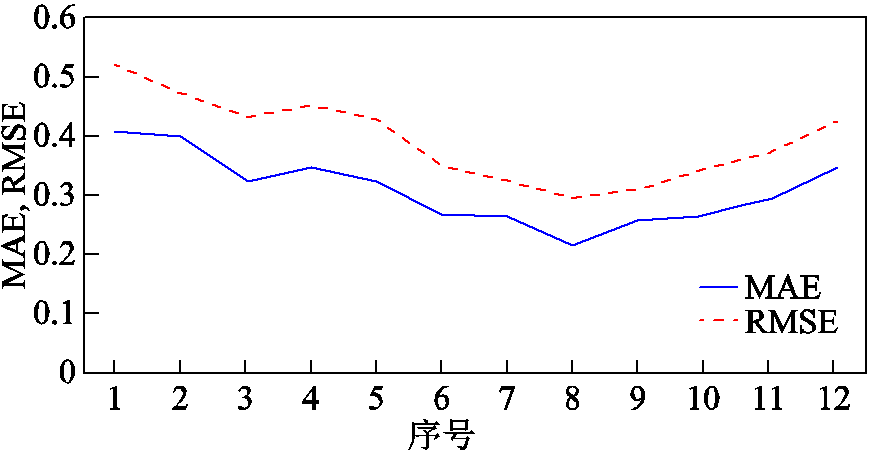
图6 不同参数配置TCN模型训练结果对比图
Fig. 6 Comparison of TCN models of different parameter settings
由图6可以看出，序号8所对应的参数配置TCN模型（即扩大因子d=8，卷积核大小K=1×5）具有最低的MAE值和RMSE值，即在12种参数配置中，序号8的配置可以获得最佳的预测精度。因此，本文TCN模型的负荷预测实验采用此参数。
3.2.2 实验与结果分析
针对第2节中的训练集数据采用TCN建模，然后对测试集数据进行预测，最终得到的误差指标值MAE和RMSE分别为0.219和0.295。与表1中其他三种机器学习方法所能获得的最佳精度相比，TCN模型的预测精度有显著提高，两个性能指标值分别提高了27.2%和24.2%。为更加直观地对比预测负荷值与实际负荷值的差异，利用式（13）对预测结果进行反归一化求解得到与真实负荷数据相同量纲的预测值，然后将其与SVR、GPR和BP神经网络的预测值以及真实负荷值一同绘制于图7中。可以看出，虽然四种模型的预测曲线都很接近实际负荷曲线，但在原始数据曲线的波峰波谷处不同模型之间的预测精度存在一定的差异。其中，SVR模型和GPR模型的预测结果出现多个“尖峰”，说明SVR模型和GPR模型在这种信息量较少的拐点处学习能力较差，而TCN模型和BP模型在“尖峰”处有更好的学习能力。进一步，以原始数据作为横坐标，以模型预测值作为纵坐标绘制四种不同机器学习模型预测结果的散点图如图8所示。对比散点图发现此四种机器学习模型的预测结果基本都能拟合出一条直线，并且各个点离对角线的垂直距离都在较小的范围内。其中SVR模型和GPR模型相对于TCN模型和BP神经网络模型离对角线的垂直距离较远，即预测误差较大；而TCN模型相比于BP神经网络模型则有更多的点落在对角线上，即误差最小。综合以上对比分析可知，基于TCN的深度学习方法在处理具有强非线性的短期电力负荷预测方面具有更优的性能。
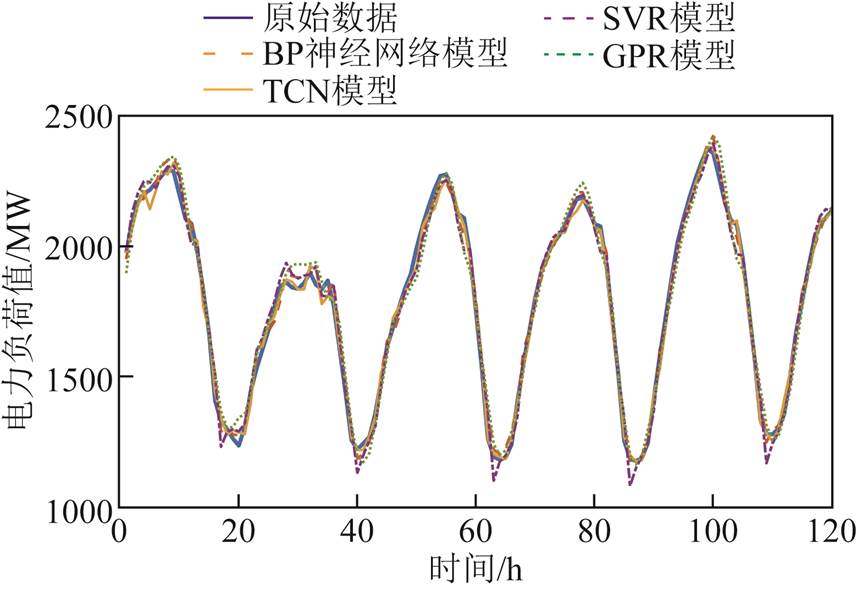
图7 负荷预测结果对比图
Fig.7 Comparison of prediction results of different models
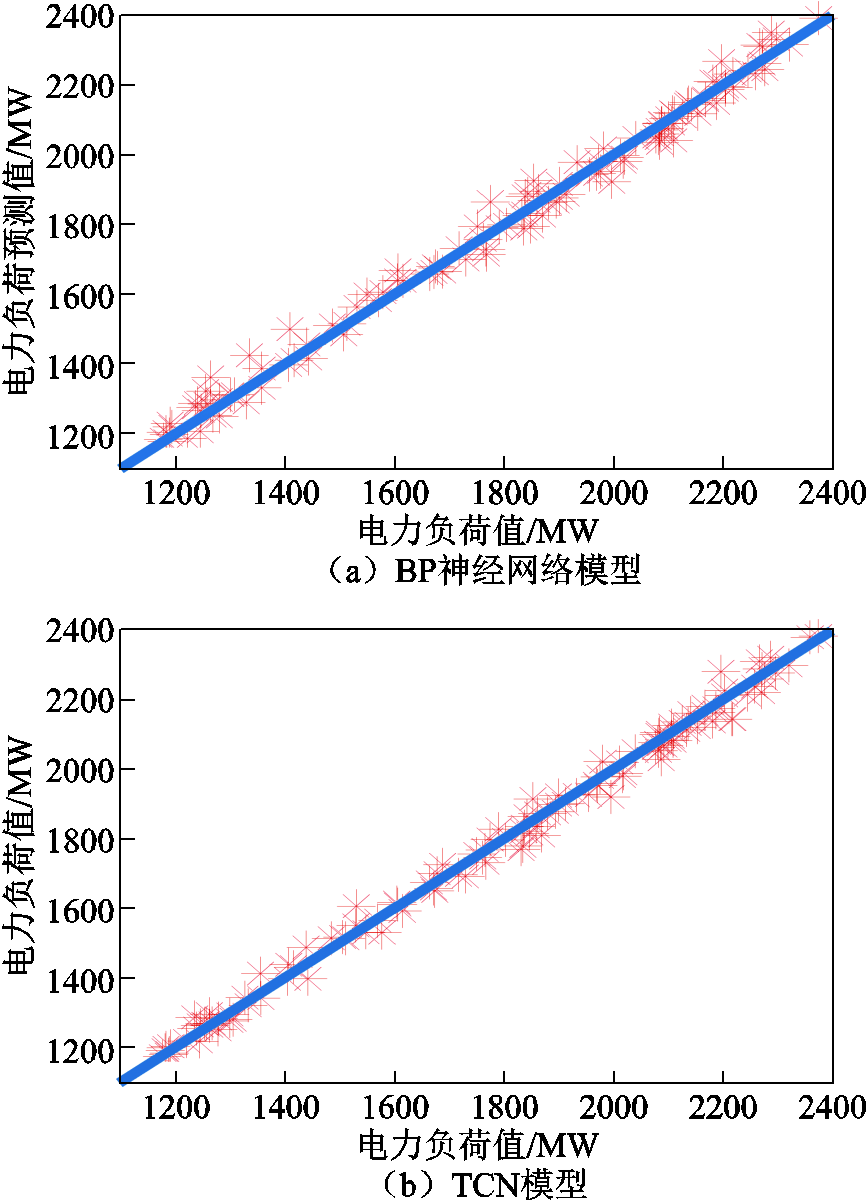
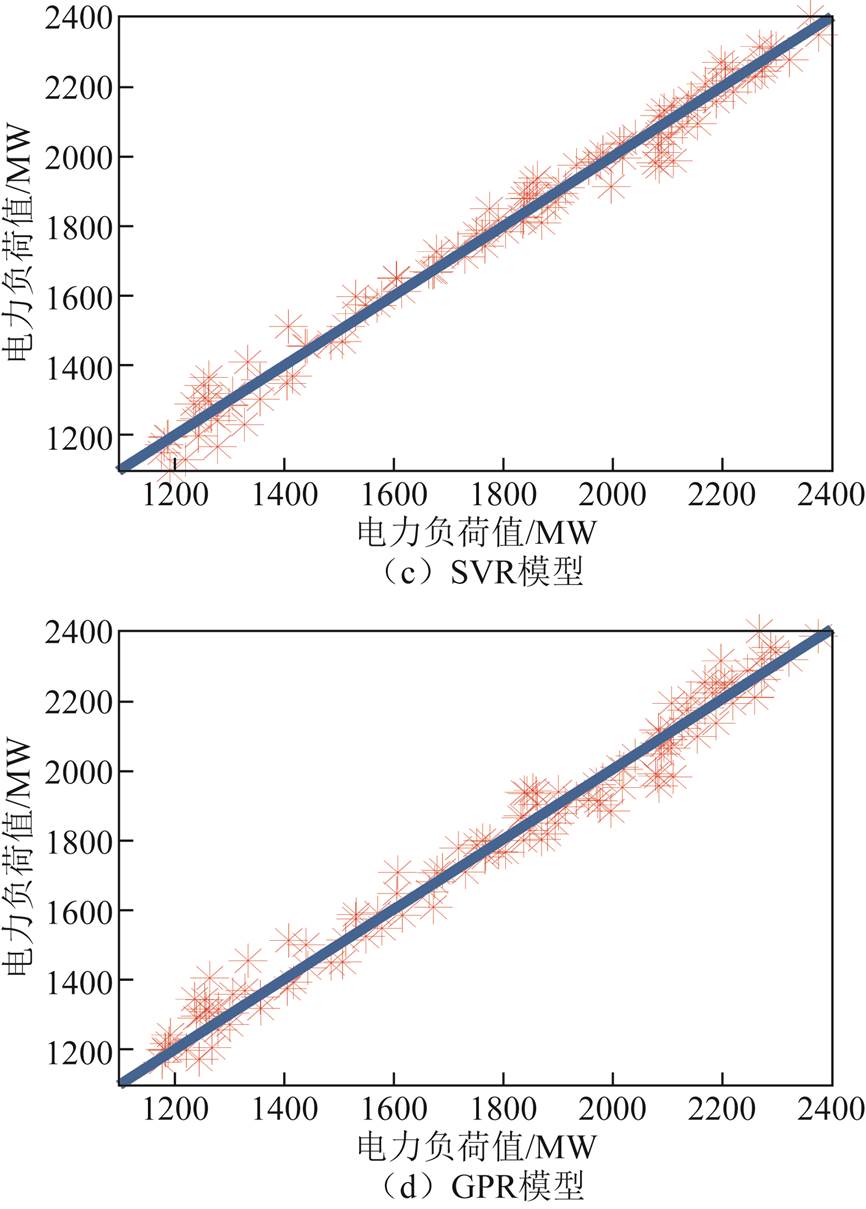
图8 预测模型散点图
Fig.8 Scatter diagram of different models
本文以短期电力负荷预测作为研究内容，对比了SVR、GPR和BP等三种经典机器学习方法各自的特点、适用性和预测效果。在此基础上，提出了采用TCN深度学习网络方法实现短期电力负荷预测。通过对真实电力负荷数据进行预测建模并分析实验结果，得出以下主要结论：
1）本文选用的各种机器学习方法在合理选择模型参数后均可以对含有非线性特征的短期电力负荷数据取得较好的预测效果。因此，机器学习方法适用于解决短期电力负荷预测问题。
2）深度学习网络相比经典机器学习方法具有更好的特征提取能力，因此可以获得更高的预测精度。由于TCN网络的构建引入了扩大因果卷积和残差块，使得该深度学习网络模型具有更好的大样本时间序列处理能力和鲁棒性，实验结果也验证了该方法的有效性和高准确性。
本文的研究内容不仅为短期电力负荷预测的方法选择提供了参考依据和选择多样性，而且对于研究电力系统领域中的其他预测问题如风力、光伏发电功率预测、储能系统中储能元件的使用寿命预测等也具有很好的借鉴意义。但是，深度学习方法通常主要适用于挖掘数据中的非线性特征，对于数据的线性特征的学习效果有时可能不如传统时间序列分析方法。而实际的电力负荷数据一般既包含线性成分又包含非线性成分，即电力负荷时间序列具有复合特征。与此同时，其他因素如天气、假日安排和用户使用习惯等与负荷数据特征之间的关系，以及对模型预测效果的影响也是需要深入关注的内容。因此，笔者未来研究工作将聚焦于设计一种可以更好地处理电力负荷数据复合特征的预测模型，以期进一步提高模型的预测精度。
参考文献
[1] Ayub N, Irfan M, Awais M, et al. Big data analytics for short and medium-term electricity load forecasting using an AI techniques ensembler[J]. Energies, 2020, 13(19): 5193-5213.
[2] Barak S, Sadegh S S. Forecasting energy consumption using ensemble ARIMA–ANFIS hybrid algorithm[J]. International Journal of Electrical Power and Energy Systems, 2016, 82: 92-104.
[3] 刘畅, 卓建坤, 赵东明, 等. 利用储能系统实现可再生能源微电网灵活安全运行的研究综述[J]. 中国电机工程学报, 2020, 40(1): 1-18.
Liu Chang, Zhuo Jiankun, Zhao Dongming, et al. A review of the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids[J]. Proceedings of the CSEE, 2020, 40(1): 1-18.
[4] 李卫国, 陈立铭, 张师, 等. 分时电价下考虑储能调度因素的短期负荷预测模型[J]. 电力系统保护与控制, 2020, 48(7): 133-140.
Li Weiguo, Chen Liming, Zhang Shi, et al. Short-term load forecasting model considering energy storage scheduling factors under time-sharing price[J]. Power System Protection and Control, 2020, 48(7): 133-140.
[5] 李培强, 丰云鹤, 李欣然, 等. 考虑超短期负荷预测的储能电池参与电网一次调频控制策略[J]. 电力系统自动化, 2019, 43(19): 87-95.
Li Peiqiang, Feng Yunhe, Li Xinran, et al. Control strategy for energy storage battery participating in primary frequency regulation of power grid considering ultra-short-term load forecasting[J]. Automation of Electric Power System, 2019, 43(19): 87-95.
[6] 张淑清, 段晓宁, 张立国, 等. Tsne降维可视化分析及飞蛾火焰优化ELM算法在电力负荷预测中应用[J]. 中国电机工程学报, 2021, 41(9): 3120-3130.
Zhang Shuqing, Duan Xiaoning, Zhang Liguo, et al. Tsne dimension reduction visualization analysis and MFOELM algorithm applied in power load forecasting[J]. Proceedings of the CSEE, 2021, 41(9): 3120-3130.
[7] Boroojeni K G, Amini M H, Bahrami S, et al. A novel multi-time-scale modeling for electric power demand forecasting: from short-term to medium-term horizon[J]. Electric Power Systems Research, 2017, 142: 58-73.
[8] 康重庆, 夏清, 刘梅. 电力系统负荷预测 [M]. 2版. 北京: 中国电力出版社, 2017.
[9] Panapakidis I P, Skiadopoulos N, Christoforidis G C. Combined forecasting system for short-term bus load forecasting based on clustering and neural networks[J]. IET Generation, Transmission & Distribution, 2020, 14(18): 3652-3664.
[10] Dai Yeming, Zhao Pei. A hybrid load forecasting model based on support vector machine with intelligent methods for feature selection and parameter optimization[J]. Applied Energy, 2020, 279: 115332-115340.
[11] Gao Xin, Li Xiaobing, Zhao Bing, et al. Short-term electricity load forecasting model based on EMD-GRU with feature selection[J]. Energies, 2019, 12(6): 1140-1157.
[12] Malekizadeh M, Karami H, Karimi M, et al. Short-term load forecast using ensemble neuro-fuzzy model[J]. Energy, 2020, 196: 117127-117136.
[13] Khwaja A S, Zhang X, Anpalagan A, et al. Boosted neural networks for improved short-term electric load forecasting[J]. Electric Power Systems Research, 2017, 143: 431-437.
[14] 王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 53-62.
Wang Zengping, Zhao Bing, Ji Weijia, et al. Short-term load forecasting method based on GRU-NN model[J]. Automation of Electric Power Systems, 2019, 43(5): 53-62.
[15] Yang Lintao, Yang Honggeng. Analysis of different neural networks and a new architecture for short-term load forecasting[J]. Energies, 2019, 12(8): 1433-1455.
[16] 储晨阳，秦川，鞠平，等. 基于优化稀疏编码的超短期负荷滚动多步预测[J]. 电工技术学报, 2021, 36(19): 4050-4059.
Chu Chenyang, Qin Chuan, Ju Ping, et al. Multi-step rolling ultra-short-term load forecasting based on the optimized sparse coding[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4050-4059.
[17] 邓带雨, 李坚, 张真源, 等. 基于EEMD-GRU-MLR的短期电力负荷预测[J]. 电网技术, 2020, 44(2): 593-602.
Deng Daiyu, Li Jian, Zhang Zhenyuan, et al. Short-term electric load forecasting based on EEMD-GRU-MLR[J]. Power System Technology, 2020, 44(2): 593-602.
[18] Liu Tongxiang, Jin Yu, Gao Yuyang. A new hybrid approach for short-term electric load forecasting applying support vector machine with ensemble empirical mode decomposition and whale optimization[J]. Energies, 2019, 12(8): 1520-1539.
[19] 徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 2021, 36(17): 3693-3704.
Xu Jianing, Ni Yulong, Zhu Chunbo. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3693-3704.
[20] Richardson R R, Osborne M A, Howey D A. Gaussian process regression for forecasting battery state of health[J]. Journal of Power Sources, 2017, 357: 209-219.
[21] Borovykh A, Bohte S, Oosterlee C W. Conditional time series forecasting with convolutional neural networks[EB/OL]. 2017, https://arxiv.org/abs/1703. 04691.
[22] Rodríguez F, Martín F, Fontán L, et al. Very short-term load forecaster based on a neural network technique for smart grid control[J]. Energies, 2020, 13(19): 5210-5228.
[23] 苏学能, 刘天琪, 曹鸿谦, 等. 基于Hadoop架构的多重分布式BP神经网络的短期负荷预测方法[J]. 中国电机工程学报, 2017, 37(17): 4966-4973.
Su Xueneng, Liu Tianqi, Cao Hongqian, et al. A multiple distributed BP neural networks approach for short-term load forecasting based on Hadoop framework[J]. Proceedings of the CSEE, 2017, 37(17): 4966-4973.
[24] 吴润泽, 包正睿, 王文韬, 等. Hadoop架构下基于模式匹配的短期电力负荷预测方法[J]. 电工技术学报, 2018, 33(7): 1542-1551.
Wu Runze, Bao Zhengrui, Wang Wentao, et al. Short-term power load forecasting method based on pattern matching in Hadoop framework[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1542- 1551.
[25] Shi Heng, Xu Minghao, Li Ran. Deep learning for household load forecasting—a novel pooling deep RNN[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5271-5280.
[26] Kong Weicong, Dong Zhaoyang, Jia Youfei, et al. Short-term residential load forecasting based on LSTM recurrent neural network[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 841-851.
[27] 赵兵, 王增平, 纪维佳, 等. 基于注意力机制的CNN-GRU短期电力负荷预测方法[J]. 电网技术, 2019, 43(12): 4370-4376.
Zhao Bing, Wang Zengping, Ji Weijia, et al. A short-term power load forecasting method based on attention mechanism of CNN-GRU[J]. Power System Technology, 2019, 43(12): 4370-4376.
[28] Bai Shaojie, Kolter J Z, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling [EB/OL]. 2018, https://arxiv.org/abs/1803.01271.
[29] Zhou Danhua, Li Zhanying, Zhu Jiali, et al. State of health monitoring and remaining useful life prediction of lithium-ion batteries based on temporal convolutional network[J]. IEEE Access, 2020, 8: 53307-53320.
[30] Wu Pin, Sun Junwu, Chang Xuting, et al. Data-driven reduced order model with temporal convolutional neural network[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 360: 112766-112778.
[31] Oord A V D, Dieleman S, Zen H, et al. WaveNet: a generative model for raw audio[EB/OL]. 2016, https://arxiv.org/abs/1609.03499v2.
[32] Wang Yongjian, Yang Ke, Li Hongguang. Industrial time-series modeling via adapted receptive field temporal convolution networks integrating regularly updated multi-region operations based on PCA[J]. Chemical Engineering Science, 2020, 228: 115956- 115971.
[33] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[EB/OL]. 2015, https://arxiv.org/abs/1512.03385.
[34] Hewage P, Behera A, Trovati M, et al. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station[J]. Soft Computing, 2020, 24(21): 16453-16482.
Temporal Convolution Network-Based Short-Term Electrical Load Forecasting
Abstract Accurate short-term electrical load forecasting plays an important role in ensuring the safe and stable operation of the power grid, optimizing energy management, improving the utilization rate of power generation equipment, and reducing operating costs. Owing to the incapability of traditional time series methods in dealing with data’s nonlinear characteristics, this article first compared the applicability and forecasting performance of classical machine learning methods in short-term electrical load forecasting. The adopted modeling methods include: support vector regression, Gaussian process regression and forward neural network; the values of metrics proved that the machine learning methods can obtain good prediction accuracy and are suitable for processing short-term load data with strong nonlinear characteristics; on this basis, a short-term electrical load forecasting method based on temporal convolutional network (TCN) deep learning method was proposed. This model has the ability to extract features from large samples of time series and realize prediction, and its structure can effectively solve the degenerate problem of deep network learning; finally, forecasting experiment was conducted on the real load data. The results showed that the TCN can acquire much higher accuracy, and the deep learning method outperforms the classical machine learning methods in non-linear feature extraction.
keywords：Short-term electrical load forecasting, machine learning, support vector regression, Gaussian process regression, temporal convolution network
DOI:10.19595/j.cnki.1000-6753.tces.210223
中图分类号：TM743
国家重点研发计划“智能电网技术与装备”重点专项资助（2017YFB0903205）。
收稿日期 2021-02-22
改稿日期 2021-06-29
赵 洋 男，1981年生，副教授，硕士生导师，研究方向为储能系统运行控制、系统建模与预测等。E-mail：simonzhaoyang@163.com（通信作者）
王瀚墨 男，1994年生，硕士研究生，研究方向为深度学习在电力负荷预测中的应用。E-mail：creepui@gmail.com
（编辑 郭丽军）