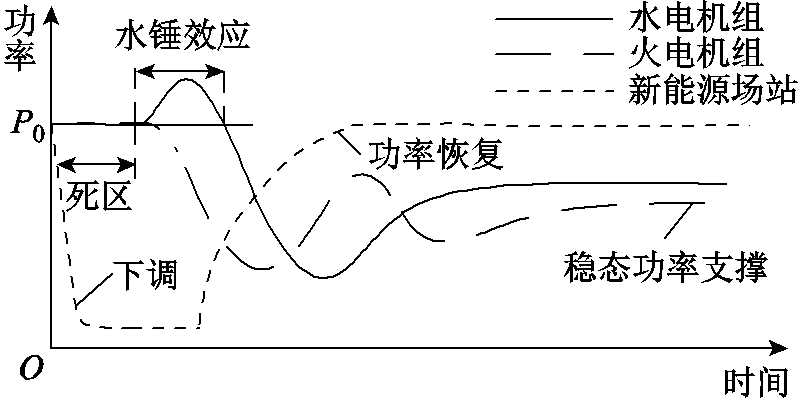
图1 不同类型机组的功率调节情况
Fig.1 Power regulation of different generators
摘要 对于含高渗透率新能源发电的送端电网,直流闭锁后可通过快速降低新能源场站功率替代高代价的切常规机组操作,来实现更加经济的频率安全控制。因此,针对送端电网直流闭锁故障,该文提出一种新能源场站协同常规机组的紧急频率控制策略优化模型,在保证频率安全的同时最小化系统控制代价。此外,考虑到直接求解上述含微分方程约束的非线性优化模型非常困难,该文提出针对该模型的系统性混合整数线性化方法,因此可用具有大规模混合整数线性规划(MILP)问题求解能力的商用软件对其进行高效求解。最后对我国西北某省级电网进行算例仿真分析,结果说明了所提优化模型的有效性以及求解过程的高效性。
关键词:直流闭锁 紧急频率控制 新能源调控 快速优化 混合整数线性规划
在区域互联电网中,特高压直流闭锁故障将对送端电网产生巨大的有功冲击[1-3],导致系统频率快速上升,处置不当甚至将可能引发波及全网的连锁性事故。目前针对直流闭锁故障的送端电网紧急频率控制措施主要为切除发电机组,并根据不同机组切除成本及控制性能的差异,对紧急切机策略进行优化。当系统较简单时,可按照启发式原则对各控制措施的优先度进行排序,经机电仿真验证决策结果,不断迭代寻找最优方案[4-6],但该方法在复杂系统中具有局限性。因此,针对大规模电网,可首先利用等值法模拟系统状态变量的波动,然后采用合适的算法对控制策略进行寻优,如文献[7-8]将复杂系统等值为单机负荷模型,获取了频率的近似解析解,但由于采用了简化的线性模型,其计算精度相对较低。部分学者进一步尝试在系统暂态频率计算过程中考虑非线性因素的影响[9],并利用人工智能算法优化紧急控制策略[10-11]。然而,这些方法虽然获得了更加精确的频率计算结果,但并未能妥善解决控制策略优化算法的计算效率问题,求解速度仍存在较大的提升空间。
随着电网中新能源发电占比的不断提升,新能源出力的波动特性也将极大地影响电网的运行方式,可能导致传统离线制定的紧急控制策略表在实际应用时出现“失配”现象。“在线预决策”则是跟踪系统运行方式变化而确保紧急控制策略有效性的重要手段[12]。波动速度非常快的新能源场站功率分量(例如1min以内时间尺度的波动分量)通常由于幅值较小而对电力系统级的调度和控制问题影响较低[13]。但是,略微低频的功率波动分量的幅值一般较大,例如,大型光伏电站在5~10min这个时间尺度上即可能出现幅值达到70%及以上额定功率的波动分量[14]。如果期望通过“在线预决策”方式来应对这种大幅功率波动,则要求紧急控制策略的生成速度要明显快于功率波动速率,对在线应用的紧急控制优化决策问题的求解效率提出了明确的挑战。
考虑切机类型时,一般情况下优先切除新能源场站[15-17]。此外,部分学者也探索了利用水电机组的精准调控参与紧急控制[18]。因此,鉴于新能源场站更加快速的功率调节能力,若在紧急控制中对部分新能源场站“以控代切”,将进一步降低控制成本。例如,文献[19]提出了光伏电站功率快速调控方案,能够保证场站级功率响应时间在100ms以内,说明了其参与紧急频率控制的潜力。此外,虽然风机功率调控的响应速度与其实际运行工况密切相关[20-21],但是已有大量研究表明风机功率调控对电力系统暂态频率支撑的有效性[22-24]。
针对上述问题,本文提出了一种切机和新能源场站功率调控协同作用的送端电网直流闭锁紧急频率控制策略优化模型及其快速求解方法。首先,该优化模型中暂态频率的计算准确计及多种重要的非线性因素,以控制成本最低为目标并考虑频率和潮流等多种约束条件;其次,该优化模型的快速求解得益于本文提出的一套系列性转换操作,将该模型规范化为可用成熟商业软件高效求解的标准混合整数线性规划(Mixed Integer Linear Programming, MILP)问题;最后,以我国西北某省电网为实例验证了该优化模型的准确性和求解过程的快速性。本文接下来将对上述模型的建立、转换及实例验证过程进行详细分析。
紧急切机是防止送端电网直流闭锁故障后暂态频率越限的有效措施,但是代价高昂,尤其是切除火电机组。此外,紧急切机操作是一项颗粒度很大的控制手段,一般会出现过切现象,造成不必要的经济损失[25]。已有研究和实践表明,现代逆变器的控制技术相对成熟,如现有光伏电站的快速功率调控技术能够在100ms以内完成站内输出功率的调整[19];风电场也能在数百毫秒内改变其输出的电磁功率,并通过调整转速提供短暂的有功支撑,即新能源功率调节速率远快于常规机组。因此,在新能源发电富集的送端电网中,直流闭锁的紧急控制措施除常规切机外还可考虑紧急连续调控部分新能源场站出力(后期新能源场站会逐渐恢复至最大功率点运行),从而用廉价的新能源场站调控替换部分常规机组切机,以更加经济的方式保证系统暂态频率安全[26-27]。事实上,新能源场站即使用“切”的方式参与紧急控制,其成本代价也要明显低于常规机组。然而,实际电网的潮流约束导致不可能简单地完全依赖新能源场站来解决紧急频率控制问题,可能必须切除部分常规机组。因此,寻求最经济的组合方式来实现常规机组切机和新能源场站“切或调”协同完成系统紧急频率控制,具有十分明显的现实意义。
由于涉及频率的暂态过程,搜索最优紧急频率控制策略需考虑如下影响因素:①水电机组的水锤效应,即水流惯性造成水电机组在调频前期出力与预想相反的现象,可见水锤效应明显不利于系统的频率暂态,不同类型机组的功率调节情况如图1所示;②常规机组的一次调频要越过死区后才启动,启动时间在2s左右,且具有功率调整上、下限。据此可推测,直流闭锁后系统频率暂态将由包含死区和饱和等强非线性特性的微分方程组描述,搜索最优紧急频率控制策略就是求解包含上述参数化微分方程约束的高维混合整数(即含有连续和离散决策变量)非线性规划问题。因此,本文建立了基于常规机组和新能源场站且考虑上述约束条件的紧急频率控制策略优化模型,并提出高效准确的求解方法。

图1 不同类型机组的功率调节情况
Fig.1 Power regulation of different generators
本文所提的送端电网直流闭锁紧急频率控制策略优化模型以控制代价最小为目标函数,并考虑暂态频率最大值和稳态频率值约束,以及线路有功潮流约束,具体描述为
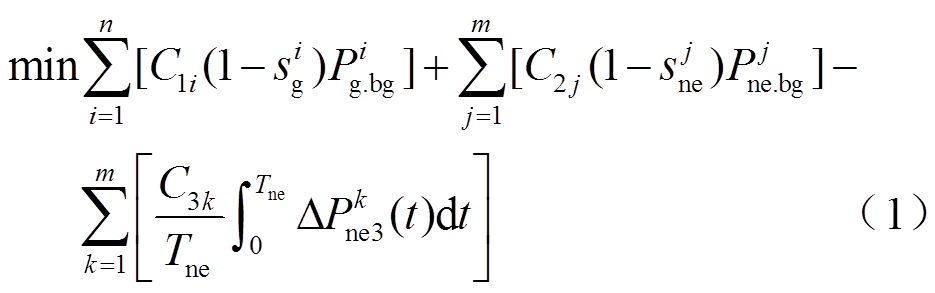
式中,n和m分别为常规机组与新能源场站的数量;C1i和C2j分别为常规机组与新能源场站的单位切除成本系数,元/104kW;C3k为新能源场站的单位调节成本系数,考虑其参与功率调节时间较短,一般取值较小,元/104kW;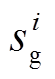 和
和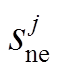 分别为常规机组和新能源场站运行状态(紧急控制策略相关变量),0为切除、1为在运;
分别为常规机组和新能源场站运行状态(紧急控制策略相关变量),0为切除、1为在运;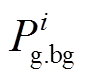 和
和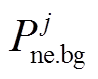 分别为机组和场站的初始运行功率;
分别为机组和场站的初始运行功率;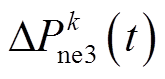 为t时刻第k个新能源场站的实际功率调控量(紧急控制策略相关变量);Tne为新能源场站参与紧急频率控制的代价计算时长。所采用的约束条件为
为t时刻第k个新能源场站的实际功率调控量(紧急控制策略相关变量);Tne为新能源场站参与紧急频率控制的代价计算时长。所采用的约束条件为
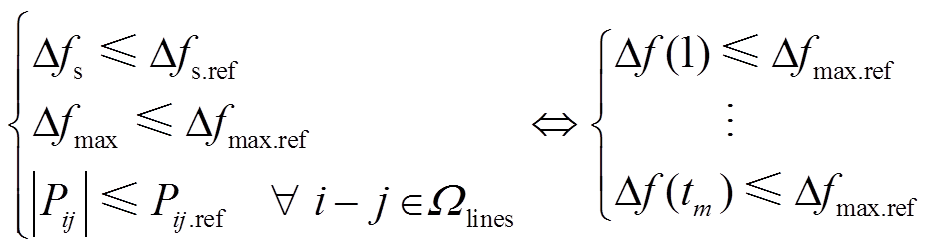 (2)
(2)
式中,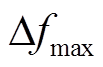 和
和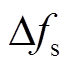 分别为暂态频率最大值和稳态频率值;
分别为暂态频率最大值和稳态频率值;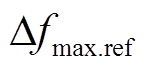 和
和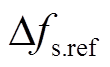 分别对应其允许的最大值(本文采用离散的切机措施与连续的功率调控手段相结合基本消除了过切的风险);
分别对应其允许的最大值(本文采用离散的切机措施与连续的功率调控手段相结合基本消除了过切的风险);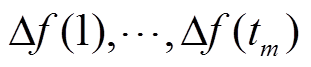 表示暂态过程中各时间断面的系统频率值;
表示暂态过程中各时间断面的系统频率值;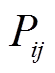 和
和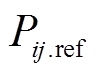 分别为各时间断面上线路i-j之间传输有功功率以及该线路允许的有功功率上限;Ωlines为电网中可能过载线路的编号集合。由于本文的研究对象是高压输电网络,故采用直流潮流模型近似计算各线路的有功功率,即
分别为各时间断面上线路i-j之间传输有功功率以及该线路允许的有功功率上限;Ωlines为电网中可能过载线路的编号集合。由于本文的研究对象是高压输电网络,故采用直流潮流模型近似计算各线路的有功功率,即
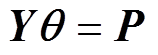 (3)
(3)
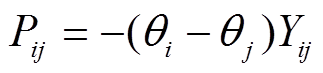 (4)
(4)
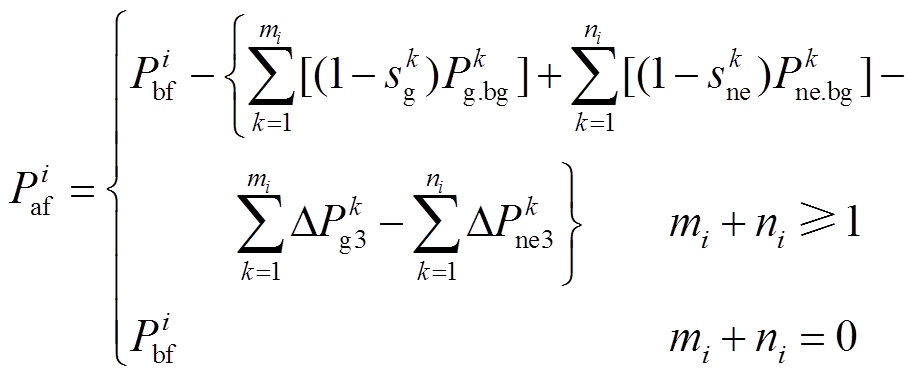 (5)
(5)
式中,P、Y和θ分别为节点注入有功功率向量、节点导纳矩阵及节点电压相位向量;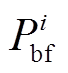 、
、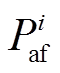 分别为正常运行时和紧急控制后各节点注入有功功率;mi和ni分别为节点i处的常规机组及新能源场站的数量;
分别为正常运行时和紧急控制后各节点注入有功功率;mi和ni分别为节点i处的常规机组及新能源场站的数量;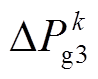 为该节点处第k台常规机组的功率调节量;
为该节点处第k台常规机组的功率调节量;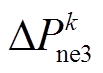 为新能源场站的功率调节量。其中直流闭锁点处的注入功率变化还需考虑闭锁功率(可实时监测获取)
为新能源场站的功率调节量。其中直流闭锁点处的注入功率变化还需考虑闭锁功率(可实时监测获取)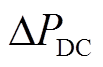 的影响。
的影响。
求解上述紧急频率控制策略优化问题的关键之一是暂态频率最大偏差值Δfmax的计算。很显然,Δfmax没有解析表达式,只能基于(以直流闭锁功率为扰动量)系统频率响应(System Frequency Response, SFR)模型[28]进行数值积分来获取,如图2所示。图2中SFR模型主要包括常规机组的一次调频环节与新能源场站的快速功率控制环节。由于针对送端直流闭锁问题,紧急控制中新能源场站功率仅允许下调。图中,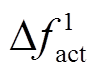 ,
, ,
,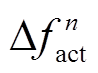 为不同机组越过死区的频率差值;
为不同机组越过死区的频率差值;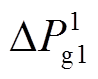 ,
, ,
,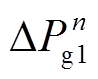 为限幅环节前的原动机功率调节指令;
为限幅环节前的原动机功率调节指令;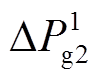 ,
, ,
,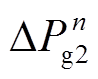 为考虑限幅环节的原动机功率响应;
为考虑限幅环节的原动机功率响应;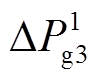 ,
, ,
,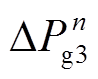 为考虑机组切除的常规机组实际功率调整量;
为考虑机组切除的常规机组实际功率调整量;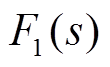 ,
, ,
,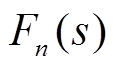 分别为不同常规机组调速器及原动机对应的传递函数(模拟其调频动态过程);
分别为不同常规机组调速器及原动机对应的传递函数(模拟其调频动态过程);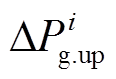 与
与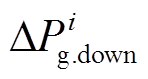 分别为不同常规机组对应的一次调频功率调节上、下限;
分别为不同常规机组对应的一次调频功率调节上、下限; ,
, ,
,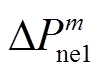 为不同新能源场站在紧急控制过程中的功率调节指令;
为不同新能源场站在紧急控制过程中的功率调节指令;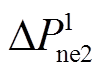 ,
, ,
,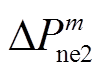 为新能源场站对功率调节指令的响应值;
为新能源场站对功率调节指令的响应值;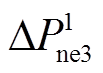 ,
, ,
,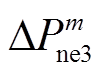 为新能源场站功率实际调整量;
为新能源场站功率实际调整量;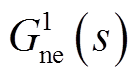 ,
, ,
,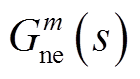 代表各个新能源场站响应紧急功率控制指令的动态模型。
代表各个新能源场站响应紧急功率控制指令的动态模型。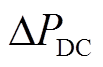 为直流闭锁功率(取正值);
为直流闭锁功率(取正值);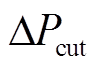 为机组(场站)切除总量(取正值);H为系统惯性常数;
为机组(场站)切除总量(取正值);H为系统惯性常数;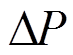 为系统不平衡功率。为提升策略优化模型求解效率,上述
为系统不平衡功率。为提升策略优化模型求解效率,上述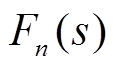 与
与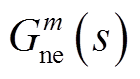 均对应着逼近详细动态模型的低阶线性传递函数。值得说明的是,本文中风机在不超速前提下采用转子动能控制方式参与抑制直流闭锁后系统暂态高频[23-24]。此外,桨距角控制则在转子动能控制会出现超速情况下(例如风机工作在恒转速区或者恒功率区)承担系统暂态频率支撑的任务[22]。桨距角控制的功率响应速率要明显慢于转子动能控制,因此对应着不同的紧急控制功率响应近似模型。更重要的是,当风机工作在最大功率跟踪区时,策略优化模型需要根据风机转速响应判断是利用转子动能控制还是桨距角控制来参与紧急控制。
均对应着逼近详细动态模型的低阶线性传递函数。值得说明的是,本文中风机在不超速前提下采用转子动能控制方式参与抑制直流闭锁后系统暂态高频[23-24]。此外,桨距角控制则在转子动能控制会出现超速情况下(例如风机工作在恒转速区或者恒功率区)承担系统暂态频率支撑的任务[22]。桨距角控制的功率响应速率要明显慢于转子动能控制,因此对应着不同的紧急控制功率响应近似模型。更重要的是,当风机工作在最大功率跟踪区时,策略优化模型需要根据风机转速响应判断是利用转子动能控制还是桨距角控制来参与紧急控制。
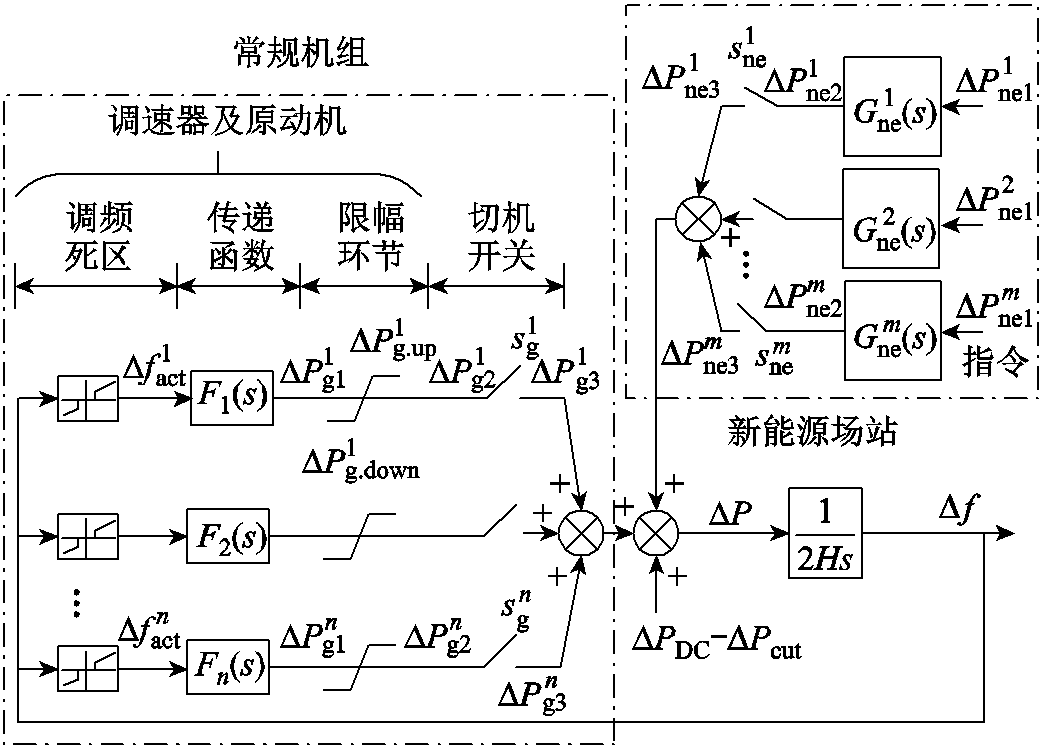
图2 考虑新能源场站功率调节的SFR模型
Fig.2 The SFR model considering power regulation of renewable energy plants
转子动能控制时风机功率会自动恢复至控制前初值,且恢复速度较快,故相应近似模型中要考虑其恢复动态。桨距角控制响应功率调节指令的速度较慢,因此本文在整个频率暂态过程中不考虑桨距角控制的功率恢复动态,即只在稳态频率偏差计算时认为风机功率已经恢复初值。如前言所述,光伏响应功率调节指令的速度非常快(100ms以内)。为尽量降低策略优化模型的复杂度,本文假设光伏电站在响应功率调节指令Tin(单位为s)后,其功率开始恢复为初值,即图2中光伏电站的功率调节指令值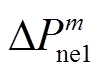 在Tin后变成零,此时近似动态模型对应光伏电站的功率恢复过程。
在Tin后变成零,此时近似动态模型对应光伏电站的功率恢复过程。
如果直接采用常规思路(如分支定界法)并结合数值积分求解上述优化问题,首先要面对的就是求解大量分支子问题,每个子问题都是一个具有死区和饱和特性的微分方程约束的非线性规划问题,且每个子问题的微分方程均被决策变量参数化,需要根据具体分支情况来形成(例如,SFR模型中系统等效惯性常数H是关于切机决策变量的函数),因此总的计算量很大且处理过程繁杂;其次,如果用数值积分处理非线性规划问题中的微分方程,将难以提供目标函数的梯度信息,基于数值摄动的近似梯度的计算将进一步增大计算量,且数值精度和稳定性差,最终可能导致搜索过程不收敛或搜索结果不理想。可以预见,对于涉及大量可切/可调单元的紧急频率控制策略优化问题,直接利用上述常规思路进行求解非常困难。
相较于上述混合整数非线性规划问题的直接求解过程具有较大困难性,混合整数线性规划问题的求解理论相对成熟,其标准形式为
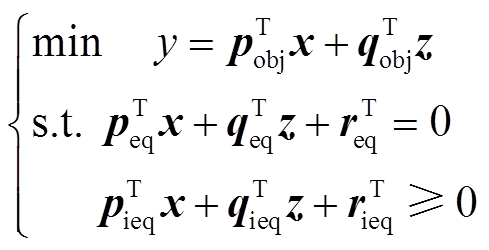 (6)
(6)
式中,y为目标函数变量;x为连续型变量;z为整数型变量;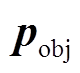 、
、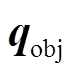 、
、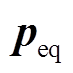 、
、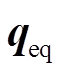 、
、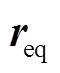 、
、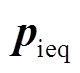 、
、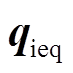 、
、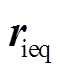 均为常系数矩阵。
均为常系数矩阵。
目前研究具备针对上述MILP问题的专用商业求解器(如CPLEX和GUROBI)能够满足大规模混合整数线性规划问题的高效稳定求解的需要[29],因此针对所提紧急频率控制策略优化模型,本文的基本思路是将计算暂态频率最大值的数值积分与优化问题搜索过程融合为一体,提出一套系列性操作将其转换为标准的混合整数线性规划问题,从而有效保障了原始控制策略优化问题求解的快速性和鲁棒性及解的质量。
图2给出了计算系统暂态频率的SFR传递函数框图。本文采用差分法对SFR模型进行离散化,并保留各时间断面上的变量值作为优化问题的中间变量,同时保持各中间变量间(以及中间变量与决策变量间)的线性关系。例如,本文利用双线性变换将常规机组原动机和调速器模型中的线性传递函数F1(s)离散化,得到对应的自回归滑动平均(Auto-Regressive Moving Average, ARMA)模型为
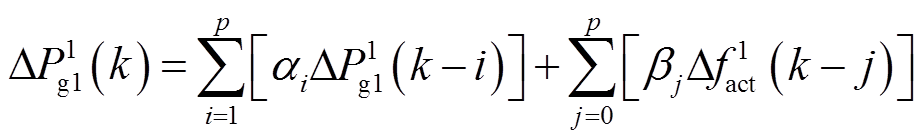 (7)
(7)
式中,k为时序变量;p为传递函数阶数;αi和βj为常系数。假设上述离散化过程的采样时间间隔恒定为T,数值积分总时长为Tmax,则对应有tm个采样时刻点,可列写方程,即
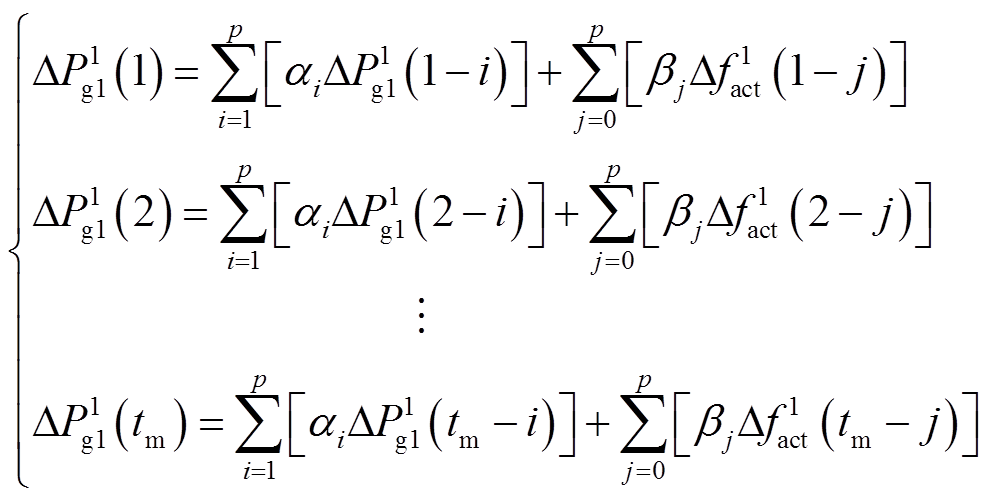 (8)
(8)
因此,式(8)中的tm个线性等式将作为控制策略优化模型的约束条件,同时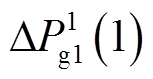 ,
, 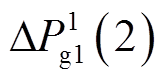 ,
, ,
,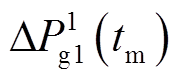 和
和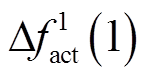 ,
,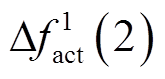 ,
, ,
,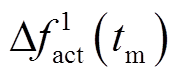 将作为MILP模型的连续型中间待优化变量(此处是区别于传统求解思路的主要内容),并且针对n台常规机组,类似式(8)的线性等式约束共有n组。针对SFR模型中其他线性传递函数,执行上述相同的离散化操作,从而将各自在Tmax时段内的积分过程分别转换为tm个衔接中间变量的等式约束。
将作为MILP模型的连续型中间待优化变量(此处是区别于传统求解思路的主要内容),并且针对n台常规机组,类似式(8)的线性等式约束共有n组。针对SFR模型中其他线性传递函数,执行上述相同的离散化操作,从而将各自在Tmax时段内的积分过程分别转换为tm个衔接中间变量的等式约束。
SFR模型的混合整数线性化过程的难点在于处理强非线性环节,例如,图3中第i台常规机组的一次调频死区和限幅环节等。事实上,从数值等效性的角度看,可以将针对该常规机组的切机操作也集成表示(即在连续的功率输出后串联一个0/1开关)。以限幅环节(饱和)和切机操作为例,本文首先将其表示为逻辑约束,即
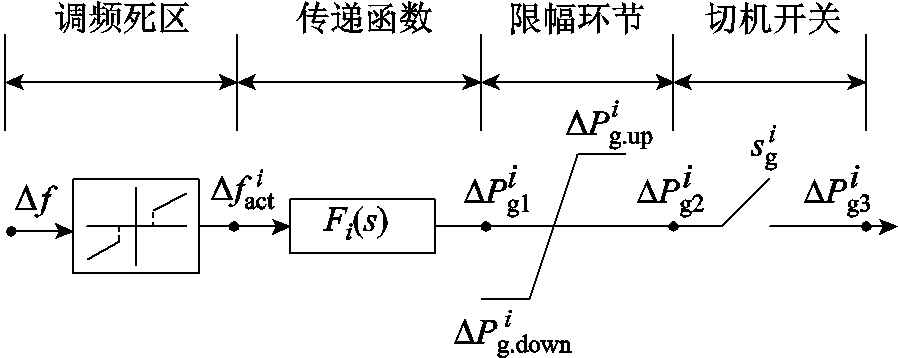
图3 第i台常规机组一次调频环节
Fig.3 The primary frequency regulation process of the ith conventional generator
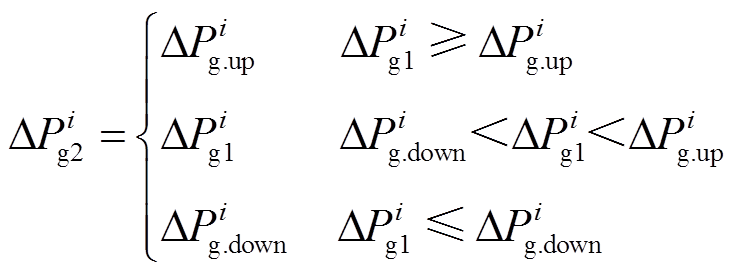 (9)
(9)
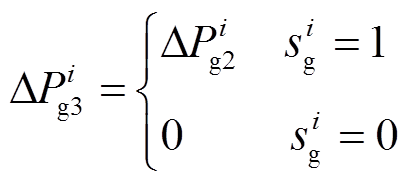 (10)
(10)
Big M法是一种实现逻辑约束向线性约束转换的有效方法,式(11)左右两边在逻辑上完全等效。
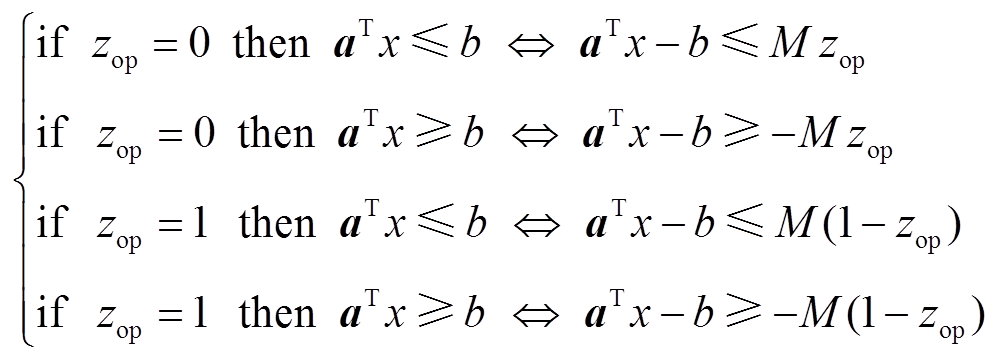 (11)
(11)
式中,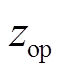 为0/1型变量;a为向量;b为常数;M为一足够大的常数。
为0/1型变量;a为向量;b为常数;M为一足够大的常数。
因此,基于Big M法的基本思路,表示限幅环节的约束(9)可进一步处理为
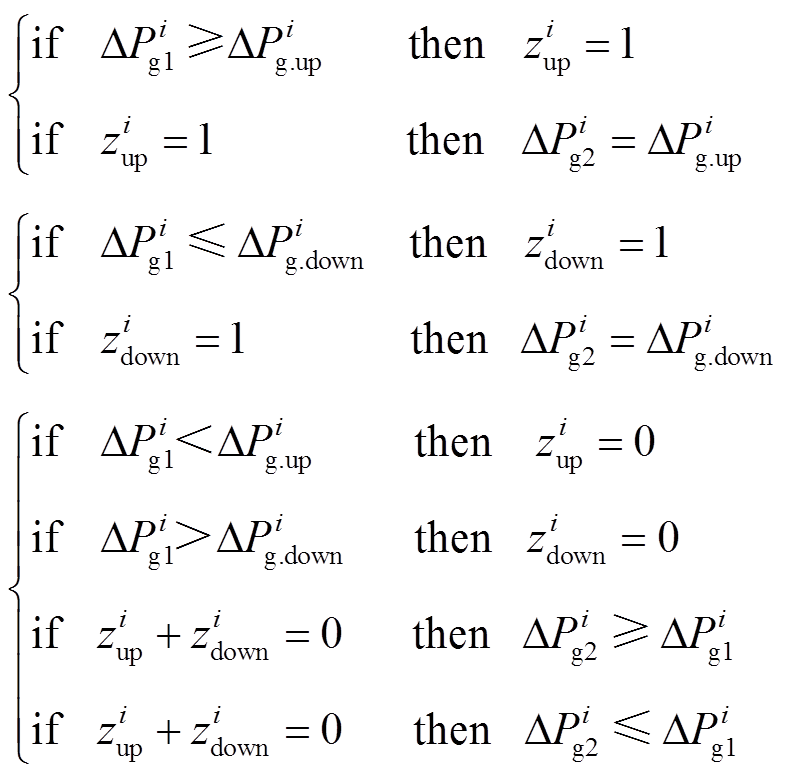 (12)
(12)
可见通过引入部分标志性变量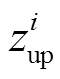 和
和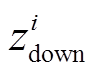 (分别标志功率调节达到上、下限),转变形式后的式(12)与式(11)中Big M法的应用形式一致,并且与约束(9)在逻辑上完全等价。并且基于式(11)中Big M法的基本原理,可以将逻辑约束(12)转换为
(分别标志功率调节达到上、下限),转变形式后的式(12)与式(11)中Big M法的应用形式一致,并且与约束(9)在逻辑上完全等价。并且基于式(11)中Big M法的基本原理,可以将逻辑约束(12)转换为
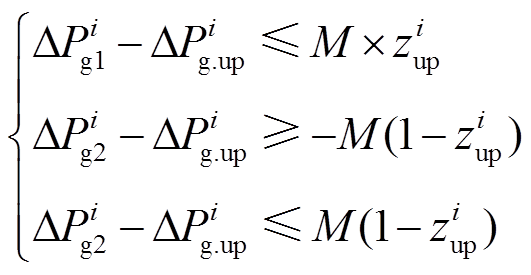
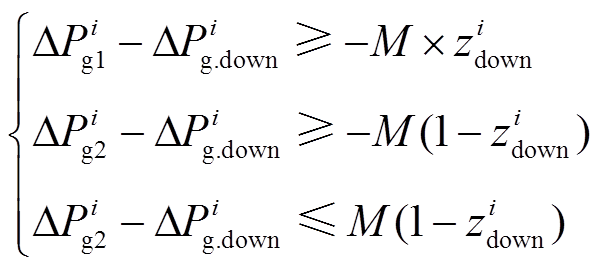 (13)
(13)
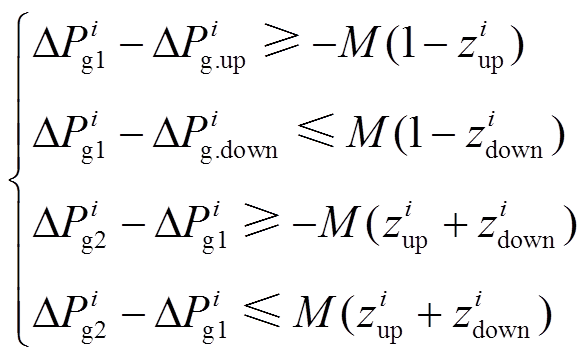
值得注意的是:式(13)中M为常量,故其为线性不等式;此外,为了与2.1节的离散化过程相接口,每个积分时间断面上都要按式(13)的形式列写对应的不等式约束,并将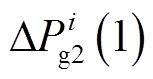 ,
,  ,
, ,
, 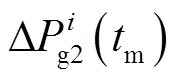 ,
,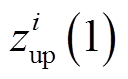 ,
, 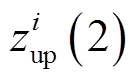 ,
, ,
,  和
和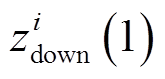 ,
, 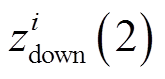 ,
, ,
, 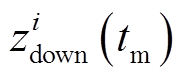 作为优化问题的中间变量(后两者为整数型待优化变量),后文不重复说明。
作为优化问题的中间变量(后两者为整数型待优化变量),后文不重复说明。
同理,常规机组的切除操作亦可转换为式(14)线性不等式约束。
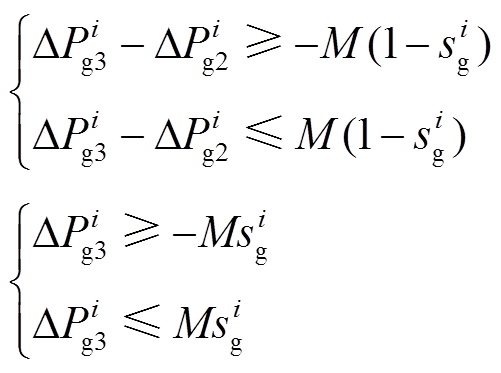 (14)
(14)
这里无需为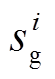 及
及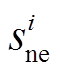 在每个积分时间断面上均设置中间变量,因为它们在每个时间断面上都是相同的。类似地,新能源场站的功率调节上下限及切除操作可表示为如式(15)、式(16)的约束。
在每个积分时间断面上均设置中间变量,因为它们在每个时间断面上都是相同的。类似地,新能源场站的功率调节上下限及切除操作可表示为如式(15)、式(16)的约束。
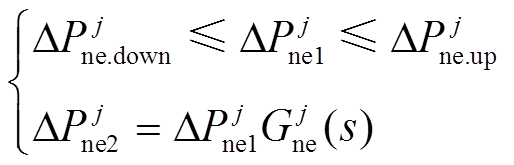 (15)
(15)
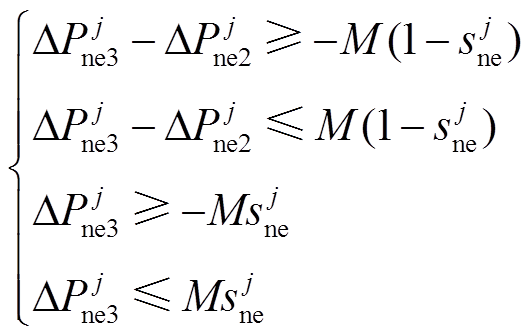 (16)
(16)
式中,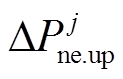 和
和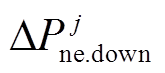 分别为新能源场站的功率调节上、下限。其中
分别为新能源场站的功率调节上、下限。其中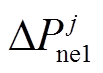 与
与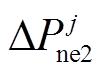 间的等式关系同样可按照式(7)的变换原理将其转换为线性等式约束,并且式(15)可能因不同类型新能源场站
间的等式关系同样可按照式(7)的变换原理将其转换为线性等式约束,并且式(15)可能因不同类型新能源场站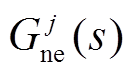 的不同而存在差异(详见算例部分)。为避免新能源场站功率在紧急控制中出现大幅波动,在紧急控制过程中对每个新能源场站仅给定一个恒定不变的功率调节参考值
的不同而存在差异(详见算例部分)。为避免新能源场站功率在紧急控制中出现大幅波动,在紧急控制过程中对每个新能源场站仅给定一个恒定不变的功率调节参考值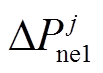 ,作为待优化变量。
,作为待优化变量。
为了避免系统正常运行时频率小幅但快速波动带来的不良影响,各类常规机组都会设置调频死区。并且部分机组的调频死区高达0.05Hz[30],这将明显降低机组对于突发频率扰动事件(例如直流闭锁)的反应速度。因此,本文在SFR模型中采用式(17)计及死区对暂态频率的影响。
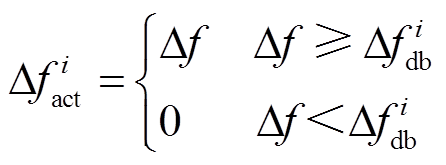 (17)
(17)
式中,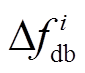 为第i台常规机组调频死区的上限。值得说明的是:送端系统频率因直流闭锁而上升,合理的频率紧急控制措施不会使频率在达到暂态最大值之前再次进入死区(或者向下穿越死区),所以式(17)从数值等效性角度是可以准确反映死区对暂态频率(最大值)的影响。同理,可以仿照上面各例将式(17)转换为线性不等式约束;根据上述常规机组各非线性环节的处理方式,可以用带逻辑判断(风机是否超速)的传递函数框图来表征“工作在最大功率跟踪区的风机是采用转子动能控制还是桨距角控制来参与紧急控制”,从而对其进行混合整数线性化处理,具体过程在此不一一赘述。
为第i台常规机组调频死区的上限。值得说明的是:送端系统频率因直流闭锁而上升,合理的频率紧急控制措施不会使频率在达到暂态最大值之前再次进入死区(或者向下穿越死区),所以式(17)从数值等效性角度是可以准确反映死区对暂态频率(最大值)的影响。同理,可以仿照上面各例将式(17)转换为线性不等式约束;根据上述常规机组各非线性环节的处理方式,可以用带逻辑判断(风机是否超速)的传递函数框图来表征“工作在最大功率跟踪区的风机是采用转子动能控制还是桨距角控制来参与紧急控制”,从而对其进行混合整数线性化处理,具体过程在此不一一赘述。
根据图2模型(其中的系统等值发电机转子运行模型),采用双线性变换离散化后的系统频率差值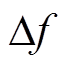 与不平衡功率
与不平衡功率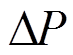 间的关系可表示为
间的关系可表示为
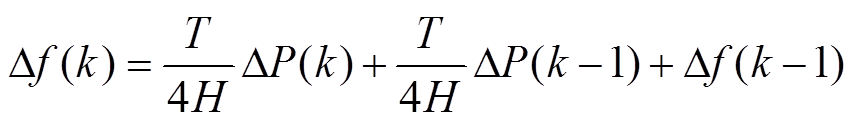 (18)
(18)
且系统的等效惯性常数H为
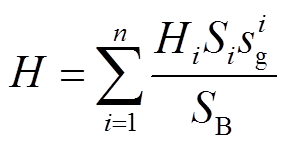 (19)
(19)
式中,Hi和Si分别为第i台常规机组的惯性常数和额定容量;SB为系统容量基值。很显然,式(18)是关于决策变量和中间变量的非线性方程。
针对上述情况,本文首先对时域下系统频率变化率与不平衡功率间的关系式进行如式(20)的变换。
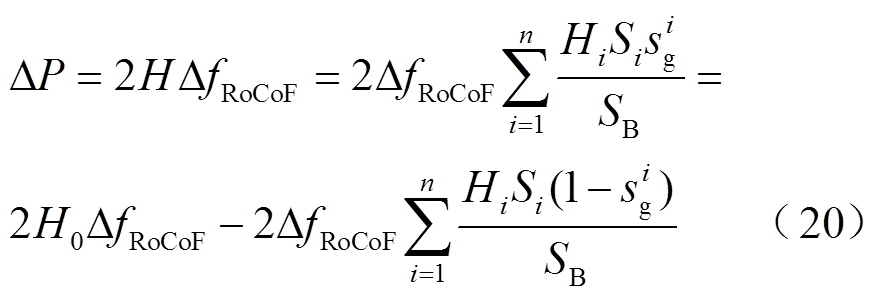
式中,H0为系统正常运行时的等效惯性常数;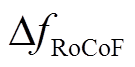 为系统频率变化率。进一步,可以将式(20)转换为等值发电机转子运动方程的传递函数框图形式,如图4所示。本文定义
为系统频率变化率。进一步,可以将式(20)转换为等值发电机转子运动方程的传递函数框图形式,如图4所示。本文定义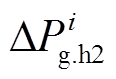 为常规机组切除引起的“惯性反馈功率”,
为常规机组切除引起的“惯性反馈功率”,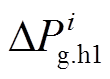 为其理论计算值。从逻辑上讲,切除常规机组一方面可以减小加速性质的不平衡功率(图4中的ΔP),从而遏制系统频率上升;另一方面由于切机而减小系统等值惯量,反而会助增频率上升的速率,这一点可以从图4中的惯性反馈功率通道反映出来。
为其理论计算值。从逻辑上讲,切除常规机组一方面可以减小加速性质的不平衡功率(图4中的ΔP),从而遏制系统频率上升;另一方面由于切机而减小系统等值惯量,反而会助增频率上升的速率,这一点可以从图4中的惯性反馈功率通道反映出来。
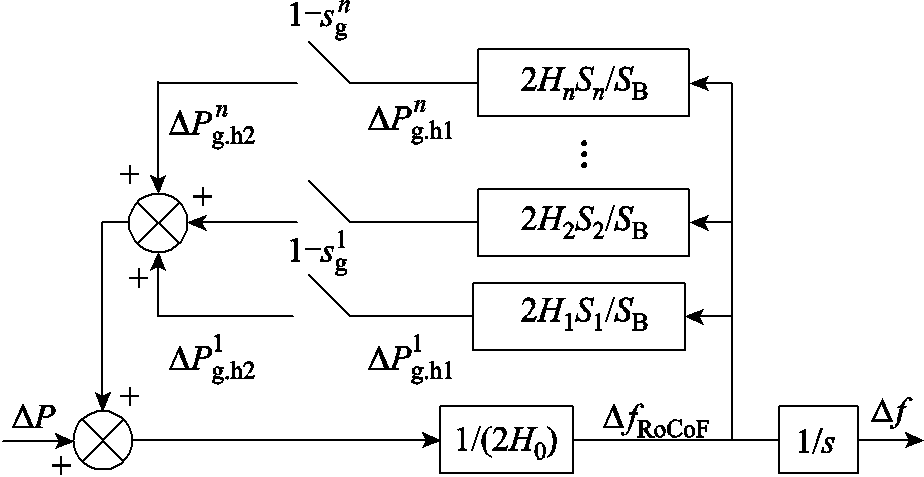
图4 考虑机组切除的发电机转子运动等值模型
Fig.4 Equivalent model of generator rotor motion considering generators tripped
图4中表征运行状态的开关同样可由Big M法转换为线性不等式约束。因此,等值发电机转子运动模型可由线性约束描述为
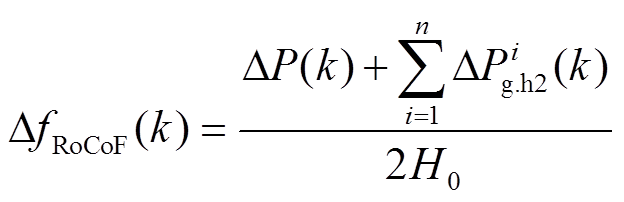 (21)
(21)
 (22)
(22)
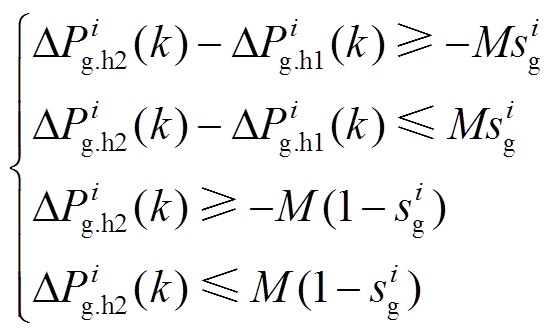 (23)
(23)
综上所述,本文所提优化模型包括三类待优化变量:①紧急控制策略相关变量:机组/场站运行状态、新能源场站功率调节指令;②系统频率动态响应模型中各个变量在离散时刻的取值:系统频率、不平衡功率、常规机组功率调整量等;③线性化过程及逻辑判断环节引入的各类中间变量在各离散时刻的取值:常规机组功率调节达到上、下限标志等。上述三类变量对应于MILP模型式(6)中的变量x、z(连续型、整数型变量),同样MILP模型的优化结果即为上述三类变量的最优取值。
至此,本文第2节已经完成对原始紧急频率控制策略优化模型(1.2节)中非线性微分方程的混合整数线性化。采用差分离散化后,目标函数(1)中的积分项很容易转换为加性求和项。因此,从理论上讲,只需对各时间断面上的频率均施加暂态频率最大值约束,并对足够长积分时间末尾的频率施加限制,就能完成对暂态频率最大值和稳态频率的上限约束,从而得到紧急频率控制策略MILP模型。事实上,实际送端大电网直流闭锁后,系统频率极大值一般出现在0~6s内,频率波动时长一般在30~60s内。取数值积分时长为60s虽然足够计算系统稳态频率,但是将产生许多的积分时间断面,相应的中间变量、线性等式和不等式也将大大增加,最终导致所生成的MILP问题的规模很大、求解难度高、计算时间长。因此,本文进一步提出如下方法来降低所生成MILP问题的规模。
1)总的积分时长取值略超过频率极大值出现时间即可,这一点可以通过分析所研究电网的历史频率波动数据来实现。此外,Tne的选取要能体现各类新能源场站参与暂态频率支撑的相对功率调控代价。由于这与新能源场站的实际功率响应曲线密切相关,故本文中取Tne等于总的积分时长Tmax。
2)系统稳态频率的计算可通过施加式(24)~式(27)约束间接实现。
 (24)
(24)
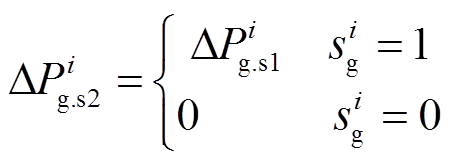 (25)
(25)
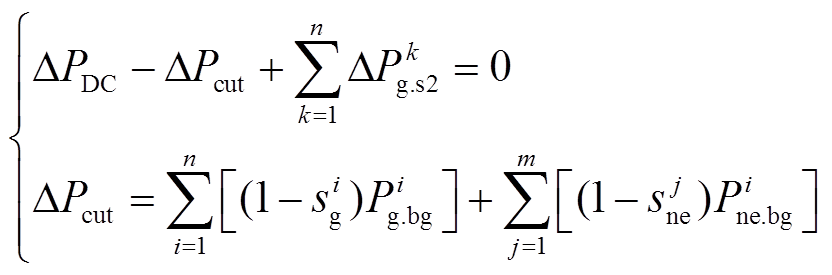 (26)
(26)
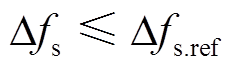 (27)
(27)
式中,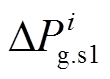 为第i台常规机组稳态功率调节量的指令值;
为第i台常规机组稳态功率调节量的指令值;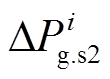 为常规机组稳态功率实际调节量;
为常规机组稳态功率实际调节量;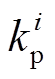 为常规机组的一次调频单位调节功率。本文暂不考虑二次调频及其影响。同样式(24)~式(26)中的逻辑约束可以通过Big M等线性化方法转换为线性不等式约束,以此构建1.2节优化模型中的稳态频率约束内容,与上述各个时间断面的暂态频率约束、潮流约束等共同构成式(6)中MILP模型的线性等式与不等式约束。在得到紧急频率控制策略MILP模型后,本文使用CPLEX对其进行求解。
为常规机组的一次调频单位调节功率。本文暂不考虑二次调频及其影响。同样式(24)~式(26)中的逻辑约束可以通过Big M等线性化方法转换为线性不等式约束,以此构建1.2节优化模型中的稳态频率约束内容,与上述各个时间断面的暂态频率约束、潮流约束等共同构成式(6)中MILP模型的线性等式与不等式约束。在得到紧急频率控制策略MILP模型后,本文使用CPLEX对其进行求解。
基于我国西北某省级电网,对上述紧急频率控制策略优化模型的有效性与求解的快速性进行验证。
该电网330kV及以上电压等级的简化网络拓扑如图5所示。该电网包含330kV及以上节点共133个(部分节点未在图中展示),其中紧急频率控制中可切(或调)的发电单元包括46个新能源场站、2台水电机组和7台火电机组。该电网直流外送线路为HL-ZMD,容量为6 000MW。算例均基于该电网部分时刻的运行监测数据(机组功率等)进行仿真,其中常规机组及新能源场站参数见附表1、附表2。
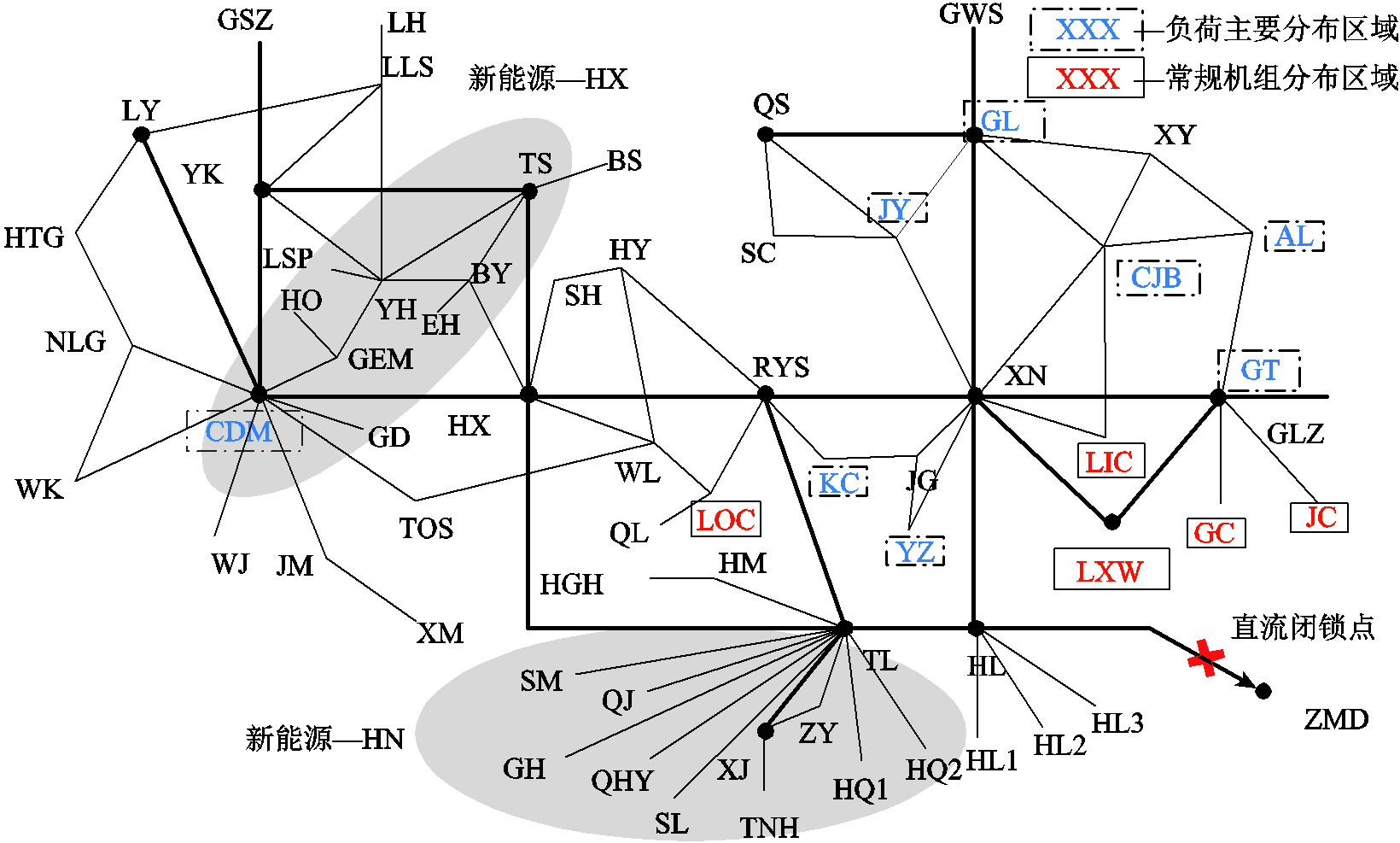
图5 中国西北某省级电网简化拓扑
Fig.5 The simplified topology of a province-sized grid in Northwest China
常规机组的切除成本系数主要考虑其切除时间及启停成本;鉴于新能源场站的启停较方便,因此仅考虑其切除时段内带来的电量损失。由于新能源场站连续调控仅参与暂态频率支撑,损失电量很少,因此相应的调控成本相比于前两项要低得多。这也说明目标函数(1)中包括第三项的主要目的是选择最经济的风机和光伏连续功率调控方式来参与紧急频率控制。结合上述省级电网实际工程统计信息及相关近似计算结果,各发电单元的单位调节/切除成本系数C1、C2、C3(假设所有常规机组/新能源场站的单位切除/调节成本相同)分别为1 500、140、3。
根据我国电能质量要求:电网频率稳态偏差应约束在0.2Hz以内;发电机组调频死区一般为0.033Hz(频率上升情况);在紧急情况下,发电厂和其他相关设备能够持续运行的频率要求范围为48.5~50.5Hz[30],因此仿真中允许的频率最大值设置为50.5Hz。考虑安全性因素及实际工程信息,本文将新能源场站的功率调整下限设置为20%额定功率;常规机组的一次调频下调功率的最大限值为15%额定功率。仿真实验均基于Matlab 2016b 软件完成,所使用的计算机系统及硬件参数为:OS: Windows10,CPU: Intel Dual Core i7-8700 3.2 GHz and RAM: 16384 MB。
为对比新能源场站通过切除和快速功率下调两种方式参与紧急控制的调控效果,本文针对HL-ZMD直流线路发生闭锁故障制定频率紧急控制措施,设置以下两组场景进行分析对比:①场景1:不考虑线路潮流约束,新能源场站仅允许切除;②场景2:考虑线路潮流约束,新能源场站允许调节或切除。
为了用尽量简洁的方式对比“切”和“调”的效果,本文假设上述两个场景中所有新能源场站均为光伏电站,其紧急功率调控方法简单易行,可用如图6所示的一阶惯性环节近似代表其紧急控制功率响应动态,并且对应的时间常数Tpv在功率下降和恢复阶段均为100ms。因此以光伏电站为例,式(15)中关于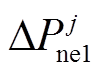 与
与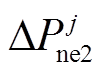 间的等式关系可线性转换为式(28),详细转换过程见附录。
间的等式关系可线性转换为式(28),详细转换过程见附录。
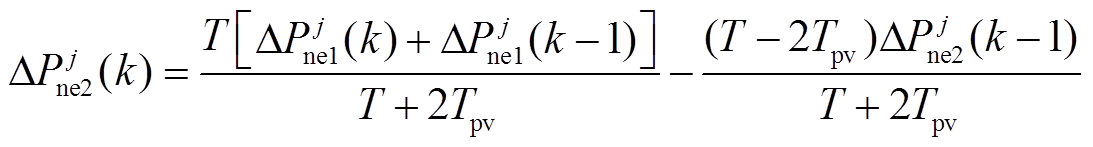 (28)
(28)
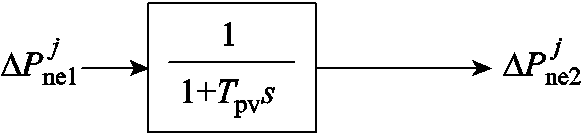
图6 光伏电站功率调整动态的等效模拟
Fig.6 Simulation of power regulation dynamics about photovoltaic plants
此外,光伏电站参与紧急控制的时间Tin=3s,数值积分总时长Tmax=6s,离散时间间隔T=0.1s。针对上述实际电网建立的原始紧急频率控制策略优化模型是一个包括46个连续决策变量(新能源场站调节指令)和55个0/1离散决策变量(切机指令),且有非线性微分方程约束条件的数学规划模型。利用本文所提方法对该模型进行混合整数线性化,两种场景下的优化模型均快速收敛到了最优解,计算耗时分别为25.7s和29.2s。上述两种场景下的紧急频率控制策略优化结果见表1。
表1 两种场景下的最优紧急控制策略
Tab.1 The optimal emergent control strategies in the two cases

场景编号切新能源场站/(104kW)切常规机组/(104kW)调新能源场站/(104 kW)控制代价/元寻优时间/s 场景1572.25008011525.7 场景2559.70012.527839529.2
1)场景1
图7首先对比了优化模型求解后获得的差分方程的解(即扰动后6s内的暂态频率)与直接对原始SFR模型进行数值积分(积分步长为0.02s)得到的频率动态曲线。可以看出,将暂态频率模型混合整数线性化并内嵌于优化问题中所获得的频率响应曲线能精确地刻画实际的频率动态。此外,系统在优化后紧急控制策略下的暂态频率最大值为50.5Hz,稳态频率(经一次调频稳态模型而非数值积分计算得到)为50.12Hz,均满足安全稳定要求。
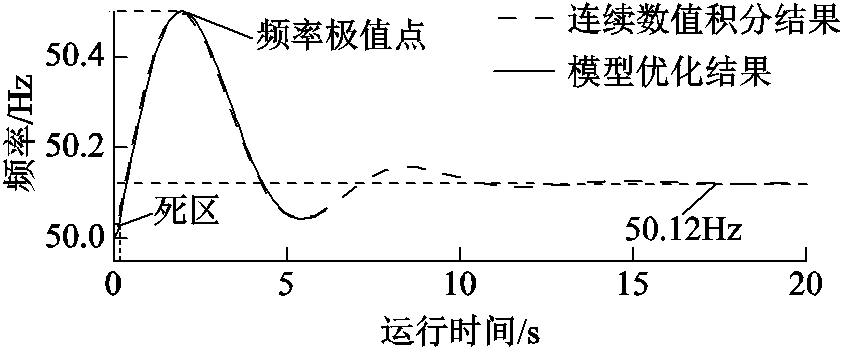
图7 场景1紧急控制后的频率波动
Fig.7 Frequency fluctuation after emergent control in Case 1
图8显示,G1、G2水电机组由于水锤效应在1.5s以前功率上调。G4、G6、G9为火电机组,在频率越过死区后,开始启动一次调频。可以看出,在故障后1s内常规机组提供的有效抑制系统频率上升的功率调节量是非常有限的,场景1主要依靠快速切除大量新能源场站实现紧急频率控制。
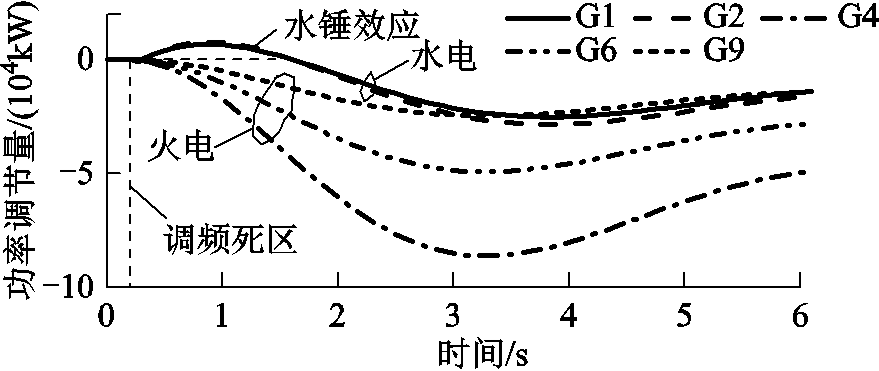
图8 场景1发电机功率调节情况
Fig.8 Power regulation of generators in Case 1
图9中标示出了场景1下主要的新能源场站切除区域。事实上,场景1下优化模型十分精准地筛选出了新能源场站的切除组合,功率调整量刚好满足紧急频率控制的需求。并且,由于未考虑线路潮流约束,为保证尽可能小的切机成本,其切机区域也相对比较分散。场景1进行紧急控制后,其部分线路暂态过程中的潮流最大值见表2。
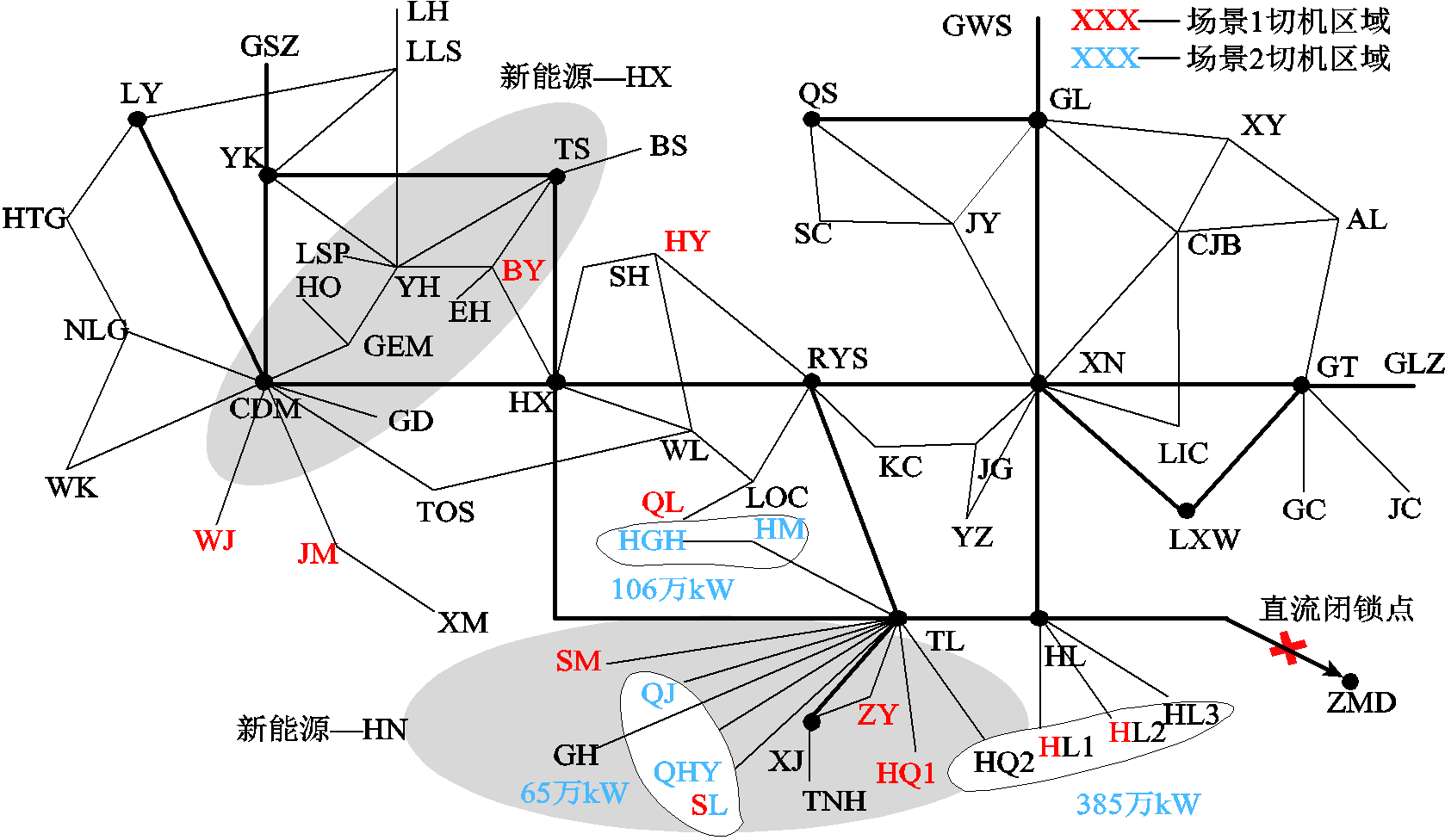
图9 场景1与场景2下切除场站的分布区域
Fig.9 The areas of plants tripped in Case 1 and Case 2
表2 场景1暂态过程中的潮流情况
Tab.2 Power flows during the transient process in Case 1
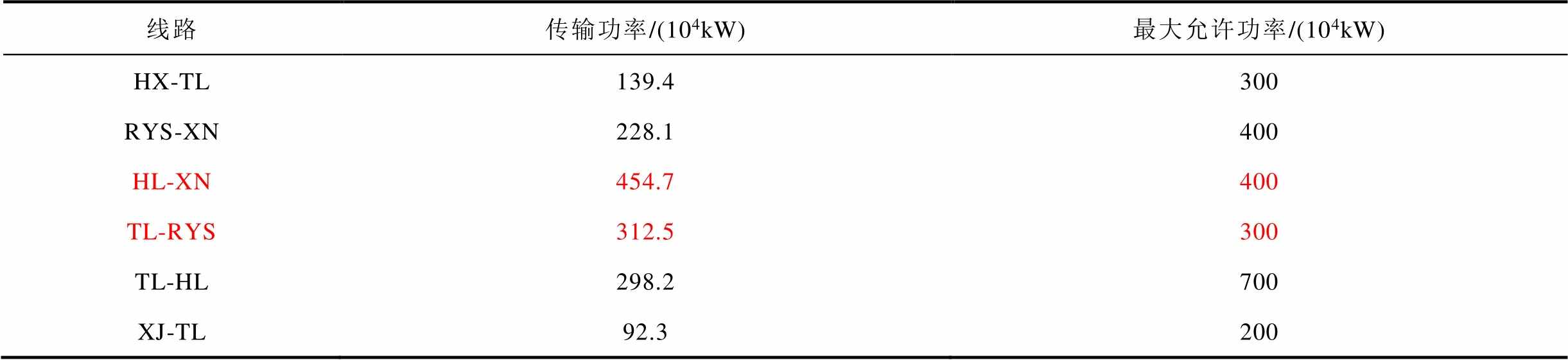
线路传输功率/(104kW)最大允许功率/(104kW) HX-TL139.4300 RYS-XN228.1400 HL-XN454.7400 TL-RYS312.5300 TL-HL298.2700 XJ-TL92.3200
从表2中可以观察到,由于未考虑潮流约束部分线路(HL-XN及TL-RYS)在暂态过程中的最大功率超过了其允许值。因为过大的线路相位差可能诱发系统功角失稳,所以从实际潮流可行及降低功角失稳风险角度看,有必要在紧急频率控制策略优化模型中显式地考虑线路潮流约束。
2)场景2
场景2优化的紧急频率控制策略对应的控制结果如图10和图11所示。
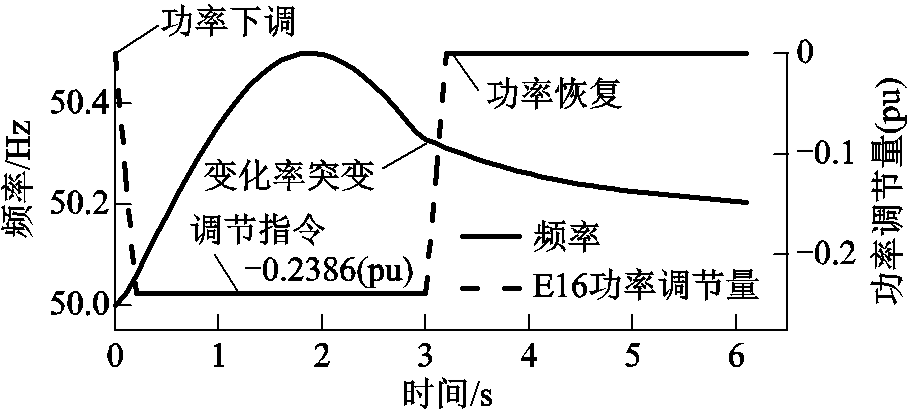
图10 场景2紧急频率控制结果
Fig.10 Results of emergent frequency control in Case 2
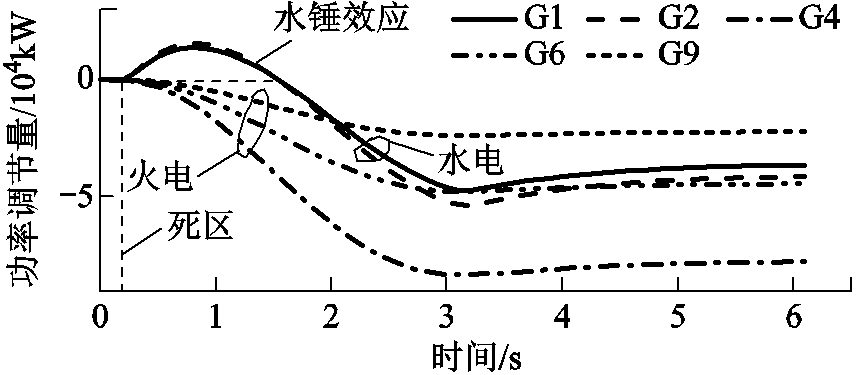
图11 场景2发电机功率调节情况
Fig.11 Power regulation of generators in Case 2
从图10可以看出,闭锁故障发生后新能源场站依据控制指令快速大幅下调了其输出功率,持续时间为3s,此后逐渐恢复至最大功率,因此系统频率在3s处因新能源功率恢复,其下降速率变小。场景2下可以利用不同区域新能源场站的连续快速调节替代粗颗粒的切除操作,因此即使相对于场景1额外增加了潮流约束,场景2下新能源场站切除量仍低于场景1,总体紧急控制代价更小(见表1)。
场景2下,各新能源场站的切除情况如图9所示,相对于场景1分散的切机区域,在线路暂态潮流的约束下,该场景下的切机区域主要集中在TL和HL地区,且保证了场景2下部分关键线路的最大功率均在允许值范围以内。图12标示出了部分线路故障前的稳态功率以及故障后暂态过程中的最大功率。可以看出,由于被切除的新能源场站主要集中在直流落点HL附近,其周围线路(包括XJ-TL、TL-HL、HL-XN等)在紧急控制前后的潮流有明显变化,其中HL-XN线路潮流(397.4万kW)已基本达到上限400万kW,而远离直流落点的新能源场站切除量较低且周围线路潮流变化较小。
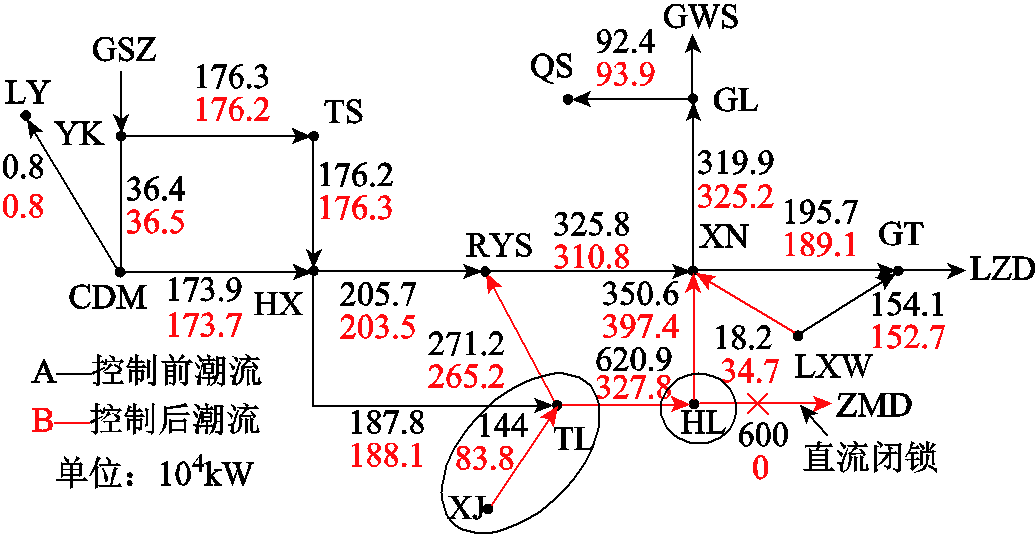
图12 控制前后线路潮流
Fig.12 Line power flows before and after control
经分析对比,上述两个场景下常规机组均未被切除。主要原因在于:该实际电网中新能源占比较高,在场景1中不考虑电网潮流约束的情况下,通过切除大量的新能源场站已基本能满足频率稳定要求;虽然在场景2下的直流闭锁可能导致闭锁点近区潮流发生大幅变化,但由于TL及HL等近闭锁点区域的新能源分布较密集,通过调节/切除的方式也基本能够满足关键线路的潮流安全约束。因此该电网在上述运行场景下执行紧急频率控制策略时,暂未切除代价较高的常规机组。
本节将通过仿真场景3展示风机在不同运行工况下参与紧急频率控制的动态过程,以及相应的系统紧急控制策略优化结果。除新能源场站包括光伏和风机(附表2)以外,场景3和场景2的设定基本相同。在场景3中,假设风电场E19~E39运行于最大功率跟踪区,E40~E46运行于恒功率区,采用转子动能控制或桨距角控制参与暂态频率支撑。试验结果表明,可用图13所示的低阶传递函数近似表征风机在转子动能控制和桨距角控制方式下参与暂态频率支撑的功率响应动态(附图2给出了针对某型风机的相应近似效果)。考虑本文关心的主要矛盾,此处简单地假设图13所示近似模型和相应参数适用于所有风机,即Twt.A1=50ms,Twt.A2= 2.3s,Twt.B= 5.7s。光伏电站仍使用图6所示模型来近似其功率响应动态,但其时间常数Tpv在功率下降和恢复阶段分别为100ms和500ms。此外,由于桨距角控制响应速度较慢,数值积分时长Tmax设置为10s。
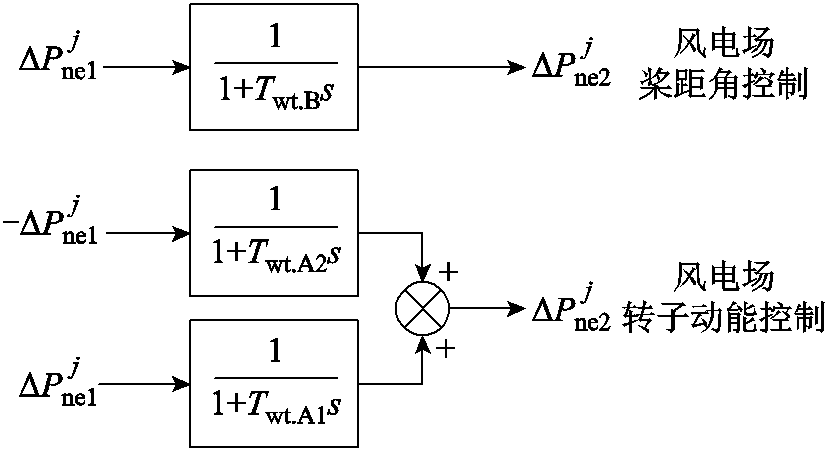
图13 风电场功率调整动态的等效模拟
Fig.13 Simulation of power regulation dynamics about wind turbine plants
在场景3下,控制策略优化模型的求解时间为39.7s,耗时略高于场景2。虽然场景3中原始策略优化模型的决策变量相对于场景2只增加了一些0/1逻辑变量,用来判断运行于最大功率跟踪区的风机是用转子动能控制还是桨距角控制来参与暂态频率支撑,但是其数值积分时间更长,混合整数线性化后产生的中间变量更多,故而求解耗时更长。尽管如此,针对本文所采用的省级电网算例,各个场景下的紧急控制策略优化模型的搜索求解时间均在30s左右,这也说明本文所提混合整数线性化方法对于快速求解策略优化模型的重要性和有效性。同时,针对省级规模电网的分钟级以下求解速度也证明了本文所提紧急控制策略优化方法可以通过在线预决策方式应对新能源场站的功率波动(波动分量主要集中在5~10min及以上时间尺度)。
场景3下紧急控制策略优化模型的求解结果见表3。可以看出,由于直流闭锁容量较大,切除新能源场站仍然是紧急控制的主要手段,且场景3和场景2下的新能源场站切除容量基本持平。然而,场景3下的新能源场站总的连续功率调整量要显著高于场景2,这是因为风机在转子动能控制方式下会出现较快速的功率恢复现象,而在桨距角控制方式下风机功率下降速度较慢,暂态降功率的效果明显不如光伏。此外,由于新能源场站的切除成本系数要显著大于连续调控成本系数,场景3下的紧急控制成本略高于场景2。
表3 场景3下的最优紧急控制策略
Tab.3 The optimal emergent control strategy in Case 3

切除新能源场站/(104kW)调节光伏电站/(104kW)桨距角控制风电场/(104kW)转子动能控制风电场/(104kW)调控成本/元 560.610.124.332.4878535
场景3下最优紧急控制策略对应的系统频率动态如图14所示,部分光伏电站和风电场的功率响应曲线如图15所示。暂态过程中系统频率的峰值为50.472Hz,而稳态频率(通过一次调频稳态模型计算得到)为50.2Hz,均满足频率安全的要求。此外可以看出,由于新能源场站的功率恢复效应(尤其是光伏和采用转子动能控制的风机),系统频率出现了较明显的二次抬升现象,但二次抬升的频率峰值要低于安全值。值得说明的是,在桨距角控制方式下,反应速度相对较慢的风机功率反而有利于抑制频率二次反弹抬升。
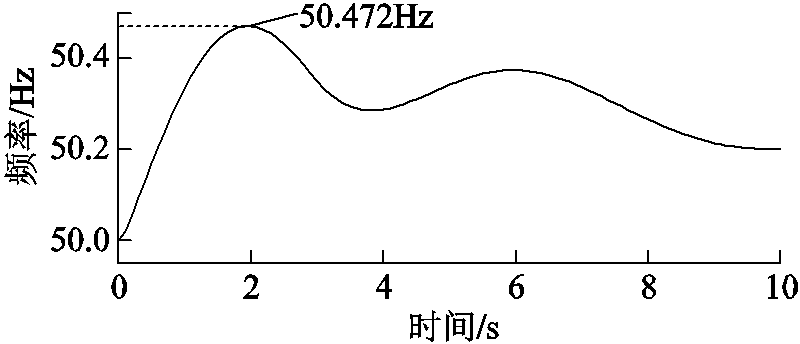
图14 场景3紧急控制后的频率波动
Fig.14 Frequency fluctuation after emergent control in Case 3
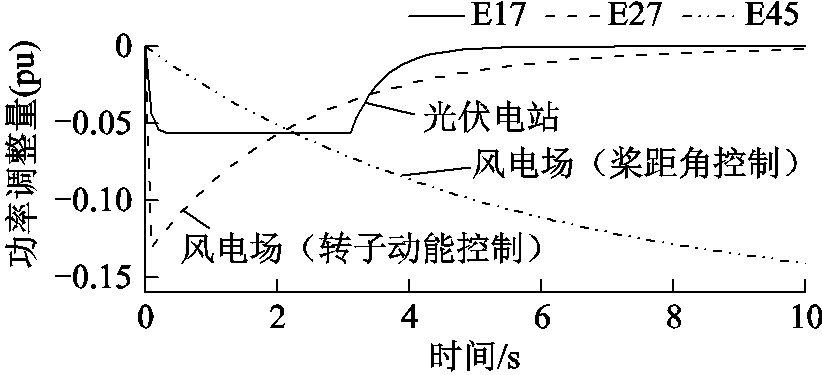
图15 新能源场站的功率调整情况
Fig 15 Power regulation of renewable energy plants
综合上述仿真和分析可知,送端电网系统可通过实时监测各场站运行状态、直流传输容量等数据,并采用本文所提优化方法,在线刷新针对直流闭锁故障的紧急控制策略,能够充分合理地利用各类调频资源,以最经济的方式降低运行场景丰富的送端电网发生直流闭锁后的系统高频风险。
利用新能源场站功率可快速连续调节的特征,本文提出了一种基于新能源场站和常规机组的协同紧急频率控制策略优化模型,能抑制送端电网直流闭锁后的暂态高频问题,并最小化整体控制代价。此外,本文提出的系统性混合整数线性化方法能将上述优化模型转换为MILP问题。在我国西北某省级电网上的仿真结果验证了优化后的紧急频率控制策略的理想控制效果,同时优化模型的求解效率较高,可以满足未来电网对紧急控制策略在线预决策的需求。
1. 常规机组的相关参数
附表1 常规机组参数
App.Tab.1 Parameters of conventional generators

名称母线P0/(104 kW)惯性常数/s类型 G1GC3005水电 G2JC3405.03水电 G3LXW343.24.58火电 G4LXW7005.86火电 G5LXW7003.6火电 G6LIC4003.48火电 G7LIC4004.64火电 G8LOC3005.43火电 G9LOC2005火电
2. 新能源场站的相关参数
附表2 新能源场站参数
App.Tab.2 Parameters of renewable energy plants
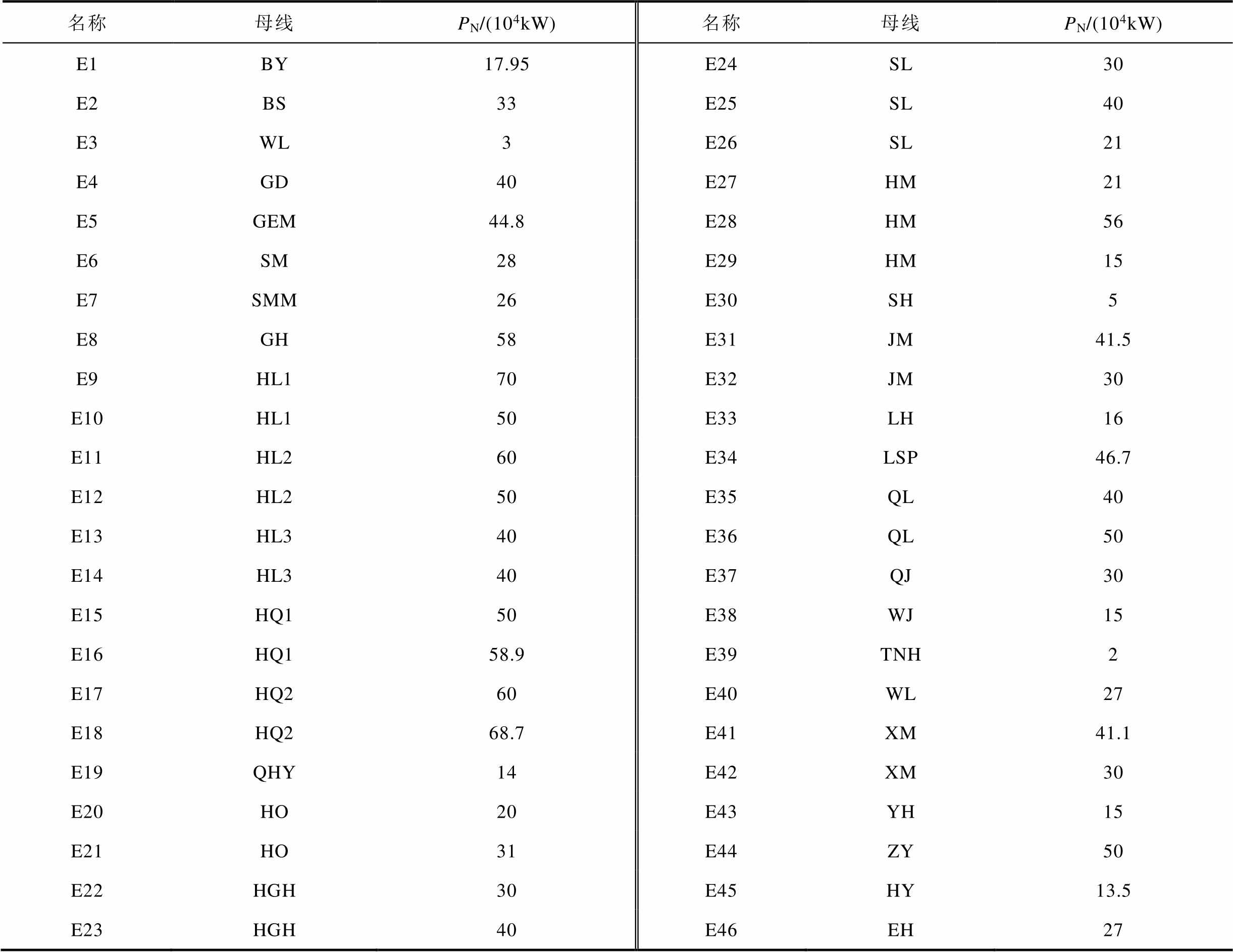
名称母线PN/(104kW)名称母线PN/(104kW) E1BY17.95E24SL30 E2BS33E25SL40 E3WL3E26SL21 E4GD40E27HM21 E5GEM44.8E28HM56 E6SM28E29HM15 E7SMM26E30SH5 E8GH58E31JM41.5 E9HL170E32JM30 E10HL150E33LH16 E11HL260E34LSP46.7 E12HL250E35QL40 E13HL340E36QL50 E14HL340E37QJ30 E15HQ150E38WJ15 E16HQ158.9E39TNH2 E17HQ260E40WL27 E18HQ268.7E41XM41.1 E19QHY14E42XM30 E20HO20E43YH15 E21HO31E44ZY50 E22HGH30E45HY13.5 E23HGH40E46EH27
注:E1~E18为光伏电站;E19~E46为风电场站。
3. 常规机组调速器及原动机模型
水电机组与火电机组调速器及原动机的数学模型及参数设置如附图1所示[31]。在该电网中,相同类型机组的调速器参数基本相近,其中: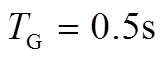 为调速器时间常数,
为调速器时间常数,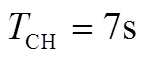 为汽轮机时间常数,
为汽轮机时间常数,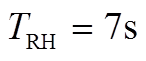 为再热时间常数,
为再热时间常数,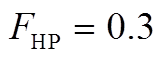 为再热系数,
为再热系数,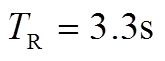 为复位时间常数,
为复位时间常数,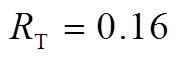 为暂时下降率,
为暂时下降率,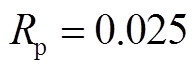 为永久下降率,单位功率调节系数
为永久下降率,单位功率调节系数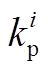 、
、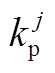 分别为30、40。
分别为30、40。
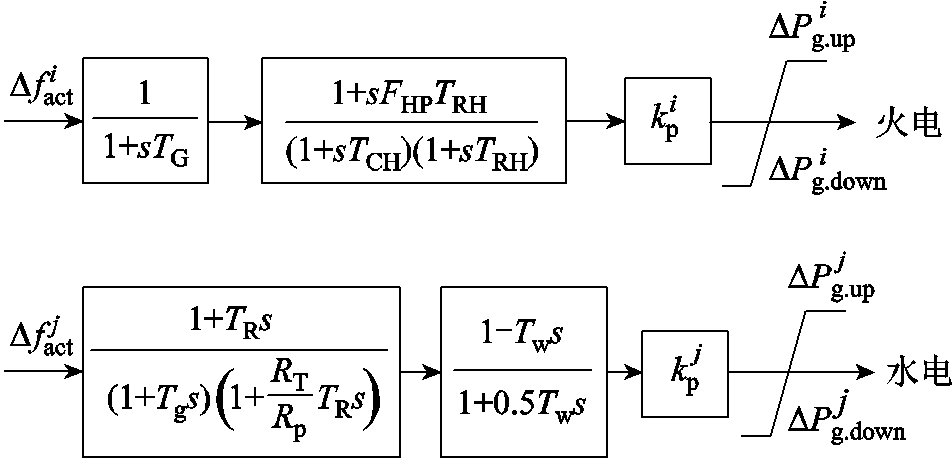
附图1 常规机组调速器及原动机数学模型
App.Fig.1 The mathematical model of governor and turbine in conventional generators
4. 部分750kV线路传输功率最大值
附表3 750kV线路传输功率上限
App.Tab.3 Upper limits of transmission lines above 750kV
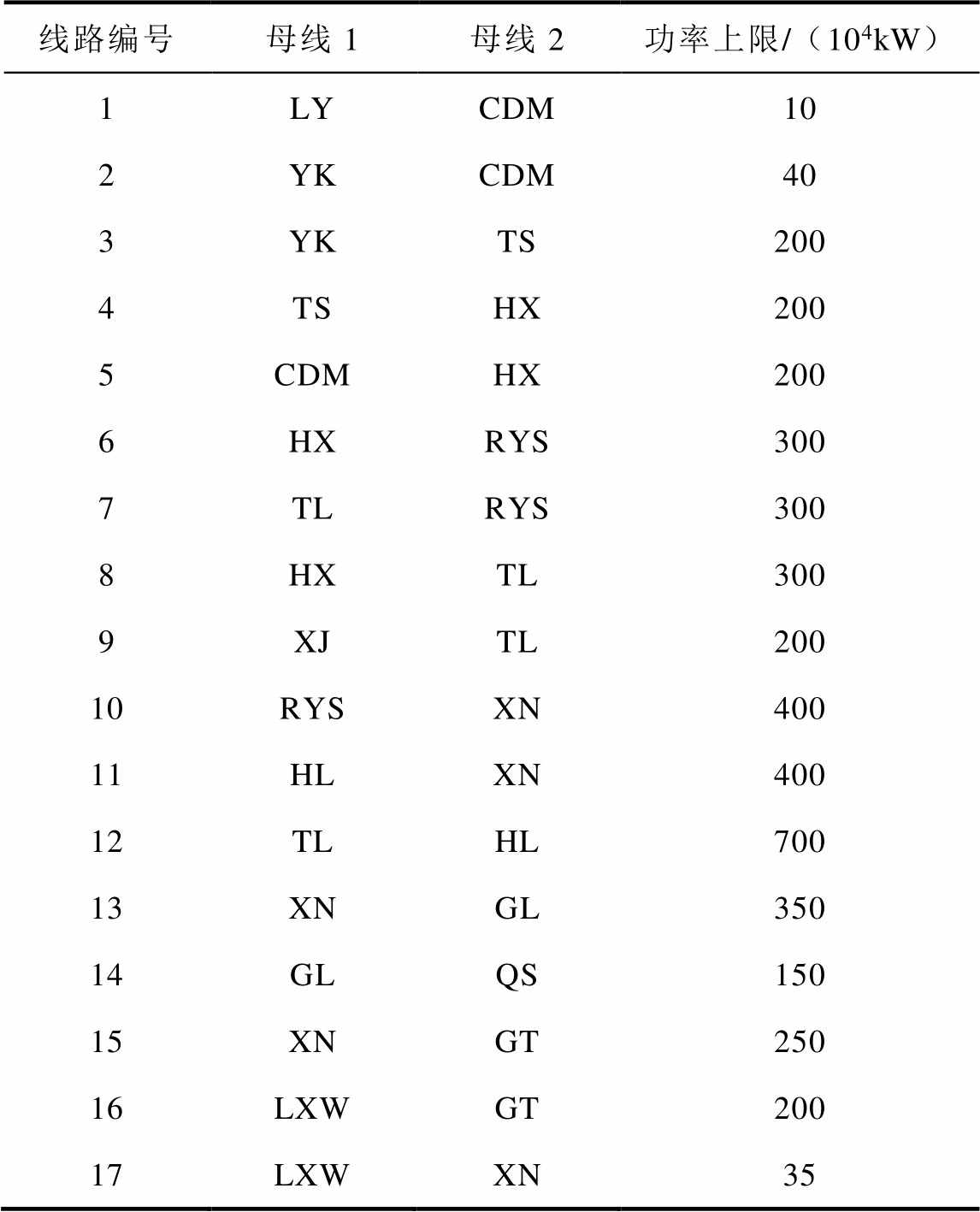
线路编号母线1母线2功率上限/(104kW) 1LYCDM10 2YKCDM40 3YKTS200 4TSHX200 5CDMHX200 6HXRYS300 7TLRYS300 8HXTL300 9XJTL200 10RYSXN400 11HLXN400 12TLHL700 13XNGL350 14GLQS150 15XNGT250 16LXWGT200 17LXWXN35
5. 风电场功率动态调整过程的近似模拟
以文献[21]所提风机为例,在不同运行工况下对应采用转子动能控制与桨距角控制对其进行功率下调仿真实验,以此拟合图13中的参数Twt.A1、Twt.A2与Twt.B(结果为Twt.A1=50ms,Twt.A2= 2.3s,Twt.B= 5.7s),一阶惯性环节近似结果与详细模型仿真结果对比如附图2所示。
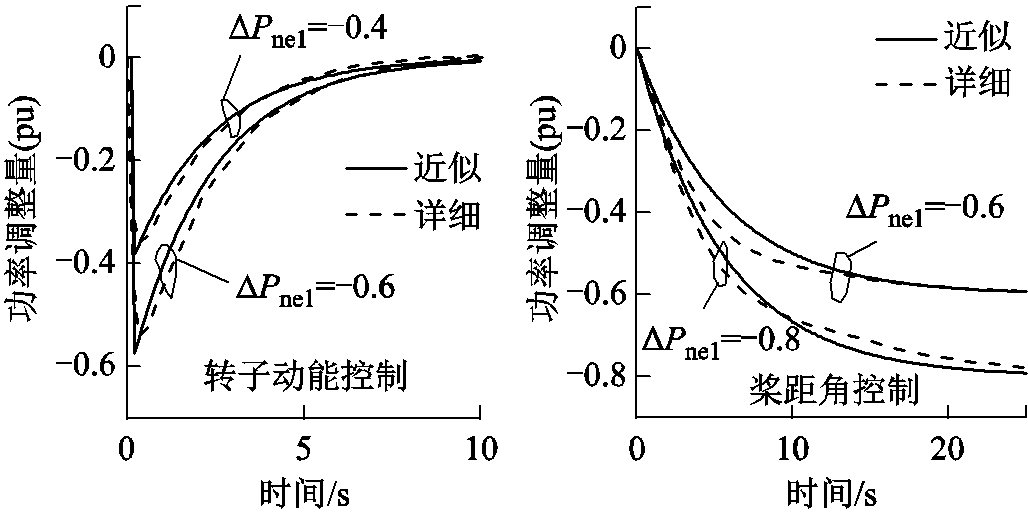
附图2 风机功率调节过程模拟
App.Fig.2 Simulation for power regulation of wind turbines
6. 双线性变换及ARMA模型的构建
双线性变换是将s域传递函数转换为z域的一种方法,具体为
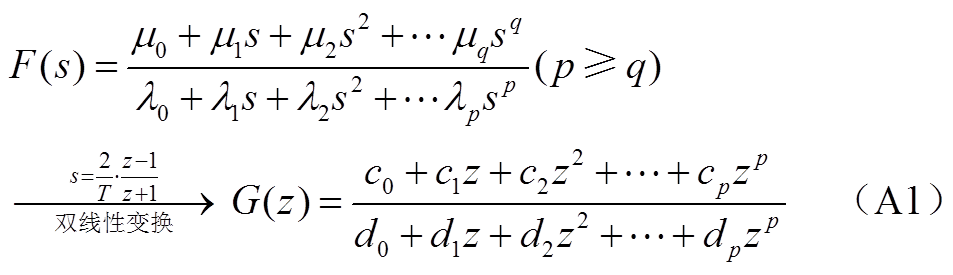
式中,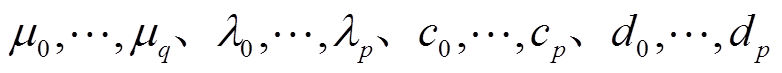 均为常系数;双线性变换中,T为离散时间步长,p、q分别为传递函数F(s)中分子、分母的阶数。并且需要注意,经过双线性变换后G(z)的分子项最高阶次也变为p。
均为常系数;双线性变换中,T为离散时间步长,p、q分别为传递函数F(s)中分子、分母的阶数。并且需要注意,经过双线性变换后G(z)的分子项最高阶次也变为p。
基于双线性变换结果,可列写时域的ARMA模型,进而构建起各变量间的等式约束关系为
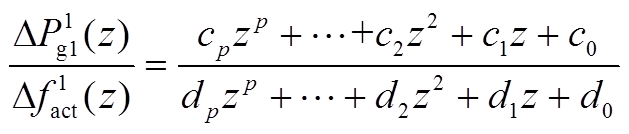 (A2)
(A2)
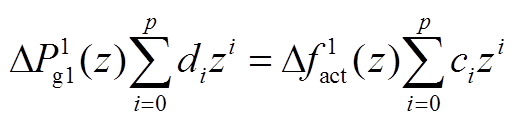 (A3)
(A3)
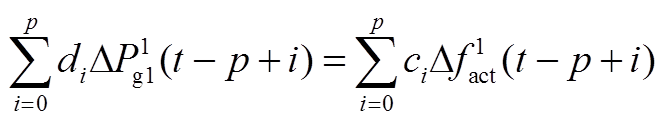 (A4)
(A4)
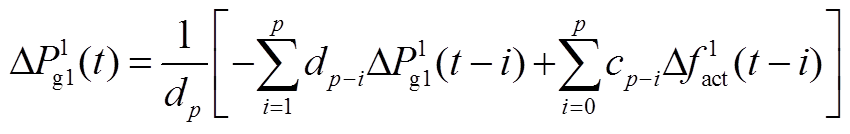 (A5)
(A5)
将式(A5)中各项系数逐次按照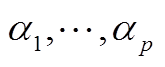 及
及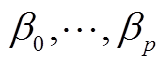 进行替换即可得如式(7)的ARMA模型。
进行替换即可得如式(7)的ARMA模型。
参考文献
[1] 张炎, 丁明, 韩平平, 等. 直流闭锁后风电送端系统暂态稳定及控制策略研究[J]. 电工技术学报, 2020, 35(17): 3714-3726.
Zhang Yan, Ding Ming, Han Pingping, et al. Study on the transient stability and control schemes of the sending-end system involving wind power after UHVDC block[J]. Transactions of China Electrote-chnical Society, 2020, 35(17): 3714-3726.
[2] 谢宇峥, 张恒旭, 李常刚, 等. 考虑风电机组频率保护的送端电网有序高频切机策略[J]. 电力系统自动化, 2021, 45(9): 153-161.
Xie Yuzheng, Zhang Hengxu, Li Changgang, et al. Ordered strategy of generators tripping for high frequency considering wind turbine frequency protec-tion[J]. Automation of Electric Power Systems, 2021, 45(9): 153-161.
[3] 李兴源, 赵睿, 刘天琪, 等. 传统高压直流输电系统稳定性分析和控制综述[J]. 电工技术学报, 2013, 28(10): 288-300.
Li Xingyuan, Zhao Rui, Liu Tianqi, et al. Research of conventional high voltage direct current transmission system stability analysis and control[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 288-300.
[4] 张志强, 袁荣湘, 徐友平, 等. 适应多回特高压直流的四川电网高频切机优化[J]. 电力系统自动化, 2016, 40(2): 141-146.
Zhang Zhiqiang, Yuan Rongxiang, Xu Youping, et al. Optimization of high frequency generator tripping strategy for multi-circuit UHVDC in Sichuan power grid[J]. Automation of Electric Power Systems, 2016, 40(2): 141-146.
[5] 钟显, 樊艳芳, 王一波, 等. 含高密度风电、交直流送端电网直流闭锁故障稳控方案研究[J]. 电力系统保护与控制, 2015, 43(13): 130-138.
Zhong Xian, Fan Yanfang, Wang Yibo, et al. Research of stability control strategies for high density wind power, AC-DC sending grid bi-pole trip[J]. Power System Protection and Control, 2015, 43(13): 130-138.
[6] 骆悦, 姚骏, 张田, 等. 大规模风电直流外送系统单极闭锁场景下送端系统协调控制策略[J]. 电工技术学报, 2019, 34(19): 4108-4118.
Luo Yue, Yao Jun, Zhang Tian, et al. Coordinated control strategy of large-scale wind power generation sending system under mono-polar block fault[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4108-4118.
[7] 赵渊, 吴小平, 谢开贵. 基于频率动态特性的电力系统频率失稳概率评估[J]. 电工技术学报, 2012, 27(5): 212-220.
Zhao Yuan, Wu Xiaoping, Xie Kaigui. Frequency instability probabilistic assessment for frequency inst- ability of power system based on frequency dynamic characteristic[J]. Transactions of China Electrotech- nical Society, 2012, 27(5): 212-220
[8] 颜自坚, 刘俊, 周海强, 等. 计及锅炉动态的直流受端系统中长期频率响应计算方法[J]. 电力系统保护与控制, 2020, 48(5): 65-71.
Yan Zijian, Liu Jun, Zhou Haiqiang, et al. Mid-term and long-term frequency calculation method for the HVDC receiving-end system considering the boiler dynamics[J]. Power System Protection and Control, 2020, 48(5): 65-71.
[9] Liu Yutian, Fan Rui, Terzija V. Power system restoration: a literature review from 2006 to 2016[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(3): 332-341.
[10] 刘威, 张东霞, 王新迎, 等. 基于深度强化学习的电网紧急控制策略研究[J]. 中国电机工程学报, 2018, 38(1): 109-119, 347.
Liu Wei, Zhang Dongxia, Wang Xinying, et al. A decision making strategy for generating unit tripping under emergency circumstances based on deep reinfor-cement learning[J]. Proceedings of the Chinese Society of Electrical Engineering, 2018, 38(1): 109-119, 347.
[11] Zhu Shaoxuan, Wang Tong, Wang Zengping. Bi-level optimized emergency load/generator shedding strategy for AC/DC hybrid system following DC blocking[J]. IET Generation, Transmission & Distribution, 2020, 14(8): 1491-1499.
[12] Zhang Xing, Jiang Han, Yu Zhihong, et al. A generator tripping control method based on trajectory sensitivity analysis and pattern search[C]//34th Chinese Control Conference (CCC), Hangzhou, 2015: 9043-9047.
[13] Lappalainen K, Valkealahti S. Output power variation of different PV array configurations during irradiance transitions caused by moving clouds[J]. Applied Energy, 2017, 190: 902-910.
[14] Omran W A, Kazerani M, Salama M M A. Investiga- tion of methods for reduction of power fluctuations generated from large grid-connected photovoltaic systems[J], IEEE Transactions on Energy Conversion, 2011, 26(1): 318-327.
[15] 杨濛濛, 郭雷, 王春华, 等. 基于改进支路暂态能量函数的风电并网暂态最优切机控制[J]. 电力系统保护与控制, 2014, 42(18): 72-77.
Yang Mengmeng, Guo Lei, Wang Chunhua, et al. Optimal transient tripping control of grid-connected wind power based on improved branch transient energy function[J]. Power System Protection and Control, 2014, 42(18): 72-77.
[16] Gautam D, Vittal V, Harbour T. Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems[J]. IEEE Transactions on Power Systems, 2009, 24(3): 1426-1434.
[17] 丁剑, 邱跃丰, 孙华东, 等. 大规模风电接入下风电机组切机措施研究(英文)[J]. 中国电机工程学报, 2011, 31(19): 25-36.
Ding Jian, Qiu Yuefeng, Sun Huadong, et al. Conside- ration of wind generator tripping under large-scale wind power integration (English)[J]. Proceedings of the CSEE, 2011, 31(19): 25-36.
[18] 周野, 刘福锁, 常海军, 等. 用于频率紧急控制的水电群精准控制策略[J]. 电力系统自动化, 2020, 44(11): 121-126.
Zhou Ye, Liu Fusuo, Chang Haijun, et al. Accurate control strategy of hydropower group for frequency emergency control[J]. Automation of Electric Power Systems, 2020, 44(11): 121-126.
[19] 王淑超, 孙光辉, 俞诚生, 等. 光伏发电系统级快速功率调控技术及其应用[J]. 中国电机工程学报, 2018, 38(21): 6254-6263, 6487.
Wang Shuchao, Sun Guanghui, Yu Chengsheng, et al. Photovoltaic power generation system level rapid power control technology and its application[J]. Proceedings of the CSEE, 2018, 38(21): 6254-6263, 6487.
[20] 章艳, 高晗, 张萌. 不同虚拟同步机控制下双馈风机系统频率响应差异研究[J]. 电工技术学报, 2020, 35(13): 2889-2900.
Zhang Yan, Gao Han, Zhang Meng. Research on difference of frequency research on frequency response difference of doubly-fed induction generator system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889-2900.
[21] 丁磊, 尹善耀, 王同晓, 等. 结合超速备用和模拟惯性的双馈风机频率控制策略[J]. 电网技术, 2015, 39(9): 2385-2391.
Ding Lei, Yin Shanyao, Wang Tongxiao, et al. Integrated frequency control strategy of DFIGs based on virtual inertia and over-speed control[J]. Power System Technology, 2015, 39(9): 2385-2391.
[22] 周志超, 王成山, 郭力, 等. 变速变桨距风电机组的全风速限功率优化控制[J]. 中国电机工程学报, 2015, 35(8): 1837-1844.
Zhou Zhichao, Wang Chengshan, Guo Li, et al. Output power curtailment control of variable-speed variable- pitch wind turbine generator at all wind speed regions[J]. Proceedings of the CSEE, 2015, 35(8): 1837-1844.
[23] 孙铭, 徐飞, 陈磊, 等. 利用转子动能的风机辅助频率控制最优策略[J]. 中国电机工程学报, 2021, 41(2): 506-514.
Sun Ming, Xu Fei, Chen Lei, et al. Optimal auxiliary frequency control strategy of wind turbine generator utilizing rotor kinetic energy[J]. Proceedings of the CSEE, 2021, 41(2): 506-514.
[24] 刘彬彬, 杨健维, 廖凯, 等. 基于转子动能控制的双馈风电机组频率控制改进方案[J]. 电力系统自动化, 2016, 40(16): 17-22.
Liu Binbin, Yang Jianwei, Liao Kai, et al. An improved frequency control strategy for DFIG based on rotor kinetic energy control[J]. Automation of Electric Power Systems, 2016, 40(16): 17-22.
[25] 陆崎, 任祖怡, 徐柯, 等. 基于隐枚举法的稳定控制优化切机方法[J]. 电力系统自动化, 2016, 40(5): 139-144.
Lu Qi, Ren Zuyi, Xu Ke, et al. An optimization method for generator tripping in stability control based on implicit enumeration method[J]. Automation of Electric Power Systems, 2016, 40(5): 139-144.
[26] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039.
Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercarpacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[27] 颜湘武, 宋子君, 崔森, 等. 基于变功率点跟踪和超级电容器储能协调控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2020, 35(3): 530-541.
Yan Xiangwu, Song Zijun, Cui Sen, et al. Primary frequency regulation strategy of doubly-fed wind turbine based on variable power point tracking and supercapacitor energy storage[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 530-541.
[28] Anderson P M, Mirheydar M. A low-order system frequency response model[J]. IEEE Transactions on Power Systems, 1990, 5(3): 720-729.
[29] Carrion M, Arroyo J M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1371-1378.
[30] GB/T 31464—2015 电网运行准则[S]. 2015.
[31] 包宇庆. 需求响应参与电力系统调频机理及控制研究[D]. 南京: 东南大学, 2015.
Rapid Optimization for Emergent Frequency Control Strategy with the Power Regulation of Renewable Energy during the Loss of DC Connection
Abstract In a power system which has highly penetrated renewable energy generators and high-voltage dc lines transmitting power to other systems, fast and continuous adjustment of the large renewable energy bases’ power outputs should be an economic replacement of the expensive countermeasure of tripping conventional generating units, for the emergent frequency control when the fault-caused loss of dc connection suddenly occurs. Therefore, an optimization model for the emergent frequency control strategy to ensure the frequency safety of the dc sending-end power system and lowest control cost, is proposed in this paper based on cooperating the renewable energy plants and conventional generators. Generally, it is very difficult to solve this optimization because it is nonlinear and with differential equation constraints. Thus, a systematic method which can convert the model to a mixed integer linear programming (MILP) problem is proposed so that it can be efficiently solved by dedicated powerful commercial software. The simulation results based on the model of a province-sized power system in North-west China prove the effectiveness of the proposed optimization model and the efficiency of the solving process.
keywords:Loss of DC connection, emergent frequency control, power regulation of renewable energy, rapid optimization, mixed integer linear programming (MILP)
DOI:10.19595/j.cnki.1000-6753.tces.210279
中图分类号:TM76
国家自然科学基金资助项目(51777143)。
收稿日期 2021-03-03
改稿日期 2021-07-15
柯德平 男,1983年生,博士,副教授,研究方向为电力系统稳定与控制、电力系统优化调度等。E-mail:kedeping@whu.edu.cn
冯帅帅 男,1997年生,硕士研究生,研究方向为新能源并网控制等。E-mail:2015302540069@whu.edu.cn(通信作者)
(编辑 赫蕾)