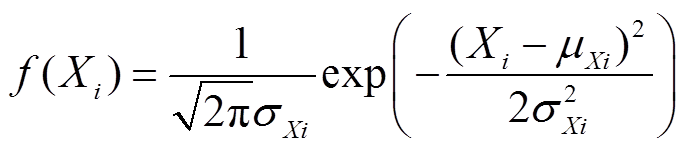（1）
摘要 随着电力系统中不确定量日益复杂，同时存在的随机与区间变量使得采用概率或区间潮流计算难以准确获取系统的运行状态。为此，提出一种基于双层代理模型的概率-区间潮流计算方法。该方法仅需较少次数的确定性潮流计算便可实现上、下层代理模型的构建，进而通过代理模型求解概率-区间潮流常规求解方法中所需要的大量确定性潮流计算，可实现输出变量的快速获取。此外，该文还提出了用于描述输出变量特征的灵敏度指标，并结合所提出的双层代理模型开展灵敏度分析，以量化输入区间变量对输出变量的影响程度。在IEEE 118节点系统中进行算例分析，通过与已有方法对比验证了所提方法的精确性和快速性，借助灵敏度分析可识别对输出变量具有显著影响的关键区间变量，有助于揭示系统运行状态与区间变量之间的关系。
关键词：不确定潮流 随机变量 区间变量 代理模型 灵敏度分析
电力系统运行中存在诸多不确定性因素[1]，例如负荷需求、线路故障等。随着以风电和光伏为代表的可再生能源大规模并网，系统运行的不确定性进一步增加[2]。因此，有必要采用适当的模型来表示各类不确定性因素，并利用不确定潮流计算对系统运行特性进行分析，从而更加准确地掌握系统的运行状态。
根据不确定量建模方式的不同，常用不确定潮流计算方法包括两种：概率潮流[3]和区间潮流[4]。概率潮流计算将输入不确定量描述为随机变量，进而采用模拟法[5]、点估计法[6]、解析法[7-8]和多项式混沌展开法[9]等获取输出变量的概率分布。区间潮流计算将输入不确定量描述为区间变量，通过仿射法[10-11]和区间泰勒展开法[12]等方法获得输出变量的上、下边界。然而，随着系统的复杂性增加，随机与区间变量往往同时存在。若采用概率潮流分析，则需假设区间变量的概率分布，导致所得结果不够准确；若采用区间潮流分析，则需丢弃随机变量的统计信息，造成对系统状态的保守估计。因此，需要研究能够同时考虑随机和区间变量的不确定潮流计算方法，即概率-区间潮流。
当随机与区间变量同时存在时，系统输出变量的波动范围为其最大、最小概率分布所围成的区域，即概率盒[13]。目前仅有少量关于概率-区间潮流计算方法的研究。文献[14]提出基于证据理论概率-区间潮流模型，并将其转换为多个区间潮流进行求解。文献[15]提出一种双层抽样法，该方法利用外层和内层抽样分别处理随机和区间变量，从而通过大量确定性潮流计算实现概率-区间潮流的求解。文献[16]将配电网中分布式电源出力和负荷需求分别视作随机和区间变量，并提出了一种基于仿射线性三相潮流的近似方法求取输出变量。文献[17]提出一种基于聚类的解析算法，该方法通过在统一最优场景下进行概率潮流计算，可快速且精确地求取单个输出变量的概率盒。针对电-气联合系统中随机与区间变量共存，文献[18]提出一种基于多项式混沌展开的概率-区间能量流计算方法。
虽然当前概率-区间潮流研究取得了一定的成果，但仍存在以下不足：一方面，算法的计算效率仍有待提升。例如双层抽样法需要进行超过106次确定性潮流计算才能得到准确的结果；基于聚类的解析算法虽然在求取单个输出变量时效率较高，但运行人员往往需要了解多个节点电压或多条支路潮流的状态。另一方面，现有研究侧重于如何获取输出变量的概率盒。然而，当系统中包含多个区间变量时会引起输出变量的波动范围较大，导致运行人员难以对系统运行状态作出准确判断。因此，有必要开展灵敏度分析来量化系统中各区间变量的影响程度，从而识别出影响系统状态的关键因素[19-20]。
针对上述不足，本文提出一种基于双层代理模型的概率-区间潮流计算方法。在所提方法中，上层代理采用径向基函数（Radial Basis Function, RBF）模型来近似系统非线性潮流方程，从而能够快速获得输出变量的边界值；基于上层代理所得结果，下层代理采用稀疏多项式混沌展开模型（sparse Polynomial Chaos Expansion, sPCE）构建输入随机变量与输出变量边界值的关系。本文所提出的双层代理模型仅需要较少次数的确定性潮流计算便可构建，进而快速求取输出变量的概率盒。此外，本文还提出了用于描述概率盒特征的灵敏度指标，并结合双层代理模型开展灵敏度分析来量化输入区间变量对输出变量概率盒的影响程度。通过在IEEE 118节点系统中进行算例分析，验证了所提方法的精确性和快速性。
在含大规模风电的电力系统中，风电出力与负荷的不确定性对系统的优化运行和稳定性产生显著影响[2]。对于负荷，其波动范围较小，预测误差通常可以采用正态分布来表示。对于风电出力，由于受到风速、风向等天气因素的影响，其波动范围较负荷更大，且预测误差的概率分布难以获得。基于上述原因，本文将负荷需求和风电出力分别表示为随机变量和区间变量。
通常有功负荷需求的波动性可采用正态分布描述，即
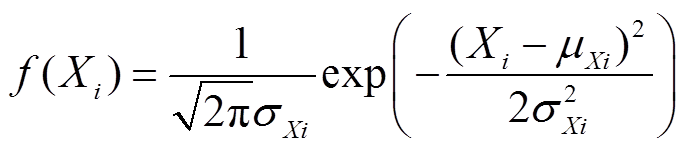（1）
式中，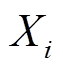
为第i个有功负荷需求；
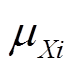和
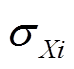分别为负荷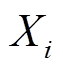的期望值和标准差。假设各节点负荷的功率因数保持不变，则无功负荷可通过有功负荷确定。与此同时，由于不同节点的负荷之间往往存在一定的相关性，通常采用Pearson相关系数[6]来描述这类相关性。
采用区间变量来描述风电出力的波动性。对于第i个风电出力Yi，其有功功率可以表示为[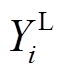
,
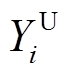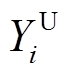]，其中和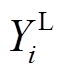分别为风电出力的上、下限。考虑到地理位置邻近的多个风电场出力之间往往具有相关性，采用如图1所示的平行四边形模型[21-22]来描述区间变量间的相关性。
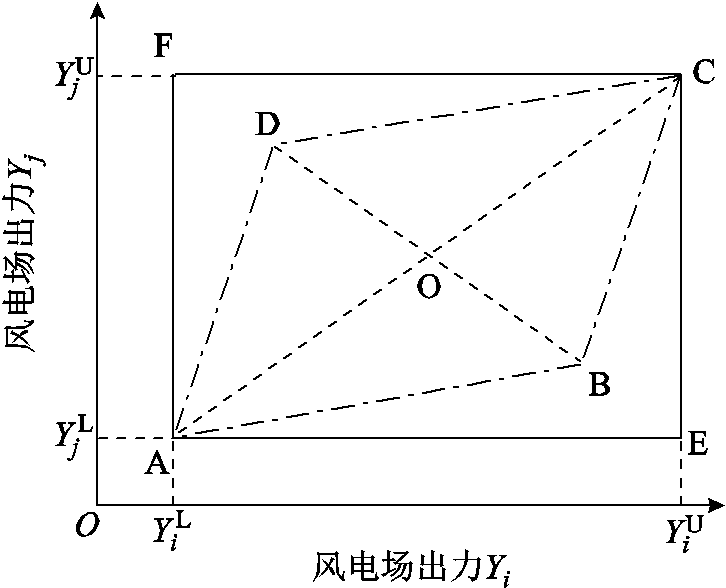
图1 区间变量的相关性
Fig.1 Correlation of interval variables
对于风电出力Yi和Yj，若忽略二者相关性，则两个风电场出力的联合采样区域为黑色实线所围成矩形AECF。当二者相关时，所构成的区域为点画线所围成的平行四边形ABCD，且相关性系数可表示为
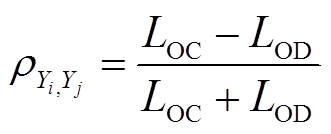（2）
式中，LOC和LOD分别为线段OC和OD的长度。
平行四边形ABCD所围成的联合采样区域[22]可表示为
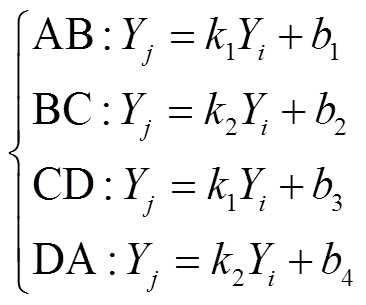（3）
式中，直线的斜率k1、k2和常数b1～b4由区间变量Yi和Yj的宽度及其相关性系数决定。
假设系统中输入变量包含m维随机变量和n维区间变量。在潮流计算中，输出变量与输入变量之间的非线性关系可以简写为
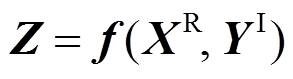（4）
式中，XR=[X1
XiXm]T为m维随机变量；YI=[Y1YiYn]T为n维区间变量；Z为节点电压和支路功率，也称为输出响应；f(·)为由潮流方程决定的输出、输入变量之间的函数关系。
由于式（4）中同时存在随机变量与区间变量，难以直接通过概率潮流或区间潮流方法进行求解。当前，双层抽样法[15]是求解概率-区间潮流最直接的方法。该方法分别在外层和内层对随机变量和区间变量进行抽样，并将样本代入到非线性潮流方程中进行求解。双层抽样法的计算步骤总结如下：
（1）在外层对m维随机变量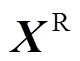
进行抽样，得到样本矩阵为xR m×M，其中M为外层抽样次数；将样本矩阵中第i个样本xR i代入式（4）中可得到
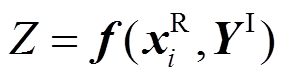（5）
式中，输出响应采用标量Z表示，代表系统中任一节点电压或支路功率。
（2）在内层对n维区间变量YI进行抽样，得到样本矩阵yI n×N，其中N为内层抽样次数；将随机变量的样本xR i与区间变量样本yI j结合并代入（5）中可得
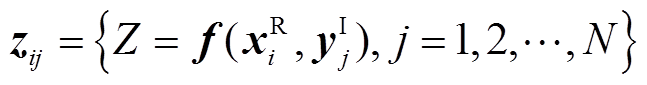（6）
（3）由步骤（2）可得输出响应zi=[zi1 zi2 
zij]T，因此，当随机变量样本为xR i时，输出变量的最大、最小值分别为zU i=max(zi)和zL i=min(zi)。
（4）重复步骤（1）～步骤（3），对于输入变量样本矩阵xR m×M中各个样本均可得到一组输出变量的边界值。因此，得到M组输出变量的边界值，即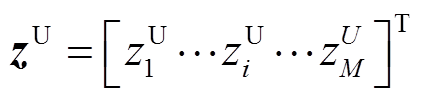
和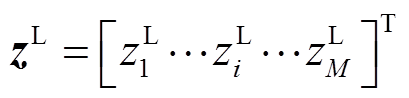
。
基于边界值zU和zL构建输出变量的概率盒如图2所示。输出变量最大概率分布Fmax(Z)和最小概率分布Fmin(Z)分别代表其下边界和上边界的概率分布。由图可知，输出变量Z的波动范围是由最大、最小概率分布所围成的区域。在概率-区间潮流中，输出变量越限事件Z＜Zlimit发生的概率为区间[Prmin, Prmax]。因此，相较于概率潮流计算，概率-区间潮流的优势在于当系统中某些节点注入功率的概率分布难以准确获取时，可将其视作区间变量，从而能够估计出输出变量超过其限值的最大、最小概率。
双层抽样法将概率-区间潮流转换为M×N次确定性潮流计算进行求解。当样本数量充足时，该方法精度较高，但大量的确定性潮流计算会导致该方法效率较低，难以应用于规模较大的系统。为了在保证精度的同时提高概率-区间潮流的计算效率，本文提出双层代理模型来近似双层抽样法中步骤（2）与步骤（4）。在所提出的双层代理模型中，采用上层代理模型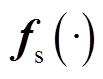
近似系统非线性潮流方程。由于代理模型能够以解析表达式近似表示输入与输出之间的关系，因此，在步骤（2）中可避免采用迭代求解的确定性潮流计算，仅需将输入变量样本代入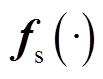即可获得输出响应zi=[zi1 zi2 … zij]T，进而得到其边界值zU i和zL i；采用下层代理模型
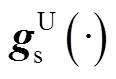和
来近似随机变量样本xR i与相对应的输出变量的上、下边界值zU i和zL i之间的关系，从而对于任意输入随机变量样本均可快速获取输出变量的边界值。在第3节中将详细介绍双层代理模型的构建过程。
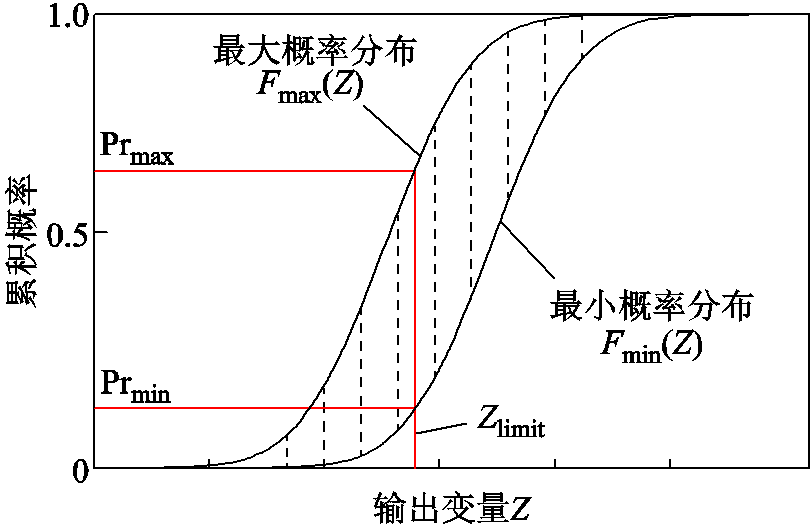
图2 输出变量Z的概率盒
Fig.2 Probability box of output variable Z
近年来，代理模型被广泛应用于多类电力系统不确定性量化分析中。常用的代理模型包括RBF模型和sPCE模型。本文以上层代理模型近似非线性潮流方程，由于需要同时考虑输入随机与区间变量，可采用RBF模型来构建；以下层代理模型近似输入随机变量与输出变量边界值的关系，此时仅需要考虑输入随机变量，可采用sPCE模型构建。
RBF代理模型也称为RBF神经网络，是一种基于多变量插值原理的前馈型神经网络，具有以任意精度逼近任意连续函数的能力，可应用于负荷与新能源预测[23-24]和潮流计算[25]。考虑输入变量为m维随机变量和n维区间变量，输出变量为任一节点电压或支路功率，则RBF代理模型的结构如图3所示。输入层包括m+n个神经元，对应于输入变量的维数；隐含层包含h个神经元，采用RBF作为激励函数；输出层对应于系统节点电压或支路功率。
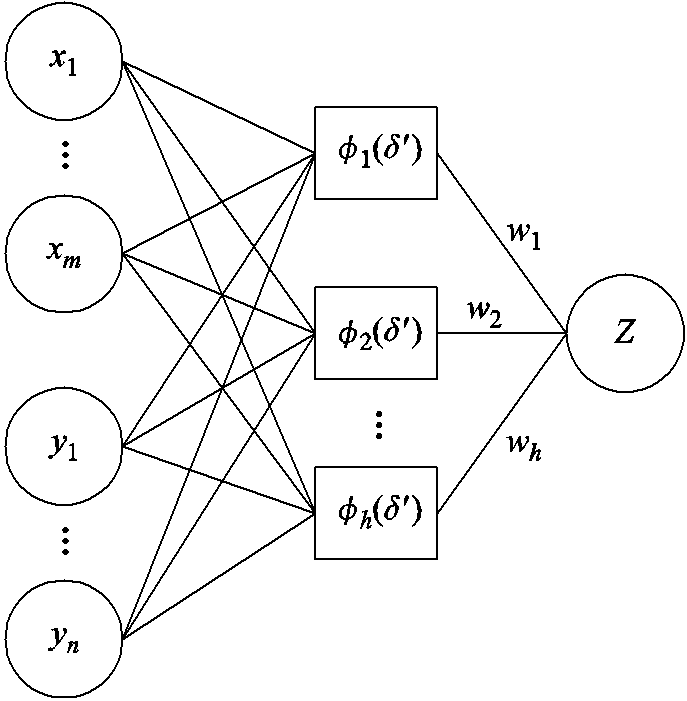
图3 RBF代理模型
Fig.3 RBF surrogate model
隐含层中RBF一般选择高斯函数形式，即
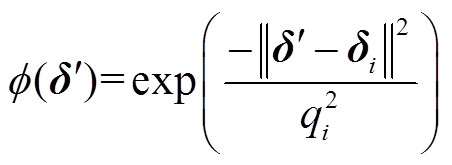（7）
式中，δ′为m+n维输入向量，δ′=[x1 xm y1 yn]T；δi为第i个隐含层神经元的中心，δi=[xi1 xim yi1 yin]T；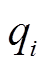
为相应神经元的扩展常数。
基于图3中RBF代理模型结构，可将输出响应表示为
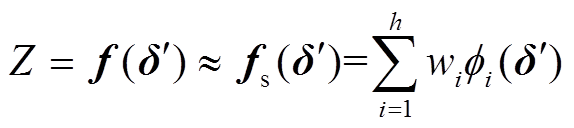（8）
式中，wi为输出层权值，表示第i个隐含层神经元对输出响应的贡献。
采用RBF代理模型来近似非线性潮流方程时，其精度取决于隐含层神经元的中心和扩展常数。为了提高构建代理模型的速度，本文以精确拟合法[25]来构建RBF模型。该方法将隐含层神经元的个数设置为输入向量的个数，从而使RBF模型能够以零误差拟合输入与输出之间的关系。
对随机变量XR和区间变量Y I进行抽样，得到h个输入向量，第i个输入向量为δi=[xi1 xim yi1 yin]T。将h个输入向量代入式（8）中，得到一组线性方程为
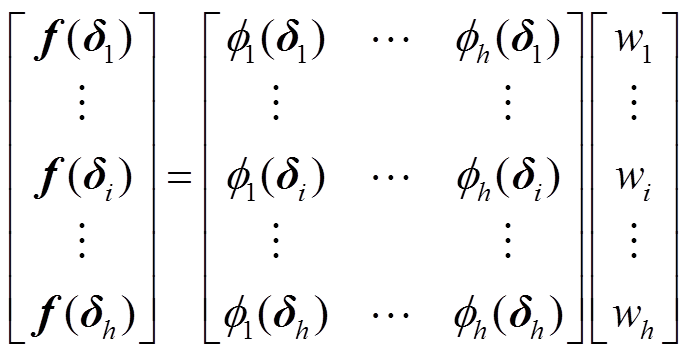（9）
式中，f(δi)为由第i个输入向量通过非线性潮流计算得到的输出响应。进一步将式（9）写为矩阵形式，即
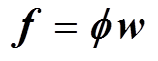（10）
式中，当各神经元的扩展常数确定时，矩阵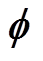
中元素均为常数，且该矩阵可逆。因此，可以得到RBF代理模型中输出层的权值为w=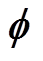-1f。
根据式（7）～式（10）可知，当RBF模型中神经元的个数h确定后，该模型输出层权值受到扩展常数的影响，因此，其拟合精度也随着选取的扩展常数不同而有所差别。扩展常数越大，RBF模型逼近曲线越光滑，但过大的扩展常数会导致模型欠缺选择性；扩展常数过小时，模型的逼近效果较差。因此，本文采用交叉验证误差（Cross-Validation Error, CVE）[26]来确定合适的扩展常数。该方法每次使用输入向量中h-1个向量来构建RBF模型，并将剩余的1个输入向量作为验证计算所得模型的误差，通过h次计算得到误差的期望值。CVE的定义为
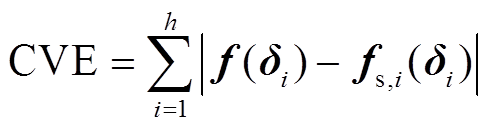（11）
式中，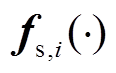
为将第i个输入向量剔除后由剩余向量构建的RBF模型。将CVE取得最小时所对应的扩展常数用作最终代理模型的构建。
在确定隐含层神经元的中心、扩展常数与输出层权值后便可得到如式（8）所示的RBF模型，从而快速地估计输出变量的边界值。采用双层抽样生成输入向量δ′，外层对随机变量XR进行抽样得到输入向量中前m个元素，内层对区间变量YI进行抽样得到剩余的n个元素，则输入向量可表示为
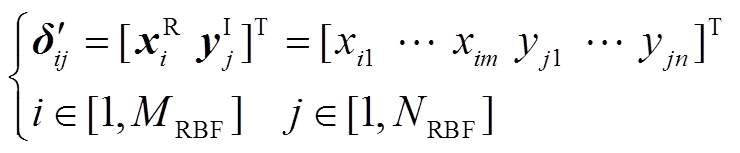（12）
式中，MRBF和NRBF分别为外层、内层的抽样次数。输出变量的边界值可以表示为
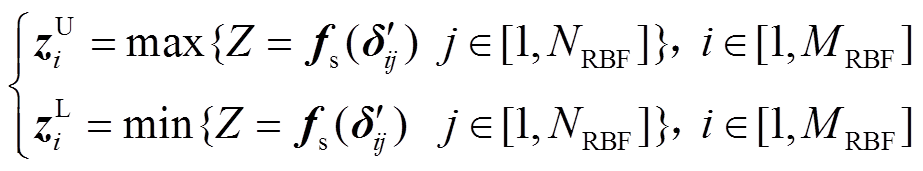（13）
采用RBF模型进行MRBF×NRBF次计算得到输出边界值zURBF=[zU1…zU i…zU MRBF]T和zL RBF=[zL1…zL i…zL MRBF]T。相较于确定性潮流计算，RBF模型仅需将输入变量样本代入其中即可得到输出响应，可极大地提高计算效率。需要指出的是，虽然将RBF代理模型与双层抽样结合能够得到输出变量边界值的样本，倘若所需计算的样本数量过多将会使总计算时间增加。因此，需要构建下层代理模型以进一步提升计算效率。
通过上层RBF模型可得到随机变量样本xR m×MRBF及其所对应的输出变量边界值样本zU RBF和zL RBF。本小节基于上述样本进一步构建下层代理模型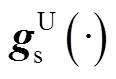和以近似描述随机变量样本与输出变量边界值之间的关系。为方便阐述，以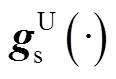为例说明下层代理模型的构建过程。
多项式混沌展开（Polynomial Chaos Expansion, PCE）是将输入随机变量和输出响应之间关系以一组正交多项式展开和的形式来近似表达。该模型被广泛应用于概率潮流计算[9,27]和全局灵敏度分析[19-20]。在构建PCE模型时，要求输入随机变量之间相互独立，因此首先需要通过Nataf变换[6]将具有相关性的输入随机变量XR=[X1…Xj…Xm]T转换为独立的标准正态分布随机变量，即ξR=[ξ1…ξj…ξm]T。同样地，要将输入随机变量样本矩阵xR m×MRBF转换为样本矩阵ξR m×MRBF。在此情况下，可采用各输入变量对应的正交多项式混沌展开来逼近输出响应，即
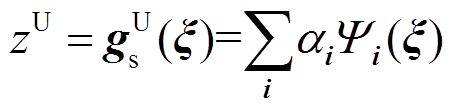（14）
式中，Ψi(ξ)为多变量多项式基函数；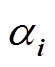
为基函数Ψi(ξ)所对应待求系数；i=[i1 i2 … im]为多阶下标，且满足|i|=i1+i2+…+im。
多变量多项式基函数Ψi(ξ)可以通过单变量多项式的张量积求取，即
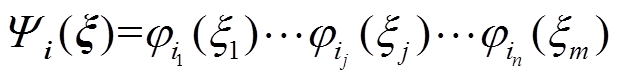（15）
式中，φij(ξj)为变量ξj的第ij阶正交多项式。通常，各输入变量对应的正交多项式取决于该变量的分布类型，本文中服从正态分布的输入变量对应的最优基函数为Hermite多项式。其他常见的连续型概率分布及其对应正交多项式体系可见文献[19]。
在实际应用中，对于式（14）中的PCE模型，通常需要设置其最高展开阶数p，将其表示为有限项截断逼近模型，即
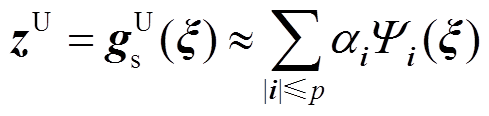（16）
截断后逼近模型的展开项数R为
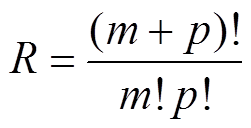（17）
一般地，最高展开阶数p取值越大，多项式展开逼近精度越高，但展开项数也会相应增加。在工程问题中，通常p取2～3即可获得较高的计算精度，在本文中取p=2。将式（16）采用向量形式表示为
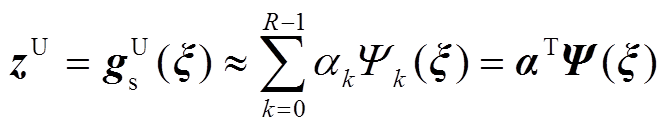（18）
式中，α=[α0α1 αR-1]T为展开系数向量，αk为第k个多项式对应的展开系数；Ψ(ξ)为基函数向量，Ψ(ξ)=[1 Ψ1(ξ) ΨR-1(ξ)]T。
为求解PCE模型中待求展开系数，需要利用上层RBF模型所得结果，即随机变量样本ξR m×MRBF及其所对应的输出变量最大值样本zU RBF，进而采用最小二乘法求解待定系数为
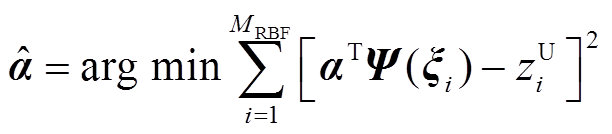（19）
式中，ξi为独立随机变量ξR的第i个样本。为保证求解精度，通常取样本数量为2R～3R。由样本系数R的计算表达式可知，当输入随机变量个数m增大时，待定系数个数R也随之快速增大，导致上层代理模型的计算量较大。由于PCE模型具有稀疏性，为了提高构建模型的效率，文献[27]提出在具有少量输入样本的情况下采用压缩感知技术实现展开系数的快速计算，从而构建sPCE模型。该方法基本思想是忽略对输出响应影响较小的展开项，仅考虑对于输出响应具有较大影响的展开项。基于展开系数向量的稀疏性，可以通过如下的优化问题进行展开系数的求解。
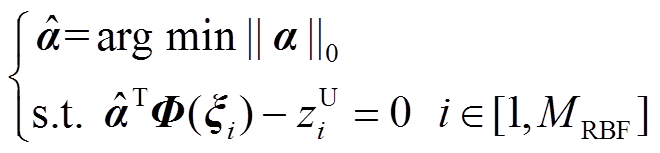（20）
式中，||α||0为待求系数向量α中非零元素的数量。通过求解式（20），使得在给定较少的样本下能够得到一组含非零项最少的展开系数向量，从而构建sPCE模型。式（20）中优化问题可采用正交匹配追踪算法来求解，文献[20, 27]给出了该算法的详细步骤，本文不再赘述。
在得到输入随机变量与其对应的输出变量最大值之间sPCE模型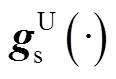后，通过产生独立随机变量ξR的样本ξR m×M，将各样本其代入αTΨ(ξ)便可获得输出变量最大值样本zU=[zU1…zU i…zU M]T。同样地，通过构建可快速地获取输出变量的最小值样本zL=[zL1…zL i…zL M]T。至此，通过双层代理模型可实现输出变量最大、最小值的快速计算，进而构建其概率盒。
在概率-区间潮流中输出变量以概率盒的形式表示，其波动范围处于最大、最小值概率分布之间。然而，当最大、最小值概率分布所涵盖的波动范围较大，则会导致其难以为运行人员提供关于系统运行状态有价值的信息。因此，需要通过开展灵敏度分析辨识出对特定输出变量影响较大的输入区间变量，以便采取措施减小其波动范围。定义描述输出变量概率盒的波动范围的平均距离指标为
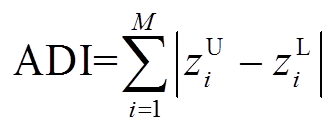（21）
式中，zU i和zL i为输出变量Z的第i组上、下边界值。
当系统中输入区间变量Yi的取值固定为其波动区间的中间值时，即Yi=(YL i+YU i)/2，输出变量的ADI也将随之减少。因此，将ADI的减少程度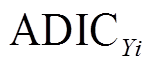
定义为变量Yi对输出变量概率盒的贡献度，即
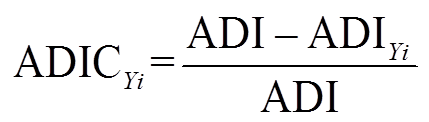（22）
式中，ADIYi为区间变量Yi的取中间值时输出变量Z的平均距离。
对于输入区间变量相互独立的情形，区间变量Yi取其中间值时，其余区间变量的波动范围未受影响，此时，ADICYi仅包含变量Yi对输出变量概率盒的贡献度。对于输入区间变量具有相关性的情形，根据图1所示平行四边形模型，区间变量Yi取其中间值时，与其相关的区间变量波动范围需要满足式（3），此时，ADICYi包含变量Yi及其相关性对输出变量概率盒的贡献度。
需要指出的是，本研究虽侧重于分析输入区间变量对输出变量概率盒的影响，但所提出的双层代理模型也可用于输入随机变量的灵敏度分析。这是因为在下层代理中利用sPCE模型建立了输入随机变量与输出变量边界值之间的关系。sPCE模型可结合用于输入随机变量灵敏度计算的Sobol分解[19]，准确且快速地得到各输入随机变量对输出响应的贡献度。利用sPCE模型开展输入随机变量灵敏度分析的具体步骤可参考文献[19-20]。
本文所提出的基于双层代理模型的概率-区间潮流计算及其灵敏度分析的计算流程如下：
（1）数据输入。包括电力系统潮流计算所需参数，输入随机变量XR的分布参数及相关性系数，输入区间变量YI的边界值参数及相关性系数。
（2）构建RBF模型。根据输入变量XR和YI生成h个样本向量δ=[δ1…δ…δh]T，并将各向量代入非线性潮流方程f(·)中得到相应的输出响应f(δ)=[f(δ1)…f(δi)…f(δh)]T，进而通过式（9）～式（11）求解RBF代理模型fs(·)中输出层的权值。
（3）基于RBF模型计算输出变量的边界值。采用拉丁超立方抽样生成对应随机变量XR的M维独立标准正态分布变量ξR的样本矩阵ξR m×MRBF，并将其经逆Nataf变换为XR的样本矩阵。将xR m×MRBF与区间变量样本矩阵YI n×NRBF通过式（12）进行组合，并代入式（13）中获取输出变量的边界值向量zURBF和zLRBF。
（4）构建sPCE模型。基于M维独立标准正态分布变量ξR的样本矩阵ξR m×MRBF以及输出变量的边界值向量zU RBF和zL RBF，采用正交匹配追踪算法计算展开系数，得到sPCE模型gU s(·)和gL s(·)。
（5）获取输出变量边界值的大量样本。产生独立随机变量ξR的样本ξR m×M，并将其代入sPCE模型 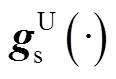和得到输出变量边界值样本zU=[zU1 zU izU M]T和zL=[zL1zL izL M]T，进而构建输出变量的概率盒。
（6）对于系统中每个输入区间变量，重复步骤（3）～步骤（5），并结合式（22）得到各区间变量对输入变量概率盒的贡献度。
本节采用IEEE 118节点系统验证所提方法的有效性。将系统中各节点有功负荷视作随机变量，且服从正态分布，期望值为原系统负荷值[28]，标准差为期望值的5%。将系统分为两个区域，区域1包含节点1～60，区域2包含节点61～118。同一区域内负荷之间的相关性系数为0.6，不同区域内负荷之间相关性系数为0.4。系统中接入八个风电场，将其分为两组，各组风电场接入节点及参数设置见表1。对于风电场的相关性，考虑以下两个场景：①场景1中不同风电出力之间相互独立；②场景2中同组风电出力之间的相关性系数为0.5，不同组风电出力之间相互独立。
表1 风电场参数设置
Tab.1 Parameters of wind farms
组号接入节点风电出力区间/MW 115, 27, 35, 45[20, 80] 280, 90, 100, 116[10, 70]
为了验证本文所提方法的有效性，对如下三种算法进行对比测试：①双层抽样法（Double Layer Monte Carlo Simulation, DLMCS）[15]。以该方法所得结果作为对比依据，将其外层、内层抽样次数均设置为2 000次，因此需要4×106次非线性潮流计算。②基于聚类的解析法（Clustering-based Analytical Method, CAM）[17]。将CAM中聚类个数设置为4个，该方法能够快速且精确地获取单个输出变量的概率盒。③本文方法，即双层代理模型法（Double Layer Surrogate Method, DLSM）。算例分析利用Matlab R2020a平台进行编程实现，程序运行的硬件环境为：R7-4750U，基准频率1.7GHz，内存为16GB。
在本文所提方法中通过上层RBF模型fs(·)来获取输出变量的边界值样本，进而将其用于下层代理模型的构建。这意味着由RBF模型所得边界值样本将直接决定所提方法的精确性。定义边界值平均误差ηγ对边界值样本的精度进行定量分析。
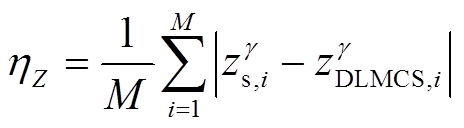（23）
式中，上标“γ”可为上、下边界值；zγs,i和zγDLMCS,i分别为通过代理模型和DLMCS所得输出变量Z的边界值样本；M为所得边界值样本的数量。
对于所得输出变量的概率盒，定义相对误差ek指标来定量分析其准确性，ek为
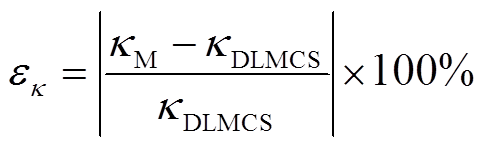（24）
式中，k为输出变量的统计矩，一般为期望值μ和标准差σ；kM和kDLMCS分别为通过待评估方法和DLMCS计算所得结果。由于同一类型的输出往往包含多个变量，采用同一类变量相对误差的平均值来表示结果的精确性。因此，分别采用εUk,mean和εLk,mean表示输出变量最大、最小值的相对误差。
本节首先验证采用RBF模型求出输出变量边界值的精确性。所用测试系统包含99个随机变量（有功负荷），8个区间变量（风电出力）。因此，在构建RBF模型中输入向量的维度为107。将RBF代理模型中神经元的数量h设置为500，即产生500个随机变量与区间变量样本作为径向基函数的中心，进而采用式（11）中CVE指标来选取合适的扩展常数。
以支路有功功率P1-2为例，图4给出了不同扩展常数下该变量的CVE指标。可以看出，当扩展常数小于0.5×104时，RBF模型拟合精度较差；而当扩展常数超过6×104后，RBF模型的拟合精度具有波动性，且呈现误差逐渐增大的趋势。当扩展常数为2.5×104时，所对应的CVE指标较低，因此本文选择该值作为用作RBF模型构建的扩展常数。
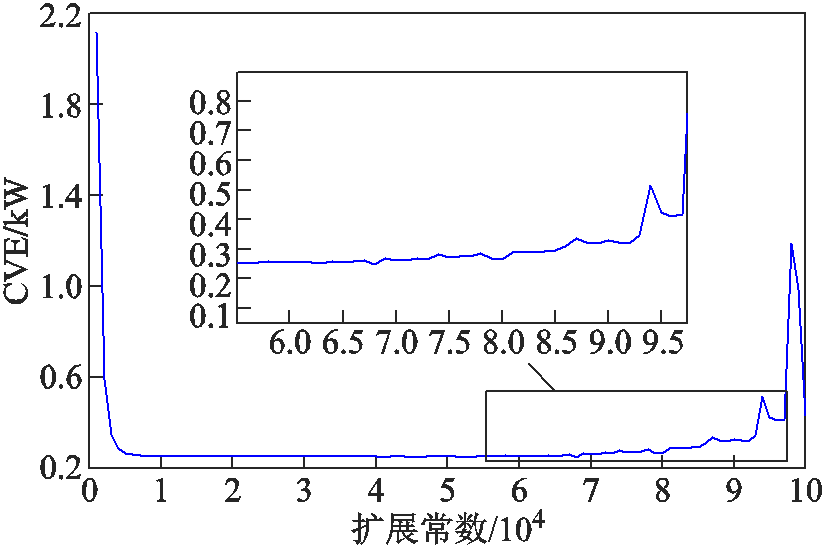
图4 不同扩展常数下的CVE
Fig.4 CVE with different scale parameters
利用所构建的RBF模型可获取输出变量边界值样本，为验证其在精确性上的优势，将其与3.2节所介绍的sPCE模型进行对比。选取sPCE模型作为对比方法的原因是其已被广泛地应用于多类电力系统不确定性量化问题[20, 27]，能够以较高精度近似表示非线性潮流方程中输入和输出变量之间的关系。在构建sPCE模型时需将系统中所包含的区间变量视作均匀分布的随机变量，并以潮流输出变量作为输出响应。将sPCE模型中最高展开阶数设置为2，输入随机变量的数量为107个，则待求解的系数为5 886项。与构建RBF代理模型类似，采用500个样本来求解sPCE模型的展开项系数。
利用所得RBF模型和sPCE模型来获取输出变量的边界值，并以DLMCS所得结果为标准计算两种代理模型的平均误差。图5给出了场景1中通过两种代理模型所得支路有功功率上、下边界值的平均误差（测试系统中包含186条支路）。对比两种代理模型所得结果的误差，可以发现RBF模型在计算精度上要高于sPCE模型，尤其是对于编号90～130支路，两者之间的精度具有明显差异。两种模型最大误差均发生在编号107支路，由RBF模型所得上、下边界值最大误差分别为0.126MW和0.176MW，而sPCE模型所得最大误差分别为1.074MW和1.305MW。此外，RBF模型所对应的边界值误差还呈现两个规律：一方面上、下边界值的误差相近，说明该模型对于求取输出变量上、下边界具有相似的精度；另一方面，不同输出变量的拟合精度有差异，例如编号30～55支路的误差较小，而编号90～130支路的误差较大，这是由于后者受输入区间变量的影响而波动范围较大，使得RBF模型的精度略有下降。
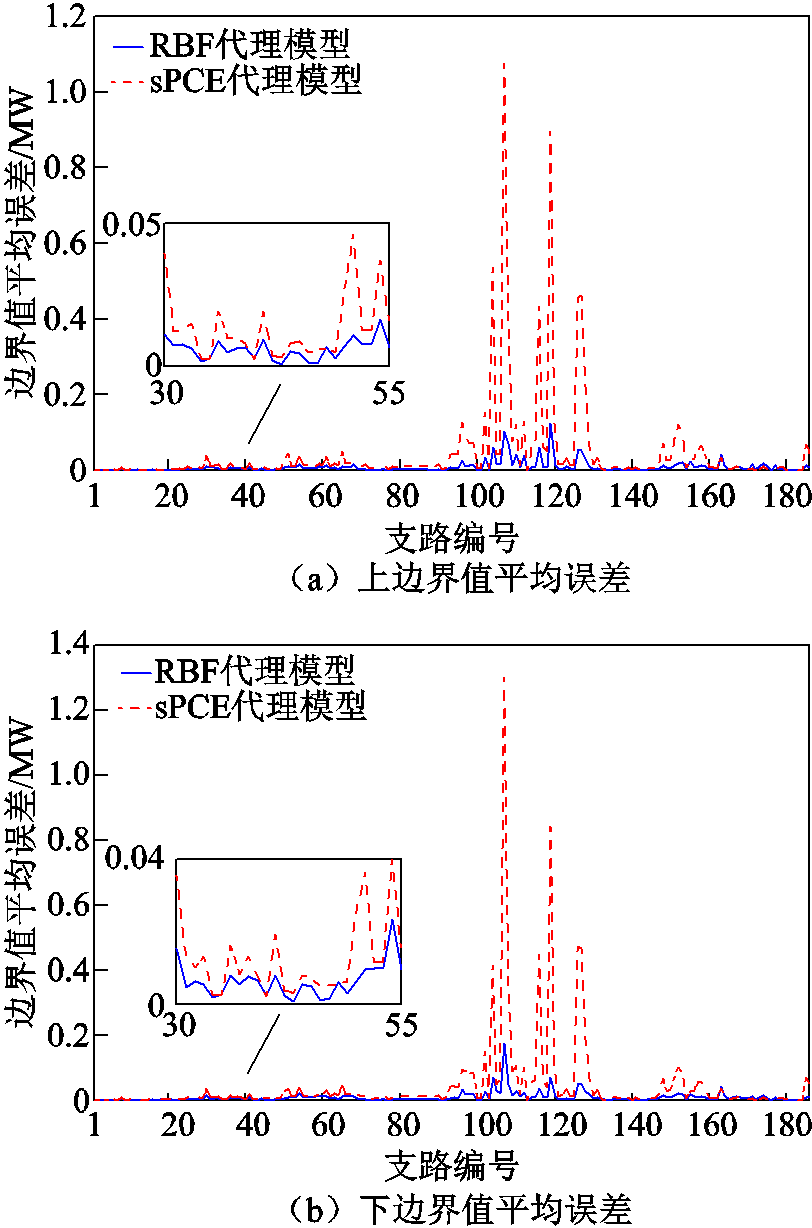
图5 不同代理模型所得结果的边界值误差
Fig.5 Boundary errors of results obtained by different surrogate models
对于sPCE模型，由于其待求展开项系数较多，通过少量样本所构建的代理模型能够较为精确地拟合输出变量的整体分布，但难以保证所得输出变量边界值的准确性。对于RBF模型，其待求的输出层权重与样本数量一致，通过扩展常数的优化选取可使其较为精确地求取实输出变量边界值。因此，在本文中将其作为上层代理模型是合理的。
在5.2节中已验证了RBF模型获取输出变量边界值的精确性。基于边界值样本可构建下层代理模型，进而得到双层代理模型，即DLSM。对于下层所采用的sPCE模型，设置其最高展开阶数为2，由于系统中存在99个随机变量，则待求解的系数包含5 050项。基于多项式混沌展开的稀疏特性，采用RBF模型产生500个边界值样本用于sPCE模型展开系数的求解。
为验证DLSM所得输出变量概率盒的精确性，采用CAM作为对比方法，以DLMCS所得结果作为标准，得到DLSM和CAM所得结果的相对误差见表2。由结果可知，在场景1和2中DLSM均能够取得与CAM相接近的计算精度。通过DLSM所得各类输出变量的期望值和标准差的相对误差均小于1%和2%，说明了所提方法能够较为精确地获取输出变量的概率盒。此外，DLSM的相对误差结果还呈现出三个规律：①同一场景中输出变量的上、下边界值的相对误差相近，表明了所提方法在求取输出变量上、下边界时具有相似的精度；②同一类型输出变量边界值的相对误差在场景1和场景2中非常接近，说明所提方法的计算精度不受是否考虑区间变量相关性的影响；③支路无功功率期望值的相对误差大于其余三种类型输出变量，这是因为系统中PV节点无功出力使得代理模拟在近似输入变量与支路无功功率之间的关系时精度有所降低。
图6～图8给出了在场景1和2中通过DLMCS和DLSM所得变量V33、P47-49和Q68-116的概率盒，选取上述变量进行分析的依据是：一方面这些变量与系统中输入区间变量所在节点邻近，受到区间变量的影响较大，可验证所提方法求取波动较大变量的计算精度；另一方面，变量V33和Q68-116不仅受到输入变量的影响，还受到邻近PV节点无功出力的影响，使得其与输入变量之间的关系更为复杂，可验证所提方法在求取该类变量时的稳健性。
表2 输出变量边界值的相对误差
Tab.2 Relative errors of output variables’ boundaries
变量类型误差(%)场景1场景2 DLSMCAMDLSMCAM VεU μ,mean0.000 70.000 10.000 50.000 1 εU σ,mean1.9031.4201.4271.656 εL μ,mean0.000 70.000 10.000 70.000 1 εL σ,mean1.4641.3141.3951.336 θεU μ,mean0.0120.0080.0100.008 εU σ,mean0.7780.8300.7660.830 εL μ,mean0.0190.0130.0260.012 εL σ,mean0.7740.8210.7590.821 PεU μ,mean0.0270.0120.0540.010 εU μ,mean1.4071.4211.4131.421 εL μ,mean0.0250.0160.0380.014 εL σ,mean1.4141.4171.4071.418 QεU μ,mean0.1290.1110.3050.111 εU μ,mean1.4761.4081.4971.431 εL μ,mean0.7290.1940.3550.134 εL σ,mean1.6291.4501.5141.436
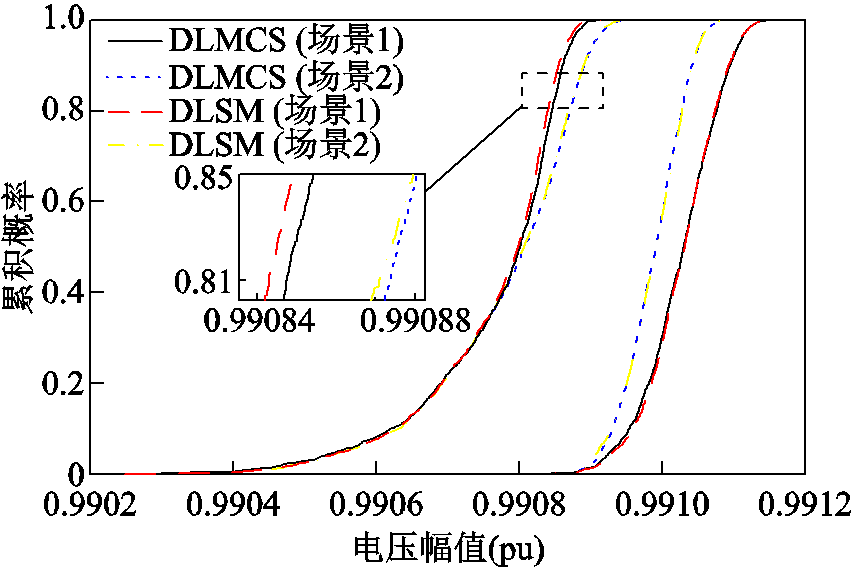
图6 节点33电压幅值的概率盒
Fig.6 Probability box of voltage magnitude of Bus 33
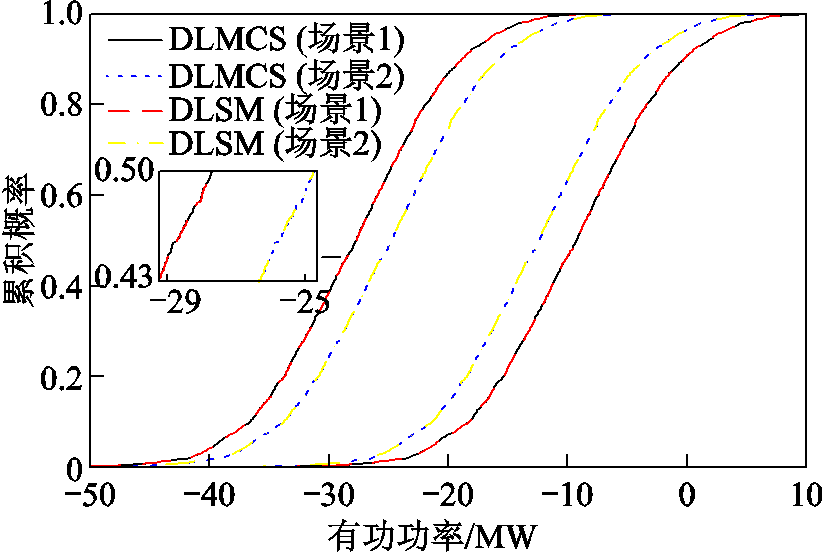
图7 支路47-49有功功率的概率盒
Fig.7 Probability box of active power of Branch 47-49
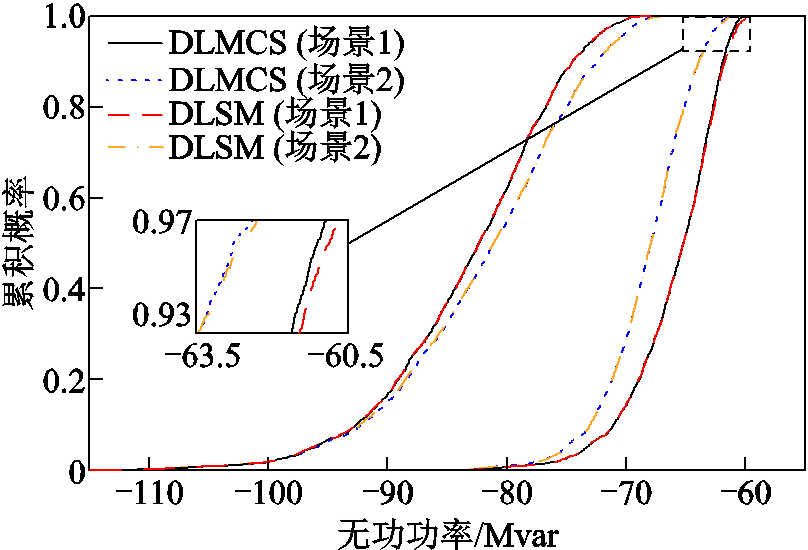
图8 支路68-116无功功率的概率盒
Fig.8 Probability box of reactive power of Branch 68-116
同一变量的概率盒包含最大、最小两条概率曲线。以DLMCS所得曲线（图中实线）作为准确结果，可以发现在场景1和场景2中由DLSM所得曲线（图中虚线）均与准确曲线非常接近。该结果表明了所提方法能够以较高的精度获取输出变量概率盒。由局部放大图可知，所得变量V33和Q68-116分布曲线的精度要低于变量P47-49，其原因在于节点电压与支路无功功率不仅与输入变量有关，还与PV节点的无功出力有关，使得代理模型在曲线局部的拟合精度略有下降。此外，同一输出变量在场景2中的概率盒被包含在场景1所得结果中，说明了输出变量最大、最小概率分布曲线之间的距离与区间变量有关，且当区间变量具有相关性时会导致输出变量概率盒变窄。
概率-区间潮流所得结果可用于分析系统中节点电压或支路功率的越限概率。表3给出了不同输出变量越限概率。由结果可知，在场景1和场景2中，通过DLSM所得变量越限概率与DLMCS和CAM的结果相近。当考虑区间变量相关性时，由于输出变量的概率盒变窄，其越限概率区间也相应地变窄。例如，变量P47-49小于-20MW的概率区间宽度从场景1中0.798减少至场景2中0.602。上述结果说明了在实际应用中考虑区间变量相关性的必要性，即避免对系统输出变量的保守估计，从而有利于运行人员做出更具针对性的决策。
表3 变量越限概率区间
Tab.3 Probability intervals of constraint violations
场景方法越限概率区间 V33＞0.990 9(pu)P47-49＜-20WMQ68-116＜-70Mvar 1DLMCS[0.003, 0.985][0.072, 0.870][0.143, 0.993] CAM[0.004, 0.982][0.072, 0.870][0.144, 0.992] DLSM[0.001, 0.988][0.072, 0.870][0.146, 0.993] 2DLMCS[0.066, 0.975][0.143, 0.744][0.291, 0.964] CAM[0.068, 0.969][0.143, 0.744][0.291, 0.961] DLSM[0.062, 0.979][0.143, 0.745][0.290, 0.962]
采用本文所提DLSM，并结合式（21）和式（22）所示指标对区间变量进行灵敏度分析。图9给出了场景1中，即区间变量相互独立时，系统中8个区间变量（以Y表示，下标代表该变量所在节点）对不同输出变量概率盒的影响程度。由结果可知，对于不同的输出变量，影响其概率盒的最关键因素是不同的。例如，对于变量P23-24而言，对其具有最大影响的变量为Y27；而对于变量P82-96具有最大影响的变量为Y100。引起该现象的主要原因是不同节点之间的电气距离存在差异。在特定节点引入的区间变量往往对与其电气联系较为紧密的节点和支路影响较大。根据灵敏度分析结果可以将区间变量按照其贡献度大小进行排序。以输出变量P75-118为例，可得到排序为：Y100＞Y90＞Y80＞Y116＞Y27＞Y45＞Y15＞Y35，其中排序前4位的区间变量的贡献度占据主导。
图9 场景1中输入区间变量的平均距离指标贡献度
Fig.9 The average distance index contributions of input interval variables in scenario 1
为了验证本文方法所得区间变量贡献度排序的正确性，将其与另外两种方法所得结果进行对比。对比方法一采用文献[29]提出的Bhattacharyya距离贡献度（以下简称BDIC）。该方法利用输出变量的最大、最小概率密度曲线的重叠面积来表征各区间变量的贡献度。某一输入区间变量所对应的BDIC越大，表明其对输出变量的影响程度越大。BDIC的定义及其具体计算步骤可见文献[29]。对比方法二采用输出变量越限概率区间宽度作为灵敏度指标。在该方法中，当某一区间变量被设置为其中间值时，输出变量越限概率区间的宽度会减少，因此，可利用其反映该区间变量的影响大小。去除某输入区间变量后输出变量的越限概率区间宽度越大，表明该区间变量对输出变量的影响程度越小。
不同方法所得区间变量贡献度结果与排序见表4。其中，对于越限概率宽度指标来说，当各输入区间变量都存在时变量P75-118＜35MW的概率为[0.229, 0.968]，该区间的宽度为0.739。由结果可以看出，基于本文所提出的平均距离指标、BDIC和越限概率区间宽度所得到的区间变量排序是一致的，从而验证了本文所提出的灵敏度指标的合理性。需要指出的是，本文所提出的平均距离指标可直接通过输出变量样本计算得到，而BDIC的计算则需要利用积分，因此，前者的计算更加方便快速。
表4 不同方法的灵敏度分析结果
Tab.4 Sensitivity analysis results of different methods
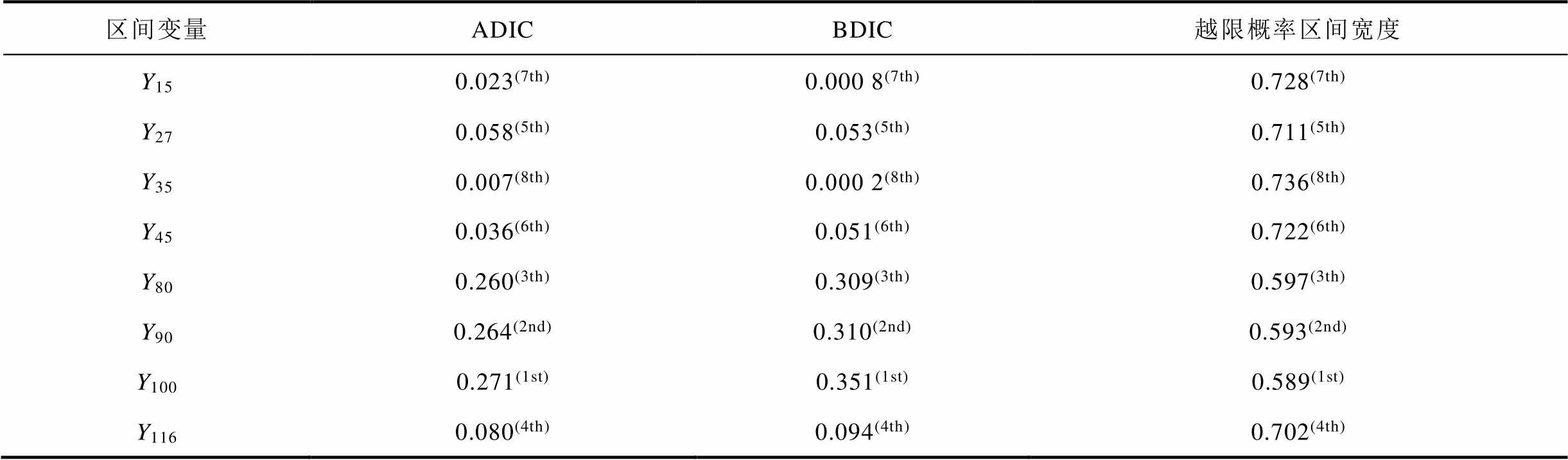
区间变量ADICBDIC越限概率区间宽度 Y150.023(7th)0.000 8(7th)0.728(7th) Y270.058(5th)0.053(5th)0.711(5th) Y350.007(8th)0.000 2(8th)0.736(8th) Y450.036(6th)0.051(6th)0.722(6th) Y800.260(3th)0.309(3th)0.597(3th) Y900.264(2nd)0.310(2nd)0.593(2nd) Y1000.271(1st)0.351(1st)0.589(1st) Y1160.080(4th)0.094(4th)0.702(4th)
图10给出了场景2下，即考虑区间变量相关性时，系统中区间变量对不同输出变量概率盒的影响程度。相较于图8中的结果，考虑相关性会使得各区间变量对输出变量概率盒的贡献度增加。这是因为当计及区间变量相关性时，区间变量Yi取其中间值时，其余区间变量的波动范围需要满足图1所示平行四边形模型。此时，ADICYi表示的变量Yi及与其具有相关性的区间变量对输出变量概率盒的贡献度之和。
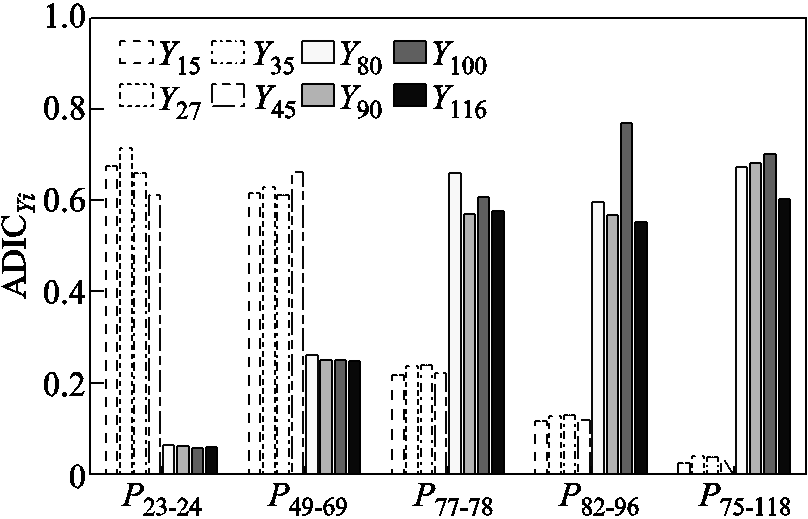
图10 场景2中输入区间变量的平均距离指标贡献度
Fig.10 The average distance index contributions of input interval variables in scenario 2
相较于场景1，考虑区间变量相关性后各变量贡献度的排序略有变化，占据主要贡献度的变量是相同的。对于输出变量P75-118，场景2中区间变量的排序为：Y100＞Y90＞Y80＞Y116＞Y27＞Y35＞Y45＞Y15，排序后3位的变量发生变化，而排序前4位的变量与场景1相同。对于场景1和场景2中占据主要贡献度的变量是相同的这一现象可结合图6～图8中曲线进行解释。虽然输出变量的概率盒在计及区间变量相关性后变窄，但其减少程度占据整体波动范围的比例仍较小。因此，相较于相关性，区间变量本身的波动范围是影响输出变量的主要因素。此外，考虑相关性后使得原本具有较大影响区间变量的贡献度进一步增加，更加突出其对输出变量的影响程度。
区间变量贡献度排序结果可为电力系统规划和运行提供新的视角。例如，为了减少变量P75-118的波动范围可以提高节点100、90、80和116处风电场功率预测精度或者安装储能装置抑制其出力的不确定性。通过上述措施还可减少变量P77-78和P82-96的波动范围，但对于变量P23-24和P49-69影响较小。
本小节对DLMCS、CAM和DLSM的计算效率进行对比。对于所提DLSM，其总耗时Ttotal由构建上、下层代理模型TRBF和TsPCE构成。TRBF包含了h次非线性潮流计算、扩展系数求取及进行MRBF×NRBF次评估的时间。TsPCE包含展开系数求解与进行M次评估的时间。TsPCE与输出变量的个数有关，可进一步表示为TsPCE=ktsPCE，其中tsPCE表示对单个输出变量构建sPCE模型及评估所需时间；k表示输出变量的个数。
以系统中所有PQ节点的电压幅值（共64个PQ节点）作为输出变量，三种方法所需计算时间见表5。由结果可知，DLMCS由于需要进行4×106次确定性潮流计算，所需计算时间最多。CAM在获取单个变量概率盒时仅需27.1s，但随着输出变量个数的增加，其计算效率也有所下降。本文所提DLSM相较于DLMCS和CAM计算效率分别提升约126倍和14倍。对于DLSM来说，仅在构建上层代理模型时需要进行少量的非线性潮流计算，并且上层代理模型得到输入随机变量和输出变量边界值样本后，下层代理模型仅需要tsPCE=1.48s（94.7/64）便可获得单个输出变量的概率盒。因此，所提方法在输出变量较多时效率方面具有更为明显的优势。
表5 不同方法的计算效率
Tab.5 The computational burden of different methods
方法TRBF/sTsPCE/sTtotal/s DLMCS——15 488.9 CAM——1 734.4 DLSM28.294.7122.9
本文针对电力系统中随机与区间变量共存时的不确定潮流计算问题，提出一种基于双层代理模型的概率-区间潮流计算方法，并基于所提方法开展了对输入区间变量的灵敏度分析。通过算例分析验证了所提方法的精确性和快速性，得到主要结论如下：
1）验证了RBF模型能够以较高的精度近似非线性潮流方程中输入变量与输出响应的关系，较为精确地获取输出响应边界值。该代理模型是本文所提方法计算精度与效率的关键所在。
2）在计算精度方面，本文所提出的DLSM能够准确地获取输出变量的概率盒，且计算误差与CAM相近；在计算效率方面，DLSM相较于DLMCS和CAM均有较大幅度的提升，且在输出变量较多时具有更为明显的优势。
3）通过灵敏度分析可识别出对输出变量影响较大的区间变量，并得到其贡献度排序。对于特定输出变量，考虑区间变量相关性与否会引起贡献度排序略有差异，而占据主要贡献度的变量仍是相同的。
参考文献
[1] Jordehi A R. How to deal with uncertainties in electric power systems? a review[J]. Renewable and Sustainable Energy Reviews, 2018, 96: 145-155.
[2] 康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11.
Kang Chongqing, Yao Liangzhong. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11.
[3] Prusty B R, Jena D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach[J]. Renewable and Sustainable Energy Reviews, 2017, 69: 1286-1302.
[4] 廖小兵, 刘开培, 乐健, 等. 电力系统区间潮流计算方法综述[J]. 中国电机工程学报, 2019, 39(2): 447-458.
Liao Xiaobing, Liu Kaipei, Le Jian, et al. Review on interval power flow calculation methods in power system[J]. Proceedings of the CSEE, 2019, 39(2): 447-458.
[5] 谢桦, 任超宇, 郭志星, 等. 基于聚类抽样的随机潮流计算[J]. 电工技术学报, 2020, 35(23): 4940-4948.
Xie Hua, Ren Chaoyu, Guo Zhixing, et al. Stochastic load flow calculation method based on clustering and sampling[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4940-4948.
[6] 韩佶, 苗世洪, 李超, 等. 计及相关性的电-气-热综合能源系统概率最优能量流[J]. 电工技术学报, 2019, 34(5): 1055-1067.
Han Ji, Miao Shihong, Li Chao, et al. Probabilistic optimal energy flow of electricity-gas-heat integrated energy system considering correlation[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1055-1067.
[7] Wang Chenxu, Liu Chengxi, Tang Fei, et al. A scenario-based analytical method for probabilistic load flow analysis[J]. Electric Power Systems Research, 2020, 181: 106193.
[8] 李聪聪, 王彤, 相禹维, 等. 基于改进高斯混合模型的概率潮流解析方法[J]. 电力系统保护与控制, 2020, 48(10): 146-155.
Li Congcong, Wang Tong, Xiang Yuwei, et al. Analytical method based on improved Gaussian mixture model for probabilistic load flow[J]. Power System Protection and Control, 2020, 48(10): 146-155.
[9] 何琨, 徐潇源, 严正, 等. 基于稀疏混沌多项式展开的孤岛微电网概率潮流计算[J]. 电力系统自动化, 2019, 43(2): 67-75.
He Kun, Xu Xiaoyuan, Yan Zheng, et al. Probabilistic
power flow calculation of islanded microgrid based on sparse polynomial chaos expansion[J]. Automation of Electric Power Systems, 2019, 43(2): 67-75.
[10] 胡健, 付立军, 马凡, 等. 基于仿射算术优化的不确定系统区间潮流快速分解法[J]. 电工技术学报, 2016, 31(23): 125-131.
Hu Jian, Fu Lijun, Ma Fan, et al. Fast decoupled power flow calculation of uncertainty system based on interval affine arithmetic optimization[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 125-131.
[11] 杜萍静, 杨明, 曹良晶, 等. 含电压源换流器交直流系统的仿射潮流算法[J]. 电工技术学报, 2020, 35(5): 1106-1117.
Du Pingjing, Yang Ming, Cao Liangjing, et al. Affine power flow algorithm for AC/DC systems with voltage source converter[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1106-1117.
[12] 廖小兵, 刘开培, 张亚超, 等. 基于区间泰勒展开的不确定性潮流分析[J]. 电工技术学报, 2018, 33(4): 750-758.
Liao Xiaobing, Liu Kaipei, Zhang Yachao, et al. Uncertain power flow analysis based on interval Taylor expansion[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 750-758.
[13] Luo Jinqing, Shi Libao, Ni Yixin. Uncertain power flow analysis based on evidence theory and affine arithmetic[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1113-1115.
[14] 鲍海波, 韦化, 郭小璇, 等. 考虑风电不确定性的概率区间潮流模型与算法[J]. 中国电机工程学报, 2017, 37(19): 5633-5642.
Bao Haibo, Wei Hua, Guo Xiaoxuan, et al. Model and algorithm of probabilistic interval power flow considering wind power uncertainty[J]. Proceedings of the CSEE, 2017, 37(19): 5633-5642.
[15] Guo Xiaoxuan, Gong Renxi, Bao Haibo, et al. Hybrid stochastic and interval power flow considering uncertain wind power and photovoltaic power[J]. IEEE Access, 2019, 7: 85090-85097.
[16] Wang Chun, Ao Xin, Fu Wenbin. Three-phase power flow calculation considering probability and interval uncertainties for power distribution systems[J]. IET Generation, Transmission & Distribution, 2019, 13(15): 3334-3345.
[17] Wang Chenxu, Liu Dichen, Tang Fei, et al. A clustering-based analytical method for hybrid probabilistic and interval power flow[J]. International Journal of Electrical Power & Energy Systems, 2021, 126: 106605.
[18] Hu Xiaoyun, Zhao Xia, Feng Xinxin. Probabilistic-interval energy flow analysis of regional integrated electricity and gas system considering multiple uncertainties and correlations[J]. IEEE Access, 2019, 7: 178209-178223.
[19] 孙鑫, 王博, 陈金富, 等. 基于稀疏多项式混沌展开的可用输电能力不确定性量化分析[J]. 中国电机工程学报, 2019, 39(10): 1-10.
Sun Xin, Wang Bo, Chen Jinfu, et al. Sparse polynomial chaos expansion based uncertainty quantification for avaiable transfer capability[J]. Proceedings of the CSEE, 2019, 39(10): 1-10.
[20] 胡潇云, 赵霞, 冯欣欣. 基于稀疏多项式混沌展开的区域电-气联合系统全局灵敏度分析[J]. 电工技术学报, 2020, 35(13): 2805-2816.
Hu Xiaoyun, Zhao Xia, Feng Xinxin. Global sensitivity analysis for regional integrated electricity and gas system based on sparse polynomial chaos expansion[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2805-2816.
[21] 鲍海波, 郭小璇. 求解含风电相关性区间潮流的仿射变换最优场景法[J]. 电力系统保护与控制, 2020, 48(18): 114-122.
Bao Haibo, Guo Xiaoxuan. Optimal scenario algorithm based on affine transformation applied interval power flow considering correlated wind power[J]. Power System Protection and Control, 2020, 48(18): 114-122.
[22] Ran Xiaohong, Leng Shipeng, Liu Kaipei. A novel affine arithmetic method with missed the triangular domain with uncertainties[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1430-1439.
[23] 陈丽娜, 张智晟, 于道林. 基于广义需求侧资源聚合的电力系统短期负荷预测模型[J]. 电力系统保护与控制, 2018, 46(15): 45-51.
Chen Lina, Zhang Zhisheng, Yu Daolin. Short-term load forecasting model of power system based on generalized demand side resources aggregation[J]. Power System Protection and Control, 2018, 46(15): 45-51.
[24] 郭茜, 匡洪海, 王建辉, 等. 单机风电功率人工智能预测模型综述[J]. 电气技术, 2020, 21(2): 1-6.
Guo Qian, Kuang Honghai, Wang Jianhui, et al. Summary of artificial intelligence prediction model for single wind power[J]. Electrical Engineering, 2020, 21(2): 1-6.
[25] Baghaee H R, Mirsalim M, Gharehpetian G B, et al. Fuzzy unscented transform for uncertainty quantification of correlated wind/PV microgrids: possibilistic-probabilistic power flow based on RBFNNs[J]. IET Renewable Power Generation, 2017, 11(6): 867-877.
[26] Li Xu, Gong Chunlin, Gu Liangxian, et al. A sequential surrogate method for reliability analysis based on radial basis function[J]. Structural Safety, 2018, 73: 42-53.
[27] Sun Xin, Tu Qingrui, Chen Jinfu, et al. Probabilistic load flow calculation based on sparse polynomial chaos expansion[J]. IET Generation, Transmission & Distribution, 2018, 12 (11): 2735-2744.
[28] Zimmerman R D, Murillo-Sanchez C E, Thomas R J. Matpower: steady-state operations, planning and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems, 2011, 26(1): 12-19.
[29] Bi Sifeng, Broggi M, Wei Pengfei, et al. The Bhattacharyya distance: enriching the P-box in stochastic sensitivity analysis[J]. Mechanical Systems and Signal Processing, 2019, 129: 265-281.
Probabilistic-Interval Power Flow and Sensitivity Analysis Using Double Layer Surrogate Method
Abstract With the increasing complexity of uncertainties in power systems, the co-existence of random and interval variables makes it challenging to accurately obtain systems’ operating states by using probabilistic or interval power flow calculations. To cope with this issue, this paper proposes a double layer surrogate method for probabilistic-interval power flow analysis. The proposed method can obtain the upper and lower surrogate models based on a few times deterministic power flow calculations. Then, the surrogate models are used to solve a large number of deterministic power flow calculations required in the conventional probabilistic-interval power flow method, and the probability boxes of output variables can be obtained with high efficiency. In addition, a sensitivity index is proposed to describe the characteristics of output variables, and the sensitivity analysis is performed using the proposed method to identify the importance of input interval variables that affect output variables. The accuracy and efficiency of the proposed method are validated on the IEEE 118-bus test system by comparing the existing methods. The sensitivity analysis can identify the key interval variables for the output variables and reveal the relationship between the operating states and the input interval variables.
keywords：Uncertain power flow, random variable, interval variable, surrogate model, sensitivity analysis
DOI:10.19595/j.cnki.1000-6753.tces.210171
中图分类号：TM744
国家自然科学基金资助项目（51977157）。
收稿日期 2021-02-01
改稿日期 2021-03-21
王晨旭 男，1996年生，博士研究生，研究方向为电力系统不确定性量化分析。E-mail：Chenxu_Wang2021@163.com
唐 飞 男，1982年生，副教授，博士生导师，研究方向为电力系统运行与控制。E-mail：tangfei@whu.edu.cn.com（通信作者）
（编辑 赫蕾）