（1）
摘要 电力牵引传动系统通常采用多模式调制策略。为了解决调制模式之间切换产生的电流和转矩冲击问题，该文对调制模式切换引起的定子磁链偏差进行研究，提出一种通用多模式调制切换策略。该策略通过分析改变开关时刻对两相静止坐标系下定子磁链的影响，计算出各相开关时刻的补偿幅度对定子磁链偏差进行补偿，从而实现多模式调制的平滑切换。该策略直接对定子磁链偏差进行补偿，不受具体调制方式和电机参数约束，可实现任意时刻无冲击切换。仿真和实验验证了定子磁链偏差补偿策略的通用性和有效性。
关键词：多模式调制 转矩冲击 切换方法 定子磁链偏差 开关时刻修正
电力牵引传动系统具有电压高、功率和电流大的特点，同时受到散热系统体积的限制，目前使用的牵引变流器的开关频率只有几百赫兹[1-5]。这对逆变器的脉冲宽度调制（Pulse Width Modulation, PWM）方法提出了更高的要求。具体表现为以下两点：①电力机车在运行过程中速度范围较宽，这将导致载波比大幅度变化，因此需要采用多种不同的调制方法以满足不同运行速度的要求；②需要实现不同的调制模式之间或者相同调制模式不同载波比之间的平滑切换，保证系统的平稳运行。
对于低载波比工况的调制模式，国内外学者已进行了大量的研究，提出了多种PWM理论及实现方法，并进行了优化，包括同步空间矢量PWM（Synchronized Space Vector PWM, SS-VPWM）、特定谐波消除PWM（Selected Harmonic Eliminated PWM, SHEPWM）和电流谐波最小PWM （Current Harmonic Minimum PWM, CHMPWM）等。实际应用中，根据各种调制方法的优缺点，采用多模式PWM方法。同时为确保系统的稳定运行，需要通过特定的切换策略保证系统在不同调制模式之间平滑过渡。
文献[6]提出一种SHEPWM的三相同步切换的策略，通过分析不同脉冲数的电流谐波特性，选择谐波冲击最小的点进行三相同步切换，但不同切换过程的电流谐波特性均不相同，分析相对复杂。文献[7-8]分别提出了基于电机定子磁链的SHEPWM和CHMPWM切换策略，通过图解法分析切换前后定子磁链轨迹，选择最接近两个磁链轨迹交点的位置进行切换，实现简单，但图解法只是从宏观上近似地判断最优切换点，并没有对具体的切换点性能进行分析。文献[9]提出一种通用的多模式调制策略切换方法，通过对比不同PWM策略的谐波磁链特性，选择定子磁链幅值和相位偏差最小点进行切换，该策略具备较好的通用性。上述文献均采用离线计算选择最优切换点的方法进行脉冲模式切换，在实际应用过程中存在以下局限性：①离线计算的固定切换点对应着固定的电压基波相位，若切换瞬间的电压指令不在最优切换点时刻，则需要等待最优切换点时刻才可进行切换；②即使是在最优切换点时刻定子磁链仍可能存在较小偏差，如果不进行合适的补偿，会使得模式切换后定子磁链轨迹在一定程度上偏离稳态优化磁链轨迹，产生转矩和电流冲击。
本文对调制模式切换引起定子磁链偏差的过程进行详细分析，提出一种通过改变开关时刻修正因调制模式切换引起的定子磁链偏差的多模式调制切换策略。该方法可以改善传统选择最优切换点方法的性能局限，实现调制模式在任意时刻无冲击的切换。该策略不依赖具体的调制方式和电机参数，具有较好的通用性。对本文所提出的切换策略进行了仿真和实验，结果验证了该方法的正确性和有效性。
多模式调制策略的切换需要保证切换前后不出现电流和转矩的冲击[10-15]。牵引电机控制系统中，更为重要的是对输出转矩的控制。由文献[9]可知，当切换前后电机转矩平稳输出时，电流不会出现冲击，因此调制模式之间平滑切换的目标是保证在调制模式切换前后电机转矩能够平稳输出。以异步电机为例，其转矩输出表达式为
（1）
式中，Te为电机的电磁转矩；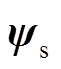
和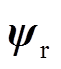
分别为定子和转子磁链矢量；Lm、Ls和Lr分别为电机互感、定子电感和转子电感；np为极对数；s为漏磁系数；g为定子磁链和转子磁链之间的夹角。
若不考虑参数变化，电机的输出转矩特性主要由转子磁链、定子磁链及定转子磁链夹角g三个因素决定。由于转子时间常数较大，电机转子磁链可以认为是一个理想的圆形，而定子磁链则包含不同次数的谐波，谐波将导致定子磁链偏离理想磁链圆。定转子磁链轨迹如图1所示。图1中，异步电机从静止加速至方波工况的过程中，转子磁链基本保持理想的圆形，而定子磁链则出现不同程度的畸变。因此在不考虑参数变化时，电机输出转矩脉动主要取决于定子磁链的幅值和相位变化。
图1 定转子磁链轨迹
Fig.1 Stator and rotor flux linkage trajectory
同步调制在稳态运行工况下存在与开关时刻表格相对应的稳态优化定子磁链，电机稳态运行时电机定子磁链一直沿稳态优化磁链轨迹运动，若电机定子磁链偏离稳态优化磁链轨迹，电机转矩将会出现振荡[14]。在调制模式发生切换过程中，切换时刻更换开关序列P(m,N)将导致定子磁链出现动态偏差，使得定子磁链在切换后无法在稳态优化磁链轨迹运行，转矩出现冲击，其中m为调制度，N为对应脉冲数。假设t=t1为初始时刻，此时调用的开关序列为P(1)(m,N1)，上标(1)表示调制模式切换前物理量。电机定子磁链沿P(1)(m, N1)对应的稳态优化磁链轨迹y(1) ss(t)运行，下标ss代表稳态值，表达式为
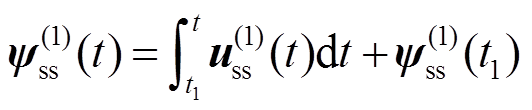（2）
式中，u(1)ss为P(1)对应的稳态定子电压；y(1) ss(t1)为定子磁链初值。
若在t=t2时刻发生调制模式切换，要求调用的开关序列变为P(2)(m, N2)，上标(2)表示调制模式切换后物理量。调制模式变化后定子磁链表达式为
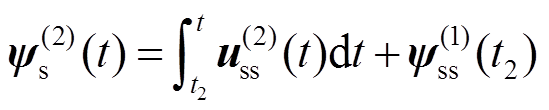（3）
式中，u(2)ss为P(2)(m,N2)对应的稳态定子电压；y(1) ss(t2)为y(1) ss(t)在t=t2的定子磁链，是计算y(2) s(t)的初值。对于开关序列P(2)(m,N2)，同样具备稳态优化磁链轨迹y(2) ss(t)，其表达式为
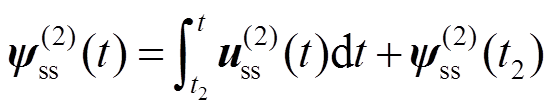（4）
式中，y(2)ss(t2)为稳态优化磁链轨迹y(2) ss(t)在t=t2的定子磁链。由于P(1)(m,N1)和P(2)(m,N1)所对应的稳态优化定子磁链不相同，即y(1) ss(t2)≠y(2) ss(t2)。因此在t＞t2时，实际定子磁链y(2) s(t2)将偏离切换后稳态优化轨迹y(2) ss(t)，产生式（5）所示的动态定子磁链偏差Dy(t)。
（5）
以三脉冲SHEPWM切换至五脉冲SHEPWM的过程为例进行分析，定子磁链动态示意图如图2所示。图2a中虚线为五脉冲SHEPWM稳态优化定子磁链轨迹，实线为三脉冲SHEPWM稳态优化定子磁链轨迹。
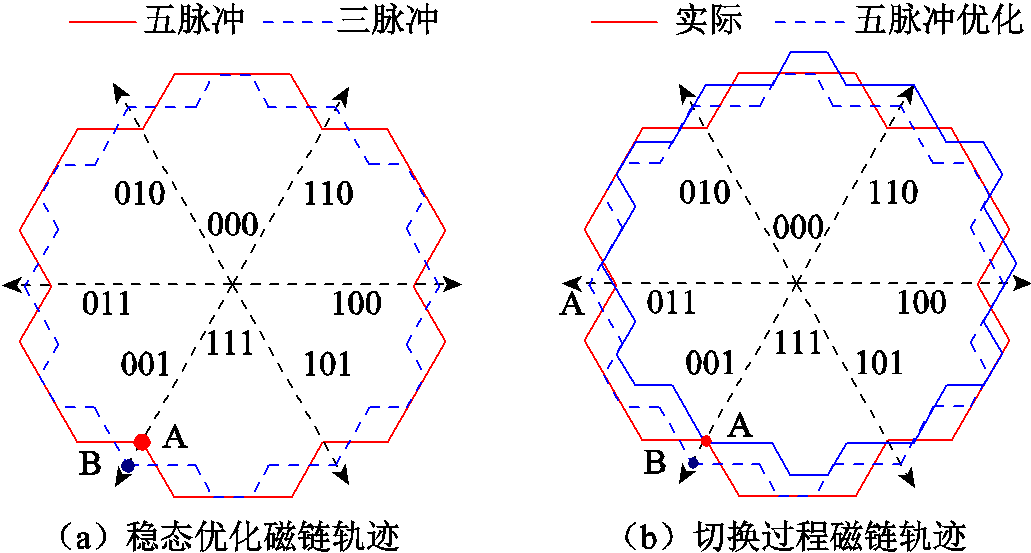
图2 定子磁链动态示意图
Fig.2 Dynamic diagram of stator flux linkage
如果三脉冲SHEPWM在图2a中A点处切换至五脉冲SHEPWM，切换过程电机定子磁链的运行轨迹将如图2b所示，图中实线为电机实际运行磁链轨迹，虚线为五脉冲SHEPWM对应的稳态优化定子磁链轨迹。切换后定子磁链的起点为三脉冲SHEPWM在切换瞬间的定子磁链A点，B点为五脉冲SHEPWM稳态优化磁链轨迹上与A点基波相位相同的定子磁链，AB两点之间存在定子磁链偏差。调制模式切换后，电机实际定子磁链将偏离五脉冲SHEPWM的稳态优化磁链轨迹，从而造成转矩和电流冲击。因此需要对定子磁链偏差进行补偿，保证切换前后的系统在两种稳态优化磁链轨迹之间平滑过渡。
对于电机控制系统，每一个采样控制周期都会输出一个参考电压指令，参考电压指令对应的开关序列P(m, N)会在下一个采样周期在逆变器产生作用。当忽略定子压降时，定子电压的积分等于定子磁链，而定子电压由施加在三相逆变器上的PWM脉冲决定。因此依据具体的定子磁链偏差，提前对开关时刻进行修正，可对调制模式切换产生的定子磁链偏差进行补偿，使得电机在切换前后两种稳态优化磁链轨迹之间平稳过渡，实现调制模式平滑切换的目的。图3为进行定子磁链偏差补偿的原理框图。
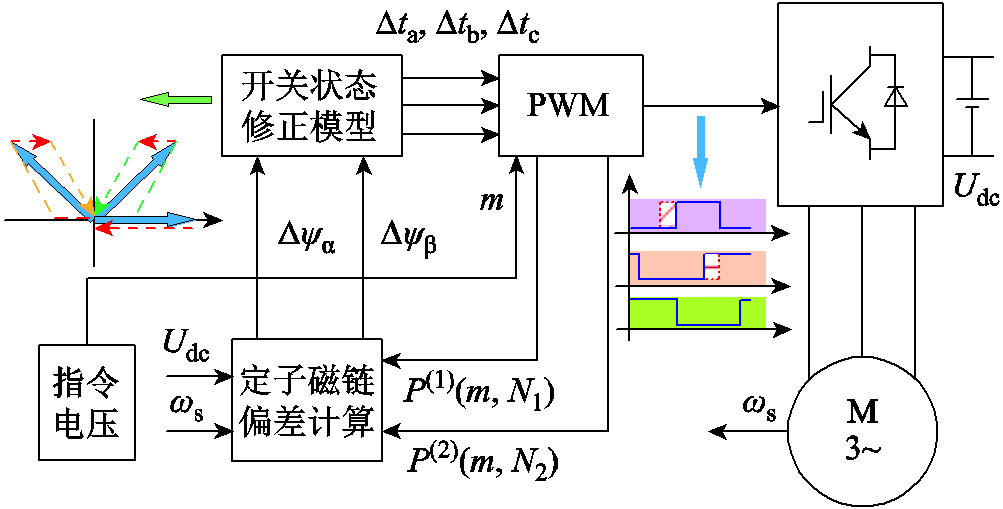
图3 定子磁链偏差补偿原理框图
Fig.3 Principle block diagram of stator flux deviation compensation
图3中定子磁链偏差计算模块的作用是计算调制模式切换瞬间的定子磁链偏差，其输入量P(1)(m,N1)为调制模式切换前对应的开关序列，P(2)(m,N2)为调制模式切换后对应的开关序列。由于P(1)(m,N1)和P(2)(m,N2)均为关于调制度m的函数，因此可通过切换瞬间的调制度m计算切换前后的开关序列，依据母线电压Udc及定子频率ws对切换瞬间的定子磁链进行离线重构及偏差计算。图3中开关修正模型的作用是计算与定子磁链偏差对应的开关时刻修正量，其输入量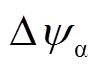
与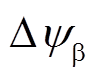
分别为a与b轴的定子磁链偏差分量，开关状态修正模型依据具体的磁链偏差，计算ABC三相开关时刻的修正大小Dta、Dtb、Dtc，通过修改PWM的开关时刻，即可达到补偿定子磁链偏差的目的，从而实现调制模式的平稳切换。
调制模式切换导致的定子磁链偏差的准确计算是实现定子磁链偏差的精确补偿的前提。根据约束目标不同，不同调制模式对应的开关序列不同，每个开关序列都存在特定的稳态优化磁链轨迹。在电机稳态运行时，电机定子磁链轨迹按各个开关序列对应的稳态优化磁链轨迹运行。从定子磁链的角度考虑，调制模式切换是两种稳态优化定子磁链轨迹之间的过渡过程，因此通过对比切换前后开关序列P(1)(m,N1)和P(2)(m,N2)对应的稳态优化磁链轨迹在不同基波相位的大小，即可得到定子磁链偏差。
首先，依据电机定子磁链与定子电压之间的关系，稳态优化定子磁链可通过对稳态定子电压uss进行积分得到，其表达式为
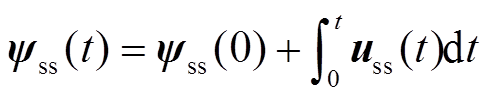（6）
式中，yss(0)为磁链初值。根据定子角频率和角度的关系，式（6）可被改写为
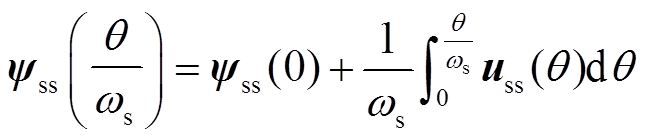（7）
式中，ws为定子角频率；q为基波相位。在忽略母线电压波动时，进一步简化式（7）可得
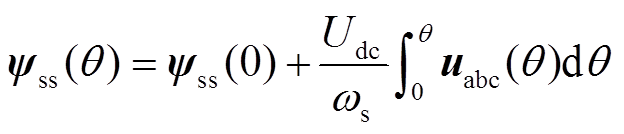（8）
式中，Udc为母线电压；uabc为三相开关波形，uabc可依据开关序列P(m,N)进行PWM脉冲重构得到。由于式（8）所计算的稳态优化定子磁链起点为零点，计算结果存在一个直流偏置，需要减去这个偏置才能得到准确的稳态优化磁链轨迹。偏置的大小为磁链在一个基波周期内的均值，其表达式为
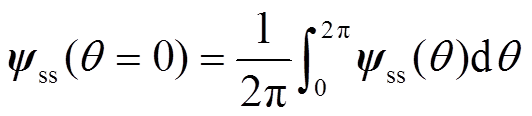（9）
最终可得到稳态优化磁链轨迹的计算公式为
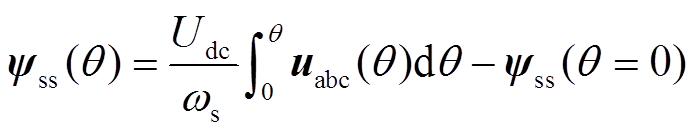（10）
图4为调制度为0.987时，五脉冲SHEPWM与三脉冲SHEPWM稳态优化磁链轨迹之间的定子磁链偏差。从图4中可知，不同相位处的定子磁链偏差大小均不相同，因此还需要特定的补偿策略对定子磁链偏差进行补偿。
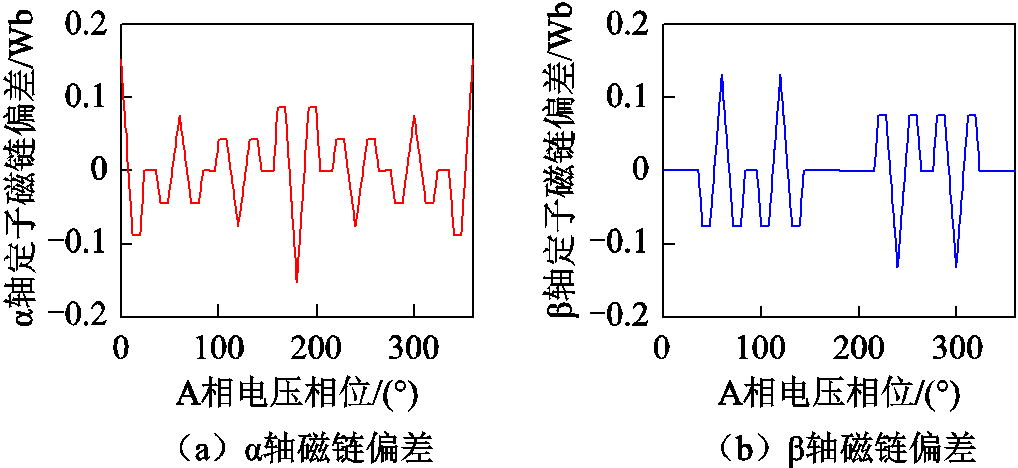
图4 五脉冲SHEPWM与三脉冲SHEPWM定子磁链偏差
Fig.4 Stator flux deviation between 5-pulse SHEPWM and 3-pulse SHEPWM
为了详细阐述定子磁链偏差补偿的原理和方法，将两电平逆变器的相关变量和物理过程进行如下定义。
（1）逆变器三相输出电压电平变化用变量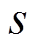
表示。sa、sb、sc分别对应A、B、C三相的电平变化。若输出电平从低电平跳变到高电平，则s=1；若输出电平从高电平跳变到低电平，则s=-1；一个采样周期内如果没有电平变化，则s=0；若一个采样周期内有多个电平变化则用下角标i作为区分不同时刻的电平变化，用si表示。
（2）将一个开关时刻时间调节量定义为Dt。若要提前开关时刻，即期望电平跳变时刻早于实际电平跳变时刻，则Dt＞0。同理，若开关时刻延迟，期望电平跳变时刻迟于实际电平跳变时刻，则Dt＜0。
图5给出了开关时刻修正示意图，根据电压积分方程可知，延长高电平持续时间可增大定子磁链，减小高电平持续时间，减小定子磁链[14]。图中Ⅰ区域与Ⅳ区域所示开关跳变相对于原始PWM波形延长了高电平持续时间，能够增大定子磁链；Ⅱ区域与Ⅲ区域所示开关跳变相对于原始PWM减小了高电平持续时间，能够减小定子磁链。通过控制开关时刻的修正大小，改变电压伏秒积，可补偿调制模式切换导致的定子磁链偏差。图5中Ts表示一个采样周期持续时间，采样周期时间大小为可修正开关时刻的范围，图中加减号对应表示磁链增加与减小。
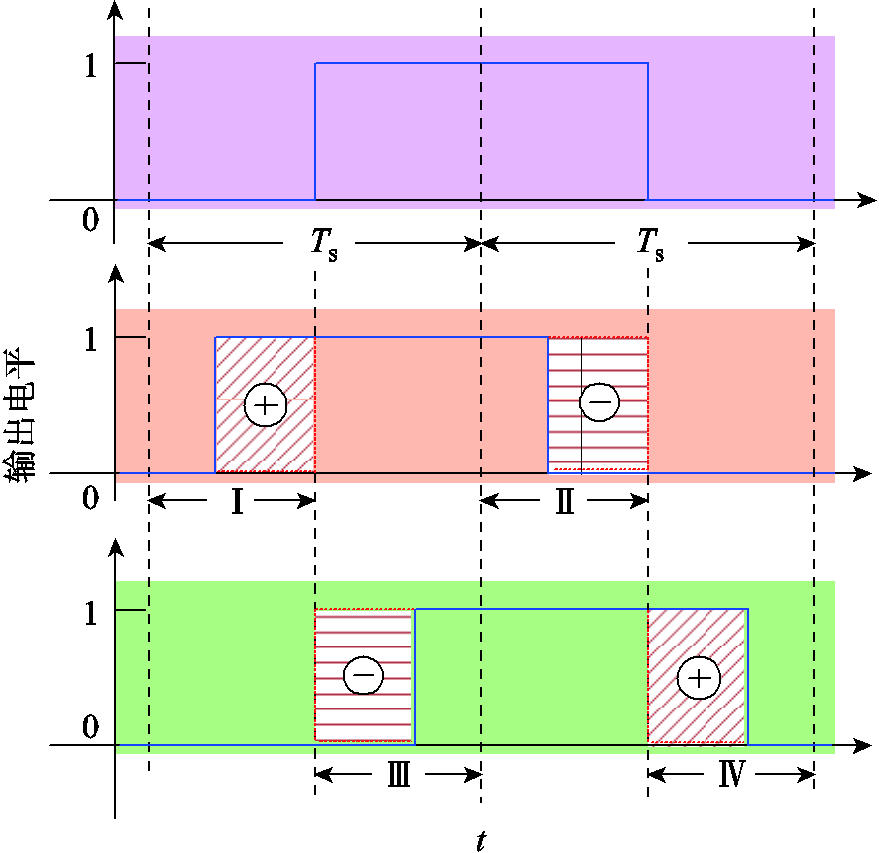
图5 开关时刻修正示意图
Fig.5 Schematic diagram of switch sequence correction
在需要增大定子磁链时，若该采样周期电平由低变高s=1（如图5中Ⅰ区域所示），则应提前电平跳变，即Dt＞0，延长高电平持续时间，图5中加号表示磁链增大；若电平由高变低s=-1（如图5中Ⅳ区域所示），则应延迟电平跳变，即Dt＜0。在需要减小定子磁链时，若该采样周期电平由高变低s=-1（如图5中Ⅱ区域所示），则应提前电平跳变时刻，即Dt＞0，缩短高电平持续时间，图中减号表示磁链减小；若电平由低变高s=1（如图5中Ⅲ区域所示），则应延迟电平跳变时刻，即Dt＜0。总结可得不同情况开关时刻修正策略为
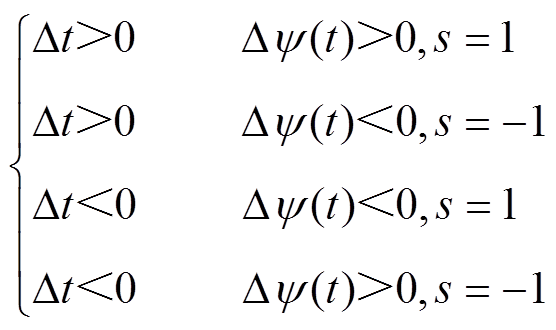（11）
根据两电平逆变器的规律，S表示逆变器三相桥臂开关状态，SA、SB、SC分别对应A、B、C三相。若上桥臂导通，则S=1，若下桥臂导通，则S=0。逆变器在两相静止ab坐标系下电压与桥臂开关状态的关系为
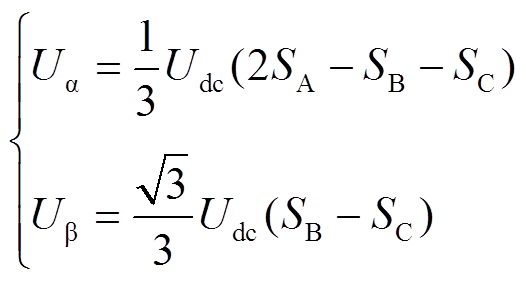（12）
式中，Ua、Ub分别为a、b轴电压。
ab两相静止坐标系下定子磁链ys表达式为
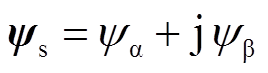（13）
式中，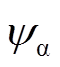
、
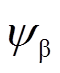分别为a、b轴定子磁链分量。依据式（12）与式（13），在一个采样周期内，第i个开关时刻的ABC各相开关时刻调整量Dtai、Dtbi、Dtci对动态磁链偏差Dy(t)的改变量为
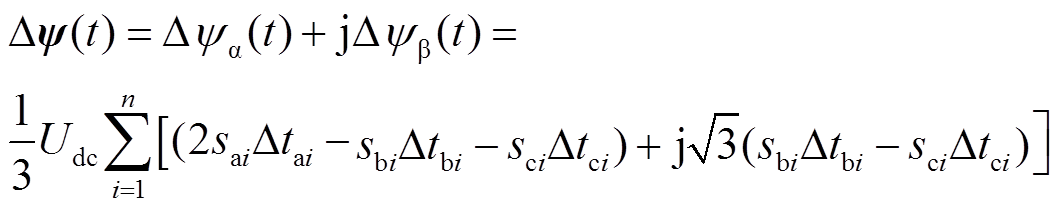（14）
对式（14）进行分析可知，A相调整量Dta只影响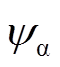的大小，B相调整量Dtb对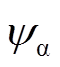和
产生的改变量正、负相异，C相调整量Dtc对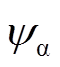和产生的改变量正、负相同。因此在定子磁链偏差补偿过程中，可先进行B相或C相的开关时刻修正计算，完全补偿b轴定子磁链偏差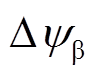
后，再进行A相开关时刻修正计算，补偿余下的a轴定子磁链偏差
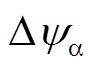，从而实现定子磁链偏差完全消除。
根据上述定子磁链偏差补偿步骤建立以下三种磁链偏差补偿原则，对具体开关时刻修正幅度进行详细计算，不同情况的磁链偏差补偿过程如图6所示，Dy(t)的下标用来区分不同情况的磁链偏差。
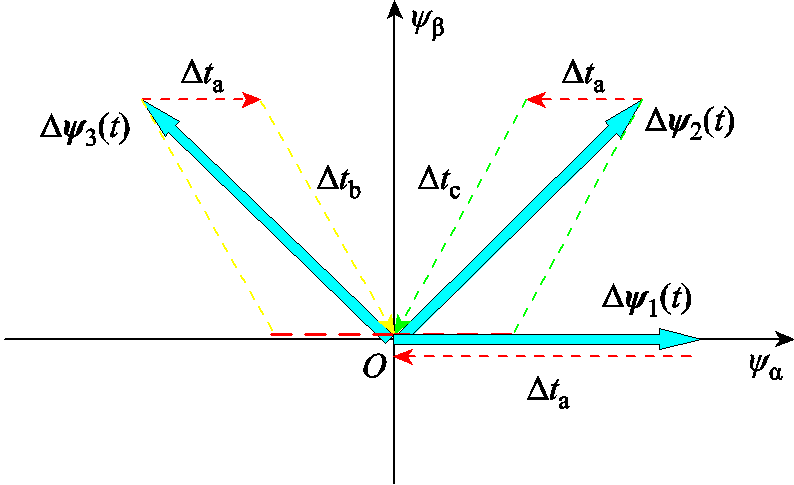
图6 误差修正原则示意图
Fig.6 Schematic diagram of error correction principle
（1）当定子磁链偏差只存在a轴磁链偏差分量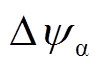
时，如图6中
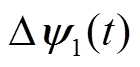所示，则可通过只修正A相开关时刻对其进行补偿。此时三相开关时刻修正幅度的计算方程为
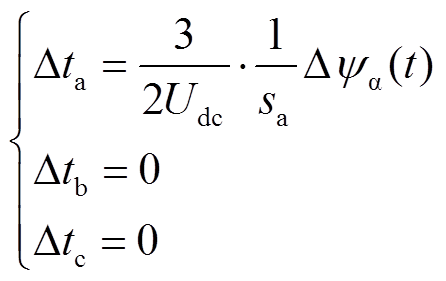（15）
（2）当a轴磁链偏差分量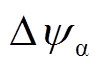(t)与b轴磁链偏差分量
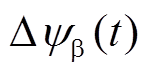符号相同时，如图6中
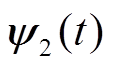所示，则通过修正A相与C相开关时刻对定子磁链偏差进行补偿。此时三相开关时刻修正幅度计算方程为
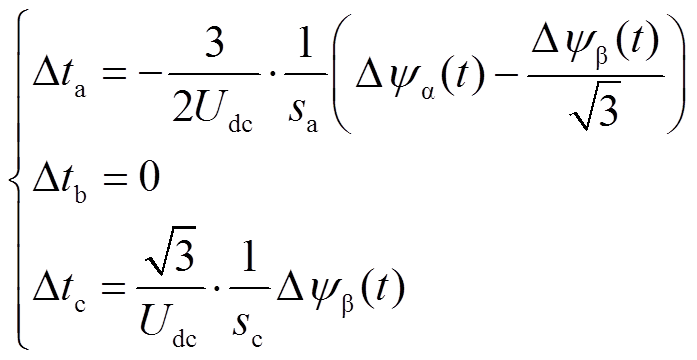（16）
（3）当a轴磁链偏差分量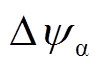(t)与b轴磁链偏差分量
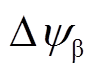(t)符号相异时，如图6中
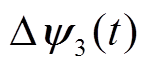所示，则通过修正A相与B相开关时刻对定子磁链偏差进行补偿。此时三相开关时刻修正幅度计算方程为
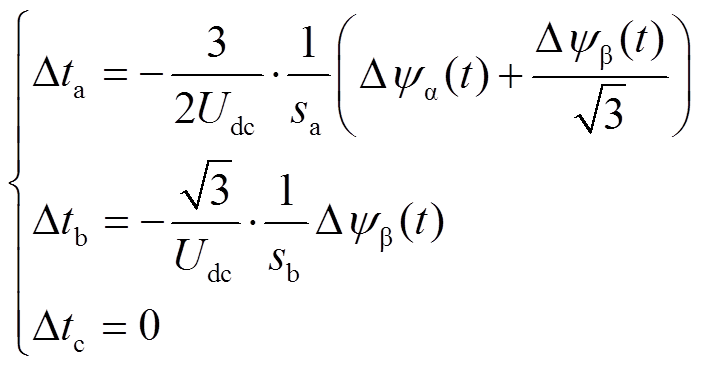（17）
上述公式计算的开关时刻修正幅度均满足不引入新的磁链偏差原则，并且此方法只用对两相开关时刻进行修正，简化了定子磁链偏差补偿的过程。
为了验证定子磁链偏差补偿方法的正确性和合理性，本文通过Matlab/Simulink对该切换策略进行仿真，并通过实验进行验证。仿真和实验的电机参数见表1。
表1 电机参数
Tab.1 Motor parameter
参数数值 额定电压/V380 额定电流/A23.2 额定功率/kW11 额定转速/(r/min)1 440 定子电阻/Ω0.279 5 转子电阻/Ω0.213 4 漏感/H0.002 6 互感/H0.064 7
以五脉冲SHEPWM切换至三脉冲SHEPWM的切换过程为例进行仿真分析。图7a为未进行开关时刻修正时，五脉冲SHEPWM切换至三脉冲SHEPWM磁链轨迹动态过程图。
传统方法选择磁链偏差最小的优化切换点，如在图7a中的A点进行切换。若在任意点实现切换，例如图7a中A点进行切换，A点位于五脉冲SHEPWM稳态优化磁链轨迹上，B点为三脉冲SHEPWM稳态优化磁链轨迹上与A点基波相位相同的定子磁链，AB两点之间存在明显的磁链偏差。从图7a中可以看出，切换后电机实际定子磁链轨迹偏离了三脉冲SHEPWM稳态优化磁链轨迹，将造成转矩和电流冲击。在A点切换电机转矩和电流波形如图7b所示，切换过程出现了9.8A的电流冲击和28N·m转矩冲击；调制模式在19.93s进行切换，约两个基波周期后在19.97s电机恢复稳态，时间较长。
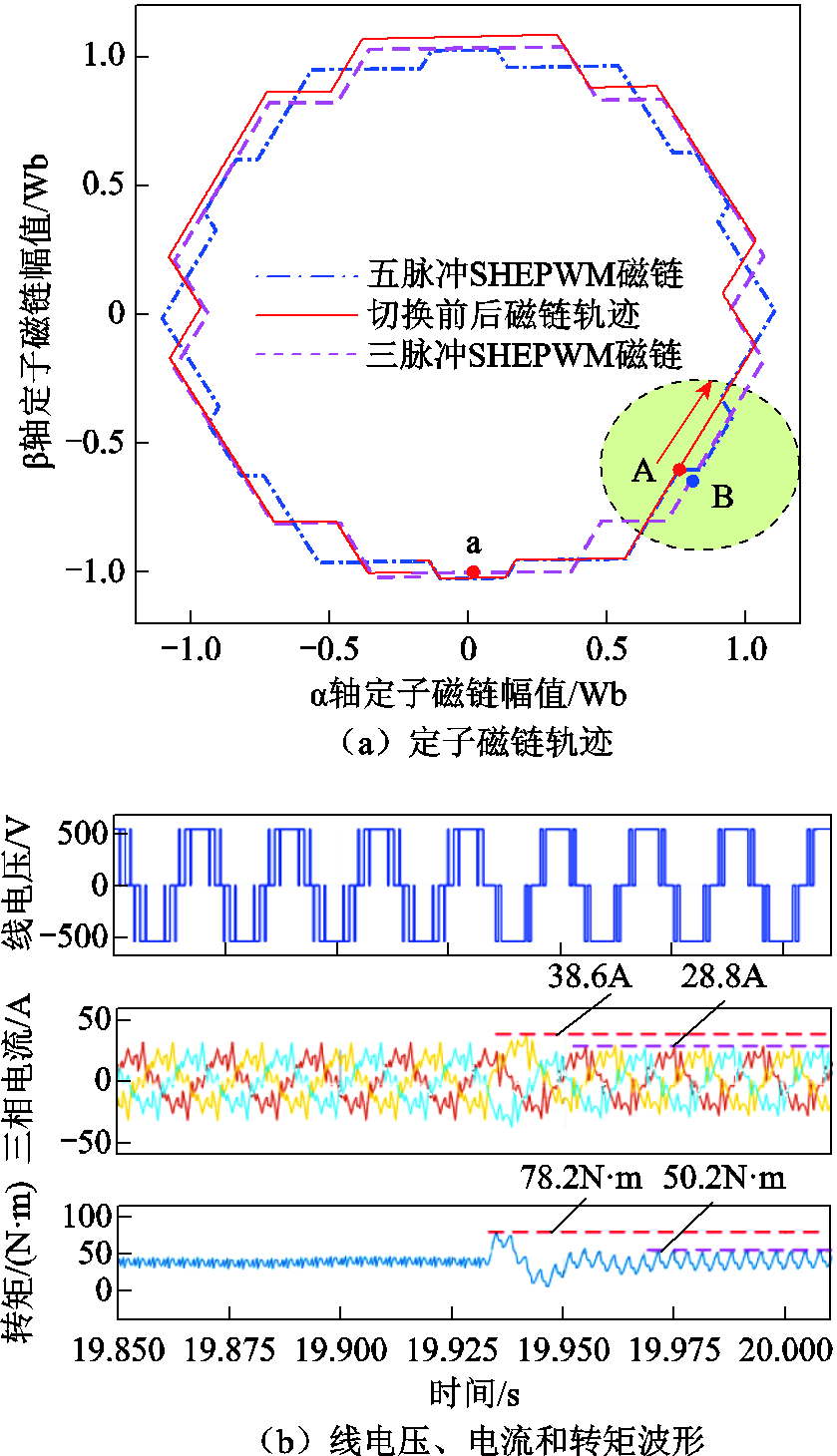
图7 未补偿切换输出特性
Fig.7 Uncompensated switching output characteristics
依据第2节中所述开关时刻修正策略对AB两点之间的定子磁链偏差进行补偿，其补偿示意图如图8所示，图8中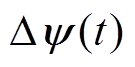
为AB两点间的定子磁链偏差，a轴磁链偏差分量
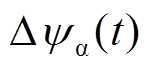与b轴磁链偏差分量
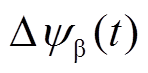符号相异，需要减小a轴磁链分量，增大b轴磁链分量。依据式（17）所示补偿原则，由于此时
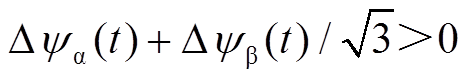，因此应缩短A相作用时间，延长B相的作用时间。
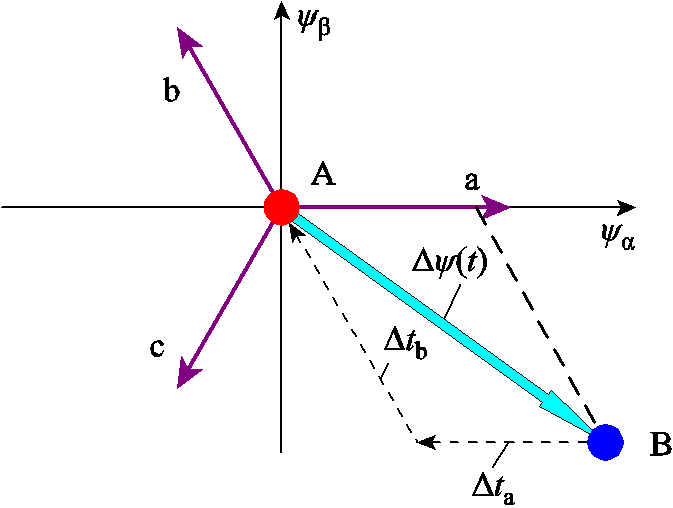
图8 定子磁链偏差补偿示意图
Fig.8 Schematic diagram of stator flux deviation compensation
依据计算所得的Dta和Dtb，提前更改PWM模块的输出脉冲，对定子磁链偏差进行补偿。施加补偿后磁链轨迹如图9a所示，切换后电机定子磁链轨迹快速恢复三脉冲SHEPWM稳态优化磁链轨迹运行，定子磁链在两种稳态优化磁链轨迹间平滑过渡。施加补偿的转矩和电流波形如图9b所示，调制模式切换过程未产生明显电流冲击和转矩冲击，系统在切换后一个采样周期即恢复稳定运行状态。
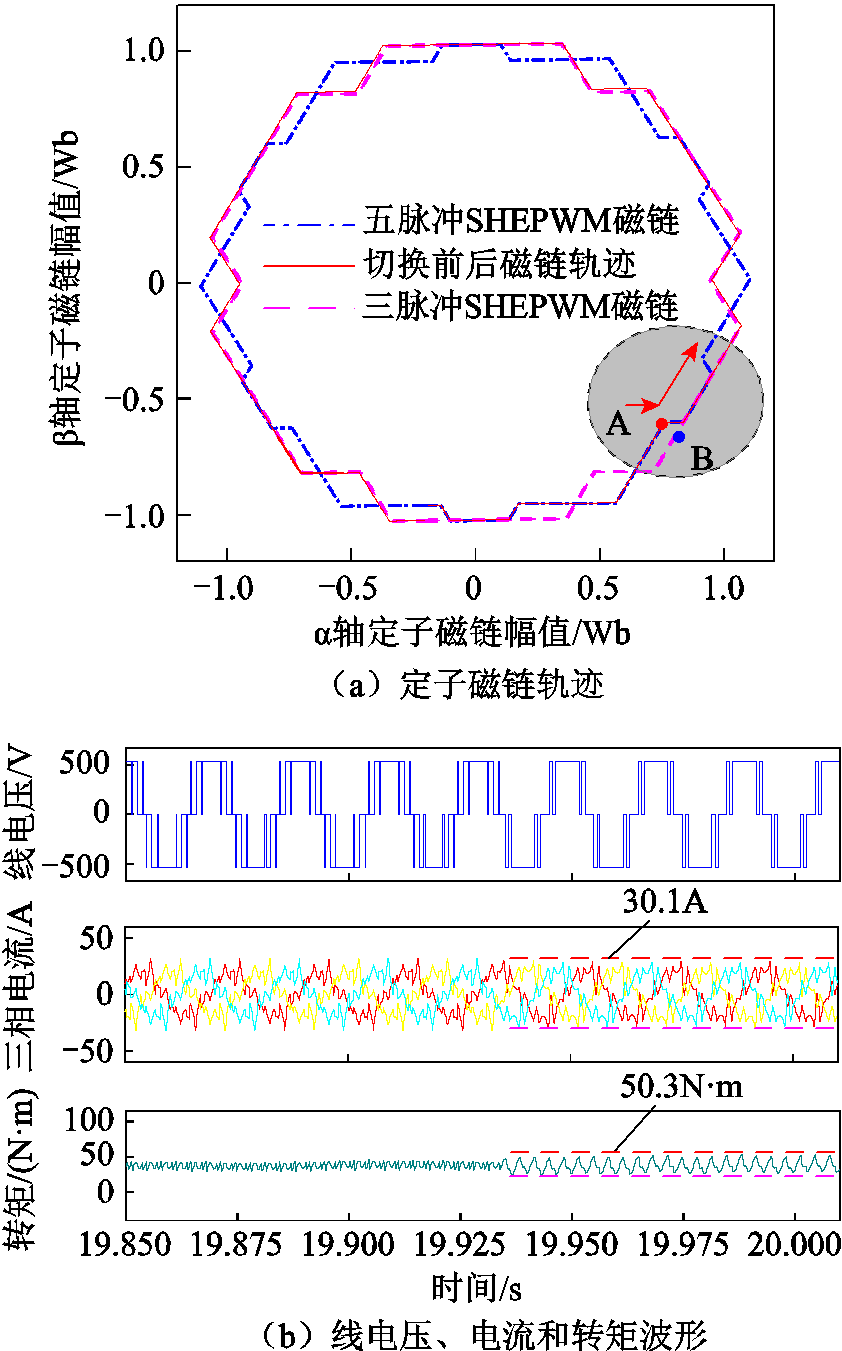
图9 补偿后切换输出特性
Fig.9 Switching output characteristics after compensation
切换前后两种调制模式不同时，由于两种调制模式的优化目标不同，电流谐波含量区别较大，产生的转矩冲击和电流冲击将更明显。以CHMPWM与SHEPWM之间的切换为例进行分析。
图10为七脉冲CHMPWM切换至五脉冲SHEPWM的动态磁链过程图，切换点A位于七脉冲CHMPWM稳态优化磁链轨迹上，B点为五脉冲SHEPWM稳态优化磁链轨迹上与A点基波相位相同的点，AB两点之间存在明显磁链偏差。
依据定子磁链偏差补偿策略对其进行补偿，图11为七脉冲CHMPWM切换至五脉冲SHEPWM的定子磁链偏差补偿示意图。图11中Dy(t)为切换点处定子磁链偏差，a轴磁链偏差分量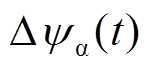与b轴磁链偏差分量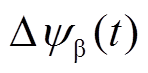符号相异，需要减小a轴磁链分量，增大b轴磁链分量。依据式（17）所示补偿原则，由于此时
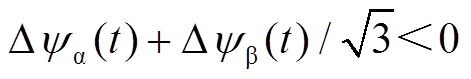，因此应延长A相和B相作用时间。
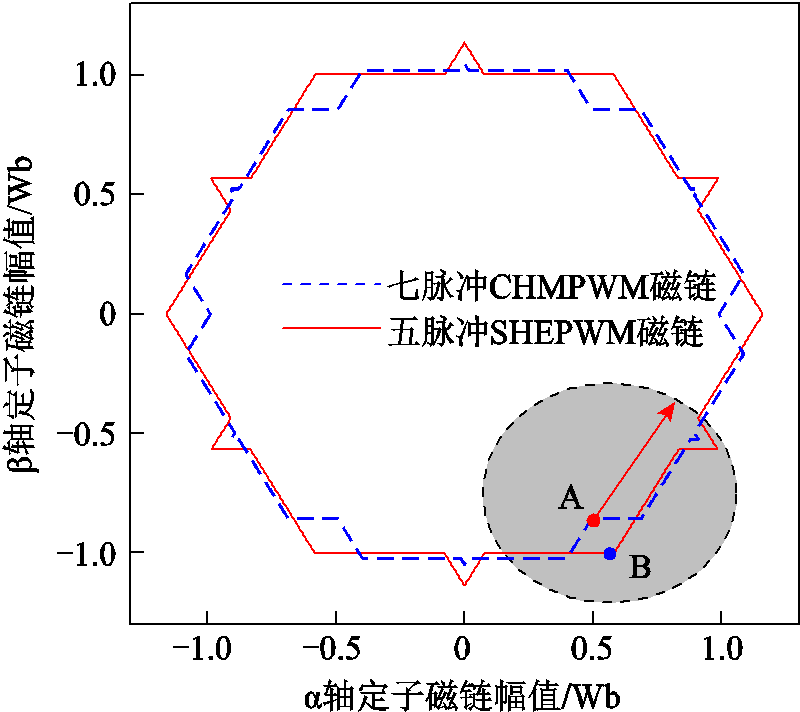
图10 切换过程定子磁链动态示意图
Fig.10 Dynamic diagram of stator flux linkage in switching process
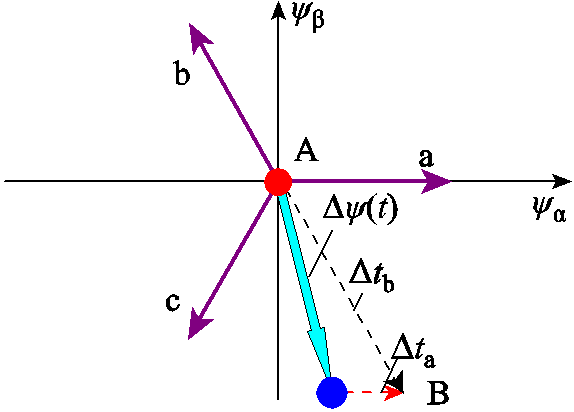
图11 定子磁链偏差补偿示意图
Fig.11 Schematic diagram of stator flux deviation compensation
图12a为未施加补偿时七脉冲CHMPWM在A点切换至五脉冲SHEPWM的转矩和电流波形，调制模式切换过程相电流冲击为13.4A，转矩冲击为54.6N·m，电流和转矩冲击均较大。依据计算所得Dta和Dtb，对定子磁链偏差进行补偿。施加补偿后转矩电流波形如图12b所示，切换过程转矩和电流未产生任何冲击，系统在切换后一个采样周期即恢复稳定运行状态。
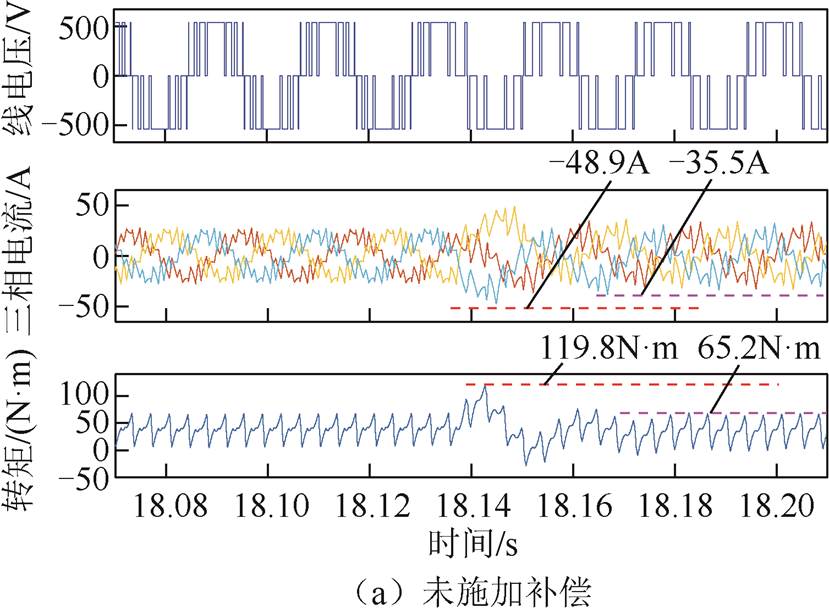
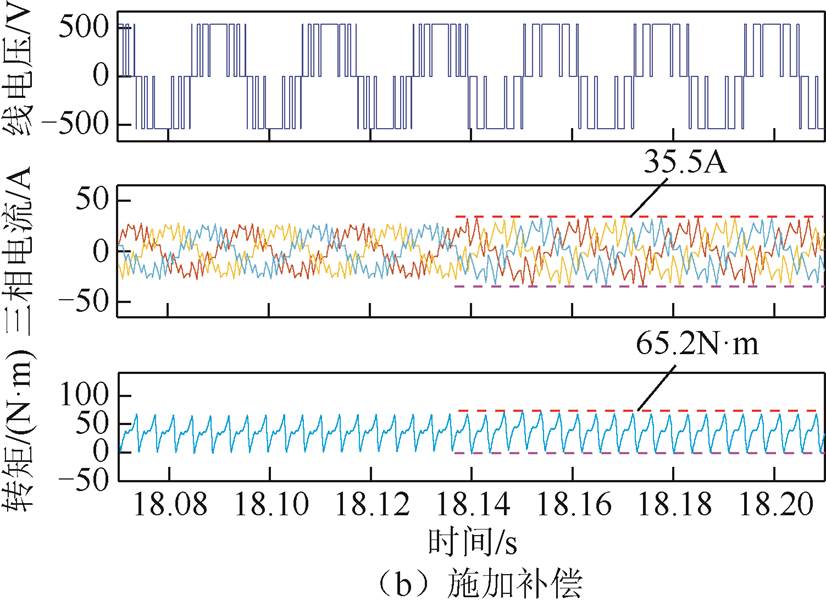
图12 七脉冲CHMPWM切换至五脉冲SHEPWM
Fig.12 Simulation result of switching 7-pulse CHMPWM to 5-pulse SHEPWM
本文实验所用平台通过电机与飞轮相连模拟机车牵引大惯量负载工况，实验平台如图13所示，实验电机所用电机参数见表1。
图13 牵引实验平台
Fig.13 Traction experiment platform
牵引电机采用转速控制模式，给定转子磁链的幅值为0.987 6Wb，转速指令通过斜坡给定，转速斜坡每秒升速为75.65r/min，实际对应的转矩大小为38.5N·m，电机从静止开始加速，在全速度范围调制策略如图14所示，当电机输出的频率低于20Hz 时采用异步SVPWM调制策略；在20Hz和30Hz之间采用15脉冲同步SVPWM调制策略；在大于30Hz时采用SHEPWM调制策略，由11脉冲SHEPWM逐渐减小脉冲数量，直至过渡方波。
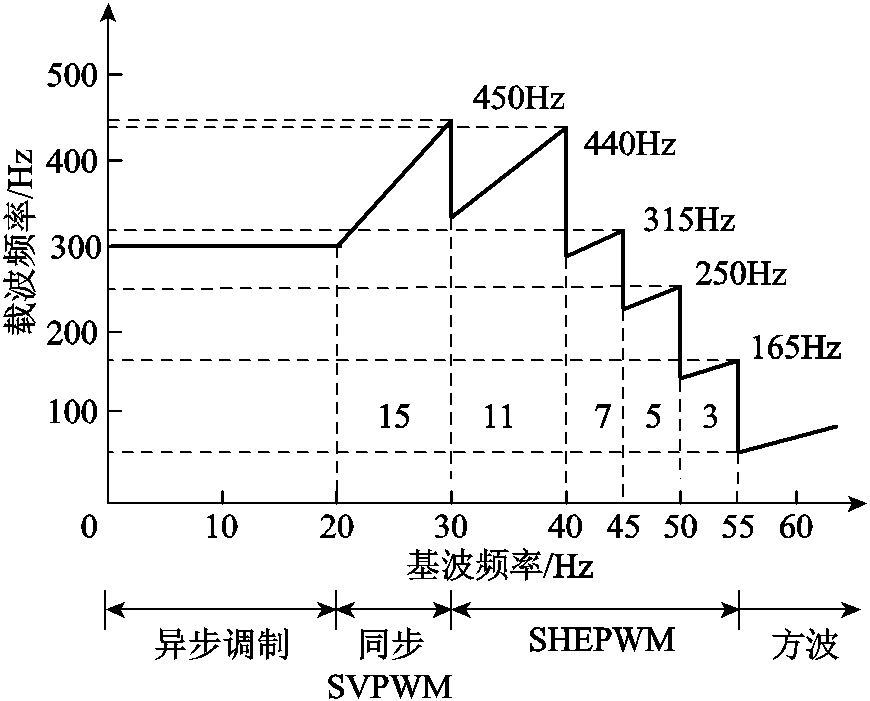
图14 全速度范围调制策略
Fig.14 Full speed range modulation strategy
未施加补偿时，五脉冲SHEPWM切换至三脉冲SHEPWM的实验波形如图15a所示，切换过程的峰值电流为55.1A，切换过程产生了12.8A的电流冲击；施加补偿后，五脉冲SHEPWM切换至三脉冲SHEPWM的实验波形如图15b所示，峰值电流为44.3A，切换过程产生的电流冲击为2.6A。相对于未加补偿的电流特性，电流冲击缩小了5倍，定子磁链偏差补偿策略的效果较为明显。
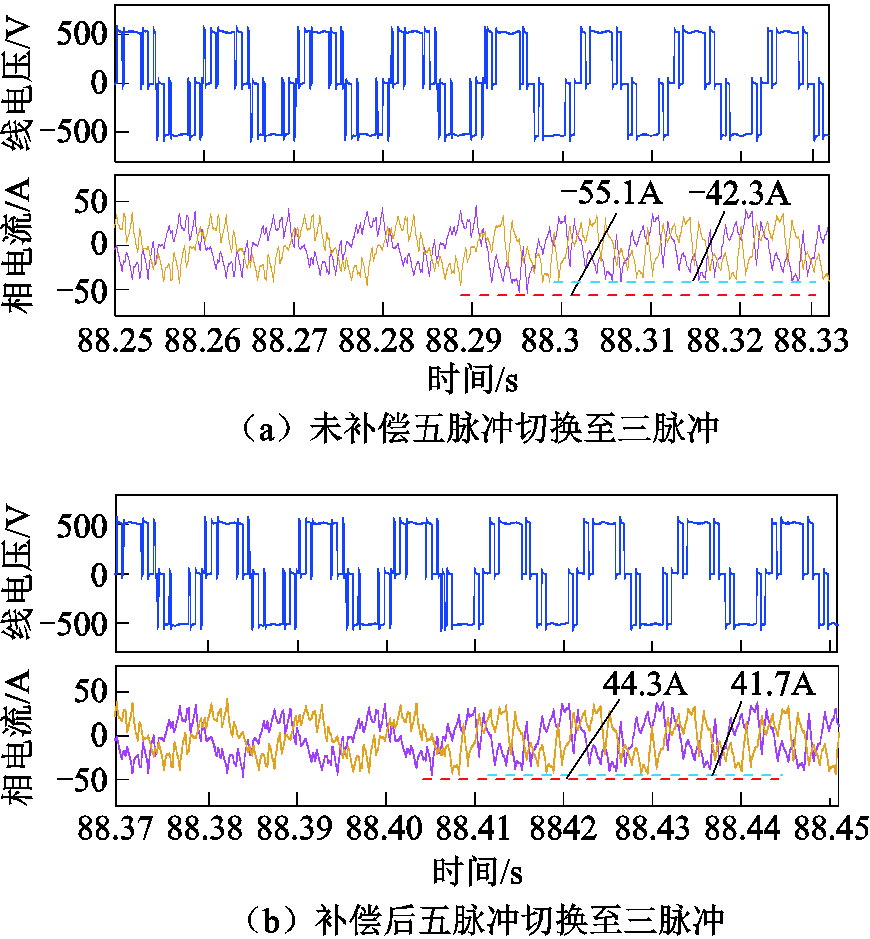
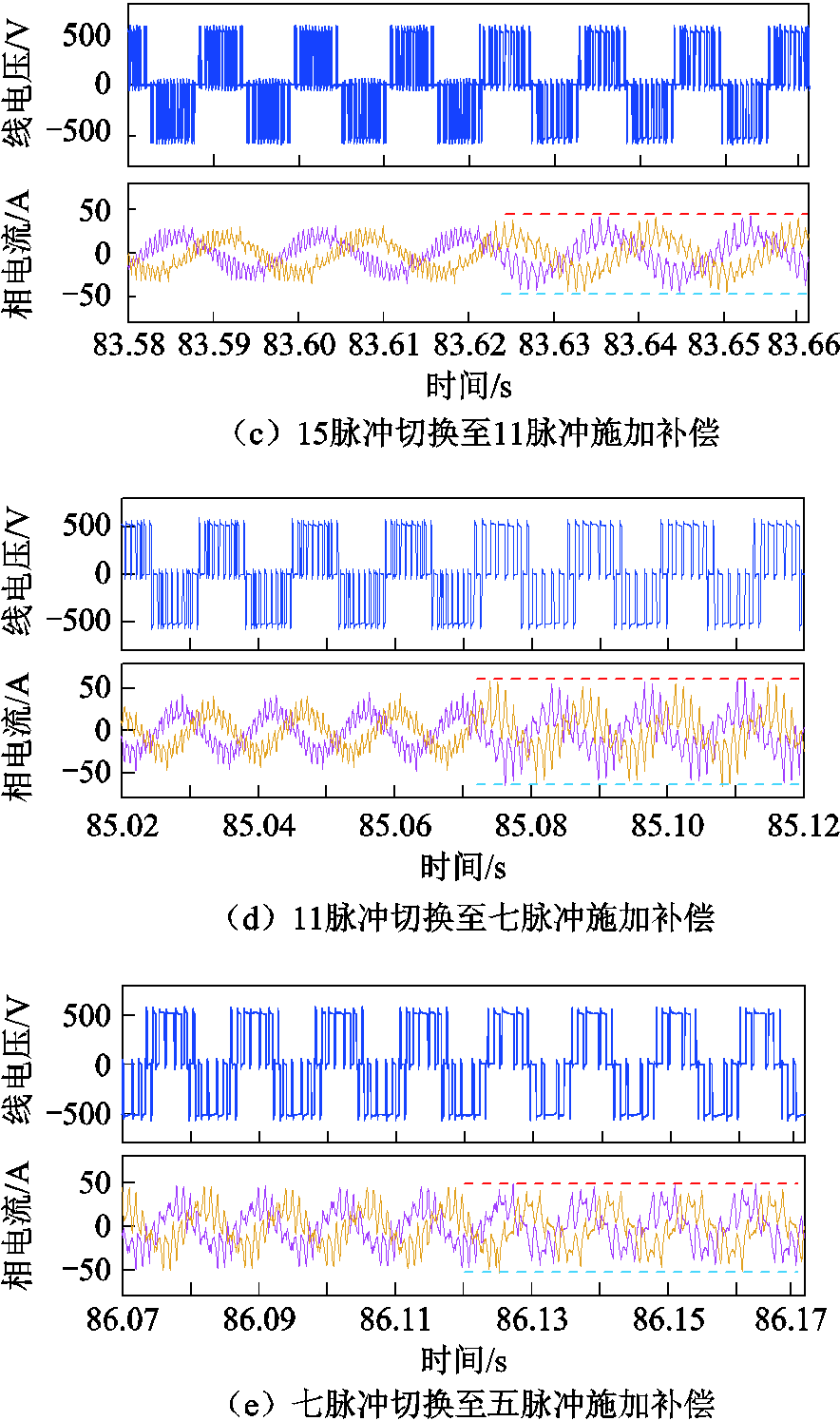
图15 切换实验结果
Fig.15 Experiment results of switching
为了验证基于开关时刻修正的多模式调制切换策略的通用性，对不同调制模式之间的切换过程进行实验验证。全速度范围其他不同切换过程实验结果如图15所示，图15c为15脉冲同步SVPWM切换至11脉冲SHEPWM的电压电流波形，图15d为11脉冲SHEPWM切换至七脉冲SHEPWM的电压电流波形，图15e为七脉冲SHEPWM切换至五脉冲SHEPWM的电压电流波形。
从以上实验结果可知，不同调制模式、相同调制模式不同脉冲数之间切换均不会产生电流冲击，在进行开关时刻修正后进行切换，不同调制模式之间均能实现平滑过渡。实验结果验证了开关时刻修正策略的通用性和有效性。
牵引传动系统在全速度范围内运行时通常采用多种调制模式混合的方式，调制模式切换会产生电流和转矩冲击问题。本文对调制模式切换引起定子磁链偏差的过程进行详细分析，提出了一种通过改变开关时刻修正因调制模式切换引起的定子磁链偏差的多模式调制切换策略。该策略在两相静止坐标系中对定子磁链偏差补偿，依据具体定子磁链偏差特性，计算出各相开关时刻修正大小，仅需对两相开关时刻进行修正即可实现对定子磁链偏差的完全补偿。该策略可以改善传统选择最优切换点方法的局限性，实现调制模式在任意时刻无冲击切换。该策略不受具体调制模式和电机参数约束，具备较好通用性。仿真和实验验证了切换策略的有效性和通用性。
参考文献
[1] 张国政, 陈炜, 谷鑫, 等. 三电平牵引变流器改进同步空间矢量调制策略[J]. 电工技术学报, 2020, 35(18): 3908-3916.
Zhang Guozheng, Chen Wei, Gu Xin, et al. An improve synchronized space vector modulation strategy for three-level inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3908-3916.
[2] 高瞻, 李耀华, 葛琼璇, 等. 低载波比下三电平中点钳位变流器改进型同步载波脉宽调制策略研究[J]. 电工技术学报, 2020, 35(18): 3894-3907.
Gao Zhan, Li Yaohua, Ge Qiongxuan, et al. Research on improved synchronized carrier based PWM for three-level neutral point clamped converter under low carrier ratio[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3894-3907.
[3] 崔恒斌, 冯晓云, 张杰, 等. 基于载波脉宽调制技术的牵引整流器谐波特性分析方法[J]. 电工技术学报, 2013, 28(9): 21-31.
Cui Hengbin, Feng Xiaoyun, Zhang Jie, et al. Harmonic characteristic analysis of carrier based pules-width modulation traction rectifier[J]. Transa-ctions of China Electrotechnical Society, 2013, 28(9): 21-31.
[4] 赵雷廷, 刁利军, 董侃, 等. 地铁牵引变流器-电机系统稳定性控制[J]. 电工技术学报, 2013, 28(6): 101-107.
Zhao Leiting, Diao Lijun, Dong Kan, et al. Stabilization control for metro traction converter-motor system[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 101-107.
[5] 刁利军, 董侃, 赵雷廷, 等. 基于双DSP-FPGA架构的城轨列车电力牵引控制系统[J]. 电工技术学报, 2014, 29(1): 174-180.
Diao Lijun, Dong Kan, Zhao Leiting, et al. Dual DSPs-FPGA structured traction control system for urban rail transit vehicle[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 174-180.
[6] 周明磊, 李强, 游小杰, 等. 基于SHEPWM的多模式调制切换策略研究[J]. 铁道学报, 2014, 36(1): 34-39.
Zhou Minglei, Li Qiang, You Xiaojie, et al. Research on SHEPWM-based switching strategy of multi-mode modulation[J]. Journal of the China Railway Society, 2014, 36(1): 34-39.
[7] 苑国锋, 陈栋, 郑春雨. 电力机车牵引传动系统的多模式调制策略及切换方法研究[J]. 电机与控制学报, 2021, 25(1): 126-135.
Yuan Guofeng, Chen Dong, Zheng Chunyu. Research on multi-mode modulation strategy and switching method of electric locomotive traction drive system[J]. Electric Machine and Control, 2021, 25(1): 126-135.
[8] 周明磊, 王琛琛, 游小杰. 基于交流电机定子磁链的CHMPWM切换策略[J]. 中国电机工程学报, 2016, 36(14): 3955-3964.
Zhou Minglei, Wang Chenchen, You Xiaojie. A switching strategy of current harmonic minimum PWM based on thestator flux trajectory of AC traction motors[J]. Proceedings of the CSEE, 2016, 36(14): 3955-3964.
[9] 周明磊, 刘伟志, 邱腾飞, 等. 适用于多模式脉宽调制的通用切换策略研究[J]. 中国电机工程学报, 2019, 39(7): 2125-2133.
Zhou Minglei, Liu Weizhi, Qiu Tengfei, et al. A genaral switching strategy for multi-mode pulse width modulation[J]. Proceedings of the CSEE, 2019, 39(7): 2125-2133.
[10] Oikonomou N, Holtz J. Closed-loop control of medium-voltage drives operated with synchronous optimal pulsewidth modulation[J]. IEEE Transactions on Industry Applications, 2008, 44(1): 115-123.
[11] Narayanan G, Ranganathan V T. Synchronised PWM strategies based on space vector approach. part I: principles of waveform generation[J]. IEEE Proceedings on Power Applications, 1999, 146(3): 267-275.
[12] Geyer T, Oikonomou N, Papafotiou G, et al. Model predictive pulse pattern control[J]. IEEE Transactions on Industry Applications, 2012, 48(2): 663-676.
[13] Holz J. Pulsewidth modulation-a survey[J]. IEEE Transactions on Industrial Electronics, 1992, 39(5): 410-420.
[14] 王治国, 郑泽东, 李永东, 等. 轨道交通车辆牵引电传动系统的调制与控制策略[J]. 电工技术学报, 2016, 31(24): 223-232.
Wang Zhiguo, Zheng Zedong, Li Yongdong, et al. Modulation and control strategy for electric traction drive system of rail transit vehicles[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 223-232.
[15] Rathore A K, Holtz J, Boller T. Synchronous optimal pulsewidth modulation for low-switching-frequency control of medium-voltage multilevel inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2374-2381.
Multi-Mode Modulation Switching Strategy Based on Switch Time Correction
Abstract Multi-mode modulation strategy is usually used in electric traction drive system. In order to solve the problem of current and torque impact caused by switching between modulation modes, this paper studies the stator flux deviation caused by switching modulation modes, and proposes a general multi-mode modulation switching strategy. By analyzing the influence of changing the switching time on the stator flux linkage in two-phase static coordinate system, the compensation amplitude of each phase switching time is calculated to compensate the stator flux linkage deviation, so as to realize the smooth switching of multi-mode modulation. The strategy compensates the stator flux deviation directly, and it is not constrained by the specific modulation mode and motor parameters, so it can achieve no impact switching at any time. The simulation and experiment verify the generality and effectiveness of the stator flux deviation compensation strategy.
keywords：Multi-mode modulation, torque impact, switching strategy, stator flux deviation, switch time correction
DOI:10.19595/j.cnki.1000-6753.tces.210084
中图分类号：TM464
北方工业大学毓优人才计划资助项目（107051360021XN083/043）。
收稿日期 2021-01-17
改稿日期 2021-08-18
苑国锋 男，1979年生，博士，高级工程师，研究方向为电力机车牵引控制、风力电机控制。E-mail：ygf@ncut.edu.cn（通信作者）
沈 阳 男，1996年生，硕士研究生，研究方向为电力机车牵引脉宽调制技术。E-mail：243772901@qq.com
（编辑 赫蕾）