基于Elmer开源有限元平台的铁氧体辅助同步磁阻电机的建模和分析
狄 冲1 鲍晓华1,2 潘 晋3 王春雨3
(1. 合肥工业大学电气与自动化工程学院 合肥 230009 2. 合肥工业大学智能制造技术研究院 合肥 230009 3. 安徽皖南新维电机有限公司 合肥 230601)
摘要 该文以一台物联网车用铁氧体辅助同步磁阻电机(FMaSynRM)为研究对象,以Elmer开源有限元平台为核心,联合运用其他开源软件建立FMaSynRM二维磁场和电路耦合的瞬态有限元模型,重点阐述了其几何建模、网格划分、磁路耦合以及后处理可视化等环节的执行逻辑。在考虑逆变器输出容量限制和主要工作点不同控制逻辑下,对FMaSynRM的铁耗、铜耗、功率因数等主要性能指标进行分析计算,并将计算结果和场图分布与商用有限元分析结果进行对比。最后对样机进行加工和测试,获得其在较宽调速范围内的输出功率图和效率图,并检验其主要性能指标,验证了Elmer在电机电磁场有限元建模计算领域的可靠性和准确性,为其他类型的电机和电磁装置的开源有限元建模提供参考和借鉴。
关键词:铁氧体辅助同步磁阻电机 开源有限元 二维电磁场 场路耦合模型
0 引言
铁氧体辅助同步磁阻电机(Ferrite Magnet assisted Synchronous Reluctance Motor, FMaSynRM)输出转矩中含有电磁转矩和磁阻转矩成分,并同时具备同步磁阻电机和永磁同步电机的主要特点[1]。FMaSynRM经过合理优化设计可以达到或者接近稀土永磁同步电机的性能,具有成本低廉、转矩密度较高、效率较高、功率因数较高等特点[2]。目前,FMaSynRM已初步应用于家用电器、电动工具、电动汽车、航空航天等领域[3-5]。鉴于其上述特性和发展潜力,在电动物联网车(即电动叉车)应用领域FMaSynRM将逐渐替代传统感应电机,成为下一代主要驱动电机。
由于FMaSynRM的拓扑结构复杂,在设计电机电磁方案时,采用解析法分析计算较难取得令人满意的结果。因此,目前学术界和工业界都采用有限元分析方法来分析、计算和设计FMaSynRM。通常,在电机电磁有限元计算领域,国内多采用商用有限元计算软件Ansys Maxwell、Altair Flux和JMAG等来建模分析[6-8]。商用有限元计算软件具有建模方便、精度高、可靠性好的特点。但具有底层代码闭源、二次可开发性能差、价格昂贵等缺点。
鉴于商用有限元软件存在上述缺点,业界对于底层代码全部公开、能够任意修改其源码、可以免费使用的电磁场开源有限元软件呼声越来越高,且相应的研究也逐渐增加。目前,已经浮现出诸如FEMM、SMEKLIB和Elmer等适用于电机电磁场分析的开源有限元软件[9-11]。其中FEMM含静磁场和时谐场求解器,但不含瞬态求解器,已经应用于同步磁阻电机设计、无刷直流电机的退磁故障分析、双馈开关磁阻电机设计等实际工程[9,12-13]。SMEKLIB虽然存在瞬态场求解器,方便进行磁场和电路相互耦合的非线性时步有限元计算,但软件的其他方面并未完善,且缺少实际工程应用案例。
Elmer是一款由芬兰IT研究中心(CSC–IT Center for Science)主导,联合当地高校和科研机构共同开发,于2005年进行开源的通用多物理场有限元分析软件[14]。其主要应用领域涉及流体力学、电磁学、声学、结构力学等多个学科,并已经应用于诸多工程实例。此外,经过十几年发展,由于Elmer的开源特性,其开发和维护已经区域国际化,其核心代码和求解器一直以较高的频率保持不断的更新和维护。
Elmer在电机电磁场分析设计领域也有相关案例报道。在感应电机分析建模方面,J. Keränen采用Elmer二维瞬态场求解器,对一台笼型转子感应电机进行建模分析,重点考察Elmer的并行计算能力,并发现采用4个及以上CPU核心能极大缩短计算时间[11]。在永磁同步电机分析建模方面,P. Ponomarev则采用Elmer二维静磁场求解器,对一台表贴式永磁同步电机进行优化设计[15]。由于其优化维度尺寸多,采用不同转子位置角的静磁场模型来代替瞬态模型,共涉及866 700个二维静磁场有限元仿真模型,因此P. Ponomarev利用超级计算机上共计200个CPU核心,耗时9h完成优化设计。上述两个案例,分别验证了采用Elmer瞬态和静磁场求解器可以对电机电磁场进行有限元建模仿真的可能性,并重点检验了其良好的并行计算能力。此外,近些年,P. Ponomarev已经逐步开始尝试采用Elmer对一台永磁同步电机进行三维电磁场有限元仿真,并成功求解电机的平均电磁转矩、铁耗、铜耗及永磁体涡流损耗,取得了一定的进展[16]。然而,这些研究重点只落在Elmer求解器本身,缺少与商用有限元软件的分析对比和样机实验的验证。
在与商用有限元软件分析对比分析方面,M. Zaheer以一台5kW的感应电机为例,对采用Elmer和商用有限元软件所计算的铁耗进行详细对比[17-18]。对比发现:在不同供电频率下,Elmer在铁耗计算方面和商用有限元软件计算结果保持高度一致,并通过样机测试验证其准确性,但其研究仅侧重于电机铁耗的建模分析,在电机其他电磁性能方面并未详细展开。
本文以电动物联网车用FMaSynRM为研究对象,主要阐述以Elmer开源有限元平台为核心建立FMaSynRM磁场和电路相耦合的有限元模型,所涉及的几何建模、网格划分、磁场和电路耦合、求解和后处理等环节皆采用开源软件执行的案例。并在各主要工作点下结合合适的控制逻辑,将利用开源平台和商用有限元软件计算得到的转矩、铁耗、功率因数等电磁性能进行详细对比,检验其计算精度。最后,对工程样机进行测试,考察电机在主要工作点的电磁性能。
1 开源平台下电机有限元建模
1.1 电机主要参数
本文研究对象为一台下一代电动物联网车用FMaSynRM。考虑其应用场景,其电磁性能方面的主要特点为需满足在空载平地、满载平地、满载爬坡和坡道起步四个特定工作点下的转矩转速特性要求,其设计要求和性能指标见表1。
表1 FMaSynRM主要设计要求和性能指标
Tab.1 Main design and performance requirements of the FMaSynRM

参数数值 直流母线电压UDC/V80 电机基波线电压ULL/V52 最大线电流Imax/A400 极对数p2 相数m3 绕组联结方式三角形 空载平地转矩/(N·m)15.1 转速/(r/min)3 700 满载平地转矩/(N·m)23.61 转速/(r/min)3 832 满载爬坡转矩/(N·m)177.51 转速/(r/min)718 坡道起步转矩/(N·m)213.01 转速/(r/min)718
表1中逆变器输出最大相电流有效值为400A,根据绕组联结方式则电机最大相电流有效值为230.94A。同时,逆变器直流母线电压为80V,则输出最大基波线电压有效值为[19]
电动物联网车平台直流侧可由蓄电池或者锂电池供电,根据实际工程经验,视其供电方式的不同,逆变器输出基波线电压有效值一般留有10%~20%的裕度。同时,为了方便更为灵活地调节电机绕组匝数,电机绕组将采用三角形联结。
此外,依据实际工程经验,在满载爬坡点的基础上将转矩提高20%,可以视作坡道起步特性,因此表1中坡道起步转矩为213.01N·m,转速为718r/min。
1.2 以Elmer为核心的开源有限元电机建模
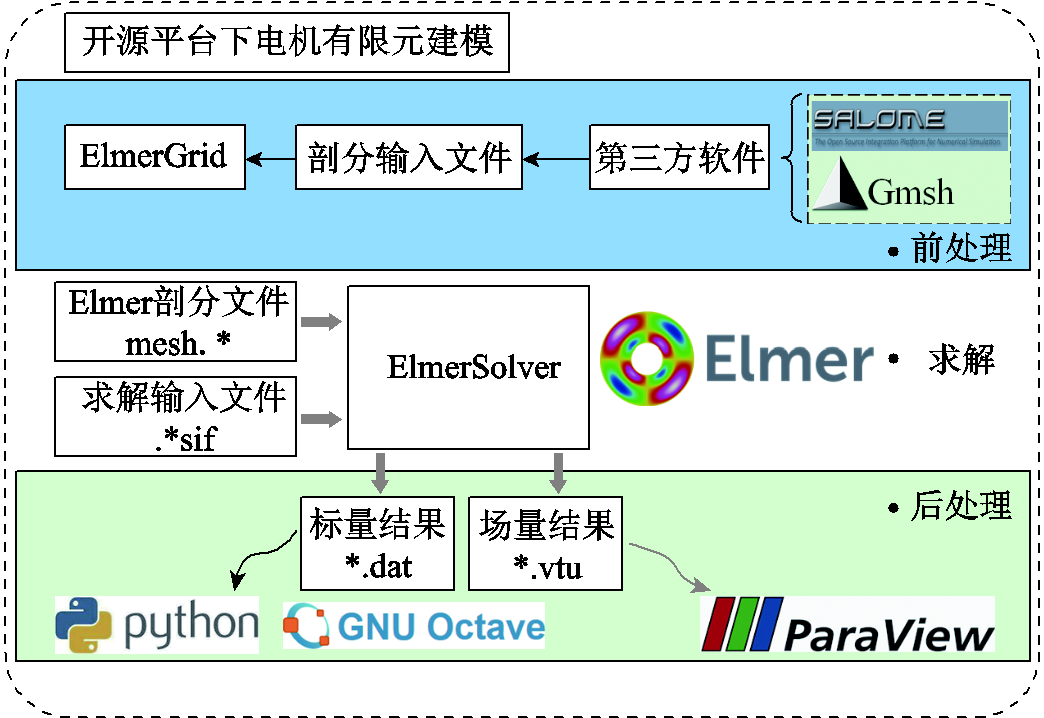
一般而言,电机电磁场有限元建模主要包括以下几个重要环节:几何模型建立、网格划分、非线性材料定义、物理面定义、运动设置、求解器设置及可视化后处理等。本文主要以Elmer(主要含网格生成器ElmerGrid、求解器ElmerSolver等核心套件)开源有限元平台为核心,联合运用其他开源有限元前处理(如Gmsh、SALOME等)和后处理(如Octave、ParaView、Python等)软件或编程语言,对电动物联网车用FMaSynRM进行建模分析,其主要建模流程如图1所示。
1.2.1 几何模型和网格
在几何模型建立以及网格划分方面,为使网格能和ElmerGrid进行对接,一般可以采用Gmsh或者SALOME进行建模及剖分。两者都是开源软件,其中SALOME可以方便读取各类CAD文件便于快速建模,而Gmsh则有利于几何尺寸的参数化建模。
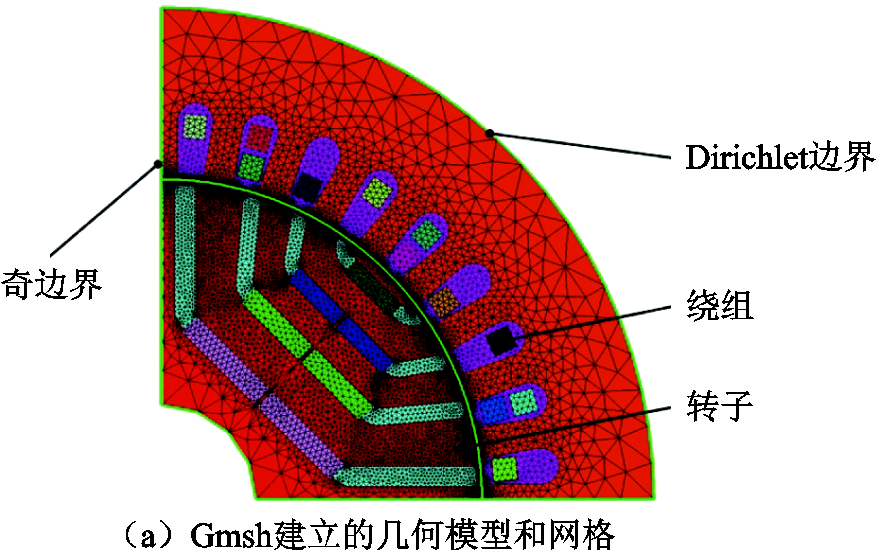
为了方便后续对电机几何尺寸进行优化,本文采用Gmsh对电机进行几何模型的建立和网格的划分,并于模型各个几何点设置剖分单元大小,其与商用软件Altair Flux所建立的几何模型和网格对比结果如图2所示。从图2中可以发现,Gmsh所建立的网格质量较高,且和Altair Flux所建立的网格较为相似。同时,两者在二维有限元分析计算过程中都可以灵活采用一阶和二阶(3节点和6节点)三角形网格单元,便于建模时对模型计算速度与精度进行取舍。此外,值得注意的是Gmsh所建立的网格需要转换为ElmerGrid所能接受的文件格式,才能进一步采用ElmerSolver求解器进行求解,进一步研究对比发现在转换过程中网格文件的网格精度没有丢失。
1.2.2 求解器和场路耦合
在求解器方面,ElmerSolver在二维电磁有限元瞬态场以磁矢位为主要求解变量,遵循下述电磁场统一方程[20]。
式中,σ为电导率,S/m;Az为z方向磁矢位,Wb/m;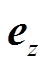 为z方向单位向量;μ为磁导率,H/m;Jz为电流密度,A/m2;M为磁化强度,A/m。其中,第一项为感生电流;第二项为动生电流;第三项为传导电流;第四项为磁化电流。
为z方向单位向量;μ为磁导率,H/m;Jz为电流密度,A/m2;M为磁化强度,A/m。其中,第一项为感生电流;第二项为动生电流;第三项为传导电流;第四项为磁化电流。
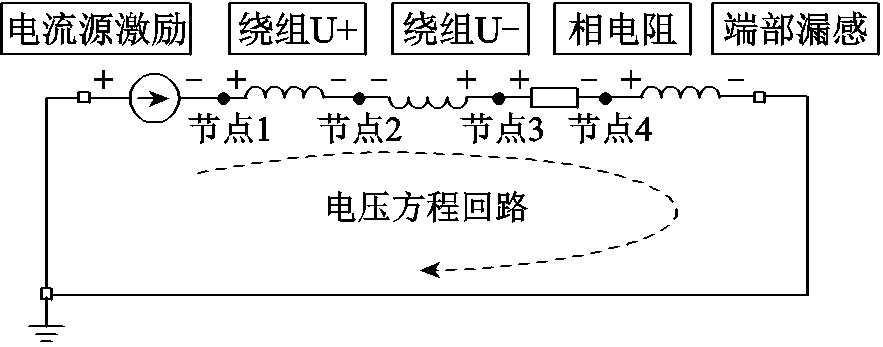
求解器经过合理部署包括:设置材料属性、定义机械运动属性、赋予物理面等,即可以进行初步分析计算。然而,为了进一步考虑绕组形式,则需要进行磁场和电路耦合仿真,根据电路各节点电流平衡和回路电压平衡列举方程,得到求解矩阵系数,并进行相应设置。FMaSynRM一般采用电流源激励进行建模仿真,且通常商用有限元建模软件(如Altair Flux)中都会将电流源三角形联结等效转换为星形联结,因为电流源三角形联结容易导致求解不收敛。同理,本文在考虑磁场和电路耦合时,也将采用上述星三角转换进行等效处理。
以U相绕组为例,其电路连接示意图如图3所示。由基尔霍夫电压定律和基尔霍夫电流定律在回路中列举电压回路方程和各节点列举电流方程,可以得到
根据上述电压电流方程,按式(4)列举矩阵方程[14],供求解器进行求解。
式中,A和B为系数矩阵;x为电路中待求解向量;f为激励源。
1.2.3 求解结果后处理和可视化
在求解结果后处理和可视化方面,如图1所示,采用ElmerSolver求解完毕后,按求解结果类型可以将其划分为标量解(如转矩曲线、电压曲线等)和矢量解(磁通密度分布、磁力线分布等)。其中标量解可采用开源软件/编程语言如Octave、Pyrthon等进行后处理并进行可视化;而矢量解则可采用开源软件ParaView进行后处理和可视化。
本节重点介绍了以Elmer为核心的开源有限元电机建模逻辑,可以发现:整个建模流程涵盖前处理、求解以及后处理,全程采用开源软件来执行。并且Elmer拥有二维瞬态求解器,能够执行磁场和电路耦合建模,满足FMaSynRM电磁场有限元建模分析的要求。
2 开源平台和商用软件的仿真结果对比
依据前文建模逻辑,本节主要对比采用开源平台和商用软件(Altair Flux)对FMaSynRM进行有限元建模的结果,并重点考察电机在空载和带载情况下的矢量解和标量解的差异。
2.1 空载情况下的仿真结果对比
FMaSynRM在空载情况下,采用Elmer和Altair Flux对其进行仿真的磁通密度和磁力线分布如图4所示。从图4中可以看出,两者磁通密度分布几乎一致,磁桥饱和处磁通密度大小较为接近。并且磁力线走向也高度相似。此外,两者建立的都是1/4模型,采用奇边界考虑其周期性,磁力线在边界附近的走向皆符合其真实物理特性。
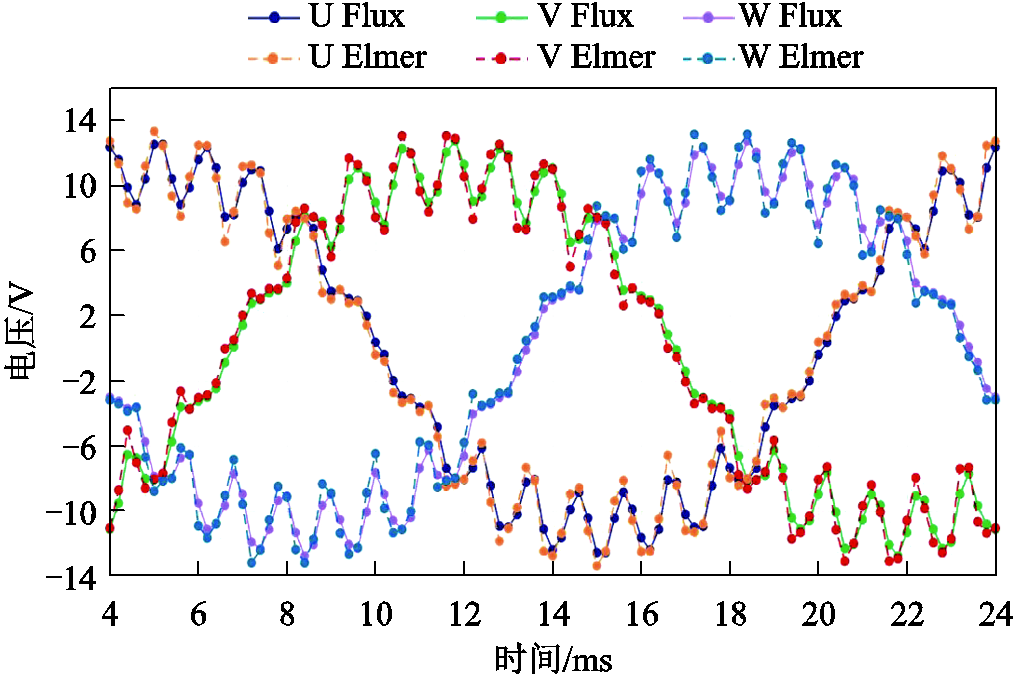
采用二维瞬态时步有限元对FMaSynRM进行仿真计算可以获得电机空载时的主要电磁性能。空载情况下电机绕组端电压随时间变化曲线对比如图5所示,对比发现,两者空载端电压误差较小,并且保证在所有时刻误差都保持在一个较小的范围内。
磁链是FMaSynRM在分析设计过程中另一项关键性能参数,Altair Flux采用式(5)来求取绕组磁链。
式中,Ns为每相串联匝数;Is为绕组相电流,A;V为对应体积所在的区域。
在ElmerSolver求解器中,由于绕组反感应电动势可以直接输出。因此,在反感应电动势基础上直接求取绕组磁链,其公式可以表示为
式中,E为绕组反感应电动势,V;t为时间,s。
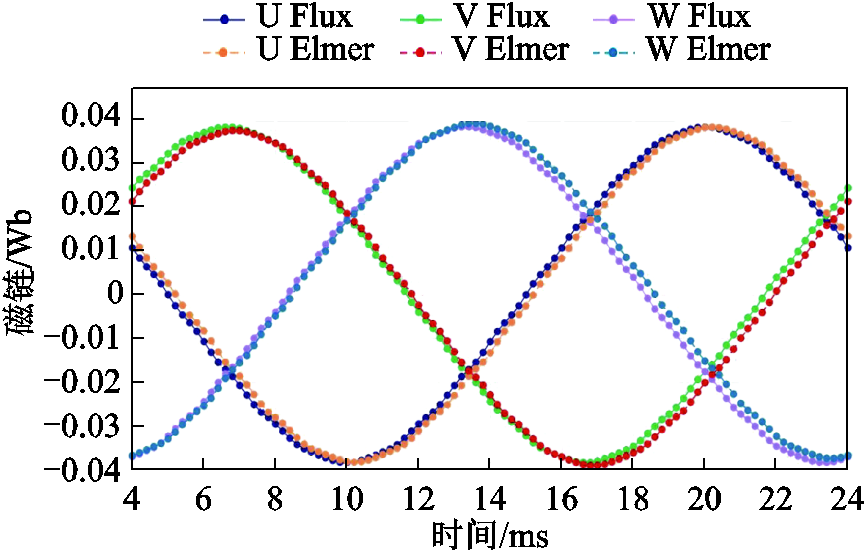
在空载情况下的电机三相绕组磁链随时间变化的曲线对比如图6所示。从图6中可以看出,Elmer和Altair Flux输出的绕组磁链幅值曲线形状较为一致。但值得注意的是,Elmer采用式(6)中逻辑所计算的绕组磁链曲线落后于Altair Flux输出的曲线半个时间步长,这是由积分处理所导致的误差。该误差可以通过减小仿真步长的方法进行有效抑制。
在电磁转矩计算方面,Elmer和Altair Flux则分别采用了虚位移法和麦克斯韦张量法(Arkko’s method)进行求解,其主要表达式为[19]
式中,B、Bn和Bt分别为气隙中的合成磁通密度、磁通密度法向分量和磁通密度切向分量,T;H为气隙中的磁场强度,A/m;θ为转子位置角,rad;μ0为真空磁导率,H/m;rs和rr分别为定转子气隙内、外半径,m;r为力臂半径,m;S为气隙所在的面域。
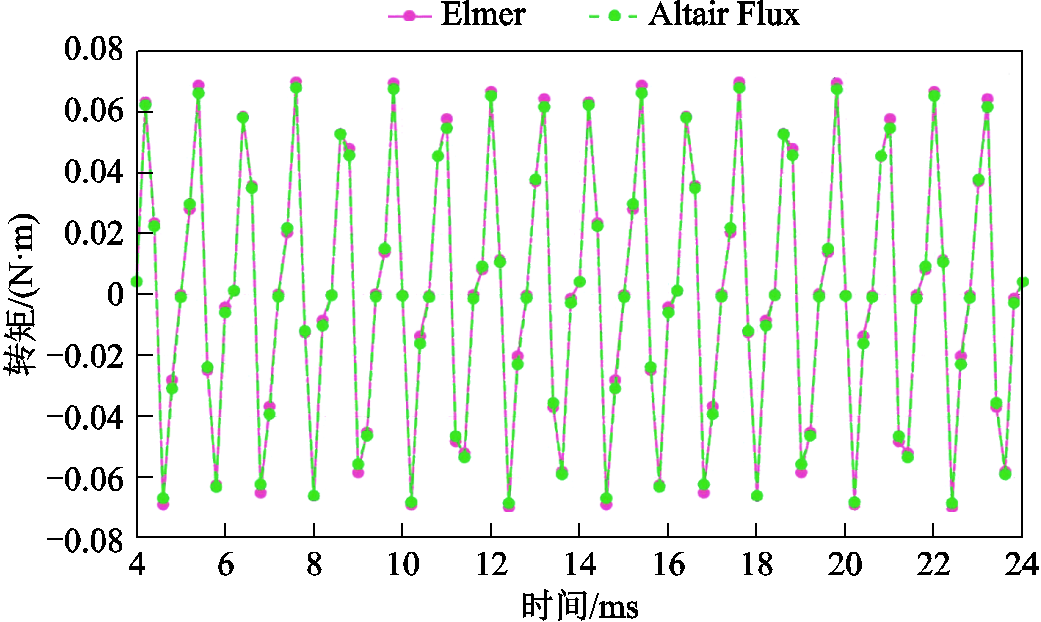
在空载情况下FMaSynRM齿槽转矩随时间变化的曲线对比如图7所示。从图7中可以发现,尽管两种软件采用不同逻辑计算转矩,但其误差时刻都保持在±2.5%以内,具有较高的精度。
2.2 带载情况下的仿真结果对比
由于学界对FMaSynRM交直轴划分并未达成统一共识,为了方便理解,本文采用永磁同步电机逻辑对FMaSynRM交直轴进行划分。为了对比开源平台和商用平台下的FMaSynRM的带载情况,下述对比都是在定子电流is = 50A,电流超前角γ = 90°(即d轴电流id = 0控制)条件下进行。
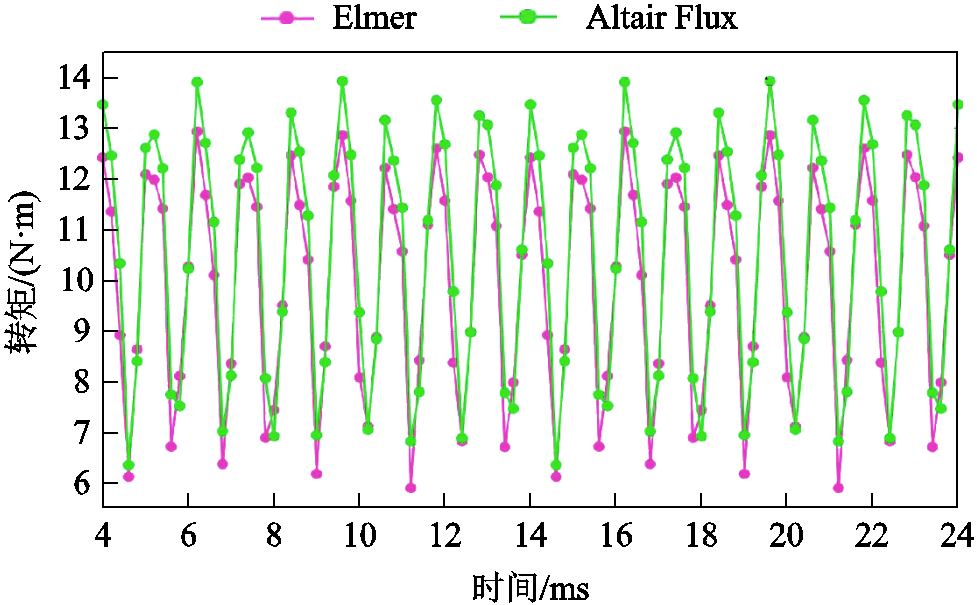
FMaSynRM在带载情况下的磁场和磁力线分布对比如图8所示。与空载情况下类似,经Elmer 和Altair Flux输出的磁场和磁力线分布都具有较高的一致性。FMaSynRM在带载情况下电磁转矩随时间变化曲线的对比如图9所示。其中经Elmer求解的平均转矩为9.92N·m,经Altair Flux求解的平均转矩为10.50N·m,两者误差为5.5%。对比转矩曲线可以发现,两个软件输出转矩具有一定的误差,这有可能是转矩求解方法和网格划分不同所导致的,但整体误差都处在一个可以接受的范围内。
3 FMaSynRM样机性能分析和实验验证
3.1 FMaSynRM样机性能分析
如表1所示,在考虑逆变器输出容量的限制下,为满足FMaSynRM在四个特定工作点特性,经过研究对比,采用正弦绕组形式可以满足上述设计要求,其中每半槽导体数采用17和9交叉设置。铁氧体采用四层结构,实测120℃下剩磁为0.335T。
依据表1中四个特定工作点,并从最大转矩电流比控制(Maximum Torque Per Ampere, MTPA)、弱磁控制(Field Weakening, FW)和最大转矩电压比控制(Maximum Torque Per Voltage, MTPV)中选择合适的控制逻辑(方法)对样机性能进行分析,其主要性能指标见表2,其中的电压和电流仍然是将三角形联结等效为星形联结进行分析计算的。
从表2中可以看出,在各工作点下,Elmer和Altair Flux采用相同的定子电流激励和电流超前角,可以得到电机电磁转矩、端电压、铜耗、铁耗和功率因数等电磁性能。对比各项性能指标可以发现,Elmer和Altair Flux两者的求解结果都较为接近,具有较小的误差,可见Elmer在电机电磁场分析计算领域具有较高的工程使用精度。其中两者铁耗采用的都是可以计及高频铁耗的改进的Bertotti模型进行求解计算[20-21],即
表2 FMaSynRM在主要工作点下的电磁性能
Tab.2 Electromagnetic performances of the FMaSynRM at the main operating points
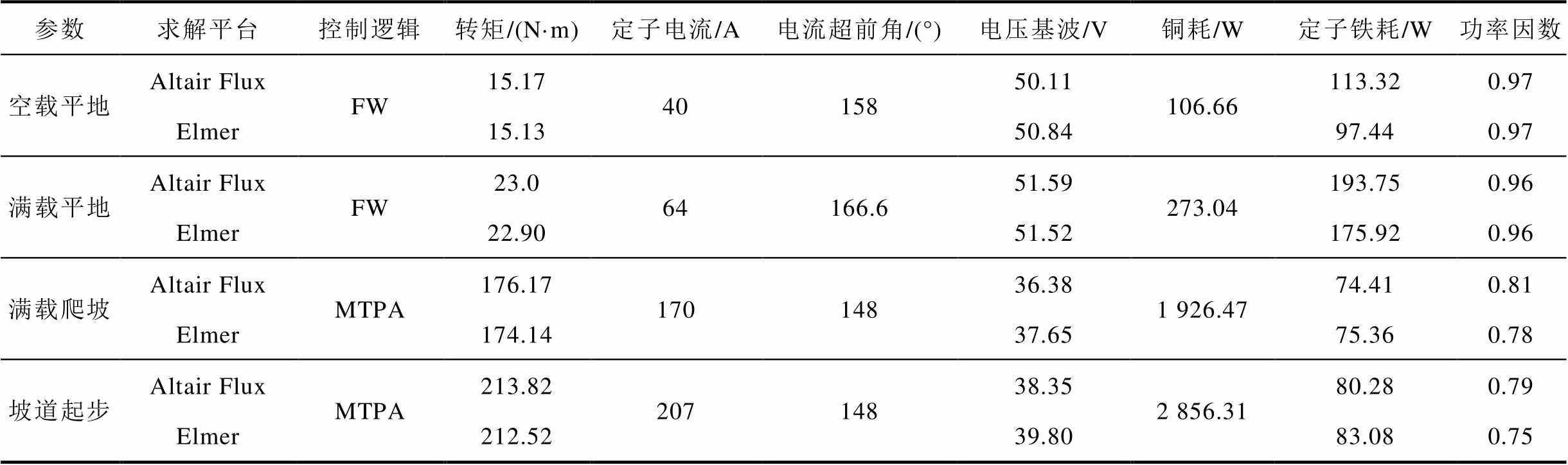
参数求解平台控制逻辑转矩/(N·m)定子电流/A电流超前角/(°)电压基波/V铜耗/W定子铁耗/W功率因数 空载平地Altair FluxFW15.174015850.11106.66113.320.97 Elmer15.1350.8497.440.97 满载平地Altair FluxFW23.064166.651.59273.04193.750.96 Elmer22.9051.52175.920.96 满载爬坡Altair FluxMTPA176.1717014836.381 926.4774.410.81 Elmer174.1437.6575.360.78 坡道起步Altair FluxMTPA213.8220714838.352 856.3180.280.79 Elmer212.5239.8083.080.75
式中,Ph、Pc和Pe分别为磁滞、涡流和杂散(此“杂散”为“excessive”,并非传统意义的“杂散损耗”)损耗,W/m3;kh[W·s/T2/m3]、kc[W/(T/s)1.5/m3]和ke[W/(T/s)2/m3]为对应损耗系数(可由多频B-P曲线拟合得到);fn为第n次磁通密度谐波的频率,Hz;Bn为第n次磁通密度谐波的幅值,T;Г为定子所在的物理面;lef为铁心轴向长度,m。
值得注意的是,一般情况下铁氧体电阻率较大约100Ω·m,因此由高频谐波引起的铁氧体感应涡流损耗可以忽略不计,所以表2中未列举铁氧体涡流损耗。
3.2 样机实验测试结果
依据电机设计优化方案,对样机进行加工,区别于其他类型电机,FMaSynRM最主要的特点为其转子拓扑结构形式的不同。本文设计加工电机的转子冲片如图10所示,可以发现该转子冲片和本文有限元所建立的模型高度一致。FMaSynRM样机的测试平台如图11所示,测试时在保证不超出逆变器容量情况下,转速由300r/min 增加到3 600r/min,步长300r/min;转矩由10N·m逐渐增加到220N·m,步长10N·m;从而获得电机功率和效率,考察电机在不同转速和转矩下的性能指标。
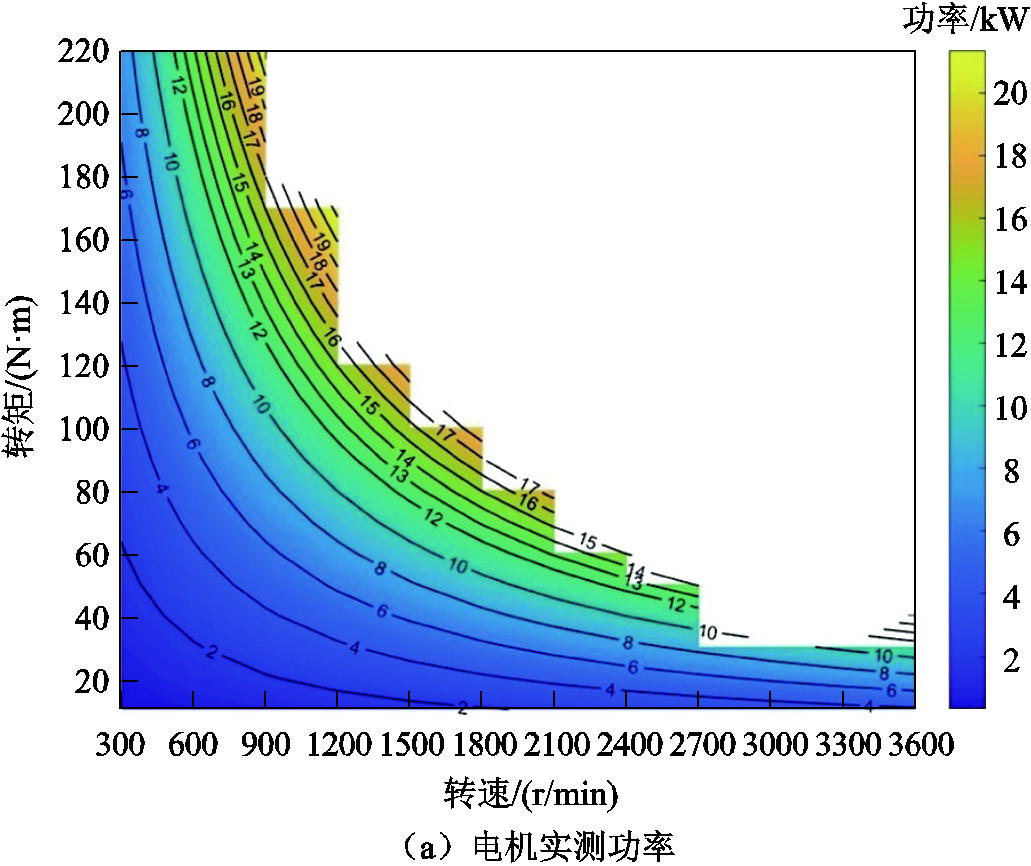
图12为样机实测输出功率和效率,从图中可以发现,该FMaSynRM在如表2所示的几个主要工作点附近的转矩输出基本符合设计要求。同时,可以发现该电机具有较宽的调速范围,且其高效运行区间同样较宽。
样机实测性能与有限元计算结果的对比见表3。表3中选择了较具代表性的工作点进行分析对比,工作点选择原则为:转速转矩都涵盖中低高范围。从表3中可以发现,实测数据和有限元仿真结果在各个工作点下都较为接近,证明了商用Altair Flux软件和开源Elmer软件都具有较高的计算精度,符合工程计算要求。此外,观察各工作点下电流可以发现,在同转矩下对比,实测电流比有限元仿真计算电流略大,原因可能是加工制造过程中的误差,以及定子采用了斜槽工艺,降低了定转子之间的电磁耦合,使得对应转矩输出能力略微下降。
表3 样机实测性能与有限元计算结果对比
Tab.3 The performance comparison of the tested and finite element simulated results of the prototype

项目转速/(r/min)转矩/(N·m)电压/V电流/A 实测30010015.33111 Altair Flux15.16104 Elmer15.17105 实测90020045.86209 Altair Flux46.95196 Elmer49.48198 实测3 0001051.7526 Altair Flux51.2924 Elmer47.8424
4 结论
本文以Elmer开源通用多物理场有限元平台为核心,详细介绍了开源平台下FMaSynRM的建模逻辑程序。具体涉及几何模型建立、网格划分、磁路耦合设置、求解结果后处理和可视化等多个方面。并将有限元仿真计算结果和商用有限元Altair Flux软件计算结果进行详细的对比。结果显示,从电机场图分布到转矩、磁链随时间变化曲线、铁耗、功率因数等电磁性能,两个平台的计算结果都保持高度一致。
此外,本文还重点考察了FMaSynRM在多个特定工作点下的性能指标,并进行实验验证。实测结果显示样机具有较宽的调速范围和高效运行区间,在不同转速下的转矩输出水平基本符合设计要求。证明了Elmer开源有限元软件在电机电磁场有限元建模领域的实用性和可靠性,为今后其他类型的电机和电磁装置的设计提供了思路。
参考文献
[1] 杨晨, 白保东, 陈德志, 等. 可变磁通永磁辅助同步磁阻电机设计与性能分析[J]. 电工技术学报, 2019, 34(3): 489-496.
Yang Chen, Bai Dongbao, Chen Dezhi, et al. Design and analysis of a variable flux permanent magnet assisted synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 489-496.
[2] 黄辉, 胡余生. 永磁辅助同步磁阻电机设计与应用[M]. 北京: 机械工业出版社, 2017.
[3] 王瑾, 李岩, 贾建国, 等. 反电动势和凸极率对高效永磁同步磁阻电机稳态特性影响分析[J]. 电工技术学报, 2020, 35(22): 4688-4698.
Wang Jin, Li Yan, Jia Jianguo, et al. Analysis of the influence of back-EMF and saliency ratio on steady-state characteristics of a high efficiency permanent magnet synchronous reluctance motor[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4688-4698.
[4] 程明, 文宏辉, 曾煜, 等. 电机气隙磁场调制行为及其转矩分析[J]. 电工技术学报, 2020, 35(5): 922-930.
Cheng Ming, Wen Honghui, Zeng Yu, et al. Analysis of airgap field modulation behavior and torque component in electric machines[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 922-930.
[5] 徐媚媚, 刘国海, 陈前, 等. 永磁辅助同步磁阻电机设计及其关键技术发展综述[J]. 中国电机工程学报, 2019, 39(23): 7033-7043.
Xu Meimei, Liu Guohai, Chen Qian, et al. Design and key technology development of permanent magnet assisted synchronous reluctance motor[J]. Proceedings of the CSEE, 2019, 39(23): 7033-7043.
[6] Turner L R. 3-D field computation: the near-triumph of commercial codes[J]. IEEE Transactions on Magnetics, 1996, 32(4): 2945-2949.
[7] Jiang W, Jahns T M, Lipo T A, et al. Machine design optimization based on finite element analysis in a high-throughput computing environment[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 2012: 869-876.
[8] Di C, Petrov I, Pyrhönen J J. Modeling and mitigation of rotor eddy-current losses in high-speed solid-rotor induction machines by a virtual permanent magnet harmonic machine[J]. IEEE Transactions on Magnetics, 2018, 54(12): 1-12.
[9] Hoffer A E, Moncada R H, Pavez B J, et al. A novel method for finite-element modeling of a commercial synchronous reluctance machine[J]. IEEE Latin America Transactions, 2018, 16(3): 806-812.
[10] Lehikoinen A, Davidsson T, Arkkio A, et al. A high-performance open-source finite element analysis library for magnetics in Matlab[C]//2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 2018: 486-491.
[11] Keränen J, Ponomarev P, Pippuri J, et al. Parallel performance of multi-slice finite-element modeling of skewed electrical machines[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.
[12] Usman A, Rajpurohit B S. Comprehensive analysis of demagnetization faults in BLDC motors using novel hybrid electrical equivalent circuit and numerical based approach[J]. IEEE Access, 2019, 7: 147542-147552.
[13] Gouda E, Salah H M. A proposed design, implementation and control of doubly fed switched reluctance motor[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 101-106.
[14] Råback P, Malinen M, Ruokolainen J, et al. Elmer models manual[M]. Helsinki: CSC–IT Center for Science, 2013.
[15] Ponomarev P, Petrov I, Bianchi N, et al. Selection of geometric design variables for fine numerical optimizations of electrical machines[J]. IEEE Transactions on Magnetics, 2015, 51(12): 1-8.
[16] Ponomarev P, Keränen J, Pasanen P. Electromagnetic transient finite element 3D modelling of electrical machines using open-source tools[C]//2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 2016: 1657-1661.
[17] Zaheer M, Lindh P, Aarniovuori L, et al. Assessment of 5 kW induction motor finite element computations with a commercial and an open-source software[C]// 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), IEEE, Istanbul, Turkey, 2019: 114-119.
[18] Zaheer M, Lindh P, Aarniovuori L, et al. Comparison of commercial and open-source FEM software: a case study[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 6411-6419.
[19] Pyrhönen J, Hrabovcova V, Semken R S. Electrical machine drives control: an introduction[M]. Chichester: John Wiley & Sons, 2016.
[20] Di C. Modeling and analysis of a high-speed solid-rotor induction machine[D]. Lappeenranta, Finland: Lappeenranta-Lahti University of Technology LUT, 2020.
[21] 张冬冬, 赵海森, 王义龙, 等. 用于电机损耗精细化分析的分段变系数铁耗计算模型[J]. 电工技术学报, 2016, 31(15): 16-24.
Zhang Dongdong, Zhao Haisen, Wang Yilong, et al. A piecewise variable coefficient model for precise analysis on iron losses of electrical machines[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 16-24.
Modelling and Analysis of a Ferrite Assisted Synchronous Reluctance Machine Based on the Open-Source Platform Elmer
Di Chong1 Bao Xiaohua1,2 Pan Jin3 Wang Chunyu3
(1. School of Electrical Engineering and Automation Hefei University of Technology Hefei 230009 China 2. Intelligent Manufacturing Institute of HFUT Hefei 230009 China 3. Anhui Wannan Xinwei Motor Co. Ltd Hefei 230009 China)
Abstract This paper takes a ferrite magnet assisted synchronous reluctance motor (FMaSynRM) as the study object. To establish the two-dimensional electromagnetic-coupled transient model of this FMaSynRM, this paper selects the open-source platform Elmer as the core solver and cooperates with some other open-source packages. The logic to build the geometry, generate the mesh, tune the electromagnet-coupled setting, conduct the post-processing is emphasized in this paper. With the consideration of the inverter’s capacity, the iron losses, copper losses, power factor etc. at main operating points are evaluated by Elmer and comparisons are made with the commercial software. Finally, the prototype is manufactured and tested. The out-put power and efficiency maps at different speeds are obtained and the results meet the design requirements. The reliability and correctness of the modelling of the FMaSynRM by Elmer is proven, which sets an example for the design of other machines and similar electromagnetic apparatus by the open-source platform.
keywords:Ferrite magnet assisted synchronous reluctance motor (FMaSynRM), open-source finite element method, two-dimensional electromagnetic field, electromagnetic-coupled model
DOI:10.19595/j.cnki.1000-6753.tces.210093
中图分类号:TM341
国家自然科学基金(51977055)、安徽省科技重大专项(201903a05020042)、高等学校学科创新引智计划(BP0719039)和中央高校基本科研业务费专项资金(JZ2021HGQA0198)资助。
收稿日期 2021-01-18
改稿日期 2021-04-10
作者简介
狄 冲 男,1991年生,博士,讲师,研究方向为电机设计和电机电磁场开源有限元建模仿真技术等。E-mail:Chong.Di@hfut.edu.cn(通信作者)
鲍晓华 男,1972年生,博士,教授,博士生导师,研究方向为电机设计理论和技术等。E-mail:baoxh@hfut.edu.cn
(编辑 赫蕾)

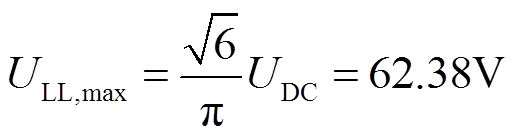 (1)
(1)

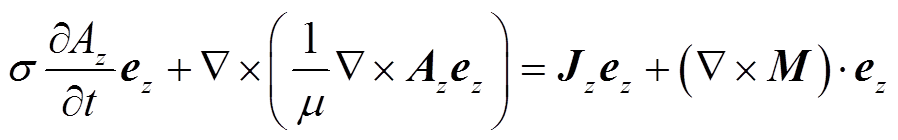 (2)
(2)
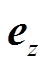 为z方向单位向量;μ为磁导率,H/m;J
为z方向单位向量;μ为磁导率,H/m;J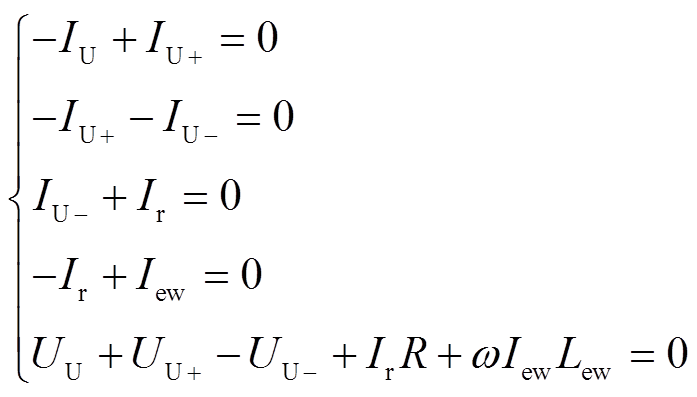 (3)
(3)
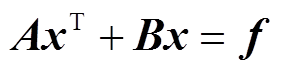 (4)
(4)

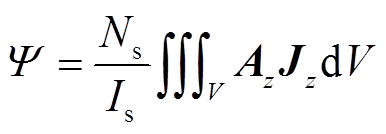 (5)
(5)
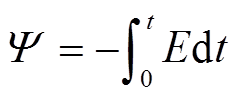 (6)
(6)
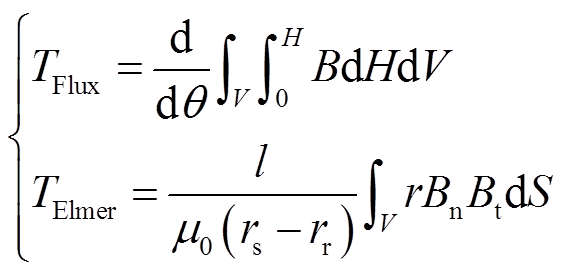 (7)
(7)


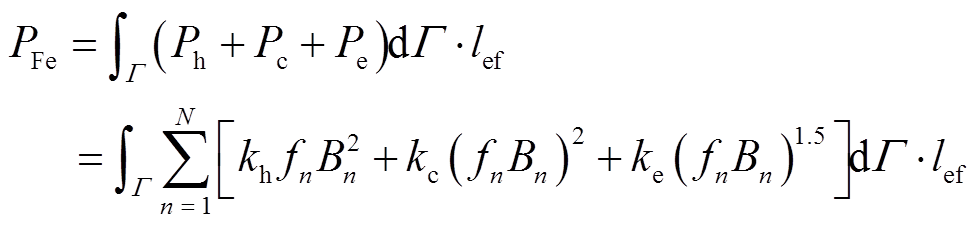 (8)
(8)