和标量位
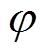用向量表示为摘要 地质勘测资料表明，地下存在电性各向异性介质，因此在研究地磁扰动（GMD）地电场时需要考虑各向异性介质的影响。建立包含各向异性介质的大地电导率模型，研究电性结构不均匀及各向异性介质对地电场分布的影响。结合新疆地区部分数据构建各向异性大地电导率模型计算GMD地电场。通过各向同性大地电导率模型对比，发现各向异性区域内主轴电导率的变化将会对该区域内相应方向上的地电场及周边的地电场产生影响，其变化规律与各向异性区域周边存在的高导或高阻体相关。结合电网结构参数得到地磁感应电流（GIC），证明虽然地下各项异性介质对地表感应地电场的大小影响较小，但由于计算GIC时通过地电场沿输电线路积分得到等效电压源，存在误差的累积，将使GIC的计算误差增大。
关键词：地电场 各向异性 大地电性结构 地磁感应电流
近些年大量研究和观测资料表明电性各向异性在地球内部已经成为不可忽视的重要现象[1-3]，否定了之前研究过程中大地导体为各向同性的假设。因此在进行磁暴对电网安全运行评估时需要考虑地下各向异性介质对地磁扰动（Geomagnetic Disturbance, GMD）地电场[4]的影响，这就要求建立能够真实反映土壤情况的各向异性大地模型。
大地电性结构模型能否真实反映地下介质的分布将直接影响GMD地电场计算结果的准确性。目前对大地电导率模型的研究，无论是只考虑电导率随深度变化的分层大地模型[5-7]，还是考虑大地电导率横向变化的分层分区模型[8-10]，用到的数据都来自基于各向同性假设的大地电磁测深（Magnetotelluric sounding, MT）反演解释资料。在工程实际中发现，应用标量电导率建立的各向同性大地电导率模型计算GMD地电场与地磁台的实测值相差较大，使地磁暴对电网安全影响评估的准确性降低。此外，随着地球物理观测技术和方法的发展，研究人员利用各向同性假设的模型无法合理解释部分大地电磁勘探数据，通过对MT响应函数的反演[11]发现不同方向的电导率不同，揭示出地下介质电性各向异性特征[12-13]，得到张量大地电导率，为研究地下各向异性介质对GMD地电场的影响提供了数据基础。
基于上述研究现状，本文采用最新的新疆地区MT实测的张量电导率数据，在建立新疆地区大地电导率模型时考虑地下各向异性介质的影响，利用地磁台监测到的地磁扰动数据研究大地电性结构不均匀及地下存在的各向异性介质对GMD地电场空间分布的影响。为计算磁暴时交流电网中的地磁感应电流（Geomagnetically Induced Currents, GIC）[14]提供更加准确的基础模型。
将大地电导率的各向异性引入涡流场全电流定律方程和电流连续性方程，矢量位和标量位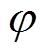用向量表示为
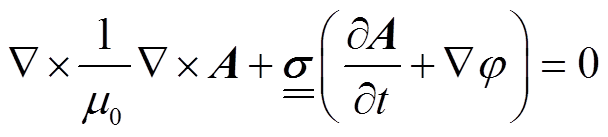（1）
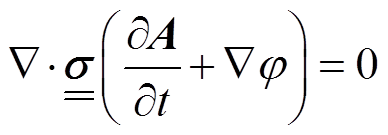（2）
式中，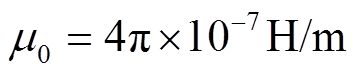
；
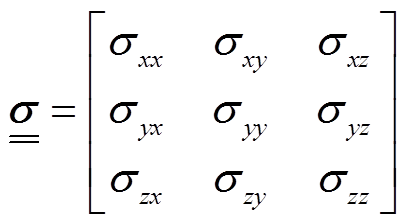为张量电导率。
伽辽金加权余量方程为
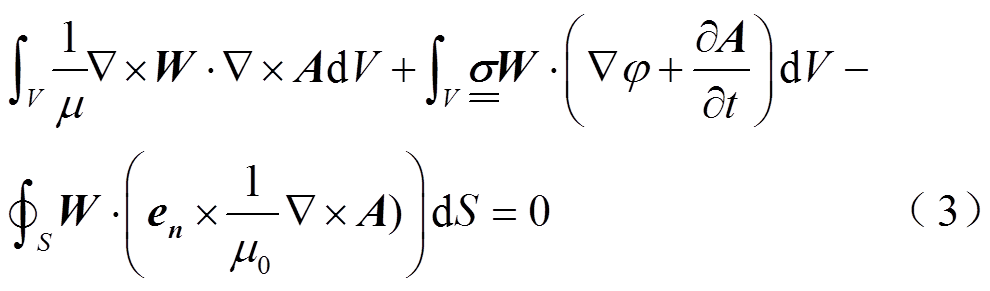
（4）
式中，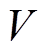
为整个求解域；
为场域边界；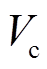
为导体区；标量权函数
为基函数，矢量函数
为与直角坐标系的单位向量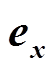
、
、
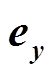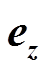相乘得到的3个矢量权函数；
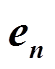为边界面的外法向。
将电导率张量进行欧拉旋转得到具有三个主值的参考电导率张量，伽辽金加权余量方程拆为三个分量式，利用形状函数在全部节点上叠加得到基函数序列，与节点上的和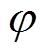组成近似函数，代入式（3）和式（4）中，求解全部节点上的和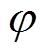，进一步计算得到电场强度和电流密度。
根据GIC 的产生过程，电网 GIC 计算可分为两个独立的步骤：①空间电流在大地中感应出电磁场，其磁场数据被地磁台测量记录，从而通过计算得到感应地电场；②地电场通过接地点作用于电网产生GIC，将此地面感应电场等效成网络中的电源，从而将电网 GIC 计算转换为一个电路问题。根据感应地电场的作用机制，线路感应电压值为感应地电场沿着该线路走向的积分值，即
（5）
式中，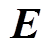
为感应地电场强度矢量；
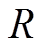为线路路径；dl为线路长度积分。
建立三维分区分块大地电导率模型后，利用有限元法计算感应地电场的分布，根据每条线路两端变电站的经纬度坐标，对线路做微元化处理，即将线路平均分为m段，得到每个微元中点的地理坐标，再转换为模型中对应的坐标，寻找每个微元中点对应的感应地电场强度。在电网GIC模型中，电网受地磁暴影响产生GIC的原理相当于在不同的变电站之间施加直流电压源，将等效电压源的积分公式简化为
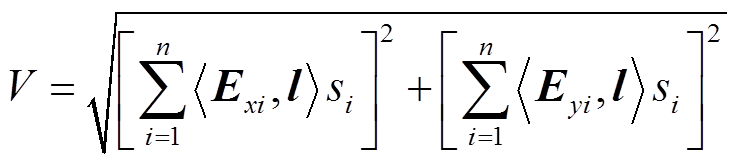（6)
式中，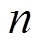
为每条线路微元的数量；
、
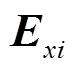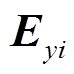为微元地电场强度分量；
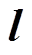为线路方向向量；
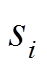为每个微元的长度。
计算得到线路感应电压值后，采用工程中应用最多的导纳矩阵法计算电网的地磁感应电流。
利用“祁连山西段及邻区电性结构及构造”以及“东昆仑-柴达木盆地过渡带深层电性结构”研究中35°N～40°N、95°E～96°E范围内电磁测深提供的张量电导率作为存在各向异性区域小范围大地电导率模型的基础数据。小范围大地电性结构模型中电阻率分布如图1所示。图1中，A1～A5区域内存在一系列高阻高导相间排列的结构，将其作为识别各向异性的标志[15]，在大地电性结构建模中将这些区域单独考虑。
图1 小范围大地电性结构模型中电阻率分布图
Fig.1 Distribution of resistivity in a small-scale geoelectric structure model
考虑到大地电导率模型的尺寸需根据被研究电网的跨度确定，模型的地理位置根据研究范围内变压器接地点的位置确定，新疆750kV电网在37°N～45°N、75°E～96°E之间，上述小范围的实测数据不能满足建模需要，所以收集了青海门源—福建宁德地学断面、内蒙阿拉善—上海奉贤地学断面、内蒙满都拉—江苏响水地学断面、格尔木—额济纳旗地学断面、新疆沙雅（天山）—哈纳斯地学断面、银川—天水地壳上地幔电性特征解释成果、格尔木—额济纳旗MT电性特征解释成果、青海大柴旦—四川大足大地电磁测深剖面的岩石圈电性结构和深部构造解释成果作为补充数据[16]。模型选取的四周边界离关心区域足够远，所以在电网对应的范围上各向四周拓展100km作为整体研究区域。虽然大地电导率在大范围内是复杂的三维分布，但其横向的变化比随深度的变化小得多，而且随着深度的增加大地电导率的分布更加均匀。
A1～A5作为可能的各向异性区域，限于计算速度和各向异性介质的原始数据，将A2作为典型各向异性区域研究其对感应地电场分布的影响。建立如图2所示的三维各向异性大地电性结构模型。不考虑地球曲率的影响，使用直角坐标系，X轴的正向为北，Y轴正向为东，Z轴正向垂直地面向下。存在各向异性区域的小范围模型南北长400km，东西长80km，深100km，整个研究区域南北长1 000km，东西长2 300km，深300km。地面边界条件如式（7）、（8）所示，式（7）指定了地面磁场的切向分量为边界条件，切向分量的取值来自于地磁台的测量数据，以面电流密度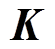
施加。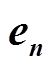
为地面的外法向单位矢量，指向Z轴的负方向。
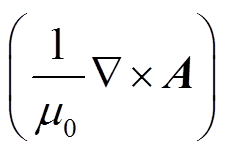为地面处的磁场强度，可由地磁台测量数据中的水平分量获得。在施加边界条件时，先利用地磁台测量得到的地磁场水平分量和磁偏角计算出地磁场南北分量和东西分量，再通过式（7）计算东西向和南北向的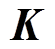，作为上边界条件[17]。
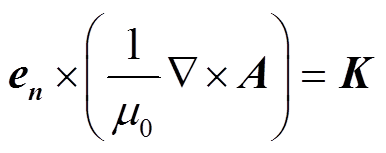（7）
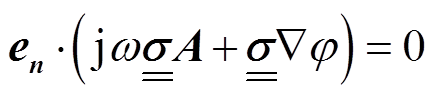（8）
图2 各向异性大地电导率模型
Fig.2 Anisotropic earth conductivity model
确定上边界条件后即可确定模型的四周边界条件，以上边界施加地磁台地磁场东向分量为例，则在整体研究区域的上表面施加北向的面电流密度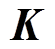。由于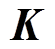施加在整个上表面，故将其作为无限大面电流密度，感应电流垂直流入南边界面，垂直流出北边界面，所以边界条件为
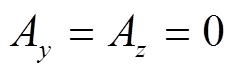。感应电流平行于东西边界面，边界条件为
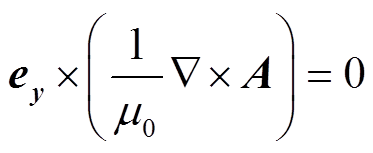。设定南北边界面的标量电位相等来满足电流连续，电磁场场量在下边界衰减至零。
对于各向同性大地电导模型，其整体尺寸和各个区块的尺寸与各向异性模型相同，只是在建模时将A1～A5区块的电导率按照之前大地电磁测深数据设置为某一定值，以便进行对比分析。
本文以2004年11月9日距离新疆最近的嘉峪关地磁台地磁场监测数据来计算GMD地电场，采样周期为1s。利用6:00:00时刻的地磁场数据研究各向异性介质对于GMD地电场的影响，使用整体模型中存在各向异性介质的部分，其模型尺寸及坐标轴设置如图2a所示，提取X=0～300km，Y=40km，Z=0km范围内（即存在各向异性区域的小范围大地电导模型上表面长300km的中心线段）的电流密度、GMD地电场强度和大地电阻率数据，如图3所示。无论是各向同性还是各向异性模型，电阻率较低的区块吸引电流，使大地电性结构模型表层的电流密度减小，因而电场强度出现一个明显的极小值。电阻率较高的区块排斥电流，使模型表层的电流密度增加，电场强度出现明显极大值。对于地下电流分布，在电阻率较小区块周围地下电流密度降低，而电阻率较大区块周围地下电流密度增加。这主要是由于地下电流在不同电阻率区块之间流通时，为了保证电流的连续性，电流密度在不同电阻率区块的边界处发生突变，并且不同区块的电阻率差异越大，电流密度突变的程度也越大。可见区块电阻率的差异会影响地下感应电流分布情况。
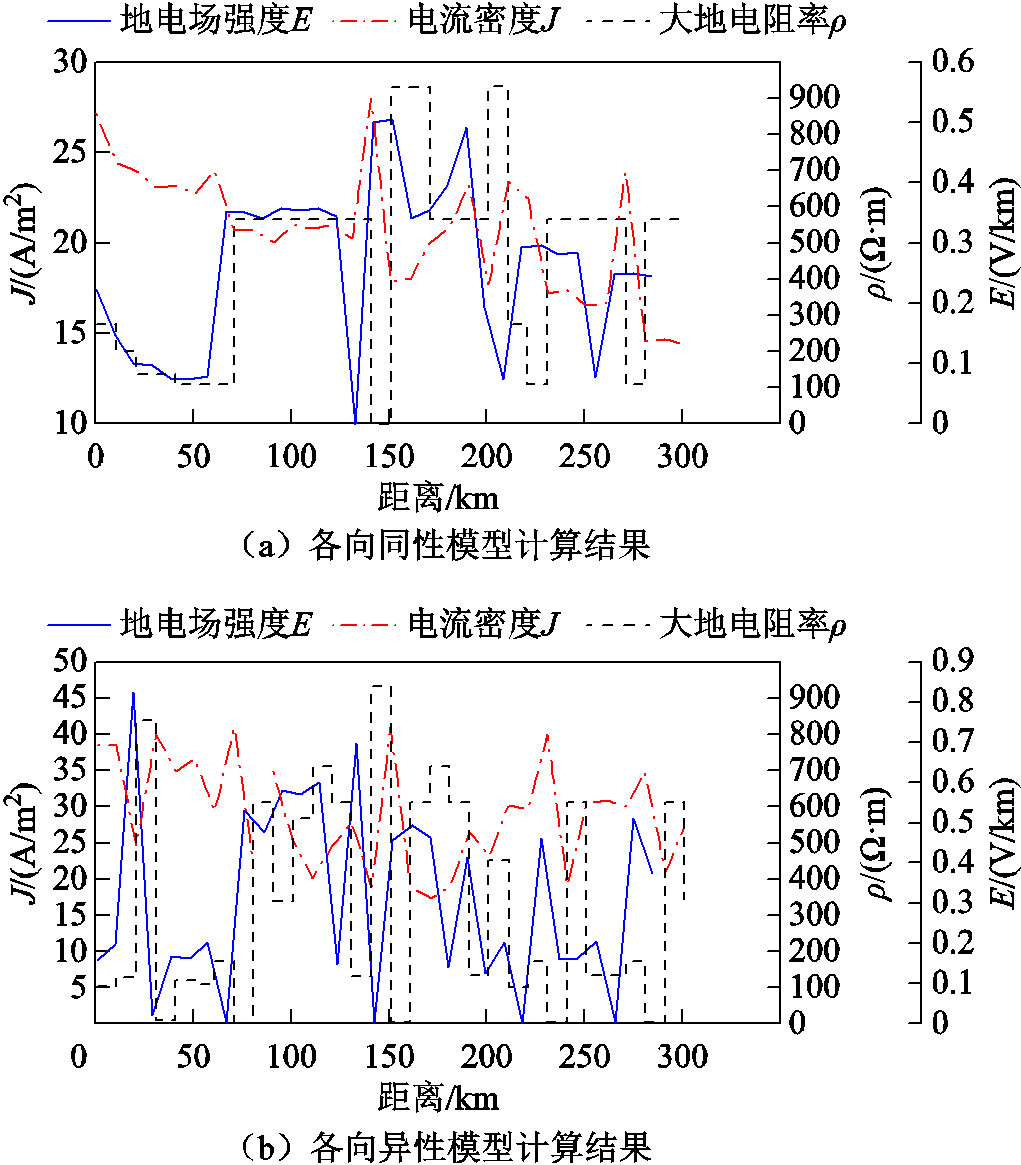
图3 计算结果
Fig.3 Calculation results
当各向异性区域的电导率取平均电阻率时，二者呈现出不同的异常幅度，各向同性模型地电场的最大异常幅度约为平均值的1.124倍，电流密度的最大异常幅度约为平均值的1.083倍，而各向异性模型地电场的最大异常幅度约为平均值的1.381倍，电流密度的最大异常幅度约为平均值的1.256倍。
将图1所示剖面按照大地电导率模型坐标系进行旋转，其中A2的左侧和右侧均为高阻区域，A5右侧为高导区域，左侧为高阻区域。通过改变A2和A5区域的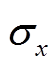
研究X轴方向电导率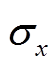对感应地电场的影响，其中X=100～300km，Y=40km，Z=0km范围内Ex如图4所示。
当A2和A5区域的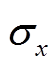发生变化时，Ex分量的振幅和相位曲线均发生不同幅度的改变。对于A5及其周边区域，由于A5右侧存在高导区块，左侧存在高阻区块，造成电磁波的衰减速度不同，所以对于存在高导区块的右侧，Ex曲线右侧随着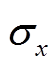的增加，Ex的振幅降低。相位曲线的右侧变化规律与振幅曲线右侧变化规律相反。对于A5左侧存在的高阻区块，其导波会影响电磁响应，致使Ex曲线和相位曲线左侧部分变化复杂且无规律。对于A2及其周边区域，其左右均为高阻区域，但是相比于右侧，左侧区域的电阻率稍低，因此A2的Ex幅值和相位曲线呈现相同的规律。
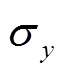对于Ex幅值和相位曲线左右支变化规律的影响与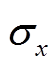相同，但是影响程度减小，即不同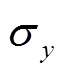对应的Ex幅值和相位曲线左右支分离程度明显减小。
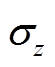对于Ex幅值和相位曲线左右支变化规律的影响程度很小，没有明显规律。因此，研究各向异性介质电导率变化对地电场的影响规律不仅结合各向异性本身的参数，也需要考虑各向异性介质区域周围高导/高阻区块的影响。
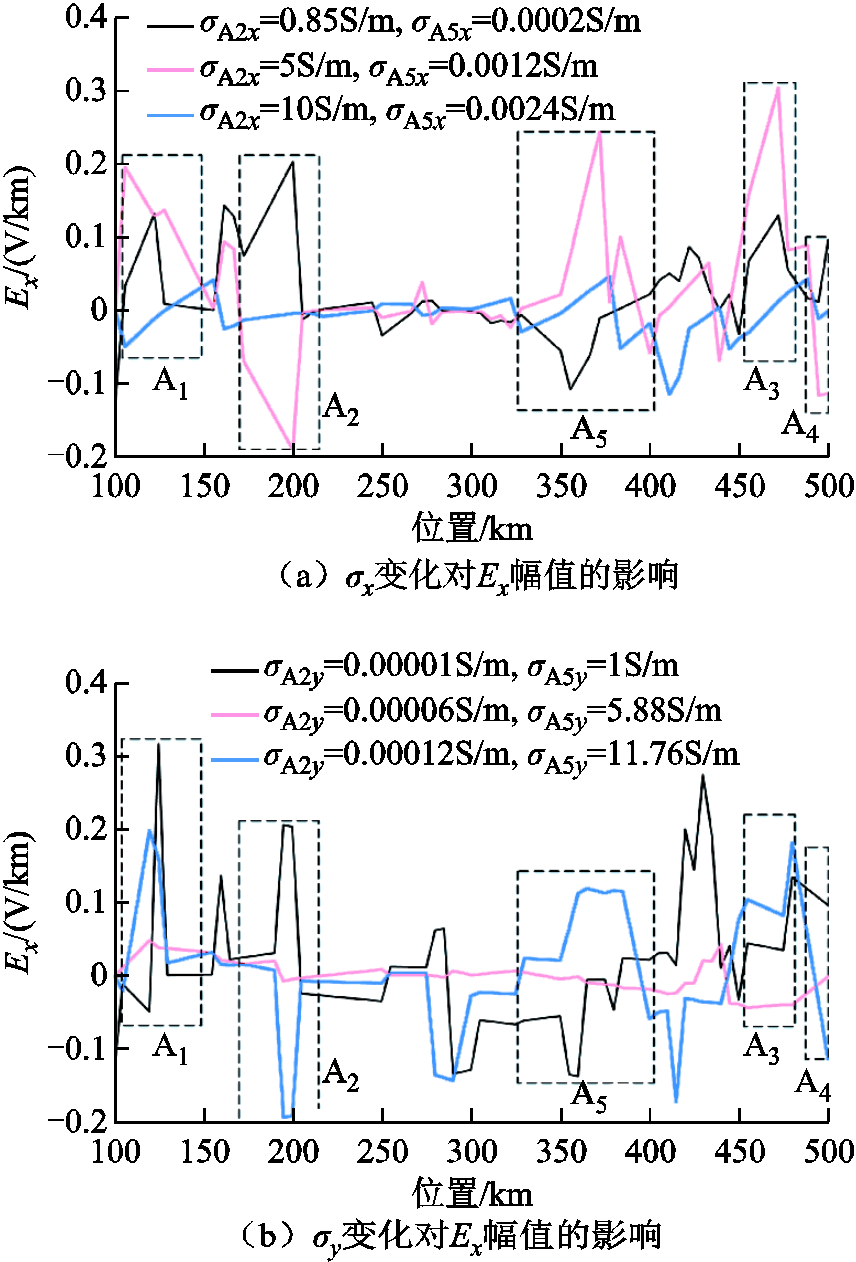
图4 电导率变化对Ex的影响
Fig.4 Effect of conductivity change on Ex
在Y=40km处做YZ切面（即沿存在各向异性区域的小范围大地电导模型上表面中心线做竖直切面），电流密度分布如图5所示。
图5 电导率变化对电流分布的影响
Fig.5 Influence of conductivity change on current distribution
竖直切面内电流方向在sx为10S/m时向X方向偏，特别是高阻区域上下，基本沿着水平方向流动，说明此时电流试图绕过高阻区域。对于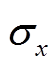为0.85S/m的情况，
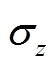相比于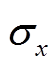为高导，所以A2区域内的电流偏向垂直方向。随着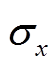的减小，电流由水平环绕、倾斜插入变为垂直穿透高阻区域。采用相同的方法研究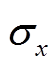变化对Ey、Jy、Ez、Jz的影响，发现无论是各向异性区域内还是周边区域，Ey、Jy、Ez、Jz受到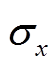影响较小。综上所述，各向异性介质不仅影响自身区域内的地电场分布，也会改变周边区域地电场。
利用2004年11月9日地磁暴乌鲁木齐地磁台的地磁扰动测量数据（事件1）、2006年12月4日地磁暴肇庆地磁台的地磁扰动测量数据（事件2）和2015年12月19日地磁暴北京地磁台的地磁扰动测量数据（事件3）研究各向异性介质对GIC的影响。基于两种大地电性结构模型计算得到X=0～400km，Y=40km，Z=0km范围内感应地电场并计算偏差如图6所示。
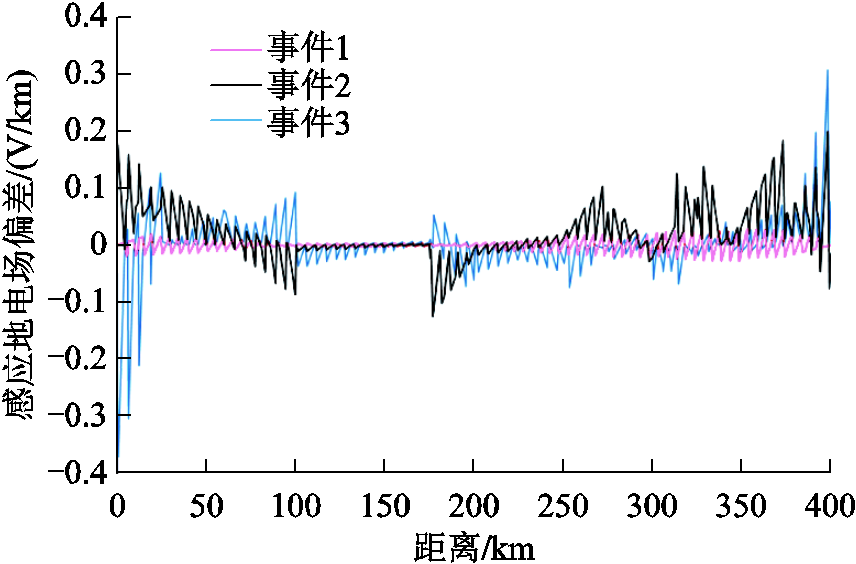
图6 不同地理位置两种模型的表层感应地电场偏差
Fig.6 Surface induced geoelectric field deviation of two models in different geographical locations
虽然不同方向的电导率变化肯定会对地电场产生影响，但在仿真结果中并没有体现出十分明显的规律，地下各向异性介质对于地表某一个位置的地电场的影响大部分会在0.1V/km范围内波动。直观地来看地电场的波动范围较小，为了体现各向异性介质对涉及地电场的问题研究价值，结合具体的工程实例进行说明。目前涉及地电场的问题包括地磁暴引起的GIC计算和接地极入地电流引起的偏磁电流计算。为了研究各向异性介质引起的感应地电场变化对相关问题的影响，引入三次地磁暴事件和哈密接地极算例进行验证。对于涉及地电场的GIC计算问题，采用如图7所示的新疆750kV电网进行分析。由于750kV线路全部采用六分裂导线，单位长度电阻远小于330kV线路，且330kV线路长度小于750kV线路，因此判断GIC主要在750kV电网流通，在建立电网等效模型时忽略330kV电网的影响。
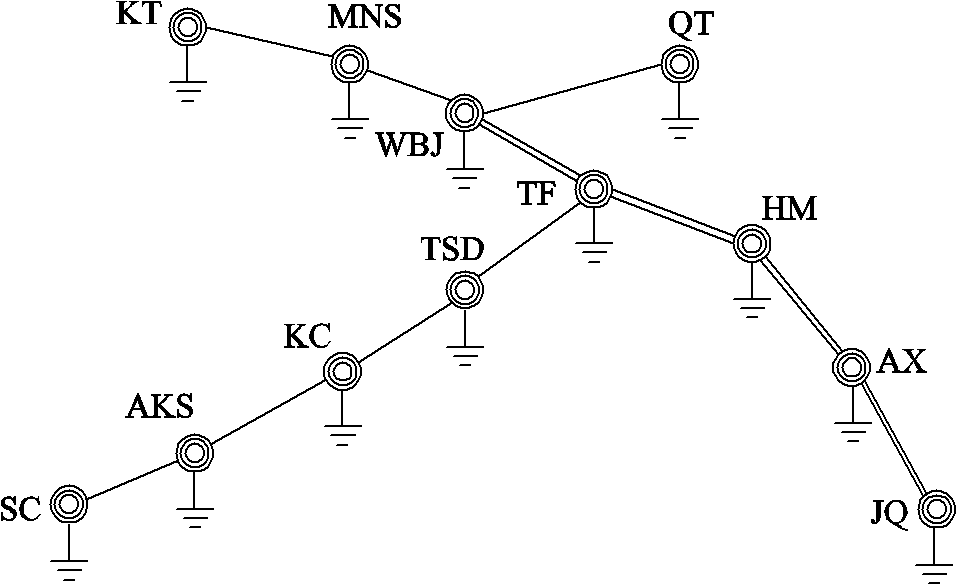
图7 2012年新疆750kV电网
Fig.7 Xinjiang 750kV power grid in 2012
利用典型线路参数和变压器参数结合文献[17]提出的电网元件等效方法，对相关变压器和线路参数进行等效，计算得到的感应地电场和GIC偏差见表1。
表1 感应地电场和GIC偏差
Tab.1 Induced geoelectric field deviation and GIC deviation
地磁暴事件最大偏差最小偏差 感应地电场强度/(V/km)GIC/A感应地电场强度/(V/km)GIC/A 事件10.104 64.032 20.003 40.067 1 事件20. 200 96.120 60.000 70.013 5 事件30.386 819.194 60.003 11.035 2
利用两种模型计算得到的GIC进行偏差分析，分别利用两种模型计算感应地电场强度的最大偏差为0.386 8V/km、最小偏差为0.000 7V/km；GIC的最大偏差为19.194 6A、最小偏差为0.013 5A。各点的地电场偏差并不大，但是建立大地电阻率模型并计算GMD地电场的最终目的是结合接地点经纬度及电网参数计算GIC。在计算等效电压源时需将地电场沿输电线路积分[7]，新疆电网750kV输电线路长度大部分在300km左右，等效电压源的平均偏差会达到80.26V，将降低GIC计算结果的准确度。
为了验证GIC的偏差是由于计算等效电压源时地电场偏差的累计造成的，利用2004年11月9日6:00:00UT至10日18:00:00UT地磁台记录数据，将新疆750kV线路的长度全部按1/10缩短，比较各个站点的GIC如图8所示。
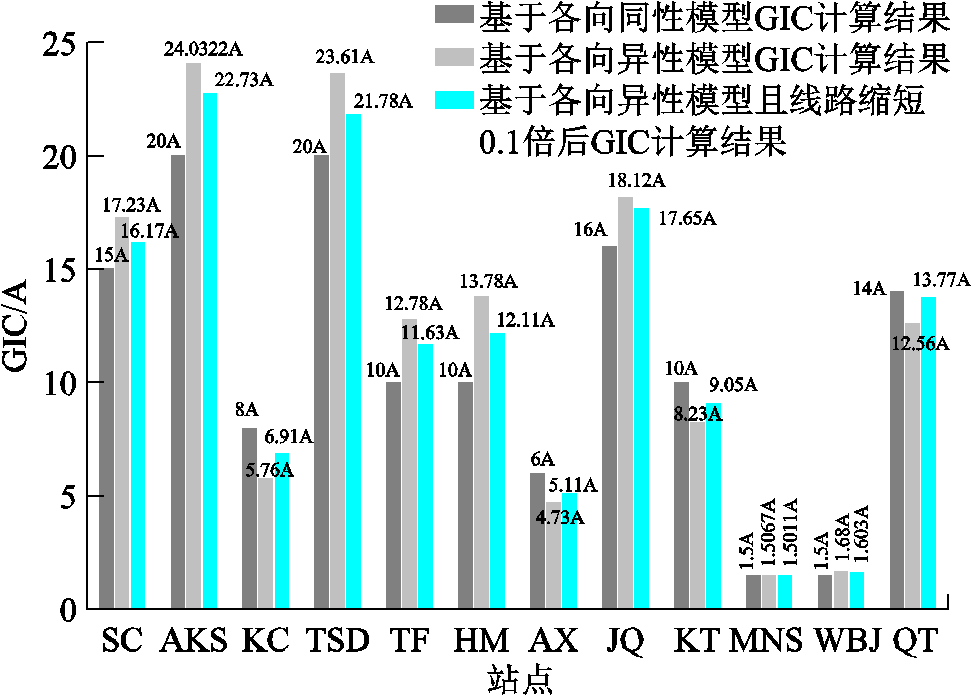
图8 新疆750kV电网各站点GIC幅值
Fig.8 GIC amplitude of stations in Xinjiang 750kV Power Grid
对线路长度缩放前后得到的GIC进行偏差分析，对于线路缩短后的网络模型，GIC的最大偏差为2.73A、最小偏差为0.001 1A，平均偏差为0.667 8A。相比于原始网络模型，各个站点的GIC偏差值均有所减小，所以线路的长短将影响地电场造成GIC偏差值的大小。
对于涉及地电场的偏磁电流计算问题，利用±800kV天中直流输电工程哈密接地极周边交流电网的偏磁电流问题，哈密接地极近区的电网结构如图9所示。需要说明的是由于哈密接地极距离大地电磁测区较远，超过了以接地极为圆心的200km范围，而哈密接地极近区又没有关于地下电性各向异性介质的数据资料，同时考虑到本文仅对地下存在的电性各向异性介质是否会对偏磁电流的计算产生影响作出定性判断，并未与实测值进行比较，故将哈密接地极近区的厂站均向大地电磁测区平移，使得哈密接地极近区的电网对应大地电磁测区位置。
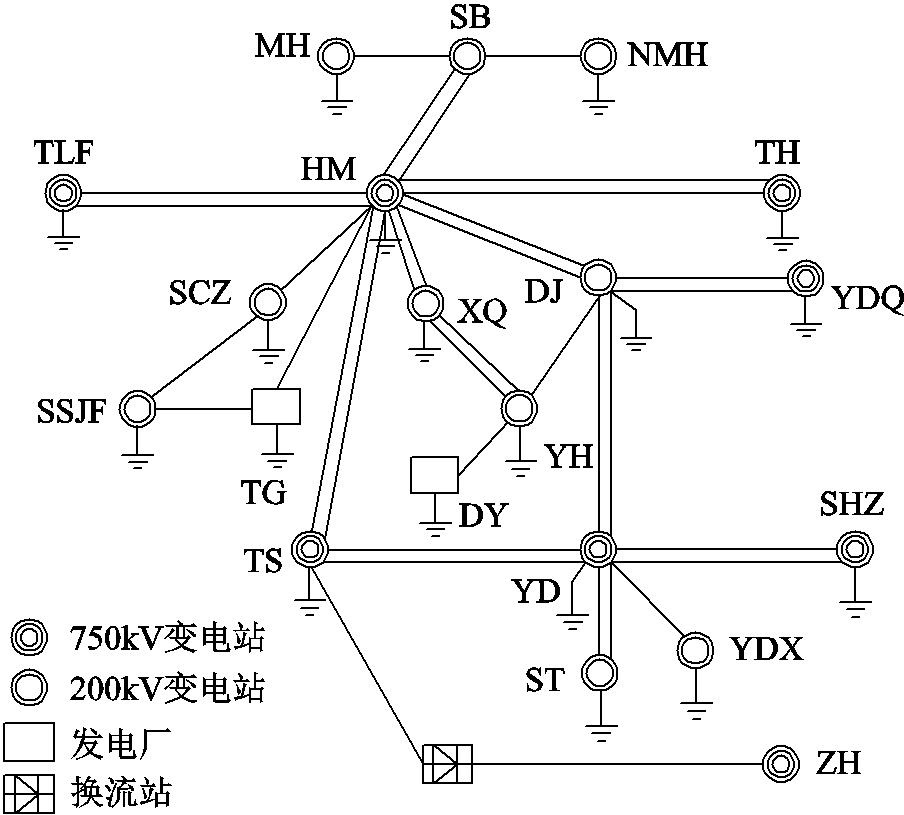
图9 哈密接地极近区电网结构图
Fig.9 Power grid structure near Hami grounding electrode
对于接地极近区交流厂站的偏磁电流，在模型的上表面提取各接地点对应坐标的电位，结合等效电网模型计算偏磁电流，哈密接地极近区交流厂站变压器接地极点地电位和偏磁电流见表2。
表2 两种模型主要变电站地电位和偏磁电流（5000A）
Tab.2 The main substation ground potential and magnetic bias current in the two models (5000A)
站点各向同性模型地电位/V各向异性模型地电位/V各向同性模型偏磁电流/A各向异性模型偏磁电流/A NMH4.1363.821-1.39-1.43 HM25.99826.1326.286.12 SCZ18.5317.970.951.21 DJ18.10317.07815.214.38 TG20.52221.006-0.36-0.43 DY11.8919.897-1.41-1.52 YDQ5.4034.9321.381.22 SB9.70110.239-2.34-2.78
对两种模型计算得到的变压器接地点电位和偏磁电流进行偏差分析，分别计算两种模型计算地电位的最大偏差为1.994V、最小偏差为0.134V、平均偏差为0.69V；偏磁电流的最大偏差为0.82A、最小偏差为0.04A、平均偏差为0.258 A，这样的差别在接地极引起的偏磁电流治理问题中并不会有太大影响。
接地极入地电流引起的偏磁电流计算过程与GIC的计算过程相似，都需要建立大地电性结构模型及等效网络模型，但两者在具体的等效电压源获取问题上有所区别。GIC的计算存在一个感应地电场沿输电线路积分的过程，从而获得线路上的等效电压源，而偏磁电流的计算直接从有限元计算结果中提取各变电站接地点的地电位，不存在累加的过程，这样就没有误差的累计。因此直流输电接地极入地电流引起的偏磁电流计算可以忽略地下存在的电性各向异性介质的影响。
将地质勘测资料中的张量电导率数据引入大地建模中，分别利用新疆地区张量电导率建立存在电性各向异性介质的大地电性结构模型计算地磁暴感应地电场，进一步结合新疆750kV电网结构参数和位置移动后的天中工程哈密接地极近区电网结构计算GIC，结果表明：
1）地下高阻介质具有排斥电流的能力，电阻率越高，排斥能力越强；高导介质具有吸引电流的能力，电阻率越低，吸引电流能力越强。由于这种特性会使地下感应电流在空间上分布不均匀，进而导致位于不同地质结构的变电站之间产生电位差，成为电网GIC的等效电压源。并且各向异性区域内主轴电导率的变化不仅会对区域内相应方向上地电场产生影响，也会对区域周边的地电场产生影响，其变化规律与各向异性区域周边存在的高导或高阻体密切相关。虽然各向异性介质对于某一位置地电场影响幅度较小，但是其会影响周边区域内地电场分布，因此影响范围较大。
2）研究磁暴时地电场分布，介质的各向异性将影响地表电场的分布，虽然在每一点的地电场强度相差并不是很大，但考虑到计算GIC时需要将地电场强度沿线路进行积分得到接地点之间的电位差，对于长输电线路会造成GIC计算准确度降低，进而影响电网受磁暴侵害评估的准确性。地下存在的电性各向异性介质同样会影响接地极入地电流产生的地表电位，但是由于线路等效电压源的计算方法不同，只需利用接地极位置和各厂站距离接地极的距离提取中性点电位即可得到等效电压源，不涉及误差的累计，所以地下存在的电性各向异性介质对偏磁电流计算偏差影响较小。
参考文献
[1] 霍光谱, 胡祥云, 黄一凡, 等. 带地形的大地电磁各向异性二维模拟及实例对比分析[J]. 地球物理学报, 2015, 58(12): 4696-4708.
Huo Guangpu, Hu Xiangyun, Huang Yifan, et al. MT modeling for two-dimensional anisotropic conductivity structure with topography and examples of comparative analyses[J]. Chinese Journal of Geophysics, 2015, 58(12): 4696-4708.
[2] 胡祥云, 霍光谱, 高锐, 等. 大地电磁各向异性二维模拟及实例分析[J]. 地球物理学报, 2013, 56(12): 4268-4277.
Hu Xiangyun, Huo Guangpu, Gao Rui, et al. The magnetotelluric anisotropic two-dimensional simulation and case analysis[J]. Chinese Journal of Geophysics, 2013, 56(12): 4268-4277.
[3] 杨淼鑫, 谭捍东, 梁盛军, 等. 对称非各向同性体大地电磁法二维异常特征[J]. 物探与化探, 2019, 43(4): 794-803.
Yang Miaoxin, Tan Handong, Liang Shengjun, et al. Two-dimensional anomaly characteristics of the magnetotelluric method for a symmetrical anisotropic body[J]. Geophysical and Geochemical Exploration, 2019, 43(4): 794-803.
[4] 王泽忠, 董博, 刘春明, 等. 华北地区大地电性结构三维建模及磁暴感应地电场有限元计算[J]. 电工技术学报, 2015, 30(3): 61-66.
Wang Zezhong, Dong Bo, Liu Chunming, et al. Three-dimensional earth conductivity structure modelling in North China and calculation of geoelectromagnetic fields during geomagnetic disturbances based on finite element method[J]. Transactions of China Electrote-chnical Society, 2015, 30(3): 61-66.
[5] Bo Dong, Wang Zezhong, Boteler D, et al. Review of earth conductivity structure modelling for calculating geo-electric fields[C]//2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, 2013: 1-5.
[6] Sun Rui, Balch C. Comparison between 1-D and 3-D geoelectric field methods to calculate geomagnetically induced currents: a case study[J]. IEEE Transactions on Power Delivery, 2019, 34(6): 2163-2172.
[7] Marti L, Yiu C, Rezaei Zare A, et al. Simulation of geomagnetically induced current with piecewise layered-earth models[J]. IEEE Transactions on Power Delivery, 2014, 29(4): 1886-1893.
[8] 司远, 王泽忠, 刘连光, 等. 基于Kriging法的直流接地极附近大地电性结构建模方法[J]. 电工技术学报, 2020, 35(21): 4448-4454.
Si Yuan, Wang Zezhong, Liu Lianguang. Modeling method of geoelectric structure near DC grounding electrode based on Kriging method[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4448-4454.
[9] 刘春明, 王璇, 刘连光, 等. 考虑海岸效应影响的电网地磁感应电流的计算方法[J]. 中国电机工程学报, 2016, 36(22): 6059-6066.
Liu Chunming, Wang Xuan, Liu Lianguang, et al. Calculation method of geomagnetically induced current in the power grid considering the influence of the coast effect[J]. Proceedings of the CSEE, 2016, 36(22): 6059-6066.
[10] Marti L, Rezaei-Zare A, Boteler D. Calculation of induced electric field during a geomagnetic storm using recursive convolution[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 802-807.
[11] Wannamaker P E. Anisotropy versus heterogeneity in continental solid earth electromagnetic studies: fundamental response characteristics and implications for physicochemical state[J]. Surveys in Geophysics, 2005, 26(6): 733-765.
[12] 殷长春, 贲放, 刘云鹤, 等. 三维任意各向异性介质中海洋可控源电磁法正演研究[J]. 地球物理学报, 2014, 57(12): 4110-4122.
Yin Changchun, Ben Fang, Liu Yunhe, et al. MCSEM 3D modeling for arbitrarily anisotropic media[J]. Chinese Journal of Geophysics, 2014, 57(12): 4110-4122.
[13] 王宁, 汤井田, 任政勇, 等. 基于有限体积法的二维大地电磁各向异性数值模拟[J]. 地球物理学报, 2019, 62(10): 3912-3922.
Wang Ning, Tang Jingtian, Ren Zhengyong, et al. Two-dimensional magnetotelluric anisotropic forward modeling using finite-volume method[J]. Chinese Journal of Geophysics, 2019, 62(10): 3912-3922.
[14] 王泽忠, 黄天超. 变压器地磁感应电流-无功功率动态关系分析[J].电工技术学报, 2021, 36(9): 1948-1955.
Wang Zezhong, Huang Tianchao. Analysis of geomagnetically induction current-reactive power dynamic relationship of transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1948-1955.
[15] 喻国. 大地电磁三维任意电各向异性正演模拟及应用研究[D]. 北京: 中国地震局地质研究所, 2018.
[16] 刘静莲. 考虑磁暴地域特征的感应地电场研究[D]. 北京: 华北电力大学, 2013.
[17] 刘连光, 郭世晓, 魏恺, 等. 基于全节点模型的三华电网地磁感应电流计算[J]. 电网技术, 2014, 38(7): 1946-1952.
Liu Lianguang, Guo Shixiao, Wei Kai, et al. Calculation of geomagnetically induced currents in interconnected north China-central China power grid based on full-node GIC model[J]. Power System Technology, 2014, 38(7): 1946-1952.
Study on the Induced Geoelectric Field of Geomagnetic Storm Considering the Underground Anisotropic Medium
Abstract Geological survey data show that there are electrically anisotropic media underground, so the influence of anisotropic media should be considered when studying the geomagnetic disturbance (GMD) geoelectric field. The earth conductivity model including anisotropic medium is established to study the influence of uneven electrical structure and anisotropic medium on the distribution of earth electric field. Combined with the data in Xinjiang, an anisotropic conductivity model is constructed to calculate the GMD geoelectric field. Compared with the isotropic earth conductivity model, it is found that the change of principal axis conductivity in the anisotropic region will affect the geoelectric field in the corresponding direction and the surrounding geoelectric field in the region, and its change law is related to the high conductivity or high resistance area around the anisotropic region. The geomagnetically induced current (GIC) is obtained by combining the structural parameters of the power grid. It is proved that although anisotropic media have little influence on the size of the surface induced geoelectric field, the calculation error of GIC will increase due to the accumulation of errors due to the equivalent voltage source obtained by integrating the geoelectric field along the transmission line when calculating the GIC.
keywords：Geoelectric field, anisotropy, geoelectric structure, geomagnetically induced current
DOI:10.19595/j.cnki.1000-6753.tces.201727
中图分类号：TM155
收稿日期 2020-12-11
改稿日期 2021-07-31
王泽忠 男，1960年生，博士，教授，博士生导师，研究方向为电力系统电磁兼容和电磁场数值计算。E-mail：wzzh@ncepu.edu.cn
司 远 男，1993年生，博士研究生，研究方向为电网安全运行与灾变控制。E-mail：siy@ncepu.edu.cn（通信作者）
（编辑 郭丽军）