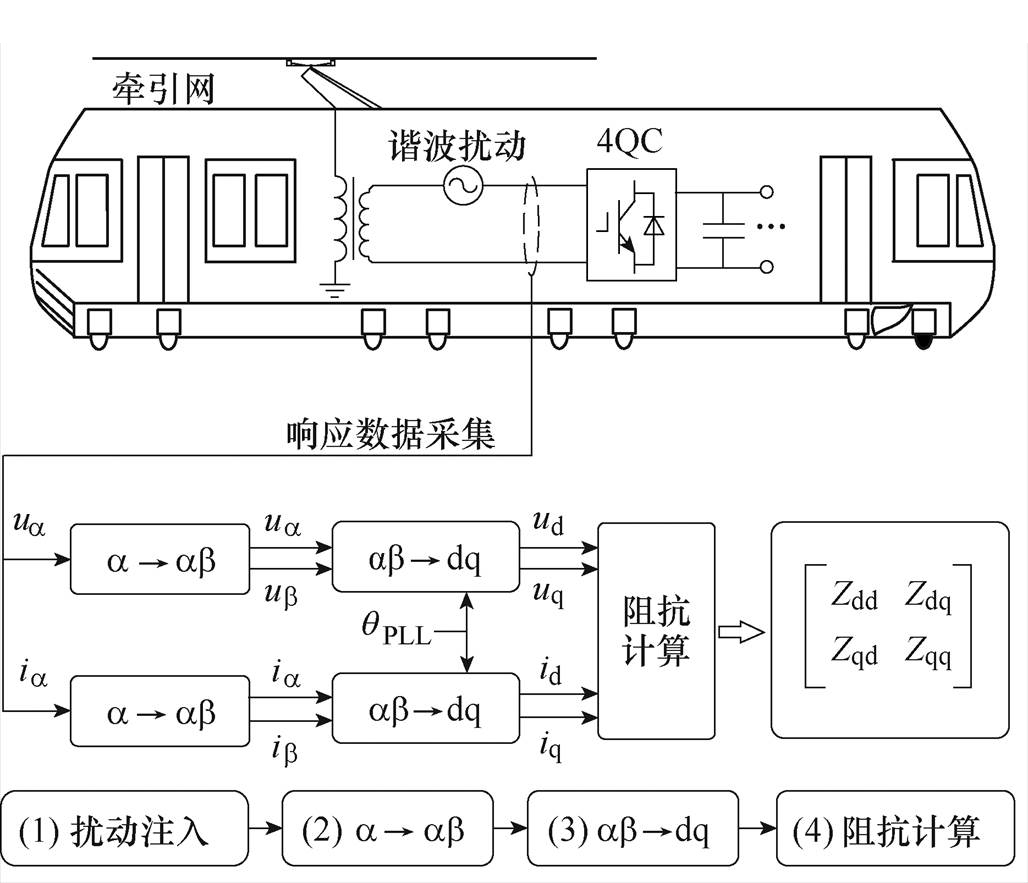
图1 高速列车4QC设备dq阻抗测量步骤
Fig.1 dq impedance measurement steps of high-speed train 4QC
摘要 高速列车以电力电子四象限变流器（4QC）作为能量转换单元，其与牵引供电网的阻抗特性不匹配将导致系统出现低频振荡、谐波放大等现象，影响电气化铁路的安全稳定运行。阻抗测量技术能够有效获取实际工程系统的阻抗特性，有较广的应用前景。现有研究表明，由4QC控制系统不对称等特性带来的频率耦合效应将干扰“宽频式”阻抗测量结果的准确性，若要避免，可选择“扫频式”的阻抗测量方法。然而，该文发现当采用“扫频式”方法进行4QC的dq阻抗测量时，其频率耦合效应同样会恶化测量结果的准确性，因此，详细分析其干扰机理并提出一种便捷有效的抑制策略。最后，基于Matlab/Simulink及硬件在环测试平台搭建详细的4QC阻抗测量模型，测量结果验证了所揭示的干扰机理及所提出的抑制策略的正确性与有效性。
关键词：高速列车 频域阻抗测量 频率扫描 频率耦合 dq阻抗
高速铁路是我国“十三五”乃至“十四五”期间的一个重大发展方向，由于其具有较高的舒适性、准时性与快速性，逐渐成为人们出行的首选形式，因而保障其安全稳定运行具有重大意义[1-5]。其中，高速列车利用具有恒功率特性的电力电子四象限变流器（Four-Quadrant Converter, 4QC）设备作为能量转换单元，其大量应用带来的负电阻特性极大地弱化“车”与“网”组成的“车网闭环系统”稳定性[6-9]。严重时导致的“弱”甚至“负”稳定性裕度，致使“车网闭环系统”发生低频振荡、谐波放大等失稳现象[6-11]，造成高速铁路保护误动、列车晚点及旅客滞留等严重后果。
现有研究表明，此类失稳现象是“并网闭环系统”频域阻抗特性不匹配造成的[12-15]。因此，获取其频域阻抗特性极为关键，目前小信号数学建模是一种比较成熟的获取阻抗特性的方法。文献[12]建立了高速列车4QC在dq旋转坐标系下的小信号阻抗模型，并利用“并网闭环系统”的主导极点判定低频振荡模态。文献[13-14]细化了4QC中锁相环（Phase Locked Loop, PLL）的小信号阻抗模型，并利用多种稳定性判据分析了系统的稳定性状态。文献[15]建立了复矢量dq旋转坐标系下的系统阻抗模型，分析了负电阻特性对其稳定性的影响规律。
然而，以上基于小信号数学建模获取“并网闭环系统”频域阻抗特性的方式需要得知系统详细的拓扑结构与运行参数。对于实际工程现场的“黑箱”型系统难以良好应用，而基于“阻抗测量”的方式无需得知被测系统具体拓扑及参数，只需采集谐波扰动后被测系统端口处的电压电流响应数据，结合dq阻抗计算公式，即可得到其频域阻抗特性。因此，阻抗测量方法更适用于获取实际工程现场的频域阻抗特性。
对于“网”的频域阻抗测量，常采用测量速度更快的“宽频式”测量技术。文献[16]提出了一种结合反并联绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）及脉冲宽度调制（Pulse Width Modulation, PWM）驱动的“宽频式”阻抗测量技术，定量分析了PWM频率与占空比对宽频频谱分布的作用机理。进一步地，为了加强“宽频式”阻抗测量技术的频谱可控性，文献[17]提出了一种“蝶形”扰动电路及“Chirp-PWM”驱动技术，能够对频带的双边限值进行有效控制，然而这种方法的宽频均匀度不够高。因此，文献[18]提出了一种模块化的扰动电路，结合“分段Chirp-PWM”驱动技术，不但能够控制频带的双边限值，而且频谱均匀度也得到极大改善。
对于“车”的频域阻抗测量，由4QC控制系统不对称等特性带来的频率耦合效应将干扰“宽频式”阻抗测量结果的准确度[19]。因此，现有研究大多采用“扫频式”阻抗测量方法进行获取4QC或者此类电力电子变流设备的频域阻抗特性。文献[19]详细阐述了频率耦合现象干扰“宽频式”阻抗测量结果准确度的原因，并采用“扫频式”的测量方法得到了电力电子变流设备的dq阻抗特性。文献[20]利用希尔伯特（Hilbert）变换及dq变换，将单相响应数据转换至dq旋转坐标系下，利用“扫频”的思路测量4QC的dq阻抗特性。文献[21]设计了一种“扫频式”的阻抗测量仪器，对4QC的dq阻抗特性进行了有效测量。
然而，研究过程中发现，这类传统的“扫频式”dq阻抗测量方法并不能完全避免频率耦合的干扰。若不考虑此时频率耦合的影响，将直接恶化测量结果的准确性。因此，本文以高速列车4QC设备为测量对象，首先，介绍了其传统dq阻抗测量方法。然后，创新性地分析了频率耦合现象对测量步骤中的“坐标变换”及“阻抗计算”的影响规律。针对此，提出了一种便捷有效的频率耦合干扰抑制策略：在对采集的响应数据进行坐标变换之前，利用快速傅里叶变换（Fast Fourier Transform, FFT）及快速傅里叶逆变换（Inverse Fast Fourier Transform, IFFT）剔除有效响应频率之外的所有干扰量，然后再进行之后的测量步骤。最后，通过Matlab/Simulink仿真和硬件在环实验验证了所揭示的干扰机理及所提出的抑制策略的正确性与有效性。
高速列车以4QC设备作为电能转换单元，其dq阻抗测量方法可分为四个步骤，如图1所示[20-21]。首先，在4QC端口处串联注入谐波电压扰动；其次，利用电压电流采集装置获取被测系统的响应数据，记为ua、ia，再将其旋转90°得到与之正交的另一组分量ub、ib；然后，利用dq变换，将静止坐标系下的ab 分量转换至旋转坐标系下，记为ud、uq、id、iq；最后，利用dq阻抗计算公式得到测量结果。
图1 高速列车4QC设备dq阻抗测量步骤
Fig.1 dq impedance measurement steps of high-speed train 4QC
谐波电压扰动常用于4QC设备的阻抗测量之中[21]。在系统最大扰动能量约束下，扫频法由于一次性只注入一个频率的扰动信号，因此，系统在该频率处的响应信号信噪比较高，所获得的测量结果准确度也相应较高。设定阻抗测量目标频率为fmes，由于4QC的多输入多输出特性，若想获取该频率处的
dq阻抗特性，则需要向被测系统分别注入频率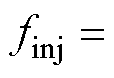
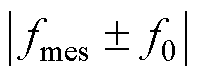的两次单频扰动[20]。值得注意的是，由于受奈奎斯特采样定理的约束，阻抗测量频率fmes一般控制在高速列车4QC设备开关频率一半以内，因此测量频率不会受到4QC设备PWM带来的特征谐波干扰。
利用电压电流采集装置对被测系统响应数据进行测量。然后，结合Hilbert变换，将单相系统a 系分量旋转90°，得到另一组b 系分量，完成“a→ab”的转换。以电流信号ia 为例，Hilbert变换公式为
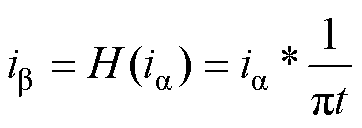（1）式中，“H”为Hilbert算子；“*”为卷积运算。
对式（1）进行傅里叶变换，其计算结果为
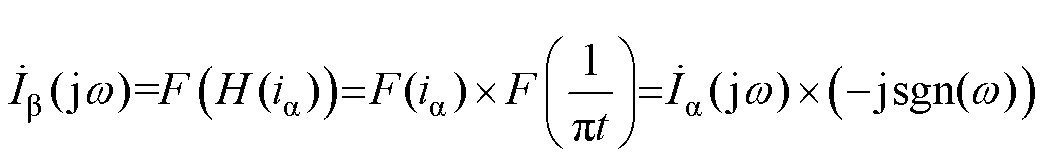（2）式中，F为傅里叶变换算子；sgn为符号函数，即
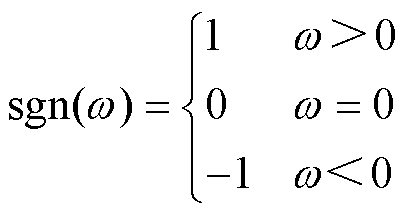（3）
将式（3）代入式（2），可得
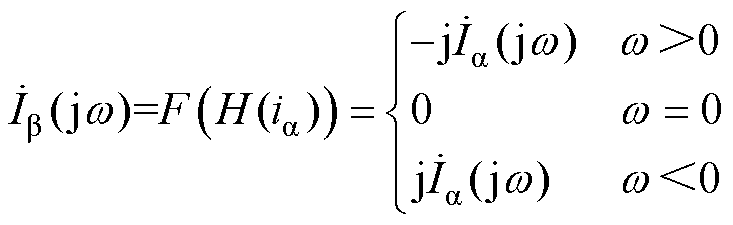（4）可见，采集的a 系响应分量通过Hilbert变换后能够对除了直流成分外的各个频率均进行相移90°的变换，从而得到与之正交的b 系分量。最终共同构成一组完整的ab 系下的分量。
通过1.2节得到ab 系下的分量后，对其进行dq变换得到旋转坐标系下的d轴及q轴分量。变换公式为
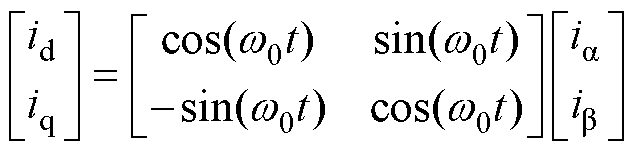（5）式中，w0为系统锁相环提供的同步角频率信号。
同理，ua 通过上述的“a→ab”“ab→dq”两级变换后，亦可得到相应的旋转坐标系下的d轴及q轴分量（ud、uq），为1.4节dq阻抗计算提供数据。
在1.1节注入的两次单频扰动下，能够得到相应的两组电压电流响应信号。然后，分别对其进行“a→ab”“ab→dq”两级变换，得到两组相应的dq系下的响应分量ud1、uq1、id1、iq1及ud2、uq2、id2、iq2。此时，4QC端口电压电流关系可表示为
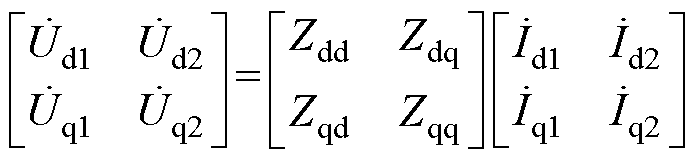（6）式中，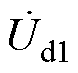
、
、
、
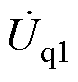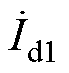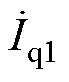为第一次单频扰动下的dq频域分量；
、
、
、
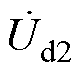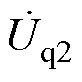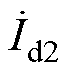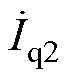为第二次单频扰动下的dq频域分量；
、
、
、
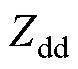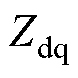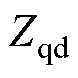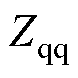为被测系统dq阻抗特性的四个元素。
因此，由式（6）变换得到其相应的dq阻抗计算公式为
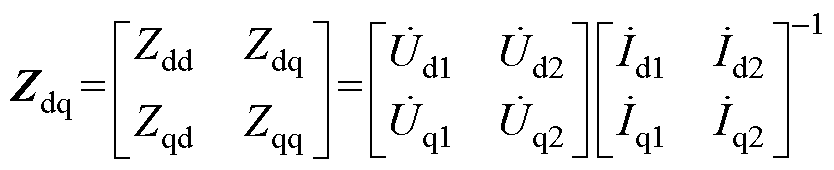（7）当设定不同的阻抗测量目标频率fmes时，可得到相应频率下的dq阻抗。因此，利用上述过程对被测对象进行“频率扫描”，即可得到设定频带内完整的频域阻抗特性。以上即为高速列车4QC设备dq阻抗“扫频式”测量的基本思路。
当向系统注入频率为finj的单频扰动时，系统在静止坐标系下的响应频率除了在理想的finj处以外，由于4QC控制系统的不对称等因素，还存在着较多的频率耦合分量，耦合频率为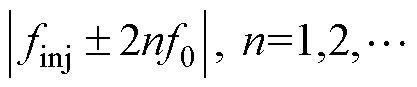
。其中，当n=1时，频率耦合分量幅值最大，为
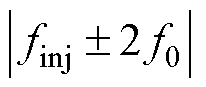，当注入频率为finj时的系统主要响应量如图2所示。下面将详细分析这两个较大分量对于dq阻抗测量的干扰机理。
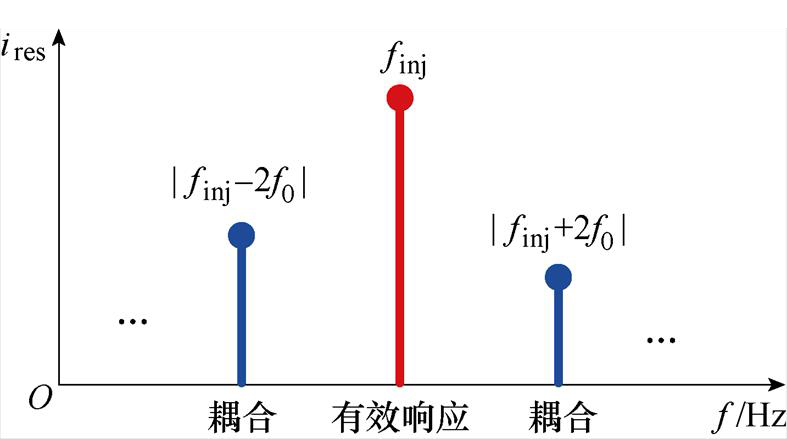
图2 当注入频率为finj时的系统主要响应量
Fig.2 Main response components when the injected frequency is at finj
当对图2所示的响应量进行dq变换时，根据不同的dq轴旋转方向，可以得到不同的dq系下的响应频率，即对静止坐标系下的响应频率进行加减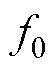
（
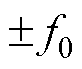）变换。
首先，分析第一种减(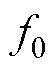
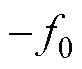)变换的情况，图2所示的三个响应量在dq旋转坐标系下的频率分别为
、
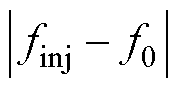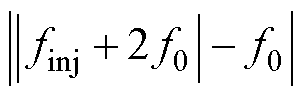及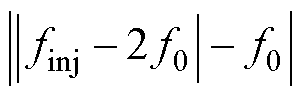
。分四类讨论finj不同取值范围下，去掉绝对值符号的表达形式。-f0变换下finj不同取值范围内的干扰分析如图3所示。
（1）当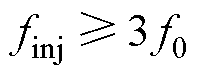
时，三者的频率去掉绝对值分别为
、
、
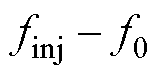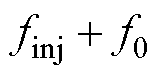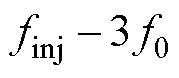，如图3a所示。
可见，响应频率间没有相互重叠的现象，即不会出现频率间的相互干扰。
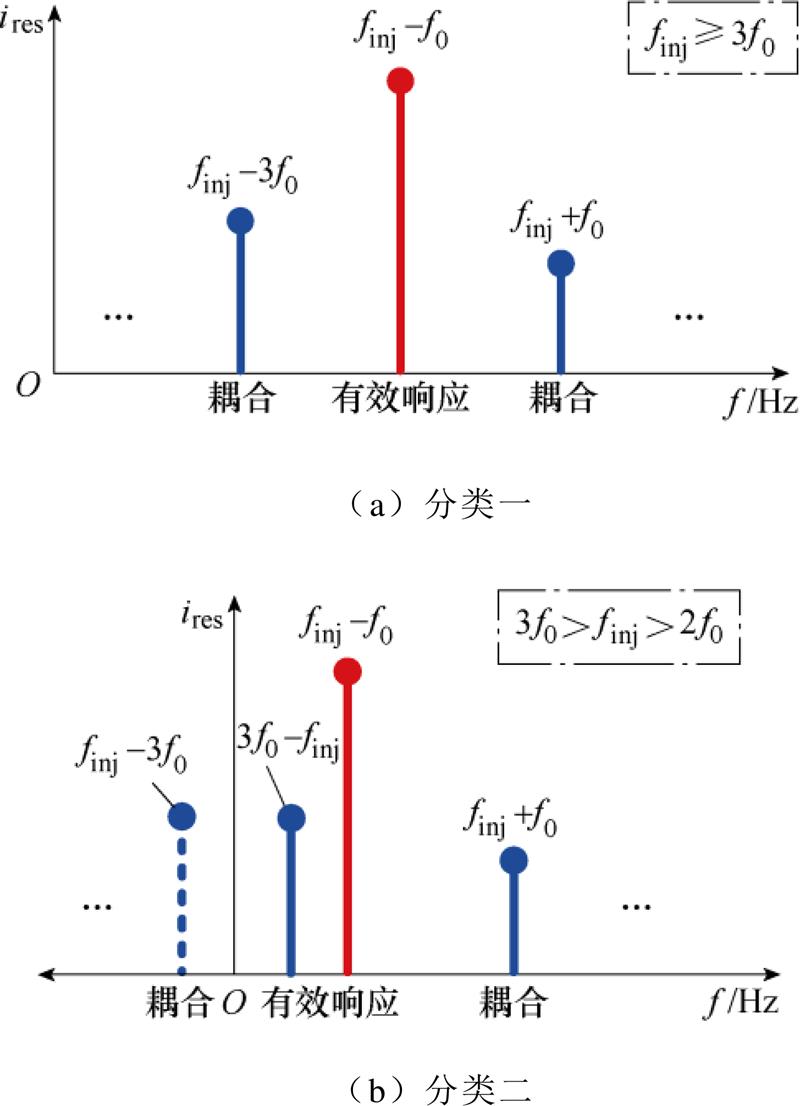
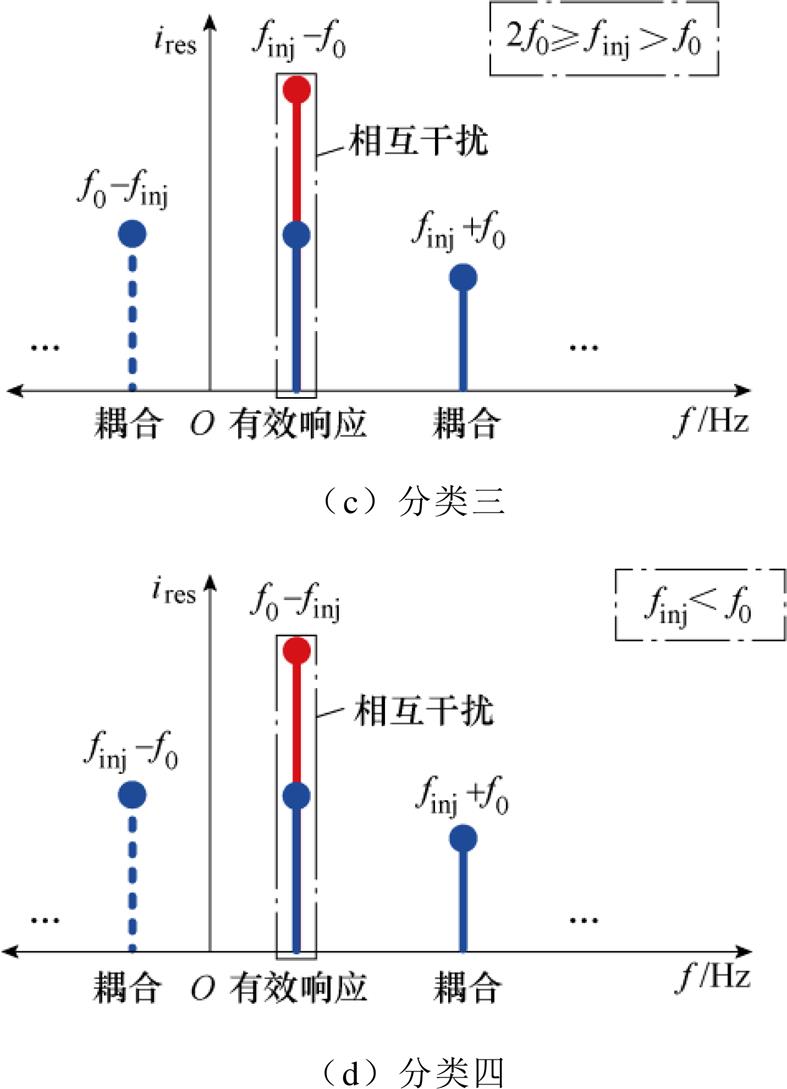
图3 -f0变换下finj不同取值范围内的干扰分析
Fig.3 Frequency interference analyses with finj in different range when under -f0
（2）当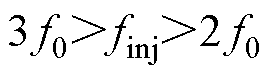
时，三者的频率去掉绝对值分别为、、
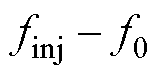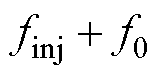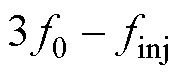，如图3b所
示。可见，响应频率间依旧没有相互重叠的现象，即不会出现频率间的相互干扰。
（3）当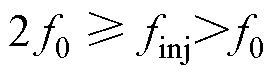
时，三者的频率去掉绝对值分别为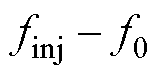、、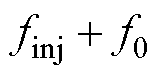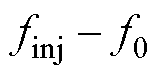，如图3c所示。
可见，响应频率间出现了相互重叠的现象，即会出现频率间的相互干扰。
（4）当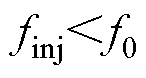
时，三者的频率去掉绝对值分别为
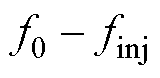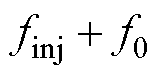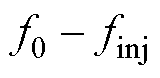、、，如图3d所示。可见，
响应频率间存在相互重叠的现象，即会出现频率间的相互干扰。
然后，分析第二种加(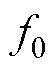
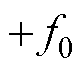) 变换的情况，此时图2所示的三个响应量在dq旋转坐标系下的频率分为
、
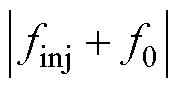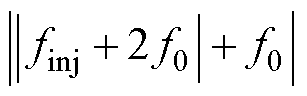及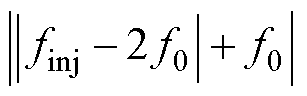
。这种情况下，可分三类讨论finj不同取值范围下，去掉绝对值符号的表达形式，+f0变换下finj不同取值范围内的干扰分析如图4所示。
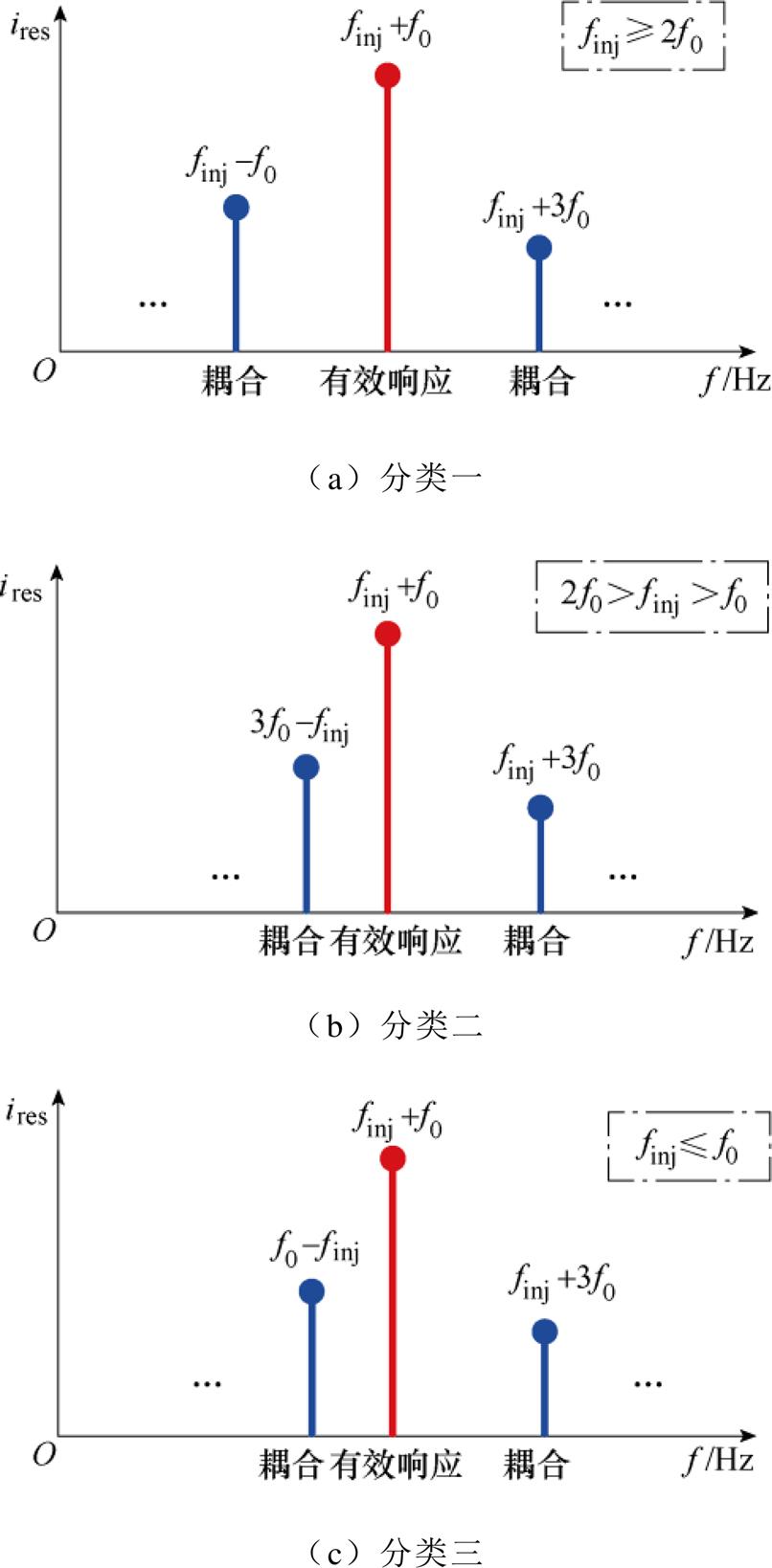
图4 +f0变换下finj不同取值范围内的干扰分析
Fig.4 Frequency interference analyses with finj in different range when under +f0
（1）当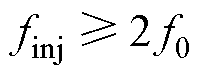
时，三者的频率去掉绝对值分别为、
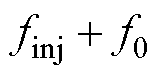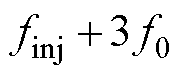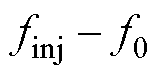、，如图4a所示。可见，响应频率间没有相互重叠的现象，即不会出现频率间的相互干扰。
（2）当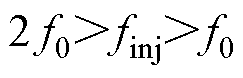
时，三者的频率去掉绝对值分别为、、
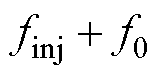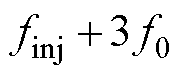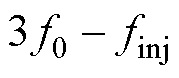，如图4b所示。可见，响应频率间仍然没有相互重叠的现象，即也不会出现频率间的相互干扰。
（3）当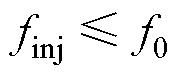
时，三者的频率去掉绝对值分别为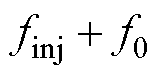、、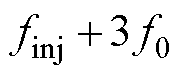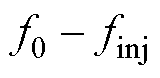，如图4c所示。可见，响应频率间依旧没有相互重叠的现象，即仍然不会出现频率间的相互干扰。
综上所述，当注入频率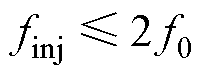
，且dq变换采用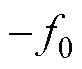变换的情况时，有效响应频率与耦合频率在dq旋转坐标系下出现重叠干扰现象，影响测量结果的准确性。
由1.1节可知，当目标dq阻抗测量频率设定为fmes时，则需要向被测系统端口注入两次单频扰动，为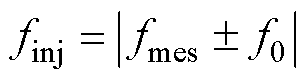
。
当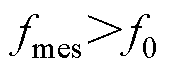
时，
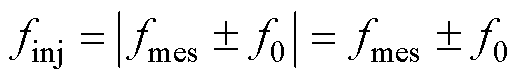。若想获得dq下频率绝对值为fmes的两组响应量，则需要对
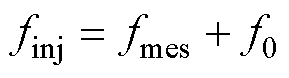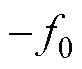进行变换形式的dq变换。由于此时
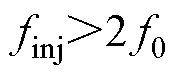，由2.1节分析可知，这种情况不会出现响应频率间的相互干扰。同理，需要对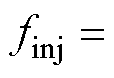 
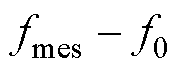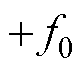进行变换形式的dq变换，这种情况也不会出现响应频率间的干扰。因此，当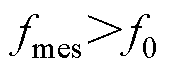时，测量结果不会被耦合频率干扰。
当
时，
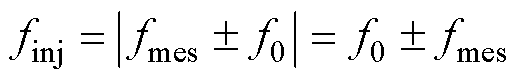。若想获得dq下频率绝对值为fmes的两组响应量，则需要对
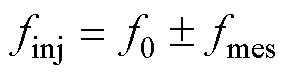均进行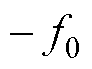
变换形式的dq变换。由于此时
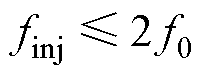，由2.1节分析可知，响应频率间会出现相互干扰现象。因此，将干扰阻抗计算 结果。
为了避免以上呈现的频率耦合量在dq坐标系下干扰系统有效响应的提取，本文提出一种便捷有效的抑制策略，高速列车4QC设备dq阻抗测量改进步骤如图5所示。点画线框外所列步骤为传统的高速列车4QC设备dq阻抗测量方法，在此基础上，点画线框内所示步骤为所提出的抑制策略。在对采集的被测系统响应电压电流数据做两级坐标变换之前，利用FFT提取并保留此时频域中的有效响应成分，剔除其他所有非有效响应量。然后，利用IFFT将此频域有效成分反变换回时域。之后再进行后面的测量步骤。
通过以上方法，由于在进行两级坐标变换之前已将所有非有效响应量全部剔除，只保留了唯一的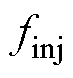
处的有效响应成分。因此，在两级坐标变换之后自然也不存在响应频率间的干扰，所提解决方案频谱分析如图6所示。经过两种不同旋转方向的坐标变换后产生的dq量1与dq量2均不会被耦合量所干扰（无耦合频谱成分）。
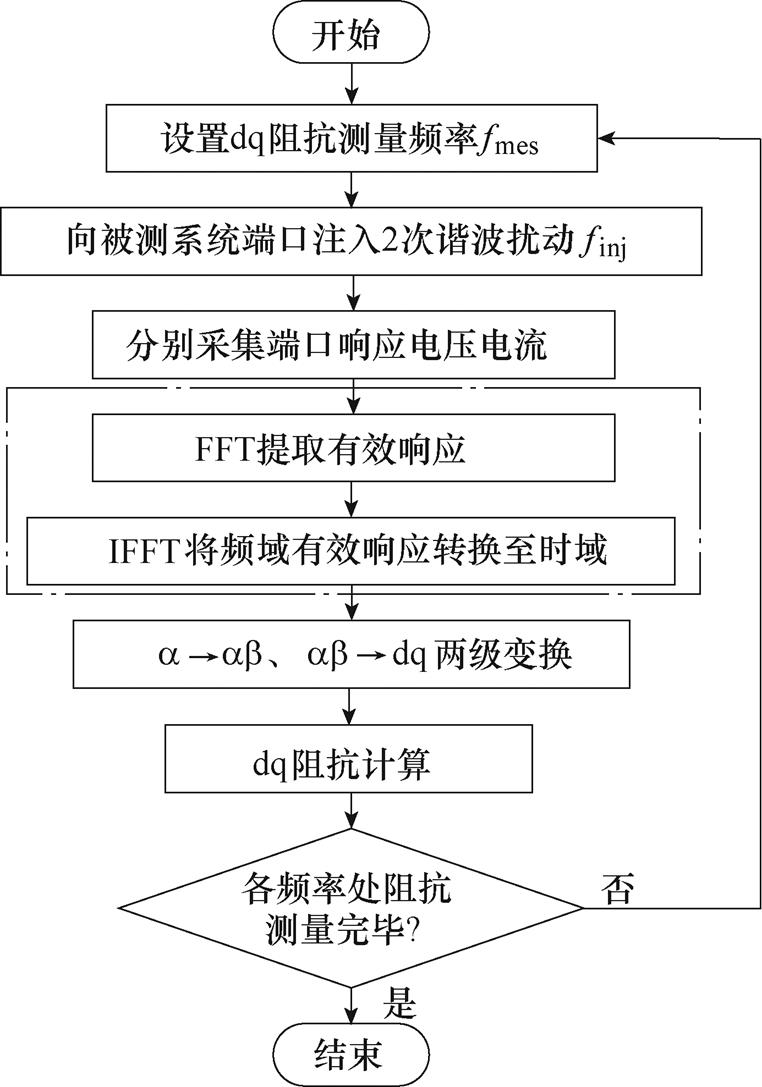
图5 高速列车4QC设备dq阻抗测量改进步骤
Fig.5 Improved dq impedance measurement steps of single-phase 4QC
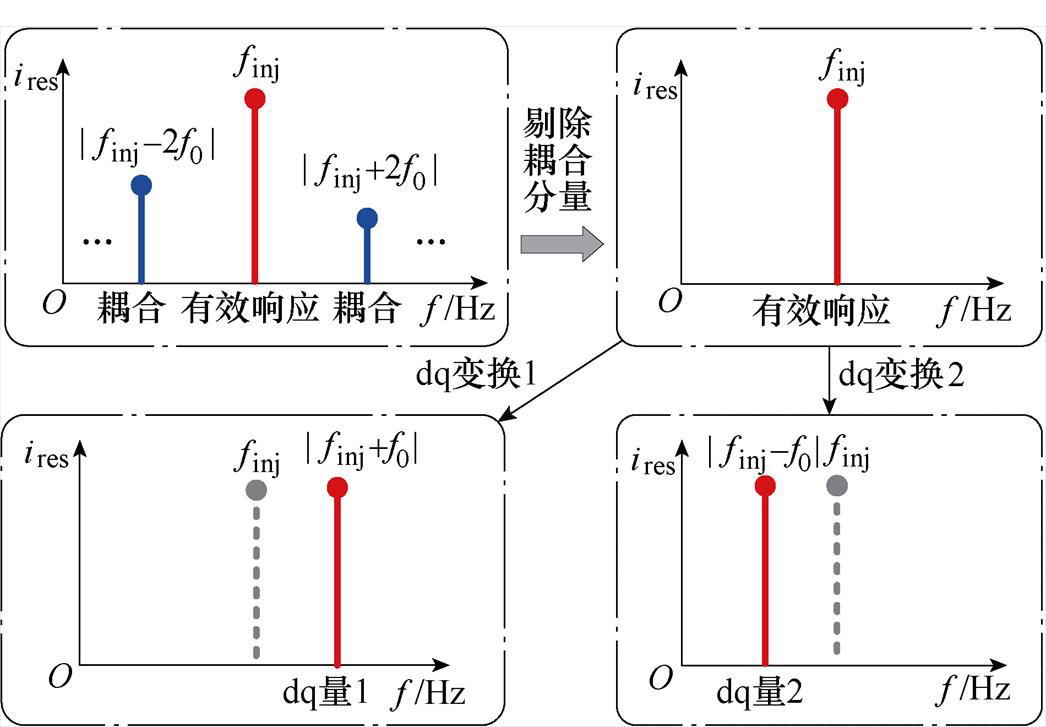
图6 所提解决方案频谱分析
Fig.6 Spectrum analysis of the proposed solution
根据文献[20-22]所呈现的高速列车4QC设备等效拓扑及控制，基于Matlab/Simulink建立其dq阻抗测量仿真模型，高速列车4QC阻抗测量等效仿真平台如图7所示。其中，控制系统由电压外环、电流内环双闭环控制结构实现。采集4QC实际直流侧电压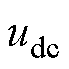
，与给定的直流电压参考值
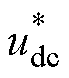作比较，其差值送入外环PI控制器进行调节，产生的量作为电流内环d轴的参考值
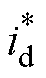。采集4QC交流侧电压
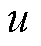，利用二阶广义积分器（Second-Order General Integr- ator, SOGI）及ab→dq变换得到q轴电压
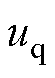，使用控制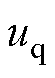=0的PLL技术得到整个控制系统的参考相位
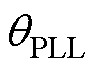。采集4QC交流侧电流
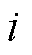，同理采用坐标变换得到d轴电流
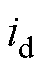与q轴电流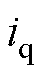
，分别和参考值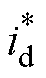与0相比较，差值使用内环的PI控制器进行调节。除此之外，在4QC端口处串联谐波电压扰动源
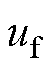，用以激发系统的谐波响应。整个仿真平台模型参数设置见表1。
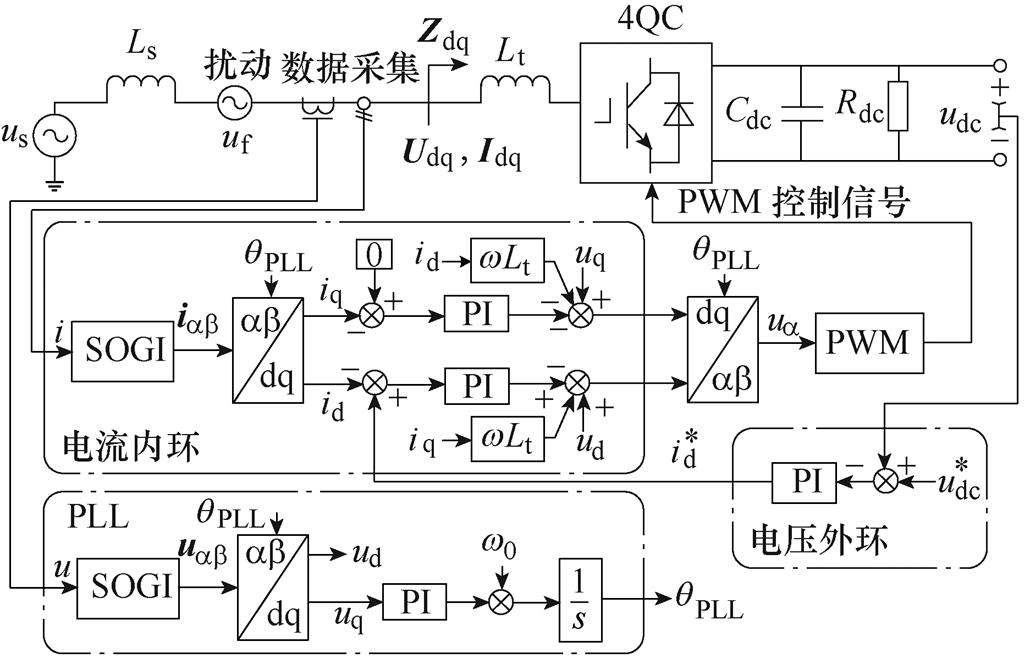
图7 高速列车4QC阻抗测量等效仿真平台
Fig.7 Equivalent simulation platform of impedance measurement for single-phase 4QC
表1 仿真平台参数设置
Tab.1 Parameters of the simulation platform
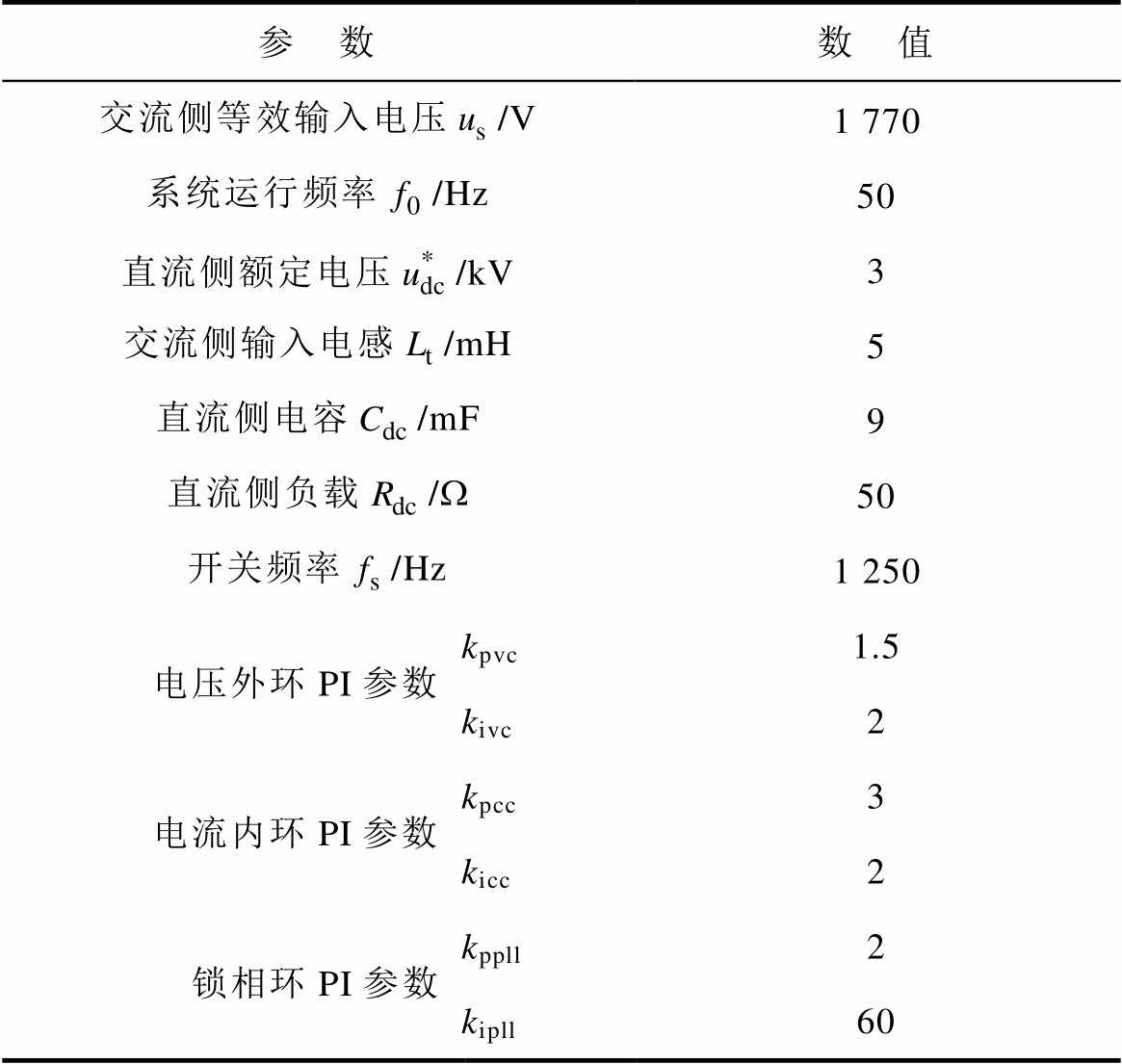
参 数数 值 交流侧等效输入电压/V1 770 系统运行频率/Hz50 直流侧额定电压/kV3 交流侧输入电感/mH5 直流侧电容/mF9 直流侧负载/W50 开关频率/Hz1 250 电压外环PI参数kpvc1.5 kivc2 电流内环PI参数kpcc3 kicc2 锁相环PI参数kppll2 kipll60
由2.1节的分析可知，当注入频率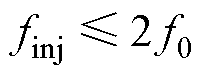，且dq变换采用
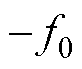变换的情况时，有效响应频率与耦合频率会在dq旋转坐标系下出现重叠干扰。设置4QC端口处注入的谐波扰动为
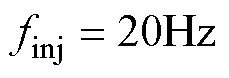。图8a为静止坐标系下的频率响应分布。可见，其主要存在着4个频率分量，分别为50Hz处的基频分量、20Hz处的有效响应、80Hz及120Hz处的两个频率耦合分量。将其进行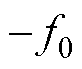形式的dq变换，得到旋转坐标系下的频率响应，如图8b所示。可见，30Hz处的响应幅值为66.208 6A，而与其相对应的图8a所示的20Hz处的有效响应幅值仅为43.021 7A。这是由于静止坐标系下除了20Hz处的成分会转换为旋转坐标系下30Hz的频率分量，80Hz处的耦合分量在旋转坐标系下也为30Hz，即静止坐标系下的有效响应频率与耦合频率转换到旋转坐标系下出现了频率间的重叠干扰现象。除此之外，旋转坐标系中的70Hz分量是静止坐标系中120Hz处的耦合分量变换而来的。以上仿真分析结果与2.1节呈现的干扰机理一致，验证了其正确性。
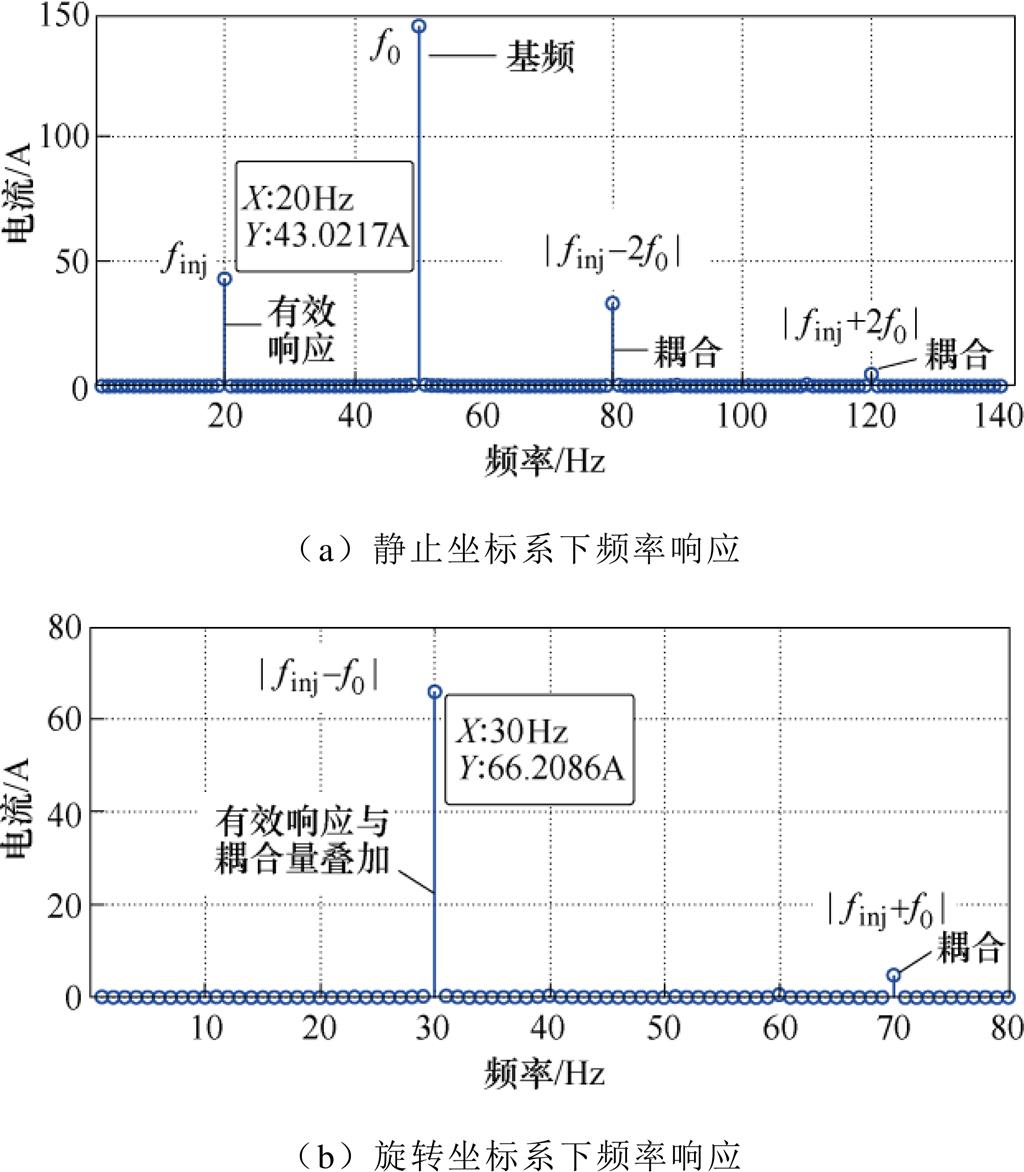
图8 传统方法注入扰动后系统频率响应分析
Fig.8 Frequency response analysis of traditional method after injecting harmonic disturbance
由2.2节的分析可知，当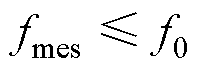
时，响应频率间会出现干扰现象，将影响阻抗计算结果。设置测量频段为1～100Hz，对所搭建的4QC等效模型进行了“扫频式”阻抗测量，测量结果如图9所示。可见，小于50Hz范围下的测量结果与大于50Hz的测量结果出现了“断层”现象，换言之50Hz频率处出现了测量结果不连续的现象。验证了扫频法中的频率耦合现象会对阻抗测量结果造成干扰。
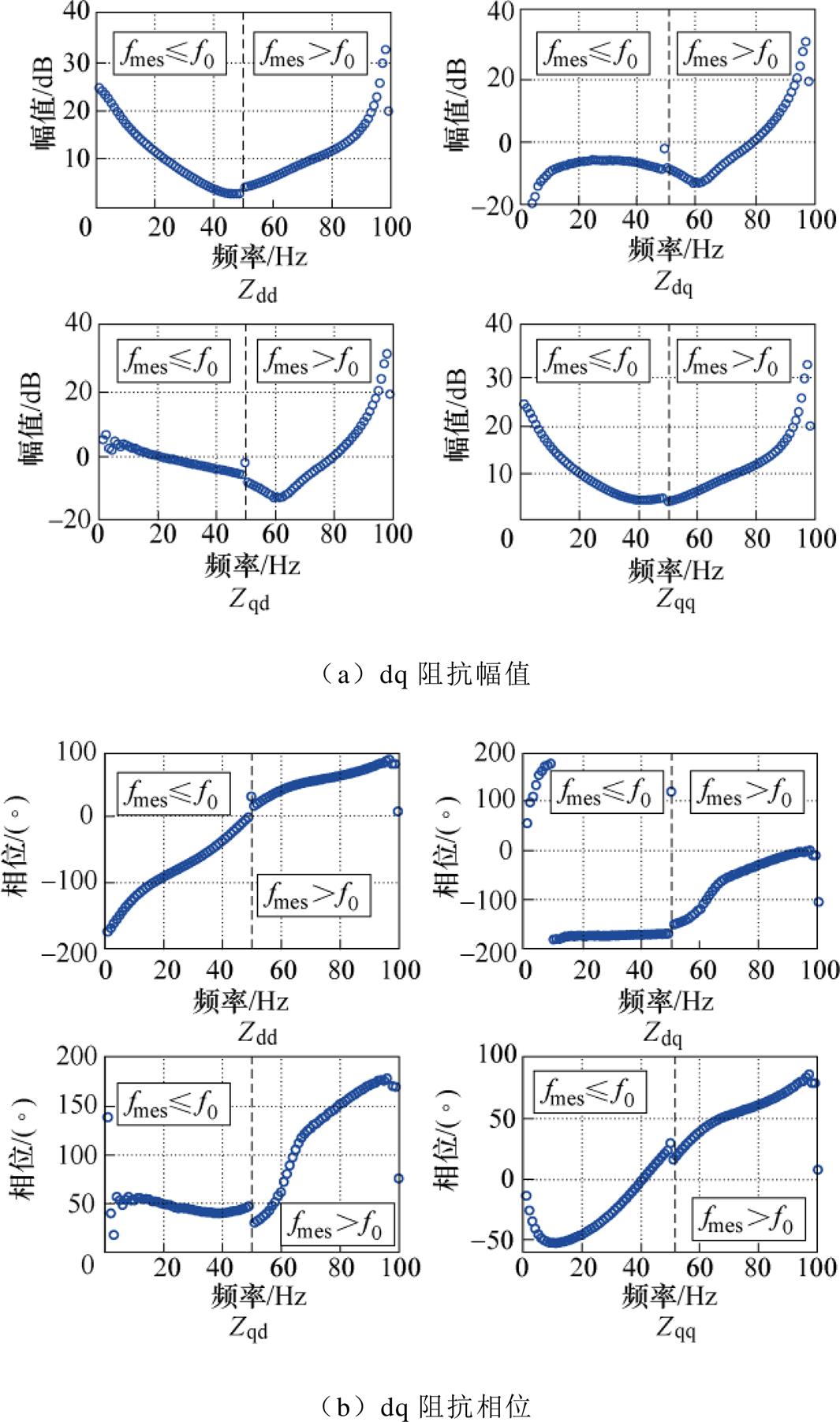
图9 传统方法频带为1～100Hz时的阻抗测量结果
Fig.9 Impedance measurement result of traditional method when setting the frequency band at 1Hz to 100Hz
采用3.1节所提解决方案对高速列车4QC等效模型进行dq阻抗测量。其中，系统在静止坐标系下的频率响应经过图5点画线框内所示步骤处理后，其结果如图10a所示。可见，此时系统只在有效频率20Hz处存在响应值，为43.021 7A，其他响应频率均被剔除。因此，将此响应变换至旋转坐标系下时，不会出现有效响应频率与耦合频率间的重叠干扰现象。如图10b所示，旋转坐标系下的有效响应值也为43.021 7A，与静止坐标系下的响应值保持一致。
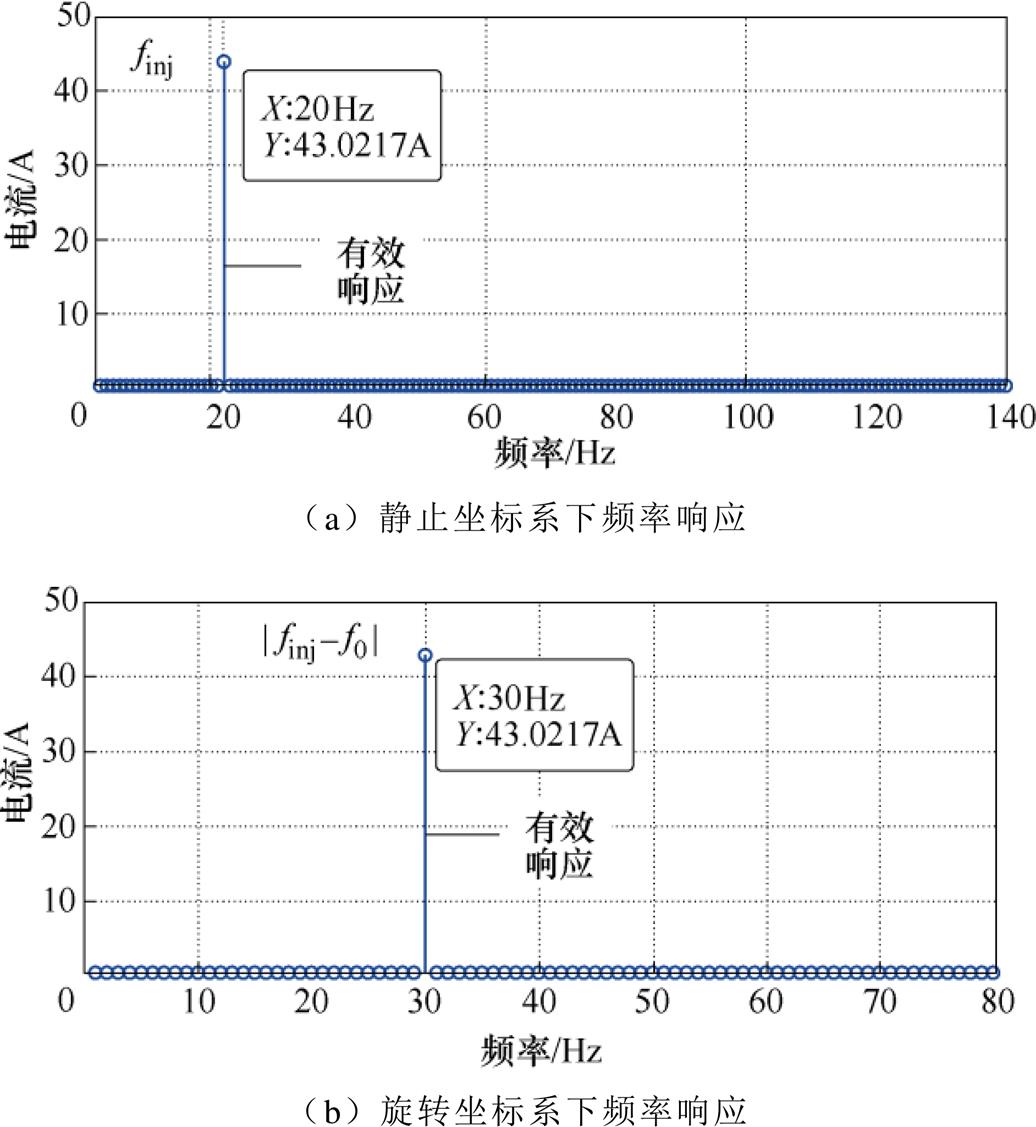
图10 所提方法注入扰动后系统频率响应分析
Fig.10 Frequency response analysis of proposed method after injecting harmonic disturbance
因此，采用所提方法进行dq阻抗计算时亦不会出现图9所示的在50Hz频率处的“断层”现象。所提方法频带为1～100Hz时的阻抗测量仿真结果如图11所示。可见，dq阻抗幅值与相位均能在频域内呈现出一条连续的曲线。由此，验证了所提方法的正确性。
为了进一步验证该方法的有效性，进行了更为实际的硬件在环验证，测试平台如图12所示。其中，阻抗测量硬件部分搭建在由Plexim公司开发的RT-Box中，系统控制算法由数字信号处理控制器（TMS320F28346）实现，PWM控制信号由现场可编程逻辑门阵列现场可编程门阵列（Field Pro- grammable Gate Array, FPGA）发出。整个测试平台参数设置见表2。
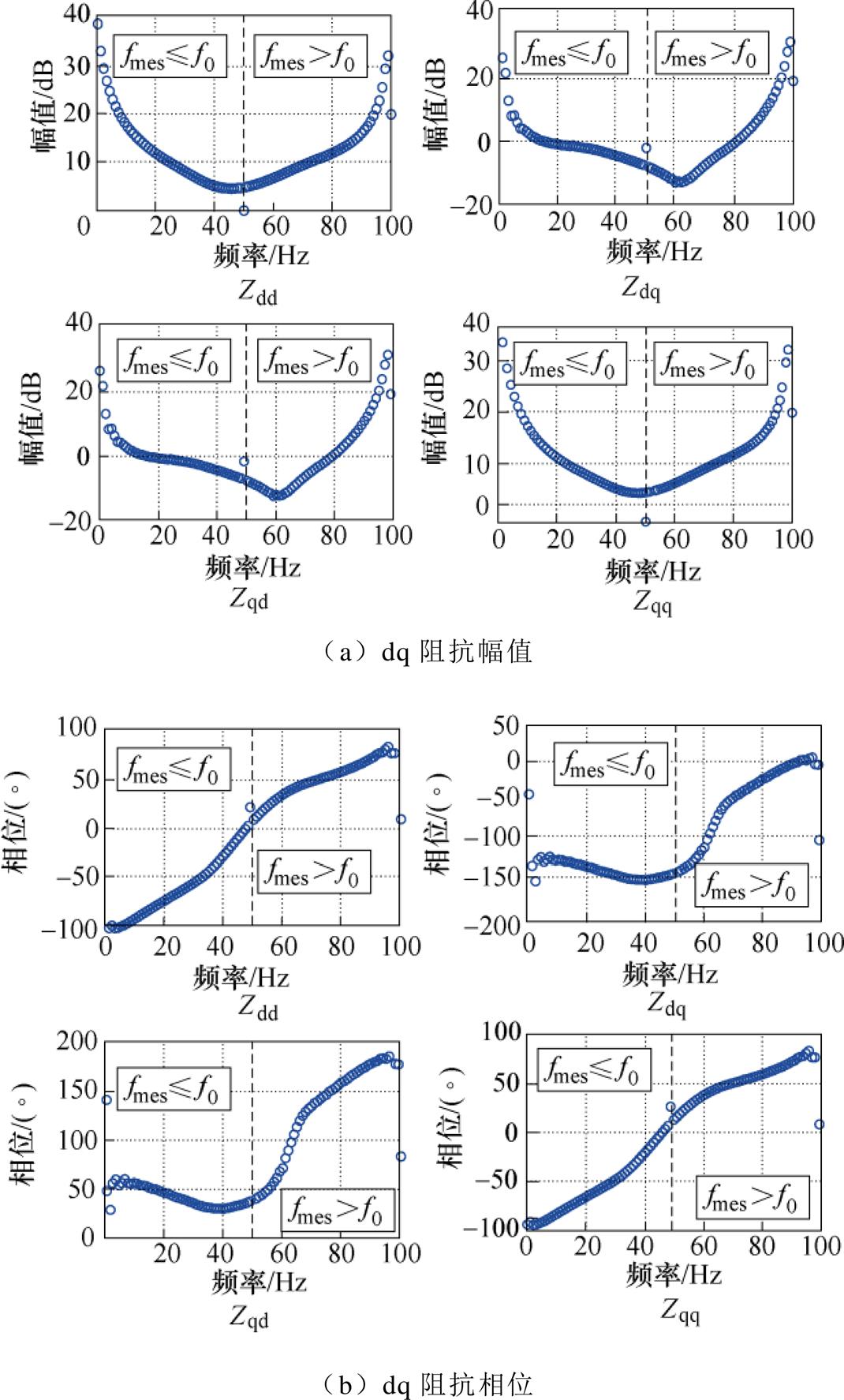
图11 所提方法频带为1～100Hz时的阻抗测量仿真结果
Fig.11 Impedance measurement simulation results of proposed method when setting the frequency band at 1Hz to 100Hz
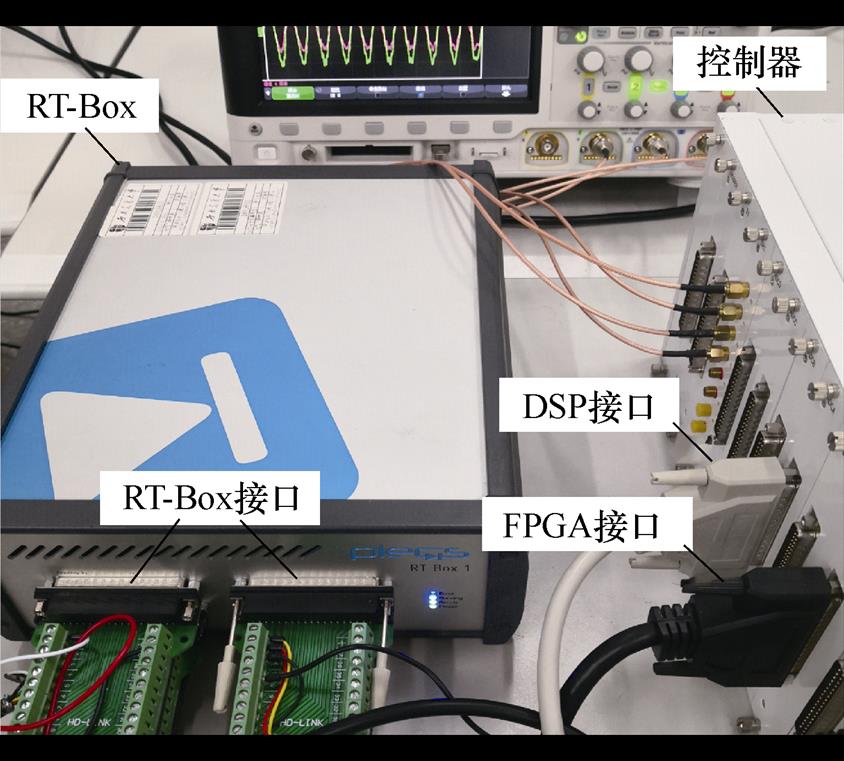
图12 高速列车4QC阻抗测量硬件在环测试平台
Fig.12 Hardware-in-the-loop test platform for measuring the high-speed train 4QC impedance
表2 测试平台参数设置
Tab.2 Parameters of the test platform
参 数数 值 RT-Box运行步长Tr/μs2 交流侧等效输入电压us/V1 770 系统运行频率f0/Hz50 直流侧额定电压/kV3.6 交流侧输入电感Lt/mH10 直流侧电容Cdc/mF9 直流侧负载Rdc/W100
（续）
参 数数 值 开关频率/Hz1 250 电压外环PI参数kpvc0.5 kivc10 电流内环PI参数kpcc5 kicc17 锁相环PI参数kppll0.09 kipll0.12
考虑频率耦合效应对阻抗测量结果的影响，采用所提抑制策略对测量对象进行频带为1～100Hz的测量工作，试验测量结果如图13所示。与仿真结果相同，由频率耦合干扰导致的50Hz处“断层”现象消失，表现为一条连续的阻抗曲线，因此进一步验证了所提测量方法的有效性。
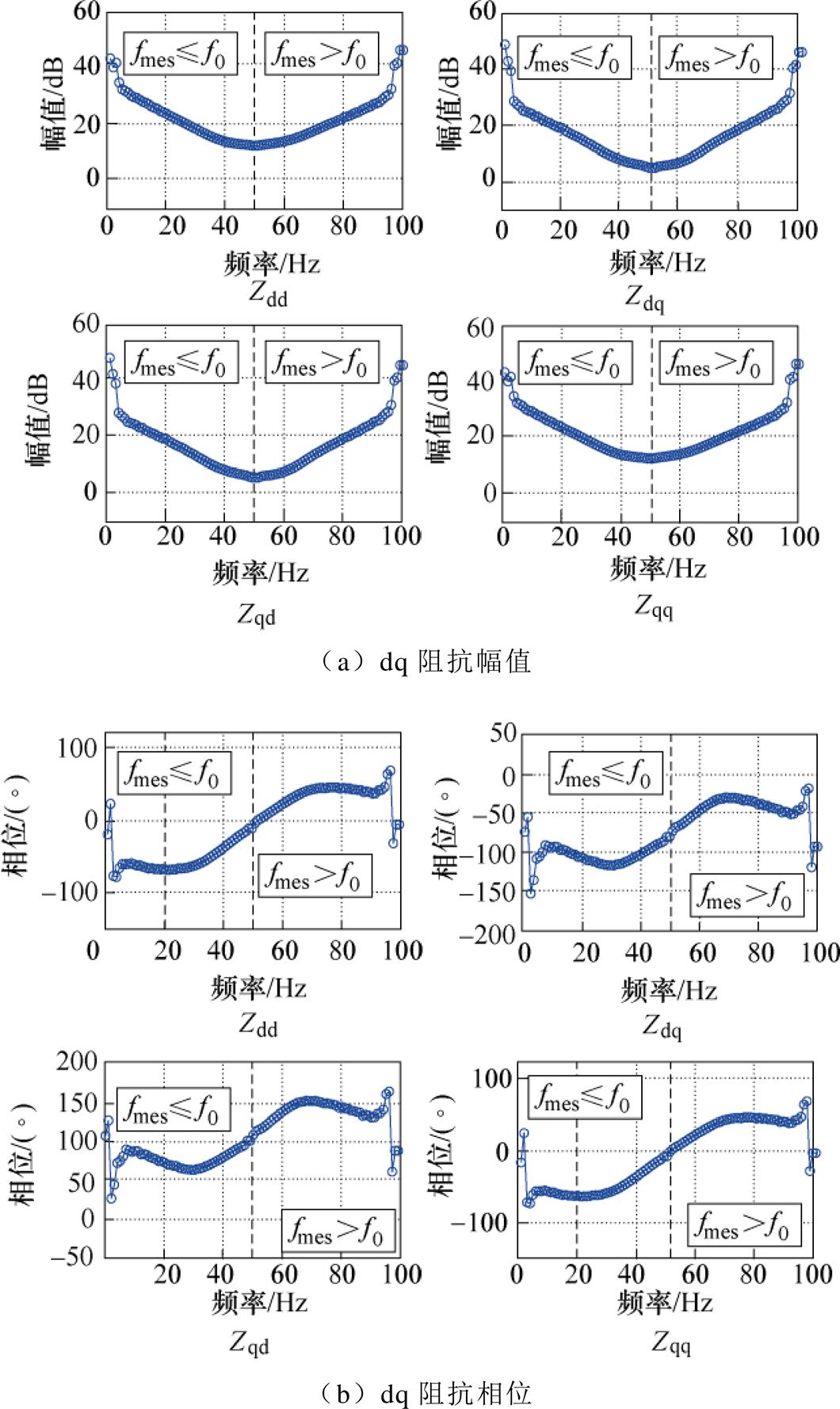
图13 所提方法频带为1～100Hz时的阻抗测量试验结果
Fig.13 Impedance measurement test results of proposed method when setting the frequency band at 1Hz to 100Hz
单相电力电子4QC设备控制系统的不对称等特性带来的频率耦合现象会干扰“宽频式”dq阻抗测量结果的准确度。因此，常采用“扫频式”方法对其进行测量。然而，研究过程中发现，此类“扫频式”dq阻抗测量法亦会受频率耦合现象的干扰。针对此，本文详细分析了测量过程中系统有效响应频率与耦合频率在坐标变换中的干扰规律，发现当注入频率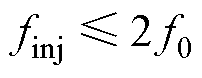
，且dq变换采用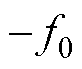变换的情况时，有效响应频率与耦合频率在dq旋转坐标系下会出现重叠干扰现象。导致当测量频率时，测量不准确，dq阻抗测量结果在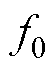
处出现“断层”现象。基于此分析，提出了一种于坐标变换之前将所有非有效响应频率剔除的抑制策略。该方法能够简单有效地避免“扫频式”dq阻抗测量中的频率耦合干扰，进而确保阻抗测量结果的准确性。
参考文献
[1] 袁佳歆, 曲锴, 郑先锋, 等. 高速铁路混合储能系统容量优化研究[J]. 电工技术学报, 2021, 36(19): 4161-4169.
Yuan Jiaxin, Qu Kai, Zheng Xianfeng, et al. Optimizing research on hybrid energy storage system of high speed railway[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4161-4169.
[2] 肖非然, 倪周, 闵永智, 等. 一种基于多智能体的多站协同高速铁路不平衡补偿方法[J]. 电工技术学报, 2020, 35(16): 3518-3528.
Xiao Feiran, Ni Zhou, Min Yongzhi, et al. Unbalanced compensation method of multi-station cooperative for high-speed railway based on multi-agent[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(16): 3518-3528.
[3] 母秀清, 王英, 陈思彤, 等. 基于改进sum-范数判据的高速铁路车网电气耦合系统稳定性研究[J]. 电工技术学报, 2019, 34(15): 3253-3264.
Mu Xiuqing, Wang Ying, Chen Sitong, et al. Stability research on high-speed railway vehicle network electric coupling system based on improved sum- norm criterion[J]. Transactions of China Electro- technical Society, 2019, 34(15): 3253-3264.
[4] 魏文婧, 胡海涛, 王科, 等. 基于铁路功率调节器的高速铁路牵引供电系统储能方案及控制策略[J]. 电工技术学报, 2019, 34(6): 1290-1299.
Wei Wenjing, Hu Haitao, Wang Ke, et al. Energy storage scheme and control strategies of high-speed railway based on railway power conditioner[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1290-1299.
[5] 魏波, 胡海涛, 王科, 等. 基于实测数据和行车运行图的高铁牵引变电站负荷预测方法[J]. 电工技术学报, 2020, 35(1): 179-188.
Wei Bo, Hu Haitao, Wang Ke, et al. Research on taction load forecasting method for high-speed railway traction substation based on measured data and train timetable[J]. Transactions of China Electro- technical Society, 2020, 35(1): 179-188.
[6] Shuai Zhikang, Cheng Huijie, Xu Jiazhu, et al. A notch filter-based active damping control method for low-frequency oscillation suppression in train- network interaction systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(4): 2417-2427.
[7] 陶海东, 胡海涛, 朱晓娟, 等. 车网耦合下的牵引供电系统谐振不稳定机理分析[J]. 中国电机工程学报, 2019, 39(8): 2315-2324.
Tao Haidong, Hu Haitao, Zhu Xiaojuan, et al. Mechanism on resonance instability of traction power supply system considering interaction between trains and networks[J]. Proceedings of the CSEE, 2019, 39(8): 2315-2324.
[8] 陶海东, 胡海涛, 姜晓锋, 等. 牵引供电低频网压振荡影响规律研究[J]. 电网技术, 2016, 40(6): 1830- 1838.
Tao Haidong, Hu Haitao, Jiang Xiaofeng, et al. Research on low frequency voltage oscillation in traction power supply system and its affecting factors[J]. Power System Technology, 2016, 40(6): 1830-1838.
[9] Hu Haitao, Zhou Yi, Li Xin, et al. Low-frequency oscillation in electric railway depot: a comprehensive review[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 295-314.
[10] Zhou Yi, Hu Haitao, Yang Jie, et al. A novel forbidden-region-based stability criterion in modified sequence-domain for AC grid-converter system[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 2988-2995.
[11] Hu Haitao, Tao Haidong, Wang Xiongfei, et al. Train-network interactions and stability evaluation in high-speed railways-part II: influential factors and verifications[J]. IEEE Transactions on Power Elec- tronics, 2018, 33(6): 4643-4659.
[12] Wang Hui, Wu Mingli, Sun Juanjuan. Analysis of low-frequency oscillation in electric railways based on small-signal modeling of vehicle-grid system in dq frame[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5318-5330.
[13] Liao Yicheng, Liu Zhigang, Zhang Han, et al. Low- frequency stability analysis of single-phase system with dq-frame impedance approach-part I: impedance modeling and verification[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4999-5011.
[14] Liao Yicheng, Liu Zhigang, Zhang Han, et al. Low- frequency stability analysis of single-phase system with dq-frame impedance approach-part II: stability and frequency analysis[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5012-5024.
[15] Zhou Yi, Hu Haitao, Yang Xiaowei, et al. Low frequency oscillation traceability and suppression in railway electrification systems[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7699-7711.
[16] Pan Pengyu, Hu Haitao, Yang Xiaowei, et al. Impedance measurement of traction network and electric train for stability analysis in high-speed railways[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10086-10100.
[17] Hu Haitao, Pan Pengyu, Song Yitong, et al. A novel controlled frequency band impedance measurement approach for single-phase railway traction power system[J]. IEEE Transactions on Industrial Electro- nics, 2020, 67(1): 244-253.
[18] Pan Pengyu, Hu Haitao, Xiao Donghua, et al. An improved controlled-frequency-band impedance mea- surement scheme for railway traction power system[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2184-2195.
[19] Gong Hong, Yang Dongsheng, Wang Xiongfei. Impact of nonlinear dynamics on converter dq impedance measurement[C]//IEEE Workshop on Control and Modeling for Power Electronics (COMPEL), Toronto, Canada, 2019: 1-6.
[20] Liao Yicheng, Liu Zhigang, Hu Xinxuan, et al. A dq-frame impedance measurement method based on Hilbert transform for single-phase vehicle-grid system[C]//IEEE Transportation Electrification Con- ference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 2017: 1-6.
[21] 肖冬华, 胡海涛, 潘鹏宇, 等. 高速列车dq阻抗测量方法及其装置设计[J]. 中国电机工程学报, 2020, 40(22): 7230-7240.
Xiao Donghua, Hu Haitao, Pan Pengyu, et al. dq impedance measurement method and its device design of high-speed train[J]. Proceedings of the CSEE, 2020, 40(22): 7230-7240.
[22] 周毅, 胡海涛, 雷科, 等. 电气化铁路低频等幅振荡机理分析[J]. 中国电机工程学报, 2021, 41(9): 3024-3036.
Zhou Yi, Hu Haitao, Lei Ke, et al. Mechanism analysis of the sustained low-frequency oscillation in the electric railway system[J]. Proceedings of the CSEE, 2021, 41(9): 3024-3036.
Frequency Coupling Interference Mechanism and Suppression Strategy for Frequency-Sweeping-Based dq Impedance Measurement of High-Speed Train Converter
Abstract High-speed train adopts four quadrant converters (4QC) as the energy conversion unit, and its mismatch in frequency-domain impedance characteristic with traction power supply network will lead to low-frequency oscillation, harmonic amplification, and other phenomena, which will affect the safe and stable operation of the electric railway. Impedance measurement technology can effectively obtain the impedance characteristics of the actual engineering system, which has a wide application prospect. Existing studies have shown that the frequency couplings caused by the asymmetric 4QC controller will interfere with the accuracy of the impedance measurement results under the wideband-based method. To avoid this interference, the frequency-sweeping-based method can be selected. However, this paper indicates that the frequency couplings will also deteriorate the accuracy of the measurement results when the frequency-sweeping-based method is used for 4QC dq impedance measurement, and the interference mechanism is analyzed in detail. Accordingly, a convenient and effective suppression strategy is proposed. Finally, the detailed impedance measurement models of 4QC are built in Matlab/Simulink and hardware- in-the-loop test platform. The results verify the correctness and effectiveness of the presented interference mechanism and suppression strategy.
keywords：High-speed train, impedance measurement in frequency domain, frequency sweeping, frequency coupling, dq impedance
DOI: 10.19595/j.cnki.1000-6753.tces.210418
中图分类号：TM721
潘鹏宇 男，1993年生，博士研究生，研究方向为牵引供电系统阻抗测量技术。E-mail: ppyswjtu@163.com
胡海涛 男，1987年生，教授，博士生导师，研究方向为牵引供电/电力系统电能质量与稳定性。E-mail: hht@swjtu.edu.cn（通信作者）
收稿日期 2021-03-28
改稿日期 2021-05-15
国家自然科学基金资助项目（52027810）。
（编辑 陈 诚）