
图1 三相交错并联降压型变换器结构
Fig.1 Three-phase interleaved Buck converter configuration
摘要 针对多相交错并联DC-DC变换器相间均流问题,该文提出一种具有动态均流能力的单电流传感器控制策略。首先,根据变换器工作模态建立全息数学模型,深入分析造成相间电流不平衡的成因,推导出稳态下各相电流与寄生电阻、负载电流及占空比解析表达式。其次,考虑器件非理想特性,利用恒定占空比交替测试法估算各相寄生电阻;将电压环控制器输出量作为基准值,引入占空比补偿因子实现相间电流均衡。然后,基于系统小信号模型利用频域法对控制环路进行分析,辅助Matlab/SISO设计工具,优化控制器零点位置与环路增益,并利用根轨迹研究负载变化对系统稳定性影响;同时增加负载电流前馈补偿环路以降低输出阻抗,进一步改善系统动态性能。最后,搭建三相交错并联Buck变换器数字控制实验样机进行稳态与动态测试,其结果验证了所提出控制策略的可行性与正确性。
关键词:交错并联变换器 单电流传感器 均流 前馈控制
目前,交错并联DC-DC变换器因具有功率密度大、瞬态响应快以及电流纹波小等优点[1-2],已广泛应用于电动汽车、光伏发电、储能系统等领域[3-5]。然而在实际系统中,由于功率半导体器件、电感、驱动器件等存在的差异性,将引起变换器各相间电流不均衡,造成对应相中热应力增加及磁饱和,从而影响系统的可靠性[6]。因此,为了保证多相交错并联变换器高效运行,每相电流的均流控制显得极为重要。
为了解决上述问题,近几年国内外研究人员提出了一些均流控制策略,主要包括下垂均流法、主从均流法和平均均流法[7-8]。其中,下垂均流法是通过改变各相外特性斜率,即调节输出阻抗实现均流,该方法易于实现,但由于每相间彼此独立,致使电压调整率较差[9]。主从均流法中主动相电流由电压外环控制,其他相电流由电压外环和均流环共同控制,可获得较好的电压调整率和均流特性。但该方法中包含多个控制环路,控制器参数设计复杂,易引起系统不稳定。然而平均均流法是将电压外环输出控制量均分作为各相电流内环的给定值,再通过PI控制器实现均流控制[5, 10-11]。
上述三种方法均需要获取各相电流值,传感器数量较多,导致系统成本、体积增加,同时均流控制策略效果易受电流传感器精度的影响。
为了抑制电流传感的不利影响,一些无传感器均流策略被相继提出[12-15]。文献[12]提出一种基于梯度估算的无传感器均流策略,但在准确估算相电流的过程中要求较大计算量。文献[13]利用输入电容电压纹波的差异代替电流采样,以减小纹波差异为目标自动调节各相占空比,从而达到均流目的。然而,该方法同样计算复杂。文献[14]提出一种通过改变各相电流分配系数来实现均流的控制方法,但该方法适用于各相电流差异较小的场合。文献[15]利用各分支电路中寄生电阻对应补偿每相中开关的占空比,该方法实现较为简单,但其动态均流性能受到限制。
在此基础上,本文提出一种单电流传感器均流控制策略,与传统均流控制策略相比,简化了系统电路,降低了成本;而与无电流传感器策略相比,改善了动态均流及过电流保护能力。主要贡献包括:①考虑器件实际损耗,利用开环恒定占空比交替测试法估算各相寄生电阻,并根据所建立的稳态电感电流解析表达式,计算出对应相占空比补偿分量;②基于系统小信号模型,利用频域法对控制环路进行分析,优化配置控制器零点位置与环路增益,并引入前馈补偿环路有效改善系统动态性能。最后,采用基于模型的设计方法完成对控制策略的功能实现,使系统具有良好的动态和稳态性能。
考虑到一般性原则,本文以三相交错并联变换器为例,研究其在降压模式下的工作原理。由此得到三相交错并联降压变换器(Three Phase Inter- leaved Buck Converter, TP-IBC)电路拓扑结构,如图1所示,三相支路分别记为P1、P2和P3。为减小负载电流波纹,设置每相驱动信号依次偏移2π/3相位。图中,S1~S6为IGBT开关管,且集成有反并联快恢复二极管;L1、L2、L3为各相的滤波电感;Ci和Co分别为输入、输出滤波电容。TP-IBC可工作在电流连续导通和断续导通两种模式,当处于断续导通模式时,由于各相电流能相互平衡而无需复杂的控制技术[16]。因此,本文仅以TP-IBC电流连续导通模式进行分析与研究。

图1 三相交错并联降压型变换器结构
Fig.1 Three-phase interleaved Buck converter configuration
为减小负载电流波纹,设置三相驱动信号依次偏移2π/3相位,即上桥臂开关管S1、S2、S3交错导通,下桥臂开关管S4、S5、S6始终关断,通过反并联二极管实现续流。
当稳态占空比分别为d<1/3、1/3≤d≤2/3以及2/3<d≤1时,开关序列呈现不同形式,不同占空比下的驱动信号序列如图2所示。图中,u1、u2、u3分别为S1、S2、S3的驱动信号。根据设计指标中输入电压(50V)、输出电压(30V)关系,系统稳态占空比(0.6)工作在1/3~2/3范围,此时变换器在一个周期内有6个开关模态。图2中,Ts为变换器的开关时间,T1~T6分别为每个模态的工作时间。
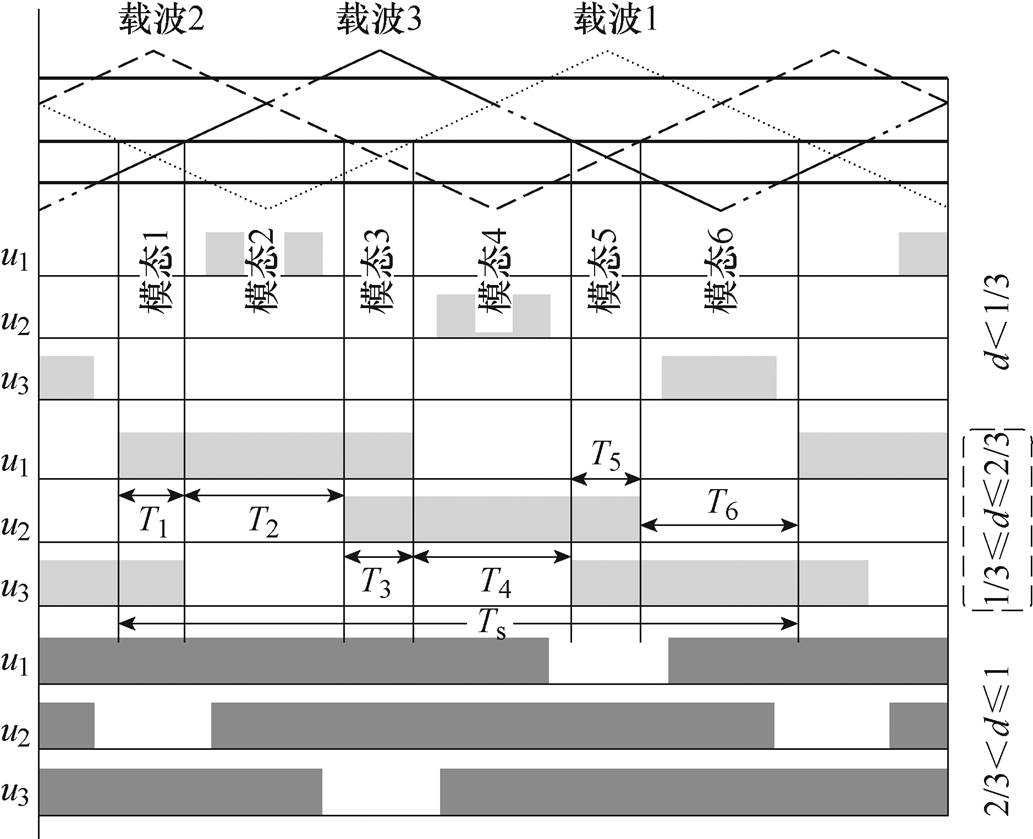
图2 不同占空比下的驱动信号序列
Fig.2 Drive signal sequences according to duty cycle
现以单相为例考虑各器件寄生参数,得到变换器单相等效电路,如图3所示。将开关管Sx等效为理想开关、正向导通压降VSx和导通电阻rSx,x= 1, 2, 3;而快恢复续流二极管等效为理想开关、正向导通压降VDy和导通电阻rDy,y=x+3;同时考虑电感绕组电阻rLx、输出滤波电容等效串联电阻rC及导线与接触等效电阻rw。当变换器稳态运行时,根据伏秒平衡原理,推导出电感电流稳态直流分量表达式为
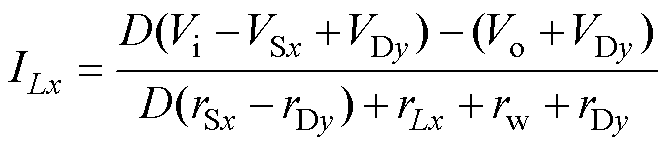 (1)
(1) 式中,D为占空比稳态值。
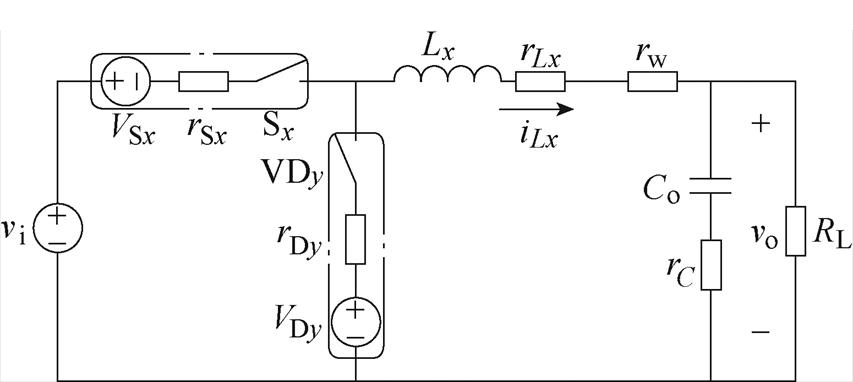
图3 变换器单相等效电路
Fig.3 Converter single phaseequivalent circuit
由式(1)可知,电感电流直流分量ILx与电感Lx和电容Co无关,而与寄生电阻以及功率开关器件正向导通压降有关。在实际电路中,由于受电感差异性和母线结构等因素的影响,TP-IBC各相间寄生参数不一致性,导致各相电流不均衡。
根据上述分析,得到TP-IBC开关模态等效电路如图4所示。由于开关器件采用高集成功率模块,因此可做近似处理,有
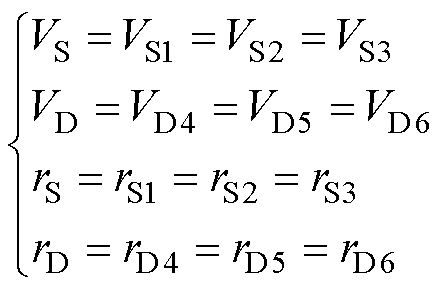 (2)
(2)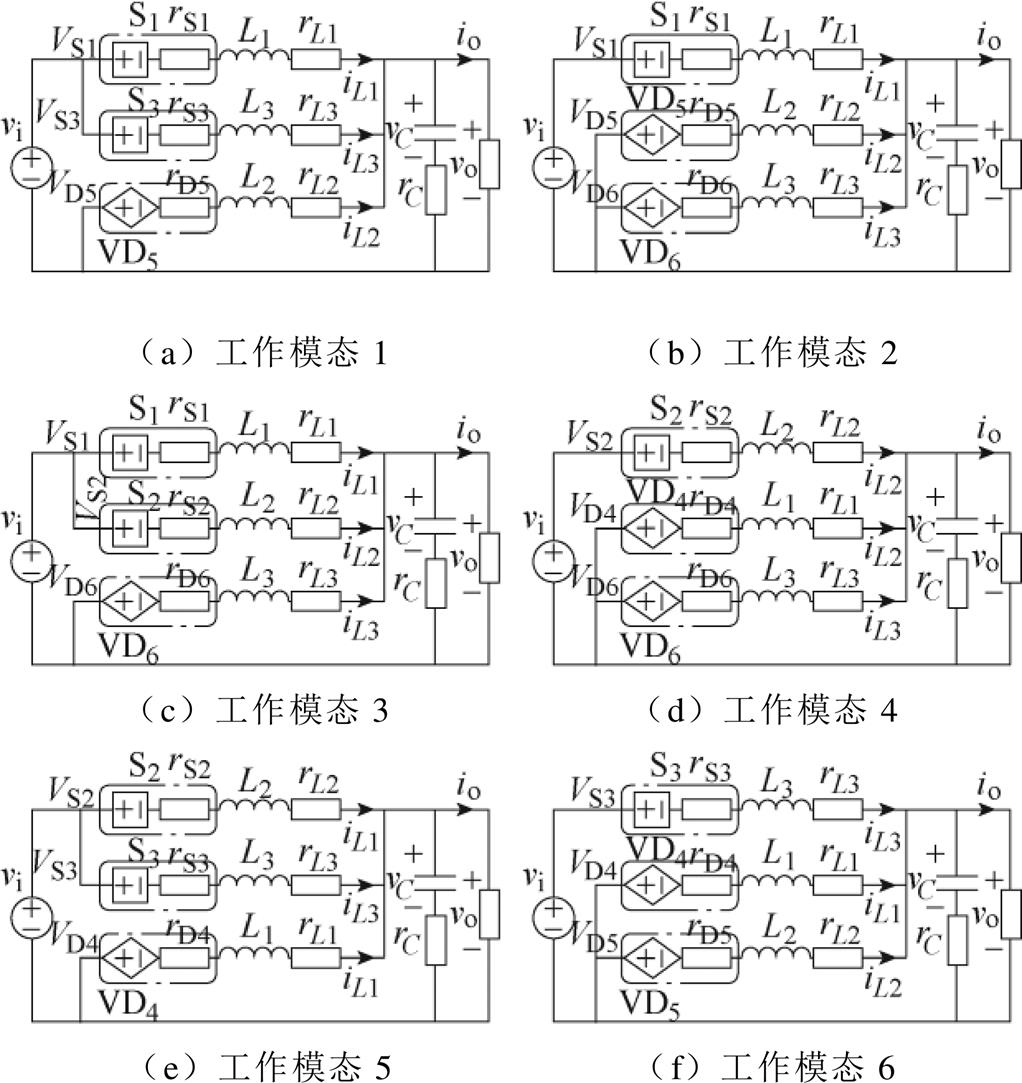
图4 TP-IBC开关模态等效电路
Fig.4 Switching modes equivalent circuit for TP-IBC
利用状态空间法方建立系统模型为
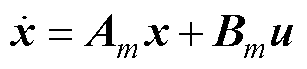 (3)
(3)式中, ;x为状态变量,x=[iL1 iL2 iL3 vC]T;u为独立输入量,u=[viVSVDio]T;Am和Bm分别为不同开关模态下的系数矩阵。
;x为状态变量,x=[iL1 iL2 iL3 vC]T;u为独立输入量,u=[viVSVDio]T;Am和Bm分别为不同开关模态下的系数矩阵。
变换器模态1等效电路如图4a所示,开关管S1、S3导通,二极管VD5续流,其状态空间方程表达式为
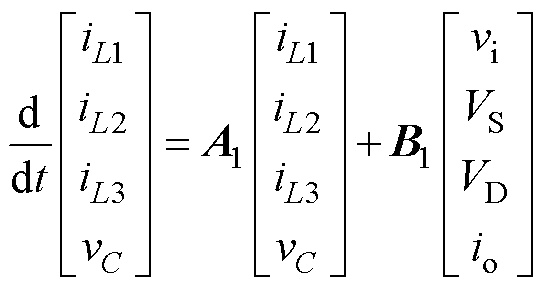 (4)
(4)其中
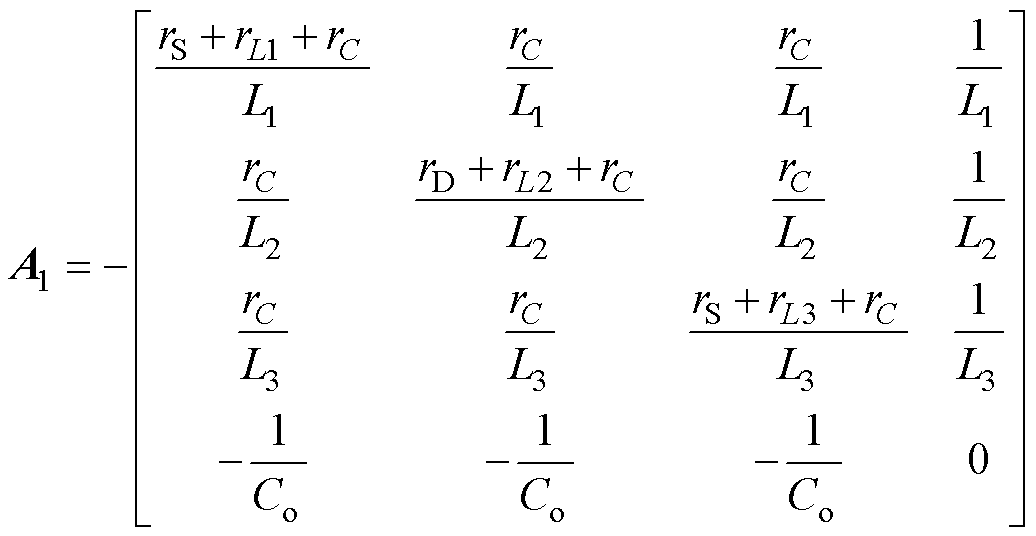 (5)
(5)
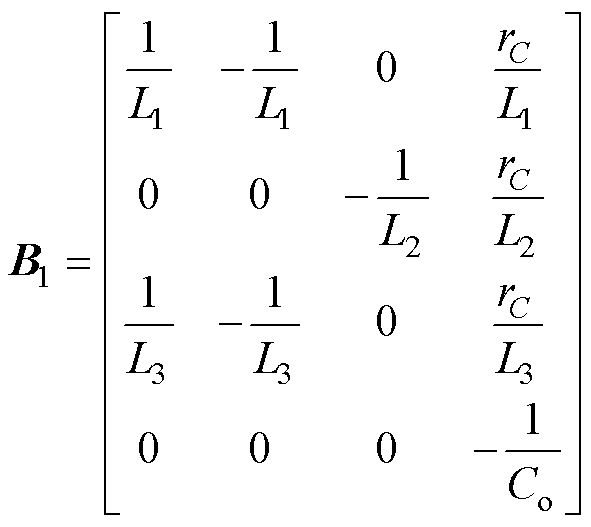 (6)
(6)同理,根据系统工作模态等效电路图4b~图4f,分别推导出系数矩阵A2~A6,B2~B6分别为
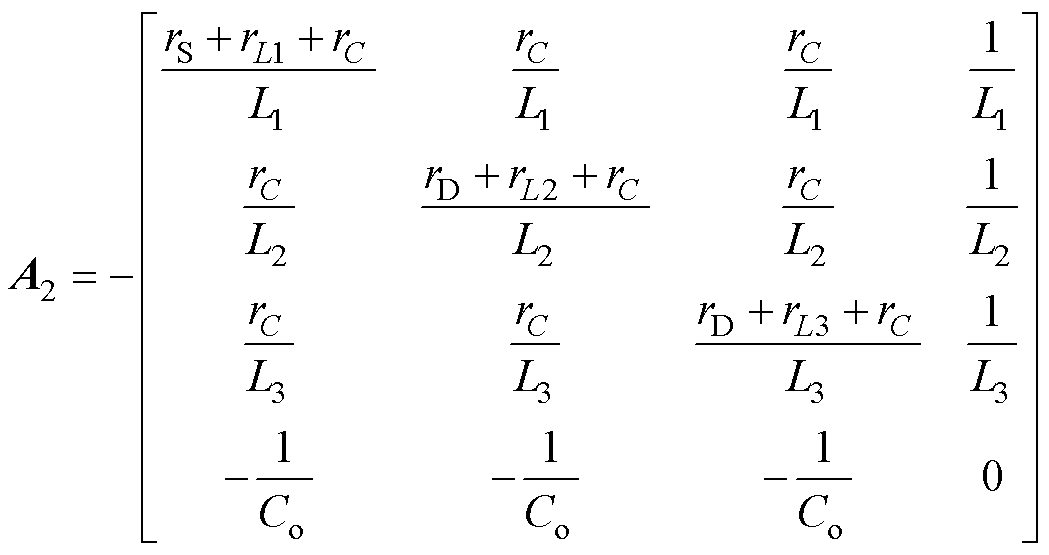 (7)
(7)
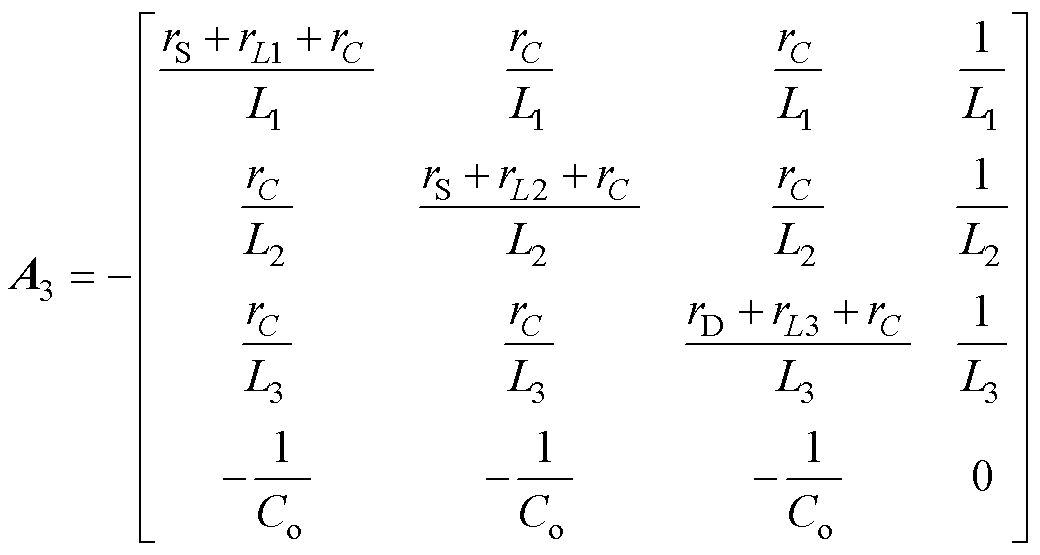 (8)
(8)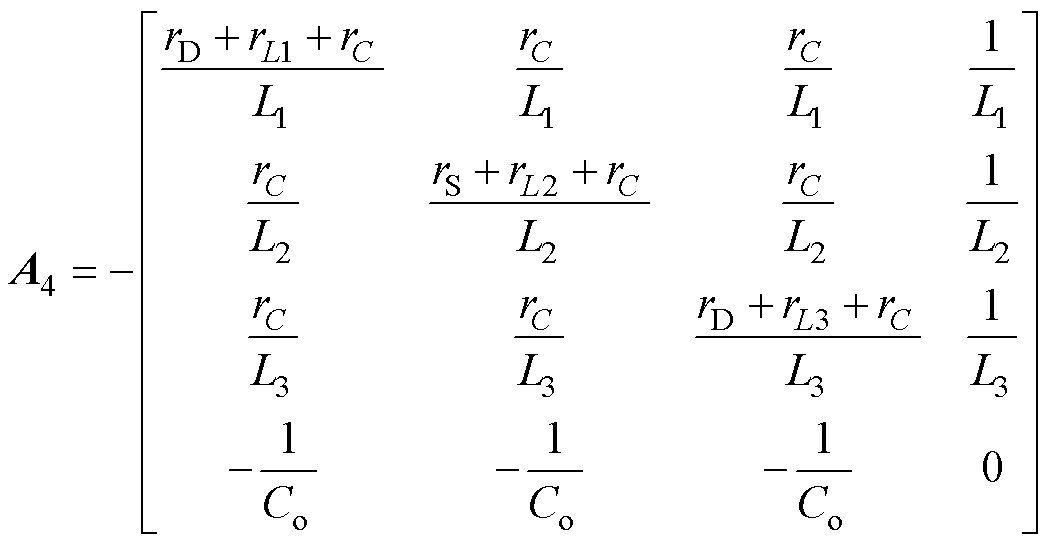 (9)
(9)
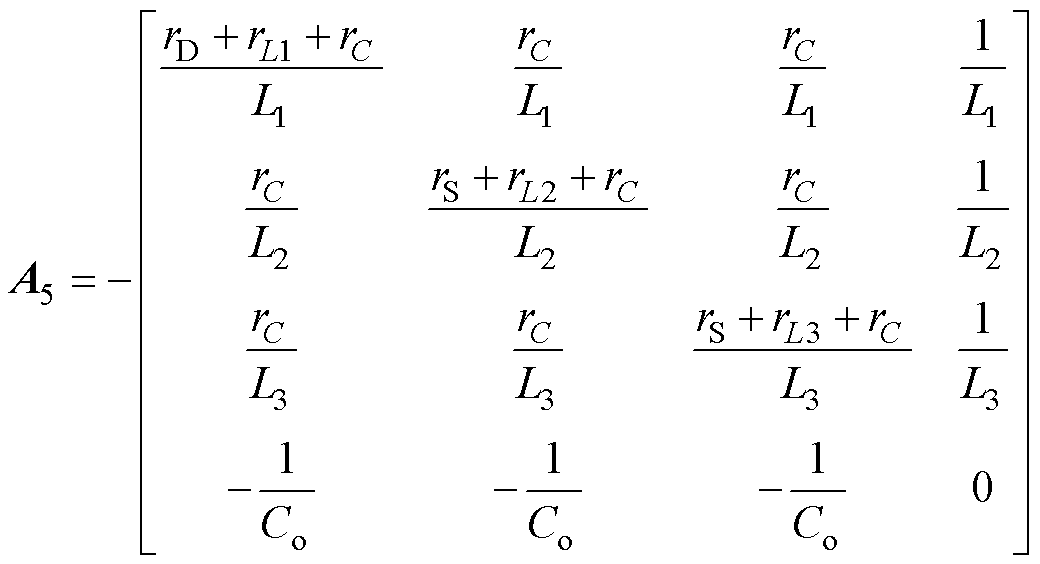 (10)
(10)
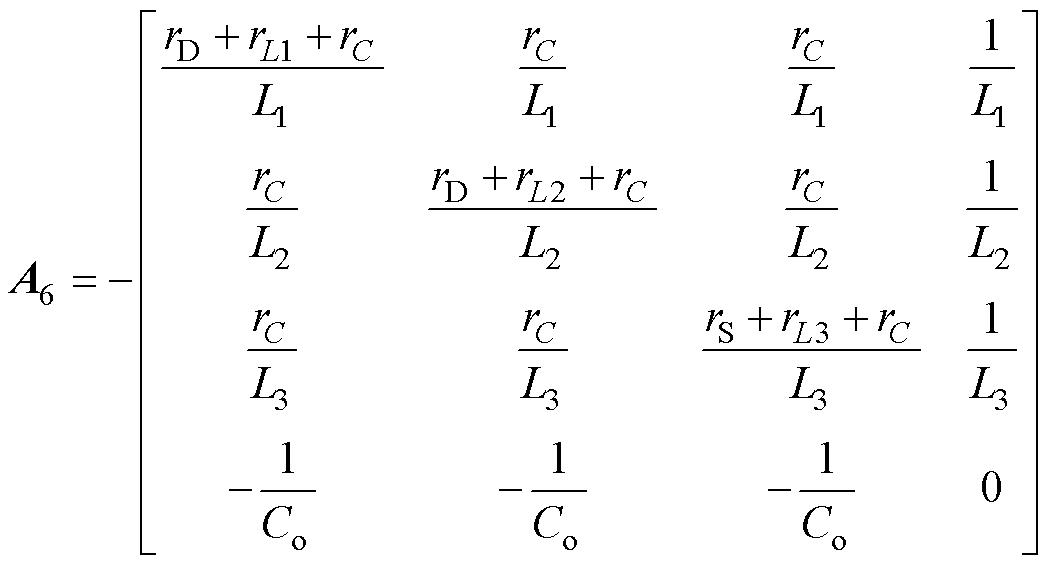 (11)
(11)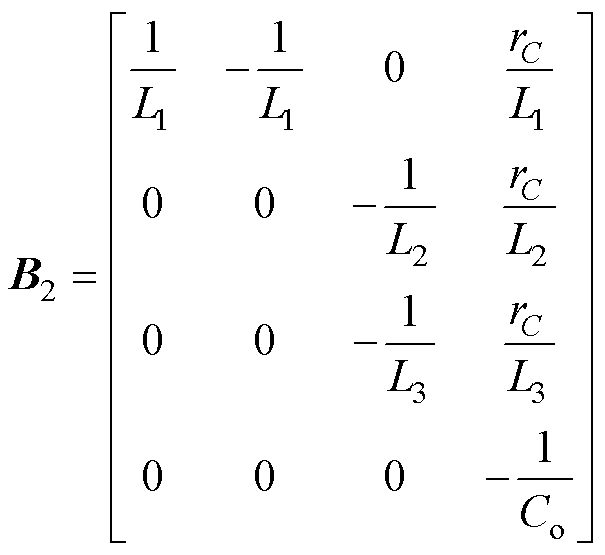 (12)
(12)
 (13)
(13)
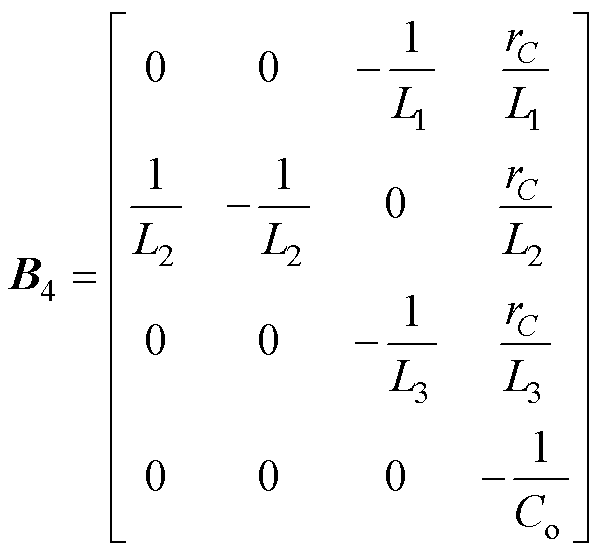 (14)
(14)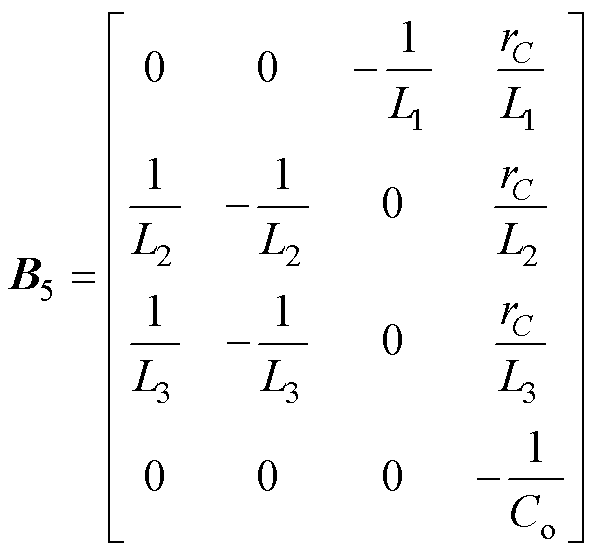 (15)
(15)
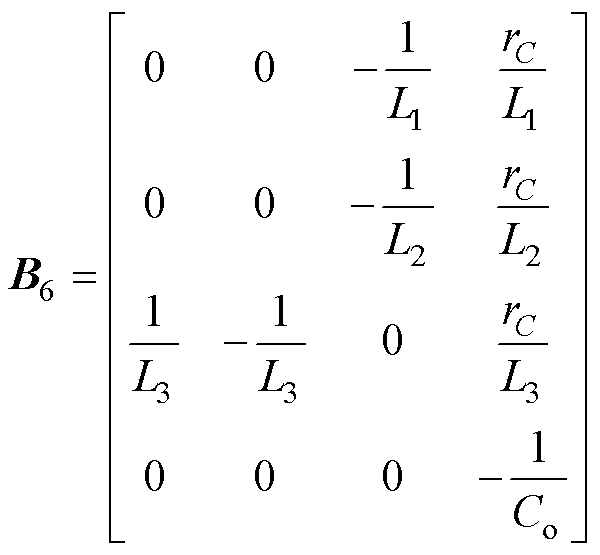 (16)
(16)
由图2可知,一个开关周期中每个开关模态作用的时间分别为
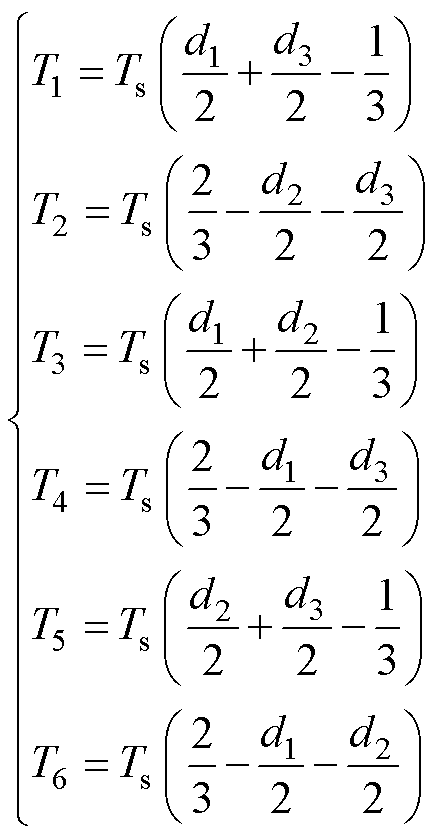 (17)
(17)式中,d1、d2、d3分别为开关管S1、S2、S3的占空比。
基于开关周期平均理论[17],联立式(4)~式(17),有
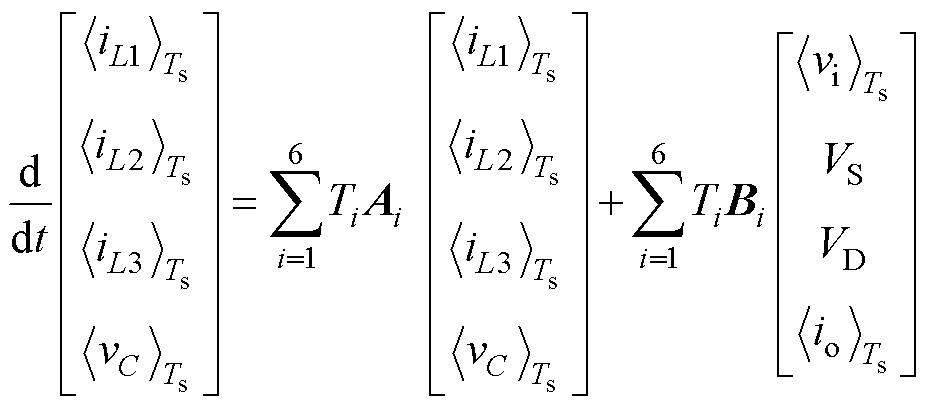 (18)
(18)式中,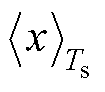 为在一个开关周期Ts内的平均值。
为在一个开关周期Ts内的平均值。
通过对式(18)中矩阵的求解,得到变换器在稳态直流静态工作点下,各相平均电感电流表示为
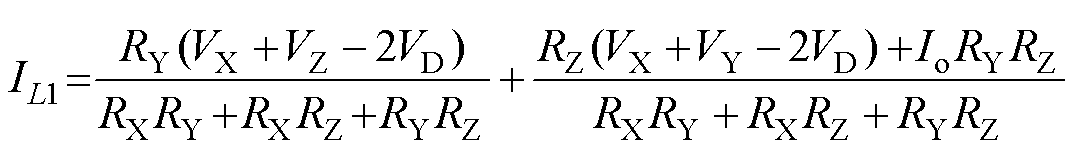 (19)
(19)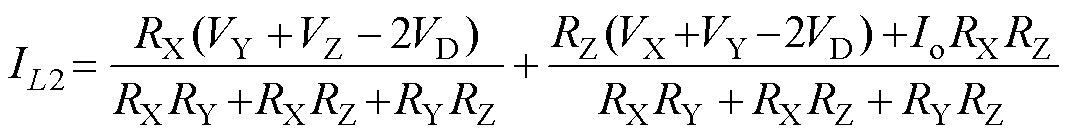 (20)
(20)
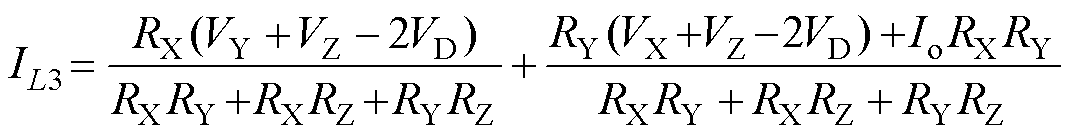 (21)
(21)
其中
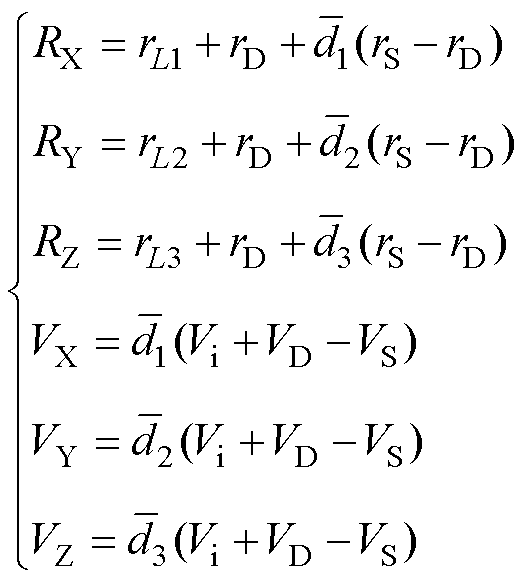
式中,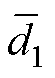 、
、 、
、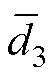 分别为d1、d2、d3的稳态直流量;Vi为输入电压vi的稳态直流量。
分别为d1、d2、d3的稳态直流量;Vi为输入电压vi的稳态直流量。
由式(19)~式(21)可知,各相平均电流不仅与本相寄生参数有关,且与其他相寄生参数有关。在实际电路中,由于各相间寄生电阻、占空比等存在差异,即RX≠RY≠RZ、VX≠VY≠VZ,从而引起IL1≠ IL2≠IL3。同时不难看出,通过合理调节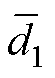 、
、 、
、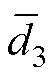 可实现各相间电流均衡。
可实现各相间电流均衡。
根据上述分析,以P1相占空比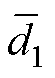 为参考基准,对P2、P3两相分别引入占空比均流补偿因子la、lb,则有以下关系成立
为参考基准,对P2、P3两相分别引入占空比均流补偿因子la、lb,则有以下关系成立
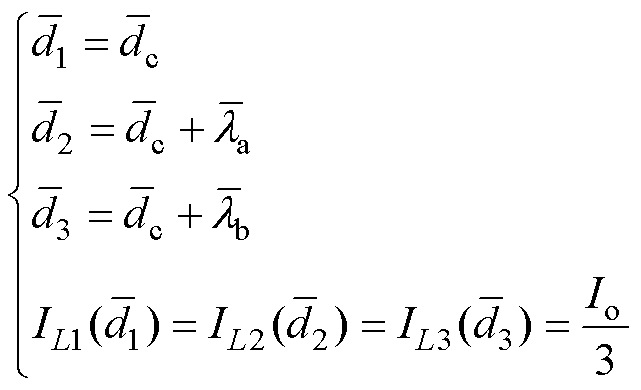 (22)
(22)式中,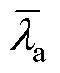 、
、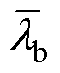 分别为la、lb的稳态值。
分别为la、lb的稳态值。
假设各相功率开关管、二极管正向导通压降与导通电阻相同,联立式(19)~式(22),求解得
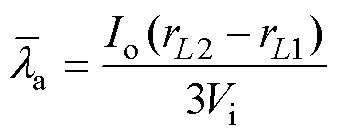 (23)
(23)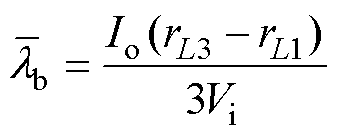 (24)
(24)
由式(23)、式(24)可知,只需获得各相寄生电阻rL1、rL2、rL3,负载电流Io和输入电压Vi,即可求出P2、P3相占空比均流补偿因子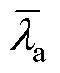 、
、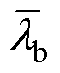 ,从而实现各相间均流输出。寄生电阻辨识方法步骤如下:
,从而实现各相间均流输出。寄生电阻辨识方法步骤如下:
(1)采用固定占空比(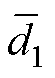 =
= =
=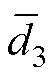 =0.6),使P1、P2、P3各相独立开环运行,并依次采样得到输出电压Vo与负载电流Io,当额定输入电压Vi=50V、负载电阻为1.5W 时,寄生电阻辨识方法如图5所示,其测量结果见表1。
=0.6),使P1、P2、P3各相独立开环运行,并依次采样得到输出电压Vo与负载电流Io,当额定输入电压Vi=50V、负载电阻为1.5W 时,寄生电阻辨识方法如图5所示,其测量结果见表1。
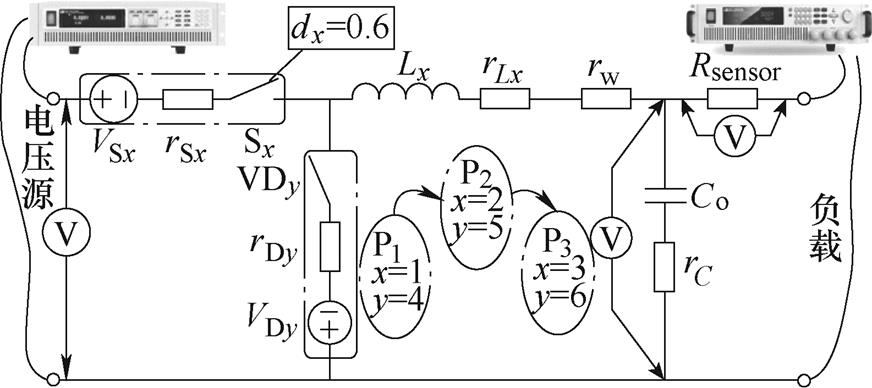
图5 寄生电阻辨识方法
Fig.5 Identification method of parasitic resistance
表1 各相寄生电阻估算值
Tab.1 Calculation parasiticresistance for each phase

相号rLx+rw/mW输入电压/V输出电压/V负载电流/A P185.249.7327.2918.19 P274.949.7227.4818.32 P398.549.7327.0818.05
(2)根据功率模块测试数据拟合得到饱和导通压降特性曲线,如图6所示。可查得不同电流下IGBT导通压降Vce=Vs+rsIo和二极管导通压降VD= Vd+rdIo。
根据步骤(1)中变换器的工作条件,其负载电流维持在18A左右,利用图6给出的拟合曲线查得, Vce=1.0V,VD=0.95V。
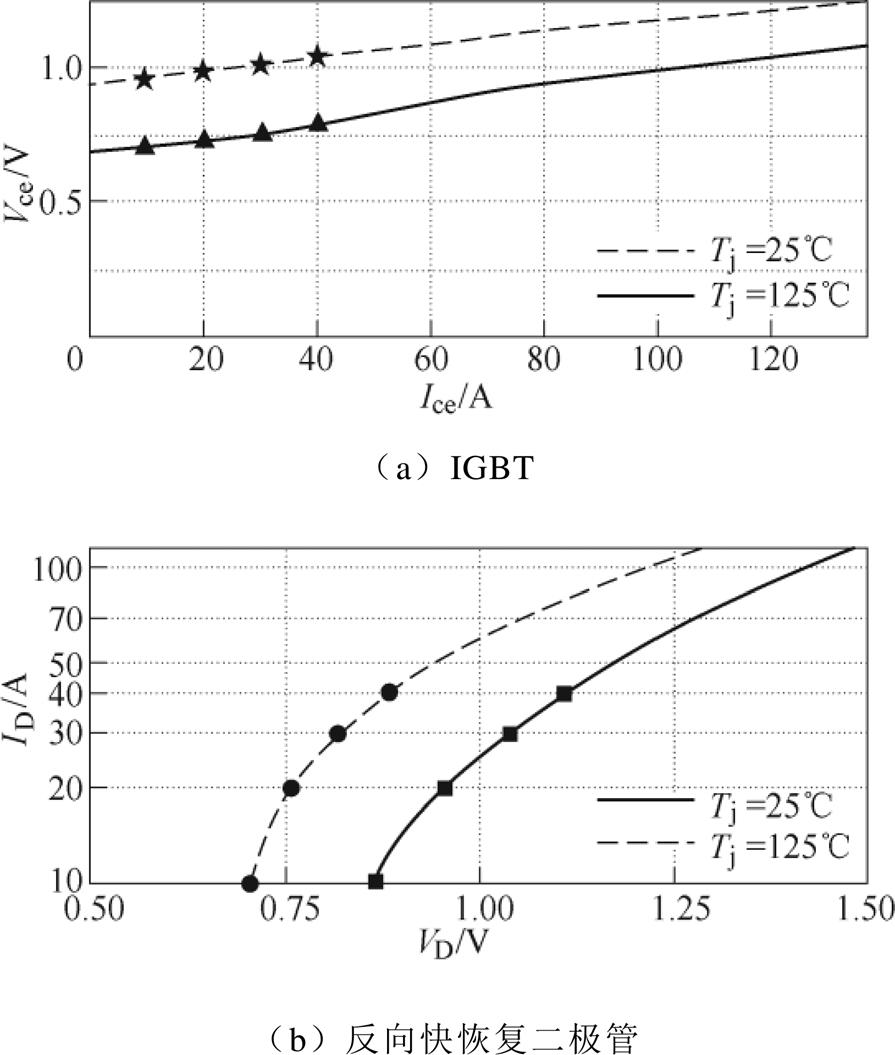
图6 功率器件正向导通特性
Fig.6 The forward characteristic of the power semiconductor
(3)基于步骤(1)、(2)中得到的数据,根据式(1),即可辨识出各相中的寄生电阻。
因此,本文提出一种采用单电流传感器的TP- IBC均流控制策略框图如图7所示。首先,将采样得到的输出电压vo与给定值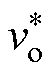 比较,其输出误差信号Dvo进入电压控制器;由于控制量为直流分量,电压控制器采用传统PI控制器即可实现对误差信号Dvo的稳态无静差控制,并得到控制量dc。同时,利用辨识得到的寄生电阻rL1、rL2和rL3,通过联立式(22)~式(24)计算出经均流补偿后的P2、P3相控制量d2、d3。
比较,其输出误差信号Dvo进入电压控制器;由于控制量为直流分量,电压控制器采用传统PI控制器即可实现对误差信号Dvo的稳态无静差控制,并得到控制量dc。同时,利用辨识得到的寄生电阻rL1、rL2和rL3,通过联立式(22)~式(24)计算出经均流补偿后的P2、P3相控制量d2、d3。
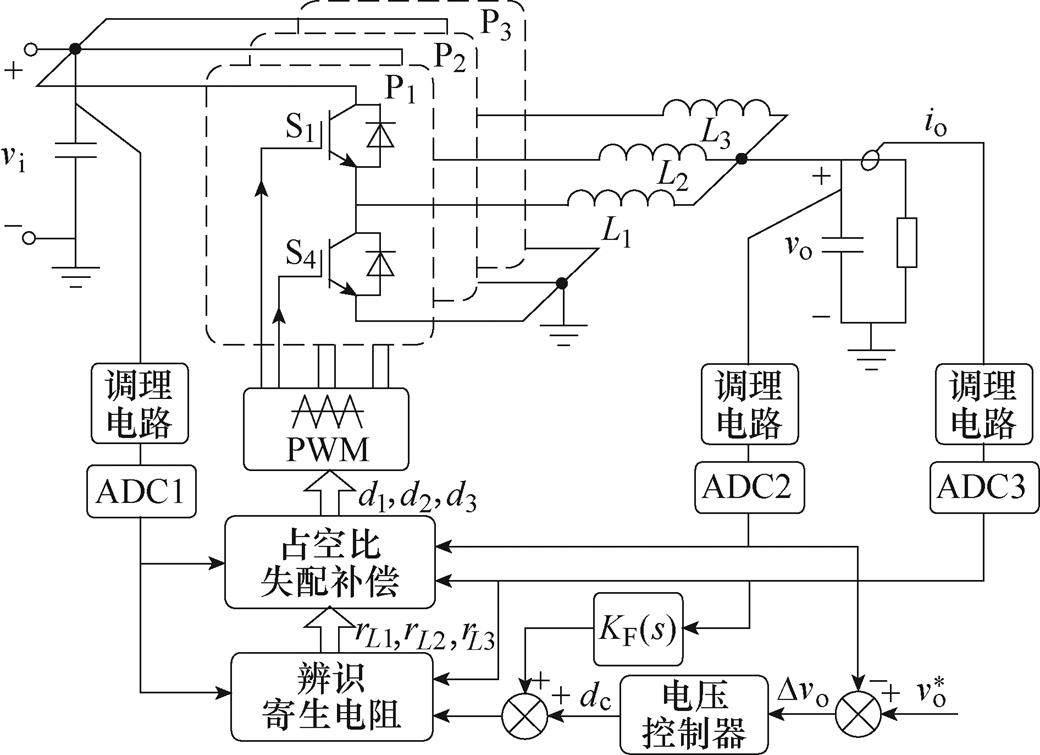
图7 单电流传感器均流控制策略框图
Fig.7 Block diagram of current sharing with single current sensor
与采用独立调节器控制每相电感电流实现均流方法相比,本文仅采用一个电流传感器,有效地降低了系统成本并提高了可靠性;与无电流传感器均流控制方法相比,本文所述的均流控制方法,增加了在线参数识别功能和直流侧电流传感器,能够根据负载电流实时补偿电流偏差量,保证系统具有良好的动态均流能力以及较好的鲁棒性。
考虑控制信号小信号扰动以及平均状态变量的小信号扰动影响,可表示为
 (25)
(25)式中,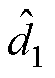 、
、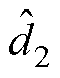 、
、 、
、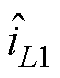 、
、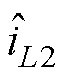 、
、 、
、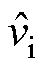 、
、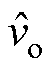 和
和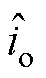 分别为各相占空比、电感电流、输入电压、输出电压和负载电流的小信号扰动量。为了降低控制系统设计过程的复杂性,假设
分别为各相占空比、电感电流、输入电压、输出电压和负载电流的小信号扰动量。为了降低控制系统设计过程的复杂性,假设
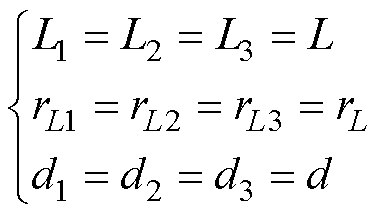 (26)
(26)
将式(25)、式(26)代入式(18),得到TP-IBC简化模型为
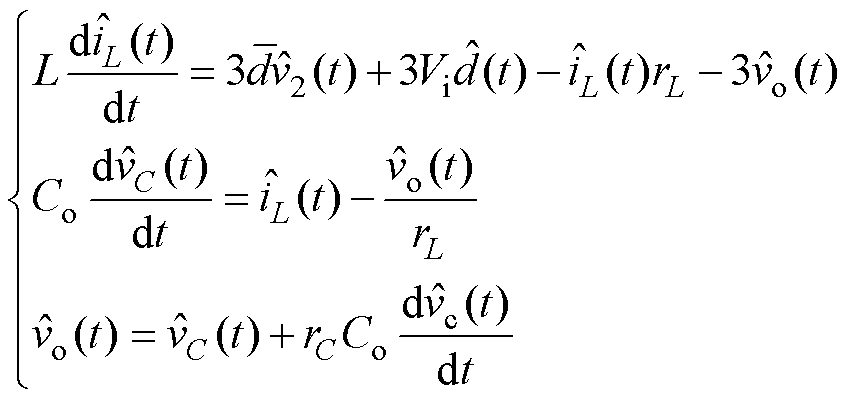 (27)
(27)式中,iL为总电感电流,iL=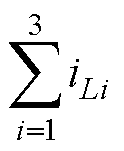 ;
;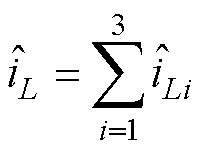 。
。
由式(27),占空比扰动量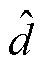 到输出电压扰动量
到输出电压扰动量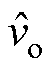 的传递函数表示为
的传递函数表示为
 (28)
(28)将输入电压和负载电流作为系统扰动量,得到基于小信号模型的TP-IBC系统控制框图,如图8所示。图中,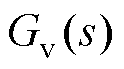 为电压控制器,KF(s)为前馈补偿环节;Gm(s)为控制与调制引起的时间延迟,采用一阶传递函数进行近似可得
为电压控制器,KF(s)为前馈补偿环节;Gm(s)为控制与调制引起的时间延迟,采用一阶传递函数进行近似可得
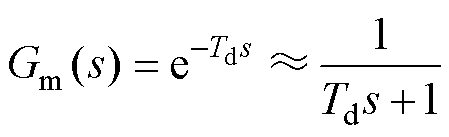 (29)
(29)
式中,Td为延迟时间。
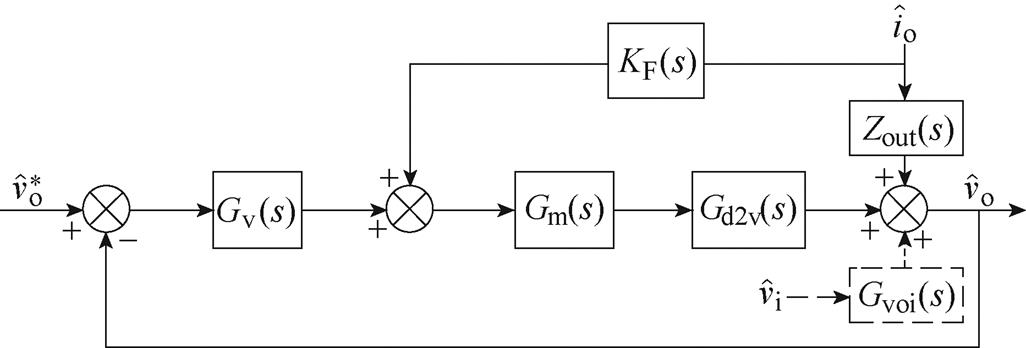
图8 基于小信号模型的系统框图
Fig.8 Block diagrams on the small-signal model
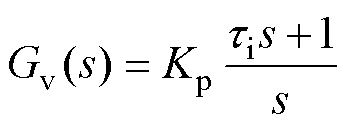 (30)
(30)根据图8所给出的系统小信号控制框图,得到系统开环传递函数与闭环传递函数为
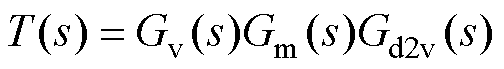 (31)
(31)
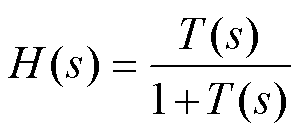 (32)
(32) 由式(32)可知,当电路参数确定时,为保证vo准确快速地跟踪给定值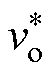 ,需要合理地设置控制器参数。由于T(s)为四阶系统,为了提高设计效率,采用Matlab/SISO设计工具,通过优化调节Gv(s)中零点位置与比例增益,以兼顾系统动态、稳态性能,最终确定控制器参数Kp=35,ti=0.17ms。经补偿后,系统开环、闭环传递函数幅频相频特性曲线如图9所示。其中开环传递函数的增益裕度为13.8dB,相位裕度为61.5°,系统带宽为580Hz,满足系统的性能要求。
,需要合理地设置控制器参数。由于T(s)为四阶系统,为了提高设计效率,采用Matlab/SISO设计工具,通过优化调节Gv(s)中零点位置与比例增益,以兼顾系统动态、稳态性能,最终确定控制器参数Kp=35,ti=0.17ms。经补偿后,系统开环、闭环传递函数幅频相频特性曲线如图9所示。其中开环传递函数的增益裕度为13.8dB,相位裕度为61.5°,系统带宽为580Hz,满足系统的性能要求。

图9 系统开环、闭环传递函数Bode图
Fig.9 Bode diagrams of open and closed-loop transfer functions
当改变负载电阻RL,使得负载电流io由1A逐渐增至30A,系统闭环传递函数极点分布情况如图10所示。共含有4个极点,包括一对共轭极点(Pa和Pb)和两个实数极点(Pc和Pd),显然所有极点均保持在左半平面,表明系统在负载规定变化范围内保持稳定,从而验证了控制器参数设计的正确性。
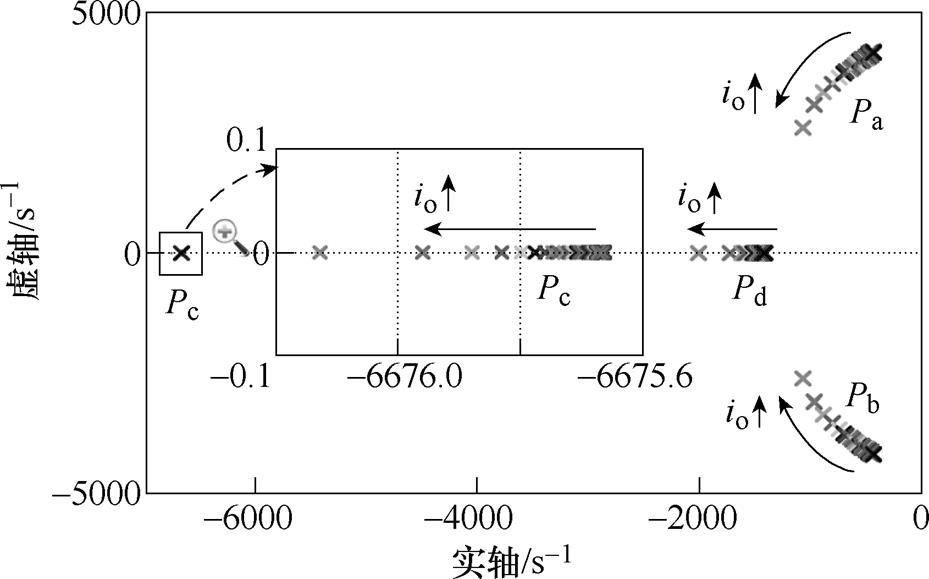
图10 不同负载情况下系统极点分布
Fig.10 System pole locations under different loads
由于输出阻抗表征了输出电压对负载电流扰动的抑制能力[18],因此减小输出阻抗能有效改善系统的动态性能。变换器开环输出阻抗、闭环输出阻抗传递函数可表示为
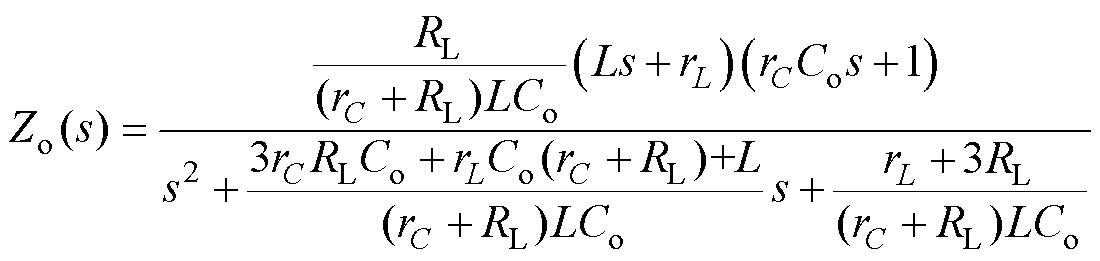 (33)
(33) (34)
(34)
由式(34)可知,当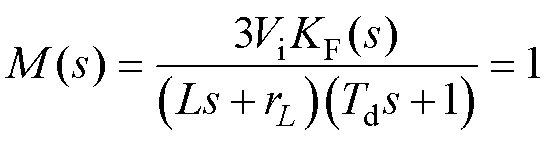 时,系统闭环输出阻抗Zcl(s)=0。令
时,系统闭环输出阻抗Zcl(s)=0。令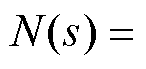
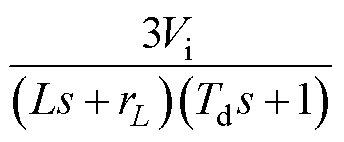 ,得到其幅频特性曲线,如图11所示,低频增益保持在62dB,随着频率增加,幅值逐渐降低。在实际应用中,考虑负载特性和数字采样环节等影响,负载电流扰动量应分布在中低频区域。针对上述问题,本文在前馈环路引入补偿函数为
,得到其幅频特性曲线,如图11所示,低频增益保持在62dB,随着频率增加,幅值逐渐降低。在实际应用中,考虑负载特性和数字采样环节等影响,负载电流扰动量应分布在中低频区域。针对上述问题,本文在前馈环路引入补偿函数为
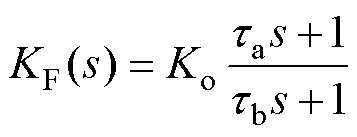 (35)
(35) 式中,Ko、ta、tb分别为前馈环路补偿函数的增益、零点系数和极点系数。
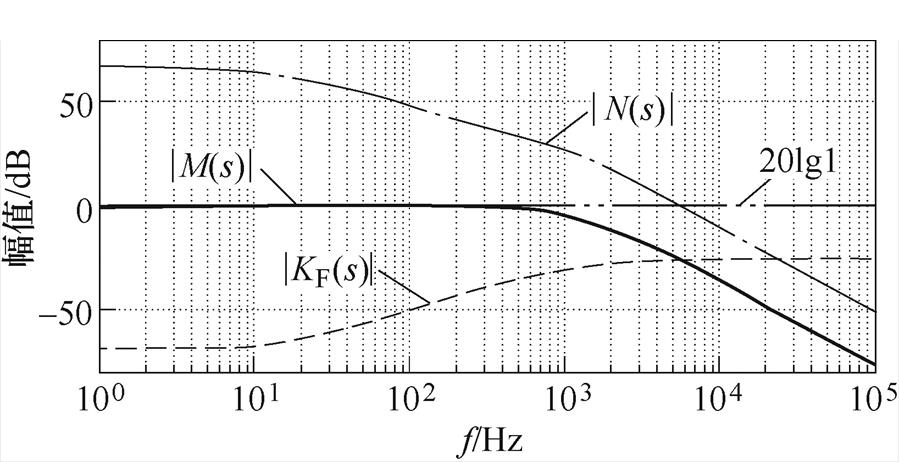
图11 N(s)、KF(s)和M(s)幅频特性曲线
Fig.11 Magnitude-frequency curves of N(s), KF(s) and M(s)
通过合理配置式(35)中零点、极点位置以及增益,使得M(s)幅值在中低频段保持近似为1,而在高频段逐渐衰减。进而得到补偿后M(s)幅值增益曲线,如图11所示,并确定优化参数Ko=4.2×10-4,ta=14ms,tb=0.1ms。
在前馈补偿环节的作用下,闭环输出阻抗幅频特性曲线如图12所示,系统闭环输出阻抗幅值在中低频段内得到显著降低,从而保证系统的抗扰性能,减小恢复时间。

图12 闭环输出阻抗幅频特性曲线
Fig.12 Magnitude-frequency curves of closed-loop output impedance
为验证提出方法在实际系统中的有效性,构建了TP-IBC实验平台,实验样机与测试设备如图13所示,包括可编程直流电源(ITECH IT6523C)、电子负载(ITECH IT8516C)、实验样机、示波器及电流探头(RIGOL DS4024/RP1003C、Tektronix A622)。TP-IBC样机由TI DSP TMS320F28335芯片作为主控制器,功率开关管采用三菱PM300CLA060,三相滤波电感采用Metglas AMCC-32 U型非晶合金磁心。
与传统手工编写代码不同,本文基于Matlab/ Simulink实时代码生成工具完成控制算法的实现。

图13 实验样机与测试设备
Fig.13 Experimental prototype and test setup
基于Embedded Target Library外设功能模块和常用算法模块构建系统模型,根据硬件环境合理配置模块,自动生成程序代码,最后通过集成开发环境将代码下载至控制芯片,基于Matlab和DSP的联合开发环境如图14所示。
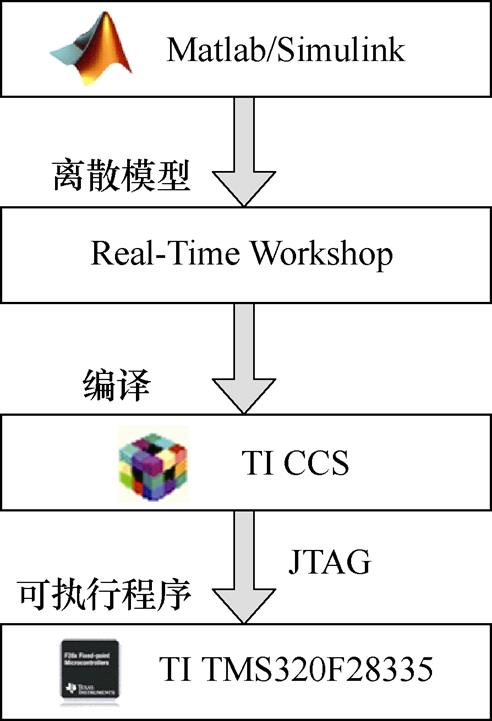
图14 基于Matlab和DSP的联合开发环境
Fig.14 Development environment based on the Matlab and DSP
控制算法快速实现的Simulink模型如图15所示,为了实现代码编译、链接与下载的自动实现,模型中需要添加F28335 eZdsp模块。而ADC模块用来采样输入电压、输出电压和负载电流,再分别进行标定处理。其中,输出电压与参考电压一同输入到带积分饱和与输出限幅功能的PID模块中,并利用计算得到的失配补偿分量对其输出结果进行修正;最终将得到的控制信号经数据格式处理后,分别送入ePWM模块生成占空比控制信号。
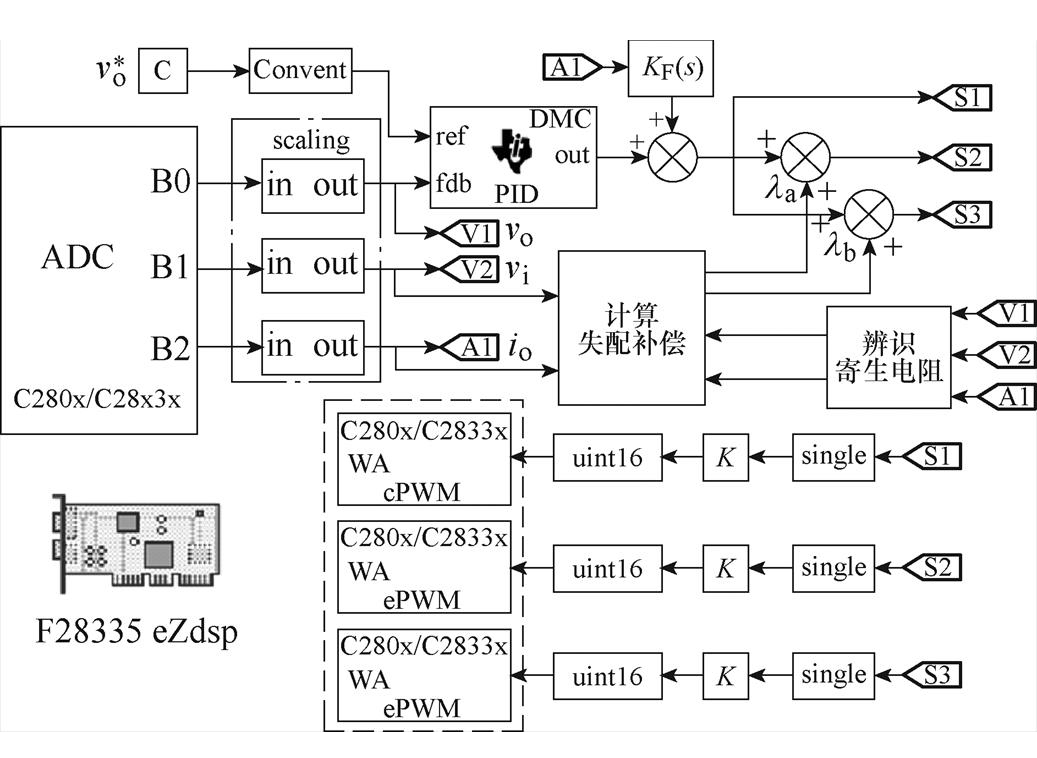
图15 控制算法快速实现的Simulink模型
Fig.15 Simulink model for control algorithms rapid implementation
依照图5给出的辨识方法,计算出各相寄生电阻值,实验参数见表2。
表2 实验参数
Tab.2 Experimental parameters

参 数数 值 输入电压vi/V50 输出电压vo/V30 开关频率fs/kHz10 输出电容Co/mF220 电容等效串联电阻rC/mW628 额定负载RL/W1.5 滤波电感L1/mH911 L2/mH877 L3/mH960
因此,得到
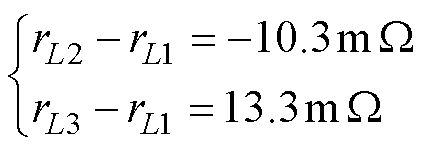 (36)
(36) 采用LCR电桥测量出各相电感直流电阻如图16所示,经过与LCR电桥测试结果对比可知,估算值与测试值保持一致,从而验证了本文所采用寄生电阻辨识方法的正确性。

图16 采用LCR电桥测量出各相电感直流电阻
Fig.16 Measured results of inductor resistance each phase with LCR meter
出于对各相电流不平衡度的合理考量,采用均流误差评价指标,不平衡度越小,表明变换器均流性能越好[19-20]。其定义为
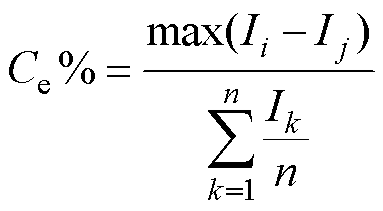 (37)
(37)式中,max(Ii-Ij)为任意两相平均电感电流的最大差异值。文中将不平衡度小于5%作为评价标准[21]。
图17和图18分别为负载电流为10A和20A工况下电感电流的稳态波形,根据波形记录数据及式(37),得出TP-IBC均流输出特性见表3。
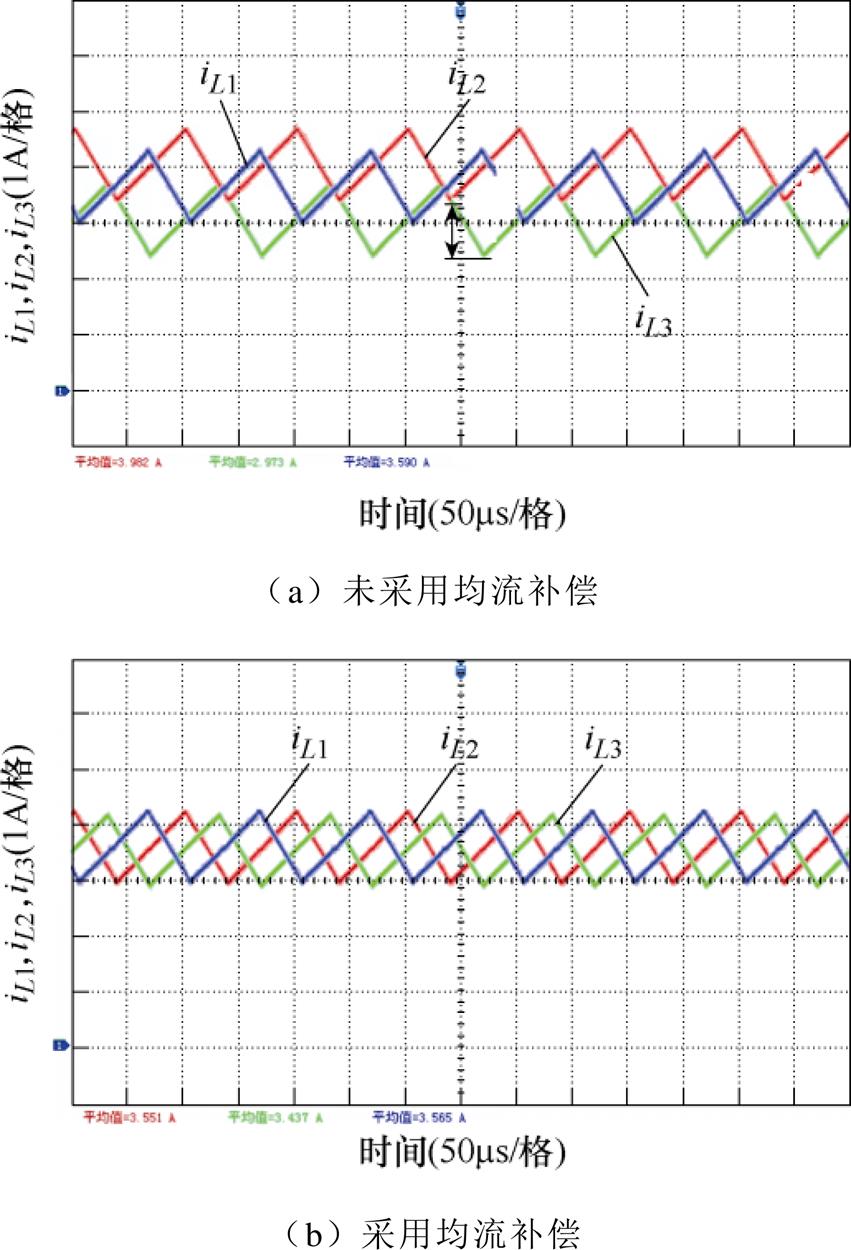
图17 负载电流10A时电感电流波形
Fig.17 Inductor current waveforms of at 10A load
当系统未采用均流控制策略时,各相电感电流差异明显,如图17a和图18a所示,两种负载下电感电流iL2和iL3差异性最为显著;由表3可知,均流误差随着负载电流增大略有增加,达到29.06%。而当采用本文所提出的均流补偿策略时,如图17b和图18b所示,两种负载下三相电感电流(iL1、iL2和iL3)幅值几乎相同,从而可有效平均分配负载电流,并满足均流误差小于5%的规定要求。
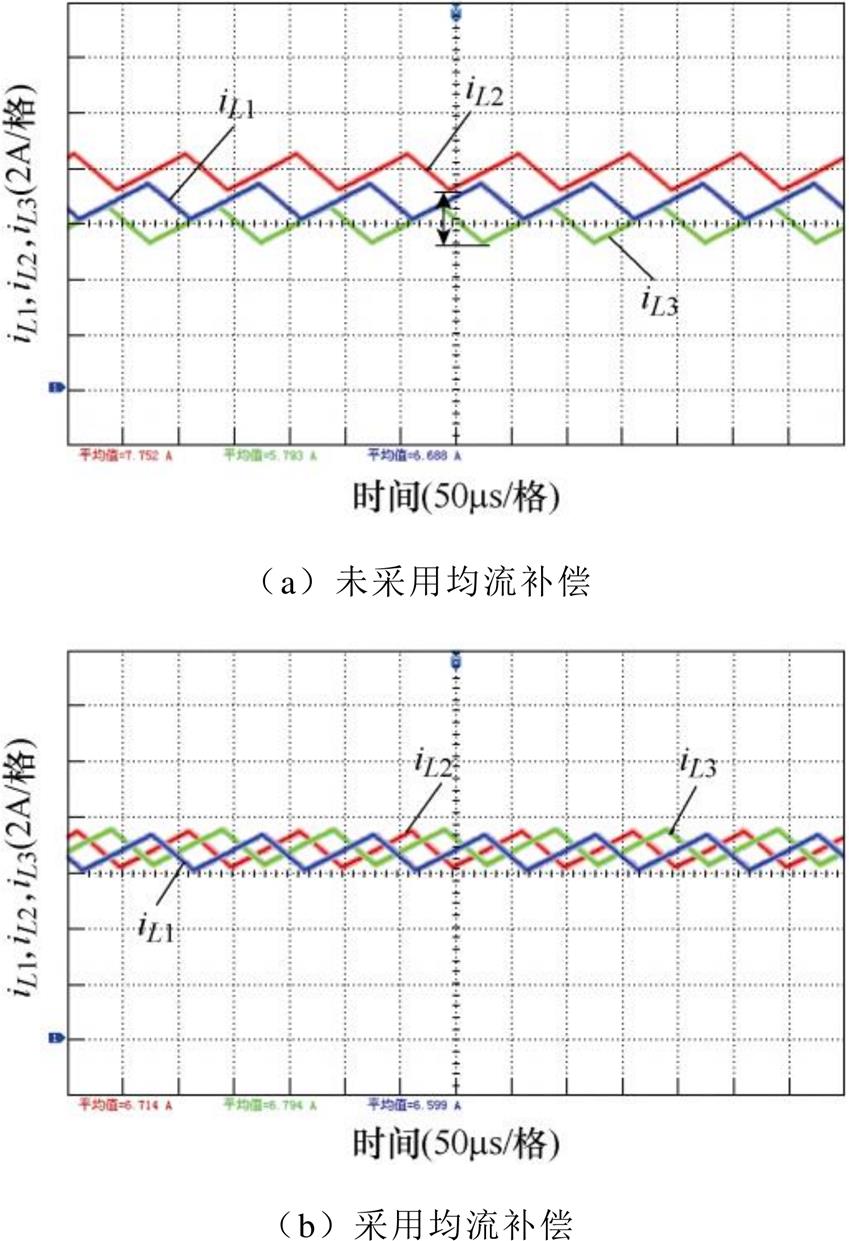
图18 负载电流20A时电感电流波形
Fig.18 Inductor current waveforms of at 20A load
表3 TP-IBC均流输出特性
Tab.3 Current sharing output performance of the TP-IBC

平均值iL1/AiL2/AiL3/Aio/ACe(%) 未补偿3.593.982.9710.5428.75 6.697.755.7920.2329.06 经补偿3.573.553.4410.563.69 6.606.716.7920.102.84
图19分别给出了负载电流由10A到20A以及20A到10A,两种阶跃响应下输出电压和负载电流的波形,可以看出,两种情况下变换器输出电压均在3ms内恢复至给定值,过冲(下冲)电压幅值较小,且在不同负载下实现无静差,表明系统具有良好的动态、稳态性能。
变换器负载电流在20A与10A之间发生阶跃变化时,各相电感电流动态响应波形如图20所示。明显在整个动态过程中,各相中的电感电流(iL1、iL2和iL3)能够始终精确均分负载电流。另外,三相电感电流恢复时间仅需10ms左右,具有较好的动态响应性能。
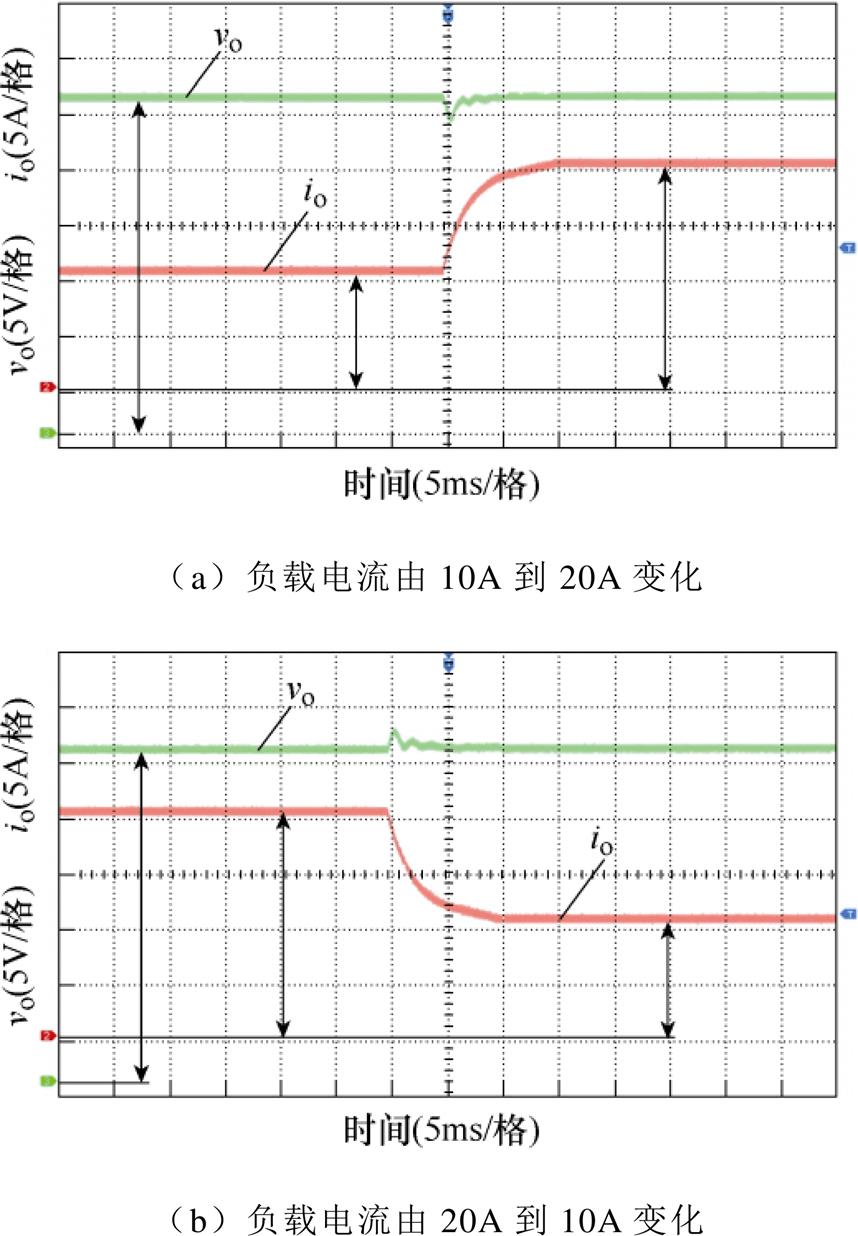
图19 负载突变时输出电压与负载电流波形
Fig.19 Output voltage and current waveforms during the load current step change
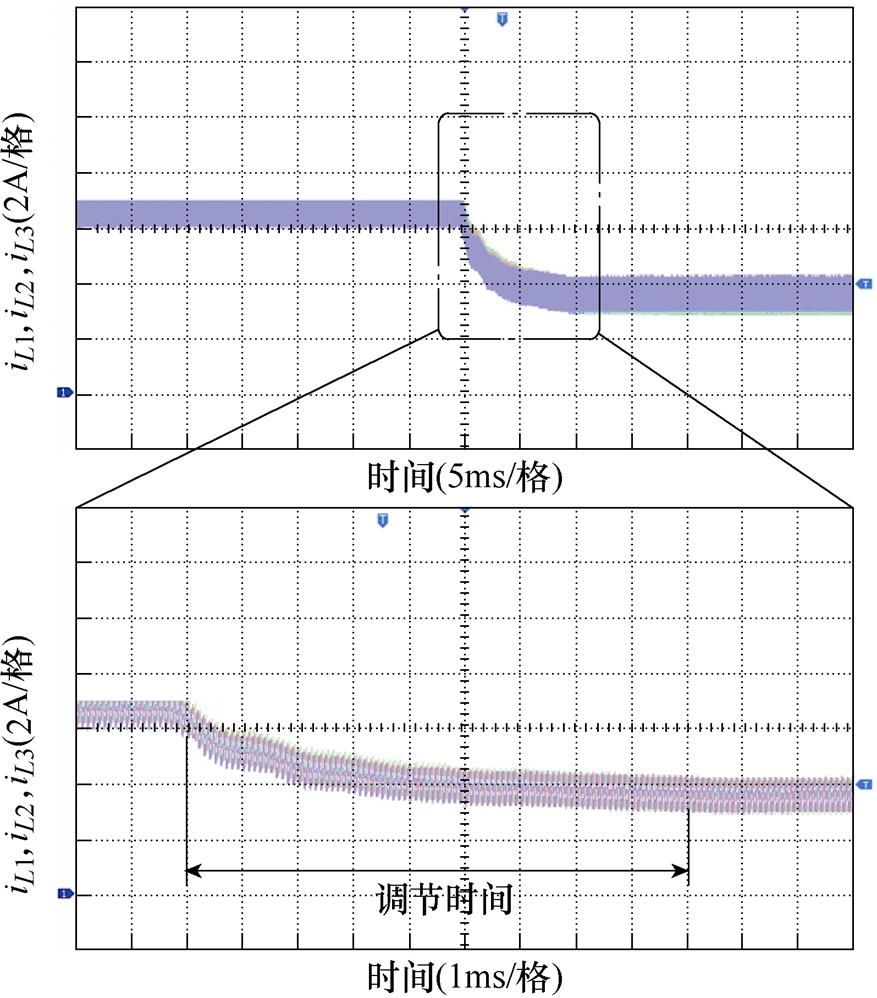
图20 负载突变时(由20A到10A)电感电流波形
Fig.20 Inductor current waveforms under 20A to 10A load current step change
本文提出一种应用于多相交错并联DC-DC变换器的单电流传感器控制策略。首先根据变换器工作模态建立全息数学模型,推导出稳态下各相电流与寄生电阻、负载电流及占空比解析表达式;其次利用恒定占空比交替测试法估算各相寄生电阻,引入占空比补偿因子实现相间电流均衡;然后基于频域法对控制器进行设计,并增加负载电流前馈补偿环路以降低输出阻抗;最后通过实验验证,得到以下结论:
1)本文所采用的控制策略能有效改善电感电流不均衡问题,保证各相电流不平衡度小于5%;当负载发生阶跃变化时,输出电压能快速恢复至给定值,各相电流始终均分负载电流。
2)相较于传统双闭环控制策略,可提高系统功率密度及节约成本,而相较于无电流传感控制策略,具有动态均流及短路保护能力,并为实际工程应用提供重要参考。
参考文献
[1] 杨玉岗, 马杰,马云巧, 等. 多相交错并联磁集成双向DC/DC变换器中耦合电感的通用设计准则[J]. 中国电机工程学报, 2015, 35(23): 6122-6134.
Yang Yugang, Ma jie, Ma Yunqiao, et al. The universal design criterion of coupled inductors in multiphase interleaving and magnetically integrated bidirectional DC/DC converters[J]. Proceedings of the CSEE, 2015, 35(23): 6122-6134.
[2] Koran A, LaBella T, Lai J. High efficiency photo- voltaic source simulator with fast response time for solar power conditioning systems evaluation[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1285-1297.
[3] Calderon-Lopez G, Scoltock J, Wang Y, et al. Power- dense bi-directional DC-DC converters with high performance inductors[J]. IEEE Transactions on Vehicular Technology, 2019, 68(12): 11439-11448.
[4] Mouli G R C, Schijffelen J H, Bauer P, et al. Design and comparison of a 10kW interleaved Boost con- verter for PV application using Si and SiC devices[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2017, 5(2): 610-623.
[5] Rocabert J, Capo-Misut R, Munoz-Aguilar R S, et al. Control of energy storage system integrating electro- chemical batteries and supercapacitors for grid- connected applications[J]. IEEE Transactions on Industry Applications, 2019, 55(2): 1853-1862.
[6] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.
Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional dc-dc converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.
[7] Meng L, Dragicevic T, Vasquez J C, et al. Tertiary and secondary control levels for efficiency optimi- zation and system damping in droop controlled DC-DC converters[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2615-2626.
[8] Chen Hungchi, Lu Cheyu, Rout U S. Decoupled master-slave current balancing control for three-phase interleaved Boost converters[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3683-3687.
[9] Huang P H, Liu Pochun, Xiao Weidong, et al. A novel droop-based average voltage sharing control strategy for DC microgrids[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1096-1106.
[10] Calderon-Lopez G, Villarruel-Parra A, Kakosimos P, et al. Comparison of digital PWM control strategies for high-power interleaved DC-DC converters[J]. IET Power Electronics, 2018, 11(2): 391-398.
[11] Tricarico T, Gontijo G F, Aredes M, et al. New hybrid-microgrid topology using a bidirectional interleaved converter as a robust power interface operating in grid-connected and islanded modes[J]. IET Renewable Power Generation, 2020, 14(1): 134- 144.
[12] Foley R F, Kavanagh R C, Egan M G. Sensorless current estimation and sharing in multiphase Buck converters[J]. IEEE Transactions on Power Elec- tronics, 2012, 27(6): 2936-2946.
[13] Huang W, Abu Qahouq J A. Input voltage ripple- based sensorless current sharing autotuning controller for multiphase DC-DC converters[J]. IEEE Transa- ctions on Industry Applications, 2016, 52(5): 4117- 4125.
[14] Abu Qahouq J A, Huang L, Huard D. A sensorless current sharing analysis and scheme for multiphase converters[J]. IEEE Transactions on Power Electro- nics, 2008, 23(5): 2237-2247.
[15] Gordillo J, Aguilar C. A simple sensorless current sharing technique for multiphase DC-DC Buck converters[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(5): 3480-3489.
[16] 杨俊杰, 刘思扬, 孙旭, 等. 多重交错并联开路电路故障检测[J]. 中国电机工程学报, 2019, 39(11): 3336-3343.
Yang Junjie, Liu Siyang, Sun Xu, et al. Multi-phase interleaved converter open circuit fault diagnosis[J]. Proceedings of the CSEE, 2019, 39(11): 3336-3343.
[17] 王朝强, 曹太强, 郭筱瑛, 等. 三相交错并联双向DC-DC变换器动态休眠控制策略[J]. 电工技术学报, 2020, 35(15): 3514-3523.
Wang Chaoqiang, Cao Taiqiang, Guo Xiaoying, et al. Dynamic dormancy control strategy of three-phase staggered parallel bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3514-3523.
[18] Sha Deshang, Zhang Jiankun, Wang Xiao, et al. Dynamic response improvements of parallel connected bidirectional DC-DC converters for electrical drive powered by low-voltage battery employing optimized feedforward control[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7783-7794.
[19] 丘东元, 张波, 韦聪颖. 改进式自主均流技术的研究[J]. 电工技术学报, 2005, 20(10): 41-47.
Qiu Dongyuan, Zhang Bo, Wei Congying. Study of paralleled Buck converters with improved automatic current-sharing technique[J]. Transactions of China Electrotechnical Society, 2005, 20(10): 41-47.
[20] 杨玉岗, 吴晗, 关婷婷. 交错并联LLC谐振变换器的磁集成均流特性[J]. 电工技术学报, 2019, 34(12): 2529-2538.
Yang Yugang, Wu Han, Guan Tingting. Magnetic integrated current sharing characteristics of inter- leaved LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2529- 2538.
[21] 任小永, 王亚坤, 陈宇, 等. 基于虚拟阻抗的LLC谐振变换器并联均流控制[J]. 电工技术学报, 2019, 34(21): 4540-4550.
Ren Xiaoyong, Wang Yakun, Chen Yu, et al. Parallel current sharing control of LLC resonant converter based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4540-4550.
Single-Sensor Sampling Current Control Strategy of Multiphase Interleaved DC-DC Converters
Abstract For multiphase interleaved DC-DC converters, current sharing among inductors is an important issue, so this paper proposes a single-sensor sampling current algorithm with current dynamic sharing capability. Firstly, a detailed mathematical model is presented according to the converter operation mode. The factors affecting current imbalance among phases are analyzed, and the analytical expressions of the phase current, parasitic resistance, load current and duty cycle are derived. Secondly, considering the non-ideal characteristics of the switches, all the parasitic resistances are estimated with constant duty-cycle test method by turning-on each phase. Taking the output of voltage loop controller as the reference value, the duty cycle compensation factors are introduced to obtain balanced inductor current. Besides, the control loop based on small-signal modeling is analyzed using the frequency-response method, and supported with the Matlab/SISO design tool, the zero position and loop gain of the controller are optimized. Stability against the load variations is investigated by means of the root locus analysis. Meanwhile, to further improve the dynamic performance, the feedforward control is implemented and the output impedance can be reduced dramatically. Finally, the experimental setup based on a three-phase interleaved Buck converter is constructed, and the steady-state and dymamic experimental results verify the correctness of the proposed control strategy.
keywords:Interleaved converter, single-current sensor, current sharing, feedforward control
DOI: 10.19595/j.cnki.1000-6753.tces.201166
中图分类号:TM46
郭 强 男,1984年生,博士,研究方向为大功率变换器及其控制技术。E-mail: guoqiang@cqut.edu.cn
谢诗云 男,1987年生,博士,研究方向为无线电能传输与电力电子变换技术等。E-mail: xieshiyun1987@cqut.edu.cn(通信作者)
重庆市教委科学技术研究计划项目(KJQN202001128)和重庆市技术创新与应用发展专项项目(cstc2019jscx-msxmX0003)资助。
收稿日期 2020-09-06
改稿日期 2020-10-09
(编辑 陈 诚)