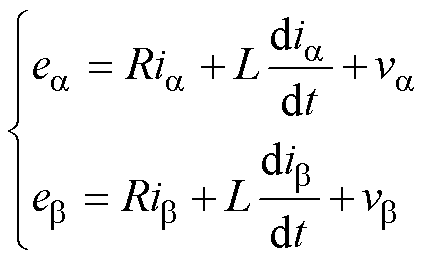（1）式中，ea、eb、va、vb、ia、ib 分别为电网电压、整流侧电压和电网电流在两相静止坐标系下a、b 轴的分量。
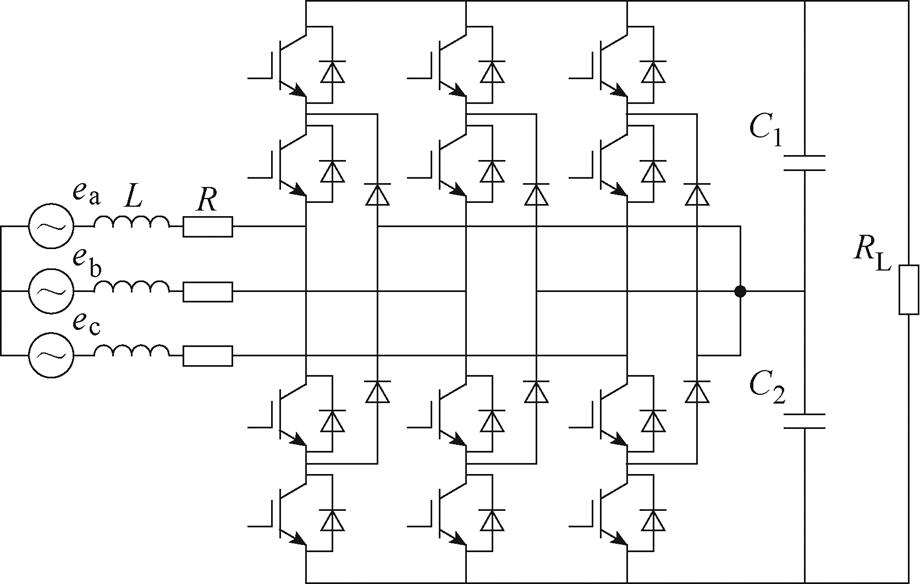
图1 三电平PWM整流器电路拓扑
Fig.1 Topology of three-level PWM rectifier
摘要 该文以三电平脉宽调制（PWM）整流器为研究对象，提出一种基于在线扰动补偿的级联式无差拍控制（CDBC）策略。该策略内外环均采用了无差拍控制方式，并建立龙伯格观测器分别对功率模型扰动和负载扰动进行估计和补偿，实现有功功率和无功功率的解耦控制以及系统快速响应。在参数设计方面，采用极点配置方法整定观测器增益，并引入期望周期数对电压环系数进行调节，从而实现内外环较高匹配性。在稳态和动态条件下，对所提控制策略进行仿真和实验，结果表明，相比于传统的无差拍功率控制（DBPC），所提控制策略可以实现更加准确的单位功率因数和更强的抗负载扰动能力。
关键词：三电平PWM整流器 在线扰动补偿 级联式无差拍控制 龙伯格观测器
目前，PWM整流器被广泛运用于风力发电、有源电力滤波器、虚拟同步机以及列车牵引等领 域[1-6]。PWM整流器的控制方法主要包括电压定向控制[7]、直接功率控制[8]、模型预测控制[9-12]等。电压定向控制通过PI控制器对电压、电流进行双闭环控制，可以实现电压、电流的无静差调节，但其动态性能受到积分器的限制。直接功率控制和有限集模型预测功率控制具有动态响应快、系统结构简单的优点，但这两种控制方法的稳态纹波大，且开关频率不固定。文献[11]提出了一种基于空间矢量调制（Space-Vector Modulation, SVM）的无差拍功率控制，相比于有限集模型预测功率控制，该方法稳态纹波小，且开关频率恒定，但其控制效果同样依赖于系统模型和参数的准确性。
模型中因近似处理产生的误差以及参数变化引起的扰动会使得受控子系统之间存在交叉耦合，这将导致被控量无法准确跟踪参考值，并且在动态过程中各个子系统之间的相互干扰会延迟系统的响应时间。为克服模型不确定性及参数失配带来的影响，文献[13-14]分别采用最小二乘法和模型参考自适应法对系统参数进行在线辨识。最小二乘法具有收敛速度快、易于编程的优点，在系统参数估计中应用较为广泛。模型参考自适应法通过自适应率使得可调模型的输出逼近实际模型的输出，从而得到待辨识参数的估计值，该方法能否构成优良的自适应控制系统与自适应律的设计有关。文献[15]在功率内环加入了基于内模原理的准积分反馈校正环节对功率的给定值进行修正，实现功率值的无差跟踪。文献[16]设计了龙伯格观测器对整流器的电流模型进行扰动补偿，该策略对参数摄动具有较强的鲁棒性。文献[17]将系统的内、外部扰动作为扩张状态变量进行重构，实现了功率之间的解耦控制。
上述方法都是从整流器的内环对系统的动态性能和稳态性能进行优化，对于电压型PWM整流器，外环通常采用PI控制器进行闭环控制，当负载发生变化时，能量交换首先发生在电容与负载之间，由于PI控制器的滞后性，导致母线电压产生较大波动。文献[18]采用了负载电流前馈控制策略提高整流器的抗负载扰动能力，但该方法需要额外的电流传感器，增大了系统的成本和体积。从文献[19-20]可知，稳态时电网的输入电流与直流母线电压的二次方更接近线性关系，因此电压环采用以直流母线电压二次方作为反馈量的PI控制器可以获得良好的控制性能。文献[21]提出了一种基于电容储能为反馈变量的控制方法，该方法与基于电压二次方为反馈的控制策略具有一定的相似性，但其物理含义更加明确。文献[22]的电压环采用了电压二次方反馈闭环的滑模控制，该策略动态响应快，但需要在控制器中给定负载的值，无法直接应用于负载变化的场合。
为了进一步改善系统的动态性能，本文对整流器的内、外环同时进行优化，提出了一种基于在线扰动补偿的级联式无差拍控制策略（Cascaded Deadbeat Control, CDBC）。其中，内环采用无差拍功率控制（Deadbeat Power Control, DBPC），并建立龙伯格观测器对功率模型扰动进行补偿，实现有功功率和无功功率之间的解耦控制。对于电压外环，推导了输入输出之间功率流动的关系，并建立龙伯格观测器对负载扰动进行观测。根据无差拍控制思想设计了一种以电压二次方为反馈量的电压控制器，并引入期望周期数对电压环的反馈增益进行调节，满足实际工程中不同的动态性能要求。最后，在仿真和实物平台上对所提出的控制策略进行验证。
三电平PWM整流器的电路拓扑如图1所示。图中，ea、eb、ec为电网侧电压，L为滤波器电感，R为滤波器等效电阻，C1、C2为直流母线滤波电容，RL为负载电阻。假设电网三相电压平衡，根据Clarke坐标变换原则，三电平PWM整流器在两相静止坐标系下的数学模型可表示为
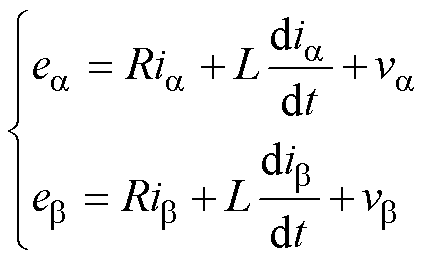（1）式中，ea、eb、va、vb、ia、ib 分别为电网电压、整流侧电压和电网电流在两相静止坐标系下a、b 轴的分量。
图1 三电平PWM整流器电路拓扑
Fig.1 Topology of three-level PWM rectifier
由瞬时功率理论可知，瞬时有功功率p和瞬时无功功率q可表示为
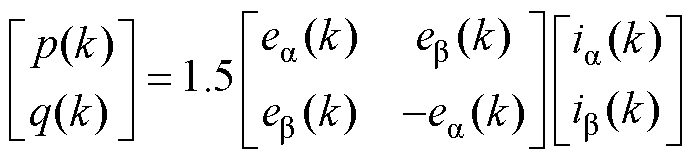（2）由于系统的采样频率远高于电网电压的频率，在一个采样周期间隔，可认为电网电压保持不变，由式（2）可得
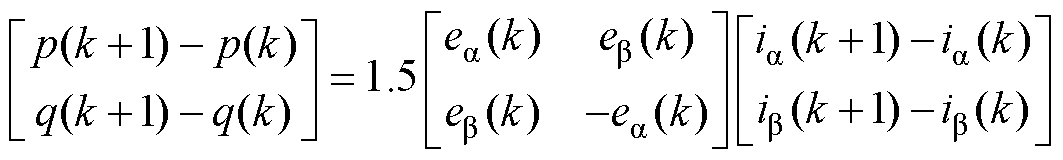（3）
忽略电阻R的影响，采用正向差分方法对式（1）进行离散化，Ts为系统控制周期，可得
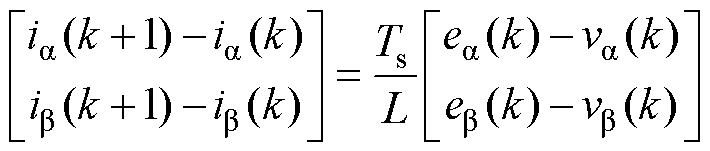（4）联立式（3）、式（4）可得瞬时功率在相邻两个控制周期改变量为
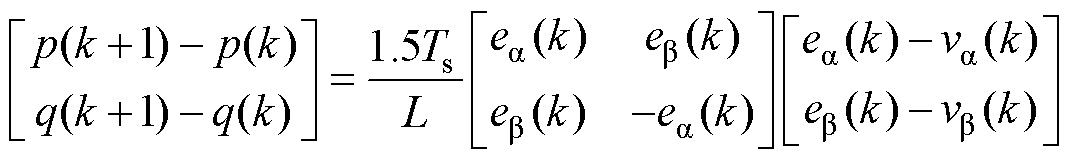（5）
图2为基于在线扰动补偿的三电平PWM整流器CDBC策略的控制框图，包括电压环控制、功率环控制以及脉宽调制部分，其中，脉宽调制策略采用含中点电位平衡控制的SVM算法。
考虑到控制模型中因近似处理产生的误差，以及参数变化引起的误差，式（5）的功率模型可重新表示为
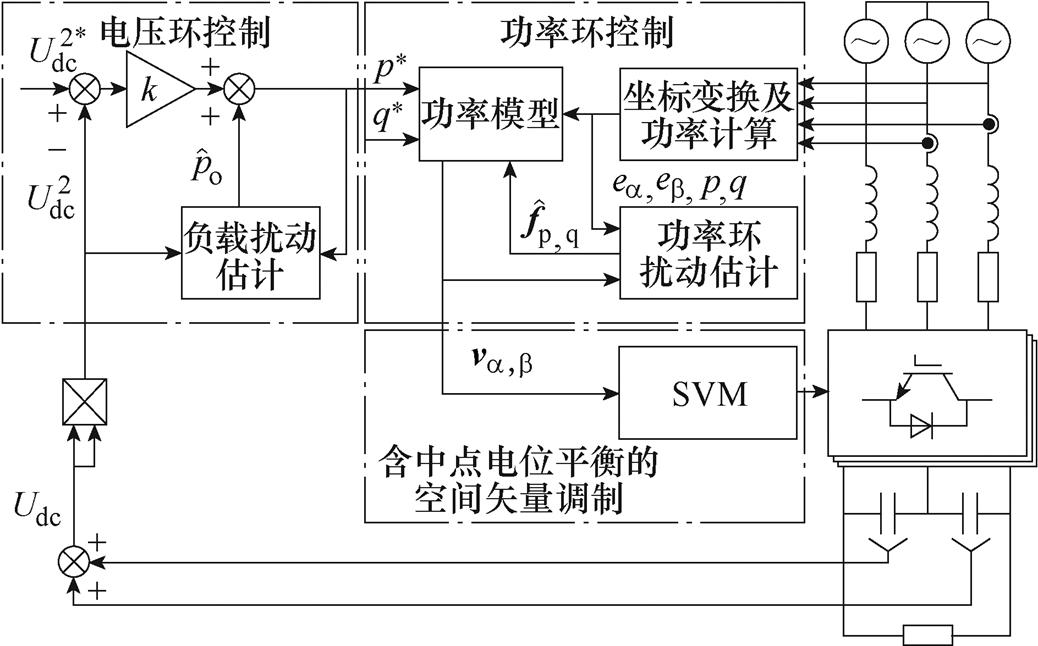
图2 基于在线扰动补偿的级联式无差拍控制框图
Fig.2 Block diagram of CDBC with online disturbance compensation
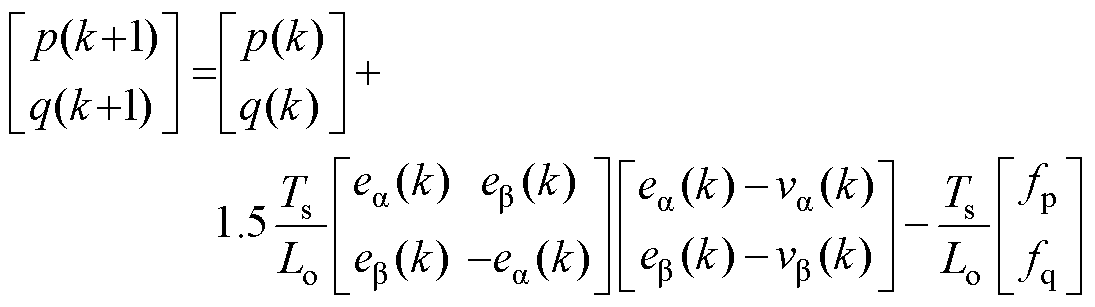（6）式中，Lo为滤波器电感的标称值；fp、fq为功率环的集总扰动，包括参数扰动及其他未建模的扰动ep、eq。记DL为滤波器电感标称值与实际值之间的误差，则fp、fq可表示为
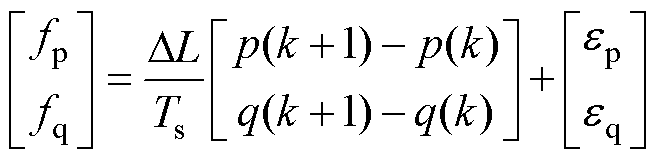（7）
为克服扰动对控制系统的影响，设计龙伯格观测器对fp、fq进行估计并补偿到控制器中。将功率和扰动量作为状态变量，l1、l2为观测器增益，则离散的龙伯格观测器可设计为
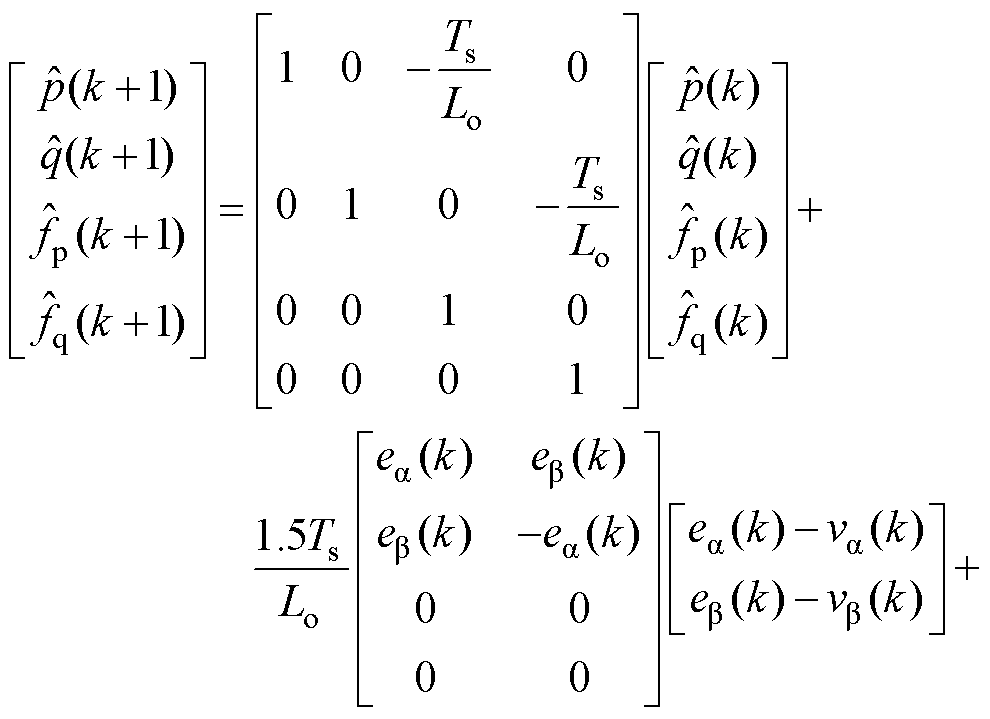
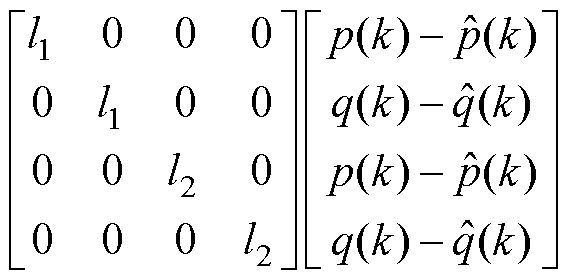（8）
根据无差拍控制原理，令下一时刻的功率为参考功率，由式（6）可推导出考虑系统扰动时输入控制电压的表达式为
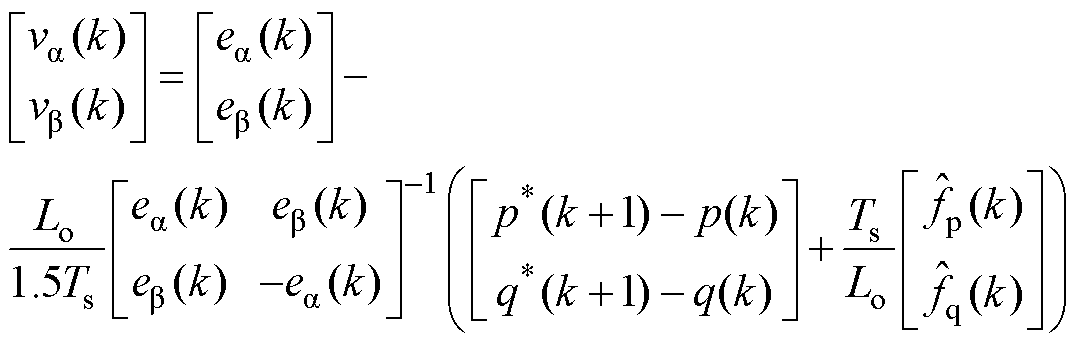（9）式中，上标“*”表示参数的参考值；上标“
”表示参数的估计值，下同。
为了简化分析，根据复空间矢量理论[23]，将式（8）观测器的表达式化为复矢量形式，即
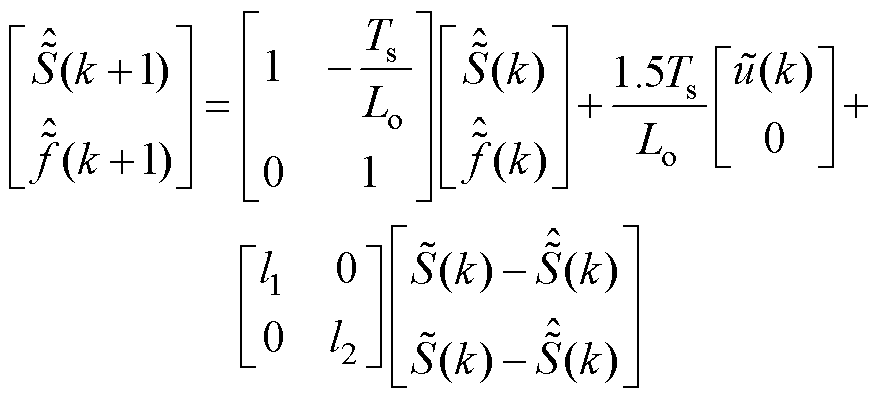（10）其中
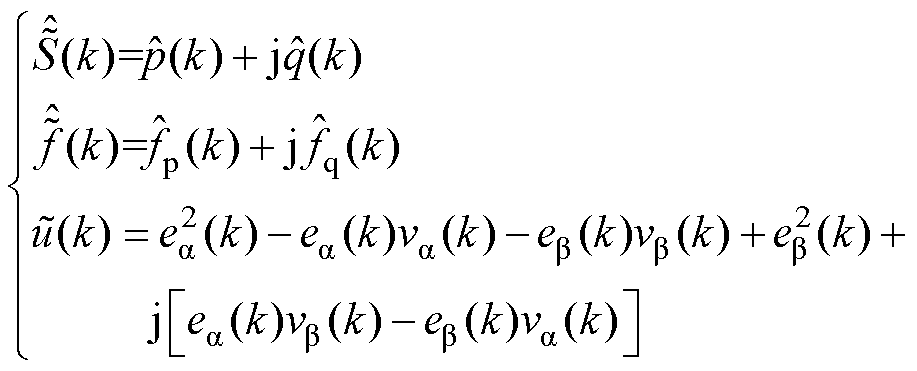
由式（10）可以得到观测器的特征多项式为
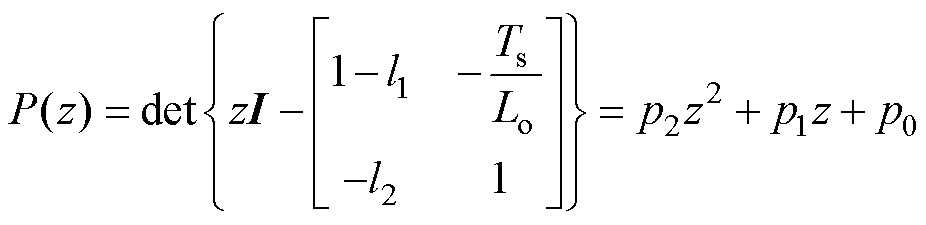（11）其中
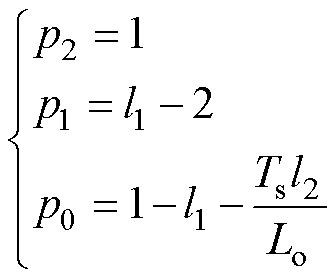
式中，I为单位矩阵。
根据离散域下的Jury稳定判据，为了保证观测器的稳定性，其特征多项式需满足以下条件
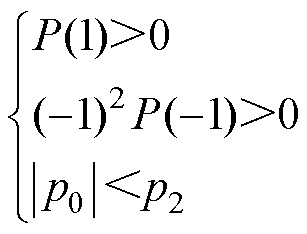（12）由式（12）可得增益l1、l2的取值范围为
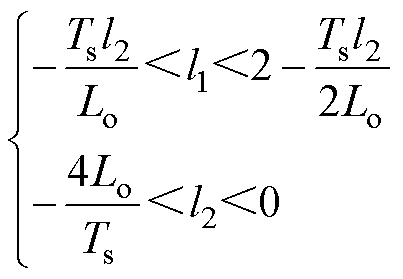（13）
通过分析观测器闭环极点的分布轨迹进一步整定观测器增益。增益变化时闭环极点分布轨迹如图3所示。由图3可知，当l1不变、l2增大时，极点首先向实轴方向移动，动态响应加快，同时阻尼系数增大，系统超调量减小；当l2继续增大时，极点向实轴两侧移动，动态响应变慢；当l2的值较小且不变、l1增大时，共轭极点首先向实轴负方向聚拢，动态响应加快，同时阻尼系数增大，系统超调量减小；当l2的值较大且不变、l1增大时，极点向实轴两侧移动，动态响应变慢。观测器的动态响应越快，对噪声越敏感，因此观测器增益的选择需要在动态响应和噪声抑制能力之间进行权衡。综合考虑系统的动态响应和抗噪声扰动能力，选取l1=2000Ts= 0.2，l2=-6000Ts=-0.6。
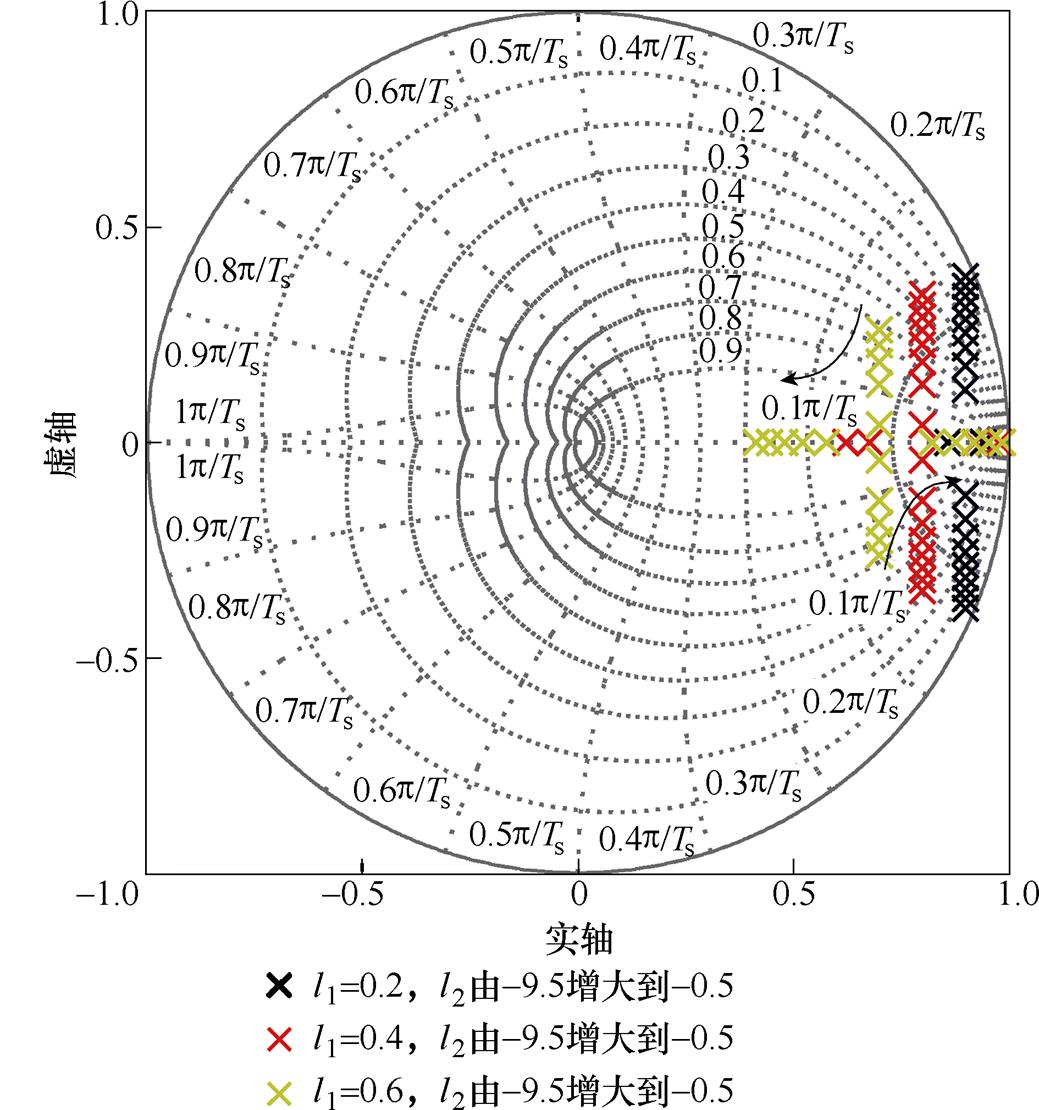
图3 增益变化时闭环极点分布轨迹
Fig.3 The rocus of closed-loop poles with gains varied
由式（1）和式（2）可得到瞬时有功功率的表达式为
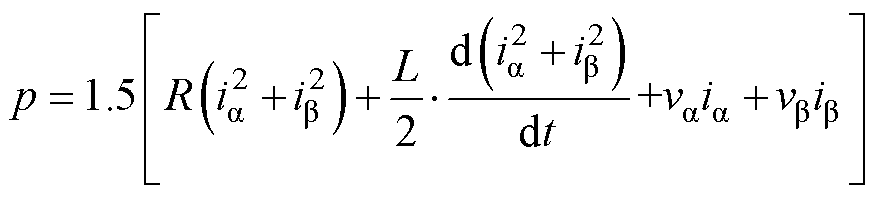（14）式中，右边第一项为滤波器等效电阻消耗的功率；第二项为滤波器电感内磁场储能吸收的功率；第三项和第四项为流动到直流侧的有功功率，包括开关器件损耗、电容储能吸收的功率以及负载消耗的 功率。
若忽略滤波器上消耗的功率和开关器件损耗，瞬时有功功率可视为电容储能吸收功率和负载功率的总和，则瞬时有功功率可表示为
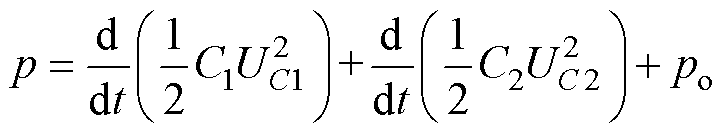（15）式中，po为负载消耗的功率；UC1、UC2分别为电容C1、C2上的电压；C1=C2=C。
稳态时输出电压Udc保持恒定，考虑到上、下电容含有低频波动且波动值与输出功率呈正相关，记中点电位Vo=UC1-UC2，式（15）可重新写为
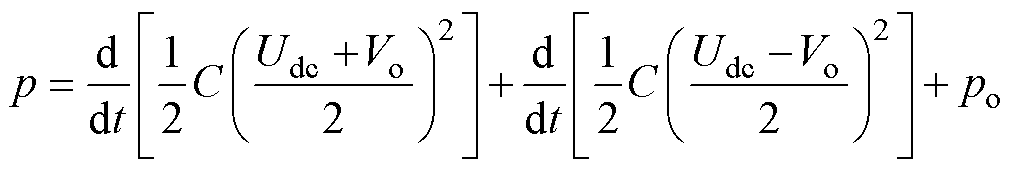
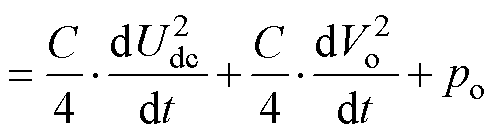（16）
式中，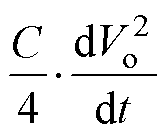
为中点电位波动引起的功率变化。当输出功率较小时，中点电位波动较小，可以认为Vo=0；当输出功率增大时，中点电位Vo的幅值增大，但是中点电位Vo是一个低频的量，所以
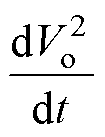是一个较小的值，当输出功率po较大时可以忽略中点电位波动引起的功率变化。因此，式（16）可化简为
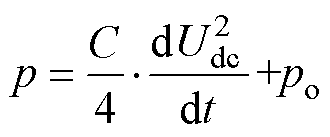（17）将式（17）离散化，可以得到离散的电压状态方程为
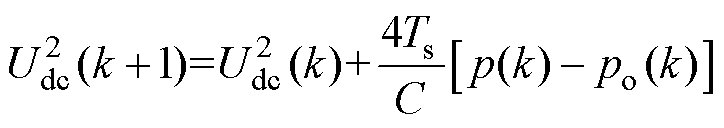（18）
根据无差拍控制原理，令下一时刻的电压为参考电压，可以得到有功功率的参考值为
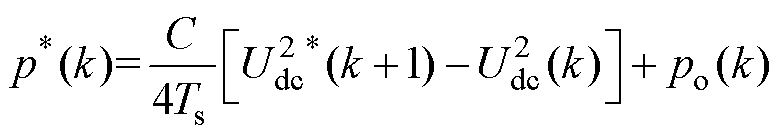（19）式（19）中，负载功率po会随着负载以及直流母线电压的变化而改变，故将负载功率po视为扰动量，并采用龙伯格观测器对其进行估计。
根据龙伯格观测器的建构原理，将电压二次方和负载功率作为状态变量，h1、h2为观测器增益，离散的龙伯格观测器可设计为
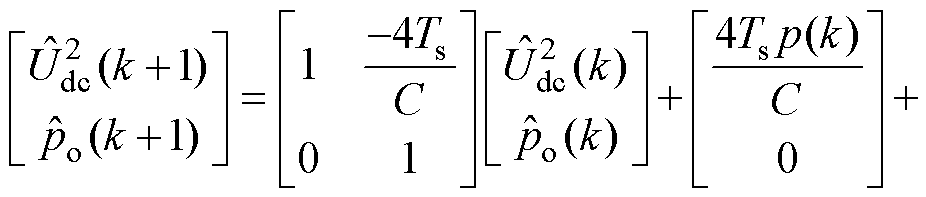
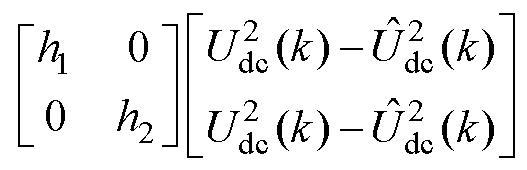（20）
因此，有功功率的参考值可重新表示为
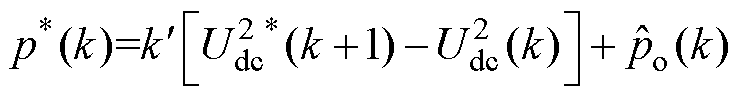（21）式中，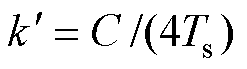
。
在本文所提的CDBC方法中，内环采用无差拍功率控制，动态响应快，实际功率可以迅速地跟踪参考功率，因此可以认为实际功率等于参考功率，即p=p*，此时，系统的响应速度主要由外环决定。若电压外环直接采用无差拍控制，即令电压的实际值在1个控制周期跟踪上参考值，当直流母线电压的实际值与参考值相差较大时，会导致输入功率急剧增大，同时系统的稳态性能变差。因此，本文令电压的实际值在N个控制周期跟踪上参考值，即令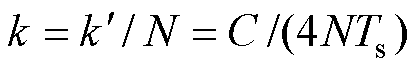
，N为直流母线电压动态调节时间的期望周期数，通过对N的合理选取可以满足实际工程中不同的动态性能要求。
电压环观测器增益的整定方法与前文中功率环观测器增益整定方法一致，最终选取h1=300Ts= 0.03，h2=-26.43Ts=-0.002 643。
为了验证本文所提控制策略的有效性，对该策略进行仿真，并与外环采用PI控制的传统无差拍功率控制进行对比，PI控制器采用电压二次方作为误差反馈量，其比例系数kp=0.05，积分系数ki=1.8。在所提的CDBC方法中，k可视为直流母线电压二次方的反馈系数，为了更好地对两者方法进行比较，在所提控制方法中，k的取值与kp相同。三电平PWM整流器的系统参数见表1。
表1 系统参数
Tab.1 System parameter
参 数数 值 滤波器电感L/mH6 直流侧电容C1,C2/mF4 700 负载电阻RL/W100 系统采样频率fs/kHz10 电网线电压有效值E/V200 电网电压频率fg/Hz50
图4为整流器的加载仿真结果，当直流侧从空载接入100W 负载后，传统DBPC方法的直流母线电压Udc降落了27.3V，经过约180ms到达稳态值；所提CDBC方法的母线电压降落了15.3V，经过约115ms到达稳态值。仿真结果表明，CDBC方法具有更小的电压降落和更快的调节速度。从图4b可知，当直流侧接入负载后，观测器估计的负载功率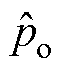
可以快速准确地自适应跟踪实际负载功率
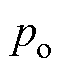，从而保证了所提控制策略具有更强的抗负载扰动能力。
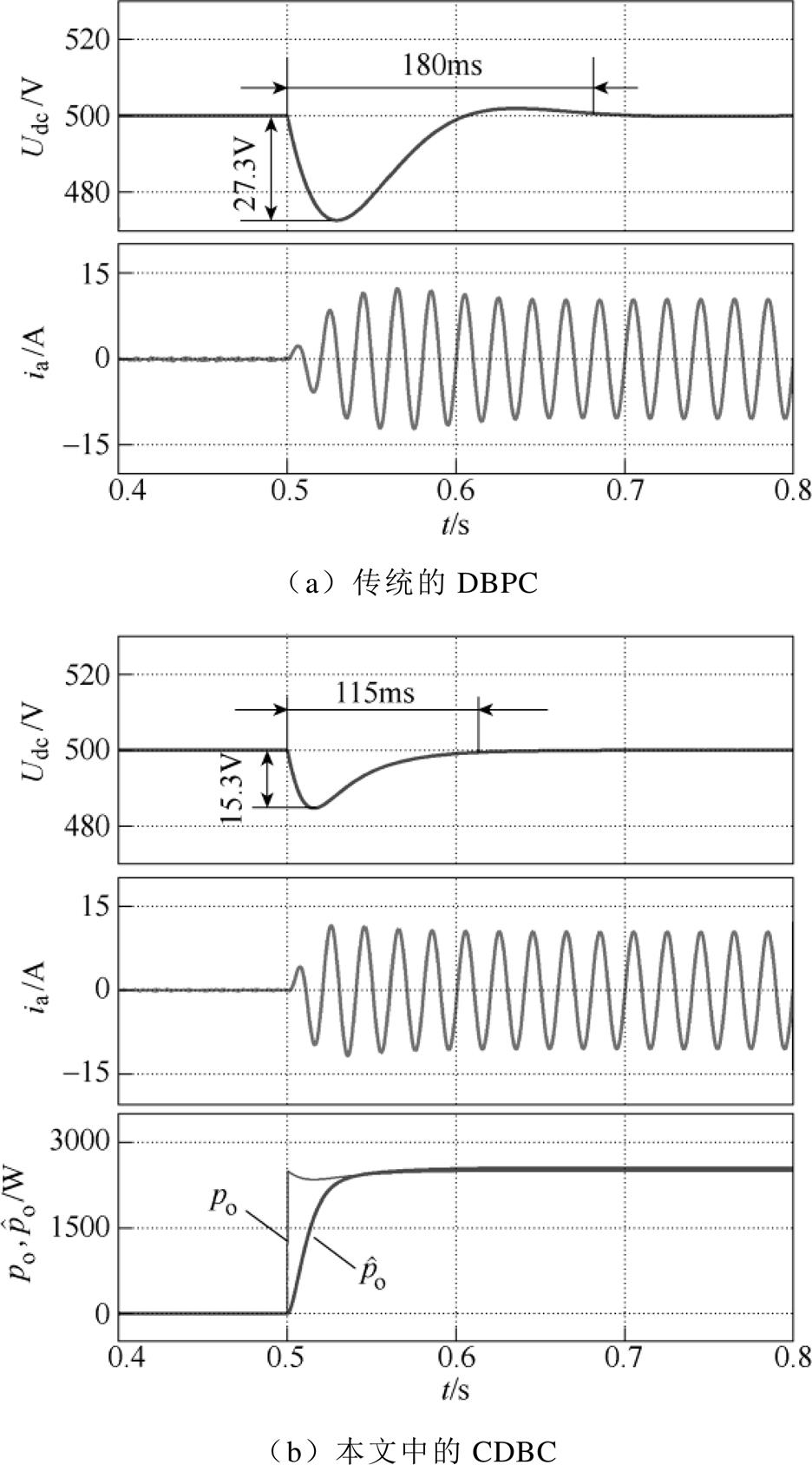
图4 加载仿真结果
Fig.4 Simulation results under sudden load
图5为整流器的直流母线电压阶跃响应仿真结果，图5中，在t=1s时刻，参考电压从500V跃变为600V，传统DBPC方法经过约150ms后直流母线电压到达稳态值，本文所提的CDBC方法经过125ms后到达稳态值；在t=1.5s时刻，参考电压从600V跃变为400V，传统DBPC方法经过约140ms后直流母线电压到达稳态值，本文所提的CDBC方法经过约128ms后直流母线电压到达稳态值。仿真结果表明，CDBC方法动态响应更快，并且在电压上升和下降的过程中没有出现超调现象。从图中的功率曲线可知，传统DBPC方法的功率无法准确跟踪参考值，并且在电压阶跃后无功功率的静差发生变化，这表明有功功率和无功功率之间存在交叉解耦，而在CDBC方法中有功功率和无功功率都可以准确地跟踪参考值，并且在动态过程中，无功功率更快地进入稳态。这是因为观测器可以对功率模型的集总扰动进行实时准确地估计，使得有功功率和无功功率实现良好的解耦控制。
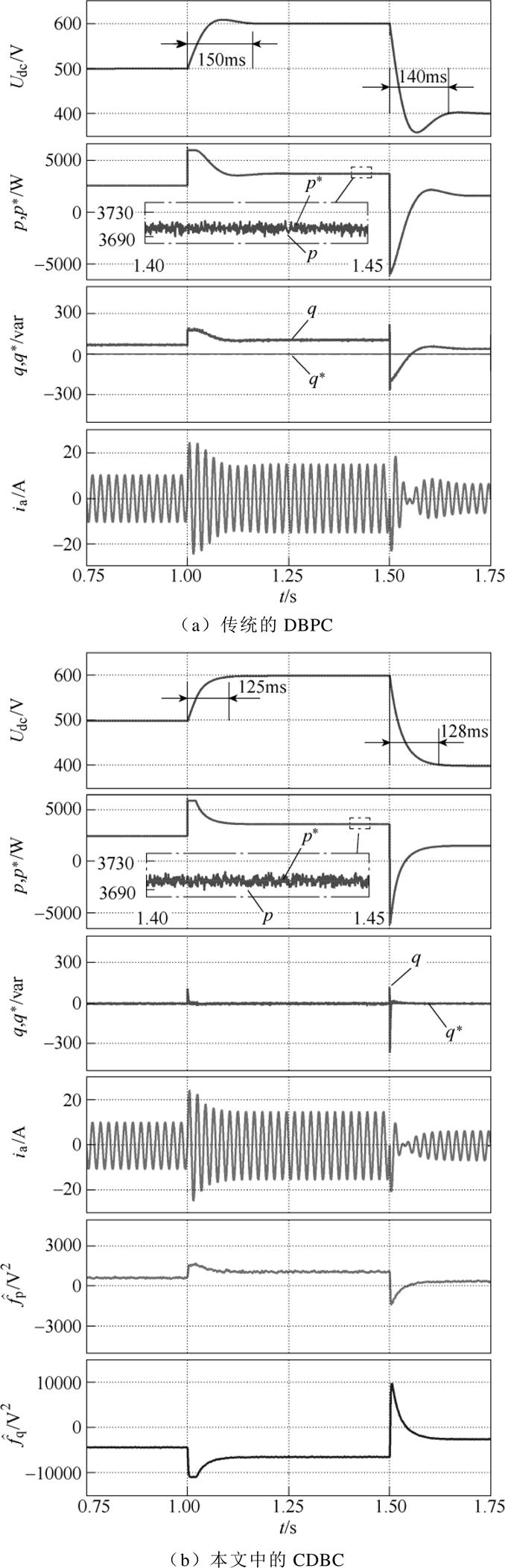
图5 直流母线电压阶跃响应仿真结果
Fig.5 Simulation results of step response for DC-link voltage
为了进一步验证该策略的有效性，在三电平PWM整流器平台上对所提控制策略进行相关实验，实验中使用的参数与仿真一致。三电平PWM整流器实验平台如图6所示，核心控制板采用TI公司的DSP芯片TMS320F28335，实验中电流量由电流探头测得，其余需要观测的量由DA芯片TLV5610输出至示波器显示。该三电平整流器系统的软启动电路由限流电阻、交流接触器和中间继电器组成，上电时通过限流电阻抑制浪涌电流，当母线电容完成预充后由DSP发出旁路切换信号将限流电阻短路，整流器进入正常运行状态。
图6 三电平PWM整流器实验平台
Fig.6 Experimental platform of three-level PWM rectifier
为了验证所提方法的抗负载扰动能力，对整流器进行加载实验。加载实验结果如图7所示，当直流侧从空载接入100W 负载后，传统DBPC方法的直流母线电压Udc降落了28V，调节时间约为100ms；所提CDBC方法的母线电压降落了17V，调节时间约为68ms。实验结果表明，相比于传统的DBPC方法，CDBC方法具有更强的抗负载扰动能力。
为了比较两种控制方法的电压跟踪性能，对整流器进行直流母线电压跃变实验，设置直流母线的参考电压从500V跃变为600V，再从600V跃变为400V。直流母线电压阶跃响应实验结果如图8所示，传统DBPC方法的调节时间分别约为125ms和140ms，本文所提的CDBC方法的调节时间分别约为113ms和120ms。实验结果表明，所提的CDBC方法动态响应更快，并且在电压上升和下降的过程中没有出现超调现象，与仿真结果基本保持一致。
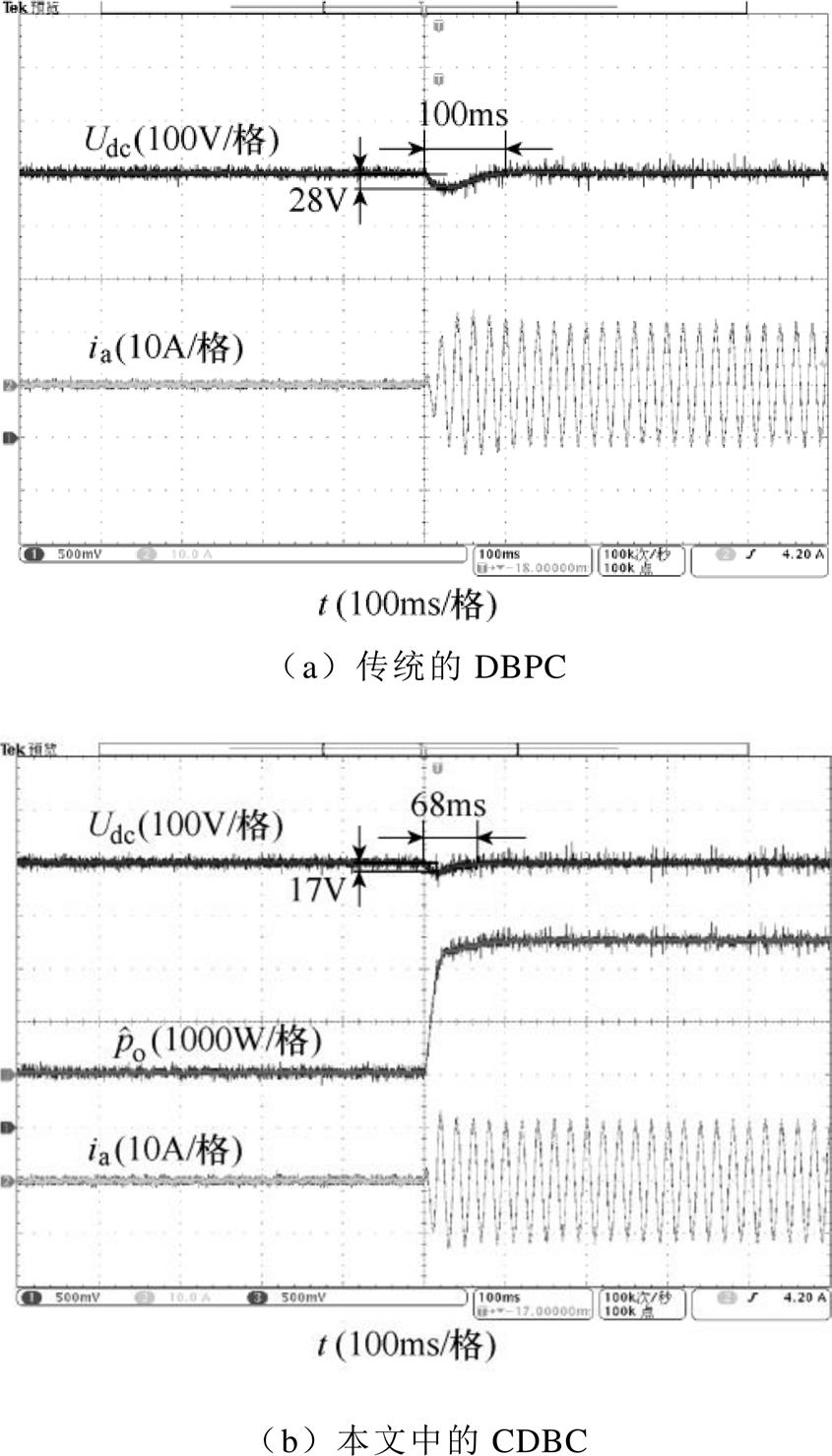
图7 加载实验结果
Fig.7 Experimental results under sudden load
为了验证CDBC方法在不同负载下的输入输出性能，图9和图10分别给出了整流器满载和半载时的稳态实验结果，设置直流母线电压参考值为500V，满载时负载电阻为100W，半载时负载电阻为200W。从图9a和图10a可知，在满载和半载时直流母线电压均可以准确跟踪参考值，同时a相电压和a相电流保持同相位，实现准确的单位功率因数。图9b和图10b为不同负载下a相电流的频谱分析，满载时总谐波畸变率（Total Harmonic Dis- tortion, THD）为4.81%，半载时THD=9.46%，具有较好的电流质量。
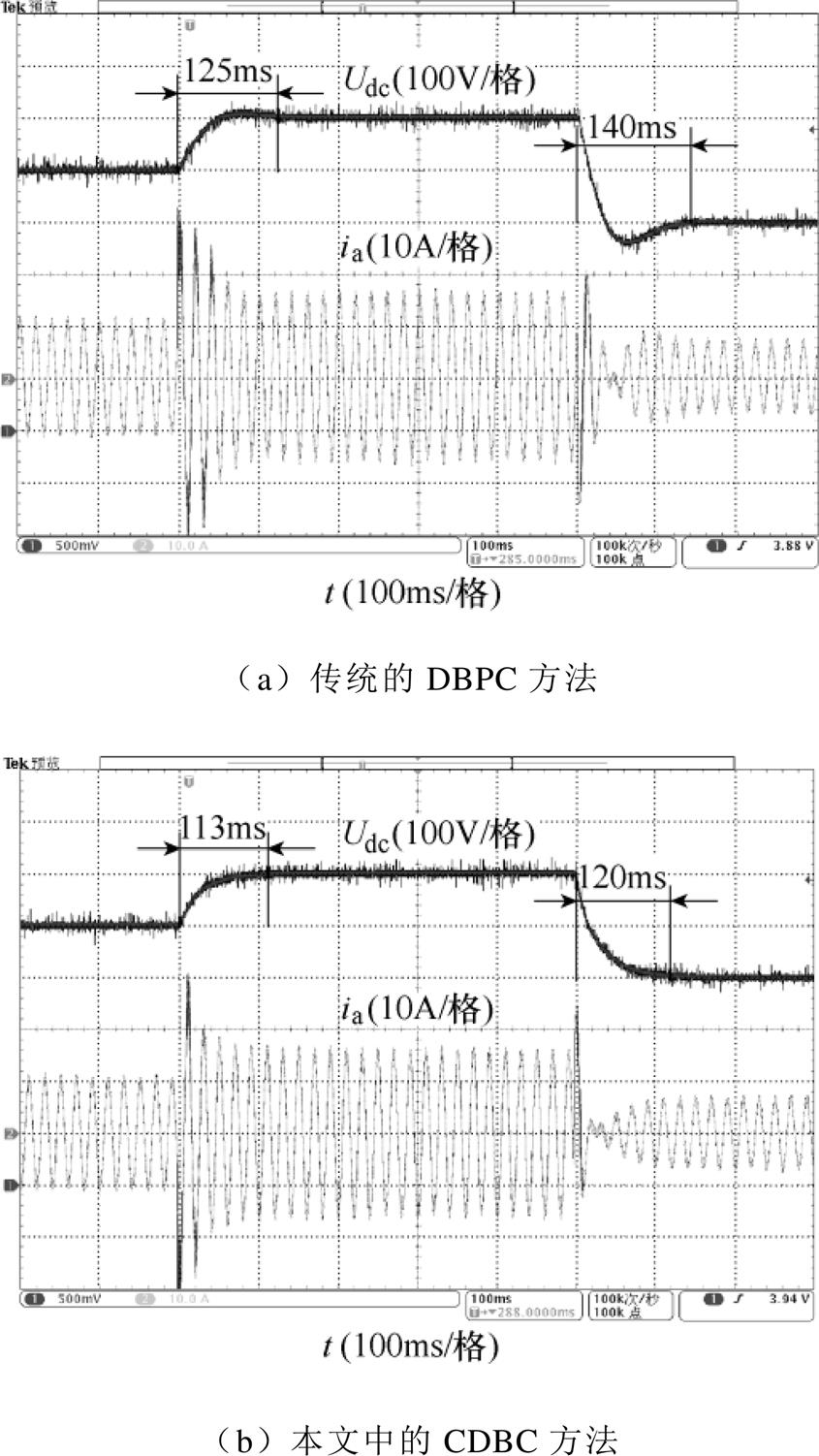
图8 直流母线电压阶跃响应实验结果
Fig.8 Experimental results of step response for DC-link voltage
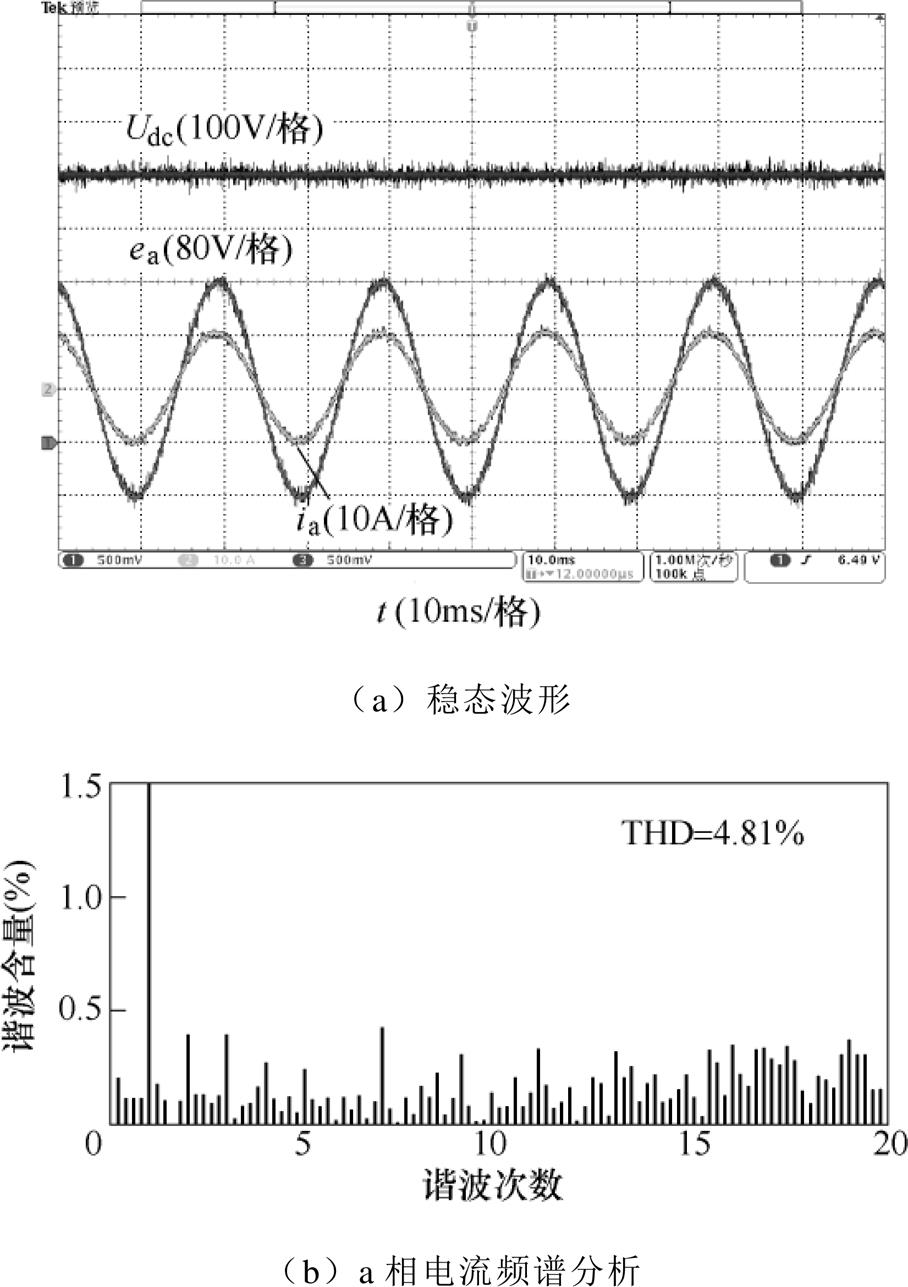
图9 满载时CDBC方法的稳态实验结果
Fig.9 Steady-state experimental results of CDBC with full load
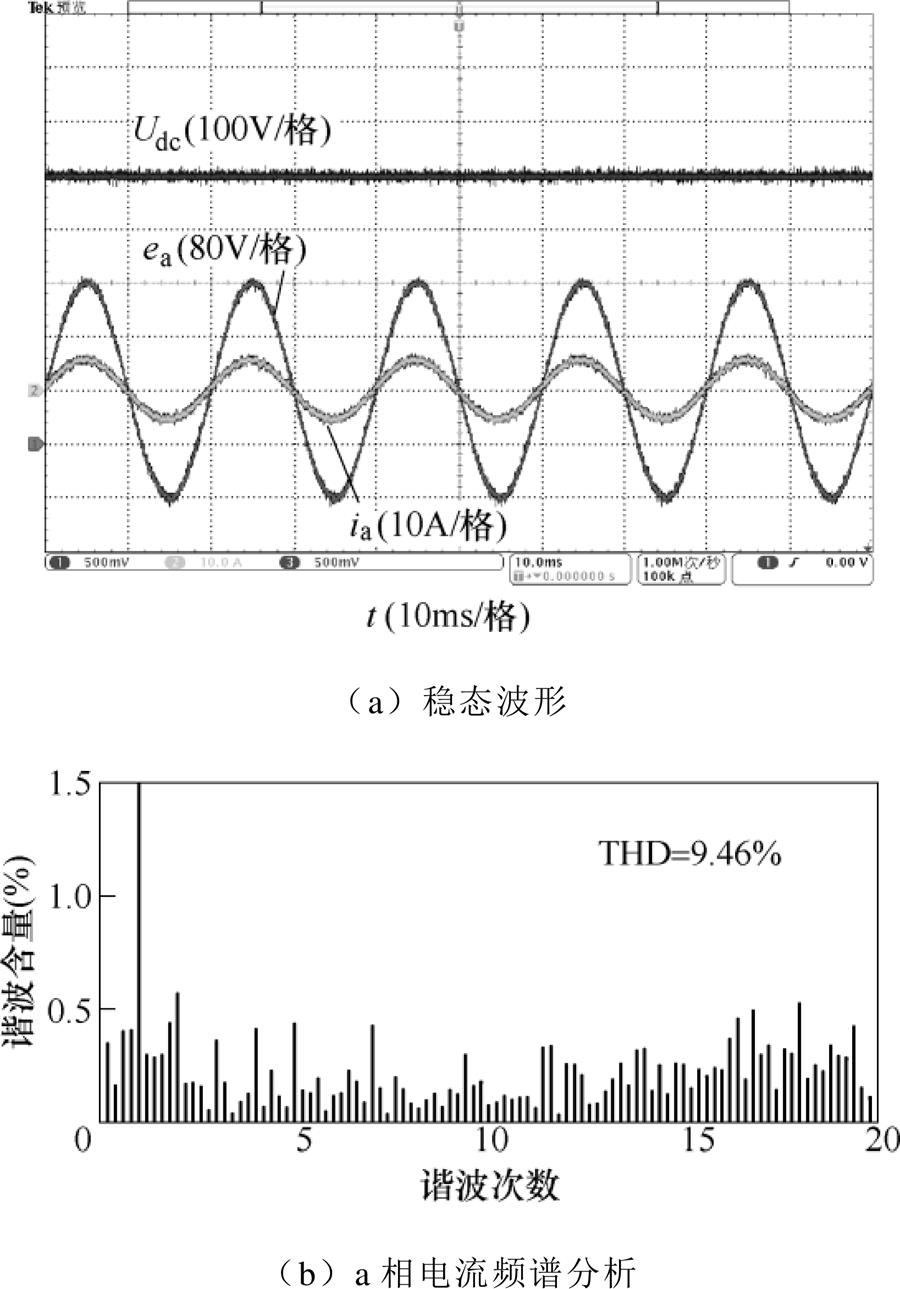
图10 半载时CDBC方法的稳态实验结果
Fig.10 Steady-state experimental results of CDBC with half load
本文分析了三电平PWM整流器的数学模型，提出了一种基于在线扰动补偿的级联式无差拍控制策略。该策略通过扰动补偿的方式实现了有功功率和无功功率的解耦控制，稳态时功率无静差。同时，克服了传统方法外环采用PI控制器时积分饱和导致的超调问题，在突加负载时具有更小的电压降落和更快的调节时间，改善了传统方法的抗负载扰动能力。
参考文献
[1] 苏晓英, 朱连成, 金石, 等. 一种复合转子无刷双馈风力发电机直接功率控制研究[J]. 电工技术学报, 2020, 35(3): 494-501.
Su Xiaoying, Zhu Liancheng, Jin Shi, et al. Research on direct power control for brushless doubly-fed wind power generator with a novel hybrid rotor[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 494-501.
[2] 梁营玉, 刘建政, 李治艳. 有源电力滤波器改进无差拍-重复控制策略[J]. 电工技术学报, 2018, 33(19): 4573-4582.
Liang Yingyu, Liu Jianzheng, Li Zhiyan. Improved deadbeat-repetitive control strategy for active power filter[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4573-4582.
[3] 张晓华, 戴碧君, 罗进, 等. 基于电流残差的有源电力滤波器故障诊断技术研究[J]. 电机与控制学报, 2019, 23(8): 50-56, 66.
Zhang Xiaohua, Dai Bijun, Luo Jin, et al. Fault diagnosis for active power filter based on current residual[J]. Electric Machines and Control, 2019, 23(8): 50-56, 66.
[4] 缪惠宇, 梅飞, 张宸宇, 等. 基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J]. 电工技术学报, 2019, 34(17): 3622-3630.
Miao Huiyu, Mei Fei, Zhang Chenyu, et al. Three phase unbalanced control strategy for virtual synchronous rectifier based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3622-3630.
[5] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
Jiang Jingya, Wang Wei, Wu Xuezhi, et al. Power decoupling strategy in virtual synchronous generator based on adaptive reactive power compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2747-2756.
[6] 孙鹏琨, 葛琼璇, 王晓新, 等. 基于硬件在环实时仿真平台的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(16): 3426-3435.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Traction control strategy of high-speed maglev train based on hardware-in-the-loop real-time simulation platform[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3426-3435.
[7] Blasko V, Kaura V. A new mathematical model and control of a three-phase AC-DC voltage source converter[J]. IEEE Transactions on Power Electronics, 1997, 12(1): 116-123.
[8] Zhang Yongchang, Li Zhengxi, Zhang Yingchao, et al. Performance improvement of direct power control of PWM rectifier with simple calculation[J]. IEEE Transactions on Power Electronics, 2013, 28(7): 3428-3437.
[9] Xia Changliang, Liu Tao, Shi Tingna, et al. A simplified finite-control-set model-predictive control for power converters[J]. IEEE Transactions on Indu- strial Informatics, 2014, 10(2): 991-1002.
[10] 夏文婧, 刘碧, 王嵩, 等. 基于输入端电压动态分量优化的PWM整流器模型预测控制[J]. 电力系统自动化, 2020, 44(1): 200-207.
Xia Wenjing, Liu Bi, Wang Song, et al. Model predictive control of PWM rectifiers based on dynamic component optimization of input-port voltage[J]. Automation of Electric Power Systems, 2020, 44(1): 200-207.
[11] Bouafia A, Gaubert J P, Krim F. Predictive direct power control of three-phase pulsewidth modulation (PWM) rectifier using space-vector modulation (SVM)[J]. IEEE Transactions on Power Electronics, 2010, 25(1): 228-236.
[12] Wang Fengxiang, Mei Xuezhu, Rodriguez J, et al. Model predictive control for electrical drive systems- an overview[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(3): 219-230.
[13] Kwak S, Moon U C, Park J C. Predictive-control- based direct power control with an adaptive parameter identification technique for improved AFE perfor- mance[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 6178-6187.
[14] Mehreganfar M, Saeedinia M H, Davari S A, et al. Sensorless predictive control of AFE rectifier with robust adaptive inductance estimation[J]. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3420-3431.
[15] 叶虹志, 姜燕, 黄守道, 等. 电压型PWM整流器无差拍预测直接功率控制[J]. 电工技术学报, 2015, 30(4): 121-128.
Ye Hongzhi, Jiang Yan, Huang Shoudao, et al. Deadbeat predictive direct power control for three- phase voltage source PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 121- 128.
[16] Xia Changliang, Wang Meng, Song Zhanfeng, et al. Robust model predictive current control of three- phase voltage source PWM rectifier with online disturbance observation[J]. IEEE Transactions on Industrial Informatics, 2012, 8(3): 459-471.
[17] Song Zhanfeng, Tian Yanjun, Yan Zhuo, et al. Direct power control for three-phase two-level voltage- source rectifiers based on extended-state obser- vation[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4593-4603.
[18] 倪靖猛, 方宇, 邢岩, 等. 基于优化负载电流前馈控制的400Hz三相PWM航空整流器[J]. 电工技术学报, 2011, 26(2): 141-146, 164.
Ni Jingmeng, Fang Yu, Xing Yan, et al. Three-phase 400Hz PWM rectifier based on optimized feedforward control for aeronautical application[J]. Transactions of China Electrotechnical Society, 2011, 26(2): 141-146, 164.
[19] 王恩德, 黄声华. 三相电压型PWM整流的新型双闭环控制策略[J]. 中国电机工程学报, 2012, 32(15): 24-30, 18.
Wang Ende, Huang Shenghua. A novel double closed loops control of the three-phase voltage-sourced PWM rectifier[J]. Proceedings of the CSEE, 2012, 32(15): 24-30, 18.
[20] 王晗, 张建文, 蔡旭. 一种PWM整流器动态性能改进控制策略[J]. 中国电机工程学报, 2012, 32(增刊1): 194-202.
Wang Han, Zhang Jianwen, Cai Xu. An improved control method of the dynamic ability for PWM rectifier[J]. Proceedings of the CSEE, 2012, 32(S1): 194-202.
[21] 姜卫东, 汪磊, 赵德勇, 等. 外环采用电容储能反馈内环采用改进无差拍控制的PWM整流器的控制方法[J]. 中国电机工程学报, 2016, 36(14): 3899- 3909.
Jiang Weidong, Wang Lei, Zhao Deyong, et al. A control method based on outer loop adopting the feedback of capacitor energy storage and internal loop adopting improved deadbeat control for PWM rectifier[J]. Proceedings of the CSEE, 2016, 36(14): 3899-3909.
[22] 马辉, 谢运祥. 基于滑模变结构的Vienna整流器新型双闭环控制策略研究[J]. 电工技术学报, 2015, 30(12): 143-151.
Ma Hui, Xie Yunxiang. A novel dual closed-loop control strategy based on sliding-mode variable structure of Vienna-type rectifier[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 143- 151.
[23] Wang Bo, Chen Xianle, Yu Yong, et al. Robust predictive current control with online disturbance estimation for induction machine drives[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4663-4674.
Cascaded Deadbeat Control Strategy with Online Disturbance Compensation for Three-Level PWM Rectifier
Abstract A cascaded deadbeat control (CDBC) strategy with online disturbance compensation is proposed for three-level pulse width modulation (PWM) rectifiers in this paper. Specifically, to realize the decoupling between active power control and reactive power control and to ensure the fast response of system, deadbeat control is adopted for both inner and outer loops, and Luenberger observers are established to estimate and compensate the disturbances brought by inaccurate power model and load variation. In terms of parameter design, the pole placement method is adopted to determine the gain of the observer, and the expected cycle value is introduced into the voltage loop for parameter adjustment, which achieves good matching between inner and outer loops. A series of simulations and experiments are carried out to test the proposed strategy under steady and dynamic conditions. It is shown that the CDBC strategy presents more accurate unity power factor and stronger robustness against load disturbance than the conventional deadbeat power control (DBPC).
keywords：Three-level PWM rectifier, online disturbance compensation, cascaded deadbeat control, Luenberger observer
DOI: 10.19595/j.cnki.1000-6753.tces.201112
中图分类号：TM46
余晨辉 男，1995年生，硕士研究生，研究方向为三电平PWM整流器模型预测控制算法。E-mail: 992413763@qq.com
汪凤翔 男，1982年生，研究员，博士生导师，研究方向为电机驱动与电力电子。E-mail: fengxiang.wang@fjirsm.ac.cn（通信作者）
收稿日期 2020-08-30
改稿日期 2020-10-21
国家自然科学基金资助项目（51877207）。
（编辑 陈 诚）