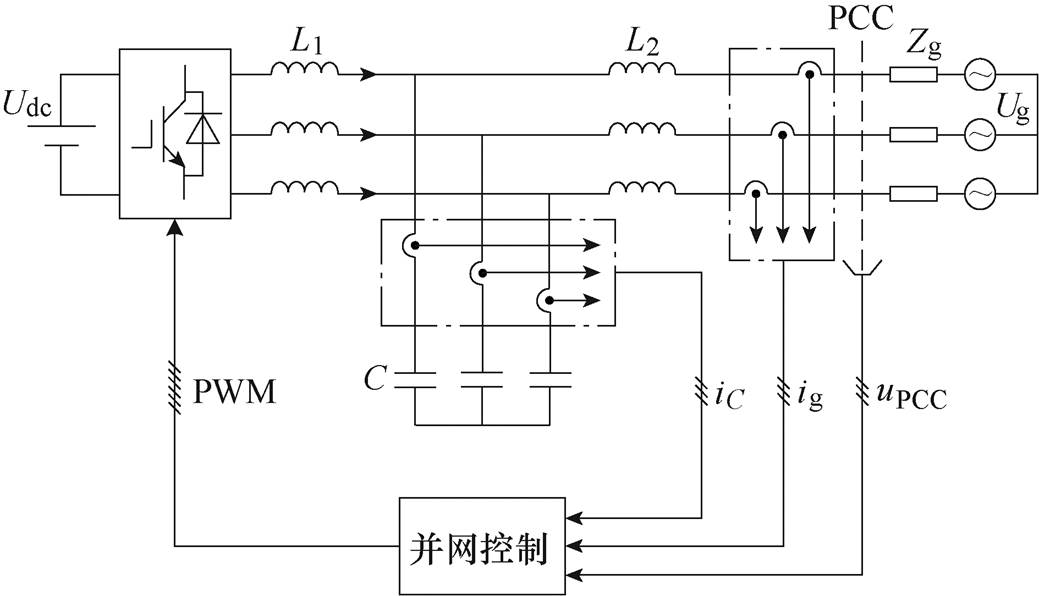
图1 LCL型并网逆变器典型拓扑
Fig.1 Typical topology of LCL-filter-based grid-connected inverter
摘要 大规模分布式新能源经逆变器接入配电网，并网逆变器与弱电网间形成复杂交互，谐波劣化问题凸显。谐波劣化分析的关键之一是并网逆变器阻抗模型的建立。白箱阻抗建模需要结构、参数、控制方式等内部信息，黑箱阻抗建模结果一般无物理意义，两种建模方法均存在应用缺陷。为弥补二者的不足，该文以白箱阻抗建模的结果为求解目标，以黑箱阻抗建模的方法为求解途径，通过有理函数逼近算法灰箱拟合并网逆变器阻抗传递函数。首先通过双模式扰动获取离散阻抗数据；然后利用矩阵束改进矢量匹配法，实现初始参数的自动获取，缩短迭代计算耗时；再次基于RT-Lab搭建半实物实时仿真平台，通过对比实验验证该文方法的有效性和优势；最后基于阻抗拟合结果开展谐波劣化分析，验证该文方法的实用性。
关键词：并网逆变器 谐波劣化 阻抗分析法 有理函数逼近 RT-Lab
多种类、多工况运行的并网逆变器（Grid- Connected Inverter, GCI）在电力电子化新能源电力系统中应用愈加广泛[1-2]。受网络阻抗特性的影响，并网逆变器并网电流中的谐波（谐波源）可能受电网中背景谐波电压（激励源）的激励而放大[3-4]，由此产生谐波劣化现象[5]。为提高并网逆变器并网电能质量，保证电网的安全稳定运行，可通过阻抗分析法[6]计算并网逆变器阻抗和电网阻抗Bode图交截频率处的相位裕度，从而开展谐波劣化分析[7]。考虑电网阻抗可通过注入各种二进制信号进行测量获取[8-9]，因此并网逆变器阻抗模型的建立是应用该方法的关键。
并网逆变器阻抗建模常基于白箱思想。通过dq轴线性化或谐波线性化，可将并网逆变器阻抗等效为阻抗传递函数的形式。其中，dq轴线性化将并网逆变器模型转换至dq轴，对稳态直流工作点进行小信号线性化分析[10]。基于这种方法，文献[11]分析了并网逆变器与电网间阻抗不匹配时的谐波劣化机理。文献[12]通过回率矩阵讨论了并网逆变器的谐波稳定性。然而，dq轴线性化在复杂系统中应用受限[13]。谐波线性化通过在系统中叠加谐波扰动，借助谐波平衡理论进行小信号近似[14]。基于这种方法，文献[15]分析了不平衡工况下的并网逆变器谐波劣化问题。文献[16]建立了考虑锁相环的并网逆变器序阻抗模型。文献[17]研究了控制及滤波器参数对并网逆变器阻抗特性的影响。
然而，上述白箱阻抗建模方法要求并网逆变器结构、参数、控制方式等内部信息已知。实际工程现场存在大量已运行但内部信息未知的并网逆变器，此时白箱阻抗建模不再适用[18]。黑箱阻抗建模虽然克服了这一缺陷，但其计算结果随机且一般无物理意义[19]，无法在其基础上进一步开展谐波劣化分析。针对两种建模思想的应用缺陷，灰箱阻抗建模[20]以白箱阻抗建模的结果为求解目标，以黑箱阻抗建模的数据驱动和数值算法为求解途径，不仅适用于并网逆变器内部信息保密的实际工程场景，而且保证求解的结果具有实际物理意义。文献[21]基于这种思想对并网逆变器的宽频域矩阵模型进行了求解，但其阻抗计算结果为离散点，无法得到阻抗传递函数的具体表达，因此无法应用阻抗分析法对其谐波劣化问题开展分析。
针对文献[21]的不足，本文从变压器铁心[22]、同轴电缆[23]等高压非线性设备的宽频建模中获取灵感。这类建模的核心思想是：对被测设备施加外部扰动信号，采集端口频率响应数据，计算测量频率下的离散阻抗值，采用有理函数逼近算法（如矢量匹配（Vector Fitting, VF）[22-23]），对阻抗传递函数进行拟合。考虑在实际工程现场中，可以通过在并网逆变器并网点串联电压扰动源或并联电流扰动源，借助频率响应分析仪采集电压/电流扰动源经并网逆变器回路后产生的电流/电压频率响应，从而获取测量频率下的离散阻抗值[24]。因此，基于这些离散阻抗数据，利用有理函数逼近算法，从灰箱角度拟合并网逆变器阻抗传递函数成为可能。然而，VF的初始极点和阶数需人为给定，最优参数需反复迭代，计算耗时较长。这些缺陷对现场人员的知识储备提出较高要求，且会直接影响并网逆变器阻抗传递函数获取的快速性和准确性。
基于上述分析，本文针对结构、参数、控制方式等内部信息未知的并网逆变器阻抗灰箱拟合问题开展研究，基于拟合结果应用阻抗分析法开展并网逆变器谐波劣化分析。首先，对并网逆变器进行概述，提出待解决的问题；然后，介绍阻抗测量的基本原理，利用双模式扰动获取并网逆变器离散阻抗数据；之后，利用矩阵束法（Matrix Pencil Method, MPM）[25-26]对VF进行改进，阐述其具体计算原理；再次，基于RT-Lab实时仿真平台，对比验证本文方法的有效性和优势；最后，基于阻抗拟合结果，通过阻抗分析法分析并网逆变器谐波劣化问题，借助上述平台验证谐波劣化现象的产生，进一步验证本文方法的实用性。
分布式电源通过并网逆变器将直流电变换成三相交流电，经滤波器组滤除并网电流中的高频谐波，将电能馈送至电网。一种LCL型并网逆变器典型拓扑如图1所示。
图1 LCL型并网逆变器典型拓扑
Fig.1 Typical topology of LCL-filter-based grid-connected inverter
图1中，Udc为直流侧电压；并网逆变器侧电感L1、网侧电感L2和滤波电容C共同组成LCL滤波器；Zg为电网等效阻抗；Ug为电网电压；iC为滤波电容电流；ig为并网逆变器并网电流；uPCC为公共连接点（Point of Common Coupling, PCC）电压。
为了运用阻抗分析法对并网逆变器进行谐波劣化分析，基于图1所示拓扑，需分别对并网逆变器和电网进行诺顿和戴维南等效，等效电路如图2所示。图中，IGCI、ZGCI分别为并网逆变器的等效电流源和等效阻抗。
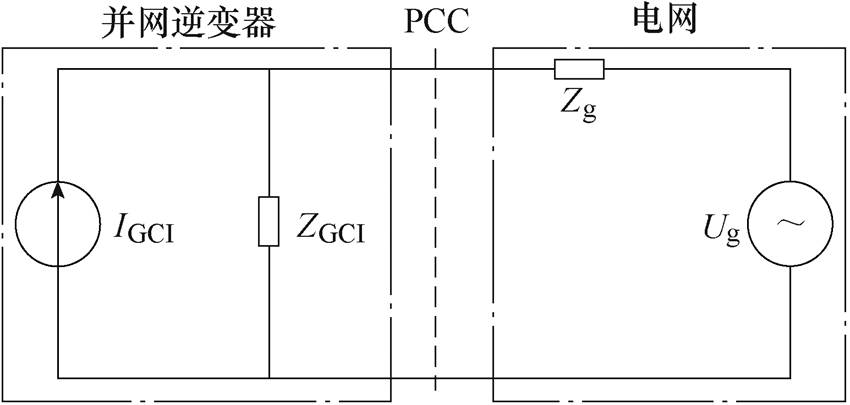
图2 阻抗分析法等效电路
Fig.2 Equivalent circuit of impedance analysis method
当并网逆变器内部信息全部已知时，根据白箱阻抗建模的结果，无论何种控制方式，ZGCI、Zg总能表示为式（1）所示的阻抗传递函数。绘制二者的Bode图，若交截频率处相位裕度小于0°，且电网中的背景谐波电压（激励源）接近该交截频率，则并网电流中该频率附近的谐波（谐波源）将被放大，产生谐波劣化现象[27-28]。然而，已并网逆变器阻抗传递函数往往因参数技术保密而未知。因此，工程应用背景下如何获取并网逆变器阻抗传递函数是亟需解决的瓶颈问题。
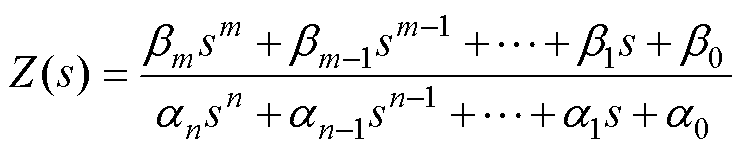（1）式中，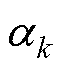
（k=1, 2,…, n）为分母多项式的各项系数；n为分母多项式的最高次数；
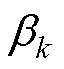（k=1, 2,…, m）为分子多项式的各项系数；m为分子多项式的最高次数；分母多项式不为0。
针对上述问题，本文参考高压非线性设备的宽频建模思路，将式（1）所示阻抗传递函数转化为式（2）所示的有理函数形式。该有理函数由Ms个实数极点项、Mf对共轭复数极点项、常数项和一次项四部分组成。
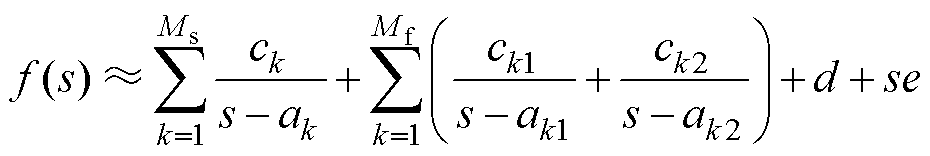（2）式中，s=jw（rad/s），j为虚数单位，w 为角频率；ak为实数极点；ck为对应实数留数；ak1、ak2为共轭复数极点；ck1、ck2为对应共轭复数留数；d和e分别为常数项和一次项实数系数。
需要说明的是：令传递函数的阶数为变量N，则N=max{n, m}，其中，max{ }为取大函数，由此，式（2）中，当m＞n时，e≠0，此时N=Ms+2Mf+1；当m≤n时，e=0，此时N=Ms+2Mf。
以式（2）所示的阻抗有理函数为拟合目标，基于并网逆变器离散阻抗数据，可借助有理函数逼近算法对其进行灰箱拟合。然而，VF初始参数需人为给定，迭代计算耗时较长，这些应用缺陷不能满足实际现场对快速精确建模的需求，因此一种克服其缺陷的有理函数逼近算法成为刚需。
借助有理函数逼近算法对并网逆变器阻抗传递函数进行灰箱拟合的前提是并网逆变器离散阻抗数据的精确获取。为了精确测量并网逆变器的宽频域离散阻抗值，同时考虑并网逆变器阻抗与电网阻抗在测量频段中的相互影响，本文参考文献[29]，采用双模式扰动对并网逆变器离散阻抗进行测量，具体原理说明如下。
并网逆变器离散阻抗测量原理如图3所示。其中，扰动注入模块连接于并网逆变器与电网间，共有串联电压扰动注入和并联电流扰动注入两种模式，注入的扰动经并网逆变器回路后产生频率响应，通过频率响应分析仪进行采集，离散阻抗表示为
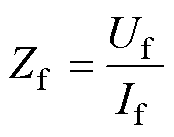（3） 式中，Zf为频率为f时并网逆变器的阻抗值；Uf、If分别为并网逆变器端口电压uabc、iabc通过快速傅里叶变换（Fast Fourier Transform, FFT）分解得到的频率f下电压、电流分量。
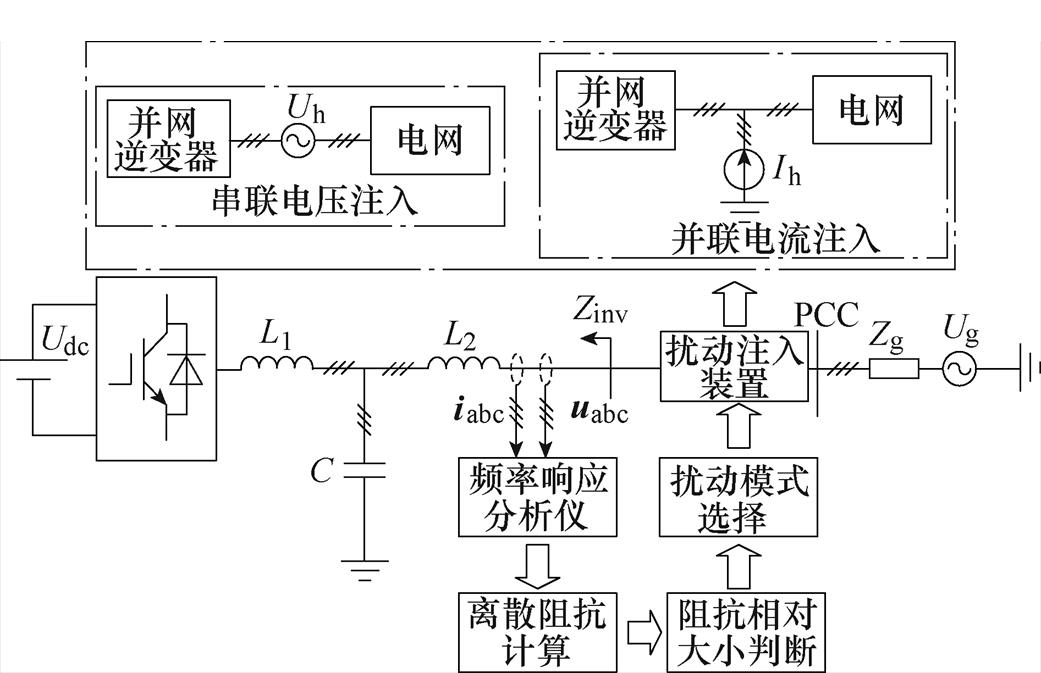
图3 离散阻抗数据测量计算原理
Fig.3 Schematic diagram of measurement and calculation of discrete impedance data
双模式扰动切换的具体操作是：①串联注入某次谐波电压，采集频率响应数据，基于式（3）得到该次谐波下并网逆变器阻抗，与同频率下电网阻抗进行比较；②当检测电网阻抗小于并网逆变器阻抗时，保存该频率点阻抗值；③检测电网阻抗大于并网逆变器阻抗时，更改扰动注入装置工作模式为并联电流注入，重新采集频率响应数据，基于式（3）对该频率下并网逆变器阻抗重新进行计算；④改变扰动注入频率，重复步骤②、③判断过程，直至对受关注频率范围内所有离散阻抗数据进行测量计算。双模式扰动注入方法具体流程可参考文献[29]，在此不再赘述。
基于第2节获取的离散阻抗数据，借助有理函数逼近算法对并网逆变器阻抗进行灰箱拟合。针对VF初始参数需人为给定、迭代计算耗时长的缺陷，本文提出一种改进矢量匹配（Improved Vector Fitting, IVF）法。其中，改进是指：本文方法首先进行MPM计算，将其结果作为VF的初始参数进行最优迭代。本文的改进既实现了VF初始参数的自动获取，也有效地减少了VF的迭代次数，缩短计算时间。详细计算原理说明如下：
1）MPM计算
MPM计算以式（4）所示时域表达式为求解目标。经Laplace变换后，式（4）中的ak、ck与式（2）中的极点和留数一一对应。
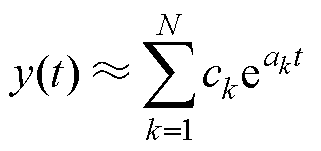（4）基于频域响应数据，计算测量频率下离散的阻抗值，设其经快速傅里叶逆变换后得到的时域数据序列为y(i)，i=1, 2,…, nt，由此建立Hankel矩阵 Y为
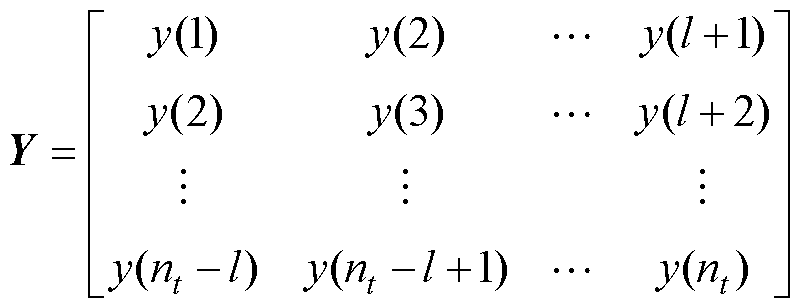（5）
式中，l为MPM参数，通常取l=nt/4以抑制采样数据中的噪声[25]。
对Y作奇异值分解（Y=UDVT）得奇异值矩阵D，D的第i个对角线元素为奇异值di，计算di的奇异熵增量[26]为
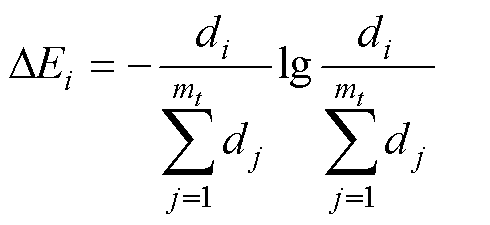（6）式中，mt=min{nt-l, l+1}。
由奇异熵增量计算k阶奇异熵Ek，Ek变化趋势图中拐点对应k值即为VF计算初始阶数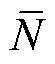
。
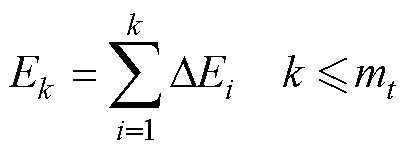（7）由D的前Nt个奇异值组成对角矩阵
，构造两个新矩阵Y1=UD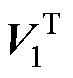
和Y2=UD
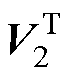。其中，V1
为V的前Nt个主导右特征向量的第1行至第l行；V2为V的前Nt个主导右特征向量的第2行至第l+1行。计算矩阵G=Y1+Y2的Nt个非零特征值
（i=1, 2,…, Nt）即可求得VF计算初始极点
。
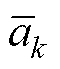2）VF迭代计算
基于MPM计算得到的初始极点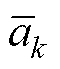和初始阶数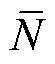。建立目标函数为
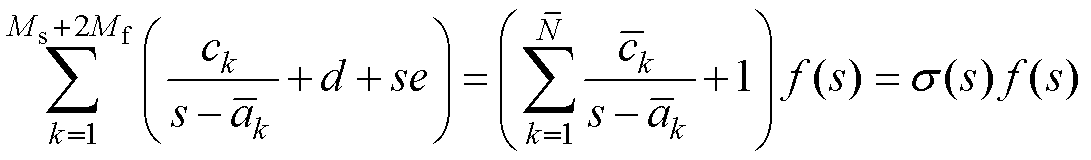（8）式中，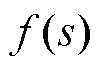
的乘积项计作辅助函数
。
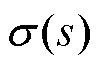对于未知参数d、e、ck、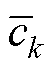
，式（8）可转化成线性方程组Ax=b[31]。通过最小二乘法解得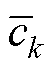，将式（8）重新整理为
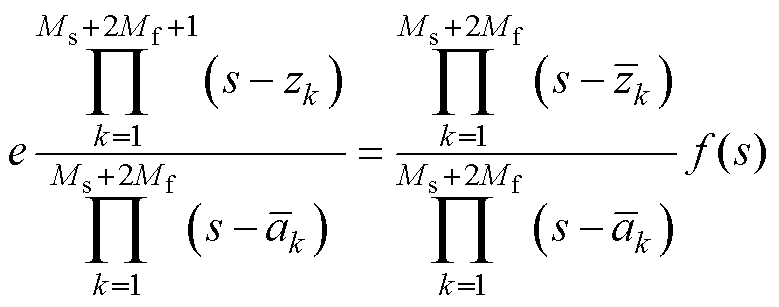（9）式中，zk和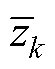
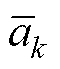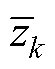为对应函数的零点。消去式（9）中的初始极点，零点即为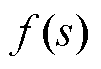
的待求极点[31]，从而实现极点更新。
基于更新后的极点，建立与Ax=b类似的线性方程组并进行最小二乘求解，实现留数、一次项、常数项的估计。
建立相对误差（Relative Error, RE）百分比
作为实测频率处，通过式（10）计算拟合结果和实测阻抗数据间的误差计算标准。可直观展现拟合误差占测量值的比重，百分比越小说明拟合误差所占的比重越小，拟合效果越好。
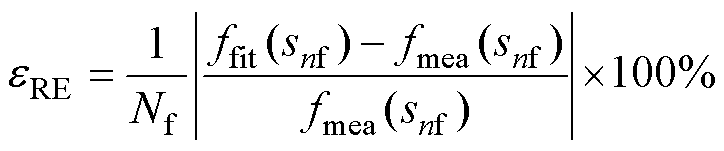（10）式中，Nf为测量值总数；snf=j2pfn，fn为第n个频率采样点的频率；下标fit表示拟合值；下标mea表示测量值。
计算一次迭代后的，对比给定阈值
。未满足时，增大阶数，同时将本次迭代得到的函数参数作为初始值重新代入VF进行迭代，直至拟合指标满足阈值。此时，本文方法获取到指定阈值下的最优参数，实现了阻抗有理函数的最优拟合。
IVF计算流程如图4所示。
基于图1所示拓扑在RT-Lab中搭建并网逆变器半实物实时仿真模型，模型具体参数见附表1，控制框图如附图1所示。实验系统原理框图和半实物实时仿真测试平台如图5所示。其中，上位机处理器参数为2.5GHz Intel Core i3；并网逆变器选用准比例谐振进行并网控制，通过OP5600实时数字仿真器实现，灰箱拟合、阻抗扫频及白箱计算均在上位机的Matlab软件中进行。
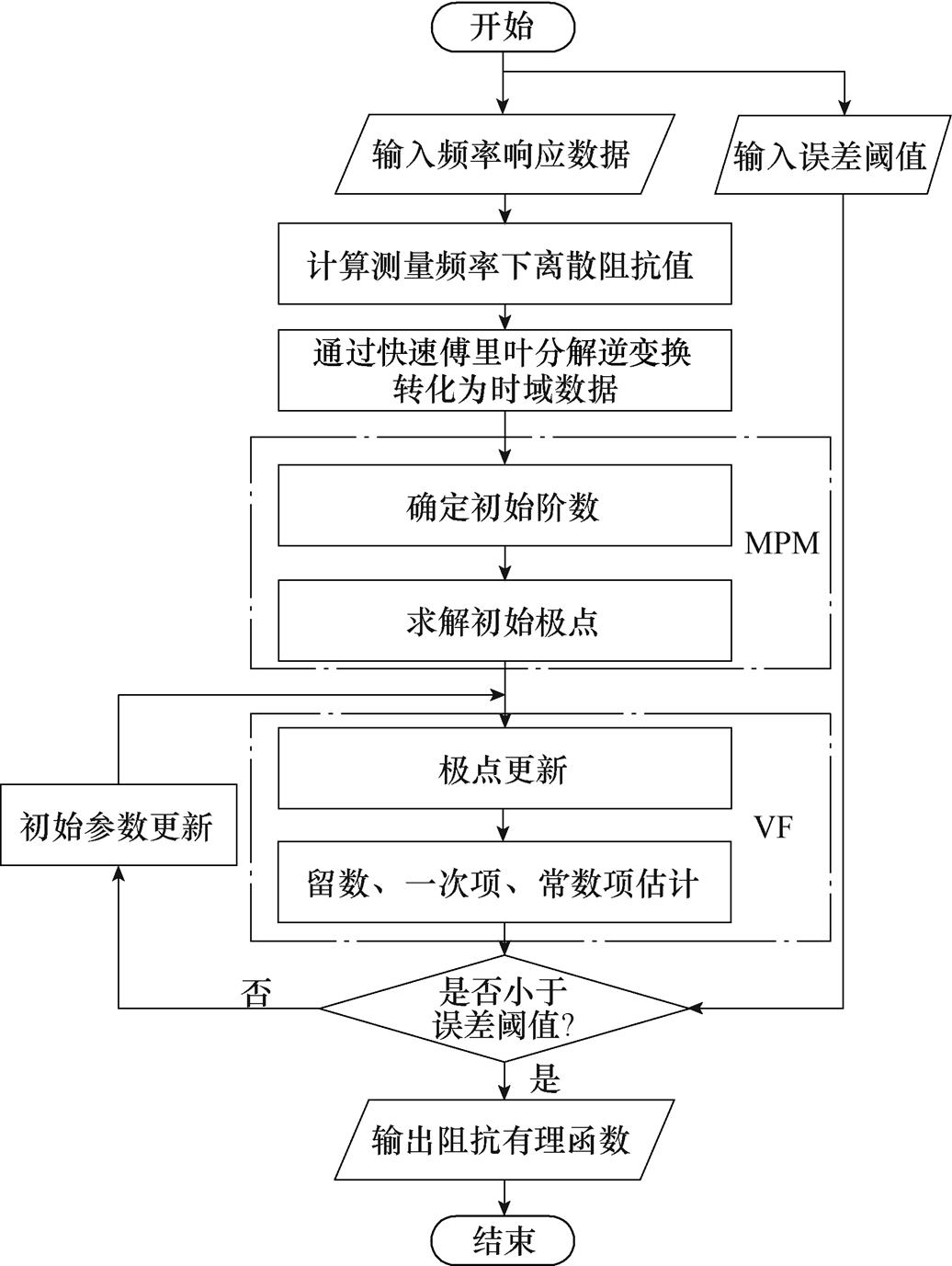
图4 IVF计算流程
Fig.4 Calculation flow chart of IVF
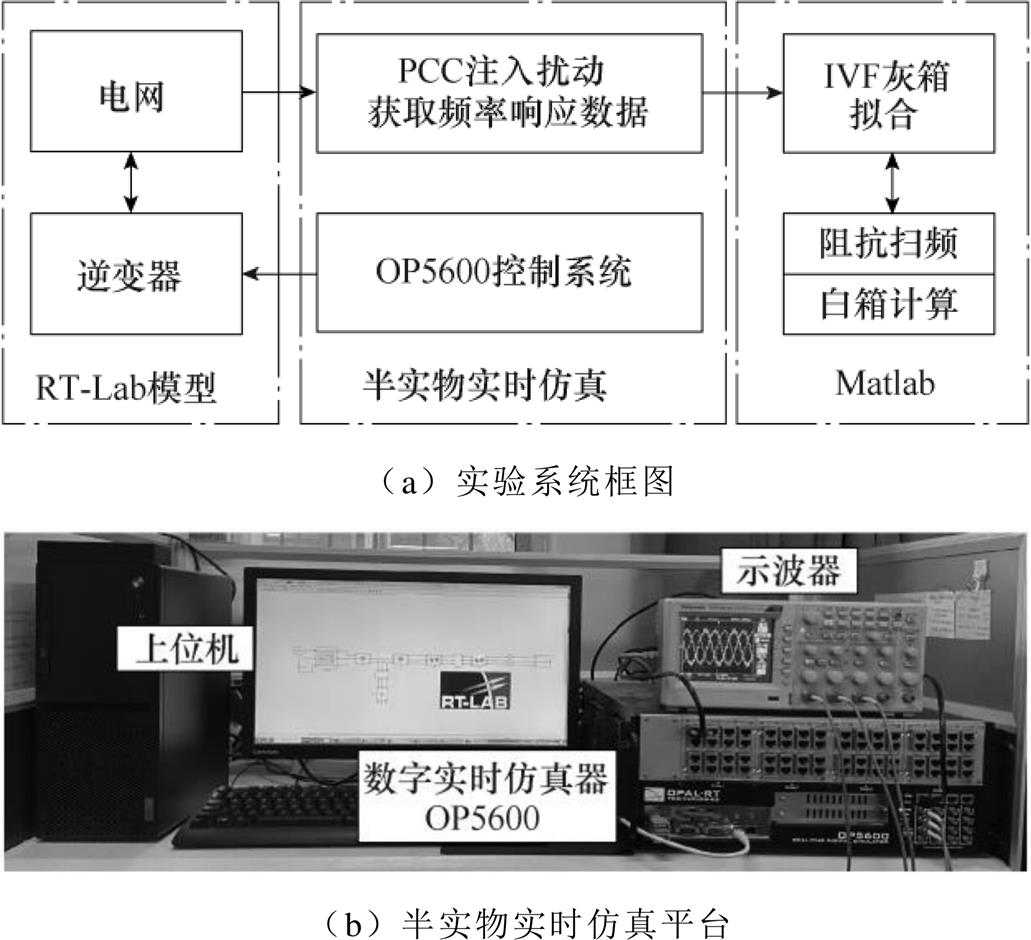
图5 系统框图及实验平台
Fig.5 System block diagram and test platform
为了保证本文所提方法的适用性和可重复性，本文基于实时仿真平台对图5b中并网逆变器施加双模式扰动，并通过电压、电流测量模块对其频率响应数据进行采集。其中，扰动源具体参数为：在PCC处串联接入12V（并网逆变器并网电压幅值的4%）2～100次宽频变化的电压扰动源，或串联接入1A（并网逆变器并网电流幅值的4%）2～100次宽频变化的电流扰动源，扰动源幅值根据文献[32]进行确定，扰动切换原则根据本文第2节介绍的原理及文献[29]进行确定。附图2a、附图2b分别给出了2～4次电压扰动源波形及对应的电流响应波形，附图2c则给出了0～1 000Hz并网逆变器离散阻抗数据点的可视化图形。
本文采用两种方法对阻抗灰箱拟合结果有效性进行分析验证。
（1）基于实时仿真平台，借助Matlab/Simulink软件中的阻抗测量模块对被研并网逆变器进行扫频。对拟合曲线与阻抗扫频数据间的进行求解计算，并将二者进行对比。
（2）对被研并网逆变器进行白箱阻抗建模，将阻抗传递函数转化为有理函数后与灰箱拟合结果进行逐项对比。需要说明的是，所有并网逆变器模型参数仅在计算白箱阻抗传递函数时使用，本文方法拟合时视作未知。
基于4.1节采集到的频率响应数据，通过式（3）计算相应频率下的离散阻抗值，运用本文提出的IVF拟合并网逆变器阻抗有理函数。其中，Ek变化趋势如图6所示，根据拐点判断VF计算初始阶数为4。阈值设置为1×10-6%，其选取标准详见附录中第3节的相关讨论。经迭代计算后各部分拟合结果见表1。绘制出灰箱拟合结果（实线）和阻抗扫频结果（虚线）如图7所示。图7亦绘制出电网阻抗曲线（点画线）以用于并网逆变器谐波劣化分析。
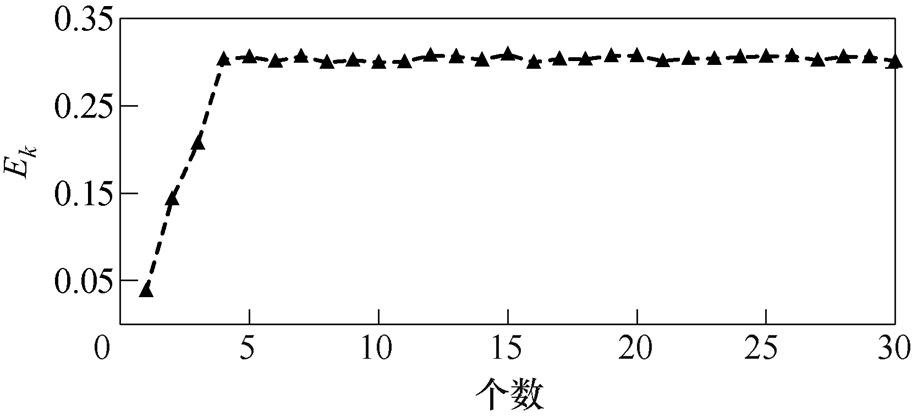
图6 Ek变化趋势
Fig.6 Change trend chart of Ek
表1 灰箱拟合结果
Tab.1 Gray-box fitting results
类型留数极点de 实数项74.14-2×105—— 2.42×104-55.57—— 共轭复数项-4.54×103±i2.58×104-5±i3.14×102—— 常数项——-1.91×10-11— 一次项———2×10-4
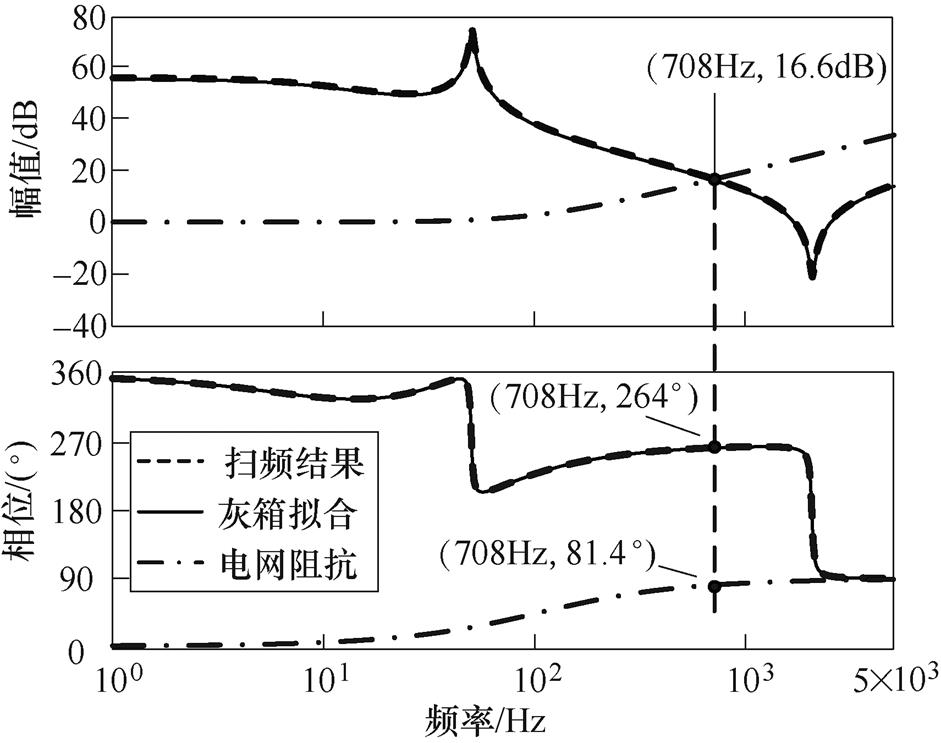
图7 拟合结果对比
Fig.7 Comparison of fitting results
经计算，本文方法拟合结果与扫频阻抗数据间=4.67×10-12%，极小的数值证明本文方法拟合精度较高。对比图7中的扫频结果（虚线）和灰箱拟合曲线（实线）可以看出，两条曲线基本完全重合，电网阻抗幅值曲线（点画线）均与二者在708Hz处产生交截。这说明，灰箱拟合结果与实际阻抗数据相契合，能够正确反映被研并网逆变器的频率响应及阻抗特性。
根据附图1给出的控制框图以及附表1给出的模型参数，采用白箱方法计算并网逆变器阻抗传递函数如式（A1）所示。将其转化为式（2）所示的有理函数形式，各部分具体计算结果见表2。
表2 白箱计算结果
Tab.2 White-box calculation results
类型留数极点de 实数项74.14-2×105—— 2.42×104-55.57—— 共轭复数项-4.54×103±i2.58×104-5±i3.14×102—— 常数项——-1.42×10-14— 一次项———2×10-4
从表1和表2的逐项对比中可以看出，并网逆变器阻抗有理函数灰箱拟合结果与白箱计算结果仅在常数项上存在偏差，考虑到该项偏差数量级较小，因此认为该误差可以忽略，灰箱拟合结果与白箱计算结果基本一致。综上所述，本文方法是有效的。
分别运用VF、MPM、IVF（本文方法）对并网逆变器离散阻抗数据进行拟合，算法对比如图8所示。绘制出VF初始拟合结果作为对比，用VF*作为标记，其中初始参数根据文献[30]按对数分布的复数进行人为给定。三种算法的运行求解均基于同一台上位机。
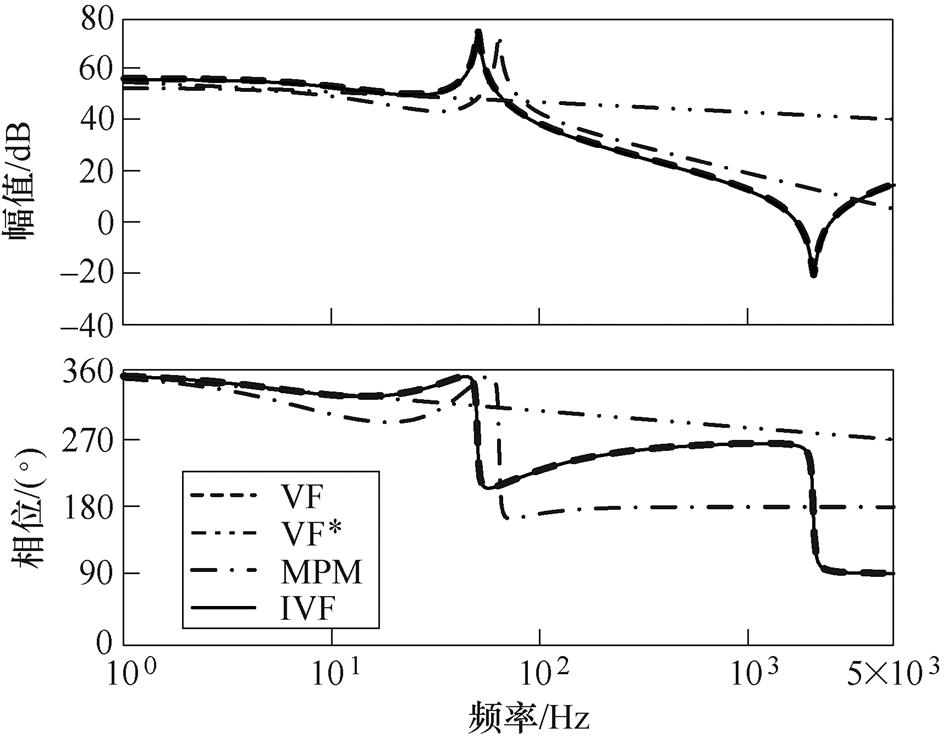
图8 不同算法对比
Fig.8 Comparison between different algorithms
统计各算法相对误差百分比见表3。为了对比各种算法的计算速度，增设10次实验平均计算用时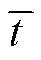
作为第2个评价指标。表3同时列举出各算法的总迭代次数作为对比。
表3 各算法评价指标值
Tab.3 Evaluation index value of each algorithm
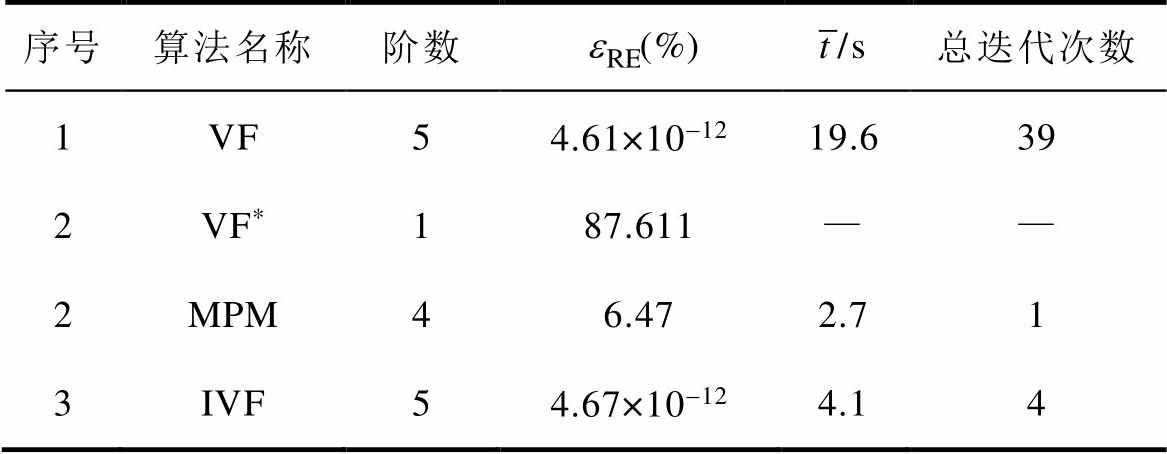
序号算法名称阶数(%)总迭代次数 1VF54.61×10-1219.639 2VF*187.611—— 2MPM46.472.71 3IVF54.67×10-124.14
首先，对VF拟合结果进行分析和讨论。从图8中可以看出，VF拟合曲线（虚线）基本与IVF（本文方法）拟合曲线（实线）重合，与初始拟合结果（双点画线）相差较大。从表2的评价指标中可以看出，VF初始拟合结果的极大，经迭代计算后，VF的极小，但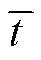数值相对较大，总迭代次数较多。这说明，受初始参数的影响，VF初始拟合效果较差，经反复迭代后最优参数下拟合精度较高，但迭代计算耗时较长。造成这一现象的根本原因在于，传统VF算法以1阶作为初始阶数，以等对数间隔的复数或实数作为初始极点。这些人为给定的参数无法针对特定逆变器产生适应性变化，因此，为了得到最终的最优拟合结果，需要反复进行迭代计算。
然后，对MPM拟合结果进行分析和讨论。从图8中可以看出，与VF初始拟合结果（双点画线）相比，MPM拟合曲线（点画线）整体趋势与VF拟合曲线（虚线）或IVF拟合曲线（实线）更为接近。
从表3中可以看出，MPM的虽不满足给定阈值，但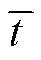数值相对较小，不存在迭代过程。这说明，单独应用MPM时虽然拟合精度较低，但其耗时短，计算速度快，拟合趋势与VF或IVF相近，拟合结果相比VF初始结果更接近于VF最终拟合结果。因此，拟合结果可以作为VF的初始参数。
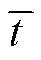最后，对IVF拟合结果进行分析和讨论。从图8中可以看出，IVF（本文方法）拟合曲线（实线）基本与VF拟合曲线（虚线）重合，从表3中可以看出，IVF的极小，与VF相近，平均计算用时和总迭代次数较VF明显减少。这说明，IVF同时继承了VF和MPM的优点，算法参数实现自动获取的同时拟合精度较高，算法迭代次数较少，计算耗时较短。
需要说明的是：①本文方法耗时要略长于MPM。这是因为本文方法为保证拟合精度，在MPM基础上再次运用VF进行了迭代计算。增加的平均时间消耗为1.4s，在工程实际应用中是可以接受的。②MPM与VF和IVF最终拟合结果阶数不同是由于MPM算法本身无法拟合常数项和一次项导致的，这也是其拟合精度不及VF和IVF的根源，但考虑到本文的算法对比基于各算法的最优拟合结果，因此，阶数不同对算法优劣结论的正确性无影响。
从图7的幅值中可以看出，708Hz处，电网阻抗曲线与并网逆变器阻抗曲线存在交截，从图7的相位中可以看出，708Hz处，电网阻抗和并网逆变器阻抗间相位差为182.6°，相位裕度为-2.6°＜0°。这说明，本文搭建的并网逆变器模型，可能在14次背景谐波电压的激励下，出现并网电流谐波劣化的现象。
为验证谐波劣化分析结论的正确性，进一步验证本文方法拟合结果的有效性和实用性，进行如下实验。工况1：电网处于无背景谐波状态，观察PCC处逆变器并网电流波形，如图9a所示；对其进行FFT，绘制频谱图如图9b所示。工况2：电网电压中出现14次背景谐波，谐波幅值为额定电压的2%，观察PCC处逆变器并网电流波形，如图9c所示；对其进行FFT，绘制频谱图如图9d所示。
电网中无背景谐波时，从图9a中可以看出，并网逆变器并网电流波形未出现明显畸变；从图9b中可以看出，并网逆变器会向电网注入宽频域谐波电流，但谐波电流含量普遍较低。当电网中出现14次背景谐波电压时，从图9c中可以看出，并网逆变器并网电流波形出现明显畸变；从图9d中可以看出，并网逆变器并网电流中的14次谐波被显著放大，谐波劣化现象产生。经计算，无背景谐波电压时，并网逆变器并网电流总谐波畸变率（Total Harmonic Distortion, THD）为0.35%，存在14次背景谐波时，THD变为8.05%。对比图9b、图9d可以发现，并网逆变器并网电流THD的显著增加主要由并网电流中被放大的14次谐波导致。
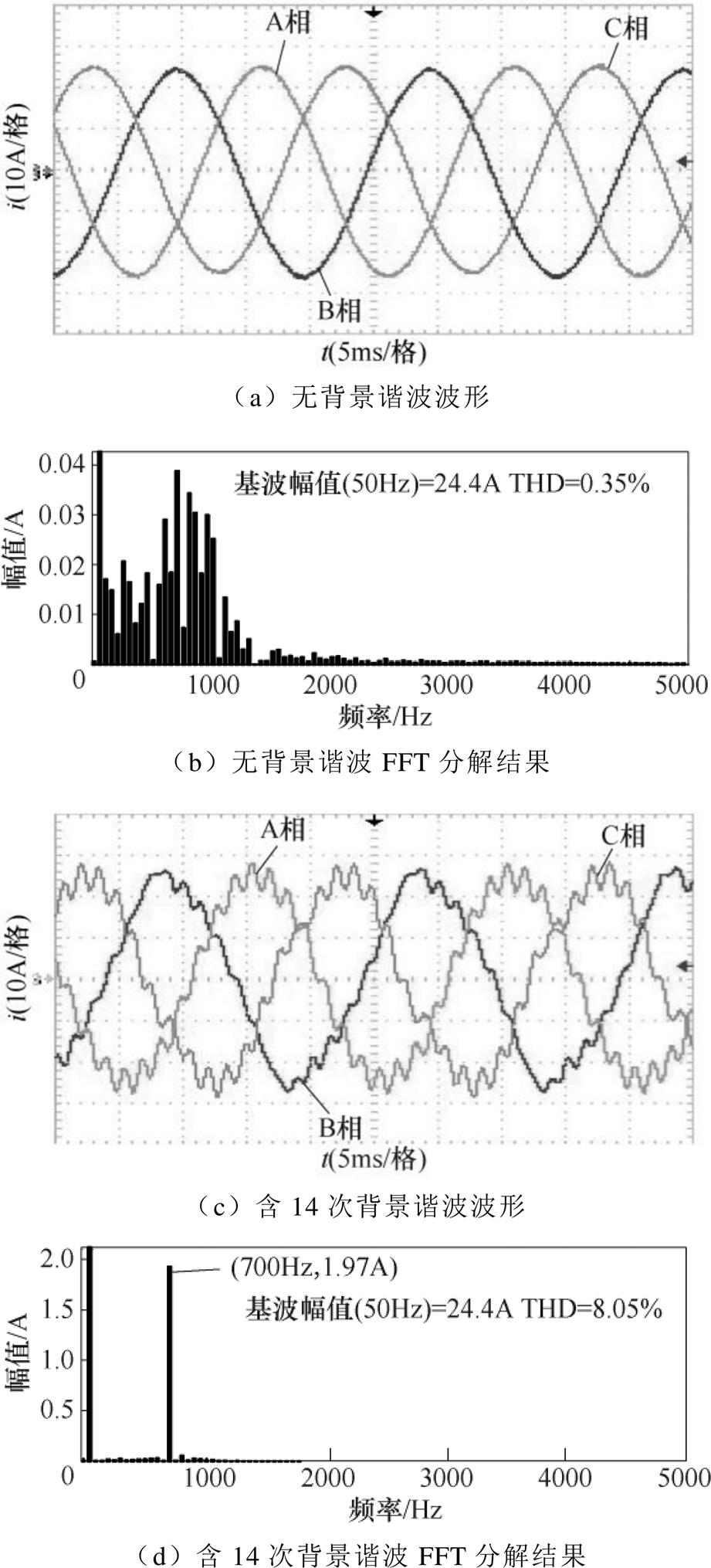
图9 谐波劣化分析验证
Fig.9 Analysis and verification of harmonic degradation
从上述实验现象中可以得出结论，14次背景谐波电压确实会使被研并网逆变器并网电流出现谐波劣化现象。谐波劣化现象及结论与基于本文方法拟合结果得到的谐波劣化分析结论一致，本文方法是有效且实用的。
本文针对结构、参数、控制方式等内部信息未知的并网逆变器阻抗灰箱拟合问题开展研究。从有理函数逼近角度，提出一种改进矢量匹配算法；基于拟合结果，开展谐波劣化分析；搭建RT-Lab实时仿真平台，通过实验得出以下结论：
1）给出了灰箱阻抗有理函数的拟合形式。将并网逆变器白箱阻抗传递函数改写为有理函数的形式，基于该形式进行阻抗灰箱拟合是谐波劣化分析的关键。
2）提出了一种改进的矢量匹配法灰箱拟合阻抗有理函数。该方法利用矩阵束拟合结果与矢量匹配最优结果相近的优势，实现了矢量匹配初始参数的自动获取，减少了迭代次数，缩短了计算耗时，可以满足实际工程现场对快速精确阻抗建模的需求。
3）复现了电网背景谐波电压影响下逆变器并网的谐波劣化现象，验证了本文方法的实用性。
基于本文提出的方法和思路，后续可继续开展的研究包括：
1）考虑谐波耦合特性对灰箱阻抗建模的影响。
2）探索本文方法在多逆变器系统中的应用，开展谐波稳定性分析等相关后续研究。
附 录
1. 模型参数说明
本文基于RT-Lab搭建半实物实时仿真平台，其中，并网逆变器模型参数见附表1，逆变器控制框图如附图1所示。
附表1 并网逆变器模型参数
App.Tab.1 Model parameters of GCI
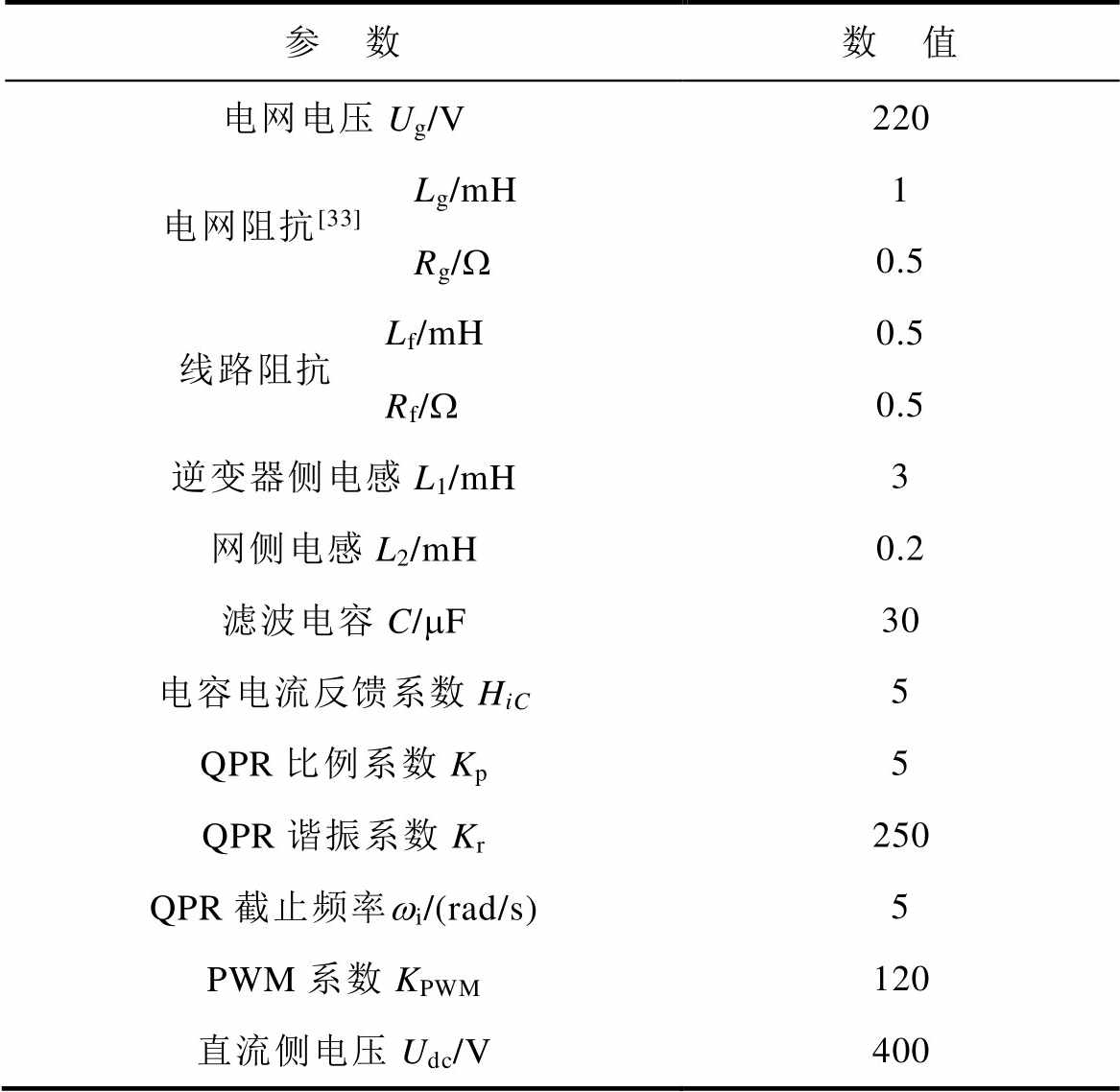
参 数数 值 电网电压Ug/V220 电网阻抗[33]Lg/mH1 Rg/W0.5 线路阻抗Lf/mH0.5 Rf/W0.5 逆变器侧电感L1/mH3 网侧电感L2/mH0.2 滤波电容C/mF30 电容电流反馈系数HiC5 QPR比例系数Kp5 QPR谐振系数Kr250 QPR截止频率wi/(rad/s)5 PWM系数KPWM120 直流侧电压Udc/V400
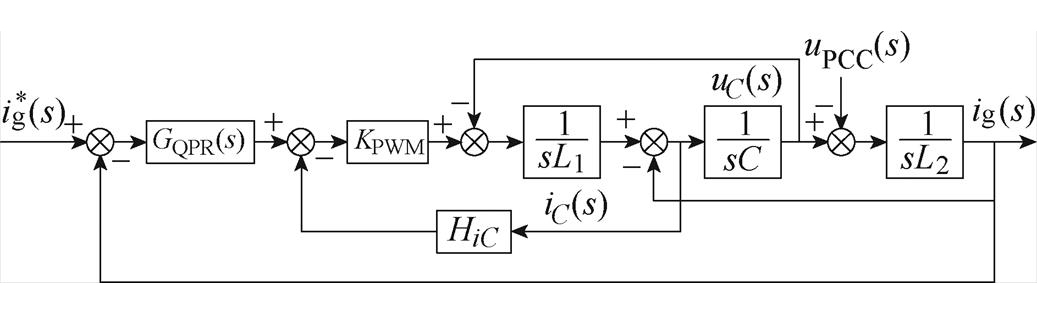
附图1 并网逆变器控制框图
App.Fig.1 Control block diagram of grid-connected inverter
根据并网逆变器模型参数及控制框图，推导其阻抗传递函数为
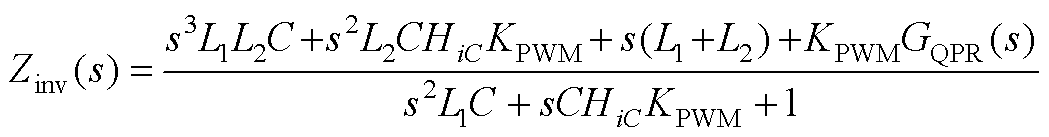（A1）其中
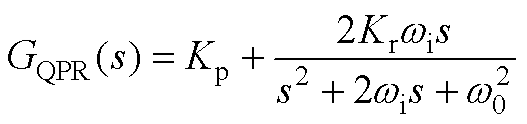
2. 部分原始数据说明
为了对本文使用的原始数据进行说明，本文绘制了2～4次电压扰动源波形及对应的电流响应波形如附图2a、附图2b所示，绘制出0～1 000Hz并网逆变器离散阻抗数据点的可视化图形如附图2c所示。
3. 误差阈值选取说明
误差阈值的选取决定了改进矢量匹配法灰箱拟合循环的结束与否，误差阈值选取越小，灰箱拟合结果越精确。然而，算法拟合存在饱和点，即当算法拟合误差达到饱和点时，误差阈值进一步减小也不会带来实际误差的显著降低，反而会导致拟合计算时间的显著增加。
为了说明上述误差饱和现象，验证本文选取1×10-6%作为误差阈值的有效性，选取1×10-10%～1×10-2%的多组误差阈值，以实际误差和拟合时间作为双重检验标准进行实验，绘制出实际误差和拟合时间对比如附图3所示。
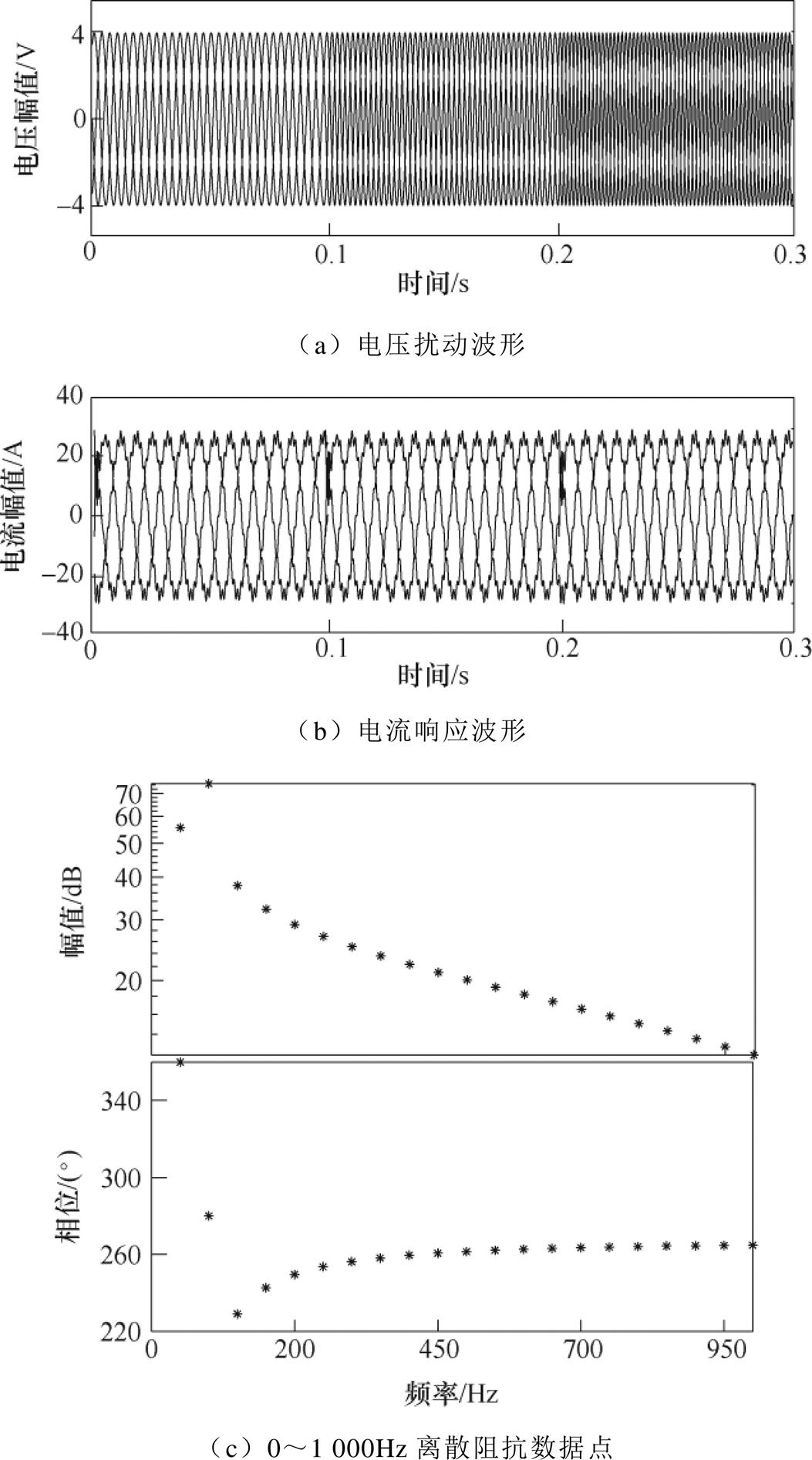
附图2 原始数据可视化（部分）
App.Fig.2 Raw data visualization (part)
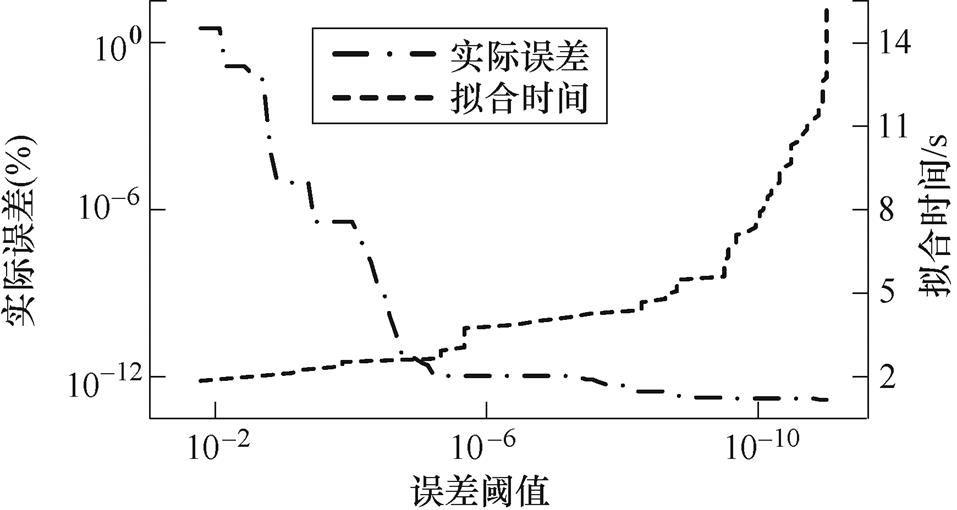
附图3 不同误差阈值下实际误差与拟合时间对比
App.Fig.3 Comparison of actual error and fitting time under different error thresholds
从附图3中可以看出，当误差阈值从1×10-6%～1×10-2%变化时，拟合实际误差随误差阈值的减小而显著降低，灰箱拟合时间普遍较短。然而，当误差阈值从1×10-10%～1×10-6%变化时，拟合实际误差随误差阈值的减小而缓慢降低，灰箱拟合时间却显著增加。因此，1×10-6%为本文算例的误差阈值饱和点。
考虑到误差阈值选取为1×10-6%时，灰箱拟合实际误差为4.67×10-12%，极小的数量级已经保证了改进矢量匹配法的灰箱拟合精度，因此，为缩短拟合时间，本文选取1×10-6%作为误差阈值进行拟合计算。
参考文献
[1] Liu Pengcheng, Wang Zheng, Wei Sanmin, et al. Recent developments of modulation and control for high-power current-source-converters fed electric machine systems[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 215-226.
[2] 胡鹏, 艾欣, 肖仕武, 等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报, 2020, 35(17): 3703-3713.
Hu Peng, Ai Xin, Xiao Shiwu, et al. Sequence impedance of static var generator and analysis of influencing factors on subsynchronous oscillation[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3703-3713.
[3] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-Inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[4] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198.
Zhao Qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5189-5198.
[5] 汪颖, 罗代军, 肖先勇, 等. 多逆变器并网下的超高次谐振特性分析[J]. 电力系统自动化, 2020, 44(1): 192-199.
Wang Ying, Luo Daijun, Xiao Xianyong, et al. Analysis on supraharmonic resonance characteristics with integration of multiple inverters[J]. Automation of Electric Power Systems, 2020, 44(1): 192-199.
[6] 陈新, 王赟程, 龚春英, 等. 采用阻抗分析方法的并网逆变器稳定性研究综述[J]. 中国电机工程学报, 2018, 38(7): 2082-2094, 2223.
Chen Xin, Wang Yuncheng, Gong Chunying, et al. Overview of stability research for grid-connected inverters based on impedance analysis methed[J]. Proceedings of the CSEE, 2018, 38(7): 2082-2094, 2223.
[7] 刘津鸣, 陈燕东, 伍文华, 等. 孤岛微电网序阻抗建模与高频振荡抑制[J]. 电工技术学报, 2020, 35(7): 1538-1552.
Liu Jinming, Chen Yandong, Wu Wenhua, et al. Sequence impedance modeling and high-frequency oscillation suppression method for island microgrid[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1538-1552.
[8] 钟佩军, 孙建军, 司学振, 等. 基于电压扰动源的并网逆变器输出阻抗测量方法[J]. 电工技术学报, 2019, 34(22): 4739-4750.
Zhong Peijun, Sun Jianjun, Si Xuezhen, et al. Measurement method of inverter output impedance based on voltage disturbance source[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4739-4750.
[9] Roinila T, Messo T. Online grid-impedance mea- surement using ternary-sequence injection[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5097-5103.
[10] Belkhayat M. Stability criteria for ac power systems with regulated loads[D]. West Lafayette: Purdue University, 1997.
[11] 严干贵, 段双明, 叶德武, 等. 基于输出阻抗的三相LCL型光伏逆变器稳定性分析[J]. 太阳能学报, 2018, 39(2): 558-566.
Yan Gangui, Duan Shuangming, Ye Dewu, et al. Stability analysis of three-phase LCL-type photo- voltaic inverter based on the output impedance[J]. Acta Energiae Solaris Sinica, 2018, 39(2): 558-566.
[12] 杨苓, 陈燕东, 周乐明, 等. 弱电网下锁相环对三相LCL型并网逆变器小扰动建模影响及稳定性分析[J]. 中国电机工程学报, 2018, 38(13): 3792-3804.
Yang Ling, Chen Yandong, Zhou Leming, et al. Effect of phase locked loop on the small-signal perturbation modeling and stability analysis for three-phase LCL-type grid-connected inverter in weak grid[J]. Proceedings of the CSEE, 2018, 38(13): 3792-3804.
[13] 李建文, 阮筱菲, 李永刚, 等. 弱电网下多并网逆变器谐振失稳研究综述[J]. 现代电力, 2020, 37(2): 187-196.
Li Jianwen, Ruan Xiaofei, Li Yonggang, et al. An overview on resonance instability of multiple grid-connected inverters in weak grid[J]. Modern Electric Power, 2020, 37(2): 187-196.
[14] Sun Jian. Small-signal methods for AC distributed power systems-a review[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2545-2554.
[15] 年珩, 杨洪雨. 不平衡运行工况下并网逆变器的阻抗建模及稳定性分析[J]. 电力系统自动化, 2016, 40(10): 76-83.
Nian Heng, Yang Hongyu. Impedance modeling and stability analysis of grid-connected inverters under unbalanced operation conditions[J]. Automation of Electric Power System, 2016, 40(10): 76-83.
[16] 王赟程, 陈新, 陈杰, 等. 基于谐波线性化的三相LCL型并网逆变器正负序阻抗建模分析[J]. 中国电机工程学报, 2016, 36(21): 5890-5898, 6033.
Wang Yuncheng, Chen Xin, Chen Jie, et al. Analysis of positive-sequence and negative-sequence impe- dance modeling of three-phase LCL-type grid- connected inverters based on harmonic lineari- zation[J]. Proceedings of the CSEE, 2016, 36(21): 5890-5898, 6033.
[17] 李奕欣, 赵书强, 马燕峰, 等. 三相LCL型并网逆变器的阻抗建模及特性分析[J]. 电力自动化设备, 2019, 39(7): 107-113.
Li Yixin, Zhao Shuqiang, Ma Yanfeng, et al. Impedance modeling and characteristic analysis of three-phase LCL-type grid-connected inverters[J]. Electric Power Automation Equipment, 2019, 39(7): 107-113.
[18] Liu Junliang, Du Xiong, Shi Ying, et al. Impedance measurement of three-phase inverter in the stationary frame using frequency response analyzer[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9390-9401.
[19] Wang Xiongfei, Blaabjerg F. Harmonic stability in power electronic-based power systems: concept, modeling, and analysis[J]. IEEE Transactions on Power Electronics, 2020, 10(3): 2858-2870.
[20] Zhou Weihua, Torres R, Wang Yanbo, et al. A gray-box hierarchical oscillatory instability source identification method of multiple-inverter-fed power systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 9(3): 3095-3113.
[21] 李建文, 吴滨源, 李永刚, 等. 分析谐波劣化机理的逆变器灰箱宽频域矩阵模型及求解方法[J]. 电力系统自动化, 2020, 44(18): 155-164.
Li Jianwen, Wu Binyuan, Li Yonggang, et al. Gray-box wide frequency domain matrix model of inverter for harmonic degradation mechanism analysis and its solution method[J]. Automation of Electric Power Systems, 2020, 44(18): 155-164.
[22] 张重远, 韩启隆. 考虑层间效应的复磁导率铁芯频变模型[J]. 高电压技术, 2019, 45(7): 2292-2298.
Zhang Chongyuan, Han Qilong. Frequency-depended modeling for the core of power transformer based on complex permeability considering interlaminar effects[J]. High Voltage Engineering, 2019, 45(7): 2292-2298.
[23] 戴宇峰, 鲁军勇, 张晓, 等. 脉冲功率同轴电缆瞬态阻抗特性研究[J]. 高电压技术, 2019, 45(6): 1915- 1920.
Dai Yufeng, Lu Junyong, Zhang Xiao, et al. Research on transient impedance characteristic of coaxial cable for pulse power[J]. High Voltage Engineering, 2019, 45(6): 1915-1920.
[24] 刘威, 刘杰, 吴小丹, 等. 风电场阻抗模型的现场测试[J]. 中国电机工程学报, 2020, 40(增刊1): 91-97.
Liu Wei, Liu Jie, Wu Xiaodan, et al. Identifying impedance models of wind farms with field tests[J]. Proceedings of the CSEE, 2020, 40(S1): 91-97.
[25] 党杰, 李勇, 徐友平, 等. 基于WAMS和奇异熵矩阵束方法的电网低频振荡仿真分析[J]. 电力系统自动化, 2010, 34(15): 14-18.
Dang Jie, Li Yong, Xu Youping, et al. Power grid low frequency oscillation simulation analysis based on WAMS and singular entropy matrix pencil method[J]. Automation of Electric Power System, 2010, 34(15): 14-18.
[26] 王印晨, 杨少兵, 宋可荐, 等. 基于滑模结构无源控制的车网耦合系统低频振荡抑制方法[J]. 电工技术学报, 2020, 35(3): 553-563.
Wang Yingchen, Yang Shaobing, Song Kejian, et al. An approach based on SMS to suppress low- frequency oscillation in the EMUs and traction network coupling system using PBC[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 553- 563.
[27] 赵普志, 李之洪, 徐交国, 等. 基于KL散度的电容器谐振研究[J]. 电气技术, 2020, 21(3): 27-30.
Zhao Puzhi, Li Zhihong, Xu Jiaoguo. Study on capacitor resonance based on KL dispersion[J]. Electrical Engineering, 2020, 21(3): 27-30.
[28] 张学广, 夏丹妮, 陈文佳, 等. 三相并网变流器弱电网下频率耦合抑制控制方法[J]. 电工技术学报, 2019, 34(21): 4559-4571.
Zhang Xueguang, Xia Danni, Chen Wenjia, et al. Frequency coupling suppression control method for three-phase grid-connected converter under weak grid[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4559-4571.
[29] 谢志为, 陈燕东, 伍文华, 等. 双模式扰动下新能源发电装备的宽频带序阻抗在线精确测量方法[J]. 中国电机工程学报, 2020, 40(9): 2903-2914.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A wide-bandwidth sequence-impedance online precise measurement method for renewable energy generation equipment with dual-mode disturbance[J]. Pro- ceedings of the CSEE, 2020, 40(9): 2903-2914.
[30] Gustavsen B, Semlyeen A. Rational approximation of frequency domain responses by vector fitting[J]. IEEE Transactions on Power Delivery, 1999, 14(3): 1052- 1061.
[31] Gustavsen B. Improving the pole relocating properties of vector fitting[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1587-1592.
[32] 涂春鸣, 李庆, 郭祺, 等. 具备电压质量调节能力的串并联一体化多功能变流器[J]. 电工技术学报, 2020, 35(23): 4852-4863.
Tu Chunming, Li Qing, Guo Qi, et al. Research on series-parallel integrated multifunctional converter with voltage quality adjustment[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4852- 4863.
[33] 张占俊, 李建文, 董耀, 等. 弱电网下多逆变器并网谐振失稳分析方法[J]. 电气技术, 2020, 21(10): 21-28.
Zhang Zhanjun, Li Jianwen, Dong Yao, et al. Method of resonance instability analysis of multiple grid- connected inverters in weak grid[J]. Electrical Engineering, 2020, 21(10): 21-28.
A Gray-Box Fitting Method of Grid-Connected Inverters Impedance for the Analysis of Harmonic Degradation
Abstract As a large number of distributed generation systems are connected to the grid through inverters, complex interactions between grid-connected inverters and weak-grids are formed, and the problem of harmonic degradation is prominent. One of the key points of harmonic degradation analysis is to establish the impedance model of the grid-connected inverter. The detailed internal information is needed in white-box impedance modeling, and the results of black-box impedance modeling are meaningless. Both methods have defects in practical engineering application. Therefore, setting the result of white-box as the goal and taking the method of black-box as the solution way, this paper presents that the impedance of the grid-connected inverters in gray-box is fitted by rational function approximation. First of all, the discrete impedance data are obtained by dual-mode disturbance, and then the matrix pencil method is used to extract the initial parameters and reduce the time of iterative calculation. An improved vector fitting is proposed. Then a hardware in the loop real-time simulation platform is built based on RT-Lab, and the effectiveness and advantages of this method are verified by comparative experiments. Finally, the analysis of harmonic degradation is carried out based on the results of impedance fitting to verify the practicability of the proposed method.
keywords：Grid-connected inverters, harmonic degradation, impedance analysis method, rational function approximation, RT-Lab
DOI: 10.19595/j.cnki.1000-6753.tces.201582
中图分类号：TM712
吴滨源 男，1998年生，博士研究生，研究方向为逆变器谐波谐振分析。E-mail: wby_ncepu@163.com
李建文 女，1983年生，博士，讲师，研究方向为配电网电能质量分析与控制、光伏并网技术。E-mail: ljw_ncepu@163.com（通信作者）
收稿日期 2020-12-04
改稿日期 2021-05-06
河北省自然科学基金（E2017502053）和中央高校基本科研业务费专项资金（2020MS095）资助项目。
（编辑 陈 诚）