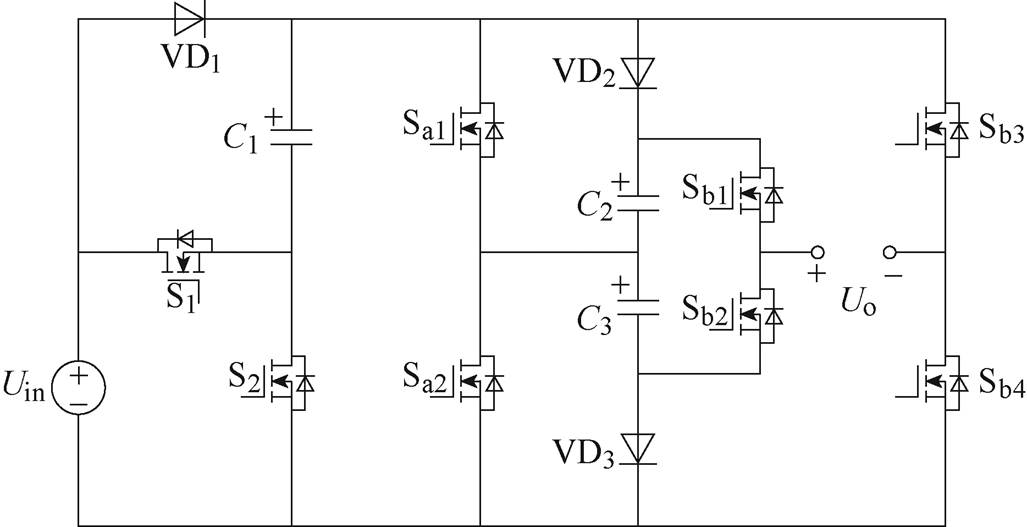
图1 提出的九电平逆变器
Fig.1 Proposed nine-level inverter
摘要 基于开关电容的多电平逆变器具有电路拓扑简单和电容电压自动平衡等优点。然而,现有开关电容型多电平逆变器存在元器件数量较多和电压应力较大等缺点。针对这些问题,该文提出一种九电平逆变器,该电路通过较少的元器件数量和较低的元器件电压应力实现了4倍升压的九电平输出,具有较低的成本和较小的体积;结合最近电平逼近法和基频调制策略来产生开关控制信号,通过开关管的有序通断实现良好的交流电输出。对九电平逆变器的工作原理、调制策略和电路参数等方面进行详细分析,最后搭建一台样机进行实验,证明了所提出电路的有效性和可行性。
关键词:多电平逆变器 开关电容 电容自均压 升压
风电和光伏等新能源发电方式具有可再生性强、环保且适用于分布式微电网等优点,其接入电网需要高性能的电力电子逆变器[1-3]。多电平逆变器因其开关管的低电压应力、输出电压谐波含量小和较低的开关频率等优点,受到了学界和工业界的广泛关注和研究[4-5]。主流的多电平逆变器主要包含中点钳位型[6-7]、飞跨电容型[8-9]、级联H桥型[10-11]和开关电容型[12-20]四类。中点钳位型和飞跨电容型的应用受限于其电容电压不平衡,以及所需开关器件的数量较多等问题;级联H桥型的缺陷主要在于需要多个独立的直流电源来产生较多的电平输出,这将会增加电路的成本以及控制与调制的复杂度;基于开关电容型的多电平逆变器因其电容的自均压特性,使用较少的开关器件和直流电源即可产生较多的电平输出以及具备自主升压功能等优点,从而具有一定的研究和应用价值。
文献[12]提出了一种基于多开关电容单元的多电平逆变器,该电路通过增加开关电容单元的数量能够实现输出电平的增加,且使用开关管数量较少,然而该电路需要较多的二极管。文献[13]提出了一种准谐振型逆变电路,该电路利用准谐振技术降低了并联充电阶段的电流尖峰,但该电路不具备升压能力。文献[14]提出了一种七电平开关电容逆变器,该电路结构和控制方法简单易行,然而其输出电平数量有限,若要得到较多的电平输出,则需将多个逆变器级联,这将增加电路的成本和体积。文献[15]提出了一种单电源自均压型九电平逆变器,该电路成本和体积较小,然而其升压能力较弱。文献[12-15]所述逆变电路均需要使用H桥来实现输出的反极性,但H桥的四个开关管所承受的电压应力为输出电压的幅值,具有较大的电压应力。为减小电压应力,文献[16]提出了一种多电平逆变器,该逆变器所有元件承受的电压应力均为输入电压,故具有较低的电压应力,但同时需要大量的开关器件。文献[17]提出了一种七电平开关电容逆变器,该电路无需H桥即可实现负电平输出,在一定程度上降低了开关管的电压应力,然而该电路使用的开关管较多。文献[18]提出了一种级联型升压逆变电路,该电路通过将开关电容和级联H桥相结合实现了较低的电压应力和较强的拓展性,然而其器件数量较多的问题仍需进一步改善。文献[19]提出了一种K型开关电容逆变器,该电路具有较少的器件数量和较低的电压应力,且可通过多个K型单元的连接实现较多的电平输出,然而该电路的升压能力较弱。文献[20]提出了一种多输入电源的开关电容逆变器,该电路通过多个输入电源实现了较多的电平输出,然而多电源结构限制了其在相关场合的应用。
针对上述现有开关电容型逆变电路所存在的问题,本文提出了一种基于开关电容的九电平逆变器。该电路拓扑结构简单易行,具有较少的器件数量和较低的器件电压应力,具备电容电压自动平衡功能和较强的升压能力,拥有一定的优越性和应用价值。本文对逆变器的工作原理、调制策略和电路相关特性等进行了理论分析,并通过实验验证了所提拓扑的可行性和有效性。
本文提出的九电平逆变器如图1所示,图中,Uin为输入直流电源。电路中器件的电压应力可分为高压、中压和低压,其中,高压为输出电压的幅值4Uin,中压为输出电压幅值的一半2Uin,低压为输入电压Uin。在该逆变器中,电容C1为低压电容,电容C2、C3为中压电容。二极管VD1为低压二极管,二极管VD2、VD3为中压二极管。开关S1、S2为低压开关,开关Sa1、Sa2、Sb3、Sb4为中压开关,开关Sb1、Sb2为高压开关。与H桥拓扑有4个高压开关相比,所提逆变器的高压开关仅为两个,因此在一定程度上降低了电压应力。该电路通过开关的有序通断实现了输入直流电源和电容的串并联切换。当处于并联状态时,电容处于充电状态;当处于串联状态时,电容和输入直流电源以不同的连接方式向负载供电,从而实现了多个电平输出。

图1 提出的九电平逆变器
Fig.1 Proposed nine-level inverter
为便于分析,对逆变器电路作出如下假设: ①开关器件和二极管均为理想器件;②电容容量足够大;③电路工作于稳态。各个电平对应的工作原理如图2所示,其相应的工作模态如下:
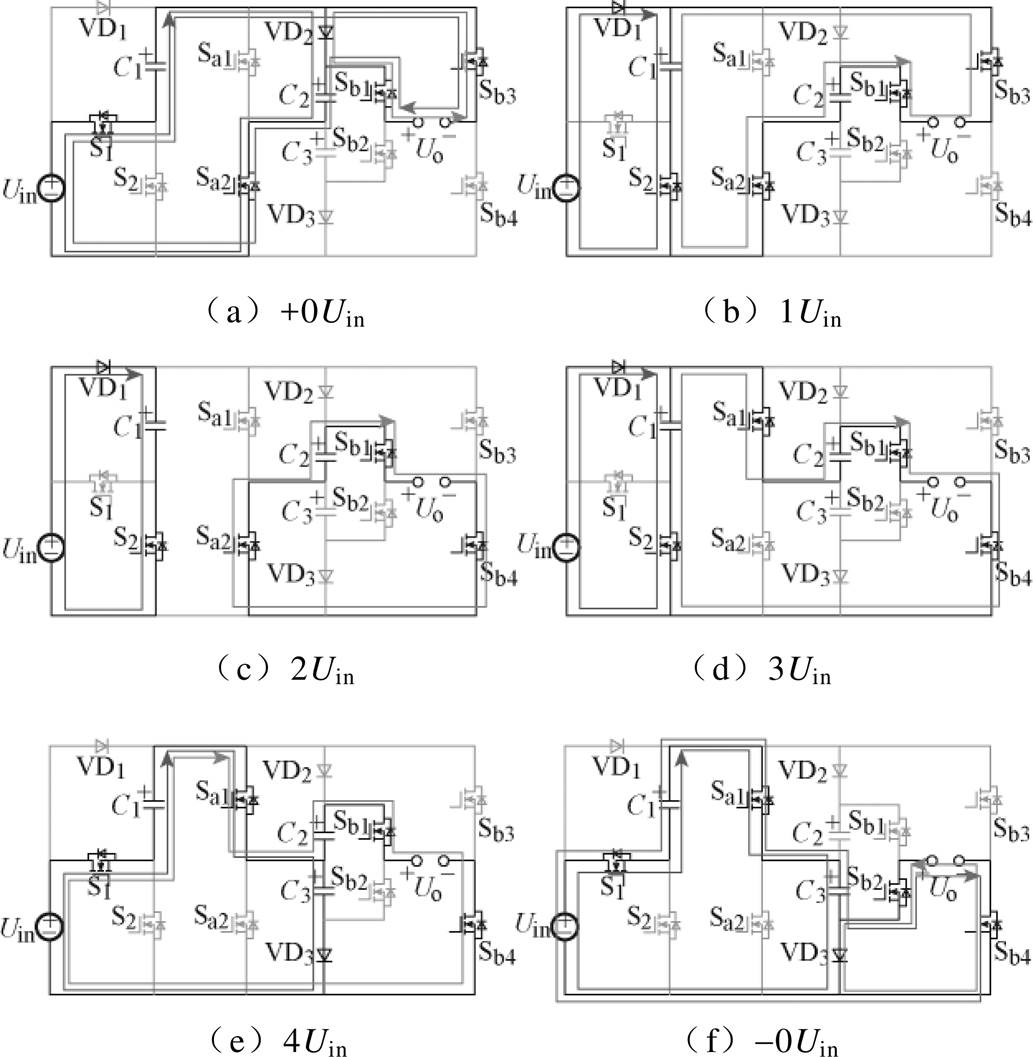
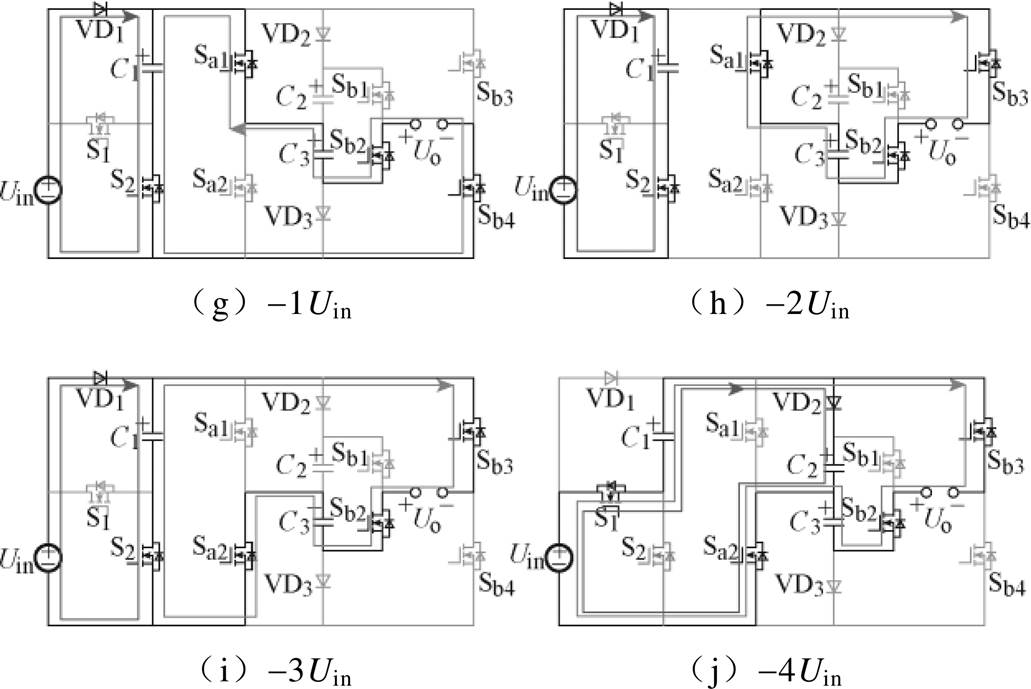
图2 工作原理
Fig.2 Operation principles
(1)+0Uin电平,如图2a所示。开关管S1、Sa2、Sb1、Sb3导通,其余开关管关断。输入电源Uin和电容C1串联共同向电容C2充电,此时电容C2的电压为2Uin,电阻负载回路为VD2-Sb1-Uo-Sb3,感性负载回路为Uin-S1-C1-Sb3-Uo-Sb1-C2-Sa2,此时输出电压Uo=0。
(2)1Uin电平,如图2b所示。开关管S2、Sa2、Sb1、Sb3导通,其余开关管关断。输入电源Uin向电容C1充电,电容C1的电压为Uin,电阻和感性负载回路为C1-S2-Sa2-C2-Sb1-Uo-Sb3,此时输出电压Uo=Uin。
(3)2Uin电平,如图2c所示。开关管S2、Sa2、Sb1、Sb4导通,其余开关管关断。输入电源Uin向电容C1充电,电容C1的电压为Uin,电阻和感性负载回路为Sa2-C2-Sb1-Uo-Sb4,此时输出电压Uo= 2Uin。
(4)3Uin电平,如图2d所示。开关管S2、Sa1、Sb1、Sb4导通,其余开关管关断。输入电源Uin向电容C1充电,电容C1的电压为Uin,电阻和感性负载回路为S2-C1-Sa1-C2-Sb1-Uo-Sb4,此时输出电压Uo=3Uin。
(5)4Uin电平,如图2e所示。开关管S1、Sa1、Sb1、Sb4导通,其余开关管关断。输入电源Uin和电容C1共同向电容C3充电,电容C3的电压为2Uin,电阻和感性负载回路为Uin-S1-C1-Sa1-C2-Sb1-Uo- Sb4,此时输出电压Uo=4Uin。
(6)-0Uin电平,如图2f所示。开关管S1、Sa1、Sb2、Sb4导通,其余开关管关断。输入电源Uin和电容C1向电容C3充电,此时电容C3的电压为2Uin,电阻负载回路为VD3-Sb4-Uo-Sb2,感性负载回路为Uin-S1-C1-Sa1-C3-Sb2-Uo-Sb4,此时输出电压Uo=0。
(7)-1Uin电平,如图2g所示。开关管S2、Sa1、Sb2、Sb4导通,其余开关管关断。输入电源Uin向电容C1充电,此时电容C1的电压为Uin,电阻和感性负载回路为C1-S2-Sb4-Uo-Sb2-C3-Sa1,此时输出电压Uo=-Uin。
(8)-2Uin电平,如图2h所示。开关管S2、Sa1、Sb2、Sb3导通,其余开关管关断。输入电源Uin向电容C1充电,电容C1的电压为Uin,电阻和感性负载回路为Sa1-Sb3-Uo-Sb2-C3,此时输出电压Uo=-2Uin。
(9)-3Uin电平,如图2i所示。开关管S2、Sa2、Sb2、Sb3导通,其余开关管关断。输入电源Uin向电容C1充电,电容C1的电压为Uin,电阻和感性负载回路为S2-C1-Sb3-Uo-Sb2-C3-Sa2,此时输出电压Uo= -3Uin。
(10)-4Uin电平,如图2j所示。开关管S1、Sa2、Sb2、Sb3导通,其余开关管关断。输入电源Uin和电容C1共同向电容C2充电,电容C2的电压为2Uin,电阻和感性负载回路为Uin-S1-C1-Sb3-Uo-Sb2-C3- Sa2,此时输出电压Uo=-4Uin。
根据上述工作模态,可得逆变器工作状态见表1。表中,“1”表示开关管导通,“0”表示开关管关断,“D”表示电容处于放电状态,“C”表示电容处于充电状态,“-”表示电容处于闲置状态。
表1 逆变器工作状态
Tab.1 Operation states of proposed inverter
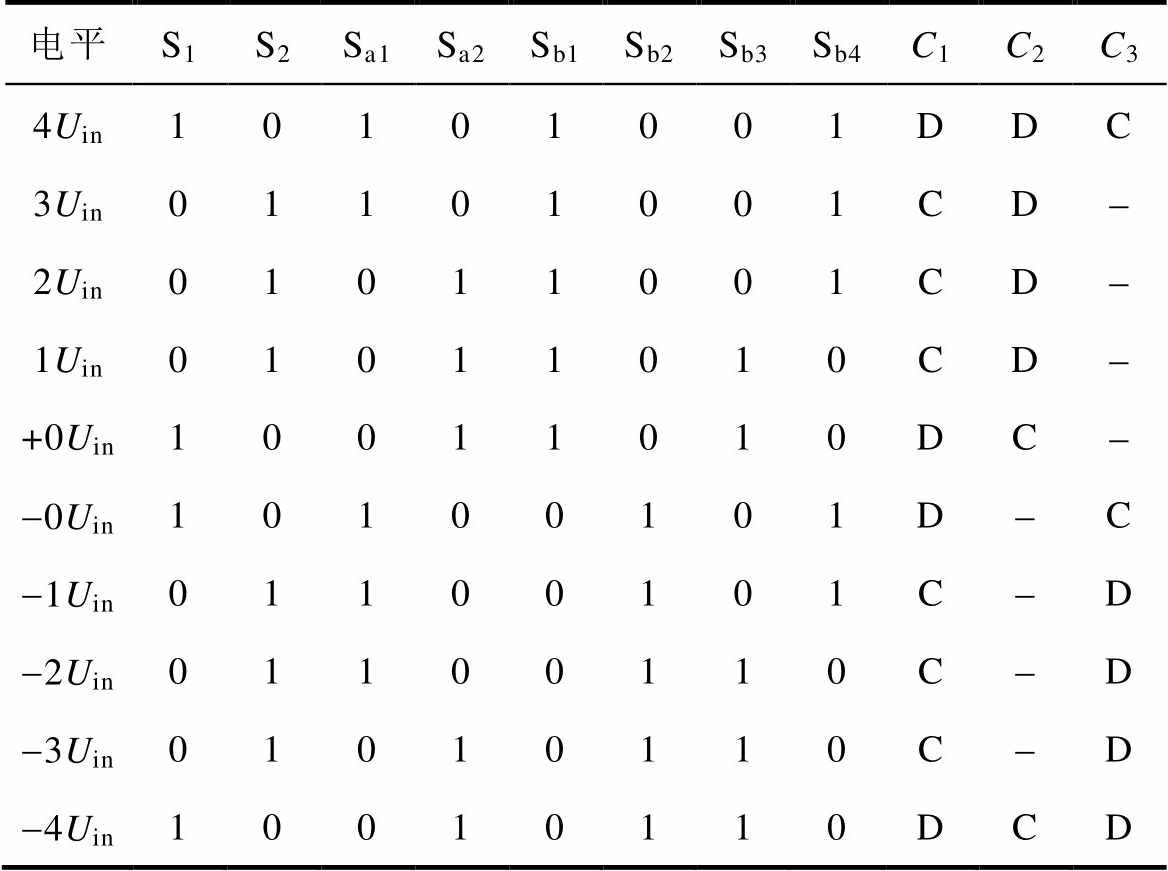
电平S1S2Sa1Sa2Sb1Sb2Sb3Sb4C1C2C3 4Uin10101001DDC 3Uin01101001CD- 2Uin01011001CD- 1Uin01011010CD- +0Uin10011010DC- -0Uin10100101D-C -1Uin01100101C-D -2Uin01100110C-D -3Uin01010110C-D -4Uin10010110DCD
本文采用最近电平逼近法来计算开关管的导通角,首先计算参考正弦波形和多电平波形的相交点所对应的角度,具体计算公式[19]为
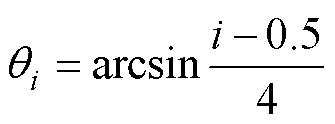 (1)
(1)式中,i为多电平波形在正半周的电平序列,对于九电平,i=1, 2, 3, 4;qi为第i电平序列对应的导通角。根据式(1)可得,q1=7°,q2=22°,q3=38°,q4=61°,由于正弦波的对称性,其余导通角可由q1~q4得出。由表1可得逆变器的工作波形,如图3所示。
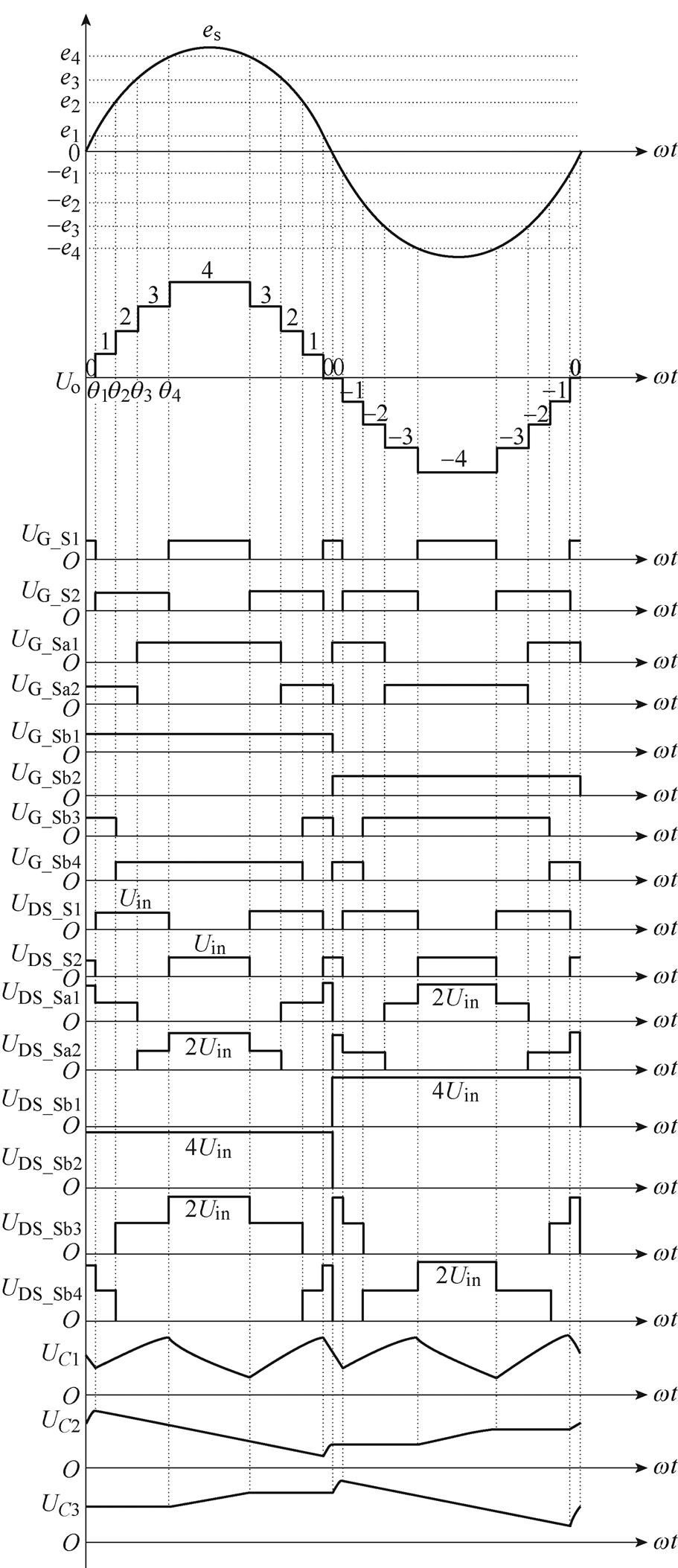
图3 工作波形
Fig.3 Operation waveforms
采用基频调制策略来产生开关的控制信号。具体实施方式如下:正弦调制波es与直线载波±ei(i=1, 2, 3, 4)相比较。载波和调制波的表达式分别为
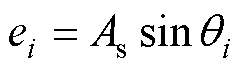 (2)
(2)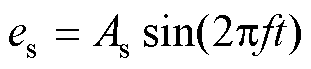 (3)
(3)
式中,As为调制波的幅值;f为调制波频率,同时也为输出电压的频率,调制逻辑如下
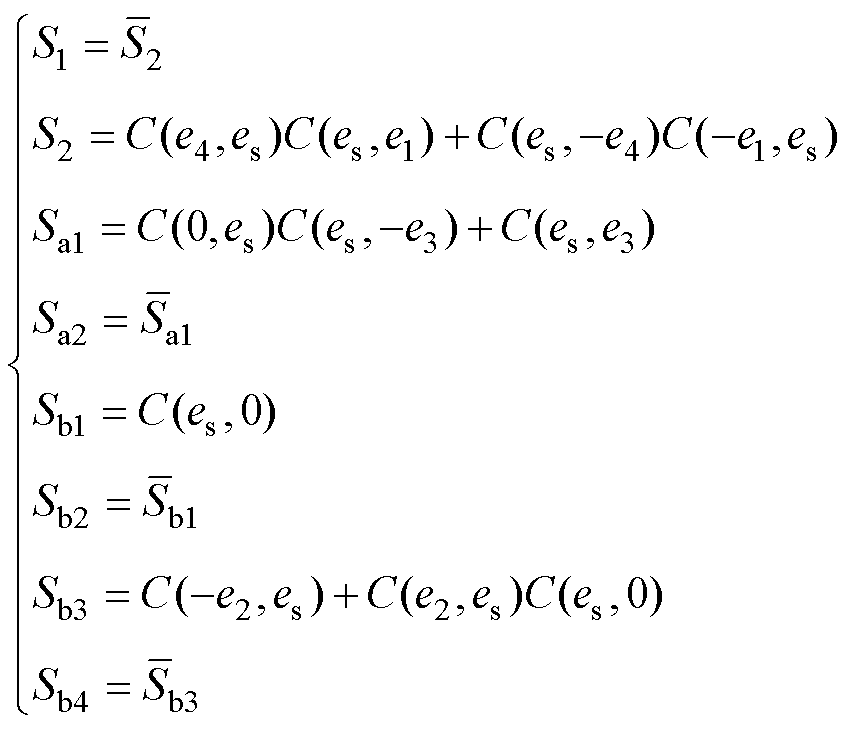 (4)
(4)式中,C(a, b)表示将a和b进行比较,当a>b时,C(a, b)=1;当a<b时,C(a, b)=0。当S=1时,开关导通;当S=0时,开关关断。由式(4)可得图4所示调制逻辑。
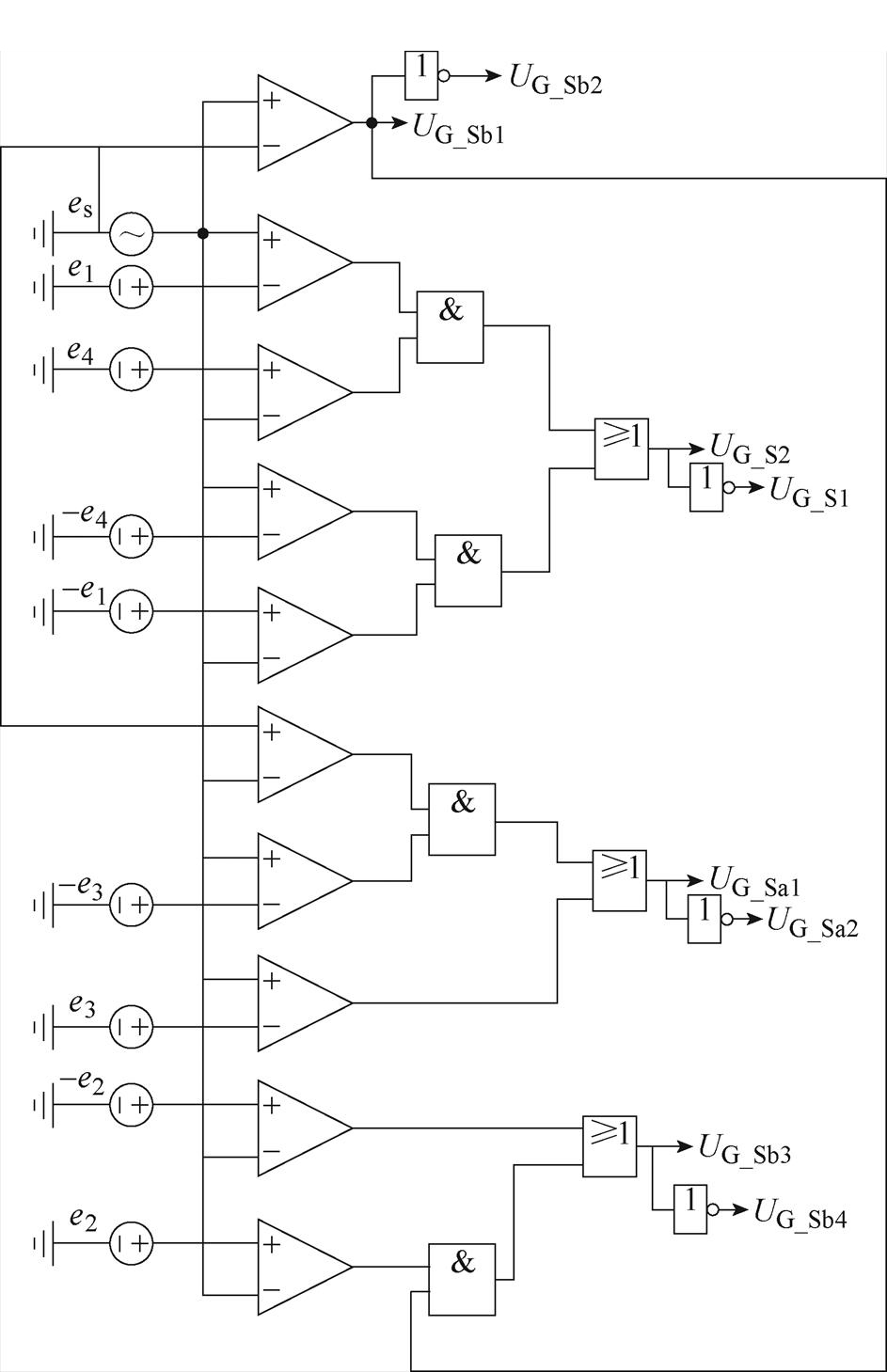
图4 调制逻辑
Fig.4 Modulation logic
由图2所示工作原理和表1所示逆变器工作状态可知,低压电容C1在输出电压为±Uin、±2Uin、±3Uin时,通过回路Uin-VD1-C1-S2被充电至Uin;而在输出电平为±0Uin和±4Uin时,与输入电源Uin串联共同向中压电容C2或C3充电,通过上述过程,C1的电压能够动态保持在Uin水平。对于中压电容C2和C3,C2在输出电压正半周和-4Uin期间被充电至2Uin并多次向负载放电,而C3则在输出电压负半周和4Uin期间被充电至2Uin,并多次向负载放电,由输出电压正负半周的对称性可知,中压电容C2和C3的充放电状态完全相同,故能够实现电容电压的自动平衡。
电容的电压纹波主要由电容的最大连续放电量决定。在所提出的逆变电路中,电容C1的最大放电区间为[q4, p-q4]或[p+q4, 2p-q4],则其最大连续放电量为
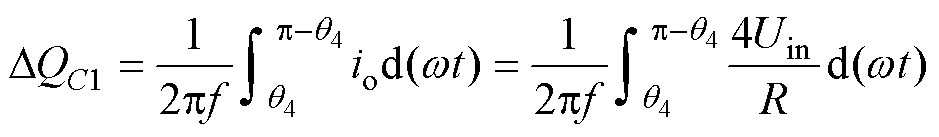
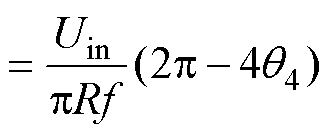 (5)
(5)
电容C1的容值需满足
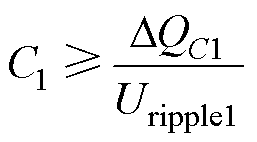 (6)
(6)式中,Uripple1为电容C1要求的电压纹波;R为负载电阻,将式(5)代入式(6)可得
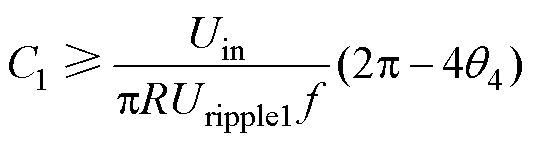 (7)
(7)
电容C2和C3的最大连续区间分别为[q1, p-q1]和[p+q1, 2p-q1],其最大连续放电量相等,即DQC2= DQC3=DQC2,3,其值为
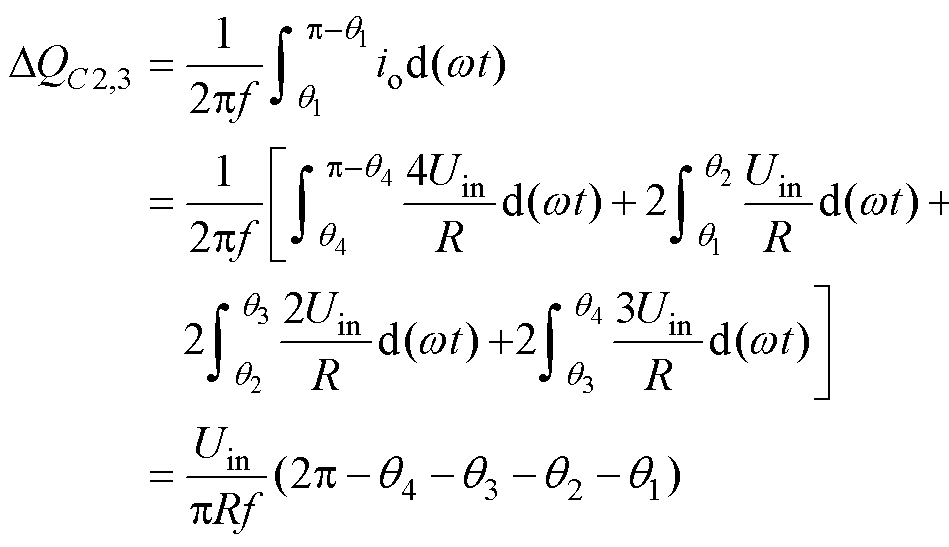 (8)
(8)电容C2和C3的容值需满足
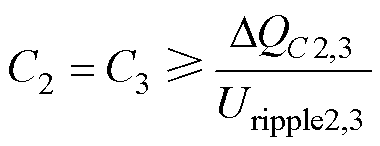 (9)
(9)
式中,Uripple2,3为电容C2、C3要求的电压纹波,将式(8)代入式(9)可得
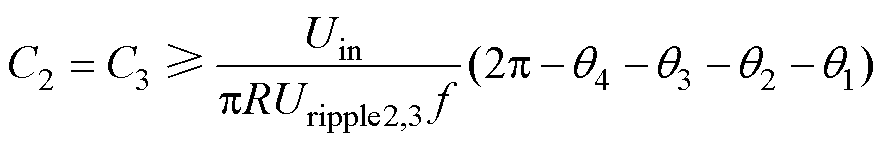 (10)
(10)根据式(7)和式(10)可知,电容的最小值与负载电阻、输出频率和要求的电压纹波成反比,与输入电压成正比。同时根据式(7)和式(10)可得,当f =50Hz时电容最小值随负载电阻的变化曲线如图5所示,当R=100W 时电容最小值随输出频率的变化曲线如图6所示,可见当逆变器的输出功率提高时需要增大电容容值,而较高的输出频率可以有效减小电容容值。
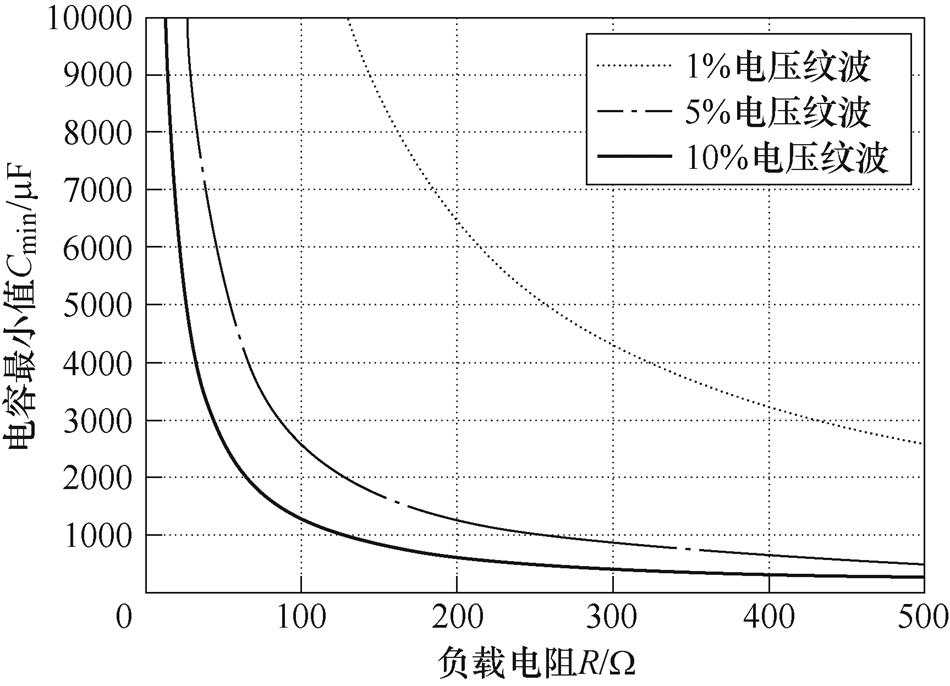
图5 当f =50Hz时电容最小值随负载电阻的变化曲线
Fig.5 Variety curves of the minimum capacitance with the load resistor when f =50Hz
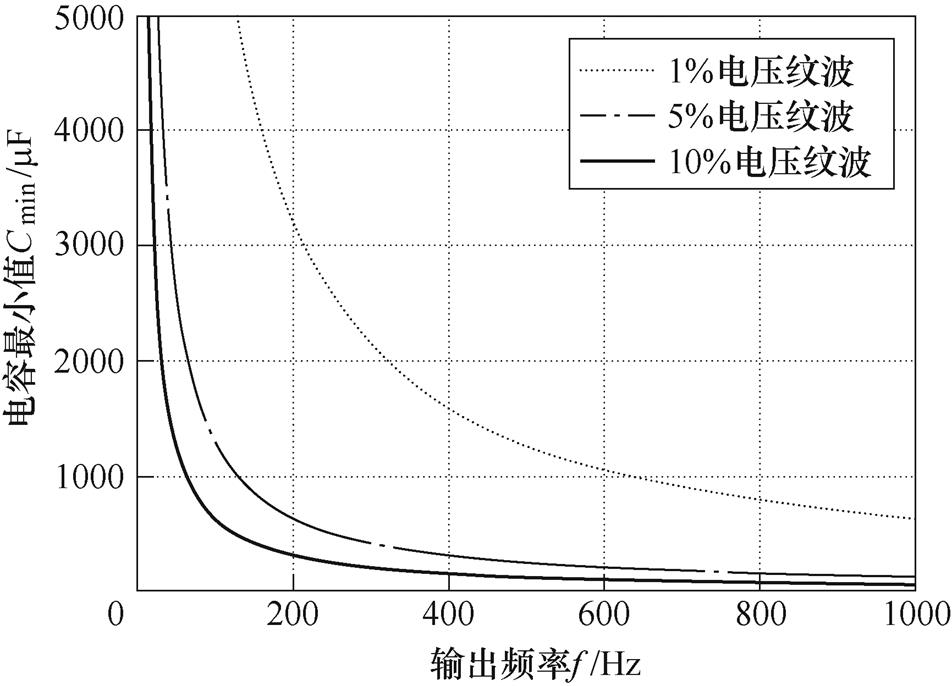
图6 当R=100W 时电容最小值随输出频率的变化曲线
Fig.6 Variety curves of the minimum capacitance with the output frequency when R=100W
多电平逆变器的损耗包括导通损耗Pcon和开关损耗Psw。导通损耗Pcon一般由开关管导通电阻RS、二极管的导通电阻RD、正向导通压降UD以及电容等效串联电阻RC构成。为方便分析,本文建立了逆变器在充电回路和放电回路等效电路,分别如图7和图8所示。图7中充电回路的电路参数可表示为
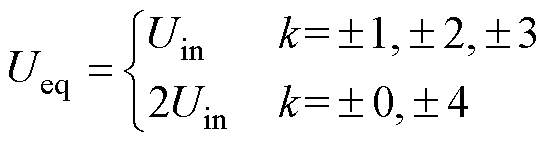 (11)
(11)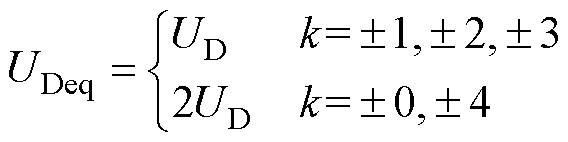 (12)
(12)
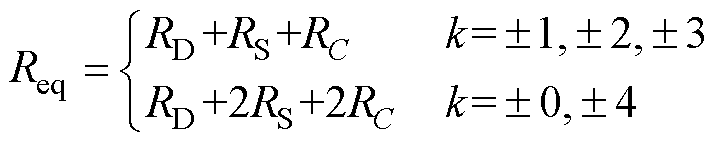 (13)
(13)
式中,k为输出波形所对应的电平序列,由式(5)可得电容C1的纹波电压为
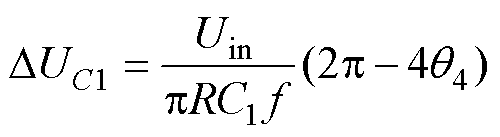 (14)
(14)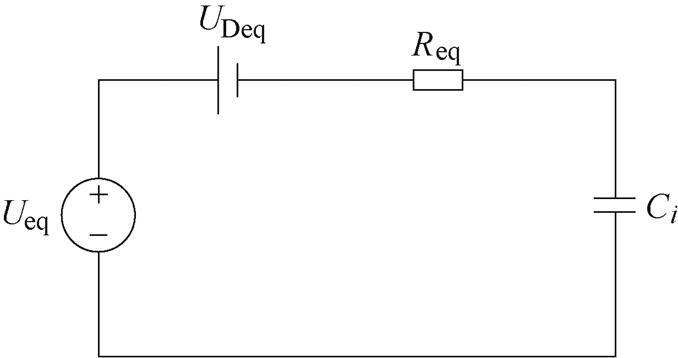
图7 充电回路等效电路
Fig.7 Equivalent circuit of charge loop
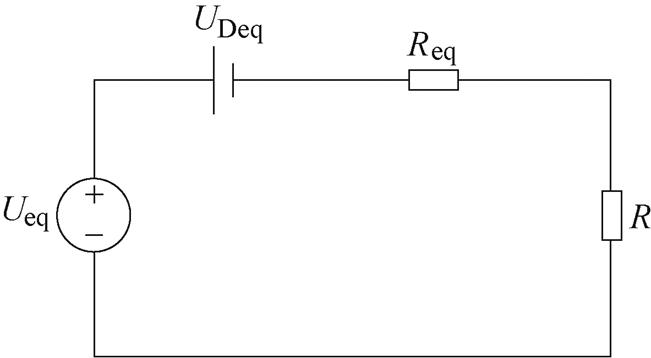
图8 放电回路等效电路
Fig.8 Equivalent circuit of discharge loop
由式(8)可得电容C2和C3的电压纹波为
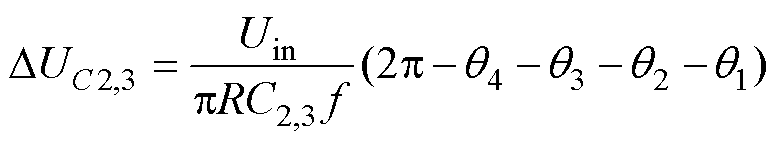 (15)
(15)当k=±1, ±2, ±3时,电容C1在一个充电阶段的能量损耗为
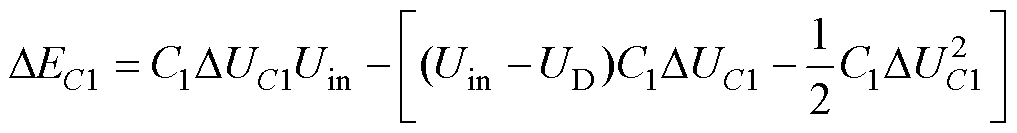 (16)
(16)
电容C1的充电损耗功率为
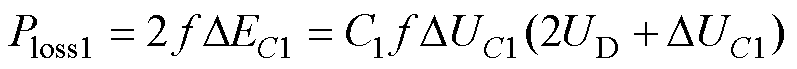 (17)
(17)当k=±0, ±4时,电容C2和C3在一个充电阶段的能量损耗为
 (18)
(18)
电容C2和C3的充电损耗功率为
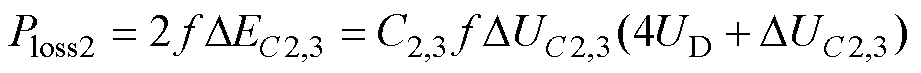 (19)
(19)在图8中,放电回路的电路参数可表示为
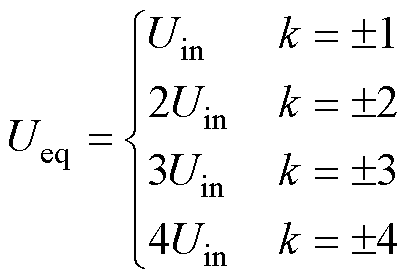 (20)
(20)
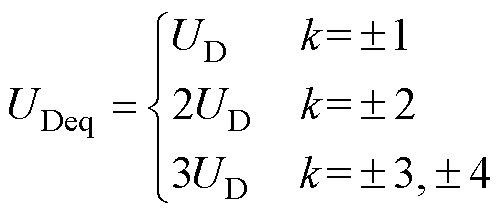 (21)
(21)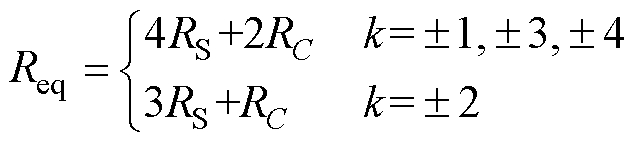 (22)
(22)
则在放电回路所造成的导通损耗为
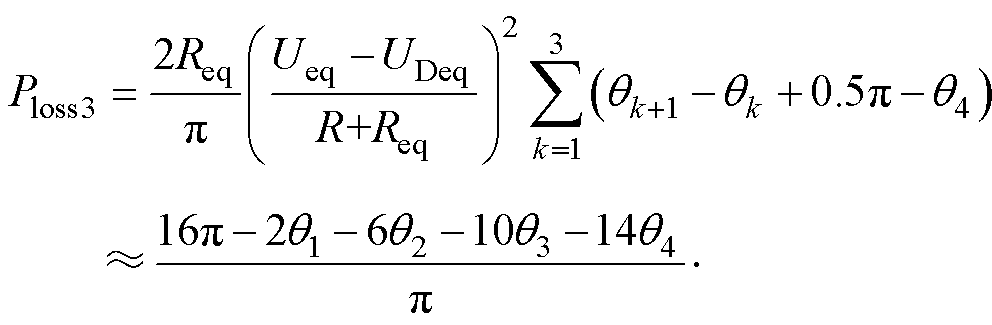
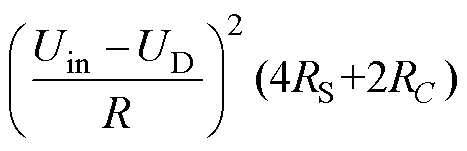 (23)
(23)
总导通损耗为
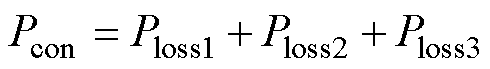 (24)
(24)开关损耗Psw一般因开关管状态切换时电压和电流的交叠处造成,其值可通过开关管漏极和源极之间寄生电容Cds的充放电过程进行估算,即
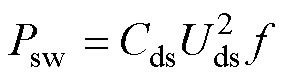 (25)
(25)
式中,Uds为开关管承受的电压应力,所提逆变器的器件电压应力见表2,则式(25)可整理为
表2 所提逆变器的器件电压应力
Tab.2 Component voltage stress of proposed inverter

器件类型电压应力 C1,VD1,S1, S2Uin C2, C3,VD2, VD3, Sa1, Sa2, Sb3, Sb42Uin Sb1, Sb24Uin
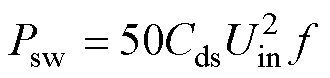 (26)
(26)各九电平逆变器参数对比见表3。表中,NSW为开关管数量,ND为二极管数量,NC为电容数量。升压系数(Boost Factor, BF)为最大输出电压和输入电压的比值,BF越大则升压能力越强。电压应力之和(Total Standing Voltage stress, TSV)为开关管和二极管的电压应力之和与最大输出电压的比值,TSV越大则器件的电压应力越大。成本函数(Cost Function, CF)能够评估多电平逆变器在成本方面的综合表现,CF越大则该电路的成本越高,其表达 式[19]为
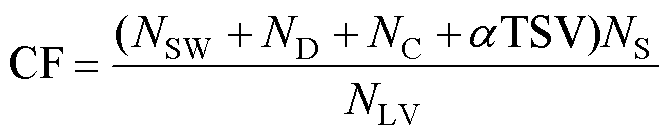 (27)
(27)式中,NLV为输出电平数量;NS为输入直流电源数量;a 为权重系数,当a>1时,表明器件电压应力较为重要;当a<1时,表明器件数量较为重要。本文选择a =1,表明器件数量和器件电压应力的重要性相同。
表3 九电平逆变器输出参数对比
Tab.3 Parameter comparisons of several nine-level inverters
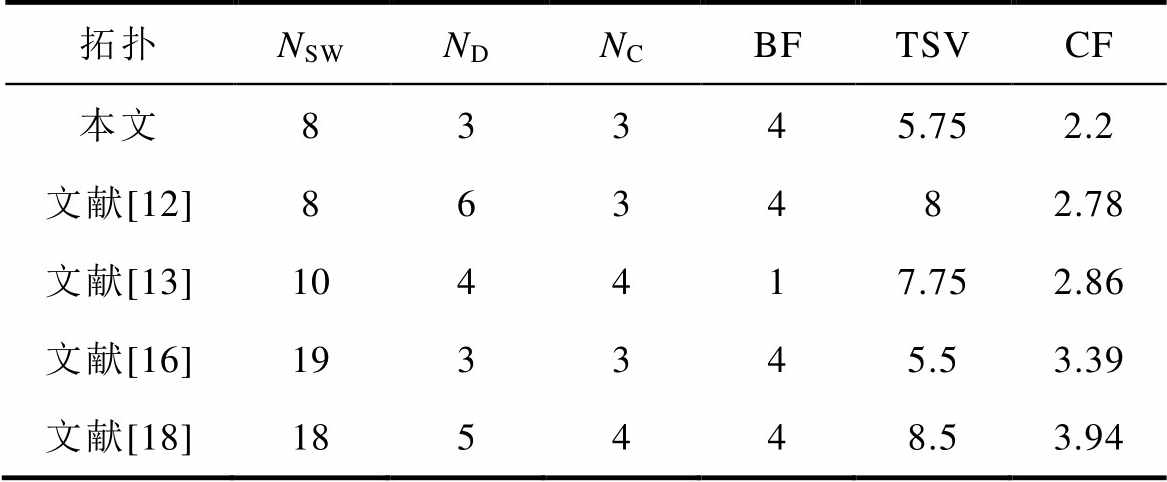
拓扑NSWNDNCBFTSVCF 本文83345.752.2 文献[12]863482.78 文献[13]104417.752.86 文献[16]193345.53.39 文献[18]185448.53.94
由表3可知,与现有九电平逆变器相比,本文所提出拓扑的器件数量和成本函数均为最小值。虽然与文献[16]相比,提出的拓扑其TSV略高,但开关管数量显著减少。故本文所提拓扑能够以较少的器件数量和较低的器件电压应力实现九电平输出。
为验证本文所提九电平逆变器的可行性和有效性,搭建了一台逆变器样机进行实验验证。实验平台如图9所示,其中开关管采用MOSFET,用dSPACE控制器来产生开关控制信号,实验元器件参数见表4。
图10为一个周期内的开关控制信号波形。可见开关S1和S2、Sa1和Sa2、Sb1和Sb2、Sb3和Sb4由四组互补导通的信号控制,与理论分析一致。

图9 实验平台
Fig.9 Experimental platform
表4 实验元器件参数
Tab.4 Parameters of experimental devices
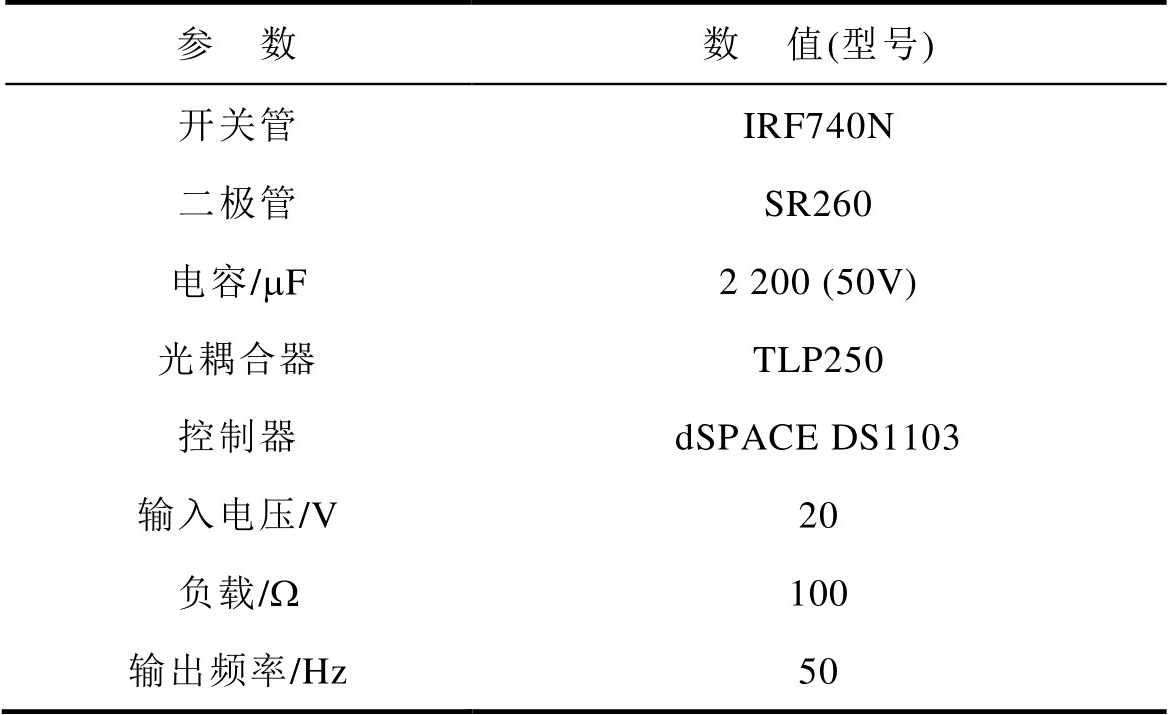
参 数数 值(型号) 开关管IRF740N 二极管SR260 电容/mF2 200 (50V) 光耦合器TLP250 控制器dSPACE DS1103 输入电压/V20 负载/W100 输出频率/Hz50

图10 开关控制信号波形
Fig.10 Waveforms of switch control signals
图11为开关管的漏极-源极电压波形,可见,开关S1和S2的电压应力为Uin,Sa1、Sa2、Sb3和Sb4的电压应力为2Uin,Sb1、Sb2的电压应力为4Uin,与有H桥逆变电路相比,承受输出电压幅值的开关管数量减半,与理论分析一致。

图11 开关漏极-源极电压波形
Fig.11 Waveforms of drain-source voltages
图12为电容电压在一个周期内的具体波形,可见,电容在一个周期内进行多次充放电且电压能够维持在相应的水平,电容的充放电区间也与理论分析一致。
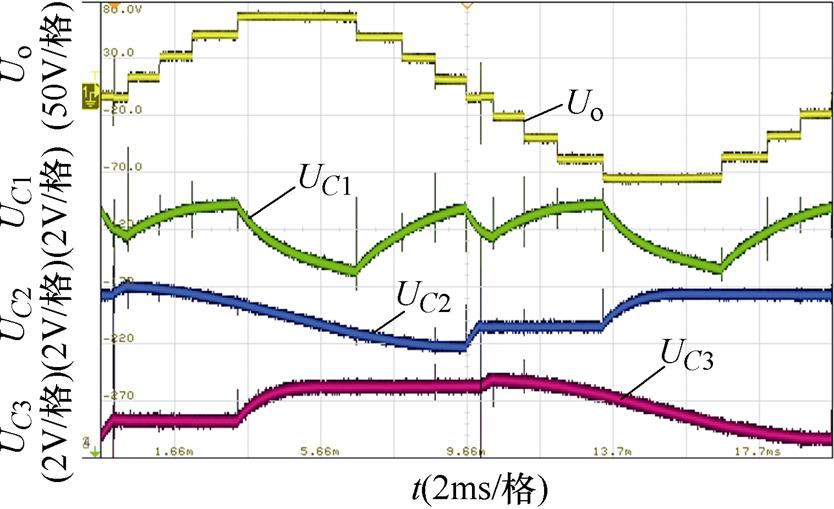
图12 电容电压的具体波形
Fig.12 Detailed waveforms of capacitor voltages
图13为逆变器输出电压和电流波形,可见,电压和电流均为理想的九电平阶梯波,其一个周期为0.02s,与理论值频率50Hz一致。其中输出电压的幅值为73V,与理论值80V基本吻合,证明本文提出的九电平逆变器能够实现4倍升压,具有正常的逆变功能。
图14为逆变器输出电压和电容电压波形,可见,电容C1~C3的电压能够分别自动维持在20V、40V和40V附近,与理论分析一致,证明了所提出九电平逆变器能够实现电容电压的自动平衡。

图13 输出频率50Hz时的输出电压和电流波形
Fig.13 Waveforms of output voltage and current when output frequency is 50Hz
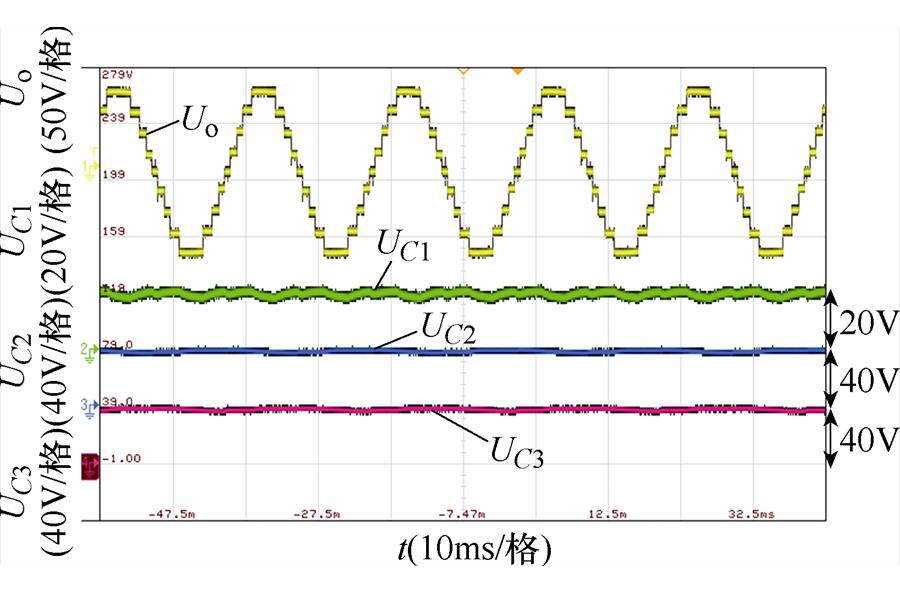
图14 输出频率50Hz时的输出电压和电容电压波形
Fig.14 Waveforms of output voltage and capacitor voltage when output frequency is 50Hz
图15为逆变器向感性负载供电时的输出电压和电流波形,其中,电阻R=100W,电感L=45mH。可见,输出电压为标准的九电平阶梯波,输出电流在电感的滤波作用下为平滑的正弦波,且输出电压和电流之间存在微小的相位差,证明提出的逆变器能够为感性负载供电。
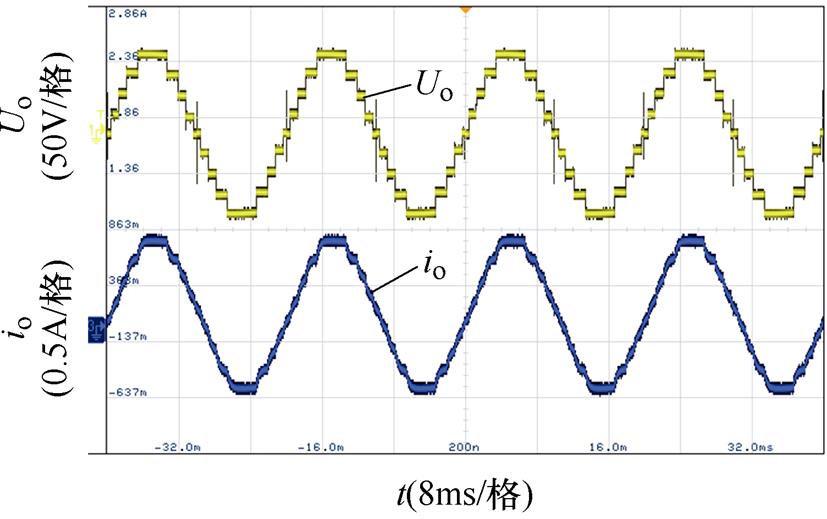
图15 带感性负载(100W-45mH)时的输出电压和电流
Fig.15 Waveforms of output voltage and current when inductive load is 100W-45mH
图16为输出频率为1kHz时的输出电压和电流波形,可见,电压和电流均为理想的九电平阶梯波,其一个周期为1ms,与理论值频率1kHz一致。其输出电压幅值基本为输入电压的4倍,实现了4倍升压的功能,证明提出的九电平逆变器能够工作在高频状态。
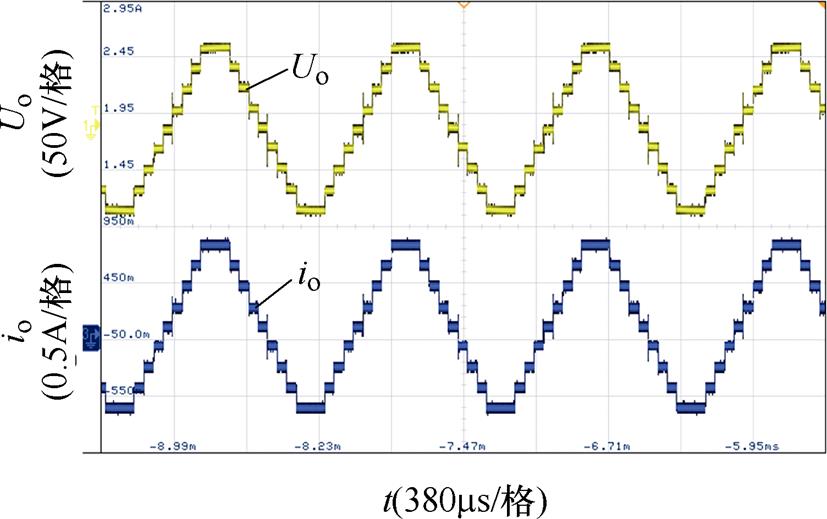
图16 输出频率1kHz时的输出电压和电流波形
Fig.16 Waveforms of output voltage and current when output frequency is 1kHz
图17为输入电压由20V变化至10V的动态波形,可见,当输入电压变化时,输出电压的幅值由73V变化至37V,电容C1~C3的电压由20V、40V和40V变化至10V、20V和20V,并稳定在该位置。证明所提九电平逆变器的输出电压和电容电压能够跟随输入正常变化,具有良好的动态性能。
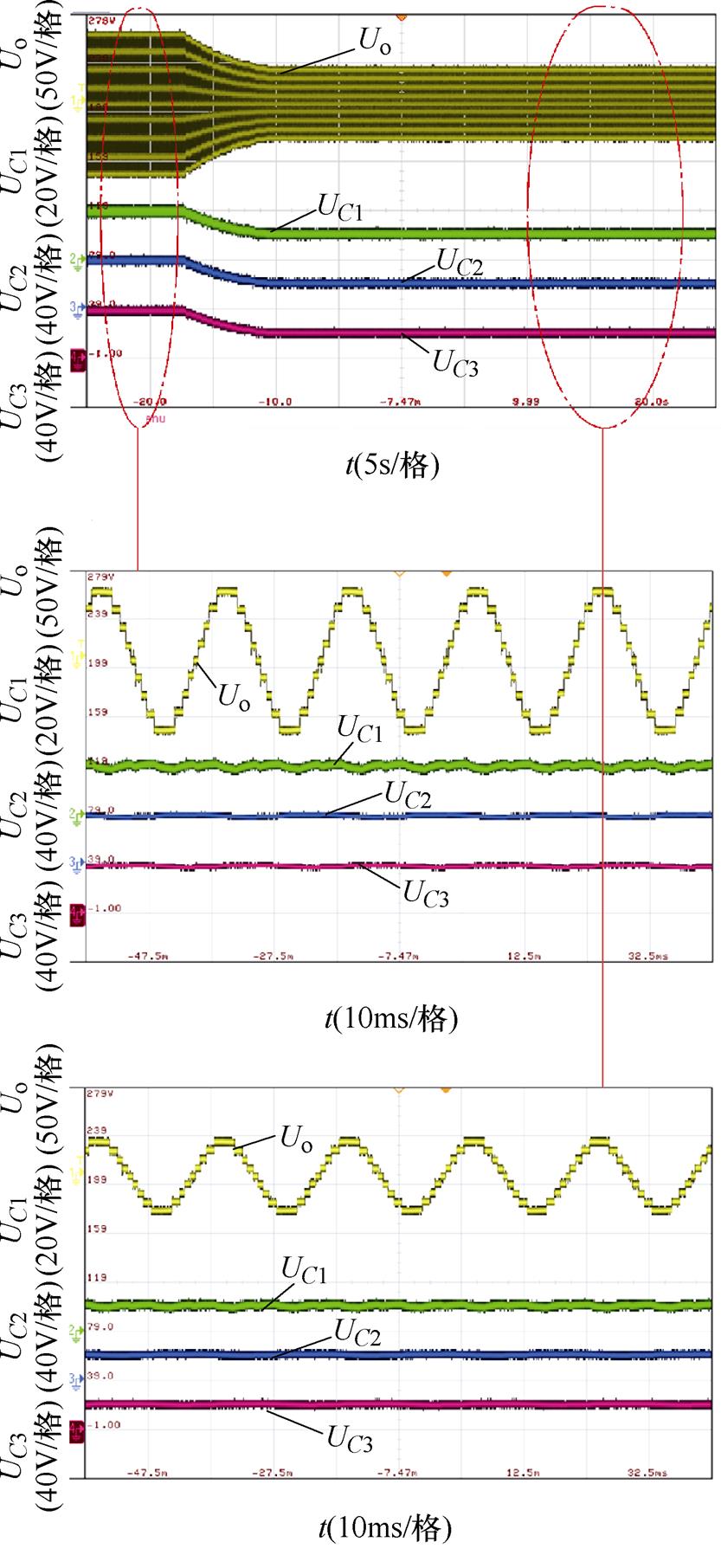
图17 输入电压由20V变化至10V的动态波形
Fig.17 Dynamic waveforms with input voltage changing from 20V to 10V
图18为负载电阻由100W 变化至50W 的动态波形,可见,当负载变化时,输出电压基本保持稳定,输出电流的幅值增大1倍,电容的电压纹波有所增大但波形依然能够保持稳定。证明所提九电平逆变器的输出电流和电容电压能够跟随负载正常变化,具有良好的动态性能。

图18 负载电阻由100W 变化至50W 的动态波形
Fig.18 Dynamic waveforms with load resistor changing from 100W to 50W
图19为所提逆变器工作在50Hz时的效率曲线,调节负载在40~100W 变化可得在不同输出功率下所对应的效率。由曲线可得,所提逆变器的最大实验效率能够达到95.1%,当输出功率增加时,由于电容的电压纹波增大,导致电容的充电损耗增加,其效率将会下降。由于在实验过程中存在线损等其他损耗,因而理论值略高于实验值。
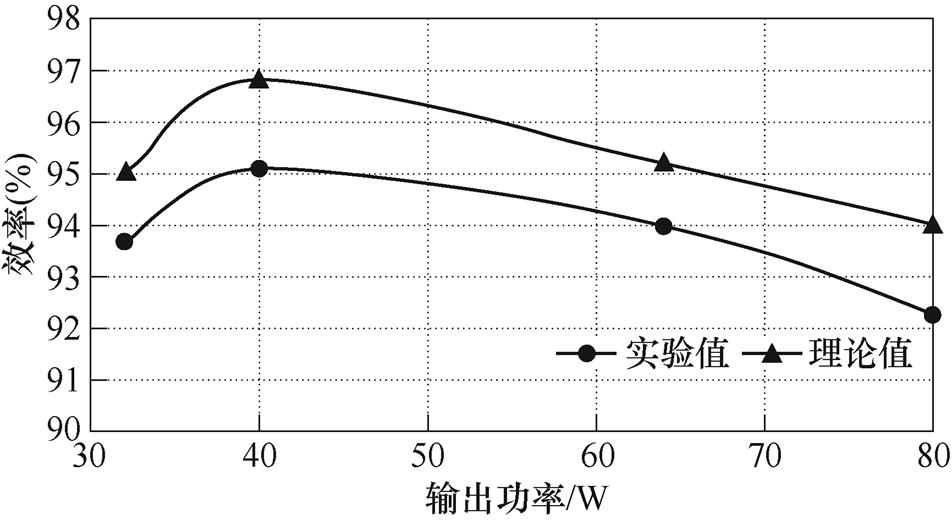
图19 逆变器效率曲线
Fig.19 Efficiency curves of proposed inverter
本文提出了一种基于开关电容的九电平逆变器。该逆变器具备较强的升压能力和电容电压自动平衡功能,使用元器件数量较少且元器件电压应力较低。首先,将最近电平逼近法和基频调制策略相结合来产生开关管的控制信号,通过控制开关管的有序通断实现了良好的电能输出。其次,对逆变器的工作原理、电容自均压特性和电容参数选择等方面进行了详细的理论分析。最后,搭建了一台样机进行实验验证,实验结果表明,所提出的九电平逆变器在工频和高频均能实现九电平阶梯波输出,且具有4倍升压和电容电压自动平衡的功能,同时在输入电压和负载变化的情况下能够正常工作,拥有良好的动态性能,适用于有逆变需求的应用场合。
参考文献
[1] 杨荣峰, 于雁南, 俞万能, 等. 新能源船舶并网逆变器电网支撑协调控制[J]. 电工技术学报, 2019, 34(10): 2141-2153.
Yang Rongfeng, Yu Yannan, Yu Wanneng, et al. New energy ship grid-connected inverter grid support and cooperative control[J]. Transactions of China Elec- trotechnical Society, 2019, 34(10): 2141-2153.
[2] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC-DC distribution net- work[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[3] Sun Xiaofeng, Wang Baocheng, Zhou Yue, et al. A single DC source cascaded seven-level inverter integrating switched-capacitor techniques[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 7184-7194.
[4] 张琦, 李江江, 孙向东, 等. 单相级联七电平逆变器拓扑结构及其控制方法[J]. 电工技术学报, 2019, 34(18): 3843-3853.
Zhang Qi, Li Jiangjiang, Sun Xiangdong, et al. Topology and control method of single-phase cas- caded seven-level inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3843-3853.
[5] Choi J S, Kang F S. Seven-level PWM inverter employing series-connected capacitors paralleled to a single DC voltage source[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3448-3459.
[6] 吴可丽, 夏长亮, 张云, 等. 二极管钳位型三电平逆变器共模电压抑制[J]. 电工技术学报, 2015, 30(24): 110-117.
Wu Keli, Xia Changliang, Zhang Yun, et al. Common- mode voltage suppression for neutral point-clamped three-level inverter[J]. Transactions of China Electro- technical Society, 2015, 30(24): 110-117.
[7] Rodriguez J, Bernet S, Steimer P K, et al. A survey on neutral-point-clamped inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2219-2230.
[8] 刘苗, 洪峰, 尹培培, 等. 复合型级联双Buck飞跨电容五电平逆变器[J]. 电工技术学报, 2015, 30(18): 35-42.
Liu Miao, Hong Feng, Yin Peipei, et al. A hybrid cascaded dual Buck flying-capacitor five-level inver- ter[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 35-42.
[9] Saccol G A, Giacomini J C, Batschauer A L, et al. Comprehensive analysis of single-phase full-bridge asymmetrical flying capacitor inverters[J]. IEEE Transactions on Industry Applications, 2019, 55(2): 1775-1786.
[10] 陈仲, 孙健博, 章修齐, 等. 级联型逆变器载波周期脉冲调整的功率均衡方法及特性分析[J]. 电工技术学报, 2019, 34(22): 4761-4771.
Chen Zhong, Sun Jianbo, Zhang Xiuqi, et al. Power balance method and characteristic analysis based on carrier period pulse adjustment for cascaded inver- ter[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4761-4771.
[11] Malinowski M, Gopakumar K, Rodriguez J, et al. A survey on cascaded multilevel inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2197-2206.
[12] Ye Yuanmao, Cheng K W E, Liu Junfeng, et al. A step-up switched-capacitor multilevel inverter with self-voltage balancing[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6672-6680.
[13] Zeng Jun, Wu Jialei, Liu Junfeng, et al. A quasi- resonant switched-capacitor multilevel inverter with self-voltage balancing for single-phase high-frequency AC microgrids[J]. IEEE Transactions on Industrial Informatics, 2017, 13(5): 2669-2679.
[14] Peng Wei, Ni Qiang, Qiu Xiaohuan, et al. Seven-level inverter with self-balanced switched-capacitor and its cascaded extension[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11889-11896.
[15] 王要强, 周成龙, 李忠文, 等. 单电源自均压九电平逆变器及其调制策略[J]. 电工技术学报, 2020, 35(4): 817-826.
Wang Yaoqiang, Zhou Chenglong, Li Zhongwen, et al. Single-source self-voltage-balancing nine-level inverter and its modulation strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 817-826.
[16] Taghvaie A, Adabi J, Rezanejad M, et al. A self- balanced step-up multilevel inverter based on switched-capacitor structure[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 199-209.
[17] Liu Junfeng, Zhu Xiangkai, Zeng Jun. A seven-level inverter with self-balancing and low-voltage stress[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 685-696.
[18] Jahan H K, Abapour M, Zare K, et al. Switched- capacitor-based single-source cascaded H-bridge multilevel inverter featuring boosting ability[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1113-1124.
[19] Zeng Jun, Lin Weijie, Cen Dehai. Novel k-type multi- level inverter with reduced components and self- balance[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, DOI: 10.1109/ JESTPE.2019.2939562.
[20] Fong Y C, Raman S R A, Ye Yuanmao, et al. Generalized topology of a hybrid switched-capacitor multilevel inverter for high-frequency AC power distribution[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2886-2897.
A Nine-Level Inverter Based on Switched-Capacitor
Abstract Multilevel inverters based on switched-capacitor have the advantages of simple circuit topology and self-balancing of capacitor voltages. However, the existing switched-capacitor based multilevel inverter has a large number of components and large voltage stress. For this reason, this paper proposes a nine-level inverter. The circuit achieves quadruple boost nine-level output through a smaller number of components and lower voltage stress, and has a lower cost and volume. Combining the nearest level modulation and the fundamental frequency modulation, the switch control signals are generated. Moreover, the satisfied AC (Alternating Current) output is realized through the orderly on-off of switches. The operation principle, modulation strategy and circuit parameters of proposed inverter are analyzed in detail. Finally, a prototype is built for experiment to prove the effectiveness and feasibility of proposed inverter.
keywords:Multilevel inverter, switched-capacitor, self-balancing of capacitor voltages, boost
DOI: 10.19595/j.cnki.1000-6753.tces.201474
中图分类号:TM464
陈思哲 男,1981年生,副教授,硕士生导师,研究方向为新能源发电控制和锂电池能量管理。E-mail: sizhe.chen@gdut.edu.cn(通信作者)
徐梦然 男,1996年生,硕士研究生,研究方向为储能系统均衡与功率变换电路。E-mail: xmr_1996@163.com
(编辑 陈 诚)