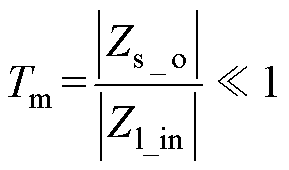（1）摘要 恒功率负载因其负阻特性，会对直流系统的稳定性产生不利影响，造成系统电压振荡。已有的稳定性研究主要针对单极性直流系统，缺少对双极性直流系统的稳定性分析及控制方法的研究。该文以采用半桥型电压平衡器架构的双极性直流系统为例，首先，对双极性直流系统的稳定性判据进行阐述；然后，采用状态空间平均法建立电压平衡器的模型，得到其控制对输出电压的传递函数；在此基础上，针对恒功率负载带来的稳定性问题，提出一种基于并联虚拟电阻的有源阻尼控制方法，以改善其稳定性；同时，还利用Lyapunov间接法分析不平衡负载对双极性系统的稳定性的影响，得出双极性系统的稳定性由系统的总输出功率决定的结论；最后，由仿真和实验验证了所提的双极性直流系统稳定性分析方法和有源阻尼方法的有效性。
关键词：双极性直流系统 恒功率负载 稳定性 半桥型电压平衡器 虚拟电阻
随着电力电子和新能源等技术的不断发展，直流系统相较于交流系统，在功率密度、灵活性和可控性上的优势愈发明显。所以，直流系统在微电网、通信、汽车、船舶、航空航天以及发输变电等领域中的应用也愈发广泛[1-4]。直流系统通常可以被分为单极性系统和双极性系统[5-7]两类。双极性系统与单极性系统相比，供电可靠性高，可以提供两个输出端口，即使某一端口故障，另一端口也可以正常运行；供电灵活性好，可以提供两个电压等级，方便不同负载和分布式电源的接入。因此，双极性直流系统得到了广泛的运用。
在直流系统中，直流负载往往通过负载变换器与源变换器相连接，因此形成级联变换器结构[8-9]。闭环控制下的负载变换器可以被视为恒功率负载（Constant Power Load, CPL）[10-11]，而恒功率负载的负阻特性有可能破坏系统的稳定性，使系统电压振荡[12]。本质上来说，恒功率负载所带来的稳定性问题是前后级变换器之间阻抗不匹配的具体体现[1]。为了解决恒功率负载所引起的直流系统的稳定性问题，有许多控制方法被提出，这些方法可以被分为有源阻尼和无源阻尼两类。与有源阻尼相比，无源阻尼会带来严重的能量耗散[13]。因此，有源阻尼是更合适的稳定性控制方法。文献[14]通过电感电流反馈的方式，在源变换器的控制环路中实现了基于电感串联虚拟电阻的有源阻尼，减小了源变换器的输出阻抗谐振尖峰，进而实现前后级变换器的阻抗匹配。与之相对的，文献[13, 15]则是针对负载变换器设计了有源阻尼控制方法，通过串并联虚拟电阻的方法，调整了负载变换器的输入阻抗。但调整负载变换器输出阻抗在控制上实现起来比较复杂，可能会降低系统可靠性。文献[16-17]针对在前后级变换器之间加有LC滤波器的直流系统进行了研究，并提出了相应的稳定性控制策略，但LC滤波器的存在会增加硬件成本和系统复杂度。上述直流系统稳定性的研究都是基于单极性直流系统，针对双极性直流系统的稳定性问题缺少系统的论述。
与单极性系统不同，双极性系统中存在不平衡工作状态，所以在进行稳定性分析及其控制方法设计时需要讨论不平衡负载的影响。在双极性直流系统中，不平衡负载会在两极间产生不平衡电压[18]。为了抑制双极性直流系统的电压不平衡问题，有许多针对电路拓扑结构的研究。文献[19-20]提出了半桥型电压平衡器拓扑，能够抑制不平衡电压。此外，还有多种两电平[6]或三电平结构[21-22]的电压平衡器拓扑被提出来用于不平衡电压抑制。相较于半桥式电压平衡器，这些拓扑虽然在性能上可能会有一定的优势，但是在拓扑结构和控制方法上会更复杂。因此，半桥型电压平衡器得到了更为广泛的研究和应用。文献[23]为半桥型电压平衡器设计了基于PI控制的控制器，提高了其电压平衡能力。文献[18]采用对称分量法实现了对半桥式电压平衡器的控制，为双极性直流系统的分析提供了一种新的思路，但没有针对恒功率负载进行讨论。
由上述分析可知，目前针对双极性直流系统的研究缺少对恒功率负载所带来的稳定性问题的论述。本文以基于半桥型电压平衡器的双极性直流系统为研究对象，提出了一种基于虚拟电阻的有源阻尼控制方法来解决恒功率负载所带来的稳定性问题。首先，分析了双极性直流系统的稳定性判据，并由半桥型电压平衡器的电路模型得到了其控制到输出电压的传递函数。然后，通过电容电流反馈的方式实现了基于并联虚拟电阻的有源阻尼方法。最后，利用Lyapunov间接法分析了不平衡负载对双极性直流系统的稳定性的影响。仿真及实验的结果证明了本文理论分析的正确性与可行性。
目前，在直流系统稳定性方面的研究主要针对单极性系统，而双极性直流系统同样面临稳定性问题。由于结构上的不同，双极性系统在使用相关稳定性判据时，有不同于单极性系统的特点，需要利用阻抗匹配原理，得到针对双极性直流系统的稳定性判据。
根据Middlebrook稳定性判据[24]，要使级联的变换器系统稳定，必须使源变换器的输出阻抗和负载变换器的闭环输入阻抗在Bode图中的幅频曲线不相交。Middlebrook稳定性判据也可以被表示为
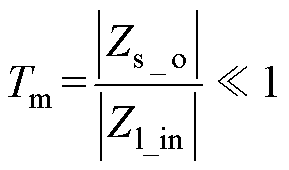（1）式中，Zs_o为源变换器闭环输出阻抗；Zl_in为负载变换器的闭环输入阻抗；Tm为整个级联系统的最小环路增益。此外，Middlebrook稳定性判据也可以通过Nyquist曲线表示出来，即要求Tm的Nyquist曲线远小于单位圆。
但是，式（1）只能描述单极性直流系统的阻抗匹配关系。在双极性直流系统中，由于不平衡工况的存在，源变换器对负载变换器的输出阻抗的变化情况和单极性系统不同。具体来说，当负极负载变化时，会造成源变换器对正极的输出阻抗的变化，反之亦然。而在单极性系统当中，负载的变化并不会改变源变换器的输出阻抗。对双极性直流系统，参考式（1），Middlebrook稳定性判据可被描述为
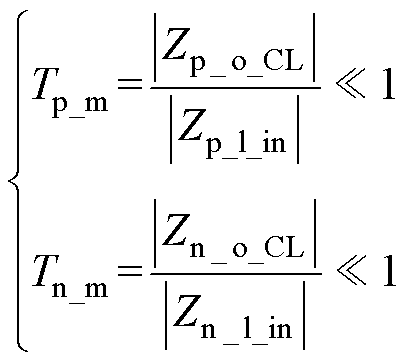（2）式中，Zp_l_in和Zn_l_in分别为正极、负极负载变换器的闭环输入阻抗；Zp_o_CL和Zn_o_CL分别为源变换器对正极负载和负极负载的闭环输出阻抗。可以看出，双极性直流系统需要正极侧和负极侧都满足Middlebrook稳定性判据。而且，由于不平衡工况的存在，在系统稳定性分析时，双极性直流系统比单极性直流系统需要考虑更多的情况。因此，在使用Middlebrook稳定性判据进行稳定性分析和稳定性控制方法设计时，双极性直流系统要比单极性直流系统更复杂。
在直流系统稳定性分析的过程当中，可以把负载变换器视作恒功率负载。而在一个给定的工作点（PCPL, VCPL）下，恒功率负载可以被等效为一个负电阻RCPL和一个恒流源ICPL相并联形成的电路，PCPL为恒功率负载所消耗的功率，VCPL为恒功率负载两端的电压[25]。而恒流源ICPL并不影响系统的稳定性[10]，所以在进行稳定性分析的时候可以将其忽略。RCPL和ICPL分别表示为
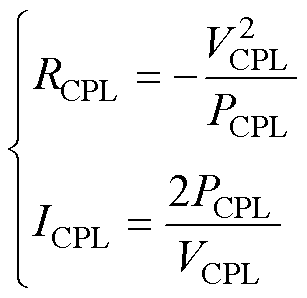（3） 所研究的系统结构如图1所示，本文以半桥型电压平衡器为源变换器，两个Buck变换器分别作为正极负载和负极负载，构成双极性直流系统。在图1b中，Buck变换器通过式（3）被简化为恒功率负载的形式。
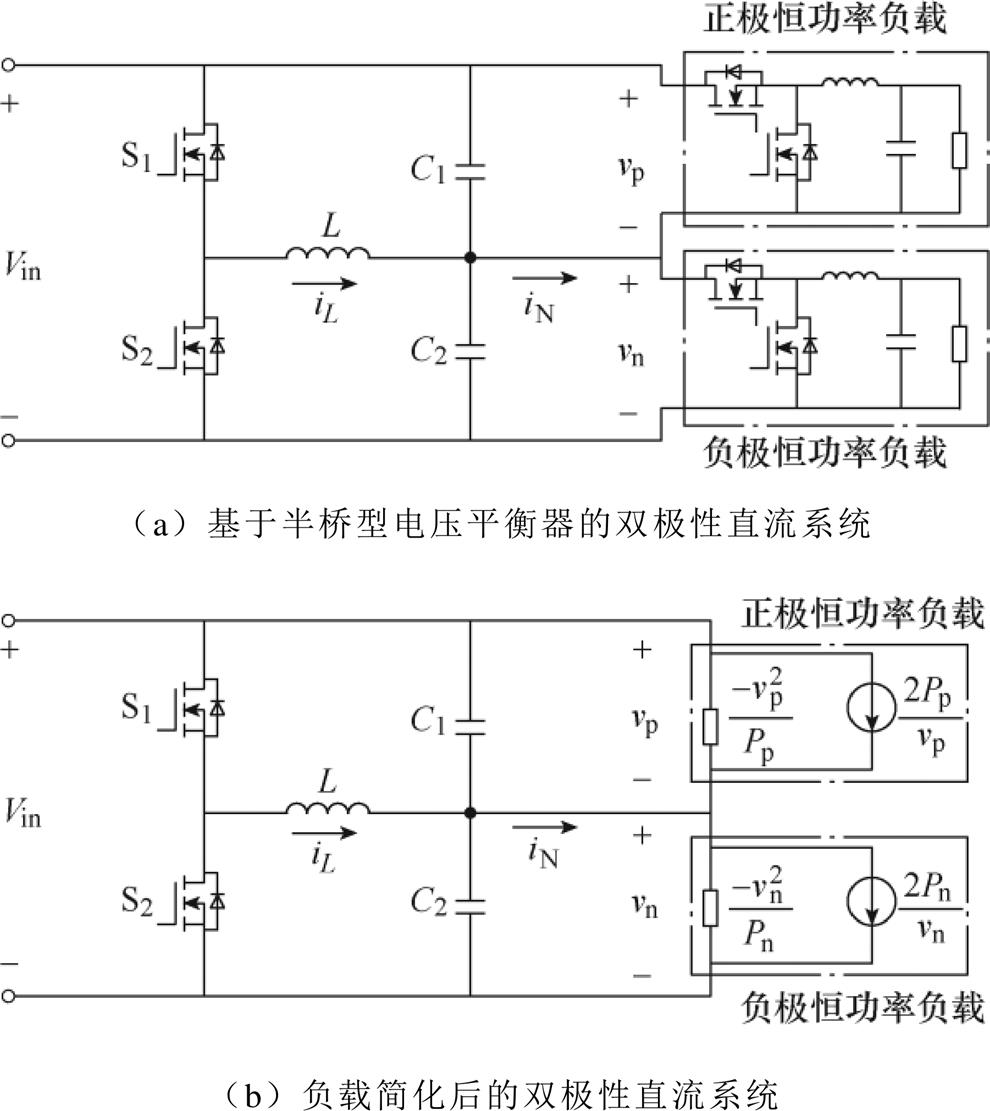
图1 所研究的系统结构
Fig.1 The structure of the studied system
为了方便表示，对图1中正负极恒功率负载的负电阻进行定义为
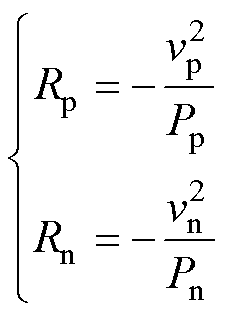（4）式中，vp和vn分别为正极输出电压和负极输出电压；Pp和Pn分别为正极输出功率和负极输出功率。采用状态空间平均法，建立半桥型电压平衡器的大信号平均模型，即
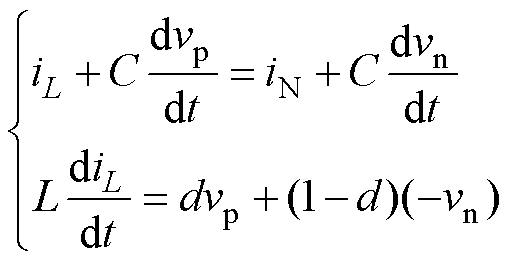（5）
式中，L为电感；C为正极输出电容C1和负极输出电容C2的容值；iL为电压平衡器电感电流；iN为电压平衡器中线电流；d为开关管S1的占空比。
由于半桥式电压平衡器电路中包含有一个纯电容回路（C1、C2和输入电压源Vin），所以系统其实是一个二阶系统，只需要两个状态变量就能描述其系统状态。电压平衡器满足
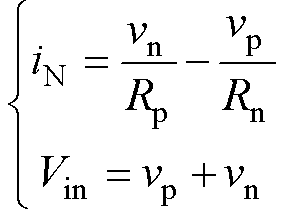（6）选取iL和vn为状态变量，把式（6）代入式（5）中，可以得到
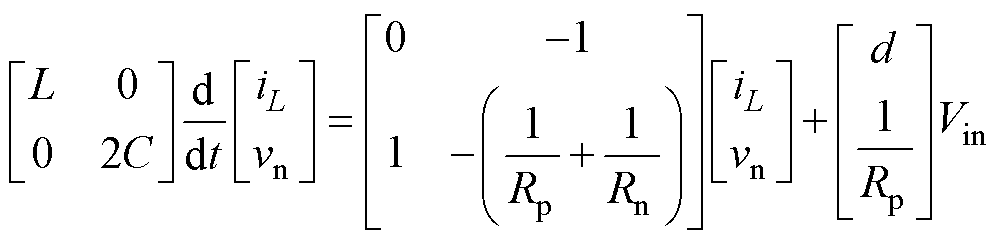（7）
通过式（7），可以得到半桥式电压平衡器的小信号模型为
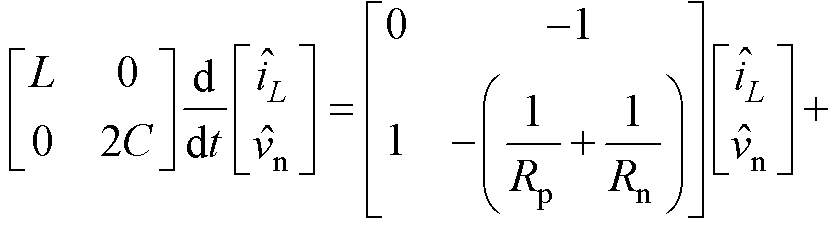
（8）
式中，
、
、
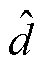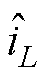和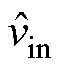
为扰动量；D、Vin为控制信号和电压的稳态值。由式（8）可得该系统控制对负极输出电压的传递函数为
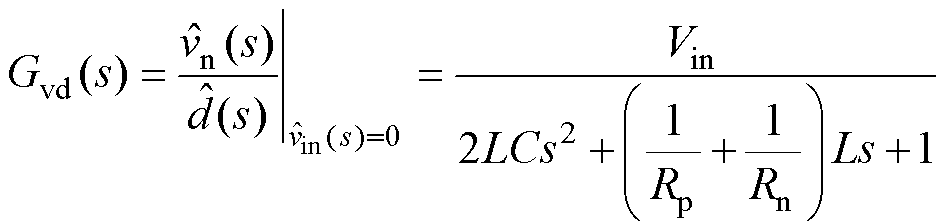（9） 系统带恒功率负载时，由于Rp和Rn的负阻特性，式（9）的分母一次项系数小于零，即系统特征方程有一项系数小于零，因此系统不稳定。本文为了解决这一稳定性问题，提出基于虚拟电阻的有源阻尼方法，其示意图如图2所示。
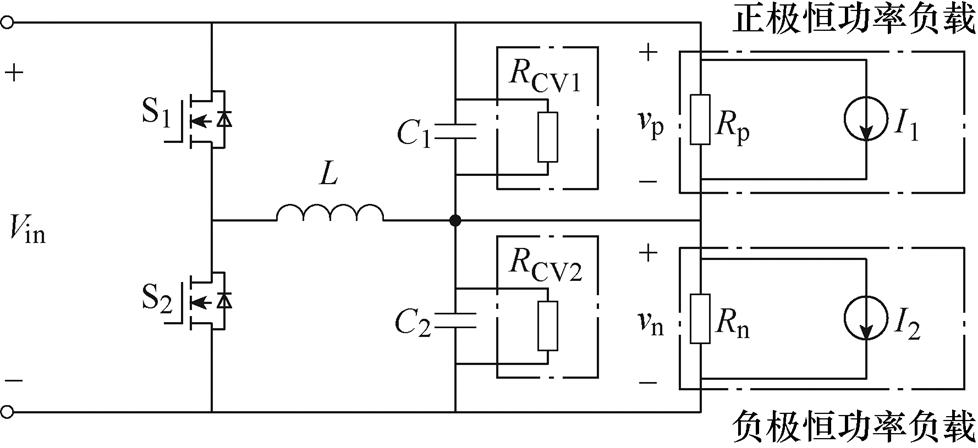
图2 虚拟电阻阻尼方法示意图
Fig.2 Circuit diagram of the virtual resister damping method
图2中，本文所提出的基于虚拟电阻的有源阻尼方法是通过在控制环路中增加适当的反馈回路，实现在正负极输出电容并联电阻的效果，从而达到阻尼电压振荡的目的。为了保证双极性直流系统的平衡，令虚拟电阻RCV1和RCV2的阻值都等于RCV。考虑虚拟电阻过后，系统的小信号模型可以表示为
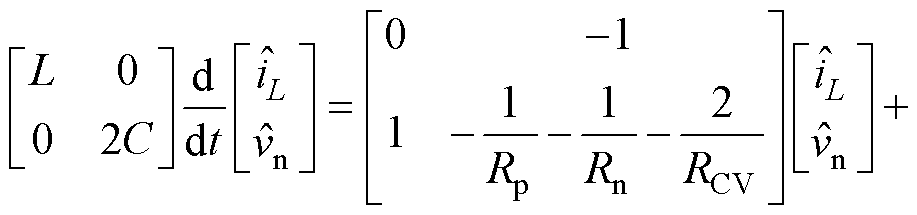
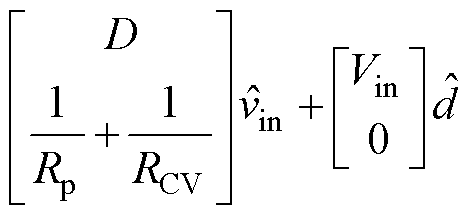（10）
由式（10）得到控制到输出电压的传递函数为
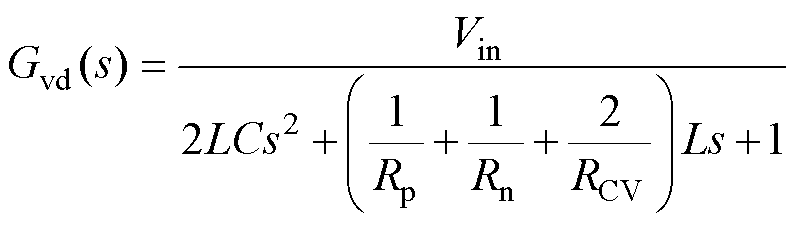（11）为了保证系统的开环稳定，式（11）的分母各项必须大于零。L、C显然大于零，因此只要保证式（12）成立就可以保证系统的开环稳定性。
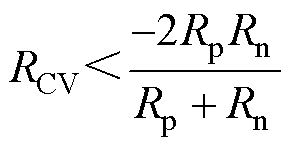（12）
半桥型电压平衡器对后级的闭环输出阻抗为
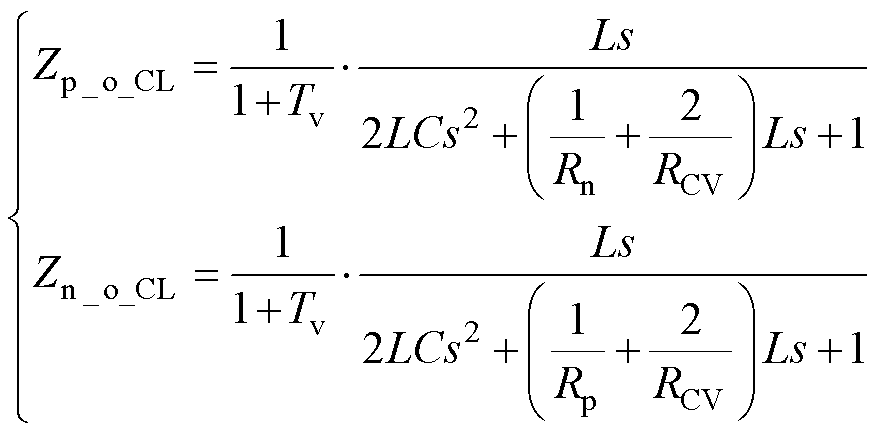（13）式中，Tv为电路平衡器的控制环路增益。把式（13）代入式（2）中，就可以利用Middlebrook稳定性判据来判断该双极性直流系统的稳定性。
图3所示为采用无源阻尼的半桥型电压平衡器闭环控制框图。图中，a为被控系统，Gc(s)和Gpwm(s)分别为PI控制器和PWM器的传递函数；b为实际的阻尼电阻的作用。
为了实现有源阻尼控制，需要在控制环路中增加一条电容电流比例前反馈回路。该比例反馈回路的作用与实际的阻尼电阻RCV的效果是等效的。和单极性直流系统只有一个输出电容不同，双极性直
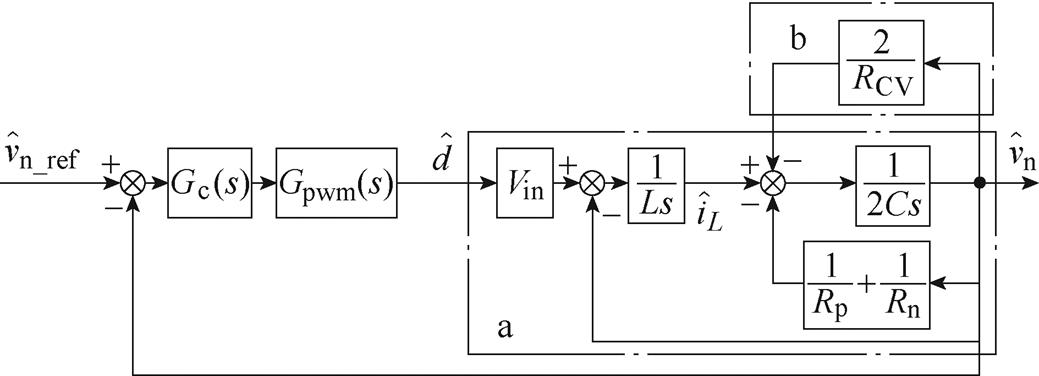
图3 无源阻尼方式的闭环控制框图
Fig.3 Closed-loop control scheme diagram of the passive damping method
流系统包含两个输出电容，所以在双极性系统中实现电容电流反馈的途径也更多样。图4给出了双极性系统中实现电容电流反馈的三种途径。这三种途径的区别在于所取的电容电流的来源不同，既可以同时取正极和负极的电容电流进行反馈，也可以只取其中一极的电容电流进行反馈。只要保证C1=C2，且图4中的反馈系数满足式（14），这三种方式的阻尼效果就是相同的。
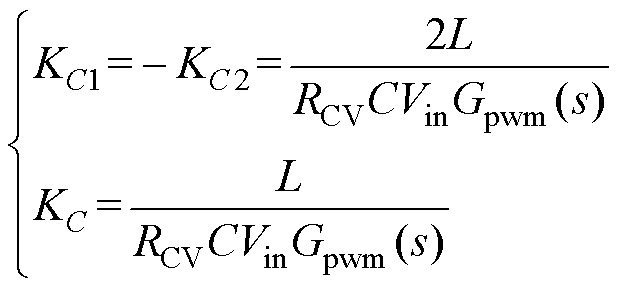（14）
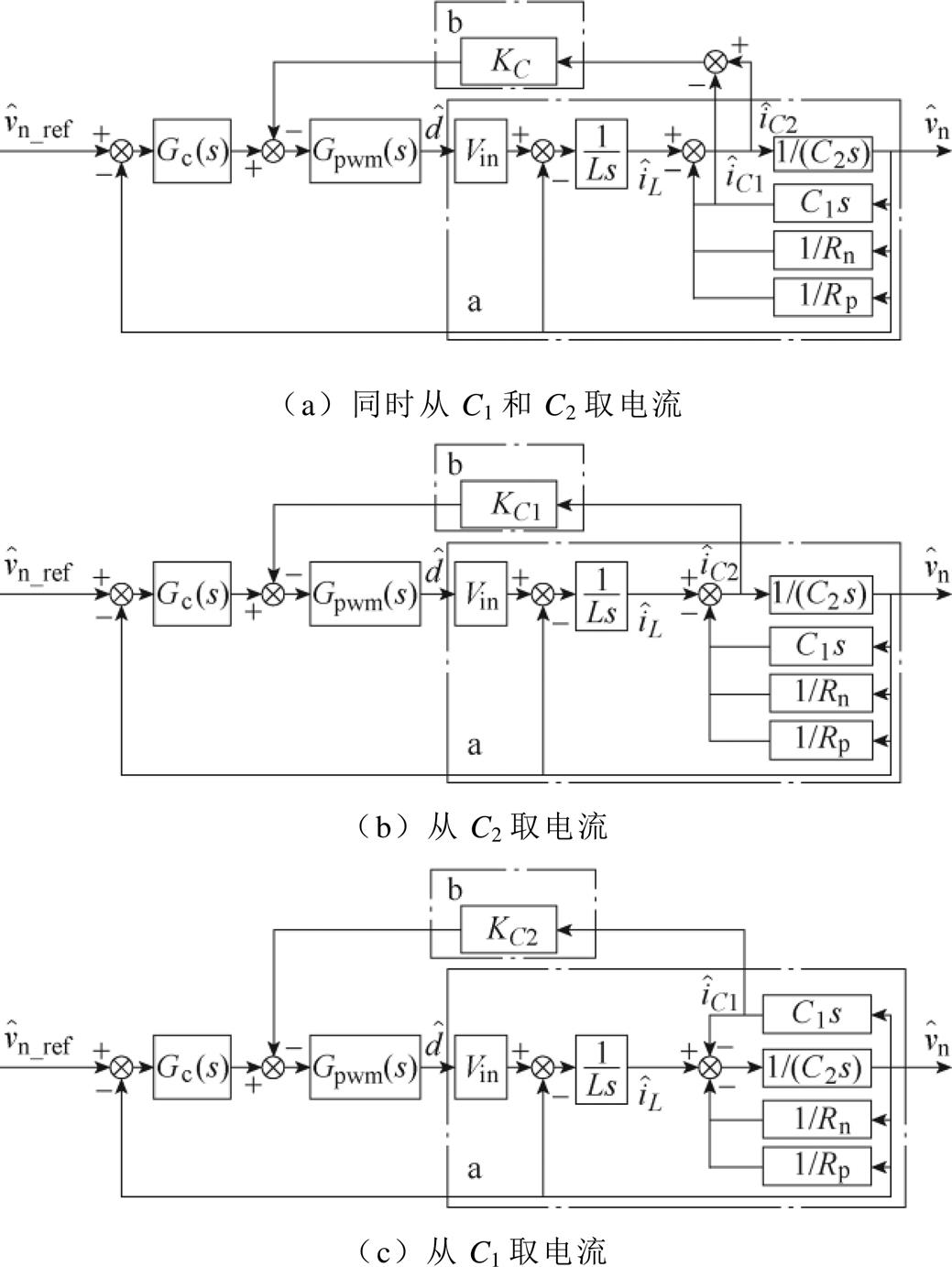
图4 三种实现有源阻尼的途径
Fig.4 Threedifferent approaches to realize the active damping method
与单极性直流系统不同，双极性直流系统需要面对不平衡负载的工况，而且，双极性系统中，前级变换器对后级变换器的输出阻抗会随着负载工况的变化而改变。因此，在通过Middlebrook稳定性判据来判别双极性直流系统的稳定性时，需要判定多个工作点的稳定性，这就增加了稳定性控制方法设计的复杂性。为了研究不平衡负载是否会影响双极性系统的稳定性，采用Lyapunov间接法对本文的系统进行分析。首先得到系统的状态方程为
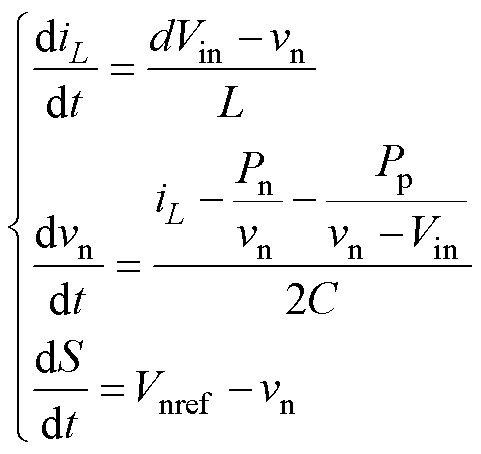（15）式中，S为闭环控制中的电压误差积分变量；Vnref为负极参考电压。正极恒功率负载和负极恒功率负载分别为Pp/(Vin-vn)和Pn/vn，即恒功率负载不再使用式（3）给出的小信号模型。式（15）中的状态变量可以表示为
（16）
该系统为一个非线性系统，为了分析系统的稳定性，需要在稳态工作点进行线性化处理。线性化处理过后，系统的状态变量可以被描述为稳态工作点Xo和交流小信号x的叠加，即
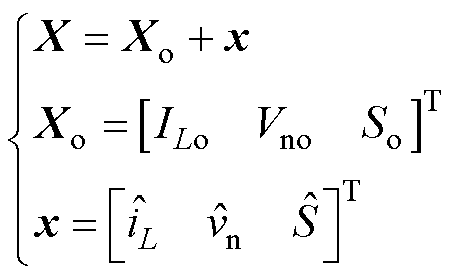（17）令式（15）左边的微分项部分全部等于零，即可得到系统状态变量的稳态工作点。把式（17）代入式（15），得到系统的线性化模型为
（18）
式中，A(Xo)为稳态工作点处的系统雅可比矩阵。针对本文所提的控制方法，式（15）中的控制信号d表示为
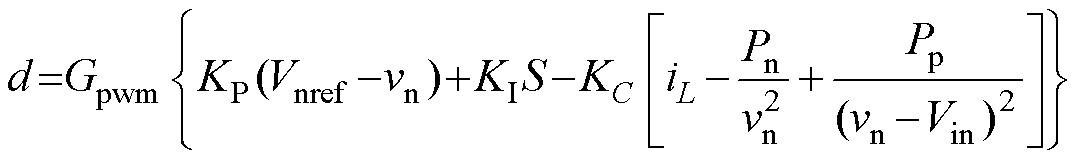（19）式中，KP和KI分别为PI控制器的比例系数和积分时间常数；KC为电容电流反馈的比例系数；Gpwm为PWM器的传递函数。由此，系统在稳态工作点处的雅可比矩阵A(Xo)可以表示为
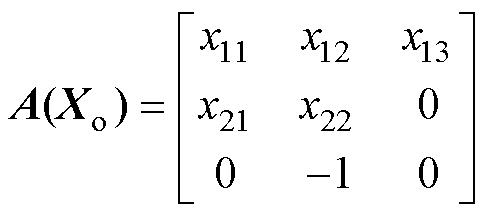（20）
（21）根据Lyapunov间接法，要使系统稳定，需要系统稳态工作点处的雅可比矩阵的所有特征值l 都位于复平面的左半平面。求解系统雅可比矩阵特征的行列式可以表示为
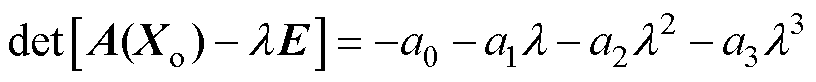（22）
根据Routh判据，针对如式（22）所示三阶多项式，要保证其所有的根都在复平面的左半平面，需要满足
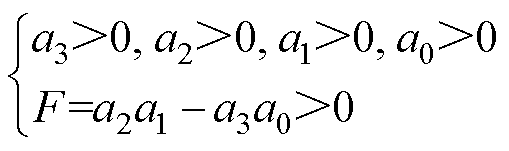（23）通过把式（20）和式（21）代入式（22）中，可求得
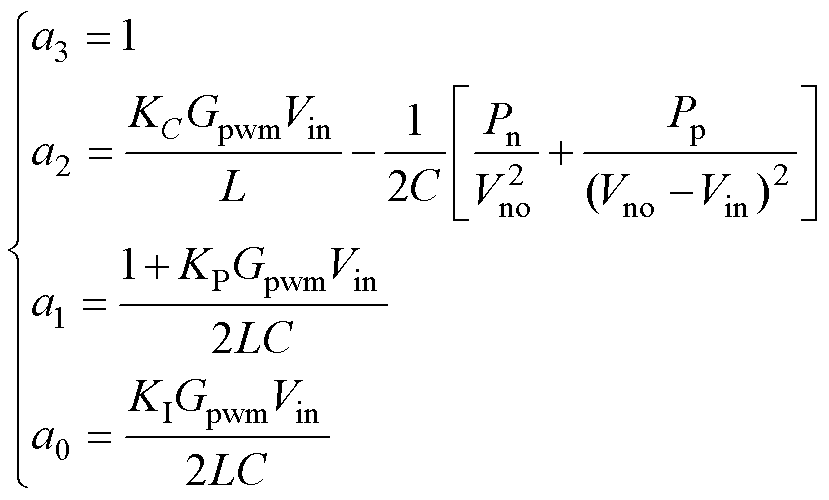（24）
把式（24）代入式（23），就可以判定出系统的稳定性。
为了分析不平衡负载对双极性直流系统稳定性的影响，本文采用了双极性直流系统参数进行讨论，本文采用的双极性直流系统参数见表1。为了定性分析，采用取特值的方法，将KC、KP和KI分别设置为0.07、0.305和599.79，再将表2中的参数代入式（23）、式（24），可以发现，a3＞0，a2＞0，a1＞0和a0＞0的条件显然是满足的。系统的稳定性将由F=a2a1-a3a0是否大于0决定。图5显示了F随正极输出功率Pp和负极输出功率Pn变化而变化的情况。
表1 本文的双极性直流系统参数
Tab.1 The parameter of the bipolar system in this paper
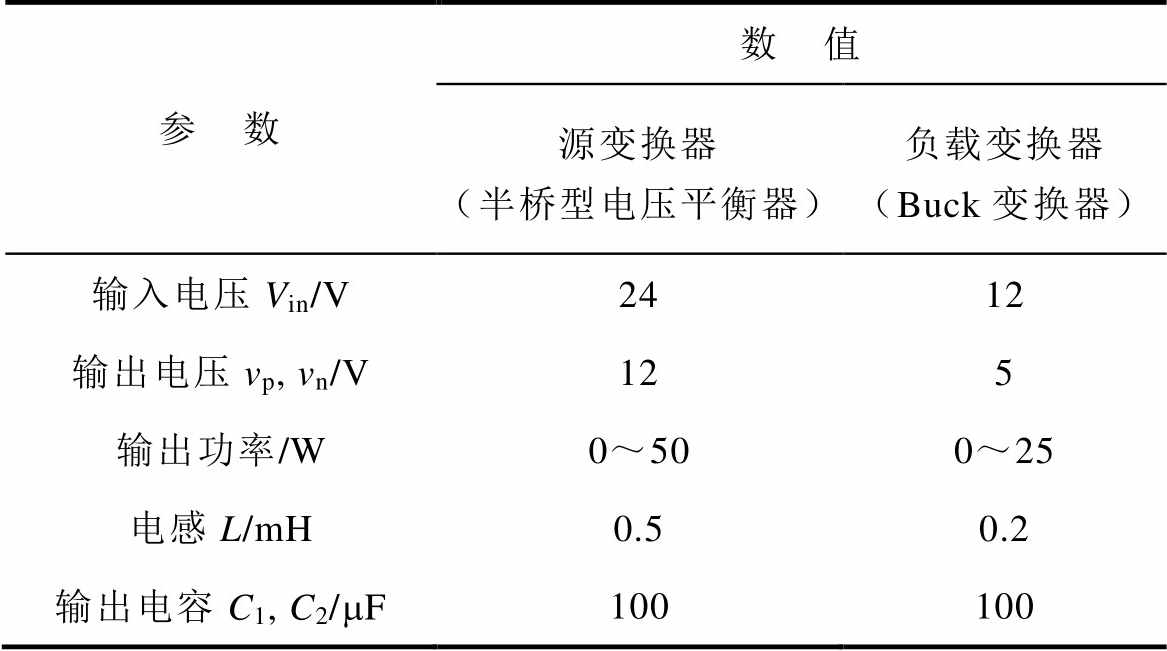
参 数数 值 源变换器（半桥型电压平衡器）负载变换器（Buck变换器） 输入电压Vin/V2412 输出电压vp, vn/V125 输出功率/W0～500～25 电感L/mH0.50.2 输出电容C1, C2/mF100100
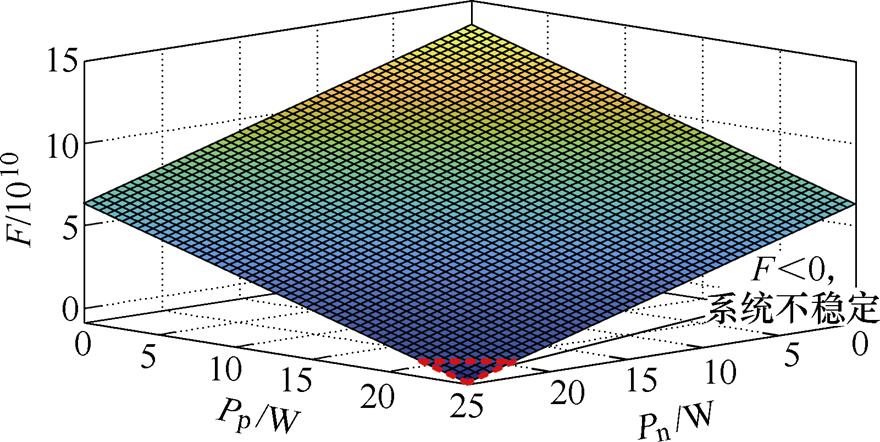
图5 F随Pp和Pn的变化情况
Fig.5 The change of F as the Pn and Pp changed
根据式（23），当F＜0时，该系统不稳定。如图5所示，F的值随着Pp和Pn之和的增加而减小，即系统最有可能在所带恒功率负载总和最大时出现不稳定，且不平衡负载的情况也并不影响系统的稳定性。所以，在分析恒功率负载对双极性直流系统稳定性的影响时，只需要考虑系统在最大功率输出点工作时的稳定性。一般情况下，双极性直流系统在最大功率点工作时，正负极负载平衡，对后级变换器的输出阻抗也相同。因此，在分析其稳定性时也只需要考虑一极的情况。换而言之，式（1）和式（2）等效，在使用Middlebrook稳定性判据判定稳定性时，双极性系统变得和单极性系统同样简洁。这一结论降低了双极性系统稳定性分析和控制环路设计的复杂性。
为验证所提出的基于虚拟阻尼的有源阻尼控制方法及稳定性分析的正确性，利用Matlab进行了仿真分析，仿真参数见表1。根据第3节的结论，只要双极性直流系统在其最大功率输出时可以稳定工作，就能确保系统在全工况范围的稳定性。系统输入、输出阻抗Bode图和Tm的Nyquist图如图6所示。
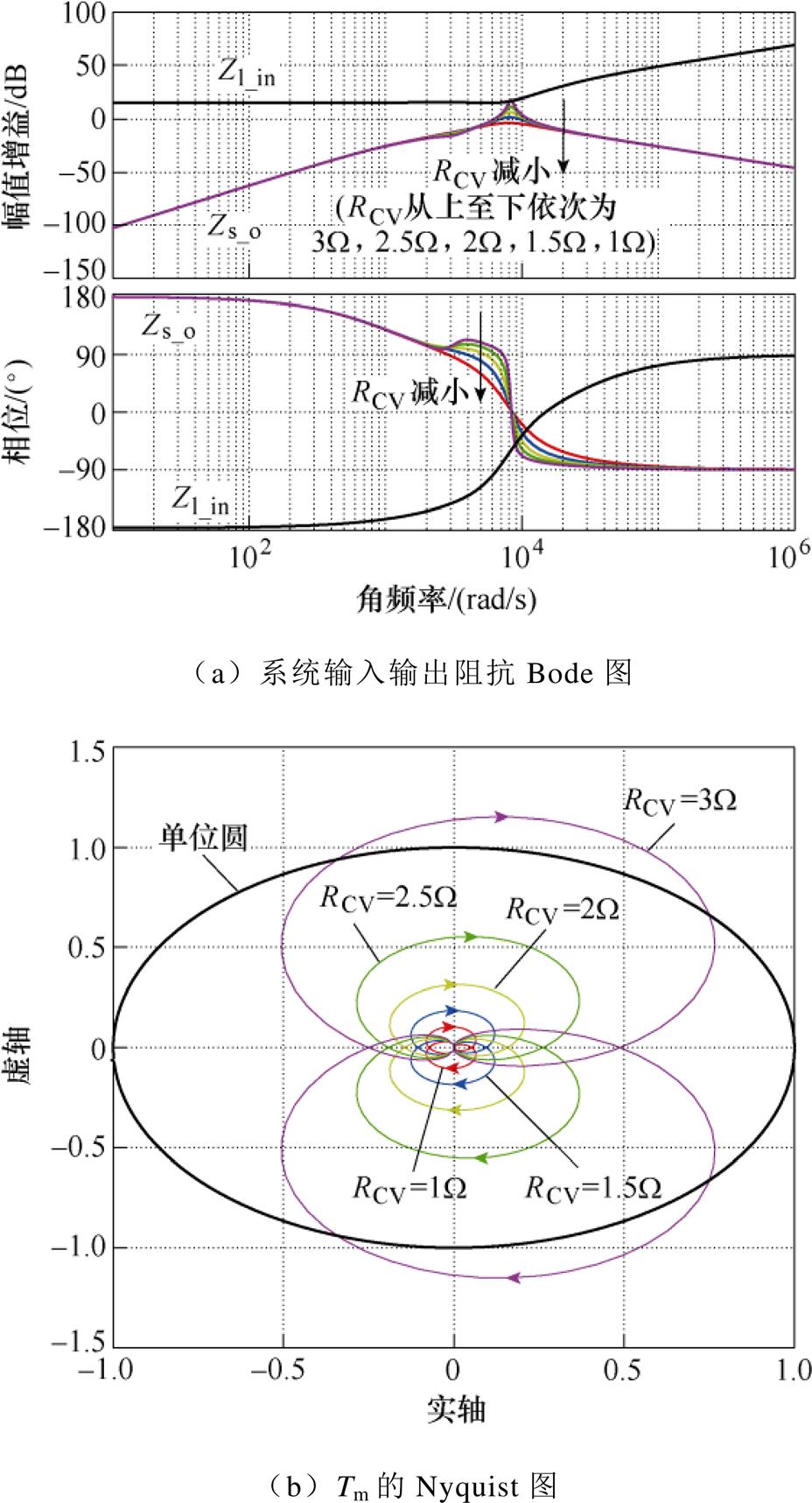
图6 系统输入、输出阻抗Bode图和Tm的Nyquist图
Fig.6 Bode plot of system input and output impendence and Nyquist plot of Tm
为了分析虚拟电阻RCV对系统稳定性的影响，图6a给出了系统源变换器（半桥型电压平衡器）的闭环输出阻抗Zs_o和负载变换器的闭环输入阻抗Zl_in的Bode图，图6b给出了系统最小环路增益Tm的Nyquist图。从图6中可以看出，随着RCV的减小，系统的稳定裕度增加。如果RCV过大，Bode图中Zs_o和Zl_in的幅频曲线就会出现交叠，Tm的Nyquist曲线也会超出单位圆的范围，造成系统不稳定。从图6b中也可以看出，当RCV减小到一定程度时，继续减小RCV对系统稳定性提升不大。
虚拟电阻RCV的存在能够提升双极性直流系统的稳定性，但对系统中源变换器的动态性能有一定的影响。图7给出了半桥型电压平衡器的环路增益Bode图。可以看出，随着RCV的增加，反映稳定性能的稳定裕度呈增加趋势，但反映动态响应速度的带宽则呈下降趋势。通过调整PI参数，能够减小其影响。
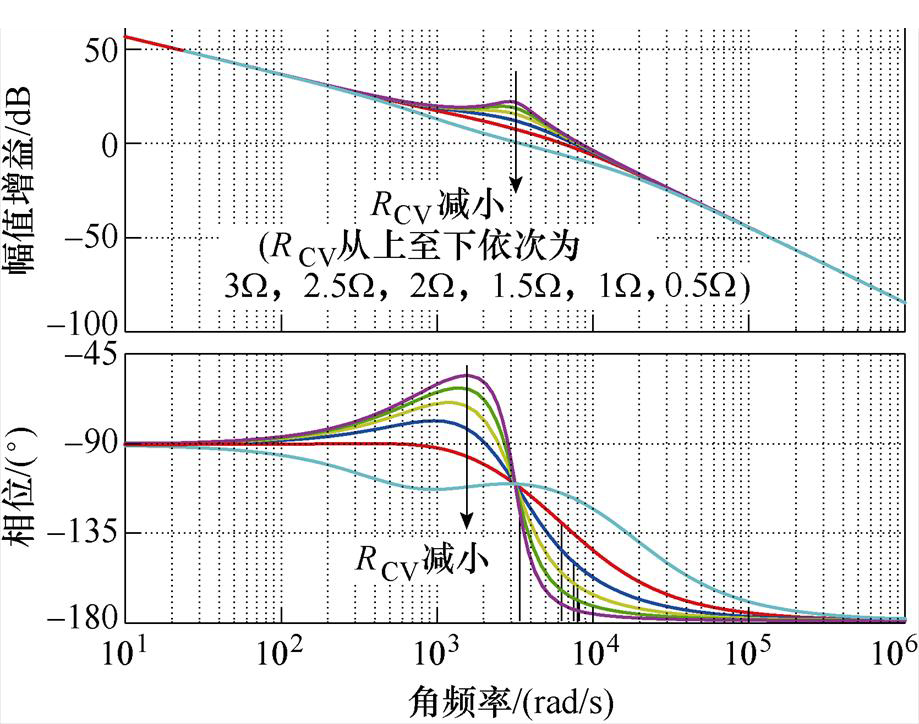
图7 半桥型电压平衡器的环路增益Bode图
Fig.7 Bode plots of the loop gain of the voltage balancer
图8对比了不同虚拟电阻阻值的阻尼效果，在0.025s之前，前后级只采用PI控制，正负极输出电压发生振荡，系统不稳定；在0.025s时加入本文所提出的有源阻尼控制方法，电压振荡被阻尼。同时，从图8中也可以发现，当RCV=1W 和RCV=0.5W时，系统的振荡阻尼效果明显，正负极的输出电压都趋于稳定。但当RCV=3W 时，即使已经加入有源阻尼控制，系统仍然存在振荡现象，系统不稳定。这一现象和图6中的结论是一致的。
通过仿真证明负载变化会造成源变换器的输出阻抗的变化这一推论，负载变化对阻抗匹配的影响仿真波形如图9所示，初始阶段正负极均为25%负载（6.25W），取RCV=3W，此时系统稳定。在0.02s负极负载切换为100%负载（25W），系统输出电压出现振荡。这说明负载切换改变了系统输入输出阻抗关系，导致正负极电压都出现振荡。这一现象也说明，在选取RCV时，要注意保证系统有足够的稳定裕度。
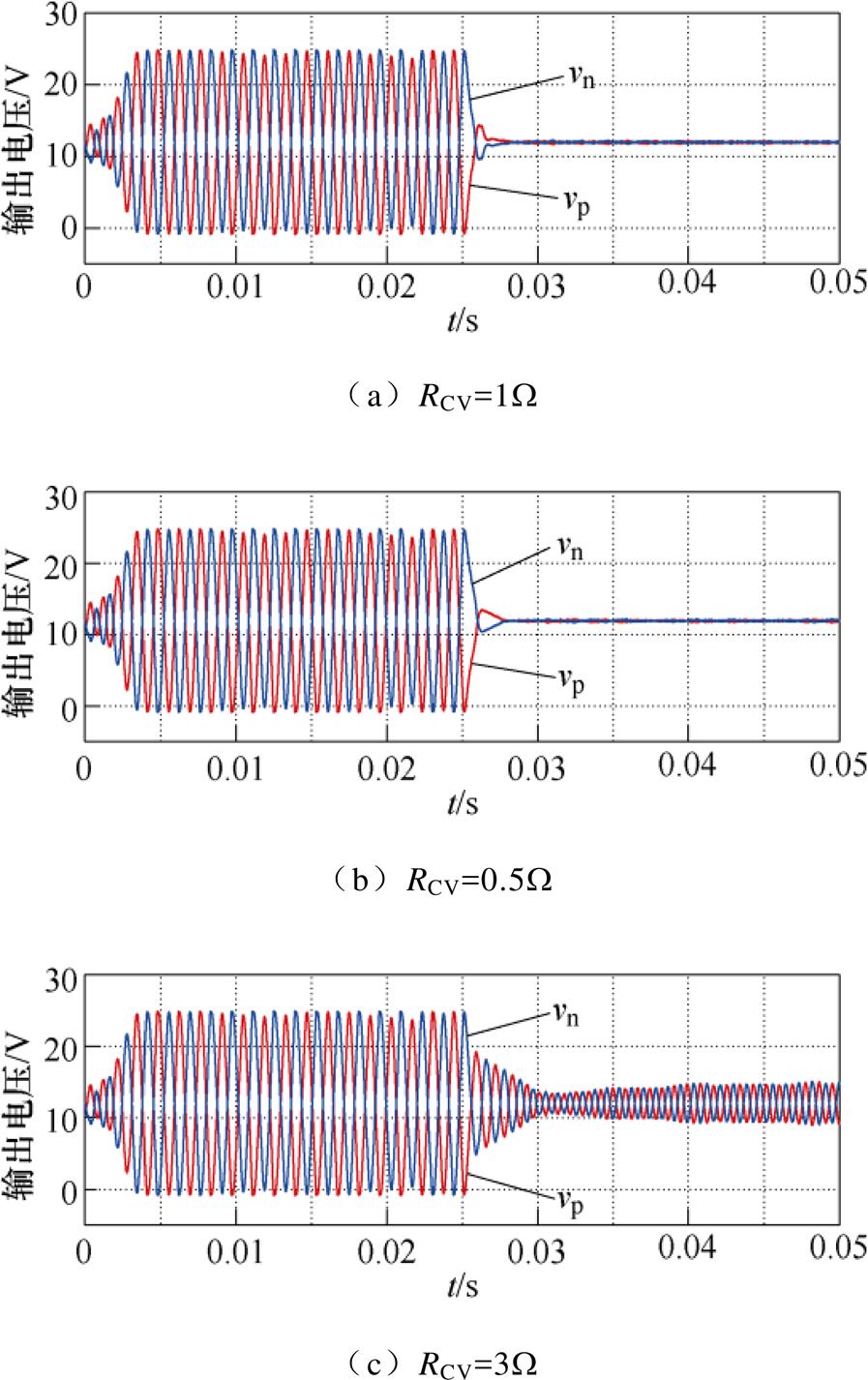
图8 不同电容并联虚拟电阻的阻尼效果仿真波形
Fig.8 Simulation waveforms of the damping effect of the different capacitor parallel virtual resistors
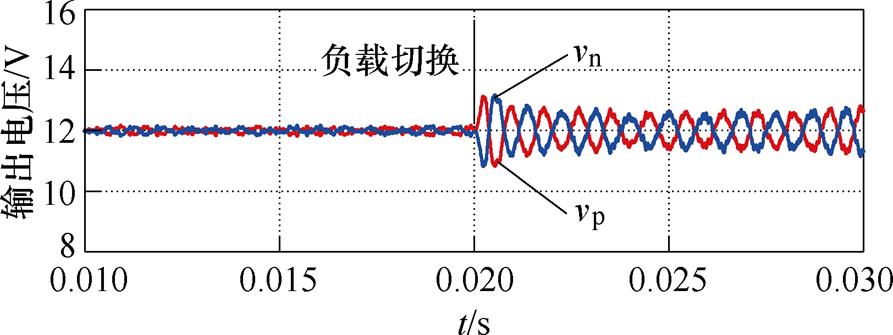
图9 负载变化对阻抗匹配的影响仿真波形
Fig.9 Simulation waveforms of the influence of load switching on impedance matching
图10反映了虚拟电阻对系统动态性能的影响，图中的两组仿真采用同样的PI参数，有源阻尼控制策略在一开始就加入控制环路当中，在0.01s时，正极恒功率负载从25%负载（6.25W）跳转到100%负载（25W），而负极恒功率负载一直保持满载（25W）输出。可以看出，虽然两种虚拟电阻阻值下系统都可以保持稳定和平衡，但是在RCV=0.5W时，系统的过渡过程时间明显更长，系统动态性能低于RCV=1W 时，这与图7中的结论一致。
为了验证系统在不平衡负载工况下的稳定性，对多种不平衡工况进行了仿真分析，不平衡负载下的仿真波形如图11所示，令RCV=1W，正极恒功率负载保持满载输出，而负极恒功率负载进行负载切换。可以看出，在不平衡负载工况下，正负极电压仍然能够保持稳定和平衡，证明了所提出的理论和方法的有效性。
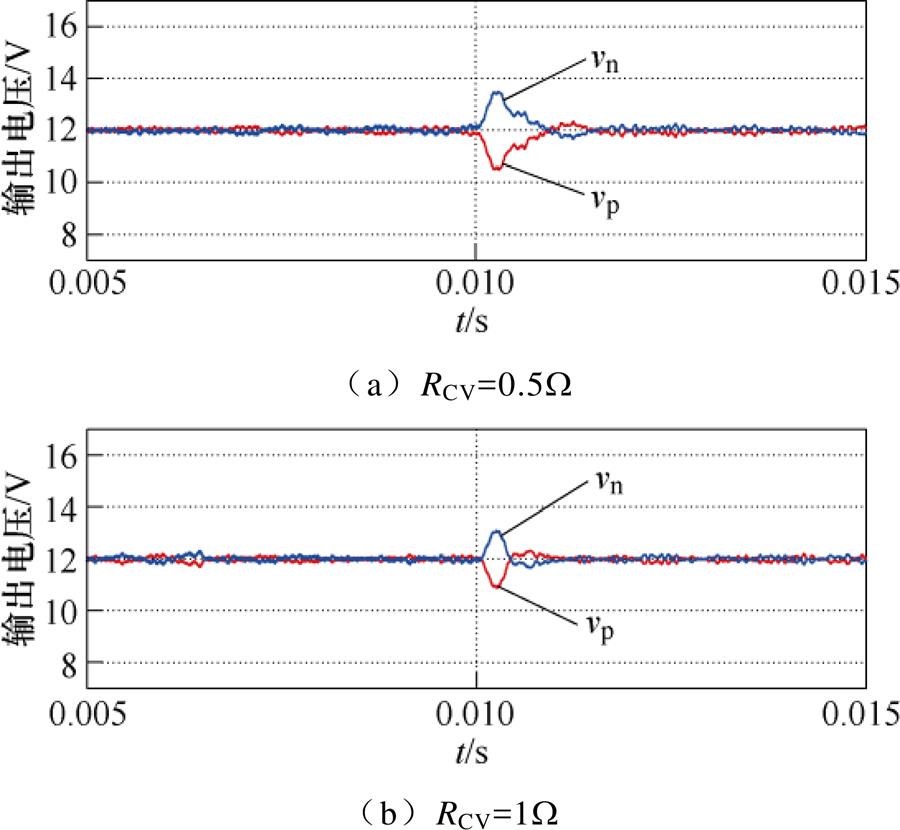
图10 有源阻尼控制对动态性能的影响仿真波形
Fig.10 Simulation waveforms of the influence of active damping control on dynamic performance
图11 不平衡负载下的仿真波形
Fig.11 Simulation waveforms of unbalanced load conditions
本文通过电容电流反馈的方式，在双极性直流系统中实现了基于电容并联虚拟电阻的有源阻尼。而在单极性直流系统中，可以采用电感电流反馈的方式实现基于电感串联虚拟电阻的有源阻尼[13]。但是对双极性系统来说，电感串联虚拟电阻的存在对电压平衡有不利的影响。电感串联虚拟电阻的阻尼仿真波形如图12所示，取电感串联虚拟电阻RLV= 9.5W，正极恒功率负载保持满载输出，而负极恒功率在0.03s从满载切换为50%负载。
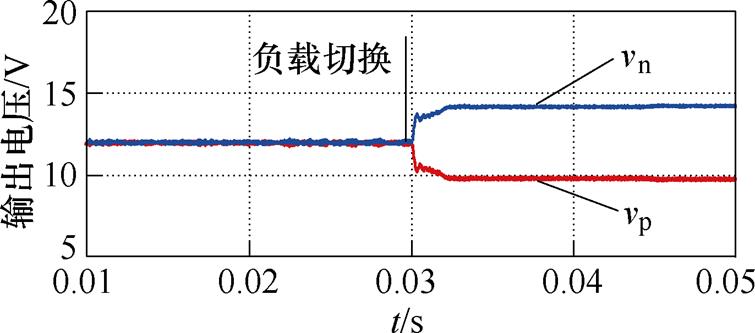
图12 电感串联虚拟电阻的阻尼仿真波形
Fig.12 Simulation waveforms of the inductor series virtual resistor
可以发现，正负极电压虽然保持稳定，但有明显的不平衡电压，这说明电感串联虚拟电阻虽然能抑制系统电压振荡，但是影响到了电压平衡器调节不平衡电压的能力。系统的稳态方程可以说明这种现象产生的原因，当采用电感串联虚拟电阻时，系统在稳态状况下，应该满足
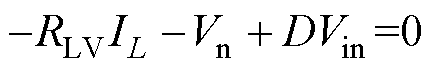（25）式中，IL、Vn分别为电感电流、负极输出电压的稳态值。由于占空比D的取值范围为0＜D＜1，当RLV和IL较大时，无法保证Vn=0.5Vin，即无法保证正负极电压平衡。
因此，适用于单极性系统的有源阻尼方法，不一定适用于双极性系统。
为了验证理论分析及仿真的有效性，搭建了双极性直流系统的实验平台，参数见表1，源变换器和负载变换器都采用TI公司的TMS320F28069型DSP作为控制器。实验平台如图13所示。
图14为控制环路加入有源阻尼控制前后的实验波形，图中，In_lo为负极Buck变换器的输出电流。实验结果与图8中的仿真波形基本相符，证明了第2节理论分析和仿真的有效性。在图14中，施加有源阻尼前后Vin有比较明显的增大。这是因为实验电源非理想电源，有较大的电源内阻。在施加有源阻尼前，电源输出电流振荡，由于电源内阻的存在，使得Vin偏小且不稳定；在施加有源阻尼后，电源输出电流不再振荡，使得Vin增大且趋于稳定。
图13 实验平台
Fig.13 Experimental platform
图14 加入阻尼控制前后的实验波形
Fig.14 Experimental waveforms before and after adding active damping control
为了验证负载变化对系统阻抗匹配的影响，参照图9中的仿真，进行了实验，负载变化对阻抗匹配的影响实验波形如图15所示。可以看到，实验结果与仿真结果相符，证明了负载变化会造成源变换器的输出阻抗的变化这一推论。
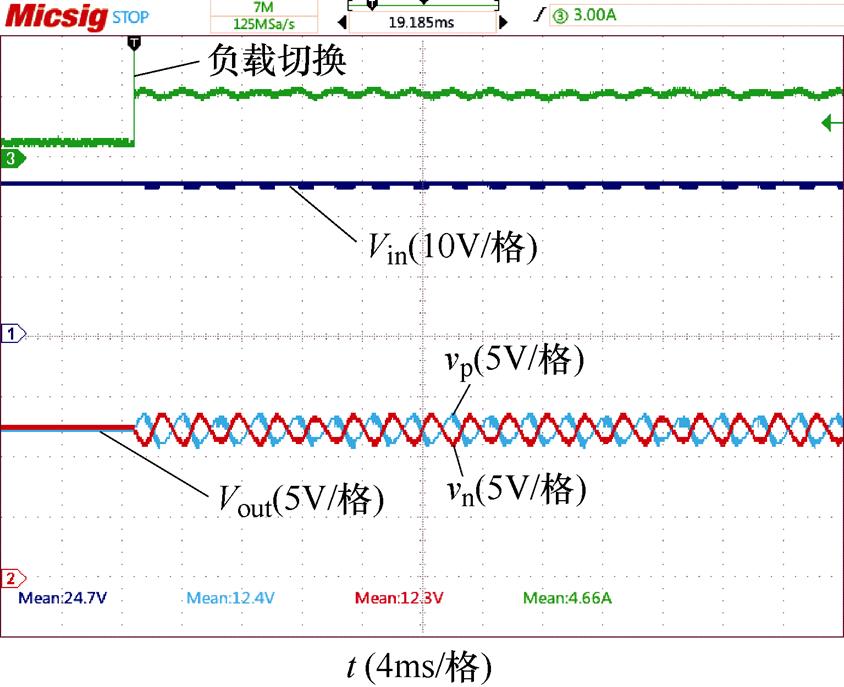
图15 负载变化对阻抗匹配的影响实验波形
Fig.15 Experimental waveforms of the influence of load switching on impedance matching
为了验证虚拟电阻对系统动态性能的影响，进行了相应的实验，有源阻尼控制对动态性能的影响实验波形如图16所示。可以看出，在RCV较小时，系统在负载切换过程中需要更长的调节时间，实验波形与图10中的仿真结果一致。
为了验证系统在不平衡负载工况下的稳定性，参照图11中的仿真，进行了不平衡仿真实验如图17所示。可以看到，实验结果与仿真结果相符，证明了所提方法在双极性直流系统稳定性的同时，也不影响其电压平衡能力。
图18给出了电感串联虚拟电阻的有源阻尼实验波形，可以发现，在不平衡负载的情况下，正负极之间出现明显的不平衡电压，这与图12中的仿真结果相符。
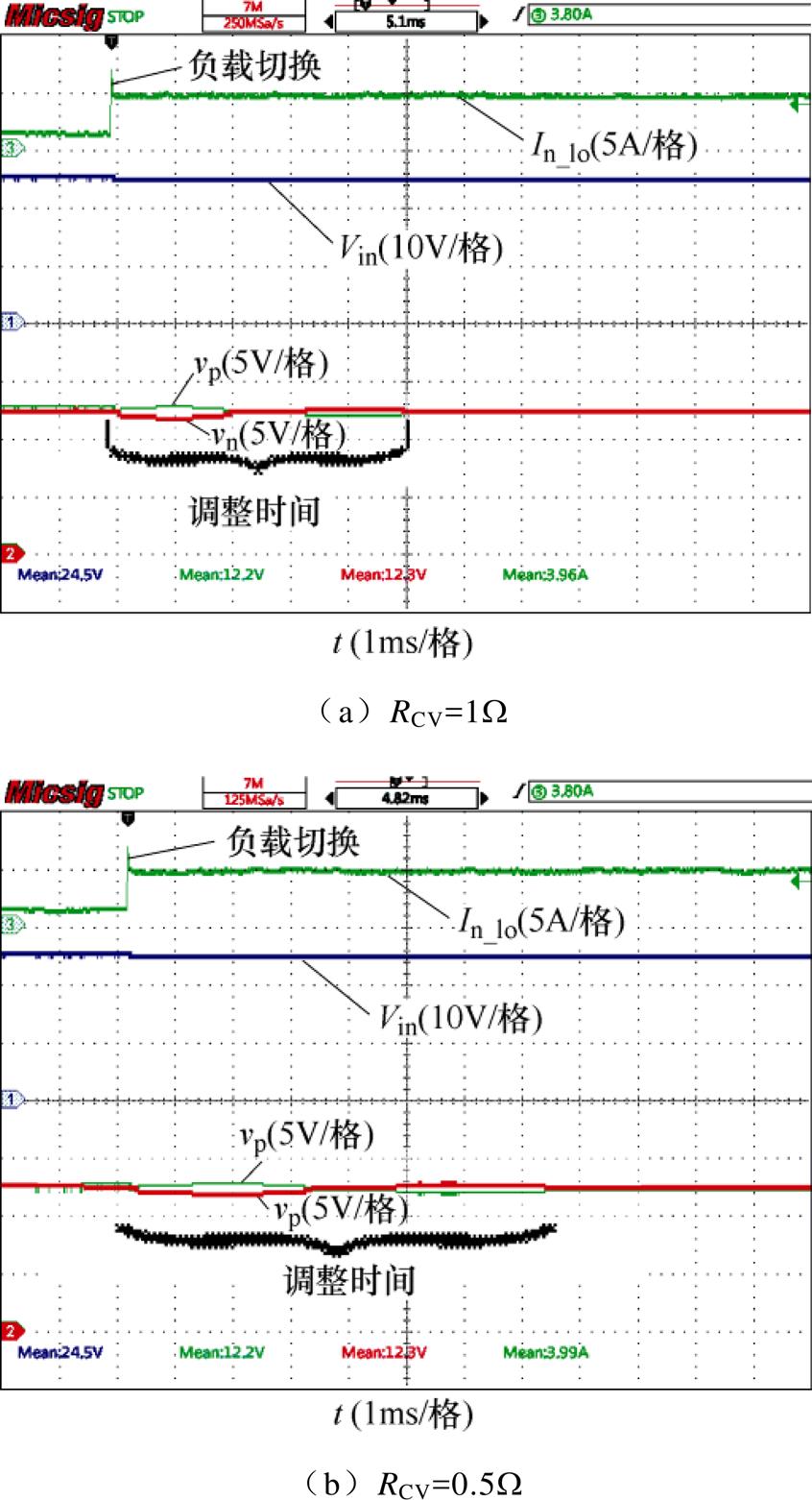
图16 有源阻尼控制对动态性能的影响实验波形
Fig16 Experimental waveforms of the influence of active damping control on dynamic performance
针对恒功率负载给双极性直流系统带来的稳定性问题，本文基于虚拟电阻的理论，提出了一种通过电容电流反馈实现的有源阻尼方法，得到了以下结论：
图17 不平衡负载下的实验波形
Fig.17 Experimental waveforms of unbalanced load conditions
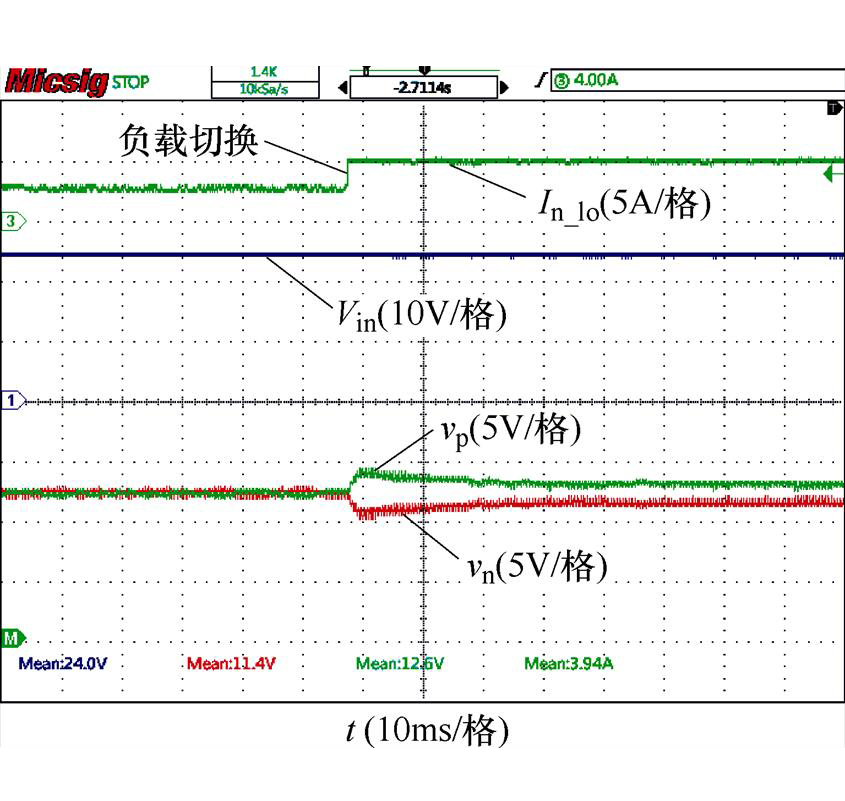
图18 电感串联虚拟电阻的阻尼实验波形
Fig.18 Experimental waveforms of the inductor series virtual resistor
1）基于输出电容并联虚拟电阻的有源阻尼方法能够抑制系统电压振荡，提升系统稳定性，且不影响双极性直流系统的电压平衡能力。
2）单极性直流系统中的有源阻尼方法（如电感串联虚拟电阻）由于没有考虑不平衡负载的影响，在双极性直流系统中可能会对电压平衡产生不利影响，因此不适用于双极性系统。
3）通过Lyapunov间接法分析不平衡负载的影响后发现：只要保证双极性直流系统在最大功率输出时的稳定性，就能确保系统在全工况范围均可以稳定工作，不平衡负载不影响系统的稳定性。
参考文献
[1] Tomislav Dragicevic, Lu Xiaonan, Juan C V, et al. DC microgrids-part I: a review of control strategies and stabilization techniques[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4876-4891.
[2] 郭力, 冯怿彬, 李霞林, 等. 直流微电网稳定性分析及阻尼控制方法研究[J]. 中国电机工程学报, 2016, 36(4): 927-936.
Guo Li, Feng Yibin, Li Xialin, et al. Study on stability analysis and damping control method of DC micro grid[J]. Proceedings of the CSEE, 2016, 36(4): 927-936.
[3] 季宇, 王东旭, 吴红斌, 等. 提高直流微电网稳定性的有源阻尼方法[J]. 电工技术学报, 2018, 33(2): 370-379.
Ji Yu, Wang Dongxu, Wu Hongbin, et al. Active damping method for improving the stability of DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 370-379.
[4] 孟建辉, 邹培根, 王毅, 等. 基于灵活虚拟惯性控制的直流微网小信号建模及参数分析[J]. 电工技术学报, 2019, 34(12): 2615-2626.
Meng Jianhui, Zou Peigen, Wang Yi, et al. Small- signal modeling and parameter analysis of the DC microgrid based on flexible virtual inertia control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2615-2626.
[5] 李霞林, 张雪松, 郭力, 等. 双极性直流微电网中多电压平衡器协调控制[J]. 电工技术学报, 2018, 33(4): 721-729.
Li Xialin, Zhang Xuesong, Guo Li, et al. Coordinated control of multiple voltage balancers in a bipolar DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 721-729.
[6] 汪飞, 雷志方, 徐新蔚. 面向直流微电网的电压平衡器拓扑结构研究[J]. 中国电机工程学报, 2016, 36(6): 1604-1612.
Wang Fei, Lei Zhifang, Xu Xinwei. Research on topologies of voltage balancers applied in DC micro- grid[J]. Proceedings of the CSEE, 2016, 36(6): 1604- 1612.
[7] 杨美辉, 周念成, 王强钢, 等. 基于分布式协同的双极直流微电网不平衡电压控制策略[J]. 电工技术学报, 2020, 36(3): 634-645.
Yang Meihui, Zhou Niancheng, Wang Qianggang, et al. Unbalanced voltage control strategy of bipolar DC microgrid based on distributed cooperation[J]. Transa- ctions of China Electrotechnical Society, 2020, 36(3): 634-645.
[8] 姚雨迎, 张东来, 徐殿国. 级联式DC/DC变换器输出阻抗的优化设计与稳定性[J]. 电工技术学报, 2009, 24(3): 147-152.
Yao Yuying, Zhang Donglai, Xu Dianguo. Output impedance optimization and stability for cascade DC/DC converter[J]. Transactions of China Electro- technical Society, 2009, 24(3): 147-152.
[9] 郭伟, 赵洪山. 基于事件触发机制的直流微电网多混合储能系统分层协调控制方法[J]. 电工技术学报, 2020, 35(5): 1140-1151.
Guo Wei, Zhao Hongshan. Coordinated control method of multiple hybrid energy storage system in DC microgrid based on event-triggered mechanism[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1140-1151.
[10] Cai Wen, Yi Fan, Eva Cosoroaba, et al. Stability optimization method based on virtual resistor and nonunity voltage feedback loop for cascaded DC-DC converters[J]. IEEE Transactions on Industry Appli- cations, 2015, 51(61): 4575-4583.
[11] 刘欣博, 高卓. 考虑恒功率负载与储能单元动态特性的直流微电网系统大信号稳定性分析[J]. 电工技术学报, 2019, 34(增刊1): 292-299.
Liu Xinbo, Gao Zhuo. Large signal stability analysis of DC microgrid system considering dynamic characteri- stics of constant power load and energy storage system[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 292-299.
[12] 朱晓荣, 孟欣欣. 直流微电网的稳定性分析及有源阻尼控制研究[J]. 高电压技术, 2020, 46(5): 1670- 1681.
Zhu Xiaorong, Meng Xinxin. Stability analysis and research of active damping control method for DC microgrids[J]. High Voltage Engineering, 2020, 46(5): 1670-1681.
[13] Zhang Xin, Ruan Xinbo, Zhong Qingchang. Improving the stability of cascaded DC/DC converter systems via shaping the input impedance of the load converter with a parallel or series virtual impedance[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7499-7512.
[14] Rahimi A M, Emadi A. Active damping in DC/DC power electronic converters: a novel method to overcome the problems of constant power loads[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1428-1439.
[15] Zhang Xin, Zhong Qingchang, Ming Wenlong. Stabi- lization of cascaded DC/DC converters via adaptive series-virtual-impedance control of the load con- verter[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6057-6063.
[16] 庞圣钊, 皇甫宜耿, 郭亮, 等. 基于Lyapunov间接法分析的恒功率负载电源变换器宽稳定控制策略[J]. 电工技术学报, 2017, 32(14): 146-154.
Pang Shengzhao, Huangfu Yigeng, Guo Liang, et al. A novel wide stability control strategy of constant power load power converter based on the analysis of Lyapunvo indirect method[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 146-154.
[17] Wu Mingfei, Dylan Dahchuan Lu. A novel stabili- zation method of LC input filter with constant power loads without load performance compromise in DC microgrids[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 62(7): 4552-4562.
[18] Gu Yunjie, Li Wuhua, He Xiangning. Analysis and control of bipolar LVDC grid with DC symmetrical component method[J]. IEEE Transactions on Power Systems, 2016, 31(1): 685-694.
[19] Kakigano Hiroaki, Miura Yushi, Ise Toshifumi. Low- voltage bipolar-type DC microgrid for super high quality distribution[J]. IEEE Transactions on Power Electronics, 2010, 25(12): 3066-3075.
[20] Kakigano Hiroaki, Miura Yushi, Ise Toshifumi, et al. DC voltage control of the DC micro-grid for super high quality distribution[C]//Power Conversion Con- ference, Nagoya, Japan, 2007: 518-525.
[21] Tan Longcheng, Wu Bin, Venkata Yaramasu, et al. Effective voltage balance control for bipolar-DC- bus-fed EV charging station with three-level DC-DC fast charger[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4031-4041.
[22] Giel Van den Broeck, Jef Beerten, Mauricio Dalla Vecchia, et al. Operation of the full-bridge three-level DC-DC converter in unbalanced bipolar DC micro- grids[J]. IET Power Electronics, 2019, 12(9): 2256- 2265.
[23] Han Byungmoon. A half-bridge voltage balancer with new controller for bipolar DC distribution systems[J]. Energies, 2016, 9(3): 1-17.
[24] Middlebrook R D. Input filter considerations in design and application of switching regulators[C]// IEEE IAS Annual Meeting, Chicago, IL, USA, 1976: 366-382.
[25] 滕昌鹏, 王玉斌, 周博恺, 等. 含恒功率负载的直流微网大信号稳定性分析[J]. 电工技术学报, 2019, 34(5): 973-982.
Teng Changpeng, Wang Yubin, Zhou Bokai, et al. Large-signal stability analysis of DC microgrid with constant power loads[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 973-982.
Stability Analysis and Active Damping Method of the Bipolar DC System with Constant Power Loads
Abstract Because of the negative incremental impedance characteristic, the constant power loads (CPLs) will adversely affect the stability of the DC system and cause system voltage oscillation. Current stability studies are mainly focusing on unipolar DC systems, and lack of research on bipolar DC systems. In this paper, a bipolar DC system based on a half-bridge voltage balancer is introduced. At first, a stability criterion for the bipolar system is illustrated. After that, the system model is derived by state space average method, and system transfer function is obtained. On this basis, a parallel virtual resistance damping method is proposed and analyzed for improving the stability of the bipolar DC system connected with CPLs. Furthermore, the Lyapunov indirect method is adopted to investigate the impact of unbalanced load on the system stability. It turns out that stability of the bipolar DC system is determined by the total output power of the system. Finally, simulation and experimental results verify the proposed method.
keywords：Bipolar DC system, constant power loads (CPLs), stability, half-bridge voltage balancer, virtual resistance
DOI: 10.19595/j.cnki.1000-6753.tces.201111
中图分类号：TM46
游逍遥 男，1996年生，硕士研究生，研究方向为DC-DC变换控制及其稳定性。E-mail: youxiaoyao@cqu.edu.cn（通信作者）
刘和平 男，1957年生，教授，博士生导师，研究方向为电力传动及其控制技术。E-mail: engineer@cqu.edu.cn
收稿日期 2020-08-30
改稿日期 2020-12-23
国家自然科学基金面上资助项目（51877017）。
（编辑 陈 诚）