
图1 L-R复合调制T型半桥LCC谐振变换器
Fig.1 T-type half bridge LCC resonant converter with L-R composite modulation
摘要 针对宽输出电压范围应用场合下,传统LCC谐振变换器变频调制调频范围宽,而采用定频调制时有软开关范围窄、轻载环流大的问题,该文基于半桥LCC谐振变换器提出一种线性-谐振(L-R)复合调制的T型半桥LCC谐振变换器。所提变换器通过添加一组Boost桥臂,在传统谐振模态中加入Boost储能模态,使得谐振电流在一个周期内呈线性、谐振型两个状态的变化,提高了传统谐振模式下的电压增益,且具有全负载范围无环流、软开关的特点。所提变换器采用脉冲频率调制-脉冲宽度调制(PFM-PWM)复合调制方式,具有谐振-线性回馈(R-LF)、线性升压-谐振(LB-R)两种工作模式,在较小的频率范围内能够实现宽范围输出,在轻载下能够保持定频PWM,提高了轻载效率。该文详细介绍了变换器的工作原理,根据时域关系推导电压增益的表达式,最后基于恒流恒压(CC-CV)充电给出设计步骤,搭建一台实验样机,实验结果验证了理论分析的正确性。
关键词:变换器 LCC谐振 宽范围输出 CC-CV充电
近年来,随着新能源的广泛发展,谐振型变换器因其优越的软开关和电磁兼容特性得到了更深入地研究。其中,LCC谐振变换器作为最早提出的三元件谐振变换器,集合了传统两元件谐振变换器的优点,同时具备输入电流具有负载相关性和空载电压可调的特性,电压调节能力强,轻载环流小,现广泛应用于静电除尘、感应加热、高压电源等场合[1-6]。
传统LCC谐振变换器采用脉冲频率调制(Pulse Frequency Modulation, PFM)。在恒流恒压(Constant Current-Constant Voltage, CC-CV)充电等需要适应宽输出电压范围和宽负载变化范围的应用场合[7-8],其工作频率需要大范围调节,不利于磁性器件设计;轻载条件下环流功率大且较高的开关频率带来严重的开关损耗及磁心损耗导致效率明显下降[9-10]。若采用定频移相调制(Phase Shift Modulation, PSM),能够避免频率大范围调节,但是存在软开关范围窄的问题。为了拓宽软开关范围,则需要设计较大的阻抗角,使得变换器环流损耗严重[11-14]。针对以上问题,目前研究的方法主要围绕调制策略和拓扑结构两个方面展开[15-21]。
在调制方法上,文献[15]提出了一种非对称移相控制策略,能够在更小的工作频率下实现软开关,但是依然存在一个较宽的环流阶段。文献[16]提出了自持移相控制,强制谐振电流滞后于谐振腔电压,但是调制载波需要与谐振电流同步,控制系统比较复杂。文献[17]提出了一种脉冲宽度调制-脉冲频率调制(Pulse Width Modulation-Pulse Frequency Modulation, PWM-PFM)混合调制策略,构建了移相角与频率的线性关系。文献[18]基于半桥LCC谐振变换器提出了一种双载波调制策略,构建了占空比与频率的线性关系。以上两种控制方式在集合了定频与变频控制优点的同时,简化了控制器的参数设计,在较小的频率变化范围内实现了较宽范围软开关,但没有解决环流损耗的问题。
在拓扑结构方面,文献[19]引入了一个开关控制,辅助谐振电感在轻载时接入谐振腔,减小调频控制下的频率变化范围。但当负载频繁变化时,系统难以稳定,且其频率调节范围依然可观。文献[20]通过在谐振腔添加无源LC辅助网络,改变流过滞后臂开关管的电流大小,实现零电压软开关(Zero Voltage Switching, ZVS)开通。其设计频率可以接近谐振频率,减小了谐振电流大小。但是只适用于全桥结构,且无源网络的加入增加了变换器的无功功率,限制了变换器效率的提升。文献[21]基于半桥结构,提出了一种Buck-Boost复合型LCC谐振变换器,将传统两级式结构并为一级,通过调节母线电压,提高增益,以适应宽范围的输出条件,但导致开关管的电压、电流应力增大,且轻载环流的问题显著。
上述方法通过减小变换器的频率调节范围、拓宽定频调节的软开关范围、提高变换器增益等方法优化了宽范围输出应用场合的变换器性能,但是并没有改变谐振变换器的传统调压机制,即通过增加回馈能量或环流能量以调节电压增益。在轻载工况时,变换器谐振腔内依然不得不流过相当一部分回馈电流或谐振环流,环流损耗问题没有得到解决。
为了优化变换器在宽范围输出应用场合的性能,变换器需要具有以下特点:①能够在全负载范围内实现软开关;②在较窄的频率范围内调压能力强;③轻载环流小。
本文为了满足以上条件,提出了一种L-R复合调制的T型半桥LCC谐振变换器。所提变换器在不同的调制方式下具有两种不同的工作模式,具备良好的电压调节能力;开关管在全负载范围内能够实现软开关,谐振腔全负载范围无环流,轻载工况下保持定频调节,有效地提升了轻载效率。文中详细分析了所提变换器的工作原理,基于时域关系得到了两种模式的电压增益曲线,详细分析了两种模式下的工作特性。最后搭建了一台具有CC-CV充电功能的实验样机,实验结果验证了其正确性。
本文提出的L-R复合调制T型半桥LCC谐振变换器如图1所示。Uin为输入电压,Iin、Io分别为输入、输出平均电流;Ci1和Ci2为两个规格相同的输入电容;辅助开关管QB1、QB2组成Boost桥臂,QR1、QR2组成谐振桥臂;谐振电感Lr位于输入电容中性点O与Boost桥臂中点A之间;串联谐振电容Cr与主变压器T1接在A、B两点之间;二次侧4个整流二极管VD5~VD8构成全桥整流结构,并联谐振电容并接在整流桥之后;后级由滤波电感Lf、滤波电容Co构成LC滤波结构,Ro为负载电阻。

图1 L-R复合调制T型半桥LCC谐振变换器
Fig.1 T-type half bridge LCC resonant converter with L-R composite modulation
为了便于分析,定义参数如下:Lm为变压器励磁电感,n为一次侧、二次侧匝比,fs为开关频率,ws为开关角频率,电容比m=Cp/(n2Cr),串联谐振频率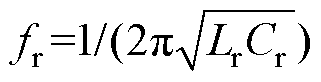 ,串联谐振角频率
,串联谐振角频率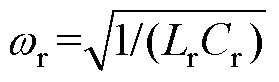 ,串并联谐振角频率
,串并联谐振角频率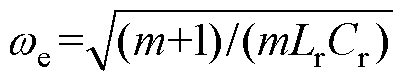 ,归一化角频率
,归一化角频率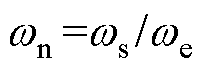 ,特征阻抗
,特征阻抗 ,品质因数
,品质因数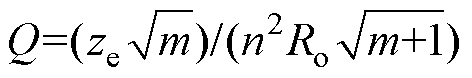 。
。
在不同的调制方式下,所提变换器具有线性升压-谐振(Linear Boost-Resonant, LB-R)和谐振-线性回馈(Resonant-Linear Feedback, R-LF)两种工作模式。其中,LB-R模式采用定频PWM。该模式通过将谐振电感复用作储能电感,在传统谐振模态之前加入Boost调制,使得电感在开始谐振之前进行线性储能,为谐振腔预注入能量,再通过谐振将能量馈送至输出侧;R-LF模式采用PFM方式。在该模式下,传统谐振过程被中断,谐振腔剩余能量将通过谐振电感直接反馈至输入侧。
图2为LB-R模式下的主要波形,图中,SB1、SB2、SR1、SR2分别为QB1、QB2、QR1、QR2的驱动信号,iLr为谐振电感电流,iB1、iB2分别为流过QB1、QB2的电流,iCr为谐振电容电流,iVD5~iVD8分别为流过VD5~VD8的电流,uCr与uCp分别为Cr和Cp上的电压。辅助开关管QB1、QB2导通占空比DL= 2fs(t1-t0),谐振开关管QR1、QR2导通占空比DT= 2fs(t3-t1),谐振过程占空比DR=2fs(t2-t1),死区时间占空比Dd=2fs(t4-t3)。工作频率为fr,采用定频PWM。Dd保持不变,通过改变DL调节电压增益。
变换器前后半周期工作原理相似,此处分析前半周期工作原理。为了简化分析,作如下假设:
(1)除考虑开关管体二极管及寄生电容外,开关管、整流二极管均为理想器件。
(2)忽略输入输出电压纹波,且两输入电容电压视为相等,均为Uin/2。
(3)Lf足够大,流过Lf的电流视为定值ILf。
(4)Lm Lr,励磁电流iLm近似为0。
Lr,励磁电流iLm近似为0。

图2 LB-R模式下主要波形
Fig.2 Main waveforms in LB-R mode
LB-R模式各阶段等效电路如图3所示,具体描述如下。
Boost储能阶段[t0, t1 :t0时刻以前,Cr、Lr、Lm通过VD2,QB1构成谐振回路,QR1两端电压为0,
:t0时刻以前,Cr、Lr、Lm通过VD2,QB1构成谐振回路,QR1两端电压为0,
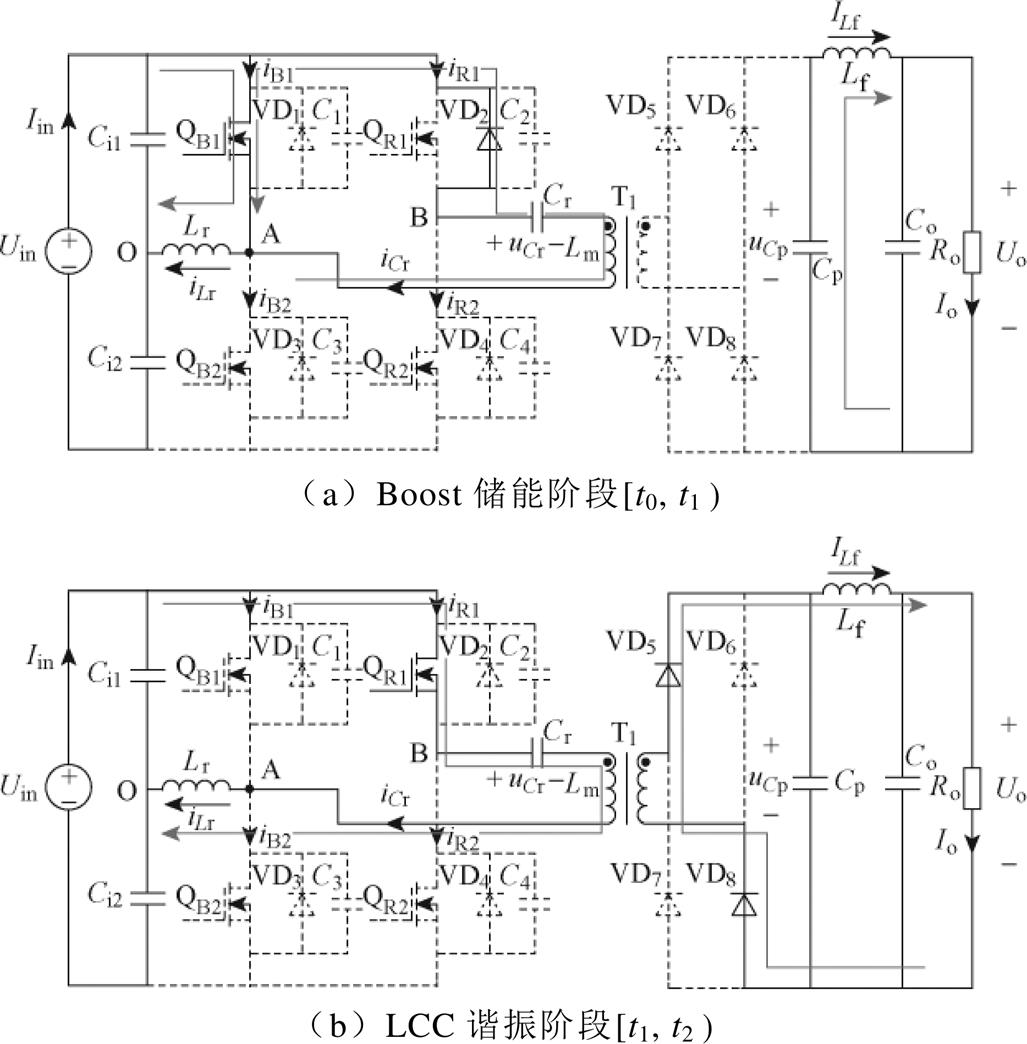
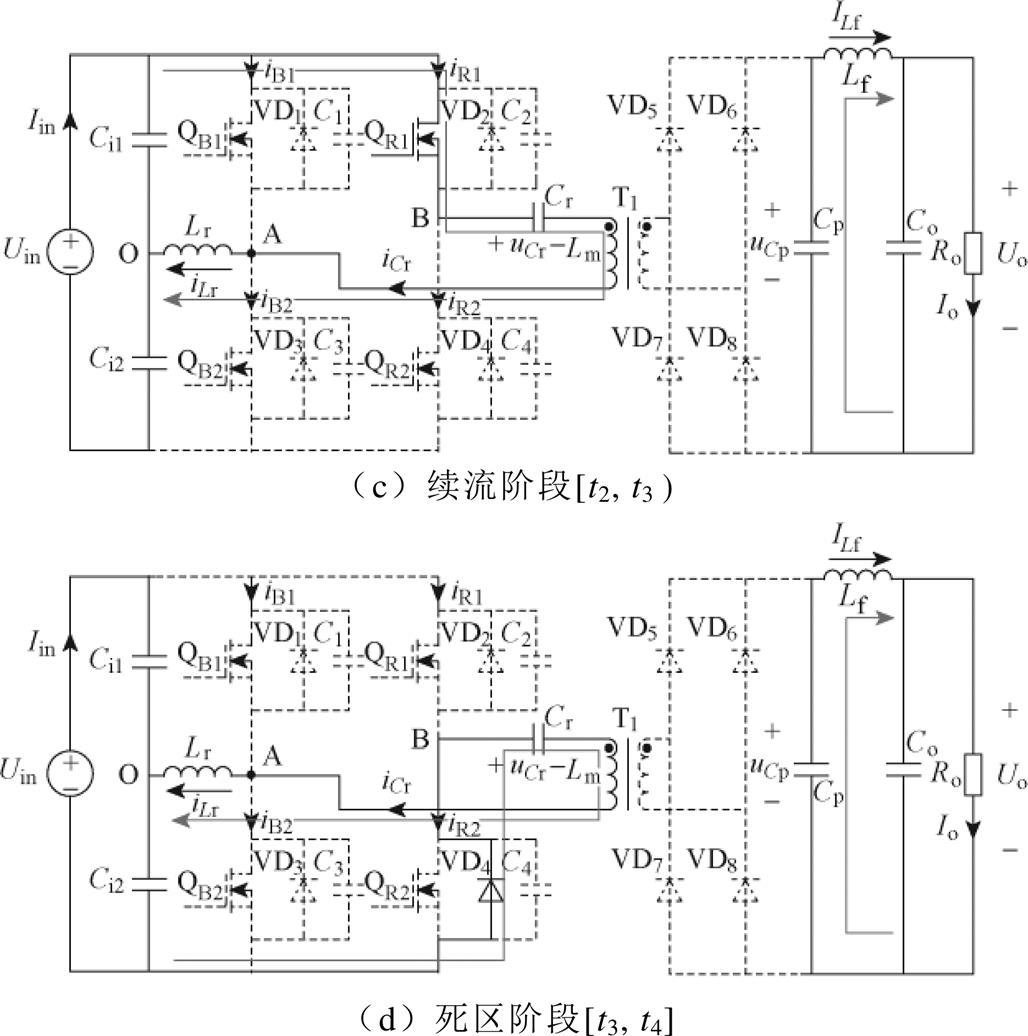
图3 LB-R模式各阶段等效电路
Fig.3 Equivalent circuit of each stage of LB-R mode
此时iCr≈0且近似保持不变。t0时刻,在Lr的作用下QB1实现零电流软开关(Zero Current Switching, ZCS)开通。Lr在Uin/2下充能,iLr线性上升。Cr与Lm通过VD2、QB1构成环流回路,Lm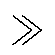 Lr,iCr依旧近似不变。VD5~VD8保持截止,Cp通过Lf释放能量,uCp线性下降。到t1时刻,QB1关断,该阶段结束。iLr(t1)表示为
Lr,iCr依旧近似不变。VD5~VD8保持截止,Cp通过Lf释放能量,uCp线性下降。到t1时刻,QB1关断,该阶段结束。iLr(t1)表示为
 (1)
(1)LCC谐振阶段[t1, t2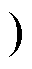 :t1时刻,QB1关断、QR1实现ZVS导通。iCr短时间内上升至iLr(t1),VD5与VD8导通。此时Lr与Cr、Cp构成LCC谐振回路开始谐振,iLr(t)由线性变化转换为谐振型变化,能量由一次侧向二次侧传输。iLr(t)、uCr(t)和uCp(t)的初始值分别为iLr(t1)、-DuCr和uCp(t1),此过程各变量表达式如下
:t1时刻,QB1关断、QR1实现ZVS导通。iCr短时间内上升至iLr(t1),VD5与VD8导通。此时Lr与Cr、Cp构成LCC谐振回路开始谐振,iLr(t)由线性变化转换为谐振型变化,能量由一次侧向二次侧传输。iLr(t)、uCr(t)和uCp(t)的初始值分别为iLr(t1)、-DuCr和uCp(t1),此过程各变量表达式如下
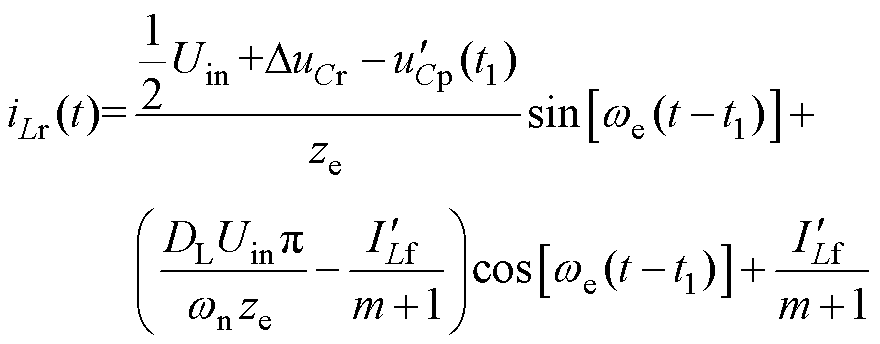 (2)
(2)

 (3)
(3)
 (4)
(4)
式中, 、
、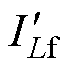 分别为uCp(t)、ILf折算至一次侧的等效值,
分别为uCp(t)、ILf折算至一次侧的等效值, =nuCp,
=nuCp,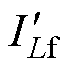 =ILf/n。到t2时刻,uCr(t)上升至DuCr,uCp上升至uCp(t2),iCr=iLm,iVD5降至0,VD5与VD8实现ZCS关断,LCC谐振过程结束。
=ILf/n。到t2时刻,uCr(t)上升至DuCr,uCp上升至uCp(t2),iCr=iLm,iVD5降至0,VD5与VD8实现ZCS关断,LCC谐振过程结束。
续流阶段[t2, t3 :t2时刻,变压器二次侧与一次侧断开,Cp向负载提供能量,ILf流过Cp,uCp线性下降,uCp(t)如式(5)所示。QR1保持导通,Cr、Lm、Lr通过QR1构成谐振回路,iCr=iLm≈0,由于Lm
:t2时刻,变压器二次侧与一次侧断开,Cp向负载提供能量,ILf流过Cp,uCp线性下降,uCp(t)如式(5)所示。QR1保持导通,Cr、Lm、Lr通过QR1构成谐振回路,iCr=iLm≈0,由于Lm Lr,iCr近似保持不变。到t3时刻,QR1近似实现ZCS关断。
Lr,iCr近似保持不变。到t3时刻,QR1近似实现ZCS关断。
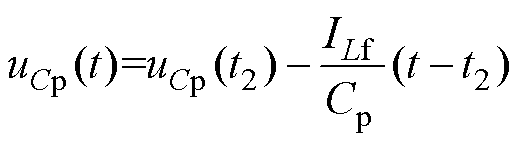 (5)
(5)死区阶段[t3, t4]:t3时刻QR1关断后,C2、C4通过iLm充放电。待QR2两端电压降至0后,VD4导通,Cr、Lm、Lr通过VD4构成谐振回路,为QR2实现ZVS导通提供条件。该阶段Cp继续向负载释放能量,到t4时刻QB2实现ZCS导通,开始下半周期工作。
在LB-R模式下变换器主要经历了Boost储能和LCC谐振馈能两个阶段。Boost储能阶段通过复用谐振电感为储能电感,为谐振腔预注入能量,此阶段谐振腔内存在通过Boost桥臂的微小环流;LCC谐振过程在将能量馈出的同时将iLr复位。在整个工作周期内,谐振电流几乎只参与传递能量,谐振腔环流近似为0。
R-LF模式采用PFM方式,该模式下Boost桥臂不工作,死区时间固定不变,QR1、QR2保持为最大占空比互补导通。
R-LF模式主要波形如图4所示,iR1、iR2分别为流过QR1、QR2的电流,a 为QR1、QR2的有效导通角,其大小对应有效谐振时间,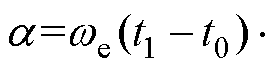
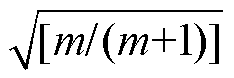 。b 为QR1、QR2的关断角,其大小对应死区时间,
。b 为QR1、QR2的关断角,其大小对应死区时间,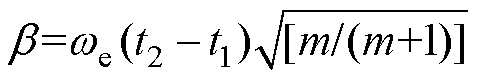 。其余变量意义与LB-R模式相同。R-LF模式各阶段等效电路如图5所示,具体原理分析如下。
。其余变量意义与LB-R模式相同。R-LF模式各阶段等效电路如图5所示,具体原理分析如下。
LCC谐振阶段[t0, t1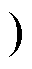 :t0时刻以前,QR1已经开通。t0时刻iLr开始正向流过QR1,VD5、VD8导通,Lr、Cr、Cp构成谐振回路开始谐振,一次侧向二次侧传输能量。到t1时刻QB1关断,该阶段结束。uCr由-DuCr上升至DuCr,uCp由uCp(t0)上升至uCp(t1)。此过程iLr(t)、uCr(t)、uCp(t)的表达式分别为
:t0时刻以前,QR1已经开通。t0时刻iLr开始正向流过QR1,VD5、VD8导通,Lr、Cr、Cp构成谐振回路开始谐振,一次侧向二次侧传输能量。到t1时刻QB1关断,该阶段结束。uCr由-DuCr上升至DuCr,uCp由uCp(t0)上升至uCp(t1)。此过程iLr(t)、uCr(t)、uCp(t)的表达式分别为
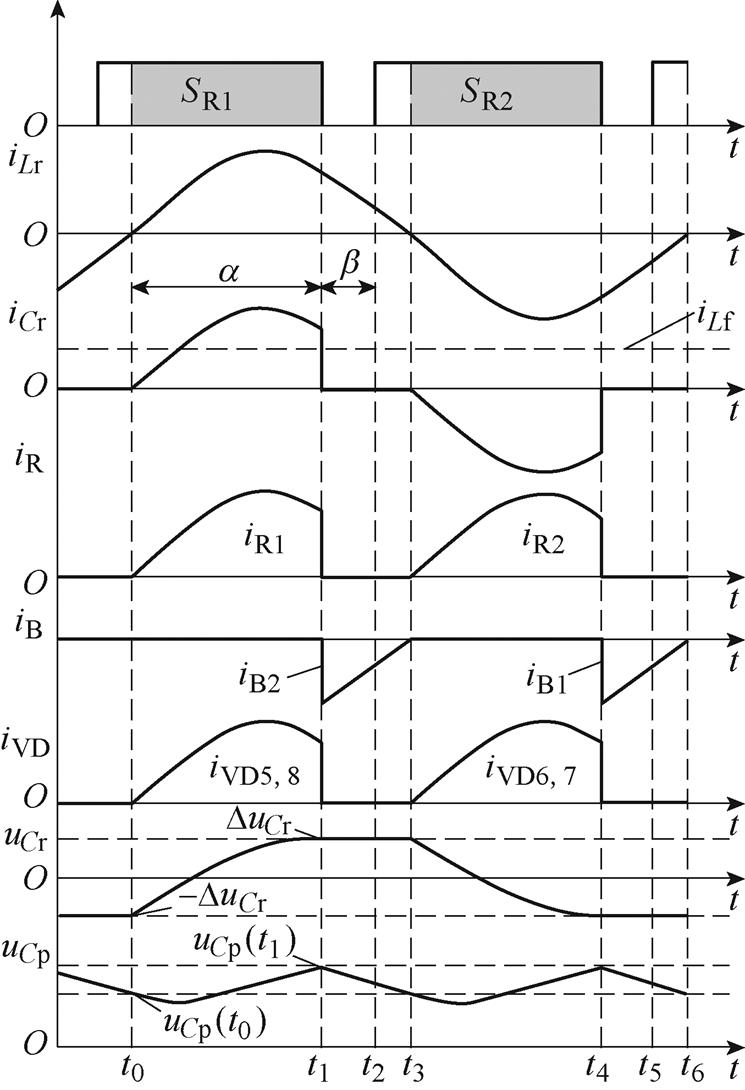
图4 R-LF模式主要波形
Fig.4 Main waveforms of R-LF mode
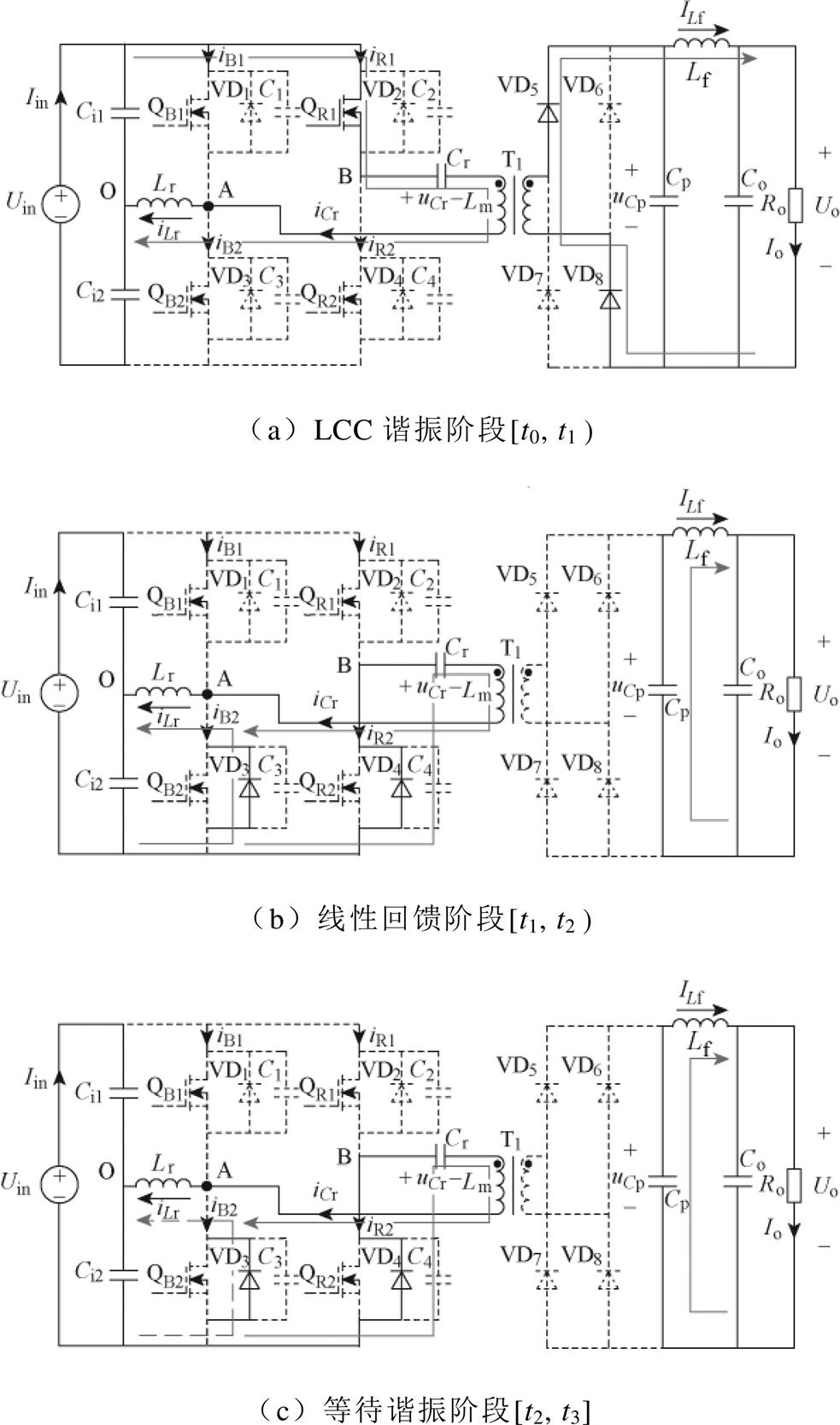
图5 R-LF模式各阶段等效电路
Fig.5 Equivalent circuit of each stage of R-LF mode
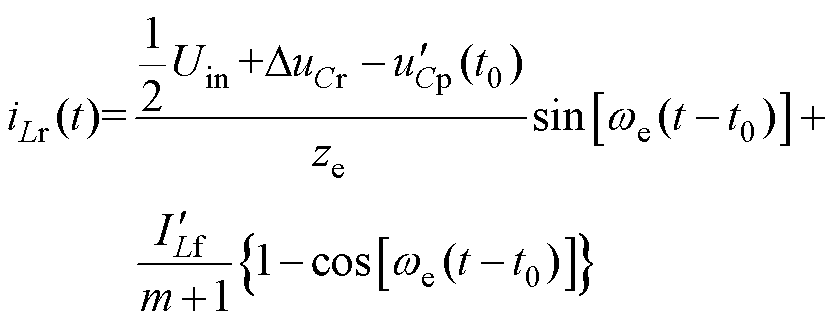 (6)
(6)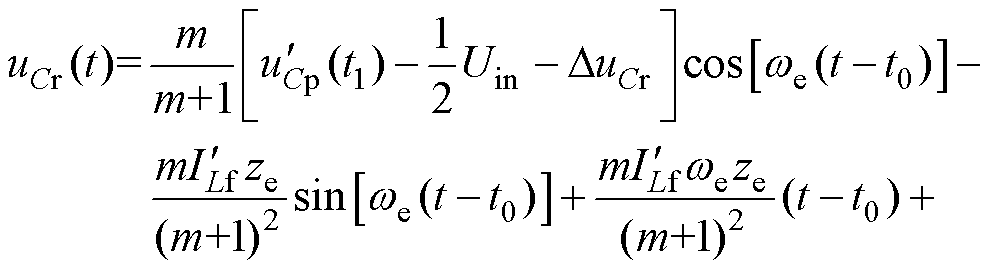
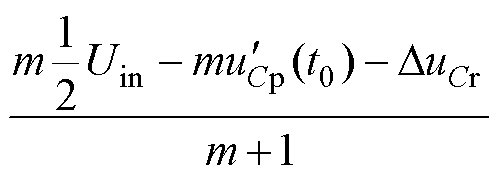 (7)
(7)
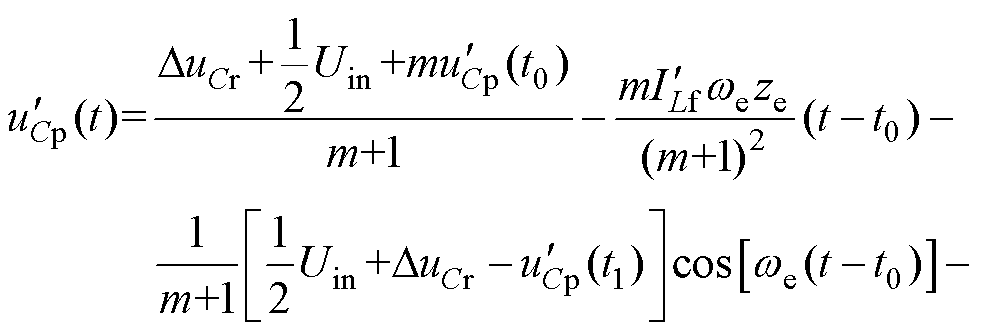
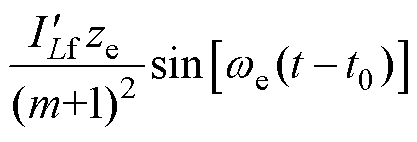 (8)
(8)
线性回馈阶段[t1, t2 :t1时刻QR1关断,变压器二次侧与一次侧断开,Cp通过Lf向负载供能,uCp线性下降,uCp(t)表示为
:t1时刻QR1关断,变压器二次侧与一次侧断开,Cp通过Lf向负载供能,uCp线性下降,uCp(t)表示为
 (9)
(9)此时在较短的时间内,VD3、VD4导通,QR2端电压被钳位至0,iCr迅速下降至iLm,谐振腔内电流转移到VD3上。Lm与Cr通过VD4构成谐振回路,由于Lm很大,iCr=iLm且近似保持不变。Lr在Uin/2作用下放电,iLr线性下降,能量回馈至输入侧。
等待谐振阶段[t2, t3]:t2时刻,QR2实现ZVS开通。此阶段各电流流向与[t1, t2]阶段相同,iLr继续下降。t3时刻iLr=0,此时Lr剩余能量全部回馈完毕,准备开始下半周期的LCC谐振。
由以上分析可知,当变换器工作在R-LF模式,能量传输关系与传统谐振变换器相似,不同之处在于,谐振腔剩余能量能够通过谐振电感直接线性回馈至输入侧,而不需要通过谐振的形式经过整个谐振腔和主变压器,减小了回馈环路的损耗。
变换器在两种模式下采用不同的调制方式,且具有不同的电压增益特性,实现软开关的方式各异。为了简化分析,取m=1分别分析两种模式下的工作特性。
由第1节分析可知,在R-LF模式中,半周期内仅LCC谐振阶段传输能量,且iCr只参与传递能量,不参与能量回馈。此时变换器电压增益与有效导通角a 的大小直接相关。
视ILf为流过滤波电感电流的平均值,定义半周期iCr的平均值为iCr_ave,根据开关周期内电容平均电流为0,得到
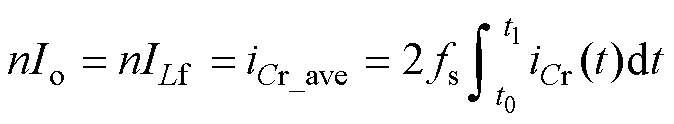 (10)
(10)由式(6)求得iCr_ave表达式为
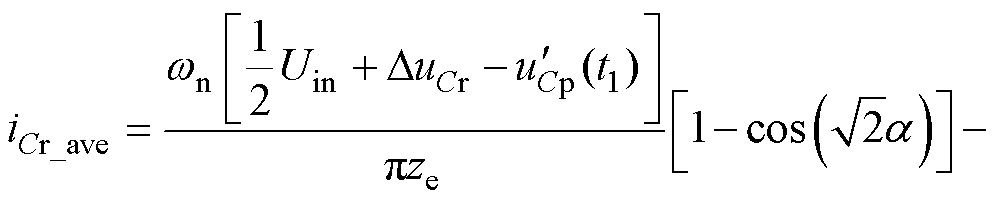
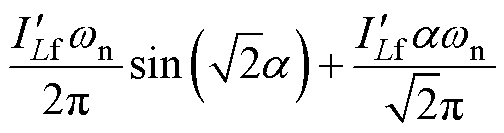 (11)
(11)由于uCr仅在谐振过程变化,结合式(10)得到DuCr表达式为
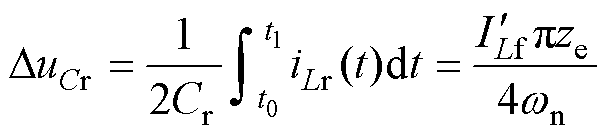 (12)
(12)
uCp在t1~t3期间由uCp(t1)线性下降至uCp(t0),该变化过程表示为
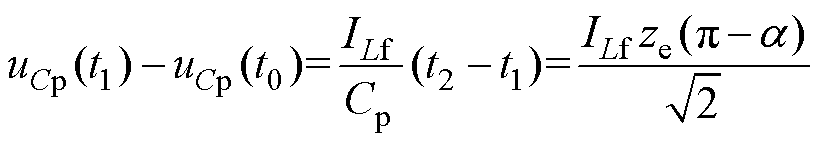 (13)
(13)由于Lf平均电压为0,输出电压Uo可以表示为
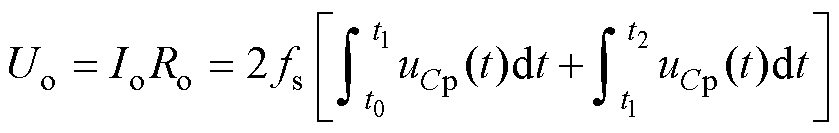 (14)
(14)
其中
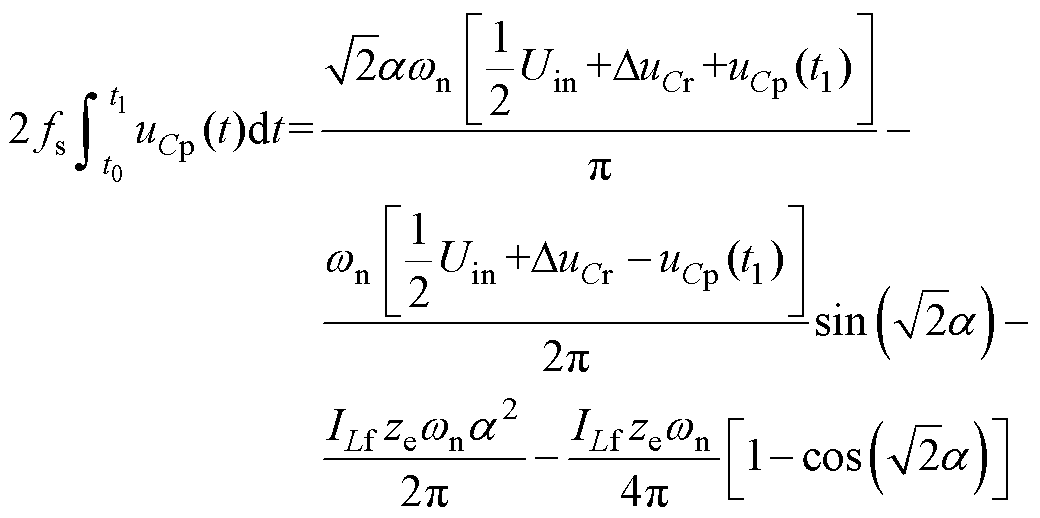 (15)
(15)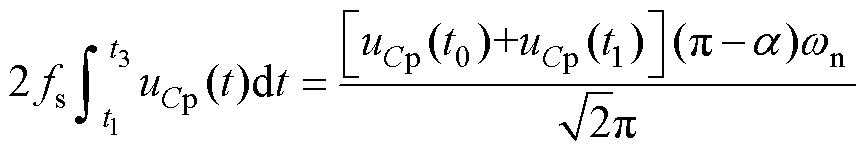 (16)
(16)
定义R-LF模式电压增益GR-LF=2nUo/Uin,结合式(10)~式(14),得到m=1时,GR-LF关于a、wn的表达式为
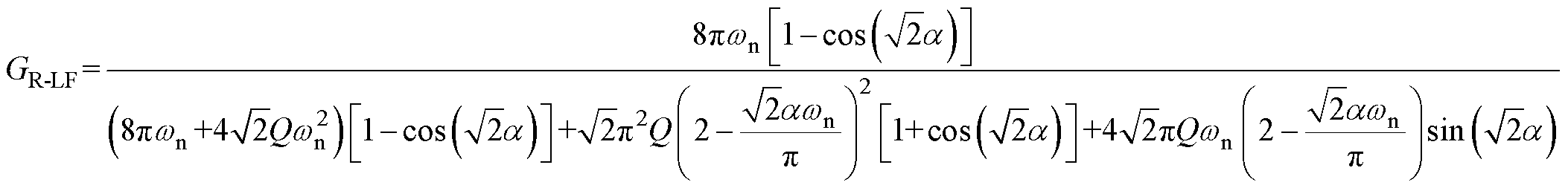 (17)
(17)由式(17)可知,R-LF模式电压增益与其导通角a 及工作频率有关,而所提变换器多模态的工作特点使得谐振电流的变化周期不同于传统谐振变换器,a 与wn的关系不能直接得到,为了建立准确的电路模型,需要分析谐振电流的特点。
定义归一化谐振电流 ,结合式(10)~式(14)可求各中间变量代入式(6)得到
,结合式(10)~式(14)可求各中间变量代入式(6)得到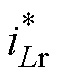 表达式为
表达式为
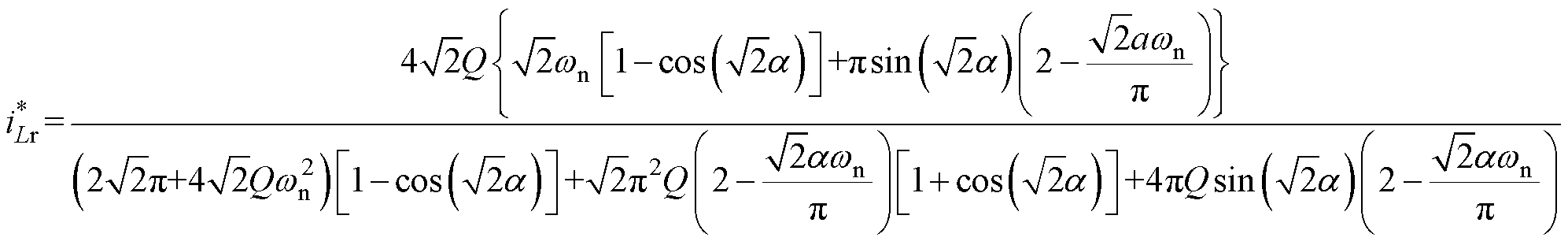 (18)
(18)根据式(18)绘制出当fs=fr且不加入Boost调制,即两模式临界状态的归一化谐振电流曲线,如图6所示。
由图6可知,在两种模式临界状态(fs=fr),谐振电流变化频率大于fr,最大导通角a_max=0.88p 且不随负载改变而变化。假设b =0.12p,则当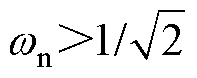 时a<0.88p,电压增益开始下降。忽略等待谐振时间,在式(18)中令
时a<0.88p,电压增益开始下降。忽略等待谐振时间,在式(18)中令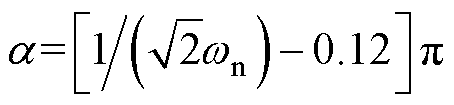 ,即得到GR-LF关于wn的表达式。
,即得到GR-LF关于wn的表达式。
图7为变换器在LB-R模式下的等效电路模型,图中,QB为辅助开关管,QR为谐振开关管。
此时谐振电感被复用作Boost储能电感,起到提升谐振腔能量的作用。经过预储能的谐振电感在辅助开关管关断后,与输入侧共同为谐振腔提供 能量。
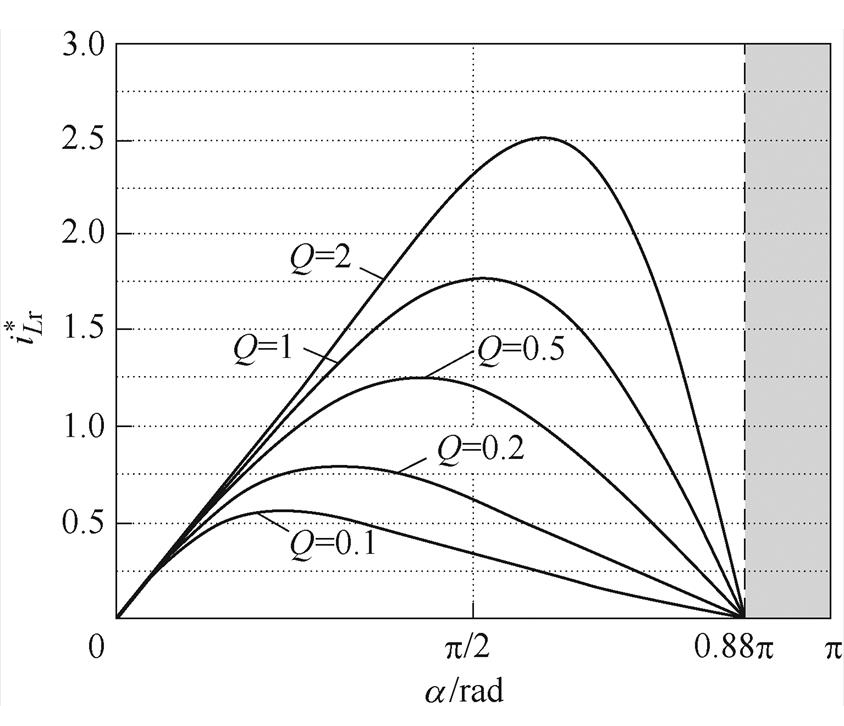
图6 R-LF模式谐振电流曲线(fs=fr)
Fig.6 Resonant current curves of R-LF mode( fs=fr)
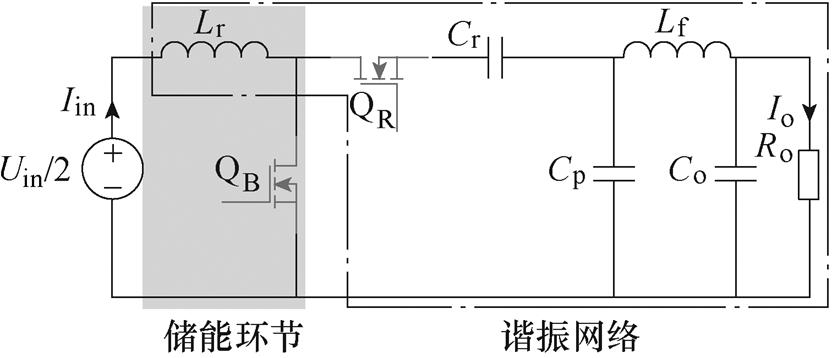
图7 LB-R模式电路模型
Fig.7 LB-R mode circuit model
根据1.1节分析可知,在半周期内,谐振腔能量将全部馈送至输出侧,忽略励磁电流的影响,谐振腔不存在环流,即在t0~t1时间段内Lr线性储能,所有能量在t1~t2谐振阶段被传输至输出侧。假设传输效率为100%,Iin与Io可以分别表示为
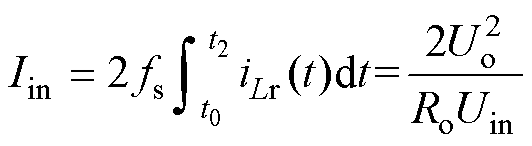 (19)
(19)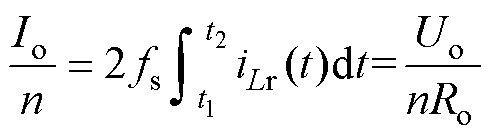 (20)
(20)
由式(19)和式(20)得到
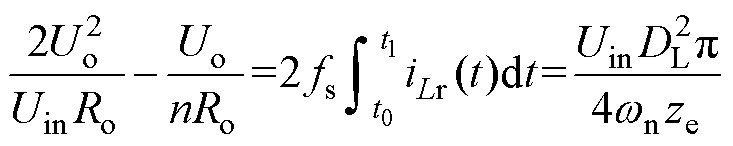 (21)
(21)定义LB-R模式下电压增益GLB-R=2nUo/Uin,由式(10)得到其表达式为
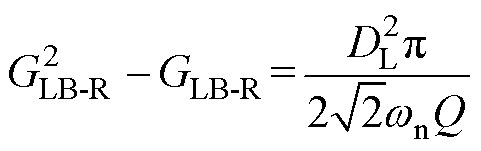 (22)
(22)
结合上述分析,由式(17)、式(22)可以分别绘制出m=1时,变换器R-LF模式与LB-R模式下的电压增益曲线GR-LF和GLB-R如图8所示。

图8 两种模式电压增益曲线(m=1)
Fig.8 Voltage gain curves of two modes (m=1)
图8中,虚线表示R-LF模式GR-LF-wn曲线,实线表示LB-R模式GLB-R-DL曲线。R-LF模式电压增益随频率减小而增大,当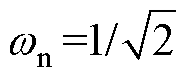 时达到最大值1;在LB-R模式下工作频率保持不变,当DL从0增大时,电压增益从1逐渐上升。从图中可以看出,所提变换器通过两种工作模式实现了较宽的电压调节范围,能够适应宽范围输出应用场合的工作要求。其中,当Q值较大时,R-LF模式在较窄的频率范围内具有良好的降压调节能力,而LB-R模式在全负载范围内具有灵活的电压调节特性和无能量反馈、无谐振环流的优点,适合轻载工作。
时达到最大值1;在LB-R模式下工作频率保持不变,当DL从0增大时,电压增益从1逐渐上升。从图中可以看出,所提变换器通过两种工作模式实现了较宽的电压调节范围,能够适应宽范围输出应用场合的工作要求。其中,当Q值较大时,R-LF模式在较窄的频率范围内具有良好的降压调节能力,而LB-R模式在全负载范围内具有灵活的电压调节特性和无能量反馈、无谐振环流的优点,适合轻载工作。
变换器在两种模式下的软开关模式见表1。
表1 软开关模式
Tab.1 Soft switching mode

模式QB1、QB2QR1、QR2 LB-RZCS开通ZVS开通;ZCS关断 R-LF不工作ZVS开通
在LB-R模式,由于QB1、QB2始终与Lr串联工作,故总能够实现ZCS开通。iCr在半周期内通过谐振复位至iLm,C2、C4通过iLm在死区和Boost时间内完成充放电以实现QR1、QR2的ZVS开通。
在R-LF模式,死区时间不变,而开关管关断电流大于iLm,即在R-LF模式能够轻易实现软开关。综上所述,变换器在实现全范围软开关条件为,在两种模式的临界状态下QR1、QR2能够实现软开关。
所提变换器电压调节能力强,软开关范围宽,适合CC-CV充电各阶段的工作要求。所提变换器基于CC-CV充电的具体的模式切换对应关系如图9所示。
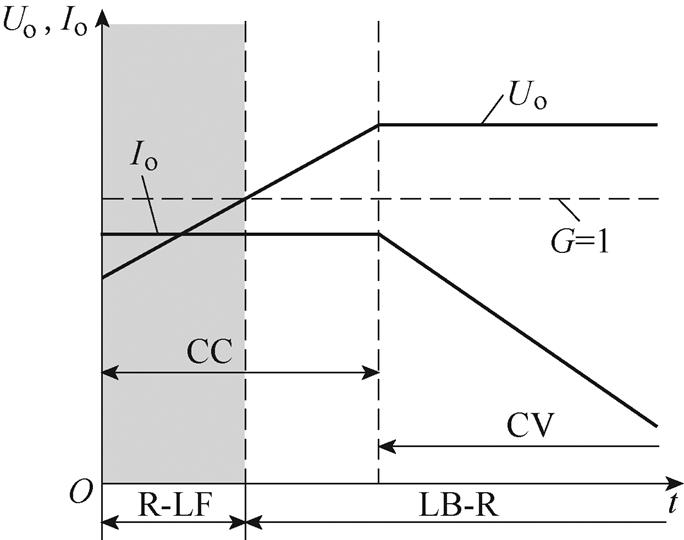
图9 模式切换
Fig.9 Mode switching
CC充电初始阶段,变换器工作在R-LF模式,此时由于负载较重,变换器能在较窄的频率范围内调节输出电压。随着负载减轻,电压增益逐渐升高,上升至1时变换器切换至LB-R模式调节,输出电压继续增大,在达到最大值后进入CV充电阶段,此后变换器保持为LB-R工作模式直到充电结束。
变换器DSP数字控制框图如图10所示。电压电流的误差信号分别通过PI控制器得到电压电流控制信号uv_con、ui_con,通过模式选择环节后,ucon被限幅并分为[0, uc 、[uc, 1]两个区间,当0≤ucon<uc时,进入R-LF模式,采用PFM,fs≥fr;当uc≤ucon≤1时,进入LB-R模式采用PWM方式,0<DL<DL_max,DL_max为辅助开关管占空比的最大值。
、[uc, 1]两个区间,当0≤ucon<uc时,进入R-LF模式,采用PFM,fs≥fr;当uc≤ucon≤1时,进入LB-R模式采用PWM方式,0<DL<DL_max,DL_max为辅助开关管占空比的最大值。
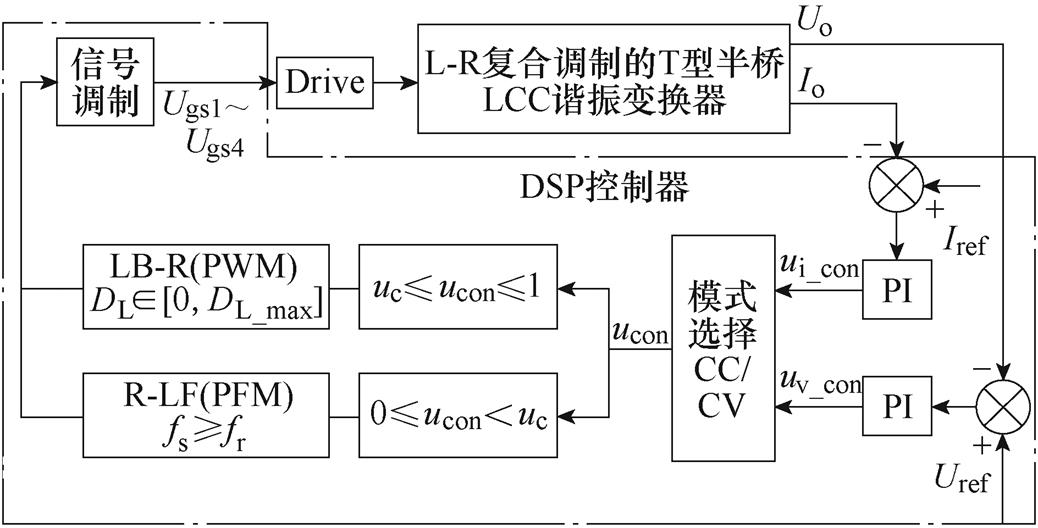
图10 闭环控制框图
Fig.10 Closed-loop control block diagram
辅助开关最大占空比DL_max直接影响Boost电流的大小。当DL值较小,无法满足高增益需求;当DL值过大,将加重辅助开关管关断损耗,过高的峰值电流不利于参数设计,且不利于整体电磁干扰(Electromagnetic Interference, EMI)优化。故DL_max折衷设计为0.3~0.4,根据增益曲线即可得到满足最大增益要求的最大功率因数Qm。
确定Qm值后,根据最大功率Pm,计算谐振原件参数为
 (23)
(23)式中,Gm为最大功率处的电压增益。
4.3.1 开关管电压应力
当变换器工作在LB-R模式下且具有最大功率时,各元件将承受最大应力。对于Boost桥臂和谐振桥臂,开关管承受最大电压应力为输入电压Uin。
4.3.2 开关管电流应力
对于谐振开关管,在一个开关周期内仅有半周期流过谐振电流,有效值iR_RMS=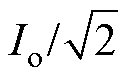 ;对于辅助开关管,在一个开关周期内仅有半周期流过Boost电流,其有效值iB_RMS为
;对于辅助开关管,在一个开关周期内仅有半周期流过Boost电流,其有效值iB_RMS为
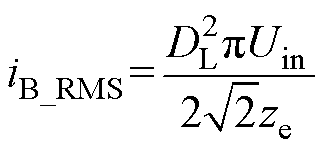 (24)
(24)由以上分析即得到功率MOSFET的设计标准。
由4.3节软开关分析可知,主变压器励磁电感Lm的设计可以在满足两模式临界状态ZVS条件的情况下尽量取大值,以最大程度降低LB-R模式下励磁电流带来的损耗。从分析中可知,在两种模式的临界状态a_max=0.88π,考虑到变压器漏感的影响,死区占空比Dd的设计应略小于0.12。为了保证死区时间内,C2、C4完成充放电过程,Lm需要满足
 (25)
(25)式中,Coss为MOSFET的输出电容。
当变换器满载工作谐振占空比DR接近谐振开关管导通占空比DT时,假设Dd+DL=1-DR,将uCp(t)近似看作线性变化,在t1~t2线性上升,t2~t5线性下降,则有如下关系:
得到uCp(t)峰峰值DuCp的表达式为
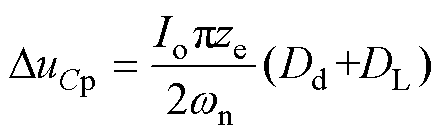 (26)
(26)iLf的峰峰值DiLf表示为
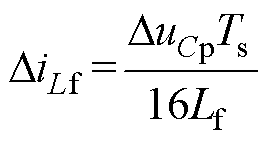 (27)
(27)
设r为滤波电感的电流纹波系数,r=DiLf/Io,得到Lf的设计表达式为
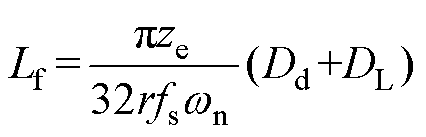 (28)
(28)半桥LCC(Half Bridge LCC, HBLCC)谐振变换器、文献[20]所提Buck-Boost半桥LCC谐振变换器与本文所提变换器的拓扑比较见表2。传统LCC谐振变换器采用调频控制,在宽范围应用场合存在调频范围宽、轻载时开关损耗大、效率低的问题。文献[20]所提变换器实际上是通过复用开关管将Buck-Boost与LCC谐振变换器的两级结构合并为一级,有利于缩小系统体积。通过升高母线电压,提高了电压增益,但也导致开关管将承受更高的电压应力,且变换器轻载环流显著;同时,由于开关管占空比同时影响前后两级,所提的双载波调制使得控制系统更加复杂。
表2 拓扑比较
Tab.2 Topology comparison

参数HBLCC谐振变换器Buck-Boost复合型LCC谐振变换器[20]L-R型LCC谐振变换器 元件MOSFET224 二极管444 谐振电感111 滤波电感111 谐振电容222 滤波电容111 开关(Q1~Q4)电压应力UinUin+UCaUin 控制方法PFMPWM+PFMPWM+PFM 软开关范围全负载范围全负载范围全负载范围 环流/回馈损耗大大接近于0
本文所提L-R型谐振变换器以向谐振注入能量的形式提高了变换器增益。对比传统LCC谐振变换器,其LB-R模式在保持定频调制的条件下能够实现全范围无环流运行,提高了整体效率。所提变换器满载Q值的设计比较小(一般为0.3~0.5),远小于传统LCC谐振变换器满载设计值(一般为4~ 5)[4],即谐振电感能够设计得比较小,在磁性器件损耗方面具有优势。对比已提出的Buck-Boost型LCC谐振变换器,所提变换器具有器件应力小、无环流、控制简单的优点。
根据第4节的设计方法,设计一台具有CC-CV充电功能,输入电压220V,输出电压80~150V,输出电流0~3.33A,最大功率500W的实验样机,样机各参数见表3。
表3 样机参数
Tab.3 Prototype Parameters

参 数数值(型号) 谐振电感Lr/mH20 谐振电容Cr/mF0.157 并联电容Cp/mF0.157 开关频率fs/kHz90~125 滤波电感/mH47 开关管Q1~Q4IPW60R120P7 整流二极管VD5~VD8F30S60S 主变压器T1EE42 Lm/mH350 变压器一次、二次侧匝比1010
当变换器工作在LB-R模式,输出电压150V,输出功率500W的LB-R模式主要波形如图11所示。
图11中,SB1、SR1分别为QB1、QR1的驱动信号;uB1、uR1分别为QB1、QR1的源漏极电压;iLr、iCr、iB1、iLf分别为流过Lr、Cr、QB1和Lf的电流;uCr、uCp分别为Cr、Cp两端的电压;Uo为输出电压。
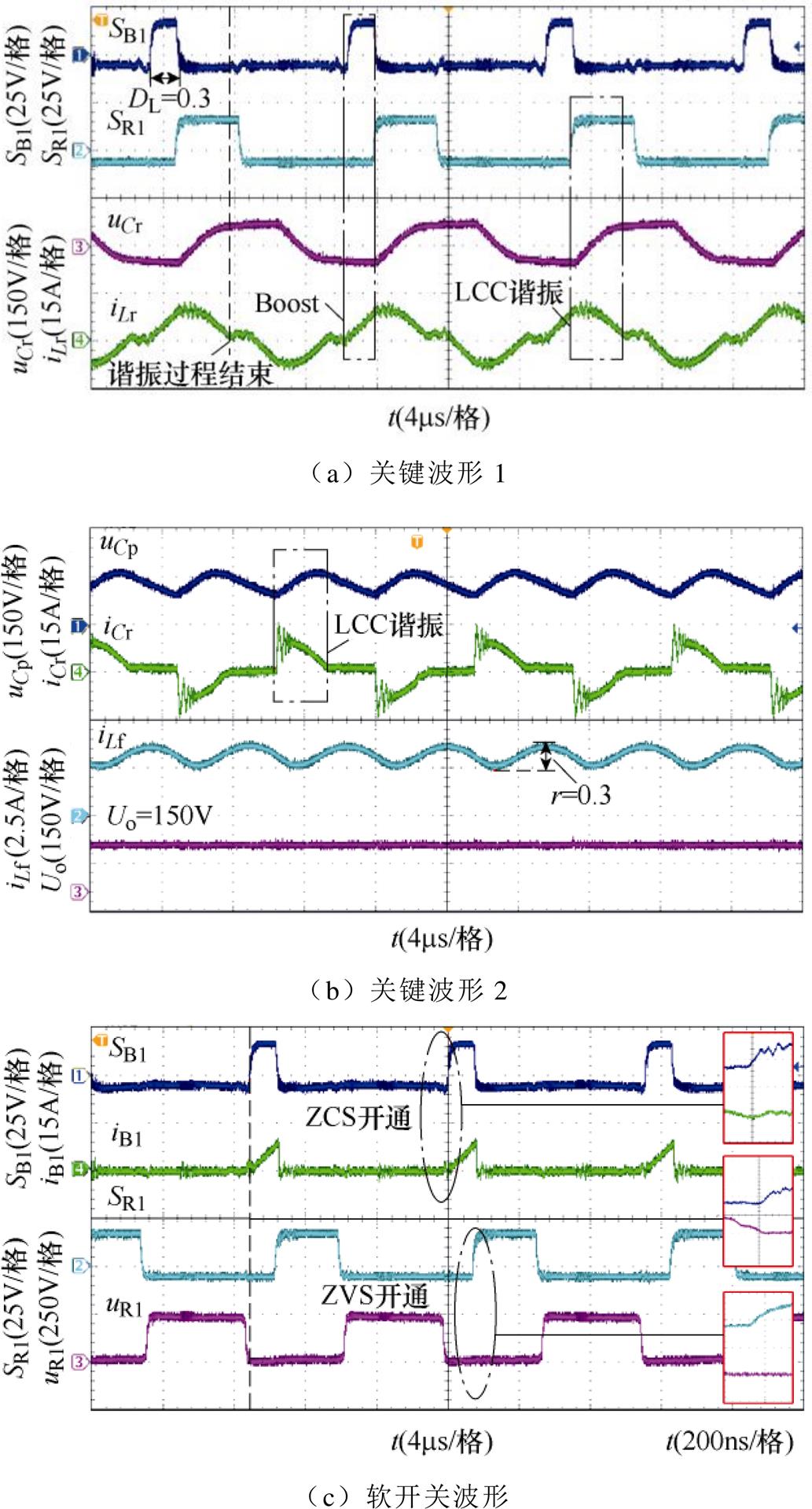
图11 LB-R模式主要波形(Uo=150V, Io=3.33A)
Fig.11 Main waveforms of LB-R mode (Uo=150V, Io=3.33A)
如图11a、图11b所示,此时DL约为0.3,输出电压150V,滤波电感电流波动系数约为0.3。在Boost储能阶段,iLr线性上升,uCr保持不变,uCp线性下降。Boost阶段结束之后进入LCC谐振阶段,uCr、iCr、uCp呈谐振规律变化。在QB2关断之前,iLr已下降至最小值,变换器在半周期内实现了完整谐振过程。如图11c所示,辅助开关管实现了ZCS开通,死区时间内,uR1下降至0,即在LB-R模式下,QR1、QR2总能实现ZVS开通和ZCS关断。
当变换器工作在R-LF模式,输出电压80V,输出功率266W的实验波形如图12所示。此时wn约为1。QR1开通之后,当iLr过0时,开始谐振。QR1关断后,uCr保持不变,iCr快速下降至iLm,iLr线性下降,当iLr重新过0时,开始下半周期的工作。由图12c可以看出,此时C2、C4在短时间内即可完成充放电过程,QR1、QR2能够轻易实现ZVS开通。
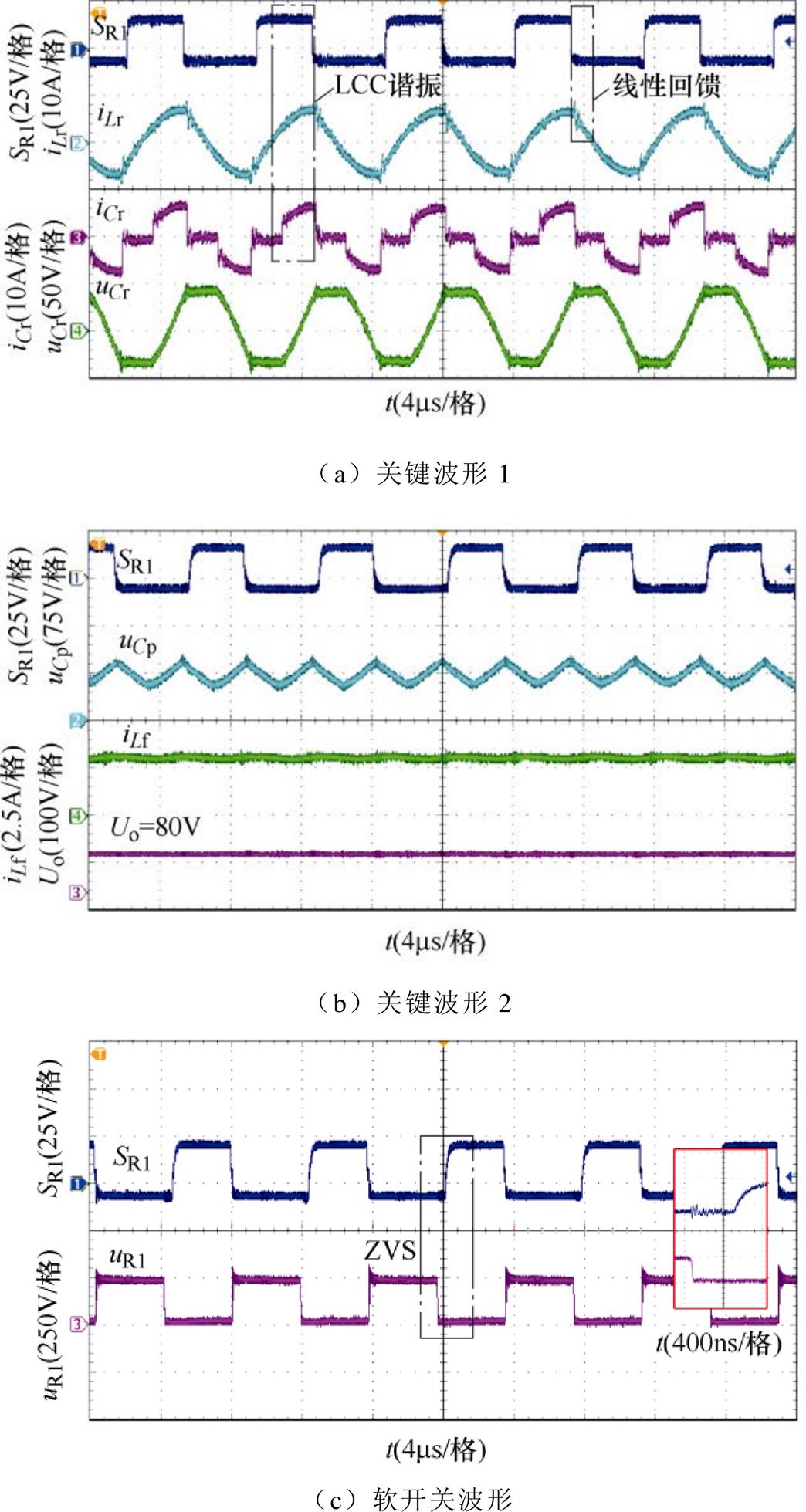
图12 R-LF模式主要波形(Uo=80V, Io=3.33A)
Fig.12 Main waveforms of R-LF mode (Uo=80V, Io=3.33A)
轻载工作主要波形如图13所示,输出电压150V,输出功率90W。此时变换器工作在LB-R模式,DL≈0.1。在Boost阶段,谐振腔环流极小,大部分谐振电流均参与能量传递。

图13 轻载工作主要波形(Uo=150V, Io=0.6A)
Fig.13 Main waveforms of light load operation (Uo=150V, Io=0.6A)
图14为变换器工作在CC模式下,负载切换的动态响应波形。此时输出电流保持为3.33A不变,当输出电压为80V,充电等效电阻Ro=24W,变换器工作在R-LF模式,QB1不工作。当负载切换至45W时,QB1开始工作,变换器进入LB-R模式。由于负载切换瞬间,输出电压不变,输出电流瞬间跌落至1.77A,随着电压上升,输出电流在短时间内稳定至3.33A。
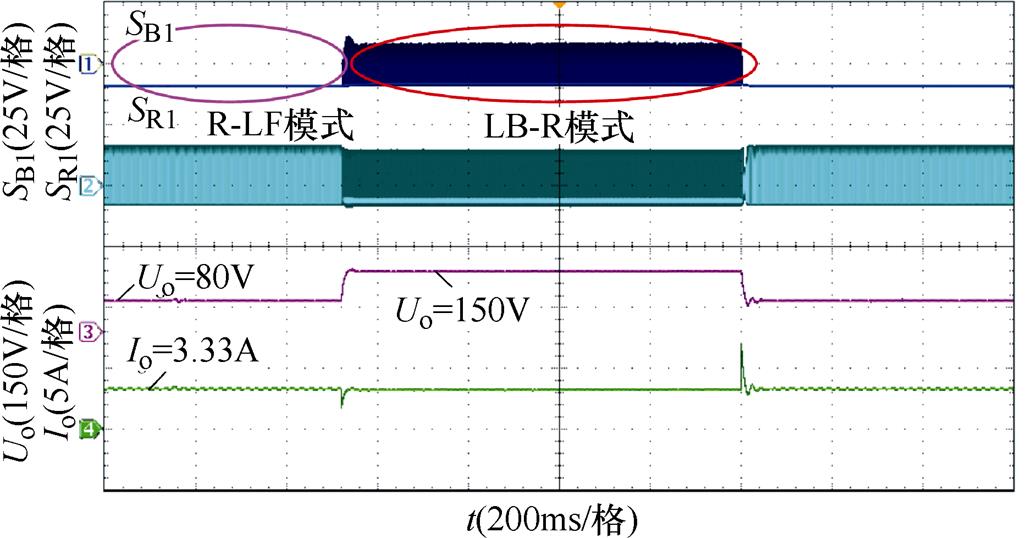
图14 CC模式动态响应波形
Fig.14 Dynamic response waveforms in CC mode
同理,当负载电阻切回时,输出电流出现一个约为6A的尖峰后逐渐稳定至3.33A。此处以大范围切换负载模拟充电等效电阻的变化,实际充电时由于充电等效电阻缓慢变化,故不会出现如实验所示的电流尖峰。
图15为变换器工作在CV模式的负载切换动态响应波形,此时变换器全程工作在LB-R模式。可以看出,辅助开关管占空比在轻载条件下明显小于工作在满载时的占空比。变换器能够在负载大范围切换时保持输出电压稳定。
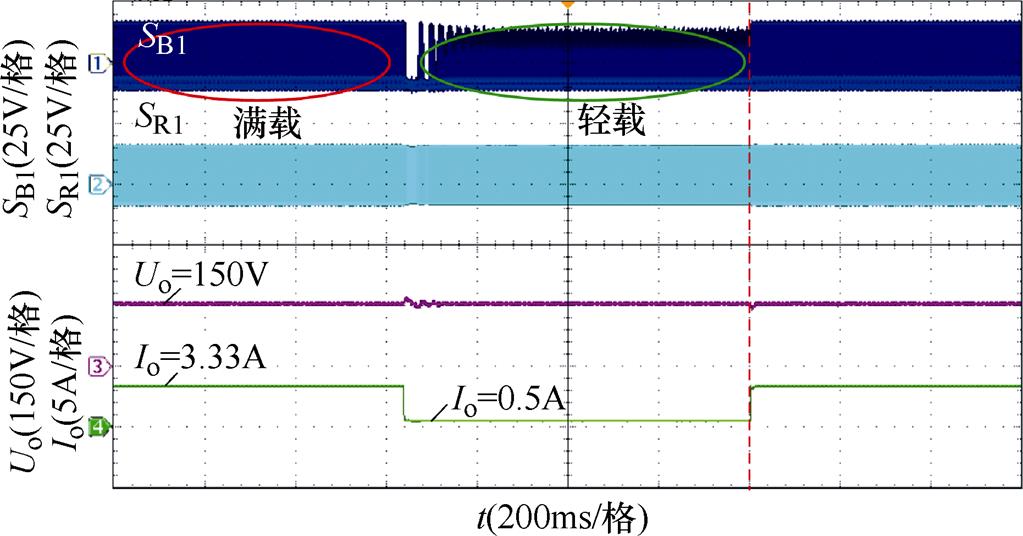
图15 CV模式动态响应波形
Fig.15 Dynamic response waveforms in CV mode
图16为实验样机与传统HBLCC谐振变换器的效率对比曲线。在全负载范围内,所提变换器相较传统HBLCC谐振变换器具有更高的效率,尤其是轻载工况下,所提变换器效率有显著提升。当变换器工作在R-LF模式,随着电压增益升高,输出功率增大,工作频率减小,效率逐渐升高;当进入LB-R模式,Boost桥臂开始工作,随着电压增益升高,辅助开关管关断损耗增大,效率略有下降。当电压增益接近1时,变换器工作在两模式的临界状态,具有最低的工作频率,且辅助开关管导通损耗与关断损耗最低,效率较高,最高为95.8%。
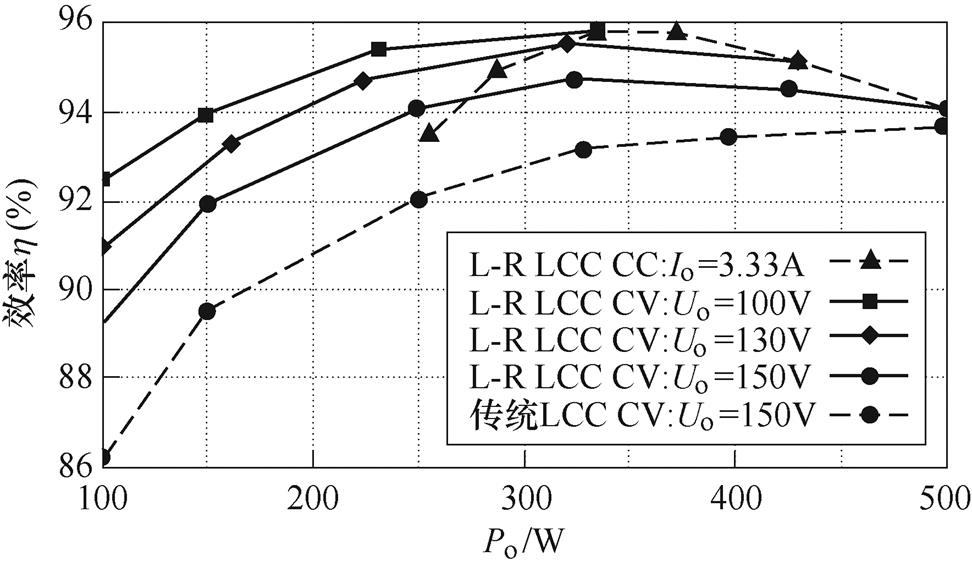
图16 实验样机效率曲线
Fig.16 Efficiency curves of experimental prototype
本文根据宽范围输出的应用要求,基于Boost复合调制原理提出了一种L-R复合调制的T型半桥LCC谐振变换器。实验结果表明,其在能够在全负载范围提高传统LCC谐振变换器的效率。主要优点如下:
1)在全负载范围内可实现无环流运行,避免了谐振腔环流损耗。
2)开关管电压应力较小,且具有全负载范围的软开关条件。
3)所采用的PFM-PWM方式易于实现,控制系统简单。
电路成本方面,所提变换器在传统HBLCC谐振变换器的基础上增加了一组桥臂,增加了一定的成本。但是两桥臂交替工作的机制减小了开关管的电流应力,故能够选择容量更小的开关器件,有利于缩减有源器件成本。综上所述,在可接受小幅提高成本的场合,所提变换器提供了一种有效的方案。
参考文献
[1] Ullah W, Khan F, Umair M. Design and optimization of segmented PM consequent pole hybrid excited flux switching machine for EV/HEV application[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 206-214.
[2] 冯兴田, 邵康, 崔晓, 等. 基于多模态切换的宽电压增益LLC谐振变换器控制策略[J]. 电工技术学报, 2020, 35(20): 4350-4360.
Feng Xingtian, Shao Kang, Cui Xiao, et al. Control strategy of wide voltage gain LLC resonant converter based on multi-mode switching[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4350- 4360.
[3] 张洪寅, 童朝南, 王泽庭. 基于临界模态的DCM- LCC谐振变换器的归一化分析与设计[J]. 电工技术学报, 2019, 34(1): 103-115.
Zhang Hongyin, Tong Chaonan, Wang Zeting. Nor- malized analysis and design of DCM-LCC resonant converter based on critical current mode[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(1): 103-115.
[4] 刘晋源, 吕林, 高红均, 等. 计及分布式电源和电动汽车特性的主动配电网规划[J]. 电力系统自动化, 2020, 44(12): 41-48.
Liu Jinyuan, Lü Lin, Gao Hongjun, et al. Planning of active distribution network considering characteristics of distributed generator and electric vehicle[J]. Auto- mation of Electric Power Systems, 2020, 44(12): 41-48.
[5] Steigerwald R L. A comparison of half-bridge resonant converter topologies[J]. IEEE Transactions on Power Electronics, 1988, 3(2): 174-182.
[6] Yang Rui, Ding Hongfa, Xu Yun. An analytical steady-state model of LCC type series-parallel resonant converter with capacitive output filter[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 328-338.
[7] Lin F, Huang Shiming, Yeh P, et al. DSP-based probabilistic fuzzy neural network control for Li-Ion battery charger[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3782-3794.
[8] 李红梅, 张恒果, 崔超. 车载充电PWM软开关DC- DC变换器研究综述[J]. 电工技术学报, 2017, 32(24): 59-70.
Li Hongmei, Zhang Hengguo, Cui Chao. Review of PWM soft-switching DC-DC converter for on-board chargers[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 59-70.
[9] 杨玉岗, 赵金升. 高增益对称双向LCLC谐振变换器的研究[J]. 电工技术学报, 2020, 35(14): 3007-3017.
Yang Yugang, Zhao Jinsheng. Normalized research on high-gain symmetric bidirectional CLC resonant converter[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3007-3017.
[10] 钱城晖, 钱挺. 辅助半桥调节的定频LLC谐振功率变换器[J]. 电工技术学报, 2019, 34(7): 1459-1467.
Qian Chenghui, Qian Ting. Fixed-frequency LLC resonant converter adjusted by auxiliary half- bridge[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1459-1467.
[11] Bhat A K S. Fixed-frequency PWM series-parallel resonant converter[J]. IEEE Transactions on Industry Applications, 1992, 28(5): 1002-1009.
[12] Czarkowski D, Kazimierczuk M K. Phase-controlled series-parallel resonant converter[J]. IEEE Transa- ctions on Power Electronics, 1993, 8(3): 309-319.
[13] Zheng Sanbo, Czarkowski D. Modeling and digital control of a phase-controlled series-parallel resonant converter[J]. IEEE Transactions on Industrial Elec- tronics, 2007, 54(2): 707-715.
[14] 陈一鸣, 许建平, 李兵兵, 等. CCVM-DCVM边界模式定频LCC谐振变换器设计[J]. 中国电机工程学报, 2018, 38(3): 850-860.
Chen Yiming, Xu Jianping, Li Bingbing, et al. Design of fixed frequency LCC resonant converter operating in CCVM-DCVM boundary mode[J]. Proceedings of the CSEE, 2018, 38(3): 850-860.
[15] 高铁峰, 张森, 赵剑锋, 等. LCC谐振变换器非对称移相控制及效率优化方法[J]. 电工技术学报, 2017, 32(8): 208-219.
Gao Tiefeng, Zhang Sen, Zhao Jianfeng, et al. Asymmetrical phase shift control and efficiency optimization strategy for LCC resonant converter[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 208-219.
[16] 高铁峰, 张森, 朱朱, 等. 自持移相LCC谐振变换器稳态分析及参数设计[J]. 电力自动化设备, 2016, 36(8): 122-129.
Gao Tiefeng, Zhang Sen, Zhu Zhu, et al. Steady-state analysis and parameter design for SSPSM-LCC resonant converter[J]. Electric Power Automation Equipment, 2016, 36(8): 122-129.
[17] 曹靖, 许建平, 陈一鸣, 等. PWM-PFM混合控制LCC谐振变换器研究[J]. 中国电机工程学报, 2018, 38(12): 3629-3637, 23.
Cao Jing, Xu Jianping, Chen Yiming. Study of PWM- PFM hybrid controlled LCC resonant converter[J]. Proceedings of the CSEE, 2018, 38(12): 3629-3637, 23.
[18] Chen Yiming, Xu Jianping, Wang Yao. A dual-carrier modulation technique for half-bridge resonant con- verter with wide soft-switching range[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 223-232.
[19] Li Zhenyu, Zhao Jun, Chen Zheng, et al. A design method for LCC resonant converter over wide load range with wide-range input and output[C]//IEEE PES Asia-Pacific Power and Energy Engineering Con- ference (APPEEC), Macao, China, 2019: 1-6.
[20] 林磊明, 许建平, 陈一鸣, 等. 一种宽范围ZVS定频LCC谐振变换器设计[J]. 中国电机工程学报, 2018, 38(16): 4846-4854, 4990.
Lin Leiming, Xu Jianping, Chen Yiming, et al. Fixed frequency LCC resonant converter design with wide zero voltage switching range[J]. Proceedings of the CSEE, 2018, 38(16): 4846-4854, 4990.
[21] Chen Yiming, Yao Shiying, Gou Jijun, et al. Analysis and design of half-bridge LCC resonant converter with Buck-Boost integration adopting dual carrier modulation[C]//2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 2019: 2190-2195.
T-Type Half-Bridge LCC Resonant Converter with L-R Composite Modulation
Abstract In the applications of wide output voltage range, the LCC resonant converter with frequency modulation has the disadvantage of wide switching frequency range, while the fixed frequency modulation has the disadvantage of narrow soft-switching range. In this paper, a T-type half-bridge LCC resonant converter with linear-resonance (L-R) composite modulation is proposed. The energy storage stage is added to the traditional resonant mode, which makes the resonant current show linear and resonant changes in one cycle. It can improve the voltage gain, and has the characteristics of soft switching and no circulating current in the full load range. The proposed converter operates in resonant-linear feedback (R-LF) and linear boost-resonant (LB-R) modes by adopting PFM-PWM composite modulation, and can achieve wide voltage gain range with narrow switching frequency. The switching frequency is fixed in the light load condition, which improves light load efficiency. In this paper, the operating principle was introduced in detail, and the expression of voltage gain was derived. The design steps based on constant current and constant voltage charging were given. Finally, an experimental prototype was built, and the results proved the correctness of the theoretical analysis.
keywords:Converter, LCC resonant, wide-range output, CC-CV charging
DOI: 10.19595/j.cnki.1000-6753.tces.201618
中图分类号:TM46
袁义生 男,1974年生,博士,教授,主要研究方向为电力电子系统及其控制。E-mail: cloudstone_yuan@aliyun.com(通信作者)
易尘宇 男,1998年生,硕士研究生,主要研究方向为电力电子与电力传动。E-mail: yichenyu0218@foxmail.com
收稿日期 2020-12-09
改稿日期 2021-04-29
国家自然科学基金资助项目(52067007)。
(编辑 陈 诚)