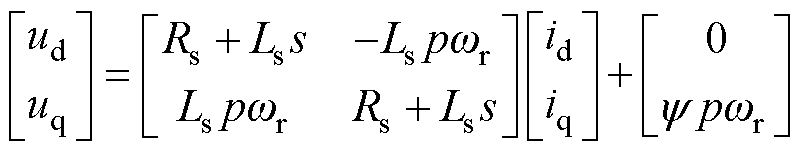 (1)
(1)摘要 由于滑模观测器的固有抖振及控制算法延迟、死区效应等非理想因素的影响,估计反电动势信号包含的谐波难以完全消除,已成为影响系统控制精度的主要因素。为了提升表贴式永磁同步电机的转子位置与转速观测精度,该文提出一种宽频带同步基频提取滤波器,提取估计反电动势基波。在此基础上,提出宽频带同步基频提取滤波器(WSFEF)与锁频环结合的信号处理方法,锁频环(FLL)的应用实现了WSFEF跟踪频率的自适应。构造基于WSFEF-FLL-锁相环(PLL)的位置与转速估计方法,将其应用到滑模控制中,增强了对谐波的抑制能力,提高了转子位置和转速估计的动态性能。仿真和实验验证了所提方法的可行性和有效性。
关键词:高速表贴式永磁同步电机 位置与转速估计 宽频带同步基频提取滤波器 锁频环 滑模观测器
无位置传感器的高速表贴式永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)系统因具有成本低、鲁棒性高等优点,而得以应用广泛[1-3]。实时获得精确的转子位置信息,保证定子绕组电流与转子位置电角度保持同步,是实现永磁同步电机精确控制的关键[4]。
在电机中高速区控制,利用反电动势估计转子角度与转速是无位置传感器控制的首选方法[5-6],其中,滑模观测器(Sliding Mode Observer, SMO)由于鲁棒性好、响应快和算法简单等优点而备受关注[7-9]。
传统滑模的抖振不能完全消除,会引入高频谐波[10]。采用二阶滑模理论设计的观测器,可以在保持鲁棒性的同时削弱抖振、减小位置和转速估算偏差[11-12]。但对于表贴式永磁同步电机,永磁体间存在的间隙,也会使反电动势中存在谐波[13]。另外,控制算法延迟、死区效应、负载扰动等非理想因素也会导致估计反电动势信号中包含谐波,影响位置与转速的检测精度[14]。
已有研究中提出相应的消除估计误差的方法。文献[15]利用自适应陷波器(Adaptive Notch Filter, ANF)-锁相环(Phase-Locked Loop, PLL)消除特定次谐波,但剩余谐波仍然影响位置估计的精度[16]。同步参考坐标(Synchronous Reference Frame, SRF)- PLL能实现电网电压基波正序分量的准确跟踪,然而不适用于信号电压存在谐波的场合[17]。文献[18]采用同步提取滤波器(Synchronous Frequency Extractor, SFE)-PLL法对霍尔信号谐波分量进行滤除,但SFE的带宽会随着基频的升高而减小,对输入信号频率依赖性强,明显影响系统的动态特性。
当电机基频较高、而控制器采样频率较低时,滑模抖振对观测精度的影响比较明显[19],引入锁相环削弱抖振的影响。利用锁相环可以较为准确地估算转子位置,但估计的转速中含有较高噪声。文献[20]采用扩展卡尔曼滤波器对转速进行估计,计算较为复杂,且实时性较差。文献[21]应用锁频环(Frequency-Locked Loop, FLL)后,频率检测响应较好,能准确获取电网电压基频。文献[22]将FLL应用到低速感应电机的转速估计中,效果良好。
本文提出一种宽频带同步基频提取滤波器(Wideband Synchronous Fundamental-Frequency Extraction Filter, WSFEF),当WSFEF中心频率与输入信号频率相等时,能实现基波提取。在此基础上,提出WSFEF-FLL结合的信号处理方法,FLL的应用实现了WSFEF跟踪频率的自适应,添加归一化频率与幅值自适应环节,进一步消除输入信号幅值、频率变化对频率检测时间的影响。构造基于WSFEF- FLL-PLL的转子位置和转速估计方法,将其应用到永磁同步电机的滑模无位置控制系统中,能有效滤除噪声与谐波,并提高位置与转速的观测精度。通过仿真和实验验证了所提方法的有效性。
1.1.1 PMSM建模
表贴式永磁同步电机(Surface PMSM, SPMSM)在dq坐标系下的电压模型可以表示为
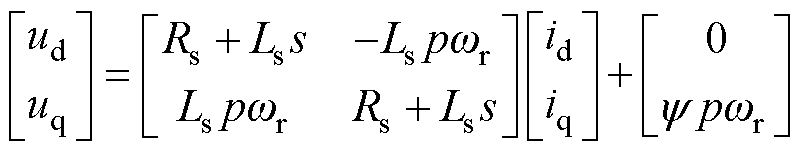 (1)
(1)式中,ud、uq分别为d、q轴定子电压;id、iq分别为d、q轴定子电流;Ls为定子相电感;Rs为定子相电阻;p为电机极对数;wr为转子机械角速度;y 为转子磁链。
将式(1)转换为ab坐标系下的电压方程为
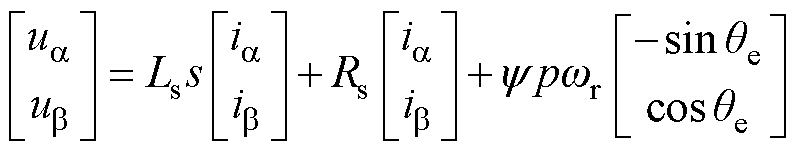 (2)
(2)式中,ua、ub 分别为a、b 轴电压分量;ia、ib 分别为a、b 轴电流分量;qe为转子电角度。
1.1.2 转子位置估计
滑模控制具有响应快、鲁棒性强的优点,可用于观测系统的未知变量,称为滑模观测器。SMO可应用于永磁同步电机无位置传感器驱动系统,通过构造观测器来生成转子位置估计的误差修正,进而计算出电机转子位置。图1为传统滑模无位置控制框图,其中符号函数被用作开关函数,低通滤波器(Low Pass Filter, LPF)用来消除开关抖振效应,相位补偿环节对LPF造成的相位延迟进行补偿。
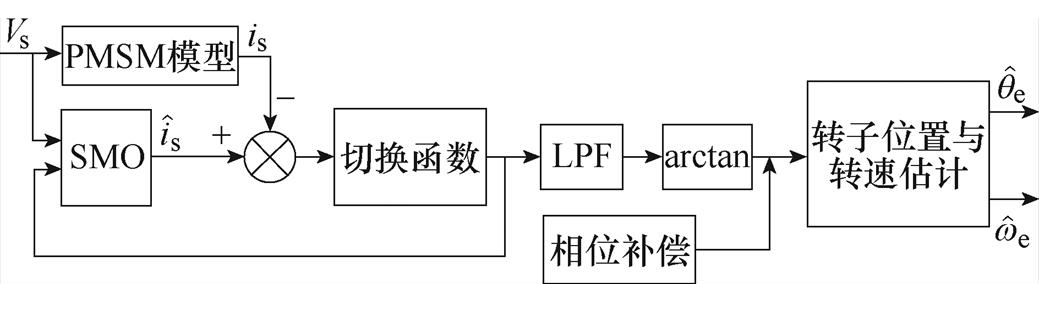
图1 传统滑模观测器控制框图
Fig.1 Conventional scheme of SMO
SMO基于PMSM的反电动势模型表示为
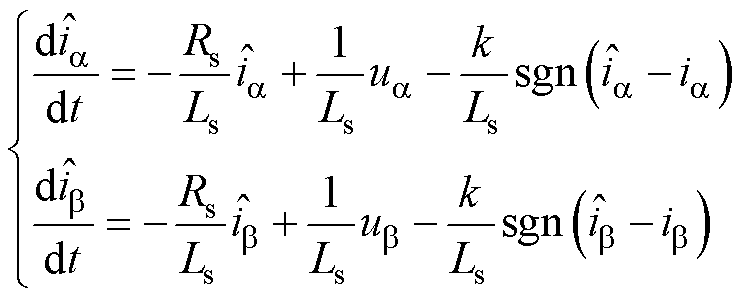 (3)
(3)式中,“ ”为估计值;k为滑模增益;sgn为符号函数。
”为估计值;k为滑模增益;sgn为符号函数。
滑模面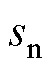 可以表示为
可以表示为
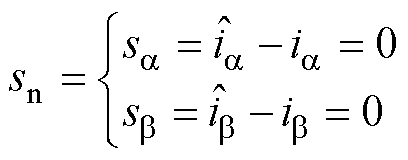 (4)
(4)式中,sa、sb 分别为a、b 轴电流估计误差。由式(2)、式(3),得动态估计偏差方程为
 (5)
(5)
式中,ea、eb 分别为a、b 轴反电动势;k>max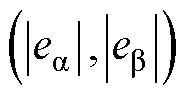 ,可以保证电流误差方程是渐近稳定的[20],这意味着在有限时间内滑模运动能收敛到
,可以保证电流误差方程是渐近稳定的[20],这意味着在有限时间内滑模运动能收敛到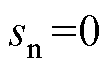 ,此时有
,此时有
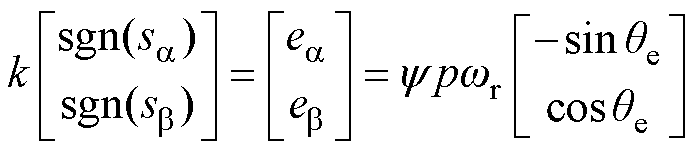 (6)
(6)从式(6)中可以看出,由于a、b 轴电流误差的高频开关信号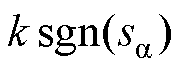 、
、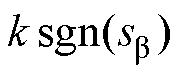 不连续,估算反电动势存在高频干扰信号,需要使用低通滤波器将高频干扰滤除,高频开关信号经过LPF处理后的数值记作
不连续,估算反电动势存在高频干扰信号,需要使用低通滤波器将高频干扰滤除,高频开关信号经过LPF处理后的数值记作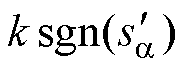 、
、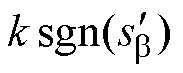 ,估计反电动势表示为
,估计反电动势表示为
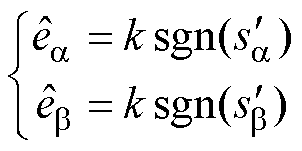 (7)
(7)
计算得估计转子位置电角度为
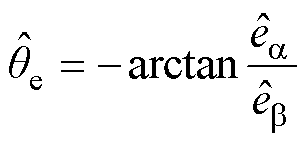 (8)
(8)在实际应用中,受延时的影响,包括控制延时和采样延时、空间延时、系统惯性和离散系统本身的限制等,开关频率不是无限高的。系统状态变量只能在稳定点附近切换,而不能稳定在平衡点,引起SMO的抖振问题,其根本原因是非线性控制函数不能实现其理想的切换,从而导致估计反电动势含有谐波分量。除此之外,由于死区效应的影响,在电压给定与实际值间引入电压差,会使反电动势发生畸变。另外,SPMSMs永磁体间气隙的存在,也会引起反电动势失真。
由于上述原因,估计反电动势总是包含大量的谐波,因此需要滤波器来进行处理,获得平滑的反电动势波形。通常利用转子角速度与LPF截止频率之比的反正切计算得相位用于补偿传统低通滤波器产生的相位延迟。但转子角速度是由转子位置信号估算得到的,反正切计算无法实现精确的相位补偿,转子位置的观测精度较差。
根据上述分析,SMO估计的原始反电动势含有大量的谐波分量,很难直接应用于永磁同步电机驱动,本文提出一种WSFEF,其结构如图2所示。其中,X(t)为输入信号,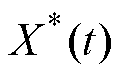 为WSFEF处理后的信号,
为WSFEF处理后的信号,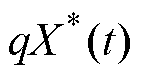 为滞后
为滞后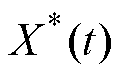 90°的正交信号,e 为滤波器增益,w0为频率检测单元对输入信号的估计频率,a(t)为X(t)与e、w0的乘积。
90°的正交信号,e 为滤波器增益,w0为频率检测单元对输入信号的估计频率,a(t)为X(t)与e、w0的乘积。

图2 宽频带同步基频提取滤波器模块
Fig.2 Structure of the WSFEF
根据图2,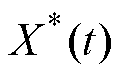 可以表示为
可以表示为
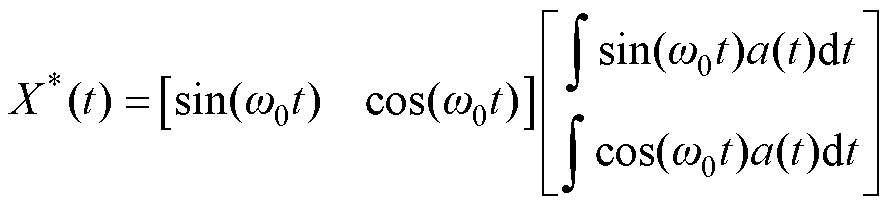 (9)
(9)式(9)的导数可以表示为
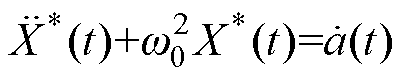 (10)
(10)
得a(t)到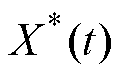 之间的传递函数G1(s)为
之间的传递函数G1(s)为
 (11)
(11)WSFEF的传递函数G(s)、Q(s)分别为
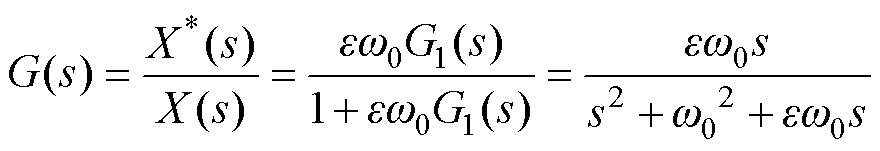 (12)
(12)
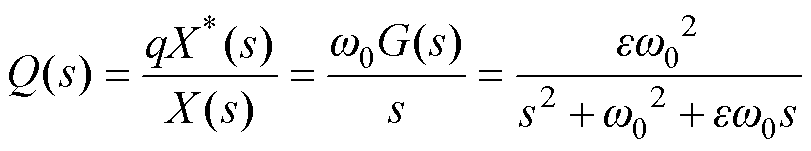 (13)
(13)由式(12)可得G(s)的品质因数Q为
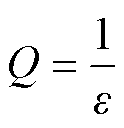 (14)
(14)
文献[17]中提出的SFE品质因数Q1为
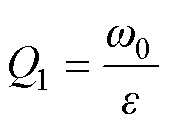 (15)
(15)与式(15)相比,Q<Q1,说明WSFEF具有较宽的通频带,使系统更容易稳定。
WSFEF的伯德图如图3所示。当WSFEF跟踪频率与输入信号频率一致(w0=w)时,WSFEF处理信号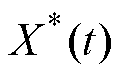 相对于输入信号
相对于输入信号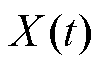 既无幅值衰减,也无相位滞后,实现了对输入信号的基波提取。
既无幅值衰减,也无相位滞后,实现了对输入信号的基波提取。
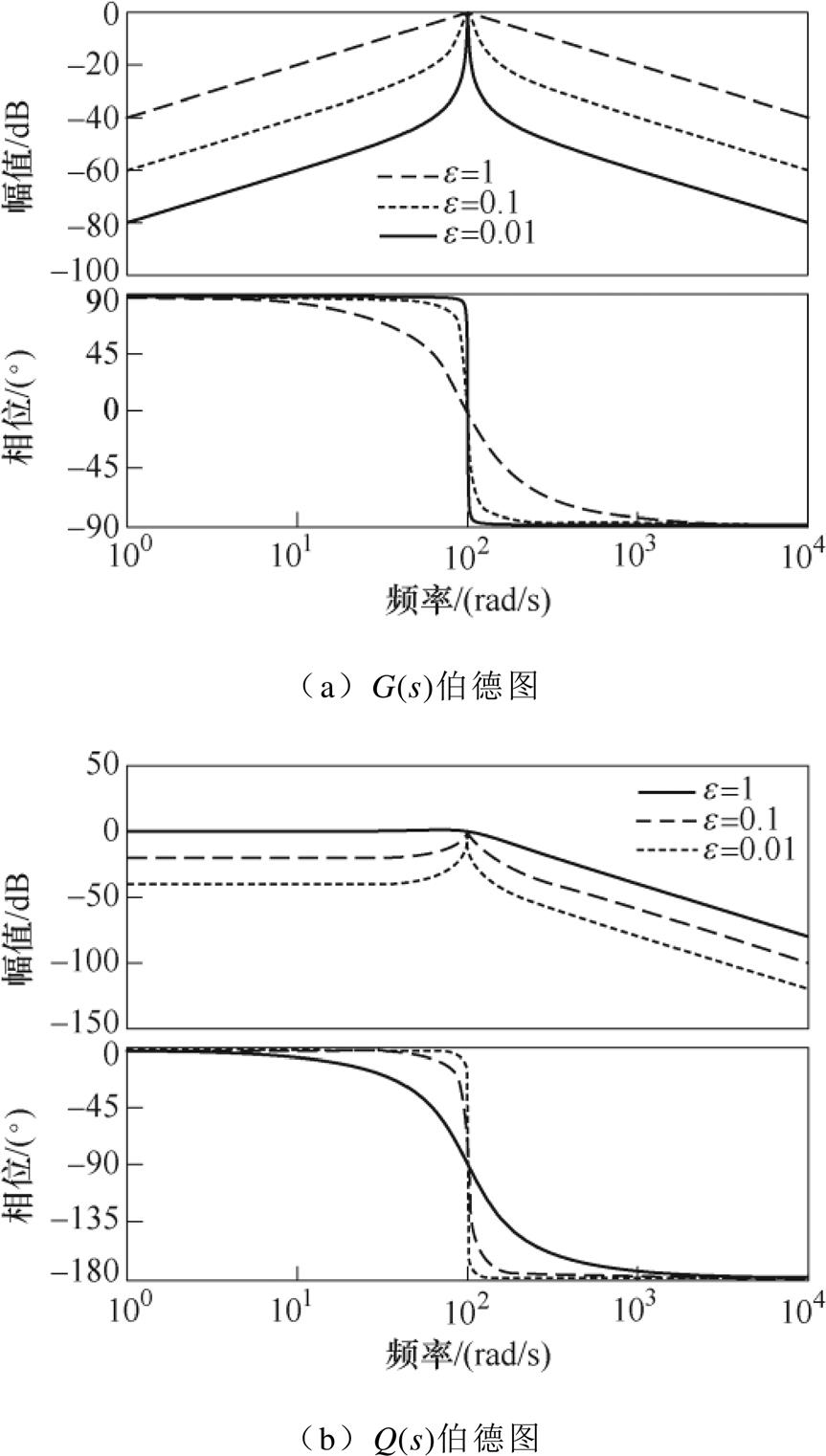
图3 WSFEF伯德图
Fig.3 Bode diagram of WSFEF
可见,WSFEF的滤波性能是由滤波器增益e 与跟踪频率w0决定的。当输入信号频率固定,即w0为固定值时,e 越小,滤波效果越好,但动态响应时间就越长。对于e 值的选择,需要权衡WSFEF的滤波效果与响应速度,一般取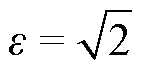 ,这也与WSFEF品质因数Q=1/e =0.707的要求一致。
,这也与WSFEF品质因数Q=1/e =0.707的要求一致。
因此,e 选定后,提升WSFEF性能的关键是提高跟踪频率w0的准确性,本文采用锁频环提升估计信号频率的准确度。基于WSFEF-FLL信号处理方法结构框图如图4所示。可知,该信号处理方法是一个闭环控制,包括WSFEF与频率检测单元两个部分;WSFEF输出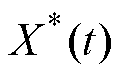 、
、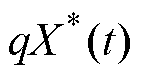 与
与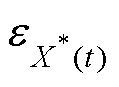 ,作为频率检测单元FLL的输入,同时锁频环输出估计频率w0反馈到滤波器输入端,构成完整的闭环控制。其中,g 为锁频环增益,
,作为频率检测单元FLL的输入,同时锁频环输出估计频率w0反馈到滤波器输入端,构成完整的闭环控制。其中,g 为锁频环增益,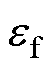 为频率估计误差,定义为滤波器估计误差
为频率估计误差,定义为滤波器估计误差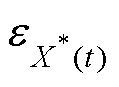 与正交分量
与正交分量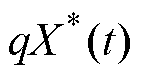 的乘积。
的乘积。
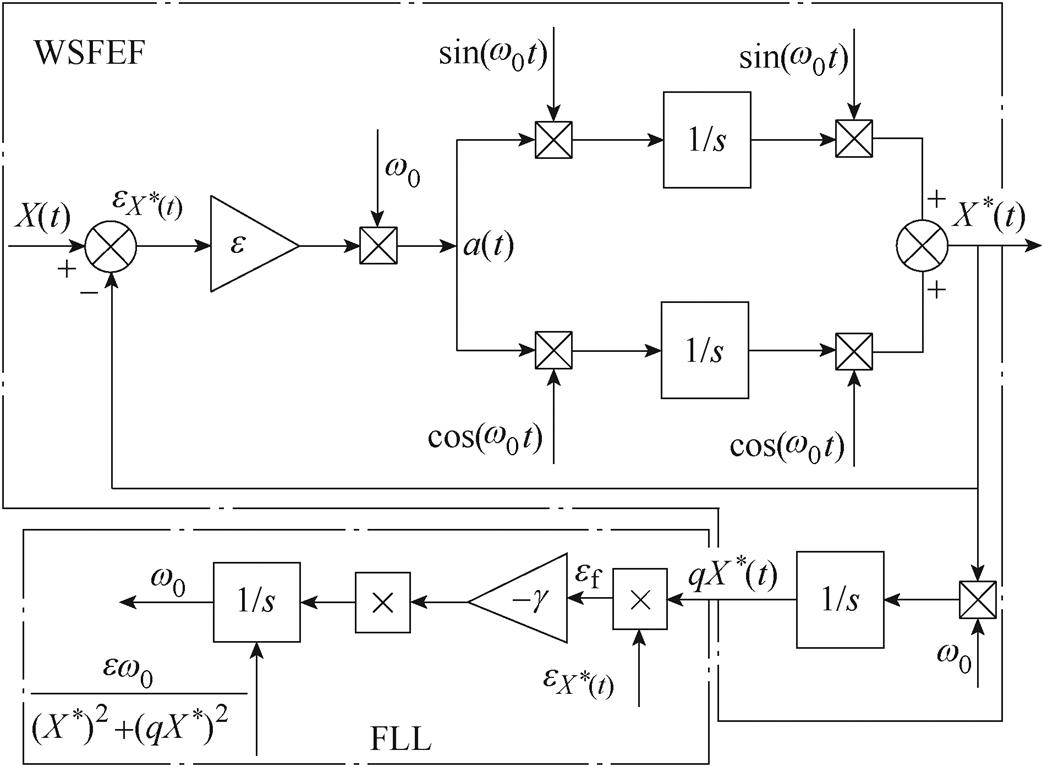
图4 WSFEF -FLL信号处理方法结构框图
Fig.4 Structure of signal processing method of WSFEF-FLL
当锁频环输出估计频率与输入信号基频一致(w0=w)时, ,
,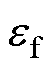 =0;当FLL估计频率大于实际输入基频(w0>w)时,
=0;当FLL估计频率大于实际输入基频(w0>w)时,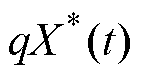 与
与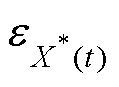 同相,
同相,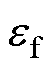 >0;当FLL估计频率低于输入信号基频(w0<w
>0;当FLL估计频率低于输入信号基频(w0<w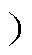 时,
时,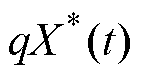 与
与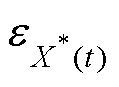 反相,
反相,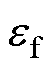 <0。本文采用一个负增益-g 的放大器和积分控制器,实现锁频环的自适应跟踪输入信号基频。另外,锁频环中加入了归一化单元,以消除输入信号的幅值、频率变化对频率检测时间的影响。
<0。本文采用一个负增益-g 的放大器和积分控制器,实现锁频环的自适应跟踪输入信号基频。另外,锁频环中加入了归一化单元,以消除输入信号的幅值、频率变化对频率检测时间的影响。
综上分析,滤波器增益e 选定后,提升WSFEF性能的关键是提高锁频环估计输入信号基频的准确性,即锁频环增益g 的选择。g 的取值根据FLL的动态性能与抗干扰能力来权衡[22],本文取g =30。
由于永磁同步电机两相反电动势的频率相等,可综合利用两个WSFEF模块的频率误差信息,只使用一个频率检测单元FLL进行频率估计,其具体结构框图如图5所示。
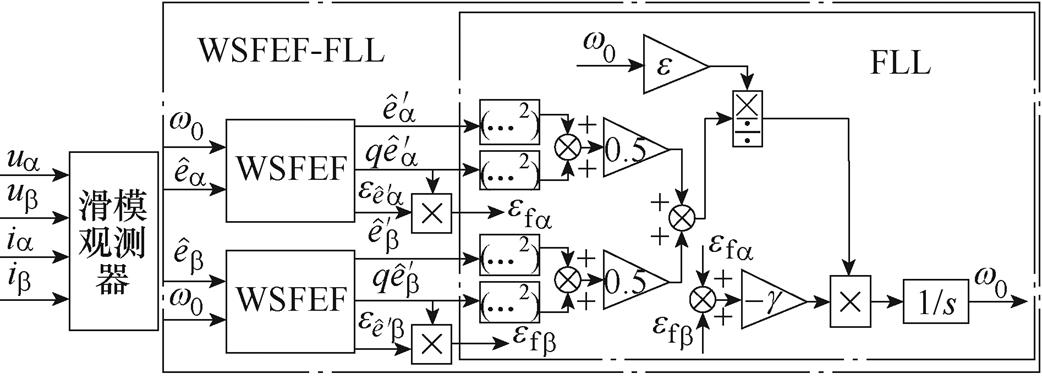
图5 双WSFEF-FLL结构框图
Fig.5 Structure of dual WSFEF-FLL
根据以上的滑模观测器及WSFEF-FLL信号处理方法特性的分析,构造了基于WSFEF-FLL-PLL的转子位置与转速估计方法,结构框图如图6所示。

图6 基于WSFEF-FLL-PLL转子位置与转速估计框图
Fig.6 Sensorless scheme of WSFEF-FLL-PLL diagram
如图6所示,三相电流经坐标变换得到α、β轴电流iα、iβ,与电流环输出的uα、uβ,共同作为SMO的输入,输出估计反电动势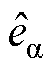 、
、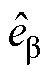 ;再经过WSFEF- FLL模块处理,估算出电机转子电角频率
;再经过WSFEF- FLL模块处理,估算出电机转子电角频率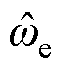 (rad/s),同时提取估计反电动势的基波信号
(rad/s),同时提取估计反电动势的基波信号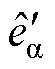 、
、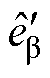 。其中,
。其中,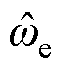 经过比例换算,得电机转子转速
经过比例换算,得电机转子转速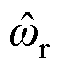 (r/min),用于电机的转速闭环控制;经过正交锁相环处理得到电机转子电角度
(r/min),用于电机的转速闭环控制;经过正交锁相环处理得到电机转子电角度 ,用于矢量控制的坐标变换。
,用于矢量控制的坐标变换。
由2.2节分析可知,经过WSFEF-FLL处理后的反电动势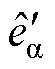 、
、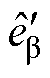 与滑模观测器估计值
与滑模观测器估计值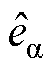 、
、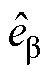 相位相同,而估计反电动势
相位相同,而估计反电动势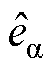 、
、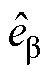 与电机实际反电动势
与电机实际反电动势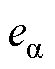 、
、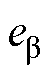 间也无相位差,因此
间也无相位差,因此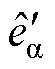 、
、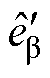 与
与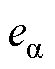 、
、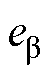 间不存在相位差。由此可得,WSFEF-FLL-PLL估计位置信号
间不存在相位差。由此可得,WSFEF-FLL-PLL估计位置信号 与电机实际位置qe之间不存在均值误差。
与电机实际位置qe之间不存在均值误差。
用于测试的高速永磁同步电机(High-Speed PMSM, HSPMSM)参数设置见表1。在Simulink中建立了采用WSFEF-FLL-PLL转子位置和转速估计方法的HSPMSM驱动系统仿真模型。
表1 高速永磁同步电机样机参数
Tab.1 The parameters of the testing HSPMSM

参 数数 值 额定功率P0/kW2.5 额定转速n/(r/min)15 000 等效相电阻Rs/W20.5×10-3 等效相电感Ls/H1.6×10-4 极对数p5 直流母线电压Udc/V120 开关频率fs/kHz40
电机运行在6 500r/min时,使用滑模观测器对反电动势进行观测,采用LPF-PLL、WSFEF-PLL法以及本文提出的WSFEF-FLL-PLL处理方法对估计反电动势进行处理,比较处理得到的反电动势、估计转速以及转子位置对比信号。
图7分别为三种方法处理后的估计反电动势仿真结果,与LPF-PLL相比,WSFEF-PLL处理后的反电动势总谐波畸变率(Total Harmonic Distortion, THD)含量明显降低,正弦度有了明显提高;应用WSFEF-FLL-PLL后,反电动势中高次谐波被滤除,波形更平滑,THD含量进一步降低,可以看出,应用FLL后提升了WSFEF的滤波性能,WSFEF-FLL- PLL信号处理方法的控制精度更高。
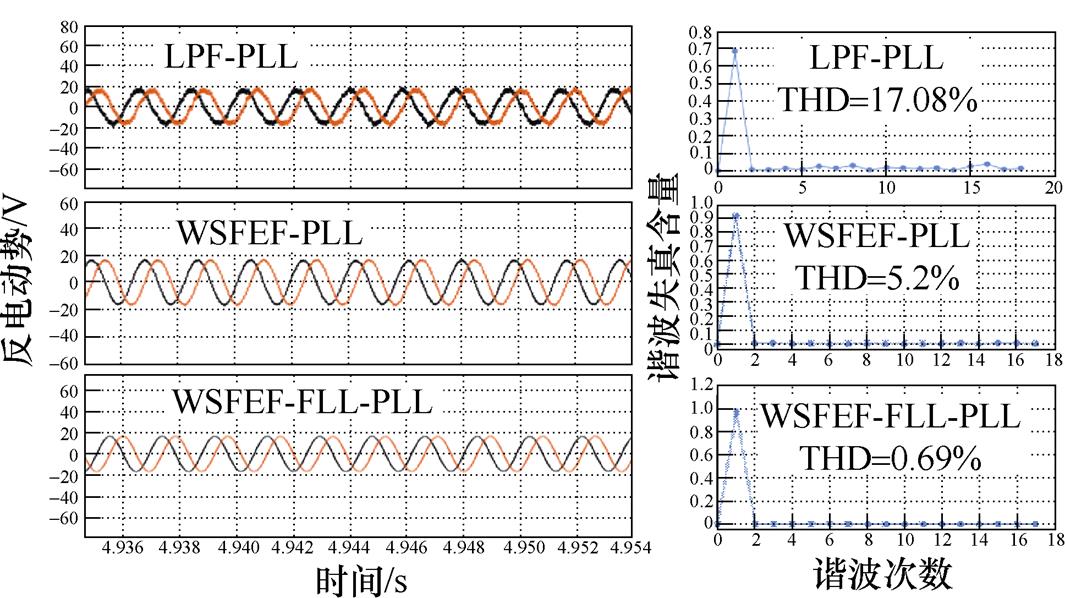
图7 估计反电动势仿真结果对比
Fig.7 Comparison of the estimated back EMF
分别采用三种信号处理方法得到的稳态位置对比波形如图8所示,LPF-PLL估计位置存在约19.5°的观测误差,WSFEF-PLL估计角度误差约为8.0°,WSFEF-FLL-PLL位置估计误差得到了有效的减小,稳态误差约2.3°。
图9给出三种方法得到的转速估计误差对比波形,可以看出,利用锁相环估计的转速中含有较高噪声,转速波动较大,而WSFEF-FLL-PLL方法估算的最大稳态误差为33r/min,波动较为平稳。
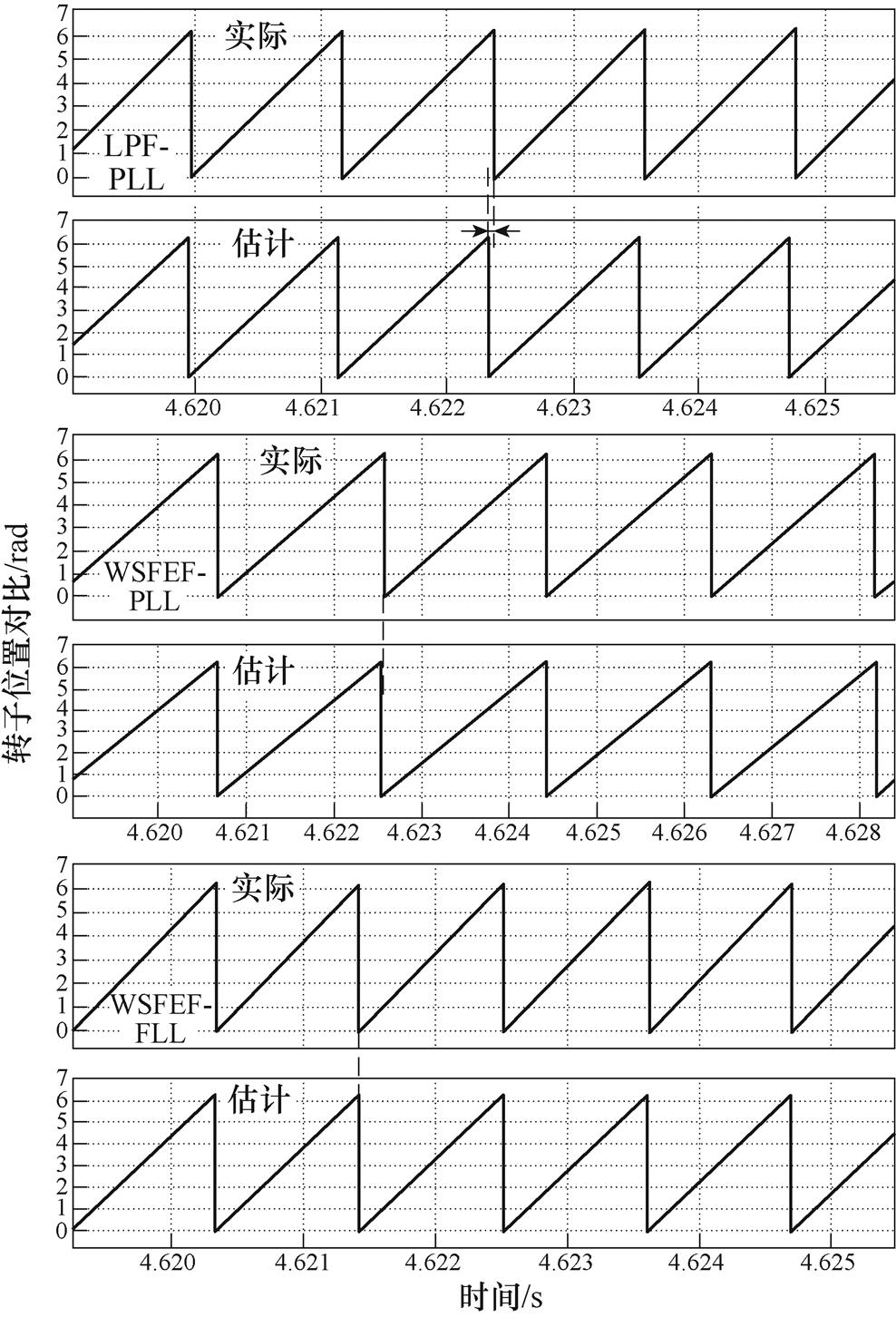
图8 稳态位置估计对比
Fig.8 Comparison of steady estimated rotor position

图9 稳态转速估计误差对比
Fig.9 Comparison of steady speed estimation error
为了检验采用WSFEF-FLL-PLL的滑模观测器无位置控制策略在0.1N·m恒负载条件下,转速变化时的性能,设置电机转速由783r/min匀速增加到6 500r/min,动态转速与位置误差波形分别如图10、图11所示。从图10可以看出,随着转速增加,LPF- PLL无论在稳态还是动态过程都存在较大波动;WSFEF-PLL对噪声抑制效果一般,最大动态转速估计误差为160r/min;WSFEF-FLL-PLL法处理的稳态速度波动小,动态时的最大误差减小到40r/min,WSFEF-FLL-PLL输出估计转速更平稳,对谐波和噪声的抑制能力更强。
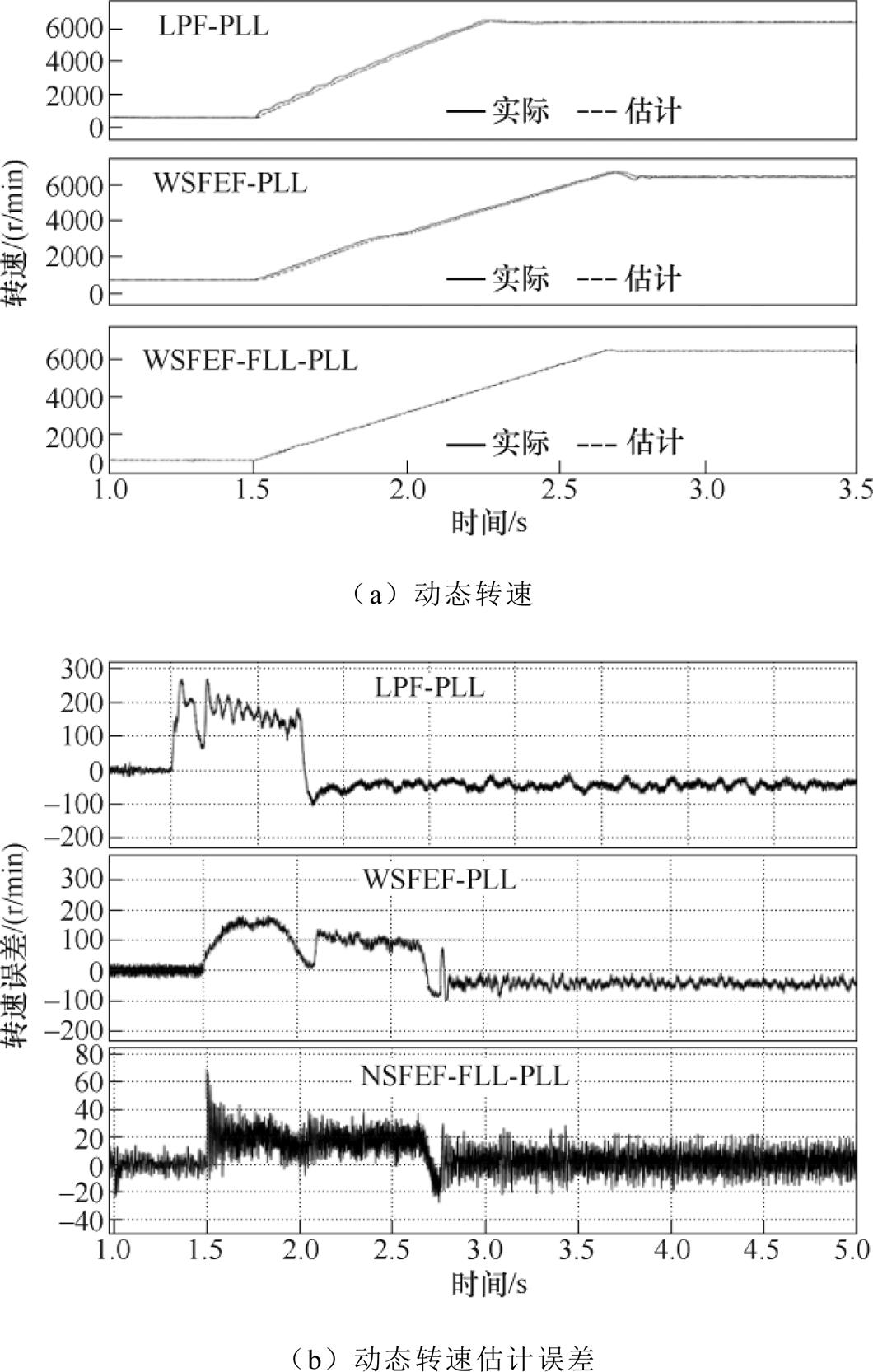
图10 动态转速估计
Fig.10 Dynamic speed estimation results

图11 动态位置估计误差
Fig.11 Dynamic rotor position estimation error
从图11的位置误差对比波形可以看出,在动态过程中,LPF-PLL会引入相位延迟,存在一定的相位误差;WSFEF处理后都能对转子位置进行有效跟踪,WSFEF-FLL-PLL的滤波精度更高,转子电角度估计误差较小。随着转速的提高,为了提升锁相环的跟踪性能,PLL的PI参数需要相应地增大,从而会放大反电动势包含的转子位置中的噪声,因此估计转子位置纹波随着转速升高而增加,但仍在可接受范围内。
仿真初步验证了本文提出的WSFEF-FLL-PLL的转子位置与转速估计方法在稳态和动态过程中的控制精度较高。
在一台表贴式永磁同步电机上对本文提出的方法进行实验验证,电机参数见表1。驱动系统采用id=0的矢量控制,DSP选用TMS320F28379D作为主控芯片,位置传感器选择两对极的旋转变压器TS2224N105E102安装在电机定子上,测量转子位置和转速。驱动系统实验平台如图12所示。

图12 永磁同步电机驱动系统实验平台
Fig.12 Experimental platform of PMSM drive system
3.2.1 稳态实验
当电机空载运行在11 000r/min时,SMO用来观测电机反电动势,分别采用LPF-PLL、WSFEF- PLL与WSFEF-FLL-PLL法来处理反电动势,实验性能如图13所示。
图13a给出11 000r/min空载稳态时的估计反电动势波形,与LPF-PLL相比,WSFEF-PLL处理后正弦度有了明显提高,WSFEF-FLL-PLL将反电动势高次谐波分量滤除,正弦度有了进一步的提高。WSFEF-PLL处理方法中,PLL估计频率含有较大纹波,作为WSFEF的跟踪频率,会影响滤波性能,从而输出估计反电动势存在失真。而FLL估计信号频率精度较高,即提升了WSFEF跟踪频率w0的准确性,从而提升WSFEF性能,反电动势对比波形与理论分析一致。
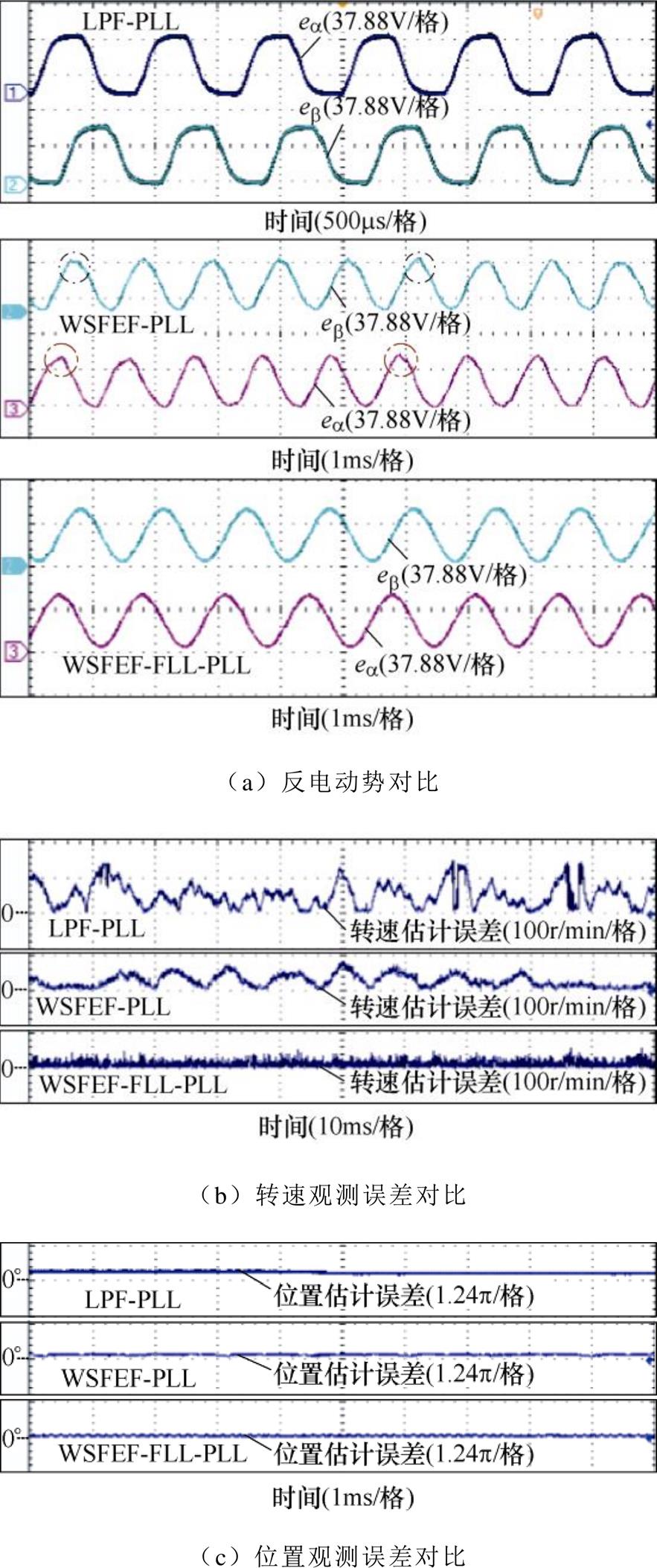
图13 稳态转速实验对比
Fig.13 Comparison of steady state experimental results
由图13b可知,转速恒定过程中,使用LPF-PLL法,转速中含有很高的噪声,最大稳态观测误差达145r/min;WSFEF-PLL对噪声的抑制效果一般,最大估计误差为80r/min;WSFEF-FLL-PLL输出的最大稳态估计误差控制在0.36%(40r/min)。
转子位置估计误差比较结果如图13c所示,使用LPF-PLL法的估计角度误差约为21.3°;WSFEF- PLL对转子位置能进行有效跟踪,由于处理后的反电动势中仍存在高次谐波,估计转子位置存在一定的相位滞后;WSFEF-FLL-PLL最大位置估计误差为2.1°左右,均值误差得到了有效的消除。
3.2.2 动态实验
为了测试所提出的基于WSFEF-FLL-PLL的转子位置与转速估计方法应用在滑模观测器中的动态性能,设定SPMSM在0.149N·m恒定负载,转速由4 000r/min阶跃到8 000r/min情况下进行实验。采用LPF-PLL、WSFEF-PLL与本文的WSFEF-FLL- PLL处理后的实验性能分别如图14中所示。
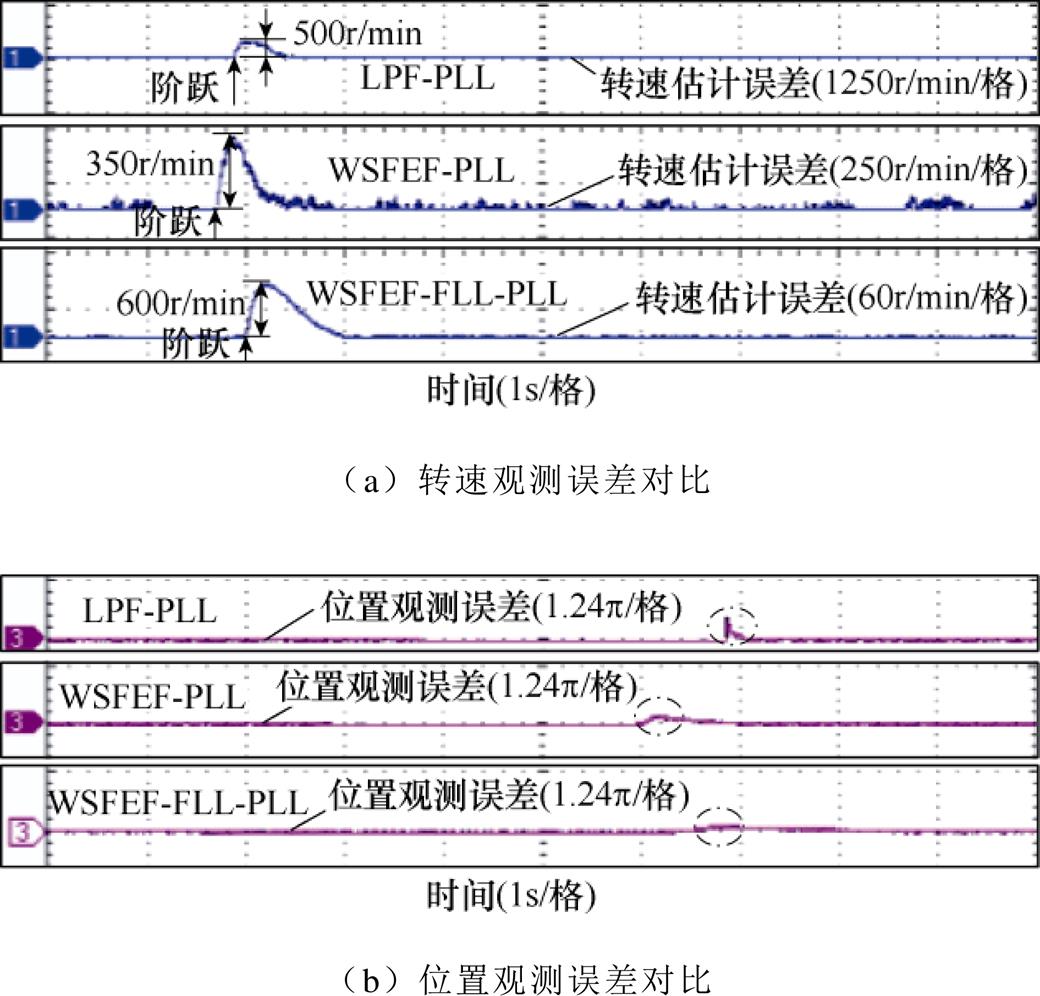
图14 0.149N·m恒负载条件下转速突变实验对比
Fig.14 Comparison of experimental results under variable speed at 0.149N·m load condition
图14a给出了滑模观测器结合LPF-PLL、WSFEF- PLL与WSFEF-FLL-PLL在恒定负载下,转速变化测试时转速估计误差结果。由图14a可知,采用了WSFEF-FLL-PLL信号处理方法的无位置控制策略,动态响应良好,转速变化过程平稳,FLL输出的最大转速估计误差控制在60r/min,估计转速能与实际波形较好地拟合。转速阶跃时的转子位置估计误差实验波形如图14b所示。随着转速增加,WSFEF- FLL-PLL输出的转子位置误差并无明显升高,动态性能较好,同时估计转子位置纹波随着转速升高略有增加,与理论分析一致。
实验结果充分验证了基于WSFEF-FLL-PLL的无位置传感器控制方案在稳态和动态下的有效性及精确性。
本文提出一种宽频带同步基频提取滤波器,在此基础上介绍了WSFEF-FLL信号处理方法,并将其引入基于SMO的HSPMSM无位置传感器控制系统中,用于消除估计反电动势中的谐波,构造WSFEF-FLL-PLL模块计算转子位置和转速。仿真和实验验证了基于WSFEF-FLL-PLL的无传感器控制方案的稳态与动态性能,与现有算法相比,该方法具有以下优点:
1)本文提出的WSFEF可以实现无相位延迟的基波提取,滤波后幅值无衰减。它具有较宽的带宽、更容易稳定、应用范围更广。
2)由WSFEF和FLL组成的信号处理方法,可以精确获得输入信号的基波频率,控制精度更高。
3)所提出的WSFEF-FLL-PLL模块,相比其他算法,转子位置和转速的估计精度更高,稳态和动态时波动更小,对谐波和噪声的抑制能力更强,从而实现了更高的系统控制精度。
参考文献
[1] 吴春, 陈科, 南余荣, 等. 考虑交叉饱和效应的变角度方波电压注入永磁同步电机无位置传感器控制[J]. 电工技术学报, 2020, 35(22): 4678-4687.
Wu Chun, Chen Ke, Nan Yurong, et al. Variable angle square-wave voltage injection for sensorless control of PMSM considering cross-saturation effect[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(22): 4678-4687.
[2] 刘伟峰, 王慧贞, 路通, 等. 六状态提前角度控制的电励磁双凸极电机带载起动方法: CN110212820A[P]. 2019-09-06.
[3] Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Elec- trical Machines and Systems, 2020, 4(2): 151-160.
[4] 陶彩霞, 赵凯旋, 牛青. 考虑滑模抖振的永磁同步电机模糊超螺旋滑模观测器[J]. 电力系统保护与控制, 2019, 47(23): 11-18.
Tao Caixia, Zhao Kaixuan, Niu Qing. Fuzzy super- spiral sliding mode observer for permanent magnet synchronous motor considering sliding mode buffe- ting[J]. Power System Protection and Control, 2019, 47(23): 11-18.
[5] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.
Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet syn- chronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.
[6] 李垣江, 董鑫, 魏海峰, 等. 表贴式永磁同步电机转速环复合PI无位置传感器控制[J]. 电工技术学报, 2020, 35(10): 2119-2129.
Li Yuanjiang, Dong Xin, Wei Haifeng, et al. Sensor- less compound PI control for surface permanent magnet synchronous motor speed regulation system[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2119-2129.
[7] 吴春, 陈子豪, 傅子俊, 等. 永磁同步电机全速范围无位置传感器控制及FPGA实现[J]. 电机与控制学报, 2020, 24(7): 121-129.
Wu Chun, Chen Zihao, Fu Zijun, et al. Sensorless control of permanent magnet synchronous machines in full speed range and FPGA implementation[J]. Electric Machines and Control, 2020, 24(7): 121-129.
[8] 章春娟, 王慧贞, 刘伟峰, 等. 一种同步基频提取滤波器: CN111181528A[P]. 2020-05-19.
[9] Wang Huimin, Liu Yongchao, Ge Xinglai. Sliding mode observer based speed sensorless vector control of linear induction motor with a parallel secondary resistance online identification[J]. IET Electric Power Applications, 2018, 12(8): 1215-1224.
[10] 刘宇博, 王旭东, 周凯. 基于滑模观测器的永磁同步电机电流偏差解耦控制[J]. 电工技术学报, 2020, 35(8): 1642-1652.
Liu Yubo, Wang Xudong, Zhou Kai. Current devia- tion decoupling control with a sliding mode observer for permanent magnet synchronous motor[J]. Transac- tions of China Electrotechnical Society, 2020, 35(8): 1642-1652.
[11] Liang Donglai, Li Jian, Qu Ronghai. Adaptive second- order sliding mode observer for PMSM sensorless control considering VSI nonlinearity[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(10): 8994- 9004.
[12] Liang Donglai, Li Jian, Qu Ronghai. Sensorless control of permanent magnet synchronous machine based on second-order sliding-mode observer with online resistance estimation[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3672-3682.
[13] Tang Qipeng, Chen Duxin, He Xiangning. Integration of improved flux linkage observer and I-f starting method for wide-speed-range sensorless SPMSM drives[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8374-8383.
[14] Nguyen A T, Rafaq M S, Choi H H, et al. A model reference adaptive control based speed controller for a surface-mounted permanent magnet synchronous motor drive[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(12): 9399-9409.
[15] Yin Guiliang, Guo Lei, Li Xiangnan. An amplitude adaptive notch filter for grid signal processing[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2638-2641.
[16] Sung-Yoon J, Kwanghee N. PMSM control based on edge-field hall sensor signals through ANF-PLL processing[J]. IEEE Transactions on Industrial Elec- tronics, 2011, 58(11): 5121-5129.
[17] Venkatramanan D, John V. Dynamic phasor modeling and stability analysis of SRF-PLL-based grid-tie inverter under islanded conditions[J]. IEEE Transa- ctions on Industry Applications, 2020, 56(2): 1953- 1965.
[18] Song Xinda, Fang Jiancheng, Han Bangcheng, et al. High-precision rotor position detection for high-speed surface PMSM drive based on linear hall-effect sensors[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4720-4731.
[19] Song Xingda, Fang Jiancheng, Han Bangcheng, et al. Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[20] 刘宁, 夏长亮, 周湛清, 等. 基于比例增益补偿的永磁同步电机转速平滑控制[J]. 电工技术学报, 2018, 33(17): 4007-4015.
Liu Ning, Xia Changliang, Zhou Zhanqing, et al. Smooth speed control for permanent magnet synchronous motor using proportional gain compen- sation[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4007-4015.
[21] 杨才伟, 王剑, 游小杰. 二阶广义积分器锁频环数字实现准确性对比[J]. 电工技术学报, 2019, 34(12): 2584-2596.
Yang Caiwei, Wang Jian, You Xiaojie. Accuracy comparison of digital implementation on the second- order generalized integrator frequency-locked loop[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2584-2596.
[22] 岳岩, 王惠民, 葛兴来. 基于锁频环的内置式永磁同步电机无传感器控制[J]. 中国电机工程学报, 2019, 39(10): 3075-3085.
Yue Yan, Wang Huimin, Ge Xinglai. Frequency- locked loop based sensorless control for interior permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2019, 39(10): 3075-3085.
Rotor Position and Speed Estimation of Permanent Magnet Synchronous Motor Based on Wideband Synchronous Fundamental- Frequency Extraction Filter
Abstract The non-ideal factors, such as the inherent chattering of sliding mode observer (SMO), the delay of control algorithm, and the dead-time effect, and so on, will produce harmonic errors of position estimation, which become the main factors affecting the accuracy of rotor position estimation. To improve the performance of the surface permanent magnet synchronous motor (SPMSM), a wideband synchronous fundamental-frequency extraction filter is proposed to extract the fundamental wave signal of the estimated back EMF. Then, a novel signal processing method combing wideband synchronous fundamental frequency extraction filter-frequency locked loop (WSFEF-FLL) is applied, and the application of FLL ensures the tracking frequency of the WSFEF adaptive. Using the WSFEF- FLL-PLL in the SMO based position estimator, the harmonics of the back EMF can be effectively eliminated, which improves the accuracy and dynamic performance of rotor position estimation. Simulation and experiment verify the feasibility and effectiveness of the proposed method.
keywords:High-speed surface permanent magnet synchronous motor, rotor position and speed estimation, wideband synchronous fundamental-frequency extraction filter, frequency-locked loop, sliding mode observer
DOI: 10.19595/j.cnki.1000-6753.tces.200913
中图分类号:TM341
章春娟 女,1996年生,硕士,研究方向为高速永磁同步电机驱动控制。E-mail: zcj086124@163.com(通信作者)
王慧贞 女,1961年生,研究员,硕士生导师,研究方向为航空起动发电。E-mail: wanghz@nuaa.edu.cn
收稿日期 2020-07-24
改稿日期 2020-09-27
(编辑 崔文静)