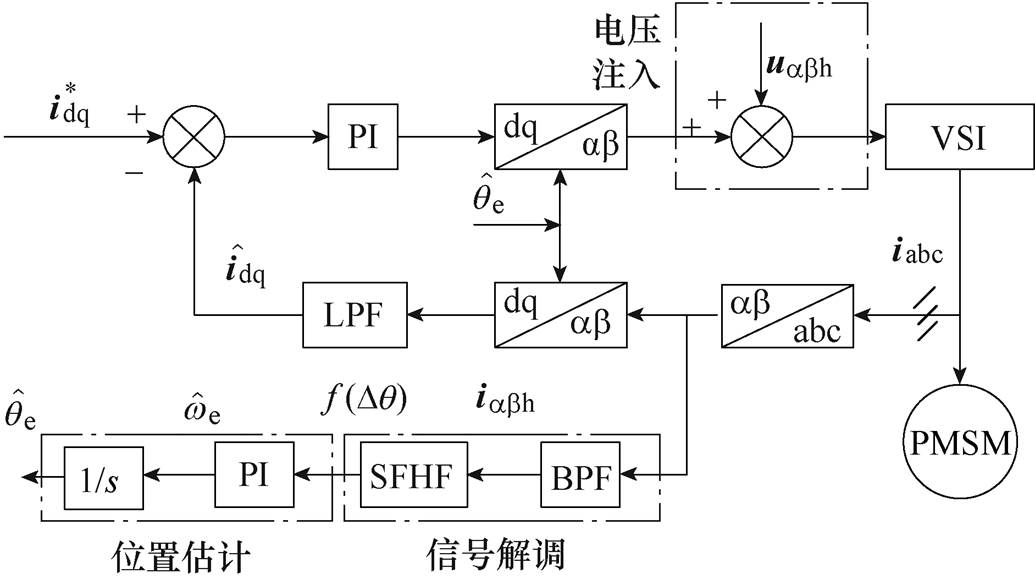
图1 高频旋转电压注入法位置估计原理框图
Fig.1 Block diagram of position estimation based on HF rotating voltage injection method
摘要 高频旋转电压注入法是一种常用的永磁同步电机零低速区转子位置估计方法，其电流解调通常采用同步轴系高通滤波器（SFHF）算法实现，但不足之处在于，不仅电流解调过程复杂，而且位置估计误差随转速的变化而变化。为此，提出一种基于估计位置反馈（EPF）的电流解调算法。一方面，利用EPF电流解调算法设计高效的位置误差补偿策略，消除转速对位置估计精度的影响；另一方面，采用该电流解调算法后系统具有独立的位置估计环路，通过在位置环采用陷波器（NF）对谐波成分陷波，有效地扩展了位置环闭环带宽，从而提高了高动态加减速工况的位置估计精度。该文回顾传统高频旋转电压注入法的实现过程，详细介绍EPF电流解调算法以及位置估计误差补偿策略，并分析利用NF对位置环带宽进行扩展的原理。最后搭建永磁同步电机实验平台对所提策略进行实验验证。
关键词：永磁同步电机 高频旋转电压注入法 同步轴系高通滤波器 电流解调 估计位置反馈
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）高性能矢量控制需要精确的转子位置信息，常用方法是使用机械式位置传感器获得，如光电编码器、霍尔传感器及旋转变压器等[1-3]。但是，机械式位置传感器存在以下不足：①由于体积和质量较大，电机的功率密度降低，价格较高，使电机成本增加[4]；②易受外部机械、电磁环境的影响，降低电机可靠性[5-6]。此外，还有一些特殊应用场合，根本无法使用机械式位置传感器，如船舶用无轴推进器是未来先进推进系统的重要发展方向之一，该类型推进器取消了电机的轮毂与主轴，使其内部的电机无法安装机械式位置传感器[1,7]。因此，PMSM无位置传感器控制技术受到越来越多的关注。
在实际工程应用中，PMSM的转速运行工况通常可分为零低速和中高速两种。零低速工况电机反电动势信号很弱甚至消失，是实现无位置传感器控制的难点[8-10]。目前，高频旋转电压注入法是PMSM零低速运行工况最常用的转子位置估计算法之一[11-17]。按照实现步骤，高频旋转电压注入法的位置估计过程可分为电压注入、电流解调及位置估计三步[11-12]。通常，电压注入及位置估计的形式相对固定，对转子位置估计性能影响不大。然而，电流解调需要对高频响应电流进行处理并解调得到转子位置误差信号，该信号包含转子位置的原始信息，因此电流解调过程的优劣将对转子位置估计性能产生严重影响。一方面，电流解调的复杂度如滤波器使用数量以及同步轴系坐标变换次数，决定了位置估计的难易程度；另一方面，采用不同的电流解调方式不仅对位置估计精度产生重要影响，而且决定了位置估计的形式属于开环或闭环。通常采用闭环的位置估计方式在动态工况下，位置估计性能往往更为优越，但必须考虑位置环带宽问题。
传统高频旋转电压注入法的电流解调采用同步轴系高通滤波器（Synchronous Frame High-pass Filter, SFHF）算法实现。但是，受到滤波器相移和数字控制延时等因素的影响，SFHF算法容易产生位置估计误差，并且采用该算法时转子位置属于开环估计，动态性能不高[12-14]。文献[15]提出一种基于自调整轴系幅值收敛（Self-adjusting Frame Amplitude Convergence, SFAC）的电流解调算法，实现了转子初始位置高精度辨识且有效地简化了电流解调过程。文献[16]分析了滤波器、数字控制相移等因素对位置估计精度的影响，并对位置估计误差进行补偿，同样实现了转子初始位置高精度辨识。但是，考虑到非零速区负序高频电流受到的相移与转速相关，而正序高频电流相移则始终保持不变，当上述两种方法应用于非零速区时，位置估计误差具有转速敏感性。文献[17]提出基于旋转坐标系的电流解调算法，消除了转子转速对位置估计精度的影响，在非零速区也获得了较高的位置估计精度。然而，文献[17]的位置估计属于闭环估计方式，却没有针对位置环带宽问题展开深入研究，理论体系有待完善。
为此，本文提出一种基于估计位置反馈（Estimated Position Feedback, EPF）的电流解调算法。该算法将估计的转子位置反馈至位置观测器的输入，并设计了一种新型解调信号，实现了转子位置误差信息直接构造，有效地简化了电流解调过程。针对位置估计误差具有转速敏感性的问题，利用EPF原理设计了一种位置估计误差补偿策略，从而消除了转速对位置估计精度的影响。采用EPF电流解调算法后转子位置估计具有独立的闭环，通过在位置环采用陷波器（Notch Filter, NF）[18-19]对谐波成分陷波，有效地扩展了位置环闭环带宽，改善了位置估计动态性能。本文对EPF电流解调算法以及位置环带宽扩展原理展开了详细分析，并搭建了实验平台，对所提策略进行实验验证。
高频旋转电压注入法的基本原理是在ab 坐标系注入一个彼此正交的高频电压激励，使电机定子产生高频电流响应，再利用特殊的信号处理手段从高频电流的相位中提取转子位置信息[11-12]，高频旋转电压注入法位置估计原理框图如图1所示。由图1可见，高频旋转电压注入法的转子位置估计过程包括电压注入、电流解调以及位置估计三个环节。
图1 高频旋转电压注入法位置估计原理框图
Fig.1 Block diagram of position estimation based on HF rotating voltage injection method
在高频电压注入工况下，PMSM高频激励数学模型通常可等效为纯电感模型，此时dq坐标系下PMSM的电压方程可表示[15]为
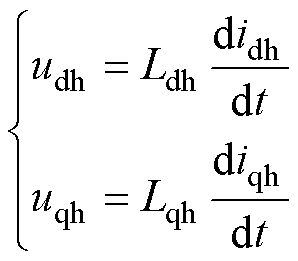（1）式中，udh和uqh分别为d、q轴的高频电压；idh和iqh分别为d、q轴的高频电流；Ldh和Lqh分别为d、q轴的高频电感。根据高频旋转电压注入原理，实际注入的高频电压可表示为
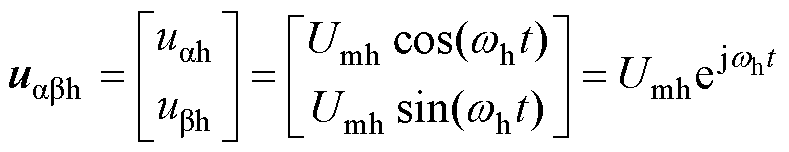（2）
式中，Umh、wh分别为注入高频电压的幅值与角频率。将式（2）变换至dq坐标系中，然后代入式（1），则dq坐标系中的高频电流响应[11-12]可表示为
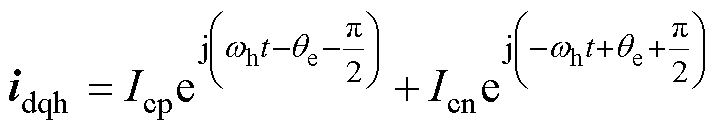（3）式中，角频率等于wh的电流成分称为正序高频电流；角频率等于-wh的电流成分称为负序高频电流；Icp与Icn分别为正序、负序高频电流幅值，二者可表示为
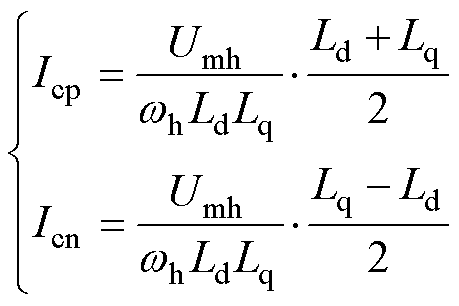（4）
对式（4）进行反Park变换，此时ab 坐标系下的高频电流响应可表示为
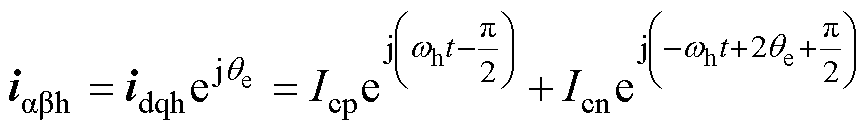（5）由式（5）可看出，ab 坐标系下负序高频电流的相位包含转子位置信息qe。
从高频响应电流的相位中初步获得转子位置误差信号的过程称为电流解调。传统高频旋转电压注入法采用基于SFHF的电流解调算法，具体包括负序高频电流提取以及利用外差法构造转子位置误差信号两个过程。图2展示了利用SFHF电流解调算法提取负序高频电流的原理框图[11-12]，该算法首先将ab 坐标系下的高频电流旋转至同步轴系，然后将输出电流进行滤波得到纯净的高频电流，最后将该电流还原得到仅含转子位置信息的负序高频电流in_ah与in_bh。
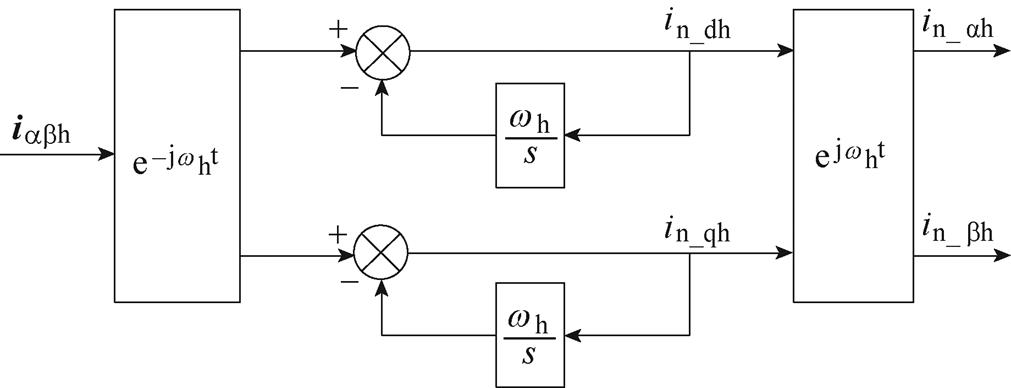
图2 SFHF电流解调算法原理框图
Fig.2 Block diagram of SFHF current demodulation algorithm
完成电流解调后，利用外差法构建转子位置误差信号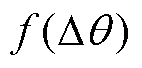
，外差法构造转子位置误差信号原理框图如图3所示，其数学实现过程为
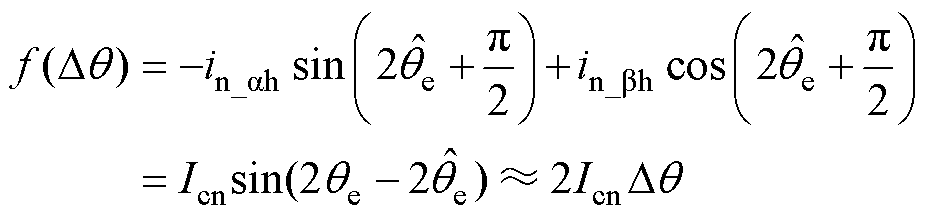（6）式中，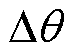
为位置误差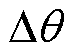，=qe-
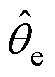；qe与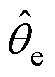分别为真实转子位置与估计转子位置。式（6）中约等号表示当位置误差信号足够小，可对其进行线性化。由图3可知，获得转子位置误差信号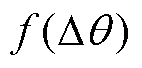后，通常利用PI调节器将其调节至零获得估计转速
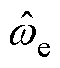，对估计转速积分后得到估计转子位置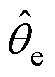[21]。
分析发现，传统的SFHF电流解调算法存在以下两点不足：
（1）对高频旋转电压注入法进行位置估计时，SFHF算法直接从负序高频响应电流的相位中提取转子位置信息。然而，受非理想因素的影响，高频电流的相位容易发生偏移，从而产生估计位置误差，其具体表现为位置估计误差随转速改变而改变。常见的非理想因素包括[11-12]：高频模型建模简化导致的相移、滤波器延迟产生的相移和PI电流调节器非线性产生的相移。
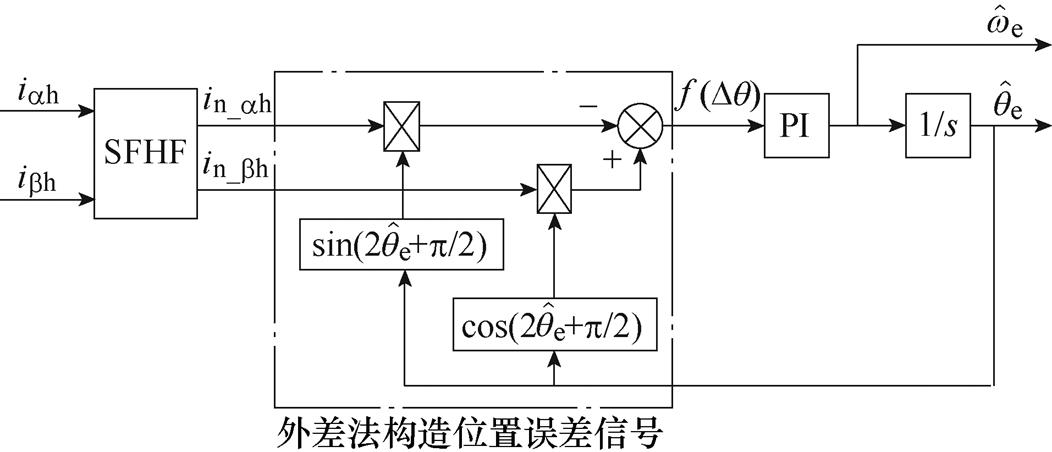
图3 外差法构造转子位置误差信号原理框图
Fig.3 Block diagram position error signal construction based on heterodyne method
（2）采用SFHF算法时，系统直接对负序高频电流进行锁相得到转子位置的估计值，属于开环估计算法。开环估计算法在高动态加减速瞬间难以快速跟随实际转子位置，使估计位置与实际位置产生偏差。若位置偏差过大，非常容易导致电机失步。
为了克服传统SFHF电流解调算法存在的不足，本文提出一种基于EPF的改进型电流解调算法，将其用于高频旋转电压注入法的位置误差信号提取。
考虑到转子位置既包含位置本身，同时也包含速度信息，因此估计与真实的转子位置可分别表示为=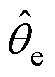
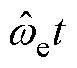, qe=wet。当位置估计过程达到稳态时，转子转速估计值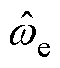非常接近真实值we，可认为二者基本相等，即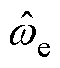≈we。
由式（5）可知，当转速不为零时，ab 坐标系下正序高频电流的频率为wh，负序高频电流的频率为wh-2we。设非理想因素对正序、负序高频电流的总相移分别为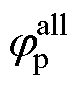
与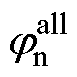
，则考虑相移后ab 坐标系下的高频电流可表示为
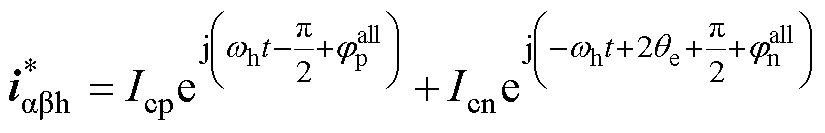（7）此外，由式（5）可知，dq坐标系下正序电流与负序电流也均含有转子位置信息。但由于真实的转子位置未知，应以估计的转子位置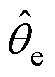代替，同时该坐标系应采用虚拟
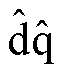坐标系表示。考虑相移后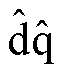，坐标系中的电流可由Park变换得到，即
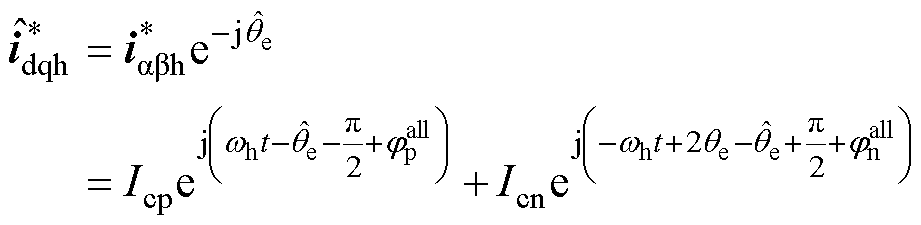
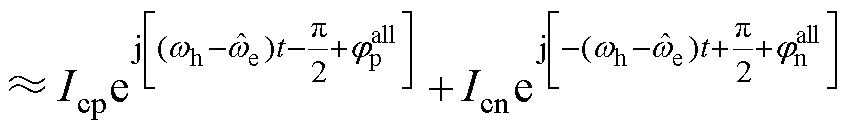（8）
由式（8）可知，在位置估计过程达到稳态时可认为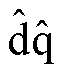坐标系中正、负序高频响应电流的频率分别为wh-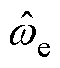与-(wh-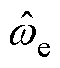)，二者具有等值异号关系。
对于ab 坐标系下的正、负序高频电流，非零速工况下二者频率的绝对值不相等，因此非理想因素对正、负序高频电流的相移之和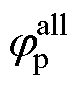+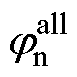≠0；对于虚拟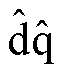坐标系下的正序、负序高频电流，非零速工况下二者频率具有等值异号关系，因此非理想因素对正、负序高频电流的相移之和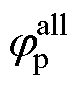+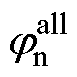=0，充分利用该结论可实现转子位置误差的精确补偿。
为了对电流相移造成的位置估计误差实现补偿，EPF电流解调算法在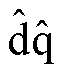坐标系下对高频电流进行处理。图4为基于EPF电流解调算法，其输入信号
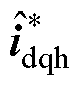源于对虚拟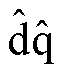坐标系下的电流
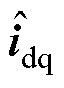进行带通滤波。
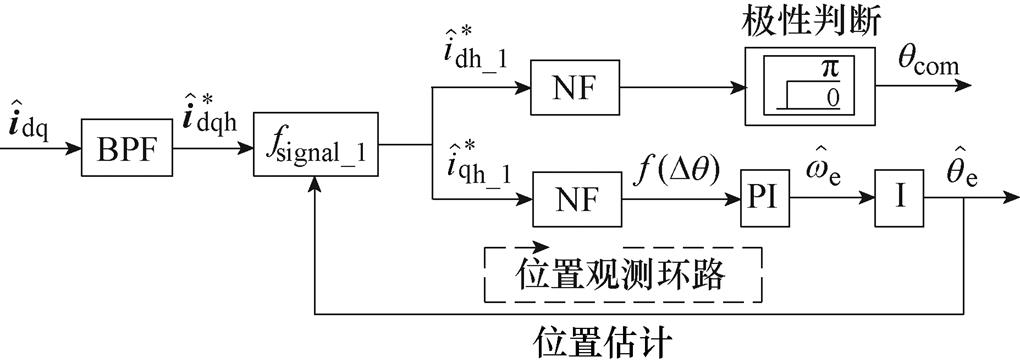
图4 EPF电流解调算法
Fig.4 Block diagram of EPF current demodulation algorithm
由图4可知，EPF电流解调算法将估计转子位置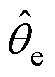反馈至位置环的输入，从而构造解调信号fsignal_1，该信号可表示为
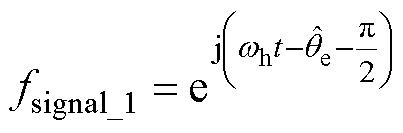（9）令虚拟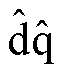坐标系下的高频电流
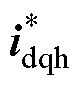与解调信号fsignal_1相乘，可得
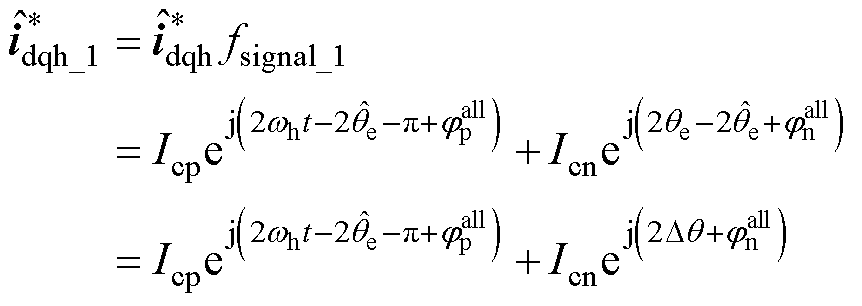（10）
式中，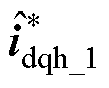
为解调后的高频电流。由式（10）可知，利用EPF电流解调算法后，正序电流变为2wh的高
频成分，负序电流直接变成含有转子位置误差的直流成分，实现了转子位置误差信息直接构造，有效地简化了电流解调过程。然后，利用NF滤除频率为2wh的正序高频电流（原因在第3节进行详述），得到的负序电流可表示为
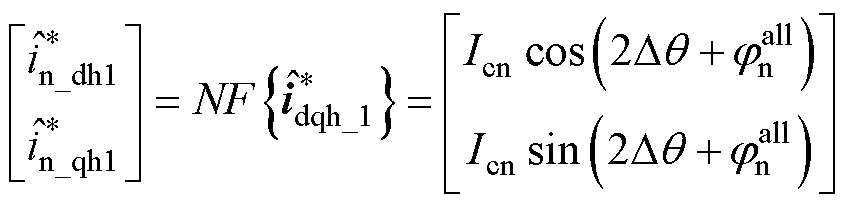（11）式中，下标“n”表示负序高频电流信号。式（11）中，对于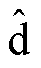
轴负序电流
，可用于初始位置检测阶段的转子磁极极性判断，具体实现过程可参考文献[15]。对于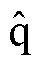
轴负序电流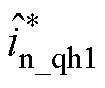
，其直接含有位置误差信息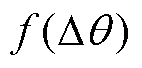，即
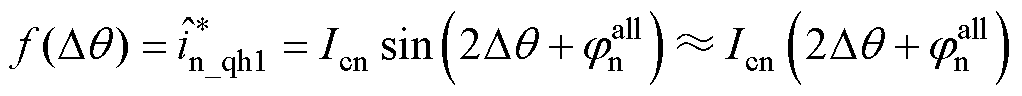（12）
完成位置误差信号提取后，利用PI调节器将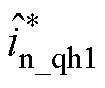调节至零，使虚拟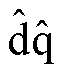坐标系与真实dq坐标系重合，即可实现转子位置估计。
由式（12）可见，初次获得的转子位置估计值含有位置误差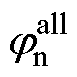，由2.1节分析可知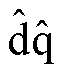，坐标系下正、负序高频电流的相移之和等于0，因此本文通过提取正序高频电流的相移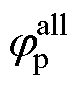对位置估计误差进行补偿。图5为考虑位置误差补偿后的转子位置估计原理框图。
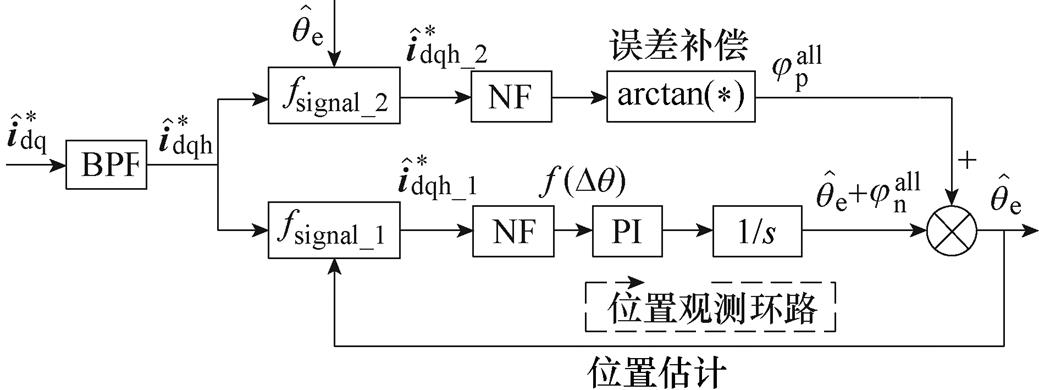
图5 考虑位置误差补偿后转子位置估计原理框图
Fig.5 Block diagram of position estimation considering position error compensation
图5中，位置误差的补偿策略利用EPF原理，设计了一个与式（9）相位相反的解调信号，即
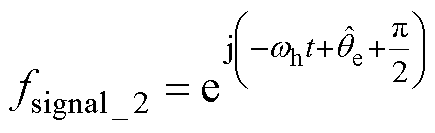（13）令虚拟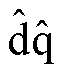坐标系下的高频电流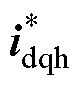与解调信号fsignal_2相乘，可得
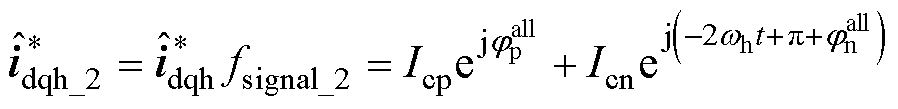（14）
由式（14）可以看出，正序电流变为含有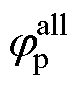的直流成分，而负序电流变成2wh的高频成分。利用NF将负序高频电流滤除，然后利用反正切函数求取正序高频电流的相移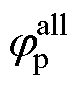，即可实现对转子位置估计误差的补偿。
值得注意的是，本文在位置观测环路中不是采用常规的一阶巴特沃斯低通滤波器（Low Pass Filter, LPF），而是采用NF滤除谐波信号。该设计的目的是为了扩展位置观测环路闭环带宽，提高动态工况下转子位置的估计性能。根据图4位置观测环路绘制等效位置环原理框图，如图6所示。图中，HF*表示式（10）中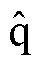轴的正序高频电流
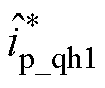，可将其视为等效位置环的扰动信号，即
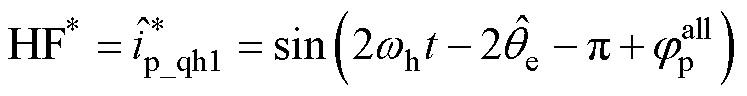（15）
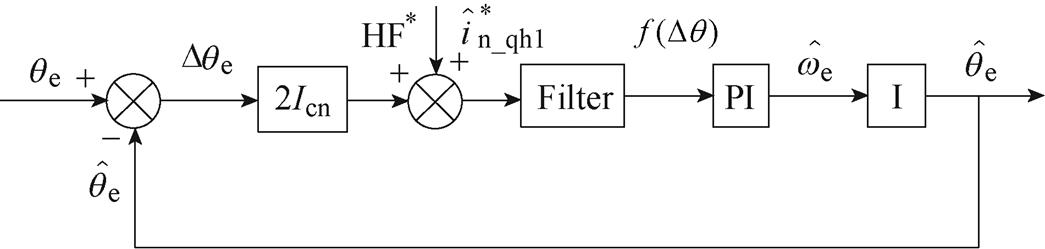
图6 等效位置环原理框图
Fig.6 Block diagram of equivalent position loop
图6中的滤波器可选择LPF或NF[18-19]，二者对应的传递函数分别为
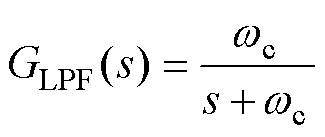（16）
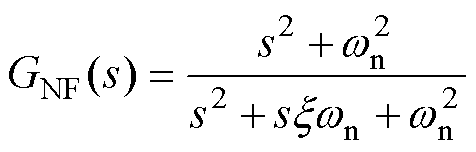（17）
式中，wc为LPF的截止频率；wn为NF的陷波频率；x 为陷波因子。那么，采用不同滤波器时位置环的闭环传递函数可分别表示为
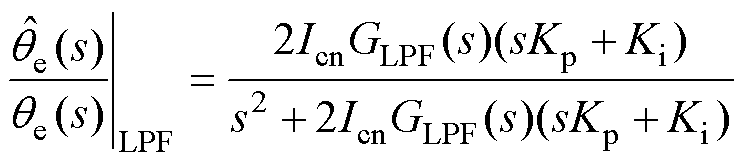（18）
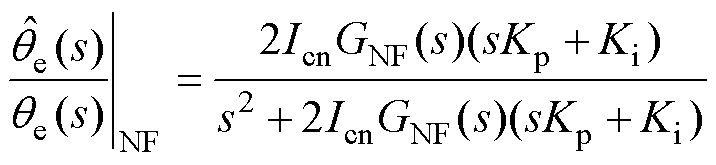（19）
不同滤波器下位置环的性能可通过闭环带宽与高频电流谐波过滤能力进行对比。在本文的实验平台中，注入高频电压的频率为300Hz，则图6中对应的高频谐波信号为600Hz。对于LPF，根据工程经验为了获得较好的滤波效果，wc的参考值可取为待滤除谐波频率的1/20，因此，wc可选为60prad/s。而对于NF，其陷波频率wn应设置为1 200prad/s，陷波因子x 可根据实际陷波效果确定，在此选定为0.3。当确定了LPF的截止频率、NF的陷波频率以及陷波因子后，位置环中仅PI调节器的比例系数Kp与积分系数Ki为待定变量。
根据式（18）与式（19），绘制位置环幅频特性曲线，如图7和图8所示。图7为基于LPF滤波的位置环幅频特性曲线，图8为基于NF滤波的位置环幅频特性曲线。绘制时设定一个谐波滤除性能指标，要求每一种滤波器对600Hz谐波的增益至少为-60dB，此时谐波信号幅值将衰减至输入的0.1%。由曲线变化规律可知，PI调节器的积分系数Ki主要影响位置环谐振峰值而几乎不影响闭环带宽fb，而比例系数Kp对闭环带宽的影响较为显著，增大Kp有助于提高闭环带宽。
图7 基于LPF滤波的位置环幅频特性曲线
Fig.7 Amplitude-frequency characteristic curves of position loop based on LPF
对比发现，若采用LPF进行滤波，当Kp＞80时，位置环对600Hz谐波的增益不足-60dB，说明系数Kp的值最大应取为80，此时对应最大的位置环闭环带宽为18Hz；反之，采用NF滤波时，得益于NF的强陷波能力，当系数Kp增大至2 000时，位置环依然对600Hz谐波保持强烈的滤波效应，此时位置环闭环带宽可达到430Hz。由上述分析可知，采用LPF滤波时由于受到滤波能力的限制，位置环带宽无法进一步提高，位置环存在动态性能与滤波精度相互矛盾的问题，而采用NF滤波时位置环则具有高带宽与强滤波能力并存的优点，这对提高高动态加减速工况的位置估计性能具有重要意义。但是，实际应用时Kp的值不宜过高，否则将减弱对开关频率次谐波的滤除能力。
图8 基于NF滤波的位置环幅频特性曲线
Fig.8 Amplitude-frequency characteristic curves of position loop based on NF
为了验证所提方法的性能，本文采用瑞士Plexim GmbH公司开发的系统级电力电子仿真软件PLECS进行仿真验证，图9为PMSM无位置传感器控制仿真模型。仿真采用PMSM参数见表1，仿真模型中逆变器开关频率为6kHz，电流采样与控制频率为12kHz。此外，高频电压的注入频率为300Hz，幅值为100V。
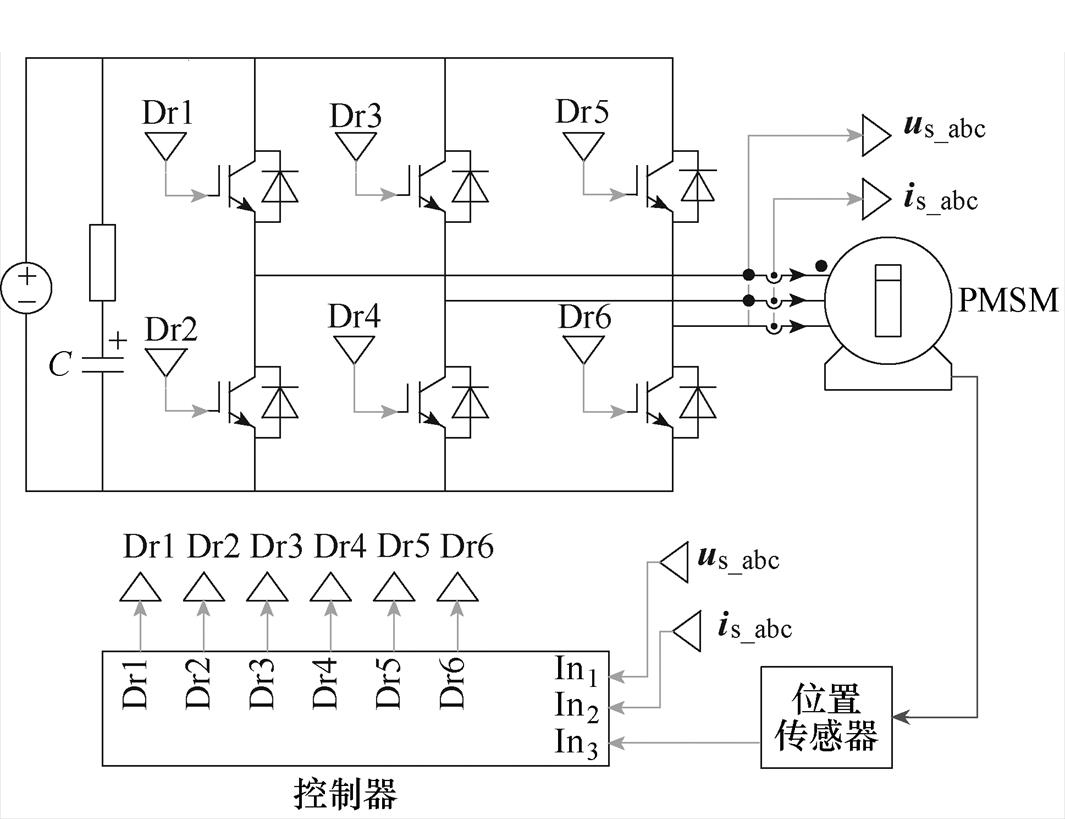
图9 PMSM无位置传感器控制仿真模型
Fig.9 Simulation model for PMSM position sensorless control
表1 永磁同步电机参数
Tab.1 Parameters of the PMSM
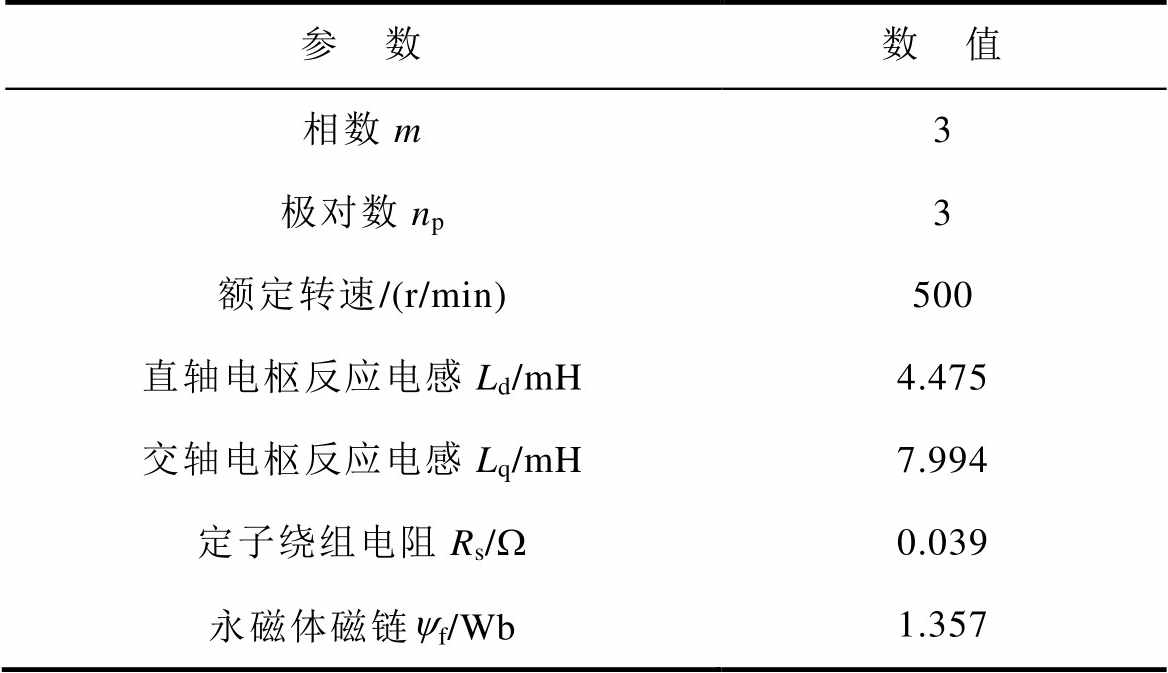
参 数数 值 相数m3 极对数np3 额定转速/(r/min)500 直轴电枢反应电感Ld/mH4.475 交轴电枢反应电感Lq/mH7.994 定子绕组电阻Rs/W0.039 永磁体磁链yf/Wb1.357
本节验证所提EPF电流解调算法及位置估计误差补偿策略的可行性，重点观察所提算法是否消除了转子转速对位置估计精度的影响。图10为传统SFHF电流解调算法在不同转速工况位置估计仿真结果，由仿真结果可知，100r/min工况下转子位置估计误差的平均值约为10°，-100r/min工况下转子位置估计误差的平均值约为-26°。可见，转子位置估计误差随转速的变化而变化，位置估计精度具有转速敏感性。
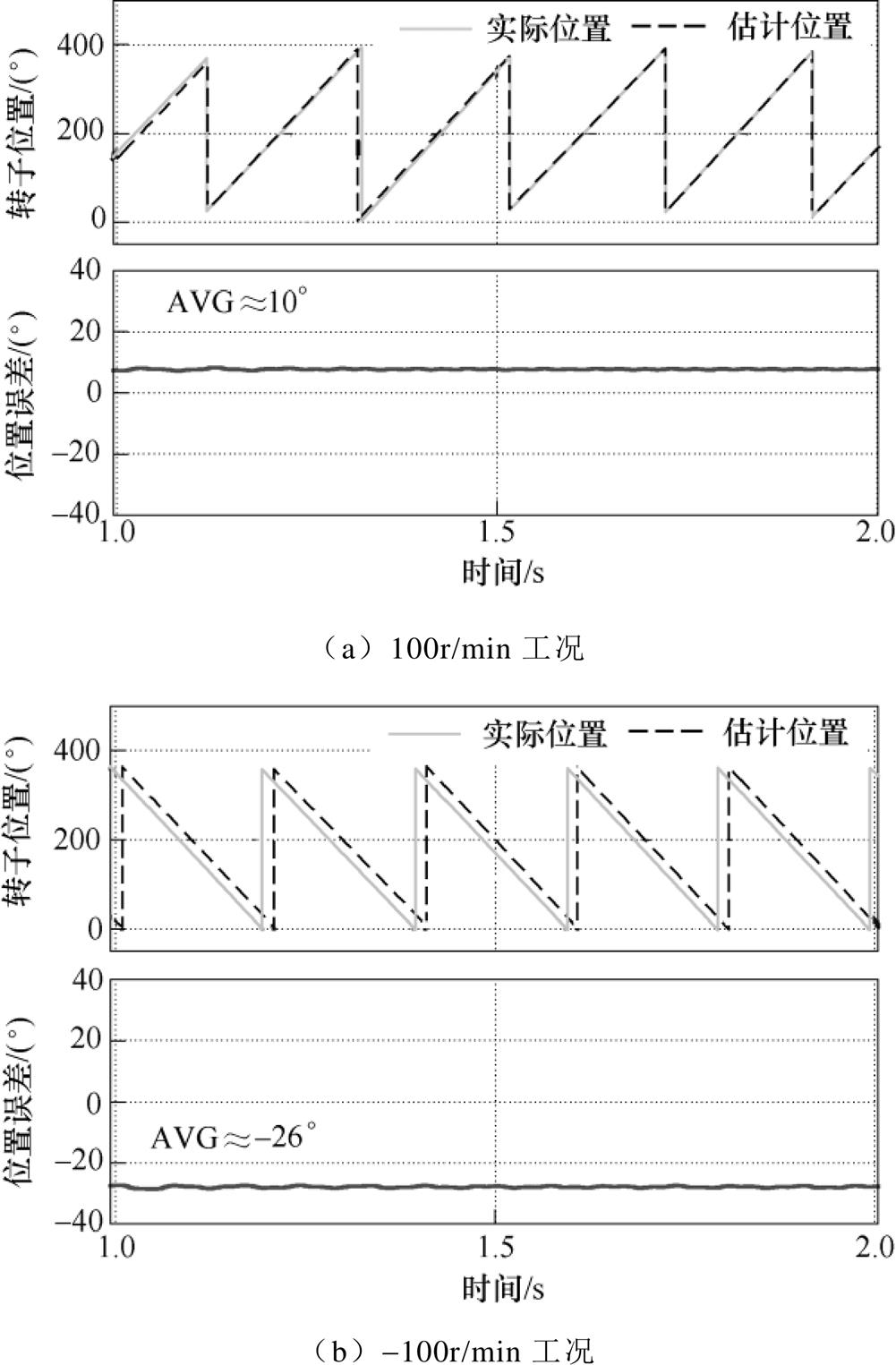
图10 传统SFHF电流解调算法在不同转速工况位置估计仿真结果
Fig.10 Simulation results of position estimation under various speed condition based on traditional SFHF current demodulation algorithm
图11为EPF电流解调算法在不同转速工况位置估计仿真结果，可以看出，采用EPF电流解调算法后，100r/min工况与-100r/min工况下转子位置估计误差的平均值分别约为2°与-2°，不仅消除了转子位置估计误差的转速敏感性，而且有效地提高了转子位置估计精度。图11的仿真结果验证了EPF电流解调算法的可行性。
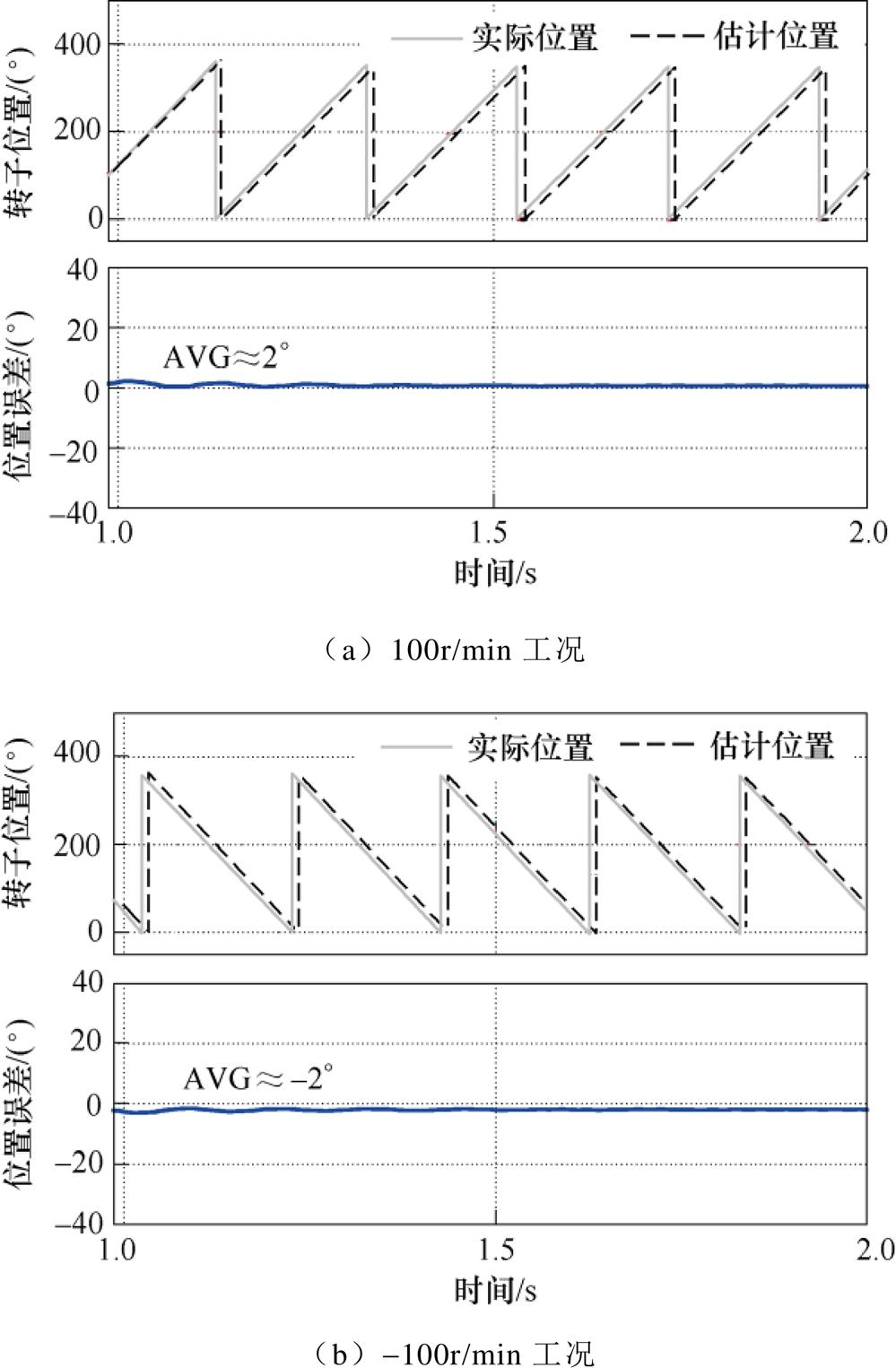
图11 EPF电流解调算法在不同转速工况位置估计仿真结果
Fig.11 Simulation results of position estimation under various speed condition based on EPF current demodulation algorithm
传统SFHF电流解调算法的位置估计精度较低，当位置估计精度无法保证时，则研究其动态过程中的位置估计性能意义不大。因此，本节仅针对本文所提的EPF电流解调算法，对比位置环分别采用LPF与NF滤波时在动态工况下的位置估计性能。
图12为位置环采用LPF在高动态加减速下位置估计仿真结果。两种穿越工况的位置估计误差平均值约为-6.3°与6.7°，可以看出，当位置环采用LPF进行滤波时，由于位置环带宽受到限制，高动态加减速工况下转子位置估计产生延迟。位置估计误差将降低电机定子电流控制精度，不利于电机长期稳定运行。若位置偏差过大，非常容易导致电机失步。
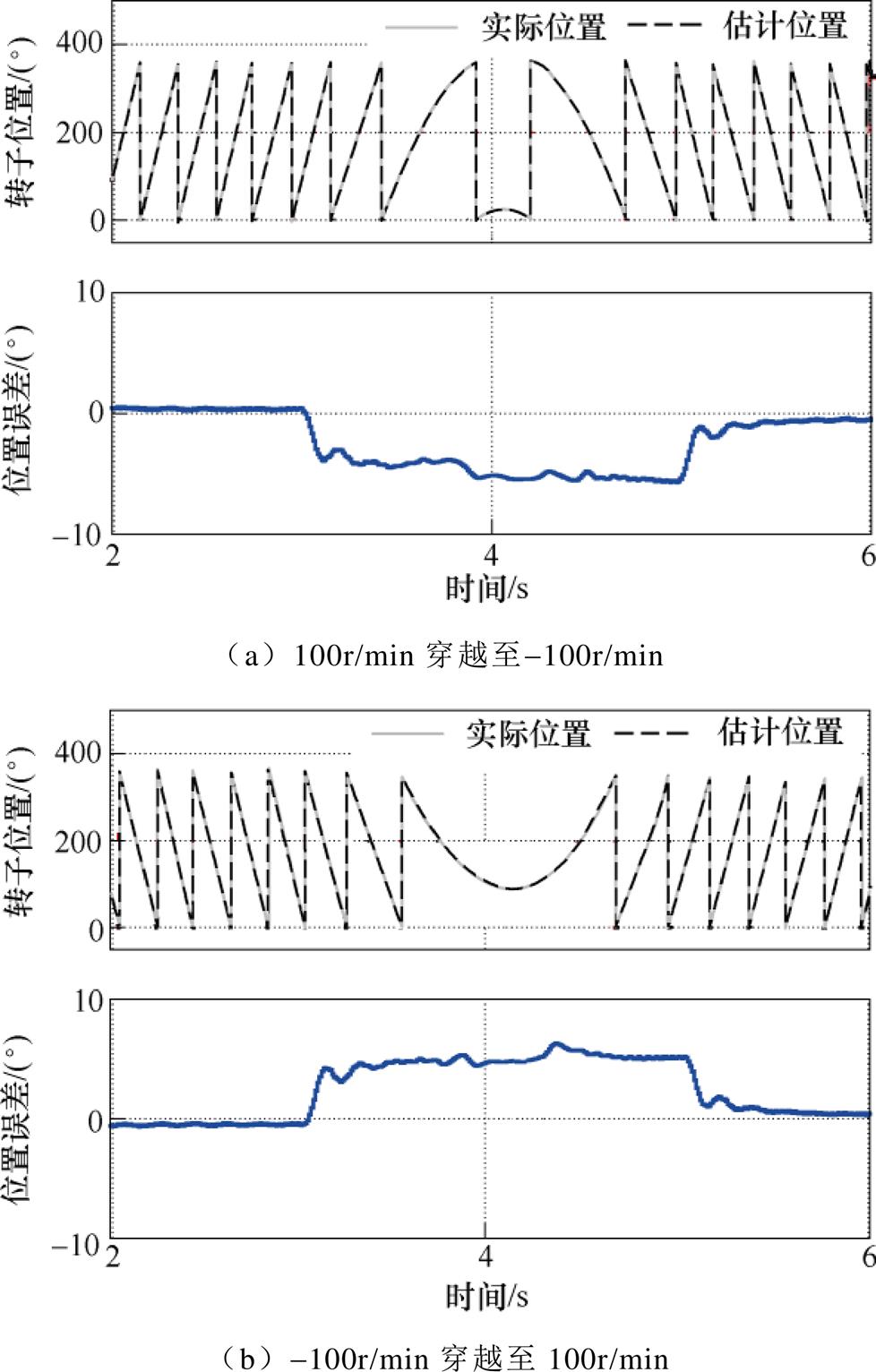
图12 位置环采用LPF在高动态加减速下位置估计仿真结果
Fig.12 Simulation results of position estimation under high dynamic acceleration and deceleration condition where LPF is employed in position loop
图13为位置环采用NF滤波在高动态加减速下位置估计仿真结果。两种穿越工况的位置估计误差平均值约为-1.4°与1.3°，可以看出，当位置环采用NF进行滤波时位置环带宽得到拓宽，高动态加减速工况下转子位置估计误差显著减小。由此说明采用NF滤波的位置环带宽扩展方法可行有效。
为了进一步验证本文所提方法的可行性，搭建PMSM实验平台对其进行验证。图14为本文采用的实验平台，电动机由变频器供电并拖动发电机产生电能，发电机电能消耗在负载电阻柜上。对于 DSP内部的转子位置、转速等信号，采用先将数据实时保存在RAM中、停机之后再将数据导出的方式进行采集，最后采用Matlab完成数据处理。实验采用电机参数见表1，变频器开关频率为6kHz，DSP内部电流采样与控制频率为12kHz。此外，高频电压的注入频率为300Hz，幅值为100V。本文的仿真平台与实验平台的工作参数一致，从而有利于进行对比验证。
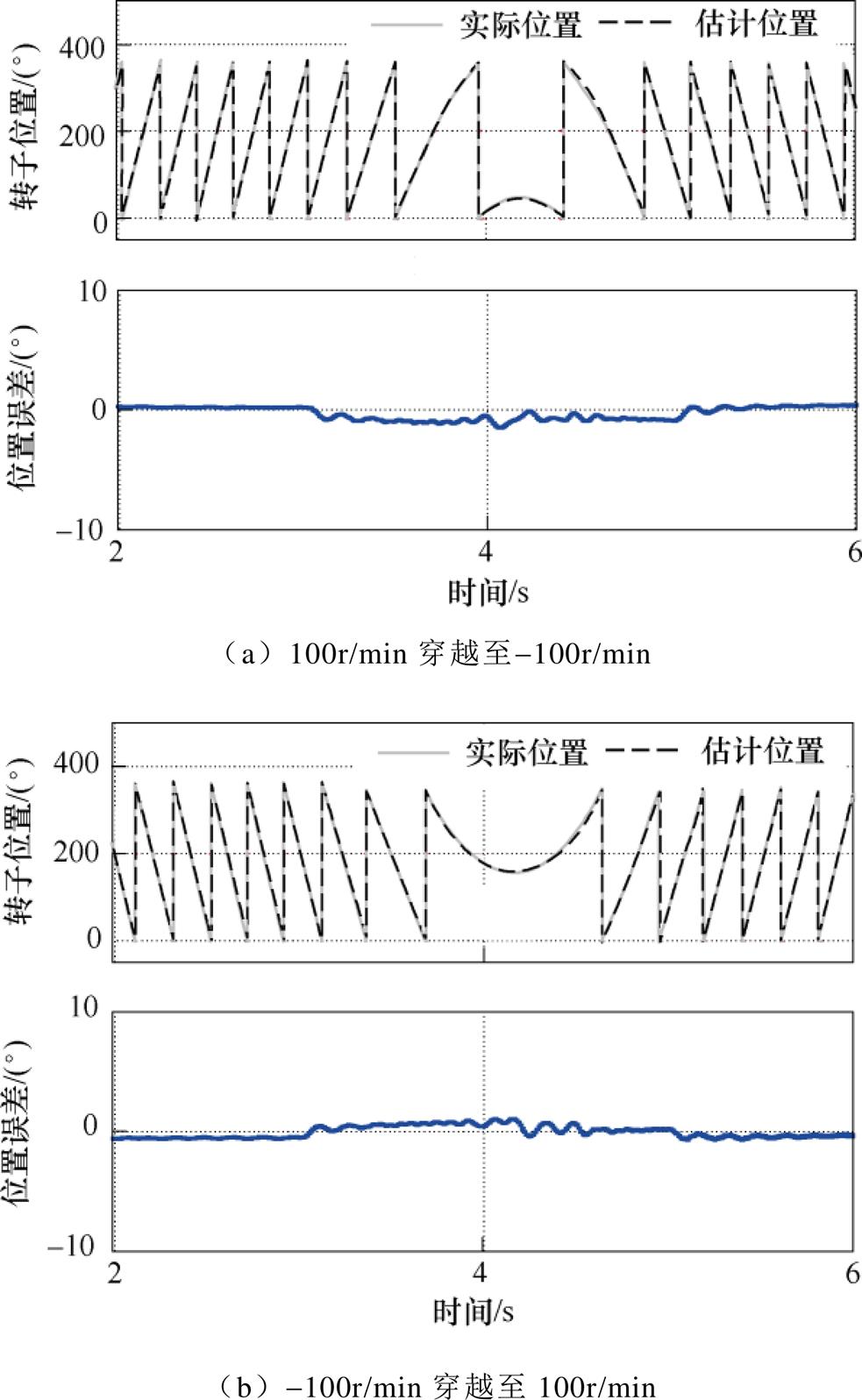
图13 位置环采用NF滤波在高动态加减速下位置估计仿真结果
Fig.13 Simulation results of position estimation under high dynamic acceleration and deceleration condition where NF is employed in position loop
图14 实验平台
Fig.14 Experimental platform
图15为传统SFHF电流解调算法在不同转速工况位置估计实验结果。可见，100r/min工况下转子位置估计误差的平均值约为12°，而-100r/min工况下转子位置估计误差的平均值约为-29°，位置估计误差随转速改变而改变。
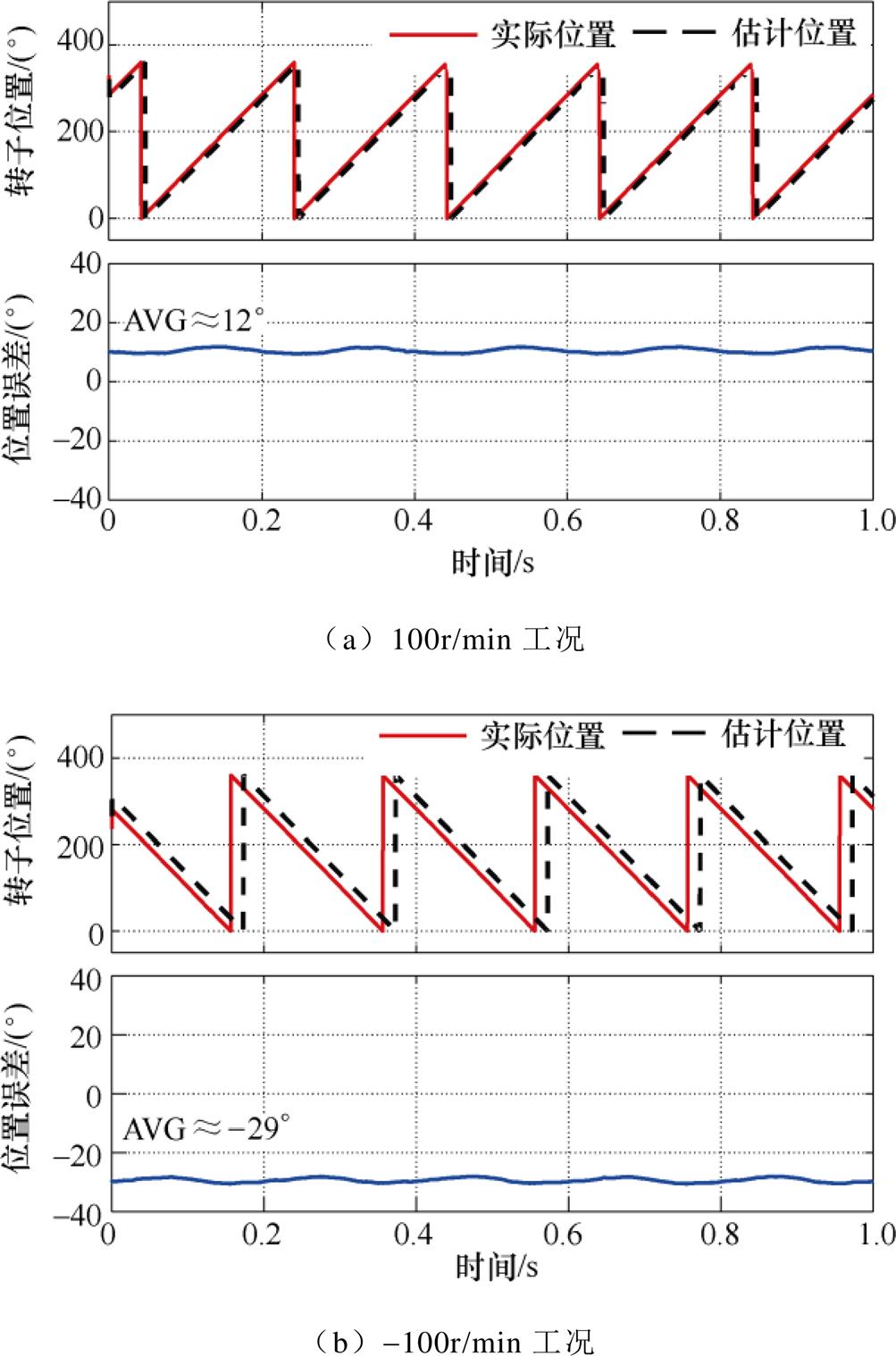
图15 传统SFHF电流解调算法在不同转速工况位置估计实验结果
Fig.15 Experimental results of position estimation under various speed condition based on traditional SFHF current demodulation algorithm
图16为EPF电流解调算法在不同转速工况位置估计实验结果。可见，100r/min工况下的转子位置估计误差的平均值约为3°，而-100r/min工况下的转子位置估计误差的平均值约为-2°。采用EPF电流算法后转子位置估计精度得到明显提高，并且基本消除了转子转速对位置估计精度的影响，实验结果与仿真结果基本一致。
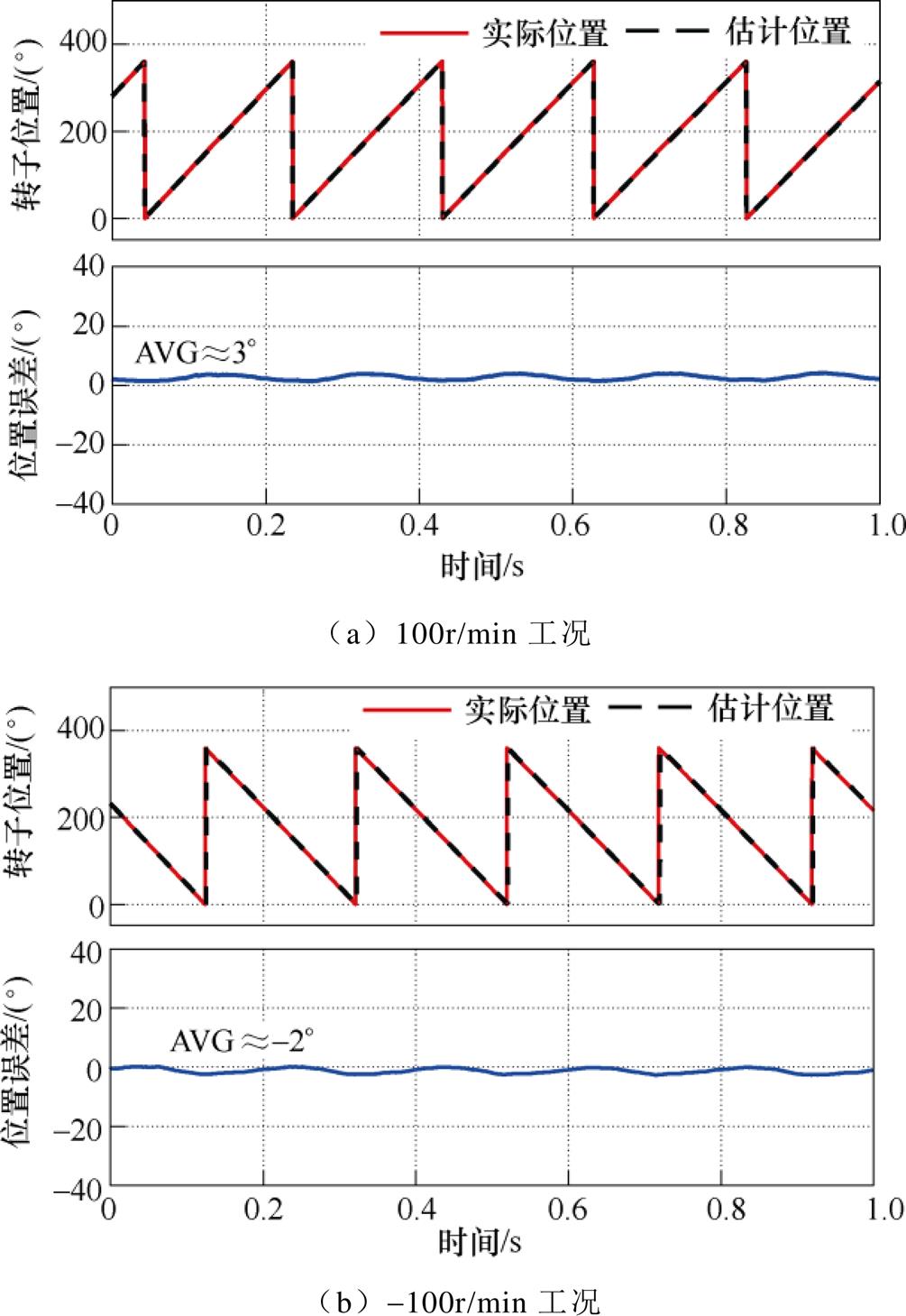
图16 EPF电流解调算法在不同转速工况位置估计实验结果
Fig.16 Experimental results of position estimation under various speed condition based on EPF current demodulation algorithm
图17为位置环采用LPF在动态加减速下位置估计性能验证实验结果。两种穿越工况的位置估计误差平均值约为-6.5°与5.3°。
图18为位置环采用NF滤波在高动态加减速下位置估计性能验证实验结果。两种穿越工况的位置估计误差平均值约为1.2°与2.0°。可见，当位置环采用NF进行滤波时位置环带宽得到拓宽，高动态加减速工况下转子位置估计误差显著减小，实验结果与仿真结果基本一致。
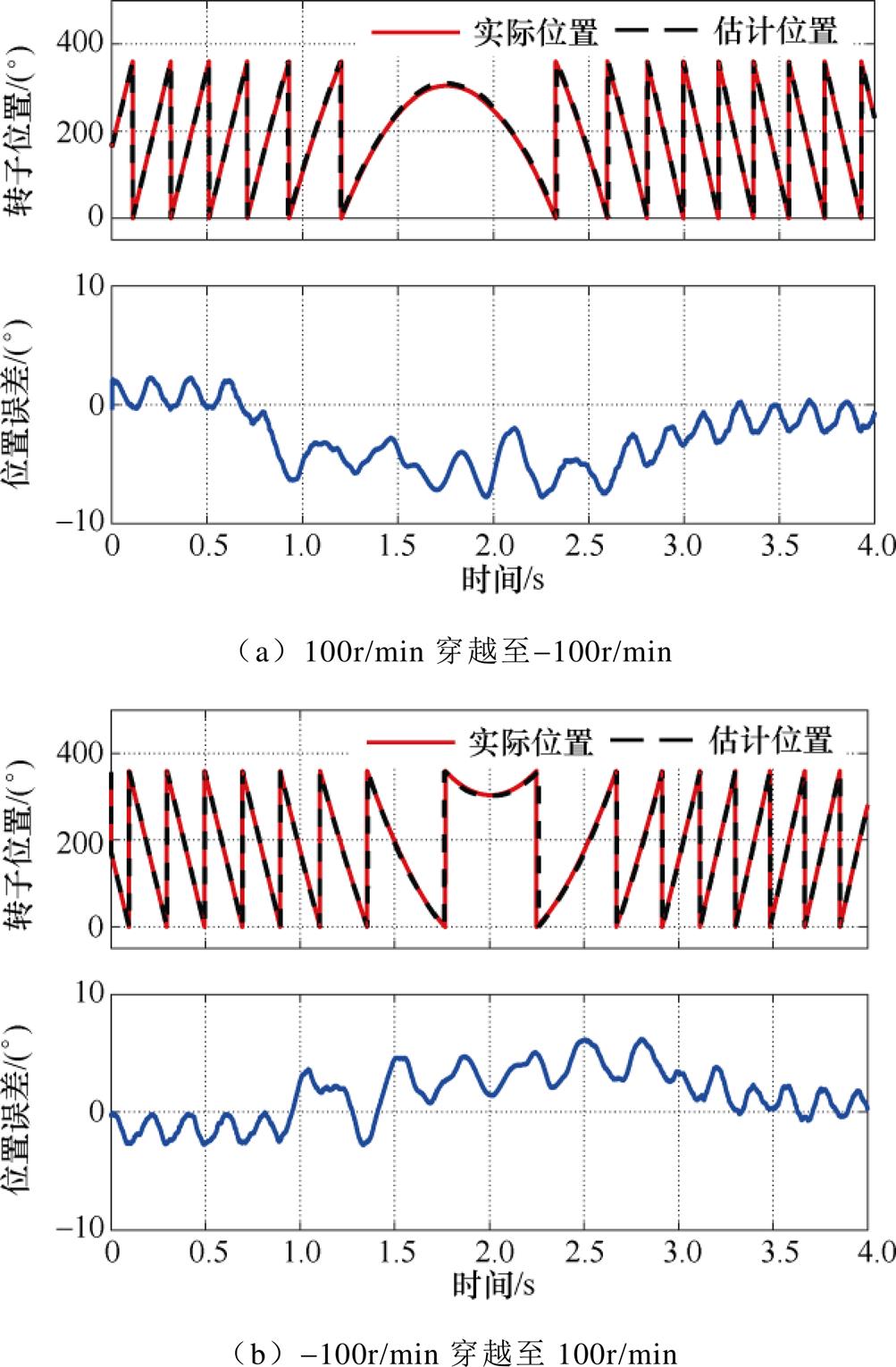
图17 位置环采用LPF在高动态加减速下位置估计实验结果
Fig.17 Experimental results of position estimation under high dynamic acceleration and deceleration condition where LPF is employed in position loop
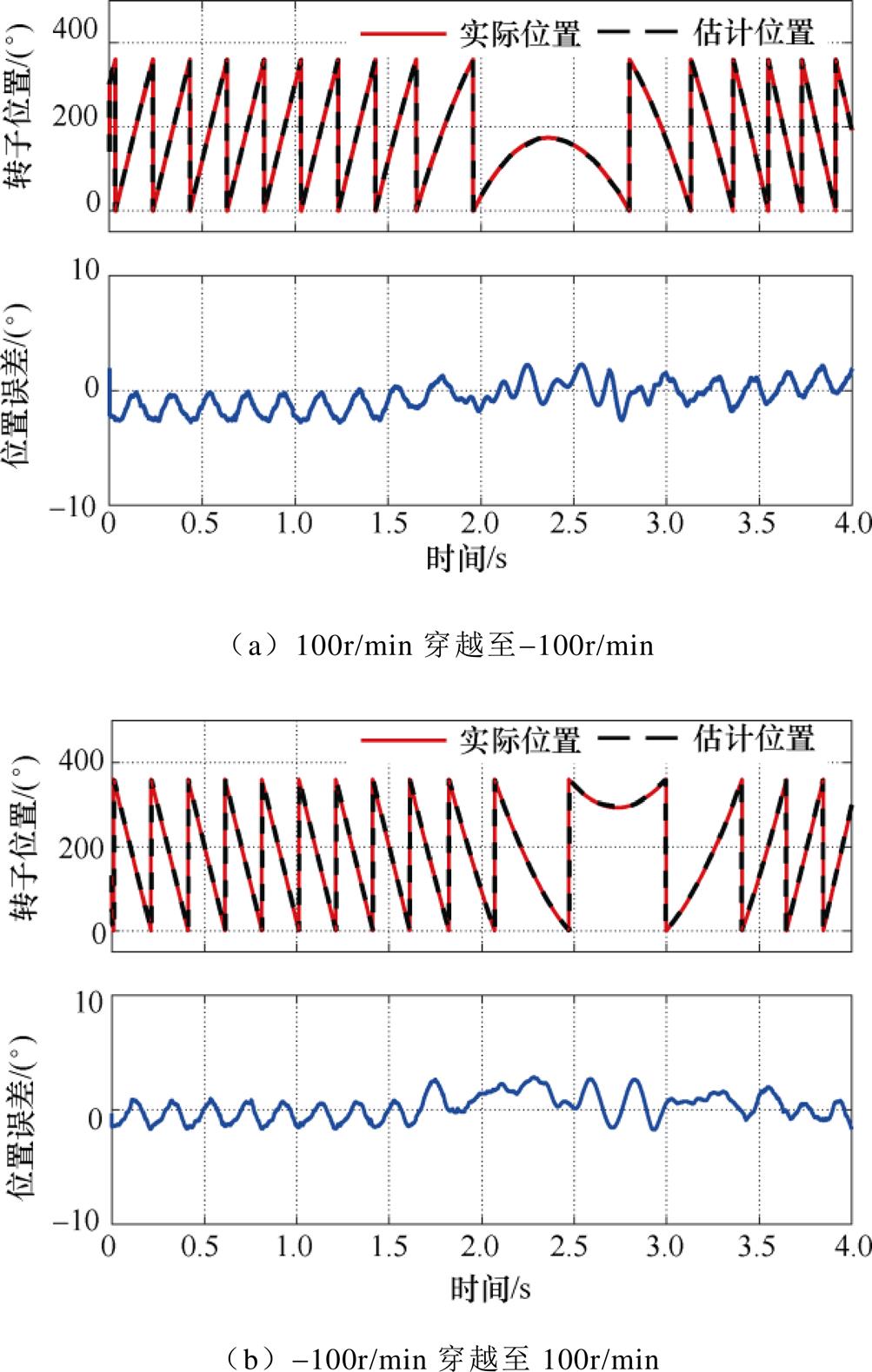
图18 位置环采用NF滤波在高动态加减速下位置估计实验结果
Fig.18 Experimental results of position estimation under high dynamic acceleration and deceleration condition where NF is employed in position loop
图19为位置环采用LPF在高动态加减速下转速估计性能分析。由图19b可以看出，局部放大后的转子转速含有大量谐波成分，如图19c所示，估计转速中600Hz的谐波含量为0.78r/min，由此说明LPF的滤波性能有限。转速谐波不仅影响电机控制精度，且易使电机驱动系统产生额外损耗。
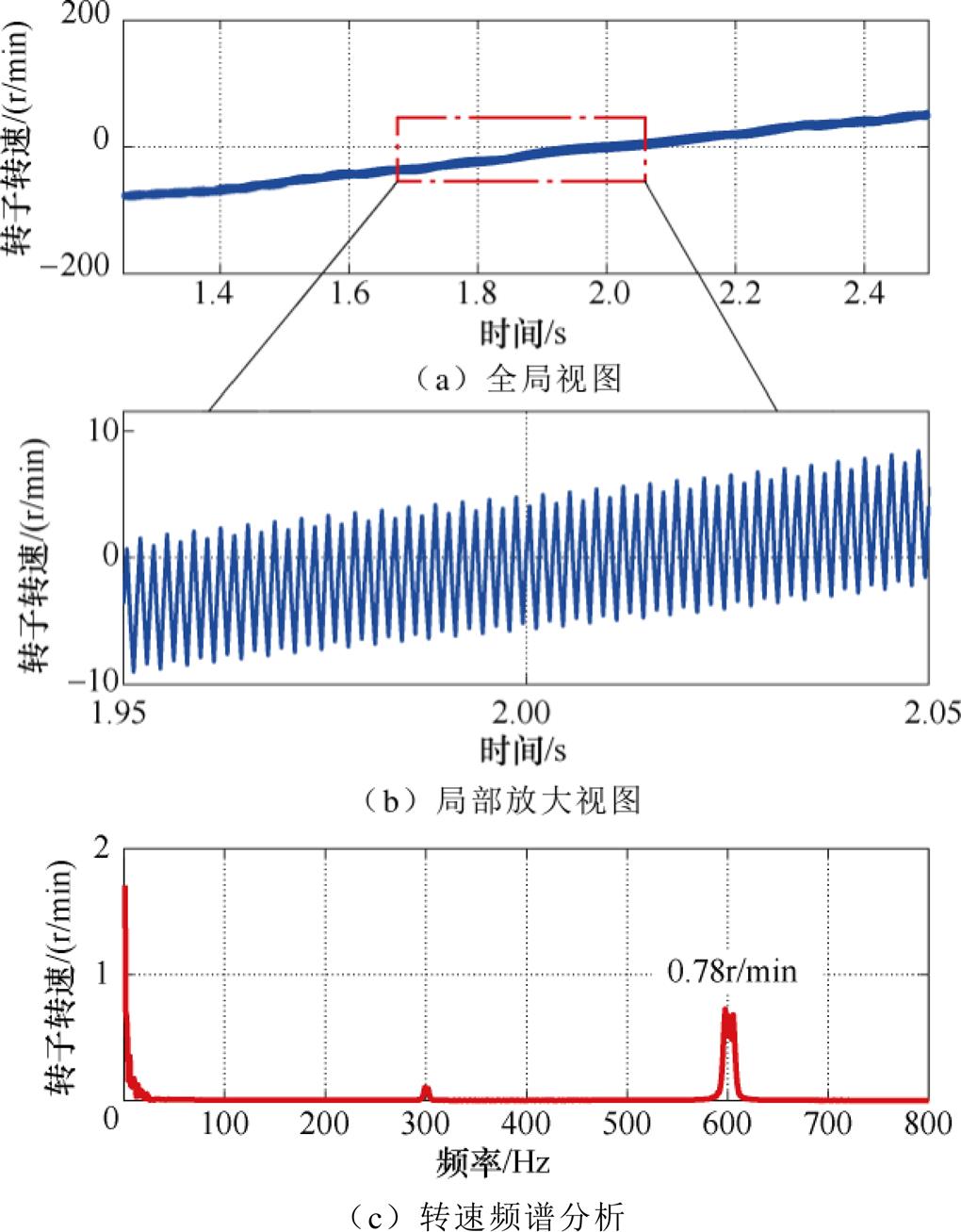
图19 位置环采用LPF在高动态加减速下估计转速性能分析
Fig.19 Performance analysis of estimated speed under fast acceleration and deceleration condition where LPF is employed in position loop
图20为位置环采用NF滤波在高动态加减速下转速估计性能分析。由图20b可以看出，局部放大后的转子转速基本不含谐波成分，如图20c所示，估计转速中600Hz的谐波含量为0.02r/min，由此证明NF具有显著的陷波性能。
位置环采用不同滤波器时综合性能对比结果见表2。对比高动态加减速下的位置误差以及转速谐波结果可知，本文所提的位置环带宽扩展策略可行有效。
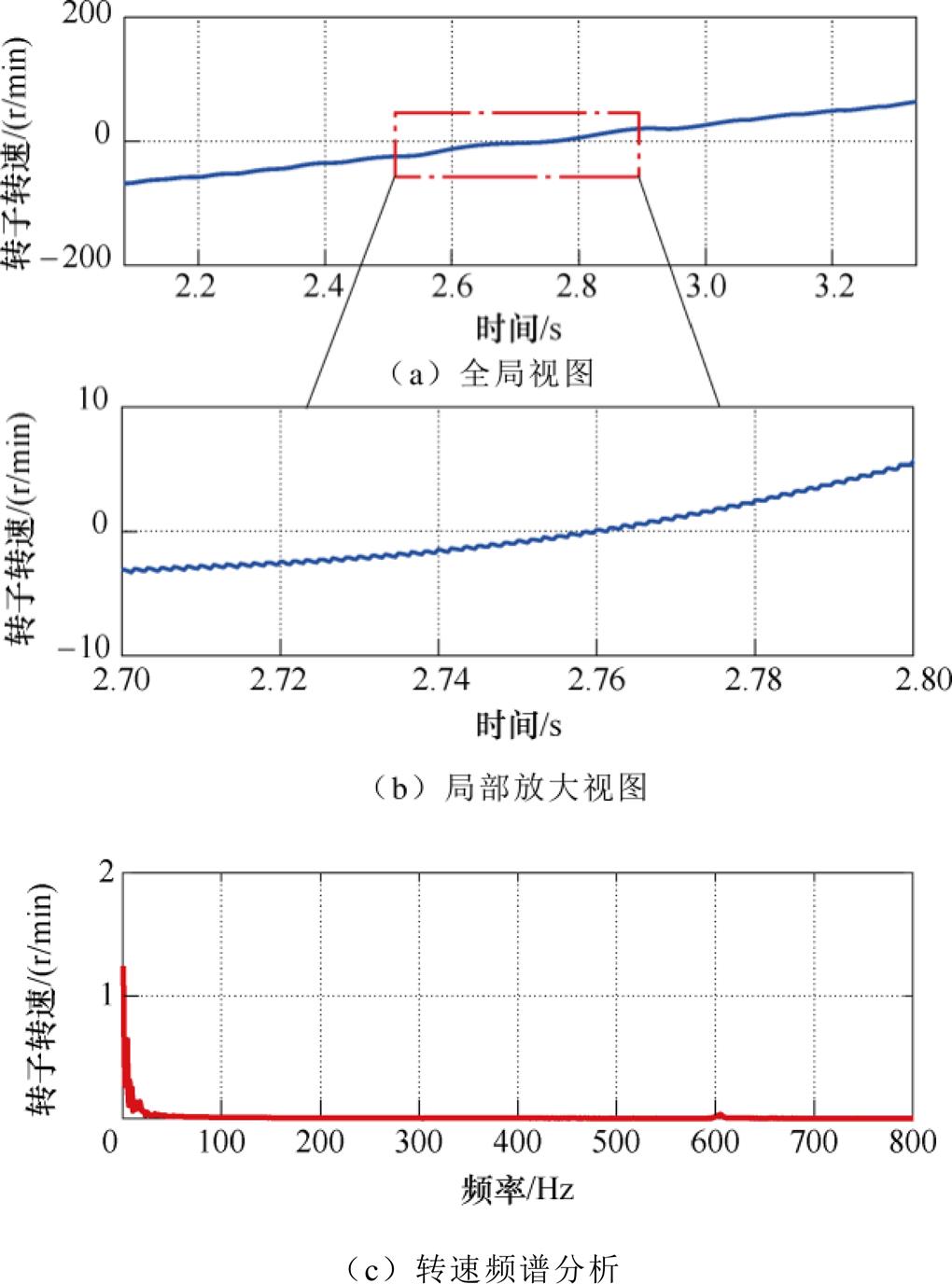
图20 位置环采用NF滤波在高动态加减速下估计转速性能分析
Fig.20 Performance analysis of estimated speed under fast acceleration and deceleration condition where LPF is employed in position loop
表2 位置环采用不同滤波器时性能对比
Tab.2 Performance comparison when various filter is employed in position loop
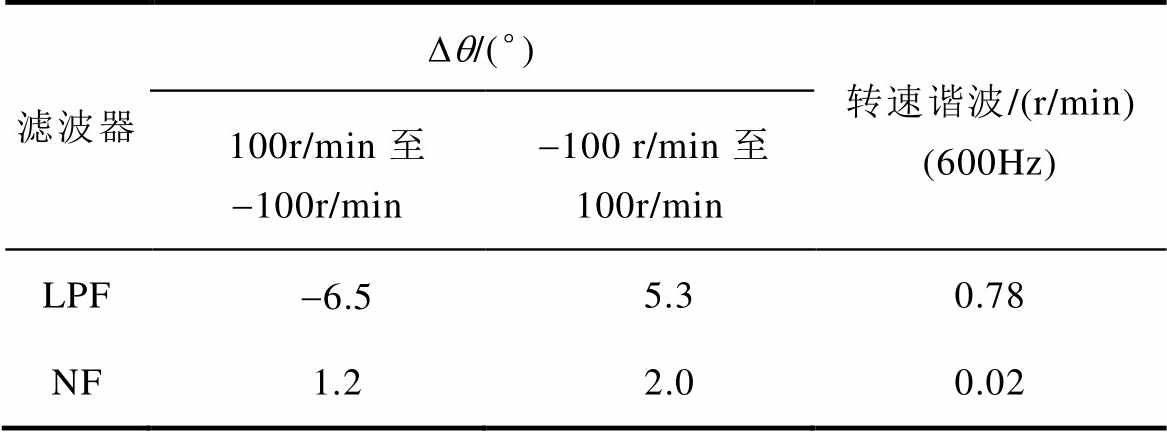
滤波器Dq/(°)转速谐波/(r/min) (600Hz) 100r/min至-100r/min -100 r/min至100r/min LPF-6.55.30.78 NF1.22.00.02
图21为电机由零速加速到额定转速的速度和转子位置实验结果，由上至下分别为转子转速与转子位置实验波形。图21中，当转速处于0～200r/min时，采用高频旋转电压注入法完成转子转速与位置估计；当转速大于200r/min时，采用有效磁链法完成转子转速与位置估计。由图21可知，电机具有四个工作阶段：P0表示电机与变频器完成备机，等待控制命令阶段；P1表示采用旋转注入法完成转子初始位置检测阶段；P2表示转速由0r/min加速到额定转速500r/min阶段，期间位置估计算法由高频旋转电压注入法自动切换至有效磁链法；P3表示电机达到额定转速的高速稳态阶段。由实验结果可以看出，电机在全转速范围无位置传感器控制下可靠运行。
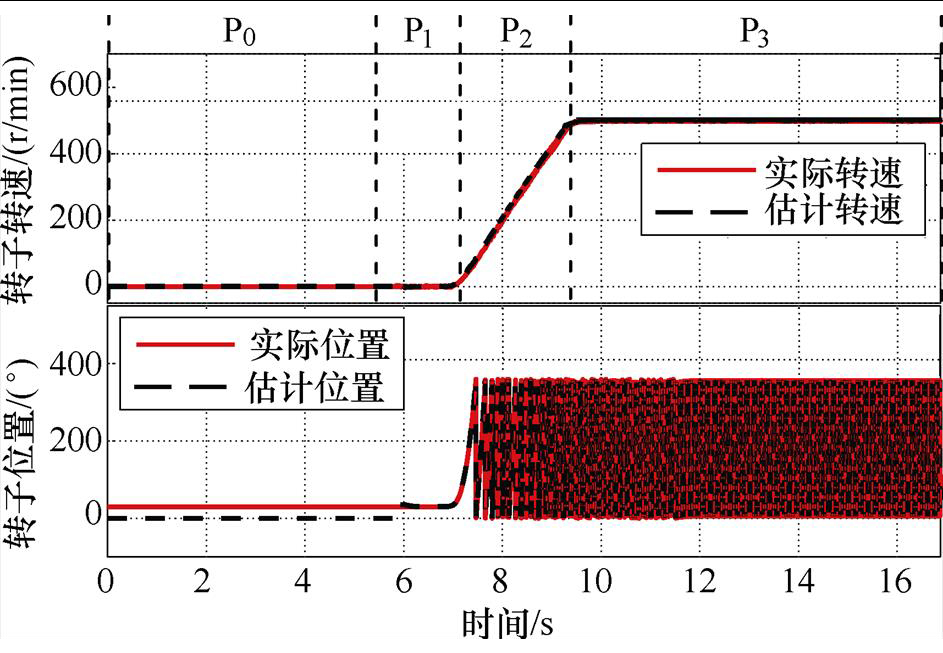
图21 电机由零速到额定转速的速度和转子位置实验结果
Fig.21 Experimental results of speed and rotor position where rotor speed changes from 0r/min to rate speed
传统高频旋转电压注入法采用SFHF算法完成电流解调，不仅电流解调过程复杂，而且转子位置估计误差随转速的变化而变化。本文分析了传统方法中引起位置估计误差的原因，提出一种基于EPF电流解调算法的改进型高频旋转电压注入法。所提方法不仅有效简化电流解调过程，消除了位置估计误差的转速敏感性，并且利用NF对位置环高频谐波进行滤波，拓宽了位置环路闭环带宽，有效地改善了高动态加减速下的位置估计性能。仿真与实验结果证明了本文所提算法的有效性。
参考文献
[1] 曹春堂, 兰志勇, 沈凡亨. 永磁同步电机无位置传感器控制系统中初始位置角检测综述[J]. 电气技术, 2020, 21(6): 1-5.
Cao Chuntang, Lan Zhiyong, Shen Fanheng. Review of initial position angle detection in sensorless control system of permanent magnet synchronous motor[J]. Electrical Engineering Magazine, 2020, 21(6): 1-5.
[2] 刘计龙, 肖飞, 麦志勤, 等. 基于双dq空间的永磁同步电机无位置传感器启动策略[J]. 电工技术学报, 2018, 33(12): 2677-2684.
Liu Jilong, Xiao Fei, Mai Zhiqin, et al. Position- sensorless startup strategy for permanent magnet synchronous motor based on double dq space[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2677-2684.
[3] Luo Xin, Tang Qipeng, Shen Anwen, et al. PMSM sensorless control by injecting HF pulsating carrier signal into estimated fixed-frequency rotating reference frame[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2294-2303.
[4] 胡静, 简优宗, 杨合民. 一阶高通滤波在发电机低频时转子位置检测角中的应用[J]. 电气技术, 2018, 19(7): 39-42.
Hu Jing, Jian Youzong, Yang Hemin. Application of first order high pass filter mathematical model of rotor position detection in low frequency of angle[J]. Electrical Engineering Magazine, 2018, 19(7): 39-42.
[5] 王海兵, 赵荣祥, 汤胜清, 等. 永磁同步电机位置检测偏差对驱动系统性能的影响研究[J]. 电工技术学报, 2018, 33(4): 911-918.
Wang Haibing, Zhao Rongxiang, Tang Shengqing, et al. Research on the influence of the position detection error to the PMSM drive system[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 911- 918.
[6] Yang S C, Hsu Y L. Full speed region sensorless drive of permanent-magnet machine combining saliency-based and back-EMF-based drive[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1092-1101.
[7] 谈微中, 严新平, 刘正林, 等. 无轴轮缘推进系统的研究现状与展望[J]. 武汉理工大学学报: 交通科学与工程版, 2015, 39(3): 601-605.
Tan Weizhong, Yan Xinping, Liu Zhenglin, et al. Technology development and prospect of shaftless rim-driven propulsion system[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2015, 39(3): 601-605.
[8] 林卫鹏, 汤宁平, 章金晶. 同步磁阻电动机无位置传感器控制的自起动方法[J]. 电气技术, 2018, 19(2): 16-21.
Lin Weipeng, Tang Ningping, Zhang Jinjing. Self- starting method for sensorless control of synchronous reluctance motor[J]. Electrical Engineering Magazine, 2018, 19(2): 16-21.
[9] Zhu Zhiqiang, Gong Liuming. Investigation of effectiveness of sensorless operation in carrier-signal- injection-based sensorless-control methods[J]. IEEE Transactions on Industrial Electronics, 2010, 58(8): 3431-3439.
[10] Zhang Xing, Li Haoyuan, Yang Shuying, et al. Improved initial rotor position estimation for PMSM drives based on HF pulsating voltage signal injection[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4702-4713.
[11] 高健伟. 基于高频注入法的永磁同步电机转子位置估计误差的分析[D]. 济南: 山东大学, 2012.
[12] 田士侠. 高频注入法永磁同步电机转子位置检测方法研究[D]. 济南: 山东大学, 2010.
[13] Wang Gaolin, Yang Lei, Zhang Guoqiang, et al. Comparative investigation of pseudorandom high frequency signal injection schemes for sensorless IPMSM drives[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2123-2132.
[14] 吴春. 永磁同步电机调速系统无位置传感器控制技术研究[D]. 西安: 西北工业大学, 2015.
[15] 李浩源, 张兴, 杨淑英, 等. 基于旋转高频注入的内置式永磁同步电机初始位置检测算法[J]. 电工技术学报, 2018, 33(8): 1724-1731.
Li Haoyuan, Zhang Xing, Yang Shuying, et al. A detecting algorithm for initial position of interior permanent magnet synchronous motor based on rotating high frequency injection[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1724- 1731.
[16] 杨健, 杨淑英, 李浩源, 等. 基于高频旋转电压注入的永磁同步电机转子初始位置估计方法[J]. 电工技术学报, 2018, 33(15): 3547-3555.
Yang Jian, Yang Shuying, Li Haoyuan, et al. Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3547-3555.
[17] 刘善宏, 杨淑英, 李浩源, 等. 基于旋转坐标系解调的内置式永磁同步电机旋转高频注入法位置观测[J]. 电工技术学报, 2020, 35(4): 709-716.
Liu Shanhong, Yang Shuying, Li Haoyuan, et al. Rotating high frequency signal injection based on interior permanent magnet synchronous motor rotor position estimation with the demodulation imple- mented on the synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 709-716.
[18] 龙丁. 交流伺服系统谐振陷波器参数自整定研究[D]. 武汉: 武汉科技大学, 2019.
[19] 郑堃, 周林, 龙贵欣, 等. 一种针对数字控制下光伏并网逆变器的陷波器滞后补偿方法[J]. 中国电机工程学报, 2019, 39(6): 1749-1757.
Zheng Kun, Zhou Lin, Long Guixin, et al. A lag compensation method based on notch filter for PV grid-connected inverter under digital control[J]. Proceedings of the CSEE, 2019, 39(6): 1749-1757.
Sensorless Control Strategy of Improved HF Rotating Voltage Injection Based on Estimated Position Feedback Current Demodulation Algorithm
Abstract High frequency (HF) rotating voltage injection method is widely used to estimate the rotor position in zero- and low-speed zone for permanent magnet synchronous motor (PMSM), where synchronous frame high-pass filter (SFHF) algorithm is employed for current demodulation. However, the disadvantage of the SFHF algorithm is that not only the current demodulation process is complicated, but also the position error changes with speed. To this end, a current demodulation algorithm based on the estimated position feedback (EPF) is proposed. On one hand, the efficient position error compensation strategy is designed with the EPF algorithm, which helps to eliminate the influence of speed on the accuracy of position estimation. On the other hand, a notch filter (NF) is employed in the position loop to eliminate the harmonic components, which expands the closed-loop bandwidth of the position loop effectively. Thus, the dynamic performance of position estimation is improved under fast acceleration and deceleration conditions. In this paper, the implementation of the traditional HF rotating voltage injection method is reviewed. Then, the EPF current demodulation algorithm and the position estimation error compensation strategy are introduced in detail. Moreover, the principle to expand the position loop bandwidth with NF is analyzed. Finally, the feasibility of the proposed strategy is verified through an PMSM experimental platform.
keywords：Permanent magnet synchronous motor, high frequency rotating voltage injection method, synchronous frame high-pass filter, current demodulation, estimated position feedback
DOI: 10.19595/j.cnki.1000-6753.tces.201210
中图分类号：TM351
麦志勤 男，1992年生，博士研究生，研究方向为永磁同步电机无位置传感器控制技术。E-mail: 827239136@qq.com
郑云波 女，1990年生，讲师，研究方向为大功率电力电子与电气传动。E-mail: 442108718@ qq.com（通信作者）
收稿日期 2020-09-18
改稿日期 2021-01-05
国防科技卓越青年基金（2018-JCJQ-ZQ-002）和国家自然科学基金青年基金（51807200）资助项目。
（编辑 陈 诚）